环氧树脂高频松弛的交流电导与双极性方波击穿特性
蒋起航1 王威望1 钟 禹1 李盛涛1 徐永生2
(1. 电力设备电气绝缘国家重点实验室(西安交通大学) 西安 710049 2. 南方电网科学研究院有限责任公司直流输电技术国家重点实验室 广州 510080)
摘要 高频非正弦电压下环氧树脂击穿表现出较强的频率依赖性,并且存在复杂的宽频电-热耦合特性。高频电压下环氧树脂交流电导,特别是载流子非线性输运过程是理解高频绝缘击穿的关键。该文以两种电工环氧树脂为研究对象,采用宽频介电谱研究环氧试样交流电导的频率与温度依赖关系,通过Almond-West模型分析得到低频下交流类直流电导率与温度的关系,低频电导随温度变化更符合Vogel-Fulcher-Tammann 模型。基于Havriliak-Negami复合介质多分散松弛极化理论,分析高频、高温下的松弛行为,认为高频交流电导率主要由松弛过程a 产生的极化损耗引起。通过高频双极性方波击穿测试平台,测试了重复频率双极性方波电压(500 Hz, 1 kHz, 2 kHz, 3 kHz)下环氧试样的击穿场强,基于三参数Weibull分布统计分析特征击穿场强随频率的关系,发现击穿场强与频率呈负相关。研究提出考虑Poole-Frenkel效应的高频高场交流电导模型,并建立高频自由体积随频率变化的击穿模型。研究指出高频下分子链段振动效应增强,导致交流电导增强;高频下分子链运动滞后于频率响应,导致总体自由体积增大,造成高频击穿场强下降。研究结果对高频绝缘破坏与可靠性研究具有重要意义。
关键词:环氧树脂 交流电导 双极性方波电压 自由体积 高频击穿
0 引言
双酚A环氧树脂因其优异的绝缘性能、热性能以及机械性能而广泛应用于绝缘子芯棒、干式变压器、盆式绝缘子、互感器等电力设备[1-3]。高频变压器作为大容量电力电子变压器的核心部件,发挥着功率传输与电压调制等功能[4]。环氧树脂是高频变压器的主要固体绝缘之一。与传统工频变压器相比,高频变压器需要承受高频DC-DC变换器电力电子电路带来的瞬态非正弦电压。通常,高频变压器绕组电压波形为双极性方波,并具有陡上升/下降沿(高dv/dt)和多谐波[5]。在这种复杂多频电压作用下,高频变压器绝缘环氧树脂需要耐受高频多谐波陡脉冲重复频率电场。此外,高频变压器铁心与绕组损耗大[6],实际运行时温升高。因此,高频变压器环氧绝缘长期承受电-热联合应力[7],环氧固体绝缘的击穿与老化概率增加[8-10],这给环氧绝缘性能提升与高频变压器设计带来了挑战。深入研究环氧树脂高频交流电导特性及其对击穿的影响,对高频变压器固体绝缘可靠性提升具有重要意义。
目前,有关环氧树脂的交流电导特性的研究多集中于微、纳米填料对交流电导特性的影响作用。张宏亮等[11]采用宽频介电谱测试研究了纳米氧化石墨烯对环氧复合材料电荷载流子特性的影响。研究指出纯环氧、单层氧化石墨烯/环氧复合材料在玻璃化转变温度Tg以上的直流电导主要由电子跳跃电导引起。陈向荣等[12]采用介电谱仪偏压模块测试了环氧树脂/碳化硅晶须复合材料的交流电导率和介电常数,分析了温度和频率对材料交流非线性电导和介电特性的影响,发现随温度升高或频率增大,其非线性交流电导率系数均减小。而在纯环氧研究方面,W. Jilani等[13]研究了环氧聚合物的交流电导机理,采用跳跃势垒模型描述Tg以上的交流电导机制,采用隧穿模型描述Tg以下的交流电导机制。但对交流电导与频率的定量分析,高频电导机制等认识不清。此外,现有的交流电导的研究方法多为宽频介电谱技术,该方法施加的正弦波电压与高频变压器环氧绝缘耐受的双极性方波电压并不相符,重复频率双极性方波电压下的交流电导特性亟待研究。
绝缘电介质的击穿特性受外施电压的影响显著[14]。研究指出交流、直流、脉冲以及高频谐波下绝缘介质击穿场强有明显差异[14-15]。在频率对绝缘击穿的影响方面,赵义焜等[16]针对高频变压器用匝间绝缘材料开展了高频方波下的击穿实验,发现随频率增加,绝缘击穿场强下降,基于热击穿理论对高频击穿结果做了定性分析。Wang Weiwang等[17]开展了固态变压器环氧绝缘高频非正弦电压下的击穿特性研究,研究指出频率与击穿场强呈负相关。然而,分析发现单纯的介质损耗发热难以导致环氧分子链断裂,热击穿不适用于解释环氧高频短时击穿现象。在高频绝缘老化破坏研究方面,Zhang Chuang等[18]研究了不同频率的双极性方波电压对环氧树脂绝缘中电树枝生长特性的影响。研究发现,高频方波电压下环氧绝缘中电树枝生长明显加快,绝缘破坏时间很短,将双极性方波电压下环氧树脂的电树枝特性归因于功率损耗、空间电荷和局部放电的协同效应。以上研究多认为高频电压下绝缘介质损耗增加导致的介质内热平衡被破坏是绝缘失效的主要原因,绝缘介质内高场电导、载流子迁移特性、自由体积等对击穿的影响尚不清晰。环氧树脂高频非正弦电压下的击穿机理亟待深入研究。
绝缘高场电导是理解绝缘击穿的关键过程。高频交流电导是决定绝缘高频击穿、局部放电、老化的重要因素。研究指出,高场下聚合物电流-电场特性服从空间电荷限制电流(Space Charge Limited Current, SCLC)机制,载流子迁移率与直流击穿场强呈负相关[19]。还有研究指出,高频电场作用下,电极-介质边界处的注入电荷密度和电场畸变率随频率的上升而增大,实际电场强度大于平均电场强度,导致绝缘击穿[20]。在击穿理论方面,自由体积理论是解释聚合物短时击穿的有效理论之一[21]。李盛涛等[22]提出了自由体积对聚合物纳米复合材料电击穿机理的影响。然而,高频下绝缘自由体积、交流电导与击穿的关联不清楚,制约了对高频击穿机理的认识。
已有研究证明双酚A环氧树脂的环氧值不同会引起分子链松弛行为的差异[23]。其根本原因可能是因为分子链长短不同导致的偶极子数目、自由体积大小存在差异。基于此,本文选取了两种环氧值不同的纯环氧树脂,采用相同的固化工艺制备出环氧固化物试样,测试与分析了两种试样的玻璃化转变温度Tg和宽频宽温度介电谱,分析了温度和频率对环氧试样交流电导率的影响。通过对双极性方波电压的傅里叶级数展开,研究了高频方波下的载流子跳跃电导与Poole-Frenkel效应。通过重复频率双极性方波击穿测试平台研究了两种试样的高频方波短时击穿特性,通过改进自由体积击穿理论提出了高频下环氧树脂交流电导对击穿的影响机制。研究结果对变频绝缘特性与失效机制、电力电子磁件的发展具有重要意义。
1 试样制备与实验方法
1.1 实验原料
选用的环氧树脂包括了两种环氧值不同的双酚A环氧树脂(美国陶氏化学生产的环氧树脂DER- 331和上海雄润生产的环氧树脂HE-1080N),选用的固化剂为嘉兴联兴公司生产的甲基四氢苯酐(JH- 910,工业级),促进剂为二甲基苄胺(BDMA,工业级)。两种环氧树脂的环氧值由盐酸-丙酮滴定法测量得到,为已知量。为方便描述,将HE-1080N、DER-331两种环氧树脂分别编号为E1、E2,两种环氧树脂的环氧值分别为0.576、0.525。
1.2 试样制备
环氧树脂固化物制备流程如下:在清洗干净的模具上均匀喷涂脱模剂(佳丹909)后放入100℃烘箱加热使脱模剂附在模具表面。将环氧基体、固化剂、促进剂按照100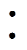 x
x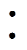 0.6(x=EV×166×0.9,EV为环氧树脂环氧值,即每100 g环氧树脂中所含的环氧基团的摩尔数,单位为mol/(100 g))的配料比加入到离心搅拌机的容器中。搅拌的程序为:搅拌分散过程转速为2 000 r/min,持续15 min,脱气过程转速为2 200 r/min,持续15 min。将搅拌均匀的混合物倒入模具中,然后将模具放入真空鼓风电热干燥箱,在常温下进行抽真空,持续脱气30 min以去除试样中的气泡,之后打开烘箱进气旋钮,在常压下进行固化。固化程序为80℃固化2 h,然后10 min升温至140℃,在140℃固化12 h。固化结束后取出试样并用酒精清洗,放入50℃的烘箱干燥备用。
0.6(x=EV×166×0.9,EV为环氧树脂环氧值,即每100 g环氧树脂中所含的环氧基团的摩尔数,单位为mol/(100 g))的配料比加入到离心搅拌机的容器中。搅拌的程序为:搅拌分散过程转速为2 000 r/min,持续15 min,脱气过程转速为2 200 r/min,持续15 min。将搅拌均匀的混合物倒入模具中,然后将模具放入真空鼓风电热干燥箱,在常温下进行抽真空,持续脱气30 min以去除试样中的气泡,之后打开烘箱进气旋钮,在常压下进行固化。固化程序为80℃固化2 h,然后10 min升温至140℃,在140℃固化12 h。固化结束后取出试样并用酒精清洗,放入50℃的烘箱干燥备用。
1.3 实验方法与平台
采用瑞士METTLER TOLEDO公司生产的DSC822E型差示扫描量热仪测试两种环氧固化物的玻璃化转变温度Tg。测试温度范围为30~200℃,升温速率为10℃/min。
采用德国Novocontrol公司的Concept 80宽带介电谱测试系统测量两种环氧绝缘的介电响应特性。测试温度范围为30~200℃,每10℃进行一次频谱图采集,频率范围为10-1~106 Hz。
采用双极性方波击穿测试系统开展双极性方波电压下的击穿实验。电极为直径25 mm的球-球电极,电极置于变压器油中以防止沿面闪络。采用分压比为1 000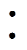 1的高压探头测量击穿时刻电压波形。测试波形被送至1 GHz带宽示波器。图1为测试系统示意图。加压措施按照标准GB/T 1408.1- 2016执行,采用升压速率为0.5 kV/s连续升压法开展高频击穿实验,记录击穿瞬间的电压值。
1的高压探头测量击穿时刻电压波形。测试波形被送至1 GHz带宽示波器。图1为测试系统示意图。加压措施按照标准GB/T 1408.1- 2016执行,采用升压速率为0.5 kV/s连续升压法开展高频击穿实验,记录击穿瞬间的电压值。
2 结果与分析
2.1 差式扫描量热分析
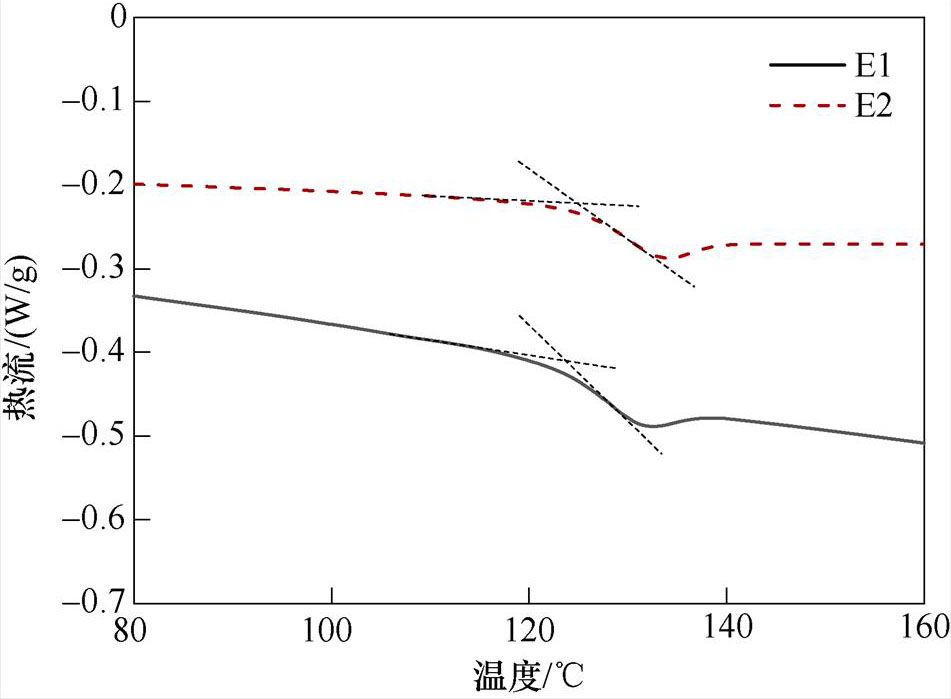
图2为两种环氧试样的DSC测试曲线。曲线截取自试样发生相变的温度范围。从图中可以看出,曲线均在120℃以上出现转折,以DSC曲线低温侧的初始基线外推与曲线最大斜率处切线的交点作为环氧树脂的玻璃化转变温度Tg,得到E1的Tg= 126.8℃,E2的Tg=127.2℃。可以看出,两种环氧树脂绝缘的Tg接近,E1的略小于E2试样。
分析认为环氧值越大,环氧分子链长度缩短,聚合度下降,苯环数量降低,分子链上可内旋转的单键比例增大即柔性链比例增大致使刚性减小。此外,分子链长度缩短使得链段间的缠结作用减弱;另一方面,环氧基团相比于分子链其他化学基团具有更大的自由体积,因此环氧值大的双酚A环氧树脂为满足分子链构象所需的温度更小,这两个因素均会使Tg随环氧值增大而不断减小。因此,E1的环氧值大,其Tg相对略小。
2.2 介电响应分析
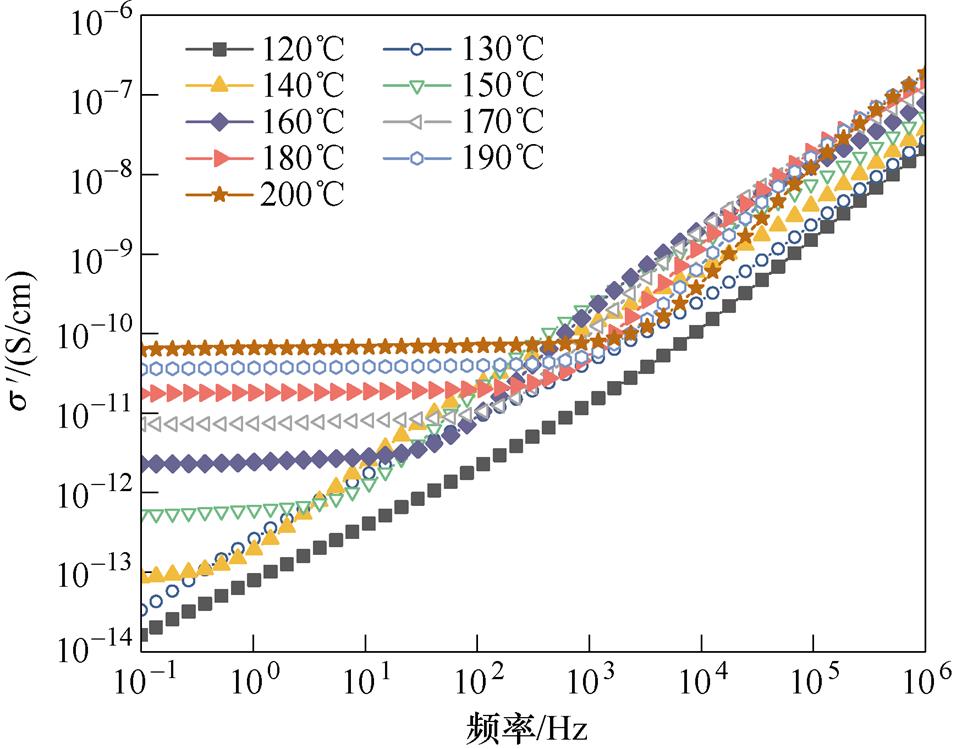
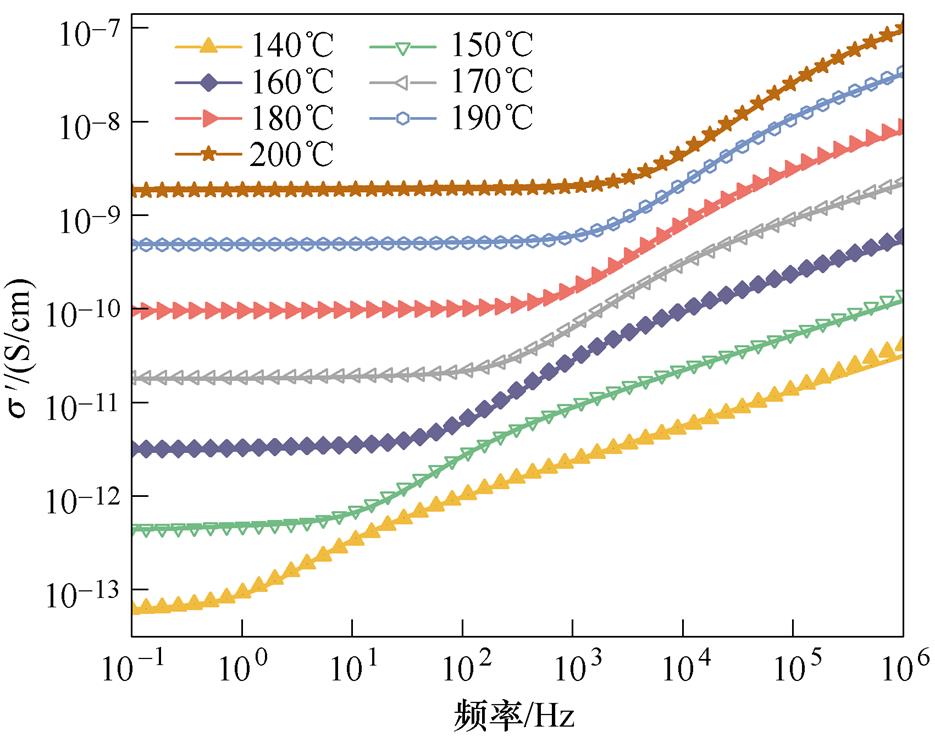
图3为E1和E2两种环氧在不同温度下复电导率实部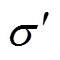 随频率的变化曲线。可以看出,在低频范围与高频范围,
随频率的变化曲线。可以看出,在低频范围与高频范围,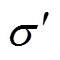 出现了不同的温度依赖性。低温下(小于140℃),
出现了不同的温度依赖性。低温下(小于140℃),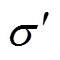 随频率的增加而增加,呈正相关。从140℃开始,两种试样的
随频率的增加而增加,呈正相关。从140℃开始,两种试样的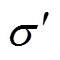 在低频区开始出现平台区,表明直流电导的影响随着温度升高而增强。此平台区的宽度随温度升高而不断变宽,在平台区内,
在低频区开始出现平台区,表明直流电导的影响随着温度升高而增强。此平台区的宽度随温度升高而不断变宽,在平台区内,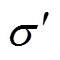 与频率关系不大,但会随温度升高而增大。在平台区结束之后,
与频率关系不大,但会随温度升高而增大。在平台区结束之后,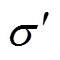 会出现一个斜率明显大于其他频段的上升过程,这是由于温度高于玻璃化转变温度以后,环氧大分子链逐渐解冻,在交变电场的作用下发生转向,出现了大分子链a 松弛过程。
会出现一个斜率明显大于其他频段的上升过程,这是由于温度高于玻璃化转变温度以后,环氧大分子链逐渐解冻,在交变电场的作用下发生转向,出现了大分子链a 松弛过程。
2.2.1 Almond-West模型
高温下,交流电导率实部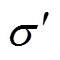 与直流电导率sdc满足Almond-West关系[24],有
与直流电导率sdc满足Almond-West关系[24],有
(a)E1
(b)E2
图3 环氧树脂在高温下的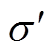
Fig.3 The 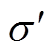 of epoxy resin under high temperature
of epoxy resin under high temperature
式中,f为测试频率;fc为在电压作用下载流子从贯穿电极的运动转变为在试样内部往复运动的起始特征频率;s为用以表征材料的松弛行为的常数,通常0≤s≤1。
由跳跃电导过程可知[25],当局域态中的电子获得了克服势垒足够的能量时,它可以从一个分子(或原子)跳到临近分子的非占据态。当频率f fc时,交流电导率实部类似直流电导率,在此频域内,直流电导主要由跳跃电导引起,频率的改变并不会影响电子运动的势能,因此电导率在此频域内与频率关系不大。
fc时,交流电导率实部类似直流电导率,在此频域内,直流电导主要由跳跃电导引起,频率的改变并不会影响电子运动的势能,因此电导率在此频域内与频率关系不大。
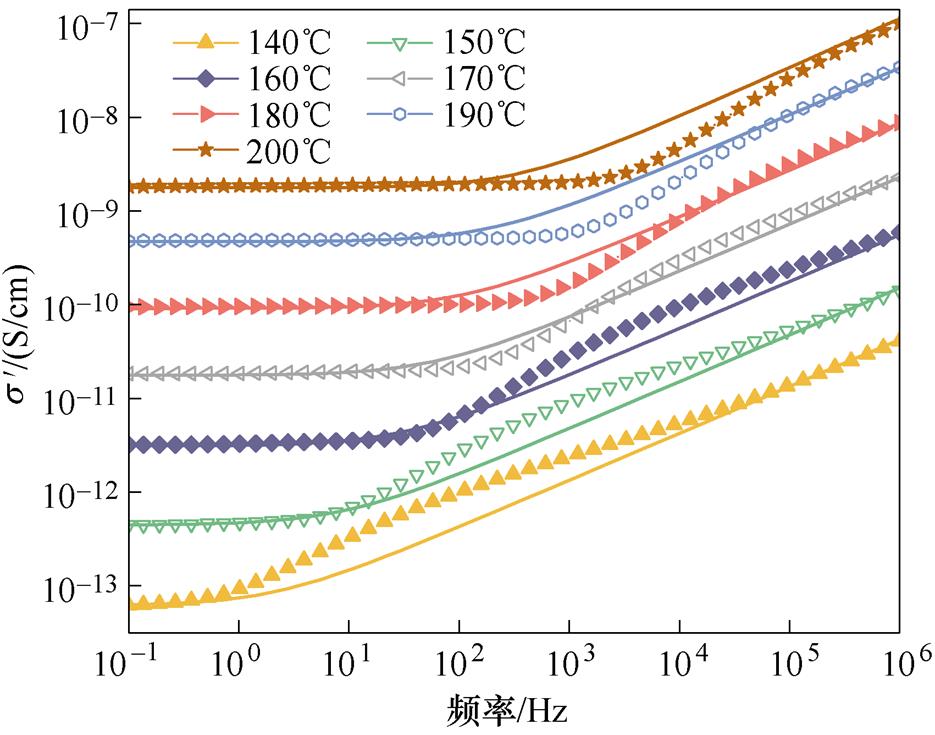
根据Almond-West模型对两种环氧试样的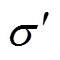 随频率的变化进行分析。对140~200℃的实验数据进行拟合。图4为E1和E2的复交流电导率实部
随频率的变化进行分析。对140~200℃的实验数据进行拟合。图4为E1和E2的复交流电导率实部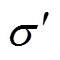 的实测结果与拟合曲线。为了清楚地表示出实验结果与拟合曲线的拟合程度,对二者进行垂直方向的平移,因此纵坐标无绝对值。从图4的拟合结果可以看出,Almond-West模型在低频与较高频段具有很好的拟合效果,但在中高频段拟合效果不好。这是因为随频率增加,大分子链松弛过程a 产生的极化损耗对高频交流电导特性产生了明显影响。
的实测结果与拟合曲线。为了清楚地表示出实验结果与拟合曲线的拟合程度,对二者进行垂直方向的平移,因此纵坐标无绝对值。从图4的拟合结果可以看出,Almond-West模型在低频与较高频段具有很好的拟合效果,但在中高频段拟合效果不好。这是因为随频率增加,大分子链松弛过程a 产生的极化损耗对高频交流电导特性产生了明显影响。
(a)E1
(b)E2
图4 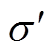 的实测数据与Almond-West拟合曲线
的实测数据与Almond-West拟合曲线
Fig.4 The measured data and Almond-West fitting curves of 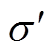
Almond-West模型对低频直流电导的拟合效果良好。表1为得到的两种环氧树脂在不同温度下的直流电导率。随温度升高,两种环氧树脂的直流电导率不断增大,E1与E2的sdc类似,二者都处于同一数量级。E1的sdc稍低于E2,这可能是因为E1环氧值大,环氧树脂内部的自由体积小,电荷迁移率小。
表1 不同温度下环氧树脂的直流电导率
Tab.1 DC conductivity at different temperatures

温度/℃sdc/(S/cm) E1E2 1406.54´10-148.02´10-14 1503.82´10-135.20´10-13 1602.64´10-122.64´10-12 1708.47´10-127.38´10-12 1802.09´10-111.80´10-11 1904.12´10-113.61´10-11 2007.14´10-116.21´10-11
为了进一步研究两种环氧树脂之间低频电导的差异,利用式(2)的Vogel-Fulcher-Tammann (VFT)公式对低频直流电导率-温度关系进行拟合[26],拟合参数见表2。
表2 VFT公式拟合参数
Tab.2 Fitting parameters of VFT formula
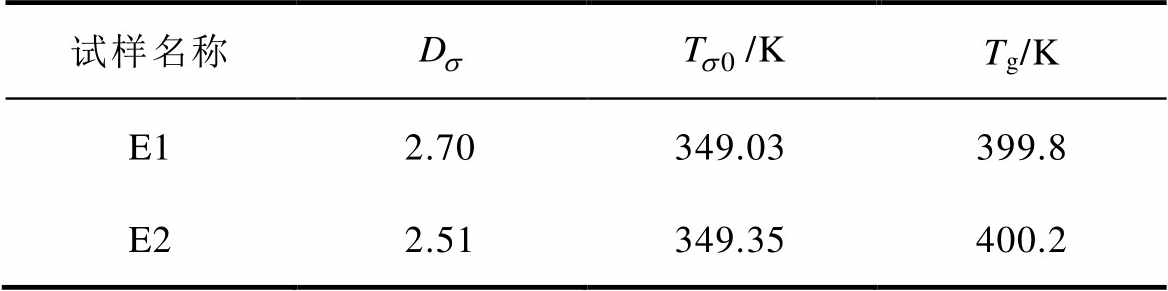
试样名称/KTg/K E12.70349.03399.8 E22.51349.35400.2
式中,sdc0为温度趋于无穷大时的直流电导率;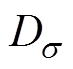 为环氧树脂内直流电导的强度系数,可以认为是无量纲活化能,
为环氧树脂内直流电导的强度系数,可以认为是无量纲活化能,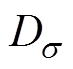 越大,分子链段热激活越困难;
越大,分子链段热激活越困难;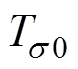 为直流电导的Vogel温度;T为热力学温度。
为直流电导的Vogel温度;T为热力学温度。
图5给出了两种环氧树脂的直流电导率随Ts0/(T-Ts0)的变化曲线。可以看出,拟合曲线与实验结果一致。Vogel温度通常比Tg小50 K[27],表2中E1、E2的Vogel温度与其对应的Tg满足此大小关系。通过Vogel温度分析计算,验证了DSC测试的Tg,表明Tg以上环氧树脂绝缘中的载流子能获得足够的能量在材料中进行迁移,从而增大低频电导。
2.2.2 Havriliak-Negami多分散松弛极化模型
通过对高温下的环氧树脂绝缘交流电导率实部的拟合发现:当频率f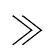 fc时,交流电导率实部与频率f之间并不满足Almond-West模型中以s为指数的幂指数关系。这表明Almond-West模型并不能反映出环氧树脂极化损耗对交流电导率的影响,尤其是在高温高频段出现的大分子链a 松弛过程。此外,Almond-West模型并不能区分电子跳跃电导和离子跳跃电导,即不能提取出松弛过程d 的影响。为了进一步研究环氧树脂绝缘高频交流电导率实部
fc时,交流电导率实部与频率f之间并不满足Almond-West模型中以s为指数的幂指数关系。这表明Almond-West模型并不能反映出环氧树脂极化损耗对交流电导率的影响,尤其是在高温高频段出现的大分子链a 松弛过程。此外,Almond-West模型并不能区分电子跳跃电导和离子跳跃电导,即不能提取出松弛过程d 的影响。为了进一步研究环氧树脂绝缘高频交流电导率实部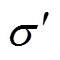 与频率和温度的关系,采用两个Havriliak-Negami(H-N)介电松弛函数分别代表松弛过程a 与松弛过程d,对140~200℃的环氧树脂复介电常数进行拟合计算,并考虑直流电导对复介电常数的影响,环氧树脂的复介电常数
与频率和温度的关系,采用两个Havriliak-Negami(H-N)介电松弛函数分别代表松弛过程a 与松弛过程d,对140~200℃的环氧树脂复介电常数进行拟合计算,并考虑直流电导对复介电常数的影响,环氧树脂的复介电常数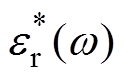 可表示为
可表示为
式中,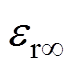 为光频介电常数;
为光频介电常数;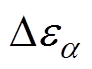 和
和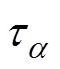 分别为松弛过程a的松弛强度和松弛时间;
分别为松弛过程a的松弛强度和松弛时间;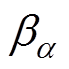 和
和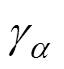 为松弛过程a 的图形参数,0<
为松弛过程a 的图形参数,0<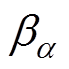 ≤1,0<
≤1,0<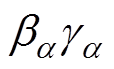 ≤1;
≤1;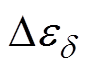 和
和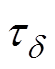 分别为松弛过程d 的松弛强度和松弛时间;
分别为松弛过程d 的松弛强度和松弛时间;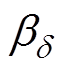 和
和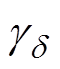 为松弛过程d 的图形参数,0<
为松弛过程d 的图形参数,0<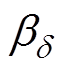 ≤1,0<
≤1,0<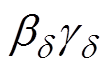 ≤1;e0为真空介电常数;j为虚数单位;
≤1;e0为真空介电常数;j为虚数单位;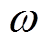 为角频率。
为角频率。
根据Maxwell方程得到复电导率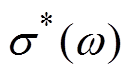 与复介电常数
与复介电常数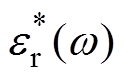 的关系[28]为
的关系[28]为
进一步得到
其中
式中,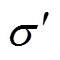 、
、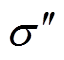 分别为复交流电导率的实部与虚部;
分别为复交流电导率的实部与虚部;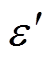 、
、 分别为复介电常数的实部与虚部;
分别为复介电常数的实部与虚部;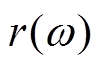 和
和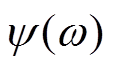 为中间项。由此根据复介电常数的拟合参数得到基于Havriliak-Negami(H-N)介电松弛函数的交流电导率
为中间项。由此根据复介电常数的拟合参数得到基于Havriliak-Negami(H-N)介电松弛函数的交流电导率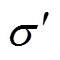 随频率的变化关系。图6为E1、E2两种试样
随频率的变化关系。图6为E1、E2两种试样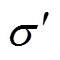 的实测数据与拟合曲线对比。从图6的拟合结果可以明显看出,采用Havriliak-Negami(H-N)函数拟合的曲线与实验结果一致性很好,表明Havriliak-Negami(H-N)函数适用于全频段的交流电导率分析。由于分别采用两个H-N介电松弛拟合函数考虑了环氧的松弛过程a 与松弛过程d,这说明在环氧树脂绝缘Tg以上,交流电导率主要由松弛过程a 引起的极化损耗和松弛过程d 引起的电导损耗共同决定。
的实测数据与拟合曲线对比。从图6的拟合结果可以明显看出,采用Havriliak-Negami(H-N)函数拟合的曲线与实验结果一致性很好,表明Havriliak-Negami(H-N)函数适用于全频段的交流电导率分析。由于分别采用两个H-N介电松弛拟合函数考虑了环氧的松弛过程a 与松弛过程d,这说明在环氧树脂绝缘Tg以上,交流电导率主要由松弛过程a 引起的极化损耗和松弛过程d 引起的电导损耗共同决定。
表3、表4分别为E1、E2在不同温度下通过H-N拟合得到的松弛过程a 对应的松弛强度Dea、松弛时间ta 以及直流电导率sdc。松弛时间随温度的变化关系说明:温度上升会导致大分子链运动增强,减小松弛时间,会导致分子链段运动频率增加,从而增大高频下交流电导。
(a)E1
(b)E2
图6 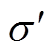 的实测数据与H-N拟合曲线
的实测数据与H-N拟合曲线
Fig.6 The measured data and H-N fitting curves of 
表3 E1试样的拟合参数
Tab.3 Fitting parameters of E1 sample
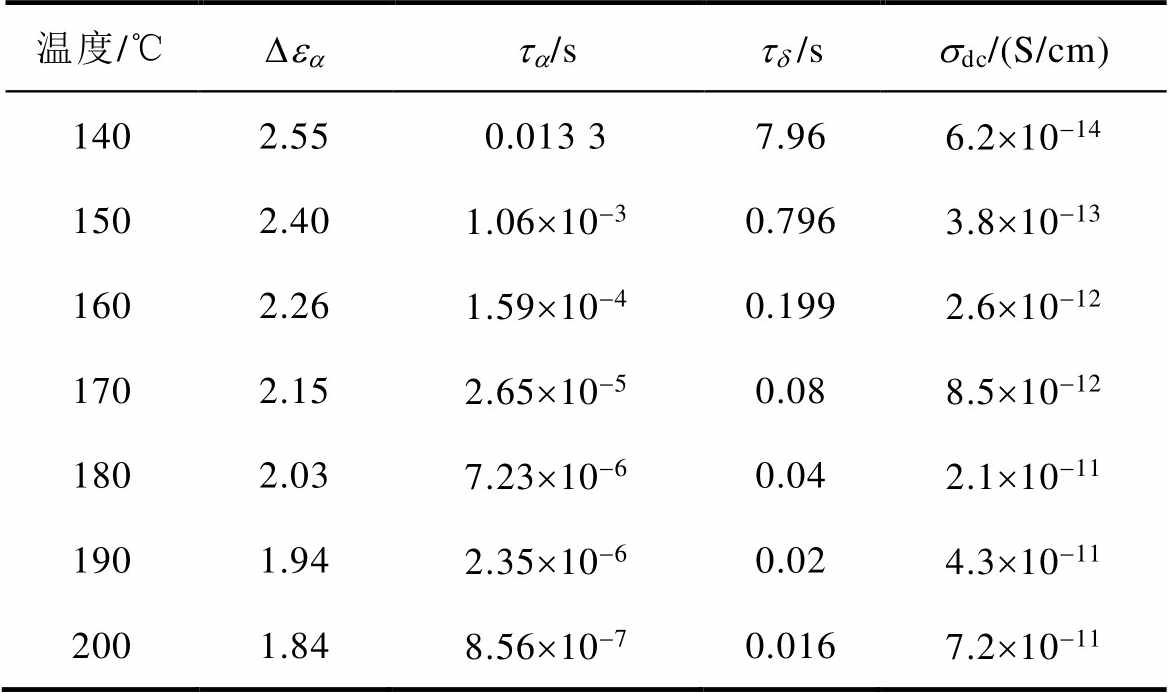
温度/℃Deata/std /ssdc/(S/cm) 1402.550.013 37.966.2´10-14 1502.401.06´10-30.7963.8´10-13 1602.261.59´10-40.1992.6´10-12 1702.152.65´10-50.088.5´10-12 1802.037.23´10-60.042.1´10-11 1901.942.35´10-60.024.3´10-11 2001.848.56´10-70.0167.2´10-11
与直流电导率相同,采用VFT公式对松弛过程a 与松弛过程d 的松弛时间进行拟合分析,两种松弛过程的松弛时间VFT公式分别表示为
表4 E2试样的拟合参数
Tab.4 Fitting parameters of E2 sample
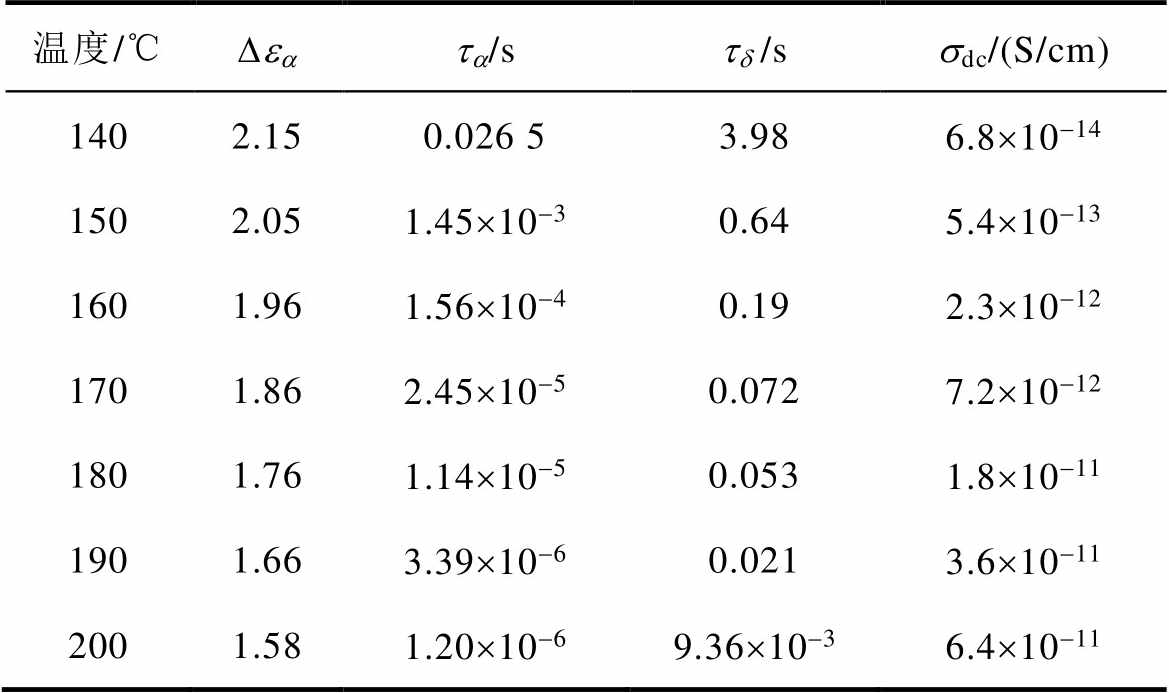
温度/℃Deata/std /ssdc/(S/cm) 1402.150.026 53.986.8´10-14 1502.051.45´10-30.645.4´10-13 1601.961.56´10-40.192.3´10-12 1701.862.45´10-50.0727.2´10-12 1801.761.14´10-50.0531.8´10-11 1901.663.39´10-60.0213.6´10-11 2001.581.20´10-69.36´10-36.4´10-11
式中,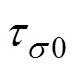 与
与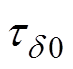 为松弛时间常数;
为松弛时间常数;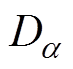 与
与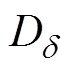 分别为松弛过程a 与松弛过程d 的强度系数,认为是一种无量纲活化能;
分别为松弛过程a 与松弛过程d 的强度系数,认为是一种无量纲活化能;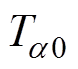 与
与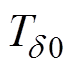 分别为松弛过程a 与松弛过程d 的Vogel温度。
分别为松弛过程a 与松弛过程d 的Vogel温度。
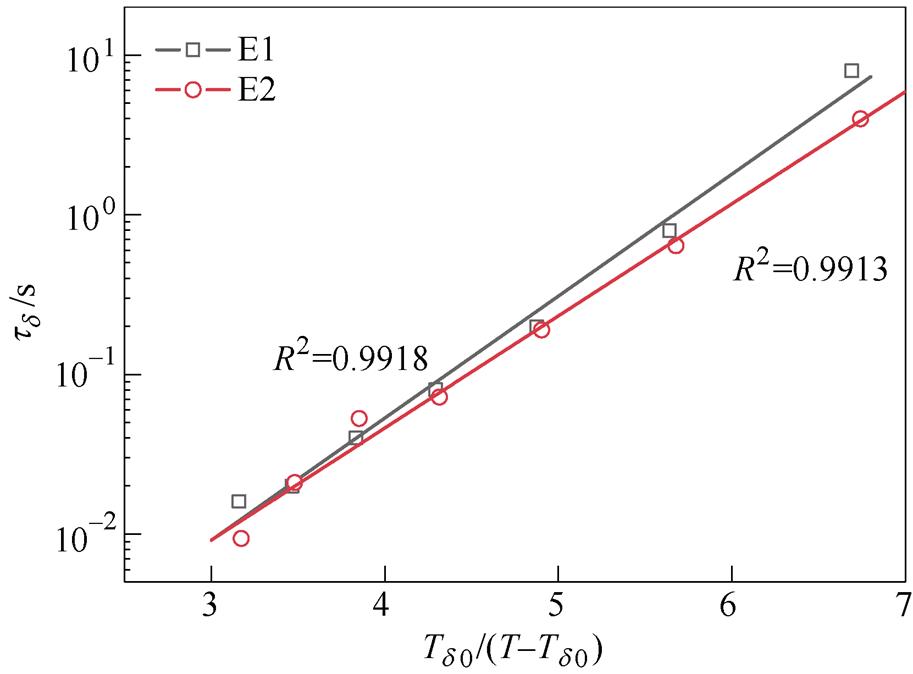
图7给出了两种环氧的松弛过程a 与松弛过程d 的松弛时间随温度的变化曲线。表5给出了各松弛过程的拟合参数。E1的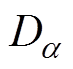 略小于E2的
略小于E2的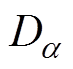 ,说明E1激活分子链运动需要的温度略低于E2,同样的温度下E1具有更大的松弛强度。对比发现,表2中的
,说明E1激活分子链运动需要的温度略低于E2,同样的温度下E1具有更大的松弛强度。对比发现,表2中的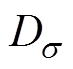 与表5中的
与表5中的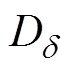 在数值上较为接近,表明松弛过程d 与直流电导过程具有密切联系,二者都与载流子跃过势垒进行迁移的过程相关。
在数值上较为接近,表明松弛过程d 与直流电导过程具有密切联系,二者都与载流子跃过势垒进行迁移的过程相关。
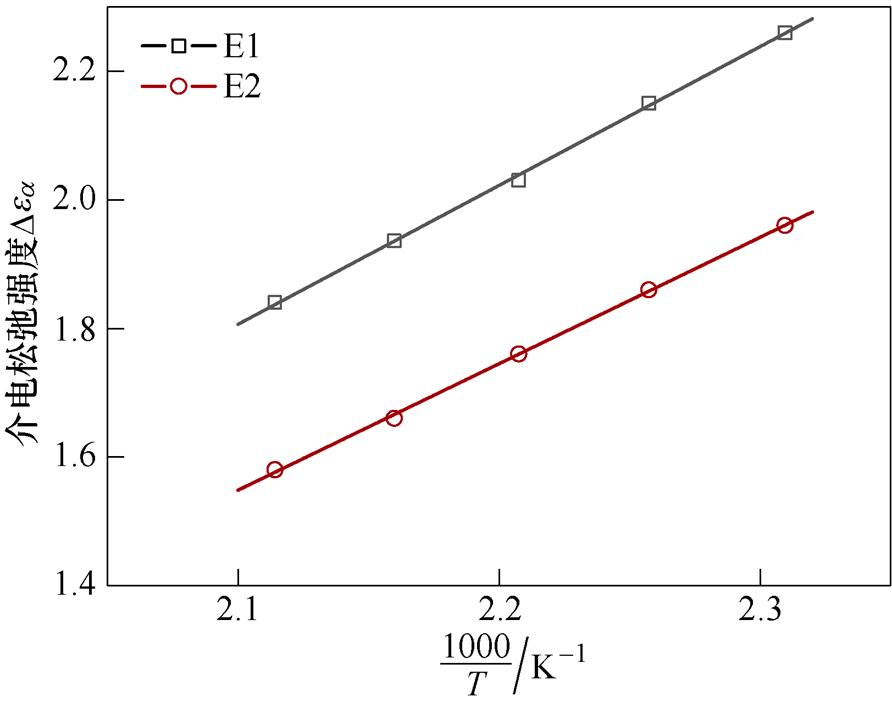
图8为松弛过程a 的介电松弛强度Dea 与温度倒数的关系曲线。对图中数据进行线性拟合,R2均大于0.999。可以看出a松弛的介电松弛强度Dea 与温度的倒数成正比,这说明松弛过程a 是由偶极子转向极化引起的,Dea 与温度的倒数满足
(a)松弛过程a
(b)松弛过程d
图7 松弛时间随温度的变化
Fig.7 Relaxation time as a function of temperature
表5 VFT公式拟合参数
Tab.5 Fitting parameters of VFT formula

试样名称T0/KDaDd E1349.33.632.33 E2349.653.682.15
式中,A为与电介质中偶极子转向极化率有关的常数。一般认为A与偶极矩和偶极子浓度成正比。计算得到E1、E2的A值分别为2 300.38和1 876.53。文献[29]将两个大分子交联点之间的分子链视为一个偶极子,因此,环氧值大的环氧树脂中偶极子浓度更高。
2.3 双极性方波电压击穿特性分析
根据高频非正弦电压下绝缘击穿测试平台与方法,研究频率对环氧试样短时击穿特性的影响。有研究[30]将三参数Weibull分布用于脉冲电压下液体击穿特性的统计,发现三参数Weibull分布能有效表征高频脉冲电压下的绝缘失效概率随电压的变化关系。三参数Weibull分布表达式为
式中,F为当电场强度小于u时的击穿概率;a1为尺度参数;b1为形状参数;g1为位置参数。a1与g1的和表示特征击穿场强,即击穿概率为63.2%的电场强度。
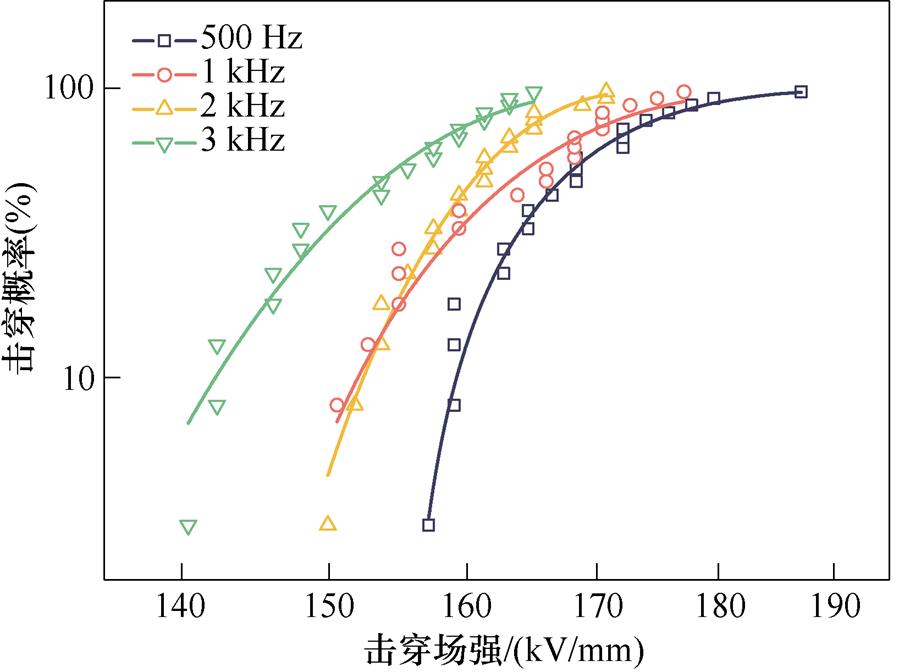
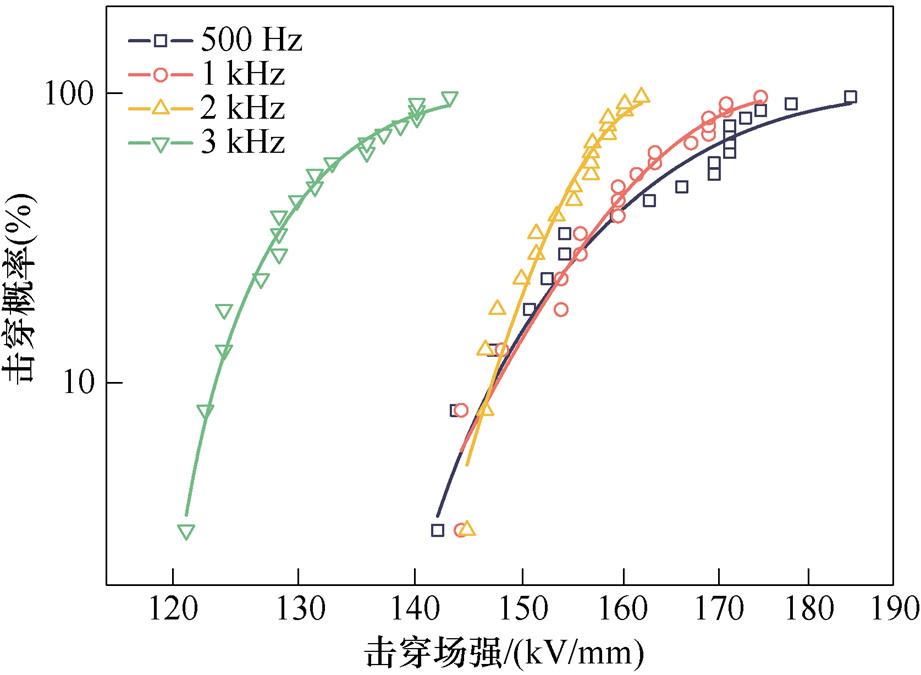
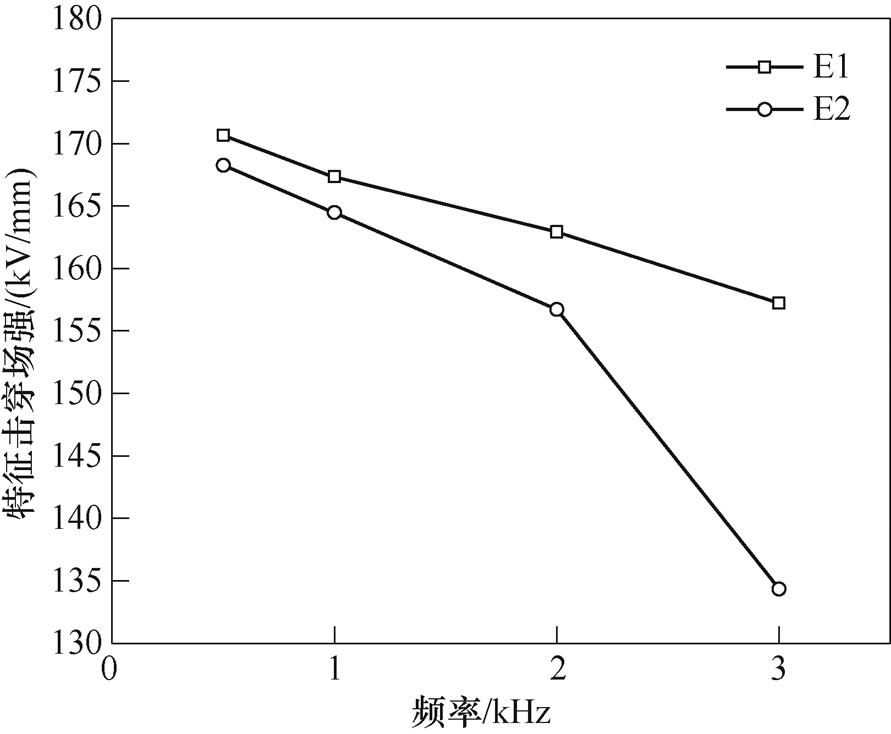
图9为不同频率下两种环氧双极性方波电压下击穿场强的三参数Weibull分布概率统计分析结果。利用式(11)对数据进行拟合,可以看出,高频方波下的环氧试样的击穿特性与三参数Weibull拟合结果吻合良好。图10为将统计分布的尺度参数与位置参数相加得到E1、E2在不同频率下的特征击穿场强。可以看出随频率增大,两种试样的特征击穿场强都降低。500 Hz时,两种环氧的击穿场强约为170 kV/mm,E1试样击穿场强略大于E2。3 kHz时,E2试样的击穿场强为134 kV/mm,相比500 Hz降低了21%,高频击穿强度出现明显下降。在每个频率处,E1试样的特征击穿场强都高于E2,且二者之间的差距随频率升高出现不断增大的趋势。当频率上升至3 kHz时,E2试样的特征击穿场强比E1低了17%,这可能是因为环氧值越大,环氧分子链长度越短,环氧固化物中交联点越多,交联点的增多会使分子链聚集成更加致密的网络,从而减小自由体积。因此,E1试样的特征高频击穿场强大于E2。
(a)E1
(b)E2
图9 不同频率下的三参数Weibull分布
Fig.9 Three parameter Weibull distribution at different frequencies
3 交流电导与高频击穿机理讨论
3.1 双极性方波电压作用下的交流电导率
不同频率下的双极性方波可通过傅里叶级数进行分解[18],双极性周期方波电压的傅里叶展开式为
式中,U(t)sq为双极性方波电压;U0为同频率单极性方波的峰值电压;fn为频率;n为正弦函数的阶数;t为时间。
在对双极性方波电压进行展开后,可认为双极性方波在电场作用下的交流电导率是不同频率不同电压幅值的正弦电压作用下的交流电导率的叠加。在交变电场作用下,电导率是与频率和电场强度相关的函数,根据低电场下的Jonscher普适介电响应特性[31]、Poole-Frenkel效应以及直流电导特性,给出电导率随频率和电场的变化关系[32]为
式中,sAC为总的交流电导率;tand0为低电场下与频率无关的损耗因数;tandPF为Poole-Frenkel(P-F)效应交流极化损耗分量;s0为低电场下偶极子转向极化引起的交流电导率;sPF为介质体内的电荷载流子P-F效应引起的交流电导率。
考虑到双极性方波的频率响应,双极性方波电压下绝缘介质总的交流电导率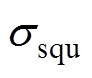 可表示为
可表示为
式中,N为所有正弦函数的谐波阶数;wn为第n阶傅里叶分解的正弦波的频率;E0为电压U0作用下的电场。
随着频率的增大,低电场下的电导率s0不断增大,这一电导率可认为与电场强度无关;对于直流电导率sdc,其与频率无关,当电场强度较低时,处于电荷注入阈值电场强度之下,直流电导率与外加电场服从欧姆定律。当电场大于电荷注入阈值电场强度,直流电导率与电场的关系服从空间电荷限制电流(SCLC)效应,sdc随电场增大而快速上升,在高电场时有显著影响。
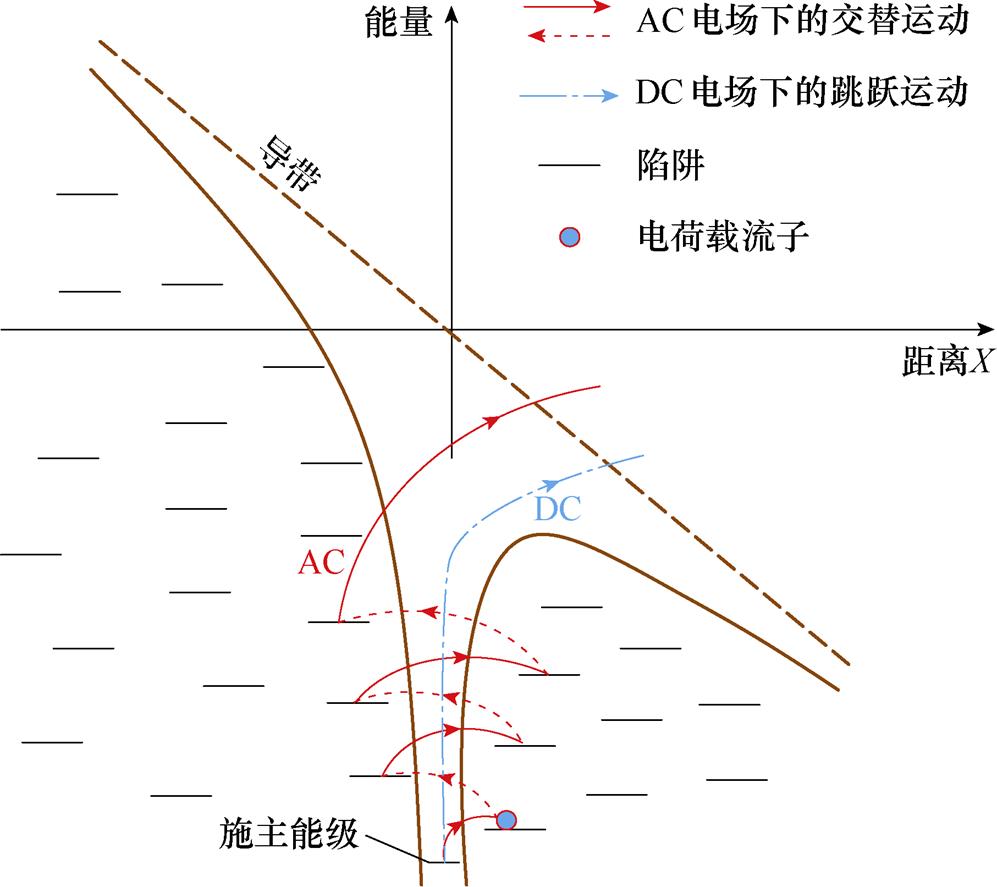
经典的Poole-Frenkel效应表示介质体内施主能级上的载流子在外施直流电场作用下,通过热激发的方式越过势垒进行迁移的热电离过程。A. K. Jonscher 和C. K. Loh等通过对经典的Poole- Frenkel效应进行修正,引入交流电导过程来描述交变电场下的电荷产生与跳跃迁移过程[33-34]。然而,已有研究对高频高电场下绝缘内部载流子迁移仍按照传统肖特基发射与直流电导处理,对交流电导率与温度特性没有仔细的区分。
图11为考虑绝缘介质高频交流电导特性的载流子输运示意图,特别是与频率和电场有关的Poole-Frenkel效应引起的交流电导。在直流电场作用下,电荷载流子朝着同一方向迁移运动,跳跃过势垒并进入导带。然而,在高频交流电压作用下,载流子在陷阱或势垒之间交替跳跃迁移,获得的能量不断累积,因此跳跃幅度不断增大,即载流子迁移率不断增大。与直流电场相比,根据绝缘介质内部载流子迁移的P-F效应,高频电场会增强载流子热激发到导带的概率。频率对交流电导率的影响体现为:随着频率的增大,电荷载流子在陷阱之间跳跃越频繁,获得的能量也会越多,热激发到导带的概率越大,因此交流电导率越大。电场对交流电导率的影响体现为:电场强度增大会降低势阱的势垒高度,载流子激发到导带需要的能量更低,同样会增大交流电导率。根据交流电场下绝缘介质电导的P-F效应可知,在高频高电场下sPF对交流电导率的贡献增加,其与电压频率和电场呈正相关。因此,随着频率增加,载流子获得的能量增加,容易越过势垒,交流电导率增加,明显高于直流下的电导率。在高电场,载流子迁移加快,从而形成足够强的碰撞电离,能量积聚迅速增加,造成分子链断裂,导致绝缘击穿。因此,高频电场下绝缘击穿场强下降。
3.2 高频电场下自由体积击穿模型
影响聚合物自由体积大小的因素包括分子链段结构、电场、温度等。当给环氧树脂两端加上不同大小的电场时,环氧分子链段发生不同程度的旋转、收缩和断裂,同时分子链段也会在空间上发生不同程度的位移,因此电场在一定程度上可以改变自由体积的大小。自由体积与温度的关系体现为:在玻璃化转变温度Tg以下,聚合物处于玻璃态,温度的升高带来的自由体积增大并不明显;在Tg以上,聚合物处于高弹态或粘流态,温度的变化会引发较大的自由体积变化,其性能会发生突变。自由体积的存在使得聚合物分子链段可以发生运动,此外,电荷也可以在自由体积间输运,因此自由体积可以影响聚合物的热学、力学、电学特性。
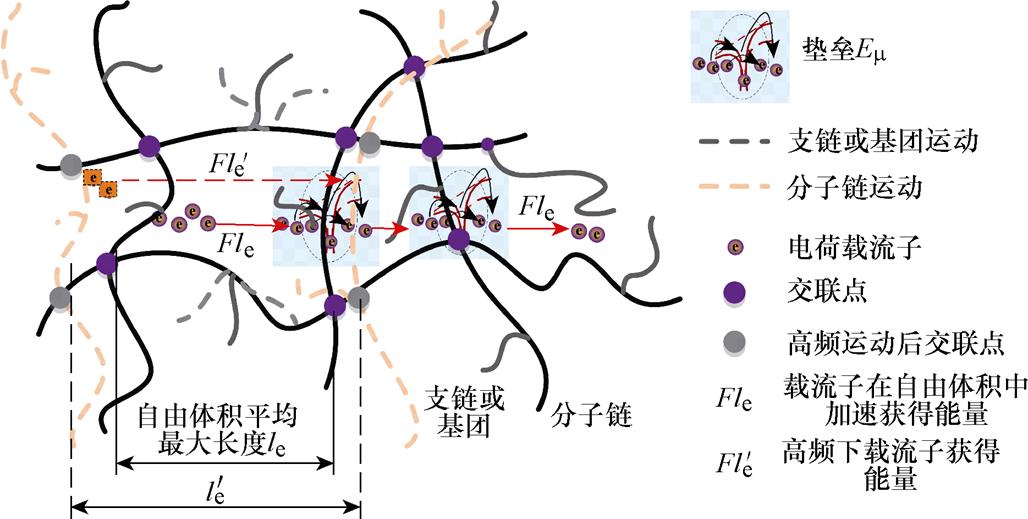
图12为交变电场下环氧树脂自由体积击穿模型示意图(高频等效自由体积平均最大长度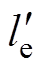 增大)。在交流电场的作用下,分子链上被束缚的电荷跟随电场方向的变化做出相应的运动,导致分子链或基团彼此之间交替性的远离或靠近,分子链上的交联点同样随着链段的伸缩振动而产生位移。在分子链运动过程中,由于分子链段运动引发不同的松弛极化特性,高频电场下分子链段运动存在迟滞效应,即分子链段运动跟不上电场变化,分子链松弛时间大于电场变化时间。高频电场下,分子链或基团朝着同一方向运动的时间即彼此靠近或远离的时间缩短,认为分子链移动的速率一定,则运动的距离越短,分子链段或基团跟不上电场变化,其运动的区域变窄,类似于在一定位置的小范围振动,因此,分子链间未被占有的区域,即自由体积相对低频下更大。根据自由体积理论,击穿强度决定于载流子在电场下加速的最大平均自由行程,而电子在自由体积中加速,其平均自由程取决于最大自由体积的长度。在本文研究频率范围内,载流子加速的最大平均自由行程随频率增大而增大,其获得能量增加,容易积聚能量,连续越过势垒,从而导致高频电场下环氧树脂击穿场强下降。另外,考虑到分子链运动和聚合物结构的复杂性,自由体积的大小与数量不断变化,高频下分子链基团的快速伸缩振动导致分子基团间距缩短,分子基团之间的势垒降低,有利于载流子跳跃,从而增加交流电导率。
增大)。在交流电场的作用下,分子链上被束缚的电荷跟随电场方向的变化做出相应的运动,导致分子链或基团彼此之间交替性的远离或靠近,分子链上的交联点同样随着链段的伸缩振动而产生位移。在分子链运动过程中,由于分子链段运动引发不同的松弛极化特性,高频电场下分子链段运动存在迟滞效应,即分子链段运动跟不上电场变化,分子链松弛时间大于电场变化时间。高频电场下,分子链或基团朝着同一方向运动的时间即彼此靠近或远离的时间缩短,认为分子链移动的速率一定,则运动的距离越短,分子链段或基团跟不上电场变化,其运动的区域变窄,类似于在一定位置的小范围振动,因此,分子链间未被占有的区域,即自由体积相对低频下更大。根据自由体积理论,击穿强度决定于载流子在电场下加速的最大平均自由行程,而电子在自由体积中加速,其平均自由程取决于最大自由体积的长度。在本文研究频率范围内,载流子加速的最大平均自由行程随频率增大而增大,其获得能量增加,容易积聚能量,连续越过势垒,从而导致高频电场下环氧树脂击穿场强下降。另外,考虑到分子链运动和聚合物结构的复杂性,自由体积的大小与数量不断变化,高频下分子链基团的快速伸缩振动导致分子基团间距缩短,分子基团之间的势垒降低,有利于载流子跳跃,从而增加交流电导率。
4 结论
本文采用宽频介电谱和双极性方波电压下的击穿测试研究了两种双酚A类环氧树脂交流电导特性和高频方波击穿特性。通过对环氧树脂高频交流电导、分子链段松弛与载流子输运特性,以及方波电压频率对短时击穿场强的影响的研究,得到如下结论:
1)高频高电场下的交流电导率由低电场下的偶极电导率、交变电场下的Poole-Frenkel效应以及直流电导率共同引起。频率升高或电场增大,都会使得交流电导率增大,且非线性程度增大。
2)频率会影响环氧分子链之间自由体积的大小,频率越高,高频电场下分子链段运动迟滞效应增加,即分子链段运动跟不上电场变化,分子链松弛时间大于电场变化时间。分子链之间未被占有的等效自由体积最大程度增加,造成击穿场强随频率的升高而下降。
参考文献
[1] 陈平, 王德中. 环氧树脂及其应用[M]. 北京: 化学工业出版社, 2004.
[2] 刘贺晨, 郭展鹏, 李岩, 等. 衣康酸基环氧树脂和双酚A环氧树脂性能对比研究[J]. 电工技术学报, 2022, 37(9): 2366-2376.
Liu Hechen, Guo Zhanpeng, Li Yan, et al. Com- parative study on the performance of itaconic acid based epoxy resin and bisphenol a epoxy resin[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2366-2376.
[3] Mohan P. A critical review: the modification, properties, and applications of epoxy resins[J]. Polymer-Plastics Technology and Engineering, 2013, 52(2): 107-125.
[4] 王威望, 刘莹, 何杰峰, 等. 高压大容量电力电子变压器中高频变压器研究现状和发展趋势[J]. 高电压技术, 2020, 46(10): 3362-3373.
Wang Weiwang, Liu Ying, He Jiefeng, et al. Research status and development trend of medium and high frequency transformer use in high-voltage and large capacity power electronic transformer[J]. High Voltage Engineering, 2020, 46(10): 3362-3373.
[5] Wang Weiwang, He Jiefeng, Liu Ying, et al. Effects of spike voltages coupling with high dV/dt square wave on dielectric loss and electric-thermal field of high-frequency transformer[J]. IEEE Access, 2021, 9: 137733-137743.
[6] 汪涛, 骆仁松, 文继峰, 等. 基于辅助绕组的高频变压器绕组损耗测量方法[J]. 电工技术学报, 2022, 37(10): 2622-2630, 2655.
Wang Tao, Luo Rensong, Wen Jifeng, et al. A measurement method of winding loss for high- frequency transformer based on auxiliary winding[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2622-2630, 2655.
[7] Wang Weiwang, Liu Ying, He Jiefeng, et al. An improved design procedure for a 10 kHz, 10 kW medium-frequency transformer considering insulation breakdown strength and structure optimization[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(4): 3525-3540.
[8] 惠苏新, 王鹏, 吴琦, 等. 重复脉冲占空比对环氧树脂电树生长特性影响研究[J]. 中国电机工程学报, 2020, 40(16): 5383-5392.
Hui Suxin, Wang Peng, Wu Qi, et al. Study of the influence of repetitive impulse voltage duty cycle on the treeing characteristics of epoxy resin electrical trees[J]. Proceedings of the CSEE, 2020, 40(16): 5383-5392.
[9] 何东欣, 张涛, 陈晓光, 等. 脉冲电压下电力电子装备绝缘电荷特性研究综述[J]. 电工技术学报, 2021, 36(22): 4795-4808.
He Dongxin, Zhang Tao, Chen Xiaoguang, et al. Research overview on charge characteristics of power electronic equipment insulation under the pulse voltage[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4795-4808.
[10] 赵波, 张宁, 李琳, 等. 大容量高频变压器磁芯损耗特性分析及结构选择[J]. 磁性材料及器件, 2016, 47(1): 39-43.
Zhao Bo, Zhang Ning, Li Lin, et al. Loss characteristics analysis and structure selection of magnetic core of high-power high-frequency transformers[J]. Journal of Magnetic Materials and Devices, 2016, 47(1): 39-43.
[11] 张宏亮, 张丝钰, 刘鹏, 等. 高温下纳米氧化石墨烯/环氧树脂复合材料的载流子特性[J]. 高电压技术, 2018, 44(12): 3814-3823.
Zhang Hongliang, Zhang Siyu, Liu Peng, et al. Characteristics of charge carrier of epoxy resin based nanocomposities filled with graphene oxide at high temperatures[J]. High Voltage Engineering, 2018, 44(12): 3814-3823.
[12] 陈向荣, 黄小凡, 王启隆, 等. 温度和频率对环氧树脂/碳化硅晶须复合材料交流非线性特性的影响[J]. 电工技术学报, 2022, 37(15): 3897-3912.
Chen Xiangrong, Huang Xiaofan, Wang Qilong, et al. Effect of temperature and frequency on AC nonlinear properties of epoxy resin/silicon carbide whisker composites[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3897-3912.
[13] Jilani W, Mzabi N, Gallot-Lavallée O, et al. Study of AC electrical conduction mechanisms in an epoxy polymer[J]. The European Physical Journal Plus, 2015, 130(11): 235.
[14] 王威望, 李盛涛. 工程固体电介质绝缘击穿研究现状及发展趋势[J]. 科学通报, 2020, 65(31): 3461- 3474.
Wang Weiwang, Li Shengtao. Research status and development of insulation breakdown in engineering solid dielectrics[J]. Chinese Science Bulletin, 2020, 65(31): 3461-3474.
[15] Ieda M, Nagao M, Hikita M. High-field conduction and breakdown in insulating polymers. Present situation and future prospects[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1994, 1(5): 934-945.
[16] 赵义焜, 张国强, 郭润睿, 等. 高频变压器用耐高温型匝间绝缘材料的击穿特性[J]. 高电压技术, 2020, 46(2): 657-665.
Zhao Yikun, Zhang Guoqiang, Guo Runrui, et al. Breakdown characteristics of heat-resistant inter-turn to insulation materials in high-frequency trans- formers[J]. High Voltage Engineering, 2020, 46(2): 657-665.
[17] Wang Weiwang, Wang Xin, He Jiefeng, et al. Dielectric breakdown characteristics of epoxy resin induced by high frequency electric stress used in solid state transformer[C]//2020 IEEE 3rd International Conference on Dielectrics (ICD), Valencia, Spain, 2021: 162-165.
[18] Zhang Chuang, Wang Shihang, Fu Hang, et al. Effect of bipolar square wave voltage with varied frequ- encies on electrical tree growth in epoxy resin[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2021, 28(3): 806-814.
[19] 李盛涛, 谢东日, 闵道敏. 聚丙烯/Al2O3纳米复合介质直流击穿特性与电荷输运仿真研究[J]. 中国电机工程学报, 2019, 39(20): 6122-6130, 6193.
Li Shengtao, Xie Dongri, Min Daomin. Namerical simulation on space charge transport and DC breakdown of polypropylene/Al2O3 nanocompo- sites[J]. Proceedings of the CSEE, 2019, 39(20): 6122-6130, 6193.
[20] 谢东日, 刘晔, 黄印, 等. 聚丙烯/BN复合介质高频击穿性能提升与电荷输运仿真研究[J]. 高电压技术, 2020, 46(2): 648-656.
Xie Dongri, Liu Ye, Huang Yin, et al. Improvement of high-frequency breakdown performance and simulation of charge transport of polypropylene/BN composite[J]. High Voltage Engineering, 2020, 46(2): 648-656.
[21] Dissado L A, Fothergill J C. Electrical degradation and breakdown in polymers[M]. London: Peter Peregrinus, 1992.
[22] 王威望, 李盛涛, 刘文凤. 聚合物纳米复合电介质的击穿性能[J]. 电工技术学报, 2017, 32(16): 25- 36.
Wang Weiwang, Li Shengtao, Liu Wenfeng. Dielectric breakdown of polymer nanocomposites[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 25-36.
[23] Li Mingru, Cai Zhuoli, Niu Huan, et al. The effect of epoxide on molecular chain relaxation on bisphenol a epoxy resin after curing[C]//2021 International Con- ference on Electrical Materials and Power Equipment, Chongqing, China, 2021: 1-4.
[24] Almond D P, Duncan G K, West A R. The deter- mination of hopping rates and carrier concentrations in ionic conductors by a new analysis of AC con- ductivity[J]. Solid State Ionics, 1983, 8(2): 159-164.
[25] Kao K C, Dielectric phenomena in solids[M]. San Diego, California: Elsevier, 2004.
[26] Diaham S, Locatelli M L. Concentration and mobility of charge carriers in thin polymers at high tempera- ture determined by electrode polarization modeling[J]. Journal of Applied Physics, 2012, 112(1): 013710.
[27] Dudowicz J, Freed K F, Douglas J F. The glass transition temperature of polymer melts[J]. The Journal of Physical Chemistry B, 2005, 109(45): 21285-21292.
[28] Kremer F, Schonhals A. Broadband dielectric spectro- scopy[M]. Berlin: Springer, 2003.
[29] Huang Yin, Min Daomin, Li Shengtao, et al. Dielectric relaxation and carrier transport in epoxy resin and its microcomposite[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(5): 3083-3091.
[30] Ushakov V I. Impulse breakdown of liquids[M]. Berlin: Springer, 2007.
[31] Jonscher A K. The ‘universal’ dielectric response[J]. Nature, 1977, 267(5613): 673-679.
[32] Tokoro T, Tohyama K, Nagao M, et al. High-field dielectric properties of polyethylene in the high- temperature region[J]. Electrical Engineering in Japan, 1992, 112(6): 10-19.
[33] Jonscher A K. Energy losses in hopping conduction at high electric fields[J]. Journal of Physics C: Solid State Physics, 1971, 4(11): 1331-1340.
[34] Jonscher A K, Loh C K. Poole-Frenkel conduction in high alternating electric fields[J]. Journal of Physics C: Solid State Physics, 1971, 4(11): 1341-1347.
AC Conductivity with High Frequency Relaxation and Breakdown Characteristics of Epoxy Resin under Bipolar Square Wave Voltage
Jiang Qihang1 Wang Weiwang1 Zhong Yu1 Li Shengtao1 Xu Yongsheng2
(1. State Key Laboratory of Electrical Insulation and Power Equipment Xi’an Jiaotong University Xi’an 710049 China 2. State Key Laboratory of HVDC Electric Power Research Institute China Southern Power Grid Guangzhou 510080 China)
Abstract As one of the solid insulation materials of high-frequency transformers (HFT), epoxy resin presents good performance under high-frequency non-sinusoidal electrical voltage.Its insulation performance depends strongly onvoltage frequency. Due to the local temperature rise in high-frequency transformers, the electrothermal effect can increase the conductivity of epoxy resin. Nevertheless, the AC conductivity fromthe dielectric spectrum measurement cannot be equivalent to the AC conductivity characteristics under high- frequency non-sinusoidal voltage. Therefore, this paper studies the AC conductivity characteristics under high-frequency square voltage by the Fourier decomposition. The mechanism underlying the AC conductivity of epoxy resin on the breakdown at high frequency is discussed by improving the free volume breakdown theory. The relationship between the AC conductivity and the high-frequency breakdown of epoxy resin is analyzedby the high-frequency relaxation characteristics and high-frequency high-field conduction theory.
Two kinds of epoxy resin samples E1 and E2 were prepared using the same process and method. According to theresults of glass transition temperature Tg andAC conductivity, the Almond-West (A-W) model and Havriliak-Negami (H-N) multi-dispersion relaxation polarization model were used to fit and analyze the AC conductivity spectrum at different temperatures, and the DC conductivity of epoxy resin at different temperatures was also obtained. Then, the temperature and frequency dependence of relaxation processes a and d are analyzed according to the fitting results of the H-N model. According to the insulation breakdown measurement results, the breakdown characteristics of two epoxy samples within 500~3 000 Hz were analyzed. Based on the statistical results of the three-parameter Weibull distribution, the relationship between the featured breakdown field strength and the frequency was obtained. According to Jonscher's universal dielectric response model, the Poole-Frenkel effect, DC conductivity, and the frequency and electric field effects on AC conductivity under bipolar square wave voltage are analyzed. The free volume breakdown model is proposed to analyze the influence of frequency on the AC conductivity and high-frequency breakdown in the epoxy resin samples.
According to the fitting results of the A-W model and the H-N model, the AC conductivity is mainly determined by the polarization loss caused by the relaxation process a above Tg. The relaxation process adepends on the dipole turning polarization, and the dipole concentration in the epoxy resin sample with a high epoxy value is high. The relaxation process d is determined by the DC conductivity process,anddprocess is related to thecarrier migration across the barrier. The breakdown strengths of two epoxy resin samples decrease with the increase in frequency.The breakdownstrength of E1 sample is greater than that of E2.
The conclusions are as follows according to the measured results, fitting results, and model analysis. (1) The AC conductivity at high frequency and high field includes dipole conductivity at low field, Poole-Frenkel emission of charge carriers under high-frequency electric field, and DC conductivity. The AC conductivity increases with the increase in frequency or electric field. (2) The hysteresis effect of movements of molecular chain segments under the high-frequency electric fields becomes obvious as the frequency increases. The maximum length of the unoccupied equivalent free volume between the molecular chains increases, reducingbreakdownstrength at high-frequency voltage. In addition, the molecular group spacing decreases with the increase in frequency, leading to the decrease of carrier hopping potential barrier and the increase in AC conductivity of epoxy resin samples.
keywords:Epoxy resin, AC conductivity, bipolar square wave voltage, free volume, high frequency breakdown
中图分类号:TM215.1
DOI: 10.19595/j.cnki.1000-6753.tces.222129
国家自然科学基金面上项目(52177025)、陕西省自然科学基础研究计划青年项目(2020JQ-045)和电力设备电气绝缘国家重点实验室中青年基础研究创新基金项目(EIPE21314)资助。
收稿日期 2022-11-11
改稿日期 2022-12-12
作者简介
蒋起航 男,1998年生,硕士,研究方向为聚合物介电与击穿性能。E-mail: jqhang@stu.xjtu.edu.cn
王威望 男,1987年生,博士,副教授,研究方向为绝缘介质理论与应用,高频磁件设计与绝缘可靠性。E-mail: weiwwang@xjtu.edu.cn(通信作者)
(编辑 陈 诚)
 x
x 0.6(x=EV×166×0.9,EV为环氧树脂环氧值,即每100 g环氧树脂中所含的环氧基团的摩尔数,单位为mol/(100 g))的配料比加入到离心搅拌机的容器中。搅拌的程序为:搅拌分散过程转速为2 000 r/min,持续15 min,脱气过程转速为2 200 r/min,持续15 min。将搅拌均匀的混合物倒入模具中,然后将模具放入真空鼓风电热干燥箱,在常温下进行抽真空,持续脱气30 min以去除试样中的气泡,之后打开烘箱进气旋钮,在常压下进行固化。固化程序为80℃固化2 h,然后10 min升温至140℃,在140℃固化12 h。固化结束后取出试样并用酒精清洗,放入50℃的烘箱干燥备用。
0.6(x=EV×166×0.9,EV为环氧树脂环氧值,即每100 g环氧树脂中所含的环氧基团的摩尔数,单位为mol/(100 g))的配料比加入到离心搅拌机的容器中。搅拌的程序为:搅拌分散过程转速为2 000 r/min,持续15 min,脱气过程转速为2 200 r/min,持续15 min。将搅拌均匀的混合物倒入模具中,然后将模具放入真空鼓风电热干燥箱,在常温下进行抽真空,持续脱气30 min以去除试样中的气泡,之后打开烘箱进气旋钮,在常压下进行固化。固化程序为80℃固化2 h,然后10 min升温至140℃,在140℃固化12 h。固化结束后取出试样并用酒精清洗,放入50℃的烘箱干燥备用。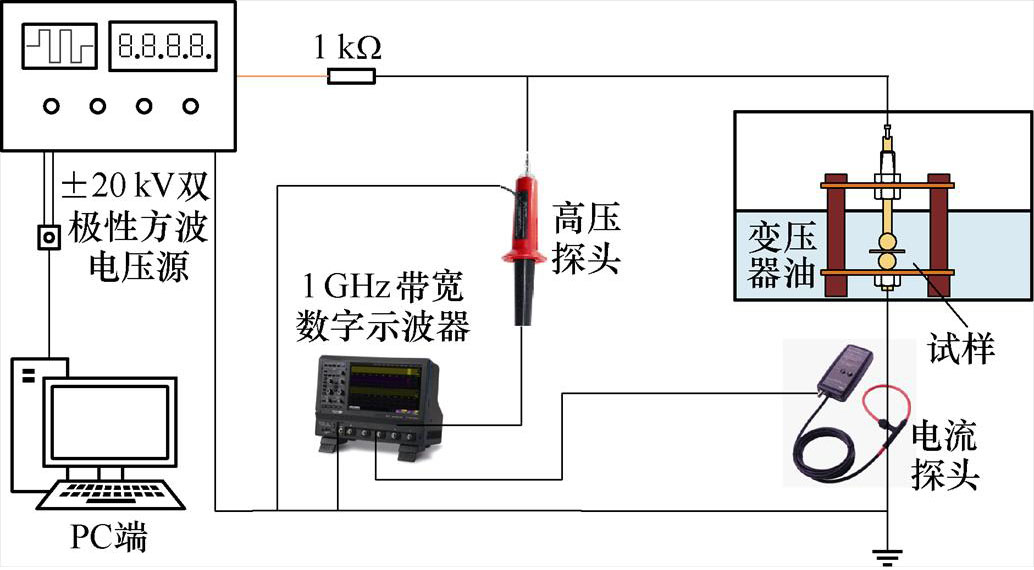
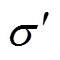 随频率的变化曲线。可以看出,在低频范围与高频范围,
随频率的变化曲线。可以看出,在低频范围与高频范围,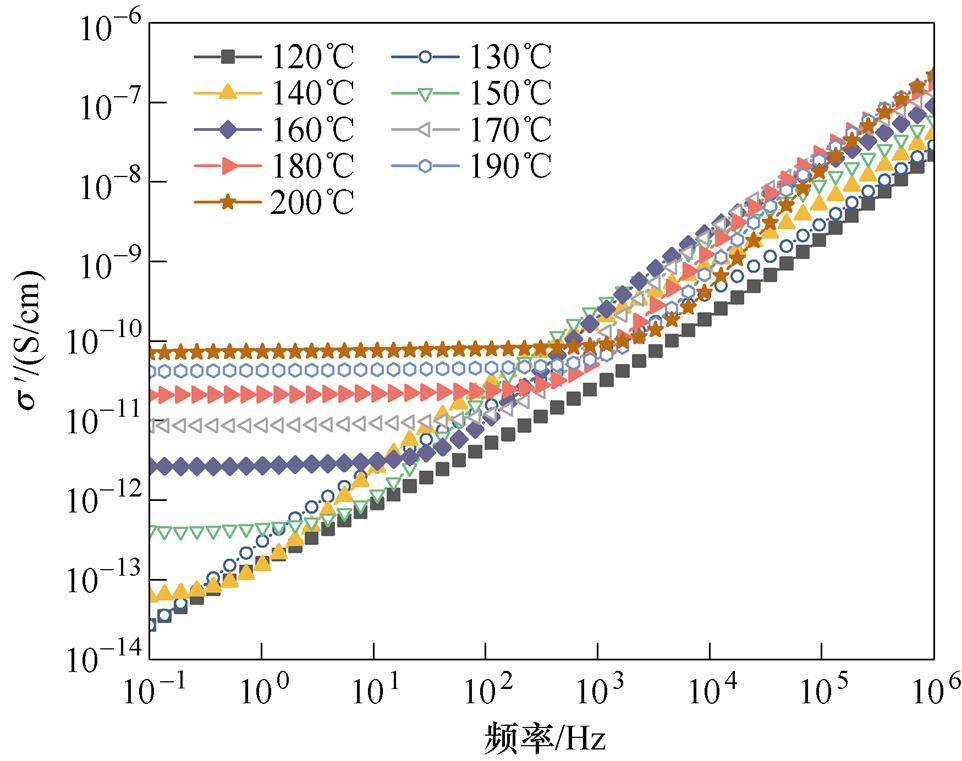
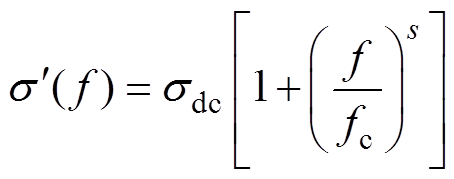 (1)
(1)
 f
f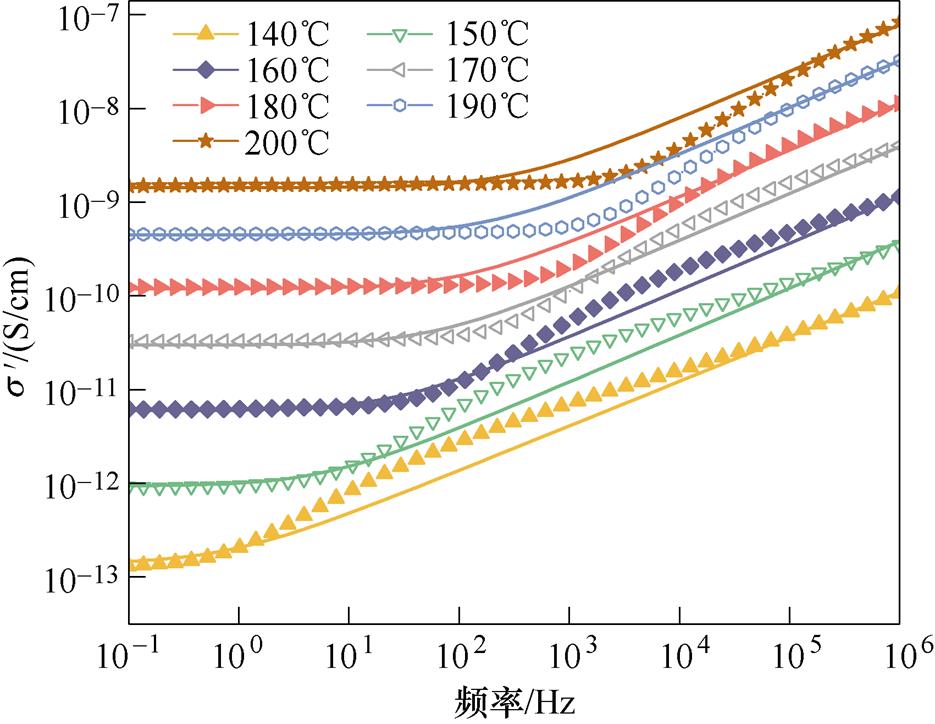


 (2)
(2)
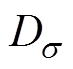 为环氧树脂内直流电导的强度系数,可以认为是无量纲活化能,
为环氧树脂内直流电导的强度系数,可以认为是无量纲活化能,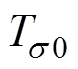 为直流电导的Vogel温度;T为热力学温度。
为直流电导的Vogel温度;T为热力学温度。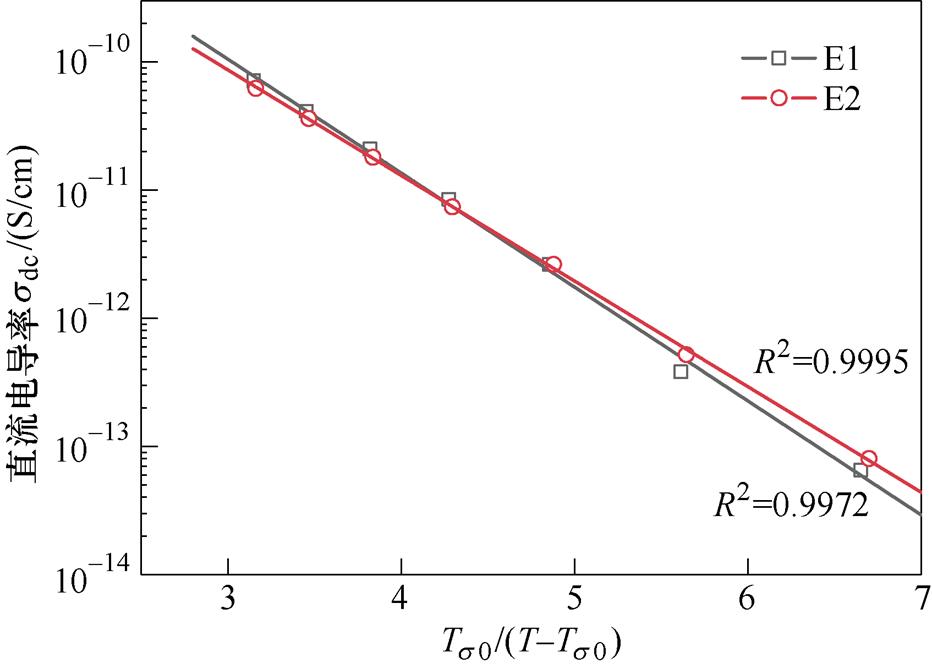
 f
f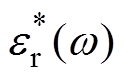 可表示为
可表示为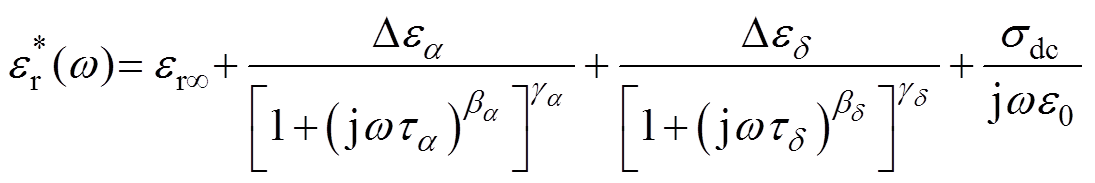 (3)
(3)
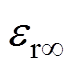 为光频介电常数;
为光频介电常数;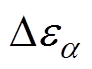 和
和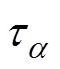 分别为松弛过程
分别为松弛过程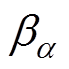 和
和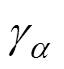 为松弛过程
为松弛过程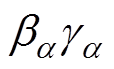 ≤1;
≤1;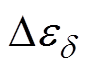 和
和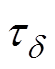 分别为松弛过程
分别为松弛过程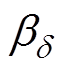 和
和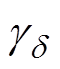 为松弛过程
为松弛过程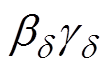 ≤1;
≤1;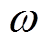 为角频率。
为角频率。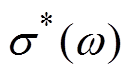 与复介电常数
与复介电常数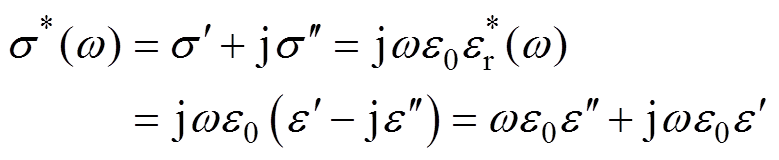 (4)
(4)
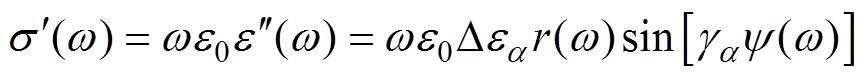 (5)
(5)
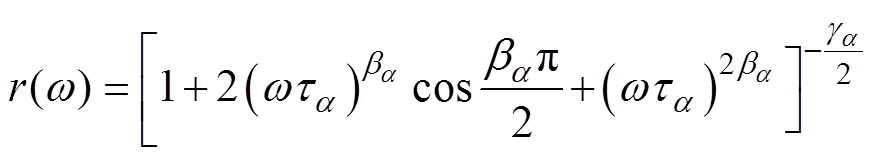 (6)
(6)
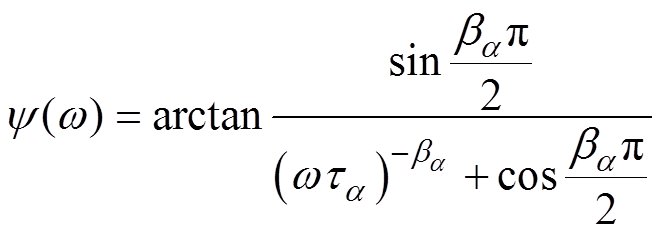 (7)
(7)
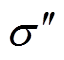 分别为复交流电导率的实部与虚部;
分别为复交流电导率的实部与虚部;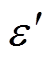 、
、 分别为复介电常数的实部与虚部;
分别为复介电常数的实部与虚部;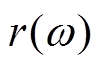 和
和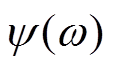 为中间项。由此根据复介电常数的拟合参数得到基于Havriliak-Negami(H-N)介电松弛函数的交流电导率
为中间项。由此根据复介电常数的拟合参数得到基于Havriliak-Negami(H-N)介电松弛函数的交流电导率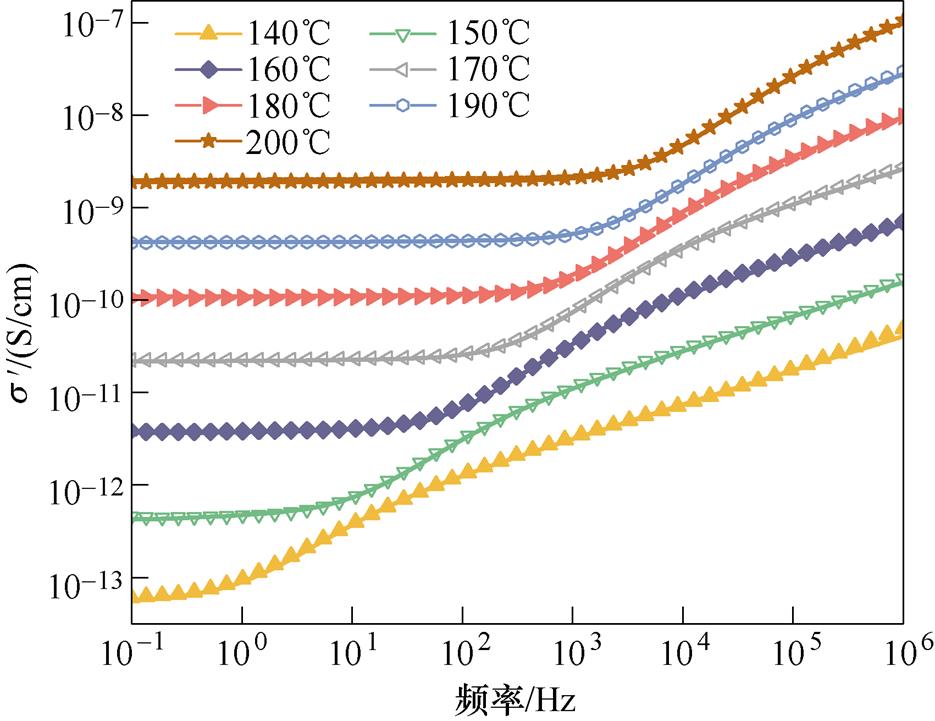


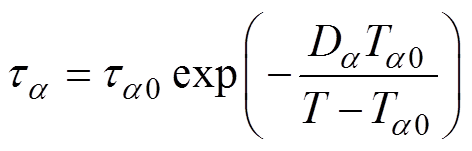 (8)
(8)
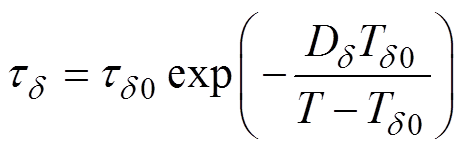 (9)
(9)
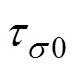 与
与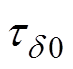 为松弛时间常数;
为松弛时间常数;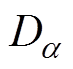 与
与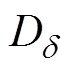 分别为松弛过程
分别为松弛过程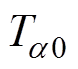 与
与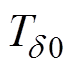 分别为松弛过程
分别为松弛过程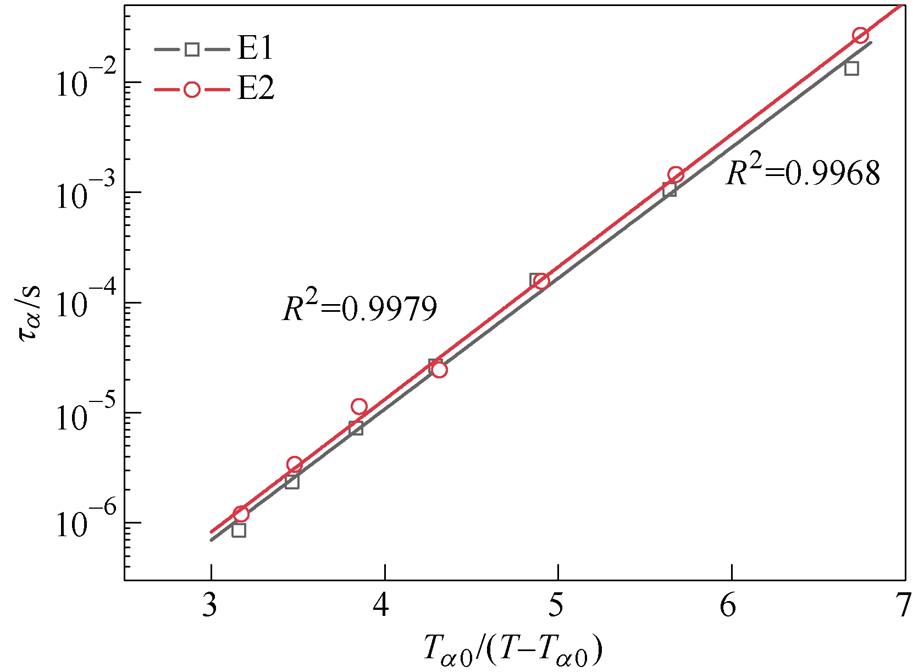

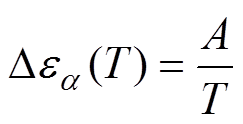 (10)
(10)
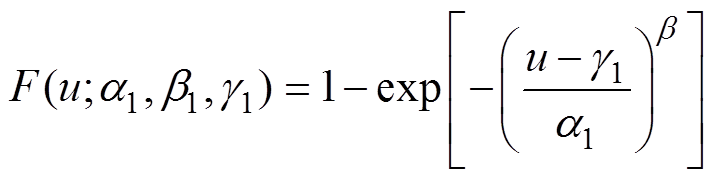 (11)
(11)
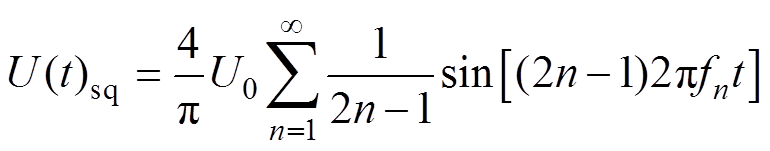 (12)
(12)
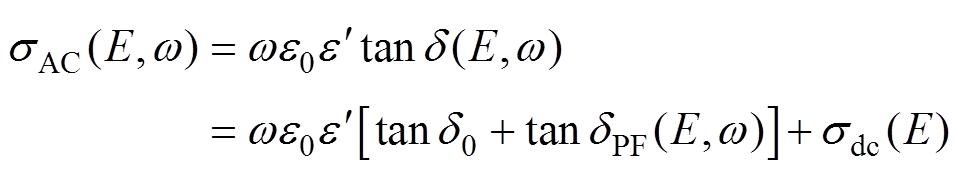
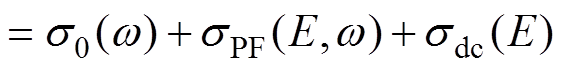 (13)
(13)
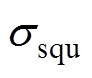 可表示为
可表示为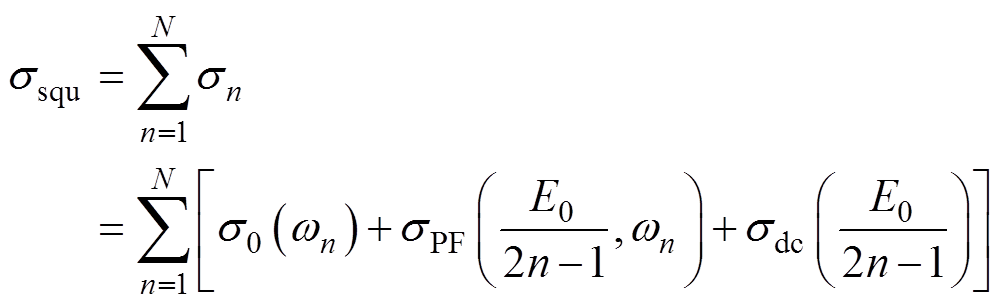 (14)
(14)
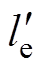 增大)。在交流电场的作用下,分子链上被束缚的电荷跟随电场方向的变化做出相应的运动,导致分子链或基团彼此之间交替性的远离或靠近,分子链上的交联点同样随着链段的伸缩振动而产生位移。在分子链运动过程中,由于分子链段运动引发不同的松弛极化特性,高频电场下分子链段运动存在迟滞效应,即分子链段运动跟不上电场变化,分子链松弛时间大于电场变化时间。高频电场下,分子链或基团朝着同一方向运动的时间即彼此靠近或远离的时间缩短,认为分子链移动的速率一定,则运动的距离越短,分子链段或基团跟不上电场变化,其运动的区域变窄,类似于在一定位置的小范围振动,因此,分子链间未被占有的区域,即自由体积相对低频下更大。根据自由体积理论,击穿强度决定于载流子在电场下加速的最大平均自由行程,而电子在自由体积中加速,其平均自由程取决于最大自由体积的长度。在本文研究频率范围内,载流子加速的最大平均自由行程随频率增大而增大,其获得能量增加,容易积聚能量,连续越过势垒,从而导致高频电场下环氧树脂击穿场强下降。另外,考虑到分子链运动和聚合物结构的复杂性,自由体积的大小与数量不断变化,高频下分子链基团的快速伸缩振动导致分子基团间距缩短,分子基团之间的势垒降低,有利于载流子跳跃,从而增加交流电导率。
增大)。在交流电场的作用下,分子链上被束缚的电荷跟随电场方向的变化做出相应的运动,导致分子链或基团彼此之间交替性的远离或靠近,分子链上的交联点同样随着链段的伸缩振动而产生位移。在分子链运动过程中,由于分子链段运动引发不同的松弛极化特性,高频电场下分子链段运动存在迟滞效应,即分子链段运动跟不上电场变化,分子链松弛时间大于电场变化时间。高频电场下,分子链或基团朝着同一方向运动的时间即彼此靠近或远离的时间缩短,认为分子链移动的速率一定,则运动的距离越短,分子链段或基团跟不上电场变化,其运动的区域变窄,类似于在一定位置的小范围振动,因此,分子链间未被占有的区域,即自由体积相对低频下更大。根据自由体积理论,击穿强度决定于载流子在电场下加速的最大平均自由行程,而电子在自由体积中加速,其平均自由程取决于最大自由体积的长度。在本文研究频率范围内,载流子加速的最大平均自由行程随频率增大而增大,其获得能量增加,容易积聚能量,连续越过势垒,从而导致高频电场下环氧树脂击穿场强下降。另外,考虑到分子链运动和聚合物结构的复杂性,自由体积的大小与数量不断变化,高频下分子链基团的快速伸缩振动导致分子基团间距缩短,分子基团之间的势垒降低,有利于载流子跳跃,从而增加交流电导率。