基于SHEPWM的三电平三相逆变器中点电位主动平衡控制策略
董志强 王琛琛 周明磊 刘明月 李 凯
(北京交通大学电气工程学院 北京 100044)
摘要 在大功率系统中,常采用特定次谐波消除脉宽调制(SHEPWM)以降低系统的开关损耗。针对三电平中点钳位(NPC)型三相逆变器在SHEPWM下的中点电位偏移问题,分析SHEPWM下逆变器输出相电压基波与3次谐波在不同电压相位范围内对中点电位的影响,设计两种在基波周期内对中点电位总充放电效果相反的开关角组合方案,并提出一种通过测量中点电位偏移值及中点电位滞环控制,选择不同的开关角组合方案进行调制的中点电位主动平衡控制策略。实验结果验证了所提出方法的实用性及有效性。
关键词:三电平中点钳位型逆变器 中点电位控制 特定谐波消除脉宽调制 3次谐波
0 引言
三电平中点钳位(Neutral Point Clamped, NPC)型逆变器[1]自被研制以来,便凭借其输出电压波形质量高、dv/dt低、可以用较低耐压的开关器件实现较高的电压输出能力等优点在中压大功率领域得到广泛应用[2-5]。然而,中点电位偏移是三电平NPC逆变器的固有问题[6],中点电位偏移值过大会导致系统输出性能变差、器件耐压过高,还会降低系统可靠性,严重时使系统损坏[2-6]。
三电平NPC常用的调制策略为规则采样正弦脉宽调制(Sinusoidal Pulse Width Modulation, SPWM)或空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM),分别可以通过注入零序电 压[7-8]和调节冗余小矢量作用时间[9-11]等方法进行中点电位平衡控制。而在较低的载波比下,如果仍然采用传统的SPWM或SVPWM,将会造成基波电压失真、相位延时增大以及低次谐波增多等诸多问 题[12]。因此,在低载波比下,三电平NPC逆变器常采用特定次谐波消除脉宽调制(Selected Harmonic Elimination PWM, SHEPWM)[13-14],其特点是可以实现准确的基波电压输出以及特定次谐波成分的消除。但是,由于三电平SHEPWM开关角个数少且计算复杂,中点电位平衡控制也更为困难。
常用的基于SHEPWM的中点电位主动平衡控制策略是根据各相负载电流极性以及中点电位偏移在各相相电压开关角的基础上叠加一个微小角度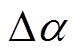 (0 °<
(0 °<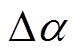 <0.2 °
<0.2 °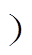 来调节各相相电压的零电平作用时间,从而实现中点电位主动平衡控制[15]。但SHEPWM较少的开关角数目,使得该方法的中点电位平衡能力十分有限,并且SHEPWM开关角数目越少,其中点电位平衡能力越弱。文献[16-18]分析了SHEPWM相电压基波以及3次谐波对中点电位的影响,并通过控制3次谐波含量来抑制中点电位波动,但是没有中点电位主动平衡效果,无法抑制中点电位偏移。文献[19-20]通过将SHEPWM看作传统的SVPWM,根据中点电位偏移情况将对中点电位有充放电效果的电压矢量用冗余矢量进行替换,从而实现中点电位主动平衡控制,但是该类方法极大地增加了系统的开关频率且计算复杂,难以实现。
来调节各相相电压的零电平作用时间,从而实现中点电位主动平衡控制[15]。但SHEPWM较少的开关角数目,使得该方法的中点电位平衡能力十分有限,并且SHEPWM开关角数目越少,其中点电位平衡能力越弱。文献[16-18]分析了SHEPWM相电压基波以及3次谐波对中点电位的影响,并通过控制3次谐波含量来抑制中点电位波动,但是没有中点电位主动平衡效果,无法抑制中点电位偏移。文献[19-20]通过将SHEPWM看作传统的SVPWM,根据中点电位偏移情况将对中点电位有充放电效果的电压矢量用冗余矢量进行替换,从而实现中点电位主动平衡控制,但是该类方法极大地增加了系统的开关频率且计算复杂,难以实现。
针对以上问题,本文通过分析相电压基波及3次谐波产生的中点电流分量在不同基波电压角度范围内对中点电位的影响,设计了两种在基波周期内对中点电位总的充放电效果相反的开关角组合方案。在此基础上,提出了一种基于SHEPWM 3次谐波含量调节的三电平NPC三相逆变器中点电位主动平衡控制策略,通过测量中点电位偏移值及中点电位滞环控制,选择不同的开关角组合方案进行调制,从而实现中点电位主动平衡控制。该方法无需进行负载电流采样,也无需进行复杂运算,且中点电位平衡速度不受开关角数目制约。实验结果验证了所提出方法的可行性及有效性。
1 三电平SHEPWM策略原理
三电平NPC三相逆变器拓扑结构如图1所示,图中,Udc为直流侧总电压,C1和C2分别为直流母线侧上、下电容,u1和u2分别为上、下母线电容电压。当直流侧中点电位稳定时,逆变器每相桥臂可以输出P、O、N三种电平状态,对应输出电压分别为Udc/2、0和-Udc/2。
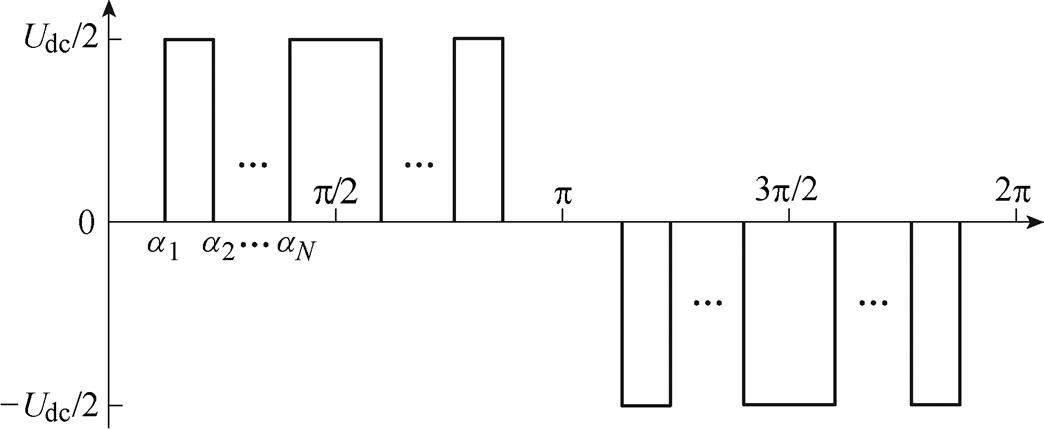
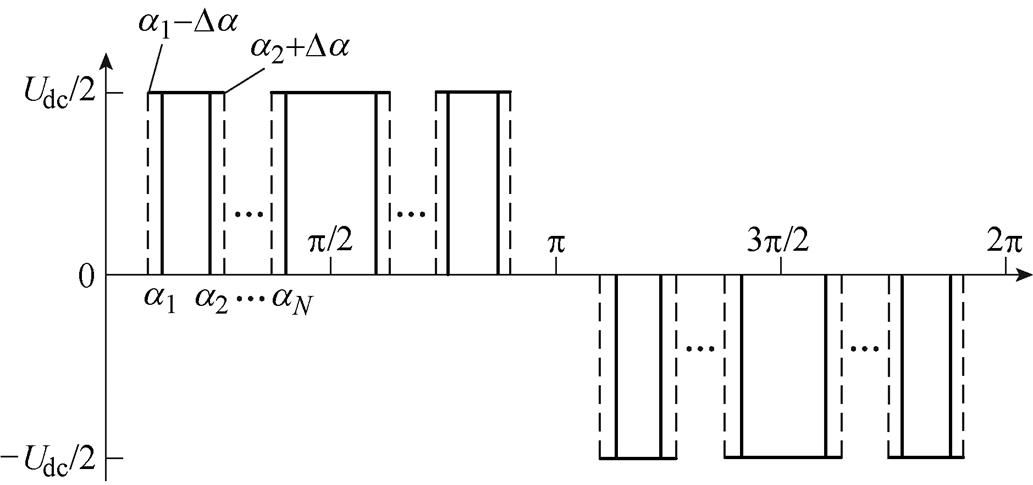
三电平NPC三相逆变器采用SHEPWM时的输出相电压波形如图2所示,图中,a1, a2,…, aN为开关角,N为开关角个数。
由于输出电压存在1/4周期对称性和半波对称性,将三电平SHEPWM相电压波形用傅里叶级数展开后可得到
式中,n为奇数;An为第n次谐波幅值,且可用开关角a1, a2,…, aN表示为
当逆变器输出侧接三相对称负载时,3及3的倍数次谐波在线电压中相互抵消,只需考虑消除6k±1(k=1, 2, 3,…)次谐波,可得基波分量(n=1)和6k±1(k=1, 2, 3,…)次谐波分量的电压幅值表达式分别为
式中,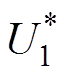 为期望的输出电压基波幅值。取直流侧总电压的一半即Udc/2为基值进行标幺化,则式(3)可转化为
为期望的输出电压基波幅值。取直流侧总电压的一半即Udc/2为基值进行标幺化,则式(3)可转化为
式中,m为调制比,m=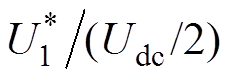 。
。
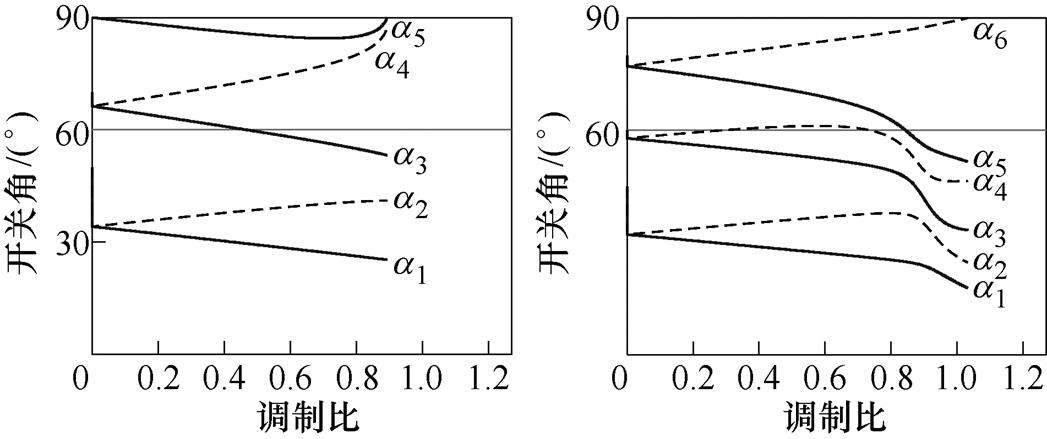
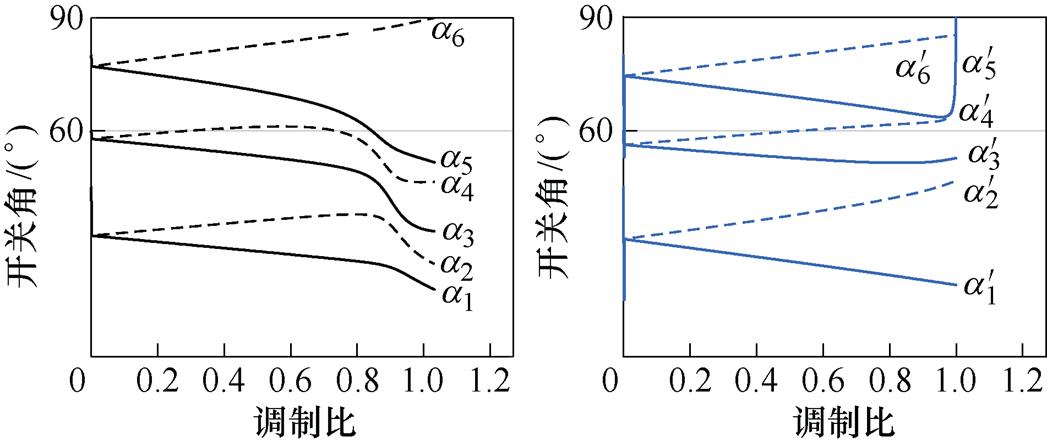
N个开关角可以构成含有N个方程的非线性方程组,通过求解式(4)的非线性方程组即可得到各个调制比下的开关角,进而在保证基波电压输出的基础上,消除N-1个特定次谐波,以N=5及N=6为例,其开关角与调制比的关系如图3所示,当N=5时,可以消除5、7、11和13次谐波;当N=6时,可以消除5、7、11、13和17次谐波。
(a)N=5 (b)N=6
图3 SHEPWM开关角与调制比的关系
Fig.3 The relationship between the switch angle of SHEPWM and the modulation index
2 三电平SHEPWM中点电流分析
当忽略掉谐波分量时,三相逆变器的参考电压标幺值及负载电流分别为
式中,q =wt,w 为输出电压基波角频率;Im为负载电流幅值;j 为负载功率因数角。
如图1所示,中点电位可以表示为直流母线电容电压之差为
式中,io为中点电流;C为上下母线电容容值。根据式(7)可以看出,中点电位的变化本质上是中点电流的变化,由三相电压及三相电流的基波分量产生的中点电流可表示[16]为
在理想情况下,三相电压和三相电流的基波分量产生的中点电流分量以3倍于基波的频率进行波动,即三电平三相逆变器的中点电位在零附近以三倍频进行波动[17]。然而实际情况中,由于不理想因素的存在,会使得中点电位产生偏移,影响系统稳定性。
3 中点电位主动平衡控制策略
目前常用的基于SHEPWM的中点电位主动平衡控制策略是在开关角度上叠加一个微小角度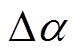 [15],SHEPWM的传统中点电位主动平衡方法如图4所示。该方法通过
[15],SHEPWM的传统中点电位主动平衡方法如图4所示。该方法通过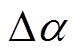 来调节相电压的零电平作用时间,进而控制中点电位。为方便数字实现以及不严重破坏输出电压的谐波特性,
来调节相电压的零电平作用时间,进而控制中点电位。为方便数字实现以及不严重破坏输出电压的谐波特性,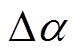 的幅值不超过0.2°[15],而
的幅值不超过0.2°[15],而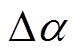 的极性则由中点电位偏移值的极性以及负载电流的极性决定。由于SHEPWM开关角数目较少,使得该方法的中点电位平衡能力十分有限,并且开关角个数越少,该方法在整个基波周期内能够进行的角度调节就越少,平衡能力就越差。
的极性则由中点电位偏移值的极性以及负载电流的极性决定。由于SHEPWM开关角数目较少,使得该方法的中点电位平衡能力十分有限,并且开关角个数越少,该方法在整个基波周期内能够进行的角度调节就越少,平衡能力就越差。
文献[16-18]分析了SHEPWM相电压中3次谐波在整个基波周期内对中点电位的影响,且该影响并不受开关角个数的限制,基于此,本文将分析不同基波电压相位范围内,相电压的基波以及3次谐波对中点电压的影响,从而实现中点电压主动平衡控制。
3.1 3次谐波含量与中点电流的关系
在三相系统中,相电压中的3次谐波不会影响线电压及输出电流的谐波性能,因此在传统SHEPWM的开关角求解中并没有对相电压3次谐波加以控制。然而对于三电平SHEPWM而言,相电压3次谐波对中点电流的影响是不可忽略的[16-18]。假设相电压3次谐波的幅值是基波电压幅值的k3倍,则求解SHEPWM开关角的方程组为
三相相电压中的3次谐波电压表达式为
联合式(5)、式(6)、式(8)和式(10)可以得到相电压的基波与3次谐波分量产生的总中点电流表达式为
为方便讨论k3与中点电流之间的关系,k3的取值需满足式(12)[16-17],以保证k3的取值不会改变式(11)中绝对值运算的符号。
将式(11)与式(12)联立,并将电压相位的0~2p 均分为六部分,分别对应r={1, 2, 3, 4, 5, 6},即可去掉式(11)中的绝对值符号并得到基波与3次谐波分量产生的总的中点电流表达式[16]为
其中
式中,io1为基波电压产生的中点电流分量;io3为3次谐波电压产生的中点电流分量。io1和io3均以3倍于基波电压的频率波动[16],因此,为方便讨论,计算基波和3次谐波各自产生的中点电流分量在0~p/3区间上的积分为
式中,Q为电流在此区间段产生的电荷量。
文献[16-17]中通过将k3的值选取为0.263 6,使得s(io3)的值,在每个p/3的区间上与s(io1)互相抵消,见表1,从而一定程度上降低了中点电位波动的幅值。同时,通过表1还可以看到,当整个基波周期内k3的取值均为0.263 6时,总的中点电流io在整个基波周期内的总积分为零,这意味着系统此时不具备中点电位主动平衡能力。
表1 k3=0.263 6时各中点电流分量积分
Tab.1 The integral of the neutral-point current components when k3=0.263 6
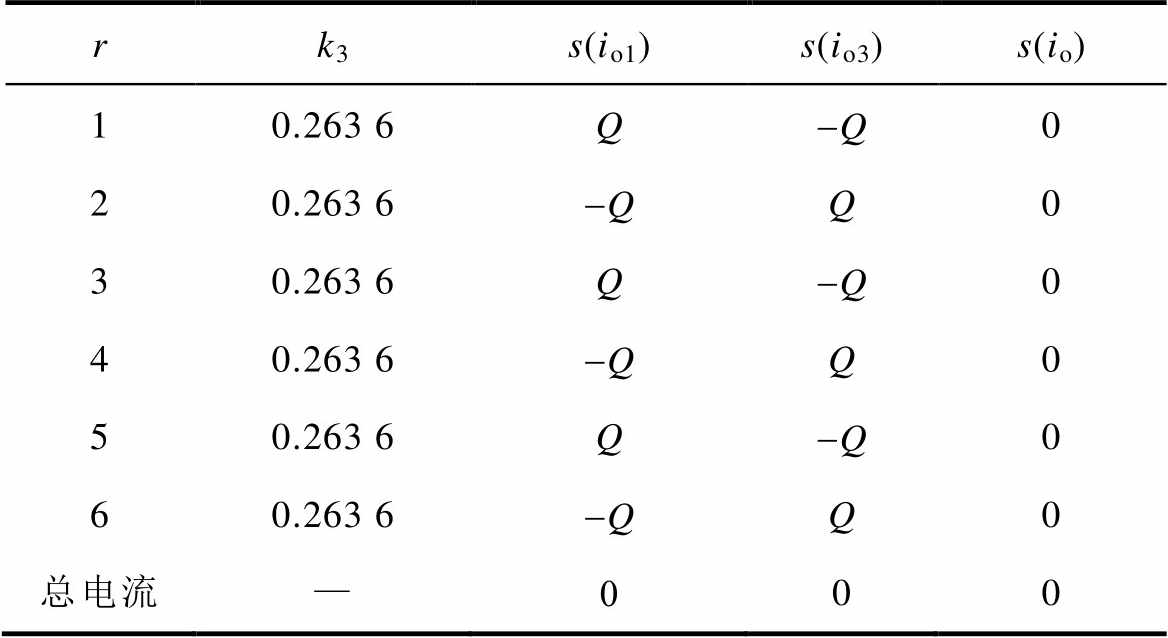
rk3s(io1)s(io3)s(io) 10.263 6Q-Q0 20.263 6-QQ0 30.263 6Q-Q0 40.263 6-QQ0 50.263 6Q-Q0 60.263 6-QQ0 总电流—000
3.2 不同3次谐波含量的开关角组合方案
根据式(14)可知,当负载功率因数大于零时,基波电压产生的中点电流分量io1在r={1, 3, 5}的区间范围内的积分均为Q,且Q>0;在r={2, 4, 6}的区间范围内的积分均为-Q。而当k3=0.263 6时,3次谐波产生的中点电流分量io3在每个p/3区间上的积分与io1的积分相反。基于此,本文设计了两种在基波周期内对中点电位总的充放电效果相反的开关角组合方案,分别见表2和表3。
表2 开关角组合方案Ⅰ
Tab.2 The switching angle combination Ⅰ
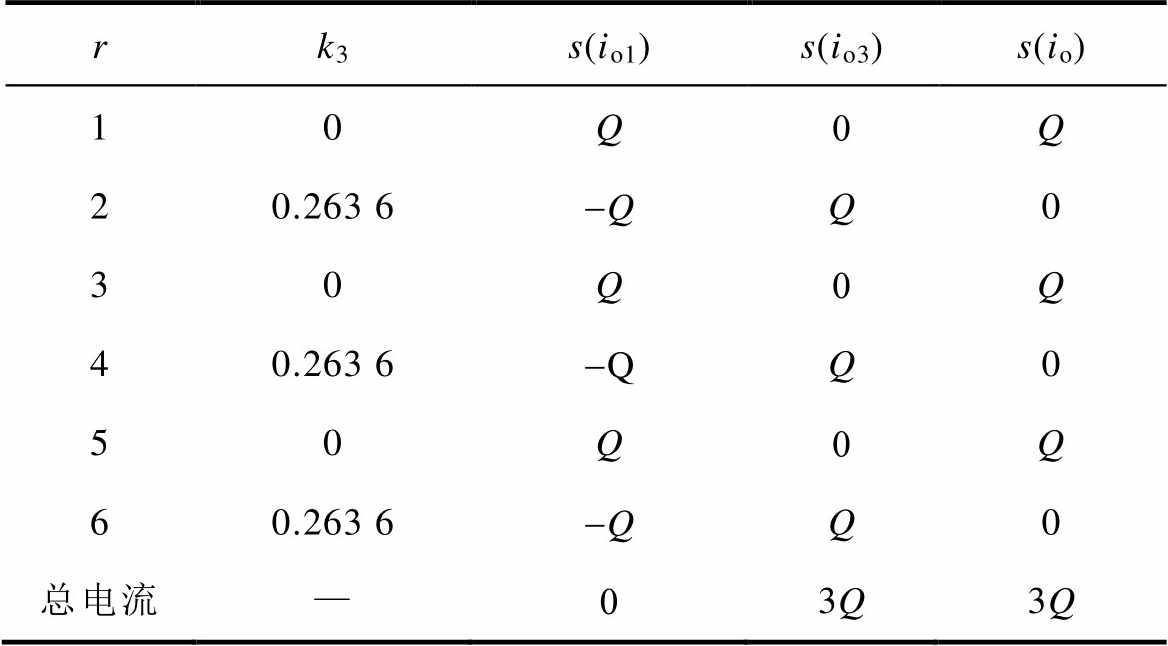
rk3s(io1)s(io3)s(io) 10Q0Q 20.263 6-QQ0 30Q0Q 40.263 6-QQ0 50Q0Q 60.263 6-QQ0 总电流—03Q3Q
表3 开关角组合方案Ⅱ
Tab.3 The switching angle combination Ⅱ
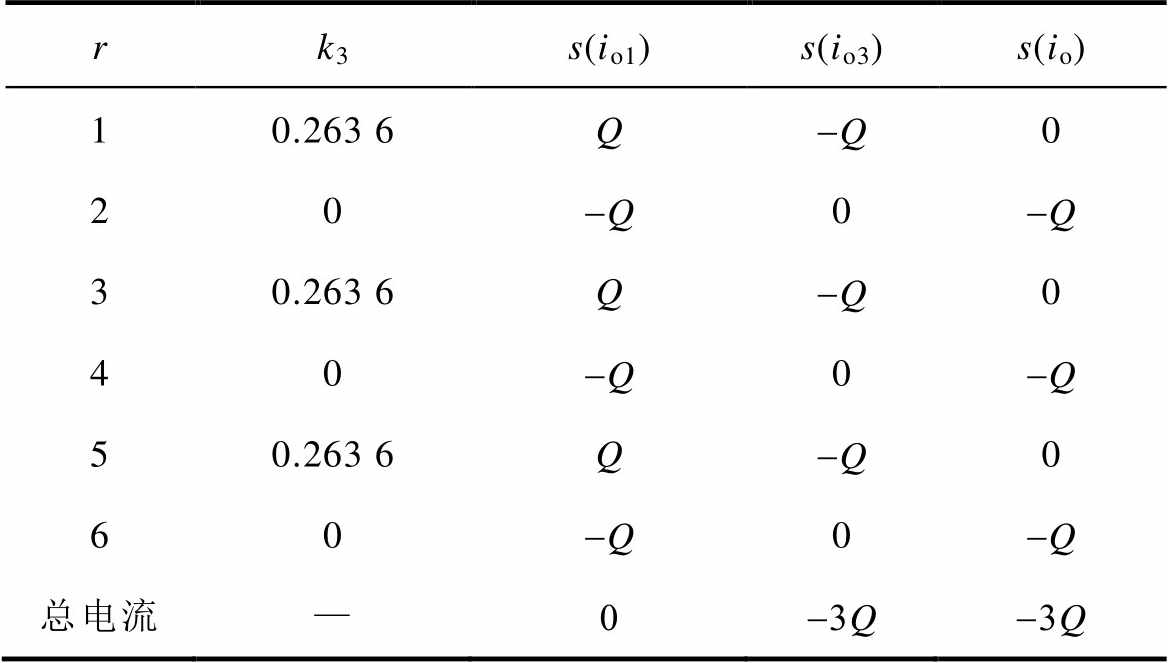
rk3s(io1)s(io3)s(io) 10.263 6Q-Q0 20-Q0-Q 30.263 6Q-Q0 40-Q0-Q 50.263 6Q-Q0 60-Q0-Q 总电流—0-3Q-3Q
开关角组合方案Ⅰ在r={1, 3, 5}的区间内采用k3=0的开关角,而在r={2, 4, 6}的区间内采用k3= 0.263 6的开关角,使得在r={1, 3, 5}的区间上中点电流积分全部为io1的积分Q,而在r={2, 4, 6}的区间上中点电流积分全部为零。
开关角组合方案Ⅱ则在r={1, 3, 5}的区间内采用k3=0.263 6的开关角,而在r={2, 4, 6}的区间内采用k3=0的开关角,使得在r={1, 3, 5}的区间上中点电流积分全部为零,而在r={2, 4, 6}的区间上中点电流积分全部为io1的积分-Q。
因此,开关角组合方案Ⅰ在一个基波周期内的中点电流积分为3Q,开关角组合方案Ⅱ在一个基波周期内的中点电流积分为-3Q,根据式(7)可以得到,开关角组合方案Ⅰ可以降低中点电位,而开关角组合方案Ⅱ可以增大中点电位。因此,根据中点电位的偏移值选取不同的开关角组合方案,即可实现平衡中点电位偏移值的效果。
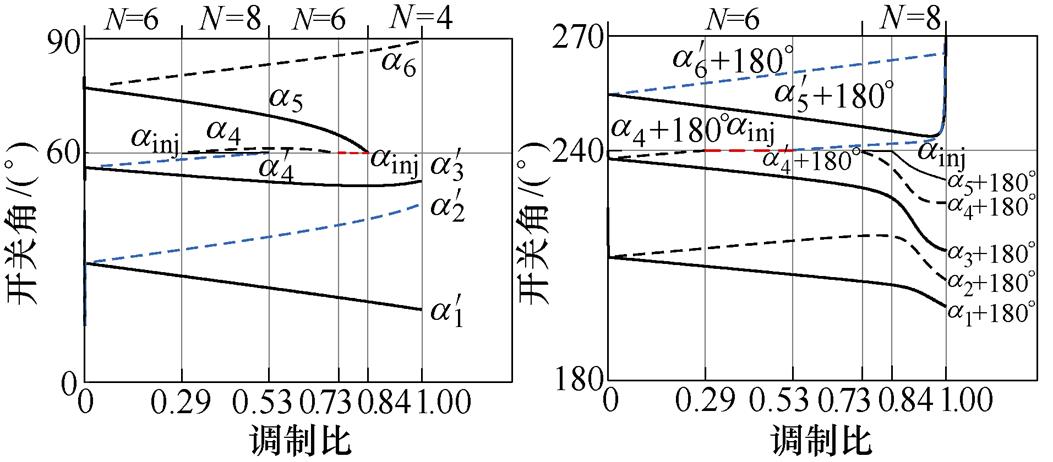
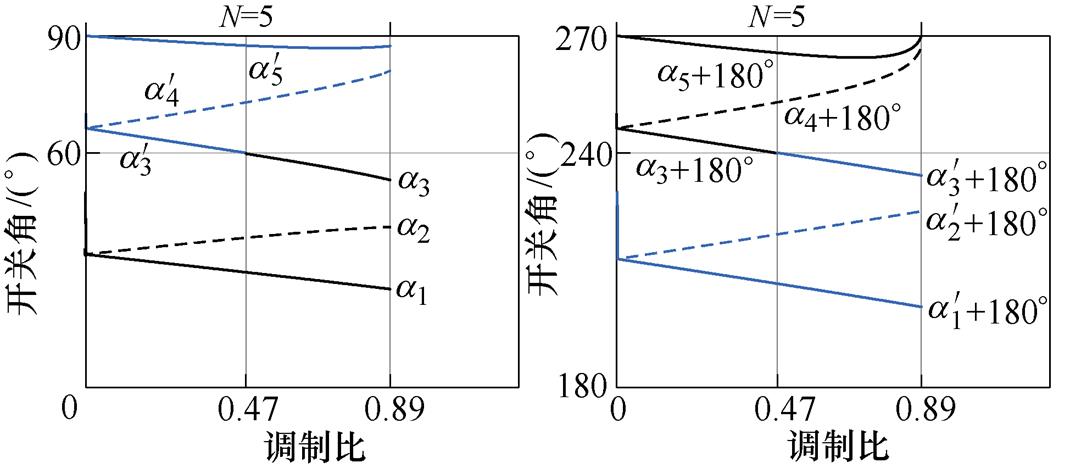
以N=5及N=6时的情况为例进行上述两种开关角组合方案设计,两种情况下k3=0以及k3=0.263 6的开关角分布分别如图5及图6所示,图中,a1~aN为k3=0时的开关角,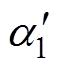 ~
~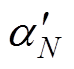 为k3=0.263 6时的开关角。
为k3=0.263 6时的开关角。
(a)k3=0 (b)k3=0.263 6
图5 N=5时的开关角随调制比变化曲线
Fig.5 The switching angle curves when N=5
(a)k3=0 (b)k3=0.263 6
图6 N=6时的开关角随调制比变化曲线
Fig.6 The switching angle curves when N=6
由于SHEPWM的输出电压存在1/4周期对称性和半波对称性,开关角组合方案Ⅰ及Ⅱ中0 °~180 °区间内(r={1, 2, 3})的输出电压关于90 °对称,180 °~360 °区间内(r={4, 5, 6})的输出电压关于270 °对称。因此,两种组合方案的开关角分布状态可以由0 °~90 °的开关角分布以及180 °~270 °的开关角分布表示。
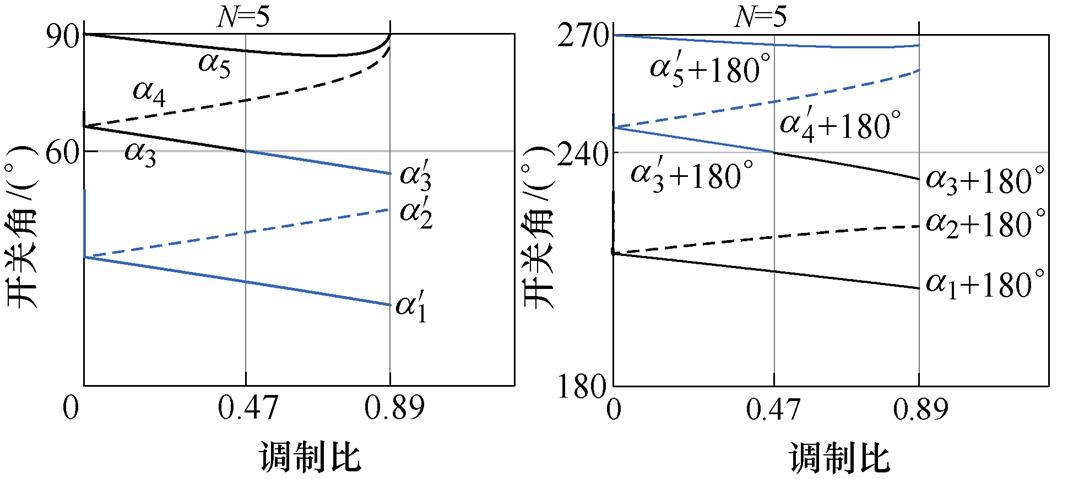
N=5时的开关角组合方案Ⅰ以及开关角组合方案Ⅱ的开关角分布分别如图7和图8所示。
(a)0 °~90 ° (b)180 °~270 °
图7 N=5时的开关角组合方案Ⅰ
Fig.7 The switch angle combination Ⅰ when N=5
(a)0 °~90 ° (b)180 °~270 °
图8 N=5时的开关角组合方案Ⅱ
Fig.8 The switch angle combination Ⅱ when N=5
通过图7及图8可以看出,开关角组合方案Ⅰ在0 °~180 °区间内的开关角分布与开关角组合方案Ⅱ在180 °~360 °区间内的开关角分布相同,开关角组合方案Ⅰ在180 °~360 °区间内的开关角分布与开关角组合方案Ⅱ在0 °~180 °区间内的开关角分布相同。同时,由于N=5时,k3=0以及k3=0.263 6的开关角中,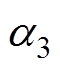 以及
以及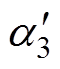 均在m=0.47处等于60 °。因此,在全调制比范围内,开关角组合方案Ⅰ以及开关角组合方案Ⅱ的开关角个数均为5个,即在N=5时采用开关角组合方案Ⅰ以及开关角组合方案Ⅱ并不增加系统的开关频率。
均在m=0.47处等于60 °。因此,在全调制比范围内,开关角组合方案Ⅰ以及开关角组合方案Ⅱ的开关角个数均为5个,即在N=5时采用开关角组合方案Ⅰ以及开关角组合方案Ⅱ并不增加系统的开关频率。
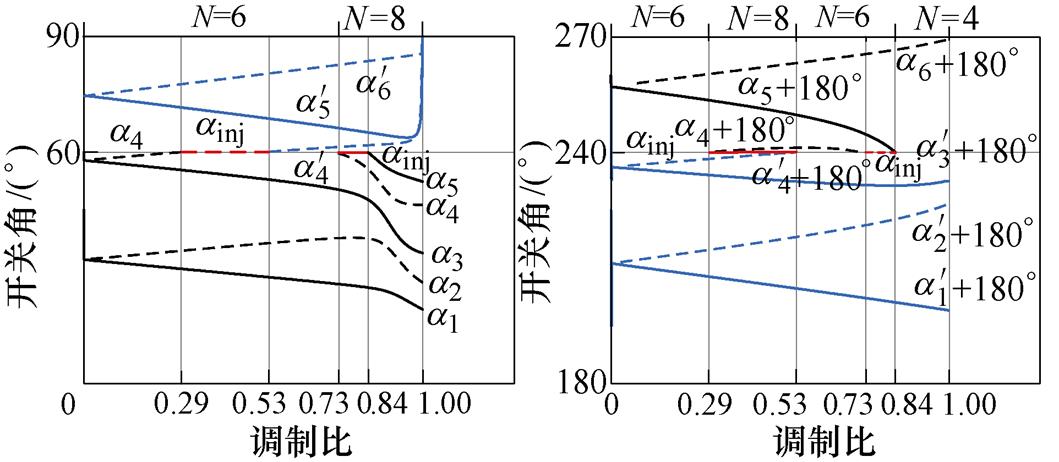
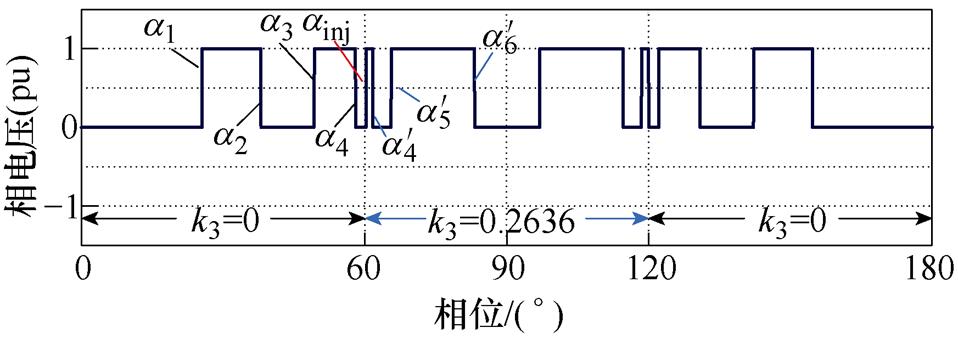
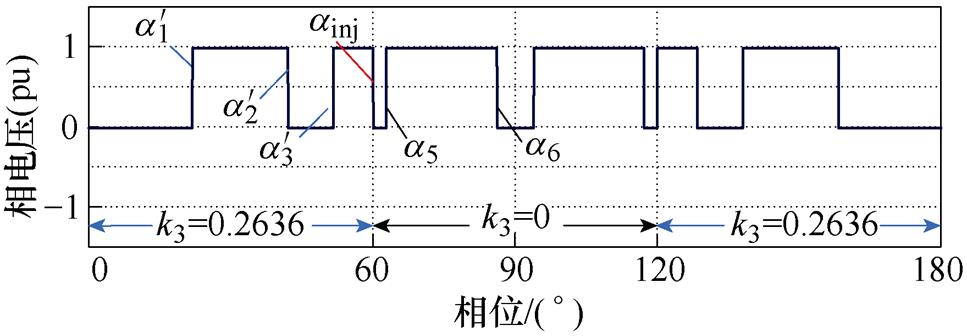
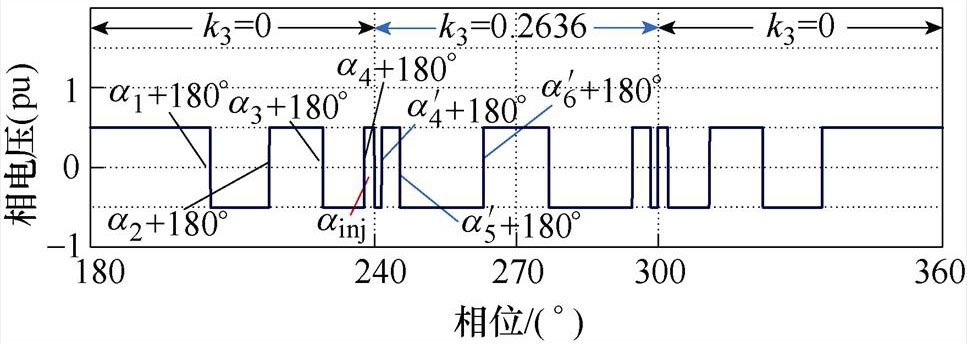
图9及图10为N=6时开关角组合方案Ⅰ以及开关角组合方案Ⅱ的开关角分布曲线。图中,ainj是为了保证不同k3含量的开关角正确切换而设置的开关角。以图11和图12所示的开关角组合方案Ⅰ及Ⅱ在m=0.8时的相电压波形为例,当开关角组合方案Ⅰ的相电压在60 °处从k3=0的开关角切换至k3=0.263 6的开关角后,下一个开关角为k3=0.263 6的开关角中的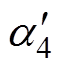 ,从60 °~
,从60 °~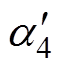 之间的相电压输出应为P状态,而60 °之前的上一个开关角为k3=0的开关角中的a4,a4之后的相电压输出O状态,因此需要在60 °处插入ainj来保证不同k3含量开关角之间的正确切换。当开关角组合方案Ⅰ的相电压在240 °处从k3=0.263 6的开关角切换至k3=0的开关角后,下一个开关角为k3=0的开关角中的a5+180 °,从240 °~a5+180 °之间的相电压输出应为O状态,而240 °之前的上一个开关角为k3=0.263 6的开关角中的
之间的相电压输出应为P状态,而60 °之前的上一个开关角为k3=0的开关角中的a4,a4之后的相电压输出O状态,因此需要在60 °处插入ainj来保证不同k3含量开关角之间的正确切换。当开关角组合方案Ⅰ的相电压在240 °处从k3=0.263 6的开关角切换至k3=0的开关角后,下一个开关角为k3=0的开关角中的a5+180 °,从240 °~a5+180 °之间的相电压输出应为O状态,而240 °之前的上一个开关角为k3=0.263 6的开关角中的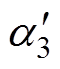 +180 °,其之后的相电压输出N状态,因此需要在240 °处插入ainj来保证不同k3含量开关角之间的正确切换。
+180 °,其之后的相电压输出N状态,因此需要在240 °处插入ainj来保证不同k3含量开关角之间的正确切换。
(a)0 °~90 ° (b)180 °~270 °
图9 N=6时的开关角组合方案Ⅰ
Fig.9 The switch angle combination Ⅰ when N=6
(a)0 °~90 ° (b)180 °~270 °
图10 N=6时的开关角组合方案Ⅱ
Fig.10 The switch angle combination Ⅱ when N=6
(a)0 °~180 °
(b)180 °~360 °
图11 N=6,m=0.8时开关角组合方案Ⅰ的相电压波形
Fig.11 The phase voltage waveforms of switching angle combination scheme Ⅰ when N=6 and m=0.8
(a)0 °~180 °
(b)180 °~360 °
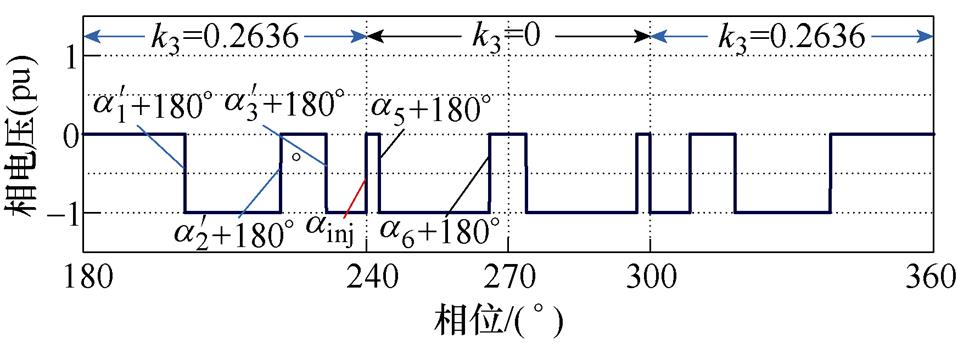
图12 N=6,m=0.8时开关角组合方案Ⅱ的相电压波形
Fig.12 The phase voltage waveforms of switching angle combination scheme Ⅱ when N=6 and m=0.8
由于开关角组合方案Ⅰ在0 °~180 °区间和180 °~360 °区间内的开关角分布分别与开关角组合方案Ⅱ在180 °~360 °区间和0 °~180 °区间内的开关角分布相同,因此,开关角组合方案Ⅱ的ainj设置与开关角组合方案Ⅰ相似,如图12所示。
通过以上分析可知,不同k3含量开关角之间的切换可能会在某些调制比范围内改变相电压总的开关动作次数。以N=6时的开关角组合方案Ⅰ为例,不同调制比范围下的开关角数目变化见表4。可以看出,N=6时的开关角组合方案Ⅰ一个基波周期最多只会增加4次开关动作。而由于开关角组合方案Ⅰ和Ⅱ的对称性,开关角组合方案Ⅱ一个基波周期最多也只会增加4次开关动作。
表4 N=6时开关角组合方案Ⅰ开关角数目变化
Tab.4 The change in the number of switching angles in switching angle combination scheme Ⅰ when N=6
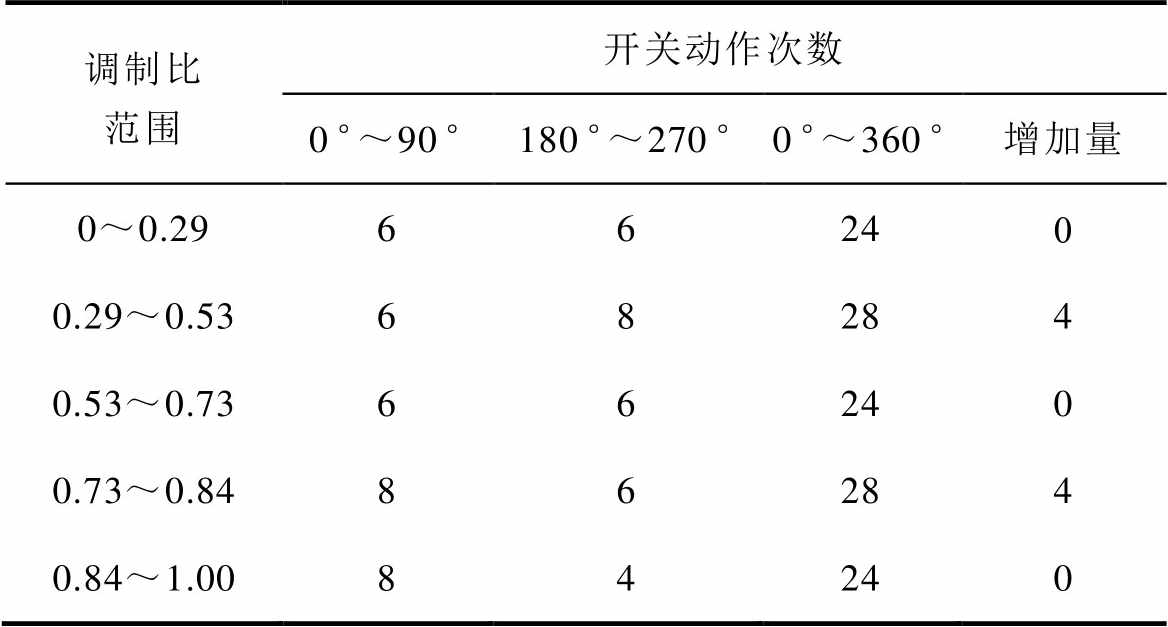
调制比范围开关动作次数 0 °~90 °180 °~270 °0 °~360 °增加量 0~0.2966240 0.29~0.5368284 0.53~0.7366240 0.73~0.8486284 0.84~1.0084240
表5中分别列出了从不同开关角个数下,所提出的两种开关角组合方案在全调制比范围内每个基波周期开关动作次数增加量的最大值。
表5 不同开关角个数下开关角组合方案开关动作次数增加量的最大值
Tab.5 The change in the number of switching angles under different pulse number
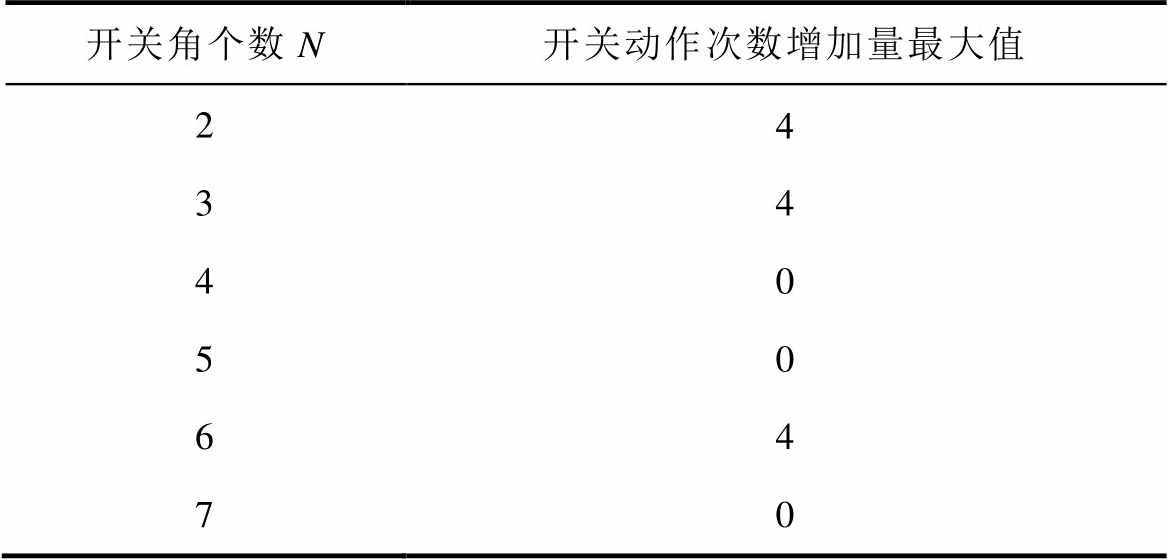
开关角个数N开关动作次数增加量最大值 24 34 40 50 64 70
通过表5可以看出,所提出的两种开关角组合方案在各个开关角数目下均不会大幅增加系统开关频率。
3.3 中点电位主动平衡控制策略
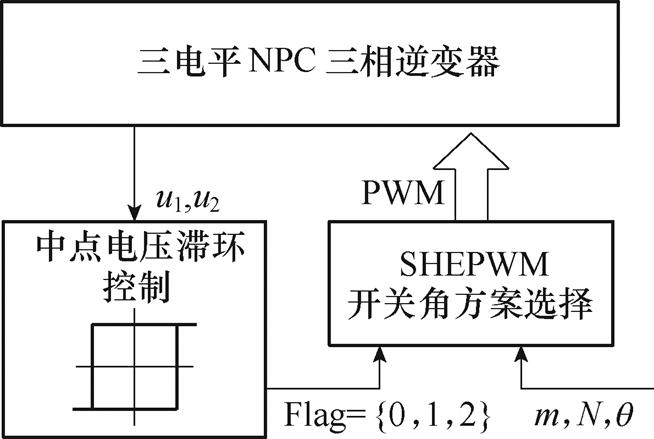
基于表2、表3设计的两种在整个基波周期内对中点电位总充放电效果相反的开关角组合方案,本文提出了一种通过检测中点电位偏移值以及中点电位滞环控制器,选择不同开关角组合方案进行调制的中点电位主动平衡控制策略,其原理如图13所示。
图13中,设中点电位滞环控制器环宽为Ulim,当中点电位偏移值小于Ulim且大于-Ulim时,滞环控制器输出Flag=0,SHEPWM选择k3=0.263 6的初始开关角来抑制中点电位波动,并且避免稳态时由于主动平衡控制策略造成的开关频率增加以及谐波性能降低;当中点电位偏移值大于Ulim时,滞环控制器输出Flag=1,SHEPWM选择开关角组合方案Ⅰ,降低中点电位值;当中点电位偏移值小于-Ulim时,滞环控制器输出Flag=2,SHEPWM选择开关角组合方案Ⅱ,提升中点电位值。Ulim的取值则根据系统所能承受的中点电位波动范围选取即可。
4 实验结果
为了验证所提出的中点电位主动平衡控制策略的实用性及有效性,本文利用三电平NPC三相逆变器实验平台在表6所示的实验参数下进行了实验验证。
表6 实验平台参数
Tab.6 Experimental platform parameters

参 数数 值 直流侧电压/V270 直流侧上下母线电容容值/mF1 000 输出电压基波频率/Hz50 中点电位偏移值/V50 中点电位滞环控制器环宽/V270×2.5% 阻感负载一 (PF≈1.0)12 W+5 mH 阻感负载二 (PF≈0.7)12 W+35 mH
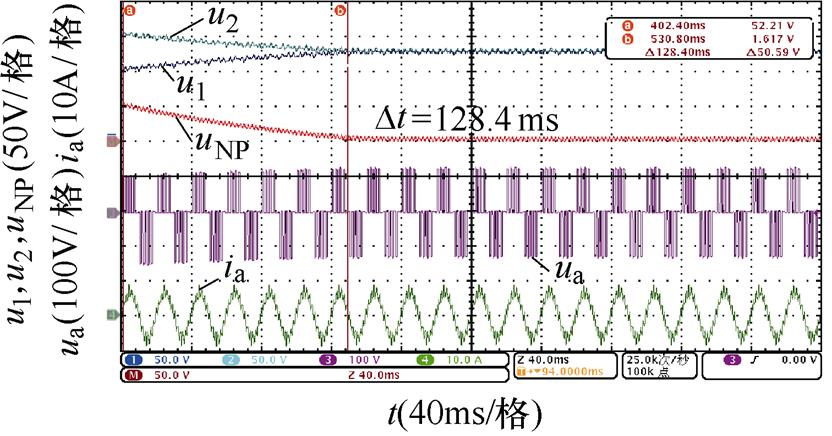
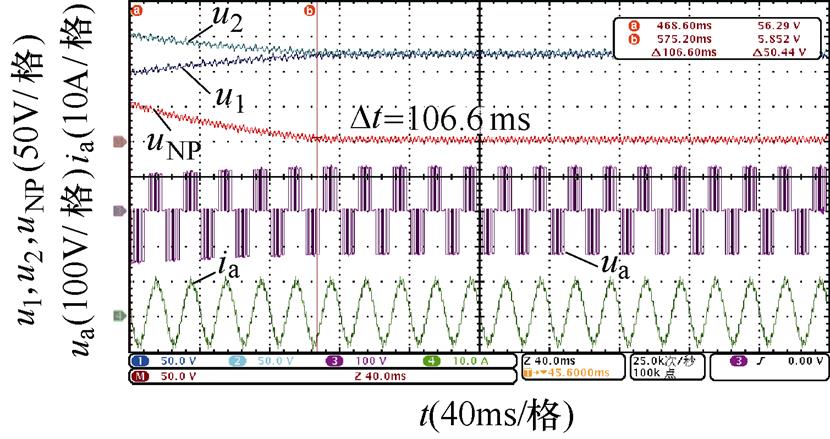
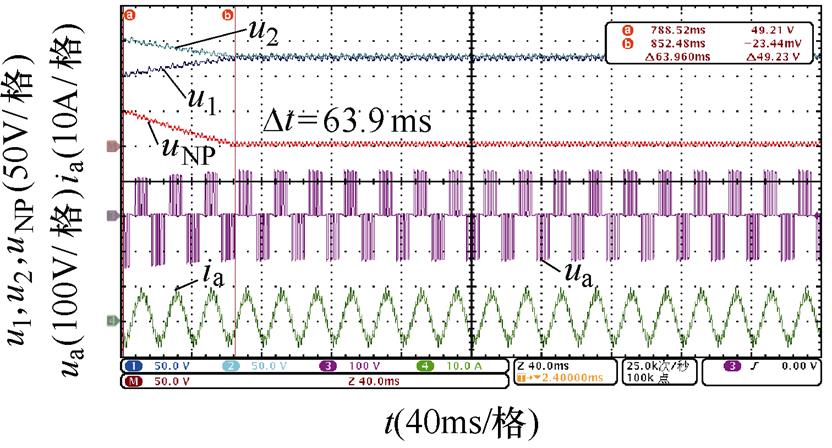
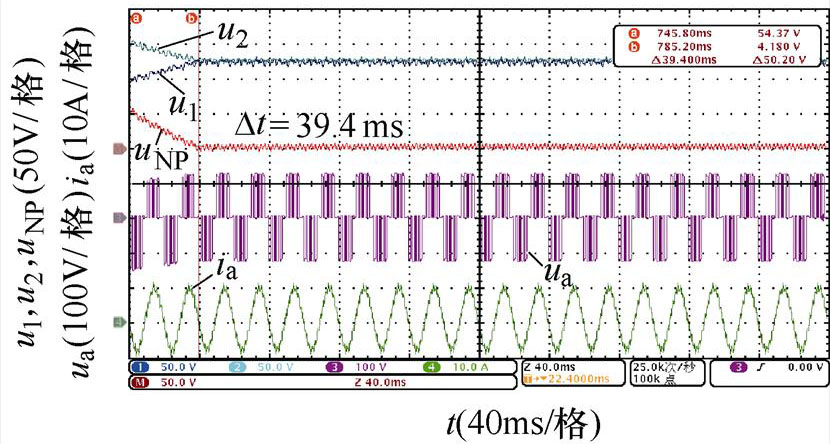
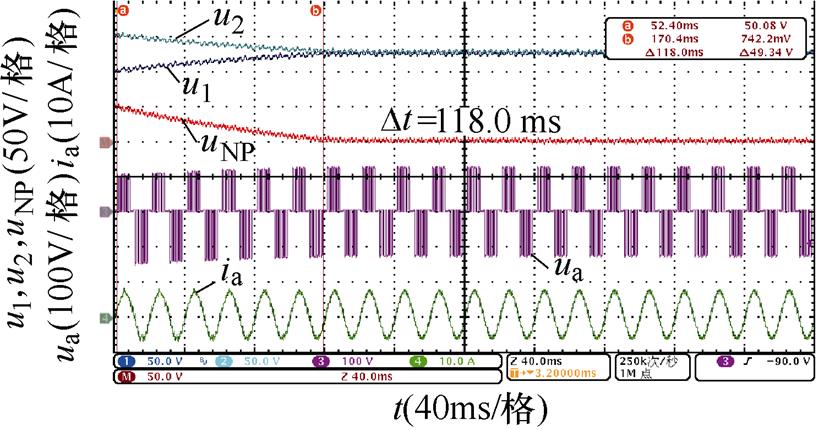
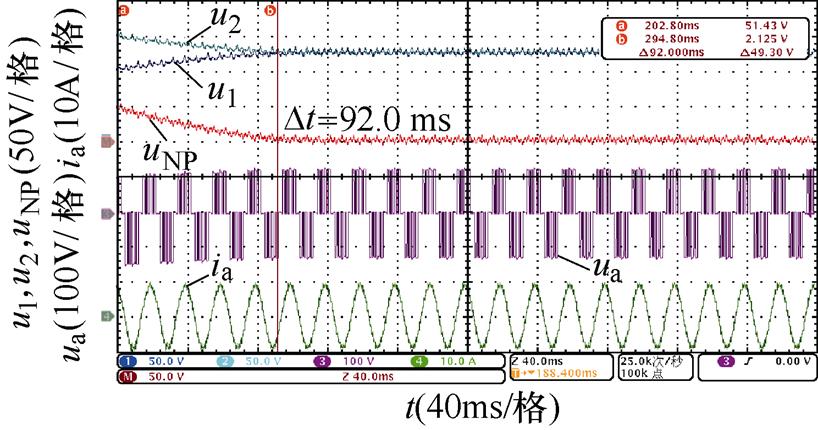
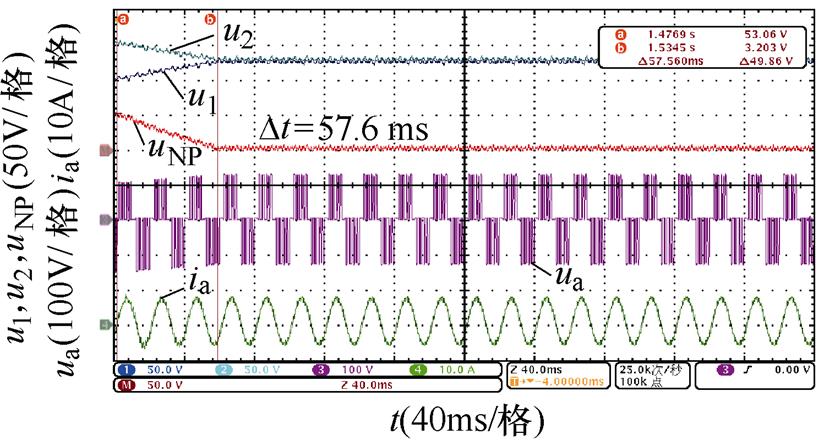
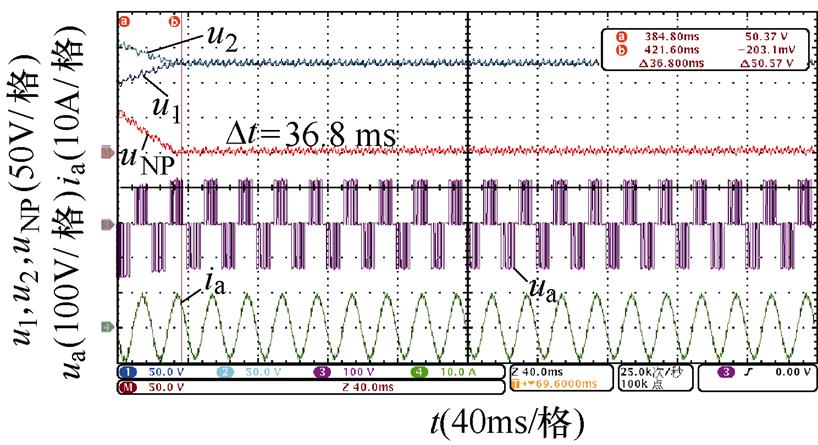
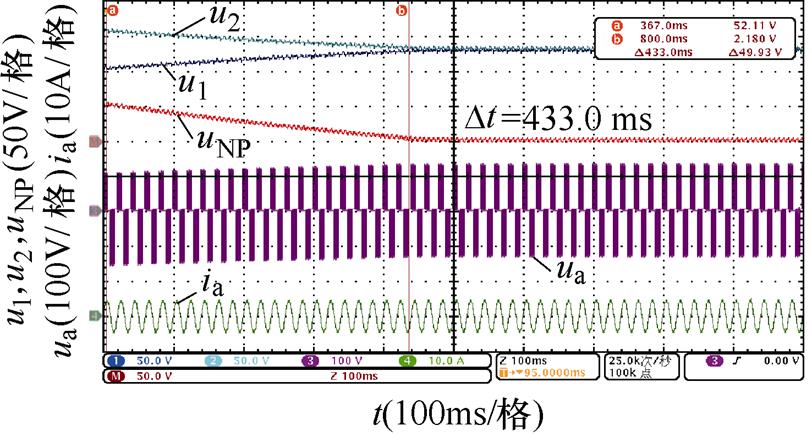
不同开关角个数、调制比以及功率因数下,基于调节微小角度的传统主动平衡方法和本文所提出的基于调节3次谐波含量的主动平衡策略的实验波形如图14~图17所示。
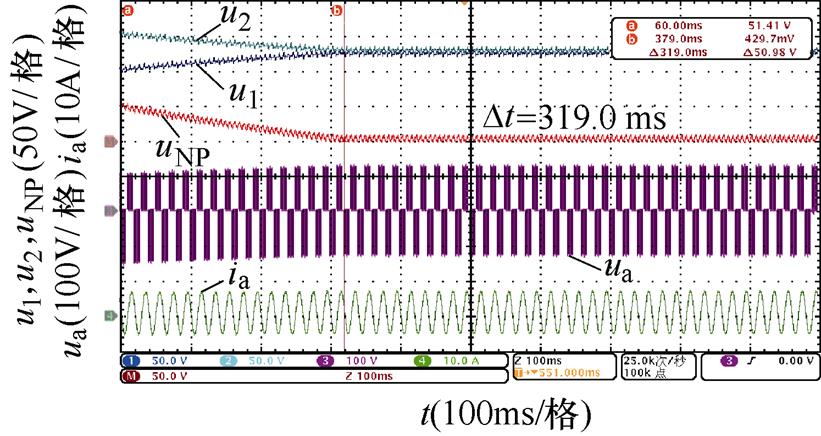
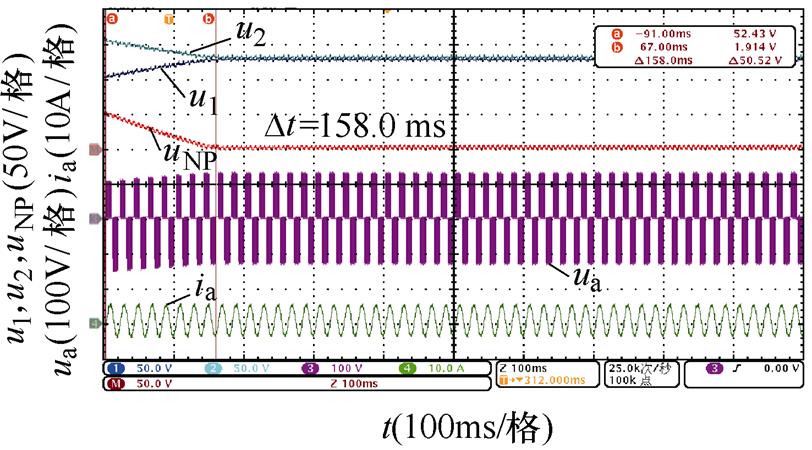
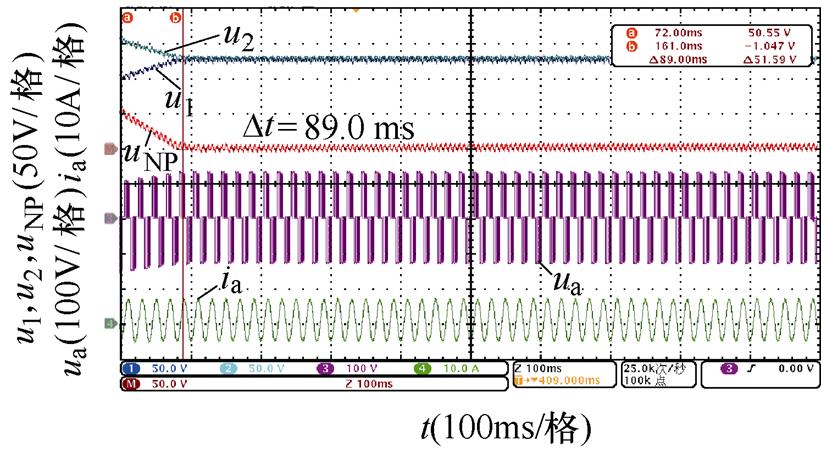
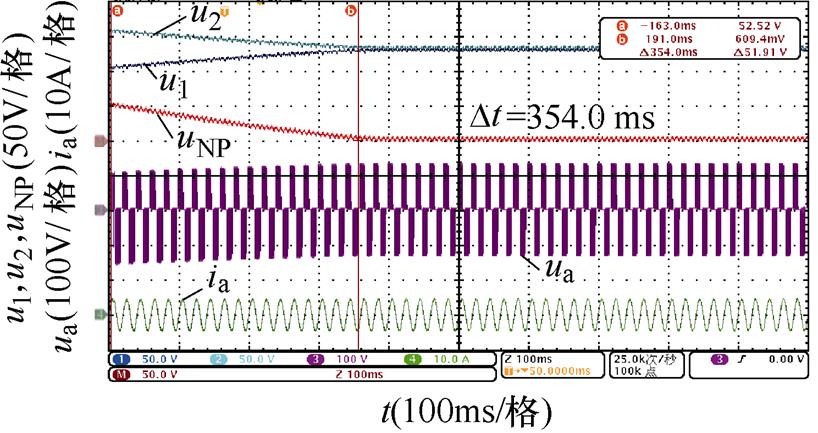
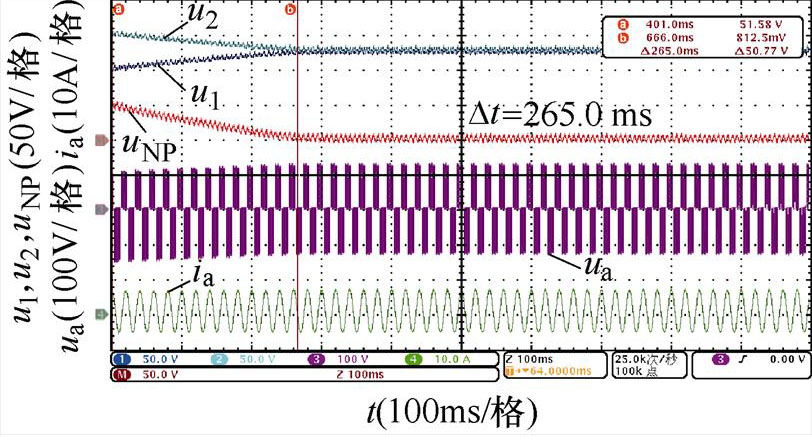
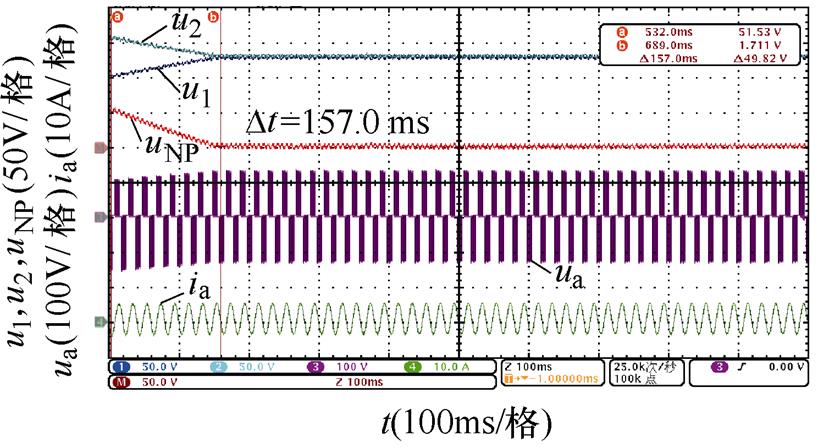
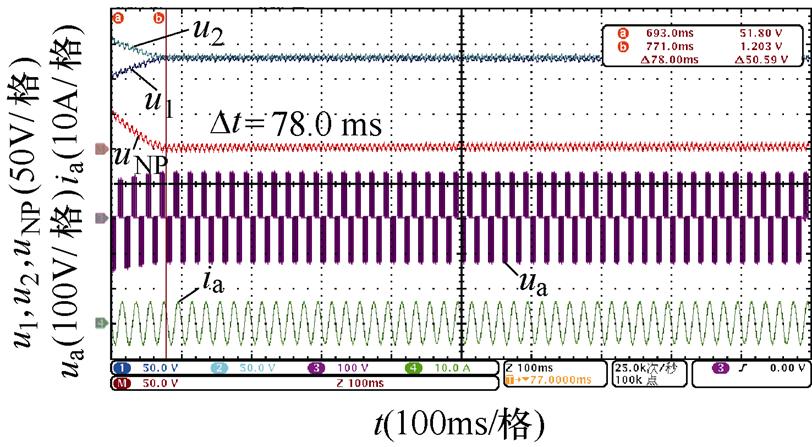
对比图14~图17,不同中点电位主动平衡策略将中点电位偏移值从50 V降低到0 V的平衡时间,可以发现,本文所提出的基于3次谐波含量调节的主动平衡策略中点电位动态平衡效果在不同开关角个数、调制比以及功率因数下均优于传统主动平衡方法,所提出方法与传统方法的平衡速度对比见表7,并且负载电流均无明显畸变。
(a)传统方法,m=0.6
(b)传统方法,m=0.8
(c)调节3次谐波含量,m=0.6
(d)调节3次谐波含量,m=0.8
图14 N=5时中点电位动态平衡实验波形(阻感负载一)
Fig.14 The NP voltage dynamic balance experiment waveforms when N=5 (the first RL load)
(a)传统方法,m=0.6
(b)传统方法,m=0.8
(c)调节3次谐波含量,m=0.6
(d)调节3次谐波含量,m=0.8
图15 N=6时中点电位动态平衡实验波形(阻感负载一)
Fig.15 The NP voltage dynamic balance experiment waveforms when N=6 (the first RL load)
(a)传统方法,m=0.6
(b)传统方法,m=0.8
(c)调节3次谐波含量,m=0.6
(d)调节3次谐波含量,m=0.8
图16 N=5时中点电位动态平衡实验波形(阻感负载二)
Fig.16 The NP voltage dynamic balance experiment waveforms when N=5 (the second RL load)
(a)传统方法,m=0.6
(b)传统方法,m=0.8
(c)调节3次谐波含量,m=0.6
(d)调节3次谐波含量,m=0.8
图17 N=6时中点电位动态平衡实验波形(阻感负载二)
Fig.17 The NP voltage dynamic balance experiment waveforms when N=6 (the second RL load)
表7 所提出方法与传统方法的平衡速度对比
Tab.7 The comparison of the balancing elapsed time between the proposed method and the traditional method
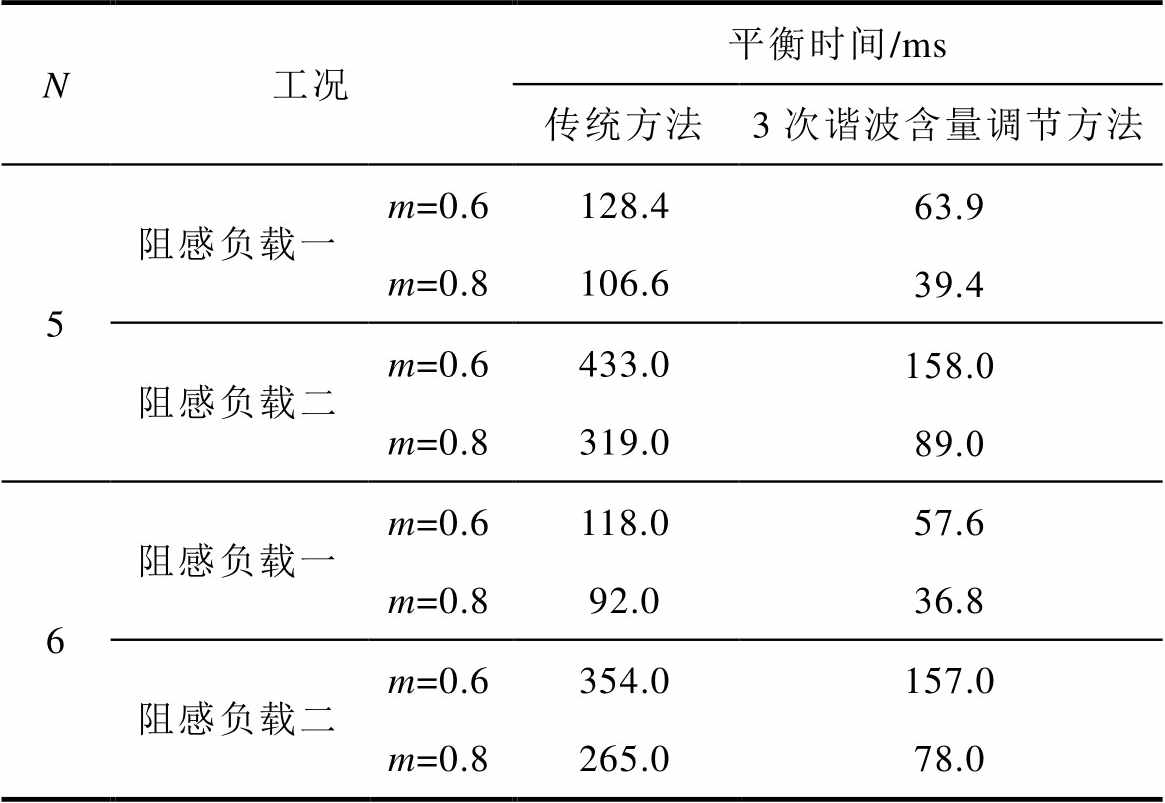
N工况平衡时间/ms 传统方法3次谐波含量调节方法 5阻感负载一m=0.6128.463.9 m=0.8106.639.4 阻感负载二m=0.6433.0158.0 m=0.8319.089.0 6阻感负载一m=0.6118.057.6 m=0.892.036.8 阻感负载二m=0.6354.0157.0 m=0.8265.078.0
同时,通过表7还可以看出,基于调节微小角度的传统主动平衡方法的平衡速度明显受到开关角个数影响,开关角个数越少,传统主动平衡方法在整个基波周期内进行的角度调节就越少,因此平衡速度越慢。而本文所提出的基于3次谐波含量调节的主动平衡策略在不同开关角个数下在整个基波周期内对中点电位的影响是确定的,因此平衡速度基本不受开关角个数的影响。
5 结论
本文针对三电平中点钳位型三相逆变器在特定次谐波消除脉宽调制下的中点电位偏移问题,提出了一种基于3次谐波含量调节的中点电位主动平衡策略,主要成果总结如下:
1)本文提出的中点电位主动平衡方法只需通过测量直流侧电容电压以及中点电位滞环控制即可实现中点电位主动平衡控制,避免了繁琐的计算和分析过程,且无需测量负载电流。
2)本文提出的中点电位主动平衡方法相对于传统的基于调节微小角度的中点电位主动平衡方法,在不同工况下均具有更好的动态平衡效果。通过实验证明了本文所提出方法的可行性及有效性。
参考文献
[1] Nabae A, Takahashi I, Akagi H. A new neutral- point-clamped PWM inverter[J]. IEEE Transactions on Industry Applications, 1981, IA-17(5): 518-523.
[2] 周汉斌, 杨建, 陈晓娇, 等. 考虑死区电压矢量的三电平变换器模型预测控制[J]. 电工技术学报, 2022, 37(20): 5290-5301.
Zhou Hanbin, Yang Jian, Chen Xiaojiao, et al. Model predictive control of three-level converter considering dead-zone voltage vector[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5290-5301.
[3] 赵牧天, 葛琼璇, 张波, 等. 高速磁悬浮牵引系统大功率三电平整流器特定谐波消除脉宽调制策略[J]. 电工技术学报, 2022, 37(16): 4180-4192.
Zhao Mutian, Ge Qiongxuan, Zhang Bo, et al. Selective harmonic elimination pulse width modu- lation for high power three-level rectifier of high- speed maglev traction system[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4180- 4192.
[4] 许嘉杰, 李锐华, 胡波. 基于三矢量模型预测控制的T型三电平整流器定频控制策略[J]. 电气技术, 2022, 23(6): 17-23, 92.
Xu Jiajie, Li Ruihua, Hu Bo. Fixed frequency control strategy of T-type three-level rectifier based on three vector model predictive control[J]. Electrical Engin- eering, 2022, 23(6): 17-23, 92.
[5] Dong Zhiqiang, Wang Chenchen, Cui Kai, et al. Neutral-point voltage-balancing strategies of NPC- inverter fed dual three-phase AC motors[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3181-3191.
[6] 罗锐, 何英杰, 陈晖, 等. 三电平变流器中点电位平衡及低开关损耗SVPWM策略[J]. 电工技术学报, 2018, 33(14): 3245-3254.
Luo Rui, He Yingjie, Chen Hui, et al. SVPWM scheme for three-level converters with neutral-point potential balancing and switching loss reduction[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3245-3254.
[7] Wang Chenchen, Li Yongdong. Analysis and calcu- lation of zero-sequence voltage considering neutral- point potential balancing in three-level NPC con- verters[J]. IEEE Transactions on Industrial Elec- tronics, 2010, 57(7): 2262-2271.
[8] 谢路耀, 金新民, 吴学智, 等. 基于零序注入的NPC三电平变流器中点电位反馈控制[J]. 电工技术学报, 2012, 27(12): 117-128.
Xie Luyao, Jin Xinmin, Wu Xuezhi, et al. Neutral point voltage feedback control based on zero sequence injection for NPC three-level converter[J]. Transactions of China Electrotechnical Society, 2012, 27(12): 117-128.
[9] Choi U M, Lee J S, Lee K B. New modulation strategy to balance the neutral-point voltage for three-level neutral-clamped inverter systems[J]. IEEE Transactions on Energy Conversion, 2014, 29(1): 91-100.
[10] Celanovic N, Borojevic D. A comprehensive study of neutral-point voltage balancing problem in three- level neutral-point-clamped voltage source PWM inverters[J]. IEEE Transactions on Power Electronics, 2000, 15(2): 242-249.
[11] 邱继浪, 何英杰, 焦乾明, 等. 非隔离型三电平逆变器漏电流抑制与中点电位平衡控制[J]. 电力系统自动化, 2021, 45(17): 161-170.
Qiu Jilang, He Yingjie, Jiao Qianming, et al. Leakage current suppression and balance control of neutral point potential for three-level transformerless inver- ter[J] Automation of Electric Power Systems, 2021, 45(17): 161-170.
[12] 徐伟, 董定昊, 葛健, 等. 基于在线参数辨识补偿的直线感应电机低开关频率模型预测控制策略[J].电工技术学报, 2022, 37(16): 4116-4133.
Xu Wei, Dong Dinghao, Ge Jian, et al. Low switching frequency model predictive control strategy based on online parameter identification compensation of linear induction motor for urban rail application[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4116-4133.
[13] 苑国锋, 沈阳. 基于开关时刻修正的多模式调制切换策略[J]. 电工技术学报, 2022, 37(5): 1171-1180.
Yuan Guofeng, Shen Yang. Multi-mode modulation switching strategy based on switch time correction[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1171-1180.
[14] 张丹, 姜建国. 高速磁悬浮永磁电机三电平无速度传感器控制[J]. 电工技术学报, 2022, 37(22): 5808- 5816.
Zhang Dan, Jiang Jianguo. Three-level sensorless control of high speed maglev permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5808-5816.
[15] Ma Dajun, Hu Cungang, Ye Qiubo, et al. Effect on harmonic performance for three-level ANPC con- verter with small change in SHEPWM switch angles[C]//IEEE 11th Conference on Industrial Electronics and Applications, Hefei, 2016: 881- 885.
[16] Guan Bo, Doki S. A current harmonic minimum PWM for three-level converters aiming at the low-frequency fluctuation minimum of neutral-point potential[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3380-3390.
[17] Guan Bo, Doki S. A suppression method of the low frequency fluctuation of the neutral point potential under 3-level SHEPWM based on 3-order harmo- nic[C]//20th International Conference on Electrical Machines and Systems, Sydney, 2017: 1-6.
[18] 谷鑫, 姜勃, 耿强, 等. 基于3次谐波控制及脉冲波动分析的三电平SHE-PWM调制优化策略[J]. 电工技术学报, 2015, 30(7): 88-96.
Gu Xin, Jiang Bo, Geng Qiang, et al. An optimal SHE-PWM modulation strategy for three-level NPC converter based on third harmonic control and pulse fluctuation analysis[J]. Transactions of China Electro- technical Society, 2015, 30(7): 88-96.
[19] Zhang Tongsheng, Du Chunshui, Qin Changwei, et al. Neutral-point voltage balancing control for three- level T-type inverter using SHEPWM[C]//IEEE 8th International Power Electronics and Motion Control Conference, Hefei, 2016: 1116-1122.
[20] Jiang Ying, Li Xiaoyan, Qin Changwei, et al. Improved particle swarm optimization based selective harmonic elimination and neutral point balance control for three-level inverter in low-voltage ride- through operation[J]. IEEE Transactions on Industrial Informatics, 2022, 18(1): 642-652.
Active Neutral-Point Voltage Balance Control Strategy for Three-Level Three-Phase Inverter Under SHEPWM
Dong Zhiqiang Wang Chenchen Zhou Minglei Liu Mingyue Li Kai
(School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China)
Abstract In the high-power system, the three-level neutral-point clamped inverter needs to adopt SHEPWM to reduce the switching power loss. The traditional neutral-point potential active balance control strategy adjusts the duty cycle of the zero-level of phase voltage by superimposing a slight angle based on the switching angle of SHEPWM from the polarity of each phase load current and neutral-point potential shift. However, the small number of SHEPWM switching angles limits the neutral-point potential balance ability. The fewer the number of SHEPWM switching angles, the weaker the neutral-point potential balance ability. Therefore, this paper analyzes the influence of the fundamental wave and the third harmonic of the output phase voltage under SHEPWM on the neutral-point potential in a different range of voltage phase angles, designs two switching angle combination schemes with opposite effects on the neutral-point potential in the fundamental wave period, and proposes a method to control the neutral-point potential by selecting different switching angle combination scheme to modulate according to the offset value and the hysteresis of the neutral-point potential.
The influence analysis of the fundamental wave and the third harmonic wave on the neutral-point current shows that the neutral-point current components generated by the fundamental wave and the third harmonic wave have triple frequency fluctuation. Moreover, when the amplitude of the third harmonic is 0.2636 times that of the fundamental wave, the integral of the neutral-point current components generated by the fundamental wave and the third harmonic cancels each other in the interval of the fundamental wave phase angle every 60 degrees. The neutral-point current integral in the whole fundamental wave cycle can be adjusted by setting the third harmonic content at every 60 degrees of the fundamental wave phase angle to control the neutral-point potential. Therefore, two switching angle combination schemes are proposed, with opposite effects on the neutral-point potential and no effect on the fundamental voltage. However, the two switching angle combination schemes may increase the number of switching times of the system because it is sometimes necessary to add extra switching angles to ensure the correct switching of the switching angles with different third harmonic content. The analysis of the switch angle combination schemes with the different numbers of switch angles shows that the proposed schemes can only increase four switching actions in the whole fundamental wave cycle at most, and will not affect the low switching frequency characteristics of SHEPWM. However, the neutral-point voltage hysteresis control is needed to determine the switching angle used to modulate. When the neutral-point voltage deviation is within the acceptable range of the system, the SHEPWM switching angle without modification is used to ensure the switching power loss and the harmonic performance of the system.
The experimental results show that compared with the traditional neutral-point potential active balancing method based on SHEPWM, the proposed method has a better dynamic balancing effect under different working conditions.
keywords:Three-level neutral-point clamped inverter, neutral-point potential control, harmonic elimination pulse width modulation (SHEPWM), third-harmonic
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.222093
北京市自然科学基金资助项目(3222056)。
收稿日期 2022-11-06
改稿日期 2022-12-02
作者简介
董志强 男,1996年生,博士研究生,研究方向为电力电子与电力传动。E-mail: 19117004@bjtu.edu.cn
王琛琛 男,1981年生,教授,博士生导师,研究方向为电力电子与电力传动。E-mail: sxf@ysu.edu.cn(通信作者)
(编辑 陈 诚)
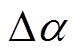 (0 °<
(0 °<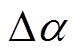 <0.2 °
<0.2 ° 来调节各相相电压的零电平作用时间,从而实现中点电位主动平衡控制[15]。但SHEPWM较少的开关角数目,使得该方法的中点电位平衡能力十分有限,并且SHEPWM开关角数目越少,其中点电位平衡能力越弱。文献[16-18]分析了SHEPWM相电压基波以及3次谐波对中点电位的影响,并通过控制3次谐波含量来抑制中点电位波动,但是没有中点电位主动平衡效果,无法抑制中点电位偏移。文献[19-20]通过将SHEPWM看作传统的SVPWM,根据中点电位偏移情况将对中点电位有充放电效果的电压矢量用冗余矢量进行替换,从而实现中点电位主动平衡控制,但是该类方法极大地增加了系统的开关频率且计算复杂,难以实现。
来调节各相相电压的零电平作用时间,从而实现中点电位主动平衡控制[15]。但SHEPWM较少的开关角数目,使得该方法的中点电位平衡能力十分有限,并且SHEPWM开关角数目越少,其中点电位平衡能力越弱。文献[16-18]分析了SHEPWM相电压基波以及3次谐波对中点电位的影响,并通过控制3次谐波含量来抑制中点电位波动,但是没有中点电位主动平衡效果,无法抑制中点电位偏移。文献[19-20]通过将SHEPWM看作传统的SVPWM,根据中点电位偏移情况将对中点电位有充放电效果的电压矢量用冗余矢量进行替换,从而实现中点电位主动平衡控制,但是该类方法极大地增加了系统的开关频率且计算复杂,难以实现。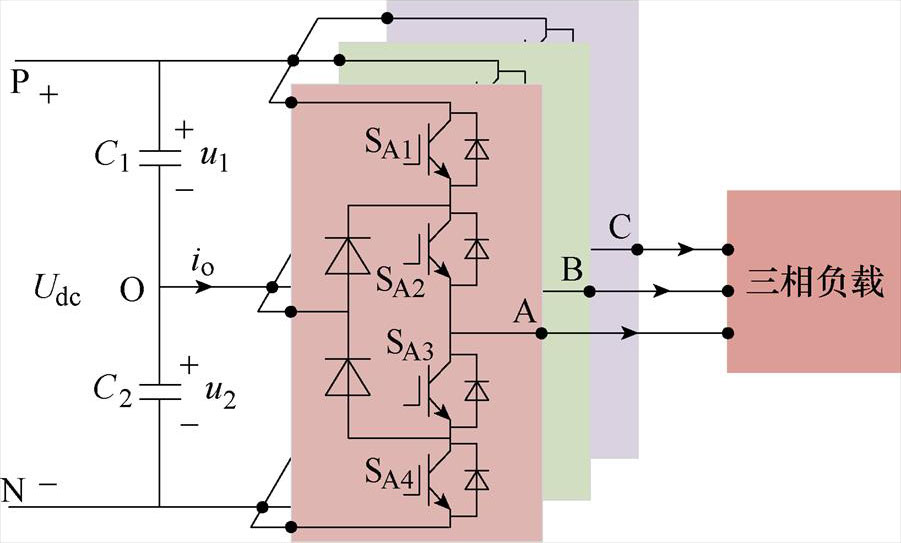
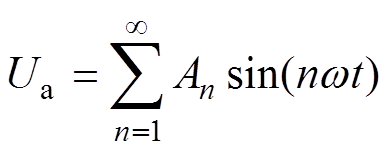 (1)
(1)
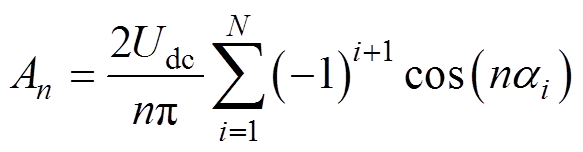 (2)
(2)
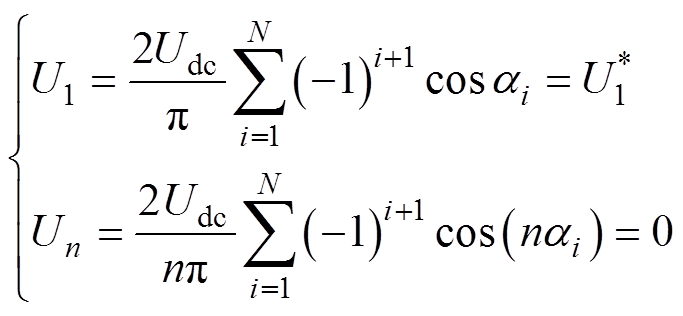 (3)
(3)
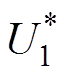 为期望的输出电压基波幅值。取直流侧总电压的一半即U
为期望的输出电压基波幅值。取直流侧总电压的一半即U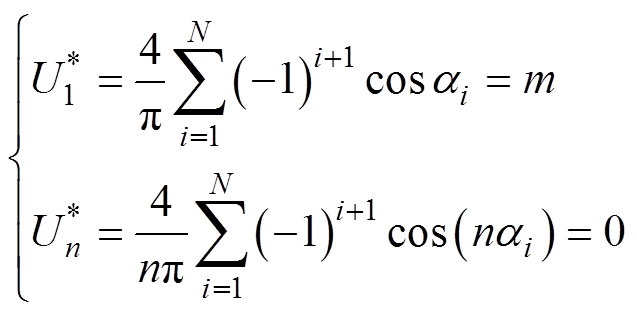 (4)
(4)
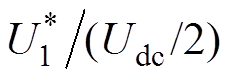 。
。
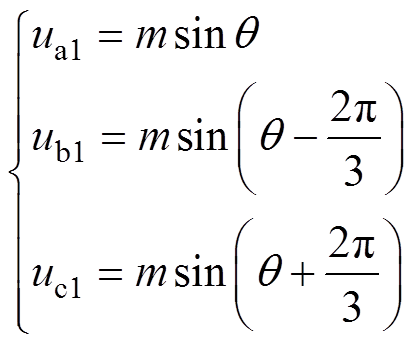 (5)
(5)
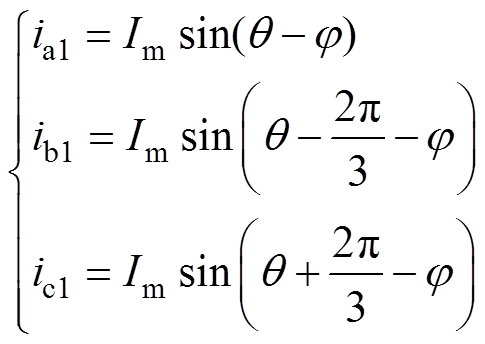 (6)
(6)
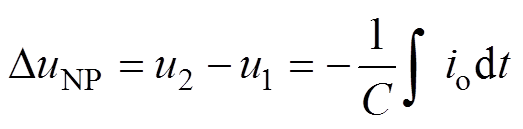 (7)
(7)
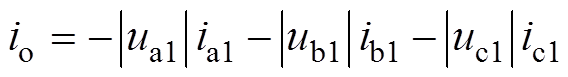 (8)
(8)
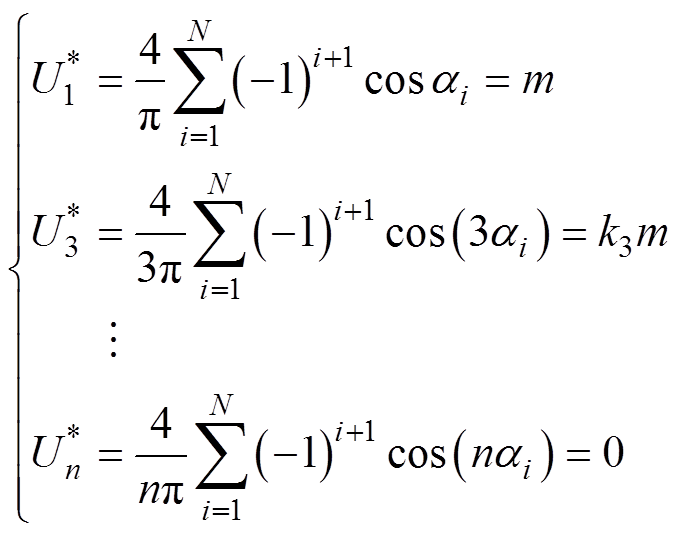 (9)
(9)
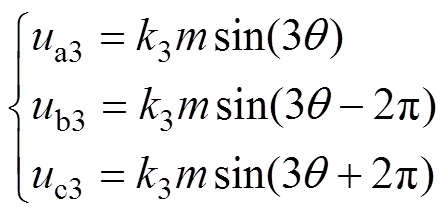 (10)
(10)
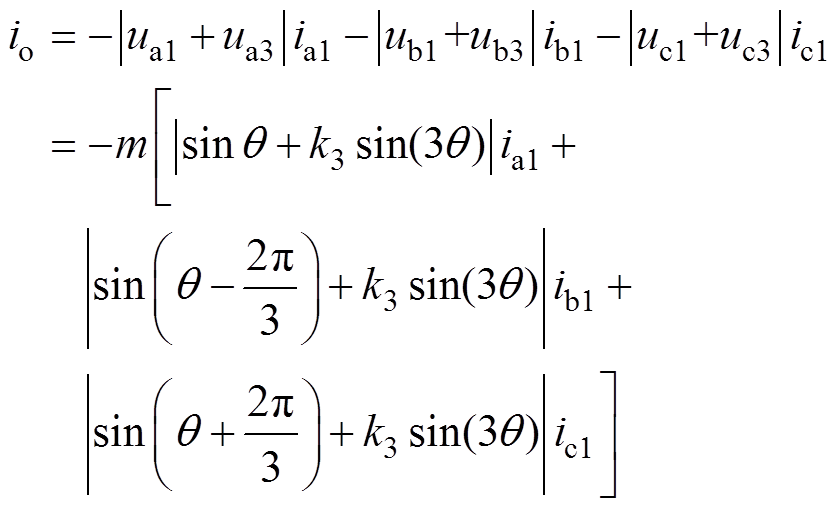 (11)
(11)
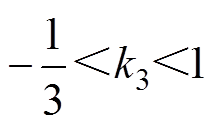 (12)
(12)
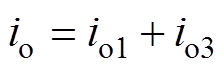 (13)
(13)
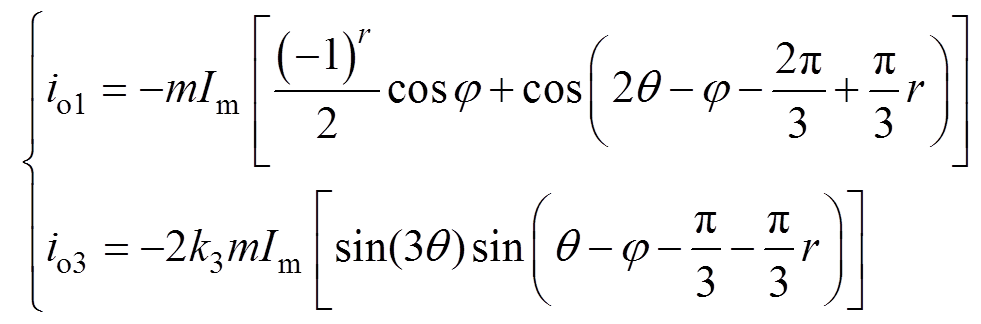
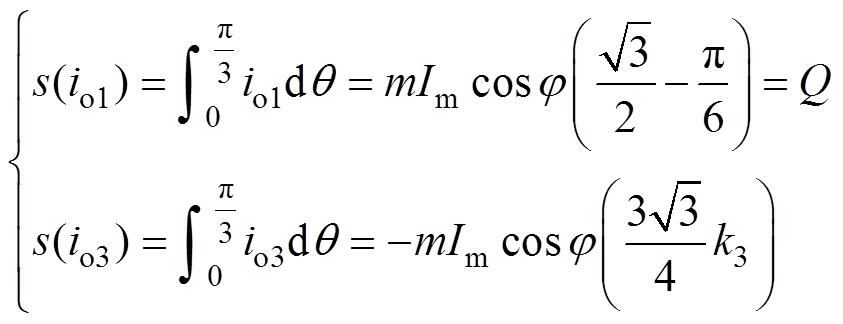 (14)
(14)



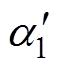 ~
~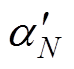 为k
为k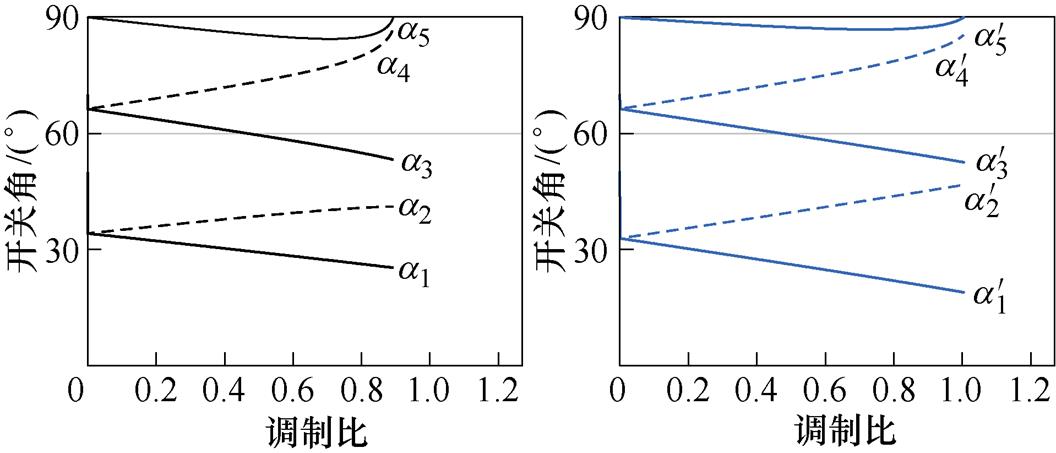
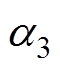 以及
以及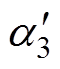 均在m=0.47处等于60 °。因此,在全调制比范围内,开关角组合方案Ⅰ以及开关角组合方案Ⅱ的开关角个数均为5个,即在N=5时采用开关角组合方案Ⅰ以及开关角组合方案Ⅱ并不增加系统的开关频率。
均在m=0.47处等于60 °。因此,在全调制比范围内,开关角组合方案Ⅰ以及开关角组合方案Ⅱ的开关角个数均为5个,即在N=5时采用开关角组合方案Ⅰ以及开关角组合方案Ⅱ并不增加系统的开关频率。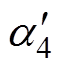 ,从60 °~
,从60 °~