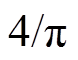 ,相比于3次谐波注入方案,两者具有更宽的稳定运行范围。但混合调制策略在SM的直流侧存在不规则且较大的电容电压波动,HCM策略具有更好的稳态性能[23]。
,相比于3次谐波注入方案,两者具有更宽的稳定运行范围。但混合调制策略在SM的直流侧存在不规则且较大的电容电压波动,HCM策略具有更好的稳态性能[23]。摘要 由于阴影遮挡、损坏等问题,基于模块化多电平变换器的光伏系统中存在光伏(PV)输出功率不平衡的现象,会使高输出功率PV对应的子模块过调制。谐波补偿调制策略是解决该问题的一种常见方案,通过向高功率PV的子模块中注入谐波而避免子模块过调制,低功率PV的子模块(称为正常子模块)则需要补偿数量相同、相位相反的谐波,使桥臂内的谐波相抵消而不会造成桥臂电压和电流畸变。然而,在PV功率严重不平衡时,为了避免高功率PV的子模块过调制,现有谐波补偿调制策略需要注入的谐波过大,会超过正常子模块的补偿范围,使正常子模块出现过调制,导致桥臂电压和电流畸变,影响系统的稳定运行。该文提出一种新型谐波补偿调制策略,在高功率PV的子模块不发生过调制的前提下避免正常子模块过调制,保证系统的稳定运行。同时,该文对不同谐波补偿调制策略稳定运行范围进行了定性和定量评估,表明所提谐波补偿调制策略能在更多PV功率不平衡工况下稳定运行。通过仿真与实验验证谐波补偿调制策略在模块化多电平变换器光伏系统中的可行性与理论分析的正确性。
关键词:模块化多电平变换器 功率不平衡 谐波补偿调制策略 过调制 稳定运行
随着能源危机与环境问题受到越来越多国家的关注与重视,发展清洁的可再生能源逐渐成为了国际社会的共识[1]。光伏发电技术因易于实现太阳能与电能的转换,受地域限制较小,而得到了广泛的关注与快速的发展[2]。
相较于两电平和三电平的光伏变换器,模块化多电平变换器(Modular Multilevel Converter, MMC)具有低开关应力、低谐波、高效率、模块化等[3-5]优势。利用MMC模块化的优势,光伏(Photovoltaic, PV)模块可以分布集成在MMC子模块(Sub-Module, SM)的直流侧,构成基于MMC的光伏系统(MMC- based Photovoltaic System, MMC-PVS),使每个PV模块实现独立的最大功率点跟踪控制,提升光伏系统的发电效率[6-7]。
阴影遮挡[8]、光照强度差异[9]、温度差异[10]或PV模块损坏等,会使部分PV模块的输出功率明显降低,导致PV输出功率不一致,称为PV功率不平衡。针对MMC-PVS的PV功率不平衡问题,一些文献研究了PV功率不平衡问题对相间和桥臂间功率平衡的影响[7, 11-12],提出MMC内部环流控制策略,通过调控MMC内部环流中的直流分量和基频交流分量实现相间和桥臂间的平衡控制。
由于MMC同一桥臂内的SM流过的电流相同,PV功率不平衡会使高功率PV对应的SM过调制[13],造成桥臂电压和电流畸变,甚至影响系统的稳定运行。该问题在MMC储能系统中也存在,SM直流侧集成电池的荷电状态均衡控制[14]、电池故障[15]等,会造成MMC储能系统中SM直流侧功率不平衡。
为了使系统能在SM直流侧功率不平衡时正常运行,文献[16-17]分别通过单独控制SM调制波的基频交流调制比和直流调制比实现不同SM直流侧功率的匹配。文献[18-19]则是同比例调控直流和基频交流分量的调制比来实现SM直流侧功率匹配。文献[20]推导了调制波中直流调制比和基频交流调制比与SM直流侧功率之间的解析关系,提出了优化分配直流和基频交流调制比的控制方案,有效拓展了MMC-BESS的稳定运行范围。同时,根据文献[20]的分析,提高基频交流调制比能够拓展MMC-BESS的稳定运行范围。然而,由于过调制的限制,上述文献中基频交流调制比最大允许值为1,极大地限制了MMC-PVS在PV功率不平衡情况下的稳定运行范围。
扩展SM的最大基频交流调制比,可以扩大PV功率不平衡情况下的稳定运行范围,在级联H桥(Cascaded H-Bridge, CHB)光伏系统中已有相关研究。文献[21-22]提出的3次谐波注入方案可以将等效基频交流调制比提升至1.155。文献[23-25]提出的谐波补偿调制(Harmonic Compensation Modulation, HCM)策略,文献[26-28]提出的混合调制策略,都能够将等效基频交流调制比提升至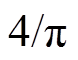 ,相比于3次谐波注入方案,两者具有更宽的稳定运行范围。但混合调制策略在SM的直流侧存在不规则且较大的电容电压波动,HCM策略具有更好的稳态性能[23]。
,相比于3次谐波注入方案,两者具有更宽的稳定运行范围。但混合调制策略在SM的直流侧存在不规则且较大的电容电压波动,HCM策略具有更好的稳态性能[23]。
根据HCM策略的基本原理,为了避免高功率PV的SM过调制,需要向其中注入谐波,同时,其余低功率PV的SM(称为正常SM)需要补偿频率相同、相位相反的谐波,从而抵消一个桥臂内注入的谐波,避免桥臂电压畸变。然而,在PV功率严重不平衡时,现有的HCM策略注入的谐波过大,会超过正常SM的补偿能力,虽然能够避免高功率PV的SM过调制,却会造成正常SM过调制,引起桥臂电压和电流畸变,影响系统的稳定运行范围。
本文提出一种新型的谐波补偿调制策略,由于注入的谐波更少,能够在保证高功率PV的SM不过调制的情况下,使低功率PV的SM也不发生过调制,避免谐波流入桥臂而导致桥臂电压和电流畸变,保证系统的稳定运行。同时,本文对不同谐波补偿调制策略稳定运行范围进行了定性和定量评估,表明所提谐波补偿调制策略能在更多PV功率不平衡工况下稳定运行。
本文所研究的MMC-PVS拓扑如图1a所示。该拓扑由三相六桥臂构成,每相由上桥臂、下桥臂和桥臂电感L0构成。每个桥臂由N个半桥型SM串联构成,每个SM的直流侧通过隔离型DC-DC变换器与光伏连接,如图1b所示。MMC-PVS的交流侧通过滤波电感Lg与交流电网相连,直流侧可以直接与直流电网相连。
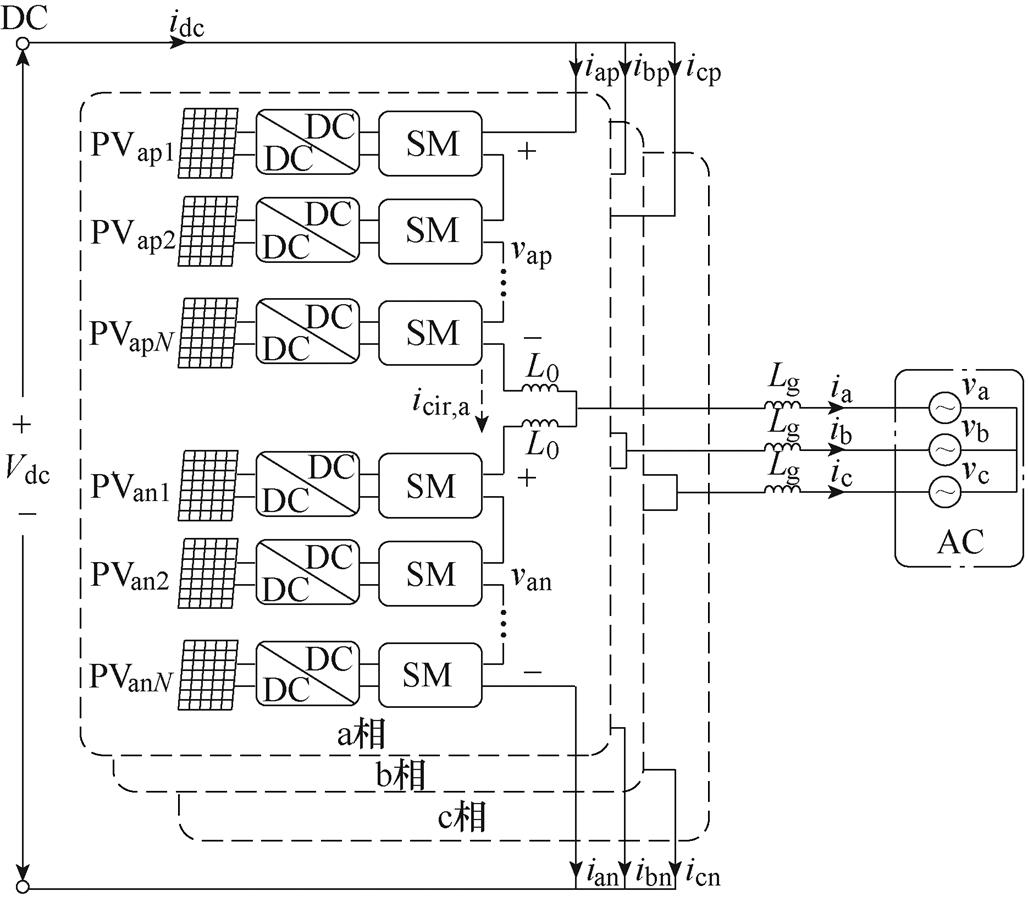
(a)基于MMC的光伏系统拓扑
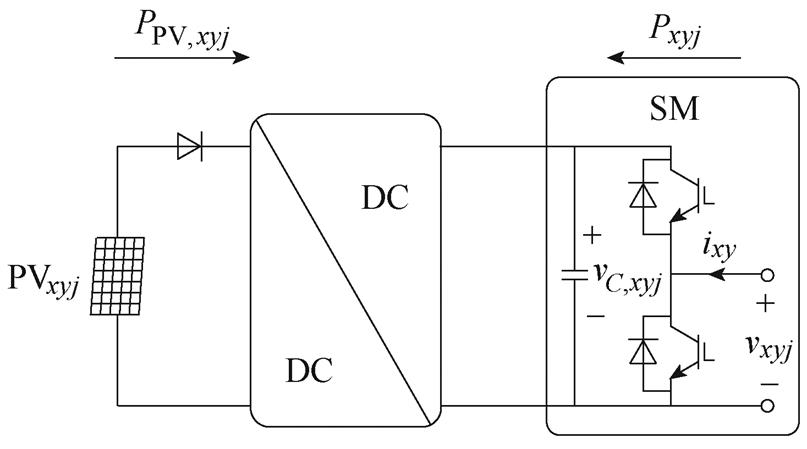
(b)基于半桥SM和隔离型DC-DC变换器的光伏模块
图1 基于MMC的光伏系统
Fig.1 MMC-based photovoltaic system
图1a中,vx和ix(x=a, b, c)分别为MMC-PVS交流侧的电压和电流,vxy和ixy(y=p, n)分别为每个桥臂的电压和电流,icir,x为每相的环流,Vdc为MMC-PVS直流侧电压。图1b中,j为桥臂内SM的序号,j=1,…, N,vxyj为SM交流端口电压,vC,xyj为SM直流侧的电容电压,其额定值为VC=Vdc/N。Pxyj和PPV,xyj分别为SM交流端口的平均功率和光伏单元的平均功率。
当同一桥臂内PV功率不平衡时,由于SM串联结构下流经每个SM的电流相同,就需要调整SM交流端口电压vxyj以匹配每个PV的输出功率。
SM的交流端口电压vxyj可以表示为
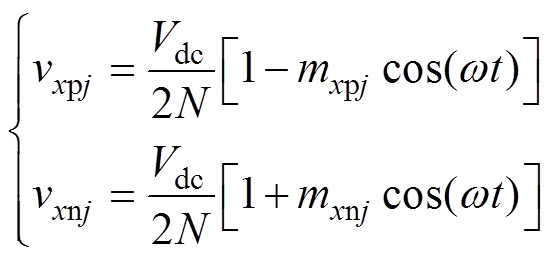 (1)
(1)
式中,mxyj为子模块的等效基频交流调制比;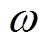 为基频角频率。
为基频角频率。
由于桥臂环流中的二倍频及以上频次的环流会增加桥臂电流应力和系统损耗,一般会采用大电容或环流抑制策略消除桥臂环流中的谐波环流,本文采用二倍频准谐振控制器对二倍频环流进行抑制[29]。同时,当PV功率不平衡时,需要调控桥臂环流中的直流和基频交流分量控制MMC-PVS的相间和桥臂间功率平衡[11]。因此,只考虑桥臂电流ixy中的直流分量和基频交流分量,ixy可以表示为
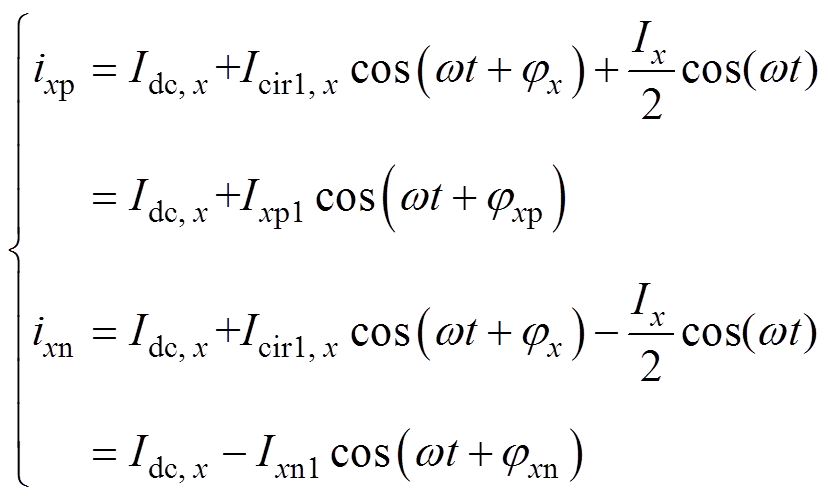 (2)
(2)
式中,Idc,x为x相桥臂环流的直流分量幅值;Icir1,x和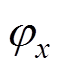 分别为桥臂环流基频分量的幅值和相位;Ixy1和
分别为桥臂环流基频分量的幅值和相位;Ixy1和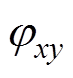 分别为桥臂电流中的基频分量的幅值和相位,表示为
分别为桥臂电流中的基频分量的幅值和相位,表示为
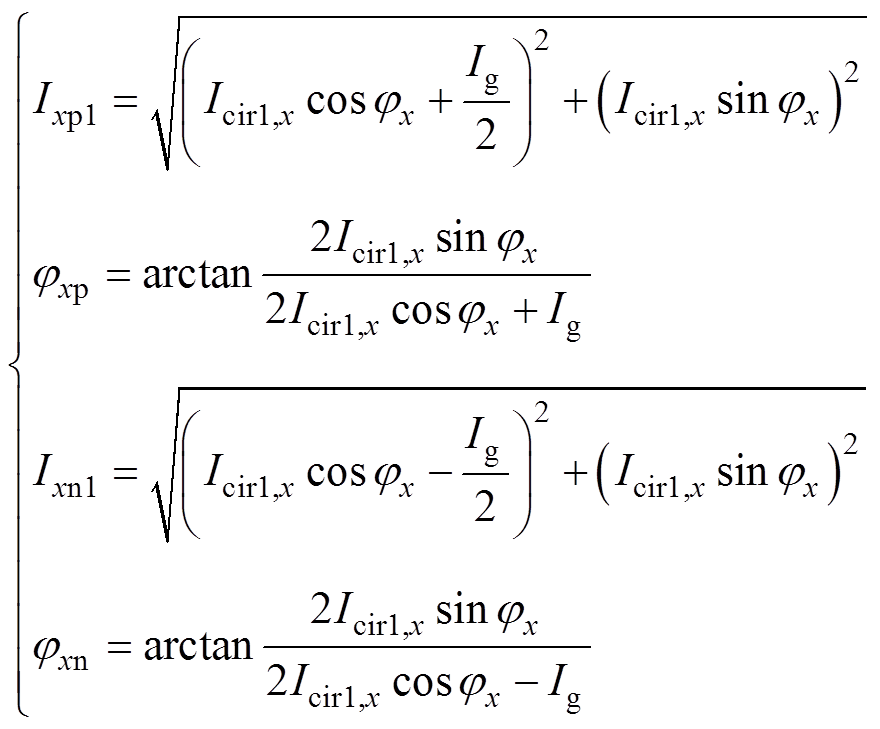 (3)
(3)
根据式(1)和式(2),SM交流端口的平均功率Pxyj可以表示为
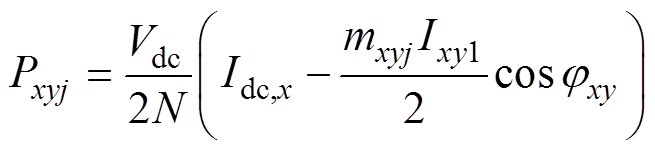 (4)
(4)
由图1b,根据功率平衡关系,SM的Pxyj和PPV,xyj满足
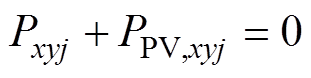 (5)
(5)
将式(5)代入式(4)中,可得mxyj为
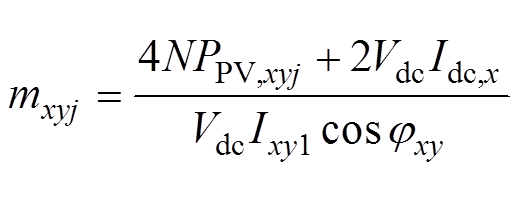 (6)
(6)
根据式(6)可知,PV功率不平衡会导致SM等效基频交流调制比出现差异。为了简化分析PV功率不平衡对SM等效基频交流调制比的影响,假定只有a相上桥臂中nPV,shaded个SM的PV模块受到阴影遮挡而导致输出功率降低,输出功率为PPV,shaded,a相其余PV模块及其他相PV模块正常运行,输出功率为PPV,normal。根据式(6),图2a为PV功率不平衡情况下SM等效基频交流调制比随PPV,shaded和nPV,shaded变化的趋势。当被遮挡的PV模块输出功率降低或数目增加时,正常运行的PV对应的SM等效基频交流调制比会随之增加,甚至出现过调制的情况。如果SM都不过调制,则mxyj≤1,对应的MMC-PVS的稳定运行范围如图2b所示。
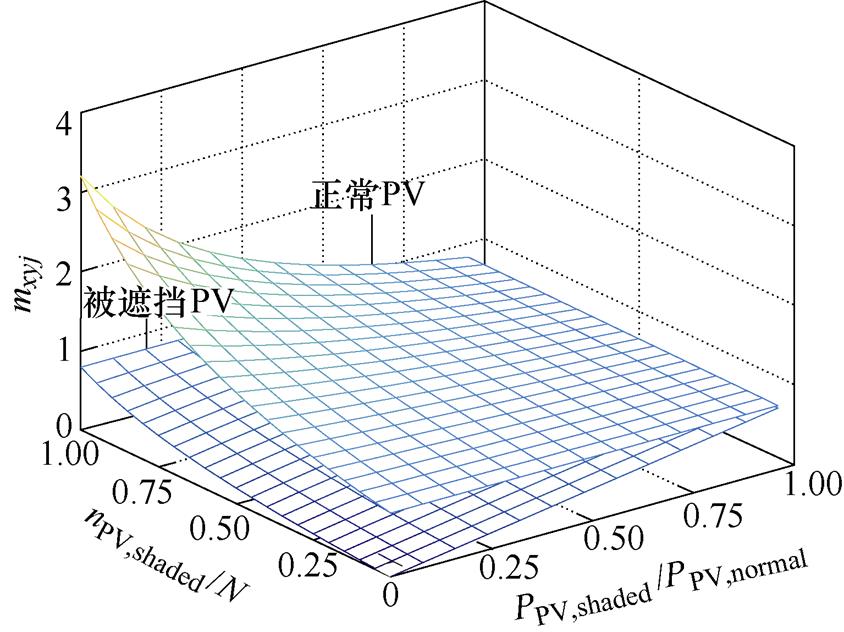
(a)mxyj随PPV,shaded和nPV,shaded的变化趋势
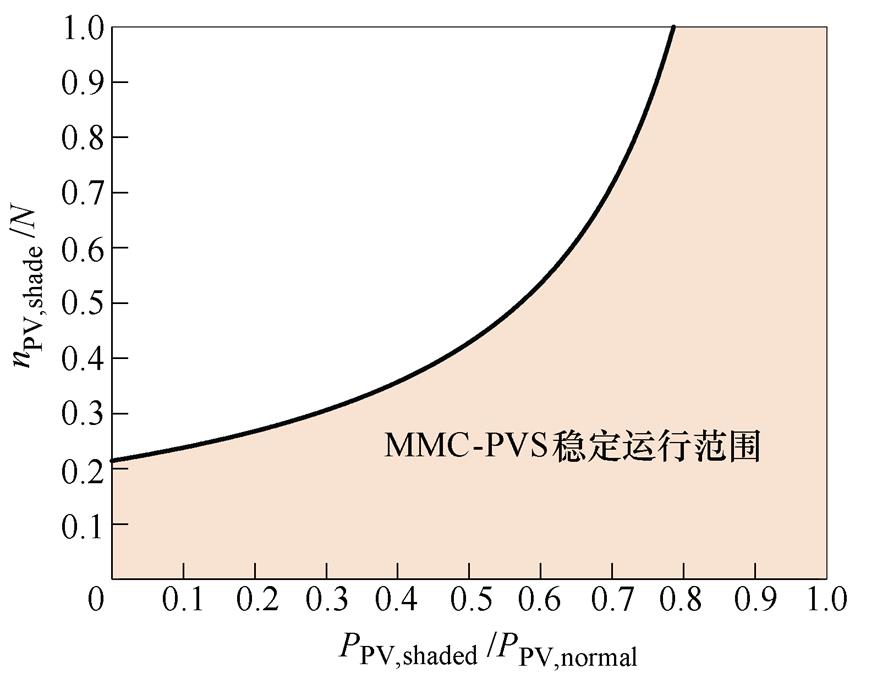
(b)MMC-PVS的稳定运行范围
图2 mxyj变化趋势和MMC-PVS稳定运行范围
Fig.2 Chart of mxyj and stable operation range of MMC-PVS
综上所述,PV功率不平衡会使SM等效基频交流调制比出现明显的差异,增加了输出功率高的PV对应SM的过调制风险,限制了MMC-PVS在PV功率不平衡情况下的稳定运行范围。
由于PV功率不平衡,导致MMC的部分SM调制波出现过调制。定义一个桥臂内出现过调制的SM(Overmodulation SM, OMSM)数目为nOM,xy,剩余SM为正常SM(Normal SM, NRSM)。假定桥臂内SM的序号按照SM等效基频交流调制比降序排列,桥臂内过调制SM的序号为j=1,…, nOM,xy,正常SM的序号为j=nOM,xy+1,…, N。为了避免桥臂电压畸变,根据式(1),同一桥臂内SM的等效基频交流调制比mxyj应满足
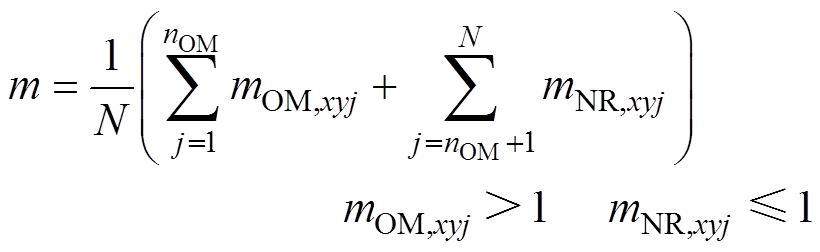 (7)
(7)
式中,m为MMC-PVS的系统调制比;mOM,xyj和mNR,xyj分别为OMSM和NRSM的子模块等效基频交流调制比。
对于OMSM,由于mOM,xyj>1,为了避免出现过调制,可以向调制波中注入一定的谐波hOM,xyj,新构成的OMSM的调制波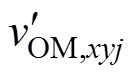 可以表示为
可以表示为
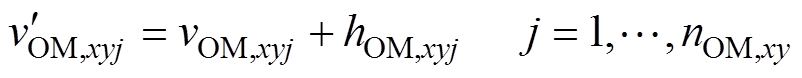 (8)
(8)
基于式(7)的约束条件,桥臂中注入NRSM的谐波补偿电压hNR,xy为
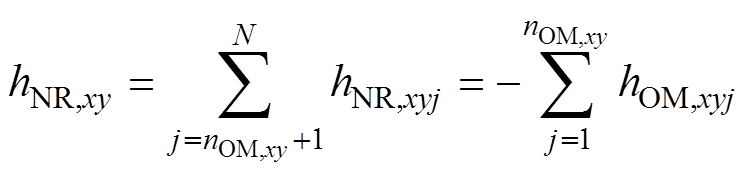 (9)
(9)
在NRSM调制波不过调制的情况下,每个NRSM允许的最大谐波补偿电压幅值HNR,xyj,max为
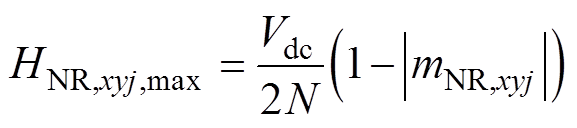 (10)
(10)
为了保证NRSM能够完全补偿注入OMSM的谐波电压,hNR,xy的幅值HNR,xy应满足
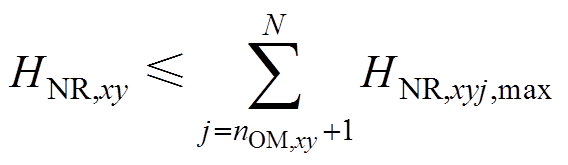 (11)
(11)
每个NRSM需要补偿的谐波电压按照对应的hNR,xyj,max比例进行分配,则每个NRSM补偿的谐波电压hNR,xyj可以表示为
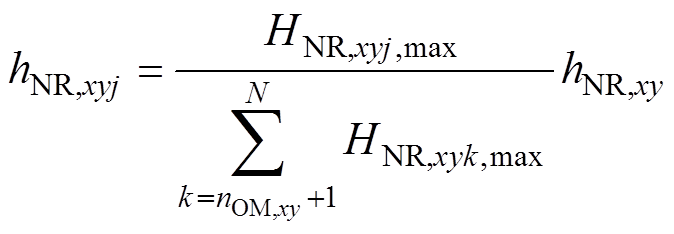 (12)
(12)
结合式(1)、式(10)和式(12),补偿谐波电压后的NRSM调制波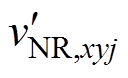 可以表示为
可以表示为
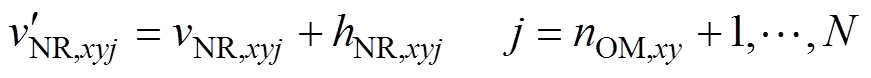 (13)
(13)
基于上述HCM策略基本原理,在图3a所示的未注入谐波电压的OMSM过调制电压vOM,xyj的基础上,本文通过注入谐波电压,提出了如图3b所示的HCM策略,新构成的OMSM调制波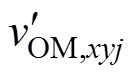 时域表达式为
时域表达式为
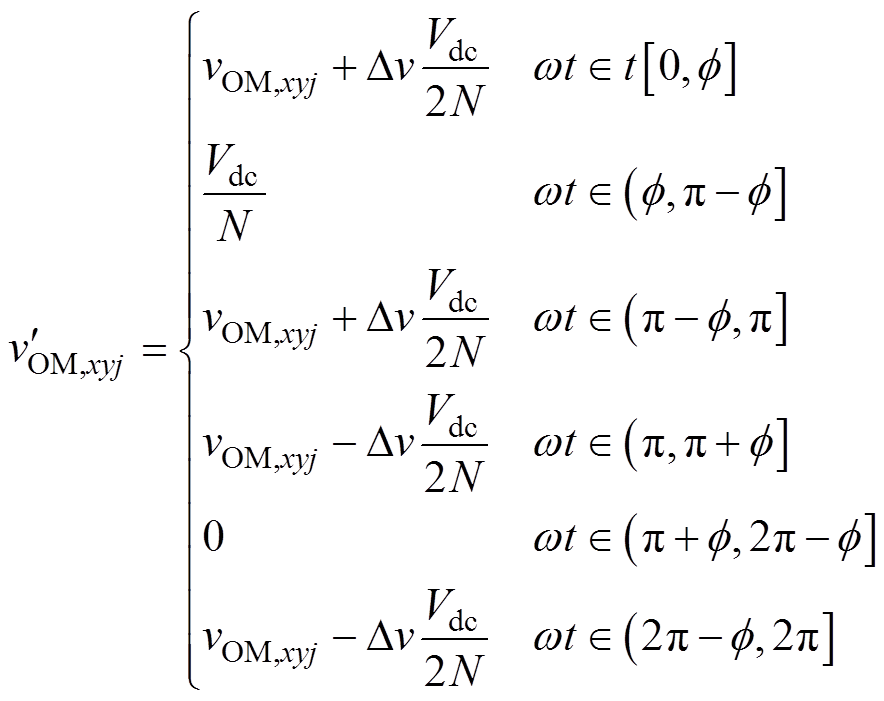 (14)
(14)
其中, 和
和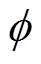 满足
满足
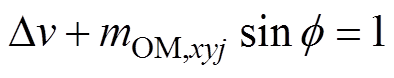 (15)
(15)
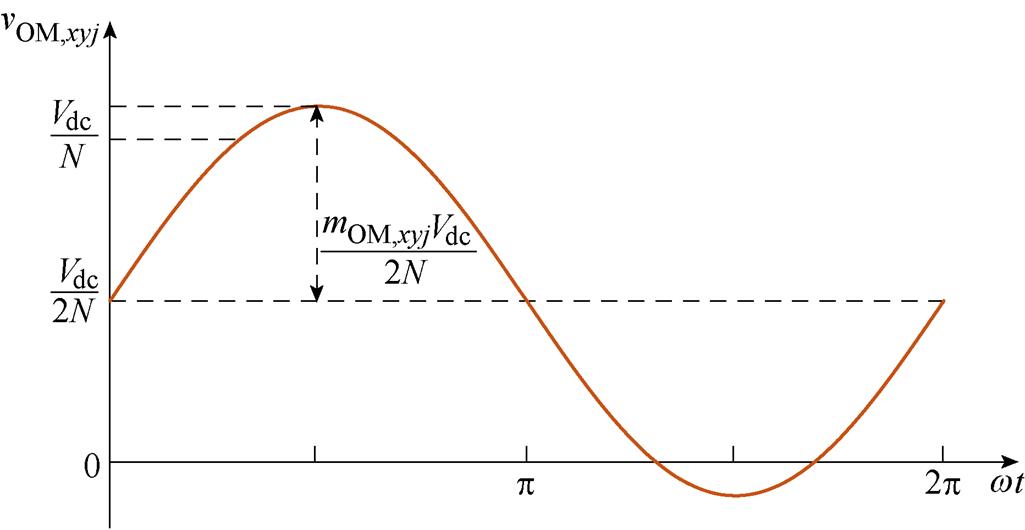
(a)未注入谐波电压的OMSM调制波vOM,xyj
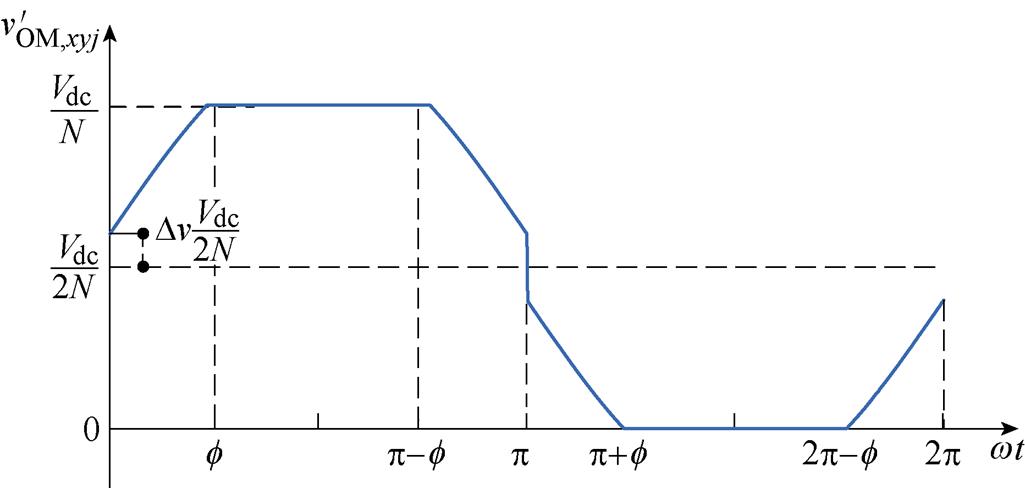
(b)注入谐波电压的OMSM调制波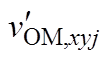
图3 所提HCM策略波形
Fig.3 Waveforms of proposed HCM strategy
将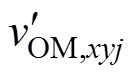 进行傅里叶分解,表示为
进行傅里叶分解,表示为
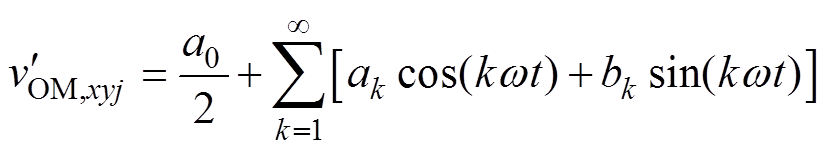 (16)
(16)
其中
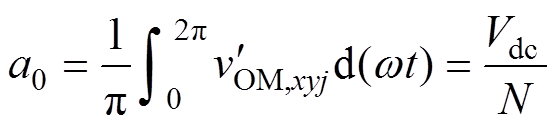
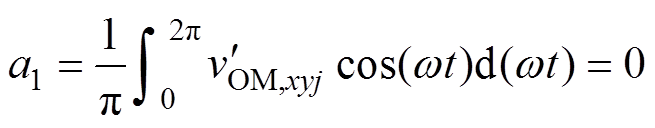
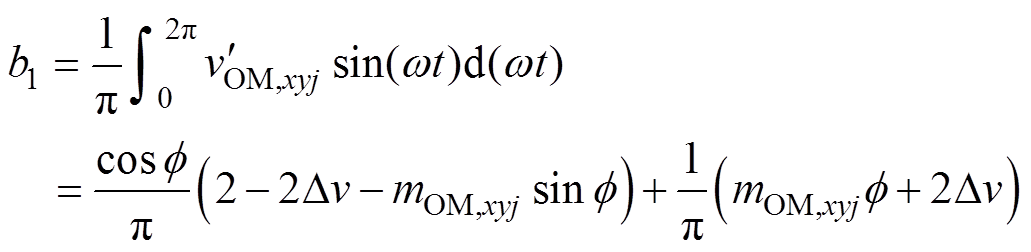
结合式(1)、式(14)~式(16),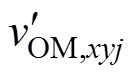 的等效基频交流调制比mOM,xyj可以表示为
的等效基频交流调制比mOM,xyj可以表示为
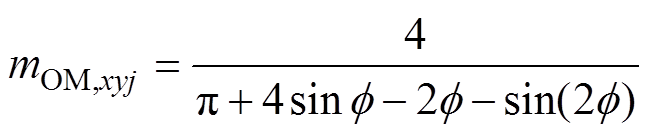 (17)
(17)
根据式(15)和式(17),图4为 与mOM,xyj的关系曲线。由图4可知,本文所提HCM策略能够将SM的等效基频交流调制比mOM,xyj扩展至
与mOM,xyj的关系曲线。由图4可知,本文所提HCM策略能够将SM的等效基频交流调制比mOM,xyj扩展至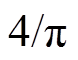 ,约为1.273,有助于扩大MMC-PVS在PV功率不平衡情况下的稳定运行范围。
,约为1.273,有助于扩大MMC-PVS在PV功率不平衡情况下的稳定运行范围。
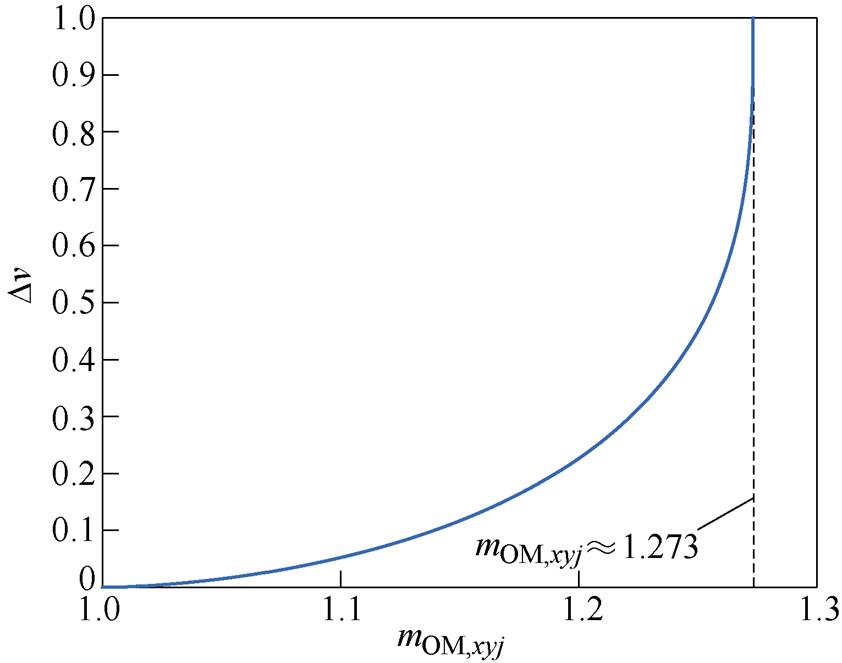
图4 Dv与mOM,xyj的关系曲线
Fig.4 Relation curve of Dv and mOM,xyj
当mOM,xyj工作于[1, 1.273]之间时,OMSM的vOM,xyj、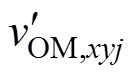 和hOM,xyj的波形如图5所示。
和hOM,xyj的波形如图5所示。
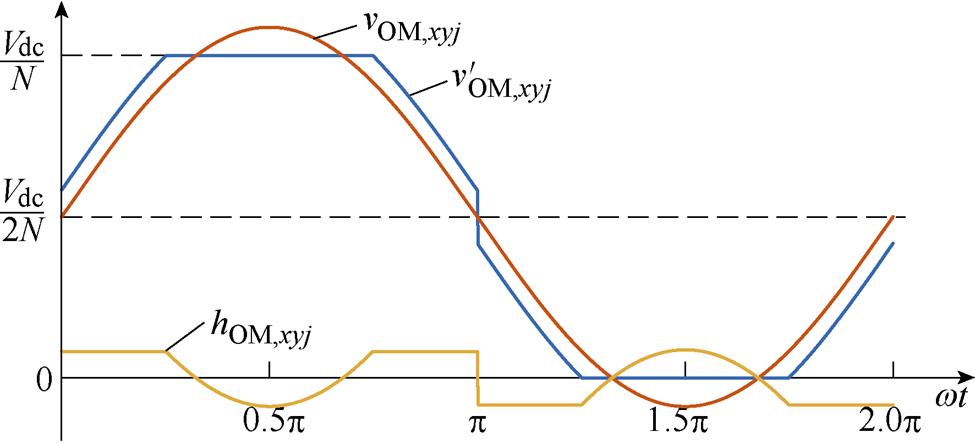
图5 所提HCM策略OMSM的调制波及谐波电压波形
Fig.5 Modulation and harmonic waveforms of OMSM of proposed HCM strategy
文献[16]的调节变量为等效基频交流调制比,本文称为正弦波调制策略。文献[23-25]提出的HCM策略分别称为策略1、策略2和策略3,本文所提HCM策略简称为所提策略。图6为策略1、策略2和策略3的OMSM对应的vOM,xyj、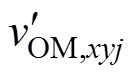 和hOM,xyj的波形。
和hOM,xyj的波形。
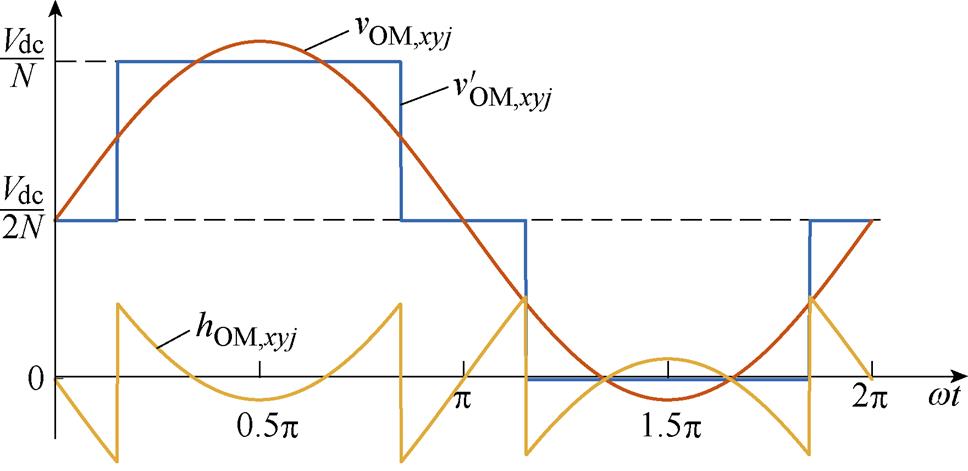
(a)策略1
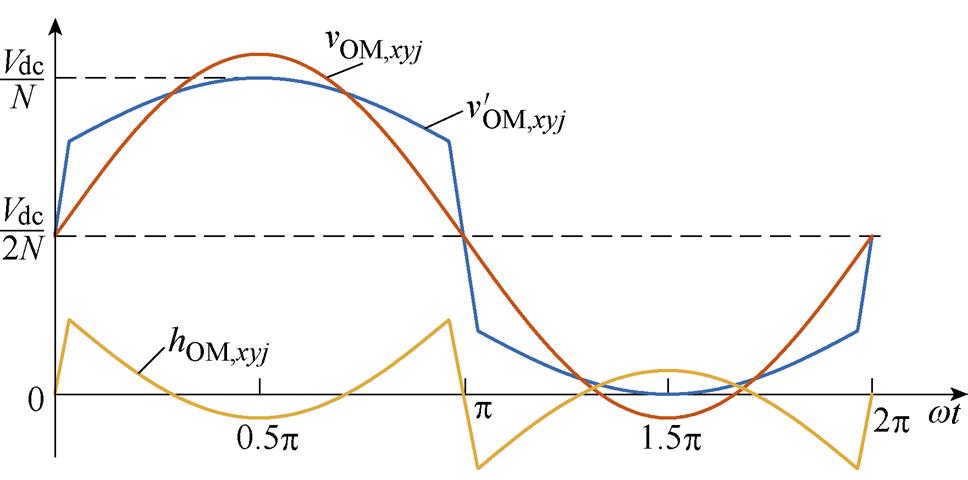
(b)策略2
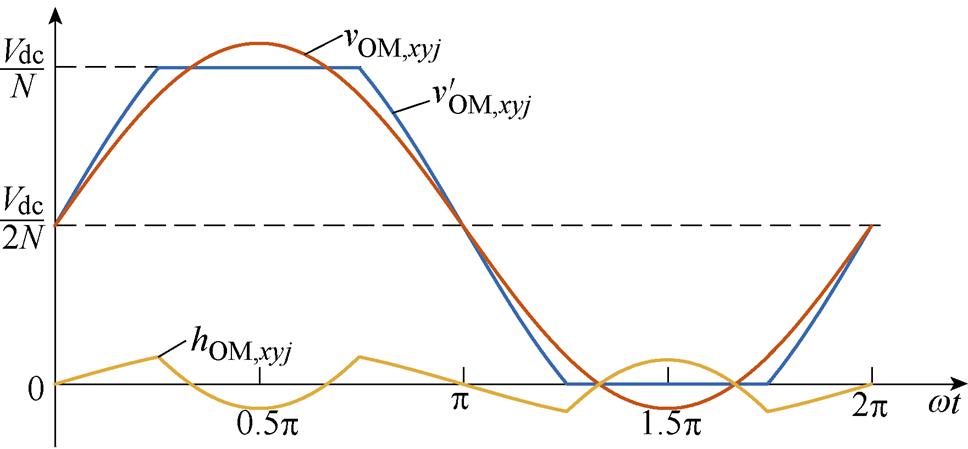
(c)策略3
图6 不同HCM策略OMSM的调制波及谐波电压波形
Fig.6 Modulation and harmonic waveforms of OMSM of different HCM strategies
根据式(9)和式(11),一个桥臂内能够注入OMSM的谐波电压应小于NRSM能补偿的谐波电压;否则,根据式(7),将导致桥臂电压发生畸变,影响MMC-PVS的稳定运行。从图5和图6可以发现,不同HCM策略注入OMSM的谐波电压存在明显差异。图7给出了不同HCM策略注入OMSM的谐波电压幅值HOM,xyj与mOM,xyj的关系曲线。
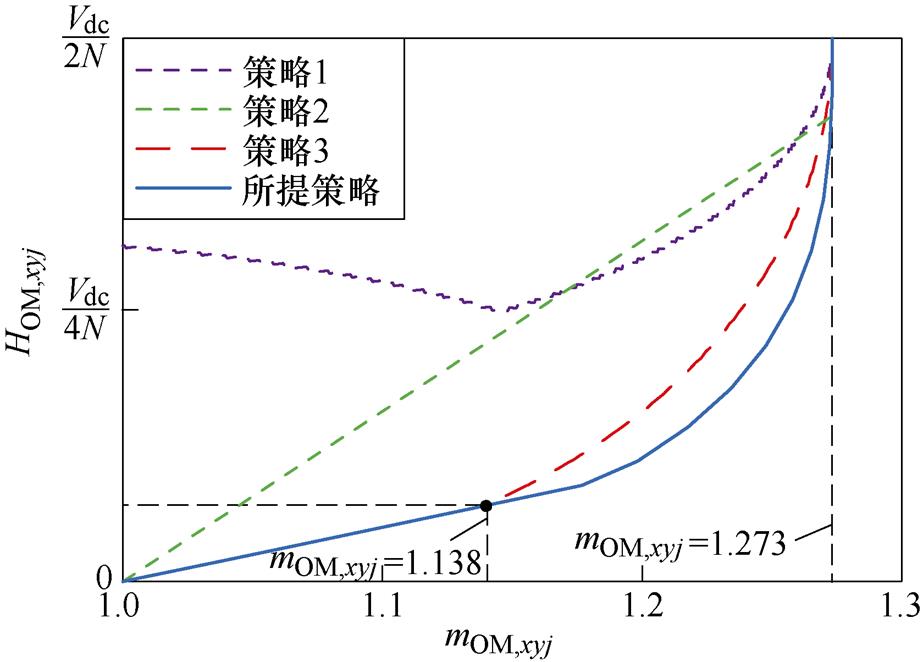
图7 不同HCM策略HOM,xyj与mOM,xyj的关系曲线
Fig.7 Relation curves of HOM,xyj and mOM,xyj for different HCM strategies
根据图7,当mOM,xyj<1.138时,策略3和所提策略具有相同且较小的HOM,xyj;当mOM,xyj>1.138时,所提策略产生的HOM,xyj明显小于策略3,具有最小的HOM,xyj。这说明在相同的PV功率不平衡情况下,所提策略注入OMSM的谐波幅值最小。相应地,需要NRSM补偿的谐波电压也最小,更易于满足式(11)的约束条件。因而,相比于策略1~3,所提策略能够适用于更多的PV功率不平衡的工况,拥有更大的MMC-PVS稳定运行范围。
考虑MMC-PVS交流侧三相对称运行的情况,定义Pr为MMC-PVS交流侧单相额定功率,Pg为运行功率。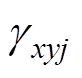 为PV功率因子,表示为
为PV功率因子,表示为
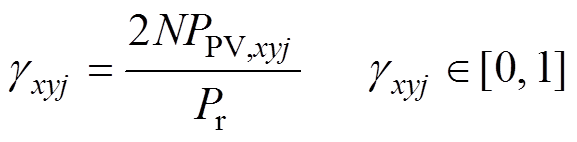 (18)
(18)
根据文献[11]和式(5),桥臂环流与PV功率的关系可以表示为
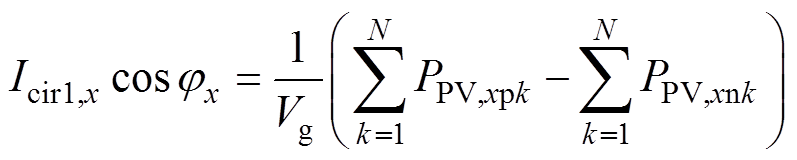 (19)
(19)
式中,Vg为MMC-PVS交流侧电压幅值,Vg=mVdc/2。
将式(18)和式(19)代入到式(6),MMC-PVS中SM的等效基频交流调制比mxyj可以表示为
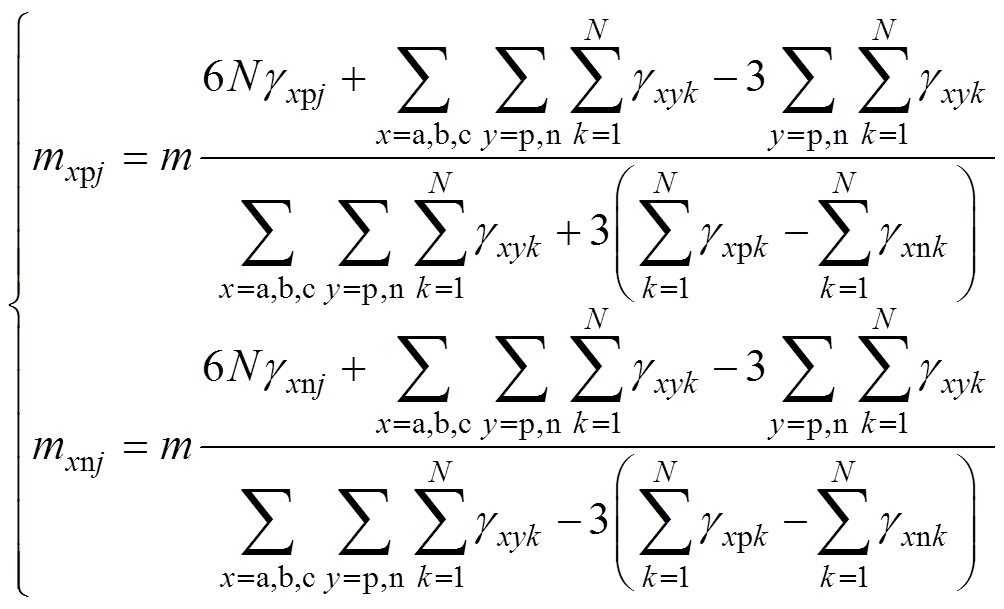 (20)
(20)
根据3.1节中的HCM策略基本原理,当桥臂内有一个或多个SM出现过调制时,可以通过向OMSM中注入谐波以提高SM的等效基频交流调制比。根据图7中不同HCM策略的HOM,xyj和mOM,xyj的关系,定义HOM,xyj=f(mOM,xyj)。根据式(9),桥臂内NRSM需要补偿的谐波幅值HNR,xy可以表示为
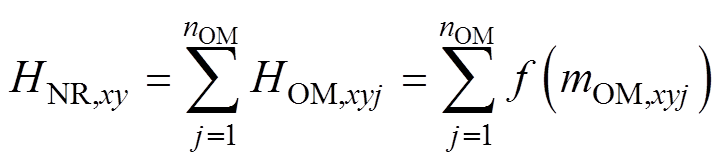 (21)
(21)
同时,结合HCM策略能够达到的最大等效基频交流调制比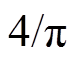 和式(11)的约束条件,基于HCM策略的MMC-PVS稳定运行的约束条件可以表示为
和式(11)的约束条件,基于HCM策略的MMC-PVS稳定运行的约束条件可以表示为
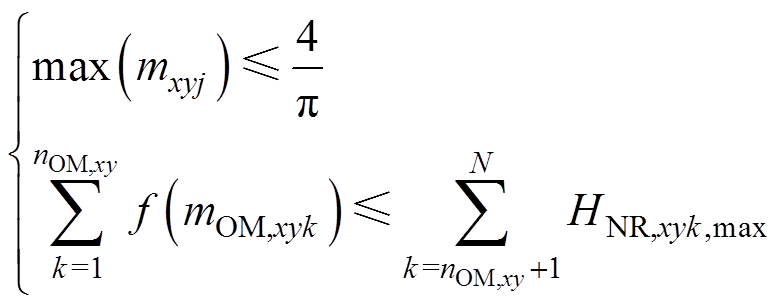 (22)
(22)
式中,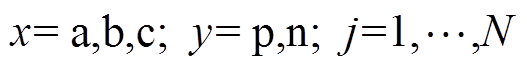 。
。
对于MMC-PVS,定义PV功率因子构成6N维向量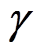 =[gap1 … gapN gan1 … ganN gbp1 … gbpN gbn1 …gbnN gcp1 … gcpN gcn1 … gcnN]。因而,在MMC-PVS中,每种PV功率分布状态都对应唯一的6N维向量
=[gap1 … gapN gan1 … ganN gbp1 … gbpN gbn1 …gbnN gcp1 … gcpN gcn1 … gcnN]。因而,在MMC-PVS中,每种PV功率分布状态都对应唯一的6N维向量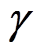 。对于任意向量
。对于任意向量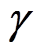 ,如果满足式(22),则为MMC-PVS的稳定运行点,而由所有稳定运行点构成的6N维空间定义为MMC-PVS的稳定运行空间(Stable Operation Space, SOS),这个6N维空间的体积定义为稳定运行因数(Stable Operation Factor, SOF)[30-31],表示为
,如果满足式(22),则为MMC-PVS的稳定运行点,而由所有稳定运行点构成的6N维空间定义为MMC-PVS的稳定运行空间(Stable Operation Space, SOS),这个6N维空间的体积定义为稳定运行因数(Stable Operation Factor, SOF)[30-31],表示为
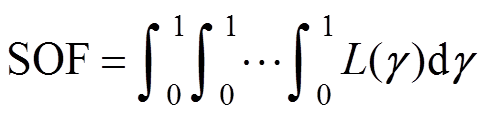 (23)
(23)
其中
 (24)
(24)
SOF反映的是所有的稳定运行点在所有可能出现的工况中的占比,能够定量评估HCM策略稳定运行范围。
为了简化分析及易于SOS的三维呈现,以N=3为例,设定a相上桥臂的部分或全部PV会出现功率下降的情况,其余桥臂PV正常运行,功率因子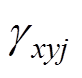 =1。
=1。
当m=0.85时,正弦波调制策略、策略1、策略2、策略3和所提策略的SOS如图8所示,对应的SOF分别为15.51%、36.51%、48.94%、69.91%和71.57%。对比正弦波调制策略,所有HCM策略都明显拓展了MMC-PVS的稳定运行范围。对比四种HCM策略,本文所提策略具有最大的SOF,表明其具有最大的稳定运行范围;策略3的SOF略小于本文策略,而明显优于策略1和策略2。另外,四种HCM策略在SOF上的差异与图7所示的谐波电压幅值的分析结果一致,说明越小的谐波电压幅值对应于更大的稳定运行范围。
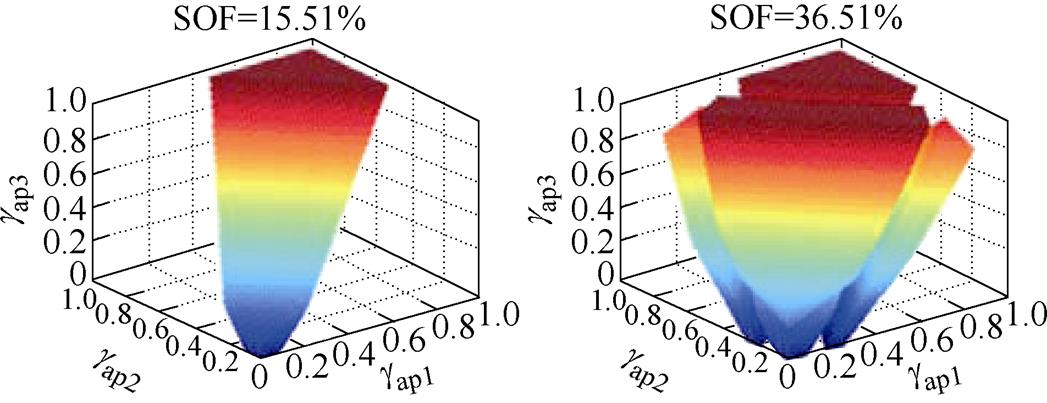
(a)正弦波调制策略 (b)策略1
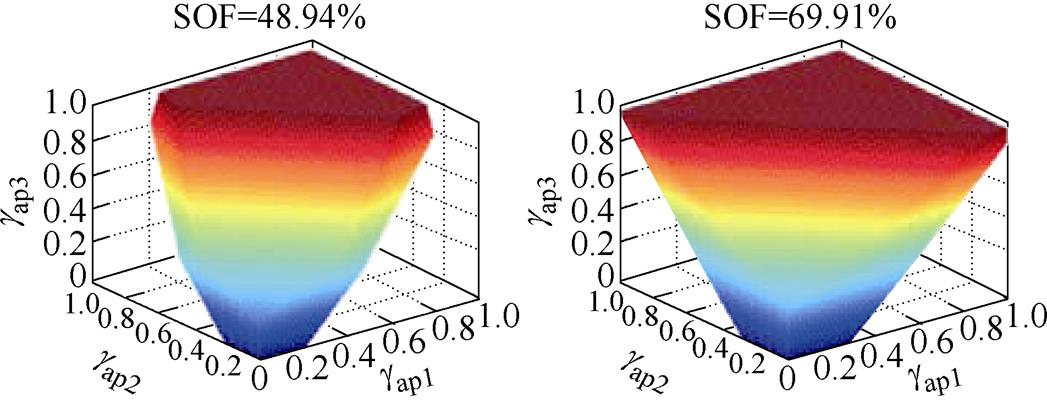
(c)策略2 (d)策略3
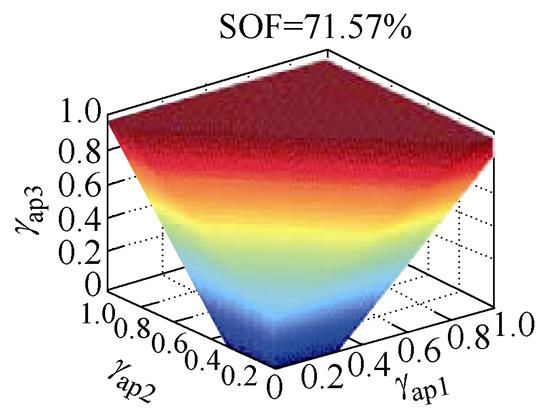
(e)所提策略
图8 m=0.85时不同策略的SOS与SOF
Fig.8 SOS and SOF of different strategies with m=0.85
图9为正弦波调制策略、策略1、策略2、策略3和所提策略的SOF随MMC-PVS的系统调制比m的变化曲线。根据图9,m对SOF具有明显的影响,并随着m的增加,不同策略的SOF都在不断降低。当m较小(m<0.48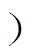 时,SOF都能够达到100%,说明MMC-PVS可以在任意的PV功率不平衡工况下稳定运行。随着m逐渐升高,正弦波调制策略的SOF急剧下降,说明正弦波调制策略的稳定运行范围急剧缩减。而四种HCM策略在m<0.7时下降趋势相同,稳定运行范围相同。当m>0.7时,四种HCM策略的SOF出现明显差异,所提策略仍具有最大的SOF,说明相比于其余HCM策略,随着m的变化,所提策略始终保持最大的稳定运行范围,与图7所示规律一致。
时,SOF都能够达到100%,说明MMC-PVS可以在任意的PV功率不平衡工况下稳定运行。随着m逐渐升高,正弦波调制策略的SOF急剧下降,说明正弦波调制策略的稳定运行范围急剧缩减。而四种HCM策略在m<0.7时下降趋势相同,稳定运行范围相同。当m>0.7时,四种HCM策略的SOF出现明显差异,所提策略仍具有最大的SOF,说明相比于其余HCM策略,随着m的变化,所提策略始终保持最大的稳定运行范围,与图7所示规律一致。
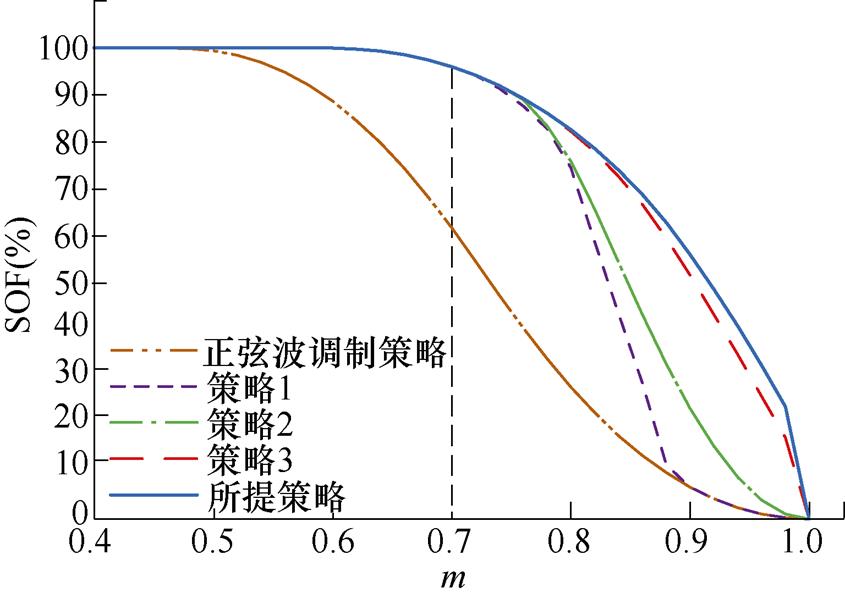
图9 不同策略SOF随m变化曲线
Fig.9 Curves of SOF along with m for different strategies
MMC-PVS控制策略框图如图10所示,图10a为MMC-PVS交流侧电流控制框图。由锁相环(Phase Locked Loop, PLL)和abc/dq变换环节获得电网侧的相位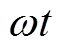 、电网电压幅值Vg、id和iq。利用图1b中的DC-DC变换器实现PV的最大功率点跟踪(Maximum Power Point Tracking, MPPT)控制,获取所有PV的总发电功率PPV。考虑MMC-PVS直流侧功率Pdc的情况下,计算MMC-PVS交流侧有功电流参考值idref,在dq坐标系下采用PI调节器实现MMC的单位功率因数并网控制。
、电网电压幅值Vg、id和iq。利用图1b中的DC-DC变换器实现PV的最大功率点跟踪(Maximum Power Point Tracking, MPPT)控制,获取所有PV的总发电功率PPV。考虑MMC-PVS直流侧功率Pdc的情况下,计算MMC-PVS交流侧有功电流参考值idref,在dq坐标系下采用PI调节器实现MMC的单位功率因数并网控制。
图10b为MMC-PVS的相间和桥臂间平衡及环流控制框图。由相间平衡控制环路得到桥臂环流直流分量参考值idc,x,ref,由桥臂间平衡控制环路及式(25)得到桥臂环流基频分量参考值icir1,x,ref。环流控制环路包含PI调节器、基频准谐振调节器(R1)和二倍频准谐振调节器(R2),能够实现桥臂环流中直流和基频分量的跟踪和二倍频分量抑制。
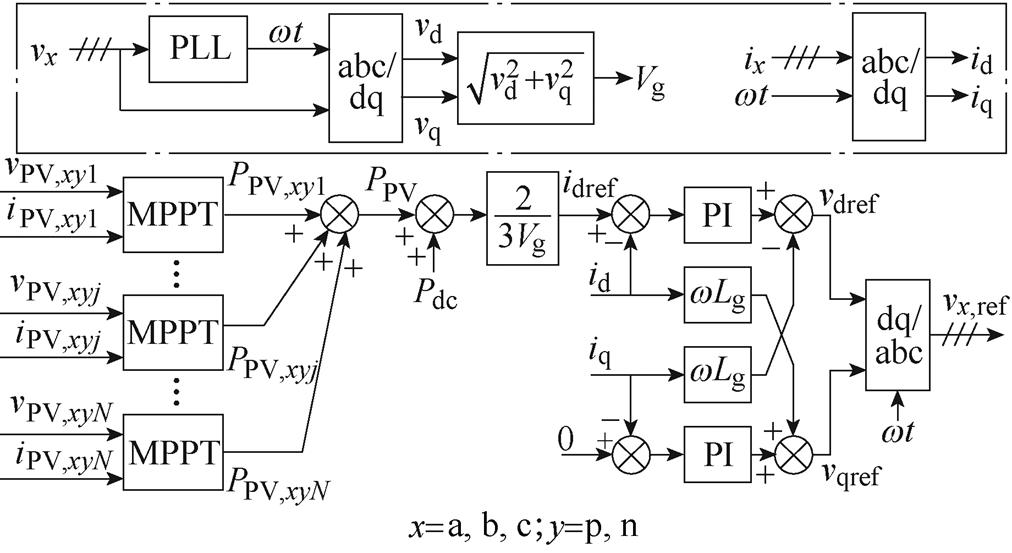
(a)MMC-PVS交流侧控制
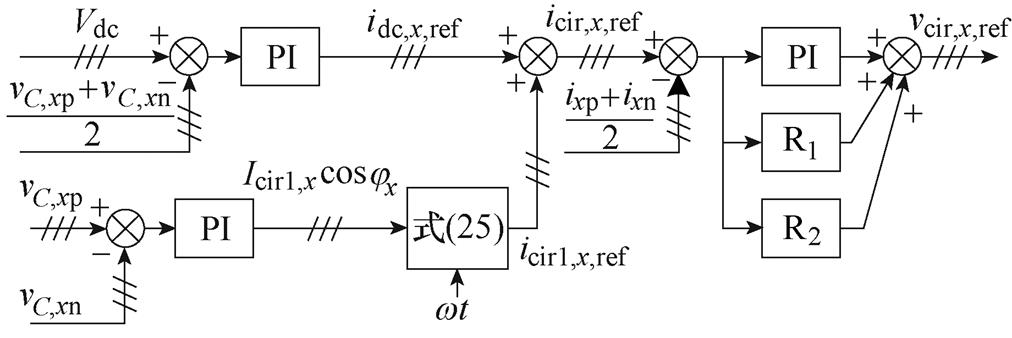
(b)MMC-PVS相间和桥臂间平衡及环流控制
(c)基于HCM策略的SM电容电压平衡控制
图10 MMC-PVS控制框图
Fig.10 Control diagram of MMC-PVS
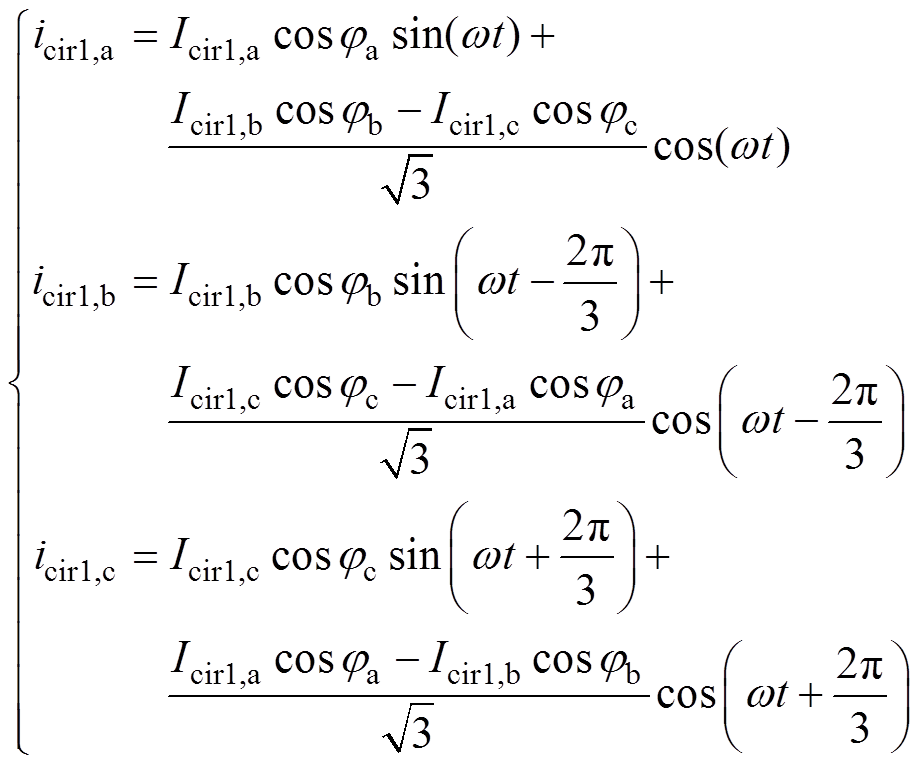 (25)
(25)
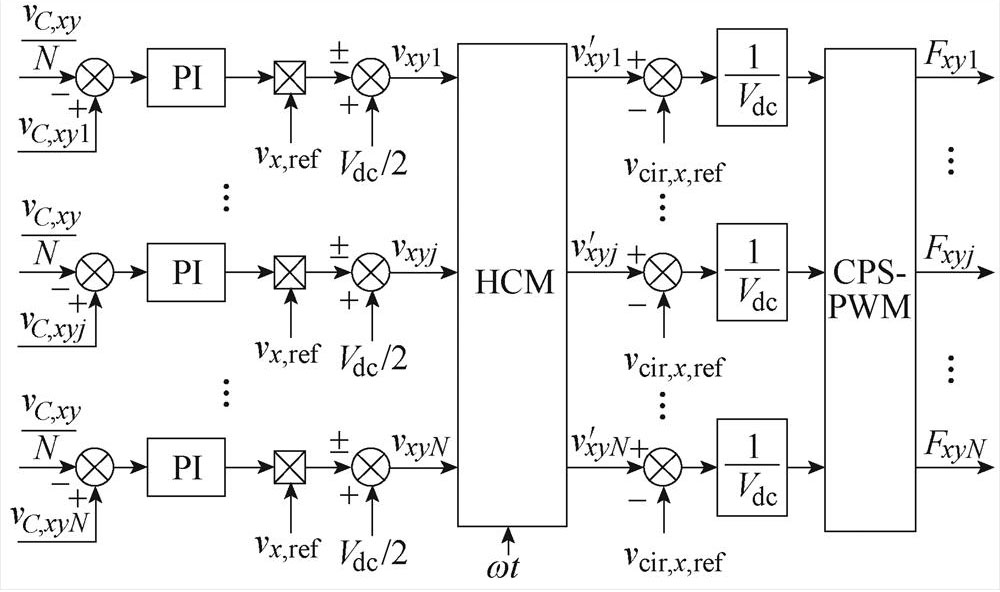
图10c为基于HCM策略的独立电压平衡控制和开关函数生成框图。每个SM电容电压与桥臂SM平均电压的误差经PI调节器后与交流侧电流控制的输出vx,ref相乘,如果y=p,其结果与Vdc/2作差,如果y=n,则与Vdc/2相加,得到谐波补偿前的SM调制波vxyj。经HCM环节,得到SM补偿后的调制波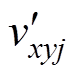 与vcir,x,ref叠加。将每个SM调制波整定并经载波移相脉宽调制(Carrier-based Phase Shift Pulse Width Modulation, CPS-PWM)环节得到SM的开关函数Fxyj,实现MMC-PVS的实时控制。
与vcir,x,ref叠加。将每个SM调制波整定并经载波移相脉宽调制(Carrier-based Phase Shift Pulse Width Modulation, CPS-PWM)环节得到SM的开关函数Fxyj,实现MMC-PVS的实时控制。
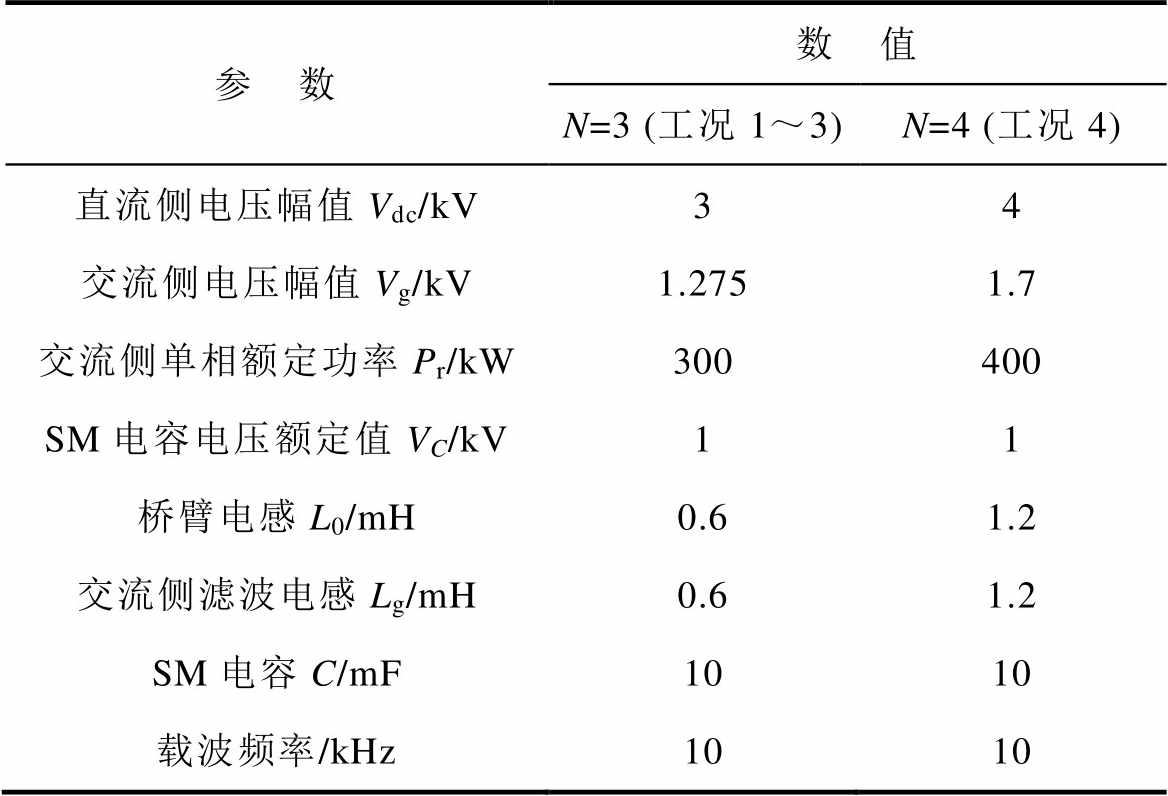
为了验证所提策略在MMC-PVS中的可行性及对比不同HCM策略的稳定运行范围差异,在Matlab/ Simulink中搭建了如图1所示的MMC-PVS仿真模型,系统仿真参数见表1。为了与图8的SOS对应,工况1~3中每个桥臂SM数目N=3,工况4为每个桥臂SM数目N=4的仿真工况。
表1 MMC-PVS仿真参数
Tab.1 Simulation parameters of MMC-PVS
参 数数 值 N=3 (工况1~3)N=4 (工况4) 直流侧电压幅值Vdc/kV34 交流侧电压幅值Vg/kV1.2751.7 交流侧单相额定功率Pr/kW300400 SM电容电压额定值VC/kV11 桥臂电感L0/mH0.61.2 交流侧滤波电感Lg/mH0.61.2 SM电容C/mF1010 载波频率/kHz1010
为了便于验证,仿真中只有a相上桥臂中的PV存在功率不平衡的情况,其余桥臂的PV功率不变,功率因子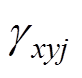 =1。同时,在所有仿真工况中,MMC- PVS直流侧功率Pdc=0。
=1。同时,在所有仿真工况中,MMC- PVS直流侧功率Pdc=0。
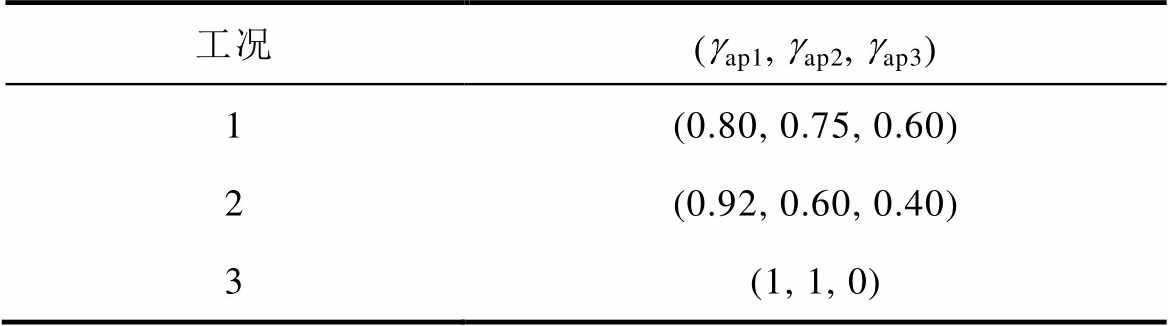
三种仿真工况中a相上桥臂PV功率因子见表2。工况1的PV运行点位于正弦波调制策略和四种HCM策略的稳定运行空间内,工况2的PV运行点位于四种HCM策略的稳定运行空间内,工况3的PV运行点只位于策略3和所提策略的稳定运行空间内。
表2 仿真工况1~3
Tab.2 Simulation conditions of Case 1 to Case 3
工况(gap1, gap2, gap3) 1(0.80, 0.75, 0.60) 2(0.92, 0.60, 0.40) 3(1, 1, 0)
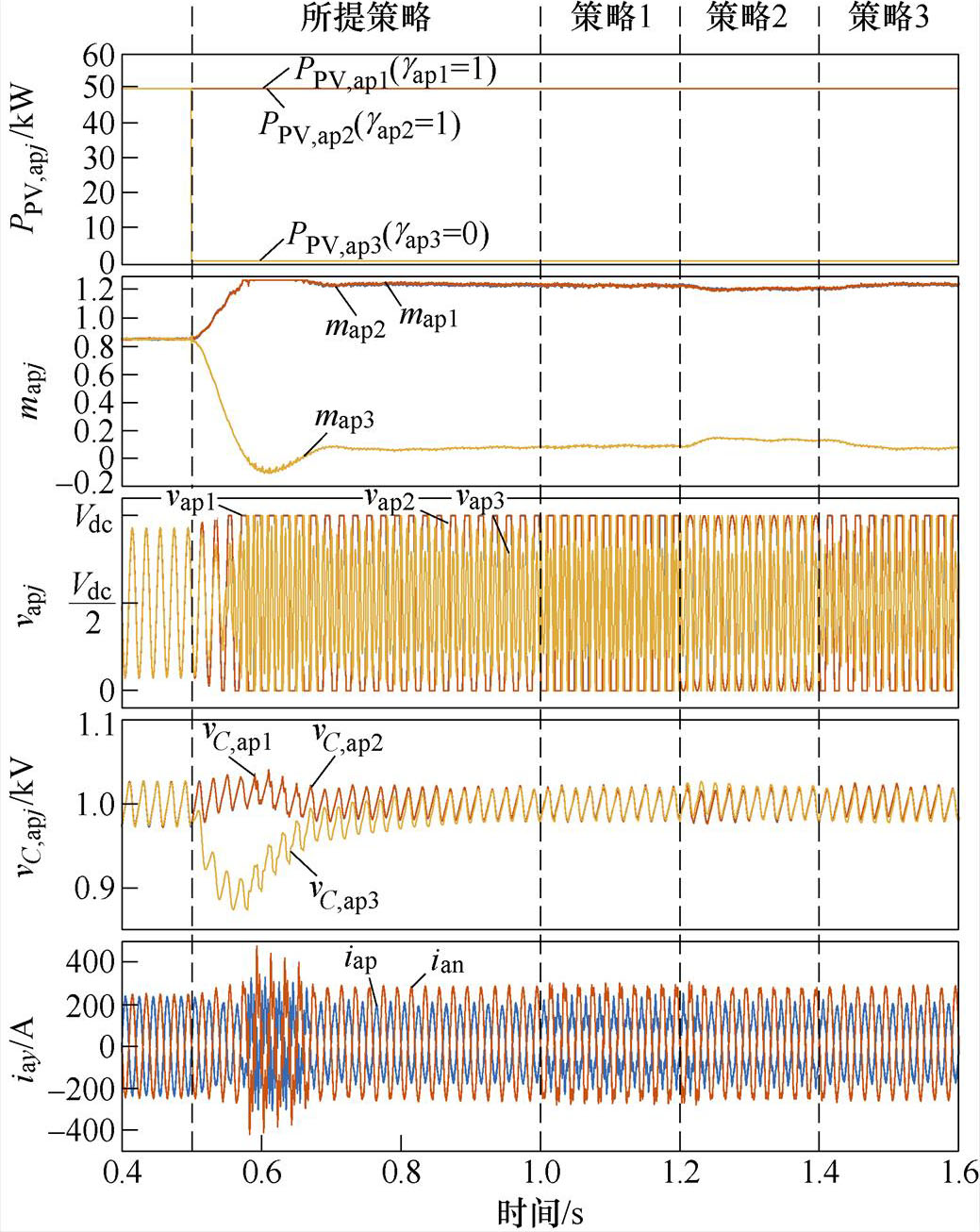
初始阶段,所有PV的功率因子相同;在0.5 s时,a相上桥臂PV出现功率不平衡现象;在[0.5 s, 1.0 s]、[1.0 s, 1.2 s]、[1.2 s, 1.4 s]和[1.4 s, 1.6 s]四个阶段依次采用所提策略、策略1、策略2和策略3。
工况1~3的仿真波形如图11~图13所示,图11a~图13a为a相上桥臂的PV功率PPV,apj、SM等效基频交流调制比mapj、SM调制波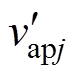 、SM电容电压vC,apj和a相上下桥臂的桥臂电流,图11b~13b为放大后四种HCM策略方案的调制电压
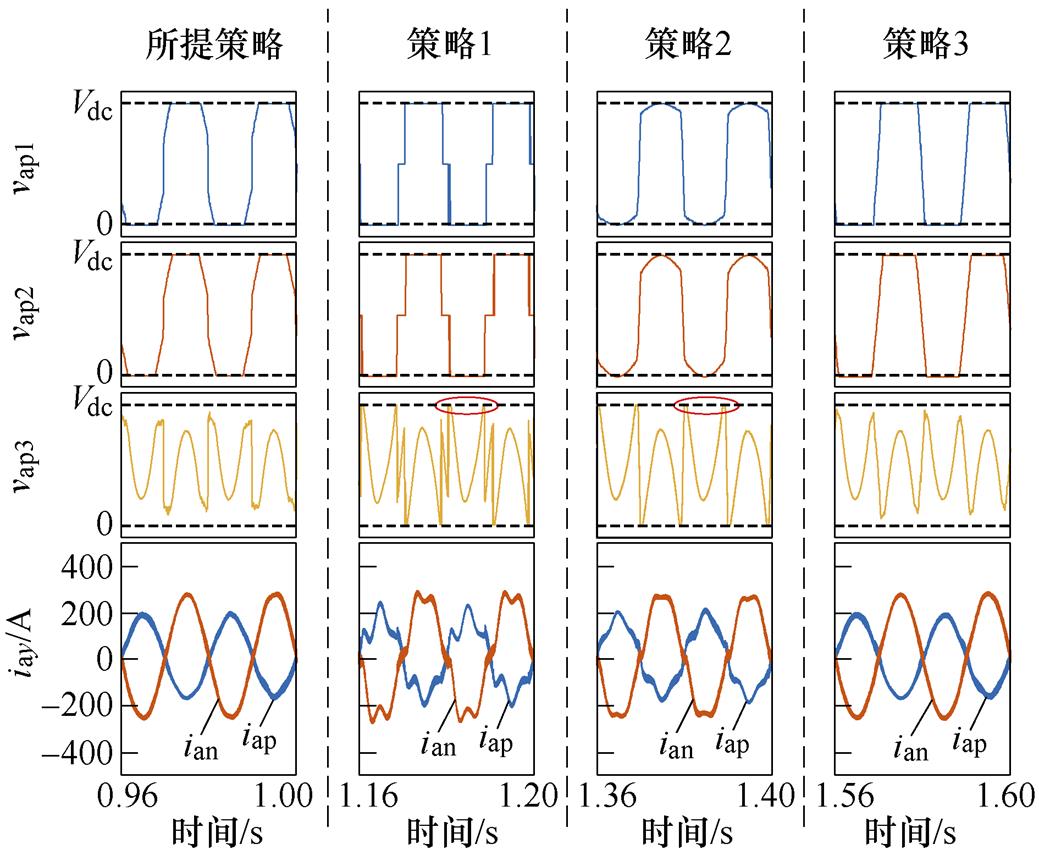
、SM电容电压vC,apj和a相上下桥臂的桥臂电流,图11b~13b为放大后四种HCM策略方案的调制电压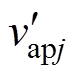 和桥臂电流的放大波形。
和桥臂电流的放大波形。
在工况1中,SM等效基频交流调制比mapj分别为0.937、0.885和0.728,没有SM过调制,MMC-PVS工作于正弦波调制策略。
在工况2中,SM等效基频交流调制比mapj为1.163、0.805和0.582,出现了过调制SM,超出了正弦波调制策略的稳定运行范围。工况2位于四种HCM策略的稳定运行空间内,均能实现MMC-PVS的稳定运行,如图12所示。
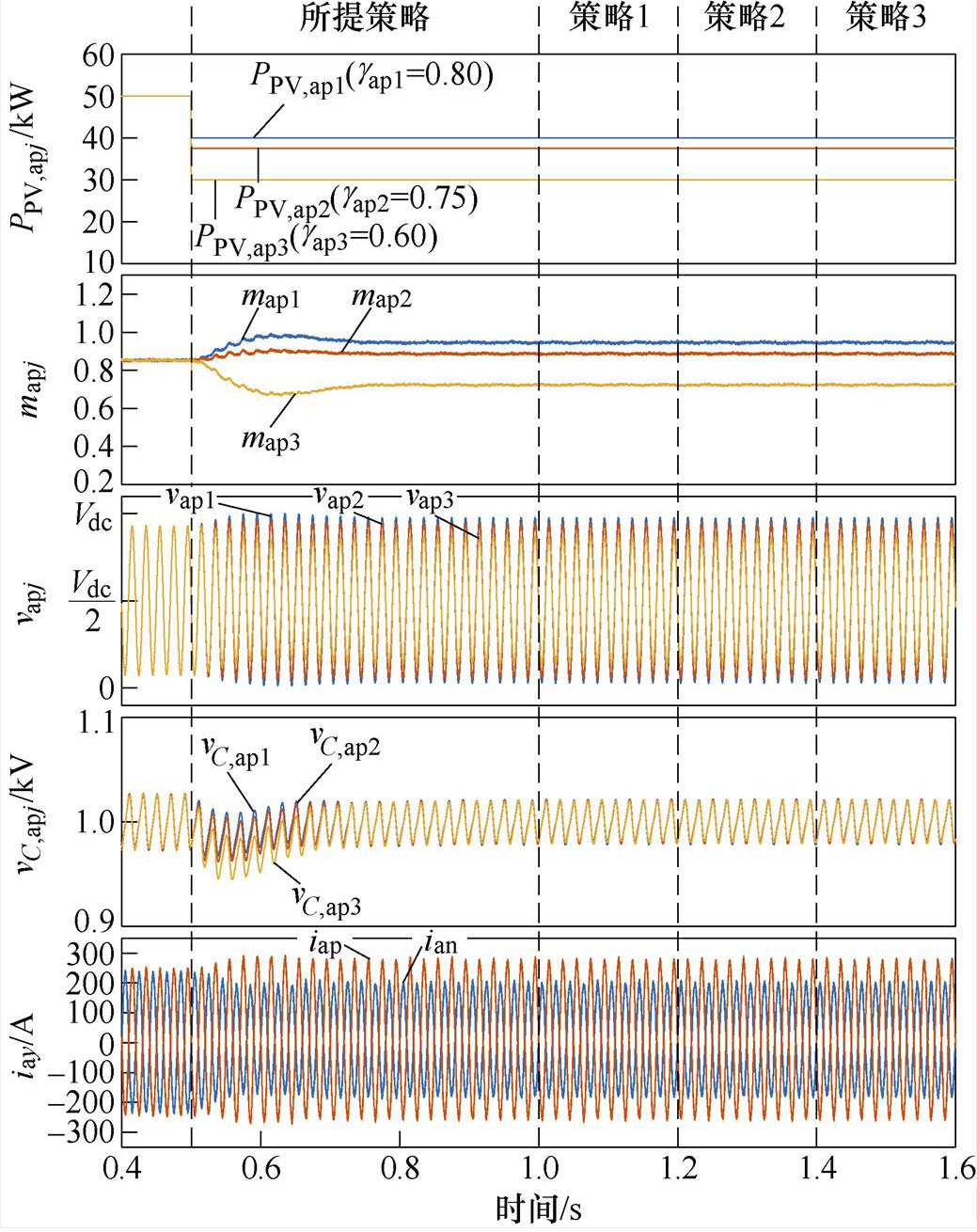
(a)不同策略动态切换波形
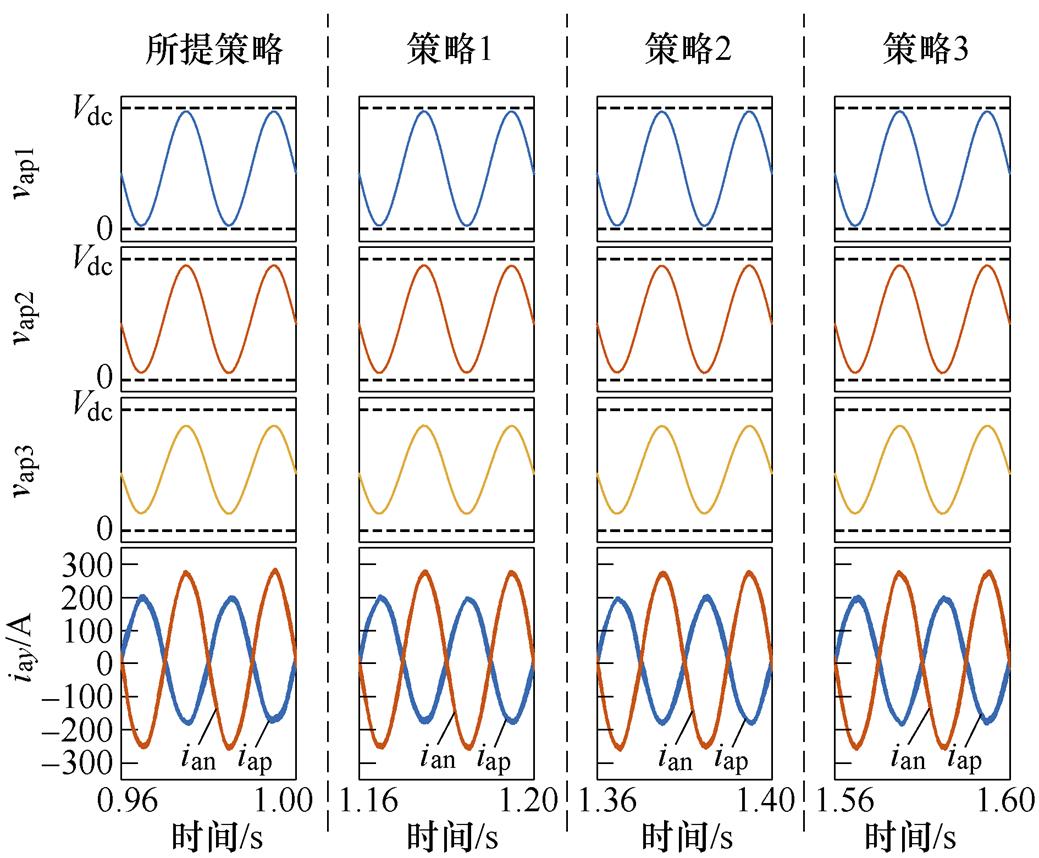
(b)不同策略稳态放大波形
图11 工况1仿真波形
Fig.11 Simulation waveforms of Case 1
在工况3中,SM等效基频交流调制比mapj为1.214、1.214和0.121,分别对应于高功率PV的SMap1、SMap2和低功率PV的SMap3。由图13b,采用策略1和策略2时,注入OMSM的谐波电压超出了NRSM能够补偿的范围,导致NRSM调制波过调制,如图13b中圆圈所示,造成了桥臂电流畸变。而根据图7,所提策略和策略3产生较小的谐波电压幅值,仍旧在NRSM能够补偿的范围内,能够实现MMC-PVS的稳定运行。
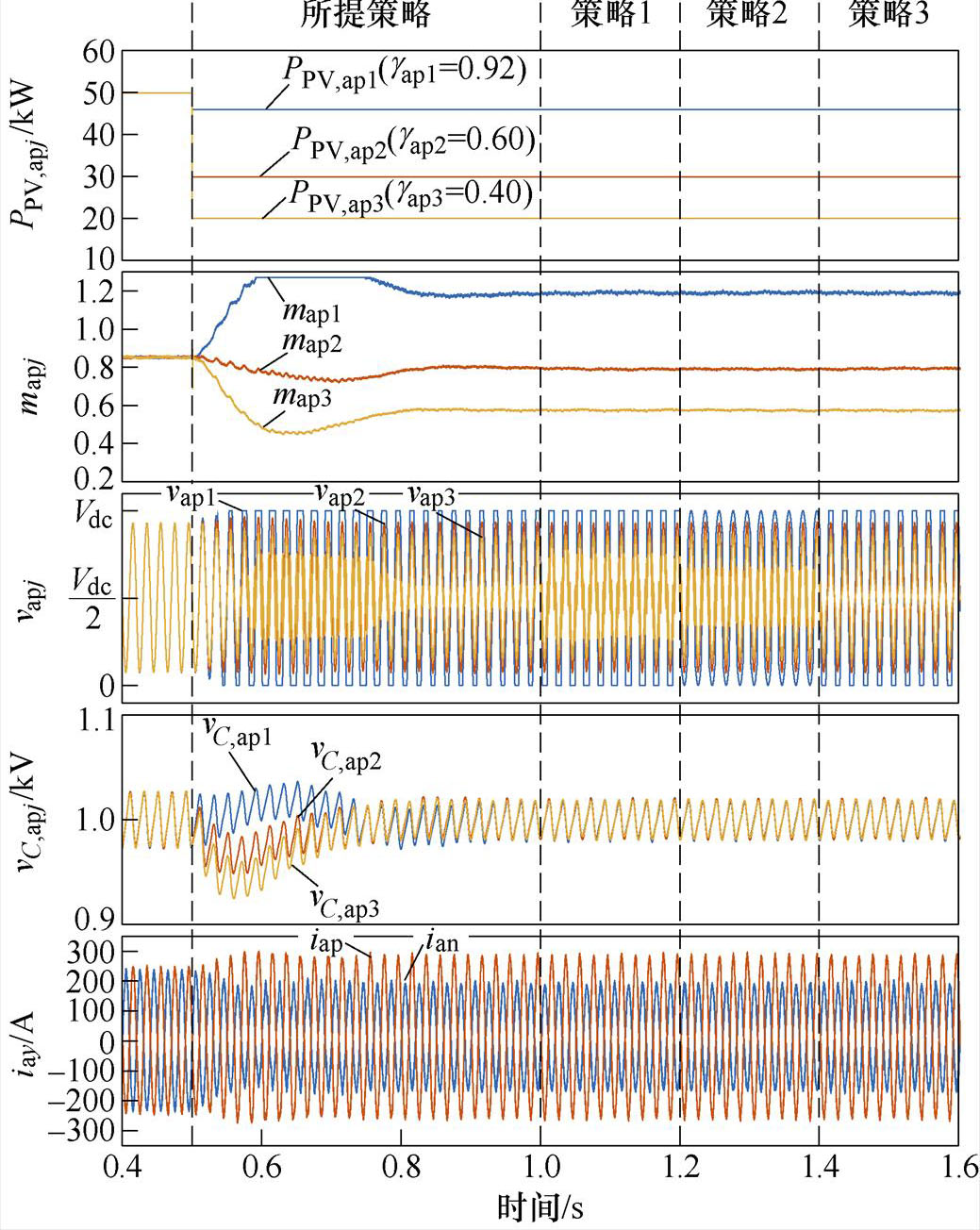
(a)不同策略动态切换波形
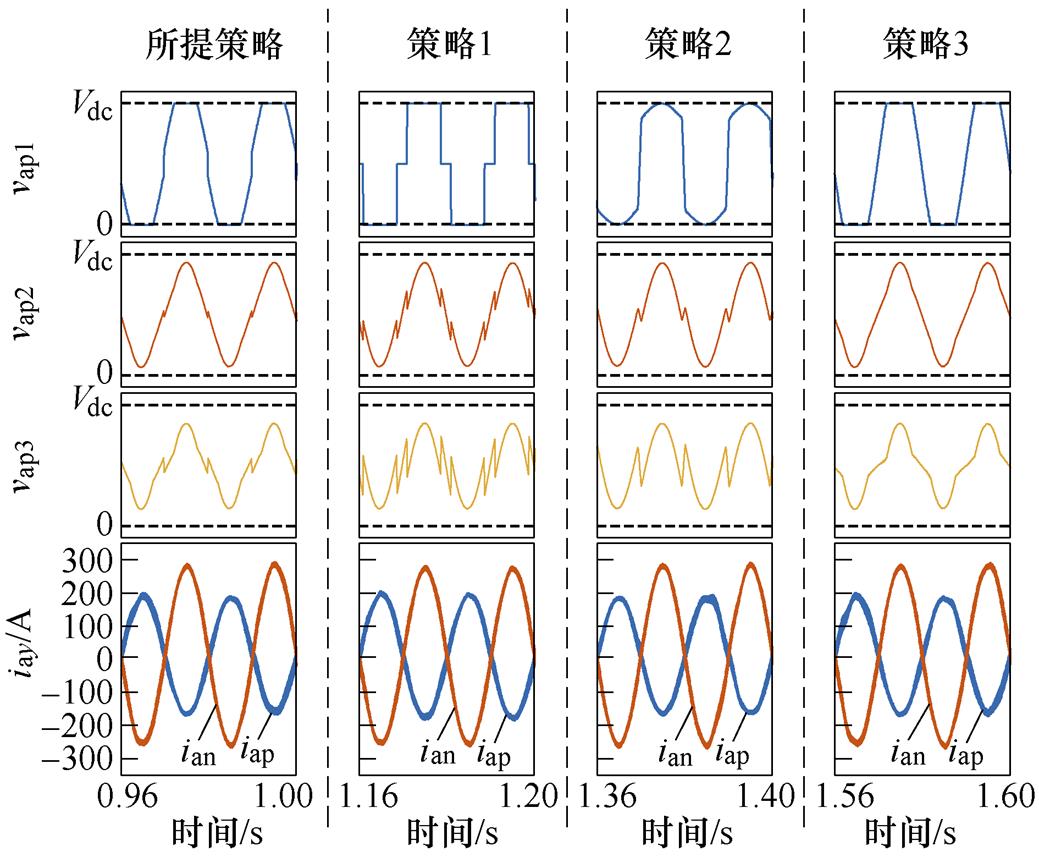
(b)不同策略稳态放大波形
图12 工况2仿真波形
Fig.12 Simulation waveforms of Case 2
工况4中,a相上桥臂四个SM中PV功率因子分别为1, 0.9, 0.74, 0,其余桥臂PV功率因子为1。基于所调策略和现有的三种策略,该工况都能满足式(22),说明工况4位于四种策略的稳定运行空间内。在该工况,SM等效基频交流调制比mapj为1.23、1.12、0.94和0.13。工况4在四种策略下都能稳定运行,没有出现NRSM调制波过调制,说明所提策略和现有的HCM策略能够用于SM数目为偶数的工况。
(a)不同策略动态切换波形
(b)不同策略稳态放大波形
图13 工况3仿真波形
Fig.13 Simulation waveforms of Case 3
根据上述仿真结果,HCM策略能够提升MMC- PVS在PV功率不平衡情况下的稳定运行范围。而相比于策略1和策略2,所提策略和策略3由于产生的谐波电压幅值较小,具有更大的稳定运行范围,验证了图8的分析结果。另外,无论MMC-PVS的桥臂SM数目为奇数还是偶数,HCM策略都能用于提升PV功率不平衡工况下的稳定运行范围。
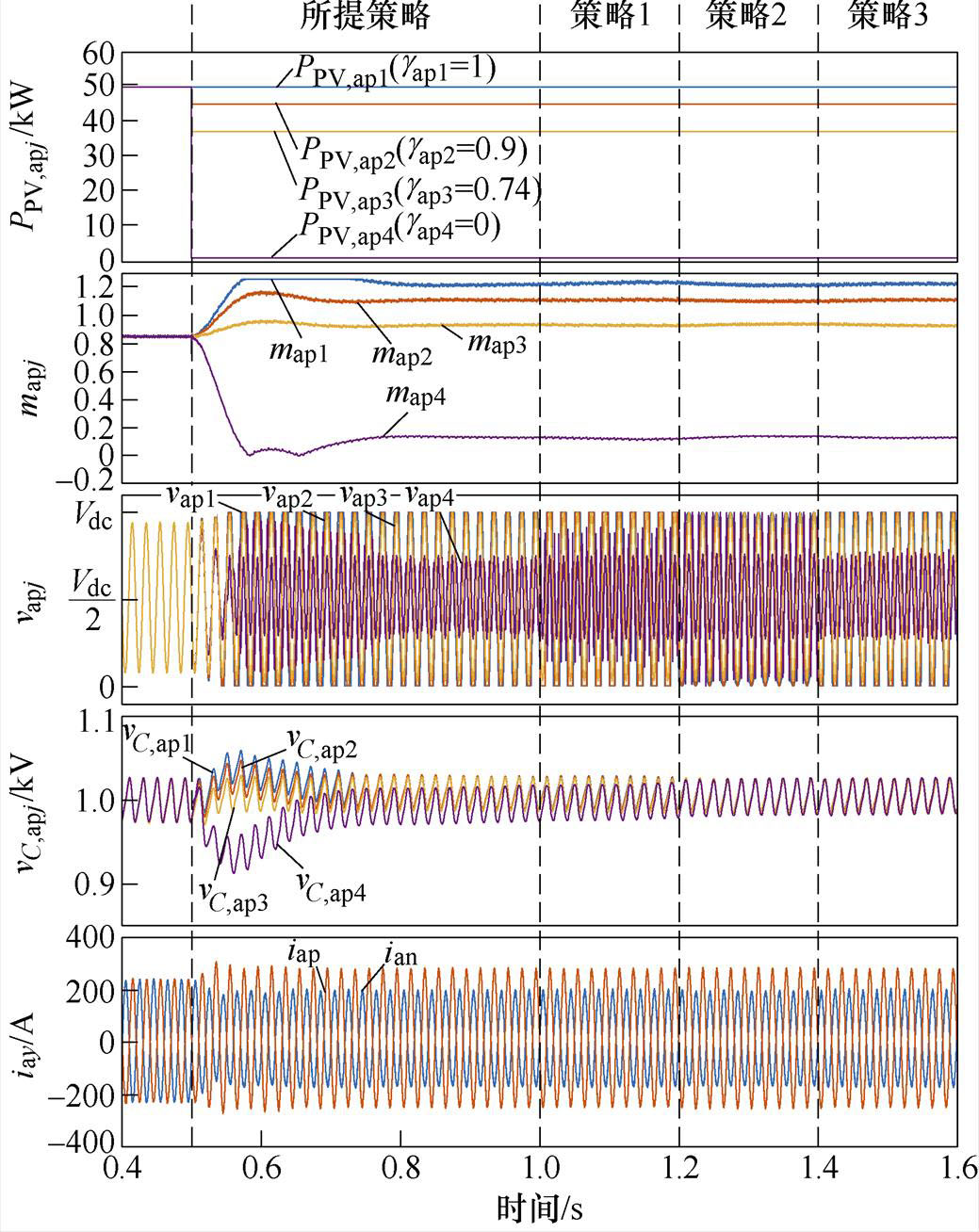
(a)不同策略动态切换波形
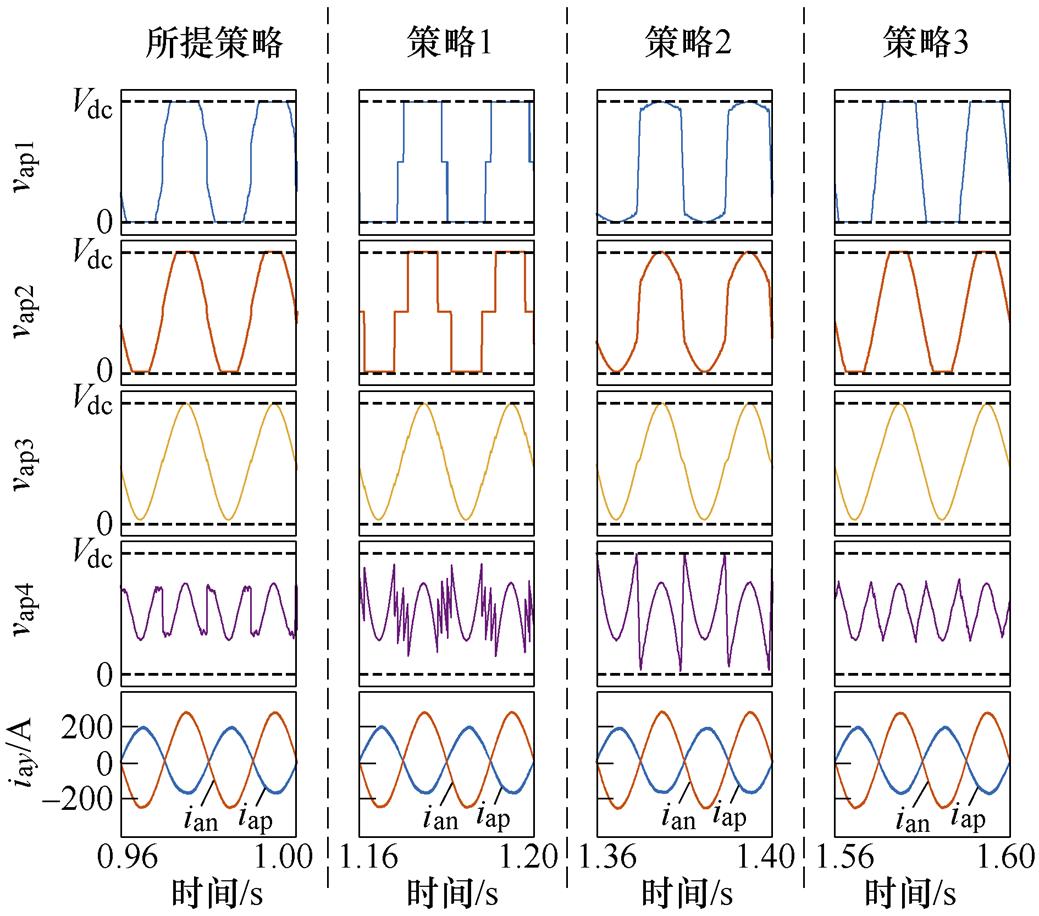
(b)不同策略稳态放大波形
图14 工况4仿真波形
Fig.14 Simulation waveforms of Case 4
为了验证HCM策略在MMC中的可行性,本文搭建了三相MMC实验样机,实验参数和实验样机见表3和如图15所示。本实验中,实验样机采用dSPACE MicroLabBox作为MMC控制器,实验平台的控制信息可以通过上位机实时修改与观测。MMC的a相上桥臂第1个SM通过DC-DC变换器与模拟光伏的直流电源相连,并通过CAN总线与dSAPCE MicroLabBox控制器通信,其余SM直流侧无DC-DC变换器相连,功率为零。MMC直流侧连接直流电源作为MMC的直流母线,交流侧连接三相电阻负载。
表3 实验平台参数
Tab.3 Experimental parameters of prototype
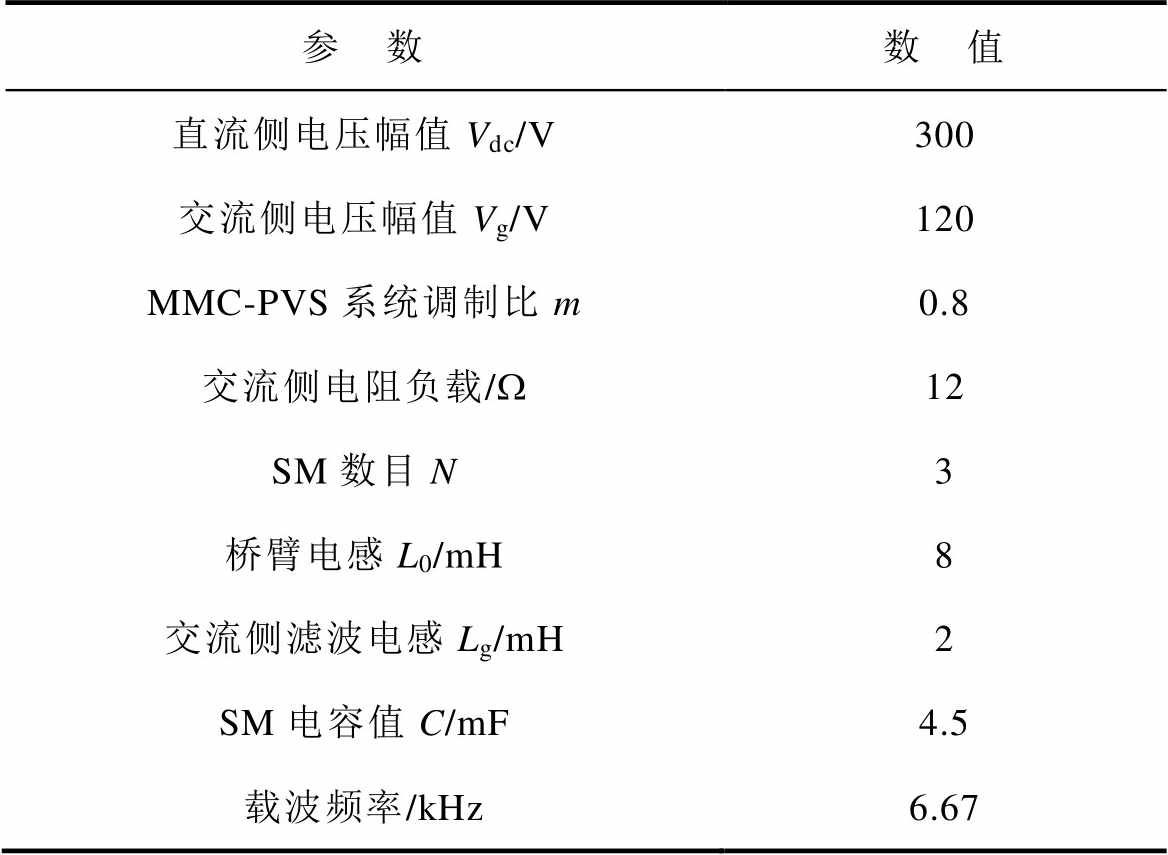
参 数数 值 直流侧电压幅值Vdc/V300 交流侧电压幅值Vg/V120 MMC-PVS系统调制比m0.8 交流侧电阻负载/W12 SM数目N3 桥臂电感L0/mH8 交流侧滤波电感Lg/mH2 SM电容值C/mF4.5 载波频率/kHz6.67

图15 三相MMC实验平台
Fig.15 Experimental prototype of three-phase MMC
图16为SMay1直流侧功率动态切换过程的实验波形。起始阶段,SMap1的直流侧功率Pap1=15 W,所有SM等效基频交流调制比都在1内,分别为map1=0.88、map2=0.78和map3=0.78。MMC工作于正弦波调制策略,SM电容电压保持平衡控制。随后,SMap1的直流侧功率由15 W提升至70 W,SMap1、SMap2、SMap3等效基频交流调制比分别为map1=1.22、map2=0.61和map3=0.60。SMap1的等效基频交流调制比超出1,出现过调制。基于图10的控制策略和图16a的实验波形,MMC由正弦波调制策略平滑的切换至所提策略,并仍旧保持SM电容电压平衡控制和交流侧电流的稳定。
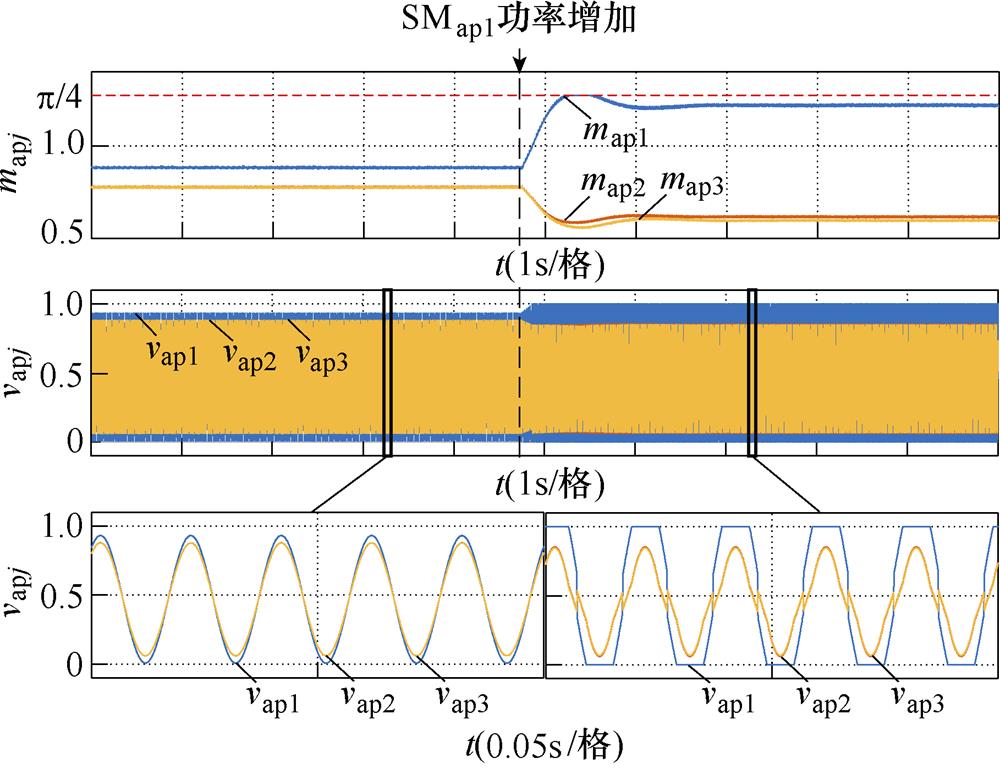
(a)mxyj和调制信号波形
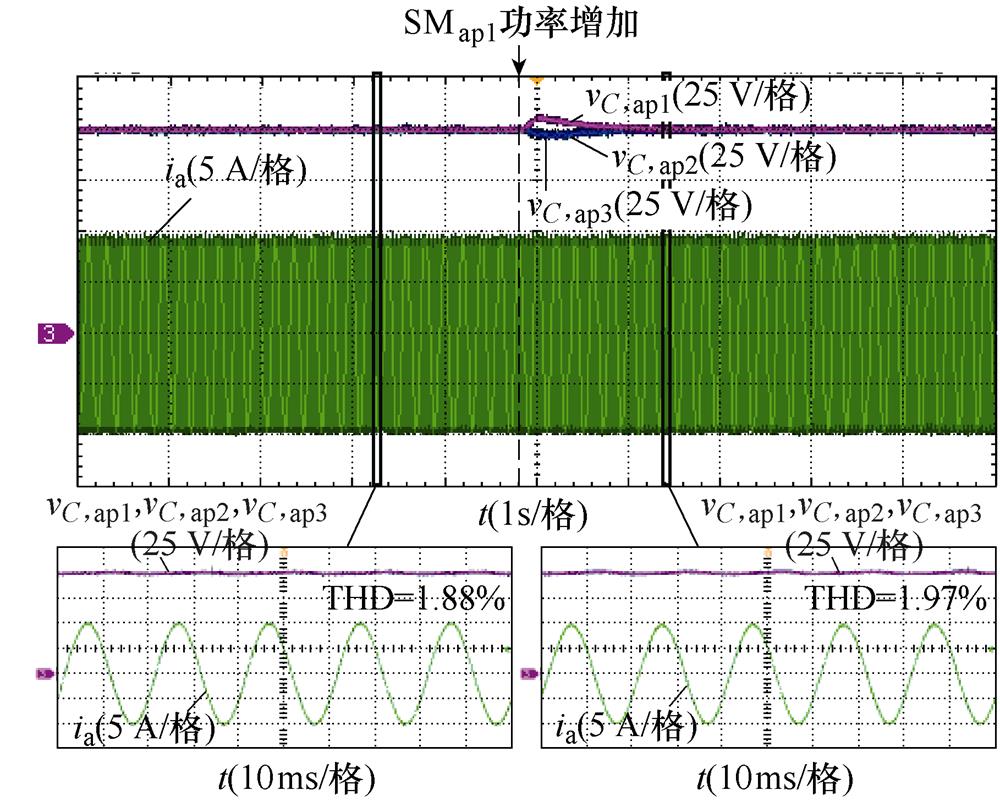
(b)子模块电容电压和交流侧电流波形
图16 所提策略动态切换波形
Fig.16 Transient waveforms of proposed strategy
SMap1直流侧功率提升至70 W后,SMap1、SMap2、SMap3等效基频交流调制比分别为map1=1.22、map2=0.61和map3=0.60。图17a和图17b分别给出了四种HCM策略稳态运行时a相上桥臂SM调制波波形、SM电容电压波形和a相交流侧电流的稳态实验波形。图17a所示HCM策略的调制波波形与理论分析和仿真结果的波形一致,图17b中四种HCM策略均能实现给定工况下MMC电容电压和交流侧电流的稳定运行。
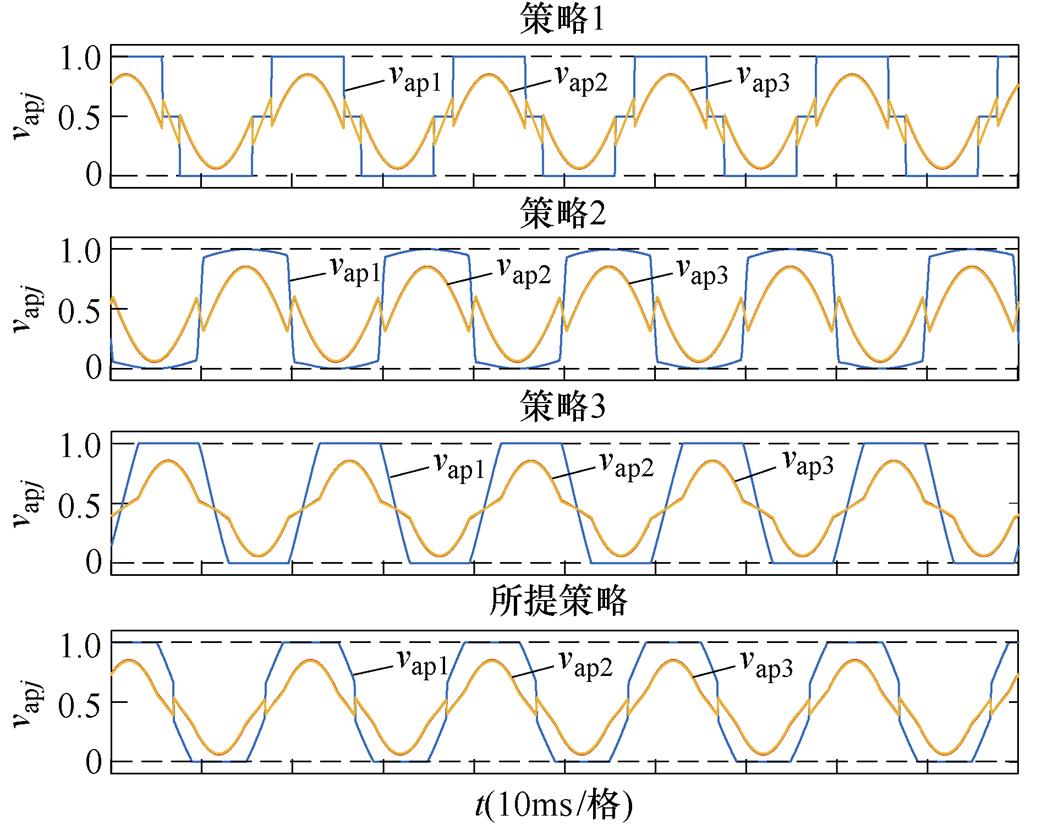
(a)稳态时SM调制波放大波形
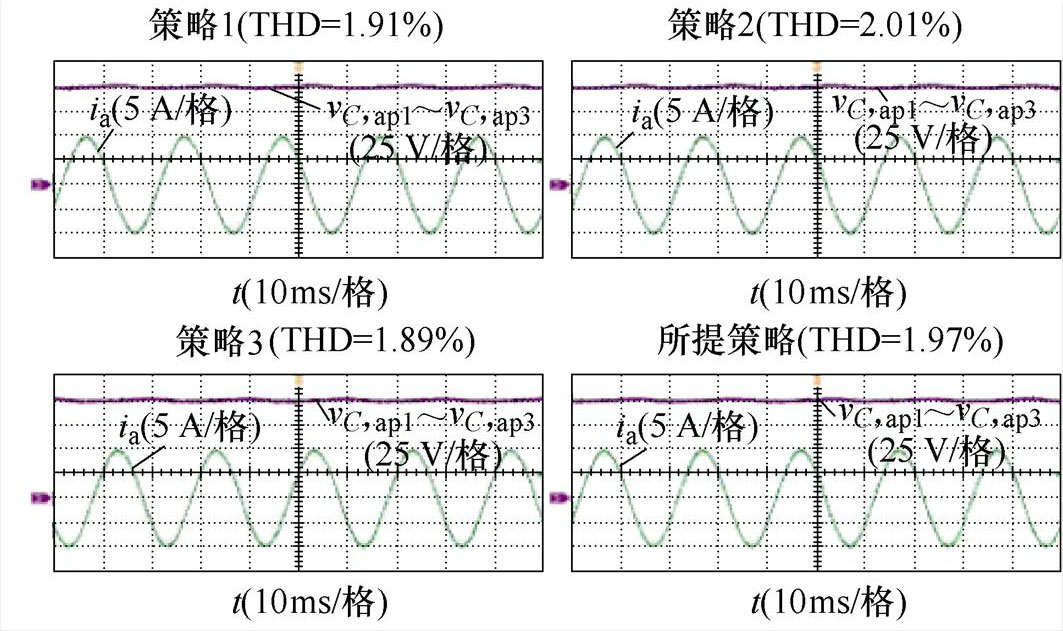
(b)稳态时SM电容电压和a相交流侧电流波形
图17 四种HCM策略稳态实验波形
Fig.17 Steady experimental waveforms of four HCM strategies
SMap1直流侧功率提升至84 W后,功率不平衡程度恶化,SMap1、SMap2、SMap3的等效基频交流调制比差异进一步扩大,使SMap1的调制比达到了极限状态。SMap1、SMap2、SMap3的等效基频交流调制比分别为map1=1.273、map2=0.695和map3=0.68。图18a和图18b分别给出了四种HCM策略稳态运行时a相上桥臂SM调制波波形、SM电容电压波形和a相交流侧电流的稳态实验波形。如图18a所示,由于map1达到了1.273,不同HCM策略中的SMap1的波形都接近于方波。图18b中四种HCM策略实现了给定工况下MMC电容电压和交流侧电流的稳定。
图16b中,采用正弦波调制策略时,交流侧电流ia的总谐波畸变率(Total Harmonic Distortion, THD)为1.88%,当切换为HCM策略后,图17b和图18b给出了不同工况下策略1、策略2、策略3和所提策略的THD分别为1.91%、2.01%、1.89%、1.97%和1.85%、1.95%、1.86%、1.89%,说明HCM策略不会明显增加MMC交流侧的谐波含量,降低电能质量。同时,上述实验结果验证了在MMC的SM直流侧功率不平衡工况下HCM策略的可行性。
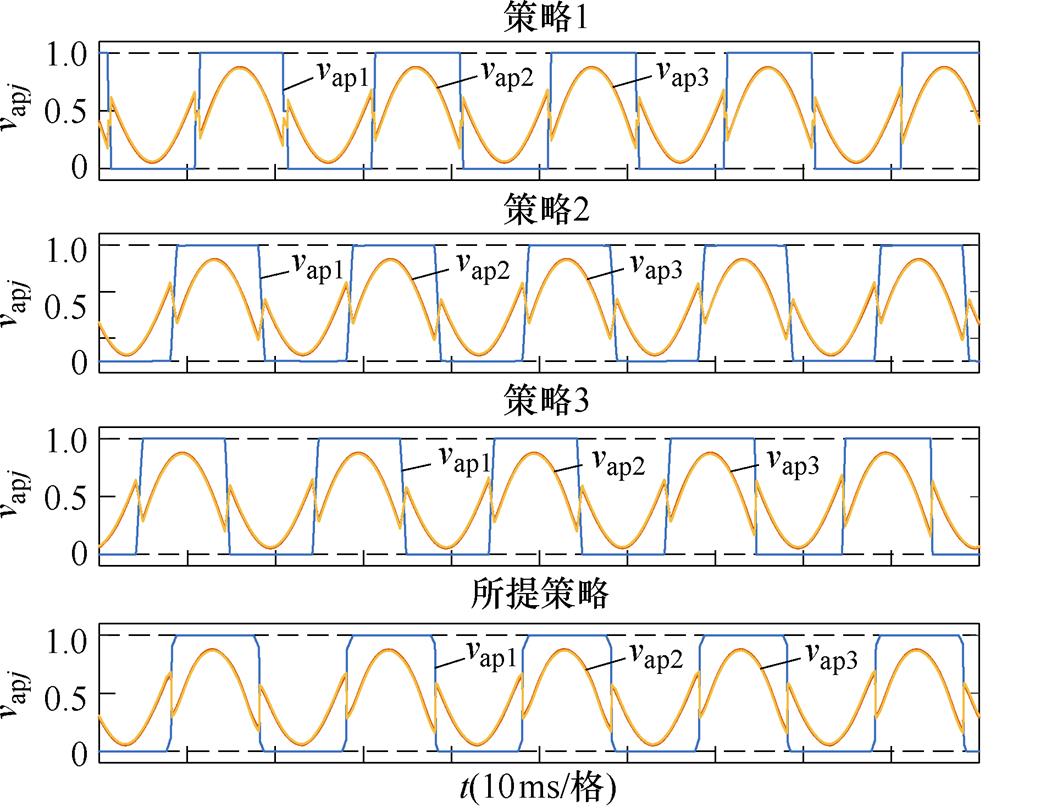
(a)稳态时SM调制波放大波形
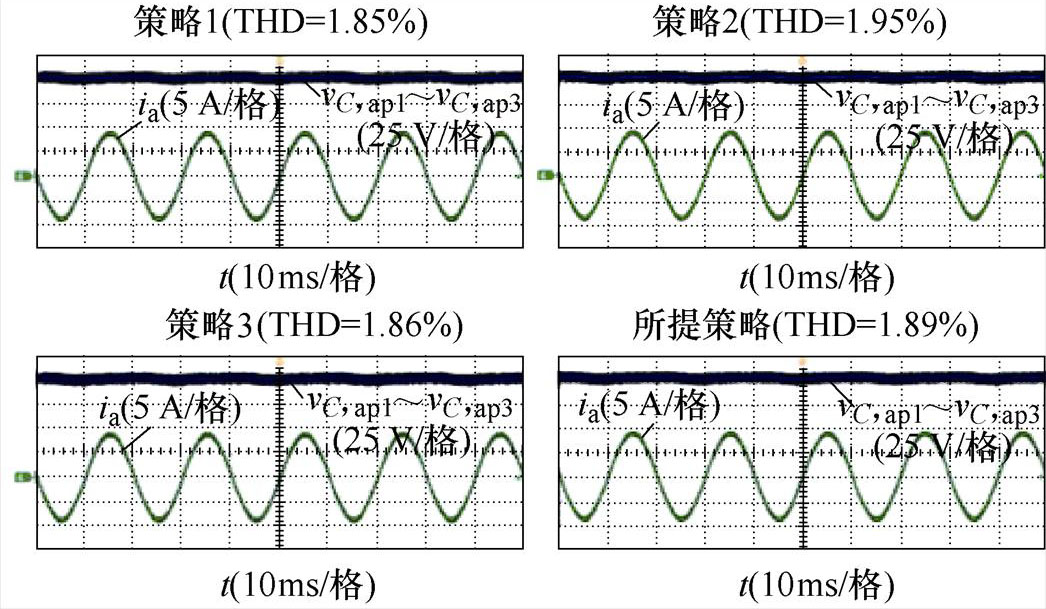
(b)稳态时SM电容电压和a相交流侧电流波形
图18 map1=1.273时四种HCM策略稳态实验波形
Fig.18 Steady experimental waveforms of four HCM strategies when map1=1.273
相比于现有的HCM策略,本文提出的HCM策略具有注入过调制SM的谐波幅值小的特点,也具备提升SM等效基频交流调制比至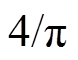 的能力。当PV功率严重不平衡时,所提HCM策略在保证高功率PV的SM不过调制的同时,也能避免正常SM过调制,保证系统的稳定运行。本文推导了HCM策略在MMC-PVS中的运行约束条件,并将其作为系统稳定运行的判定条件。结合SOS和SOF,定性和定量地评估了HCM策略的稳定运行范围,为所提HCM策略能在PV功率严重不平衡工况下正常运行提供了理论依据。最后,通过仿真与实验验证了所提HCM策略的可行性与理论分析的正确性。
的能力。当PV功率严重不平衡时,所提HCM策略在保证高功率PV的SM不过调制的同时,也能避免正常SM过调制,保证系统的稳定运行。本文推导了HCM策略在MMC-PVS中的运行约束条件,并将其作为系统稳定运行的判定条件。结合SOS和SOF,定性和定量地评估了HCM策略的稳定运行范围,为所提HCM策略能在PV功率严重不平衡工况下正常运行提供了理论依据。最后,通过仿真与实验验证了所提HCM策略的可行性与理论分析的正确性。
参考文献
[1] 王灿, 张羽, 田福银, 等. 基于双向主从博弈的储能电站与综合能源系统经济运行策略[J]. 电工技术学报, 2023, 38(13): 3436-3446, 3472.
Wang Can, Zhang Yu, Tian Fuyin, et al. Economic operation of energy storage power stations and integrated energy systems based on bidirectional master-slave game[J]. Transactions of China Elec- trotechnical Society, 2023, 38(13): 3436-3446, 3472.
[2] 张兴, 吴孟泽, 王明达, 等. 单相光伏级联多电平逆变器漏电流抑制与功率均衡控制综述[J]. 电力系统自动化, 2023, 47(9): 202-215.
Zhang Xing, Wu Mengze, Wang Mingda, et al. Review on leakage current suppression and power balance control of single-phase photovoltaic cascaded multilevel inverter[J]. Automation of Electric Power Systems, 2023, 47(9): 202-215.
[3] 武鸿, 王跃, 刘熠, 等. 基于广义电容电压不平衡度的MMC子模块开路故障诊断策略[J]. 电工技术学报, 2023, 38(14): 3909-3922.
Wu Hong, Wang Yue, Liu Yi, et al. Open circuit fault diagnosis strategy of MMC sub-module based on generalized capacitor voltage unbalance[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(14): 3909-3922.
[4] 滕甲训, 赵巍, 潘禹卓, 等. 基于开关电容结构的MMC子模块波动功率耦合方案及其参数约束[J]. 中国电机工程学报, 2021, 41(21): 7449-7464.
Teng Jiaxun, Zhao Wei, Pan Yuzhuo, et al. A fluctuating power coupling method for submodules of MMC based on switched-capacitors and its para- meters constraint[J]. Proceedings of the CSEE, 2021, 41(21): 7449-7464.
[5] 滕甲训, 潘禹卓, 卜泽敏, 等. 基于谐振式推挽结构的三端口MMC-SST波动功率耦合方案研究[J]. 中国电机工程学报, 2022, 42(6): 2308-2321.
Teng Jiaxun, Pan Yuzhuo, Bu Zemin, et al. Research on fluctuating power coupling scheme of three-port MMC-SST based on resonant push-pull structure[J]. Proceedings of the CSEE, 2022, 42(6): 2308- 2321.
[6] Teng Jiaxun, Sun Xiaofeng, Liu Xinlei, et al. Power mismatches elimination strategy for MMC-based photovoltaic system and lightweight design[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 11614-11629.
[7] Barcellona S, Barresi M, Piegari L. MMC-based PV three-phase system with distributed MPPT[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 1567-1578.
[8] 周亮, 武美娜, 胡安. 局部遮挡下光伏阵列的快速建模及极值点分布特征研究[J]. 电工技术学报, 2021, 36(增刊2): 572-581.
Zhou Liang, Wu Meina, Hu An. Fast modeling and analysis of power peaks characteristics of PV arrays under partial shading conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 572- 581.
[9] 李桐, 韩学山. 时变追踪并网光伏电站最大输出功率的无功优化方法[J]. 电工技术学报, 2023, 38(11): 2921-2931.
Li Tong, Han Xueshan. Reactive power optimization for time-varying tracking of maximum output power of grid-connected photovoltaic power station[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2921-2931.
[10] 赵斌, 谭恒, 何锁盈, 等. 高原高寒地区光伏组件背板冷却对输出功率影响的实验研究[J]. 太阳能学报, 2022, 43(8): 122-129.
Zhao Bin, Tan Heng, He Suoying, et al. Experimental study on influence of backplane cooling on power output of photovoltaic modules in frigid plateau region[J]. Acta Energiae Solaris Sinica, 2022, 43(8): 122-129.
[11] Bayat H, Yazdani A. A power mismatch elimination strategy for an MMC-based photovoltaic system[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 1519-1528.
[12] Debnath S, Marthi P R V, Xia Qianxue, et al. Renewable integration in hybrid AC/DC systems using a multi-port autonomous reconfigurable solar power plant (MARS)[J]. IEEE Transactions on Power Systems, 2021, 36(1): 603-612.
[13] 赵涛, 张兴, 毛旺, 等. 基于无功补偿的级联H桥光伏逆变器功率不平衡控制策略[J]. 中国电机工程学报, 2017, 37(17): 5076-5085, 5227.
Zhao Tao, Zhang Xing, Mao Wang, et al. Control strategy for cascaded H-bridge photovoltaic inverter under unbalanced power conditions based on reactive compensation[J]. Proceedings of the CSEE, 2017, 37(17): 5076-5085, 5227.
[14] 刘红锐, 李海瑞, 韦向阳, 等. 一种模块化的高性能蓄电池均衡器研究[J]. 电工技术学报, 2023, 38(17): 4574-4585.
Liu Hongrui, Li Hairui, Wei Xiangyang, et al. Research on a modular high performance battery equalizer[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4574-4585.
[15] Soong T, Lehn P W. Assessment of fault tolerance in modular multilevel converters with integrated energy storage[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4085-4095.
[16] Mao Meiqin, Ding Yong, Chang Liuchen, et al. Multi-objective power management for EV fleet with MMC-based integration into smart grid[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1428- 1439.
[17] Cupertino A F, Farias J V M, Pereira H A, et al. Comparison of DSCC and SDBC modular multilevel converters for STATCOM application during negative sequence compensation[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 2302-2312.
[18] Yasuda T, Miyashita M, Kumagai T, et al. Input current balancing control method under imbalanced load for three-phase multi-port converter based on modular multilevel converter[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 2021: 1278-1284.
[19] Yasuda Takumi, Itoh Jun-ichi, Guidi Giuseppe, et al. Power distribution control between cells with imbalanced load for modular multilevel multiport converter[C]//2021 IEEE 12th Energy Conversion Congress & Exposition-Asia, Singapore, Singapore, 2021: 775-780.
[20] Wang Zhe, Lin Hua, Ma Yajun. Improved capacitor voltage balancing control for multimode operation of modular multilevel converter with integrated battery energy storage system[J]. IET Power Electronics, 2019, 12(11): 2751-2760.
[21] Hu Yuhua, Zhang Xing, Mao Wang, et al. An optimized third harmonic injection method for reducing DC-link voltage fluctuation and alleviating power imbalance of three-phase cascaded H-bridge photovoltaic inverter[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 2488-2498.
[22] Zhao Tao, Zhang Xing, Mao Wang, et al. An optimized third harmonic compensation strategy for single-phase cascaded H-bridge photovoltaic inver- ter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8635-8645.
[23] Wang Mingda, Zhang Xing, Zhao Tao, et al. Harmonic compensation strategy for single-phase cascaded H-bridge PV inverter under unbalanced power conditions[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10474-10484.
[24] Li Jinyu, Chen Jie, Gong Chunying. An optimized reactive power compensation strategy to extend the working range of CHB multilevel grid-tied inver- ters[J]. IEEE Transactions on Power Electronics, 2023, 38(4): 5500-5512.
[25] Zhao Tao, Zhang Xing, Mao Wang, et al. Harmonic compensation strategy for extending the operating range of cascaded H-bridge PV inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1341-1350.
[26] Moosavi M, Farivar G, Iman-Eini H, et al. A voltage balancing strategy with extended operating region for cascaded H-bridge converters[J]. IEEE Transactions on Power Electronics, 2014, 29(9): 5044-5053.
[27] Miranbeigi M, Iman-Eini H. Hybrid modulation technique for grid-connected cascaded photovoltaic systems[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(12): 7843-7853.
[28] Wang Cheng, Zhang Kai, Xiong Jian, et al. A coordinated compensation strategy for module mismatch of CHB-PV systems based on improved LS-PWM and reactive power injection[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2825-2836.
[29] Li Shaohua, Wang Xiuli, Yao Zhiqing, et al. Cir- culating current suppressing strategy for MMC- HVDC based on nonideal proportional resonant controllers under unbalanced grid conditions[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 387- 397.
[30] Yang Siwei, Zhang Xing, Mao Wang, et al. Quanti- tative comparison and analysis of different power routing methods for single-phase cascaded H-bridge photovoltaic grid-connected inverter[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(4): 4134- 4152.
[31] Yu Yifan, Konstantinou G, Townsend C D, et al. Comparison of zero-sequence injection methods in cascaded H-bridge multilevel converters for large- scale photovoltaic integration[J]. IET Renewable Power Generation, 2017, 11(5): 603-613.
A Harmonic Compensation Modulation Strategy for Extending Steady Operation Range of Modular Multilevel Converter-Based Photovoltaic System
Abstract Harmonic compensation modulation (HCM) strategies are commonly used solutions for photovoltaic (PV) power imbalance conditions of a modular multilevel converter-based photovoltaic system (MMC-PVS). The maximum equivalent fundamental-frequency modulation index is extended to 1.273, and the system’s stable operation range is expanded. According to the principle of HCM strategy, harmonics are injected into submodules (SMs) with high-power PVs to prevent over-modulation, and the rest of SMs corresponding to low-power PVs (referred as normal SMs) compensate for the same amount of opposite harmonics to avoid distortions on phase arm voltages and currents. However, existing HCM strategies may lead to over-modulation on normal SMs and distortions on phase arm voltages and currents when facing severe PV power imbalance. This paper proposes a novel HCM strategy to prevent the over-modulation on SMs and normal SMs simultaneously.
The principle of HCM strategy is introduced, and an HCM strategy for expanding the system’s stable operation range is proposed. Then, relationships between the injected harmonic amplitude and equivalent fundamental-frequency modulation index in over-modulation SM are analyzed. On this basis, operation constraints of HCM strategies in MMC-PVS are derived as the criteria of system stable operation. Combined with the concepts of stable operation space (SOS) and stable operation factor (SOF), stable operation ranges of different HCM strategies are evaluated qualitatively and quantitatively. The results show that the SOF of the proposed HCS strategy is improved by up to 71.57%, which is 4.61 times that of the traditional sinusoidal pulse width modulation (SPWM) strategy and significantly larger than those of most existing HCM strategies.
When PV power is slightly imbalanced, the proposed HCM strategy and existing HCM strategies achieve smooth transitions under various working conditions with negligible current distortion. Under severe PV power imbalance, the proposed HCM strategy maintains system stability, while other HCM strategies exhibit current distortions. The HCM strategies can normally operate when the number of SMs of each phase arm is 3 and 4, respectively.
Compared with the existing HCM strategies, the proposed HCM strategy extends the stable operation range of MMC-PVS, avoiding over-modulation on normal SMs and SMs with high power PVs simultaneously. The HCM strategies maintain the normal operation of MMC-PVS with odd or even numbers of SMs in each phase arm under PV power imbalance conditions. The proposed HCM strategy can also be applied in cascaded H-bridge converter-based PV systems with the capability of stable operation range extension.
keywords:Modular multilevel converter, power imbalance, harmonic compensation modulation (HCM) strategy, over-modulation, stable operation
中图分类号:TM615
DOI: 10.19595/j.cnki.1000-6753.tces.231254
河北省重点研发计划项目(19214405D)和河北省自然科学基金重点项目(E2021203162)资助。
收稿日期 2023-08-03
改稿日期 2023-09-19
潘 尧 男,1993年生,博士研究生,研究方向为多电平变换器控制。E-mail: 798968001@qq.com
孙孝峰 男,1970年生,教授,博士生导师,研究方向为变流器拓扑及波形控制技术、功率因数校正与有源滤波技术、新能源发电与组网技术。E-mail: sxf@ysu.edu.cn(通信作者)
(编辑 陈 诚)