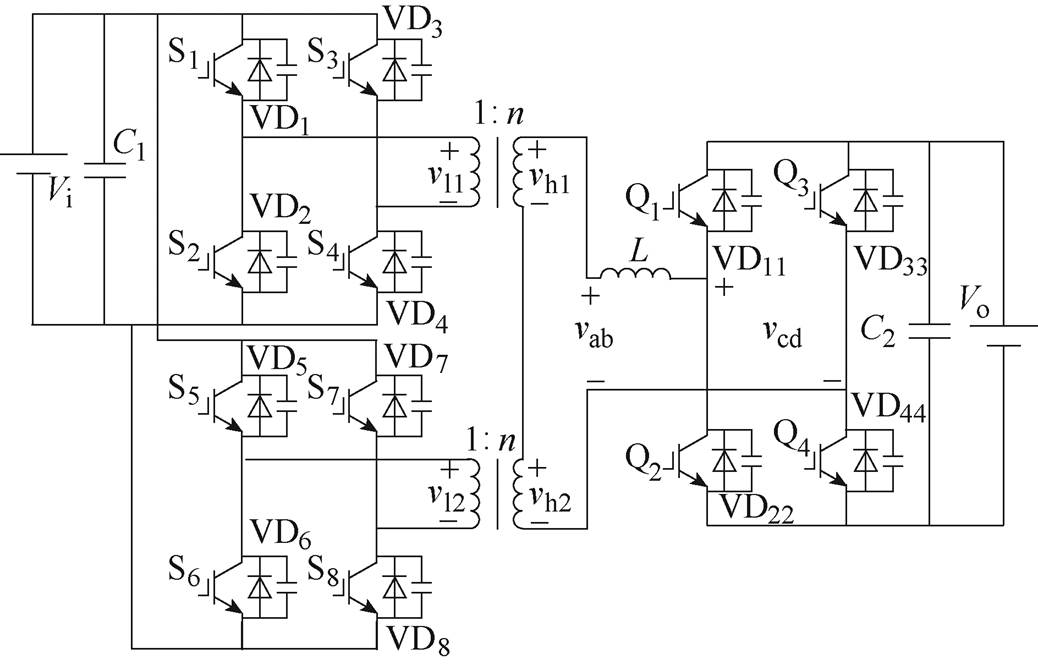
图1 LPHS DAB变换器主电路
Fig.1 Main circuit diagram of LPHS DAB converter
摘要 针对双有源全桥（DAB）直流变换器在功率突变时产生的电流偏置问题，该文提出一种新的瞬态直流偏置抑制策略。首先，以基于全移相调制的双有源全桥直流变换器为研究对象，分析DAB变换器产生直流偏置的原因及危害。然后，在全局电感电流应力最优结果的基础上，对功率在四个工作区域突变时产生的瞬态直流偏置问题进行详细分析，推导各种电流突变情况下的直流偏置表达式，并据此提出一种新的过渡态引入方法，对于不同的功率突变状态可以得到统一的过渡移相角表达式，简化了控制过程。接着，根据所得过渡态结果，提出统一的载波调制方法，并对调制策略的适用性进行分析。最后，通过实验平台验证了所提方法可以有效消除功率突变时产生的电流偏置。
关键词：双有源全桥（DAB）变换器 功率突变 瞬态直流偏置抑制 全移相控制 载波调制
随着全球新能源技术的快速发展，双向DC-DC变换器广泛应用在新能源发电、不间断电源、储能系统、航空航天电源系统以及电动车能量管理系统等电能变换领域中[1-2]，其中双有源全桥（Dual Active full Bridge, DAB）变换器具有能量双向传输、电气隔离、软开关、控制简单灵活等优点，引起了学者的广泛研究。
近年来，关于DAB变换器的移相控制策略及其相关拓展已被广泛研究，其中包括单移相（Single- Phase-Shift, SPS）控制[3-4]、扩展移相（Extended- Phase-Shift, EPS）控制[5-9]、双移相（Dual-Phase-Shift, DPS）控制[10-13]和三移相（Triple-Phase-Shift, TPS）控制[14-18]，文献[19]又在此基础上提出了基于矩阵变压器的全移相控制策略，上述方法可在一定程度上减小DAB变换器的电感电流应力和回流功率，从而提高系统的传输效率，但当传输功率突变或负载突变时，这些传统的移相策略都不可避免地导致电路电流产生直流偏置，使得电感电流应力增加，变压器发生偏磁现象。为了抑制功率突变造成的电流偏置，文献[20-21]在SPS控制的基础上分别引入不同的过渡态，当功率突变时以不同的方式改变开关信号的占空比，均能有效抑制电流偏置，但不适用于其他移相策略。文献[22]提出了一种暂态EPS控制策略，在功率突变后引入相应的过渡态，能够在半个开关周期内消除直流偏置，具有较快的动态响应，但所得结果不适用于TPS控制。针对TPS控制的DAB变换器，文献[23]从调制过程入手，通过错开一次侧和二次侧的比较值来减小暂态直流偏置电流，这种调制方案适用于所有移相控制方式，但是只有当电压传输比等于1时才能完全消除直流偏置，与引入过渡态相比动态响应时间较长。文献[24]对损耗不平衡和瞬态直流偏置问题进行了综合分析，相邻周期采用不同的移相占空比，且通过调节零电平时间来抑制直流偏置，由于相邻周期采用不同的移相策略，且抑制直流偏置时需要判断零电平时间是否满足要求，所以实现算法较为复杂。文献[25]将电感电流从三个移相角中解耦，分解出三段互相独立的等价电流分量，并分别处理各个移相角等效作用下的瞬态直流偏置，该分析方法可用于所有的移相状态，但所得结论涉及区域判断过多，过渡时三个移相角均需改变，控制实现复杂，且并未分析引入过渡态后对原来调制方式有效性的影响。文献[26]以混合三电平DAB变换器为研究对象，提出了一种基于TPS控制的开关序列重构的瞬态电流优化策略，该方法可以在功率突变时使电感电流快速达到稳态，但是该方法针对不同的突变状态采用不同的过渡移相角，增加了控制的复杂性，且没有分析功率反向突变的情况。文献[27-28]通过改进变压器设计、增加额外电路以及使用特殊的电流传感器进行辅助控制，来抑制电路中产生的直流偏置，但会增加电路的复杂性和实现成本。
本文对电流偏置控制策略进一步完善，以基于矩阵变压器的DAB变换器为研究对象进行深入分析，变压器采用低压侧并联、高压侧串联（Low- voltage side in Parallel and High-voltage side in Series, LPHS）的电路结构，该结构可以减小低压侧损耗，提高整机效率。然后在文献[19]的全移相（Full-Phase-Shift, FPS）全局电感电流最优控制算法的基础上，引入新的过渡态来解决由功率突变引起的直流偏置问题，在维持全局电感电流应力最小的同时，实现瞬态电流偏置的抑制。当功率在4个最优区域中突变时均可得到统一的过渡态移相角，相比于其他控制方法极大地简化了调制过程。文中首先对直流偏置的原因以及引入过渡态后的数学模型进行详细分析，并提出了相应的调制方法，实验表明，此方法能够有效去除直流偏置。
基于矩阵变压器的双有源全桥DC-DC变换器主电路如图1所示。矩阵变压器采用LPHS的结构，以此来平分低压侧的大电流和高压侧大电压，可以降低开关器件的耐流等级。此外采用两个变压器设计时，每个变压器的电压比为原来的一半，从而简化了变压器的设计。
图1 LPHS DAB变换器主电路
Fig.1 Main circuit diagram of LPHS DAB converter
图1中，vl1、vl2为两变压器一次电压，vh1、vh2为两变压器二次电压，vab为串联侧变压器电压之和，vcd为高压侧H桥产生的方波电压，n为两变压器电压比，Vi为低压侧输入电压，Vo为高压侧输出电压，并且令Vo=k2nVi，k为电压传输比，L为传输电感，C1为低压侧电容，C2为高压侧电容，S1～S8为低压侧开关管，Q1～Q4为高压侧开关管，VD1～VD8为低压侧续流二极管，VD11～VD44为高压侧续流二极管。
由于这种结构采用多个高频变压器一起工作，所以每个变压器的正常运行是保证电路稳定工作的关键，而造成高频变压器异常工作的主要原因就是偏磁问题。此外，电路的稳定运行还和电感电流应力有关，在一个开关周期内，如果电感L两端电压伏秒积不为零，就会使得电感电流发生直流偏置，造成电流应力增加，流过器件的瞬态电流增大，严重时还会损坏器件。变压器两端电压的伏秒积不平衡会导致励磁电流偏置，随着时间的累计，进一步使得变压器偏磁，严重时还会产生磁饱和现象，使得电路无法正常工作。所以，为了保证电路的正常工作，需要抑制电感电流和变压器励磁电流的偏置现象。
对于DAB变换器，造成电路电流产生直流偏置的原因有多种，可分为硬件和软件控制两种：
（1）硬件方面：①开关特性参数不一致，如开关速度、通态压降以及导通电阻的差异；②电路分布参数的不对称性，如驱动信号的延迟不同。这些原因会使得电感两端电压以及变压器两端电压正负幅值不一致或电压不对称，导致一个周期内电压伏秒积不为0，从而使得电流出现直流偏置现象。对于原因①，在设计电路时应选择同厂家、同批次的功率管，以使得开关差异尽可能小；对于原因②，在设计电路时，要保证主电路以及驱动电路的对称性，使得驱动信号到达开关管的时间接近同步。除此之外在设计变压器时要选择合适的磁心型号，对磁心体积留有一定的裕度，以保证高频变压器的稳定运行。
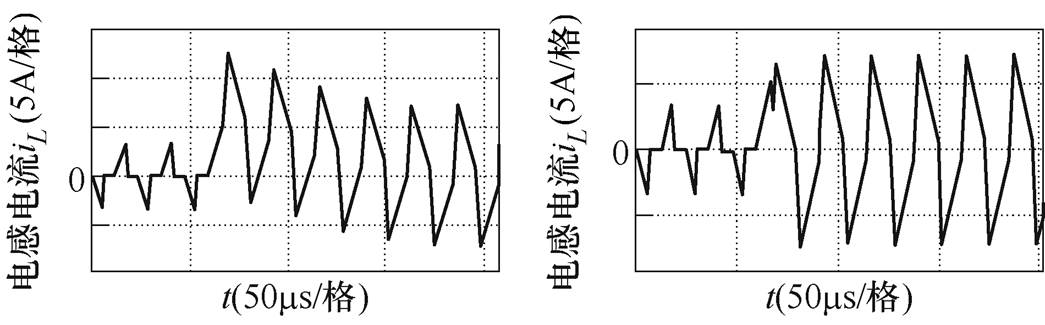
（2）软件控制方面：DAB变换器在正常运行时，如果输出功率突变并依然采用和突变之前相同的调制策略时，就会导致相邻半周期电压不对称，使电流产生瞬态直流偏置，需要经过多个调制周期才能恢复到平衡状态。功率每次突变都会导致电路电流发生不同程度的偏置，随着时间的累计必然会影响到电路的正常工作，降低功率输出效率，所以要通过改进调制策略避免这种电流偏置现象产生。功率突变时，有无直流偏置的电感电流波形对比如图2所示。
（a）有直流偏置 （b）无直流偏置
图2 有无直流偏置的电感电流波形对比
Fig.2 Comparison of inductive current waveforms with and without DC bias
图2为电感电流iL从3.4 A反向突变到7.4 A的电流波形，图2a为存在直流偏置的电感电流波形，由图中可以看出，由于功率突变时未引入合适的控制策略，电流产生了较大的偏置，最大电流约为12.6 A，远超于稳定后的7.4 A，此冲击电流可能造成设备的损坏；除此之外，造成的最大直流偏置约为5 A，过大的直流偏置易使变压器产生偏磁问题，影响设备正常运行。图2b为无直流偏置的电流波形，由于引入了适当的瞬态控制，所以在功率突变时电感电流不会偏置。由此可得，为了防止功率突变造成的上述不良影响，必须引入合适的瞬态控制策略，进而有效抑制电流突变带来的潜在危害。
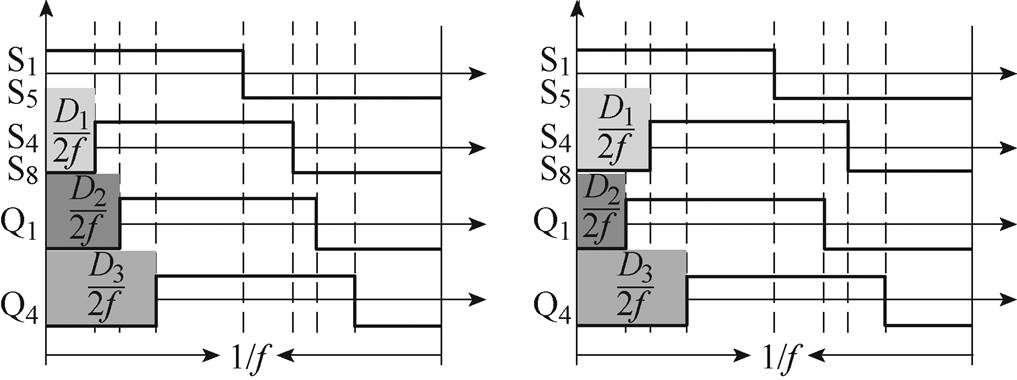
对于全移相控制的LPHS DAB变换器，经过优化控制后共存在三种移相角，分别为低压侧S1、S4之间以及S5、S8之间的移相角q1，低压侧S1和高压侧Q1之间的移相角q2，低压侧S1和高压侧Q4之间的移相角q3，同一桥臂的开关互补导通。取开关频率为f，则开关周期为1/f，再取三个移相角的半开关周期占空比分别为D1、D2、D3，则三个移相角对应的移相时间分别为D1/(2f)、D2/(2f)、D3/(2f)，各个开关对应的工作波形如图3所示。图中高电平表示开关管开通，低电平表示开关管关断，S1、S5同时发波，S4、S8同时发波，同一桥臂其余开关管与图中对应的开关管互补导通。
（a）移相状态1 （b）移相状态2
图3 各个开关对应的工作波形
Fig.3 Working waveforms corresponding to each switch
图3中三个占空比均可在0～1之间取值，其中状态1对应的占空比关系为0≤D1≤D2≤D3≤1，状态2对应的占空比关系为0≤D2≤D1≤D3≤1。除图中两种状态之外还存在多种不等关系，根据这些移相关系，文献[19]以电感电流应力最小为目标，对LPHS DAB变换器的所有移相状态进行综合分析，最后得出全移相下电感电流应力的全局最优解，见表1。
表1 电感电流应力全局最优解
Tab.1 Global optimal solution of inductor current stress
0＜k＜1k≥1
表1中结果共分为4个区域，当0＜k＜1时，标幺化后的传输功率P0以2(k-k2)为分界线；当0＜P0＜2(k-k2)时，设为区域1；当2(k-k2)≤P0≤1时，设为区域2。当1≤k时，P0以(-2+2k)/k2为分界线；当0＜P0＜(-2+2k)/k2时，设为区域3；当(-2+2k)/k2≤ P0≤1时，设为区域4。其中选取的功率标幺基准值为nViVo/(4fL)。每个区域对应的最优移相占空比和标幺化后的电感电流应力ILm均在表1中给出，其中电流的标幺基准值为nVi/(4fL)。由表1可见，不同区域对应不同的移相关系，当功率在不同区域之间突变时会产生更为明显的电流偏置现象，使得电感电流应力增加，进而会对电路产生较大的潜在影响，所以必须采取措施予以消除。
根据图3中状态1和状态2的移相关系并通过计算分析易得，表1中区域1和区域3为状态2的特例，区域2和区域4为状态1的特例。所以为了得到统一的结论，分别对状态1、状态2对应的功率突变情况进行分析，即可得到每个区域的直流偏置结果。下面以k≥1时为例，对两种状态对应的直流偏置问题进行分析。
取功率由低压侧向高压侧传输时为正常传输，对于移相状态1，当功率正向流动突增时的工作波形如图4所示。
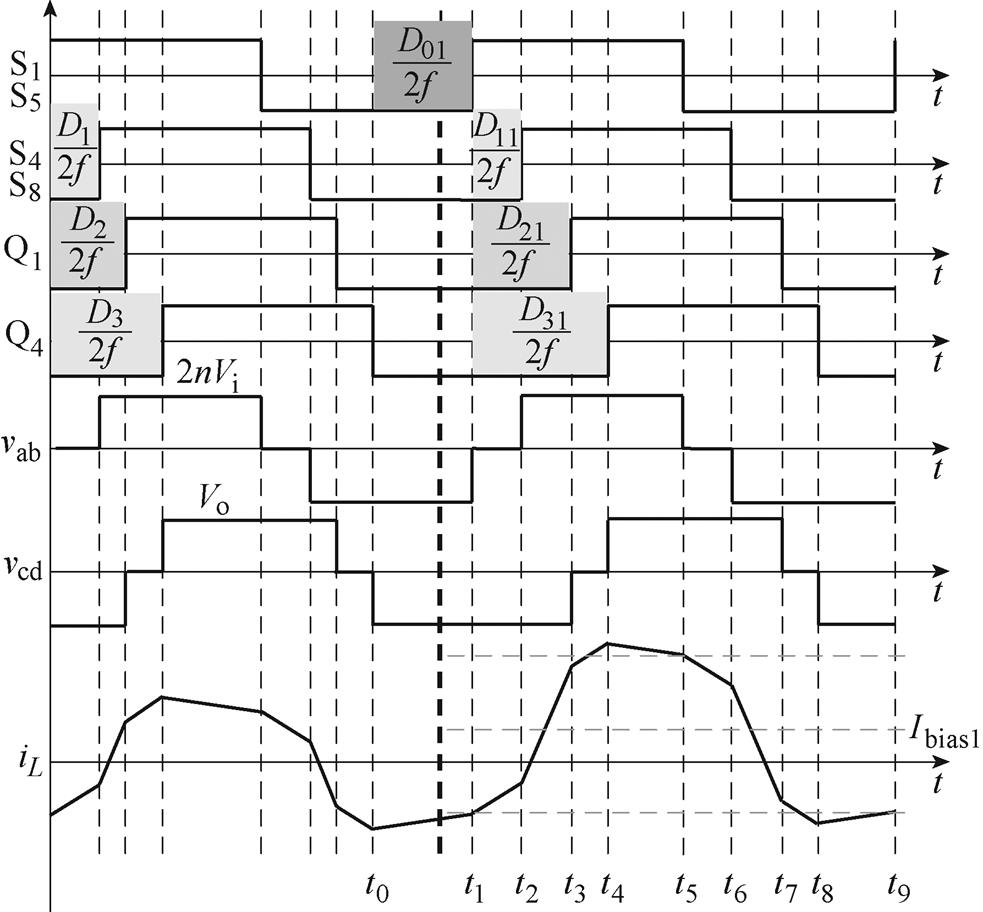
图4 状态1，功率正向流动突增时的工作波形
Fig.4 State 1, the working waveforms when the power is suddenly increased in the positive direction
图4中，vab、vcd均在图1中标出，两者的电压差为电感两端电压，iL为电感电流，t0～t9为电流波形在不同转折点处对应的时刻，粗虚线左侧为前一开关周期的工作波形，粗虚线右侧为因功率突变而改变移相大小之后的工作波形，定义功率突变后原来三个移相占空比由D1、D2、D3分别变为D11、D21、D31，D01为t0～t1时间间隔的半开关周期占空比，如图4中阴影部分所示，其中t0为粗虚线前一开关周期的iL最后转折时刻，t1为粗虚线后一开关周期的iL首次转折时刻。由图4可以看出，由于功率突变，移相角发生改变，使得粗虚线前半开关周期电压和后半开关周期电压不对称，导致功率突变后电压伏秒积不为0，进而使得变换器电流发生偏置，直流偏置电流大小如图中Ibias1所示，Ibias1为t1和t5时刻电流对应的平均值。
由图4可以计算出D01的表达式为
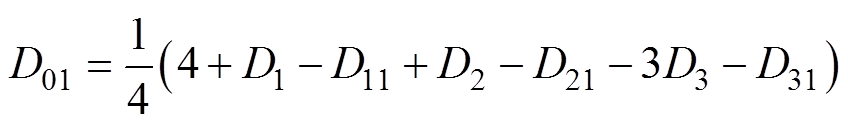（1）
且由文献[19]可得功率突变之前t0时刻的电感电流可表示为
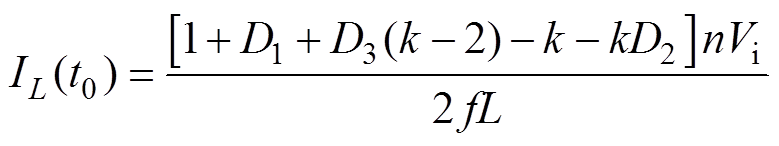（2）
由图2中各个时间段的vab和vcd的电压差可求得电感两端电压DVL，结合电感电流和电压的关系可知DIL=DVLDt/L，DIL为电感电流的变化量，Dt为图4中相邻时间变化量，那么功率突变后各个时刻的电感电流可表示为
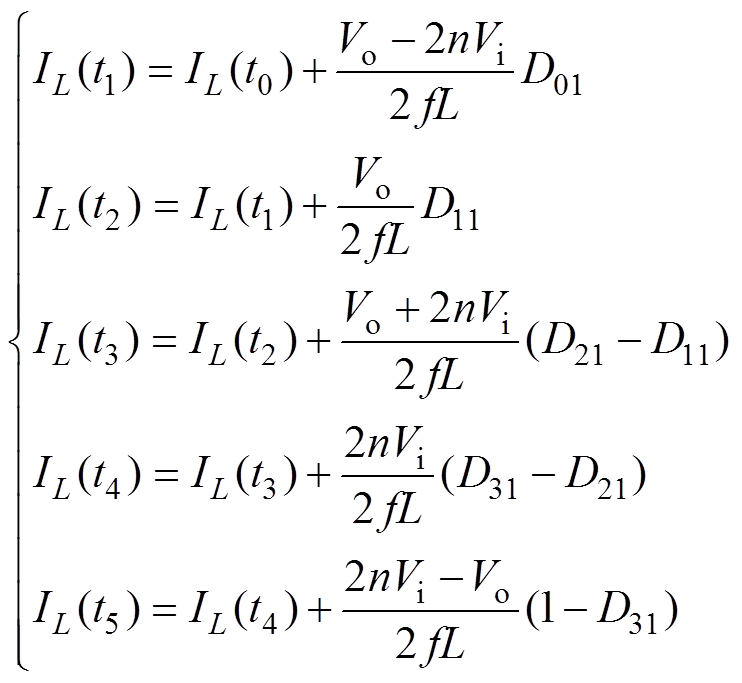（3）
由图4中细横虚线可以看出，功率突变后产生的直流偏置为
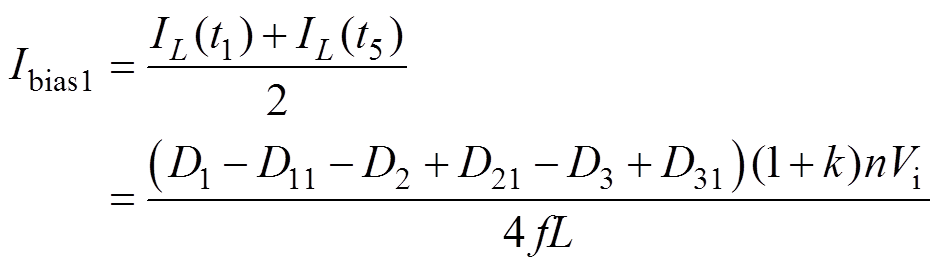（4）
式中，IL(t1)和IL(t5)分别为t1和t5时刻的电感电流。当功率由状态2同向突变到此状态时，经计算t0时刻的电感电流表达式不变，D01的表达式也不变，所以最后得到的偏置电流的表达式和式（4）相同。
当功率由负向流动突变为正向流动时，工作波形如图5所示。这种情况会造成更大程度的电压不对称，使得直流偏置更加明显，如图5中Ibias2所示。
无论负向流动的波形处于状态1还是状态2，t0时刻的电感电流表达式均为
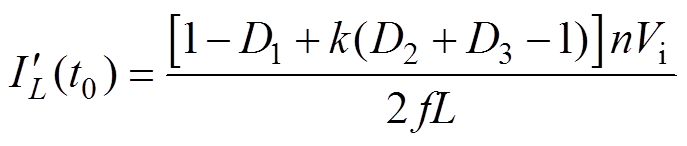（5）
t0～t1之间的半周期占空比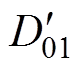
的表达式为
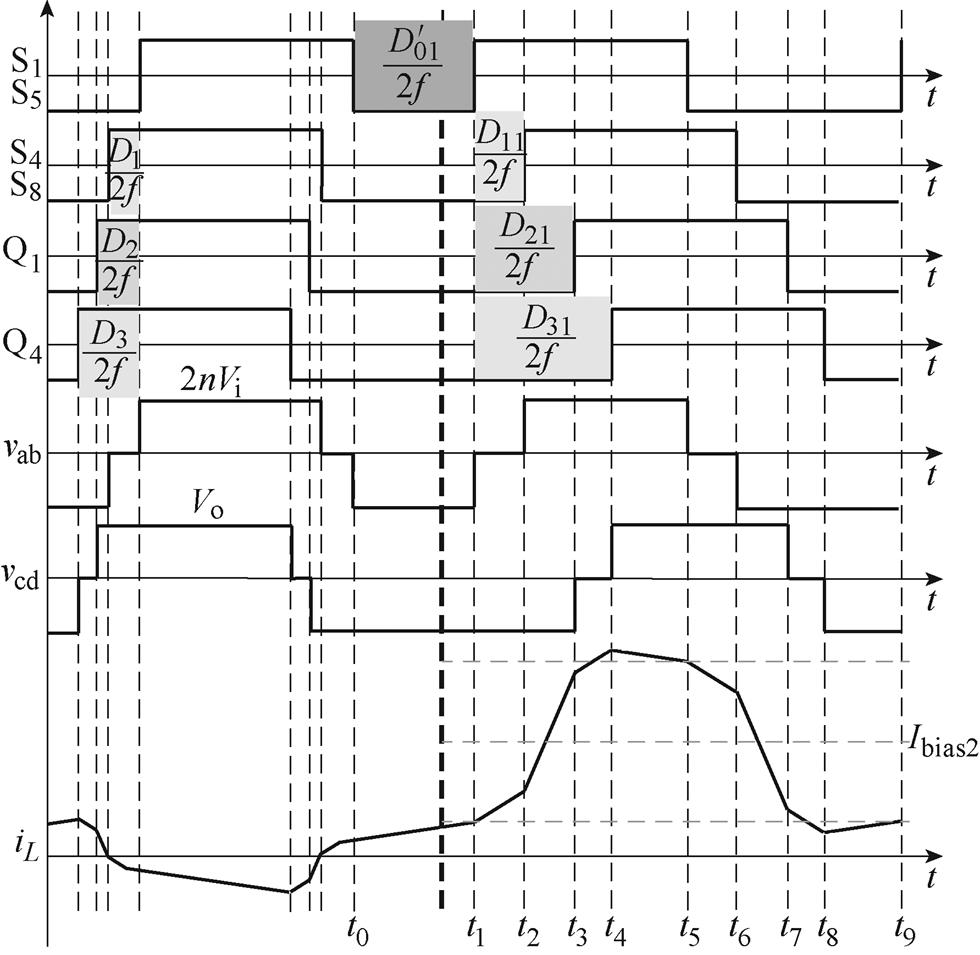
图5 状态1，功率由负向突变到正向时的工作波形
Fig.5 State 1, the working waveforms when the power suddenly changes from negative to positive
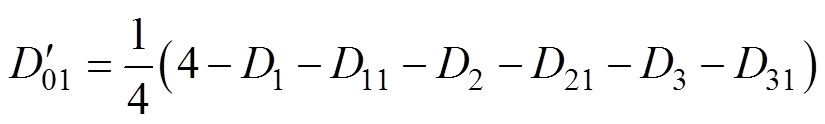（6）
将此时的
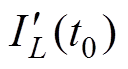和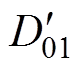重新代入方程组式（3），可得功率流动方向突变时产生的直流偏置为
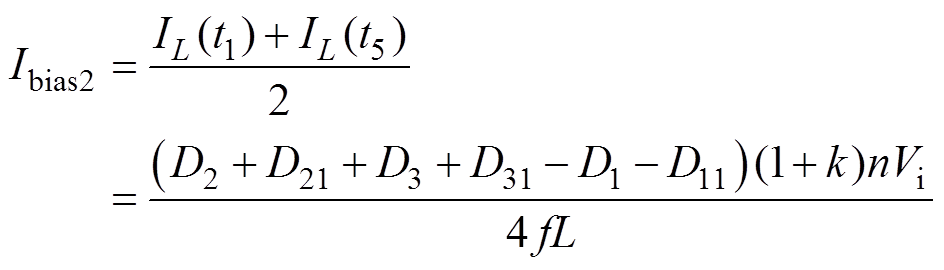（7）
对于移相状态2，功率流动方向和移相状态均不改变时，功率突然增加后的工作波形如图6所示。
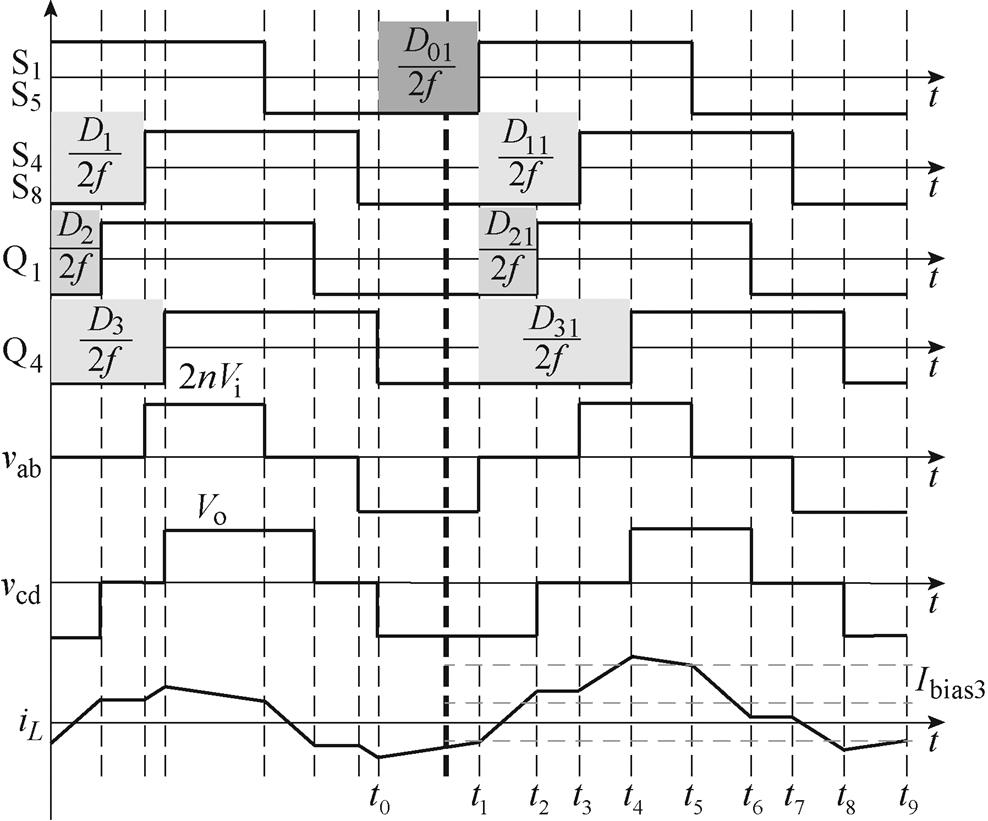
图6 状态2，功率正向突增时的工作波形
Fig.6 State 2, the working waveforms when the power is suddenly increased in the positive direction
经计算，此种情况下，D01的表达式与式（1）相同，t0时刻电流的表达式和式（2）相同，那么功率突变后各个时刻的电感电流可表示为
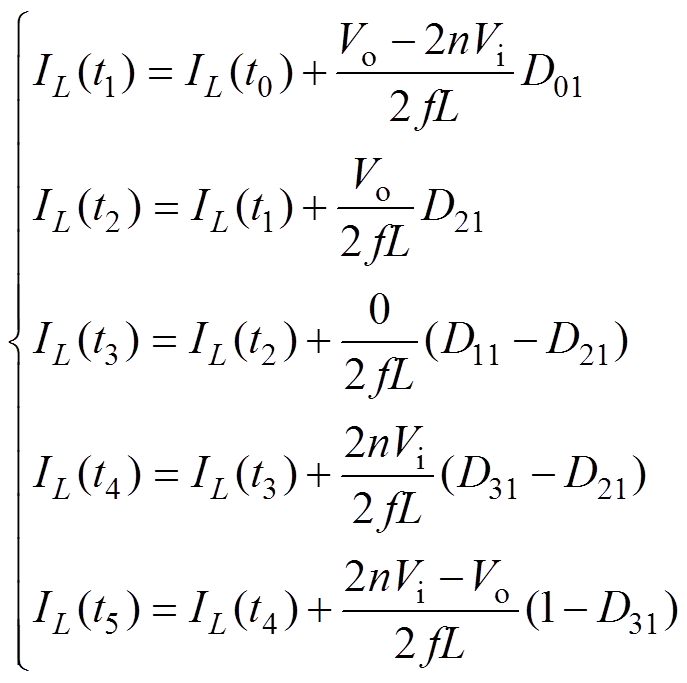（8）
由方程组式（8）求解出各个时刻的电流后，可计算出偏置电流的表达式为
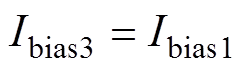（9）
式（9）说明图6功率突变的偏置电流结果和图4相同。对于状态2还存在功率由状态1同向突变到状态2的情况，经计算，此时方程组式（8）仍然成立，所以偏置电流表达式也不变，仍为式（9）所示。
当功率由负向流动突变为正向流动时的工作波形如图7所示。
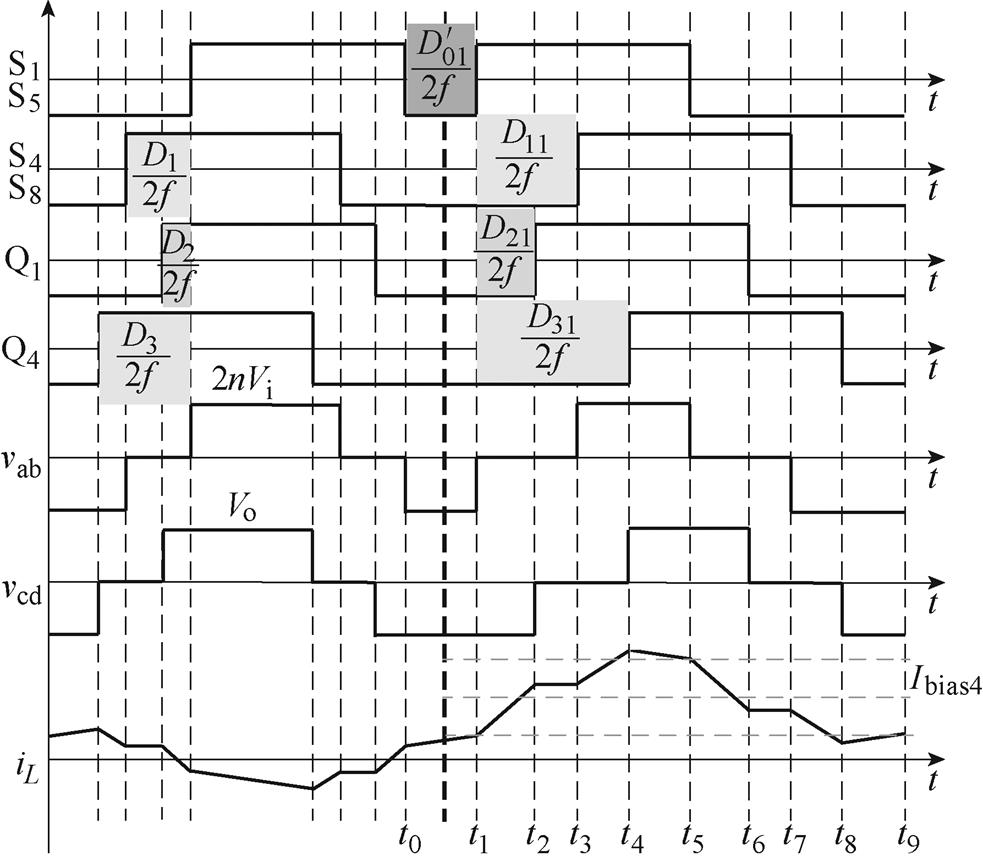
图7 状态2，功率由负向突变到正向时的工作波形
Fig.7 State 2, the working waveforms when the power suddenly changes from negative to positive
此时，无论负向流动时处于状态1还是状态2，经计算t0时刻的电流表达式均与式（5）相同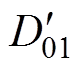，与式（6）相同，且方程组式（8）仍成立，将表达式（5）、式（6）代入方程组式（8）可解得
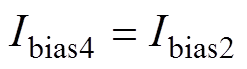（10）
通过上面的结果可得，功率同向突变或反向突变时，状态1和状态2均具有同样的直流偏置表达式，但两个突变方向对应的表达式不同。取电流基准值为nVi/(4fL)，标幺化之后的电流偏置表达式为
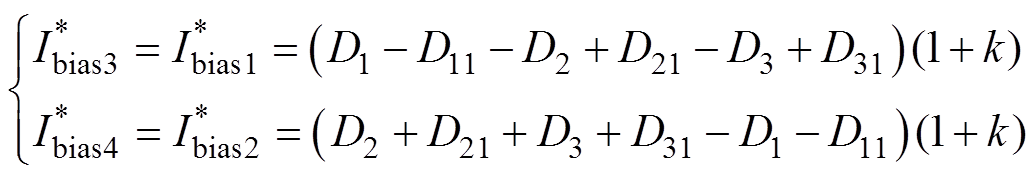（11）
分别取k=0.8和k=1.25，当功率同方向流动由P1突变成P2时，将表1中k≥1的两个区域和0＜ k＜1的两个区域对应的移相值代入式（11）中，可得到关于P1、P2的直流偏置表达式，绘制成三维曲面如图8所示。
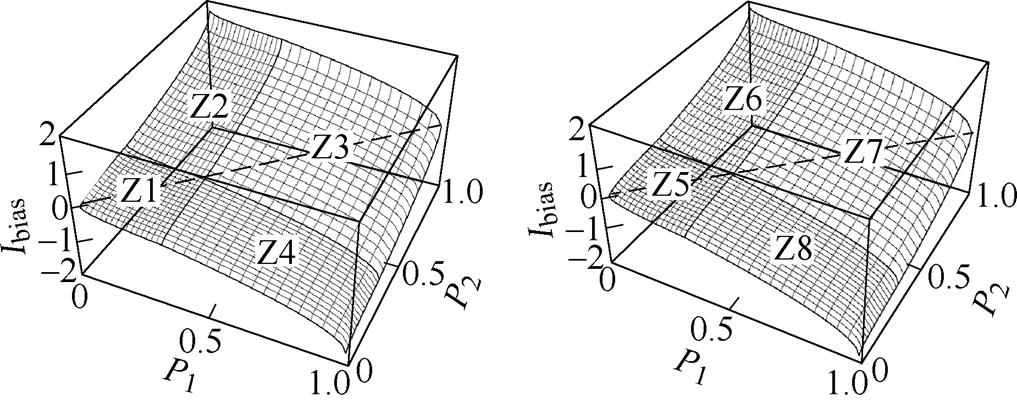
（a）k=0.8 （b）k=1.25
图8 功率同向突变时在各个区域产生的直流偏置
Fig.8 DC bias generated in each region when the power suddenly changes in the same direction
图8中，Z1～Z8四部分对应表1中相同区域或不同区域之间的功率突变情况，P1表示负向功率绝对值大小，P2表示正向功率大小。其中，Z1部分为功率在区域1内部突变，Z2部分为功率从区域1突变到区域2，Z3部分为功率在区域2内部突变，Z4部分为功率从区域2突变到区域1，Z5部分为功率在区域3内部突变，Z6部分为功率从区域3突变到区域4，Z7部分为功率在区域4内部突变，Z8部分为功率从区域4突变到区域3。图中虚线表示直流偏置正负分界线，且正负值关于这条线对称，说明功率以相同的大小突增或突减时产生的直流偏置绝对值大小是一样的。从图中还可以看出，功率突增时会产生正的直流偏置，功率突减时会产生负的直流偏置，尤其是功率在不同区域之间突变时会产生更大的电流偏置，如图8中Z2、Z4、Z6和Z8部分。
在上述k值条件下，功率从负向流动突变到正向流动产生的直流偏置的三维曲面如图9所示。
图9中，各部分对应的功率突变区域与图8一致。由图9可得，功率由负突变到正后，全部产生正的直流偏置，功率由正突变到负后产生的直流偏置与图9相反。结合图8和图9可知，功率突变时会产生不同程度的偏置电流，且功率反向突变会比同向突变产生更大的直流偏置，对电路的影响就会更大。所以必须采取措施来抑制功率突变时的瞬态直流偏置。
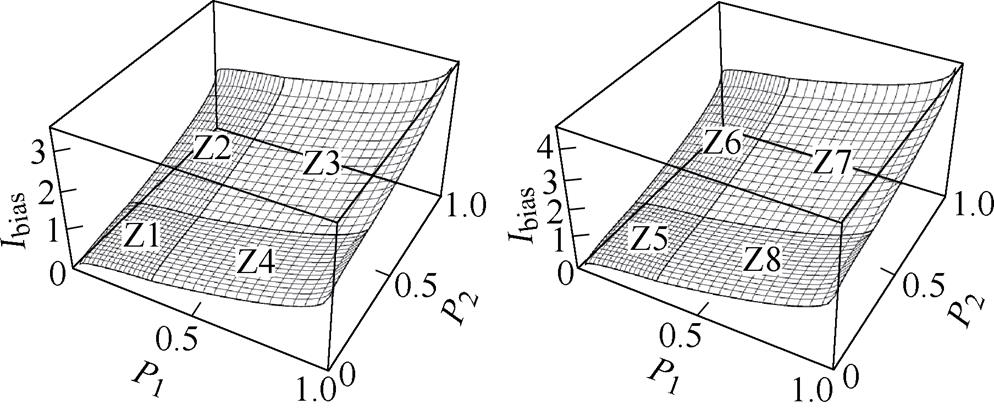
（a）k=0.8 （b）k=1.25
图9 功率反向突变时在各个区域产生的直流偏置
Fig.9 DC bias generated in various regions when the power is reversed suddenly
由第2节分析可得，因为功率突变后仍采用原来的移相方式进行调制，从而导致电压伏秒积不平衡，进而产生直流偏置现象。所以如果在功率突变后能够引入一个过渡态来调整移相值，使得此周期直流偏置为0，然后再恢复为原来的移相方式即可消除直流偏置。
在传统单移相调制策略中，功率突变后通常保持一次侧的开关波形不变，改变二次侧的方波占空比，进而抑制直流偏置，如文献[20-21]所示。但是本文涉及三个移相角，且存在不同状态的功率突变，如果引入不恰当的过渡态，最终得到的结果可能比较复杂，不利于调制和控制芯片实现。所以本文提出一种新的引入过渡态的方式，对于不同的突变状态可以得到统一的结果，易于调制。
观察工作波形图4～图7可得，对于移相状态1，功率突变后t2～t3时间段电流的斜率最大，对电流的增减起决定性作用，所以可以通过调节这段时间来改变电流的增减趋势，从而抵消直流偏置。同理，对于移相状态2，t1～t2和t3～t4时间段对电流的增减起决定性作用，为了和状态1的调制方式保持一致，仍可以调节t2～t3的时长来改变电流的增减趋势，当这段时间增加时，t1～t2和t3～t4的时间就减小，则电流会减小；反之，则电流增加。所以根据上述分析，可得到引入过渡态的方式如下：
（1）定义功率突变后引入过渡态的半周期占空比为Dtx，其中，x=1, 2, 3, 4表示不同的状态。
（2）功率突变后的新一周期，在新的移相值基础上，让低压侧S1、S4、S5、S8的上升沿同时移动Dtx/(2f)时间，当Dtx为正时同时左移；反之，右移。
（3）功率突变后的新一周期，让高压侧Q1、Q4的上升沿也同时移动Dtx/(2f)时间，当Dtx为正时同时右移；反之，左移，即与式（2）的移动方向相反，大小相同。其他时刻保持不变。
经过上述过渡以后，若功率突变后电流负向偏置，则可计算出Dtx为正，加入Dtx后会使得电流减小的速度变慢，抵消电流的负向偏置；若功率突变后电流正向偏置，则Dtx为负，加入Dtx后会使得电流增加的速度变慢，抵消电流的正向偏置。以此为基础，下面分别对不同的突变状态引入过渡过程。
对于移相状态1，功率同方向突增后引入过渡态的工作波形如图10所示。
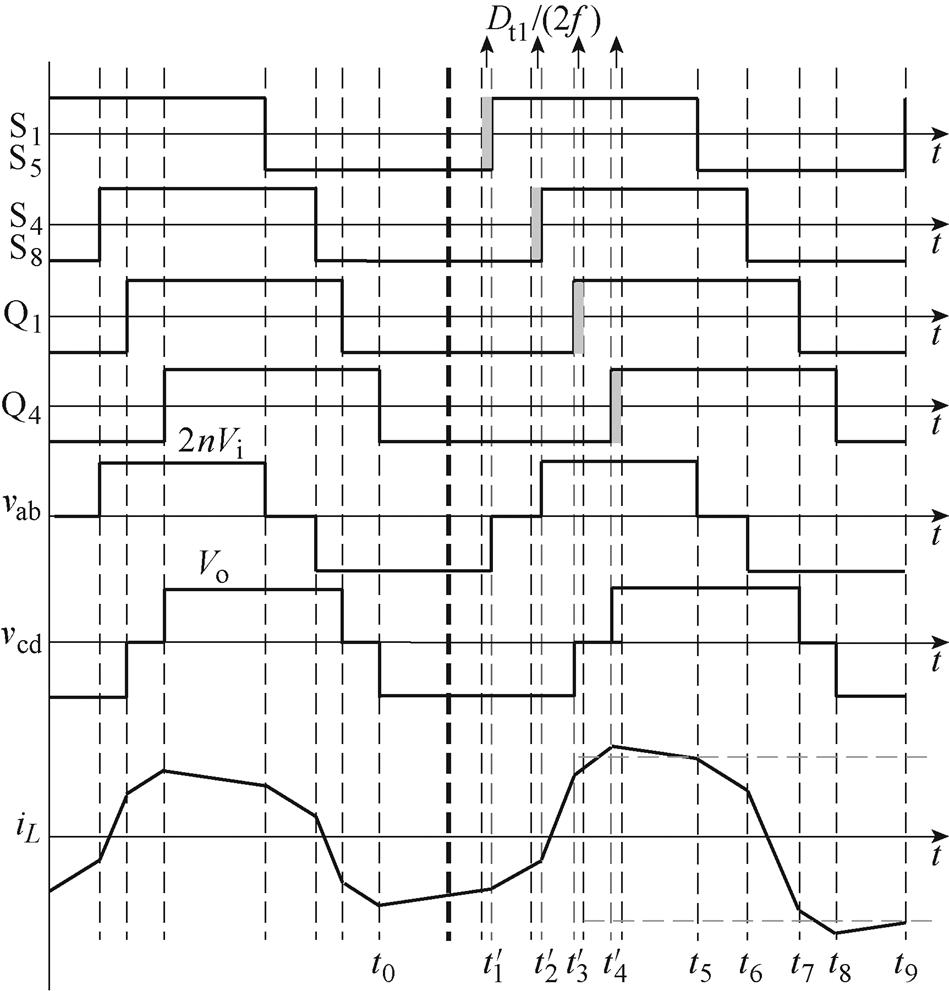
图10 状态1，功率同向突变时过渡后的工作波形
Fig.10 State 1, the working waveforms after transition when the power suddenly changes in the same direction
图10中，Dt1/(2f)为引入的过渡时间，经分析可知，功率突增后，电流会正向偏置，所以此时Dt1为负，可以将S1、S4、S5、S8上升沿同时右移，Q1、Q4的上升沿同时左移，移动大小如图10阴影部分所示。移动之后的上升沿对应阴影附近虚线处对应的时刻变为
、
、
、
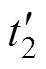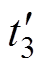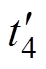。t0时刻的电流和式（2）相同，其余各个时刻的电流表达式见表2。
引入过渡态并不会影响t5时刻之后的电流波形，所以如果能保证式（12）成立，则直流偏置为0，后续电压每周期伏秒积保持为0，直流偏置被消除。
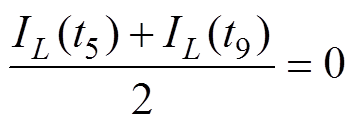（12）
式中，IL(t9)为t9时刻的电感电流。将表2中IL(t5) 和IL(t9)对应的表达式代入式（12）可解得，引入的过渡态占空比Dt1为
表2 状态1，引入过渡态后的电流表达式
Tab.2 State 1, the current expression after introducing the transition state
时刻电流表达式
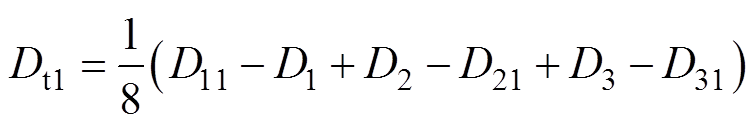（13）
当功率从状态2突变到状态1时，表2中的表达式保持不变，最后过渡态结果仍然为式（13）。
当功率由反向流动突变成正向流动时，引入过渡态的波形如图11所示。
图11中，Dt2/(2f)为引入的过渡时间，由第2.1节可得，无论突变前处于状态1还是状态2，t0时刻的电流均和式（5）相同，D01和式（6）相同，代入表2中各个电流表达式，并将IL(t5)和IL(t9)对应的表达式代入式（12），可解得引入的过渡态移相占空比Dt2为
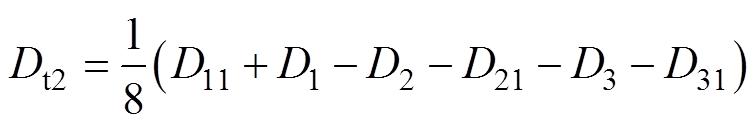（14）
对于状态2，功率同方向突增后引入过渡态的波形如图12所示。
图12中，Dt3/(2f)为此突变状态下引入的过渡时间，由第2.1节可得，无论功率突变前处于状态1还是状态2，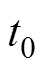
时刻的电流均和式（2）相同。引入过渡态后其余各个时刻电流值见表3。
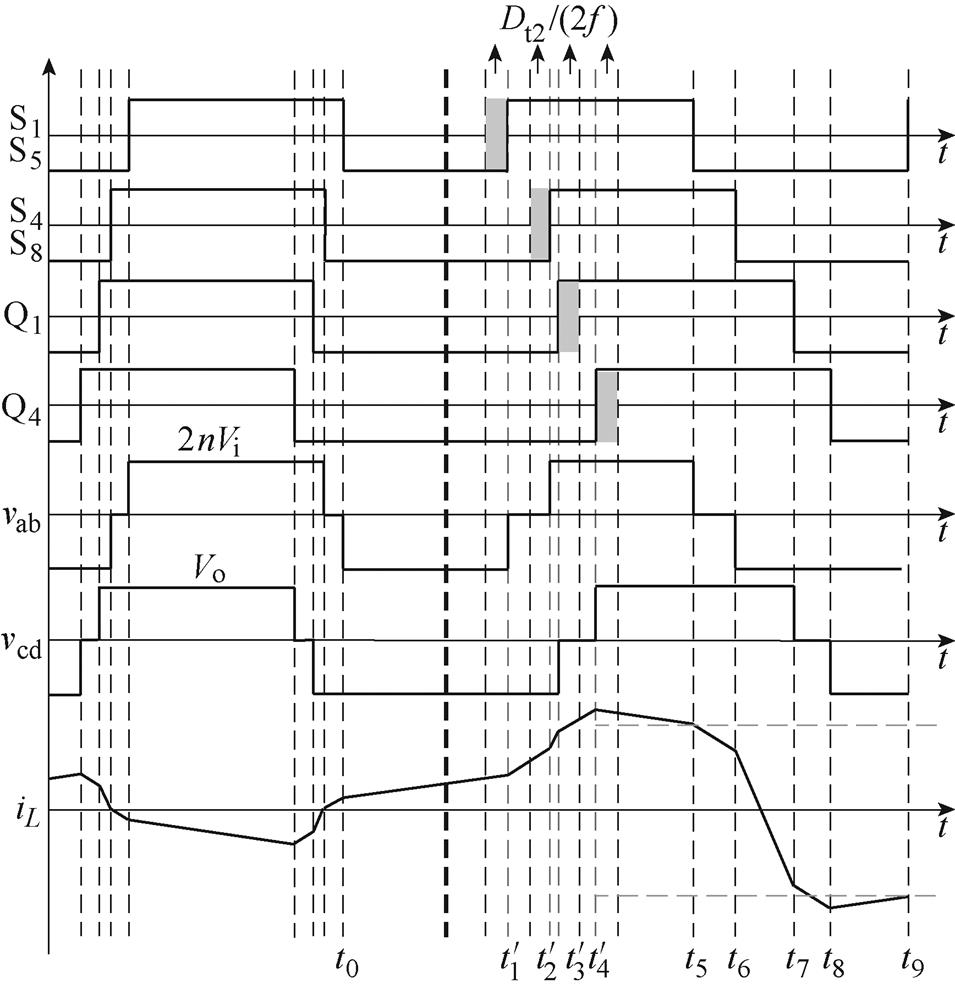
图11 状态1，功率反向突变时过渡后的工作波形
Fig.11 State 1, the working waveforms after the transition when the power is reversed suddenly
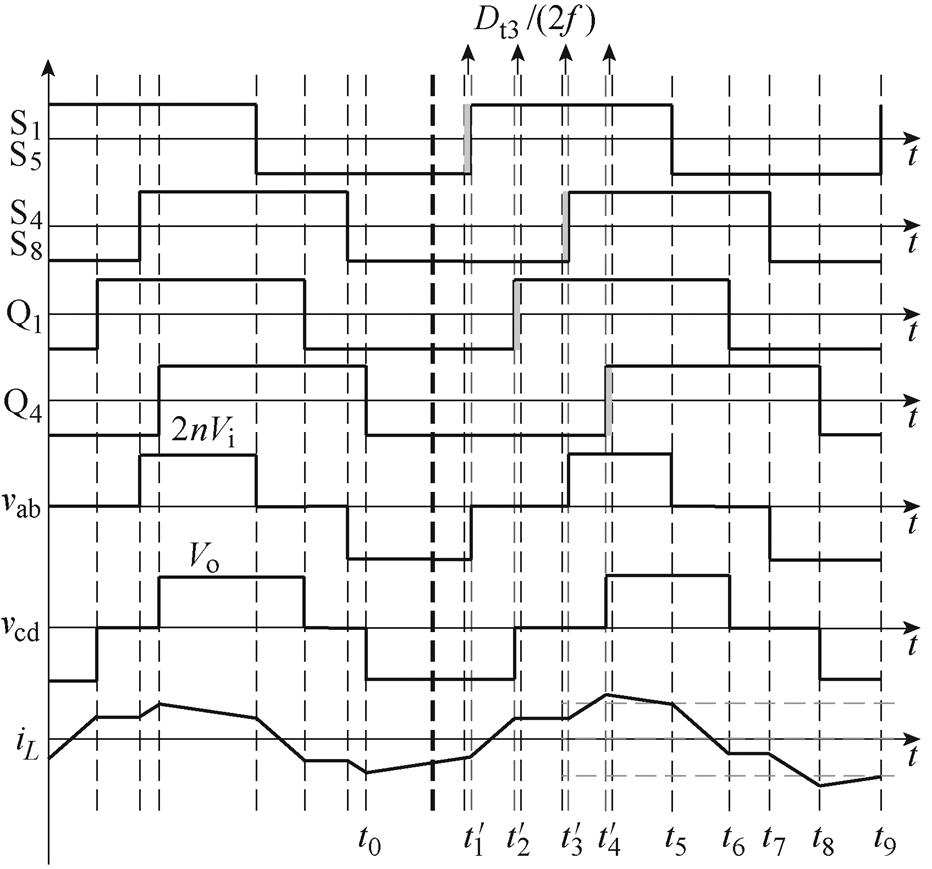
图12 状态2，功率同向突变时过渡后的工作波形
Fig.12 State 2, the working waveforms after the transition when the power is suddenly changed in the same direction
将表3中IL(t5)和IL(t9)对应的表达式代入式（12），可解得引入的过渡态移相占空比Dt3为
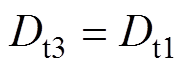（15）
由式（15）可以看到，最后得到和状态1相同的过渡态移相值，可以进行统一调制，以实现不同状态之间的切换。
功率反向突变后，引入过渡态的波形如图13所示。
图13中，Dt4/(2f)为此突变状态下引入的过渡时间，由第2.1节可得，无论突变前处于状态1还是状态2，t0时刻的电流均和式（5）相同，D01和式（6）相同，代入表3中各个电流表达式，并将IL(t5)和IL(t9)对应的表达式代入式（12）可解得，引入的过渡态移相占空比Dt4为
表3 状态2，引入过渡态后的电流表达式
Tab.3 State 2, the current expression after introducing the transition state
时刻电流表达式
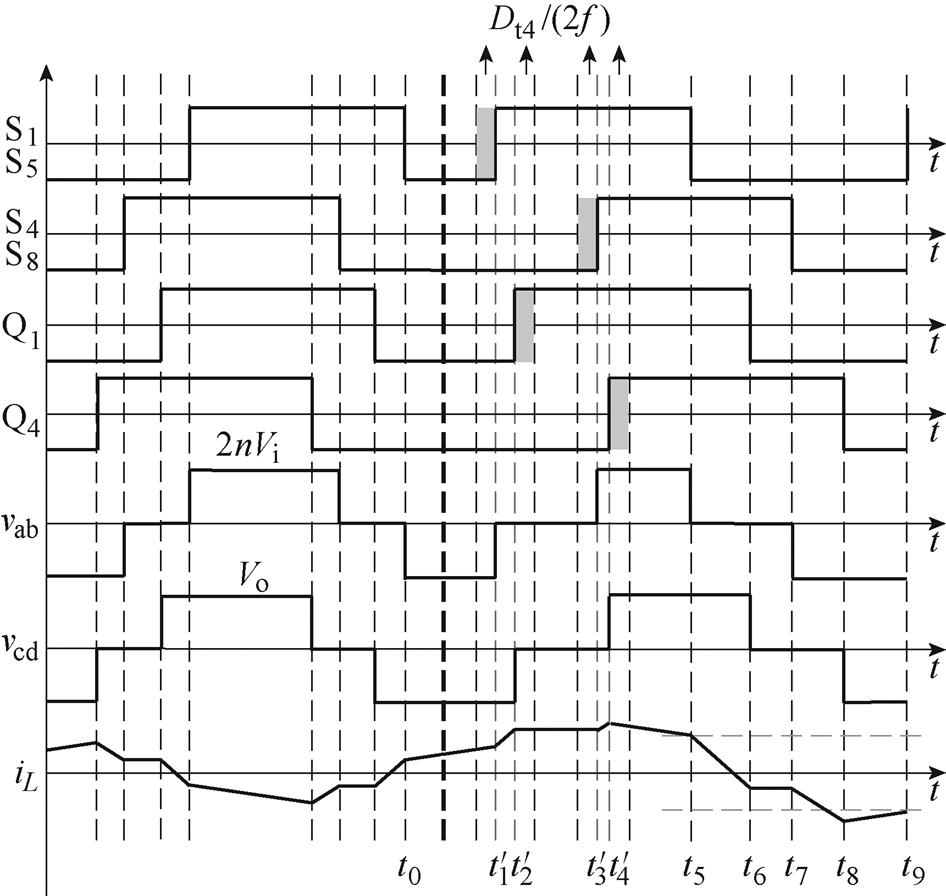
图13 状态2，功率反向突变时过渡后的工作波形
Fig.13 State 2, the working waveforms after transition when the power is reversed suddenly
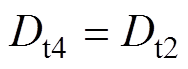（16）
综上所述，功率同向突变时，不论是处于什么状态，最后引入的过渡态表达式均为Dt1；功率反向突变时，最后引入的过渡态表达式均为Dt2，而且它们和k值无关，为调制提供了便利性。值得注意的是，当引入的过渡态稍大时，会出现移相状态和状态1、状态2不符合的情况，但是经过计算，结果仍然和上述分析相同。由此可得，本文提出的过渡方式可以实现统一的调制，仅在功率反向突变的时候使用不同的过渡公式，与文献[24-26]相比，在快速实现偏置电流抑制的同时，极大地简化了控制过程，能够有效节省控制芯片资源，提高工作频率。与文献[23]相比，本文的偏置电流抑制效果与电压传输比k值无关，且应用范围更广，具有更快的动态性能。
由表1可得，每个区域都存在三个移相角，且大小各不相同，需要使用统一的调制策略，以方便引入过渡态。为了简化调制计算，将低压侧内移相角占空比定义为Dp，高压侧内移相角占空比定义为Dq，两桥产生的方波之间的移相角占空比定义为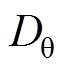
，上述占空比均为半开关周期占空比。将各个占空比对应的移相时间作用到开关脉冲波形，如图14所示。
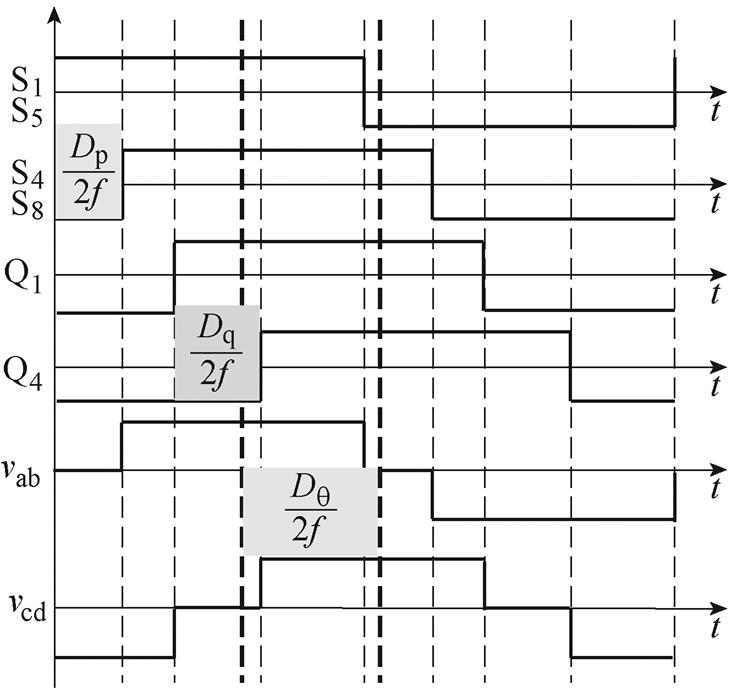
图14 重新定义移相值后的波形
Fig.14 The waveforms after redefining the phase shift value
图14中，粗虚线表示vab、vcd的中线，无论处于何种移相状态均有
（17）
为了使得载波和调制波易于比较，本文以锯齿波作为载波，最终调制结果如图15所示。
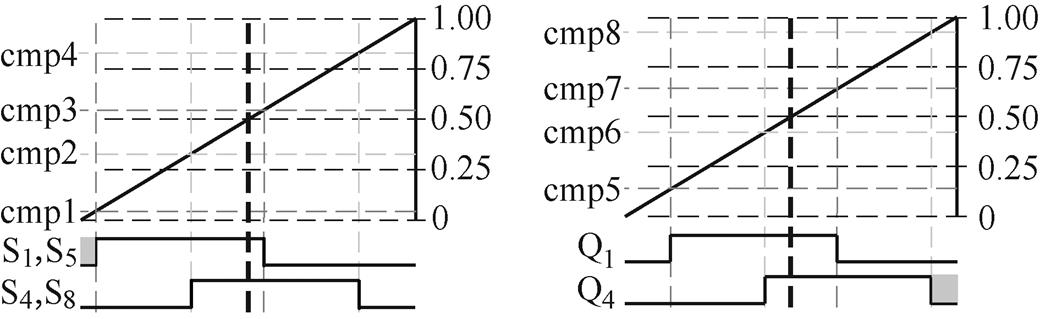
（a）低压侧调制波形 （b）高压侧调制波形
图15 载波调制波形
Fig.15 Carrier modulation waveforms diagram
图15中，cmp1～cmp8分别为各个开关对应的调制信号，其中，cmp1和cmp3决定S1、S5的开通和关断，cmp2和cmp4决定S4、S8的开通和关断，cmp5和cmp7决定Q1的开通和关断，cmp6和cmp8决定Q4的开通和关断，其余开关互补导通。在移相过程中，先让S1、S4、S5、S8的高电平位于载波中心，即载波大于0.25小于0.75的部分为高电平，然后让S1、S5左移(Dp/2)/(2f)，S4、S8右移同样的时间，由此可得一次侧桥的内移相占空比Dp。同理二次侧桥的内移相角可通过相互移动(Dq/2)/(2f)得到。然后再让S1、S4、S5、S8同时左移(Dθ/2)/(2f)，Q1、Q4同时右移(Dθ/2)/(2f)，可得到一次侧和二次侧之间的移相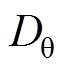，从而使得所有脉冲波形按照计算的移相角工作。
使用图15所示的调制策略时，要求图中阴影部分的时间要大于0，否则就会出现调制失效的现象。分别将左、右侧阴影部分的半开关周期占空比定义为Dl、Dr，以功率正向流动时为例，可计算得各种移相情况对应的Dl、Dr的表达式分别为
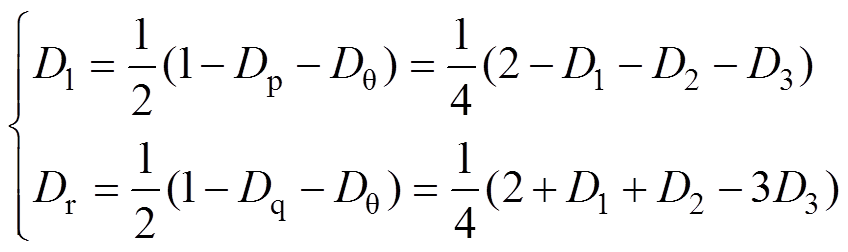（18）
当功率反向流动时，Dl、Dr的结果与式（18）相反。通常电压传输比k工作在0.5～2之间，否则传输相同功率时会产生较大的电感电流应力。k在此范围时，将表1中4个区域的移相值分别代入式（18），并画出对应的三维曲面如图16所示。
由图16可以得，经过调制后Dl、Dr均大于0，不会出现失调的现象，证明本调制策略可以有效工作。
考虑引入的过渡态并结合图15，可分别计算得到图15中的8个调制信号的表达式见表4。
表4中，dir表示功率流动的方向，功率正向流动时dir值为1，功率负向流动时值dir为-1。因为最后需把原来设定的半开关周期移相占空比转化成全开关周期的占空比，所以表4中的占空比的表达式要除以2。得到8个调制信号后按照图15的调制方式就可得到对应的开关脉冲信号，从而控制开关管的开通和关断。
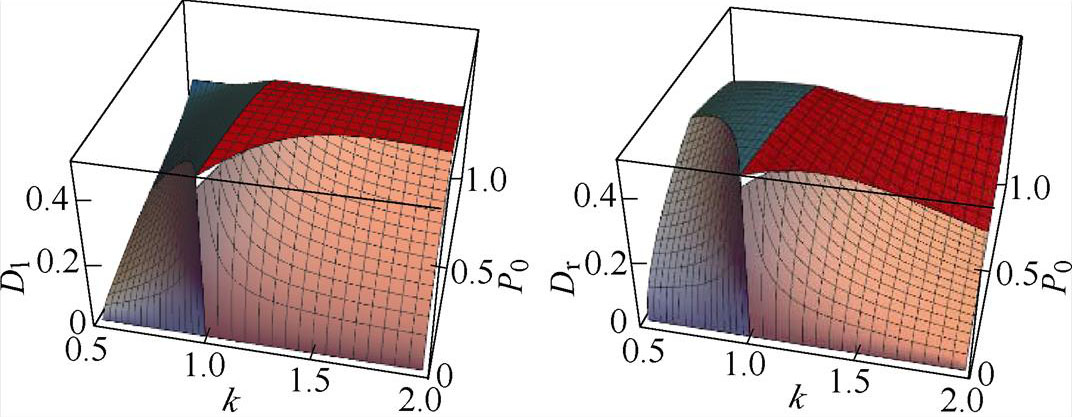
（a）Dl的三维曲面 （b）Dr的三维曲面
图16 Dl、Dr的三维曲面
Fig.16 3D surface plots of Dl and Dr
表4 8个调制信号的表达式
Tab.4 Expressions for eight modulated signals
调制信号表达式 cmp1 cmp2 cmp3 cmp4 cmp5 cmp6 cmp7 cmp8
综上所述，将取直流两侧电压和目标功率为输入量，开关信号为输出量，可得到总的控制流程如图17所示。
图17中，通过采样得到低压侧和高压侧的直流电压Vi和Vo，再结合给定功率Pref，根据表1判断电路的工作区域，计算出D1、D2、D3、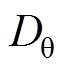，然后根据功率突变情况引入相应的过渡态Dt1或Dt2，结合表4可计算出所需8个调制信号，然后通过统一的载波调制得到所需的开关脉冲信号。由此可得，和文献[26]相比，本文所提调制策略可以实现统一调制，只需在对应的载波比较值上引入统一的Dtx即可完成调制，而不是每种突变状态都采用不同的过渡移相角，简化了调制过程。而文献[23]一个载波周期需要更新两次比较值，对控制器的计算能力要求较高，在同等计算能力的情况下，本文所提调制策略载波频率可以达到更高。与文献[24]相比，本调制策略不涉及复杂的状态机判断，更易于实现。和文献[25]相比，调制时减少了判断次数，节省了运算时间。
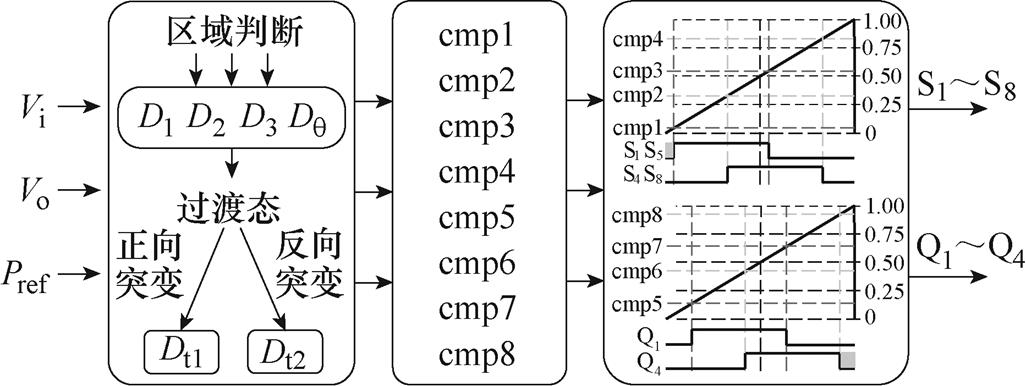
图17 控制流程
Fig17 Control flow chart
首先搭建LPHS DAB变换器实验平台，包括控制模块和主电路模块，在基于ARM芯片（STM32G474）和FPGA芯片（LCMX02-2000HC-4TG144I）的控制板及储能DC-DC的主电路板上来完成本文的实验验证。实验平台如图18所示。
图18 实验平台
Fig.18 Experimental platform
低压侧两H桥和高压侧H桥电路分开布局，为了隔离高低压信号，将控制电路和主电路布局在不同的电路板上。此型号的ARM芯片内部具有高精度定时器HRTIM，可以将计数频率提高到GHz等级，从而可以提高移相角的分辨率，能够实现更为微小的移相过程；利用FPGA芯片的高速特性，在出现过电流等故障时可以实现快速的脉冲封锁，而且此型号的FPGA芯片具有低功耗、低成本特性，所以此实验平台具有一定的普适性。实验参数见表5。
表5 实验参数
Tab.5 Experimental parameters
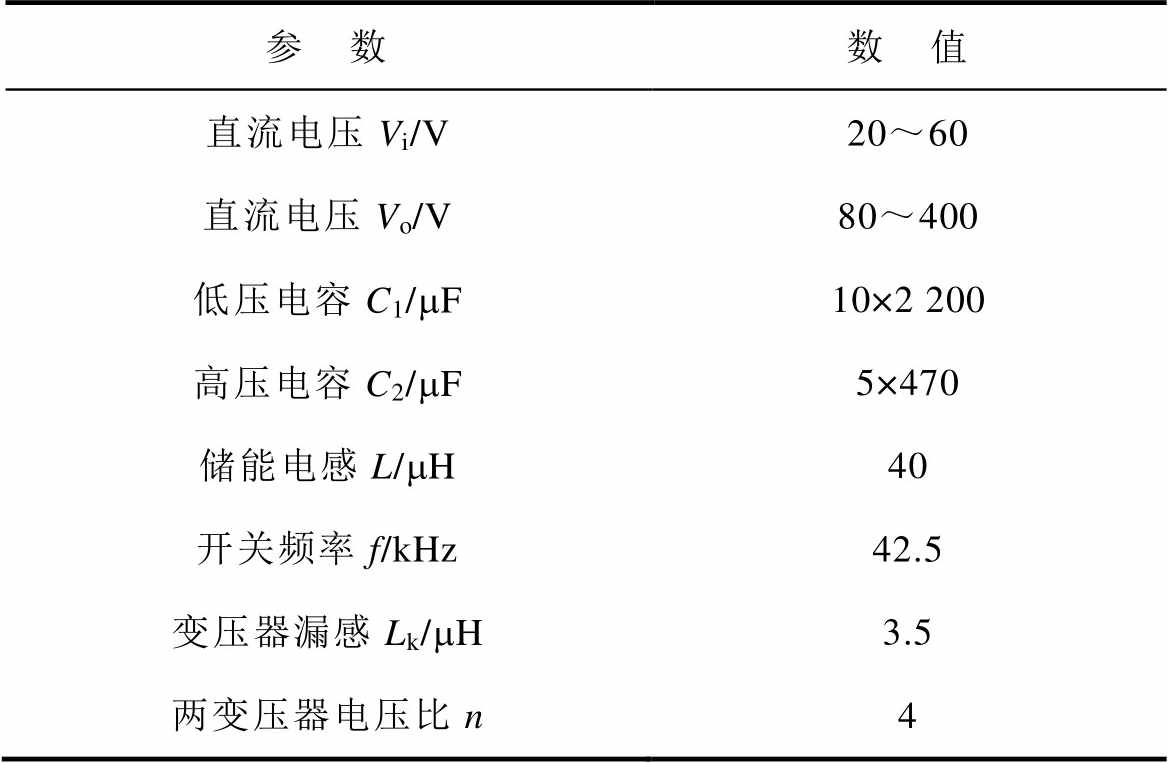
参 数数 值 直流电压Vi/V20～60 直流电压Vo/V80～400 低压电容C1/mF10×2 200 高压电容C2/mF5×470 储能电感L/mH40 开关频率f/kHz42.5 变压器漏感Lk/mH3.5 两变压器电压比n4
首先以电压传输比k=0.8为例，分别分析功率在相同区域同向突变和不同区域同向突变时的输出波形，观察功率突变时电流的变化情况，以此来验证引入过渡态后对FPS控制方法的优化效果。实验波形对比如图19所示。
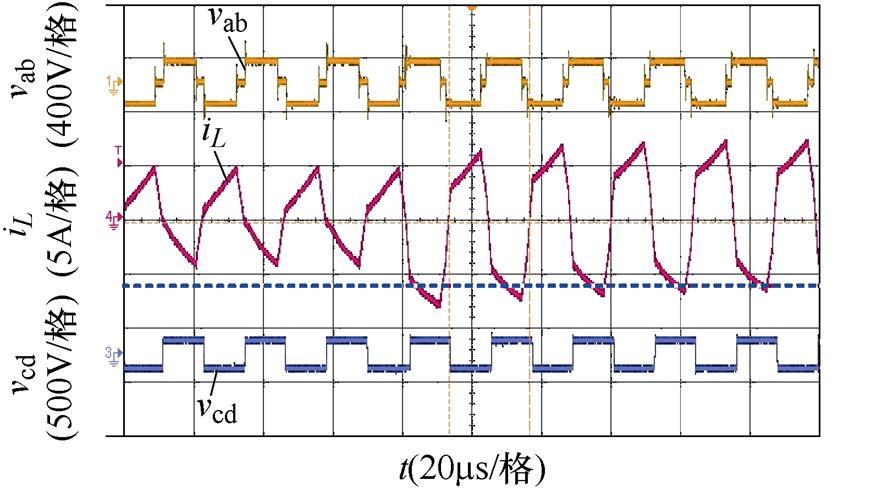
（a）k=0.8，Pref =0.35(pu)突变到Pref =0.6(pu)，未引入过渡态
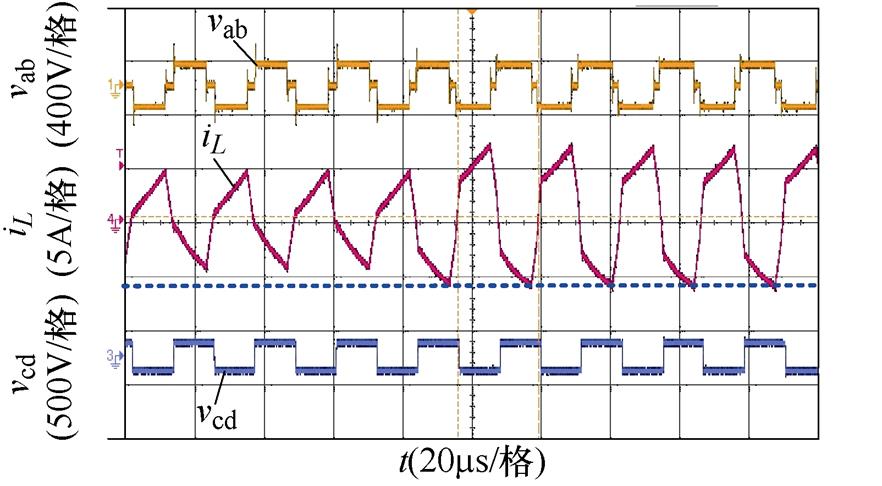
（b）k=0.8，Pref =0.35(pu)突变到Pref =0.6(pu)，引入过渡态
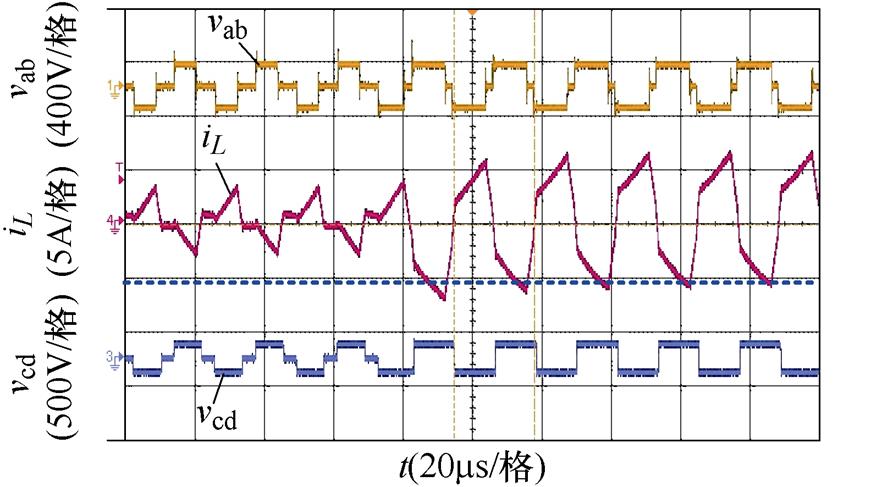
（c）k=0.8，Pref =0.15(pu)突变到Pref =0.5(pu)，未引入过渡态
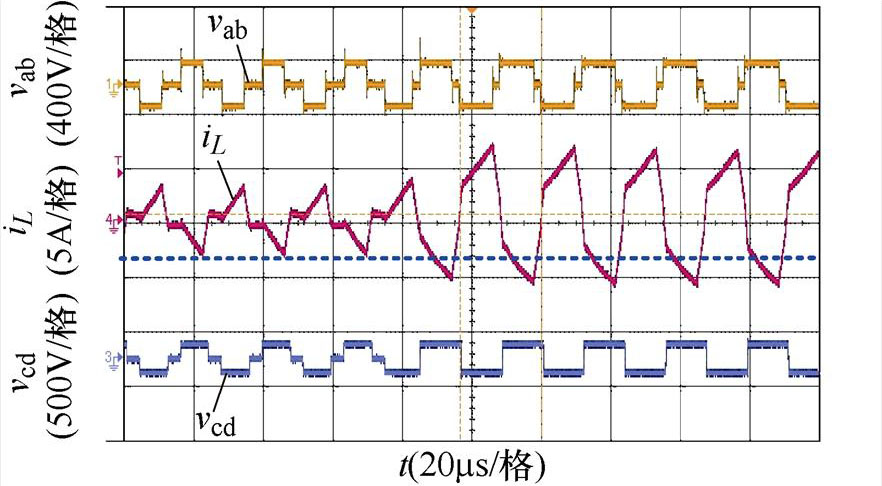
（d）k=0.8，Pref =0.15(pu)突变到Pref =0.5(pu)，引入过渡态
图19 功率同向突变，引入过渡态前后的实验波形对比
Fig.19 Comparison of experimental waveforms before and after the introduction of transition states in the case of same power mutation
图19中，低压侧输入电压Vi=20 V，高压侧输出电压Vo=128 V，此时最大传输功率Pm约为1.28 kW，以此功率为基准功率，进行功率突变的实验验证。Pref为标幺化后的给定功率，图19a、图19b为Pref从0.35(pu)突变到0.6(pu)的实验波形，将k=0.8代入表1中功率分界线2(k-k2)，可以计算得到区域1和区域2的分界功率标幺值为0.32(pu)，所以图19a、图19b为功率在区域2内同向突变的波形对比。其中图19a为未引入过渡态的FPS控制实验结果，图中虚线对应稳定后的最小电感电流，从图19a中可以看出，在功率突变时电感电流明显地偏离了虚线位置，产生了直流偏置，如果功率突变范围增加则产生的电感电流偏置更大，将会带来更多不利影响。图19b为引入过渡态后的FPS控制实验结果，由于在调制过程中加入了本文提出的过渡态移相角，所以并未产生电流偏置，经过半周期的调节基本达到了稳定状态，实现了较好的直流偏置抑制效果和动态性能。图19c、图19d为Pref从0.15(pu)同向突变到0.5(pu)的实验波形，突变功率分布在分界功率点两侧，所以是功率从区域1同向突变到区域2的情况；图19c为未引入过渡态时的实验波形，从图中可以看到，突变后电流仍偏离虚线位置，产生直流偏置；图19d为引入过渡态后的实验波形，从图中可以看出，引入过渡态后可以在半周期内消除直流，功率在不同区域突变时同样可以实现良好的效果。
为了进一步验证本文所提方法的有效性，再对功率反向突变的情况进行分析，分别对比不同区域功率反向突变和相同区域功率反向突变的实验结果，以此全面观察功率反向突变时对电感电流应力的影响。实验波形如图20所示。
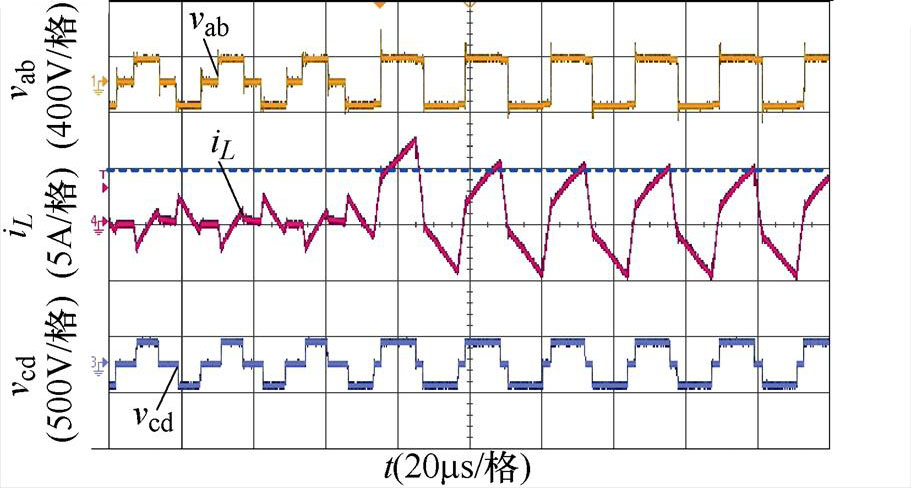
（a）k=1.2，Pref =0.1(pu)突变到Pref =-0.35(pu)，未引入过渡态
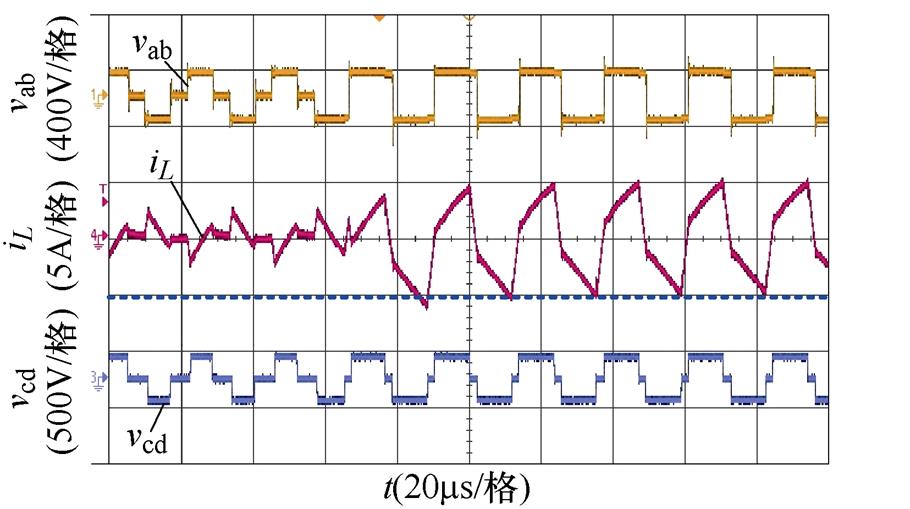
（b）k=1.2，Pref =0.1(pu)突变到Pref =-0.35(pu)，引入过渡态
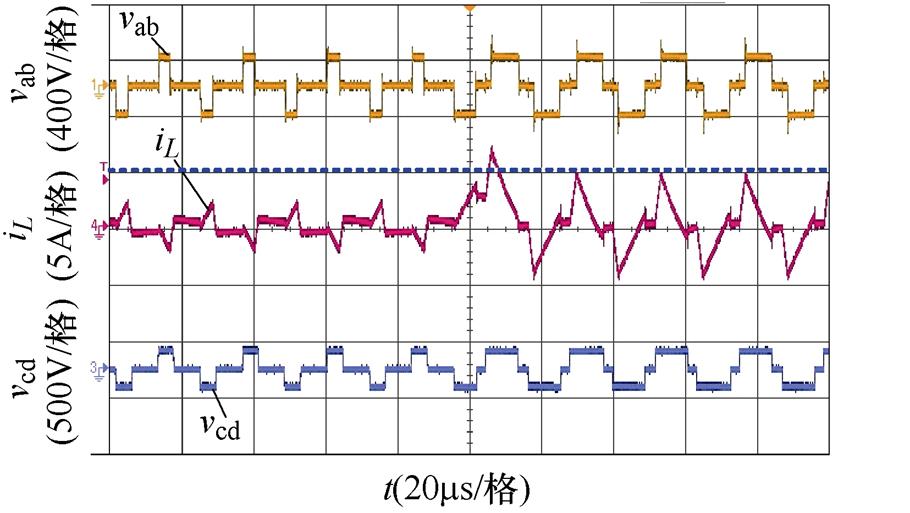
（c）k=0.8，Pref =0.05(pu)突变到Pref =-0.2(pu)，未引入过渡态
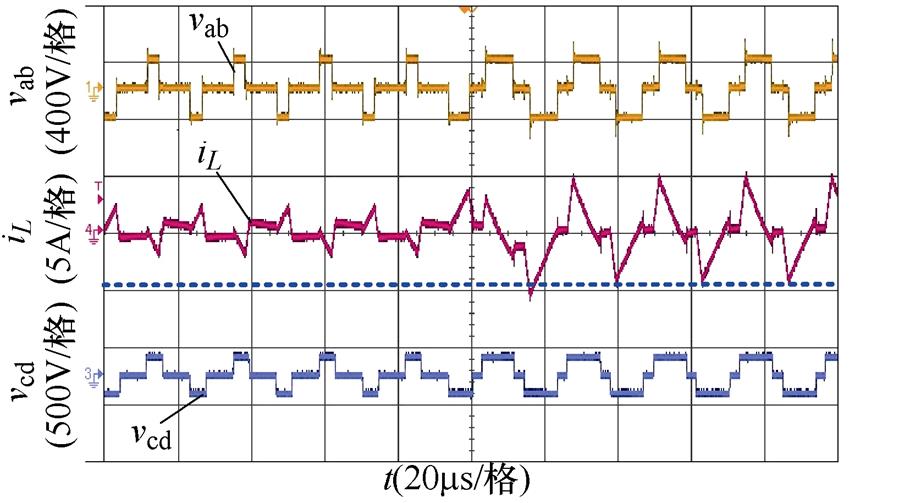
（d）k=0.8，Pref =0.05(pu)突变到Pref =-0.2(pu)，引入过渡态
图20 功率反向突变，引入过渡态前后的实验波形对比
Fig.20 Comparison of experimental waveforms before and after the introduction of transition states in the case of reverse power mutation
对于图20a、图20b，输入电压Vi=20 V，输出电压Vo=192 V，电压传输比k=1.2，此时最大传输功率Pm约为1.92 kW，以此功率为基准功率，将k=1.2代入表1中功率分界线(-2+2k)/k2可得区域3和区域4的分界功率标幺值P0=0.28(pu)。图20a、图20b为Pref从0.1(pu)反向突变到0.35(pu)的实验波形，即功率从区域3突变到区域4的情况，图20a为未引入过渡态的情况，从图中可以看出，功率反向突变时会造成更为明显的电流偏置，形成较大的电流冲击；图20b为引入过渡态后的实验波形，从图中可见，由于存在过渡态的调节，功率突变后并不会导致电流过冲，具有较好的动态响应。对于图20c、图20d，输入电压Vi=25 V，输出电压Vo=160 V，电压传输比k=0.8，最大传输功率Pm约为2 kW，由前文可得，k=0.8时对应的标幺功率分界值为0.32(pu)，图20c、图20d为Pref从0.05(pu)反向突变到0.2(pu)的实验波形，即功率在区域1内突变的情况，图20c为未引入过渡态的实验波形，由波形可以看出，即使功率反向突变范围较小，但是在突变后仍然产生明显的电流尖峰。图20d为引入过渡态的实验波形，由图可得，引入过渡态后电流偏置得到抑制，能够快速恢复稳态。
当反向功率突变范围较大时，采用未引入过渡态的FPS控制方法则有可能产生严重的偏置电流冲击，导致电路停止工作，如图21所示。
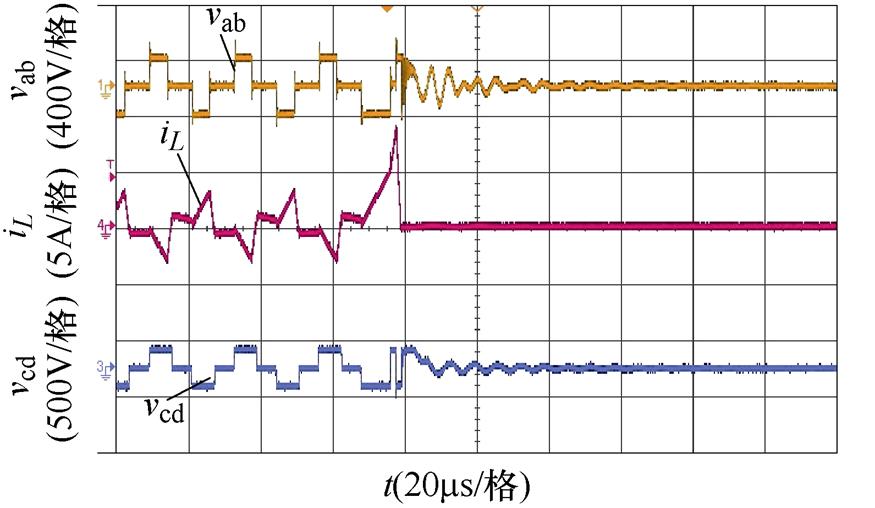
（a）k=0.8，Pref =0.1(pu)突变到Pref =-0.4(pu)，未引入过渡态
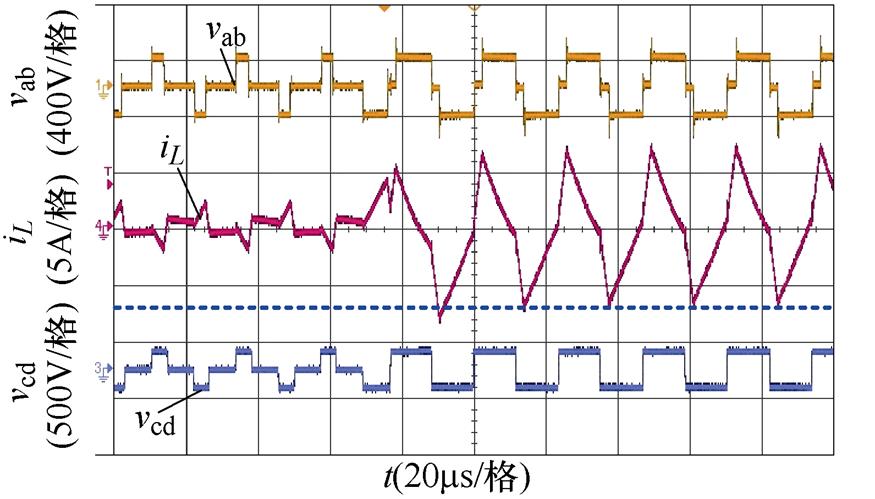
（b）k=0.8，Pref =0.1(pu)突变到Pref =-0.4(pu)，引入过渡态
图21 标幺功率从0.1(pu)突变到-0.4(pu)时的实验波形对比
Fig.21 Comparison of experimental waveforms when the unit power jumps from 0.1(pu) to -0.4(pu)
图21中，低压侧输入电压Vi=25 V，高压侧输出电压Vo=160 V，电压传输比k=0.8，最大传输功率Pm约为2 kW，以此功率基准功率，图21为给定标幺功率Pref从0.1(pu)反向突变到0.4(pu)的实验波形，为从区域1反向突变到区域2的情况，且反向突变范围较大。图21a为未引入过渡态的功率突变波形，此时因为功率反向突变较大，造成了较大的电流偏置，产生大的电流尖峰，进一步触发了控制器中的过电流保护，使得功率突变后电路停止工作，如果没有过电流保护，则可能会使器件损坏，造成不必要的损失。图21b为引入过渡态后的功率突变实验波形，从图中可以看到，引入过渡态后，电感电流经过半个周期的调整即恢复到平衡状态，基本不会产生偏置，更不会触发过电流保护，保证电路的可靠运行性。
通过上述不同的实验结果均可证明，在FPS控制的基础上引入本文提出的过渡态，可以有效抑制功率突变时造成的电感电流偏置现象，功率在不同工作区域以及不同方向突变时均可有效抑制电流偏置，消除了功率突变时的电流过冲，提高了电路运行的可靠性。
本文以基于全移相控制的DAB变换器为研究对象，对功率在不同工作区域突变时产生的电感电流直流偏置问题进行全面分析，经过一系列计算和实验可得出：
1）传统的移相调制策略在功率突变时会产生电流偏置现象，尤其是功率跨区域突变和反向突变时直流偏置更为明显。
2）提出的新的引入过渡态方式可以有效地解决直流偏置现象，且不同移相状态以及不同工作区域均可以得到统一的结果，简化了调制过程，在保证电感电流应力全局最优的同时实现了稳定过渡。
3）通过一种新的载波调制方法生成开关脉冲，在一个周期内即可完成直流偏置的抑制，且不会出现失调的现象。
参考文献
[1] 赵彪, 安峰, 宋强, 等. 双有源桥式直流变压器发展与应用[J]. 中国电机工程学报, 2021, 41(1): 288- 298.
Zhao Biao, An Feng, Song Qiang, et al. Development and application of DC transformer based on dual- active-bridge[J]. Proceedings of the CSEE, 2021, 41(1): 288-298.
[2] 孙志峰, 肖岚, 王勤. 输出并联型双有源全桥变换器控制技术研究综述[J]. 中国电机工程学报, 2021, 41(5): 1811-1831.
Sun Zhifeng, Xiao Lan, Wang Qin. Review research on control technology of output parallel dual- active-bridge-converters[J]. Proceedings of the CSEE, 2021, 41(5): 1811-1831.
[3] 涂春鸣, 管亮, 肖凡, 等. 双有源桥DC-DC变换器的模态分析方法[J]. 中国电机工程学报, 2019, 39(18): 5468-5479, 5595.
Tu Chunming, Guan Liang, Xiao Fan, et al. Modal analysis method of dual active bridge DC-DC converter[J]. Proceedings of the CSEE, 2019, 39(18): 5468-5479, 5595.
[4] 杨柯欣, 宋文胜, 安峰, 等. 双向有源全桥DC-DC变换器电流源模式的快速动态响应控制方法[J]. 中国电机工程学报, 2018, 38(8): 2439-2447, 2553.
Yang Kexin, Song Wensheng, An Feng, et al. Rapid dynamic response control method of dual-active- bridge DC-DC converters in current source mode[J]. Proceedings of the CSEE, 2018, 38(8): 2439-2447, 2553.
[5] 侯旭, 曾正, 冉立, 等. 基于扩展移相控制的双向有源桥变换器回流功率优化[J]. 中国电机工程学报, 2018, 38(23): 7004-7014, 7134.
Hou Xu, Zeng Zheng, Ran Li, et al. Backflow power optimization of dual active bridge converter based on extended-phase-shift control[J]. Proceedings of the CSEE, 2018, 38(23): 7004-7014, 7134.
[6] 王攀攀, 徐泽涵, 高利强, 等. 新扩展移相角下的双有源桥DC-DC变换器优化控制策略[J]. 中国电机工程学报, 2023, 43(2): 727-738.
Wang Panpan, Xu Zehan, Gao Liqiang, et al. Optimal control strategy for dual active bridge DC-DC converter with new extended-phase-shift angle[J]. Proceedings of the CSEE, 2023, 43(2): 727-738.
[7] 郭华越, 张兴, 赵文广, 等. 扩展移相控制的双有源桥DC-DC变换器的优化控制策略[J]. 中国电机工程学报, 2019, 39(13): 3889-3899.
Guo Huayue, Zhang Xing, Zhao Wenguang, et al. Optimal control strategy of dual active bridge DC-DC converters with extended-phase-shift control[J]. Pro- ceedings of the CSEE, 2019, 39(13): 3889-3899.
[8] 刘飞龙, 郑智文, 孙孝峰, 等. 双有源桥变换器低平均电流的调制研究[J]. 中国电机工程学报, 2019, 39(16): 4884-4891, 4990.
Liu Feilong, Zheng Zhiwen, Sun Xiaofeng, et al. A modulation study on low rectified average current of dual active bridge converter[J]. Proceedings of the CSEE, 2019, 39(16): 4884-4891, 4990.
[9] 王武, 雷文浩, 蔡逢煌, 等. 结合电流应力优化的双有源全桥DC-DC变换器自抗扰控制[J]. 电工技术学报, 2022, 37(12): 3073-3086.
Wang Wu, Lei Wenhao, Cai Fenghuang, et al. Active disturbance rejection control of dual-active-bridge DC-DC converter with current stress optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3073-3086.
[10] 杨向真, 孔令浩, 杜燕, 等. 基于动态矩阵控制的DAB变换器电流应力与回流功率优化方法[J]. 电力系统自动化, 2021, 45(17): 153-160.
Yang Xiangzhen, Kong Linghao, Du Yan, et al. Optimization method of current stress and backflow power of DAB converter based on dynamic matrix control[J]. Automation of Electric Power Systems, 2021, 45(17): 153-160.
[11] 王仁龙, 杨庆新, 操孙鹏, 等. 一种优化电流应力的双有源桥式DC-DC变换器双重移相调制策略[J].电工技术学报, 2021, 36(增刊1): 274-282.
Wang Renlong, Yang Qingxin, Cao Sunpeng, et al. An optimized dual phase shift modulation strategy for dual active bridge DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 274-282.
[12] 曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J]. 电工技术学报, 2019, 34(12): 2507-2518.
Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of dual-active full bridge converter based on dual phase shift control[J]. Transactions of China Electrotech- nical Society, 2019, 34(12): 2507-2518.
[13] 胡燕, 张天晖, 杨立新, 等. 双重移相DAB变换器回流功率优化与电流应力优化的对比研究[J]. 中国电机工程学报, 2020, 40(增刊1): 243-253.
Hu Yan, Zhang Tianhui, Yang Lixin, et al. Com- parative study of reactive power optimization and current stress optimization of DAB converter with dual phase shift control[J]. Proceedings of the CSEE, 2020, 40(S1): 243-253.
[14] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720- 4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[15] 蔡逢煌, 石安邦, 江加辉, 等. 结合电流应力优化与虚拟电压补偿的双有源桥DC-DC变换器三重移相优化控制[J]. 电工技术学报, 2022, 37(10): 2559- 2571.
Cai Fenghuang, Shi Anbang, Jiang Jiahui, et al. Triple-phase-shift optimal control of dual-active- bridge DC-DC converter with current stress optimi- zation and virtual voltage compensation[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(10): 2559-2571.
[16] 任强, 艾胜. 全工况范围的DAB三自由度优化控制策略[J]. 中国电机工程学报, 2020, 40(11): 3613- 3622.
Ren Qiang, Ai Sheng. A three degree freedom optimal control strategy of dual-active-bridge converters for full range operations[J]. Proceedings of the CSEE, 2020, 40(11): 3613-3622.
[17] 费跃, 李若愚, 雷园, 等. 宽输入电压双有源桥变换器电流有效值最小控制方法研究[J]. 中国电机工程学报, 2019, 39(19): 5656-5665, 5893.
Fei Yue, Li Ruoyu, Lei Yuan, et al. Minimize RMS current method of wide input voltage dual active bridge converter[J]. Proceedings of the CSEE, 2019, 39(19): 5656-5665, 5893.
[18] 高宇, 李若愚, 李林柘, 等. 三重移相调制模式下双有源变换器的直接功率控制[J]. 电工技术学报, 2022, 37(18): 4707-4719.
Gao Yu, Li Ruoyu, Li Linzhe, et al. Triple phase shift modulation-based direct power control strategy for a dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4707-4719.
[19] 吴春华, 陈修淋, 李智华, 等. 基于矩阵变压器的全移相双有源全桥直流变换器的电流应力优化方法[J/OL]. 中国电机工程学报, 2022, DOI: 10.13334/ j.0258-8013.pcsee.213271.
Wu Chunhua, Chen Xiulin, Li Zhihua, et al. Current stress optimization method of full-phase-shift dual- active full-bridge DC converter based on matrix transformer[J/OL]. Proceedings of the CSEE, 2022, DOI: 10.13334/j.0258-8013.pcsee.213271.
[20] Takagi K, Fujita H. Dynamic control and performance of a dual-active-bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7858-7866.
[21] Zhao Biao, Song Qiang, Liu Wenhua, et al. Transient DC bias and current impact effects of high- frequency-isolated bidirectional DC-DC converter in practice[J]. IEEE Transactions on Power Electronics, 2015, 31(4): 3203-3216.
[22] Dai Tianli, Qin Jinggang, Ge Gao, et al. Research on transient DC bias analysis and suppression in EPS DAB DC-DC converter[J]. IEEE Access, 2020, 8(1): 61421-61432.
[23] Yang Caiwei, Wang Jian, Wang Chenchen, et al. Transient DC bias current reducing for bidirectional dual-active-bridge DC-DC converter by modifying modulation[J]. IEEE Transactions on Power Elec- tronics, 2021, 36(11): 13149-13161.
[24] Wang Shien, Li Chi, Wang Kui, et al. Loss imbalance and transient DC-bias mitigation in dual active bridge DC/DC converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1399-1409.
[25] Yang Guoliang, Zhang Deqiang, Yang Xitong, et al. Transient DC bias suppression and general dynamic modulation for dual active bridge converter[C]//2022 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Guangzhou, China, 2022: 527-532.
[26] Du Chunshui, Guo Wenchen, Guo Song, et al. Transient current optimal control of the hybrid three level dual active bridge converters based on triple- phase-shifting control[C]//2021 IEEE 12th Inter- national Symposium on Power Electronics for Distributed Generation Systems (PEDG), Chicago, IL, USA, 2021: 1-8.
[27] Shu Liangcai, Chen Wu, Song Zhanfei. Prediction method of DC bias in DC-DC dual-active-bridge converter[J]. CPSS Transactions on Power Electro- nics and Applications, 2019, 4(2): 152-162.
[28] Qiu Guanqun, Ran Li, Feng Hao, et al. A fluxgate- based current sensor for DC bias elimination in a dual active bridge converter[J]. IEEE Transactions on Power Electronics, 2022, 37(3): 3233-3246.
Transient Current Bias Suppression Strategy of Full Phase Shifting Dual Active Full Bridge DC Converter
Abstract The research on dual active full-bridge (DAB) converters mainly focuses on phase-shifting methods, topology, and dynamic response. Among them, phase shift methods include single phase shift, double phase shift, extended phase shift, and triple phase shift. These different phase-shifting methods correspond to different inductor current stress and reflux power, but the ultimate goal is to obtain higher transmission efficiency.
When the transmission power changes suddenly, the traditional phase shifting method will cause the circuit current to generate a DC bias. This biased current will increase the current stress of the inductor, and in severe cases, it will also cause the transformer to be biased. Therefore, a transition state is introduced to suppress the DC bias when the power changes suddenly. Firstly, the DAB converter based on full phase-shift modulation is taken as the research object. The current of the bridge arm on the low-voltage side of the DAB converter with this structure is reduced by half, and the voltage of the transformer on the secondary side is also reduced by half. Therefore, the conduction loss can be reduced, and the transmission efficiency can be improved. The global optimal solution of inductor current stress can be obtained by full phase shift modulation. The optimal solution is divided into four regions, and the sudden current change in each optimal region is analyzed. Two kinds of phase shifting states are divided, and each phase shifting state corresponds to a different relationship between the magnitude of the phase shifting angle. The sudden power change is discussed in the same direction and reverses sudden change in these two phase-shifting states. The corresponding current bias results can be obtained when the power changes suddenly in the full range. This result with a three-dimensional surface diagram fully reflects the magnitude of the inductor current bias generated when the power changes suddenly. Then, a new DC bias suppression strategy is proposed, which adopts a unified transition state introduction method for all power mutation situations. For all phase-shifting states, the pulse signals of the same group of switches are changed to facilitate the realization of unified modulation. Moreover, with the goal of no DC bias after power mutation, the transition-state phase shift angles corresponding to various sudden changes are calculated. It is shown that the same transition state results can be obtained by power mutation in different regions without changing the power mutation direction. Thus, the controller implementation is simplified, and fewer control chip resources are occupied while maintaining a fast dynamic response. Finally, a unified carrier modulation strategy is proposed. The applicability of the modulation strategy is analyzed, and the modulation method is applied to the experimental platform. During the experiment, the power is mutated in the same direction and reversed in the four optimal regions. The experimental results show that the method proposed can effectively suppress the DC bias when the power changes suddenly, and the dynamic response is relatively stable.
Through the above analysis and verification, the following conclusions can be obtained: (1) The traditional phase-shift modulation strategy will produce a current bias phenomenon when the power changes suddenly. In particular, the DC bias is more apparent when the power is suddenly changed across regions and reversed. (2) The proposed method of introducing a transition state can effectively solve the DC bias phenomenon. In addition, different phase shift states and working areas can obtain consistent results, simplifying the modulation process. A stable transition is achieved while ensuring the global optimum of the inductor current stress. (3) Switching pulses are generated by a new carrier modulation method. The suppression of the DC bias can be completed within one cycle, and no imbalance will occur. The experimental results are consistent with the theoretical analysis, which verifies the proposed method.
keywords：Dual active full bridge (DAB) converter, sudden change of power, transient DC bias suppression, full phase shift control, carrier modulation
中图分类号：TM614
DOI: 10.19595/j.cnki.1000-6753.tces.222091
国家自然科学基金资助项目（51677112）。
收稿日期 2022-11-06
改稿日期 2022-12-30
吴春华 男，1978年生，副教授，研究方向为光伏发电、电力变换等。E-mail: wuchunhua@shu.edu.cn
陈修淋 男，1998年生，硕士研究生，研究方向为新能源发电、电力电子变换等。E-mail: xiulin1998@shu.edu.cn（通信作者）
（编辑 陈 诚）