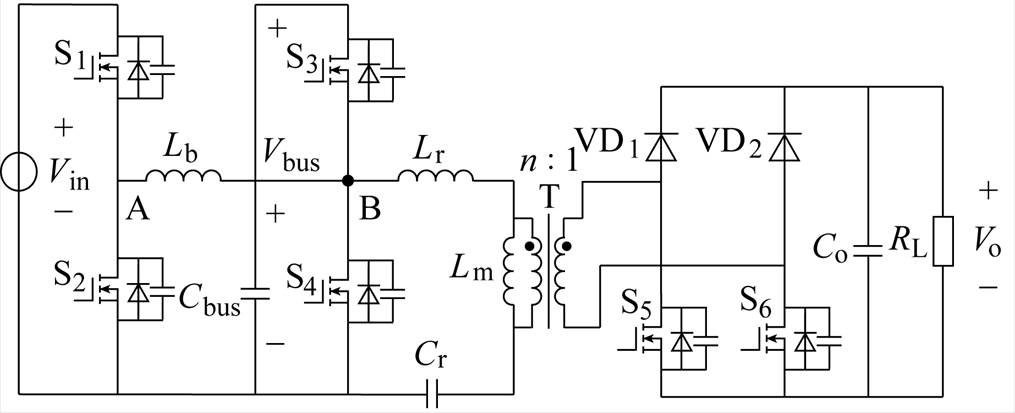
图1 级联式四开关Buck-Boost LLC变换器拓扑
Fig.1 Cascaded four-switch Buck-Boost LLC converter
摘要 为了解决变频控制的桥臂共用型四开关Buck-Boost LLC级联变换器磁性元件设计和优化困难的问题,提出一种二次侧为特殊全桥整流结构的级联式四开关Buck-Boost LLC变换器。通过控制二次侧开关管的交叠导通时间以拓宽变换器的电压增益。该变换器可根据不同的输入电压范围工作在交叠模式和整流模式;在不改变变换器参数的条件下将增益显著提高,能够适应更宽范围的输入电压,同时保持了变换器较高的工作效率。在两种工作模式的基础上,采用移相控制使变换器所有开关管实现零电压导通(ZVS),二极管实现零电流关断(ZCS)。结合状态平面轨迹分析法,对定频控制的级联式四开关Buck-Boost LLC变换器进行模态分析,并推导两种工作模式下的输入-输出表达式和开关管的软开关实现条件。最后,通过研制一台70~280 V输入、240 W/28 V输出的实验样机,验证了理论分析的正确性。
关键词:宽输入电压范围 四开关Buck-Boost LLC变换器 移相控制 软开关
随着能源危机和环境问题的日益严重,燃料电池由于具有能源安全性、环境亲和性、燃料多样性等优点成为分布式电源系统及电动汽车中最有前景的能源技术之一[1]。锂离子电池过充或亏电需要宽输入范围的DC-DC变换器来改善输出特性[2]。电动汽车动力电池组也需要宽输入电压范围的车载DC- DC变换器[3]。在这些应用场合中,宽电压范围DC- DC变换器的隔离性、效率和参数优化均需考虑[4]。因此,研究宽输入电压范围、高效率的DC-DC变换器具有重要意义。
常用的DC-DC变换器软开关设计困难、开关损耗大、效率难以提高[5]。对于软开关拓扑的使用越来越广泛,而其中移相全桥变换器和谐振变换器对其应用较广。移相全桥变换器在轻载工况下易丢失软开关,并且存在环流损耗较大的缺点[6-7]。谐振变换器在特定的工作频率下,谐振电感、谐振电容与变压器构成谐振腔,无须借助其他电路与控制手段实现软开关[8]。传统LLC谐振变换器是通过调频来调节输出电压,变压器的励磁电感需足够小以达到宽输入电压范围的要求;但谐振电流将因此增大,从而使开关管损耗与变压器损耗增加,不利于效率提升,并且变压器优化设计困难[9-10]。
综合宽输入电压范围和效率两方面的考虑,文献[11-15]在LLC谐振变换器的基础上提出两级式DC-DC变换器,而级联式非隔离型DC-DC+LLC级联变换器也得到了广泛关注。在非隔离型DC-DC变换器中,Buck变换器只具备降压功能;LLC谐振变换器的输入电压越高,效率越高;使用Buck变换器作为前级变换器不利于整体工作效率优化。传统Buck-Boost变换器和Cuk变换器的输入输出电压极性相反。因此,传统Buck变换器、Buck-Boost变换器和Cuk变换器均不适合级联变换器的前级方案。文献[11-13]采用了级联式Boost LLC变换器,但前级Boost变换器只有升压功能,实现开关器件的零电压导通(Zero Voltage Switching, ZVS)困难,并且后级LLC谐振变换器的开关器件需承受更高的电压应力。文献[14]提出交错并联Boost变换器与双谐振槽LLC谐振变换器级联而成的新拓扑,但当输入电压范围较宽时,LLC谐振变换器的工作频率范围也随之变宽,并且双谐振槽结构复杂和成本高。文献[15]对集成Buck-Boost LLC级联变换器进行了增益分析、双频控制与同频移相控制研究,但LLC谐振变换器均被当作直流变压器(DC Transformer, DCX),未充分发挥LLC谐振变换器的优势,并且该拓扑在输入与输出极端情况下将出现电感电流过大的问题。文献[8]基于传统变频控制LLC变换器,提出一种改进型LLC变换器,将二次侧全桥整流桥的两个二极管换成开关管,通过二次侧开关管同时导通使谐振电感充电,进而拓宽电压输入范围。
综合以上变换器的优势与不足,本文提出一种二次侧为特殊全桥整流结构的级联式四开关Buck- Boost LLC变换器,以解决LLC谐振变换器在频率变化时带来的磁性元件设计和优化的问题,并使变换器在定频控制下拓宽输入范围。该变换器可根据不同的输入电压范围工作在交叠模式和整流模式,同时对变换器采用移相控制,改变前级四开关Buck- Boost变换器中间电感电流的波形形状,实现一次侧开关管的软开关。结合状态轨迹模型[16-18],对两种模式下的工作模态进行分析,并通过实验样机对理论分析加以验证。
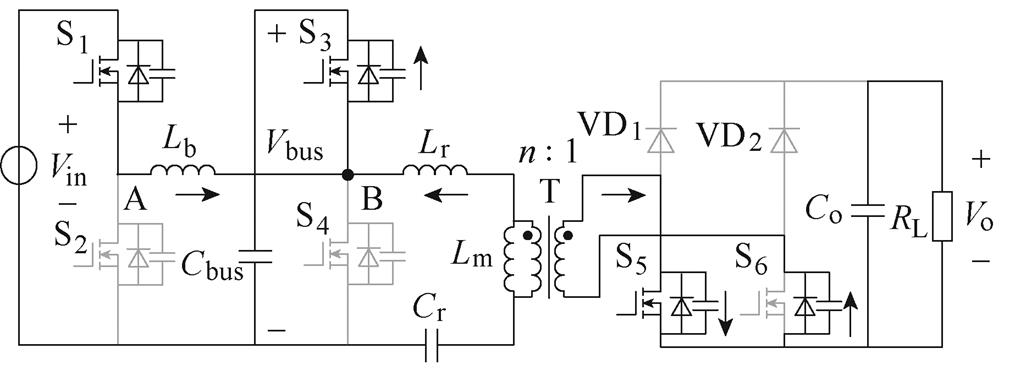
二次侧为特殊全桥整流结构的级联式四开关Buck-Boost LLC变换器拓扑如图1所示。

图1 级联式四开关Buck-Boost LLC变换器拓扑
Fig.1 Cascaded four-switch Buck-Boost LLC converter
桥臂S1、S2与桥臂S3、S4构成前级四开关Buck-Boost变换器,桥臂S3、S4与二次侧开关器件VD1、VD2、S5和S6构成后级半桥LLC谐振变换器;Lb为中间电感,uAB为两端电压;Cbus为中间电容,Vbus为电压;T为变压器,电压比为n 1,Lm为励磁电感;Lr为谐振电感,Cr为谐振电容,两者构成谐振腔的谐振频率为fr;Co为输出滤波电容;RL为负载;Vin为直流输入电压,Vo为输出电压。
1,Lm为励磁电感;Lr为谐振电感,Cr为谐振电容,两者构成谐振腔的谐振频率为fr;Co为输出滤波电容;RL为负载;Vin为直流输入电压,Vo为输出电压。
变换器的特殊全桥整流结构为二次侧两个二极管被替换成开关管S5、S6。S5与S6同时导通使变压器二次侧短路,谐振电感存储能量,从而在定频控制下提高变换器增益,为方便分析,将二次侧开关管S5、S6同时导通时间称为交叠导通时间。
桥臂S1、S2与桥臂S3、S4上下开关管互补导通,开关管S1占空比为d1,共用桥臂S3、S4占空比为0.5,那么变换器输入-输出关系为
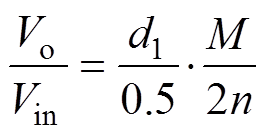 (1)
(1)
需要注意的是:本文中增益M表示后级LLC变换器的增益,是不同于输出-输入电压比的量。
以临界输入电压Vin_thre为分界,变换器根据不同输入电压范围有两种工作模式:①当Vin≤Vin_thre时,S1占空比d1恒为最大值d1max,变换器调节二次侧开关管S5、S6的交叠导通时间使增益M>1,从而稳定输出电压,记为交叠模式;②当Vin>Vin_thre时,二次侧开关管交叠导通时间为零,其占空比均为0.5,增益M=1,起整流作用,变换器对开关管S1进行脉冲宽度调制(Pulse Width Modulation, PWM)以稳定输出电压,记为整流模式。
四开关Buck-Boost变换器与半桥LLC谐振变换器进行了桥臂集成共用[19],但各自的工作状态不受影响。输入电压Vin与中间电容电压Vbus决定着中间电感电流iLb的波形,中间电容电压Vbus与谐振电容电压vCr决定谐振电流iLr的波形。桥臂S1、S2与桥臂S3、S4驱动信号进行移相是实现其软开关的重要方式,移相控制下,变换器的输入-输出关系不受影响。
基于变换器工作效率考虑,使级联式变换器定频工作于谐振频率,那么开关频率fs为
 (2)
(2)
图2为变换器交叠模式的模态波形,一个周期内前半周期与后半周期工作原理类似,在此分析前半周期t0~t6。S1的脉冲信号与S3的脉冲信号形成移相,移相值为p;S5与S6占空比相同,S3与S6开始导通时刻相同,S4与S5开始导通时刻相同;二极管VD1与VD2的电流分别为iD1与iD2。
图3为前半周期各模态的工作电路,设开关管Si的体二极管与结电容分别为VDoi、Cossi(i=1, 2, 3, 4, 5, 6),各模态工作原理分析如下。

图2 变换器交叠模式的模态波形
Fig.2 Modal waveforms of overlapping mode
模态a1[t0, t1 :t0时刻,开关管S1保持导通,S4关断,S3进入死区时间,二极管VD1与VD2未导通;中间电感Lb两端电压uAB由Vin变化为Vin-Vbus,电感电流iLb线性下降;谐振电流为负,电流iLb与iLr均流向点B,此模态下两电流对Coss3放电、Coss4充电。死区时间内,Coss3放电完成,体二极管VDo3导通,S3在其脉冲信号到来时刻t1实现ZVS。
:t0时刻,开关管S1保持导通,S4关断,S3进入死区时间,二极管VD1与VD2未导通;中间电感Lb两端电压uAB由Vin变化为Vin-Vbus,电感电流iLb线性下降;谐振电流为负,电流iLb与iLr均流向点B,此模态下两电流对Coss3放电、Coss4充电。死区时间内,Coss3放电完成,体二极管VDo3导通,S3在其脉冲信号到来时刻t1实现ZVS。

(a)模态a1[t0, t1
(b)模态a2[t1, t2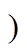

(c)模态a3[t2, t3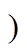
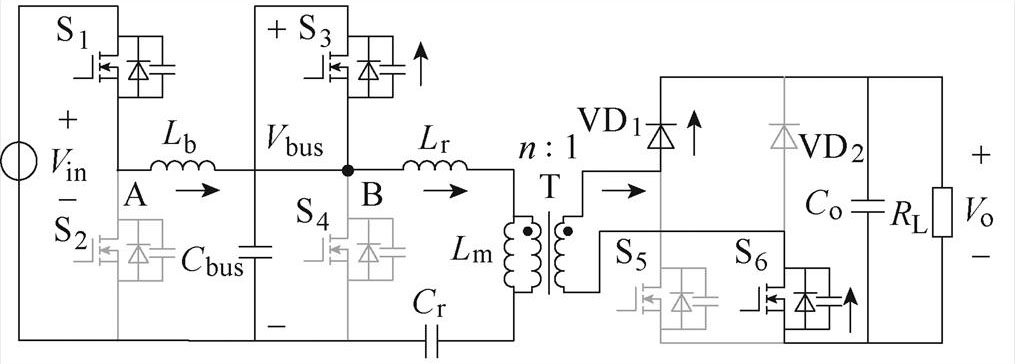
(d)模态a4[t3, t4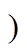

(e)模态a5[t4, t5
(f)模态a6[t5, t6]
图3 交叠模式前半周期各模态的工作电路
Fig.3 Operating circuit for each mode in first half cycle of overlapping mode
模态a2[t1, t2 :t1时刻,开关管S1保持导通,S3 ZVS导通;二次电流流通路径为:变压器绕组上端→S5→VDo6→变压器绕组下端,S6漏源极间电压已为零,则S6在其脉冲信号到来时刻t2实现ZVS。
:t1时刻,开关管S1保持导通,S3 ZVS导通;二次电流流通路径为:变压器绕组上端→S5→VDo6→变压器绕组下端,S6漏源极间电压已为零,则S6在其脉冲信号到来时刻t2实现ZVS。
模态a3[t2, t3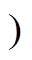 :t2时刻,开关管S1与S3保持导通;二次侧S5保持导通,S6ZVS导通,进入交叠导通时段。由图3c可知,变压器二次侧短路与励磁电感Lm被短路,模态a3的谐振腔简化电路如图4所示。
:t2时刻,开关管S1与S3保持导通;二次侧S5保持导通,S6ZVS导通,进入交叠导通时段。由图3c可知,变压器二次侧短路与励磁电感Lm被短路,模态a3的谐振腔简化电路如图4所示。
根据图4所示电路列写电路方程为
 (3)
(3)
 (4)
(4)
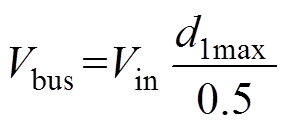 (5)
(5)
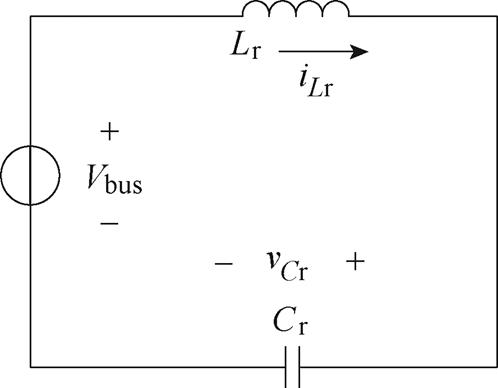
图4 模态a3的谐振腔简化电路
Fig.4 Simplified circuit of resonant cavity for mode a3
联立式(3)~式(5),可解得谐振电流与谐振电容电压为
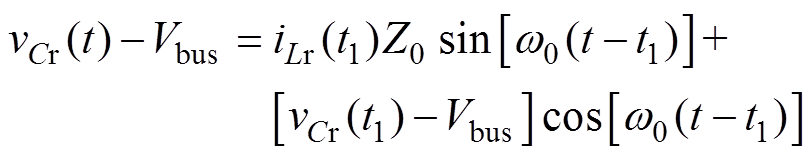 (6)
(6)
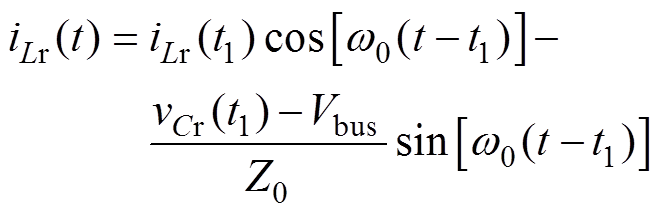 (7)
(7)
其中
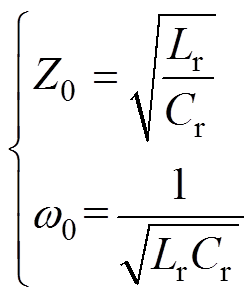 (8)
(8)
根据式(6)、式(7),模态a3的状态轨迹曲线方程为
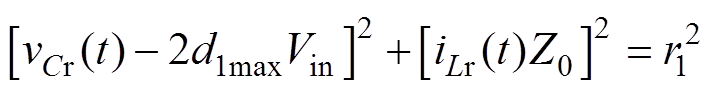 (9)
(9)
其中
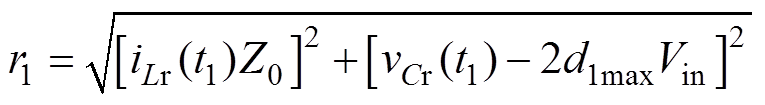 (10)
(10)
对谐振腔进行状态轨迹分析,以谐振电容电压vCr为横坐标,Z0iLr为纵坐标,交叠模式的状态轨迹图如图5所示。模态a2与模态a3的状态轨迹为图中AB段圆弧,其圆心为(2d1maxVin, 0),半径为r1。
模态a4[t3, t4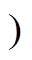 :t3时刻,开关管S1与S3保持导通;S5关断,S6保持导通,二极管VD1承受正向电压导通,S5与S6脱离交叠导通时段,变压器二次侧与励磁电感不再被短路,变压器一次侧被钳位至nVo,模态a4的谐振腔简化电路如图6所示。
:t3时刻,开关管S1与S3保持导通;S5关断,S6保持导通,二极管VD1承受正向电压导通,S5与S6脱离交叠导通时段,变压器二次侧与励磁电感不再被短路,变压器一次侧被钳位至nVo,模态a4的谐振腔简化电路如图6所示。
同理,模态a4的状态轨迹曲线方程为
 (11)
(11)
其中
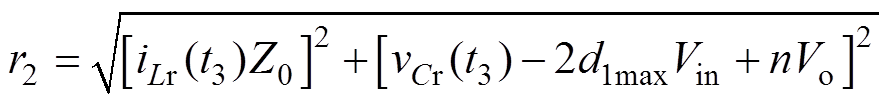 (12)
(12)
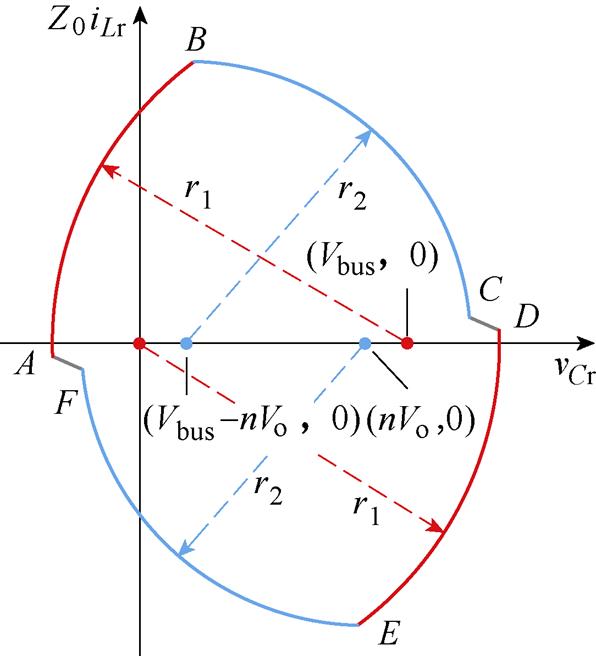
图5 交叠模式下谐振腔的状态轨迹图
Fig.5 State trajectory diagram of resonant slot in overlapping mode
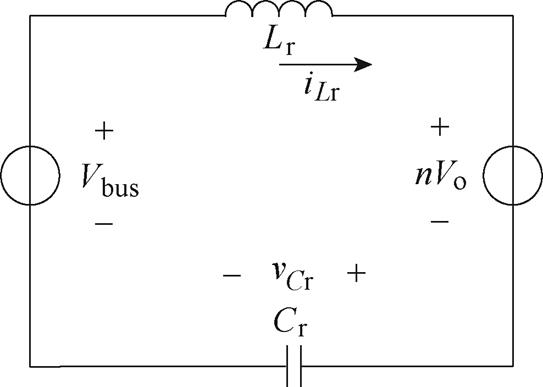
图6 模态a4的谐振腔简化电路
Fig.6 Simplified circuit of resonant cavity for mode a4
变压器二次侧未被短路,励磁电感Lm两端电压被钳位至nVo,根据伏秒平衡可得
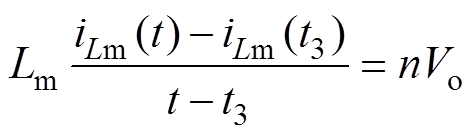 (13)
(13)
模态a5[t4, t5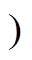 :t4时刻,开关管S1关断,死区时间内,电感电流iLb对S2的结电容完成放电,体二极管VDo2导通,在接下来的脉冲信号到来时刻实现ZVS;S3保持导通,uAB由Vin-Vbus变化为-Vbus,电感电流iLb由正向负线性减小;模态a5的谐振腔等效电路与模态a4相同。
:t4时刻,开关管S1关断,死区时间内,电感电流iLb对S2的结电容完成放电,体二极管VDo2导通,在接下来的脉冲信号到来时刻实现ZVS;S3保持导通,uAB由Vin-Vbus变化为-Vbus,电感电流iLb由正向负线性减小;模态a5的谐振腔等效电路与模态a4相同。
模态a4与模态a5的状态轨迹曲线为BC段圆弧,其圆心为(2d1maxVin-nVo, 0),半径为r2。
模态a6[t5, t6 :t5时刻,开关管S2与S3保持导通,谐振电流iLr下降至与励磁电流iLm相交,电感电流iLb在t6时刻下降至最小值;二极管电流iD1在t5时刻自然到零,VD1实现ZCS,励磁电感不再被钳位于nVo。模态a6的谐振腔简化电路如图7所示。
:t5时刻,开关管S2与S3保持导通,谐振电流iLr下降至与励磁电流iLm相交,电感电流iLb在t6时刻下降至最小值;二极管电流iD1在t5时刻自然到零,VD1实现ZCS,励磁电感不再被钳位于nVo。模态a6的谐振腔简化电路如图7所示。
同理,模态a6的状态轨迹曲线方程为
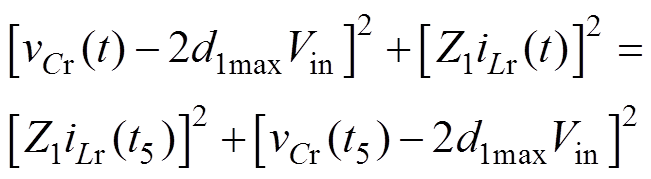 (14)
(14)
其中
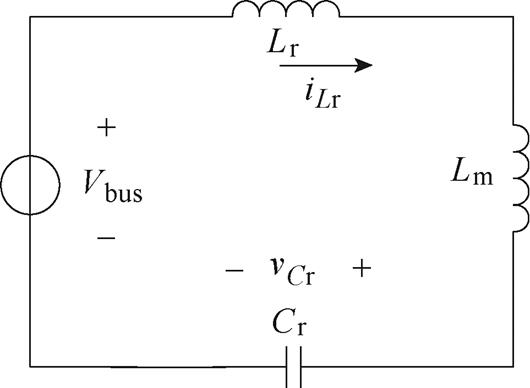
图7 模态a6的谐振腔简化电路
Fig.7 Simplified circuit of resonant cavity for mode a6
 (15)
(15)
模态a7[t6, t7]:模态a7为后半周期的开始模态,在t6时刻,开关管S2保持导通,S3关断,谐振电流与励磁电流相等,S3的结电容Coss3充电,S4的结电容放电;uAB由-Vbus变化为0,电感电流iLb保持负值不变。死区时间内,电流iLb与iLr共同对结电容Coss4完成放电,使S4在下一模态开始时刻t7实现ZVS。
模态a6与模态a7的状态轨迹为图5中CD段椭圆弧。
后半周期工作模态原理类似,不作赘述。图5中,DE段圆弧圆心为(0, 0),半径为r1;图5中,EF段圆弧圆心为(nVo, 0),半径为r2;FA为椭圆弧。
在整流模式下,开关管S5、S6交叠导通时间为零,占空比均为0.5,与二极管功能相同。后级变换器作DCX作用,其增益M保持为1,谐振频率下,谐振电流为标准正弦波,整流模式的模态波形如图8所示。
模态b1[t0, t1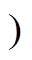 :t0时刻,开关管S1保持导通,S2保持关断,S4关断,谐振电流对S3的结电容放电;uAB由Vin变化为Vin-Vbus,电感电流iLb开始线性上升。
:t0时刻,开关管S1保持导通,S2保持关断,S4关断,谐振电流对S3的结电容放电;uAB由Vin变化为Vin-Vbus,电感电流iLb开始线性上升。
模态b2[t1, t2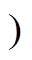 :t1时刻,S3结电容完成放电,其体二极管VDo3导通,S3实现零电压导通,二极管VD1导通。
:t1时刻,S3结电容完成放电,其体二极管VDo3导通,S3实现零电压导通,二极管VD1导通。
模态b3[t2, t3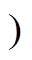 :t2时刻,S1关断,uAB由Vin-Vbus变化为-Vbus,电感电流iLb由正向负线性下降,并对S2的结电容放电,S3与S6保持导通,S4与S5保持关断。
:t2时刻,S1关断,uAB由Vin-Vbus变化为-Vbus,电感电流iLb由正向负线性下降,并对S2的结电容放电,S3与S6保持导通,S4与S5保持关断。
模态b4[t3, t4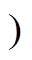 :t3时刻,S2结电容完成放电,其体二极管VDo2导通,S2实现零电压导通。
:t3时刻,S2结电容完成放电,其体二极管VDo2导通,S2实现零电压导通。
模态b5[t4, t5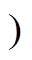 :t4时刻,S2保持导通,S3关断,uAB由-Vbus变化为0,电感电流iLb保持负值不变;谐振电流iLr对S4的结电容Coss4放电,同时下降至与励磁电流相交,电流iD1自然到零,二极管VD1实现ZCS。
:t4时刻,S2保持导通,S3关断,uAB由-Vbus变化为0,电感电流iLb保持负值不变;谐振电流iLr对S4的结电容Coss4放电,同时下降至与励磁电流相交,电流iD1自然到零,二极管VD1实现ZCS。

图8 整流模式的模态波形
Fig.8 Modal waveforms of rectification mode
模态b6[t5, t6]:t5时刻,S2保持导通,S4结电容放电完成,其体二极管VDo4导通,S4实现ZVS,二极管VD2导通。后半周期工作原理类似,不作赘述。
在交叠模式下,开关管S1占空比d1保持为最大值d1max不变,变换器通过改变交叠占空比doverlap来调节增益M的值,doverlap定义为
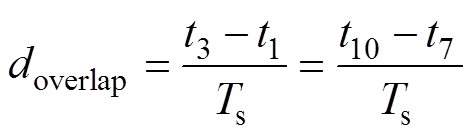 (16)
(16)
式中,Ts为开关周期。
定频模式下,励磁电感远大于谐振电感,因t5~t6时间段极短,该段时间内可认为励磁电流极小且未变化,并假设其值为ILm,那么ILm满足
 (17)
(17)
为简化分析,忽略励磁电流[20],谐振电流和谐振电容电压在t1与t5时刻的关系为
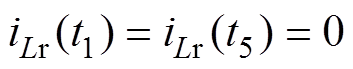 (18)
(18)
 (19)
(19)
交叠模式下的中间电容电压满足式(5)。
变换器输出功率可表示为
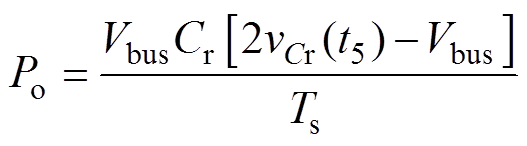 (20)
(20)
图5所示的状态轨迹图中,t3时刻对应着轨迹曲线AB段圆弧的B点,结合式(18)、式(19),t3时刻的谐振电流与谐振电容电压分别为
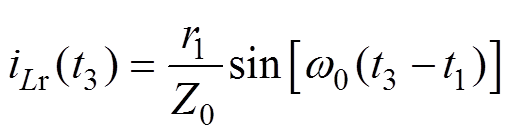 (21)
(21)
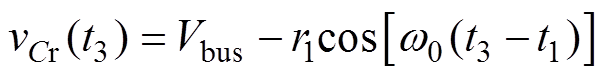 (22)
(22)
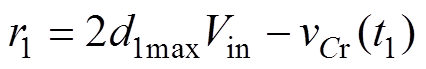 (23)
(23)
B点又在BC段圆弧上,那么t3时刻谐振电流与谐振电容电压的另一种表达式为
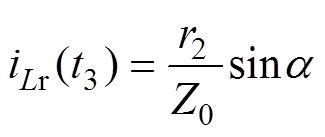 (24)
(24)
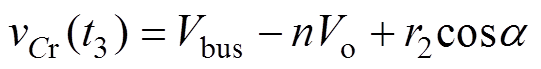 (25)
(25)
式中,a 为这一阶段的初始角度。
根据模态a5的状态轨迹曲线方程式(11),t5时刻有
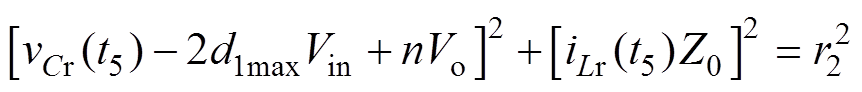 (26)
(26)
联立式(12)、式(16)和式(18)~式(26)可以得到增益M和交叠占空比doverlap的关系为
 (27)
(27)
采用以下实验参数:变压器电压比n=3;谐振电感Lr=15.134 mH;谐振电容Cr=168 nF;输出电压Vo=28 V,开关周期Ts=10 ms,绘制交叠模式下不同输出功率时变换器增益M与交叠占空比doverlap的关系曲线,如图9所示。从关系曲线可知,变换器可在谐振频率下改变交叠占空比doverlap可调节增益M的值。
值得注意的是:交叠占空比doverlap存在限制,其极限值为0.25。以谐振电流iLr变化率的角度分析,在半个周期内,模态a3为交叠导通时间存在的模态,其谐振电流变化率为|Vbus-vCr|/Lr;模态a4与模态a5为结束交叠导通状态后向二次侧及负载传输能量的模态,其谐振电流变化率为|Vbus-vCr-nVo|/Lr,而|Vbus-vCr|/Lr>|Vbus-vCr-nVo|/Lr,那么交叠导通时间段(t1~t3)的谐振电流变化率大于能量传输时间段(t3~t5)的变化率。因励磁电流较小,谐振电流在半个周期内始于励磁电流,回归励磁电流,那么交叠导通时间应小于能量传输时间;在半个周期内,交叠导通时间应满足t3-t1<Ts/4,根据式(16)所示的交叠导通时间定义,doverlap<0.25。
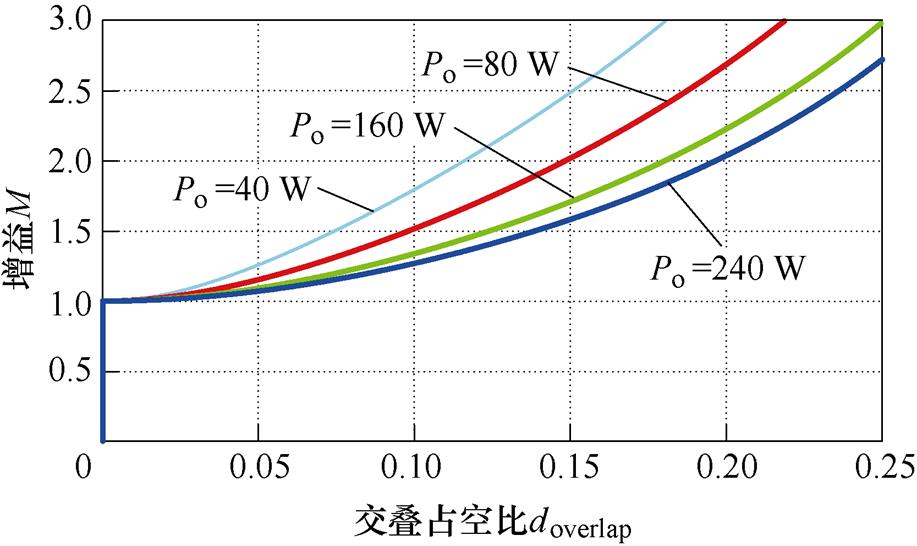
图9 增益M与交叠占空比doverlap关系曲线
Fig.9 Graph of gain M versus overlap duty ratio doverlap
根据式(27)与图9所示的关系曲线,当变换器参数开关周期Ts、变压器电压比n与谐振电容Cr确定后,存在以下两种情况。
(1)变换器输出功率Po≤160 W的情况下,增益M可在doverlap的限制范围内达到较大值;在同一输出功率所在的曲线上,增益M需求较大时,通过增加交叠占空比doverlap使M变大;但是在轻载情况下,负载越轻,增益曲线变化率越大,变换器可能会因DSP分辨率限制而出现调节精度的问题。
(2)变换器输出功率Po>160 W的情况下,增益M在doverlap的限制范围内不能达到3;在同一输出功率所在增益曲线上,增益M需求较大时,在一定交叠占空比裕度内的需求可得到满足。
所以,变换器功率调节范围也存在限定,在变换器硬件参数设计时,应该综合考虑输入-输出范围与图9所示关系曲线,合理设定变换器功率以满足增益M的需求,并且注意交叠占空比doverlap需要留出一定的裕度。
在整流模式下,变换器通过改变开关管S1的占空比d1稳定输出电压,二次侧开关管S5、S6互补导通且占空比均为0.5,交叠导通时间为零,增益M=1,那么整流模式下输入-输出关系式为
 (28)
(28)
全输入电压范围内,开关管S1占空比d1与交叠导通占空比doverlap分别为
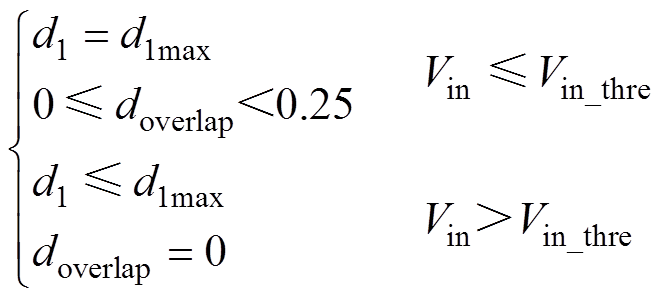 (29)
(29)
以开关管S1开始导通时刻为零时刻,移相值p为S1脉冲信号超前S3脉冲信号的时间与工作周期之比,则电感电流iLb表达式为
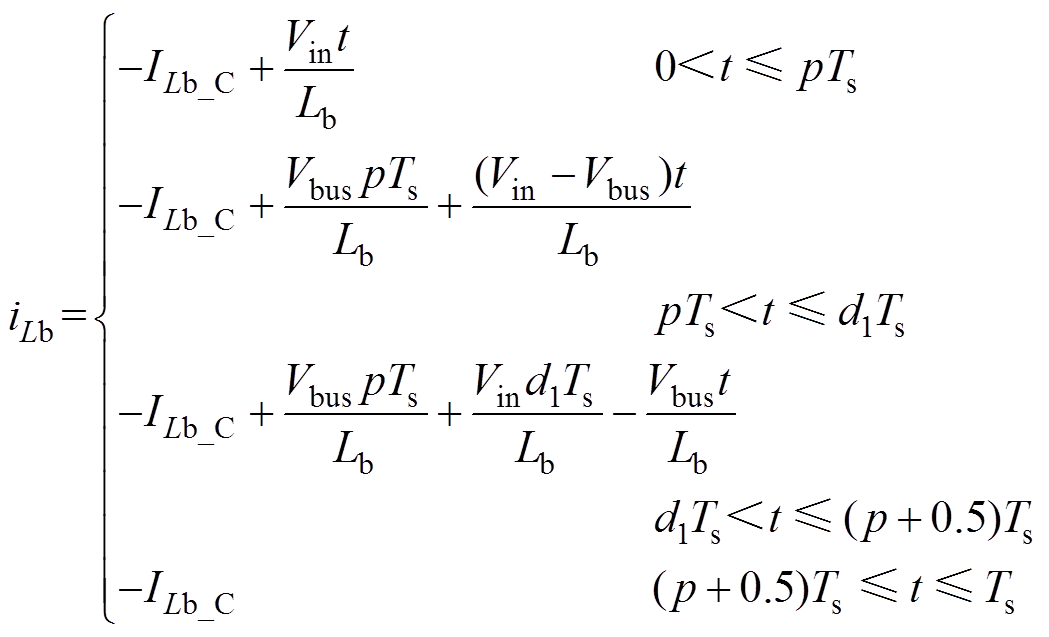 (30)
(30)
忽略变换器的功率传输损耗,传输功率[21]为
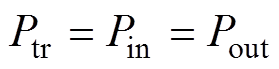 (31)
(31)
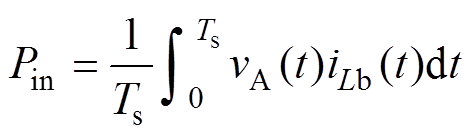 (32)
(32)
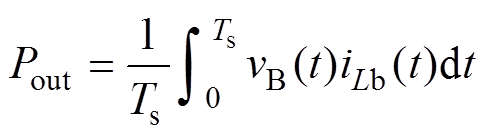 (33)
(33)
式中,vA(t)为开关管S2的漏源极间电压;vB(t)为开关管S4的漏源极间电压,计算得传输功率为
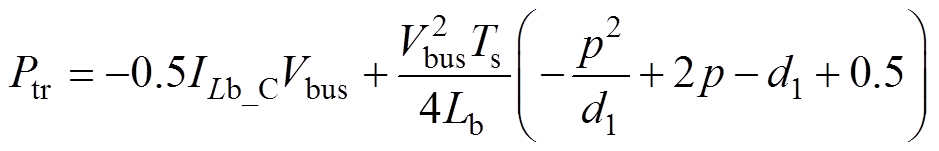 (34)
(34)
根据式(34),当工作周期Ts、电感Lb、传输功率Ptr确定时,d1、Vbus、p、ILb_C存在着制约关系,在确定的输入电压下,d1与Vbus也确定,式(34)为p与ILb_C的关系式。死区时间内,电流iLb和iLr对开关管结电容充放电,ILb_C实现软开关的最小值为IZVS,IZVS为
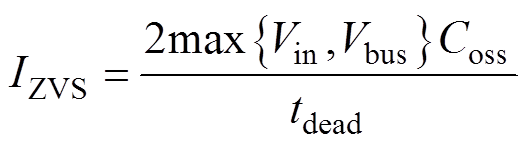 (35)
(35)
变换器工作于谐振频率时,变压器励磁电流iLm分别在开关管S5关断时刻与S3关断时刻达到最小值-ILm与最大值ILm,并且等于谐振电流iLr,那么关于ILm的表达式为
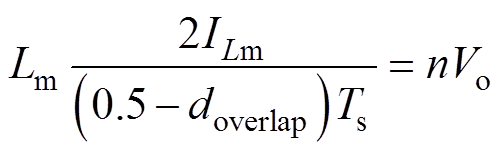 (36)
(36)
开关管S1与S2的软开关实现由电感电流iLb决定;S3与S4的软开关实现由电感电流iLb和谐振电流iLr共同决定,变换器一次侧开关管S1~S4实现软开关的条件为
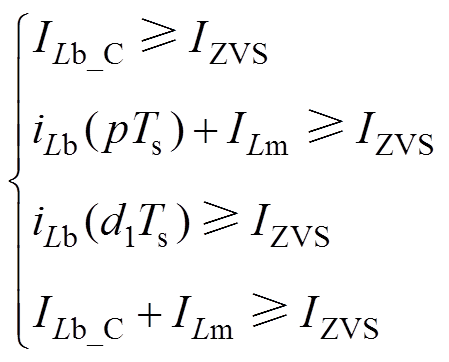 (37)
(37)
将电感电流iLb表达式(30)~式(37)联立,可解得变换器的软开关条件为
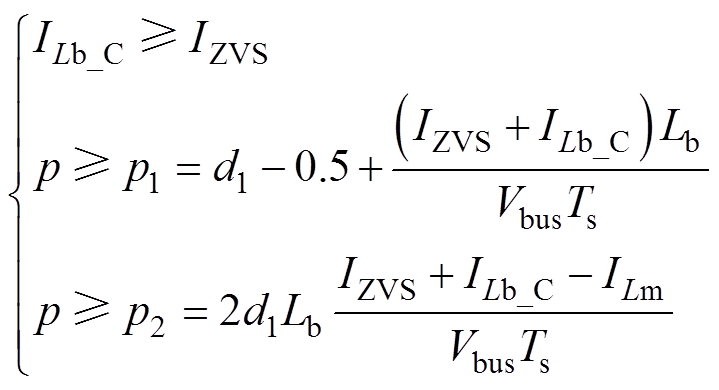 (38)
(38)
1)中间电感Lb
前级四开关Buck-Boost变换器可能处于降压状态或升压状态,那么中间电感的表达式为
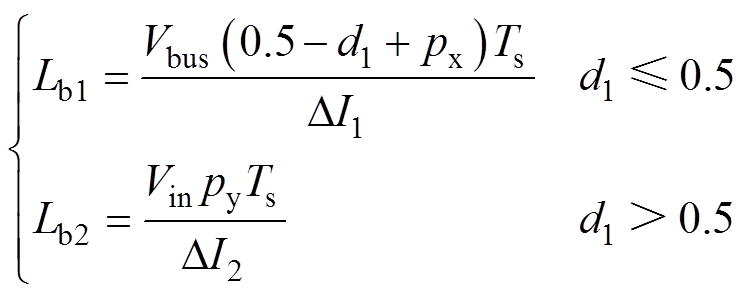 (39)
(39)
式中,px与py为两种状态下的移相值;DI1与DI2为两种状态下的电流波动值,为满足全输入电压范围内电感电流波动值,Lb取较大的值为
 (40)
(40)
2)变压器电压比n
变换器输入电压为临界输入电压Vin_thre时,增益M=1,d1为最大值,那么变压器电压比n为
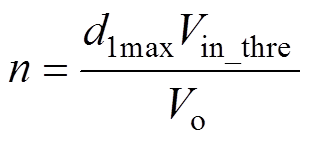 (41)
(41)
3)谐振腔参数
根据输出功率表达式(20),谐振电容Cr为
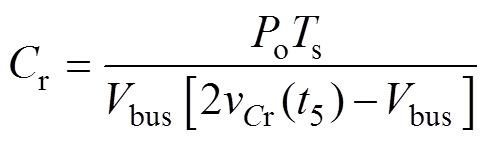 (42)
(42)
谐振电容在输出功率最大、中间电容电压Vbus最小时选取,当谐振电容确定后,谐振电感Lr为
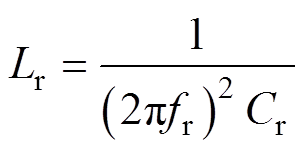 (43)
(43)
变换器采用定频控制,为减小变压器损耗提高效率,励磁电感Lm应尽可能大,但考虑到软开关的实现,根据式(36),励磁电感在交叠占空比为设定最大值doverlap_max时选取,那么励磁电感Lm为
 (44)
(44)
为了验证本文提出的二次侧为特殊全桥整流结构的级联式四开关Buck-Boost LLC变换器理论分析,搭建了一台240 W的实验样机,如图10所示。样机的主要实验参数见表1。
表1 级联式四开关Buck-Boost LLC变换器实验参数
Tab.1 Experiment parameters of cascaded four-switch Buck-Boost LLC converter

参 数数 值 输入电压Vin/V70~280 临界输入电压Vin_thre/V120 谐振电感Lr/mH15.13 谐振电容Cr/nF167 励磁电感Lm/mH120 变压器电压比n31 开关频率fs/kHz100 中间电容Cbus/mF150×4 输出滤波电容Co/mF470×2 输出电压Vo/V28 最大输出功率Po/W240
变换器输入电压范围为70~280 V,临界输入电压为120 V。当输入电压在70~120 V范围内时,变换器工作于交叠模式;当输入电压在120~280 V范围内时,变换器工作于整流模式。

图10 实验样机
Fig.10 Experimental prototype
各实验波形中,vgsi与vdsi分别表示开关管Si(i=1, 2, 3, 4, 5, 6)的栅极驱动电压与漏源极间电压,图11为输入电压Vin=70 V时变换器的实验波形。
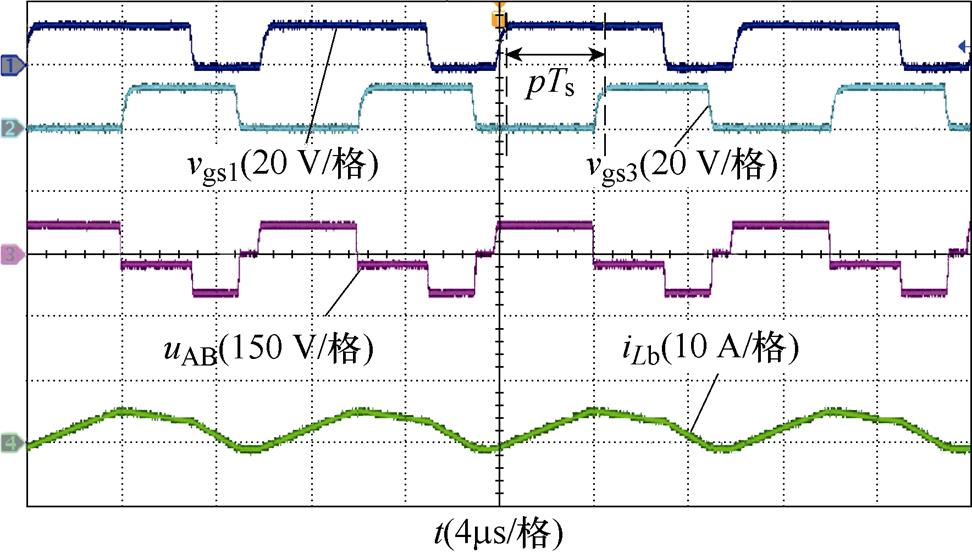
(a)中间电感电压与电流波形
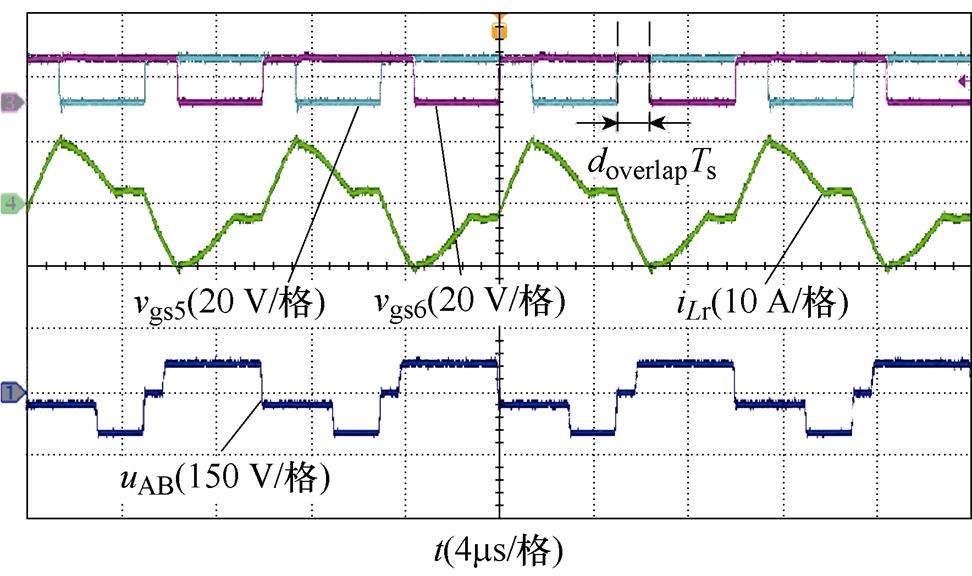
(b)二次侧交叠导通信号与谐振电流波形
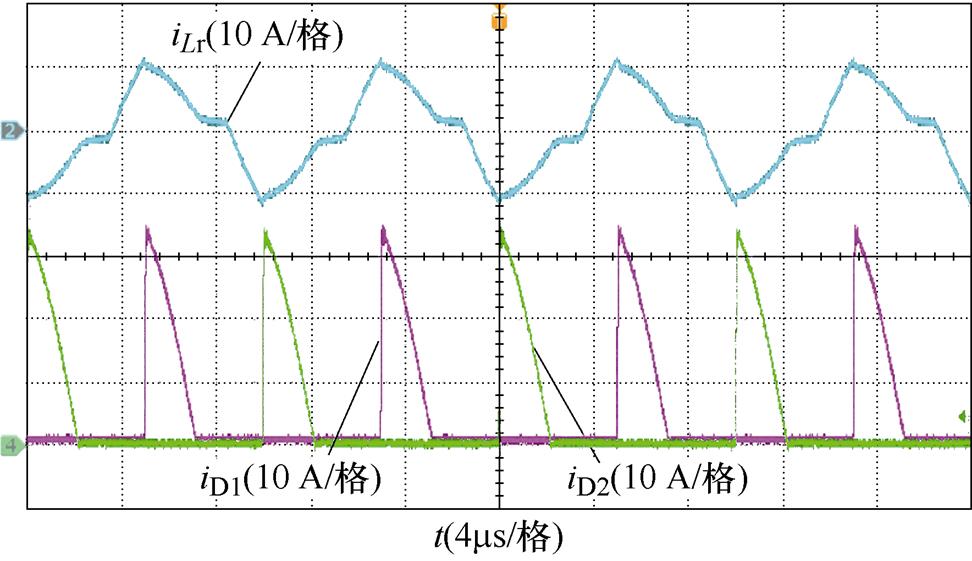
(c)谐振电流与二极管电流波形
图11 输入电压为70 V时变换器的实验波形
Fig.11 Experimental waveforms of the converter with Vin=70 V
如图11a所示,合适的移相值改变电流iLb的波形形状,实现开关管S1与S2的软开关。图11b为开关管S5与S6交叠导通信号,谐振电流在交叠导通时间内振幅大,因而变化率较大,在交叠导通时间外,谐振电流为与整流模式相同的正弦波。如图11c所示,二极管VD1与VD2的电流自然到零,实现零电流关断。
图12为输入电压Vin=70 V时变换器的软开关实验波形。变换器所有开关管均实现了零电压导通,并且S5与S6实现软开关的时间裕度较大。
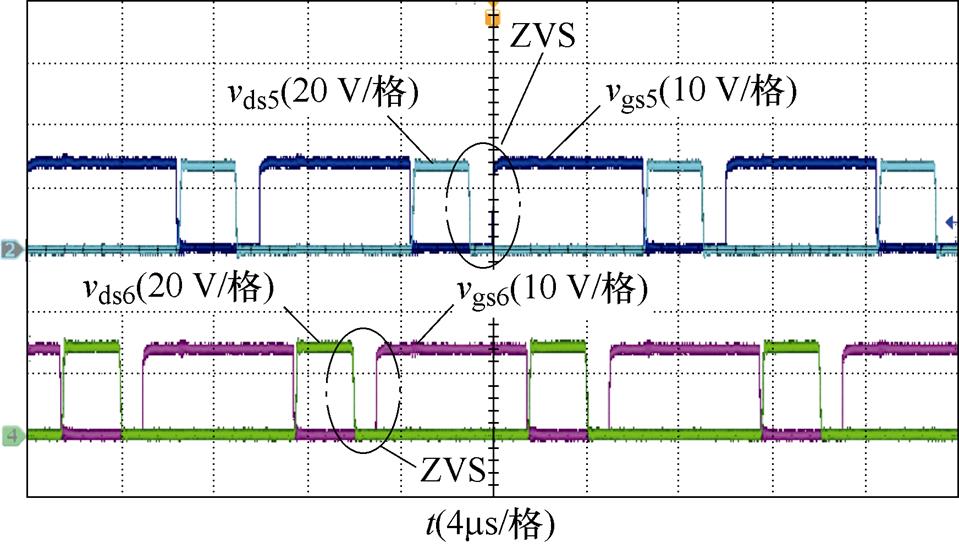
(a)二次侧开关管软开关波形
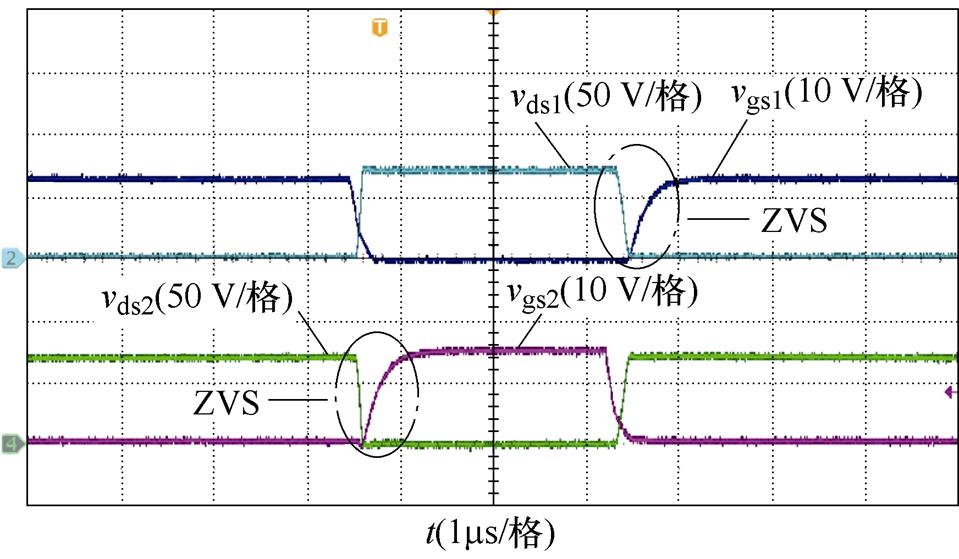
(b)一次侧开关管S1与S2软开关电流波形
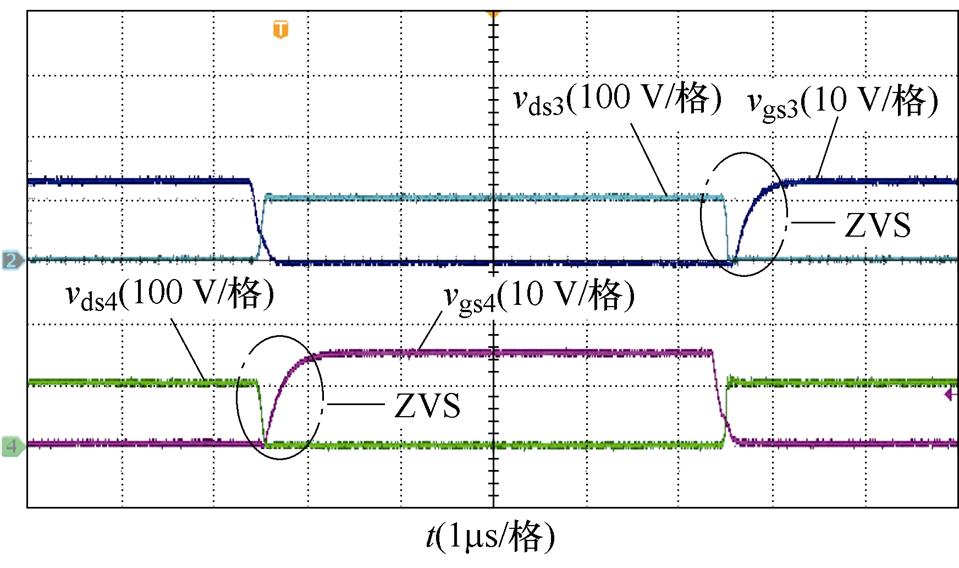
(c)一次侧开关管S3与S4软开关电流波形
图12 输入电压为70 V时变换器的软开关实验波形
Fig.12 Soft switching experimental waveforms of the converter with Vin=70 V
图13为输入电压Vin=120 V时变换器的实验波形。此时,变换器工作于整流模式,前级变换器为升压状态,一次侧两桥臂间仍有移相以实现软开关。
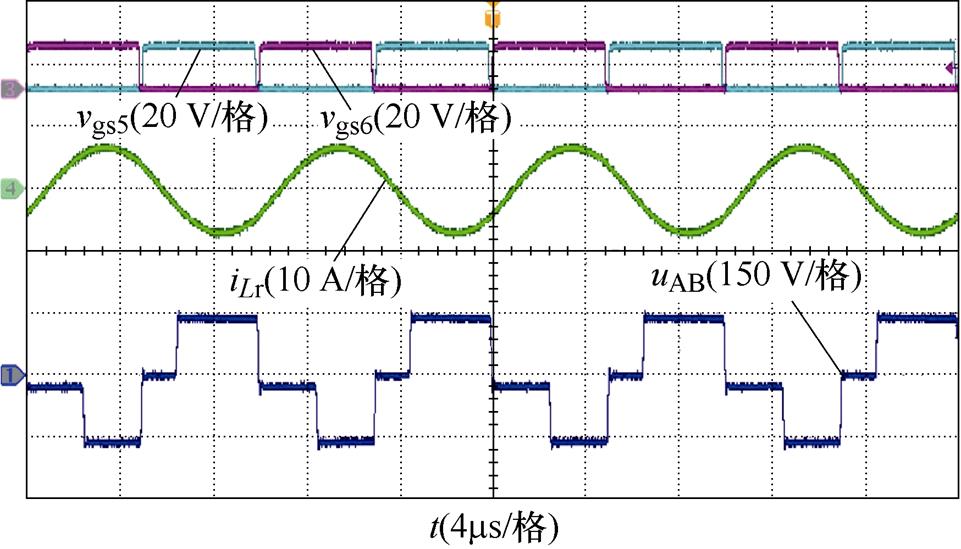
(a)二次侧开关信号与谐振电流波形
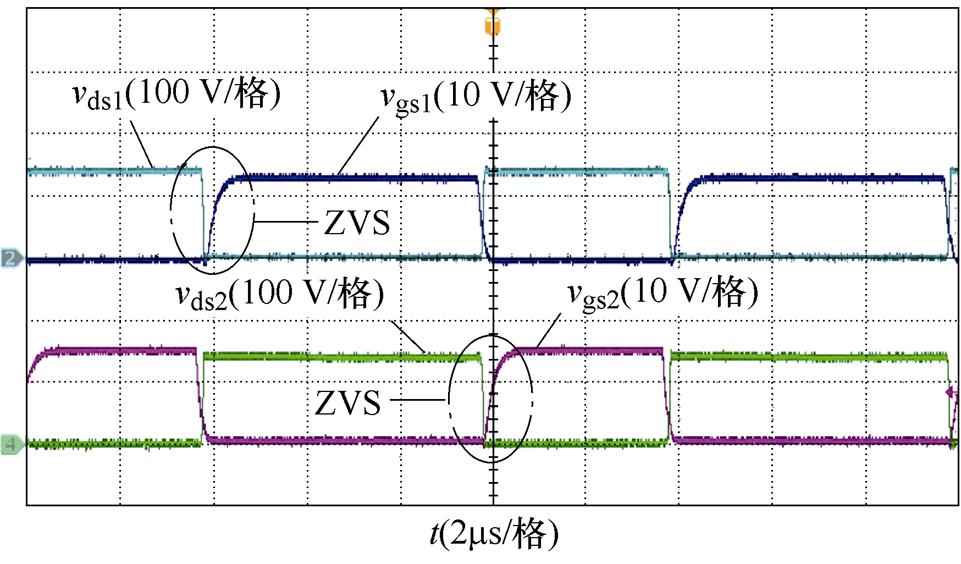
(b)一次侧开关管S1与S2软开关电流波形
图13 Vin=120 V时变换器的实验波形
Fig.13 Experimental waveforms of the converter with Vin=120 V
如图13a所示,S5与S6占空比均为0.5,交叠导通时间为零。谐振电流为正弦波,那么后级LLC变换器开关管实现ZVS,二极管电流自然到零实现ZCS,如图13b所示,在合适的移相值下,桥臂(S1、S2)实现了ZVS。
图14为输入电压Vin=280 V时变换器的实验波形。此时,变换器工作于整流模式,前级变换器为降压状态,所有开关管与二极管均实现了软开关。
图15为变换器在三个实验输入电压下不同输出功率的效率曲线。由曲线可知,半载至满载时,变换器效率在90%以上,实验测试效率曲线在输入电压为280 V、输出功率为160 W时达到峰值效率94.4%。变换器工作于交叠模式时,一个周期内存在四个模态二次侧开关器件未作用,输入-输出能量传输时间变小,开关管S1占空比d1保持最大值,中间电感电流应力较大。变换器工作于整流模式时,一个周期内存在两个模态二次侧开关器件未作用,能量传输时间比交叠模式多,开关管S1占空比在0.5附近,中间电感电流应力较小,整体效率略高于交叠模式,但在半载以上时,效率非常接近。
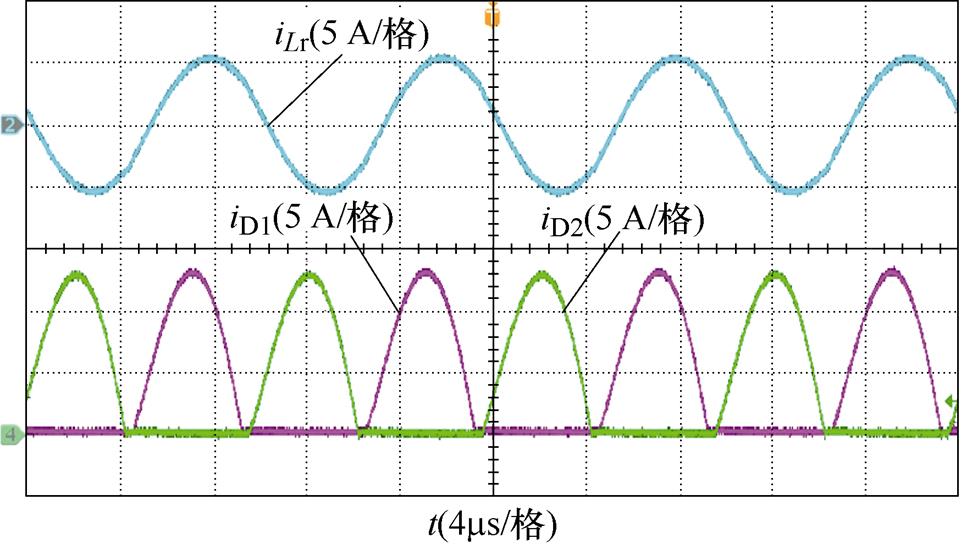
(a)谐振电流与二极管电流波形
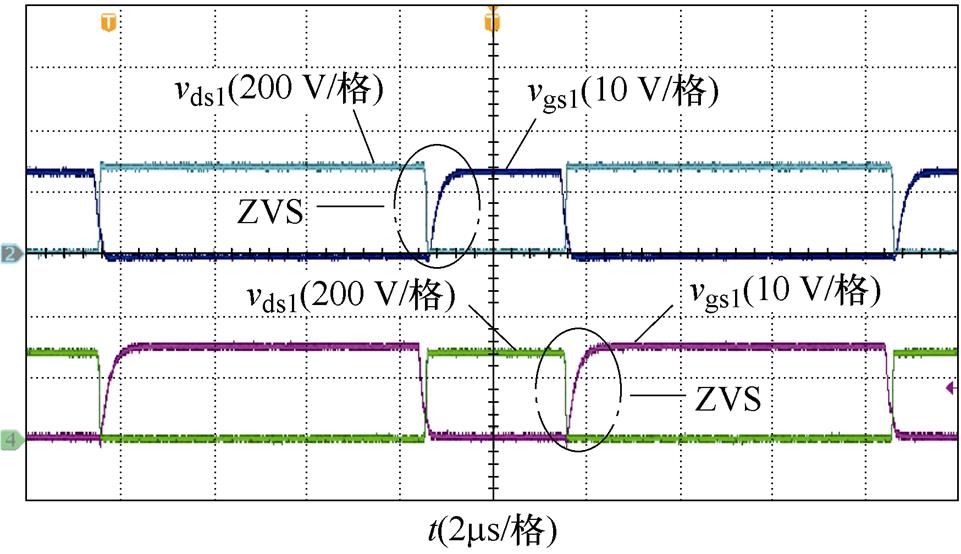
(b)一次侧开关管S1与S2软开关电流波形
图14 Vin=280 V时变换器的实验波形
Fig.14 Experimental waveforms of the converter with Vin=280 V
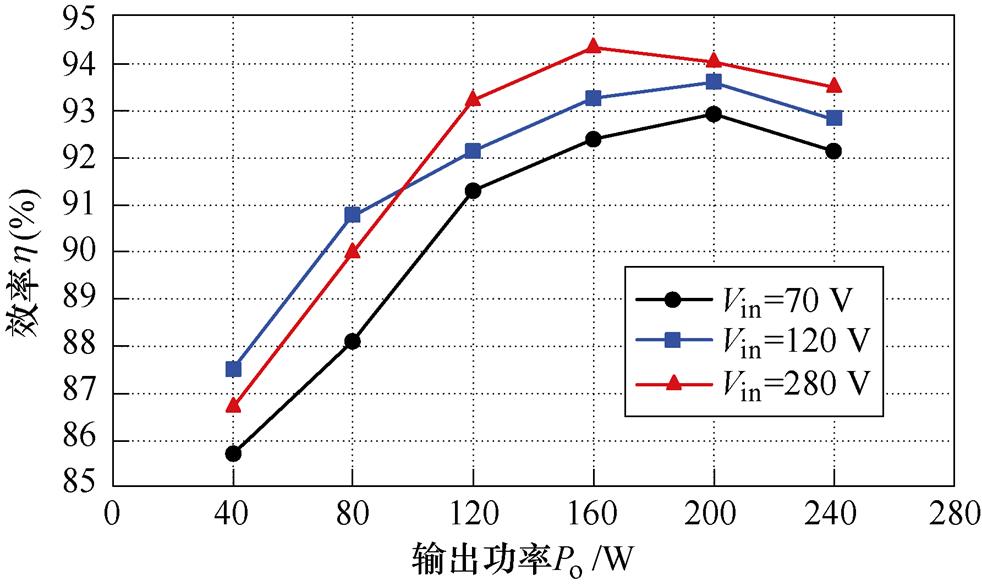
图15 不同输入电压下的效率曲线
Fig.15 Efficiency curves at different input voltages
图15所示94.4%的效率值是在输入电压为280 V、输出功率为160 W功率的条件下得到的,故94.4%为整流模式的峰值效率;当输入电压为70~120 V时,变换器工作于交叠模式,交叠模式下的峰值效率逼近于输入电压为120 V时的峰值效率,以输入电压为120 V的效率曲线中的峰值效率93.6%作为交叠模式的峰值效率。
表2给出了四种宽输入电压范围LLC类变换器的控制自由度、输入电压范围、输入电压倍数和峰值效率等性能指标对比数据,其中输入电压倍数为最大输入电压与最小输入电压之比。
由表2的对比可知,文献[15]的后级LLC变换器仅作DCX作用,且变压器二次侧为双绕组,不利于磁性元件的设计,其输入电压倍数和峰值效率均较低。文献[8]的控制自由度为3,峰值效率最高,输入电压倍数为3.33,交叠模式下本文具有与文献[8]相近的峰值效率,并且具有更大的输入电压倍数。文献[22]与本文的输入电压倍数均为4,但峰值效率略低于本文,且控制自由度为2。综合比较,本文提出的级联式四开关Buck-Boost变换器在控制自由度、输入电压倍数和效率方面具有较大优势。
表2 四种LLC类变换器的性能指标对比
Tab.2 Comparison of performance indexes of 4 types of LLC-type converters

LLC类变换器控制自由度输入电压范围/V输入电压倍数峰值效率(%) 移相控制集成Buck-Boost LLC级联变换器[15]2200~4502.2590.5 混合模式定频控制改进型LLC变换器[8]3120~4003.3394.6 二极管钳位全桥三电平LLC变换器[22]2100~400492.5 级联式四开关Buck-Boost LLC变换器(本文)370~280493.6
本文提出一种二次侧为特殊全桥整流结构的定频控制级联式四开关Buck-Boost LLC变换器。根据不同输入电压范围,变换器工作于交叠模式与整流模式:工作于交叠模式时,变换器控制交叠占空比调节增益M,稳定输出电压;工作于整流模式时,交叠占空比为零,增益M为定值1,通过对一次侧桥臂S1、S2进行PWM控制来稳定变换器的输出电压。在这两种工作模式的基础上,对一次侧两个桥臂采用移相控制,实现所有开关管与二极管的软开关。该变换器在传统拓扑基础上拓宽了输入范围,可设计在4倍以上的输入电压倍数并且具有较高效率。在今后的工作中,应考虑优化变换器的移相控制,使其切换平滑、算法简单。
参考文献
[1] Mazumder S K, Burra R K, Huang Rongjun, et al. A universal grid-connected fuel-cell inverter for resi- dential application[J]. IEEE Transactions on Indu- strial Electronics, 2010, 57(10): 3431-3447.
[2] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of Lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[3] 丁超, 李勇, 姜利, 等. 电动汽车直流充电系统LLC谐振变换器软开关电压边界分析[J]. 电工技术学报, 2022, 37(1): 3-11.
Ding Chao, Li Yong, Jiang Li, et al. Analysis of soft switching voltage boundary of LLC resonant con- verter for EV DC charging system[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 3-11.
[4] 焦健, 郭希铮, 游小杰, 等. LLC谐振变换器的改进型电流解析方法[J]. 电工技术学报, 2021, 36(23): 5002-5013.
Jiao Jian, Guo Xizheng, You Xiaojie, et al. An improved current analytical method for LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 5002-5013.
[5] 童军, 吴伟东, 李发成, 等. 基于GaN器件的高频高效LLC谐振变换器[J]. 电工技术学报, 2021, 36(增刊2): 635-643.
Tong Jun, Wu Weidong, Li Facheng, et al. High frequency and high efficiency LLC resonant converter based on GaN device[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 635-643.
[6] 沙德尚, 李斌, 袁文琦, 等. 基于负载自适应的辅助LC网络宽范围零电压开通的输入串联输出并联移相全桥DC-DC变换器[J]. 中国电机工程学报, 2016, 36(13): 3558-3564, 3374.
Sha Deshang, Li Bin, Yuan Wenqi, et al. Loads adaptive input-series-output-parallel phase shift full bridge derived DC-DC converters with auxiliary LC networks to achieve wide zero voltage switching range[J]. Proceedings of the CSEE, 2016, 36(13): 3558-3564, 3374.
[7] Shi Yong, Gui Xuwei, Xi Ji, et al. Large power hybrid soft switching mode PWM full bridge DC-DC con- verter with minimized turn-on and turn-off switching loss[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11629-11644.
[8] 周国华, 范先焱, 许多, 等. 具有宽范围输入和高效率的改进型LLC谐振变换器[J]. 电机与控制学报, 2020, 24(10): 9-18.
Zhou Guohua, Fan Xianyan, Xu Duo, et al. Improved LLC resonant converter with wide range input and high efficiency[J]. Electric Machines and Control, 2020, 24(10): 9-18.
[9] 郭兵, 张一鸣, 张加林, 等. 基于直接移相角控制的移相全桥LLC变换器混合控制策略[J]. 电工技术学报, 2018, 33(19): 4583-4593.
Guo Bing, Zhang Yiming, Zhang Jialin, et al. Hybrid control strategy of phase-shifted full-bridge LLC converter based on digital direct phase-shift control[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4583-4593.
[10] 李辉, 黄樟坚, 廖兴林, 等. 一种抑制SiC MOSFET桥臂串扰的改进门极驱动设计[J]. 电工技术学报, 2019, 34(2): 275-285.
Li Hui, Huang Zhangjian, Liao Xinglin, et al. An improved SiC MOSFET gate driver design for crosstalk suppression in a phase-leg configuration[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 275-285.
[11] Kim B C, Park K B, Kim C E, et al. LLC resonant converter with adaptive link-voltage variation for a high- power-density adapter[J]. IEEE Transactions on Power Electronics, 2010, 25(9): 2248-2252.
[12] Musavi F, Craciun M, Gautam D S, et al. An LLC resonant DC-DC converter for wide output voltage range battery charging applications[J]. IEEE Transa- ctions on Power Electronics, 2013, 28(12): 5437- 5445.
[13] Musavi F, Craciun M, Gautam D S, et al. Control strategies for wide output voltage range LLC resonant DC-DC converters in battery chargers[J]. IEEE Transactions on Vehicular Technology, 2014, 63(3): 1117-1125.
[14] Kim E S, Yoon K H, Phum S, et al. Operation characteristics of two-stage DC/DC converter for photovoltaic system[C]//Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Expo- sition, Orlando, FL, USA, 2012: 681-685.
[15] 孙孝峰, 仇江峰, 栗晓华, 等. 一种具有宽输入电压范围的集成Buck-Boost LLC级联变换器[J]. 中国电机工程学报, 2016, 36(6): 1667-1673.
Sun Xiaofeng, Qiu Jiangfeng, Li Xiaohua, et al. An integrated Buck-Boost LLC cascaded converter with wide input voltage range[J]. Proceedings of the CSEE, 2016, 36(6): 1667-1673.
[16] Zhao Xiaonan, Zhang Lanhua, Bron R, et al. A high-efficiency hybrid resonant converter with wide- input regulation for photovoltaic applications[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 3684-3695.
[17] LaBella T, Yu Wensong, Lai J S, et al. A bi- directional-switch-based wide-input range high effici- ency isolated resonant converter for photovoltaic applications[J]. IEEE Transactions on Power Elec- tronics, 2014, 29(7): 3473-3484.
[18] Kim J W, Moon G W. A new LLC series resonant converter with a narrow switching frequency variation and reduced conduction losses[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4278-4287.
[19] Liu Qi, Qian Qinsong, Ren Bowen, et al. A two-stage Buck-Boost integrated LLC converter with extended ZVS range and reduced conduction loss for high- frequency and high-efficiency applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 727-743.
[20] Hu Zhiyuan, Liu Yanfei, Sen P C. Cycle-by-cycle average input current sensing method for LLC resonant topologies[C]//IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 2013: 167-174.
[21] Waffler S, Kolar J W. A novel low-loss modulation strategy for high-power bidirectional Buck + Boost converter[J]. IEEE Transactions on Power Electronics, 2009, 24(6): 1589-1599.
[22] 孙明波, 马运东, 温海涛. 应用于超宽输入的LLC谐振变换器设计[J]. 电源学报, 2019, 17(1): 1-9.
Sun Mingbo, Ma Yundong, Wen Haitao. Design of LLC resonant converter used in ultra-wide input applications[J]. Journal of Power Supply, 2019, 17(1): 1-9.
Abstract In new energy resource and electric vehicle fields, DC-DC converters are required to have more advantages, such as wide gain range, isolation, and high efficiency. Therefore, a cascaded four-switch Buck- Boost LLC converter with power switch integration is selected by discussing the advantages and disadvantages of various DC-DC converters. The cascaded converter has a four-switch Buck-Boost converter in the pre-stage and a half-bridge LLC resonant converter in the post-stage. Since designing and optimizing the magnetic components of the cascaded converter controlled by variable frequency is difficult, a special full bridge rectifier structure on the transformer’s secondary side is proposed. The cascaded converter with a special full bridge rectifier structure can widen the input voltage range under fixed frequency control and realize the wide gain range, isolation, high efficiency, and parameter optimization.
The low-side switching devices of the special full bridge rectifier structure on the transformer’s secondary side are switches. The simultaneous on-time of the low-side switches is called the overlapping turn-on time. The gain of the cascaded converter can be improved by controlling the overlapping turn-on time. Therefore, the gain range can be widened, and the efficiency is optimized under fixed frequency control. The gain of the converter that the parameters are unchanged is increased significantly so that the cascaded converter could be adapted to a wider input voltage range and maintain higher efficiency simultaneously. When the input voltage is less than or equal to the threshold input voltage, the cascaded converter adjusts the overlapping turn-on time to stabilize the output voltage. This mode is called overlapping mode. When the input voltage exceeds the threshold input voltage, the overlapping turn-on time is zero, and the cascaded converter performs pulse width modulation on the input leg on the primary side to stabilize the output voltage. This mode is called rectification mode. Based on the two modes, the phase shift control technique is applied to the two-leg on the primary side of the cascaded converter. The waveform shape of the middle inductor current of the pre-stage four-switch Buck-Boost converter is changed by the phase shift control technique, which can achieve zero voltage switching (ZVS) of switches and zero current switching (ZCS) of diodes. The modal analysis of the cascaded four-switch Buck-Boost LLC converter with fixed frequency control was carried out using the state plane trajectory analysis method, and the input-output expressions and the soft switching conditions of the switches in two modes were derived.
In order to verify the correctness of the theoretical analysis, an experimental prototype with 70~280 V input voltage and 240 W/28 V output was designed. The experimental tests included the wide input range, operating mode, phase shift control technique, soft switching, and efficiency of the converter. The peak efficiency was 93.6% in overlapping mode and 94.4% in rectification mode. In addition, it was experimentally verified that both operating modes could achieve soft switching, and there was a large soft switching time margin in the overlapping mode. The cascaded four-switch Buck-Boost LLC converter with a special full bridge rectifier structure on the secondary side had wide gain and high efficiency compared with the same type of converter.
The following conclusions can be drawn from the theoretical analysis and experiments. The proposed cascaded converter works under fixed frequency control, solving the difficulty of designing and optimizing the magnetic components controlled by variable frequency. The cascaded converter has a wide gain range and high efficiency, and can realize soft switching of all switches and diodes. In addition, the converter can be designed for more than four times of input voltage multiplier. In future work, the phase shift control technique of the converter will be optimized to make it smoother and simpler.
keywords:Wide input voltage range, four-switch Buck-Boost, LLC converter, phase shift, soft switching
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.222252
国家自然科学基金资助项目(62271417, 61771405)。
收稿日期 2022-12-05
改稿日期 2023-02-03
周国华 男,1983年生,教授,博士生导师,研究方向为电力电子调制与控制技术、数字控制技术、建模与稳定性分析,电力电子技术在新能源发电系统中的应用等。E-mail: ghzhou-swjtu@163.com(通信作者)
邱森林 男,1996年生,硕士研究生,研究方向为开关变换器拓扑及其控制技术。E-mail: slqiu_pece@163.com
(编辑 陈 诚)