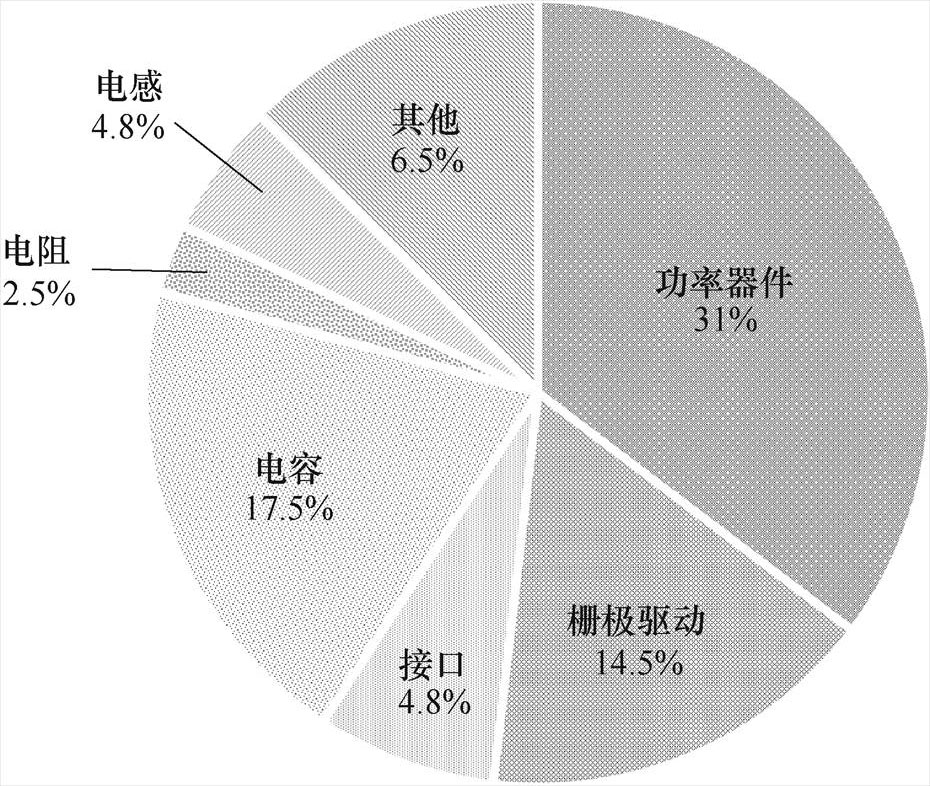
图1 变流器系统故障源分布
Fig.1 Distribution of fault sources in converter systems
摘要 为了防止绝缘栅双极型晶体管（IGBT）突发性失效而影响电力电子设备安全可靠运行，急需对IGBT剩余寿命做出精确预测，这对现有预测模型在高准确性和低不确定性方面提出了挑战。该文提出一种优化模型，该模型通过利用逐次变分模态分解（SVMD）技术来提取退化特征，并采用贝叶斯方法优化长短期记忆（LSTM）神经网络的超参数以提高预测性能。首先，该模型通过SVMD技术将退化特征数据分解为多个模态后将有用模态重构从而提取和增强退化特征；其次；利用贝叶斯优化方法通过高斯过程（GP）代理模型和期望改进（EI）采集函数对LSTM预测模型超参数实现全局寻优；最后，基于SVMD特征提取技术和贝叶斯优化LSTM网络的预测模型通过实际IGBT退化特征数据证明了模型的有效性和优越性。结果表明，所提模型与传统优化模型相比，提高了13%的寿命预测准确性，并减少了34%的预测不确定性。
关键词：IGBT 可靠性 寿命预测 模态分解 失效分布
绝缘栅双极型晶体管（Insulated Gate Bipolar Transistors, IGBT）是电力电子系统实现电能转换和控制的核心部件。变流器系统故障源分布如图1所示，变流器系统中IGBT失效引发的故障率[1]高达31%，电容和栅极驱动故障仅占17.5%和14.5%。事实上，据工业统计数据显示，用于高可靠性领域的IGBT由于复杂环境和工况致使其可靠性并不像预期的那样高[2]。
为了提高IGBT可靠性并保障电力电子设备安全可靠运行，急需对IGBT进行精确的寿命预测。寿命预测是预测IGBT的寿命终点（End of Lifetime, EOL）或剩余使用寿命（Remaining Useful Lifetime, RUL）的过程，这有助于安排维修工作，减少非计划停机造成的经济损失，提高变流器的可靠性。目前，典型的寿命预测模型包括失效物理（Physics of Failure, PoF）模型[3-6]、数据驱动模型[7-13]等。PoF模型充分考虑了IGBT失效机理具有直接的物理含义，但考虑到不同的失效模式，很难在实际系统中获得准确的模型[14]；数据驱动模型具有节省计算时间、提高准确度和加速设计过程等优势[7]，可在失效机理不明情况下预测寿命，是目前IGBT寿命预测的热点[15]。文献[8]使用一个包含递归神经网络（Recurrent Neural Network, RNN）的预测方法进行IGBT寿命估计，该方法依靠经验试凑来确定RNN的超参数，导致模型可能并非具有最优性能，从而影响预测准确性。M. Baharani等将长短期记忆（Long Short-Term Memory, LSTM）深度学习用于Si MOSFET寿命预测，其预测方法与卡尔曼滤波[9]和粒子滤波[10]方法相比性能更好[11]，由于原始数据存在的噪声可能会对预测产生影响。Zheng Shuai等[13]利用基于LSTM的RUL预测方法，在数据集上的结果表明LSTM比支持向量回归[12]等浅层学习算法表现更好。S. Y. Fu等基于LSTM方法评估电子器件封装结构的可靠性并与RNN方法对比，发现LSTM在长期预测方面优势更明显[7]。然而，传统LSTM的局限性在于依靠经验选取模型的超参数并非最优超参数组合，并且LSTM网络的输入包含了大量干扰噪声，这些方面在很大程度上会制约预测准确性并导致预测的不确定性增大[16-17]。
图1 变流器系统故障源分布
Fig.1 Distribution of fault sources in converter systems
为了解决基于传统LSTM的IGBT寿命模型预测准确性低和预测不确定性大的问题，本文提出了基于优化LSTM网络的IGBT寿命预测方法，将LSTM网络与逐次变分模态分解（Successive Variational Mode Decomposition, SVMD）技术、贝叶斯优化（Bayesian Optimization, BO）方法相结合。首先，通过SVMD技术将退化特征数据分解为多个模态并将有用模态重构从而提取和增强退化特征。然后，利用贝叶斯方法通过高斯过程代理模型和期望改进采集函数对LSTM网络超参数（隐含层层数Nh、隐含层细胞数Nu和初始学习率Ri）实现全局寻优。最后，利用优化后的LSTM网络对重构数据进行退化特征之间时间相关性规律的挖掘并实现IGBT寿命预测。本文在IGBT加速老化数据集上进行效果验证，结果表明，与传统优化方法相比，本文方法不仅显著减小了预测不确定性，而且提高了预测的准确性，可为制定IGBT器件运维方案提供理论支撑。
本文采用的优化LSTM网络的IGBT预测模型是基于IGBT性能退化过程中反映退化规律的历史数据。因此，进行IGBT寿命预测需要详细的退化数据，此数据必须真实地反映IGBT性能退化的时间相关性。
一般而言，包含不同退化特征的数据所反映的失效模式存在差异，不同的失效模式所诱发的失效机理也不同。在实际研究中，结到壳热阻Rth-jc、通态压降Vce(on)和瞬态尖峰电压Vce(peak)等退化特征量常被用于IGBT寿命预测研究[18-21]。其中，通态压降Vce(on)的变化大多归因于键合线开裂和脱落，结到壳热阻Rth-jc的变化多归因于IGBT焊料层疲劳退化，瞬态尖峰电压Vce(peak)变化多是由于IGBT退化过程中寄生参数的变化。考虑到数据获取方式有限，本文采用美国国家航空航天局卓越预测中心公开的IGBT加速老化数据集[22]，以瞬态尖峰电压Vce(peak)为例进行IGBT寿命预测模型的分析和研究。该数据集记录了10 kHz开关频率、40%占空比条件下IRG4BC30K器件的栅极电压、集电极电流和开通关断电压等高速测量结果。在IGBT关断期间，由于杂散电感等寄生元件的存在会产生一个瞬态电压，它与器件的关断电压共同产生的瞬态峰值电压如图2所示。这个电压将随着IGBT的性能退化而降低直至发生闩锁效应，此特征较好地反映了IGBT性能退化规律，可视作研究其寿命预测的一般案例。
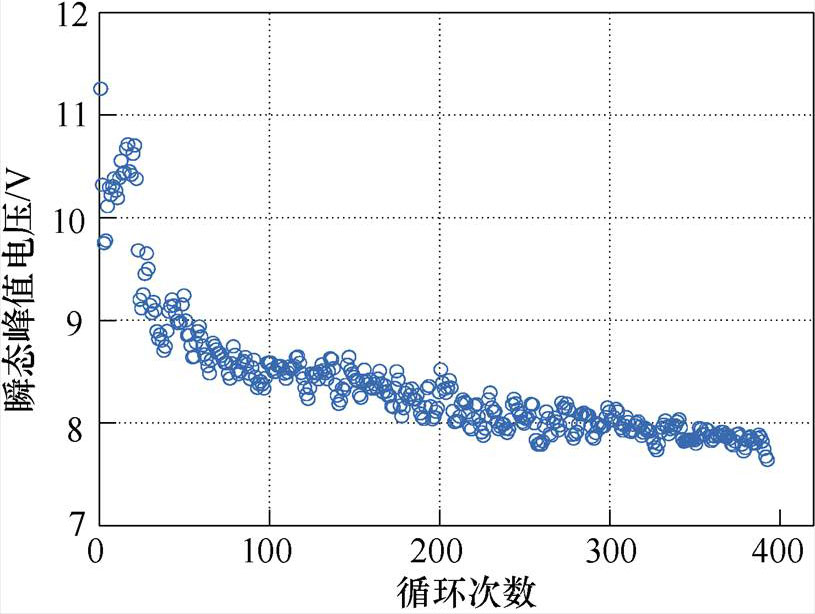
图2 全寿命周期内IGBT退化数据
Fig.2 The IGBT degradation data in full life cycle
鉴于LSTM神经网络在长期预测方面的突出优势，本文采用LSTM神经网络作为IGBT寿命模型的基础进行建模。此外，针对基于传统LSTM的IGBT寿命预测模型在预测准确性低和不确定性大的问题上，本文采用两种优化方法对其进行优化。
基于此，本节首先将从传统LSTM的IGBT寿命预测模型出发描述模型建立过程；然后针对传统模型预测准确性低和不确定性大这两个问题对模型进行两方面优化提升；最后给出IGBT寿命预测模型的预测流程。
基于传统LSTM的IGBT寿命预测模型的核心在于LSTM神经网络建立，建立之前需要对IGBT退化数据进行预处理。
2.1.1 IGBT退化数据预处理
首先，为了减少数据采样中异常值对模型性能的干扰，需要将采集数据的异常值剔除。然后，将包含退化特征的数据进行标准化处理并构建时间序列向量。最后，将时间序列向量按照如图3所示的IGBT全寿命周期数据比例进行划分[23-24]，依次划分为训练集、验证集和测试集，分别用于IGBT寿命预测模型的训练、验证和未来寿命的预测。
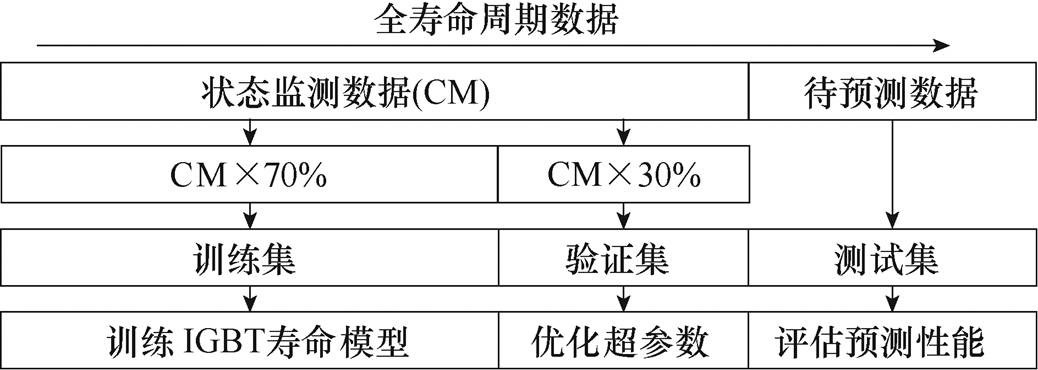
图3 IGBT全寿命周期数据划分
Fig.3 IGBT degradation data division in full life cycle
2.1.2 寿命预测模型建立
IGBT寿命预测模型的核心是LSTM神经网络，它是一种特殊的RNN，在RNN基础上增加了遗忘门、输入门和输出门，LSTM的循环单元结构如图4所示。LSTM神经网络可以选择性地记忆有效信息并删除无效信息，有效地克服了RNN梯度消失或爆炸问题[20-21]。由于门控机制的引入，使LSTM模型具备一定长期预测能力[25]，目前被广泛应用于能源负荷预测和光伏功率预测等领域[26-28]。
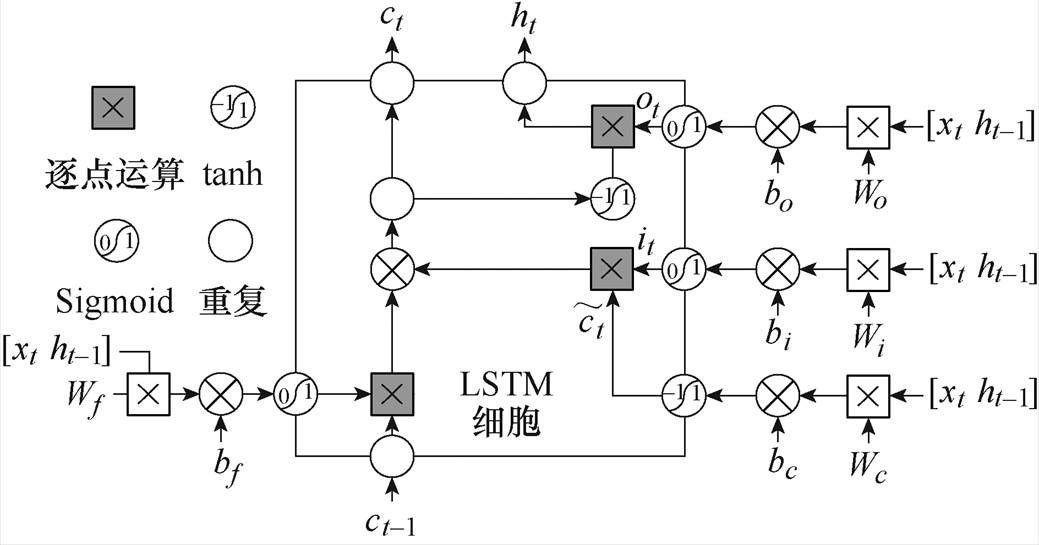
图4 IGBT寿命预测模型中LSTM的结构
Fig.4 Structure of LSTM in IGBT life prediction model
LSTM的循环结构实现过程分为三步：①首先利用上一时刻的外部状态ht-1和当前时刻的输入xt，计算出输入门it、遗忘门ft、输出门ot以及候选状态ct；②结合ft和it来更新记忆单元ct；③结合ot，将内部状态的信息传递给外部状态ht。通过LSTM循环单元，整个网络可以建立较长距离的时序依赖关系。LSTM的前向计算过程具体表示为
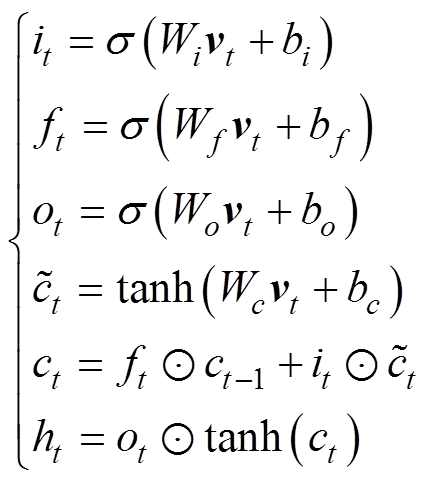（1）
式中，s(x)为sigmoid函数；ql 为权重和偏置向量，ql=[WiWf Wc Wo bibf bc bo]，是待训练的神经网络参数；vt=[xt ht-1]；
代表两个向量的Hadamard运算。
2.1.3 剩余寿命预测
IGBT寿命预测模型基于历史数据构成的时间序列向量不断进行滚动迭代预测[29]，实现退化特征的长期预测，将该过程多次重复得到IGBT在寿命终点处的失效分布。然后，引入高斯过程GP(m, s2)对寿命终点的失效分布进行高斯拟合得到期望和方差[30]，期望作为IGBT预测的循环次数，方差决定了所预测IGBT循环次数的预测区间（Prediction Interval, PI）。由高斯过程的特性可知，高斯过程经线性变换后生成的随机过程仍是高斯过程，所以RUL也满足高斯分布规律。最后，估计IGBT的RUL并给出RUL的失效概率分布。RUL和预测区间计算分别为
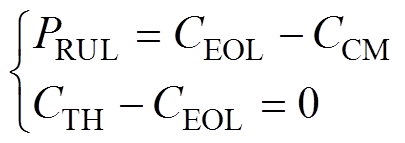（2）
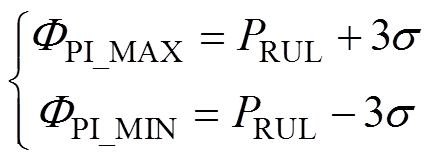（3）
式中，PRUL为预测的RUL循环次数；CEOL为预测的寿命终点循环次数；CCM为状态监测的循环次数；CTH为IGBT寿命失效阈值；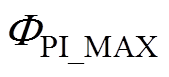
和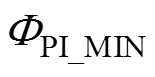
为预测RUL的上、下限。
本节从数据驱动模型的核心出发，将“数据”和“模型”这两大关键因素作为优化对象对传统模型进行优化和提升。针对“数据”方面，数据采集设备由于环境干扰和测量技术的局限性造成原始监测数据中包含大量呈现异常的“脏”数据[31]。与此同时，IGBT器件发生退化或出现故障时监测数据也会出现异常，该监测数据包含表征器件退化和故障的重要信息，不可将其与噪声数据、异常数据等“脏”数据同步处理。针对“模型”方面，超参数和网络参数对模型的预测效果都有很大的影响[32]。网络参数一般由模型不断迭代训练获得，超参数则一般由人工调试的方式进行反复试验来搜索。其中，超参数的选择和调优非常重要，不同的超参数组合将会导致不同的预测性能。此外，各个超参数对预测模型的影响并不相互独立，如何为模型选取一组好的超参数一直是机器学习领域的难题之一[33]。针对传统LSTM网络在预测准确性低和不确定性大这两方面的问题，本文在基于传统LSTM的IGBT寿命预测模型基础上对模型进行两方面的优化，具体优化原理如图5所示。
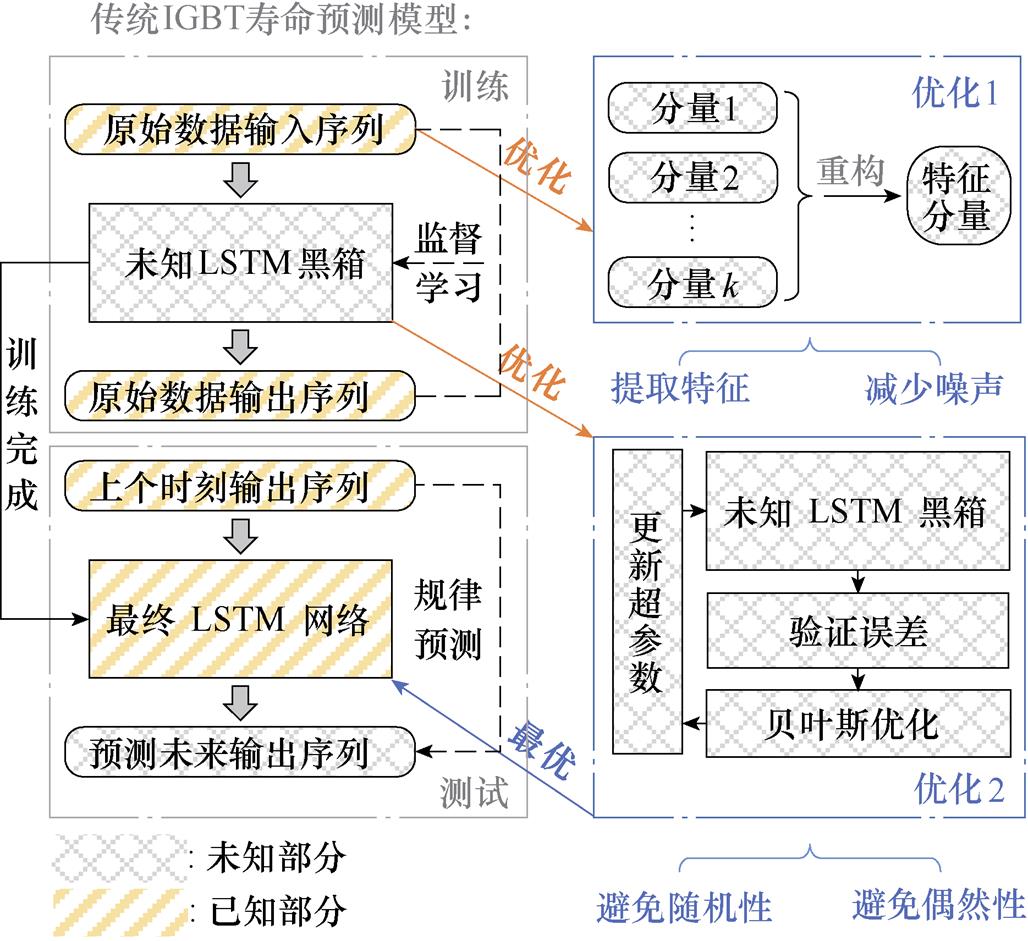
图5 IGBT寿命预测模型优化原理
Fig.5 IGBT life prediction model optimization principles
首先，针对IGBT早期退化特征较弱，在“脏”数据背景下难以有效提取重要信息导致预测准确性差的问题，为了减弱或避免“脏”数据中噪声和异常值对预测精度的影响，需要在原始数据中提取并增强IGBT退化特征，本文采用SVMD技术对退化数据进行模态分解，并对有用模态重构达到特征提取的效果。
其次，LSTM神经网络的拟合能力和训练效果与其网络超参数的选择有很大关系，针对传统 LSTM网络的超参数都是依靠经验调节进而降低预测模型的性能和精度这一问题，本文采用贝叶斯方法对网络超参数进行最优化选择，在避免繁琐试错过程的同时，最大限度地保证模型预测的准确性。
2.2.1 SVMD提取IGBT退化特征
为了避免原始数据中噪声影响神经网络参数进而干扰预测精度，在LSTM建模之前需要提取原始退化数据的特征趋势和变化规律，即对原始信号中的有用信号进行单独提取。
SVMD技术[34]被视为变分模态分解（Variational Mode Decomposition, VMD）的连续实现和扩展，相比基于VMD技术提取IGBT数据特征[35]，避免了由于模态分量数目不确定导致的模态混叠问题。因此，本文引入SVMD技术对IGBT退化数据进行顺序分解。该过程将持续到所有的模态分量被提取出来，或者重构误差（输入信号和各模态分量之和的误差）小于阈值。将IGBT瞬态峰值电压退化数据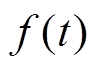
分解成两个部分，即第L个瞬态峰值电压分量uL(t)和残余电压fr(t)，即
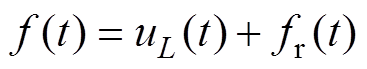（4）
式中，fr(t)为除uL(t)以外的电压分量，包含两个部分：先前提取的IGBT瞬态峰值电压分量之和与未处理的电压分量，即
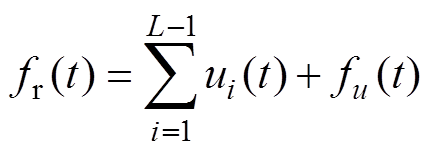（5）
为了得到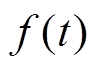中的第一个电压分量，SVMD的迭代表达式为
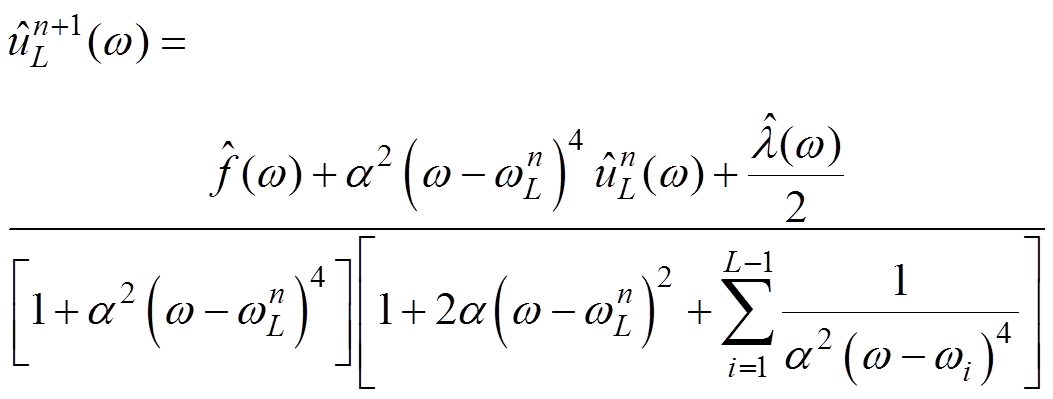（6）
式中，a 为数据保真度约束的平衡参数，其值通常非常大[34]，因此更新wL的方程将近似为
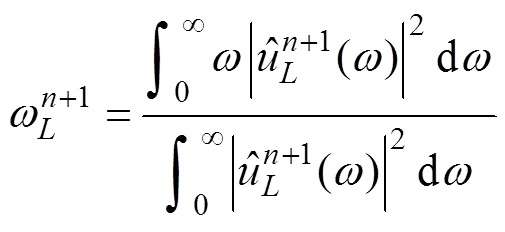（7）
拉格朗日乘子l 表示为
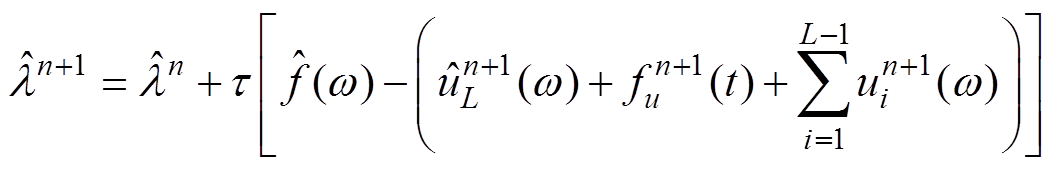（8）
最后，使用双重上升法得到修正表达式为
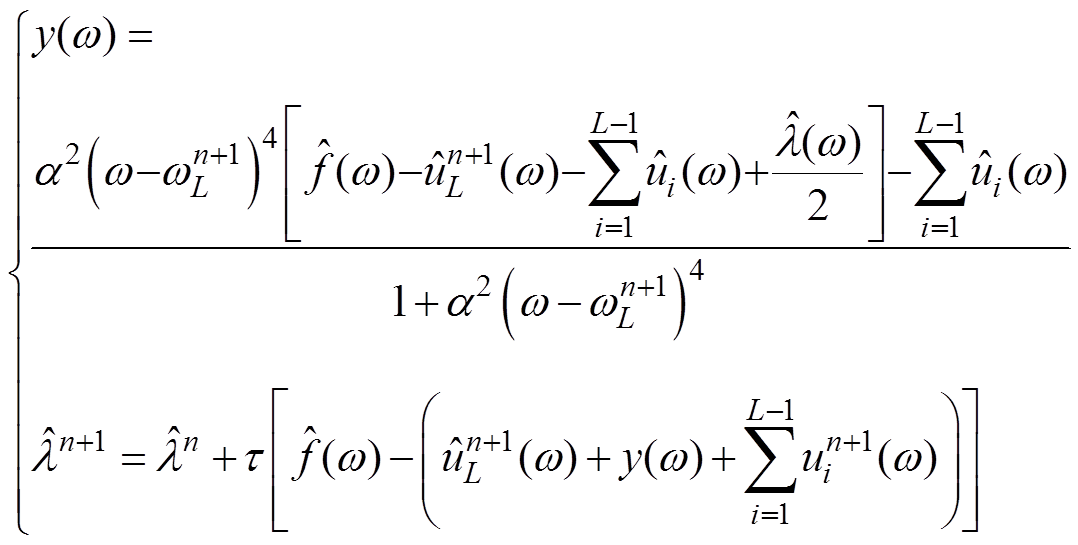（9）
式中，t 为更新参数；wL为中心频率。
通过上述过程不断提取IGBT瞬态峰值电压退化数据的电压分量，直到重构误差小于设定阈值。图2中IGBT电压退化数据分解结果如图6所示。
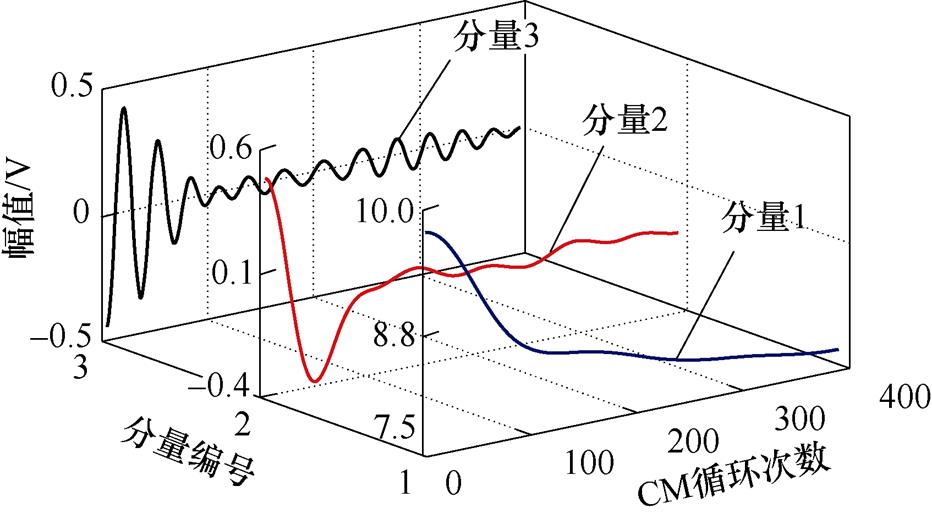
图6 经过SVMD提取的IGBT退化特征
Fig.6 IGBT degradation feature extraction by SVMD
可以看出，IGBT瞬态峰值电压退化数据被分解为三个包含不同特征的电压分量，其中分量1、分量2和分量3按照频率由低到高被依次提取。
2.2.2 贝叶斯优化IGBT寿命模型超参数
通常情况下，IGBT寿命预测模型的LSTM神经网络超参数（隐含层层数Nh、隐含层细胞数Nu和初始学习率Ri）选择需要依赖经验确定，有较大的随机性和偶然性。针对这一问题，BO方法能有效地对超参数空间进行全局搜索，对超参数组合实现快速寻优[36-37]。因此，本文通过贝叶斯方法对IGBT寿命预测模型的LSTM网络超参数Nh、Nu和Ri进行优化，其寻优过程表示为
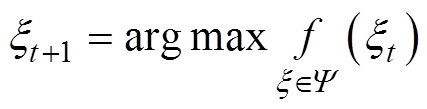（10）
式中，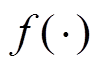
为用于评价性能的目标函数；
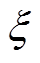为IGBT寿命模型的超参数组合；
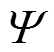为超参数空间。贝叶斯优化源于贝叶斯定理[38]，它使用贝叶斯公式来建立优化过程的概率分布。
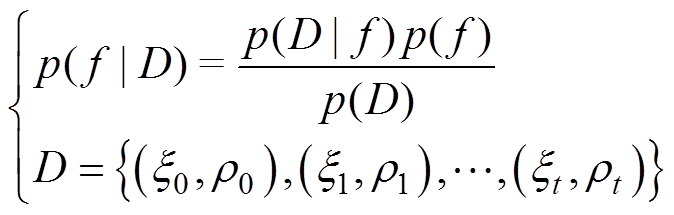（11）
式中，D为超参数观测值的集合；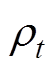
=
为超参数组合的评价，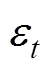
为观测噪声；
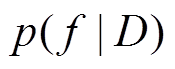为f的后验概率分布；
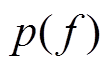为f的先验概率分布；
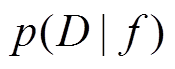为观测值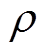
的似然分布；
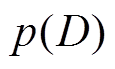为边际似然分布。
贝叶斯优化神经网络超参数由两大核心部分组成，分别是概率代理模型和采集函数表达。本文采用高斯过程（Gaussian Process, GP）为代理模型、采用期望改进（Expectation Improvement, EI）作为采集函数，优化IGBT寿命模型中LSTM超参数过程如图7所示。
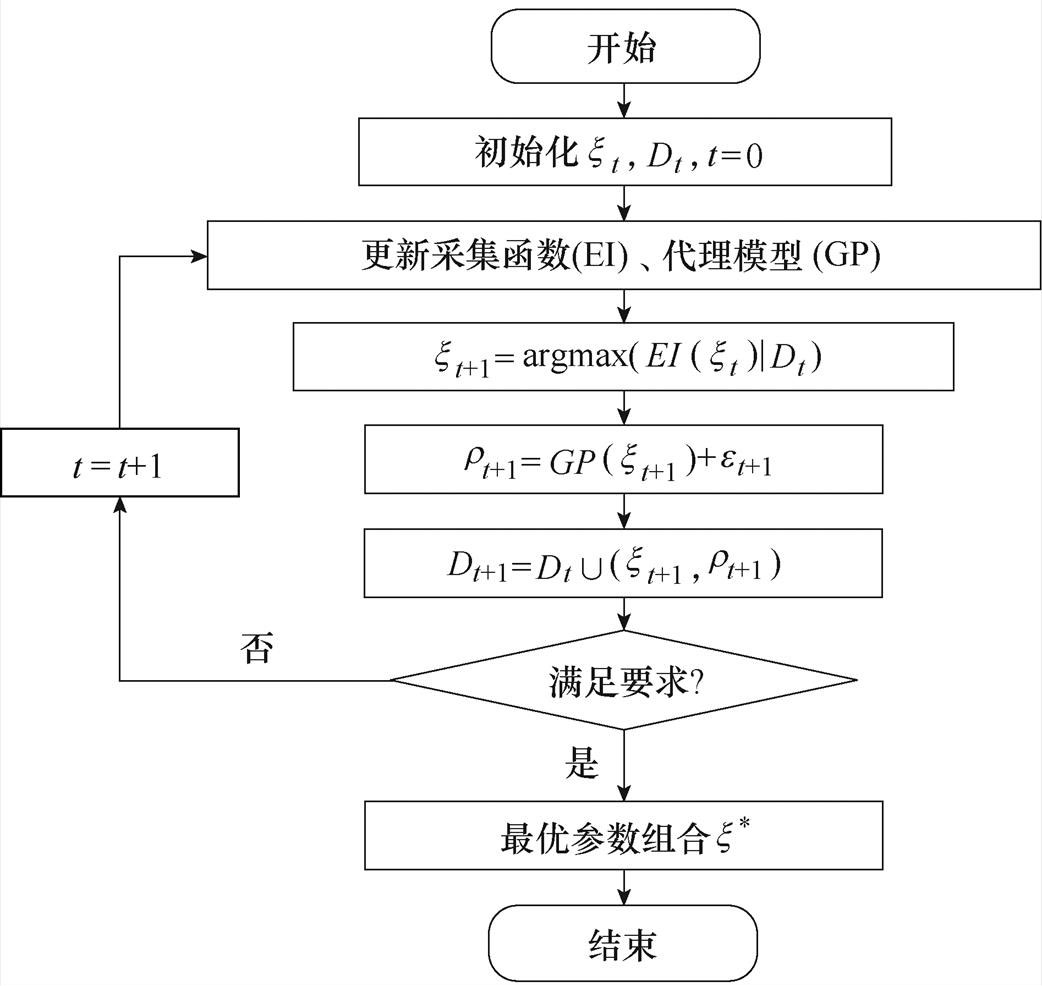
图7 贝叶斯优化IGBT寿命模型中LSTM超参数过程
Fig.7 Bayesian optimization process of LSTM hyperparameter in IGBT lifetime model
基于优化LSTM神经网络的IGBT寿命预测模型如图8所示。
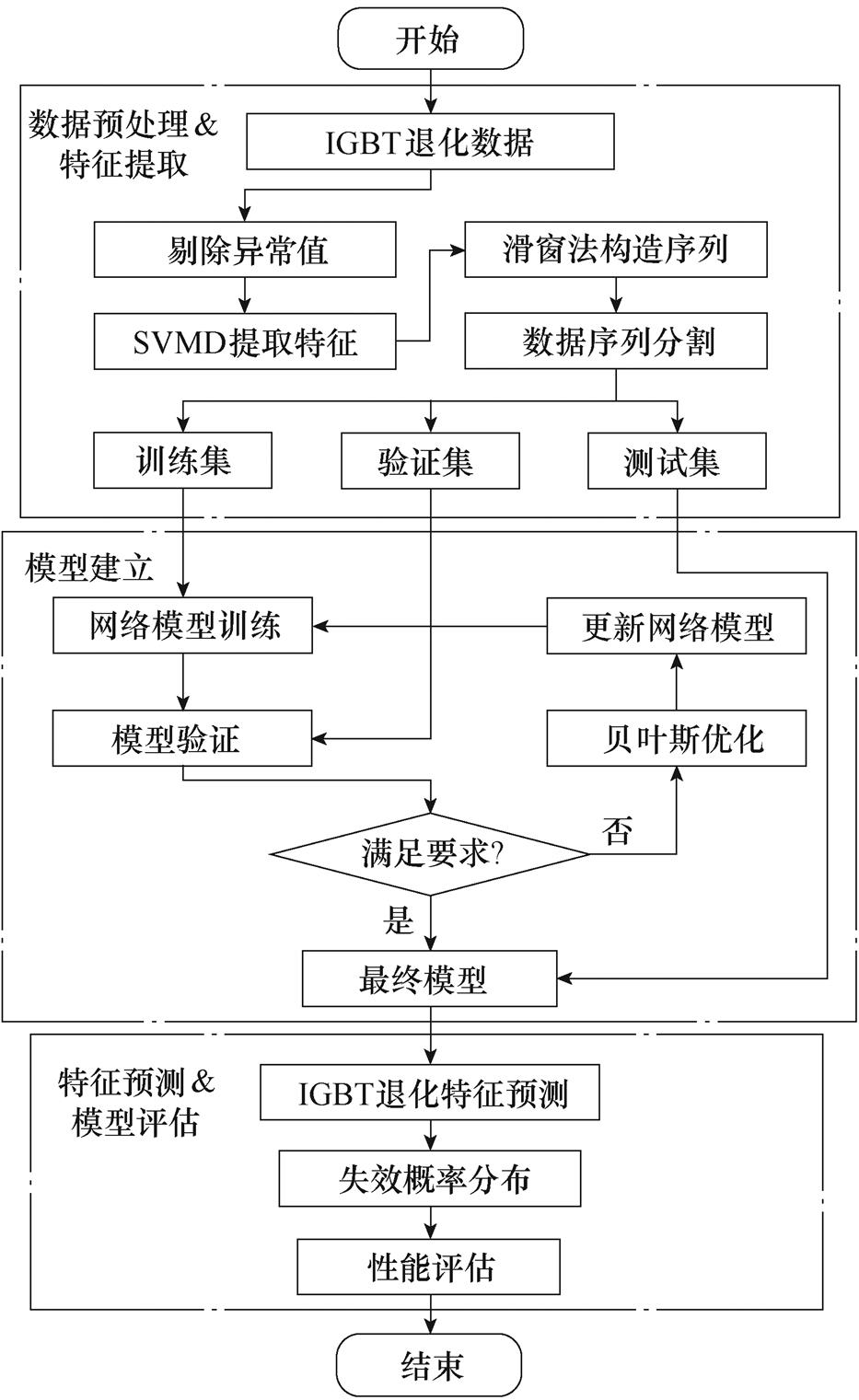
图8 本文所提的IGBT寿命预测模型
Fig.8 The IGBT life prediction model proposed
模型由三部分构成：数据预处理及特征提取、网络模型建立、退化特征预测及模型评估。图8包含了本文区别于基于传统LSTM的IGBT寿命预测模型的两个优化方面：优化一在于利用SVMD技术对IGBT寿命模型的输入数据进行特征提取，以便在降低数据噪声的同时增强模型的鲁棒性；优化二是采用BO方法对IGBT寿命模型中的LSTM网络超参数进行全局寻优，以便发挥模型最优性能。
为了预测IGBT的寿命，设置IGBT寿命预测模型的主要参数见表1。该模型在一台配备英特尔Core i5-10600k CPU、16 GB内存和微软Windows 10 64位操作系统的Matlab®R2020a上进行训练、验证和测试。
表1 IGBT寿命预测模型参数设置
Tab.1 Parameter setting of IGBT life prediction model
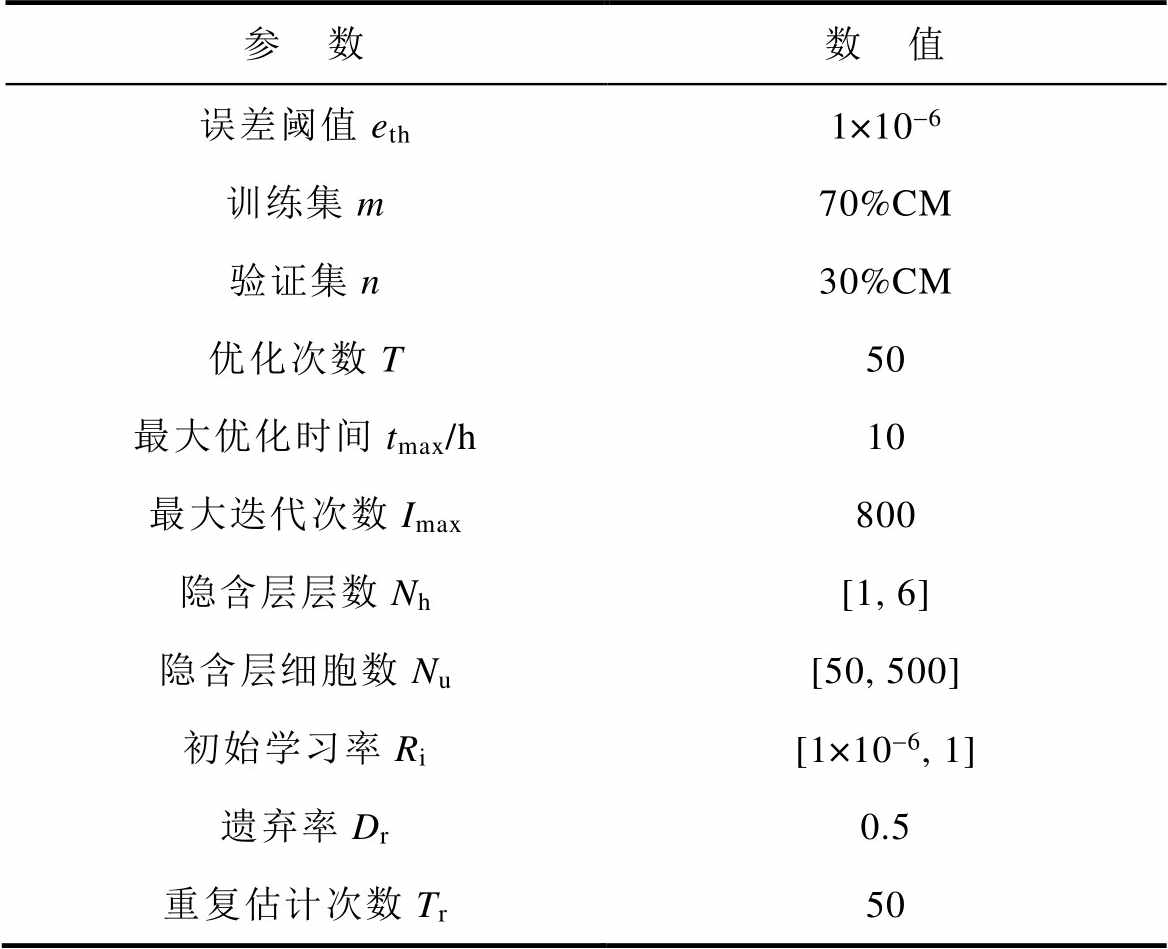
参 数数 值 误差阈值eth1×10-6 训练集m70%CM 验证集n30%CM 优化次数T50 最大优化时间tmax/h10 最大迭代次数Imax800 隐含层层数Nh[1, 6] 隐含层细胞数Nu[50, 500] 初始学习率Ri[1×10-6,1] 遗弃率Dr0.5 重复估计次数Tr50
经过贝叶斯方法对预测模型超参数组合的不断迭代优化以及不同参数组合下寿命模型的不断训练，获得最优超参数组合见表2。考虑到RNN[8]、LSTM[11]在IGBT及MOSFET寿命预测中被广泛选择为预测模型，因此，RNN、LSTM作为对比模型来分析所提模型的性能和预测能力。为了保障结果的严谨性，除超参数外其余参数设置各模型保持一致。
表2 IGBT寿命预测模型的最优超参数组合
Tab.2 The optimal hyperparameter combination for IGBT life prediction model
参 数数 值 初始学习率0.019 隐含层层数3 隐含层细胞数89
不同状态监测（Condition Monitoring, CM）循环次数下IGBT寿命预测结果如图9所示。以图9a为例，图中实线代表IGBT实际循环次数，虚线和曲线分别代表不同模型预测的IGBT循环次数和失效概率分布。其中，预测循环次数越接近实线表明准确性越高，概率分布越集中表明不确定性越小。可以看到，本文方法预测准确性最高，预测不确定性最小。当CM循环次数增加时同样具有类似的结果，随着CM循环次数的增加，不同模型预测的循环次数距离实际循环次数越来越接近，并且失效概率分布也越来越集中。这说明随着监测数据的增加，IGBT寿命预测模型的预测精度逐渐提高，预测不确定性逐渐降低。整体来看，就预测不确定性而言，本文方法的失效概率分布形状更陡峭，表明其预测区间跨度更少，预测的循环次数更集中，说明该方法预测不确定性更小；就预测准确性而言，相比传统未优化模型，本文方法预测的IGBT循环次数始终距离实际循环次数更近，说明该方法预测准确性更高，尤其是当CM循环次数较小时这一优势尤为明显。
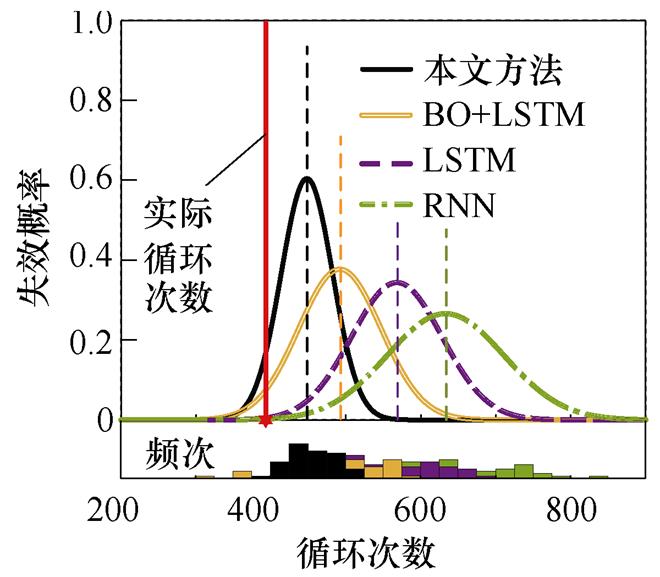
（a）CCM=160
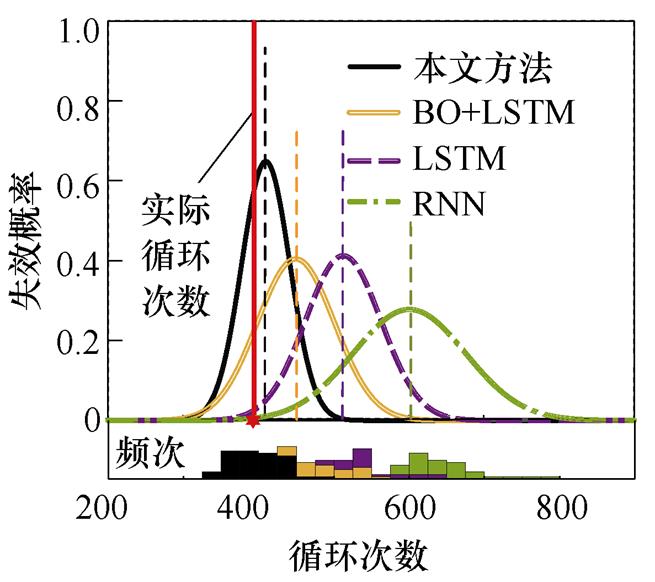
（b）CCM=190
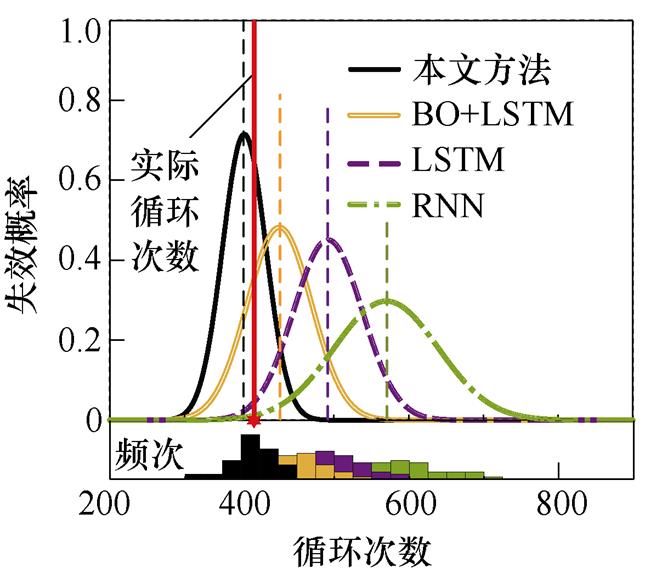
（c）CCM=220
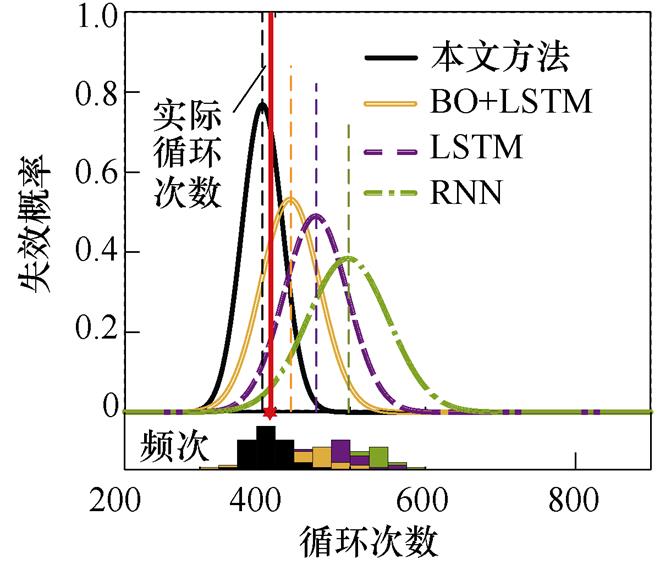
（d）CCM=250
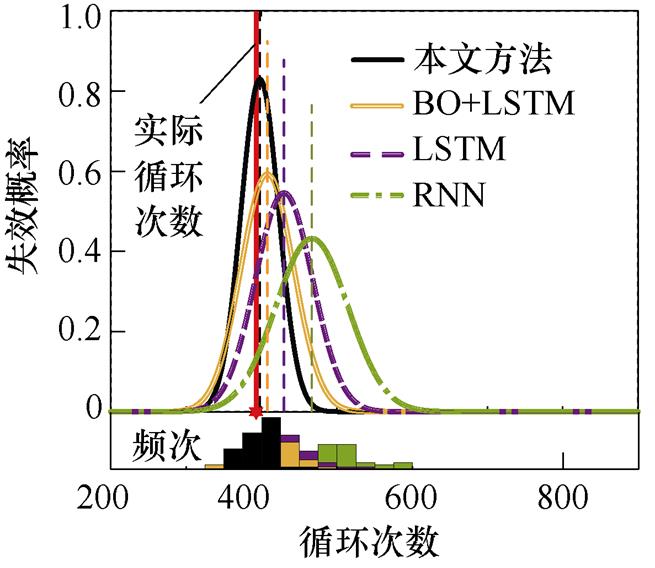
（e）CCM=280
（f）CCM=310
图9 不同CM循环次数下的IGBT寿命预测结果（CEOL）
Fig.9 The IGBT life prediction results under different CM cycles (CEOL)
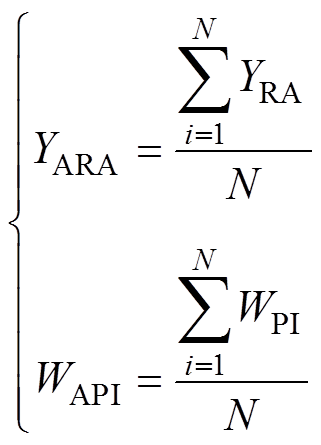
为更好地反映不同IGBT寿命预测模型预测的准确性、不确定性，本文选取相对精度YRA[39]和预测区间宽度WPI[40]为评价指标对不同CM循环次数下的预测性能进行评价。另外，本文选用文献[39]中的平均相对精度YARA作为本文的整体评价指标，来评价模型预测的准确性。同时，为了整体评价模型预测的不确定性，本文参考平均相对精度和相对精度的关系定义了平均预测区间宽度WAPI这一指标，该指标将不同CM循环次数下的预测区间宽度取平均以整体反映模型预测的不确定性。不同指标的计算公式分别如式（12）、式（13）所示，其中，YRA和YARA越大越好，越大表示模型预测的准确性越高；WPI和WAPI越小越好，越小表明模型预测的不确定性越小；不同模型预测的RUL见表3。
表3 IGBT剩余寿命预测结果
Tab.3 The IGBT residual life prediction results
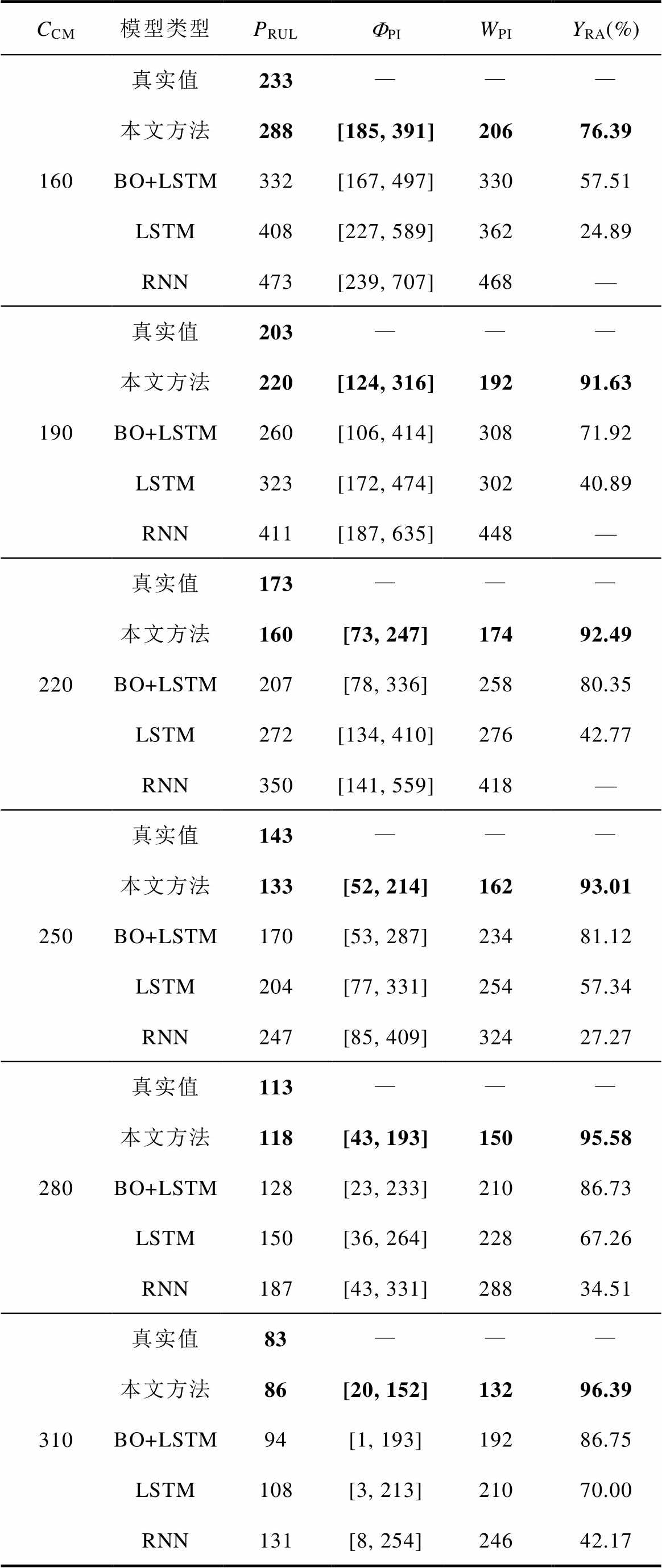
CCM模型类型PRULFPIWPIYRA(%) 160真实值233——— 本文方法288[185, 391]20676.39 BO+LSTM332[167, 497]33057.51 LSTM408[227, 589]36224.89 RNN473[239, 707]468— 190真实值203——— 本文方法220[124, 316]19291.63 BO+LSTM260[106, 414]30871.92 LSTM323[172, 474]30240.89 RNN411[187, 635]448— 220真实值173——— 本文方法160[73, 247]17492.49 BO+LSTM207[78, 336]25880.35 LSTM272[134, 410]27642.77 RNN350[141, 559]418— 250真实值143——— 本文方法133[52, 214]16293.01 BO+LSTM170[53, 287]23481.12 LSTM204[77, 331]25457.34 RNN247[85, 409]32427.27 280真实值113——— 本文方法118[43, 193]15095.58 BO+LSTM128[23, 233]21086.73 LSTM150[36, 264]22867.26 RNN187[43, 331]28834.51 310真实值83——— 本文方法86[20, 152]13296.39 BO+LSTM94[1, 193]19286.75 LSTM108[3, 213]21070.00 RNN131[8, 254]24642.17
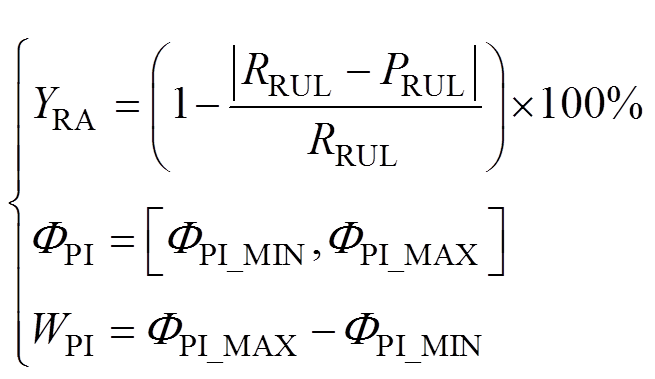（12）
（13）
式中，PRUL为预测剩余寿命；RRUL为实际剩余寿命；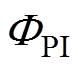
为预测区间；
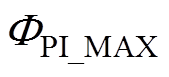和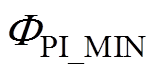
分别为预测区间最大和最小值。
表3中，ΦPI的跨度越大，WPI越大，说明预测的不确定性就越高。相比之下，使用本文方法的预测准确性和预测不确定性要好得多。此外，实际IGBT循环寿命RRUL和预测循环寿命PRUL之间也有更好的一致性。这些都表明，利用SVMD提取退化特征来提高IGBT寿命预测模型性能的做法得到了预测效果的支撑。
就寿命预测的指导意义而言，为了满足估计的要求，有研究指出，RUL的预测误差应不超过实际RUL的±30%[41-42]。不同的IGBT寿命预测模型的RUL预测值如图10所示，灰色区域代表实际RUL± 30%的误差区间。可以看出，使用BO方法优化LSTM预测的RUL并不接近实际的RUL，甚至在CM循环次数为160个周期时不能满足寿命预测误差30%的要求。相比之下，其他两种方法的预测误差更大，而使用本文所提模型预测的RUL误差在全部CM循环次数下都满足要求。
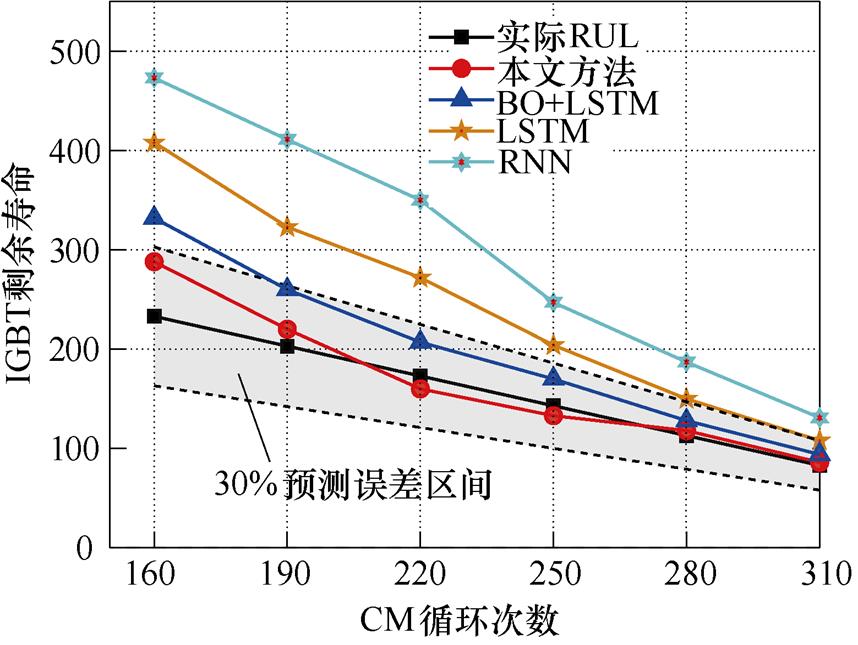
图10 IGBT剩余寿命的预测误差
Fig.10 Prediction error of IGBT remaining life
本文所提模型中的BO优化在提高预测准确性的同时不会增加不确定性，并且SVMD优化在降低预测不确定性的同时不会降低准确性，两者优化效果不会相互制约，其性能提升效果如图11所示。阴影部分面积表示SVMD优化下和BO优化下的性能提升效果。可以看出，SVMD 优化对于提升预测准确性和降低不确定性都有一定效果，从提升效果来看，SVMD优化对降低预测不确定性作用更大；BO优化对于提升预测准确性和降低不确定性也都有一定影响；BO优化对提高预测准确性作用更大。此外，这两种优化是可以同时实现的，即图中上、下两部分阴影面积相加后表示性能提升效果。
根据式（13）对不同IGBT寿命模型的整体性能评价结果见表4。
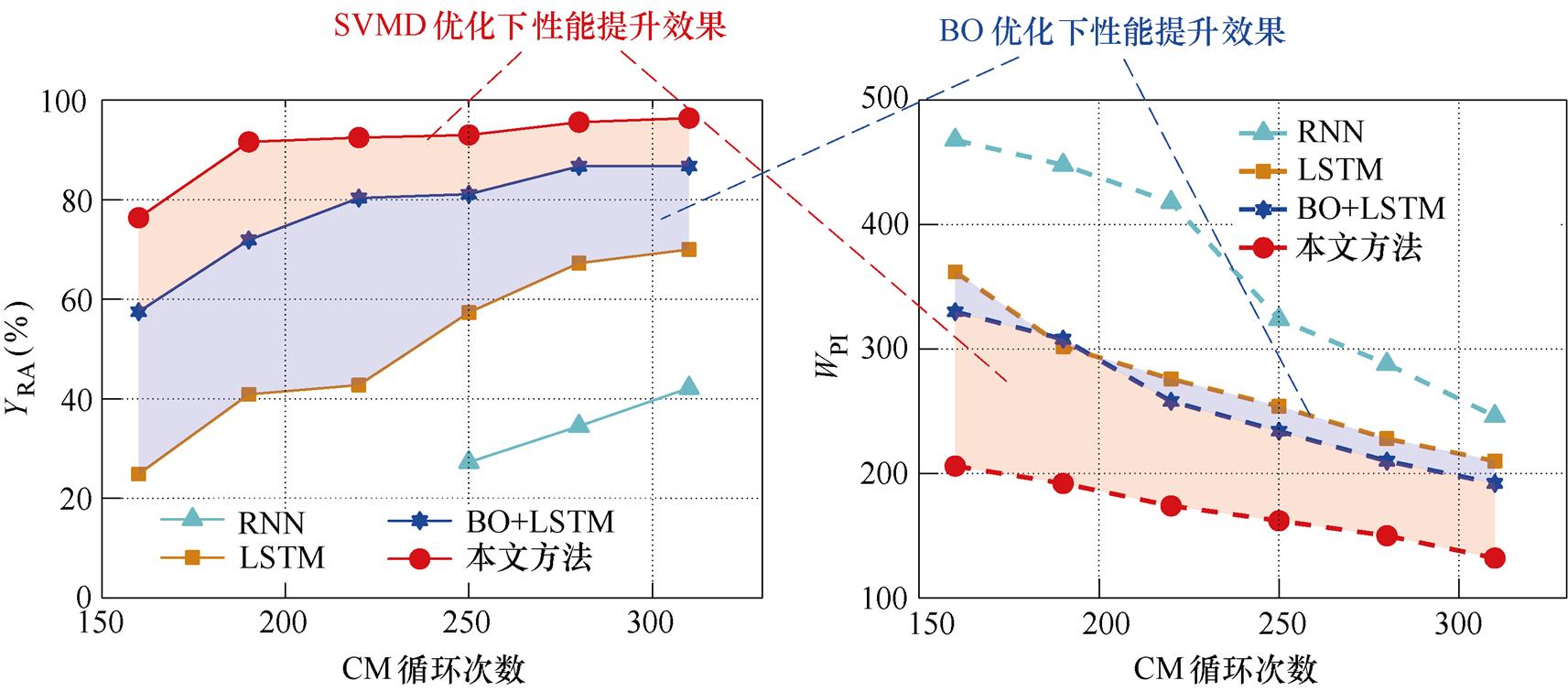
（a）相对精度YRA （b）预测区间宽度WPI
图11 两种优化下模型性能提升效果
Fig.11 Performance improvement with two optimizations
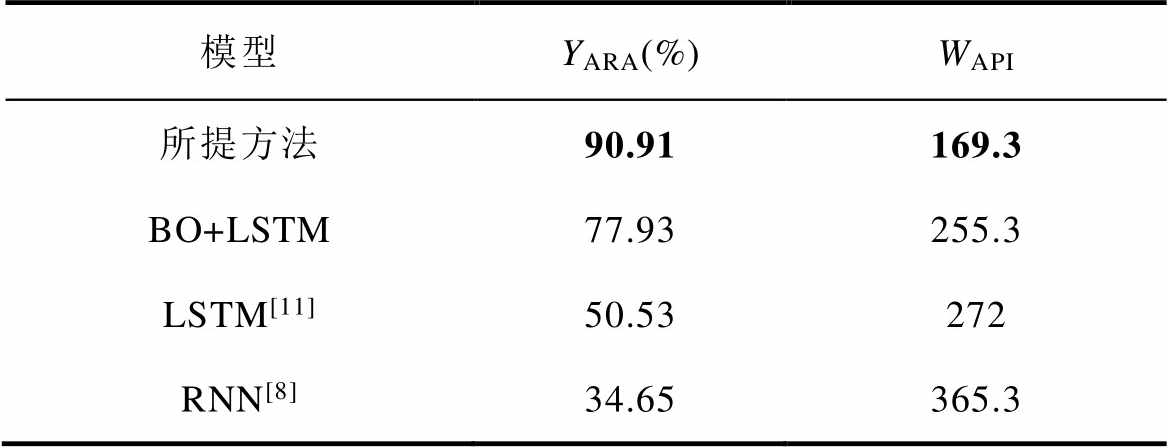
表4 所提IGBT寿命预测模型评价
Tab.4 Evaluation of the proposed IGBT life model
模型YARA(%)WAPI 所提方法90.91169.3 BO+LSTM77.93255.3 LSTM[11]50.53272 RNN[8]34.65365.3
表4中平均相对精度YARA越大越好，平均预测区间宽度WAPI越小越好。由评价结果可知，基于RNN的IGBT寿命预测模型的预测效果并不理想，通过其平均相对精度和平均预测区间宽度可以证明这一点。作为RNN的改进型，基于LSTM的IGBT寿命模型预测性能有所提高，表现为平均相对精度从RNN的34.65%提高至50.53%，平均预测区间宽度从365.3个循环减少到272个。相比之下，经过BO方法优化LSTM的IGBT寿命预测模型在平均相对精度和平均预测区间宽度方面表现更为出色。更进一步地，本文在BO方法优化LSTM的IGBT寿命预测模型基础上增加了SVMD提取退化特征，这使平均相对精度提高到90.91%，平均预测区间宽度降低到169.3个循环，在几个模型中准确率最高并且预测不确定性最小。定量分析后发现，相比基于贝叶斯优化LSTM的IGBT寿命预测模型，本文的预测模型提高了13%的寿命预测准确性，并减少了34%的预测不确定性。
在实际的电力电子设备中，由于不同工况下电压、电流、占空比等运行条件有所不同，导致它们可能以方波或正弦波等任意规律变化。这样可能会引起功率损耗的差异，然后通过热网络影响器件工作时的温度最终影响器件寿命消耗。这样的参数变化对基于解析模型相关方法的寿命消耗情况是有影响的。然而，本文所采用的LSTM神经网络模型本质上属于数据驱动类模型，数据驱动类模型建模时重点关注的两部分分别是“数据”和“模型”。当建模过程的方法已经确定后，“模型”部分的整体性能（包括预测准确性和不确定性）基本上也已经确定。除此之外，不同CM循环次数下模型预测的准确性和不确定性与CM循环次数密切相关，即与输入模型的数据量密切相关。为此，只要采集的退化数据量足够多，模型预测的准确性和不确定性基本上不会受到占空比等变化的影响。
一般来说，电力电子装置是使用同一批次的IGBT器件构建的。在这种情况下，器件的一致性较好，参数分布性带来的影响几乎可以忽略，因此不必对每个器件进行单独分析。然而，在某些情况下如用于维护和更换，需要使用不同批次的器件。众所周知，不同批次生产的IGBT器件由于制造商的生产工艺和材料等原因导致实际的热电参数可能会存在差异，这可能会影响寿命预测模型输入数据的初始大小。值得一提的是，数据驱动模型是对数据变化规律和趋势进行预测，数据初始值的大小并不会对本文模型产生影响，也不会对退化数据趋势产生实质的影响。故理论上器件参数的分布对预测不确定性的影响基本可以忽略。
针对现有IGBT寿命预测模型存在预测准确性低、预测不确定性大的问题，本文提出了一种基于优化LSTM的IGBT寿命预测模型。该模型通过SVMD技术将IGBT退化数据分解为多个模态并将有用模态重构达到提取和增强IGBT退化特征的效果。此外，不同于传统IGBT寿命预测模型依靠经验试错法进行超参数选取，该模型采用BO方法对IGBT寿命模型中LSTM的超参数进行全局寻优以提高模型的预测性能。本文所提模型在实际IGBT退化特征数据上进行验证，证明了该模型在性能提升方面的有效性和优越性。通过不同模型对比分析，可以得出以下结论：
1）采用BO方法对IGBT寿命预测模型中LSTM网络的隐含层层数、隐含层细胞数和初始学习率进行优化，提高了IGBT寿命预测模型的精度。
2）利用SVMD技术提取IGBT的退化特征，能够降低IGBT寿命模型预测的不确定性并提高准确性。
3）所提模型在监测数据较少的条件下，同样能够较为准确地预测IGBT的剩余使用寿命，其长期预测性能较好，可为IGBT复杂环境下的监测和运维提供参考。
参考文献
[1] Yang Shaoyong, Bryant A, Mawby P, et al. An industry based survey of reliability in power elec- tronic converters[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1441-1451.
[2] 张军, 张犁, 成瑜. IGBT模块寿命评估研究综述[J]. 电工技术学报, 2021, 36(12): 2560-2575.
Zhang Jun, Zhang Li, Cheng Yu. Review of the lifetime evaluation for the IGBT module[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(12): 2560-2575.
[3] 曾文彬, 宋梁, 张西应, 等. 基于Coffin-Manson模型功率半导体器件可靠性评估[J]. 电力电子技术, 2022, 56(7): 138-140.
Zeng Wenbin, Song Liang, Zhang Xiying, et al. Reliability evaluation for power semiconductor device using Coffin-Manson model[J]. Power Elec- tronics, 2022, 56(7): 138-140.
[4] 赖伟, 陈民铀, 冉立, 等.老化实验条件下的IGBT寿命预测模型[J]. 电工技术学报, 2016, 31(24): 173-180.
Lai Wei, Chen Minyou, Ran Li, et al. IGBT lifetime model based on aging experiment[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 173-180.
[5] Ceccarelli L, Kotecha R M, Bahman A S, et al. Mission-profile-based lifetime prediction for a SiC MOSFET power module using a multi-step condition- mapping simulation strategy[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 9698-9708.
[6] Shen Yanfeng, Liivik E, Blaabjerg F, et al. Reliability evaluation of an impedance-source PV microcon- verter[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018: 1104-1108.
[7] Fu S Y, Tseng Y C, Chiang K N. Study on data effect of using RNN model to predict reliability life of wafer level packaging[C]//2020 15th International Micro- systems, Packaging, Assembly and Circuits Tech- nology Conference (IMPACT), Taipei, China, 2020: 200-203.
[8] Mei Wenjuan, Liu Zhen, Su Yuanzhang. MRPM: multistep robust prediction machine for degradation time series projection[C]//2021 IEEE International Instrumentation and Measurement Technology Con- ference (I2MTC), Virtual, Glasgow, UK, 2021: 1-7.
[9] Dusmez S, Duran H, Akin B. Remaining useful lifetime estimation for thermally stressed power MOSFETs based on on-state resistance variation[J]. IEEE Transactions on Industry Applications, 2016, 52(3): 2554-2563.
[10] Celaya J, Saxena A, Saha S, et al. Prognostics of power MOSFETs under thermal stress accelerated aging using data-driven and model-based methodo- logies[C]//Annual Conference of the Prognostics and Health Management Society, Montreal, QC, Canada, 2011: 443-452.
[11] Baharani M, Biglarbegian M, Parkhideh B, et al. Real-time deep learning at the edge for scalable reliability modeling of Si-MOSFET power electronics converters[J]. IEEE Internet of Things Journal, 2019, 6(5): 7375-7385.
[12] 李畸勇, 张伟斌, 赵新哲, 等. 改进鲸鱼算法优化支持向量回归的光伏最大功率点跟踪[J]. 电工技术学报, 2021, 36(9): 1771-1781.
Li Jiyong, Zhang Weibin, Zhao Xinzhe, et al. Global maximum power point tracking for PV array based on support vector regression optimized by improved whale algorithm[J]. Transactions of China Electro- technical Society, 2021, 36(9): 1771-1781.
[13] Zheng Shuai, Ristovski K, Farahat A, et al. Long short-term memory network for remaining useful life estimation[C]//2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 2017: 88-95.
[14] Ni Ze, Lü Xiaofeng, Yadav O P, et al. Overview of real-time lifetime prediction and extension for SiC power converters[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(8): 7765-7794.
[15] 唐圣学, 张继欣, 姚芳, 等. IGBT模块寿命预测方法研究综述[J]. 电源学报, 2023, 21(1): 177-194.
Tang Shengxue, Zhang Jixin, Yao Fang, et al. Rerview of lifetime prediction methods for IGBT power modules[J]. Journal of Power Supply, 2023, 21(1): 177-194.
[16] 石怀涛, 尚亚俊, 白晓天, 等. 基于贝叶斯优化的SWDAE-LSTM滚动轴承早期故障预测方法研究[J]. 振动与冲击, 2021, 40(18): 286-297.
Shi Huaitao, Shang Yajun, Bai Xiaotian, et al. Early fault prediction method combining SWDAE and LSTM for rolling bearings based on Bayesian optimization[J]. Journal of Vibration and Shock, 2021, 40(18): 286-297.
[17] 姚艳, 曹健. 一种成本有效的面向超参数优化的工作流执行优化方法[J]. 计算机集成制造系统, 2020, 26(6): 1628-1635.
Yao Yan, Cao Jian. Cost-effective workflow execu- tion strategy for hyperparameter search[J]. Computer Integrated Manufacturing Systems, 2020, 26(6): 1628-1635.
[18] 葛建文, 黄亦翔, 陶智宇, 等. 基于Transformer模型的IGBT剩余寿命预测[J]. 半导体技术, 2021, 46(4): 316-323.
Ge Jianwen, Huang Yixiang, Tao Zhiyu, et al. Residual useful life prediction of IGBTs based on Transformer model[J]. Semiconductor Technology, 2021, 46(4): 316-323.
[19] 白梁军, 黄萌, 饶臻, 等. 基于GARCH模型的IGBT寿命预测[J]. 中国电机工程学报, 2020, 40(18): 5787-5796.
Bai Liangjun, Huang Meng, Rao Zhen, et al. Lifetime prediction of IGBT based on GARCH model[J]. Proceedings of the CSEE, 2020, 40(18): 5787-5796.
[20] 高伟, 张琼洁, 李长留, 等. 基于LSTM网络的牵引变流器IGBT故障预测方法研究[J]. 电子器件, 2020, 43(4): 804-808.
Gao Wei, Zhang Qiongjie, Li Changliu, et al. A fault prediction method of IGBT in traction converter based on LSTM[J]. Chinese Journal of Electron Devices, 2020, 43(4): 804-808.
[21] 王飞, 黄涛, 杨晔. 基于Stacking多模型融合的IGBT器件寿命的机器学习预测算法研究[J]. 计算机科学, 2022, 49(增刊1): 784-789.
Wang Fei, Huang Tao, Yang Ye. Study on machine learning algorithms for life prediction of IGBT devices based on Stacking multi-model fusion[J]. Computer Science, 2022, 49(S1): 784-789.
[22] Celaya J, Wysocki P, Goebel K. IGBT accelerated aging data set, NASA prognostics data reposi- tory[DB/OL]. NASA Ames Research Center, Moffett Field, CA, 2009, https://www.nasa.gov/content/ prognostics-center-of-excellence-data-set-repository.
[23] 石耀霖, 李林芳, 程术. 运用LSTM神经网络对川滇地区的地震中期预报: 回溯性预测2008年汶川Ms8.0地震的探索[J]. 中国科学院大学学报, 2022, 39(1): 1-12.
Shi Yaolin, Li Linfang, Cheng Shu. Application of LSTM neural network for intermediate-term earth- quake prediction: retrospective prediction of 2008 Wenchuan Ms8.0 Earthquake[J]. Journal of Univer- sity of Chinese Academy of Sciences, 2022, 39(1): 1-12.
[24] 罗仁泽, 李阳阳. 一种基于RUnet卷积神经网络的地震资料随机噪声压制方法[J]. 石油物探, 2020, 59(1): 51-59.
Luo Renze, Li Yangyang. Random seismic noise attenuation based on RUnet convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 51-59.
[25] 于永进, 姜雅男, 李长云. 基于鲸鱼优化-长短期记忆网络模型的机-热老化绝缘纸剩余寿命预测方法[J]. 电工技术学报, 2022, 37(12): 3162-3171.
Yu Yongjin, Jiang Yanan, Li Changyun. Prediction method of insulation paper remaining life with mechanical-thermal synergy based on whale optimi- zation algorithm-long-short term memory model[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3162-3171.
[26] 王琛, 王颖, 郑涛, 等. 基于ResNet-LSTM网络和注意力机制的综合能源系统多元负荷预测[J]. 电工技术学报, 2022, 37(7): 1789-1799.
Wang Chen, Wang Ying, Zheng Tao, et al. Multi- energy load forecasting in integrated energy system based on ResNet-LSTM network and attention mechanism[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1789-1799.
[27] 葛磊蛟, 赵康, 孙永辉, 等. 基于孪生网络和长短时记忆网络结合的配电网短期负荷预测[J]. 电力系统自动化, 2021, 45(23): 41-50.
Ge Leijiao, Zhao Kang, Sun Yonghui, et al. Short- term load forecasting of distribution network based on combination of Siamese network and long short-term memory network[J]. Automation of Electric Power Systems, 2021, 45(23): 41-50.
[28] 杨晶显, 张帅, 刘继春, 等. 基于VMD和双重注意力机制LSTM的短期光伏功率预测[J]. 电力系统自动化, 2021, 45(3): 174-182.
Yang Jingxian, Zhang Shuai, Liu Jichun, et al. Short- term photovoltaic power prediction based on varia- tional mode decomposition and long short-term memory with dual-stage attention mechanism[J]. Automation of Electric Power Systems, 2021, 45(3): 174-182.
[29] 黄凯, 丁恒, 郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766.
Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753-3766.
[30] Tamssaouet F. Towards system-level prognostics: modeling, uncertainty propagation and system remaining useful life prediction[D]. Toulouse: Institut National Polytechnique de Toulouse, 2020.
[31] 代杰杰, 宋辉, 杨祎, 等. 基于栈式降噪自编码器的输变电设备状态数据清洗方法[J]. 电力系统自动化, 2017, 41(12): 224-230.
Dai Jiejie, Song Hui, Yang Yi, et al. Cleaning method for status data of power transmission and trans- formation equipment based on stacked denoising autoencoders[J]. Automation of Electric Power Systems, 2017, 41(12): 224-230.
[32] 史佳琪, 马丽雅, 李晨晨, 等. 基于串行-并行集成学习的高峰负荷预测方法[J]. 中国电机工程学报, 2020, 40(14): 4463-4472, 4726.
Shi Jiaqi, Ma Liya, Li Chenchen, et al. Daily peak load forecasting based on sequential-parallel ensemble learning[J]. Proceedings of the CSEE, 2020, 40(14): 4463-4472, 4726.
[33] 李兵, 梁舒奇, 单万宁, 等. 基于改进正余弦算法优化堆叠降噪自动编码器的电机轴承故障诊断[J]. 电工技术学报, 2022, 37(16): 4084-4093.
Li Bing, Liang Shuqi, Shan Wanning, et al. Motor bearing fault diagnosis based on improved sine and cosine algorithm for stacked denoising autoen- coders[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4084-4093.
[34] Nazari M, Sakhaei S M. Successive variational mode decomposition[J]. Signal Processing, 2020, 174: 107610.
[35] 张鑫. 基于信号处理的牵引逆变器系统故障诊断算法研究[D]. 成都: 西南交通大学, 2021.
[36] 李亚茹, 张宇来, 王佳晨. 面向超参数估计的贝叶斯优化方法综述[J]. 计算机科学, 2022, 49(增刊1): 86-92.
Li Yaru, Zhang Yulai, Wang Jiachen. Survey on Bayesian optimization methods for hyper-parameter tuning[J]. Computer Science, 2022, 49(S1): 86-92.
[37] 黄梓欣, 林湘宁, 马啸, 等. 含风电继电保护应用中的电流互感器饱和电流重构方法[J]. 电工技术学报, 2022, 37(19): 4823-4834.
Huang Zixin, Lin Xiangning, Ma Xiao, et al. Reconstruction method of saturation current of current transformer in relay protection application related to wind power[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4823-4834.
[38] 孟晓承, 韩学山, 许易经, 等. SF6高压断路器机械故障概率的非精确条件估计[J]. 电工技术学报, 2019, 34(4): 693-702.
Meng Xiaocheng, Han Xueshan, Xu Yijing, et al. Imprecise estimation for conditional mechanical outage probabilities of SF6 high voltage circuit breakers[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 693-702.
[39] Wang Xiang, Wei Weiwei, Zhang Yanhui, et al. A data-driven lifetime prediction method for thermal stress fatigue failure of power MOSFETs[J]. Energy Reports, 2022, 8: 467-473.
[40] Su Xiaohong, Wang Shuai, Pecht M, et al. Pro- gnostics of lithium-ion batteries based on different dimensional state equations in the particle filtering method[J]. Transactions of the Institute of Measure- ment and Control, 2017, 39(10): 1537-1546.
[41] 郭稳. 功率MOSFET剩余使用寿命预测方法及热疲劳建模研究[D]. 南昌: 华东交通大学, 2020.
[42] Chen Weiqiang, Zhang Lingyi, Pattipati K, et al. Data-driven approach for fault prognosis of SiC MOSFETs[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(4): 4048-4062.
IGBT Lifetime Prediction Model Based on Optimized Long Short-Term Memory Neural Network
Abstract Insulated gate bipolar transistors (IGBTs) are the core components of power electronic systems for converting and controlling electrical energy. However, the reliability of IGBT is lower than expected due to the complex environment and operating conditions, and the sudden failure of IGBT will lead to unplanned downtime of the entire system. Therefore, assessing the remaining useful lifetime (RUL) of IGBT will help guide regular maintenance and reduce economic losses. To prevent the sudden failure of IGBT, it is urgent to accurately predict the RUL of IGBT, but most existing methods have low prediction accuracy and high uncertainty. Therefore, this paper proposes an IGBT life prediction model based on optimized long short-term memory (LSTM). Starting from the two cores of the data-driven model, “data” and “model” are optimized and upgraded, which can effectively improve the accuracy and reduce the uncertainty of the model prediction.
Firstly, the original condition monitoring (CM) data often contain many contaminated data that appear abnormal due to environmental interference and limitations of measurement technology. Meanwhile, CM data may also appear abnormal when IGBT devices degrade or fail, containing important information to characterize the degradation and failure of IGBT. It cannot be processed simultaneously with contaminated data. The proposed model extracts and enhances degraded features by decomposing the IGBT degraded data into multiple modes using the successive variational mode decomposition (SVMD) technique and then reconstructing the useful modes. Secondly, selecting the model’s hyperparameters will greatly affect the model’s learning ability and training effect. Traditionally, the selection of hyperparameters by the empirical trial-and-error method has contingency and randomness, seriously affecting the performance of the model. The proposed model uses the Bayesian optimization (BO) method to realize the global optimization of multiple hyperparameters in the model through the Gaussian process (GP) proxy model and expectation improvement (EI) acquisition function. Finally, the effectiveness and superiority of the LSTM prediction model based on SVMD and BO are verified with real data.
The results show that the predicted RUL is not close to the real RUL by the BO+LSTM method and cannot even meet the 30% error requirement at CM is 160 cycles. In contrast, the errors of the conventional LSTM and RNN methods are large, while the predicted RUL errors using the proposed model meet the requirements for all CM cycles. In addition, the evaluation of the overall performance of the model shows that as an improvement on the RNN, the average relative accuracy (YARA) of the LSTM method improves from 34.65% of RNN to 50.53%, and the average width of prediction interval (WAPI) reduces from 365.3 cycles to 272 cycles. In comparison, the BO+LSTM method has a better prediction performance. Furthermore, the YARA of the proposed model improves to 90.91%, and the WAPI decreases to 169.3 cycles, which is the best performance among several models. Quantitative analysis shows that the proposed model improves the lifetime prediction accuracy by 13% and reduces the prediction uncertainty by 34% compared to the BO+LSTM model.
The conclusions can be drawn: (1) The BO algorithm is used to optimize the hyperparameters of the LSTM, which improves the prediction accuracy of the model. (2) The SVMD is used to extract the degraded features of the IGBT, which reduces the uncertainty and improves the accuracy of the model prediction. (3) Compared with other models, the proposed model can maintain a high prediction accuracy with less CM data, and its long-term prediction performance is better.
keywords：IGBT, reliability, lifetime prediction, mode decomposition, failure distribution
中图分类号：TN322.8; TM46
DOI: 10.19595/j.cnki.1000-6753.tces.222231
国家杰出青年科学基金（52125704）和中央高校基本科研业务费专项资金（2022CDJHLW009）资助项目。
收稿日期 2022-11-29
改稿日期 2023-02-12
任宏宇 男，1997年生，硕士研究生，研究方向为电力电子变流器可靠性。E-mail: rhy@cqu.edu.cn
余瑶怡 女，1994年生，博士研究生，研究方向为电力电子变流器可靠性等。E-mail: yuyaoyi@cqu.edu.cn（通信作者）
（编辑 陈 诚）