（1）
摘要 重复控制器凭借其具有多个谐振峰而广泛应用于电流谐波抑制领域，然而在实际电机控制系统中，由于系统采样频率固定而电流谐波频率随电机转速而变化，会导致重复控制器中出现分数阶延时环节，而该环节在实际控制器中无法实现。对此，该文针对现有分数阶处理方法进行讨论，分析了插值逼近方法中插值系数对重复控制器整体频率特性的作用，据此提出基于几何约束优化的分数阶重复控制器，通过优化各插值系数，电机在全转速范围内都可以保证谐振频率和电流谐波频率相吻合，并且谐振峰值更符合电机谐波组成规律；还分析了滤波器所处反馈回路位置对频率特性的影响，作为组合滤波器设计依据；为保证系统稳定，对包含PI、重复控制器以及离散电机模型的电流控制系统进行稳定性分析，并作为控制参数选取依据。最后，通过台架实验验证了该文所提出的方法的谐波抑制性能是更优的。
关键词：分数阶延时环节 重复控制器 控制稳定性 谐波抑制 永磁同步电机（PMSM）
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）因其功率密度高、运行效率高、动态响应快、结构简单，从而在新能源汽车电驱动系统、航空航天等高性能领域被广泛应用[1]。然而，由于电机本体结构存在齿槽效应、绕组非正弦分布、永磁体缺陷和磁路磁饱和效应等缺陷，将导致电机气隙磁场畸变，同时驱动系统中的逆变器死区时间和开关器件固有管压降等非线性因素致使输出电压波形失真，这两方面因素都会导致定子电流中存在电流谐波分量[2-3]。电流谐波会直接导致电机发热严重，同时还造成电机电磁转矩发生波动，影响平顺性，并且在采用无位置传感器控制的电机系统中，电流谐波同时还影响转子位置估计精度，进而影响控制系统稳定性[4]。
针对定子中的电流谐波问题，国内外研究学者展开了大量的研究工作，抑制电流谐波的思路可以划分为优化电机本体结构[5-6]、加入输出滤波器[7]、专用拓扑结构[8]和谐波抑制算法[9-18]四个方面。谐波抑制算法无需在已有系统结构上做出改动并且效果明显，从而被广泛使用，主要算法包括谐波电压补偿[9]、多旋转PI控制[10]、自抗扰控制[11]、比例谐振控制[12-13]和重复控制[14-18]等。重复控制由于结构简单、谐波抑制效果好、具有多个谐振频率、可通过设计内模系数来调节谐振带宽和峰值，从而在并网逆变器、电机控制等领域中广泛应用。
重复控制在实际应用过程中存在如下问题，当系统采样频率与电流谐波频率之比值不为整数时，重复控制器中会存在分数阶延时环节，实际控制器若将该分数阶延时环节四舍五入到附近的整数阶，会导致重复控制器多个谐振频率发生集体偏移，与电流谐波频率不一致，从而造成谐波抑制性能急剧降低。针对此问题，武永燎等采用二阶拉格朗日插值对频率比值小数部分构成的分数阶延时环节进行插值逼近，提高了电流控制系统谐波抑制性能[16]；陈东等基于线性插值法设计了可逼近分数阶延时环节的数字滤波器，提升了对电网频率变化的适应 性[17]；徐群伟等提出了双分数阶快速重复控制策略，将传统内模重新塑造为有限个阶次相邻、权重系数不同的整数阶内模，改善了分数阶以及电网频率偏移时的适应性问题[18]。
上述几位学者在处理分数阶问题时，本质上都是采用了拉格朗日插值逼近，针对插值逼近来处理分数阶问题，有关插值系数对重复控制器的影响、如何设计插值系数来优化谐波抑制性能等相关研究缺失；有关含有重复控制器的电流控制系统稳定性分析不够详实具体，或只讨论重复控制器自身稳定性。对此，本文对传统拉格朗日插值逼近分数阶进行改进，根据插值系数对重复控制器频率特性影响的相关分析，提出了基于几何约束优化的重复控制器。相较于传统方法，实现了更少的谐振频率偏移，更符合电机各阶次谐波组成规律的谐振峰值分布；分析了滤波器所处反馈回路位置对频率特性的影响，以此为依据在回路外设计了组合滤波器，进一步改善了重复控制器幅频特性；将所改进的分数阶重复控制器置入电流控制系统，考虑系统采样和计算延迟，对整个电流控制系统稳定性进行了分析，以此给出相关参数选择依据。通过台架实验验证了本文所提方法的谐波抑制性能是更优的。
理想电机运行在稳态工况时，三相电流应当为正弦波且相位相差120°，但是由于电机本体缺陷以及驱动电路含有各种非线性因素，三相电流中会含有各阶次谐波且主要为6k±1（k为正整数）次，此时三相电流组成可近似表示为
（1）
式中，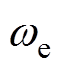
为电机三相电流频率；
、
、
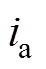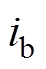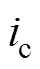分别为A、B、C相电流；
、
、
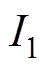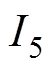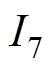分别为基波电流、5次、7次谐波电流幅值；
、
、
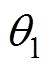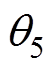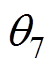分别为A相基波电流、5次、7次谐波电流初始相位。
根据幅值不变约束条件，式（1）坐标变换到两相旋转坐标系下可得
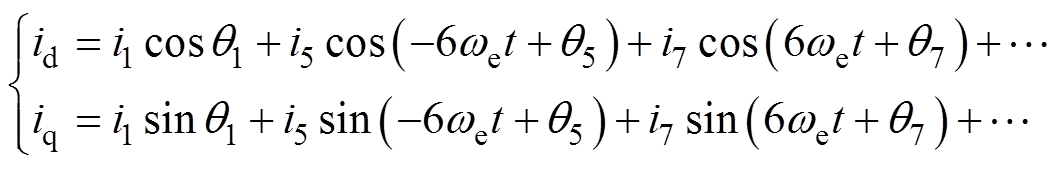（2）
式中，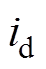
、
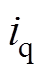分别为两相旋转坐标系下d、q轴电流。
由式（2）可知，自然坐标系下6k±1次谐波分量坐标变换到两相旋转坐标系下表现为6k次周期性扰动。传统永磁同步电机矢量控制系统中电流环仅含有PI控制器，而PI控制器只能实现对直流分量无误差跟踪，当电流环中含有电流谐波类周期性扰动时，PI控制器不能有效地抑制电流谐波。
重复控制是基于控制理论中的内模原理，所谓内模原理，其本质是如果闭环控制系统中包含外部输入信号的动力学模型，则此系统可以无静差跟踪输入信号。对于无静差系统，当控制器输入的误差信号为零时，内模可以起到信号发生器的作用，不依赖外部变量持续不断地给出相应控制信号。图1为理论重复控制器框图，其传递函数为
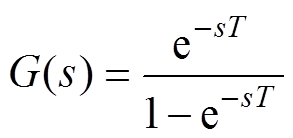（3）
式中，T为给定信号周期。
该传递函数本质上是周期延时正反馈环节，而从内模的角度理解，延时环节和正反馈构成了谐波信号发生器，将输入信号延时特定周期后再次输入，符合电流谐波周期性出现的特点，并且还可以不断输出给定基准频率任意整数倍的谐波信号，因此在两相旋转坐标系下加入给定频率为6倍相电流频率的重复控制器可以有效抑制电流谐波。
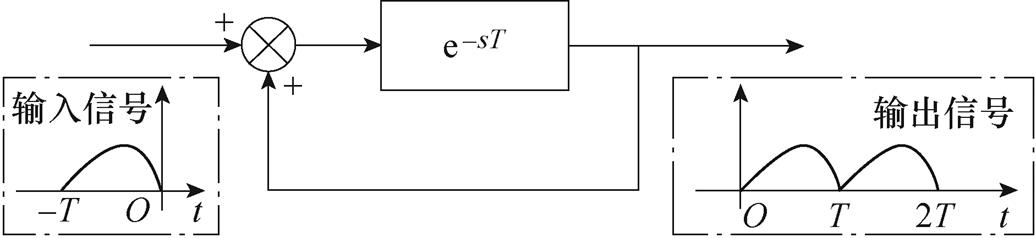
图1 理论重复控制框图
Fig.1 Theoretical repetitive controller block diagram
为抑制电流谐波，可以将1/6相电流周期作为给定信号周期的重复控制器和PI控制器在电流环中并联，但由于理论重复控制器在给定频率整数倍处具有无穷增益，为防止其将误差信号中高频干扰成分一并放大从而造成电流控制系统不稳定，需要对重复控制器内模进行改进，通过在反馈回路加上小于1的常数或者低通滤波器，来减弱重复控制器对频率波动变化的敏感度，提高系统稳定性[19]；并且由于实际控制器无法实现纯延时环节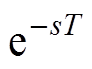
，因此还需将重复控制器改写成离散形式，有
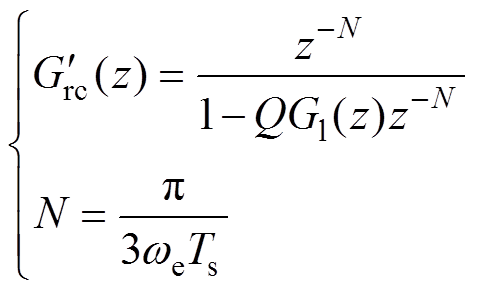（4）
式中，Q为内模系数，0＜Q＜1；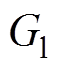
为低通滤波函数；N为控制器延时周期；
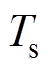为控制器采样周期。
以q轴为例，图2a、图2b分别为传统、改进后的重复控制器框图，在电流控制系统中重复控制器输入为q轴电流误差。传统结构中延时环节位于前向通道，控制量与电流误差的关系在理想内模下可以改写为式（5），能看到重复控制器控制律由之前时刻的电流误差决定；而若将延时环节移到反馈通道，两者关系可以改写为式（6），控制律由当前时刻误差量决定，考虑到电机实际运行过程中电流谐波组成时刻发生变化，后者系统动态性能相较于前者会更好，因此将延时环节移至反馈通道上。相较于传统结构，本文还将低通滤波器移至反馈回路外，减少谐振频率偏移，并在回路外设计了高通滤波器
以实现组合滤波，具体分析见后文。
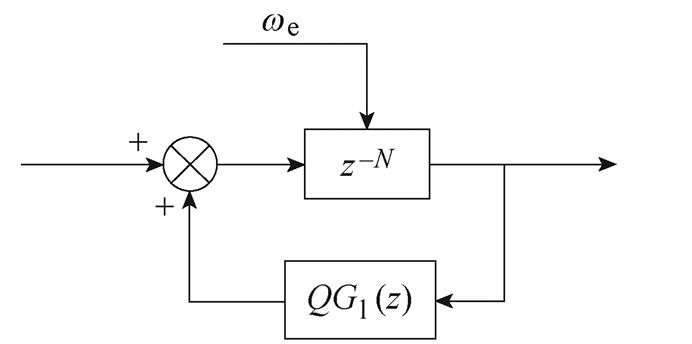
（a）传统重复控制器结构
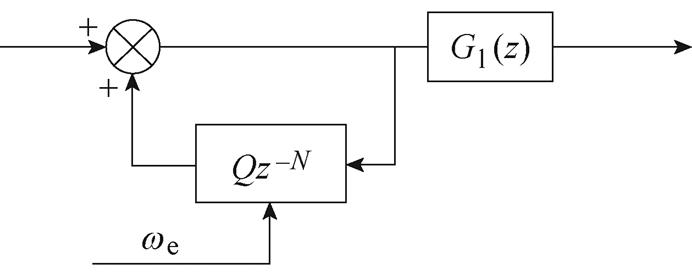
（b）改进重复控制器结构
图2 改进前后的重复控制器框图
Fig.2 Block diagram of repetitive controller before and after improvement
（5）
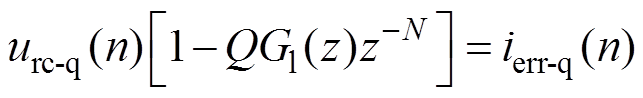（6）
式中，urc-q(n)为当前时刻q轴重复控制器计算出的控制量；ierr-q(n)、ierr-q(n-N) 分别为当前n时刻、n-N时刻q轴电流误差。
当电流频率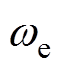确定时，两相旋转坐标系下电流谐波频率与其成6k倍，而延时周期与电流频率唯一对应，因此N决定了重复控制器能抑制的电流谐波频率。由于电机在运行过程中电流频率会时刻变化，N可以看作由整数部分N0和小数部分N1组成，而实际控制器只能将信号延时整数倍采样周期，因此如何处理分数阶延时环节
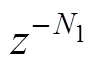至关重要。
2.3.1 不同分数阶处理方式对幅频特性的影响
本文后续所采用永磁同步电机极对数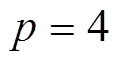
，系统采样周期为50 ms，根据电机常用转速区间，后续分析时选用延时周期
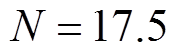进行，对应电流频率约为1 196.8 rad/s。内模系数Q对重复控制器幅频特性的影响如图3所示，内模系数不会改变谐振频率，但随着Q逐渐向1逼近，谐振峰值快速增大至无穷大、谐振带宽范围收窄至0。考虑到实际运行中电流谐波频率存在着微弱变化，峰值过大将造成系统不稳定，而过小不利于谐波抑制性能，因此在后续分析、设计过程中初步选取内模系数
。
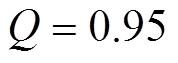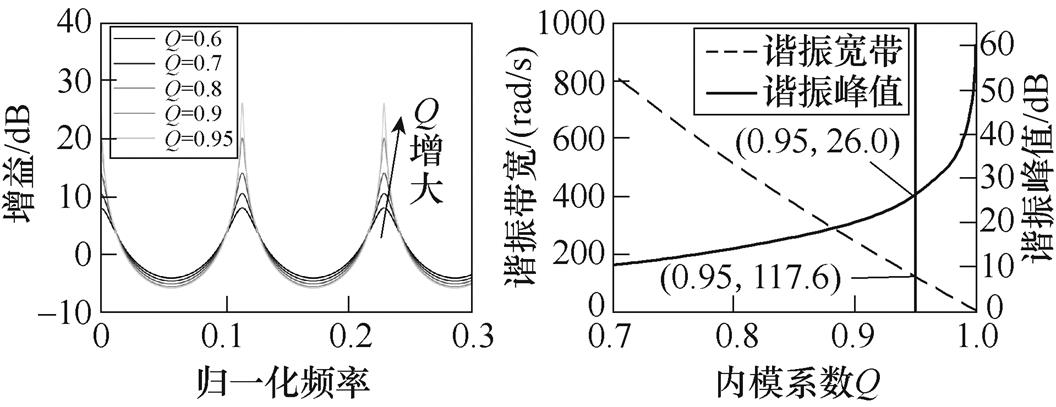
（a）不同内模系数Q下的 幅频特性（b）谐振带宽、峰值和内模 系数Q之间的关系
图3 内模系数Q对重复控制器幅频特性的影响
Fig.3 Influence of internal model coefficient Q on amplitude frequency characteristics of repetitive controller
现有研究对分数阶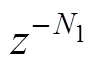的处理方法可以归结为两类：①N1四舍五入为0或者1，这将直接导致被抑制电流谐波频率发生偏移，会极大损失谐波抑制性能；②拉格朗日插值逼近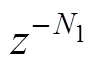，采用多个整数阶延时环节（
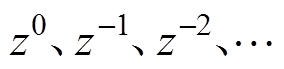）乘以拉格朗日插值系数，从而对分数阶实现插值逼近。
基于插值逼近的分数阶重复控制器传递函数为
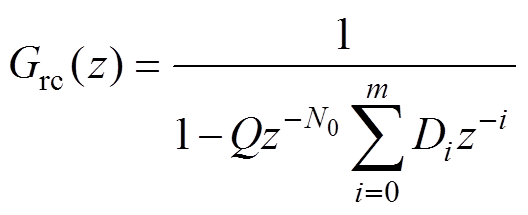（7）
当采用拉格朗日插值时，其插值系数为
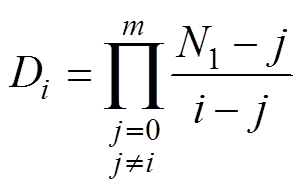（8）
式中，m为插值阶次；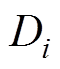
为插值系数。
不同分数阶处理方式对重复控制器的影响如图4所示。图4a可以看到，将N1四舍五入后，对谐振峰值没有影响，但是谐振频率发生了偏移，并且k越大偏移越多。这是因为N1四舍五入可以等效于反算出的电流频率发生变化，谐振频率与电流频率成6k倍数关系，因此k越大谐振频率偏移越严重。由图4b可以看到，对分数阶采用拉格朗日插值后，重复控制器谐振峰普遍存在着向左偏移，且k越大偏移越多；但随着插值阶次提高，谐振频率偏移程度、峰值变化程度并没有明显改善，反而呈现出不确定性变化规律。
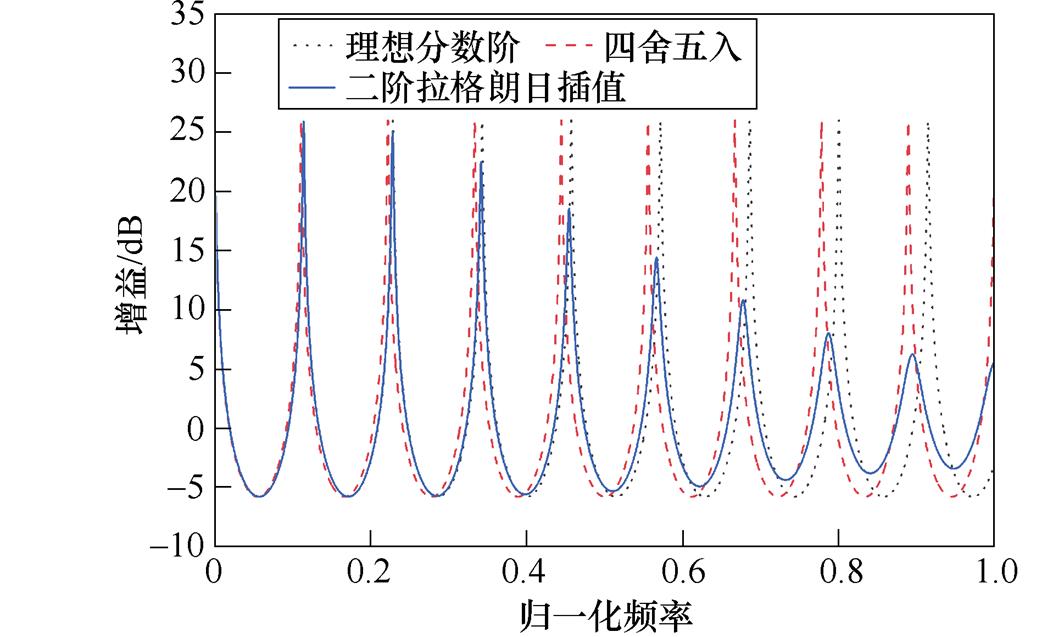
（a）不同分数阶处理方式对幅频特性的影响
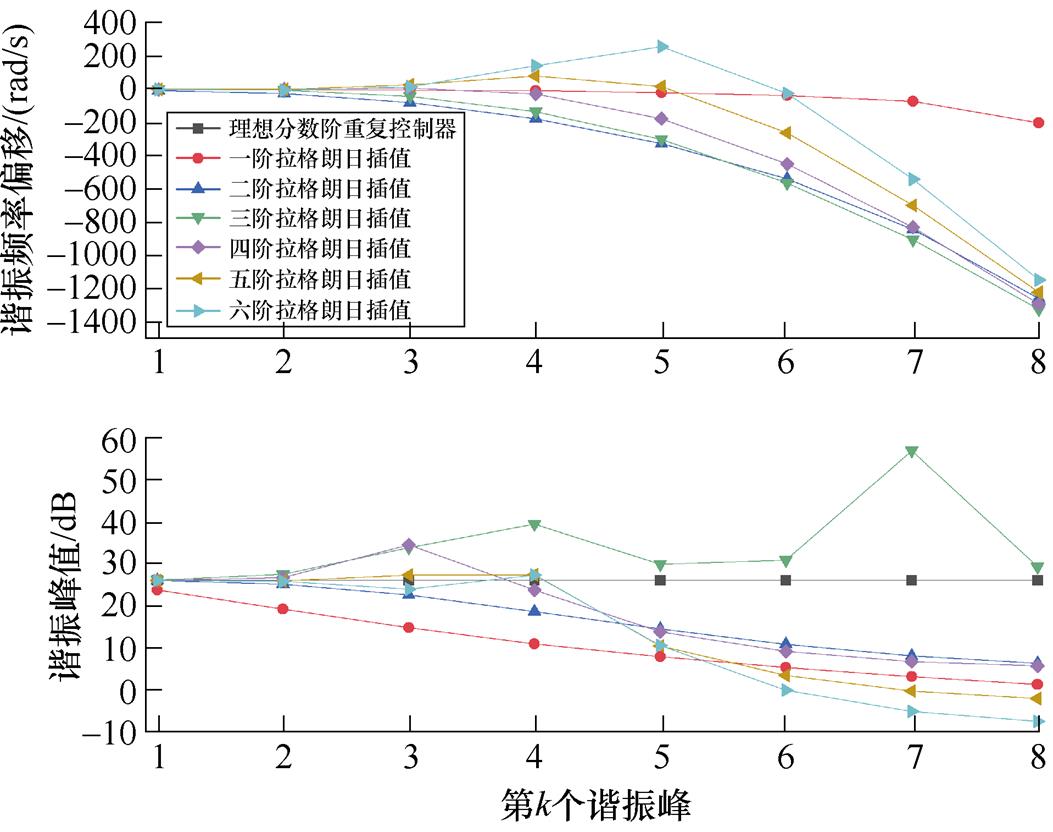
（b）不同阶次拉格朗日插值所造成的频率偏移、谐振峰值变化
图4 不同分数阶处理方式对重复控制器的影响
Fig.4 Influence of different fractional order processing methods on repetitive controller
2.3.2 拉格朗日插值系数分析
采用拉格朗日插值对分数阶进行逼近时，插值系数是直接套用式（8）得来的，其实际含义为：现有m+1个插值节点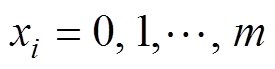
，对应有m+1个拉格朗日插值基函数
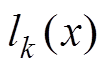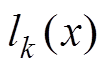，其中在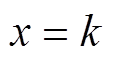
处等于1，剩下插值节点都等于0，这些基函数在
处取值为对应的拉格朗日插值系数。以二阶拉格朗日插值为例，具体取值过程如图5所示。
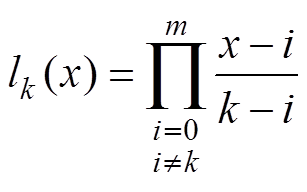（9）
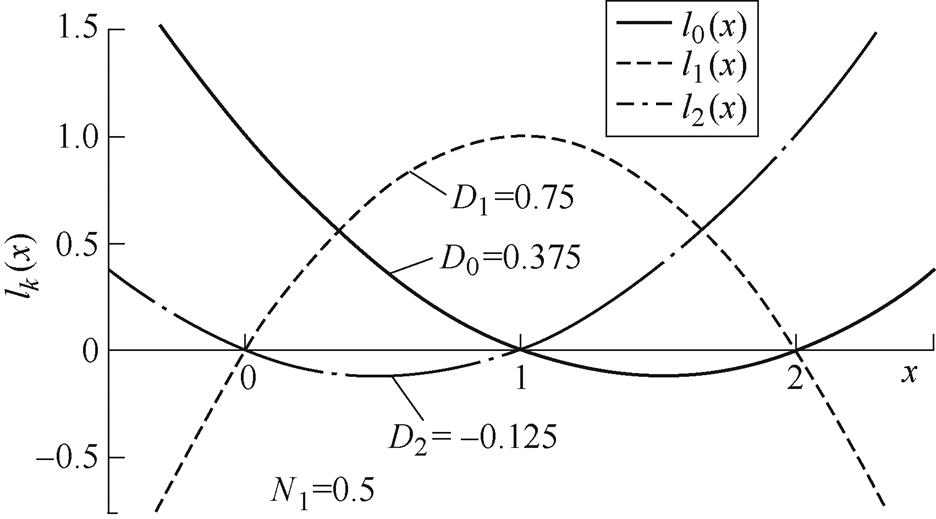
图5 拉格朗日插值系数取值过程
Fig.5 The value process of lagrange interpolation coefficient
假设有待进行拉格朗日多项式插值的函数为
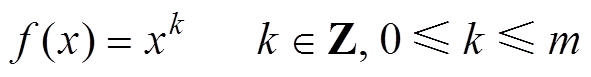（10）
根据插值余项定理可知
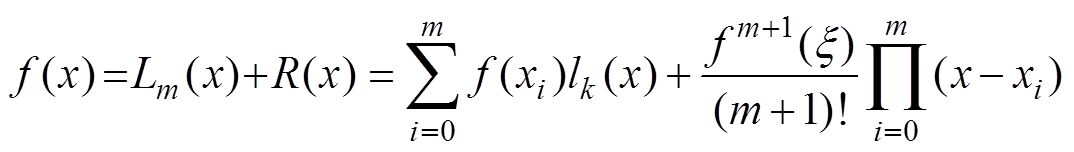（11）
由于待进行拉格朗日插值的函数为k次多项式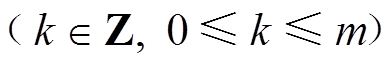
，因此有
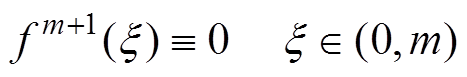（12）
将待插值函数在节点上的取值代入式（11），有
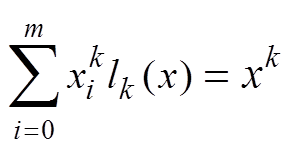（13）
由图5可知，拉格朗日插值系数为其对应插值基函数在处的取值，N1与拉格朗日插值系数唯一对应，这是因为m+1个插值系数之间存在式（13）所示m+1个约束，这些约束与重复控制器幅频特性（其决定了谐波抑制性能）没有直接联系，而通过合理配置插值系数能够实现较拉格朗日插值更好的谐波抑制效果。
将电流谐波视作电流环中的误差信号，则重复控制器是将电流频率6k倍处的误差信号放大，得到控制量，因此决定重复控制器谐波抑制性能的是其幅频特性，准确地讲是其谐振频率以及峰值。针对分数阶问题，基于重复控制器幅频特性展开研究是直切要害的。
基于插值逼近的分数阶重复控制器在连续域的传递函数为
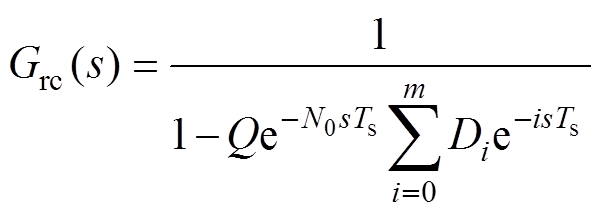（14）
在式（14）中令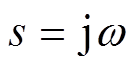
，并基于欧拉公式展开后可得到一般形式见式（15），对其分别取模和相位即可得到重复控制器幅频特性和相频特性。
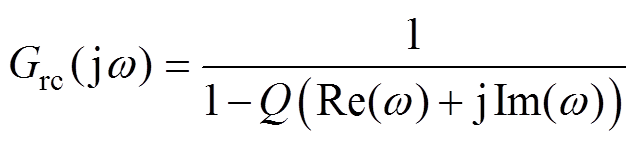（15）
式中，
和
分别为重复控制器中所有延时环节按照欧拉公式展开后所得到的实部和虚部。
3.1.1 幅频特性
以实部Re、虚部Im分别作为横纵坐标，对式（15）取模后可得
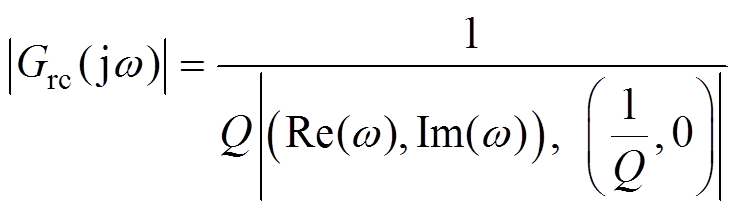（16）
根据式（16）可得如图6所示重复控制器幅频特性曲面，该曲面由内模系数Q唯一确定，且在（1/Q, 0）点具有无穷大增益，并且曲面上某点的增益值仅由该点离（1/Q, 0）距离决定，距离越远增益越小。
当插值系数确定后，、取值由频率唯一确定，其函数关系推导得
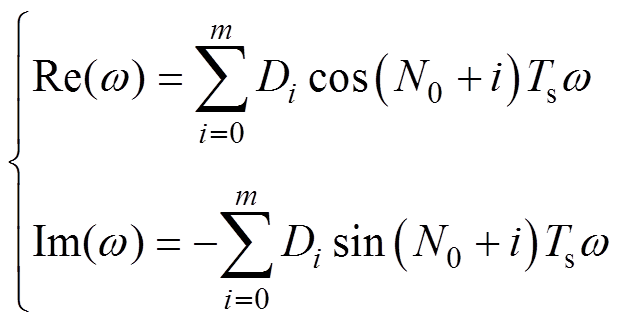（17）
式（17）可以等效为复合圆周运动，若将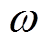
视为自变量，其运动规律由
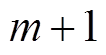个半径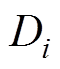为、角频率为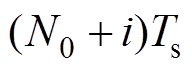
的圆周共同决定。当频率从零逐渐增大到无穷大，取点按照如图7所示复合圆周运动，该点投影到幅频特性曲面上就得到对应频率处的幅值。简言之，插值系数决定了取点在幅频特性曲面上的运动规律，进而决定了该插值系数下重复控制器的幅频特性。
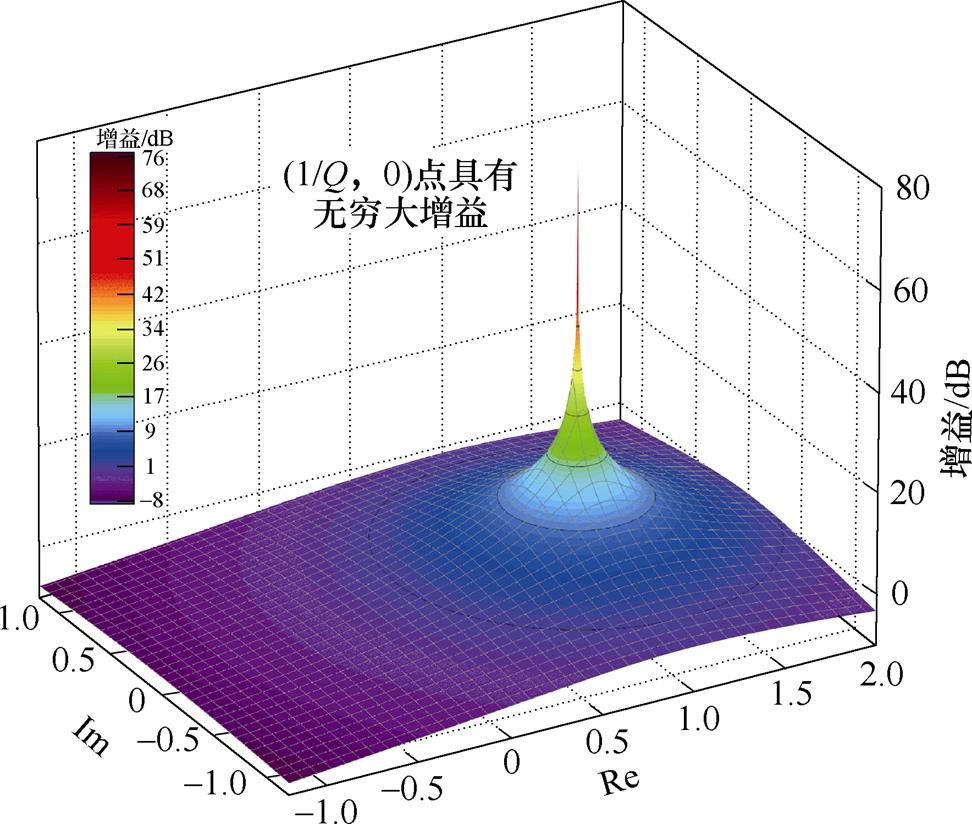
图6 重复控制器幅频特性曲面
Fig.6 Amplitude frequency characteristic surface of repetitive controller
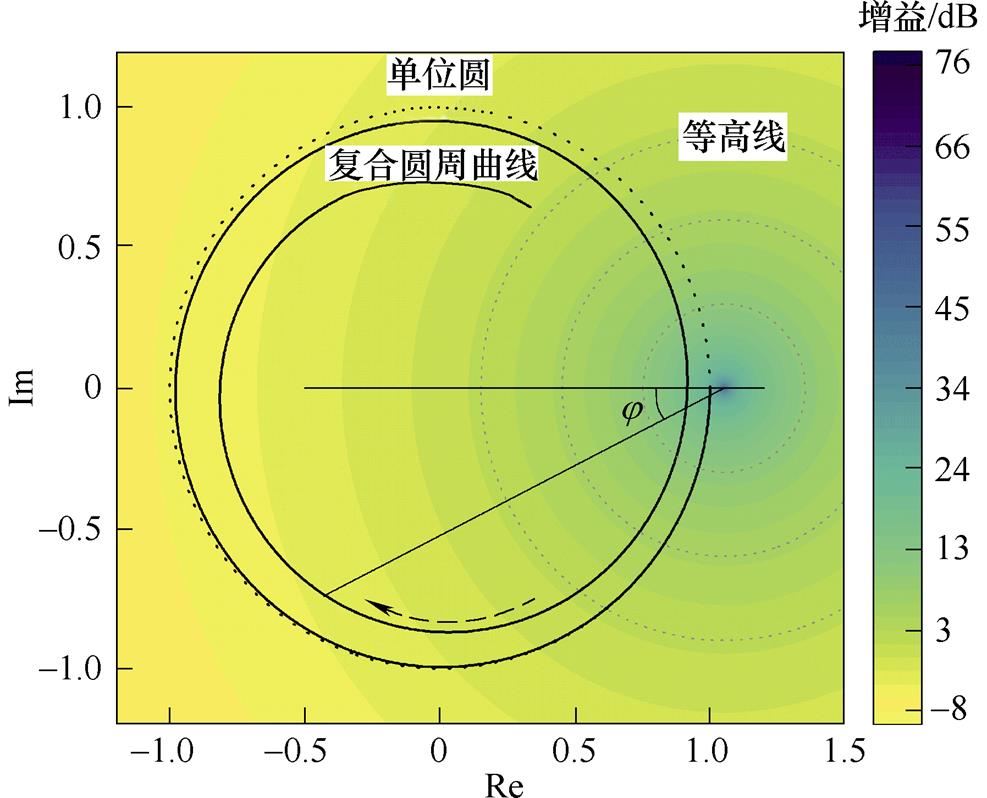
图7 复合圆周运动示意
Fig.7 Schematic of compound circular motion
由图7可以看到，幅频特性曲面等高线是以（1/Q, 0）为圆心的同心圆。理想分数阶重复控制器的运动曲线为以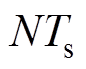
为角频率的单位圆，而基于插值逼近的分数阶重复控制器其运动曲线表现为在单位圆附近运动。因此，谐振频率偏移可归结为等于6k倍电流频率时，式（17）复合圆周曲线未与等高线相切，若此时曲线朝着靠近（1/Q, 0）方向运动则谐振频率增大，反之则减小；同理可得，谐振峰值变化是因为复合圆周曲线与等高线相切时，离（1/Q, 0）距离发生了变化。
这进一步说明了相较于套用计算式（8），可以通过合理配置插值系数来优化复合圆周曲线，进而实现更少的谐振频率偏移以及更符合电流谐波分布规律的谐振峰值，进而提升重复控制器的电流谐波抑制性能。
3.1.2 相频特性
对式（15）取相位后可得
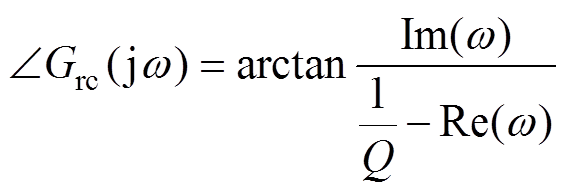（18）
式（18）在复平面上可表示为（1/Q, 0）和当前取点连线与实轴负方向之间的夹角。因此可以得知，当复合圆周曲线仅在（1/Q, 0）左侧穿越实轴时，相位会在-90°～90°之内来回振荡，这能保证重复控制器自身具有足够的相位裕度，而相位接近90°具体程度则由1/Q和复合圆周曲线共同决定，并且可以通过减小Q或者整体缩小插值系数来减小相位振荡范围；当复合圆周运动曲线在（1/Q, 0）右侧穿越实轴时，穿越前后会发生相位从-180°～180°突变，因此在设计插值系数时应当保证
。
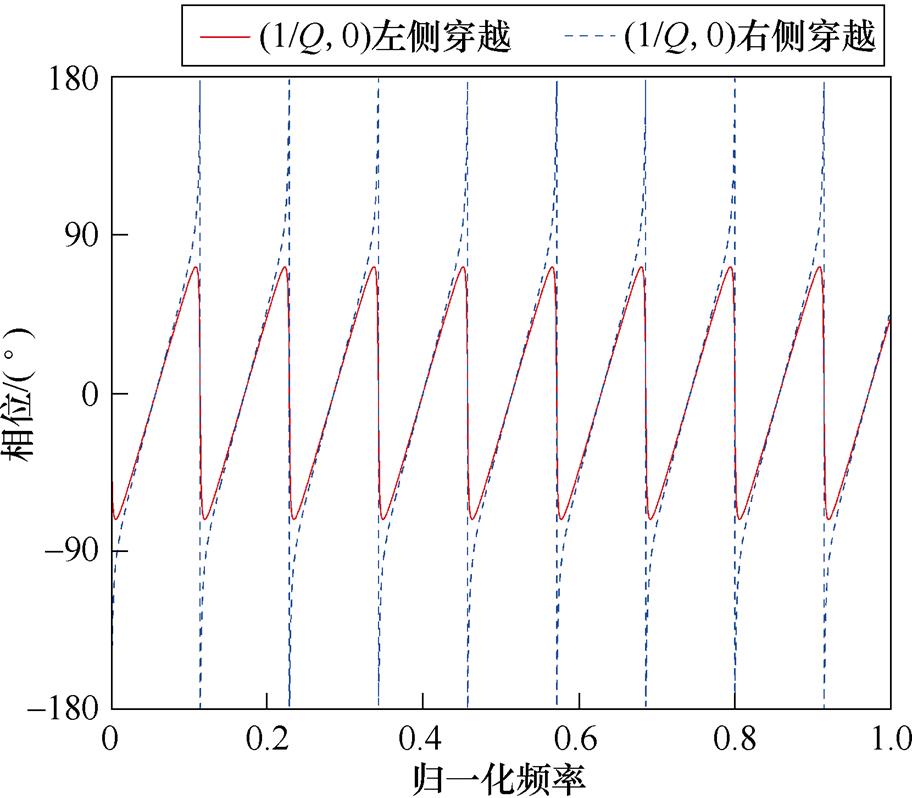
图8 穿越点对相频特性的影响
Fig.8 Influence of crossing coordinates on phase frequency characteristics
在进行插值系数优化时，由于获得重复控制器幅频特性需要计算所有频率下的增益，因此本文将插值系数优化转化为复合圆周曲线几何约束问题，谐振频率优化等效于频率为电流频率6k倍时复合圆周曲线是否和等高线相切，谐振峰值优化问题则等效于频率为电流频率6k倍时曲线至（1/Q, 0）距离。通过将问题转化，将插值系数优化过程中节省大量计算资源，进而实现更优的参数设计。
当复合圆周曲线和等高线相切时，曲线切线斜率和该点与（1/Q, 0）连线斜率之乘积为-1，因此引入式（19）用来评价谐振频率偏移程度；由于增益和该点与（1/Q, 0）距离成反比，引入式（20）用来评价谐振峰值变化程度。综合考虑插值效果和优化难度，采用二阶插值对分数阶进行逼近。图9所示为本文设计的几何约束优化算法，以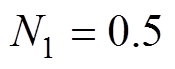
为例，先在拉格朗日插值系数附近初始化Di，如果前三处谐振频率偏移都小于
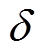，计算频率偏移、峰值变化的综合损失，若综合损失小于过往循环最小值，就将Di记为当前最优插值系数，然后在该系数附近生成新的Di，直至循环次数满足要求。考虑到电机电流谐波分布规律，算法中仅优化前三处谐振峰，并且可以通过调节kj来实现各谐振峰值与6、12、18次电流谐波成量相吻合。
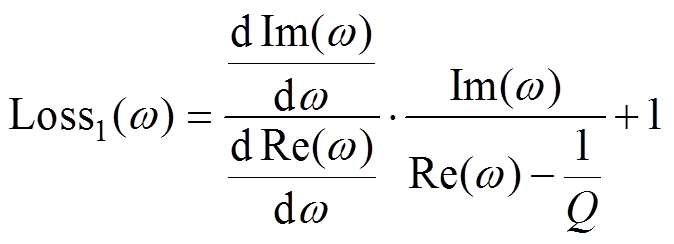（19）
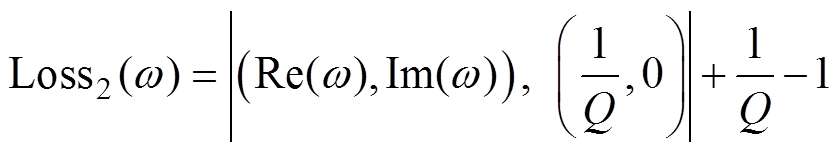（20）
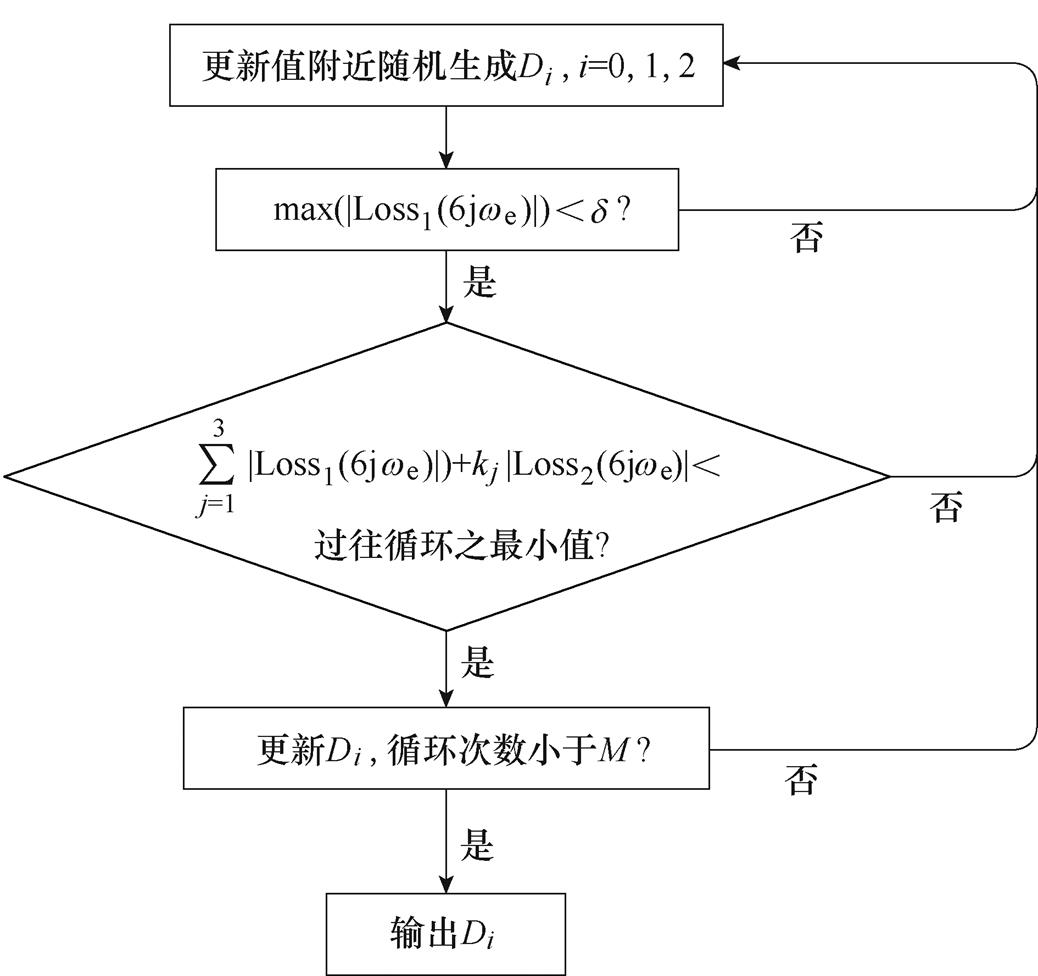
图9 几何约束优化算法结构
Fig.9 The proposed algorithm structure of geometric constraint optimization
图10为插值系数优化结果，可看到相较于传统拉格朗日插值，改进分数阶重复控制器具有更少的谐振频率偏移，且谐振峰值更低，从而系统稳定性提升，且由于谐振频率偏移更少，6k次电流谐波频率处增益反而更高，因此提升稳定性的同时还提升了谐波抑制性能。关于图10，需要特别说明的是，插值系数优化前后在高频部分均出现了较大的谐振频率偏移以及峰值变化，这是由于实际控制器本身就无法实现分数阶延时，采用整数阶插值逼近分数阶时并不能在全频率段都完美复现分数阶重复控制器的幅频特性，只能通过插值系数优化来尽量复现。这意味着重复控制器在实现过程中，可以同时抑制前几处较低阶次谐波，但在高频处由于出现了不可避免的谐振频率偏移，因此高次谐波抑制性能比较有限，并且如果后面几处谐振峰值较高但谐振频率偏移严重的话，不仅不能起到谐波抑制作用反而会危害系统稳定性。
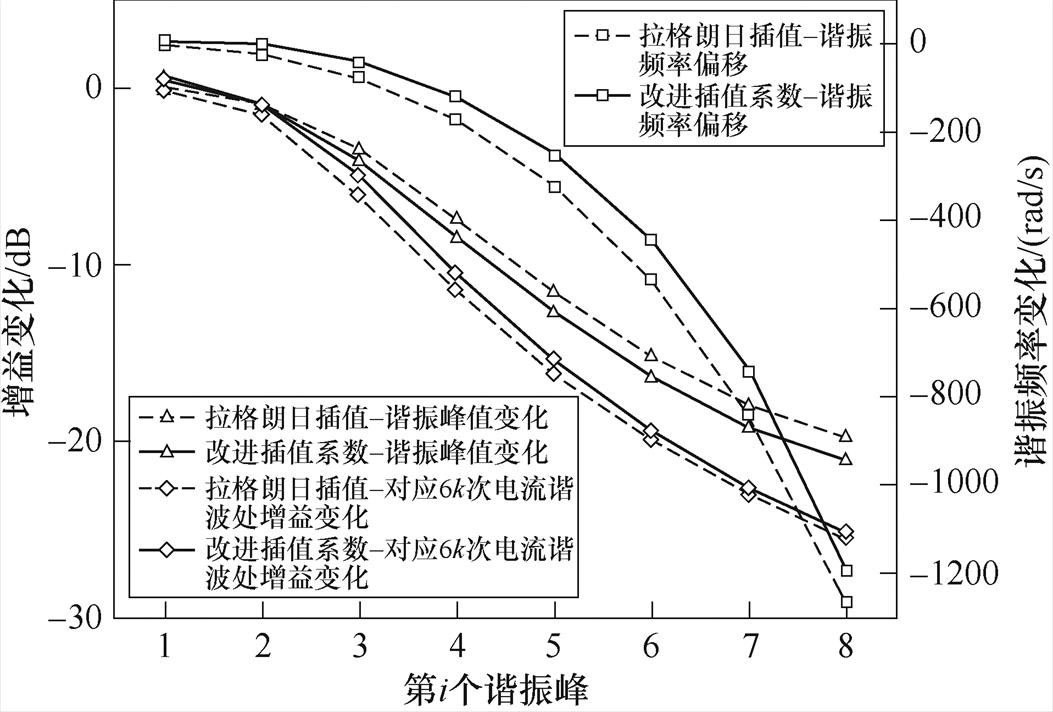
图10 改进分数阶重复控制器相较基于拉格朗日插值的幅频特性对比
Fig.10 Comparison of amplitude frequency characteristics between proposed fractional order repetitive controller and lagrangian interpolation based controller
3.3.1 滤波器所处回路位置的影响
当低通滤波器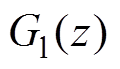
位于重复控制器反馈回路外时，如式（21）所示，其传递函数为原先传递函数直接乘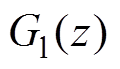，因此认为反馈回路外加上低通滤波器不会影响谐振频率，会削弱高频处谐振峰值。
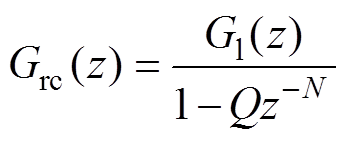（21）
当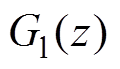位于反馈回路内时，传递函数如式（22）所示，
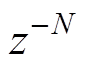在复平面上按单位圆进行运动，由于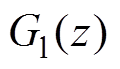在过渡带内随着频率增大而增益减小，此时
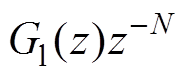在复平面上是向内螺旋的，这会造成曲线在穿越实轴前和等高线相切而导致谐振频率减小；即使在通带内，由于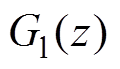存在通带纹波，同样会造成谐振频率增大或减小，从而极大降低了谐波抑制性能；且随着频率增大，由于曲线是向内螺旋的，穿越实轴的位置离（1/Q, 0）越来越远，而（1/Q, 0）附近增益衰减非常明显，因此反馈回路内的低通滤波器还会极大地降低高频处谐振峰值。
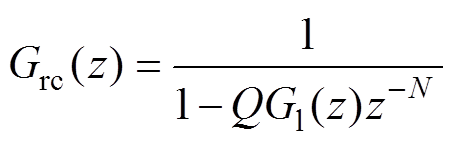（22）
上述分析是以低通滤波器为例，而高通滤波器具有类似结论，因此得出结论，为避免谐振频率偏移而极大损失了谐波抑制性能，应将滤波器移至反馈回路外。
3.3.2 组合滤波器设计
结合复合圆周运动规律可知，重复控制器幅频特性必然存在周期性规律，因此前几处谐振峰较大的峰值会在高频处反复出现。为避免将高频噪声放大后作为控制量一并输入系统，从而造成系统不稳定，需要在重复控制器中加入低通滤波器，在较高频率处适当地削弱谐振峰值，因此低通滤波器选用一阶低通滤波器，截止频率为8 000 Hz。
重复控制器直接目的是在电流频率6k倍处放大dq轴电流误差量，但观察图4a可知，当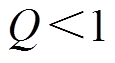
时，在零频率附近总会存在半个谐振峰，这意味着重复控制器同样会将附近频率的误差放大很多倍后输入控制系统，这是不利于控制稳定性以及谐波抑制效果的，因此还需要引入高通滤波器来消除这半个谐振峰。同时注意到，半个谐振峰增益总是在首个谐振频率的特定比例处附近降至0 dB，因此选用一阶高通滤波器，通过试凑后截止频率定义为
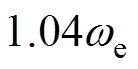，实现随电流频率自动调整通带范围，消除半个谐振峰。
图11为在不同位置引入组合滤波器后的基于几何约束优化的重复控制器幅频特性，可见在反馈回路内引入组合滤波器后谐振频率偏移严重，而在回路外引入时，仅在前几处低次谐波频率处保留了较大增益且谐振频率未发生偏移，考虑到通过实验得知电机仅前几处低次谐波成分较大，因此可认为在回路外引入组合滤波器提高系统稳定性的同时还极大地保留了谐波抑制性能。
电流控制系统框图如图12所示，电流控制系统中含有重复控制器
、PI控制器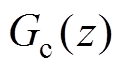
以及电机模型
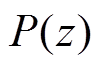，因此仅分析重复控制器稳定性并不能保证整个电流控制系统稳定，考虑到控制算法是数字实现的，因此本文基于离散域分析系统稳定性。
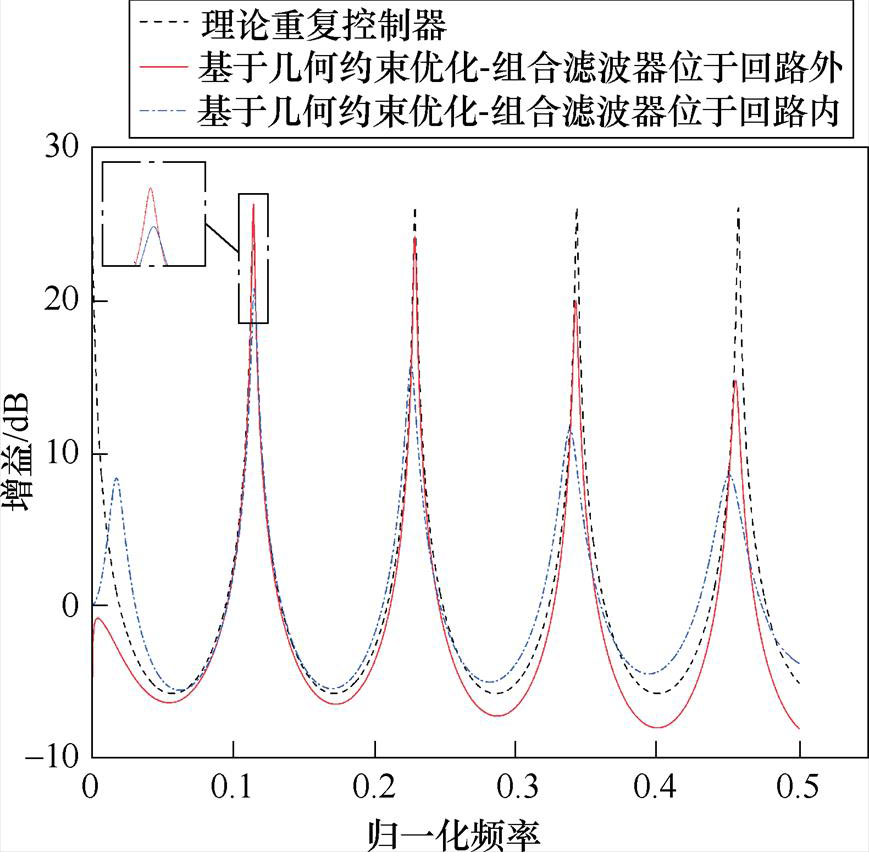
图11 引入组合滤波器后基于几何约束优化的分数阶重复控制器幅频特性
Fig.11 Amplitude frequency characteristics of fractional order repetitive controller based on geometric constraint optimization with combined filter
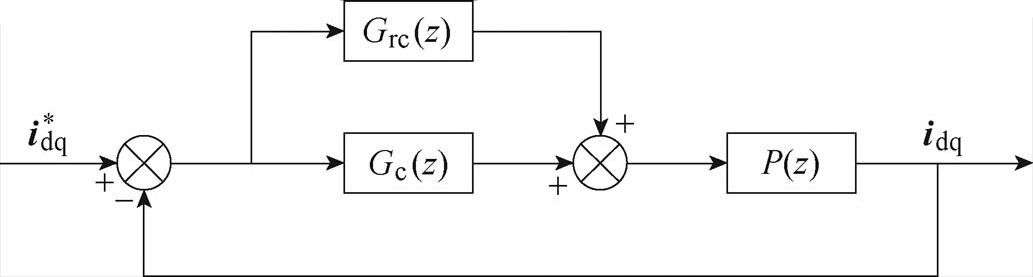
图12 电流控制系统框图
Fig.12 Block diagram of current control system
模型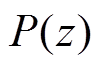，因此仅分析重复控制器稳定性并不能保证整个电流控制系统稳定，考虑到控制算法是数字实现的，因此本文基于离散域分析系统稳定性。
电机控制器采样方式为起点采样终点更新，所更新的电压命令值有一个脉冲宽度调制（Pulse Width Modulation, PWM）周期的角度延迟，如图13所示。对延迟角度进行补偿后，电机在两相旋转坐标系下的离散数学模型P(z)可表示为
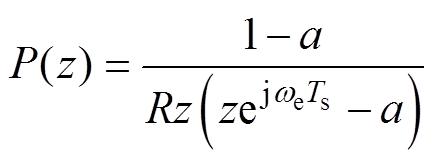（23）
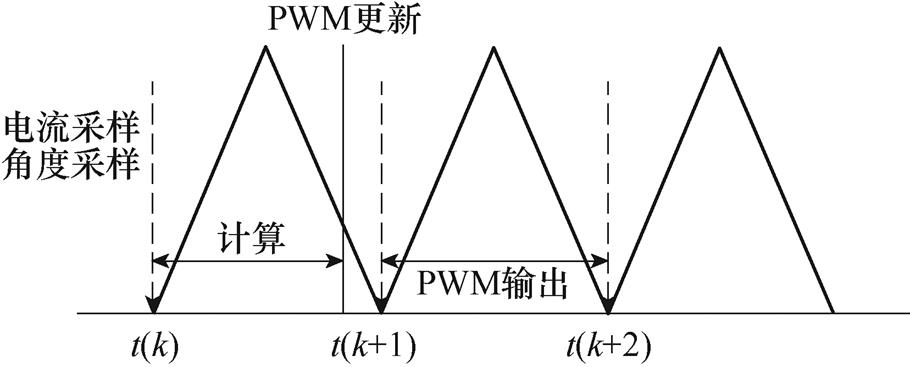
图13 控制器采样更新示意图
Fig.13 Diagram of sample and update for controllers
其中
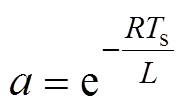
式中，R为定子电阻；L为定子电感。
结合图12，可知电流控制系统开环传递函数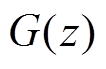
表示为
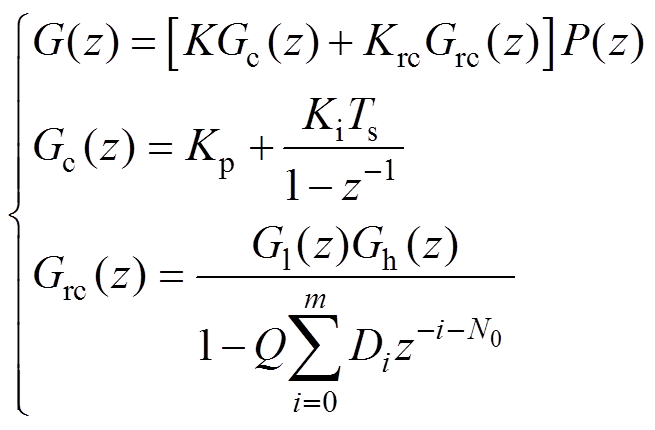（24）
式中，Kp和Ki分别为电流环PI控制器比例、积分增益；K为PI控制器增益；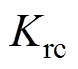
为重复控制器增益。
本节稳定性分析的相关参数取值在表1中给出，除此之外电流控制系统可以调节的参数包括：
PI控制器增益K、重复控制器增益、内模系数Q，其稳定性分析以及参数选择流程为：没有重复控制器时K取值的稳定性分析，确定K取值后，再分别讨论和Q取值对稳定性的影响，据此确定两者取值；由于电机运行工况会发生变化，还需要讨论在不同电机转速下的电流控制系统稳定性。
表1 稳定性分析的相关参数
Tab.1 Relevant parameters of stability analysis
参 数数 值 电机极对数4 定子电阻/W0.015 定子电感/H0.000 77 系统采样周期/ms50 电流环PI控制器比例增益Kp2.55 电流环PI控制器积分增益Ki285.5
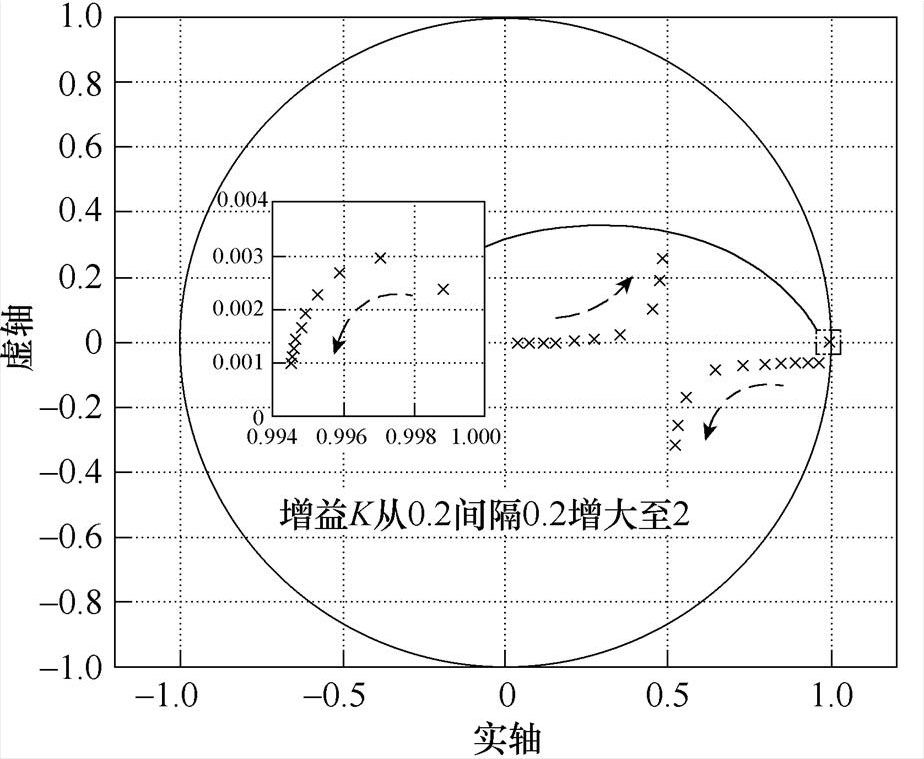
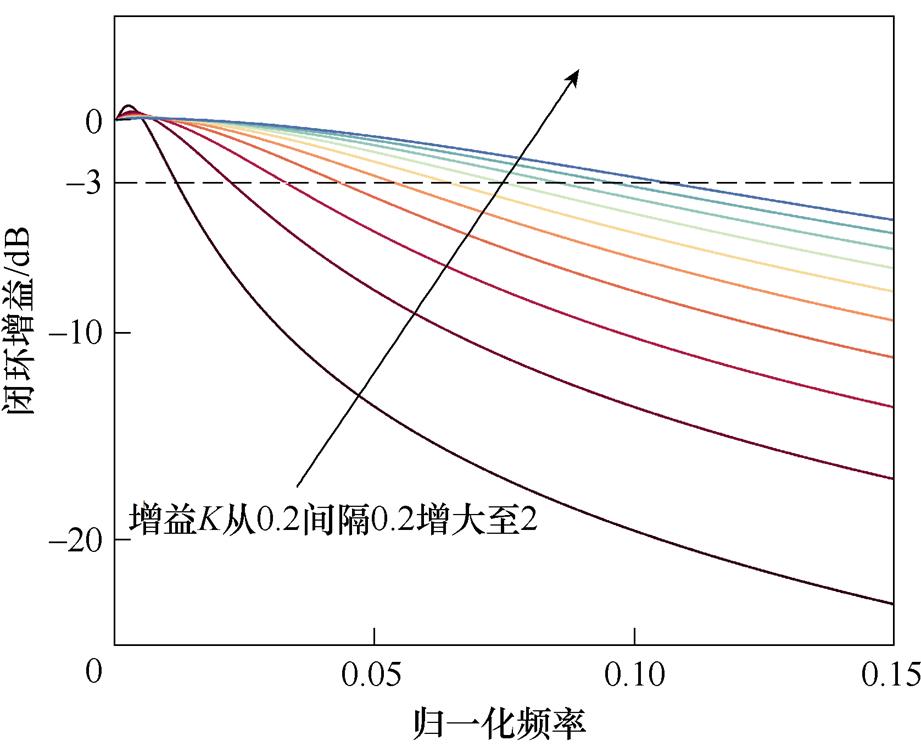
图14a、图14b分别为随着增益K增大，仅含PI控制器电流控制系统的闭环极点分布和带宽变化情况，可以看到，随着K从0.2增大至2，距离单位圆最近的黑色“×”所示极点逐渐远离单位圆，因此系统稳定性增强，但同时电流环带宽随着K增大而增大，系统抗干扰能力变弱，综合考量后选取PI控制器增益K=1。
当在电流控制系统中引入带有组合滤波器的重复控制器后，闭环极点数量达到
，根据闭环极点分布来分析不够直观，因此在分析过程中引入奈奎斯特图，并以奈奎斯特曲线至（-1, j0）距离min|1+G(z)|来分析系统稳定性。
（a）闭环极点分布
（b）系统带宽
图14 增益K对仅含PI控制器闭环系统的影响
Fig.14 Influence of gain K on closed loop system with PI controller only
据闭环极点分布来分析不够直观，因此在分析过程中引入奈奎斯特图，并以奈奎斯特曲线至（-1, j0）距离min|1+G(z)|来分析系统稳定性。
电流指令、电流误差之间的传递函数可表示为
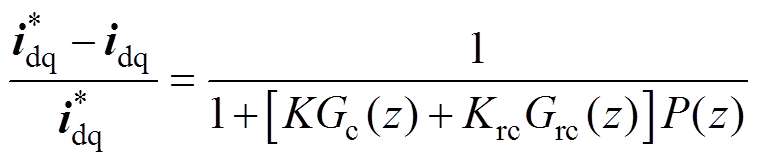（25）
式（25）同样定义为灵敏度函数
[20]，当扰动作用在被负反馈回路所包含的前向通道上时，闭环系统对于扰动所造成传递函数或参数变化的灵敏度是开环系统的倍，因此灵敏度函数的模可用来衡量电流控制系统稳定性，其模越大，开环传递函数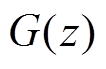距离（-1, j0）越近，电流输出对扰动越敏感，系统越不稳定。
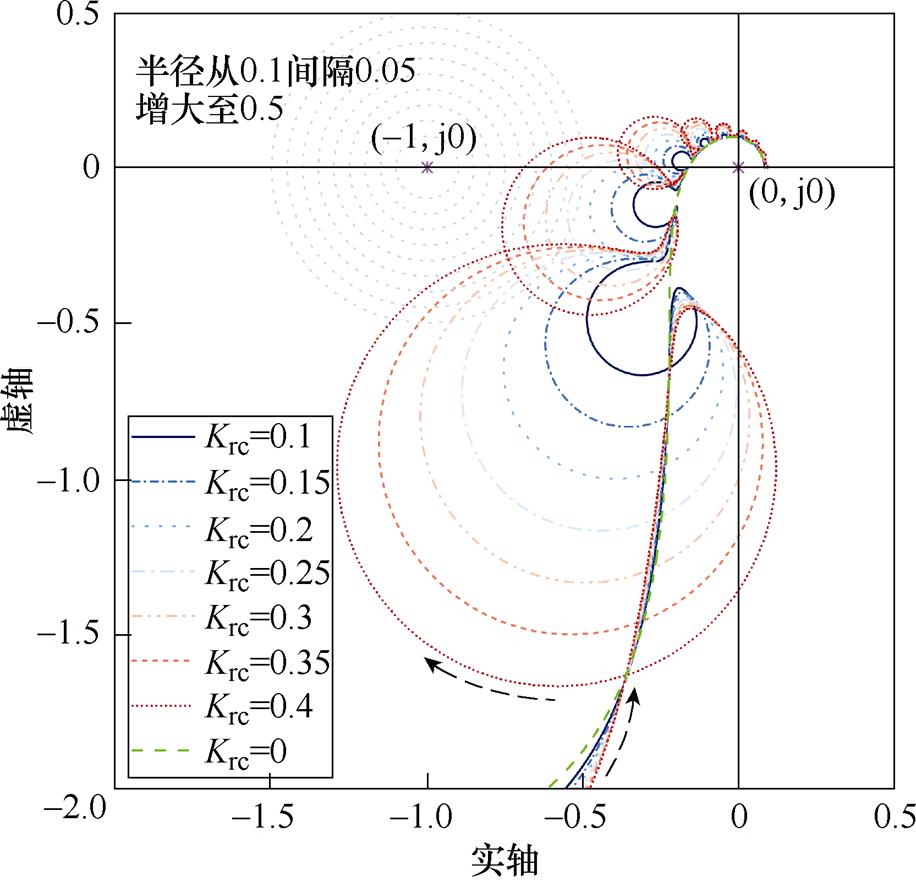
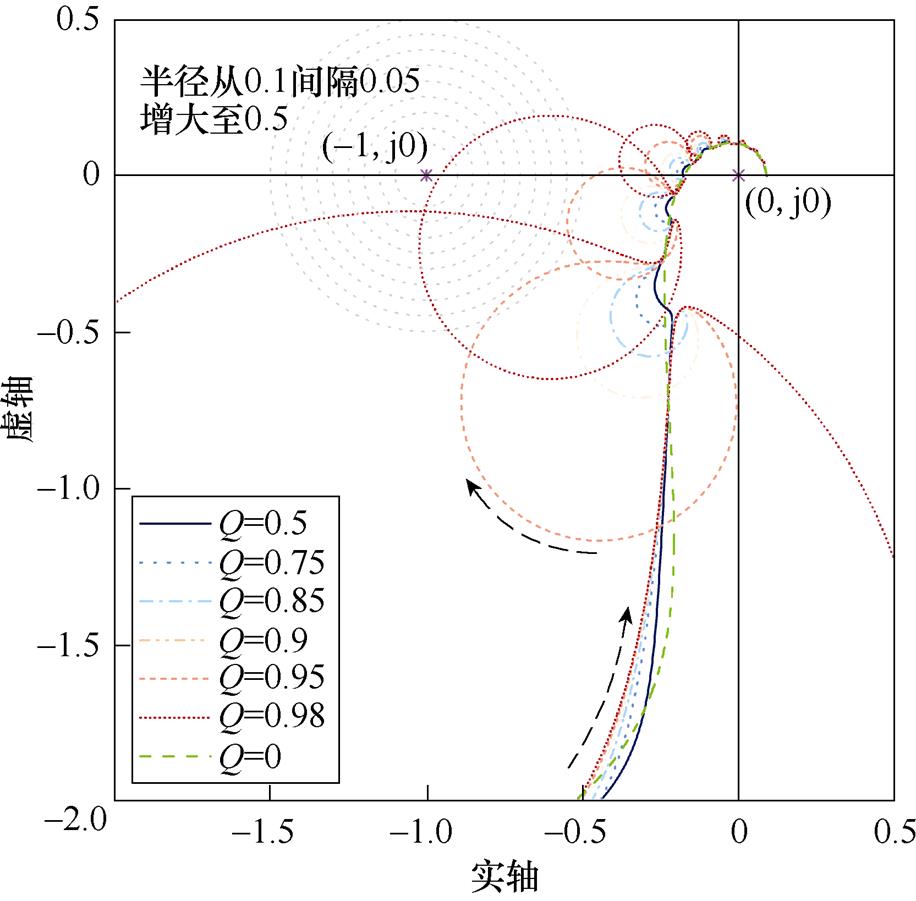
图15为重复控制器增益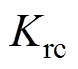和内模系数Q变化时，开环系统奈奎斯特曲线分布，当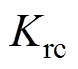变化时，Q=0.95，而当Q变化时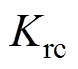，=0.25。图15a可以看到，当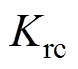=0时，绿色虚线为仅含PI控制器的电流控制系统奈奎斯特曲线；而当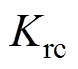＞0时，奈奎斯特曲线在绿色虚线基础上，往实轴负方向出现了很多个“鼓包”，其每个都对应了重复控制器谐振峰；随着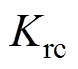增大，“鼓包”向着（-1, j0）靠近，min|1+G(z)|减小，系统稳定性下降。由图15b可以看到，同样是在Q=0所示绿色虚线基础上往实轴负方向出现了很多“鼓包”；但和图15b不同的是，随着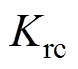增大“鼓包”向（-1, j0）靠近得比较线性，而系统对内模系数Q更为敏感，随着Q增大，“鼓包”向（-1, j0）快速靠近，min|1+G(z)|减小，系统稳定性下降。
（a）重复控制器增益变化
（b）内模系数变化
图15 奈奎斯特曲线随重复控制增益和内模系数变化
Fig.15 Influence of repetitive controller gain and internal model coefficient on nyquist curves
为直观地获取重复控制器增益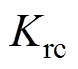和内模系数Q两者对系统稳定性的影响，便于控制参数选取，分别以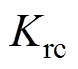、Q为横纵坐标，绘制出如图16所示min|1+G(z)|分布，可以看到，在大部分区域随着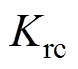、Q增大，min|1+G(z)|减小，系统稳定性下降；但在图片右上角，min|1+G(z)|变化趋势并不规律，这是因为图中两条白色虚线所对应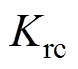、Q取值时奈奎斯特曲线恰好经过（-1, j0），此时min|1+G(z)|=0，而当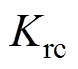、Q取值远离两条白色虚线时，min|1+G(z)|增大，系统稳定性相对增强。为保证系统稳定性，不考虑在图16右上角区域选取控制参数，综合考虑系统稳定性、谐振带宽以及峰值后，选取
，
。
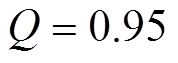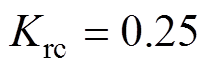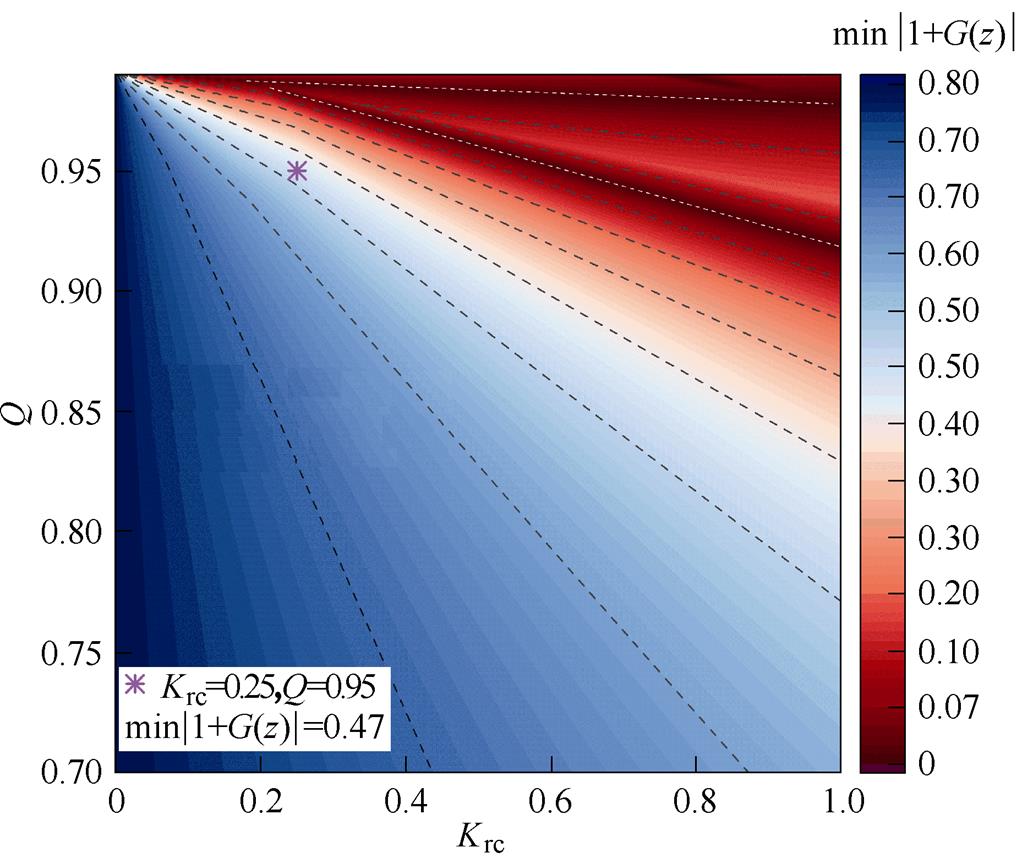
图16 min|1+G(z)|受重复控制器增益和内模系数影响分布
Fig.16 Influence of repetitive controller gain and internal model coefficient on min|1+G(z)|
图17为电流控制系统在不同电机转速下奈奎斯特曲线到（-1, j0）的最小距离变化曲线，可以看到，大致规律是随着转速增高，min|1+G(z)|增大，系统稳定性增强；曲线在200～300 rad/s、300～600 rad/s转速区间内，图17中曲线均出现向下凹，这是因为当电机转速增大时，图15所示“鼓包”在绿色虚线上沿着奈奎斯特曲线方向逐渐向上移动，当实轴恰好穿过两个“鼓包”中间时，min|1+G(z)|有局部最大值，对应电机转速约为300 rad/s；而在较小转速范围内，min|1+G(z)|存在波动，这是因为几何约束优化过程中是以固定步长进行插值逼近的，而局部波动范围约为0.02，在可接受范围内。总体而言，引入了本文所提出的基于几何约束优化分数阶重复控制器的电流控制系统在不同转速下均具有较好的稳定性。
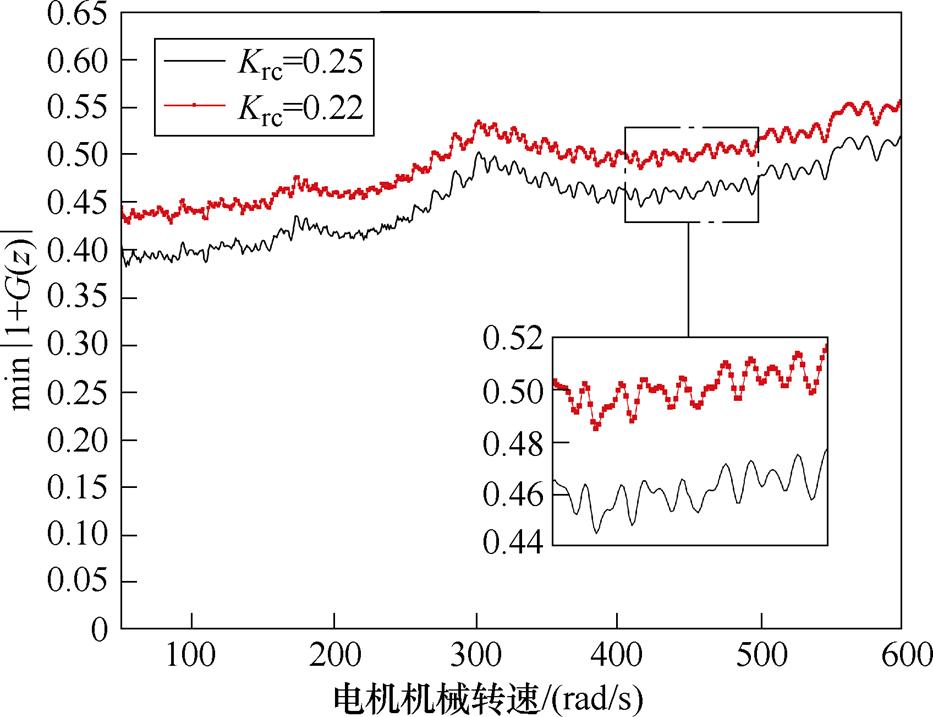
图17 min|1+G(z)|随电机转速变化曲线
Fig.17 Influence curves of motor speed on min|1+G(z)|
600 rad/s转速区间内，图17中曲线均出现向下凹，这是因为当电机转速增大时，图15所示“鼓包”在绿色虚线上沿着奈奎斯特曲线方向逐渐向上移动，当实轴恰好穿过两个“鼓包”中间时，min|1+G(z)|有局部最大值，对应电机转速约为300 rad/s；而在较小转速范围内，min|1+G(z)|存在波动，这是因为几何约束优化过程中是以固定步长进行插值逼近的，而局部波动范围约为0.02，在可接受范围内。总体而言，引入了本文所提出的基于几何约束优化分数阶重复控制器的电流控制系统在不同转速下均具有较好的稳定性。
为验证本文所提出基于几何约束优化的重复控制器的谐波抑制性能，本文进行了电机台架测试验证，实验平台如图18所示，主要包括负载电机、被测电机、电机控制器、数据采集及标定设备。其中，控制被测电机基于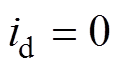
矢量控制算法且采用双采样双更新策略，控制系统框图如图19所示，相关参数见表2。
图18 电机实验台架
Fig.18 Motor test bench
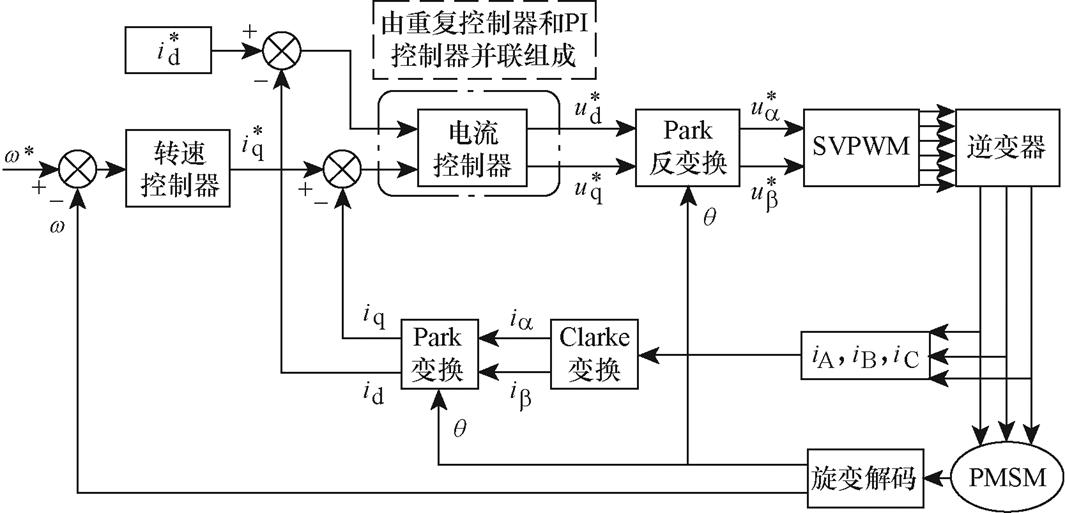
图19 永磁同步电机矢量控制系统框图
Fig.19 Block diagram of vector control system for PMSM
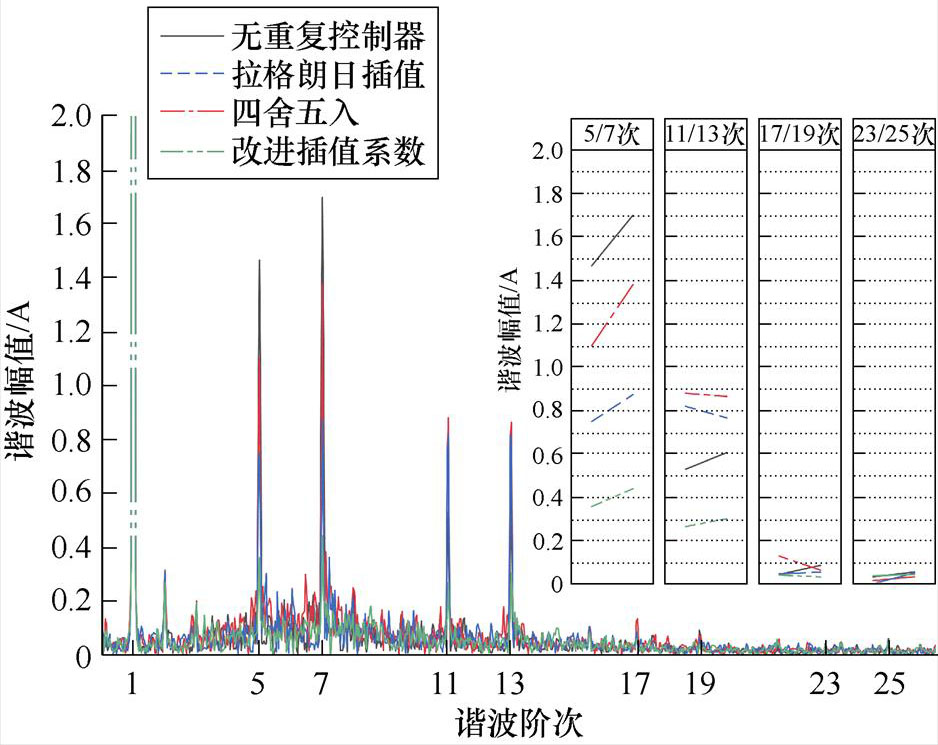
令被测电机q轴电流指令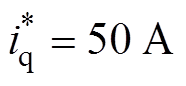
，负载电机机械转速分别为1 000、1 980、3 000、4 000 r/min时进行谐波抑制性能对比实验，对比无重复控制器、针对分数阶四舍五入、基于拉格朗日插值逼近以及改进插值系数后的相电流和谐波组成，实验结果如图20所示。特别说明，各转速工况下分数阶其小数部分
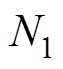分别为0、0.253、0.667、0.5，若将第二个转速工况设置为2 000 r/min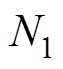，同样为0，由于此时并不存在分数阶环节，因此为了凸显不同分数阶处理方法之间谐波抑制性能差异，将第二个转速工况设置为1 980 r/min。
表2 永磁同步电机控制系统参数
Tab.2 Parameters of PMSM control system
参 数数 值 (型号) 电机额定功率/kW35 电机额定转速/(r/min)3 000 电机控制芯片Infineon Aurix TC277 PWM频率/kHz10
改进插值系数后的相电流和谐波组成，实验结果如图所示。特别说明，各转速工况下分数阶其小数部分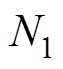分别为0、0.253、0.667、0.5，若将第二个转速工况设置为2 000 r/min，
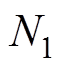同样为0，由于此时并不存在分数阶环节，因此为了凸显不同分数阶处理方法之间谐波抑制性能差异，将第二个转速工况设置为1 980 r/min。
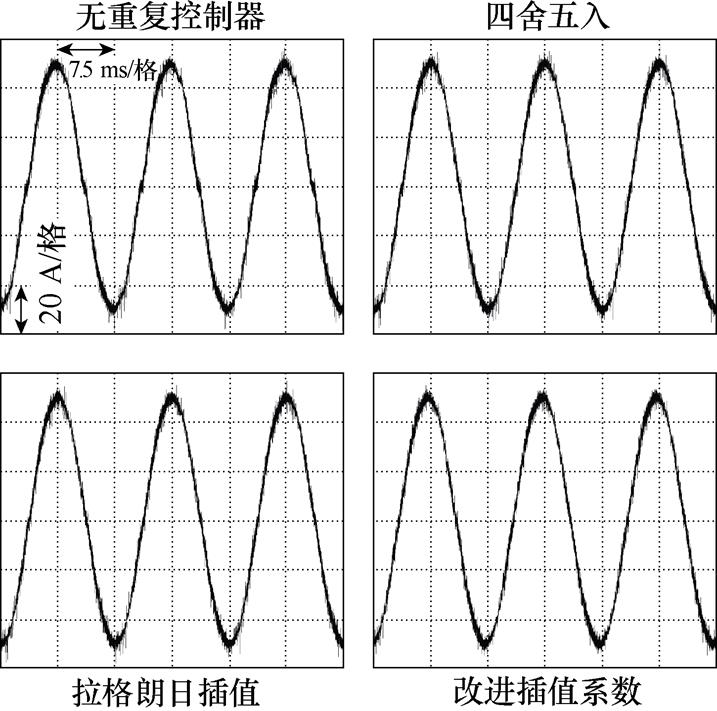
（a）1 000 r/min相电流波形
（b）1 000 r/min谐波组成分析
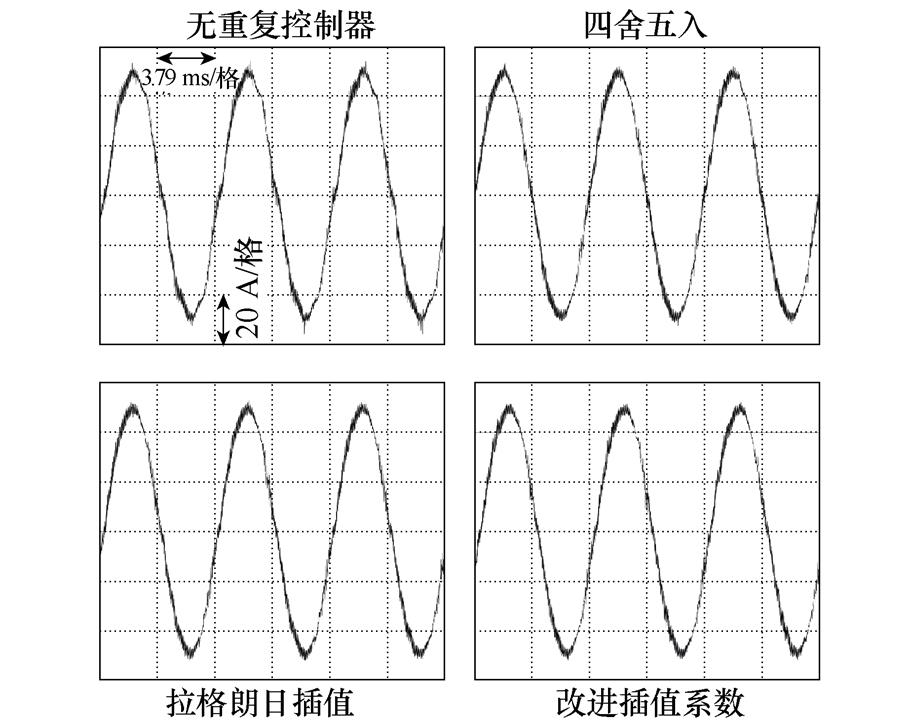
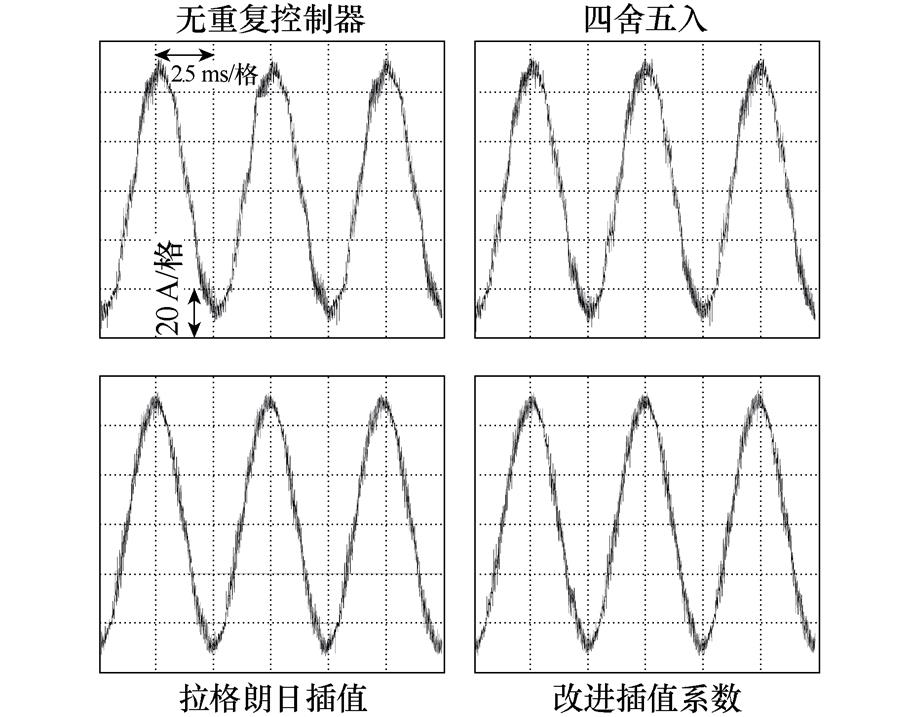
（c）1 980 r/min相电流波形
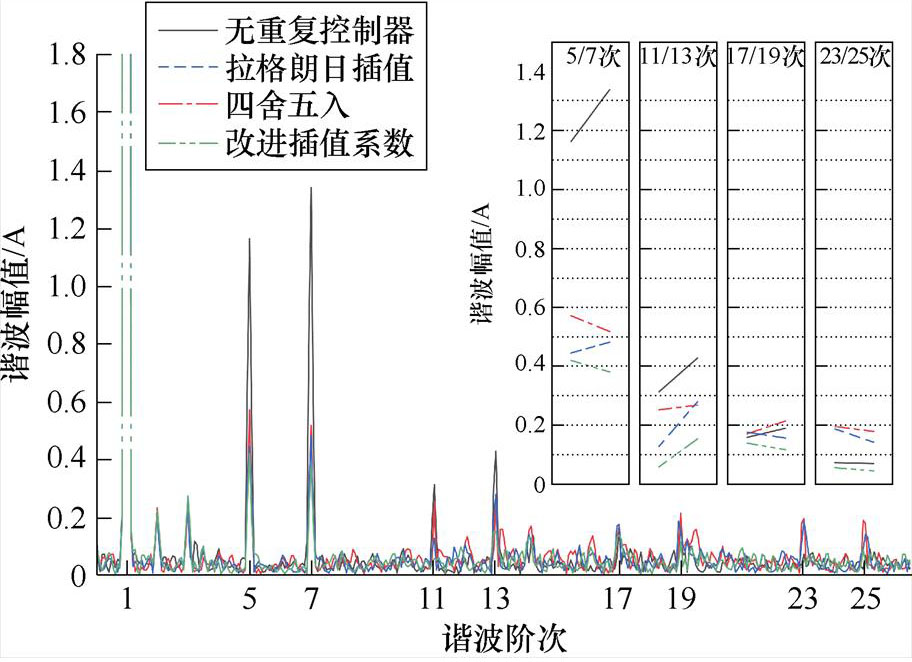
（d）1 980 r/min谐波组成分析
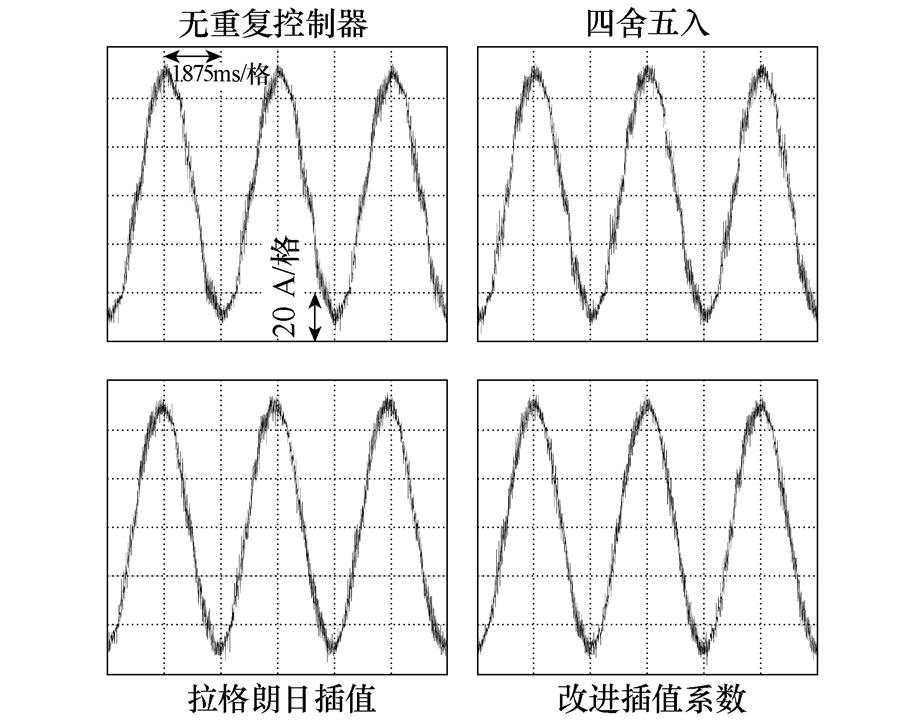
（e）3 000 r/min相电流波形
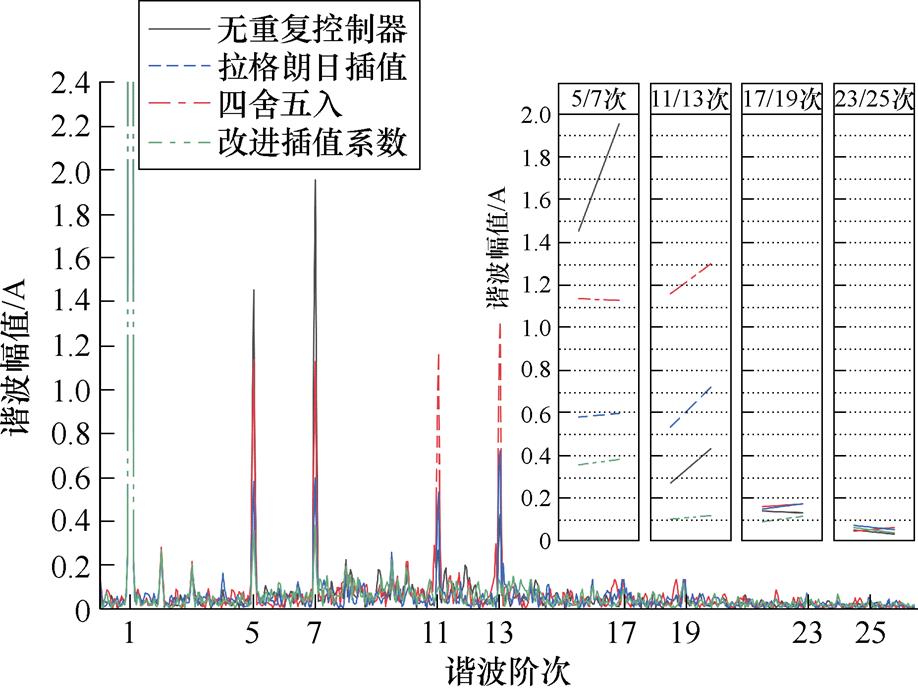
（f）3 000 r/min谐波组成分析
（g）4 000 r/min相电流波形
（h）4 000 r/min谐波组成分析
图20 不同转速下相电流波形及谐波组成分析
Fig.20 Phase current waveforms and harmonic analysis at different motor speeds
由图20a、图20c、图20e、图20g可以看到，没有采用重复控制器的电流控制系统均出现较为严重的相电流波形畸变，由对应转速下谐波组成分析可以看出，这是由于相电流中存在较大5、7次谐波分量。
在电机机械转速为1 000 r/min时，由于此时延时周期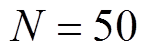
并不存在小数部分，此时三种对分数阶采用不同处理方式的重复控制器本质上是相同的。由图20b可以看到，三者都可以对6k±1次谐波进行有效抑制且三者谐波抑制性能几乎相同，其中针对谐波成分较大的5、7、11、13次电流谐波抑制效果更为明显。在电机机械转速为1 980、3 000、4 000 r/min时，存在分数阶延时环节，三者不同分数阶处理方法在谐波抑制性能上出现了差异。由图20d、图20f、图20h可以看到，对于5、7次谐波，四舍五入、拉格朗日插值逼近以及改进插值系数这三者谐波抑制性能逐渐增强。而在相同转速下随着谐波阶次提高或者相同谐波阶次下随着电机转速提高，四舍五入、拉格朗日插值逼近其谐波抑制性能随之下降，甚至出现了相较于无重复控制器时更高的现象，在1 980 r/min-23/25次、3 000 r/min-11/13次、4 000 r/min-11/13次尤为明显，出现此实验结果是因为在相同转速下随着谐波阶次提高，四舍五入、拉格朗日插值这两者谐振频率偏移越严重，从图4a可以看到，四舍五入谐振频率偏移相较于拉格朗日插值更严重，在谐波组成分析结果右上角分组图内反映为红色点画线位于蓝色虚线之上；相同谐波阶次下随着电机转速提高，谐振频率偏移同样随之变多。由于本文所提出基于几何约束优化的重复控制器能够实现谐振频率偏移更少、6k次电流谐波频率处增益更高，因此谐波抑制性能更优，在分组图上体现为绿色双点画线位于最下方；并且从谐波组成分析可以看出，随着转速增高，绿色双点画线和蓝色虚线之间的距离随之增大，这证明本文所提出的改进重复控制器对电流频率变化具有更强的适应性。
针对系统采样频率固定而电流谐波频率变化从而导致重复控制器中所出现的分数阶延时环节实际控制器无法实现的问题，本文提出了基于几何约束优化的分数阶重复控制器，在分析、设计以及实验验证过程中得出如下结论：
1）以3.1节理论分析为依据，改进插值系数后实现了相较于拉格朗日插值谐振频率偏移更少、谐振峰值更低、6k次电流谐波频率处增益更高，从而提升系统稳定性的同时还提升了谐波抑制性能。
2）理论分析了滤波器所处反馈回路位置对于谐振频率、幅值的影响，根据分析结论在反馈回路外设计了组合滤波器，不影响谐振频率的同时对谐振峰值进行了修正，从而进一步提升系统稳定性。
3）将所提出的改进重复控制器放入电流控制系统并在离散域进行了系统稳定性分析，分析不同控制参数对系统稳定性的影响，并且给出控制参数选取依据，保证电流控制系统稳定运行。
4）通过实验结果验证了本文提出的改进重复控制器对于不同阶次电流谐波均具有更优的谐波抑制性能且电流频率适应性更强。
参考文献
[1] 赵文祥, 刘桓, 陶涛, 等. 基于虚拟信号和高频脉振信号注入的无位置传感器内置式永磁同步电机MTPA控制[J]. 电工技术学报, 2021, 36(24): 5092- 5100.
Zhao Wengxiang, Liu Huan, Tao Tao, et al. MTPA control of sensorless IPMSM based on virtual signal and high-frequency pulsating signal injection[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5092-5100.
[2] Sun Tongze, Liu Xiping, Zou Yongling, et al. Design and optimization of a mechanical variable-leakage- flux interior permanent magnet machine with auxiliary rotatable magnetic poles[J]. CES Transa- ctions on Electrical Machines and Systems, 2021, 5(1): 21-29.
[3] 黄科元, 周佳新, 刘思美, 等. 考虑逆变器非线性永磁同步电机高频注入电感辨识方法[J]. 电工技术学报, 2021, 36(8): 1607-1616.
Huang Keyuan, Zhou Jiaxin, Liu Simei, et al. Inductance identification method of permanent magnet synchronous motor considering inverter nonlinearity based on high-frequency injection[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1607-1616.
[4] Zhang Guoqiang, Wang Gaolin, Xu Dianguo, et al. ADALINE-network-based PLL for position sensorless interior permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1450-1460.
[5] Zhou Min, Zhang Xinxing, Zhao Wenxiang, et al. Influence of magnet shape on the cogging torque of a surface-mounted permanent magnet motor[J]. Chinese Journal of Electrical Engineering, 2019, 5(4): 40-50.
[6] Wu D, Zhu Z Q. Design tradeoff between cogging torque and torque ripple in fractional slot surface- mounted permanent magnet machines[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4.
[7] 谭广军. 高速永磁同步电机驱动控制关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
[8] 杜鹏程. 高速永磁同步电机电流谐波抑制技术[D]. 哈尔滨: 哈尔滨工业大学, 2020.
[9] 陈杰, 章新颖, 闫震宇, 等. 基于虚拟阻抗的逆变器死区补偿及谐波电流抑制分析[J]. 电工技术学报, 2021, 36(8): 1671-1680.
Chen Jie, Zhang Xinying, Yan Zhenyu, et al. Dead- time effect and background grid-voltage harmonic suppression methods for inverters with virtual impedance control[J]. Transactions of China Elec- trotechnical Society, 2021, 36(8): 1671-1680.
[10] 廖勇, 甄帅, 刘刃, 等. 用谐波注入抑制永磁同步电机转矩脉动[J]. 中国电机工程学报, 2011, 31(21): 119-127.
Liao Yong, Zhen Shuai, Liu Ren, et al. Torque ripple suppression of permanent magnet synchronous motor by the harmonic injection[J]. Proceedings of the CSEE, 2011, 31(21): 119-127.
[11] 李思毅, 苏健勇, 杨贵杰. 基于自抗扰控制的永磁同步电机弱磁控制策略[J]. 电工技术学报, 2022, 37(23): 6135-6144.
Li Siyi, Su Jianyong, Yang Guijie. Flux weakening control strategy of permanent magnet synchronous motor based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6135-6144.
[12] 黄仁志, 全相军, 吴在军, 等. 基于多重谐振控制器的参考值前馈自适应控制[J]. 电工技术学报, 2022, 37(16): 4212-4224.
Huang Renzhi, Quan Xiangjun, Wu Zaijun, et al. A multiple resonant based on reference feedforward adaptive voltage control of three-phase inverter[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4212-4224.
[13] 夏薇, 王凯, 张建亚, 等. 基于谐振控制器的谐波削极型永磁同步电机转矩脉动抑制策略[J]. 中国电机工程学报, 2019, 39(18): 5499-5508, 5598.
Xia Wei, Wang Kai, Zhang Jianya, et al. Torque ripple suppression of permanent magnet synchronous motor with harmonic shaped rotors based on resonance controllers[J]. Proceedings of the CSEE, 2019, 39(18): 5499-5508, 5598.
[14] Tian Minghe, Wang Bo, Yu Yong, et al. Discrete-time repetitive control-based ADRC for current loop disturbances suppression of PMSM drives[J]. IEEE Transactions on Industrial Informatics, 2022, 18(5): 3138-3149.
[15] Tang Mi, Gaeta A, Formentini A, et al. A fractional delay variable frequency repetitive control for torque ripple reduction in PMSMs[J]. IEEE Transactions on Industry Applications, 2017, 53(6): 5553-5562.
[16] 武永燎, 李红, 宋欣达, 等. 基于改进型重复控制器的永磁同步电机电流谐波抑制方法研究[J]. 电工技术学报, 2019, 34(11): 2277-2286.
Wu Yongliao, Li Hong, Song Xinda, et al. Suppression of harmonic current in permanent magnet synchronous motors using improved repetitive controller[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2277-2286.
[17] 陈东, 张军明, 钱照明. 一种具有频率变化适应性的并网逆变器改进型重复控制方法[J]. 电工技术学报, 2014, 29(6): 64-70.
Chen Dong, Zhang Junming, Qian Zhaoming. An improved repetitive control scheme for grid- con- nected inverter with frequency-varying adaptability[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 64-70.
[18] 徐群伟, 吴俊, 吕文韬, 等. 基于双分数阶快速重复控制的有源电力滤波器电流控制策略[J]. 电工技术学报, 2019, 34(增刊1): 300-311.
Xu Qunwei, Wu Jun, Lü Wentao, et al. Current control strategy of active power filter based on double fractional-order rapid repetitive control[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(S1): 300-311.
[19] 刘兴亚. 永磁同步电机电流谐波抑制策略的研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
[20] Yepes A G, Freijedo F D, Lopez Ó, et al. Analysis and design of resonant current controllers for voltage-source converters by means of Nyquist diagrams and sensitivity function[J]. IEEE Transa- ctions on Industrial Electronics, 2011, 58(11): 5231- 5250.
Abstract Due to the structural defects of the permanent magnet synchronous motor and various nonlinear factors in the driving circuit, the three-phase current in the motor contains current harmonics of various orders, which are mainly (6k±1) (k is a positive integer) orders. These current harmonics of (6k±1) orders in the natural coordinate system will be displayed as 6k orders after the coordinate is changed to the two-phase rotating coordinate system. At the same time, the transfer function of the repetitive controller has multiple resonance peaks, and its resonance frequency is a multiple relationship. Thus, the repetitive controller is widely used for suppressing the current harmonics of permanent magnet synchronous motors.
However, the sampling period of the motor controller is fixed in the actual control system, and the current harmonic frequency changes with the motor speed, causing a fractional delay link in the repetitive controller. The most commonly used method to solve this problem is Lagrange interpolation to approximate the fractional delay link. This paper first analyzes the shortcomings of this method, and then discusses the method of Lagrange interpolation to approximate fractional order with numerical analysis. There are unnecessary specific constraints between Lagrange interpolation coefficients, and a better harmonic suppression effect can be achieved by reasonably configuring the interpolation coefficients.
Then, the coefficient in the interpolation approximation method is mapped to compound circular motion, combined with the amplitude-frequency characteristic surface of the proposed repetitive controller. The effects of the interpolation coefficient on the resonant frequency and harmonic peak value of the repetitive controller are analyzed, and a fractional-order repetitive controller based on geometric constraint optimization is proposed. The resonance frequency and current harmonic frequency of the motor can be guaranteed to coincide in a broader range of speeds. Moreover, the resonance peak value is consistent with the harmonic composition of the motor, thus achieving a better harmonic suppression effect. The repetitive controller with a large resonance peak in the high-frequency part will cause system instability. This paper also introduces the combined filter, and discusses the influence of the feedback loop position of the filter on the resonance frequency and peak.
This paper introduces the sensitivity function and combines the Nyquist curve to analyze the stability of the current control system, including PI, repetitive controller, and discrete motor model. First, the influence of PI controller gain K on the system’s stability without a repetitive controller is analyzed. After determining the value of K, the influence of repetitive controller gain Krc and internal model coefficient Q on the stability of the system is discussed, and the values of Krc and Q are determined. After all parameters are determined, the stability of the current control system at different motor speeds is also discussed.
Finally, the experiments of no repetitive controller, rounding, Lagrange interpolation, and the improved repetitive controller proposed in this paper are carried out on the motor bench at different speeds. The current waveform and FFT analysis verify that the harmonic suppression performance of the proposed method is good.
keywords：Fractional order delay, repetitive controller, control stability, harmonic suppression, permanent magnet synchronous motor (PMSM)
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.222202
江西省重点研发计划-产业链科技创新联合体资助项目（20224BBE52003）。
收稿日期 2022-11-23
改稿日期 2023-02-14
朱 元 男，1976年生，博士，副教授，研究方向为汽车电子嵌入式软件、车用永磁同步电机控制。E-mail: yuan.zhu@tongji.edu.cn（通信作者）
朱醴亭 男，1999年生，硕士研究生，研究方向为车用永磁同步电机控制。E-mail: 2131592@ tongji.edu.cn
（编辑 崔文静）