 (1)
(1)
摘要 在复杂环境、多变负载工况中,由于时变电感参数、磁场耦合、铁心饱和等影响,电机控制精度及可靠性下降。为解决以上问题,该文充分利用时间序列模型反映电机电压、电流等状态变量之间关系,消除传统参数化建模的影响,提出基于超局部化时间序列的无模型预测电流滑模控制(SMC)方法。该方法将时间序列数据驱动模型超局部化,提升传统超局部模型精度,并采用递归最小二乘法(RLS)在线估计和更新模型中全部待定系数,实时精准响应当前系统工作状态。在此基础上,结合超局部时间序列模型,生成滑模控制函数,并设计Lyapunov方法验证函数趋近条件。实验结果表明,与传统控制方法相比,提出方法具有更强的鲁棒性、更优的电流质量和较低的系统噪声。
关键词:无模型滑模控制 超局部化时间序列模型 递归最小二乘算法 数据驱动模型
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有功率密度高、可靠性强、结构简单等优点,在新能源汽车领域中得到应用。近年来,随着新能源汽车的快速发展,对于系统动静态性能、噪声、振动等性能要求日益提升[1]。但由于电机系统运行环境恶劣、工况复杂多变,其物理参数实时变化,传统控制策略难以充分满足严苛要 求[2]。针对该问题,多种先进控制方法在电机系统中运用,如模型预测控制[3]、模糊控制[4]、滑模控制(Sliding Mode Control, SMC)[5]等。其中,由于SMC使系统状态量沿着滑模面滑动,控制本质稳定,有抵抗参数摄动能力强、结构简单等优势,得到国内外研究人员的广泛关注[6]。
传统SMC由于不连续开关特性导致系统产生抖振,严重限制其在高端场合应用。为了解决这一问题,研究者从不同的角度进行了改进:一种思路是优化切换增益,即在控制过程中通过调整切换增益来消除抖振[7];另一种思路是增加扰动观测器,通过对系统扰动的观测估计,实现抖振消除[8];此外,使用人工智能算法对SMC进行优化,可通过改进控制精度抑制抖振[9]。文献[10]通过在滑模面和趋近律中引入状态变量,并在SMC中引入负载转矩自适应逻辑,使滑模面跟随负载转矩调整,有效抑制系统抖振并提升动态性能;文献[11]设计一种非奇异快速终端滑模(Fast Non-singular Terminal Sliding Mode, FNTSM)面,并结合扰动观测器,有效降低系统抖振并提升系统敛散性和抗扰性;文献[12]提出一种基于自适应模糊神经网络时变滑模控制(Adaptive Fuzzy Neural Network Time-varying SMC, AFNNTSMC),通过模糊神经网络在线调整时变滑模面斜率,提高系统响应速度和鲁棒性。此外,滑模方法可转化为非线性观测器,用于估算部分可测或不可测系统中扰动量。文献[13]采用快速终端积分滑模(Fast-Terminal Integral Sliding Mode, FTISM)观测器,对集总扰动进行补偿,提升系统鲁棒性;文献[14]提出新型离散域二阶超螺旋滑模观测器,在无位置传感器系统中估算反电动势并抑制抖振的同时,得到电机转子位置和转速。
虽然先进SMC可获得较强的鲁棒性,但随着其逐步向专有控制发展,受先验模型有限精度的影响愈发明显,在某些复杂、多变的高端装备中,无法建立完整和准确的模型,需要控制策略有更强的灵活性和鲁棒性。无模型控制(Model Free Control, MFC)是一种获得强鲁棒性的有效方案,该方法采用采样数据直接建立数据驱动模型替代先验模型描述当前电机系统状态,完全消除电机物理参数及其对模型精度的影响[15-16]。无模型思想与多种控制策略结合,在保持原有性能特性基础上,增强系统鲁棒性,如无模型自适应控制[17]、无模型预测控制[18]、无模型滑模控制[19]等。
选择合适的数据驱动模型结构是MFC获得高品质控制性能的关键核心。超局部模型由于结构简单、实现容易,通常用于描述电机系统。该模型将系统中未知部分汇总为单一变量,并设计合适的代数算法或观测器对变量进行在线估算,保持模型拟合度[20-21];时间序列模型采用离散传递函数结构推演电机系统当前工况,其中各阶系数通过递归最小二乘法(Recursive Least Square, RLS)在线调整。该模型符合电机机械特性,有更好的控制精度。但由于连续集控制函数设计复杂,通常用于无模型预测控制中[22];动态线性化模型通过引入伪导数概念,将电机系统进行偏格式、紧格式或全格式变换描述为非线性时变系统,通常用于无模型自适应控制策略[23]。此外,一些模型结构适合表达特殊场合中电机系统运行状态。文献[24]通过离散空间矢量方法将电机系统拟合为一种新型无参数自适应模型,通过双RLS估算模型架构,获得良好的控制精度和动静态性能;文献[25]提出对白箱(White Box, WB)模型建模误差进行实时补偿,使其在自调试驱动器中有适当的计算负担和准确性。
由于多数高拟合度数据驱动模型设计滑模控制函数困难,目前在无模型滑模控制中多基于超局部模型描述电机系统,获得强鲁棒性和抗扰性[19, 26-27]。但受制于超局部结构本质有限的拟合度,控制性能难以提升。为进一步改进无模型SMC的控制精度,本文提出一种基于超局部化时间序列的无模型预测电流滑模控制方法。该方法将时间序列模型巧妙地超局部化,简化模型结构并提升模型精度;将模型中所有待定系数汇总为递归向量,采用RLS算法对包括增益系数的全部待定系数进行在线精准估算,保持模型对系统当前工作状态的高拟合度。在此基础上,结合幂次趋近律和Lyapunov方法产生滑模控制函数。将本文提出的基于超局部化时间序列的无模型滑模控制策略记为提出方法,将文献[28]中基于超局部的无模型滑模控制方法应用至电流控制,并设定为传统控制策略。通过仿真与实验和传统控制策略进行综合比较,验证提出方法的有效性及其在鲁棒性、电流质量和系统噪声方面的优势。
在dq坐标系下,PMSM状态方程可描述为
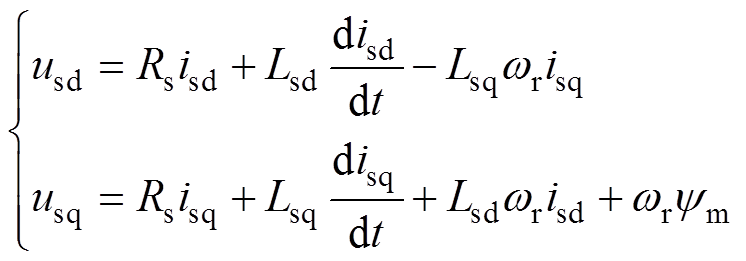 (1)
(1)
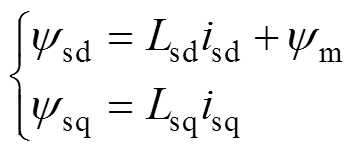 (2)
(2)
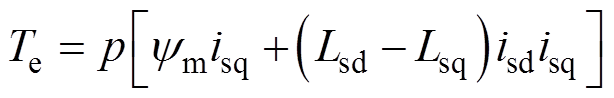 (3)
(3)
式中,下标d和q表示分量所处坐标轴;us为定子电压;is为定子电流;Rs为定子电阻;Ls为定子电感;ym为永磁体磁链;p为极对数;wr为转子角速度。
根据式(1)中变量关系,在无模型控制中,将电机系统描述为如下超局部结构。
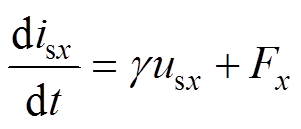 (4)
(4)
式中,下标x为d或q分量;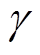 为输入增益,根据文献[29],该增益通常选定为1/Ls;Fx为电机系统未知成分,需要设计观测器或代数方法进行估算。
为输入增益,根据文献[29],该增益通常选定为1/Ls;Fx为电机系统未知成分,需要设计观测器或代数方法进行估算。
对于PMSM时间序列模型,可表示为
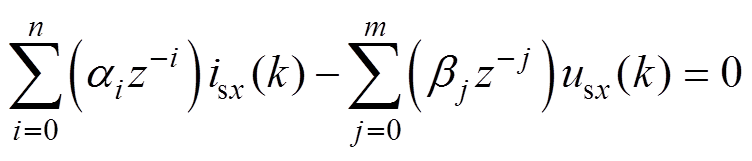 (5)
(5)
式中,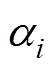 和
和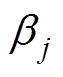 为待定系数;n和m为模型阶数;k为趋近律系数。为使系统构成因果关系,系数
为待定系数;n和m为模型阶数;k为趋近律系数。为使系统构成因果关系,系数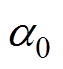 选定为1。
选定为1。
将采样数据和待定系数分别构成回归向量,有
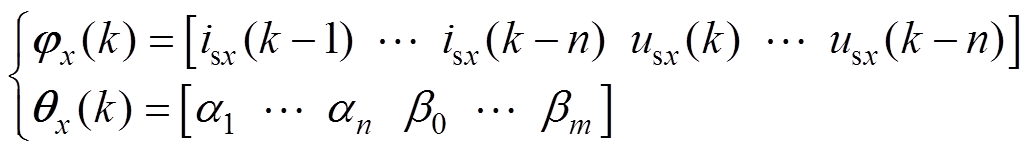 (6)
(6)
通过RLS在线估算待定系数向量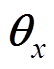 为
为
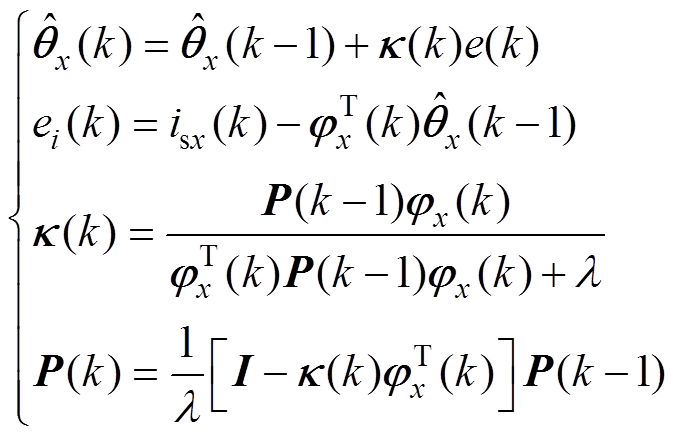 (7)
(7)
式中,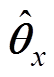 为
为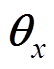 的估计值;ei为电流采样值与估算值误差;
的估计值;ei为电流采样值与估算值误差;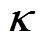 为增益递归矩阵;P为协方差递归矩阵;
为增益递归矩阵;P为协方差递归矩阵;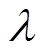 为遗忘因子。在每个采样周期内,待定系数均得到更新,保持模型对电机系统的高度适配。
为遗忘因子。在每个采样周期内,待定系数均得到更新,保持模型对电机系统的高度适配。
由于采样周期Ts取值小,更新向量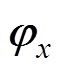 至第k+1个采样周期,预测变量可通过时移得到,有
至第k+1个采样周期,预测变量可通过时移得到,有
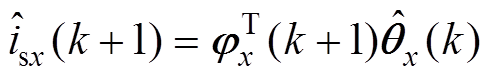 (8)
(8)
式中,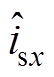 和
和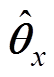 分别为isx和
分别为isx和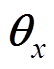 的估算值。将回归向量中的usx(k+1)设定为电压参考
的估算值。将回归向量中的usx(k+1)设定为电压参考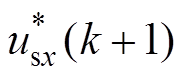 ,并由拉格朗日法获得,有
,并由拉格朗日法获得,有
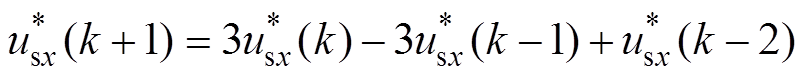 (9)
(9)
结合式(8),式(5)中模型结构可变化为
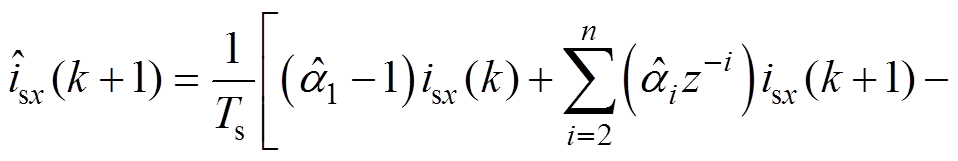
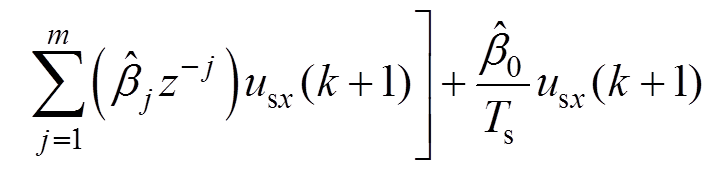 (10)
(10)
式中,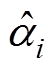 和
和![]() 为
为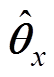 中元素。第一项可视作未知项Fx的估算,即
中元素。第一项可视作未知项Fx的估算,即
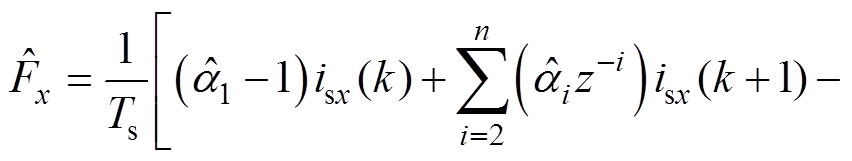
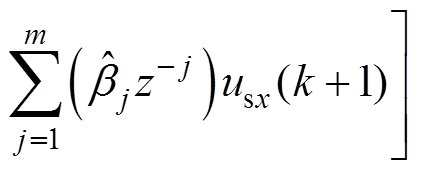 (11)
(11)
第二项可视为输入增益g 的估算,即
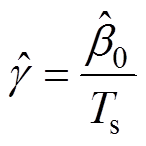 (12)
(12)
则时间序列模型变化为超局部架构,对应的电压参考为
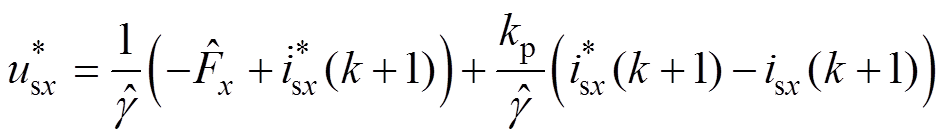 (13)
(13)
式中,kp为比例系数。
未来的电流参考值均通过拉格朗日法获得,有
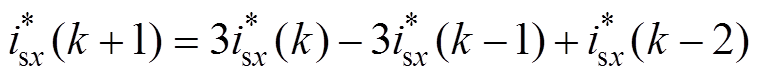 (14)
(14)
各模型建模过程中所需参数见表1。表中,w 为参数估计中观测器增益设计所需带宽。与超局部模型相比,参数输入增益g 同未知项Fx统一进行在线估计,无需物理参数参与计算。
表1 建模所需参数
Tab.1 Required coefficients in the modeling process

先验模型超局部模型[28]提出模型 建模系数Rs, Lsd, Lsq, ymg (1/Ls), wn, m, l
融入滑模信号uSMx,将电压参考改进设计为
式中,ex为实际电流误差。
代入超局部化时间序列模型,控制函数变化为
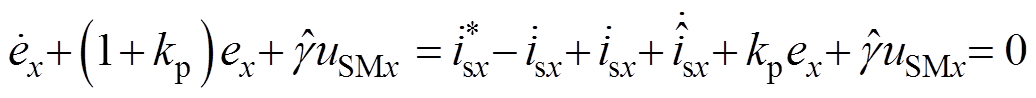 (16)
(16)
即
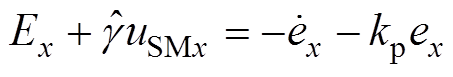 (17)
(17)
其中
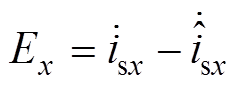
分别定义状态变量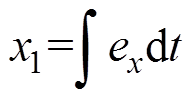 和x2=ex,可获得状态方程为
和x2=ex,可获得状态方程为
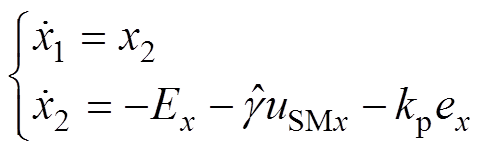 (18)
(18)
选择滑模面为s=cx1+x2和带饱和函数的幂次趋近律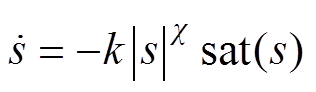 ,其中c为滑模面系数,
,其中c为滑模面系数,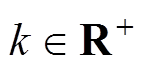 、
、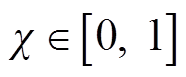 。滑模面的导数为
。滑模面的导数为
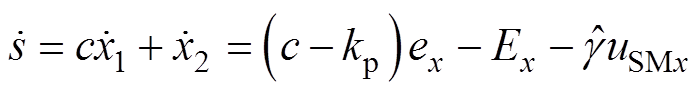 (19)
(19)
则滑模信号可设计为
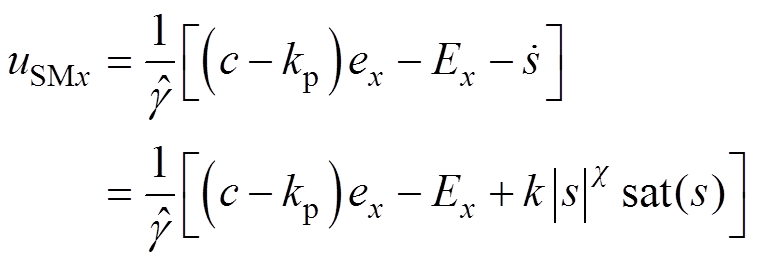 (20)
(20)
使用控制函数时,Ex使用其上界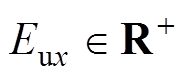 代替,即
代替,即
设计Lyapunov函数为
其导数为
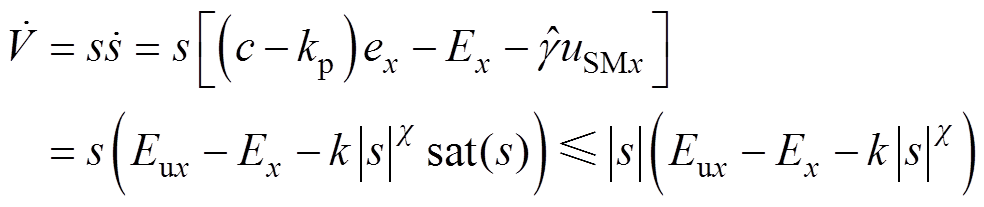 (23)
(23)
若 ,系统满足趋近条件
,系统满足趋近条件![]() 。提出方法的结构和实现流程分别如图1和图2所示。
。提出方法的结构和实现流程分别如图1和图2所示。
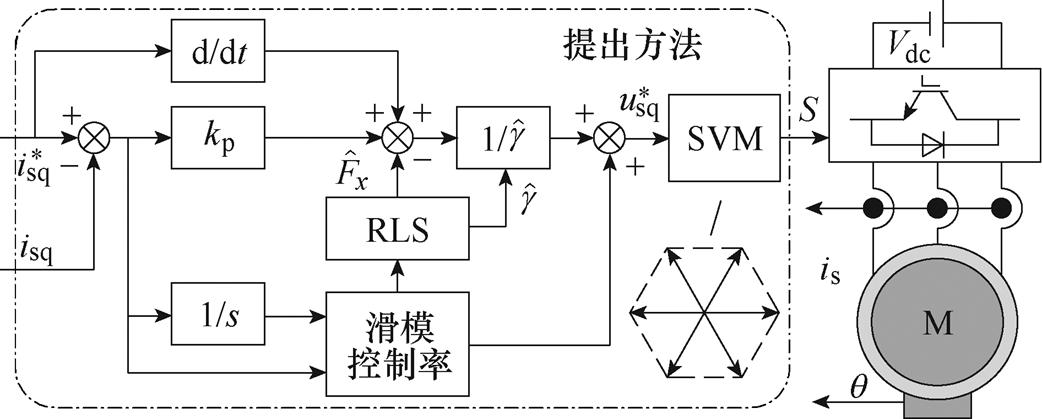
图1 提出方法结构
Fig.1 Structure of the proposed method
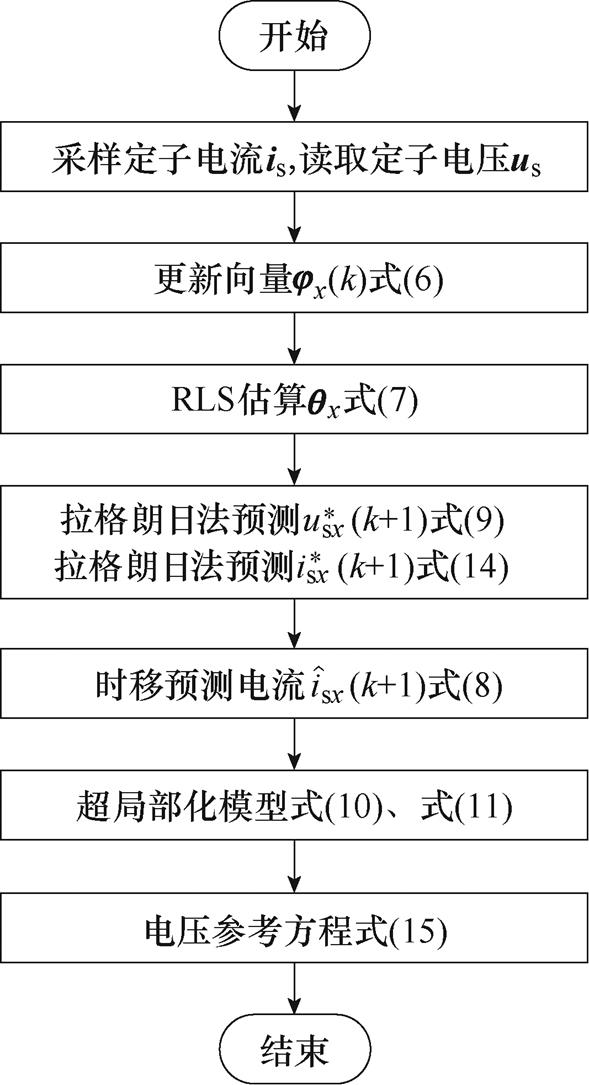
图2 提出方法实现流程
Fig.2 Realizing flow chart of the proposed method
为验证上述基于超局部化时间序列的无模型预测电流SMC效果,结合4.8 kW PMSM搭建实验平台,如图3所示,PMSM的数据驱动模型及控制算法在DSP F28379D中运行。主要参数见表2。

图3 实验平台
Fig.3 Experimental platform
表2 主要系统参数
Tab.2 Main system parameters
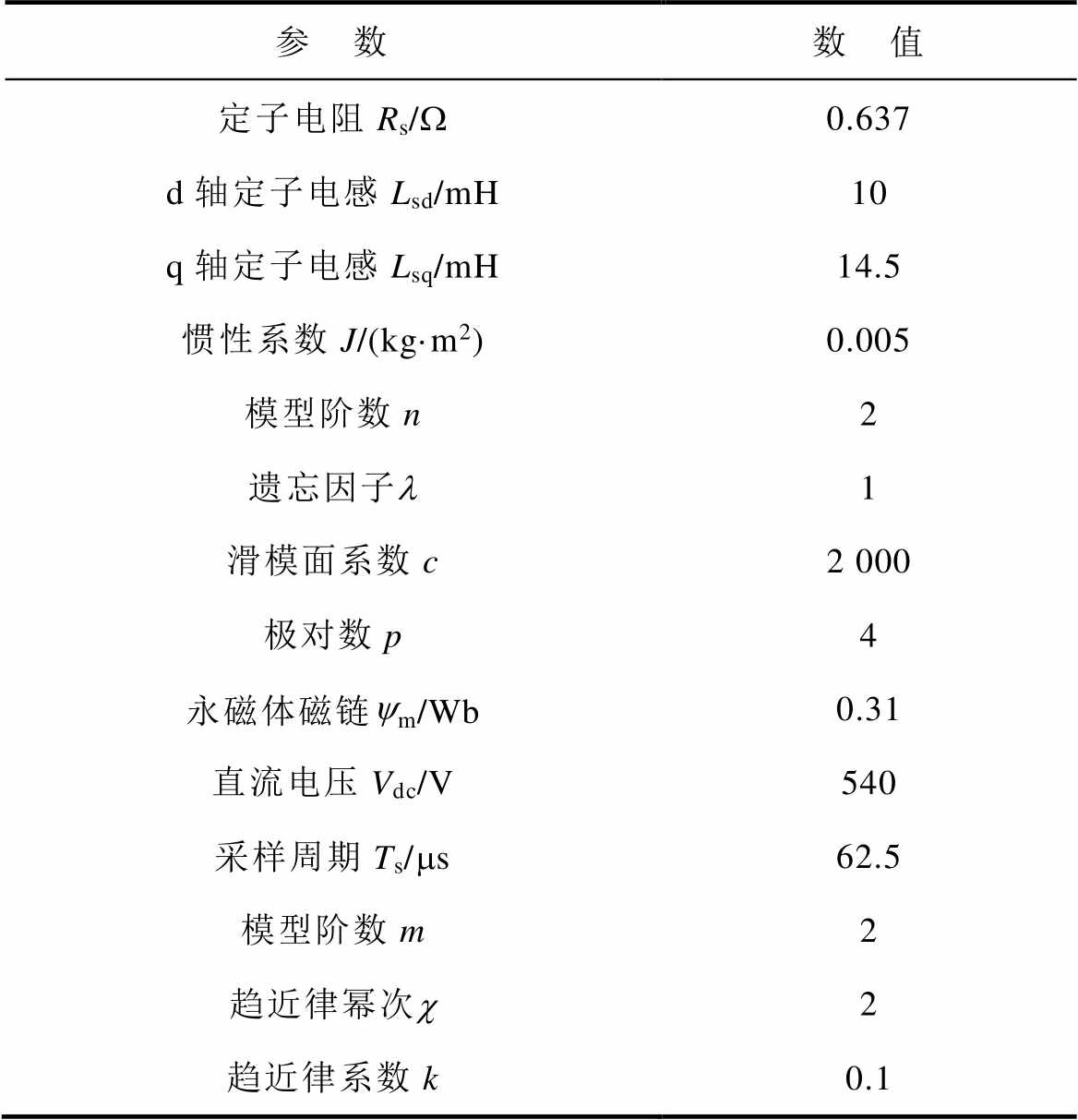
参 数数 值 定子电阻Rs/W0.637 d轴定子电感Lsd/mH10 q轴定子电感Lsq/mH14.5 惯性系数J/(kg·m2)0.005 模型阶数n2 遗忘因子l1 滑模面系数c2 000 极对数p4 永磁体磁链ym/Wb0.31 直流电压Vdc/V540 采样周期Ts/ms62.5 模型阶数m2 趋近律幂次c2 趋近律系数k0.1
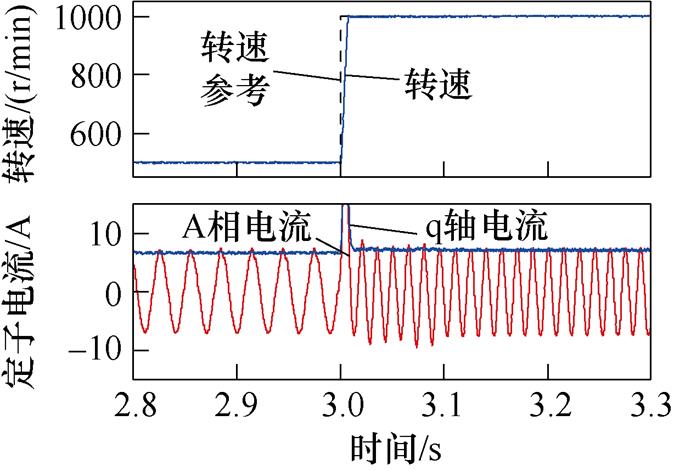
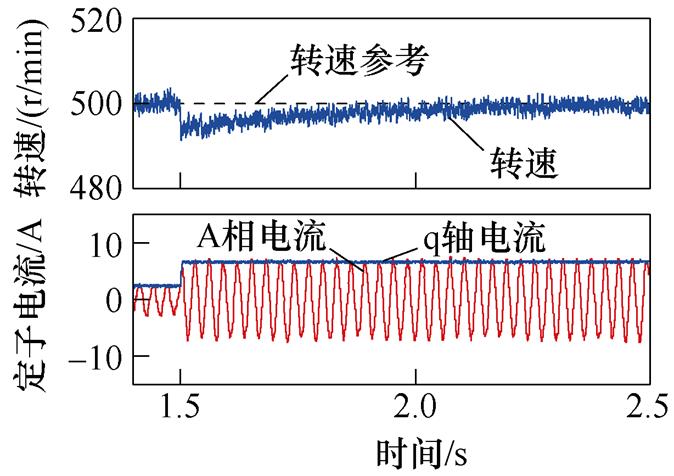
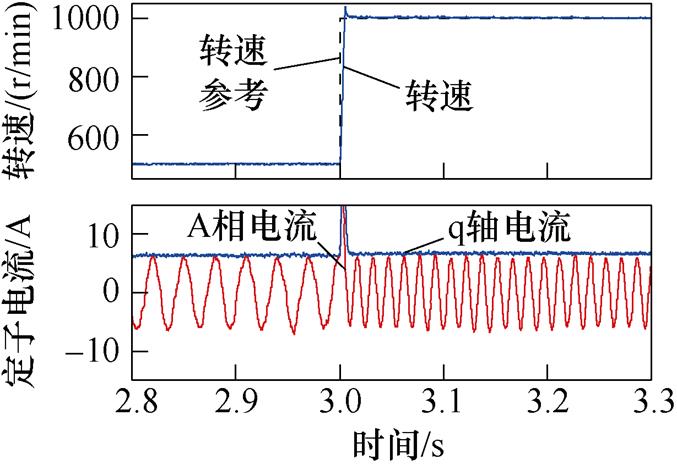
在无参数失配条件下,将转速参考从500 r/min调整至1 000 r/min,负载转矩从空载增加至11.5 N·m。提出方法所得转速、q轴电流和A相电流实验波形如图4所示。可见提出方法可有效跟随参考运行,并抵抗负载扰动。在转速参考变化过程中,系统在经过1.85 s的调整时间ts1后恢复稳态,超调量s1约1.64%;在负载转矩变化过程中,系统调整时间ts2为6.18 s,超调量s2约16.0%。稳态过程定子电流总谐波畸变率(Total Harmonic Distortion, THD)值为3.14%。
在相同趋近律和滑模面条件下,基于超局部模型的传统无模型SMC方法实验波形如图5所示。可见传统方法在转速参考变化过程中调节时间ts1和超调量s1分别为2.0 s和1.72%,在负载转矩变化过程中调节时间ts2和超调量s2分别为6.60 s和17.8%,稳态过程定子电流THD为3.55%。然而,根据电流放大波形,运行过程中有明显畸变,相较于提出方法正弦度下降。
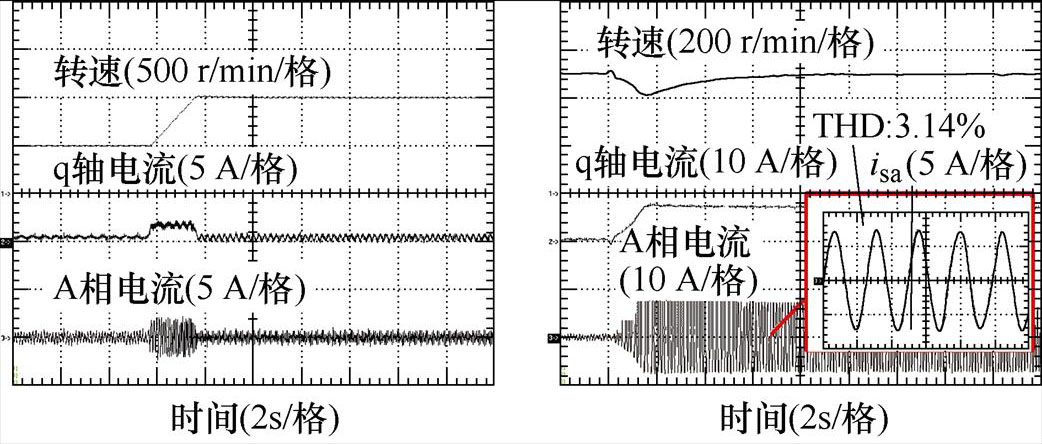
(a)转速参考变化 (b)负载转矩变化
图4 提出方法实验波形
Fig.4 Experimental waveforms of the proposed method
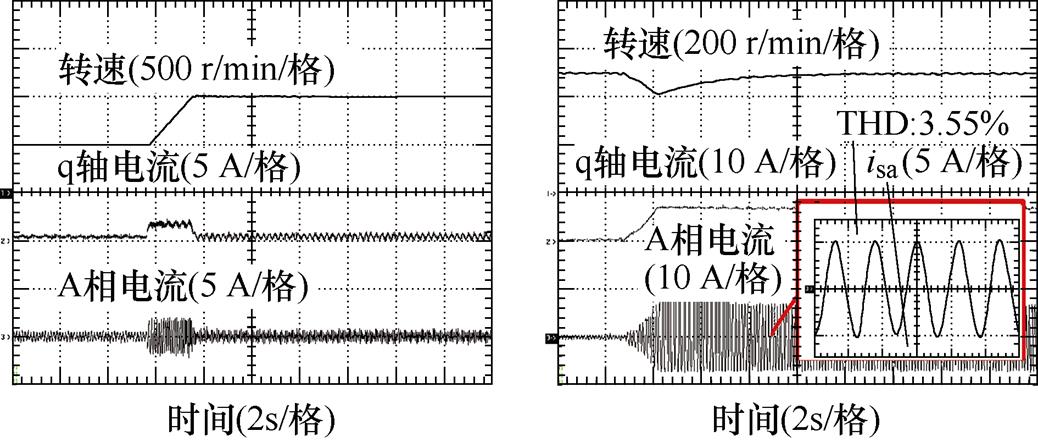
(a)转速参考变化 (b)负载转矩变化
图5 传统方法实验波形
Fig.5 Experimental waveforms of the conventional method
对相电流进行傅里叶分析,谐波含量如图6a所示。可以看出,提出方法所得主要谐波有所降低,如5次、7次和13次谐波;由连续傅里叶分析得到的统计小提琴图如图6b所示。两个控制方法覆盖面积基本相同,所得电流质量稳定程度相似。相较于传统方法,提出方法所得THD覆盖范围及其中位数较低,有较好的电流质量。
对连续1 000个采样周期内q轴电流误差进行累积,结果如图7所示,d轴电流累计误差结果与q轴结果类似。实验结果显示,相比传统方法中超局部模型,提出方法中超局部化时间序列模型能更加精准地描述电机系统的运动特性和工作状态,可获得较低的电流累积误差。通过高度适配模型设计的滑模控制律所得的控制变量,能更加精准地控制系统,达到更优秀的控制效果。
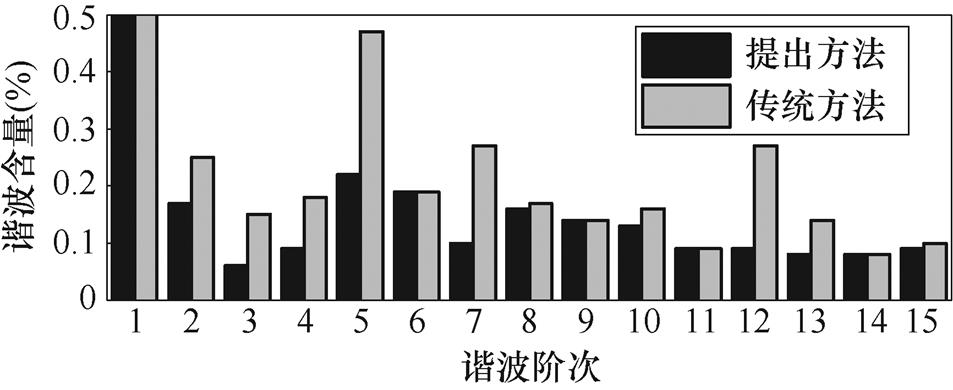
(a)傅里叶分析结果
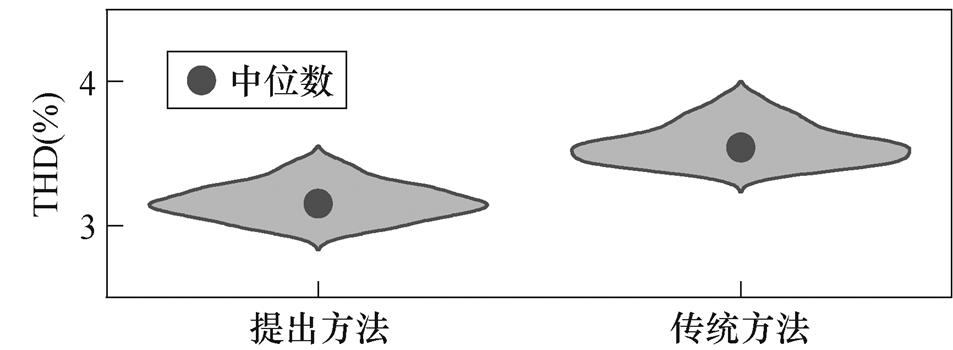
(b)连续傅里叶结果
图6 相电流傅里叶分析结果
Fig.6 Fourier analysis results for the phase currents
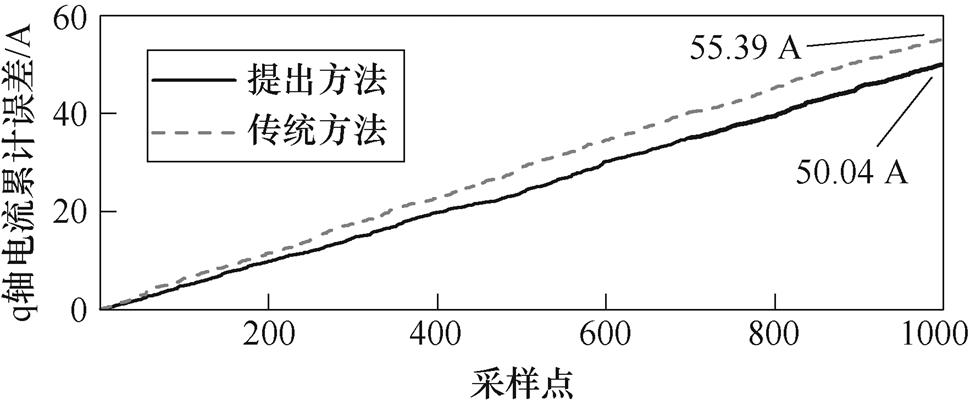
图7 q轴电流累计误差实验波形
Fig.7 Experimental waveforms of accumulated errors on q-axis current
两种控制策略所得性能见表3,其中转速综合实践与绝对误差(Integrated Time and Absolute Error, ITAE)值对稳态过程中连续5 000个采样点累加获得。由于相同的转速控制器,系统动态性能指标基本相同;相较于经典超局部模型,由于超局部化时间序列模型有更高精度,精准反映电机系统运行状态,提出方法转速ITAE提升16.04%,电流THD提升11.55%,控制精度有所提升。
表3 系统性能
Tab.3 System performances
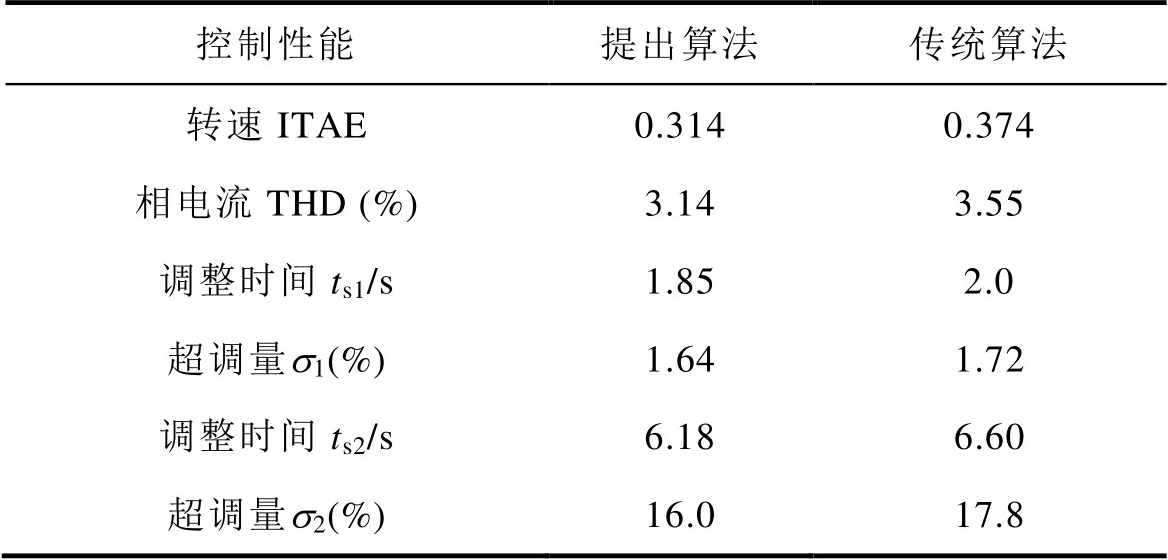
控制性能提出算法传统算法 转速ITAE0.3140.374 相电流THD (%)3.143.55 调整时间ts1/s1.852.0 超调量s1(%)1.641.72 调整时间ts2/s6.186.60 超调量s2(%)16.017.8
在不同转速条件下,空载和带载时两种控制策略所得系统噪声如图8所示。可见,随着转速上升,系统产生的噪声脉冲幅值和密度均有所增加;电机带载运行时比空载运行产生更多噪声。在相同转速和带载条件下,相较于传统方法,提出方法产生的噪声脉冲幅值和密度明显得到优化。在2 000 r/min带载运行条件下,传统方法最大噪声幅值为46.88 dB,提出方法为39.06 dB,降低16.68%。
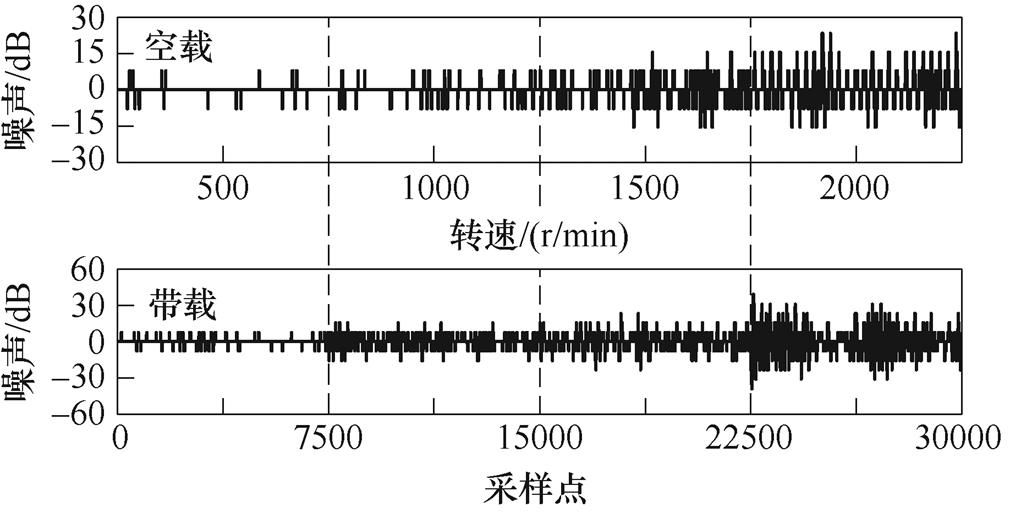
(a)提出方法噪声结果
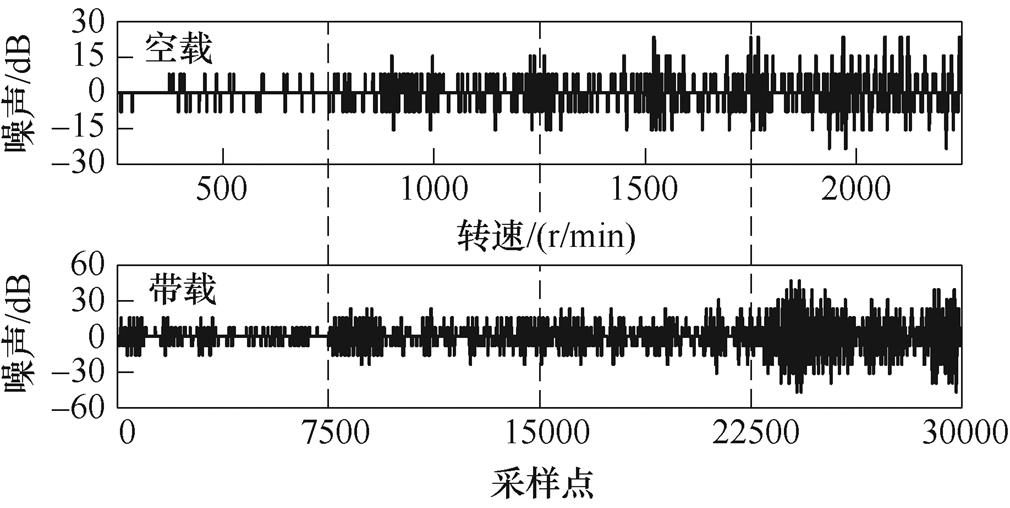
(b)传统方法噪声结果
图8 系统噪声测试结果
Fig.8 System noise test results
对运行过程中系统噪声幅值求取平均值,所得结果如图9所示。可见,无论系统处于何种运行条件下,提出方法所得系统噪声均小于传统方法,特别在带载运行时,系统噪声优化程度更高。同样在带载2 000 r/min条件下,传统方法平均噪声幅值为8.3 dB,提出方法为11.9 dB,降低30.25%。
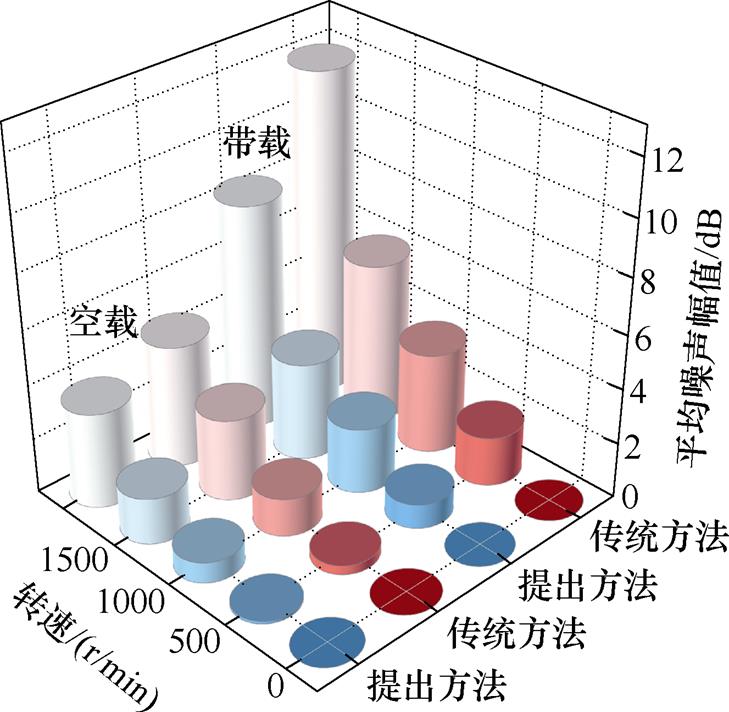
图9 平均系统噪声幅值
Fig.9 Average amplitudes of the system noises
在不同倍率的输入增益下,传统方法电流质量如图10所示。根据测试结果,以及式(4)和文献[30]所述,传统方法鲁棒性和稳态性能受到输入增益和定子电感参数取值的直接影响。定义Lsqe为控制策略中Lsq的取值,在1 000 r/min运行,参数失配设定为Lsqe/Lsq=2时,相电流实验波形和连续傅里叶分析结果如图11所示,在运行过程中切换控制策略观察相电流质量。可以看出,传统方法受到参数正失配(Lsqe/Lsq>1)的严重影响,相电流中存在大量谐波,THD中位数达到36.09%;而提出方法基本不受参数失配影响,电流质量与图4中无参数失配实验结果相似,THD中位数为3.807%。
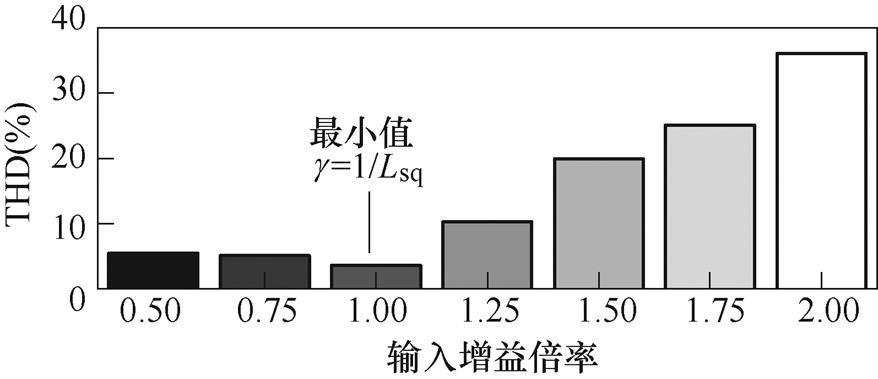
图10 不同输入增益倍率下传统方法电流质量结果
Fig.10 Results for the current quality with different times of input gain of the conventional method
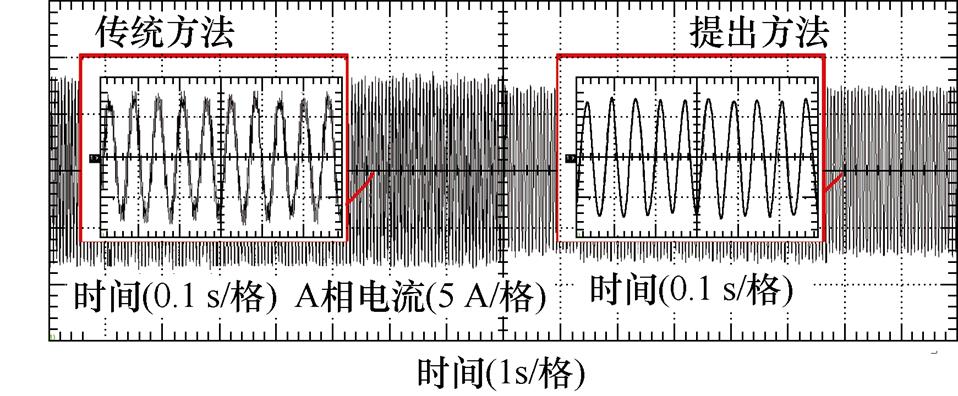
(a)相电流实验波形
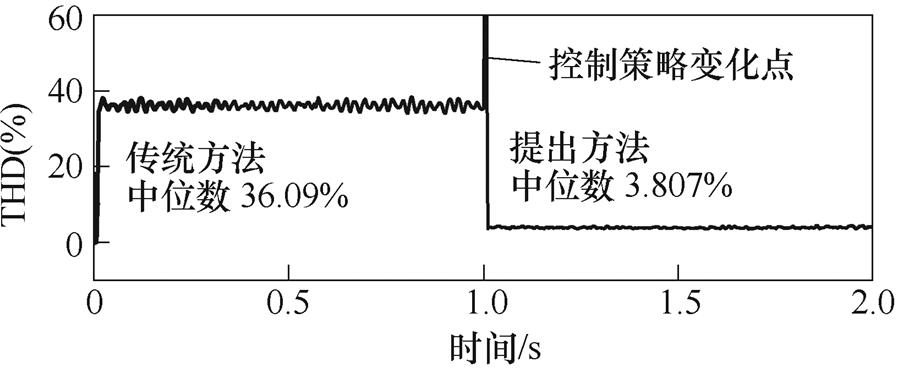
(b)连续傅里叶结果
图11 q轴定子电感正失配条件下相电流实验结果
Fig.11 Experimental results of the phase current with q-axis stator inductance positive mismatch
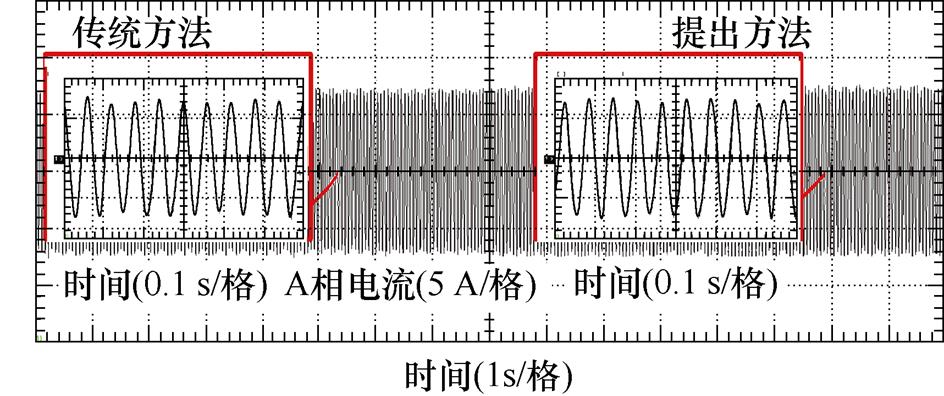
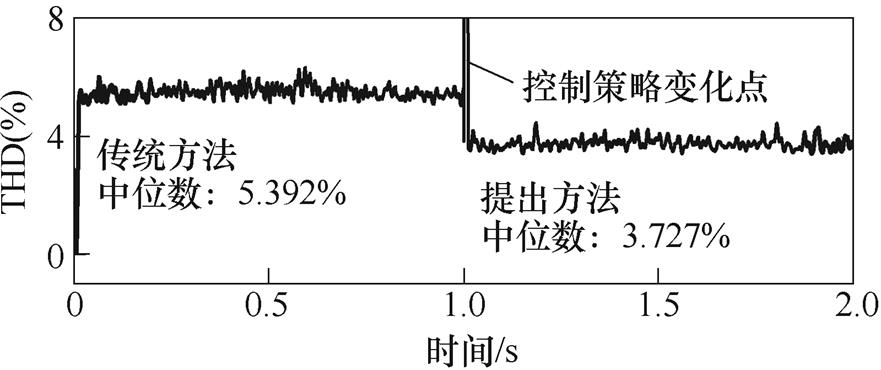
参数失配设定为Lsqe/Lsq=0.5,相电流实验波形和连续傅里叶分析结果如图12所示。在q轴定子电感负失配(Lsqe/Lsq<1 条件下,传统方法受到影响较弱,仅在部分正弦幅值位置处存在畸变,相电流THD中位数为5.392%;提出方法同样不受影响,所得THD中位数为3.727%。
条件下,传统方法受到影响较弱,仅在部分正弦幅值位置处存在畸变,相电流THD中位数为5.392%;提出方法同样不受影响,所得THD中位数为3.727%。
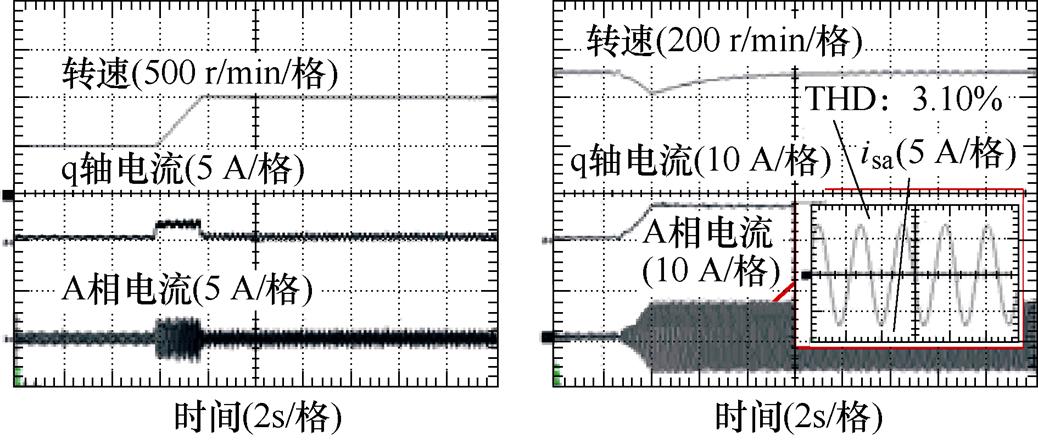
将提出算法的幂次控制律中饱和函数修改为符号函数,即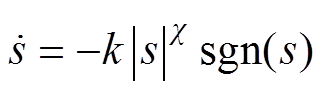 。在相同条件下对控制性能进行验证,实验结果如图13所示。可以看出,变换控制律后系统可稳定运行。在转速参考变化过程中,系统调整时间和超调量分别约1.90 s和1.52%;在负载转矩变化过程中,系统调整时间和超调量分别约6.50 s和17.68%。稳态过程定子电流THD为3.10%。各项性能指标与带有饱和函数趋近律的提出方法相近。因而在提出方法中,数据驱动模型的变化幅度不足以引发系统鲁棒性下降问题。
。在相同条件下对控制性能进行验证,实验结果如图13所示。可以看出,变换控制律后系统可稳定运行。在转速参考变化过程中,系统调整时间和超调量分别约1.90 s和1.52%;在负载转矩变化过程中,系统调整时间和超调量分别约6.50 s和17.68%。稳态过程定子电流THD为3.10%。各项性能指标与带有饱和函数趋近律的提出方法相近。因而在提出方法中,数据驱动模型的变化幅度不足以引发系统鲁棒性下降问题。
(a)傅里叶分析结果
(b)连续傅里叶结果
图12 q轴定子电感负失配条件下相电流实验结果
Fig.12 Experimental results of the phase current with q-axis stator inductance negative mismatch
(a)转速参考变化 (b)负载转矩变化
图13 不同控制律的提出方法实验波形
Fig.13 Experimental waveforms of the proposed method with different control law
为充分验证提出方法的优势性,搭建仿真模型进行验证,模型参数与表2相同。分别设定负载转矩在1.5 s从4 N·m增加至11.5 N·m、转速参考值在3 s从500 r/min增加至1 000 r/min。
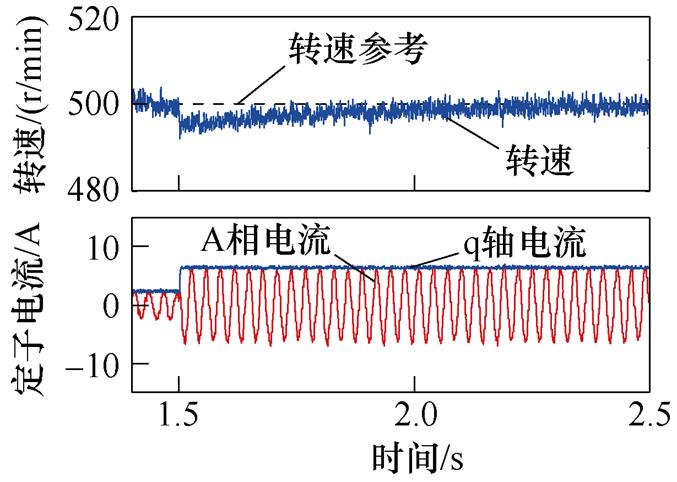
提出方法和传统方法的转速、A相电流和q轴电流仿真结果如图14和图15所示。在转速参考变化过程中,提出方法的转速调整时间为7.38 ms,超调量为0.24%,传统方法的调整时间为12.38 ms,超调量为4.07%;在负载转矩变化过程中,提出方法的转速调整时间为5.88 ms,超调量为1.70%,传统方法的调整时间为7.56 ms,超调量为1.79%。二者相电流THD值分别为5.03%和6.32%,1 s内稳态转速ITAE值分别为0.424和0.52。通过改进的模型结构,提出方法有良好的电流质量和动态性能。
(a)转速参考变化
(b)负载转矩变化
图14 提出方法仿真波形
Fig.14 Simulation waveforms of the proposed method
(a)转速参考变化
(b)负载转矩变化
图15 传统方法仿真波形
Fig.15 Simulation waveforms of the conventional method
对不同趋近幂次下的提出算法进行验证,转速ITAE和定子电流THD测试结果如图16所示。可以看出,在趋近幂次选择[0, 2]范围内,系统稳定性得到有效保持。随着d轴和q轴趋近幂次增大,转速ITAE逐渐降低,而电流THD呈现先增加后降低的趋势。综合考虑性能指标,本文选取趋近幂次为2。
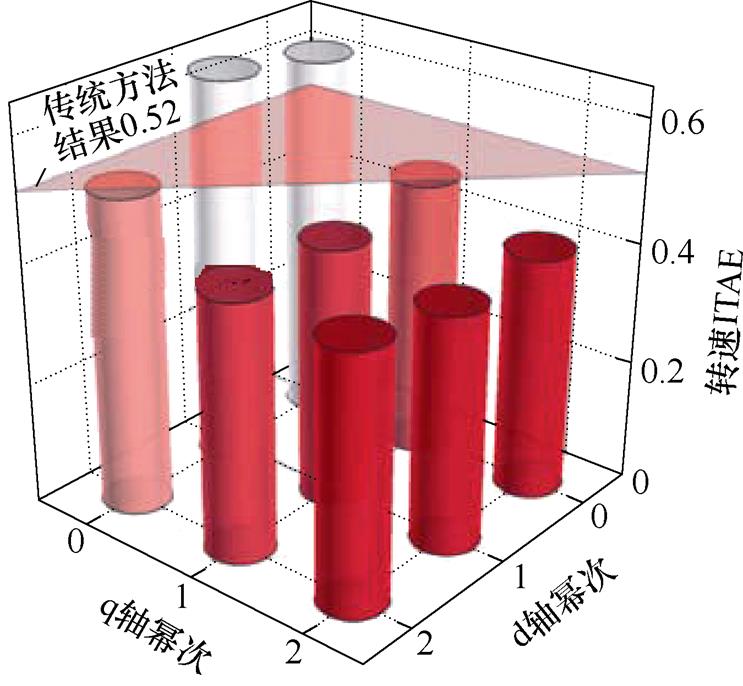
(a)转速ITAE结果
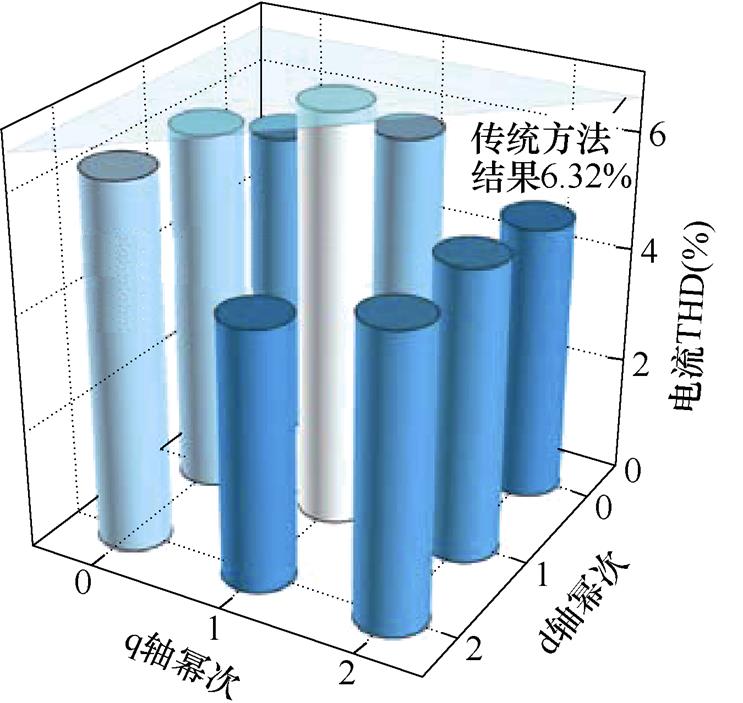
(b)定子电流THD结果
图16 不同趋近幂次的提出方法仿真测试结果
Fig.16 Simulation results with different approaching orders for the proposed method
本文提出一种基于超局部化时间序列的无模型预测电流滑模控制方法,并将其应用至永磁同步电机驱动系统中。该方法利用超局部化时间序列模型简化模型结构、提高精度,并结合RLS实时更新模型,使其保持对电机系统的高度适配。在此基础上,结合幂次趋近律和Lyapunov方法生成滑模控制函数。实验结果验证了提出方法的有效性,并在相同条件下与传统无模型滑模控制进行综合性能比较,证明了提出方法可获得更优的电流质量、更低的系统噪声幅值和平均值,以及更强的鲁棒性。
在低采样频率条件下,数据驱动模型精度降低,直接影响系统的控制性能。然而,在本文的研究框架下,方法尚不能充分解决该问题。在未来的研究中,将低采样频率视作一种规律性的数据缺失,结合数据的时间序列特性和数据填补思想,从而提高模型精度和控制性能,为低采样频率可靠运行提供更好的解决方案。
参考文献
[1] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online para- meter identification of permanent magnet syn- chronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[2] 李晓华, 赵容健, 田晓彤, 等. 逆变器供电对电动汽车内置式永磁同步电机振动噪声特性影响研究[J]. 电工技术学报, 2020, 35(21): 4455-4464.
Li Xiaohua, Zhao Rongjian, Tian Xiaotong, et al. Study on vibration and noise characteristics of interior permanent magnet synchronous machine for electric vehicles by inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455-4464.
[3] Rodriguez J, Garcia C, Mora A, et al. Latest advances of model predictive control in electrical drives-part I: basic concepts and advanced strategies[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 3927-3942.
[4] Tang Mi, di Benedetto M, Bifaretti S, et al. State of the art of repetitive control in power electronics and drive applications[J]. IEEE Open Journal of Industry Applications, 2021, 3: 13-29.
[5] Yu Xinghuo, Feng Yong, Man Zhihong. Terminal sliding mode control-an overview[J]. IEEE Open Journal of the Industrial Electronics Society, 2020, 2: 36-52.
[6] 黄依婷, 沈建新, 王云冲, 等. 基于递推最小二乘法观测器的永磁同步伺服电机变参数滑模控制[J]. 中国电机工程学报, 2022, 42(18): 6835-6846.
Huang Yiting, Shen Jianxin, Wang Yunchong, et al. Variable parameter sliding mode control of permanent magnet synchronous servo machine based on recursive least square observer[J]. Proceedings of the CSEE, 2022, 42(18): 6835-6846.
[7] 付东学, 赵希梅. 永磁直线同步电机自适应反推全局快速终端滑模控制[J]. 电工技术学报, 2020, 35(8): 1634-1641.
Fu Dongxue, Zhao Ximei. Adaptive backstepping global fast terminal sliding mode control for per- manent magnet linear synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(8): 1634-1641.
[8] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[9] El-Sousy F F M, Alenizi F A F. Optimal adaptive super-twisting sliding-mode control using online actor-critic neural networks for permanent-magnet synchronous motor drives[J]. IEEE Access, 2021, 9: 82508-82534.
[10] 韩国强, 陆哲, 吴孟霖, 等. 基于改进滑模控制策略的开关磁阻电机直接瞬时转矩控制方法[J]. 电工技术学报, 2022, 37(22): 5740-5755.
Han Guoqiang, Lu Zhe, Wu Menglin, et al. Direct instantaneous torque control method for switched reluctance motor based on an improved sliding mode control strategy[J]. Transactions of China Electro- technical Society, 2022, 37(22): 5740-5755.
[11] Yuan Lei, Jiang Yunhao, Xiong Lu, et al. Sliding mode control approach with integrated disturbance observer for PMSM speed system[J]. CES Transa- ctions on Electrical Machines and Systems, 2023, 7(1): 118-127.
[12] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for per- manent magnet linear synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(4): 861-869.
[13] Wang Fengxiang, He Long. FPGA-based predictive speed control for PMSM system using integral sliding-mode disturbance observer[J]. IEEE Transa- ctions on Industrial Electronics, 2021, 68(2): 972- 981.
[14] 王琛琛, 苟立峰, 周明磊, 等. 基于改进的离散域二阶滑模观测器的内置式永磁同步电机无位置传感器控制[J]. 电工技术学报, 2023, 38(2): 387- 397.
Wang Chenchen, Gou Lifeng, Zhou Minglei, et al. Sensorless control of IPMSM based on improved discrete second-order sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 387-397.
[15] 魏尧, 柯栋梁, 黄东晓, 等. 基于时间序列的永磁同步电机连续控制集无模型预测电流控制[J/OL]. 电工技术学报, 2023, DOI: 10.19595/j.cnki.1000- 6753.tces.230159.
Wei Yao, Ke Dongliang, Huang Dongxiao, et al. A continuous-control-set type model-free predictive current control based on time-series for PMSM drives[J/OL]. Transactions of China Electrotechnical Society, 2023, DOI: 10.19595/j.cnki.1000-6753.tces. 230159.
[16] 米阳, 伦雪莹, 孟凡斌, 等. 基于无模型算法和电动汽车辅助调节的新能源电力系统频率协调控制[J]. 电力系统保护与控制, 2021, 49(24): 13-20.
Mi Yang, Lun Xueying, Meng Fanbin, et al. Frequency coordinated control of a new energy power system based on a model-free algorithm and EV auxiliary regulation[J]. Power System Protection and Control, 2021, 49(24): 13-20.
[17] 曹荣敏, 郑鑫鑫, 侯忠生. 基于改进多入多出无模型自适应控制的二维直线电机迭代学习控制[J]. 电工技术学报, 2021, 36(19): 4025-4034.
Cao Rongmin, Zheng Xinxin, Hou Zhongsheng. An iterative learning control based on improved multiple input and multiple output model free adaptive control for two-dimensional linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4025- 4034.
[18] Wang Fengxiang, Wei Yao, Young H, et al. Continuous-control-set model-free predictive funda- mental current control for PMSM system[J]. IEEE Transactions on Power Electronics, 2023, 38(5): 5928-5938.
[19] Zhao Kaihui, Yin Tonghuan, Zhang Changfan, et al. Robust model-free nonsingular terminal sliding mode control for PMSM demagnetization fault[J]. IEEE Access, 2019, 7: 15737-15748.
[20] Mousavi M S, Davari S A, Nekoukar V, et al. Predictive torque control of induction motor based on a robust integral sliding mode observer[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 2339-2350.
[21] 汪凤翔, 杨奥, 于新红, 等. 基于自适应超螺旋滑模观测器的三相Vienna整流器无模型预测电流控制[J/OL]. 电工技术学报, 2023, DOI: 10.19595/ j.cnki.1000-6753.tces.222213.
Wang Fengxiang, Yang Ao, Yu Xinhong, et al. Model-free predictive current control for three-phase Vienna rectifier based on adaptive super-twisting sliding mode observer[J/OL]. Transactions of China Electrotechnical Society, 2023, DOI: 10.19595/j.cnki. 1000-6753.tces.222213.
[22] Wei Yao, Young H, Wang Fengxiang, et al. Gen- eralized data-driven model-free predictive control for electrical drive systems[J]. IEEE Transactions on Industrial Electronics, 2023, 70(8): 7642-7652.
[23] 刘国海, 陈仁杰, 张多, 等. 两电机调速系统的神经网络逆无模型自适应鲁棒解耦控制[J]. 中国电机工程学报, 2019, 39(3): 868-874, 965.
Liu Guohai, Chen Renjie, Zhang Duo, et al. Model- free adaptive robust control for two motor drive system based on neural network inversion[J]. Pro- ceedings of the CSEE, 2019, 39(3): 868-874, 965.
[24] Bolognani S, Carlet P G, Tinazzi F, et al. Current ripple minimisation in deadbeat parameter-free predictive control of synchronous motor drives[J]. IEEE Open Journal of Industry Applications, 2021, 2: 278-288.
[25] Brosch A, Hanke S, Wallscheid O, et al. Data-driven recursive least squares estimation for model predictive current control of permanent magnet synchronous motors[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2179-2190.
[26] 赵凯辉, 刘文昌, 刘智诚, 等. 一种永磁同步电机无模型高阶滑模控制算法[J]. 电工技术学报, 2023, 38(6): 1472-1485.
Zhao Kaihui, Liu Wenchang, Liu Zhicheng, et al. Model-free high sliding mode control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1472-1485.
[27] 赵凯辉, 戴旺坷, 周瑞睿, 等. 基于扩展滑模扰动观测器的永磁同步电机新型无模型滑模控制[J]. 中国电机工程学报, 2022, 42(6): 2375-2386.
Zhao Kaihui, Dai Wangke, Zhou Ruirui, et al. Novel model-free sliding mode control of permanent magnet synchronous motor based on extended sliding mode disturbance observer[J]. Proceedings of the CSEE, 2022, 42(6): 2375-2386.
[28] 赵凯辉, 殷童欢, 张昌凡, 等. 永磁同步电机无模型滑模控制方法研究[J]. 电子测量与仪器学报, 2018, 32(4): 172-180.
Zhao Kaihui, Yin Tonghuan, Zhang Changfan, et al. Research on model-free sliding mode control of permanent magnet synchronous motor[J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(4): 172-180.
[29] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model- free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[30] Li Wanrong, Yuan Huawei, Li Sinan, et al. A revisit to model-free control[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14408-14421.
Model-Free Predictive Sliding Mode Control Using Ultra-Localized Time-Series for Permanent Magnet Synchronous Motor Drives
Abstract The limited flexibility and robustness of the typical sliding mode control (SMC) fail to meet the demands of complex environments with variable loads and the influence of time-varying inductance parameters, magnetic field coupling, core saturation, and other factors. On the contrary, the model-free SMC strategy is more effective. This paper proposes a model-free predictive SMC strategy utilizing an ultra-localized time-series model for a permanent magnet synchronous motor (PMSM) driving system. By representing the motor as a collection of discrete-time linear functions and maintaining high model accuracy through an online estimation algorithm, the proposed strategy is better aligned with the motion characteristics of the motor system.
Firstly, this approach establishes an ultra-localized time-series model and updates the regressive vector, which only summarizes input and output signals based on sampled data. Secondly, all undetermined coefficients in the model are estimated using the recursive least square (RLS) algorithm. Consequently, the current operating state of the motor driving system is described as a collection of discrete-time linear functions and converted into the ultra-local structure to generate the sliding mode signal. Finally, control functions are designed based on the power-reaching rule, and the reaching conditions are verified using the Lyapunov method. This ultra-localized time-series model is easily implemented within the SMC strategy, offering good accuracy and addressing the issues caused by time-varying physical parameters in the plant model of the typical SMC and input gain of the conventional observer-based ultra-local model.
Simulation and experimental results on a PMSM driving system demonstrate the effectiveness of the proposed method in resisting disturbances and successfully tracking the reference. The disturbances primarily include changed parameter mismatches and load torque. Fourier analysis and accumulated error comparisons between the proposed and conventional model-free SMC strategies show that the proposed method reduces the total harmonic distortion (THD) by 3.14%. Compared to the conventional strategy, the proposed method exhibits the minimum ascending slope of accumulated error for current and lower operating noise amplitudes in various speed references and load torques. Experimental results with different parameter mismatches of the stator inductance further verify its robustness.
The validations provide the following conclusions: (1) The proposed method adopts an ultra-localized time-series model to represent the current operating state of the motor driving system. Unlike the conventional strategy that utilizes an ultra-local approach, this model formulates the system as a collection of discrete-time linear functions. (2) The ultra-localized time-series model significantly improves current quality, accumulated current error, and system noise. This improvement is attributed to the high accuracy of the ultra-localized time-series model and the eliminated influences of the unsuitable input gain. (3) By employing a designed estimation algorithm and sampled data, the ultra-localized time-series model replaces the physical model, which involves multiple time-varying physical parameters, enabling more accurate modeling and updating processes.
keywords:Model-free sliding mode control, ultra-localized time series model, recursive least square algorithm, data-driven model
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.230301
国家自然科学基金(52277070)、中国博士后科学基金(2023M730598)和福建省科技计划(2021I0039)资助项目。
收稿日期 2023-03-16
改稿日期 2023-06-09
魏 尧 男,1993年生,博士,研究方向为新能源汽车电控系统、交流电机伺服系统及其先进控制。E-mail: yao.wei@fjirsm.ac.cn
汪凤翔 男,1982年生,博士,研究员,博士生导师,研究方向为电力电子与电力传动。E-mail: fengxiang.wang@fjirsm.ac.cn(通信作者)
(编辑 崔文静)