（1）
摘要 在电动汽车电驱动系统中，逆变器中的高频开关动作是产生开关损耗影响逆变器效率的主要因素，特别是为适应驱动电机高速化的趋势，不得不采用较高的开关频率，从而在低速时产生不必要的开关损耗，使逆变器效率偏低。因此，该文提出一种基于三状态脉冲宽度调制（TSPWM）的多模式调制策略来减少逆变器的开关损耗，提高全工况范围的逆变器效率。根据工况动态改变调制模式：在不同转速下采取变载频分段异步TSPWM；根据电机的相电流幅值动态地改变TSPWM不连续调制的钳位模式，使电流幅值较大的相保持在钳位状态以减小损耗。为了解决不同模式切换时相位突变导致电流或转矩冲击的问题，提出一种基于载波周期角度计算的电压矢量相位补偿算法，通过精确分析调制模式改变时刻对电压矢量角的影响，计算出切换后的补偿角度对空间电压矢量角进行补偿，从而实现不同模式的平滑切换。最后，通过算法仿真和电机实验验证了所提策略的有效性。结果表明，采用基于TSPWM的多模式调制策略的电机驱动系统，其逆变器效率得到了显著提升，且具有较小的共模电压。
关键词：三状态脉冲宽度调制（TSPWM） 多模式调制 分段变载波比调制 共模电压 电机驱动 电动汽车
三相两电平脉冲宽度调制（Pulse Width Modu- lation, PWM）逆变器广泛应用于中小容量的变频驱动系统中，如工业通用变频器及电动汽车驱动电机控制系统等[1-2]。在中小容量场合，为了获得优良的动静态调速性能，逆变器中金属氧化物半导体场效应管（Metal Oxide Semiconductor Field Effect Transistor, MOSFET）或绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）器件的开关频率通常可以达到10 kHz或几十kHz以上。另外，由于在数字化控制系统中控制周期固定实现起来更方便等原因，通常变频调速系统中的PWM开关频率是固定的。
但高频PWM技术的使用，在为逆变器带来优良控制性能的同时，也产生一些负面效应。首先，高频PWM会产生较高的开关损耗。其次，高频PWM会在逆变器输出端产生高频交变的共模电压（Common Mode Voltage, CMV）。高频共模电压是产生轴电压的元凶，而电机轴电流正是在轴电压的作用下，穿透轴承油膜，最终破坏轴承、危及电机系统的运行[3-6]。文献[7-9]中提出的三状态脉冲宽度调制（Tri-Sate PWM, TSPWM）算法，通过合理使用零矢量，将共模电压的高频分量降低到了直流母线电压的1/3。
要降低开关损耗，最直接的措施是适当降低开关频率。可供借鉴的是，在开关频率较低的大容量机车牵引系统中，普遍采用分段同步调制[10-13]、优化PWM等变载频PWM技术[14-16]。如在文献[10-12]中均用到了基于空间矢量脉冲宽度调制（Space Vector Pulse Width Modulation, SVPWM）的同步调制技术，或使用分段同步调制结合异步调制的混合调制算法。文献[14-15]详细介绍了基于特定谐波消除脉冲宽度调制（Selective Harmonic Elimination Pulse Width Modulation, SHEPWM）的多模式调制原理。韩坤等在文献[13]中采用的方法是低速用异步调制、中高速使用基于SHEPWM的同步调制、最高速过渡到方波调制模式。段宇航设计了一种在中频段采用同步SVPWM、高频段采用SHEPWM的多模式调制算法[17]。王堃等从磁链轨迹、线电压谐波分布及数字化实现难易等方面对比了同步SVPWM和SHEPWM，认为SHEPWM计算复杂，需要较多的存储空间，而SVPWM计算简单，容易数字化实现；但SHEPWM可以保证基波幅值的准确性并且可以消除大量低频谐波[18]。苑国锋等提出了综合性能最为全面、几乎囊括了几种常用策略的多模式调制方法，即从异步调制切换至同步SVPWM、再到同步SHEPWM直至方波调制[19]。
对多模式PWM而言，不同PWM模式之间的平滑切换是关键问题之一，不少文献对此进行了研究。文献[10]给出了一种简单的分段同步调制方法，在一个调制波周期结束后进行切换，其优点是不会产生任何相位上的突变，缺点是载波比切换的延时相对于载波频率而言相对较高，实时性差。文献[13, 20-23]等对基于SHEPWM的多模式调制策略之间如何平滑过渡进行了研究，例如，从异步调制切换到SHEPWM，采用的办法是在电压相位90°时同时切换三相，但实时性普遍较低。
现有文献中的多模式PWM技术通常针对机车牵引等大容量场合，其在电动汽车电驱动系统中的应用研究目前在文献报道中还很罕见。如果目标系统开关频率发生变化（如用SiC器件取代IGBT），调制模式也要针对性地优化调整[24]。而电动汽车驱动系统的开关频率远高于机车牵引系统，因此需要改进研究、提出更合适的多模式PWM算法。另外，如基于SVPWM设计调制策略，开关次数仍相对较多，且会产生较大的共模电压。
鉴于此，本文提出一种基于TSPWM技术的多模式调制新策略。针对电动汽车电驱动系统等中小功率变频调速系统开关频率相对较高的特点，综合考虑效率和电流波形质量来优化不同速度段的调制模式和载波比，进行分段异步TSPWM；根据功率因数改变钳位模式进一步减小开关损耗；在不同载频模式切换时对空间电压矢量相位进行准确补偿使电机电流过渡平滑。最后，通过Simulink仿真和电机台架实验对所提策略进行了验证。
在机车牵引系统中采用多模式PWM策略，通常是针对交流电力机车牵引传动系统开关频率低（通常只有几百赫兹）的特点，利用有限的开关频率尽可能消除电流中的低次谐波[19]。而在电动汽车电机驱动系统中，开关频率一般可以达到10～20 kHz左右。例如，近年来由于电动汽车驱动电机具有高速化的趋势，从每分钟几千转到上万转、再到1.6万r/min、1.8万r/min甚至2万r/min，逆变器也不得不采用较高的开关频率，或逐步采用SiC器件。在较高的开关频率下，即便采用异步调制，其波形不对称产生的非特征谐波也可以忽略，并没有采用同步调制或SHEPWM的紧迫需求。而且在高频情况下，对计算时间要求也高，如在20 kHz的情况下，需要全部电机控制算法在50 ms内完成。因此，过去通常采用比较方便数字化系统实现的固定载频异步调制策略。
但车用电机的调速范围宽，并不总在额定转速附近运行。当电机转速较低时，仍然采用较高的开关频率就会造成不必要的开关损耗，影响逆变器效率。随着电动汽车电驱动系统高速化、高频化的趋势和提高续驶里程的要求，进一步优化PWM模式、减小逆变器损耗、提高效率显得非常必要。逆变器损耗主要包括IGBT的导通损耗和开关损耗。IGBT的导通损耗为
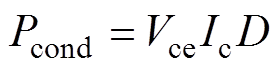（1）
IGBT的开关损耗为
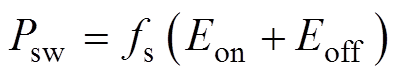（2）
可以看出，导通损耗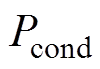
主要与饱和压降
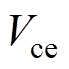、集电极电流
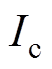和导通时间占空比
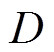有关，和频率或转速无关；开关损耗
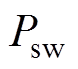主要与开关频率
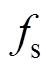、开通损耗
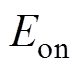和关断损耗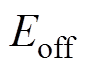
有关。而：逆变器效率为输出功率/输入功率，低速时逆变器损耗没有明显减少，但输出功率很小，所以效率很低；如果减少开关频率，就可以减少开关次数，大幅减小开关损耗。因此，减少开关次数可以改善逆变器效率，特别是电机处于低速状态下。
另一方面，高频PWM会产生高频共模电压。电机驱动系统的共模等效电路如图1所示。图中，N为电机中性点，通常对地悬空；A、B、C为逆变器三相输出点。Udc为直流母线电压；G1～G6均为IGBT；VD1～VD6均为反并联二极管；Cwf、Cwr、Crf分别为三相绕组和定子铁心之间、三相绕组和转子铁心之间、定转子铁心之间的分布电容；Cb为电机轴承油膜的等效电容，和油膜厚度、压力等因素有关；Rb为电机轴电流通道的等效电阻，也是非线性的。共模电压定义为
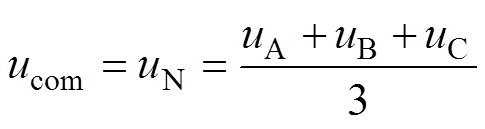（3）
式中，
、
、
、
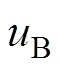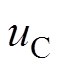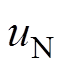分别为A、B、C、N点对地（即O点处）电压。
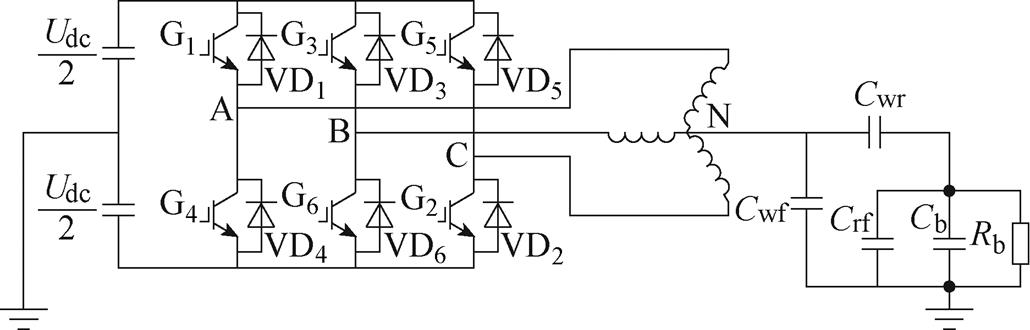
图1 电机驱动系统逆变器主电路原理
Fig.1 Equivalent circuit of motor drive system
普通SVPWM在调制过程中需要频繁使用两个零矢量（000、111），根据式（3）可知，逆变器在零矢量时将分别产生大小为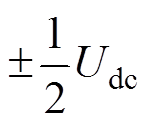
的共模电压。峰峰值为
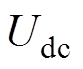、开关频率相关频次的共模电压通过分布电容在转子侧感应出轴电压，击穿轴承油膜产生轴电流腐蚀轴承，危及系统安全运行。此外，高频的共模电压还会对周围电子设备产生严重的电磁干扰。由于共模电压主要是通过对地分布电容耦合产生作用的，因此需要尽量抑制共模电压中的高频分量。
根据以上分析，针对电动汽车电驱动系统开关频率较高的特点，提出一种基于TSPWM的多模式PWM新策略，目的是减小开关损耗并兼顾共模电压抑制。主要思路和措施如下。
TSPWM具有抑制共模电压的优点，且在同样载频下开关次数比SVPWM的减少1/3左右[7-9]，因此首先将TSPWM算法应用到多模式调制策略中。
原始TSPWM有两种模式。在高调制比模式下，使用左、中、右（V6、V4和V5）3个相邻非零矢量合成参考电压矢量。TSPWM矢量合成原理如图2所示。图2中，kl、kc、kr分别为左、中、右非零矢量的作用系数。由于没有使用零矢量，其共模电压在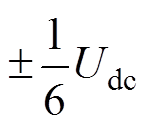
之间，峰峰值仅为SVPWM的1/3。在低调制比区使用两个相差120°的左、右非零矢量加一个（相邻的中间）零矢量来合成参考电压矢量。如图2中的V6、V5和V7（111），这种情况下共模电压在
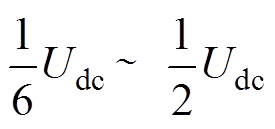之间，即其波动的峰峰值在一个扇区内也是直流电压的1/3，从而共模电压的高频分量幅值得到了显著的抑制。且两种模式有统一的计算公式，不增加计算量[25]。
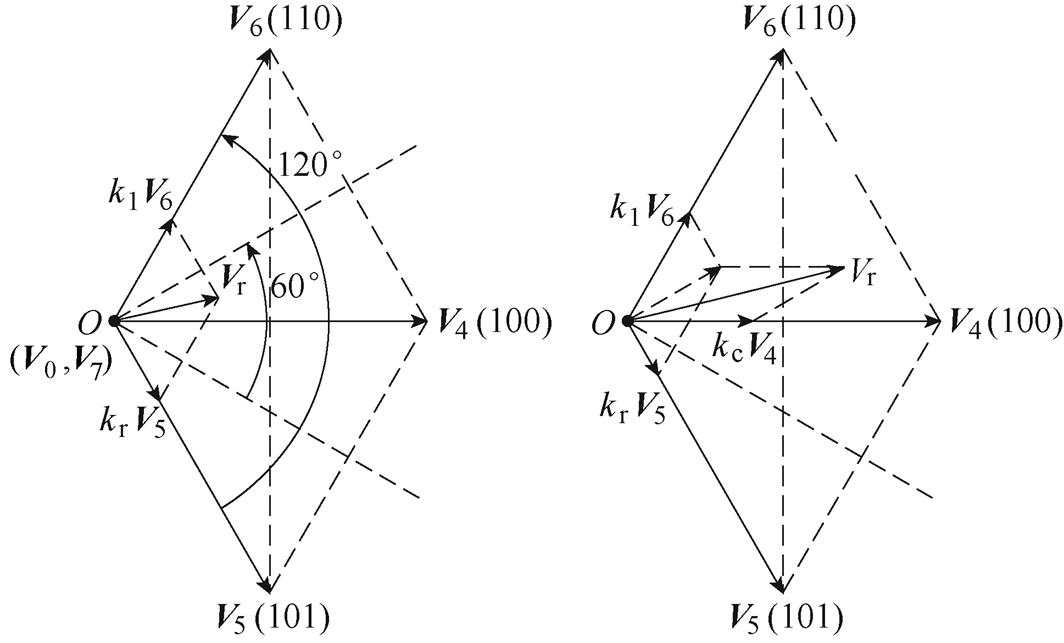
（a）低调制比 （b）高调制比
图2 TSPWM矢量合成原理
Fig.2 Principle of TSPWM
此外，无论高、低调制比模式，总有一相的开关不动作而是被钳位在正/负母线上，只有两相有开关动作，所以在PWM周期不变的前提下，开关次数少了1/3。因此，预期相比使用普通SVPWM算法，开关损耗可以减少1/3左右[9]。
如上所述，作为一种不连续调制方式，TSPWM总有一相处于钳位状态，以图2的情况为例，几个开关状态中A相总是“1”，即A相钳位到正母线。图2的矢量合成模式有效跨度为120°，原始TSPWM将-30°～30°的范围作为一个扇区，使用V6、V5作为左右矢量，只用了60°。可见，钳位角有60°的自由度。文献[26]首先提出利用在±30°的钳位角自由度范围内动态跟踪负载阻抗角的思路来进一步减小开关损耗，但未能很好地处理阻抗角大于30°的情况。后来还有其他文献提出类似的思路，动态划分扇区，但局限性更大，只有±24.7°的范围，甚至对调制比还有限制[8, 27]。
本文再略作改进，换一种思路来理解、利用TSPWM钳位角的自由度。不划分动态扇区，而是固定电压矢量的扇区划分如图3所示。但在每个扇区内，合成参考电压矢量所用的基本电压矢量不是固定的，有两种模式。例如，在扇区⑤的参考电压矢量，可以使用V6、V5合成使A相钳位，也可以使用V2、V4合成使C相钳位。具体采用哪种钳位模式，则判断：如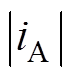
＞
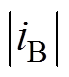，采取A相钳位模式；反之采取C相钳位模式。这样，被钳位的相没有开关动作，只产生导通损耗，不产生开关损耗。因为总是选择电流幅值较大的相进行钳位，这样减少开关损耗的效果是最好的。本方法不需要通过计算电流阻抗角进行动态扇区划分，实现简单；且对阻抗角和调制比的大小都没有限制。
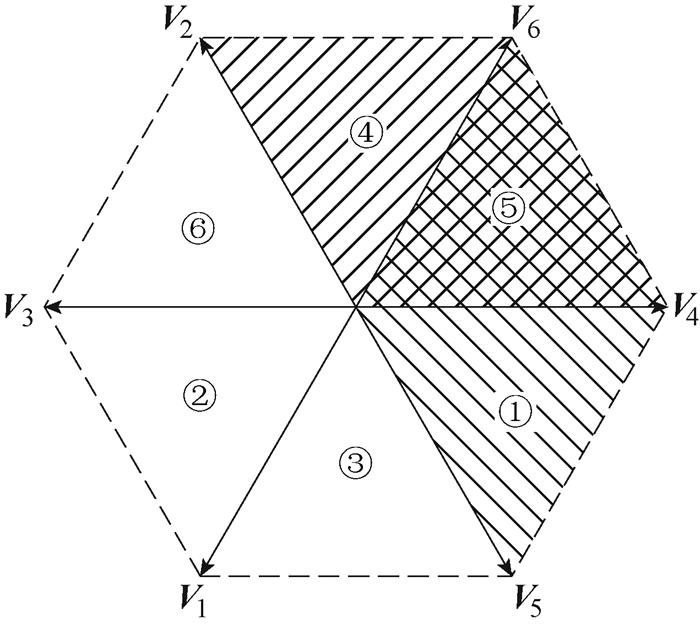
图3 改进TSPWM扇区划分
Fig.3 Modified TSPWM sector division
由于电动汽车驱动电机的调速范围宽，控制器开关频率较高，如果使用定载频的调制算法，当电机处于低速运行状态时，过高的开关频率则会导致不必要的开关损耗，最终影响驱动系统的整体效率。
根据电动汽车电驱动系统开关频率较高的特点，即使在高速工况下载波比通常也能达到20左右，使用SHEPWM等方法的必要性不大。另外，电动汽车电驱动系统控制周期短，这些PWM算法复杂且对电流闭环控制系统的架构有一定影响，给微控制单元（Microcontroller Unit, MCU）造成较大的计算负担。为进一步优化开关频率、降低逆变器损耗，又兼顾异步调制PWM周期固定、计算实现简单的优点，故本文采用分段变载波比的异步调制策略，如图4所示。图中，fr为基波频率，fc为载波频率。在不同的速度段分别采用不同的载波频率，在一个速度段内仍保持异步调制的优点。
分段异步调制策略组合的一般原则为随着电机频率上升逐步提高开关频率，但如何细分速度区间以及各区间的载频需要视具体电机而定。本文优化设计分段调制方案的原则是，综合考虑效率和电流波形质量来优化不同速度段的调制模式和载波比。一般开关频率越低，IGBT器件开关损耗越小，使得逆变器的效率越高。但开关频率也不能无限制降低，太低的开关频率会使电流波形质量下降，电流纹波变大，增加电机的谐波损耗影响电机效率进而影响驱动系统的整体效率。且载频变低也会导致电流环响应变慢，影响系统动态性能。一般地，在异步调制过程中载波比大于等于20时调制效果较好，电流波形的质量能得到一定保证。开关频率高，电流波形质量好，电机效率也较高，但逆变器效率会降低。根据以上分析，为了在不严重影响电流波形质量的前提下尽量降低载波比，使系统效率较高，通过标定的方式在某个速度段按照如下方式找到相对的平衡点。
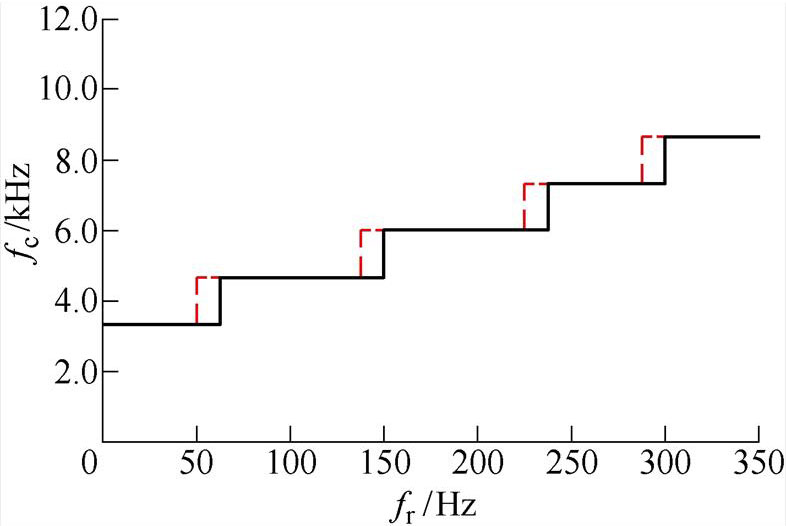
图4 分段可变载波比调制
Fig.4 Piecewise variable carrier wave ratio modulation
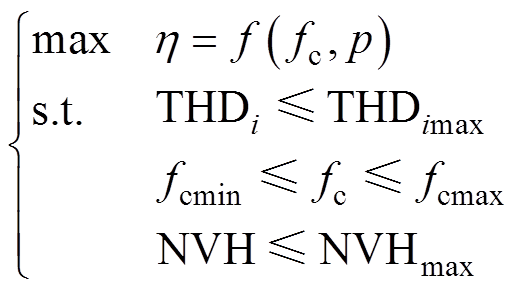
这里几个约束的含义是：为电流总谐波畸变率（Total Harmonic Distortion, THD）设定一个上限以免波形太差，下标i代表电流；开关频率设定上、下限；噪声、振动与声振粗糙度（Noise、Vibration、Harshness, NVH）指标满足需求；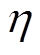
为系统效率；
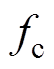为开关频率；p（pattern）为PWM模式，例如可以选择TSPWM或者SVPWM。
不同PWM模式或载波比的平滑切换是实现多模式PWM的基础。采用分段改变载波比的调制技术，在电机加/减速过程中会涉及载波比/开关频率的切换，如处理不好就会造成实际电压相位的突变，引起电流或转矩的冲击。
本文在分析数字化控制周期对电压矢量角度影响的基础上，提出一种对空间电压矢量角进行准确补偿的算法，在载波比切换过程中，既可以兼顾切换相位的平滑性和稳定性，又可以保证实时性。
在数字化控制系统中，用以控制计算的采样值（电流、转速等），数字化控制周期的影响如图5所示，第k周期的电流ik是在之前第k-1周期的中点时刻采样的。因此，矢量控制计算的id、iq及d轴位置等，均是以该时刻的采样值作为基准的。
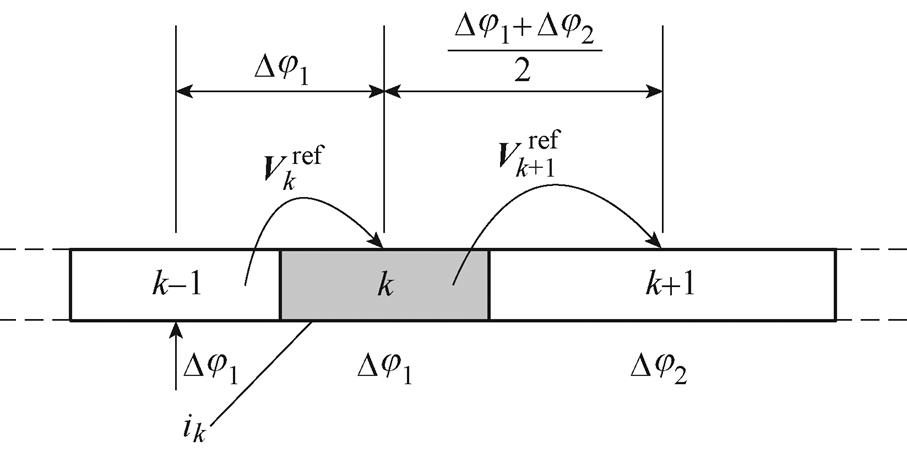
图5 数字化控制周期的影响
Fig.5 Influence of digital control cycle
当前正在执行的PWM波形对应电压指令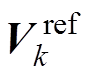
，是在上一个周期计算出来的；而当前周期计算所得到的电压指令，要到下一个周期才能发出，其等效作用时间在k+1周期的中点时刻。根据k-1周期的数据计算得到的d、q轴电压，从逻辑上来说也是相对于k-1周期的转子位置来说的，但实际上该电压矢量起作用时时间已经差不多过去了两个PWM周期，因此需要对电压矢量角进行补偿。
设切换前载波周期为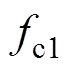
，载波比为
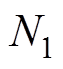，载波周期对应的相位变化为
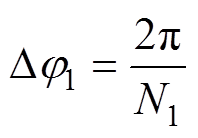。因为切换过程相对较快，认为在切换过程中电机转速即基波周期近似保持不变。切换后载波周期为
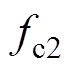，载波比为
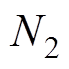，载波周期对应的相位变化为
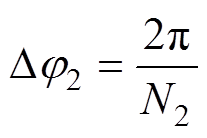。载波切换时刻电压相位变化如图6所示。由图6中可以看出，从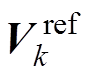到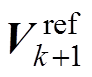
，角度跨度应为
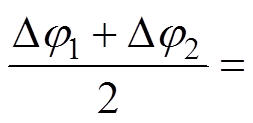
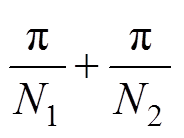。相对k-1周期的角度，补偿相位则应为
。
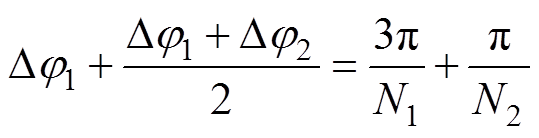根据数字周期对电压矢量角进行角度补偿后，在载波比切换前后补偿角度随载频周期变化，就可以保证电压矢量的相位不发生突变，满足了模式实时切换的要求。
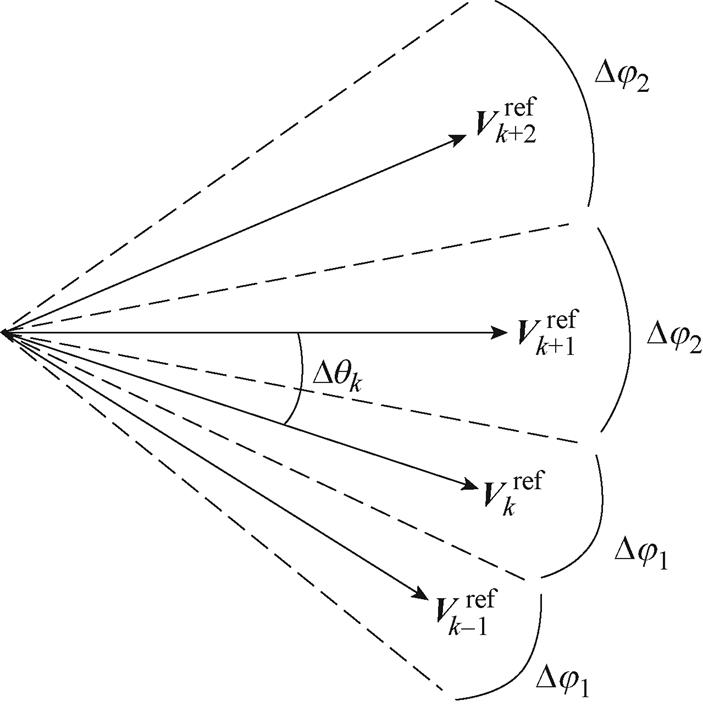
图6 载波切换时刻电压相位变化
Fig.6 Voltage phase angle change at the time of carrier switching
本文首先在Matlab/Simulink仿真软件中验证不同的载频模式切换时能否平滑过渡。表1为TSPWM算法仿真中使用的各区段开关频率情况。
表1 分段调制频率
Tab.1 Switching frequency of each section
基波频率/Hz调制方式开关频率/kHz 0～30异步2 30～50异步4 50～100异步6
图7为0.6 s切换时刻载波波形，由于此时调制波频率由30 Hz变为31 Hz，开关频率由2 kHz变为4 kHz，均使用异步调制。2 kHz切换至4 kHz时的电流波形如图8所示。由图8可以看出，切换时刻过程电流平滑过渡，没有出现电流冲击的现象。切换完成后，由于载波比变大，电流纹波减小。切换前后的相电流（除去了基波分量和直流分量）频谱图如图9所示。从图9中可以看出，切换后载波比的提高使得电流波形质量变好，电流谐波含量下降。此外，实测的电流THD值也从3.29%降为2.07%。
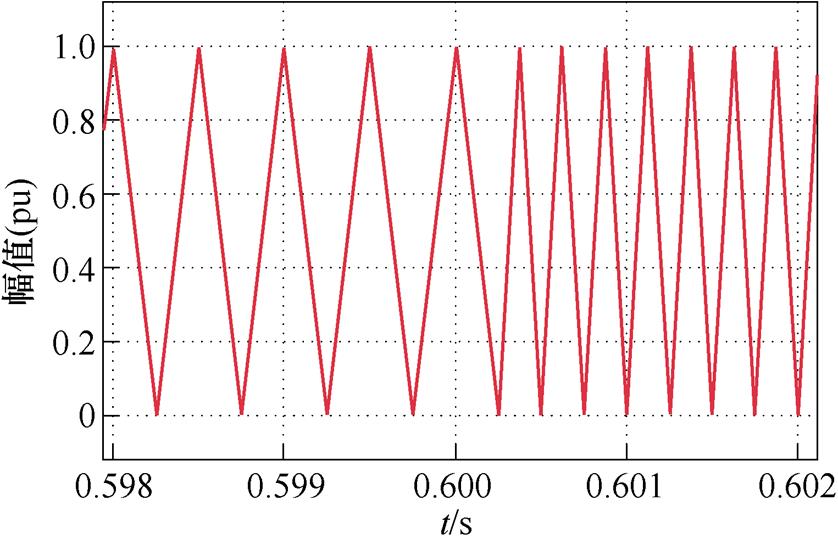
图7 0.6 s切换时刻载波波形变化
Fig.7 Carrier wave change during 0.6 s switching
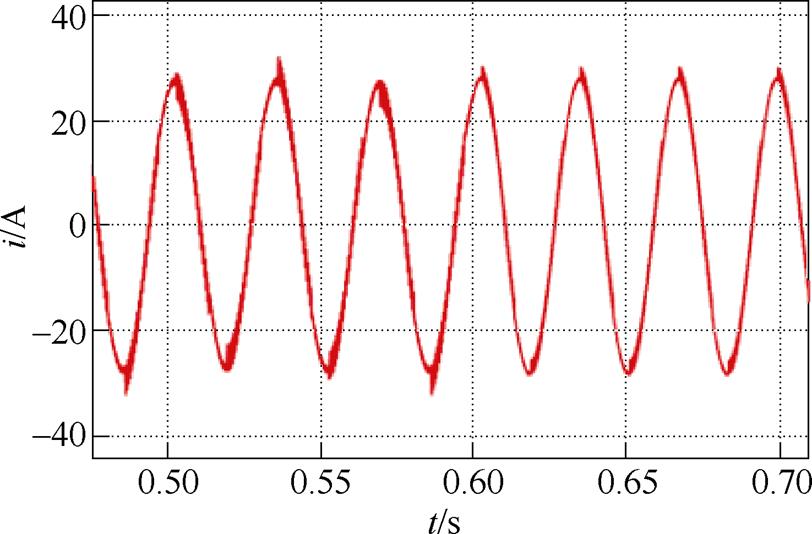
图8 2 kHz切换至4 kHz时的电流波形
Fig.8 Current waveform switching from 2 kHz to 4 kHz
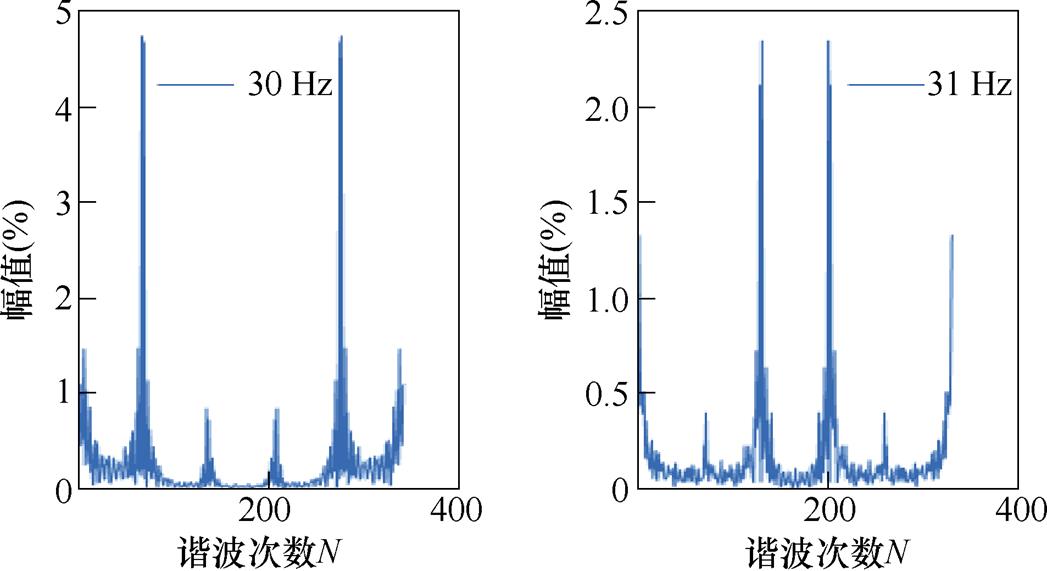
图9 切换前后电流频谱图
Fig.9 Current spectrum before and after switching
仿真结果表明，本文提出的电压矢量相位补偿方式可以使参考电压相位在载波切换时不突变，实现多模式PWM策略中不同PWM模式的平滑过渡。
为了验证本文多模式PWM策略的效果，搭建了永磁同步电机矢量控制实验平台。所用电机为一台乘用车减速轮毂永磁同步电机，控制策略为矢量控制，参数见表2。因实验条件所限，所用逆变器为一台旧的风冷IGBT控制器，以TI 28335 DSP为主控芯片，设计开关频率为10 kHz，故本文未开展10 kHz以上实验。
表2 被测电机参数
Tab.2 Parameters of tested motor
参 数数 值 额定功率/kW12.5 额定转速/(r/min)5 000 峰值电流/A100 峰值功率/kW25 极对数6
图10～图12分别为SVPWM及TSPWM低、高调制模式下产生的共模电压。从这三张图可以得出SVPWM产生的是高频交变的共模电压，而TSPWM在低调制比区和在高调制比区用于合成参考矢量的基本电压矢量不同，造成了两者共模电压波形不一致，但无论电压矢量位于低调制比区还是位于高调制比区，每个PWM周期内TSPWM控制算法产生的共模电压均为SVPWM控制算法所产生共模电压的1/3。
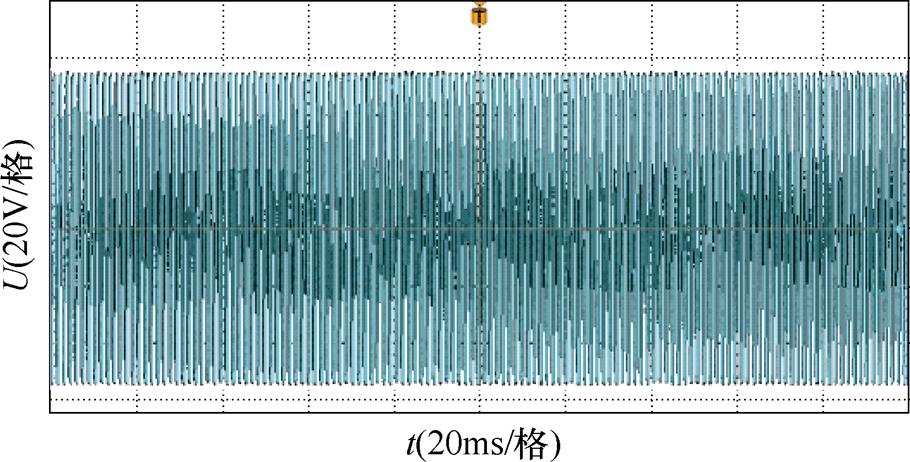
图10 SVPWM算法产生的共模电压
Fig.10 CMV generated by SVPWM algorithm
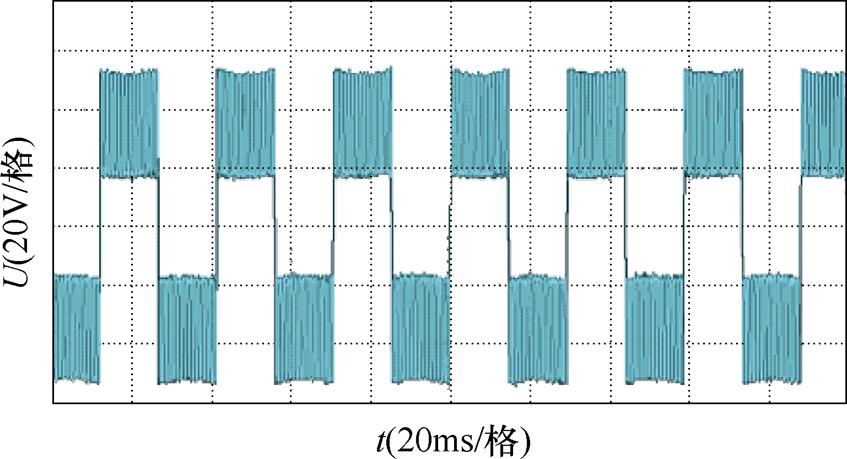
图11 低调制比区TSPWM算法产生的共模电压
Fig.11 CMV generated by TSPWM algorithm in low modulation ratio region
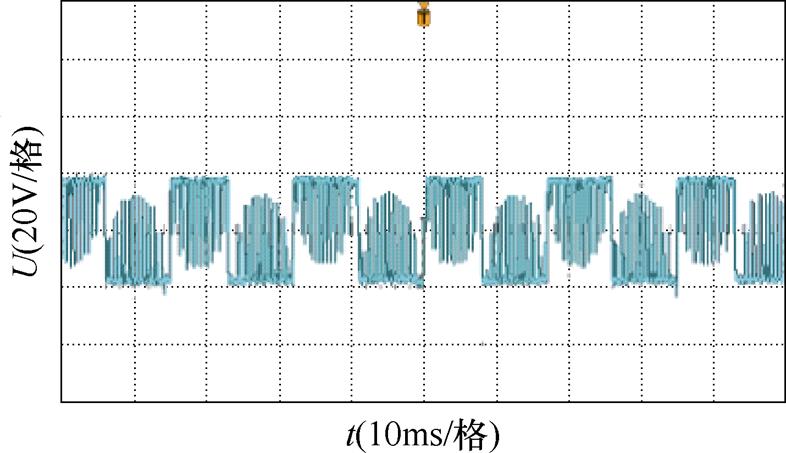
图12 高调制比区TSPWM算法产生的共模电压
Fig.12 CMV generated by TSPWM algorithm in high modulation ratio region
高频共模电压还会产生电磁干扰（Electro- magnetic Interference, EMI）干扰。本课题组在某无轨电车公司实车验证两种PWM算法的EMI干扰情况。在同一辆无轨公交车上，分别采用不同的PWM策略，用万用表交流电压档测量控制器壳体与车架之间的电压（控制器壳体与车架之间做了二次绝缘，低压控制电24 V负极接车架），并分别在电池供电和采用受电弓通过电网供电两种模式下重复该实验，共模EMI干扰对比见表3。可见，采用普通SVPWM算法，逆变器工作时产生的高频EMI可在壳体上感应出高压电，如电气隔离处理不当可能会造成人身安全问题，而TSPWM可以将干扰产生的感应电压降到安全电压以下，有效地抑制了PWM开关产生的共模EMI干扰。
表3 共模EMI干扰对比
Tab.3 Comparison of common mode EMI（单位: V）
供电类型干扰产生的电压 SVPWMTSPWM 电池供电1969～26 受电弓供电28011～36
图13a为原始TSPWM算法的A相PWM波形和A相电流波形。从图中可以看出，电流最大峰值点不在A相钳位区段的中心时刻，使得部分开关动作出现在相电流很大甚至最大的时刻。经过改进后，从图13b可以看出，相电流峰值和钳位区段中心时刻对齐，电流最大的区段只有导通损耗，没有开关损耗，开关动作都发生在电流相对较小的时段内，这样开关损耗就得到了进一步地降低。
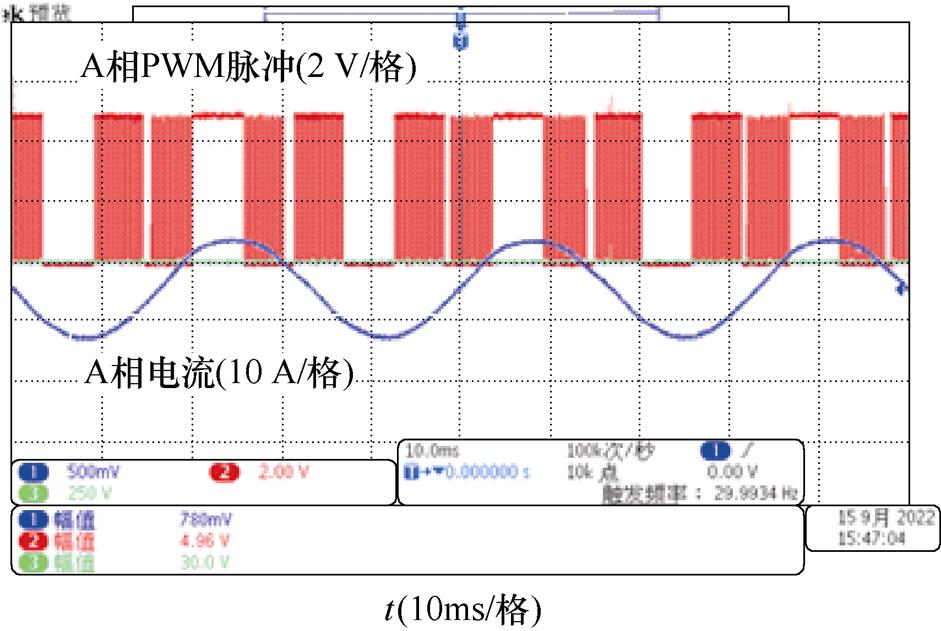
（a）原始TSPWM
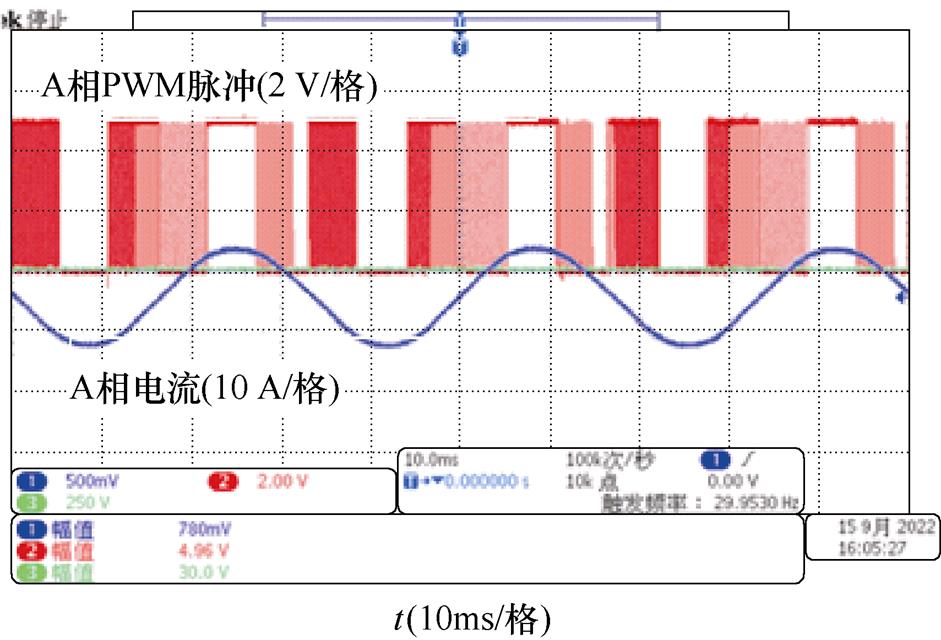
（b）最大电流相钳位后的TSPWM
图13 TSPWM算法的PWM波形和电流波形
Fig.13 PWM waveforms and current waveforms of TSPWM
为了定量验证最大电流相钳位措施的效果，对逆变器效率进行了对比测试。在相同转速（1 000 r/min）、相同开关频率（8 kHz）下，改变转矩以便改变功率因数，测量改进前后的逆变器效率见表4。最大电流相钳位后的TSPWM得到的逆变器效率高于原始TSPWM，验证了最大电流相钳位措施对逆变器开关损耗的抑制效果。故后续实验中均默认使用改进后的TSPWM。
表4 逆变器效率对比
Tab.4 Inverter efficiency comparison
电机转矩/(N·m)效率(%) 原始TSPWM最大电流相钳位TSPWM 4.763.1967.06 9.571.6274.10 14.573.0575.20
以下实测本文相位补偿算法在载频切换中的效果。图14为在电机加速过程中，当电机在1 000 r/min载频切换时刻的相电流波形。为了使对比更明显，将开关频率从2 kHz切换到10 kHz。图14a为未采用角度补偿的电流波形，从图中可以看出，电流有明显的振荡过程。同时，从数据采集系统检测到9%左右的转矩波动。图14b为角度补偿之后的电流切换波形，从图中可以看到，在开关频率切换瞬间没有出现电流冲击的现象。同时，系统采集到的转矩波动小于2%。此外，还完成了开关频率从高频到低频的切换、SVPWM和TSPWM算法之间的切换等，均可以实现平滑过渡。实验表明，本文提出基于数字化控制周期角度补偿的载波比切换策略，可以实现不同开关频率或PWM模式间的平滑切换。
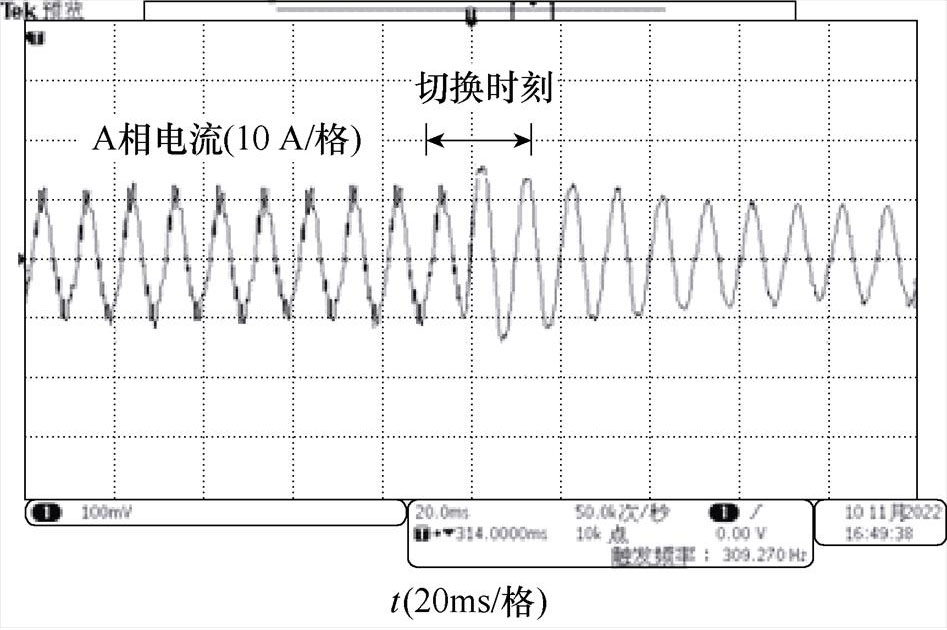
（a）无角度补偿
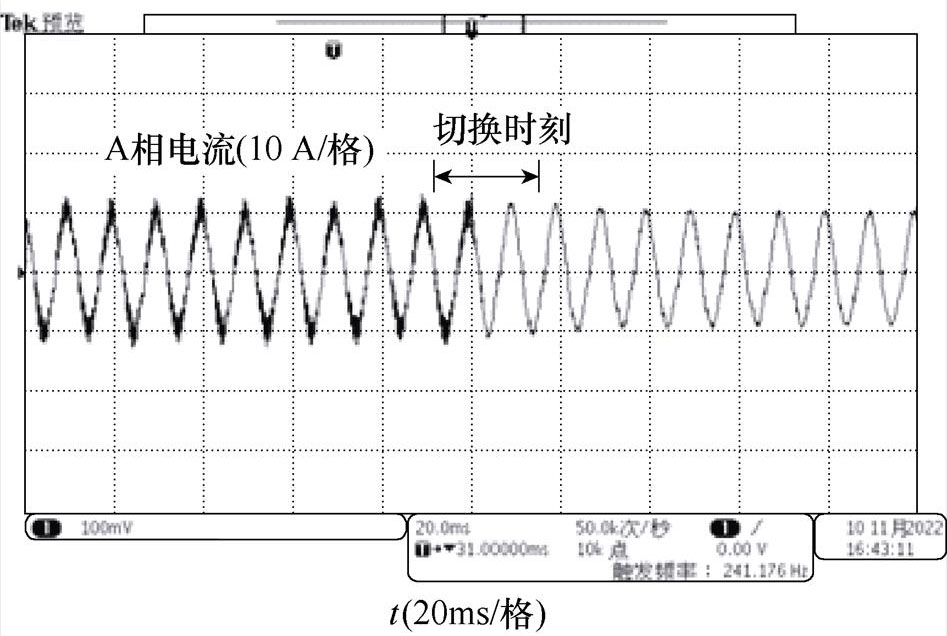
（b）有角度补偿
图14 载频从2 kHz切换至10 kHz时的电流波形
Fig.14 Current waveforms of carrier frequency 2 kHz switching to 10 kHz
为了系统、全面地测试本文基于TSPWM的多模式调制算法的效果，特别是与不采用多模式调制的普通SVPWM进行不同转速转矩下的效率对比，在测功机台架上进行完整测试。本次实验转速范围为0～4 800 r/min，转矩范围为0～20 N·m。
为避免区间段划分过于细致频繁而增加切换过程，实验中分段调制的相邻区间段开关频率差设定为1 kHz。本文采用的多模式调制策略所用开关频率为1～10 kHz。在每个速度段，按第2节的原则在电流波形质量和效率之间权衡选择优化载波比，在电流波形质量不大幅下降的前提下尽量选择效率高的开关频率。
传统SVPWM算法下的逆变器效率云图如图15所示，开关频率固定为10 kHz。使用变载频SVPWM策略的逆变器效率云图如图16所示。使用本文多模式TSPWM策略的逆变器效率云图如图17所示。
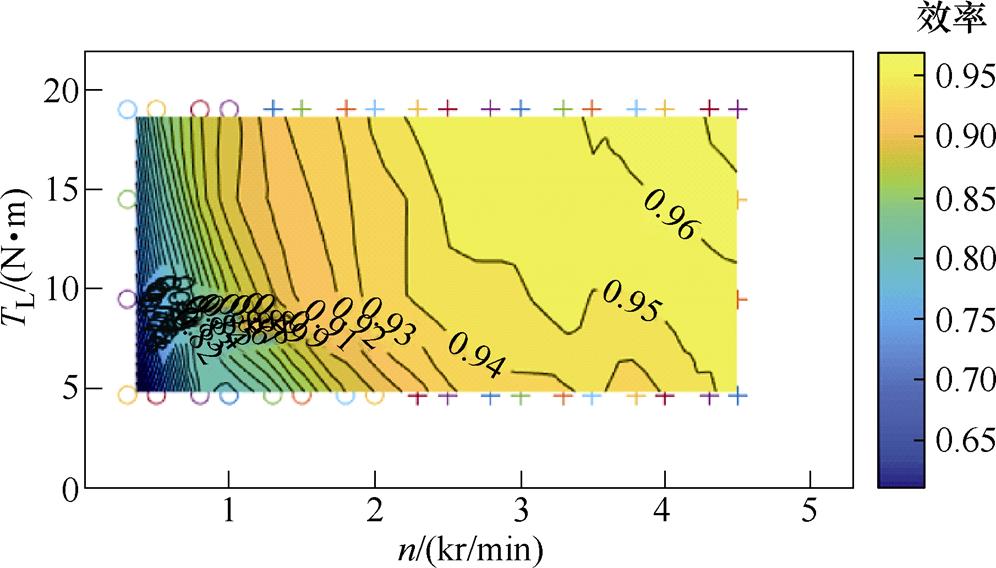
图15 传统定载频SVPWM的逆变器效率云图
Fig.15 Efficiency map of traditional SVPWM inverter
相比传统SVPWM，多模式TSPWM的逆变器最高效率约提升1%；全范围逆变器效率平均可增加5%。
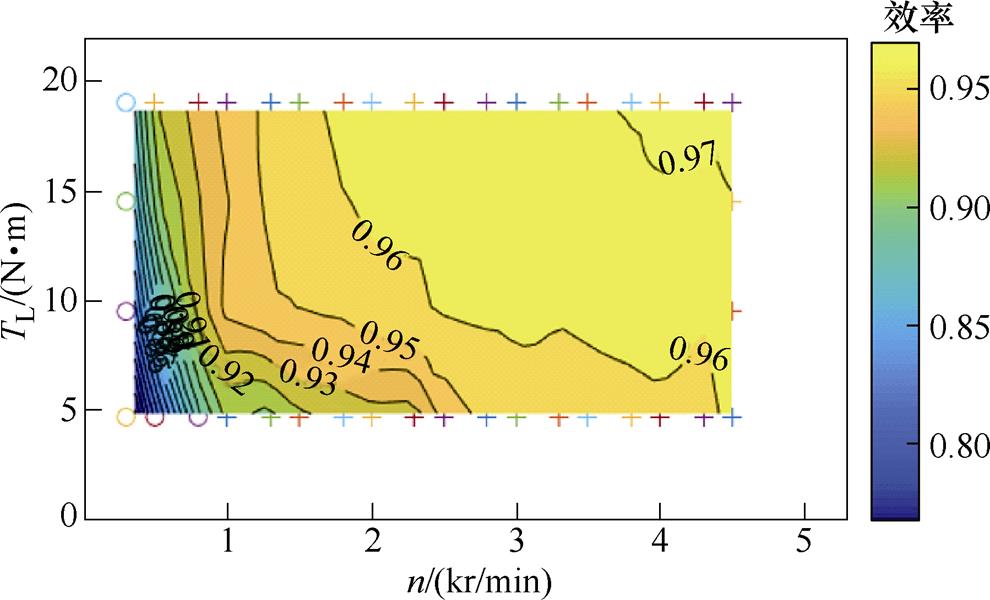
图16 变载频SVPWM逆变器效率云图
Fig.16 Inverter efficiency map of multi-mode strategy based on SVPWM
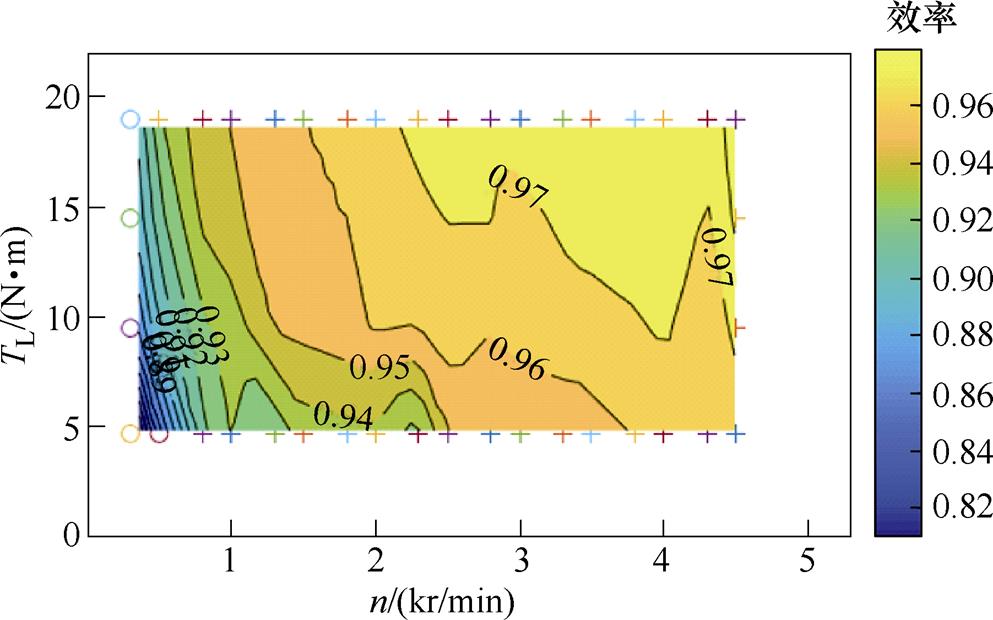
图17 基于TSPWM的多模式策略的逆变器效率云图
Fig.17 Inverter efficiency map of multi-mode strategy based on TSPWM
定义逆变器效率95%及以上的区域为高效区。可以计算得到，定载频SVPWM策略控制得到的高效区面积约占整体区域的33%；变载频SVPWM的高效区面积比为68.3%；而本文基于TSPWM的多模式策略控制得到的高效区面积比为73.1%。
实验表明，由于开关损耗在逆变器损耗中占有较大的比重，通过优化开关频率、减少开关次数来提高逆变器效率具有显著的效果；而在同等条件下，基于TSPWM的调制算法又比基于SVPWM的算法进一步提高了逆变器效率。
为了减少电动汽车电机控制器中高频PWM产生的开关损耗和高频共模电压，本文提出了一种基于TSPWM算法的多模式调制策略。针对车用驱动系统开关频率相对较高的特点，综合考虑效率和波形质量，优化分段异步调制的开关频率选择；引入并改进TSPWM，根据电流幅值选择钳位模式；提出一种基于载波周期角度计算的电压矢量相位补偿算法，对载频变化时空间电压矢量相位的跳变进行准确的补偿。
仿真和实验验证了本文所提出基于TSPWM的多模式PWM策略的有效性：从减少开关次数和减小开关动作时的电流幅值这两个维度减少开关损耗，能显著改善逆变器效率并可抑制高频共模电压；不同模式间实现了平滑切换、无冲击。本文算法不仅适用于电动汽车电驱动系统中，还可以推广到家电、并网等其他应用领域。
参考文献
[1] 陈杰, 沈禹廷, 沈佳茜, 等. 三相VIENNA整流器的混合空间矢量脉宽调制策略[J]. 电工技术学报, 2021, 36(增刊2): 665-675.
Chen Jie, Shen Yuting, Shen Jiaqian, et al. Hybrid space vector pulse width modulation strategy for three-phase VIENNA rectifier[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 665-675.
[2] 肖蕙蕙, 魏苏东, 郭强, 等. 优化开关序列的PWM整流器模型预测控制策略[J]. 电工技术学报, 2022, 37(14): 3665-3675, 3700.
Xiao Huihui, Wei Sudong, Guo Qiang, et al. Model predictive control strategy for PWM rectifier with optimized switching sequence[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3665- 3675, 3700.
[3] 吕照瑞, 胡文彪. 电力有源滤波器的共模电压抑制方法研究[J]. 电气技术, 2015, 16(3): 30-33.
Lü Zhaorui, Hu Wenbiao. Common-voltage reduction research for APF[J]. Electrical Engineering, 2015, 16(3): 30-33.
[4] Guo Leilei, Zhang Xing, Yang Shuying, et al. A model predictive control-based common-mode voltage suppression strategy for voltage-source inverter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6115-6125.
[5] 郭磊磊, 金楠, 李琰琰, 等. 电压源逆变器虚拟矢量模型预测共模电压抑制方法[J]. 电工技术学报, 2020, 35(4): 839-849.
Guo Leilei, Jin Nan, Li Yanyan, et al. Virtual vector based model predictive common-mode voltage redu- ction method for voltage source inverters[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 839-849.
[6] 夏帅, 郑京港, 陈瑞成, 等. 低共模电压双三电平变换器中点电位主动控制调制策略[J]. 电工技术学报, 2022, 37(24): 6388-6398.
Xia Shuai, Zheng Jinggang, Chen Ruicheng, et al. Low common mode voltage strategy with active neutral point voltage control of dual three level converters[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6388-6398.
[7] Lu Haifeng, Cheng Xiaomeng, Qu Wenlong, et al. A three-phase current reconstruction technique using single DC current sensor based on TSPWM[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1542-1550.
[8] 倪荣来, 李军伟, 陆海峰, 等. 基于TSPWM的车用交流感应电机控制器设计[J]. 微特电机, 2016, 44(10): 64-69.
Ni Ronglai, Li Junwei, Lu Haifeng, et al. Design of AC induction motor controller for vehicle based on TSPWM[J]. Small & Special Electrical Machines, 2016, 44(10): 64-69.
[9] 倪荣来. 基于TSPWM的车用感应电机控制系统开发[D]. 淄博: 山东理工大学, 2017.
[10] 谷杨心. 基于DSP的逆变器分段同步调制算法的研究[J]. 电测与仪表, 2010, 47(6): 73-76.
Gu Yangxin. Sub-synchrony modulation method study of inverter based on DSP[J]. Electrical Measurement & Instrumentation, 2010, 47(6): 73-76.
[11] Xiao Lifan, Li Jian, Chen Junhua, et al. Synchronous SVPWM for field-oriented control of PMSM using phase-lock loop[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 4324-4331.
[12] 张文涛. 低开关频率下的矢量控制系统SVPWM同步调制策略[D]. 西安: 西安理工大学, 2019.
[13] 韩坤, 宋玉明, 余彬, 等. 牵引逆变器多模式分段同步调制算法FPGA程序设计与实现[J]. 电工技术学报, 2019, 34(20): 4314-4322.
Han Kun, Song Yuming, Yu Bin, et al. Traction inverter multi-section synchronous SVPWM strategy FPGA program design and implementation[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(20): 4314-4322.
[14] 康雪峰. 基于SHEPWM的交流调速系统多模式脉宽调制方法研究[D]. 大连: 大连交通大学, 2020.
[15] Jing Tao, Maklakov A, Radionov A, et al. Research on hybrid SHEPWM based on different switching patterns[J]. International Journal of Power Electronics and Drive Systems (IJPEDS), 2019, 10(4): 1875.
[16] 董志强, 王琛琛, 周明磊, 等. 基于SHEPWM的三电平三相逆变器中点电位主动平衡控制策略[J/OL]. 电工技术学报, 2023: 1-10. https://doi.org/10.19595/ j.cnki.1000-6753.tces.222093.
Dong Zhiqiang, Wang Chenchen, Zhou Minglei, et al. Active NP voltage balance control strategy for three- level three phase inverter under SHEPWM[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-10. https://doi.org/10.19595/j.cnki.1000-6753.tces. 222093.
[17] 段宇航. 低开关频率下永磁同步电机驱动系统控制技术研究[D]. 大连: 大连理工大学, 2021.
[18] 王堃, 游小杰, 王琛琛, 等. 低开关频率下SHEPWM和SVPWM同步调制策略比较研究[J]. 电工技术学报, 2015, 30(14): 333-341.
Wang Kun, You Xiaojie, Wang Chenchen, et al. Research on the comparison of synchronized modu- lation of SHEPWM and SVPWM under low switching frequency[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 333-341.
[19] 苑国锋, 陈栋, 郑春雨. 电力机车牵引传动系统的多模式调制策略及切换方法研究[J]. 电机与控制学报, 2021, 25(1): 126-135.
Yuan Guofeng, Chen Dong, Zheng Chunyu. Multi- mode modulation strategy and switching method of electric locomotive traction drive system[J]. Electric Machines and Control, 2021, 25(1): 126-135.
[20] Zhang Hang, Liu Weiguo, Chen Zhe, et al. Smooth transition of multimode synchronous modulation for IPMSM sensorless drives in rail-transit appli- cations[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(1): 128-138.
[21] Li Guibin, Zheng Zedong, Li Yongdong, et al. Multi- mode SHEPWM with low switch frequency for traction application[C]//2017 19th European Con- ference on Power Electronics and Applications (EPE'17 ECCE Europe), Warsaw, Poland, 2017: 1-8.
[22] 余彬, 宋文胜, 赵雷廷, 等. 基于SHEPWM的多模式调制切换算法[J]. 西南交通大学学报, 2020, 55(2): 450-458.
Yu Bin, Song Wensheng, Zhao Leiting, et al. Switching scheme of multi-mode modulation based on selected harmonic elimination pulse width modu- lation[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 450-458.
[23] 苑国锋, 沈阳. 基于开关时刻修正的多模式调制切换策略[J]. 电工技术学报, 2022, 37(5): 1171-1180.
Yuan Guofeng, Shen Yang. Multi-mode modulation switching strategy based on switch time correction[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1171-1180.
[24] 胡亮, 付翔宇, 吕永灿, 等. 一种SiC牵引逆变器高频-低频混合型多模式PWM调制方法[J]. 控制与信息技术, 2022(3): 39-45.
Hu Liang, Fu Xiangyu, Lü Yongcan, et al. A frequency hybrid multi-mode PWM modulation method for SiC traction inverter[J]. Control and Information Technology, 2022(3): 39-45.
[25] Lu Haifeng, Qu Wenlong, Cheng Xiaomeng, et al. A novel PWM technique with two-phase modulation[J]. IEEE Transactions on Power Electronics, 2007, 22(6): 2403-2409.
[26] Cheng Xiaomeng, Qu Wenlong, Lu Haifeng, et al. An improved two-phase PWM strategy for inverters in electric vehicle[C]//2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 2008: 1-5.
[27] 张兴, 汪天呈, 王付胜, 等. 一种具有共模电压抑制能力的改进型调制策略[J]. 电力电子技术, 2015, 49(8): 89-92.
Zhang Xing, Wang Tiancheng, Wang Fusheng, et al. An improved reduced common-mode voltage pulse width modulation strategy[J]. Power Electronics, 2015, 49(8): 89-92.
Research on Multi-Mode Modulation Strategy of Motor Drive System Based on Tri-State PWM in EV
Abstract Two-level inverters are widely used in variable frequency motor drive systems of electric vehicles. High-frequency PWM modulation technology can generate high-frequency and high amplitude common mode voltage in the inverter, which will endanger the normal operation of the motor. Especially at low speeds, using traditional fixed switching frequency asynchronous modulation PWM will result in high switching losses with low output power and inverter efficiency. Therefore, a multi-mode modulation strategy is proposed based on TSPWM (Tri-State PWM). By improving the TSPWM modulation algorithm and adopting a segmented variable carrier wave ratio modulation strategy, the inverter efficiency of the motor drive system is significantly improved, and the common mode voltage is reduced.
Firstly, the TSPWM algorithm, which uses three switch states to synthesize the reference voltage in each PWM cycle, reduces the number of switching actions by one-third. Secondly, select the clamping phase according to the amplitude of the current, increase the overlap time between the maximum current and the inactivity of the switching device, and reduce the switching loss of the inverter. Thirdly, considering the system efficiency and current waveform quality, the carrier frequency is optimized at different speed ranges. Moreover, based on the calculation of carrier period angle, a phase angle compensation algorithm of the voltage vector is proposed to avoid the current shock when the modulation mode is switched. By accurately analyzing the impact of changing the modulation mode on the voltage vector angle, the compensation angle after switching is calculated and compensated to the reference space voltage angle, thus achieving smooth switching of different modes.
The experimental results show that the common-mode voltage of TSPWM in a PWM period is one-third of that of SVPWM, whether the voltage vector is in a high or low modulation ratio region. Using the maximum current phase clamping technique, the clamping phase is precisely the phase with the maximum phase current, and the vertex position of the current amplitude is in the middle of the clamping region. The simulation results show that the angle compensation algorithm of the voltage vector can achieve a smooth transition of the angle of the voltage vector during the carrier frequency switching process. Through the experimental results of the multi-mode modulation strategy based on TSPWM at different switching frequencies, the current waveform oscillation without angle compensation is significant, and about 9% of torque ripple is detected during the modulation mode switching. The current waveform using angle compensation has no impact on the switching process, and the torque fluctuation collected by the system is less than 2%, which verifies the feasibility of the switching strategy based on angle compensation.
Compared with the traditional SVPWM algorithm, the proposed multi-mode modulation algorithm based on TSPWM can increase the maximum efficiency of the inverter by about 10%, and the overall efficiency of the inverter can be improved by an average of 5%. The high-efficiency area, where the inverter efficiency is 95% or more, has increased by 40.1%.
The following conclusions can be drawn through simulation and experiments. (1) Compared with the traditional SVPWM strategy, this paper optimizes the switching frequency at different speeds and adopts TSPWM to reduce the number of switching actions, significantly reducing the switching loss and improving the efficiency of the inverter. (2) The switching loss can be further reduced by dynamically changing the clamping mode according to the magnitude of the phase current. (3) The angle compensation algorithm of the voltage vector effectively overcomes the voltage phase hopping problem in the PWM modulation mode switching to realize the smooth transition. (4) The proposed algorithm can also reduce the peak-to-peak value of high-frequency common mode voltage in one PWM cycle. Therefore, it is suitable for small and medium-sized inverters with a 100 kW or less power output, represented by electric vehicle drive systems.
keywords：Tri-state PWM (TSPWM), multi-mode modulation, piecewise variable carrier wave ratio modulation, common mode voltage, motor drive, electric vehicle
中图分类号：TM921
清华大学－潍柴动力智能制造联合研究院资助项目（JIIM04, 2021）。
收稿日期 2022-12-05
改稿日期 2023-02-22
DOI: 10.19595/j.cnki.1000-6753.tces.222255
夏 衍 男，1997年生，硕士研究生，研究方向为汽车电子。E-mail: xy95216@163.com
陆海峰 男，1976年生，副教授，硕士生导师，研究方向为新能源与电动汽车电驱动技术、高性能电机控制、电力电子变换器新型调制技术、宽禁带器件应用等。E-mail: luhaifeng@mail.tsinghua.edu.cn（通信作者）
（编辑 崔文静）