图1 试验现场布置
Fig.1 Test site layout
摘要 2018—2019年夏季在广州从化开展了火箭引雷试验，雷击对象分为两种，分别是架空线路和地面。对比了两种引雷情况下各阶段雷电流的电流波形参数的差异，发现引雷至地面情况下初始阶段的最大电流、平均电流、转移电荷、作用积分分别是引雷至架空线路情况下的2.8、2.4、2.0、5.3倍。引雷至地面情况下回击的上升时间几何均值为0.25 µs，小于引雷至线路情况下的0.60 µs，而对于电流峰值等其他回击波形参数而言，差异不明显。M分量与初始连续电流脉冲类似，引雷至线路情况下的电流峰值、转移电荷、连续电流水平均小于引雷至地面情况下的。基于诺顿电流源等效电路模型分析两种引雷情况下雷电流不同阶段存在差异的原因，可能是雷电在不同电流阶段时其通道等效阻抗不一样所导致的。
关键词：火箭引雷 架空线路 雷电流 回击
雷电灾害是影响电力系统安全稳定运行的重要因素，获取真实的雷电参数对电力系统雷电防护具有重要意义[1-4]。火箭引雷技术可以在特定的时间和地点进行引雷，并且能够把雷电引向指定的被击对象，很好地解决了自然闪电随机性强、难观测的问题[5]。相关学者研究了火箭引雷和自然闪电的相似性，证明火箭引雷回击可以用来模拟自然闪电的继后回击[6-8]。目前积累的火箭引雷雷电观测数据绝大部分来自直击地面的闪电，关于雷击架空线路的观测资料还比较少。
雷电流是雷电研究的重要参数，对雷电防护研究非常有益。例如，它可以用来估算先导携带的电荷量。测量雷电流的主要方法有通过带测量仪器的高塔、人工引雷、闪电定位系统估算和磁场反演等[9-11]。一次人工触发闪电的电流波形主要可以分为初始阶段（Initial Stage, IS）、回击（Return Stroke, RS）和M分量三部分。人工触发闪电的初始阶段是自然下行地闪所不具备的，但研究人工触发闪电的初始阶段可以帮助理解从高大结构（如高塔、输电线路、山区架空线路）上始发的自然上行闪电。M. Miki等[12]比较了人工触发闪电初始阶段电流参数和高塔始发的自然上行闪电的相应参数，认为两者基本相似。Qie Xiushu等[13]于2014年报告了在中国山东测量的6次火箭引雷的初始阶段电流参数，而Zheng Dong等[14]于2017年报告了在中国广东测量的45次火箭引雷的初始阶段电流参数。初始阶段会叠加一些明显的脉冲，这些脉冲被称为初始连续电流脉冲（Initial Continuing Current Pulse, ICCP）。
回击是闪电电流波形中最受关注的部分，V. A. Rakov等[15]于1998年报道了不同接地电阻情况下的回击电流峰值。J. Schoene等[16]于2009年报道了1999—2004年在佛罗里达州Camp Blanding获得的回击电流数据。Zheng Dong等[14]于2017年报道了2008—2016年在广州从化测得的50个触发闪电的回击电流波形参数。
M分量是发生在回击之后叠加在连续电流之上的脉冲，首次由D. J. Malan进行研究并命名[17]。Zhang Yijun等[18]总结了2006—2016年在广州从化获取的M分量电流波形参数。Ma Zilong等[19]基于2005—2017年在山东滨州进行的火箭引雷试验，分析了109个M分量的电流波形参数。
相关研究已经表明被击物体的属性会影响雷电的参数，例如，当闪电击中数百米的高塔时，雷电流会在高塔的阻抗不连续处发生折反射，这会增强高塔内部的雷电流，增强的雷电流会辐射出更强的电磁场[20-23]。闪电直接击中地面与闪电直接击中架空线路两种情况下雷电流的泄流路径非常不同，获取真实的架空线路直击雷的雷电参数并分析它与地面直击雷雷电参数的异同，对电力系统雷电防护十分有益。本文将比较分析引雷至地面和引雷至架空线路两种情况下火箭引雷的初始阶段、回击及M分量的电流参数特征，并分析产生差异的原因。
2018—2019年夏季，武汉大学雷电防护与接地技术教育部工程研究中心与广东电科院、中国气象局合作，在广州野外雷电实验基地开展了国内首次引雷至架空线路的火箭引雷试验。
火箭引雷的基本过程如下：使用大气电场仪、气象雷达等设备，判断环境电场合适时，向雷暴云发射一枚小火箭，小火箭尾部连接着数百米长的金属导线。由于金属导线的快速上升，小火箭头部的电场会发生强烈畸变，从而在火箭头部诱发上行先导。当上行正先导发展至雷暴云内后，会诱使雷暴云沿着这条通道发生强烈的放电，类似于自然闪电的箭式先导-继后回击的放电过程。
雷击对象分为两种，一种是架空线路，另一种是地面。图1给出了试验现场的布置图。当引雷至地面时，雷电流由引流杆引入安装在地面发射架中的电流测量设备，经测量后直接流入土壤（接地电阻为6.7 Ω）。当引雷至架空线路时，雷电流首先由引流杆引入安装在塔发射架顶部的电流测量设备，测量后经一根导线流入10 kV架空线路，最后绝大部分的雷电流经最近的两基杆塔流入土壤。架空线路每级杆塔采用单根垂直接地体接地，杆塔接地电阻为25～110 Ω。架空线路总长为1 513 m，共包含22基杆塔，杆塔高度为10 m，间距为70 m。
图1 试验现场布置
Fig.1 Test site layout
电流测量设备为1 mΩ同轴分流器（Hilo公司ISM系列同轴分流器），3 dB带宽为DC～200 MHz，可测量雷电流的范围为-50～50 kA。电流信号由光纤传输采集系统（HBM公司ISOBE5600）传输至控制室内，由日本横河高速多通道数字示波器（DL850E）进行采样，采样率为设备上限50 MHz，采样时间为2 s。整个电流测量系统的带宽为20 MHz。2018—2019年共成功触发了60次闪电，其中34次雷击对象为地面，26次雷击对象为架空线路。总回击数为225次，其中引雷至地面的回击数为105次，引雷至架空线路的回击数为120次。
一次典型的触发闪电的电流波形如图2所示。
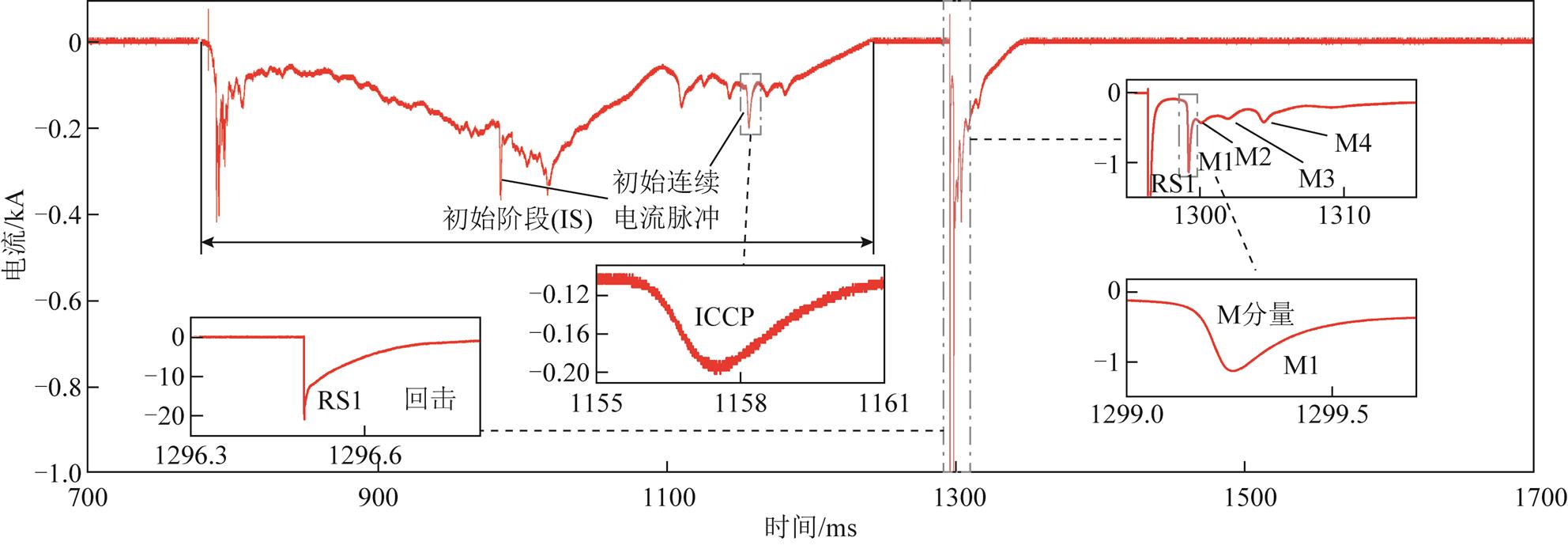
图2 一次典型触发闪电的电流波形
Fig.2 A typical triggered lightning current waveform
火箭引雷的电流波形主要由初始阶段电流（其中包含初始阶段电流脉冲ICCP）、回击阶段电流和回击之后叠加在连续电流之上的M分量组成。
可供定量分析的初始阶段电流波形样本为30个，其中15个为击中架空线路的情况，15个为击中地面的情况。为了定量分析初始阶段电流波形，定义了5个波形参数[14]，分别是最大电流Imax（kA）、平均电流Iave（A）、转移电荷Q（C）、作用积分AI（103 A2·s）、持续时间TD（ms）。转移电荷指的是电流的积分，而作用积分是指电流二次方的积分，定义式分别为
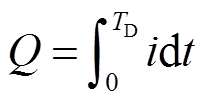（1）
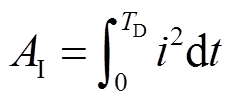（2）
平均电流的定义为转移电荷除以持续时间，表达式为
（3）
这30个初始阶段电流波形参数的分布如图3所示。采用箱线图来展示数据的分布，能够直观地显示数据的最大值、最小值、上四分位点、下四分位点及中位数。
如图3a所示，引雷至地面情况下，初始阶段的平均电流的算术均值和几何均值分别为198.0 A和133.9 A，引雷至架空线路情况下则分别为64.9 A和56.2 A。引雷至地面情况下初始阶段的平均电流约为引雷至架空线路情况下的2.4倍。
类似地，从图3b～图3d可以看出，引雷至地面情况下初始阶段的最大电流、转移电荷和作用积分同样远大于引雷至架空线路情况下。当引雷至地面时，几何均值分别为1.7 kA、29.5 C和8.0×103 A2·s。当引雷至线路时，几何均值分别为0.6 kA、15.0 C和1.5×103 A2·s。
而从图3e中可以发现，在两种引雷情况下，初始阶段的持续时间没有明显差异。引雷至地面时，初始阶段持续时间的算术均值和几何均值分别为275.7 ms和220.2 ms，引雷至架空线路时，初始阶段持续时间的算术均值和几何均值分别为300.7 ms和267.1 ms。
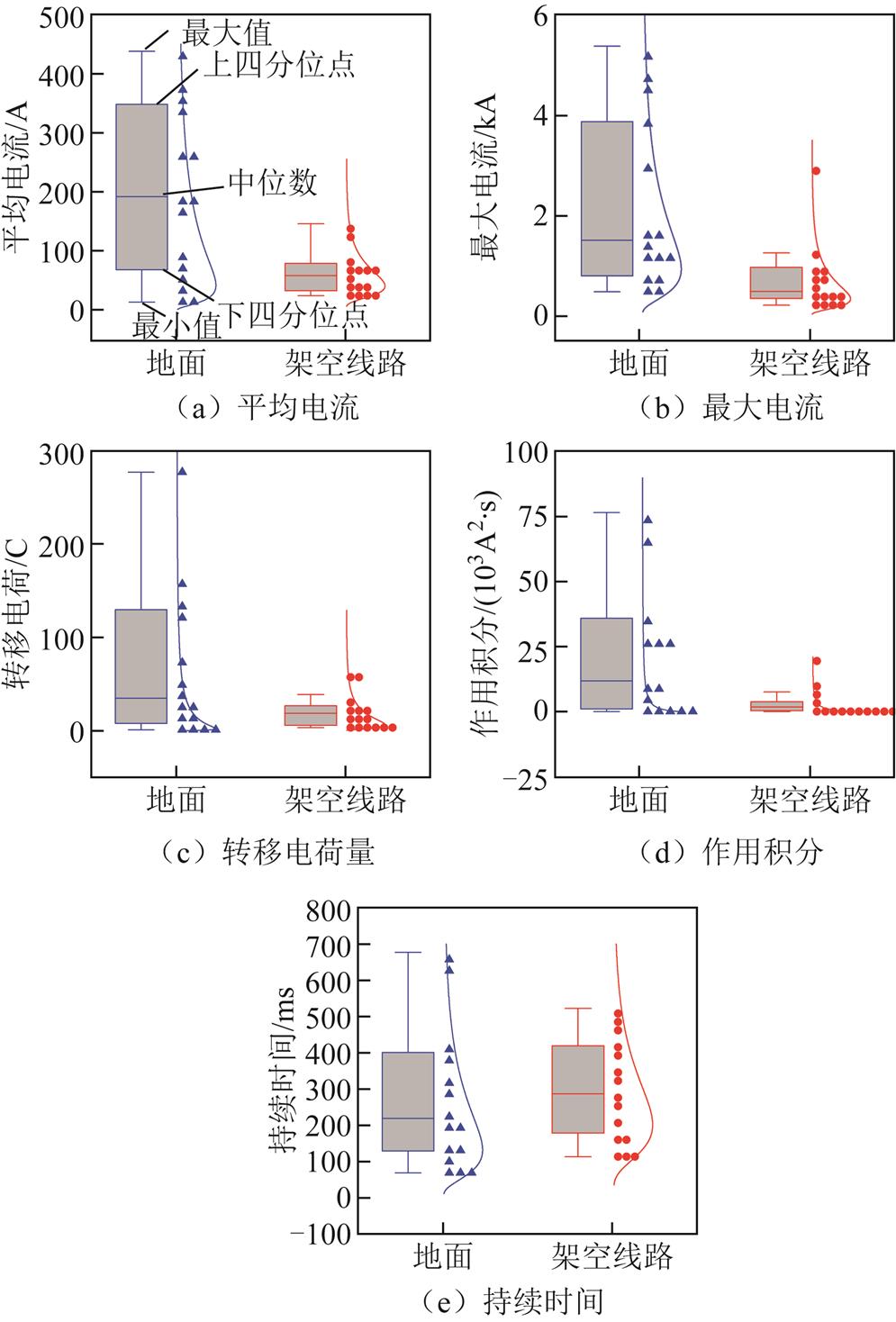
图3 初始阶段电流波形参数分布
Fig.3 Distribution of initial stage current waveform parameters
需要注意的是，Zheng Dong等[14]的试验地点与本文的试验地点相同，试验情况是引雷至地面，所得到的初始阶段的平均电流、最大电流、转移电荷、作用积分和持续时间的几何均值分别为132.5 A、1.3 kA、45.1 C、10.0×103 A2·s和347.9 ms，与本文中引雷至地面的结果相似，但与引雷至架空线路的结果有很大不同。这意味着架空线路的存在大大降低了初始阶段的最大电流、平均电流、转移电荷和作用积分，却并不影响初始阶段的持续时间。
本文可供定量分析的ICCP样本一共有52个，其中引雷至地面有31个，引雷至架空线路有21个。为了定量分析ICCP电流波形，参照Zhou Fangcong等[24]的参数定义，对6个波形参数进行了统计，分别是电流峰值IP（A）、10%～90%上升时间T10-90（µs）、半峰值宽度THPW（µs）、持续时间TD（µs）、转移电荷Q（C）和连续电流水平ICC（A）。其中，连续电流水平指ICCP发生时背景电流的大小。
两种引雷情况下ICCP波形参数的分布如图4所示。这里采用小提琴图来展示数据，以便于观察数据的密度分布。图4还给出了所有数据点的值以及数据的算术均值±1 SD（SD为标准差），为了方便对比，还将两种引雷情况数据的算术均值用虚线进行连接。
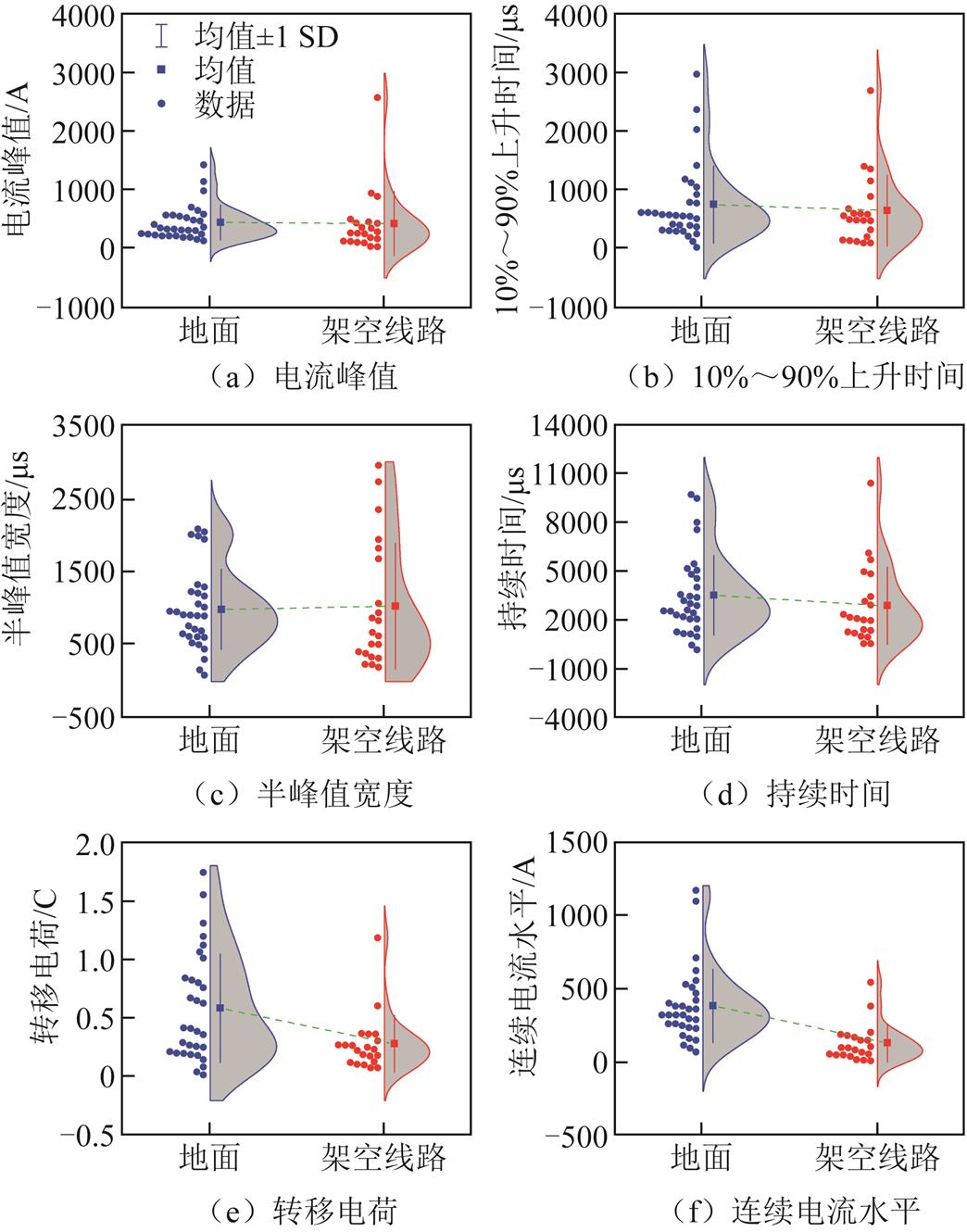
图4 初始连续电流脉冲波形参数分布
Fig.4 Distribution of initial continuing current pulse waveform parameters
引雷至地面情况下，ICCP电流峰值的算术均值和几何均值分别为444.1 A和373.6 A，引雷至架空线路工况下则分别为424.8 A和256.8 A。两种情况的算术均值很接近，几何均值有明显差别，这是因为引雷至架空线路情况下有一个样本的值为2 583.3 A，明显偏大。如果排除这个异常样本，对比几何均值，可以认为引雷至架空线路情况下ICCP的电流峰值要小于引雷至地面情况下的，约小31%。
从图4b～图4d来看，两种引雷情况下ICCP的10%～90%上升时间、半峰值宽度和持续时间的差别都较小。引雷至地面情况下，ICCP转移电荷的算术均值和几何均值分别为0.59 C和0.40 C，引雷至架空线路情况下分别为0.28 C和0.22 C，后者明显小于前者。这可能与引雷至架空线路情况下ICCP的电流峰值更小以及持续时间略微偏小有关。
引雷至地面情况下，ICCP的连续电流水平的算术均值和几何均值分别为380.2 A和315.0 A，引雷至架空线路情况下分别为126.8 A和78.8 A，后者明显小于前者。从图4f可以看出，引雷至地面情况下ICCP连续电流水平的值主要分布于250～500 A区间，而引雷至架空线路情况下则主要分布于0～250 A区间。造成这种差别的原因与上文分析的引雷至架空线路情况下初始阶段的平均电流明显低于引雷至地面情况下的有关，也就是说引雷至架空线路情况下ICCP发生时所处的背景电流水平更低。
回击是雷电最受关注的阶段，因为回击的上升时间很短，电流幅值很大，能够辐射出强烈的电磁场，容易对被击物体或近距离物体造成破坏性损害。本文可供定量分析的回击电流样本一共157个，其中击中地面的样本87个，击中架空线路的样本一共70个。为了定量分析回击电流波形特征，定义了7个波形参数，即电流峰值IP（kA）、10%～90%上升时间T10-90（µs）、半峰值宽度THPW（µs）、回击间隔时间TIN（ms）、1 ms内转移电荷Q1ms（C）、1 ms内作用积分AI-1ms（103 A2·s）。回击的1 ms内转移电荷和1 ms内作用积分的定义与初始阶段的转移电荷和作用积分定义相同，只是积分间隔是在回击开始时刻后的1 ms内。回击间隔时间是指两次相邻回击的时间间隔。这些参数的分布如图5所示。
引雷至地面情况下，回击电流峰值的算术均值和几何均值分别为14.6 kA和13.4 kA，而引雷至架空线路情况下则分别为18.0 kA和16.4 kA。看起来架空线路的存在增加了测得的回击电流峰值，但V. A. Rakov[20]比较了雷电击中不同高度物体时测得的雷电回击电流峰值发现，测量的回击电流峰值不会受到物体本身的影响。J. Schoene等[16]对全长628 m的架空线路开展了引雷实验，也得到了类似的结论，雷击架空线路的回击电流峰值和雷击地面的比较接近，几何均值分别为12.4 kA和11.1 kA。Zheng Dong等[14]的试验地点与本文相同，试验工况为引雷至地面，测得的回击电流峰值的算术均值和几何均值分别为17.7 kA和16.4 kA，与本文的引雷至架空线路情况下测得的回击电流峰值较一致。图5a显示两种引雷情况下回击电流峰值的分布模式是相似的，样本最大分布区间均为8～16 kA，均占30%以上。
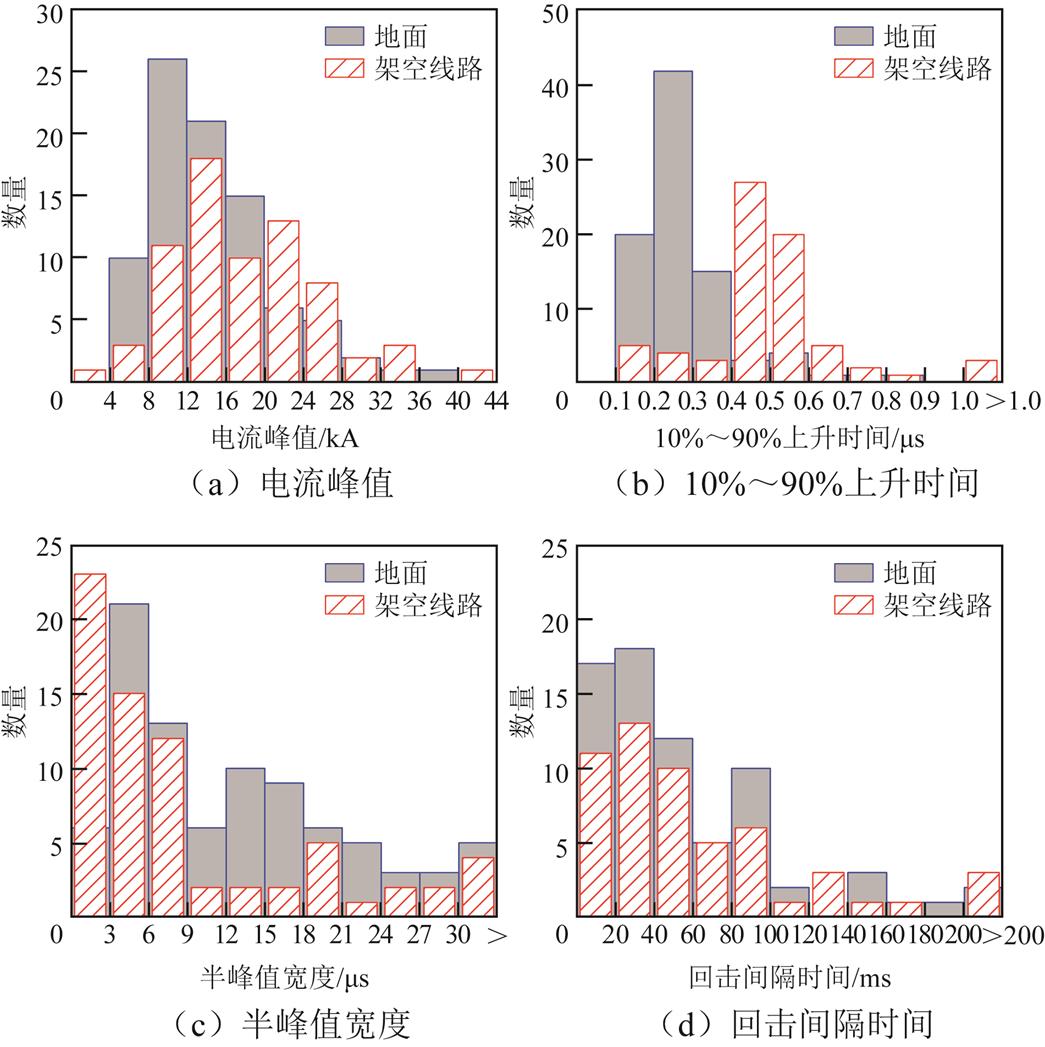
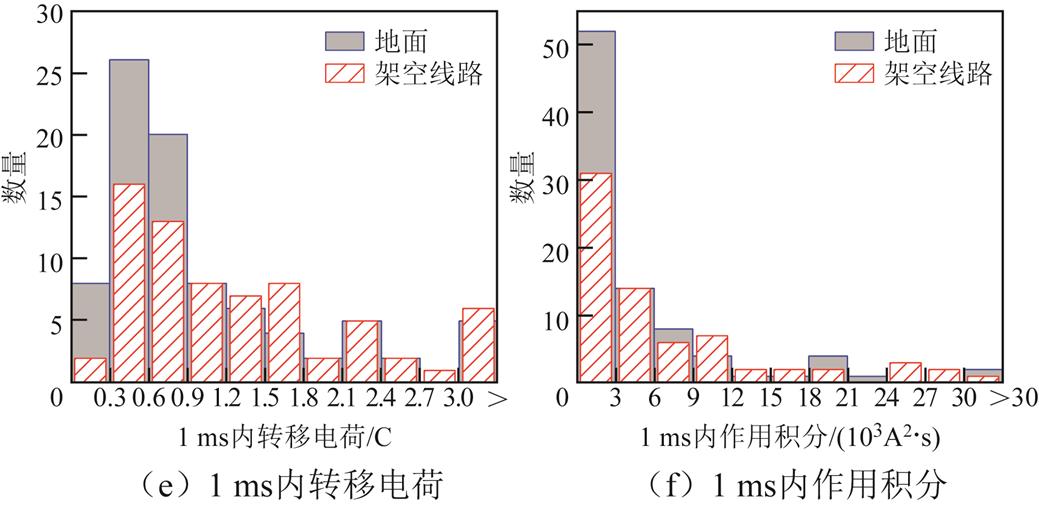
图5 回击电流波形参数分布
Fig.5 Distribution of return stroke current waveform parameters
当引雷至架空线路时，回击电流10%～90%上升时间的几何均值为0.6 μs，是引雷至地面情况（0.25 μs）的2.4倍。如图5b所示，对于引雷至地面的情况，大多数回击的10%～90%上升时间都分布在0.1～0.3 μs之内，占71%。对于引雷至架空线路的情况，占比最大的范围是0.4～0.6 μs，占68%。在J. Schoene等[16]的比较试验中，当引雷至地面时，回击电流10%～90%上升时间的几何均值为0.4 μs，引雷至架空线路时则为1.2 μs，同样表明架空线路的存在增加了回击电流的10%～90%上升时间。这种增加效应很可能是由于引雷至架空线路时雷电流遇到了较大的线路特征阻抗（数百欧姆）所造成的。
引雷至地面时，半峰值宽度的算术均值和几何均值分别为13.1 μs和9.9 μs；引雷至架空线路时，半峰值宽度的算术均值和几何均值为12.0 μs和6.8 μs。架空线路的存在似乎降低了回击电流的半宽时间，但这种差异不够明显，特别是从算术均值来看。图5c显示引雷至架空线路时半峰值宽度的最大分布区间为0～3 μs，占33%，引雷至地面时半峰值宽度最大分布区间为3～6 μs，占24%。
两种引雷情况下回击间隔时间没有明显差异。当引雷至架空线路时，回击间隔时间的几何均值为38.2 μs，引雷至地面时的几何均值为41.9 μs。回击间隔时间的最小值为2.4 ms，最大值达到499.9 ms，
本文的回击1 ms内转移电荷的几何均值在引雷至地面时为0.8 C，引雷至架空线路时为1.1 C，这与Qie Xiushu等[13]测得的0.86 C较为接近。在 J. Schoene等[16]的比较试验中，当引雷至地面时，回击电流的1 ms内转移电荷的几何均值为0.8 C，引雷至架空线路时则为1.1 C，与本文的测量结果接近。作用积分表征了雷电流的电阻能量，本文的回击1 ms内作用积分的几何均值在引雷至地面时为2.6×103 A2·s，引雷至架空线路时为3.5×103 A2·s。引雷至架空线路情况下1 ms内转移电荷和1 ms内作用积分的几何均值比引雷至地面情况下的略高，这是因为引雷至架空线路情况下回击的电流峰值略微更高造成的，有研究表明电流峰值越大的回击转移的电荷也越多[14]。
回击的下降沿有时会存在持续时间约为数十毫秒的连续电流，在连续电流上会叠加一些脉冲，这些脉冲的主要特点是上升时间长（约为几百微秒），幅值小（约为几百安培），波形近似对称，这种脉冲被称为M分量。本文可供定量分析的M分量电流波形样本为147个，其中引雷至地面的有44个，引雷至架空线路的有103个。针对M分量电流波形定义了6个波形参数，分别为电流峰值IP（A）、10%～90%上升时间T10-90（µs）、半峰值宽度THPW（µs）、持续时间TD（µs）、转移电荷Q（C）、连续电流水平ICC（A）。这些波形参数的定义方法与R. Thottappillil等[25]的定义方法一致。M分量电流波形参数的分布如图6所示。
如图6a所示，引雷至地面情况下，M分量电流峰值的算术均值和几何均值分别为952.9 A和553.1 A，引雷至架空线路情况下则分别为877.9 A和398.4 A。两种情况下电流峰值的算术均值很接近，几何均值有明显差别，是因为引雷至架空线路情况下有两个样本的值大于6 kA，明显偏大。如果排除这两个样本，对比几何均值，可以认为引雷至架空线路情况下M分量的电流峰值要小于引雷至地面情况下的，约小28%。
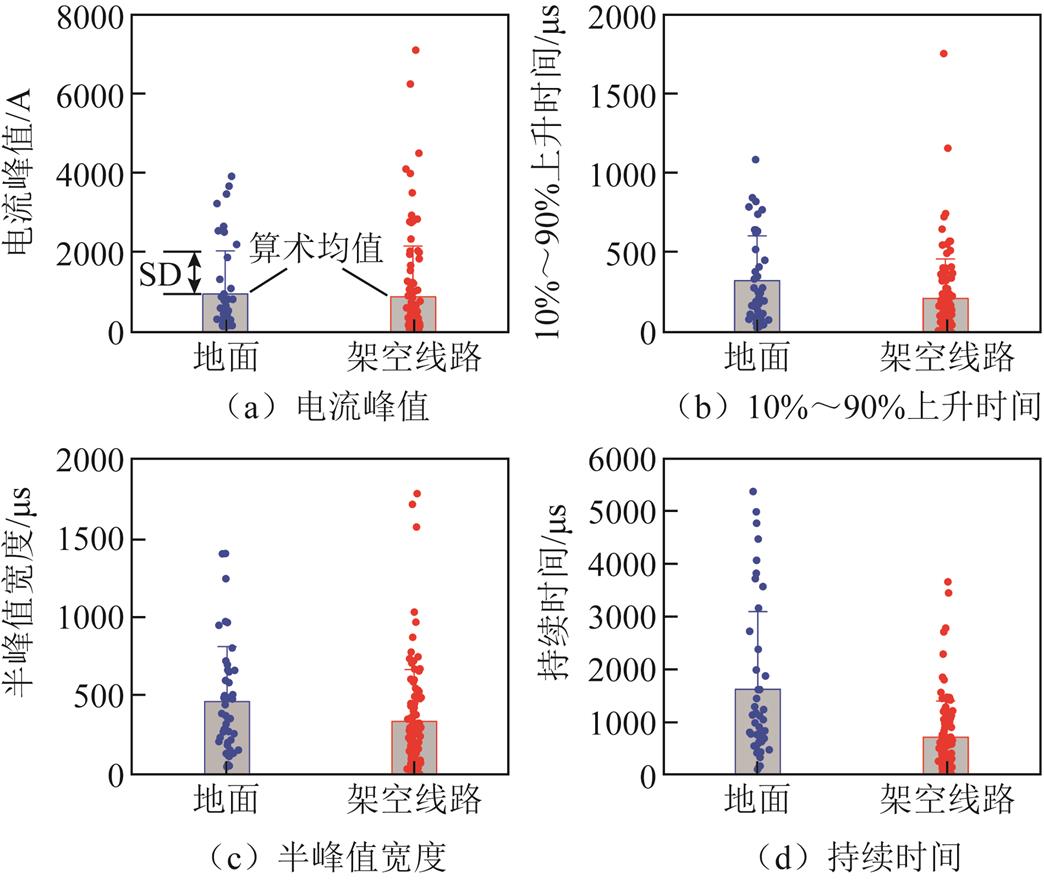
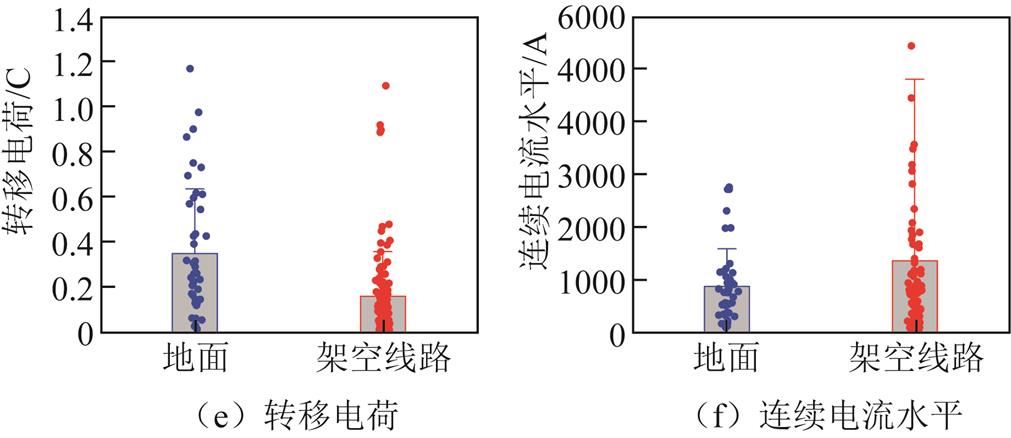
图6 M分量电流波形参数分布
Fig.6 Distribution of M-component current waveform parameters
两种引雷情况下M分量的10%～90%上升时间、半峰值宽度、持续时间的异同规律是一致的，都是引雷至架空线路情况下的偏小，分别见图6b～图6d。引雷至架空线路情况下，这三个参数明显分布得更紧密，更偏向0轴。这三个参数两种引雷情况下表现出一样的异同规律可能是因为M分量的电流波形是近乎对称的，这样更小的上升时间意味着M分量的下降时间也会更小，从而会有更小的脉冲宽度和持续时间。
如图6e所示，引雷至地面情况下，M分量转移电荷量的算术均值和几何均值分别为0.35 C和0.24 C，引雷至架空线路情况下则分别为0.16 C和0.08 C。引雷至架空线路情况下的转移电荷明显低于引雷至地面情况下的，根据转移电荷的定义，这样的结果是合理的。因为引雷至架空线路情况下M分量的电流峰值、10%～90%上升时间、半峰值宽度、持续时间均更小，所以转移的电荷会更少。注意到部分M分量的转移电荷很多，引雷至地面情况下最大值可达1.17 C，引雷至架空线路情况下最大值可达1.09 C。因此，部分M分量幅值大、上升时间小、转移电荷多，并且M分量的数量往往比回击的数量多，所以在雷电防护工作中，M分量也是一个需要考虑的因素。
图6f给出了M分量连续电流水平的条形图以及数据点的分布。引雷至地面情况下，M分量连续电流水平的算术均值和几何均值分别为895.6 A和674.0 A，引雷至架空线路情况下则分别为1 375.6 A和471.7 A。引雷至架空线路情况下算术均值远大于几何均值是由于存在3个远大于6 kA的数据样本值，明显偏大，并没有在图6f中展示。如果不考虑这3个值，引雷至架空线路情况下M分量所处的背景电流水平更低，这可能意味着架空线路的存在不仅会降低初始阶段的平均电流，同样降低了回击之后连续电流阶段的平均电流。
上述分析表明架空线路的存在极大地影响了雷电流的电流参数，且架空线路的存在对雷电流不同阶段的影响不同。本节基于图7所示的诺顿等效电路研究各种物体对雷电流参数的影响，该简化模型忽略了非线性过程[20]。
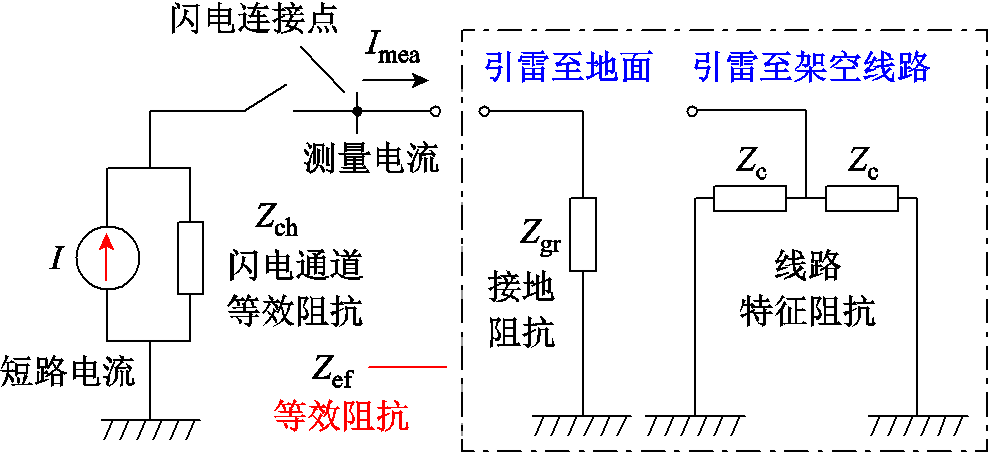
图7 闪电击中不同物体的诺顿等效电路
Fig.7 Norton equivalent circuit diagrams for lightning strikes on different objects
图7中所示的闪电连接点在闪电通道底部，也就是引流杆的顶部，本文测量电流的位置在引流杆的下方。当引雷至地面时，接地电阻（Zgr）为6.7 Ω；引雷至架空线路时，雷电流遇到的阻抗是架空线路的特征阻抗（Zc）。本文采用CIGRE技术手册549（2013）所提出的参数，即400 Ω。当引雷至架空线路时，大部分雷电流从最接近雷击点的两基杆塔流入地面，所以图7中的模型只包含两基杆塔，雷电流注入点为架空线路中点，因此在引雷至架空线路情况下，雷电流遇到的有效波阻抗约为200 Ω。两种工况下雷电不同阶段的Zch和Zef见表1。
表1 两种工况下雷电不同阶段的Zch和Zef
Tab.1 Zch and Zef at different stages of lightning under two conditions
雷电阶段闪电通道等效阻抗Zch/Ω等效阻抗Zef/Ω 地面架空线路地面架空线路 初始阶段≈145≈1456.7200 回击阶段＞2 000＞2 0006.7200 ICCP阶段≈445≈4456.7200 M分量阶段≈514≈5146.7200
Zch为闪电通道的等效阻抗，在本模型中假定它是恒定的。I为短路电流，也被称为“未受干扰”的电流，即当Zch=∞和Zgr=0时的电流。Imea为雷击点的实际测量电流，计算式为
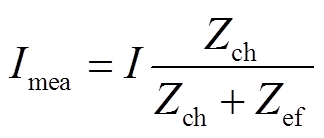（4）
对于初始阶段电流来说，架空线路的存在使初始阶段的最大电流、平均电流、转移电荷和作用积分分别降低至引雷至地面情况下的35%、42%、51%和19%。架空线路对初始阶段电流参数有很大影响。根据图7中的模型，只有当初始阶段的闪电通道等效阻抗小于线路特征阻抗（200 Ω）时，才会出现这种现象。根据平均电流的降低系数，初始阶段闪电通道等效阻抗的估算值为145 Ω（远大于6.7 Ω）。
对于初始连续电流脉冲来说，架空线路的存在使初始连续电流脉冲的电流峰值和转移电荷量分别降低至引雷到地面情况下的69%和55%。只有当初始连续电流脉冲的闪电通道等效阻抗与线路特征阻抗处于同一个数量级时，才会出现这种现象。根据初始连续电流脉冲电流峰值的降低量，初始连续电流脉冲的闪电通道等效阻抗的估算值为445 Ω。
对于回击电流，除了10%～90%上升时间增加为地面情况的2.4倍以外，架空线路的存在对回击电流峰值没有明显影响或者不会降低回击电流峰值。根据图7所示模型，只有当回击阶段的闪电通道等效阻抗都非常大时，才会出现这种现象，即对回击而言，Zch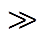
Zef，此时，可以把回击阶段的闪电通道视为一个理想的电流源，其闪电通道等效阻抗的准确值无法确定，但本文认为它至少为200 Ω的10倍以上。
对于M分量来说，架空线路的存在对电流的影响与初始连续电流脉冲类似，电流峰值和转移电荷量分别降低至引雷到地面情况下的72%和33%。根据电流峰值的降低量，M分量的闪电通道等效阻抗的估算值为514 Ω。
2018—2019年夏天在广州开展了引雷至架空线路与引雷至地面两类的火箭引雷试验，分析了两种情况下闪电各阶段的雷电流波形特征，主要结论如下：
1）引雷至地面情况下初始阶段的最大电流、平均电流、转移电荷、作用积分分别是引雷至架空线路情况下的2.8、2.4、2.0、5.3倍。两种引雷情况下初始阶段的持续时间没有明显差异。
2）两种引雷情况下回击电流波形上升时间存在明显差异，引雷至地面情况下几何均值为0.25 µs，引雷至架空线路情况下则为0.60 µs。两种引雷情况下回击的其他电流波形参数差异不明显。
3）引雷至架空线路情况下M分量与ICCP的电流峰值、转移电荷、连续电流水平均略小于引雷至地面情况下的。此外，M分量的上升时间、半峰值宽度、持续时间也小于引雷至地面情况下的，前者分别约为后者的56%、59%、40%。
4）人工引雷试验中，雷电在不同电流阶段其通道的等效阻抗存在显著差异，基于诺顿电流源等效电路模型推测等效阻抗初始阶段雷电通道约为100 Ω，在ICCP阶段约为400 Ω，在M分量阶段约为500 Ω，在回击阶段大于2 000 Ω。
参考文献
[1] Uman M A. The Art and Science of Lightning Protection[M]. Cambridge: Cambridge University Press, 2008.
[2] 王红斌, 程思, 范伟男, 等. 雷暴活动全闪电定位及空间演变过程分析[J]. 电工技术学报, 2021, 36(2): 373-379.
Wang Hongbin, Cheng Si, Fan Weinan, et al. Total lightning location of thunderstorm activities and spatial evolution process analysis[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 373-379.
[3] 张文锋, 李志伟, 张国建, 等. 山区35kV架空线路雷击特性仿真分析[J]. 电气技术, 2022, 23(9): 19-28.
Zhang Wenfeng, Li Zhiwei, Zhang Guojian, et al. Simulation analysis on lightning strike characteristics of 35kV overhead lines in mountainous area[J]. Electrical Engineering, 2022, 23(9): 19-28.
[4] 孟国栋, 折俊艺, 应琪, 等. 微米尺度气体击穿的数值模拟研究进展[J]. 电工技术学报, 2022, 37(15): 3857-3875.
Meng Guodong, She Junyi, Ying Qi, et al. Research progress on numerical simulation of gas breakdown at microscale[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3857-3875.
[5] 蔡力, 柯逸丰, 李进, 等. 基于高速摄像观测的风电场雷击风机发展过程和特性分析[J]. 电工技术学报, 2021, 36(增刊1): 303-310.
Cai Li, Ke Yifeng, Li Jin, et al. Development process and characteristic analysis of the natural lightning strike on wind turbine based on high-speed camera observation[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 303-310.
[6] Fieux R P, Gary C H, Hutzler B P, et al. Research on artificially triggered lightning in France[J]. IEEE Transactions on Power Apparatus and Systems, 1978, PAS-97(3): 725-733.
[7] Hubert P, Laroche P, Eybert-Berard A, et al. Triggered lightning in new Mexico[J]. Journal of Geophysical Research: Atmospheres, 1984, 89(D2): 2511-2521.
[8] Fisher R J, Schnetzer G H, Thottappillil R, et al. Parameters of triggered-lightning flashes in Florida and Alabama[J]. Journal of Geophysical Research: Atmospheres, 1993, 98(D12): 22887-22902.
[9] 刘亚坤, 戴明秋, 毕晓蕾, 等. 三种冲击电流连续作用下铝3003合金的损伤特性[J]. 电工技术学报, 2020, 35(6): 1173-1180.
Liu Yakun, Dai Mingqiu, Bi Xiaolei, et al. Damage characteristics of Al alloy 3003 suffered from three continuous impulse currents[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1173-1180.
[10] 周蜜, 丁文汉, 王建国, 等. 闪电连接高度对地面电场波形的影响[J]. 电工技术学报, 2021, 36(4): 857-868.
Zhou Mi, Ding Wenhan, Wang Jianguo, et al. Effect of lightning junction height on ground electric field waveform[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 857-868.
[11] 张亮, 何聪, 李军浩, 等. 振荡雷电冲击电压下气体绝缘组合电器中极不均匀场击穿特性研究[J]. 电工技术学报, 2020, 35(12): 2672-2680.
Zhang Liang, He Cong, Li Junhao, et al. Breakdown characteristics study of non-uniform field in gas insulated switchgear under oscillating lightning impulses[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2672-2680.
[12] Miki M. Initial stage in lightning initiated from tall objects and in rocket-triggered lightning[J]. Journal of Geophysical Research: Atmospheres, 2005, 110(D2): D02109.
[13] Qie Xiushu, Jiang Rubin, Yang Jing. Characteristics of current pulses in rocket-triggered lightning[J]. Atmospheric Research, 2014, 135/136: 322-329.
[14] Zheng Dong, Zhang Yijun, Zhang Yang, et al. Characteristics of the initial stage and return stroke currents of rocket-triggered lightning flashes in Southern China[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(12): 6431-6452.
[15] Rakov V A, Uman M A, Rambo K J, et al. New insights into lightning processes gained from triggered-lightning experiments in Florida and Alabama[J]. Journal of Geophysical Research: Atmospheres, 1998, 103(D12): 14117-14130.
[16] Schoene J, Uman M A, Rakov V A, et al. Characterization of return-stroke currents in rocket-triggered lightning[J]. Journal of Geophysical Research: Atmospheres, 2009, 114(D3): D03106.
[17] Malan D J, Schonland B F J. Progressive lightning. VII. Directly-correlated photographic and electrical studies of lightning from near thunderstorms[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1947, 191(1027): 485-503.
[18] Zhang Yijun, Lü Weitao, Chen Shaodong, et al. A review of advances in lightning observations during the past decade in Guangdong, China[J]. Journal of Meteorological Research, 2016, 30(5): 800-819.
[19] Ma Zilong, Jiang Rubin, Sun Zhuling, et al. Characteristics of impulsive currents superimposing on continuous/continuing current of rocket-triggered lightning[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(4): 1200-1208.
[20] Rakov V A. Transient response of a tall object to lightning[J]. IEEE Transactions on Electromagnetic Compatibility, 2001, 43(4): 654-661.
[21] Pavanello D, Rachidi F, Janischewskyj W, et al. On the current peak estimates provided by lightning detection networks for lightning return strokes to tall towers[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(3): 453-458.
[22] Rachidi F, Janischewskyj W, Hussein A M, et al. Current and electromagnetic field associated with lightning-return strokes to tall towers[J]. IEEE Transactions on Electromagnetic Compatibility, 2001, 43(3): 356-367.
[23] 陈怀飞, 王宇, 孙通, 等. 风机回击电磁场波形特征及辐射增强效应研究[J]. 高电压技术, 2020, 46(6): 2122-2130.
Chen Huaifei, Wang Yu, Sun Tong, et al. Study on waveform characteristics and radiation enhancement effect of lightning return stroke initiated from wind turbine[J]. High Voltage Engineering, 2020, 46(6): 2122-2130.
[24] Zhou Fangcong, Zhang Yijun, Lu Weitao, et al. Characteristics of initial continuous and continuing current processes in rocket-triggered lightning[C]// XV International Conference on Atmospheric Electricity, Norman, Oklahoma, USA, 2014: 1-12.
[25] Thottappillil R, Goldberg J D, Rakov V A, et al. Properties of M components from currents measured at triggered lightning channel base[J]. Journal of Geophysical Research: Atmospheres, 1995, 100(D12): 25711-25720.
Abstract Most of the current rocket-triggered lightning experiments are conducted with lightning strikes on the ground. Related studies have shown that the properties of the struck object affect the parameters of the lightning. The paths of the lightning flow are very different between direct lightning strikes on the ground and direct lightning strikes on overhead line. It is necessary to obtain the lightning parameters of a real overhead line direct strike and analyze the similarities and differences between them and the ground direct strike lightning parameters for power system lightning protection.
Rocket-triggered lightning experiments were conducted at the Guangzhou Field Experiment Site for Lightning Research and Testing in Conghua, Guangzhou, during the summer of 2018 and 2019. Lightning strikes objects are divided into two kinds, one is overhead line and the other is ground. When lightning strikes on the ground, the lightning current is introduced by the inducing rod to the current measuring equipment installed in the ground launcher, and flows directly into the soil after measurement (grounding resistance is 6.7 Ω). When the lightning strikes on overhead line, the lightning current is first introduced by the current measuring equipment installed in the top of the tower launcher, measured and then flows into the 10 kV overhead line via a wire, and finally the majority of the lightning current flows into the soil via the two nearest towers (the characteristic impedance of the overhead line is about 200 Ω). The current parameters characteristics of the initial stage, return strokes and M-components in the case of lightning to ground and lightning to overhead line are analyzed to compare whether they differ and to analyze the reasons for the differences.
The maximum current, average current, transfer charge, and action integral of the initial stage in the case of lightning to the ground are 2.8, 2.4, 2.0, and 5.3 times those of the lightning to the overhead line. There is no significant difference in the duration of the initial stage between two conditions. The geometric mean of the rise time of the return stroke when the lightning strikes the ground is 0.25 μs, which is much smaller than 0.60 μs when the lightning strikes the overhead line. For other waveform parameters of return strokes such as the current peak, the difference is not obvious. The M-components are similar to the initial continuing current pulses, and the current peak value, transfer charge, continuing current level in the case of lightning to the overhead line are all smaller than those of the lightning to the ground. The rise time, half-peak width, and duration of the M-components are also smaller than those of the lightning to the ground, with the former being about 0.56, 0.59, and 0.40 times the latter. Analysis based on Norton current source equivalent circuit model. The reason for the difference in lightning current between the two lightning conditions is that the equivalent impedance of the lightning channel is different in each stage.
keywords：Rocket triggered lightning, overhead line, lightning current, return stroke
中图分类号：TM863
DOI:10.19595/j.cnki.1000-6753.tces.222127
国家自然科学基金（52177154）和中央高校基本科研业务费专项资金（2042023kf0183）资助项目。
收稿日期 2022-11-11
改稿日期 2022-12-01
蔡 力 男，1987年生，教授，博士生导师，研究方向为雷电防护与接地技术，雷电物理与雷电探测。E-mail：cail@whu.edu.cn（通信作者）
杜懿阳 男，2000年生，硕士研究生，研究方向为雷电物理与雷电防护。E-mail：dyy0318@163.com
（编辑 李 冰）