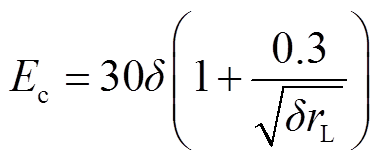 (1)
(1)
摘要 该文研究了大气条件下棒-板间隙中流注放电的产生与发展机理。首先,基于Raether判据和Meek判据,建立了在给定放电条件下流注的发展长度与由电子球表面电场表示的空间电场强度之间的关系,可用其判断流注放电的发展过程;然后,建立了流注放电的等离子体化学反应仿真模型,分析了流注放电发展过程中带电粒子、平均电子能量及电场强度的分布规律;最后,开展了大气条件下负直流棒-板放电实验,分析了流注型电晕放电的发展过程。研究表明,等离子体化学反应模型用于计算厘米级间隙的流注放电的可靠性较高,放电初期以氮气和氧气的电离反应为主,且只有主放电通道的电子崩在放电中期发展为流注,而放电后期负离子层变厚形成鞘层。实验结果表明,流注型电晕由流注和漫射辉光区域组成,且流注的形状、位置随加压时间发生变化,负离子层的积聚是漫射辉光区域形成的主要原因。该文所得结论可为明确负极性电晕放电中流注放电的产生与发展机制,以及等离子体的制备等提供理论依据。
关键词:流注型电晕 辉光放电 Raether判据 Meek判据 离子鞘 棒-板间隙
在直流输电工程中,由于架空线表面存在强电场,因此在导线周围的空气间隙内极易发生电晕放电。具有流注性质的电晕放电在局部产生大量带电粒子,进而畸变空间电场并加速空间电离反应,促进流注放电的发展。流注通道一旦形成,极易引起输电线路与周围空气发生闪络,不仅耗费大量电能,还威胁电力系统的安全运行[1]。厘米级空气间隙中的流注放电会产生大量的等离子体和自由基团,且放电产物具有优异的化学性能,故厘米级间隙的流注放电常用于点火助燃、废气处理及毒剂洗消[2-4]。因此,研究厘米级间隙电晕放电过程中流注的产生与发展机制,对提高直流输电系统运行可靠性以及等离子体的工业生产制备具有重要意义。
大气条件下流注放电的发展速度极快,气相反应复杂。由于缺乏更高精度的观测和测量系统,在实验中很难完整地记录流注放电过程并准确地测量流注放电参数[5],流注放电起始和发展的机理研究还未完善。极性效应使得负极性条件下的起晕电压低,流注更易产生。因此,研究大气条件下厘米级间隙的负极性流注放电的产生与发展机制能够丰富和发展气体放电理论。
计算机模拟技术、设备检测和观测技术的迅速发展为流注放电的实验与仿真研究提供了有力支撑。实验方面,利用超高速摄像机ICCD(intensified charge coupled device)可在宏观上研究流注放电的发展过程。例如,文献[6]观察到电晕放电中心由大量喷射状细丝组成;文献[7]拍摄了0.5 cm间隙中流注放电的放电形态;文献[8]分析了大气条件下一次流注与二次流注放电过程中自由基的产生数量,并实测了流注半径;文献[9]测量了不同压强下厘米级棒-板空气间隙的击穿电压,发现负直流条件下板电极表面的电荷积聚是极性效应反转的主要原因;文献[10]发现在8 cm的空气间隙下,湿度越大,流注发展所需的电场强度越大,气压越小,流注发展所需的电场强度越小;文献[11]研究表明,在1.6 cm空气间隙中氮氧比例能直接决定光电离的速率,且氧气含量越少,光电离效率越低,越容易产生分支;文献[12]对高压直流实验的回路设计进行了详细说明,有助于正确搭建实验平台。
借助于计算机模拟,可深入探究流注放电的微观机理。现有流注仿真模型主要包括动力学模型、流体力学模型和混合模型,其中流体力学模型因其较高的计算可靠性被广泛应用[13-14]。但流注放电的微观研究主要集中在毫米级间隙,鲜有对厘米级间隙下流注放电的仿真研究。同时,传统流体仿真模型[15]仅由三个连续性方程和一个泊松方程组成,其计算所用的放电参数是在毫米级间隙条件下得到的拟合结果,因此其用于厘米级间隙流注仿真计算的有效性尚待检验。
为提高计算模型的可靠性,本文对大气条件下厘米级棒-板间隙负极性电晕中流注的产生与发展机理进行研究。首先,分析流注的产生与发展机制,然后建立流注放电的等离子体化学反应仿真模型,并开展实验研究。本文通过求解玻耳兹曼方程得到电子能量分布函数,为减小计算量,给定电子迁移率。电子能量分布函数仅用于求解电离反应的反应速率,然后将计算结果代入流体方程求解流体模型。此外,基于Raether判据和Meek判据的理论基础,发展了在极不均匀场下流注的发展长度与电子崩头部的电场强度之间的关系,可用于检验仿真模型准确性和计算流注长度。
1.1.1 起晕场强
F. W. Peek[16]最早给出了大气压下25℃时导线起晕场强的计算式,如式(1)所示。但由式(1)计算的正电晕放电及球电极放电的起晕场强与实际测量值间的误差较大,故J. J. Lowke等[17]对其进行了修正,得出了式(2)所示球电极的起晕场强表达式。
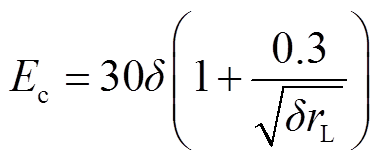 (1)
(1)
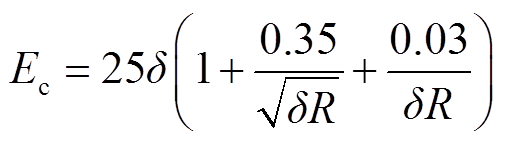 (2)
(2)
式中,Ec为起晕场强,kV/cm;δ为相对空气密度;rL和R分别为导线半径和球电极半径,cm。
虽然利用式(1)和式(2)确定厘米级间隙的起晕场强简单易行,但是其仅可用于分析放电起始阶段的起晕场强,尚不能对流注放电的产生及发展过程进行详细描述。
1.1.2 流注起始判据
随着棒-板间隙中电压的升高,电晕放电加剧,在靠近棒电极的电离区内产生大量空间电荷,倘若畸变的空间电场能够维持流注产生,则负电晕开始向负流注转变。目前广泛认可的流注起始判据有Raether判据、Meek判据和光电离判据[18-19]。其中Raether判据和Meek判据是基于均匀场下的流注放电起始判据,不适于本文棒-板电极下的流注放电起始判定;而光电离判据是基于流注形成过程建立的数学模型,理论性强,但其模型中的多个变量取值困难,不易对其进行定量求解。为此,本文流注放电的起始判据将根据流注仿真研究的经验,认为当电子密度达到1018 m-3时,流注起始。进一步,基于Raether判据和Meek判据中可利用空间电场强度与外施电场的比值关系判定流注起始的基本思想,发展了确定流注发展长度的方法。
当棒-板间隙之间的电压低于击穿电压时,流注的发展过程如图1所示,此时流注放电由流注茎、主流注通道、流注丝组成。
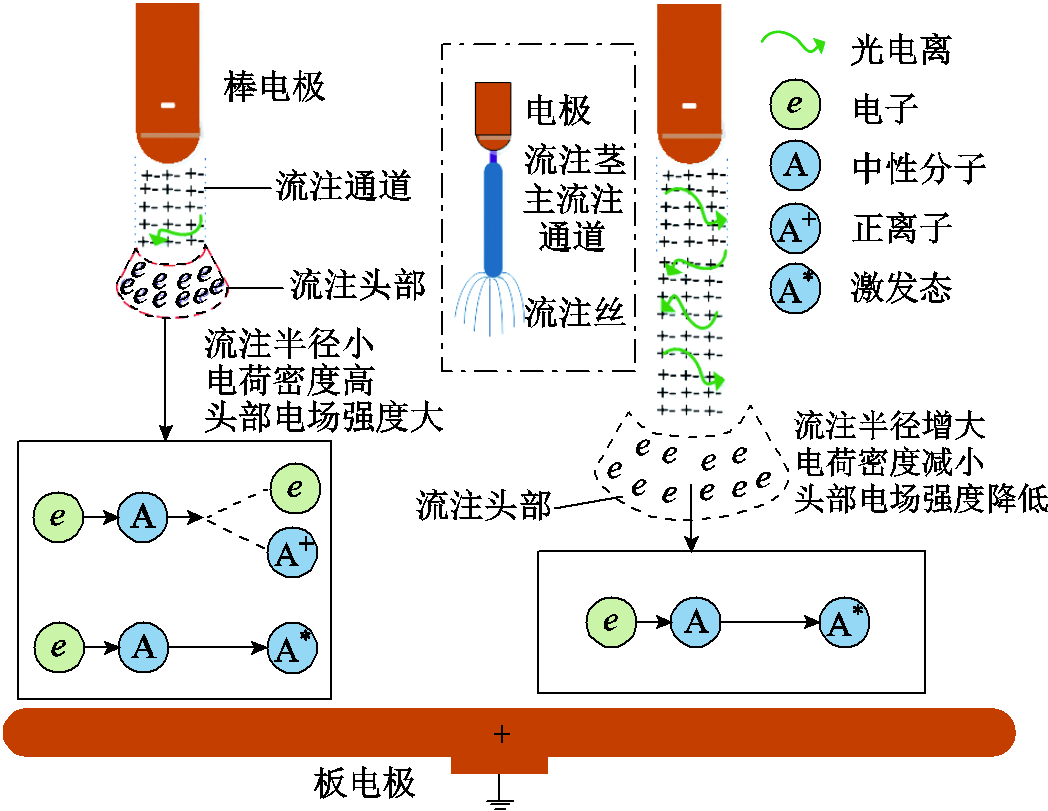
图1 流注放电示意图
Fig.1 Schematic diagram of streamer discharge
图1中,将流注茎与主流注通道的长度作为流注的长度。极不均匀电场下,电离系数α随流注发展的位置而发生变化,在靠近棒电极的周围,流注头部空间电荷数量多、电场强度高、电离和激发速率快,且流注的半径较小,因此光电离提供的种子电子容易在高电场强度作用下产生电子崩维持流注发展。当流注发展至远离棒电极时,由于电源电场本身的不对称性及电子发射角度的随机性,使得流注半径在发展过程中增大,流注头部空间电场强度降低,电离减弱,流注发展变得困难。
为探究流注的发展长度与空间电场强度两者间的关系,本文提出在极不均匀场下流注长度的计算方法。具体地,首先,假设流注发展过程中流注头部的电子都聚集在一个半径为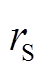 的球内,并以电子球表面的电场强度Es作为空间电场强度。其次,当电子球内的电子数为n时,用式(3)计算球体表面的电场强度Es,即得到能够维持流注发展的空间电场强度模值。因流注发展过程中,流注头部的电子数量并非均匀分布,而是由无限个不同数密度的小区域组成,故可将式(3)中的电子数n表示为电子数密度与体积的乘积关系,如式(4)所示。再次,用式(5)近似计算流注半径
的球内,并以电子球表面的电场强度Es作为空间电场强度。其次,当电子球内的电子数为n时,用式(3)计算球体表面的电场强度Es,即得到能够维持流注发展的空间电场强度模值。因流注发展过程中,流注头部的电子数量并非均匀分布,而是由无限个不同数密度的小区域组成,故可将式(3)中的电子数n表示为电子数密度与体积的乘积关系,如式(4)所示。再次,用式(5)近似计算流注半径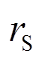 [20],并将其代入式(3)中,得到流注长度l与空间电场强度Es的一一对应关系,进而可根据空间电场强度确定流注长度。
[20],并将其代入式(3)中,得到流注长度l与空间电场强度Es的一一对应关系,进而可根据空间电场强度确定流注长度。
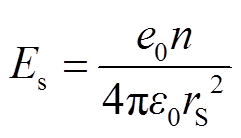 (3)
(3)
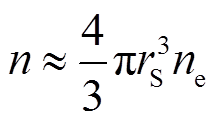 (4)
(4)
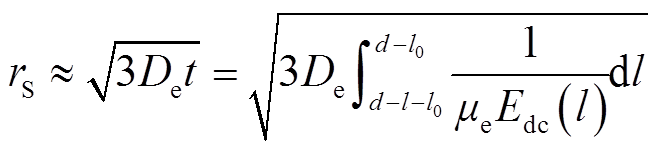 (5)
(5)
式中,Es为电子球表面电场强度,V/m;n为球体内的电子数;ε0为真空介电常数,ε0=8.85×10-12 F/m;e0为元电荷量,C;ne为球体内电子数密度,m-3;De为电子扩散系数,m2/s;Edc(l)为外施电源电场强度,V/m;μe为电子迁移率;l0和l分别为流注起始位置和发展长度,cm;d为间隙距离,cm;t为流注发展为l长度所需的时间,s;。
通常,μe和De满足爱因斯坦关系式(6),故可将式(3)进一步表征为式(7)。
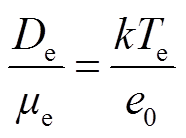 (6)
(6)
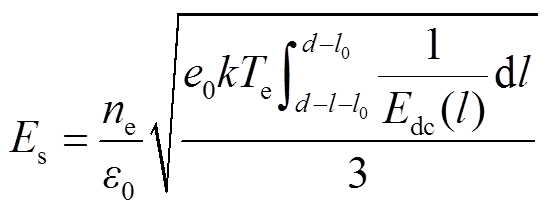 (7)
(7)
式中,Te为电子温度,eV;k为玻耳兹曼常数。
显然,式(7)可定量表征流注发展长度l与维持其发展所需的空间电场强度Es之间的关系。通过求解流注放电等离子体化学反应仿真模型,确定式(7)中的参数变量,并将电子球表面电场强度Es与流注放电仿真模型中由泊松方程计算的空间场强进行对比,进而可以判定流注发展是否截止。
本文采用基于流体力学的等离子体化学反应模型[21]进行流注放电的数值模拟。模型由电子连续性方程,电子能量方程,正、负离子及中性分子输运方程和泊松方程组成,并耦合光电离计算模型。
电子的迁移和扩散过程由连续性方程表示为
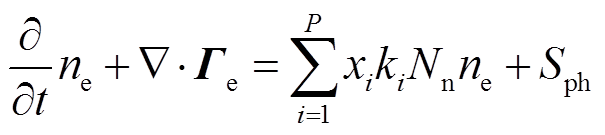 (8)
(8)
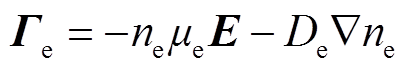 (9)
(9)
式中,Гe为电子通量;Sph为光电离速率,m3/s;P为使目标物质产生或减少的反应数目;i为不同的反应;xi为目标物质的摩尔分数;ki为反应速率,m3/s,电子碰撞反应的反应速率通过求解电子能量分布函数,并对能量进行积分求取,表达式见2.2节式(21);E为电场强度,V/m。
电子能量的传输过程由电子能量密度方程表示为
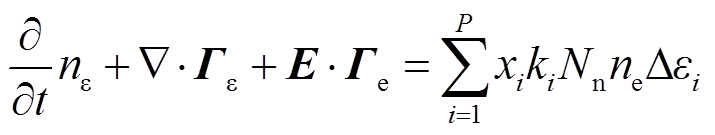 (10)
(10)
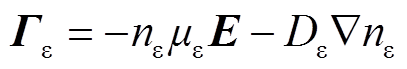 (11)
(11)
式中,Гε为电子能量通量;nε为电子能量密度,eV/m3;Δεi为碰撞反应i产生的能量损失,eV;με为电子能量迁移率,m2/(V·s);Dε为电子能量的扩散系数。本文取电子迁移率μe=3.74×1024(1021E)-0.22[20],电子输运系数之间的关系满足
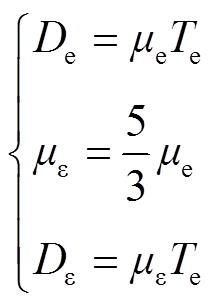 (12)
(12)
正离子、负离子、中性分子的迁移与扩散过程由重粒子多组分输运方程表示,即
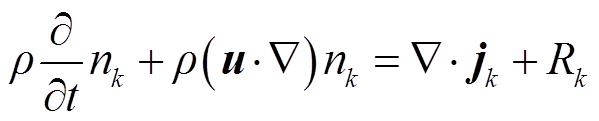 (13)
(13)
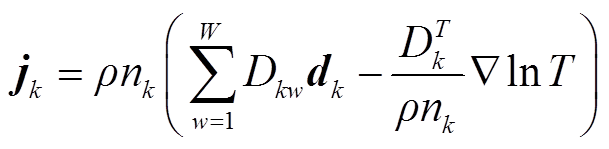 (14)
(14)
式中,ρ为空气密度,kg/m3;nk为重粒子k数密度,m-3;u为平均流体矢量,m/s;jk为粒子k扩散通量矢量,kg/(m2·s);Rk为粒子k由于化学反应造成的速率变化,kg/(m3·s);Dkw和dk分别为多组分扩散系统中粒子k的Maxwell-Stefan扩散系数和扩散驱动力;W为粒子k扩散系数的总个数;DT k为热扩散系数;T为气体温度。
空间电场分布由泊松方程式(15)和式(16)求解。
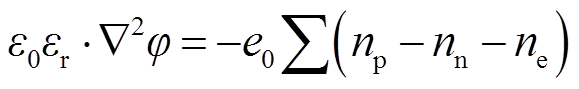 (15)
(15)
式中,εr为相对介电常数;np、nn分别为正、负离子数密度,m-3;φ为电势,V。
光电离是流注生成与发展不可或缺的因素,目前空气中放电的光电离速率主要由传统积分模型[22]确定,其表达式为
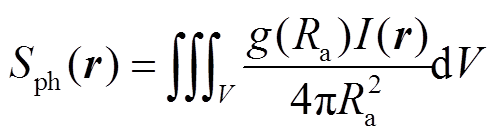 (17)
(17)
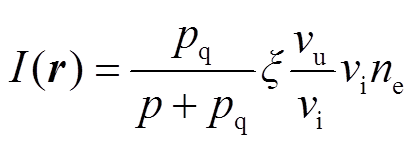 (18)
(18)
式中,g(Ra)为光子的吸收函数;Ra为光子产生与被吸收之间的距离;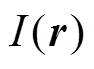 为光子的产生函数;r为方向矢量;ξ为光电离效率;p为大气压强,p=760 Torr(1 Torr=133.3 Pa);pq为激发态气体熄灭压强,pq= 30 Torr;vu为电子的激发频率;vi为电离频率。本文ξvu/vi取值为0.06[23]。
为光子的产生函数;r为方向矢量;ξ为光电离效率;p为大气压强,p=760 Torr(1 Torr=133.3 Pa);pq为激发态气体熄灭压强,pq= 30 Torr;vu为电子的激发频率;vi为电离频率。本文ξvu/vi取值为0.06[23]。
传统光电离模型计算采用积分运算形式,为减少计算量,本文采用对光子的吸收函数作三指数拟合的Helmholtz微分方程做近似计算,计算式见式(19)和式(20),拟合系数取值[24]见表1。
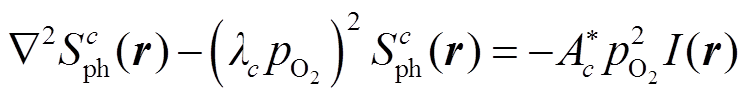 (19)
(19)
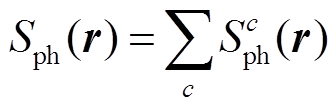 (20)
(20)
式中,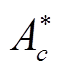 、
、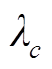 为拟合系数;
为拟合系数;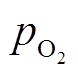 为氧气分压,取150 Torr。
为氧气分压,取150 Torr。
表1 拟合参数取值
Tab.1 Value of fitting coefficient

c/(cm-2·Torr-2)/(cm-1·Torr-1) 12×10-45.37×10-2 23.6×10-31.317×10-1 31.255×10-15.602×10-1
由于空气中某些气体的碰撞截面数据尚不明确,为简化计算模型,本文仅考虑氮气与氧气的混合气体(N2:O2=0.79:0.21),其包含N2、O2、O、O3、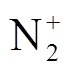 、
、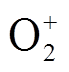 、
、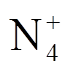 、
、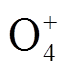 、
、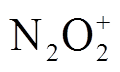 、
、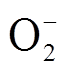 、电子e共11种组分,可形成23组反应[25],具体见表2。表2中,M代表N2或O2,当R9~R11、R17、R18分别考虑N2或O2时,共计23组反应;NA为阿伏伽德罗常数;反应速率单位对于二体反应为m3/(s·mol),三体反应为m6/(s·mol2),其中k1和k2通过求解电子能量分布函数,并对能量进行积分求取,表达式为
、电子e共11种组分,可形成23组反应[25],具体见表2。表2中,M代表N2或O2,当R9~R11、R17、R18分别考虑N2或O2时,共计23组反应;NA为阿伏伽德罗常数;反应速率单位对于二体反应为m3/(s·mol),三体反应为m6/(s·mol2),其中k1和k2通过求解电子能量分布函数,并对能量进行积分求取,表达式为
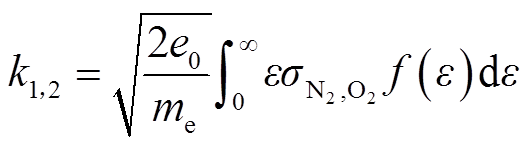 (21)
(21)
式中,me为电子质量,kg;ε为电子能量;σN2、σO2分别为电子与N2和O2的碰撞截面,截面数据来自LXCat数据库[26-27];f(ε)为电子能量分布函数,采用玻耳兹曼-两项近似(线性)方法求解。
表2 本文考虑的化学反应过程
Tab.2 Chemical reaction processes considered in research

序号反应反应速率Δε/eV 电离反应 R1k115.6 R2k212.1 附着反应 R3 复合反应 R4 R5 R6 R7 R8 R9 R10 电荷转移反应 R11 R12 R13 R14 R15 R16 R17 R18
本文所用模型包含电极边界和空气开放边界:电极边界采用反应壁边界条件;气体边界设置为零电荷、零通量边界。
电子在电极上的边界条件为
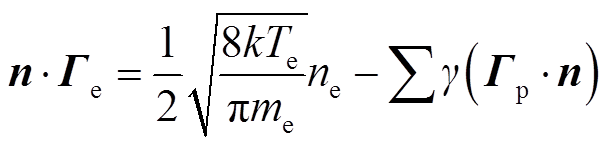 (22)
(22)
式中,n为边界法向量;Гp为正离子的通量;γ为二次电子发射系数,在板电极取0,棒电极取0.02。
电子能量在电极上的边界条件为
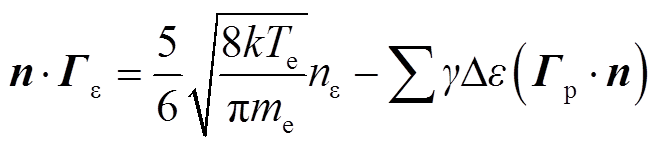 (23)
(23)
所有正离子、负离子、中性分子在电极边界上满足式(24)。
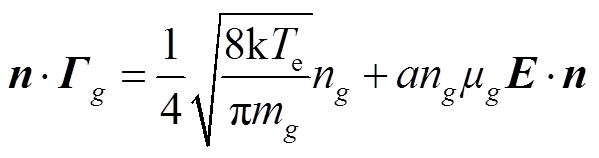 (24)
(24)
式中,Гg为第g类粒子的通量;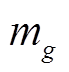 为粒子质量,kg;ng为其数密度,m-3;μg为其迁移率,m2/(V·s);a为系数。对于正、负离子,当离子向异性电极方向迁移时a=1,同性电极边界a=0;中性分子在电极边界取0。
为粒子质量,kg;ng为其数密度,m-3;μg为其迁移率,m2/(V·s);a为系数。对于正、负离子,当离子向异性电极方向迁移时a=1,同性电极边界a=0;中性分子在电极边界取0。
为保证计算模型的准确性,边界条件与文献[24]保持一致。
本文使用COMSOL Multiphysics 5.6中等离子体模块、数学模块和静电模块,建立二维轴对称仿真模型。本文构建的几何模型中,棒电极半径为0.75 cm,棒电极尖部半径为0.075 cm,板电极半径为8 cm。外施电压上升沿为5 ns,峰值为-80 kV。板电极接地,间隙为18 cm。气压为1 atm(1 atm=760 Torr=101.3 kPa),温度为293 K。为提高模型的收敛性,本文对求解域网格进行了一定的设置,网格平均单元质量为0.92,所建立的几何模型如图2所示。
3.2.1 带电粒子数密度分布及发展过程
由式(2)计算出本文放电电极的起晕场强约为75.3 kV/cm,在外施电压达到峰值时,棒电极尖部产生的电场强度约为200 kV/cm,因此在棒电极处电晕放电剧烈,自由电子获得能量,当其能量高于气体分子的电离能时,气体分子将被电离。
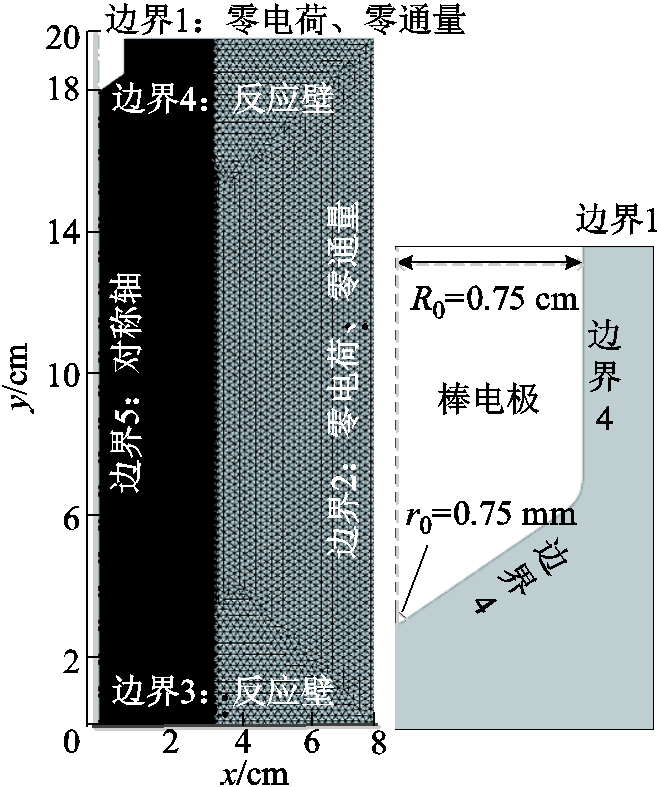
图2 几何模型
Fig.2 Geometric model
在整个流注发展过程中,对称轴线上正、负离子及电子的整体密度分布随时间的发展曲线如图3所示。由图3可看出,每一时刻电子密度峰值存在于流注头部,同样在流注头部存在大量电离产生的正离子,而负离子的产生稍滞后于电子和正离子,其原因是负离子主要在流注经过的通道内产生,而流注头部由于电场强度高、电子能量大,难以发生附着反应。为深入研究流注发展过程中带电粒子的动作行为及分布特性,本文将整个流注放电的发展过程分为三个具有代表性的时间点,分别对应流注的起始、发展与预击穿时刻,其对应时间分别为t=3 ns、t=10 ns、t=29 ns。
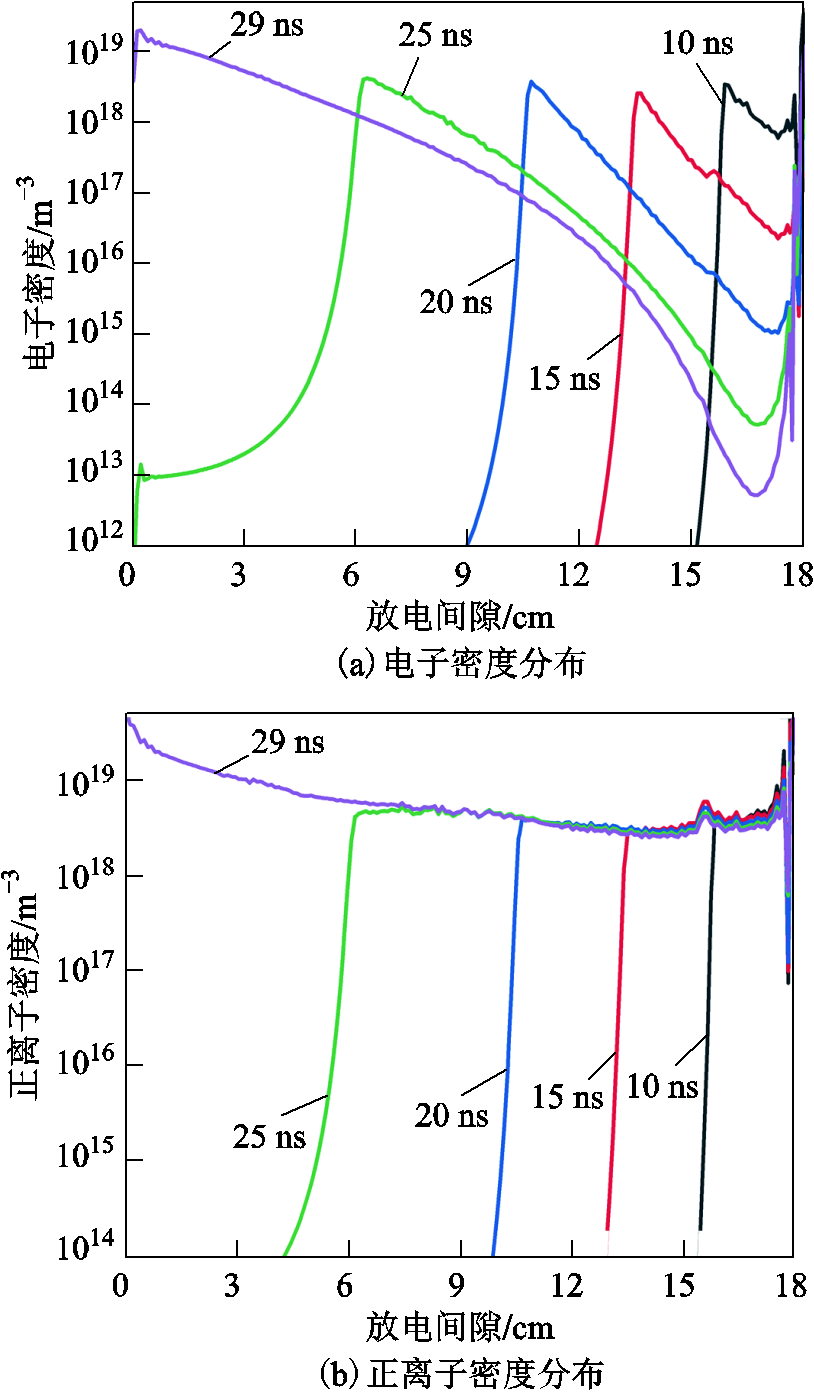
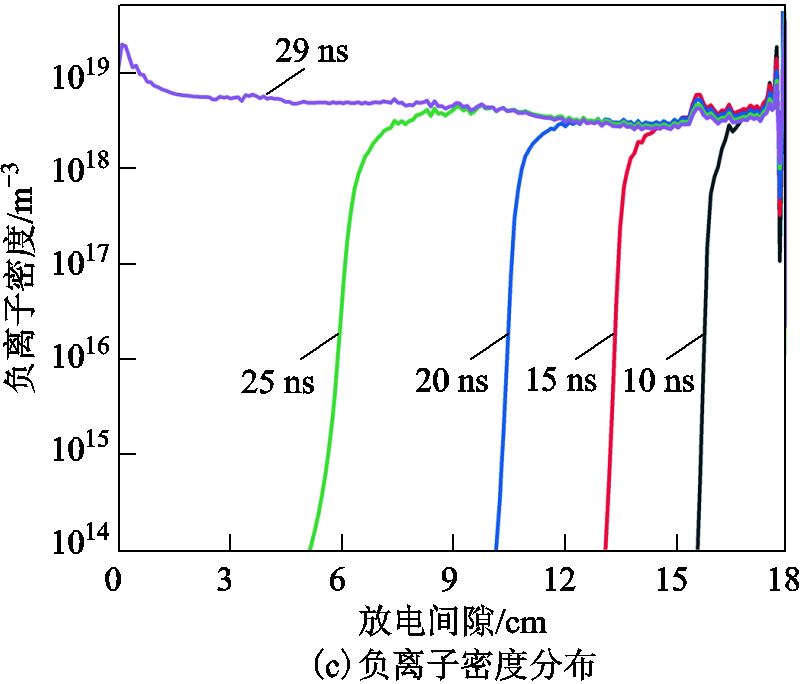
图3 不同时刻带电粒子数密度分布曲线
Fig.3 Density distribution curve of charged particles at different times
t=3 ns时,间隙内电子密度分布和对称轴线上带电粒子数密度分布如图4所示。图4中以板电极的圆心作为x=0的位置,此时电压幅值约为-70 kV。由图4a可看出,此时电子密度峰值仅分布在棒电极尖部及两侧拐角处,通道内电子数密度仅为1010 m-3量级。由图4b、图4c可发现,在靠近棒电极约 1 mm的间隙内,电子和正离子数量最多,负离子数量较少,其中电子数密度为3.9×1021 m-3,正离子数密度为6.1×1019 m-3。正离子中,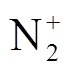 、
、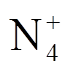 、
、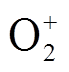 占比最高,据此可推断出靠近棒电极处以电离反应R1、R2为主,且其数值大于电子崩到流注起始的临界粒子数密度1018 m-3,因此流注产生。在电离区以外的区域,电场强度较小,正、负离子发生复合,并发射光子引发光电离,光电子因无法形成新电子崩而生成负离子。
占比最高,据此可推断出靠近棒电极处以电离反应R1、R2为主,且其数值大于电子崩到流注起始的临界粒子数密度1018 m-3,因此流注产生。在电离区以外的区域,电场强度较小,正、负离子发生复合,并发射光子引发光电离,光电子因无法形成新电子崩而生成负离子。
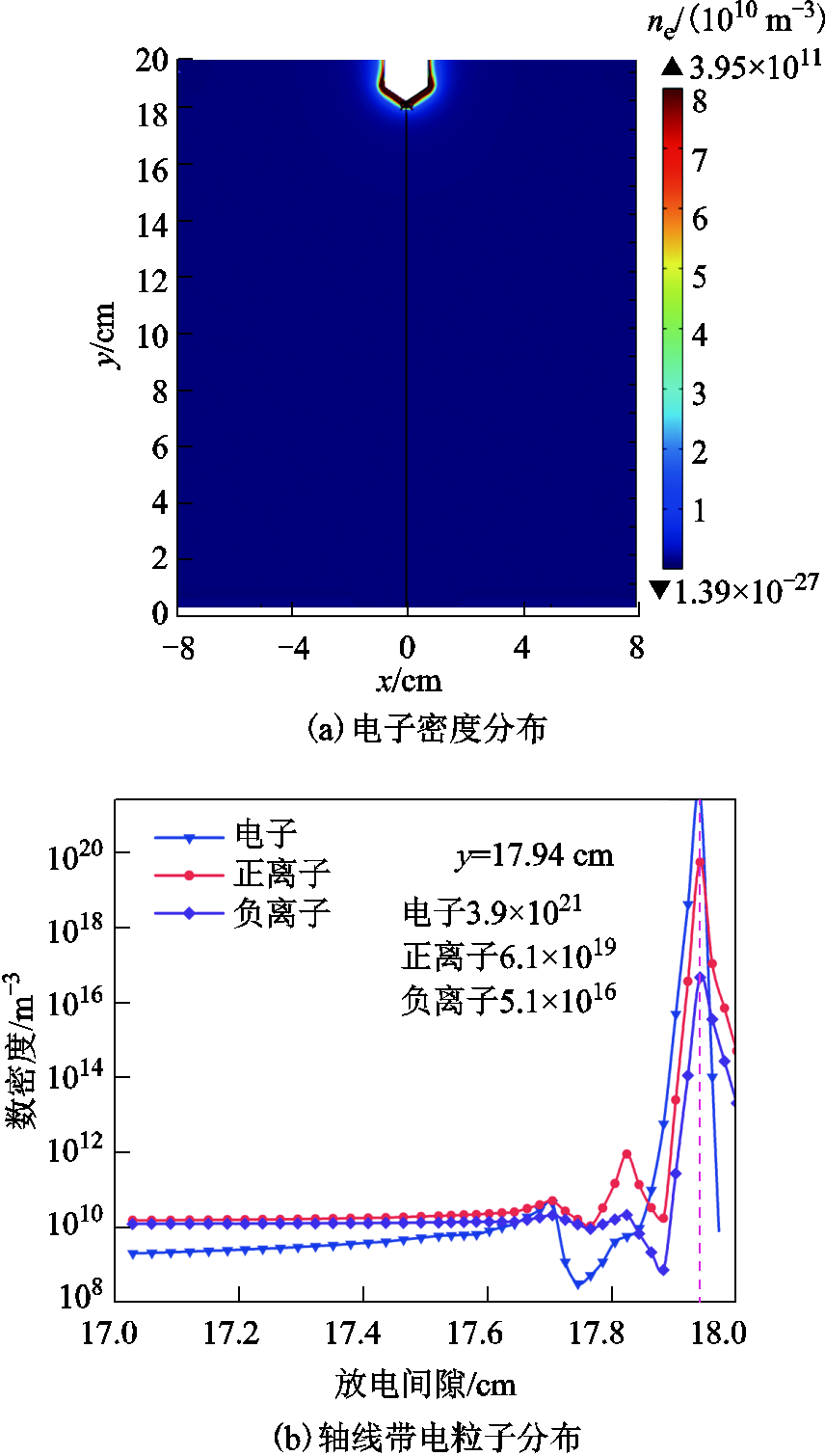
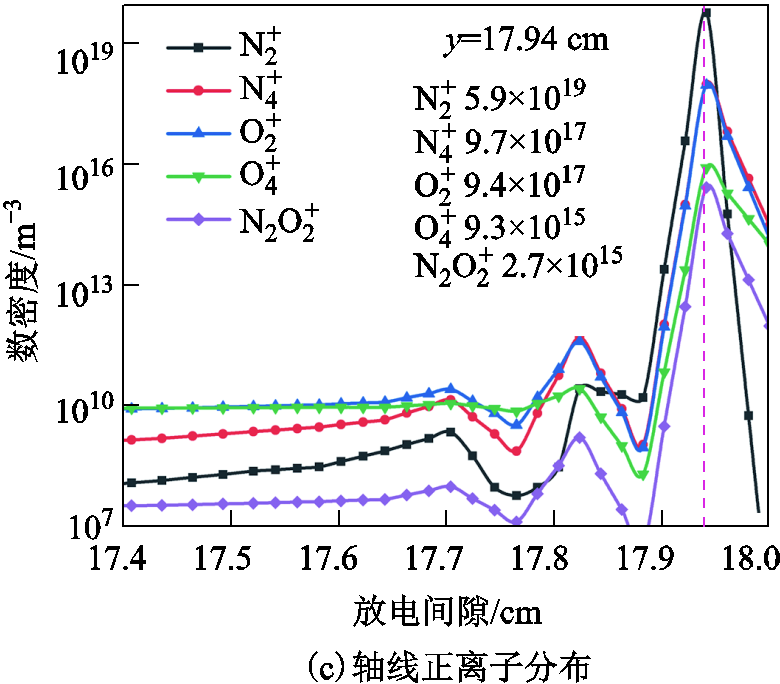
图4 t=3 ns时带电粒子分布
Fig.4 Distribution of charged particles at t = 3 ns
t=10 ns、外施电压为-80 kV时,间隙内电子密度分布和对称轴线上带电粒子数密度分布如图5所示。由图5a可看出,由于棒电极尖部与两侧曲率大,靠近其周围的气体分子几乎全部被电离,并形成了三个方向的电子崩;电极两侧电场强度小,无法持续产生有效电子来维持电子崩发展,最终只有主放电通道的电子崩发展为流注。由图5b可知,此刻对称轴线上靠近棒电极处的电子密度较t=3 ns时明显降低,峰值为3.7×1019 m-3,负离子数密度大幅提高,峰值达6.4×1020 m-3。分析其原因是,前期产生的自由电子有一部分被附着为负离子,并形成负离子层,负离子层削弱了与棒电极之间的电场并使得净电离速率降低。此时流注头部在y=15.85 cm位置,由于流注头部空间电荷密度足够高(1018 m-3量级),空间电场能够维持流注头部内的电离反应,因此流注头部电子密度和正离子数密度要高于负离子数密度。由图5c可知,在流注头部正离子占比最多的是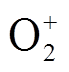 、
、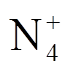 ,这是因为流注头部空间电场畸变程度大,且O2电离能低于N2,所以O2更易被电离。在流注经过的通道内
,这是因为流注头部空间电场畸变程度大,且O2电离能低于N2,所以O2更易被电离。在流注经过的通道内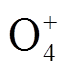 、
、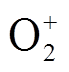 占比最多,这是由于O2易吸收光子而引发光电离,产生的
占比最多,这是由于O2易吸收光子而引发光电离,产生的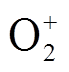 发生电荷转移生成
发生电荷转移生成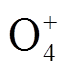 。本文各类正、负离子的分布规律与文献[21,28]结果基本一致,其原因是流注的产生与发展强调的是空间电场及光电离对维持流注头部电离反应的影响。故毫米级间隙下流注的产生与发展机理同样能够解释厘米级间隙的流注放电。
。本文各类正、负离子的分布规律与文献[21,28]结果基本一致,其原因是流注的产生与发展强调的是空间电场及光电离对维持流注头部电离反应的影响。故毫米级间隙下流注的产生与发展机理同样能够解释厘米级间隙的流注放电。
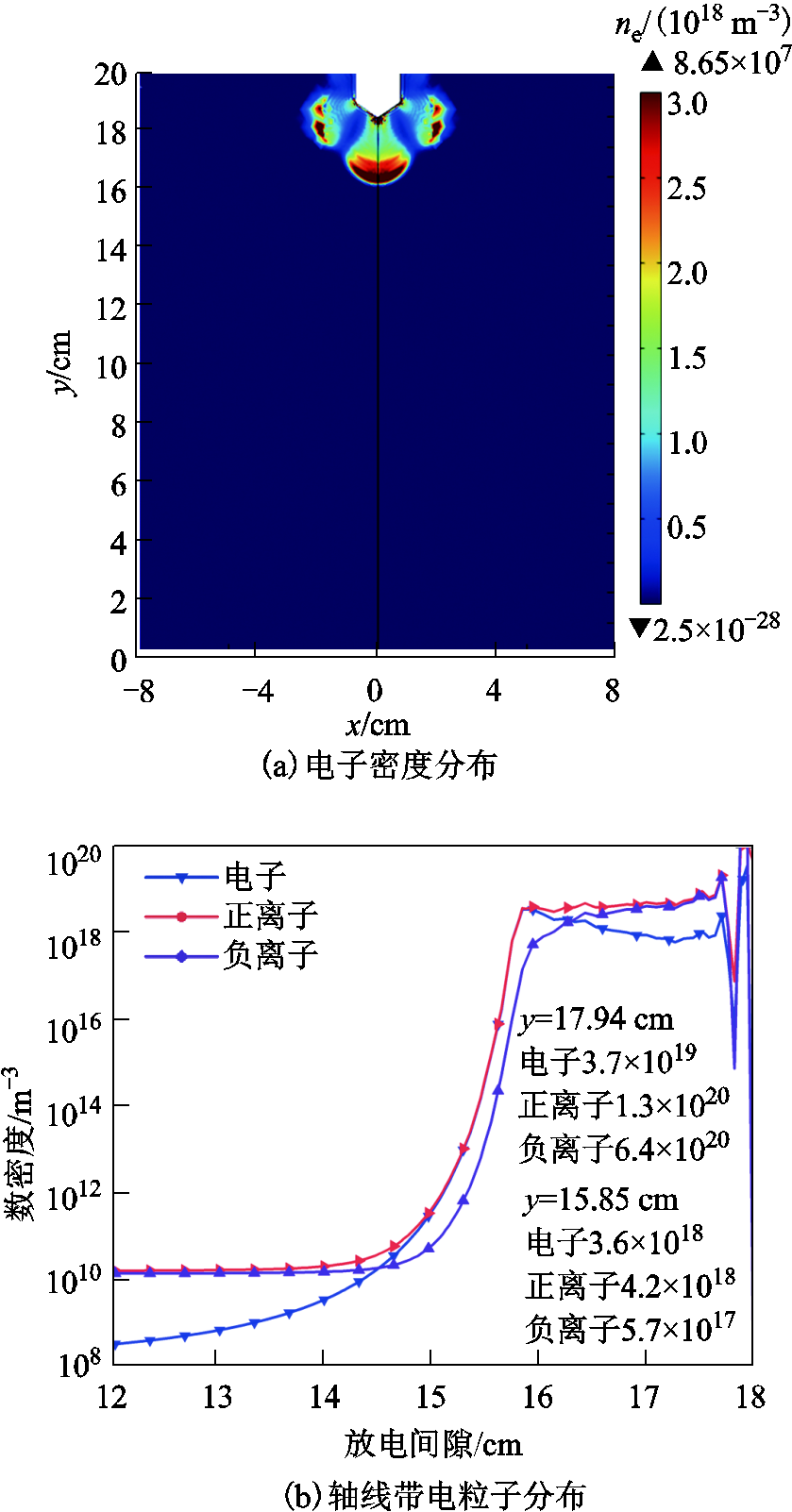
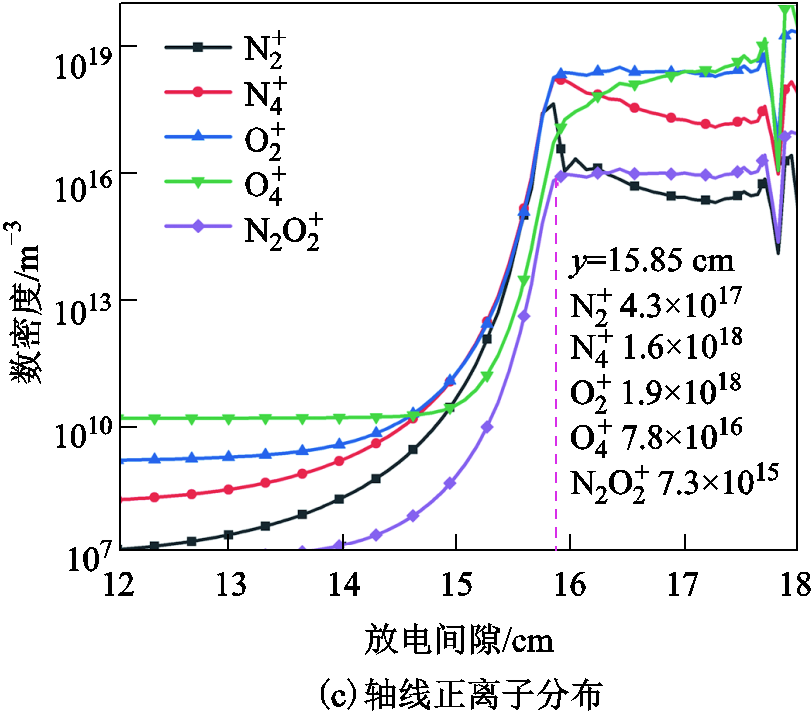
图5 t=10 ns时带电粒子分布
Fig.5 Distribution of charged particles at t = 10 ns
t=29 ns时带电粒子分布如图6所示。由图6a可看出,此时流注头部已到达板电极,其电子数密度峰值为3.01×1019 m-3。由轴线上的带电粒子数密度分布曲线图6b可知,在棒电极处存在大量正离子,正离子碰撞棒电极会产生二次发射电子,二次电子在畸变电场下将形成电子崩。在流注通道内正、负离子数值稳定,形成等离子体正柱区,此时流注的放电形态如图6c所示。在板电极处,负离子和电子数密度增加,这是由于负离子受电场迁移在板电极聚集,随着时间的延长,负离子层变厚,且电荷之间相互排斥,因此形成鞘层。鞘层的出现增加了板电极处的电场畸变,造成电离速率升高,电子和正离子增多。
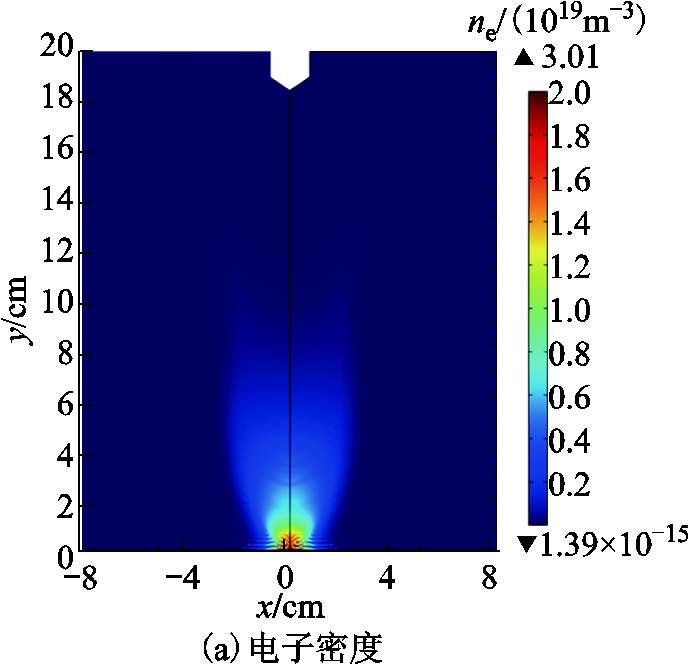
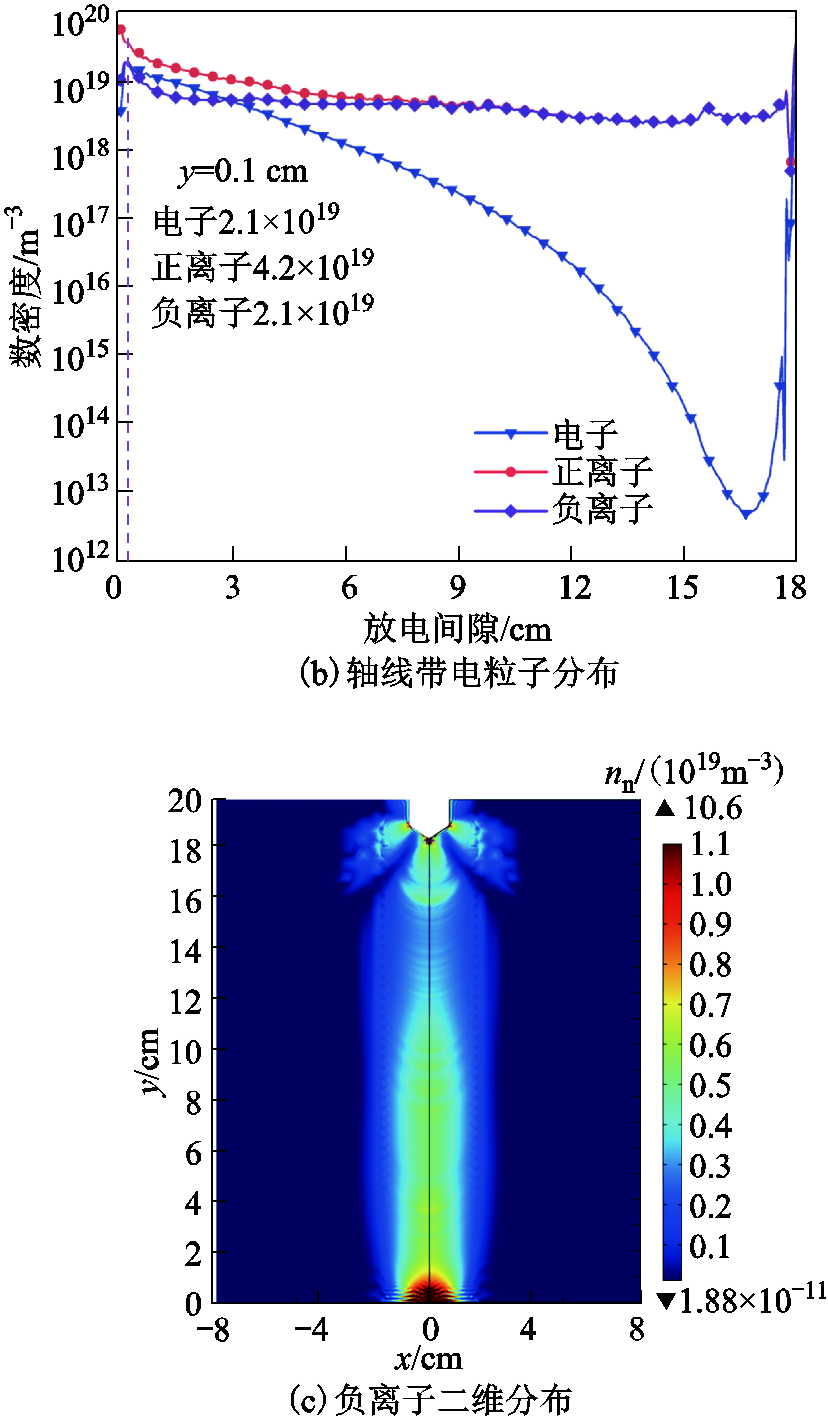
图6 t=29 ns时带电粒子分布
Fig.6 Distribution of charged particles at t = 29 ns
3.2.2 平均电子能量与电场强度的分布及发展过程
电子在电场作用下能量升高,高能电子通过与重物质的碰撞过程进行能量传递,由高能电子碰撞引发的电离过程会直接影响带电粒子的位置分布,进而影响空间电场的分布,因此空间电场的畸变程度及其分布和发展规律是研究流注放电的关键。
轴线上不同时刻平均电子能量的分布如图7所示。由图7可知,在流注发展初期,流注的起始依赖外施强电场,当t=4 ns时,在棒电极处电场强度高达上百kV/mm,因此棒电极处的平均电子能量约为16.5 eV,远高于通道内的平均电子能量。当流注发展至远离棒电极时,电场畸变则主要由流注头部的空间电荷引起,其在流注发展过程中较为均匀,因此通道内的平均电子能量也较为均匀,约为6.2~6.8 eV,这将会造成氮气分子的电子能级以及转动和振动能级发生跃迁,由于其能级不稳定,能量将以光子的形式释放,产生的光子极易被氧气分子吸收而发生光电离,进而维持流注的发展。在靠近板电极处,平均电子能量开始增加,原因是此处的空间电场强度增强。为探究电场强度增强的原因,计算得到空间电场强度与负离子数密度的二维分布如图8所示。
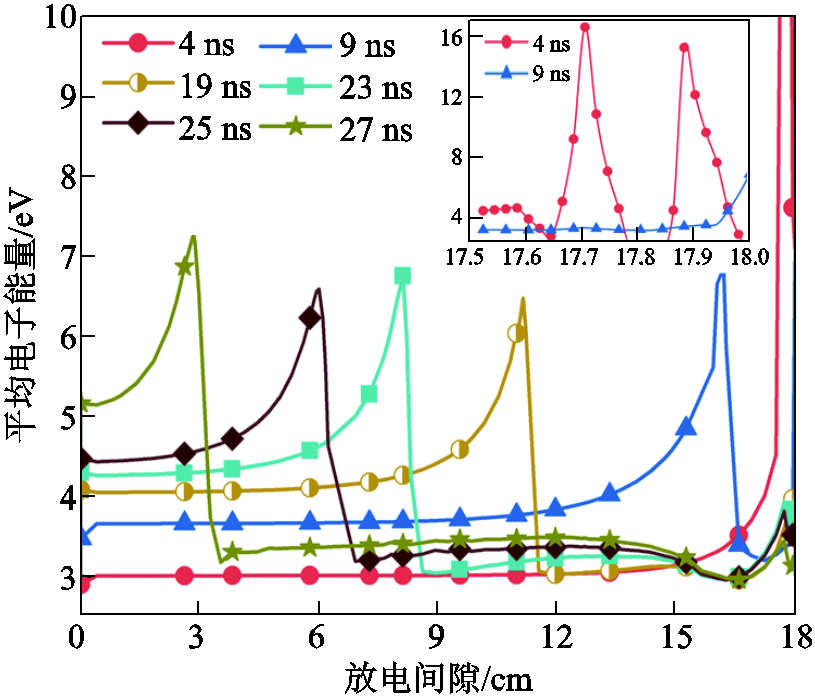
图7 不同时刻轴线处的平均电子能量分布
Fig.7 Average electron energy distribution at different times along the axis
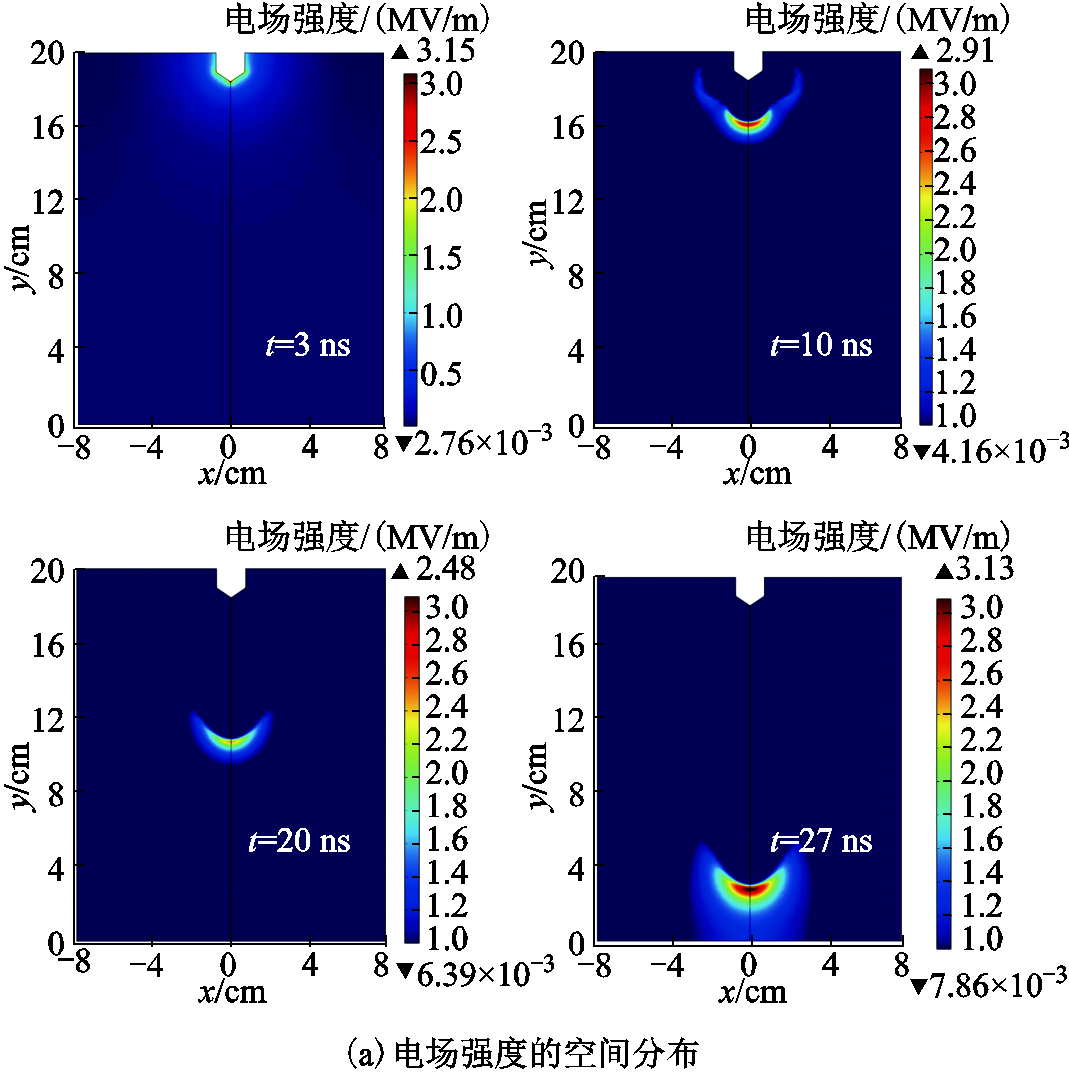
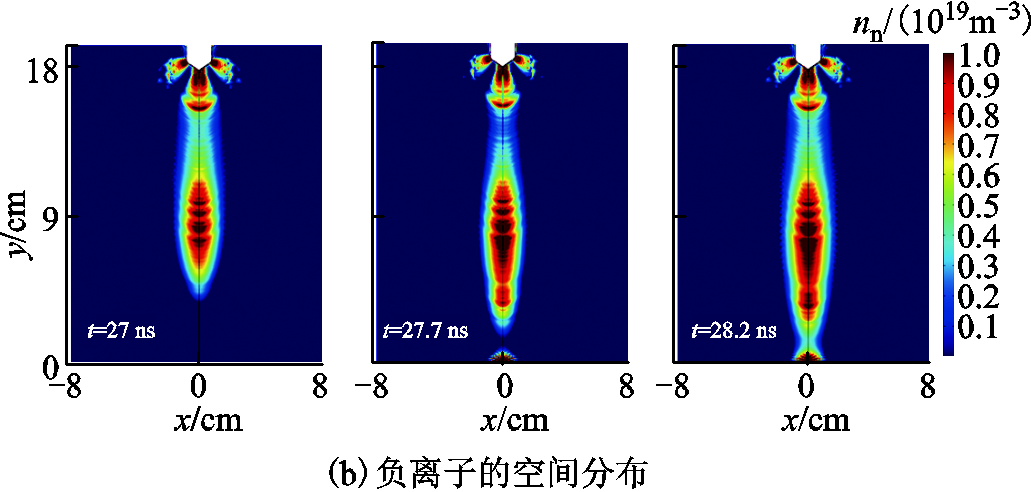
图8 不同时刻电场强度及负离子的空间分布
Fig.8 Spatial distribution of electric field strength and negative ion number density at different times
由图8a可知,电场强度随空间电荷的移动而发生变化,净空间电荷密度分布决定了电场的分布规律。当t=3 ns时,棒电极处存在大量带电粒子,其电场强度峰值为3.15 MV/m。之后由于负离子层的存在使得棒电极与流注头部之间的电场强度降低,因此在t=10 ns时,流注头部电场强度峰值为2.91 MV/m。当t>10 ns时,流注头部距棒电极较远,放电通道内带电粒子密度和电子能量较为均匀,因此其电场强度相对平缓,约为2.3~2.5 MV/m。当流注头部靠近板电极时,空间电场强度明显增强,约为3.13 MV/m。从图8b可看出,当流注头部靠近板电极时,流注通道内已存在大量的负离子,由于同性电荷之间相互排斥及质量大等原因,其运动速率较电子慢得多,因此其积聚会使得流注头部与板电极之间的电场强度增强;同时负离子层的存在会削弱与棒电极之间的电场强度,使得流注经过的通道内的电场强度降低,自由电子更易被附着,负离子数目会继续增加,进一步增大与板电极之间的电场强度,此时流注头部的自由电子在前向通道内的电离反应将更为激烈,将会产生更多的空间电荷和有效电子,流注头部的电场强度也随之增强,而最先到达板电极的部分电子,会在电场作用下发生放电,使得板电极附近出现放电现象。此时,板电极处的放电现象有别于流注通道内的放电,其放电强度与负离子层的积聚程度有关。
3.2.3 流注发展长度的确定方法
为量化表征电子球的表面电场强度Es与流注长度l之间的对应关系,本文绘制了外施电压在轴线上的电场分布曲线,如图9所示。图中,Edc为外施电压在轴线上产生的电场强度分量;Eav定义为平均电场强度,其值为外施电压幅值与间隙距离的比值,本文取为0.44 MV/m。
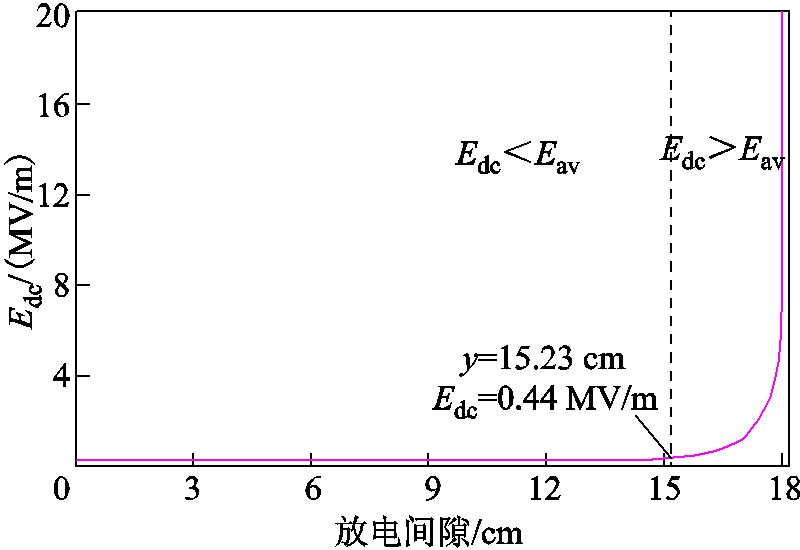
图9 电源电场的轴线分布
Fig.9 Axial distribution of power field
由图9可知,外施电压产生的电场在靠近棒电极的区域内变化较大,而在通道内较为均匀,距离板电极约15.23 cm处的电场强度值等于Eav。将Edc(单位为V/m)取倒数并进行三次多项式拟合为流注长度l(单位为cm)的函数,即
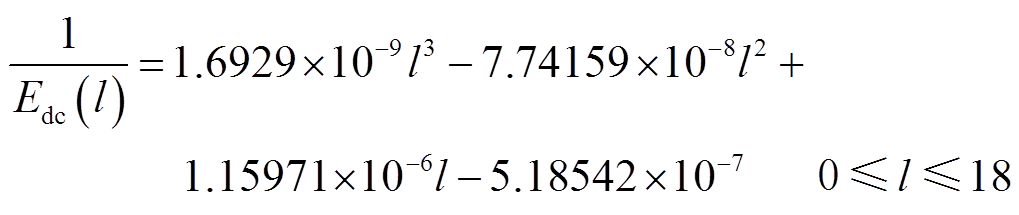 (25)
(25)
因Raether判据中的l代表电子崩发展的临界长度,本文为将其转换为流注长度作如下假设。
1)外施电压能够满足在棒电极放电起始时刻,电子崩放电转变为流注放电,因此式(7)中l0=0。
2)在式(7)成立的条件下,将式中电子密度ne、电子温度Te及式(25)中Edc(l)倒数的拟合函数取值为流注放电仿真模型中的计算值,并采用描坐标点法得到Es与l的关系曲线,如图10所示。
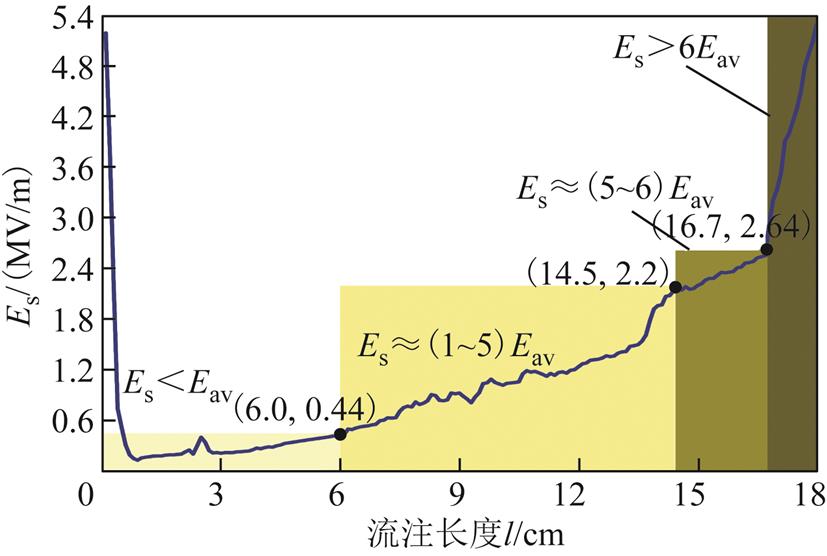
图10 Es与l的关系曲线
Fig.10 Relationship curve between Es and l
由图10可得,在流注起始阶段Es较高,意味着流注起始需要较高的电子密度,此时崩头内电场强度要高于52 kV/cm才能满足条件。随后Es迅速降低,这是由于流注起始阶段的光电离效率高,光电离为流注发展提供大量种子电子,并且流注起始阶段存在分支,在轴线方向上碰撞电离速率较低。在流注发展过程中,电子球表面电场强度由于电荷的积累和汇聚作用而缓慢升高。当流注头部电场畸变程度小于1倍平均电场强度时,流注发展长度小于6 cm;当流注头部电场畸变程度为1~5倍平均电场强度时,流注发展长度小于14.5 cm;当流注头部电场畸变程度大于12倍平均电场强度时,流注将击穿棒-板间隙。
3.3.1 实验设计
为验证仿真模型,本文进一步搭建了棒-板间隙下的电晕放电实验平台,并开展了实验研究。实验用棒、板电极均由金属铜材料制成,棒电极半径为0.75 cm,尖部半径为0.075 cm;板电极直径为16 cm,厚度为1 cm。采用HY-DC300型高压直流电源供电,最高输出电压为±300 kV,放电间隙设置为18 cm,环境温度为20℃,限流电阻为40 kΩ。放电时采用照相机对放电现象进行拍摄。放电结构示意图如图11所示。
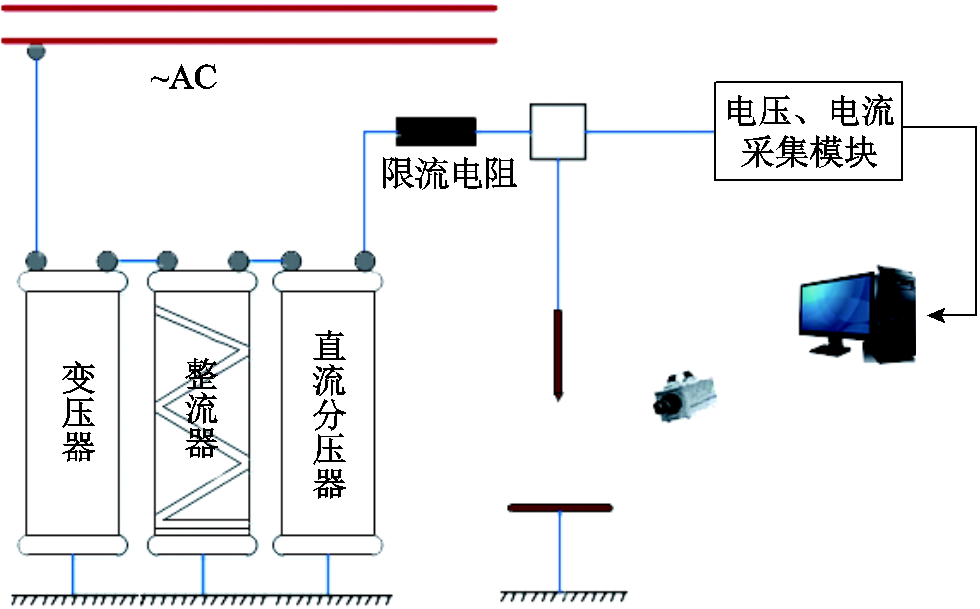
图11 放电结构示意图
Fig.11 Discharge structure diagram
3.3.2 实验结果与分析
采用匀速升压方式,当电压升至约-60 kV时,棒电极处产生蓝紫色微弱的晕光,如图12所示。

图12 实验中的电晕放电
Fig.12 Corona discharge in experiment
经分析知,此阶段为电晕起始阶段,其形成原因是棒电极尖部的电场强度达到了起晕场强,在棒电极周围造成局部的气体击穿并生成正离子和电子,由于电场强度不高,电子被中性分子附着为负离子,正、负离子发生复合反应并发射光子,因此在棒电极尖部周围形成晕光。
当电压升高为-70 kV时,棒电极尖部的晕光愈加明亮,光圈变大且有外扩趋势,此时并伴随着放电的“呲呲”声,棒电极放电呈喷射状,即刷状放电。分析其成因,一方面是由于微观上电极尖部存在微小缺陷,这些缺陷在强电场作用下将先发生放电;另一方面,靠近棒电极周围存在大量高能电子,电子碰撞反应以电离和激发反应为主,由激发态回归基态释放的光子容易被氧气分子捕捉继而发生光电离并形成电子崩,而电子崩头部的二次电子由于放电强度不高且距棒电极较远,因此易被附着为负离子,使得放电难以向深处发展。由于带电粒子受电场迁移而进入棒电极,电流幅值会略有提升,其放电现象如图13所示。
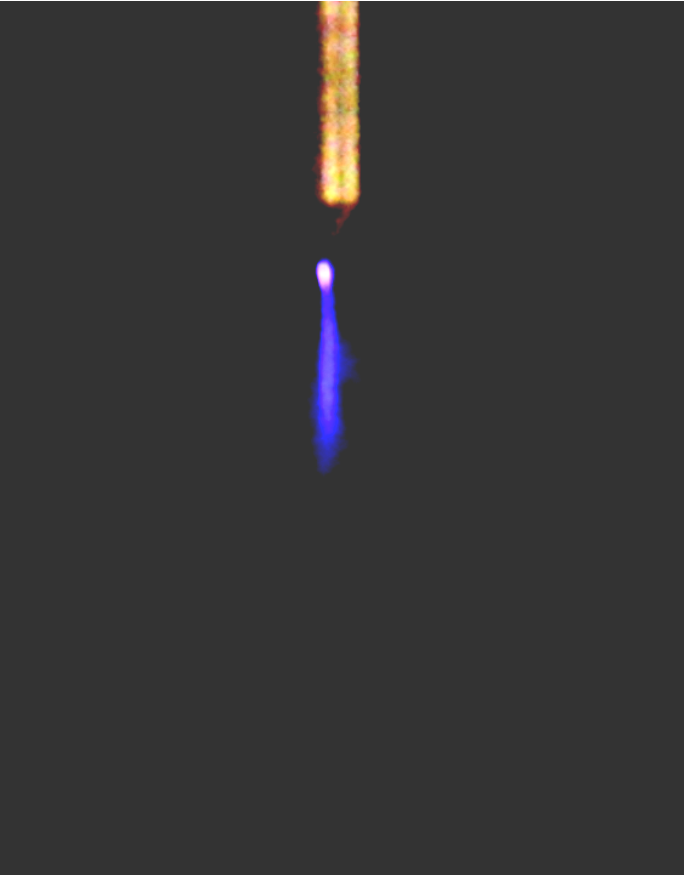
图13 流注放电起始现象
Fig.13 Streamer discharge initiation
由于流注起始阶段在棒电极尖部发生多次流注放电,此时空间电荷对空间电场的畸变作用已经不容忽视,大量负离子在电场作用下向板电极移动。当电压升至约-82 kV时,放电通道瞬时明亮,蓝紫流光瞬间贯穿棒-板间隙,且光束呈现窄口圆柱状,靠近棒电极处明亮耀眼,沿棒电极下方出现喷射状流注,由大量流注丝汇聚组成,其长度与棒电极和负离子层之间的放电强度相关,放电强度越强,电子在空间内电离反应越剧烈,流注的长度越长。此时放电现象如图14所示。

图14 实验中的流注放电现象
Fig.14 Streamer discharge in experiment
由图14可知,流注在起始和发展过程中存在大量分支,原因是由空间电荷引起的电场畸变位置与带电粒子的分布并不完全一致,因此光电子及二次碰撞电子在极不均匀电场作用下引发二次电子崩的位置不同。随着流注的发展,所有分支都向主放电通道靠拢,因流注半径较小的分支与流注半径较大分支在空间上的发展速度不同,半径小的分支极易受主放电通道内的电荷吸引被电场驱动而并入主通道。由于流注发展过程很快,现有相机无法准确地捕捉到其最大发展长度,因此在图14中展示了其近似的最大长度时的照片。图14中将整个放电通道划分为流注(放电)区和漫射(辉光)区,其中漫射区为靠近板电极上方具有弥漫发光形式的区域,流注区的长度约为16.66 cm。
流注头部电场强度的仿真结果与电子球表面电场强度的对比如图15所示。根据图10中电子球表面电场强度Es与流注长度l的关系,当流注长度为16.66 cm时,电子球表面电场强度为2.63 MV/m,与仿真结果3.03 MV/m相差13.2%。另外,在靠近棒电极的小范围内,轴线上的电场强度仿真结果低于理论计算结果。其原因是,在流注的起始阶段,电场呈极不均匀分布,轴线上的电场不能完全表征此时的空间电场,所以在流注放电的起始阶段两者存在一定的误差。随着时间的延长,流注放电变得均匀。当流注长度小于16.9 cm时,仿真计算的电场强度始终大于能够维持流注发展的电子球表面的电场强度,由此可佐证仿真模型的合理性;当流注长度大于16.9 cm时,仿真计算结果与理论值相差无几,表明在本文放电条件下,沿棒电极向下发展的流注在长度为16.9 cm时,将难以继续维持其发展。而在剩余间隙内,随着负离子积聚逐渐增多,电场强度逐渐增强,将在板电极处产生漫射区,此区域在满足一定条件时可以转变为阳极流注区,此时整个通道将更容易被击穿。
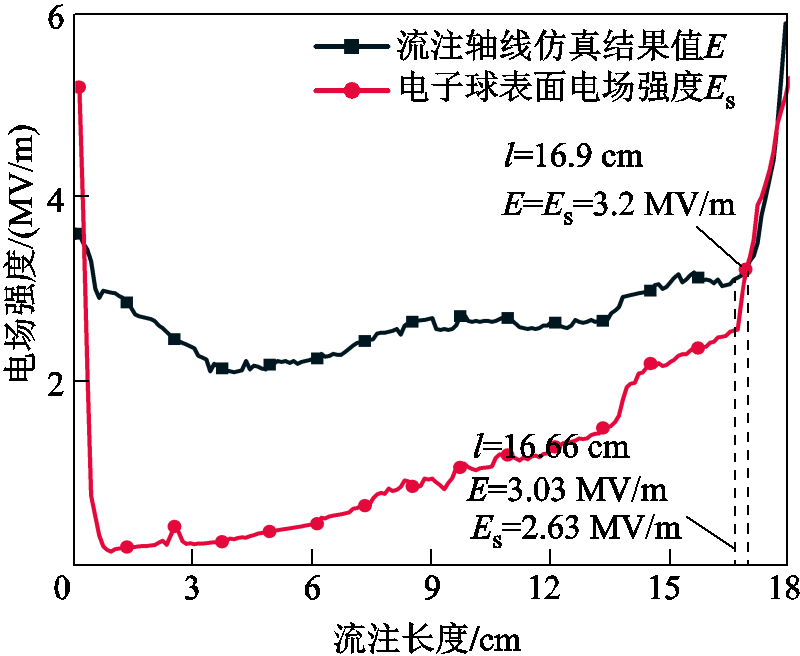
图15 流注头部电子球表面电场Es与流注仿真模型计算电场E对比
Fig.15 Comparison between the surface electric field Es of the electron sphere at the streamer head and the calculated electric field E of the streamer simulation model
为验证仿真模型的有效性,本文得到实验与仿真放电电流峰值随外施电压幅值的变化曲线如图16所示。其中,流注放电模型中放电电流可由式(26)确定。
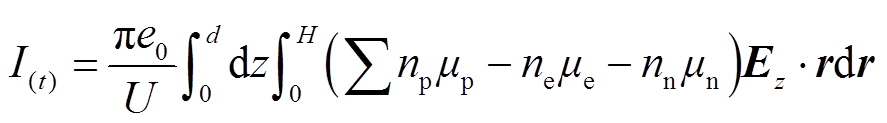 (26)
(26)
式中,U为外施电压幅值,kV;H为放电区域的半径,cm;Ez为电场强度的垂直分量,kV/cm。
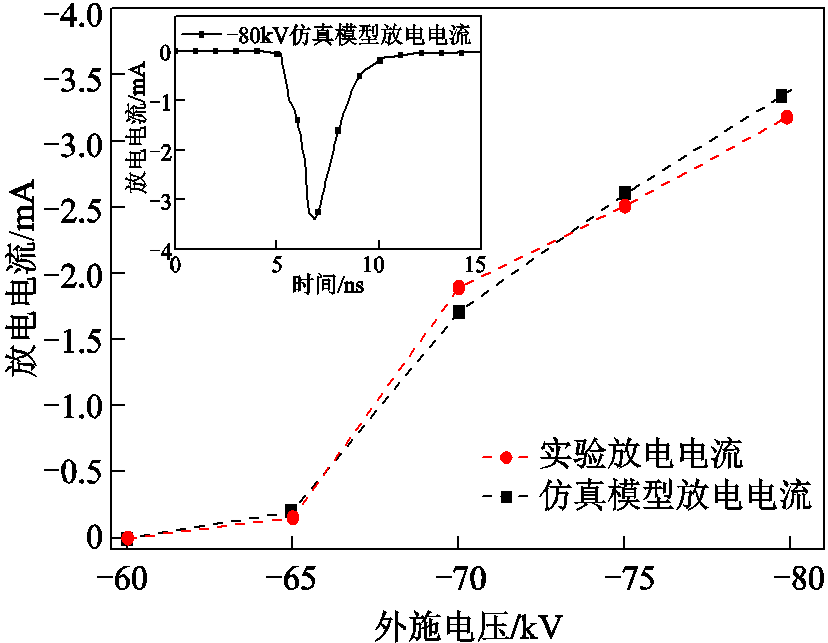
图16 实验与仿真的放电电流的对比
Fig.16 Comparison of discharge current between experiment and simulation
由图16可知,当在外施电压约为-70 kV时,电流才显著增大,而此时恰是流注起始时对应的电压幅值,大量带电粒子开始流入棒电极,因此电流幅值升高。此后随着外施电压的升高,更多的带电粒子流入电极,电流幅值升高。仿真计算的放电电流与实验测量到的放电电流具有较好的一致性,可以证明流注计算模型的可靠性。
本文探究了在大气条件下厘米级棒板间隙负电晕放电中流注放电的产生与发展机制,探究了其带电粒子、平均电子能量及电场强度的分布规律及变化过程,并发展了在极不均匀场情况下流注发展长度的确定方法,得出如下结论:
1)基于流体力学的等离子体化学反应仿真模型对求解大气条件下厘米级间隙的流注放电仍然具有很好的准确性。
2)在流注发展过程中,高能电子主要产生于流注头部,而负离子主要产生于流注经过的区域内。对于正离子,在流注头部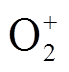 、
、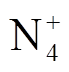 最多;在流注通道内
最多;在流注通道内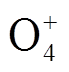 、
、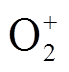 最多,计算结果与毫米级间隙流注放电的带电粒子分布特征保持一致。
最多,计算结果与毫米级间隙流注放电的带电粒子分布特征保持一致。
3)流注放电的起始过程需要产生较高的电子密度,而流注的发展长度取决于空间电场的畸变程度。本文放电条件下,当流注头部电场强度小于1倍平均电场强度时,流注长度小于6 cm;当流注头部电场强度为1~5倍平均电场强度时,流注长度小于14.5 cm;当流注头部电场强度大于12倍平均电场强度时,流注将击穿棒-板间隙。
4)负离子层积聚是漫射区产生的主要原因。这是由于负离子层造成板电极区域内电场增强,使得电子更容易获取能量,加剧了电离和激发反应。
参考文献
[1] 张贵新, 李大雨, 王天宇. 交流电压下气固界面电荷积聚与放电特性研究进展[J]. 电工技术学报, 2022, 37(15): 3876-3887.
Zhang Guixin, Li Dayu, Wang Tianyu. Progress in researching charge accumulation and discharge characteristics at gas-solid interface under AC voltage[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3876-3887.
[2] 王瑞雪, 李忠文, 虎攀, 等. 低温等离子体化学毒剂洗消技术研究进展[J]. 电工技术学报, 2021, 36(13): 2767-2781.
Wang Ruixue, Li Zhongwen, Hu Pan, et al. Review of research progress of plasma chemical warfare agents degradation[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2767-2781.
[3] Masuda S. Pulse corona induced plasma chemical process: a horizon of new plasma chemical technologies[J]. Pure and Applied Chemistry, 1988, 60(5): 727-731.
[4] Starikovskaia S M. Plasma assisted ignition and combustion[J]. Journal of Physics D: Applied Physics, 2006, 39(16): R265-R299.
[5] 宋辉, 孟祥麟, 盛戈皞, 等. 短空气间隙流注放电的实验观测技术综述[J]. 电网技术, 2022, 46(2): 774-785.
Song Hui, Meng Xianglin, Sheng Gehao, et al. Overview of experimental observation technology for short air gap streamer discharge[J]. Power System Technology, 2022, 46(2): 774-785.
[6] Loeb L B, Brown S C. Electrical coronas: their basic physical mechanisms[J]. Physics Today, 1966, 19(1): 109-111.
[7] Ono R, Oda T. Ozone production process in pulsed positive dielectric barrier discharge[J]. Journal of Physics D: Applied Physics, 2007, 40(1): 176-182.
[8] Eichwald O, Ducasse O, Dubois D, et al. Experimental analysis and modelling of positive streamer in air: towards an estimation of O and N radical production[J]. Journal of Physics D: Applied Physics, 2008, 41(23): 234002.
[9] 杨亚奇, 李卫国, 夏喻, 等.低气压下长间隙交直流放电特性研究[J]. 电工技术学报, 2018, 33(5): 1143-1150.
Yang Yaqi, Li Weiguo, Xia Yu, et al. Research of AC and DC discharge characteristics of long gap under low pressure[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1143-1150.
[10] 孟晓波, 惠建峰, 卞星明, 等. 低气压下流注放电特性的研究[J]. 中国电机工程学报, 2011, 31(25): 139-149.
Meng Xiaobo, Hui Jianfeng, Bian Xingming, et al. Research on the characteristic of streamer discharge at low air pressure[J]. Proceedings of the CSEE, 2011, 31(25): 139-149.
[11] Chen She, Wang Feng, Sun Qiuqin, et al. Branching characteristics of positive streamers in nitrogen-oxygen gas mixtures[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(3): 1128-1134.
[12] 夏喻, 李卫国, 陈艳. 高空下棒-板间隙直流放电特性及电压校正[J]. 电工技术学报, 2018, 33(9): 2115-2120.
Xia Yu, Li Weiguo, Chen Yan. DC discharge performance and voltage correction of air gaps under high altitude[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2115-2120.
[13] 董曼玲. 直流条件下厘米级间隙流注特性数值仿真及实验研究[D]. 武汉: 华中科技大学, 2012.
Dong Manling. Numerical simulation and experimental research of DC corona streamer in centimeter-level air gap[D]. Wuhan: Huazhong University of Science and Technology, 2012.
[14] Davies A J, Davies C S, Evans C J. Computer simulation of rapidly developing gaseous discharges[J]. Proceedings of the Institution of Electrical Engineers, 1971, 118(6): 816.
[15] Nikonov V, Bartnikas R, Wertheimer M R. Surface charge and photoionization effects in short air gaps undergoing discharges at atmospheric pressure[J]. Journal of Physics D: Applied Physics, 2001, 34(19): 2979-2986.
[16] Peek F W. Dielectric Phenomena in High-Voltage Engineering[M]. 3rd ed. New York: McGraw-Hill book company, inc., 1929.
[17] Lowke J J, D'Alessandro F. Onset corona fields and electrical breakdown criteria[J]. Journal of Physics D: Applied Physics, 2003, 36(21): 2673-2682.
[18] 刘鹏, 郭伊宇, 吴泽华, 等. 特高压换流站大尺寸典型电极起晕特性的仿真与试验[J]. 电工技术学报, 2022, 37(13): 3431-3440.
Liu Peng, Guo Yiyu, Wu Zehua, et al. Simulation and experimental study on corona characteristics of large size typical electrodes used in UHV converter station[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3431-3440.
[19] Xiao Dengming. Gas Discharge and Gas Insulation[M]. Berlin, Heidelberg: Springer, 2016.
[20] 李向荣, 王飞鹏, 黄正勇, 等. 光电离对天然酯绝缘油流注放电影响规律[J]. 电工技术学报, 2023, 38(12): 3350-3365.
Li Xiangrong, Wang Feipeng, Huang Zhengyong, et al. Impact of photoionization on streamer discharge in natural ester insulating oil[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3350-3365.
[21] 程晨, 陈维江, 贺恒鑫, 等. 基于脉冲定量纹影系统的正先导放电起始阶段通道瞬态温度测量[J]. 电工技术学报, 2023, 38(23): 6483-6493.
Cheng Chen, Chen Weijiang, He Hengxin, et al. Experimental measurement on the transient temperature evolution of positive initial leader channel based on pulse-driven quantitative schlieren system[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6483-6493.
[22] Zhelezniak M B, Mnatsakanian A, Sizykh S. Photoionization of nitrogen and oxygen mixtures by radiation from a gas discharge[J]. High Temperature Science, 1982, 20(3): 357-362.
[23] Bourdon A, Pasko V P, Liu N Y, et al. Efficient models for photoionization produced by non-thermal gas discharges in air based on radiative transfer and the Helmholtz equations[J]. Plasma Sources Science and Technology, 2007, 16(3): 656-678.
[24] 蔡新景, 王新新, 邹晓兵, 等. 基于Helmholtz模型的流注放电过程光电离快速计算[J]. 中国电机工程学报, 2015, 35(1): 240-246.
Cai Xinjing, Wang Xinxin, Zou Xiaobing, et al. Fast computation of photoionization in streamer discharges based on Helmholtz model[J]. Proceedings of the CSEE, 2015, 35(1): 240-246.
[25] 彭长志, 董旭柱, 赵彦普, 等. 正极性先导起始与发展过程中的等离子体特征[J]. 电工技术学报, 2023, 38(2): 533-541.
Peng Changzhi, Dong Xuzhu, Zhao Yanpu, et al. Plasma characteristics of positive leader inception and development[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 533-541.
[26] Pitchford L C, Alves L L, Bartschat K, et al. LXCat: an open-access, web-based platform for data needed for modeling low temperature plasmas[J]. Plasma Processes and Polymers, 2017, 14(1/2): 1600098.
[27] Carbone E, Graef W, Hagelaar G, et al. Data needs for modeling low-temperature non-equilibrium plasmas: the LXCat project, history, perspectives and a tutorial[J]. Atoms, 2021, 9(1): 16.
[28] Pancheshnyi S V, Yu Starikovskii A. Stagnation dynamics of a cathode-directed streamer discharge in air[J]. Plasma Sources Science and Technology, 2004, 13(3): B1-B5.
Abstract The genesis and development mechanisms of streamers during centimeter gap corona discharge should be thoroughly studied in order to increase the DC transmission system's dependability and plasma output on a commercial scale. Few investigations have been done so far on the streamer discharge in the centimeter-level air gap. Using atmospheric circumstances and an 18 cm rod-plate gap, a simulation model of the plasma chemistry of streamer discharge is built in this article. To check the accuracy of this simulation model, an experimental platform is being developed.
Both the Raether and the Meek criteria are predicated on the uniform field, making them inappropriate for determining the flow discharge start at the bar-plate electrode. And the photoelectric ionization criteria is a mathematical model that is based on the highly theoretical flow formation process. Quantitatively solving the model is challenging due to the complexity of the various variable values. The flow is therefore assumed to begin when the electron density exceeds 1018 m-3 in this research based on the experience of flow modeling.
This work examines the distribution and development law of charged particles, average electron energy, and electric field intensity in the growth of streamer discharge based on the simulation results. The findings demonstrate that high-energy electrons are mostly present in the head of the streamer, where their ionization reaction leads in a significant production of positive ions, which distorts the spatial electric field. As a result, both the distribution of the spatial electric field and the average electron energy are compatible with the distribution of electron density.
The maximum development length l of the streamer and the electric field intensity Es at the head of the streamer under a very uneven electric field are determined in this work using the Raether and Meek criterion as inspirations. The findings indicate that the length of the streamer is less than 6 cm when the electric field distortion of the streamer head is less than one times the average electric field, less than 14.5 cm when the electric field distortion is one to five times the average electric field, and less than 12 times the average electric field when the streamer will break through the rod plate gap. The creation of diffuse zone is mostly caused by the accumulation of negative ion layer. This is due to the negative ion layer's augmentation of the electric field in the plate electrode region, which makes it simpler for electrons to get energy, as well as the intensification of the ionization and excitation reactions.
The negative DC rod plate discharge experiment is conducted to ensure the simulation model's accuracy, and the calculated discharge current and experimental discharge current are compared. According to the experimental findings, the streamer and anode glow regions make up the streamer corona. The shape and placement of the streamer, which has a length of approximately 16.66 cm, change depending on the voltage being used. Anode glow area development is mostly due to the distortion of the anode electric field brought on by the negative ion sheath.
In summary, the insights reached in this work can serve as a theoretical foundation for explaining the mechanism of streamer discharge formation and development in negative polarity corona discharge as well as plasma preparation.
keywords:Streamer corona, glow discharge, Raether criterion, Meek criterion, ion sheath, rod-plate gap
中图分类号:TM851
DOI:10.19595/j.cnki.1000-6753.tces.222186
山东省重点研发计划资助项目(2019GGX102049)。
收稿日期 2022-11-21
改稿日期 2022-12-21
李长云 男,1974年生,工学博士,副教授,研究方向为高压电气设备运行与故障诊断、能源互联网中的绝缘技术。E-mail:sdlcyee@sdust.edu.cn(通信作者)
李岩青 男,1998年生,硕士研究生,研究方向为高电压气体放电。E-mail:874752886@qq.com
(编辑 李 冰)