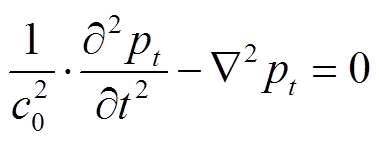（1）
摘要 基于到达时间差（TDOA）的声源定位方法是当前气体绝缘输电线路（GIL）故障定位的主要方式，声波在GIL结构上的传输特性深刻影响着定位结果的准确性。为进一步提升故障定位精度，该文提出了考虑导波频散与多模态特性的GIL壳体声传输分析模型，以典型220 kV GIL管段为研究对象，建立声波传输有限元模型，研究了导波特性对故障定位的影响，确定了适用于故障定位的超声导波模态以及GIL非直管结构对该模态导波的衰减与时延量，通过现场定位试验验证了分析模型的可行性，为GIL声源故障定位系统的传感器配置与定位阈值设置提供了计算依据。结果表明，在20～60 kHz频带内，F(1, 1)模态导波具有能量高、波形形状稳定、抗干扰能力强等特点，使用该模态导波进行故障定位精度较高。GIL非直管结构会对F(1,1)模态导波造成较大的幅值衰减与一定程度的时延，在故障定位中考虑非直管结构衰减与时延影响可以使定位误差降低60%以上。
关键词：气体绝缘输电线路（GIL） 故障定位 到达时间差（TDOA） 超声导波 传播特性
伴随着我国“双碳”目标的逐步推进以及新型电力系统建设的进一步加快，开发并接纳更高比例的新能源势在必行。作为一种新型的电能输送方式，气体绝缘输电线路（Gas-Insulated transmission Line, GIL）可针对性地解决新能源开发中能量密度低、占地面积大、源端环境复杂等特性带来的电能送出难问题[1-2]，已广泛应用于我国水电站、核电站建设中，在大规模海上风电场电能汇集与特高压输电通道特殊地形跨越等方面也存在广阔的应用前景[3-4]。
GIL在结构上类似于气体绝缘开关设备（Gas-Insulated Switchgear, GIS）母线，但其长度远超后者，同时还包含大量的伸缩节、气隔单元等非直管结构，应用在GIS上的一系列在线监测方法需根据GIL自身结构特点做进一步的改进与优化，以满足监测系统可靠性与经济性的要求。相比于人工监听法、化学检测法等传统GIS故障定位方法，基于到达时间差（Time Difference of Arrival, TDOA）的声源定位方法作为一种非侵入式的在线监测方式，可较好地兼顾GIL绝缘故障定位快速性与精确性的需求，已逐步配置于近年新建GIL项目中[5-7]。
声波自声源发出后，受被测物结构限制主要在其结构内传播，声波在结构中的传播特性是影响基于TDOA定位方法准确度的主要因素。20世纪90年代以来，国内外学者对声波在短距离GIS母线中的传播理论[8-10]、传播路径[11-12]与幅值衰减情况[13-15]开展了相应的研究。近年来，为完善GIL声定位理论，一些学者分析了GIL直管区段的声场分布[16]、声频谱特性[17]，以及GIL伸缩节、气隔单元等非直管结构的声衰减量[18]与时延量[19]。实际上，声波沿GIL壳体传输时具有频散与多模态特性，频散指声波速度随着频率的变化而改变；多模态指沿GIL壳体传播的声波存在多种模态，同频率下不同模态的声波具有不同的声速。现阶段研究一般将GIS/GIL内传播的声波简化为速度恒定的横、纵波，未考虑频散与多模态特性对声波传输带来的复杂影响，研究成果与实际存在偏差，难以对定位系统精度的提升形成有效指导。
鉴于此，本文提出了一种考虑导波频散与多模态特性的GIL壳体声传输分析模型，通过声-结构耦合数值仿真研究声波在GIL典型区段的传播特性，确定适用于故障定位的超声模态以及该模态经过GIL伸缩节、气隔盆子等非直管结构的衰减与时延情况，为GIL声源定位系统配置提供指导，对于GIL故障定位精度的提升具有重要的意义。
GIL内部发生放电性故障时，故障点附近的SF6发生膨胀压缩，产生以球状波阵面形式扩散传播的声波[20]。声波在SF6中传播时仅有纵波一种形式，到达GIL壳体后将转换为纵向波、扭转波、弯曲波等多种形式，以不同的速度沿着GIL壳体传播，其波形转换情况遵循声波的折反射定律[21]。
声波从声源传播至位于GIL壳体表面的声发射传感器存在多种路径，由于金属介质中声波传播速度快且损耗小，从声源点以直线最短距离传播至GIL壳体并沿壳体继续传播的直达声波将最早到达传感器并用于故障定位[22]。因为该声波的传播路径主要位于GIL壳体，因此其在GIL壳体内的传播特性决定着故障定位结果的准确度。
直达声波的传播路径涉及SF6气体与GIL金属壳体两类介质。将GIL内的SF6看作理想气体，可以用声压波动方程描述声波在SF6中传播的基本规律[23]，即
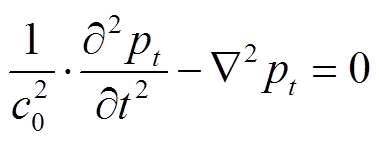（1）
式中，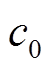
为SF6中声波的传播速度，m/s；
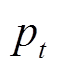为声压，Pa。相比于标准大气压，GIL内0.4～0.6 MPa的工作气压会使声波在SF6中的传播速度略微下降，由于直达声波在SF6中的传播距离很短，因此GIL内气压大小对故障定位的影响可以忽略。
将GIL金属壳体看作线弹性体，根据弹性动力学的位移解法，可以用以位移表示的运动微分方程描述声波在GIL壳体中传播的基本规律[24]。
（2）
式中，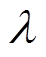
、
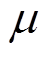分别为拉梅第一、第二系数，Pa；
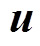为位移矢量，m；
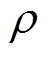为固体介质密度，kg/m3。
在流-固交界面上，两种介质所满足的边界条件可以用式（3）表示，其中上标A表示固体介质，上标B表示流体介质。
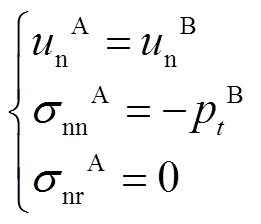（3）
式中，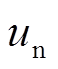
为法向位移，m；
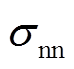为法向应力，Pa；
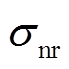为切向应力，Pa。
GIL壳体可近似为长距离圆柱壳波导结构，存在内、外两个流-固交界面，沿GIL壳体传播的声波不断在两个交界面发生折、反射，横波与纵波干涉耦合形成声导波，其在GIL壳体中的传播情况如图1所示。
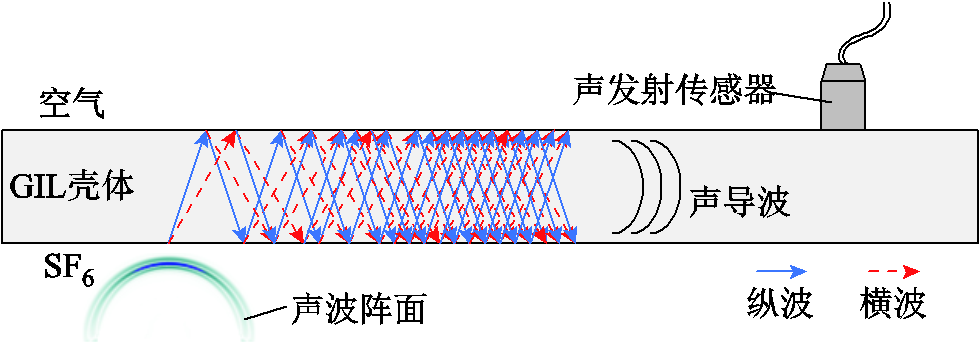
图1 声导波在GIL壳体中的传播情况
Fig.1 Propagation of guided wave in GIL shell
声导波的传播特性与波导边界条件有关。将时谐波通解与圆柱壳内、外表面的应力边界条件引入式（2），经过变换得到描述GIL壳体中导波传播情况的频率方程[25]为
（4）
式中，Cij为6×6系数矩阵中的元素，描述了波数、角频率、GIL壳体内外径及壳体材料参数间的复杂关系。通过数值方法求解上述隐式超越方程，可以得到描述波速度和频率之间关系的频散曲线。
根据国产某型220 kV GIL结构尺寸，绘制导波在其壳体中传播的群速度频散曲线，如图2所示。
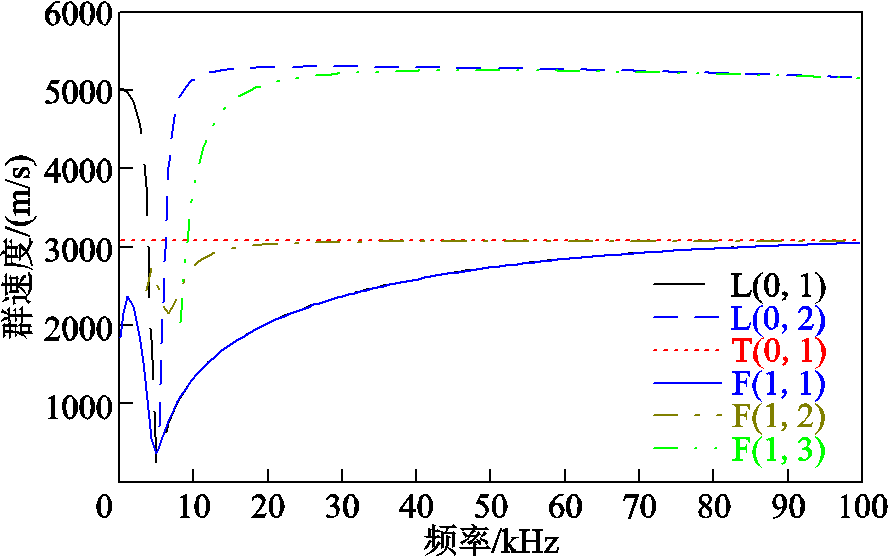
图2 220 kV GIL壳体内导波群速度频散曲线
Fig.2 Guided wave group velocity dispersion curve in 220 kV GIL shell
图2中的每一条曲线代表导波的一种模态，可以看出，在0～100 kHz范围内，沿GIL壳体结构传播的导波模态主要有六种，包括纵向波L(0, 1)和 L(0, 2)，扭转波T(0, 1)，弯曲波F(1, 1)、F(1, 2)和F(1, 3)。当导波频率在5 kHz以下时，GIL中只存在低阶的纵向波L(0, 1)、扭转波T(0, 1)及弯曲波 F(1, 1)三种模态，其中纵向波和弯曲波存在频散情况，而扭转模态波的群速度和频率无关；当频率上升到5 kHz以上时，逐渐出现L(0, 2)、F(1, 2)和F(1, 3)等新的模态，各模态的能量分布与激励方式有关。
根据图2可以看出，GIL壳体内传播的导波在同一频率下存在多种模态。为探究导波模态对GIL声源故障定位的影响，按上述220 kV GIL结构尺寸构建40 m长GIL直管段声-结构耦合有限元仿真模型，在模型两端添加声吸收边界减少声波的反射，在GIL壳体中央添加径向力模拟最先到达的声波波阵面对GIL壳体的激励作用。GIL直管段仿真模型示意图如图3所示。
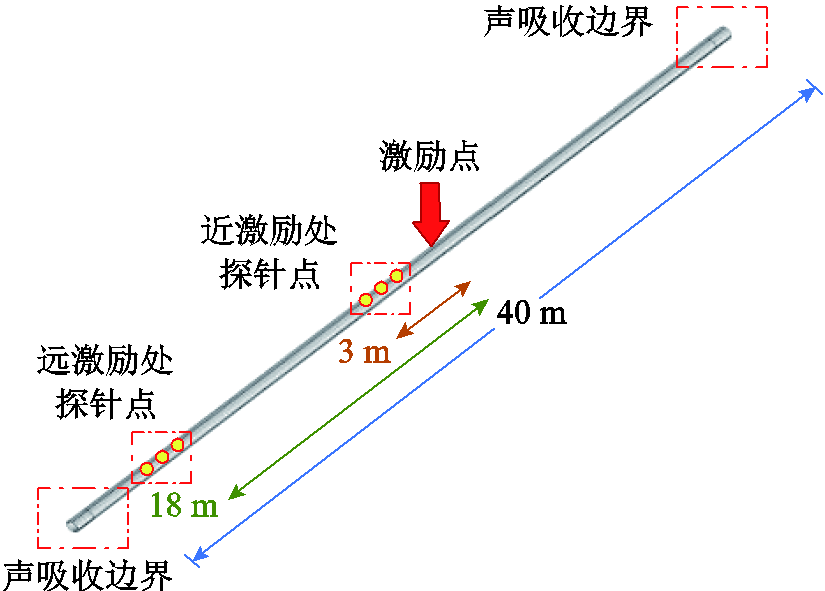
图3 GIL直管段仿真模型示意图
Fig.3 Schematic diagram of GIL straight pipe simulation model
为避免导波的频散特性对仿真结果造成影响，激励信号选用声发射测试中常用的汉宁窗调制正弦信号[26-27]，该信号的频带较窄，能量主要集中在中心频率附近。由于模型的网格尺寸与计算时间步长取决于结构内传播的导波波长，因此结合模型规模与硬件条件将激励信号中心频率设定为10 kHz，周期数设为10，激励信号时域波形如图4所示。
参考实际GIL声源定位系统传感器的安装位置，在距离声源较近的1 m、2 m、3 m及较远的16 m、17 m、18 m处壳体顶部表面布置探针点，绘制加速度时域波形表征声导波的传播状态。由于激励点两侧的仿真结果具有对称性，因此探针点均设置在激励点同一侧。
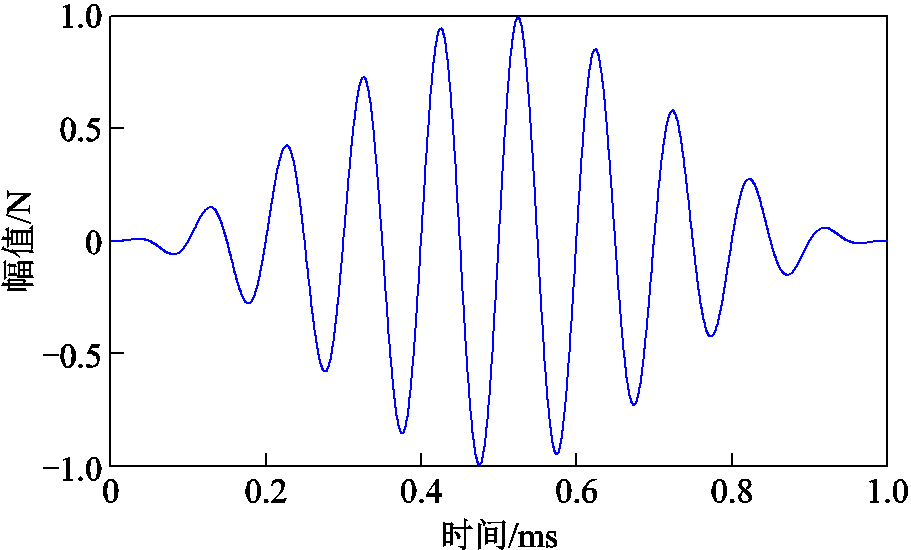
图4 中心频率为10 kHz的汉宁窗调制正弦波激励信号
Fig.4 Hanning window modulated sine wave excitation signal with center frequency of 10 kHz
近激励处三个探针点的时域波形如图5所示。可以看出，激励点附近的声导波主要由激励直接产生的一次声波和一次声波在GIL壳体上下边界来回反射产生的二次声波组成，整体呈现衰减振荡形态。
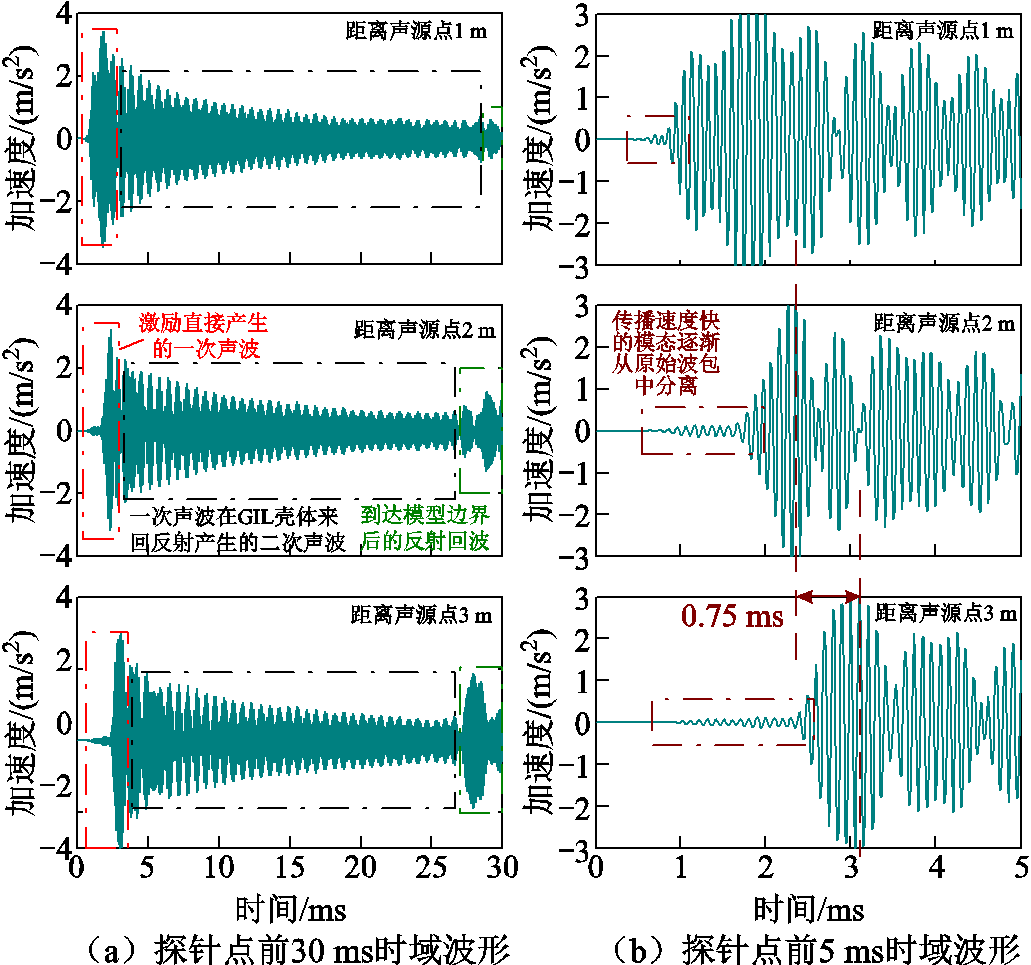
图5 近激励处各位置的声导波时域波形
Fig.5 Time-domain waveforms of guided wave at various positions near the excitation
由激励直接产生的一次声波的原始波包一开始包含多种声模态，随着传播距离的增加，传播速度有所差异的各模态将逐渐从中分离，原始波包形状在此期间变化剧烈。
在声模态能量分布方面，计算得到的一次声波原始波包速度约为1 300 m/s，与图2中弯曲波F(1, 1)和纵向波L(0, 1)在10 kHz处的波速相对应，说明这两种模态或其中之一占一次声波能量的主要部分。
远离激励处三个探针点的时域波形如图6所示。可以看出，传播一定距离后，由激励直接产生的一次声波的原始波包已分离成若干个幅值各异的波包，使声能量分散在更宽的时域空间中。
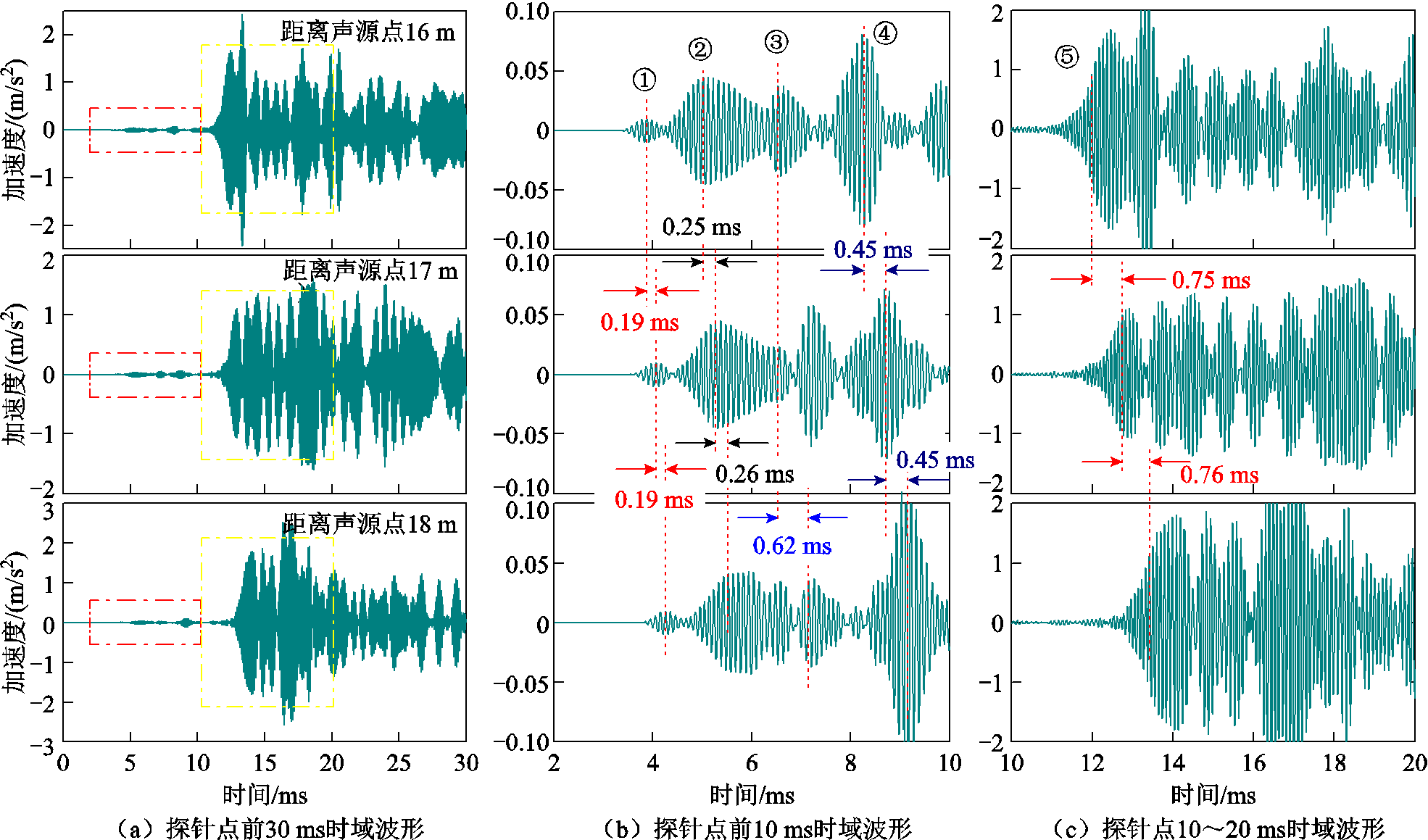
图6 远激励处各位置的声导波时域波形
Fig.6 Time-domain waveforms of guided wave at various positions away from the excitation
图6中，各探针点波形前方由幅值较小的波包①～④以及幅值较大的波包⑤构成，计算得到的传播速度分别为5 300、3 900、3 200、2 300、1 300 m/s，分别与图2中的L(0, 2)、F(1, 3)、T(0, 1)、F(1, 2)以及F(1, 1)和L(0, 1)模态在10 kHz处的波速相近，证明本文所建立的仿真模型遵循导波的传播理论可有效表征GIL壳体内导波的传播过程。
在模态波波形方面，纵向波L(0, 2)和弯曲波 F(1, 3)因传播速度明显快于其他模态而所受干扰较小，传播过程中波包形状最为稳定且易于区分；扭转波T(0, 1)和弯曲波F(1, 2)由于波速较慢且相近，在传播过程中易受到彼此以及后方二次声波中 L(0, 2)与F(1, 3)等波速较快模态的干扰，传播时波包形状变化较大，增大了区分的难度；弯曲波 F(1, 1)和纵向波L(0, 1)传播速度相近，这两种模态对应的波包⑤幅值是前方波包①～④幅值的20余倍，传播过程中波包形状基本稳定。
为了明晰F(1, 1)与L(0, 1)模态的声能量占比，在模型上重新施加中心频率为2 kHz的汉宁窗调制正弦信号激励，计算得到一次声波原始波包的传播速度约为2 000 m/s，对应F(1, 1)模态在 2 kHz处的波速，表明在沿径向激励GIL壳体的情况下，低阶弯曲波F(1, 1)的能量占一次声波能量的主要部分。
GIL声源定位属于被动监测，不能同超声探伤一样选择输出单一的声模态，必须确定用于故障定位的有效模态[28]。对基于直接时延估计的TDOA定位方法而言，位于前方的一次声波L(0, 2)、F(1, 3)等传播速度较快的模态虽然波包形状稳定，理论定位精度高，但其幅值较小，加之GIL现场环境噪声复杂，定位系统的信噪比往往难以满足要求；位于后方的二次声波受扩散、反射及干涉等情况影响，模态混叠现象严重，在传播过程中变化剧烈的波包形状难以满足定位精度的要求。相比之下，一次声波F(1, 1)模态具有能量大、抗噪声及模态干扰能力强、波包形状较稳定等优点，在GIL声源故障定位方面具备优势。
GIL发生放电性故障时产生的声信号频带很宽，沿GIL壳体传播的导波不但存在多种模态，还会在传播过程中发生频散现象。为了降低导波的频散特性对GIL声源故障定位的影响，需要确定合适的定位频带。
在GIS放电性故障模拟试验装置壳体上布置声发射传感器，通过装置内部故障模型产生放电，测试壳体上声波的频带能量分布，试验布置如图7所示。
在测试中分别记录GIS内部放电、周围环境风机、人员说话声等激励下声波信号时域波形。因为GIL壳体中传播的声波信号属于机械振动信号，因此选用振动信号处理中常用的db7小波对被测信号进行7层小波分解，计算对应的近似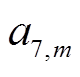系数
与细节系数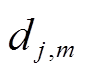
(j=1～7)。由于测试中使用的信号采样频率为1 MHz，其对应的奈奎斯特频率为500 kHz，信号7层分解下得到8个频带见表1。
图7 GIL放电性故障声波特性测试
Fig.7 Acoustic characteristic test of GIL discharge fault
表1 不同激励下GIL壳体内声波频带能量分布
Tab.1 Energy distribution of sound wave band in GIL shell under different excitations
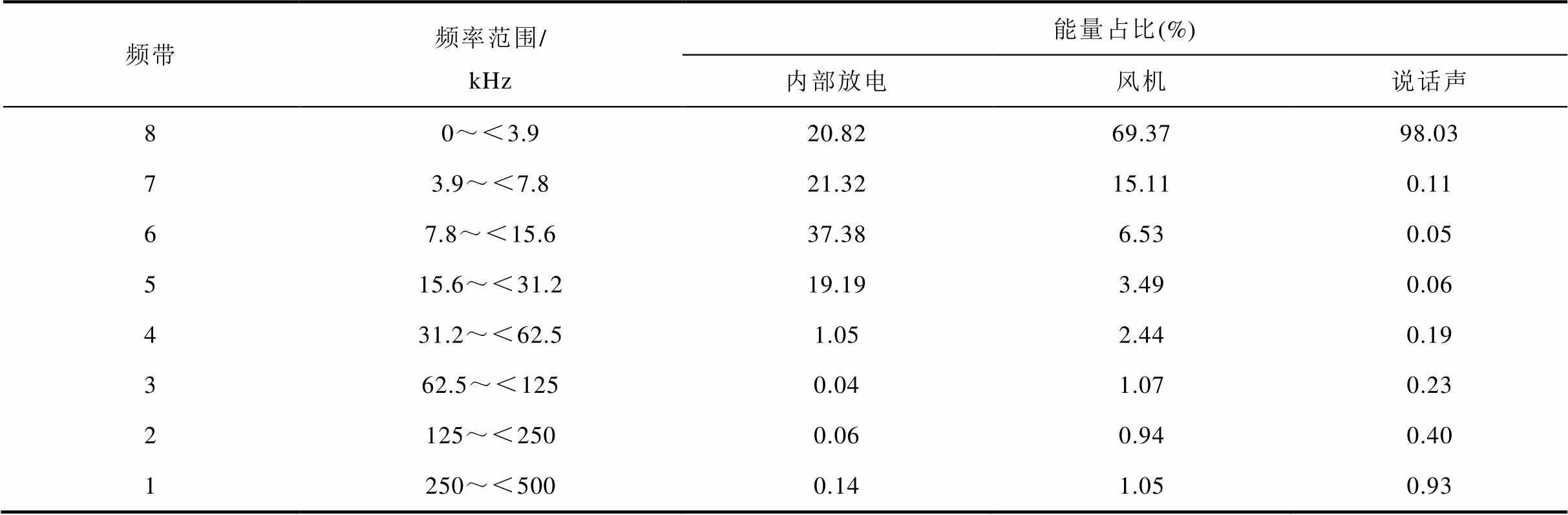
频带频率范围/ kHz能量占比(%) 内部放电风机说话声 80～＜3.920.8269.3798.03 73.9～＜7.821.3215.110.11 67.8～＜15.637.386.530.05 515.6～＜31.219.193.490.06 431.2～＜62.51.052.440.19 362.5～＜1250.041.070.23 2125～＜2500.060.940.40 1250～＜5000.141.050.93
频带8能量占比的计算表达式为
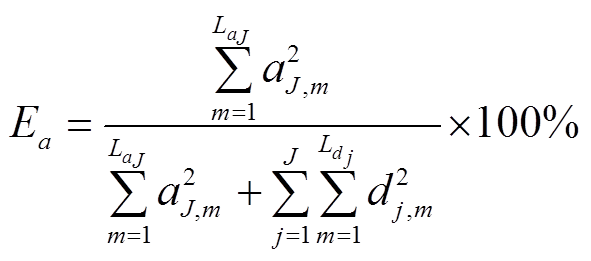（5）
式中，J为小波分解的层数；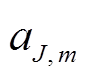
为第J层对应的第m个近似系数；dj,m为第j层对应的第m个细节系数；
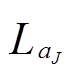为第J层近似系数的长度；
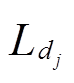为第j层细节系数的长度。
频带1～7能量占比Ed, j的计算表达式[29]为
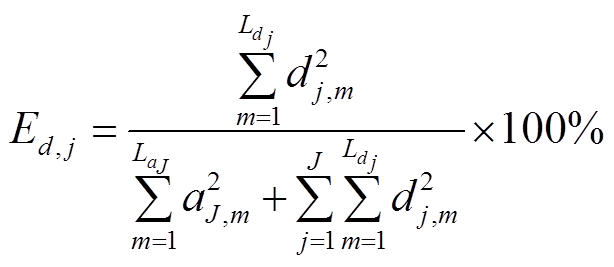（6）
根据式（5）与式（6）计算各频带的能量占比，结果见表1。
从表1可以看出，排除信号采集设备自身引入的高频噪声，GIL内部放电产生的声波能量主要集中在第4～8频带范围，基本位于60 kHz以内；风机、说话声等环境干扰主要集中在第7～8频带范围，基本位于10 kHz以下的低频带。图2所示的频散曲线中，GIL壳体内各模态波速在0～20 kHz频带内随频率变化剧烈，在20～100 kHz频带内基本保持平稳。基于上述两点，应选择20～60 kHz频带作为GIL声源故障定位的监测频带，可以有效地降低环境噪声与导波频散特性对GIL声源故障定位的影响。
使用上述40 m长GIL直管段仿真模型分析宽频带超声导波在GIL直管区段的传播情况，将激励施加于距模型右侧边界10 m处，在激励点左侧2～27 m位置内布置6个探针点，整体模型示意图如图8所示。
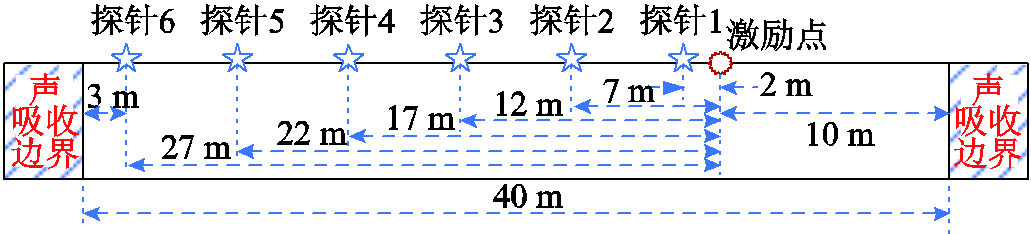
图8 GIL直管段超声导波传播特性模型示意图
Fig.8 Schematic diagram of ultrasonic guided wave propagation characteristic model in GIL straight pipe
锤击法作为GIS/GIL故障定位测试中常用的一种声波激励方法[30-31]，通过压电式冲击力锤对GIS/GIL壳体施加瞬间冲击模拟内部放电时壳体受到的激励作用，同时根据力锤内置传感器输出的冲击力波形的幅值对锤击强度进行描述。在图7所示装置上分别采用加压放电与力锤敲击壳体的方式激励声波，根据两种激励方式下到达传感器的声波时域波形最大幅值，确定接近放电强度的锤击强度及对应的冲击力波形，同时将带通滤波与归一化处理后的传感器输出信号频谱进行比较，结果如图9所示。可以看出，在所确定的20～60 kHz定位频带内，力锤激励与放电激励的声波频谱均在25 kHz左右达到峰值，两者在分布上具有相似性。因此，在模型激励信号的选取上，将力锤输出的冲击力波形经三次样条插值平滑化处理后作为激励施加在模型之上。
将各探针点获得的声波信号按所确定的定位频带进行带通滤波处理，所得到的时域波形如图10所示。
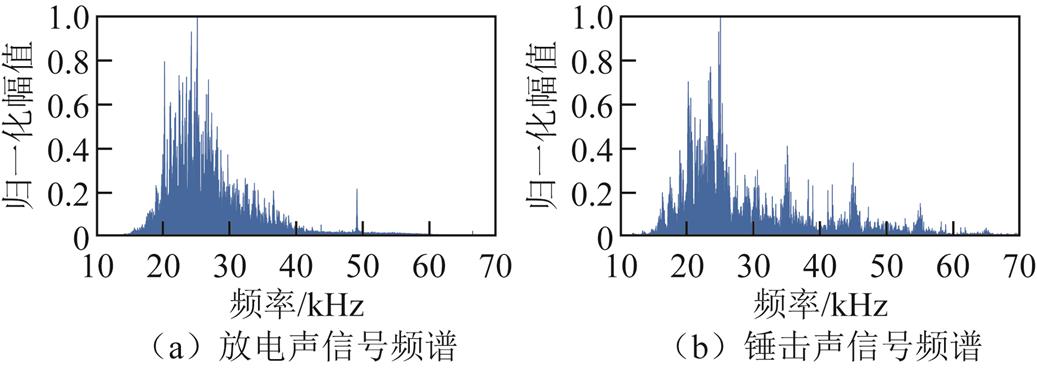
图9 放电与锤击激励下声信号频谱
Fig.9 Spectrum of acoustic signal under discharge and hammer excitation
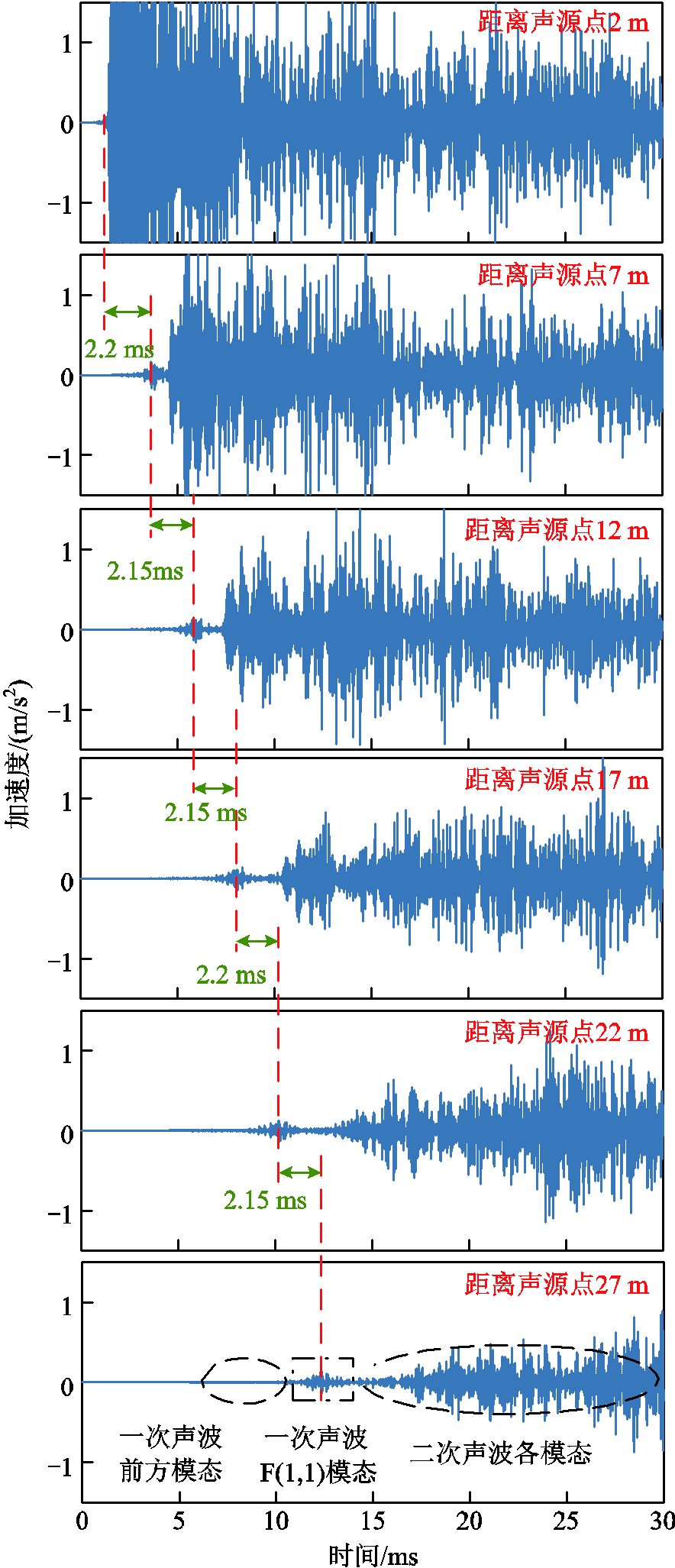
图10 各探针点超声导波时域波形
Fig.10 Time-domain waveforms of ultrasonic guided wave at each probe point
从图10可以看出，在所选定位频带内，沿GIL壳体传播的超声导波在时域上可以分为一次声波L(0, 2)、F(1, 3)等前方模态、一次声波F(1, 1)模态及二次声波三部分，各部分在幅值与波包形状方面区分明显，受频散干扰较小。
其中，一次声波前方模态在传播过程中波包形状稳定，幅值衰减小，但其幅值仅为一次声波F(1, 1)模态的1/20；二次声波相比窄频带激励下包含更多的模态导波，整体幅值高，但在传播过程中波包形状变化剧烈，幅值衰减较快。
对于一次声波F(1, 1)模态，其自原始波包分离所需的传播距离在2 m以内，在传播过程中幅值衰减较慢，10 m幅值衰减量约为30%，在时空分布上与前方及后方模态导波混叠程度低，波包形状整体稳定，易于定位算法辨别区分。因此，应选用弯曲波F(1, 1)作为GIL声源故障定位的有效模态。
在波形能量方面，一次声波F(1, 1)模态导波的传播速度约为2 300 m/s，在图2频散曲线中所对应的频率为25 kHz，与图9锤击声信号频谱峰值对应频率一致，说明定位频带内能量最高的频率成分对一次声波F(1, 1)模态导波的形成起主要贡献，由此可根据声信号频谱与频散曲线确定用于故障定位的F(1, 1)模态导波的传播速度。
工程经验表明，GIL伸缩节、气隔盆子等非直管结构对沿壳体传播的导波信号具有明显的幅值衰减与时延作用，展现出与直管段截然不同的声传输特性，需要在GIL声源故障定位中特别考虑。
为研究F(1, 1)模态导波经过GIL非直管结构的传播特性，对国产该型220 kV GIL单级伸缩节、双级伸缩节、气隔盆子等非直管结构单元进行三维结构建模，并与直管结构模型组合形成GIL非直管区段声波传输仿真模型。将探针点布置在待测非直管结构两侧，同时在距离待测结构较远处施加力锤冲击激励。220 kV GIL非直管结构及仿真模型如图11所示，模型布置示意图如图12所示，探针点时域波形如图13所示。
图11 220 kV GIL非直管结构及仿真模型
Fig.11 220 kV GIL non-straight pipe structure and simulation model
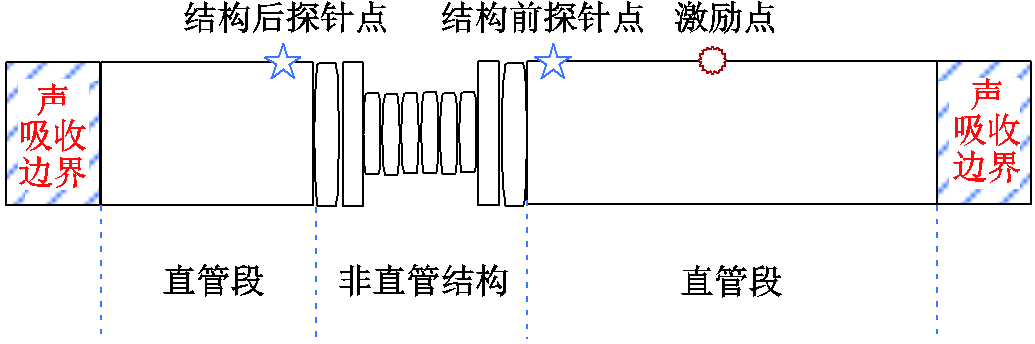
图12 GIL非直管区段声波传输模型布置示意图
Fig.12 Schematic diagram of the acoustic wave transmission model in GIL non-straight pipe section
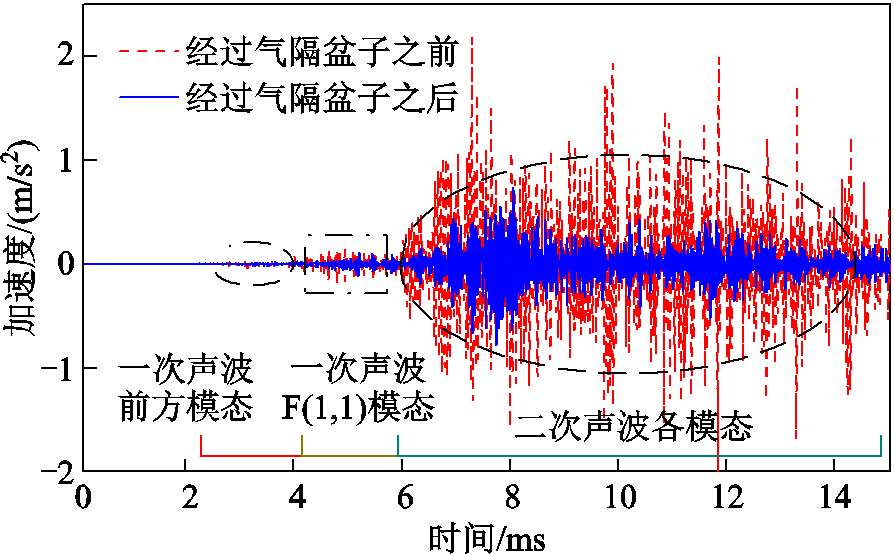
图13 超声导波经过气隔盆子前后对比
Fig.13 Comparison of ultrasonic guided wave before and after passing through gas basin insulator
从图13可以看出，经过GIL非直管结构前后的超声导波在时域上仍可分为上述三部分，但受非直管结构与直管段间声阻抗不匹配的影响，一次声波前方模态出现混叠，难以对单一模态进行辨别；二次声波各模态波包形状变化仍十分剧烈，不具备故障定位优势；相比之下，一次声波F(1, 1)模态同其他模态混叠程度低，易于从幅值上区分，经非直管结构后波包幅值仍保持在一次声波前方模态4倍以上，具有辨识度高、经过非直管结构后波形形状变化小等优点，在含非直管结构的GIL定位区段保持上述故障定位优势。
以经过非直管结构前后的F(1, 1)模态导波波包幅值为基准计算声衰减量，以F(1, 1)模态导波在直管上的传播速度为基准计算声时延量，计算得到的弯曲波F(1, 1)经过GIL非直管结构的传播特性见表2。
表2 弯曲波F(1, 1)经过GIL非直管结构的传播特性
Tab.2 Propagation characteristics of bending wave F(1, 1) through GIL non-straight pipe structure
GIL结构结构长度/m声衰减量(%)传播波速/(m/s)声时延量/ ms 单级伸缩节0.61907000.6 双级伸缩节0.99966501.1 气隔盆子0.38602 0000.03
结果表明，GIL伸缩节与气隔盆子均会对F(1, 1)模态导波造成较大的幅值衰减，但F(1, 1)模态导波经过气隔盆子时的传播速度基本不会下降，因此伸缩节是造成F(1, 1)模态导波时延的主要因素。
为了验证本文所提出的分析模型的正确性，在某GIL生产现场开展故障定位测试，如图14所示。试验所用的GIL由5节8 m长直管段与1节单级伸缩节组合而成，在伸缩节附近的导体上内置缺陷模型，用于产生放电性声信号。在声源两侧10 m距离处的GIL壳体表面布置传感器，构成一个20 m长的定位区间，记录到达的声波信号。
图14 220 kV GIL故障定位测试现场
Fig.14 220 kV GIL fault location test site
基于直接时延估计的TDOA定位方法通过所设定的定位阈值确定时域波形信号前方的定位特征点，根据特征点对应时刻计算声波到达定位区间两侧传感器的时间差，并根据设定的声波波速推算声源点位置，定位原理如图15所示。由于缺乏相关标准及确切的研究数据，工程上多采用经验法确定定位阈值与计算波速。对于包含非直管结构的定位区间，工程上一般采用纯直管简化或定位区间等效波速两种方法考虑非直管结构对故障定位造成的影响。
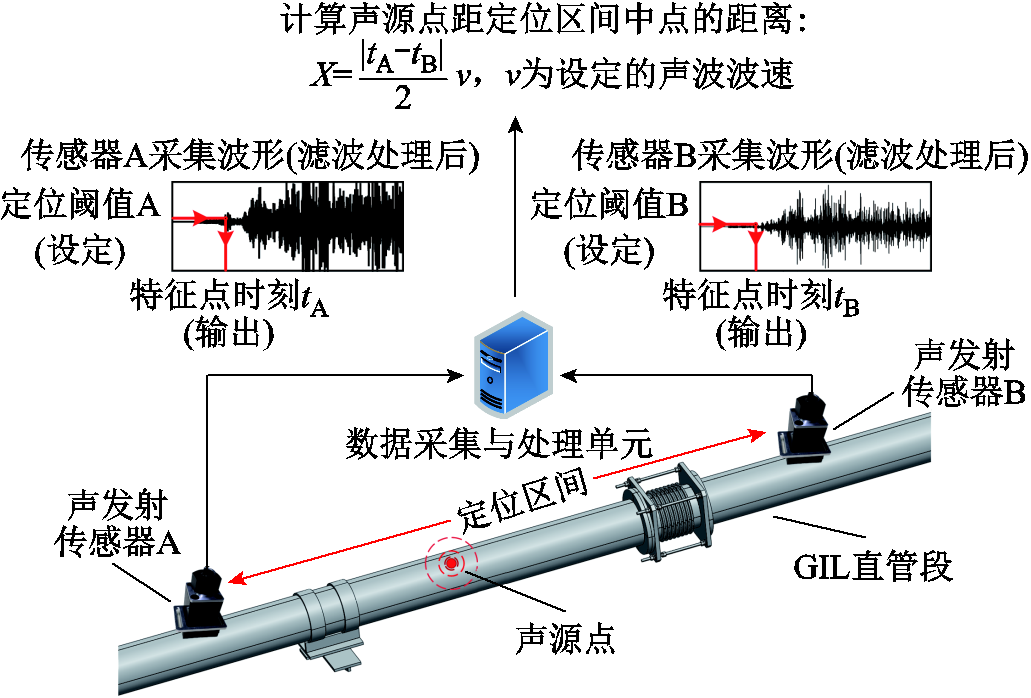
图15 基于直接时延估计的TDOA定位方法原理
Fig.15 Principle of TDOA location method based on direct time delay estimation
基于本文提出的分析模型，在测试中根据F(1, 1)模态导波特点及单级伸缩节对其造成的声衰减量确定定位区间两侧的定位阈值及声波波速，以便使用F(1, 1)模态导波进行故障定位。同时，提出在到达时间差中减去非直管结构声时延量的新方法考虑GIL非直管结构对故障定位造成的影响，并与上述两种方法的定位结果进行对比。三种方法的定位结果见表3。
表3 GIL故障定位结果
Tab.3 GIL fault location results
GIL定位方法定位变量 到达时差/ms设定波速/(m/s)定位误差/m 纯直管简化0.92 3001.035 等效波速0.91 9000.855 考虑时延0.32 3000.345
可以看出，使用F(1, 1)模态导波进行故障定位精度较高，在此基础上考虑非直管结构衰减与时延的影响可以使GIL故障定位误差进一步降低60%以上。定位试验验证了本文提出的分析模型的合理性。
基本本文成果，应选择20～60 kHz定位频带内一次声波F(1, 1)模态波包作为计算特征点，根据波包幅值确定定位阈值，并结合信号频谱与GIL壳体导波频散曲线确定该模态导波的传播速度。
由于GIL总体长度较长，声源定位系统需布置大量的传感器并形成多个定位区间。根据GIL非直管结构声衰减量计算结果，一个定位区间内应包含不多于两个气隔盆子或一个伸缩节单元，否则F(1, 1)模态导波幅值可能衰减至噪声水平以下。当定位区间内存在伸缩节单元时，需考虑结构时延量对故障定位造成的影响。
此外，一次声波F(1, 1)模态在声源点附近尚未从原始波包分离，不易确定计算特征点，因此在配置GIL故障定位系统时应尽量避免在GIL气隔盆子等放电故障易发生处2 m以内位置布置传感器。
针对GIL声源故障定位机理不明、精度不高这一工程实际问题，本文结合理论分析与数值仿真，对超声导波在GIL壳体内的传播情况与传播规律进行了研究，确定了适用于故障定位的超声模态以及该模态导波经过GIL非直管结构的衰减与时延特性，并得到如下结论：
1）本文提出的GIL壳体声传输分析模型能够考虑声波传播过程中频散与多模态特性带来的影响，所得声波传播规律与导波理论及试验结果可有效对应。
2）综合GIL内部放电声信号频带能量分布与GIL壳体导波频散曲线，选择20～60 kHz作为故障定位的监测频带可有效减少导波频散与环境干扰对GIL声源故障定位的影响。
3）GIL壳体内传播的声导波具有多种模态，其中F(1, 1)模态兼具稳定性与易识别性，使用该模态进行故障定位精度较高。GIL非直管结构会对F(1, 1)模态导波造成较大的幅值衰减与一定程度的时延，在故障定位中考虑非直管结构衰减与时延影响可以使定位误差降低60%以上。
参考文献
[1] 邱玥, 陆帅, 陆海, 等. 综合能源系统灵活性：基本内涵、数学模型与研究框架[J]. 电力系统自动化, 2022, 46(17): 16-43.
Qiu Yue, Lu Shuai, Lu Hai, et al. Flexibility of integrated energy system: basic connotation, mathematical model and research framework[J]. Automation of Electric Power Systems, 2022, 46(17): 16-43.
[2] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4808-4822.
[3] 杜伯学, 董佳楠, 梁虎成. 特高压GIL非均匀热气流特性与三支柱绝缘子绝缘裕度分析[J]. 电工技术学报, 2023, 38(6): 1678-1686.
Du Boxue, Dong Jianan, Liang Hucheng. Non-uniform gas convection in UHV-GIL and insulation margin analysis for tri-post insulator[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1678-1686.
[4] 薛乃凡, 李庆民, 刘智鹏, 等. 微纳粉尘运动行为与微弱放电探测技术研究进展[J]. 电工技术学报, 2022, 37(13): 3380-3392.
Xue Naifan, Li Qingmin, Liu Zhipeng, et al. Research advances of the detection technology for kinetic behavior and weak discharge of the micro-nano dust[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3380-3392.
[5] 刘通, 腾云, 杨景刚, 等. 基于可听声的GIL设备交流耐压击穿放电定位研究[J]. 高压电器, 2021, 57(1): 26-32, 40.
Liu Tong, Teng Yun, Yang Jinggang, et al. Study on AC withstand voltage breakdown discharge location of GIL equipment based on audible-signal[J]. High Voltage Apparatus, 2021, 57(1): 26-32, 40.
[6] 李玉杰, 王枭, 杨景刚, 等. 基于DOA估计的GIL击穿放电定位方法研究[J]. 高压电器, 2022, 58(9): 94-101.
Li Yujie, Wang Xiao, Yang Jinggang, et al. Research on location method of GIL breakdown and discharge based on DOA estimation[J]. High Voltage Apparatus, 2022, 58(9): 94-101.
[7] 罗楚军, 岳浩, 李健, 等. 基于超声波法的长距离超高压GIL电弧故障定位[J]. 电力与能源, 2021, 42(1): 39-45, 136.
Luo Chujun, Yue Hao, Li Jian, et al. Long-distance UHV GIL arc fault location based on ultrasonic method[J]. Power & Energy, 2021, 42(1): 39-45, 136.
[8] Lundgaard L E. Partial discharge. XIII. Acoustic partial discharge detection-fundamental considerations[J]. IEEE Electrical Insulation Magazine, 1992, 8(4): 25-31.
[9] Kranz H G. Fundamentals in computer aided PD processing, PD pattern recognition and automated diagnosis in GIS[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(1): 12-20.
[10] 李成榕, 王浩, 郑书生.GIS局部放电的超声波检测频带试验研究[J]. 南方电网技术, 2007, 1(1): 41-45.
Li Chengrong, Wang Hao, Zheng Shusheng. Experiment research on ultrasonic band selection of GIS partial discharge detection[J]. Southern Power System Technology, 2007, 1(1): 41-45.
[11] 陈隽, 刘文浩, 卢军, 等. GIS中不同位置电晕放电的超声波信号特性[J]. 高电压技术, 2011, 37(12): 3006-3011.
Chen Jun, Liu Wenhao, Lu Jun, et al. Acoustic signal characteristics of corona discharge in different location of GIS[J]. High Voltage Engineering, 2011, 37(12): 3006-3011.
[12] 刘君华, 姚明, 黄成军, 等. 采用声电联合法的GIS局部放电定位试验研究[J]. 高电压技术, 2009, 35(10): 2458-2463.
Liu Junhua, Yao Ming, Huang Chengjun, et al. Experimental research on partial discharge localization in GIS using ultrasonic associated with electromagnetic wave method[J]. High Voltage Engineering, 2009, 35(10): 2458-2463.
[13] 宋蓓华. 基于声电联合的GIS局部放电带电检测技术研究[D]. 上海: 上海交通大学, 2012.
Song Beihua. Based on the UHF and UE combined GIS partial discharge on-line detection technology research[D]. Shanghai: Shanghai Jiao Tong University, 2012.
[14] Lundgaard L E, Runde M, Skyberg B. Acoustic diagnosis of gas insulated substations: a theoretical and experimental basis[J]. IEEE Transactions on Power Delivery, 1990, 5(4): 1751-1759.
[15] 黎大健, 梁基重, 步科伟, 等. GIS中典型缺陷局部放电的超声波检测[J]. 高压电器, 2009, 45(1): 72-75.
Li Dajian, Liang Jizhong, Bu Kewei, et al. Ultrasonic detection of partial discharge on typical defects in GIS[J]. High Voltage Apparatus, 2009, 45(1): 72-75.
[16] 腾云, 杨景刚, 马勇, 等. GIL击穿放电低频声场仿真[J]. 高电压技术, 2020, 46(3): 906-914.
Teng Yun, Yang Jinggang, Ma Yong, et al. Low frequency acoustic field simulation of GIL disruptive discharge[J]. High Voltage Engineering, 2020, 46(3): 906-914.
[17] 李永亮, 唐俊, 党冬, 等. 苏通GIL综合管廊声传播特性仿真研究[J]. 声学技术, 2018, 37(4): 297-302.
Li Yongliang, Tang Jun, Dang Dong, et al. Simulation study of acoustic propagation characteristics in Suzhou-Nantong GIL multi-utility tunnel[J]. Technical Acoustics, 2018, 37(4): 297-302.
[18] Fei Ye, Liu Yunpeng, Chen Jiangbo, et al. The attenuation and propagation law of ultrasonic wave in UHV gas insulated line[J]. IEEE Access, 2020, 8: 163308-163315.
[19] 杜志叶, 郝兆扬, 郝乾, 等. 220kV GIL复杂壳体结构振动传播特性分析[J]. 湖南大学学报(自然科学版), 2022, 49(2): 125-134.
Du Zhiye, Hao Zhaoyang, Hao Qian, et al. Analysis on vibration propagation characteristics of 220kV GIL complicated shell structure[J]. Journal of Hunan University (Natural Sciences), 2022, 49(2): 125-134.
[20] 伍企舜. GIS声学诊断的理论与实验基础[J]. 高压电器, 1991, 27(2): 55-61.
[21] (美)伊文. 层状介质中的弹性波[M]. 刘光鼎, 译.北京: 科学出版社, 1966.
[22] 薛建议, 朱明晓, 邵先军, 等. 特高压GIS局部放电超声波传播特性仿真[J]. 高压电器, 2018, 54(9): 67-75.
Xue Jianyi, Zhu Mingxiao, Shao Xianjun, et al. Simulation on ultrasonic propagation characteristics of partial discharge in ultra-high voltage GIS[J]. High Voltage Apparatus, 2018, 54(9): 67-75.
[23] 邵长金, 杨振清, 周广刚. 场与波[M]. 东营: 中国石油大学出版社, 2015.
[24] 程祖依. 弹性动力学基础[M]. 武汉: 中国地质大学出版社, 1989.
[25] 侯云霞. Lamb波和管中导波的传播特性研究[D]. 大连: 大连理工大学, 2009.
Hou Yunxia. Study on propagation characteristics of Lamb wave and guided wave in pipes[D]. Dalian: Dalian University of Technology, 2009.
[26] 张清华, 张登科, 崔闯, 等. 基于超声导波的钢桥面板纵肋对接焊缝疲劳裂纹检测方法[J]. 中国公路学报, 2022, 35(6): 101-112.
Zhang Qinghua, Zhang Dengke, Cui Chuang, et al. Fatigue crack detection method based on ultrasonic-guided waves for the longitudinal rib butt weld of steel decks[J]. China Journal of Highway and Transport, 2022, 35(6): 101-112.
[27] 栗霞飞, 刘飞, 赵满全, 等. 基于超声导波检测管道缺陷的数值模拟[J]. 声学技术, 2019, 38(2): 164-169.
Li Xiafei, Liu Fei, Zhao Manquan, et al. Numerical simulation of pipeline defects detection based on ultrasonic guided wave[J]. Technical Acoustics, 2019, 38(2): 164-169.
[28] 姚睿丰, 王妍, 高景晖, 等. 压电材料与器件在电气工程领域的应用[J]. 电工技术学报, 2021, 36(7): 1324-1337.
Yao Ruifeng, Wang Yan, Gao Jinghui, et al. Applications of piezoelectric materials and devices in electric engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1324-1337.
[29] 魏东, 刘侃, 丁荣军, 等. 基于多重同步压缩变换的永磁同步电机初期匝间短路故障检测[J]. 电工技术学报, 2022, 37(18): 4651-4663.
Wei Dong, Liu Kan, Ding Rongjun, et al. A multi-synchrosqueezing transformation based early stage detection of inter-turn short circuit fault in permanent magnet synchronous machine[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4651-4663.
[30] 徐鹏, 苏勇令, 贺林, 等. 振动测试技术在GIS耐压试验故障定位中的应用研究[J]. 华东电力, 2014, 42(1): 23-27.
Xu Peng, Su Yongling, He Lin, et al. Vibration test system using in breakdown location of GIS withstand voltage test[J]. East China Electric Power, 2014, 42(1): 23-27.
[31] 马文长, 马博辉, 何宁辉, 等. 基于声源信号的GIL击穿性放电定位研究[J]. 宁夏电力, 2021(2): 28-34.
Ma Wenchang, Ma Bohui, He Ninghui, et al. Research on location of GIL breakdown discharge based on acoustic signal[J]. Ningxia Electric Power, 2021(2): 28-34.
Research on Propagation Characteristics of Gas-Insulated Transmission Line Ultrasonic Guided Wave for Sound Source Localization
Abstract The sound source localization method based on time difference of arrival (TDOA) is currently the mainstream method for fault location of gas-insulated transmission line (GIL). The GIL shell is similar to the cylindrical shell, and the acoustic wave propagating along the shell has the dispersion and multi-modal characteristics, which increases the difficulty of precise positioning. In recent years, people have studied the acoustic wave transmission process on GIL, but most of the studies have ignored the influence of guided wave characteristics on the transmission of acoustic wave, and the research results are deviated from the actual situation. In order to solve these problems, this paper proposes a GIL shell acoustic transmission analysis model considering guided wave dispersion and multi-modal characteristics, determines the guided wave mode suitable for GIL fault location and the attenuation and time delay caused by GIL non-straight tube structure, which effectively improves the fault location accuracy of GIL.
Firstly, the dispersion curve of guided wave in the typical 220 kV GIL shell is drawn, and the guided wave modes in the frequency range of 0～100 kHz are determined. Secondly, a finite element model of acoustic wave transmission in the long-distance GIL straight pipe is established, and the propagation characteristics of guided waves are studied by applying different excitation to the model. According to the simulation results and the requirements of GIL sound source localization, the effective frequency band and guided wave mode suitable for fault location are determined. Thirdly, in order to study the location advantages of the selected guided wave mode in the GIL non-straight pipe section and the attenuation and time delay by the GIL non-straight pipe structure, the expansion joint, gas basin insulator and other non-straight pipe structures are added to the long-distance GIL straight pipe model. Finally, the selected guided wave mode is used for GIL field location test, and the influence of the attenuation and time delay of the GIL non-straight pipe structure are considered in the localization algorithm. The effectiveness of the analysis model is verified according to the location results.
The results show that the propagation distance required for F(1,1) mode to separate from the original wave packet is within 2 m in the 20～60 kHz frequency band. In the GIL straight pipe section, the amplitude of F(1,1) mode is about 20 times that of the front modes, and the amplitude is attenuated up to 30% after 10m of propagation. In the process of propagation, the shape of F(1,1) mode is more stable than the modes of the rear secondary acoustic wave. In terms of temporal and spatial distribution, it is easy to distinguish with the front and rear modes, and can be used as the preferred mode for fault location. For F(1,1) mode, GIL non-straight pipe structures such as single-stage expansion joints, double-stage expansion joints, and gas basin insulator will cause 90%, 96%, and 60% attenuation, and 0.6 ms, 1.1 ms, 0.03 ms delay. The error of using F(1,1) mode for fault location in an interval with the length of 20 m is about 1 m. Further considering the influence of the attenuation and time delay of the GIL non-straight pipe structure, the positioning error can be reduced to about 0.3 m, which proves the effectiveness of the analysis model in improving the fault location accuracy of GIL.
The following conclusions can be drawn from the results: (1) The GIL shell acoustic transmission analysis model can effectively consider the influence of guided wave dispersion and multi-modal characteristics on GIL sound source localization, and the F(1, 1) mode has great fault location advantage. (2) The location frequency band of 20～60 kHz reduces the interference of guided wave dispersion and environmental noise to GIL sound source localization, which helps to improve the accuracy of fault location. (3) The GIL non-straight pipe structure will cause a large amplitude attenuation and a certain degree of time delay to the F(1,1) mode. Considering the influence of the attenuation and time delay of the GIL non-straight pipe structure in fault location can make the positioning error is further reduced by more than 60%.
keywords：Gas-insulated transmission line (GIL), fault location, time difference of arrival (TDOA), ultrasonic guided wave, propagation characteristics
中图分类号：TM755
DOI:10.19595/j.cnki.1000-6753.tces.221902
国家自然科学基金资助项目（51977152）。
收稿日期 2022-10-08
改稿日期 2022-10-26
杜志叶 男，1974年生，教授，博士生导师，研究方向为智能电气设备、特高压直流输电关键技术、电磁多物理场耦合计算技术。E-mail：Duzhiye@126.com
郝兆扬 男，1998年生，硕士研究生，研究方向为气体绝缘输电线路故障定位。E-mail：haozhaoyang.whu@foxmail.com（通信作者）
（编辑 李 冰）