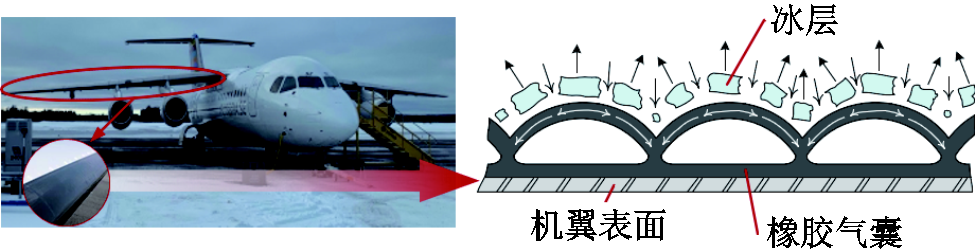
图1 橡胶气囊除冰示意图
Fig.1 Diagram of rubber pneumatic boots de-icing
摘要 叶片结冰影响风力发电机的安全稳定运行,现有的叶片热力除冰、涂料防冰技术分别存在能耗高、耐候性差等问题,均无法大面积推广应用。受飞机机翼气囊除冰方法启发,该文提出一种新结构式的气动脉冲除冰方法。利用Abaqus商业软件对该方法的简化模型进行除冰过程的数值仿真,对比分析了不同脉冲充气气压下覆冰厚度对除冰效果的影响。同时,通过人工覆冰与除冰试验,对仿真结果进行验证。仿真与试验结果表明:在低充气气压下,冰层越薄越容易破碎脱落,覆冰厚度的增加有利于提升低充气气压下的脱冰率;在相同充气气压下,冰层厚度的增加可以降低结构表面形变。
关键词:风力发电机 覆冰 数值仿真 气动脉冲除冰 覆冰试验
风能在推进新能源及低碳社会建设中扮演着重要角色[1-5]。全球风能理事会在2021年的报告中指出,2020年全球新增风力发电装机容量超过900 GW,相比2019年增长了53%。高寒地区气温低、空气密度大,可用风能比其他地区高约10%[6]。然而,低温带来的覆冰问题严重削弱了风机的输出功率,并影响风机的安全稳定运行[7-8]。
目前,热空气技术和电热技术是风机防/除冰的主要手段。然而,上述方法会随着环境温度的降低和来流风速的提升消耗更多能量,且除冰周期增加[9]。与之相比,机械式的气动除冰方法更加直接高效,且能耗较低[10]。1980年以来,该方法被广泛用于直升机旋翼和民用机机翼除冰方面[11]。由于风机叶片与机翼结构相似,气动除冰方法在风机叶片除冰方面具有较好的应用前景。
机翼上的气动除冰方法主要依靠粘贴在表面的橡胶气囊实现,如图1所示。气囊充气时会产生6~10 mm的形变,持续时间为1~4 s,表面冰层在弯曲力的作用下破碎并在剪切力的作用下被剥离[12]。

图1 橡胶气囊除冰示意图
Fig.1 Diagram of rubber pneumatic boots de-icing
为减少外部粘贴气囊长时间大形变对叶片气动性能的影响,本文提出一种新结构式的气动脉冲除冰方法,即将气囊浇注于叶片内部来减少表面形变和除冰时长。为研究该方法在不同覆冰厚度下的除冰效果,采用Abaqus商业软件对新结构简化模型的除冰过程进行数值仿真;同时,设计并制作气动脉冲除冰样板,通过人工覆冰与除冰试验验证仿真结果的准确性。仿真与试验结果证明,该方法在表面最大位移小于2 mm、气动脉冲时间为4 ms的条件下能够实现除冰。
图2为气动脉冲除冰样板设计示意图,其结构参数见表1。样板采用与风机叶片相同材质的玻璃纤维增强环氧树脂制成;树脂板上开有一凹槽,沿其中线粘结尼龙复合材料制成的扁平气囊;利用聚醚胺改性的环氧树脂将气囊浇注于凹槽内部,环氧树脂固化后会形成具有良好韧性的弹性层;为保护弹性层,在其外侧粘贴一层薄铝合金蒙皮。
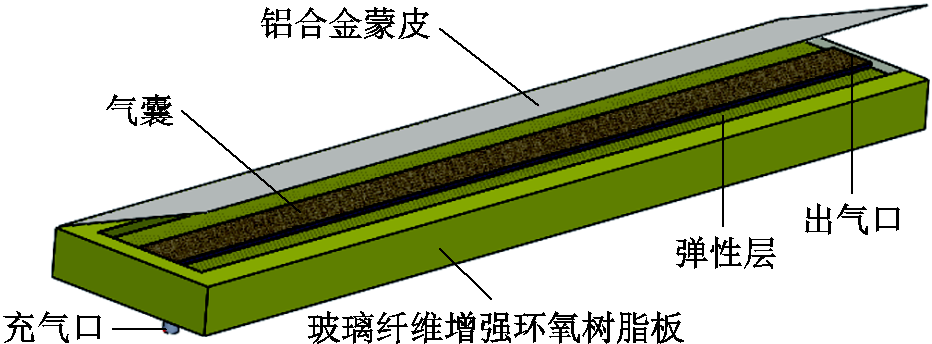
图2 气动脉冲除冰样板设计示意图
Fig.2 Design of pneumatic impulse de-icing sample
表1 除冰样板结构参数
Tab.1 The structure parameters of the de-icing sample

部件长×宽×厚/(mm×mm×mm) 环氧树脂板300×80×20 凹槽298×60×4 铝合金蒙皮300×80×0.4 气囊298×8.5×0.5
气动脉冲除冰原理如图3所示。当铝合金蒙皮表面开始结冰,通过充气口向气囊内部通入脉冲高压气体,气囊迅速膨胀并对弹性层/铝合金蒙皮/冰层复合层产生极强冲击力。由于冰层在快速加载条件下呈现出脆性断裂特点,当冲击力足够大时,冰层会在弯曲力的作用下发生断裂,而铝合金蒙皮表面弯曲产生的横向剪切应力可以将破碎冰层剥离。当脉冲气体从出气口逸出后,在弹性层的作用下,结构表面恢复初始平整状态。
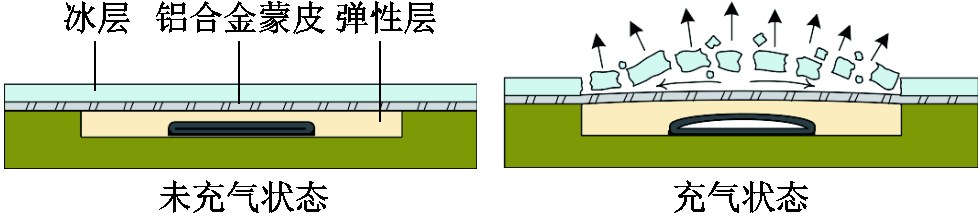
图3 气动脉冲除冰原理
Fig.3 Principle of pneumatic impulse de-icing
气动脉冲除冰过程涉及结构动力学问题,利用有限单元法,将模型离散成微小单元,并对各单元动力变化过程进行计算分析,从而获得模型整体结构动力响应。结构有限元的运动方程[13]为
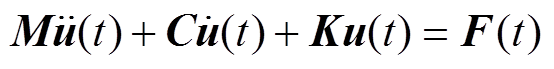 (1)
(1)
式中,M、C和K分别为结构的质量、阻尼和刚度矩阵;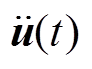 、
、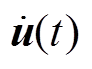 和
和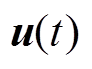 分别为单元节点的加速度、速度和位移矢量;
分别为单元节点的加速度、速度和位移矢量;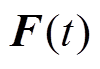 为单元节点的总外力矢量。利用中心差分显示积分方法对式(1)进行求解计算,可得节点的加速度矢量为
为单元节点的总外力矢量。利用中心差分显示积分方法对式(1)进行求解计算,可得节点的加速度矢量为
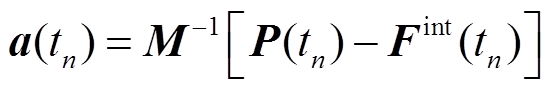 (2)
(2)
式中,Fint(tn)为内力矢量;P(tn)为外力矢量;n为第n个增量步。对应节点的速度和位移矢量表达式分别为
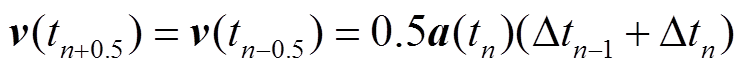 (3)
(3)
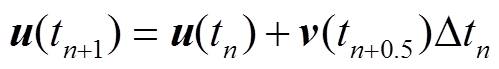 (4)
(4)
为了提高计算的效率和收敛性,假设材料均为各向同性,其本构方程[14]可写为
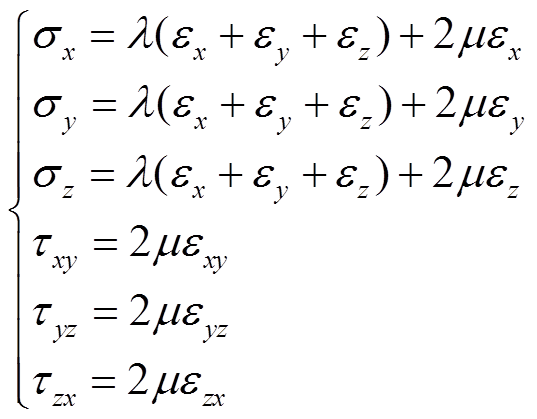 (5)
(5)
式中,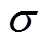 为正应力;
为正应力;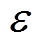 为正应变;
为正应变;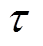 为切应力;下标x, y, z分别代表各物理量在该方向上的分量;λ和μ为拉梅弹性常数,二者与弹性模量E和泊松比
为切应力;下标x, y, z分别代表各物理量在该方向上的分量;λ和μ为拉梅弹性常数,二者与弹性模量E和泊松比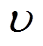 的关系分别为
的关系分别为
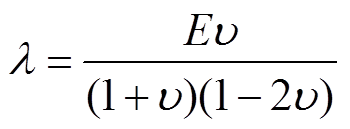 (6)
(6)
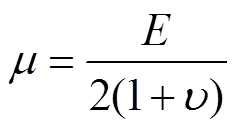 (7)
(7)
当冰层最大主拉应力超过其抗拉强度时就会产生裂纹。冰层脆性断裂符合朗肯准则,其主要基于Ⅰ型断裂原理。根据弹性断裂力学理论,Ⅰ型裂纹的裂尖应力场及其位移场的极坐标表达式[13,15]为
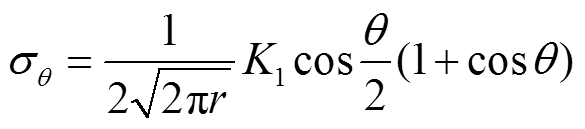 (8)
(8)
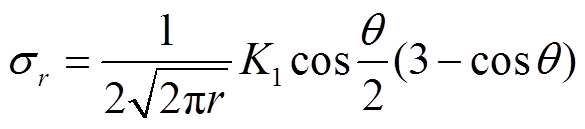 (9)
(9)
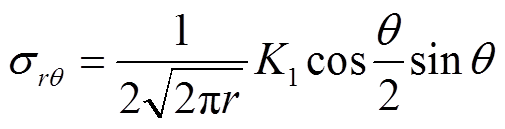 (10)
(10)
式中,K1为应力强度因子;r为裂尖区域中强度因子控制区的极半径;θ为以裂尖为圆心的方位角。
为了模拟冰层Ⅰ型断裂,需要用到拉伸软化模型中的断裂能准则。其原理是先设置单元失效时的最大位移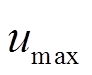 ,通过计算判断最大位移
,通过计算判断最大位移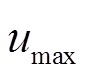 与模型单元位移
与模型单元位移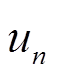 的大小关系来决定模型是否断裂。当
的大小关系来决定模型是否断裂。当 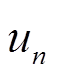 >
>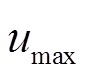 时,单元应力赋值为0,单元被删除,裂纹产生。
时,单元应力赋值为0,单元被删除,裂纹产生。
利用商业软件Abaqus 6.14中的显示动力求解方案可实现上述除冰过程的数值仿真研究。为提高计算效率和收敛性,且考虑到除冰过程中起主要作用的结构为弹性层、铝合金蒙皮和冰层,本文将仿真的几何模型进行简化处理,如图4所示。图4a中,虚线构图为简化忽略部分,实线构图为简化仿真几何模型。根据表1可知气囊外径为8.5 mm,厚度为0.5 mm,弹性层厚度为4 mm。在考虑到气囊厚度对简化模型的影响后,气压作用区域宽度设置为8 mm(图4显示蓝色区域宽度),弹性层厚度设置为3.5 mm。简化后的模型尺寸参数见表2。
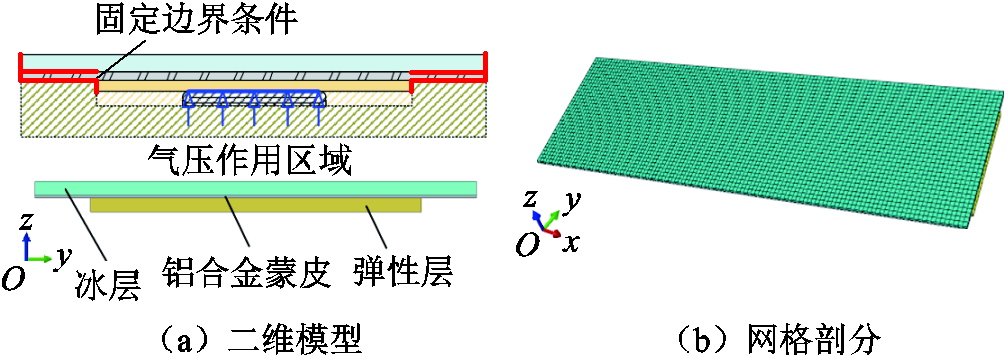
图4 仿真简化几何模型
Fig.4 Simplified simulation geometric model
表2 简化模型的尺寸参数
Tab.2 Size parameters of the simplified model

材料名称长×宽×厚/(mm×mm×mm) 弹性层298×60×3.5 铝合金蒙皮300×80×0.4 冰层300×80×1/2/3
由于覆冰环境参数不同,冰层的力学参数是在一定范围内波动的,参考文献[16-19],本文设定冰层的弹性模量为2 GPa,泊松比为0.30,弯曲强度为0.27 MPa,断裂位移为5×10-5 mm,冰层在铝合金蒙皮的横向剪切应力为0.5 MPa。弹性层弹性模量为0.8 GPa,泊松比为0.34。铝合金蒙皮弹性模量为70 GPa,泊松比为0.33。
根据样板结构特点,对图4a红线标记处沿x轴扩展的平面设置为固定边界条件;在保证单元节点相互连接的条件下,设定划分网格大小为2.5 mm;气压作用区域施压大小包括0.5、1、1.5、2、2.5 MPa,作用脉冲时长为4 ms。
覆冰与除冰试验在国家重点实验室的低温低气压人工气候室展开,如图5所示。试验室全长3.8 m,内径2.0 m。利用制冷控制系统,控制内部温度在-1.1~-36℃范围内可调。腔体顶端安装IEC标准喷头,通过加压空气雾化水流来提供过冷却水滴。

图5 人工气候室
Fig.5 The artificial climate chamber
除冰试验设备如图6所示。其中,集气瓶用于存储高压气体,电磁阀用于控制样板的充气动作,通过继电器控制电源对电磁阀的供电开断和供电时长,从而产生具有规定时长的脉冲气压。

图6 除冰试验设备
Fig.6 De-icing test equipments
雨凇质地坚硬、粘结力强,其带来的影响最为恶劣。根据雪峰山野外科学观测研究站长期对风机覆冰的气候条件记录发现,叶片出现雨凇的温度基本在-5℃左右,风速范围为5~6 m/s[20];当风机叶片覆冰厚度分别为1、2和3 mm时,其功率分别降低了10.9%、13.8%和16.8%[21]。因此,在对除冰样板进行覆冰时,气候室温度控制在-5℃左右,风速设置为6 m/s,平均覆冰厚度主要包括1、2和3 mm三种工况。除冰样板表面覆冰为均匀覆冰,覆冰期间每隔10 min利用游标卡尺分别测量样板中间及两边冰层厚度,并求取平均值。当样板平均覆冰厚度达到要求值时,关闭喷淋系统,将样板继续在-5℃条件下冷冻10 min后再进行除冰操作。
仿真过程分别采用了1、1.5、2、2.5、3 MPa的脉冲充气气压,其脉冲宽度均为4 ms。利用脱冰率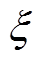 来反映除冰效果,其表达式为
来反映除冰效果,其表达式为
式中,Ni为脱落冰层单元个数;Na为冰层单元总个数。
利用仿真计算获得不同冰厚下样板的脱冰率如图7所示,样板表面形变的最大位移如图8所示。
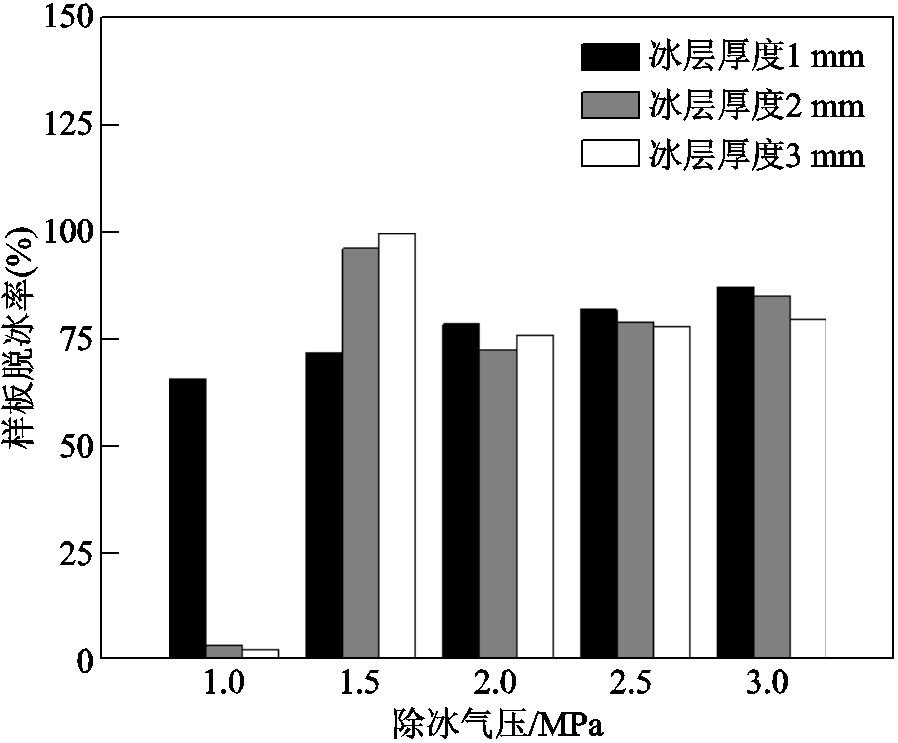
图7 不同冰厚下样板的脱冰率
Fig.7 De-icing ratio of samples under different ice thicknesses
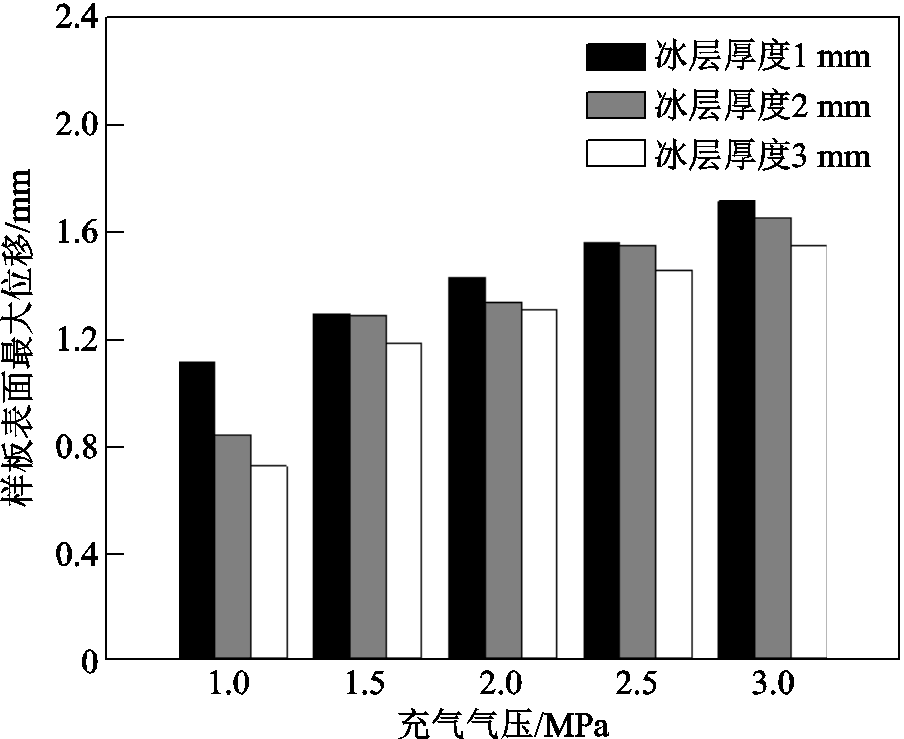
图8 不同冰厚下样板表面的最大位移
Fig.8 The maximum displacement of samples surface under different ice thicknesses
由图7可知:
1)当冰厚为1 mm时,采用1 MPa的充气气压,样板脱冰率为65.4%;当冰厚为 2 mm和3 mm时,在1 MPa充气气压下样板无法除冰,仅在冰层出现裂纹,上述仿真结果如图9所示。

图9 充气气压1 MPa仿真结果
Fig.9 Simulation results under 1 MPa inflation pressure
2)当冰厚为1 mm时,随着充气气压的增加,脱冰率呈现递增趋势,当气压增至3 MPa时,脱冰率达到了86.8%;然而当冰厚为2 mm和3 mm时,随着充气气压从1.5 MPa开始增加,脱冰率出现先大幅降低后缓慢增加的趋势。
出现上述结果的分析如下:
1)冰层越薄越容易断裂。当冰厚为1 mm时,较小的充气气压即可使其发生断裂,最大位移出现在样板中心线。根据弯曲梁正应力分布特点,冰层受到的横向剪切应力也从样板中心线向两端逐渐递减,因此会有中间冰层大面积脱落,而两端依然有破碎冰层残留的现象。随着充气气压增加,最大位移增大(见图8),导致蒙皮表面横向剪切应力也相应增大,这是1 mm冰层随气压增加时脱冰率递增的主要原因。
2)当冰厚为2 mm或3 mm时,由弹性层、蒙皮和冰层组成的整体,其结构刚度增大,因此在 1 MPa气压作用下最大位移较小(见图8),这是导致2 mm或3 mm冰层在1 MPa气压下无法脱落的主要原因。
3)当气压增至1.5 MPa时,在冰厚2 mm和 3 mm的工况下,蒙皮最大位移分别增至1.285 mm和1.184 mm(见图8)。在增大的横向剪切应力作用下,冰层由中间裂纹处逐渐向两端被剥离。然而由于冲击压力较小,结构刚度较大,冰层上产生的裂纹数目较少,虽然靠近两端的冰层受到被剥离的剪切应力很小,但是它们会在已被剥离冰层的带动下脱落,如图10所示。这是导致2 mm和3 mm冰层在1.5 MPa气压下除冰率很高的主要原因。
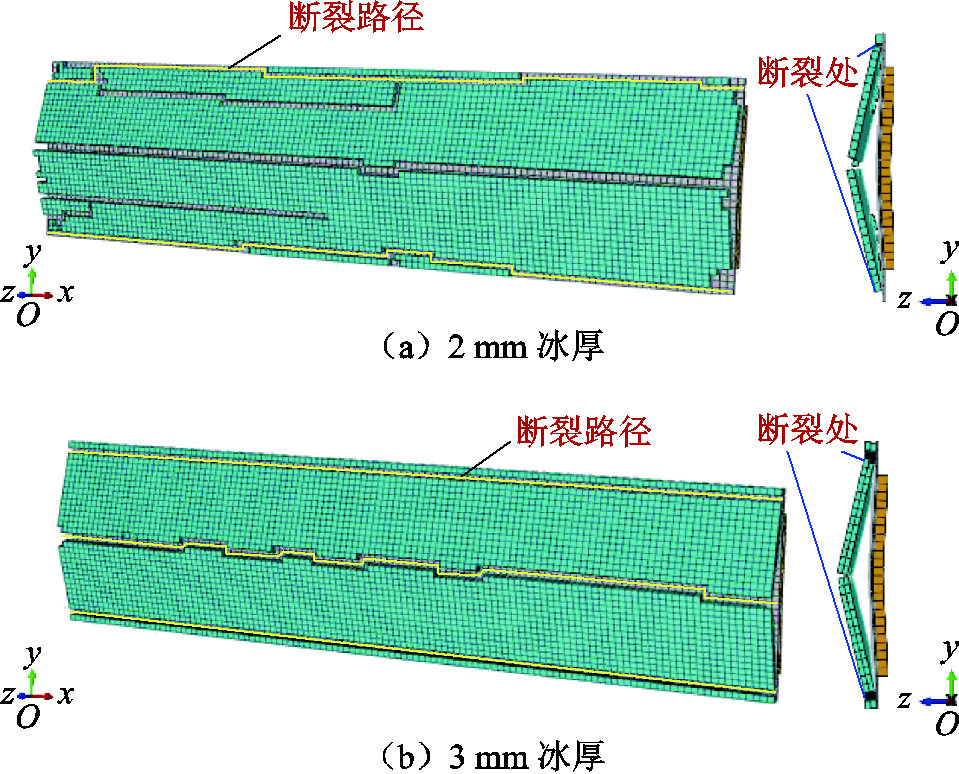
图10 充气气压1.5 MPa仿真结果
Fig.10 Simulation results under 1.5 MPa inflation pressure
4)当气压增至2 MPa时,2 mm和3 mm冰层裂纹增多,两端冰层无法在被剥离冰层的带动下脱离蒙皮表面,如图11所示,这将导致2 mm和3 mm冰层脱冰率明显降低。当气压继续增加,两端破碎冰层受到的剪切应力不断提升,使得2 mm和3 mm冰层脱冰率开始增加,如图12所示。

图11 充气气压2 MPa仿真结果
Fig.11 Simulation results under 2 MPa inflation pressure
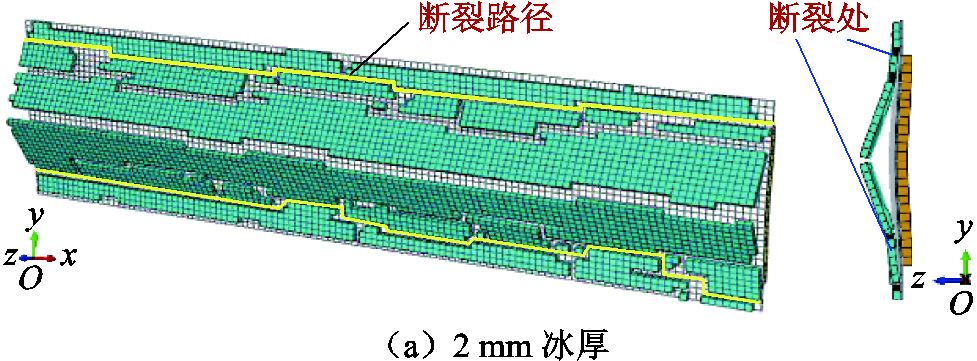

图12 充气气压3 MPa仿真结果
Fig.12 Simulation results under 3 MPa inflation pressure
根据表1中的结构参数,设计制作了除冰样板,样板的除冰效果如图13~图15所示。

图13 充气压力1 MPa的脱冰效果
Fig.13 De-icing effects under 1 MPa inflation pressure

图14 充气压力1.5 MPa的脱冰效果
Fig.14 De-icing effects under 1.5 MPa inflation pressure


图15 充气压力3 MPa的脱冰效果
Fig.15 De-icing effects under 3 MPa inflation pressure
1)由图13可知,当充气压力为1 MPa时, 2 mm和3 mm冰层均未脱落。其中,通过增加图像对比度可以发现,2 mm冰层上的裂纹明显多于 3 mm冰层,这说明在相同充气气压下,冰层越厚,产生的裂纹越少,与仿真结果相吻合。
2)由图14可知,当充气压力为1.5 MPa时,2 mm和3 mm冰层发生大面积脱落,且脱冰面积明显大于1 mm冰层,与仿真结论一致。其中,2 mm冰层存在一小块未断裂并粘结在蒙皮表面,它是由于充气接口设计位置导致气体只能向单侧传递造成。
3)由图15可知,当充气压力为3 MPa时,1 mm冰层脱冰面积明显提升,2 mm和3 mm冰层脱冰面积相比1 MPa作用气压有所降低,该试验结果符合仿真规律。
本文提出一种将气囊浇注于叶片内部的新结构式的气动脉冲除冰方法,通过仿真模拟和试验验证得出结论如下:
1)与粘贴在翼型表面的气囊除冰方法相比,新结构式的气动脉冲除冰方法能够在减小表面形变位移和形变时长的条件下实现除冰目的,其中,表面形变最大位移不超过2 mm,形变时长为4 ms。
2)在较低的充气气压下,覆冰厚度越薄,冰层越容易破碎和脱落,但是脱冰率偏低,可以通过增大充气气压来提升冰层受到的横向剪切应力,从而达到提升脱冰率的目的。
3)当充气气压相同时,冰层厚度的增加有利于减小表面形变,同时冰层变厚有利于提升低充气气压下的脱冰率。在工程应用时,可以考虑在覆冰达到一定厚度时,利用合适的低充气气压实现大面积除冰操作,其主要原理是利用被剥离冰层带动两端冰层一起脱落。
参考文献
[1] 陆秋瑜, 马千里, 魏韡, 等. 基于置信容量的风场配套储能容量优化配置[J]. 电工技术学报, 2022, 37(23): 5901-5910.
Lu Qiuyu, Ma Qianli, Wei Wei, et al. Optimal configuration of energy storage parameters based on confidence capacity of wind farms[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5901-5910.
[2] 沈小军, 聂聪颖, 吕洪. 计及电热特性的离网型风电制氢碱性电解槽阵列优化控制策略[J]. 电工技术学报, 2021, 36(3): 463-472.
Shen Xiaojun, Nie Congying, Lü Hong. Coordination control strategy of wind power-hydrogen alkaline electrolyzer bank considering electrothermal charact-eristics[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 463-472.
[3] 程明, 许利通, 曹政, 等. 级联式无刷双馈电机的矢量控制系统和功率流研究[J]. 电工技术学报, 2022, 37(20): 5164-5174.
Cheng Ming, Xu Litong, Cao Zheng, et al. Study on vector control system and power flow of cascaded brushless doubly-fed induction generator[J]. Transactionsof China Electrotechnical Society, 2022, 37(20): 5164-5174.
[4] 朱东海, 邹旭东, 胡家兵, 等. 双馈风电机组无撬棒故障穿越技术研究综述[J]. 电工技术学报, 2022, 37(19): 4895-4910.
Zhu Donghai, Zou Xudong, Hu Jiabing, et al. Review of crowbarless fault ride through technology for doubly-fed induction generator-based wind turbines[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4895-4910.
[5] 王晨, 寇鹏, 王若谷, 等. 利用多空间尺度下时空相关性的点云分布多风机风速预测[J]. 电力系统自动化, 2021, 45(22): 65-73.
Wang Chen, Kou Peng, Wang Ruogu, et al. Wind speed forecasting for multiple wind turbines with point cloud distribution using spatio-temporal correlation on multiple spatial scale[J]. Automation of Electric Power Systems, 2021, 45(22): 65-73.
[6] Fortin G, Perron J, Ilinca A. Behaviour and modeling of cup anemometers under icing conditions[C]// International Workshop on Atmospheric Icing of Structure XI, Canada, Montreal, 2005: 1-6.
[7] Madi E, Pope K, Huang Weimin, et al. A review of integrating ice detection and mitigation for wind turbine blades[J]. Renewable and Sustainable Energy Reviews, 2019, 103: 269-281.
[8] 胡琴, 王欢, 邱刚, 等. 风力发电机叶片覆冰量化分析及其应用[J]. 电工技术学报, 2022, 37(21): 5607-5616.
Hu Qin, Wang Huan, Qiu Gang, et al. Quantitative analysis of wind turbine blade icing and its application[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5607-5616.
[9] Wei Kexiang, Yang Yue, Zuo Hongyan, et al. A review on ice detection technology and ice elimination technology for wind turbine[J]. Wind Energy, 2020, 23(3): 433-457.
[10] Parent O, Ilinca A. Anti-icing and de-icing techniques for wind turbines: critical review[J]. Cold Regions Science and Technology, 2011, 65(1): 88-96.
[11] Palacios J, Wolfe D, Bailey M, et al. Ice testing of a centrifugally powered pneumatic deicing system for helicopter rotor blades[J]. Journal of the American Helicopter Society, 2015, 60(3): 1-12.
[12] Weisend N A. Design of an advanced pneumatic deicer for the composite rotor blade[J]. Journal of Aircraft, 1989, 26(10): 947-950.
[13] 马健钧. 海冰弯曲破坏的数值模拟方法研究[D]. 天津: 天津大学, 2013.
Ma Jianjun. Methodology research on the numerical simulation of the bending failure of sea ice[D]. Tianjin: Tianjin University, 2013.
[14] 李群, 欧卓成, 陈宜亨. 高等断裂力学[M]. 北京: 科学出版社, 2017.
[15] 杨新辉. 脆性/韧性断裂机理与判据及裂尖变形理论研究[D]. 大连: 大连理工大学, 2005.
Yang Xinhui. Study on mechanism and criterion for brittle/ductile fracture and theory of crack-tip deformation[D]. Dalian: Dalian University of Technology, 2005.
[16] 蒋兴良, 舒立春, 孙才新. 电力系统污秽与覆冰绝缘[M]. 北京: 中国电力出版社, 2009.
[17] Gupta V, Bergström J S. A progressive damage model for failure by shear faulting in polycrystalline ice under biaxial compression[J]. International Journal of Plasticity, 2002, 18(4): 507-530.
[18] Dong W, Ding J, Zhou Z X. Experimental study on the ice freezing adhesive characteristics of metal surfaces[J]. Journal of Aircraft, 2014, 51(3): 719-726.
[19] 季顺迎, 王安良, 苏洁, 等. 环渤海海冰弯曲强度的试验测试及特性分析[J]. 水科学进展, 2011, 22(2): 266-272.
Ji Shunying, Wang Anliang, Su Jie, et al. Experimental studies and characteristics analysis of sea ice flexural strength around the Bohai Sea[J]. Advances in Water Science, 2011, 22(2): 266-272.
[20] 梁健. 风力机叶片覆冰预测模型研究[D]. 重庆: 重庆大学, 2017.
Liang Jian. Research on ice prediction model of wind turbine blade[D]. Chongqing: Chongqing University, 2017.
[21] 舒立春, 李瀚涛, 胡琴, 等. 自然环境叶片覆冰程度对风力机功率损失的影响[J]. 中国电机工程学报, 2018, 38(18): 5599-5605.
Shu Lichun, Li Hantao, Hu Qin, et al. Effects of ice degree of blades on power losses of wind turbines at natural environments[J]. Proceedings of the CSEE, 2018, 38(18): 5599-5605.
Numerical Simulation and Experimental Verification of the Influences of Icing Thicknesses on Pneumatic Impulse De-Icing Effects
Abstract With the expansion of wind farm construction in cold regions around the world, more and more attention has been paid to anti-/de-icing technologies used on wind turbine blades. The common ice protection methods for wind turbine blades mainly include super-hydrophobic coating (SHC) anti-icing method and thermal anti-/de-icing methods. However, the hydrophobic property of SHC will be weakened as the number of icing increases and the thermal methods will consume a lot of time and energy with the ambient temperature goes down.Compared withthe methods mentioned above, mechanical de-icing method has better de-icing performances with lower energy consumption. Inspired by the airfoil de-icing boot, a new structured pneumatic impulse de-icing method suitable for wind turbine blade is proposed. This method uses the modified epoxy resin to pour the inflatable tube inside the protected structure. By applying an impulse of high pressure gas to produce a rapid impact force, the ice accumulated on the protected structure surface will be crushed and removed. Compared with the de-icing boot used on airfoil, the new structured pneumatic impulse de-icing method has shorter operation time and smaller surface deformation displacement.
For identifying the de-icing effects of the new structured pneumatic impulse de-icing method under different icing thicknesses, the dynamic simulation of de-icing process based on the simplified model of this new method was carried out by the commercial software Abaqus. The simulation adopted inflation pressures include 1 MPa, 1.5 MPa, 2MPa, 2.5 MPa and 3 MPa with the impulse duration is 4 ms. To verify the accuracy of simulation results, the pneumatic impulse de-icing samples were manufactured, and the icing and de-icing tests were carried out in the artificial climate chamber. The icing temperature in the climate chamber is controlled at 5℃, the wind velocity is set at 6 m/s, and the average icing thicknesses mainly include 1 mm, 2 mm and 3 mm.
The simulation and tests results show that: (1) With the increase of inflation pressure, the de-icing ratio of sample with 1 mm ice layer shows an increasing trend, and this is caused by the enhancement of transverse shear stress working at the ice/metal interface. (2) When the inflation pressure increases from 1.5 MPa to 3 MPa, the de-icing ratio of sample with 2 mm or 3 mm ice layer decreases firstly and then increases. The reason for the better performance using 1.5 MPa inflation pressure is that there is less cracks on the ice layer and the ice layer near the sample sides will be dragged off by the middle shed ice layer. When the inflation pressure is 2 MPa, more cracks appears, which makes it impossible to pull the ice off near the sample sides. With the inflation pressure further rises, the increase of transverse shear stress contributes more to the improvement of de-icing ratio. (3) The increase of ice thickness could reduce the surface deformation displacement and increase the de-icing ratio under low inflation pressure. This indicates that the new structured pneumatic impulse de-icing method has better de-icing effects by increasing the ice thickness during de-icing operation properly.
keywords: Wind turbine, icing, numerical simulation, pneumatic impulse de-icing, icing test
中图分类号:TM315
DOI:10.19595/j.cnki.1000-6753.tces.222097
国家自然科学基金资助项目(52077020, 51977016)。
收稿日期 2022-11-06
改稿日期 2022-11-30
于 周 男,1994年生,博士研究生,研究方向为风力发电机覆冰及防护。E-mail:yuzhoucqu@163.com
舒立春 男,1964年生,博士,教授,博士生导师,研究方向为高电压与绝缘技术、输电线路和风力发电机覆冰及防护。E-mail:lcshu@cqu.edu.cn(通信作者)
(编辑 李 冰)