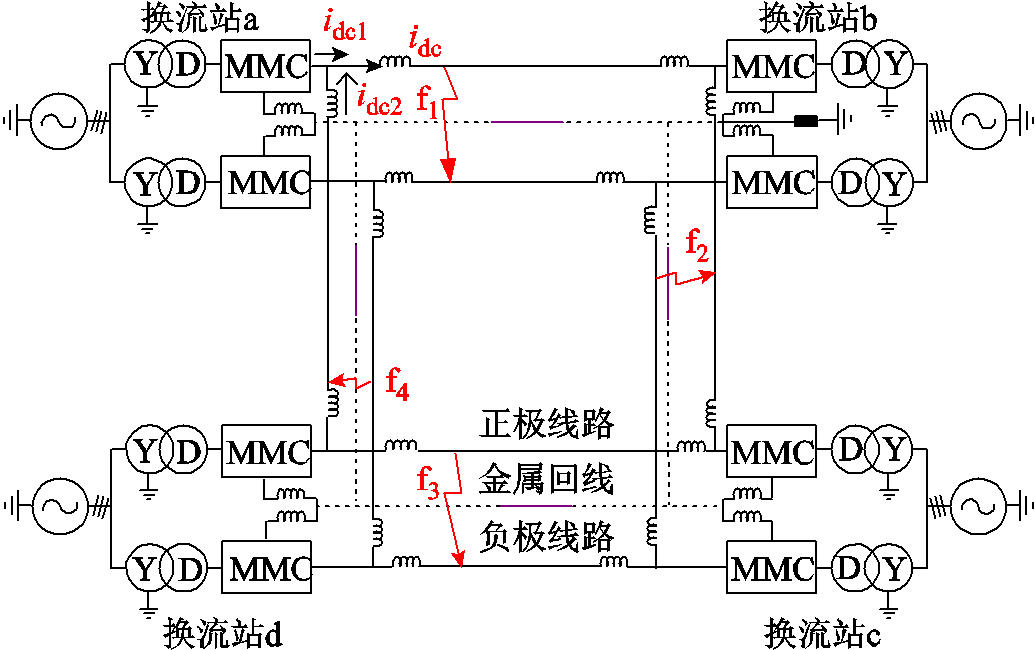
图1 基于半桥型的四端MMC-HVDC电网拓扑结构
Fig.1 Topology of the-four terminal MMC-HVDC grid based on half-bridge
摘要 传统的MMC-HVDC电网直流短路故障电流计算一般采用等效RLC电路方法。但是该方法没有考虑主动限流控制(ACLC)对等效电路RLC参数的影响,因此无法直接用于含ACLC的MMC-HVDC电网的直流短路故障电流的解析计算问题。该文通过将ACLC的控制效果等效为虚拟阻抗产生的压降,建立了体现ACLC的控制影响的等效RLC电路,以包含电流变化率限流环节的典型ACLC算法为例,推导了直流双极短路故障条件下ACLC的控制参数与虚拟阻抗的映射关系以及相应的直流故障电流解析表达式。最后,以基于含ACLC的半桥型四端MMC-HVDC电网为例,建立PSCAD/EMTDC仿真模型,对采用ACLC的直流双极短路故障电流解析计算结果进行了验证。结果表明:故障后10 ms内直流短路故障电流的PSCAD仿真结果与所提出的含ACLC的等效RLC电路解析计算结果的平均误差在8.29%以内,最大误差在10.99%。因此,使用所提出的方法具有工程实用性。
关键词:模块化多电平换流器 主动限流控制 虚拟阻抗 RLC电路 直流短路故障电流计算
基于模块化多电平换流器的高压直流(Modular Multi-level Converter based on High Voltage Direct Current, MMC-HVDC)电网具备有功功率、无功功率快速解耦、无换相失败等优点,被认为是未来解决高比例可再生能源并网消纳问题的关键技术之一[1-2]。
采用半桥型子模块(Half Bridge Sub-Module,HBSM)的MMC系统,以其成本优势成为目前MMC-HVDC电网的主流。然而这种结构不具备故障自清除能力,必须依靠直流断路器(DC Circuit Breakers, DCCB)切断故障线路实现故障清除与恢复。MMC-HVDC电网发生直流短路故障时,故障回路等值阻抗小,直流故障电流上升率快,峰值大,对直流断路器开断速度和容量要求高[3]。直流断路器开断速度的提高和开断容量的增加均意味着其制造成本的不断攀升。因此直流短路故障电流的抑制是半桥型MMC-HVDC电网保护的关键技术之一[4]。
综合现有文献,目前所提出的直流短路故障限流方法可以分为实体限流技术和虚体限流技术两类[5]。第一类实体限流技术,通过在实际电路中串联限流电阻、限流电感等物理限流元件构成故障限流器(Fault Current Limiter, FCL),从而减小故障电流峰值和上升率[6-8]。采用实体限流技术能够有效地抑制直流短路故障电流的上升率和峰值,但是会额外增加系统的建设成本。
而第二类虚体限流技术主要通过在MMC控制算法上附加故障线路短路电流的主动限流控制(Active Current Limiting Control, ACLC)功能[9-10]。ACLC方法大大减少了硬件投资,因而受到广泛关注。现有文献所提出的ACLC方法可以分为四类:在电压外环控制器增设虚拟阻抗[11-12]、改变环流抑制器[13]、减小子模块投入数[14-15]、减小桥臂参考电压[16-18]。ACLC控制本质是通过减小换流站出口直流电压达到降低故障电流的目的。但是使用ACLC抑制MMC-HVDC电网的直流短路故障电流,往往为了较大程度地减小电流会使子模块投入数减小过多,系统可能会出现桥臂过电流闭锁以及换流站出口直流电压减小过大而引起系统崩溃[19]。因此对考虑ACLC的MMC-HVDC电网的故障电流计算分析至关重要。
关于MMC-HVDC电网的直流短路故障电流的准确计算问题,目前已有较多文献对此进行了研究,如对双端MMC-HVDC电网直流侧的短路和断线故障特性分析[20-22],所采用的典型方法是根据故障类型和阶段对MMC-HVDC电网建立等效RLC电路模型,进而得到直流故障电流的时域解析表达式[23-24]。文献[25]考虑交流侧对故障回路的影响,采用递推公式对短路电流进行计算,且可以得到较为准确的电流计算结果。对于多端MMC-HVDC电网,文献[26]在简化等效电路的基础上,对电网的各支路列写了电压微分方程和电流方程,通过解微分方程的方式来最终获得故障电流的计算结果。文献[27]提出一种基于伴随电路的MMC-HVDC电网的故障电流计算方法,文献不仅考虑了交流侧电流的注入问题,建立了MMC-HVDC电网的等效模型,并以张北工程为例验证了方法的准确性。但是多端柔性直流电网,随着直流电网换流站端数的增加,导致微分方程阶次较高求解复杂。因此一些文献研究能快速求解出线路短路故障电流的近似解析式[28-30]。其中,文献[28]提出了一种MMC-HVDC电网的近似解析计算方法,该方法忽略距离点较远的换流站的子模块电容放电,以此简化故障回路。文献[29]针对四端柔性直流电网,通过计算故障后附加电压源的等效RLC电路的直流电流的故障分量,再叠加正常运行的电流分量,即得到故障电流的近似解析式。文献[30]将直流短路故障电流分为稳态时和故障时的直流电流,然后将基于半桥型四端直流电网进行不同形式的拆分,得到不同的等效RLC电路,进而得到不同情况下的直流短路故障电流的工程实用计算方法,为MMC-HVDC电网直流短路故障特性的研究奠定了较好的基础。
但是,上述等效RLC电路的方法,大多没有考虑直流短路故障后故障限流措施投入的影响。文献[31-32]针对含电感型故障限流器的MMC-HVDC电网,根据直流电网的双极短路故障后的电容快速放电机理,分析了电感型故障限流器投入前后故障电流的变化情况,提出了一种含直流故障限流装置特性的MMC-HVDC电网直流短路故障电流的通用等效RLC计算方法。但是,针对含ACLC的MMC-HVDC电网的直流短路故障电流的等效RLC电路模型研究,现有文献鲜有涉及。
因此,本文通过对含ACLC的MMC-HVDC电网的直流双极短路故障回路分析,建立换流站出口直流电压的压降与虚拟阻抗产生的压降之间的映射关系,推导了含ACLC控制的直流双极短路等效RLC电路和故障后10 ms内直流短路故障电流时域解析表达式;通过在PSCDA/EMTDC搭建含ACLC的基于半桥型四端MMC-HVDC电网的仿真模型,验证了所提方法的有效性。
图1所示的电路结构是一个含ACLC的基于半桥型的四端MMC-HVDC电网。

图1 基于半桥型的四端MMC-HVDC电网拓扑结构
Fig.1 Topology of the-four terminal MMC-HVDC grid based on half-bridge
稳态工作下,三相桥臂始终处于对称状态,每相上、下桥臂投入的子模块数量之和相同,并保持不变,以维持直流电压稳定。上、下桥臂子模块数量分配根据桥臂参考电压,采用最近电平逼近调制(Nearest Level Modulation, NLM)方法动态确定,即
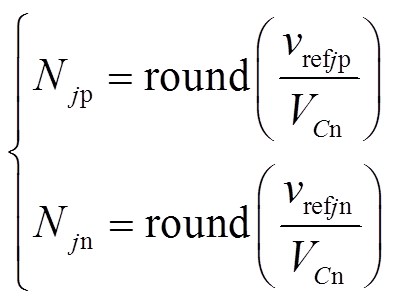 (1)
(1)
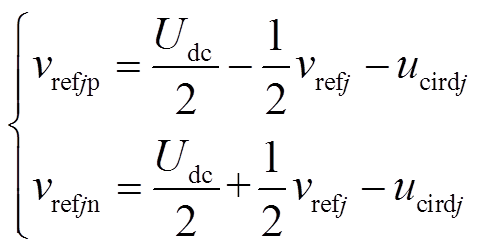 (2)
(2)
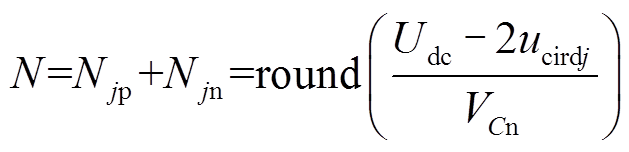 (3)
(3)
式中,Udc为MMC直流侧电压额定值;vrefj分别为j(j=a,b,c)相单元输出交流电压参考值;vrefjp、vrefjn为上、下桥臂电压的参考值;Njp、Njn分别为投入上、下桥臂的子模块数;VCn为单个子模块电容额定电压;ucirdj为j相的环流抑制器输出的环流电压;N为系统稳态时的子模块投入数目。
由式(3)可知,单相上、下桥臂投入的子模块总数与直流侧电压额定值、单个子模块电容额定电压以及与环流抑制器输出的环流电压有关。但不论系统是在稳态运行状态还是故障状态下,直流侧电压额定值、单个子模块电容额定电压都是定值,而环流电压ucirdj随系统运行状态不同而不同,因此 -2ucirdj值会影响上、下桥臂投入的子模块总数。为了考虑-2ucirdj对单相桥臂子模块总数的影响程度,本文对MMC-HVDC电网稳态运行情况进行电磁暂态仿真,其参数依照附表1选取。PSCAD电磁暂态仿真结果表明,环流电压的值在 0.05(pu)~0.05(pu)之间,则环流控制产生的子模块数变化值在8以内,因此式(3)中计算子模块数时忽略环流电压,则单相桥臂投入的子模块总数为
0.05(pu)~0.05(pu)之间,则环流控制产生的子模块数变化值在8以内,因此式(3)中计算子模块数时忽略环流电压,则单相桥臂投入的子模块总数为
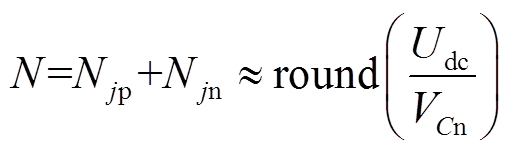 (4)
(4)
MMC-HVDC系统发生直流短路故障后利用ACLC方法抑制故障电流,其限流控制原理本质就是使MMC-HVDC电网发生故障后的数毫秒内,投入换流站中的子模块数将主动减小至n(n<N)。其直流出口电压变化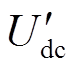 为
为
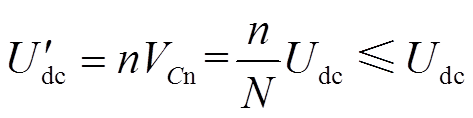 (5)
(5)
MMC出口直流电压迅速下降,从而实现减小故障电流上升率和峰值目的。
1.2.1 含ACLC的MMC等效RLC电路模型
如图1所示,直流侧发生双极短路故障情况下,MMC在故障后、闭锁前的短时间内,在电容电压平衡控制作用下,子模块电容通过故障点迅速放电。此时,MMC直流侧故障电流特性主要由子模块电容放电电流决定。而半桥型MMC-HVDC投入主动限流控制后,子模块投入数减小,迫使MMC直流输出电压降低,使子模块电容放电电流减小。根据电流通路可以得到含ACLC故障闭锁前MMC的等效RLC电路,如图2所示。图2中,MMC拓扑结构如图2的左图所示。每个MMC都是由6个桥臂组成,每个桥臂由1个桥臂电感和n个子模块组成。图2中的电容初始电压由故障前的Udc变为nUdc/N。R′C、LC、C′C分别为故障后、闭锁前含ACLC的MMC等效电路的串联电阻、电感、电容。
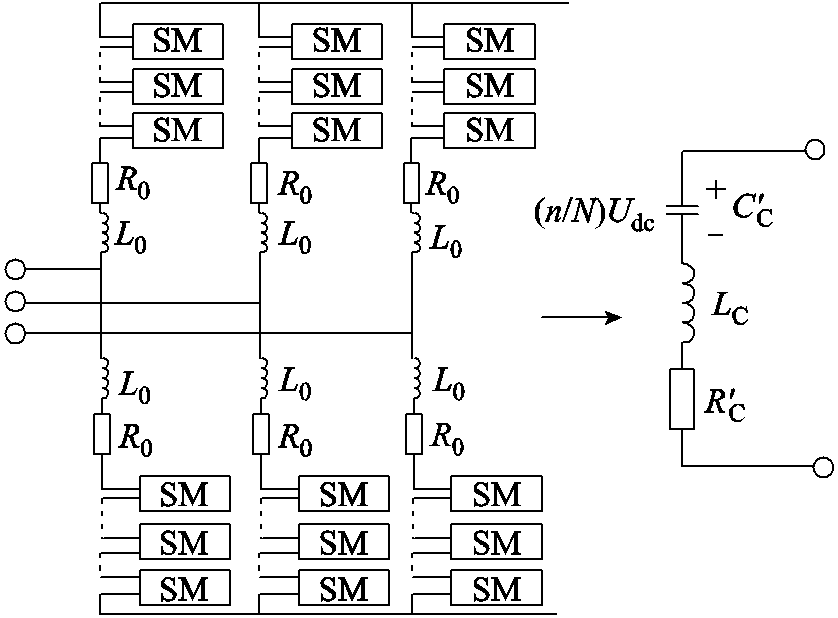
图2 MMC等效电路
Fig.2 MMC equivalent circuit
在分析未投入主动限流控制时系统的故障RLC回路时,可以利用储能相等原则计算等效电容。其中储能相等原则是指将单相的2N个子模块的电容用1个电容器来等效。其中单相2N个子模块的电容器储能与等效的1个电容器储存的能量相同以及承受的总电压不变[22]。但是当故障后换流站投入的子模块数由N减小到n,此时的子模块数并非是一个固定值,所以使用储能相等原则计算等效电容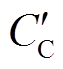 的方法将不再适用。同时,故障发生后,等效电阻值
的方法将不再适用。同时,故障发生后,等效电阻值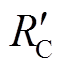 随子模块数减小而减小。因此,传统的等效RLC电路方法不能直接用于分析含ACLC的MMC-HVDC电网的直流短路故障电路。
随子模块数减小而减小。因此,传统的等效RLC电路方法不能直接用于分析含ACLC的MMC-HVDC电网的直流短路故障电路。
针对上述问题,本文首先建立了含ACLC的MMC-HVDC电网换流站出口压降与虚拟阻抗的压降的映射关系。该映射关系认为故障后投入桥臂中的子模块总数等效不变,即此时MMC等效电路中的子模块数仍为N,仍然满足传统的等效RLC电路,同时将ACLC控制作用等效为RLC电路中增设的虚拟阻抗消耗的压降,如图3所示。
图3中,ACLC的控制效果映射在MMC子模块虚拟电阻Rvir和电感Lvir的部分。由虚拟阻抗产生的压降为Δu。
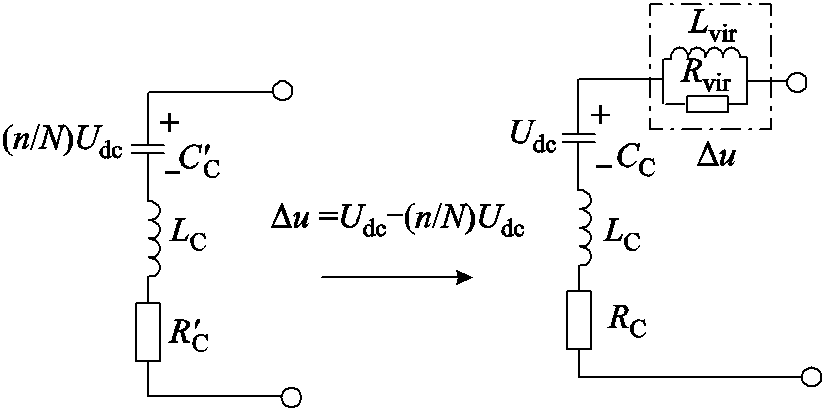
图3 含虚拟阻抗的MMC等效RLC电路
Fig.3 Equivalent RLC circuit of MMC with virtual impedance
MMC等效电路中虚拟阻抗产生的压降Δu一般形式为如式(6)所示。
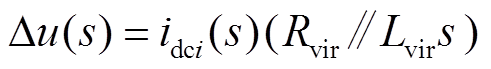 (6)
(6)
式中,idci为换流站i(i=a, b, c, d)的出口直流电流。
若等效虚拟阻抗只有电感或者电阻、电感并联形式,则相应产生的压降值分别为
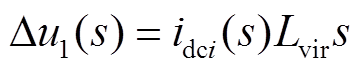 (7)
(7)
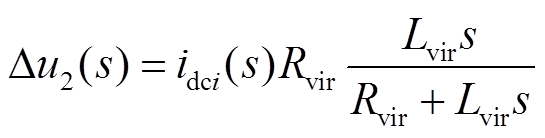 (8)
(8)
因此,主动限流控制的效果被等效成如图3的右图中RLC电路中新增的虚拟阻抗的压降,RLC电路中电容的总电压值不变,投入的子模块数仍为N,故等效电容CC就能遵循储能相等原则,并且等效电阻与故障前电阻相等,即等效电阻RC、电感LC、电容CC可满足
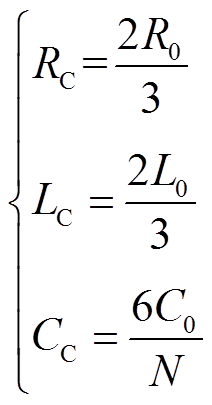 (9)
(9)
式中,R0,L0、C0分别为MMC的桥臂电阻和每个桥臂开关导通的总等效电阻值、桥臂电感值、子模块电容。
1.2.2 含ACLC换流站的等效RLC电路模型
对图1所示的基于半桥型的四端MMC-HVDC电网的正、负极换流站进行等效变换,每个换流站的正、负极是通过中性线电抗器连接。换流站的等效电路如图4所示。
图4中,换流站的等效RLC电路的电阻和Rsum、电感和Lsum、电容和Csum计算式为
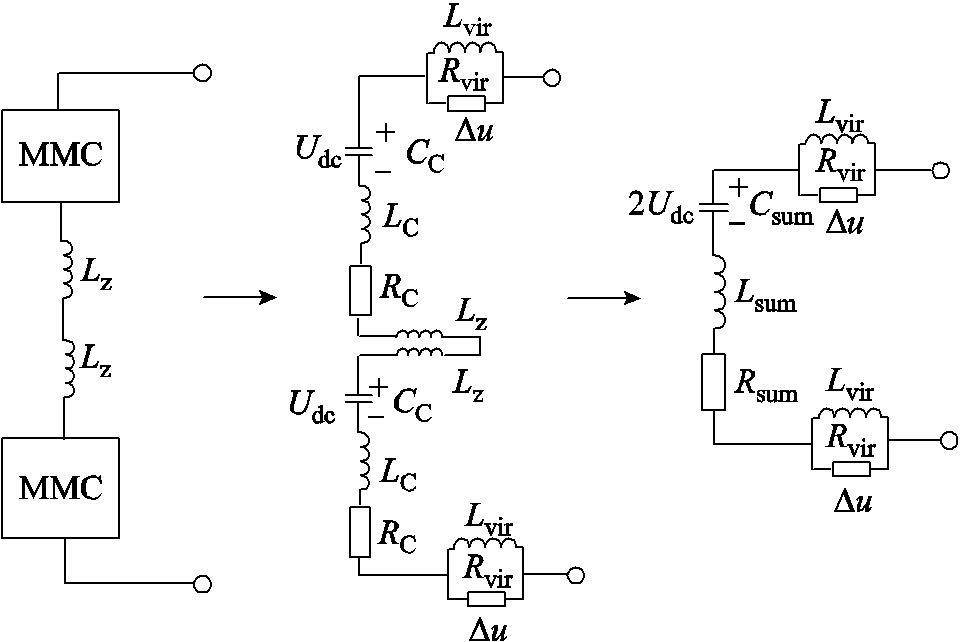
图4 含虚拟阻抗的换流站的等效电路
Fig.4 Equivalent circuit of converter station with virtual impedance
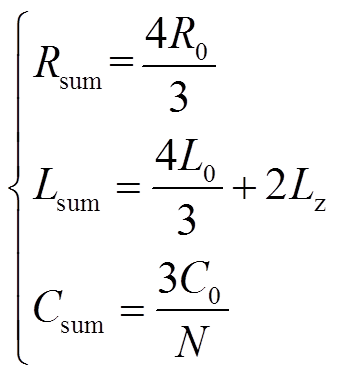 (10)
(10)
式中,Lz为中性线电抗器的电感值。
1.2.3 含ACLC的四端MMC-HVDC电网双极短路故障等效RLC模型
基于半桥型四端MMC-HVDC电网发生直流双极短路故障时,各换流站之间存在通过线路相互充放电的直接耦合关系,同时还存在子模块电容对故障点放电回路存在重叠而造成的耦合作用。但由于故障后换流站闭锁前的时间一般在10 ms以内,且并联换流站之间通过直流线路相互充放电导致的耦合作用基本可以忽略[25],因此本文只考虑故障后存在并联关系的换流站子模块电容对故障点的放电回路存在重叠关系造成的耦合作用。假设故障点在f1处,则故障后的MMC-HVDC电网按如图5所示进行拆分。为了便于分析,将距离故障点近的换流站定义为近端换流站,与近端换流站并联的换流站定义为次近端换流站。
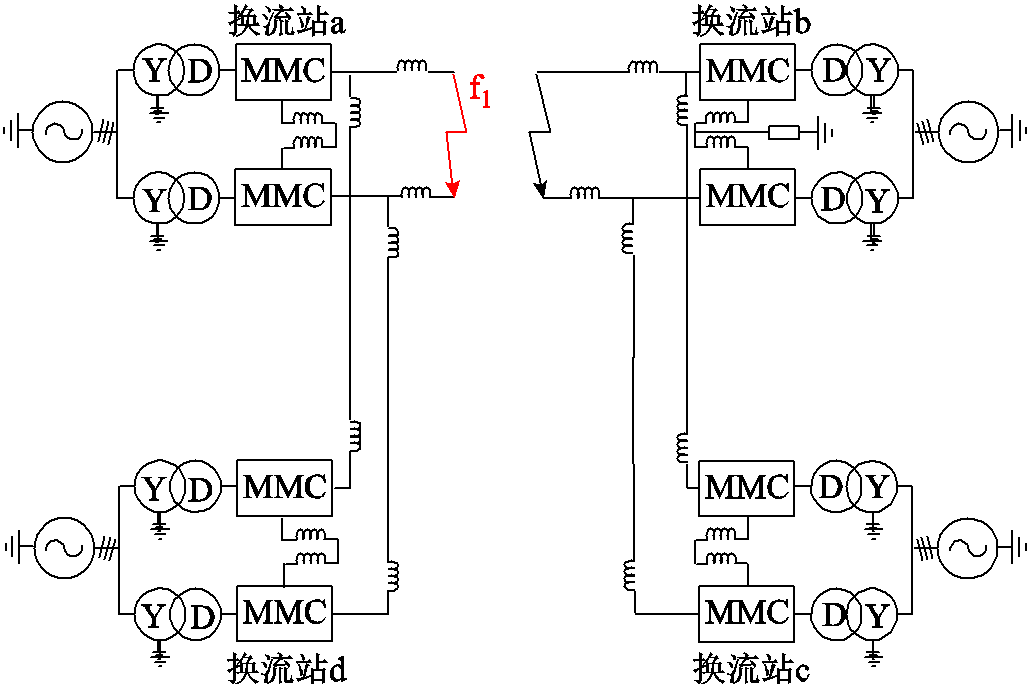
图5 故障后MMC-HVDC电网的简化方式
Fig.5 Simplified method of MMC-HVDC grid after fault
因此含ACLC的基于半桥型的四端MMC-HVDC电网在f1处的左侧故障回路的等效RLC电路如图6所示。
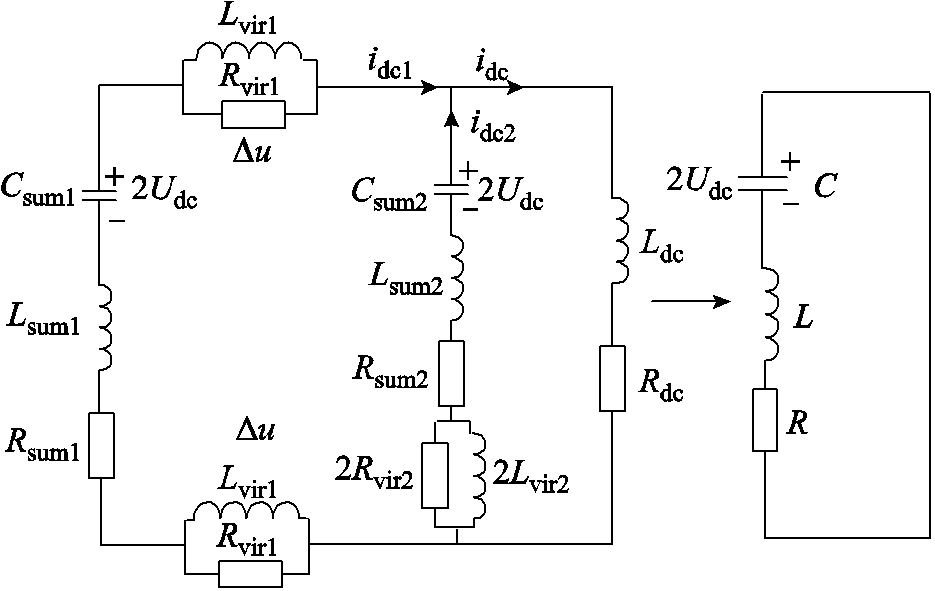
图6 基于半桥型的四端MMC-HVDC电网的含虚拟阻抗的等效RLC电路
Fig.6 Equivalent RLC circuit with virtual impedance on four-terminal MMC-HVDC grid based on half bridge
图6中,支路1为近端换流站的等效RLC支路,支路2为次近端换流站的等效RLC支路。idc1、idc2分别为支路1和2的直流故障电流。由此可见,并联换流站的子模块电容对故障点的放电回路重叠造成的耦合作用与换流站参数及放电回路中的线路参数有关。
为便于分析,将图6中虚拟电感和虚拟电阻的并联形式等效成串联形式,如图7所示。
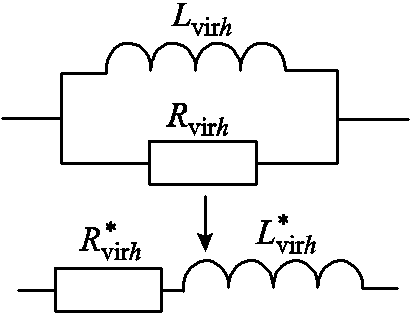
图7 虚拟电感、虚拟电阻的并串联转换
Fig.7 Parallel and series conversion of virtual inductance and virtual resistance
根据阻抗串并联的表达式转换,可得到并联形式的虚拟阻抗转化为串联形式的虚拟阻抗的关系式为
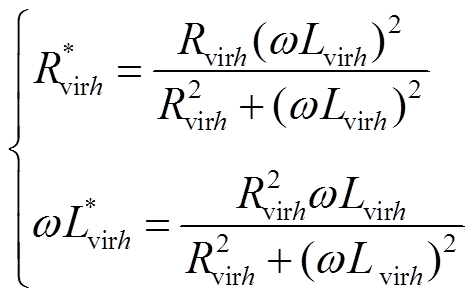 (11)
(11)
式中,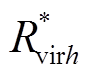 、
、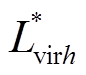 (h=1,2为支路1或者支路2)分别为等效电路中的虚拟电阻、虚拟电感串联形式值时对应;ω为直流故障回路角频率。
(h=1,2为支路1或者支路2)分别为等效电路中的虚拟电阻、虚拟电感串联形式值时对应;ω为直流故障回路角频率。
此时对应图6的等效RLC电路支路1的等效电阻、电感和电容分别为Rsum1、Lsum1、Csum1,支路2的等效电阻、电感和电容分别为Rsum2、Lsum2、Csum2,其各自的值为
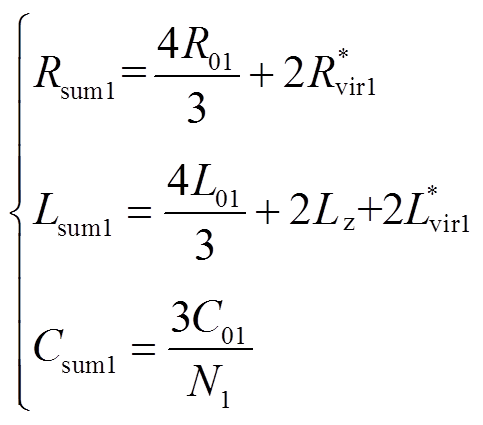 (12)
(12)
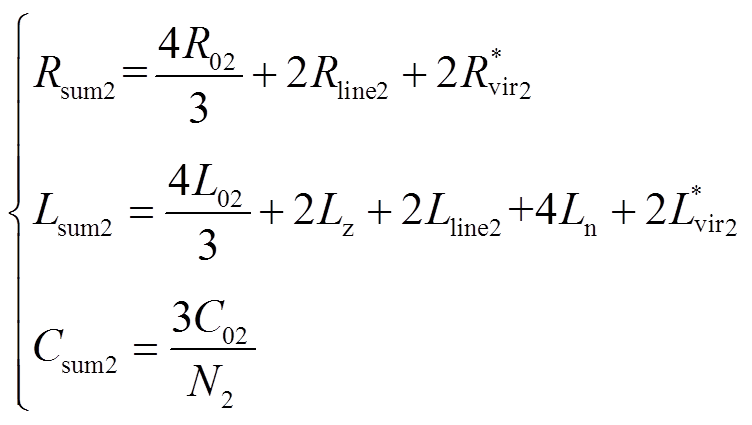 (13)
(13)
式中,R01、L01、C01、N1为近端换流站的桥臂电阻、桥臂电感、子模块电容、子模块投入数;R02、L02、C02、N2为次近端换流站的桥臂电阻、桥臂电感、子模块电容、子模块投入数;Rline2、Lline2为次近端换流站到近端换流站的线路电阻、线路电感;Ln为换流站出口处的平波电抗器;Rdc、Ldc分别为故障线路上总的电阻值、电感值。因此等效电路中的RLC电气参数分别为
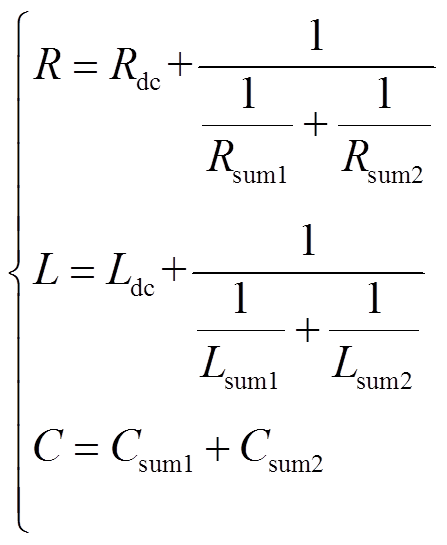 (14)
(14)
可得图6右侧故障回路暂态过程的故障电流解析解为
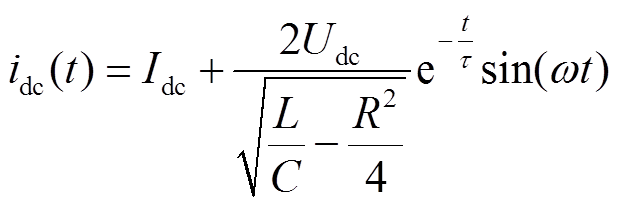 (15)
(15)
其中,电容初始时刻电压和回路初始时刻电流分别为故障前的直流电压Udc和故障前的线路直流电流Idc。式中参数时间常数τ,角频率ω分别为
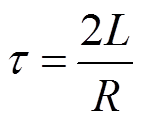 (16)
(16)
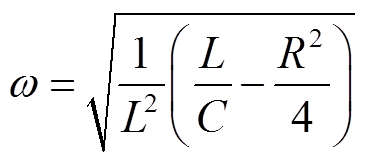 (17)
(17)
根据第1节含ACLC的MMC-HVDC电网直流双极短路故障电路的分析可知,只要能得到等效RLC电路中的虚拟阻抗值,就可以得到计及ACLC的直流短路故障电流的解析表达式。
因此本节采用文献[15]中的基于主动限流控制环节:以电流变化率限流的ACLC算法为例进行分析,确定控制参数与虚拟阻抗的对应关系,从而得到具体的故障电流解析式。图8为基于电流变化率限流的ACLC算法的控制框图。从图8中看出,主动限流控制算法的完整控制器有有功、无功外环控制,内环电流控制,环流抑制器、电流变化率限流控制环节。其中换流站a、c、d的外环控制器选择模式Ⅰ:定有功功率和定无功功率控制;换流站b的外环控制器选择模式Ⅱ:定直流电压控制、定无功功率控制,通过外环有功、无功控制获得内环的电流指令值。所采用的电流变化率限流算法由微分控制环节和滞环比较器组成。其原理为:换流站i(i为换流站a、b、c或者d)的直流母线电流idci先进行标幺化,再经过微分环节得到直流电流变化率didc/dt,将didc/dt通过滞环比较器得到动作信号,再将didc/dt乘以时间常数Td以及动作信号得到Δk,最后由上限幅值1.0减去Δk并经过限幅环节,得到该限流环节的输出k。其中,滞环比较器在输入大于动作值时输出为1,小于返回值时输出为0,动作值根据换流器直流电压和限流电感计算得到的变化率进行整定,返回值初步选定为0。其中Δk、k的表达式分别为
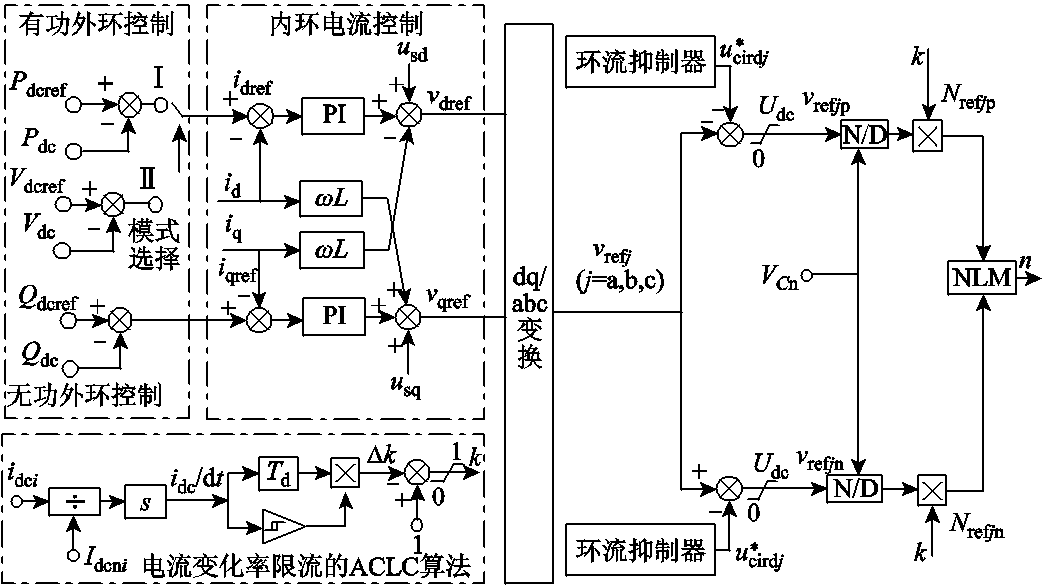
图8 电流变化率限流的ACLC算法控制框图
Fig.8 Control block diagram of ACLC algorithm for current change rate limiting
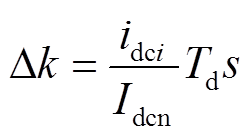 (18)
(18)
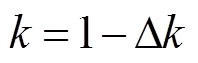 (19)
(19)
式中,Td为限流控制的时间常数;Idcn为换流站的出口直流电流的额定值。
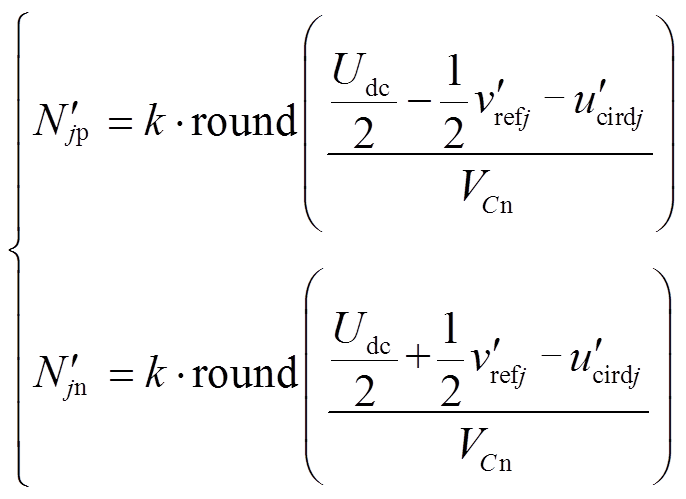
稳态时,主动限流控制不起作用,子模块数n=N,换流站出口直流电压值没有改变,则系统维持正常运行模式;双极短路故障发生后,电流变化率didc/dt>0,k<1,n随之逐渐减小,换流站出口直流电压值减小,达到减小直流短路故障电流的目的。因此,考虑了限流控制之后,在直流短路故障发生后,投入换流站的上、下桥臂的子模块数变为
 (20)
(20)
式中,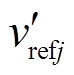 为含主动限流控制的MMC-HVDC系统的j(j=a,b,c)相单元输出交流电压参考值;
为含主动限流控制的MMC-HVDC系统的j(j=a,b,c)相单元输出交流电压参考值;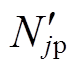 、
、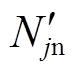 分别为上桥臂投入的子模块数、下桥臂投的子模块数;
分别为上桥臂投入的子模块数、下桥臂投的子模块数;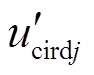 为环流抑制器的输出环流电压。
为环流抑制器的输出环流电压。
此时单相桥臂中投入的子模块数n为
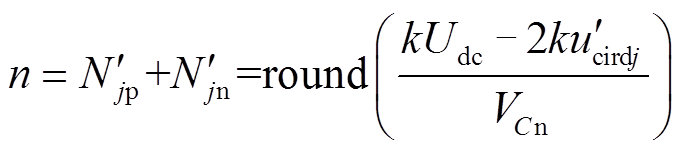 (21)
(21)
由式(21)可以看出,单相上、下桥臂投入的子模块数与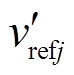 无关,而与
无关,而与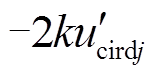 有关。根据PSCAD电磁暂态仿真结果,发生故障后10 ms内,环流电压
有关。根据PSCAD电磁暂态仿真结果,发生故障后10 ms内,环流电压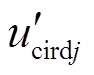 的值在-0.15(pu)~0.2(pu)之间,则环流控制产生b相子模块数变化值在18以内,因此
的值在-0.15(pu)~0.2(pu)之间,则环流控制产生b相子模块数变化值在18以内,因此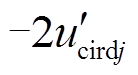 对b相子模块投入总数存在一定的影响,但是为了后续虚拟阻抗的RLC电路的等效,简便起见,本文忽略
对b相子模块投入总数存在一定的影响,但是为了后续虚拟阻抗的RLC电路的等效,简便起见,本文忽略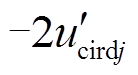 对单相子模块投入总数的影响。因此,式(21)中计算子模块数时忽略环流电压,则单相桥臂投入的子模块总数为
对单相子模块投入总数的影响。因此,式(21)中计算子模块数时忽略环流电压,则单相桥臂投入的子模块总数为
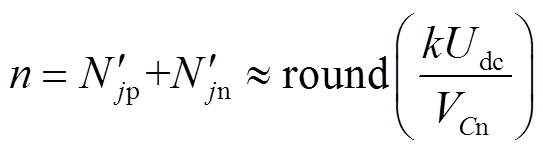 (22)
(22)
因此换流站出口直流电压减小的压降Δu1为
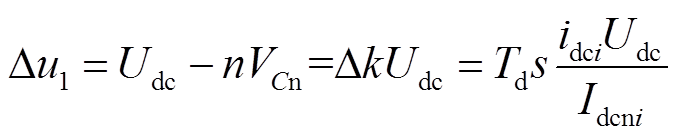 (23)
(23)
由第1节分析可知,ACLC算法的限流控制效果可以等效成虚拟电感的压降,也可以等效成虚拟电阻和虚拟电感压降。但是文献[15]中的基于电流变化率限流的ACLC算法采用微分控制环节,其限流效果等效成虚拟电感。因此,为了验证该等效RLC电路的广泛性,现使用超前滞后惯性环节,则限流效果等效为虚拟阻抗产生的压降。因此改进的基于电流变化率限流的ACLC算法的控制框图如图9所示。
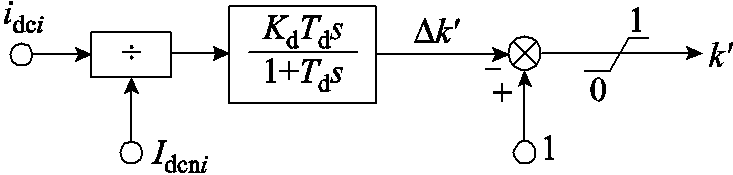
图9 改进的基于电流变化率限流的ACLC算法的控制框图
Fig.9 Control block diagram of improved ACLC algorithm for current change rate limiting
图9所示改进的基于电流变化率限流算法由超前滞后惯性环节组成。其原理为:换流站i(i为换流站a、b、c或者d)的直流母线电流idci先进行标幺化,再经过比例微分环节得到Δk',最后由上限幅值1.0减去Δk'并经过限幅环节,得到该限流环节的输出k'。相应的Δk'、k'的表达式为
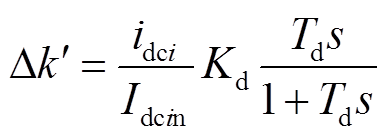 (24)
(24)
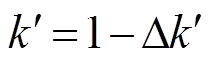 (25)
(25)
式中,Kd为限流控制的增益系数。
同理,采用超前滞后惯性环节时,换流站出口直流电压减小的压降Δu2如式(26)所示。
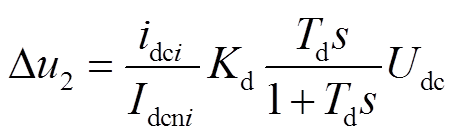 (26)
(26)
2.2.1 虚拟电感值确定
本节以基于电流变化率限流的ACLC算法为例讨论虚拟电感值确定方法。基于电流变化率限流的ACLC算法使用了微分控制环节,其等效压降在等效RLC电路中体现为虚拟电感的压降。即根据式(7)与式(23)有
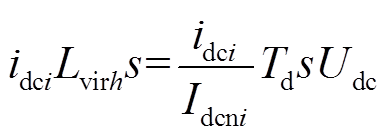 (27)
(27)
则虚拟电感值为
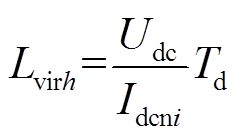 (28)
(28)
由式(12)~式(17)和式(28)得到限流控制参数Td与电流idc的关系,从而计算出故障电流。
2.2.2 虚拟电阻、电感值确定
同样,改进的基于电流变化率限流控制的ACLC算法,其中使用了超前滞后惯性环节,其压降将在等效RLC电路中等效为虚拟电感和电阻并联的压降。则根据式(8)与式(26)有
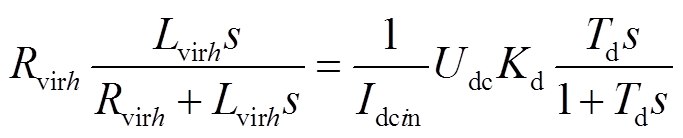 (29)
(29)
则虚拟电阻和电感值为
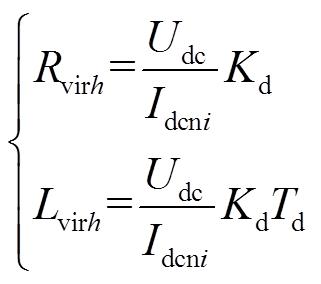 (30)
(30)
由式(11)~式(17)和式(30)可以得到限流控制参数Td、Kd与直流故障电流idc的关系,从而计算出故障电流。
本文在PSCAD/EMTDC上搭建了如图1所示的含ACLC的基于半桥型四端MMC-HVDC电网的电磁暂态仿真模型,四端MMC-HVDC正常运行时,换流站a、d为送端换流站,换流站b、c为受端换流站,因此以功率从换流站a向b,换流站d向c流入的方向为正方向。其中,电网参数参照文献[30]选取,其参数见附表1,以基于电流变化率限流环节的ACLC方法为例验证本方法的准确性。
考虑到验证该方法的广泛性,采取两组实验。实验一为限流环节使用了微分控制环节,其限流效果映射为虚拟电感的压降,即故障回路为含虚拟电感的等效RLC电路;实验二为电流变化率环节使用了超前滞后惯性环节,其限流效果映射为虚拟电感与虚拟电阻并联的压降,即故障回路为含虚拟阻抗的等效RLC电路。并且针对这两组实验,设置不同的故障点、以及不同的控制参数,分别采用PSCAD电磁暂态仿真和含基于电流变化率限流的ACLC算法的等效RLC电路解析计算得到直流电路故障电流仿真结果与计算结果。其不同仿真场景见表1。实验一中的Td=0.001 s按照文献[15]选取。
表1 场景设置
Tab.1 Scene setting
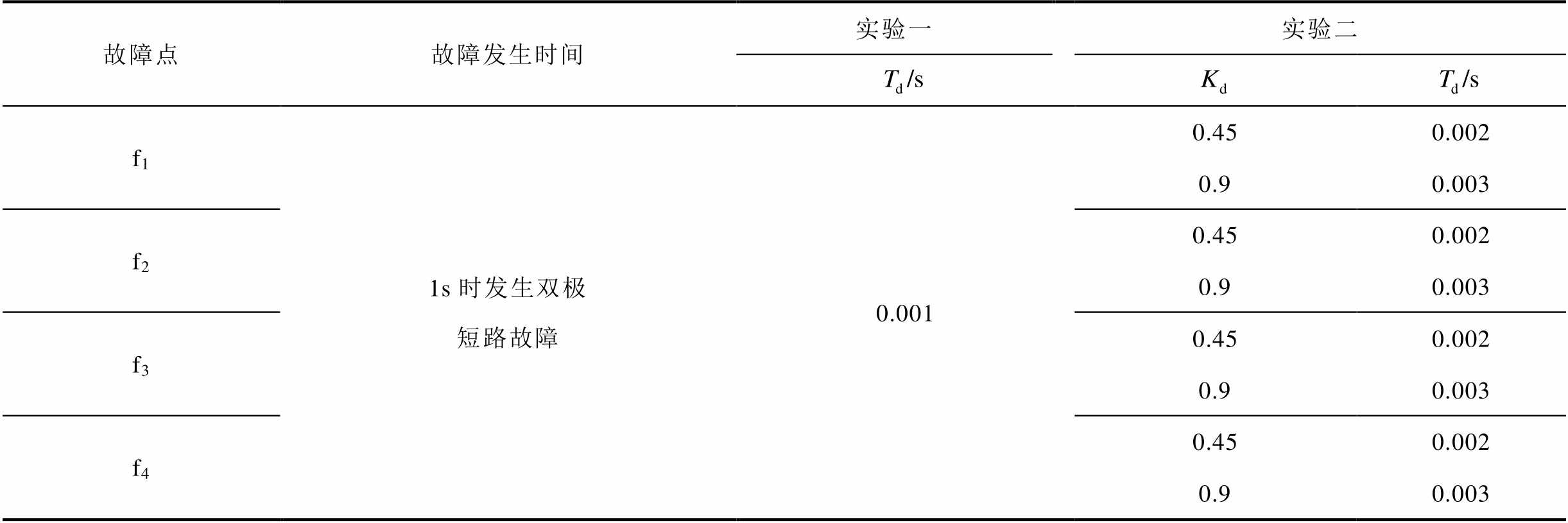
故障点故障发生时间实验一实验二 f11s时发生双极短路故障0.0010.450.002 0.90.003 f20.450.002 0.90.003 f30.450.002 0.90.003 f40.450.002 0.90.003
1)实验一:含虚拟电感的等效RLC电路仿真结果
图10为实验一的直流短路故障电流在不同故障处的仿真结果与计算结果对比。由图可以看出,4个故障处的故障电流计算的相对误差最大为 7.87%,平均误差为3.31%。
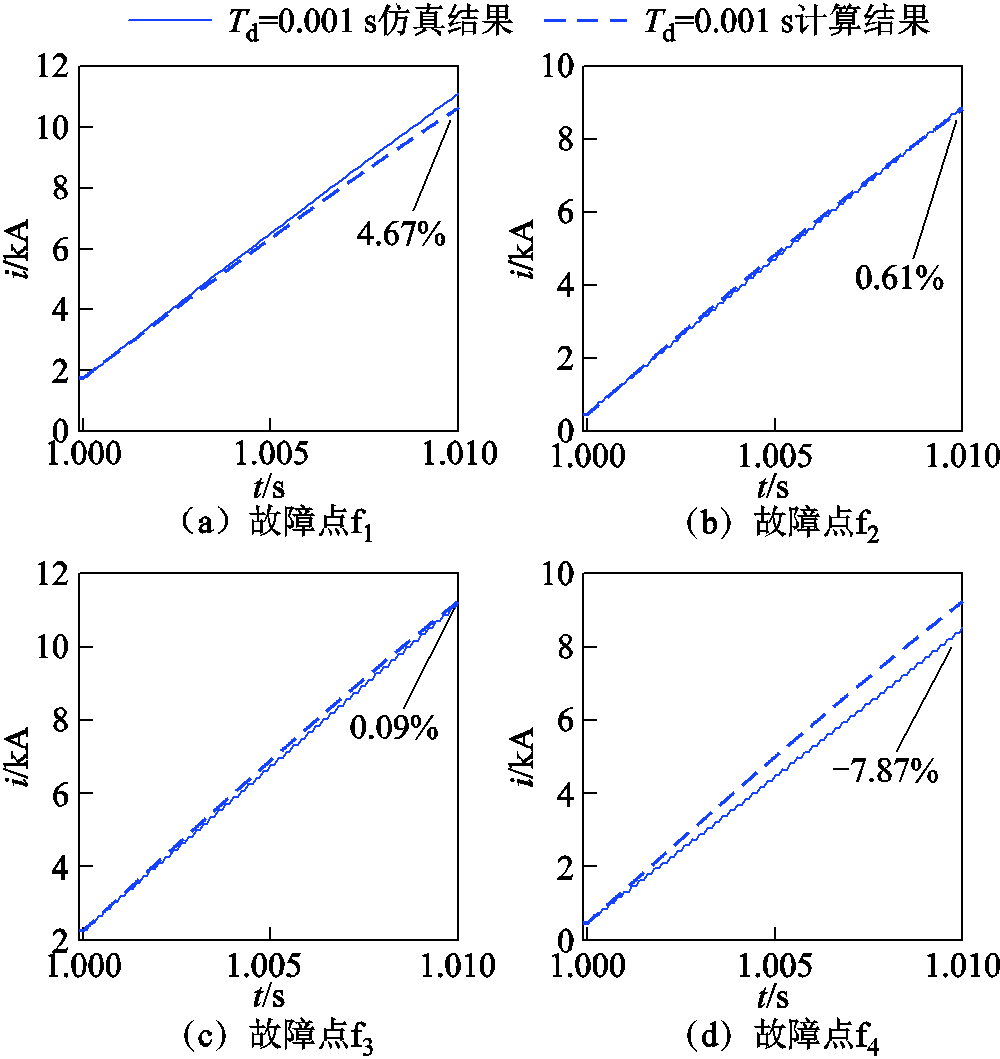
图10 实验一:故障电流在不同故障点处的验证结果
Fig.10 Verification results of fault current at different fault points in experiment 1
2)实验二:含虚拟阻抗的等效RLC电路仿真结果
实验二中由于使用超前滞后惯性环节实现ACLC的限流效果,在控制效果中会存在控制延迟的问题。因此,在故障电流解析计算式中,考虑在故障1~1.5 ms之间虚拟阻抗不起作用,则使用无限流控制时的故障电流计算解析式;在故障1.5 ms后,虚拟阻抗起作用,使用含虚拟阻抗的故障电流计算解析式。对应的故障电流仿真结果与计算结果如图11所示。
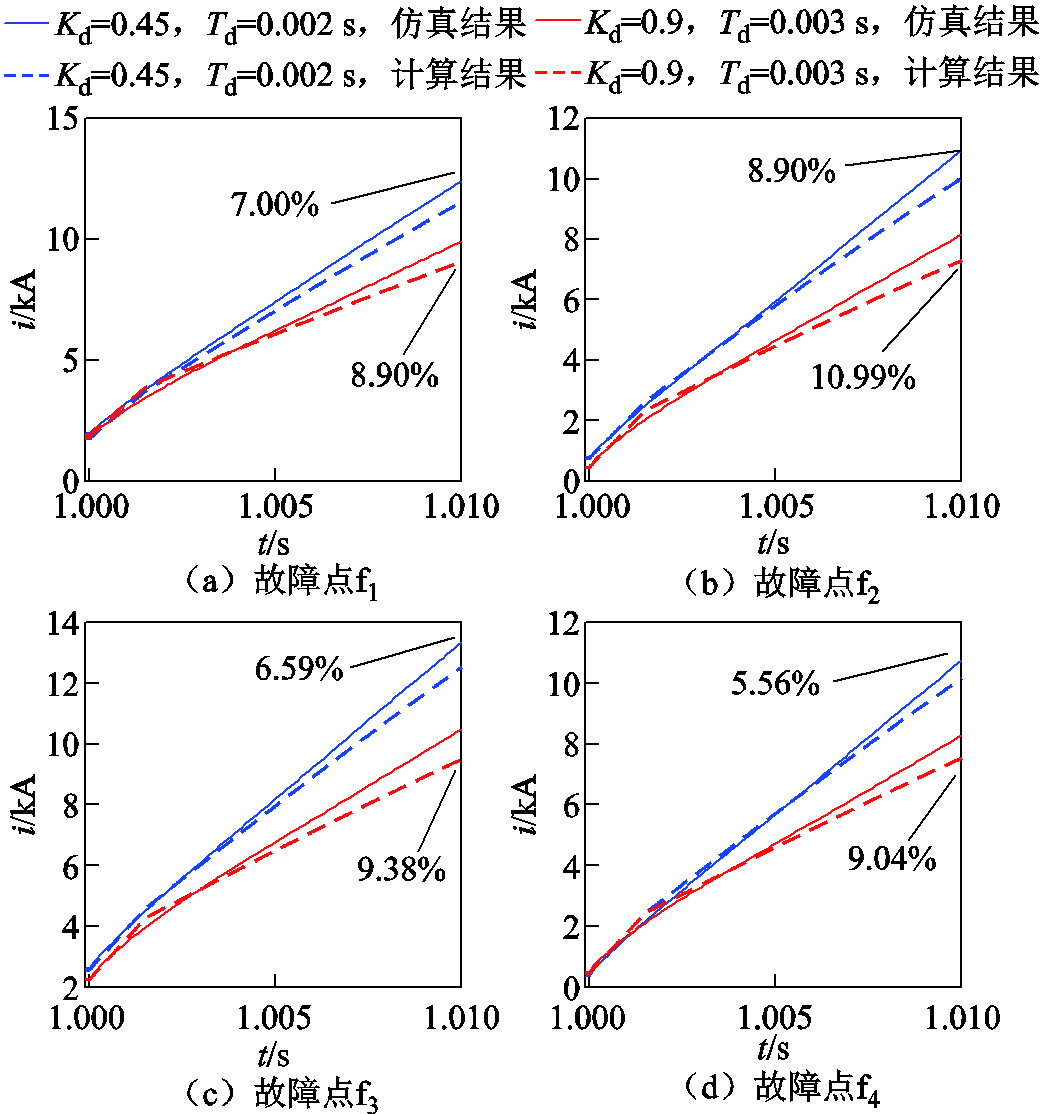
图11 实验二:故障电流在不同场景的验证结果
Fig.11 Verification results of fault current in different scenarios in experiment 2
图11为实验二在4个故障点处以及选取不同参数下的直流短路故障电流仿真结果与计算结果对比。4个场景中的故障电流计算的相对误差最大为10.99%,平均误差为8.29%。实验二中限流控制器参数选取Kd=0.9,Td=0.003 s,分别在4个不同故障点下进行电流计算,与实验一相比,其计算结果较仿真结果都具有较大的误差,可能的原因是控制器参数取值大导致k在故障10 ms内就到达上限幅值1.0,使得采用PSCAD仿真的故障电流比解析计算的故障电流大。其两组实验的电流仿真结果与计算结果的误差见表2。
表2 两组实验-不同场景电流的仿真与计算结果误差
Tab.2 Two sets of experiments - error of current simulation and calculation results in different scenarios
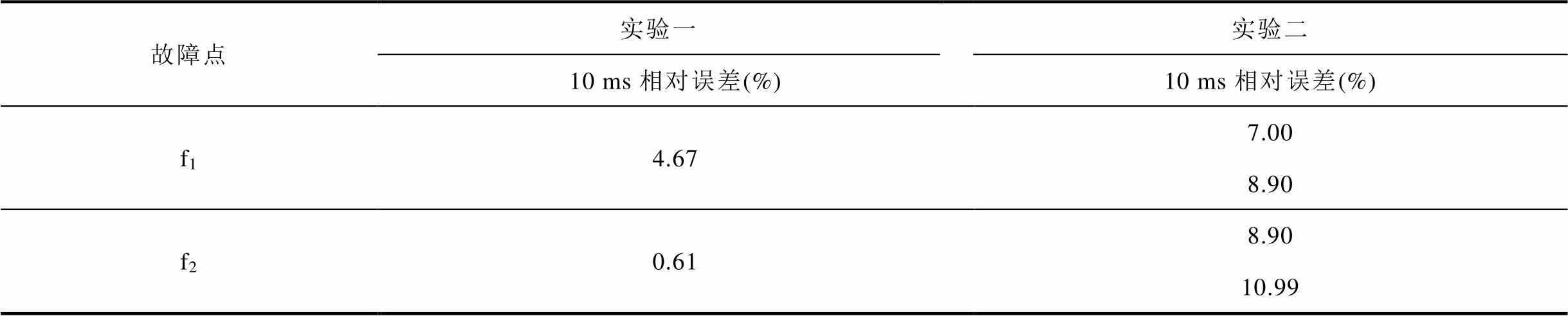
故障点实验一实验二 10 ms相对误差(%)10 ms相对误差(%) f14.677.00 8.90 f20.618.90 10.99
(续)
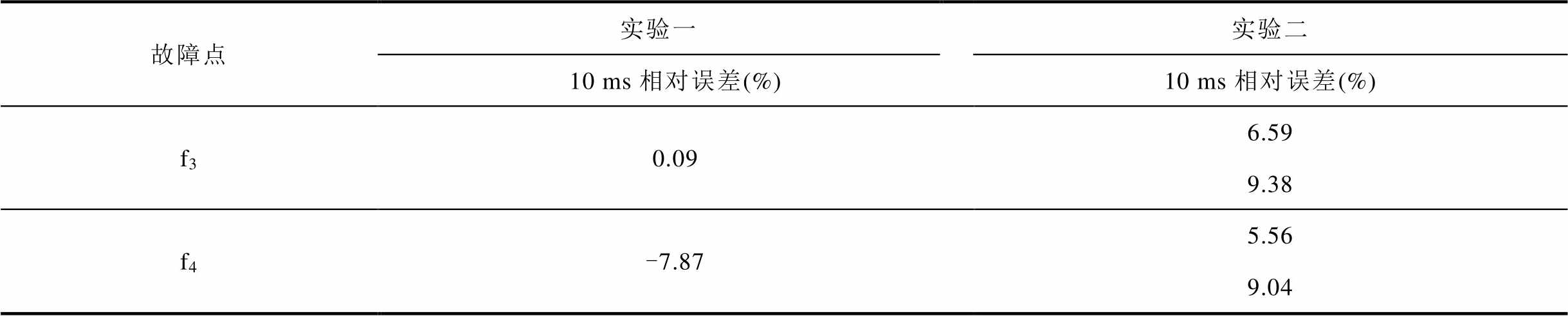
故障点实验一实验二 10 ms相对误差(%)10 ms相对误差(%) f30.096.59 9.38 f4-7.875.56 9.04
从两组实验中都可以看出,使用含虚拟阻抗的等效RLC电路分析ACLC的MMC-HVDC电网的故障电流仿真结果与计算结果误差都小于11%,其分析方法具有一定的准确性。
3)与现有典型故障电流计算方法比较
为了体现本方法的优势,本节按照文献[15]的仿真模型和仿真参数,增加了文献[15]中电流变化率限流控制的故障电流计算方法的仿真和计算结果,并与本文提出的计算方法的计算结果进行比较,结果如图12所示。其中,MMC-HVDC系统在1 s时发生双极短路故障。从图中看出文献[15]中的故障电流计算最大相对误差为-2.89%,本文提的故障电流计算最大相对误差为3.06%,两种方法都能较为准确地计算出故障10 ms内的直流短路电流。但是文献[15]从单个换流站的角度分析故障电流特性,因此只适用于计算单端换流器系统的故障电流。而本文的故障电流计算考虑了多端换流器投入主动限流控制对故障电流的影响,因此本文提出的故障电流计算方法不仅能计算单端换流器系统的故障电流,还可以计算多端换流器系统的直流短路故障电流。
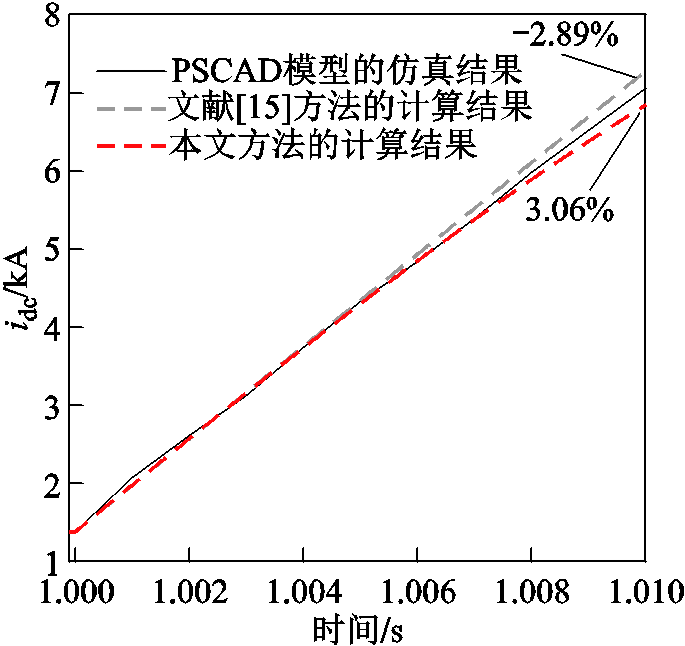
图12 与现有典型故障电流计算方法对比
Fig.12 Comparison with existing typical fault current calculation methods
4)与传统等效RLC电路方法计算结果比较
传统的等效RLC电路未考虑到主动限流控制投入系统中对故障电流的影响,本文提出的计算方法考虑了主动限流控制投入系统中对故障电流的影响。因此为了体现本文提出的电流计算方法在准确度上的优势,本节增加了采用传统等效RLC电路计算方法[30]计算的直流短路故障电流与电磁暂态仿真模型仿真结果对比,如图13所示。其中的电磁暂态仿真模型、参数选取与仿真结果与实验一中选取相同,并且选取了4个不同故障点位置的双极短路的故障场景。从图13可以看出,在故障发生后 10 ms时,使用传统等效RLC电路方法计算的直流短路故障电流和电流仿真结果相对误差最大能达到-49.55%,最小的电流相对误差也达到了-22.72%,而本文提出的电流计算方法相对误差在10.99%以下。因此,传统的等效RLC电路计算方法计算的误差较大,无法用于分析含ACLC的多端MMC-HVDC电网的直流短路故障电流。
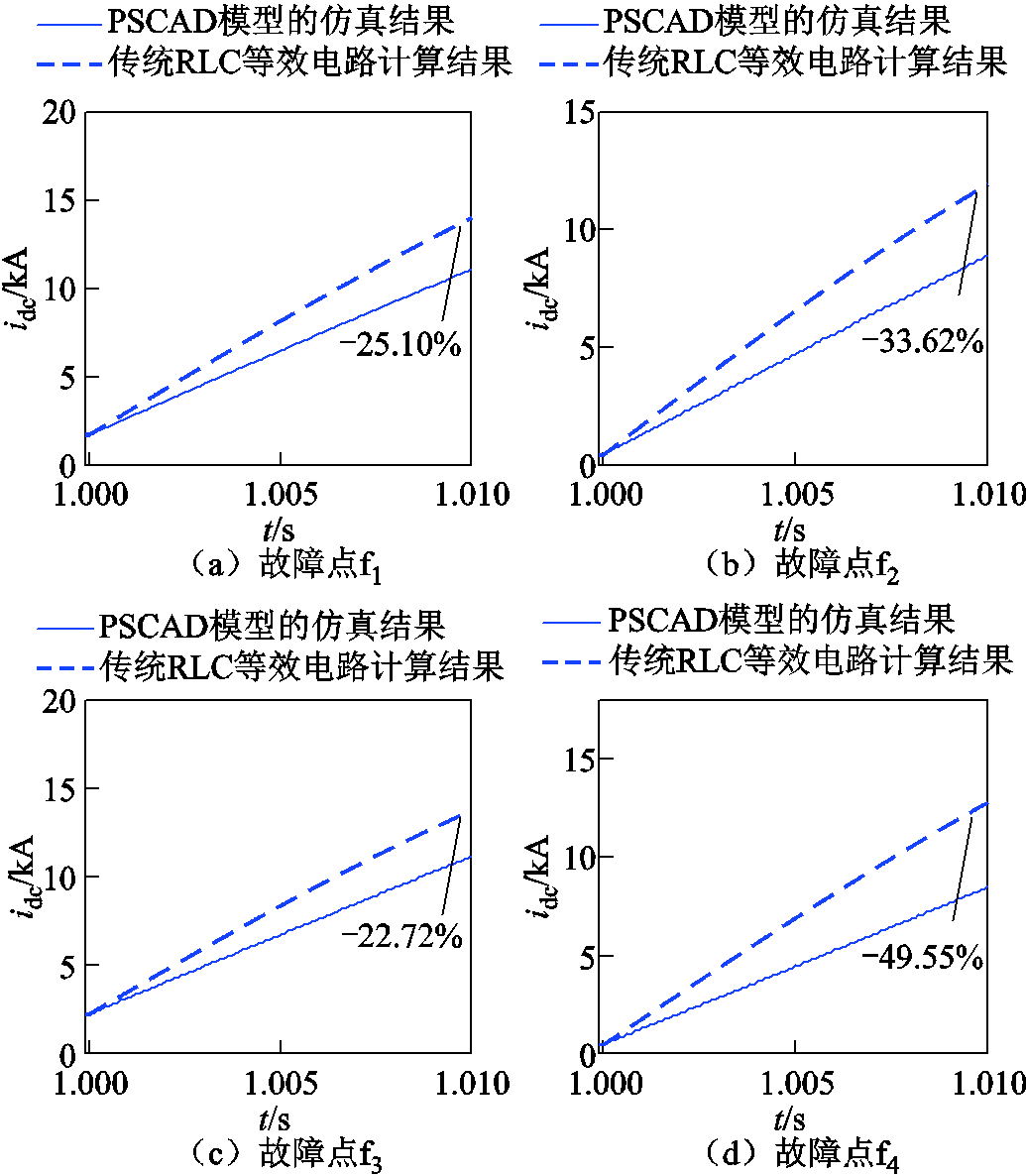
图13 传统RLC等效电路方法计算的直流短路故障电流与电流仿真结果对比
Fig.13 Comparison between DC short-circuit fault current calculated by traditional RLC equivalent circuit method and current simulation value
本文提出了含ACLC的MMC-HVDC电网直流短路故障电流的等效RLC模型和时域解析解,以电流变化率限流环节的ACLC和四端MMC-HVDC电网为例,在PSCAD环境下建立了电磁暂态仿真模型,通过对比电磁暂态模型和含ACLC的等效RLC解析模型的结果,得到如下结论:
1)ACLC投入后,通过将换流站出口直流电压降映射为虚拟阻抗产生的压降,直流双极短路故障回路可等效为含虚拟阻抗的RLC放电电路,从而建立含ACLC特性的等效RLC电路模型。
2)采用虚拟电感映射方法(实验一)在不同直流短路故障场景下,10 ms内故障电流计算平均相对误差都在3.31%以下;采用虚拟阻抗映射方法(实验二)在不同直流短路故障场景下,10 ms内故障电流计算平均相对误差都在8.29%以下,因此该计算方法具有较好的工程实用性。
3)本文在分析虚拟阻抗的等效RLC电路时,忽略了环流抑制器在故障情况下的动态特性对等效虚拟阻抗的影响。因此后续工作可以考虑环流抑制器对故障电流计算方法的影响,以进一步提高计算方法的准确度。
4)尽管本文采用具体电流变化率的限流环节类型的ACLC算法,展示了所提出方法的思想,但该方法可以推广到分析其他类型的主动限流控制的短路故障电流计算问题。
附 录
附表1 四端MMC-HVDC电网参数
App.Tab.1 The parameters of the four-terminal MMC-HVDC grid
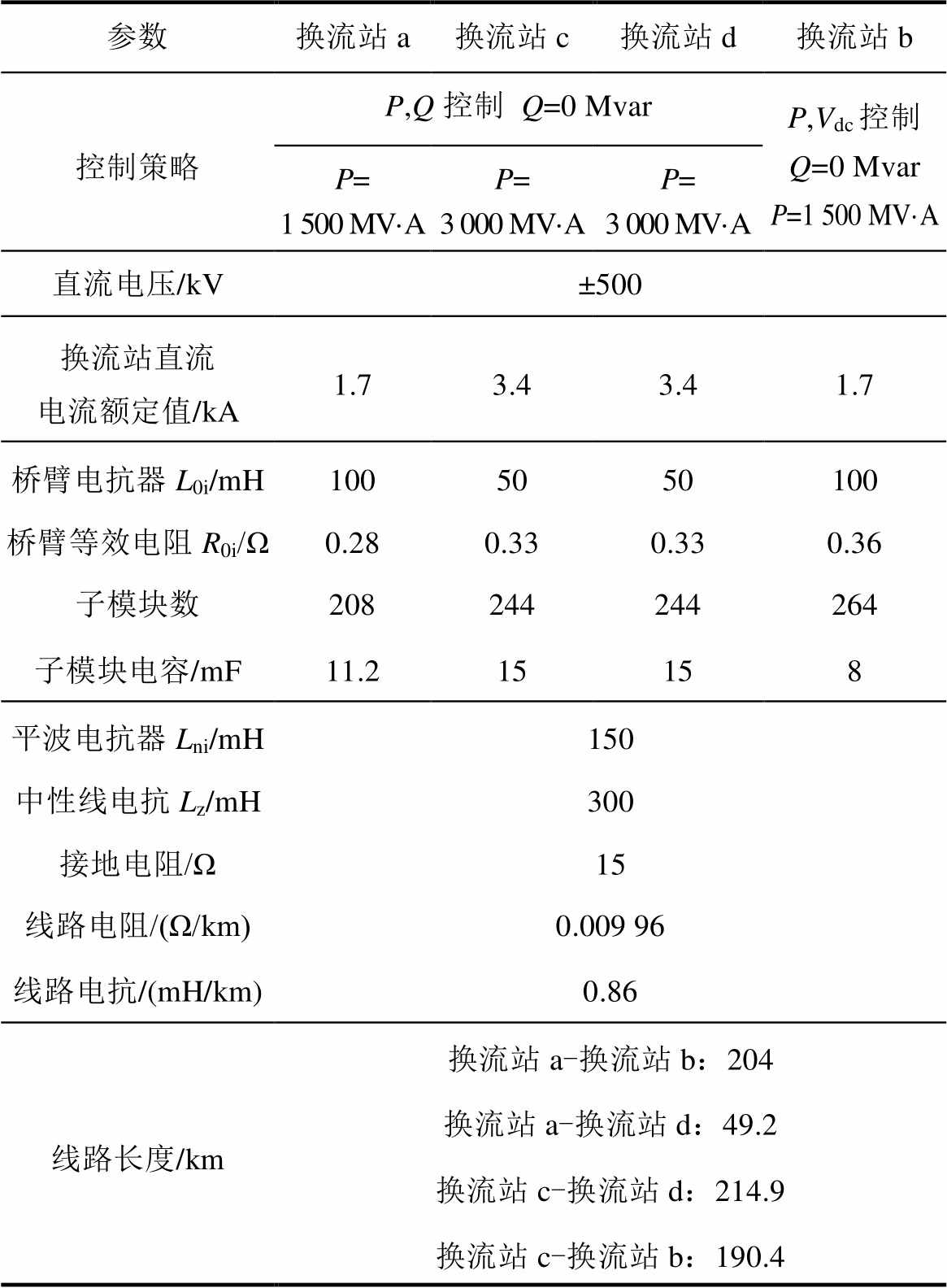
参数换流站a换流站c换流站d换流站b 控制策略P,Q控制Q=0 MvarP,Vdc控制Q=0 MvarP=1 500 MV·A P=1 500 MV·AP=3 000 MV·AP=3 000 MV·A 直流电压/kV±500 换流站直流电流额定值/kA1.73.43.41.7 桥臂电抗器L0i/mH1005050100 桥臂等效电阻R0i/Ω0.280.330.330.36 子模块数208244244264 子模块电容/mF11.215158 平波电抗器Lni/mH150 中性线电抗Lz/mH300 接地电阻/Ω15 线路电阻/(Ω/km)0.009 96 线路电抗/(mH/km)0.86 线路长度/km换流站a-换流站b:204 换流站a-换流站d:49.2 换流站c-换流站d:214.9 换流站c-换流站b:190.4
参考文献
[1] 严胜, 罗湘, 贺之渊. 直流电网核心装备及关键技术展望[J]. 电力系统自动化, 2019, 43(3): 205-215.
Yan Sheng, Luo Xiang, He Zhiyuan. Prospect of core equipment and key technology for DC power grid[J]. Automation of Electric Power Systems, 2019, 43(3): 205-215.
[2] CICRE B4-52 Working Group. HVDC grid feasibility study[R]. Melbourne: International Council on Large Electric Systems, 2013.
[3] 陈继开, 孙川, 李国庆, 等. 双极MMC-HVDC系统直流故障特性研究[J]. 电工技术学报, 2017, 32(10): 53-60, 68.
Chen Jikai, Sun Chuan, Li Guoqing, et al. Study on characteristics of DC fault in bipolar MMC-HVDC system[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 53-60, 68.
[4] 黄强, 邹贵彬, 高磊, 等. 基于HB-MMC的直流电网直流线路保护技术研究综述[J]. 电网技术, 2018, 42(9): 2830-2840.
Huang Qiang, Zou Guibin, Gao Lei, et al. Review on DC transmission line protection technologies of HB-MMC based DC grids[J]. Power System Technology, 2018, 42(9): 2830-2840.
[5] 陈磊, 何慧雯, 王磊, 等. 基于半桥型MMC的柔性直流电网故障限流方法综述[J]. 电力系统保护与控制, 2021, 49(21): 175-186.
Chen Lei, He Huiwen, Wang Lei, et al. Review of the fault current limiting approaches for a flexible DC grid based on a half-bridge MMC[J]. Power System Protection and Control, 2021, 49(21): 175-186.
[6] 茆美琴, 程德健, 袁敏, 等. 基于暂态能量流的模块化多电平高压直流电网接地优化配置[J]. 电工技术学报, 2022, 37(3): 739-749.
Mao Meiqin, Cheng Dejian, Yuan Min, et al. Optimal allocation of grounding system in high voltage direct current grid with modular multi-level converters based on transient energy flow[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 739-749.
[7] 周光阳, 李妍, 何大瑞, 等. 含限流器的多端柔直系统故障保护策略[J]. 电工技术学报, 2020, 35(7): 1432-1443.
Zhou Guangyang, Li Yan, He Darui, et al. Protection scheme for VSC-MTDC system with fault current limiter[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1432-1443.
[8] Mao Meiqin, Lu Hui, Cheng Dejian, et al. Optimal allocation of fault current limiter in MMC-HVDC grid based on transient energy flow[J]. CSEE Journal of Power and Energy Systems, 2023, 9(5): 1786-1796.
[9] 郑涛, 吴琼, 吕文轩, 等. 基于主动限流控制的直流配电网保护及故障隔离方案[J]. 电力系统自动化, 2020, 44(5): 114-121.
Zheng Tao, Wu Qiong, Lü Wenxuan, et al. Protection and fault isolation scheme based on active current-limiting control for DC distribution network[J]. Automation of Electric Power Systems, 2020, 44(5): 114-121.
[10] 韩杰祥, 张哲, 冉启胜, 等. 低压直流配电网主动限流控制及保护方案[J]. 电力系统自动化, 2022, 46(9): 182-190.
Han Jiexiang, Zhang Zhe, Ran Qisheng, et al. Active Current-limiting control and protection scheme for low-voltage DC distribution network[J]. Automation of Electric Power Systems, 2022, 46(9): 182-190.
[11] 张帆, 许建中, 苑宾, 等. 基于虚拟阻抗的MMC交、直流侧故障过电流抑制方法[J]. 中国电机工程学报, 2016, 36(8): 2103-2113.
Zhang Fan, Xu Jianzhong, Yuan Bin, et al. Over Current suppression control for AC and DC faults of modular multilevel converters based on virtual impedance[J]. Proceedings of the CSEE, 2016, 36(8): 2103-2113.
[12] 唐欣, 海帆, 湛若水. 直流配电网中送端换流器的故障限流控制策略[J]. 高电压技术, 2021, 47(10): 3424-3429.
Tang Xin, Hai Fan, Zhan Ruoshui. Fault current limiting control strategy of converter at the sending end in DC distribution network[J]. High Voltage Engineering, 2021, 47(10): 3424-3429.
[13] 吴琼. 柔性直流配电网故障特性分析及保护原理研究[D]. 北京: 华北电力大学, 2020.
Wu Qiong. Research on fault characteristic analysis and protection principle of flexible DC distribution network[D]. Beijing: North China Electric Power University, 2020.
[14] 樊强, 赵西贝, 赵成勇, 等. 模块化多电平换流器自适应故障限流控制策略[J]. 电力系统自动化, 2021, 45(17): 126-133.
Fan Qiang, Zhao Xibei, Zhao Chengyong, et al. Adaptive fault current limiting control strategy for modular multilevel converter[J]. Automation of Electric Power Systems, 2021, 45(17): 126-133.
[15] 倪斌业, 向往, 周猛, 等. 半桥MMC型柔性直流电网自适应限流控制研究[J]. 中国电机工程学报, 2020, 40(17): 5609-5619.
Ni Binye, Xiang Wang, Zhou Meng, et al. Research on adaptive-current-limiting control of VSC-HVDC grid based on half-bridge MMC[J]. Proceedings of the CSEE, 2020, 40(17): 5609-5619.
[16] 李国庆, 杨勇, 辛业春, 等. 基于桥臂电压控制的MMC直流短路主动限流方法[J]. 电网技术, 2021, 45(1): 144-152.
Li Guoqing, Yang Yong, Xin Yechun, et al. Active Current-limiting method of MMC to handle DC short-circuit based on bridge arm voltage control[J]. Power System Technology, 2021, 45(1): 144-152.
[17] Fang Xiongfeng, Hu Zeyu, Xing Yongfei, et al. A DC fault current limiting method for HB-MMC without losing control of AC currents[C]//2021 IEEE 12th Energy Conversion Congress & Exposition - Asia (ECCE-Asia), Singapore, 2021: 279-284.
[18] 丁然, 梅军, 管州, 等. 适用于MMC型直流变压器的直流故障主动限流控制方法[J]. 电力系统自动化, 2018, 42(21): 131-138.
Ding Ran, Mei Jun, Guan Zhou, et al. Active current limiting control method for DC fault of MMC based DC transformer[J]. Automation of Electric Power Systems, 2018, 42(21): 131-138.
[19] Mei Jun, Fan Guangyao, Ge Rui, et al. Research on coordination and optimal configuration of current limiting devices in HVDC grids[J]. IEEE Access, 2019, 7: 106727-106739.
[20] Yang Haiqian, Zeng Hongyan. Modeling on transient characteristic and suppression control of DC fault in MMC-HVDC system[J]. IOP Conference Series: Materials Science and Engineering, 2018, 394(4): 042117.
[21] 裴翔羽, 汤广福, 张盛梅, 等. 双极柔性直流电网短路电流暂态特性分析[J]. 全球能源互联网, 2018, 1(4): 403-412.
Pei Xiangyu, Tang Guangfu, Zhang Shengmei, et al. Analysis on transient characteristics of short-circuit current for bipolar VSC-based DC grid[J]. Journal of Global Energy Interconnection, 2018, 1(4): 403-412.
[22] 徐政, 肖晃庆, 张哲任. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017.
[23] 和敬涵, 黄威博, 李海英, 等. FBMMC直流故障穿越机理及故障清除策略[J]. 电力自动化设备, 2017, 37(10): 1-7.
He Jinghan, Huang Weibo, Li Haiying, et al. FBMMC DC fault ride-through mechanism and fault clearing strategy[J]. Electric Power Automation Equipment, 2017, 37(10): 1-7.
[24] 张建坡, 赵成勇, 黄晓明, 等. 基于模块化多电平高压直流输电系统接地故障特性仿真分析[J]. 电网技术, 2014, 38(10): 2658-2664.
Zhang Jianpo, Zhao Chengyong, Huang Xiaoming, et al. Simulation research on earth fault characteristics of modular multilevel converter based high voltage direct current transmission system[J]. Power System Technology, 2014, 38(10): 2658-2664.
[25] 王威儒, 贺之渊, 李国庆, 等. 含交流影响的MMC-HVDC直流故障电流递推计算方法[J]. 中国电机工程学报, 2019, 39(增刊1): 313-320.
Wang Weiru, He Zhiyuan, Li Guoqing, et al. Recursive calculation method of MMC-HVDC DC fault current with AC effect[J]. Proceedings of the CSEE, 2019, 39(S1): 313-320.
[26] Li Chengyu, Zhao Chengyong, Xu Jianzhong, et al. A pole-to-pole short-circuit fault current calculation method for DC grids[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4943-4953.
[27] Gao Shilin, Ye Hua, Liu Yutian. Accurate and efficient estimation of short-circuit current for MTDC grids considering MMC control[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1541-1552.
[28] 刘麒麟, 张英敏, 张明奇, 等. 直流电网输电线路短路故障的单端化近似解析计算方法[J]. 电测与仪表, 2023, 60(3): 47-52.
Liu Qilin, Zhang Yingmin, Zhang Mingqi, et al. A single terminal approximate analytical method for short-circuit fault of transmission lines in DC power grid[J]. Electrical Measurement & Instrumentation, 2023, 60(3): 47-52.
[29] 汤兰西, 董新洲. MMC直流输电网线路短路故障电流的近似计算方法[J]. 中国电机工程学报, 2019, 39(2): 490-498.
Tang Lanxi, Dong Xinzhou. An approximate method for the calculation of transmission line fault current in MMC-HVDC grid[J]. Proceedings of the CSEE, 2019, 39(2): 490-498.
[30] 郝亮亮, 李伟杰, 王卓雅, 等. MMC-HVDC电网输电线路双极短路故障电流的实用计算[J]. 电力系统自动化, 2020, 44(5): 68-76.
Hao Liangliang, Li Weijie, Wang Zhuoya, et al. Practical calculation for bipolar short-circuit fault current of transmission line in MMC-HVDC grid[J]. Automation of Electric Power Systems, 2020, 44(5): 68-76.
[31] Xu Jianzhong, Zhu Sicheng, Li Chengyu, et al. DC fault current calculation method in MMC-HVDC grid considering current-limiting devices[J]. The Journal of Engineering, 2019, 2019(16): 3188-3195.
[32] 茆美琴, 何壮, 陆辉, 等. 含故障限流器投入的MMC-HVDC系统直流短路故障电流解析计算[J]. 电网技术, 2022, 46(1): 81-89.
Mao Meiqin, He Zhuang, Lu Hui, et al. DC fault current analytical calculation of MMC-HVDC system including fault current limiter[J]. Power System Technology, 2022, 46(1): 81-89.
Analytical Calculation of DC Short-Circuit Fault Current of Modular Multi-Level Converter-HVDC Grid with Active Current Limiting Control
Abstract The traditional short-circuit fault current analytical calculation of modular multi-level converter based on light voltage direct current (MMC-HVDC) grid generally uses equivalent RLC circuit method. However, this method does not consider the influence of active current limiting control (ACLC) on the RLC parameters of the equivalent circuit, thus it can not be directly applied to the analytical calculation for MMC-HVDC grid with an ACLC. To fill this gap, this paper proposes an analytical calculation method for DC short-circuit fault current of MMC-HVDC grid with an ACLC by establishing the relationship between the control effect and RLC parameters in the equivalent RLC circuit. Firstly, the control principle of the typical ACLC is analyzed, concluding that the essence of ACLC’s principle is to reduce the outlet DC voltages of converter stations by dynamically reducing the inputting number of sub-modules of the converters. Secondly, by mapping the voltage drop resulted from ACLC to the voltage drop generated by the introduced virtual impedance in the equivalent RLC circuit, the DC short-circuit fault loop can be equivalent to the RLC circuit with the virtual impedance within 10 ms after the pole to pole short-circuit fault occurs. Then, the virtual impedance value can be determined according to the parameters of the current limiting controller, and the analytical solution of the DC short-circuit fault current can be found according to the known RLC parameters and the derived virtual impedance value. Thirdly, taking the four-terminal MMC-HVDC grid with the ACLC with current limiting link of current change rate as an example, the equivalent RLC circuit with the virtual impedance is derived according to the relationship between the control parameters of the ACLC and the virtual impedance, thus, the analytical solution of the DC short-circuit fault current is obtained. Finally, taking the four-terminal MMC-HVDC grid based on half bridge as an example, the PSCAD/EMTDC simulation model is established to validate the proposed method. The calculation results of DC short-circuit fault current of MMC-HVDC grid with ACLC by the proposed method arecompared with the electromagnetic transient simulation results of DC short-circuit fault current under different fault points and different parameters by PSCAD/EMTDC model.
According to the simulation analysis results, the following conclusions are obtained:
(1) By mapping the DC voltage drop at the outlet of the converter station with the ACLC to the voltage drop generated by the equivalent virtual impedance, the pole to pole short-circuit fault circuit can be equivalent to the RLC discharge circuit with virtual impedance, thus the equivalent RLC circuit model with ACLC characteristics can be derived. (2)Using the virtual inductance mapping method (Experiment 1), the average relative error of DC fault current within 10 ms is below 3.31% under different DC short-circuit fault scenarios. Using the virtual impedance mapping method (Experiment 2), the average relative error of fault current within 10 ms is below 8.29% under different DC short-circuit fault scenarios. Thus, the calculation method proposed in this paper has good engineering practicability. (3) But,when analyzing the equivalent RLC circuit with virtual impedance, the influence of the dynamic characteristics of circulating current suppressor on the equivalent virtual impedance is ignored. Therefore, the influence of circulating current suppressor on fault current calculation method can be considered in future work to further improve the calculation accuracy of the DC fault current by the proposed method. (4) Although this paper uses specific ACLC algorithm of current limiting link type with current change rate to show the idea of the proposed method, this method can be extended to analyze the short-circuit fault current calculation problem of other types of ACLC algorithms.
keywords:Modular multi-level converter (MMC), active current limiting control, virtual impedance, RLC circuit, DC short circuit fault current calculation
中图分类号:TM721.1
DOI:10.19595/j.cnki.1000-6753.tces.222081
国家重点研发计划(2018YFB0904600)和高等学校学科创新引智计划(BP0719039)资助项目。
收稿日期 2022-11-03
改稿日期 2022-11-29
吴丽丽 女,1996年生,硕士研究生,研究方向为柔性直流输电技术。E-mail:1930406944@qq.com
茆美琴 女,1961年生,博士,教授,研究方向为电力电子技术在可再生能源发电系统中的应用、微电网系统。E-mail:mmqmail@163.com(通信作者)
(编辑 郭丽军)