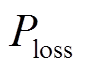计算公式为摘要 统计线损率是衡量电力系统经济运行的重要指标。然而，用户用电数据采集异常、数据传输中断等因素会导致统计线损率异常或缺失，这严重阻碍了智能配电网的线损精益化管理与经济高效运行。针对馈线统计线损率合理值的估计问题，该文提出了一种基于集成树和混合专家系统（MoE）的馈线统计线损率双层估计模型。首先，使用最大信息系数以更有效地分析统计线损率与其相关特征间的非线性关系，并采用鲁棒性强的K-Medoids聚类算法对馈线进行精细划分；然后，使用Stacking集成学习框架，基于基估计和元估计双层模型对馈线统计线损率进行两阶段估计，选用决策树和各类集成树模型作为基估计模型对统计线损率进行初步估计，将各基估计模型输出结果输入元估计模型MoE中进行最终估计，使用方均根误差（RMSE）和平均绝对误差（MAE）来衡量模型所估计统计线损率的合理性；最后，通过算例分析表明，与其他模型相比，该文所提馈线统计线损率双层估计模型具有更低的RMSE和MAE，对馈线统计线损率的估计效果更好。
关键词：统计线损率 线损率估计 机器学习 集成树 混合专家系统
降低线损是电力企业节能增效、实现双碳目标的重要途径。据统计，2021年，南方电网通过降低线损率减少了350万t碳排放量[1]，而馈线线损占电网总线损的50%以上[2]。因此，开展配电网馈线线损分析研究具有重要意义。
统计线损率是电网进行线损精细化管理的重要指标[3]。用户用电数据采集异常、数据传输中断等因素会导致统计线损率异常或缺失，从而使统计线损率无法反映线损的真实情况[4-5]。为此，需要对馈线统计线损率的合理值进行估计。
随着智能配电网的建设和人工智能技术的发展，基于数据驱动的线损率估计模型成为研究热点[6-9]。该类模型分为单一估计模型[10-15]和多模型融合[16-21]。文献[10]使用快速独立成分分析进行特征选取，然后通过支持向量回归（Support Vector Regression, SVR）对馈线线损进行估计。文献[11]使用粒子群优化算法来优化SVR的参数，一定程度上提升了线损估计精度。文献[12]使用灰色关联分析对特征进行筛选，然后使用BP（back propagation）神经网络对线损率进行估计。文献[13]使用降噪自编码器（Denoising Autoencoder, DAE）对特征进行重构，然后使用长短期记忆网络（Long Short-Term Memory, LSTM）对馈线日线损率进行估计。文献[14]提出一种深度迁移学习网络，实现对含分布式电源的电网线损进行估计。考虑到馈线种类繁多，文献[15]首先使用模糊C均值聚类对馈线进行聚类，然后对每一个类馈线进行线损估计，实现了对馈线线损更精细化的管理。文献[10-15]均使用单一估计模型进行线损率估计，其估计精度有待提升。
多模型融合是提升模型性能的有效方法[16]，其在线损率估计领域也有所应用[17-21]。文献[17]使用基于Bagging集成学习思想的随机森林模型对台区线损率进行估计。文献[18]使用基于Boosting集成学习思想的极限梯度提升树[19]（eXtreme Gradient Boosting, XGBoost）对馈线统计线损率进行估计。文献[20-21]将Stacking集成学习分别应用到馈线线损和台区线损估计，各基估计模型均选用机器学习模型，元估计模型均采用梯度提升树（Gradient Boosting Decision Tree, GBDT）。文献[17-21]在一定程度上提高了线损率估计的准确性。然而，其所用模型均为机器学习模型，该类模型应用到线损率估计等复杂场景时，存在特征挖掘不充分、泛化能力较差的问题。深度神经网络在理论上可以拟合任何数据间的非线性关系，经过训练可以具有良好的泛化能力[22]。谷歌提出一种混合专家系统神经网络，针对一个估计任务同时训练多个高度专业化的专家神经网络模型，从而可以深入挖掘数据间的潜在联系，进一步提高估计准确性[23]。
为此，本文基于Stacking集成学习思想，提出一种基于集成树和混合专家系统的馈线统计线损率双层估计模型。首先使用最大信息系数对所选特征有效性进行验证；然后使用K-Medoids聚类算法对馈线进行聚类；最后针对每一类馈线训练统计线损率双层估计模型。选用决策树、随机森林、极限随机树[24]（Extremely Randomized Tree, ExtraTree）、GBDT、自适应提升树[25]（Adaptive Boosting Tree, AdaBoost）和XGBoost模型作为基估计模型对线损率进行初步估计，并使用元估计模型混合专家系统（Mixture of Experts, MoE）对基估计模型结果进行深度融合，得到统计线损率最终估计结果。
在实际应用中，统计线损为供电量与售电量之差。由于不同馈线的统计线损量级相差较大，为此，通常采用统计线损率作为电力系统线损的评估指标。统计线损率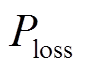计算公式为
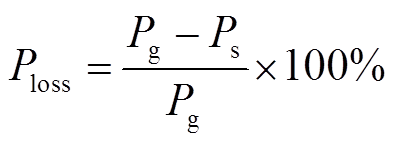（1）
式中，Pg为供电量；Ps为售电量。
统计线损是由理论线损和管理线损共同组成。因此，将理论线损率作为统计线损率估计的一个特征。而理论线损是通过潮流计算某段时间内已投运的变压器和线路上产生的线损，与线路和变压器有关的运行数据有线路总长度、线路供电量、线路投运时间、配电变压器额定容量与配变投运时间等，这些指标也间接影响着统计线损率，为此也将上述特征作为统计线损率估计的特征。
通过上述物理层面的分析可知，统计线损率与其各特征之间并非简单的线性关系，下面从数据角度进行量化分析。最大信息系数[26]（Maximal Information Coefficient, MIC）是一种基于信息论的相关性检验方法。与基于统计学理论的相关系数相比，最大信息系数可以更有效地衡量变量间的非线性关系。为此，选取最大信息系数对统计线损率与各特征之间的相关性进行分析。
设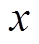
为与统计线损率相关的某个特征，y为统计线损率。绘制该特征与统计线损率的散点图，并进行网格划分，设i和j分别为x和y方向上所划分的网格数。在给定的i和j的情况下，计算该特征与统计线损率在网格中的最大互信息值
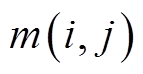，计算公式为
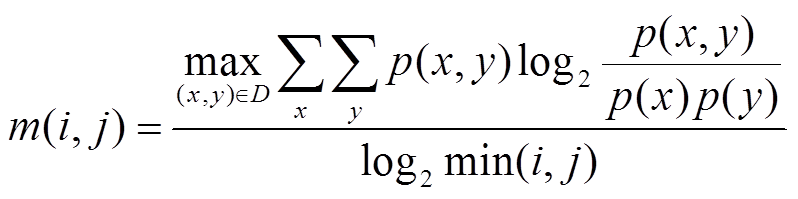（2）
式中，p(x,y)为x与y的联合概率分布；p(x)和p(y)分别为x与y的边缘概率分布；D为二元集合。
根据式（3）的约束改变i和j，计算不同网格数下的最大互信息值，其中最大值即为最大信息系数，有
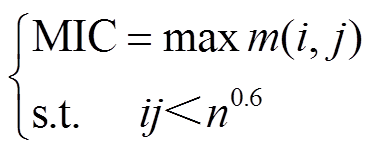（3）
式中，n为馈线数量。MIC的取值范围为[0,1]，特征与统计线损率之间的MIC越大，则该特征与统计线损率之间的相关性越强；MIC越小，则相关性越弱。
在进行聚类或统计线损率估计时，每条馈线将用一个向量表征，输入聚类模型或者估计模型中。馈线进行聚类与统计线损率估计时所用输入向量有所不同，聚类时，输入向量为统计线损率与其特征向量拼接所得，而进行统计线损率估计时，输入向量即为特征向量。
不同馈线的线路供电量、配电变压器（简称“配变”）额定容量等特征可能差别较大，这会影响模型对馈线统计线损率的估计性能。因此，将所选馈线特征输入到聚类模型，确定馈线类别后再分别进行估计。K-Medoids聚类算法是一种基于划分思想的聚类算法，该算法超参数少，且鲁棒性高[27]。因此，使用K-Medoids聚类算法对馈线进行聚类。算法具体流程如图1所示。
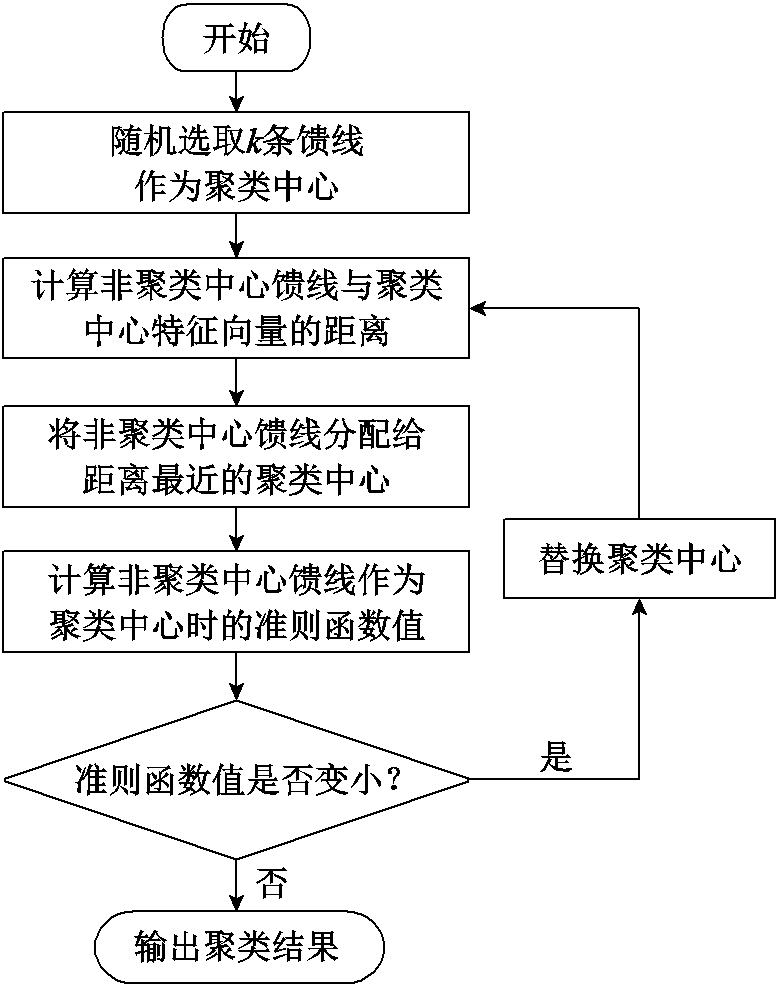
图1 K-Medoids聚类算法流程
Fig.1 The flow chart of K-Medoids clustering algorithm
准则函数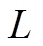
为
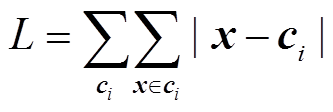（4）
式中，x为非聚类中心馈线的特征向量；ci为第i个聚类簇中心馈线的特征向量。
聚类效果的评价指标为戴维森堡指数（Davies-Bouldin Index, DBI）和Calinski-Harabz指数（Calinski-Harabaz Index, CHI），计算公式分别为
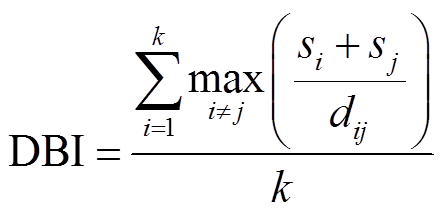（5）
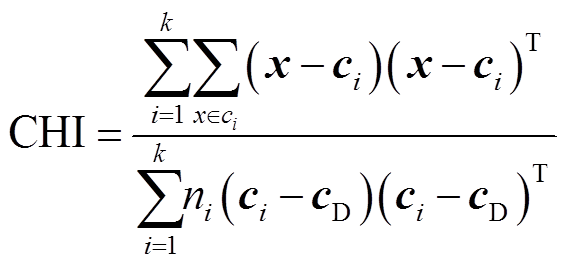（6）
式中，k为聚类簇数；i为第i个聚类簇；j为第j个聚类簇；s为第i个簇内数据点到该簇质心的距离；dij 为聚类簇i和j之间的距离；cD为馈线数据集的中心馈线。当DBI越小，CHI越大时，类内间距越小，类间间距越大，聚类的效果越好。
由于馈线种类复杂，单一估计模型往往只能对一部分馈线线损率具有较好的估计效果。Stacking集成估计模型可以融合多个估计模型优势，该模型分为两层，第一层为多个基估计模型，第二层为元估计模型。基于Stacking集成学习思想，本文提出基于集成树和混合专家系统的双层估计模型对各类型馈线统计线损率进行估计。首先，将馈线特征向量输入各基估计模型（决策树和集成树模型）。然后将各基估计模型的估计结果送入元估计模型（混合专家系统）进行二次估计，得到最终的统计线损率估计结果。
本文主要选用决策树（Decision Tree, DT）及集成树模型作为基估计模型。对于线损率估计任务，估计模型的误差主要来源于两方面：一方面是估计偏差，另一方面是估计方差，两者共同构成估计模型的估计误差。
Bagging是并行集成方法，其每个基模型之间相互独立，可以降低方差。随机森林（Random Forest, RF）是基于Bagging思想的模型，给每一个基模型随机分配相同数量的馈线，从而可以降低方差。ExtraTree与随机森林相似，但ExtraTree直接使用所有馈线进行训练，且线损率特征完全随机分裂。随机性的增强可以进一步减小估计方差，但可能会造成偏差增大。为此，将两种估计模型均作为基估计模型来平衡方差和偏差，进而减小估计误差。
Boosting是串行集成方法，每个弱估计器根据上一个弱估计器的估计结果进行权重更新，从而不断改进模型，降低偏差。AdaBoost、GBDT、XGBoost是基于Boosting思想的三种模型。AdaBoost采用自适应策略，减少估计误差大的馈线的权重，增大估计误差小的馈线的权重。不同于AdaBoost通过调整馈线权重的方式训练模型，GBDT是通过减少损失函数的梯度来更新权重，以最快的速度最小化馈线线损估计值与真实值之间的误差为目标对估计模型进行拟合。考虑到AdaBoost和GBDT分别是从不同的角度降低偏差，为此将两个模型均作为基估计模型。此外，XGBoost将GBDT的目标函数进行二阶泰勒展开，同时加入了正则项，可以防止过拟合，也将其作为一个基估计模型。
由于估计模型复杂度的上升可能会导致估计方差变大，从而会导致过拟合，反而使估计效果变差。为此，将决策树也作为一个基估计模型来平衡方差和偏差。综上所述，本文选取决策树、随机森林、ExtraTree、GBDT、AdaBoost和XGBoost为馈线统计线损率估计基模型。
模型融合是一种提高模型估计效果的有效方法。谷歌提出一种稀疏门控混合专家系统神经网络，通过建立多个高度专业化的专家神经网络深入挖掘数据中的潜在联系，并使用稀疏门控网络控制各专家系统的输出，防止模型过拟合。MoE网络结构如图2所示。
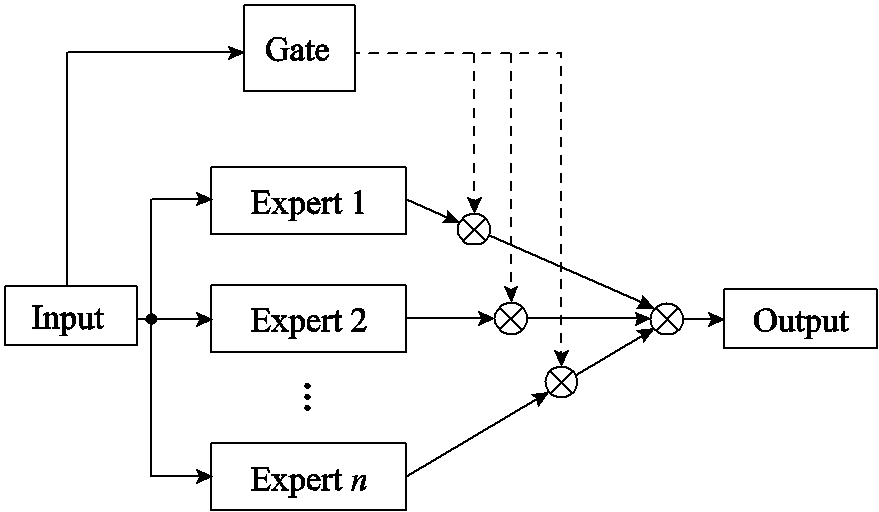
图2 MoE网络结构
Fig.2 Network structure of MoE
将训练数据输入各个专家网络（图2中的Expert 1～Expert n）和稀疏门控网络（图2中Gate），根据训练数据不断更新参数，建立起输入与输出之间的函数关系，实现每个专家系统的高度专业化。然后通过稀疏门控网络控制各专家系统的输出，最终的输出y可以表示为
（7）
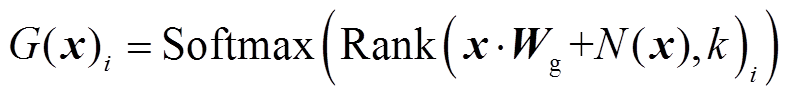（8）
（9）
式中，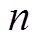
为专家网络个数；x为输入特征向量；
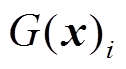为门控网络的第i个输出权重；
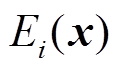为第i个专家网络输出结果；Softmax函数将函数值映射到[0,1]，Rank函数对专家网络进行排序，保留k个专家网络；
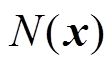为噪声项，用来均衡负载；v为门控网络的初始输出；
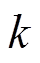为保留的专家网络数；Wg为权重矩阵。
在确定馈线所属类别后，使用基于集成树模型和MoE的双层估计模型对馈线统计线损率进行两阶段估计。该模型架构如图3所示。首先构建馈线的特征向量，记为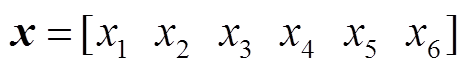
，然后将x输入各个基估计模型，得到各基估计模型的统计线损率估计结果向量，记为
。
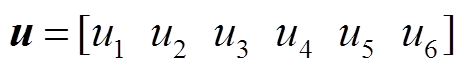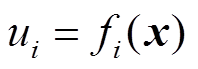（10）
式中，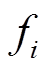
为各基估计模型抽象成的非线性函数；
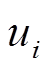为各基估计模型估计结果。
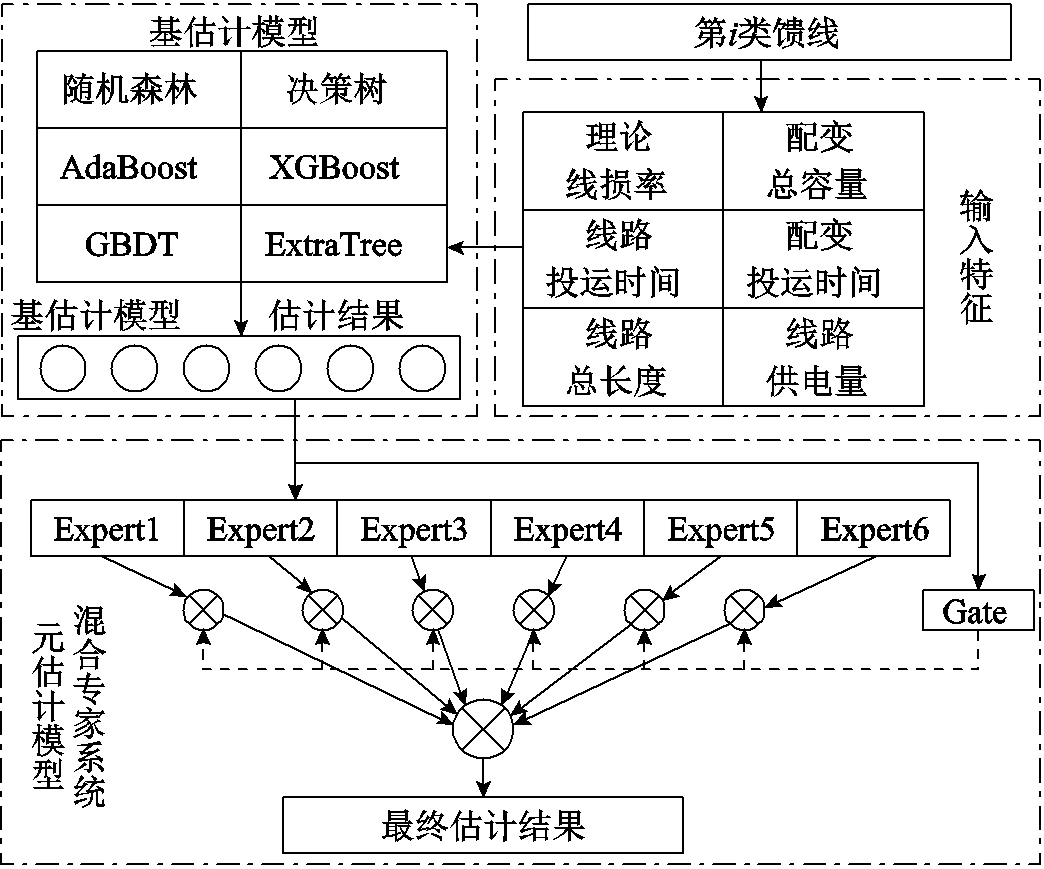
图3 所提估计模型架构
Fig.3 The proposed estimation model
经过各基估计模型的估计后，将基估计模型估计结果向量u输入元估计模型（混合专家系统）中，得到最终的线损率估计结果ypred为
（11）
为了评估模型估计所得统计线损率的合理性与准确性，本文采用方均根误差（Root Mean Square Error, RMSE）和平均绝对误差（Mean Absolute Error, MAE）来衡量各估计模型的估计误差。RMSE对数据异常值敏感，可以放大估计偏差较大点的误差，MAE可以防止因正负误差抵消而导致的误差减小，其公式分别为
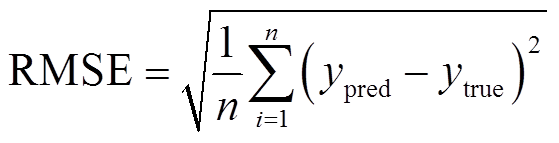（12）
（13）
式中，n为馈线条数；ypred为统计线损率估计值；ytrue为统计线损率真实值。由MAE和RMSE公式可知，估计模型的两个指标值越小，其所估计的线损率越合理和准确。
本文选取某市1 117条馈线对上述所提方法的有效性进行验证。所采集数据均为线损管理系统中质量码无问题的数据，每条馈线包含的记录数据有统计线损率、理论线损率、线路总长度、线路供电量、线路投运时间、配变额定容量与配变投运时间。为了增强结果可信性，基于交叉验证的思想，将数据分为10份。将数据集按照7:2:1比例划分为训练集、验证集和测试集，取10次交叉验证结果的均值作为模型的最终估计结果[15]。文中所涉及的机器学习模型基于Scikit-learn进行搭建，深度学习模型基于Keras和TensorFlow进行搭建。
下面使用1.1节介绍的最大信息系数进行特征有效性检验，各个特征与统计线损率之间的最大信息系数如图4所示，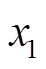
,
,
,
,
,
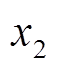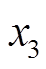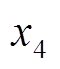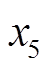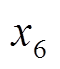分别是理论线损率、线路总长度、线路供电量、线路投运时间、配变额定容量与配变投运时间。
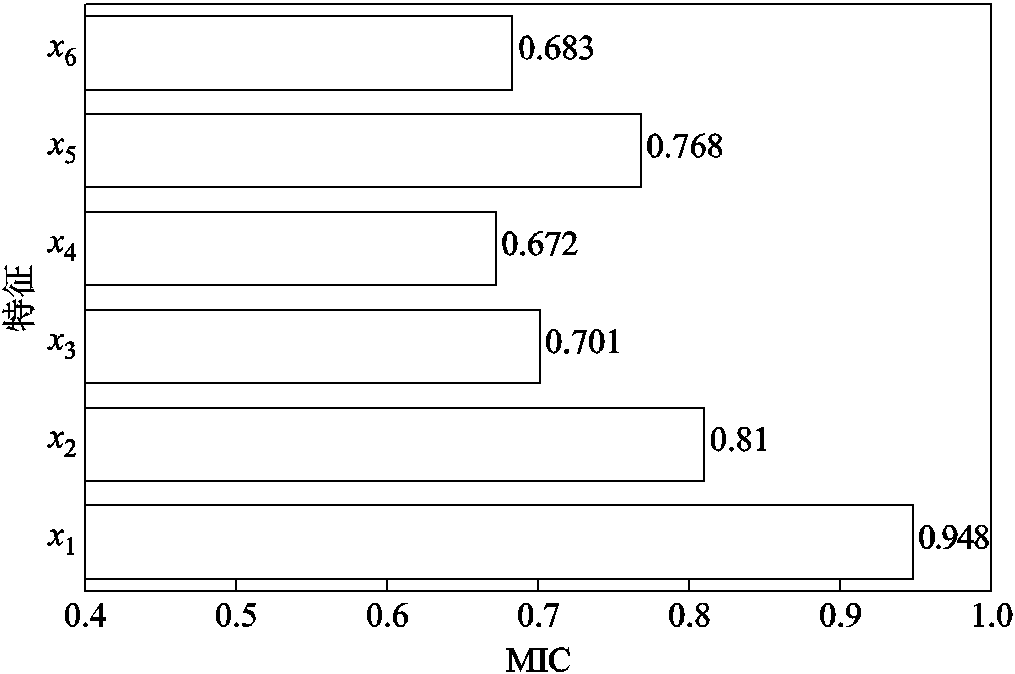
图4 各特征最大信息系数
Fig.4 Maximal information coefficient of each feature
可以看到，理论线损率的最大信息系数为0.948，这从数据角度验证了理论线损率与统计线损率之间的强相关关系。此外，其余各特征的MIC均在65%以上，这证明各特征与统计线损率之间均具有较高相关性，故可以将各特征作为馈线聚类和统计线损率估计的特征。
使用K-Medoids聚类算法对馈线进行聚类，分别计算馈线为2～9个类别时的CHI和DBI，CHI和DBI与聚类簇数的关系如图5所示，当聚类簇为3时，CHI最大，DBI最小。亦即此时各类馈线之间的间距大，每类馈线内部各条馈线之间的间距小，聚类效果最优。因此，将馈线聚类为三类。其中，第1类馈线有588条，第2类馈线有355条，第3类馈线有174条。
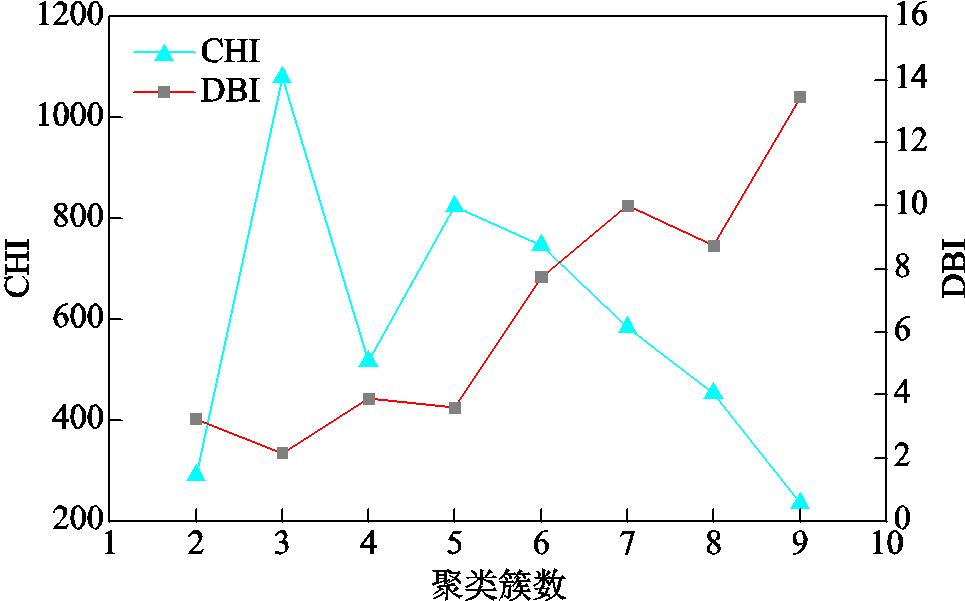
图5 CHI和DBI与聚类簇数的关系
Fig.5 Relationship between CHI, DBI and cluster number
为了验证聚类对统计线损率估计效果的提升作用，本文将不同估计模型聚类前的RMSE和MAE与聚类后对三类馈线估计的总体RMSE和MAE进行对比，结果见表1。
表1 基估计模型聚类前后RMSE和MAE对比
Tab.1 Comparison of RMSE and MAE before and after base estimator clustering
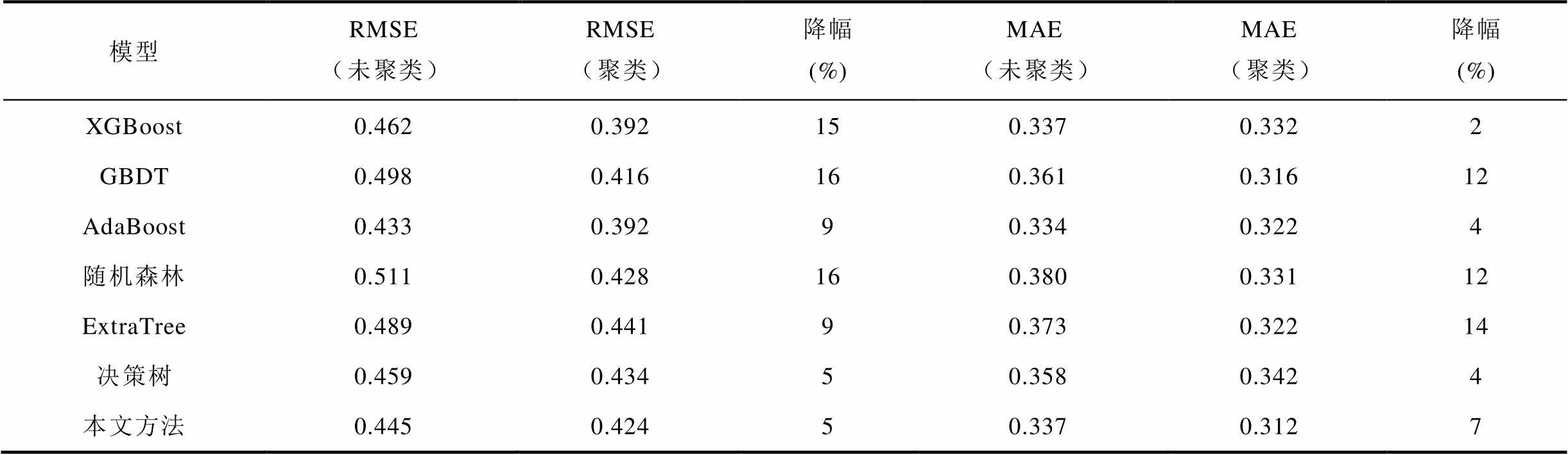
模型RMSE（未聚类）RMSE（聚类）降幅 (%)MAE（未聚类）MAE（聚类）降幅 (%) XGBoost0.4620.392150.3370.3322 GBDT0.4980.416160.3610.31612 AdaBoost0.4330.39290.3340.3224 随机森林0.5110.428160.3800.33112 ExtraTree0.4890.44190.3730.32214 决策树0.4590.43450.3580.3424 本文方法0.4450.42450.3370.3127
与未聚类时相比，经过聚类后，各基估计模型的RMSE和MAE均有所下降。其中，随机森林和GBDT的RMSE下降了16%，ExtraTree的MAE下降了14%。本文所提方法的RMSE和MAE也下降了5%和7%。因此，对馈线进行聚类之后再估计，可以提高馈线统计线损率估计准确性。
为了验证本文所提方法具有更好的估计效果，除了与各基估计模型的效果进行对比，本文还与线性加权模型进行对比。线性加权模型为
（14）
式中，wm为各基估计模型所分配的权重；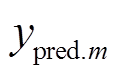
为各基估计模型的估计结果。
采取两种方式进行权重分配，第一种为简单加权（Simple Weighting, SW），即按照各基估计模型的估计误差进行排序，本文选取估计误差最小的四个模型，按照误差降序分配0.1、0.2、0.3、0.4权重（见附表1～附表3）。第二种采用粒子群优化加权算法（Particle Swarm Optimization Weighting, PSOW），通过建立以估计误差最小为目标的优化函数，使用粒子群算法寻优得到最优权重。优化函数为
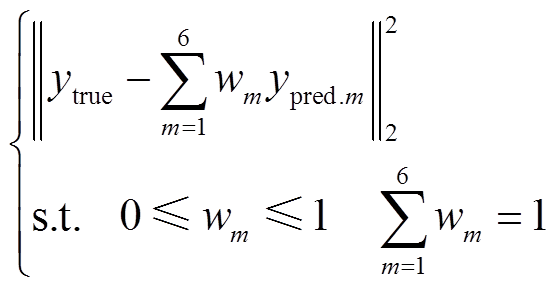（15）
下面对各模型在三类馈线测试集上的表现进行分析，表2为各个模型进行线损率估计的RMSE和MAE对比，图6、图7和图8分别为不同模型对各类馈线中每条馈线的线损估计误差。
表2 各模型RMSE和MAE对比
Tab.2 RMSE and MAE comparison of each model
模型名称第一类馈线第二类馈线第三类馈线 RMSEMAERMSEMAERMSEMAE XGBoost[14]0.521 0.369 0.443 0.305 0.438 0.328 GBDT0.503 0.360 0.427 0.318 0.425 0.339 AdaBoost0.513 0.376 0.448 0.351 0.446 0.351 随机森林[13]0.482 0.367 0.421 0.328 0.432 0.364 ExtraTree0.499 0.382 0.476 0.329 0.380 0.312 决策树0.544 0.396 0.425 0.339 0.503 0.365 SW0.480 0.356 0.409 0.301 0.415 0.333 PSOW0.505 0.352 0.419 0.298 0.486 0.360 本文方法0.458 0.327 0.389 0.284 0.387 0.295
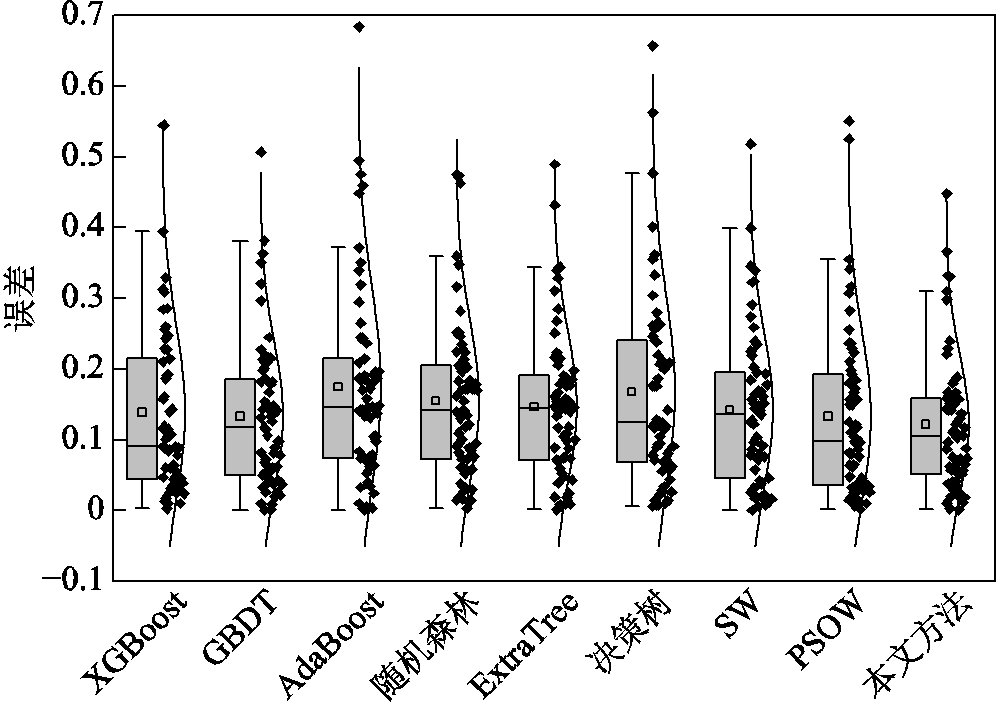
图6 第一类馈线线损率误差分布
Fig.6 The error distribution of the first kind of feederline loss rate
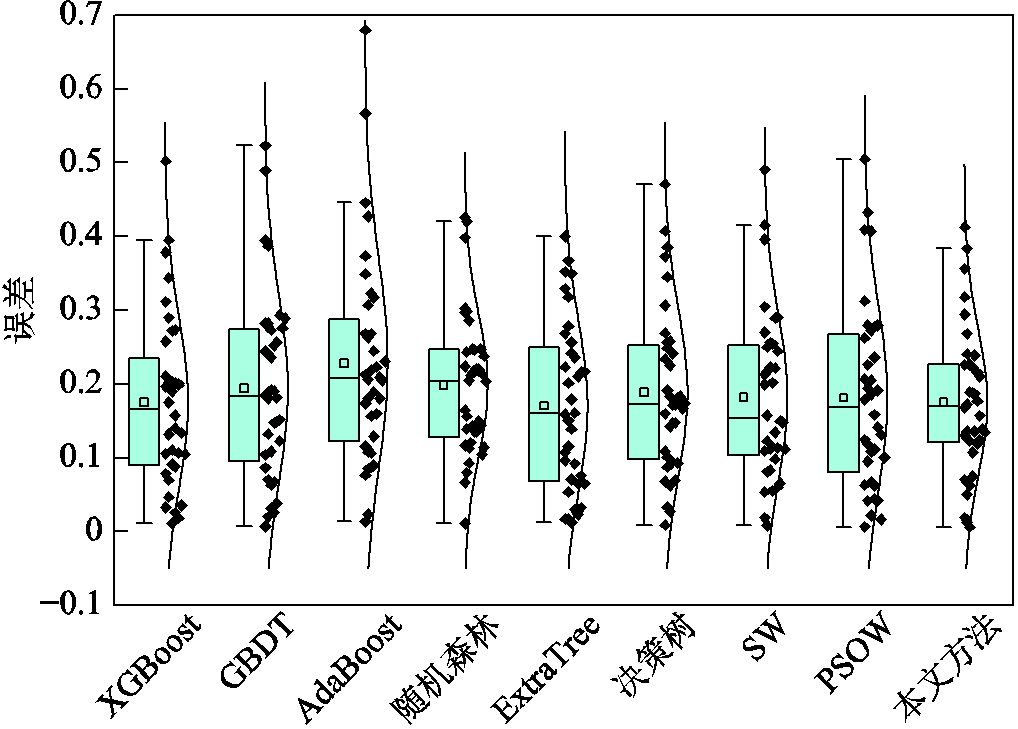
图7 第二类馈线线损率误差分布
Fig.7 The error distribution of the second kind of feeder line loss rate
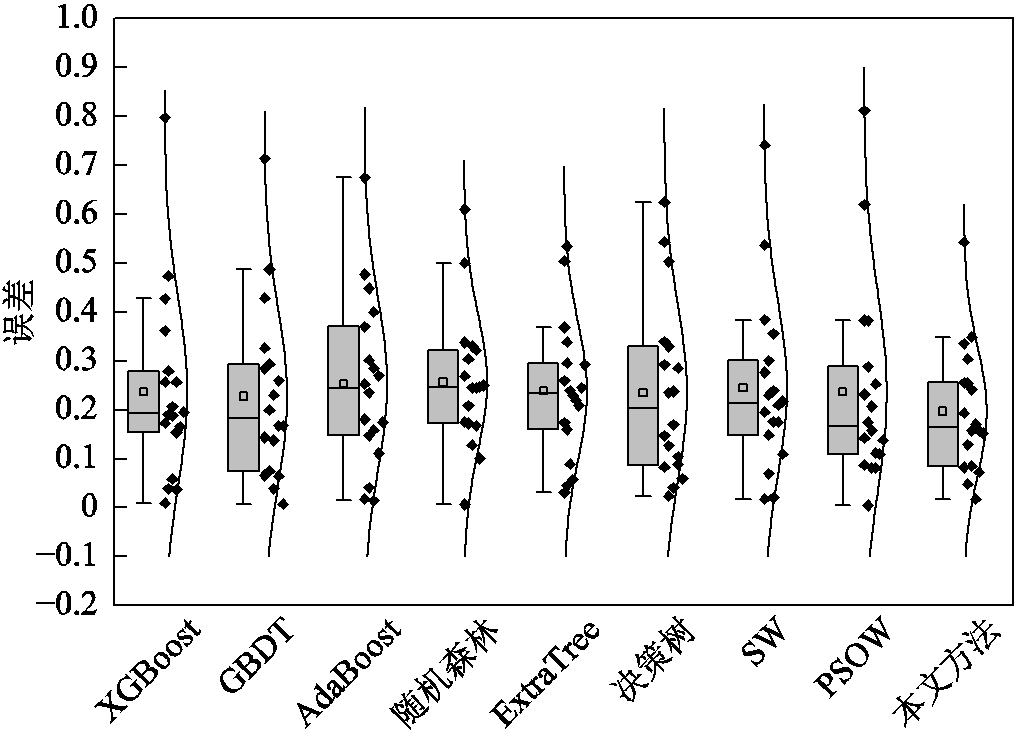
图8 第三类馈线线损率误差分布
Fig.8 The error distribution of the third kind of feeder line loss rate
首先分析各基估计模型对于不同类别馈线的估计结果。在六个基估计模型中，随机森林模型对第一类和第二类馈线估计的RMSE均为最小。但在对第三类馈线进行估计的基模型中，随机森林表现欠佳，ExtraTree的RMSE最小，其值为0.38。此外，在对第三类馈线进行估计时，ExtraTree的MAE也为最小。这是因为图8中ExtraTree的线损估计误差大部分分布在0.2～0.3附近，且离群点的离群程度较低。但在对第一类馈线和第二类馈线进行估计时，ExtraTree的性能不是最优。这说明，单个基估计模型只能对某些类别馈线线损率进行准确估计。
对比线性加权模型与各基模型，在对第一类和第二类馈线进行估计时，与各类馈线最优基模型（评估指标值最小的基估计模型）对比，线性加权模型的RMSE和MAE均有所下降，这是因为线性加权模型对估计结果进行二次集成，从而使估计准确性得到进一步提高。但在对第三类馈线进行线损率估计时，线性加权模型的RMSE与MAE均不如最优基估计模型，这是由于第三类馈线的数量较少，导致训练过程中出现了严重过拟合，从而使得线性加权模型在测试集上效果变差。
由上述分析可知，与单一估计模型相比，线性加权估计模型能进一步提高馈线统计线损率估计准确性，但其还不能充分挖掘数据间的潜在关系，在对数量较少的第三类馈线进行线损率估计时易产生过拟合。因此，各单一估计模型和线性加权模型均不能实现对多种类型馈线线损率的准确估计。
本文所提模型在一定程度上解决了模型过拟合问题，实现了对各类馈线更准确的估计。在对第一类和第二类馈线进行线损率估计时，本文方法的RMSE分别比各类馈线最优基模型低5%和8%。这是因为，不同于SW和PSOW的线性加权，专家神经网络中的不同专家可以深入挖掘线损数据的非线性关系，对于训练样本充足的第一类和第二类馈线，本文方法估计准确性高于各类馈线基估计模型和线性加权模型。在对训练数据较少的第三类馈线进行估计时，虽然本文方法比ExtraTree的RMSE高1.8%，但其比线性加权模型降低了6.77%，在一定程度上防止了过拟合。
对比线性加权模型，在估计三类馈线时，由表2可知，本文方法的MAE分别下降7%、5%和11%。与各类馈线最优基估计模型相比，本文方法估计三类馈线统计线损率时，其MAE分别下降8%、7%和5%。由图6～图8也可以看到，在对每一类馈线进行线损率估计时，与其他模型相比，本文方法的误差分布更集中于低误差区域，而且本文方法的误差分布中位数与平均值相近，这说明本文所提统计线损率估计模型的准确性和稳定性更好。
为了进一步验证本文方法的可行性，选取文献[15]和文献[16]的方法对比，RMSE和MAE对比结果见表3。
表3 RMSE和MAE对比
Tab.3 RMSE and MAE comparison
方法第一类馈线第二类馈线第三类馈线 RMSEMAERMSEMAERMSEMAE 文献[20]0.482 0.369 0.403 0.300 0.406 0.325 文献[21]0.477 0.362 0.396 0.294 0.425 0.332 本文方法0.458 0.327 0.389 0.284 0.387 0.295
由表3可知，本文方法的RMSE和MAE较其他两种算法更低。在对第一类馈线进行估计时，本文方法比文献[20]方法的MAE下降了11%。在对第三类馈线进行估计时，本文方法的RMSE比文献[21]下降了9%。因为文献[20]和文献[21]的元估计模型为机器学习模型，其对数据挖掘的能力弱于混合专家系统。综上可知，与现有的线损估计模型相比，本文所提基于集成树模型和MoE的双层估计模型对不同类型馈线统计线损率均有更好的估计效果。
本文针对馈线统计线损率数据质量差的问题，提出了一种基于集成树和MoE的馈线统计线损率双层估计模型，得到以下主要结论：
1）使用最大信息系数选取理论线损率及相关馈线特征为馈线聚类和统计线损率估计的特征指标，并验证了K-Medoids聚类可以提高馈线统计线损率估计准确性。
2）基于Stacking集成学习思想，使用集成树模型和混合专家系统对馈线统计线损率进行两阶段估计。选用决策树及不同集成树模型作为基估计模型进行初步估计，使用混合专家系统网络作为元估计模型进行最终估计。相比于其他集成估计模型，本文所提估计模型对馈线统计线损率具有更好的估计效果。
3）对于训练样本较少的第三类馈线，本文方法存在一定程度的过拟合，后续可围绕小样本集下的馈线统计线损率估计进行研究。
附 录
附表1 第一类馈线各模型参数
App.Tab.1 Model parameters of the first kind of feeder
模型名称模型参数 XGBoostmax_depth = 25, n_estimators=30 GBDTn_estimators=25,max_depth=15,min_samples_leaf=15,min_samples_split=10 AdaBoostn_estimators=50,max_depth=10,min_samples_leaf=15,min_samples_split=10 随机森林n_estimators=50,max_depth=15,min_samples_leaf=10,min_samples_split=10 ExtraTreen_estimators=50,max_depth=5,min_samples_leaf=5,min_samples_split=10 决策树max_depth=8,min_samples_leaf=10,min_samples_split=10 SW权重向量w=[0,0.1,0.2,0.4,0.3,0] PSOW权重向量w=[0.75,0.21,0,0,0.04,0] MoE特征共享层：units=100, num_experts=6任务层：Dense层（units=64,32,16,1）
附表2 第二类馈线各模型参数
App.Tab.2 Model parameters of the second kind of feeder
模型名称模型参数 XGBoostmax_depth = 10,n_estimators=10 GBDTn_estimators=50,max_depth=15,min_samples_leaf=15,min_samples_split=10 AdaBoostn_estimators=50,max_depth=10,min_samples_leaf=15,min_samples_split=10 随机森林n_estimators=60,max_depth=15,min_samples_leaf=15,min_samples_split=10 ExtraTreen_estimators=15,max_depth=20,min_samples_leaf=15,min_samples_split=10 决策树max_depth=10,min_samples_leaf=5,min_samples_split=10 SW权重向量w=[0.1,0.2,0,0.3,0,0.4] PSOW权重向量w=[0.2,0,0.32,0,0.38,0.1] MoE特征共享层：units=30, num_experts=6任务层：Dense层（units=16,8,1）
附表3 第三类馈线各模型参数
App.Tab.3 Model parameters of the third kind of feeder
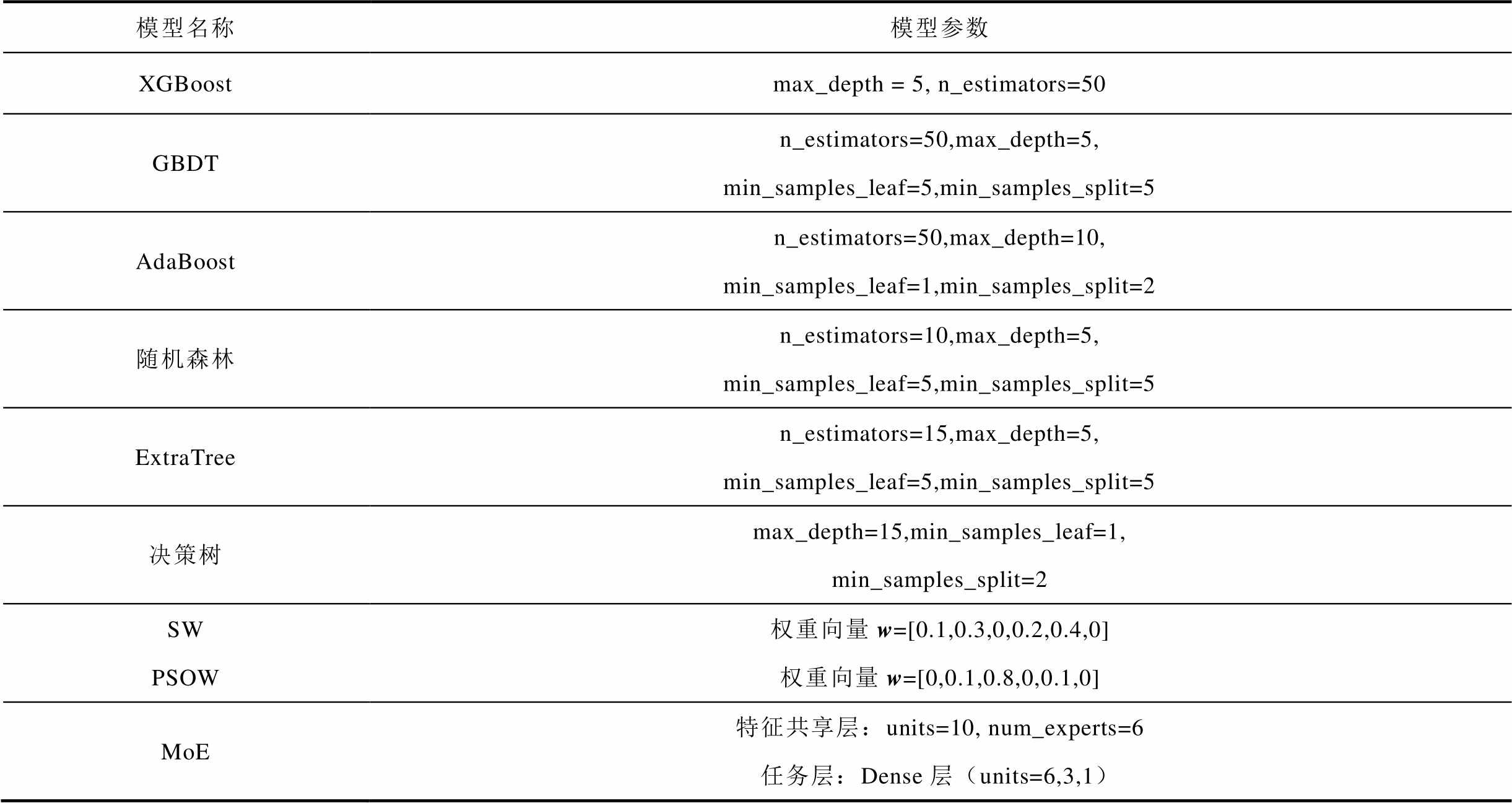
模型名称模型参数 XGBoostmax_depth = 5, n_estimators=50 GBDTn_estimators=50,max_depth=5,min_samples_leaf=5,min_samples_split=5 AdaBoostn_estimators=50,max_depth=10,min_samples_leaf=1,min_samples_split=2 随机森林n_estimators=10,max_depth=5,min_samples_leaf=5,min_samples_split=5 ExtraTreen_estimators=15,max_depth=5,min_samples_leaf=5,min_samples_split=5 决策树max_depth=15,min_samples_leaf=1,min_samples_split=2 SW权重向量w=[0.1,0.3,0,0.2,0.4,0] PSOW权重向量w=[0,0.1,0.8,0,0.1,0] MoE特征共享层：units=10, num_experts=6任务层：Dense层（units=6,3,1）
参考文献
[1] 南方电网公司. 2021年绿色低碳发展年刊[EB/OL]. (2022-06-13)[2022-10-20].https://www.csg.cn/shzr/ zrbg/202206/P020220613351130050261.
[2] 马喜平, 贾嵘, 梁琛, 等. 高比例新能源接入下电力系统降损研究综述[J]. 电网技术, 2022, 46(11): 4305-4315.
Ma Xiping, Jia Rong, Liang Chen, et al. Review of researches on loss reduction in context of high penetration of renewable power generation[J]. Power System Technology, 2022, 46(11): 4305-4315.
[3] 王方雨, 刘文颖, 陈鑫鑫, 等. 基于“秩和”近似相等特性的同期线损异常数据辨识方法[J]. 电工技术学报, 2020, 35(22): 4771-4783.
Wang Fangyu, Liu Wenying, Chen Xinxin, et al. Abnormal data identification of synchronous line loss based on the approximate equality of rank sum[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4771-4783.
[4] 唐登平, 李俊, 孟展, 等. 统计线损数据准确性研究[J]. 电力系统保护与控制, 2018, 46(24): 33-39.
Tang Dengping, Li Jun, Meng Zhan, et al. Research on accuracy of statistical line losses[J]. Power System Protection and Control, 2018, 46(24): 33-39.
[5] 黄彦钦, 余浩, 尹钧毅, 等. 电力物联网数据传输方案：现状与基于5G技术的展望[J]. 电工技术学报, 2021, 36(17): 3581-3593.
Huang Yanqin, Yu Hao, Yin Junyi, et al. Data transmission schemes of power Internet of Things: present and outlook based on 5G technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3581-3593.
[6] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636.
Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[7] 刘晟源, 章天晗, 林振智, 等. 数据赋能低压配用电系统精益化运行的关键技术与算法[J]. 电力系统自动化, 2023, 47(3): 187-199.
Liu Shengyuan, Zhang Tianhan, Lin Zhenzhi, et al. Key technologies and algorithms of data empowerment for lean operation of low-voltage power distribution and consumption system[J]. Automation of Electric Power Systems, 2023, 47(3): 187-199.
[8] 李鹏, 习伟, 蔡田田, 等. 数字电网的理念、架构与关键技术[J]. 中国电机工程学报, 2022, 42(14): 5002-5017.
Li Peng, Xi Wei, Cai Tiantian, et al. Concept, architecture and key technologies of digital power grids[J]. Proceedings of the CSEE, 2022, 42(14): 5002-5017.
[9] 徐焕增, 孔政敏, 王帅, 等. 基于动态线损及FMRLS算法的智能电表误差在线评估模型[J]. 中国电机工程学报, 2021, 41(24): 8349-8358.
Xu Huanzeng, Kong Zhengmin, Wang Shuai, et al. Online error evaluation model of smart meter based on dynamic line loss and FMRLS algorithm[J]. Proceedings of the CSEE, 2021, 41(24): 8349-8358.
[10] 彭建春, 李春晖, 祁学红, 等. 基于快速独立成分分析和支持向量回归的混合馈线线损估算[J]. 电力系统保护与控制, 2012, 40(3): 51-55.
Peng Jianchun, Li Chunhui, Qi Xuehong, et al. Loss estimation of power distribution systems based on fast independent component analysis and support vector regression[J]. Power System Protection and Control, 2012, 40(3): 51-55.
[11] 徐茹枝, 王宇飞. 粒子群优化的支持向量回归机计算配电网理论线损方法[J]. 电力自动化设备, 2012, 32(5): 86-89, 93.
Xu Ruzhi, Wang Yufei. Theoretical line loss calculation based on SVR and PSO for distribution system[J]. Electric Power Automation Equipment, 2012, 32(5): 86-89, 93.
[12] 张义涛, 王泽忠, 刘丽平, 等. 基于灰色关联分析和改进神经网络的10 kV配电网线损预测[J]. 电网技术, 2019, 43(4): 1404-1410.
Zhang Yitao, Wang Zezhong, Liu Liping, et al. A 10 kV distribution network line loss prediction method based on grey correlation analysis and improved artificial neural network[J]. Power System Technology, 2019, 43(4): 1404-1410.
[13] 周王峰, 李勇, 郭钇秀, 等. 基于DAE-LSTM神经网络的配电网日线损率预测[J]. 电力系统保护与控制, 2021, 49(17): 48-56.
Zhou Wangfeng, Li Yong, Guo Yixiu, et al. Daily line loss rate forecasting of a distribution network based on DAE-LSTM[J]. Power System Protection and Control, 2021, 49(17): 48-56.
[14] 卢志刚, 杨英杰, 李学平, 等. 基于深度迁移学习理论含风电光伏系统的地区电网网损率计算[J]. 中国电机工程学报, 2020, 40(13): 4102-4111.
Lu Zhigang, Yang Yingjie, Li Xueping, et al. A deep migration learning based power loss rate calculation method for distributed power system with wind and solar generation[J]. Proceedings of the CSEE, 2020, 40(13): 4102-4111.
[15] 欧阳森, 冯天瑞, 安晓华. 考虑馈线聚类特性的中压配网线损率测算模型[J]. 电力自动化设备, 2016, 36(9): 33-39.
Ouyang Sen, Feng Tianrui, An Xiaohua. Line-loss rate calculation model considering feeder clustering features for medium-voltage distribution network[J]. Electric Power Automation Equipment, 2016, 36(9): 33-39.
[16] 徐建军, 黄立达, 闫丽梅, 等. 基于层次多任务深度学习的绝缘子自爆缺陷检测[J]. 电工技术学报, 2021, 36(7): 1407-1415.
Xu Jianjun, Huang Lida, Yan Limei, et al. Insulator self-explosion defect detection based on hierarchical multi-task deep learning[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1407-1415.
[17] 王守相, 周凯, 苏运. 基于随机森林算法的台区合理线损率估计方法[J]. 电力自动化设备, 2017, 37(11): 39-45.
Wang Shouxiang, Zhou Kai, Su Yun. Line loss rate estimation method of transformer district based on random forest algorithm[J]. Electric Power Automation Equipment, 2017, 37(11): 39-45.
[18] Wang Shouxiang, Dong Pengfei, Tian Yingjie. A novel method of statistical line loss estimation for distribution feeders based on feeder cluster and modified XGBoost[J]. Energies, 2017, 10(12): 2067.
[19] 马良玉, 程善珍. 基于支持向量数据描述和XGBoost的风电机组异常工况预警研究[J]. 电工技术学报, 2022, 37(13): 3241-3249.
Ma Liangyu, Cheng Shanzhen. Abnormal state early warning of wind turbine generator based on support vector data description and XGBoost[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3241-3249.
[20] 邓威, 郭钇秀, 李勇, 等. 基于特征选择和Stacking集成学习的配电网网损预测[J]. 电力系统保护与控制, 2020, 48(15): 108-115.
Deng Wei, Guo Yixiu, Li Yong, et al. Power losses prediction based on feature selection and Stacking integrated learning[J]. Power System Protection and Control, 2020, 48(15): 108-115.
[21] 董美娜, 刘丽平, 王泽忠, 等. 基于Stacking集成学习的有源台区线损率评估方法[J]. 电测与仪表, 2023, 60(6): 134-139.
Dong Meina, Liu Liping, Wang Zezhong, et al. A line loss rate evaluation method based on Stacking ensemble learning for transformer district with DG[J]. Eleetrical Measurement & Instrumentation, 2023, 60(6): 134-139.
[22] Khodayar M, Liu Guangyi, Wang Jianhui, et al. Deep learning in power systems research: a review[J]. CSEE Journal of Power and Energy Systems, 2020, 7(2): 209-220.
[23] Shazeer N, Mirhoseini A, Maziarz K, et al. Outrageously large neural networks: the sparsely-gated mixture-of-experts layer[EB/OL]. 2017: arXiv: 1701.06538. https://arxiv.org/abs/1701.06538.
[24] Sambasivam G, Amudhavel J, Sathya G. A predictive performance analysis of vitamin D deficiency severity using machine learning methods[J]. IEEE Access, 2020, 8: 109492-109507.
[25] 贾科, 宣振文, 林瑶琦, 等. 基于Adaboost算法的并网光伏发电系统的孤岛检测法[J]. 电工技术学报, 2018, 33(5): 1106-1113.
Jia Ke, Xuan Zhenwen, Lin Yaoqi, et al. An islanding detection method for grid-connected photovoltaic power system based on adaboost algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1106-1113.
[26] 邱高, 刘俊勇, 刘友波, 等. 风电外送通道极限传输能力的自适应向量机估计[J]. 电工技术学报, 2018, 33(14): 3342-3352.
Qiu Gao, Liu Junyong, Liu Youbo, et al. Adaptive support vector machine estimation for total transfer capability of wind power exporting corridors[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3342-3352.
[27] 胡聪, 徐敏, 洪德华, 等. 基于改进K-medoids聚类和SVM的异常用电模式在线检测方法[J]. 国外电子测量技术, 2022, 41(2): 53-59.
Hu Cong, Xu Min, Hong Dehua, et al. Online detection method for abnormal electricity model behavior based on improved K-medoids clustering and SVM[J]. Foreign Electronic Measurement Technology, 2022, 41(2): 53-59.
Double-Layers Stacking Estimation Model for Feeder Statistical Line Loss Rate Based on Tree-Based Ensemble Learning and MoE
Abstract Reducing line loss is important for power grids to save energy and achieve carbon neutrality. Statistical line loss rate is an important indicator for the refined management of line loss in the power grid. However, abnormal data collection of power consumption, interruption of data transmission and other factors lead to the abnormality or missing of statistical line loss rate. At present, the ensemble learning framework is applied to the field of line loss estimation, but models used for estimation are all machine learning models, so the estimation accuracy needs to be improved. In order to improve the accuracy of statistical line loss rate estimation, a double-layers estimation model for feeder statistical line loss rate based on tree-based ensemble learning and mixture of experts (MoE) is proposed.
Firstly, the maximum information coefficient (MIC) is used to effectively analyze the nonlinear relationship between the statistical line loss rate and its correlated features, so as to build a feature set of statistical line loss rate. Secondly, the feature vector of each feeder is input to the robust K-Medoids clustering algorithm to realize the fine division of feeders. Thirdly, using the Stacking integrated learning framework, the feeder statistical line loss rate is estimated in two stages based on the base estimation and meta estimation double-layer models. The decision tree, gradient boosting decision tree (GBDT), adaptive Boosting (AdaBoost), extreme gradient Boosting (XGBoost), random forest and extremely randomized tree (ExtraTree) are selected as base estimation models for preliminary estimation of the statistical line loss rate, and the output results of each base estimation model are input into the meta estimation model MoE for final estimation.
A comprehensive set of experiments has been conducted on a real-world feeder statistical line loss rate dataset (1) The MIC values of statistical line loss rate and theoretical line loss rate, total length of line, line power supply, line operation time, rated capacity of distribution transformer, operation time of distribution transformer are respectively 0.948, 0.81, 0.701, 0.672, 0.768 and 0.683, which demonstrates the high correlation between each feature and the statistical line loss rate. (2) Feature vectors are fed into the K-medoids algorithm, feeders are divided into three parts. Through clustering, the total RMSE and MAE of statistical line loss rate estimated by the proposed model are decreased by 5% and 7% respectively. (3) Compared with other models, the error distribution of proposed model is concentrated in the low error area, and the between the median value and the mean value is closer, which means the proposed model has better accuracy and stability. The comparison between the proposed model and other ensemble model which has the best performance shows that, the RMSE of each type of feeders estimated by the proposed model are reduced by 4%, 2%, 5% respectively, and the MAE of each type of feeders estimated by the proposed model are reduced by 10%, 3%, 9% respectively.
The following conclusions can be drawn from the simulation analysis: (1) The maximum information coefficient is used to verify the rationality of using the theoretical line loss rate and its related features for feeder clustering and statistical line loss rate estimation. (2) Compared with direct estimation, the estimation accuracy of statistical line loss rate can be improved by clustering feeders using K-medoids algorithm. (3) Compared with the existing ensemble estimation model, the estimation model proposed in this paper has lower RMSE and MAE, which means the statistical line loss rate estimated by the proposed model is more reasonable.
keywords：Statistical line loss rate, line loss rate estimation, machine learning, tree-based ensemble learning, mixture of experts
中图分类号：TM744
DOI:10.19595/j.cnki.1000-6753.tces.221994
国家自然科学基金资助项目（U2166202）。
收稿日期 2022-10-20
改稿日期 2023-01-27
王守相 男，1973年生，博士，教授，博士生导师，研究方向为分布式发电、微网与智能配电网等。E-mail：sxwang@tju.edu.cn。
郭陆阳 男，1995年生，博士研究生，研究方向为智能配电网。E-mail：guoluyang@tju.edu.cn（通信作者）
（编辑 赫 蕾）