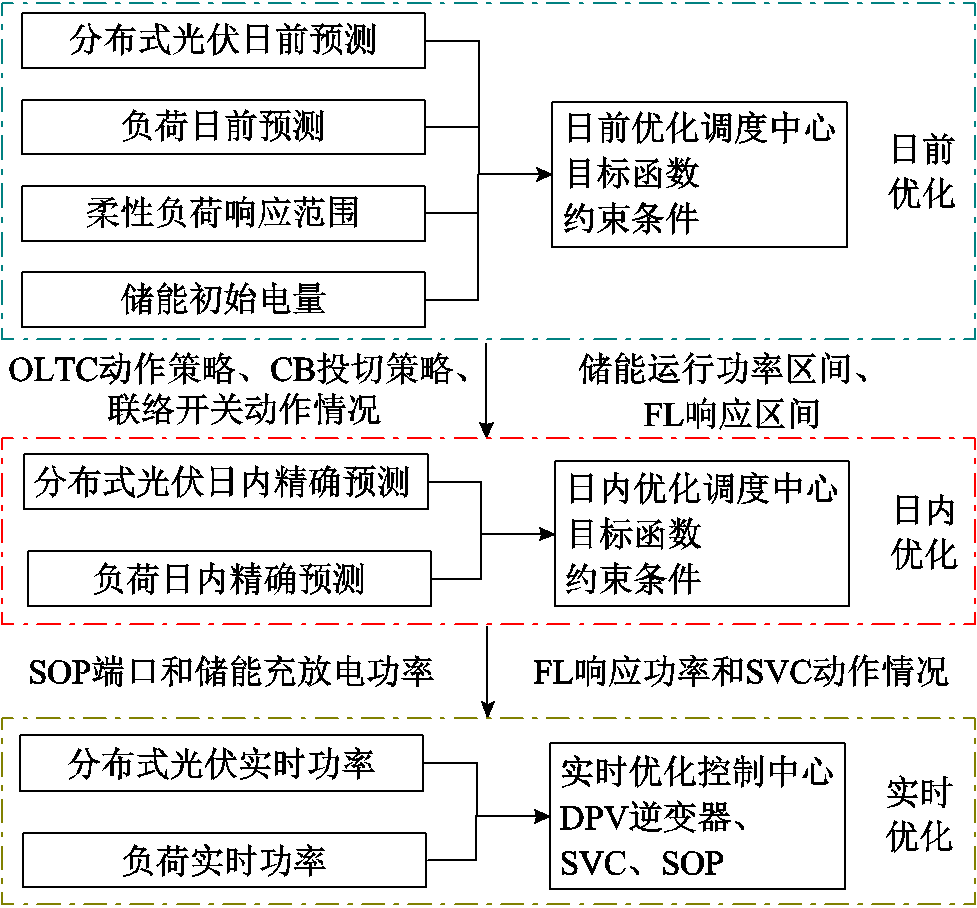
图1 多时间尺度优化控制框架
Fig.1 Framework of multi-time scale optimization control
摘要 为优化储能型智能软开关(E-SOP)、传统网侧调控设备的运行策略,提升高渗透率光伏配电网运行水平,提出了基于网侧资源协调的自储能柔性互联配电系统日前-日内优化模型。首先,提出了“源网荷储”下多种网侧资源协调利用的多时间尺度优化控制架构;其次,在日前阶段构建计及有载调压变压器、无功补偿装置、联络开关、E-SOP和柔性负荷的长时间有功-无功联合优化模型,在日内阶段建立多目标滚动优化模型,并采用线性化方法将模型转换为混合整数线性规划模型;然后,基于KL散度构建源荷不确定性模糊集,给出日前两阶段分布鲁棒优化模型转化过程和基于列与约束生成算法的求解方法;最后,算例仿真验证所提方法的有效性。
关键词:储能型智能软开关 柔性互联配电系统 分布鲁棒优化 滚动优化 日前-日内优化
在“碳达峰、碳中和”目标的推动下,分布式电源(Distributed Generation, DG)规模迅速发展,高渗透率可再生能源DG将成为新型配电系统的重要特征之一。然而,大量DG接入配电网后,其出力的随机性和波动性极易造成系统双向潮流、电压越限、线路过载等问题[1]。主动配电网通过网侧有载调压变压器(On-Load Tap Changer, OLTC)调节、电容器组(Capacitor Bank, CB)投切、拓扑重构优化、DG有功-无功控制等实现系统运行优化[2-3]。而智能软开关(Soft Open Point, SOP)作为可替换联络开关的新型电力电子设备,接入配电网可实现馈线间潮流精准控制、动态无功补偿和供电方式灵活切换等功能[4]。考虑到当前SOP的成本仍然较高,有必要研究SOP和传统调控设备的协调优化以实现配电网多时间尺度经济安全运行。
国内外针对SOP与传统调控设备协调参与配电网运行优化已开展了一定研究。文献[5]建立了联络开关和SOP并存时配电网运行的时序优化模型;文献[6]构建了含SOP和CB的双层运行优化模型;文献[7]提出了考虑SOP和CB、OLTC的电压和无功优化协调控制模型;文献[8]建立了考虑SOP、需求侧响应、储能优化和网络重构的配电网日前优化模型;文献[9]建立了SOP与联络开关协调的日前-日内滚动两阶段优化模型。上述文献均基于确定性优化模型展开研究,忽略了新型源荷大规模接入带来的不确定性影响。
文献[10]建立了基于场景分析法的有源配电网DG与SOP三层协调规划模型,并采用并行遗传算法与锥规划混合算法求解模型;文献[11]建立了DG和负荷的时序多状态随机场景模型,并提出了协调DG、CB和SOP的机会约束规划模型。文献[12]建立了考虑高渗透光伏接入的主动配电网两阶段SOP鲁棒优化模型;文献[13]构建了一种含SOP、OLTC和CB的柔性互联配电网三阶段鲁棒电压控制模型。然而,随机优化方法的不确定性参数概率分布获取困难,而鲁棒优化在最恶劣情况下进行决策,计算结果过于保守[14]。近年来,分布鲁棒优化(Distributionally Robust Optimization, DRO)开始受到广泛关注。文献[15]采用综合范数约束不确定性场景概率分布置信集合,构建了基于数据驱动的含SOP配电网多目标DRO调度模型。文献[16]建立源荷预测误差的不确定性概率集合,计及OLTC和CB运行约束构建了柔性互联配电网两阶段分布鲁棒机会约束优化模型。DRO方法通过寻找不确定变量最恶劣概率分布下的解[17],可确保优化方案的经济性和鲁棒性。因此,本文将引入DRO方法进行柔性互联配电网不确定性优化问题的研究。
储能和SOP的联合优化能充分应对源荷的不确定性,提升配电网运行经济性[18]。相对于独立配置储能和SOP,储能型SOP(Soft Open Points with Energy Storage, E-SOP)具备更为灵活的时空调节能力,且具有更小的体积和成本[19]。文献[20]构建了协调DG、E-SOP的柔性互联配电网多目标优化调度模型,重点分析了日前优化阶段E-SOP的有效性。文献[3]提出了协调OLTC和E-SOP的日前-日内两阶段区间优化调度模型,日前阶段优化得到储能荷电状态(State of Charge, SOC)区间和OLTC状态,日内滚动优化得到储能SOC和SOP各端功率。文献[19]建立了协调OLTC、CB和E-SOP的自储能柔性互联配电网多时间尺度电压优化模型。文献[3]和[19]的结果表明多时间尺度优化调度能更好地协调各种可调度资源,提升配电网运行经济性和安全性。然而,以上文献对网侧多类型调控资源的考虑还不够全面,多时间尺度协调运行策略还需进一步研究。
此外,传统网侧调控资源的离散性、快慢特性和E-SOP的时序性决定了自储能柔性互联配电网优化调度模型是一个多时段强耦合的混合整数非线性规划模型,且源荷的不确定性使得模型求解难度进一步加大。文献[21]通过凸松弛和线性化将混合整数非线性模型转化为混合整数线性规划模型进行求解,文献[14]采用列与约束生成(Column and Constraint Generation, C&CG)算法求解考虑不确定性的两阶段混合整数线性规划模型以提升求解效率,本文同样引入凸松弛、线性化方法转化模型,并采用C&CG算法进行优化求解。
综上所述,为发挥传统网侧调控资源和E-SOP的综合优势并提升高渗透率分布式光伏(Distributed Photovoltaic, DPV)配电网的运行效益,本文提出了基于网侧资源协调的自储能柔性互联配电系统日前-日内优化方法。首先,提出了日前-日内优化框架;其次,建立日前长时间尺度不确定性优化模型和日内多目标滚动优化模型,并将模型线性化;然后,基于KL散度构建源荷不确定性模糊集,将日前两阶段优化模型转化为分布鲁棒优化模型,并分别利用C&CG算法和理想点法求解日前和日内优化模型;最后,算例仿真验证所提方法的正确性和有效性。
本文以含高渗透率DPV的自储能柔性互联配电系统为研究对象,该系统包含基础负荷和柔性负荷(Flexible Load, FL),网侧资源包含OLTC、CB、静止无功补偿器(Static Var Compensator, SVC)、联络开关与E-SOP,其中E-SOP可替换联络开关与配电网节点相连,其典型结构如附图1所示。为充分协调发挥多种资源的快慢调节特性,提出了多时间尺度优化控制框架如图1所示,由日前优化、日内优化和实时优化三个阶段组成。本文侧重于网侧资源协调利用,主要从日前和日内两个时间尺度进行分析。

图1 多时间尺度优化控制框架
Fig.1 Framework of multi-time scale optimization control
在配电网实际运行中,OLTC和CB等离散装置不做连续调节,网络拓扑也不能频繁调整,需要在日前阶段给出其运行方案。此外,储能系统也需要调度中心预先下发充放电控制指令。根据DPV和负荷的预测不确定性集合,采用两阶段DRO方法进行日前优化,优化时间间隔为1 h。然后,将日前网络重构方案、小时级的OLTC及CB动作情况、储能充放电时刻和柔性负荷响应时刻提前一天交付给运行控制人员。同时,日前阶段要将优化得到的储能运行区间和FL响应区间(即SOC上、下限和FL削减率的上、下限值)传递给日内阶段,作为日内优化模型的储能和FL运行约束。
日内优化阶段,DPV和负荷的短期预测能获得更为精确的结果,以15 min为间隔循环滚动求解各装置的运行策略。基于日前优化阶段传递的调度策略,以E-SOP各端口出力、SVC无功功率、DPV无功出力和FL响应功率作为控制变量,以系统网损和电压偏移最小为目标建立优化模型,获取各控制量的日内分钟级运行策略。需要说明的是,实时优化阶段可以利用DPV无功调节、SVC和SOP控制实现就地电压控制以减少高低电压越限问题。
2.1.1 目标函数
日前阶段,以1 h为时间间隔,以最小化运行成本为目标函数,制定优化调度方案。配电网运行成本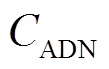 由四部分组成:购电成本
由四部分组成:购电成本![]() 、网损成本
、网损成本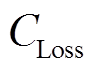 、FL响应成本
、FL响应成本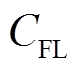 和储能退化成本
和储能退化成本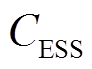 。
。
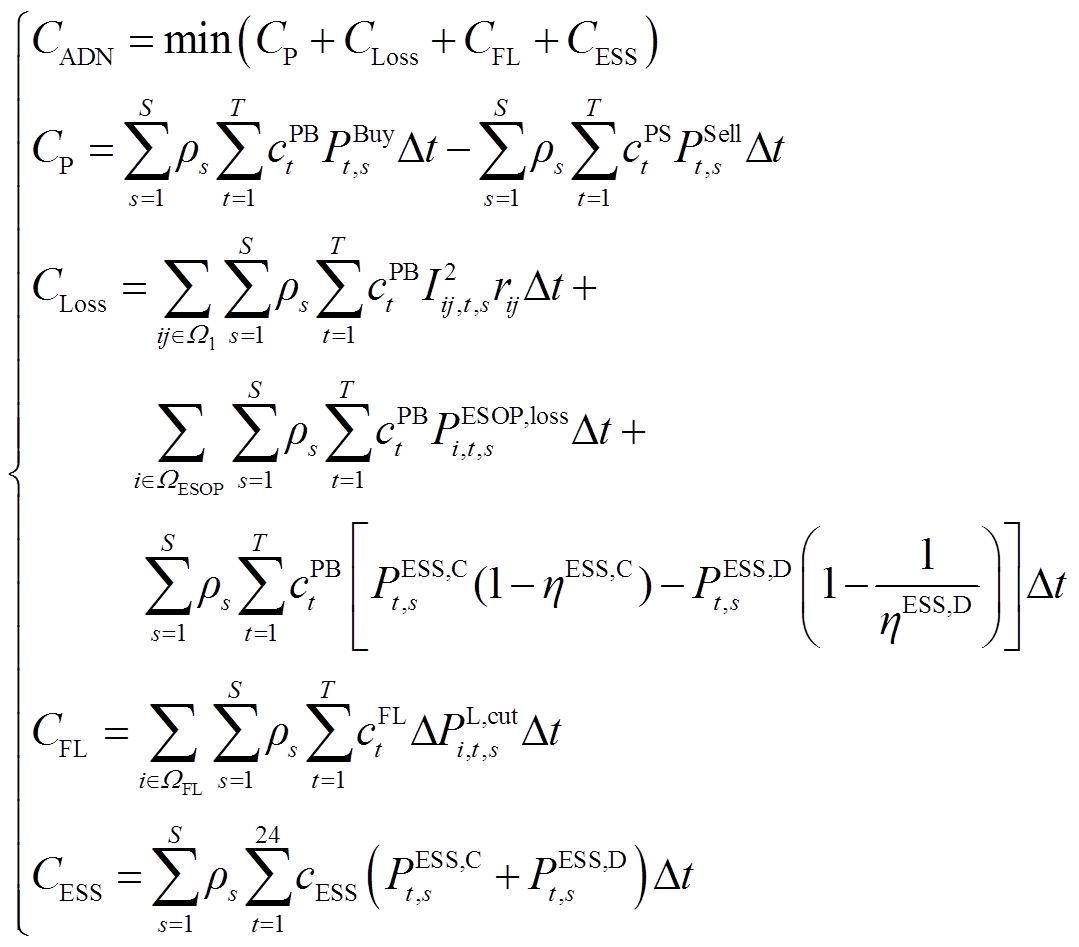 (1)
(1)
式中,t为时段;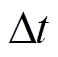 表示时间间隔;s为场景;
表示时间间隔;s为场景;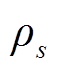 为场景s的概率,具体分析见3.1节;
为场景s的概率,具体分析见3.1节;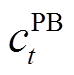 、
、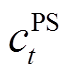 分别为配电网单位购、售电分时价格;
分别为配电网单位购、售电分时价格;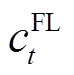 为FL单位补偿成本系数;
为FL单位补偿成本系数;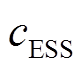 为ESS退化成本系数;
为ESS退化成本系数;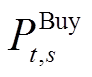 和
和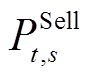 分别为配电网的单位购电、售电量;
分别为配电网的单位购电、售电量;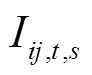 为支路ij的电流;
为支路ij的电流;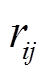 为支路ij的电阻;
为支路ij的电阻;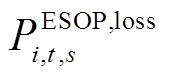 为E-SOP的有功功率损耗;
为E-SOP的有功功率损耗;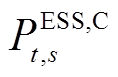 和
和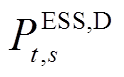 分别为E-SOP中储能的充、放电功率;
分别为E-SOP中储能的充、放电功率; 和
和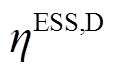 分别为储能的充、放电效率;
分别为储能的充、放电效率;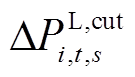 为FL削减量;
为FL削减量;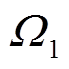 、
、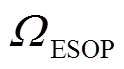 和
和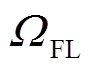 分别为线路集、E-SOP接入节点集和FL节点集。
分别为线路集、E-SOP接入节点集和FL节点集。
2.1.2 约束条件
1)潮流约束[21]
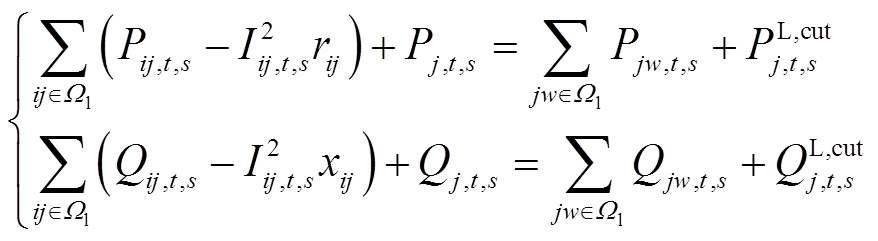 (2)
(2)
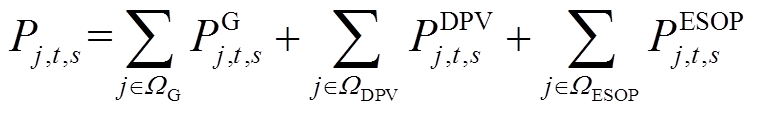 (3)
(3)
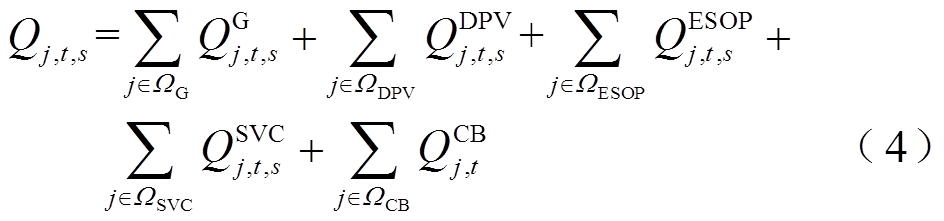
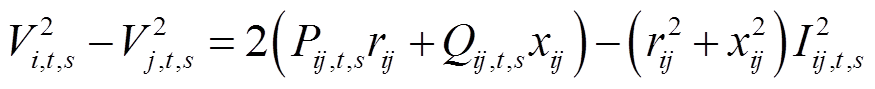 (5)
(5)
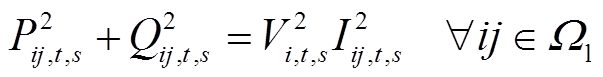 (6)
(6)
式中,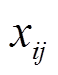 为支路ij的电抗,支路jw与支路ij相连;
为支路ij的电抗,支路jw与支路ij相连;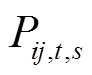 和
和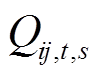 分别为支路ij的有功和无功传输功率;
分别为支路ij的有功和无功传输功率;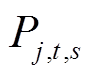 和
和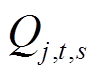 分别为注入节点j的有功和无功总功率;
分别为注入节点j的有功和无功总功率;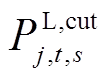 和
和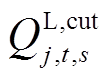 分别为负荷削减后的有功和无功功率;
分别为负荷削减后的有功和无功功率; 和
和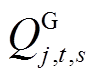 分别为发电机输出的有功和无功功率;
分别为发电机输出的有功和无功功率; 和
和 分别为DPV输出的有功和无功功率;
分别为DPV输出的有功和无功功率;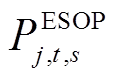 和
和 分别为E-SOP注入节点j的有功和无功功率;
分别为E-SOP注入节点j的有功和无功功率;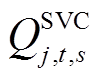 和
和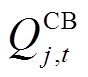 分别为SVC和CB输出的无功功率;
分别为SVC和CB输出的无功功率;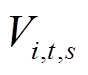 为节点i的电压。
为节点i的电压。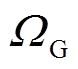 、
、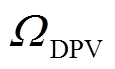 、
、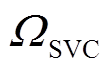 、
、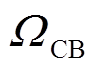 分别为发电机、DPV、SVC和CB接入节点集。
分别为发电机、DPV、SVC和CB接入节点集。
2)安全约束
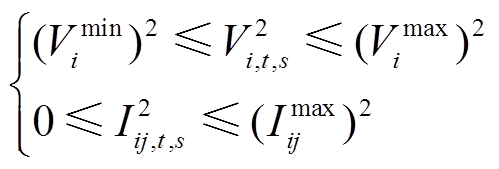 (7)
(7)
式中,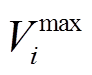 和
和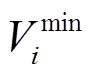 分别为节点i电压的上、下限;
分别为节点i电压的上、下限;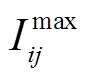 为支路ij电流的上限。
为支路ij电流的上限。
3)DPV无功约束[22]
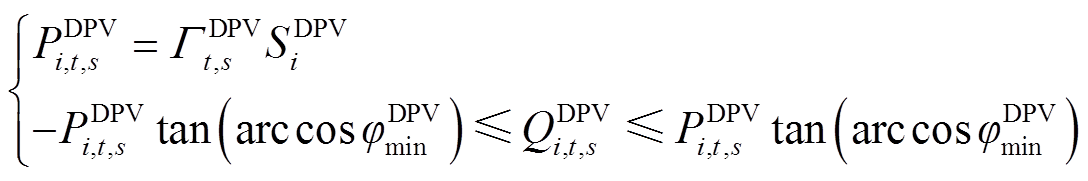 (8)
(8)
式中,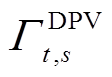 为DPV出力标幺值;
为DPV出力标幺值;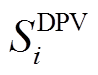 为节点i的DPV安装容量;
为节点i的DPV安装容量;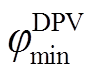 为DPV逆变器的最小功率因数。
为DPV逆变器的最小功率因数。
4)E-SOP运行约束
多端E-SOP的数学模型可表示为
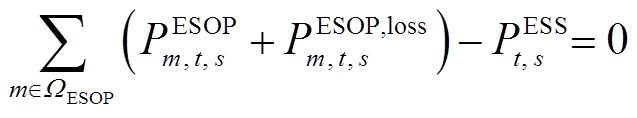 (9)
(9)
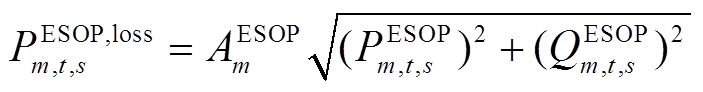 (10)
(10)
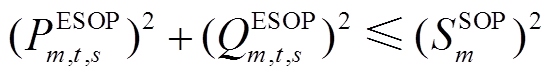 (11)
(11)
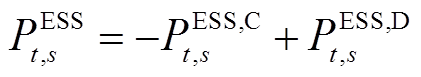 (12)
(12)
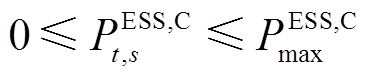 (13)
(13)
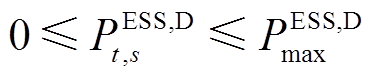 (14)
(14)
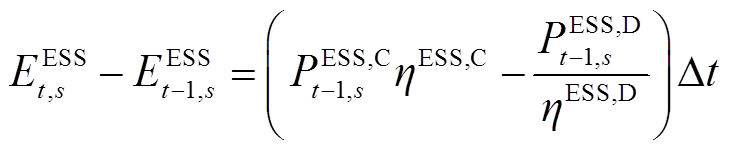 (15)
(15)
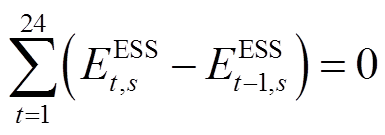 (16)
(16)
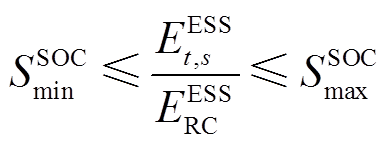 (17)
(17)
式中,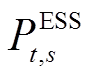 为储能输出功率;
为储能输出功率; 为E-SOP的损耗系数;
为E-SOP的损耗系数;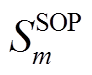 为SOP安装容量;
为SOP安装容量;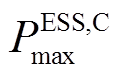 和
和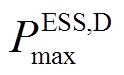 分别为充、放电最大功率;
分别为充、放电最大功率;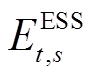 为t时刻储能剩余电量;
为t时刻储能剩余电量;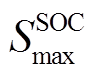 、
、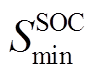 分别为储能SOC的上、下限;
分别为储能SOC的上、下限;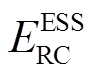 为储能额定容量。
为储能额定容量。
为了保证在日内优化阶段储能运行策略能满足全时段最优,即能满足各源荷不确定性场景,本部分引入储能功率区间约束[3],即
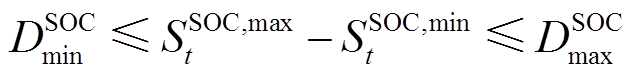 (18)
(18)
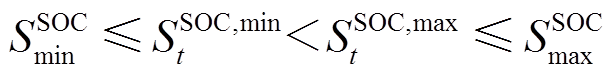 (19)
(19)
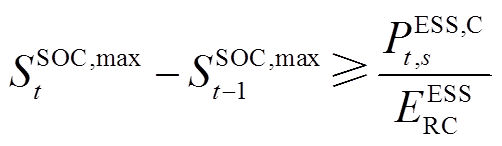 (20)
(20)
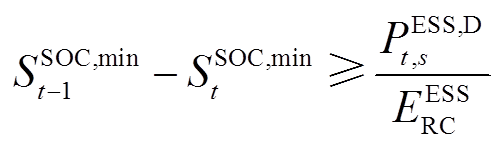 (21)
(21)
式中, 、
、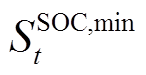 分别为优化得到的储能SOC各时刻上、下限;
分别为优化得到的储能SOC各时刻上、下限;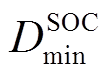 和
和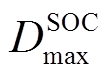 为定值,分别为各时刻储能SOC的最小值和最大值。
为定值,分别为各时刻储能SOC的最小值和最大值。
5)网络重构约束
配电网络需满足辐射状与连通性约束,约束可表示为[8]
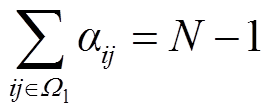 (22)
(22)
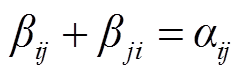 (23)
(23)
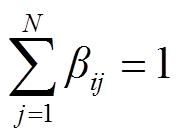 (24)
(24)
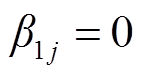 (25)
(25)
式中,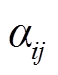 为0-1变量,表示线路状态,
为0-1变量,表示线路状态,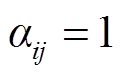 即线路是闭合的,
即线路是闭合的,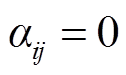 即线路断开;
即线路断开;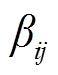 为0-1变量,节点i为节点j的父节点时取1,否则取0。本文设定日前优化阶段网络重构仅发生一次。
为0-1变量,节点i为节点j的父节点时取1,否则取0。本文设定日前优化阶段网络重构仅发生一次。
考虑网络重构后,潮流方程可改写成
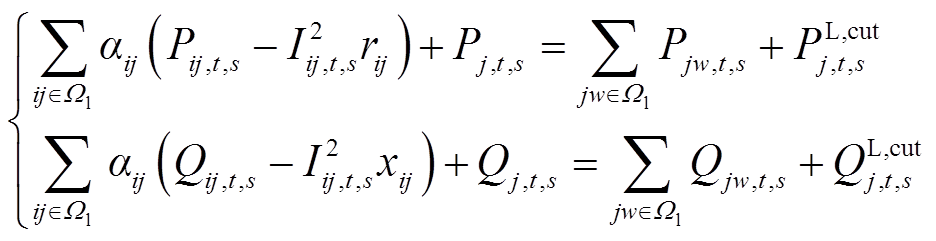 (26)
(26)
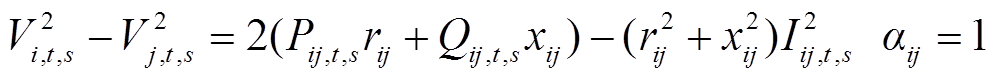 (27)
(27)
 (28)
(28)
上述改写的潮流方程是非凸的,采用大M法引入不等式约束对其进行松弛。此时,对断开支路来说,其有功功率、无功功率和支路电流为0,而对于闭合支路该约束不起作用。
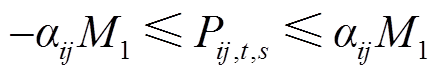 (29)
(29)
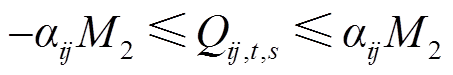 (30)
(30)
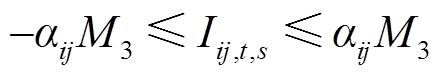 (31)
(31)
于是潮流方程可转换为
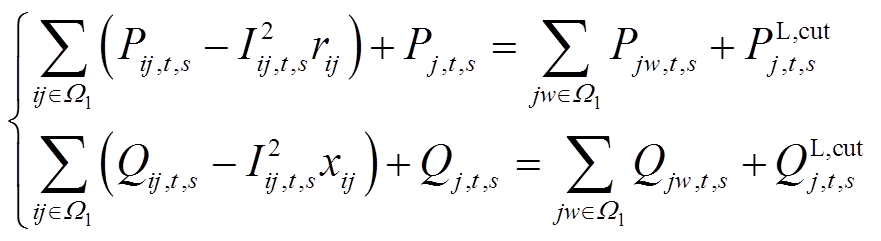 (32)
(32)
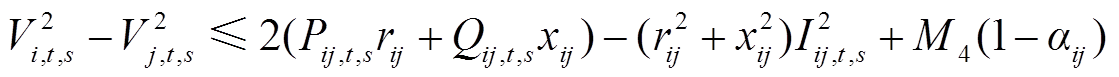 (33)
(33)
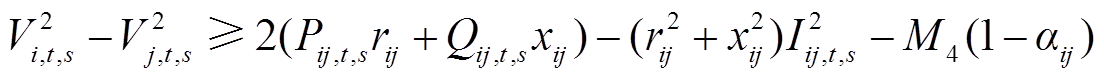 (34)
(34)
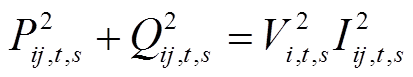 (35)
(35)
式中,M1~M4为大M法引入的足够大的正数。
6)其他约束
OLTC、SVC、CB和FL等运行约束可参考文献[21],如附录所示。
在日内优化阶段,超短期DPV出力和负荷预测相对准确,DPV出力和负荷采用点预测值。以15 min为时间间隔,依据2 h的超短期源荷预测结果,对日前计划进行修正,前一时段结束后更新预测信息重新进行优化求解,不断向前推移时段、循环滚动,直至24 h结束,实现日内滚动优化[23]。
1)目标函数
以网损和电压偏移最小为目标,即
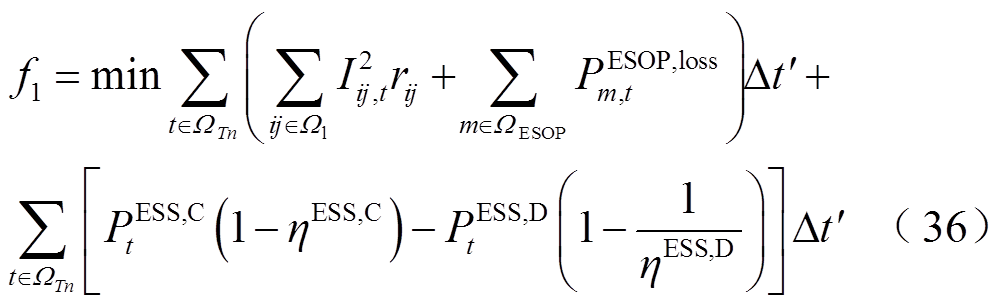
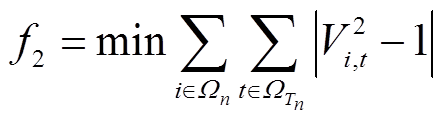 (37)
(37)
式中,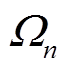 为节点集合;
为节点集合;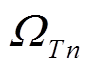 为滚动优化时段集合;
为滚动优化时段集合;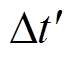 为时间间隔。
为时间间隔。
2)约束条件
日内优化的潮流约束、安全约束、SVC约束、DPV无功约束和E-SOP约束,与日前优化一致。除此之外,还应包含日前优化得到的OLTC和CB动作状态、联络开关动作方案、储能和FL区间约束。
需要说明的是,上述日前、日内优化模型建立后,采用文献[21]的线性化方法将其转换为混合整数线性规划模型,转换过程见附录。
为处理源荷日前预测的不确定性,本文提出了基于数据驱动的两阶段自储能柔性互联配电网DRO模型。将2.1.1节中模型式(1)改写为min-max-min形式。
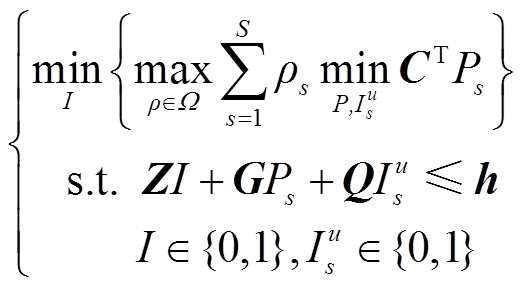 (38)
(38)
式中,I、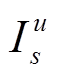 分别为第一和第二阶段优化模型的0-1变量;Ps为第二阶段优化问题的连续变量;CT、Z、h、Q、G均为常数系数矩阵,表示上文变量相应的矩阵或向量形式;Ω为DPV和负荷的模糊集。
分别为第一和第二阶段优化模型的0-1变量;Ps为第二阶段优化问题的连续变量;CT、Z、h、Q、G均为常数系数矩阵,表示上文变量相应的矩阵或向量形式;Ω为DPV和负荷的模糊集。
本文研究中,第一阶段以OLTC和CB控制策略、联络开关动作情况为决策变量;而第二阶段则以DPV和负荷的不确定性出力场景概率分布、FL响应功率为变量,不含二进制变量。第一阶段和第二阶段交替迭代求解,第一阶段得到最优决策量传递给第二阶段,第二阶段优化计算得到最差场景概率分布并返回给第一阶段,给出日前调度方案。
3.1.1 基于KL散度的模糊集
由于各时段DPV和负荷出力具有随机性和波动性,假设其不确定性出力分别为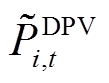 、
、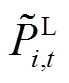 。分布鲁棒优化方法处理不确定性变量
。分布鲁棒优化方法处理不确定性变量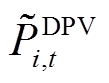 、
、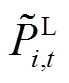 是在t时段构建出变量的所有可能的概率分布模糊集W。基于距离的所有可能概率分布的模糊集W的构建方法如下。
是在t时段构建出变量的所有可能的概率分布模糊集W。基于距离的所有可能概率分布的模糊集W的构建方法如下。
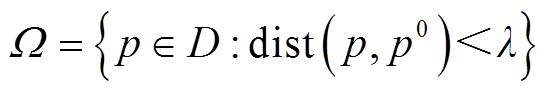 (39)
(39)
式中,D为所有可能的概率分布;λ为参考概率分布![]() 与真实概率分布p之间的最大误差水平;
与真实概率分布p之间的最大误差水平;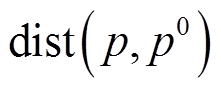 表示距离函数。
表示距离函数。
通过统计DPV和负荷历史数据,构建基于KL散度的DPV和负荷模糊集。具体步骤如下:
1)通过对大量历史数据进行估计构造参考概率分布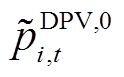 、
、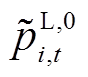 。假设选取某地区单位容量DPV和负荷时段t的联合出力数据有Mt个样本,根据特征将其分类为N个子区间,则各对应子区间的样本分别为
。假设选取某地区单位容量DPV和负荷时段t的联合出力数据有Mt个样本,根据特征将其分类为N个子区间,则各对应子区间的样本分别为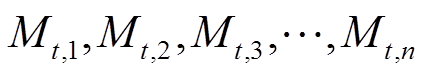 ,显然有
,显然有
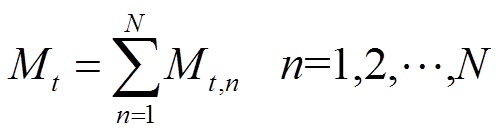 (40)
(40)
当样本数量足够大时,可用式(41)计算得到的离散概率分布作为某个时段t单位容量DPV(或负荷)的参考概率分布[24]。
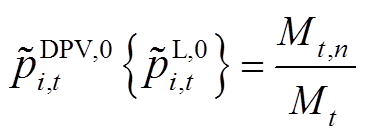 (41)
(41)
2)本文采用KL散度表征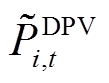 、
、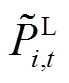 参考概率分布与真实概率分布之间距离的量度。以
参考概率分布与真实概率分布之间距离的量度。以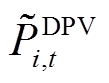 为例,则模糊集表示为[24]
为例,则模糊集表示为[24]
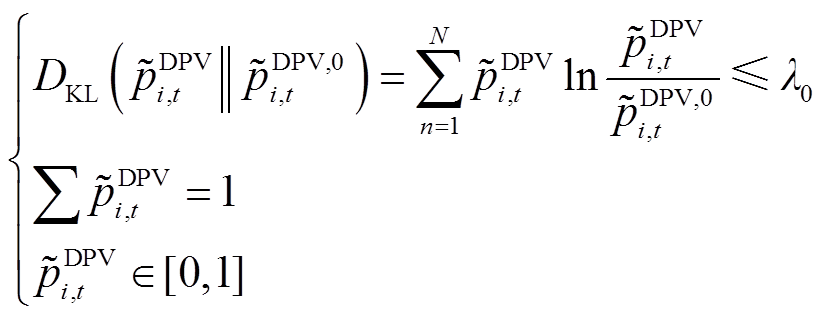 (42)
(42)
式中,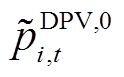 为根据光伏历史数据得到的
为根据光伏历史数据得到的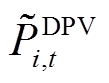 的参考概率分布;
的参考概率分布; 为
为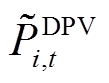 的真实概率分布;
的真实概率分布;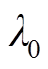 为KL散度阈值;DKL为真实概率分布与参考概率分布之间的KL散度值,距离越小表明两个分布越相似,特别地,当DKL=0时,真实概率分布与参考概率分布相同,此时分布鲁棒优化模型将退化为传统的随机规划模型。需要说明的是,
为KL散度阈值;DKL为真实概率分布与参考概率分布之间的KL散度值,距离越小表明两个分布越相似,特别地,当DKL=0时,真实概率分布与参考概率分布相同,此时分布鲁棒优化模型将退化为传统的随机规划模型。需要说明的是,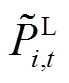 的分析过程类似。
的分析过程类似。
综上所述,由式(42)建立基于KL散度的DPV和负荷概率分布模糊集,既考虑了变量的参考概率分布,又避免了直接选取某一分布的盲目性,且所有的模糊集与样本集误差都保持在误差水平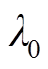 内。
内。
3.1.2 日前分布鲁棒优化模型求解
针对式(38)的DRO模型,本文采用C&CG算法求解,将模型解耦为、子问题和主问题迭代求解[14]。
1)子问题
子问题是以主问题优化确定的决策变量为已知量,在3.1.1节所求的不确定性模糊集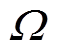 内,找到最严重的场景分布概率并返回给主问题,其模型为
内,找到最严重的场景分布概率并返回给主问题,其模型为
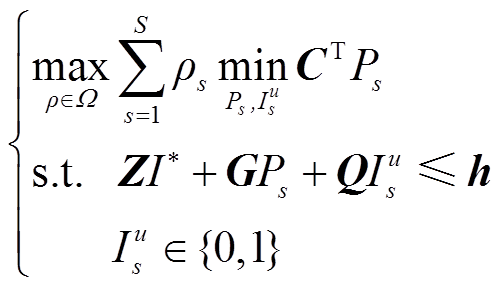 (43)
(43)
式中,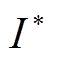 为主问题中得到的第一阶段变量的值,其在子问题中为常数。需要注意到,此时子问题目标函数存在由
为主问题中得到的第一阶段变量的值,其在子问题中为常数。需要注意到,此时子问题目标函数存在由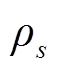 和
和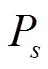 相乘的非线性项,一般难以直接采用KKT或强对偶条件转换。因此,本文将该子问题解耦为两个独立的步骤,具体步骤如下:
相乘的非线性项,一般难以直接采用KKT或强对偶条件转换。因此,本文将该子问题解耦为两个独立的步骤,具体步骤如下:
(1)先求解下层S个混合整数线性规划模型,如式(44)所示。
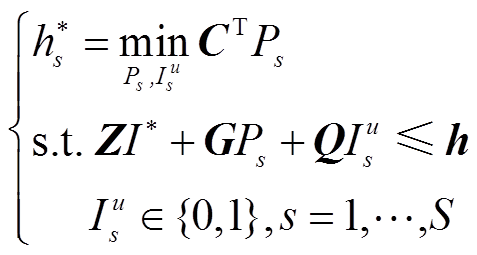 (44)
(44)
(2)将下层模型求得的最优值代入上层模型,此时优化得到的目标函数值即为原问题的上界。
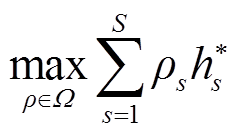 (45)
(45)
通过上述两个步骤,子问题可求得最差场景概率分布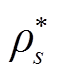 ,并将其返回给主问题。
,并将其返回给主问题。
2)主问题
主问题以子问题传来的DPV和负荷的不确定性场景变量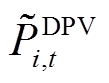 、
、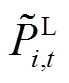 为已知量,进行自储能柔性互联配电网调度策略求解,模型如式(46)所示。此时,主问题优化得到的值为原问题更新下界值。
为已知量,进行自储能柔性互联配电网调度策略求解,模型如式(46)所示。此时,主问题优化得到的值为原问题更新下界值。
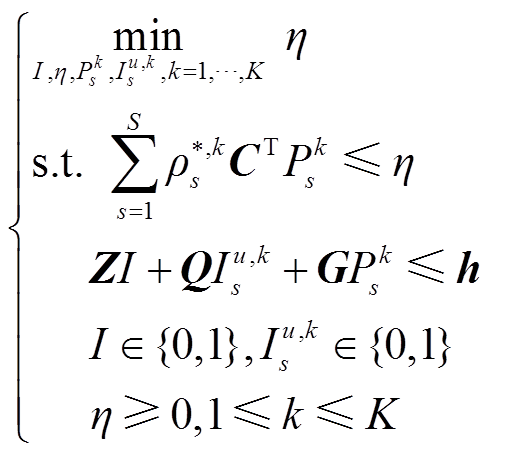 (46)
(46)
式中,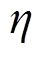 为中间变量,表示对子问题的预估值;K、k分别表示外层循环的总次数和第k次;
为中间变量,表示对子问题的预估值;K、k分别表示外层循环的总次数和第k次;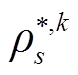 为第k次迭代时找到的最严重场景分布概率。
为第k次迭代时找到的最严重场景分布概率。
3)C&CG算法求解步骤
采用C&CG算法求解上述模型的步骤如下:
(1)初始化DPV和负荷出力场景,设置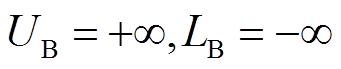 ,迭代次数k=0。
,迭代次数k=0。
(2)求解主问题,得到第一阶段决策变量初始值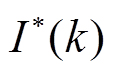 及目标函数值
及目标函数值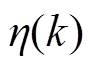 ,传递给子问题,并更新下界值LB。
,传递给子问题,并更新下界值LB。
(3)求解两步解耦后的子问题,将最差场景概率分布传递给主问题,并更新上界值UB。
(4)当上界和下界满足一定误差时,模型达到收敛标准,如式(47)所示。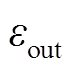 为很小的正数。否则,k=k+1,返回步骤(2)。
为很小的正数。否则,k=k+1,返回步骤(2)。
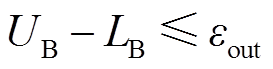 (47)
(47)
求解流程如图2所示。
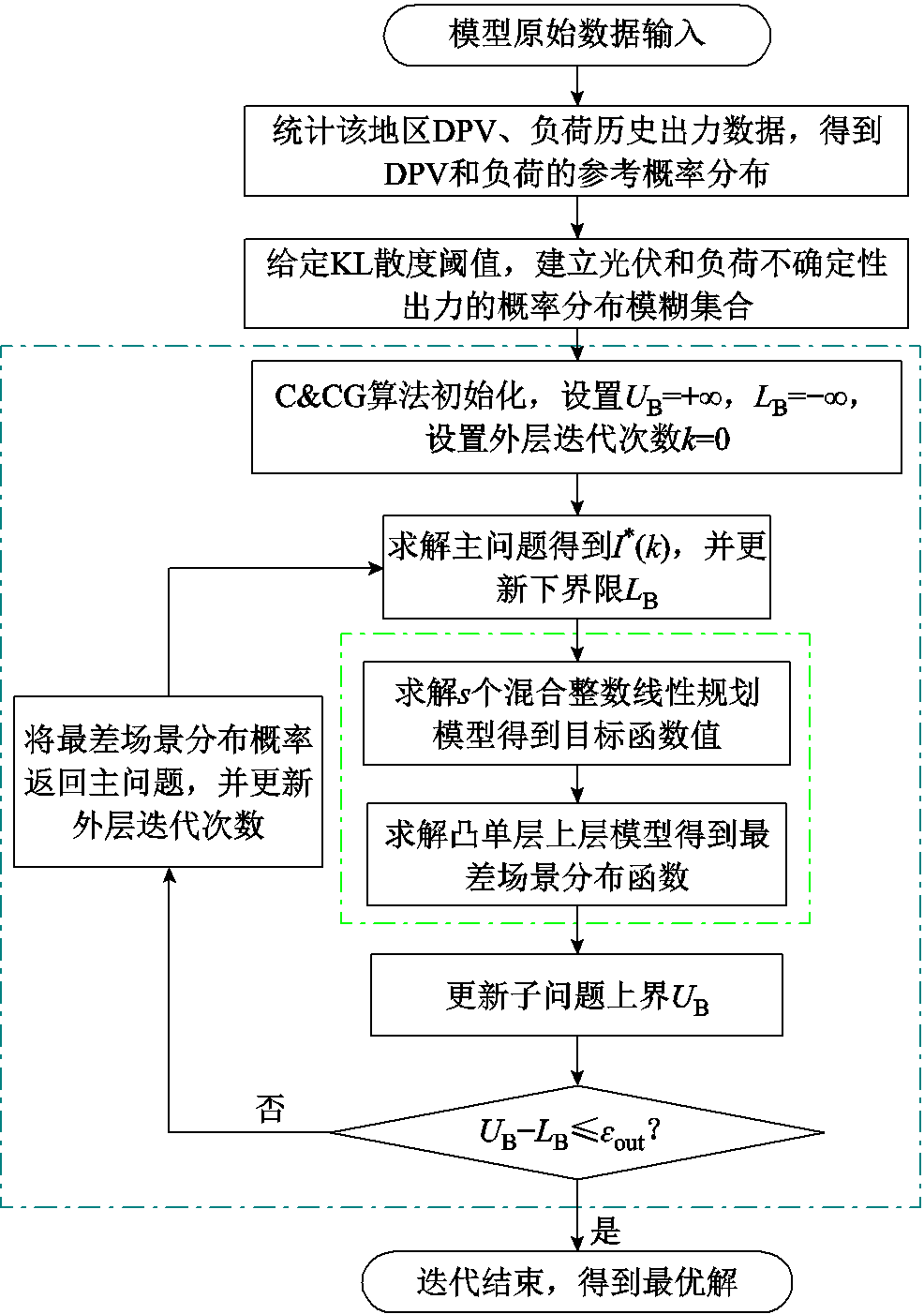
图2 日前优化算法求解流程
Fig.2 Flow chart of day-ahead optimization algorithm
日内滚动优化为多目标优化问题,本文采用理想点法将其转换为单目标优化问题。
理想点法利用各个目标的最优解将目标函数与最优解的距离作为新的目标函数,即
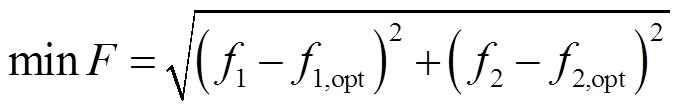 (48)
(48)
式中,F为新构建的目标函数;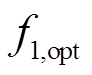 和
和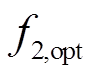 分别为两个子目标的最优值。
分别为两个子目标的最优值。
上述基于欧式距离的理想点法为非线性的,引入曼哈顿距离对求解方程进行修正,则可以得到
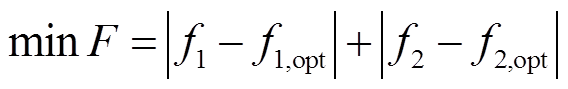 (49)
(49)
经过上述转换后,式(49)中仍存在绝对值非线性项,同样采用附录的绝对值线性化处理方法。
将日前优化阶段的优化结果传递给日内优化阶段后,根据2.2节所述的求解流程,更新DPV和负荷预测结果以及各设备运行状态值进行滚动求解。
本文以改进的中国某51节点农村配电网进行算例分析,系统如附图2所示[21]。DPV接入位置及容量见附表1,且逆变器最小功率因数为0.9;E-SOP各端分别与节点14、32、48相连,容量均设置为600 kV∙A,损耗系数为0.02,储能参数见附表2;OLTC抽头可调节范围为±4×1.25%;假设节点11、33、47、51为FL,最大削减率为1,削减速率系数为0.3;SVC安装位置为节点14、48,可调范围为-500~500 kvar;CB安装位置为节点9、31,单位容量为100 kvar,共安装5组;设置5条联络线路,其中2条由E-SOP替代,如附图2所示。购售电分时电价见附表3[25]。FL补偿成本系数为0.6元/(kW×h)[22]。日前DPV和负荷典型场景、日内滚动预测结果分别如附图3a、附图3b所示。本文模型采用GAMS软件调用CPLEX求解器进行优化求解。C&CG算法迭代收敛判据常数取0.01。
日前优化阶段,设置4个案例进行仿真分析。案例1:考虑CB、SVC和E-SOP优化;案例2:考虑CB、SVC、E-SOP优化和网络重构;案例3:考虑CB、SVC、E-SOP和OLTC优化;案例4:考虑CB、SVC、E-SOP、OLTC优化和网络重构。
4.2.1 运行经济性分析
各算例运行成本结果见表1。相比案例1,案例2、3、4的总运行成本分别降低1.0%、7.42%和8.03%,且E-SOP、OLTC和网络重构协调优化(即案例4)对运行成本的降低是最优的。由案例2、3的结果可知,OLTC相比网络重构优化对系统运行成本的降低效果更优。相比案例2,案例3、4对系统网损成本降低效果更为明显,分别降低了0.082 6万元和0.088 4万元,这是因为OLTC通过调节系统首端电压优化了系统全局电压分布情况,从而更好地降低系统网损。
表1 不同案例运行成本
Tab.1 Operating costs of different cases (单位:万元)

案例购电成本网损成本FL补偿成本储能退化成本总成本 11.182 60.196 10.072 50.021 01.472 2 21.179 00.186 60.070 50.021 11.457 2 31.154 80.113 50.073 90.020 81.363 0 41.151 60.107 70.073 80.020 91.354 0
4.2.2 CB、OLTC和网络重构结果分析
案例1~4的CB投切组数情况如附图4所示。由附图4可知,各案例中节点9和节点31处的CB投切组数是不一致的,其中不考虑OLTC优化的案例1、2中CB投切组数较多,且CB投切动作较频繁,这是因为为了保持系统电压在允许范围内且降低网损,网侧需要提供更多的无功支撑。
案例3、4的OLTC调节情况如图3所示。由图3可知,光伏出力较高时,系统整体电压水平较高以减少系统网损,两案例中OLTC也维持在较高挡位;且两案例中OLTC的挡位均是大于4的,这是为了保证在光伏不出力时,系统末端节点也能维持较高的电压水平以确保配电网安全运行。
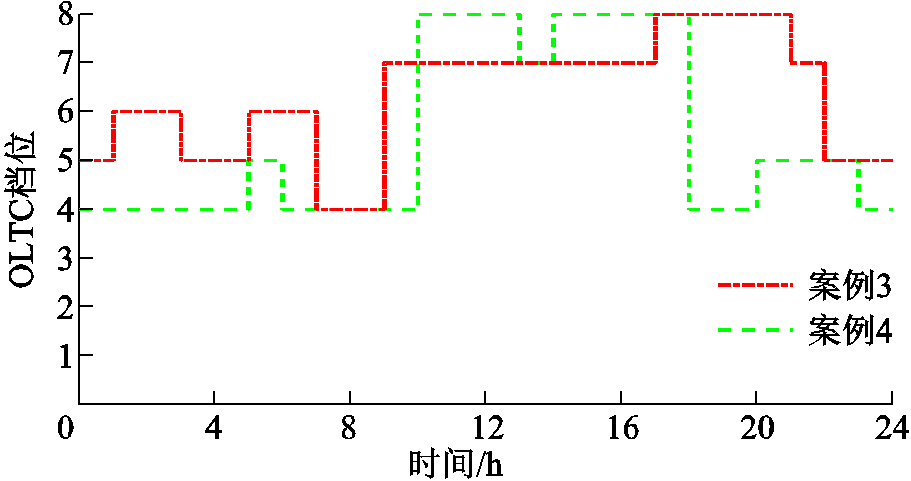
图3 不同案例OLTC挡位优化结果
Fig.3 Optimized OLTC tap position in different cases
案例2和4网络重构后的系统拓扑如附图5所示。由附图5可知,两种案例下网络重构结果是不一致的,但系统仍然满足辐射状运行约束。
4.2.3 储能和FL区间结果分析
案例4储能SOC优化区间和FL响应时间/区间分别如附图6和附图7所示。由附图6可知,优化得到的初始SOC值为0.2~0.6,且储能SOC值的区间宽度在0.2和0.4之间变化。由附图7可知,4个FL节点的响应时刻均为光伏出力较小的时刻,且此时段削减补偿费用是低于配网购电价格的,此时FL进行需求响应以维持系统运行经济性。需要说明的是,与储能SOC区间优化不同,为应对所有不确定性场景,FL区间结果是由所有场景下的FL响应结果叠加得到的。
4.3.1 多目标优化结果分析
为说明本文多目标优化的有效性,本部分引入单目标优化进行对比验证,对比结果见表2。其中,网损单目标优化中,电压偏差根据96个时间段的实际电压分布情况计算得到;电压单目标优化中,网损值则根据优化后的潮流分布计算得到。由表2可知,采用多目标优化的网损值和电压偏差介于两个单目标的优化结果之间,多目标优化可兼顾系统网损优化和电压优化,确保系统具有较好的经济性和安全性。
表2 多目标与单目标优化结果对比
Tab.2 Comparison results of multi-objective and single-objective optimization

类型网损f1 (pu)电压偏差f2 (pu)求解时间/s 网损单目标5.692295.96622 电压单目标54.78480.92023 多目标优化15.59393.214127
此外,系统所有节点96个时间段的电压分布情况如附图8所示。由附图8可知,网损单目标优化中,电压水平整体相对较高,且电压波动较大;而电压单目标优化和多目标优化中,电压水平相对较低且电压波动较小,这进一步说明多目标优化具有更好的网损和电压优化效果。此外,日内多目标优化的求解时间为127 s,而日内滚动优化的时间尺度为15 min,满足日内运行阶段的时间要求。
4.3.2 日内各设备运行策略
日内快速调控设备SVC、SOP、储能和FL的出力情况如附图9、附图10和图4、图5所示。
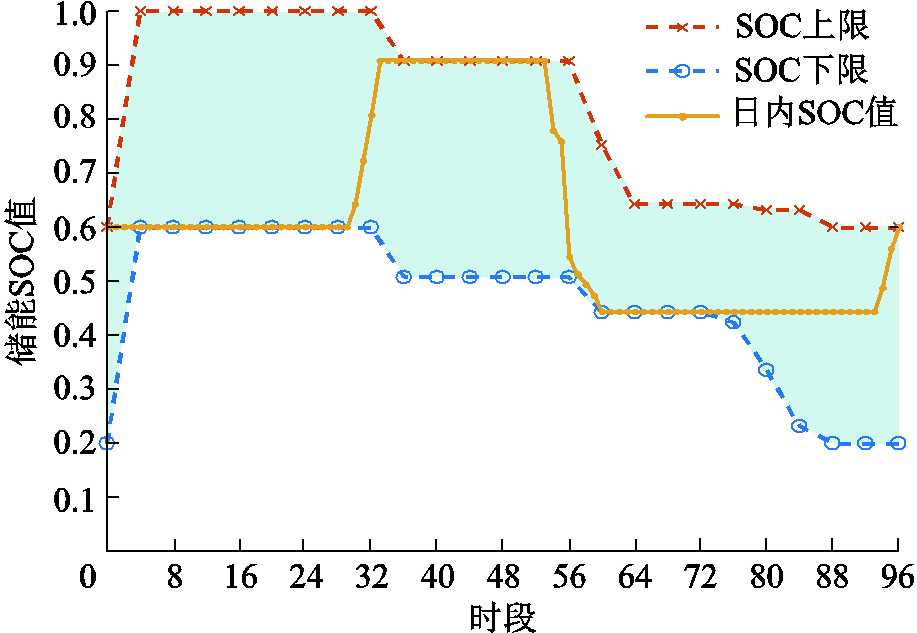
图4 日内优化SOC变化情况
Fig.4 SOC changes of intra-day optimization
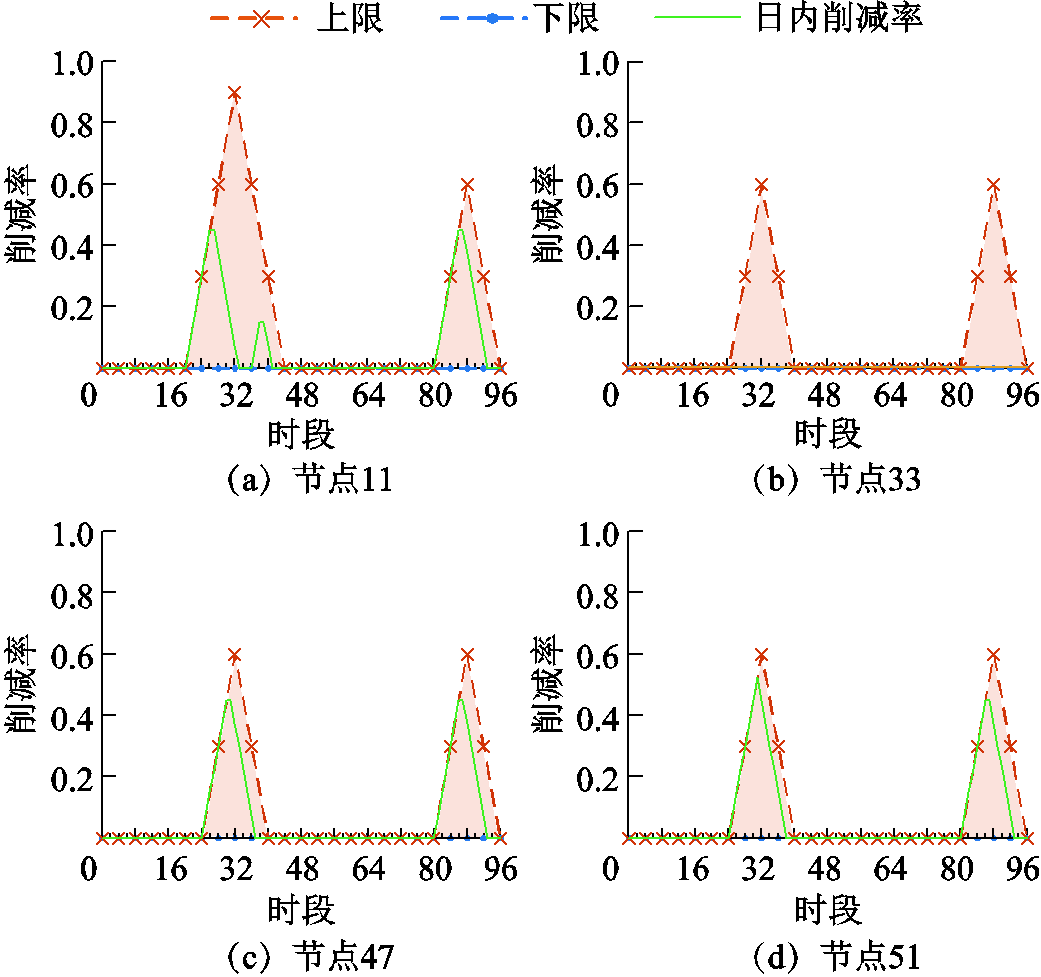
图5 日内优化FL响应情况
Fig.5 FL response of intra-day optimization
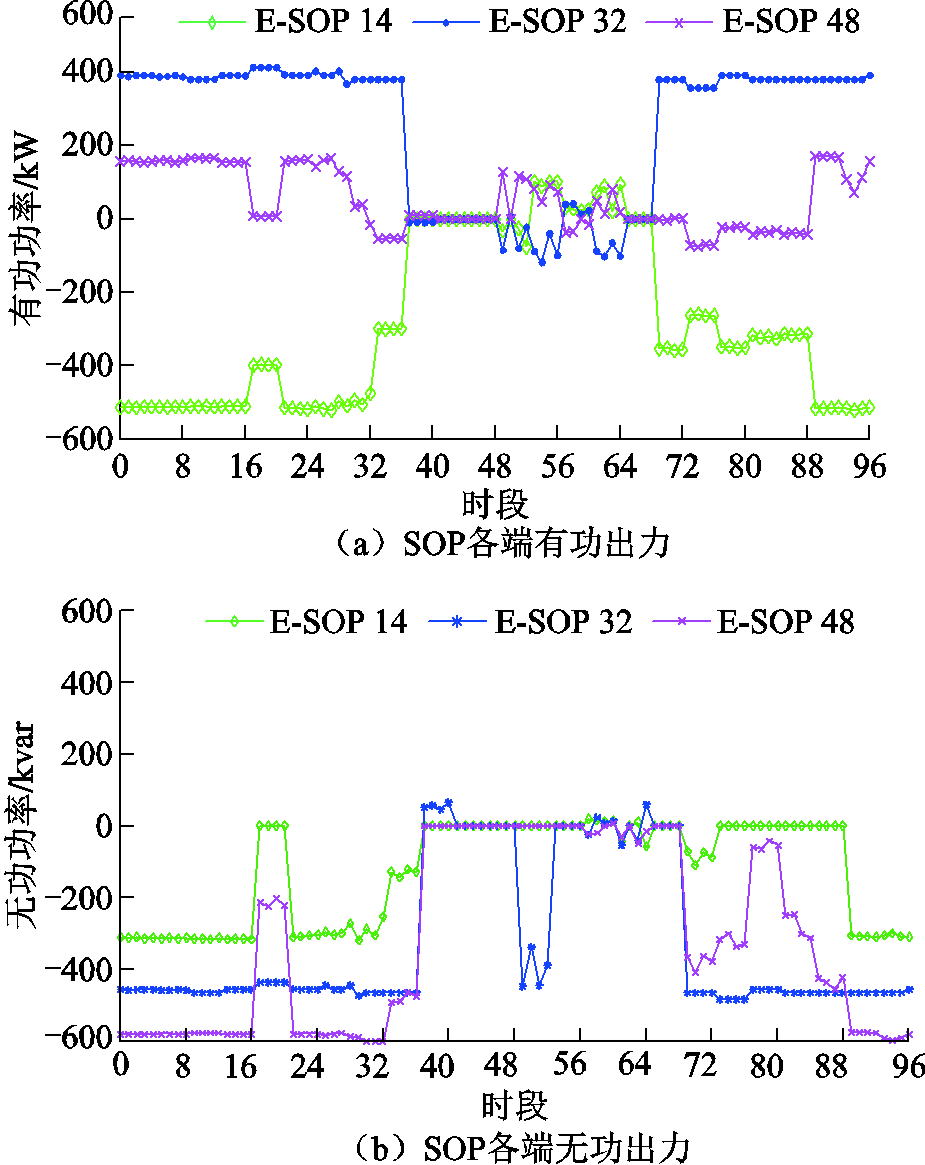
为保证馈线功率分布最优,通过SOP实现有功功率快速转移,并且SOP具有一定的无功支撑能力,如附图10所示。由附图5b和附图10可知,光伏出力较小时,由于14节点所在线路较长且负荷较大,为减少系统有功损耗,需要14节点所在馈线转移有功功率到节点32和节点48所在馈线;而光伏出力较大时,可为各条馈线提供较充足的有功功率,各馈线间有功功率转移较少。此外,由附图9和附图10可知,为改善系统电压分布并降低网损,SVC和SOP在光伏出力较小时或光伏不出力时发出无功进而提供无功支撑;而在光伏出力较大时,由于附图8c节点电压较高,基本不需要SOP提供无功支撑,SVC还吸收了无功以优化系统网损和电压。
由图4可知,储能在0 h—7.25 h不进行充放电,在7.25 h—8.25 h进行充电,8.25 h储能SOC值已达到上限,虽然8.25 h—13.25 h光伏出力较大,但储能不进行充放电行为;储能在13.25 h—14.25 h进行快速放电,并在14.25 h达到日前优化得到的最大放电深度,这是因为此时配电网分时电价较高,储能放电以降低系统运行成本。由图5可知,各节点FL在日前响应时间和削减率约束下进行日内响应,且每15 min对FL响应情况更新一次。日内FL削减时段均为配电网外购电价较高的时刻,而此时负荷需求较大而光伏出力较小,通过负荷有功削减能降低线路上的功率损耗并通过与网侧调控设备的协调改善系统电压分布。
4.3.3 日内配电网购售电情况
日内优化阶段配电网购售电情况如附图11所示。由附图11可知,由于本文配电网DPV渗透率较高,光伏出力较大的9:15—18:00,光伏发电量不能完全被本地负荷消纳,配电网向上级电网售电。
为分析DRO方法处理日前不确定性优化问题的有效性,本文选取文献[14]提到的随机优化(Stochastic Optimization, SO)方法与DRO方法进行对比分析。案例3和案例4的仿真结果如图6所示。由图6可知,SO方法对应的总成本是小于DRO方法的,且DRO购电成本是高于SO方法的,DRO模型使得配电网向上级电网购买了更多电能以应对DPV和负荷的不确定性,说明DRO方法相比SO方法具有更强的鲁棒性。
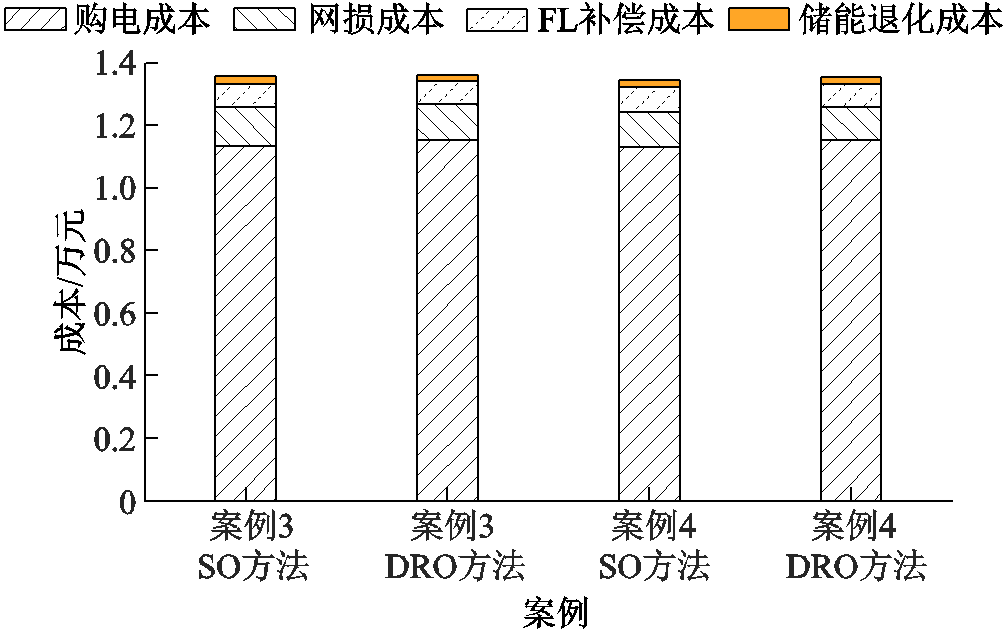
图6 SO和DRO方法运行成本对比
Fig.6 Operating costs of SO and DRO method
图7给出了案例3和案例4典型场景的概率分布变化情况。由图7可知,场景1、3的概率分别由0.205上升到0.393、0.391,由0.303上升到0.330、0.333,而场景2的概率由0.492降低到0.277、0.276,这是因为考虑不确定性后,为了找到最差概率对应的场景从而保证优化结果的鲁棒性,DRO模型使得运行成本较低的场景概率变小,而运行成本较高的场景概率则相应增大。
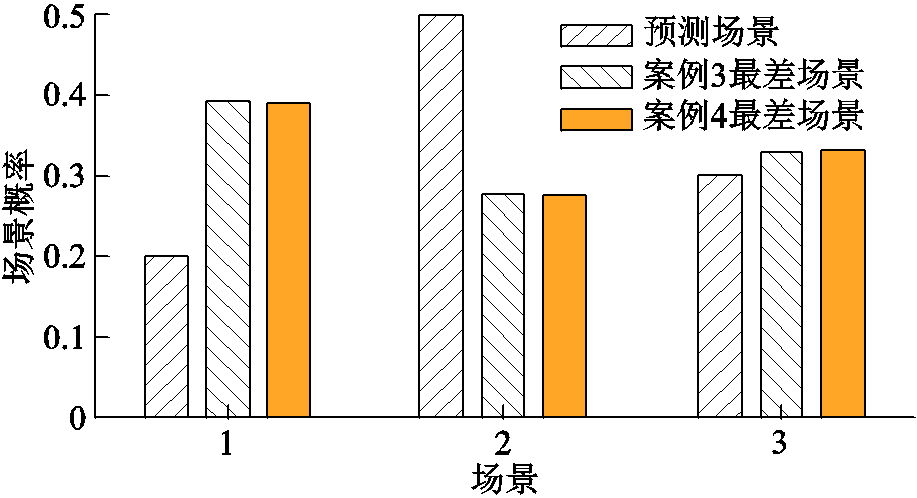
图7 各场景概率分布变化情况
Fig.7 Probability distribution changes of each scenario
本文采用C&CG算法将DRO模型解耦为主问题和子问题后进行优化求解,案例3和案例4均经过2次迭代即满足收敛要求,其中第二次迭代的上、下界差值分别为0.001 7和0.002 7。采用GAMS软件调用CPLEX求解所提优化模型,案例3求解时间为0.52 h,而案例4由于网络重构问题引入了大量0-1变量,求解时间较长,为8.81 h。结合表1结果可知,案例3的运行成本仅比案例4高90元,但求解效率更高,因此如果要同时兼顾运行成本和求解效率,可忽略网络重构优化问题,重点协调利用网侧OLTC、CB、SVC和E-SOP。
此外,KL 散度阈值决定了实际概率分布的不确定集合的范围,也反映了决策者的风险偏好。图8给出了不同KL散度阈值对应的案例3日前优化结果。由图8可知,配电网日前总运行成本会随KL散度阈值增大而增大,这是因为KL 散度阈值越大,不确定性集合的分布函数簇范围也越大,而分布鲁棒优化方法是在分布函数簇中求解最坏情况下的配电网日前优化运行成本结果。
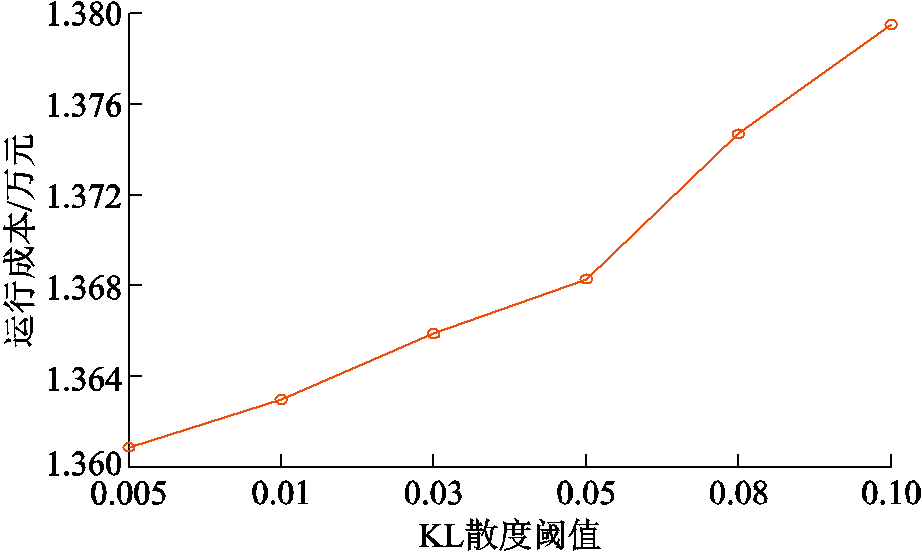
图8 不同KL散度阈值的运行结果影响
Fig.8 Impact on operation results under different thresholds
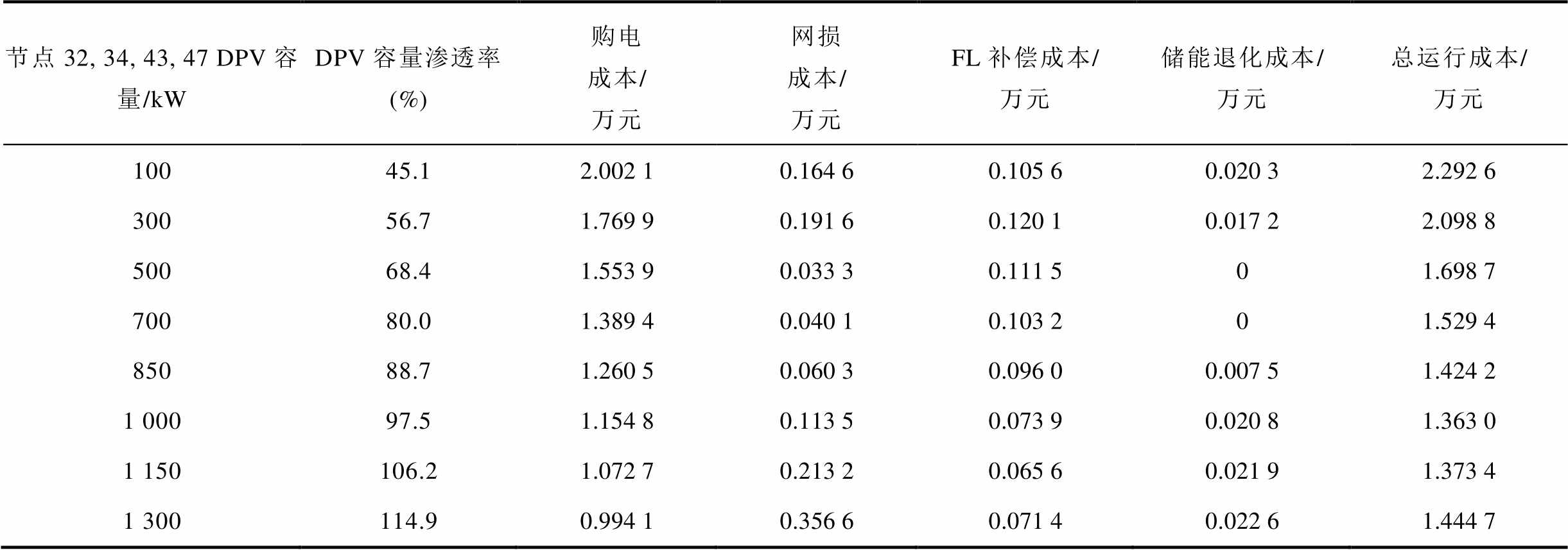
为分析DPV容量渗透率对系统优化运行的影响,本节以4.2节案例3为基础,改变节点32、34、43、47的DPV接入容量,其他节点DPV配置情况不变,DPV接入容量设置情况和仿真结果见附表4。由附表4可知,随着DPV渗透率不断增大,配网总运行成本先降低后升高,这是因为当DPV渗透率升高时,网侧资源调控能力不足,导致系统运行成本增加。当DPV渗透率为97.5%时,总运行成本是最低的,此时网损成本也是相对较小的。
下面分析SOC不同区间宽度设置对日前优化运行成本的影响。SOC区间宽度设置情况和对应的仿真结果见附表5。由附表5可知,储能SOC区间宽度设置越大,系统总运行成本越小,这是因为储能SOC区间宽度越大,其可控范围越大,其能为配电网提供的有功调节能力越大。对比附表5中定值区间0.2、0.3、0.4和对应可变区间的日前优化阶段总运行成本可知,可变的区间宽度相比固定的区间宽度对降低配电网总运行成本作用更为明显。此外,不同区间宽度下优化得到的SOC初值是不一致的。
本文在网侧资源协调利用框架下,考虑源荷的不确定性,提出了基于分布鲁棒优化的日前长时间两阶段优化调度模型和基于滚动优化的日内多目标优化模型,得到以下结论:
1)基于网侧资源协调的日前-日内优化能够充分发挥网侧调控设备的快慢调节特性,提升配电网运行效益。
2)日前阶段的E-SOP、OLTC和网络重构协调优化运行总成本相比E-SOP单独优化降低了约8.04%。
3)日内多目标滚动优化能够兼顾网损和电压优化,且可得到更为精确的日内各快速调控设备运行策略。
本文仅针对日前、日内两个时间尺度进行网侧资源协调利用,下一步将考虑DPV有功削减、SVC和SOP控制等进行“日前优化-日内滚动-实时校正”的多时间尺度运行优化。
附 录
含高渗透率DPV的E-SOP配电系统的典型结构如附图1所示。
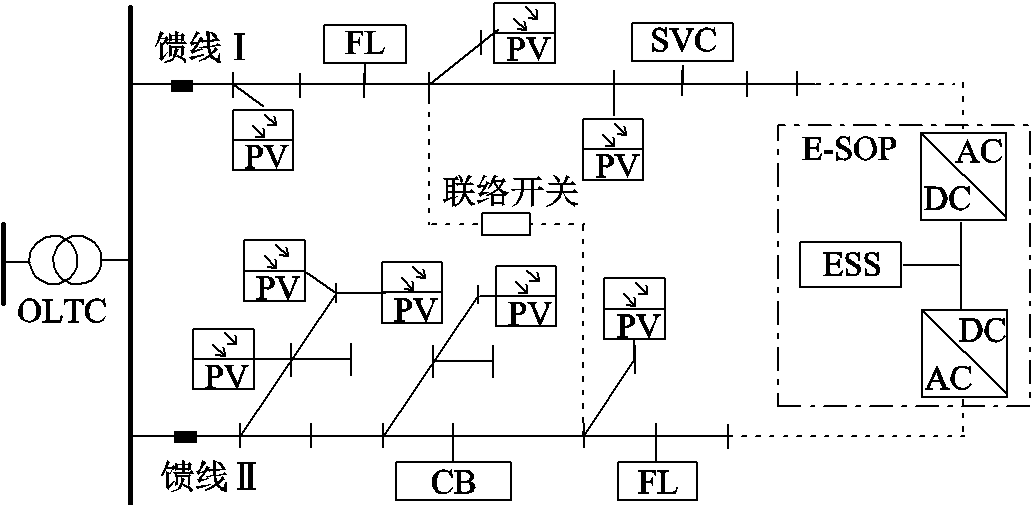
附图1 含E-SOP配电系统结构
App.Fig.1 Structure of distribution system with E-SOP
采用文献[21]的线性化方法将其转换为混合整数线性规划模型,转换过程如下。
1. 其他运行约束
1)OLTC运行约束
用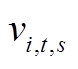 和
和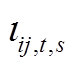 代替电压、电流二次方
代替电压、电流二次方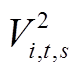 和
和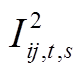 ,代入式(5),得到
,代入式(5),得到
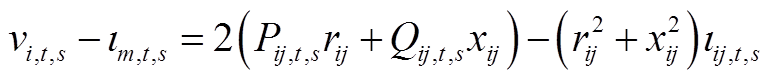 (A1)
(A1)
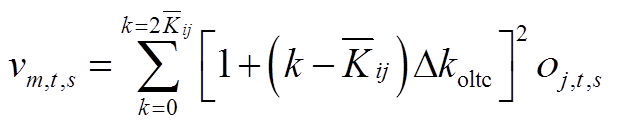 (A2)
(A2)
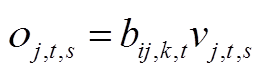 (A3)
(A3)
 (A4)
(A4)
式中,m为描述OLTC两端电压的关系而引入的虚拟母线; 为二进制变量,
为二进制变量,![]() 为单位调节步长;
为单位调节步长;![]() 为DLTC档位调节最大值;当
为DLTC档位调节最大值;当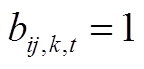 时,表示OLTC挡位k闭合,当
时,表示OLTC挡位k闭合,当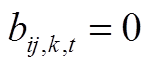 时,表示OLTC挡位k断开;
时,表示OLTC挡位k断开;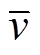 和
和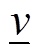 分别为电压幅值二次方的上、下限;
分别为电压幅值二次方的上、下限;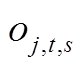 为线性化OLTC末端节点电压幅值二次方而引入的中间变量。
为线性化OLTC末端节点电压幅值二次方而引入的中间变量。
同时,需对OLTC每日动作次数进行限制,即
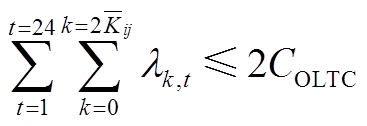 (A5)
(A5)
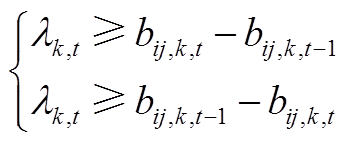 (A6)
(A6)
式中,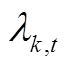 为二进制变量,表示OLTC的第k个调节挡位是否有变化,有变化则
为二进制变量,表示OLTC的第k个调节挡位是否有变化,有变化则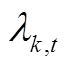 =1,不变化则为0;
=1,不变化则为0;![]() 为每天OLTC可以动作的最大次数。
为每天OLTC可以动作的最大次数。
2)SVC运行约束
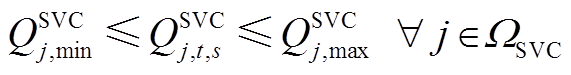 (A7)
(A7)
式中,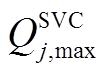 和
和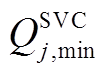 分别为SVC无功功率上、下限。
分别为SVC无功功率上、下限。
3)CB运行约束
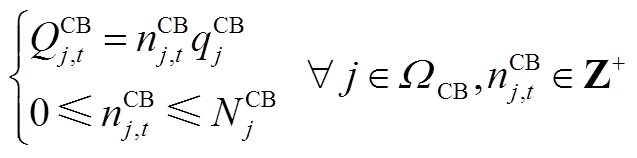 (A8)
(A8)
式中,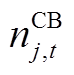 为投入使用的CB组数;
为投入使用的CB组数;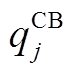 为单组CB的容量;
为单组CB的容量;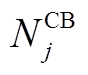 为能投入的最大CB组数。同样需对CB每日动作次数进行限制:
为能投入的最大CB组数。同样需对CB每日动作次数进行限制:
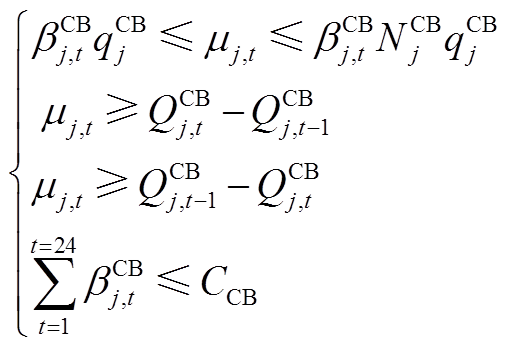 (A9)
(A9)
式中,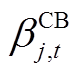 为二进制变量,表示CB在t时刻是否动作,若
为二进制变量,表示CB在t时刻是否动作,若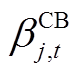 =1,则CB动作,反之不动作;
=1,则CB动作,反之不动作;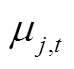 是从t-1到t的时间段内CB无功出力变化的绝对值;
是从t-1到t的时间段内CB无功出力变化的绝对值;![]() 为每天CB可以动作的最大次数。
为每天CB可以动作的最大次数。
4)FL运行约束
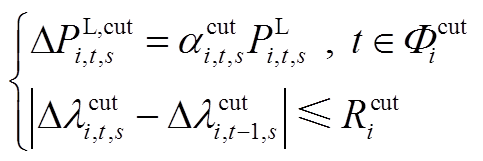 (A10)
(A10)
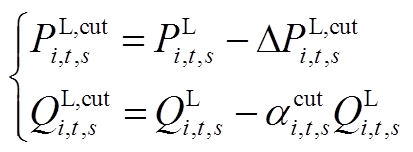 (A11)
(A11)
式中,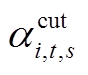 为可削减阈值系数,取值为0~1;
为可削减阈值系数,取值为0~1;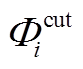 为可削减时段集合;
为可削减时段集合;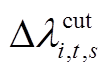 、
、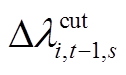 分别为时段t和t-1的削减比例系数,
分别为时段t和t-1的削减比例系数,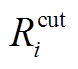 为FL允许的削减速率系数。
为FL允许的削减速率系数。
2. 线性化方法
潮流方程是非线性的,采用如下方式处理。
用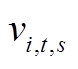 和
和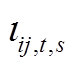 代替电压、电流二次方
代替电压、电流二次方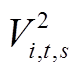 和
和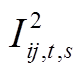 ,有
,有
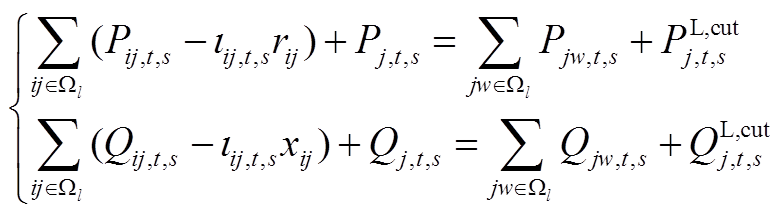 (A12)
(A12)
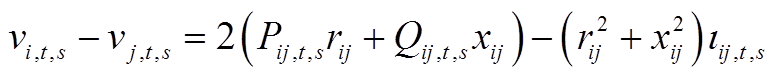 (A13)
(A13)
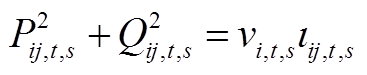 (A14)
(A14)
对式(A14)进行二阶锥松弛,得到
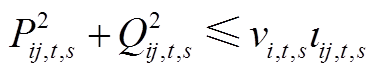 (A15)
(A15)
此时,式(A15)的右部可以表述为
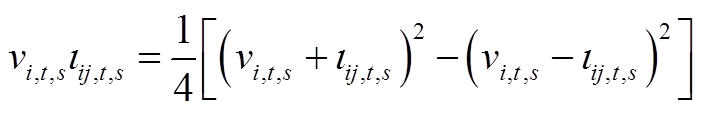 (A16)
(A16)
相应地,式(A15)则可以等价为
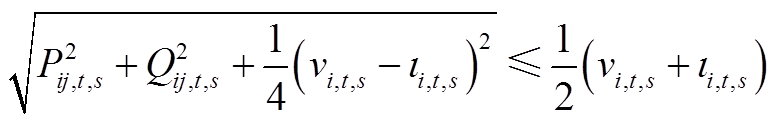 (A17)
(A17)
然后,式(A17)可以分解为两个旋转锥约束式。
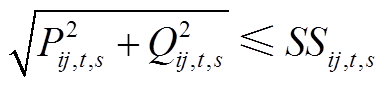 (A18)
(A18)
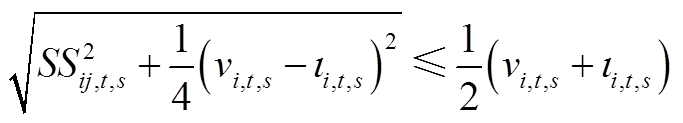 (A19)
(A19)
式(A18)和式(A19)具有相同的一般形式,即
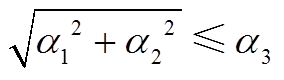 (A20)
(A20)
基于多面体近似方法,式(A20)可转换为
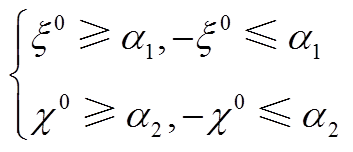 (A21)
(A21)
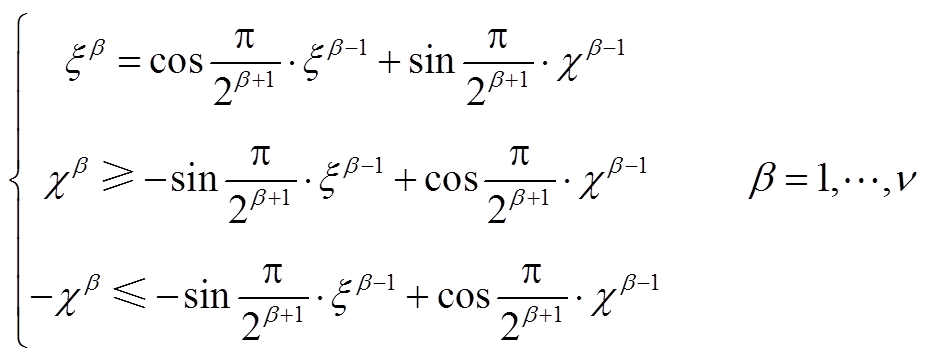 (A22)
(A22)
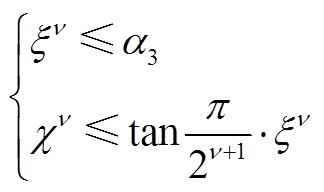 (A23)
(A23)
式中,参数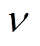 决定了为线性化式而应该添加的额外约束和变量的数量。需要说明的是,E-SOP运行约束式可同样采取上述方法线性化。
决定了为线性化式而应该添加的额外约束和变量的数量。需要说明的是,E-SOP运行约束式可同样采取上述方法线性化。
此外对于绝对值项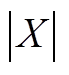 ,引入非负中间变量
,引入非负中间变量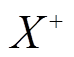 和
和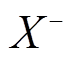 替换X,即
替换X,即
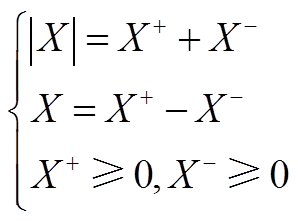 (A24)
(A24)
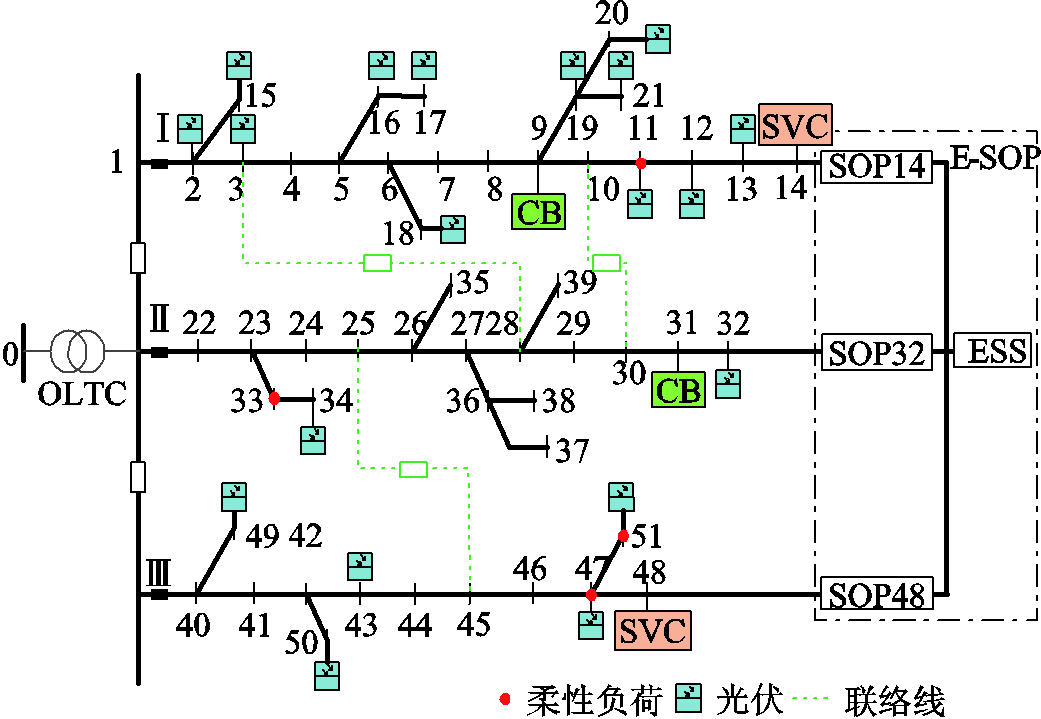
附图2 中国某51节点农村配电网改进系统
App.Fig.2 Improved 51-node system of a rural distribution network in China
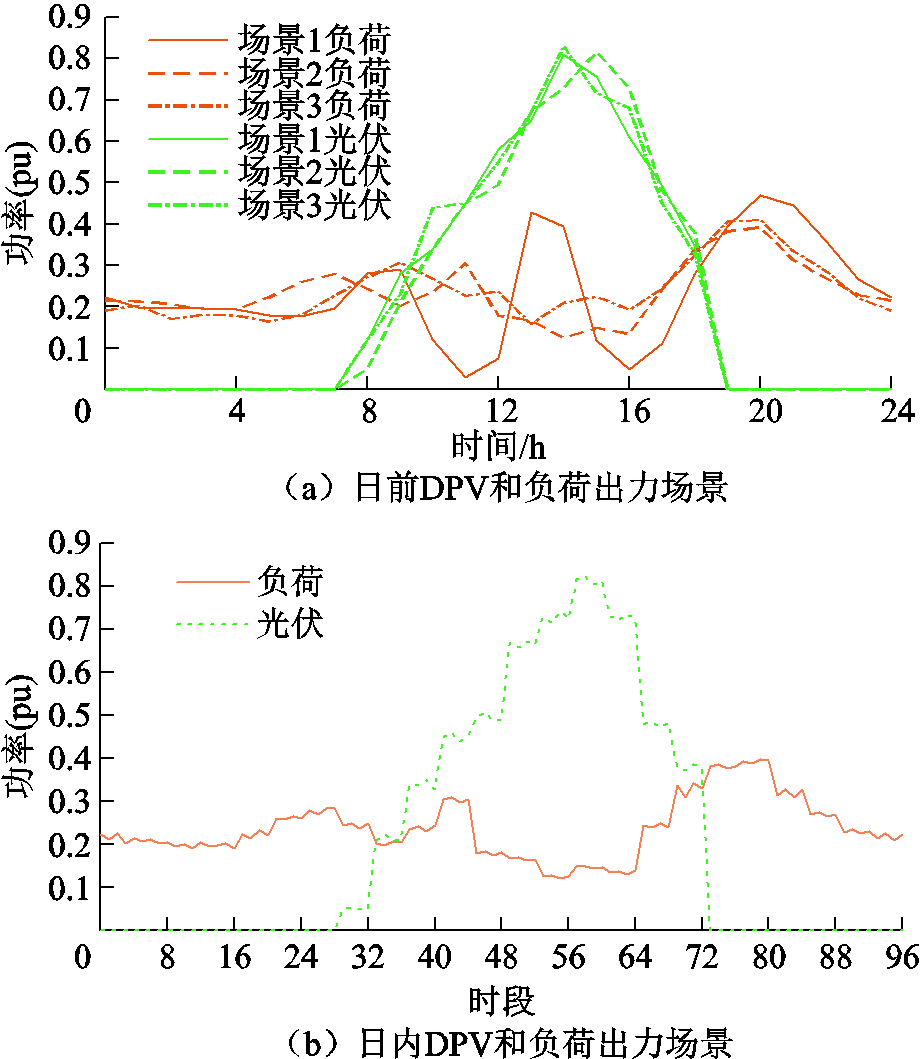
附图3 DPV出力和负荷需求情况
App.Fig.3 DPV output and load demand
附表1 DPV接入位置及容量
App.Tab.1 Accessed location and capacity of DPV

接入节点231112131516171819202132344347495051 容量/kW606018060120901206060901801201 0001 0001 0001 000300600600
附表2 储能参数
App.Tab.2 Energy storage system parameters

参数数值 储能安装容量/(kW×h)1 000 最大充电功率/kW300 最大放电功率/kW300 储能充电效率(%)70 储能放电效率(%)70 储能放电深度(%)90 储能优化充放电区间宽度0.2~0.4 储能退化成本系数/[元/(kW×h)]0.5
附表3 分时电价
App.Tab.3 The time-of-use electricity price

交易方式价格/[元/(kW×h)] 0:00—8:008:00—12:0012:00—15:0015:00—19:0019:00—23:0023:00—24:00 购电0.4880.7791.2410.7791.2410.488 售电0.3570.3570.3570.3570.3570.357
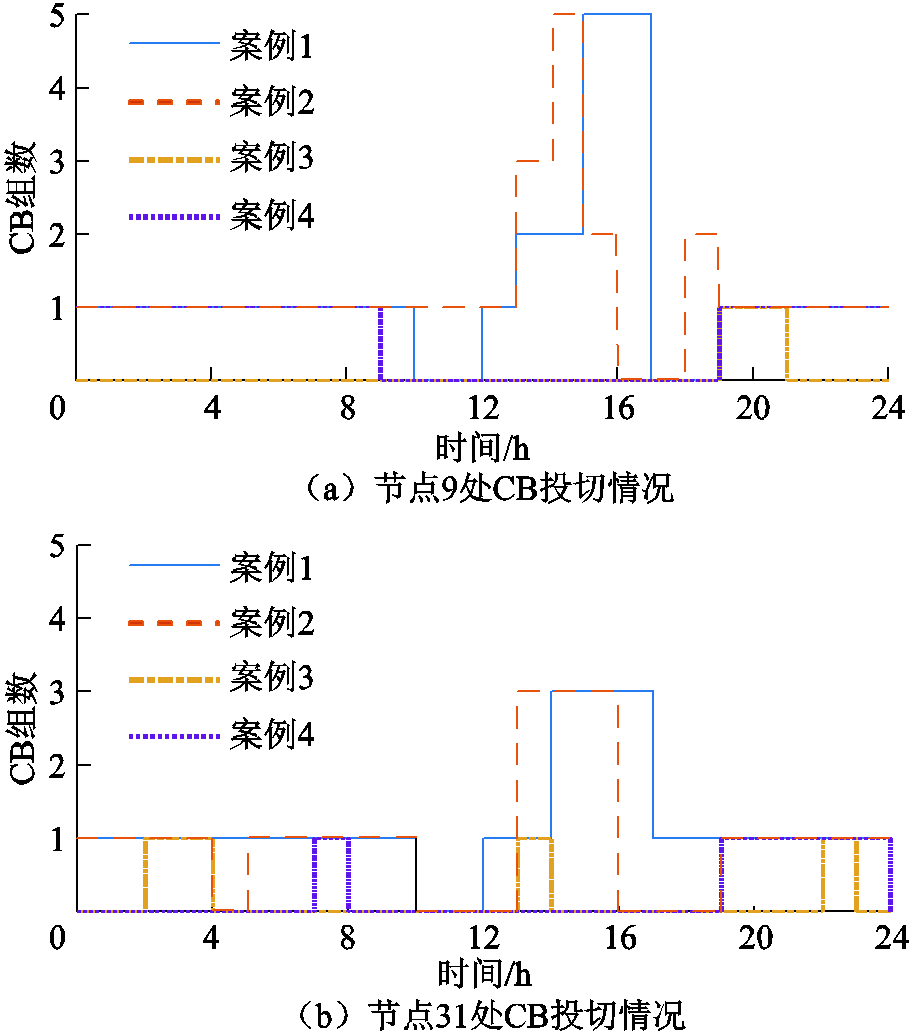
附图4 不同案例两节点处CB投切情况
App.Fig.4 CB situations of two nodes in different cases
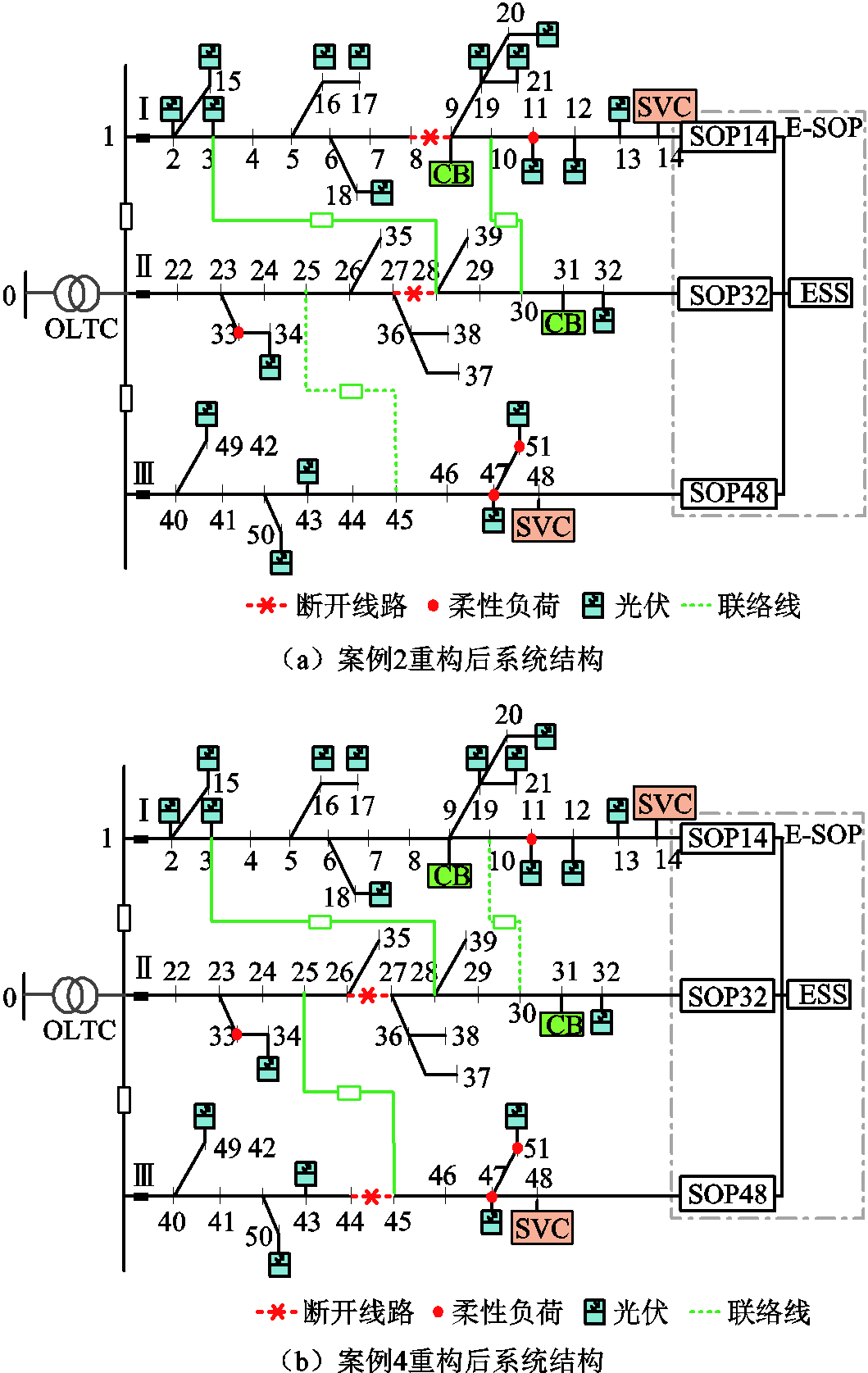
附图5 网络重构后系统结构
App.Fig.5 System diagram after network reconfiguration
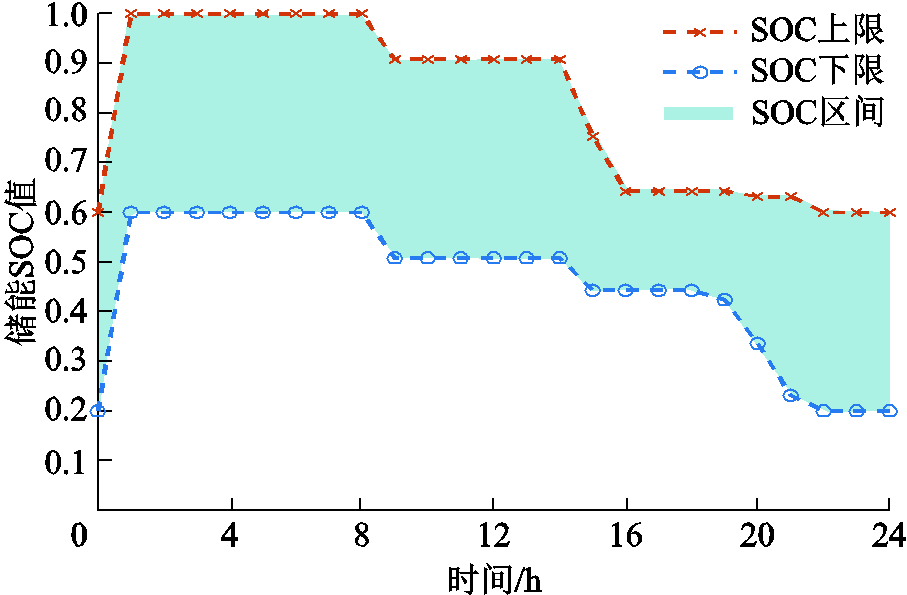
附图6 日前SOC区间优化结果
App.Fig.6 The optimized SOC range of day-ahead optimization
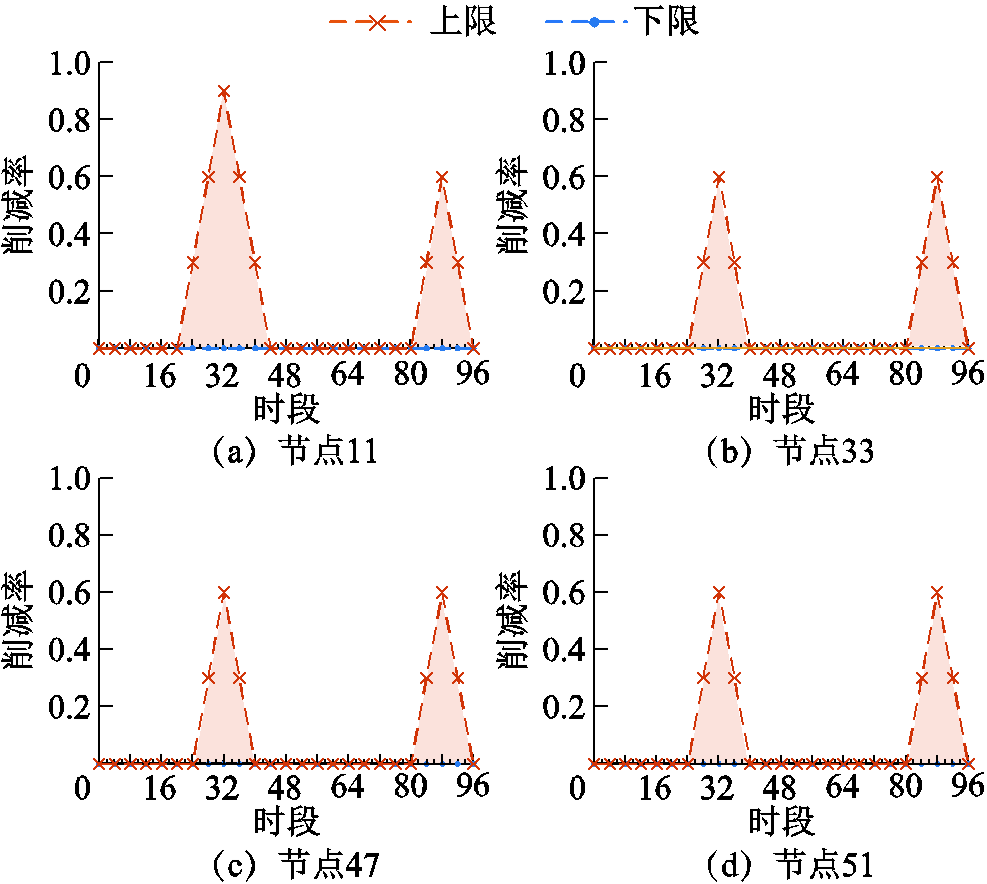
附图7 FL响应时刻和区间
App.Fig.7 Response time and interval of FL
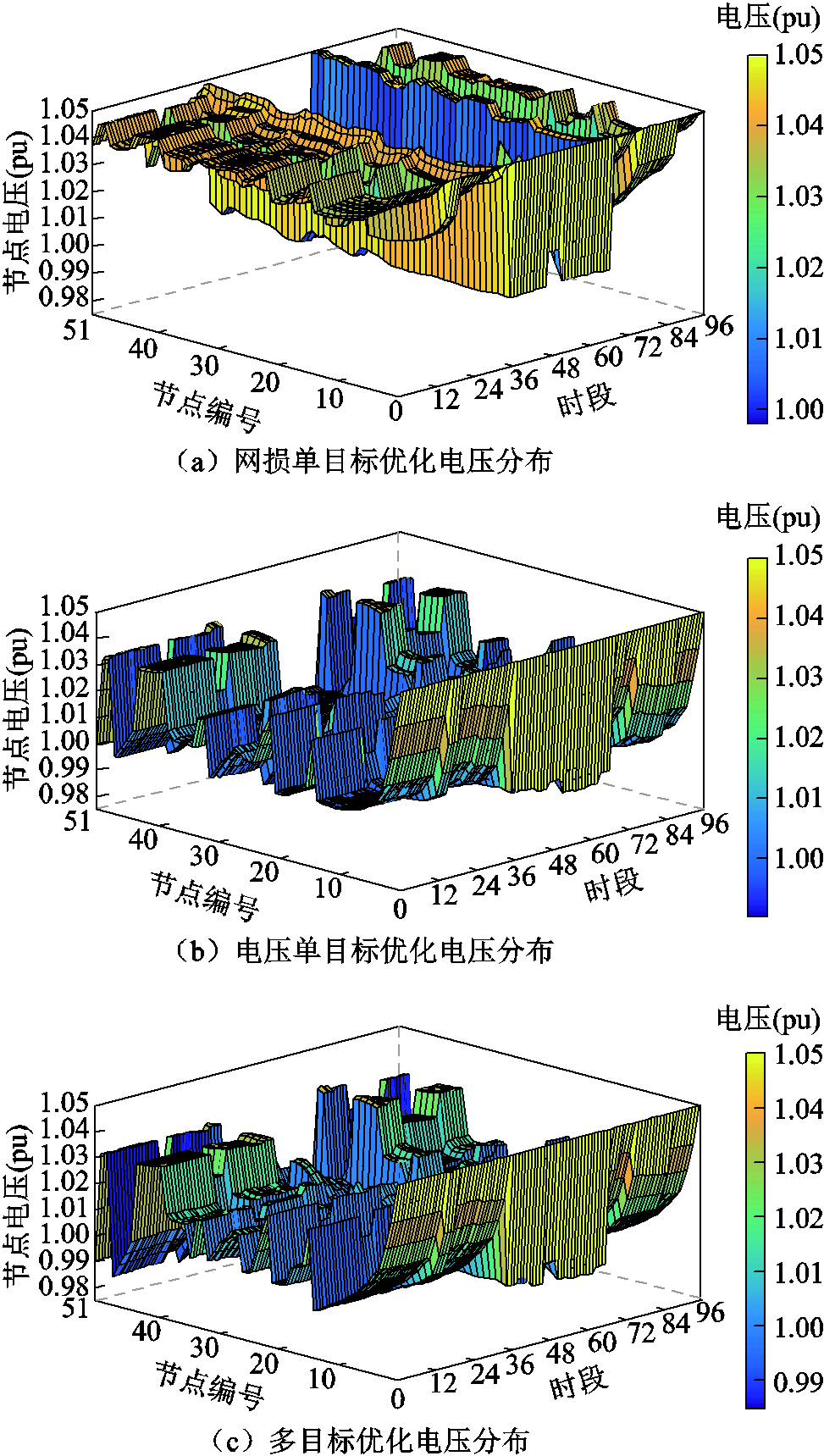
附图8 不同方法下电压分布比较
App.Fig.8 Comparisons of voltage distribution under different methods
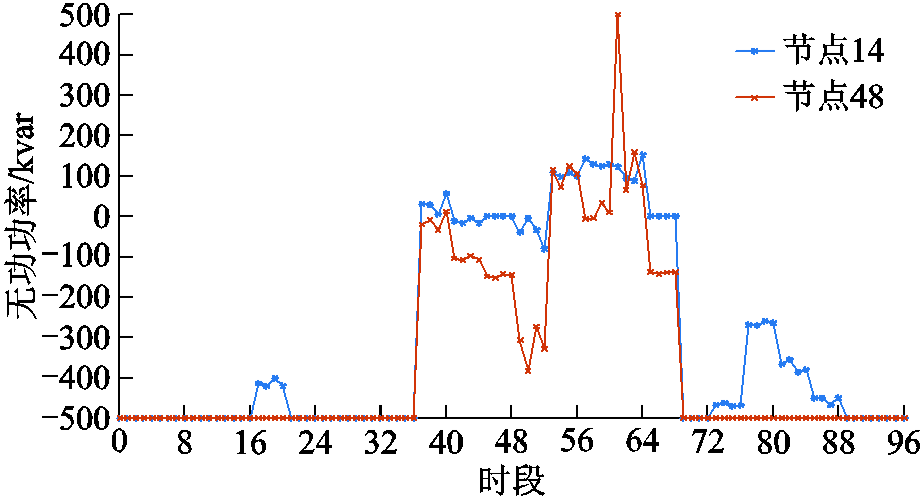
附图9 SVC无功功率出力
App.Fig.9 Reactive power output of SVC
附图10 SOP各端有功/无功出力情况
App.Fig.10 Active and reactive power of each SOP port
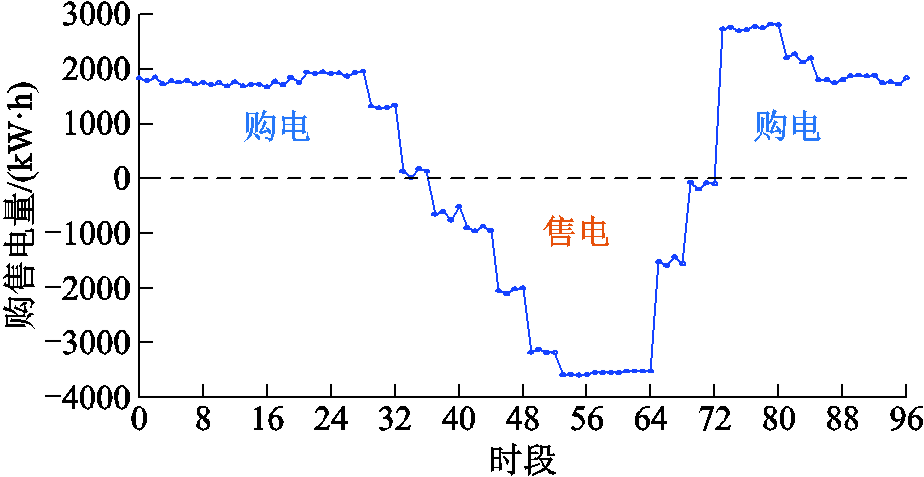
附图11 日内阶段购售电情况
App.Fig.11 Electricity purchase and salein in tra-day stage
附表4 不同DPV渗透率下日前运行成本对比
App.Tab.4 Comparison of costs in day-ahead optimization under different DPV permeabilities

节点32, 34, 43, 47 DPV容量/kWDPV容量渗透率(%)购电成本/万元网损成本/万元FL补偿成本/万元储能退化成本/万元总运行成本/万元 039.32.139 20.200 30.105 40.017 22.462 1
(续)
节点32, 34, 43, 47 DPV容量/kWDPV容量渗透率(%)购电成本/万元网损成本/万元FL补偿成本/万元储能退化成本/万元总运行成本/万元 10045.12.002 10.164 60.105 60.020 32.292 6 30056.71.769 90.191 60.120 10.017 22.098 8 50068.41.553 90.033 30.111 501.698 7 70080.01.389 40.040 10.103 201.529 4 85088.71.260 50.060 30.096 00.007 51.424 2 1 00097.51.154 80.113 50.073 90.020 81.363 0 1 150106.21.072 70.213 20.065 60.021 91.373 4 1 300114.90.994 10.356 60.071 40.022 61.444 7
附表5 不同SOC区间下日前运行成本对比
App.Tab.5 Comparison of costs in day-ahead optimization under different SOC ranges

SOC区间宽度购电成本/万元网损成本/万元FL补偿成本/万元储能退化成本/万元总运行成本/万元 0~0.11.178 70.112 10.073 90.005 31.369 9 0~0.21.169 90.112 20.073 90.010 81.366 8 0.2 (定值)1.175 40.112 30.073 90.006 71.368 3 0.1~0.31.161 40.112 30.073 90.016 51.364 1 0.3 (定值)1.169 40.112 70.073 90.010 41.366 4 0.2~0.41.154 80.113 50.073 90.020 81.363 0 0.1~0.41.143 80.112 40.073 90.027 81.357 9 0.4 (定值)1.163 00.112 00.073 90.014 11.363 0
参考文献
[1] 刘佳, 程浩忠, 姚良忠, 等. 混合输配电系统的分布式随机优化规划[J].电工技术学报, 2019, 34(10): 1987-1998.
Liu Jia, Cheng Haozhong, Yao Liangzhong, et al. A distributed stochastic optimization method for planning transmission and distribution systems[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 1987-1998.
[2] Wang Bo, Zhang Cuo, Dong Zhaoyang. Interval optimization based coordination of demand response and battery energy storage system considering SOC management in a microgrid[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2922-2931.
[3] Hu Ruonan, Wang Wei, Wu Xuezhi, et al. Interval optimization based coordinated control for distribution networks with energy storage integrated soft open points[J]. International Journal of Electrical Power and Energy Systems, 2022, 136: 107725(1-16).
[4] 王成山, 宋关羽, 李鹏, 等. 基于智能软开关的智能配电网柔性互联技术及展望[J]. 电力系统自动化, 2016, 40(22): 168-175.
Wang Chengshan, Song Guanyu, Li Peng, et al. Research and prospect for soft open point based flexible interconnection technology for smart distribution network[J]. Automation of Electric Power Systems, 2016, 40(22): 168-175.
[5] 王成山, 宋关羽, 李鹏, 等. 一种联络开关和智能软开关并存的配电网运行时序优化方法[J]. 中国电机工程学报, 2016, 36(9): 2315-2321.
Wang Chengshan, Song Guanyu, Li Peng, et al. A hybrid optimization method for distribution network operation with SNOP and tie switch[J]. Proceedings of the CSEE, 2016, 36(9): 2315-2321.
[6] 郑焕坤, 石甜静. 基于智能软开关和无功补偿装置的配电网双层优化[J]. 电力系统自动化, 2019, 43(19): 117-123.
Zheng Huankun, Shi Tianjing. Bi-level optimization of distribution network based on soft open point and reactive power compensation device[J]. Automation of Electric Power Systems, 2019, 43(19): 117-123.
[7] Li Peng, Ji Haoran, Wang Chengshan, et al. Coordinated control method of voltage and reactive power for active distribution networks based on soft open point[J]. IEEE Transactions on Sustainable Energy,2017,8(4):1430-1442.
[8] 章博, 刘晟源, 林振智, 等. 高比例新能源下考虑需求侧响应和智能软开关的配电网重构[J]. 电力系统自动化, 2021, 45(8): 86-94.
Zhang Bo, Liu Shengyuan, Lin Zhenzhi, et al. Distribution network reconfiguration with high penetration of renewable energyconsidering demand response and soft open point[J]. Automation of Electric Power Systems, 2021, 45(8): 86-94.
[9] 丛鹏伟, 唐巍, 娄铖伟, 等. 含高渗透率可再生能源的主动配电网两阶段柔性软开关与联络开关协调优化控制[J]. 电工技术学报, 2019, 34(6): 1263-1272.
Cong Pengwei, Tang Wei, Lou Chengwei, et al. Two-stage coordination optimization control of soft open point and tie switch in active distribution network with high penetration renewable energy generation[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1263-1272.
[10] 马丽, 薛飞, 石季英, 等. 有源配电网分布式电源与智能软开关三层协调规划模型[J]. 电力系统自动化, 2018, 42(11): 86-93.
Ma Li, Xue Fei, Shi Jiying, et al. Tri-level coordinated planning model of distributed generator and intelligent soft open point for active distribution network[J]. Automation of Electric Power Systems, 2018, 42(11): 86-93.
[11] Zhang Lu, Shen Chen, Chen Ying, et al. Coordinated allocation of distributed generation, capacitor banks and soft open points in active distribution networks considering dispatching results[J]. Applied Energy, 2018(231): 1122-1131.
[12] Ji Haoran, Wang Chengshan, Li Peng, etal. Robust operation of soft open points in active distribution networks with high penetration of photovoltaic integration[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 280-289.
[13] 胡若男, 王玮, 吴学智, 等. 含智能软开关的主动配电网3阶段鲁棒电压控制方法[J]. 高电压技术, 2020, 46(11): 3752-3761.
Hu Ruonan, Wang Wei, Wu Xuezhi, et al. Three-stage robust voltage control method for active distribution network with soft open points[J]. High Voltage Engineering, 2020, 46(11): 3752-3761.
[14] 魏梅芳, 吴燕, 黎跃龙, 等. 基于分布鲁棒优化的微电网日前经济运行模型与求解方法[J].电力系统及其自动化学报, 2022, 34(12): 81-90.
Wei Meifang, Wu Yan, Li Yuelong, et al. Economic operation model and solution method of microgrid based on distributionally robust optimization[J/OL]. Proceedings of the CSU-EPSA. 2022, 34(12): 81-90.
[15] 马望, 高红均, 李海波, 等. 考虑智能软开关的配电网灵活性评估及优化调度模型[J]. 电网技术, 2019, 43(11): 3935-3943.
Ma Wang, Gao Hongjun, Li Haibo, et al. Flexibility evaluation and optimal dispatch model of distribution network considering soft open point[J]. Power System Technology, 2019, 43(11): 3935-3943.
[16] 蔡晖, 窦飞, 万文文, 等. 计及源荷不确定性的柔性互联配电系统两阶段电压优化[J]. 电网技术, 2022, 46, 4(4): 1566-1574.
Cai Hui, Dou Fei, Wan Wenwen, et al. Two-stage voltage optimization of flexible interconnected distribution system considering source and load uncertainty[J]. Power System Technology, 2022, 46(4): 1566-1574.
[17] 贺帅佳, 阮贺彬, 高红均, 等. 分布鲁棒优化方法在电力系统中的理论分析与应用综述[J]. 电力系统自动化, 2020, 44(14): 179-191.
He Shuaijia, Ruan Hebin, Gao Hongjun, et al. Overview on theory analysis and application of distributionally robust optimization method in power system[J]. Automation of Electric Power Systems, 2020, 44(14): 179-191.
[18] 孙充勃, 李敬如, 原凯, 等. 基于区间优化的配电网智能软开关与储能系统联合优化方法[J]. 高电压技术, 2021, 47(1): 45-54.
Sun Chongbo, Li Jingru, Yuan Kai, et al. Two-stage optimization method of soft open point and energy storage system in distribution network based on interval optimization[J]. High Voltage Engineering, 2021, 47(1): 45-54.
[19] 褚国伟, 张友旺, 葛乐, 等. 自储能柔性互联配电网多时间尺度电压优化[J].电力系统自动化, 2021, 45(9): 71-79.
Chu Guowei, Zhang Youwang, Ge Le, et al. Multi-time-scale voltage optimization of flexible interconnected distribution network with self-energy storage[J]. Automation of Electric Power Systems, 2021, 45(9): 71-79.
[20] Baghban-Novin S, Hamidi A, Golshannavaz S, et al. E-SOP’s contribution in a techno-economic and clean operation of distribution networks: A multi-objective optimization approach based on linear models[J]. International Transactions on Electrical Energy Systems, 2020, 30(2): 1-21.
[21] 李勇, 姚天宇, 乔学博, 等. 基于联合时序场景和源网荷协同的分布式光伏与储能优化配置[J]. 电工技术学报, 2022, 37(13): 3289-3303.
Li Yong, Yao Tianyu, Qiao Xuebo, et al. Optimal configuration of distributed photovoltaic and energy storage system based on joint sequential scenario and source-network-load coordination[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3289-3303.
[22] 姚天宇, 李勇, 乔学博, 等. 计及安全边界和智能软开关协同配置的配电网分布式光伏准入容量优化[J]. 电力自动化设备, 2022, 42(04): 63-70.
Yao Tianyu, Li Yong, Qiao Xuebo, et al. Hosting capacity optimization of distributed photovoltaic in distribution network considering security boundary and coordinate configuration of SOP[J]. Electric Power Automation Equipment, 2022, 42(04): 63-70.
[23] 曾飞, 苏伟, 徐广开, 等. 含快充负荷的低压直流互联配电网多时间尺度经济调度[J]. 电网与清洁能源, 2022, 38(1): 14-23.
Zeng Fei,Su Wei,Xu Guangkai, et al. Multi-time scale economic dispatch of LVDC distribution network with fast charging load[J]. Power System and Clean Energy, 2022, 38(1): 14-23.
[24] CaoYang, Wei Wei, WangJianhui, et al. Capacity planning of energy hub in multi-carrier energy networks: A data-driven robust stochastic programming approach[J]. IEEE Transactions on Sustainable Energy. 2020, 11(1): 3-14.
[25] 芮涛, 李国丽, 王群京, 等. 配电侧多微电网日前电能交易纳什议价方法[J]. 电网技术, 2019, 43(7): 2576-2585.
Rui Tao, Li Guoli, Wang Qunjing, et al. Nash bargaining method for multi-microgrid energy trading in distribution network[J]. Power System Technology, 2019, 43(7): 2576-2585.
Day-Ahead and Intra-Day Optimization of Flexible Interconnected Distribution System with Self-Energy Storage Based on the Grid-Side Resource Coordination
Abstract The integration of high-permeability distributed photovoltaic (DPV) has introduced new technical challenges for the operation and control of distribution networks. Soft open point (SOP), a typical flexible interconnection equipment that can replace traditional interconnection switches, is capable of accurately controlling power flow between feeders, as well as dynamic reactive power compensation. It provides a new approach to improving the operation level of distribution networks with high-permeability photovoltaics. However, the current cost of SOP remains high, making it necessary to investigate coordinated operating strategies between SOP and traditional grid-side control equipment, and achieve economic and efficient distribution network operations across multiple time scales. Therefore, this paper proposes a day-ahead and intra-day optimization model of flexible interconnected distribution system with self-energy storage based on grid-side resource coordination.
Firstly, a multi-time scale optimization control framework is proposed to facilitate the coordinated utilization of multiple grid-side resources within the 'source-network-load-storage' paradigm.In the day-ahead stage, this paper puts forward a long time-scale optimization model that coordinates the active and reactive power considering various devices such as on-load tap changers (OLTC), reactive power compensation devices, interconnection switches, E-SOP, and flexible loads (FL). For the intra-day stage, a comprehensive multi-objective rolling optimization model is presented, which is subsequently transformed into a mixed integer linear programming model through the application of linearization techniques. Moreover, a fuzzy set representing the uncertainties associated with source and load is developed using KL-divergence. The transformation process of the two-stage distributionally robust optimization (DRO) model is proposed, and the solution method based on the column and constraint generation (C&CG) algorithm for the day-ahead stage is provided. The multi-objective intra-day model is solved using the ideal point method.
The numerical results demonstrate that, in the day-ahead stage, the coordinated optimization of E-SOP, OLTC, and network reconfiguration proves beneficial in reducing operational costs. Moreover, it is observed that OLTC has a more significant impact on network loss reduction compared to network reconfiguration. Additionally, the utilization of the distributionally robust optimization (DRO) method allows for a balance between economic efficiency and robustness in the day-ahead optimization scheme. During the intra-day stage, the multi-objective optimization results in network loss values and voltage deviations that lie between those obtained from the two single-objective optimizations. This ensures that the distribution network attains improved economic efficiency while maintaining security. The operation strategy for rapid control equipment is optimized at 15-minute intervals. SOP plays a crucial role in swiftly transferring active power between feeders to optimize power flow and voltage distribution within the distribution network. It works in conjunction with SVC to provide reactive power support. Furthermore, energy storage charging/discharging and flexible load (FL) responses also contribute to network loss reduction and enhanced voltage distribution.
The following conclusions can be drawn from the study: (1) The day-ahead and intra-day optimization based on the grid-side resource coordination can give full play to the fast and slow regulation characteristics of the grid side control equipment, and improve the operation efficiency of the distribution network. (2) In the day-ahead stage, the total operation cost of coordinated optimization of E-SOP, OLTC and network reconfiguration is about 8.0% lower than that of E-SOP alone. (3) In the intra-day stage, multi-objective rolling optimization can take into account the network loss and voltage optimization, and can obtain more accurate operation strategies of various rapid control equipment.
This paper only aims at the coordinated utilization of grid-side resources in the day-ahead and intra-day stage. The next step is to research on the multi-time scale operation optimization of “day-ahead optimization, intra-day rolling and real-time correction”.
Keywords:Soft open points with energy storage, flexible interconnected distribution system, distributionally robust optimization, rolling optimization, day-ahead and intra-day optimization
中图分类号:TM732
DOI:10.19595/j.cnki.1000-6753.tces.221929
国家自然科学基金联合基金重点支持项目(U22B200134)、国家重点研发计划政府间国际科技创新合作重点项目(2022YFE0129300)和南方电网公司科技项目(030400KK52210064(GDKJXM20210061))资助。
收稿日期 2022-10-09
改稿日期 2023-02-24
李 勇 男,1982年生,教授,博士生导师,研究方向为能源/电力系统优化运行与控制、电能变换系统与装备。E-mail:yongli@hnu.edu.cn
乔学博 男,1992年生,博士后,研究方向为智能配电网运行优化与规划、柔性直流配电技术。E-mail:qiaoxb@csg.cn(通信作者)
(编辑 郭丽军)