图1 基于风电场景生成的绿氢储能规划方法
Fig.1 The green hydrogen energy storage planning method based on wind power scenario generation
摘要 以条件生成对抗网络(CGAN)为代表的半监督学习可计及风电波动并生成出力场景集合,生成的数据可输入氢气储能容量配置模型以支撑优化求解。为此,该文首先设计一种校正条件生成对抗网络(CCGAN),并基于风电预测误差构建条件校正器,对预测失准事件和风电爬坡事件下输入生成器的标签信息进行识别和校正;然后,以储能定容的综合成本和各风场弃风成本为目标函数,构建绿氢储能容量配置的多目标优化模型,并引入基于切比雪夫距离的膝区域数学概念,以指导多目标优化算法设计;最后,以新英格兰39节点系统为例进行算例分析,结果表明未经校正的条件信息将导致定容决策偏离实际,而CCGAN能生成计及风电不确定性的高置信出力场景,使得容量配置结果兼顾鲁棒性和经济性。
关键词:校正条件生成对抗网络 绿氢储能 容量配置 场景生成 风电预测误差
“双碳”目标指导下,我国的风电渗透率不断提高。为实现风电的高效消纳,以风电制氢气为典型的绿氢储能系统正成为能量存储的重要载体[1]。该储能形式在构建清洁低碳、安全高效的能源体系进程中的潜力亟待挖掘[2-3]。然而,风电日内出力本身的间歇性、随机性和波动性给绿氢制备与存储造成了困难。如何精确地刻画风电日内出力的波动,并为绿氢储能规划提供数据驱动力是有待解决的关键问题。
风电出力场景是风氢储能规划中的数据基础,常用统计学方法描述其出力的不确定性。该方法通过拟合风电历史数据求解模型的参数,再进行抽样以生成风电出力场景。统计理论下的风电场景生成方法包括:蒙特卡洛抽样[4]、场景树[5]、动态场景树[6]和马尔可夫链[7-8]等方法。采用统计理论描述风电出力需假设先验及固定的概率模型,而风电出力的模糊性和随机性难以满足不变的概率模型,若使用这种统计方法刻画风电的不确定性,生成的场景数据将存在特征模态单一、精度欠佳等问题。
随着深度学习的发展,以生成对抗网络(Generative Adversarial Network, GAN)为代表的黑盒模型为风电场景生成提供了新的技术路线。该技术可学习训练集内的潜在分布特征,通过博弈训练,生成符合历史样本分布的新数据[9-10]。已有相关研究将GAN生成的场景用于驱动电力系统规划工作的开展。文献[11]设计了基于深度卷积生成对抗网络的间歇分布式电源优化配置方法;文献[12]针对风光资源的不确定性,提出一种基于Wasserstein距离的GAN,模拟风光资源场景以设计新能源电源容量配置模型。针对独立型微网的容量优化配置,文献[13]提出一种基于GAN场景模拟和条件风险价值(Conditional Value at Risk, CVaR)的容量随机优化配置模型。上述GAN模型的应用场景都应用于电源容量规划。规划方案实施前,目标风场尚未投运,进而无实际的目标风电场本体历史运行数据,需要借助历史气象数据或同类邻近场站的历史运行数据作为参考。而此类方法无法直接应用于储能在目标风电场下的容量配置。因此,储能规划背景下,基于GAN技术的风电场景生成问题有待解决。此外,风电预测误差作为风电不确定性、波动性的重要评价指标[14-15],其在GAN模型中作为标签信息的潜力有待进一步挖掘。
氢气储能规划方面,目前的研究侧重于分析制氢过程对定容的影响。文献[16]在风氢容量配置中考虑了电解槽的间歇性工况和热交换。文献[17]设计了考虑热平衡的风-氢混合系统,构建了考虑电解槽、燃料电池间歇工作模式热平衡的氢储能系统模型。文献[18]以天然气-风-光-氢综合能源系统为规划对象,考虑了供电辐射区域的电动汽车随机充电需求。文献[19]考虑了阶梯碳价对制氢储能规划的影响。文献[20]对风电出力不确定性的描述较为粗糙,仅使用单个典型日描述风电出力,无法全面地刻画风电出力的强不确定性。上述研究中制氢的能量来源并非完全来自风电,也就无法实现氢气制备的绿色化。在以风电制氢为代表的储能规划问题中,尽管文献[21]和文献[17,22]分别从数据驱动和模型驱动的角度分析了风电对氢气储能规划的影响,但忽略了风电历史预测数据的统计价值和风电爬坡事件对制氢过程的影响,在实际运行中难以达到预期的运行效果。
完全以风电供能的绿氢储能规划需要计及风电出力的不确定性。传统的规划方法多是采用鲁棒优化[23]、随机优化[24]和分布鲁棒优化[17]的方法处理风电出力的不确定性,但鲁棒优化的忽略了历史出力的统计价值,易导致规划结果过于保守;在实际工程中,统计模型难以精确地建立导致随机优化的可靠性降低;分布鲁棒优化的模糊集理论欠缺可解释性,优化结果依赖参数的人为选取。基于深度学习的场景生成的规划方法提供了新的技术路线[12-13]。GAN在考虑风电出力随机性的场景生成问题中初显优势[11-14],却罕有研究能将场景生成的结果应用于解决该实际氢气储能规划问题。这类深度学习驱动下的规划新范式的可行性也有待进一步探究。
针对以上问题,本文首先设计了基于风电场景生成的绿氢储能容量规划框架,提出基于校正条件生成对抗网络(Corrected Conditional Generative Adversarial Networks, CCGAN)的风电场景生成模型。在网络中设计了基于改进旋转门算法的校正器,对预测失准和风电爬坡事件下的预测数据进行识别与清洗,以保证条件信息高度的可参考性。同时在生成器和判别器中嵌入膨胀卷积操作克服常规卷积感受野不足的问题。对绿氢制备、储存施加约束,构建绿氢储能系统容量配置多目标优化模型,引入切比雪夫距离下的膝区域定义,并设计基于膝区域的非支配排序算法(Knee Region-NSGA-Ⅲ, kr-NSGA-Ⅲ)对容量配置模型进行求解。最后基于新英格兰39节点系统进行仿真,验证了生成场景的精确性和规划模型的有效性。
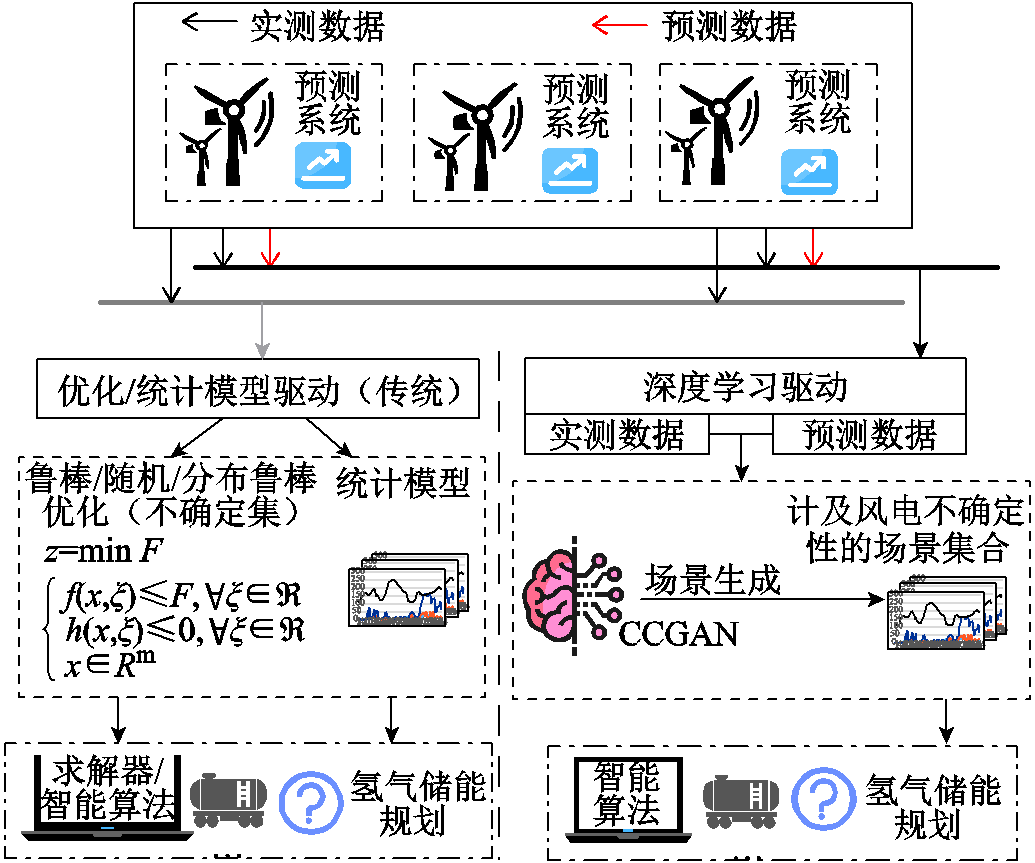
本文构建一种基于风电场景生成的绿氢储能容量规划方法,与传统储能规划框架对比如图1所示。

图1 基于风电场景生成的绿氢储能规划方法
Fig.1 The green hydrogen energy storage planning method based on wind power scenario generation
图1左侧为氢气储能的传统规划方法。风电的随机性是通过不确定性优化理论或统计模型刻画的[17]。以鲁棒优化为代表的不确定优化缺乏对历史数据的统计检验[20]。传统统计模型难以体现风电出力的多模态特征[21]。绝大多数规划模型仅使用了实测数据[19-22],忽略了历史预测数据的参考价值,无法全面地描述风电不确定性出力的高维特征。
本文设计一个基于深度学习驱动的绿氢储能框架来替代上述传统的规划范式。借助深度神经网络拟合高维非线性映射的能力,建立该随机变量的隐式模型。通过将风电的实测数据和历史预测数据同时输入CCGAN提取风电的波动特性,使该网络能够学习到风电出力的波动特征,能够精确地生成风电出力场景集合。最后将该计及风电不确定性和波动性的场景数据输入多目标优化算法,以支撑该绿氢储能容量规划问题的求解。由于风电爬坡事件是风电不确定性的主要表现形式,而该类事件持续时间多为小时级。因此,本文重点研究日内风电出力不确定性对绿氢规划的影响。
CGAN是基于博弈论提出的半监督生成模型。本文借鉴文献[15]提出的CGAN结构进行原理说明并进一步改进。CGAN的基本结构及原理如图2所示。
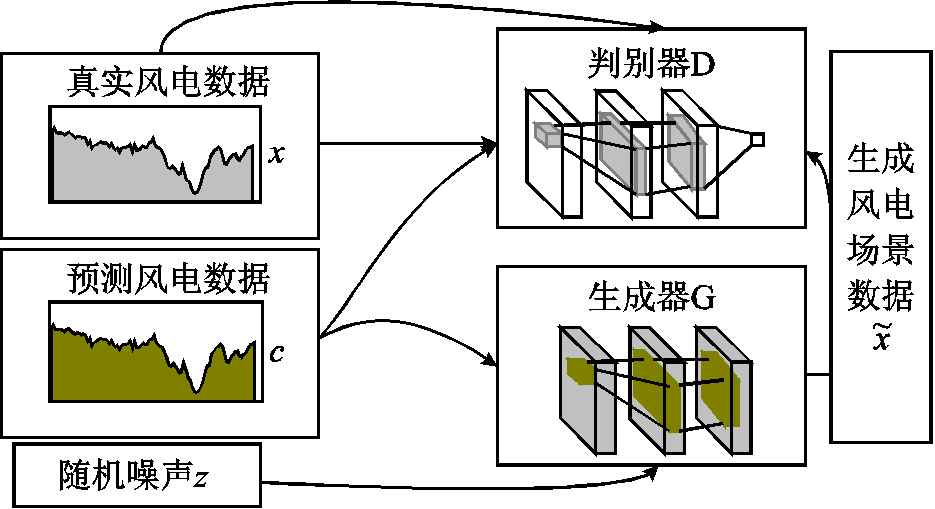
图2 CGAN结构及原理
Fig.2 The structure of CGAN
图2的CGAN包括两个深度神经网络:判别器(Discriminator, D)和生成器(Generator, G)[15]。生成器通过学习风电预测数据的潜在分布将随机噪声映射到生成的样本中;判别器尽可能判断输入数据是真实的风电历史数据还是标签信息下生成的数据。图2中,风电预测数据为条件信息c,该信息输入判别器使其区别于常规的无监督GAN。生成器和判别器的内部层次结构还可包括卷积层、池化层和全连接层。其中包括了卷积、激活函数(ReLU, LReLU, Tanh)和批标准(Batch Normalization)等操作,实现对风电时序和幅值特征信息的提取和识别。
算法原理上,噪声信号z和条件信息c需要合成输入生成器G,而生成器将生成含条件信息的场景样本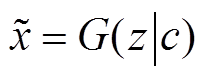 。判别器D有两个任务:①判断生成样本是否满足条件信息c;②判断生成样本的分布与真实分布之间的概率距离。可采用Wasserstein距离描述,该概率距离
。判别器D有两个任务:①判断生成样本是否满足条件信息c;②判断生成样本的分布与真实分布之间的概率距离。可采用Wasserstein距离描述,该概率距离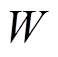 定义为
定义为
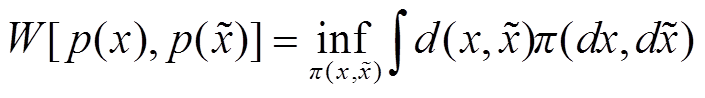 (1)
(1)
式中,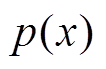 、
、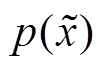 分别为真实分布和生成分布;
分别为真实分布和生成分布;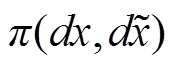 为满足真实分布和生成分布的联合概率密度分布;
为满足真实分布和生成分布的联合概率密度分布;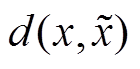 为分布间的概率测度。
为分布间的概率测度。
根据1-Lipschitz连续和梯度罚函数变换[15],该概率测度下判别器D的目标函数为
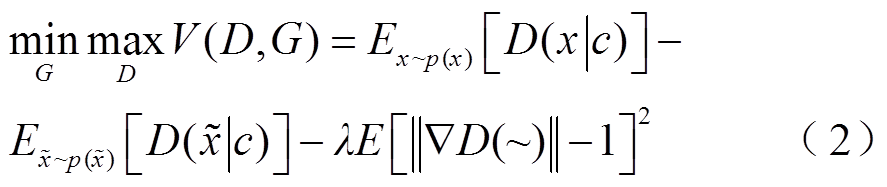
式中,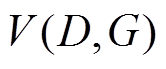 为生成器和判别器中样本的差距;E为不同分布的期望值;D(·)为判别器的目标函数;
为生成器和判别器中样本的差距;E为不同分布的期望值;D(·)为判别器的目标函数;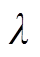 为惩罚项系数。式(2)可理解为一个带条件信息的两人极大极小值博弈问题,生成器G希望提升生成样本被判别器D判断为真的概率,而判别器D希望尽可能提升其自身判断出生成器G生成的样本为假的概率。经过反复博弈,生成器G可生成符合条件信息并接近真实风电样本的场景数据。
为惩罚项系数。式(2)可理解为一个带条件信息的两人极大极小值博弈问题,生成器G希望提升生成样本被判别器D判断为真的概率,而判别器D希望尽可能提升其自身判断出生成器G生成的样本为假的概率。经过反复博弈,生成器G可生成符合条件信息并接近真实风电样本的场景数据。
根据2.1分析可知,条件信息作为生成器的输入是具有标签作用的。在实际风电预测问题中,风电本身的随机性、模糊性,以及预测间隔等问题都会造成预测精度不理想。若盲目采用预测精度较差的数据作为条件信息输入生成器,将引入错误的标签信息,导致生成器生成偏离实际的场景数据。因此,本文在CGAN的基础上引入条件校正器构成如图3的CCGAN网络结构。
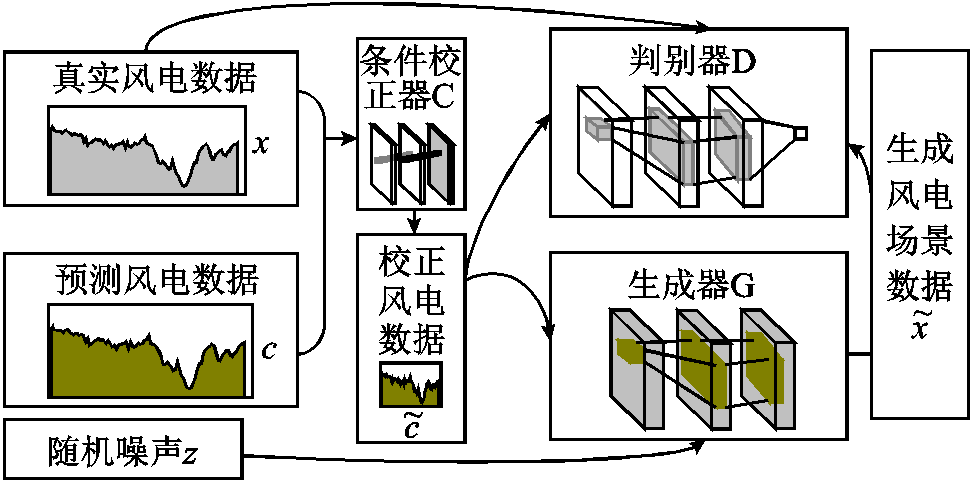
图3 CCGAN架构
Fig.3 The structure of CCGAN
对比图2和图3中风电预测数据不再直接输入生成器G,而是先与真实风电数据x输入条件校正器C,由条件校正器C进行数据校正,生成校正后的风电样本数据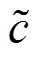 再分别输入生成器和判别器。生成器的多层卷积不断提取校正样本数据
再分别输入生成器和判别器。生成器的多层卷积不断提取校正样本数据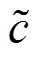 的分布特征。同理,判别器D也不再使用未经校正的条件信息,同样经过多层卷积操作,完成校正条件后的数据与生成数据之间的分类监督学习任务。最终,通过反复的博弈可达到Nash均衡,生成器G可生成符合校正条件并接近真实风电数据的场景数据。
的分布特征。同理,判别器D也不再使用未经校正的条件信息,同样经过多层卷积操作,完成校正条件后的数据与生成数据之间的分类监督学习任务。最终,通过反复的博弈可达到Nash均衡,生成器G可生成符合校正条件并接近真实风电数据的场景数据。
判别器和生成器中均有卷积操作。本文为提升卷积操作捕捉风电出力在纵向和横向相关性的能力,引入膨胀卷积(Dilated Convolution)[25],通过修改“膨胀率”,不同的膨胀率对应不同的感受野,即卷积核中填充0,进而获得样本的高维信息。图4为不同膨胀率的卷积示意。
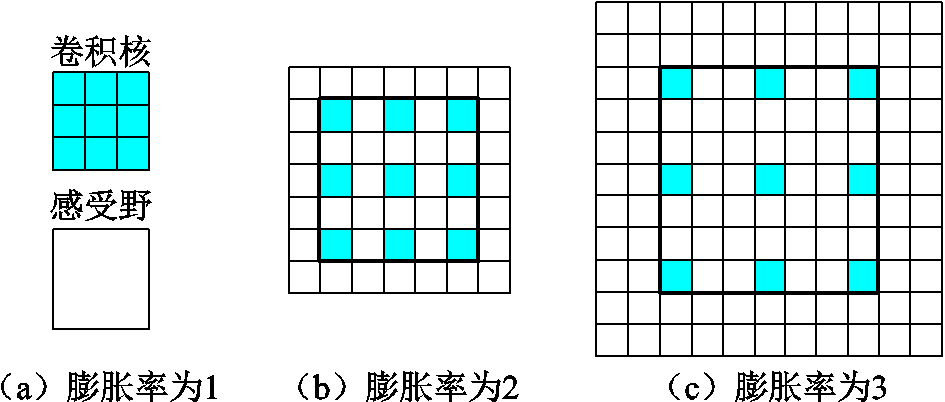
图4 膨胀卷积操作
Fig.4 Dilated convolution operation
尽管膨胀卷积可以提高感受野的大小,获取更高维度的上下连续信息,但多次叠加膨胀卷积也会导致局部信息丢失。为平衡卷积性能,本文设定膨胀率为2,且判别器和生成器均只进行一层膨胀卷积操作。
风电功率的实测值和预测值之间存在差异。国家能源局发布的《风电功率预测误差系统功能规范》中做了相关规定[26]。预测误差et定义为
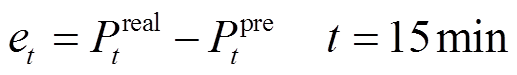 (3)
(3)
式中,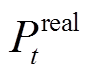 、
、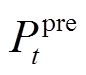 分别为t时刻风电功率的实际值和预测值;时间分辨率为15 min。该规范中仅要求预测系统的月方均根误差率(Root Mean Square Error, RMSE)应小于20%,具体分配到每个预测间隔内的预测数据的方均根误差率也应低于20%。基于预测误差的定义,本文将预测值不等于实测值的情况分类为两个事件:预测失准A1、预测合理A2。这两类事件可表示为
分别为t时刻风电功率的实际值和预测值;时间分辨率为15 min。该规范中仅要求预测系统的月方均根误差率(Root Mean Square Error, RMSE)应小于20%,具体分配到每个预测间隔内的预测数据的方均根误差率也应低于20%。基于预测误差的定义,本文将预测值不等于实测值的情况分类为两个事件:预测失准A1、预测合理A2。这两类事件可表示为
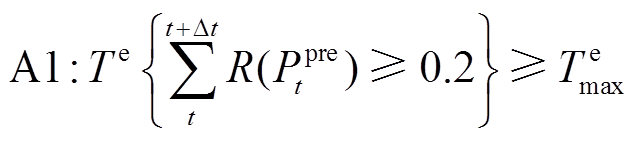 (4)
(4)
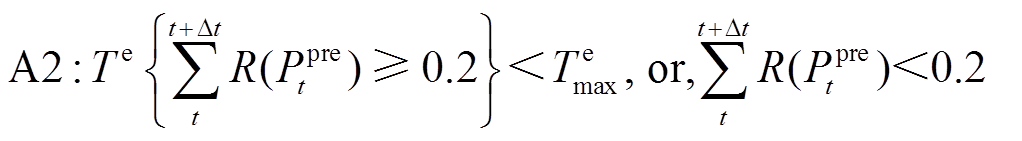 (5)
(5)
式中,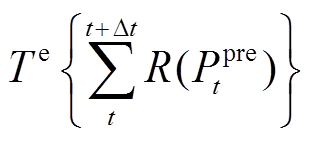 为预测误差方均根误差
为预测误差方均根误差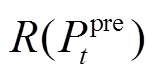 持续的时长;
持续的时长;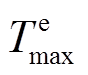 为预测误差满足上限时可接受的时长。式(4)表明,当预测误差长期的RMSE都超过固定规范值,可认为这是一次预测失准事件,这类事件下风电预测功率是无法提供可靠的预测信息的。换言之,预测值已经超出了风电合理的波动范围。而式(5)则可理解为预测值在风电合理的波动区间内,或短暂误差较大但持续时长可以接受。
为预测误差满足上限时可接受的时长。式(4)表明,当预测误差长期的RMSE都超过固定规范值,可认为这是一次预测失准事件,这类事件下风电预测功率是无法提供可靠的预测信息的。换言之,预测值已经超出了风电合理的波动范围。而式(5)则可理解为预测值在风电合理的波动区间内,或短暂误差较大但持续时长可以接受。
预测失准事件A1定义中需要排除一类特殊情况,即风电爬坡事件。风电爬坡事件A3是指短时间风电功率急剧地上升和下降,可表示为
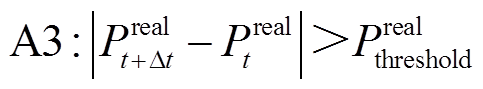 (6)
(6)
式中, 为爬坡事件的门槛值;
为爬坡事件的门槛值;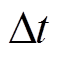 为时间间隔。风电爬坡是一类小概率突发事件,且难以挖掘其统计规律,这种情况下实际风电出力往往会极大地偏离合理的风电波动区间。由于发生概率低,这种情况下仍可认为预测系统给出的预测数据是可靠的,是风电本身的强随机性产生了过大的预测误差。
为时间间隔。风电爬坡是一类小概率突发事件,且难以挖掘其统计规律,这种情况下实际风电出力往往会极大地偏离合理的风电波动区间。由于发生概率低,这种情况下仍可认为预测系统给出的预测数据是可靠的,是风电本身的强随机性产生了过大的预测误差。
根据以上对预测事件的划分,为校正条件信息,图5设计了基于预测误差的条件校正器。
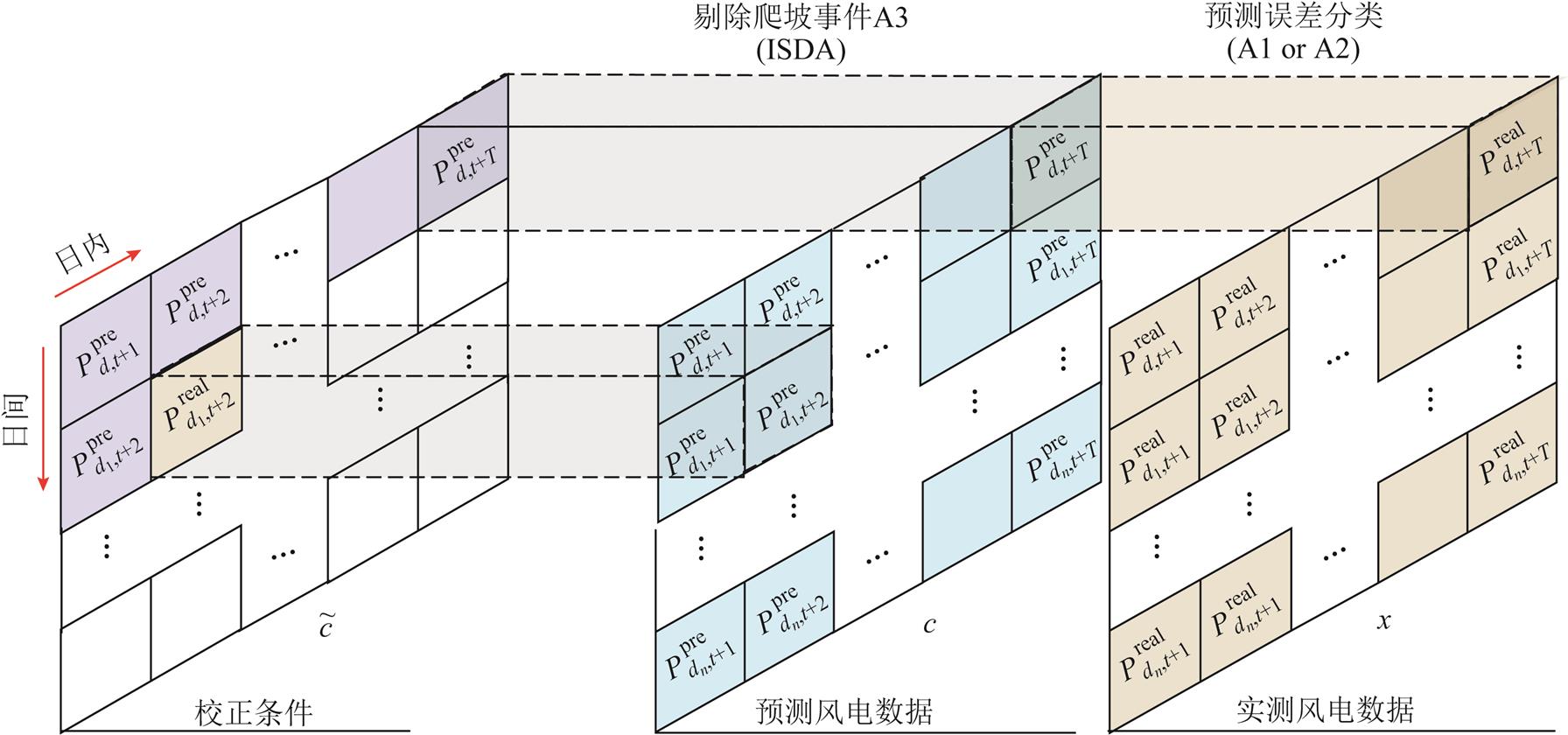
图5 条件校正器工作原理
Fig.5 Principle of condition corrector
图5中的条件校正器由两层网络构成,首先根据预测误差判断预测失准事件A1是否发生,当检索完A1事件后,启动改进旋转门算法(Improved Swinging Door Algorithm, ISDA),用于识别A1事件下的风电爬坡事件A3[27]。
ISDA可将风电时序的趋势化特征识别。首先需构造得分函数S,而爬坡事件的检测可转换为求解得分函数最大值的动态优化问题,该问题的目标函数J及其约束为
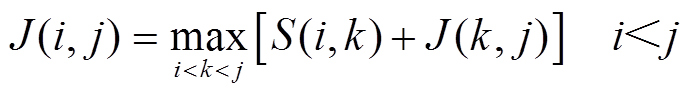 (7)
(7)
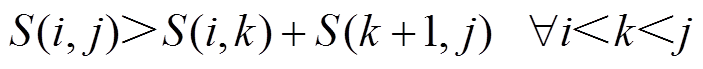 (8)
(8)
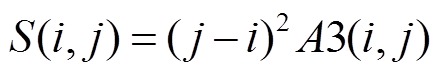 (9)
(9)
式中,目标函数J(i, j)为在子区间内需取得最大值;S(i, k)为子区间中的得分值。爬坡趋势需满足式(8)。得分函数可具体表达为式(9)。A3(i, j)为子区间(i, j)上的爬坡事件标志位,为0-1变量,取值为1代表爬坡事件发生,而取0时表示在该子区间上未发生爬坡事件。
ISDA识别爬坡事件A3后,剔除预测失准时间段内的风电爬坡事件。最后进行数据拼接得到校正条件数据,当预测失准时使用实测数据替代预测数据,如图5中以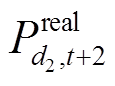 替代
替代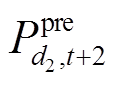 ,表达式为
,表达式为
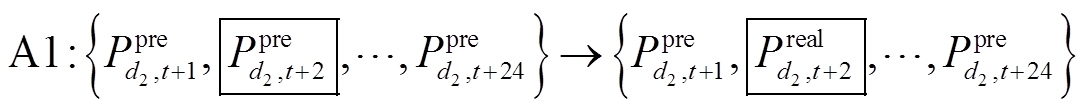 (10)
(10)
风电爬坡事件A3和预测合理事件A2的时段内仍将预测数据作为条件样本输入生成器和判别器。表达式为
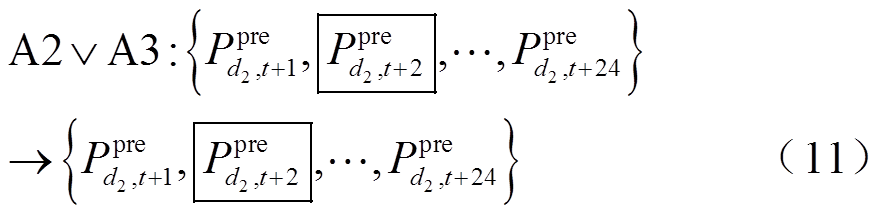
通过该条件校正操作实现对数据的精细化、分类化清洗,为生成器和判别器的反复博弈过程提供可靠的参考信息。
本文构建储能容量配置的多目标优化模型,分别最小化绿氢储能投资、运行成本及各风场弃风惩罚成本。
绿氢储能的年化投资和运行成本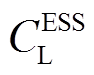 [21]为
[21]为
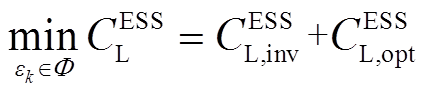 (12)
(12)
式中,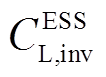 、
、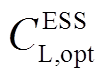 分别为绿氢储能设备的年化投资成本和运行成本;
分别为绿氢储能设备的年化投资成本和运行成本;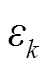 、
、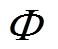 分别为GAN生成的场景和场景集合。另一类目标函数,即各风场的弃风成本为
分别为GAN生成的场景和场景集合。另一类目标函数,即各风场的弃风成本为
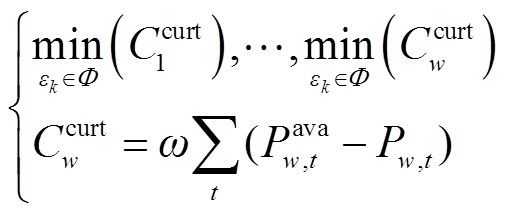 (13)
(13)
式中,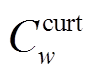 为风电场w的年弃风惩罚成本;
为风电场w的年弃风惩罚成本;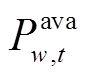 为风电场w在t时刻的可发功率;
为风电场w在t时刻的可发功率;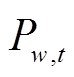 为风电场w在t时刻的上网功率;
为风电场w在t时刻的上网功率;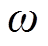 为弃风惩罚价格。
为弃风惩罚价格。
式(12)中第一项还可具体表示为
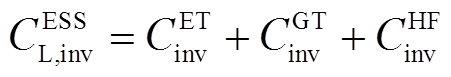 (14)
(14)
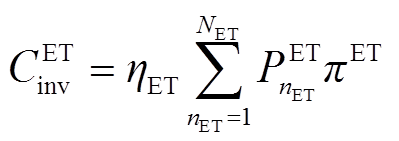 (15)
(15)
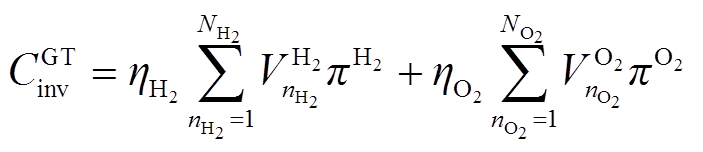 (16)
(16)
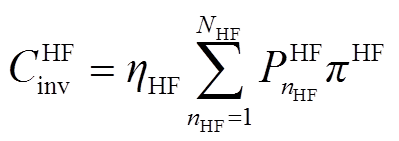 (17)
(17)
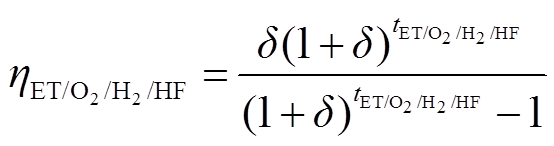 (18)
(18)
式中, 、
、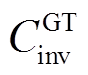 、
、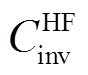 分别为电解槽(Electrolytic Tank, ET)、储气罐(Gas Tank, GT)和燃氢机组(Hydrogen Fuel, HF)投资成本[28];
分别为电解槽(Electrolytic Tank, ET)、储气罐(Gas Tank, GT)和燃氢机组(Hydrogen Fuel, HF)投资成本[28];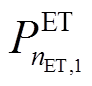 、
、![]() 分别为电解槽的功率和单位功率投资价格;
分别为电解槽的功率和单位功率投资价格;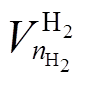 、
、![]() 分别为储氢罐体积和单位体积价格;
分别为储氢罐体积和单位体积价格;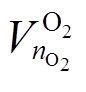 、
、![]() 分别为储氧罐体积和单位体积价格;
分别为储氧罐体积和单位体积价格;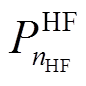 、
、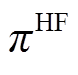 分别为燃氢机组功率和单位功率的投资价格;
分别为燃氢机组功率和单位功率的投资价格;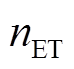 、
、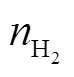 、
、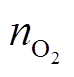 、
、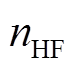 分别为对应风场将安装的电解槽、储氢罐、储氧罐和燃氢机组的编号;
分别为对应风场将安装的电解槽、储氢罐、储氧罐和燃氢机组的编号;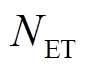 、
、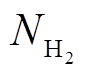 、
、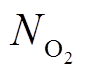 、
、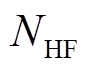 分别为计划投资的电解槽、储氢罐、储氧罐和燃氢机组个数;
分别为计划投资的电解槽、储氢罐、储氧罐和燃氢机组个数;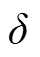 为折现值;
为折现值;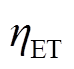 、
、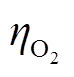 、
、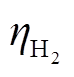 、
、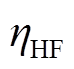 分别为电解槽、储氢罐、储氧罐和燃氢机组年化折算系数;
分别为电解槽、储氢罐、储氧罐和燃氢机组年化折算系数;![]() 、
、![]() 、
、![]() 、
、![]() 分别为计划投资的电解槽、储氢罐、储氧罐和燃氢机组的预估使用寿命。
分别为计划投资的电解槽、储氢罐、储氧罐和燃氢机组的预估使用寿命。
绿氢储能的年运行成本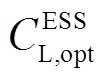 为
为
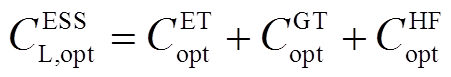 (19)
(19)
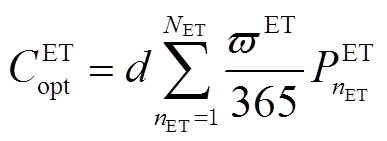 (20)
(20)
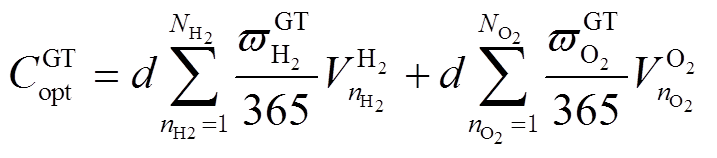 (21)
(21)
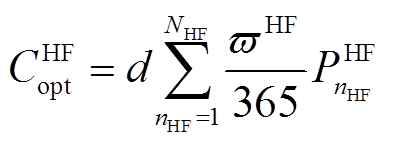 (22)
(22)
式中,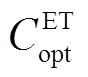 、
、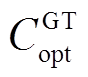 、
、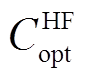 分别为电解槽、储气罐和燃氢机组年运行成本;
分别为电解槽、储气罐和燃氢机组年运行成本;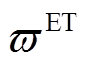 、
、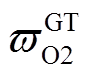 、
、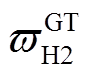 、
、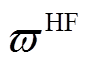 分别为电解槽、储氧罐、储氢罐和燃氢机组的单位功率/体积年运行成本;d为典型日天数。
分别为电解槽、储氧罐、储氢罐和燃氢机组的单位功率/体积年运行成本;d为典型日天数。
1)负荷平衡约束
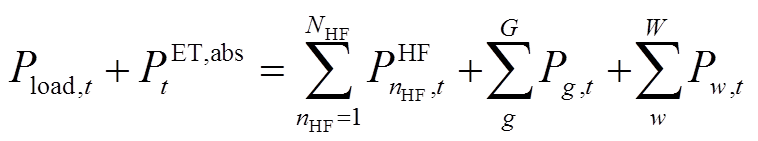 (23)
(23)
式中,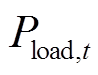 、
、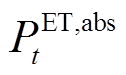 分别为t时刻负荷功率和电解槽功率;
分别为t时刻负荷功率和电解槽功率;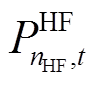 、
、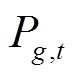 、
、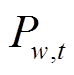 分别为t时刻燃氢机组
分别为t时刻燃氢机组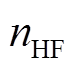 、常规火电机组g、风电场w的出力;w和W分别为风电场的编号和集合;g和G分别为常规火电的编号和集合。
、常规火电机组g、风电场w的出力;w和W分别为风电场的编号和集合;g和G分别为常规火电的编号和集合。
2)绿氢制备约束
制氢过程中有能量损耗,该过程可表示为
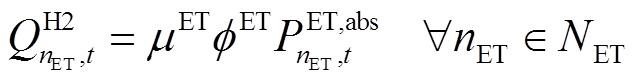 (24)
(24)
式中,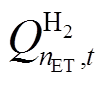 、
、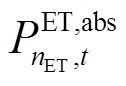 分别为电解槽
分别为电解槽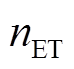 的产氢量和输入功率;
的产氢量和输入功率;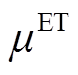 、
、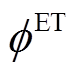 分别为电解槽的制氢转换率及电解槽效率。绿氢的制造过程必须满足供能来源于可再生能源,因此在满足整个系统负荷平衡式(23)的基础上,电解槽的供电功率必须满足
分别为电解槽的制氢转换率及电解槽效率。绿氢的制造过程必须满足供能来源于可再生能源,因此在满足整个系统负荷平衡式(23)的基础上,电解槽的供电功率必须满足
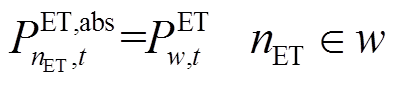 (25)
(25)
式中,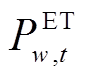 为风电场w在t时刻对电解槽
为风电场w在t时刻对电解槽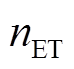 的供给功率。
的供给功率。
3)绿氢燃烧约束
燃氢过程同样存在能量损耗,需满足
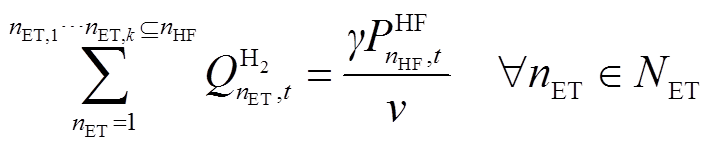 (26)
(26)
式中,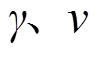 分别为单位发电量的耗氢量和燃氢机组的发电效率;
分别为单位发电量的耗氢量和燃氢机组的发电效率;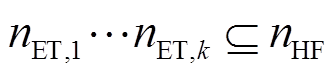 表示燃氢机组
表示燃氢机组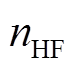 所对应的电解槽
所对应的电解槽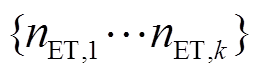 。
。
4)绿氢存储状态约束
绿氢储能的储氢罐的状态可表示为
式中,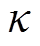 为氢气罐的存储效率;
为氢气罐的存储效率;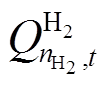 为t时刻储氢罐的氢气量;
为t时刻储氢罐的氢气量;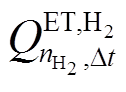 为
为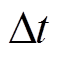 时间间隔下电解槽的电解氢气量。储氧罐的状态可表示为
时间间隔下电解槽的电解氢气量。储氧罐的状态可表示为
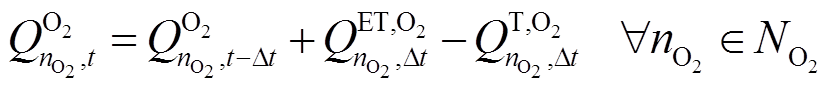 (28)
(28)
式中,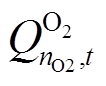 为t时刻储气罐的氧气量;
为t时刻储气罐的氧气量;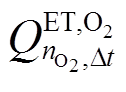 为
为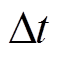 时间间隔电解槽的电解氧气量;
时间间隔电解槽的电解氧气量;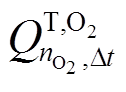 为
为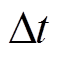 时间间隔输送的氧气量。氢气和氧气还受气罐体积的影响,需满足
时间间隔输送的氧气量。氢气和氧气还受气罐体积的影响,需满足
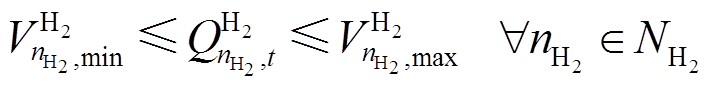 (29)
(29)
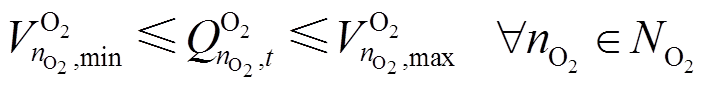 (30)
(30)
式中,![]() 、
、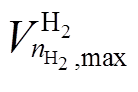 分别为氢气罐的可存储的氢气体积下、上限;
分别为氢气罐的可存储的氢气体积下、上限;![]() 、
、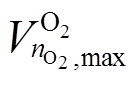 分别为氧气罐可存储的氧气体积的下、上限。
分别为氧气罐可存储的氧气体积的下、上限。
5)风电出力约束
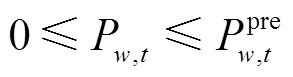 (31)
(31)
式中,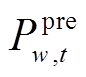 为风电场w在t时段的预测功率。
为风电场w在t时段的预测功率。
6)火电爬坡约束
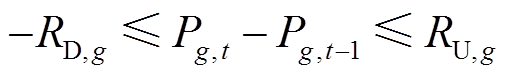 (32)
(32)
式中,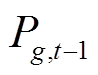 为常规火电机组在t-1时段的出力;
为常规火电机组在t-1时段的出力;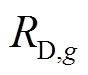 为机组g的下爬坡速率;
为机组g的下爬坡速率;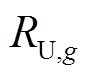 为机组g的上爬坡速率。
为机组g的上爬坡速率。
7)直流潮流约束
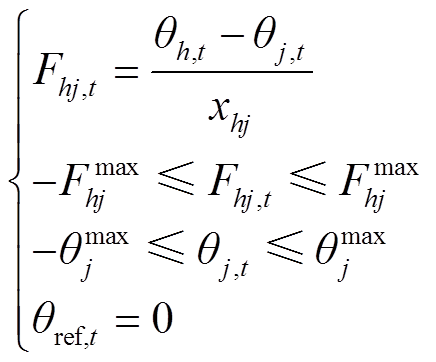 (33)
(33)
式中,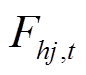 为线路
为线路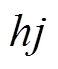 的电力潮流,正负值表示潮流方向;
的电力潮流,正负值表示潮流方向;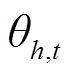 和
和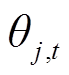 分别为节点h和j的电压相角;
分别为节点h和j的电压相角;![]() 为线路
为线路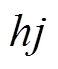 的电抗;
的电抗;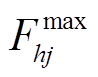 为线路
为线路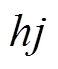 的最大传输容量值;
的最大传输容量值;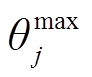 为电压相角限值;
为电压相角限值;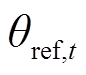 为平衡节点电压相角[28]。
为平衡节点电压相角[28]。
本文所建储能容量配置模型归纳为多目标优化问题,需要同时最小化弃风成本和绿氢储能容量投资运行成本。为提升模型求解效率,本节引入膝区域的数学定义。膝区域在多目标优化理论中代表该区域解在优化目标上存在较好的平衡性,在缺乏先验知识的情况下能引导算法收敛。定义膝区域需要先引入膝点的概念,首先给出了基于切比雪夫距离(Chebyshev Distance, CD)膝点的数学定义。在图6给出了基于曼哈顿距离和CD的膝区域几何解释。
切比雪夫距离:假设存在两个向量A、B,其维数同为m维,则可用无穷范数表示二者间的距离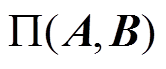 。具体表示为
。具体表示为
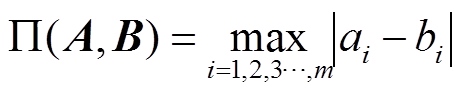 (34)
(34)
式中,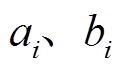 分别为向量A和B的第i个分量。
分别为向量A和B的第i个分量。
膝点:假设帕累托前沿(Pareto Front, PF)上的理想点为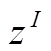 ,解向量在目标函数归一化的表现各有差别,若能最小化性能并提升解向量的最大值,可定义为基于CD的膝点,记为
,解向量在目标函数归一化的表现各有差别,若能最小化性能并提升解向量的最大值,可定义为基于CD的膝点,记为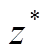 。膝点的折中性表现在:相比于理想点
。膝点的折中性表现在:相比于理想点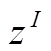 ,
,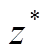 对目标函数归一化后性能的改变不偏向于任何目标,该特性有助于平衡储能投资和弃风惩罚两个目标之间的效益冲突。数学形式为
对目标函数归一化后性能的改变不偏向于任何目标,该特性有助于平衡储能投资和弃风惩罚两个目标之间的效益冲突。数学形式为
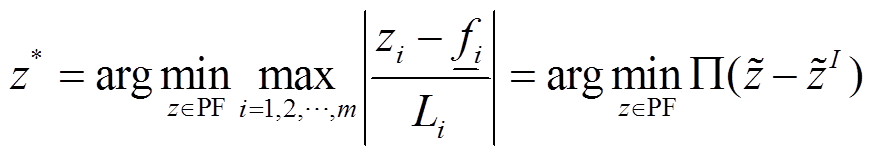 (35)
(35)
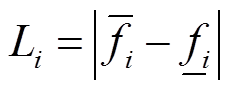 (36)
(36)
式中,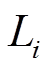 为解向量中各分量最大差值;
为解向量中各分量最大差值;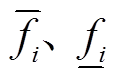 分别为该向量的目标值上、下限;
分别为该向量的目标值上、下限;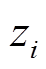 为膝点的第i个分量;
为膝点的第i个分量;![]() 分别为归一化向量点。
分别为归一化向量点。
基于CD的膝区域定义:如采用圆形表示膝区域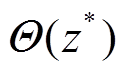 ,则该区域可表示为
,则该区域可表示为
 (37)
(37)
式中,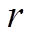 为膝区域半径。具体到本文的两个目标函数中,归一化后,对弃风成本和绿氢储能投资成本不存在偏好,从数学上实现最佳的性能折中。为辅助说明基于切比雪夫距离的膝点定义,还需引入基于曼哈顿距离(Manhattan Distance, MD)的膝点定义。定义
为膝区域半径。具体到本文的两个目标函数中,归一化后,对弃风成本和绿氢储能投资成本不存在偏好,从数学上实现最佳的性能折中。为辅助说明基于切比雪夫距离的膝点定义,还需引入基于曼哈顿距离(Manhattan Distance, MD)的膝点定义。定义![]() 为基于曼哈顿距离的膝点。如图6所示,基于CD的膝点与原点的直线Lz将垂直于经过基于MD膝点的切平面Bu。则基于MD的膝点可定义为
为基于曼哈顿距离的膝点。如图6所示,基于CD的膝点与原点的直线Lz将垂直于经过基于MD膝点的切平面Bu。则基于MD的膝点可定义为
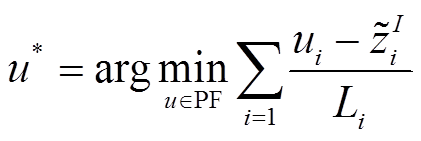 (38)
(38)
式中,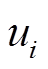 为
为![]() 的第i个分量。MD和CD的膝点有如下关系。定义平面簇
的第i个分量。MD和CD的膝点有如下关系。定义平面簇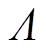 为
为
式中,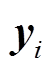 为构成超平面的向量;
为构成超平面的向量;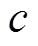 为平面簇的系数。MD定义下膝点的切平面Bu,与该切平面垂直的直线并与PF相交,交点即为基于CD的膝点。膝点与膝区域的几何表示如图6所示。图6还表示了PF为凸集和凹集下的膝点和膝区域。图6中,基于CD的膝点是唯一的,而基于MD的膝点不唯一,该特点有助于加速算法收敛。此外,基于该定义的算法也能同时应对非凸PF问题,提高了算法求解非凸问题的效率。
为平面簇的系数。MD定义下膝点的切平面Bu,与该切平面垂直的直线并与PF相交,交点即为基于CD的膝点。膝点与膝区域的几何表示如图6所示。图6还表示了PF为凸集和凹集下的膝点和膝区域。图6中,基于CD的膝点是唯一的,而基于MD的膝点不唯一,该特点有助于加速算法收敛。此外,基于该定义的算法也能同时应对非凸PF问题,提高了算法求解非凸问题的效率。
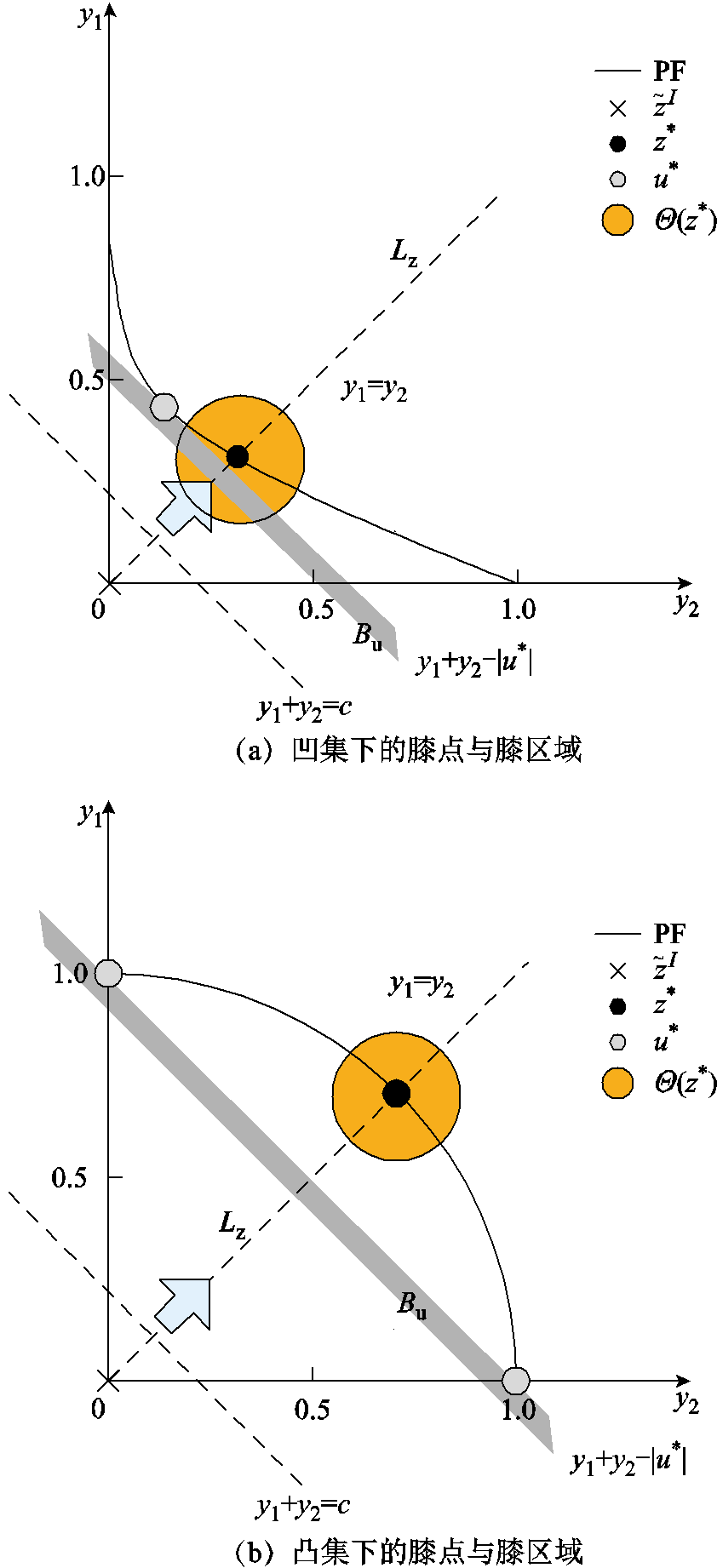
图6 膝点与膝区域的几何表示
Fig.6 Geometric representation of knee point and knee region
本文借鉴文献[29]中对膝点的定义方法,设计基于膝区域的多目标优化算法流程如图7所示。图7具体步骤如下:
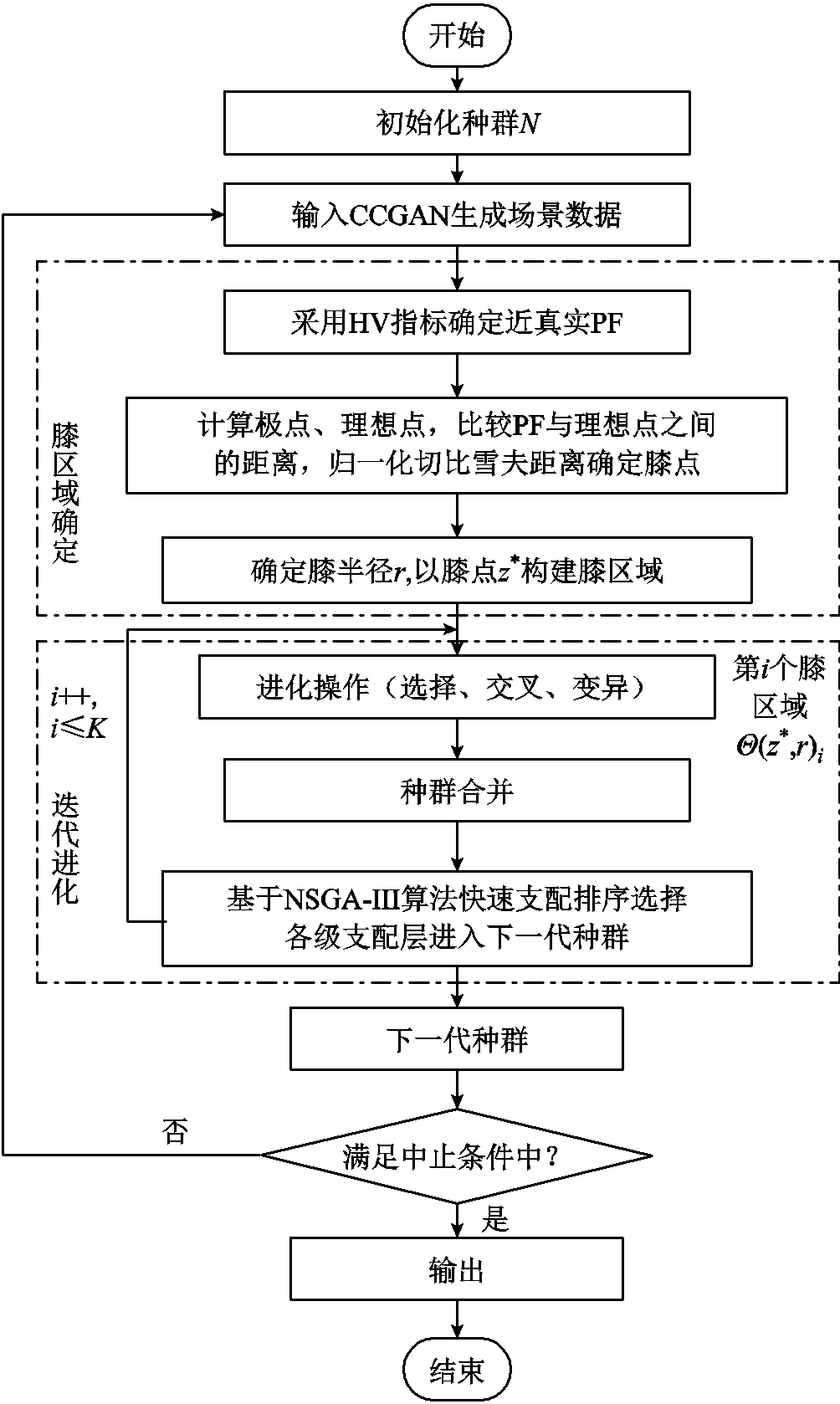
图7 kr-NSGA-Ⅲ算法流程
Fig.7 Algorithm procedure of kr-NSGA-Ⅲ
1)输入基于CCGAN生成的风电场景数据,负荷数据,绿氢储能投资及运行相关参数,绿氢制备、燃烧和储存约束所涉及参数,风电爬坡约束和直流潮流约束所涉及参数。
2)采用超体积(Hyper Volume, HV)指标得到关于风电弃风成本和绿氢储能投资运行成本的虚拟PF。
3)根据两类成本构成的PF计算极点、理想点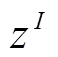 和切比雪夫距离,归一化得到弃风成本和绿氢储能投资运行成本函数的膝点
和切比雪夫距离,归一化得到弃风成本和绿氢储能投资运行成本函数的膝点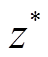 。
。
4)设置膝半径r,确定膝区域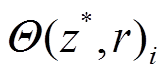 。
。
5)启动迭代进化部分,包括选择、交叉、变异等操作,合并种群。
6)基于NSGA-Ⅲ算法的快速支配排序选择各级支配层进入下一代种群。
7)若满足迭代收敛(进化代数达到上限),则输出结果;若不满足,则返回重复步骤2)~步骤6)继续迭代求解。
8)输出求解结果: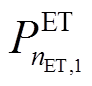 、
、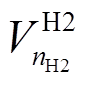 、
、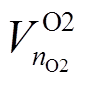 、
、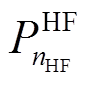 、
、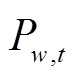 。
。
算例选用Pytorch作为CGAN和CCGAN的深度学习框架,基于CUDA调用图形处理器加速并行计算。计算机CPU Intel core i9 12 900 K 3.9 GHz,内存64 GB,GPU NVIDIA 3080Ti,显存12 GB,CUDA核心10 240,Boost clock 1.67 GHz。
场景生成部分:本文选用中国内蒙古地区两个风场的历史实测数据和历史预测数据,预测数据来自风场群的内部的预测系统,数据尺度从2017年1月1日—2019年12月31日,时间分辨率为15 min。经数据清洗,选择800天作为训练集样本,100天作为测试集样本,训练后完成k-fold交叉验证,k=10。作为对比验证,CGAN和CCGAN各生成1年数据,采用k-means聚类削减场景[5],生成四类典型日,每个典型日下对生成数据削减至20组。
规划计算部分:本文选用新英格兰39节点改进系统进行分析,系统如图8所示。在节点5和39接入发电功率为175 MW和66 MW风场群(WF1, WF2),同时绿氢储能系统所含电解槽、氢气罐、氧气罐和燃氢机组均接于对应风场下。算例参数见表1,典型日负荷数据如图9所示。kr-NSGA-Ⅲ算法参数设置如下:编码方式为实值编码,交叉算子采用模拟二进制,个体选择概率0.9,交叉率1,迭代次数100次,种群数为1 000,膝半径为0.05。
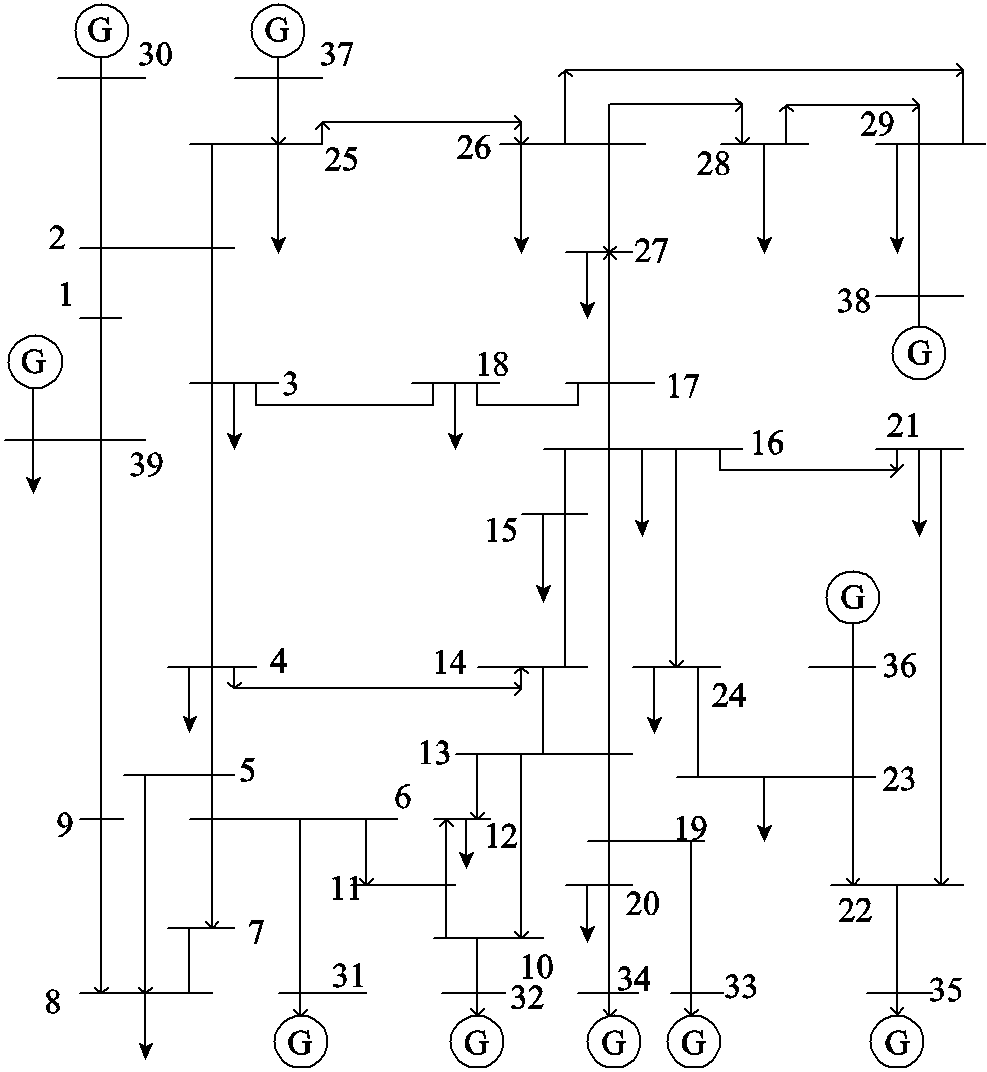
图8 新英格兰39节点系统
Fig.8 The New England 39 bus system
表1 算例参数
Tab.1 Parameters of case study

参数数值 电解槽功率成本/(元/kW)2 210[30] 高压储氢罐投资系数/(元/m3)2 000[21] 氧气罐投资系数/(元/m3)600[21] 储氢、储氧罐年运行成本/(元/m3)100 制氢转换率(%)75[31] 折现率(%)5 电解槽使用寿命/a10[32] 储氧罐使用寿命/a15[31] 储氢罐压力/MPa75 储氧罐压力/MPa0.8 燃氢机组投资系数/(元/kW)5 180[29] 燃氢机组年运行成本/(元/kW)5.94 氢气充放效率(%)98[30] 燃氢效率(%)40[31] 储氢罐使用寿命/a15[31] 燃氢机组使用寿命/a15[31]
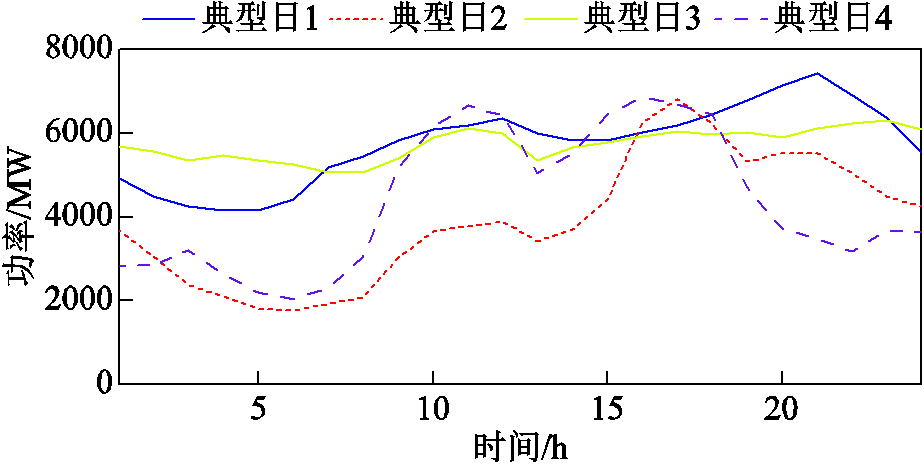
图9 典型日负荷数据
Fig.9 Typical daily load
通过模型训练后,CGAN和CCGAN的损失函数如图10和图11所示。图10未经条件校正,部分时段预测值与实际值相差过大,导致训练网络梯度波动较大,难以实现收敛。图11为经条件修正后的CCGAN,表现出了良好的收敛性,生成器与判别器的损失函数趋于一致,实现了Nash均衡。
从测试集随机生成100个日出力场景,并选择发生预测失准事件和爬坡事件的日出力场景进行对比分析。图12为CGAN和CCGAN在发生预测失准事件时生成的日出力场景集合。
图12中,灰色区域为生成场景。77~88时刻发生预测失准事件,预测值与实际值相差较大,且预测误差大于基准值的时长较长,约4 h。CGAN使用了不可靠的条件信息,随机噪声仅模拟预测值,生成值相对于实测值最大偏离约42 MW,波动区间叠加于预测值本身,生成场景对实测值的覆盖率较差。CCGAN在该时段校正了条件信息,生成的场景集合对实测值覆盖率更高。在41~72时刻,CGAN受限于感受野限制,生成场景质量较差,而CCGAN的膨胀卷积操作增大了感受野,生成的场景覆盖率高,拟合效果更佳。可见在预测失准事件下,该方法仍可生成逼近真实值的场景集合。
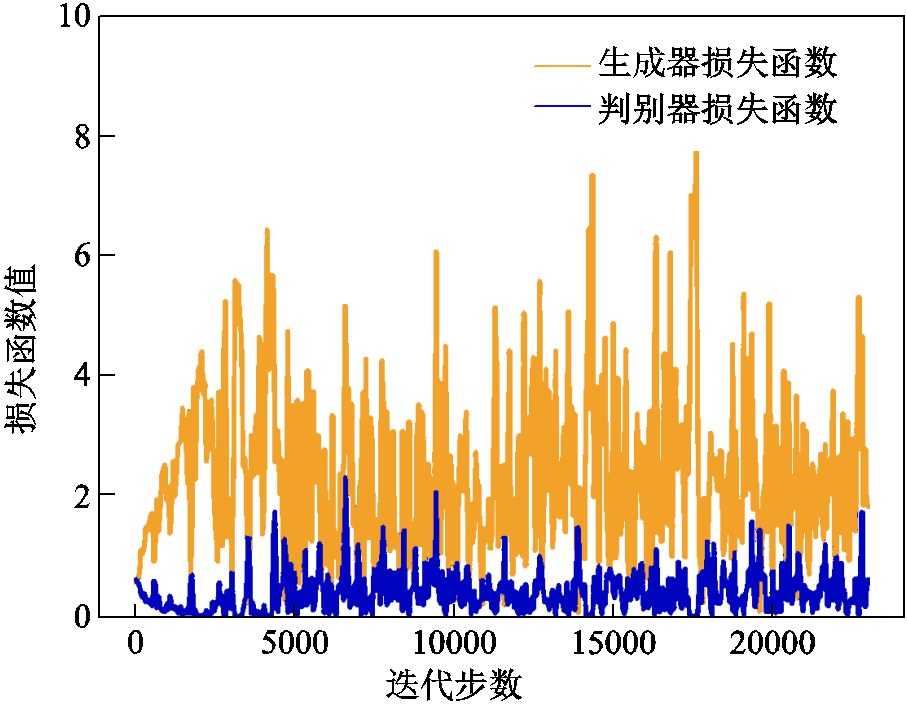
图10 CGAN损失函数
Fig.10 Loss function of CGAN
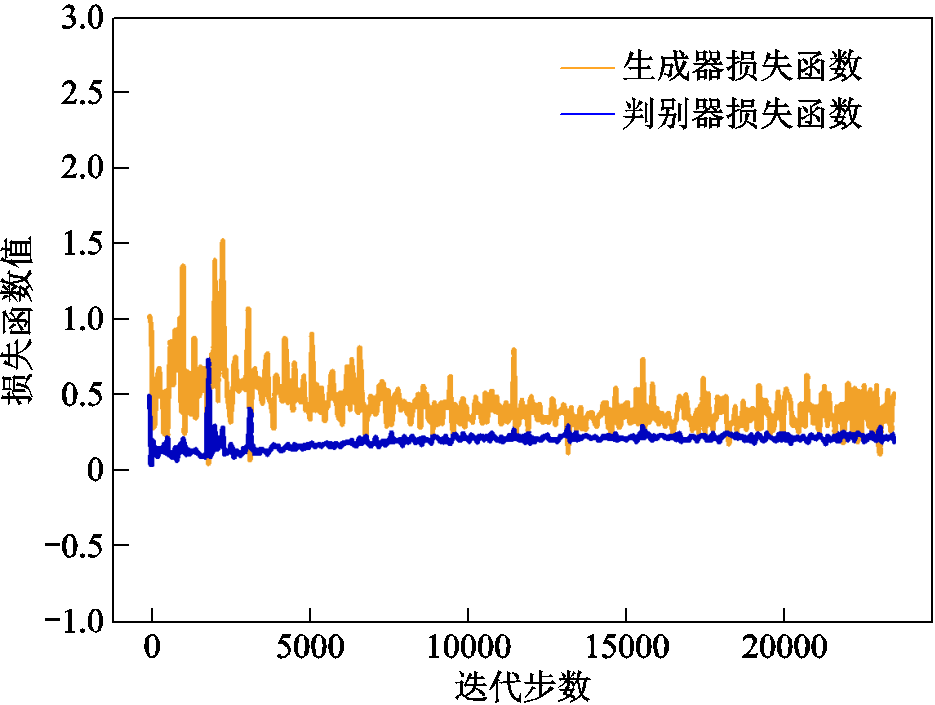
图11 CCGAN损失函数
Fig.11 Loss function of CCGAN
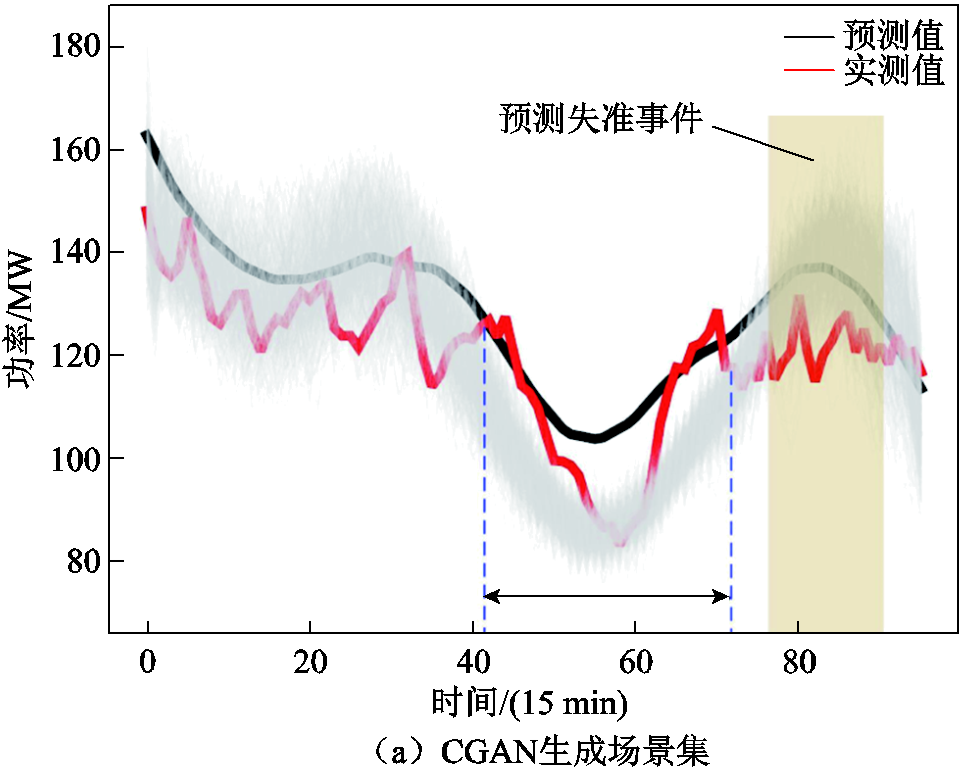
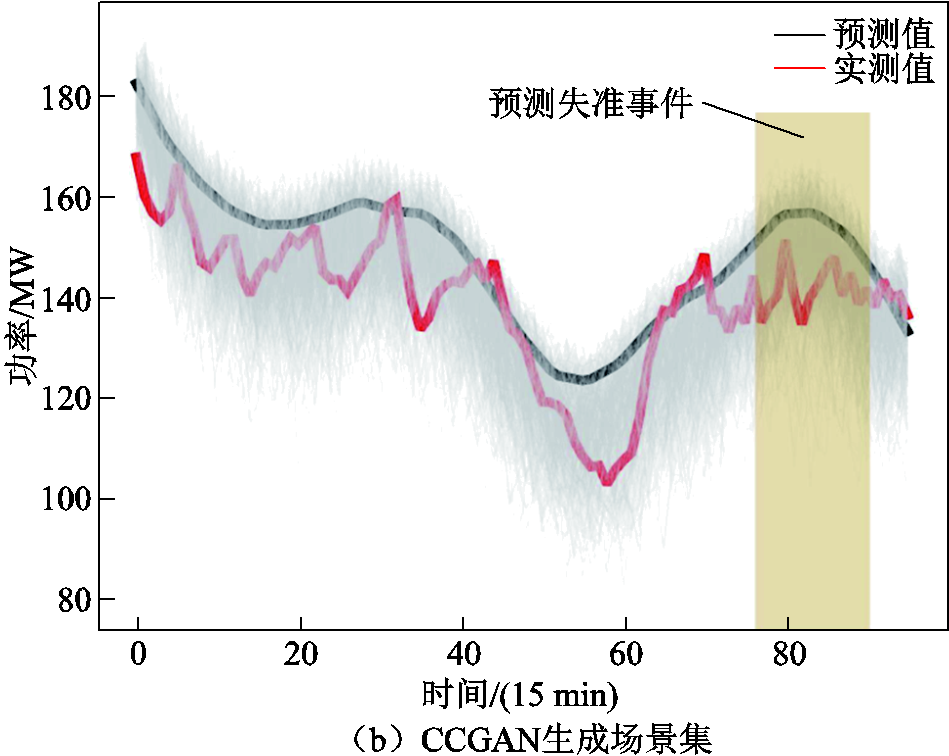
图12 预测失准事件下风电生成场景对比(WF1)
Fig.12 Comparison of wind power generation scenarios under prediction misalignment (WF1)
图13为CGAN和CCGAN在发生风电爬坡事件时生成的日出力场景集合。
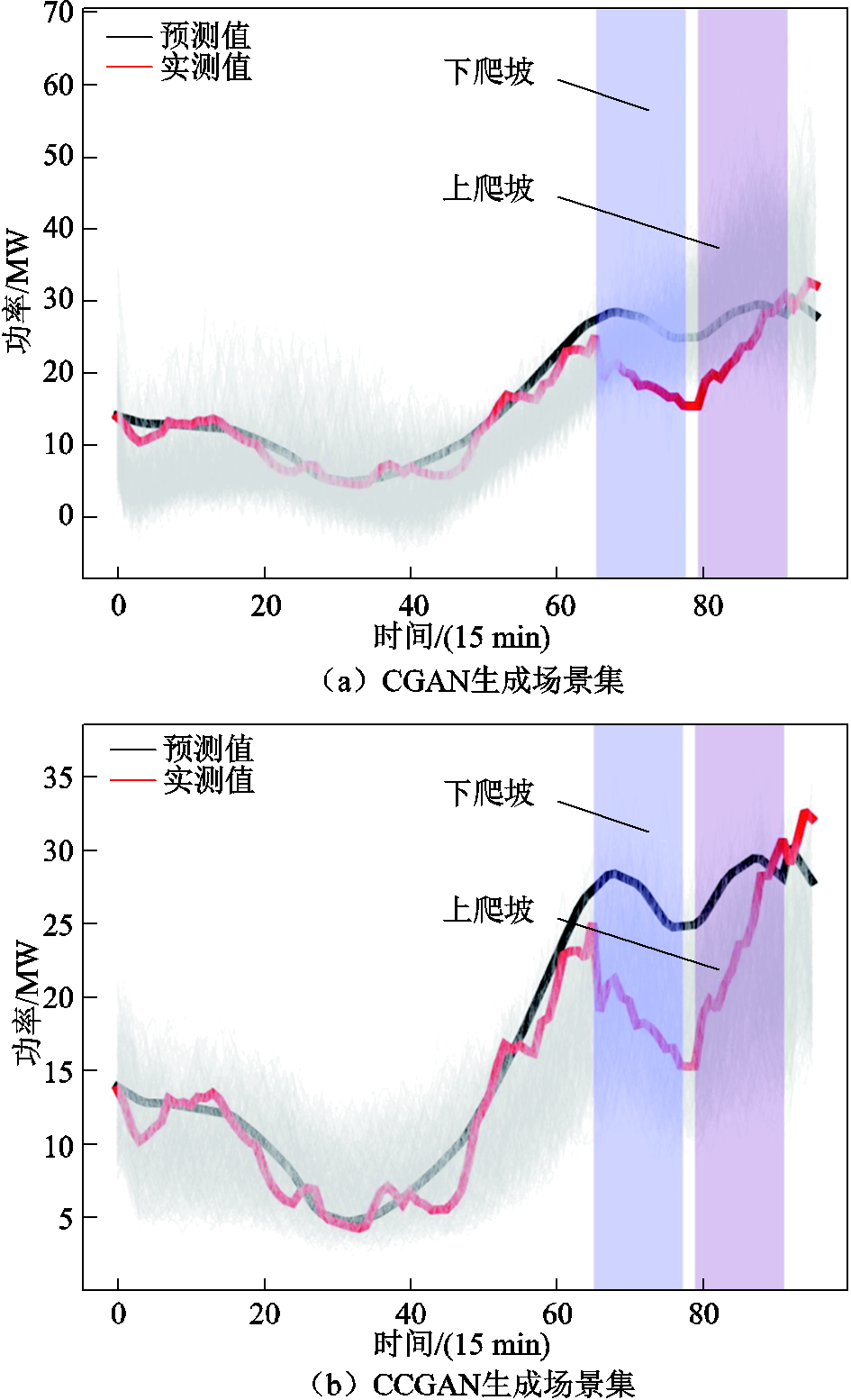
图13 风电爬坡事件下风电生成场景对比(WF2)
Fig.13 Comparison of wind power generation scenarios under ramp event (WF2)
图13中,在66~77时刻发生了下爬坡事件,79~91时刻发生了上爬坡事件。上、下爬坡率分别为15.6%和23.8%。CGAN由于仍输入预测值作为条件信息,生成场景过度拟合该不可靠的预测信息,66~91时刻生成的场景集合整体趋势变为上升。而CCGAN通过条件校正器对风电爬坡事件进行识别和数据的清洗,该时段充分利用了实测信息和预测误差的映射关系,生成的场景可捕捉爬坡事件特点。即使上、下爬坡事件连续发生这种小概率情况下,CCGAN依旧可生成对实测值覆盖效果较好的场景集合。综上所述,CCGAN在预测失准和爬坡事件问题上都可有效地学习预测误差波动的非线性关系,可生成更接近实测值的高质量场景集合。
为综合量化分析CGAN和CCGAN生成性能,本文选用平均绝对误差(Mean Absolute Percentage Error, MAPE)、覆盖率(Cover Rate, CR)、波动区间宽度(Fluctuation Interval Width, FIW)三类指标分析生成数据的精度[15]。MAPE值越小,精度越高。CR可评价置信区间对实测值的覆盖效果,FIW用于评价生成场景捕捉波动模糊性的能力。CR和FIW需联合作为一组评价指标,且当CR越高FIW越小时,生成数据的精度越高,捕捉风电波动随机性的能力越强。
生成场景指标对比分析(WF1)见表2。由表2可知,在预测合理事件下,CGAN和CCGAN都有较高的覆盖率,在相同的置信度下,CCGAN给出的功率波动区间更小,反映了该方法对随机波动捕捉的精准性更高。在预测失准事件下,CCGAN的覆盖率远高于CGAN,100%置信度下,波动区间降低12.4 MW。在风电爬坡事件下,CCGAN的优势进一步得到体现,生成数据的MAPE保持在30%以内。90%置信度下,覆盖率仍大于80%,体现了该方法对风电的短时急剧功率变化的刻画能力。
表2 生成场景指标对比分析(WF1)
Tab.2 Comparative analysis of scenarios (WF1)
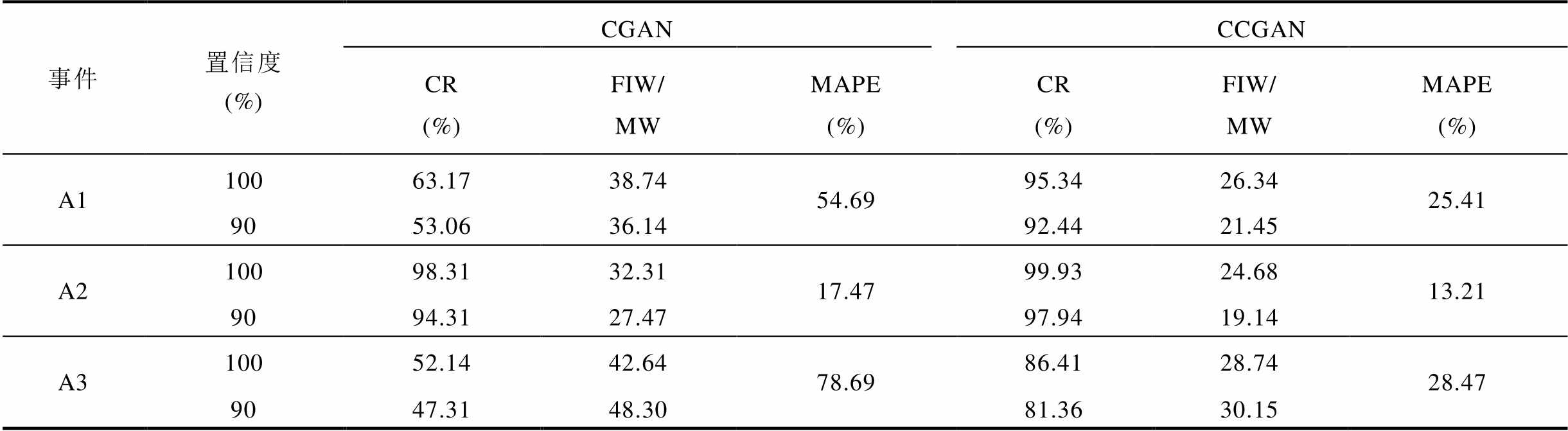
事件置信度 (%)CGANCCGAN CR(%)FIW/MWMAPE(%)CR(%)FIW/MWMAPE(%) A110063.1738.7454.6995.3426.3425.41 9053.0636.1492.4421.45 A210098.3132.3117.4799.9324.6813.21 9094.3127.4797.9419.14 A310052.1442.6478.6986.4128.7428.47 9047.3148.3081.3630.15
通过方法对比可看出本文所提CCGAN模型可更加精确地描述风电出力的随机性,并在预测失准和风电爬坡两类特殊事件发生时,纠正预测误差,提高生成模型对实际出力的逼近程度,为下一步规划提供可靠的数据支撑。
采用本文所提CCGAN对两个风场进行四个典型日场景生成,典型日出力如图14~图21所示,并代入容量配置模型进行计算。
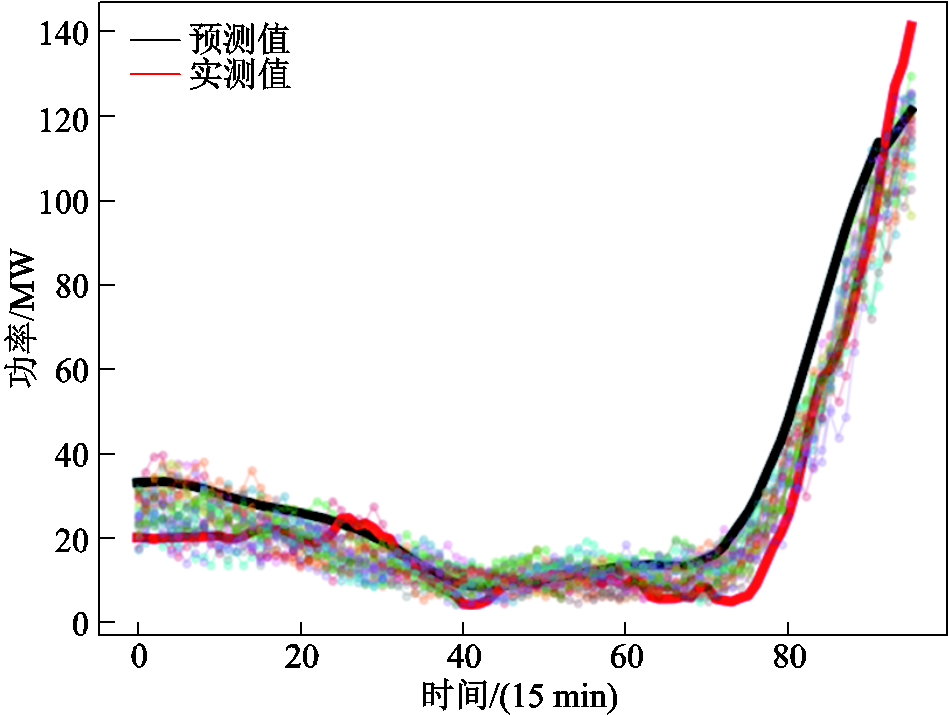
图14 风场1典型日1生成场景
Fig.14 Typical scenario of day 1 (WF1)
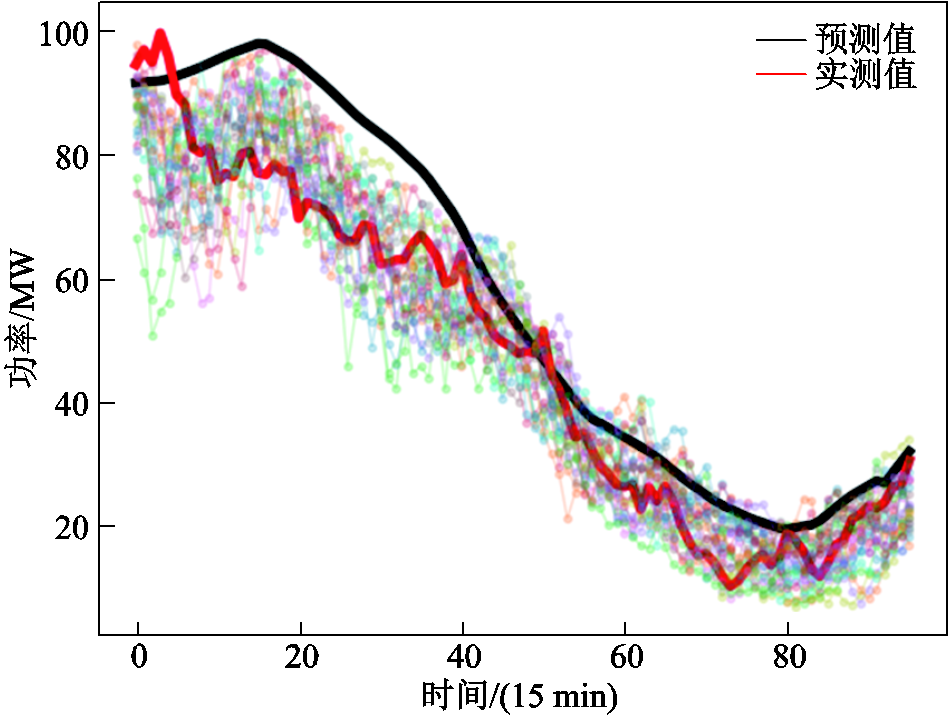
图15 风场1典型日2生成场景
Fig.15 Typical scenario of day 2 (WF1)
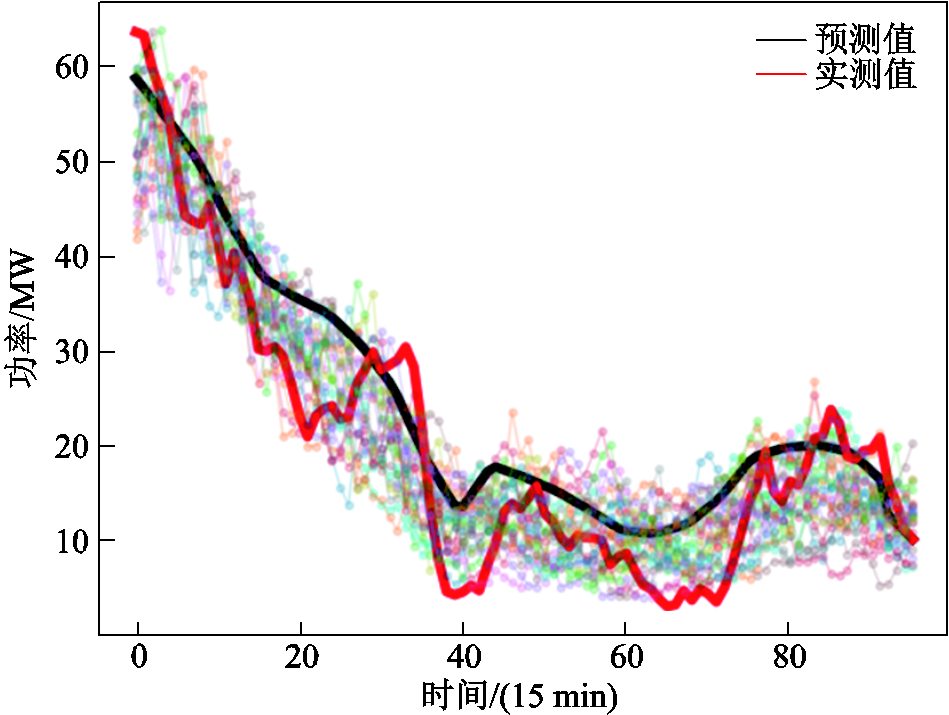
图16 风场1典型日3生成场景
Fig.16 Typical scenario of day 3 (WF1)
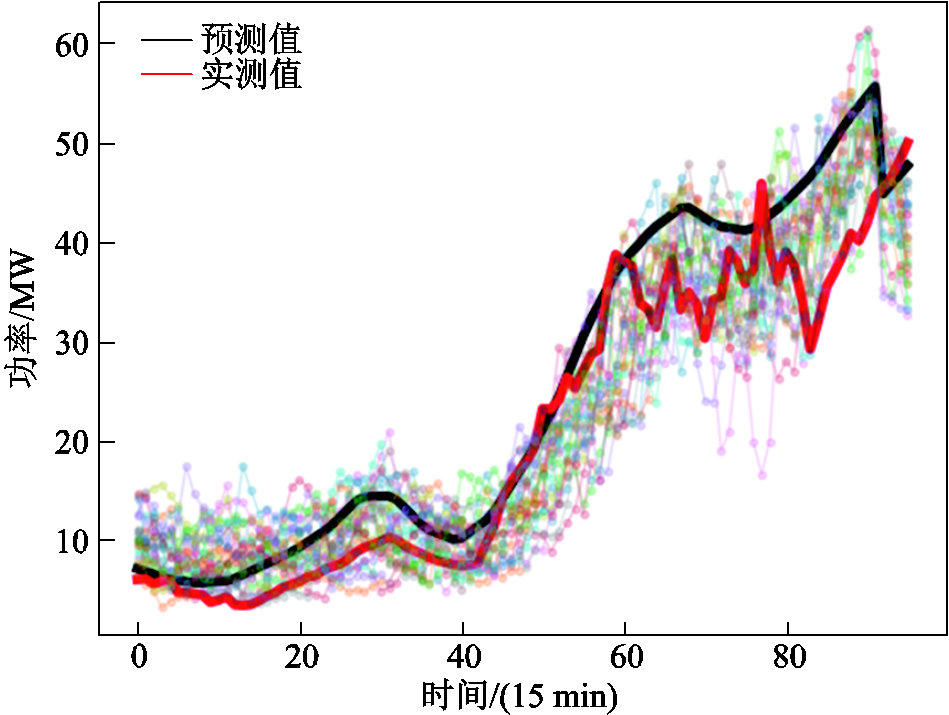
图17 风场1典型日4生成场景
Fig.17 Typical scenario of day 4 (WF1)
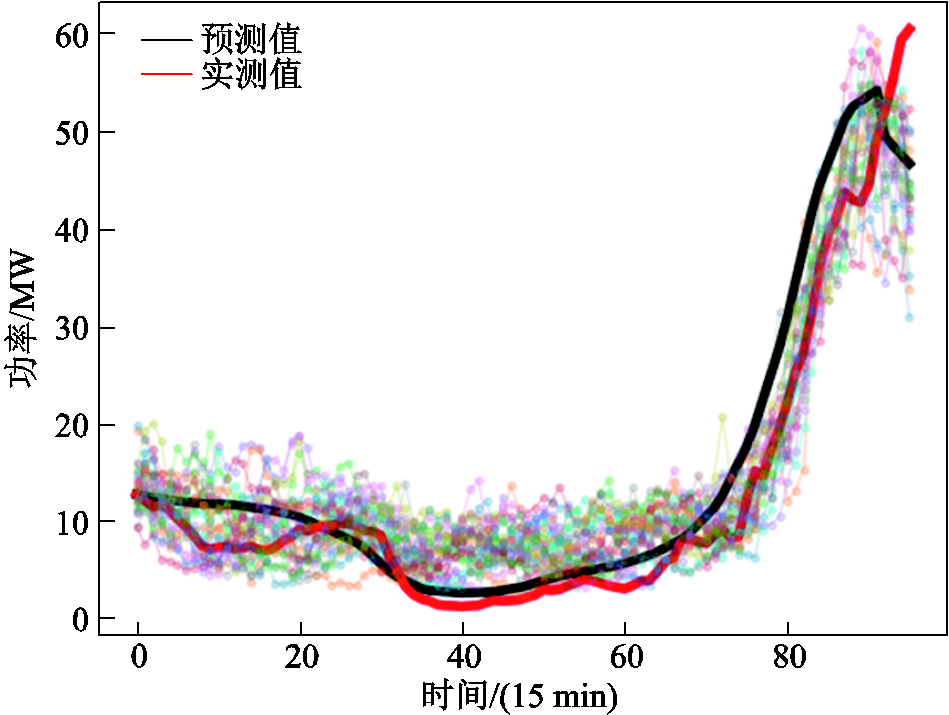
图18 风场2典型日1生成场景
Fig.18 Typical scenario of day 1 (WF2)
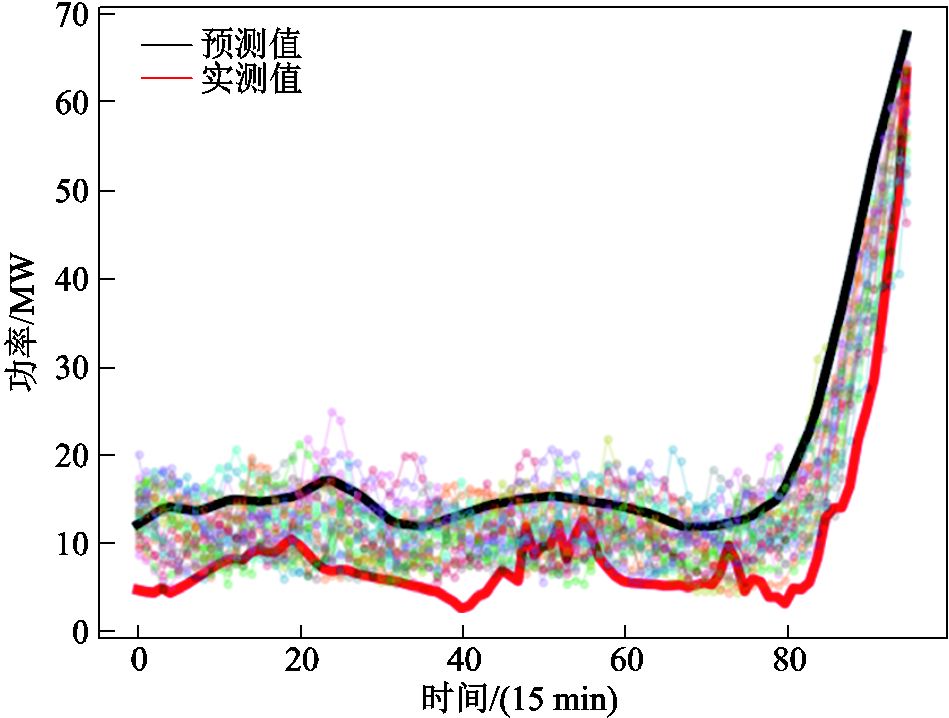
图19 风场2典型日2生成场景
Fig.19 Typical scenario of day 2 (WF2)
图22给出了NSGA-Ⅲ和kr-NSGA-Ⅲ得到的Pareto前沿。尽管传统NSGA-Ⅲ的非支配解分布分散,但对于该实际决策问题,决策者更加关注的是膝点解,这类解能为储能决策提供指导。
由图22可以看出,本文所提算法能收敛到膝区域,而传统的NSGA-Ⅲ无法收敛到该区域。此外,本文所提算法得到的大量非支配解分布于膝区域内,解集更集中化,在该三维的实际优化问题上的区域可控性强,收敛性能更好。对应也给出更多的解析信息,对决策方案的选择更具针对性。
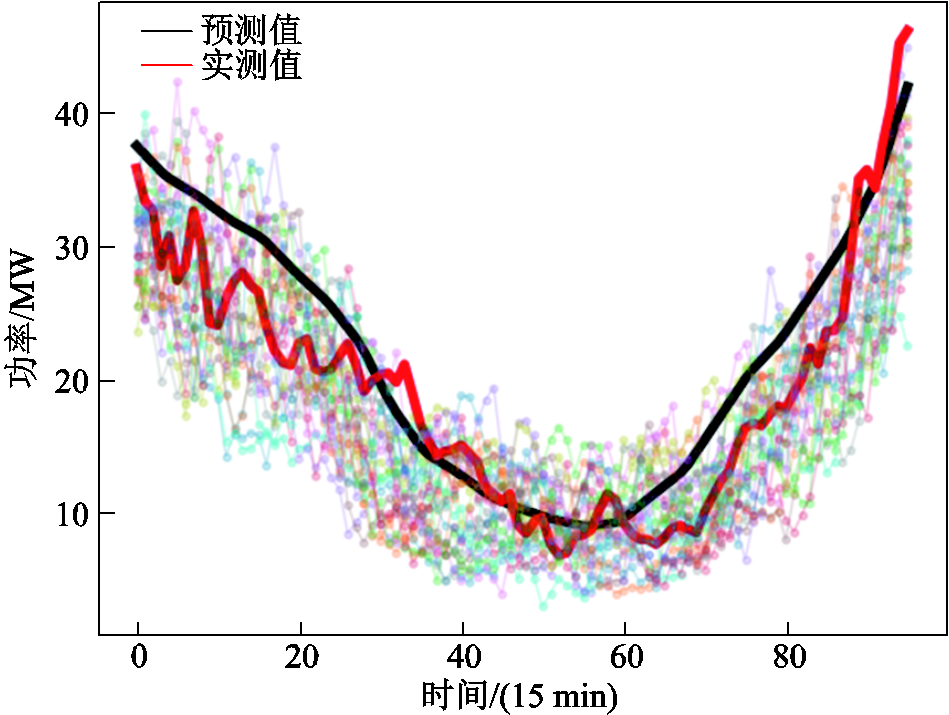
图20 风场2典型日3生成场景
Fig.20 Typical scenario of day 3 (WF2)
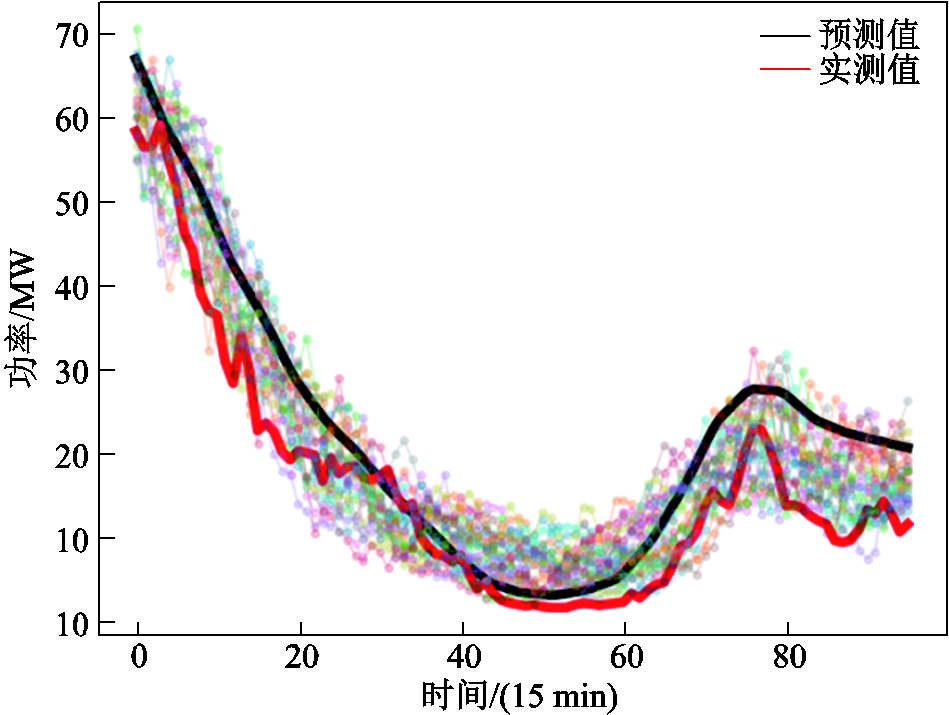
图21 风场2典型日4生成场景
Fig.21 Typical scenario of day 4 (WF2)
表3和表4分别给出了两种算法在风电实测值、鲁棒优化、马尔可夫蒙特卡洛模拟(Markov Chain Monte Carlo, MCMC)、CGAN和CCGAN五类数据来源下的绿氢储能系统配置结果。
1)对比两表中在实测值下的配置结果,NSGA-Ⅲ给出的折中解相比于kr-NSGA-Ⅲ的膝点解中,绿氢储能系统中各类设备的容量值、体积值均更高,且两个风场的年弃风成本也略高。相比于折中解,引入切比雪夫距离的膝点解可进一步引导解的搜索,收敛得到更逼近真实帕累托前沿的解。该系统中线路传输容量充足,可满足各种配置结果的功率传输需要,避免了因功率越限而导致优化模型无法得到可行解的问题。
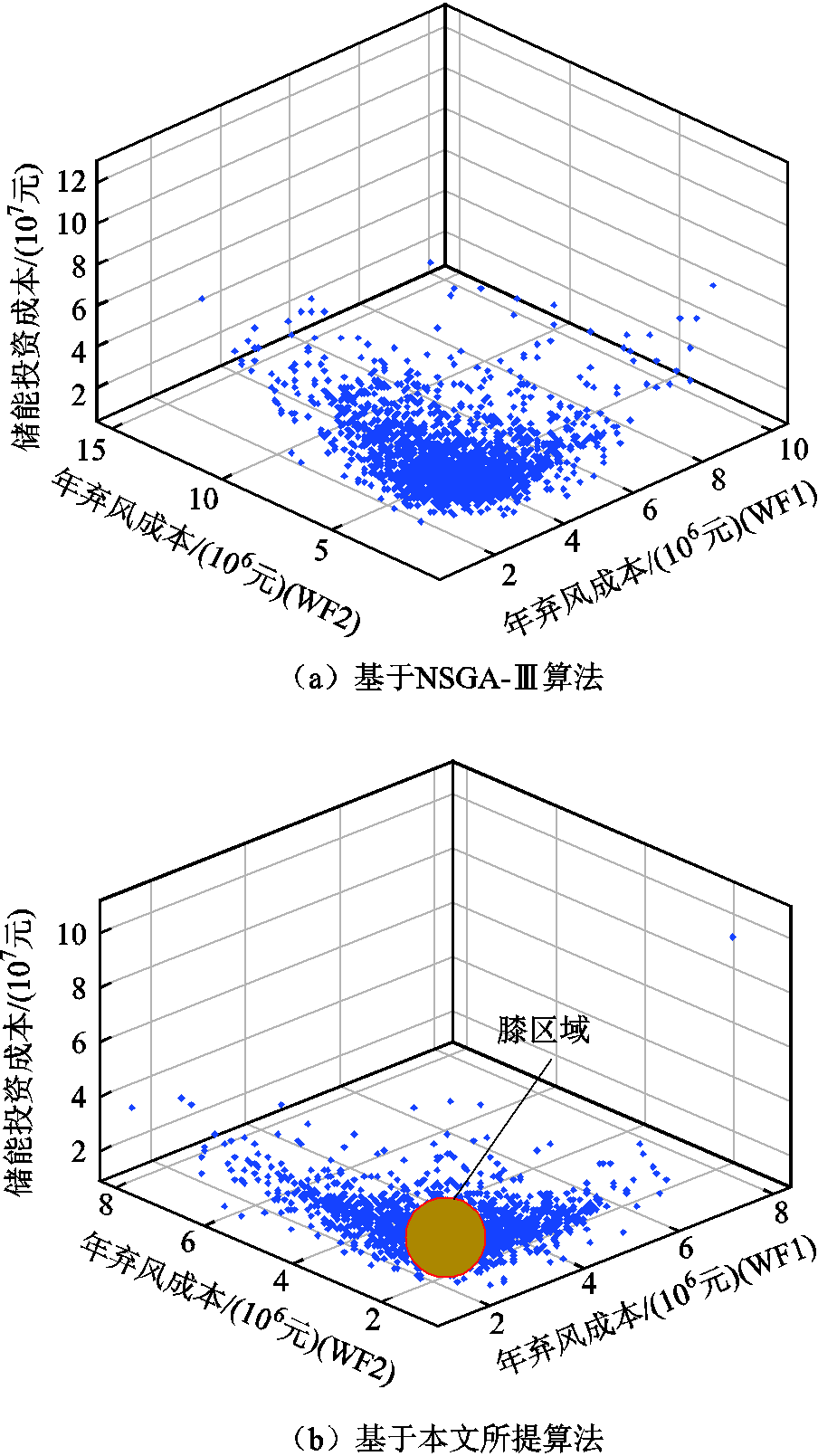
图22 两种算法的Pareto前沿
Fig.22 Pareto frontier of two algorithms
表3 基于NSGA-Ⅲ的绿氢储能配置结果
Tab.3 Green hydrogen storage sizing based on NSGA-Ⅲ
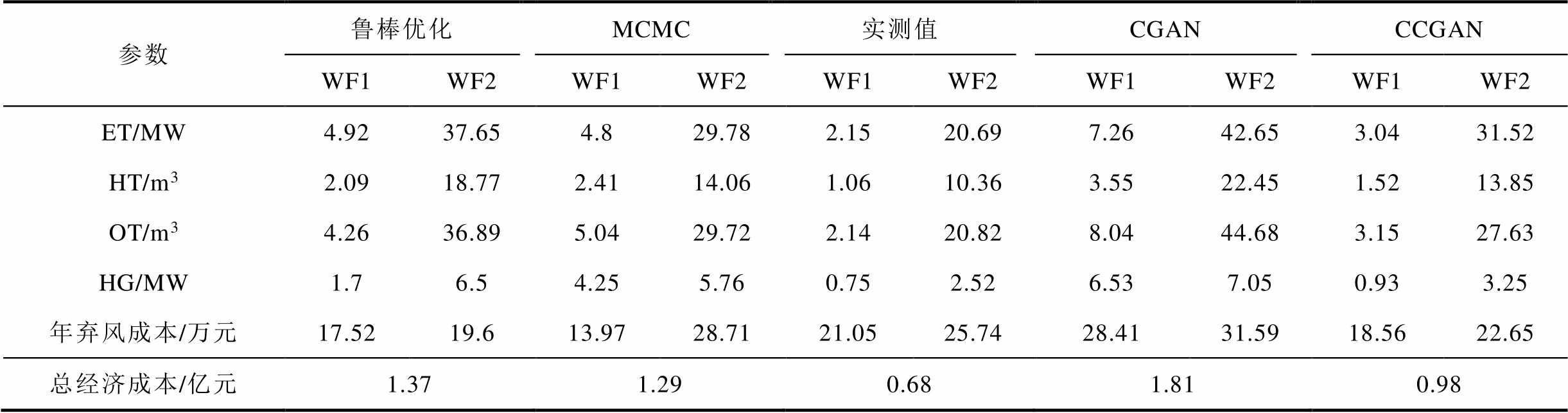
参数鲁棒优化MCMC实测值CGANCCGAN WF1WF2WF1WF2WF1WF2WF1WF2WF1WF2 ET/MW4.9237.654.829.782.1520.697.2642.653.0431.52 HT/m32.0918.772.4114.061.0610.363.5522.451.5213.85 OT/m34.2636.895.0429.722.1420.828.0444.683.1527.63 HG/MW1.76.54.255.760.752.526.537.050.933.25 年弃风成本/万元17.5219.613.9728.7121.0525.7428.4131.5918.5622.65 总经济成本/亿元1.371.290.681.810.98
表4 基于kr-NSGA-Ⅲ的绿氢储能配置结果
Tab.4 Green hydrogen storage sizing based on kr-NSGA-Ⅲ
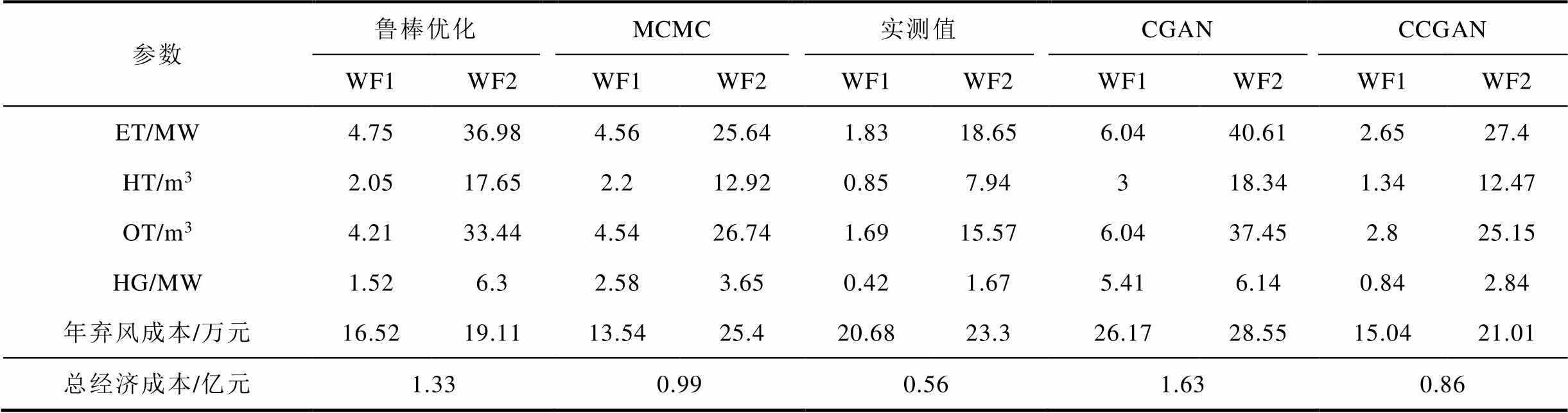
参数鲁棒优化MCMC实测值CGANCCGAN WF1WF2WF1WF2WF1WF2WF1WF2WF1WF2 ET/MW4.7536.984.5625.641.8318.656.0440.612.6527.4 HT/m32.0517.652.212.920.857.94318.341.3412.47 OT/m34.2133.444.5426.741.6915.576.0437.452.825.15 HG/MW1.526.32.583.650.421.675.416.140.842.84 年弃风成本/万元16.5219.1113.5425.420.6823.326.1728.5515.0421.01 总经济成本/亿元1.330.990.561.630.86
2)在本文所提算法(kr-NSGA-Ⅲ)中,对比CGAN和真实值输入下的该绿氢储能系统配置结果,CGAN生成的风电场景输入下,两个风场电解槽的功率总和提高了26.17 MW,WF1和WF2中的燃氢机组发电功率至5.41 MW和6.14 MW。反映了CGAN生成场景的功率波动区间较宽,需要投入较多储能设备应对风电的波动,以降低风场的弃风成本。
3)在四种生成型场景下,将CCGAN的配置结果与实测值、CGAN、鲁棒优化和MCMC进行综合对比,CCGAN的配置结果总体小于CGAN和鲁棒优化,但大于实测值,总经济成本也低于MCMC。鲁棒优化和MCMC由于未使用历史预测值的统计价值,容易高估风电的不确定性。而本文方法生成的场景在实测值的基础上合理地计及了风电的波动,配置结果在鲁棒性和经济性上有所协调。可以看到,CGAN在WF1的燃氢机组功率约为实测值配置结果的13倍,但CCGAN仅为实测值的2倍,这是由于WF1的历史数据中预测失准事件A1发生频率高,CGAN的生成器输入了大量错误的条件信息,迫使生成的数据严重偏离了实测值,风电出力场景的可靠性较低,已无法支撑该系统的规划计算,造成规划方案过鲁棒化,投资效率下降。可见在该深度学习框架下条件校正是必要的。
4)相比于WF1,CGAN对WF2的生成场景相对可靠。对比CCGAN,尽管CGAN配置了较大容量储能,但年弃风成本相比实测值反而提高。鲁棒优化额外多配置了11.68 MW的电解槽,才能比CCGAN的弃风成本减少0.42万元。而CCGAN更为精准地捕捉了风电的波动特征,特别是在高置信度下仍可缩小风电波动的范围,配合kr-NSGA-Ⅲ的膝区域搜索策略,以较少的储能投资,获得更大的弃风成本缩减率,进一步验证了CCGAN可为该储能规划问题提供可靠、精确的场景支撑。
本文针对基于半监督学习技术CGAN生成风电场景对实测值拟合效果差、预测精度低等问题,提出了一种基于风电预测误差的校正条件生成对抗网络,并构建了绿氢储能系统容量规划模型。通过算例分析得到以下结论:
1)通过引入改进旋转门算法,CCGAN的校正器能精确地识别预测失准和风电爬坡事件,对输入生成器的条件信息进行针对性校正,为数据生成提供了可靠的标签信息。
2)本文所提基于CCGAN的风电场景生成方法,相比于传统的鲁棒优化、MCMC和CGAN,可捕捉风电出力的波动特征,平均绝对误差可降低29.2%~50.2%,生成数据可兼顾高置信度与较窄波动区间,为储能规划提供高质量的场景集合。
3)绿氢储能容量配置结果表明,预测失准频发的样本下,CGAN的生成场景将导致规划结果偏离实际,相比鲁棒优化,本文所提方法的规划结果可降低约0.47亿元的经济成本,并使决策结果兼顾鲁棒性和经济性。
本文提出的半监督学习技术可为绿氢储能规划提供可靠的风电日内出力数据。随着季节性氢气储能技术的普及,后续研究将结合该深度学习技术研究风电长期出力不确定性对季节性绿氢储能的影响。
参考文献
[1] 李争, 张蕊, 孙鹤旭, 等. 可再生能源多能互补制-储-运氢关键技术综述[J]. 电工技术学报, 2021, 36(3): 446-462.
Li Zheng, Zhang Rui, Sun Hexu, et al. Review on key technologies of hydrogen generation, storage and transportation based on multi-energy complementary renewable energy[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 446-462.
[2] 张鹏成, 徐箭, 柯德平, 等. 氢能驱动下钢铁园区能源系统优化配置[J]. 电力系统自动化, 2022, 46(14): 1-10.
Zhang Pengcheng, Xu Jian, Ke Deping, et al. Optimal configuration of energy system in iron and steel park driven by hydrogen energy[J]. Automation of Electric Power Systems, 2022, 46(14): 1-10.
[3] 孙鹤旭, 李争, 陈爱兵, 等. 风电制氢技术现状及发展趋势[J]. 电工技术学报, 2019, 34(19): 4071-4083.
Sun Hexu, Li Zheng, Chen Aibing, et al. Current status and development trend of hydrogen production technology by wind power[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4071-4083.
[4] 赵书强, 金天然, 李志伟, 等. 考虑时空相关性的多风电场出力场景生成方法[J]. 电网技术, 2019, 43(11): 3997-4004.
Zhao Shuqiang, Jin Tianran, Li Zhiwei, et al. Wind power scenario generation for multiple wind farms considering temporal and spatial correlations[J]. Power System Technology, 2019, 43(11): 3997-4004.
[5] 张俊涛, 程春田, 申建建, 等. 考虑风光不确定性的高比例可再生能源电网短期联合优化调度方法[J]. 中国电机工程学报, 2020, 40(18): 5921-5932.
Zhang Juntao, Cheng Chuntian, Shen Jianjian, et al. Short-term joint optimal operation method for high proportion renewable energy grid considering wind-solar uncertainty[J]. Proceedings of the CSEE, 2020, 40(18): 5921-5932.
[6] 仉梦林, 胡志坚, 王小飞, 等. 基于动态场景集和需求响应的二阶段随机规划调度模型[J]. 电力系统自动化, 2017, 41(11): 68-76.
Zhang Menglin, Hu Zhijian, Wang Xiaofei, et al. Two-stage stochastic programming scheduling model based on dynamic scenario sets and demand response[J]. Automation of Electric Power Systems, 2017, 41(11): 68-76.
[7] 马燕峰, 李鑫, 刘金山, 等. 考虑风电场时空相关性的多场景优化调度[J]. 电力自动化设备, 2020, 40(2): 55-65.
Ma Yanfeng, Li Xin, Liu Jinshan, et al. Multi-scenario optimal dispatch considering temporal-spatial correlation of wind farms[J]. Electric Power Automation Equipment, 2020, 40(2): 55-65.
[8] 董雷, 孟天骄, 陈乃仕, 等. 采用马尔可夫链—多场景技术的交直流主动配电网优化调度[J]. 电力系统自动化, 2018, 42(5): 147-153.
Dong Lei, Meng Tianjiao, Chen Naishi, et al. Optimized scheduling of AC/DC hybrid active distribution network using Markov chains and multiple scenarios technique[J]. Automation of Electric Power Systems, 2018, 42(5): 147-153.
[9] Zhang Wenjie, Luo Yonghong, Zhang Ying, et al. SolarGAN: multivariate solar data imputation using generative adversarial network[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 743-746.
[10] 于文家, 丁世飞. 基于自注意力机制的条件生成对抗网络[J]. 计算机科学, 2021, 48(1): 241-246.
Yu Wenjia, Ding Shifei. Conditional generative adversarial network based on self-attention mechanism[J]. Computer Science, 2021, 48(1): 241-246.
[11] 顾洁, 刘书琪, 胡玉, 等. 基于深度卷积生成对抗网络场景生成的间歇式分布式电源优化配置[J]. 电网技术, 2021, 45(5): 1742-1751.
Gu Jie, Liu Shuqi, Hu Yu, et al. Optimal allocation of intermittent distributed generation based on deep convolutions generative adversarial network in scenario generation[J]. Power System Technology, 2021, 45(5): 1742-1751.
[12] 马燕峰, 傅钰, 赵书强, 等. 基于WGAN风光资源场景模拟和时序生产模拟的新能源电源容量配置[J]. 电力自动化设备, 2020, 40(11): 77-86.
Ma Yanfeng, Fu Yu, Zhao Shuqiang, et al. Capacity allocation of new energy source based on wind and solar resource scenario simulation using WGAN and sequential production simulation[J]. Electric Power Automation Equipment, 2020, 40(11): 77-86.
[13] 李康平, 张展耀, 王飞, 等. 基于GAN场景模拟与条件风险价值的独立型微网容量随机优化配置模型[J]. 电网技术, 2019, 43(5): 1717-1725.
Li Kangping, Zhang Zhanyao, Wang Fei, et al. Stochastic optimization model of capacity configuration for stand-alone microgrid based on scenario simulation using GAN and conditional value at risk[J]. Power System Technology, 2019, 43(5): 1717-1725.
[14] Zhang Ning, Kang Chongqing, Xia Qing, et al. Modeling conditional forecast error for wind power in generation scheduling[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1316-1324.
[15] 董骁翀, 孙英云, 蒲天骄. 基于条件生成对抗网络的可再生能源日前场景生成方法[J]. 中国电机工程学报, 2020, 40(17): 5527-5536.
Dong Xiaochong, Sun Yingyun, Pu Tianjiao. Day-ahead scenario generation of renewable energy based on conditional GAN[J]. Proceedings of the CSEE, 2020, 40(17): 5527-5536.
[16] 邓智宏, 江岳文. 考虑制氢效率特性的风氢系统容量优化[J]. 可再生能源, 2020, 38(2): 259-266.
Deng Zhihong, Jiang Yuewen. Optimal sizing of a wind-hydrogen system under consideration of the efficiency characteristics of electrolysers[J]. Renewable Energy Resources, 2020, 38(2): 259-266.
[17] 司杨, 陈来军, 陈晓弢, 等. 基于分布鲁棒的风-氢混合系统氢储能容量优化配置[J]. 电力自动化设备, 2021, 41(10): 3-10.
Si Yang, Chen Laijun, Chen Xiaotao, et al. Optimal capacity allocation of hydrogen energy storage in wind-hydrogen hybrid system based on distributionally robust[J]. Electric Power Automation Equipment, 2021, 41(10): 3-10.
[18] 周建力, 乌云娜, 董昊鑫, 等. 计及电动汽车随机充电的风-光-氢综合能源系统优化规划[J]. 电力系统自动化, 2021, 45(24): 30-40.
Zhou Jianli, Wu Yunna, Dong Haoxin, et al. Optimal planning of wind-photovoltaic-hydrogen integrated energy system considering random charging of electric vehicles[J]. Automation of Electric Power Systems, 2021, 45(24): 30-40.
[19] 肖白, 刘健康, 张博, 等. 考虑阶梯碳交易和需求响应的含氢储能的并网型微电网优化配置[J]. 电力自动化设备, 2023, 43(1): 121-129.
Xiao Bai, Liu Jiankang, Zhang Bo, et al. Optimal configuration of grid-connected microgrid with hydrogen energy storage considering ladder-type carbon trading and demand response[J]. Electric Power Automation Equipment, 2023, 43(1): 121-129.
[20] 江岳文, 杨国铭, 朱振山. 考虑交通流量捕获的风-氢-电耦合网络规划[J]. 电力系统自动化, 2021, 45(22): 19-28.
Jiang Yuewen, Yang Guoming, Zhu Zhenshan. Wind-hydrogen-electricity coupled network planning considering traffic flow capture[J]. Automation of Electric Power Systems, 2021, 45(22): 19-28.
[21] 袁铁江, 曹继雷. 计及风电-负荷不确定性的风氢低碳能源系统容量优化配置[J]. 高电压技术, 2022, 48(6): 2037-2044.
Yuan Tiejiang, Cao Jilei. Capacity optimization allocation of wind hydrogen low-carbon energy system considering wind power-load uncertainty[J]. High Voltage Engineering, 2022, 48(6): 2037-2044.
[22] Zheng Yi, You Shi, Bindner H W, et al. Incorporating optimal operation strategies into investment planning for wind/electrolyser system[J]. CSEE Journal of Power and Energy Systems, 2022, 8(2): 347-359.
[23] 叶畅, 曹侃, 丁凯, 等. 基于广义储能的多能源系统不确定优化调度策略[J]. 电工技术学报, 2021, 36(17): 3753-3764.
Ye Chang, Cao Kan, Ding Kai, et al. Uncertain optimal dispatch strategy based on generalized energy storage for multi-energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3753-3764.
[24] 田坤鹏, 孙伟卿, 韩冬, 等. 满足非水可再生能源发电量占比目标的“源-网-储”协调规划[J]. 电力自动化设备, 2021, 41(1): 98-108.
Tian Kunpeng, Sun Weiqing, Han Dong, et al. Coordinated planning of “generation-grid-storage” to satisfy proportion target of non-hydro renewable energy generation[J]. Electric Power Automation Equipment, 2021, 41(1): 98-108.
[25] Zhu Hu, Qiao Yiming, Xu Guoxia, et al. DSPNet: a lightweight dilated convolution neural networks for spectral deconvolution with self-paced learning[J]. IEEE Transactions on Industrial Informatics, 2020, 16(12): 7392-7401.
[26] 国家能源局. 风电功率预测系统功能规范NB/T 31046—2013[S]. 北京: 新华出版社, 2014.
[27] Cui Mingjian, Zhang Jie, Florita A R, et al. An optimized swinging door algorithm for identifying wind ramping events[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 150-162.
[28] 崔杨, 曾鹏, 王铮, 等. 考虑碳捕集电厂能量转移特性的弃风消纳多时间尺度调度策略[J]. 中国电机工程学报, 2021, 41(3): 946-961.
Cui Yang, Zeng Peng, Wang Zheng, et al. Multiple time scales scheduling strategy of wind power accommodation considering energy transfer characteristics of carbon capture power plant[J]. Proceedings of the CSEE, 2021, 41(3): 946-961.
[29] Vallee F, Brunieau G, Pirlot M, et al. Optimal wind clustering methodology for adequacy evaluation in system generation studies using nonsequential Monte Carlo simulation[J]. IEEE Transactions on Power Systems, 2011, 26(4): 2173-2184.
[30] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[31] 马榕谷, 陈洁, 赵军超, 等. 非并网风氢互补系统的容量多目标优化[J]. 太阳能学报, 2019, 40(2): 422-429.
Ma Ronggu, Chen Jie, Zhao Junchao, et al. Multi-objective optimization for capacity of non-grid-connected wind/hydrogen hybrid power system[J]. Acta Energiae Solaris Sinica, 2019, 40(2): 422-429.
[32] 李奇, 赵淑丹, 蒲雨辰, 等. 考虑电氢耦合的混合储能微电网容量配置优化[J]. 电工技术学报, 2021, 36(3): 486-495.
Li Qi, Zhao Shudan, Pu Yuchen, et al. Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 486-495.
Abstract The wind power penetration rate in China is increasing. In order to realize the efficient consumption of wind power, the green hydrogen energy storage system (ESS) is becoming an essential carrier of energy storage. However, the intermittence, randomness, and volatility of wind intraday power make it difficult to produce and store green hydrogen. Providing scenario data for green hydrogen ESS planning and displaying the intraday output fluctuation of wind power is a critical challenge. To address these issues, this paper designs a green hydrogen ESS capacity planning framework based on wind power scenario generation. The corrected-conditional generative adversarial network (CCGAN) is constructed to generate scenario data.
Firstly, a corrector based on the improved revolving door algorithm is designed in the CCGAN to identify and clean the prediction data under the prediction misaim and wind power ramp events to ensure the high reference of conditional information. Secondly, the dilated convolution is embedded in the generator and discriminator to overcome the problem of the insufficient receptive field. Thirdly, by imposing constraints on the production and storage of green hydrogen, a multi-objective optimization model for green hydrogen ESS sizing is developed. The definition of knee region under Chebyshev distance is introduced. The non-dominated sorting genetic algorithm based on knee region (kr-NSGA-Ⅲ) is designed to solve the capacity sizing model. Finally, the simulation based on the New England 39-bus system verifies the generated scenario’s accuracy and the planning model’s effectiveness.
Simulation results on the actual wind farm data show that, when predictions are accurate, both conditional generative adversarial network (CGAN) and CCGAN have higher coverage for measured data. At the same confidence level, the power fluctuation range given by CCGAN is smaller, which reflects that the method has higher accuracy for random fluctuation. Under the prediction misaim event, the coverage of CCGAN is much higher than that of CGAN, and the fluctuation range is reduced by 12.4 MW at a 100% confidence level. Under the wind power ramp event, the mean absolute percentage error of the scenario data generated by CCGAN is kept within 30%. At a 90% confidence level, CCGAN can still have a coverage of more than 80%, reflecting the ability to characterize the short-term fluctuation of wind power. In the four generative scenarios, the sizing results of CCGAN are compared with the measured values, CGAN, robust optimization, and Markov chain Monte Carlo (MCMC). The sizing results of CCGAN are generally smaller than CGAN and robust optimization but larger than the measured values, and the total economic cost is also lower than MCMC. Robust optimization and MCMC are easy to overestimate the uncertainty of wind power because these methods do not use the statistical value of prediction data. The scenario generated by the proposed method reasonably considers wind power fluctuation based on measured data, and the sizing result is a tradeoff between robustness and economy.
The following conclusions can be drawn from the simulation analysis: (1) By employing the improved revolving door algorithm, the CCGAN’s corrector can accurately identify the prediction misaim and wind power ramp events and perform targeted correction on the conditional information of the input generator, providing a reliable label for data generation. (2) Compared with the robust optimization, MCMC, and CGAN, the wind power scenario generation based on CCGAN can capture the fluctuation characteristics of wind power, and the generated data can consider both high confidence and narrow fluctuation range, providing a high-quality scenario set for green hydrogen ESS planning. (3) The results of green hydrogen ESS sizing show that under the samples with frequent prediction misaim events, the scenario of CGAN will lead to the deviation of planning results from reality. Compared with robust optimization, the planning results of the proposed method can reduce investment costs.
Keywords:Corrected-conditional generative adversarial network, green hydrogen energy storage, capacity sizing, scenario generation, wind power forecasting error
中图分类号:TM614
DOI:10.19595/j.cnki.1000-6753.tces.222009
甘肃省科技计划(21ZD8JA001)、智能电网保护和运行控制国家重点实验室开放课题(考虑风功率波动和调频能力的风电场站储能配置与运行优化技术)资助项目。
收稿日期 2022-10-26
改稿日期 2022-12-28
朱 玲 女,1986年生,硕士,高级工程师,研究方向为新能源电力系统稳定及控制,储能规划与运行。E-mail:zhuling@sgepri.sgcc.com.cn(通信作者)
李 威 男,1976年生,博士,研究员级高级工程师,研究方向为电力系统安全稳定分析与控制。E-mail:liwei10@sgepri.sgcc.com.cn
(编辑 赫 蕾)