 (1)
(1)
摘要 多微电网中的环境状态、控制资源及偶然事件均具有强不确定性,而电动汽车在参与电网削峰填谷的同时也给发电控制带来了挑战。为此,该文提出一种基于可进化模型预测控制(LBMPC)的含电动汽车多微电网发电控制策略。首先,基于控制器交互的多微电网互联结构,考虑了发电机端电压调节和负荷频率控制(LFC)之间的耦合关系,建立含电动汽车多微电网的发电控制模型;然后,设计了一种基于多智能体的控制器参数自适应算法:频率控制器以实时频偏和EV站输出功率边界为状态集,以模型预测控制(MPC)控制器的可调参数矩阵Qx作为动作集,以频率偏差为奖励函数指标,电压控制器同理,从而实现MPC与PI控制器权重参数的自适应调整;最后,仿真结果表明,自动调压(AVR)回路增加了有功功率干扰,对LFC控制器提出了更高的要求,与传统控制和MPC算法相比,应用于控制器互联结构的可进化模型预测控制器能够在子微电网之间进行信息交换,并且根据环境状态实时更新控制器参数,显著提高了多微电网频率控制过程的鲁棒性和快速性。同时,与纯深度确定性策略梯度(DDPG)控制器相比,该文提出的双层控制结构在机器学习智能体出现故障无法正常输出动作时,能更好地保证系统的安全稳定运行。
关键词:多微电网负荷频率控制 电动汽车 发电机端电压 多智能体算法 模型预测控制
在“碳达峰”与“碳中和”的国家能源战略背景下[1],以化石能源为驱动力的常规发电机组逐渐被风力发电与光伏发电等可再生能源发电机组所代替[2]。而具有开发和延伸特性的微电网能够充分促进这类具有强随机性的分布式电源的大规模接入,从而得到了高速的发展建设[3]。同时,发展电动汽车(Electric Vehicle, EV)是保障低碳能源的趋势,我国也将电动汽车作为战略性新兴产业,微电网的发展也促使电动汽车开始广泛应用于电网的削峰填谷、抑制功率波动中[4]。
但是,在大规模电动汽车接入微电网的同时,孤岛运行的微电网的电能质量也会下降,从而引起整个微电网的不稳定[5]。因此,新型微电网结构与稳定控制策略必须能够自适应地应对各类外部环境状态、控制资源及偶然事件中的强不确定性。
为了解决孤岛单一微电网容量有限,容易受到各种非线性随机波动的影响的问题[6-7],各子微电网之间存在功率耦合关系的多微电网系统(Multi-Microgrid System, MMS)逐步被广泛应用。但是,多微电网的结构组成复杂,其稳定控制面临着更大的挑战[8],系统的频率与发电机端电压的稳定是衡量电能质量的标准。而现有研究也将PID[9-12]、模糊控制[13-15]等经典控制方法应用到多微电网的传统结构中,以此改善孤岛微电网系统的运行效果。但是,上述研究中,所选取的多微电网模型均只包含联络线间的功率交互,控制器之间不存在信息交互,难以实现各子微电网之间“去中心化”的协调控制;同时,上述研究中仅有文献[12, 15]考虑了电动汽车参与微电网调控的情况,且相应的控制模型没有考虑电动汽车站输出边界的随机性。而事实上,电动汽车在参与电网削峰填谷、抑制功率波动的同时,其输出功率约束边界会受到用户出行需求[16]、用户充电行为[17]、电动汽车移动性[18]等因素的影响。进而,文献[9,12-15]在负荷频率控制(Load Frequency Control, LFC)过程中,忽略了发电机端电压对系统有功功率平衡的影响,在实际情况中,两者的调节过程具有强耦合性。而文献[10-11]虽然考虑了端电压调控过程所引起的有功功率扰动,但其与上述研究所采用的方法均依赖权重的优化求解、参数的设置或隶属函数的建立,难以在控制模型中设定控制系统中的各类约束条件,对多微电网复杂拓扑结构变化、电动汽车与分布式电源的强随机性的适应性不足。
此外,也有相关研究开始基于这些方法完成逆变器设计[19],以实现微电网负荷频率控制,例如文献[20]提出了一种多重逆变器复杂控制策略用于微电网的运行控制,但可控负载和高比例新能源单元会给这类转换器的设计过程带来巨大挑战。
基于此,能够将控制过程转换为求解优化问题,从而很好地适应分布式电源与电动汽车的强随机性的鲁棒模型预测控制(Model Predictive Control, MPC)[21]被应用于含电动汽车多微电网的控制中。文献[22]则基于鲁棒模型预测控制理论,设计了一种改进的带有线性二次调节器的鲁棒模型预测控制器,可用于含电动汽车多微电网的频率控制;文献[23]提出了一种新的自适应智能模型预测控制方案,能够在考虑到电动汽车电池荷电状态(State of Charge, SOC)控制的情况下完成多微电网系统的稳定性控制。但是,上述多微电网模型均没有考虑发电机端电压调节和系统频率控制之间的耦合关系,且传统的鲁棒模型预测控制在面对电动汽车站输出边界发生周期性变化、端电压调控引起有功干扰,以及系统遭遇极端扰动等强非线性影响时,已经整定好参数的控制器不具有进化性能,其控制性能会受到较大影响,甚至导致闭环系统不稳定;同时,各控制器独立存在于各个子微电网中,不存在信息耦合关系,因此各子微电网之间无法根据实时运行环境提前实现协调互助和“去中心化”协调控制。
现今,具备在线学习与经验回放能力的强化学习智能算法已经得到了深入的研究[24],其可通过数据的有效积累保证控制能力在训练过程能够持续的进化。机器学习在微电网中的研究更多地集中在单一智能体在微电网控制中的应用,文献[25]与文献[26]分别基于R(λ)学习与深度Q学习算法,设计出能够应对孤岛单一微电网中分布式电源随机性的负荷频率控制器,但这些算法的动作空间是非连续性,在应用于含电动汽车多微电网这种复杂场景时,可能会出现动作空间“维数爆炸”的问题。同时,多智能体算法具有“集中式训练、分布式执行”的协调控制思想[27],能够更好地适应分布式电源的强随机特性、系统频率与发电机端电压耦合作用与电动汽车的随机输出功率约束。文献[28]将多智能体深度确定性策略梯度(Multi-Agent Deep Deterministic Policy Gradient, MA-DDPG)应用于多微电网系统的负荷频率协同控制中,能够很好地保证多微电网系统的整体稳定性。但是,文献[28]与文献[25-26]中的机器学习控制器的输出直接连接并决定了各调频机组的出力,其主要基于数据的有效积累,以保证控制能力在训练过程能够持续的进化。该过程可被视为黑盒子,当这类机器学习控制器一旦遇到训练中未曾遇到的复杂场景,则无法保证正常输出,将直接影响到微电网中调频机组的正常运行,难以应用到含电动汽车多微电网这种安全性要求比较高的工程应用中。
因此,本文提出一种基于可进化模型预测控制的含电动汽车多微电网智能发电控制策略。
1)在系统模型设计方面,基于控制器互联的新型多微电网控制结构,考虑了发电机端电压调节和系统频率控制之间的耦合关系,为实现系统频率与发电机端电压在孤岛微电网运行下的自治协调控制提供模型基础,更加符合实际场景。
2)在算法设计方面,设计出可进化的MPC与PI参数自适应控制器。控制器中的DDPG多智能体组可以在经验积累的基础上不断进化,从而根据含电动汽车多微电网的复杂运行场景对MPC与PI控制器的权重参数进行自适应调整;同时在“集中式训练、分布式执行”的架构下,能够根据实时运行状态信息实现各子微电网之间的协同控制。
3)在安全运行方面,当上层机器学习智能体故障无法正常输出动作时,下层MPC与PI控制器能够采用提前整定好的参数完成控制过程,直到上层控制器恢复正常,在提高控制效果的同时保证了系统的安全性。
在电力系统中自动发电控制主要包含频率控制与电压控制,两者的调节过程具有一定耦合关系。本节将依次完成微电网系统的负荷频率控制模型与自动调压(Automatic Voltage Regulation, AVR)模型,以及相应的耦合模型。微电网中分布式电源较多,主要包含微型燃气轮机(Micro Turbine, MT)、电动汽车站与新能源机组(以风力发电为主)。
电动汽车充电站能够作为灵活储能参与微电网的频率调控过程中,但是其会因为所具有的移动性与用户行为随机性,而影响到实时的输出功率边界,由此影响到电动汽车充电站的频率调控过程;而充电站内电动汽车的实时状态与分布情况受到用户行为随机性的影响,其主要包括电动汽车的日常驾驶里程和出发/返回时间。根据文献[26],建立相应的概率密度函数,有
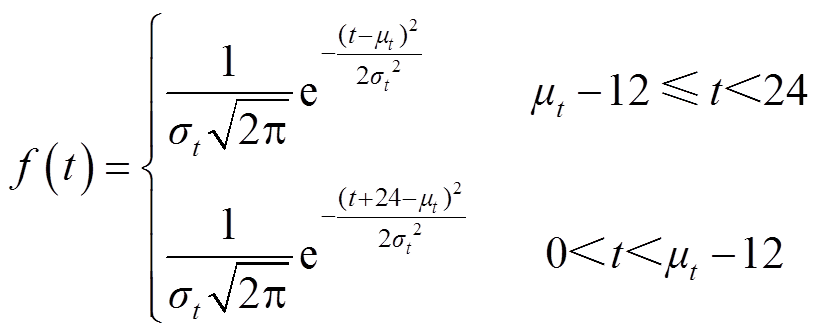 (1)
(1)
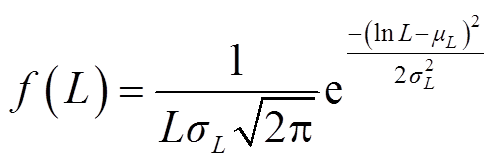 (2)
(2)
式中,μ为平均值;σ为标准差,其具体值受区域类型影响;t为时间;L为距离。
此外,电动汽车进入充电站后的初始充电过程会一直持续到充电状态达到SOCm(该值的含义为保证电动汽车拔掉电源后有足够的电量完成正常行驶过程)。由此可根据日行驶里程计算出进站后,电池荷电状态到SOCm所需的时间Tc为
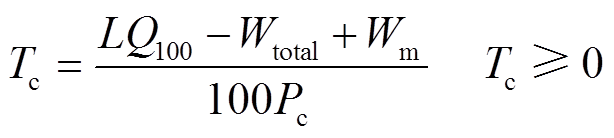 (3)
(3)
式中,Pc为充电功率;Q100为百公里耗电量;Wtotal为EV的平均满功率;Wm为SOC=SOCm时EV的平均功率。
进而,EV在站内的停滞时间可以定义为ΔT,离开充电站的时间定义为Tleave,并满足约束
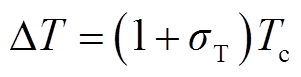 (4)
(4)
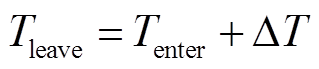 (5)
(5)
式中,σT为正随机数,取值可根据用户出行习惯确定;Tenter为进入EV站的时间。
综上所述,电动汽车输出功率边界模型如图1所示,可根据SOC0状态对进站的EV进行分类。如图1a所示,当SOC0<SOCm时,EV将进行强制充电并至少持续到荷电量达到SOCm。如图1b所示,当SOC0≥SOCm时,电动汽车可以直接参与微电网的调节过程,且这一放电过程不会使SOC低于SOCm。而SOCmax是保证电池寿命的最大SOC值,Thalfway是EV离站前的时间。即,而不同荷电状态的电动汽车将具有不同充放电状态,处于“强制充电”状态的车辆无法参与到微电网的频率控制过程中,而处于充电边界与放电边界之间的电动汽车,则能够根据微电网的实际情况,参与到微电网的调控过程中。
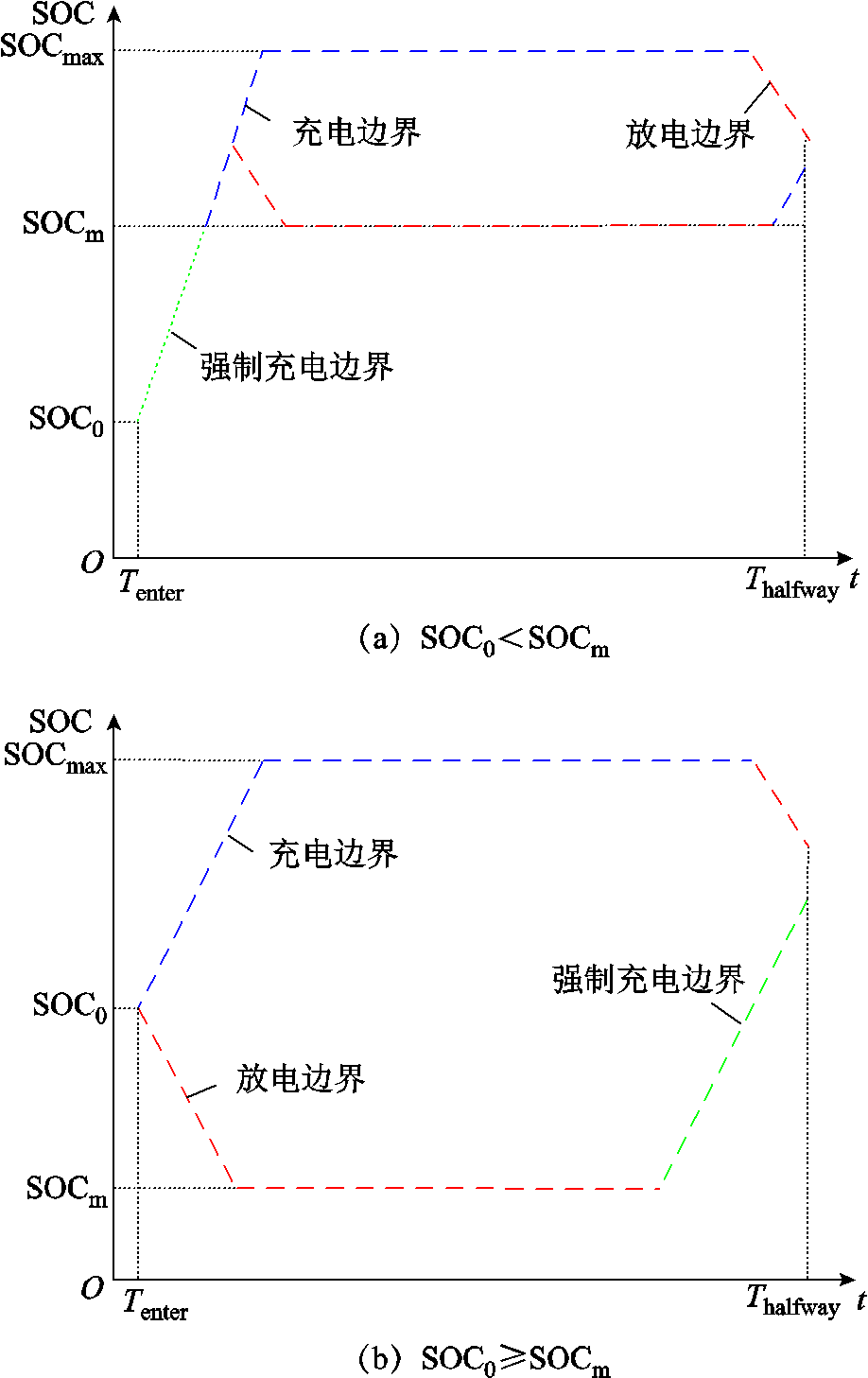
图1 电动汽车输出功率边界模型
Fig.1 Boundary model of electric vehicle output power
因此,在时间t时,站内共有n辆EV,且有i辆EV处于强制充电状态(SOC<SOCm),j辆EV的SOC达到SOCmax,所以处于不可充电状态,而剩余的EV(SOCm<SOC<SOCmax),处于可充可放的状态。由此可得EV站的输出上、下边界分别为
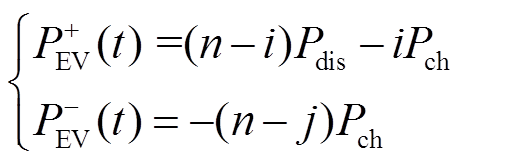 (6)
(6)
式中,Pdis和Pch分别为单体EV的平均放电和充电功率。
综上所述,电动汽车站负荷频率控制模型如图2所示,由电动汽车SOC模型、充放电边界计算中心与控制器共同组成:控制器将根据微电网实时情况发出控制指令,而该控制指令所代表的输出功率变化则受到电动汽车站实际情况的限制。图2中,ΔuEV为控制器发送给EV站的控制信号,Te为EV站时间常数,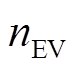 为电动汽车的数量。
为电动汽车的数量。
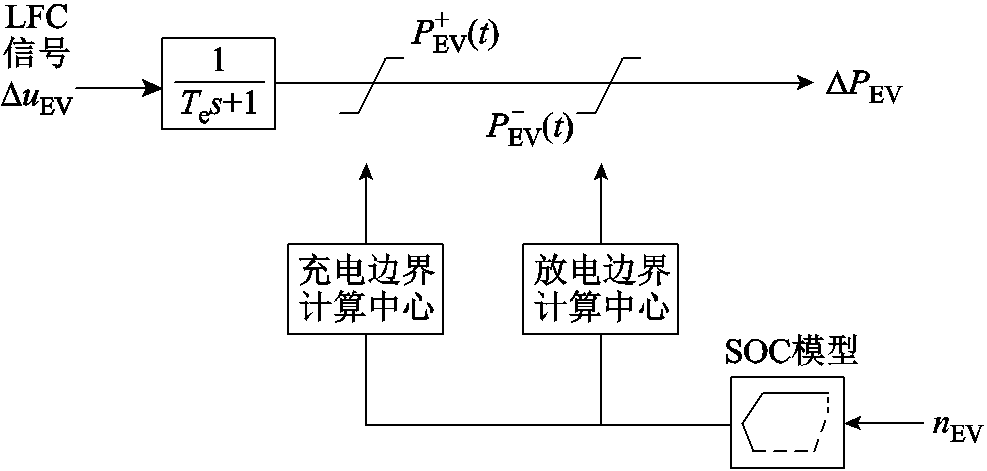
图2 电动汽车负荷频率控制模型
Fig.2 Load frequency control model of electric vehicle
本文的新能源机组以风力发电为例,且由于其频率响应特性具有极强的随机性,故可视作扰动源。此外,将微型燃汽轮机[26]作为主调频机组加入到多微电网系统中,以保证调控过程的稳定性。
由此,在不考虑发电机自动调压装置与系统频率之间的耦合情况下,可得到孤岛单一微电网的负荷频率控制模型,如图3所示。图3中,ΔPw为风电扰动功率,ΔPL为负荷扰动功率,ΔPMT为微型燃气轮机的输出功率增量,ΔPEV为EV站的输出功率增量,Ht是微电网的惯性常量,ΔuMT为控制器发送至燃气轮机的LFC信号,ΔXMT为燃料系统的阀门位置变化的增量,Tf、Tt分别为燃料系统和涡轮机的时间常数,R为调速器系数,±δmt为功率爬坡约束的上、下限,±μmt为功率增量约束的上、下限。风力发电与负载一同向系统输入扰动功率,而微型燃气轮机与电动汽车站一起作为微电网的调频机组。
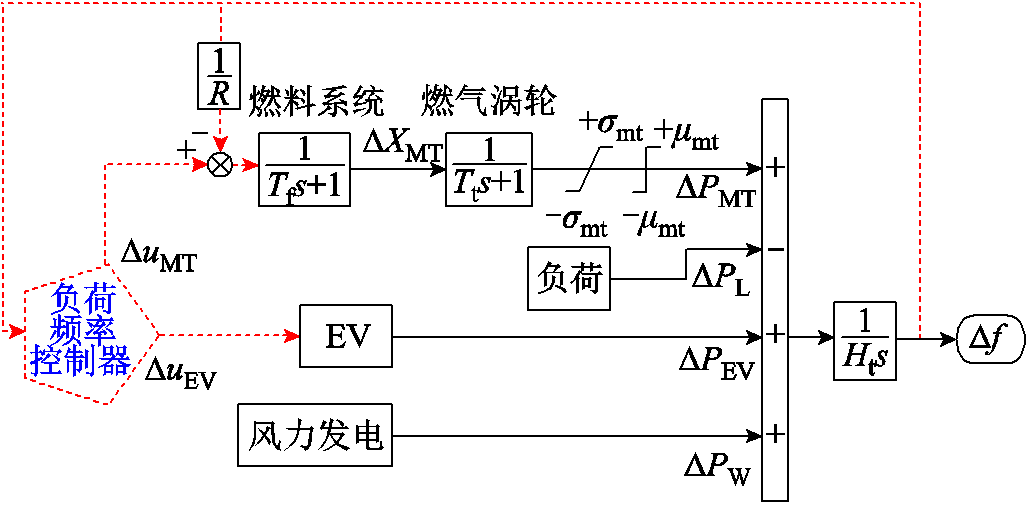
图3 含电动汽车的微网负荷频率控制模型
Fig.3 Load frequency control model of microgrid with EVs
而发电机自动调压装置能够对发电机端电压进行调控。发电机自动调压模型如图4所示,包含电压控制器、放大器、励磁装置、发电机及电压传感器。图4中,Vref为参考电压,Vt为实时实际电压,∆V为电压偏差,KA、KE和KG分别为放大器、励磁装置和发电机的增益,TA、TE和TG分别为放大器、励磁装置和发电机的时间常数。将传感器所捕获到的实时电压值与电压标准值进行比对,其生成的差值会发送给调压控制器,由此控制器发送调节信号并经过放大器、励磁装置,最终调节发电机端的励磁,从而保证无功功率的平衡,完成电压的调控过程。
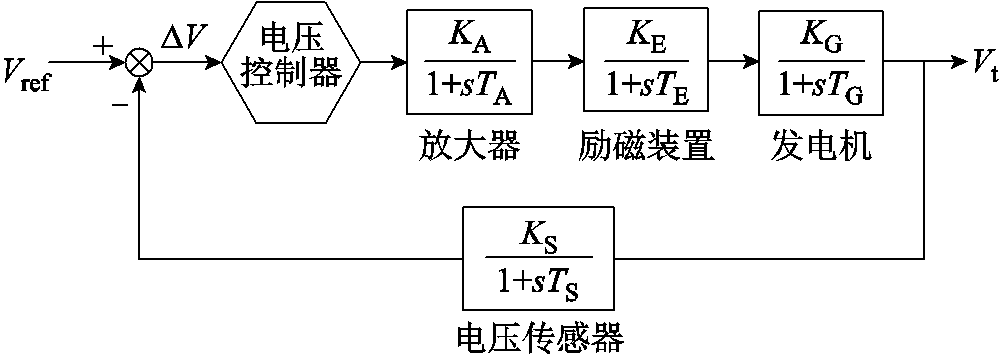
图4 发电机自动调压模型
Fig.4 Automatic voltage regulation model of generator
由此,可将微电网的负荷频率控制(LFC)与自动调压(AVR)模型进行耦合处理,所得到的耦合调控模型如图5所示。图5中,随机与负荷功率波动会通过引起频率偏差而影响到端电压的控制过程;同样地,在对端电压进行调整的过程中,AVR回路也会给微电网系统造成有功功率干扰ΔPAVR,并作用于LFC过程。由此,可搭建出多微电网系统的频率控制模型架构如图6所示。图6中,AVR方框代表发电机电压耦合调控模块,ΔPAVR为AVR回路向微电网系统输出的有功功率干扰,而ΔPti为子微网向联络线输出的功率增量。同时,本文提出了一种双层耦合控制器结构和一种控制器互连的多微电网结构。传统的联络线电力模型可以实现微电网之间的电力传输,如图6右侧点画线框中的绿色连接线所示,可以传输和连接各个微电网的电力。然而,这种传统的联络线电力模型无法在MMS中实现控制器之间的信息交换,对分布式电源即插即用、微电网拓扑变换等复杂运行环境的适应性较差。因此,本文中的MMS采用了多智能体控制。每个子微电网中的DDPG控制器之间存在互联,共享决策信息,如图6中的左侧控制器互联蓝色连接线所示。此外,每个微电网的频率偏差也反馈给每个DDPG与MPC控制器,如图所示由图6中的橙色粗虚线和频率偏差输出侧的红色虚线组成。由此,MA-DDPG 控制器组可以判断每个微电网的工作状态是否正常,并以MMS的整体稳定性为最大目标,以实现协调控制每个子微电网。
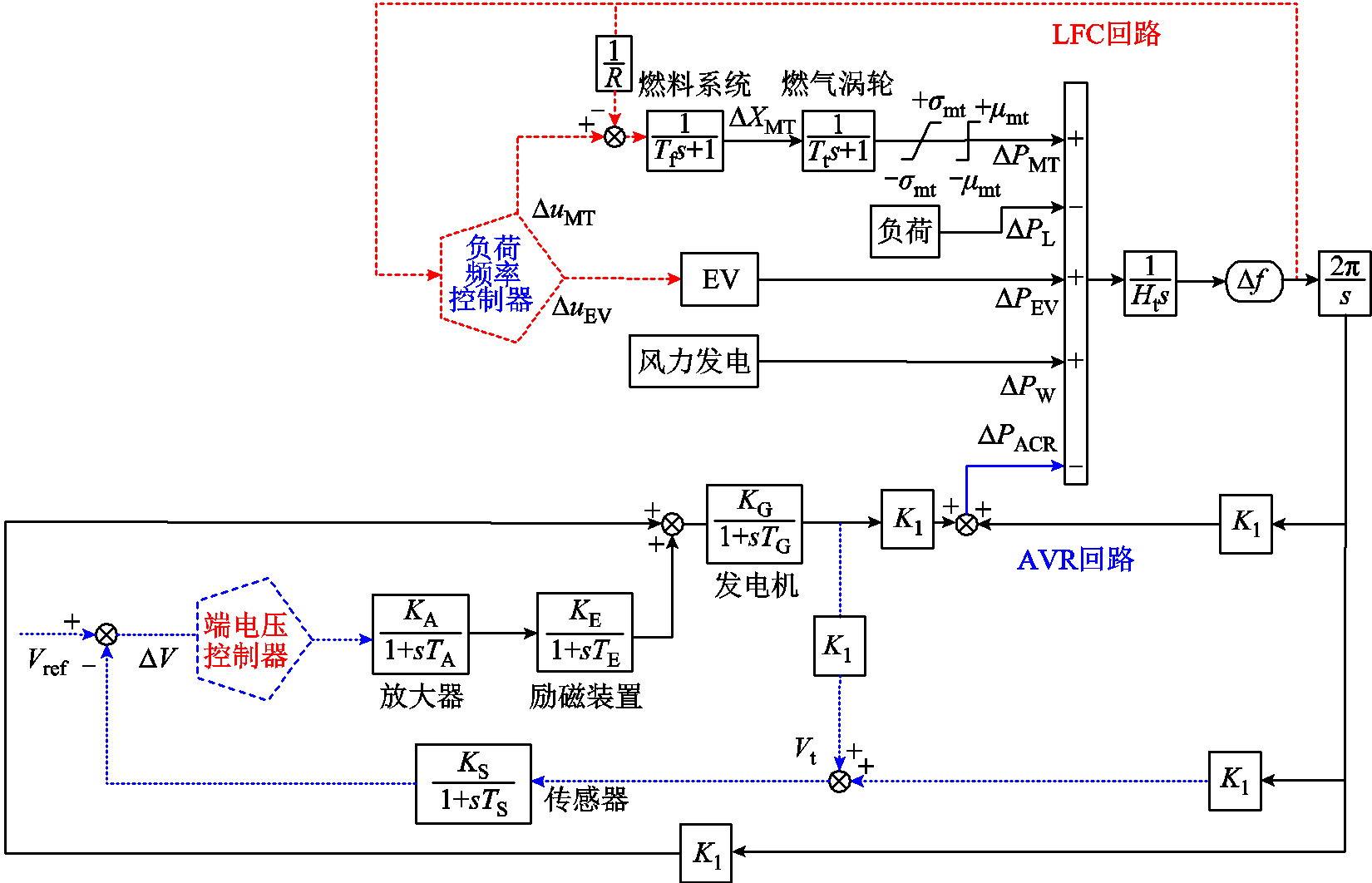
图5 负荷频率与发电机电压耦合调控模型
Fig.5 Coupling regulation model of load frequency and generator voltage
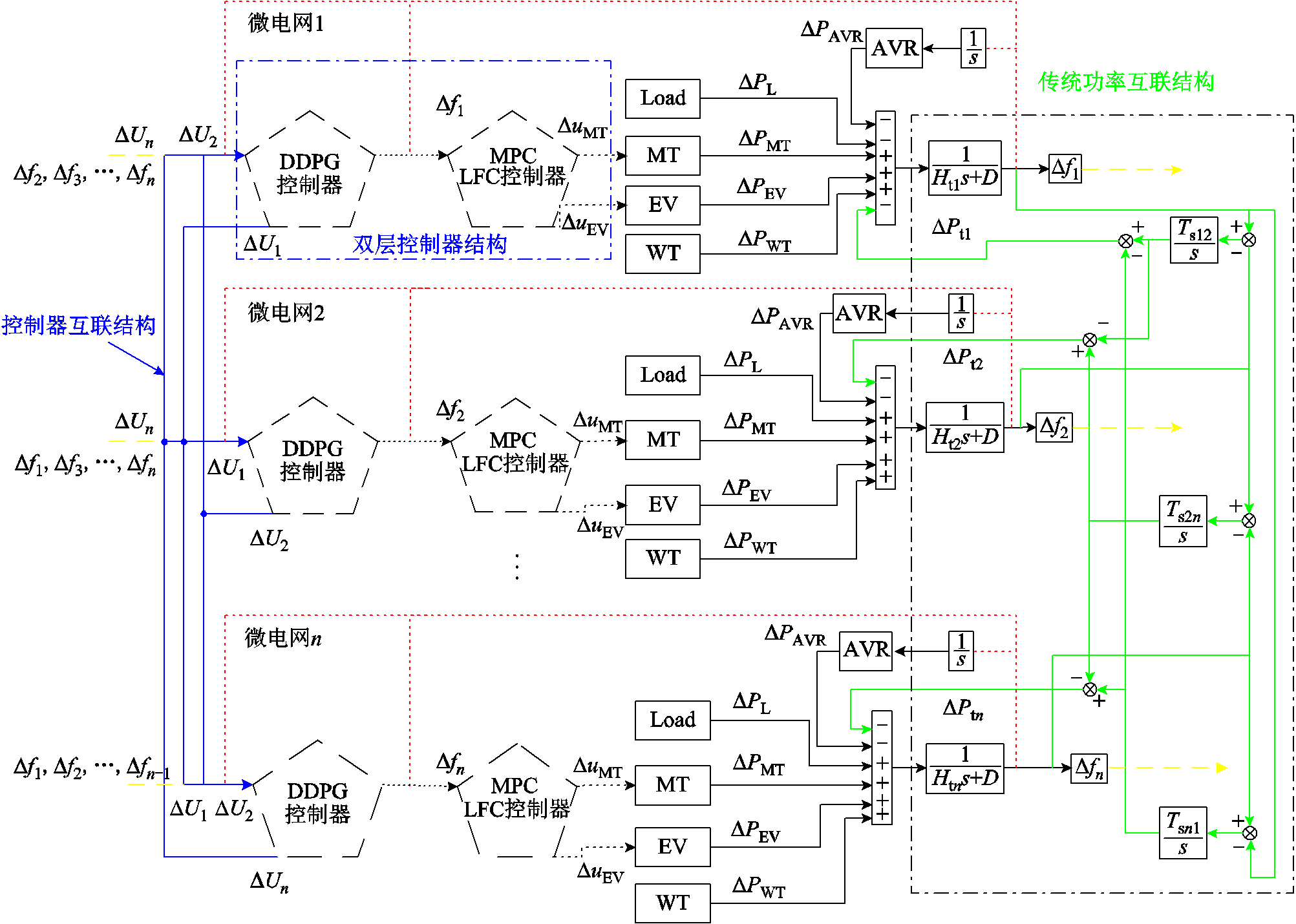
图6 考虑AVR的多微电网负荷频率控制模型结构
Fig.6 The structure of multi-microgrid load frequency control model considering AVR
进而,为了保证智能控制器的运行安全,本文提出了一种双层耦合控制器结构。如图6紫框所示,两层控制器的上层由机器学习代理组成,下层是MPC 控制器。当机器学习智能体组正常运行时,下层MPC控制器通过接收上层命令调整控制参数,根据状态空间信息调整系统单元的输出,实现频率控制;当机器学习智能体发生故障无法正常输出动作时,下层MPC控制器也可以使用预先设置的参数完成频率控制过程,直到上层控制器恢复正常。
传统的MPC不具备进化能力,其物理模型和控制参数不会随着被控对象和运行环境的变化进行自适应调整。而强化学习具备在线学习与经验回放能力,能够根据有效数据的积累,使得自身的预测能力在理论上不断进化,但其控制过程被视为黑匣子,对于很多安全性要求较高的项目来说是无法接受的。由此可见,MPC和强化学习可以相得益彰。本文采用DDPG算法实现MPC控制器中输出权重矩阵Qx的自适应调整,设计出一种基于可进化MPC的负荷频率控制器来保持多微电网的稳定性。
当鲁棒模型预测控制策略应用于多微电网控制时,各子微电网的状态空间方程需要设置为
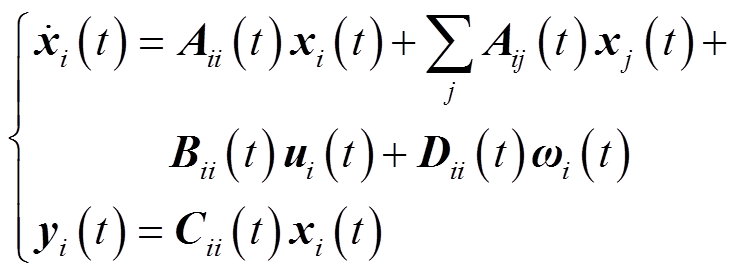 (7)
(7)
式中,ui为子微电网i的输入;xi为子微电网i的状态变量;xj为子微电网j的状态变量;yi为输出的子微电网i;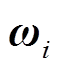 为MMS的扰动;Aii、Aij、Bii、Cii和Dii为状态空间方程的系数矩阵,其具体表达式由实际系统确定。
为MMS的扰动;Aii、Aij、Bii、Cii和Dii为状态空间方程的系数矩阵,其具体表达式由实际系统确定。
具体来说,xi为
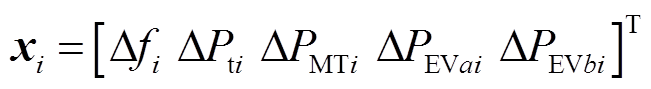 (8)
(8)
式中,Δfi为频率偏差;ΔPti为联络线功率变化;ΔPMTi为燃气轮机功率变化;ΔPEVi为电动汽车站功率变化;a和b为电动汽车站。因此,通过组合多个子微电网的状态变量,可以得到多微电网系统的状态变量为
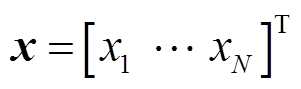 (9)
(9)
式中,N为MMS中子微电网的总数。
多微电网系统的输入、输出和扰动可以设置为
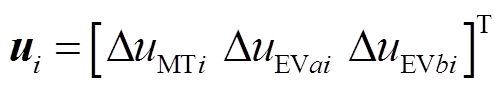 (10)
(10)
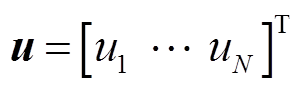 (11)
(11)
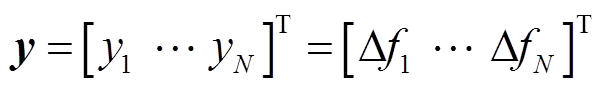 (12)
(12)
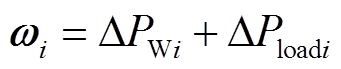 (13)
(13)
式中,输入量u为给MT和EV站的LFC信号;输出量y为MMS中各子微电网的频率偏差;扰动量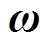 为风电随机扰动与负荷扰动。
为风电随机扰动与负荷扰动。
因此,结合上面建立的各调频单元的LFC模型和状态空间方程,状态空间矩阵可以表示为
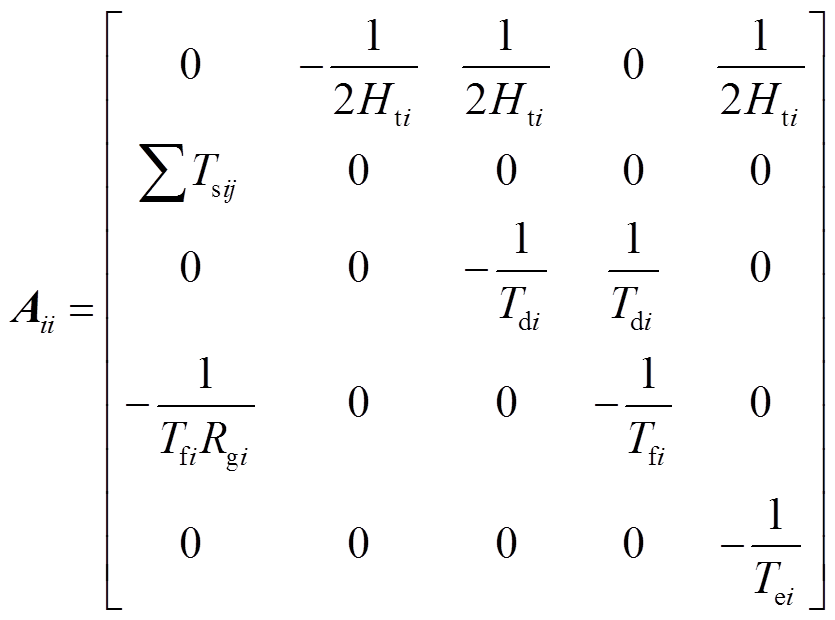 (14)
(14)
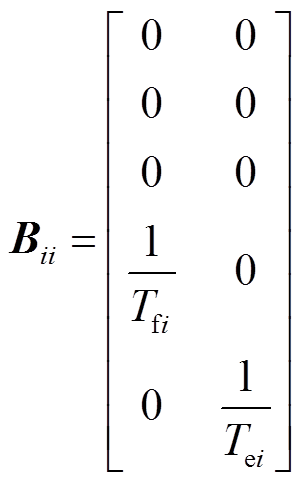
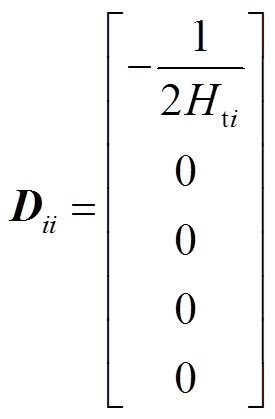 (15)
(15)
在此基础上,可以得到多微电网系统集成离散后的状态空间方程为
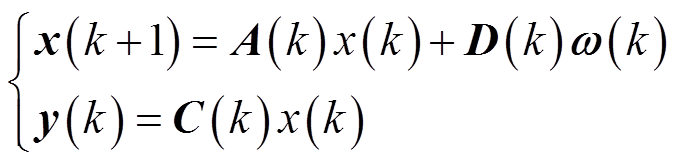 (16)
(16)
式中,A(k)、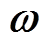 (k)、C(k)和D(k)为离散状态系数矩阵。
(k)、C(k)和D(k)为离散状态系数矩阵。
为了保证子微电网i的频率稳定性,目标函数可设置为
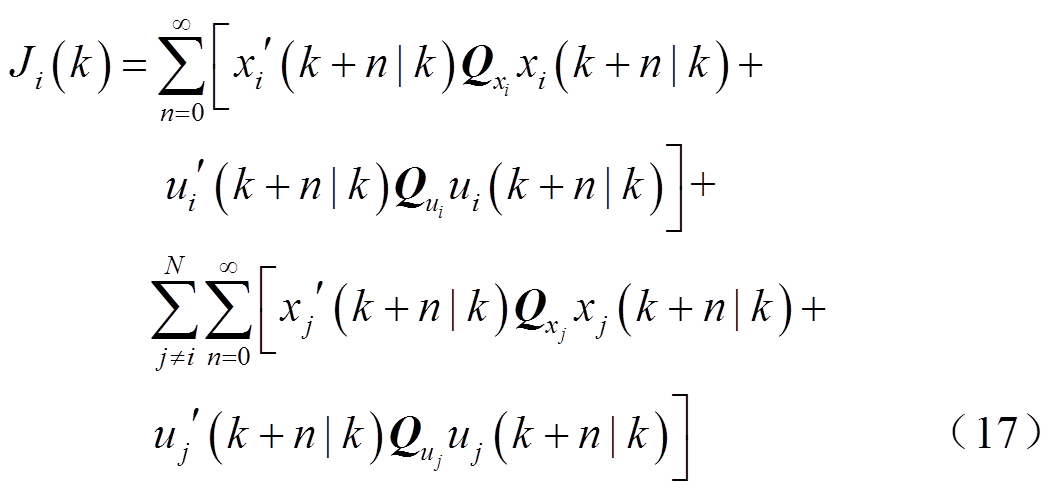
式中,Qx和Qu为权重矩阵,Qx权重矩阵的选择对优化目标的实现有非常重要的影响。因此,状态权重矩阵Qx中的qf、qt、qmt、qev是系统状态下Δf、ΔPt、ΔPMT和ΔPEV的权重。其中qf和qt可以设置为固定参数,受环境状态影响不大。而qmt和qev应该是可以随状态变化的自适应参数。此外,在式(17)中,n为预测长度,mxi和mui为状态量和输入量的数目。此外,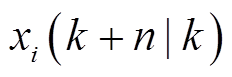 与
与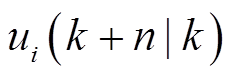 表示子微电网i在时间k+n (n>0)的预测状态和输入量,它们是系统基于时间k时的信息得到的。
表示子微电网i在时间k+n (n>0)的预测状态和输入量,它们是系统基于时间k时的信息得到的。
综上所述,微电网的频率控制过程可以转换为一个优化问题,即目标是最小化目标函数的上限,并添加对多微电网、分布式电源和电动汽车的约束[22],有
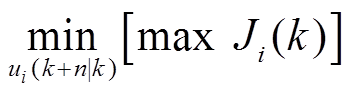 (18)
(18)
作为一种深度强化学习,DDPG可以实现MPC算法中输出权重矩阵Qx的自适应调整。控制器结构对比示意图如图7所示。图7a显示了以机器学习算法为核心的单层控制器的结构设计[28]。强化学习控制器直接与微电网相连,并向微电网的各个调频单元发送控制信号。如果强化学习控制器遇到没有学习过的极端场景时,其控制能力就会失效,无法输出合理的动作,导致微电网系统不稳定。因此,本文提出了一种基于DDPG与MPC的双层耦合控制结构,如图7b所示,当强化学习智能体出现故障时,MPC控制器也可以使用预先设置的参数完成频率控制过程,直到强化学习智能体恢复正常。
此外,如图7b所示,以子微网MG1中的智能体1为例,智能体1可以检测到每个采样周期内的当前环境信息,包括每个子微电网的频率偏差集ΔF=[Δf1 Δf2 Δfn]和其余智能体的输出动作集ΔU=[Δu2 Δu3
Δfn]和其余智能体的输出动作集ΔU=[Δu2 Δu3 Δun]。在获取环境信息后,智能体会输出动作集ΔU1=[qmt qev],以实现对MPC控制器控制参数的调整。进而,MPC控制器将根据环境信息向微电网发送实时LFC信号ΔAi=[ΔuMTi ΔuEVi],从而控制子微电网中各调频单元的输出功率,实现有功功率平衡,抑制系统频率波动。
Δun]。在获取环境信息后,智能体会输出动作集ΔU1=[qmt qev],以实现对MPC控制器控制参数的调整。进而,MPC控制器将根据环境信息向微电网发送实时LFC信号ΔAi=[ΔuMTi ΔuEVi],从而控制子微电网中各调频单元的输出功率,实现有功功率平衡,抑制系统频率波动。
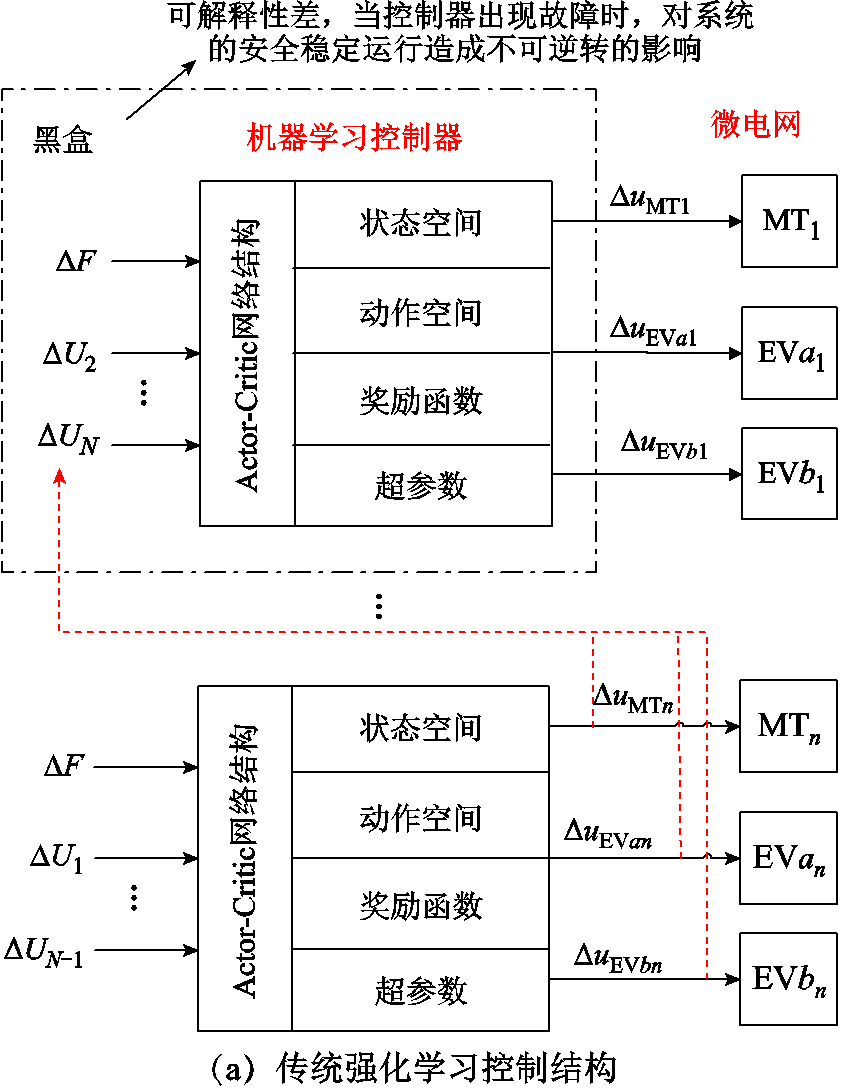
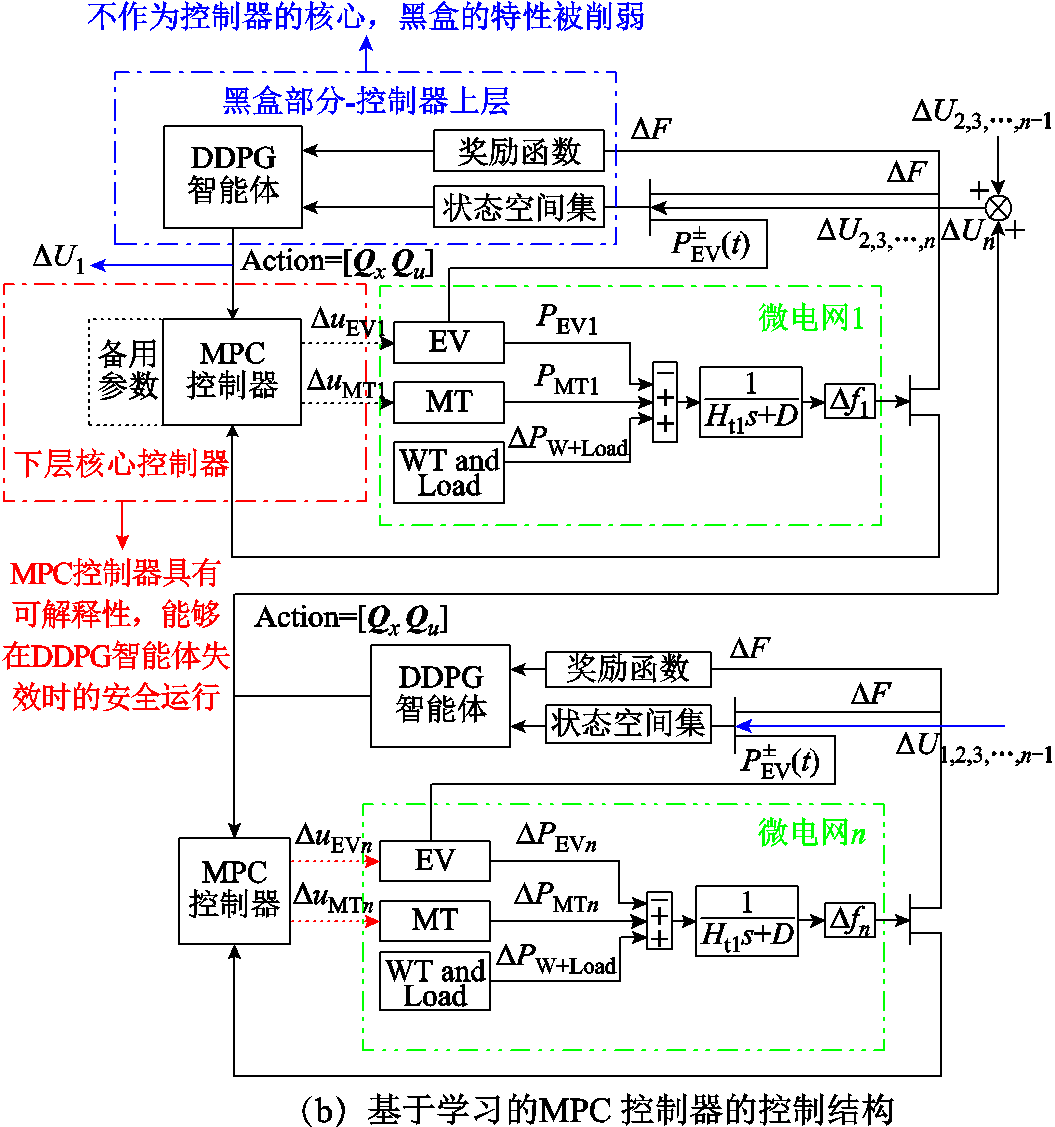
图7 控制器结构对比示意图
Fig.7 Schematic diagram of the controller structure comparison
综上所述,DDPG算法中的动作集U代表了智能体在当前环境状态S下所执行的动作,本文DDPG智能体的动作集可以定义为MPC控制器的可调输出权重矩阵,即
同时,根据实际情况,权重矩阵的值应该是大于等于0的实数,且权重上限过大会引起动作空间过大。因此,对动作空间的约束设置合适的基准值后,标幺化后的动作集可以设置为
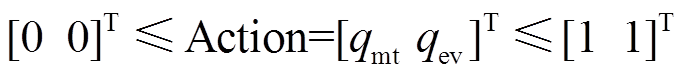 (20)
(20)
而智能体的环境空间则为微电网频率控制闭环系统的状态量:实时频率偏差ΔF(t)、实时上下限约束集和电动汽车充电站充电功率。由此,状态空间S可以定义为
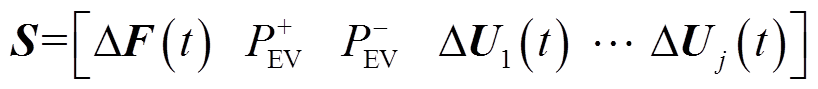 (21)
(21)
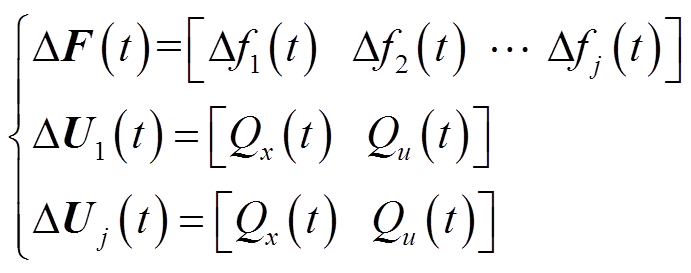 (22)
(22)
此外,优秀的奖励函数可以提高强化学习的训练收敛速度,不合理的奖励规则甚至会导致平均奖励曲线出现振荡。因此,根据我国电力安全工作规定的原则,并考虑一定的调整死区,以微电网1中的智能体为例,其奖励函数可设计为
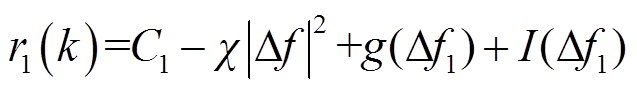 (23)
(23)
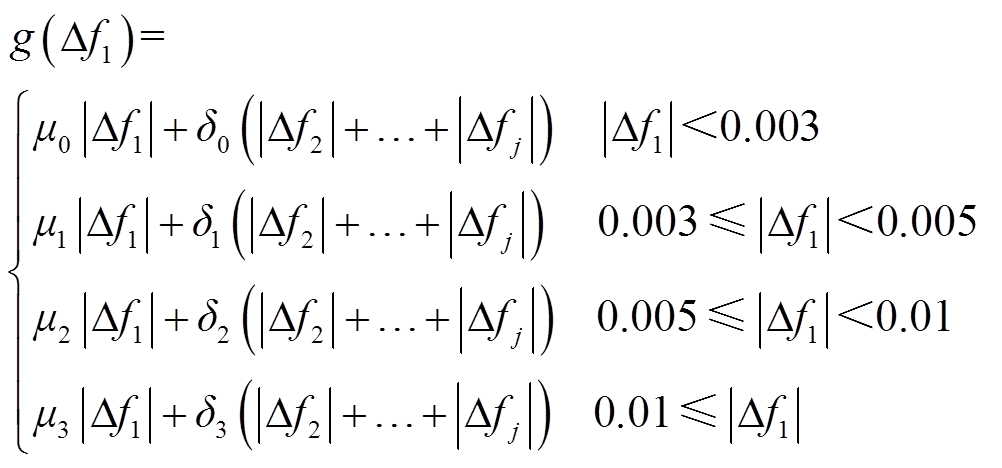 (24)
(24)
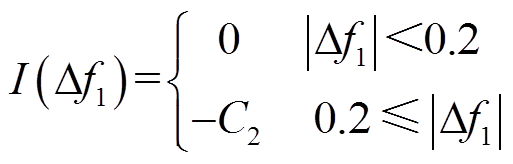 (25)
(25)
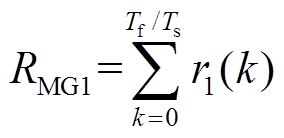 (26)
(26)
式中,μ0、μ1、μ2和μ3为子微电网1频率偏差所对应的权重系数;δ0、δ1、δ2和δ3为其余子微电网频率的权重系数;C1为循环过程中的固定奖励:一个循环中的总步长越长,固定奖励的总值就越大,从而鼓励智能体尽可能避免训练暂停的情况;χ为固定惩罚因子,以对频率波动进行惩罚;g(Δf)为不同频率波动死区下的惩罚值;I(Δf)为终止惩罚,当触发该惩罚项时,系统会自动停止训练;C2为终止惩罚值,该惩罚值的数额极大,远大于其余类型的惩罚值。
可见,当某个子微网的的智能体环境满足终止状态时,所有智能体都将结束本轮训练,即无法输出动作并获取奖励值。只有当各智能体协调配合,保证系统中没有任何一个智能体环境满足终止条件,才能在整体上获得高额奖励值。而最终的参数取值需要通过大量的基于实例的仿真验证来获得,以保证学习的收敛速度和效果。
进而,需要设计位于各个子微电网之中的发电机自动调压控制器,各AVR回路相互独立,仅对本子微电网的LFC过程造成直接性的影响。因此其控制难度低于LFC过程,仅需应用基于DDPG的PI算法,以减少设计难度与建设成本。
DDPG智能体的状态空间可设置为:实际电压与参考电压误差的标幺值DV,实际电压的标幺值V、电压误差的标幺值的积分∫DV。
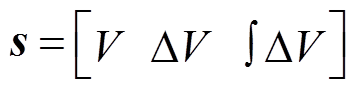 (27)
(27)
式中,DV=V-1。
因此,DDGP的输出动作将对PI控制参数进行实时调节,即为比例系数KP与积分系数KI。
电压控制器的奖励函数的设计思路与前文类似,实时电压偏差越大,智能体所得到的惩罚值越大。因此可得所有电压控制器的奖励函数为
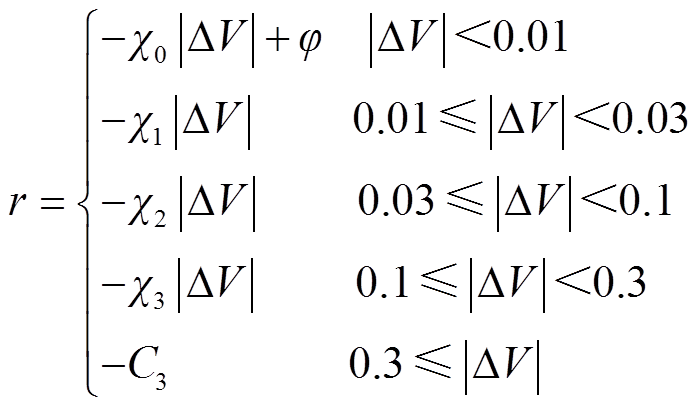 (29)
(29)
式中,χ0、χ1、χ2、χ3为不同电压偏差区间对应的惩罚系数;φ为正奖励值;C3为智能体进入终止状态时获得的最大惩罚值。
为了评估上述策略的控制效果,构建了一个包含3个子微电网的多微电网系统,其具体构架如图8所示。子微电网编号分别为MG1、MG2、MG3,具体机组参数设置见表1。
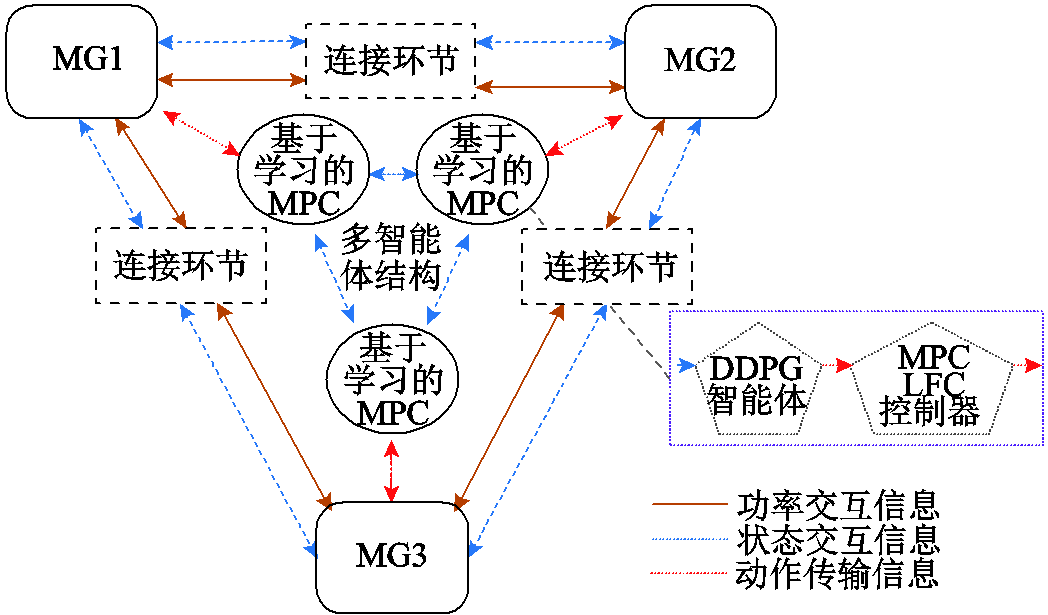
图8 本文多微电网系统结构
Fig.8 Structure diagram of multi-microgrid system
表1 多微电网LFC模型的系统参数
Table1 System parameters of multi-piconet LFC model
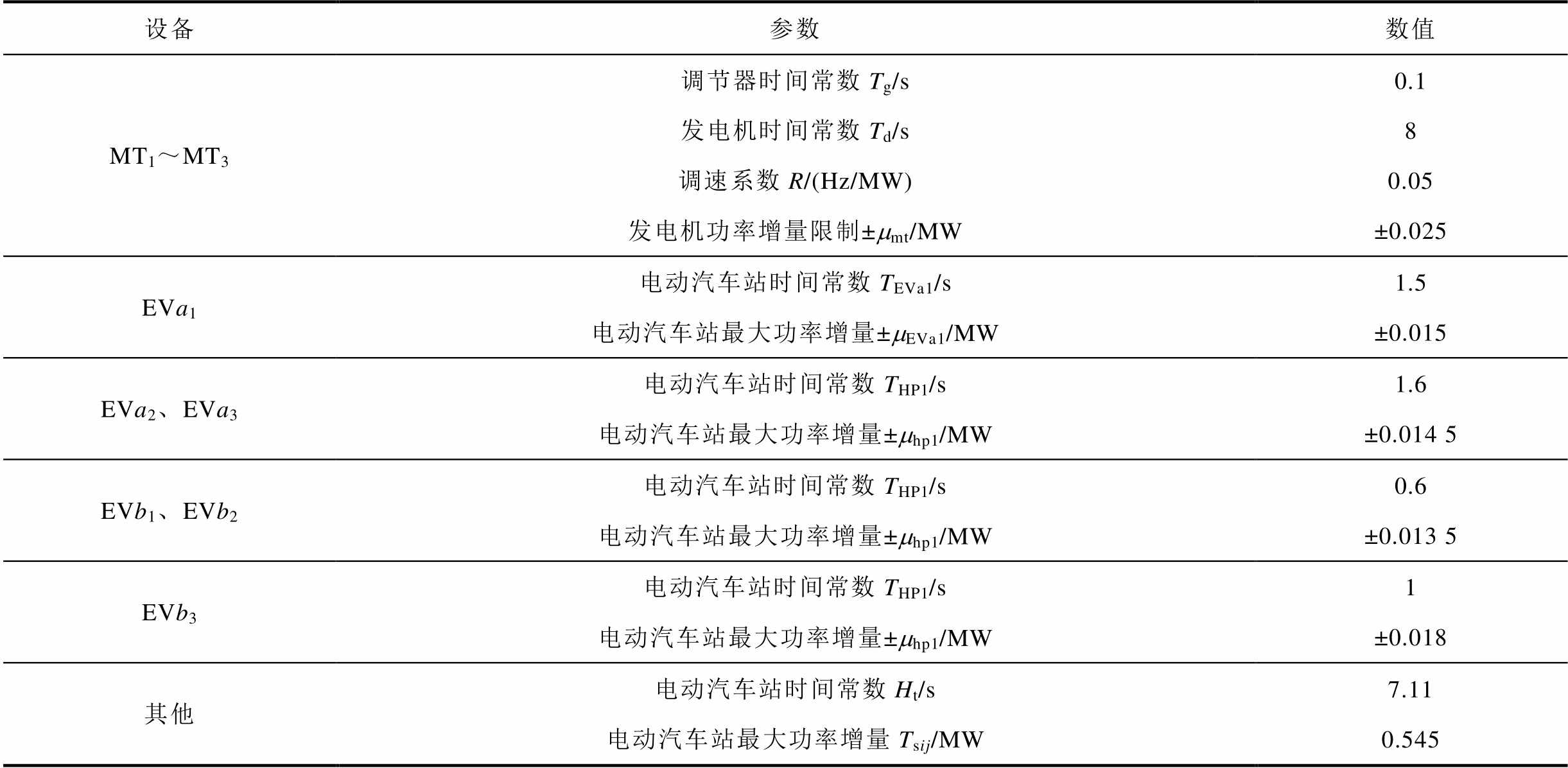
设备参数数值 MT1~MT3调节器时间常数Tg/s0.1 发电机时间常数Td/s8 调速系数R/(Hz/MW)0.05 发电机功率增量限制±mmt/MW±0.025 EVa1电动汽车站时间常数TEVa1/s1.5 电动汽车站最大功率增量±mEVa1/MW±0.015 EVa2、EVa3电动汽车站时间常数THP1/s1.6 电动汽车站最大功率增量±mhp1/MW±0.014 5 EVb1、EVb2电动汽车站时间常数THP1/s0.6 电动汽车站最大功率增量±mhp1/MW±0.013 5 EVb3电动汽车站时间常数THP1/s1 电动汽车站最大功率增量±mhp1/MW±0.018 其他电动汽车站时间常数Ht/s7.11 电动汽车站最大功率增量Tsij/MW0.545
基于此,本文基于多微电网结构进行大量仿真测试,能够获得奖励函数中各权值及超参数的具体取值:μ0、μ1、μ2和μ3为0.18、0.08、0.03、0.01;δ0、δ1、δ2和δ3为0.1、0.04、0.015与0.005;χ0、χ1、χ2与χ3为1、5、10与15; C1=0.01,C2=10,χ=10,φ=5,C3=200;折扣因子g为0.9,学习率a为0.001。
DDPG算法隶属于一种深度强化学习,该控制器在投入使用前需要经过一段随机试错的预训练阶段。在该阶段,智能体能够根据大量有效数据完成经验的积累,从而获得最优值函数Q网络[30],并由此保证其投入运行后的稳定性。以MG1中的频率控制器为例,其具体的训练过程如图9所示。
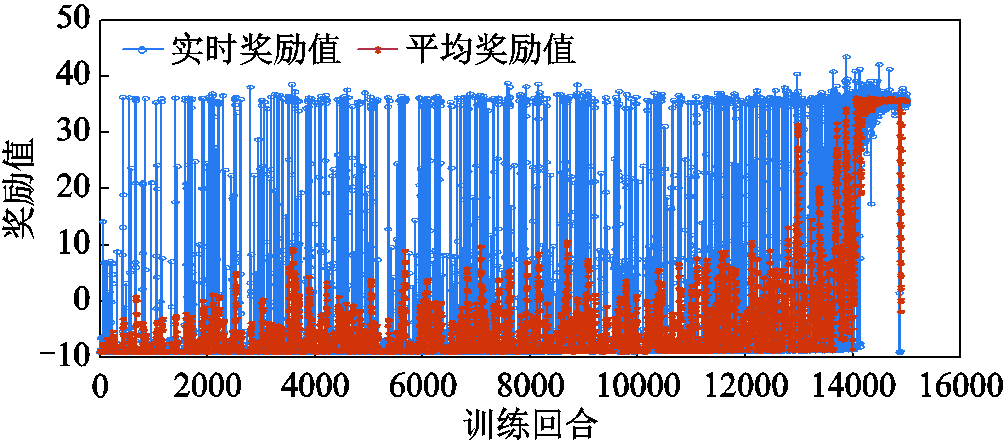
图9 频率控制器的智能体训练过程
Fig.9 Agent training process of frequency controller
由图9可见,频率控制智能体训练了15 000回合,共耗时163 457 s。在整个训练过程中,频率控制器的智能体起初无法适应AVR回路、电动汽车和分布式电源的随机性带来的非线性效应,实时奖励函数波动很大,且平均奖励仍然很低。而在训练后期,智能体逐渐进化,其输出动作的质量得到显著提升,实时奖励函数和平均奖励函数均达到了高水平,这意味着所设计的控制器收敛速度快、振荡小、在线学习能力强,可用于多微电网不同情况下的稳定性仿真。
经过预学习后的DDPG-PI控制器可以根据发电机端电压变化,实时地调整控制参数,使端电压更快达到额定值。为体现DDPG-PI控制器的优越性,引入传统PI控制器进行对比,如图10所示。
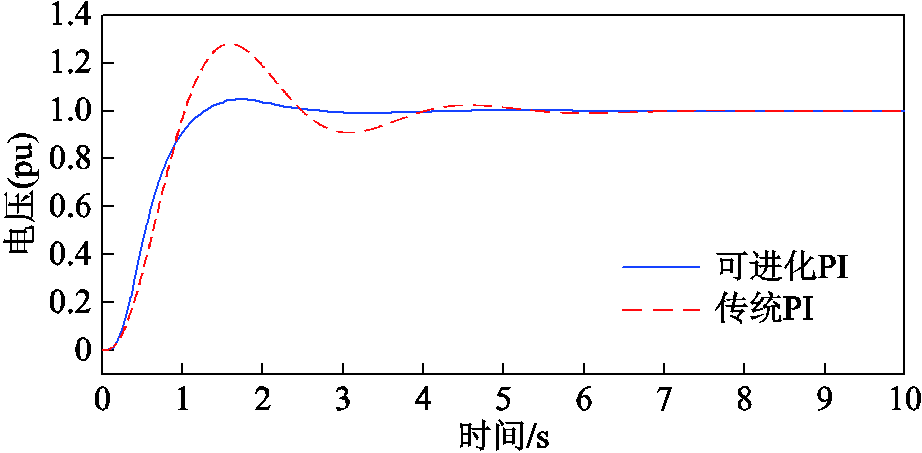
图10 微电网AVR回路端电压
Fig.10 The terminal voltage regulation process of the AVR loop of the microgrid
可见,传统PI控制具有较大的超调量且响应速度较慢,而可进化PI控制器下的电压响应速度较快,且不存在超调量,电压更易稳定。同时,DDPG控制器对PI控制器参数实时优化的结果如图11所示。
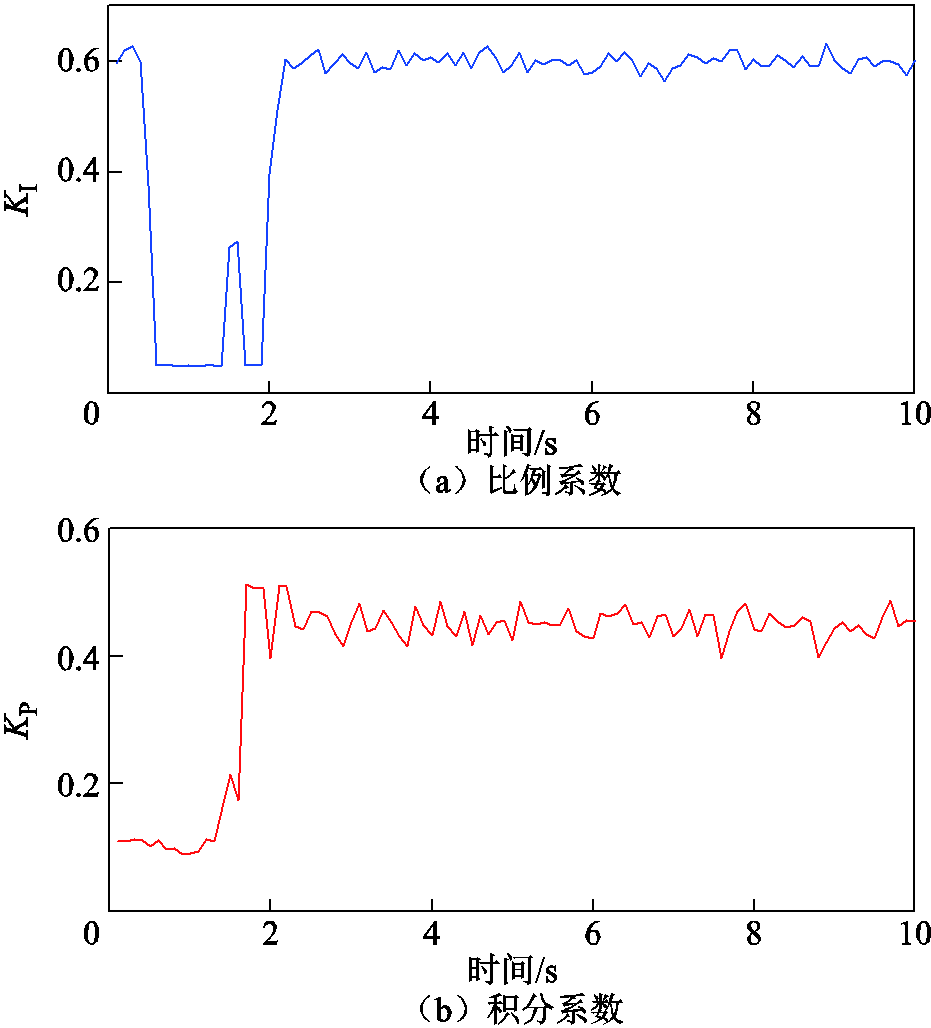
图11 PI控制器参数优化结果
Fig.11 PI controller optimization parameters
可见,DDPG-PI控制器能够实现控制器参数自适应,在不同的阶段选择不同的比例-积分系数。同时,为了验证AVR回路和LFC回路存在一定程度上的耦合,可在传统控制下的多微电网中,于0 s时对子微电网1施加0.04(pu)的有功功率干扰,分析AVR回路对LFC的影响,考虑与不考虑AVR耦合时的频率偏移如图12所示。
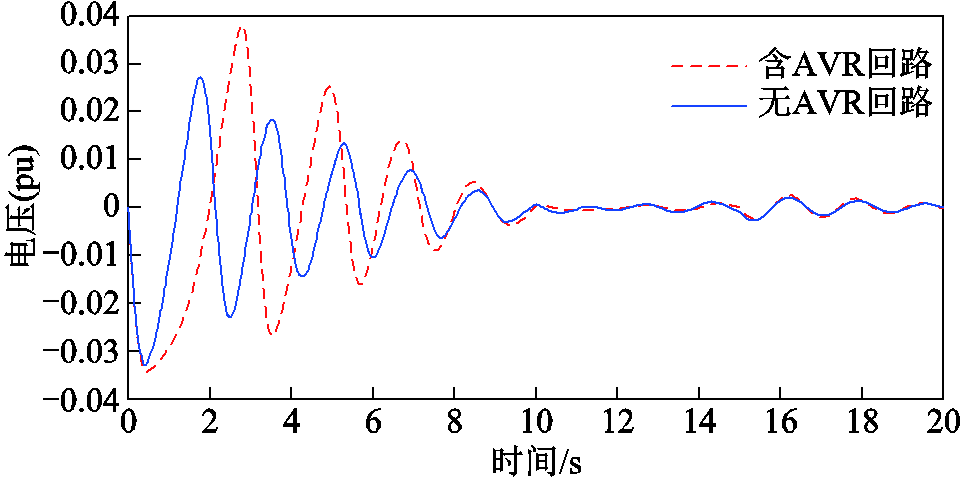
图12 考虑与不考虑AVR耦合时的频率偏移
Fig.12 Frequency deviation with and without AVR coupling
可见,AVR回路增加了多微电网系统的有功功率干扰,从而使得负荷频率发生了更大的偏移,这对LFC控制器提出了更高的要求。而后文有关负荷频率控制相关的算例场景中,所使用的多微电网模型均将考虑AVR回路的影响。
假设某工作日0:00,对稳态微电网系统的随机扰动包括负荷扰动和风电扰动,且组合扰动的具体情况如图13所示。可见,负荷扰动呈现2次相反的阶跃,因此在50 s后即为0,此后总扰动完全与风电扰动重合。而在85 s后,为了能够在扰动逐渐消失后,比较各控制算法下微电网频率的恢复速度,作者在原有的风电历史数据后,加入了一段稳态过程。并假设MG1在60 s发生极端故障,微型燃气轮机无法输出功率,即ΔP=0。
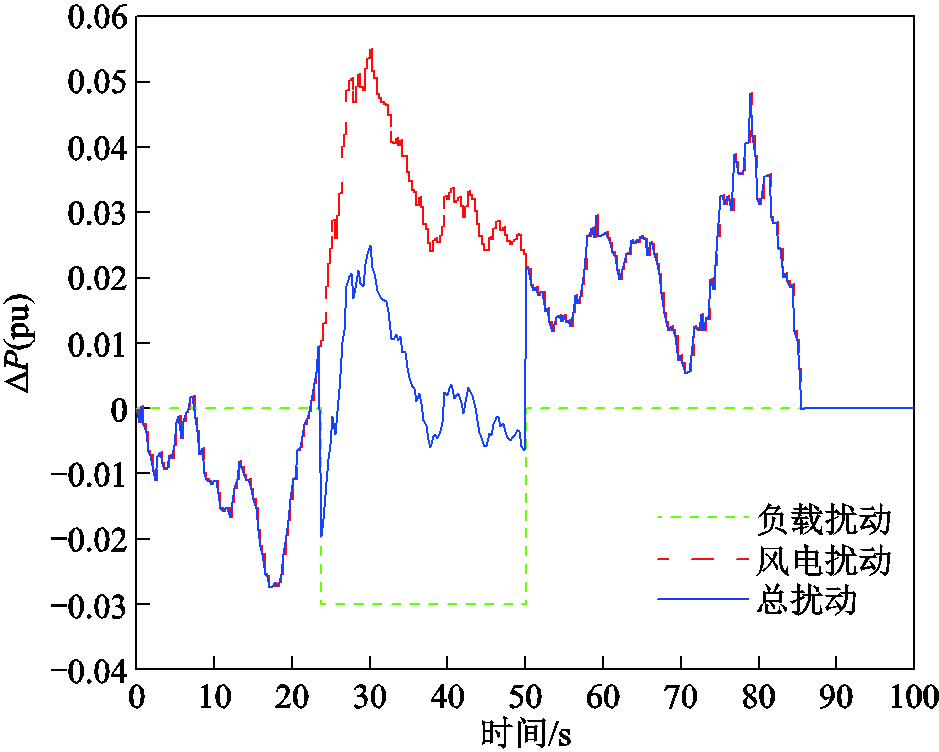
图13 多微电网系统受到的强随机扰动
Fig.13 Strong random disturbance to multimicrogrids
基于此,以子微电网1为例,在不同控制器管控下的频率波动如图14、图15所示。与 PID 控制、模糊控制和传统的 MPC相比(控制器参数与结构见附录),本文提出的基于学习的MPC控制器具有最好的性能。同时,可将MG1的频率偏移绝对值作为考核对象,考核优秀率阈值可设置为±0.01 Hz,85 s后恢复至0.005 Hz以下所需时间定义为恢复时间。从而得到此场景下的频率控制效果分析见表2、表3。
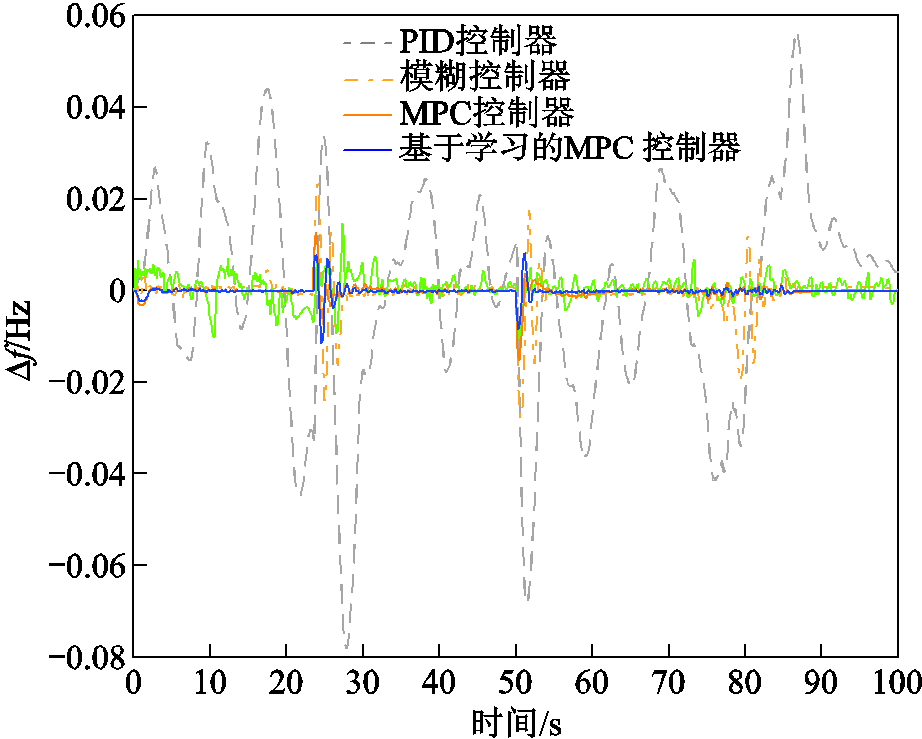
图14 强随机扰动下的多微电网系统频率偏差
Fig.14 Frequency deviation of multi-microgrid system under strong random disturbance
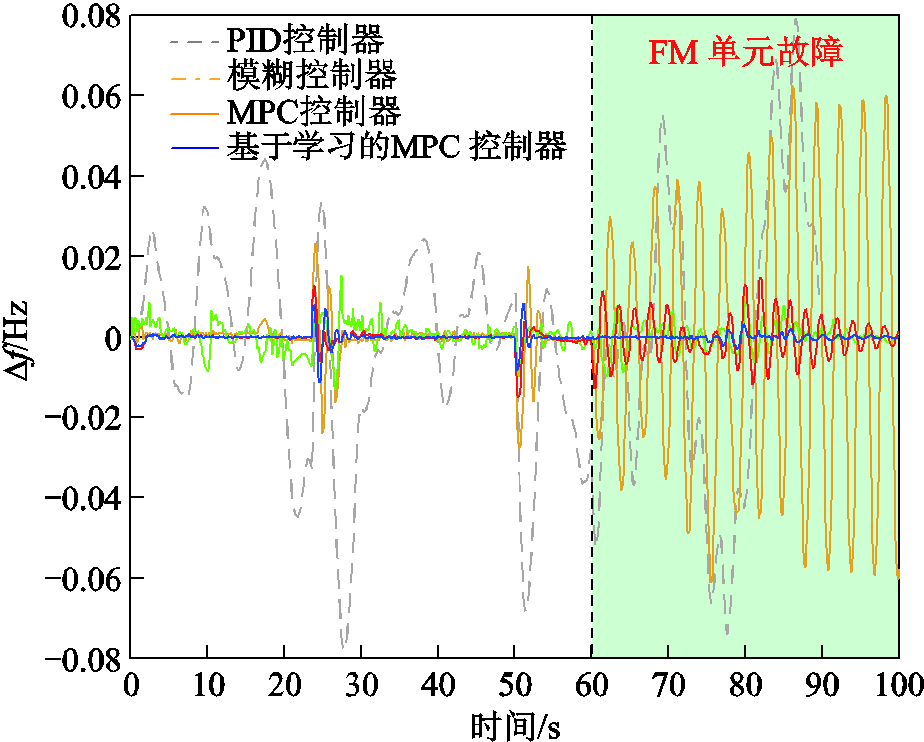
图15 发生极端故障时的多微电网系统频率偏差
Fig.15 Frequency deviation of multi-microgrid system under strong random disturbance
表2 强随机扰动下的微电网1的控制结果(0:00)
Tab.2 Control results of microgrid 1 at 0:00

控制类型平均值/Hz最大值/Hz恢复时间/s优秀率(%) PID控制器0.018 590.077 97>1035.00 模糊控制器0.0020.0277 4<194.25 DDPG控制器0.001 3440.012 6<199.05 MPC控制器0.000 5810.015 03<199.26 可进化MPC0.000 5650.011 2<199.80
表3 发生极端故障时的的微电网1控制结果
Tab.3 Microgrid 1 control results in case 1

控制类型平均值/Hz最大值/Hz恢复时间/s优秀率(%) PID控制器0.022 680.078 37>1032.31 模糊控制器0.013 250.062 48>1064.15 DDPG控制器0.002 0590.012 6<199.05 MPC控制器0.002 2670.015 2>593.06 可进化MPC0.000 8420.011 2<199.80
由此可知,当MG1受到随机扰动与负载扰动,且部分调频机组出现极值故障时,PID、模糊和传统MPC控制下的微电网频率稳定性受到极大影响,频率控制优秀率分别下跌至32.31%、64.15%和93.06%。同时,恢复时间也均不理想:三者均达5 s以上。而深度强化学习智能体组能够以MMS整体稳定性最大化为目标,提前协调MPC控制组对MG2和MG3的功率输出进行调整,以辅助MG1防止功率失控,因此可见DDPG控制器与可进化MPC控制器管控下的微电网频率优秀率处于较高水平,但基于各评价指标的全面性分析,可进化MPC控制器依然优于纯机器学习控制器。而其管控下微电网的各设备及连线的具体功率变化如图16所示。
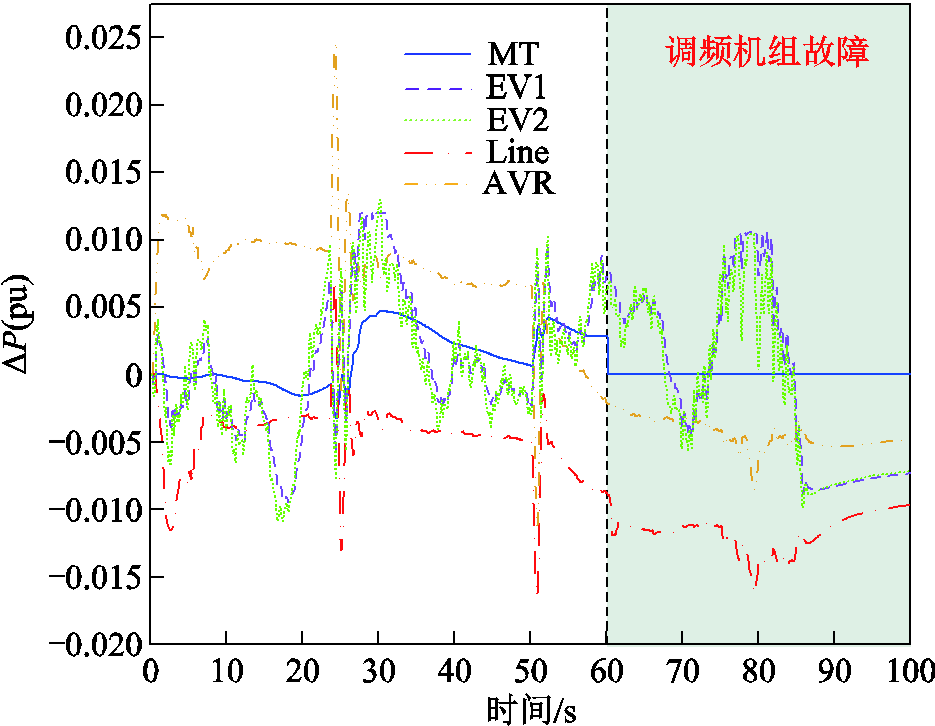
图16 场景1的微电网1中各机组输出功率增量
Fig.16 Output power increment of each unit in MG1
从图16可见,当某次微电网的调频单元遇到极端故障时,MT机组无法调节功率增量,电动汽车作为辅助调频机组,出力也得到了一定提升,而微电网之间电力交换的增加与变化尤为显著,这是通过控制器互连和输电线路实现的。此外,图16中的绿色、紫色线条呈现出明显的锯齿状,以EV1为例,其有功出力在30 s与80 s时因输出边界而发生明显的突变,发生数次小型阶跃型突变。由此可见电动汽车输出功率限幅受到用户行为的随机影响。
在实际系统中,电动汽车站的输出功率边界会在一天内发生相应变化。为了探索电动汽车对频率控制的影响,并验证所设计的控制器在面对电动汽车随机性时的鲁棒性,本节基于场景1中的仿真,并假设扰动发生在17:00,且60 s时不再发生极端故障。易知,在0:00时,几乎所有电动汽车均停留在充电站并能够参与到调频中,而在17:00时,大部分电动汽车已经离开充电站,并处于返程的行驶过程中,无法参与微电网的调频。在这种情况下,传统控制器将无法适应电动汽车站输出功率边界的阶段性突变,从而影响频率控制效果。而本文所提出的基于学习的MPC控制器能够基于预学习过程中积累的经验,实时改变MPC控制器参数以适应一日内所发生的EV站输出功率边界的变化。
在0:00和17:00时,DDPG智能体动作集的动态变化如图17所示(标幺化后)。可以看出,在每个时段内,MPC控制器的参数不会因为随机扰动而发生剧烈变化。但在一天中的不同时段中,DDPG 智能体能够分阶段调整MPC控制器的参数,以适应电动汽车站输出功率边界的周期性变化。此外,根据场景1中的评估标准,计算在没有极端故障时,三组控制器在17:00的仿真结果见表4。可以看出,在17:00,MG1 在 PID、模糊和传统MPC控制器控制下的频率调节能力明显低于凌晨0:00。但在基于学习的MPC下,MG1的频率偏移仍能保持在0.01 Hz以内,达到98.95%的优秀率,这是通过参数自适应和协调控制实现的。
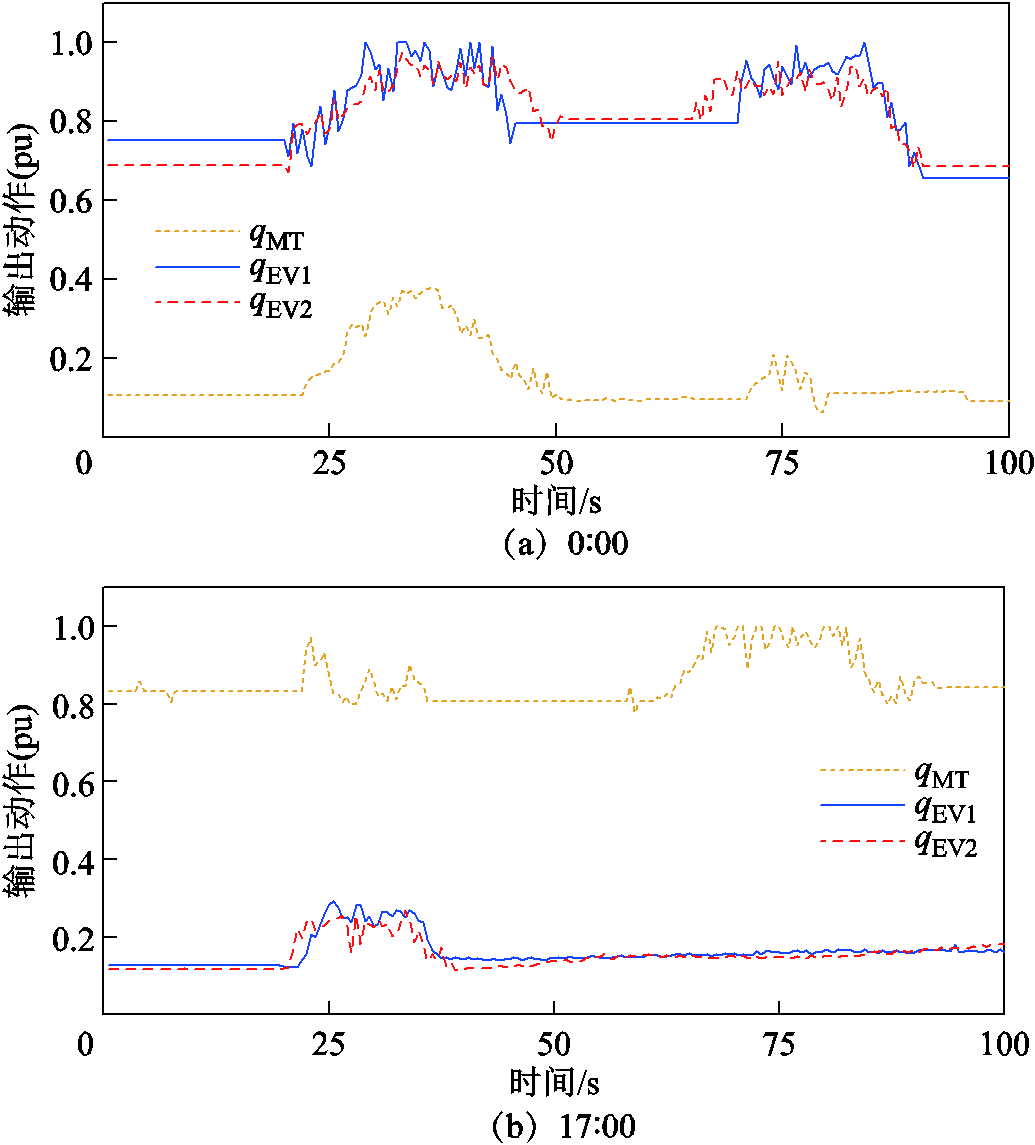
图17 DDPG智能体动作集的动态变化
Fig.17 Dynamic changes of action sets of DDPG Agents
表4 在17:00时微电网1的控制结果
Tab.4 Control results of microgrid 1 at 17:00

控制类型平均值/Hz最大值/Hz恢复时间/s优秀率(%) PID控制器0.021 960.090 16>1029.77 模糊控制器0.011 940.059 27>1070.84 DDPG控制器0.001 8550.013 2<197.13 MPC控制器0.002 0070.019 8>390.06 可进化MPC0.000 6320.012 4<198.95
进而,为了验证双层控制结构对微电网控制过程安全性的保证,在基于学习的MPC控制器和DDPG控制器之间进行了对比实验。基于场景1(调频机组不发生极端故障),假设两组系统中的DDPG控制器均在40 s时面对“未曾学习过”的复杂场景而发生故障,无法正常输出动作,并在80 s时恢复。比较两组控制器的频率控制效果,如图18所示。
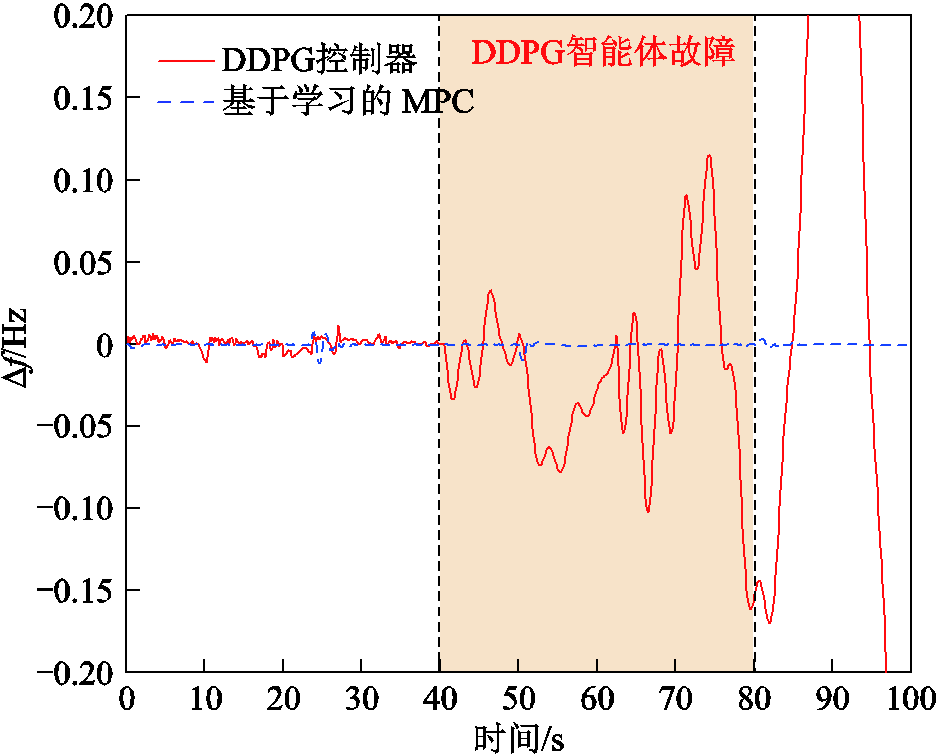
图18 机器学习控制器故障时的多微电网系频率偏差
Fig.18 Frequency deviation of multi-microgrid system when machine learning controller fails
可见,DDPG控制下的微电网系统在故障期间完全丧失了调频能力,因为DDPG智能体无法正常输出动作,不能向系统的调频单元下达指令。因此,在DDPG智能体恢复后,系统稳定性也难以恢复,严重影响微电网运行过程的安全性。而基于学习的MPC控制器采用了双层控制结构,当DDPG控制器出现故障时,MPC控制器可以在预先设定的控制参数下正常运行:在40 s时,频率发生了极小的波动,100%的频率控制优秀率在整个控制过程中依然能得到保证。
深度强化学习算法控制器在正常运行场景下的稳定性是值得肯定的,本文作者与其他学者均已在该领域建立了大量研究基础[25-26,28-29]。机器学习算法所具有的黑盒特性是其主要缺陷,在面对“未曾学习过”的复杂场景时,则有可能出现本节所描述的故障,而本文同样通过“双层控制器结构”解决了该缺陷引起的安全性问题,凸显了所提策略的优越性。
本文提出了一种可进化的模型预测控制的含电动汽车多微电网智能发电控制策略,得到结论如下:
1)与传统多微电网模型相比,考虑了控制器互联结构,并在传统负荷频率控制模型中增加了自动电压调节系统,考虑了发电机端电压调节和系统频率控制之间的耦合关系,更符合实际场景。
2)与PID和模糊控制相比,可进化的MPC控制器不仅可以根据被控对象的历史信息和未来输入预测系统的未来输出;还可以将频率控制过程转换为求解优化问题,从而很好地适应多微电网系统中的随机场景。在负载扰动和风电扰动下,基于学习的MPC控制器下的微电网频率控制效果明显优于传统控制器。
3)与传统MPC相比,基于学习的MPC控制器可以应用于控制器互联的多微电网系统,从而实现多微电网的协调控制;还可以通过DDPG智能体基于实时运行环境状态调整MPC参数,从而更好地适应系统各类复杂工况。当系统发生各类极端故障时,所提出的控制器仍能将微电网的频率波动控制在0.01 Hz以内,控制优秀率仍能达到99.8%,恢复时间小于1 s,显著增强了多微电网的稳定性。
4)与DDPG控制器相比,所提出的双层保护结构具有更强的安全性和稳定性。当机器学习智能体遭遇未学习过的环境,不能正常输出动作时,MPC控制器可以利用预先设置的参数完成频率控制过程,直到机器学习控制器恢复正常,确保微电网的频率波动控制在0.01 Hz以内,明显优于DDPG控制器。
参考文献
[1] 何晨可, 朱继忠, 刘云, 等. 计及碳减排的电动汽车充换储一体站与主动配电网协调规划[J]. 电工技术学报, 2022, 37(1): 92-111.
He Chenke, Zhu Jizhong, Liu Yun, et al. Coordinated planning of electric vehicle charging-swapping-storage integrated station and active distribution network considering carbon reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 92-111.
[2] Pascual J, Arcos-Aviles D, Ursúa A, et al. Energy management for an electro-thermal renewable–based residential microgrid with energy balance forecasting and demand side management[J]. Applied Energy, 2021, 295: 117062.
[3] 周玮, 蓝嘉豪, 麦瑞坤, 等. 无线充电电动汽车V2G模式下光储直流微电网能量管理策略[J]. 电工技术学报, 2022, 37(1): 82-91.
Zhou Wei, Lan Jiahao, Mai Ruikun, et al. Research on power management strategy of DC microgrid with photovoltaic, energy storage and EV-wireless power transfer in V2G mode[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 82-91.
[4] 随权, 魏繁荣, 林湘宁, 等. 一种基于可控负荷效率控制的孤岛微网新型调度策略[J]. 中国电机工程学报, 2019, 39(24): 7168-7178, 7490.
Sui Quan, Wei Fanrong, Lin Xiangning, et al. A novel dispatching strategy for isolated microgrid based on controllable load efficiency control[J]. Proceedings of the CSEE, 2019, 39(24): 7168-7178, 7490.
[5] 李长云, 徐敏灵, 蔡淑媛. 计及电动汽车违约不确定性的微电网两段式优化调度策略[J]. 电工技术学报, 2023, 38(7): 1838-1851.
Li Changyun, Xu Minling, Cai Shuyuan. Two-stage optimal Scheduling strategy for micro-grid considering EV default uncertainty[J]. Journal of Electrotechnical Technology, 2023, 38(7): 1838-1851.
[6] 刘迎澍, 陈曦, 李斌, 等. 多微网系统关键技术综述[J]. 电网技术, 2020, 44(10): 3804-3820.
Liu Yingshu, Chen Xi, Li Bin, et al. State of art of the key technologies of multiple microgrids system[J]. Power System Technology, 2020, 44(10): 3804-3820.
[7] Bevrani H, Feizi M R, Ataee S. Robust frequency control in an islanded microgrid: H∞and m-synthesis approaches[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 706-717.
[8] 张释中, 裴玮, 杨艳红, 等. 基于柔性直流互联的多微网集成聚合运行优化及分析[J]. 电工技术学报, 2019, 34(5): 1025-1037.
Zhang Shizhong, Pei Wei, Yang Yanhong, et al. Optimization and analysis of multi-microgrids integration and aggregation operation based on flexible DC interconnection[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1025-1037.
[9] Khokhar B, Dahiya S, Singh Parmar K P. Load frequency control of a microgrid employing a 2D Sine Logistic map based chaotic sine cosine algorithm[J]. Applied Soft Computing, 2021, 109: 107564.
[10] Esmaeili Karkevandi A, Daryani M J, Usta O. ANFIS-based intelligent PI controller for secondary frequency and voltage control of microgrid[C]//2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 2018: 1-6.
[11] 崔明勇, 曹朋, 朱大伟, 等. 基于FOPI+FOPD控制器的单区域电力系统频率控制及电压调节[J]. 燕山大学学报, 2022, 46(2): 157-165, 176.
Cui Mingyong, Cao Peng, Zhu Dawei, et al. Frequency control and voltage regulation of single area power system based on FOPI+FOPD controller[J]. Journal of Yanshan University, 2022, 46(2): 157-165, 176.
[12] Jan M U, Ai Xin, Abdelbaky M A, et al. Adaptive and fuzzy PI controllers design for frequency regulation of isolated microgrid integrated with electric vehicles[J]. IEEE Access, 2020, 8: 87621-87632.
[13] Mohammadzadeh A, Kayacan E. A novel fractional-order type-2 fuzzy control method for online frequency regulation in ac microgrid[J]. Engineering Applications of Artificial Intelligence, 2020, 90: 103483.
[14] Mahdi M M, Ahmad A Z. Load frequency control in microgrid using fuzzy logic table control[C]//2017 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Cadiz, Spain, 2017: 318-323.
[15] 项雷军, 陈昊, 郭新华, 等. 基于模糊分数阶PID的含电动汽车的多能源微电网二次频率控制[J]. 电力自动化设备, 2021, 41(11): 74-80.
Xiang Leijun, Chen Hao, Guo Xinhua, et al. Secondary frequency control of multi-energy microgrid with electric vehicles based on fuzzy fractional-order PID[J]. Electric Power Automation Equipment, 2021, 41(11): 74-80.
[16] Yang Jun, Zeng Zhili, Tang Yufei, et al. Load frequency control in isolated micro-grids with electrical vehicles based on multivariable generalized predictive theory[J]. Energies, 2015, 8(3): 2145-2164.
[17] Fan Peixiao, Ke Song, Kamel S, et al. A frequency and voltage coordinated control strategy of island microgrid including electric vehicles[J]. Electronics, 2021, 11(1): 17.
[18] Mounce R, Nelson J D. On the potential for one-way electric vehicle car-sharing in future mobility systems[J]. Transportation Research Part A: Policy and Practice, 2019, 120: 17-30.
[19] Chen Lei, Lu Xiaomin, Min Yong, et al. Optimization of governor parameters to prevent frequency oscillations in power systems[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4466-4474.
[20] 王敏, 李想, 张程飞. 基于多重逆变器复杂控制策略的微电网运行控制[J]. 现代电力, 2016, 33(5): 24-29.
Wang Min, Li Xiang, Zhang Chengfei. The operation and control of microgrid based on the complex control strategy of multiple inverters[J]. Modern Electric Power, 2016, 33(5): 24-29.
[21] Hu Jianchen, Ding Baocang. Output feedback robust MPC for linear systems with norm-bounded model uncertainty and disturbance[J]. Automatica, 2019, 108: 108489.
[22] Rao Yingqing, Yang Jun, Xiao Jinxing, et al. A frequency control strategy for multimicrogrids with V2G based on the improved robust model predictive control[J]. Energy, 2021, 222: 119963.
[23] Khokhar B, Singh Parmar K P. A novel adaptive intelligent MPC scheme for frequency stabilization of a microgrid considering SoC control of EVs[J]. Applied Energy, 2022, 309: 118423.
[24] 刘全, 翟建伟, 章宗长, 等. 深度强化学习综述[J]. 计算机学报, 2018, 41(1): 1-27.
Liu Quan, Zhai Jianwei, Zhang Zongchang, et al. A survey on deep reinforcement learning[J]. Chinese Journal of Computers, 2018, 41(1): 1-27.
[25] 余涛, 梁海华, 周斌. 基于R(λ)学习的孤岛微电网智能发电控制[J]. 电力系统保护与控制, 2012, 40(13): 7-13.
Yu Tao, Liang Haihua, Zhou Bin. Smart power generation control for microgrids islanded operation based on R(λ) learning[J]. Power System Protection and Control, 2012, 40(13): 7-13.
[26] 范培潇, 杨军, 肖金星, 等. 基于深度Q学习的含电动汽车孤岛微电网负荷频率控制策略[J]. 电力建设, 2022, 43(4): 91-99.
Fan Peixiao, Yang Jun, Xiao Jinxing, et al. Load frequency control strategy based on deep Q learning for island microgrid with electric vehicles[J]. Electric Power Construction, 2022, 43(4): 91-99.
[27] 赵星宇, 丁世飞. 深度强化学习研究综述[J]. 计算机科学, 2018, 45(7): 1-6.
Zhao Xingyu, Ding Shifei. Research on deep reinforcement learning[J]. Computer Science, 2018, 45(7): 1-6.
[28] 范培潇, 柯松, 杨军, 等. 基于改进多智能体深度确定性策略梯度的多微网负荷频率协同控制策略[J]. 电网技术, 2022, 46(9): 3504-3515.
Fan Peixiao, Ke Song, Yang Jun, et al. Load frequency coordinated control strategy of multi-microgrid based on improved MA-DDPG[J]. Power System Technology, 2022, 46(9): 3504-3515.
[29] Fan Peixiao, Ke Song, Yang Jun, et al. A load frequency coordinated control strategy for multimicrogrids with V2G based on improved MA-DDPG[J]. International Journal of Electrical Power & Energy Systems, 2023, 146: 108765.
[30] 李捷, 余涛, 潘振宁. 基于强化学习的增量配电网实时随机调度方法[J]. 电网技术, 2020, 44(9): 3321-3332.
Li Jie, Yu Tao, Pan Zhenning. Real-time stochastic dispatch method for incremental distribution network based on reinforcement learning[J]. Power System Technology, 2020, 44(9): 3321-3332.
A Multi Microgrid Intelligent Generation Control Strategy with Electric Vehicles Based on Evolutionary Model Predictive Control
Abstract Under the background of the national energy strategy of "carbon peaking" and "carbon neutrality", conventional generators driven by fossil energy are gradually replaced by renewable energy units such as wind power and photovoltaics. The microgrid with the characteristics of development and extension can fully promote the large-scale access of such distributed power sources with strong randomness, thus achieving rapid development and construction. At the same time, the development of electric vehicles (EV) is a trend to ensure low-carbon energy. China also regards the development of electric vehicles as a strategic emerging industry. The development of microgrids has also prompted electric vehicles to be widely used in power grid shaving peaks and valleys, and curb power fluctuations. However, when large-scale electric vehicles are connected to the microgrid at the same time, it may also lead to the degradation of the power quality of the islanded microgrid, and even the instability of the entire microgrid. To this end, a multi-microgrid power generation control strategy with electric vehicles based on evolvable model predictive control (MPC) is proposed in this paper.
Firstly, based on the multi-microgrid interconnection structure of controller interaction, considering the coupling relationship between generator terminal voltage regulation and system frequency control, a power generation control model with multiple microgrids with electric vehicles is established. Secondly, an adaptive algorithm of controller parameters based on MA-DDPG is designed: the frequency controller takes the real-time frequency offset and EV station output power boundary as the state set, and the adjustable parameter matrix Qxof the MPC controller as the action set, and the frequency deviation is used as the reward function index, and the voltage controller takes the real-time voltage as the state set, the proportional-integral coefficient of the PI controller as the action set, and the voltage offset as the reward function index; so as to realize the adaptive adjustment of the weight parameters of the MPC and the PI controller. Meanwhile, under the architecture of "centralized training and distributed execution", the intelligent agent group can realize the cooperative control between the sub-microgrids according to the real-time operating status information.
The simulation results show that, the automatic voltage regulation loop increases the active power disturbance, which puts forward higher requirements for the load frequency controller. Under the load disturbance and wind power disturbance, the microgrid frequency control effect under the learning-based MPC controller is significantly better than that of the traditional controller. When various extreme faults occur in the system, the proposed controller can still control the frequency fluctuation of the microgrid within 0.01 Hz through coordinated control and parameter self-adaptation, the control excellence rate can still reach 100%, and the recovery time is still less than 1 s, the robustness of the multi-microgrid performance is significantly enhanced, and the performance is better than the traditional MPC controller in all aspects. In addition, when the machine learning controller fails, the proposed two-layer controller structure can still ensure that the frequency fluctuation of the microgrid is controlled within 0.01 Hz, and the control excellence rate can reach 100%, which is significantly better than the DDPG controller.
The following conclusions can be drawn from the simulation analysis: (1) Compared with PID and fuzzy control, the evolvable MPC controller can transform the frequency control process into solving an optimization problem, and thus well adapt to the stochastic scene in the multi-microgrid system. (2) Compared with the traditional MPC, the DDPG agent can adjust the MPC and PI control parameters according to the real-time operating environment state, so as to better adapt to the complex working conditions where the system parameters and structure change with time. (3) Compared with the DDPG controller, the proposed double-layer protection structure has stronger security and stability. When the machine learning agent fails and cannot output actions normally, the MPC controller can use the preset parameters to complete the frequency control process until the machine learning controller returns to normal.
keywords:Multi-microgrid load frequency control, electric vehicle, generator terminal voltage, MA-DDPG algorithm, model predictive control
中图分类号:TM727
DOI:10.19595/j.cnki.1000-6753.tces.222138
国家自然科学基金资助项目(51977154)。
收稿日期 2022-11-13
改稿日期 2023-02-16
范培潇 男,1999年生,硕士研究生,研究方向为微电网智能控制。E-mail:whufpx0408@163.com
杨 军 男,1977年生,教授,博士生导师,研究方向为电动汽车、电力系统运行安全与稳定等。E-mail:JYang@whu.edu.cn(通信作者)
(编辑 赫 蕾)