为蓄电池输出功率，
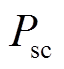为超级电容输出功率，
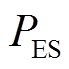为混合储能总输出功率，
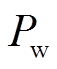为风电原始功率，
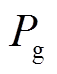为风电并网功率。本文选用磷酸铁锂电池-超级电容器混合储能系统配置于风电场出口处，储能功率控制器通过采集风电原始出力、风电并网功率及储能SOC等信息对储能输出功率进行调节，通过DC-DC变换器单电流环控制、DC-AC变换器电压电流双环控制[23]使混合储能平抑风电功率波动符合并网要求。摘要 混合储能系统能够较好地应对复杂的风电波动，有效地提高电网的稳定性和安全性。在混合储能平抑风电功率波动的典型应用场景下，该文首先提出一种计及荷电状态（SOC）自恢复的混合储能平抑风电功率波动控制方法，在满足风电平抑需求的情况下，通过模型预测控制快速调节储能在平抑功率过程中的荷电状态，提高储能持续稳定运行能力；然后，为提高混合储能系统协调运行能力，设计了加权滑动平均（WMA）-模糊控制策略对超级电容和蓄电池功率进行动态分配；最后，结合实际风电功率数据，通过仿真验证了所提策略能有效平衡储能寿命和平抑风电波动的矛盾，能充分考虑两种储能设备的特性差异并提高功率分配的合理性。
关键词：风电功率波动 混合储能 模型预测控制 加权滑动平均 模糊控制
在“双碳”目标下，风力发电因技术较为成熟，成为最具开发规模和商业发展前景的新能源发电方式[1-2]。但由于风本身具有间歇性、波动性和随机性等特征，随着其并网渗透水平的提升将会对电力系统的安全稳定运行造成严重影响[3-4]。储能系统由于响应迅速、操作灵活，通过控制能较好地吸收和释放电能，在应对复杂风电波动时可极大地提高风电并网功率的平稳度，从而降低风电直接并网对电网带来的不利影响[5]。
储能设备根据其介质的不同分为以蓄电池为代表的能量型储能和以超级电容器、飞轮储能和超导储能为代表的功率型储能[6]。在风电波动较为复杂的场景中，越是大容量、高功率密度、响应速度快的储能设备平抑风电波动的效果越好，单一配置某一种储能设备无论是从经济还是技术上都无法同时满足要求。因此，许多专家学者提出利用能量型与功率型相结合的混合储能系统来平抑风电输出功率，如蓄电池-超级电容[7-8]、全钒液流电池-压缩空气储能[9]、飞轮-蓄电池[10]等混合储能系统。
为保证电网的稳定运行，促进新能源的消纳，越来越多的预测方法被用于风电系统平抑目标功率预测中[11]，文献[12]利用随机森林预测法预测后续风功率，以此对储能进行充放电控制。文献[13]采用卷积神经网络方法结合所提风速矩阵时空关联分解重构策略提高风电预测精度。一些学者将模型预测控制（Model Predictive Control, MPC）引入多变量且高维复杂的风电系统控制中。文献[14]将风电输电断面的容量状态划分为安全、预警及警戒区，以此划分断面功率的不同波动情况，根据当前实际风电集群有功输出功率与划分区域的关系决定未来风电集群功率是否需要增减，最后通过模型预测控制进行功率调节。文献[15]提出一种基于风电预测的储能模型预测控制策略，设计了随风速变化而自动调整动态荷电状态（State of Charge, SOC）初始值的优化函数，有效改善了风速随机性和预测误差对风电调频能力的影响。为实现对储能功率的控制，文献[16]提出一种双层模型预测方法，外层确定下一时刻的预期目标功率，内层通过充放电约束关系使实际输出功率跟随目标功率，通过反馈实时修正储能功率。
以平抑风电功率波动为主要目标，如何有效地发挥功率型和能量型储能设备各自的优点，合理分配平抑目标功率，关系着储能控制的高效与经济。其中，最为常用的目标功率分配方法是滤波类方法。文献[17]采用一阶低通滤波算法实现了储能电池和超级电容器之间的功率分配。文献[18]提出一种具有可变滤波器时间常数的两阶段低通滤波器控制策略，优化混合储能的功率分配。文献[19]针对混合储能不同工作模式提出不同最大输出功率及等效SOC的评估方法，基于离散一致性算法设计储能功率分配分层控制策略。文献[20]提出基于自适应权重和模拟退火策略的鲸鱼优化算法功率分配策略，有效降低了储能电池单元的运行成本和折损率。此外，经验模态分解与加权滑动平均法等也被应用在储能功率分配控制中，利用并网功率波动要求对分解方法进行自适应改进，结合储能能量状态约束其功率指令，将储能荷电状态维持在合理范围内[21]。文献[22]利用滑动平均滤波法确定平抑目标，再结合模态分解与模糊控制规则修正储能设备的充放电功率，提高了平抑水平和储能系统经济性。
综上所述，对风电平抑目标功率的预测结果将直接影响混合储能系统对风电波动的平抑效果，同时，平抑目标功率的分配将直接影响各储能设备的放电深度及充放电次数，进而对其寿命产生影响。因此，合理地确定混合储能系统的平抑目标功率，以及平抑目标功率在不同储能设备之间的协调分配至关重要。为在平抑风功率波动的同时兼顾储能系统的寿命，本文首先在考虑储能系统荷电状态基础上建立了系统MPC模型，通过引入充放能力饱和函数提出考虑SOC自恢复的储能系统MPC优化控制目标，利用滚动优化的方法确定了风电平抑目标功率；然后提出基于加权滑动平均（Weighted Moving Average, WMA）-模糊控制的混合储能功率分配策略，将过去已知的储能系统实际功率与MPC预测的未来平抑目标功率进行计算，动态调整混合储能系统的功率分配，从而实现在满足平抑功率需求的同时充分发挥储能元件各自的性能优势这一控制目标；最后，根据实际风电数据，从并网波动、储能充放电裕度以及累计充放电量等多指标评价体系，验证本文所提方法在平抑风电并网功率波动和改善全局储能出力水平的有效性。
风储联合控制系统具有非线性、多变量耦合、多约束、不确定性等特点，传统控制方法难以精确描述其数理模型，控制效果有限。MPC为一种实时控制手段，通过预测系统未来的动态信息对一定预测时域的控制目标进行优化，具有良好的快速性和鲁棒性。本节工作是在平抑风电功率波动的同时兼顾储能系统的寿命，建立了考虑混合储能系统SOC自恢复的MPC预测模型和优化目标，通过滚动优化算法最终确定了混合储能系统平抑的目标功率。
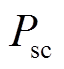用于平抑风电功率波动的风储联合系统结构如图1所示。图1中为蓄电池输出功率，为超级电容输出功率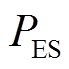，为混合储能总输出功率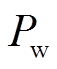，为风电原始功率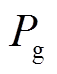，为风电并网功率。本文选用磷酸铁锂电池-超级电容器混合储能系统配置于风电场出口处，储能功率控制器通过采集风电原始出力、风电并网功率及储能SOC等信息对储能输出功率进行调节，通过DC-DC变换器单电流环控制、DC-AC变换器电压电流双环控制[23]使混合储能平抑风电功率波动符合并网要求。
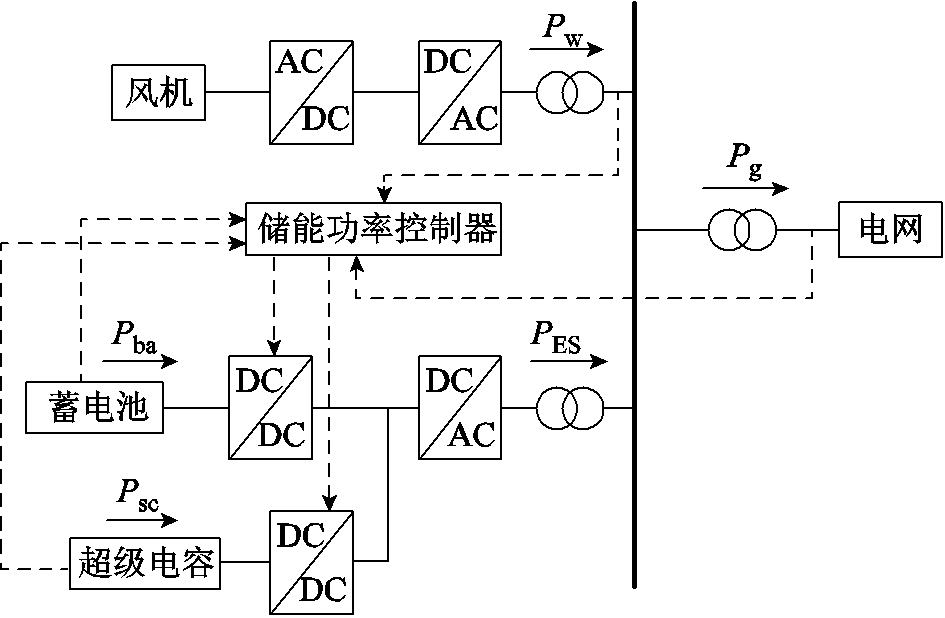
图1 风储联合系统结构
Fig.1 Structure of wind-storage combined system
以图1给定的功率方向为参考，可得
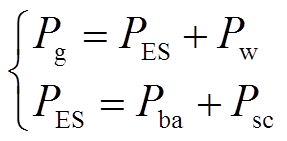（1）
基于状态空间理论，k时刻的状态变量、控制变量、扰动变量可分别表示为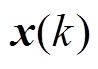
、
和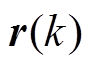
，系统的离散时间状态方程[24]为
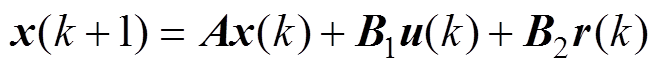（2）
式中，A、B1、B2为系数矩阵。
在不考虑蓄电池和超级电容器充放电效率以及换流器等损耗情况下，对式（1）进行离散化处理可得
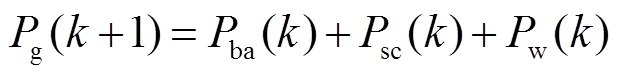（3）
式中，
为控制的时间节点。
由式（3）可知，风电并网功率、蓄电池平抑功率、超级电容平抑功率相互关联，而储能系统出力受荷电运行状态影响，离散后的蓄电池和超级电容的荷电运行状态分别为
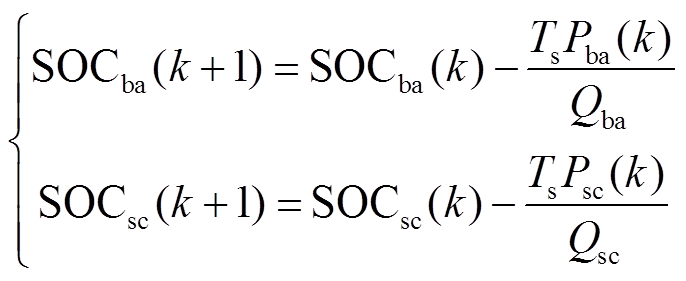（4）
式中，
和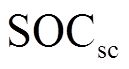
分别为蓄电池和超级电容的荷电状态值；
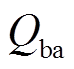和
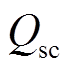分别为蓄电池和超级电容的额定容量；
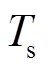为控制周期。
混合储能系统以大容量的蓄电池为主体，因此混合储能系统的SOC基本由蓄电池SOC决定，故对蓄电池SOC进行调节可视为对混合储能系统SOC的调节。由此可将式（4）统一写为
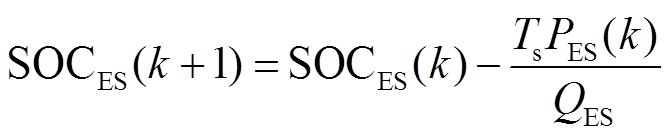（5）
式中，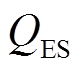
为混合储能总额定容量，
；
为混合储能系统的荷电状态，有
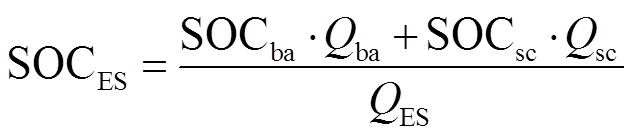（6）
结合式（2）、式（3）、式（5），令系统的状态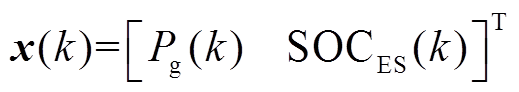变量
，控制变量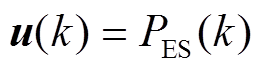
，系统的可测扰动输入量
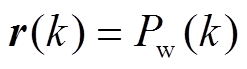，得到考虑混合储能SOC的MPC预测模型为
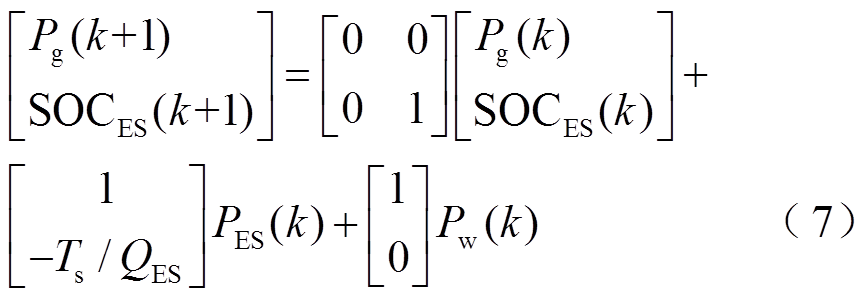
对比式（2）和式（7），可得式（2）中各系数矩阵为
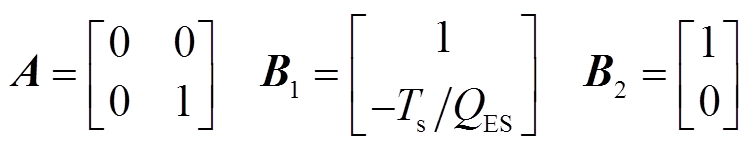（8）
1.2.1 考虑SOC的充放电饱和能力函数
混合储能平抑风电功率的过程中，蓄电池SOC运行状态影响着储能设备的充放电裕度及寿命。蓄电池SOC区域划分如图2所示，蓄电池在不同SOC区间的充放电能力不同，当SOC处于区域1时（该区域的SOC上、下界分别为a、b，且满足
），蓄电池的充放电裕度最大，对于各种不同的功率波动都具备较大的平抑能力，为最优运行区间；当SOC偏离0.5处于区域2时，蓄电池虽然有一定的充放电裕度但不适合长时间运行；若SOC接近上、下限，达到区域3时，蓄电池基本没有充放电裕度，且在这个区间充放电会极大地提高其寿命损耗。由于不良运行状态的存在使蓄电池充放电裕度不足、功率不足等，将导致蓄电池的放电深度及充放电转换次数增加，影响蓄电池的长期稳定运行，最终导致寿命快速消耗，并且无法达到理想的风电平抑效果。
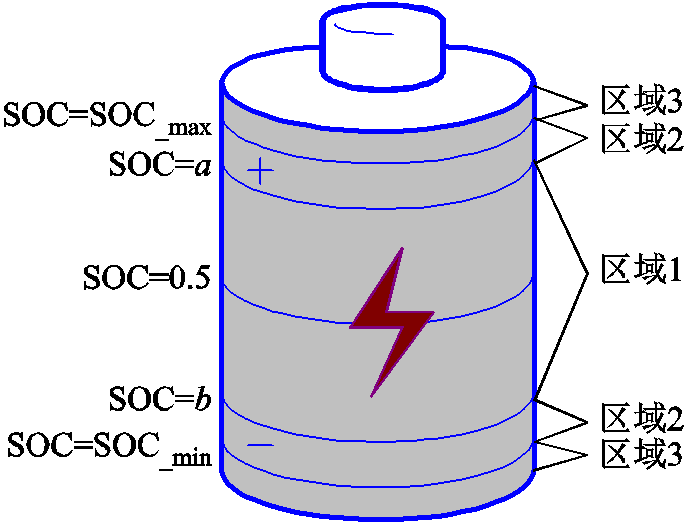
图2 蓄电池SOC区域划分
Fig.2 Battery SOC area division
由此，为保证良好的风电平抑效果及蓄电池的长期稳定运行，本文针对蓄电池运行提出两点要求：①蓄电池应工作在充放电裕度较大的区域；②蓄电池SOC最优运行区间不能过大或过小，需根据外界功率需求适时调整SOC的运行区间。为此，基于Logistics函数提出充放电饱和能力函数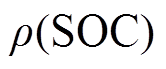
用以表征不同SOC值与储能充放电裕度关系。
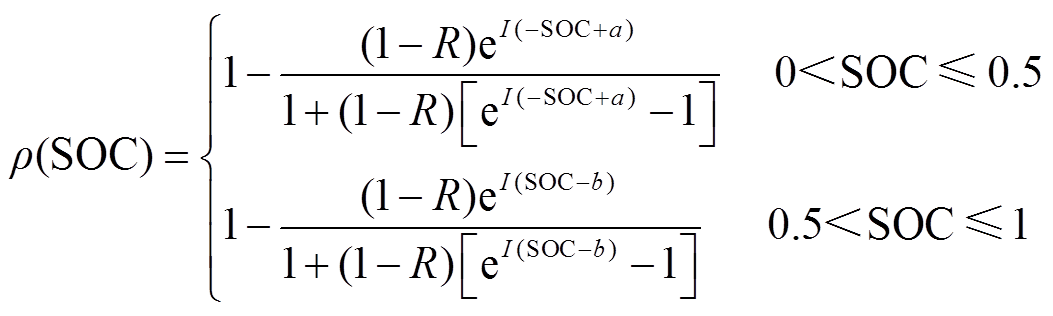（9）
式中，R为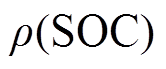初始值且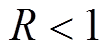
；I用以控制函数的变化快慢。
由式（9）可知，当SOC介于[a,b]之间时，函数值大于或等于R，此时充放电饱和度较高，属于良好的充放电SOC范围，并且对函数求导可得SOC在0.5附近的斜率变化较小，即SOC轻微变化对饱和度影响不大。当SOC小于a或大于b时，函数值小于R且快速变化至趋近于0，表明饱和度过低，不利于电池的运行，需进行SOC调节。
1.2.2 混合储能系统MPC优化目标
从风电并网功率和储能SOC的相互关系出发，当储能有足够大出力裕度时，应尽可能地平抑风电的波动；当储能出力裕度较小时，可以适当减小风电波动平抑的标准来恢复储能的出力裕度，以降低储能的寿命损耗。基于上述考虑，将充放电饱和能力函数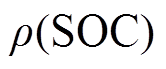以权重系数形式引入MPC优化目标函数。
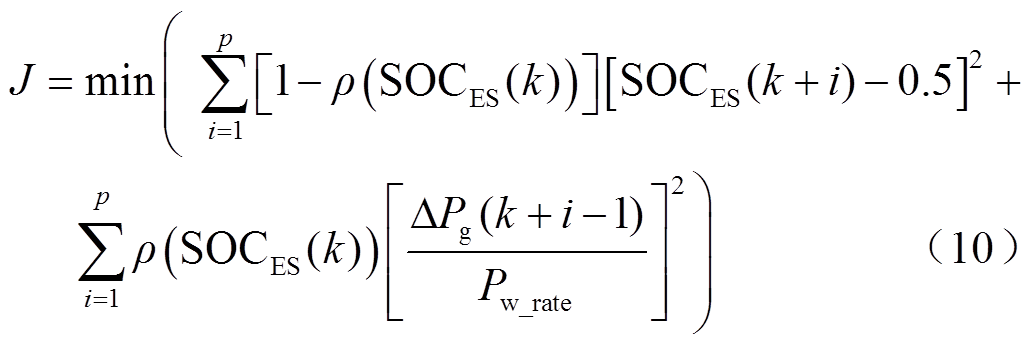
式中，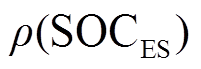
为混合储能系统充放电饱和能力函数；
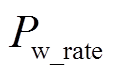为风电装机容量；
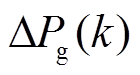为风电功率并网功率增量，
；
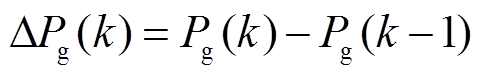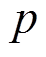为预测时域。
式（10）的MPC优化目标函数包括调节储能SOC和调节并网功率增量两部分，通过改变权重即充放电饱和能力函数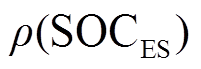来实现对两个控制目标的调节。当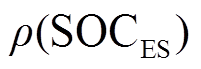较小时，储能系统充放电饱和度低，控制目标以恢复储能SOC为主，使得储能SOC尽量处于区域1并调节在0.5附近；当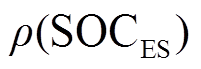较大时，储能系统充放电饱和度较高，储能SOC处于良好的运行区间，控制目标主要以风电并网功率增量最小化为主，以提高风电并网功率的平滑程度。而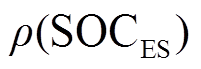的大小与参数a、b、I、R有关，因此，通过对充放电饱和能力函数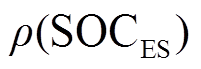进行参数调节，即可灵活调节储能SOC和并网功率增量的控制比重。
风储联合系统除满足MPC优化目标函数外，还需满足混合储能SOC约束、充放电功率约束以及并网功率约束，即
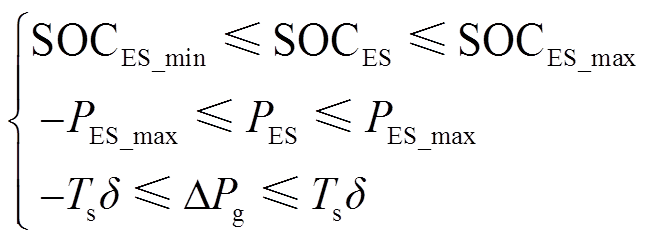（11）
式中，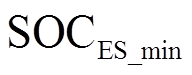
、
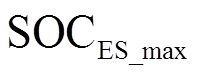分别为混合储能的SOC最小、最大限值；
为混合储能最大功率；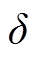
为单位时间的波动限值，本文设定为2%。
根据MPC原理，结合混合储能预测模型式（2）、优化目标式（10）及系统约束式（11），可将其转换为二次规划形式进行求解，得到现在及未来一段时间的控制变量序列，即混合储能系统平抑的目标功率。
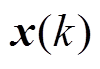为已知的k时刻实际状态值，根据式（2）可得k+1时刻的状态变量
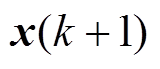，进一步可用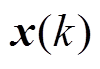计算出k+2时刻的状态变量为
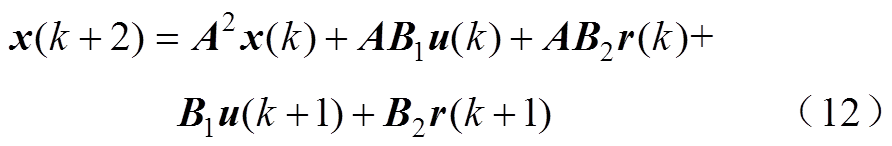
以此类推，可根据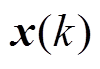得到每一时刻状态变量的表达式，都由已知的状态量、扰动量和待求的控制变量组成。设状态变量序列、控制变量序列及扰动量序列分别为
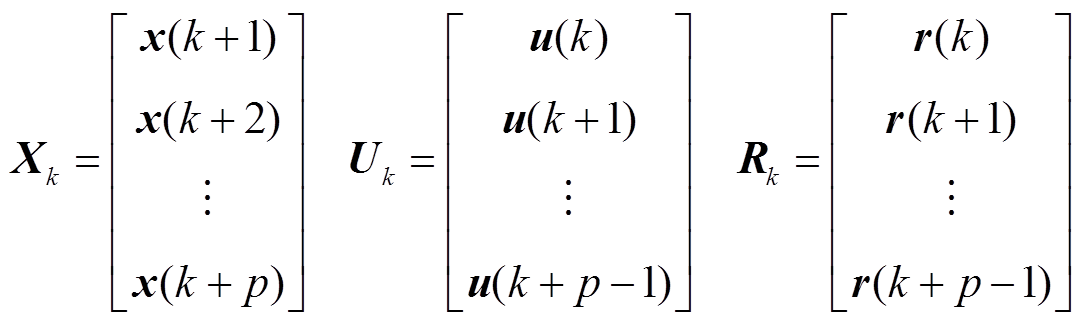（13）
记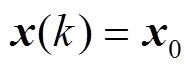
，则式（2）可以拓展为
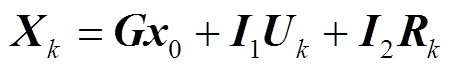（14）
其中，各系数矩阵分别为
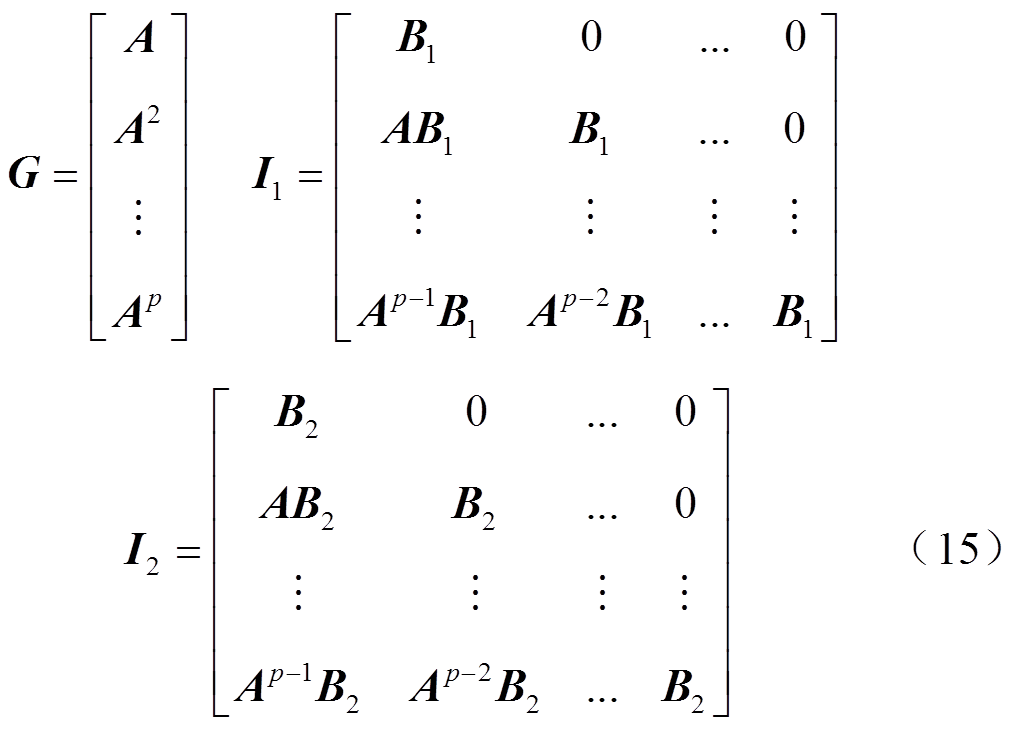
通过矩阵运算，优化目标中所有状态变量可由控制变量表示，由于常数项不参与优化故可省略，因此，可将目标函数转换为标准的二次规划形式，有
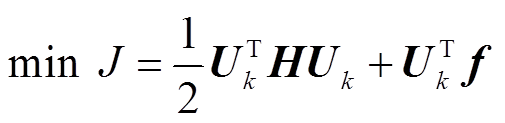（16）
式中，H为待求控制变量的二次项参数矩阵；f为待求控制变量的一次项参数矩阵。
通过数学求解，可得到满足优化条件与约束条件的最优控制变量序列
，即混合储能平抑目标功率
、
、
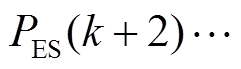。理论上，若实际系统模型与建立的数理模型一致，且预测足够精确，则该控制序列代入实际系统所得结果将与理论得到的预测状态变量一致。但由于存在模型误差及扰动等因素，为提高控制精度，控制过程需进行滚动优化：在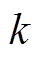时刻求解最优混合储能目标功率、、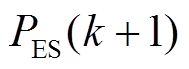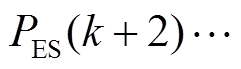时，越靠近当前时刻的预测信息越精确，故每次优化只选取序列的第一项作用于被控系统。当系统进入
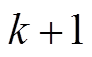时刻，更新状态序列进行预测，以此类推，反复修正控制过程中的各种误差，以此提高控制精度。
通过模型预测控制求解得到的混合储能系统平抑的目标功率，初步满足了风电功率波动及动态恢复储能SOC的需求，但为了充分发挥混合储能系统中锂电池和超级电容器各自的性能优势，需要对混合储能目标功率进行协调分配。在这个过程中，需考虑利用蓄电池的大容量特性对大幅度的功率进行平抑，同时，充分利用超级电容器快速响应能力和频繁转换充放电能力，让其承担高频变化的功率，从而适当降低蓄电池充放电的转换次数，提高蓄电池的使用寿命。因此，本节首先改进加权滑动平均法对平抑的目标功率进行分配，然后利用模糊控制对相关参数进行调整，以提高该方法的自适应性。
WMA法是以滑动窗口为参考区域来计算加权平均的一种办法。传统WMA法只包含对过去数据的分析，缺少对未来预测数据的快速跟踪，同时固定的滑动窗口长度限制了计算的灵活性。MPC正好可以弥补传统WMA法前瞻性的不足，根据预测未来数据变动情况动态调节滑动窗口长度，从而实现灵活分配蓄电池和超级电容的功率。因此，结合MPC法的预测结果提出一种改进的WMA法，其时间轴的划分如图3所示，将时间轴以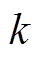时刻为分界线，向前和向后划分过去和未来两个时间区域，区域长度各为
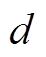，即总滑动窗长度为
。
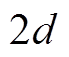图3 改进WMA法时间轴的划分
Fig.3 Partition of the timeline by WMA method
首先计算过去和未来各部分单独的参考值。
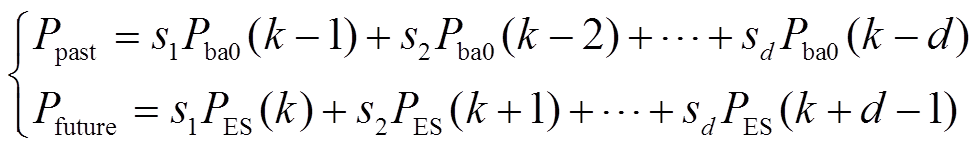（17）
式中，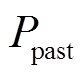
为过去的功率参考值；
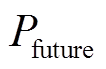为未来的功率参考值；
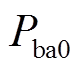为蓄电池输出的实际功率；
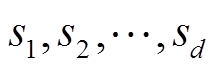分别为各部分权重系数，
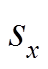取值为
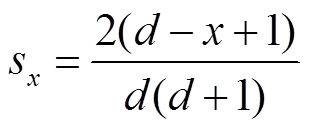（18）
则蓄电池和超级电容的参考功率分别为
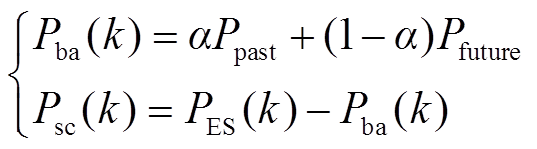（19）
式中，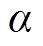
为过去和未来参考值的权重，
。
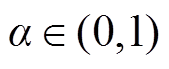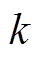时刻的蓄电池参考功率由过去已知的蓄电池实际功率和MPC未来预测的混合储能功率通过WMA法进行计算，从而弥补了传统MWA法前瞻性不足的缺点。结合式（17）和式（19）可知，通过改变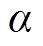和d的大小，可以动态调整蓄电池和超级电容的分配功率，从而提高平抑功率需求较大时蓄电池的出力水平。
为提高蓄电池和超级电容对不同目标功率及不同荷电运行状态的适应性，体现能量型与功率型储能设备之间的差异性，采用模糊控制对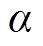和d两个参数进行动态调整。
对模型预测得到的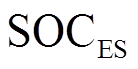，以预测时域p为尺度计算未来混合储能的荷电状态变化情况，即
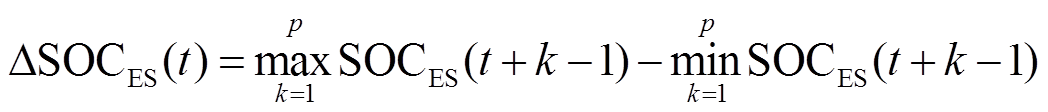（20）
混合储能未来目标功率的变化同步影响着储能系统未来荷电状态的变化，因此以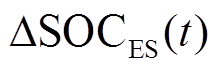
的大小表征未来混合储能目标功率的变化情况，并将其划分为四种工况。考虑到超级电容的容量远小于蓄电池，平抑裕度较差，因此除了考虑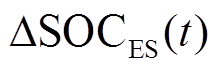外，还需结合超级电容的荷电状态
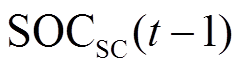设计不同工况下模糊控制器基本逻辑。
工况①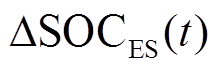，非常小：希望超级电容承担主要出力，蓄电池出力较小且保持与前一时刻功率基本相同，对应的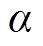与d都较大。
工况②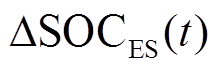，较小：若超级电容SOC平抑裕度较高，超级电容仍承担主要出力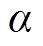，与d都较大；若超级电容裕度较低，减小d以减少超级电容出力，提高蓄电池出力。
工况③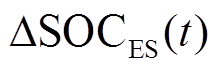，较大：由超级电容和蓄电池共同承担平抑功率，则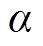与d取值适中。
工况④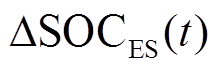，非常大：蓄电池承担主要出力且跟随未来波动变化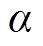，与d取值较小。因超级电容能量密度小，易过充过放，当超级电容SOC接近上下限时，进一步减小d。
根据上述模糊控制器基本逻辑，将超级电容前一时刻的荷电状态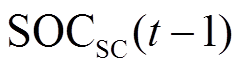和未来混合储能的荷电状态变化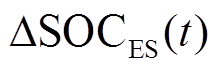作为模糊控制器的输入量，以滑动窗口长度d及过去和未来参考值的权重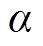作为输出，建立模糊控制器的隶属度函数如图4所示。
图4 模糊控制输入/输出隶属函数
Fig.4 Input/output membership functions of fuzzy controller
超级电容荷电状态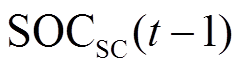模糊集论域为[0,1]，对应的模糊子集为{VS, S, M, B, VB}，分别表示很小、小、中、大、很大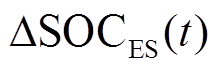；论域为[0,1]，对应模糊子集为{SS, MS, MB, BB}，分别表示非常小、较小、较大、非常大。输出权重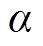的论域为[0,1]，对应模糊子集{VL, L, H, VH}，分别表示很低、低、高、很高；输出滑动窗口d为离散域{5, 10, 15, 20, 25}，对应模糊子集为{VS, S, M, B, VB}。
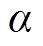和d的模糊控制规则分别见表1和表2。
表1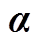 
模糊控制规则
Tab.1 Fuzzy control rule of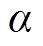
ΔSOCES(t)SOCSC(t-1) VSSMBVB SSHVHVHVHH MSLHHHL MBVLLLLVL BBVLVLVLVLVL
表2 d模糊控制规则
Tab.2 Fuzzy control rule of d
ΔSOCES(t)SOCSC(t-1) VSSMBVB SSBVBVBVBB MSMBVBBM MBSMMMS BBVSSMSVS
由此得到本文所提混合储能平抑风电功率波动控制流程如图5所示。
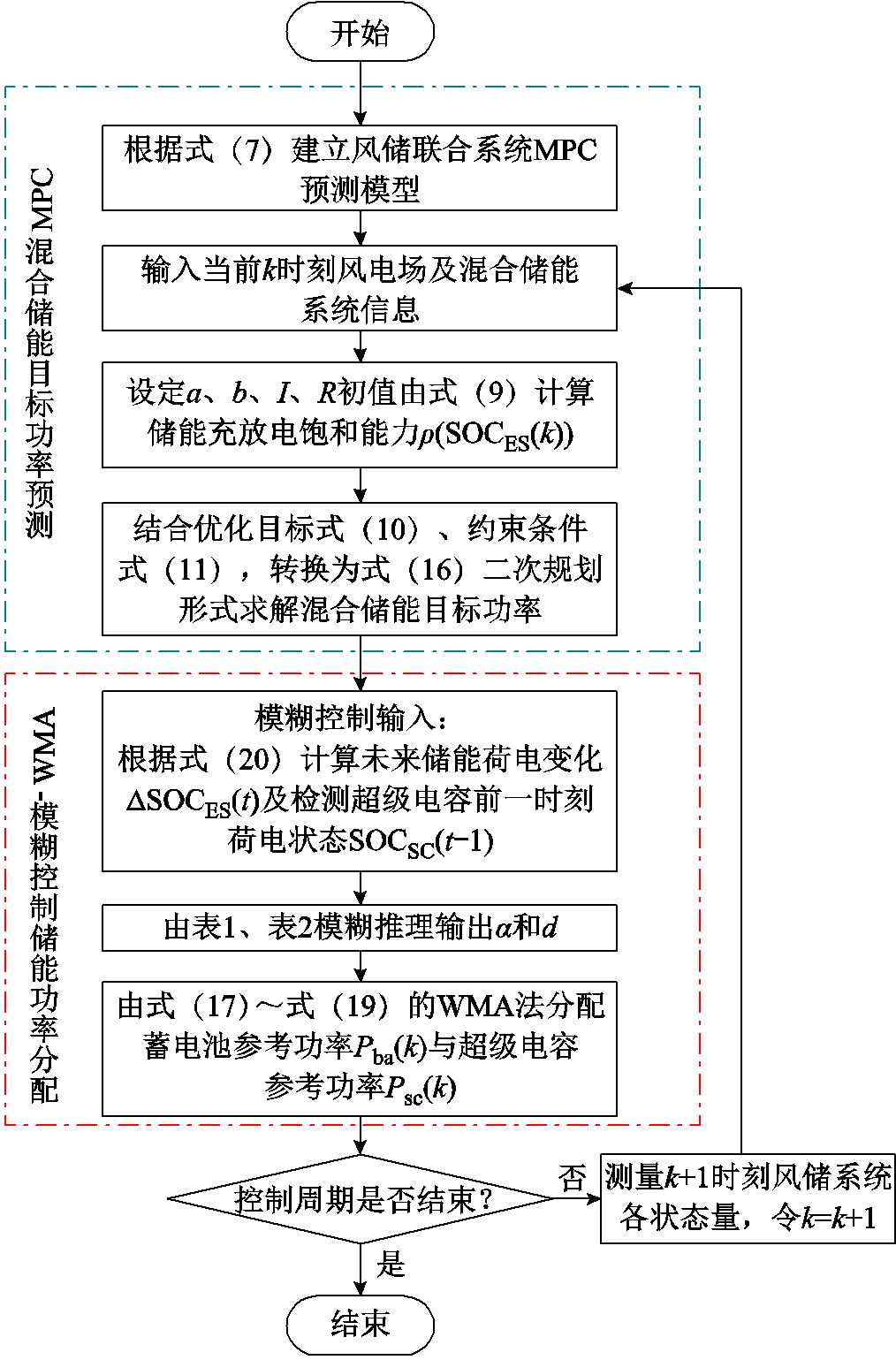
图5 混合储能平抑风电功率波动控制流程
Fig.5 Hybrid energy storage to smooth out wind power fluctuations control process
为验证所提策略的有效性，按照我国标准GB/T 19963—2011所规定的电力系安全稳定运行准则，风电功率变化量需要满足在1 min和10 min两个时间尺度上不超过所规定的限值[25]，在Matlab上建立图1所示风储联合模型进行仿真，采用装机容量为32 MW的某风电特征天风电数据作为输入，风电数据采样周期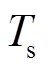为1 min，研究时长T为24 h。采用文献[26]以蓄电池全寿命周期成本最小为目标的计算方法，配置功率6 MW、能量15
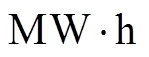的蓄电池储能，取蓄电池与超级电容能量配置比为25:1[27]，即配置功率6 MW、能量0.6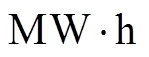的超级电容储能。
采用平均充放电裕度等指标评价储能系统的运行情况及风电平抑效果。
1）平均充放电裕度
利用一段时间内储能充放电饱和能力平均值来表征一段时间以内的储能平均充放电裕度，即
（21）
2）累积充放电量
定义累积充放电量Eb为
（22）
Eb用于表示储能系统能量交换的总量，该值越大表征储能的寿命损耗越多。
3）并网平均波动率
并网功率在研究周期T内的平均波动率可表示为
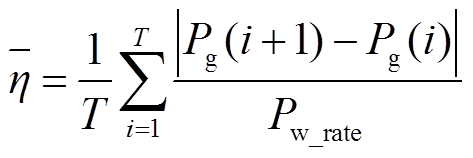（23）
3.1.1 风功率平抑效果与储能SOC调节仿真
基于上述参数和相关指标，采用三种MPC方法对混合储能系统的平抑功率及风电并网功率进行控制，分别为：①MPC方法1，以混合储能实时的SOC状态接近0.5为优化目标；②MPC方法2，以并网风电功率波动率最小为优化目标；③MPC方法3，即本文优化方法，实时考虑风电平抑效果和储能SOC状态进行动态优化。MPC方法3控制过程中，设定a=0.3，b=0.7，I=30，R=0.5，蓄电池和超级电容的SOC初始值均为0.5，SOC上、下限分别为0.9和0.1。
1）并网功率及其波动频率对比
图6和图7分别为三种控制方法下的并网功率及并网功率波动频率分布。
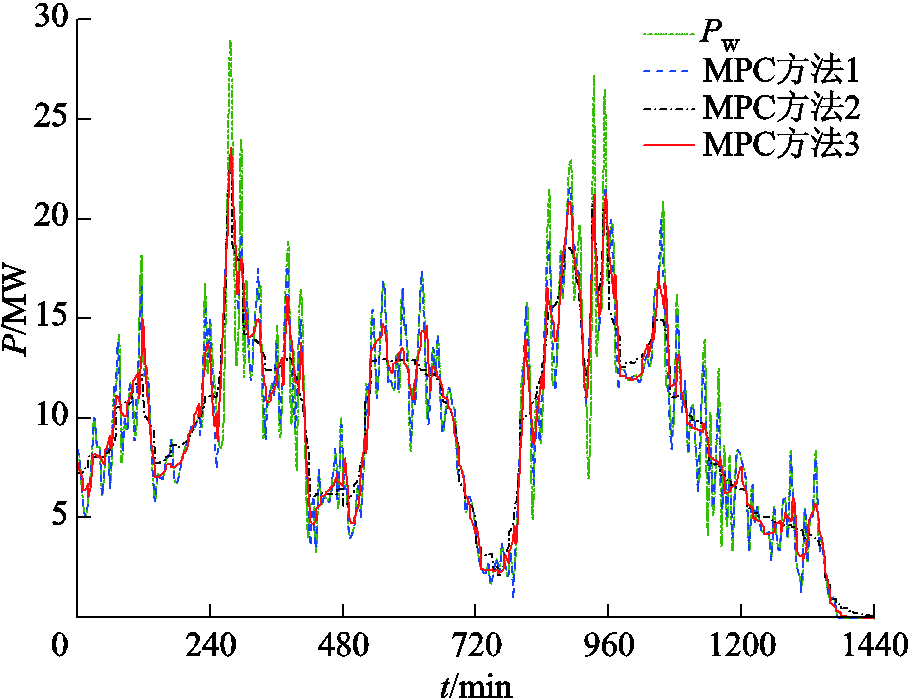
图6 并网功率对比
Fig.6 Comparison of grid-connected power
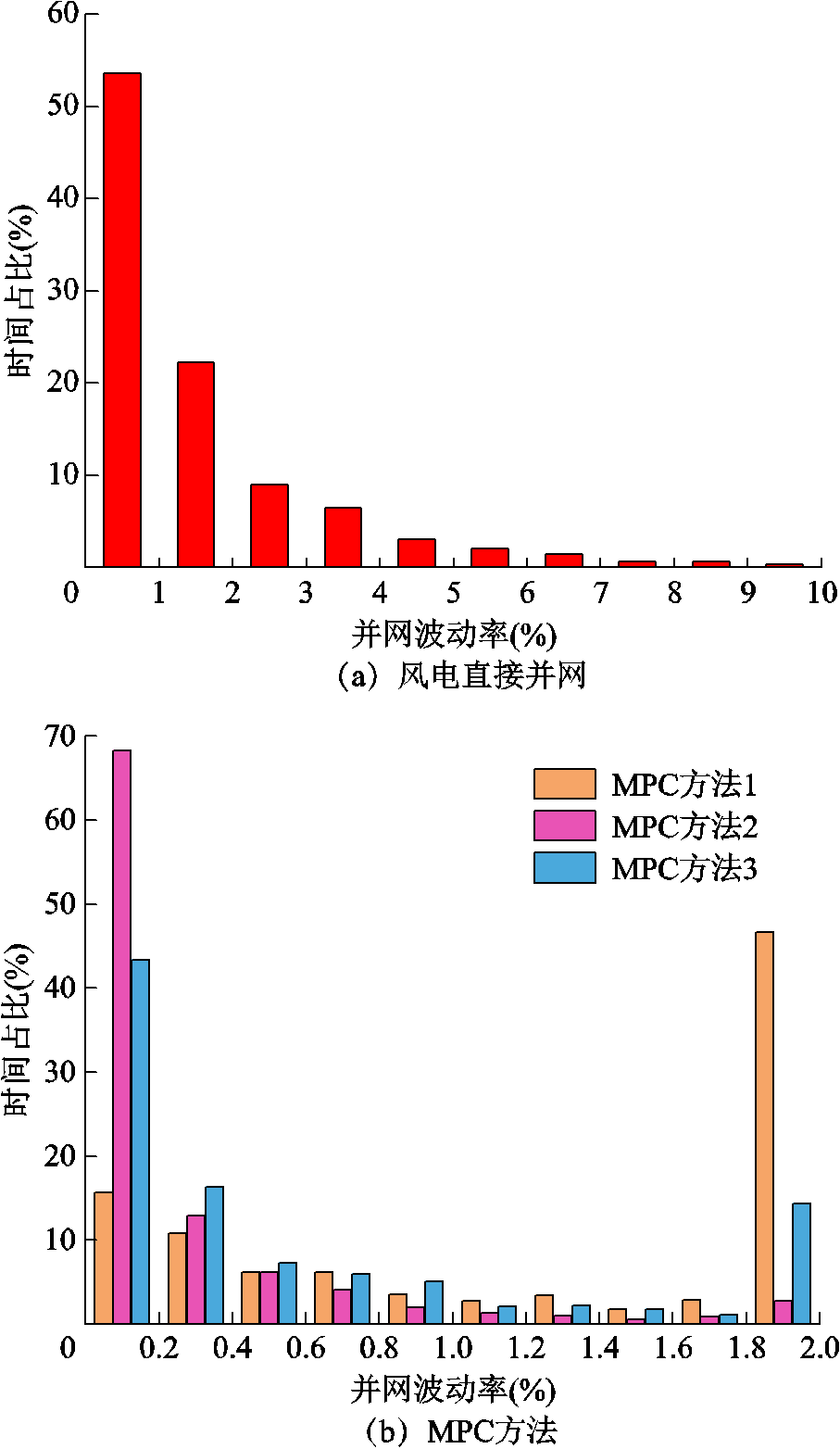
图7 并网功率波动率分布对比
Fig.7 Comparison of grid-connected power volatility distribution
图6中，对比原始风电功率PW可以看出，三种方法都有效地实现了对风电并网功率波动的平抑。相比于风电直接并网，对比图7a与图7b可知，原始风电并网波动率大于2%的时间约占24.2%，平抑后的风电并网功率波动率都被限制在2%以内，满足并网要求。就平抑效果而言，以并网功率波动率最小为控制目标的MPC方法2的效果最好，68.2%的波动率分布在0.2%以下；其次是本文方法，43.4%的波动率分布在0.2%以下；平抑效果最差的是方法1，仅有15.7%的波动率分布在0.2%以下，多数波动率分布在0.2%～2%范围内。
2）混合储能SOC调节对比
在控制储能系统平抑风电功率过程中，风电并网功率波动率不能作为衡量控制策略优劣的单一标准，储能系统的运行状态影响着储能元件的使用寿命、系统整体经济性及长期的风电平抑效果。图8为三种控制策略下混合储能SOC变化情况对比，图9为对应图8中混合储能SOC的分布对比。
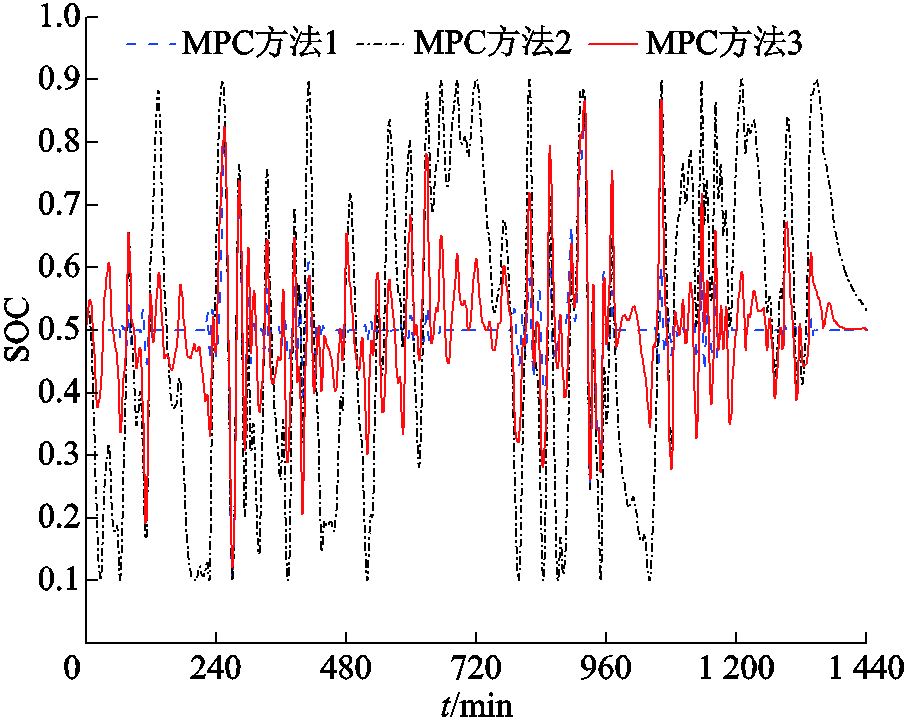
图8 混合储能SOC变化对比
Fig.8 Comparison of hybrid energy storage SOC changes
图9 混合储能SOC分布对比
Fig.9 Comparison of hybrid energy storage SOC distribution
由图8和图9可以看出，三种控制方法下的混合储能SOC随时间的变化情况存在较大差异。MPC方法1控制下的储能SOC超过90%的时间维持在[0.4,0.6]的高充放电裕度区域，仅在风电功率波动较大的时间段有所动作，符合MPC方法1的优化目标策略。对应MPC方法2，虽然能够将储能SOC限制在允许的运行区间[0.1,0.9]之内，但SOC的变化幅度较大且接近30%的时间处于充放电裕度较低的区域，存在风电功率波动无法平抑以及由此带来的加速储能寿命消耗的风险。采用本文控制策略MPC方法3时，储能SOC的工作区间得到很大改善，约90%的时间SOC保持在[0.3,0.7]之间。如图8在480～720 min和1 200～1 440 min等时间段，相较于MPC方法2，储能SOC的运行范围更加良好。而相较于MPC方法1，如在0～240 min和1 200～1 440 min等时间段，本文方法控制下的储能可以提供更多的充放电功率来对风电功率进行平抑，改善平抑效果。
本文所提MPC方法3对SOC的动态调整过程如图10所示。
图10 不同初始荷电状态下混合储能SOC调节过程
Fig.10 Hybrid energy storage SOC regulation process for different initial SOC
由图10可见，对于不同的混合储能初始SOC值，在本文所提MPC方法3控制调节下，储能的SOC能够随着时间逐渐恢复到0.5附近，并最终跟随初始SOC=0.5对照组的SOC变化。初始SOC越偏离0.5其恢复到0.5附近的速度越快，说明本文控制策略能够根据储能SOC所处区间动态调整SOC的恢复速度，从而保证储能运行在良好的荷电运行区间。
3）评价指标对比
图6中原始风功率的平均波动率为1.52%，三种控制方法的评价指标对比见表3，对比表中数据可得：①三种方法的平均波动率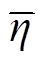
均小于原始风电波动率，说明三种方法对风电功率的波动均有平抑效果，与图7所得结论一致。其中方法2并网平均波动率最低，方法1最高，本文方法介于二者之间。②比较混合储能充放电总能量
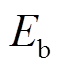，本文方法为28.93 MW·h，远低于方法2的47.67 MW·h，说明本文方法在一定程度上降低了储能系统在平抑风电波动过程中的输出，减少了寿命损耗。③对比混合储能平均充放电裕度
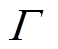，本文方法为0.948 6，与方法1的0.978 7接近，而远高于方法2的0.591 4。综合比较三组指标，说明本文方法在满足风电波动平抑要求的同时兼顾了储能的充放电能力，有效地提高了储能的持续稳定运行能力，其原因在于本文所提的控制策略中将表征储能系统SOC的充放电饱和能力函数作为权重系数引入MPC优化目标函数中，根据SOC的状态动态调整并网功率增量和储能SOC调节两个控制目标。
表3 控制方法结果评价指标对比
Tab.3 Comparison of indicators for evaluating the results of control methods
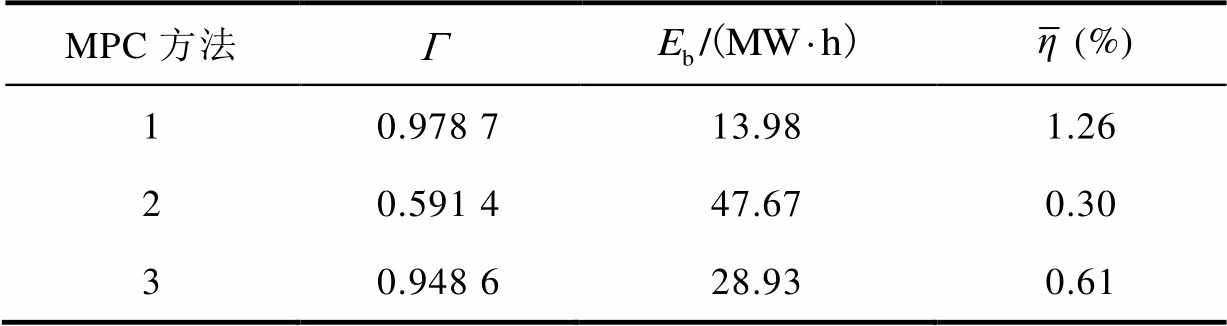
MPC方法(%) 10.978 713.981.26 20.591 447.670.30 30.948 628.930.61
3.1.2 充放电饱和能力函数对混合储能MPC调节的影响
本文所提考虑混合储能SOC自恢复的MPC方法中，储能系统充放电饱和能力函数作为调节储能SOC及风电并网波动的权重系数引入优化目标，其参数a、b、I、R的选取将影响储能SOC和并网功率增量二者的控制比重。本节仿真时，I分别取值20、30、40，R分别取值0.3、0.5、0.7，对比不同[a, b]取值范围下的评价指标分别列于表4～表6。
表4 I=20时参数调节对比
Tab.4 Comparison of different parameters for I=20
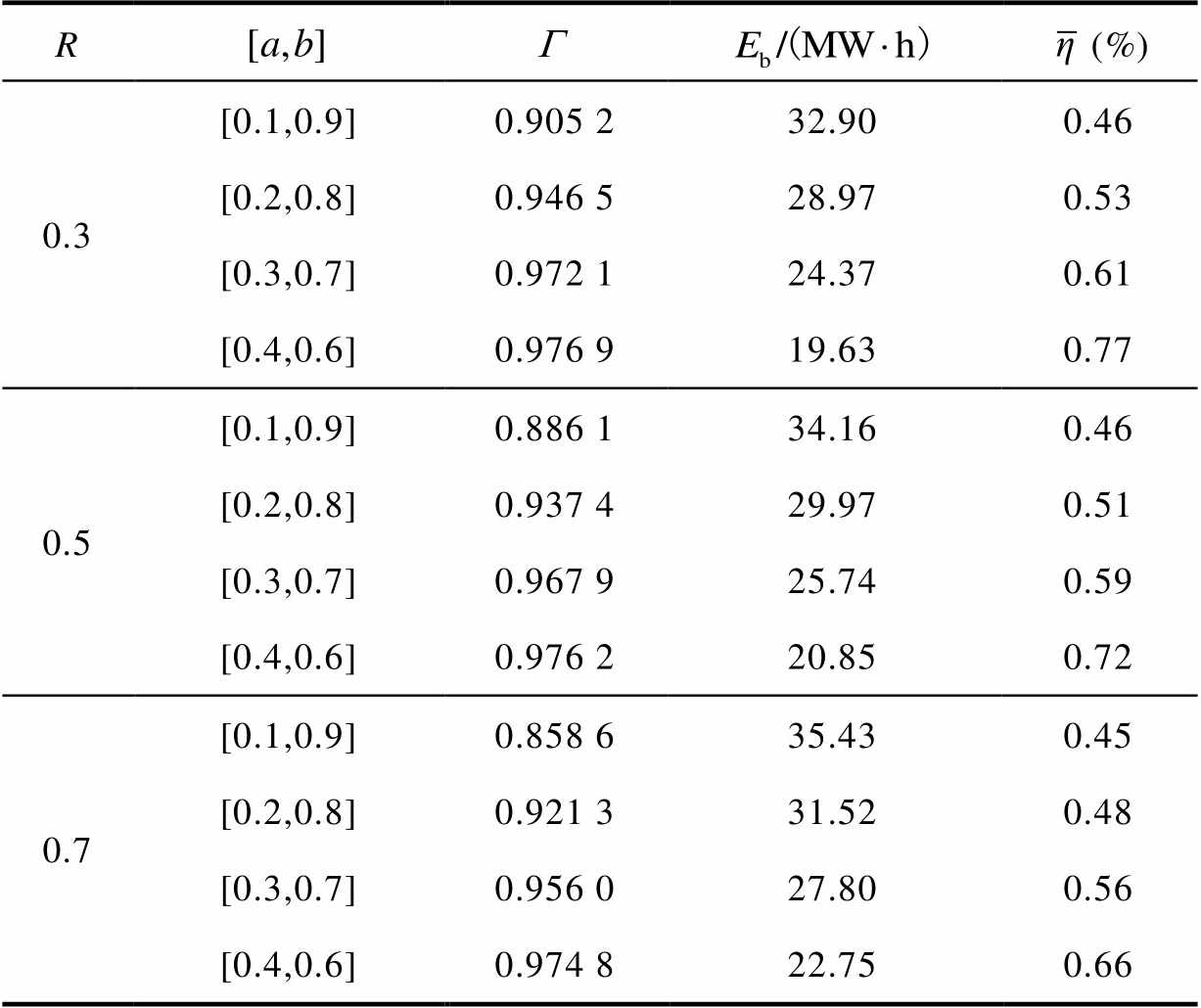
R(%) 0.3[0.1,0.9]0.905 232.900.46 [0.2,0.8]0.946 528.970.53 [0.3,0.7]0.972 124.370.61 [0.4,0.6]0.976 919.630.77 0.5[0.1,0.9]0.886 134.160.46 [0.2,0.8]0.937 429.970.51 [0.3,0.7]0.967 925.740.59 [0.4,0.6]0.976 220.850.72 0.7[0.1,0.9]0.858 635.430.45 [0.2,0.8]0.921 331.520.48 [0.3,0.7]0.956 027.800.56 [0.4,0.6]0.974 822.750.66
表5 I=30时参数调节对比
Tab.5 Comparison of different parameters for I=30
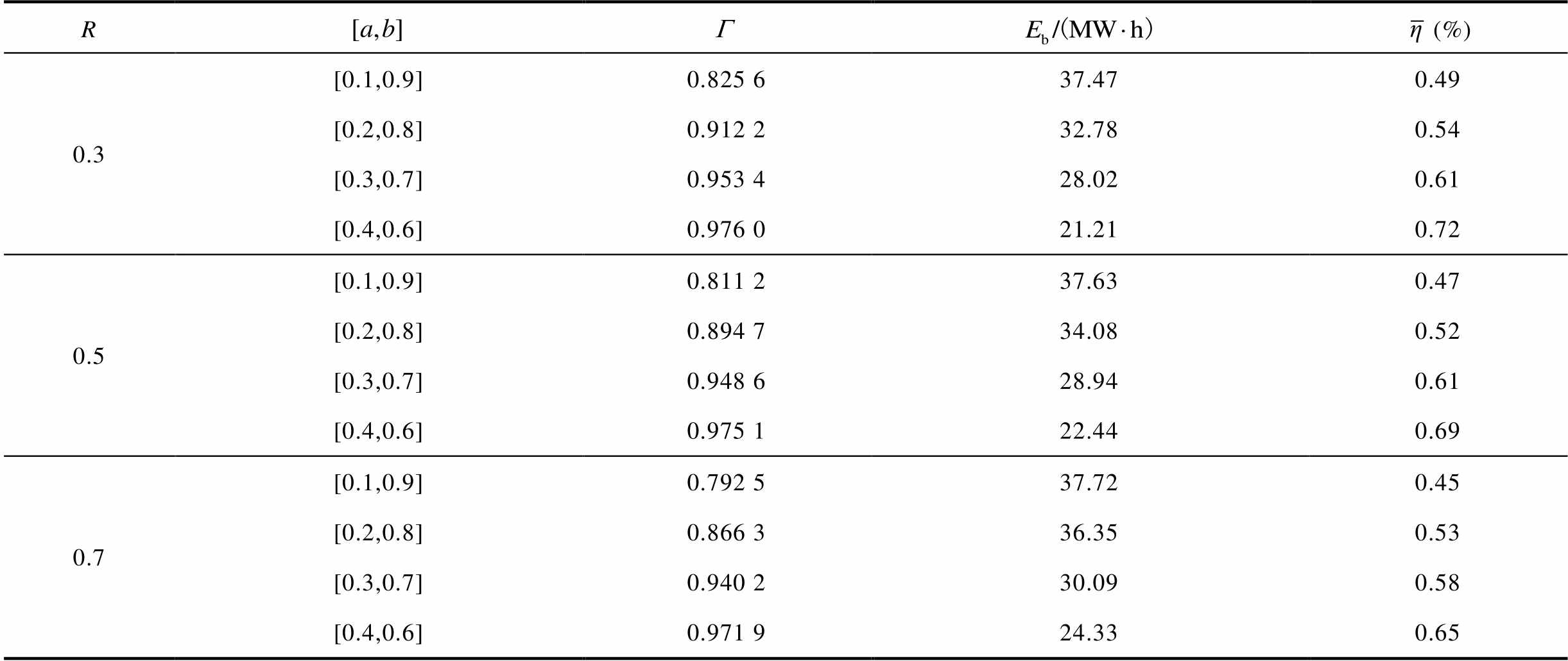
R(%) 0.3[0.1,0.9]0.825 637.470.49 [0.2,0.8]0.912 232.780.54 [0.3,0.7]0.953 428.020.61 [0.4,0.6]0.976 021.210.72 0.5[0.1,0.9]0.811 237.630.47 [0.2,0.8]0.894 734.080.52 [0.3,0.7]0.948 628.940.61 [0.4,0.6]0.975 122.440.69 0.7[0.1,0.9]0.792 537.720.45 [0.2,0.8]0.866 336.350.53 [0.3,0.7]0.940 230.090.58 [0.4,0.6]0.971 924.330.65
表6 I=40时参数调节对比
Tab.6 Comparison of different parameters for I=40
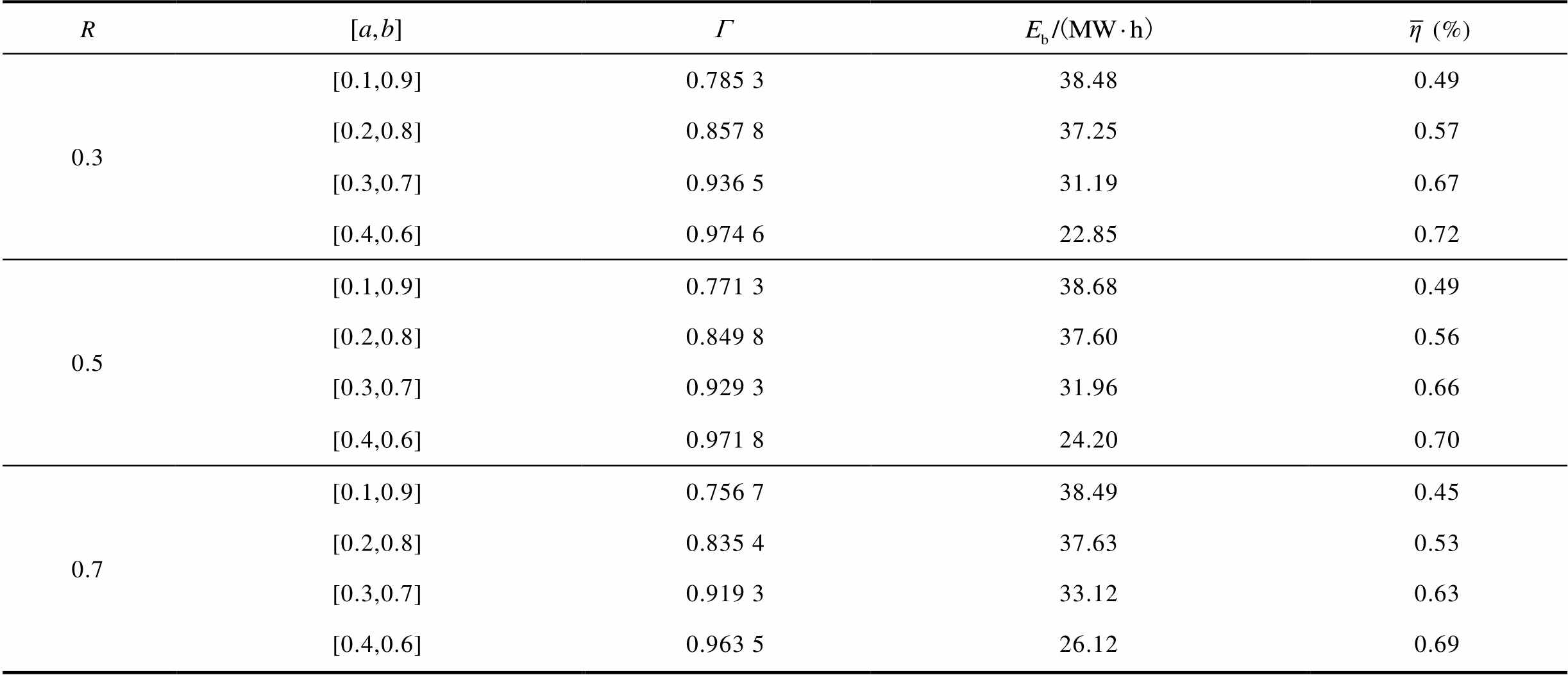
R(%) 0.3[0.1,0.9]0.785 338.480.49 [0.2,0.8]0.857 837.250.57 [0.3,0.7]0.936 531.190.67 [0.4,0.6]0.974 622.850.72 0.5[0.1,0.9]0.771 338.680.49 [0.2,0.8]0.849 837.600.56 [0.3,0.7]0.929 331.960.66 [0.4,0.6]0.971 824.200.70 0.7[0.1,0.9]0.756 738.490.45 [0.2,0.8]0.835 437.630.53 [0.3,0.7]0.919 333.120.63 [0.4,0.6]0.963 526.120.69
对比表4～表6可知，随着I值的增大，充放电饱和能力函数变化加快，储能更加频繁地调节，平均充放电裕度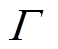减小，储能累积充放电量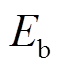增加，且风电并网波动率
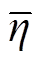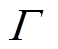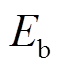也有所增加，因此，对于I的取值不宜过大。对比同一I值下的各参数，R值较小时，相比于同一[a,b]下的其他对照组来看，更大，更小，但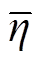较高，说明这种控制过程更加侧重于调节储能SOC；反之，在R值取值较大时则侧重于调节风电波动。但对比评价指标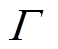和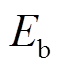，各结果差异较小，因此，可以根据风电功率平抑需求适当增大R的取值。对比同一I和R取值下的各[a,b]对照组可以看出，当[a,b]取值在[0.1,0.9]时的平均波动率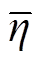最小，但是平均充放电裕度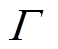过低，不利于储能系统的长期稳定运行；而当取值在[0.4,0.6]时的风电平均波动率过大，即平抑风电波动效果较差。因此，比较良好的[a,b]取值范围应该在小于[0.1,0.9]而大于[0.4,0.6]。
采用本文所提的改进WMA-模糊控制功率分配策略对MPC滚动优化得到的混合储能目标功率进行分配，蓄电池和超级电容功率调节过程如图11所示。蓄电池的功率变化相较于超级电容较为平缓，仅在240～480 min和720～960 min目标功率需求较大的时间段内功率变化较大。可见在整个风电平抑过程中，蓄电池分配了大幅度的波动功率，而超级电容分配了较为频繁的小幅度波动功率，发挥了锂电池和超级电容器各自的性能优势。
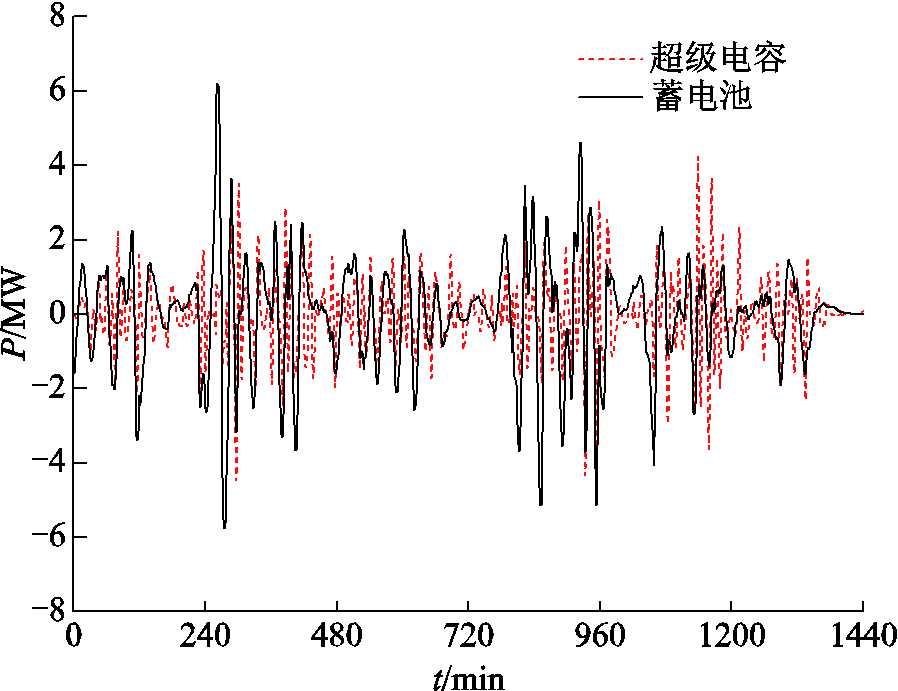
图11 各储能元件功率分配情况
Fig.11 Power distribution of energy storage components
图12为在分配目标功率时各储能元件SOC的变化情况，可以看出蓄电池和超级电容都在规定的SOC运行区间内工作，超级电容SOC变化频率和幅度相对于蓄电池更高，符合两种储能元件的特点。
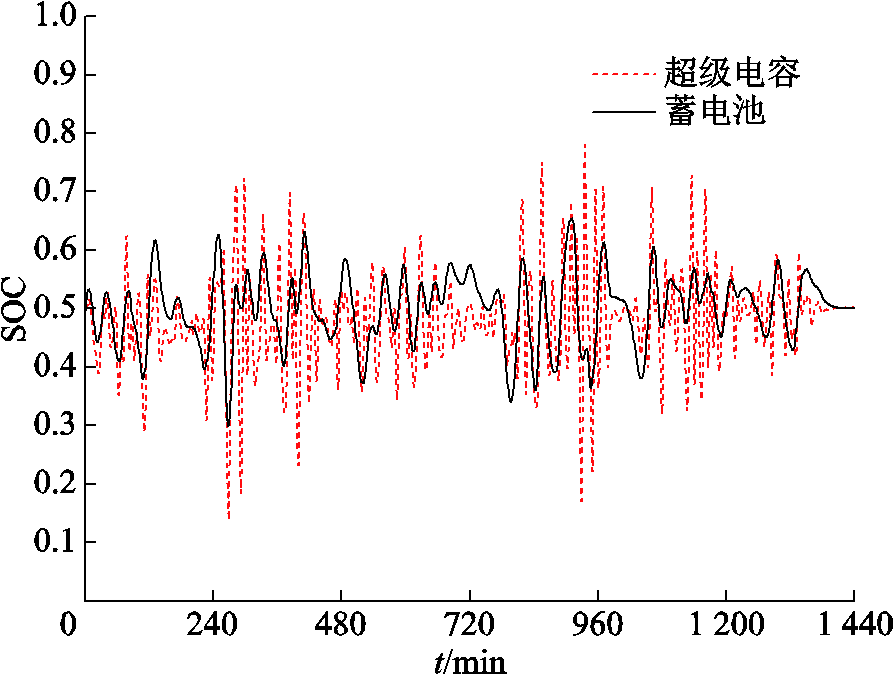
图12 各储能元件SOC变化情况
Fig.12 Changes in SOC of energy storage components
为进一步提高储能对未来功率变化的适应性，采用模糊控制对WMA参数进行调节。图13展示了在有/无模糊控制调节WMA参数下截取的第200～600 min的混合储能功率和蓄电池功率。
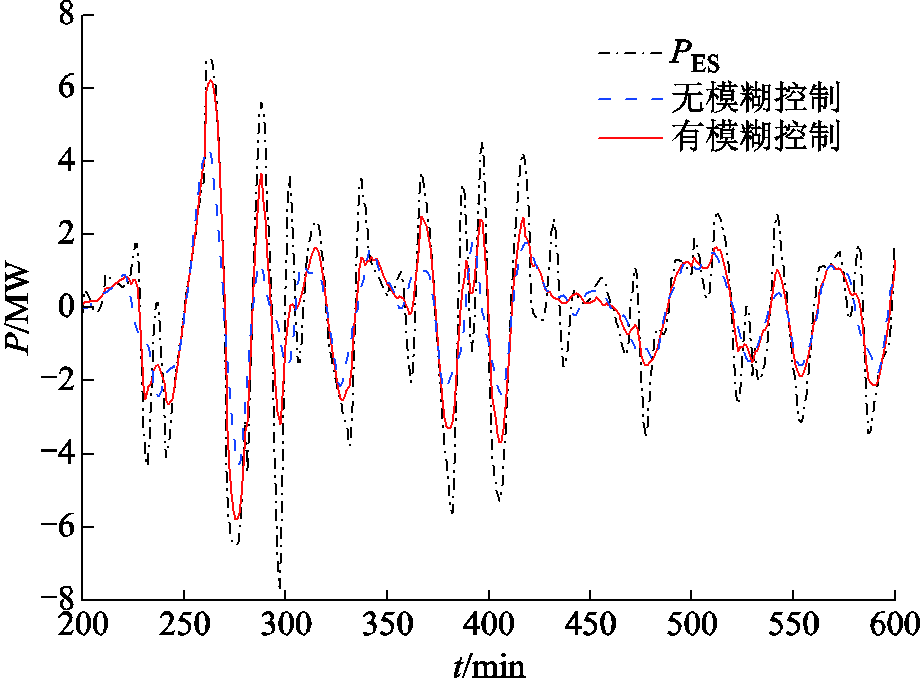
图13 200～600 min有/无模糊控制的蓄电池功率
Fig.13 Battery power with/without fuzzy control in 200～600 min
由图13可知，由于无模糊控制时WMA参数没有变化，因此在各个时段的蓄电池功率都相对平稳，但在混合储能目标功率较大时，如250～300 min，由于WMA参数不可调导致蓄电池不能快速地跟随目标功率进行调整，不能按需提供充足的功率，剩余功率只能由超级电容承担，不利于风电功率的平抑。而引入模糊控制后，在混合储能功率较小时，如图中200～230 min及440～470 min等时段，蓄电池的功率变化不大，基本和无模糊控制时一致，减小了蓄电池在低出力水平下的放电深度及充放电次数。而当储能功率需求较大时，如图13中250～300 min及370～420 min等时段，通过参数调节蓄电池能够快速跟踪大幅度功率变动，提供更多的功率以减小超级电容的功率负担。综上所述，本文的功率分配方法能够在一定程度上根据未来不同功率波动需求调整储能的功率分配，从而更加有效地对风电波动进行平抑。
为实现风储联合系统中风电并网功率波动的平抑，同时提升储能系统的长期稳定运行能力，本文应用磷酸铁锂电池和超级电容混合储能系统，结合MPC理论与WMA-模糊控制完成了混合储能目标功率预测和动态分配，通过理论分析与仿真验证得出以下主要结论：
1）提出了混合储能充放电饱和能力函数，并将其作为控制权重设计了兼顾储能系统SOC恢复和并网功率波动平抑能力的MPC策略。仿真结果表明，在平抑风电波动过程中，所提控制方法不仅能有效平抑风电功率波动，同时也能有效优化储能SOC运行区间，降低储能的寿命损耗。
2）基于MPC预测的储能目标功率，本文利用改进加权滑动平均法对蓄电池及超级电容的功率进行动态分配，并且设计了基于SOC反馈的模糊控制器动态调节MPC中的多目标优化比例。仿真结果表明，本文方法能根据功率需求自适应调整储能功率的分配，在低水平出力下降低蓄电池的放电深度与频繁转换充放电状态，降低对寿命的损耗，而在平抑功率需求较大时提高蓄电池出力，减小超级电容的输出压力，提高功率分配的合理性。
本文围绕风储联合系统风功率波动平抑及混合储能系统的协调配合与稳定运行展开了研究，但仍存在一些未涉及或仍待后续研究解决的问题，如优化混合储能的容量配置进一步发挥超级电容的性能优势；若有条件增加实验验证等。
参考文献
[1] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804.
Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1791-1804.
[2] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[3] 周博, 艾小猛, 方家琨, 等. 计及超分辨率风电出力不确定性的连续时间鲁棒机组组合[J]. 电工技术学报, 2021, 36(7): 1456-1467.
Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.
[4] 杨立滨, 曹阳, 魏韡, 等. 计及风电不确定性和弃风率约束的风电场储能容量配置方法[J]. 电力系统自动化, 2020, 44(16): 45-52.
Yang Libin, Cao Yang, Wei Wei, et al. Configuration method of energy storage for wind farms considering wind power uncertainty and wind curtailment constraint[J]. Automation of Electric Power Systems, 2020, 44(16): 45-52.
[5] Lin Li, Jia Yuanqi, Ma Minghui, et al. Long-term stable operation control method of dual-battery energy storage system for smoothing wind power fluctuations[J]. International Journal of Electrical Power & Energy Systems, 2021, 129: 106878.
[6] 谢小荣, 马宁嘉, 刘威, 等. 新型电力系统中储能应用功能的综述与展望[J]. 中国电机工程学报, 2023, 43(1): 158-169.
Xie Xiaorong, Ma Ningjia, Liu Wei, et al. Functions of energy storage in renewable energy dominated power systems: review and prospect[J]. Proceedings of the CSEE, 2023, 43(1): 158-169.
[7] Wan Can, Qian Weiting, Zhao Changfei, et al. Probabilistic forecasting based sizing and control of hybrid energy storage for wind power smoothing[J]. IEEE Transactions on Sustainable Energy, 2021, 12(4): 1841-1852.
[8] Elmorshedy M F, Elkadeem M R, Kotb K M, et al. Optimal design and energy management of an isolated fully renewable energy system integrating batteries and supercapacitors[J]. Energy Conversion and Management, 2021, 245: 114584.
[9] 齐晓光, 姚福星, 朱天曈, 等. 考虑大规模风电接入的电力系统混合储能容量优化配置[J]. 电力自动化设备, 2021, 41(10): 11-19.
Qi Xiaoguang, Yao Fuxing, Zhu Tiantong, et al. Capacity optimization configuration of hybrid energy storage in power system considering large-scale wind power integration[J]. Electric Power Automation Equipment, 2021, 41(10): 11-19.
[10] Guo Tingting, Liu Youbo, Zhao Junbo, et al. A dynamic wavelet-based robust wind power smoothing approach using hybrid energy storage system[J]. International Journal of Electrical Power & Energy Systems, 2020, 116: 105579.
[11] 万灿, 崔文康, 宋永华. 新能源电力系统概率预测:基本概念与数学原理[J]. 中国电机工程学报, 2021, 41(19): 6493-6509.
Wan Can, Cui Wenkang, Song Yonghua. Probabilistic forecasting for power systems with renewable energy sources: basic concepts and mathematical principles[J]. Proceedings of the CSEE, 2021, 41(19): 6493-6509.
[12] 刘颖明, 王维, 王晓东, 等. 结合风功率预测及储能能量状态的模糊控制策略平滑风电出力[J]. 电网技术, 2019, 43(7): 2535-2543.
Liu Yingming, Wang Wei, Wang Xiaodong, et al. A fuzzy control strategy combined with wind power prediction and energy storage SOE for smoothing wind power output[J]. Power System Technology, 2019, 43(7): 2535-2543.
[13] 潘超, 李润宇, 蔡国伟, 等. 基于时空关联分解重构的风速超短期预测[J]. 电工技术学报, 2021, 36(22): 4739-4748.
Pan Chao, Li Runyu, Cai Guowei, et al. Multi-step ultra-short-term wind speed prediction based on decomposition and reconstruction of time-spatial correlation[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4739-4748.
[14] 路朋, 叶林, 裴铭, 等. 风电集群有功功率模型预测协调控制策略[J]. 中国电机工程学报, 2021, 41(17): 5887-5900.
Lu Peng, Ye Lin, Pei Ming, et al. Coordinated control strategy for active power of wind power cluster based on model predictive control[J]. Proceedings of the CSEE, 2021, 41(17): 5887-5900.
[15] 陈长青, 李欣然, 谭庄熙. 考虑风电不确定性的风储调频能力[J]. 高电压技术, 2022, 48(6): 2128-2139.
Chen Changqing, Li Xinran, Tan Zhuangxi. Frequency modulation capability of wind storage considering wind power uncertainty[J]. High Voltage Engineering, 2022, 48(6): 2128-2139.
[16] Cao Minjian, Xu Qingshan, Qin Xiaoyang, et al. Battery energy storage sizing based on a model predictive control strategy with operational constraints to smooth the wind power[J]. International Journal of Electrical Power & Energy Systems, 2020, 115: 105471.
[17] 孙玉树, 唐西胜, 孙晓哲, 等. 基于MPC-HHT的多类型储能协调控制策略研究[J]. 中国电机工程学报, 2018, 38(9): 2580-2588, 2826.
Sun Yushu, Tang Xisheng, Sun Xiaozhe, et al. Research on multi-type energy storage coordination control strategy based on MPC-HHT[J]. Proceedings of the CSEE, 2018, 38(9): 2580-2588, 2826.
[18] Wu Tiezhou, Yu Wenshan, Guo Linxin. A study on use of hybrid energy storage system along with variable filter time constant to smooth DC power fluctuation in microgrid[J]. IEEE Access, 2019, 7: 175377-175385.
[19] 刘忠, 杨陈, 蒋玮, 等. 基于一致性算法的直流微电网储能系统功率分配技术[J]. 电力系统自动化, 2020, 44(7): 61-69.
Liu Zhong, Yang Chen, Jiang Wei, et al. Consensus algorithm based power distribution technology for energy storage system in DC microgrid[J]. Automation of Electric Power Systems, 2020, 44(7): 61-69.
[20] 付华, 陆鹏, 张俊男. 基于A-SA-WOA算法的直流微电网全钒液流电池储能系统功率分配策略[J]. 电工技术学报, 2023, 38(7): 1826-1837.
Fu Hua, Lu Peng, Zhang Junnan. Power allocation strategy of DC microgrid all vanadium redox flow battery energy storage system based on A-SA-WOA algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1826-1837.
[21] 付菊霞, 陈洁, 滕扬新, 等. 基于集合经验模态分解的风电混合储能系统能量管理协调控制策略[J]. 电工技术学报, 2019, 34(10): 2038-2046.
Fu Juxia, Chen Jie, Teng Yangxin, et al. Energy management coordination control strategy for wind power hybrid energy storage system based on EEMD[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2038-2046.
[22] 李亚楠, 王倩, 宋文峰, 等. 混合储能系统平滑风电出力的变分模态分解-模糊控制策略[J]. 电力系统保护与控制, 2019, 47(7): 58-65.
Li Yanan, Wang Qian, Song Wenfeng, et al. Variational mode decomposition and fuzzy control strategy of hybrid energy storage for smoothing wind power outputs[J]. Power System Protection and Control, 2019, 47(7): 58-65.
[23] 王宇. 超级电容与蓄电池混合储能系统的能量管理与控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
Wang Yu. Study on energy management and control of a supercapacitor and battery hybrid energy storage system[D]. Harbin: Harbin Institute of Technology, 2016.
[24] 孙玉树, 张国伟, 唐西胜, 等. 风电功率波动平抑下的MPC双储能控制策略研究[J]. 电工技术学报, 2019, 34(3): 571-578.
Sun Yushu, Zhang Guowei, Tang Xisheng, et al. Research on MPC and daul energy storage control strategies with wind power fluctuation mitigation[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 571-578.
[25] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 风电场接入电力系统技术规定: GB/T 19963—2011[S]. 北京: 中国标准出版社, 2012.
[26] 朱丽云. 考虑充放电能量不均衡的双电池系统容量配置与控制策略研究[D]. 重庆: 重庆大学, 2018.
Zhu Liyun. Study on the capacity configuration and control strategy of dual battery system considering charging and discharging unbalanced energy[D]. Chongqing: Chongqing University, 2018.
[27] 李学斌, 刘建伟. 采用二阶滤波的混合储能系统实时功率分配方法[J]. 电网技术, 2019, 43(5): 1650-1657.
Li Xuebin, Liu Jianwei. Real-time power distribution method adopting second-order filtering for hybrid energy storage system[J]. Power System Technology, 2019, 43(5): 1650-1657.
Abstract The increase in penetration of new energy sources such as wind power poses a huge threat to the security and stability of the power grid operation. This paper used a hybrid energy storage system with a battery and supercapacitor to cope with the complex fluctuations of wind power. To achieve the smoothing of grid-connected power fluctuations while reducing the lifetime losses of the storage system, this paper proposed a hybrid energy storage control method taking into account the state of charge (SOC) self-recovery to smooth out wind power fluctuations, including model predictive control (MPC) to predict the target power of hybrid storages and weighted moving average (WMA) method with fuzzy control to allocate target power.
This paper first established the MPC optimization target function combining SOC recovery for energy storage systems and grid-connected power fluctuation smoothing capability. To characterize the relationship between the SOC and the charge and discharge margin of the energy storage system, a charge and discharge saturation capacity function was proposed. This function was also introduced as a weighting factor into the MPC optimization target function, achieving rapid adjustment of the SOC during power smoothing and improving the long-term stable operation capability of energy storage. An improved WMA method was then proposed to distribute the MPC-predicted target power between supercapacitor and battery power. Considering the small capacity of supercapacitor which is easy to overcharge and over-discharge, the SOC of the supercapacitor at the previous moment and the change of SOC of future hybrid energy storage were taken as fuzzy control inputs. According to the different operating conditions, the fuzzy control rules were designed to dynamically adjust the WMA sliding window length d and the α weighted of past and future reference values, thus improving the adaptability of the battery and supercapacitor to different target power and different SOC.
A wind-storage joint model was developed in Matlab, and the simulation compared the control effects of three methods of optimization targets. Method 1 is SOC closed to 0.5 at real-time. Method 2 is minimizing the fluctuation rates of grid-connected power. Method 3 is the optimization method for this paper. The simulation results show that the fluctuation rates of grid-connected power are less than 2% by method 3, in which 43.4% of the fluctuation rates are below 0.2%, and the average fluctuation rate is 0.61%, which is between the other two methods. The total charge and discharge energy of the hybrid energy storage is 28.93, which is much lower than the 47.67 of method 2. The average charge and discharge margin of 0.948 6 is close to 0.978 7 for method 1, but much higher than 0.591 4 for method 2. For different initial SOC, the SOC can gradually recover to around 0.5 and eventually follow the change of the control group with the initial value of SOC=0.5. Simulations were then carried out to verify the power allocation strategy with improved WMA-fuzzy control. The results show that the power variation of the battery is relatively gentle compared to that of the supercapacitor, and only varies greatly in the time of 240 min to 480 min and 720 min to 960 min when the power demand is high.
The simulation analysis leads to the following conclusions. Firstly, the proposed model predictive control for the target power of hybrid energy storage can effectively smooth out wind power fluctuations, and also effectively optimize the operation interval of SOC and reduce the lifetime loss of energy storage. Secondly, the designed allocation strategy adaptively adjusts the distribution of energy storage power according to the power demand. This strategy reduces the depth of discharge and the charge-to-discharge transition state of the battery at low levels of power output, thus reducing the loss of life. In contrast, increasing the battery output when the power demand is high. It reduces the pressure on the supercapacitor and improves the rationality of the power distribution.
Keywords：Wind power fluctuations, hybrid energy storage, model predictive control, weighted moving average, fuzzy control
中图分类号：TM614
DOI:10.19595/j.cnki.1000-6753.tces.221976
收稿日期 2022-10-18
改稿日期 2022-12-05
林 莉 女，1974年生，副教授，硕士生导师，研究方向为电力系统运行与控制。E-mail：linli@cqu.edu.cn（通信作者）
林雨露 女，1999年生，硕士研究生，研究方向为微电网与储能协调运行与控制。E-mail：yulu_lyl@163.com
（编辑 赫 蕾）