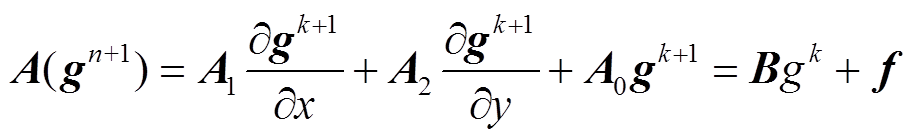 (1)
(1)
摘要 油浸式电力变压器绕组温升监测是保证其安全稳定运行的重要手段。为了改善采用有限元方法计算油浸式电力变压器绕组瞬态温升时存在效率不高的问题,提出一种结构保留的本征正交分解(SPOD)与离散经验插值方法(DEIM)相结合的计算策略。首先,该文采用最小二乘有限元法(LSFEM)与迎风有限元法(UFEM)构建变压器绕组瞬态温升计算控制方程;其次,针对控制方程的特点,引入SPOD方法,通过将采样时间内的计算结果构成快照矩阵,建立降阶模型,降低有限元刚度矩阵的计算阶数,提高求解有限元方程的效率;然后,为了改善本征正交分解方法对于非线性问题效率提升不高的缺陷,结合DEIM算法,对有限元方程中的非线性项进行插值处理,从而减少每一时步形成总体刚度矩阵的时间,进一步提高总体计算效率。为了验证文章所提算法的精确性及高效性,根据油浸式电力变压器绕组的基本特点,建立了单分区分匝绕组传热模型,对其瞬态传热过程进行计算,结果表明:基于SPOD-DEIM的有限元降阶计算能够在保证精度的前提下有效提高计算效率,与全阶计算结果相比,流场与温度场的计算误差均不超过1.5%,且计算效率提升5.1倍。同时,为了充分说明SPOD-DEIM算法在工程应用中的价值,该文基于110 kV变压器绕组搭建了温升实验平台,建立了八分区分匝绕组数值计算模型,对算法的精度、效率及工程应用价值进行了验证及讨论,计算及实验结果表明:精度方面,降阶计算较全阶计算的瞬态全过程计算误差小于2.5%,且与实验结果相比,误差不超过5.41 K;效率方面,降阶计算的全过程计算时间为54.28 h,与全阶计算相比,计算效率提升至10.57倍,与商业仿真软件Fluent相比,效率提升至6.37倍,充分说明所提算法的高效性及工程应用价值,为大型电力设备快速仿真提供新思路。
关键词:绕组瞬态温升 结构保留 本征正交分解 离散经验插值 降阶计算 温升实验
电力变压器作为电力系统当中的主要电气设备,其稳定性和安全性需要得到切实的保证。在实际运行过程中,变压器绕组产生的欧姆损耗与涡流损耗使得绕组温度上升,一旦绕组温度过高,就会面临损坏甚至烧毁的风险,因此对于变压器绕组温升的监测至关重要。针对油浸式电力变压器,绕组温升的监测手段目前主要包括三种:直接测量法[1-3]、代理模型法[4-6]及数值计算法[7-9]。其中,数值计算方法是较为主要的方法。
数值计算方法通过建立流热耦合场的控制方程,对温升问题进行数值计算,从而得到绕组整体的温度分布或者变化曲线。针对变压器绕组温升问题的计算目前采用较多的数值计算方法有有限元法、有限体积法等。相较于有限体积法,有限元法具有灵活性高、直观性强、求解精度高等诸多优势,应用前景更为广泛。同时,随着有限元方法的不断发展,迎风有限元(Upwind Finite Element Method, UFEM)[10]、最小二乘有限元(Least Squares Finite Element Method, LSFEM)等[11-12]方法克服了传统有限元算法在数值上的不稳定性,极大地提高了数值模型的计算精度,使其更加逼近实际结果。然而,计算时间成本过高是阻碍该类方法应用于工程实际的关键问题。
有限元法的瓶颈在于计算效率与模型剖分的精细程度相关。在实际工程问题当中,为了精确计算,需要对模型剖分的网格数量非常多,从而导致计算中的有限元刚度矩阵规模特别大,这对计算机内存和计算效率提出了考验。为了提高计算绕组温升计算的速度,谢裕清[13-14]、荣世昌等[15]提出采用本征正交分解(Proper Orthogonal Decomposition,POD)的方法得到降阶正交基,降低有限元方程阶数,进而提高计算效率,该方法效果显著且计算成本较低。然而,当有限元方程中涉及的物理量较多且彼此之间量级相差较大时,传统的POD方法可能需要更多的正交基才可以保证精度,因此,Shuai Yan等[16-17]提出采用结构保留的本征正交分解方法(Structure-Preserved Proper Orthogonal Decomposition, SPOD),这种方法的好处在于简化问题的同时能够保证完整问题的块结构,更适用于物理量较多的有限元计算。
另一方面,SPOD方法虽然能够降低方程的阶数,使得有限元方程能够在一个阶数较低的子空间内求解,但是,由于非线性项的存在,其在形成刚度矩阵的过程中仍然需要遍历所有单元,这是另一个限制计算效率的瓶颈问题。为了克服这一问题,本文结合采用了S. Chaturantabut和D. S. Sorensen[18]提出的离散经验插值方法(Discrete Empirical Interpolation Method, DEIM),该方法不需要将非线性项中的所有元素进行回代计算,其仅需通过贪婪算法选取方程非线性项中的部分元素,进而用少量元素对全体进行插值,从而达到提高计算效率的目的。
综上所述,本文首先结合LSFEM以及UFEM推导油浸式电力变压器流固耦合传热过程的瞬态控制方程;然后详细介绍SPOD与DEIM的算法原理,并将其引入所推导的瞬态控制方程中,得到降阶计算模型;最后根据110 kV电力变压器结构特点,搭建了油浸式电力变压器绕组温升实验平台,并建立二维数值传热模型, 结合相关实验,提出并讨论了SPOD-DEIM算法的相关性能及实际应用价值。
油浸式电力变压器绕组的温升过程显然是一个流热耦合计算问题。对于其中反映油流变化的流场,基于流体力学中的质量守恒与动量守恒定律,结合涡量ω,同时对时间项采用Crank-Nicolson方法进行离散,其二维瞬态控制方程可表示为[19]
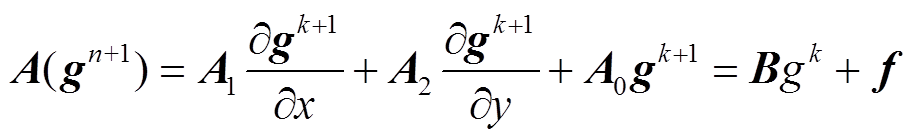 (1)
(1)
其中
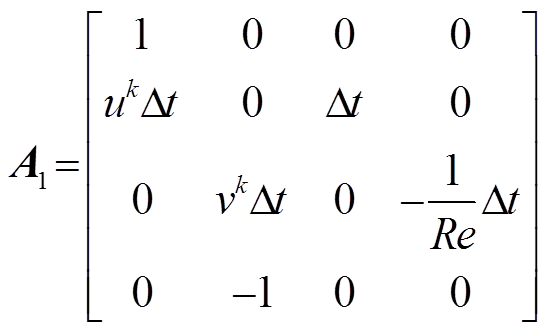
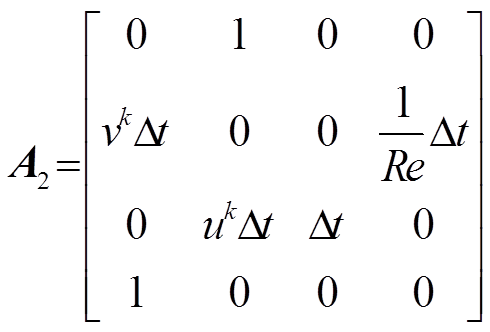
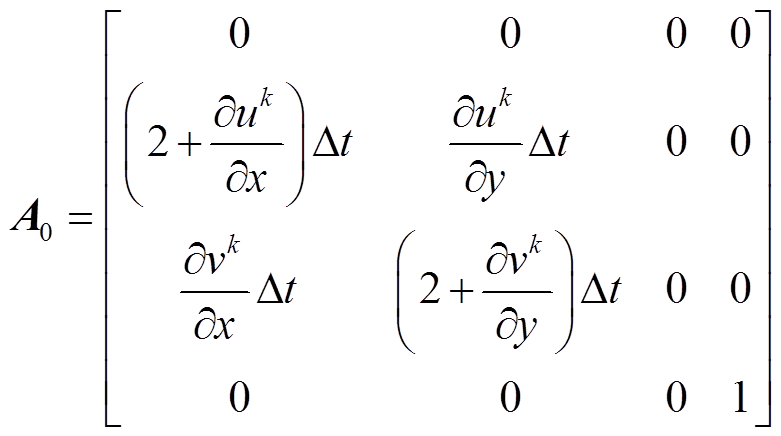
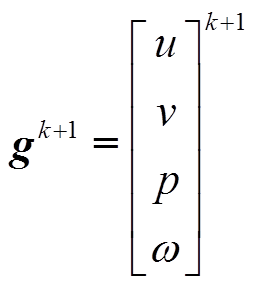
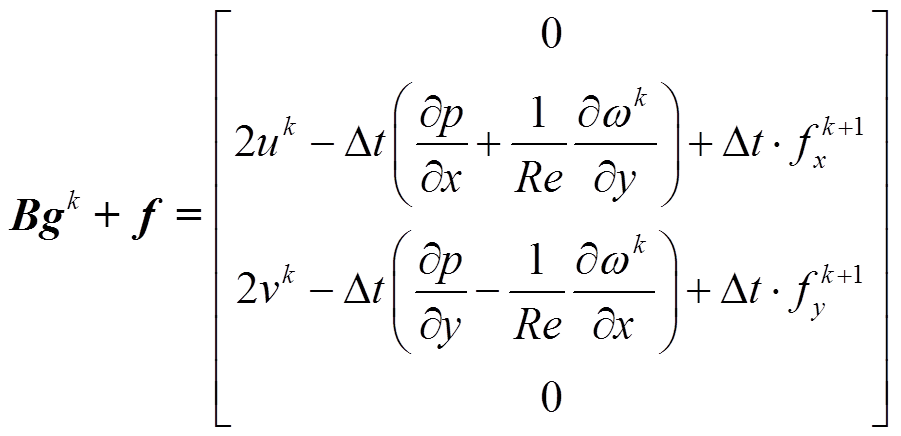
式中,k+1为瞬态计算当中的第k+1个时间步;k为第k个时间步;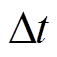 为时间步长;u、v分别为流体的横向与纵向速度,m/s;p为流体压力,Pa;ρ为密度,kg/m3,此处为流体密度;Re为雷诺数;f为外力密度矢量,不考虑重力项时,可以取0。
为时间步长;u、v分别为流体的横向与纵向速度,m/s;p为流体压力,Pa;ρ为密度,kg/m3,此处为流体密度;Re为雷诺数;f为外力密度矢量,不考虑重力项时,可以取0。
采用LSFEM方法对式(1)进行空间离散,得到其有限元求解格式为
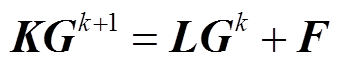 (2)
(2)
其中
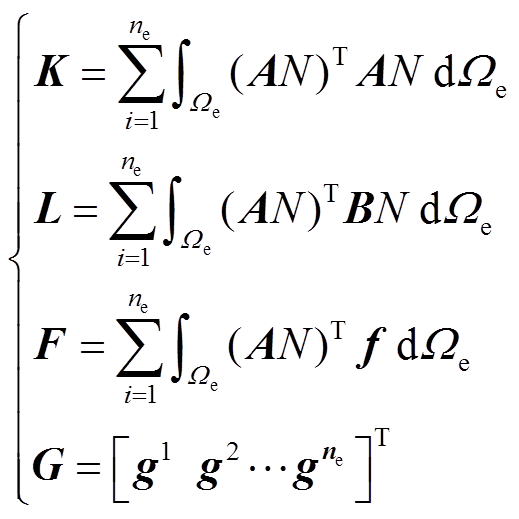
式中,ne为有限单元总数;Ωe为求解场域;N为有限元形函数;G为各节点的自由度矩阵。
对于温度场,基于能量守恒定律,采用UFEM方法得到其瞬态温度场控制方程为[19]
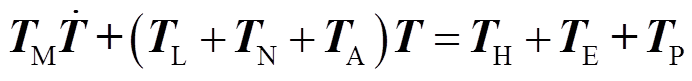 (3)
(3)
其中
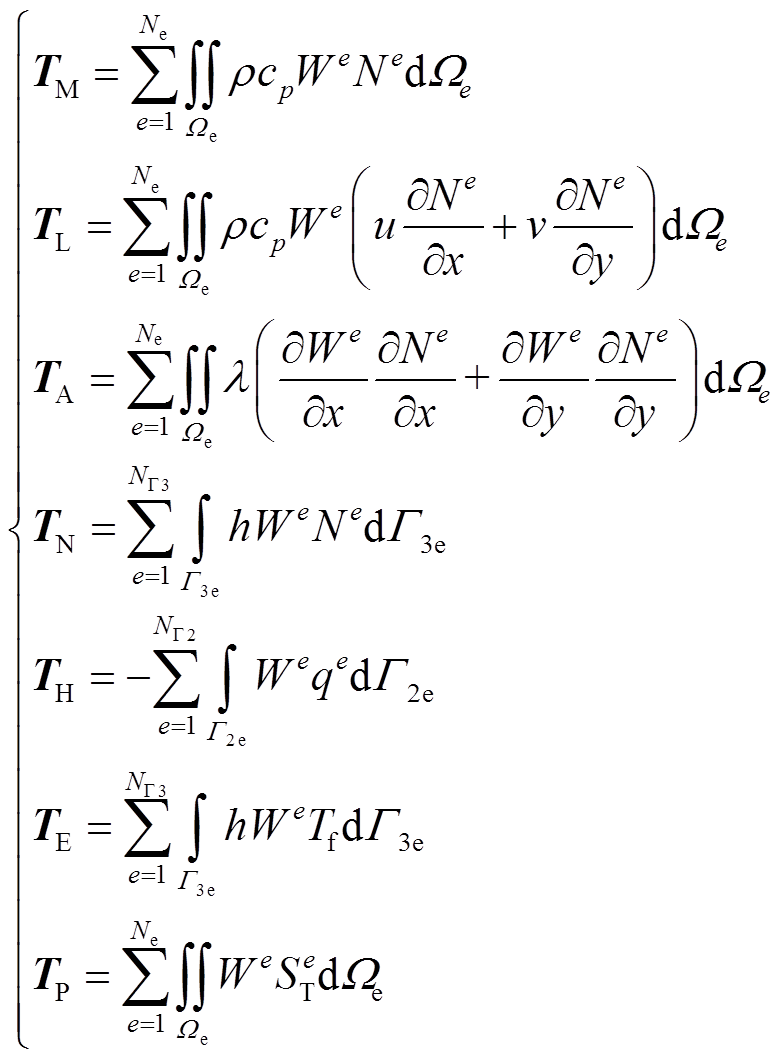
式中,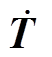 表示时间偏导项,
表示时间偏导项,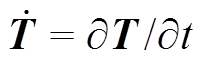 ;Ne为总单元数;NΓ2为第二类边界条件单元数;NΓ3为第三类边界条件单元数;q为热流密度,W/m2;Γ2e为第二类边界;Γ3e为第三类边界;W为迎风算子;N为有限元形函数;ρ为密度,kg/m3,此处为介质密度;cp为比定压热容,J/(kg·K);λ为导热系数,W/(m·K);ST为热源密度,W/m3;h为表面传热系数,W/(m2·K);Tf为环境温度,K。
;Ne为总单元数;NΓ2为第二类边界条件单元数;NΓ3为第三类边界条件单元数;q为热流密度,W/m2;Γ2e为第二类边界;Γ3e为第三类边界;W为迎风算子;N为有限元形函数;ρ为密度,kg/m3,此处为介质密度;cp为比定压热容,J/(kg·K);λ为导热系数,W/(m·K);ST为热源密度,W/m3;h为表面传热系数,W/(m2·K);Tf为环境温度,K。
同样采用Crank-Nicolson方法对其中的时间项进行离散,可以得到式(3)的最终求解格式为
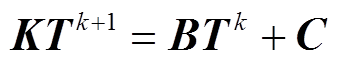 (4)
(4)
其中
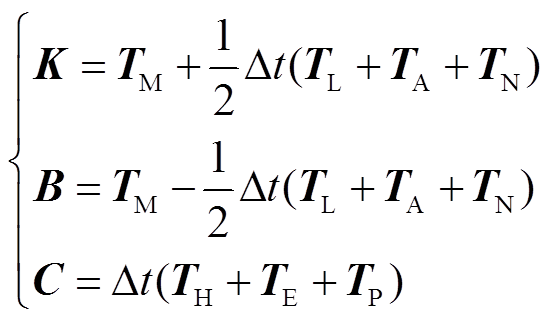
将式(2)与式(4)联立,结合相应的边界条件与初始条件,即可以得到油浸式电力变压器绕组瞬态温升计算方程。根据LSFEM-UFEM结合的有限元方法即可较为精确地获得绕组瞬态温升变化过程中的流场及温度场分布。然而,在实际工程应用中,模型的网格规模和节点数量一般较大,采用有限元方法进行求解面临时间成本过高的问题,因此,需要考虑引入降阶技术,降低计算规模,从而提高计算效率。本文采用结构保留的本征正交分解方法与离散经验插值方法改善该问题。
本征正交分解方法原理是通过将一组数值计算得到的场域求解结果组成快照矩阵,基于奇异值分解的原理获得正交基,选取其中反映系统特征较多的部分组成降阶子空间,最后通过投影定理,将原系统投影至降阶子空间中完成降阶模型的构建。假设一组由计算结果构成的快照矩阵数据集为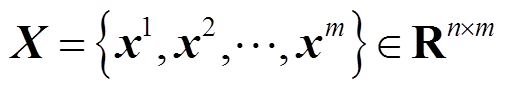 ,若需要一组m维正交基表示该组数据集,且使得误差最小,则有
,若需要一组m维正交基表示该组数据集,且使得误差最小,则有
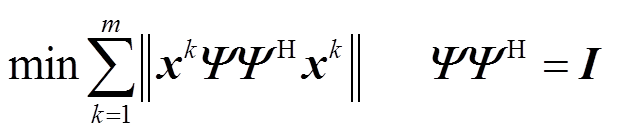 (5)
(5)
式中, 表示矩阵
表示矩阵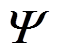 的共轭转置。
的共轭转置。
基于变分方法与拉格朗日乘子法[20],可以将上述最优问题转化为式(6)的矩阵特征值计算问题。
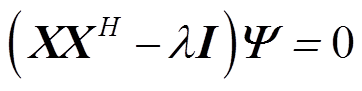 (6)
(6)
通过计算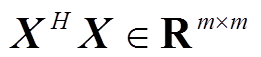 的特征值可以较为便利地得到
的特征值可以较为便利地得到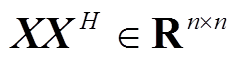 的特征向量,二者的对应关系为
的特征向量,二者的对应关系为
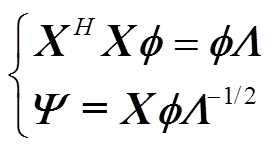 (7)
(7)
式中,Λ为特征值矩阵,Λ=[λ1 λ2 ××× λm],且λ1>λ2>×××>λm。该算法的截断误差可以表示为[21]
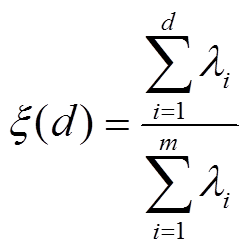 (8)
(8)
式中,λi为Λ中的第i个特征值,其可以表征第i个POD正交基向量Ψi对系统特征的贡献。式(8)的意义在于,当选择的正交基个数为前d阶时,其所包含的数据特征占系统总特征的百分比。因此,一般情况下,选取能够占到系统总特征约99.9%的正交基数量,即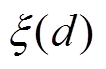 >99.9%,再结合投影定理,可在由正交基构成的降阶子空间中很好地反映原系统特征,使得模型阶数由n维降低至d维。
>99.9%,再结合投影定理,可在由正交基构成的降阶子空间中很好地反映原系统特征,使得模型阶数由n维降低至d维。
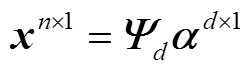 (9)
(9)
可以看出,在每个迭代步内,系统方程由全阶计算时的n阶降低为了d阶,矩阵计算规模得以减少,能够很好地提高求解效率。然而,对于非线性问题而言,刚度矩阵K的形成与前一时间步的物理量有关,因此每时刻计算都需要遍历所有单元重新形成K,这是降低计算效率的另一瓶颈问题,结合离散经验插值算法可以对其做出改善。
离散经验插值源于经验插值,其主要针对非线性问题提出了一种离散点插值思路,从而减小非线性计算引起的效率降低。
对于非线性项F(xk)∈Rn×1,通过奇异值分解选取一组正交基U,使其可以表示为
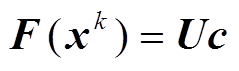
 (10)
(10)
上述方程对于求解c,其未知数有d个,方程有n组,属于超定方程组,因此需要剔除U中的n-d行。采用的方法是引入布尔矩阵P,有
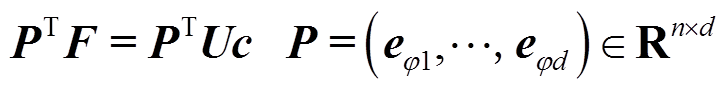 (11)
(11)
式中,eφ1为第φ1个元素为1的单位向量。通过引入布尔矩阵,可以使得矩阵可逆,从而求得c为
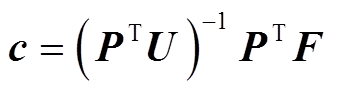 (12)
(12)
再将c的求解结果代入式(10),则有
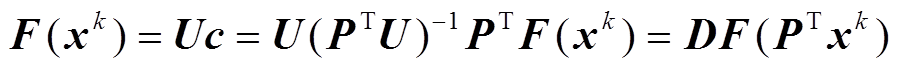 (13)
(13)
式中,D为DEIM插值矩阵,在求解过程中仅需计算一次。同时,由于布尔矩阵P的选择作用,实际运算中仅仅需要F中的d个离散点,而其他n-d个点的值则由插值得到。布尔矩阵P的形成与d个插值点的选取通过基于贪婪算法的搜索完成,其搜索思路为:将第一个插值点的位置选择为U中的第一个基向量u1绝对值最大元素的位置,然后依次用当前的基向量组表示下一基向量,选择残差向量的最大元素位置作为下一个插值点的位置。程序伪代码见表1。
特别地,在有限元方法中,由于插值点表示的是有限元剖分区域内的节点,其值的大小与该节点所属的所有单元均有关,因此在形成总体刚度矩阵时需要注意,将选择的插值点属于的所有单元刚度矩阵均进行计算并组装,如图1所示。
综上所述,仅需提前计算一次POD正交基及DEIM插值矩阵和插值点,即可从有限元方程降阶和非线性项插值两个方面提高原系统的计算效率。
然而,对于本文所探讨的流场问题而言,其节点自由度包含四个物理量:横向及纵向速度、压力、涡量,且四个物理量之间量纲不同,数量级不同,四者均为构成流场的重要特征。因此,在降阶模型中,需要保持这四个物理量在有限元矩阵中原本的块结构,本文采用了SPOD-DEIM方案。
表1 DEIM插值点搜索算法
Tab.1 DEIM interpolation point search algorithm
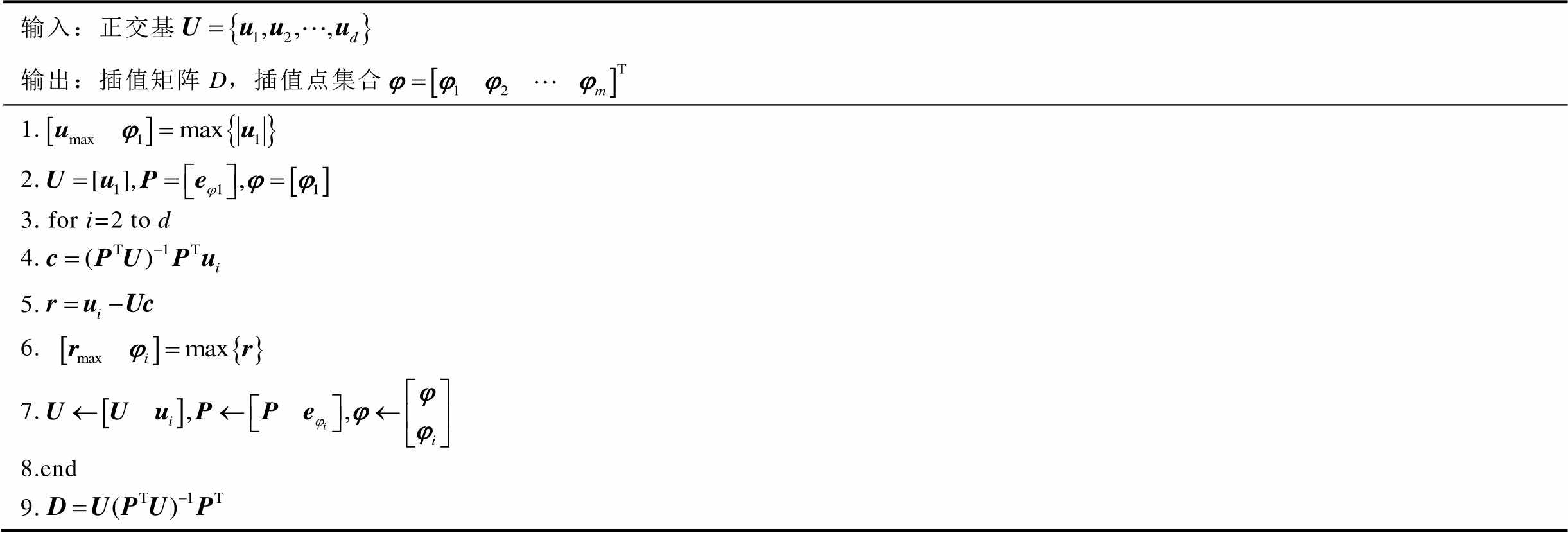
输入:正交基 输出:插值矩阵D,插值点集合 1. 2. 3. for i=2to d 4. 5. 6. 7. 8.end 9.
注:max()表示max函数,其输出结果依次表示为最大值以及最大值所在位置序号。
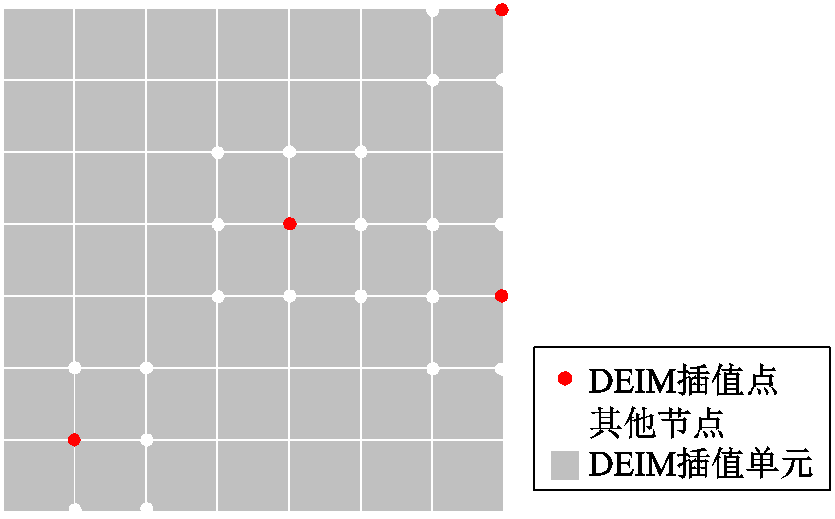
图1 DEIM算法应用于有限元
Fig.1 Application of DEIM in finite element method
油浸式电力变压器绕组温升计算涉及流场与温度场的耦合,因此,引入降阶算法需要同时考虑温升计算中的流场控制方程与温度场控制方程。首先,对于反映变压器油流分布的瞬态流场计算方程,根据式(2),其离散形式可以用矩阵表示为
式中,K、L为有限元刚度矩阵,矩阵中各元素根据油流场中各节点的物性参数、位置以及时间步长形成;F为有限元右端项矩阵,与各节点的油流速度有关;Gk+1与Gk分别为第k+1时间步和第k时间步的变压器油状态参数,包括横向速度u、纵向速度v、压强p以及涡量ω。通过设置入口油流速度等边界条件、场域内油流初始速度等初始条件即可通过式(14)计算得到瞬态过程中油流的速度变化。
按照传统POD降阶模型构建方法,选取前S个时间步的流场全阶计算结果构成快照矩阵,则有Snapshot=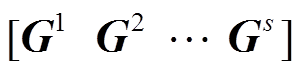 ,接着对其进行奇异值分解即可获得降阶正交基,进而通过降阶正交基保留的原系统数据特征构建降阶计算模型。然而,实际计算过程中,各状态参数的大小往往差异很大,如:u、v与p、ω相比一般较小,这就使得基于全局的POD降阶正交基选取不能很好地反映各状态参数的数据特征,且传统的POD方法通常是对整个数据集进行分解,仅能够反映数据集的统计特征,而无法保留物理特征,使得降阶模型的可解释性低。因此本文采用了一种“数据结构保留”的降阶计算策略,通过变换矩阵Q,将快照矩阵Snapshot的数据结构调整为
,接着对其进行奇异值分解即可获得降阶正交基,进而通过降阶正交基保留的原系统数据特征构建降阶计算模型。然而,实际计算过程中,各状态参数的大小往往差异很大,如:u、v与p、ω相比一般较小,这就使得基于全局的POD降阶正交基选取不能很好地反映各状态参数的数据特征,且传统的POD方法通常是对整个数据集进行分解,仅能够反映数据集的统计特征,而无法保留物理特征,使得降阶模型的可解释性低。因此本文采用了一种“数据结构保留”的降阶计算策略,通过变换矩阵Q,将快照矩阵Snapshot的数据结构调整为
 (15)
(15)
式中,上标表示时间步,下标表示节点号,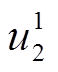 即表示第二个节点在第一个时刻的横向速度。变换矩阵Q的作用在于将快照矩阵中属于同一物理属性(横/纵向速度、压强、涡量)的数据聚合到一起,形成块结构U、V、p、ω。对不同的块结构分别进行奇异值分解形成SPOD降阶正交基Ψu∈
即表示第二个节点在第一个时刻的横向速度。变换矩阵Q的作用在于将快照矩阵中属于同一物理属性(横/纵向速度、压强、涡量)的数据聚合到一起,形成块结构U、V、p、ω。对不同的块结构分别进行奇异值分解形成SPOD降阶正交基Ψu∈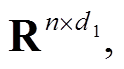 Ψv∈
Ψv∈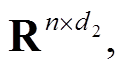 Ψp∈
Ψp∈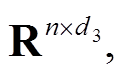 Ψω∈
Ψω∈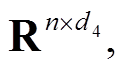 (d1, d2, d3, d4
(d1, d2, d3, d4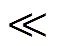 n),其中各块结构正交基的个数d由该部分的数据特征决定,并将各物理量分别表示为
n),其中各块结构正交基的个数d由该部分的数据特征决定,并将各物理量分别表示为
u=Ψuαu v=Ψvαv p=Ψpαp ω=Ψωαω
这样通过块分解的方式即可合理选择各部分降阶正交基的阶数,充分提取并保留各物理量的数据特征,同时也使得构建的降阶模型更具有物理意义。
获得降阶正交基后,为了降低计算阶数,将原系统投影至降阶子空间中,采用伽辽金投影方法,将系统方程重构为
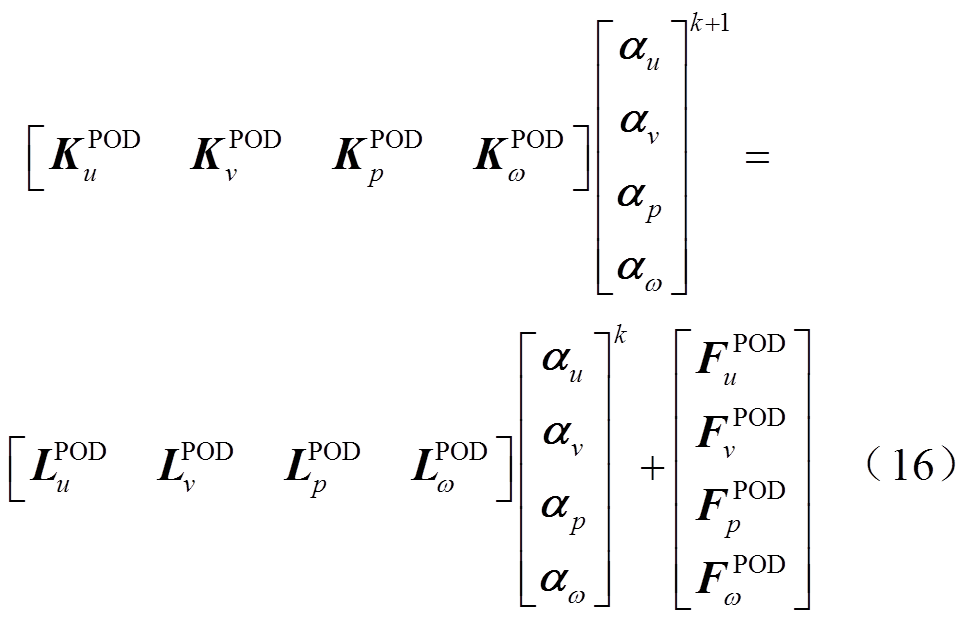
其中
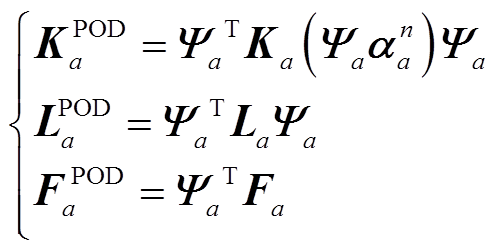
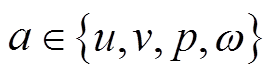
在此基础上,基于DEIM算法思路,分别选取非线性项Kuu、Kvv、Kpp、Kωω、Luu、Lvv、Lpp、Lωω前s个时间步的数值计算结果形成快照矩阵,通过奇异值分解得到正交基,再利用搜索算法得到d个插值点对应的布尔矩阵P以及插值矩阵D。综上所述,采用SPOD-DEIM算法的流场计算方程为

其中
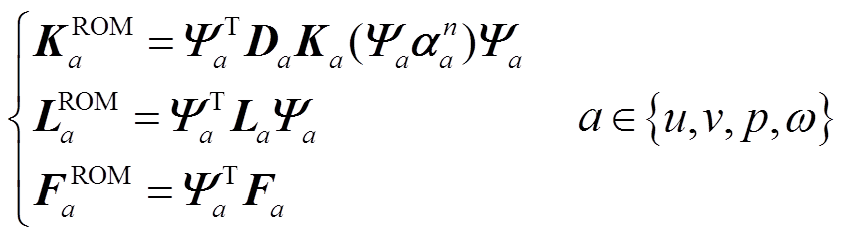
式中,KuROM、KvROM、KpROM、KωROM、LuROM、LvROM、LpROM、LωROM分别为四个物理量在SPOD-DEIM降阶模型中的块结构。各部分的数据特征及物理特征在降阶计算方程中得到了充分保留。
同理,绕组温度场计算方程参考式(4)可以表示为
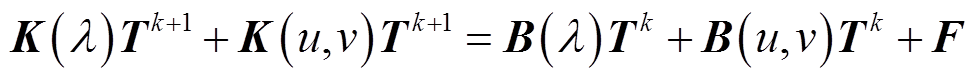 (18)
(18)
式中,K(λ)、B(λ)为与材料物性参数(如导热系数λ等)相关的刚度阵;K(u,v)、B(u,v)为与流体速度相关的刚度阵;F为右端项。同样地,采用SPOD-DEIM方法对其进行降阶,将控制方程重构为
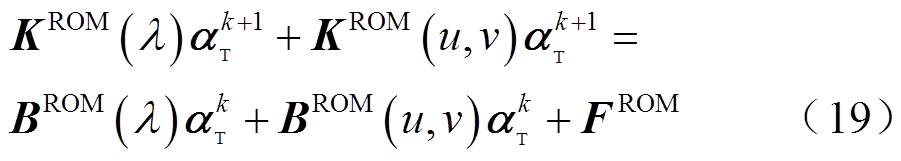
其中
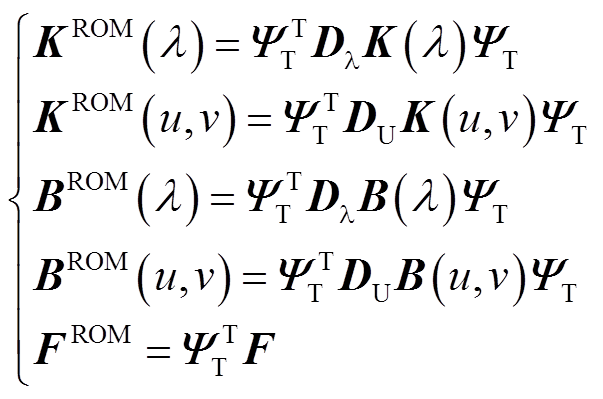
式中,ΨT为应用SPOD方法获得的正交基矩阵,由于温度场的解向量中不存在类似于流场的多种状态量,因此此处的ΨT与采用传统POD方法得到的正交基相同;Dλ与DU为采用DEIM方法获得的插值矩阵。
综上所述,结合SPOD和DEIM方法的油浸式电力变压器绕组瞬态温升降阶计算流程如图2所示。
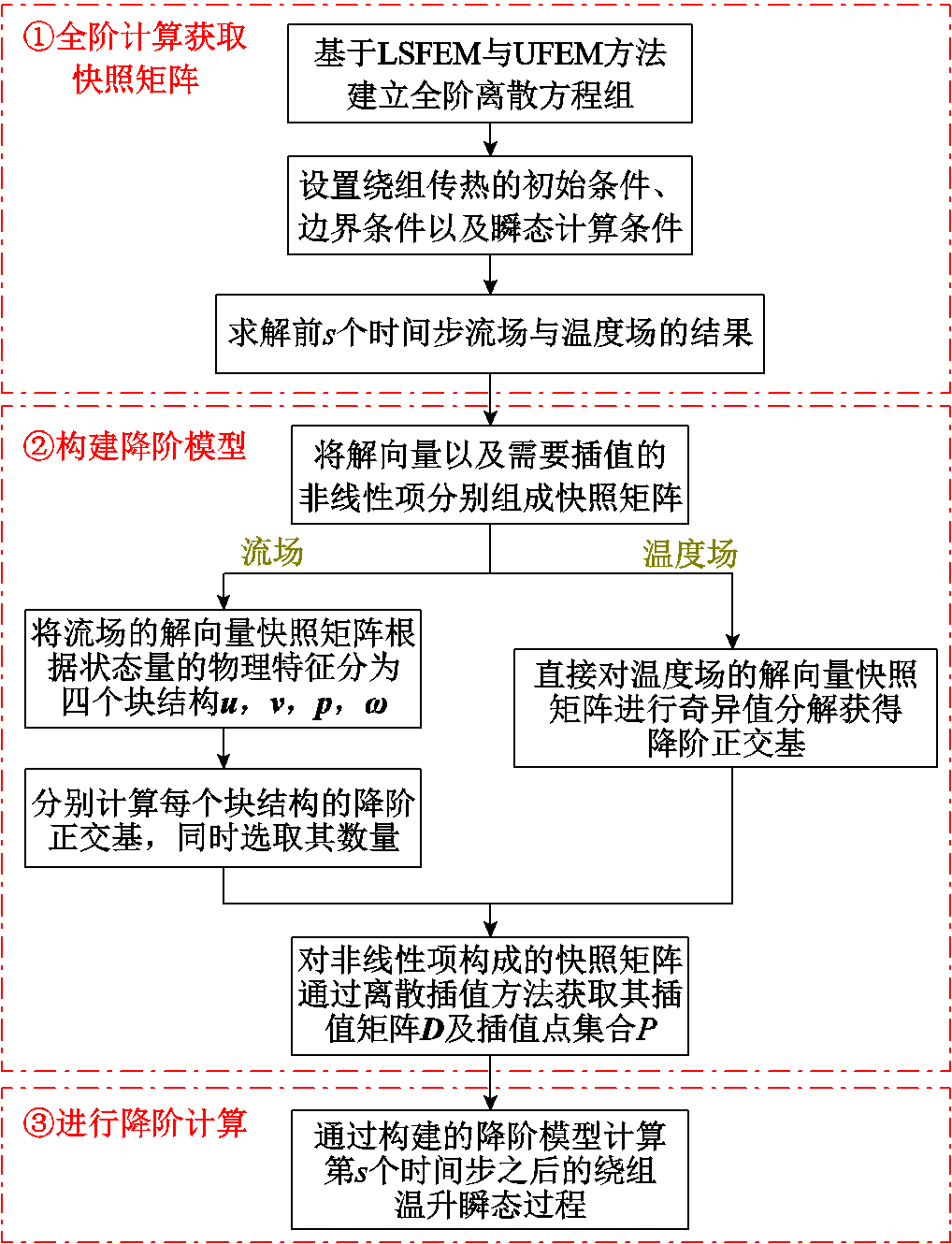
图2 SPOD-DEIM算法流程
Fig.2 Schematic diagram of SPOD-DEIM
显然,随着模型的节点与网格规模逐渐增大,降阶模型相较于全阶模型的效率提升也将逐渐增加。
为了讨论SPOD-DEIM算法应用于油浸式电力变压器温升计算时的适用性及高效性,参考油浸式电力变压器结构特点,建立了单分区分匝绕组传热模型对其精度和效率进行了讨论。同时,为了进一步验证该算法的实用价值,文章基于110 kV变压器绕组基本结构,搭建了产品级油浸式电力变压器绕组温升实验平台,并根据其结构参数建立了二维绕组传热模型,在此基础上进行计算分析。
3.1.1 二维单分区分匝绕组模型建立
油浸式电力变压器的基本结构如图3所示,绕组内部的挡板将绕组分成了几个结构大致相同的分区,各分区内油流均从入口进入,以S形线路与绕组充分接触后从出口流出,因此在初步验证算法有效性时,可以选取其中一个单分区绕组模型进行讨论。
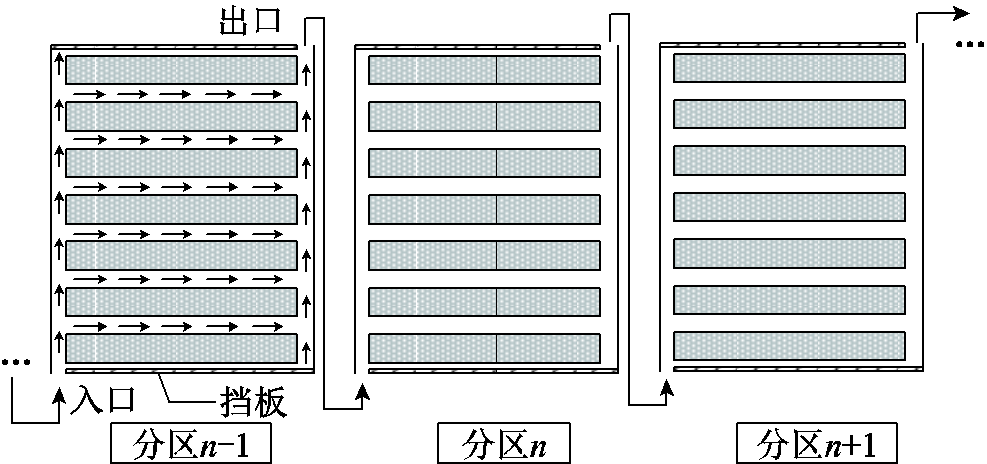
图3 油浸式电力变压器绕组一般结构
Fig.3 General structure of oil-immersed power transformer windings
二维单分区分匝绕组模型如图4所示,该分区包含九个线饼,十条油道,将线饼从上至下标号为线饼1~9,将油道从上至下标号为油道1~10。模型的总体尺寸为155.5 mm × 154.2 mm,油流入口宽度为10 mm,出口宽度为8 mm,除1号油道为3 mm外,其余油道均为6 mm。
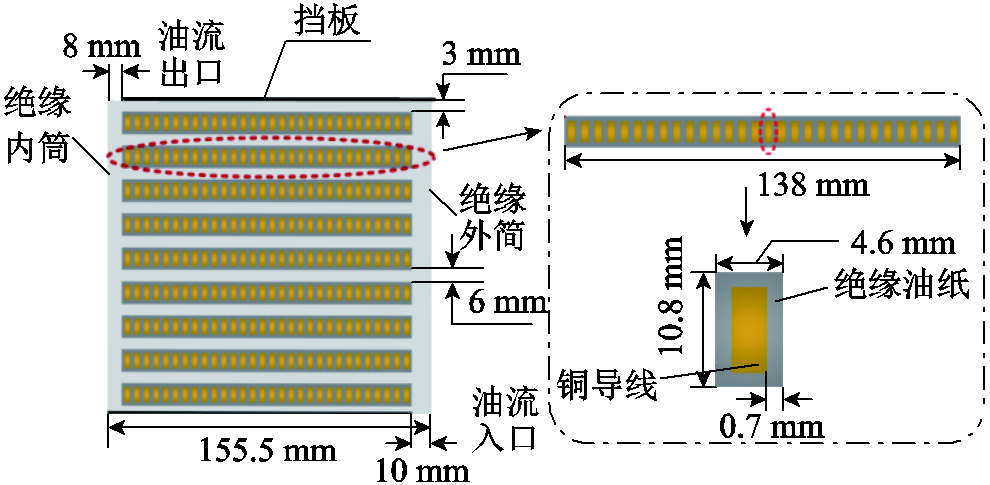
图4 二维单分区分匝绕组模型
Fig.4 2-D single zone winding model
设置出口为压力边界条件,压力为0 Pa;将绝缘筒壁与挡板设置为无滑移壁面边界条件,即速度为0 m/s;该模型的热源为绕组的欧姆损耗,考虑温度对绕组电阻的影响,给出损耗计算公式[12]为
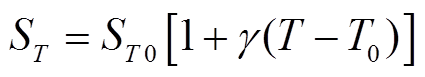 (20)
(20)
式中,ST0为绕组在T0温度下的损耗密度,在本算例中参考了文献[12]取值为227 000 W/m3,并在Fluent软件中通过udf设置与自编程程序相同的热源;γ为导体温度系数,对于铜导体一般可以取为0.003 93 K-1[22]。相关材料的物性参数见表2。
表2 模型物性参数
Tab.2 Model physical parameters

对象物性参数数值 变压器油密度/(kg/m3)1 098.72-0.712T 比热容/[J/(kg·K)]807.163+3.28T 动力粘度/(Pa·s)0.084 6-4×10-4T+5×10-7T2 导热系数/[W/(m·K)]0.150 9-7.101×10-5T 铜导线密度/(kg/m3)8 900 比热容/ [J/(kg·K)]381 导热系数/[W/(m·K)]387.6 绝缘油纸密度/(kg/m3)980 比热容/[J/(kg·K)]2 000 导热系数/[W/(m·K)]0.25 挡板密度/(kg/m3)700 比热容/[J/(kg·K)]2310 导热系数/[W/(m·K)]0.17
3.1.2 全阶算法正确性验证
由于本文所采用的降阶算法均以式(2)与式(4)为基础,因此在进行降阶算法的验证之前,有必要对基于LSFEM-UFEM的全阶算法正确性进行说明。设置单分区绕组入口油流速度为0.05 m/s,初始温度为290 K,分别采用仿真软件Fluent和基于LSFEM-UFEM的自编程程序对该绕组模型的瞬态温升过程进行计算,模型网格数量为46 827,节点数量为187 783。本文所采用的算法编程与计算软件为:Matlab R2021a,计算机配置为:CPU Intel Core i9-12900KF,内存128 GB。当绕组的传热过程达到稳态时,流场与温度场的云图对比如图5所示。
从图5中可以看出,本文所采用的全阶计算方法与Fluent的计算结果大致相同,各线饼及油道的最高温升和最大流速如图6所示。

图5 稳态云图对比
Fig.5 Comparison of steady cloud images
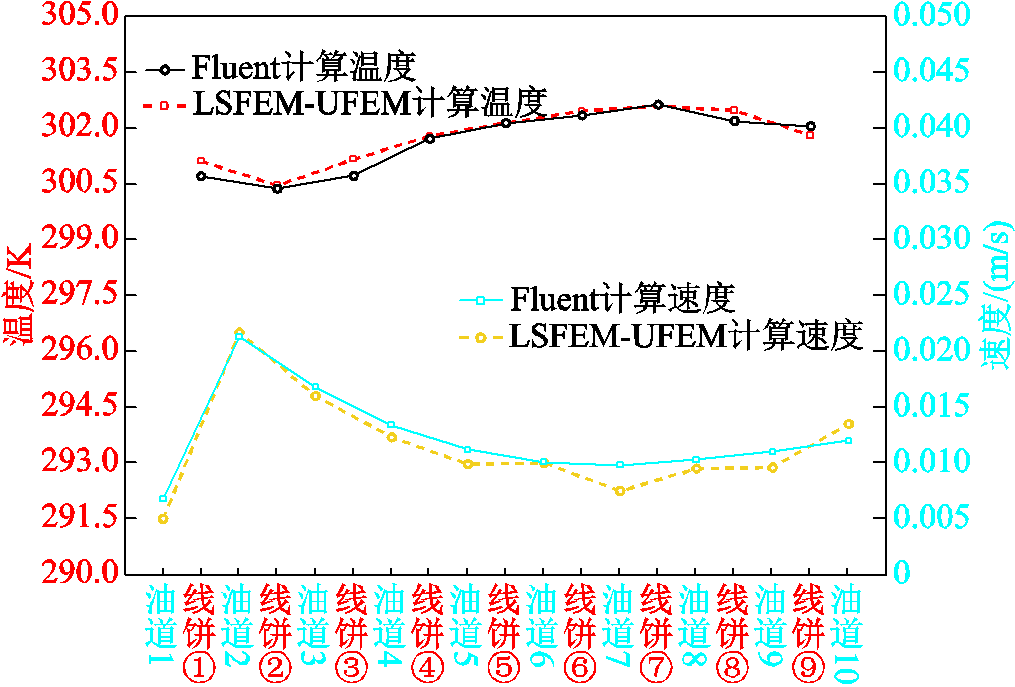
图6 各线饼(油道)最高温升(最大油速)
Fig.6 Maximum temperature rise (maximum oil speed) of each thread cake (oil passage)
可以看出,二者的计算结果几乎一致,流场最大误差为0.002 3 m/s;温度场的最大误差为0.443 0 K。选取油速最快的第2油道以及温度最高的第7线饼的中心位置为监测点,将油流流速与绕组温度的瞬态变化过程绘图如图7所示。
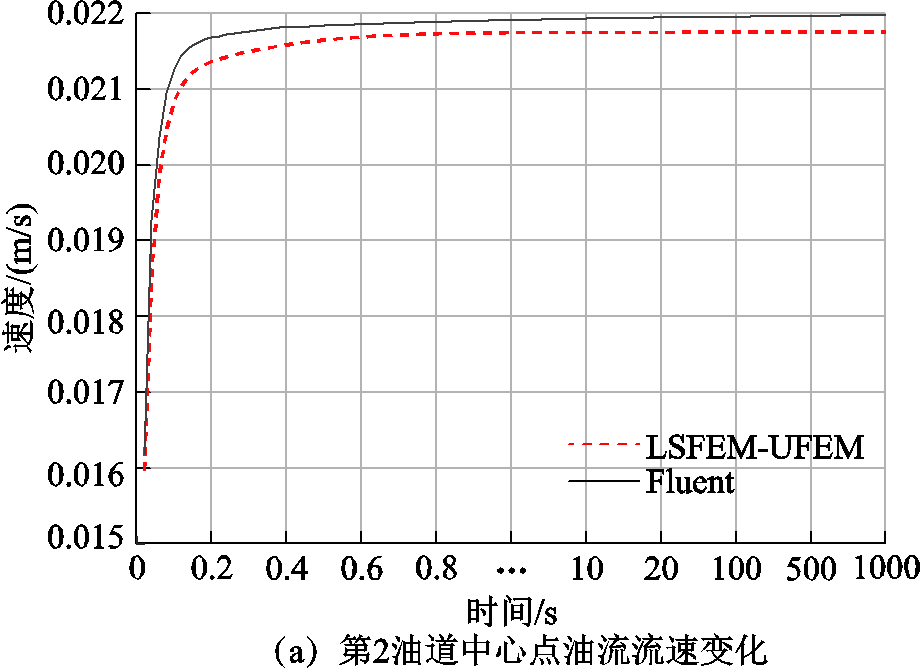
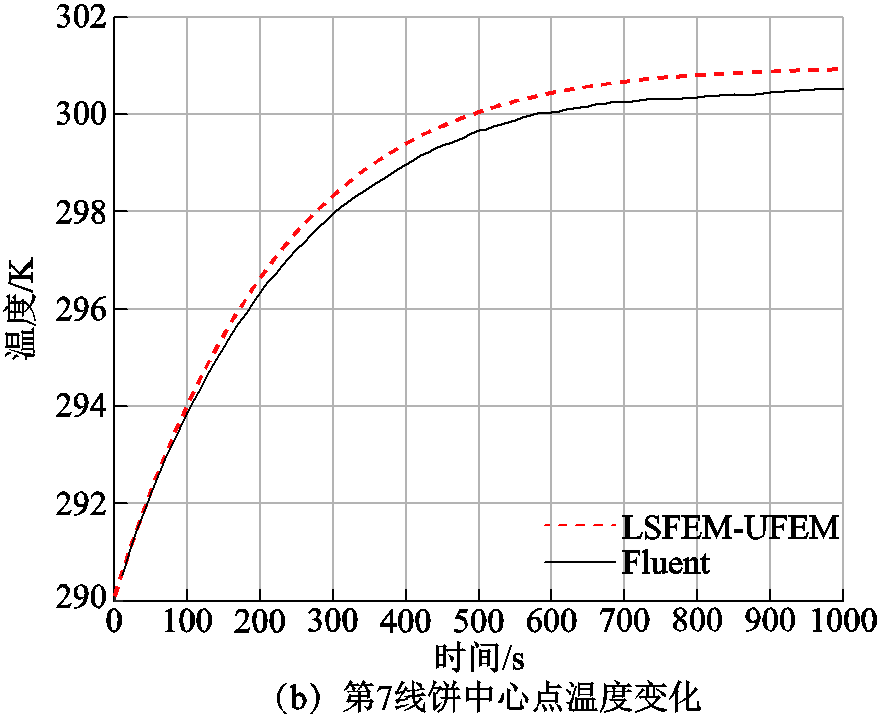
图7 参考点油流流速及温度变化
Fig.7 Velocity and temperature change at reference point
在监测点的瞬态变化过程中,第2油道的流速最大误差出现在第0.04 s,为0.000 7 m/s,相对误差为3.6%;第7线饼的温度最大误差出现在第870 s,为0.470 1 K,摄氏温标相对误差为1.75%。由于仿真软件Fluent采用的数值计算方法为有限体积法,而本文的自编程方法为LSFEM-UFEM结合的有限元法,因此二者的计算过程中必然会存在一定误差,但根据前文的分析可以看出,这个误差处在可以接受的范围内,因此,可验证本文所采用的基于LSFEM-UFEM全阶算法的正确性,在该算法的基础上进行降阶计算具有一定可信度。
3.1.3 降阶算法正确性验证
基于3.1.2节中采用的全阶计算模型,以绕组温升从0~100 s的计算数据为样本数据,各物理量根据式(8)选取模态能量大于99.9%的SPOD正交基数量,并选取不会使得计算发散的最小DEIM插值点数量,基于式(16)与式(18)构造流场与温度场的降阶模型并进行降阶计算,将计算结果与全阶计算结果进行对比。
计算达到稳态时,全阶计算与SPOD-DEIM降阶计算的流场和温度场对比如图8所示。
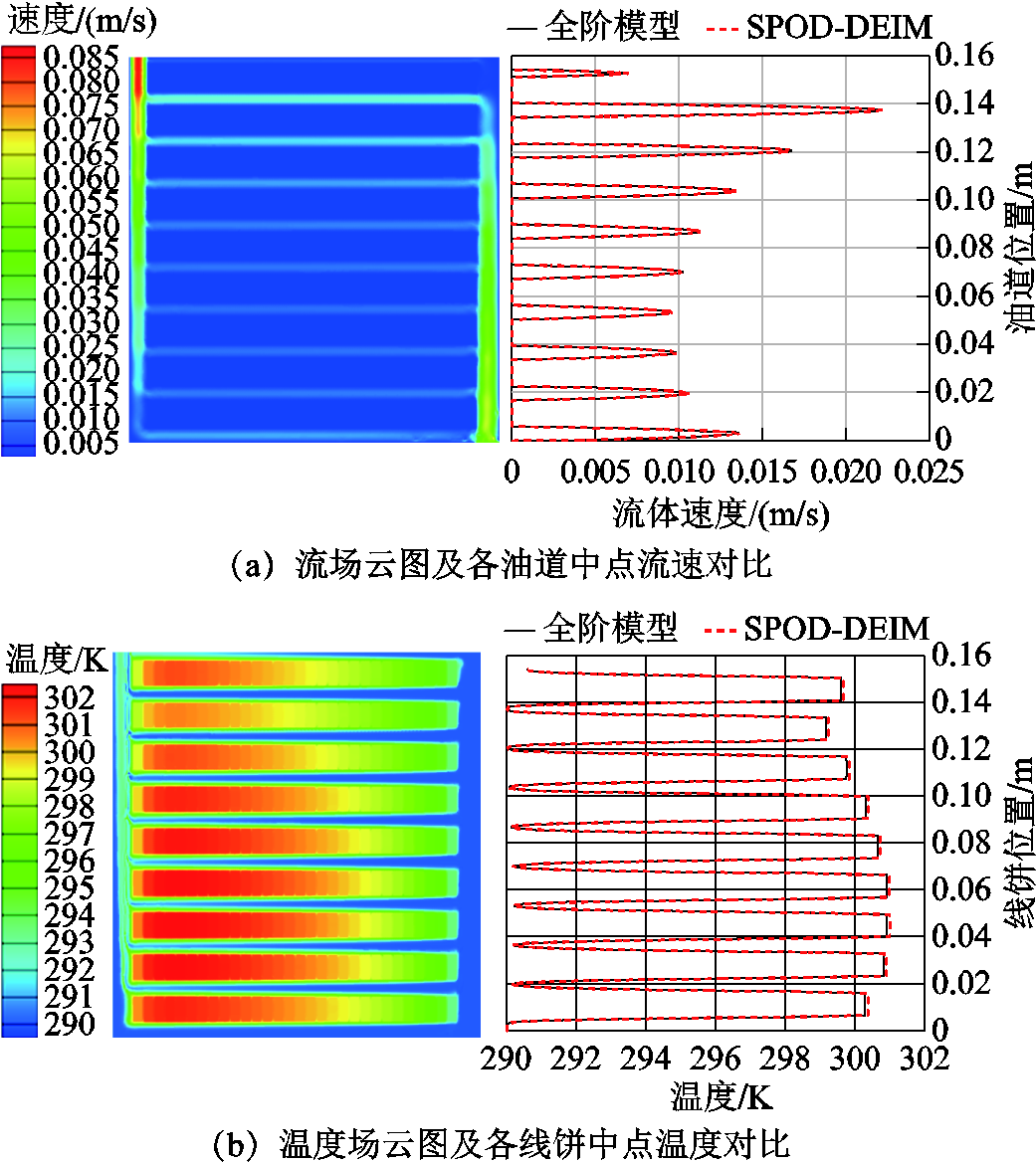
图8 稳态结果对比
Fig.8 Steady state results comparison
图8a与图8b表示分区各线饼和油道中心线上的温度与速度大小。从图8可以看出,全阶计算模型与降阶计算模型达到稳态时的计算结果几乎完全相同,其中,速度场的最大误差出现在第2油道,为0.000 01 m/s;温度场的最大误差出现在第4线饼,为0.067 K。
定义第k时间步的降阶误差为
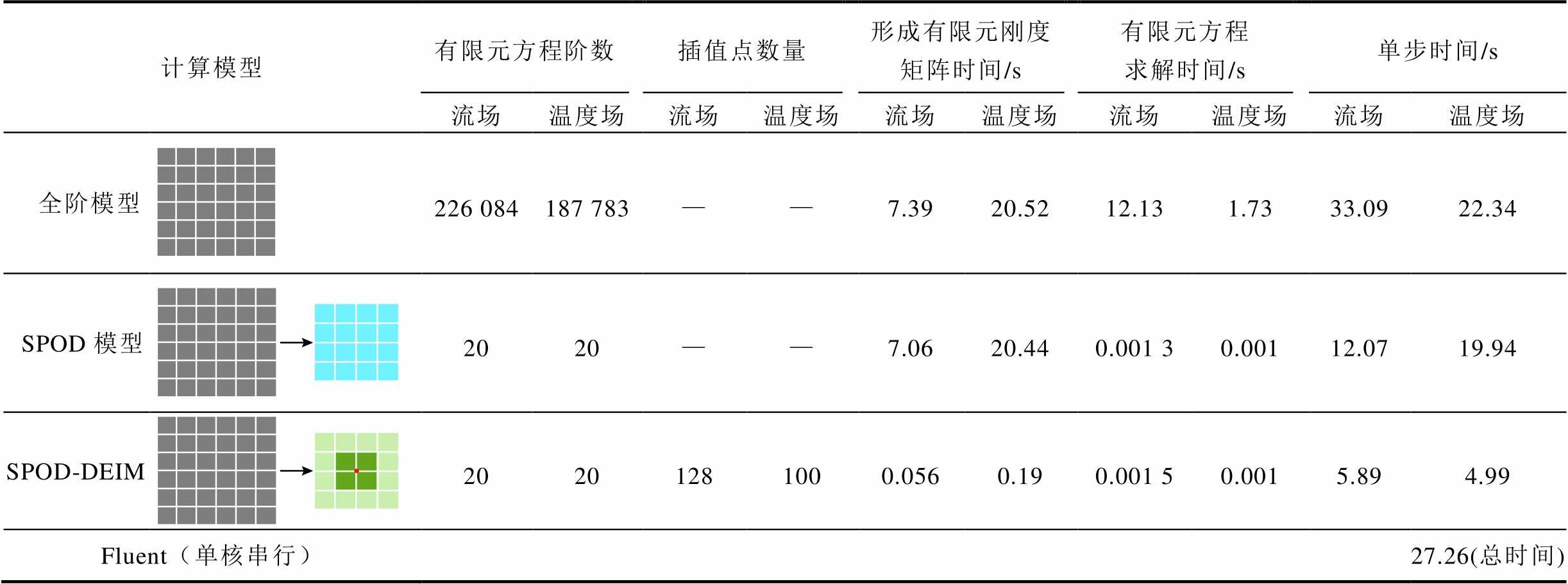
表3 计算效率对比
Tab.3 Calculation efficiency comparison
计算模型有限元方程阶数插值点数量形成有限元刚度矩阵时间/s有限元方程求解时间/s单步时间/s 流场温度场流场温度场流场温度场流场温度场流场温度场 全阶模型226 084187 783——7.3920.5212.131.7333.0922.34 SPOD模型2020——7.0620.440.001 30.00112.0719.94 SPOD-DEIM20201281000.0560.190.001 50.0015.894.99 Fluent(单核串行)27.26(总时间)
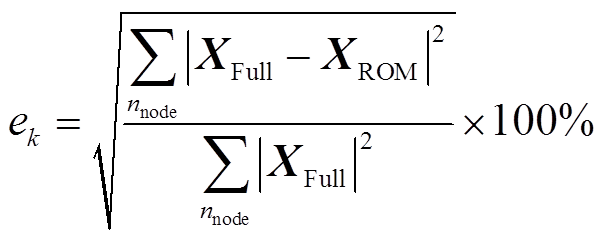 (21)
(21)
式中,X为求解变量,X∈(U,T);下标Full表示全阶计算结果,ROM表示降阶计算结果;nnode为流场域或温度场域所有节点数量。计算瞬态计算过程中各个时间步下的降阶误差如图9所示。
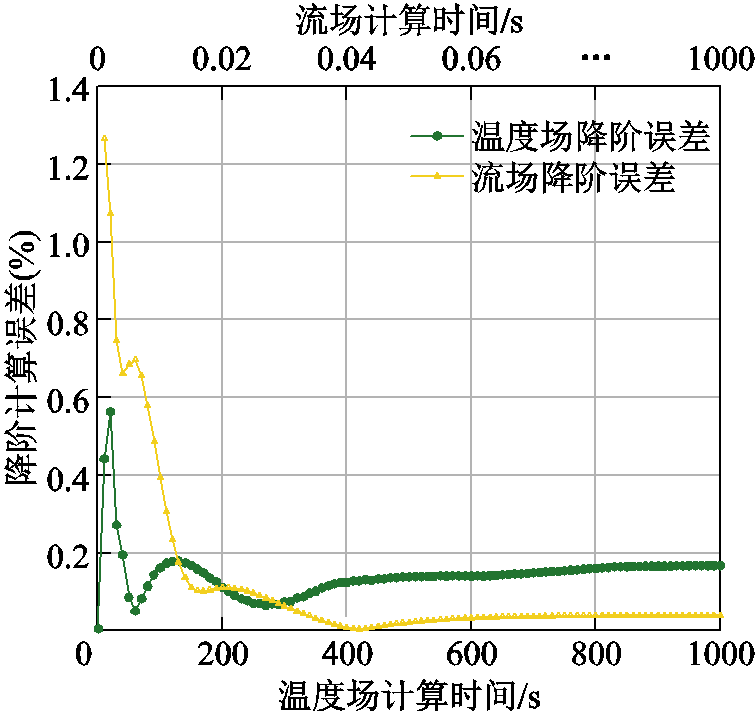
图9 流场及温度场降阶计算误差
Fig.9 Reduced order calculation error of flow field and temperature field
可以看出,在该过程中,流场降阶计算误差最大为1.26%,温度场降阶计算误差最大为0.56%。两场的降阶计算精度均处于可接受范围内,由此可初步说明降阶算法的正确性。同时,为了反映SPOD-DEIM算法的计算效率,将全阶计算、SPOD降阶计算、SPOD-DEIM降阶计算以及Fluent单线程计算的平均单步计算时间记录于表3中。表中“单步总时间”列计算时间由流场和温度场两部分计算时间构成,如全阶模型“单步总时间”中流场计算时间为33.09 s,温度场计算时间为22.34 s,总计算时间为55.43 s。
从表3中可以看出,通过引入SPOD算法,能够有效降低有限元方程的阶数,极大地提高有限元方程求解时间,但从单步计算时间来看,流场计算时间从33.09 s降低至12.07 s,后者为前者的36.47%;温度场计算时间从22.34 s降低到19.94 s,降阶后计算时间为前者的89.26%。效率提升并不明显,这是由于流固耦合问题具有的强非线性,使得每一时步的有限元刚度矩阵需要重新形成,耗费较多时间。
在结合了DEIM插值方法之后,SPOD-DEIM降阶计算较SPOD降阶计算在形成有限元刚度矩阵方面效率得到了进一步提高。以流场为例,刚度矩阵的形成时间从7 s左右减少到0.056 s;同时,对于单步计算时间,较全阶计算模型,流场计算时间从33.09 s降低至5.89 s,减少为原先的17.78%,温度场计算时间从22.34 s降低至4.99 s,减少为原先的22.33%,SPOD-DEIM降阶总体计算时间为全阶计算的19.63%。
大幅度减少了计算时间。且与仿真软件Fluent的串行计算速度相比,降阶模型的效率也提升近2倍。这说明了本文所采用降阶算法的高效性。
可以看到,在单分区分匝模型中,降阶的瞬态计算与全阶计算效率提升并不是很高,这是由于该模型的规模较小,降阶计算的效率提升并不明显。从2.3节中可以得到,降阶模型效率的提升显然与降阶之后节点与网格数量减少的倍数有关,因此,随着全阶模型的网格与节点规模逐渐扩大,基于SPOD-DEIM算法的降阶计算相较于全阶计算将有更为明显的效率优势,这一点将在3.2节的温升实验中加以验证。
为了充分讨论SPOD-DEIM算法应用于实际油浸式电力变压器温升计算时的适用性及高效性,参考110 kV电力变压器结构特点,本文搭建了产品级油浸式电力变压器绕组温升实验平台,并根据其结构参数建立了二维绕组传热模型,在此基础上进行计算分析。
该实验平台由空心饼式无感线圈、器身绝缘、隔热油箱、片式散热器、油泵、风机、导油管路和热电偶等部件组成。图10与图11为实验模型整体布置外观图与示意图。

图10 温升实验平台
Fig.10 Temperature rise experimental platform
绕组整体分为8个分区,从顶端到底端依次编号为分区1~8,其中,分区1~3各有7个线饼,分区4~8各有9个线饼,为了便于比较与说明,将构成绕组的线饼依次编号为1~66。每个线饼由15匝导线组成,每匝导线由2根扁铜导线并绕而成,由内轴向到外轴向将每个线饼中的导线依次编号为线匝1~30。
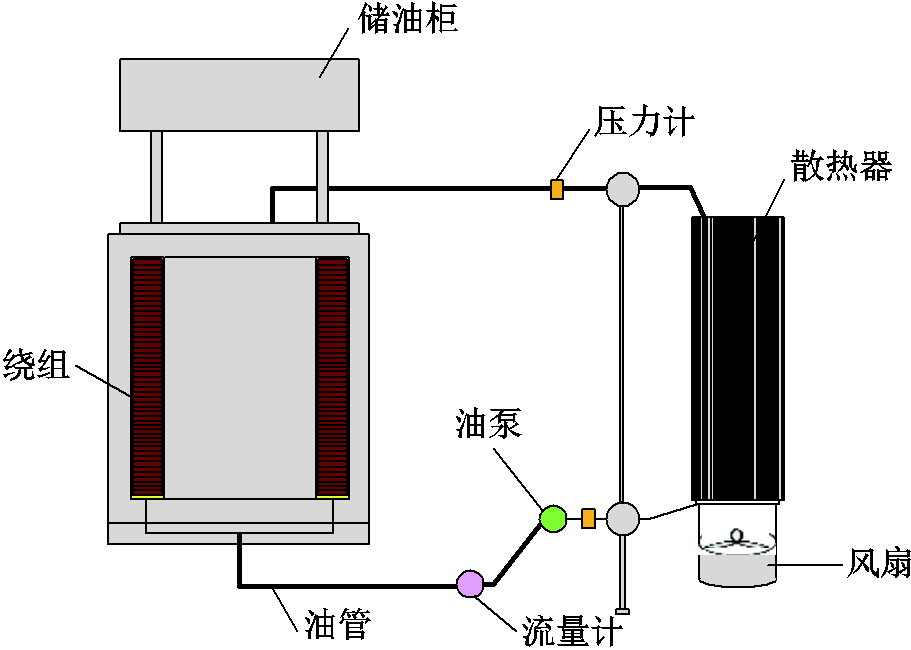
图11 实验平台示意图
Fig.11 Schematic diagram of experimental platform
根据实验采用的饼式绕组轴对称的结构特点,构造二维等效数值模型如图12所示。为精确数值计算的结果,该模型考虑了饼式绕组的分匝结构以及绝缘纸、挡板等对绕组温升有显著影响的结构件。变压器油、挡板以及绝缘纸的物性参数同表2。
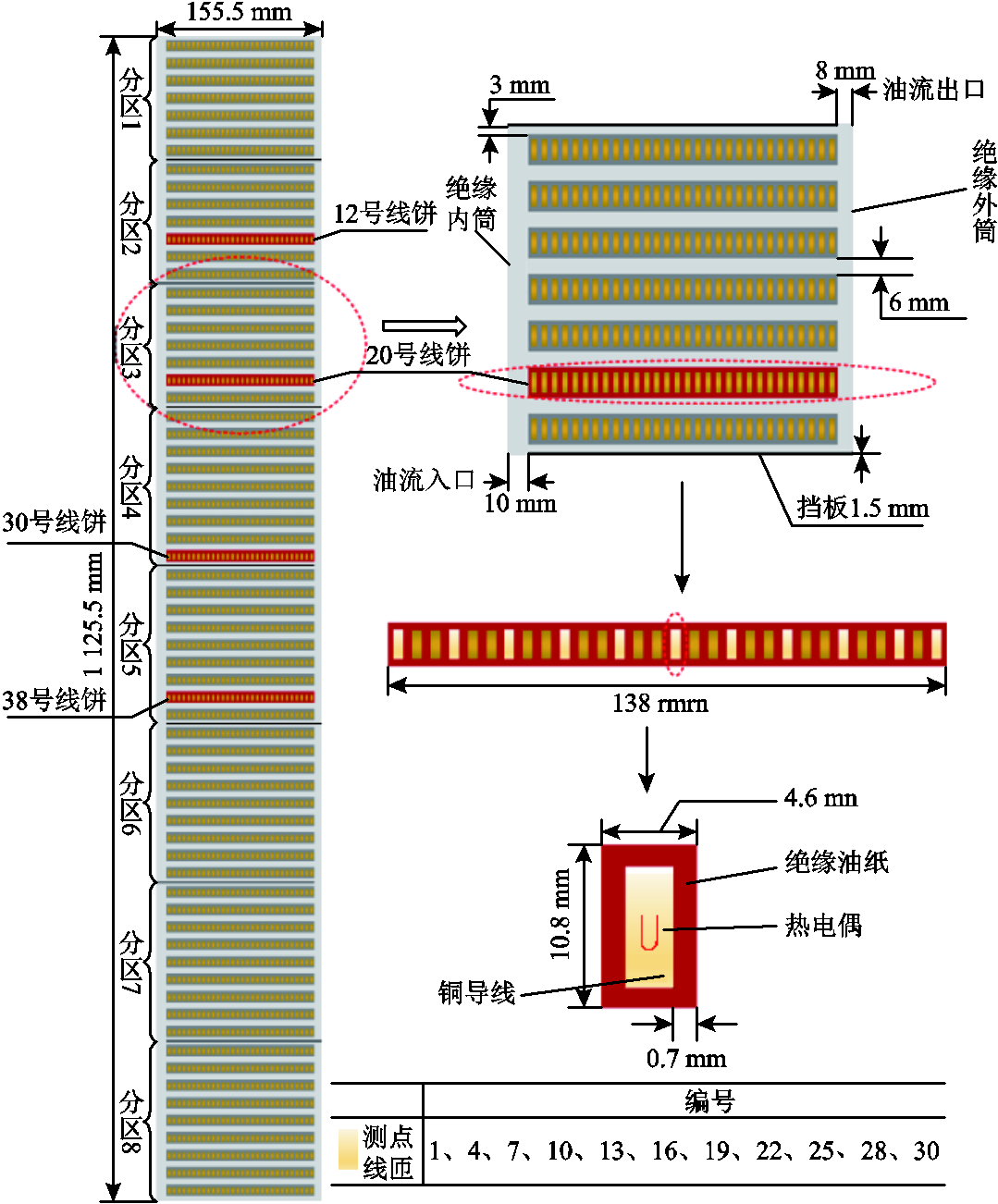
图12 二维八分区分匝绕组模型
Fig.12 2-D eight zone winding model
实验条件设置如下:
1)本实验的测温装置为热电偶,分别布置于12、20、30与38号线饼,同时,每个测温线饼上设置11个测点,分别为1、4、7、10、13、16、19、22、25、28、30号线匝。
2)本实验的目的在于测量油浸式电力变压器绕组在强油散热条件下的温升变化趋势,记录进口油量为14.4m3/s,进口油温随时间变化,根据入口处的热电偶记录每一时刻的油温用以仿真计算,初始油温为16.24℃,功率分析仪得到绕组的功率为25.000 4 kW ,其功率因数测量为0.999 82,可以假定作为热源的绕组损耗中只有欧姆损耗,计算过程中热源密度同式(19)。电源和进口流量保持恒定。
3)温度记录仪每10 s采集一次各测点的绕组温度。当顶层油温变化率为1℃/h并维持2 h,认为油温达到稳定状态。实验共进行了7.66 h,收集各测点数据2 758组。
进行温升实验的同时,采用图12所示的八分区二维轴对称模型进行仿真分析,模型网格数量为211 613,节点数量为846 211,设置时间间隔Δt=10 s,并以0~1 000 s的全阶计算结果作为样本数据形成降阶子空间,基于SPOD-DEIM方法对绕组的温升全过程进行降阶计算。将Fluent软件的仿真结果、基于SPOD-DEIM算法的自编程结果、实验结果进行对比,做如下讨论。
达到稳态时,12号、20号、30号、37号线饼上绕组温度的分布如图13所示。
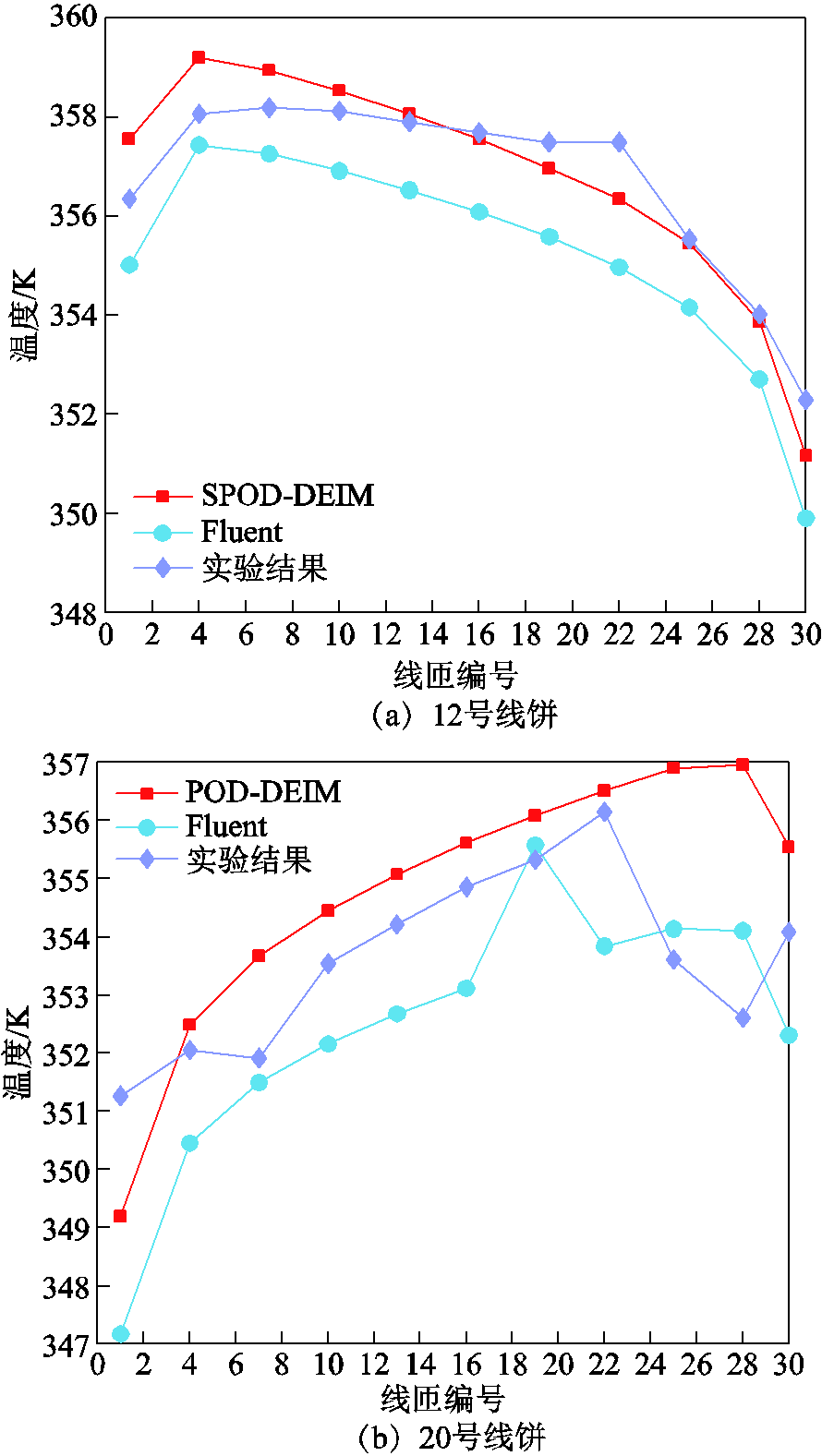
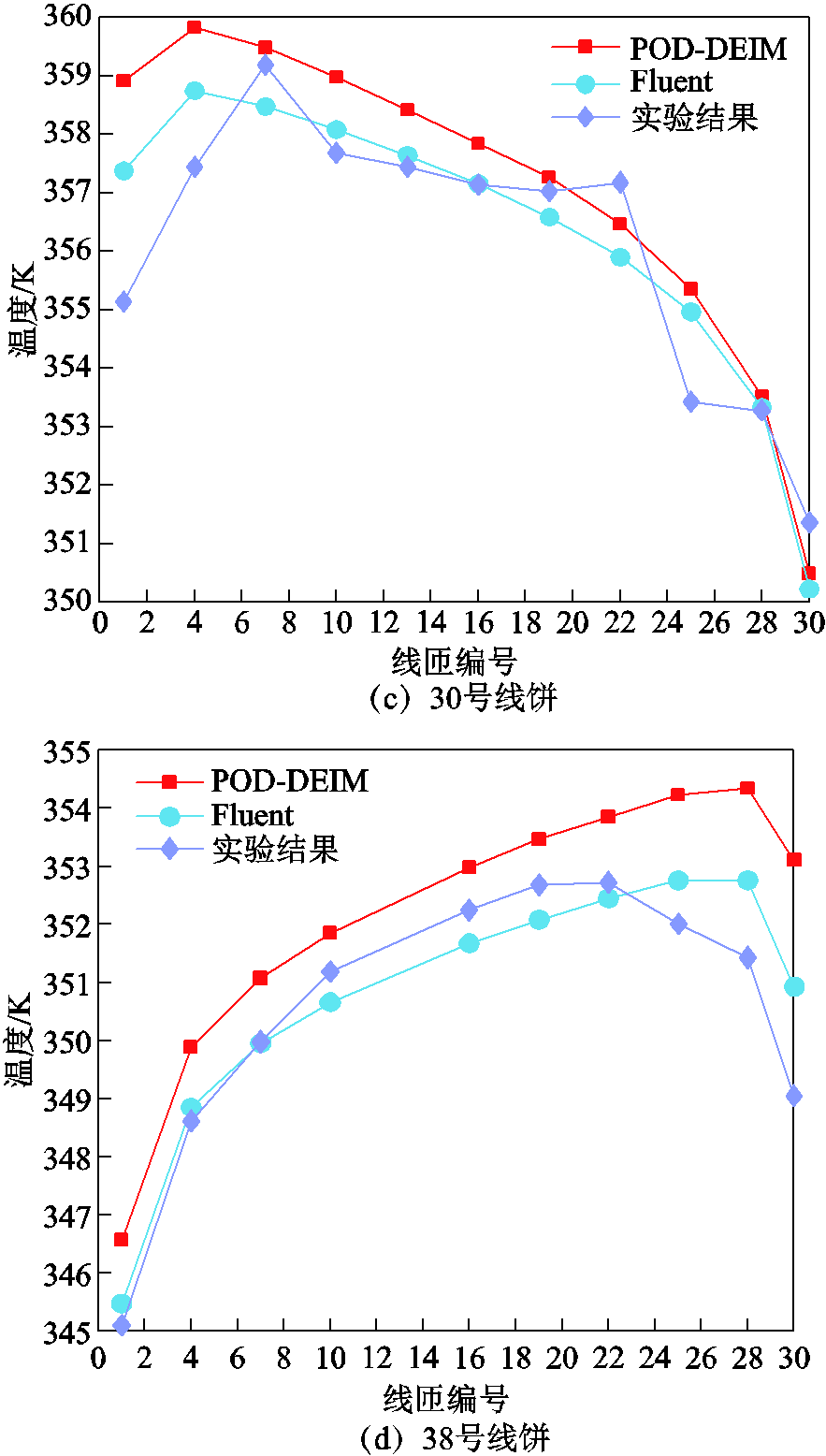
图13 稳态时各线饼监测点温度分布
Fig.13 Temperature distribution of monitoring points of each line cake in steady state
从图13可以看出,三种方法达到稳态时的温度差异不大,本文所采用的SPOD-DEIM降阶算法与实验结果的最大误差出现在20号线饼28号测点上,为4.4 K,在工程上属于可接受的范围。同时,与Fluent算法的计算结果相比,本文自编程结果在这几个测点上更接近于实验结果,初步说明了本文所提出算法的正确性。
选择12号绕组4号测点、20号绕组22号测点、30号绕组4号测点与38号绕组28号测点,导出其运行过程中的温度变化数据,并绘制温度变化曲线如图14所示。
可以看出,在这几个测点上,三种方式所得到的温度变化趋势近乎一致,且差异不大。SPOD-DEIM算法与实验结果的最大误差出现于2 500 s左右,在12号线饼4号测点上,为5.41 K,Fluent仿真结果与实验结果的最大误差出现在12号线饼4号测点上,为7.13 K,与Fluent相比,本文算法更加接近于实际结果,考虑实验过程中的不可控因素,该误差在可接受范围内。为进一步说明算法的精度,以12号线饼各测温点为例,将实验过程中,降阶计算与全阶计算在各个时间点根据式(20)计算得到的计算误差记录如图15所示。
由于采用前1 000 s的计算结果作为样本数据,因此,前100个时间步的计算误差为0。可以看出,SPOD-DEIM降阶计算过程中,与全阶计算相比最大计算误差不超过2.5%,这进一步说明了本文所采用的基于SPOD-DEIM降阶方法的混合有限元算法的高精确性。为了分析采用SPOD-DEIM降阶算法之后,模型计算的效率提升,将计算时间记录见表4。
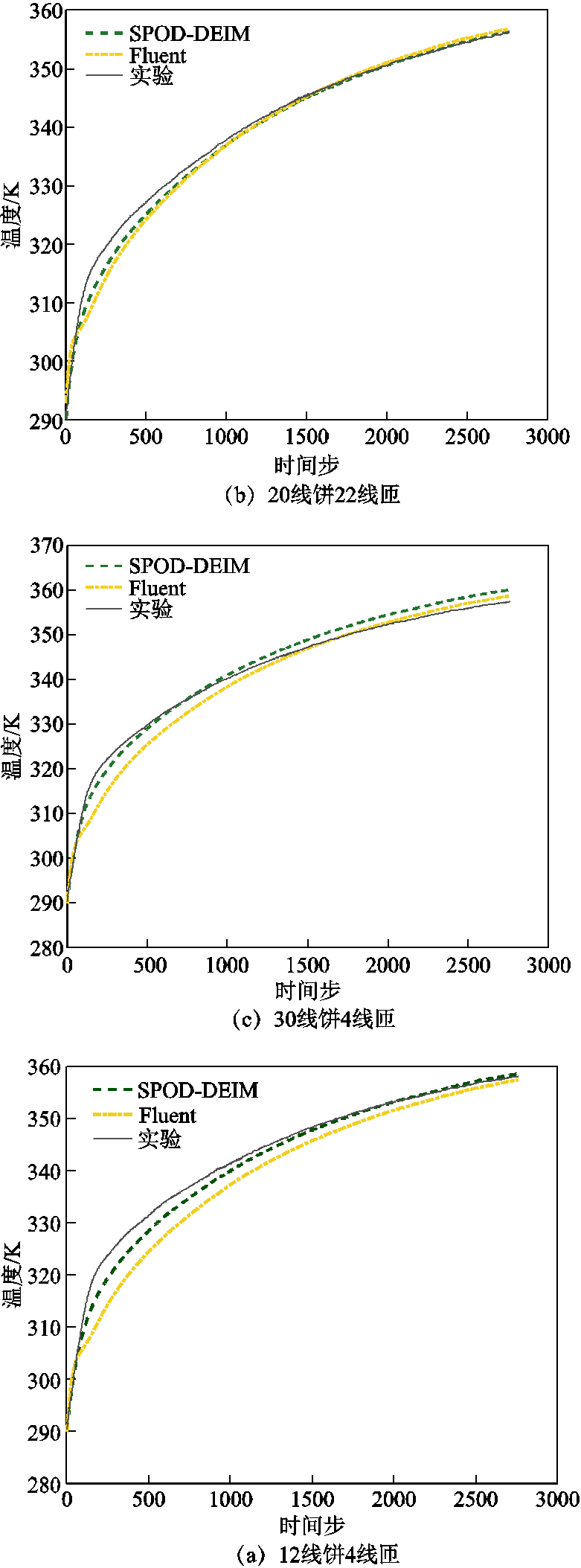
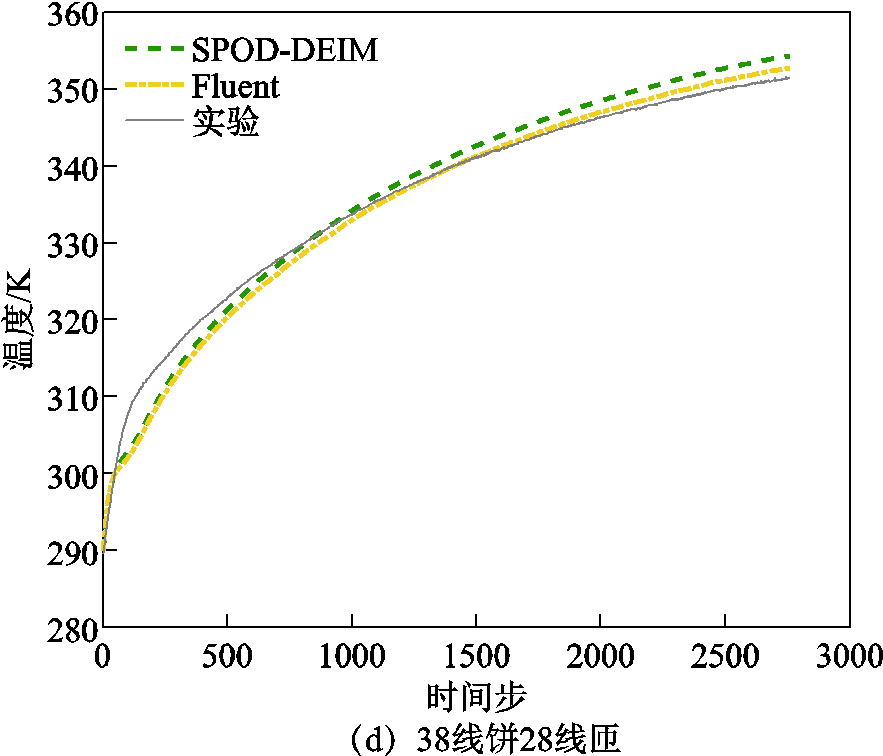
图14 瞬态时各线饼监测点温度变化
Fig.14 Temperature change of each line cake monitoring point during transient
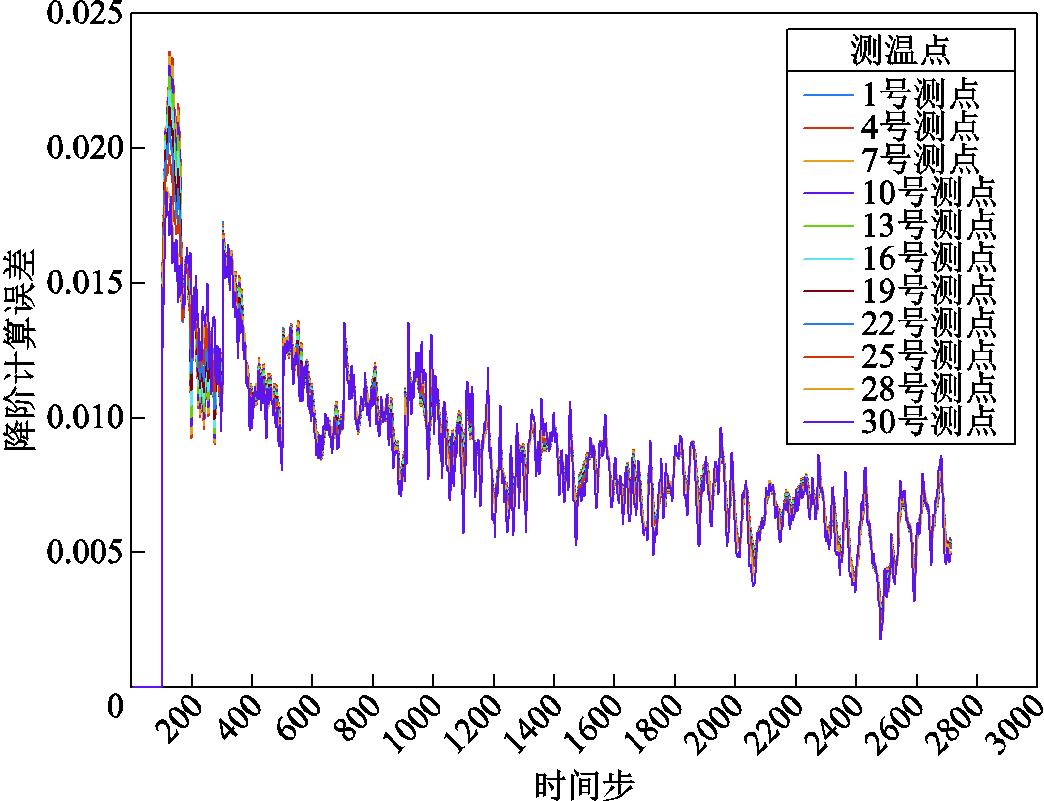
图15 12线饼各线匝监测点降阶计算误差
Fig.15 Order reduction calculation error of each turn monitoring point of 12 cake
表4 计算时间对比
Tab.4 Calculation time comparison(单位:h)

计算模型全阶计算时间降阶计算时间预处理时间总时间 全阶模型573.59573.59 SPOD-DEIM20.7833.500.0154.29 Fluent(单核)346.27346.27
表4中,预处理时间表示形成降阶正交基与插值矩阵的时间,在降阶计算中,二者均只需形成一次便可用于全过程瞬态计算;SPOD-DEIM降阶模型中的全阶计算时间表示形成快照矩阵的时间,该算例中将0~100时间步的全阶计算结果组成快照矩阵。由表4可知,对实验的全过程采用全阶模型计算,计算时间约为573.59 h,而若采用基于SPOD-DEIM的降阶算法计算,则包括预处理时间在内的计算时间仅为54.28 h,较全阶计算模型有大幅度提高,计算效率为后者的10.57倍。且相较于商业仿真软件Fluent的单核串行运算,该算法的效率提升也在6.37倍以上。由此可说明,基于SPOD-DEIM的降阶算法针对实际工程模型也有较好的应用价值,能够在可接受的误差范围内有效地提高温升计算效率。同时与3.1.3节中得到的结论相比也进一步说明随着实际工程模型规模的逐渐增大,降阶计算模型的效率提升也将更加明显。
本文针对油浸式电力变压器绕组瞬态温升过程,采用LSFEM-UFEM混合有限元方法建立了二维绕组温升数值模型,研究并讨论了将SPOD-DEIM算法应用于其中的潜在能力,相关计算及实验结果表明:
1) 精度和效率方面,本文根据油浸式电力变压器绕组基本结构,建立了二维绕组单分区分匝绕组传热模型,基于SPOD-DEIM混合有限元方法对绕组的瞬态温升过程进行计算,结果表明:在1 000 s的仿真时间中,降阶计算的结果与全阶计算几乎完全相同,其流场最大误差不超过1.26%,温度场最大误差不超过0.56%,同时,效率方面降阶计算效率较全阶计算效率提升了5倍以上,且相较于仿真软件Fluent的单核串行运算,该算法的计算效率也提升了近2倍。这初步说明了SPOD-DEIM降阶算法的有效性。
2)工程应用方面,本文基于110 kV油浸式电力变压器绕组基本结构,搭建了温升实验平台,并基于平台绕组建立了二维八分区分匝绕组传热模型进行数值计算,将实验结果、SPOD-DEIM混合有限元算法计算结果、Fluent仿真结果进行对比,结果表明:精度方面,在绕组的瞬态温升实验过程中,与实验结果相比,基于SPOD-DEIM混合有限元算法在监测点的最大误差仅为5.41 K,考虑实验过程中的不可控因素,该误差在可接受范围内;效率方面,全阶计算模型的全过程计算时间为573.59 h,而SPOD-DEIM降阶算法包括预处理时间在内的计算时间仅为54.29 h,后者较前者效率提升约为10.57倍。同时,相较于同等网格规模的Fluent单核串行计算,本文所采用的算法效率提升也在6.37倍以上。由此可充分说明本文所提算法具有较高的工程应用价值。
参考文献
[1] 刘云鹏, 李欢, 高树国, 等. 分布式光纤传感在大型变压器温度和绕组变形监测中的应用研究[J]. 中国电机工程学报, 2022, 42(16): 6126-6135.
Liu Yunpeng, Li Huan, Gao Shuguo, et al. Research on application of distributed optical fiber sensing in monitoring of temperature and winding deformation of large transformer[J]. Proceedings of the CSEE, 2022, 42(16): 6126-6135.
[2] 徐征宇, 张书琦, 廖和安, 等. 传感光纤与变压器电磁线一体化技术[J]. 中国电机工程学报, 2021, 41(19): 6816-6826.
Xu Zhengyu, Zhang Shuqi, Liao Hean, et al. Integration technology of sensing optical fiber and transformer electromagnetic wire[J]. Proceedings of the CSEE, 2021, 41(19): 6816-6826.
[3] Liu Yunpeng, Li Xinye, Li Huan, et al. Experimental and numerical investigation of the internal temperature of an oil-immersed power transformer with DOFS[J]. Applied Sciences, 2020, 10(16): 5718.
[4] 唐钊, 刘轩东, 陈铭. 考虑流体动力学的干式变压器热网络模型仿真分析[J]. 电工技术学报, 2022, 37(18): 4777-4787.
Tang Zhao, Liu Xuandong, Chen Ming. Simulation analysis of dry-type transformer thermal network model considering fluid dynamics[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4777-4787.
[5] 骆仁松, 汪涛, 文继峰, 等. 大功率高频变压器三维温升计算及优化设计方法[J]. 电工技术学报, 2023, 38(18): 4994-5005, 5016.
Luo Rensong, Wang Tao, Wen Jifeng, et al. Three dimensional temperature rise calculation and optimization design method for high-power high-frequency transformers[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4994-5005, 5016.
[6] 彭道刚, 陈跃伟, 钱玉良, 等. 基于粒子群优化-支持向量回归的变压器绕组温度软测量模型[J]. 电工技术学报, 2018, 33(8): 1742-1749, 1761.
Peng Daogang, Chen Yuewei, Qian Yuliang, et al. Transformer winding temperature soft measurement model based on particle swarm optimization-support vector regression[J]. Transactions of China Electrote-chnical Society, 2018, 33(8): 1742-1749, 1761.
[7] 刘刚, 郝世缘, 胡万君,等. 基于SCAS时间匹配算法油浸式变压器绕组瞬态温升计算方法[J/OL]. 电工技术学报, 2023: 1-14. https://doi.org/10.19595/ j.cnki.1000-6753.tces.222137.
Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Transient temperature rise calculation of oil immersed transformer winding based on SCAS time matching algorithm[J]. Transactions of China Electrotechnical Society, 2023: 1-14. https://doi.org/10.19595/j.cnki.1000-6753.tces.222137.
[8] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.
Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal-fluid model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4483-4491.
[9] 王泽忠, 李明洋, 宣梦真, 等. 单相四柱式变压器直流偏磁下的温升试验及仿真分析[J]. 电工技术学报, 2021, 36(5): 1006-1013.
Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al. Temperature rise test and simulation of single-phase four-column transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(5):1006-1013.
[10] Hendriana D, Bathe K J. On upwind methods for parabolic finite elements in incompressible flows[J]. International Journal for Numerical Methods in Engineering, 2000, 47(1/2/3): 317-340.
[11] 靳立鹏, 刘刚, 任增强, 等. 无量纲最小二乘有限元法GPU实现及其在变压器绕组流场仿真中的应用研究[J/OL]. 华北电力大学学报(自然科学版), 2022: 1-9. http://kns.cnki.net/kcms/detail/13.1212.TM. 20220715.0954.002.
Jin Lipeng,Liu Gang,Ren Zengqiang,et al. Research on dimensionless least square finite element method GPU implementation and its application in transformer winding flow field simulation[J/OL]. Journal of North China Electric Power University (Natural Science Edition): 2022: 1-9. http://kns.cnki. net/kcms/detail/13.1212.TM.20220715.0954.002.
[12] 谢裕清, 李琳, 宋雅吾, 等. 油浸式电力变压器绕组温升的多物理场耦合计算方法[J]. 中国电机工程学报, 2016, 36(21): 5957-5965.
Xie Yuqing, Li Lin, Song Yawu, et al. Multi-physical field coupled method for temperature rise of winding in oil-immersed power transformer[J]. Proceedings of the CSEE, 2016, 36(21): 5957-5965.
[13] 谢裕清, 李琳, 王帅兵. 瞬态Navier-Stokes方程的最小二乘有限元降阶计算方法[J]. 华北电力大学学报(自然科学版), 2017, 44(3): 74-80.
Xie Yuqing, Li Lin, Wang Shuaibing. Reduced-order method for the transient Navier-Stokes equation based on least-squares finite element method[J]. Journal of North China Electric Power University, 2017, 44(3): 74-80.
[14] 谢裕清, 李琳. 基于本征正交分解的换流变压器极性反转电场降阶模型[J]. 中国电机工程学报, 2016, 36(23): 6544-6551.
Xie Yuqing, Li Lin. A reduced order model via proper orthogonal decomposition for polarity reverse electric fields in converter transformers[J]. Proceedings of the CSEE, 2016, 36(23): 6544-6551.
[15] 刘刚, 荣世昌, 武卫革, 等. 基于混合有限元法和降阶技术的油浸式变压器绕组2维瞬态流-热耦合场分析[J]. 高电压技术, 2022, 48(5): 1695-1704.
Liu Gang, Rong Shichang, Wu Weige, et al. Two-dimensional transient flow-thermal coupling field analysis of oil-immersed transformer windings based on hybrid finite element method and reduced-order technology[J]. High Voltage Engineering, 2022, 48(5): 1695-1704.
[16] Yan Shuai, Tang Zuqi, Henneron T, et al. Structure-preserved reduced-order modeling for frequency-domain solution of the Darwin model with a gauged potential formulation[J]. IEEE Transactions on Magnetics, 2020, 56(1): 1-4.
[17] Lall S, Krysl P, Marsden J E. Structure-preserving model reduction for mechanical systems[J]. Physica D: Nonlinear Phenomena, 2003, 184(1/2/3/4): 304-318.
[18] Chaturantabut S, Sorensen D C. A state space error estimate for POD-DEIM nonlinear model reduction[J]. SIAM Journal on Numerical Analysis, 2012, 50(1): 46-63.
[19] Jiang Bonan. The least-squares finite element method: theory and applications in computational fluid dynamics and electromagnetics[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 1998.
[20] 陈刚, 吕计男, 龚春林, 等. 计算流固耦合力学[M].北京: 科学出版社, 2021.
[21] Sato Y, Igarashi H. Model reduction of three-dimensional eddy current problems based on the method of snapshots[J]. IEEE Transactions on Magnetics, 2013, 49(5): 1697-1700.
[22] 廖才波, 阮江军, 刘超, 等. 油浸式变压器三维电磁-流体-温度场耦合分析方法[J]. 电力自动化设备, 2015, 35(9): 150-155.
Liao Caibo, Ruan Jiangjun, Liu Chao, et al. Comprehensive analysis of 3-D electromagnetic-fluid-thermal fields of oil-immersed transformer[J]. Electric Power Automation Equipment, 2015, 35(9): 150-155.
Abstract In order to improve the efficiency problem of using finite element method to calculate the transient temperature rise of oil immersed power transformer windings, this paper proposes a calculation strategy that combines structure preserved property orthogonal decomposition (SPOD) with discrete empirical interpolation method (DEIM). Firstly, the article uses the least squares finite element method (LSFEM) and upwind finite element method (UFEM) to construct the control equation for calculating the transient temperature rise of transformer windings. The finite element method combined with LSFEM-UFEM can accurately obtain the flow field and temperature field distribution during the transient temperature rise change process of the winding; However, in practical engineering applications, the mesh size and number of nodes of the model are generally large, and using finite element method to solve faces the problem of high time cost. Therefore, in order to reduce the computational scale and improve computational efficiency, the article introduces a reduction method based on the characteristics of the control equation. The traditional POD method usually decomposes the entire dataset and only reflects the statistical characteristics of the dataset, However, the inability to preserve physical features results in low interpretability of the reduced order model. Therefore, this article adopts a reduced order calculation strategy of "data structure preservation" to improve the efficiency of solving finite element equations; At the same time, in order to improve the efficiency improvement of the intrinsic orthogonal decomposition method for nonlinear problems, the DEIM algorithm is combined to interpolate the nonlinear terms in the finite element equation, thereby reducing the time for forming the overall stiffness matrix at each step and further improving the overall computational efficiency. In order to verify the accuracy and efficiency of the algorithm proposed in the article, a single zone split turn winding heat transfer model was established and its transient heat transfer process was calculated. The results showed that the finite element reduced order calculation based on SPOD-DEIM can effectively improve the calculation efficiency while ensuring accuracy. Compared with the full order calculation results, the calculation errors of the flow field and temperature field are not more than 1.5%, and the calculation efficiency is increased by 5.1 times. At the same time, in order to fully demonstrate the value of SPOD-DEIM algorithm in engineering applications, the article built a temperature rise test platform based on 110 kV transformer windings, and established an eight zone split turn winding numerical calculation model to verify and discuss the accuracy, efficiency, and engineering application value of the algorithm. The calculation and experimental results show that in terms of accuracy, the transient whole process calculation error of reduced order calculation is less than 2.5% compared to full order calculation, and compared with experimental results, The error shall not exceed 5.41 K; In terms of efficiency, the entire process calculation time of reduced order calculation is 54.28 h, which increases the calculation efficiency to 10.57 times compared to full order calculation and 6.37 times compared to commercial simulation software Fluent. This fully demonstrates the efficiency and engineering application value of the algorithm proposed in this article.
keywords:Transient temperature rise of winding, structure-preserved, proper orthogonal decomposition (SPOD), discrete empirical interpolation method (DEIM), reduced order calculation, temperature rise experiment
中图分类号:TM411
DOI:10.19595/j.cnki.1000-6753.tces.222155
国家重点研发计划(2021YFB2401703)和中央高校基本科研业务费专项资金(2022MS073)资助项目。
收稿日期 2022-11-05
改稿日期 2023-04-03
刘 刚 男,1985年生,副教授,硕士生导师,研究方向为电气设备多物理场建模及仿真、电力系统时域仿真和电磁场理论及其应用等。E-mail:liugang_em@163.com(通信作者)
胡万君 男,1999年生,硕士研究生,研究方向为多物理场快速计算等。E-mail:1366320104@qq.com
(编辑 郭丽军)