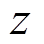轴上对称分布，选取xOy平面上的上下两测点，测量其径向（
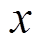轴辐向）漏磁分量。摘要 针对变压器绕组变形、轻微匝间故障等早期故障，传统的保护方案一般难以进行有效的诊断，根据变压器绕组漏磁场变化可以灵敏地检测出绕组的早期故障，但缺乏适用于工程应用的绕组漏磁场分析的解析方法和在线测量方案。针对这些问题，该文计算了简化模型下的变压器绕组漏磁场分布，通过测量绕组上、下表面和中部的漏磁感应强度，提出故障分量磁平衡保护的整定方法和判别逻辑。最后，建立了Ansys的仿真模型和动模实验模型，验证了保护方案具有不受负荷变化及不受励磁涌流的影响，并且区内故障检测灵敏度高的优点。
关键词：变压器保护 匝间短路 绕组变形 磁平衡保护
变压器在电力系统中担任转换和分配电能的作用，当其受到多次外部短路电动力的冲击后，绕组可能会发生不可逆的形变[1]。一旦长期运行在轻度绕组变形下，极易导致变压器绕组出现匝间故障[2]。在绕组匝间故障的初期，传统的差动保护灵敏度较低，难以对变压器形成有效保护，一旦任其长期运行在故障状态，极易使得故障进一步发展为层间短路，甚至发生相间短路，最终导致变压器烧毁[3]。据相关统计，绕组匝间短路在变压器绕组故障中约占50%～60%[4]。因此，有必要提出一种新型保护方案，能够检测变压器的绕组变形和轻微匝间故障，对变压器的检修维护都具有重要意义。
当前，变压器的绕组变形、匝间绝缘损坏、轻微及间歇性匝间短路等早期故障诊断方法主要包括变压器油中溶解气体分析法、局部放电检测法、漏电感法和漏磁检测法等[5-8]。溶解气体分析法和局部放电检测法为不确定性检测法，通过检测结果反向推演故障原因，对运行人员的经验要求较高。当变压器绕组结构发生变化时（如绕组变形、匝间故障），漏磁场分布会发生变化，因此可利用绕组漏磁分布特征量对变压器早期故障进行研究。文献[9]提出了漏磁场探测线圈的在线检测方法，对绕组绝缘破坏进行了检测。文献[10]利用探测线圈检测漏磁场的方法，判别绕组发生匝间故障并确定故障位置。文献[11]建立了变压器绕组的三维有限元模型，并针对其漏磁场分布特征进行了相应分析。由于探测线圈在油浸式变压器中有短路风险，因此，文献[12-14]提出在变压器制造的同时埋入光纤，根据光纤受力变形的原理，进行变压器绕组变形在线监测，但是这种方法实际应用困难。采用漏磁场能量积分法可计算出绕组漏感，因此也有文献[15]利用漏感参数辨识法识别绕组变形。文献[16]建立了一种不同状态下的漏感迭代计算的变压器多状态模型，为早期故障识别提供了新思路。文献[17-18]利用漏感参数变化识别绕组匝间故障。文献[19]利用在线计算短路阻抗的变化，识别绕组匝间故障。但是漏磁场能量积分法计算的漏感参数误差大，难以准确在线辨识漏感参数。
上述文献在变压器发生绕组变形和匝间故障的情况下，在绕组漏感参数的变化规律、漏磁场特征量的故障判据、用于变压器故障缺陷检测的光纤在线检测技术等方面的研究取得了一定的成果，为利用绕组漏磁场变化检测变压器绕组变形、轻微匝间故障的研究奠定了基础，但在以下几方面的研究仍存在不足：
1）缺乏适用于变压器早期故障保护的绕组漏磁场在线测量方案，以及高灵敏的绕组变形、轻微匝间故障的保护方案。
2）缺乏适用于工程应用的变压器绕组变形、轻微匝间故障的解析分析方法，以及对变压器早期故障保护的定值整定方法。
本文通过简化模型下的分离变量解析计算方法，求取变压器故障绕组漏磁场分布解析公式。同时提出不受负荷和励磁涌流影响、高灵敏度的工频故障分量磁平衡保护的动作逻辑，并根据绕组变形、轻微匝间故障漏磁场解析公式对保护定值进行了整定和校验。最后，通过仿真模型和动模实验验证了本文所提保护方案的正确性和有效性。
本文磁平衡保护的依据绕组漏磁感应强度对称性的变化，传统的继电保护故障特征量采用电流、电压等电气量，只有闭合回路才能形成故障电流，变压器差动保护基于基尔霍夫定理，节点流入电流等于流出电流，但是如果不忽略励磁电流，差动保护并不满足基尔霍夫定理，所以具有励磁涌流闭锁逻辑；而漏磁场空间分布符合麦克斯韦方程组，磁通线回路中包含磁势、磁阻，和电流回路一样也是闭合回路。不包含电流的闭合空间类似于基尔霍夫定理中的电流节点，穿入的磁通线一定等于穿出的磁通线，因此可以通过对闭合空间内，两个通过相同磁通线边界上的对称点磁感应强度的测量（一进一出），构成磁平衡保护。对称测量系统原理如图1所示。光纤测量传感器安装在如图1所示的位置，由于漏磁通在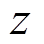轴上对称分布，选取xOy平面上的上下两测点，测量其径向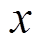（轴辐向）漏磁分量。
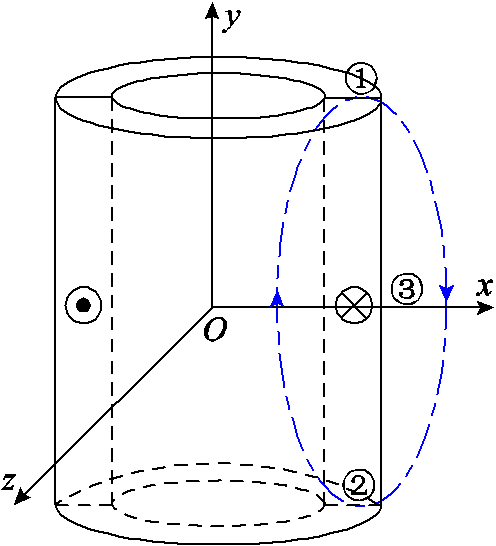
图1 对称测量系统原理
Fig.1 Schematic of a symmetrical measurement system
根据文献[20-22]，由于变压器绕组、铁心、铁轭结构的对称性，漏磁场在空间中呈对称分布。漏磁场的磁通线会经过绕组附近空间、夹件、铁轭、油箱壁、铁心等部分形成闭合回路，而漏磁场的磁平衡保护关注于绕组空间测点漏磁场的平衡性。在图1中，①、②点绕组中流过穿越性电流使得漏磁感应强度平衡；③点由于绕组结构对称，在绕组结构没有被破坏前，其辐向漏磁感应强度接近为0。因此，为便于工程实现，可以以漏磁场对称性分析为关注点，对绕组的漏磁路进行简化，将复杂的三维模型简化为二维模型进行分析。
发生上端绕组变形时，单相绕组和铁心二维剖面图如图2所示，设高压绕组变形后的电流密度为
；绕组正常运行时高压绕组的电流密度为
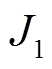。由于漏磁场分布于空气中，根据叠加原理，将故障分量的高压绕组分为变形区域和未变形区域，电流密度分别为
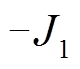和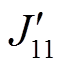
。其中正常分量仍保持漏磁场对称，故障分量的漏磁不平衡量是本研究的重点。
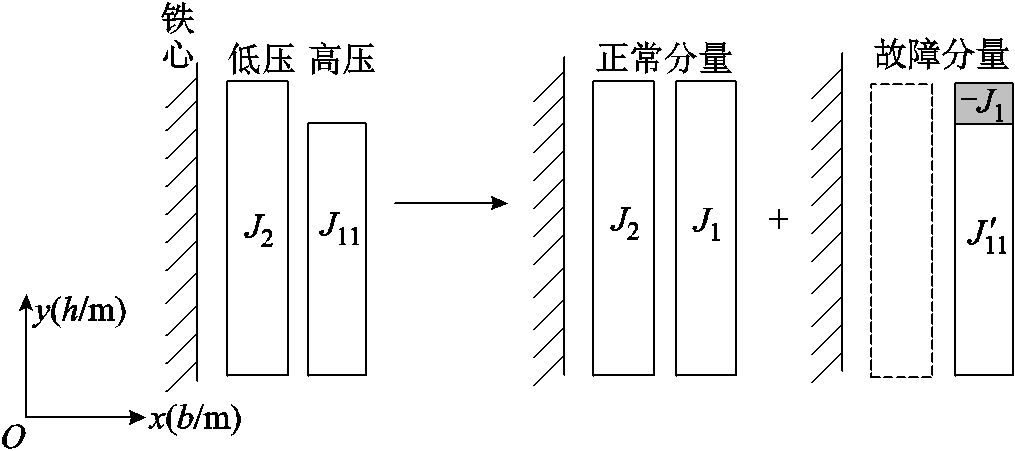
图2 绕组变形故障绕组分解示意图
Fig.2 Schematic of decomposition of the winding deformation faulty winding
具体的绕组变形故障区域划分如图3所示。绕组电流密度利用傅里叶级数分解法，对每一频率分量通过偏微分方程的解析法分段求解漏磁感应强度，将分段后的各分量的求解结果叠加获得漏磁感应强度的空间分布函数。由于轻度绕组变形仍能保持正常运行，因此整个绕组仍能满足安匝平衡，同时故障分量绕组区域也满足安匝平衡，则
图3 绕组变形故障分量电流密度分解示意图
Fig.3 Schematic of current density decomposition of the winding deformation faulty winding
（1）
式中，h为绕组高度。
利用镜像原理构造出偶延拓的傅里叶级数，其绕组电流密度的分解公式为
（2）
式中，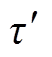
为上下铁轭之间的距离。
在区域Ⅱ和Ⅲ中，电流密度为0；在区域Ⅰ内，电流密度不为0，向量磁位AzI满足泊松方程为
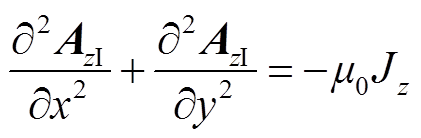（3）
式中，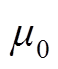
为真空磁导率。
解出区域Ⅰ的辐向漏磁感应强度为
（4）
式中，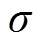
为铁心与故障绕组的距离，=
；
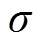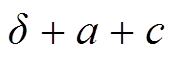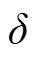为高压绕组和铁心的距离，a为高压和低压绕组间隔的距离，c为低压绕组的厚度；
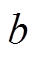为故障绕组宽度。
发生端部匝间短路单相绕组和铁心二维剖面图如图4所示。
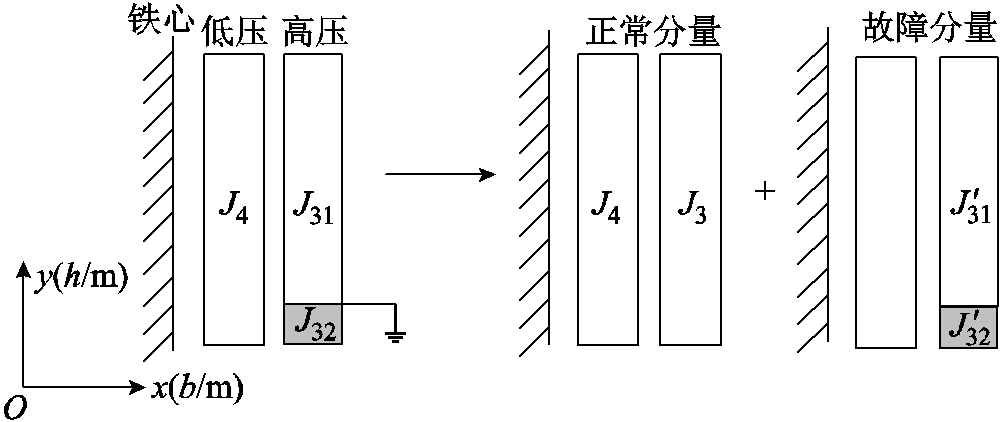
图4 匝间故障绕组分解示意图
Fig.4 Schematic of decomposition of the inter-turn faulty winding
由于发生匝间短路后，原有的安匝平衡状态被破坏，则电流密度分解后出现了直流分量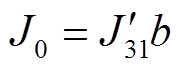
。
匝间故障绕组电流密度分解示意图如图5所示。根据图5可知，谐波分量计算表达式为
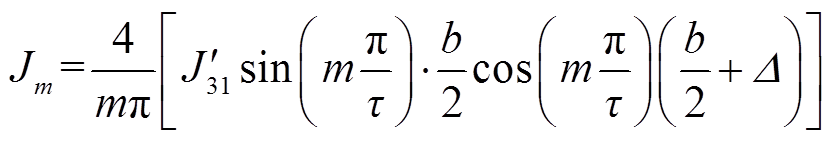（5）
式中，t为极距，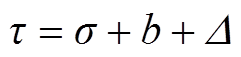
；Δ为故障绕组与中性面的距离。
采用分离变量法求解区域Ⅰ′、Ⅱ′、Ⅲ′，获得辐向漏磁感应强度关于空间坐标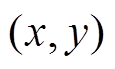
表达式见附录式（A1），最终未短路匝绕组故障分量与短路匝绕组故障分量进行叠加，求得所需空间的故障分量漏磁场分布。
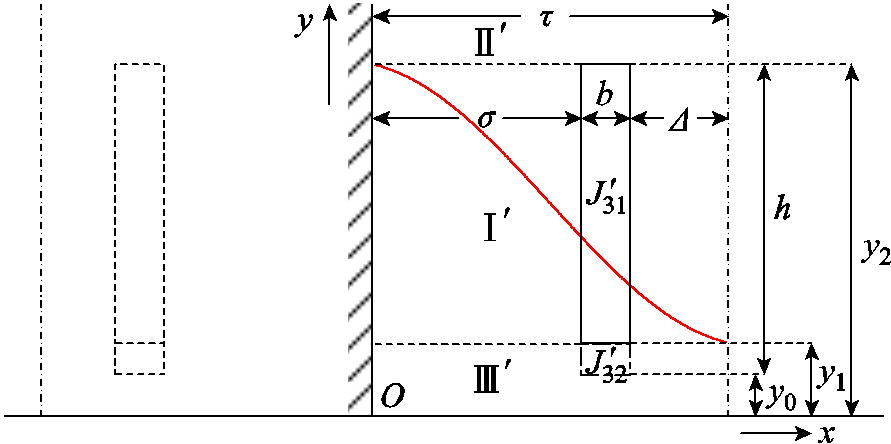
图5 匝间故障绕组电流密度分解示意图
Fig.5 Schematic of current density decomposition of the inter-turn faulty winding
光纤漏磁场测量原理采用基于法拉第效应的磁光原理[23-24]。
本文采用巴特沃斯带通滤波器，对光纤漏磁传感器采样数据进行滤噪处理。其幅频平方函数为
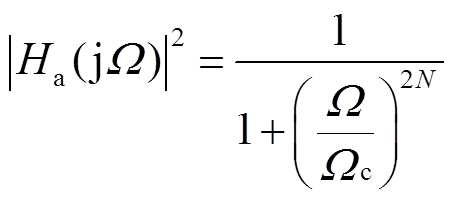（6）
式中，
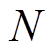为阶数；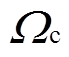
为截止频率。当滤波频率W在截止频率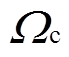以内时，幅频特性
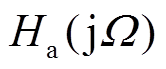越接近1。
本文使用Matlab自带的工具箱设计巴特沃斯带通滤波器，阶数设置为最低阶，取采样频率Fs= 5 000 Hz，通带频率Fpass=40 Hz，阻带频率Fstop= 60 Hz，通带内波动Dpass=0.057 5 dB，阻带内最小衰减Dstop=0.000 1 dB，密度因子dens=20。由此完成滤波器的设计，并对光纤漏磁传感器采样数据进行处理，提取工频量。
假设绕组截面电流密度均匀分布，只要绕组结构不改变、绕组两端流过穿越性电流，那么穿过两个边界测点的磁通线相同，两个测点的磁感应强度就相同，不平衡量为0。如果内部发生故障，漏磁场分布对称性发生变化，就会出现很大的故障不平衡量，由于励磁涌流、区外故障电流对单侧绕组来说为穿越性电流，故障不平衡量仍为0，所以磁平衡保护能够躲过励磁涌流和穿越性故障电流的影响。由于负荷电流为穿越性电流，其产生的漏磁感应强度在测点①、②和测点③均是平衡的，但由于测量、安装位置误差，会对不平衡量产生影响，因此采用故障分量的辐向漏磁感应强度作为故障特征量，提高检测灵敏度。具体的保护逻辑框图如图6所示。
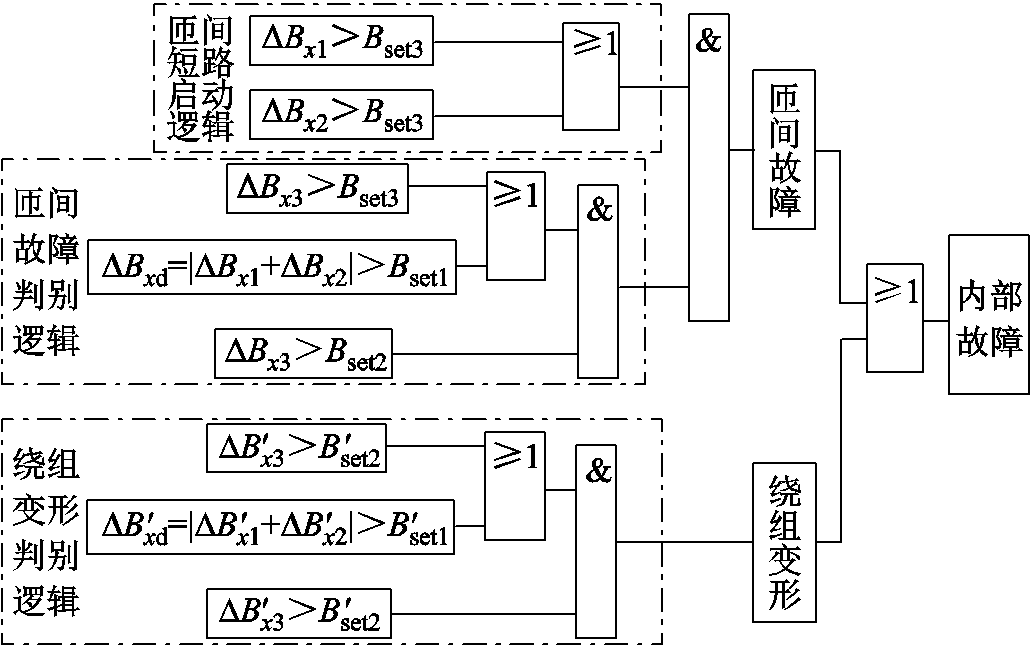
图6 磁平衡保护逻辑框图
Fig.6 Logic block diagram of magnetic balance protection
图6中，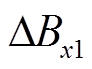
、
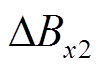分别为匝间故障下绕组上下两端辐向漏磁故障分量，
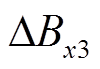为匝间故障下绕组中部辐向漏磁故障分量，
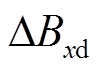为匝间故障下绕组上下两端辐向漏磁故障不平衡量，
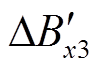为绕组变形下绕组中部辐向漏磁故障分量，
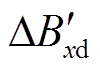为绕组变形下绕组上下两端辐向漏磁故障不平衡量。
本文动模变压器光纤漏磁传感器安装位置如图7所示。具体的磁平衡保护流程如图8所示。磁平衡护通过检测绕组上下端和中部是否存在辐向漏磁故保障分量，并按照故障分量是否为突变的形式，分别进行匝间短路与绕组变形的故障逻辑判别，并与其对应的整定计算值比较，进行保护动作。
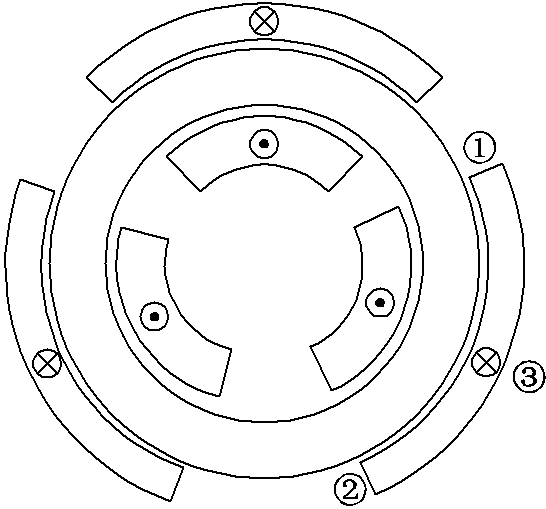
图7 动模变压器传感器安装位置示意图
Fig.7 Schematic diagram of the installation position of the dynamic mode transformer sensor
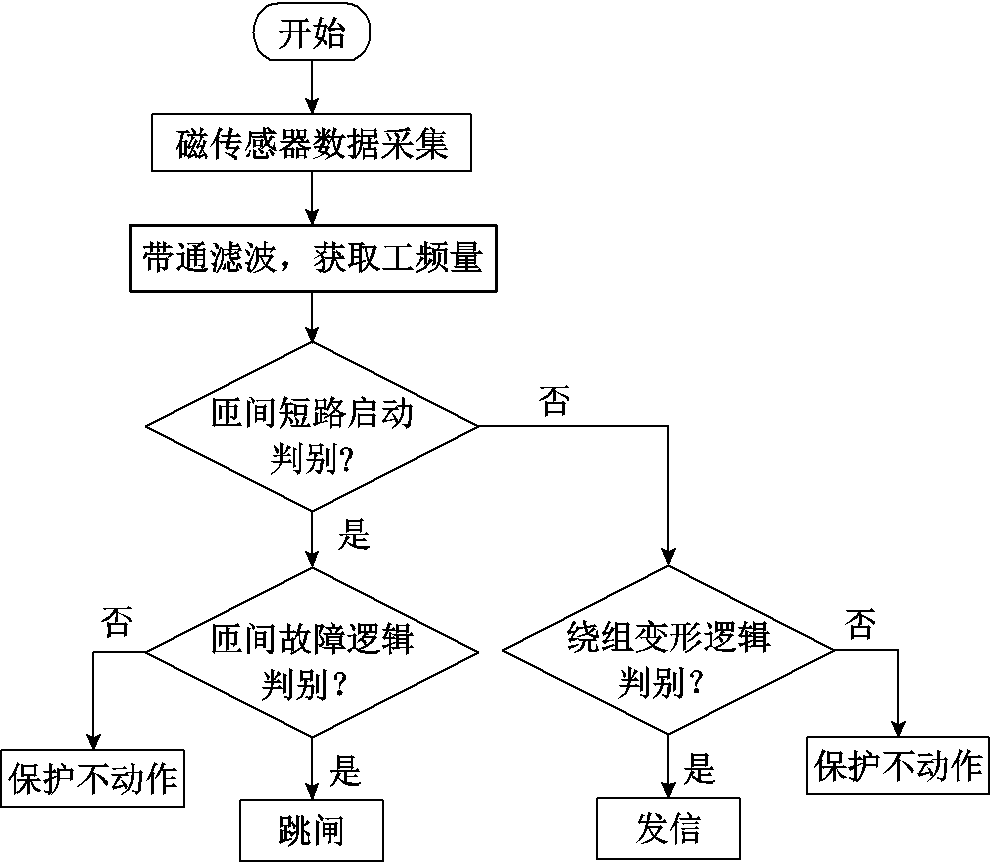
图8 磁平衡保护流程
Fig.8 Flow chart of magnetic balance protection
2.3.1 绕组变形整定值设定
本文将磁光传感器安装在绕组上下两端的中间，则绕组变形后的故障不平衡量
整定公式为
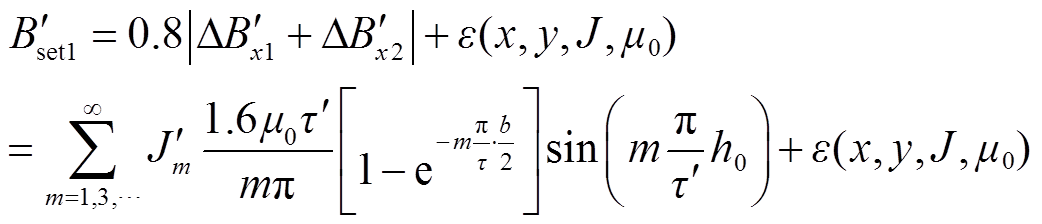（6）
式中，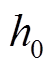
为铁轭到绕组之间的距离。
根据式（7）可知，当上、下测点的垂直位置一致时，位置参数固定，对于故障不平衡量的影响因素只有电流密度的分布，随着轴向变形程度加深，故障不平衡量逐渐增大，所以保护为过量保护。由于在进行解析计算时，将绕组附近空间、夹件、油箱壁等复杂磁路，均等效为空气磁路，因此需要考虑增加一个误差项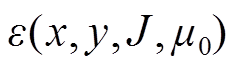
，此误差项主要与位置、电流密度、材料的磁导率有关。
同理，中间测点整定值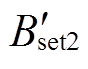
的表达式为
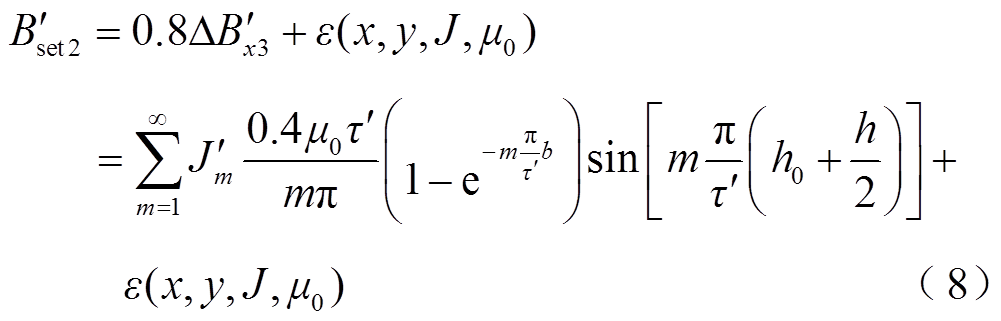
由于磁光测量传感器精度的限制，本文选取了5%的绕组变形进行整定，计算出心式变压器绕组变形整定值，
=29.9 mT，
=4.1 mT。
2.3.2 匝间短路整定值设定
本文磁平衡保护启动值选择为0.2倍的上、下端额定辐向漏磁感应强度的变化量[25]，即
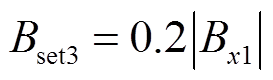（9）
式（9）具体见附录式（A2）和（A3）。对于不同电压等级的变压器，需要根据相应的额定电流进行启动值整定。
当短路位置发生在中间段时，其上、下测点故障分量之和极小，考虑可靠系数后上、下测点故障不平衡量的整定公式为
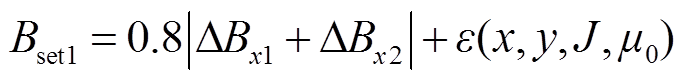（10）
同理，中间测点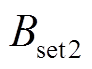
选取故障发生2匝接地短路的故障分量进行整定，放置在绕组中部右端。利用前述的计算方法，求得在动模变压器的径向漏磁感应强度的整定数值，
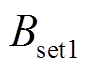=0.182 mT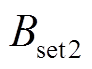，=0.109 mT，
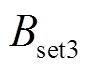=0.087 mT。
2.3.3 误差分析
由于受结构件或其他进出线的电磁干扰，变压器正常运行时内部漏磁场并不对称（即可认为在安装位置对称的情况下，上、下测点的辐向漏磁感应强度不平衡量不为0，中间测点辐向漏磁感应强度大于0），但是本文考虑的是故障情况下与正常情况下漏磁场的变化量，实际上当绕组出现故障后，相应的漏磁场反映的变化趋势并没有改变，仍然可认为是一个过量保护。误差项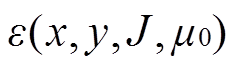
会使得绕组上、下和中间不平衡量不为0。当发生绕组故障时，误差项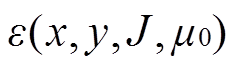能够提高不平衡量的整定值，一定程度上防止保护误动。但是对于磁光传感器而言，安装位置是影响磁平衡保护的关键因素。相关分析如下。
1）绕组变形时上、下安装位置误差分析
假设上下测点的垂直位置不一致，相差为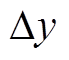
，则误差公式为
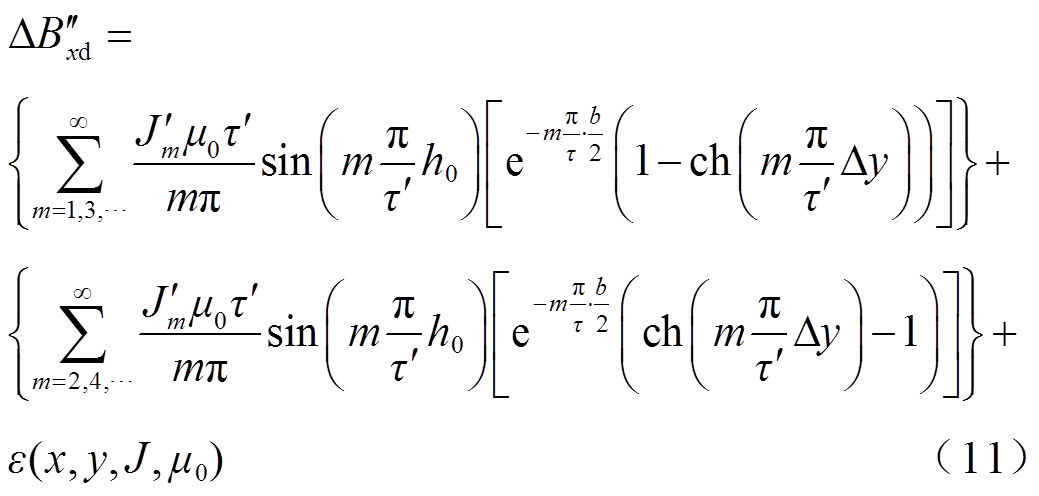
当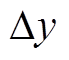增大时，
为单调增函数，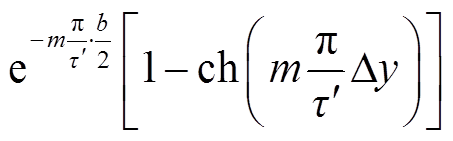
为单调减函数，同理，
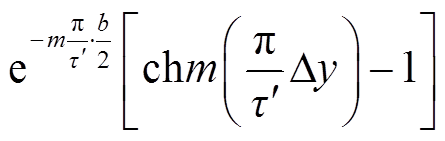为单调增函数，由于偶数次谐波变化量更大，所以式（11）随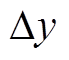增大而增大。上、下安装位置的不一致，会导致在区外故障不平衡量过大而越限，但是利用中间测点的不平衡量可以实现穿越性电流的闭锁，防止保护误动。
2）匝间短路时上、下安装位置误差分析
匝间短路以辐向漏磁故障分量的突变作为启动依据，因此只需考虑在变压器发生空载合闸情况下，上、下测点不平衡量不越限。一般来说，变压器空载电流为额定电流的5～8倍，则取10倍的变压器额定电流，计算上、下测点垂直相距0.05b的不平衡量，具体公式为
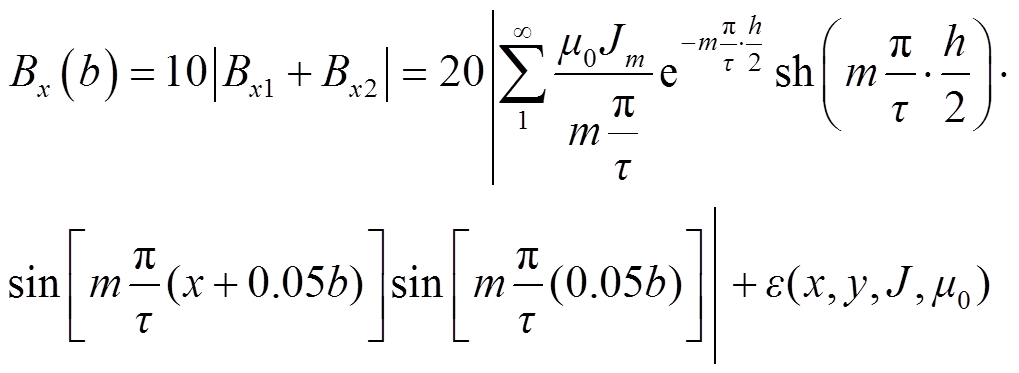（12）
动模变压器计算出的误差值为0.084 mT。当正常运行时上、下测点不平衡量超过误差值时，可通过给单独的上测点或下测点采样数进行修正，保证上、下测点不平衡量在允许误差内。
3）中间测点安装位置误差分析
由于中间测点的不平衡量能够可靠反应绕组结构的变化，发生区外故障时的穿越性电流远大于励磁涌流，可选择20～40倍的额定电流对中部测点进行误差计算，具体为
式中，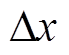
代表安装位置与绕组中点的误差，此误差较小，一般取0.05
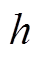，心式变压器计算出的误差值为0.5 mT，动模变压器计算误差为0.02 mT。正常情况下，中间测点的辐向漏磁分量受到安装位置的影响较小，保护动作的可靠性高。利用这一特性可实现两种故障类型区外故障的可靠闭锁。
因此在面对复杂的实际漏磁场分布时，具体的应对措施为：①提高整定值，通过牺牲一定的灵敏度确保保护的可靠性；②若正常时的不平衡量过大，影响到空载合闸或外部故障的保护闭锁，可根据端口电流求得的辐向磁感应强度值对采集量进行补偿修正，保证其误差不超过阈值。
本文将建立变压器三相心式仿真模型和动模变压器仿真模型。其中三相心式仿真模型将用来验证上文所提故障分量漏磁计算的准确性，动模变压器仿真模型既可以作为不同结构变压器磁平衡保护的补充，又可以弥补动模实验中匝间故障短路匝有限的缺陷。通过心式模型、动模模型和动模实验分别验证磁平衡保护具有广泛的适用性。
3.1.1 心式变压器仿真模型
首先以一台心式三相双绕组变压器为例，对变压器内部绕组匝间短路故障情况进行仿真分析。具体模型参数、建模图和漏磁云图见附录，为了保证计算速度，采用Maxwell二维模型。
采用故障分量的思想，将上端绕组变形后的辐向漏磁强度计算值与Ansys仿真值进行比较，验证辐向漏磁故障分量的正确性。图9为不同变形程度下计算值与仿真值的比较。
图9 不同变形程度下计算值与仿真值的比较
Fig.9 Comparison of calculated and simulated values at different deformation degrees
由图9可知，计算值与仿真值存在一定的误差， 但是数据变化的趋势一致。利用此计算原理，可以快速计算出磁平衡保护整定值，便于工程实践应用。
3.1.2 动模变压器仿真模型
动模变压器仿真模型按照动模实验系统进行建模，具体的组合式变压器建模图和漏磁云图如附图1和附图2所示，可以对动模实验数据进行比较研究。
3.1.3 动模实验模型
动模实验系统接线如图10a所示，无穷大电源系统参数：E=1 kV，忽略系统内阻。线路参数如下：r1=0.012 7 Ω/km，x1=0.174 7 Ω/km，c1=0.033 6 µF/km，长度L=200 km。此系统中的试验变压器为三相三绕组变压器，采用YN/YN/d11接线，变压器T参数如下：额定容量为10 kV×A，额定电压U1/U2/U3=1 000 V/ 1 000 V/380 V，频率f=50 Hz，归算至高压侧的绕组参数为R1=R2=R3=0.42 Ω，X1=X2=X3=10.76 Ω。负荷参数为ZL=(159.987+j1.358)Ω。匝间短路故障设置在高压侧A3、A4之间和A8、A9之间，短路抽头如图10b所示，通过故障录波仪记录变压器的电流和电压。
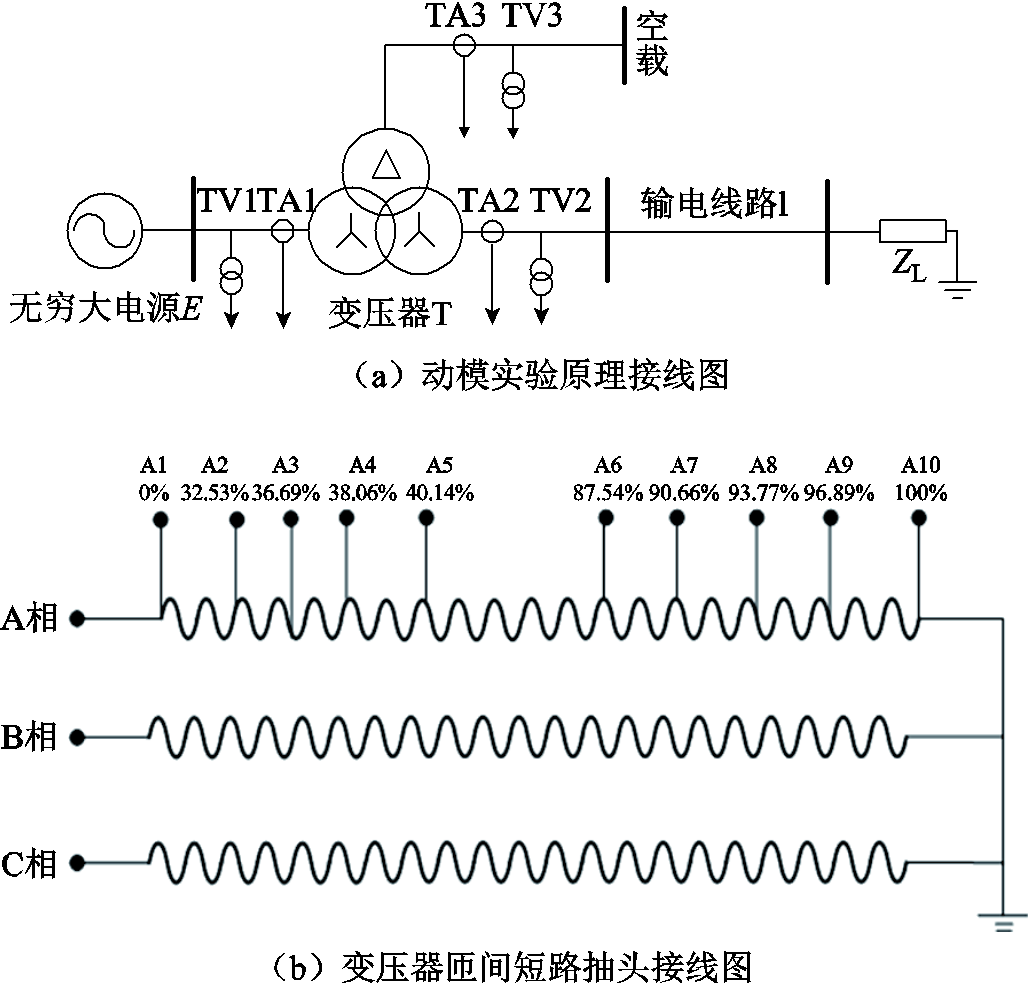
图10 变压器动模实验平台
Fig.10 Dynamic model experiment platform of transformer
本文所研发的光纤磁场的测量系统如图11所示，磁光传感器如图11a所示，磁平衡保护光纤信号采集、数据处理硬件如图11b所示。
在完成动模实验平台搭建后，需要在变压器A相绕组上安装磁光传感器，搭建图12所示磁平衡保护平台。
图11 光纤漏磁场测量系统
Fig.11 Optical fiber leakage magnetic field measurement system
图12 磁平衡保护平台
Fig.12 Platform of magnetic balance protection
3.1.4 动模变压器仿真模型和动模实验模型的比较
由于试验变压器所能实现的匝间故障程度有限，故建立了动模变压器仿真模型用于验证磁平衡保护的灵敏性与速动性。图13为变压器空载下匝间短路实测与仿真波形对比。图13匝间故障位置设置在A8、A9之间。利用此仿真模型模拟动模实验不能实现轻微匝间短路，完善磁平衡保护的高灵敏度验证。
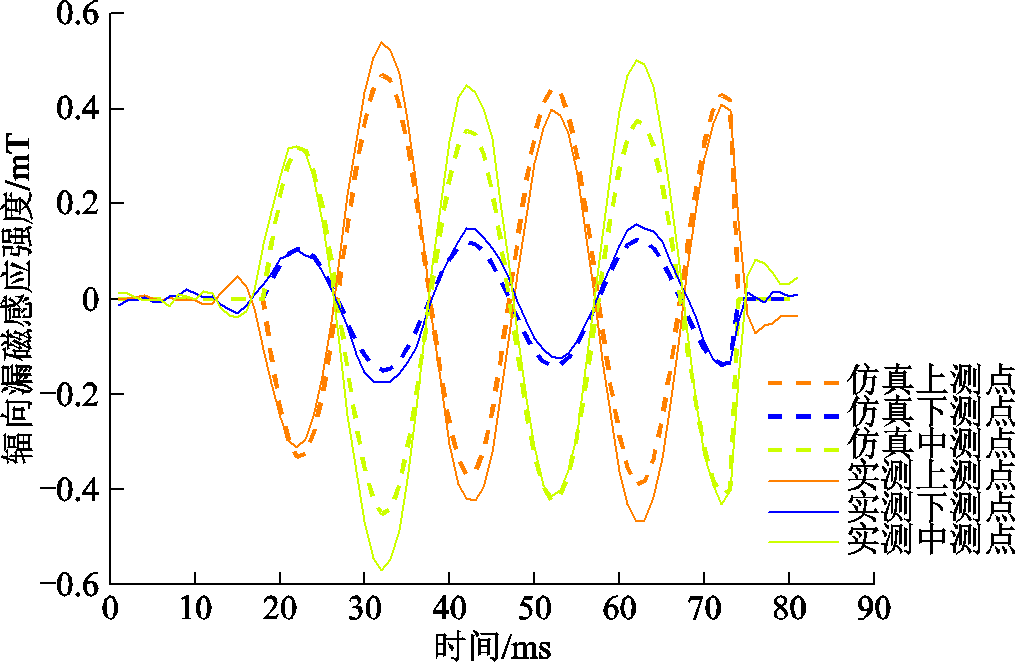
图13 空载下匝间短路实测与仿真波形对比
Fig.13 Comparison of measured and simulated waveforms of inter-turn short circuit under no load
由于动模实验中只能实现匝间短路，因此绕组变形的磁平衡保护验证主要依靠芯式的仿真模型。图14为5%上端绕组变形仿真测量和故障分量的漏磁波形。
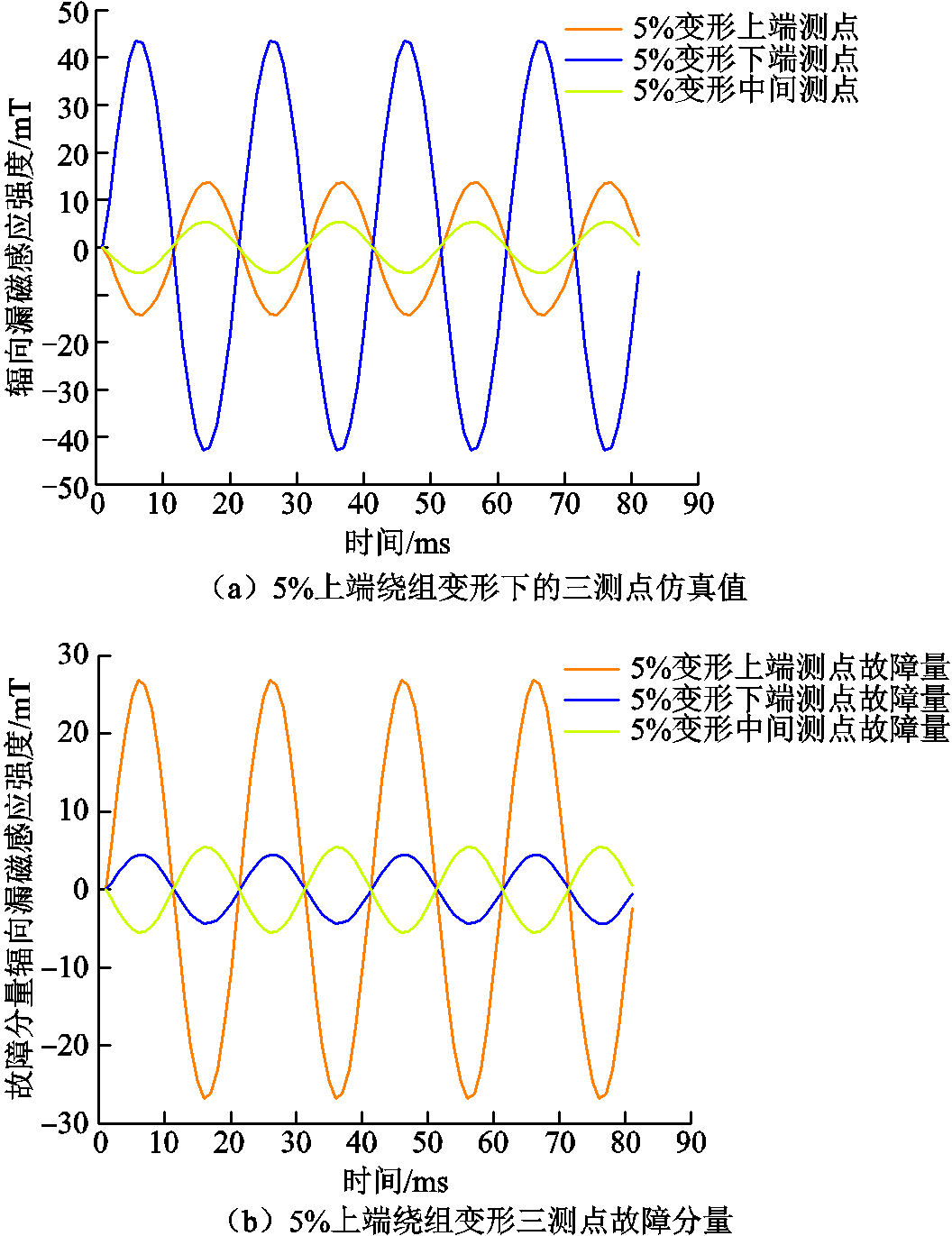
图14 5%上端绕组变形仿真测量和故障分量的漏磁波形
Fig.14 5% upper winding deformation simulation measurement and leakage flux waveforms of fault component
5%上端绕组变形磁平衡保护检验曲线如图15所示。由图15可知，发生轻度绕组变形时，在一段时间内上、下不平衡量几乎维持在31.4 mT，中间测点故障量为5.5 mT。根据上述的动作曲线情况可知，磁平衡保护可以准确动作。
本次动模验证实验主要包括三个方面，分别为空载合闸实验、空投匝间实验以及带载下的匝间短路实验。实验中匝间故障位置设置在A3、A4之间。
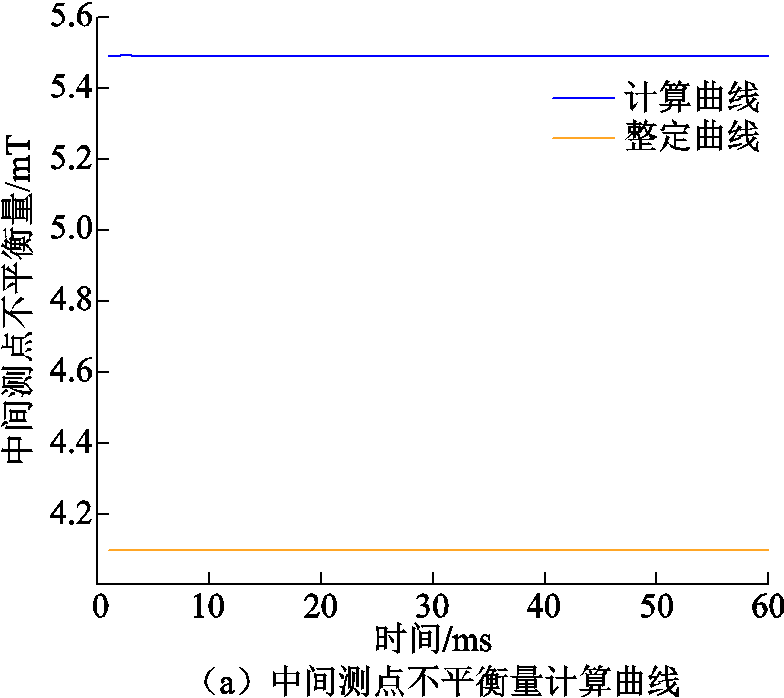
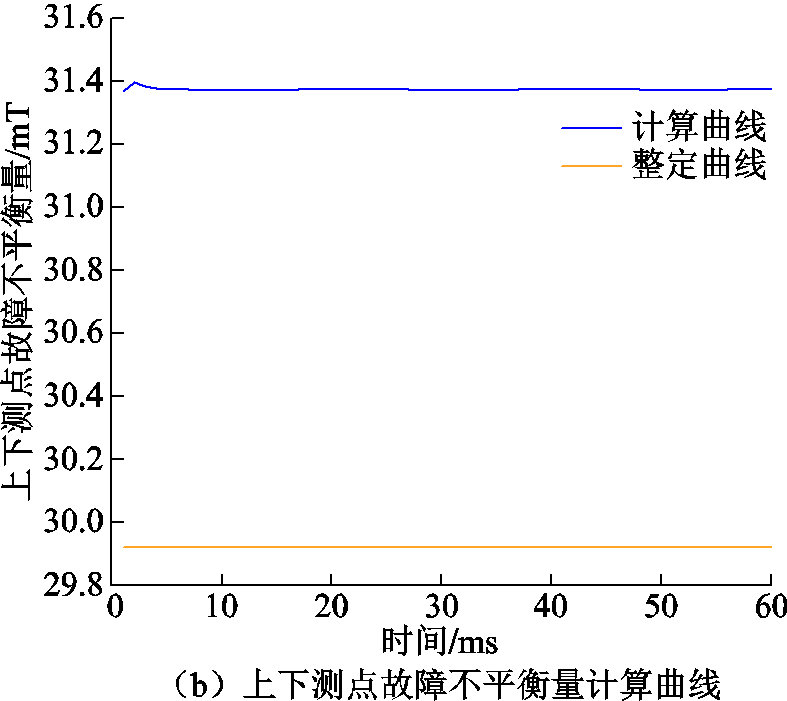
图15 5%上端绕组变形磁平衡保护检验曲线
Fig.15 5% upper winding deformation magnetic balance protection test curve
3.3.1 空载合闸
当变压器处于空载合闸状态下时，其内部结构仍然对称，磁平衡保护应不受励磁涌流的影响。图16为空载合闸下实测采样和滤波后的漏磁波形。
当变压器进行空载合闸时，其合闸产生的励磁涌流是正常运行时电流的数倍，因而监测的辐向漏磁感应强度也会随之增大。但是由于变压器绕组对称，上、下测点形成的故障不平衡量和中间测点故障不平衡量均小于门槛值，保护闭锁，具体如图17空载合闸磁平衡保护检验曲线所示，可知保护不受励磁涌流的影响。
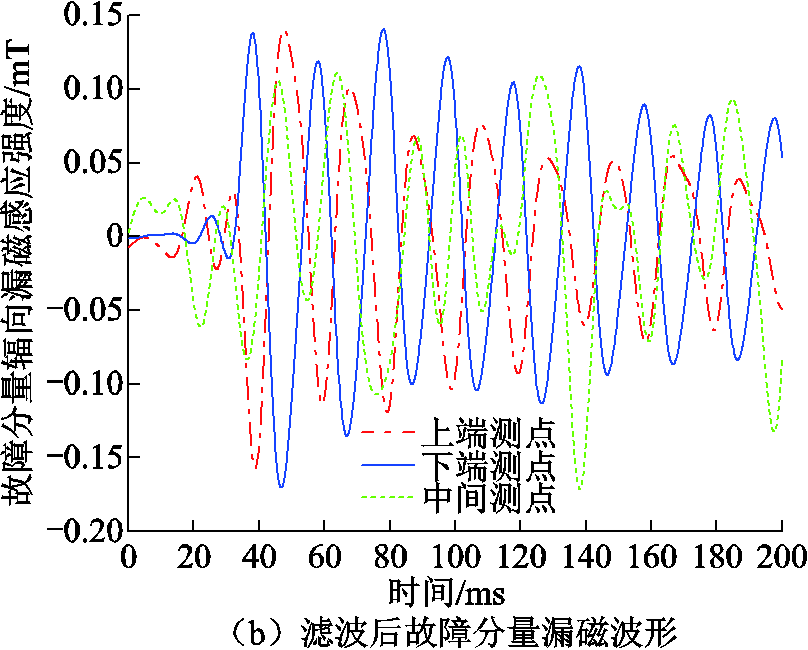
图16 空载合闸实测采样和滤波处理后的波形
Fig.16 The waveforms after the measured sampling and filtering of the no-load closing
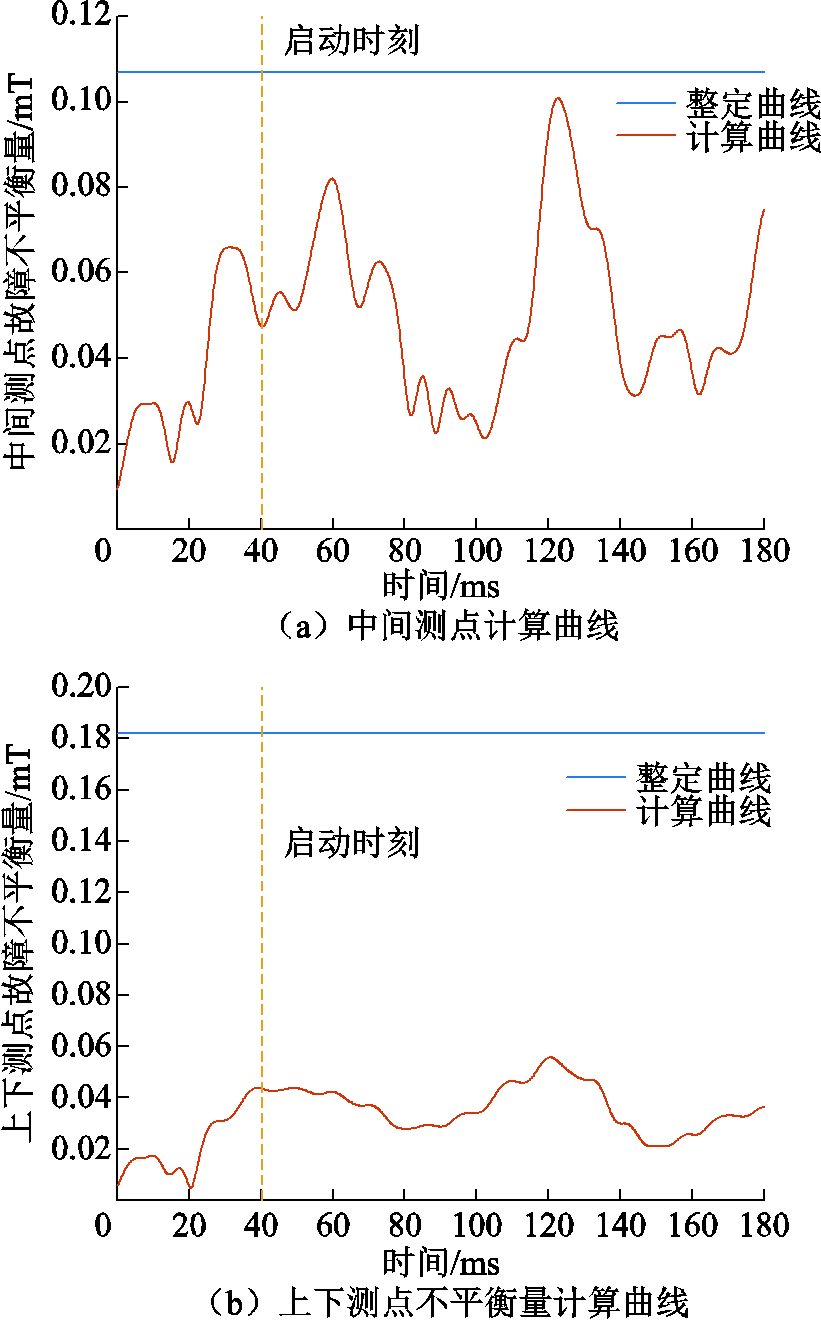
图17 空载合闸磁平衡保护检验曲线
Fig.17 Verification curves of the no-load closing of magnetic balance protection
3.3.2 空投匝间短路
变压器发生空投匝间故障时，由于励磁涌流的存在，传统电流差动保护会进行谐波闭锁，导致延时切除故障，造成变压器损坏。图18为空投匝间故障实测采样和滤波漏磁感应强度波形。
空投匝间磁平衡保护检验曲线如图19所示。由图19可知，在45.7 ms检测到上、下测点的辐向漏磁发生突变，保护随即启动，经过20 ms的傅里叶计算数据窗延时，上、下测点故障不平衡量和中间测点故障不平衡量大于门槛值，满足保护出口逻辑，保护动作。
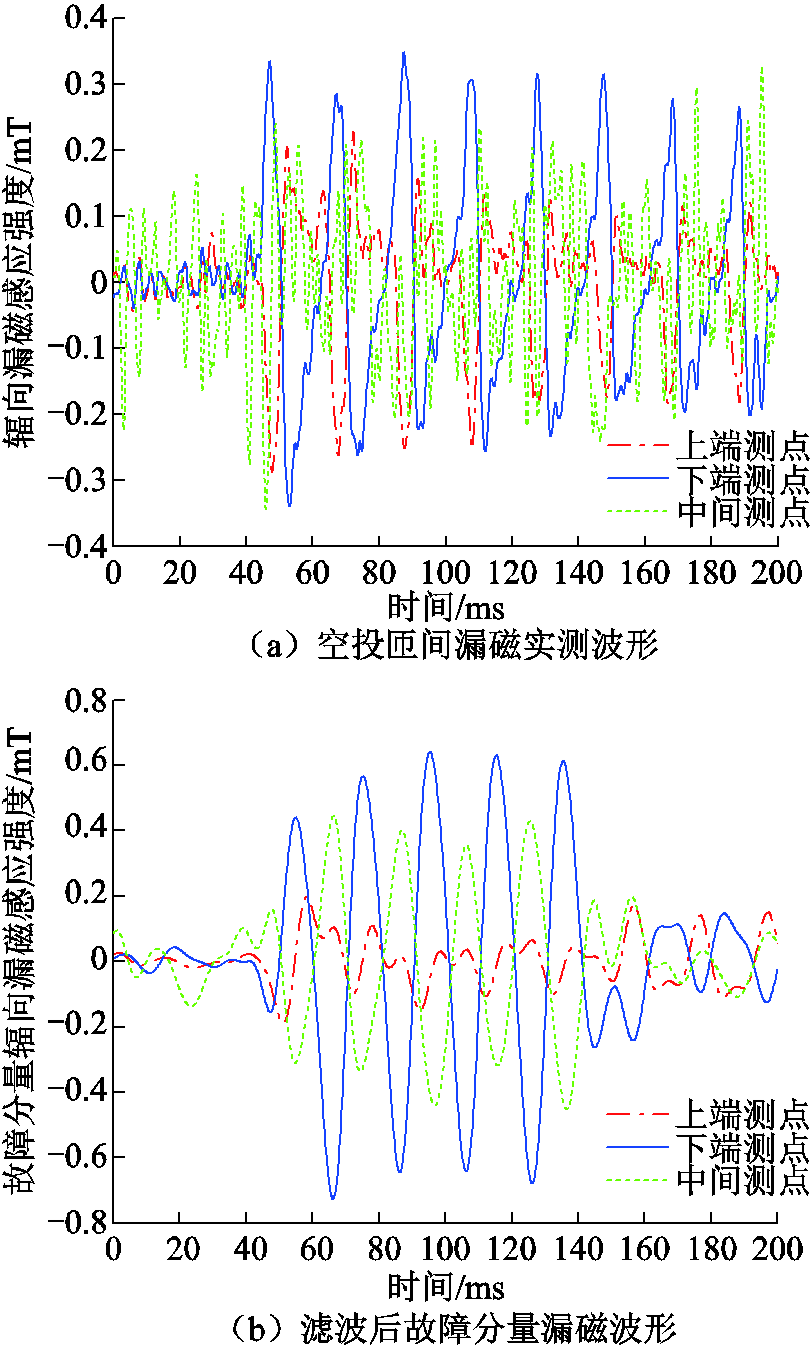
图18 空投匝间实测采样和滤波处理后的波形
Fig.18 The waveforms after the measured sampling and filtering of the inter-turn short circuit fault by energizing no-load
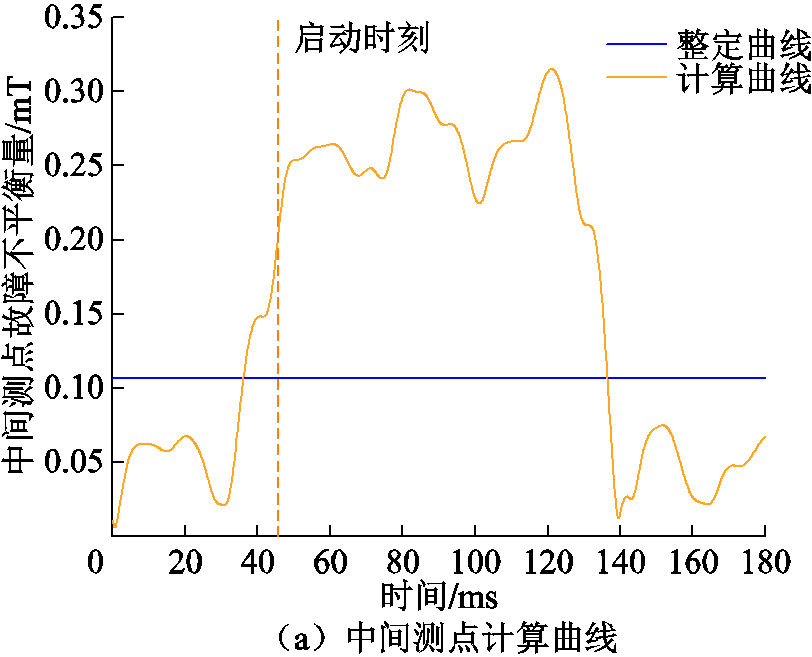
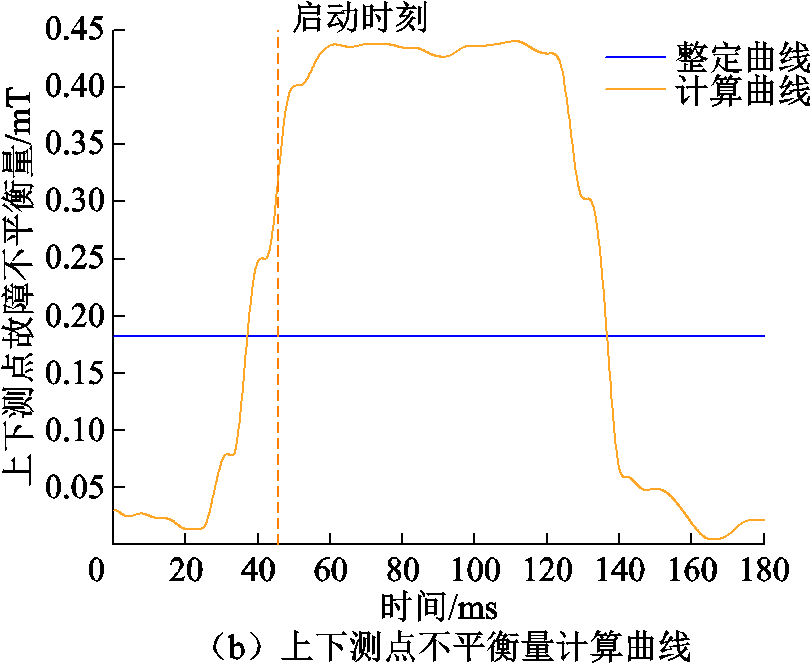
图19 空投匝间磁平衡保护检验曲线
Fig.19 Verification curves of inter-turn short circuit fault by energizing no-load of magnetic balance protection
3.3.3 带载匝间故障
本文选取了包含10个周波采样的故障数据，在满足辐向漏磁故障分量启动Bset3的条件后，经过计算上、下测点不平衡量和中间测点不平衡量均大于门槛值，保护动作，具体动模实验中不同工况下保护的比较数据见表1。
表1 不同工况下磁平衡保护的比较
Tab.1 Comparison of magnetic balance protection under different working conditions
工况类型磁平衡保护/mT动作情况 空载合闸0.0440.048不动作 空投匝间故障0.3230.20220 ms动作 带载匝间故障0.3900.18220 ms动作
本文通过动模实验，验证了在变压器不同工况下所提出基于故障分量的磁平衡保护的有效性。不仅能检测出轻微的匝间短路情况，而且能够躲避励磁涌流影响，保护能够迅速出口。
3.4.1 磁平衡保护对绕组变形的优越性验证
参数辨识法是指通过建立变压器稳态和暂态模型来辨识出绕组漏电感、励磁电感等参数，并依此判断绕组是否发生变形。在建立参数辨识方程时假定三相绕组电阻和漏电感相等，便于消去励磁支路建立线性辨识方程。在变压器空载合闸导致的极端涌流场景下，由于消去了励磁绕组的影响，无法利用励磁支路信息，同时绕组电流很大使得辨识方程误差很大，参数计算产生较大误差。但是磁平衡保护可以利用光纤传感器实时监测绕组辐向漏磁场的变化，利用构建的保护逻辑进行发信，及早实现变压器的检修，保证其安全运行。表2为心式变压器绕组变形的仿真数据。
表2 心式变压器不同位置绕组变形仿真验证
Tab.2 Simulation verification of winding deformation in different positions of core transformer （单位：mT）
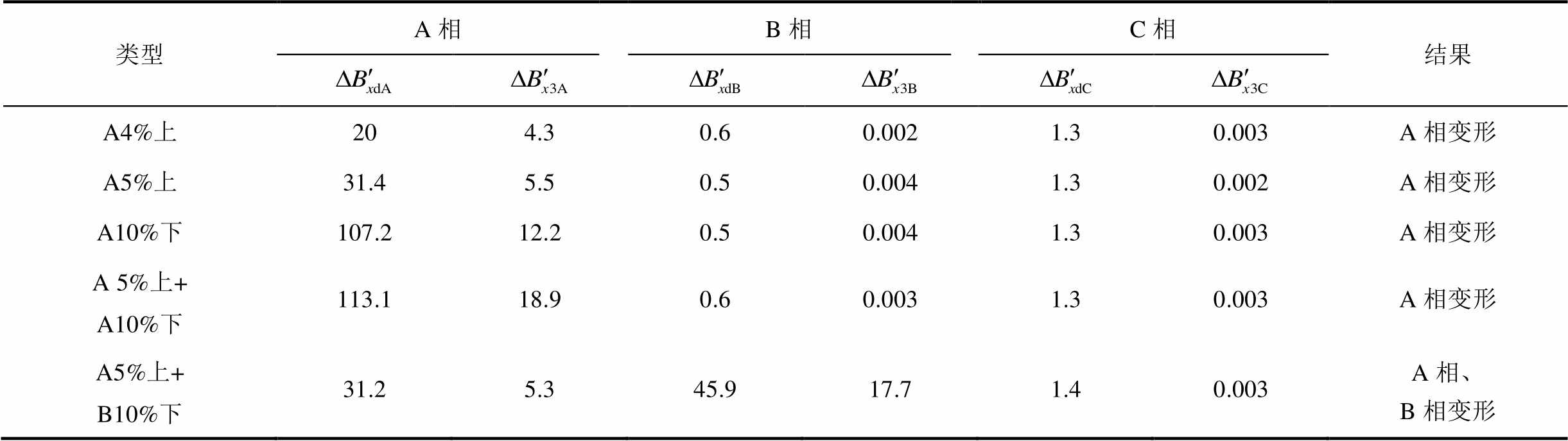
类型A相B相C相结果 A4%上204.30.60.0021.30.003A相变形 A5%上31.45.50.50.0041.30.002A相变形 A10%下107.212.20.50.0041.30.003A相变形 A 5%上+A10%下113.118.90.60.0031.30.003A相变形 A5%上+B10%下31.25.345.917.71.40.003A相、 B相变形
由表2可知，磁平衡保护可以有效地检测出5%以上的绕组变形，同时可以确认出绕组变形的故障相，提高了检修效率。
3.4.2 磁平衡保护对匝间短路的优越性验证
如果整层绕组短路，整层绕组电流密度均匀，测点处漏磁场仍然对称，本文中早期故障判据不动作。传统降压变压器低压绕组一般绕1～3层，因其线径粗，层数不宜太多，高压绕组电压较高所以绕组较多，一般要超过2层，有时甚至达到4～5层。以5层来说，整个层间短路可导致20%匝间故障，传统的差动保护可识别2%以上的匝间故障，此时端口电流变化已经很明显，由传统的差动保护动作。本文方法着眼于研究变压器早期故障的保护，可以与传统差动保护形成互补，提高变压器运行的安全性。
1）动模实验比较
根据变压器保护整定原则，差动保护整定值为7.37 A。空投于变压器发生1.38%匝间短路时，传统差动保护不会启动，而本文方法均可启动，具体可见表3。
表3 不同负载下发生1.38%匝间短路动模实验比较
Tab.3 Comparison of 1.38% inter-turn short circuit between the two methods under different loads
类型磁平衡保护/mT传统差动保护/A 结果结果 空载0.332 50.193 8动作5.04不动作 轻载0.401 50.162 3动作4.93不动作 带电阻负载0.381 30.170 4动作4.94不动作 带阻感负载0.239 20.239 2动作4.8不动作
由表3可知，在变压器发生1.38%匝间故障时，传统保护处于保护死区，无法动作，而本文方法均能使得保护动作，灵敏度更高。
差动保护在轻微匝间故障判别时会受到励磁涌流的影响，特别是变压器发生空投匝间故障时，保护会受2次谐波闭锁影响延迟动作，甚至拒动，具体分析如下。图20为空投匝间故障的差动电流波形。在匝间短路时，差动保护应该动作。但是由于此时处于空载合闸期间，二次谐波制动使得保护动作闭锁，具体谐波占比如图21所示，此时保护一直闭锁，根据单相制动三相的原则，在延时500 ms后，退出保护。
综上所述，本文方法相比于传统方法具有更快的速动性和更高灵敏性。
2）仿真分析比较
由于实际动模匝间故障设置存在物理限制，因此通过动模变压器仿真模型模拟更多的轻微匝间短路情况，并比较本文方法的优越性。
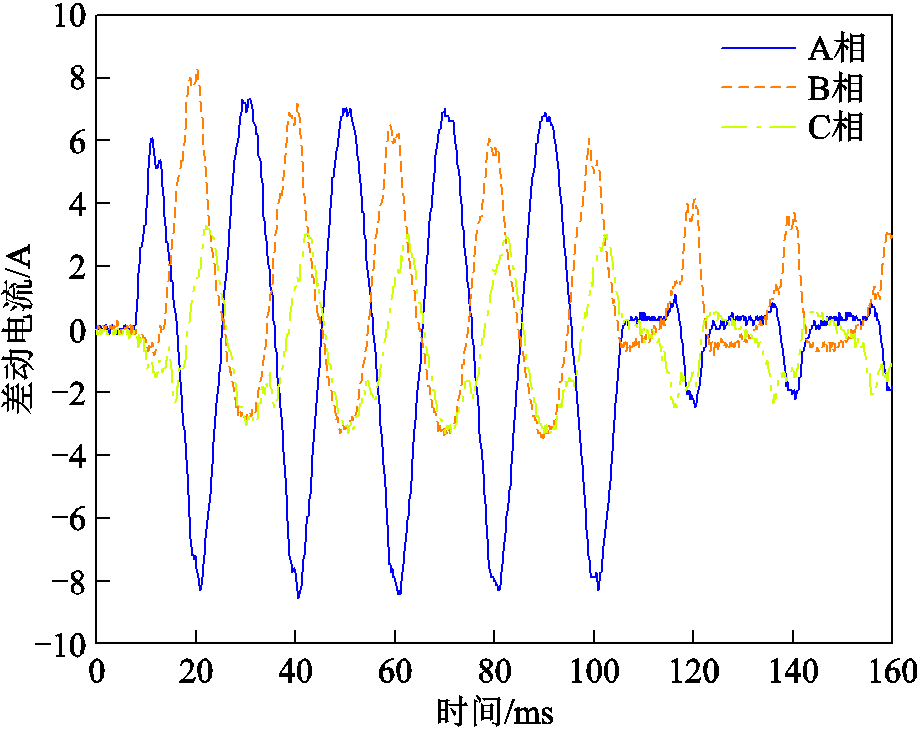
图20 空投匝间短路的差动电流波形
Fig.20 Differential current waveforms of airdrop inter-turn short circuit
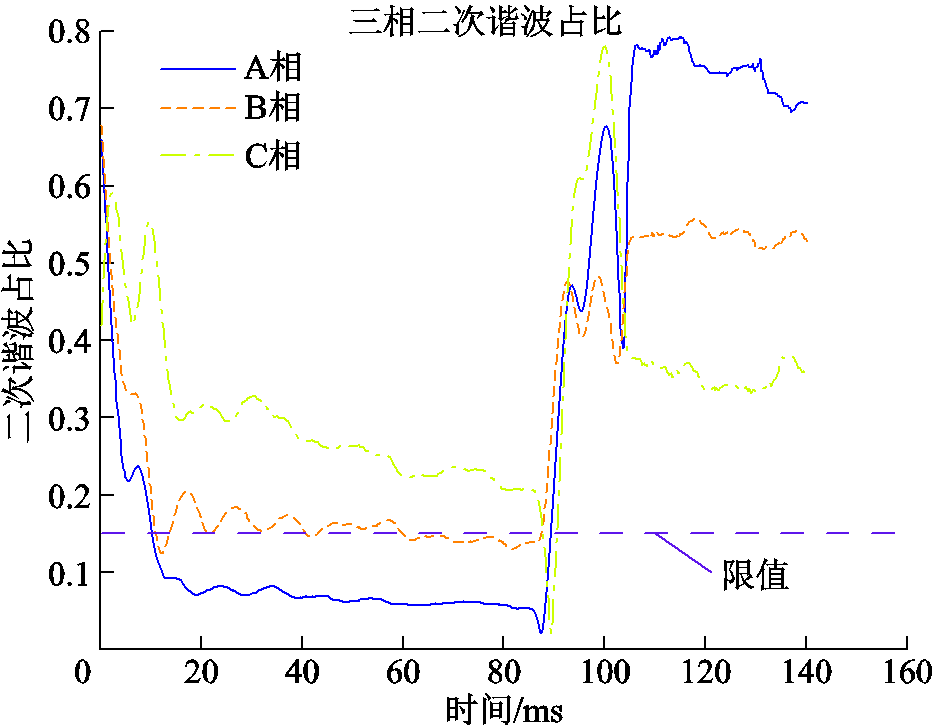
图21 空投匝间短路三相差流二次谐波占比
Fig.21 Second harmonic ratio of airdrop inter-turn short-circuit of three-phase difference flow
以仿真模型空载下的匝间短路为例，由于空载电流极小，可认为其为0，那么匝间短路下差动电流可认为是完全的差动量。具体如图22所示。
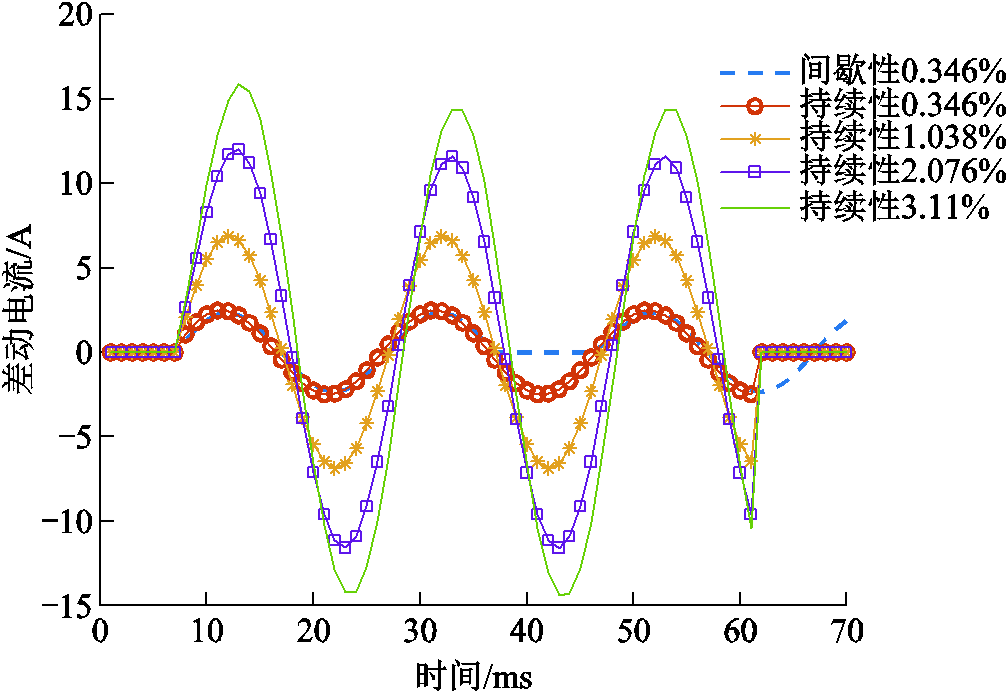
图22 空载下不同匝数匝间短路差动电流波形
Fig.22 Differential short-circuit current waveforms between turns with different turns under no-load
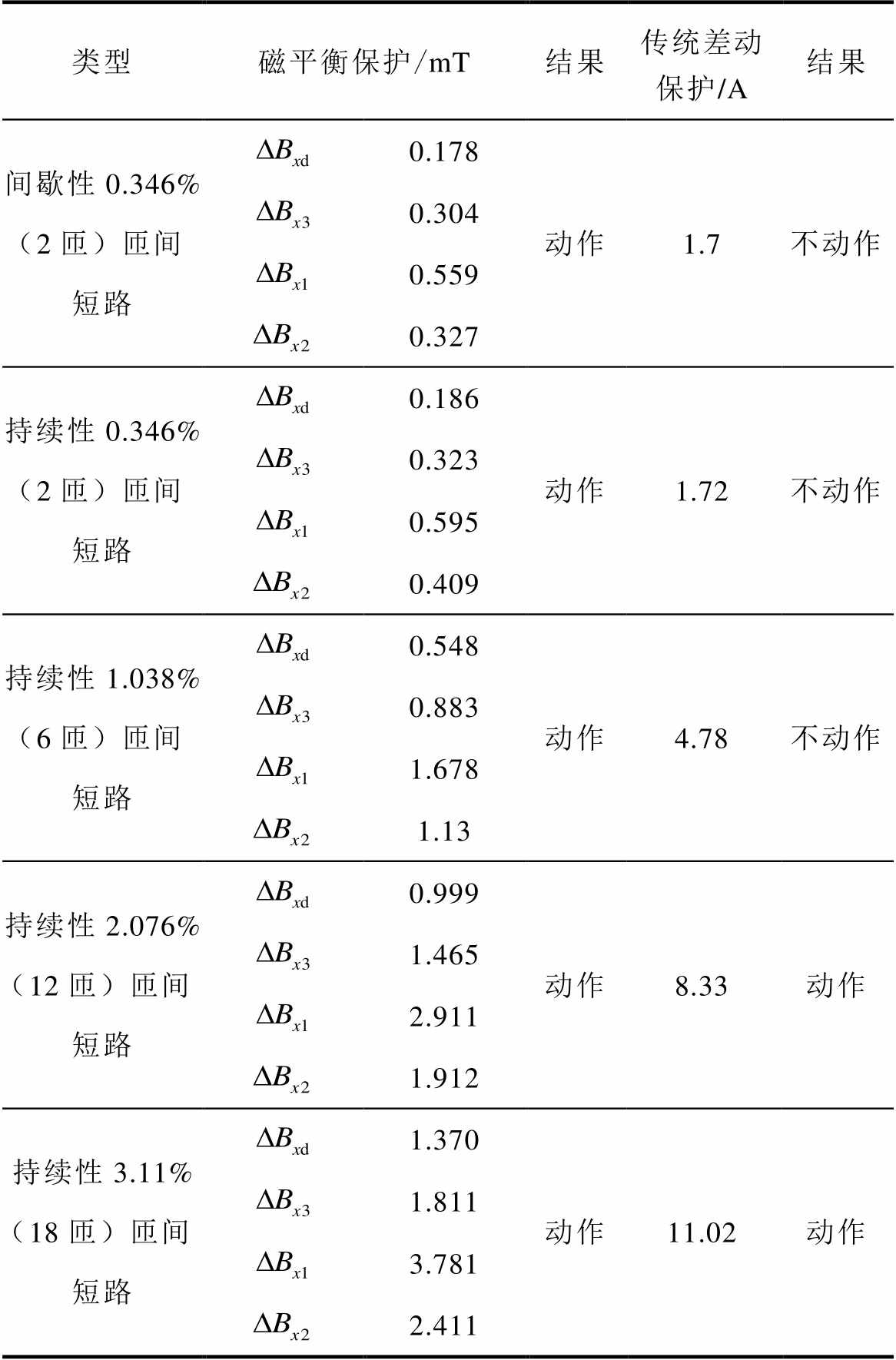
不同短路匝数下工频变化量磁平衡保护与传统差动保护仿真数据比较见表4。
表4 磁平衡保护与传统差动保护仿真数据比较
Tab.4 Simulation data comparison of magnetic balance protection with traditional differential protection
类型磁平衡保护/mT结果传统差动保护/A结果 间歇性0.346%（2匝）匝间短路0.178动作1.7不动作 0.304 0.559 0.327 持续性0.346%（2匝）匝间短路0.186动作1.72不动作 0.323 0.595 0.409 持续性1.038%（6匝）匝间短路0.548动作4.78不动作 0.883 1.678 1.13 持续性2.076%（12匝）匝间短路0.999动作8.33动作 1.465 2.911 1.912 持续性3.11%（18匝）匝间短路1.370动作11.02动作 1.811 3.781 2.411
从表4可知，差动保护在轻微匝间故障判别的灵敏度不够，而磁平衡保护漏磁特征变化明显，灵敏度高于差动保护。
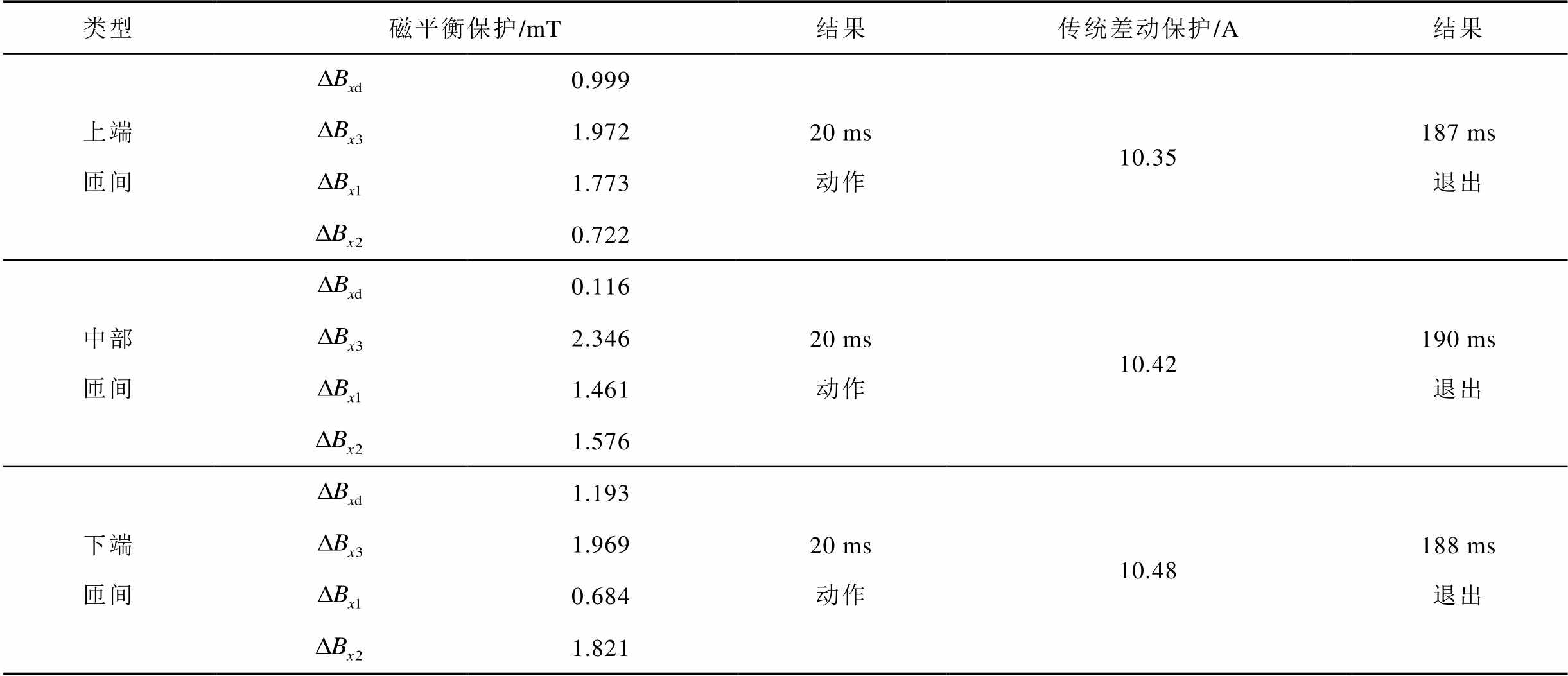
为验证本文方法不受励磁涌流影响，相比于传统保护具有更高的速动性，选择利用仿真模型进行高压绕组不同位置发生3%的空投匝间短路故障来比较两种方法的动作时间，匝间故障时间设置为前200 ms，总仿真时间为400 ms，具体见表5。
由表5可知，当发生两种保护均能启动的空投匝间故障时，由于传统保护受到励磁涌流的影响，在保护启动初期，单相二次谐波占比超过15%，根据实际单相制动三相的原则，传统保护不能快速动作，当匝间故障消失，励磁涌流衰减到动作值以下，保护退出，此时可能已造成变压器绕组损毁。
表5 高压绕组不同位置发生3%的空投匝间仿真数据分析
Tab.5 Simulation data analysis of 3% of the inter-turn short circuit fault by energizing no-load at different locations of high-voltage windings
类型磁平衡保护/mT结果传统差动保护/A结果 上端匝间0.99920 ms动作10.35187 ms退出 1.972 1.773 0.722 中部匝间0.11620 ms动作10.42190 ms退出 2.346 1.461 1.576 下端匝间1.19320 ms动作10.48188 ms退出 1.969 0.684 1.821
3）实验总结
首先通过不同工况下动模实验数据在磁平衡保护中的动作情况，验证了本文方法的保护动作逻辑的正确性。然后通过不同负载下的匝间短路动模实验比较本文方法与传统方法，本文磁平衡保护法具有更高的灵敏度和更少的动作时间。最后通过仿真模型来进行两种方法在不同匝数下的匝间故障比较，得出本文方法不受励磁涌流影响。根据上述仿真与动模实验的相互验证补充，体现出磁平衡保护的优越性。
针对变压器早期故障的保护问题，本文采用变压器漏磁场磁平衡原理，提出了用于检测变压器绕组变形、轻微匝间故障的绕组早期故障的保护原理，得出了以下几点结论：
1）采用空间磁平衡测量的思路，简化了漏磁场的计算模型，利用分离变量解析法建立了绕组变形、匝间故障漏磁计算模型，用于保护的整定和分析。
2）提出了基于每个绕组3个测量点的变压器绕组变形、轻微匝间故障的磁平衡保护逻辑及整定和校验方法。
3）分别建立了心式变压器、动模实验变压器仿真模型并搭建了动模实验系统，对本文提出的磁平衡保护进行了仿真和动模实验验证，实验证实磁平衡保护能够检测出5%以上的绕组变形和1%以下的匝间短路。
附 录
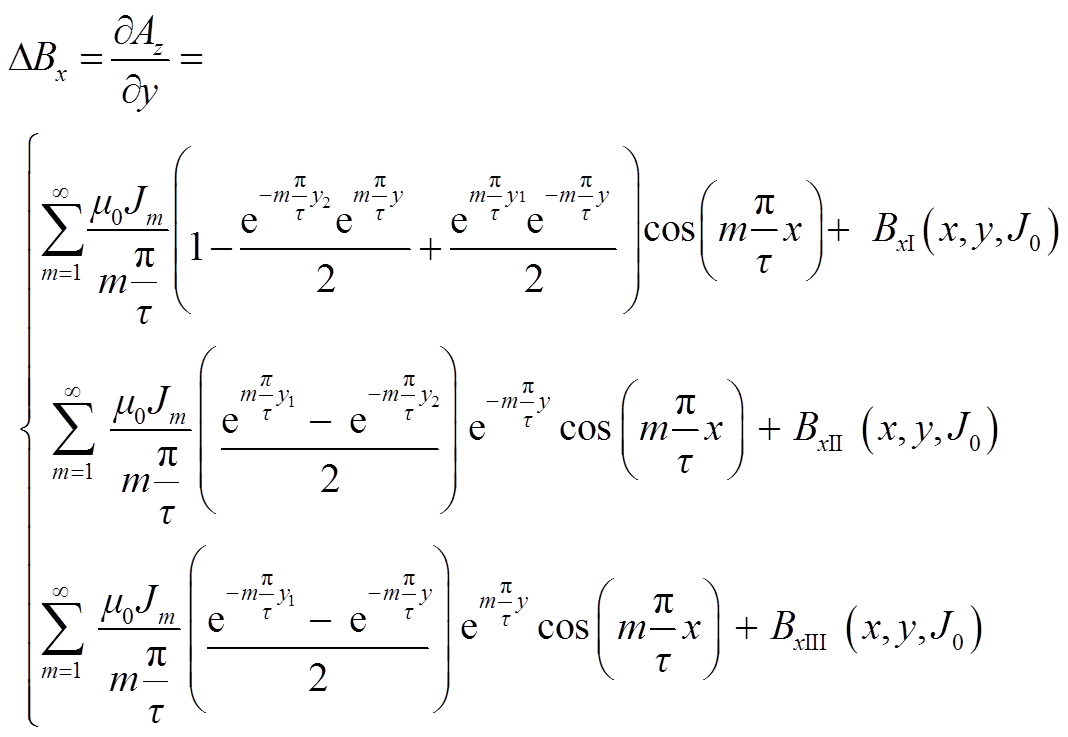（A1）
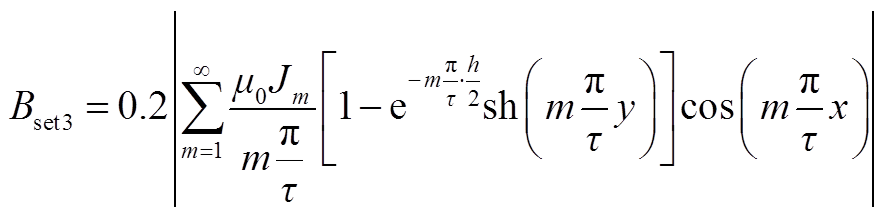（A2）
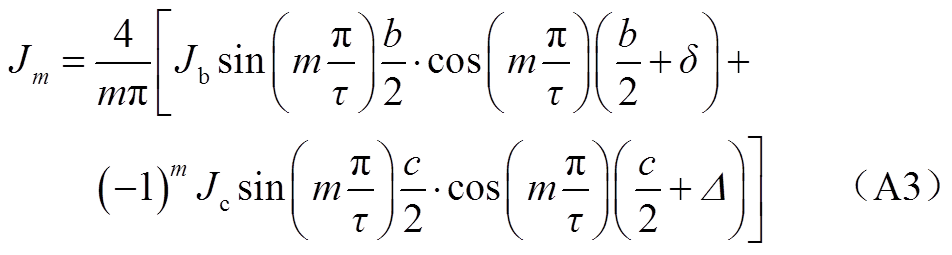
式中，t为极距，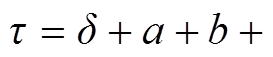
。
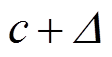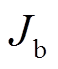和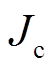
分别为一次绕组和二次绕组的电流密度。
附表1 心式变压器的电气参数
App.Tab.1 Electrical parameters of core transformer
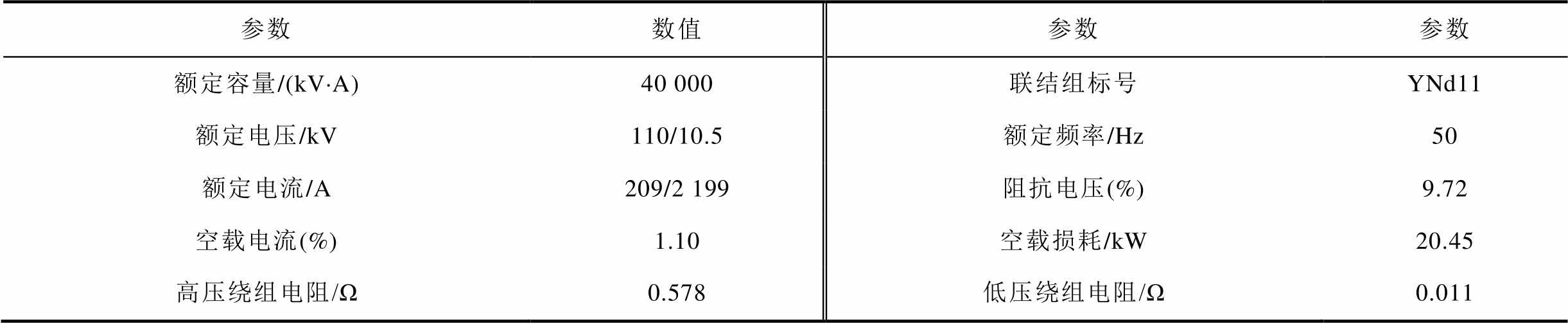
参数数值参数参数 额定容量/(kV×A)40 000联结组标号YNd11 额定电压/kV110/10.5额定频率/Hz50 额定电流/A209/2 199阻抗电压(%)9.72 空载电流(%)1.10空载损耗/kW20.45 高压绕组电阻/Ω0.578低压绕组电阻/Ω0.011
附图1 心式变压器仿真模型
App.Fig.1 Simulation model of core transformer
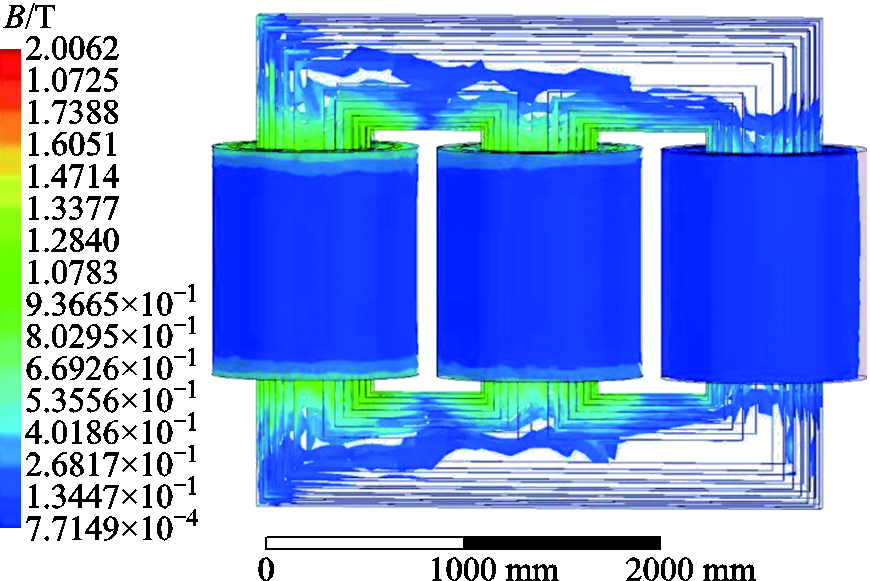
附图2 心式变压器漏磁云图
App.Fig.2 Magnetic leakage cloud map of core transformer
附图3 动模变压器仿真模型
App.Fig.3 Simulation model of dynamic mode transformer
附图4 动模变压器漏磁云图
App.Fig.4 Magnetic leakage cloud map of dynamic mode transformer
参考文献
[1] 钱国超, 王丰华, 王劭菁, 等. 大型变压器绕组振动频响特性的试验研究[J]. 高电压技术, 2018, 44(3): 821-826.
Qian Guochao, Wang Fenghua, Wang Shaojing, et al. Experimental research of vibration frequency response features of transformer winding[J]. High Voltage Engineering, 2018, 44(3): 821-826.
[2] 邓祥力, 谢海远, 熊小伏, 等. 基于支持向量机和有限元分析的变压器绕组变形分类方法[J]. 中国电机工程学报, 2015, 35(22): 5778-5786.
Deng Xiangli, XieHaiyuan, XiongXiaofu, et al. Classification method of transformer winding deformation based on SVM and finite element analysis[J]. Proceedings of the CSEE, 2015, 35(22): 5778-5786.
[3] 唐治平, 彭敏放, 李光明, 等. 基于重复脉冲法的变压器绕组匝间短路故障诊断[J]. 电力自动化设备, 2018, 38(10): 153-158.
Tang Zhiping, Peng Minfang, Li Guangming, et al. Diagnosis of inter-turn short circuit fault of transformer winding based on repetitive surge oscillograph[J]. Electric Power Automation Equipment, 2018, 38(10): 153-158.
[4] 金文龙, 陈建华, 李光范, 等. 全国110 kV及以上等级电力变压器短路损坏事故统计分析[J]. 电网技术, 1999, 23(6): 70-74, 77.
JinWenlong, Chen Jianhua, Li Guangfan, et al. Statistics and analysis on power tranformer damages caused by short circuit fault in 110 kV and higher voltage classes[J]. Power System Technology, 1999, 23(6): 70-74, 77.
[5] 张鹏, 齐波, 李成榕, 等. 电力变压器油中溶解气体特性影响因素的量化分析[J]. 中国电机工程学报, 2021, 41(10): 3620-3631, 3686.
Zhang Peng, Qi Bo, Li Chengrong, et al. Quantitative analysis of influence factors of dissolved gas characteristics in power transformer oil[J]. Proceedings of the CSEE, 2021, 41(10): 3620-3631, 3686.
[6] 郑书生, 陈金祥, 李成榕, 等. 变压器绕组对局部放电特高频定位方法的影响[J]. 高电压技术, 2013, 39(2): 324-329.
Zheng Shusheng, Chen Jinxiang, Li Chengrong, et al. Influence of windings on locating partial discharge in transformers by using ultra-high frequency method[J]. High Voltage Engineering, 2013, 39(2): 324-329.
[7] 索南加乐, 焦在滨, 康小宁, 等. Y/Δ接线变压器漏感参数的识别方法[J]. 中国电机工程学报, 2008, 28(13): 84-90.
SuoNanjiale, Jiao Zaibin, Kang Xiaoning, et al. Algorithm to identify leakage inductances of power transformer with Y-delta connection[J]. Proceedings of the CSEE, 2008, 28(13): 84-90.
[8] Haghjoo F, Mostafaei M, Mohammadi H. A new leakage flux-based technique for turn-to-turn fault protection and faulty region identification in transformers[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 671-679.
[9] Cabanas M F, Melero M G, Pedrayes F, et al. A new online method based on leakage flux analysis for the early detection and location of insulating failures in power transformers: application to remote condition monitoring[J]. IEEE Transactions on Power Delivery, 2007, 22(3): 1591-1602.
[10] Athikessavan S C, Jeyasankar E, Manohar S S, et al. Inter-turn fault detection of dry-type transformers using core-leakage fluxes[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1230-1241.
[11] 潘超, 石文鑫, 孟涛. 单相变压器匝间短路电磁特性研究[J]. 高电压技术, 2020, 46(5): 1839-1856.
Pan Chao, Shi Wenxin, Meng Tao. Study on electromagnetic characteristics of interturn short circuit of single-phase transformer[J]. High Voltage Engineering, 2020, 46(5): 1839-1856.
[12] 刘云鹏, 李欢, 田源, 等. 基于分布式光纤传感的绕组变形程度检测[J]. 电工技术学报, 2021, 36(7): 1347-1355.
Liu Yunpeng, Li Huan, Tian Yuan, et al. Winding deformation detection based on distributed optical fiber sensing[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1347-1355.
[13] 刘云鹏, 李昕烨, 李欢, 等. 内置分布式光纤传感的35 kV油浸式变压器研制[J]. 高电压技术, 2020, 46(6): 1886-1894.
Liu Yunpeng, Li Xinye, Li Huan, et al. Development of 35 kV oil-immersed transformer with built-in distributed optical fiber[J]. High Voltage Engineering, 2020, 46(6): 1886-1894.
[14] 刘云鹏, 王博闻, 李欢,等. 结合载纤绕组形变测量法的大型变压器绕组多次短路冲击暂态声纹特征[J]. 中国电机工程学报, 2022, 42(1): 434-447.
Liu Yunpeng, Wang Bowen, Li Huan, et al. Transient acoustics characteristics of large transformer windings under multiple short-circuit impulse combined with fiber-carrying winding deformation measurement[J]. Proceedings of the CSEE, 2022, 42(1): 434-447.
[15] 郑涛, 树玉增, 董淑惠, 等. 基于漏感变化的变压器式可控高抗匝间保护新原理[J]. 电力系统自动化, 2011, 35(12): 65-69.
Zheng Tao, Shu Yuzeng, Dong Shuhui, et al. Interturn fault protection for transformer type controllable shunt reactor based on leakage inductance change[J]. Automation of Electric Power Systems, 2011, 35(12): 65-69.
[16] 邓祥力, 朱慧, 杨梅, 等. 基于多状态模型的变压器绕组早期故障保护方法研究[J]. 中国电机工程学报, 2022, 42(18): 6704-6715.
Deng Xiangli, Zhu Hui, Yang Mei, et al. Research on early fault protection method of transformer winding based on multi-state model[J]. Proceedings of the CSEE, 2022, 42(18): 6704-6715.
[17] 刘校销, 郑涛, 黄婷. 基于等效漏电感参数辨识的磁控式并联电抗器匝间故障保护方案[J]. 电工技术学报, 2020, 35(1): 134-145.
Liu Xiaoxiao, Zheng Tao, Huang Ting. Protection scheme based on the identification of equivalent leakage inductance against turn-to-turn fault of magnetically controlled shunt reactor[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 134-145.
[18] 邓祥力, 王传启, 张哲. 基于回路平衡方程和励磁电感的特高压变压器保护[J]. 中国电机工程学报, 2012, 32(1): 6, 147-153.
Deng Xiangli, Wang Chuanqi, Zhang Zhe. UHV transformer protection based on equivalent circuit equation and excitation inductance[J]. Proceedings of the CSEE, 2012, 32(1): 6, 147-153.
[19] 李振华, 蒋伟辉, 喻彩云, 等. 基于短路阻抗及DU-I1轨迹特征联合分析的变压器绕组变形故障在线检测方法[J]. 电力自动化设备, 2021, 41(7): 203-209, 217.
Li Zhenhua, Jiang Weihui, Yu Caiyun, et al. Online detection method of transformer winding deformation based on combined analysis of short circuit impedance and DU-I1 locus characteristics[J]. Electric Power Automation Equipment, 2021, 41(7): 203-209, 217.
[20] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.
Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal-fluid model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4483-4491.
[21] 郑玉平, 龚心怡, 潘书燕, 等. 变压器匝间短路故障工况下的漏磁特性分析[J]. 电力系统自动化, 2022, 46(15): 121-127.
Zheng Yuping, Gong Xinyi, Pan Shuyan, et al. Analysis on leakage flux characteristics of turn-to-turn short-circuit fault for power transformer[J]. Automation of Electric Power Systems, 2022, 46(15): 121-127.
[22] 孙佳安, 李琳. 考虑次同步分量下时间周期问题的三维定点有限元法及变压器电磁特性分析[J]. 电工技术学报, 2022, 37(14): 3475-3486.
Sun Jia'an, Li Lin. 3D fixed-point finite element method for time periodic problems with subsyn-chronous components and analysis of transformer electromagnetic characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3475-3486.
[23] Liu Shiming, Zhang Luliang, Fu Chuanshun, et al. A new two-port network model-based pilot protection for AC transmission lines[J]. IEEE Transactions on Power Delivery, 2020, 35(2): 473-482.
[24] Liu Shiming, Wang Bo, Zhao Yongsen, et al. Novel differential protection approach of UHV AC transmission lines based on tellegen’s quasi-power theorem[J]. IEEE Transactions on Power Delivery, 2022, 37(2): 1264-1274.
[25] 汤蕴璆, 梁艳萍. 电机电磁场的分析与计算[M]. 北京: 机械工业出版社, 2010.
Magnetic Balance Protection of Transformers Based on Optical Fiber Leakage Magnetic Field Measurement
Abstract Traditional differential protection has difficulty responding effectively to early faults such as transformer winding deformation and minor inter-turn faults.Early winding faults can be sensitively detected according to the changes of transformer winding leakage field, but analytical methods and online measurement solutions suitable forwinding leakage field analysis of engineering applications are scarce. To address the above problems, this paper proposes a model for calculating the leakage field distribution of transformer windings under the simplified model, and puts forward a corresponding early fault protection scheme based on the magnetic balance principle of transformer leakage field.
Firstly, the faulty winding with uneven current density distribution is divided into unfaulty turn winding and short-circuited turn winding by superposition theorem, and the Fourier series decomposition method is applied to the winding current density by using the mirror image current method and ignoring the effect of the core.For each frequency component, the leakage induction intensity is solved by the separation of variables method.The results of each frequency component are superimposed to obtain the spatial distribution function of the leakage induction intensity.Secondly, since the transformer winding, core and yoke are symmetrical in structure, the leakage field is symmetrically distributed in space. Magneto-optical sensors are set at the upper and lower end points and the middle of the winding, then the principle of magnetic balance protection based on transformer leakage field is proposed.When the transformer is in normal operation, the sum of radial magnetic induction intensity at the upper and lower end points of the winding is 0, and the radial magnetic induction intensity at the middle point is close to 0. If a fault occurs inside the transformer, the symmetry of the leakage magnetic field distribution changes, and a large amount of fault unevenness will appear at the upper and lower measurement points and the middle point, according to which early winding faultscan bedetected.Finally, the correctness of the magnetic balance protection scheme is verified by establishing the core simulation model of Ansys and the dynamic mode combined transformer model, and the advantages of magnetic balance protection under early faults are demonstrated by comparing the traditional differential protection with the method in this paper.
The following conclusions are drawn from the simulations and dynamic mode experiments: (1) Based on three measurement points per winding, the transformer winding magnetic balance protection logic method can respond to the transformer winding early faults sensitively. (2) Magnetic balance protection is able to detect winding deformations above 5% and inter-turn short circuits below 1%. (3) The protection scheme is not affected by changes in load and inrush current.
keywords：Transformer protection, inter-turn short circuit fault, winding deformation, magnetic balance protection
中图分类号：TM41
DOI:10.19595/j.cnki.1000-6753.tces.221959
国家自然科学基金资助项目（51777119）。
收稿日期 2022-10-10
改稿日期 2022-11-17
邓祥力 男，1973年生，副教授，硕士生导师，研究方向电力系统稳定与控制。E-mail：xiangli_deng@163.com
朱宏业 男，1996年生，硕士研究生，研究方向为变压器保护、电力系统继电保护等。E-mail：mmqmail@163.com（通信作者）
（编辑 郭丽军）