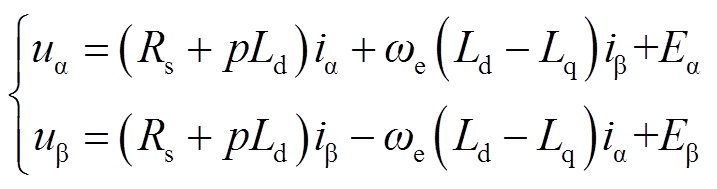 (1)
(1)
摘要 滑模观测器具有响应速度快、鲁棒性强等优点,已广泛应用于表贴式永磁同步电机无位置传感器的中、高速控制系统。然而,具有固定参数的滑模观测器很难在宽速度范围内保持一致的估算精度,而采用基于速度观测器带宽限制的方法进行噪声和扰动抑制会降低电机的动态性能。针对上述问题,该文首先分析滑模观测器估算表贴式永磁同步电机转子位置的误差产生机理,提出一种新型位置误差观测器,主要思想是基于磁链观测进行位置误差连续估算,并采用最速梯度下降法对积分过程进行反馈校正;然后,通过变增益循环迭代优化提高位置误差观测器的速度与准确性;最后搭建表贴式永磁同步电机加载测试平台进行实验,结果验证了所提方法具有位置观测精度高、鲁棒性强的特点。
关键词:表贴式永磁同步电机 变增益最速梯度下降法 滑模观测器 估算位置修正策略
表贴式永磁同步电机(Surface mounted Permanent Magnet Synchronous Motor, SPMSM)具有高效率、高功率密度、宽调速范围等优点,广泛应用于电动汽车、航空航天、伺服驱动等领域。在进行SPMSM磁场定向控制时需要转子位置信息。传统方法通过在电机轴端部安装旋转变压器、光电编码器等传感器进行位置测量,但是位置传感器会导致系统成本的增加和可靠性的降低。因此,SPMSM的无位置传感器控制技术研究具有重要意义[1-3]。PMSM无位置传感器控制技术可以分为两类:一类是高频信号注入法,通过注入高频信号并提取高频响应获取转子位置,适用于零速、低速,如脉振高频注入、正弦高频注入等[4-5];另一类是基于电机数学模型的方法,通过提取反电动势进行转子位置估算,适用于中高转速,如扩展卡尔曼滤波法、滑模观测器(Sliding Mode Observer, SMO)法、模型参考自适应法、非线性观测器法等。其中,滑模观测器法由于具有算法简单、动态响应快、鲁棒性强等优点,得到了广泛应用[6-7]。但采用滑模观测器进行转子位置估算时,由于测量噪声和信号相位延迟等导致估算的转子位置存在偏差,该位置偏差会使得系统动态和静态性能下降[8]。针对上述问题,学者们进行了深入研究,提出的解决方法可以分为两类:一类侧重于提高反电动势观测器的性能;另一类是优化位置与速度的估算方法。
在提高反电动势观测器性能的研究中,文献[9]提出了一种在线参数自适应的离散时间SMO,根据负载转矩和转速自适应地调节饱和函数的边界和观测器增益,实现对扩展反电动势的准确观测。文献[10]提出了一种自适应同步频率观测器,能够在频率变动时自适应地跟踪定子电流,通过定子电流误差收敛保证观测器输出的反电动势平滑。文献[11]将扩展反电势估算值反馈到定子电流观测中,同时采用消除旋转影响的锁相环(Phase Locked Loop, PLL)改善滑模观测器的抖振问题。文献[12]采用串联高阶滑模结构保证输出反电动势的连续光滑,以此削弱SMO中高频切换带来的抖振。这些方法通常需要调整多个参数来设计自适应方案,实际工程应用中调试过程较为复杂。
在优化位置与速度观测方法的研究中,文献[13]通过建立SMO的非线性等效模型来分析和补偿SMO引起的位置估计偏差,并采用前馈锁相环来抑制变速操作下的稳态位置跟踪误差。文献[14]提出通过建立独立位置和速度误差观测器来消除负载干扰的影响,该方法降低了速度和负载转矩瞬变时的位置估计误差。上述两种方法都需要额外的速度观测器,使控制系统变得复杂。此外,在暂态过程中,位置和速度观测器很难同时保证快速收敛。文献[15]提出采用三阶非线性观测器代替正交锁相环,采用非线性反馈机制提高收敛速度,然而该方法需要准确的系统惯性参数,否则会出现明显的位置估算误差。文献[16]提出一种双重锁相环,通过对延迟重构信号与初始估算位置进行二次锁相以补偿位置误差。文献[17]以最小电流为优化目标,调整锁相基准调节补偿角度,这两种方法实现简单且对参数依赖较小,但是在稳态时存在电流抖振。
针对以上方法的局限性,本文首先对环路滤波器、锁相环跟踪滞后等非理想因素所造成的转子位置估算误差进行分析,研究转子位置估算误差补偿方法,建立估算坐标系下SPMSM数学模型;然后提出基于最速梯度下降法的位置误差观测器,并利用变增益循环迭代方法提高观测器的收敛速度与准确性;最后基于一台SPMSM进行实验研究,验证本文所提策略的正确性和有效性。
PMSM在α-β坐标系下的电压方程用反电动势形式可表示为
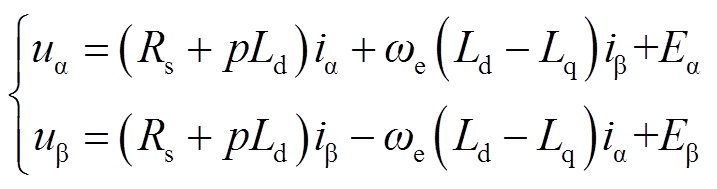 (1)
(1)
式中,uα、uβ,iα、iβ分别为α、β轴定子电压和电流;Rs为定子电阻; Ld、Lq分别为d、q轴电感,在SPMSM中Ld=Lq,后文中二者均用Ls表示;ωe为电机的电角速度;p为微分算子;Eα和Eβ为反电动势,可表示为
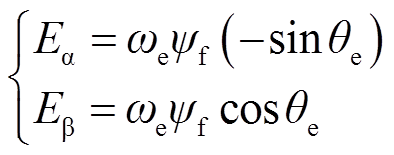 (2)
(2)
式中,θe为转子的电角度;ψf为永磁体磁链。
由于反电动势中包含转子位置信息θe,因此可通过反电动势进行转子位置估算。以电流作为状态变量设计滑模观测器,根据电压方程(1)得到状态方程(3)。
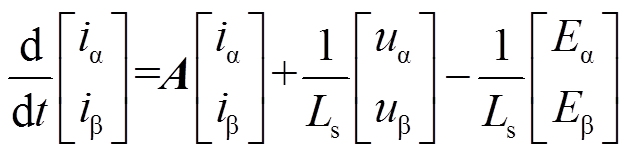 (3)
(3)
式中,A为转移矩阵,有
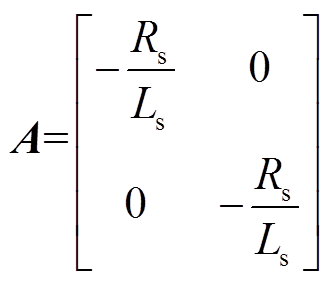 (4)
(4)
基于状态方程(3),设计滑模观测器表达式为
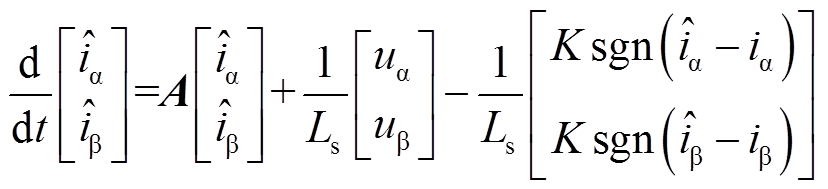 (5)
(5)
式中,上标ˆ表示估算值;K为滑模控制律增益;sgn为符号函数。通过式(3)和式(5),获得电流误差方程为
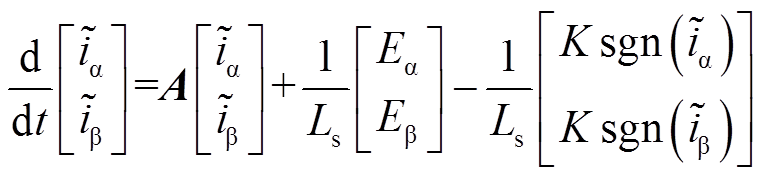 (6)
(6)
式中,上标~表示估算误差;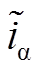 和
和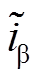 分别为α轴和β轴下的电流估算误差,
分别为α轴和β轴下的电流估算误差,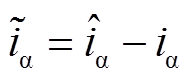 ,
,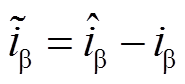 。
。
当观测器的状态变量到达滑模面后,观测器状态将在滑模面附近保持平衡稳定运行。在稳定的滑动模态下,估算反电势的表达式为
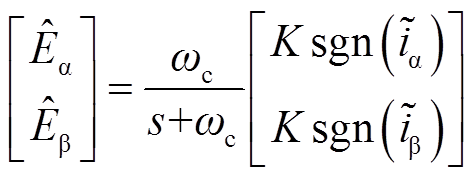 (7)
(7)
式中,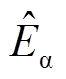 和
和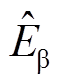 为α-β坐标系下的反电动势估算值;ωc为低通滤波器截止频率;s为拉普拉斯变换算子。
为α-β坐标系下的反电动势估算值;ωc为低通滤波器截止频率;s为拉普拉斯变换算子。
为减小高频抖振现象对估算位置带来的影响,采用锁相环(PLL)提取转子位置。PLL的结构框图如图1所示。
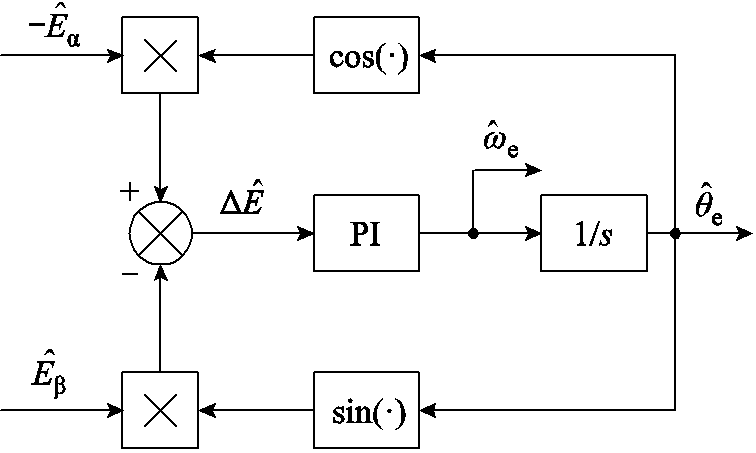
图1 锁相环结构框图
Fig.1 Structure block diagram of PLL
PLL的表达式为
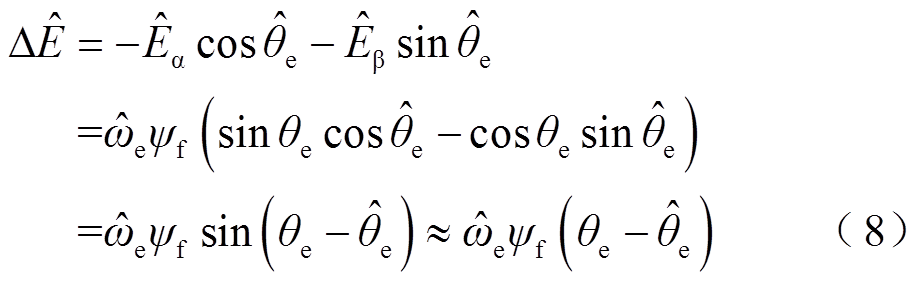
根据式(8),当估算角度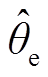 与实际角度
与实际角度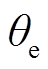 差值较小时,
差值较小时,![]() 近似为估算角度误差的线性函数。将
近似为估算角度误差的线性函数。将![]() 作为输入,利用比例积分(Proportional Integral, PI)进行调节,获得电机的电角速度,通过电角速度积分得到转子位置。
作为输入,利用比例积分(Proportional Integral, PI)进行调节,获得电机的电角速度,通过电角速度积分得到转子位置。
在基于滑模观测器的SPMSM闭环调速系统中,一些非理想因素如低通滤波器引起的相位滞后、环路延迟和锁相环跟踪延迟会影响位置估算精度。以下分别对其进行详细分析。
1)低通滤波带来的相位滞后
滑模观测器估算的反电动势有较大的开关噪声,需要设置低通滤波器进行处理;通过锁相环得到的转速估算值,也需要进行低通滤波。上述滤波器的使用,均会带来估算转速与估算位置的误差,虽然能够对其进行相位补偿,但系统变化时很难计算精确的补偿值,这种影响在电机高速运行时尤为明显。
2)环路延迟
在数字控制系统中,需要在一个周期内完成电流采样、滑模观测器及矢量控制运算,并更新下一周期的脉宽调制(Pulse Width Modulation, PWM)输出占空比,其处理时序如图2所示。
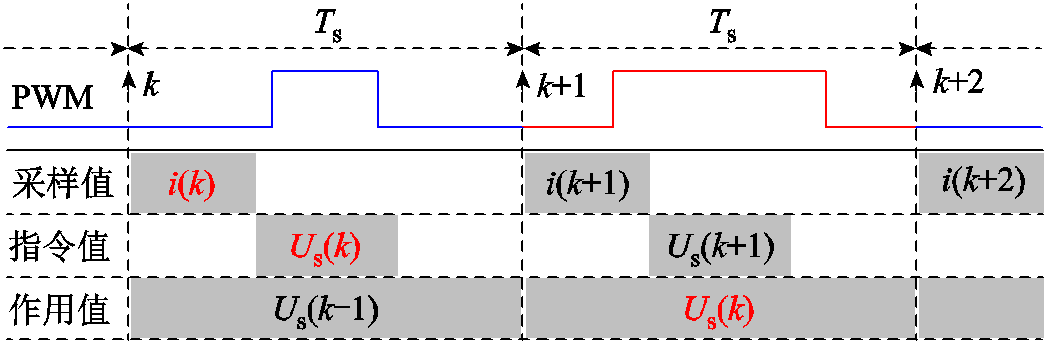
图2 数字采样、运算及更新PWM时序
Fig.2 Timing chart of digital sampling, operation and updating PWM
图2中,信号采样与控制指令存在时序限制要求,本周期的控制指令需要在下一周期执行并进行采样。在该过程中,控制信号在印制电路板线路和电气隔离芯片上传输时存在的信号延迟、功率器件存在的开通关断过程、电流采样时传感器上升下降时间、采样信号低通滤波相位延迟等都会造成控制环路的延迟。由于控制环路的复杂性,难以实时准确计算出环路延迟造成的位置估算误差。在高速运行时,载波比较低,环路延迟将进一步增大位置估算误差。
3)锁相环跟踪过程
由于锁相环的PI调节器具有低通滤波属性,导致电机在动态运行过程中会产生时滞效应,如图3所示。因此在动态运行过程中会产生不可避免的估算转速跟踪及收敛过程,这会导致估算转子位置偏差增大。
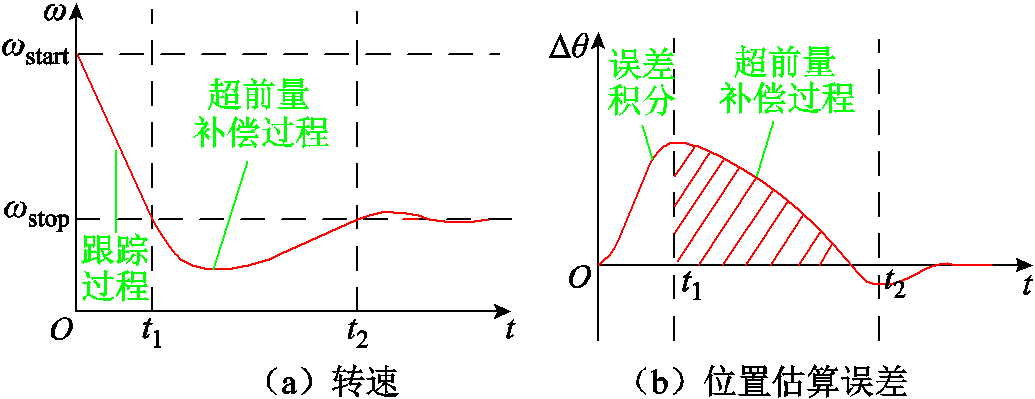
图3 锁相环跟踪过程
Fig.3 Tracking process of phase-locked loop
在SPMSM无位置传感器控制系统中,实际转子位置和滑模观测器估算转子位置空间关系如图4所示,图中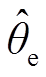 表示估算的转子位置,θerr表示实际位置和估算位置间的误差,沿
表示估算的转子位置,θerr表示实际位置和估算位置间的误差,沿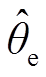 方向定义γ-δ坐标系。当低通滤波器的截止频率足够高时,可以近似忽略低通滤波器的收敛过程,并且基于前述优化后的锁相环结构,γ-δ坐标系的旋转角速度
方向定义γ-δ坐标系。当低通滤波器的截止频率足够高时,可以近似忽略低通滤波器的收敛过程,并且基于前述优化后的锁相环结构,γ-δ坐标系的旋转角速度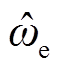 与电机的电角速度ωe一致。在图4中,实际转子位置θe由两个部分组成:估算位置
与电机的电角速度ωe一致。在图4中,实际转子位置θe由两个部分组成:估算位置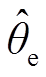 和位置误差θerr。估算位置
和位置误差θerr。估算位置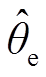 由滑模观测器进行估算。如果能估算位置误差θerr并对SMO的观测角度进行补偿,就能实现准确的转子位置估算。
由滑模观测器进行估算。如果能估算位置误差θerr并对SMO的观测角度进行补偿,就能实现准确的转子位置估算。
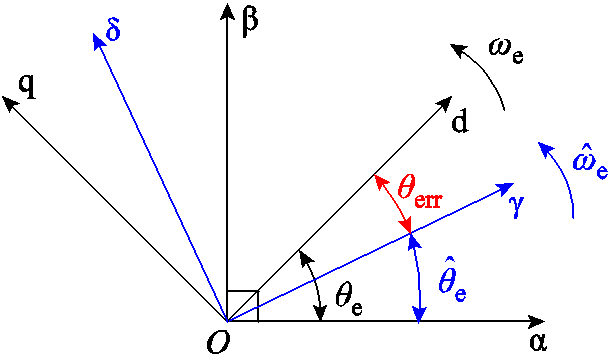
图4 实际位置与估算位置空间关系
Fig.4 Spatial relationship between actual location and estimated location
在Park变换中采用估算位置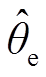 作为转子位置角进行坐标变换。由于估算位置
作为转子位置角进行坐标变换。由于估算位置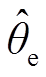 与实际转子位置θe存在角度差,无位置传感器矢量控制实质是在γ-δ坐标系下进行的。首先建立SPMSM在γ-δ坐标系下的数学模型,基于d-q坐标系下SPMSM的电压方程,对位置误差θerr进行Park变换,计算位置误差θerr。
与实际转子位置θe存在角度差,无位置传感器矢量控制实质是在γ-δ坐标系下进行的。首先建立SPMSM在γ-δ坐标系下的数学模型,基于d-q坐标系下SPMSM的电压方程,对位置误差θerr进行Park变换,计算位置误差θerr。
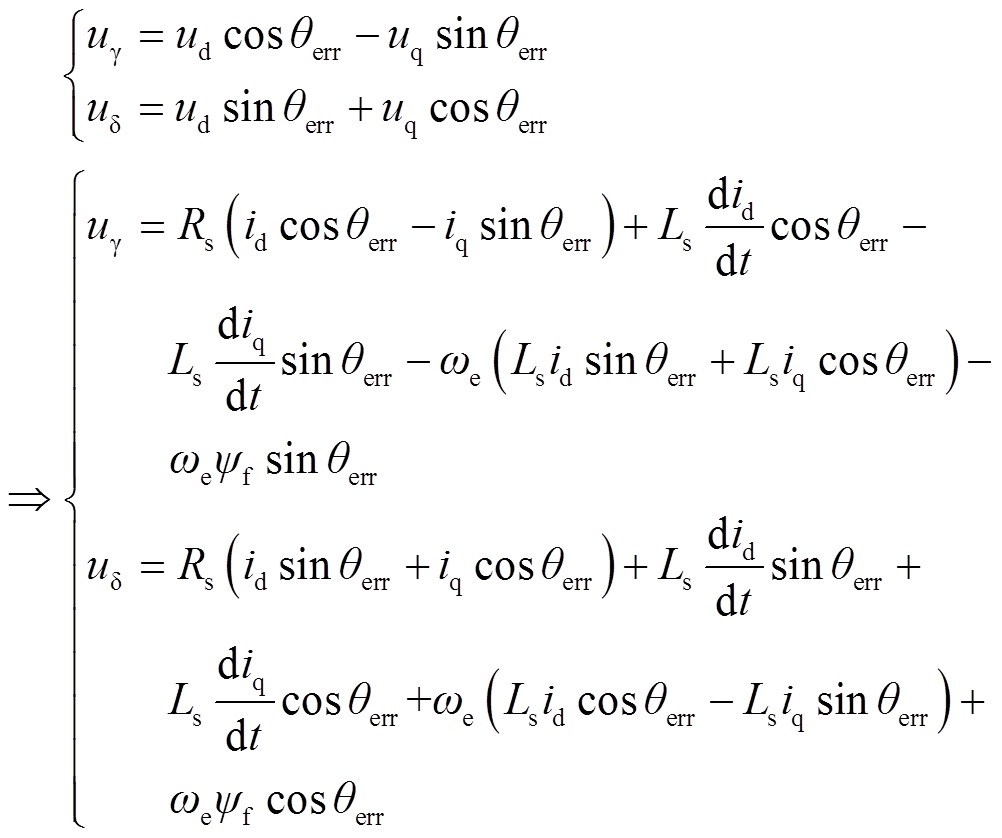 (9)
(9)
式中,uγ、uδ分别为估算坐标系下的γ轴和δ轴电压。
位置误差θerr在电机稳态运行时保持不变,因此θerr为常值,即
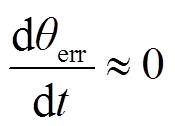 (10)
(10)
结合式(9)与式(10),得到γ-δ坐标系下SPMSM的电压方程为
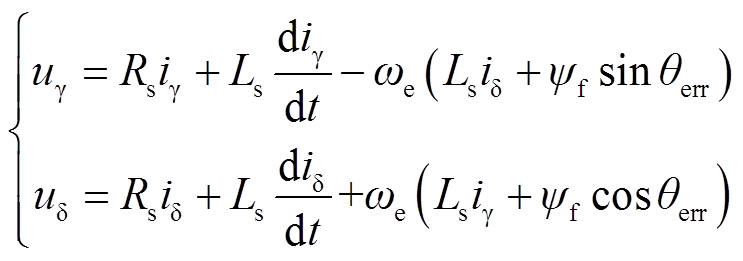 (11)
(11)
式中,iγ、iδ分别为估算坐标系下γ轴和δ轴电流。
为能够准确观测到角度误差并提高位置修正过程对电机参数变化的鲁棒性,本文提出基于磁链观测器进行位置误差连续估算,并采用最速梯度下降法对积分过程进行反馈校正。基于γ-δ轴电压方程(11),定义新的状态变量和输入变量分别为
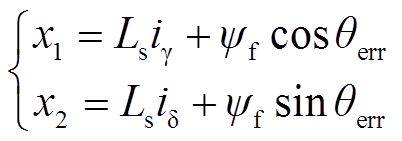 (12)
(12)
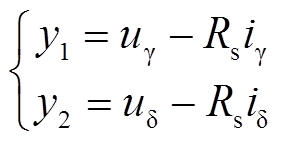 (13)
(13)
式中,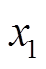 、
、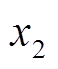 为定义的状态变量,代表γ-δ轴下的电机磁链,该状态变量包含位置估算误差;
为定义的状态变量,代表γ-δ轴下的电机磁链,该状态变量包含位置估算误差;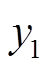 、
、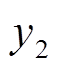 为定义的输入变量。
为定义的输入变量。
对式(12)求导得到
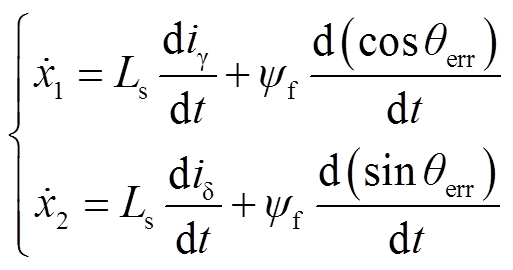 (14)
(14)
根据式(10)、式(11)、式(13),得到
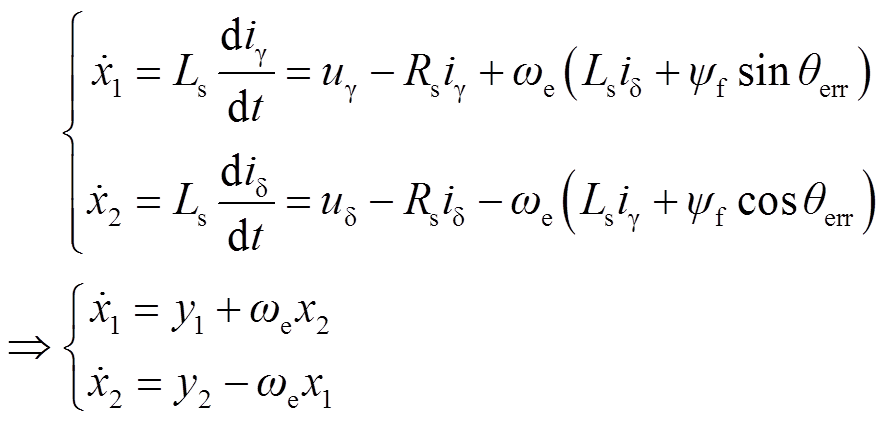 (15)
(15)
为提取状态变量x1、x2中的转子位置信息,定义向量函数η(x),该向量函数是永磁体磁链在γ-δ轴系下的投影。向量模为磁链幅值,向量角为γ-δ轴系与d-q转子坐标系的角度差,即观测角误差。
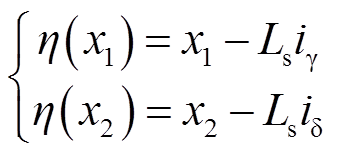 (16)
(16)
对于状态变量x1和x2的估算值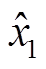 和
和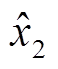 ,有
,有
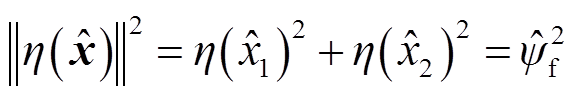 (17)
(17)
式中,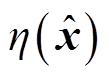 为状态量估算值的向量函数;
为状态量估算值的向量函数;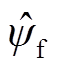 为磁链的估算幅值。
为磁链的估算幅值。
为减小式(15)积分过程中由于初始转子磁链、检测误差等引起的直流偏移和谐波问题,本文基于最速梯度下降法的思想设计位置误差观测器。通过向控制系统损失函数梯度的反方向进行迭代更新,使控制系统达到目标函数的局部极小值。
控制系统损失函数的设计至关重要,目前常用的损失函数有0-1损失函数、绝对值损失函数、平方损失函数和对数损失函数。其中0-1损失函数是一个非凸函数,不适用于梯度下降法;绝对值损失函数收敛速度恒定,在最小值点有振荡;对数损失函数收敛速度快,但计算量较大;平方损失函数的收敛速度较快,在最小值附近不易振荡,计算量适中。因此本系统选择平方损失函数。设计的损失函数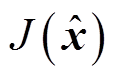 参见式(18)。式中的1/4是为简化计算过程设置的常数项。
参见式(18)。式中的1/4是为简化计算过程设置的常数项。
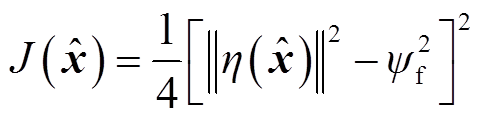 (18)
(18)
设计的位置误差观测器为
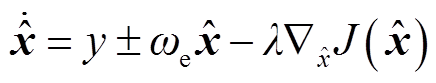 (19)
(19)
损失函数的梯度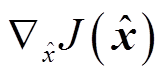 为
为
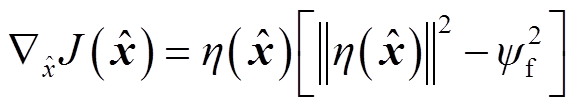 (20)
(20)
因此,位置误差观测器的微分方程为
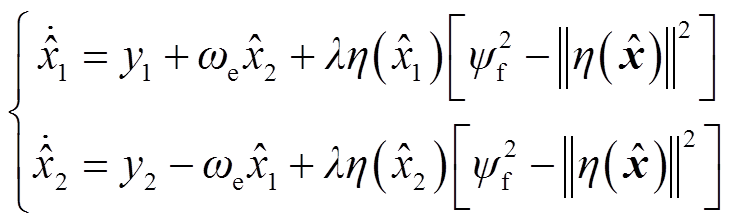 (21)
(21)
式中,λ为观测器增益,用于控制梯度下降过程的整体幅度。
通过估算的状态变量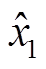 和
和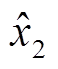 ,利用式(22)重构得到位置误差估算值为
,利用式(22)重构得到位置误差估算值为
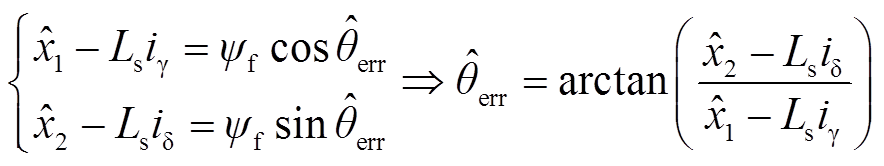 (22)
(22)
在式(22)中通过反正切函数计算位置误差。但工程实践中反正切方法对噪声敏感,而锁相环方法对高频噪声具有抑制作用,因此最终采用锁相环方法进行位置解算。
设计的位置误差观测器总体结构框图如图5所示,将滑模观测器的估算转速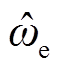 作为位置误差观测器的输入转速。
作为位置误差观测器的输入转速。
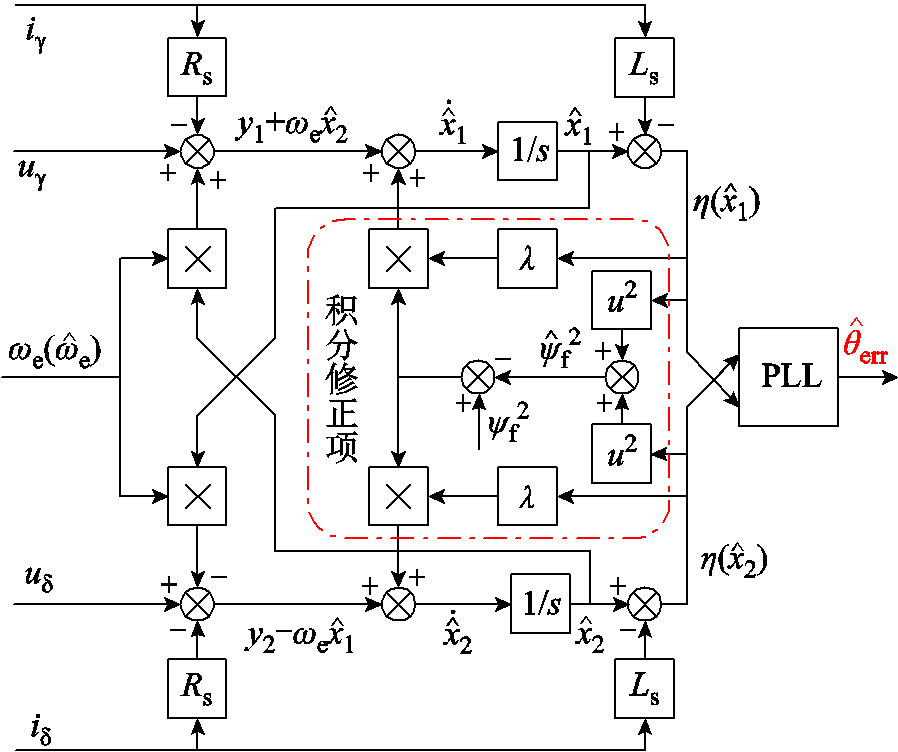
图5 基于梯度下降法的位置误差观测器结构框图
Fig.5 Structural block diagram of position error observer based on gradient descent method
在图5中,位置误差观测器选择较为稳定的转子磁链作为参考值,将磁链估算值作为反馈项,通过梯度下降法对状态方程(15)的积分项进行实时修正,使估算磁链收敛到与实际磁链一致,从而降低误差估算过程中对电阻和电感参数变化的敏感度。
定义观测器误差为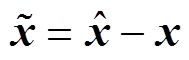 ,根据式(15)~式(21),对观测器误差求导得到
,根据式(15)~式(21),对观测器误差求导得到
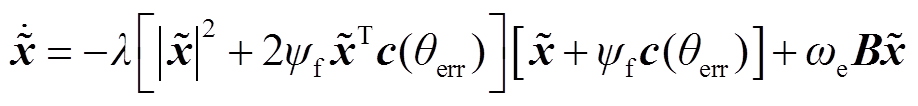 (23)
(23)
其中
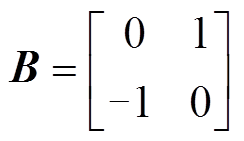
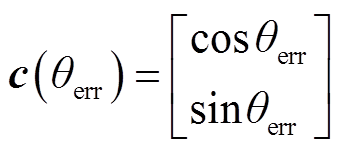
有如下结论:
1)全局渐进稳定性。对于任意速度,存在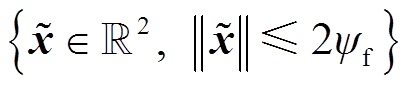 使系统是全局渐进稳定的,式(23)中所有的轨迹都会收敛到该圆。
使系统是全局渐进稳定的,式(23)中所有的轨迹都会收敛到该圆。
2)在任意非零恒定转速下的稳定性。对于任意非零恒定速度满足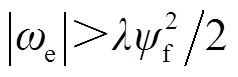 时,系统是全局渐进稳定的。
时,系统是全局渐进稳定的。
证明1:定义观测器状态变量带旋转因子和幅值变化的观测误差的状态变量χ为
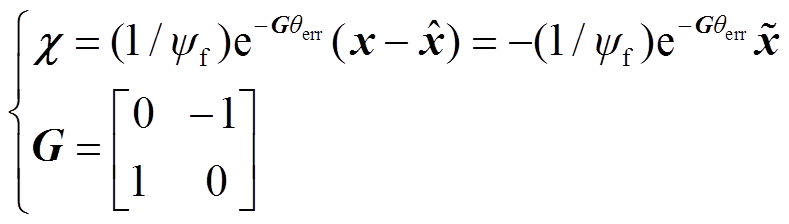 (24)
(24)
对状态变量χ求导得到
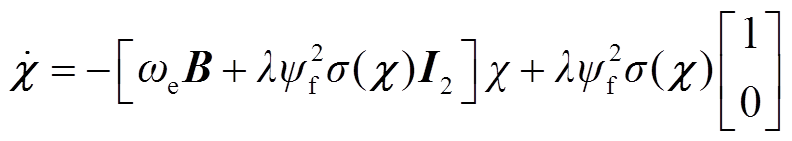 (25)
(25)
式中,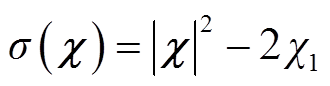 ;I2为二阶单位矩阵。为简化公式,定义新的时间刻度z和速度刻度Ω(z),分别为
;I2为二阶单位矩阵。为简化公式,定义新的时间刻度z和速度刻度Ω(z),分别为
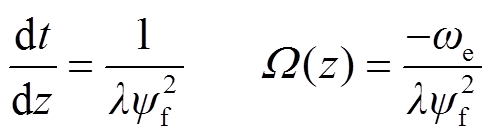 (26)
(26)
式(25)可表示为
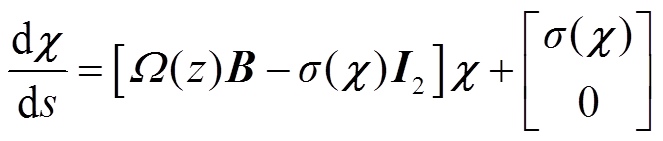 (27)
(27)
根据式(27)可得到新的状态方程式(28)。
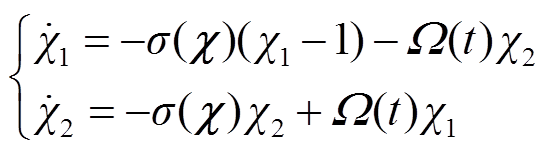 (28)
(28)
定义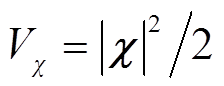 ,并推导
,并推导 的导数为
的导数为
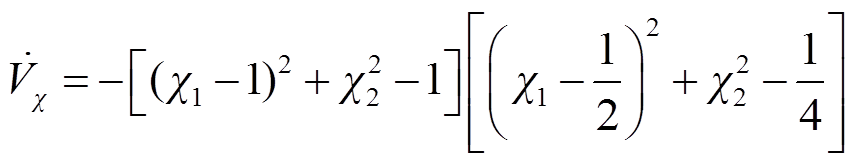 (29)
(29)
由式(29)可知,表达式的前半部分代表半径为1、圆心位置为(1, 0)的一个圆;后半部分代表半径为0.5、圆心位置为(0.5, 0)的一个圆。显而易见,当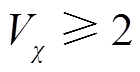 时,两个部分均大于或等于0,此时
时,两个部分均大于或等于0,此时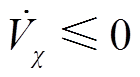 。在该情况下有
。在该情况下有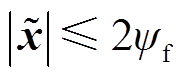 ,满足该条件时,系统是渐进稳定的。
,满足该条件时,系统是渐进稳定的。
证明2:针对式(28)所表示的系统,根据参考文献[18],假设电机转速为定值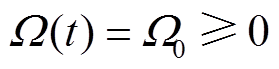 ,如果Ω0>1/2,系统渐进稳定且收敛至(0,0)点。在(0,0)点,根据χ的定义,即系统渐进稳定并收敛到幅值和相位差为零的点。
,如果Ω0>1/2,系统渐进稳定且收敛至(0,0)点。在(0,0)点,根据χ的定义,即系统渐进稳定并收敛到幅值和相位差为零的点。
根据Ω定义,在Ω0>1/2时有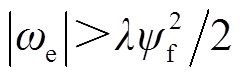 ,即满足该条件时系统渐进稳定。
,即满足该条件时系统渐进稳定。
在SPMSM动态运行过程中,通过梯度下降法对磁链观测误差进行负反馈调节,位置误差观测器只有观测器增益λ一个可调参数。增大观测器增益λ有利于提高收敛速度,但在稳态时电流或电压噪声会造成输出的波动增大;减小观测器增益λ虽可减小稳态时的波动,但会降低收敛速度。
为解决观测器收敛速度与稳态波动间的矛盾,提出基于磁链观测误差幅值自动调整观测器增益λ,并在单个电流环控制周期内多次迭代以加速收敛,称该方法为变增益循环迭代优化。其在单控制周期内的算法执行流程及迭代过程如图6所示。
算法具体计算过程阐述如下:
1)根据本周期iγ、iδ、uγ、uδ,基于上一控制周期中状态变量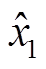 和
和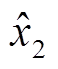 进行磁链估算。对磁链估算值与实际值的平方差取绝对值,当该值超过设定范围
进行磁链估算。对磁链估算值与实际值的平方差取绝对值,当该值超过设定范围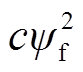 时(其中c为大于零小于1的常数),对差值进行限幅,并调整观测器增益为kλ0(其中k为大于1的常数,λ0为初始设置的观测器增益)。上述λ0、c、k、N需要根据仿真和实验测试择优选取参数值。
时(其中c为大于零小于1的常数),对差值进行限幅,并调整观测器增益为kλ0(其中k为大于1的常数,λ0为初始设置的观测器增益)。上述λ0、c、k、N需要根据仿真和实验测试择优选取参数值。
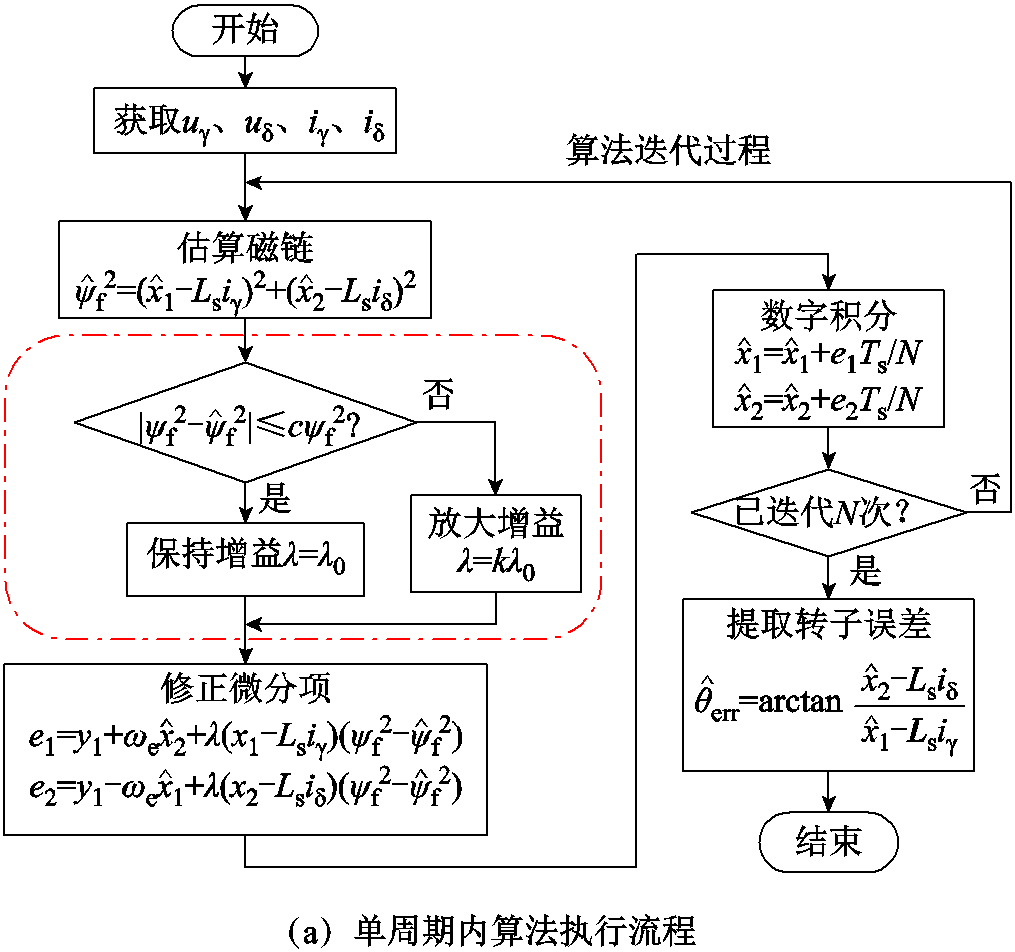
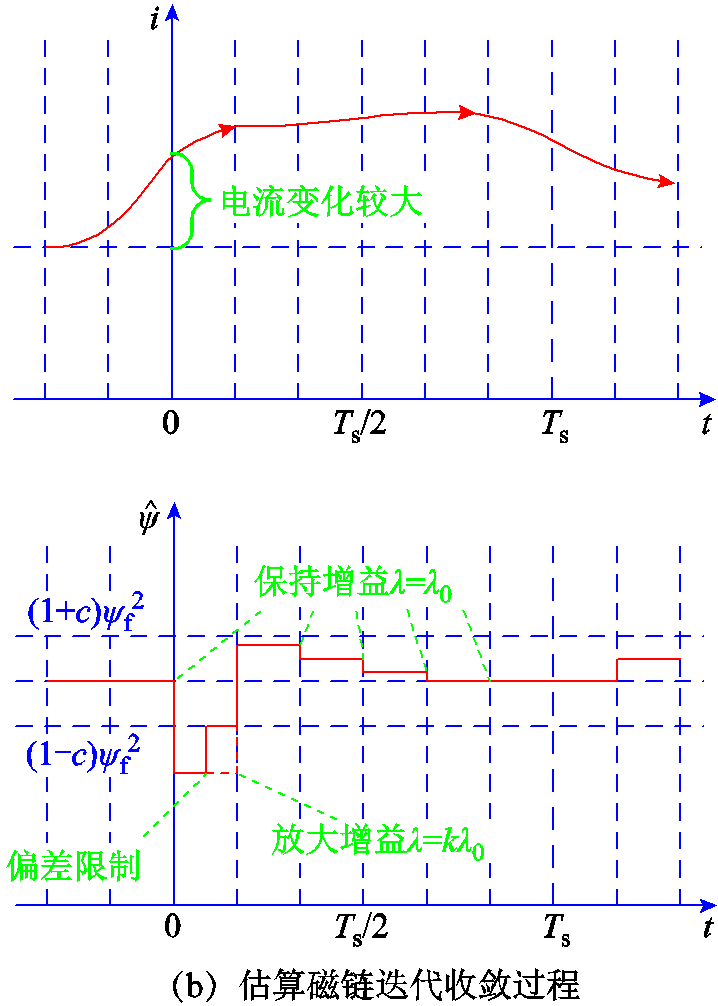
图6 变增益循环迭代优化算法单周期信号处理过程
Fig.6 Single cycle signal processing process of using variable gain cyclic iterative optimization algorithm
2)根据上一步计算的估算磁链和观测器增益,通过状态方程(21)计算状态微分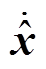 ;然后根据式(30)计算状态变量的单次迭代估算值。
;然后根据式(30)计算状态变量的单次迭代估算值。
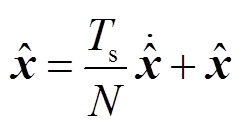 (30)
(30)
式中,Ts为电流环控制周期;N为单个周期内循环迭代次数。
3)重复前两步N次,以加速估算磁链向设定磁链收敛的速度,然后根据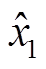 和
和 使用锁相环计算位置误差。
使用锁相环计算位置误差。
基于提出的位置误差观测器对估算位置进行实时连续修正的信号处理过程如图7所示。图7中Park变换是将α-β坐标系下的变量转换到γ-δ坐标系,用于后续位置误差估算。
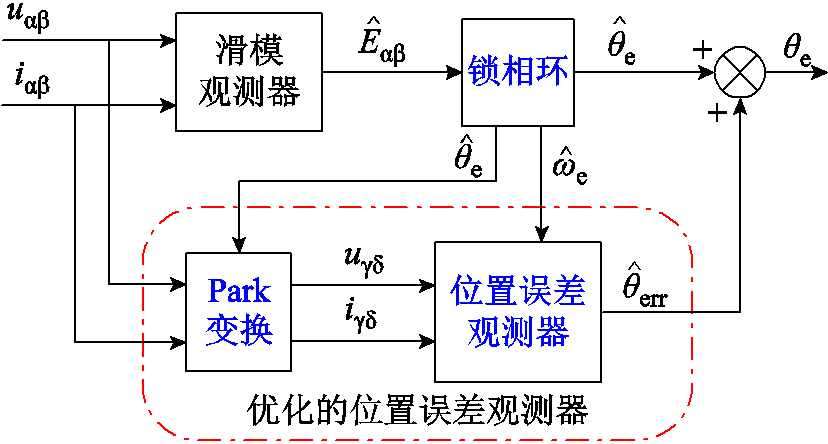
图7 采用估算位置修正策略滑模观测器信号处理过程
Fig.7 Signal processing process of sliding mode observer based on estimated position correction strategy
在重构的γ-δ坐标系下,通过观测器得到位置误差估算值后,用此误差估算值对滑模观测器的输出进行实时连续修正,修正后的估算位置更加准确,将其用于矢量控制能够有效提高系统的动静态性能。
为验证所提出的估算位置修正策略的有效性,以TMS320F2812为主控芯片搭建了SPMSM无位置传感器系统实验平台,如图8所示。

图8 电机控制系统实验平台
Fig.8 Experimental platform of motor control system
图8中,实验用SPMSM的参数见表1。在该电机的轴端安装有旋转变压器,其测得的转子位置数据仅用来与估算的转子位置进行比对;负载为额定扭矩10 N·m的磁粉制动器,转矩传感器为JN338-20 A。驱动器的PWM频率和电流采样频率均为10 kHz,死区时间为3.5 ms。控制板通过RS422和控制器域网总线与上位机进行数据交互。
表1 表贴式永磁同步电机参数
Tab.1 Test SPMSM parameters

参数数值 额定线电压/V220 额定功率/W750 额定转速/(r/min)3 000 相电阻/Ω1.44 直轴电感/mH3.2 交轴电感/mH3.2 磁链/Wb0.097 极对数4 转动惯量/(kg·m2)1.82×10-3
图9给出了负载转矩保持0.5 N∙m,转速由800~3 000 r/min时的实验波形。位置误差观测器的参数设置为:初始增益λ0=1 750,单周期迭代次数N=6,增益变化倍数k=10,误差限幅系数c=0.2。图9中,上图为整个调速过程的转速曲线(蓝色)和修正后的位置误差曲线(红色)。下图为位置误差局部放大图,蓝色曲线是初始估算误差曲线,代表滑模观测器估算位置与旋转变压器测量的转子位置间的误差;棕色曲线是位置补偿值,取值直接为位置误差观测器的输出;红色曲线是位置误差,等于位置补偿值减去初始估算误差,该曲线表征了观测器估算精度。
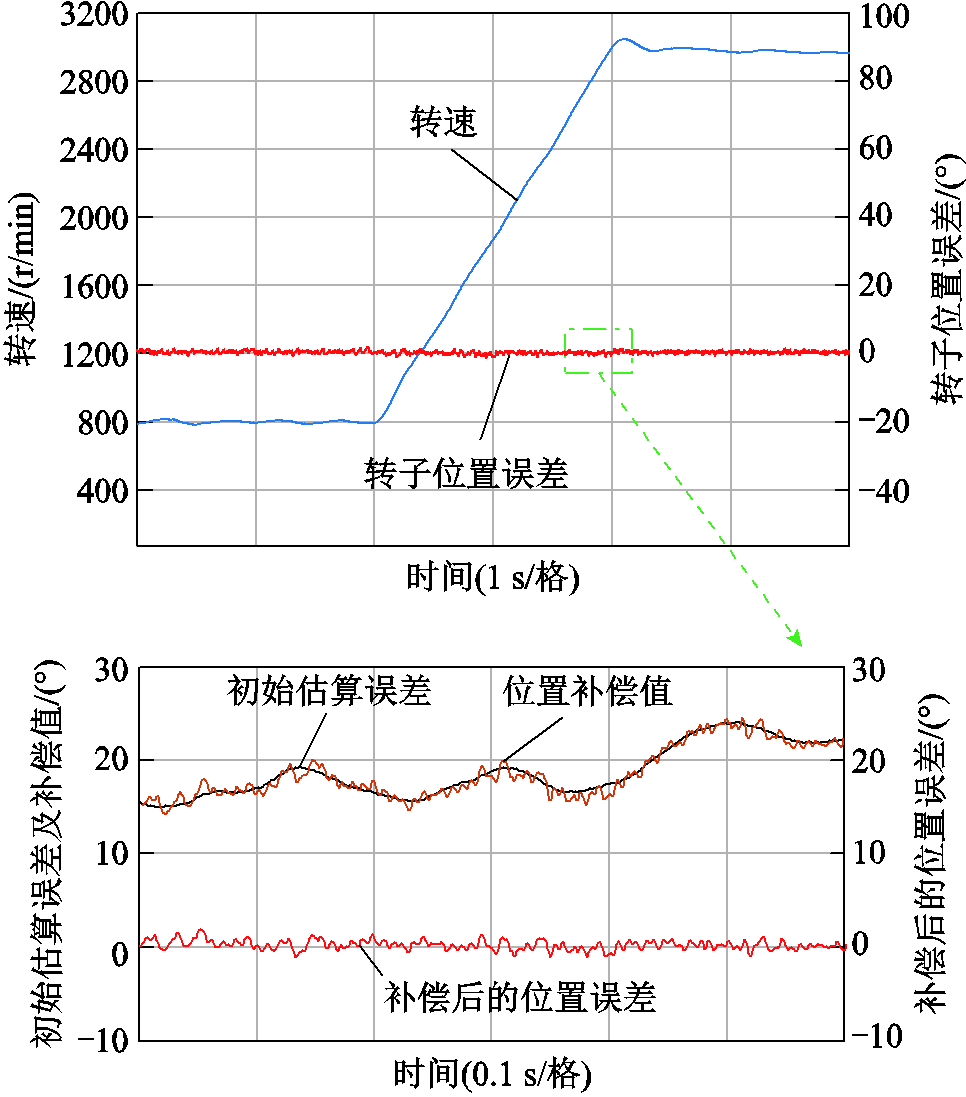
图9 调速过程中使用估算位置修正策略的实验波形
Fig.9 Experimental waveforms of using estimated position correction strategy during speed regulation
由实验波形可知,在运动过程中位置误差观测器能实时跟踪转子位置误差,观测器输出值修正后,转子位置误差最大为2°,运行过程中无明显的振荡现象。
图10给出了电机在3 000 r/min运行时,负载转矩从0.5 N∙m增加至2.4 N∙m时的实验波形。
图10中位置误差是旋变检测位置与采用观测器输出修正后的位置误差。初始估算误差曲线代表滑模观测器估算位置与旋转变压器测量的转子位置间的误差;位置补偿值直接为位置误差观测器的输出;位置误差等于位置补偿值减去初始估算误差,该曲线表征了观测器估算精度。
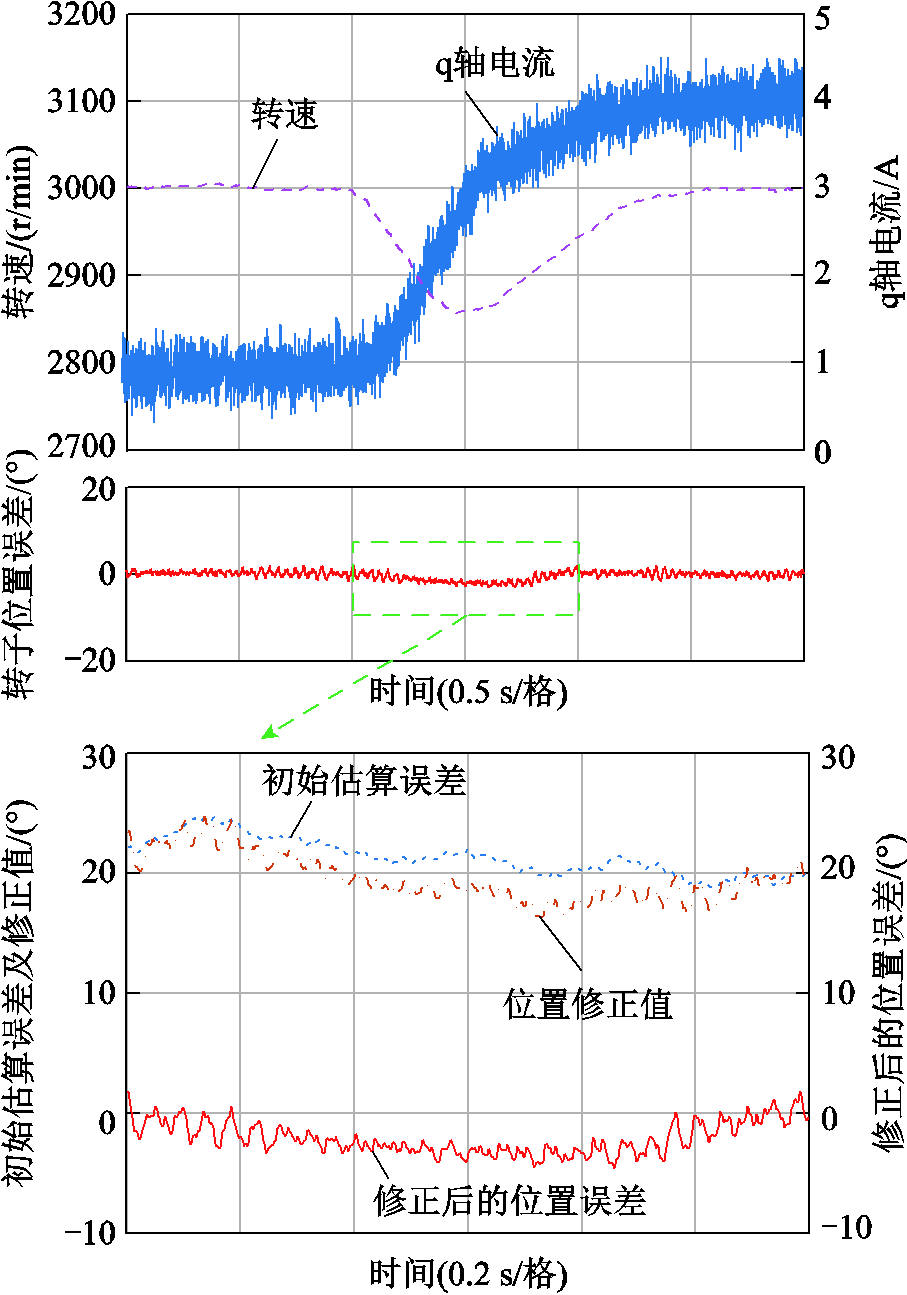
图10 负载变化过程中使用估算位置修正策略的实验波形
Fig.10 Experimental waveforms of using estimated position correction strategy during load changes
由实验波形可知,负载转矩从0.5 N∙m增加至2.4 N∙m时,q轴电流从0.8 A上升至4.0 A,过程中转速有最大140 r/min的转速跌落。位置误差曲线表明,当负载变化较大时,误差跟踪会发生一小段偏移,这主要是由q轴电流的较大变化及转速估算误差所引起,此过程中位置误差最大约为3°且很快收敛到0°附近。
图11给出了电机在2 000 r/min、负载转矩0.5 N∙m运行时,通过增减滑模观测角度,测试位置误差观测器响应速度的实验波形。在30 ms处,将滑模观测器角度输出减10°,在70 ms处将滑模观测器角度输加10°,测试结果表明在4 ms内,修正后的位置误差减小到1°内。
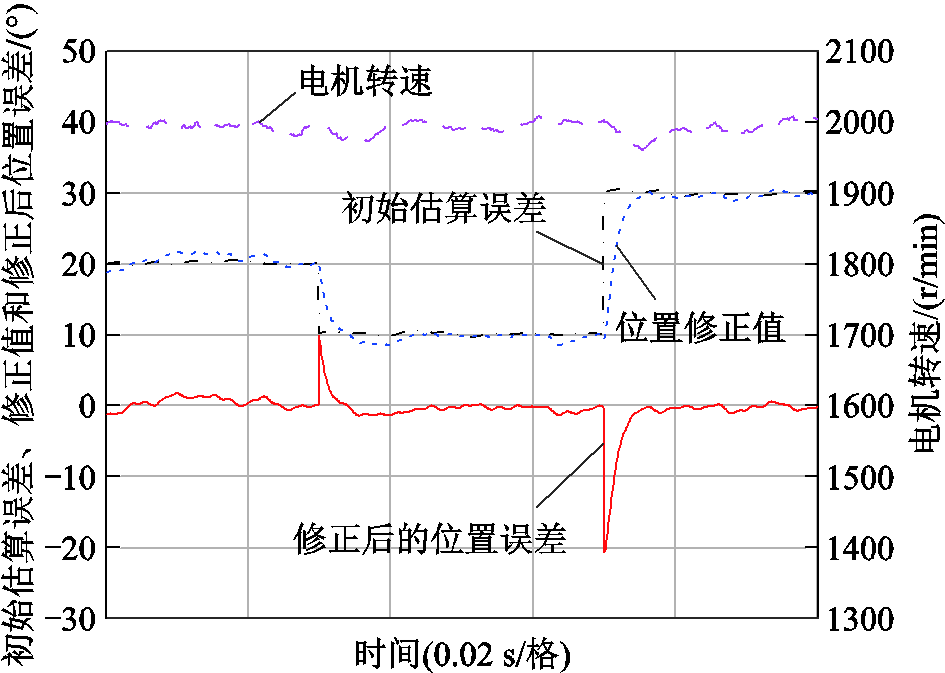
图11 角度突变下的观测器响应实验波形
Fig.11 Experimental waveforms of observer response under angle sudden change
图12a、图12b分别为电阻值增大50%、电阻值减小50%的位置误差曲线。SPMSM运行转速为2 000 r/min、负载转矩为2.4 N∙m。电阻变化的方法是将观测器中电阻值设置为实际电阻值的指定倍数。图中实际位置是通过旋转变压器检测获得,估算位置是滑模观测器输出并经过估算位置修正后的角度,位置误差为估算位置减去实际位置。
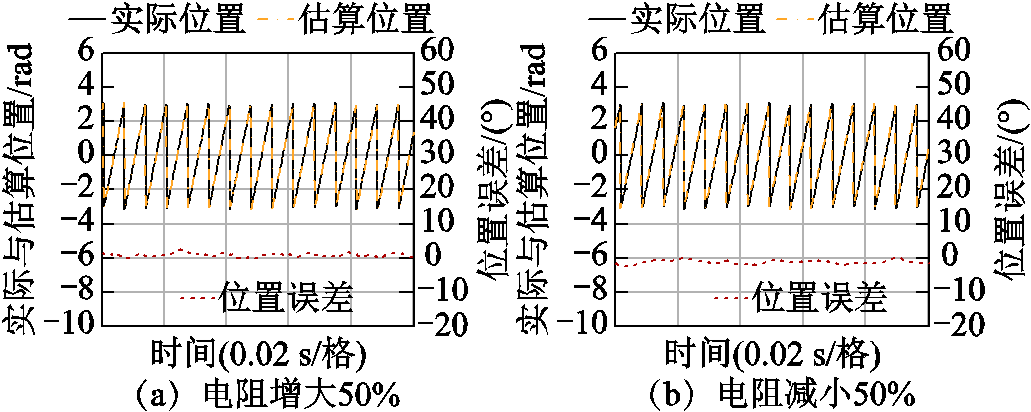
图12 电阻变化时使用估算位置修正策略位置误差
Fig.12 Position error of using estimated position correction strategy when resistance change
实验结果表明,电阻值增大50%,位置误差中心值为1.5°,位置误差范围为0°~3°;电阻值减小50%,位置误差中心值为-1.5°,位置误差范围为0°~-3°。
图13a、图13b分别为电感值增大50%、电感值减小50%的位置误差曲线。SPMSM运行条件、电感值调整方法与电阻敏感性测试方法一致。
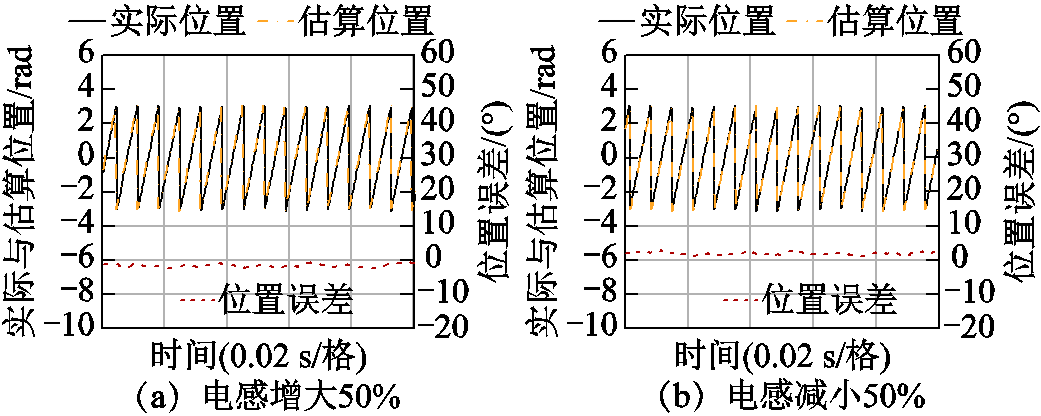
图13 电感变化时使用估算位置修正策略位置误差
Fig.13 Position error of using estimated position correction strategy when inductance change
实验结果表明电感值增大50%,位置误差中心值为-2.5°,位置误差范围为-1.5°~-4.5°;电感值减小50%,位置误差中心值为2.5°,位置误差范围为1°~4.5°。
以上是对参数敏感性的台架实验,接下来对参数敏感性进行详细的仿真计算和分析。首先推导观测器在参数变化后稳态点方程,根据该方程分析影响观测误差的条件;然后仿真计算在各种条件下电阻、电感参数变动导致的观测误差并分析观测误差达极值时的条件。
首先在相电阻值变为Rs+ΔR、其他参数均不变的条件下,标记电阻变化前的稳态点为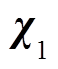 (
(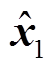 ,
,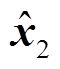 ),电阻值变化后的稳态点为
),电阻值变化后的稳态点为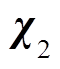 (
(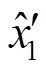 ,
,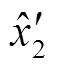 )。在稳态点
)。在稳态点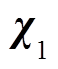 处根据式(22)计算估算位置。在稳态点χ2,设该点的磁链估算值为
处根据式(22)计算估算位置。在稳态点χ2,设该点的磁链估算值为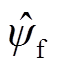 ,则有
,则有
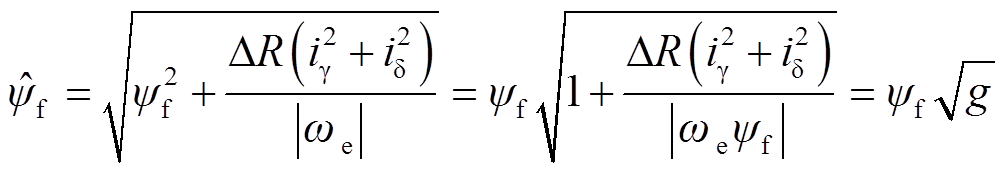 (31)
(31)
式中,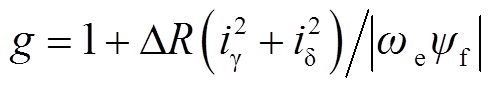 。将式(31)代入式(21)得
。将式(31)代入式(21)得
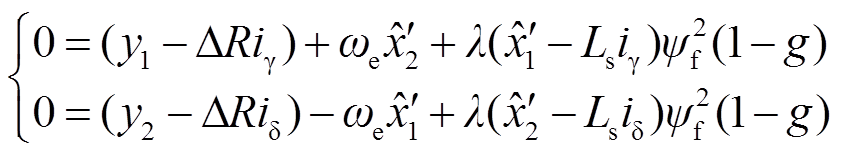 (32)
(32)
根据式(31)仿真计算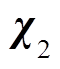 点的状态(
点的状态(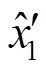 ,
,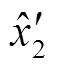 ),使用式(22)计算观测角度。从式(31)可知在电阻变化条件下,影响观测误差的条件有电流和转速。由于电流越大观测误差越大,因此在q轴电流为 4 A、不同转速条件下,对观测器中Rs变化导致的观测误差进行仿真计算并绘图。具体如图14所示。图中转速范围800~3 000 r/min,ΔR变化范围为标称电阻值的±50%,观测误差等于观测器估算位置减去实际位置偏差,图中最大观测误差为5.13°,出现在最低转速和电阻变化为极值的坐标点。
),使用式(22)计算观测角度。从式(31)可知在电阻变化条件下,影响观测误差的条件有电流和转速。由于电流越大观测误差越大,因此在q轴电流为 4 A、不同转速条件下,对观测器中Rs变化导致的观测误差进行仿真计算并绘图。具体如图14所示。图中转速范围800~3 000 r/min,ΔR变化范围为标称电阻值的±50%,观测误差等于观测器估算位置减去实际位置偏差,图中最大观测误差为5.13°,出现在最低转速和电阻变化为极值的坐标点。
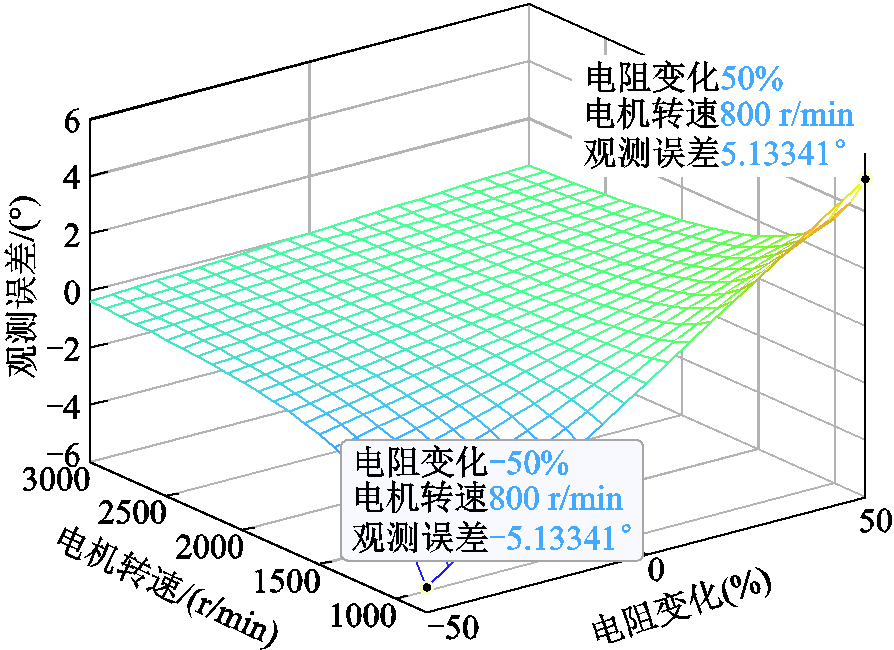
图14 不同转速下电阻变化导致的观测误差仿真
Fig.14 Simulation results of observation error at different speeds when resistance change
在电感值变化为Ls+ΔL、其他参数均不变的情况下,标记电感值变化前的稳态点为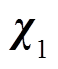 (
(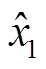 ,
,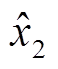 ),电感值变化后的稳态点为
),电感值变化后的稳态点为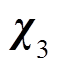 (
(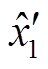 ,
,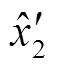 )。由于电感处于积分值的输出端,对
)。由于电感处于积分值的输出端,对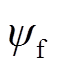 幅值影响有限,即估算磁链与实际磁链的二次方差近似为零,代入式(21)得到
幅值影响有限,即估算磁链与实际磁链的二次方差近似为零,代入式(21)得到
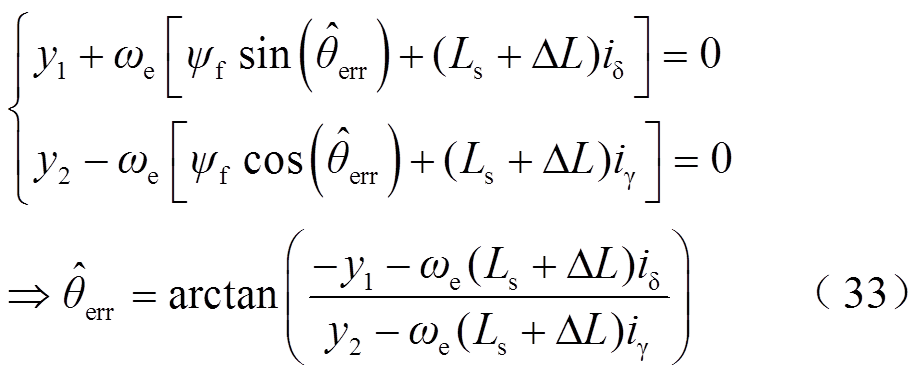
从式(33)可知,电感值变化时观测误差主要受电流幅值的影响。因此对不同q轴电流条件下、Ls变化的观测误差进行计算并绘图,如图15所示。图15中iq变化范围为±4 A,电感变化范围为电感标称值的±50%,观测误差等于观测器估算位置减去实际位置偏差,图中最大观测误差为3.77°,出现在q轴电流和电感变化同时为极值的坐标点处。
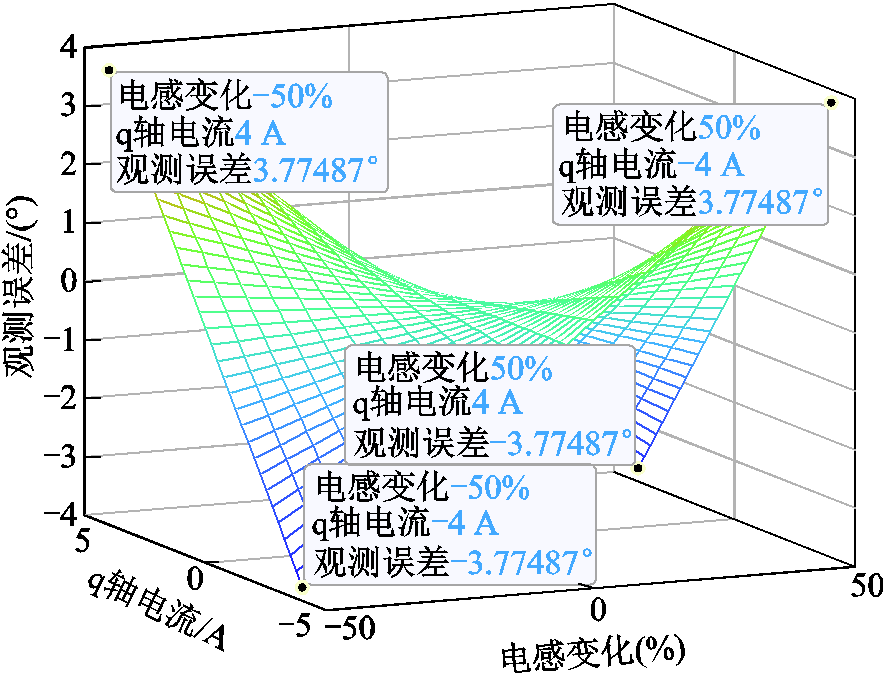
图15 不同iq时电感变化导致的观测误差仿真
Fig.15 Simulation results of observation error at different iq when inductance changes
本文以表贴式永磁同步电机为研究对象,重点分析讨论了各种非理想因素对滑模观测器位置估算误差的影响,并提出了提高位置估算精度的优化策略,主要研究成果如下:
1)本文分析了表贴式永磁同步电机控制系统中滑模观测器转子位置估算误差的产生机理,其主要由于滤波算法及数字运算环路延时等因素,造成了难以准确计算并补偿的转子位置误差。锁相环的跟踪滞后及积分过程会进一步增大转子位置误差。
2)本文以转子估算位置构造γ-δ坐标系,建立包含转子位置误差的数学模型,提出了基于最速梯度下降法和磁链观测器的转子位置误差观测器,用于对转子位置误差进行实时跟踪和补偿,并通过变增益循环迭代优化算法提升转子位置修正过程的速度和准确性。
3)通过搭建表贴式永磁同步电机加载测试平台,对本文提出的控制策略进行测试验证。测试结果表明所提的估算位置修正策略提高了转子位置估算精度,且在动稳态运行中均表现出良好的性能。
参考文献
[1] Kwon Y C, Sul S K, Baloch N A, et al. Improved design of IPMSM for sensorless drive with absolute rotor position estimation capability[J]. IEEE Transactions on Industry Applications, 2016, 52(2): 1441-1451.
[2] 麦志勤, 刘计龙, 肖飞, 等. 基于估计位置反馈电流解调算法的改进型高频旋转电压注入无位置传感器控制策略[J]. 电工技术学报, 2022, 37(4): 870-881, 891.
Mai Zhiqin, Liu Jilong, Xiao Fei, et al. Sensorless control strategy of improved HF rotating voltage injection based on estimated position feedback current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 870-881, 891.
[3] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet synchronous motor based on adaptive notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[4] Kim S, Ha J I, Sul S K, et al. PWM switching frequency signal injection sensorless method in IPMSM[J]. IEEE Transactions on Industry Applications, 2012, 48(5): 1576-1587.
[5] 薛哗, 魏佳丹, 周波. 三级式同步电机低速阶段无位置传感器起动控制高频信号注入法的对比[J]. 电工技术学报, 2018, 33(12): 2703-2712.
Xue Hua, Wei Jiadan, Zhou Bo. Comparative investigation on sensorless control of three-stage synchronous motor based on high-frequency injection method at low speed[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2703-2712.
[6] 姜燕, 李博文, 吴轩, 等. 基于比例谐振滤波的改进永磁同步电机转子位置观测器[J]. 电工技术学报, 2020, 35(17): 3619-3630.
Jiang Yan, Li Bowen, Wu Xuan, et al. An improved rotor position observer for permanent magnet synchronous motors based on proportional resonant filtering[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3619-3630.
[7] 陈思溢, 皮佑国. 基于滑模观测器与滑模控制器的永磁同步电机无位置传感器控制[J]. 电工技术学报, 2016, 31(12): 108-117.
Chen Siyi, Pi Youguo. Position sensorless control for permanent magnet synchronous motor based on sliding mode observer and sliding mode controller[J]. Transactions of China Electrotechnical Society, 2016, 31(12): 108-117.
[8] Hejny R W, Lorenz R D. Evaluating the practical low-speed limits for back-EMF tracking-based sensorless speed control using drive stiffness as a key metric[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1337-1343.
[9] Zhao Yue, Qiao Wei, Wu Long. An adaptive quasi-sliding-mode rotor position observer-based sensorless control for interior permanent magnet synchronous machines[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5618-5629.
[10] Bao Danyang, Pan Xuewei, Wang Yi, et al. Adaptive synchronous-frequency tracking-mode observer for the sensorless control of a surface PMSM[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6460-6471.
[11] 申永鹏, 刘安康, 崔光照, 等. 扩展滑模观测器永磁同步电机无传感器矢量控制[J]. 电机与控制学报, 2020, 24(8): 51-57, 66.
Shen Yongpeng, Liu Ankang, Cui Guangzhao, et al. Sensorless filed oriented control of permanent magnet synchronous motor based on extend sliding mode observer[J]. Electric Machines and Control, 2020, 24(8): 51-57, 66.
[12] 陶彩霞, 赵凯旋, 牛青. 考虑滑模抖振的永磁同步电机模糊超螺旋滑模观测器[J]. 电力系统保护与控制, 2019, 47(23): 11-18.
Tao Caixia, Zhao Kaixuan, Niu Qing. Fuzzy super-spiral sliding mode observer for permanent magnet synchronous motor considering sliding mode buffeting[J]. Power System Protection and Control, 2019, 47(23): 11-18.
[13] Liu Gang, Zhang Haifeng, Song Xinda. Position-estimation deviation-suppression technology of PMSM combining phase self-compensation SMO and feed-forward PLL[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 335-344.
[14] Lee Y, Sul S K. Model-based sensorless control of an IPMSM with enhanced robustness against load disturbances based on position and speed estimator using a speed error[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1448-1459.
[15] Xu Zhuang, Zhang Tianru, Bao Yuli, et al. A nonlinear extended state observer for rotor position and speed estimation for sensorless IPMSM drives[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 733-743.
[16] 顾聪, 王晓琳, 邓智泉. 一种基于双重锁相环的高速永磁同步电机转子位置估计误差全补偿方法[J]. 中国电机工程学报, 2020, 40(3): 962-970.
Gu Cong, Wang Xiaolin, Deng Zhiquan. A rotor position estimated error correction method for high-speed permanent magnet synchronous motor based on dual-phase-locked-loop[J]. Proceedings of the CSEE, 2020, 40(3): 962-970.
[17] 王晓琳, 刘思豪, 顾聪. 基于自适应基准锁相环的高速永磁电机转子位置误差全补偿方法[J]. 电工技术学报, 2021, 36(20): 4308-4317.
Wang Xiaolin, Liu Sihao, Gu Cong. A rotor position error compensation algorithm for high-speed permanent magnet motor based on phase-locked loop with adaptive reference[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4308-4317.
[18] Ortega R, Praly L, Astolfi A, et al. Estimation of rotor position and speed of permanent magnet synchronous motors with guaranteed stability[J]. IEEE Transactions on Control Systems Technology, 2011, 19(3): 601-614.
Estimated Position Correction Algorithm for Surface-Mounted Permanent Magnet Synchronous Motor Based on Variable Gain Steepest Gradient
Abstract Due to its high robustness and simplicity, sliding mode observer (SMO) has been widely used in sensorless control of surface mounted permanent magnet synchronous motor (SPMSM) at medium and high speeds. However, various non-ideal factors in actual control systems will lead to calculation errors and control delays, which will seriously affect the position estimation accuracy of SMO. To solve the above problem, this paper first analyzes the mechanism of position estimation error, and establishes the mathematical model in the error coordinate; Then, the steepest gradient descent position error observer based on nonlinear flux observer is proposed, and the variable gain cyclic iteration method is proposed to improve the speed and accuracy of the estimated position correction process. Finally, the accuracy and robustness of the proposed algorithm are verified through an SPMSM experimental platform.
Firstly, the SMO principle and the rotor position estimation error mechanism in SPMSM sensorless control system are analyzed. Secondly, the mathematical model including the estimated position error is established at the observation error coordinate system (γ-δ frame). Thirdly, a rotor position error observer based on the steepest gradient descent method and nonlinear flux observer at the γ-δ frame is proposed, and the observer’s stability is proved. Finally, variable gain and one cycle iterative algorithm are proposed to improve the speed of the position correction process. Because the proposed observer only needs the rotor angle and speed information calculated by the SMO, it has no coupling with the current control loop and can be configured and adjusted more conveniently.
Experimental results on the 750 W SPMSM experimental platform show that, when the load torque is kept at 0.5 N∙m and the speed is adjusted from 800 r/min to 3 000 r/min, the maximum rotor position error is 2° and the average error is 0°. At 3 000 r/min, when the load torque increases from 0.5 N∙m to 2.4 N∙m (rated torque), the maximum rotor position error is 3°; after the speed is stable, the average error is 0° and the maximum error is 2°. When the estimated angle of the rotor suddenly changes ±10°, the position error corrected by the observer is reduced to within 1° within 4ms. During the parameter sensitivity bench test, the resistance changes by ±50%, and the position error deviate from the center point by ±1.5°. The inductance changes by ±50%, and the position error deviates from the center point by ±2.5°. Then the theoretical analysis of parameter sensitivity is carried out. The analysis results show that the maximum position error of 5.13° occurs at the lowest speed and maximum current when the resistance changes, and the maximum position error of 3.77° occurs at the maximum current when the inductance changes.
The following conclusions can be drawn from the experimental results and theoretical analysis: (1) The proposed algorithm can be configured and adjusted conveniently, due to the decoupling of SMO and the current control loop. (2) The proposed algorithm can effectively track the position error when changing speed and load. In case of a sudden change of angle, it can realize rapid observation of angle error. (3) The proposed algorithm has good robustness when the resistance and inductance parameters change.
keywords:Surface mounted permanent magnet synchronous motor (SPMSM), variable gain steepest gradient descent method, sliding mode observer (SMO), estimated position correction algorithm
中图分类号:TM341
DOI:10.19595/j.cnki.1000-6753.tces.221934
国防科技工业核动力技术创新中心(HDLCXZX-2021-ZH-016)和核反应堆系统设计技术重点实验室运行基金(HT-KFKT-24-2021016)资助项目。
收稿日期 2022-10-09
改稿日期 2022-12-29
王益明 男,1985年生,博士研究生,研究方向为同步电机的驱动和控制技术。E-mail:20141103096@cqu.edu.cn
罗凌雁 女,1984年生,工程师,研究方向为特种电机设计与控制、电动汽车电驱动系统、混合动力的控制与仿真。E-mail:luoly@cqu.edu.cn(通信作者)
(编辑 赫 蕾)