图1 纯电动乘用车数据类型
Fig.1 Pure electric passenger cars
摘要 为充分挖掘电动汽车大数据监控平台海量数据应用潜力,提升锂离子电池组传统故障诊断方法在异常检测、故障电池定位和故障诊断等方面的效率,该文提出一种基于数据挖掘和大数据分析的电动汽车高效单体电池异常检测、定位与电池系统故障诊断方法。首先,使用t-SNE对采集的动力电池历史运行数据可视化降维,利用K均值聚类算法结合Z分数方法设计电压异常诊断系数,完成异常单体的准确检测和异常定位,并结合熵权-变异系数法进行单体电池性能评估,实现不同单体电池异常程度的综合评定;其次,采用3s-MSS算法以概率形式计算电池组中单体电池端电压的异常变化,并通过不同电池故障概率统计分析,利用数理统计方法实现电池系统故障与突发故障的统计分类,在时间维度上进行电池系统的故障诊断;最后,基于该文所提出的故障诊断与异常检测方法,对监控平台上四辆电动汽车三年的运行数据进行了异常特性诊断,并按照春、夏、秋、冬四季对其故障特征进行了分析。诊断结果显示,在四个季节故障概率分布中,电动汽车各单体电池最高故障概率分别为1.99%、4.95%、3.67%、9.52%,平均故障概率为1.54%、4.31%、3.07%、4.59%,夏、冬两季电池故障发生概率高于春、秋两季。相关诊断结果可为动力电池稳定运行提供维护建议,为提升电动汽车的可靠性和优化设计提供参考。
关键词:动力电池 数据挖掘 大数据 异常检测 故障诊断
近年来,随着全球对环境和能源问题的日益关注,电动汽车作为一种清洁能源交通工具,受到广泛推崇[1-2]。锂离子电池因其具有功率密度大、能量密度高、自放电率低等优异性能而成为当前电动汽车电能存储装置的首选[3-4]。然而,因锂离子电池系统故障并导致电动汽车热失控的事故时有发生,其使用安全性备受关注[5]。由于自身工作特性影响,锂离子电池需维持在一定的电压与温度范围内才能稳定工作,相比于无约束的电动汽车行驶工况,锂电池的安全工作窗口显得较为狭窄与严苛,致使其在复杂不确定交通环境中故障风险凸显[6]。此外,锂离子电池随着循环充放电而退化,导致电池容量下降、锂库存损失、活性物质损失和电阻增加,影响电池的整体性能,增加了电池故障的风险[7]。同时,由于锂电池单体本身在制造过程中存在初始不一致性问题,随着使用次数的积累,从而加剧单体间的初始不一致性,最终导致系统中单体电池发生过充、过放或内部短路(Internal Short Circuit, ISC)等故障,影响电池系统的正常工作[8]。当前,电动汽车运行监控平台被广泛应用,基于平台可获取海量整车及动力电池运行数据,利用先进的大数据挖掘和分析技术,检测电池系统异常变化,定位发生异常的单体电池,及时诊断其运行过程中发生的或未发生的故障,从而保证电池组安全高效运行,具有重要价值和意义[9]。
目前已经有大量学者对电池系统故障诊断展开研究,主要包括基于解析模型的方法、基于数据驱动的方法和基于数理统计分析的方法[10]。基于解析模型的方法需要借助于精确的电池系统数学模型,当建立的模型较为准确时,该方法可以准确反映出系统的动态变化过程并实时开展故障诊断[11]。文献[12]采用一阶RC等效电路模型分析电池故障状态,基于Simscape模拟电池组接触故障,通过理论分析得知串联电池组电压变化异常的故障原因为电池接触故障或电池内阻异常增加。文献[13]采用改进的扩展卡尔曼滤波器(Extended Kalman Filter, EKF)在线获取开路电压,首先,构建了曲线与电池荷电状态(State of Charge, SOC)之间的关系,从而在实时不更新关系的情况下节省时间;其次,通过插值获得“中间电池”和“最小电池”之间的SOC差异;最后,通过在线拟合拐点前的差异曲线来计算外部软短路电流和电阻,能够有效地检测外部软短路故障。文献[14]提出了一种基于电压输入、电流输出模型的电流传感器故障诊断方法,利用最小二乘法结合无迹卡尔曼滤波估计电流传感器的故障电流,通过将估计的故障电流与诊断阈值进行比较,实现了电流传感器的快速故障诊断。然而,对于复杂的高度非线性时变系统来说,精确的电池系统建模和其所带来的计算负担是目前电池管理系统所面临的一个重要挑战[15]。模型易受电池老化、环境等因素的影响,且参数需频繁标定,使其诊断精度低、实现困难。另外,该方法只适用于特定的电池故障,需要分别对电池的不同故障进行大量的测试和建模训练,导致适用性窄、鲁棒性差[16]。
基于数据驱动的电池故障诊断方法由于具有良好的非线性映射特性,在电池故障检测领域得到了广泛应用[17]。此类诊断方法不需要对电池系统进行精确建模,通过将电池系统的可测量参数或者信号如电流、电压、温度等作为算法模型的输入,将对应的故障类型进行编码作为模型输出,利用大量的离线数据对相应的机器学习算法模型进行训练,来学习输入特征与编码故障之间的映射关系,然后用训练好的模型或者建立好的映射关系进行系统在线故障诊断[18]。文献[19]提出基于在线序列超限学习机和主成分分析的蒸汽冷却型燃料电池系统快速故障诊断方法,使用在线序列超限学习机对故障特征向量进行分类,能有效提高模型诊断正确率并降低运算时间。文献[20]通过检测移动窗口内电池电压序列的修正样本熵,能够诊断并预测电池短路和开路等不同的早期故障,同时预测故障发生的时间。然而,在锂电池复杂的应用条件下,满足训练要求的同类型故障数据量较少,因此历史运行数据的丰富性和可靠度成为了该类方法在实际应用的主要障碍[21]。同时,大量的数据训练不仅增大了系统的计算负担,而且用于算法模型训练的数据的质量也很难得到保证[22]。
基于数理统计分析的方法直接利用信号采集系统获取的电流、电压和温度数据,运用信息熵、正态分布等统计工具进行深入分析,通过设定恰当的异常系数或阈值,能够有效实现对电池故障的诊断[23]。随着大数据分析技术的快速发展,学者们正在尝试利用更先进的大数据统计分析技术来推进与电池安全管理相关的研究[24-25]。文献[26]提出用组内相关系数法计算电池包中相邻电芯之间的电压相关系数来进行电压故障诊断和定位。此类方法计算复杂度低,执行效率高,但往往仅能实现故障检测,难以对故障类型进行识别。为了提高故障诊断的鲁棒性与准确性,文献[27]基于新能源汽车监控平台运行数据,利用BP神经网络算法和3s 多层次筛选算法(3s-Multi-level Screening Strateyy-3s-MSS),提出了一种新的系统故障和缺陷诊断方法,通过故障概率分析定义了系统故障与实际运行故障,并总结了概率变化对电池性能造成的影响。当前,针对电动汽车电动化、智能化、网联化以及数字化发展趋势,利用机器学习与大数据分析方法相结合的电池智能故障诊断方法,是未来动力电池故障诊断的重要研究方向[28]。
综上所述,现阶段电池故障诊断方法仍存在实际车载应用中检测与定位故障效率低下、鲁棒性不强、难以检测到因电池参数变化而发生的微小故障等限制。为弥补传统方法中检测异常电池效率低下、定位异常或故障电池困难等缺点,本研究基于电动汽车云监控平台采集动力电池运行数据,采用数据挖掘与大数据分析技术,提出了一种电池故障诊断与异常检测方法,实现了电池电压潜在异常变化检测。基于熵权-变异系数法进行单体电池性能评估,实现了不同单体电池异常程度的综合评定。为进一步分析故障原因,基于3s-MSS筛选策略,建立故障诊断模型,利用数据挖掘方法进行故障统计分类,实现异常单体电池异常检测-定位-诊断的全面分析。通过局部离群因子(Local Outlier Factor, LOF)算法和聚类离群诊断(Connectivity-based Outilier Factor, COF)算法两种方法代替3s-MSS算法,对比和验证大数据统计模型性能。此外,基于所构建电池故障诊断模型,对大数据平台上四辆电动汽车三年的电池运行数据进行诊断,并就季节变化对电池性能和故障概率的影响进行了分析。
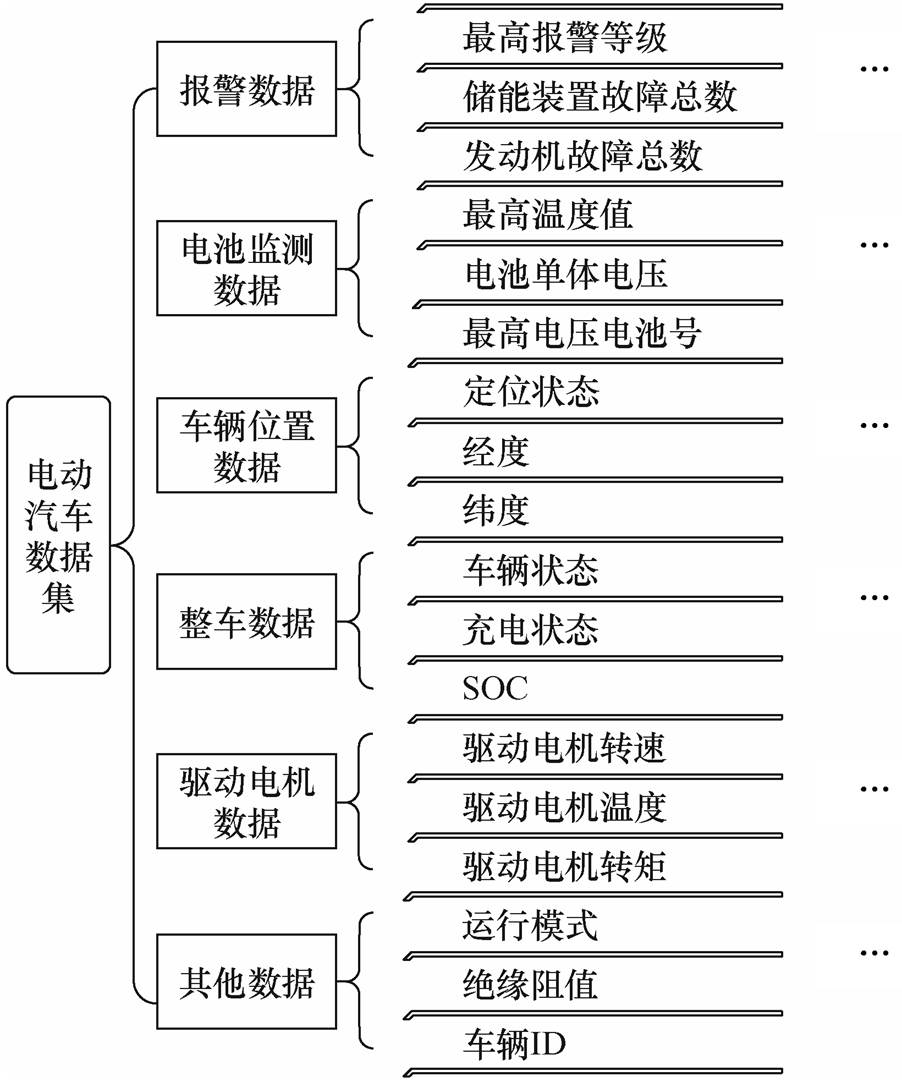
为保障锂电池车载应用安全性,除在电池组电池管理系统(Battery Management System, BMS)中内置故障诊断系统外,一个实时监控电池运行情况,为最终用户和制造商提供决策参考的管理平台也是一种可行的解决方案。为高效监控电动汽车运行状态,收集电动汽车实时运行数据,进一步优化产品,厂家一般均建立云监控平台。监控平台的数据采集是通过安装在车辆上的车载数据采集终端从车辆CAN总线中实时收集车辆运行状态的关键信息,包括从电池状态、能量利用效率到车辆位置等多维度数据。这些数据的采集有助于精准评估车辆性能,提升维护效率,为用户提供更安全、高效、可靠的出行体验。云监控平台目前具备数据存储、数据分析、运行安全报警等主要功能模块,对企业电动汽车运行监控与管理、性能分析与技术提升等发挥着重要作用。本研究使用了某企业监控平台收集的时间跨度为三年的纯电动乘用车的运行监控数据,包括纯电动乘用车电池的报警数据、电池监测数据、车辆位置数据、整车数据、驱动电机数据等50多种数据,数据采样间隔为10 s,具体数据类型如图1所示。

图1 纯电动乘用车数据类型
Fig.1 Pure electric passenger cars
在车辆运行数据收集过程中,存在多种干扰因素,如车载传感器、信号线缆和传输网络干扰等,导致原始数据质量较差,因此需要对原始数据进行预处理。由于平台数据存储的限制,同一车辆不同年份数据存储在不同文件中。为此,首先需要整合不同文件中时间、单体电压、SOC等数据,统一进行规范化处理。另外,由于数据传输干扰问题,原始数据中出现许多无效、重复和缺失值,因此需要进行数据清洗。具体的清洗流程包括:对整合后的单体电压等数据进行连续性校验,判定是否出现连续时间超过1 min的数据错误或缺失;如果超过1 min,直接删除相关数据;如果未超过1 min,则结合车辆前后状态数据,使用拉格朗日插值法来更新有问题的数据,以便于后续开发和验证诊断模型。
本节根据数据格式和统计算法,建立了电动汽车单体电池电压异常检测与故障诊断模型,其故障诊断流程如图2所示。首先利用t分布随机近邻嵌入(t-distributed Stochastic Neighbor Embedding, t-SNE)方法对单体电池电压数据进行了可视化降维处理,将高维电池电压数据压缩为低维数据;其次利用K均值聚类算法(K-Means Algorithm, KMA)对降维数据进行聚类分析,有效地识别了单体电池异常;再次结合高斯分布原理和Z分数(Z-score)法设计诊断系数对异常电池进行定位;然后利用熵权-变异系数法评估了各个单体电池的异常程度;最后利用3s-MSS筛选策略对样本中的故障数据点进行剔除,建立诊断标准,通过对故障矩阵进行统计处理,可以得到动力电池的故障概率和类别,实现对不同类型的电池故障诊断,同时在时间维度上进行了故障概率统计,分析了季节变化对电池性能和故障概率的影响。
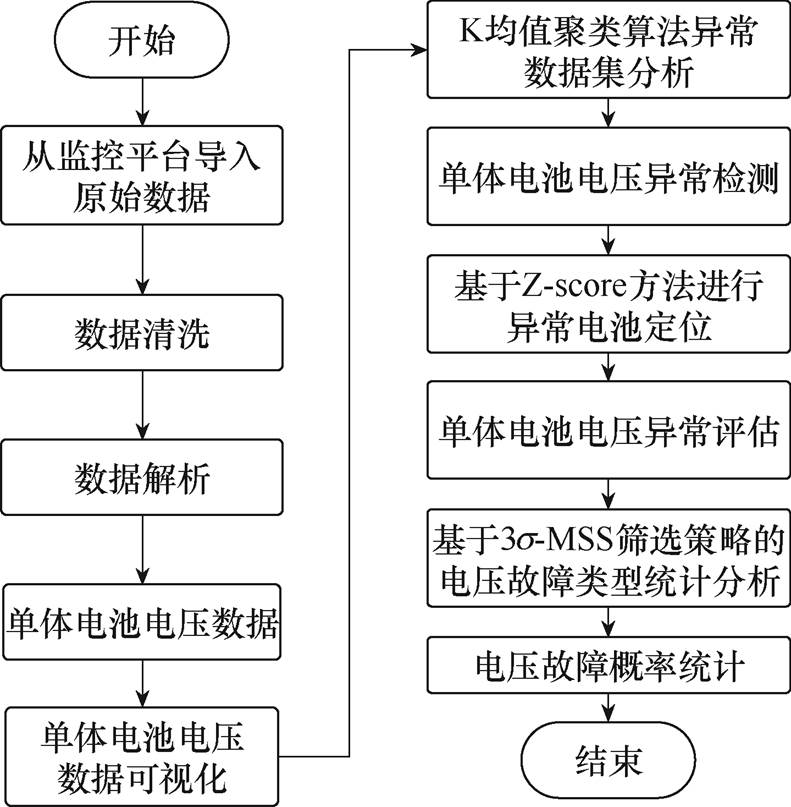
图2 异常检测与诊断流程
Fig.2 Anomaly detection and diagnosis flowchart
数据降维与可视化是进行大体量数据处理的常用技术,其目的是通过降维,减少数据集的维度,从而简化数据结构,提高计算效率,同时可以更容易地识别数据中的集群,通过将数据降维到二维空间,可以将数据可视化,能够更直观地理解数据,有助于观察数据的分布、趋势和异常值。电动汽车运行过程中为保障电池组的安全性和可靠性,往往需要监测每个单体电池的运行状态。然而对每个单体电池的电压进行诊断和分析可能会导致计算负担过大,同时降低了实时故障检测的效率。为应对这一问题,本节采用t-SNE技术,将所有单体电池的高维电压数据(每个电池的电压数据被视为一维)压缩为二维数据。t-SNE方法通过保留数据样本之间的局部结构,将高维数据映射到一个低维空间,以便能够更好地展示数据的相似性和差异性。相较于传统降维方法,t-SNE在处理非线性关系方面表现出色,因此特别适用于复杂数据集的可视化[29]。本文使用t-SNE方法对预处理后的电池数据进行降维处理,其核心思想是基于原始数据点在高维空间中相似性和低维空间中相似性之间的差异,通过优化目标函数来实现映射。具体流程如下:
(1)准备数据:准备要进行降维可视化的单体电池电压数据集。
(2)特征提取和归一化:将数据集进行特征提取和归一化,保证特征向量的长度一致。
(3)计算相似度矩阵:使用二次方根欧氏距离计算样本之间的相似度或距离,并将计算结果保存在相似度矩阵中。
(4)降维:使用t-SNE算法对相似度矩阵进行降维,并得到低维空间的嵌入向量。
(5)可视化:使用优化过程完成后,得到了低维空间中的数据点位置,使用散点图方式将这些数据点进行可视化,以展示原始数据的结构和相似性关系。
将降维后的电压数据集使用K均值算法聚类分析,有助于直观检测到单体电池是否发生异常。K均值聚类可以用于异常数据集分析,该算法通过迭代优化,将数据点划分到不同的簇中,使得同一簇内的数据点相似度较高,不同簇之间的相似度较低。通过将降维后的单体电池数据划分为不同的簇,并计算每个簇的中心点,可以识别出异常簇和异常点,从而实现异常检测[30]。这意味着,如果降维后的电压数据点与其所属簇的中心点的距离过大,且与所属簇的分布呈现出离散状态,那么它可能被认为是异常数据。
为了利用K均值聚类来分析异常数据集,可以采取以下步骤:
(1)选择K值:需要确定要分成多少个簇(K值)。较大的K值有助于更好地检测异常数据点。
(2)执行K均值聚类:使用K值执行K均值聚类,将数据集分成K个簇。
(3)检测异常点:对于每个簇,计算每个数据点到该簇的中心点的欧氏距离,对所有数据点计算它们到簇中心的距离的平均值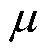 和标准差
和标准差 ,将距离超出某个阈值的数据点标记为异常数据点,其中异常值的阈值
,将距离超出某个阈值的数据点标记为异常数据点,其中异常值的阈值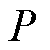 的计算公式为
的计算公式为
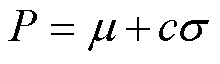 (1)
(1)
式中,c为控制异常值的敏感度系数;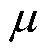 为所有样本平均值;
为所有样本平均值; 为样本标准差。根据本文数据,c =1.5。
为样本标准差。根据本文数据,c =1.5。
(4)分析结果:分析被标记为异常的数据点,探索它们是否具有共同的特征或模式。
通过K均值聚类算法分析,可以检测到降维后的异常数据簇以及异常数据点。
利用K均值聚类算法进行电压数据异常检测后,异常数据可指示电池组中的特定单体电池存在的问题,通过分析异常电压数据的来源和模式,即可获取异常电池位置和编号,从而提升电池组的整体性能和安全性。在车辆运行期间,故障情况相对较少见,仅占据全部运行数据的一小部分。然而,当拥有充足的数据量时,电池组参数的变化应该近似符合高斯分布,因此本文采用高斯分布来表征各个单体电池电压数据的分布特性。利用基于高斯分布建立的诊断准则来检测异常原因,高斯分布建立的准则为
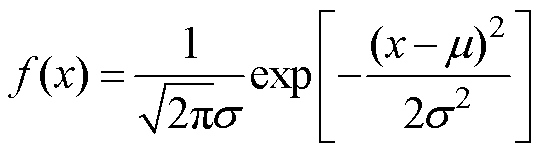 (2)
(2)
式中,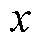 为目标样本。
为目标样本。
由于各单体电池的电压变化存在一定程度的差异,而故障单体电池的电压波动可能在某个时间段内表现得较快,亦或是较缓慢。因此,仅依据标准差和均值所计算得到的电压概率密度可能难以准确地探测电压方面的异常情况。鉴此,本文通过建立基于概率密度函数的电压异常诊断指标,同时根据Z分数法设计的异常诊断系数可以有效定位发生异常的单体。Z分数法常被用于异常诊断和异常系数的设计,Z分数直观地表示了一个数据点相对于平均值的偏离程度,大的Z分数意味着数据点偏离了平均值,因此可能是异常值,这使得异常点的检测变得相对直观和易于理解。同时该方法对于大样本数据的异常诊断效果较好,当样本容量足够大时,大部分数据点的Z分数会在一定范围内集中,有助于更准确地确定异常值。其具体为
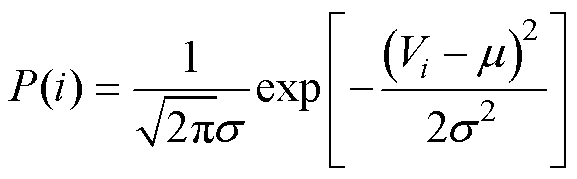 (3)
(3)
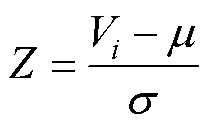 (4)
(4)
式中,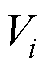 为每个时刻的单体电压,
为每个时刻的单体电压,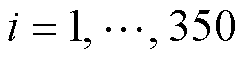 ;
; 值表示目标样本与基于标准差的原始样本平均值之间的距离。当目标样本值低于平均值时,
值表示目标样本与基于标准差的原始样本平均值之间的距离。当目标样本值低于平均值时, 为负数;否则,为正。
为负数;否则,为正。
基于Z分数设计异常诊断系数并通过分析各单体电池的 值的偏离程度可以准确定位异常单体,即
值的偏离程度可以准确定位异常单体,即
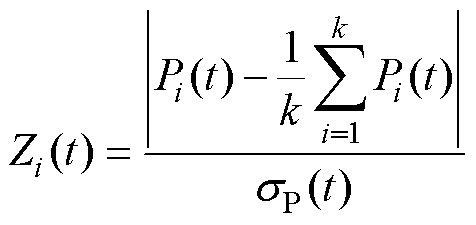 (5)
(5)
式中,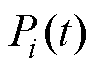 为
为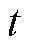 时刻第
时刻第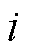 个单体电池电压的概率密度值;
个单体电池电压的概率密度值;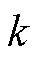 为电池个数,
为电池个数,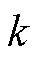 =30;
=30;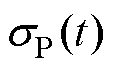 为
为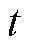 时刻所有电芯电压概率密度值的标准差。当计算得到了每个电芯电压的
时刻所有电芯电压概率密度值的标准差。当计算得到了每个电芯电压的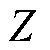 值,则可根据
值,则可根据 值的大小来判断是哪一个电芯发生异常。
值的大小来判断是哪一个电芯发生异常。
对异常电池单体进行异常检测并定位后,进行电池在时间维度上的异常程度综合评估是为了更全面地了解电池系统的整体状态,可以判断单体电池的异常状态,了解各单体电池的异常程度。基于熵权-变异系数法进行单体电压性能评估的方法是一种有效的多标准决策分析技术,用于评估电池单体的工作稳定性和性能。本节基于熵权-变异系数法对定位异常的单体电池进一步开展了异常程度综合性能评估,计算每个单体电池的综合评价分值,能够更全面地反映单体电池的异常程度。其中,得分上限和得分下限分别代表了指标最优和最差的情况,是为了考虑指标值的变异性和范围,使评分结果更加合理和可信。评分上限和评分下限的作用在于确定指标的归一化范围,确保所有指标的得分在相同的尺度上,这有助于避免某个指标由于数值范围的不同而对最终评价结果产生不合理的影响,使各个指标在计算熵值时具有可比性,有助于更全面地评估综合指标的表现。具体评估策略如图3所示。
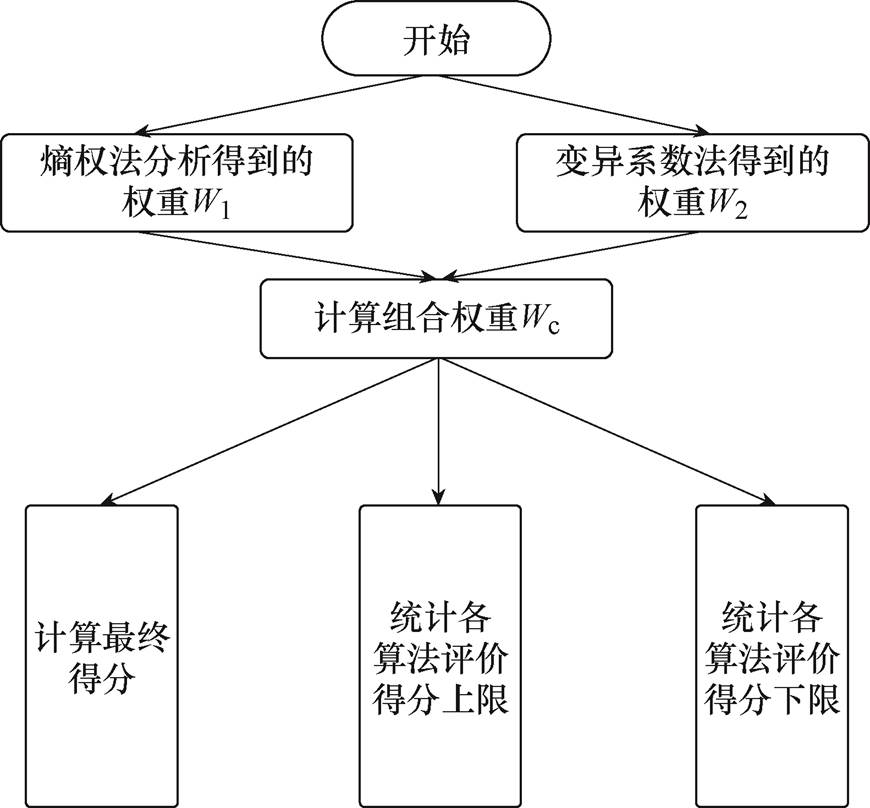
图3 单体电池异常程度评估策略
Fig.3 Cell voltage anomaly evaluation strategy
根据熵权-变异系数法进行单体电池异常程度评估的具体计算过程如下。
2.4.1 熵权法
在熵权法中将每个时刻当作一个指标,每个指标下包含各单体的电压值。首先对采集到的数据进行预处理后形成电压矩阵 为
为
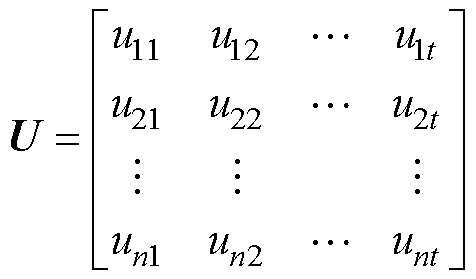 (6)
(6)
式中,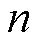 为单体数目;
为单体数目;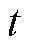 为某个时刻。
为某个时刻。
计算第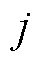 项时刻指标下第
项时刻指标下第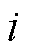 个单体电压值占该时刻指标的比重
个单体电压值占该时刻指标的比重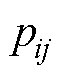 并构成评价矩阵
并构成评价矩阵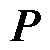 为
为
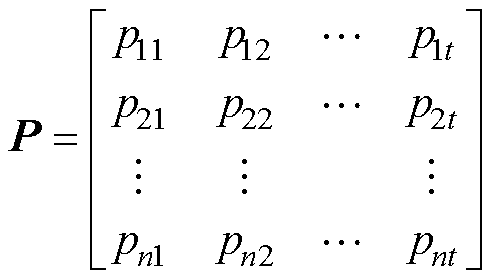 (7)
(7)
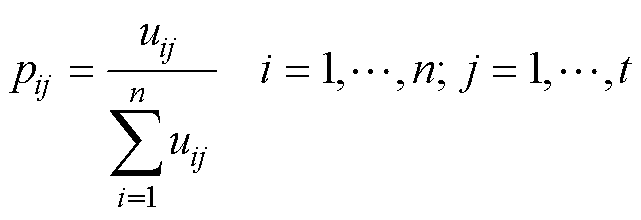 (8)
(8)
式中,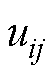 为第j项时刻指标下第i个单体的电压值。
为第j项时刻指标下第i个单体的电压值。
计算评价矩阵中每个指标的相对熵,用于衡量指标的重要性。相对熵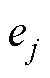 计算公式为
计算公式为
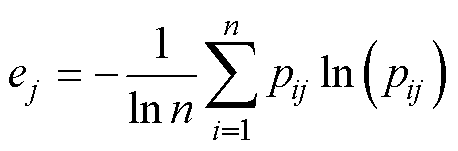 (9)
(9)
将每个时刻指标下各单体的差异可以用权重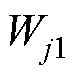 表示,时刻指标下权重差别越大,对评价的意义越大,即当熵权重值越大时,说明相应时刻指标对整体评价的贡献越大。权重的计算公式为
表示,时刻指标下权重差别越大,对评价的意义越大,即当熵权重值越大时,说明相应时刻指标对整体评价的贡献越大。权重的计算公式为
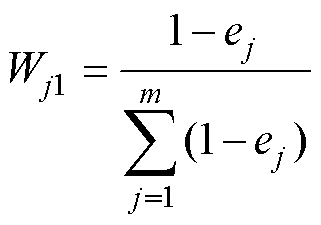 (10)
(10)
式中,m为时刻指标的总数量,m=350。
2.4.2 变异系数法
计算全部单体电压的均值为
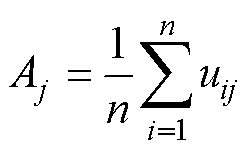 (11)
(11)
计算全部单体电压的标准差为
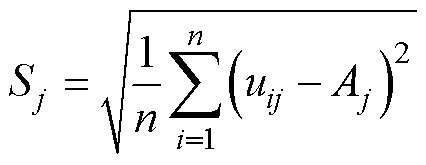 (12)
(12)
计算全部单体电压的变异系数为
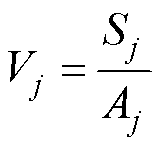 (13)
(13)
根据变异系数法计算其权重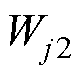 为
为
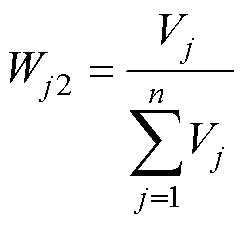 (14)
(14)
2.4.3 熵权-变异系数法
根据熵权法和变异系数法计算得到的权重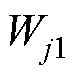 和
和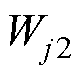 ,求出熵权-变异系数法的组合权重
,求出熵权-变异系数法的组合权重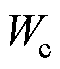 为
为
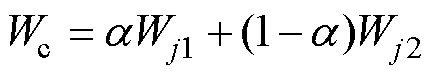 (15)
(15)
式中,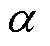 为一个权重调整系数,根据相关数据与算法调试结果,本文设置
为一个权重调整系数,根据相关数据与算法调试结果,本文设置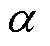 =0.4。
=0.4。
可以得到评分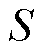 为
为
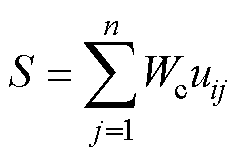 (16)
(16)
计算得分上限和下限分别为
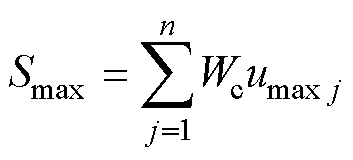 (17)
(17)
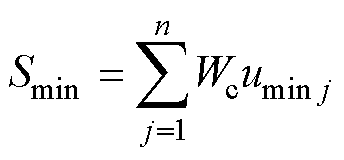 (18)
(18)
式中,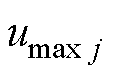 为第j项时刻指标下的电压最大值;
为第j项时刻指标下的电压最大值;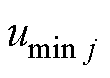 为第j项时刻指标下的电压最小值。
为第j项时刻指标下的电压最小值。
计算评分均值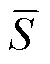 为
为
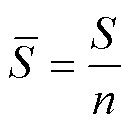 (19)
(19)
最终计算每个单体的得分差值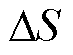 为
为
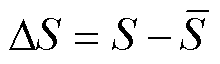 (20)
(20)
为了进一步分析定位异常的单体电池发生异常或故障的类别,本节利用3s-MSS多级筛选策略采用高斯分布概率特征对所有单体电池电压数据进行集中筛选并实现了故障概率统计。
3s-MSS多级筛选策略的筛选过程是通过多次筛选寻找最优数据中心点并筛选出异常值的方法。与传统3s 筛选准则相比,3s-MSS多级筛选准则充分考虑了测量值与平均值之间的偏差,以及其他统计量影响,通过多次筛选寻找到最优数据中心点,达到准确区分正常离群点与真正异常值的目的。
通常中心点识别算法往往基于数据的数字特征,如中位数或者均值,然而这两个数字特征往往会受到数据中离群点的较大影响,导致最终计算出的中心值偏离理想的中心点。如图4所示为使用3s-MSS多级筛选策略进行第一次筛选并寻找最优数据中心点的结果。图4中,C1为根据初始数据集计算的数据中心点,C2为首次使用3s-MSS算法剔除P3、P4、P5等离群点后建立的数据中心点。可以明显看出,在初始圆内P1、P2未被定义为异常数据点,但偏离中心点C1较远;根据第一次异常数据筛选后,重新建立的标准数据圆中,P1、P2被定义为异常数据点,由此可见中心点C2比中心点C1更加合理,集群中的数据点较为分散地分布在数据点C2周围。表明多级筛选策略能够有效地实现理想数据中心点的标准构建,并用于识别与该中心点相差较大的数据点,通过对异常数据的多次筛选计算获取故障数据出现的概率。
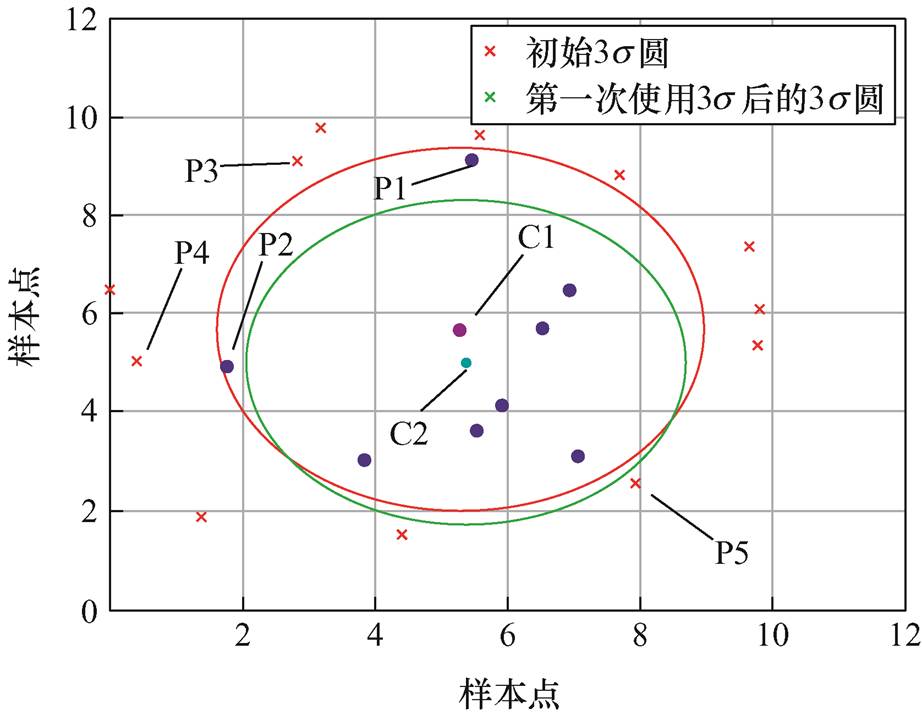
图4 剔除离群点后的中心点对比
Fig.4 Comparison of center points after removing outliers
根据3s-MSS原则进行故障数据筛选并进行故障频率统计的计算流程如下:
(1)根据电动汽车的实时电压数据计算电芯电压的平均值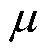 和标准差
和标准差 ,构造
,构造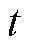 个时刻
个时刻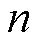 个单体电压原始数据的矩阵为
个单体电压原始数据的矩阵为
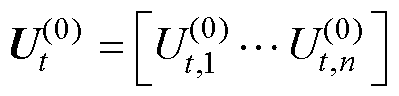 (21)
(21)
(2)根据所有样本数据计算电芯电压的平均值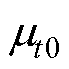 和标准差
和标准差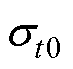 ,计算每一个时刻电芯电压数据
,计算每一个时刻电芯电压数据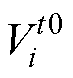 与
与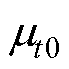 的差值,即
的差值,即
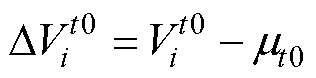 (22)
(22)
(3)通过对比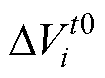 的绝对值与3
的绝对值与3 的大小,可以得到一个新的电压数据矩阵为
的大小,可以得到一个新的电压数据矩阵为
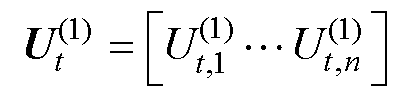 (23)
(23)
(4)根据所有样本数据计算电芯电压的平均值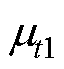 和标准差
和标准差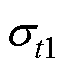 ,计算每一个时刻电芯电压数据
,计算每一个时刻电芯电压数据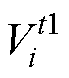 与
与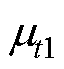 的差值,即
的差值,即
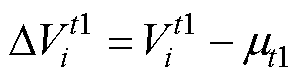 (24)
(24)
(5)对数据筛选处理重复步骤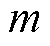 次。得到最终的高斯分布,通过对比
次。得到最终的高斯分布,通过对比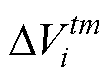 与3
与3 的绝对值的大小,可以得到最终的电压数据矩阵为
的绝对值的大小,可以得到最终的电压数据矩阵为
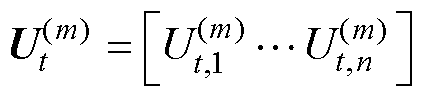 (25)
(25)
(6)判断收敛条件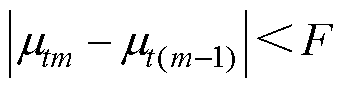 是否成立,F为相似相容度,根据本文数据,F=0.001;若不满足,则迭代计算步骤(5)。
是否成立,F为相似相容度,根据本文数据,F=0.001;若不满足,则迭代计算步骤(5)。
(7)根据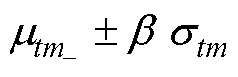 比较最终矩阵中的数据。其中,
比较最终矩阵中的数据。其中,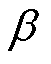 为经验系数,
为经验系数,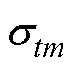 为达到收敛条件时的最终矩阵
为达到收敛条件时的最终矩阵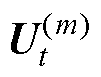 的标准差。在此范围之外,诊断模型返 回1。在此范围内,诊断模型返回0,如式(26)所示。该过程构建超出t时刻电压数据阈值的故障矩阵用式(27)表示。
的标准差。在此范围之外,诊断模型返 回1。在此范围内,诊断模型返回0,如式(26)所示。该过程构建超出t时刻电压数据阈值的故障矩阵用式(27)表示。
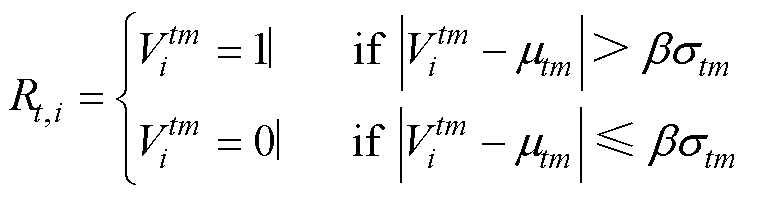 (26)
(26)
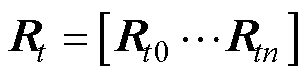 (27)
(27)
对于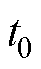 ~
~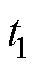 时期的数据,从步骤(1)~步骤(6)进行循环计算,得到这段时间的故障矩阵为
时期的数据,从步骤(1)~步骤(6)进行循环计算,得到这段时间的故障矩阵为
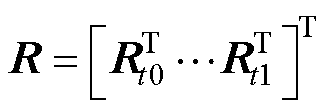 (28)
(28)
通过对故障矩阵的故障概率统计分析,可以得到电池包内各单体电池在一段运行时间内的故障概率变化情况。分析电池单体的故障概率,可以推测电池故障概率异常变化的原因,同时可以评估整个电池包的可靠性。这有助于设计更可靠、稳定的电池系统,并为电池系统改进提供数据支持。
本节以监控平台中某一辆电动车电池组内某一电池包中30串单体电池一个月的运行数据为例,基于本文提出的电池异常检测与诊断方法对其中一个电池包中的30个串联单体进行了结果分析。其中每个采样时刻可以采集到30个单体电池的电压数据。
首先利用t-SNE算法对该电池包中的30串单体电池电压数据进行降维,可视化结果如图5所示。可知30串单体电池电压数据组成的数据集被压缩成了二维,能够直观地在平面中观察数据点的分布情况,所有的高维电压数据大致被压缩成了二维平面中三个数据簇,通过观察发现,其中部分数据簇呈现出与主要数据簇远离的趋势,如图5中的数据簇1与数据簇2,同时部分数据点也呈现出远离数据簇的趋势,如图5中的数据点1和数据点2,相比于高维的电压数据分布,此类数据簇和数据点可能是由于数据异常导致,利用t-SNE技术进行电压数据降维可视化后,有助于发现数据中的聚类结构,即相似的数据点在降维后可能会聚集在一起,这有助于识别潜在的群集或类别,同时提高了数据计算效率。通过t-SNE进行电压数据降维后可以观察到所有单体电池的数据分布情况以及聚类结构,需要进一步进行聚类分析来检测单体电池是否发生异常。
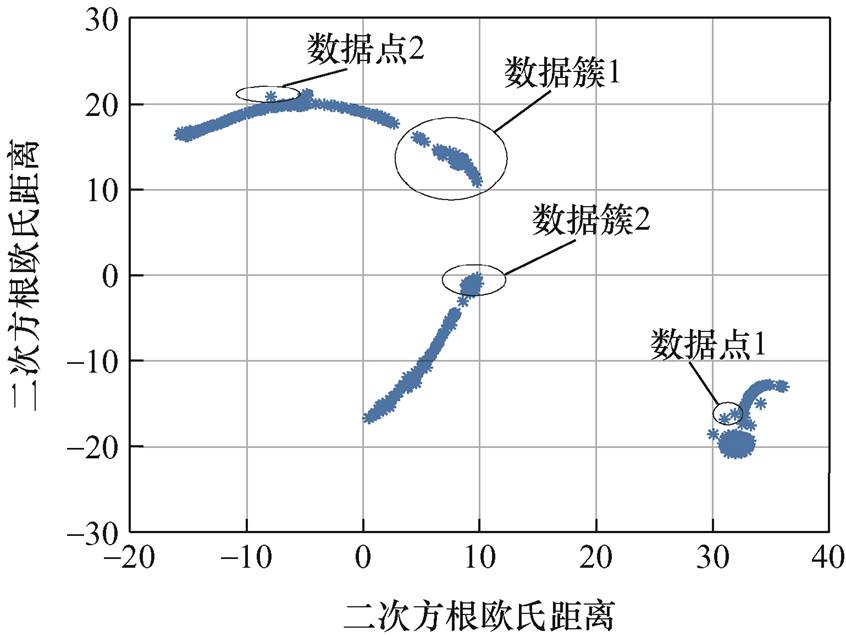
图5 数据降维可视化
Fig.5 Visualization of data dimensionality reduction
利用K均值聚类算法对降维后的30串单体电池电压数据进一步聚类分析,相关的聚类结果如图6所示。可知降维后的电压数据点由于彼此之间的相似性和距离被划分为了三个集群,数据集群分布特点集中且距离数据中心点较近的数据集群为正常集群,如图6中的集群1;集群中一小部分数据独立集成一个群并且与其他群相隔较远,集群中所含数据量较少,这种集群很可能是数据异常导致的,如图6中的异常数据簇1;同一个集群中离正常集群较远,呈现出远离集群的趋势,且数据点分布相比于正常集群比较分散,这些数据则为异常数据,如图6中的异常数据点1和异常数据点2。对该部分异常数据检测分析发现,其来源于该电动车中某电池包2020年6月22日运行期间,后面将进一步对该部分数据进行分析,以便于更为准确地定位到异常单体电池。
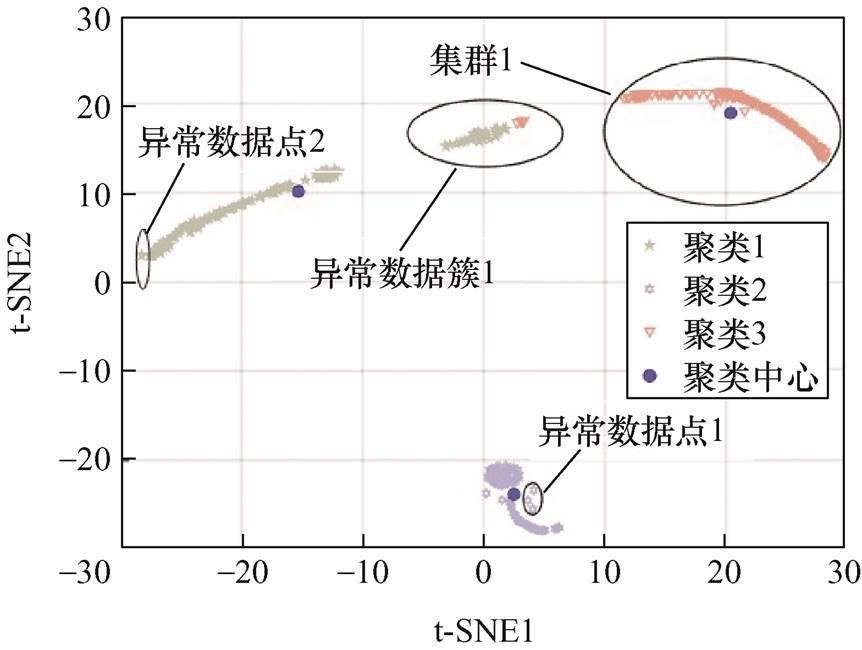
图6 基于t-SNE的K均值聚类分析
Fig.6 K-means cluster analysis based on t-SNE outliers
由于仅根据K均值聚类分析结果,仍无法判断哪些单体发生了异常,为此基于2.3节介绍的Z分数方法对K均值聚类找到的异常数据进行了异常单体的定位。图7为30串单体电池在2020年6月22日一段时间内的电压变化曲线,图8为根据Z分析法计算得到的单体电池异常诊断系数(Z值)结果。
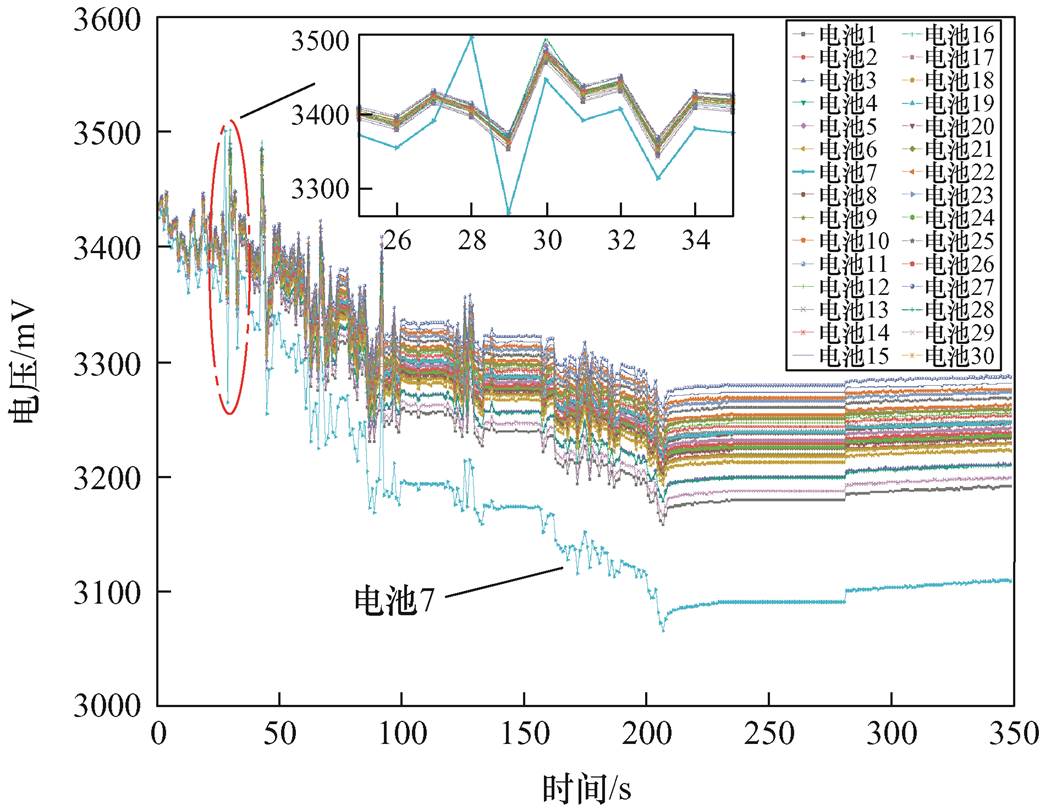
图7 单体电池电压变化曲线
Fig.7 Voltage curves of a single battery
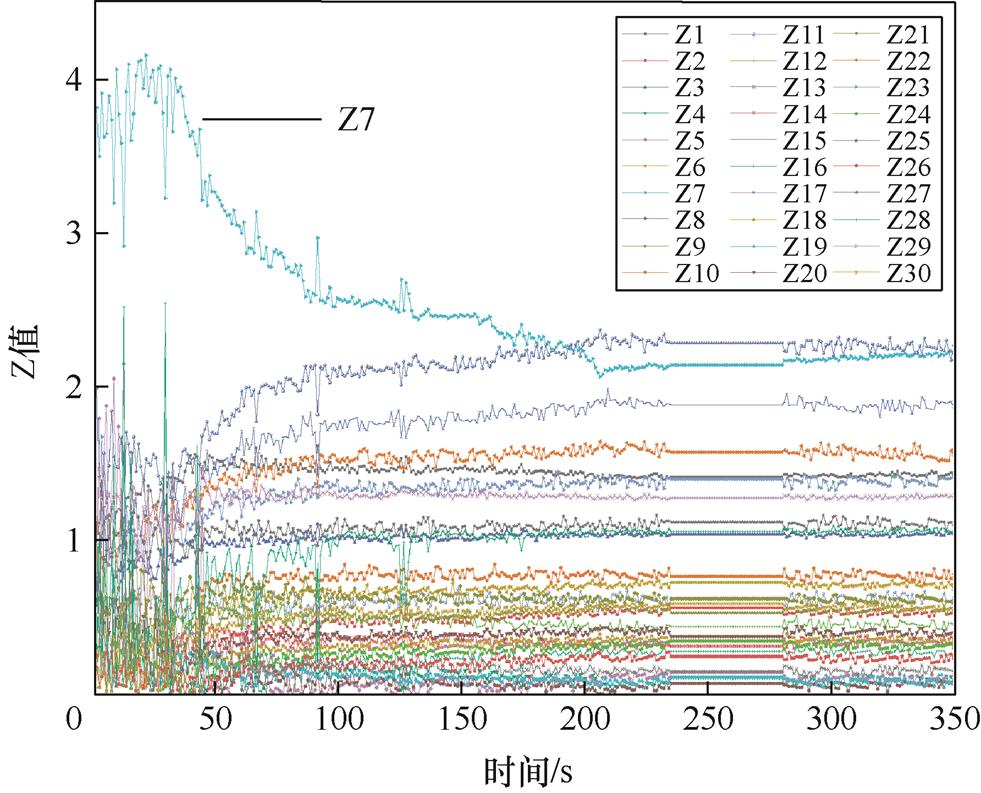
图8 Z值变化曲线
Fig.8 Z-value change curves
从图7可以明显看出,电池包中第7串单体电池的电压为这段时间内所有电压的最小值,电压值明显偏离了其他电芯电压曲线,且第7串单体电池的电压曲线波动较大,在28 s时电压迅速下降,最大压差达到了236 mV,在第207 s时电压降低到最小值3 067 mV。分析认为,这可能是第7串电芯发生故障导致其电气性能下降,所以造成了放电压差过大。根据图8中各单体电池异常诊断系数(Z值)可知,第7串单体电池电压的Z值同样远远大于其他单体电池,且波动较大,进一步说明第7串单体电池发生异常,也表明本文设计的电压异常诊断方法能准确诊断出电压异常并且对故障单体电池进行准确定位。
获取异常电芯编号及位置后,进一步基于2.4节所介绍的熵权-变异系数法对异常单体电池异常程度进行了评估。为分析一段时间内,单体电池数据波动程度,首先根据该电池包内30个单体电池在2020年6月22日的端电压数据,计算获得各单体电池各时刻指标下的权重值,计算结果如图9所示。其中,权重值越低表示单体电池在该时刻的混乱程度越高,权重值越高表明单体电池电压数据越集中。由图9可知,对应的各时刻指标中,第28 s的权值最低,权重值为0.002 4,表明在该时刻电池发生明显波动,可能发生异常或故障。为进一步明确发生故障单体电池的异常程度,根据熵权-变异系数法计算得到各单体电池综合评价分值和综合评价分数差值,结果如图10和图11所示,各单体电池综合得分、得分上限与得分下限计算结果见表1。
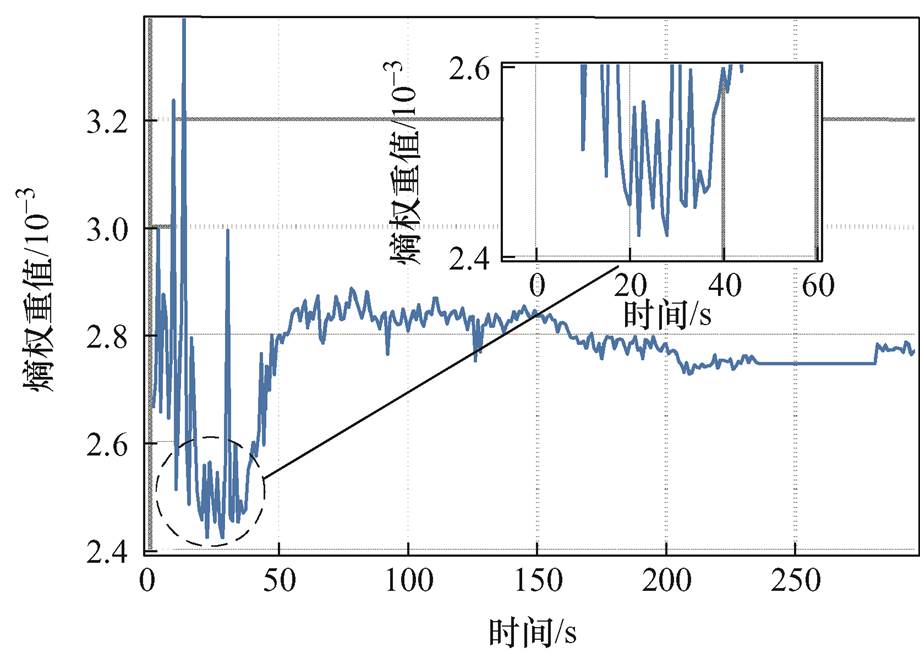
图9 时刻指标下的综合权值
Fig.9 The comprehensive weight under the time metric
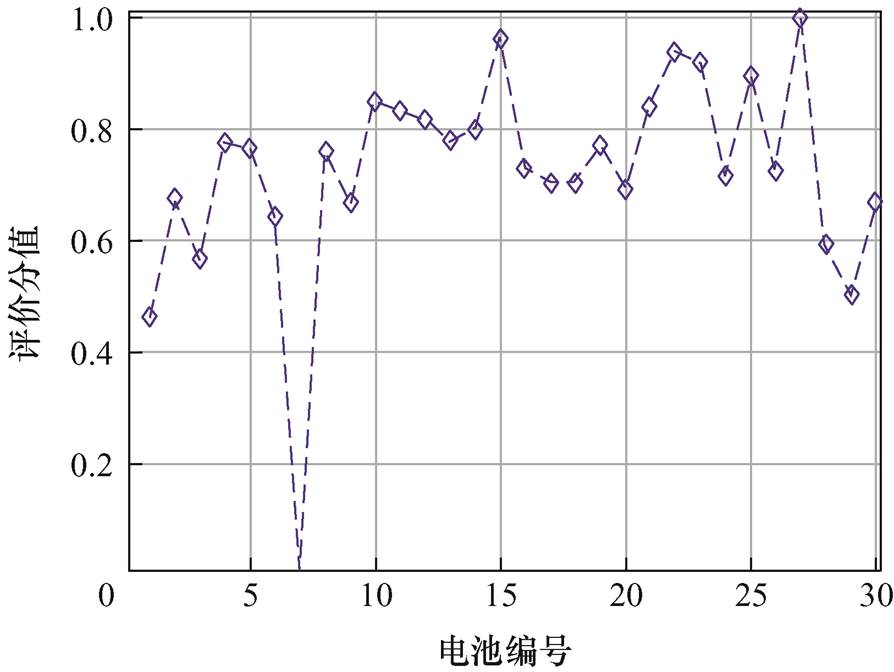
图10 综合评价分值
Fig.10 Comparison of center points after removing outliers
根据表1中部分单体的综合得分、得分上限和得分下限的统计结果可知,各单体之间的得分差值较小,显示出它们在不同指标上的得分相对一致,这反映了各单体在评分上的相似性。也表明它们在受评估指标方面具有相近的表现,得分的上限和下限之间的差异很小,评分的波动范围相对较窄。综合以上结果表明,本文提出的评估方法相对稳定一致,评分结果较为合理和可信。
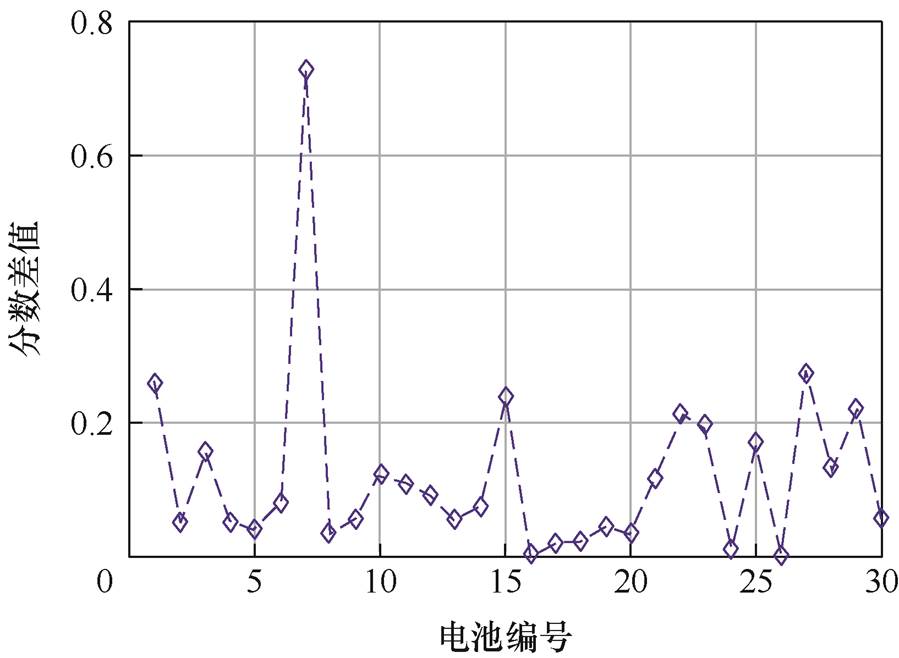
图11 综合评价分数差值
Fig.11 Difference in overall evaluation score
表1 各单体电池综合得分、得分上限与得分下限计算结果
Tab.1 The calculation results for the overall score, upper limit, and lower limit of each individual battery
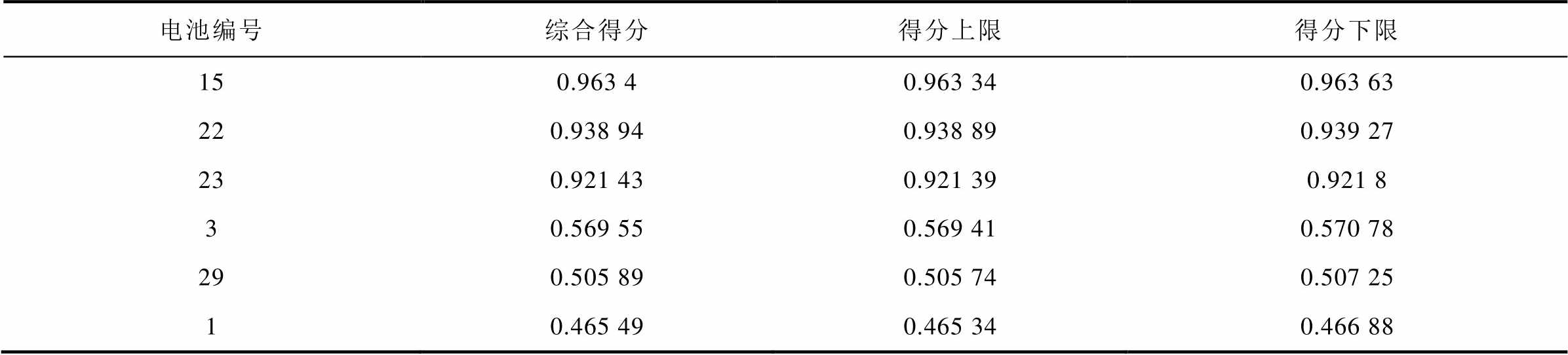
电池编号综合得分得分上限得分下限 150.963 40.963 340.963 63 220.938 940.938 890.939 27 230.921 430.921 390.921 8 30.569 550.569 410.570 78 290.505 890.505 740.507 25 10.465 490.465 340.466 88
通过分析单体电池的综合性能,发现第7串单体电池的评分最低,分数差值最大,达到了0.727的分差,这与设计的异常诊断系数判断定位单体电池异常相对应,同时验证了设计的异常诊断系数能准确定位发生故障的单体电池。
为了判断第7串单体电池是否一直表现出异常性,利用平台获取电动汽车在2020年6月22日、2020年7月9日和2020年7月14日的部分数据源。经过2.4节的处理方法得到各个单体的在该时间段的评价分数差值,见表2。
表2 第7串单体电池在三个时间段的分数差值对比
Tab.2 Comparison of the difference in the scores of the 7 th string of cells in three time periods
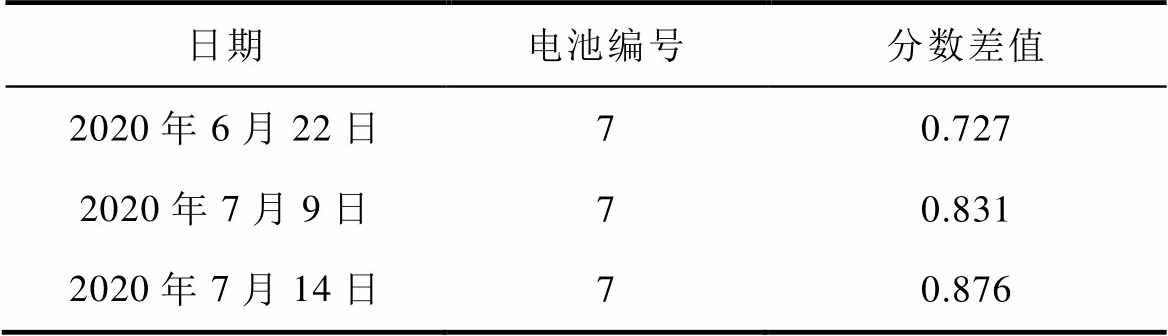
日期电池编号分数差值 2020年6月22日70.727 2020年7月9日70.831 2020年7月14日70.876
从表2中可以看出,随着时间的增加,第7串单体电池出现性能下滑的情况。
通过设计的异常检测与定位方法,检测并定位了发生电压异常变化的电池单体,基于2.5节介绍的基于3s-MSS筛选策略进行了异常电芯的故障概率统计分析,以便进一步地分析导致单体异常及故障的具体原因。
相关文献研究表明,纯电动乘用车的故障类型包括系统性故障和突发性故障[31]。系统性故障是在电动汽车或动力电池的生产过程中,由于电池材料以及设计方案的影响,导致动力电池在性能或质量方面存在差异,造成单体电池在充放电过程中表现出一定程度的不一致性[32],由这类原因导致的电池故障相对比较稳定,电池电压变化相对稳定,由3s-Mass筛选策略统计计算的故障概率也相对地保持在一个稳定区间。突发性故障指车辆在运行过程中,由于遭遇事故等原因造成电池电性能急剧变化的过程,在这种条件下,电池参数发生急剧变化[33],由3s-Mass筛选策略计算的部分单体电池故障概率就会发生相对的巨大变化。图12为同一类型四辆纯电动乘用车在一个月内所有单体电池的故障概率统计结果,根据故障概率分析,总结出以下两种故障情况:
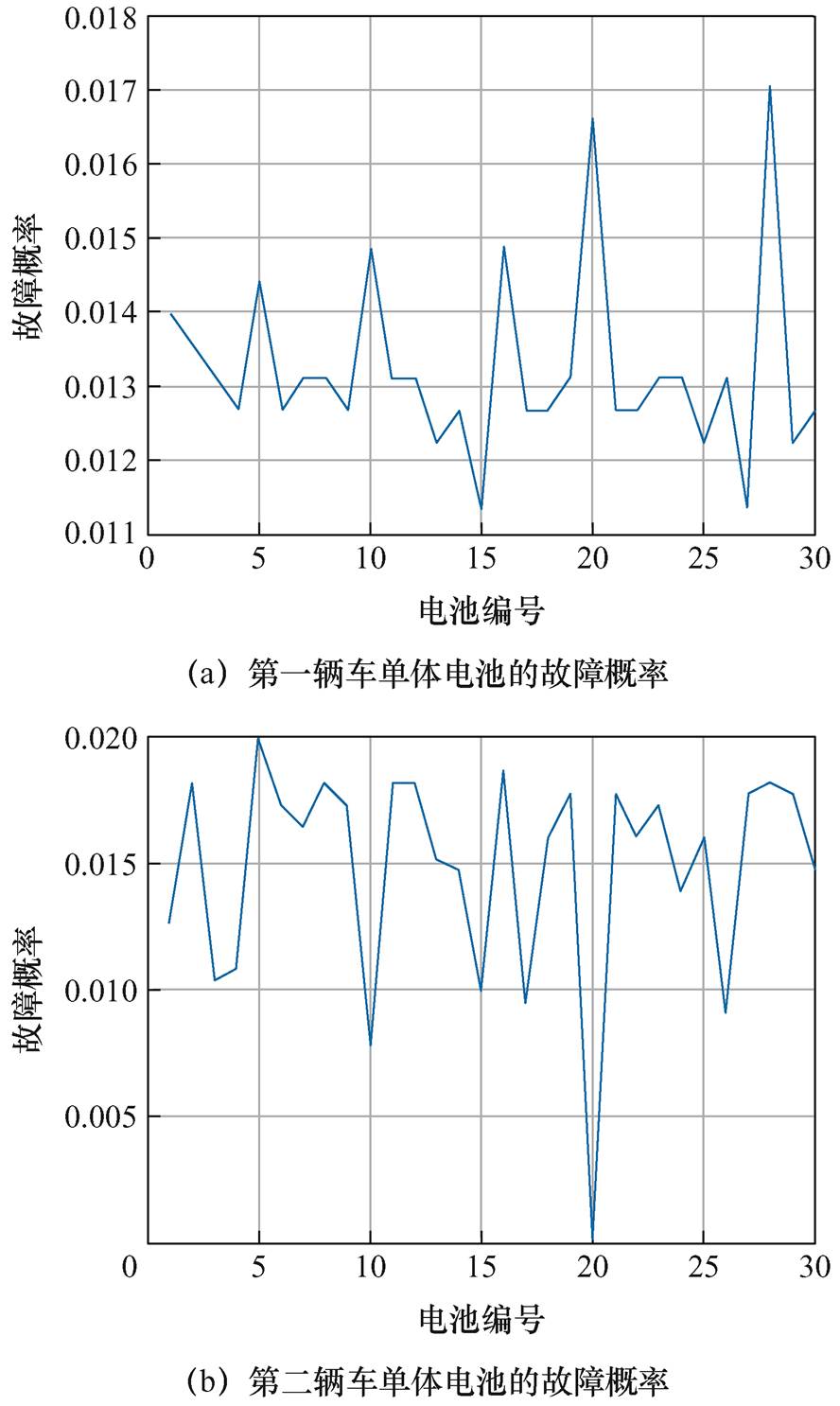
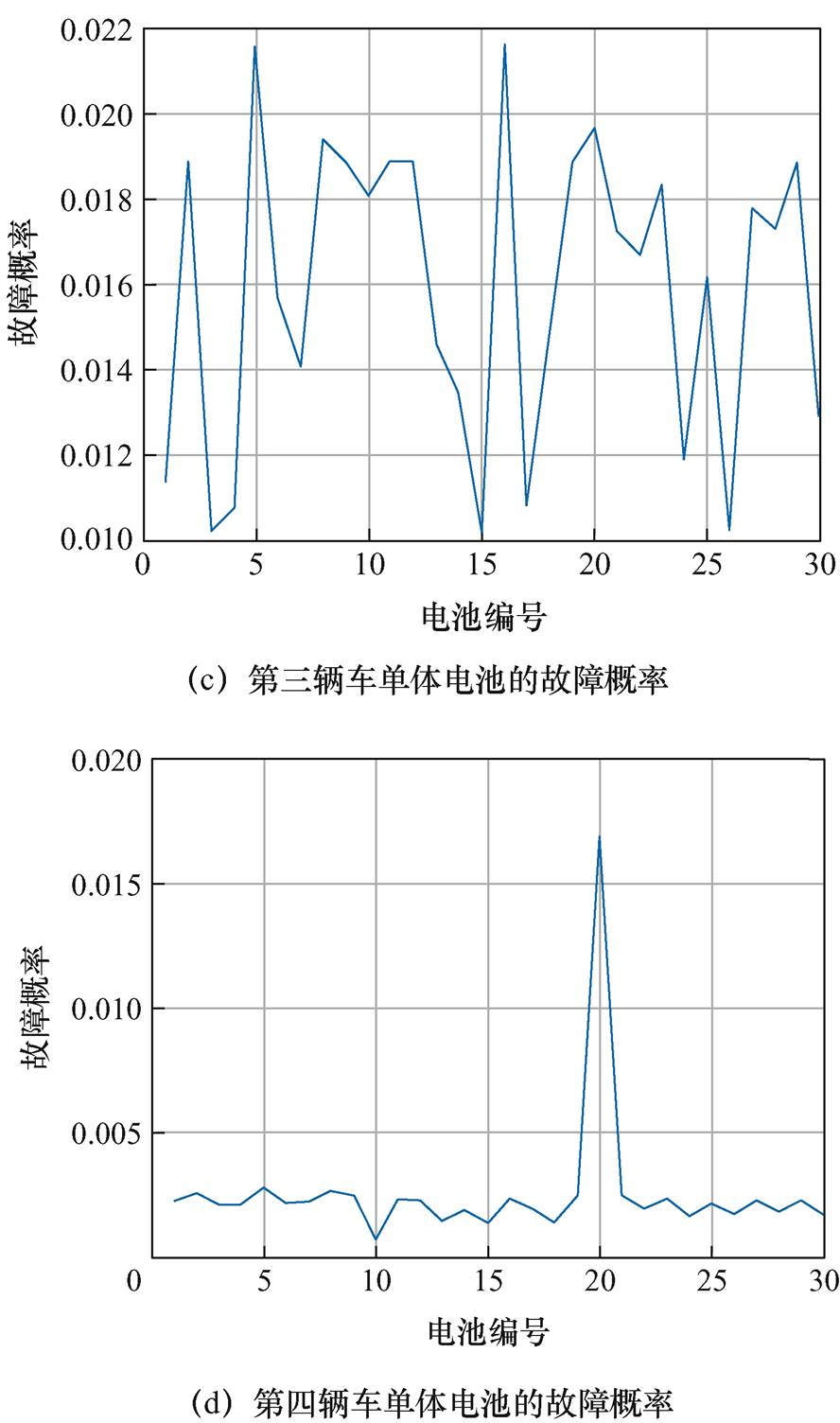
图12 两种故障类型对比
Fig.12 Comparison of the two fault types
(1)一小部分车辆的电池电压往往超过3s 区间,故障概率超过1.5%,且位置并不固定,这种故障极可能是由于电池发生某些意外事故造成的,图12d中,该电池包内除编号为20的电池故障概率为1.7%,其他单体电池的故障概率都在0.5%以下,由此将该类故障定义为突发性故障。
(2)有很大一部分车辆的故障概率在2%以下,且该类型的故障位置是固定的,如图12a、图12b和图12c所示,电池包所有单体电池的故障概率相差较小,且保持在一个较低的水平,这种故障可能是由车辆设计缺陷或某些固有问题引起的,由此将此类故障定义为系统性故障。
为进一步验证本文采用3s-MSS算法进行故障诊断的效果,使用相同的电动汽车电池运行数据与另外两种核心算法对结果进行了比较和验证,包括聚类异常因子(COF)诊断算法,局部离群因子(LOF)诊断算法。该两种诊断算法在数据挖掘和异常检测领域均被广泛应用[34],COF算法通过对数据进行聚类分析,识别数据集中不同聚类之间的异常因子,从而有效地检测出异常样本,其基本思想是利用聚类结构的信息,将异常性定义为样本与其簇内部和其他簇之间的距离之比,从而提高了异常检测的准确性和稳定性。然而,由于COF算法基于簇内数据的方差进行异常评分,对于密度差异较大的簇可能不够敏感,因此在处理包含不同密度簇的数据集时可能表现不佳[35]。相比之下,LOF算法则注重于局部异常检测,通过评估每个样本与其邻近样本之间的密度比来确定异常程度,能够有效地发现那些相对于其周围环境而言密度较低的数据点,从而实现对局部异常的敏感检测。其独特的局部观察方式使得LOF算法在处理复杂数据分布和多密度区域的场景中表现出色,然而,LOF算法对于高维数据的计算复杂度较高,且在处理全局异常时稳定性不够高[36]。需要说明的是,三种方法所采用的数据预处理方法是一致的,动力电池故障诊断结果如图13所示,表3则展示了三类算法的概率最大值和最小值。
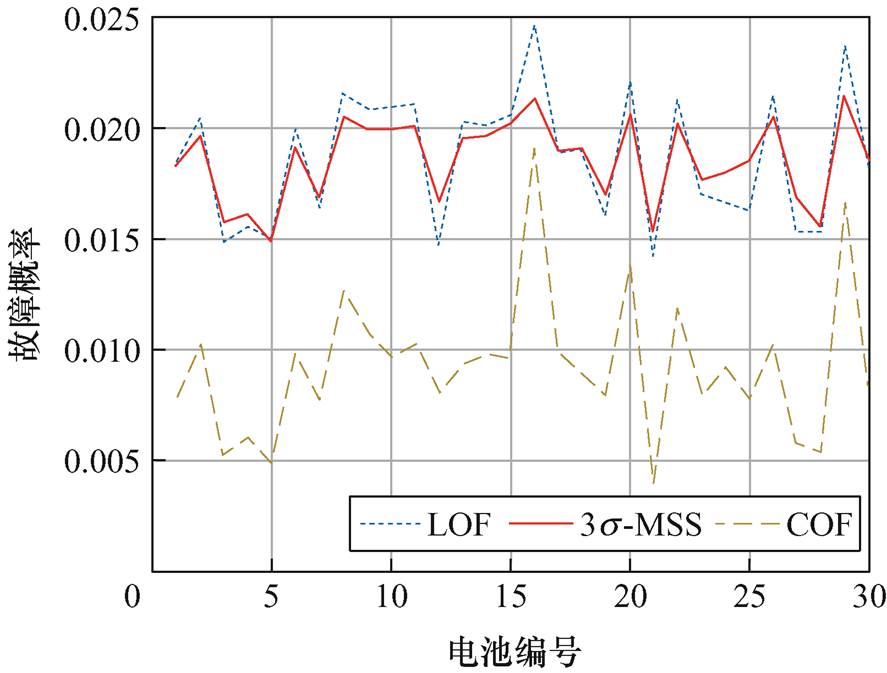
图13 三类算法的故障概率最大值与最小值对比
Fig.13 Fault frequency statistics of the three methods
表3 三类算法的故障概率最大值与最小值对比
Tab.3 The comparison of maximum and minimum fault frequencies among three types of algorithms

算法类型最大值最小值 3s-MSS0.021 30.015 3 COF0.019 10.004 0 LOF0.024 70.014 3
由图13可知,三种方法的结果非常相似,表明三种方法均能实现对单体电池故障的诊断和定位。然而,COF算法故障概率明显偏低,表明其对于低故障概率事件诊断不准确,出现这种情况的主要原因是当离群点的数量很小时,聚类的数量是冗余的。由三种方法的诊断来看,各单体电池最高频率和最低频率都分别发生在第16串和第21串单体电池中。根据表2中三类算法的概率最大值与最小值对比可知,在故障概率较高的情况下,LOF算法诊断结果偏高,与3s-MSS、COF两种算法的最大值差值较大,分别达到了0.003 4与0.005 6;在概率较低的情况下,LOF的算法诊断结果适中,与3s-MSS算法诊断结果接近,差值仅为0.001 0,表明LOF算法在低概率故障下性能更好,但在高故障概率下不稳定,易导致故障概率结果诊断过高。3s-MSS算法的结果则在高和低故障概率统计中都相对稳定,表明本文选择的3s-MSS算法用于电池单体的故障诊断与概率统计分析具有更好的表现。
为了分析电动汽车电池故障在长时间内的特征和变化,基于本文所建立的故障诊断与异常检测模型,在季节性时间维度上开展了电池故障诊断分析,以获取不同季节下动力电池故障特征,为动力电池安全使用提供参考。将采集的10辆同类型纯电动乘用车三个年度内动力电池数据按春、夏、秋、冬四个季节进行诊断统计,获取的故障频率诊断分布结果如图14所示。同时,对其中第四辆车三个年度内电池运行数据进行了故障频率诊断,其分布结果如图15所示。
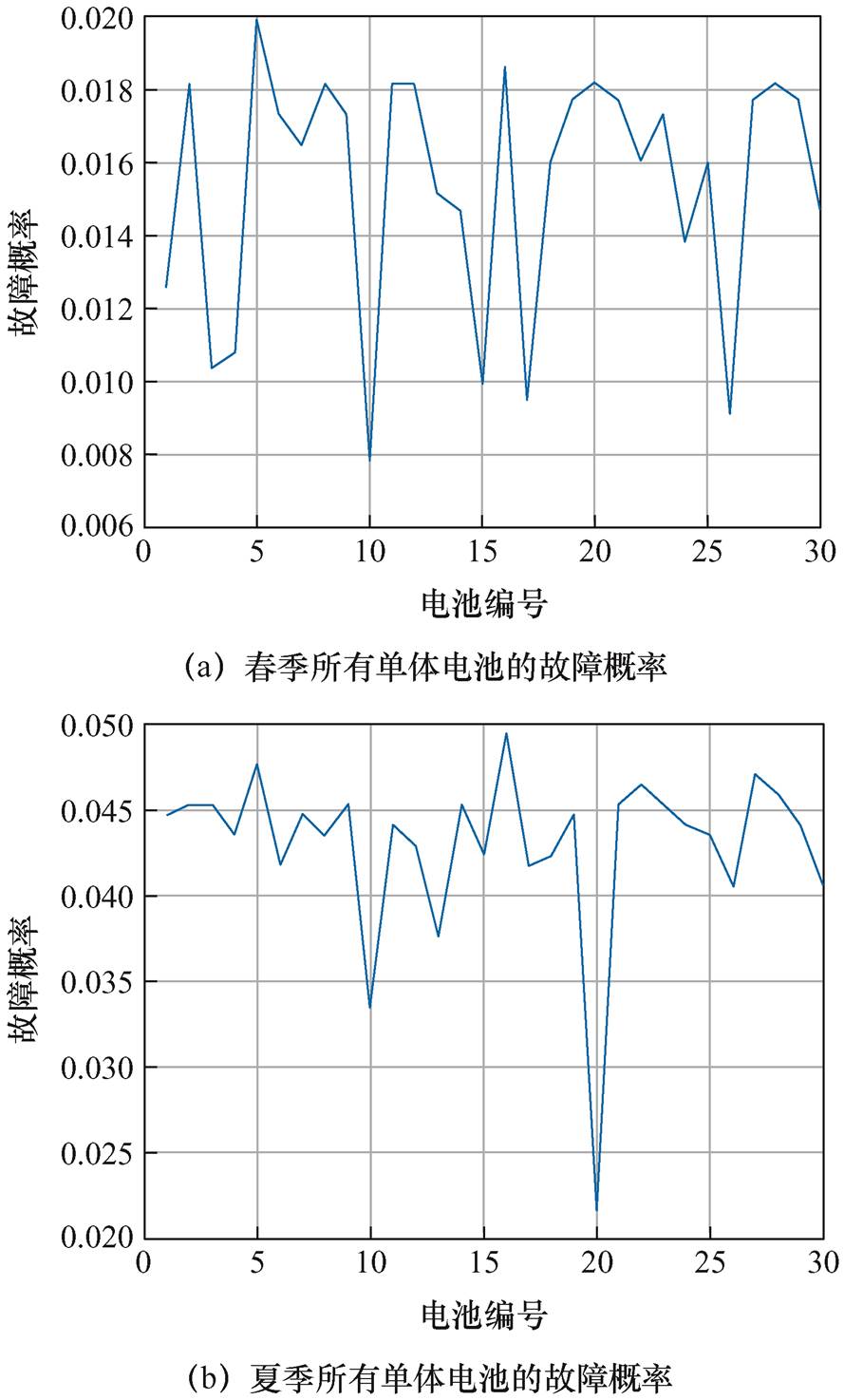
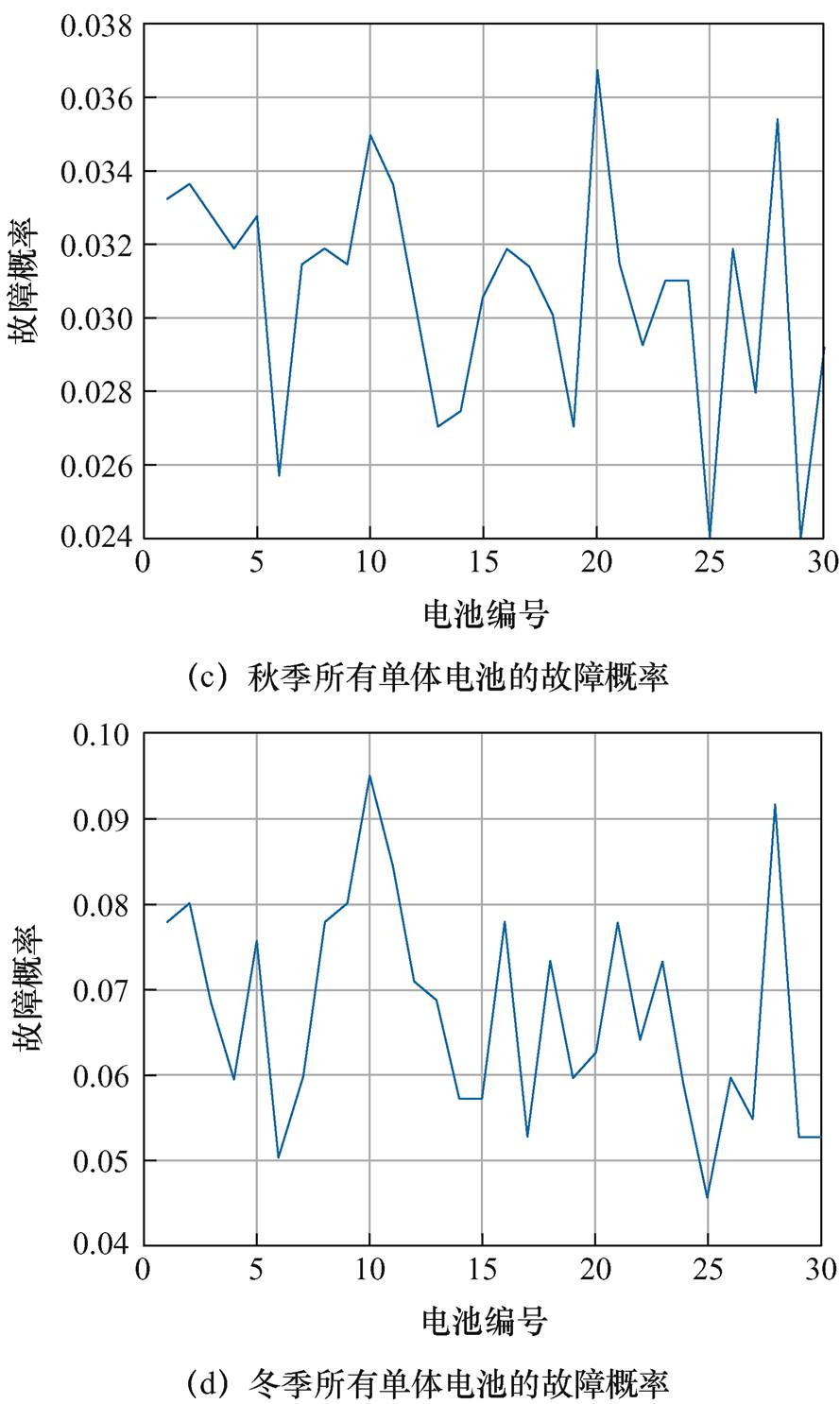
图14 不同季节故障概率统计分布
Fig.14 Statistical distribution of failure probability in different seasons
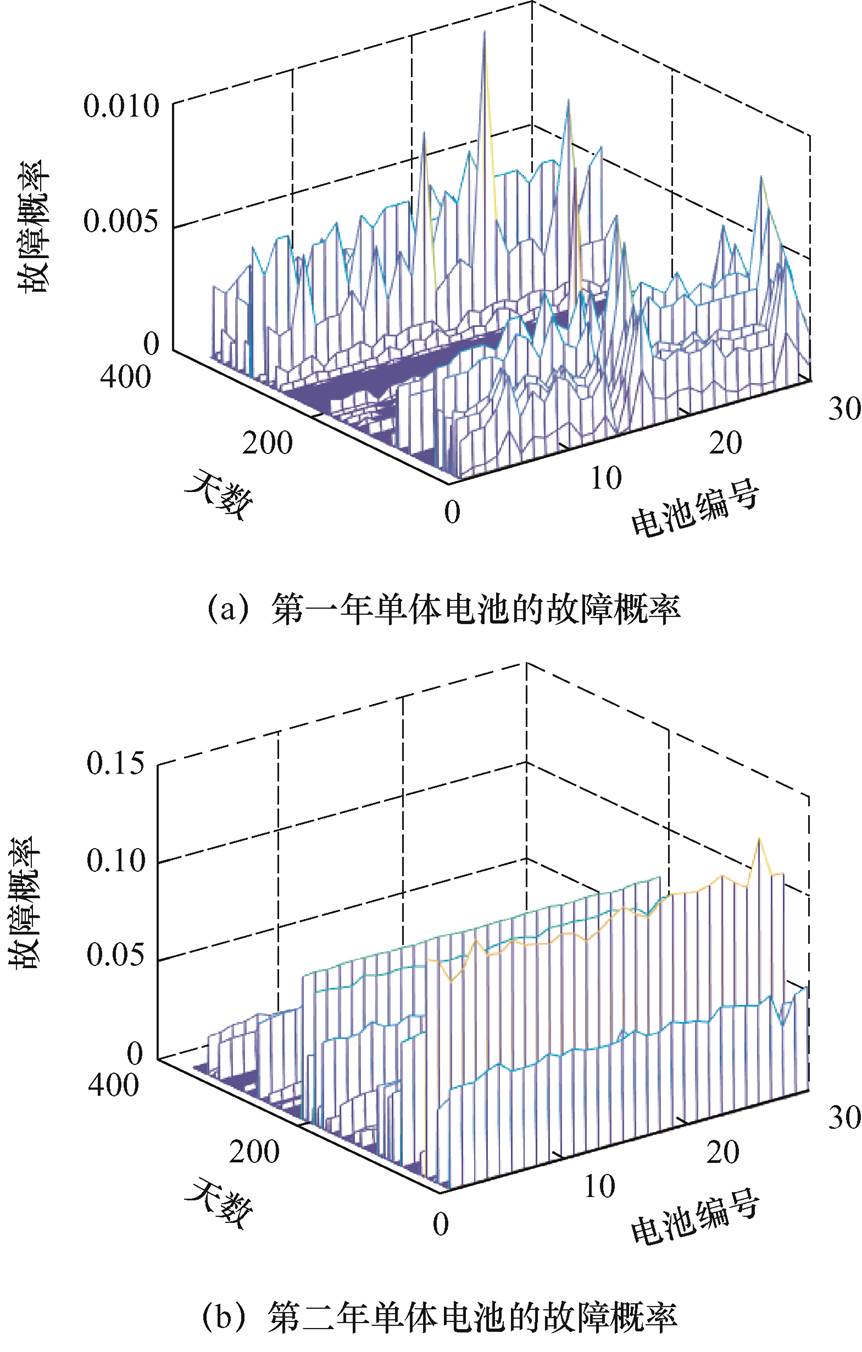
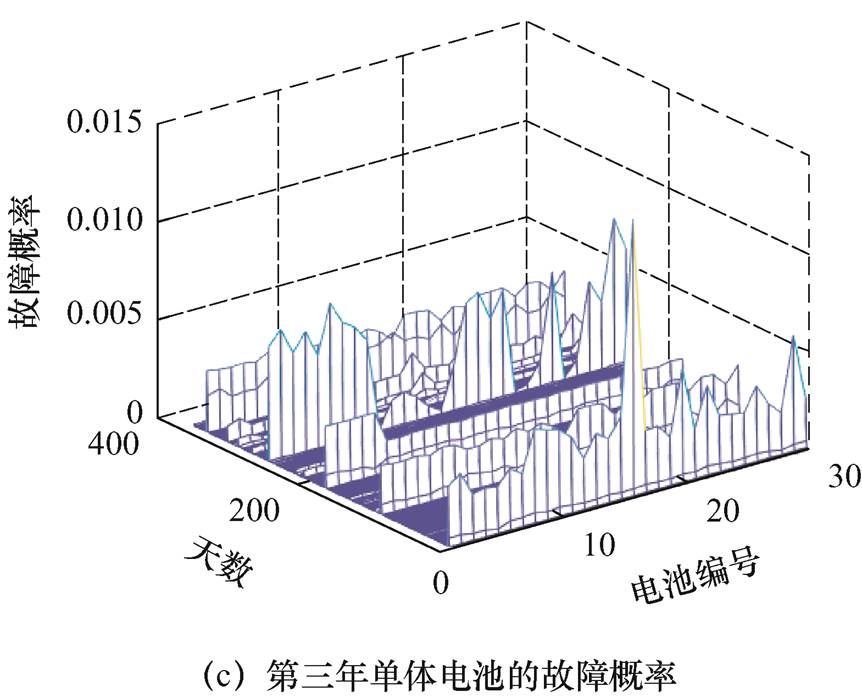
图15 第四辆车三年内电池数据的故障概率统计分布
Fig.15 Statistical distribution of failure probability for all data acquisition cycles
由图14可知,车辆在春、夏、秋、冬四个季节故障概率分布中,最高故障概率分别为1.99%、4.95%、3.67%、9.52%,平均故障概率为1.54%、4.31%、3.07%、4.59%。根据故障概率统计可知,夏、冬两个季节平均故障概率普遍偏高,且出现最高故障概率的单体电芯也在这两个季节,这是由于夏季高温可能导致电池包内温度升高,这对电池的性能和寿命都有负面影响,高温会加速电池自身的化学反应,导致电池容量下降和电阻增加,在高温条件下,电池的循环寿命可能缩短,且更容易发生内部故障,例如,正极和负极之间的短路。冬季低温可能导致电池在起动和工作时性能不佳,甚至在极端情况下可能无法正常工作。此外,低温还可能导致电池包中的电解液变得粘稠,影响电池的正常充放电过程,例如,发生过充、过放等故障。在夏、冬两个季节的温度变化过程中,容易导致电池性能下降,故障概率升高。在图14a~图14c中,各单体电池的故障概率变化相对较小,最高故障概率与平均故障概率差值最大为0.64%,由于单体间的不一致性影响,各单体间的故障概率又有所区别,在图14d中,第10串和第28串单体电池的故障概率与平均故障概率差值达到了4.93%和4.58%,可能是由于电池发生某些意外事故造成的。
为进一步分析不同季节下电池故障频率特性,对其中第四辆车三个年度内电池运行数据进行了故障频率诊断,其分布结果如图15所示。由诊断结果可知,第一年中第19串电池在第281天故障概率最高,为2%;基于3s-MSS的电池故障诊断结果表明,该类故障概率较低,且在整个故障概率统计周期内的故障概率都低于2%,可能是由于车辆设计缺陷或某些固有问题引起的造成的。第二年中第28串电池在第36天故障概率最高,为12.69%;基于3s-MSS的电池故障诊断结果表明,该类故障与同一天的所有单体电池的平均故障概率4.17%相比,故障概率差值达到了8.52%,可能是由于电池发生某些意外影响造成的。第三年中第16串电池在第6天故障概率最高,为14.14%;基于3s-MSS的电池故障诊断结果表明,该类故障与同一天的所有单体电池的平均故障概率3.71%相比,故障概率差值达到了10.43%,可能是由于电池发生某些意外影响造成的。以上分析综合表明,本文所设计的基于数据挖掘与大数据分析的电池故障诊断与异常检测方法可以实现对电池异常状态的准确定位,计算故障概率,并估计故障类型。通过对大数据平台大量运行数据的持续故障分析与诊断,有助于针对性的采取相应电池安全管理措施,保证车辆稳定安全运行。
本文基于数据监控平台收集的数据,提出了一种基于数据挖掘和大数据分析的车载动力电池故障诊断方法。该方法相比于传统的故障诊断方法,无需建立复杂的电池模型,易于实现,能够完成异常单体电池的异常检测-定位-诊断的全方面分析,异常检测与故障诊断方面效率高,鲁棒性较强,具有明显的优势。同时,本文对所提出的故障诊断与异常检测方法的原理进行了详细阐述,并应用于实车数据中。基于K均值聚类算法与Z分数方法设计异常诊断系数,再通过熵权法和异常系数法进行单体电池的综合性能评估,实现了异常单体电芯的准确定位与有效检测,利用3s-MSS算法,建立了电池故障诊断无故障电池终端电压的标准,准确定义了两种异常电压故障类型,其中通过一段时间内的概率统计结果表明,一小部分车辆的电池电压往往超过3s 区间,故障概率超过15%,且位置并不固定,这种故障极可能是由于电池发生某些意外事故造成的;有很大一部分车辆的故障概率在2%以下,且该类型的故障位置是固定的,这种故障可能是由车辆设计缺陷或某些固有问题引起的。
通过与聚类离群分析和局部离群因子分析两种故障诊断方法对比,进一步验证了诊断模型的有效性和准确性。此外,从全年平台运行数据对不同季节的单体电池进行了故障概率分析,车辆在春、夏、秋、冬四个季节故障概率分布中,单体电池最高故障概率分别为1.99%、4.95%、3.67%、9.52%,平均故障概率为1.54%、4.31%、3.07%、4.59%,春、秋两季故障发生概率差异不大,故障发生的概率相对较低。然而,在夏、冬两季电池故障发生概率相对较高。针对不同季节下电池故障概率可以针对性地优化维护策略,以确保系统的可靠性并降低维护成本。未来将更加关注夏季、冬季电池故障的发生,挖掘故障高发的原因。此外,如何实现对突发故障的提前预警,降低突发故障发生的频次也是未来研究关注的重要方向之一。
参考文献
[1] 王震坡, 李晓宇, 袁昌贵, 等. 大数据下电动汽车动力电池故障诊断技术挑战与发展趋势[J]. 机械工程学报, 2021, 57(14): 52-63.
Wang Zhenpo, Li Xiaoyu, Yuan Changgui, et al. Challenge and prospects for fault diagnosis of power battery system for electrical vehicles based on big-data[J]. Journal of Mechanical Engineering, 2021, 57(14): 52-63.
[2] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[3] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和降噪自编码器-长短时间记忆的锂离子电池剩余寿命预测[J].电工技术学报, 2024, 39(1): 289-302.
Yin Jie, Liu Bo, Sun Guobing, et al. Transfer learning denoising autoencoder-long short term memory for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 289-302.
[4] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342.
Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium- ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342.
[5] Sun Zhenyu, Wang Zhenpo, Liu Peng, et al. An online data-driven fault diagnosis and thermal runaway early warning for electric vehicle batteries[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12636-12646.
[6] Tran M K, Fowler M. A review of lithium-ion battery fault diagnostic algorithms: current progress and future challenges[J]. Algorithms, 2020, 13(3): 62-80.
[7] Chen Kui, Liao Qiang, Liu Kai, et al. Capacity degradation prediction of lithium-ion battery based on artificial bee colony and multi-kernel support vector regression[J]. Journal of Energy Storage, 2023, 72: 108160.
[8] 杨梦洁, 杨爱军, 叶奕君, 等. 基于气体分析的锂离子电池热失控早期预警研究进展[J]. 电工技术学报, 2023, 38(17): 4507-4538.
Yang Mengjie, Yang Aijun, Ye Yijun, et al. Research progress on early warning of thermal runaway of Li-ion batteries based on gas analysis[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4507-4538.
[9] Jiang Jiuchun, Li Taiyu, Chang Chun, et al. Fault diagnosis method for lithium-ion batteries in electric vehicles based on isolated forest algorithm[J]. Journal of Energy Storage, 2022, 50: 104177.
[10] Jiang Jiuchun, Cong Xinwei, Li Shuowei, et al. A hybrid signal-based fault diagnosis method for lithium-ion batteries in electric vehicles[J]. IEEE Access, 2021, 9: 19175-19186.
[11] XiongRui, Pan Yue, Shen Weixiang, et al. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: recent advances and perspectives[J]. Renewable and Sustainable Energy Reviews, 2020, 131: 110048.
[12] 徐佳宁, 梁栋滨, 魏国, 等. 串联电池组接触电阻故障诊断分析[J]. 电工技术学报, 2017, 32(18): 106-112.
Xu Jianing, Liang Dongbin, Wei Guo, et al. Series battery pack’s contact resistance fault diagnosis analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 106-112.
[13] Ma Mina, Duan Qiangling, Li Xiaoyu, et al. Fault diagnosis of external soft-short circuit for series connected lithium-ion battery pack based on modified dual extended Kalman filter[J]. Journal of Energy Storage, 2021, 41: 102902.
[14] Yu Quanqing, Dai Lei, Xiong Rui, et al. Current sensor fault diagnosis method based on an improved equivalent circuit battery model[J]. Applied Energy, 2022, 310: 118588.
[15] Wang Yujie, Tian Jiaqiang, Chen Zonghai, et al. Model based insulation fault diagnosis for lithium-ion battery pack in electric vehicles[J]. Measurement, 2019, 131: 443-451.
[16] Feng Xuning, Pan Yue, He Xiangming, et al. Detecting the internal short circuit in large-format lithium-ion battery using model-based fault-diagnosis algorithm[J]. Journal of Energy Storage, 2018, 18(4): 26-39.
[17] Schmid M, Gebauer E, Hanzl C, et al. Active model-based fault diagnosis in reconfigurable battery systems[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 2584-2597.
[18] Chatterjee S, Kumar Gatla R, Sinha P, et al. Fault detection of a Li-ion battery using SVM based machine learning and unscented Kalman filter[J]. Materials Today: Proceedings, 2023, 74: 703-707.
[19] 刘嘉蔚, 李奇, 陈维荣, 等. 基于在线序列超限学习机和主成分分析的蒸汽冷却型燃料电池系统快速故障诊断方法[J]. 电工技术学报, 2019, 34(18): 3949-3960.
Liu Jiawei, Li Qi, Chen Weirong, et al. Fast fault diagnosis method of evaporatively cooled fuel cell system based on online sequential extreme learning machine and principal component analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3949-3960.
[20] Shang Yunlong, Lu Gaopeng, Kang Yongzhe, et al. A multi-fault diagnosis method based on modified sample entropy for lithium-ion battery strings[J]. Journal of Power Sources, 2020, 446: 227275.
[21] Samanta A, Chowdhuri S, Williamson S S. Machine learning-based data-driven fault detection/diagnosis of lithium-ion battery: a critical review[J]. Electronics, 2021, 10(11): 1309-1326.
[22] 黄凯, 丁恒, 郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766.
Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753-3766.
[23] Zhou Shiyao, Chen Ziqiang, Lin Tiantian. Lithium- ion battery cell open circuit fault diagnostics: methods, analysis, and comparison[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 2493-2505.
[24] Yao Lei, Fang Zhanpeng, Xiao Yanqiu, et al. An intelligent fault diagnosis method for lithium battery systems based on grid search support vector machine[J]. Energy, 2021, 214: 118866.
[25] Yao Lei, Xiao Yanqiu, Gong Xiaoyun, et al. A novel intelligent method for fault diagnosis of electric vehicle battery system based on wavelet neural network[J]. Journal of Power Sources, 2020, 453: 227870.
[26] Li Xiaoyu, Wang Zhenpo. A novel fault diagnosis method for lithium-ion battery packs of electric vehicles[J]. Measurement, 2018, 116: 402-411.
[27] Zhao Yang, Liu Peng, Wang Zhenpo, et al. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods[J]. Applied Energy, 2017, 207: 354-362.
[28] Yao Lei, Xu Shiming, Xiao Yanqiu, et al. Fault identification of lithium-ion battery pack for electric vehicle based on GA optimized ELM neural network[J]. IEEE Access, 1809, 10: 15007-15022.
[29] Kobak D, Berens P. The art of using t-SNE for single-cell transcriptomics[J]. Nature Communications, 2019, 10: 5416.
[30] Kuraria A, Jharbade N, Soni M. Centroid selection process using WCSS and elbow method for K-mean clustering algorithm in data mining[J]. International Journal of Scientific Research in Science, Engineering and Technology, 2018, 4(11): 190-195.
[31] Xiong Rui, Sun Wanzhou, Yu Quanqing, et al. Research progress, challenges and prospects of fault diagnosis on battery system of electric vehicles[J]. Applied Energy, 2020, 279: 115855.
[32] Qiu Yishu, Cao Wenjiong, Peng Peng, et al. A novel entropy-based fault diagnosis and inconsistency evaluation approach for lithium-ion battery energy storage systems[J]. Journal of Energy Storage, 2021, 41: 102852.
[33] Lan Jiamei, Wei Ruichao, Huang Shenshi, et al. In-depth bibliometric analysis on research trends in fault diagnosis of lithium-ion batteries[J]. Journal of Energy Storage, 2022, 54: 105275.
[34] 刘座辰, 林磊, 殷天翔, 等. 一种模块化多电平换流器子模块开路故障的快速检测与诊断方法[J]. 电工技术学报, 2022, 37(19): 4883-4894.
Liu Zuochen, Lin Lei, Yin Tianxiang, et al. A fast open-circuit fault detection and diagnosis method for sub-modules of modular multilevel converters[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4883-4894.
[35] Nowak-Brzezińska A, Horyń C. Exploration of outliers in if-then rule-based knowledge bases[J]. Entropy, 2020, 22(10): 1096.
[36] Wang Hongzhi, Bah M J, Hammad M. Progress in outlier detection techniques: a survey[J]. IEEE Access, 2019, 7: 107964-108000.
Abstract Due to various environmental and operating conditions,traditional battery fault diagnosis is challenging with the development of electrification, intelligence, connectivity, and digitization in the automotive industry. This paper proposes a battery fault diagnosis and anomaly detection method based on data mining and extensive data analysis. The approach involves operational data collection from the power battery through an electric vehicle cloud monitoring platform and a comprehensive analysis of anomaly detection, localization, and diagnosis for individual battery cells.
Firstly, t-SNE is used to visualize the dimension reduction of battery cell data, compressing high- dimensional cell voltage data into low-dimensional data. Then, the K-means algorithm is applied for clustering analysis. Combined with the principles of Gaussian distribution and Z-score, diagnostic coefficients are designed to locate abnormal batteries. Subsequently, the entropy-weighted coefficient of the variation method is used to assess the degree of abnormality for each battery cell. Finally, a diagnostic standard is established using the 3s-MSS filtering strategy. Compared to the COF and LOF algorithms based on statistical processing of the fault matrix, the proposed method compresses the voltage data of 30 series of individual batteries into two dimensions and effectively detects abnormal battery cells. For a specific period, the voltage curve of the 7th series of individual batteries exhibits significant fluctuations, with a rapid voltage drop at the 28th and 207th seconds, reaching a maximum voltage difference of 236 mV. The Z-value in the diagnostic coefficient designed based on the Z-score for the 7th series of individual batteries is significantly higher than other cells, indicating an anomaly. The overall score for the 7th series in the battery comprehensive evaluation shows a score difference of 0.727. Using the 3s-MSS filtering strategy for fault probability statistics, a small percentage of vehicles show a battery fault probability exceeding 15% with variable positions likely resulting from unexpected accidents. Most vehicles have a fault frequency below 2%, and the positions of such faults are fixed, possibly due to vehicle design defects or inherent issues. According to the diagnostic results, the 3s-MSS filtering strategy is suitable for fault probability statistics in batteries. In the time dimension of fault probability statistics, the fault probabilities in spring, summer, autumn, and winter are 1.99%, 4.95%, 3.67%, and 9.52%, respectively, with average fault probabilities of 1.54%, 4.31%, 3.07%, and 4.59%.
In conclusion, (1) using t-SNE and K-means for dimension reduction and clustering analysis can effectively detect whether individual battery cells experience anomalies. Additionally, the diagnostic coefficient designed based on the Z-score accurately diagnoses voltage anomalies and locates faulty cells. (2) Compared to LOF and COF algorithms, the 3s-MSS filtering strategy has more apparent advantages and can further identify and diagnose battery fault types for fault probability statistics. (3) Accordingl to the three-year historical operational data of different vehicles, the frequency of faults does not differ significantly between spring and autumn. However, in summer and winter, the frequency of battery faults is relatively high, which provides maintenance recommendations for the stable operation of vehicles.
Keywords:Power battery, data mining, big data, anomaly detection, fault diagnosis
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.231983
云南省基础研究计划项目(202301AT070423)、国家自然科学基金项目(52367021, 52267022)和昆明理工大学自然科学研究基金项目(KK23202202021)资助。
收稿日期2023-12-27
改稿日期 2024-01-10
申江卫 男,1984年生,高级实验师,硕士生导师,研究方向为新能源汽车动力电池管理。E-mail: shenjiangwei6@kust.edu.cn
陈 峥 男,1982年生,教授,博士生导师,研究方向为新能源汽车节能控制与动力电池管理、智能网联汽车优化控制。E-mail: chen@kust.edu.cn(通信作者)
(编辑 陈 诚)