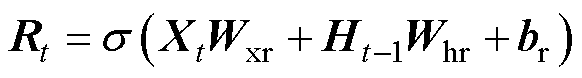 (1)
(1)
摘要 准确的电池健康状态估计可以保证锂离子电池可靠安全运行,减少系统不必要的维护成本。采用机器学习算法虽然能够获得精确的电池健康状态(SOH),但是其估计精度严重依赖于算法中的参数,普适性差,且会受到传感器噪声的影响。该文提出一种结合降噪自编码器(DAE)和门控递归单元的递归神经网络(GRU-RNN)的混合模型进行电池的SOH估计,以提高算法估计精度及抗干扰能力。首先,利用电压-容量模型来重构电池恒流充电和放电阶段的电压曲线,以减小传感器噪声对SOH估计的影响;其次,从电压曲线和增量容量(IC)曲线中提取相关特征作为SOH估计模型的输入;再次,利用DAE对带有噪声的输入特征进行无监督的训练,可以增强模型的鲁棒性;最后,在输入特征含有噪声的情况下,利用提出的DAE-GRU-RNN算法与其他SOH估计算法进行对比验证。结果表明,该文提出的算法精度更高,相对误差比GRU-RNN和深度神经网络(DNN)模型小6.39%~23.23%。利用部分电压曲线获得的特征数据进行电池SOH预测时,该算法依然具有较高的电池SOH估计精度。
关键词:电池健康状态估计 降噪自编码器 门控递归单元的递归神经网络 无监督训练
锂离子电池具有能量密度高、续航能力强、标称电压高、自放电率低、循环时间长、无记忆效应等优点,在纯电动汽车、混合电动汽车、卫星、航空等领域发挥着越来越重要的作用[1-4]。在使用过程中,由于副反应和机械应力的作用,电池会出现容量衰减和内阻增加的现象,可以用健康状态(State of Health, SOH)和剩余使用寿命(Remaining Useful Life, RUL)两个指标来表征这种老化现象[5-7]。SOH定义为当前充放电容量占额定容量的百分比;RUL定义为当SOH下降到80%以下或内阻翻倍时,从当前周期到寿命结束所剩下的循环次数。SOH和RUL的精确估计对确保电池的安全可靠运行有着重要意义[8-9]。近年来,很多学者进行了电池SOH估计和RUL预测的相关研究,可分为基于模型的方法和基于数据驱动的方法两大类,这些方法在准确性、计算复杂度和鲁棒性等方面各有优缺点[10-11]。基于模型的方法通过双指数模型、经验模型、等效电路模型等获取电池衰减的长期依赖性,并结合卡尔曼滤波算法和粒子滤波算法进行模型参数估计[12-16]。A. Allam等[17]提出一种基于电化学模型的自适应互联观测器来估算电池模型参数和容量。尽管电化学模型可以获得较高的估计精度,但是电化学模型参数较多且计算成本较高[18]。因此,一些研究利用双卡尔曼滤波算法和等效电路模型对电池荷电状态(State of Charge, SOC)、模型参数和容量进行实时估计[19-20]。但是以上方法的电池SOH估计精度高度依赖于电池模型的精度。此外,该方法还容易受到外界环境干扰,鲁棒性较差。基于数据驱动的算法采用人工神经网络(Artificial Neural Network, ANN)、支持向量机(Support Vector Machine, SVM)、门控递归(Gated Recurrent Unit, GRU)神经网络、极限学习机(Extreme Learning Machine, ELM)等机器学习算法将可测量信号或老化特征映射到容量退 化[21-23]。Shen Sheng等[24]提出了一种基于深度卷积神经网络集成学习和迁移学习(Deep Convolution Neural Network Ensemble and Transfer Learning, DCNN-ETL)的容量估计方法,解决了数据量小导致的预测不准的问题。Pang Hui等[25]通过贝叶斯优化算法确定了双向长短期记忆(Bidirectional Long Short-Term Memory, BiLSTM)网络的关键超参数,并与传统的长短时记忆(Long Short-Term Memory, LSTM)神经网络进行了比较,提高了模型估计的精度。这些方法都是在直接获得电池可用容量的基础上得到的,但是在电池实际应用中其容量不可测量。为了解决这个问题,Wang Zhenpo等[26]从差分热伏安法曲线中选择4个高质量特征作为模型的输入,然后利用GPR模型来估算电池的SOH。Gou Bin等[27]提出了一种基于集成学习方法和极限学习机方法的SOH估计方法,特征因素选择为相同充电电压范围内的持续时间。在两个公共数据集上的测试验证了该方法的正确性。以上方法均是在一个电池上进行数据集划分,并取得了良好的估计效果。但是存在一个问题,但是在一个电池上进行训练和测试不符合实际应用需求。Shen Sheng等[28]从充电阶段的电流和电压数据中提取特征,然后利用深度CNN模型在不同的电池数据集上进行了仿真验证,从而实现了电池SOH的在线估计。
电池在实际工作过程中会受到环境和传感器精度的影响,测量信号中往往含有大量的噪声。这将给电池SOH健康指标的提取造成一定困难,提取的特征难以获得理想的估计效果。例如,从原始的电流和电压数据中获得的容量增量(Incremental Capacity, IC)曲线存在大量的噪声,将无法准确识别每个峰值的特征信息。为了解决这一问题,一些研究采用了多种滤波方法,如自动平均值滤波算法、高斯滤波算法、Savitzky Golay滤波算法[29-30]。虽然这些方法比较简单,可以消除大部分的噪声,保留了基本的IC轮廓信息。但是以上方法对滤波器的参数较为敏感,不同大小的滤波窗口会有不同的滤波效果。一些研究利用基于模型的方法来获得IC曲线上的峰值、峰值位置和峰面积,如基于高斯函数和洛伦兹函数的电压-容量(Voltage-Capacity, VC)模型[31]。通过重构恒流充电阶段的电压-容量的曲线获得的IC曲线明显要比利用滤波的方式更加平滑,更容易通过获得特征来描述电池的退化现象。Bian Xiaolei等[32]通过人工添加噪声的方式来验证VC模型的可行性和鲁棒性。三个公开数据集的测试结果表明,即使在电流和电压存在噪声的情况下,依然可以获得精确的VC曲线。
机器学习算法虽然能够获得精确的电池SOH,但是模型估计精度严重依赖于算法中的参数。有时训练后的模型在一个测试集上具有较好的估计效果,但在另一个测试集上估计效果就非常差,并不具有一定的普适性。此外,由于电池材料差异或实验设备操作不当等原因,提取的特征数据总会出现一些异常值点,严重偏离电池实际的老化轨迹曲线。为了弥补以上方法在电池SOH估计上的缺陷,本文提出一种新的估计框架来实现电池SOH的精确估计。其主要贡献如下:
(1)利用VC模型来重构恒流充电和放电阶段的电压曲线,并从电压曲线和IC曲线中提取相关的特征作为估计模型的输入。重建后的电压曲线可更容易地获取其IC曲线,而且更容易识别IC曲线上的各个特征。
(2)利用降噪自编码器(Denoising Auto Encoder, DAE)功能对带有噪声的输入特征进行了无监督的训练,从损坏的数据中学习更稳健和有用的特征信息,使得估计模型具有更强的鲁棒性。
(3)利用结合DAE和门控递归单元的递归神经网络(GRU-RNN)网络模型来估计电池SOH。在输入特征含有噪声的情况下,本文提出的方法依然具有较高的电池SOH估计精度。
门控循环神经网络是在简单的循环神经网络的基础上加入了门控机制,用来控制神经网络中信息的传递,以更好地捕捉时间序列中步距较大的依赖关系,解决长期记忆和反向传播中的梯度消失或爆炸问题。相比于LSTM网络,GRU网络具有参数较少、结构简单、计算效率更高等优点,更适用于构建较大的网络[33]。GRU网络工作过程简单描述如下
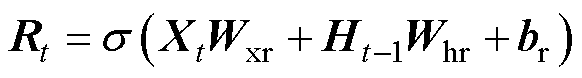 (1)
(1)
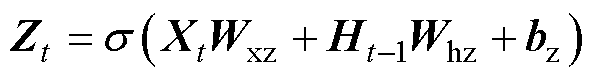 (2)
(2)
 (3)
(3)
 (4)
(4)
式中,Xt∈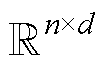 为小批量输入样本,n为样本个数,d为输入个数;Rt∈
为小批量输入样本,n为样本个数,d为输入个数;Rt∈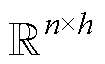 为重置门的输出,h为隐藏单元个数;Zt∈
为重置门的输出,h为隐藏单元个数;Zt∈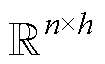 为更新门的输出Wxr和Wxz∈
为更新门的输出Wxr和Wxz∈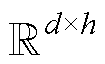 、Whr和Whz∈
、Whr和Whz∈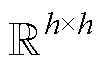 、Wxh∈
、Wxh∈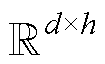 和Whh∈
和Whh∈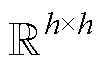 均为网络权重参数;br、bz和bh为网络偏置参数;s 为Sigmoid激活函数,其主要作用是将重置门和更新门中的每个元素的值域都转换到0~1之间;tanh激活函数的作用是将所有元素值域转换到[-1, 1]之间;
均为网络权重参数;br、bz和bh为网络偏置参数;s 为Sigmoid激活函数,其主要作用是将重置门和更新门中的每个元素的值域都转换到0~1之间;tanh激活函数的作用是将所有元素值域转换到[-1, 1]之间;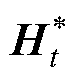 ∈
∈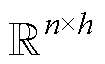 为候选隐藏状态;Ht为当前时刻的隐藏层状态;Ht1为上一时刻的隐藏状态;
为候选隐藏状态;Ht为当前时刻的隐藏层状态;Ht1为上一时刻的隐藏状态;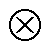 为向量中各个元素乘积。
为向量中各个元素乘积。
GRU网络的输出以及相应的损失函数为
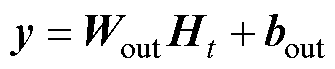 (5)
(5)
式中,Wout为网络输出层的权重参数;bout为网络输出时的偏置参数;y为网络的输出。
自动编码器(Auto Encoder, AE)神经网络是一种具有无监督学习的神经网络。其输入向量和输出向量同维度,通过隐含层对原始输入数据进行有效编码和训练,从而保留和获得更好的特征信息[34]。P. Vincent等[35]提出一种降噪自编码器,主要是在普通AE的基础上对输入数据添加噪声,然后强制AE从损坏的数据中学习一些更稳健和有用的特征信息,使得AE具有更强的鲁棒性。DAE网络在训练过程中采用随机梯度下降的方式对网络中的参数进行更新,以此来减小原始输入数据和损坏输入数据的误差。其详细步骤如下:
(1)假定输入样本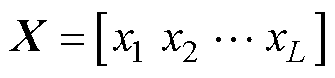 ,L为输入特征向量的个数,按照一定的比例对输入样本X加入噪声干扰,得到损坏的输入样本
,L为输入特征向量的个数,按照一定的比例对输入样本X加入噪声干扰,得到损坏的输入样本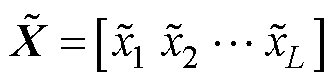 。
。
(2)将损坏的样本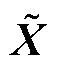 通过非线性激活函数进行编码,获得隐含层的输出HDE为
通过非线性激活函数进行编码,获得隐含层的输出HDE为
 (6)
(6)
式中,Wencoder为输入层与编码层之间的权值矩阵;bencoder为编码层偏置向量;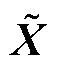 为添加噪声之后的各个输入样本。
为添加噪声之后的各个输入样本。
(3)将隐含层输出HDE进行解码,得到DAE网络重构后的输入样本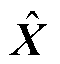 为
为
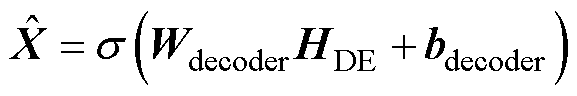 (7)
(7)
式中,Wdecoder为隐含层与输出层之间的权值矩阵;bdecoder为解码层偏置向量。
引入KL散度来衡量某个隐含层神经元节点的平均激活输出和设定的稀疏度之间的相似性,得
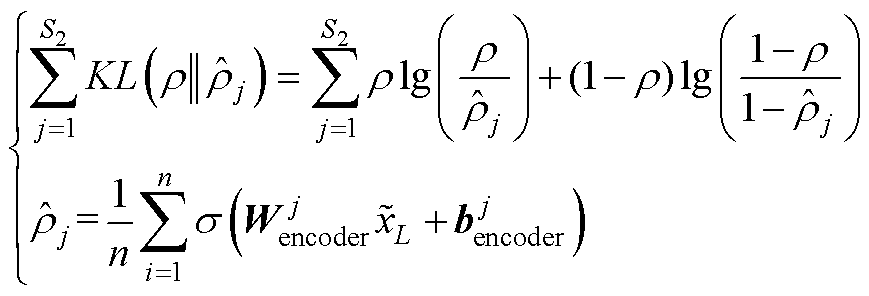 (8)
(8)
式中,r 为稀疏性参数,r 越接近于0,中间层平均激活度越小;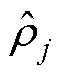 可以近似地作为第j个神经元被激活的概率;S2为神经元数目;KL散度表示平均激活度和目标值的差异。
可以近似地作为第j个神经元被激活的概率;S2为神经元数目;KL散度表示平均激活度和目标值的差异。
当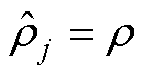 时,KL散度的最小值为0;当
时,KL散度的最小值为0;当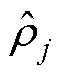 接近于0或者1的时候,KL散度将会变得非常大。总体的代价函数可以表示为
接近于0或者1的时候,KL散度将会变得非常大。总体的代价函数可以表示为
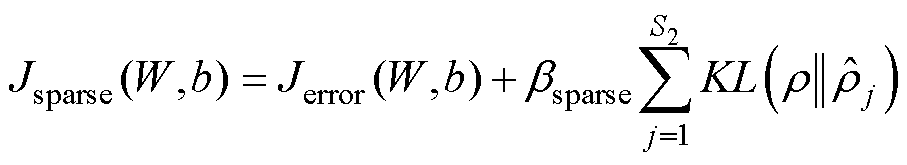 (9)
(9)
式中,bsparse为控制稀疏性惩罚因子的权重;Jerror(W,b)为原来DAE网络中的损失函数;Jsparse(W,b)为稀疏DAE网络中的损失函数;W和b分别为网络中的权值系数和偏置。
通过训练稀疏DAE网络可以转换输入数据的分布信息,但是稀疏DAE网络并不具备分类或者回归功能。为了实现以上功能,需要在其顶层添加分类或回归器,如SVM、ELM、LSTM和GRU等网络结构。稀流DAE-GRU-RNN预测框架如图1所示,当稀疏DAE网络训练完毕后,去掉输出层及相应的权重和偏置,只保留输入层和隐含层,然后将隐含层获得的特征信息输入GRU-RNN网络,通过GRU-RNN网络的非线性拟合能力来预测时间序列数据。
本文DAE部分为单独的网络结构,主要作用为数据集特征转换和降噪。DAE属于无监督学习网络,一旦训练完成,将编码器的输出部分直接输入GRU网络中,并未用到DAE的解码器的网络输出。
选用马里兰大学的先进生命周期工程中心(Center for Advanced Life Cycle Engineering, CALCE)采集的开源电池寿命数据集作为研究对象[36]。电池型号为CS和CX,CS型号电池的额定容量为1.1 A·h,CX型号电池的额定容量为1.35 A·h。电池实测过程的温度为25℃。两种型号的电池正极均是LiCoO2和微量Mn,负极均是石墨,形状均是棱柱形。电池测试实验主要分为两个阶段:恒流-恒压(Constant Current-Constant Voltage, CC-CV)充电阶段和恒流(Constant Current, CC)放电阶段。在充电过程中,两款电池分别以0.5C的恒定电流进行CC模式充电,直至达到充电截止电压4.2 V,然后再以CV模式充电,直到电流下降到0.05 A。在放电过程中,两款电池分别以不同倍率的恒定电流进行CC模式放电,直至达到放电截止电压2.7 V。CS2-35、CS2-36、CS2-37和CS2-38电池的放电电流为1.1 A,CS2-33电池的放电电流为0.55 A。CX2-34、CX2-36、CX2-37和CX2-38电池的放电电流为1.35 A,CX2-35电池的放电电流为0.675 A。
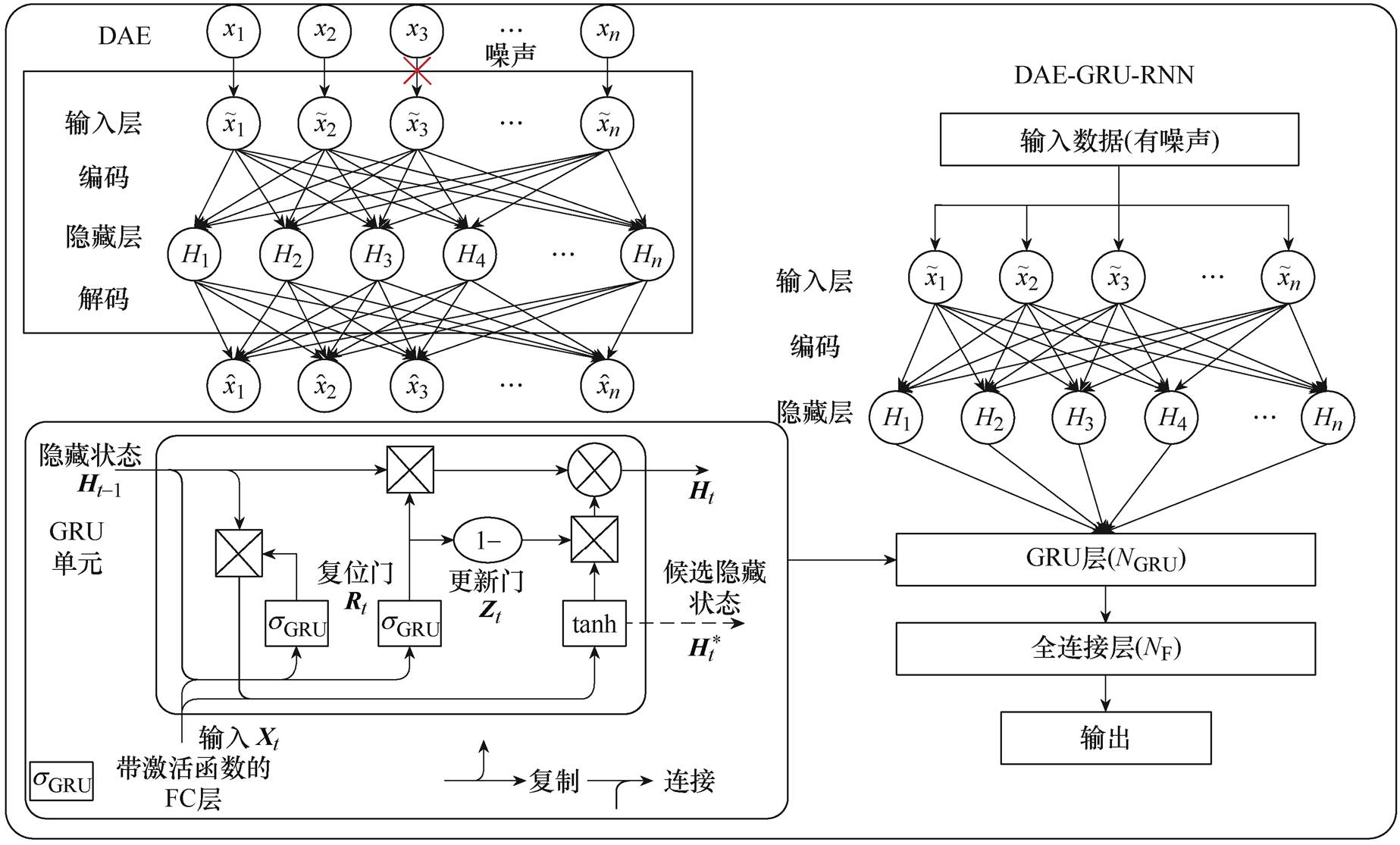
图1 稀疏DAE-GRU-RNN预测框架
Fig.1 Sparse DAE-GRU-RNN prediction framework
采用一阶RC电池模型进行电压重构,其欧姆内阻和RC支路可以很好地反映电池内部的化学反应。在CC模式充电和放电阶段,电池两端的开路电压Uoc可以表示为
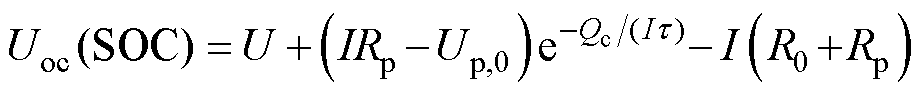 (10)
(10)
式中,Uoc为电池的开路电压;SOC为每个时间步的电池荷电状态;U为测量电压;I为测量电流;Rp为电池极化内阻;Up,0为极化电压;Qc为充电容量值;R0为欧姆内阻;t 为时间常数。
电池SOC为当前循环时刻的剩余容量与最大可用容量的比值。其表达式为
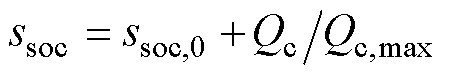 (11)
(11)
式中,ssoc为电池当前时刻的SOC值;ssoc,0为电池初始时刻的SOC值;Qc,max为电池当前充放电循环的最大容量值。
电池在不同充放电循环下的SOC-OCV曲线是相对稳定的,受电池老化状态和外界环境影响较小。利用多项式的集总参数热模型来描述温度对电池OCV曲线的影响。其表达式[37]为
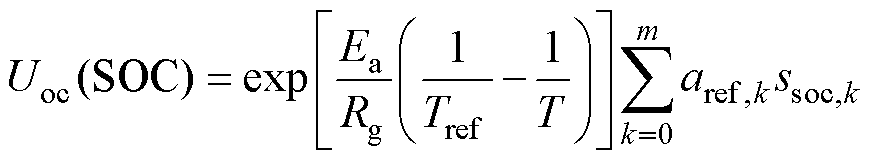 (12)
(12)
式中,Ea为电池的活化性能;Rg为气体的常数;Tref为计算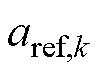 时的参考温度,
时的参考温度,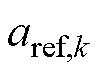 为拟合系数常量;T为温度值;m为SOC-OCV多项式的阶数;ssoc,k为k时刻的电池SOC值。
为拟合系数常量;T为温度值;m为SOC-OCV多项式的阶数;ssoc,k为k时刻的电池SOC值。
综合式(10)~式(12),电池充电电压和充电容量的关系表达式为
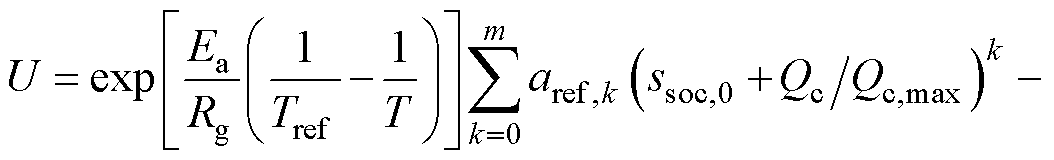
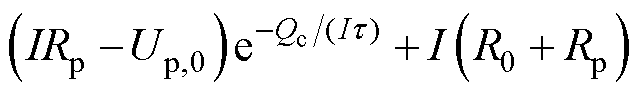 (13)
(13)
经过简化,将式(13)改写为
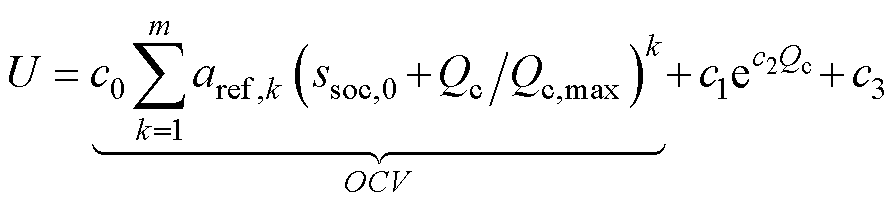 (14)
(14)
式中,c0、c1、c2和c3为同一循环时刻下的常数值。
常数c0,…, c3、aref,1,…, aref,m、ssoc,0和Qc,max主要是根据电池负载测量电压和CC阶段充电容量的关系进行参数辨识所得。本文选用非线性最小二乘法对上述参数进行辨识,其优化方式选择Trust-region-reflective算法。本文为了整个电池寿命期间电压都能获得良好的拟合效果,每次充放电循环都对以上参数进行参数辨识,且Qc,max并不一定是CC期间最大的充电容量。为了提高计算效率和模型的预测精度,需要对上述参数添加约束。根据文献[23]给出的经验范围值,取k=10,上述两个电池型号的其他参数范围为
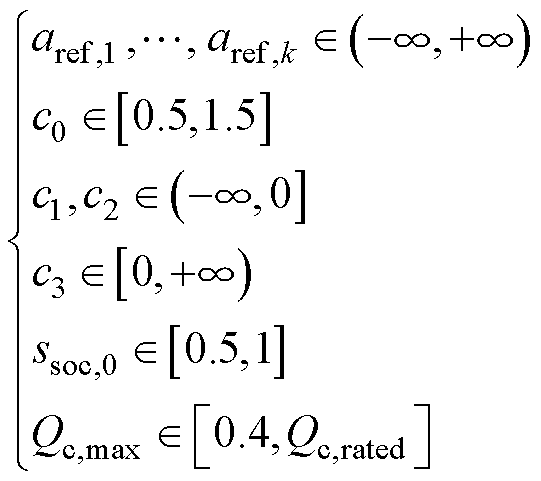 (15)
(15)
式中, 为电池额定容量。
为电池额定容量。
以CS-36电池为例,详细对比几种重构电压的方式。利用SVR算法重构电压曲线时,核函数为径向基核函数,核尺寸参数类型为“auto”,求解器为序列最小优化(Sequence Minimum Optimization, SMO)算法。也有将电流、温度和SOC值作为特征,并利用ELM算法来预测电压数据的电压重构方法。本文的研究重点主要是重构CC段的电压数据,其方式主要为拟合形式。因此,SVR和ELM模型的训练集和测试集均相同,其输入均为充电容量,输出均为电压。ELM模型的激活函数为Sigmoid函数,神经元数量为10。NN模型的输入为时间序列,输出为电压。多形式拟合电压的优化方式为Trust-Region-Reflective(TRR)算法,多项式模型的阶数为9。aref,1,…,aref,m的参数可以根据首次充电循环的充电容量和电压确定,这一组参数值在后续的充电循环过程中不变。所有模型参数采用非线性最小二乘法进行参数辨识,优化方式选择Levenberg-Marquardt算法,将其命名为RC-Fixed。但是在整个电池寿命衰减期间,固定的参数值可能获得不好的电压拟合效果。因此,本文在每次充电循环中对所有参数进行辨识,其优化方式选择TRR算法,将其命名为RC-Variable。
电池在工作过程中,外界未知环境对电流和电压的采集会产生一定的影响,此外,不同型号的电流和电压传感器也存在一定的偏差。因此,本文也参照文献[26]对电流和电压添加噪声的方式对电压曲线进行重构,以此来验证电压重构方法在噪声干扰下的鲁棒性。对电流和电压添加不同倍率的高斯噪声,其表达式为
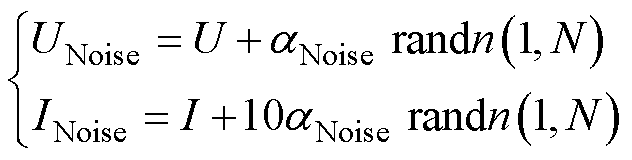 (16)
(16)
式中,UNoise和INoise分别为添加噪声之后的电压和电流数据;U和I分别为原始测量的电压和电流数据;aNoise为高斯噪声的倍率;randn为均值为0、方差为1的正态分布。
图2为CX-38电池在噪声倍率aNoise=0.03时的测量和模拟Q-V曲线。
通过图2中不同循环时刻的拟合效果可以看出,即使在噪声倍率aNoise= 0.03时,拟合的电压曲线也都能够与理想的电压曲线相吻合。噪声倍率aNoise= 0.01时的模拟最大误差都在1%以内,噪声倍率aNoise= 0.03时的模拟最大误差都在2%以内。
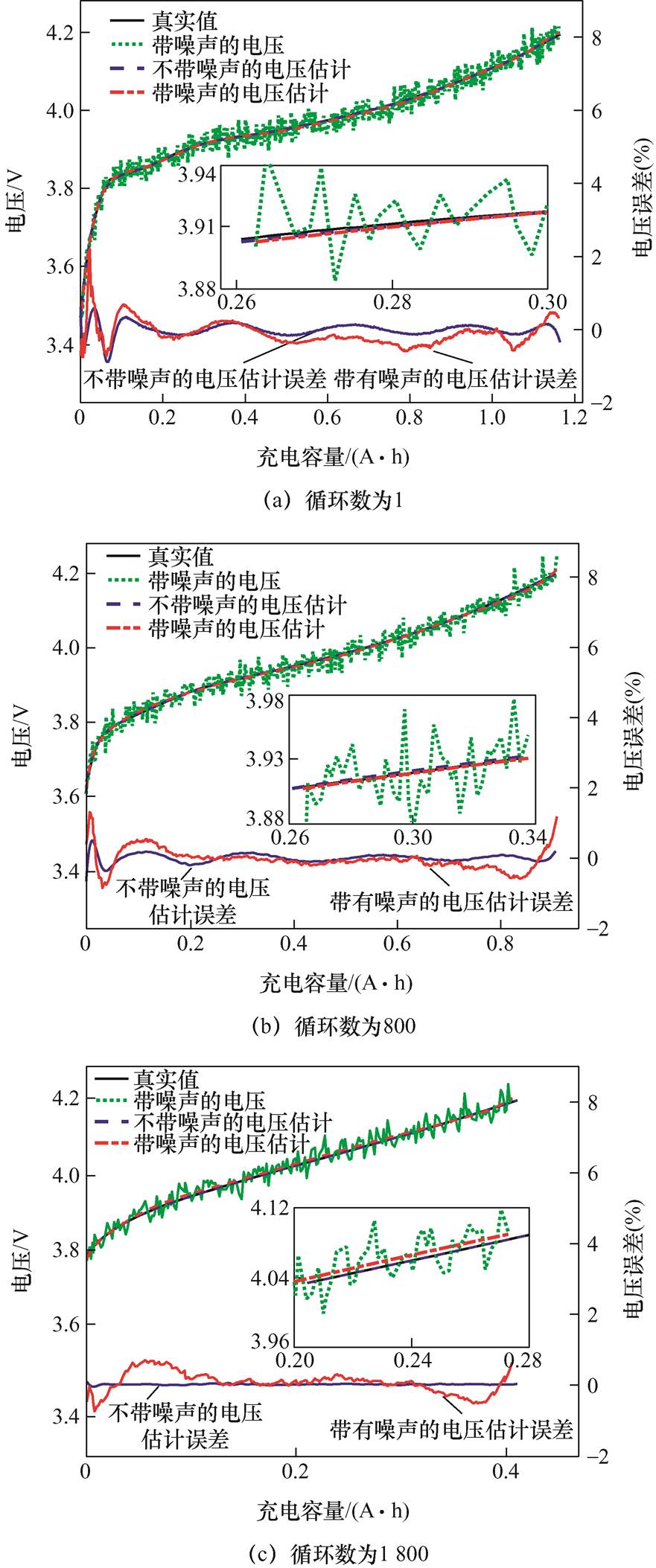
图2 CX-38电池的测量和模拟Q-V曲线
Fig.2 Measurement and simulation of Q-V curves of CX-38 battery
在电动汽车上的电池,其充电工况一般是固定不变的,放电工况较为随机。因此,一般可以从充电工况的电流、电压和时间的测试数据中提取相应的特征值,然后利用提出的稀疏DAE-GRU-RNN网络对电池SOH进行预测。现以CS-35电池为例,对这些特征值及其提取过程进行详细的描述。
1)与电压相关的特征值
等充电电压上升的时间间隔(Time Interval of Equal Charge Voltage Rise, TI-ECVR)、等充电电压上升的充电容量(Charge Capacity of Equal Charge Voltage Rise, CC-ECVR)和充电电压曲线的斜率(Slope of Charge Voltage Curve, SCVC)都可以反映电池的老化现象。但是TI-ECVR和CC-ECVR的数据在标准化之后,相差较小,有些数据点几乎是一样的。因此本文利用充电电压曲线下的面积(Area under Charging Voltage Curve, ACVC)来替代CC-ECVR值作为模型的输入。不同老化时刻电池充电时期的电压曲线如图3所示。
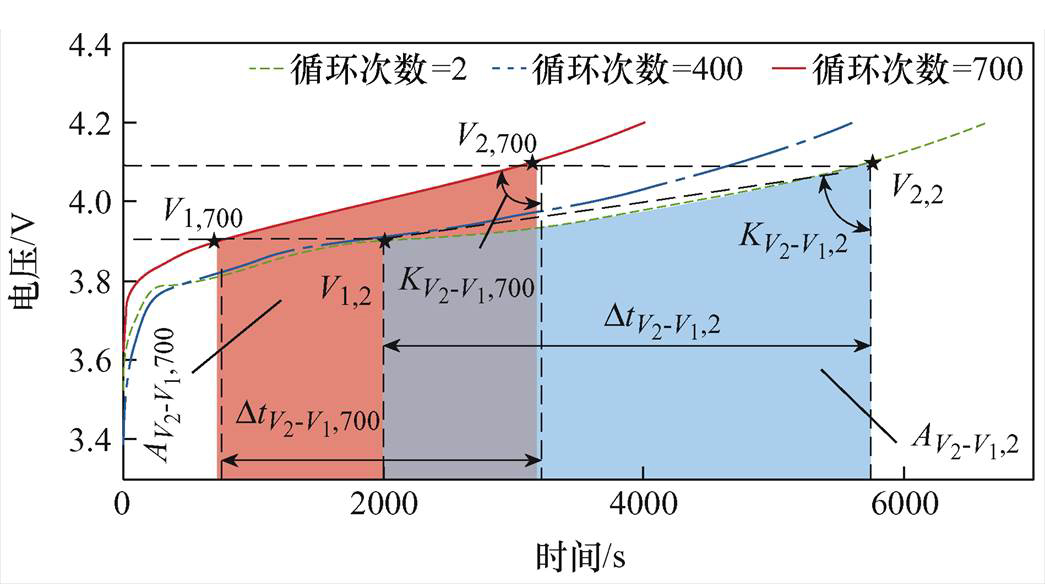
图3 不同老化时刻电池充电时期的电压曲线
Fig.3 Voltage curves of battery charging at different aging times
不同充放电循环下,相同充电电压间隔下的三个特征值会随着充放电次数的增加呈减小的趋势。为了能获得更多的数据输入来提高模型的预测精度,分别从不同的充电电压片段中提取以上特征值作为模型的输入。选取的电压片段范围分别为3.73~3.9 V、3.73~4.0 V、3.73~4.1 V、3.73~4.2 V、3.8~4.0 V、3.8~4.1 V、3.8~4.2 V、3.9~4.1 V、3.9~4.2 V、4.0~4.2 V。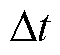 为对应上述电压片段的TI-ECVR值;
为对应上述电压片段的TI-ECVR值; 为上述电压片段的ACVC值;
为上述电压片段的ACVC值;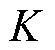 为两个电压点的斜率值,其计算公式为
为两个电压点的斜率值,其计算公式为
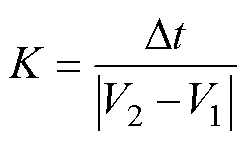 (17)
(17)
2)与容量增量曲线相关的特征值
锂离子电池IC曲线分析是锂离子电池衰退机理分析常用的方法。该方法能够将平缓的电压平台转化为IC曲线中的峰值。通过电池循环过程中的实验数据,能够计算容量增量曲线,曲线能够反映出电池内部电化学变化的特征。相较于差动电压(Differential Voltage, DV)曲线,基于IC曲线的分析方法相对简单,且提供了电压与容量之间的关系,特别是容量的变化率,可以更直观地反映电池的健康状态。本文主要从充电阶段的IC曲线中提取IC最高点(IC Peak, ICP)、IC最高点的位置(IC Peak Location, ICPL)和IC曲线内的面积(Area in the IC Curve, AICC)三个特征值作为研究对象。原始的IC曲线是根据传感器采集的电流、电压和时间的数据提取的,通过对Q-V曲线应用导数运算,其获取方式还可以利用近似的差分运算表示为
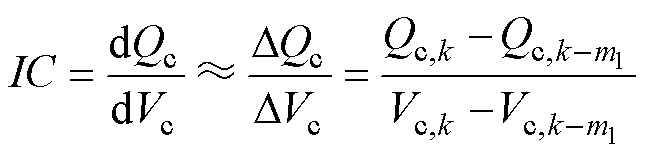 (18)
(18)
式中,Qc,k和Vc,k分别为k时刻的充电容量和充电电压;m1为IC曲线上的采样间隔,其作用是避免数值相差较小造成明显的异常值。
但是原始的IC曲线上包含大量的噪声,且IC曲线上的峰值对噪声高度敏感,很难捕捉到有效的特征值对电池SOH进行估算。本文采用三次样条差值法对原始的数据集进行数据扩充,以便从IC曲线中获得更稳健的数据特征。两款电池通过重构Q-V曲线的方式获得的IC曲线上有两个主峰,峰的强度和电压位置信息可以揭示电池内部活性物质的损失,进而来反映电池容量退化趋势。
图4a为CS-36电池整个老化测试过程的IC曲线。图中结果显示,两个IC曲线峰值随着充放电循环次数的增加呈下降的趋势,且电压位置信息也随着循环次数的增加逐渐向高电压偏移,两个波峰的面积也呈逐渐减小的趋势。在充放电循环初期,峰值、峰值位置和波峰面积偶然出现了个别异常的现象,但整体而言,从IC曲线中提取的这6个特征信息在一定程度上可以反映电池老化的趋势。图4b为提取6个特征值的示意图,第一个ICP为ICpeak1,ICPL为V3,AICC为ICarea1;第二个ICP为ICpeak2,ICPL为V4,AICC为ICarea2。第一个波峰面积的电压范围为3.73~3.85 V,第二个波峰面积的电压范围为3.85~4.1 V。从图中可以看出,在电池整个充放电周期,第二个峰值点的特征信息与电池老化轨迹的关系较为明确,各个特征信息的提取也相对容易。第一个峰值点的特征信息在充放电初期也具有明显的位置信息,但是随着电池充放电次数的增加,第一个峰值点出现了淹没现象,并不能有效提取峰值和电压位置的相关特征信息,只能计算电压3.73~3.85 V范围内的面积。为了获得更多的有用特征信息,现将两个波峰面积之和也纳入预测模型的输入,即ICarea3=ICarea1+ICarea2。因此,本文采用ICarea1、ICarea2、ICarea3、V4和ICpeak2作为预测模型的输入。
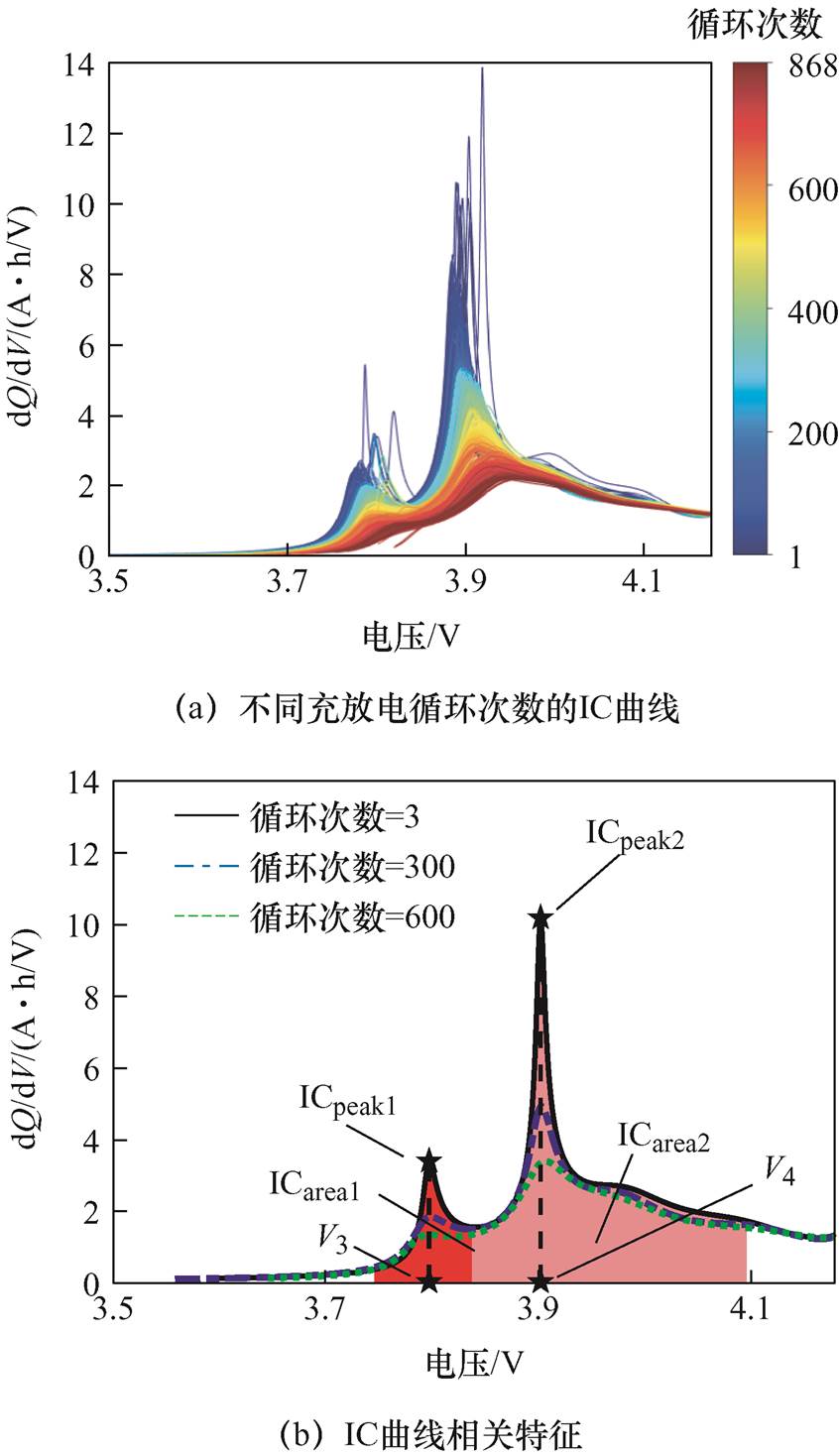
图4 CS-36电池IC曲线及特征
Fig.4 CS-36 battery IC curves and its characteristics
选用Pearson相关系数来分析各个特征值与实际电池SOH的关联程度。
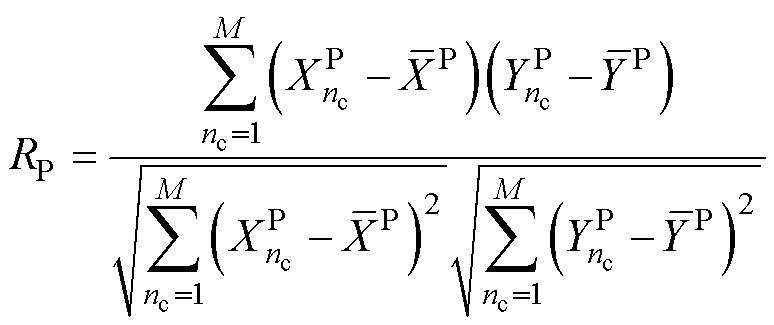 (19)
(19)
式中,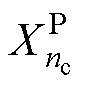 为电池每次循环实际的SOH值;
为电池每次循环实际的SOH值;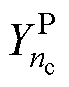 为充电阶段提取的特征数据;RP为Pearson相关系数;
为充电阶段提取的特征数据;RP为Pearson相关系数;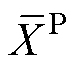 和
和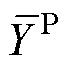 为样本数据的均值;
为样本数据的均值;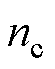 为当前充放电循环次数;M为总的充放电循环次数。
为当前充放电循环次数;M为总的充放电循环次数。
表1为部分电池的特征值与电池SOH相关系数。可以看出,CX-34电池的特征信息与电池SOH的相关系数基本上都在0.9以上,这表明从充电阶段的电压、电流和时间数据中提取的大部分特征信息与电池SOH都有着高度的相关性。而在CS-35电池中,从电压范围4.0~4.2 V内提取的特征信息与电池SOH的相关系数在0.39~0.40之间,这表明它们之间的关系为弱相关性。CS-35电池的特征信息与电池SOH的相关系数都在0.87以上,均表现为强相关性。为了验证本文算法的可行性以及输入数据结构的完整性,在预测CS型号电池SOH的时候,将电压片段4.0~4.2 V内提取的特征信息剔除,不作为预测模型的输入。
表1 部分电池特征信息与电池SOH的Pearson相关系数
Tab.1 Pearson correlation coefficient between each characteristic information and battery SOH

特征数据电池编号特征数据电池编号 CS-35CX-34CS-35CX-34 Dt10.945 60.975 9Dt70.995 40.999 0 K10.943 90.976 4K70.989 80.997 0 A10.929 00.971 1A70.994 90.998 9 Dt20.992 90.991 9Dt80.910 20.995 4 K20.995 70.994 0K80.896 10.992 9 A20.983 20.985 9A80.909 10.995 3 Dt30.996 20.998 2Dt90.900 40.993 5 K30.997 10.999 0K90.879 20.989 0 A30.983 80.994 1A90.899 80.993 6 Dt40.997 30.999Dt100.400 50.922 2 K40.996 60.998 1K100.397 10.921 8 A40.985 70.995 8A100.403 20.922 7 Dt50.995 20.993 4ICarea10.970 80.973 5 K50.994 40.994 6ICarea20.995 20.998 7 A50.994 70.993 7ICarea30.996 40.998 3 Dt60.995 80.998 8V40.949 30.928 0 K60.992 50.998 5ICpeak20.898 30.969 5 A60.995 30.998 8
电池SOH的预测流程如图5所示,预测步骤如下:
(1)将电池测试数据进行充电电压重构后进行特征因素提取,并利用Pearson相关系数法剔除弱相关度特征信息。
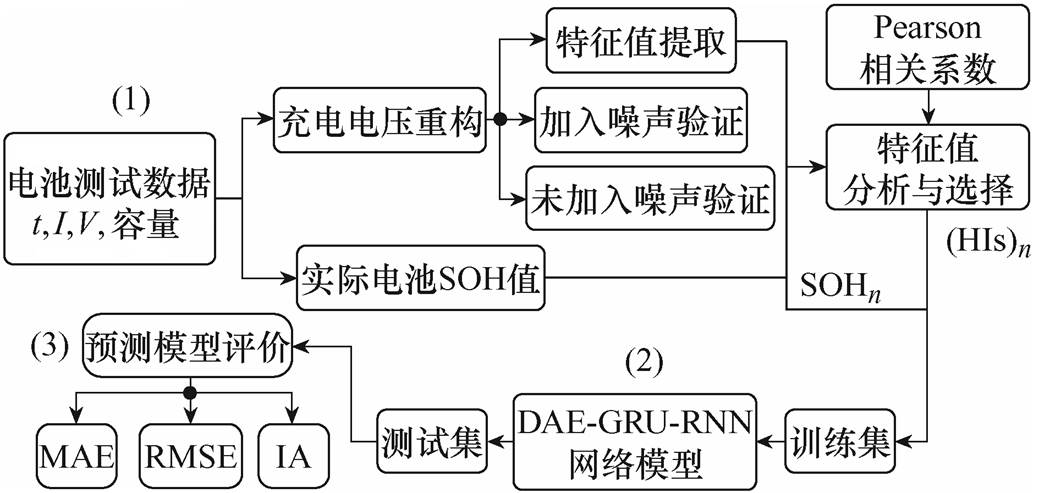
图5 电池SOH的预测流程
Fig.5 Flow chart of battery SOH prediction
(2)利用降噪自编码器对带有噪声的输入特征进行了无监督训练,结合门控递归单元的递归神经网络形成DAE-GRU-RNN算法,并进行训练集和测试集的划分。
(3)进行模型训练及预测,并进行预测模型评价。
对于电池短期SOH预测,利用三个度量指标对模型的稳定性和精确性进行验证,即平均绝对误差(Mean Absolute Error, MAE)、方均根误差(Root Mean Square Error, RMSE)和协议指数(Index of Agreement, IA)。三个指标分别为
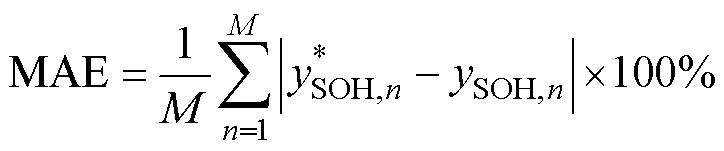 (20)
(20)
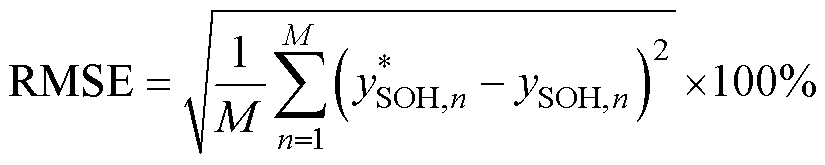 (21)
(21)
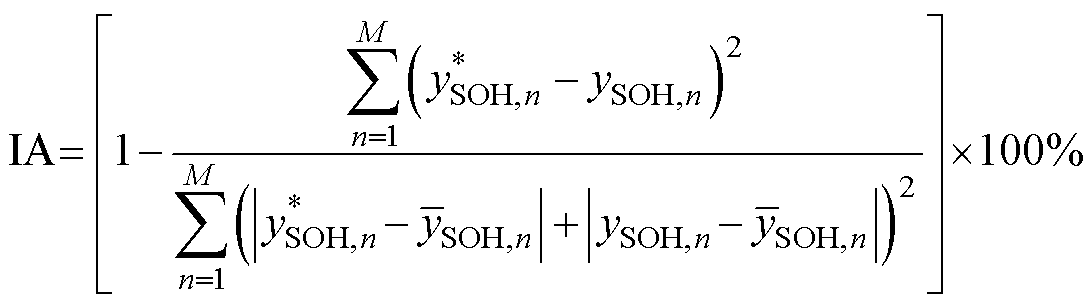 (22)
(22)
式中,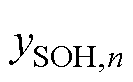 为电池实际的SOH值;
为电池实际的SOH值;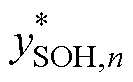 为模型预测的SOH值;
为模型预测的SOH值;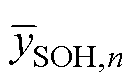 为实际SOH的平均值;M为测试集中总的循环次数。
为实际SOH的平均值;M为测试集中总的循环次数。
对各个电池提取的特征数据添加噪声来评估提出算法的预测精度和泛化能力。值得注意的是,文中只是对归一化之后的特征数据添加高斯噪声,噪声倍率aNoise=0.03。实验过程采取交叉验证的方式来对比不同算法的预测性能,即训练数据和测试数据均采用不同的电池数据集。采用模型对比和部分充电曲线下测试两个实验来验证算法的可行性。
引入普通的三层深度神经网络(Deep Neural Networks, DNN)和普通GRU-RNN网络模型与提出的模型在特征数据含有噪声的情况下进行比较。所用到的两组电池数据集均采用留一法对电池SOH进行预测。例如,当预测CS-35电池的SOH值时,所用到的训练集为CS-36、CS-37和CS-38;同理,当预测CS-36电池的SOH值时,所用到的训练集为CS-35、CS-37和CS-38。CS-35和CX-34电池SOH预测结果如图6所示。
图6a和图6d分别为三种算法在CS-35和CX-34电池上的SOH预测结果。图中结果显示,三种算法获得的电池SOH的预测结果都能很好地追踪真实的SOH值。图6b和图6e分别为CS-35和CX-34电池SOH预测误差。图6c和图6f分别为CS-35和CX-34电池SOH预测误差的概率密度曲线。从预测误差结果可以看出,两个电池利用DAE- GRU-RNN网络模型获得的SOH误差最小,除了个别循环时刻的误差较大之外,在CS-35电池上,其余时刻的误差都在0.02以内,在CX-34电池上,在前1 500循环时刻,误差范围也大部分都在0.02以内,在1 500充电循环之后,由于电池容量再生现象的出现,实际的电池SOH也随之出现了较大的波动,但误差也基本上控制在0.04以内。从误差概率密度可以看出,DAE- GRU-RNN网络模型预测误差概率密度曲线比其他两个网络模型呈现出高和窄的趋势。
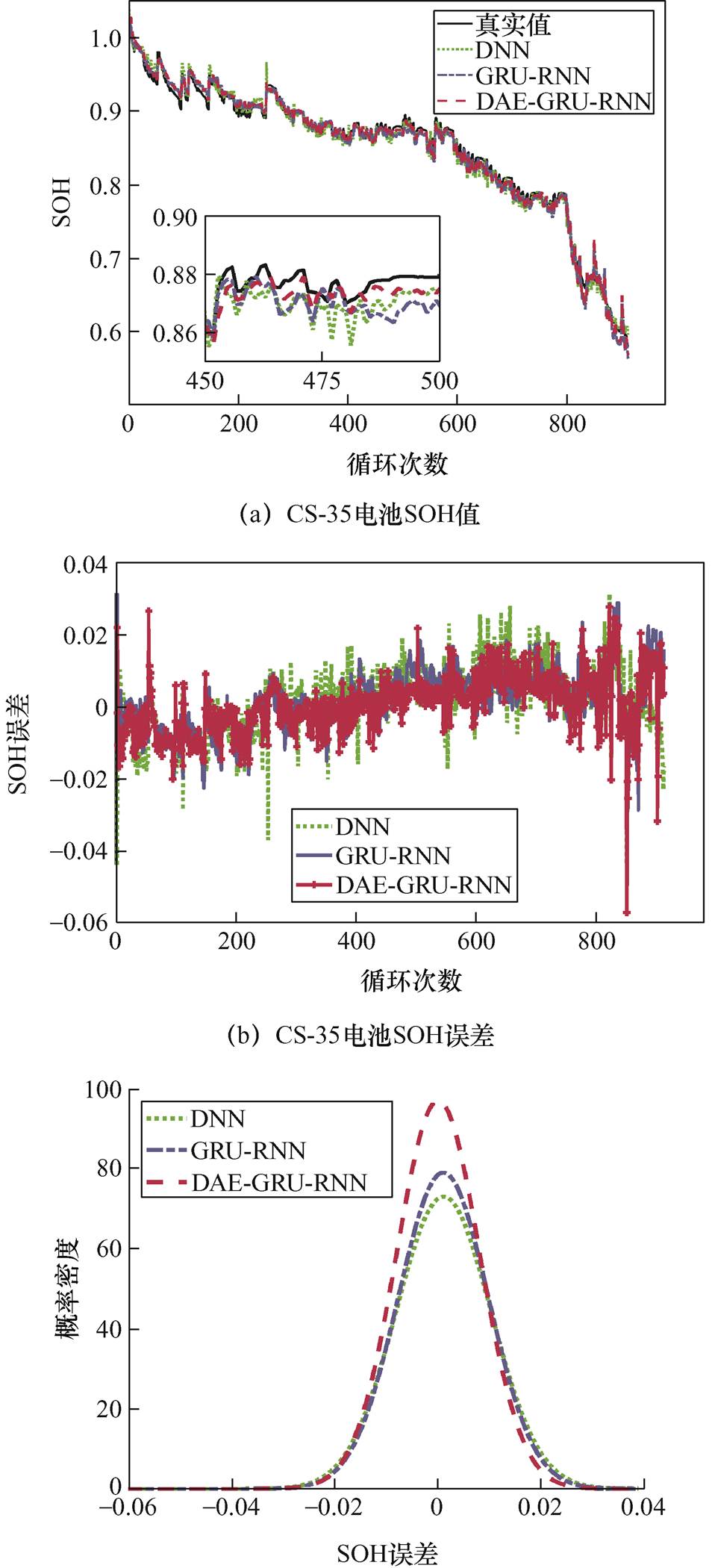
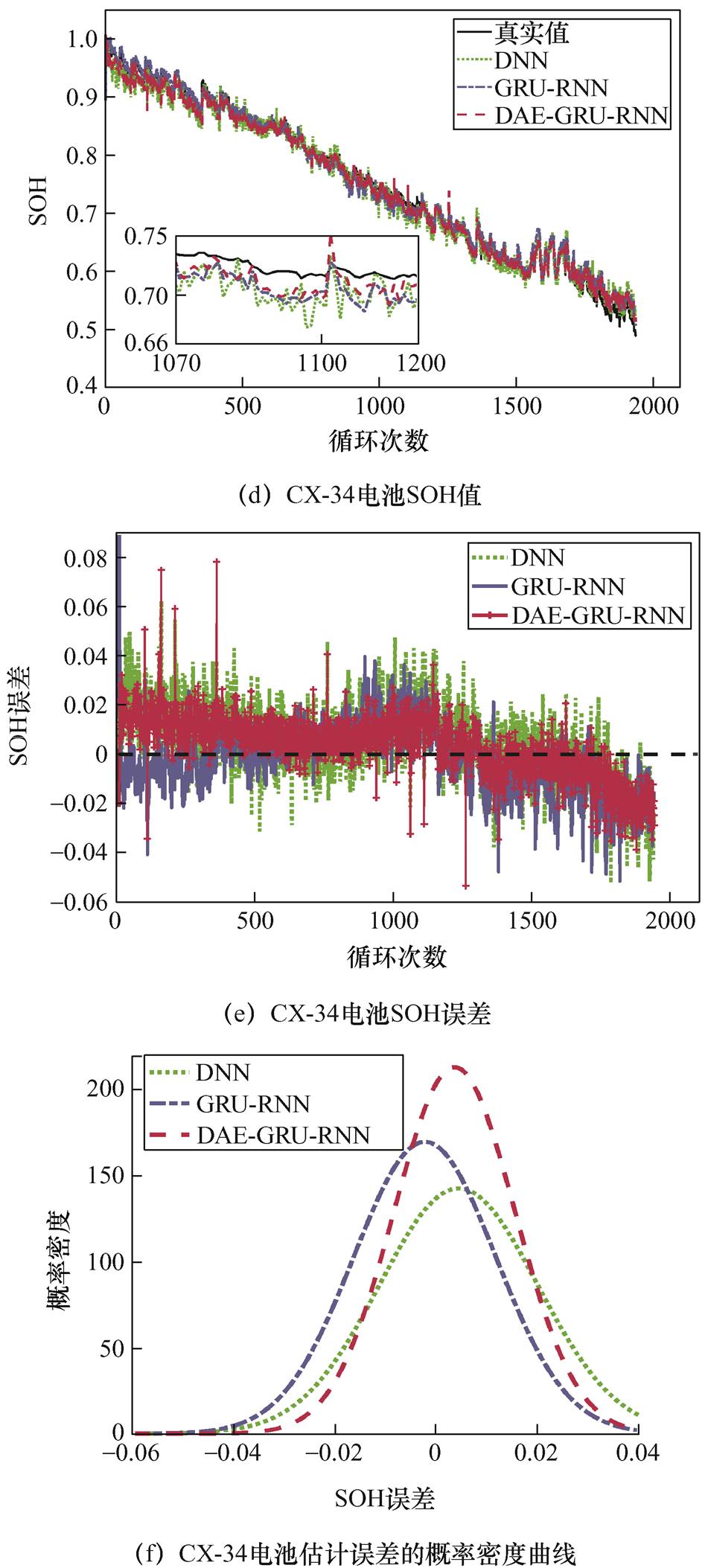
图6 CS-35和CX-34电池SOH预测结果
Fig.6 SOH prediction results of CS-35 and CX-34 battery
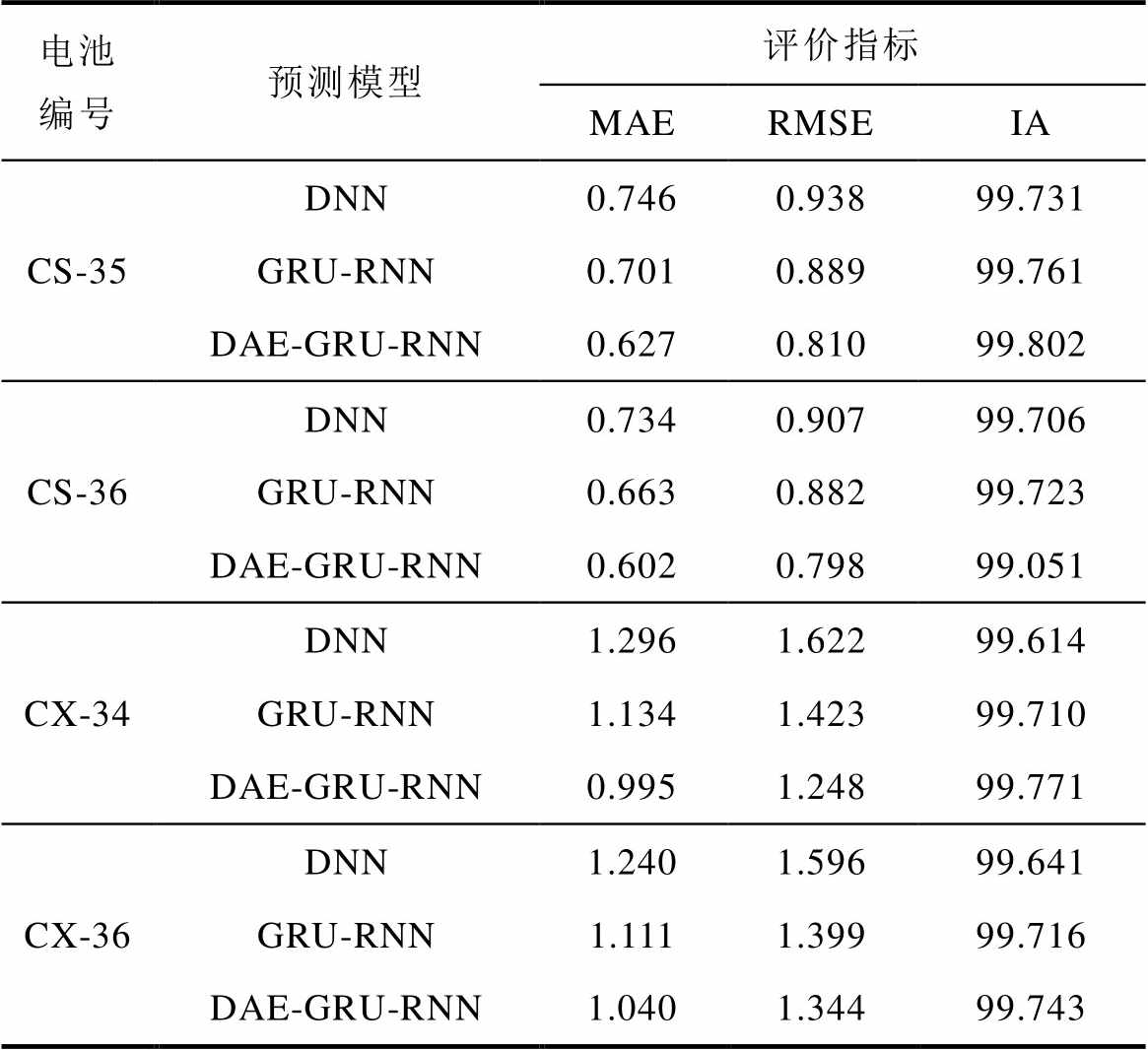
表2为4电池型号的SOH预测误差统计结果。
表2 电池SOH预测结果
Tab.2 Battery SOH prediction results (%)
电池编号预测模型评价指标 MAERMSEIA CS-35DNN0.7460.93899.731 GRU-RNN0.7010.88999.761 DAE-GRU-RNN0.6270.81099.802 CS-36DNN0.7340.90799.706 GRU-RNN0.6630.88299.723 DAE-GRU-RNN0.6020.79899.051 CX-34DNN1.2961.62299.614 GRU-RNN1.1341.42399.710 DAE-GRU-RNN0.9951.24899.771 CX-36DNN1.2401.59699.641 GRU-RNN1.1111.39999.716 DAE-GRU-RNN1.0401.34499.743
结果表明,利用三种网络模型获得的CS-35和CS-36电池SOH估计误差的MAE和RMSE均在1%以内,而CX-34和CX-36电池SOH估计误差的MAE和RMSE相对较高,误差范围也都控制在2%以内。以CS-35电池为例,三种算法预测的电池SOH的MAE分别为0.627%、0.701%和0.746%;RMSE分别为0.810%、0.889%和0.938%;IA分别为99.802%、99.761%和99.731%。提出算法的MAE误差相较GRU-RNN和DNN算法降低了10.55%和15.95%。这表明,DAE-GRU-RNN网络模型通过DAE层可以充分学习数据特征的分布情况,利用网络重新获得更有利于预测模型的输入数据,以提高GRU- RNN网络模型的预测精度。
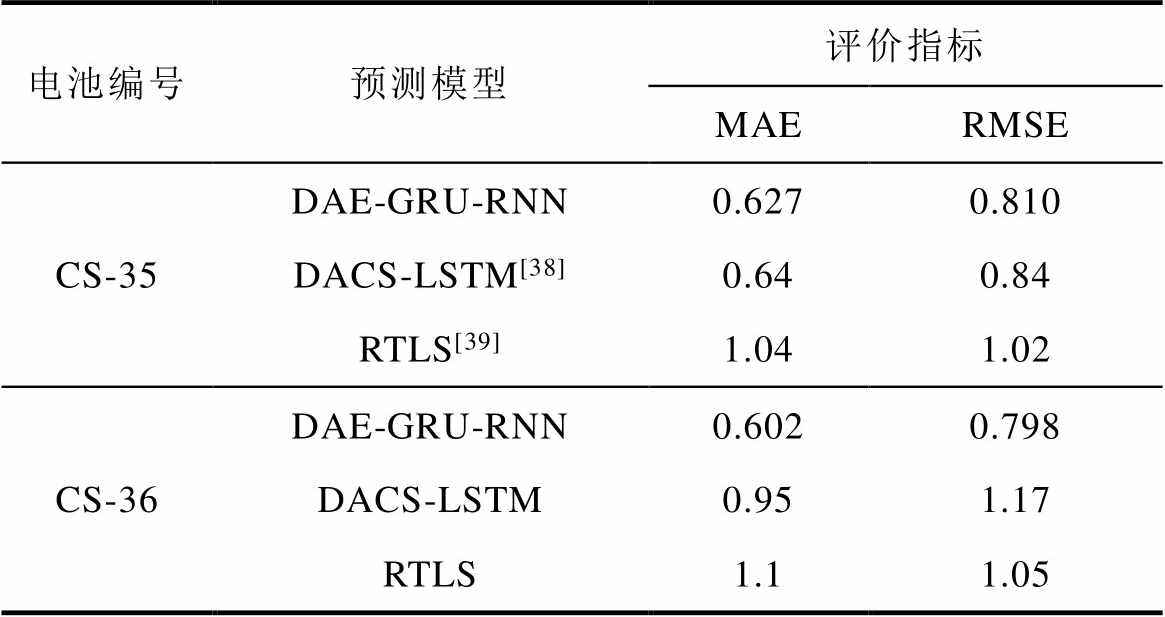
表3给出了提出的算法和一些最新SOH估计方法的预测精度对比。从表3中可以看出,和一些最新的方法相比-动态自适应杜鹃搜索优化长短期记忆神经网络(Dynamic Adaptive Cuckoo Search Long Short-Term Memory, DACS-LSTM)和重构迁移学习策略(Rebuilding Transfer Learning Strategies, RTLS),本文提出的算法预测效果更好。
表3 提出算法和文献报道电池SOH预测精度对比
Tab.3 comparison of battery SOH prediction accuracy between the proposed algorithm and that reported in the literature (%)
电池编号预测模型评价指标 MAERMSE CS-35DAE-GRU-RNN0.6270.810 DACS-LSTM[38]0.640.84 RTLS[39]1.041.02 CS-36DAE-GRU-RNN0.6020.798 DACS-LSTM0.951.17 RTLS1.11.05
在实际应用中电池满充满放的情况较少,不可能每次都获得完整的CC充电曲线。因此,有必要验证一下部分充电曲线提取的特征信息是否可以满足电池SOH的预测。此外,实验2还验证了所提出的算法训练出来的模型是否可以应用于多个电池SOH的估算。在CS型号的电池中,利用CS-35和CS-36电池作为训练集获得一个预测模型,然后利用该模型同时在CS-37、CS-38和CS-33电池上进行预测。同理,利用CX-34和CX-36电池作为训练集获得一个预测模型,然后利用该模型同时在CX-37、CX-38和CX-35电池上进行预测。值得注意的是,CS-33和CX-35电池的放电工况与上述两组工况不同。实验2以最短电压片段内的特征数据为模型的输入特征对电池SOH进行预测,即电压片段为3.73~3.9 V、3.8~4.0 V、3.9~4.1 V和4.0~4.2 V,分别对应测试条件Case 1、Case 2、Case 3和Case 4。现将完整CC曲线上获得的特征值来预测电池SOH作为对比,对应测试条件Case 5。
图7为CS-33、CS-37和CS-38电池的SOH预测结果。表4为CS-33、CS-37和CS-38三个电池的误差统计结果。
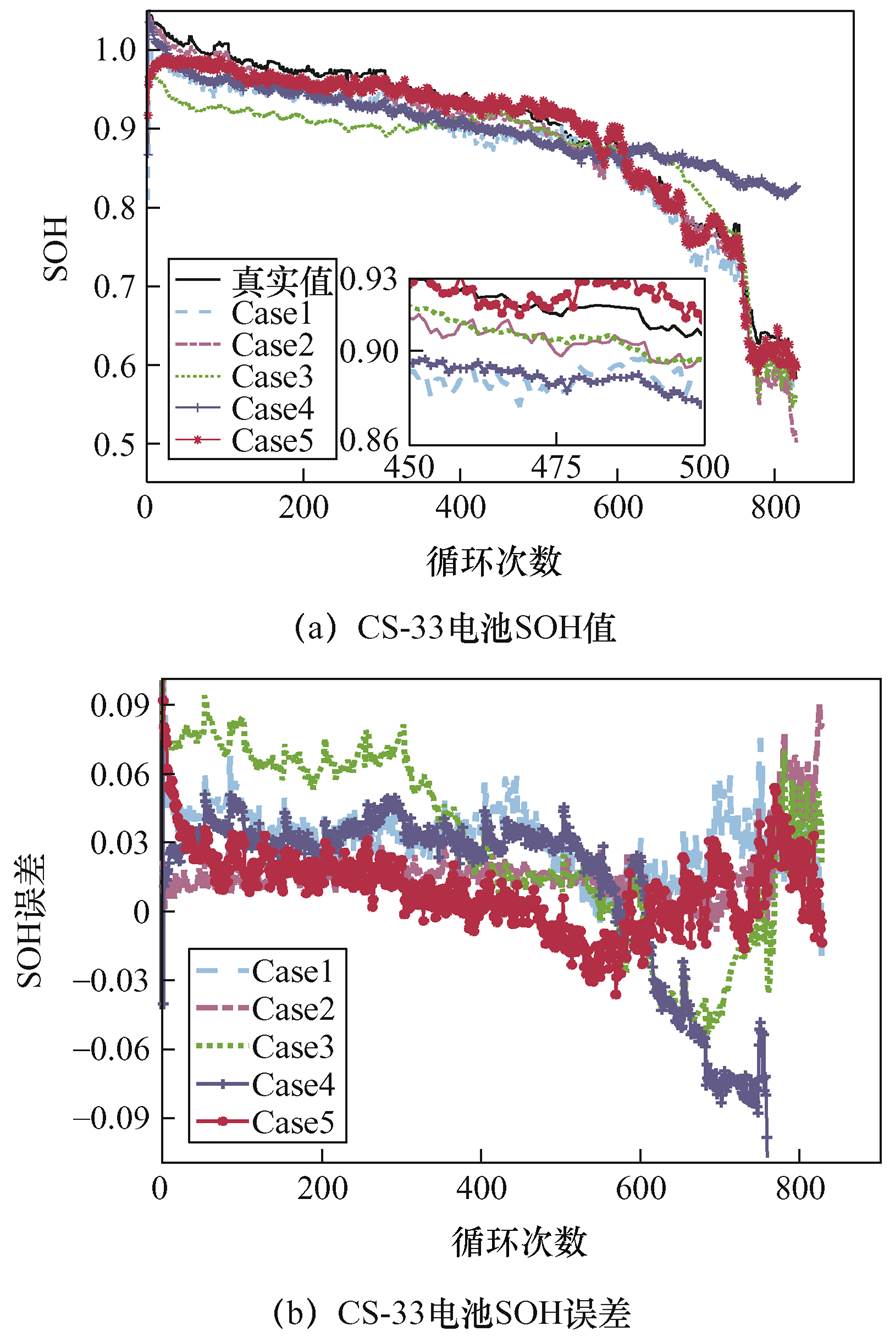
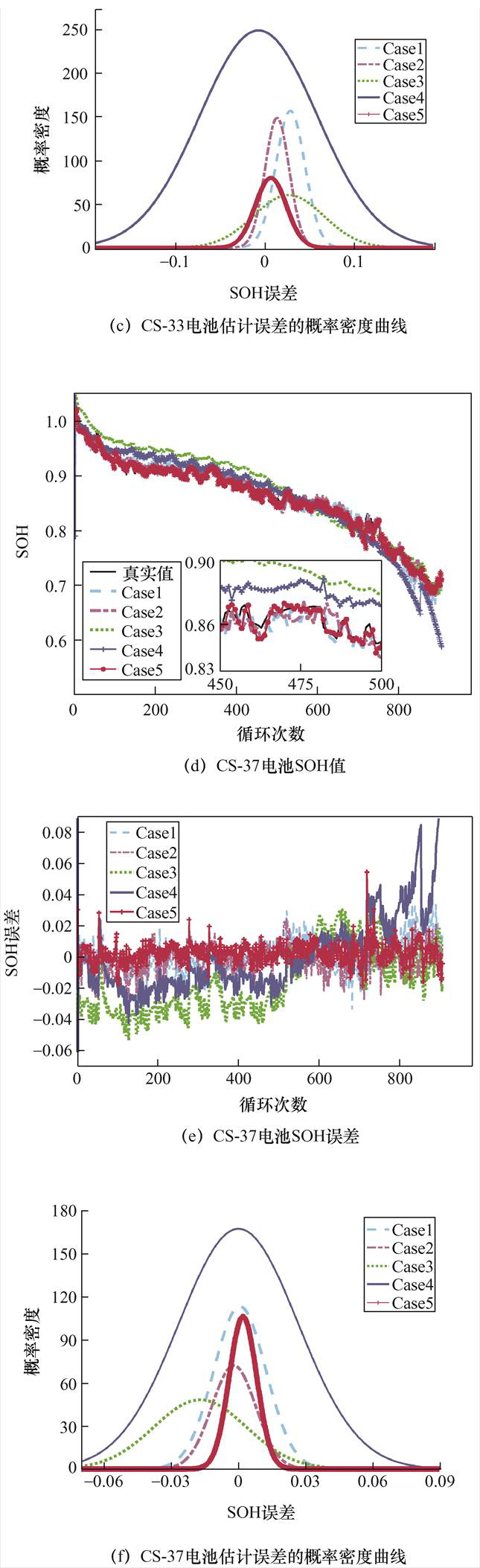
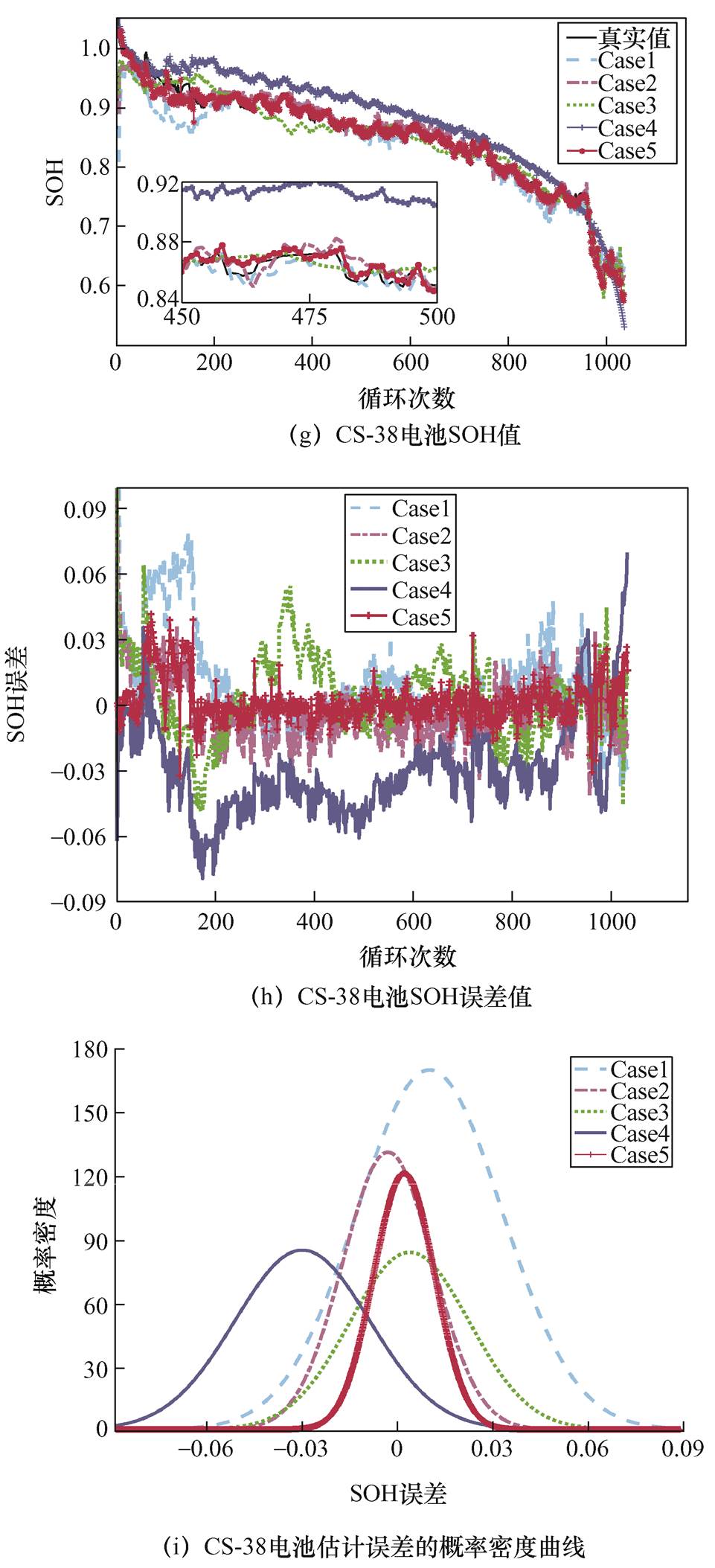
图7 CS-33、CS-37和CS-38电池SOH预测结果
Fig.7 SOH prediction curves of CS-33、CS-37 and CS-38 batteries
当利用完整电压数据提取特征值进行预测时,训练模型在CS-37和CS-38电池上都获得了较高的预测精度,误差结果的MAE都在0.7%以内,RMAE都控制在1%以内,IA也高达99.67%以上。由于放电工况不同,导致数据分布差异较大,预测模型在CS-33电池上的预测误差较大,但也都控制在了2%以内,其MAE为1.285%,RMSE为1.621%,IA为99.655%。这表明所提出的算法利用训练集训练出一个模型可以应用于不同数据集的测试。当利用部分电压曲线获得的特征数据进行电池SOH预测时,三个电池预测的误差都有不同程度的增加。这主要是因为电压片段内提取的特征个数较少,严重影响了预测模型的预测精度。相比于其他电压片段,电压片段在3.8~4.0 V之间的特征数据预测的电池SOH误差较小,其MAE基本上控制在1.5%以内,RMSE在2%以内。电压片段在4.0~4.2 V内提取的特征数据预测结果最差,预测的SOH衰减曲线严重偏离真实的SOH值,在CS-37和CS-38电池上预测误差的MAE分别为1.952% 和3.329%,RMSE分别为2.661%和3.651%;在CS-33电池上,预测误差的MAE高达4.775%,RMSE高达6.619%。这是由于在电池高电压区提取的特征值变化并不明显,高电压区的Pearson相关系数较小,低电压区的Pearson相关系数较大。
表4 实验2的CS型号电池SOH预测结果
Tab.4 SOH prediction results of CS batteries for experiment 2 (%)
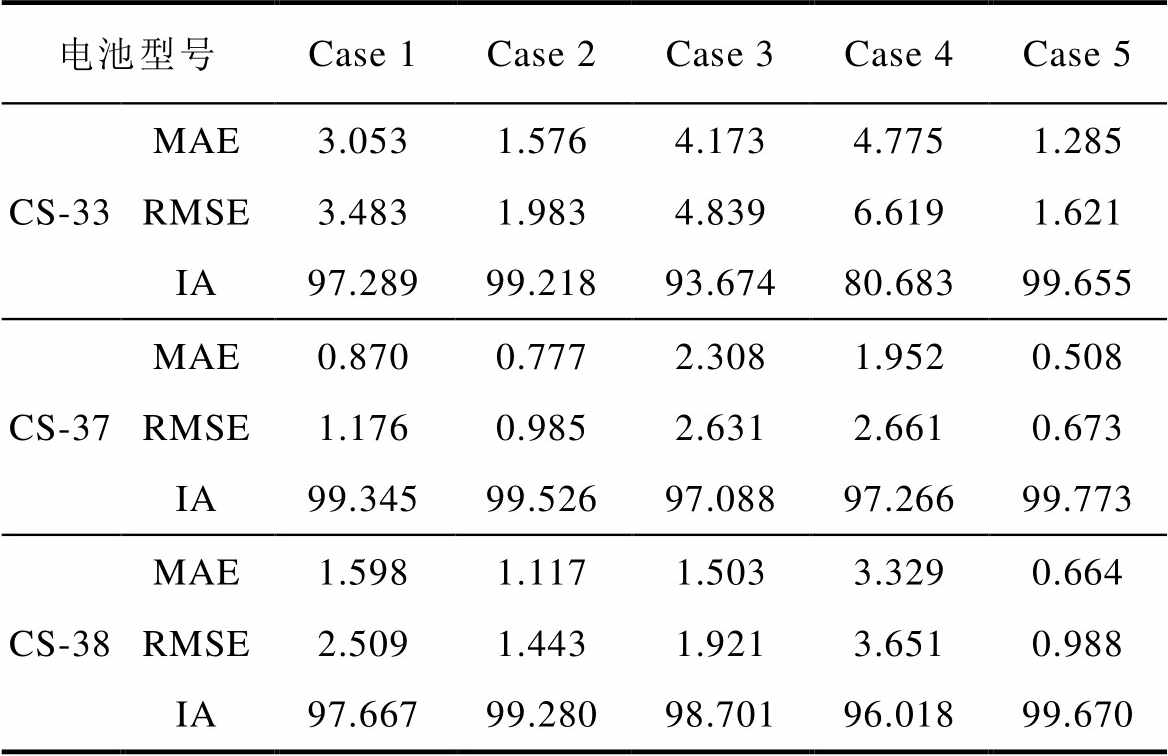
电池型号Case 1Case 2Case 3Case 4Case 5 CS-33MAE3.0531.5764.1734.7751.285 RMSE3.4831.9834.8396.6191.621 IA97.28999.21893.67480.68399.655 CS-37MAE0.8700.7772.3081.9520.508 RMSE1.1760.9852.6312.6610.673 IA99.34599.52697.08897.26699.773 CS-38MAE1.5981.1171.5033.3290.664 RMSE2.5091.4431.9213.6510.988 IA97.66799.28098.70196.01899.670
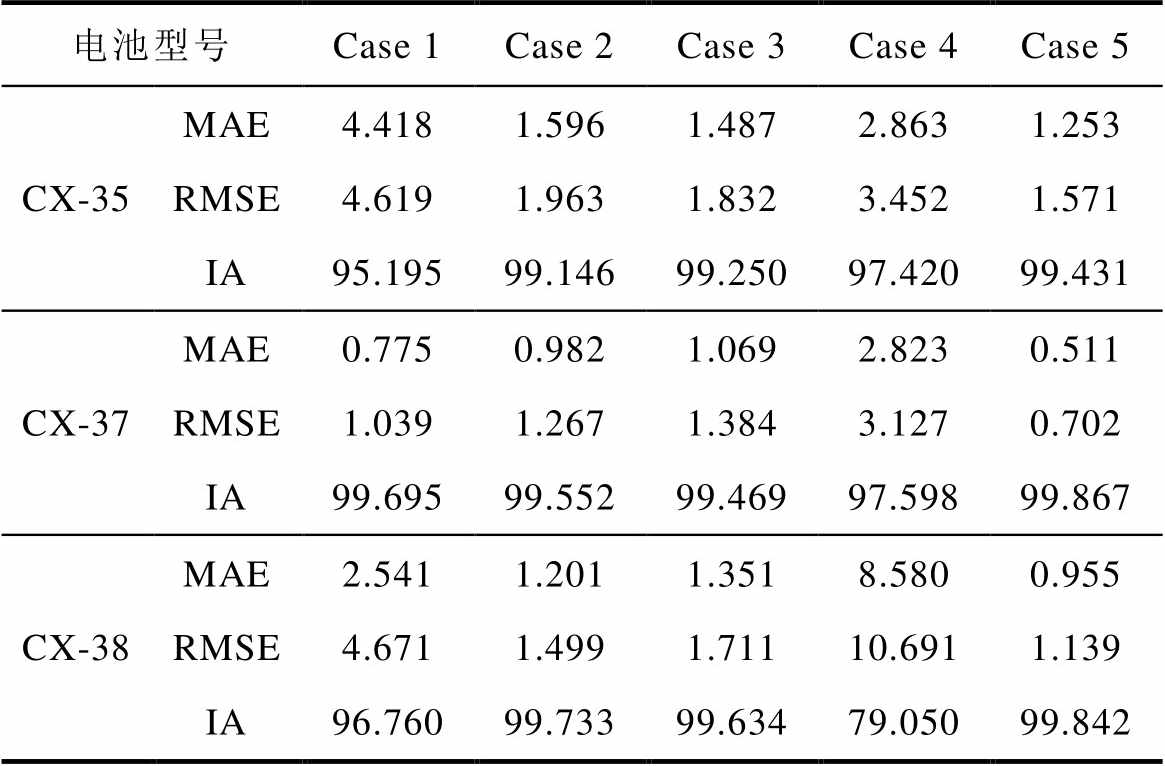
图8为CX-35、CX-37和CX-38电池的SOH估计结果。表5为CX-35、CX-37和CX-38电池的误差统计结果。当利用完整电压数据提取特征值进行预测时,训练模型在CX-37和CX-38电池上都获得了较高的预测精度,误差结果的MAE都在1%以内,RMAE都控制在1.2%以内,IA也高达99.842%以上。与CS型号电池一样,预测模型在CX-35电池上的预测误差较大,但其MAE和RMSE也都在2%以内。当利用部分电压曲线获得的特征数据进行电池SOH预测时,三个电池预测的误差都有不同程度的增加。不同于CS型号的三个电池,电压片段在3.8~4.0 V和3.9~4.1 V之间的特征数据预测的电池SOH误差较小,CX型号的电池误差的MAE基本上在1.6%以内,RMSE在2%以内。在CX-35电池上,电压片段在3.73~3.9 V提取的特征值预测的电池SOH效果最差,其MAE为4.418%,RMSE为4.619%,IA为95.195%。而对于CX-37和CX-38电池,电压片段在4.0~4.2 V之间提取的特征值预测的电池SOH效果最差,CX-37电池误差结果的MAE为2.823%,RMSE为3.127%,CX-38电池的效果直接偏离实际的SOH值,其误差结果MAE高达8.580%,RMSE高达10.691%。



图8 CX-35、CX-37和CX-38电池SOH预测结果
Fig.8 SOH prediction results of CX-35、CX-37 and CX-38 batteries
表5 实验2的CX型号电池SOH预测结果
Tab.5 SOH prediction results of CX batteries for experiment 2 (%)
电池型号Case 1Case 2Case 3Case 4Case 5 CX-35MAE4.4181.5961.4872.8631.253 RMSE4.6191.9631.8323.4521.571 IA95.19599.14699.25097.42099.431 CX-37MAE0.7750.9821.0692.8230.511 RMSE1.0391.2671.3843.1270.702 IA99.69599.55299.46997.59899.867 CX-38MAE2.5411.2011.3518.5800.955 RMSE4.6711.4991.71110.6911.139 IA96.76099.73399.63479.05099.842
由于传感器精度差异,在采集电压和电流时容易受到噪声干扰,提取的IC曲线不易获得峰值和峰值位置信息。此外,在电池完整的寿命测试期间,由于外界环境因素以及充放电工况并不一定都是完整过程,导致提取的特征信息容易出现偏离退化轨迹。本文提出了一种DAE-GRU-RNN混合模型进行电池的SOH估计以解决上述问题。首先利用电压-容量的VC模型来重构恒流充电阶段的电压曲线,并对该方法在不同的充放电循环时刻进行了模型验证。即使在噪声倍率aNoise=0.03时,模拟误差的MAE依然控制在0.5%以内,RMSE在0.6%以内。表明该方法具有较强的抗干扰能力。与采用滤波器对IC曲线数据预处理的方式相比,利用重构后的电压曲线获得的IC曲线更平滑,其峰值位置信息更加明确。从电压曲线中选取10个电压片段提取等充电电压上升的时间间隔TI-ECVR、充电曲线下的面积ACVC和两个电压点的斜率值K作为预测模型的输入。然后利用Pearson相关系数法对所有的特征信息进行了详细的分析。采用人工添加噪声的方式来对模型的输入特征进行噪声干扰,再利用DAE- GRU-RNN网络模型在不同的电池数据集上进行SOH预测。从预测结果可以看出,提出的算法相对误差比GRU-RNN和DNN模型小6.39%~23.23%。实验2为利用全部特征数据对电池SOH进行预测,两个型号的电池误差MAE和RMSE均在2%以内,IA均在99.4%以上。当利用部分电压曲线获得的特征数据进行预测时,电池SOH预测误差均有不同程度的增加。两个实验表明,所提出的方法可以在带有噪声的输入数据集中学习一些更稳健的特征信息来提高模型的预测精度,训练一个模型可以在多个测试集上进行预测,无需再对模型进行参数调整,具有较强的泛化能力。
参考文献
[1] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et al. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551- 4563.
[2] 刘素贞, 陈云龙, 张闯, 等. 融合多维超声时频域特征的锂离子电池荷电状态估计[J]. 电工技术学报, 2023, 38(17): 4539-4550, 4563.
Liu Suzhen, Chen Yunlong, Zhang Chuang, et al. State of charge estimation of lithium-ion batteries fused with multidimensional ultrasonic time-frequency domain features[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4539-4550, 4563.
[3] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703- 1725.
[4] 张闯, 王泽山, 刘素贞, 等. 基于电化学阻抗谱的锂离子电池过放电诱发内短路的检测方法[J]. 电工技术学报, 2023, 38(23): 6279-6291, 6344.
Zhang Chuang, Wang Zeshan, Liu Suzhen, et al. Detection method of overdischarge-induced internal short circuit in lithium-ion batteries based on electrochemical impedance spectroscopy[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6279-6291, 6344.
[5] Li Xiaoyu, Yuan Changgui, Wang Zhenpo, et al. A data-fusion framework for lithium battery health condition estimation Based on differential thermal voltammetry[J]. Energy, 2022, 239: 122206.
[6] 戴俊彦, 夏明超, 陈奇芳. 基于双重注意力机制的电池SOH估计和RUL预测编解码模型[J]. 电力系统自动化, 2023, 47(6): 168-177.
Dai Junyan, Xia Mingchao, Chen Qifang. Encoding and decoding model of state of health estimation and remaining useful life prediction for batteries based on dual-stage attention mechanism[J]. Automation of Electric Power Systems, 2023, 47(6): 168-177.
[7] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342.
Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium- ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342.
[8] Chang Chun, Wu Yutong, Jiang Jiuchun, et al. Prognostics of the state of health for lithium-ion battery packs in energy storage applications[J]. Energy, 2022, 239: 122189.
[9] 周才杰, 汪玉洁, 李凯铨, 等. 基于灰色关联度分析-长短期记忆神经网络的锂离子电池健康状态估计[J]. 电工技术学报, 2022, 37(23): 6065-6073.
Zhou Caijie, Wang Yujie, Li Kaiquan, et al. State of health estimation for lithium-ion battery based on gray correlation analysis and long short-term memory neural network[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6065-6073.
[10] Guo Yongfang, Huang Kai, Hu Xiaoya. A state- of-health estimation method of lithium-ion batteries based on multi-feature extracted from constant current charging curve[J]. Journal of Energy Storage, 2021, 36: 102372.
[11] Yang Duo, Zhang Xu, Pan Rui, et al. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve[J]. Journal of Power Sources, 2018, 384: 387-395.
[12] Chen Yuan, He Yigang, Li Zhong, et al. A combined multiple factor degradation model and online verification for electric vehicle batteries[J]. Energies, 2019, 12(22): 4376.
[13] Ahmadian A, Sedghi M, Elkamel A, et al. Plug-in electric vehicle batteries degradation modeling for smart grid studies: review, assessment and conceptual framework[J]. Renewable and Sustainable Energy Reviews, 2018, 81: 2609-2624.
[14] Yang Shichun, Hua Yang, Qiao Dan, et al. A coupled electrochemical-thermal-mechanical degradation modelling approach for lifetime assessment of lithium-ion batteries[J]. Electrochimica Acta, 2019, 326: 134928.
[15] Hu Minghui, Li Yunxiao, Li Shuxian, et al. Lithium- ion battery modeling and parameter identification based on fractional theory[J]. Energy, 2018, 165: 153-163.
[16] Pang Hui, Guo Long, Wu Longxing, et al. A novel extended Kalman filter-based battery internal and surface temperature estimation based on an improved electro-thermal model[J]. Journal of Energy Storage, 2021, 41: 102854.
[17] Allam A, Onori S. Online capacity estimation for lithium-ion battery cells via an electrochemical model-based adaptive interconnected observer[J]. IEEE Transactions on Control Systems Technology, 2021, 29(4): 1636-1651.
[18] Wu Longxing, Liu Kai, Pang Hui. Evaluation and observability analysis of an improved reduced-order electrochemical model for lithium-ion battery[J]. Electrochimica Acta, 2021, 368: 137604.
[19] 申江卫,高承志, 舒星, 等. 基于迁移模型的锂离子电池宽温度全寿命SOC与可用容量联合估计[J]. 电工技术学报, 2023, 38(11): 3052-3063.
Shen Jiangwei, Gao Chengzhi, Shu Xing, et al. Joint estimation of SOC and usable capacity of lithium-ion battery with wide temperature and full life based on migration model[J]. Transactions of China Electro- technical Society, 2023, 38(11): 3052-3063.
[20] Shi Haotian, Wang Shunli, Wang Liping, et al. On- line adaptive asynchronous parameter identification of lumped electrical characteristic model for vehicle lithium-ion battery considering multi-time scale effects[J]. Journal of Power Sources, 2022, 517: 230725.
[21] Duan Wenxian, Song Shixin, Xiao Feng, et al. Battery SOH estimation and RUL prediction framework based on variable forgetting factor online sequential extreme learning machine and particle filter[J]. Journal of Energy Storage, 2023, 65: 107322.
[22] Feng Xuning, Weng Caihao, He Xiangming, et al. Online state-of-health estimation for Li-ion battery using partial charging segment based on support vector machine[J]. IEEE Transactions on Vehicular Technology, 2019, 68(9): 8583-8592.
[23] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和降噪自编码器-长短时间记忆的锂离子电池剩余寿命预测[J].电工技术学报, 2024, 39(1): 289-302.
Yin Jie, Liu Bo, Sun Guobing, et al. Transfer learning denoising autoencoder-long short term memory for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 289-302.
[24] Shen Sheng, Sadoughi M, Li Meng, et al. Deep convolutional neural networks with ensemble learning and transfer learning for capacity estimation of lithium- ion batteries[J]. Applied Energy, 2020, 260: 114296.
[25] Pang Hui, Wu Longxing, Liu Jiahao, et al. Physics- informed neural network approach for heat generation rate estimation of lithium-ion battery under various driving conditions[J]. Journal of Energy Chemistry, 2023, 78: 1-12.
[26] Wang Zhenpo, Yuan Changgui, Li Xiaoyu. Lithium battery state-of-health estimation via differential thermal voltammetry with Gaussian process regression[J]. IEEE Transactions on Transportation Electrification, 2021, 7(1): 16-25.
[27] Gou Bin, Xu Yan, Feng Xue. An ensemble learning- based data-driven method for online state-of-health estimation of lithium-ion batteries[J]. IEEE Transactions on Transportation Electrification, 2021, 7(2): 422-436.
[28] Shen Sheng, Sadoughi M, Chen Xiangyi, et al. A deep learning method for online capacity estimation of lithium-ion batteries[J]. Journal of Energy Storage, 2019, 25: 100817.
[29] Li Yi, Abdel-Monem M, Gopalakrishnan R, et al. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter[J]. Journal of Power Sources, 2018, 373: 40-53.
[30] Li Xiaoyu, Yuan Changgui, Wang Zhenpo. Multi- time-scale framework for prognostic health condition of lithium battery using modified Gaussian process regression and nonlinear regression[J]. Journal of Power Sources, 2020, 467: 228358.
[31] Li Xue, Jiang Jiuchun, Wang Leyi, et al. A capacity model based on charging process for state of health estimation of lithium ion batteries[J]. Applied Energy, 2016, 177: 537-543.
[32] Bian Xiaolei, Wei Zhongbao, He Jiangtao, et al. A novel model-based voltage construction method for robust state-of-health estimation of lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 12173-12184.
[33] Cho K, Courville A, Bengio Y. Describing multimedia content using attention-based encoder- decoder networks[J]. IEEE Transactions on Multimedia, 2015, 17(11): 1875-1886.
[34] Choi H, Kim M, Lee G, et al. Unsupervised learning approach for network intrusion detection system using autoencoders[J]. The Journal of Supercomputing, 2019, 75(9): 5597-5621.
[35] Vincent P, Larochelle H, Lajoie I, et al. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11: 3371-3408.
[36] Xing Yinjiao, Ma E W M, Tsui K L, et al. An ensemble model for predicting the remaining useful performance of lithium-ion batteries[J]. Microelectronics Reliability, 2013, 53(6): 811-820.
[37] Bian Xiaolei, Wei Zhongbao, Li Weihan, et al. State- of-health estimation of lithium-ion batteries by fusing an open circuit voltage model and incremental capacity analysis[J]. IEEE Transactions on Power Electronics, 2022, 68(2): 2226-2236.
[38] Ren Pu, Wang Shunli, Chen Xianpei, et al. A novel multiple training-scale dynamic adaptive cuckoo search optimized long short-term memory neural network and multi-dimensional health indicators acquisition strategy for whole life cycle health evaluation of lithium-ion batteries[J]. Electrochimica Acta, 2022, 435: 141404.
[39] Huang Kai, Yao Kaixin, Guo Yongfang, et al. State of health estimation of lithium-ion batteries based on fine-tuning or rebuilding transfer learning strategies combined with new features mining[J]. Energy, 2023, 282: 128739.
Abstract The state-of-health (SOH) estimation of lithium-ion batteries is a key technology in battery management systems, which can ensure the safe operation of the battery system. In practical applications, sensors for voltage and current collection are susceptible to external environmental interference, and the collected data often contains a large amount of noise. The estimation accuracy of the battery SOH model largely depends on the parameters in the algorithm, and some methods are usually not universal. In addition, the charging and discharging conditions of the battery are not complete, so the extracted feature information can easily deviate from the degradation trajectory. Such issues can lead to inaccurate estimation of SOH. This paper proposes a new framework based on the denoising autoencoder (DAE) and gated recurrent unit recurrent neural network (GRU-RNN) with the gated recurrent unit.
Firstly, the voltage-capacity (VC) model is used to reconstruct the voltage curve during the constant current charging stage, and the least squares method is used for model parameter identification. The incremental capacity (IC) curve is obtained from the reconstructed voltage curve. Subsequently, relevant features are extracted from the reconstructed voltage and IC curves as inputs of the SOH estimation model. The reconstructed voltage curve can easily obtain the IC curve of the battery and identify its feature information. Even when the noise ratio is 0.03, the reconstructed voltage curve is consistent with the real voltage curve, which shows that this method has strong noise anti-jamming ability.
Then, the reconstructed voltage curve is divided into different voltage segments, and relevant features are extracted from different voltage segments and IC curves. The Pearson correlation coefficient method is used, and features with high correlation are selected as inputs for the estimation model. Subsequently, a denoising autoencoder is used to train input features with noise in an unsupervised manner and learn more robust and valuable feature information from the damaged data.
Finally, two experiments are performed to verify the effectiveness of the proposed method. When the features contain noise, the proposed algorithm battery has high SOH prediction accuracy, and the relative error is 6.39% to 23.23% lower than that of the GRU-RNN and deep neural network (DNN) models. When the battery SOH is predicted using all the features, the battery’s MAE and RMSE errors of the two models are less than 2%, and the IA is more than 99.4%. When the features are obtained from part of the voltage and IC curve, the prediction error of the battery SOH increases. Two experiments show that the proposed method can learn more robust feature information from noisy data to improve the model’s prediction accuracy and has strong generalization ability. A model can be trained on multiple test sets without adjusting the model’s parameters.
Keywords: State-of-health estimation, denoising autoencoder, gated recurrent unit recurrent neural network, unsupervised training
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.231644
国家自然科学基金重点项目(51637004)和国家重点研发计划“重大科学仪器设备开发”项目(2016YF0102200)资助。
收稿日期 2023-10-02
改稿日期 2024-01-09
陈 媛 女,1990年生,博士,硕士生导师,研究方向为电池管理系统状态估计与故障诊断。E-mail:cumtjiangsucy@126.com
段文献 男,1988年生,博士,研究方向为电池管理系统状态估计与故障诊断。E-mail:dwx342977542@126.com (通信作者)
(编辑 陈 诚)