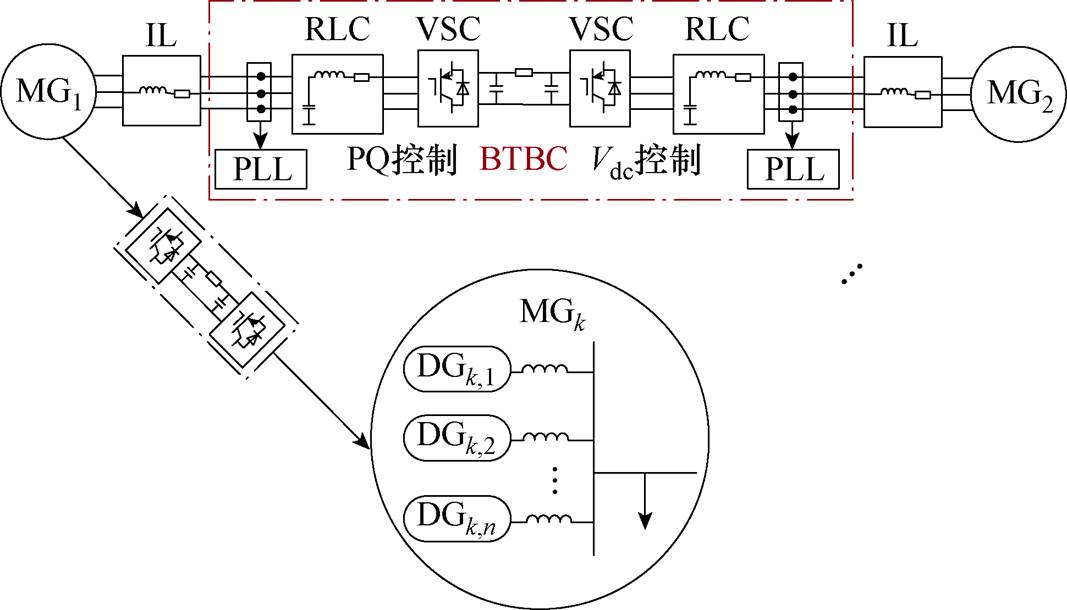
图1 基于BTBC柔性互联的微电网群拓扑结构
Fig.1 Topological structure of microgrid cluster based on BTBC flexible interconnection
摘要 在基于背靠背变流器柔性互联的交流微电网群中，传统的分层控制架构可以实现各微电网（MG）单元内的频率/电压无差恢复和功率均分的控制目标，但无法实现微电网群全局层面的有功均分控制目标，因此，亟须提出柔性互联微电网群的分层协同控制方法，并分析其小信号稳定性。该文提出一种柔性互联微电网群全新的分层分布式协同控制架构，各背靠背变流器可通过两侧MG单元有效交互实现集群层面的全局控制目标，实现全局层面的有功均分。进一步建立分层分布式控制架构下微电网群系统的小信号模型，分析其稳定性的主导失稳模态，并与已有文献方法进行了功率传输稳定性的比较分析。最后，利用Matlab/Simulink搭建了仿真模型，验证了控制策略的有效性和优越性。
关键词：背靠背变流器 柔性互联 微电网群 分层协同控制 小信号稳定性分析
微电网群（Microgrid Cluster, MGC）将地理空间上毗邻的多个微电网（Microgrid, MG）整合成紧密的整体，从而更好地应对单一微电网备用容量小、稳定性差的问题[1-3]，还能有效提高分布式电源（Distributed Generator, DG）的消纳水平。MGC系统存在多种互联形式，在传统的阻抗线路互联方式下，各MG单元间的扰动不能相互隔离，且交互功率也只能通过间接方式调节。而基于背靠背变流器（Back-To-Back Converter, BTBC）柔性互联方式下的MGC系统，由于具备区域间潮流连续调节、故障分区缓冲等功能[4-6]，是近年来的研究焦点。
然而与传统阻抗互联的MGC系统相比，柔性互联MGC系统中各MG单元间无法形成有效的“频率信号”传递[7-10]，其本质是一个可分区异步运行的互联系统。在此范式下，柔性互联MGC系统中，各MG单元的频率扰动平抑任务只能由区域内的可调节电源独自承担，不利于MGC整体的控制性能提升。虽然BTBC具备一定的受控调节能力，但若不对其施加合适且正确的传输功率指令[11-12]，MGC系统集群层面整体的扰动均衡控制目标任务难以实现。
MGC系统基本的控制任务一般包括[13-17]：①频率和电压的无差恢复控制；②集群层面的功率均分控制。上述控制目标仅通过各DG采用的本地控制模式无法完全实现，必须构建完善的通信控制架构。目前，在阻抗互联MGC系统中，控制策略一般设计为各DG采用本地下垂控制+分布式/集中式二次协同控制；通信架构一般设计为微电网单元层+集群层的两层架构。代表性的研究有文献[15-16]，建立了一类分层分布式的二次控制架构，实现了频率/有界电压无差恢复和有功/无功均分控制的目标。但上述针对阻抗互联MGC系统的分层协同控制的研究中，控制对象仅有采用下垂控制的DG，而柔性互联的MGC系统中，控制对象还包括BTBC。因此需要研究包含BTBC的分层协同控制架构和方法。
现有直接针对基于BTBC柔性互联MGC系统分层协同控制的相关文献较少，但注意到基于BTBC柔性互联MGC系统与柔性交直流互联微电网/微电网群、柔性直流多端互联MGC系统之间存在某些相似性，相关研究可以一同作为参考。例如，文献[18]针对多端柔性直流互联的微电网群系统，将各AC-DC变流器端口纳入分层协同控制架构，提出一种适用于直流互联孤岛MGC系统的分层分布式控制策略，但由于多端柔性互联架构下，必有一个变流器工作在直流电压控制模式，因此该方法仅能实现N-1个微电网的有功均分控制。文献[19]针对交直流互联微电网，提出了一种基于协调因子均衡的分层控制策略，实现了交/直流微电网内的交流电压/频率、直流电压的恢复控制，以及功率均分控制，该控制方法具有借鉴意义，但需要针对交流柔性互联场合进行重新设计。文献[20]针对BTBC互联的MGC系统，设计了全新的集中-分布式混合的分层协同控制通信网络架构，能够实现上述控制目标。但该方法过于依赖实时测量各MG内的本地负荷，方法的实用性欠佳。
此外，柔性互联模式下MGC系统的稳定性也值得重点关注，特别是，引入分层协同控制架构对MGC系统稳定主导特征的影响。文献[21]针对分层协同控制架构下的常规阻抗互联MGC系统，开展了完整的小信号建模和稳定主导分析，指出分层协同控制架构下系统会增加更多的低频稳定主导极点。文献[22-23]则以BTBC互联的MGC系统为研究对象，发现除各MG内DG的下垂增益外，BTBC的控制器参数和物理电路参数都对MGC稳定性有直接影响。文献[24-25]针对柔性互联系统中BTBC装置的双向交互稳定性开展分析，指出BTBC不同传输方向下有着截然不同的稳定特性。上述的稳定分析结果可提供有益的参考，但目前鲜有文献开展分层控制下柔性互联MGC系统的小信号稳定分析研究。
综上所述，当前基于BTBC互联的MGC系统存在显著缺陷，主要表现为缺少有效的分层协同控制架构设计以及缺少分层协同控制下稳定主导特征分析等。本项目拟设计一种包含BTBC的分层分布式协同控制架构，实现柔性互联MGC系统频率/有界电压无差恢复以及全局有功均分控制的目标。进一步建立该控制架构下柔性互联MGC系统的完整小信号模型，分析其稳定性的主导失稳模态，并与已有控制方法进行了稳定性差异比较。最后通过仿真验证了本文研究的正确性。
本文研究的柔性互联MGC系统结构如图1所示，它由N个交流子MG单元及各单元间q个背靠背变流器型FMSS组成。根据图1的连通度理论，为满足N个子MG单元间的功率互济，BTBC-FMSS的个数q需满足q≥N-1的条件。若综合考虑控制效果和成本因素，本文假定q=N，即MGC系统中各MG单元采用“手拉手”柔性环形互联的方式。
图1 基于BTBC柔性互联的微电网群拓扑结构
Fig.1 Topological structure of microgrid cluster based on BTBC flexible interconnection
此外本文研究的孤岛微电网群由下垂控制下的DG主导，不含同步发电机。由于PQ控制下的DG可被简化为负荷，故不单独分析。在所提控制策略时间尺度内，新能源DG一次能源侧波动视为外部给定常数。
仅采用一次控制的微电网单元利用本地的下垂控制恢复DG的频率、电压稳定性和实现功率均分[14-17]，但是本地下垂控制只能实现有差调节，负荷不间断扰动下无法使频率、电压精确地保持在额定值，同时电压恢复与无功控制间也存在固有矛盾。为解决这一问题，本文借鉴文献[16]中传统方法，在微电网单元的DG之间引入了通信网络，在下垂控制基础上通过分布式二次控制进一步实现微电网单元频率、有界电压的无差调节和有功、无功功率的均分控制。
在基于BTBC柔性互联的MGC系统中，由于BTBC的隔离作用，频率、电压扰动无法像在传统的交流线路互联MGC系统中一般可于各MG单元间自由传递，导致各MG单元内部的扰动只能通过各自的DG进行平抑，无法做到全局性的有功均分控制。因此解决问题的核心思路在于，如何合理控制互联BTBC的传输功率，在MG单元实施不同控制（一次/二次）模式下，都能实现MGC系统层面的有功均分。
为解决上述问题，本文设计了一种分层分布式控制架构，提出的系统控制架构可分为两层。底层为图1所示的柔性互联微电网群物理层，其中MG通过由两个电压源变流器背靠背连接构成的BTBC连接；上层为图2所示实现柔性互联微电网群内稀疏通信的信息层，其中MG内部相邻的DG进行通信，MG之间由领导DG代表其所在MG单元与其相连BTBC进行通信，BTBC扮演类似“桥接器”角色。
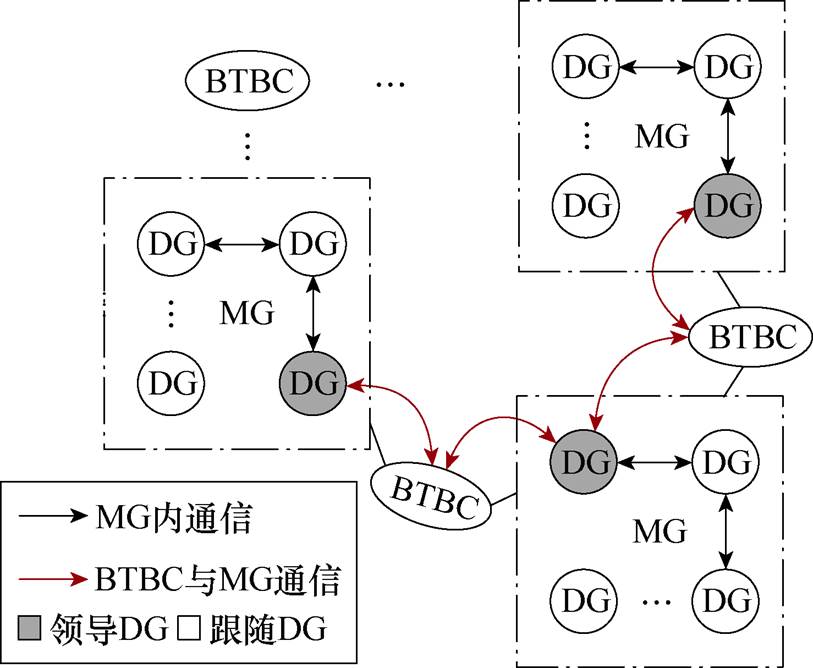
图2 BTBC-IMGs的通信拓扑结构
Fig.2 The communication topology of BTBC-IMGs
本文拟采用所提出的分层协同传输功率控制架构，包含对MG单元内以及MGC系统中MG之间的控制，具体控制目标如下：
1）MG单元内的控制目标
目标1：实现MG单元内各DG频率/端口有界电压的二次恢复控制，即
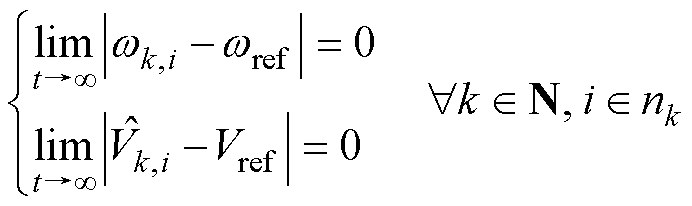（1）
式中，下标k为MG编号；i为DG编号；wk,i、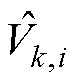
分别为MGk中DGk,i的频率、有界输出电压；wref、Vref分别为频率、输出电压的参考值；nk为微电网单元内DG的个数。
目标2：实现MG单元内各DG之间的有功和无功功率均分控制，使各DG按照自身有功容量（即有功/无功下垂系数）出力，以实现扰动均担。即
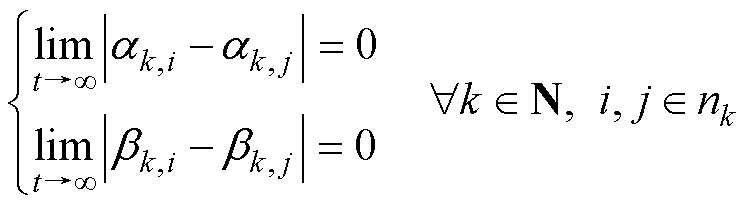（2）
式中，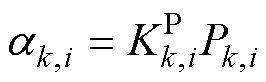
，
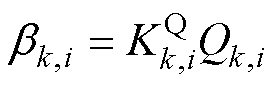分别表示第k个MG中第i台DG按照下垂系数的有功和无功出力比率，
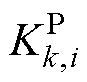和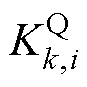
分别为DGk,i的有功和无功下垂系数，Pk,i和Qk,i分别为MGk中DGk,i的有功功率和无功功率。
2）柔性互联MGC系统的控制目标
目标3：全局有功功率均分控制，协调各BTBC传输功率实现不同MG单元间按照各自容量出力。
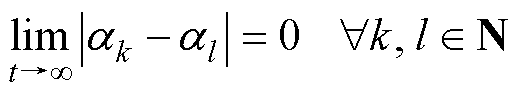（3）
式中，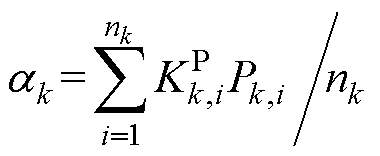
、
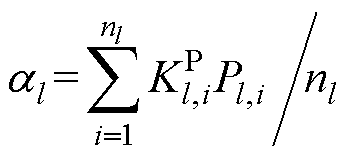分别表示第k个与第l个MG单元稳态下平均有功出力比率；nl为第l个微电网单元内DG的个数。
2.1.1 MG单元的一次控制
本文中，DG采用如图3所示的带有下垂特性的一次控制以实现微电网单元内无通信的电压、频率控制，具体[22]表示为
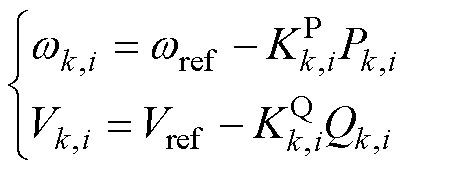（4）
其中
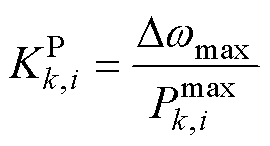
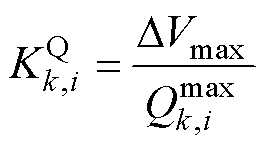
式中，Dwmax与DVmax分别为允许的最大频率、电压偏差；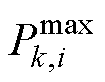
和
分别为额定有功功率、无功功率。
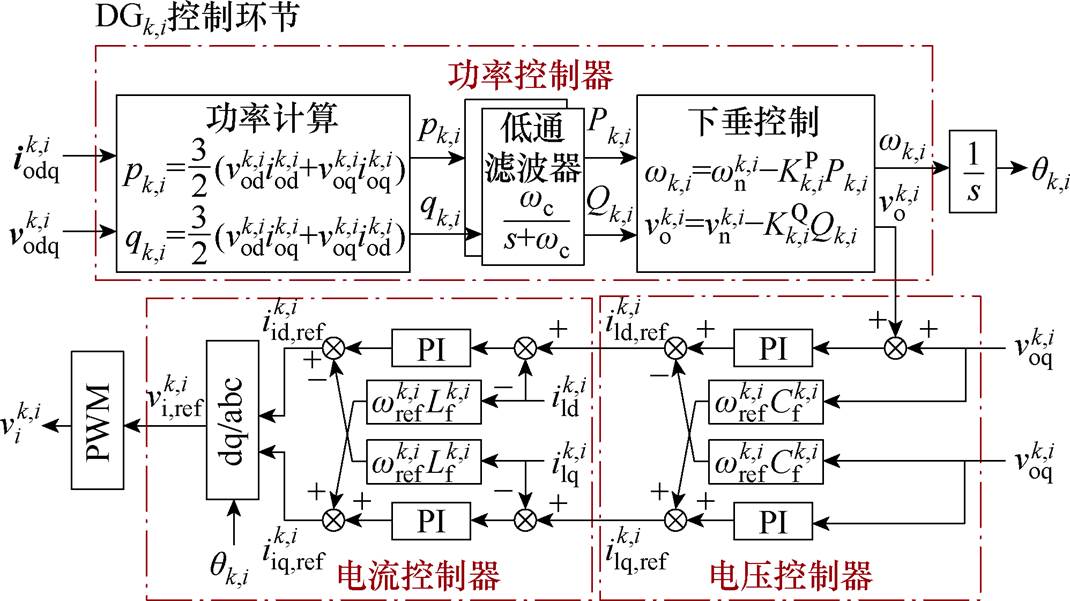
图3 电压控制逆变型DG的控制框图
Fig.3 Control block diagram of inverter based DG with voltage control
2.1.2 MG单元的分布式二次控制
由于本地下垂控制下的控制效果存在固有偏差，为实现MG单元内如式（1）和式（2）所示的无差调节目标，本文参考文献[26-27]方法设计了分布式二次控制策略，采用多智能体一致性算法实现MG单元内的控制目标。
以图4为例，考虑存在虚拟节点的通信网络，采用一致性算法[15]的频率恢复控制补偿值设计为
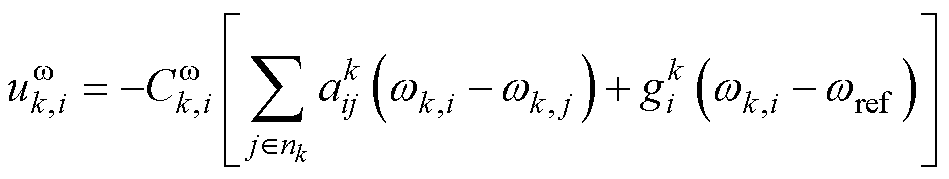（5）
式中，
为频率控制比例系数且为正值；
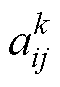为MGk中DGk,i到DGk,j的相邻权重，若DGk,i与DGk,j通信则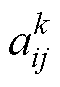为1，否则为0；
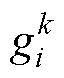为MGk中虚拟节点DG0～DGk,i的权重值，若虚拟节点DG0与DGk,i通信，则
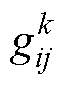为1，否则为0。
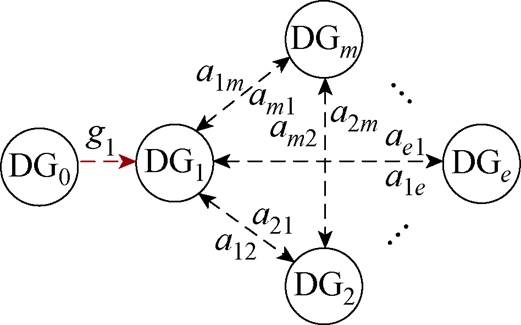
图4 MG单元通信网络拓扑
Fig.4 MG unit communication network topology
有功功率均分控制补偿值可设计为
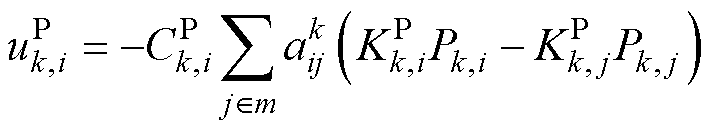（6）
式中，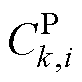
为有功功率补偿值增益且为正值。
定义分布式二次控制频率有功调节量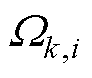
为
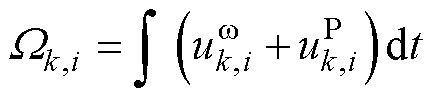（7）
由式（1）、式（7）可得加入分布式二次控制的频率控制器为
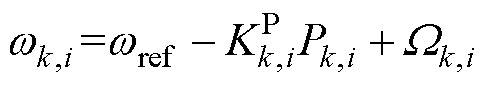（8）
由于线路阻抗失配，MG单元中的DG具有不同的输出电压，造成电压恢复和精确的无功功率均分之间始终存在矛盾[14-15]，通过控制方法只能精确实现两者中的一项。本文选择在各MG单元的DG之间实现精确的无功功率均分和有界输出电压恢复。为得到各DG的有界输出电压，设计了分布式电压观测器来估计每个DG的有界电压，使估计值收敛于MG单元内所有DG的加权平均电压，估算过程可以简单地表示[26]为
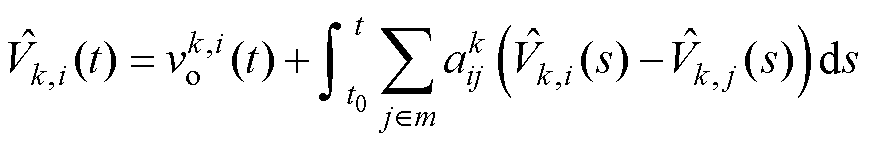（9）
式中，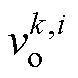
为DGk,i端口电压；
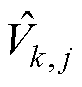为DGk,j的有界输出电压。
与频率、有功功率的二次控制类似，有界电压恢复控制补偿值可设计为
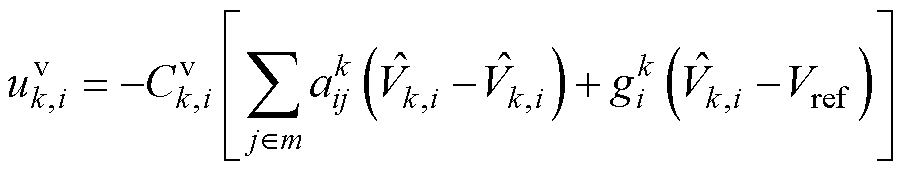（10）
式中，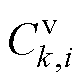
为电压补偿值增益且为正值。
无功功率补偿控制值可设计为
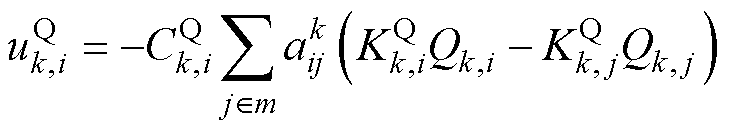（11）
式中，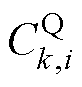
为无功功率补偿值增益且为正值。
定义分布式二次控制有界电压无功调节量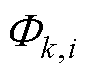
为
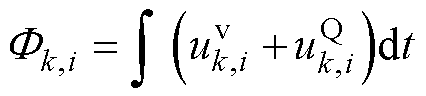（12）
由于在dq旋转坐标系下进行控制，故采用d轴电压定向策略，将输出电压的q轴分量设置为0，从而便于电压的定向控制。即电压控制器设计为
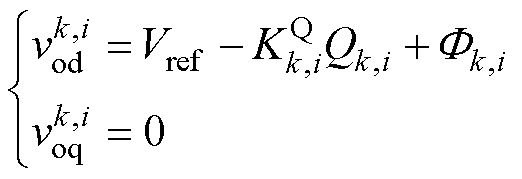（13）
在MG单元中增加频率、有界电压以及有功和无功的分布式二次控制后，控制目标1和2得以完全实现。
在MGC系统的控制层面，各MG单元利用BTBC进行“桥接”后实现柔性互联MGC系统层面的协同控制。其主要目标在于充分调控BTBC有功出力能力实现各MG单元间能量的互联互济，最终实现目标3——全局有功均分控制。
值得指出的是，BTBC的结构特性决定了其本质上是一个双向无功电源，而传输有功功率只能由一端向另一端传递。此外，电力系统中频率-有功的耦合特性具有全局性，而电压-无功耦合特性只具有局域性。因此本文不讨论基于BTBC柔性互联MGC系统的全局无功均分控制问题，各BTBC两端输出的无功功率统一设为0。
BTBC一般一个端口采用PQ控制，而另一端口采用VdcQ控制。PQ控制端口可基于本地控制或接受上级电网的调度指令，根据需求，完成不同时间尺度（s级、min级或h级）内的功率传输控制；而VdcQ控制端口则通过反馈控制方式，动态抑制直流电压扰动，维持其运行在恒定值。其相应的控制框图如图5所示。
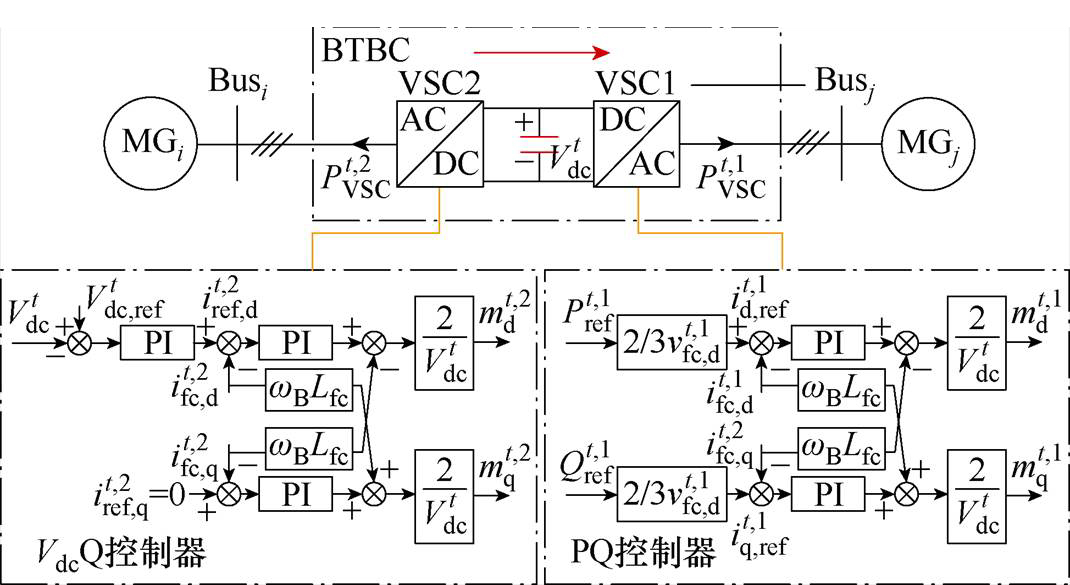
图5 BTBC控制策略图
Fig.5 BTBC control strategy diagram
与传统方式不同，本文所研究的柔性互联MGC系统并不具有传统意义上类似文献[20]上级集中调度的微电网中央控制器，而采用分布式控制的方式。总结来说，BTBC获取有功传输指令存在下列两种控制模式。
1）BTBC的本地控制
各MG单元仅采用本地下垂控制时，BTBC利用两侧VSC端口的PLL得到相连两侧MG单元的频率差值信号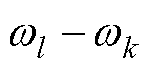
，对该差值信号进行PI控制即可得到BTBC的有功传输指令。该控制模式可完全不依赖通信且易于实现，其控制式为
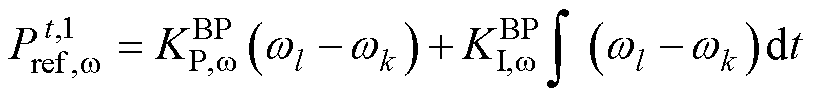（14）
式中，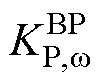
、
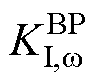分别为BTBC基于两侧MG频率差值设计的有功控制器的比例、积分调节系数。
2）BTBC的分层协同控制
当各MG单元分别启动分布式二次恢复控制后，两侧MG单元的频率信号逐步恢复至额定值，但两侧MG单元的平均有功出力比率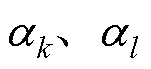
仍不相同，BTBC失去了利用两侧MG单元频率误差信号来计算传输有功指令的优势。此时，应根据两侧MG单元的平均有功出力比率差值
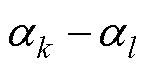来计算。相应地，对该差值信号进行PI控制即可得到BTBC的有功传输指令为
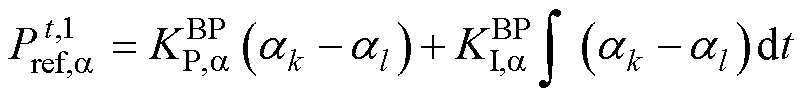（15）
式中，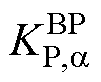
、
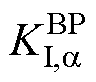分别为BTBC基于两侧MG有功出力比率差值设计的有功控制器的比例、积分调节系数。
两侧MG平均有功出力比率的信号需要获取MG单元内部所有机组的信息，若实时精确计算需要占用过多的通信资源。但考虑到各MG单元内各DG始终遵循下垂控制的控制率。则在准稳态阶段，各MG内有功出力比率是一致的。存在
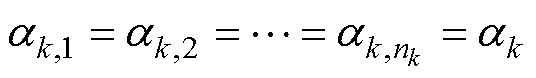（16）
因此，选用任意一台机组的有功出力比率都可以作为各MG整体有功出力比率的代表，本文选取各MG单元编号1号的DG作为代表。则式（15）可改写为
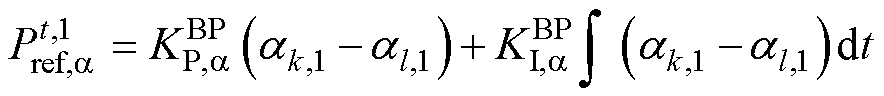（17）
显然用DGk,1的有功出力比率动态代表MGk的整体动态，必然存在控制性能上的差异，但稳态控制结果不存在差异，这是一个综合考虑通信成本和控制性能的折中方案。
综上所述，当各MG单元采用一次控制时，BTBC可采用本地控制模式，其优点为无需通信即可实现MGC全局层面的有功均分；缺点为该模式依赖BTBC两侧频率差计算功率传输指令，故无法与频率无差控制并行。当各MG单元采用二次控制时，BTBC可采用分层协同控制模式，此模式优点为不与MG二次控制冲突，可同时实现MG内频率的无差控制与MGC全局层面的有功均分；缺点为依赖通信。
上述两种控制模式均可实现MGC全局层面的有功均分，可依据实际情况灵活选择不同的控制模式。则BTBC的传输功率指令计算式可由式（14）、式（17）表示为
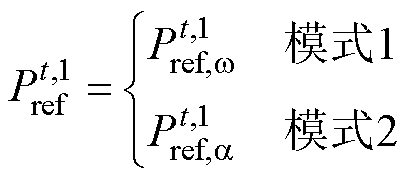（18）
根据dq参考系变换和d轴输出电压定向原理，PQ控制侧VSC的内电流控制器的电流参考值[20]相应设置为
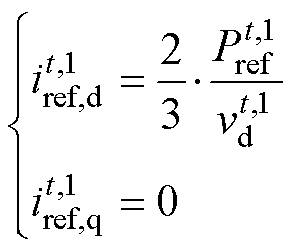（19）
对于VdcQ控制侧VSC，其电流内环的d轴电流参考值主要基于直流侧电压偏差通过PI得到，表示为
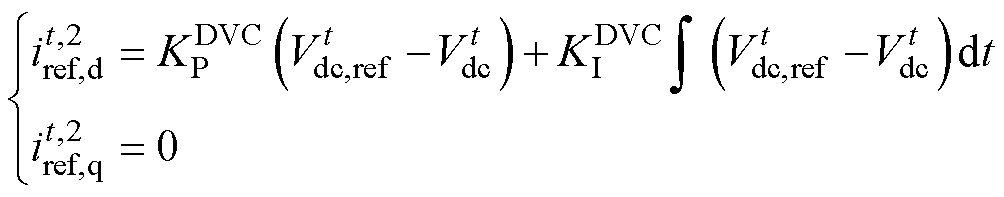（20）
式中，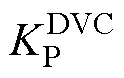
、
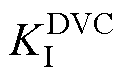分别为VdcQ控制侧VSC电压外环控制的比例、积分调节系数。
本节将首先构建分层协同控制架构下的柔性互联MGC系统的完整动态模型，并在稳定运行点进行线性化，得到整个MGC系统的小信号模型[28-30]。值得指出的是，文献[21, 24]已构建了不含分层控制架构的柔性互联MGC系统小信号模型，为简化分析过程，本节在文献[21, 24]工作基础上，重点给出分层协同控制相关模态的建模过程。
考虑包含m个DG的微电网单元建模，由式（8）、式（13）可知，微电网单元引入分布式二次控制后系统新增状态变量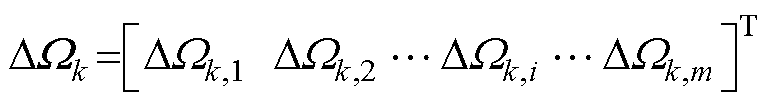
，
=
。
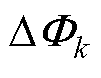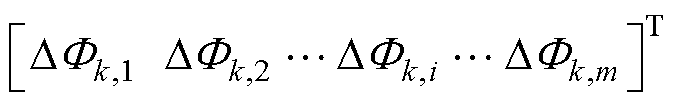需要特别说明的是，考虑MG单元内的无功功率均分控制，对微电网内m个DG引入有界电压控制，仅新增m-1个状态变量。
对式（8）求导可得
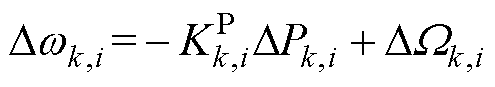（21）
对式（7）求导，并将式（21）代入可以得到
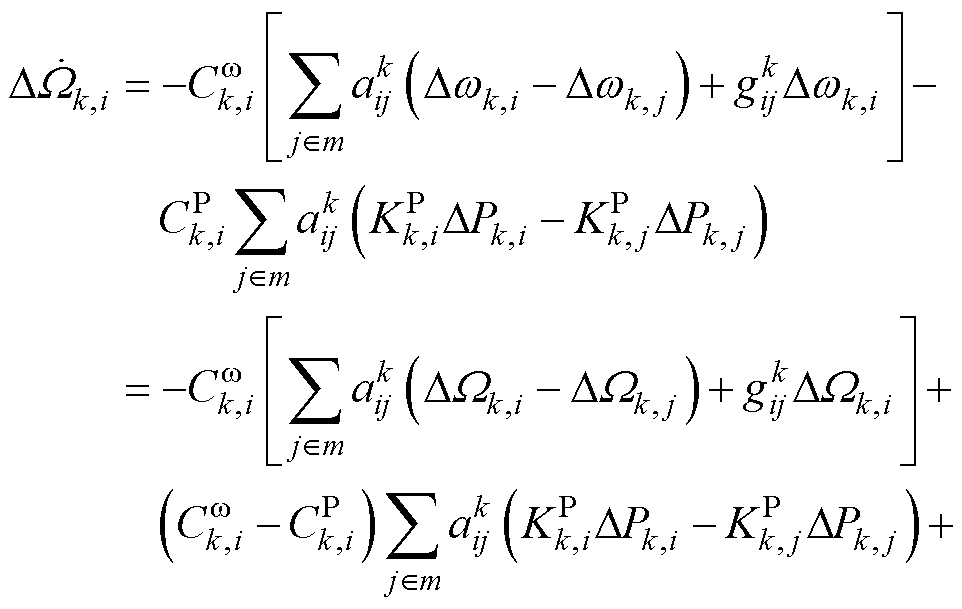
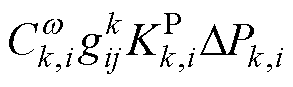（22）
令同一个MG内不同DG的频率/有功功率补偿增益相同，即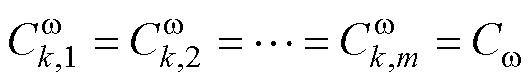
，
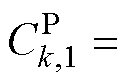
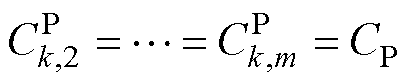，结合图论基本概念可得
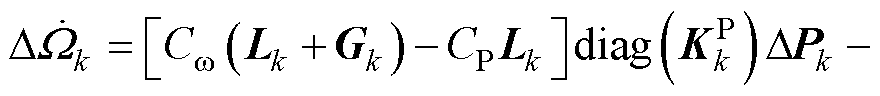
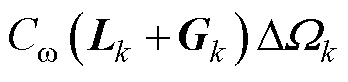（23）
式中，Lk为MGk通信网络的拉普拉斯矩阵；Gk为MGk通信网络中领导节点的邻接矩阵；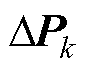
= 
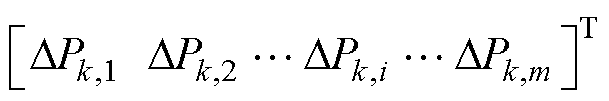为MGk中各DG的有功功率状态变量；
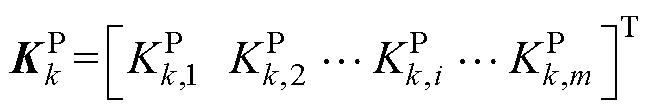为MGk中各DG的有功下垂系数。
对式（12）求导可得
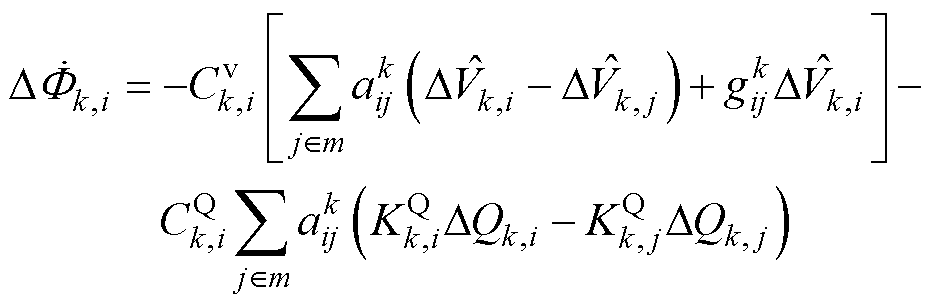（24）
在同一个微电网单元中设置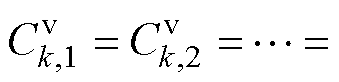
，
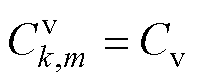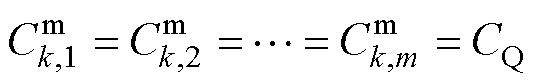，可得
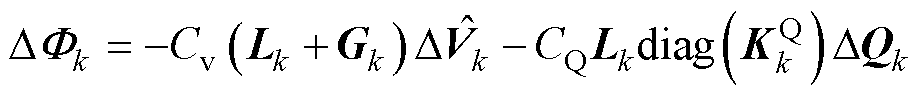（25）
式中，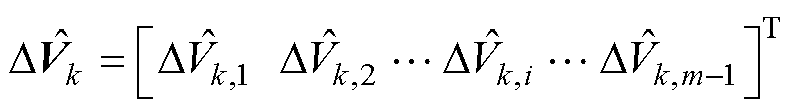
为MG单元内各DG的有界输出电压；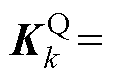
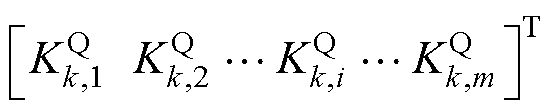为MGk中各DG的有功下垂系数；
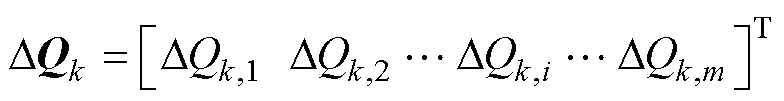为MGk中各DG的无功功率状态变量。
将式（23）、式（25）添加到一次控制微电网小信号模型就可得到增加分布式二次控制的微电网单元小信号模型如下
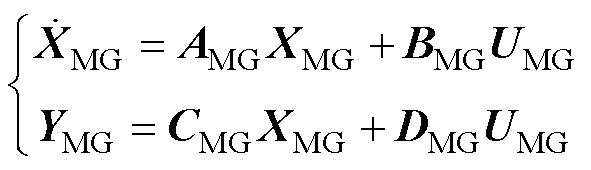（26）
式中，AMG、BMG、CMG、DMG分别为微电网状态空间小信号模型的系统矩阵、控制矩阵、输出矩阵和直接传递函数矩阵；UMG、YMG分别为状态空间模型的输入与输出向量。
MG中作为公共参考坐标系的DG1状态变量为XDG1，含12个状态变量，分别为输出有功功率、输出无功功率、电压外环控制积分器输出dq分量、电流内环控制积分器输出dq分量、电感电流dq分量、输出电压与电流dq分量；其余DG状态变量为XDGi（1＜i≤m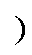
，其在DG1的基础上增加与参考坐标系的夹角为状态变量，故含13个状态变量；MG分布式二次控制中w-P与v-Q droop控制补偿量对应的状态变量分别为
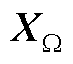与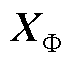
，各含m个状态变量；有界电压控制含m-1个状态变量；故MG状态变量XMG共包含16m-2个状态变量。
采用BTBC分层控制策略后，线性化式（14）及式（17）可得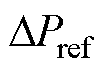
的表达式为
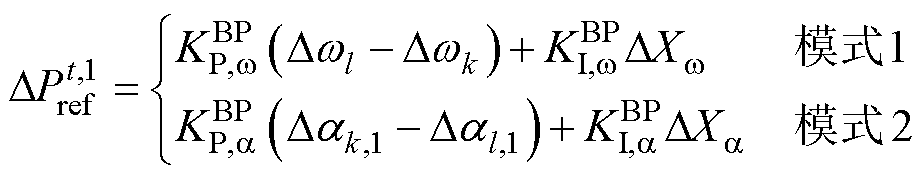（27）
式中，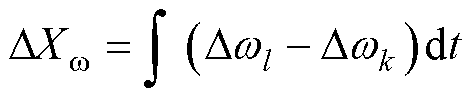
为BTBC两侧MG的频率差值的积分量；
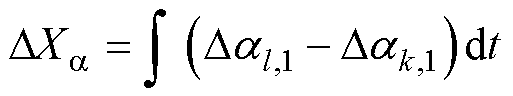为BTBC两侧MG领导DG的有功出力比率差值。
在BTBC状态空间方程中添加状态变量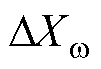
或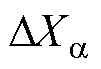
，并将式（27）添入BTBC状态空间方程组，即可得到修改控制策略的背靠背变流器小信号模型，状态空间如下
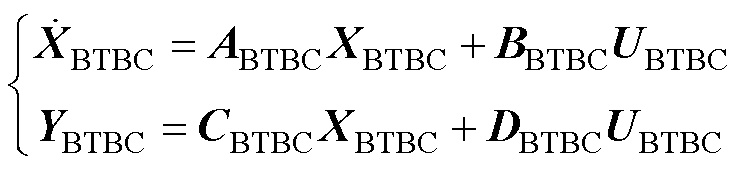（28）
式中，XBTBC为包含20个状态变量的列向量，即在原有的BTBC状态变量上新增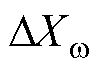
或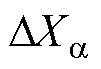
；ABTBC、BBTBC、CBTBC、DBTBC分别为BTBC状态空间小信号模型的系统矩阵、控制矩阵、输出矩阵和直接传递函数矩阵；UBTBC、YBTBC分别为状态空间模型的输入与输出向量。
建立互联线路IL的小信号模型，其状态空间为
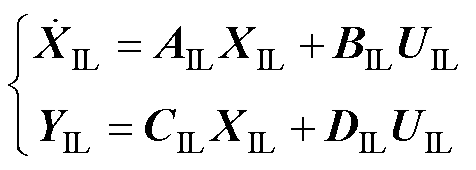（29）
式中，XIL=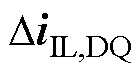
；AIL、BIL、CIL、DIL分别为互联线路状态空间小信号模型的系统矩阵、控制矩阵、输出矩阵和直接传递函数矩阵；UIL、YIL分别为状态空间模型的输入与输出向量。
将N个MG、BTBC与2N个IL模块按如图6所示的互联关系连接，可得MGC状态空间为
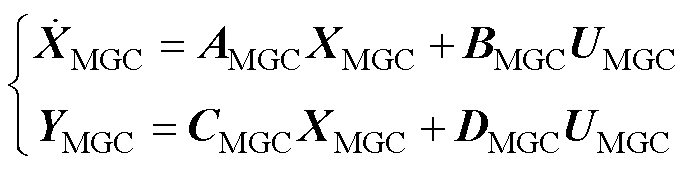（30）
式中，XMGC包含16mN+22N-1个状态变量；AMGC、BMGC、CMGC、DMGC分别为微电网群状态空间小信号模型的系统矩阵、控制矩阵、输出矩阵和直接传递函数矩阵；UMGC、YMGC分别为状态空间模型的输入与输出向量。
需要指出，由于本文构建的模型为N个MG通过q=N个BTBC环形连接，故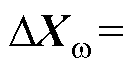
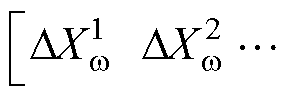
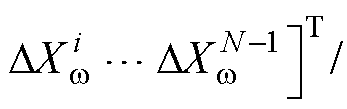
仅有N-1个状态变量，N个BTBC仅有20N-1个状态变量。
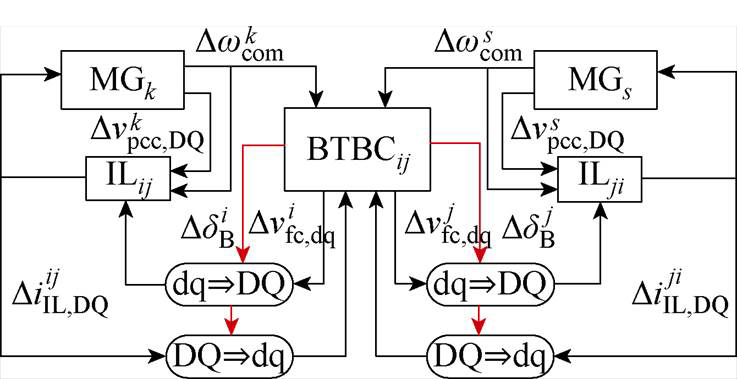
图6 MGC各模块间的输入输出关系
Fig.6 Input and output relationships between MGC modules
考虑本文所提MG分布式二次控制与BTBC的两种功率传输控制均为外环控制，为研究本文所提控制策略对MGC系统稳定性的影响，现构建通过BTBC环形连接的三MG系统小信号模型，其仿真模型的拓扑如图7所示。
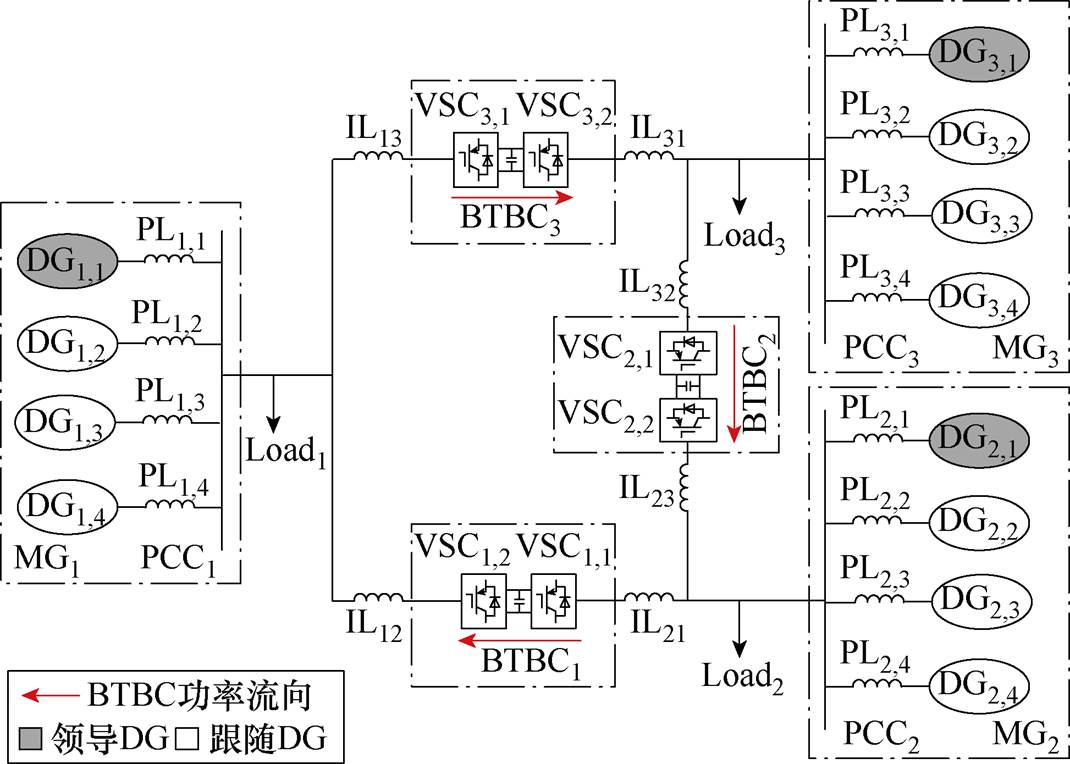
图7 BTBC-MGC的仿真模型拓扑结构
Fig.7 Example of simulation model of BTBC-MGC
设置表1所示的四种控制模式，进行相应主导稳定模式以及功率传输稳定性的比较。其中文献[22]控制与本文所提本地控制相似，即不需要构建分层协同的控制架构，但两种方法均无法实现频率/电压的无差恢复。文献[20]控制与本文所提分层协同控制对应，二者在MG内均采用分层协同的控制架构，能实现包括MGC全局层面有功均分在内的所有本文所提控制目标；不同点在于本文对BTBC采用分布式的分层协同控制而文献[20]利用集中式的集群层控制实时采集各MG数据并计算出BTBC传输功率指令。
表1 主导模态分析中的控制模式
Tab.1 Control modes in dominant modal analysis
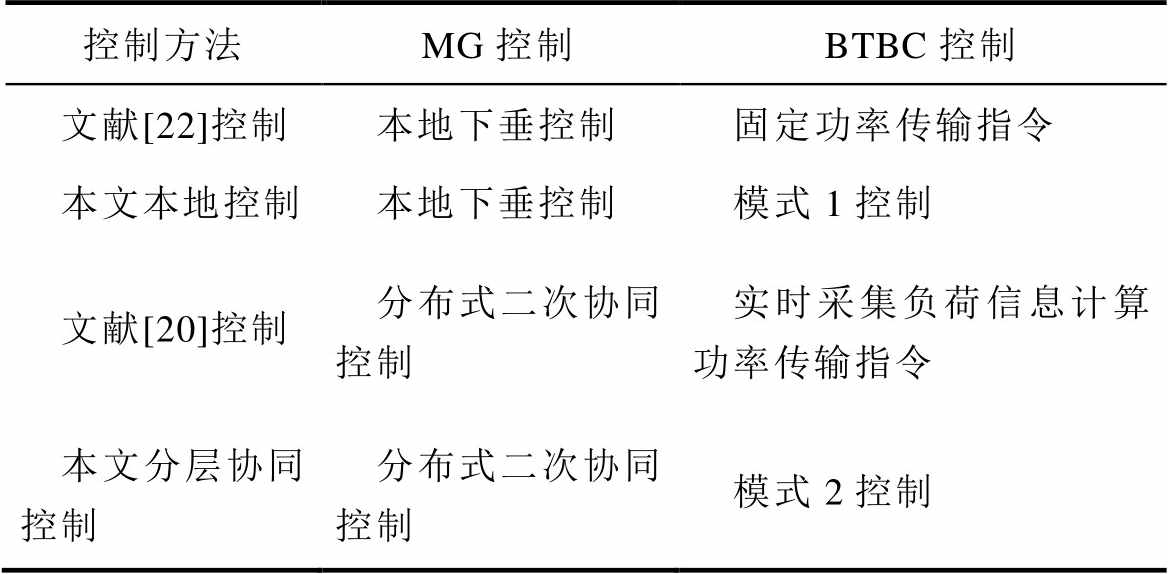
控制方法MG控制BTBC控制 文献[22]控制本地下垂控制固定功率传输指令 本文本地控制本地下垂控制模式1控制 文献[20]控制分布式二次协同控制实时采集负荷信息计算功率传输指令 本文分层协同控制分布式二次协同控制模式2控制
由于文献[22]控制较其他各控制相对基础，无特殊控制环，故表2仅给出其余三种控制的独有控制环参数。四种控制建模下均保持物理电路参数与相同控制环的参数一致，详细数据见附表1与附表2。此外，为方便后续的小信号分析，表3中给出了各主导极点的模态及其对应的控制环节。
表2 BTBC互联环形微电网群独有控制参数
Tab.2 Common control parameters for different control methods in BTBC-MGC
系统参数数值 本文本地控制BTBC频率恢复控制PI参数0 1 500 本文分层协同控制MG二次控制比例参数频率/(1/s)60 有功功率/[rad/(kW·s2)]20 电压/(1/s)30 无功功率/(V/kvar)200 BTBC有功均分控制PI参数0 1 600 文献[17]控制MG二次控制比例参数频率/(1/s)60 有功功率/[rad/(kW·s2)]20 电压/(1/s)30 无功功率/(V/kvar)200
首先进行文献[22]控制与本文本地控制特征根分布对比分析，研究本文所提出的BTBC基于两侧MG频率差值的有功传输策略对MGC系统稳定性的影响。出于控制变量考虑，文献[22]中给定的BTBC功率传输指令在数值上与本地控制由控制策略求出的功率传输指令一致。
分析图8所示两种控制下的特征根分布可知，在MG采用传统一次下垂控制时引入基于BTBC两侧MG单元的平均有功出力比率差值控制策略后，该控制模态所主导的两个特征根出现在实部-1左右，较文献[22]更加靠近坐标系虚轴，稳定性有所降低。为分析该控制策略对系统小信号稳定性的影响程度，现作控制参数根轨迹分析。需要说明的是，控制策略中的比例环节虽然能加快控制速度，但无助于实现控制目标的无差调节，故这里假设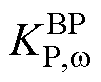
= 0，仅对功率传输控制积分系数
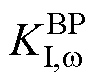变化下的主导极点根轨迹进行分析。
表3 小信号分析中的图例与备注
Tab.3 Legends and remarks in small signal analysis
图 例备 注 DxMG内有界电压控制 Dd各DG功角 DW频率二次控制补偿量 DF电压二次控制补偿量 DXwBTBC两侧频差积分 DXaBTBC两侧有功均分积分 vQMG内v-Q下垂控制 wPMG内w-P下垂控制 PQVSC PQ控制 DCBTBC直流部分 PLLBTBC内锁相环 VdcQVSC VdcQ控制 LPF低通滤波器 VCDGDG内电压控制 RLCBTBCBTBC-RLC电路
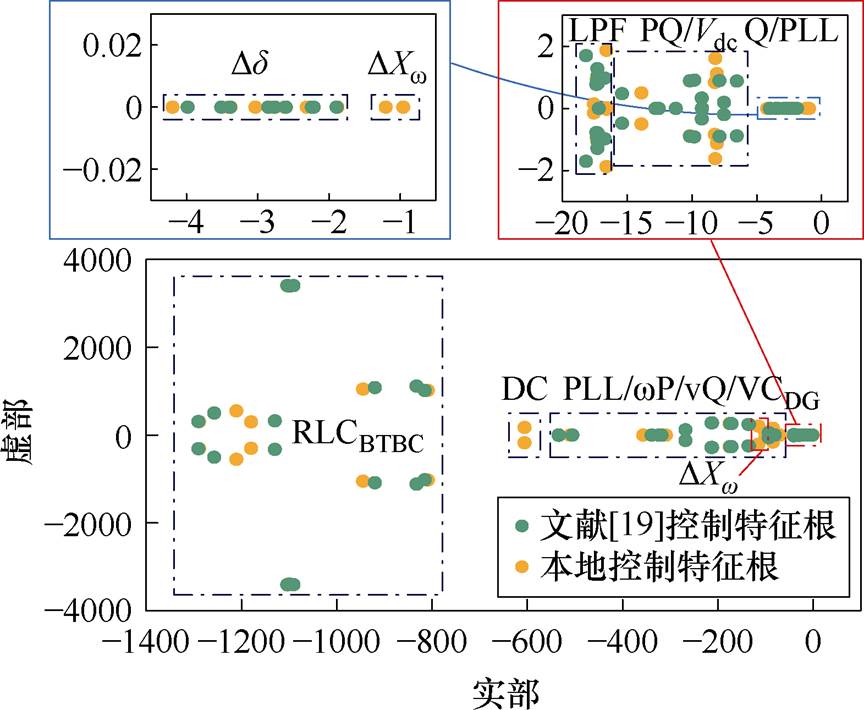
图8 文献[22]与本地控制下的特征值分布比较
Fig.8 Eigenvalues distribution comparison between control in Ref.[22] and local control in this article
分析图9可知，BTBC功率传输控制积分系数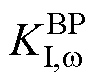从1增长至7 200的过程中，影响系统稳定性的特征根由BTBC两侧频率-传输功率控制模态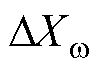主导，且在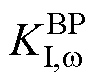=7 150时达到临界稳定。故认为在本地控制下，关键参数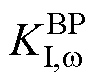取值范围为 (1, 7 150)。
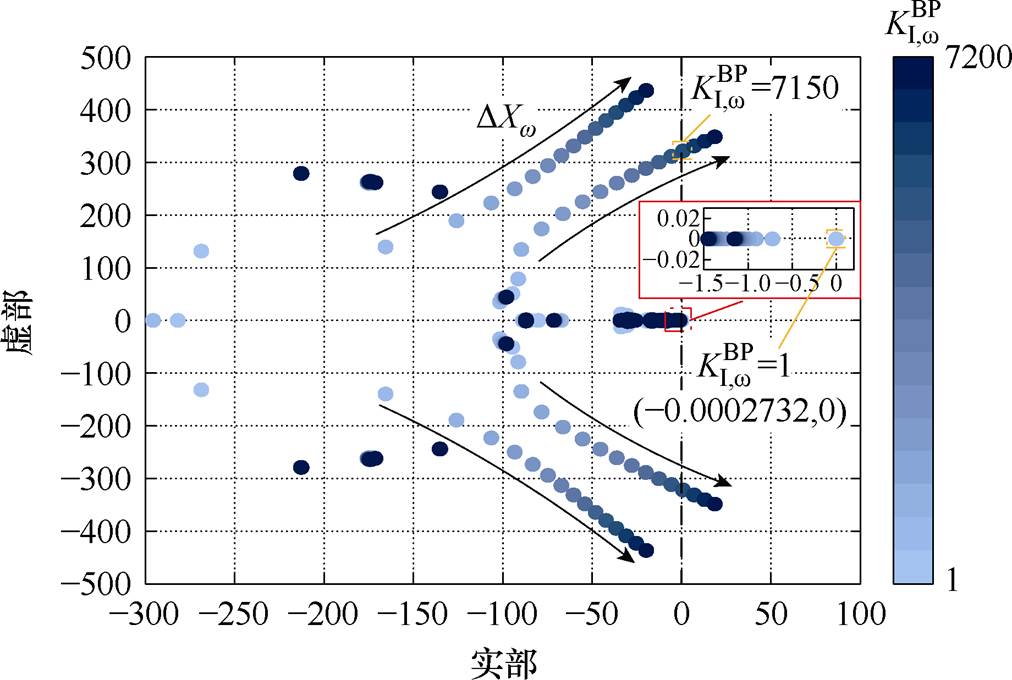
图9 本地控制下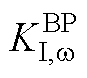
变化的主导极点根轨迹
Fig.9 The dominated pole root locus diagram of 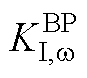variation under local control
继续进行文献[20]控制与分层协同控制的特征根分布对比分析，研究基于背靠背变流器柔性互联微电网群的分层协同控制对MGC系统稳定性的影响。此对比中，文献[20]给定的BTBC功率传输指令与分层协同控制自发求出的指令一致，硬件参数设置一致。
与前文类似，由图10可知分层协同控制存在较文献[20]控制更为接近虚轴的低频主导极点，这些极点由MG内有界电压控制、DG与参考坐标系功角差等模态主导。考虑相关控制环节中的参数影响系统小信号稳定性的可能，以BTBC功率传输控制的积分系数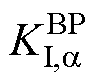
为代表，画出其动态变化下主导极点的根轨迹。
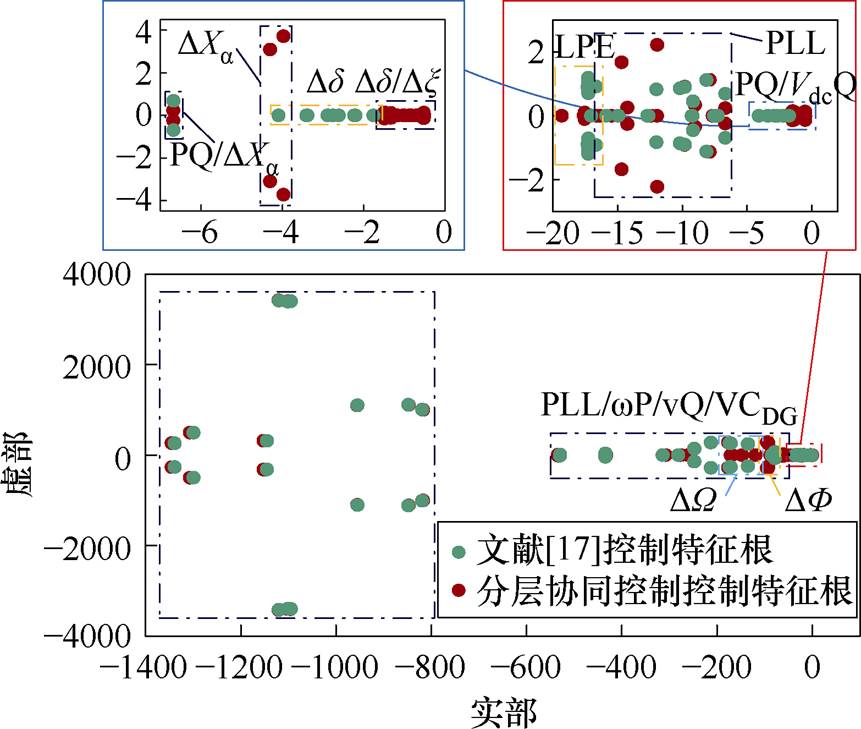
图10 文献[20]与分层协同控制下的特征值分布比较
Fig.10 Eigenvalues distribution comparison between control in Ref.[20] and hierarchical cooperative control
由图11可知，BTBC功率传输控制积分系数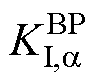从1增长至22 000的过程中，根轨迹出现明显变化。且该主导极点的模态与BTBC两侧有功均分-传输功率控制及MG有功下垂控制有关，且当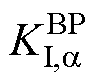= 21 730时系统临界稳定。显然，在本算例下，关键参数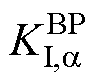的取值范围为 (1, 21 730)。
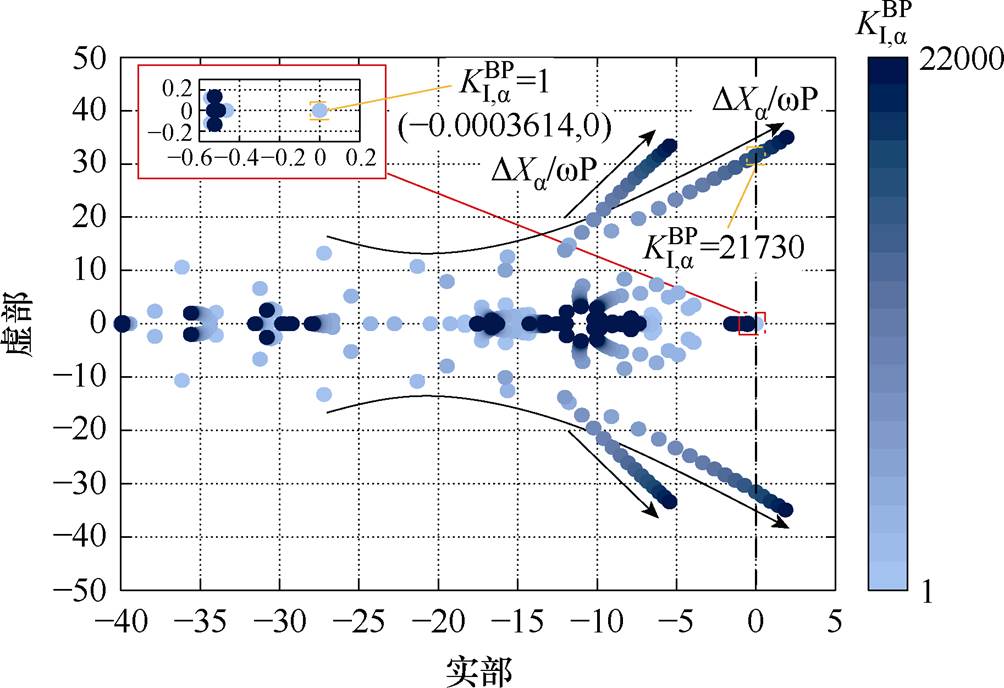
图11 分层协同控制下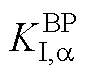
变化的主导极点根轨迹
Fig.11 The dominated pole root locus diagram of 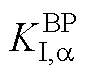variation under hierarchical cooperative control
将本文所提分层协同控制与文献[20]所提控制策略进行功率传输稳定性分析比较。各MG单元的基础负荷设置见附表2。其中MG1从基荷开始逐步增加有功负荷，MG2与MG3分别保持基荷不变，可得本文分层协同控制与文献[20]控制下MG1的临界有功负载及对应的BTBC传输功率极限（取临界失稳的BTBC此时传输的功率）。做根轨迹分析如图12所示，可知文献[20]控制下主导模态与BTBC两侧有功均分-传输功率控制、VSC PQ控制及MG有功下垂控制有关；本文分层协同控制下主导模态与VSC PQ控制及MG有界电压控制有关。同理，可得MG2/MG3的临界有功负荷及BTBC临界传输功率，一并整理见表4。
由表4可知，本文模式2下分层协同控制与文献[20]控制在MG临界负载及BTBC传输功率极限的表现极为相似，可见两种控制稳定性极其接近。
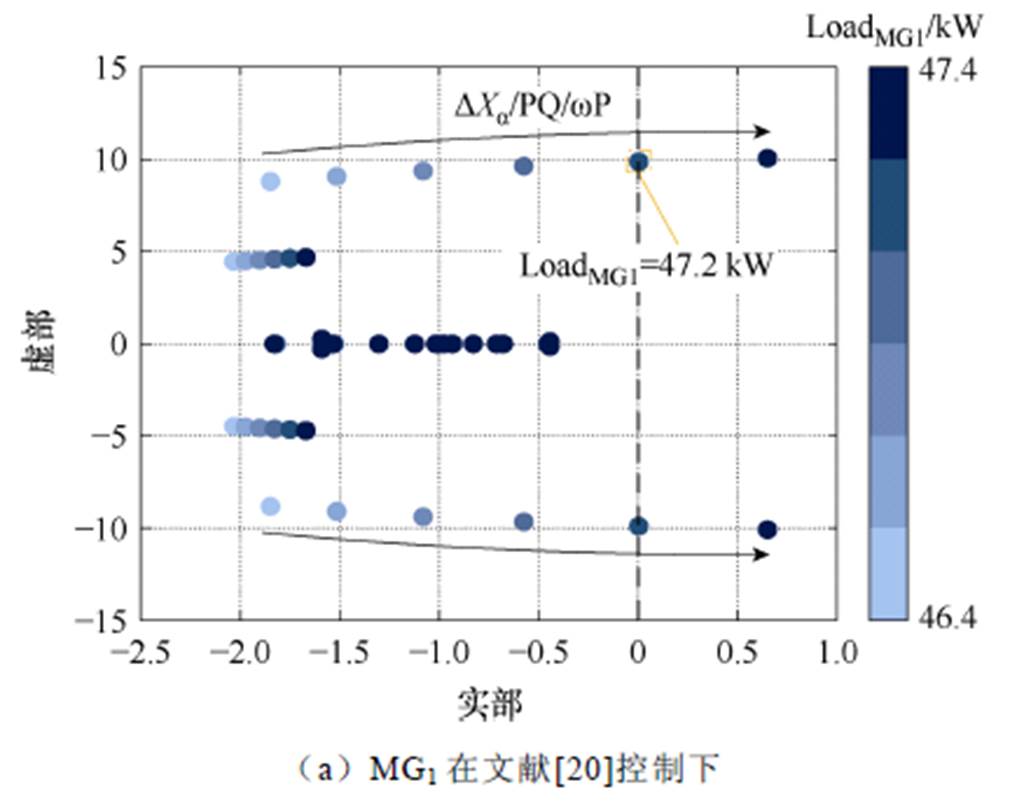
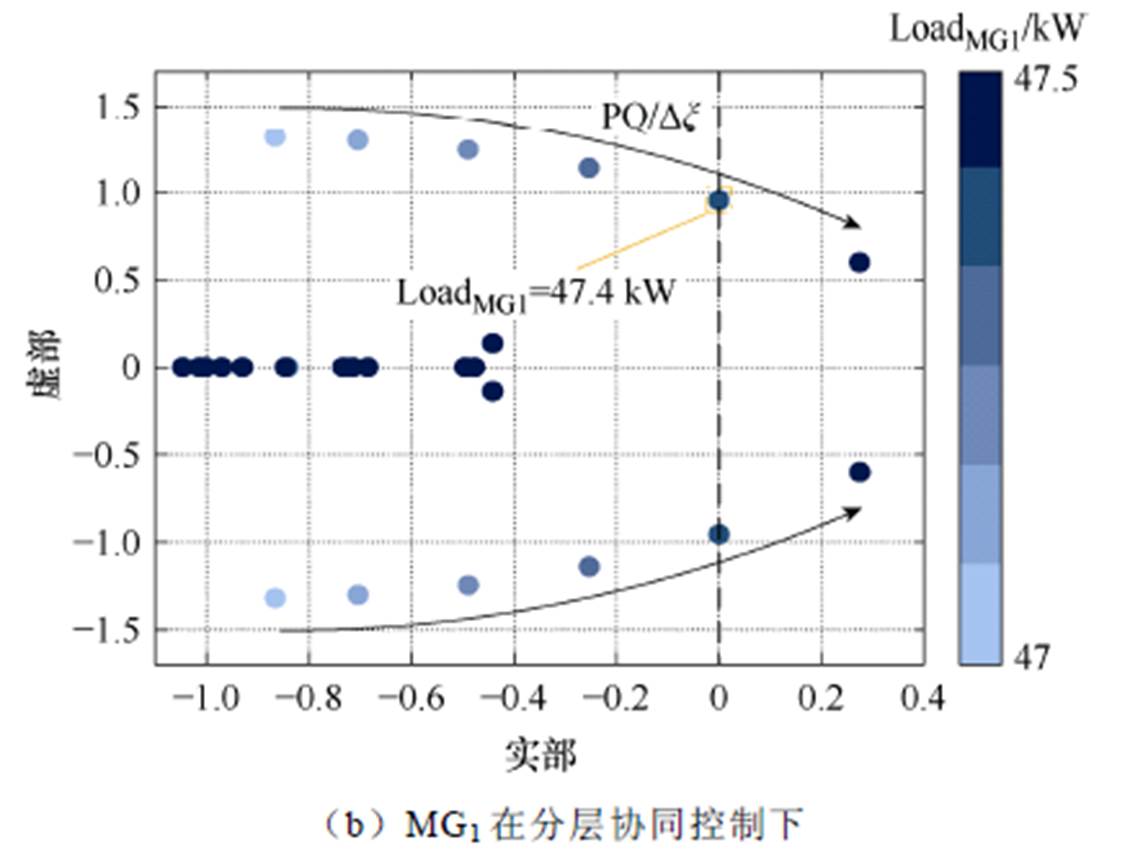
图12 MG1文献[20]和分层协同控制下不同有功负载的根轨迹分析
Fig.12 Root locus analysis of MG1 under control in Ref.[20] and hierarchical cooperative control with load variations
表4 文献[20]和分层协同控制下的临界负载及对应的BTBC传输功率极限
Tab.4 The critical active load and the corresponding BTBC transmission power limit of each MG under control in Ref.[20] andhierarchical cooperative control （单位: kW）
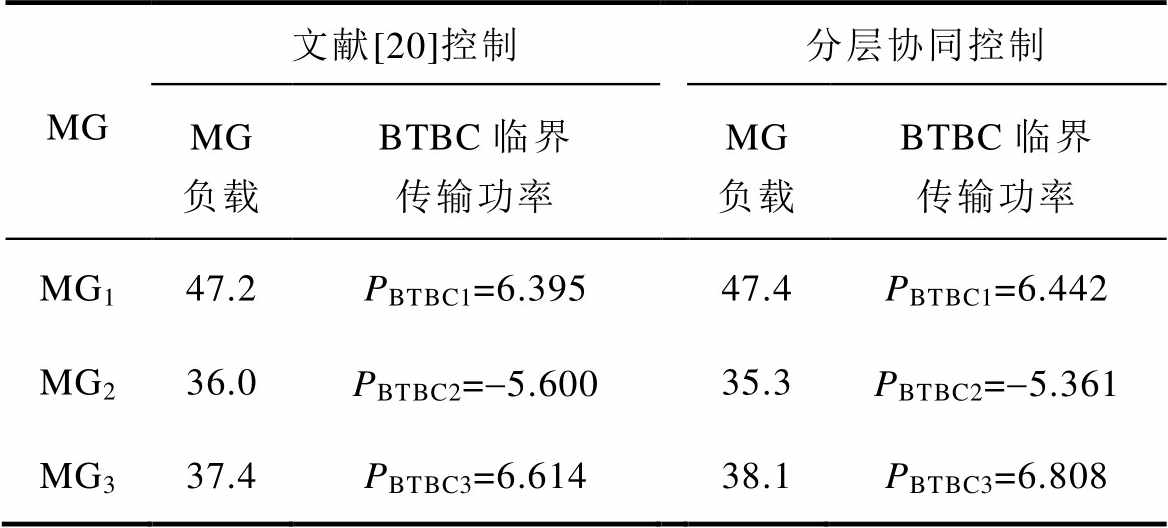
MG文献[20]控制分层协同控制 MG负载BTBC临界传输功率MG负载BTBC临界传输功率 MG147.2PBTBC1=6.39547.4PBTBC1=6.442 MG236.0PBTBC2=-5.60035.3PBTBC2=-5.361 MG337.4PBTBC3=6.61438.1PBTBC3=6.808
但本文所提方法相比文献[20]，无需实时测量负荷，仅需要根据各MG单元内的领导节点DG获取有功均分比率值，显然更具有实用性。此外，本文方法不会出现文献[20]无确定解问题。
为了验证所提出的柔性互联MGC系统分层协同控制策略的效果，在Matlab/Simulink中对如图7所示的系统模型进行仿真。本节所构模型的结构及参数与第4节所构模型一致，详细的参数设置亦见于表2及附录。
仿真结果验证了该方法在一系列控制变化下的性能，详细的五个阶段验证过程如下：
（1）阶段1：t=0～5 s，准备阶段，所有BTBC的功率传输指令设置为0。
（2）阶段2：t=5～10 s，在5 s时刻，各BTBC的模式1控制启动，MGC运行在本地控制模式。
（3）阶段3：t=10～15 s，在10 s时刻，各MG单元的二次控制启动，但BTBC仍保持模式1。
（4）阶段4：t=15～20 s，在15 s时刻，MG1内突增5 kW+j5 kvar的负载。
（5）阶段5：t=20～25 s，各BTBC的模式2控制启动，MGC运行在分层协同控制模式。
以MGC中的MG1为例分析本文所提控制策略对MG单元的控制效果，MG1内DG仿真输出曲线如图13所示。MG1内各DG频率曲线如图13a所示，0～10 s内各DG频率保持一致但低于额定频率50 Hz，t=10 s时MG单元启动分布式二次控制，使得各DG频率恢复至额定值50 Hz，并在随后的阶段中稳态下频率稳定在50 Hz。MG1内各DG的有界输出电压与有功出力比率变化如图13b、图13c所示，控制过程中所有DG均保持一致。MG1内各DG的无功出力比率曲线如图13d所示，各DG稳态下无功出力比率在t=10 s时启动分布式二次控制后达到一致。图13所示仿真曲线说明本文所提基于背靠背变流器柔性互联微电网群的分层协同控制实现了第1节所提MG单元内的控制目标：目标1与目标2。
图13 MG1内DG仿真输出曲线对比
Fig.13 DG simulation output curves in MG1
由于微电网内各DG有功出力比率在各控制下均一致，故以微电网内第一组DG为代表，展示各MG有功出力比率仿真输出曲线，具体如图14所示。阶段1内各MG有功出力比例未保持一致，阶段2启用BTBC模式1控制后各MG有功出力比例趋于一致；阶段4在MG二次控制启动后增加MG1负载，由于BTBC失去了利用两侧MG单元频率误差信号来计算传输有功指令的优势，使得MG1与MG2、MG3有功出力比率不再一致；阶段5启用BTBC的模式2控制后各MG有功出力比率恢复一致。图14证明本文所提基于背靠背变流器柔性互联微电网群的分层协同控制实现了第1节所提柔性互联MGC系统的控制目标：目标3。
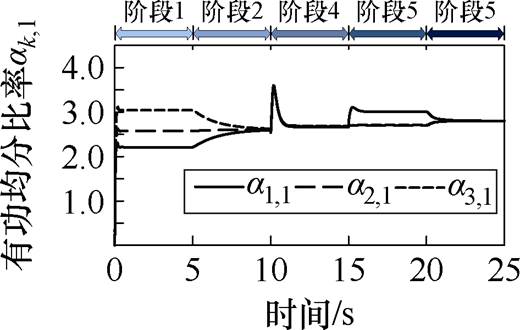
图14 各MG有功出力比率仿真输出曲线对比
Fig.14 Comparison of active power sharing rates among MGs
为验证本文第4节对分层协同控制与文献[20]控制两种控制所进行的小信号稳定分析结论，现构建仿真模型，分别采用分层协同控制与文献[20]控制的微电网群仿真模型，具体参数见表2及附录。两种控制对应的仿真模型除采用控制策略不同，其余参数、结构均相同。
1）分层协同控制仿真过程设置
t=0 s仿真开始；t=1 s启动微电网二次控制；t=3 s启动BTBC模式2控制；t=5 s后MG1有功负载在20 kW的基础上每间隔2 s增加10 kW直至系统失稳。
2）文献[20]控制仿真过程设置
t=0 s仿真开始；t=1 s启动微电网二次控制；t=3 s启动给定的功率传输指令控制，其指令数值上与控制3相同负载下BTBC稳态传输功率相同；t= 5 s后MG1有功负载在20 kW的基础上每间隔2 s增加10 kW直至系统失稳。
分层协同控制与文献[20]控制下微电网群系统仿真输出曲线如图15所示，分层协同控制与文献[20]控制在MG1 20 kW/30 kW/40 kW负载下均保持稳定，在50 kW负载下均失稳，该结果验证了第4节中对两种控制小信号稳定性分析比较的结论，即分层协同控制与文献[20]控制稳定性接近。同时还可以看出，由于文献[20]方法是通过测量负荷直接计算各BTBC功率的方式实现控制目标，其动态响应较快，但各状态量的冲击也大。而本文所提分层分布式控制架构下，各控制的时间尺度分布更为合理，动态响应较为平缓，有利于提升控制性能。
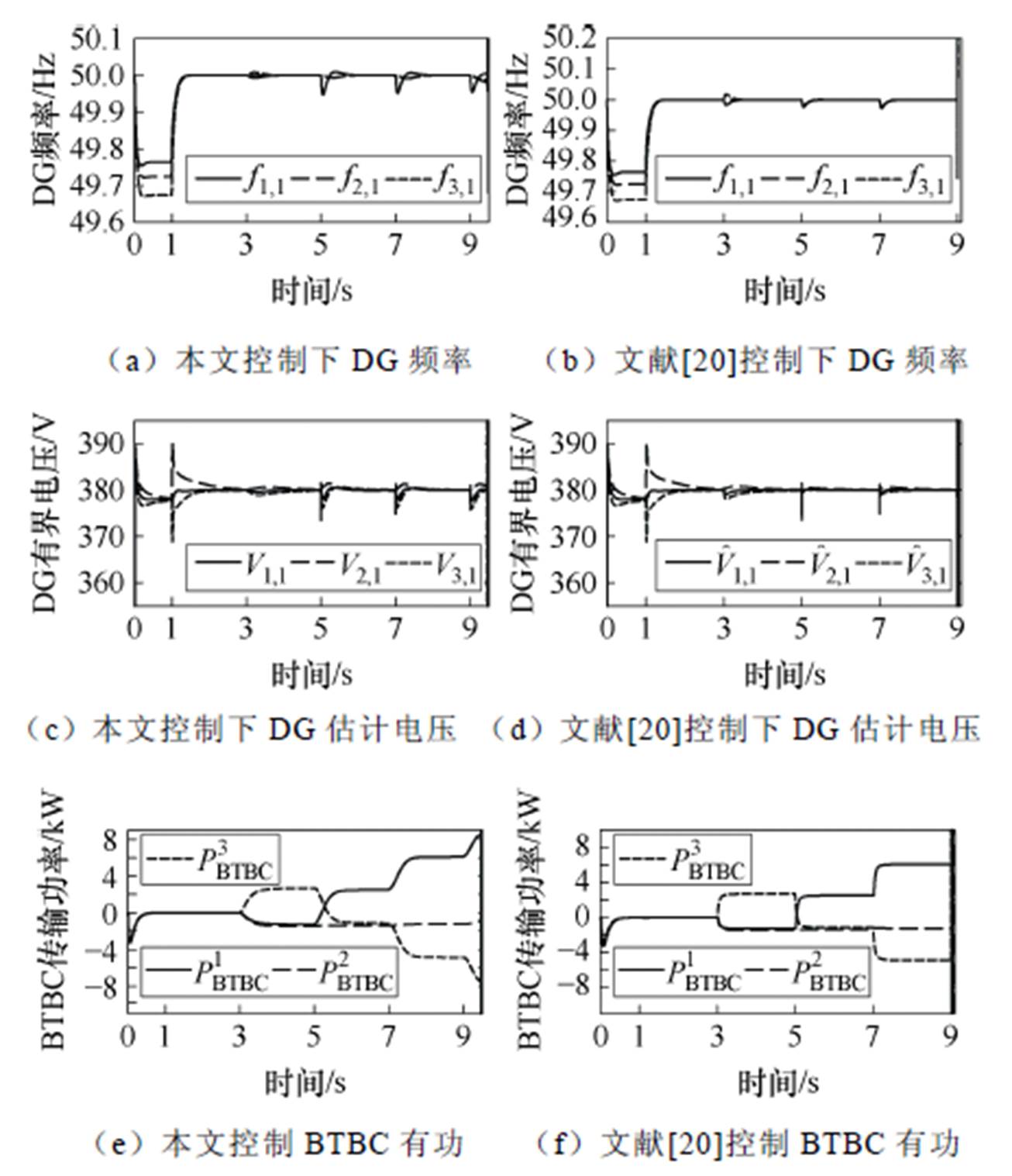
图15 分层协同控制与文献[20]控制下微电网群系统仿真输出曲线
Fig.15 Dynamics of microgrid cluster system under hierarchical cooperative control and control in Ref.[20]
文献[24]利用BTBC两侧MG有功基荷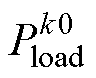
、
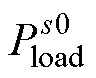及BTBC端口频率变化量
、
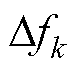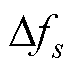，由式（31）计算出BTBC传输功率指令
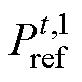，从而减小BTBC两侧MG有功均分的差异。
（31）
式中，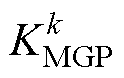
、
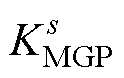分别为MGk/s的等效下垂系数，其可表示为
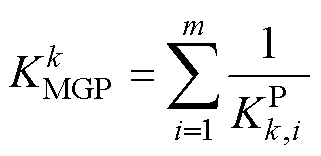，m为MGk所含DG数量；
、
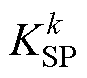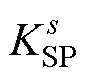分别代表MGk/s的系统单位调节功率，可表示为=+
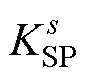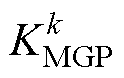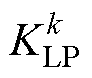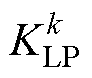，为MGk负荷单位调节功率，由历史运行数据估计得到。
以5.1节所用MGC模型为基础，分别采用文献[24]控制及本文本地控制。所设模型中MG1、MG2、MG3有功基荷分别为20 kW、22 kW、25 kW。仿真过程设置如下：
t=0 s仿真开始，BTBC传输功率指令为0；t=3 s时MG3增加5 kW有功负载；t=6 s BTBC分别启动文献[24]控制及本文本地控制，开始传输功率；t=9 s时MG3再次增加5 kW有功负载。仿真分析结果如图16所示。
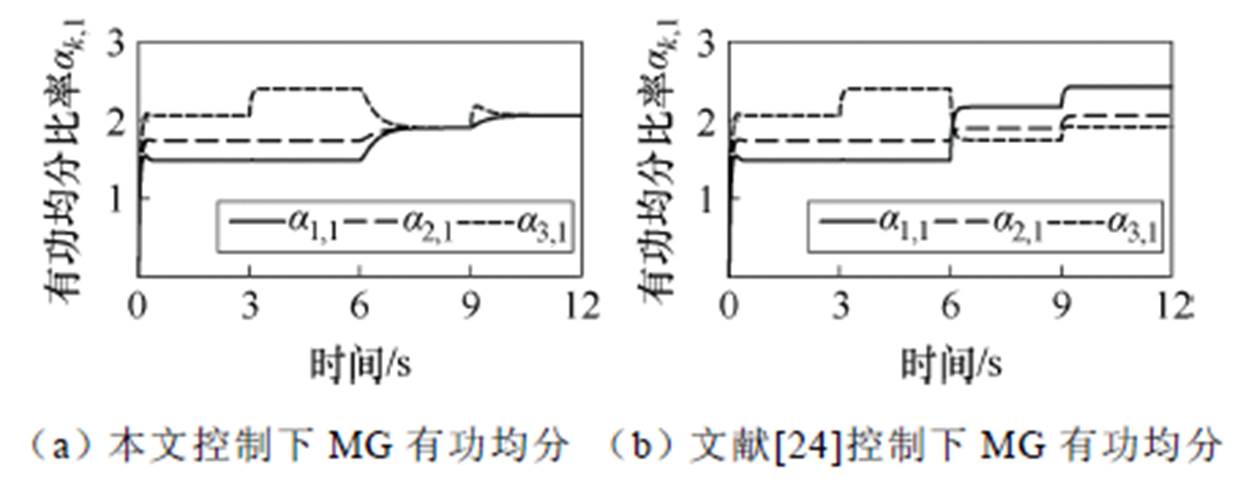
图16 本文本地控制与文献[24]控制下微电网群系统MG有功均分比率输出曲线
Fig.16 Output curves of MG active power equalizing ratio of microgrid group system under hierarchical cooperative control and reference Ref.[24] control
t=3 s MG3增加负载后两种控制下的MGC均仅有MG3有功均分比率增加；t=6 s启动控制后本文本地控制将MGC有功均分比率控制至相同水平，而文献[24]仅能缩小MG间有功均分比率的差距，不能实现无差调节；t=9 s再次增加MG3负载，此时本文控制下的各MG有功均分比率仍然保持一致，而文献[24]控制下的各有功均分比率差值进一步扩大。显然，本文所提本地控制策略对MGC全局层面的有功均分控制效果优于文献[24]控制。
本文提出了一种基于背靠背变流器柔性互联微电网群的分层协同控制，建立了包含微电网单元二次控制和BTBC改进功率传输控制的微电网群小信号模型，实现了MGC全局层面的有功均分，分析了该控制对系统小信号稳定性的影响。最后，在Matlab/Simulink中验证了本文提出控制方法的有效性。得到的主要结论及成果如下：
1）本文提出两种互补的MGC全局有功均分控制策略：即不依赖通信但无法与DG频率无差恢复控制并行的策略及依赖通信但兼容DG频率无差恢复控制的策略。
2）对引入基于背靠背变流器柔性互联微电网群的分层协同控制的MGC系统进行小信号建模，厘清了分层协同控制下系统的稳定主导模态。
3）将本文所提出的分层协同控制策略与文献[20]所提控制策略进行比较，两种控制下功率传输稳定性接近，但本文所提分层协同控制策略无需实时测量（或估计）本地负荷、不存在无确定解问题，更易于实际应用。
附 录
附表1 BTBC互联环形微电网群物理元件参数
App.Tab.1 Physical element parameters of ring-shaped BTBC-MGC
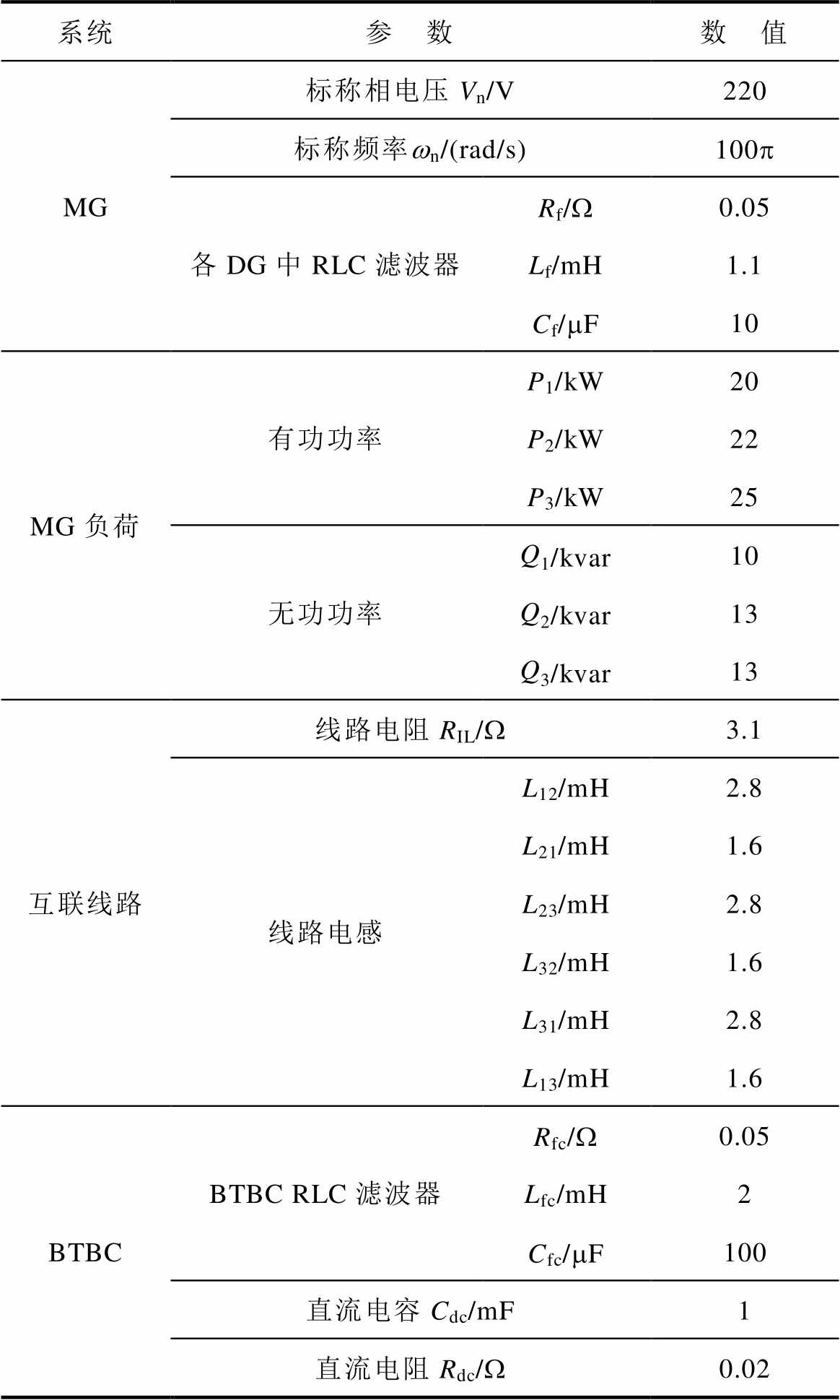
系统参 数数 值 MG标称相电压Vn/V220 标称频率wn/(rad/s)100p 各DG中RLC滤波器Rf/W0.05 Lf/mH1.1 Cf/mF10 MG负荷有功功率P1/kW20 P2/kW22 P3/kW25 无功功率Q1/kvar10 Q2/kvar13 Q3/kvar13 互联线路线路电阻RIL/W3.1 线路电感L12/mH2.8 L21/mH1.6 L23/mH2.8 L32/mH1.6 L31/mH2.8 L13/mH1.6 BTBCBTBC RLC滤波器Rfc/W0.05 Lfc/mH2 Cfc/mF100 直流电容Cdc/mF1 直流电阻Rdc/W0.02
附表2 BTBC互联环形微电网群共有控制参数
App.Tab.2 Common control parameters for different control methods in BTBC-MGC
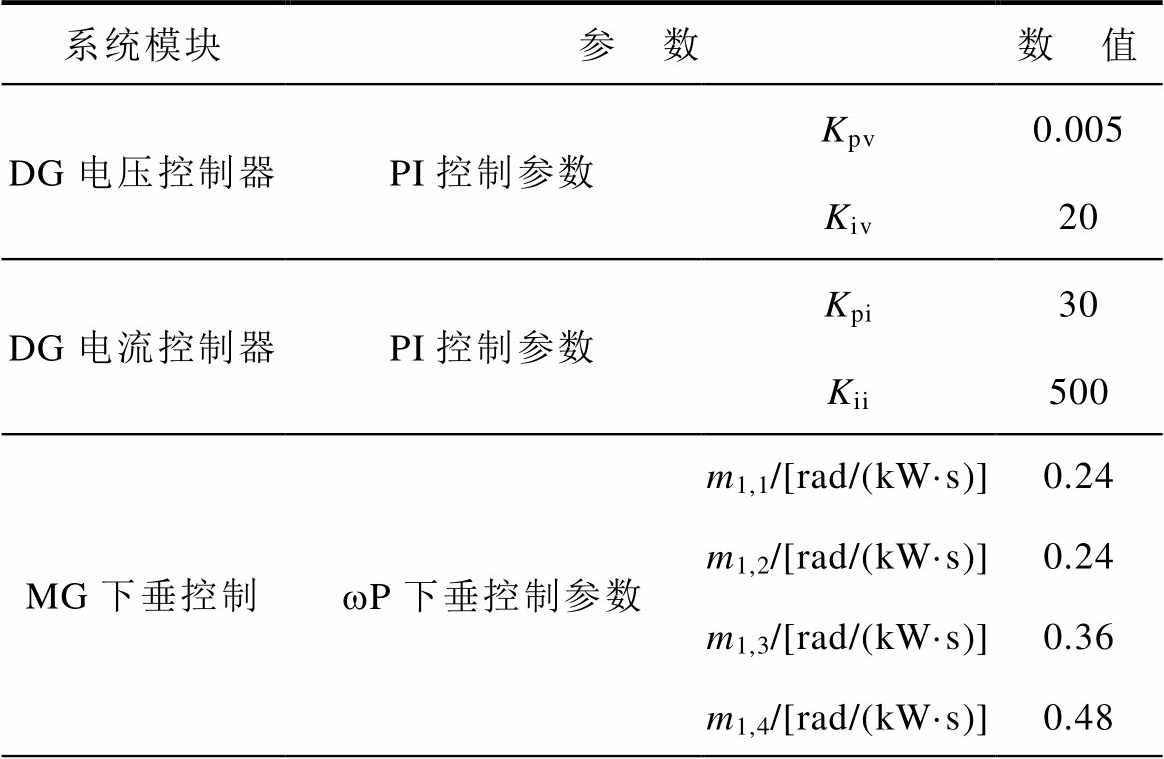
系统模块参 数数 值 DG电压控制器PI控制参数Kpv0.005 Kiv20 DG电流控制器PI控制参数Kpi30 Kii500 MG下垂控制wP下垂控制参数m1,1/[rad/(kW·s)]0.24 m1,2/[rad/(kW·s)]0.24 m1,3/[rad/(kW·s)]0.36 m1,4/[rad/(kW·s)]0.48
（续）
系统模块参 数数 值 MG下垂控制wP下垂控制参数m2,1/[rad/(kW·s)]0.24 m2,2/[rad/(kW·s)]0.36 m2,3/[rad/(kW·s)]0.36 m2,4/[rad/(kW·s)]0.48 m3,1/[rad/(kW·s)]0.24 m3,2/[rad/(kW·s)]0.36 m3,3/[rad/(kW·s)]0.48 m3,4/[rad/(kW·s)]0.48 vQ下垂控制参数n1,1/(V/kvar)2.4 n1,2/(V/kvar)2.4 n1,3/(V/kvar)3.6 n1,4/(V/kvar)4.8 n2,1/(V/kvar)2.4 n2,2/(V/kvar)3.6 n2,3/(V/kvar)3.6 n2,4/(V/kvar)4.8 n3,1/(V/kvar)2.4 n3,2/(V/kvar)3.6 n3,3/(V/kvar)4.8 n3,4/(V/kvar)4.8 BTBC电流控制器PI参数KpBpc20 KpBvc200 KiBpc20 KiBvc200 直流电压控制器PI参数KpDVC2 KiDVC20
参考文献
[1] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207.
Zheng Zhong, Miao Shihong, Li Chao, et al. Coor- dinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy Internet[J]. Transactions of China Electro- technical Society, 2022, 37(1): 192-207.
[2] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impe- dance[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[3] 董雷, 杨子民, 乔骥, 等. 基于分层约束强化学习的综合能源多微网系统优化调度[J]. 电工技术学报, 2024, 39(5): 1436-1453.
Dong Lei, Yang Zimin, Qiao Ji, et al. Optimal scheduling of integrated energy multi-microgrid system based on hierarchical constrained reinfor- cement learning[J]. Transactions of China Electro- technical Society, 2024, 39(5): 1436-1453.
[4] 徐殿国, 刘瑜超, 武健. 多端直流输电系统控制研究综述[J]. 电工技术学报, 2015, 30(17): 1-12.
Xu Dianguo, Liu Yuchao, Wu Jian. Review on control strategies of multi-terminal direct current trans- mission system[J]. Transactions of China Electro- technical Society, 2015, 30(17): 1-12.
[5] 赵书强, 王慧, 田娜, 等. 基于模型预测控制的直流微电网虚拟惯性优化方法[J]. 电工技术学报, 2023, 38(12): 3264-3276.
Zhao Shuqiang, Wang Hui, Tian Na, et al. Model predictive control based DC microgrid virtual inertia optimal method[J]. Transactions of China Electro- technical Society, 2023, 38(12): 3264-3276.
[6] 王成山, 王丹, 周越. 智能配电系统架构分析及技术挑战[J]. 电力系统自动化, 2015, 39(9): 2-9.
Wang Chengshan, Wang Dan, Zhou Yue. Framework analysis and technical challenges to smart distribution system[J]. Automation of Electric Power Systems, 2015, 39(9): 2-9.
[7] Guan Yajuan, Wei Baoze, Guerrero J M, et al. An overview of the operation architectures and energy management system for multiple microgrid clusters[J]. iEnergy, 2022, 1(3): 306-314.
[8] 陈倩, 王维庆, 王海云. 计及需求响应和混合博弈含多微网主动配电网协调优化[J]. 电力系统自动化, 2023, 47(9): 99-109.
Chen Qian, Wang Weiqing, Wang Haiyun. Coor- dinated optimization of active distribution network with multiple microgrids considering demand response and mixed game[J]. Automation of Electric Power Systems, 2023, 47(9): 99-109.
[9] 蔡瑶, 卢志刚, 潘尧, 等. 计及多重差异的交直流混合多能微网多时间尺度优化调度[J]. 电工技术学报, 2024, 39(11): 3392-3410.
Cai Yao, Lu Zhigang, Pan Yao, et al. Multi-time-scale optimal scheduling of AC-DC hybrid multi-energy microgrid considering multiple differences[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(11): 3392-3410.
[10] 黄文焘, 吴攀, 邰能灵, 等. 基于混合公共连接单元的柔性互联多微网结构与控制方法[J]. 中国电机工程学报, 2019, 39(12): 3499-3514.
Huang Wentao, Wu Pan, Tai Nengling, et al. Architecture design and control method for flexible connected multiple microgrids based on hybrid unit of common coupling[J]. Proceedings of the CSEE, 2019, 39(12): 3499-3514.
[11] 王杰, 黄文焘, 余墨多, 等. 柔性互联微网模式紧急切换平滑控制策略[J]. 中国电机工程学报, 2022, 42(21): 7695-7706.
Wang Jie, Huang Wentao, Yu Moduo, et al. Smooth control strategy for emergency switching of inter- connected microgrids via FMS[J]. Proceedings of the CSEE, 2022, 42(21): 7695-7706.
[12] 杨万里, 涂春鸣, 兰征, 等. 基于储能型柔性多状态开关的直流微电网与交流配电网柔性互联策略[J]. 电力自动化设备, 2021, 41(5): 254-260.
Yang Wanli, Tu Chunming, Lan Zheng, et al. Flexible interconnection strategy between DC microgrid and AC distribution network based on energy storage flexible multi-state switch[J]. Electric Power Auto- mation Equipment, 2021, 41(5): 254-260.
[13] Zhao Daduan, Zhang Chenghui, Sun Yue, et al. Distributed robust frequency restoration and active power sharing for autonomous microgrids with event- triggered strategy[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 3819-3834.
[14] Li Zhongwen, Cheng Zhiping, Liang Jing, et al. Distributed event-triggered secondary control for economic dispatch and frequency restoration control of droop-controlled AC microgrids[J]. IEEE Transa- ctions on Sustainable Energy, 2020, 11(3): 1938- 1950.
[15] Wu Xiangyu, Xu Yin, He Jinghan, et al. Pinning- based hierarchical and distributed cooperative control for AC microgrid clusters[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9865-9885.
[16] Lu Xiaoqing, Lai Jingang, Yu Xinghuo. A novel secondary power management strategy for multiple AC microgrids with cluster-oriented two-layer cooperative framework[J]. IEEE Transactions on Industrial Informatics, 2021, 17(2): 1483-1495.
[17] 范培潇, 杨军, 温裕鑫, 等. 基于可进化模型预测控制的含电动汽车多微电网智能发电控制策略[J]. 电工技术学报, 2024, 39(3): 699-713.
Fan Peixiao, Yang Jun, Wen Yuxin, et al. Intelligent generation control strategy of multi-microgrid with electric vehicles based on evolutionary model predictive control[J]. Transactions of China Elec- trotechnical Society, 2024, 39(3): 699-713.
[18] 于国星, 宋蕙慧, 侯睿, 等. 柔性直流互联孤岛微网群的分布式频率协同控制[J]. 电力系统自动化, 2020, 44(20): 103-111.
Yu Guoxing, Song Huihui, Hou Rui, et al. Distributed cooperative frequency control for flexible DC interconnected island microgrid cluster[J]. Auto- mation of Electric Power Systems, 2020, 44(20): 103-111.
[19] Brandao D I, dos Santos R P, Silva W W A G, et al. Model-free energy management system for hybrid alternating current/direct current microgrids[J]. IEEE Transactions on Industrial Electronics, 2021, 68(5): 3982-3991.
[20] 孟潇潇, 邵冰冰, 韩平平, 等. 基于背靠背变流器柔性互联的微网群分层协同恢复控制策略[J]. 中国电机工程学报, 2023, 43(20): 7812-7827.
Meng Xiaoxiao, Shao Bingbing, Han Pingping, et al. Hierarchical cooperative recovery control strategy for flexible interconnected microgrid cluster based on back-to-back converters[J]. Proceedings of the CSEE. 2023, 43(20): 7812-7826.
[21] He Jinghan, Wu Xiaoyu, Wu Xiangyu, et al. Small- signal stability analysis and optimal parameters design of microgrid clusters[J]. IEEE Access, 2019, 7: 36896-36909.
[22] Naderi M, Khayat Y, Shafiee Q, et al. Interconnected autonomous AC microgrids via back-to-back con- verters: part I: small-signal modeling[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(5): 4728-4740.
[23] Naderi M, Khayat Y, Shafiee Q, et al. Interconnected autonomous AC microgrids via back-to-back con- verters: part II: stability analysis[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(11): 11801- 11812.
[24] 周念成, 张茂凡, 孟潇潇, 等. 基于背靠背变流器互联的微网间传输功率控制及稳定性分析[J]. 电力系统自动化, 2023, 47(2): 34-41.
Zhou Niancheng, Zhang Maofan, Meng Xiaoxiao, et al. Control and stability analysis of power trans- mission between microgrids based on back-to-back converter interconnection[J]. Automation of Electric Power Systems, 2023, 47(2): 34-41.
[25] 田艳军, 彭飞, 王毅, 等. AC/DC-DC/AC级联变流器DC与AC双侧双向交互稳定性分析及协调优化控制[J]. 高电压技术, 2021, 47(7): 2434-2446.
Tian Yanjun, Peng Fei, Wang Yi, et al. Bidirectional interactive stability analysis of DC and AC sides for AC/DC-DC/AC cascade converter and coordinative optimization control[J]. High Voltage Engineering, 2021, 47(7): 2434-2446.
[26] Lai Jingang, Lu Xiaoqing, Yu Xinghuo, et al. Cluster- oriented distributed cooperative control for multiple AC microgrids[J]. IEEE Transactions on Industrial Informatics, 2019, 15(11): 5906-5918.
[27] Lu Xiaoqing, Lai Jingang, Liu Guoping. Master-slave cooperation for multi-DC-MGs via variable cyber networks[J]. IEEE Transactions on Cybernetics, 2021, 52(8): 8425-8438.
[28] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation Modes’Participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[29] 张泽华, 宋桂英, 张晓璐, 等. 考虑恒功率负载的直流微电网稳定性与鲁棒性控制策略[J]. 电工技术学报, 2023, 38(16): 4391-4405.
Zhang Zehua, Song Guiying, Zhang Xiaolu, et al. Stability and robustness control strategy of DC microgrid considering constant power load[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(16): 4391-4405.
[30] 王力, 谭振杰, 曾祥君, 等. 基于改进等效电路模型的直流微电网大信号稳定性分析[J]. 电工技术学报, 2024, 39(5): 1284-1299.
Wang Li, Tan Zhenjie, Zeng Xiangjun, et al. Large signal stability analysis of DC microgrid based on improved equivalent circuit model[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1284- 1299.
Abstract A single microgrid (MG) has a small capacity and poor stability problems. Combining multiple microgrids adjacent to each other in geographical space into a more compact whole, that is, microgrid cluster (MGC), is an effective way to improve the distributed power supply (DG) consumption level. The traditional interconnection mode has the defect that the disturbance between MG units cannot be isolated from each other, and the interactive power can only be adjusted indirectly. Although the flexible interconnection based on back-to-back converters (BTBC) has the advantages of inter-regional power flow continuous regulation and fault zone buffering, the flexible interconnection MGC system cannot form an effective “frequency signal” transmission among MG units. It is difficult to achieve active power sharing at the global level of microgrid clusters. The current MGC system based on BTBC interconnection has significant defects, mainly manifested as the lack of effective hierarchical cooperative control architecture design and stable dominant characteristics analysis under hierarchical cooperative control. A new control method based on the flexible interconnection of BTBC needs to be proposed.
Firstly, this paper proposes a novel distributed hierarchical coordinated control architecture, including a physical layer of flexible interconnected microgrid cluster and an information layer with sparse communication in a two-layer structure. Under this control architecture, the control objectives can be realized, such as secondary restoration control, reactive power sharing control, and global active power sharing control for each DG frequency/port bounded voltage in the MG unit. Secondly, two control strategies are proposed to achieve global active power sharing. Local control is independent of communication but cannot be parallel with frequency invariant control, and hierarchical cooperative control depends on communication but can realize frequency invariant control at the same time. Thirdly, a full-order small signal model of the system is established, and the dominant modes are analyzed. Finally, Matlab/Simulink simulation is carried out to verify the effectiveness and superiority of the proposed control strategies.
The conclusions are as follows. (1) Compared with the traditional hierarchical cooperative control and local control, the proposed strategy can achieve both MG frequency/voltage restorations and active/reactive power-sharing management. (2) The stable dominant modes of the proposed hierarchical cooperative control are the voltage and power angle dynamics in each MG. The stable dominant modes of local control are the dynamics in BTBCs. (3) The stability of the proposed hierarchical cooperative control strategy is close to the strategy mentioned in the literature [15]. It does not need to measure (or estimate) the local load in real-time, has no undefined solution problem, is easy to apply in practice.
keywords：Back-to-back converters, flexible interconnection, microgrid cluster, hierarchical cooperative control, small signal stability analysis
中图分类号：TM46; TM73
DOI: 10.19595/j.cnki.1000-6753.tces.240313
国家自然科学基金（52207087）和安徽省自然科学基金（2108085QE236）资助项目。
收稿日期 2024-02-28
改稿日期2024-03-11
孟潇潇 男，1992年生，讲师，硕士生导师，研究方向为新型电力系统的稳定分析与控制、微电网控制技术等。E-mail: mxxfreedom@hfut.edu.cn（通信作者）
尤泽豪 男，2000年生，硕士研究生，研究方向为微电网稳定分析与控制。E-mail: 2022170506@mail.hfut.edu.cn
（编辑 陈 诚）