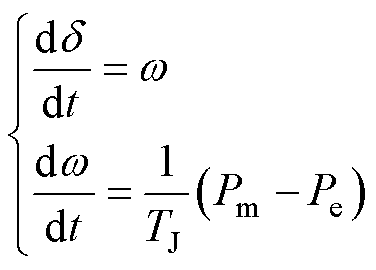 (1)
(1)
摘要 基于响应驱动的暂态功角稳定分析方法具有不依赖模型和参数、计算量小、能够实时量测和实时判别等突出优势。首先,该文针对单机无穷大系统挖掘出发电机电流和角速度蕴含的暂态功角稳定信息,建立了故障后电流与角速度的关联关系,揭示了两电气量存在的暂态稳定性特征;其次,利用信息量测技术得到发电机电流与角速度的关系曲线,通过分析关系曲线特性,提取出系统功角稳定和功角失稳关键特征,并探究了风机接入后对关系曲线特性的影响,提出了一种暂态功角稳定新判据;最后,通过比较故障清除后机端母线电压相位差变化率的大小识别临界机群,将该文方法应用于多机系统暂态稳定性判别。仿真算例结果表明了所提方法能够简单快速地判断出暂态功角稳定态势。
关键词:电力系统 暂态功角稳定 稳定判别 响应信息 关键特征
电力系统暂态稳定问题历来受到电力领域学术界和工业界的高度重视[1-3]。近年来,大量间歇性新能源和电力电子设备接入电网,改变了传统电力系统的系统结构,对系统受到大扰动后的暂态稳定动态特性造成了深刻的影响[4-7]。传统的电力系统暂态稳定分析方法,如时域仿真法[8]和直接法[9-11],对电力系统的参数、模型和运行时刻的网络结构的依赖较为严重,较难满足现代电网的实时性需求。随着信息量测技术的快速发展和完善,实现了全网实时同步数据的监测和获取,使得基于响应信息的暂态稳定性分析方法能够有效避免对系统运行方式、模型和参数的依赖[12],更易满足现代电网“实时决策,实时控制”的需求[13-15]。
基于响应信息的暂态稳定研究主要包括暂态稳定关键特征提取[16-22]和暂态稳定趋势预测及判别[23-29]两方面。在暂态稳定关键特征提取方面,文献[16]研究了相平面上轨迹的凹凸性与系统暂态稳定性的关系。文献[17]发现发电机相轨迹与支路相轨迹几何特征具有一致性,提出了基于交流关键支路受扰相轨迹凹凸性的暂态稳定判别方法。文献[18]研究了网络中节点电压幅值与相位在时空上的分布及功率传输特征,构建了一种可表征暂态功角稳定态势的简化支路暂态输电能力(simplified Branch Transient Transmission Capability, sBTTC)指数。也有学者利用暂态功角失稳时发电机转速特征,提出了基于发电机转速轨迹在线判别两群暂态功角失稳的新方法[12]。文献[19]基于广义角速度和广义角加速度构成的扩展相平面的物理特征,提出了一种新的暂态稳定判别方法,能充分利用系统的响应信息。
除了轨迹几何特征,学者们还研究基于其他暂态稳定特征的暂态稳定判别方法。文献[20]基于单机能量变化率与多摆稳定性关系进行暂态稳定判别,可有效利用量测得到的实时同步响应信息。文献[21]将最大李雅普诺夫指数的特征与暂态功角稳定特征相结合,实现了暂态功角稳定在线辨识。文献[22]从数据相关性角度提出了基于量测数据时序谱分布特性的电力系统暂态功角稳定判别方法。上述方法应用时需要对响应信息进行较繁琐的计算处理或坐标变换,难免产生计算或变换上的误差,影响暂态稳定判别结果的准确性。
在暂态稳定趋势预测和判别方面,主要有人工智能法和轨迹预测法。文献[23-25]将神经网络、支持向量机和决策树的机器学习方法应用于暂态稳定评估。文献[26]提出了自适应神经模糊推理系统(Adaptive Network based Fuzzy Inference System, ANFIS)的稳定判别模型,针对人工智能可解释性和泛化能力差等缺点进行了改进。尽管如此,人工智能稳定判别方法固有的物理意义不明确和泛化能力差以及训练模型无法覆盖所有电网实际运行场景等缺陷仍然难以从根本上解决,限制了该类方法在工程实际中的应用。文献[27]对量测数据进行数值运算,通过Taylor级数展开式获得未来时刻发电机转子角和角速度以实现对系统未来轨迹的预测。文献[28]基于同步相量测量单元引入虚拟负荷实现多机系统受扰轨迹预测。文献[29]应用参数辨识理论辨识系统故障后导纳参数,提出了受扰轨迹快速积分预测新方法,对经典模型具有较好的预测精度。但轨迹预测方法受电网规模扩大的影响难以实现快速仿真,预测误差愈加严重。
针对上述判别方法存在的缺点,本文提出了一种基于发电机电流与角速度响应关联特征的新能源电力系统暂态功角稳定判别方法。该方法不受系统参数、模型和运行时刻网络结构的影响,不需要过多的量测信息和复杂的计算,所用到的发电机电流和角速度以及机端母线电压相位均是简单、易于量测的电气量,方法简单、快速、可靠。本文首先挖掘出发电机电流和角速度蕴含的暂态功角稳定信息,建立了故障后电流与角速度的关联关系,揭示了两电气量存在的暂态稳定性特征。其次,通过分析关系曲线特性,提取出系统暂态稳定和失稳关键特征,并探究了风机接入后对关系曲线特性的影响,提出了一种新的暂态功角稳定判据。最后,通过比较故障清除后机端母线电压相位差变化率大小识别临界机群,将所提判据推广到多机系统,并通过仿真算例验证了本文方法的有效性。
在如图1所示的单机无穷大系统中,假设发电机模型为二阶经典模型,其微分方程(不计阻尼)表示为
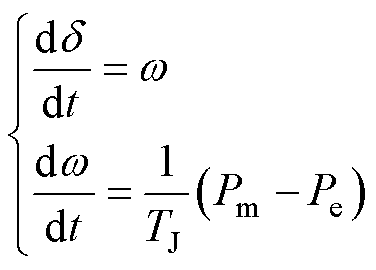 (1)
(1)
式中,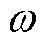 为角速度偏差,是相对于选定参考轴的角速度;
为角速度偏差,是相对于选定参考轴的角速度;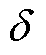 为功角;
为功角;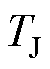 为惯性时间常数;
为惯性时间常数;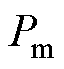 为恒定机械功率;
为恒定机械功率;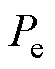 为发电机电磁功率。
为发电机电磁功率。

图1 单机无穷大测试系统示意图
Fig.1 Illustration of one machine infinite bus test system
不同时段的功角特性曲线如图2所示,电力系统在稳定运行、故障期间和故障清除后其发电机功角特性曲线会经历从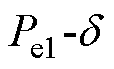 变为
变为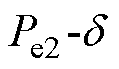 再变为
再变为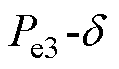 的过程,这三个过程存在各自的实时响应信息,反映各个过程发电机的状态乃至整个系统的暂态稳定性。
的过程,这三个过程存在各自的实时响应信息,反映各个过程发电机的状态乃至整个系统的暂态稳定性。
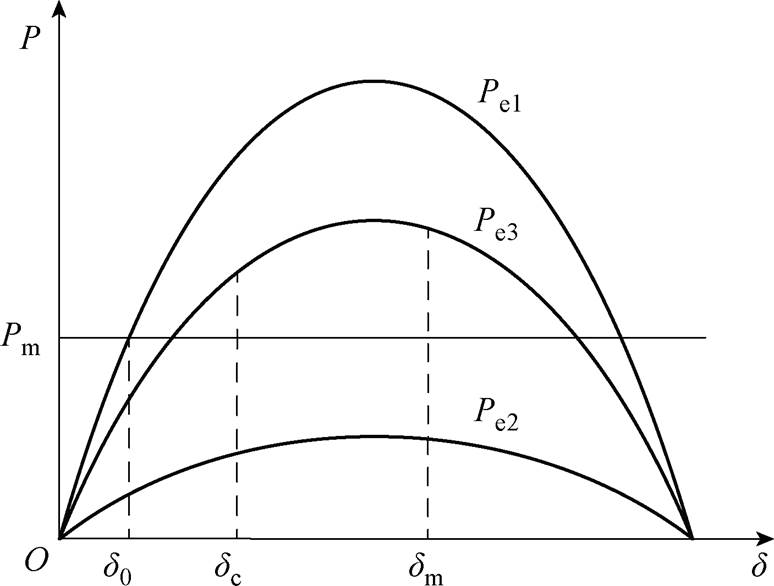
图2 不同时段的功角特性曲线
Fig.2 Power angle characteristic curves in different periods
本文按故障前、故障期间和故障后三个阶段将机端电流划分为三段,如图3所示:①系统稳定运行时,机端电流为负荷电流,记为IL;②故障持续期间的电流为短路电流,记为IK;③系统清除故障后的机端电流为故障后电流,记为IZ。
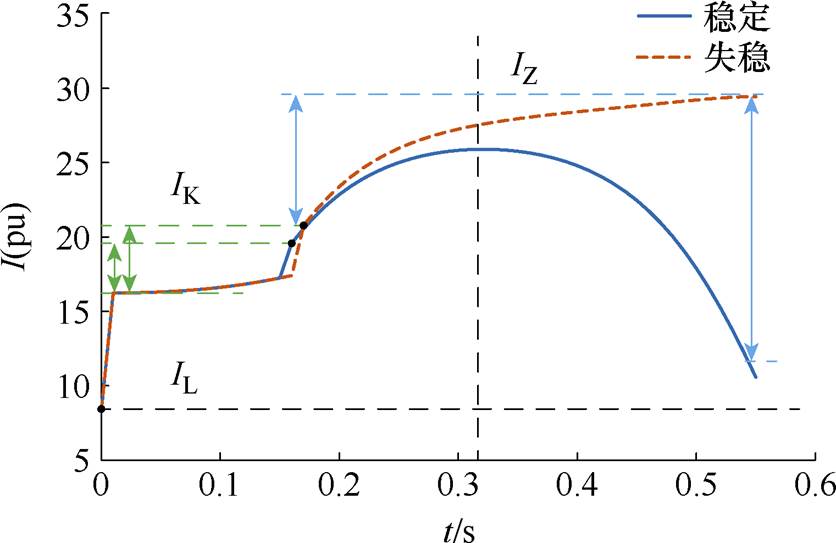
图3 电流分段示意图
Fig.3 Illustration of current segmentation
对比图3中系统稳定和失稳两种情况下的各段电流,可知故障后电流IZ在较短时间内表现出明显的差异性,即系统稳定时,故障后电流在快速到达峰值后是持续减小的;而系统失稳时,故障后电流持续增大。故障后电流具有的明确的暂态稳定和失稳特征是本文识别系统暂态稳定性的关键。
由式(2)可知,短路电流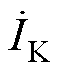 可以看作由负荷电流
可以看作由负荷电流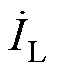 和故障附加电流
和故障附加电流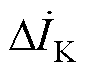 两部分组成[30],有
两部分组成[30],有
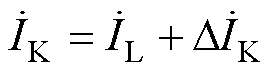 (2)
(2)
则故障期间的发电机电磁功率可以表示为
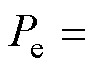
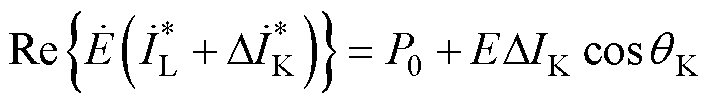 (3)
(3)
式中,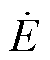 和
和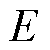 分别为发电机内电动势相量和幅值;
分别为发电机内电动势相量和幅值;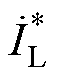 和
和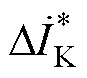 分别为
分别为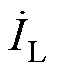 和
和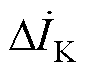 的共轭值;
的共轭值;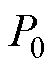 为正常运行时的发电机电磁功率;
为正常运行时的发电机电磁功率;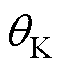 为
为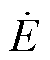 和
和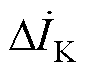 的角度差。
的角度差。
同样地,将故障后电流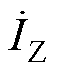 看作由负荷电流
看作由负荷电流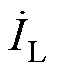 和故障后附加电流
和故障后附加电流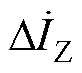 两部分组成,有
两部分组成,有
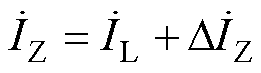 (4)
(4)
则故障后的发电机电磁功率为
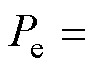
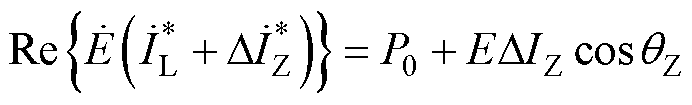 (5)
(5)
式中,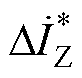 为
为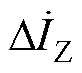 的共轭值;
的共轭值;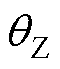 为
为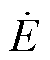 和
和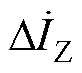 的角度差。
的角度差。
结合式(4)和式(5)可得
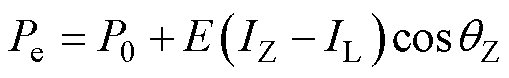 (6)
(6)
将式(6)代入式(1)可得
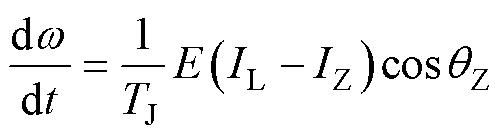 (7)
(7)
由此,本文建立了发电机电流与角速度的关联关系,如式(7)所示,角速度的变化趋势由电流差值符号和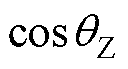 符号共同决定,因此,在探究角速度与暂态稳定性关系时,需要进一步分析暂态过程中的角速度变化趋势与电流差值符号和
符号共同决定,因此,在探究角速度与暂态稳定性关系时,需要进一步分析暂态过程中的角速度变化趋势与电流差值符号和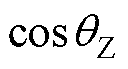 符号的对应关系,进而实现利用电流差值描述角速度的变化,为后续暂态功角稳定判据的建立提供理论依据。
符号的对应关系,进而实现利用电流差值描述角速度的变化,为后续暂态功角稳定判据的建立提供理论依据。
本文结合发电机功角特性曲线,对发电机电流和角速度与系统暂态稳定性之间的关联关系进行探究,以挖掘出适用于暂态稳定判别的暂态稳定性特征。
暂态稳定性关键特征提取原理如图4所示。图4中的点k为稳定平衡点,点h为不稳定平衡点,点f为假设的发电机转子转速到达同步转速时的运行点位置。过程1为系统稳定过程,该过程对应的发电机角速度的变化为先减小后增大,会在功角特性曲线的稳定平衡点出现角速度拐点,且角速度拐点附近的电流持续减小;过程2为系统失稳过程,该过程对应的发电机角速度的变化同样为先减小后增大,但此时的角速度拐点是功角特性曲线的不稳定平衡点,且角速度拐点附近的电流是持续增大的。由于系统稳定和系统失稳过程发电机角速度呈现的变化特性相同,故在描述系统暂态稳定性时,无法单靠角速度拐点判别出暂态稳定性,还需要结合角速度拐点附近的电流变化趋势,借助电流变化的差异性实现系统稳定和系统失稳情况的区分。
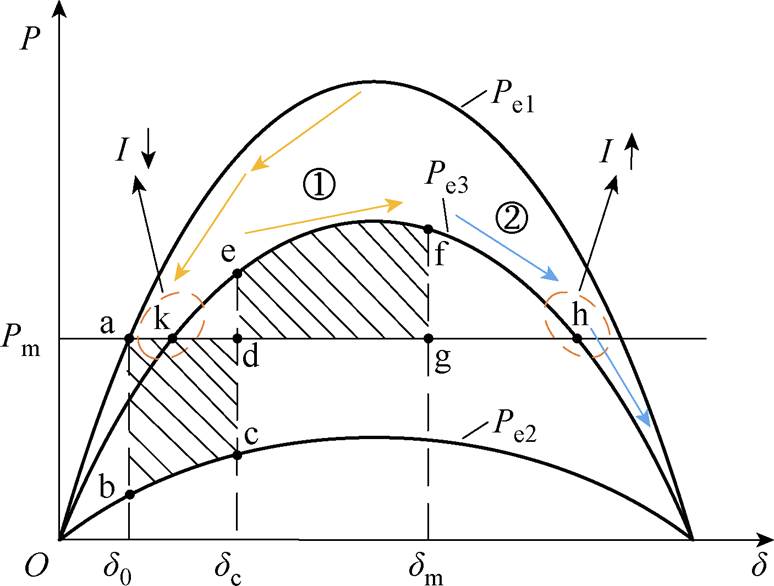
图4 暂态稳定性关键特征提取原理
Fig.4 Principle diagram of key features extraction of transient stability
结合图4和式(7)对关键特征进行分析,在稳定平衡点附近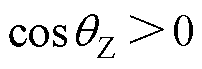 ,角速度减小的过程中,有
,角速度减小的过程中,有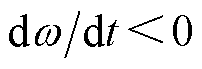 ,
,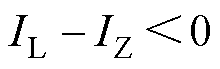 ,经过角速度拐点后出现角速度增大的过程,有
,经过角速度拐点后出现角速度增大的过程,有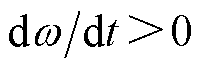 ,
,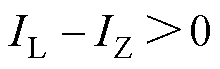 ,可知,整个过程电流对应角速度的变化呈现电流持续减小的特性,与图4分析一致。
,可知,整个过程电流对应角速度的变化呈现电流持续减小的特性,与图4分析一致。
由于电压大幅度跌落使得电流急剧跃升,在到达不稳定平衡点时电流已不再是稳定运行时的负荷电流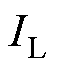 而变成了远大于
而变成了远大于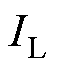 的电流
的电流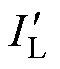 。此时,不稳定平衡点附近的电流与角速度关系变为
。此时,不稳定平衡点附近的电流与角速度关系变为
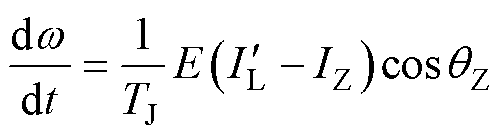 (8)
(8)
由此,在不稳定平衡点附近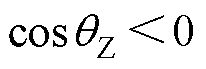 ,角速度减小的过程,有
,角速度减小的过程,有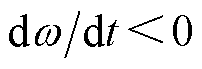 ,
,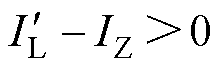 ,经过角速度拐点后角速度增大的过程,有
,经过角速度拐点后角速度增大的过程,有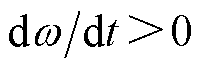 ,
,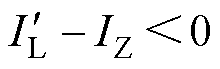 ,整个过程电流对应角速度的变化持续增大,与图4的分析一致。
,整个过程电流对应角速度的变化持续增大,与图4的分析一致。
由上述分析可知,在角速度拐点确定之后,故障后电流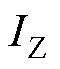 与负荷电流
与负荷电流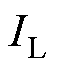 、电流
、电流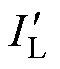 大小的比较可以作为暂态稳定性判据的条件之一,与角速度拐点附近的电流变化趋势共同构成本文暂态稳定性判据。理想情况下,系统稳定时,发电机角速度拐点正是故障后电流
大小的比较可以作为暂态稳定性判据的条件之一,与角速度拐点附近的电流变化趋势共同构成本文暂态稳定性判据。理想情况下,系统稳定时,发电机角速度拐点正是故障后电流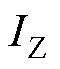 和负荷电流
和负荷电流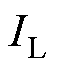 相等的点;系统失稳时,发电机角速度的拐点是故障后电流
相等的点;系统失稳时,发电机角速度的拐点是故障后电流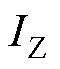 和电流
和电流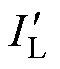 相等的点。在实际应用中,角速度拐点处的
相等的点。在实际应用中,角速度拐点处的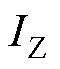 与
与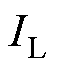 、
、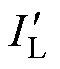 可能并不完全相等,可以设定阈值
可能并不完全相等,可以设定阈值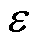 ,以便应用于工程实际。
,以便应用于工程实际。
综上所述,所提取的系统暂态稳定性特征有两个:①角速度拐点;②角速度拐点附近的电流变化趋势。本文后续将故障后电流和角速度的关系绘制成发电机I-w 关系曲线,简化了系统暂态功角稳定判别过程,有助于更好地阐明本文方法。
在单机无穷大系统中设置三相短路接地故障,调整不同故障时间,绘制系统稳定和失稳时电流与角速度的关系曲线即发电机I-w 关系曲线,如图5所示。
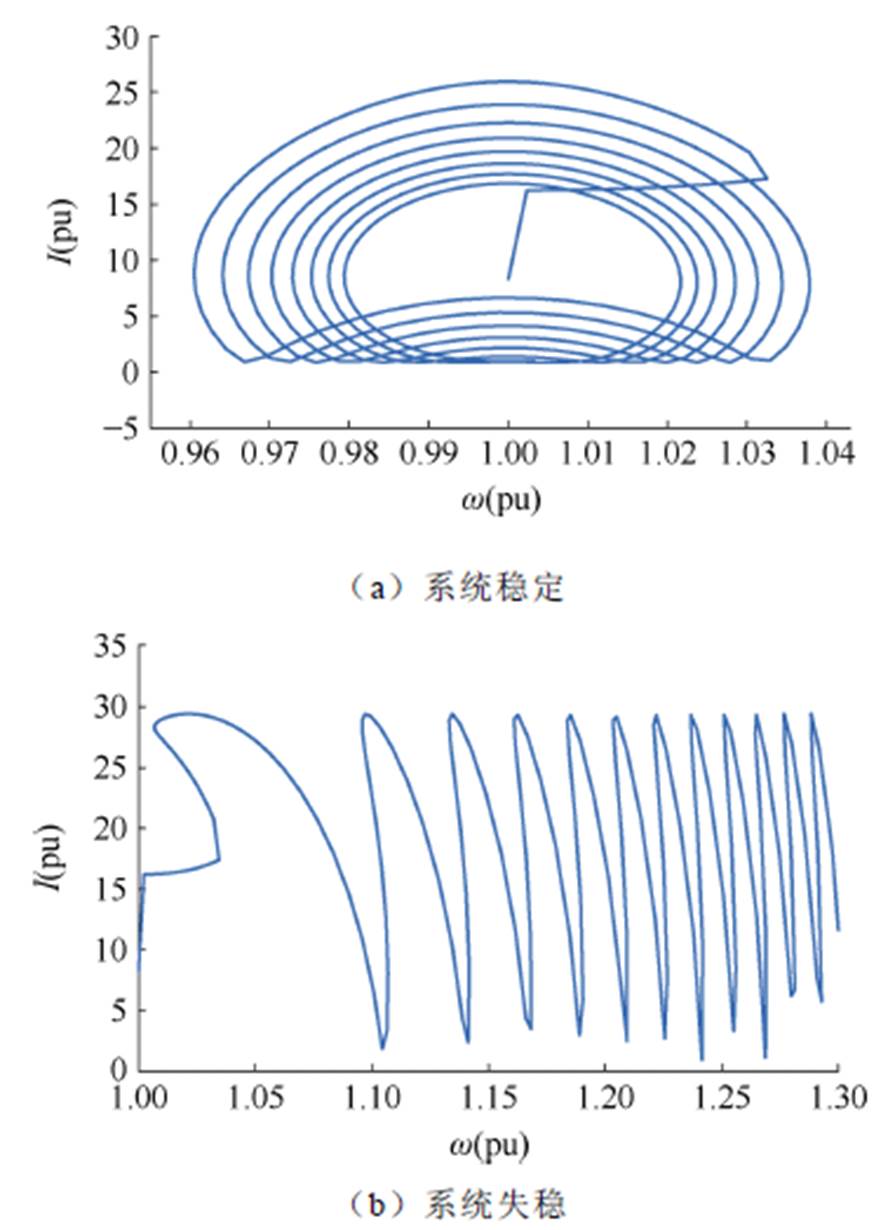
图5 稳定和失稳情况I-w 关系曲线
Fig.5 I-w relationship curves of system at stability and instability
对比图5a和图5b可知,当系统稳定时,I-w 关系曲线表现出“收敛”态势;当系统失稳时,I-w 关系曲线表现出崩溃的“发散”态势。这表明I-w 关系曲线与系统暂态稳定性紧密关联,其中蕴含着丰富的系统暂态稳定信息。同时,关系曲线中包含着第1节中挖掘的两个暂态稳定性特征:角速度拐点和角速度拐点附近的电流变化趋势。从I-w 关系曲线中提取关键特征,并利用稳定和失稳关键特征判别电力系统的暂态稳定态势,将电力系统暂态功角稳定的判别过程简化为I-w 关系曲线关键特征监测和辨识的过程。
无论系统稳定还是系统失稳,I-w 关系曲线均会在较短的时间内出现角速度拐点,在经过该角速度拐点后,I-w 关系曲线的收敛和发散特性逐渐表现出来。同时,该角速度拐点附近的电流在稳定和失稳时总是表现出明显的差异,即系统稳定时角速度拐点附近的电流持续减小,系统失稳时角速度拐点附近的电流持续增大。可见,通过I-w 关系曲线较易提取暂态稳定性关键特征,对暂态稳定性判据的提出具有重要意义。
角速度拐点是反映发电机运行点状态和系统稳定性态势的关键点,同时考虑到暂态稳定分析对于快速性的需求,想要判别系统暂态稳定性仅需关注包含角速度拐点的局部I-w 关系曲线,如图6所示。
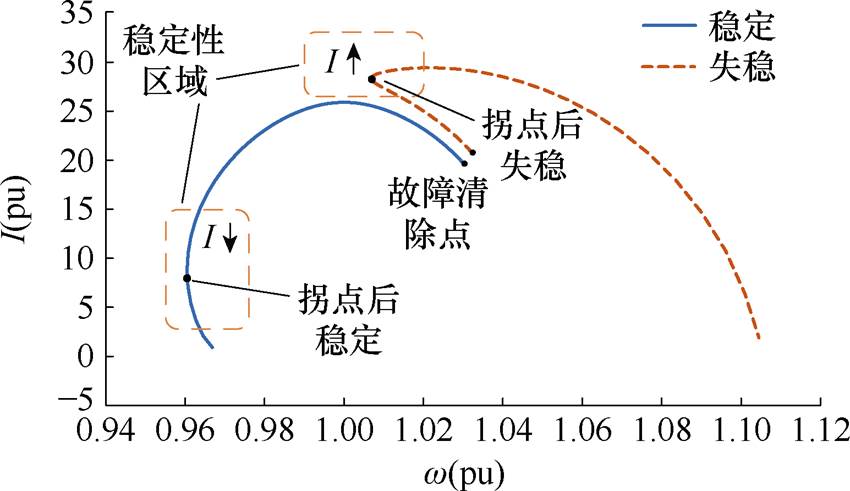
图6 故障后稳定与失稳情况I-w关系曲线对比
Fig.6 Comparison diagram of I-w relationship curve of system at stability and instability after fault
结合第1.2节探究的发电机电流与角速度存在的关联关系,本文将I-w 关系曲线中出现的角速度先减小后增大的第一个角速度拐点(角速度第一个极小值点)定义为稳定性拐点,记为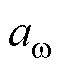 ,并将以稳定性拐点
,并将以稳定性拐点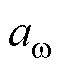 为中心
为中心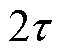 范围的区域定义为稳定性区域,记为
范围的区域定义为稳定性区域,记为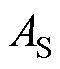 ,用故障后电流
,用故障后电流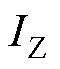 表示为
表示为
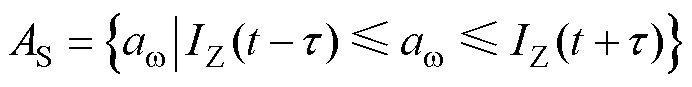 (9)
(9)
式中,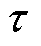 为响应信息量测的间隔,本文
为响应信息量测的间隔,本文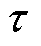 为设置的仿真间隔,
为设置的仿真间隔,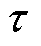 =10 ms。
=10 ms。
由图6可知,稳定性区域内包含稳定性拐点,同时也包含着电流的变化趋势。系统稳定时,稳定性区域内电流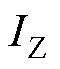 是持续减小的,则该区域为稳定区域;系统失稳时,稳定性区域内电流
是持续减小的,则该区域为稳定区域;系统失稳时,稳定性区域内电流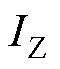 是持续增大的,则该区域为失稳区域,故可以通过识别稳定性区域是稳定区域还是失稳区域实现电力系统暂态稳定性的判别。
是持续增大的,则该区域为失稳区域,故可以通过识别稳定性区域是稳定区域还是失稳区域实现电力系统暂态稳定性的判别。
考虑到近年来风电并网规模不断扩大,为探究风电接入系统后对I-w 关系曲线特性的影响,本文对风电并网系统进行探究,在图1所示的单机无穷大系统的源侧接入双馈风电机组,系统结构如图7所示。
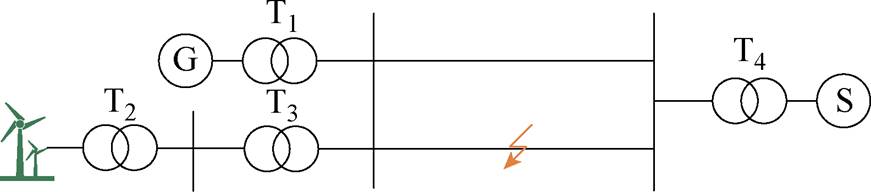
图7 单机无穷大系统接入风机示意图
Fig.7 Illustration of one machine infinite bus system connected to wind turbine
在接入风电的单机无穷大系统中改变风电渗透率,使风电渗透率分别为0%、25%、50%、75%,分析不同比例风电接入系统后对I-w 关系曲线特性的影响。在保持故障工况与未接风电单机无穷大系统相同的前提下,同样得到系统稳定和系统失稳情况故障后电流与角速度的关系曲线,其局部I-w 关系曲线如图8和图9所示。
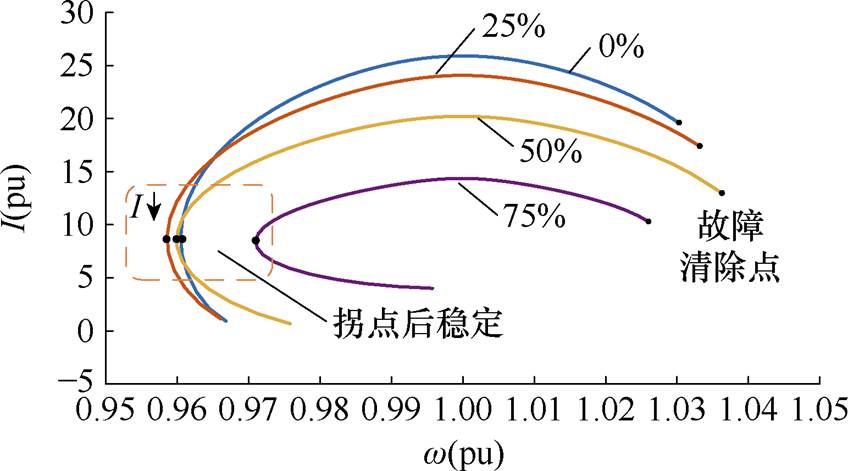
图8 不同比例风电接入系统故障后稳定时I-w 关系曲线
Fig.8 I-w relationship curves of different proportions of wind power access system when the system is stable after failure
对比图6和图8、图9可知,接入不同比例的风电后,系统的I-w 关系曲线特性不变,暂态关键特征仍然存在,稳定性拐点的定位和稳定性区域的辨识仍可适用,表明了在风电大规模接入电力系统的场景下,本文方法仍能很好地判别系统的暂态稳定性。
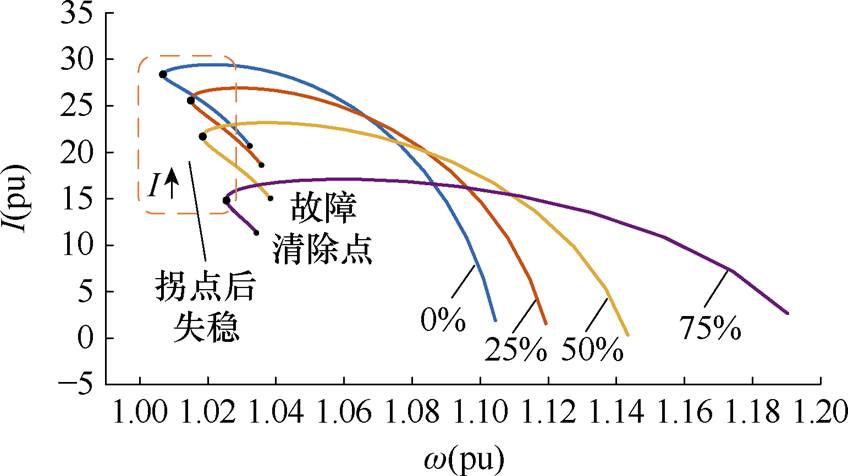
图9 不同比例风电接入系统故障后失稳时I-w 关系曲线
Fig.9 I-w relationship curves of different proportions of wind power access system when the system is instable after failure
由第2.1节可知,I-w 关系曲线蕴含着丰富的暂态稳定信息,其中的关键特征提取有两个关键环节:①稳定性拐点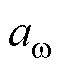 的监测和识别;②稳定性区域内电流IZ的变化趋势的识别。基于这两个关键环节,本文提出了一种基于发电机电流与角速度关联特征的新能源电力系统暂态功角稳定判别方法。
的监测和识别;②稳定性区域内电流IZ的变化趋势的识别。基于这两个关键环节,本文提出了一种基于发电机电流与角速度关联特征的新能源电力系统暂态功角稳定判别方法。
本文方法通过识别关键特征,迅速定位稳定性拐点,找到稳定性区域,并计算电流变化率,根据正负号判断稳定性区域内电流的变化趋势,确定稳定性区域是稳定区域还是失稳区域,最终确定电力系统暂态稳定性。本文提出的暂态功角稳定性判据如下所示。
1)系统稳定
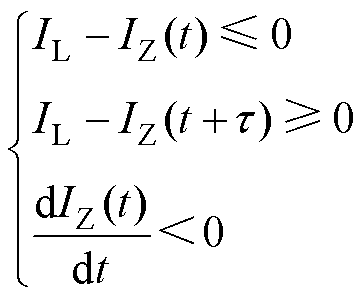 (10)
(10)
2)系统失稳
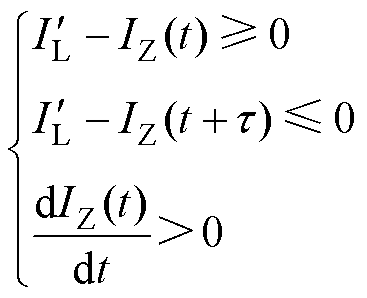 (11)
(11)
式中,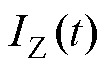 为
为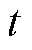 时刻测得电流;
时刻测得电流;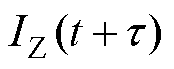 为
为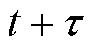 时刻的电流;
时刻的电流;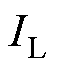 为稳定拐点时刻量测电流;
为稳定拐点时刻量测电流;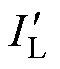 为失稳拐点时刻量测电流。
为失稳拐点时刻量测电流。
多机系统的暂态功角稳定性通常可由系统中最快加速或减速失步机组组成的局部稳定性表征,即机群稳定性。故障清除后系统中最快加速或减速失步的一台或多台机组为受扰严重机组,将这些机组划分为一群,称为临界机群,其余机组划分为另一群,称为剩余机群。临界机群与剩余机群之间的稳定情况直接表征多机系统的暂态稳定性。
受扰系统的稳定情况取决于临界机群、剩余机群及两者之间的相对稳定性,临界机群中任意一台机组失稳且相对于剩余机群失稳则系统失稳,临界机群中所有机组稳定且相对于剩余机群稳定则系统稳定。多机系统暂态稳定性的判别实际是对临界机群中一台或多台机组稳定和失稳情况的识别。
发电机组分群的本质是将具有相似动态响应行为的机组归为一群,经典分群方法通常利用功角角度摆开程度的大小实现分群,但在短时间内根据功角很难准确实现临界机群的识别[3, 31-32]。实际上,角速度可直接表征受扰后发电机自身的动态变化行为。已有学者[20, 33]利用角速度偏差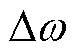 或角速度变化率
或角速度变化率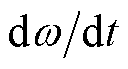 确定受扰最严重机组(对)。考虑到电力系统中相量测量单元(Phasor Measurement Unit, PMU)局部配置的现状和机端母线电压相位差变化特性与发电机功角变化具有一致性的特点[17],本文利用故障清除后机端母线电压相位差
确定受扰最严重机组(对)。考虑到电力系统中相量测量单元(Phasor Measurement Unit, PMU)局部配置的现状和机端母线电压相位差变化特性与发电机功角变化具有一致性的特点[17],本文利用故障清除后机端母线电压相位差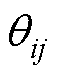 代替角速度进行发电机组分群。
代替角速度进行发电机组分群。
相较于利用角速度偏差或角速度变化率分群的方法,本文方法利用的母线电压相位比角速度更易于测量,它既可以通过电网配置的PMU来采集,又可以采用电流互感器进行测量,实现全局母线电压相位的准确提取,避免了当PMU配置过少或位置缺乏代表性时利用角速度偏差或角速度变化率分群的方法失效的情况,同时也为继电保护技术参与到电力系统暂态稳定分析的过程提供了新的思路。
本文将机端母线电压相位差变化率作为发电机分群指标,用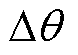 表示,如式(12)所示。在故障清除后,系统中稳定机群的机端母线电压相位差变化比较平稳,通常表现为小幅度增加或者减小,即
表示,如式(12)所示。在故障清除后,系统中稳定机群的机端母线电压相位差变化比较平稳,通常表现为小幅度增加或者减小,即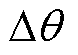 为较小的正值或为负值,而失稳机群的机端母线电压相位差变化剧烈,呈现大幅增加态势,即
为较小的正值或为负值,而失稳机群的机端母线电压相位差变化剧烈,呈现大幅增加态势,即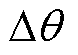 为较大的正值,利用稳定机群和失稳机群的分群指标的差异性实现系统机组的划分,以此作为所提分群方法的分群标准。值得注意的是,该方法目前无法给出确定的数值来划分机群,只能通过实时计算
为较大的正值,利用稳定机群和失稳机群的分群指标的差异性实现系统机组的划分,以此作为所提分群方法的分群标准。值得注意的是,该方法目前无法给出确定的数值来划分机群,只能通过实时计算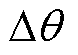 并进行比较的方式识别临界机群。综上所述,通过实时量测机端母线电压相位、计算分群指标并比较其大小能够实现临界机群的识别。该临界机群识别方法具有实时性,不受系统结构变化影响,能保证临界机群的识别精度。
并进行比较的方式识别临界机群。综上所述,通过实时量测机端母线电压相位、计算分群指标并比较其大小能够实现临界机群的识别。该临界机群识别方法具有实时性,不受系统结构变化影响,能保证临界机群的识别精度。
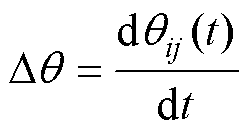 (12)
(12)
在多机系统中,电流与角速度的关联关系、系统稳定关键特征和系统失稳关键特征同样存在,本文以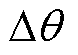 的大小作为分群的依据,形成了适用于多机系统的暂态稳定性判别方法,其判别具体流程如图10所示,具体步骤如下:
的大小作为分群的依据,形成了适用于多机系统的暂态稳定性判别方法,其判别具体流程如图10所示,具体步骤如下:
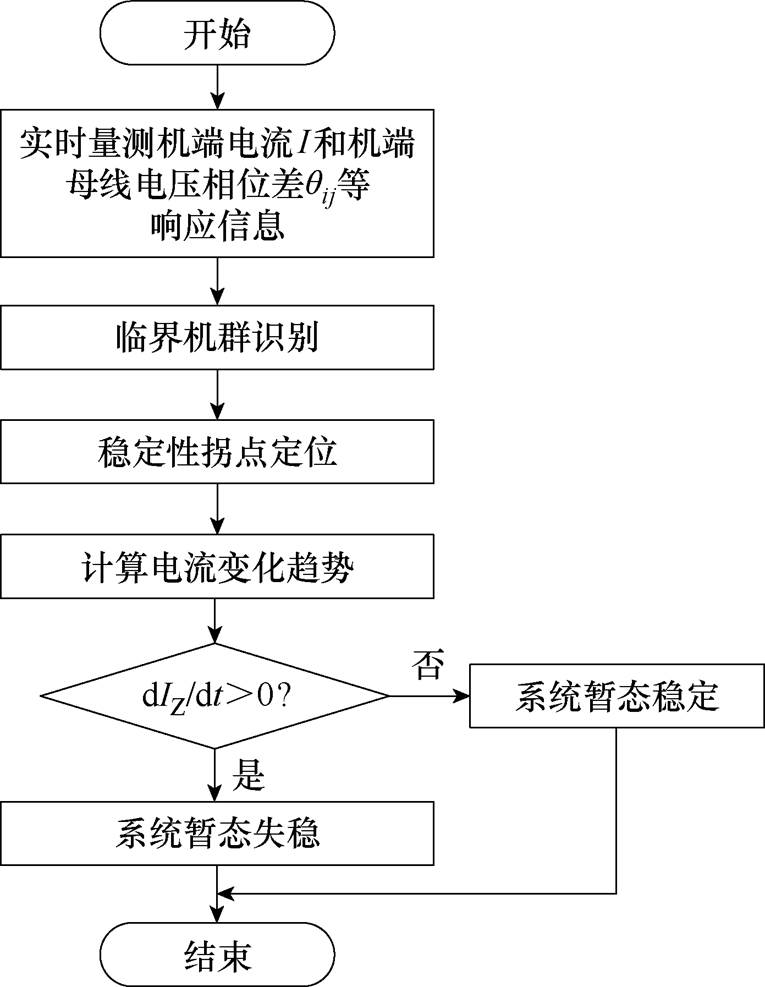
图10 暂态稳定性判别流程
Fig.10 Transient stability discriminant flow chart
(1)利用信息量测技术实时测量发电机端口电流和机端母线电压相位差等响应信息,比较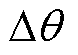 的大小实现临界机群识别。
的大小实现临界机群识别。
(2)快速定位角速度拐点,比较拐点时刻电流与实测电流的大小并计算拐点附近电流变化趋势。
(3)利用本文所提判据对临界机群中受扰严重机组进行暂态稳定性判别,通过判断机群间的暂态稳定性得到整个系统的暂态稳定性。
为验证方法的有效性,在图11所示的节点25和28分别接入250 MW双馈风电机组的新英格兰10机39节点系统上进行仿真试验。发电机为二阶经典模型,负荷采用恒定阻抗模型,以发电机G2作为参考机。在PSASP仿真软件中设置仿真时长为5 s,仿真步长为10 ms,以仿真输出的发电机电流和角速度的数据来模拟实测数据,输出间隔为10 ms。在线路24-16的50%处设置三相短路故障,0 s接入故障,通过调整故障清除时间模拟不同的故障严重程度,当故障后0.53 s清除故障,系统是稳定的;当故障后0.54 s清除故障,系统失稳。故障持续时间由实际仿真情况得到。
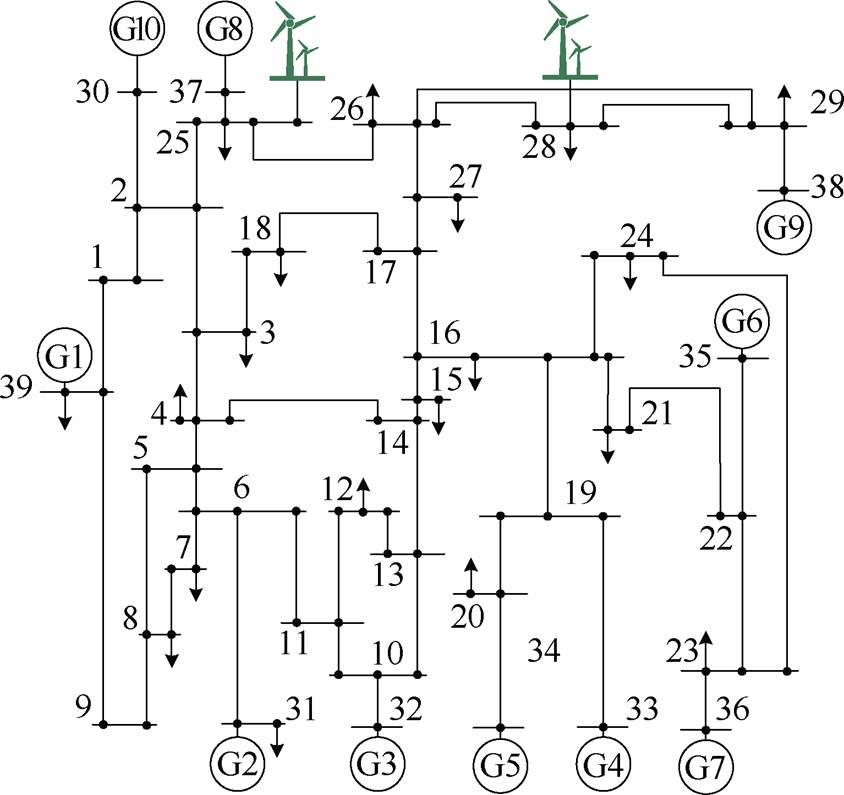
图11 改进的新英格兰10机39节点测试系统示意图
Fig.11 Illustration of the improved New England 10-machine 39-bus test system
分别计算系统稳定和失稳情况下故障清除后各发电机端口母线电压相位差变化率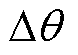 ,见表1和表2,根据
,见表1和表2,根据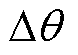 的大小实现机组分群,{G4, G5, G6, G7}的
的大小实现机组分群,{G4, G5, G6, G7}的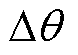 大小相近且均大于0,表明这四台发电机具有相似的动态响应行为,相位差呈现较大幅度增长;其余发电机的
大小相近且均大于0,表明这四台发电机具有相似的动态响应行为,相位差呈现较大幅度增长;其余发电机的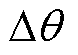 大小相近且明显小于{G4, G5, G6, G7},相位差呈现小幅度增长趋势或减小趋势,故可由此将系统中发电机分为两群,{G4, G5, G6, G7}为临界机群,其余发电机为剩余机群。
大小相近且明显小于{G4, G5, G6, G7},相位差呈现小幅度增长趋势或减小趋势,故可由此将系统中发电机分为两群,{G4, G5, G6, G7}为临界机群,其余发电机为剩余机群。
表1 稳定情况利用机端母线电压相位差变化率分群
Tab.1 Grouped by the change rate of the phase angle difference of the terminal bus voltage when the system is stable
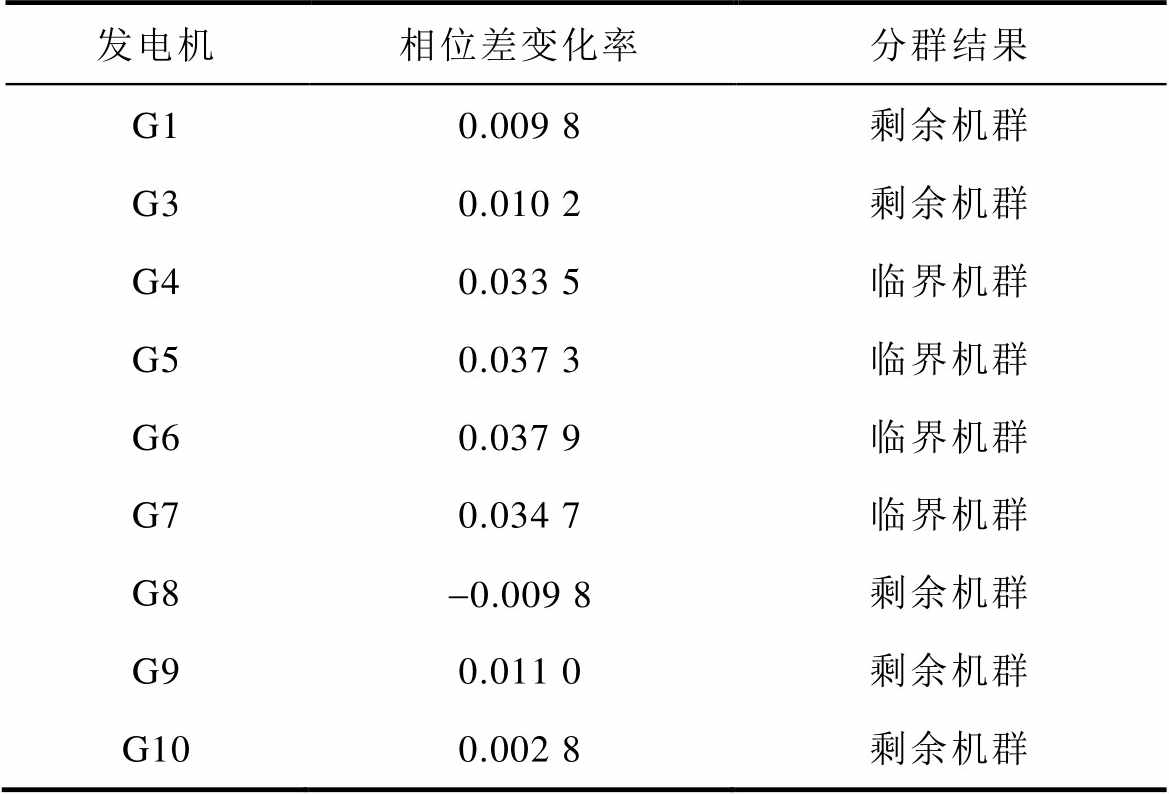
发电机相位差变化率分群结果 G10.009 8剩余机群 G30.010 2剩余机群 G40.033 5临界机群 G50.037 3临界机群 G60.037 9临界机群 G70.034 7临界机群 G8-0.009 8剩余机群 G90.011 0剩余机群 G100.002 8剩余机群
表2 失稳情况利用机端母线电压相位差变化率分群
Tab.2 Grouped by the change rate of the phase angle difference of the terminal bus voltage in the instable system
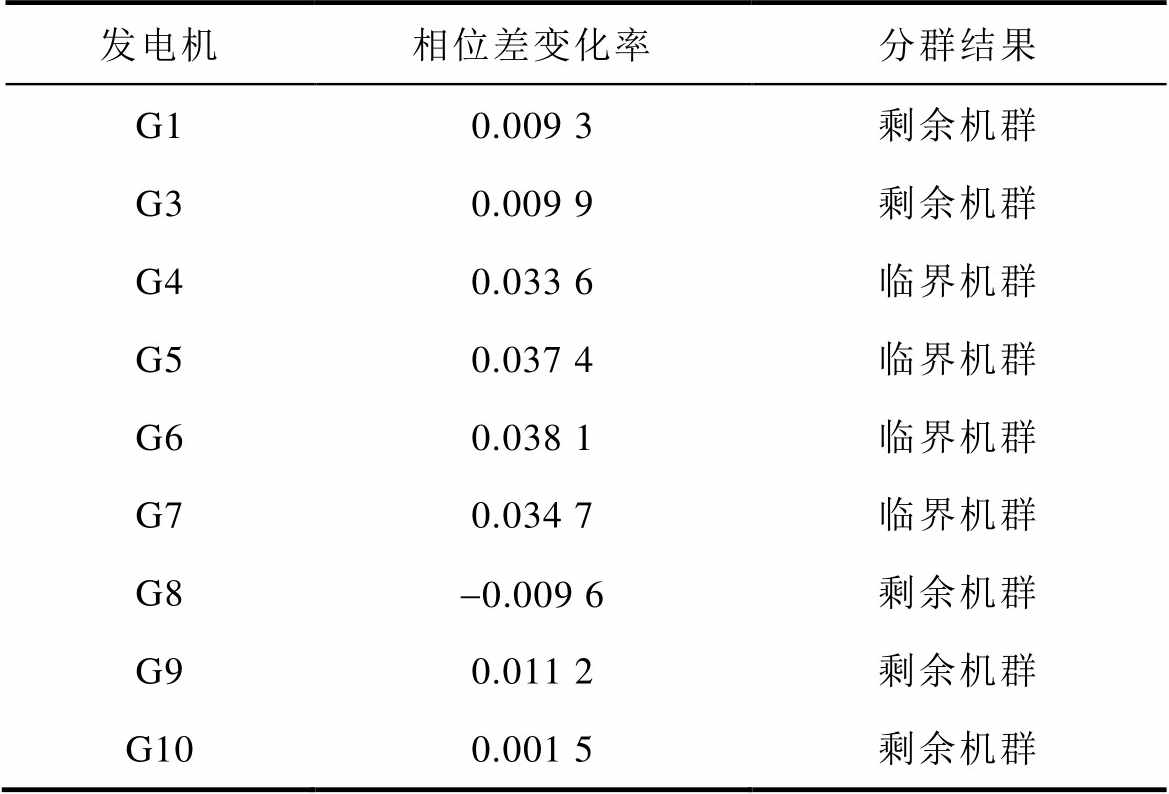
发电机相位差变化率分群结果 G10.009 3剩余机群 G30.009 9剩余机群 G40.033 6临界机群 G50.037 4临界机群 G60.038 1临界机群 G70.034 7临界机群 G8-0.009 6剩余机群 G90.011 2剩余机群 G100.001 5剩余机群
将仿真输出的故障后电流和角速度的数据作为实测数据,利用本文所提暂态功角稳定判别方法对该系统进行暂态稳定性判别。
1)0.53 s清除故障
实时量测发电机响应信息,以临界机群中发电机G6为例,绘制其I-w关系曲线和功角时域曲线,如图12所示,关系曲线呈现角速度拐点附近电流持续减小的特征,利用本文判据判别此工况下系统暂态功角稳定性,结果表明,0.53 s清除故障,发电机G6的I-w关系曲线满足系统稳定判据,判定系统是稳定的,与仿真结果一致。
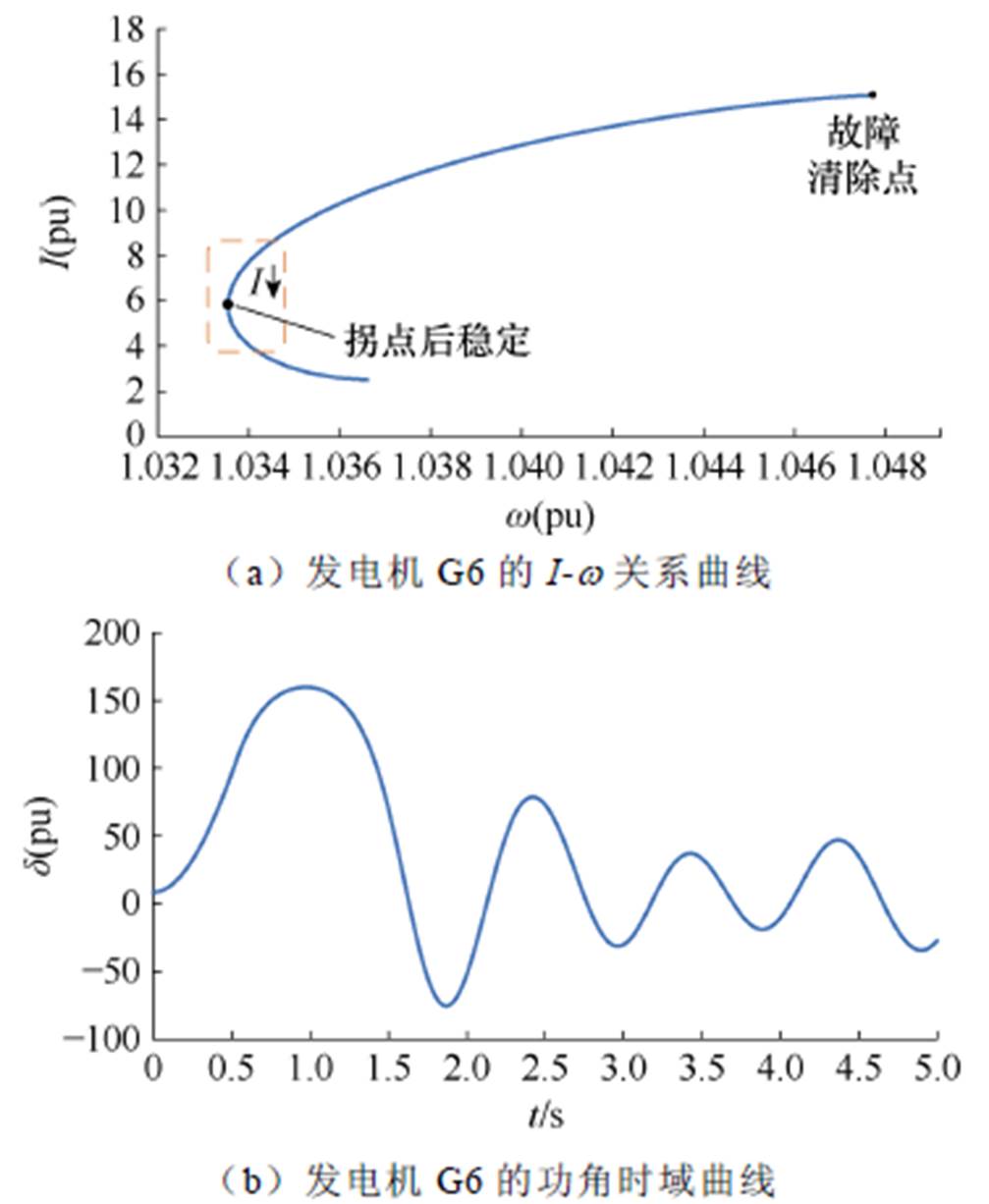
图12 0.53 s清除故障后系统的暂态稳定性判别
Fig.12 Discrimination of system transient stability after clearing the fault in 0.53 s
2)0.54 s清除故障
以临界机群中发电机G6为例,绘制发电机G6的I-w 关系曲线和功角时域曲线,如图13所示,关系曲线呈现角速度拐点附近电流持续增大的特征,利用本文判据判别此工况下的系统暂态功角稳定性,结果表明,0.54 s清除故障,发电机G6的I-w 关系曲线满足系统失稳判据,系统失稳,与仿真结果一致。
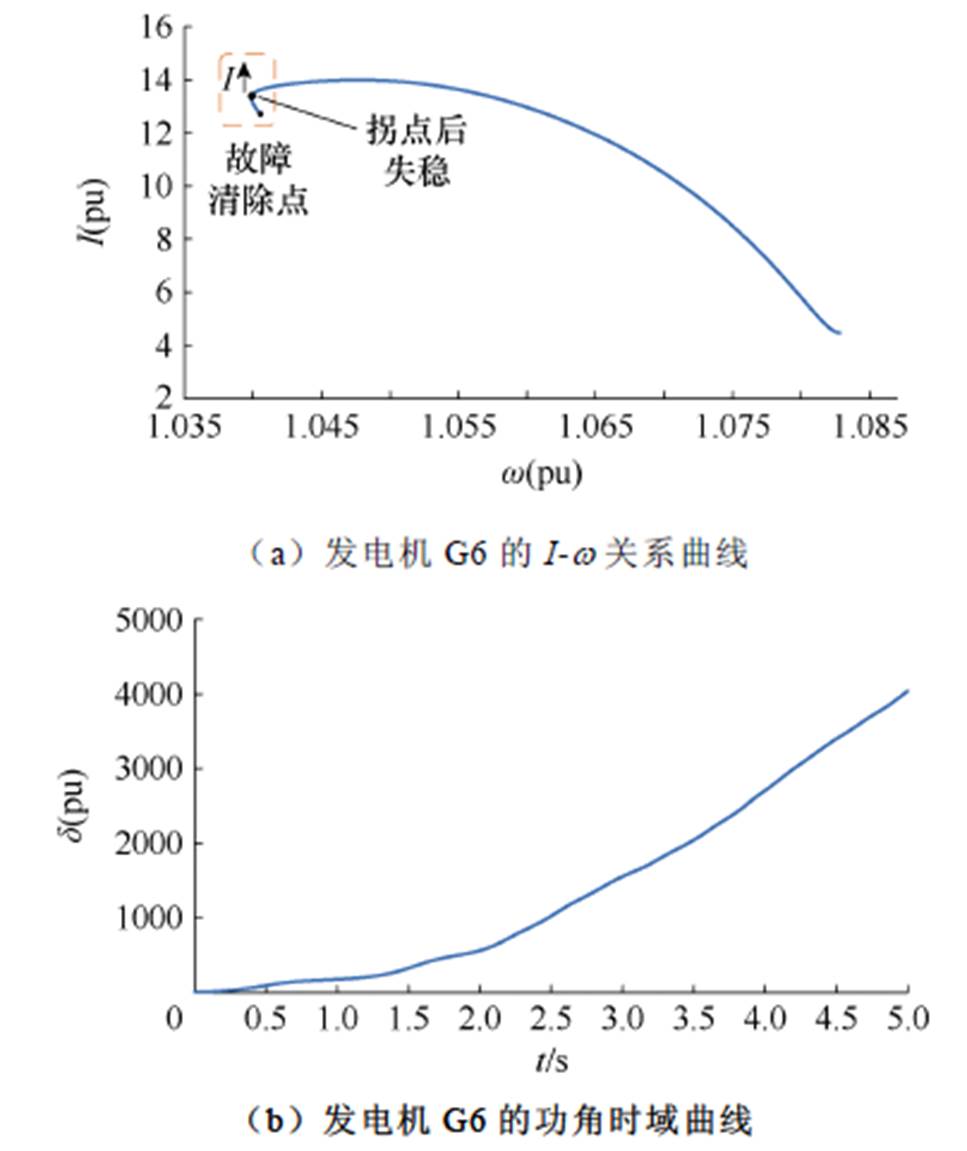
图13 0.54 s清除故障后系统的暂态稳定性判别
Fig.13 Discrimination of system transient stability after clearing the fault in 0.54 s
上述测试结果表明了本文方法能有效准确地判别出系统暂态稳定性。所提方法的临界机群识别时间以实际测量数据的输出间隔为准,文中设置输出间隔为10 ms,则临界机群识别时间为10 ms,为方便描述和比较,将临界机群识别和功角稳定判别两个过程的时间合计描述为暂态稳定判别时间。表3为本文方法与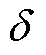 >180°工程判据法失稳判别时间的对比。相较于
>180°工程判据法失稳判别时间的对比。相较于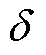 >180°工程判据法,本文方法仅用80 ms的时间准确地判别出系统失稳,快速性大大提高,很大程度地缩短了失稳判别时间,能为紧急控制争取更多的时间。
>180°工程判据法,本文方法仅用80 ms的时间准确地判别出系统失稳,快速性大大提高,很大程度地缩短了失稳判别时间,能为紧急控制争取更多的时间。
表3 10机39节点系统中两种方法暂态失稳判别效果比较
Tab.3 Comparison of transient instability discrimination time of two methods in 10-machine 39-bus system (单位: s)

故障清除时刻d >180°工程判据法判别时刻本文方法判别时刻 0.541.020.62
另外,本文方法能够较快识别出系统稳定,而工程功角判据则需要持续监测功角变化足够长时间,可见,本文判据使稳定判别更加快速,避免了长时间的数据提取和计算,减轻了数据处理系统负担。此外,由于完全基于响应,本文方法能反映系统故障后真实的暂态稳定特性,同时基于电气量本身构建暂态功角稳定性判据和临界机群识别方法,使得系统暂态稳定性判别更加简单易行,也保证了判别结果的准确性。
为了进一步证实判据的适用性,在东北某地区实际电网中进行测试验证,图14为东北某地区实际电网500 kV接线。截至2021年5月末,该地区新能源发电装机容量达1 454万kW,区域4、区域7和区域8是该地区的风电场,有大规模风力发电机组接入电网,同时有其他区域的能源基地通过直流向该地区负荷中心送电。可见,该地区电网已成为规模化新能源并网交直流混联电力系统。
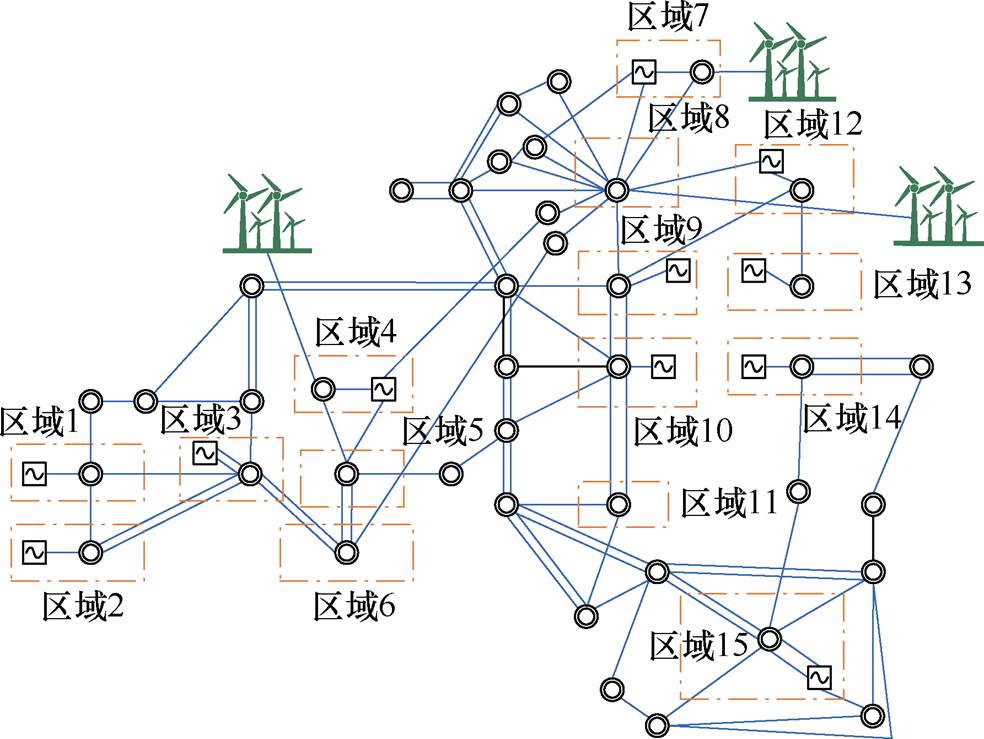
图14 东北某地区实际电网500 kV接线
Fig.14 500 kV wiring diagram of actual power grid in a certain area of Northeast China
选取图14区域11内部的一条线路——LYKC220- LFJ220线路,在该线路的50%处设置三相短路故障,0 s接入故障,通过调整故障清除时间模拟不同的故障严重程度,当故障后0.20 s清除故障,系统是稳定的;当故障后0.21 s清除故障,系统失稳。区域11内部的发电机LYKC-G1和LYKC-G2受故障影响严重,系统中其他发电机均受扰较轻,利用本文临界机群识别方法对系统中所有发电机组进行分群,同调机组分群情况:{LYKC-G1, LYKC-G2}为临界机群,其余机组组成剩余机群。
利用本文方法对实际电网算例中稳定和失稳情况进行暂态稳定性判别,以临界机群中发电机LYKC-G1为例,其稳定性判据结果及对应发电机功角时域曲线如图15和图16所示。
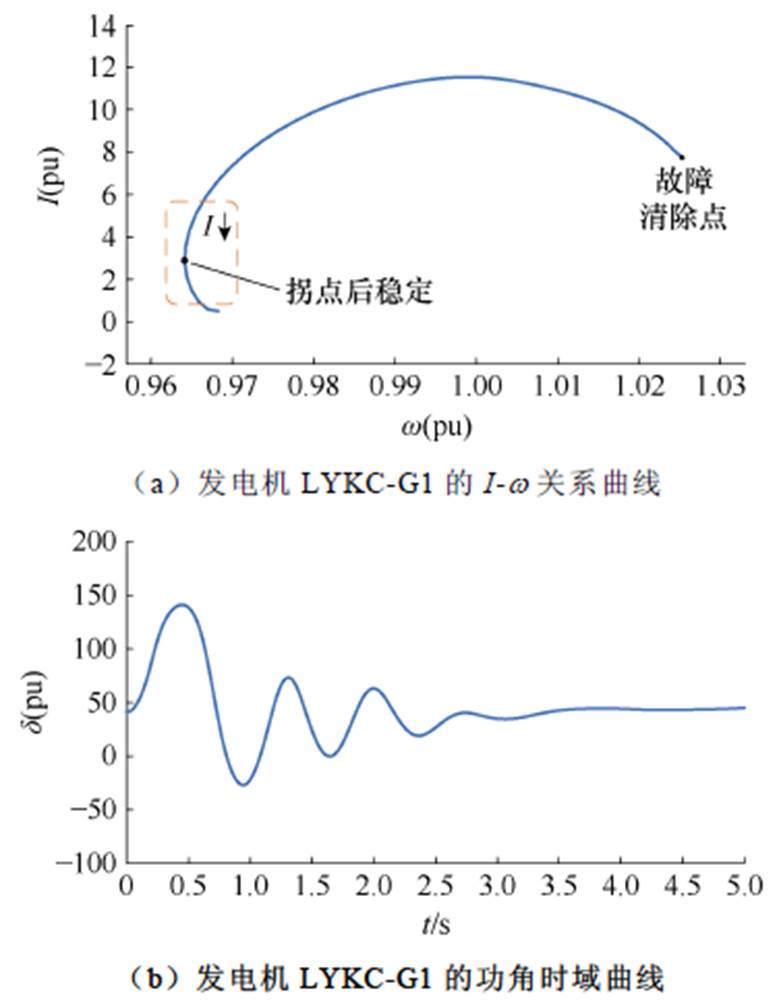
图15 0.20 s清除故障后系统的暂态稳定性判别
Fig.15 Discrimination of system transient stability after clearing the fault in 0.20 s
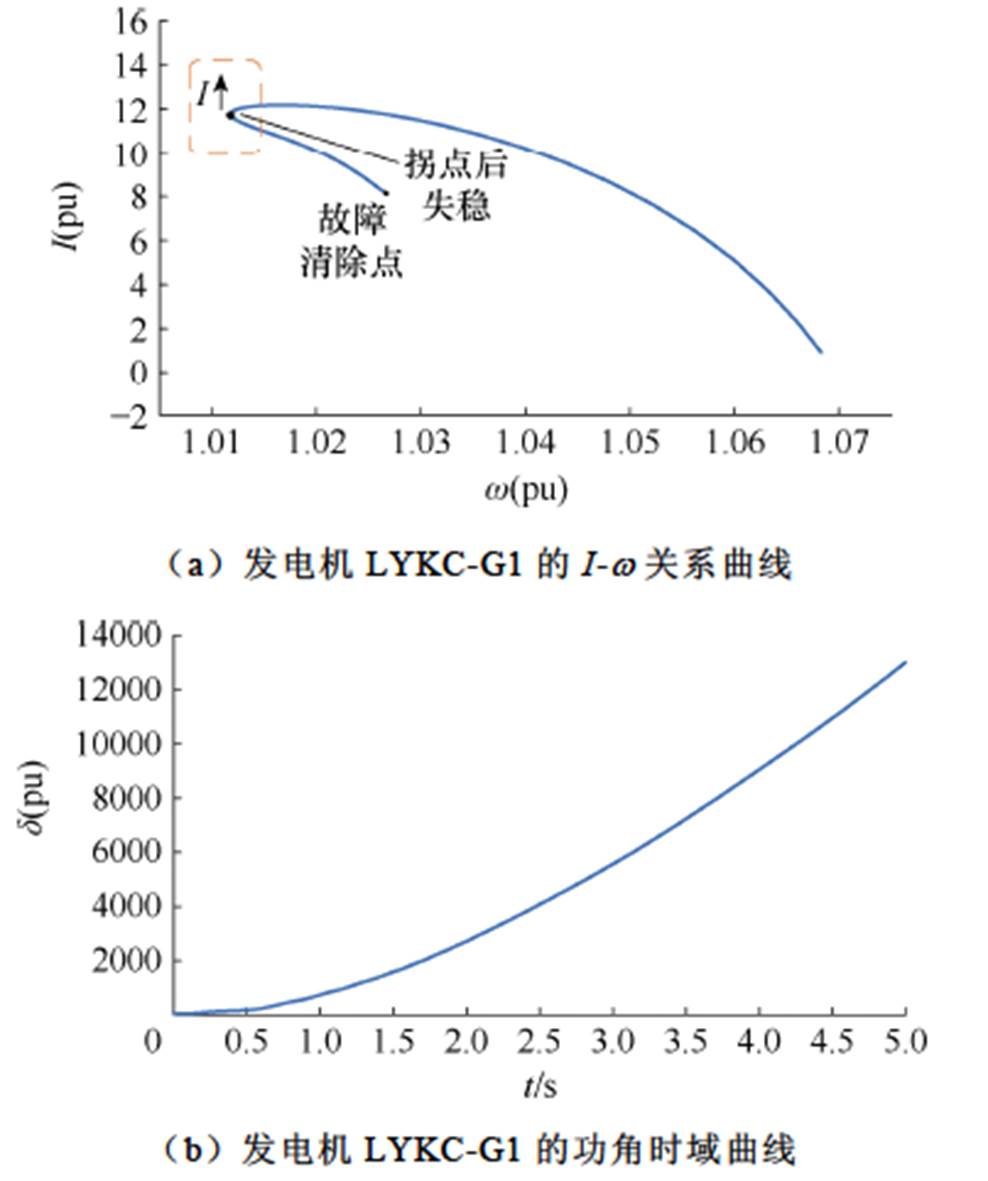
图16 0.21 s清除故障后系统的暂态稳定性判别
Fig.16 Discrimination of system transient stability after clearing the fault in 0.21 s
图15中关系曲线呈现角速度拐点附近电流持续减小的特征,图16中关系曲线呈现角速度拐点附近电流持续增大的特征。根据本文判据,0.20 s清除故障,发电机LYKC-G1的I-w 关系曲线满足系统稳定判据,系统是稳定的,与仿真结果一致;0.21 s清除故障,发电机LYKC-G1的I-w 关系曲线满足系统失稳判据,系统失稳,与仿真结果一致。
上述测试结果表明,本文判据能够有效准确地判别东北某地区电网的暂态功角稳定性,验证了本文所提方法在应用于复杂的含规模化新能源并网交直流混联的实际大电网时仍具有很好的适用性、有效性和准确性。将本文判据的判稳时间与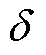 >180°工程功角判据的判稳时间进行对比,见表4。本文方法对于系统失稳情况仅需要190 ms即可准确判别出系统失稳,再次证实所提方法具有良好的快速性和准确性。
>180°工程功角判据的判稳时间进行对比,见表4。本文方法对于系统失稳情况仅需要190 ms即可准确判别出系统失稳,再次证实所提方法具有良好的快速性和准确性。
表4 东北某地区实际电网两种方法暂态失稳判别效果比较
Tab.4 Comparison of transient instability discrimination time of two methods in actual power grid in an area of Northeast China(单位: s)

故障清除时刻d >180°工程判据法判别时刻本文方法判别时刻 0.210.510.40
本文提出了一种基于发电机电流与角速度响应关联特征的新能源电力系统暂态功角稳定判别新方法,该方法能充分利用实测响应信息对系统暂态功角稳定性快速准确地判别。该方法具有不受系统运行方式、网络结构、模型和参数的影响,不需要复杂的计算、计算量和量测信息量小等优点。本文主要研究结论如下:
1)挖掘出发电机电流和角速度蕴含的暂态功角稳定信息,建立了故障后电流与角速度的关联关系,并揭示了两电气量与系统暂态稳定性间的联系。
2)基于实时量测的响应信息绘制发电机I-w 关系曲线,从关系曲线中提取出系统稳定和失稳关键特征,定义了稳定性拐点和稳定性区域,并探究了风机接入后对关系曲线特性的影响,提出了基于I-w 关联特征的暂态功角稳定新判据,该判据简化了电力系统暂态功角失稳的判别过程,能够快速准确地判别系统的暂态功角稳定性。
3)本文方法不仅能够准确判别出系统暂态失稳,还大大缩短了判别时间,快速性好。由于该方法稳定性判别时刻显著早于系统失稳时刻,还能为后续的紧急控制争取更多的时间。
4)通过比较故障清除后机端母线电压相位差变化率大小识别临界机群,形成了多机系统暂态稳定性判别流程,使本文方法可以推广到多机系统。方法在改进的新英格兰10机39节点系统和东北某地区实际电网中均能准确判别系统暂态功角稳定性,验证了本文方法的有效性,也体现了本文方法具有较好的普适性。
附录 算例参数
附表1 新英格兰10机39节点系统发电机参数
App.Tab.1 Generator parameters of New England 10-machine 39-bus system (pu)

发电机名称节点节点类型有功功率P电压V参数组视在功率Sn G1030PV2.51.047 5101 000 G231Slack00.9822700 G332PV6.50.983 13800 G433PV6.320.997 24800 G534PV5.081.012 35600 G635PV6.51.049 36800 G736PV5.61.063 57700 G837PV5.41.027 88700 G938PV8.31.026 591 000 G139PV101.0311 000 风G140PQ0.541.085 710250 风G244PQ0.541.085 710250
附表2 新英格兰10机39节点系统发电机参数组
App.Tab.2 Generator parameter sets of New England 10-machine 39-bus system (pu)

参数组号直轴同步电抗Xd直轴暂态电抗交轴同步电抗Xq交轴暂态电抗直轴短路暂态时间常数交轴短路暂态时间常数发电机惯性时间常数Tj 92.1060.572.050.5874.791.966.9 82.030.3991.960.63776.70.416.942 72.0650.3432.0441.3025.661.57.542 62.0320.41.9280.65127.30.48.7
(续)

参数组号直轴同步电抗Xd直轴暂态电抗交轴同步电抗Xq交轴暂态电抗直轴短路暂态时间常数交轴短路暂态时间常数发电机惯性时间常数Tj 54.020.7923.720.9965.40.448.666 42.0960.348 82.0641.3285.691.57.15 31.9960.424 81.8960.700 85.71.58.95 22.0650.487 91.9741.196.561.58.658 120.61.90.870.710 1010.310.690.510.208.4
附表3 新英格兰10机39节点系统变压器参数
App.Tab.3 Transformer parameters of New England 10-machine 39-bus system (pu)
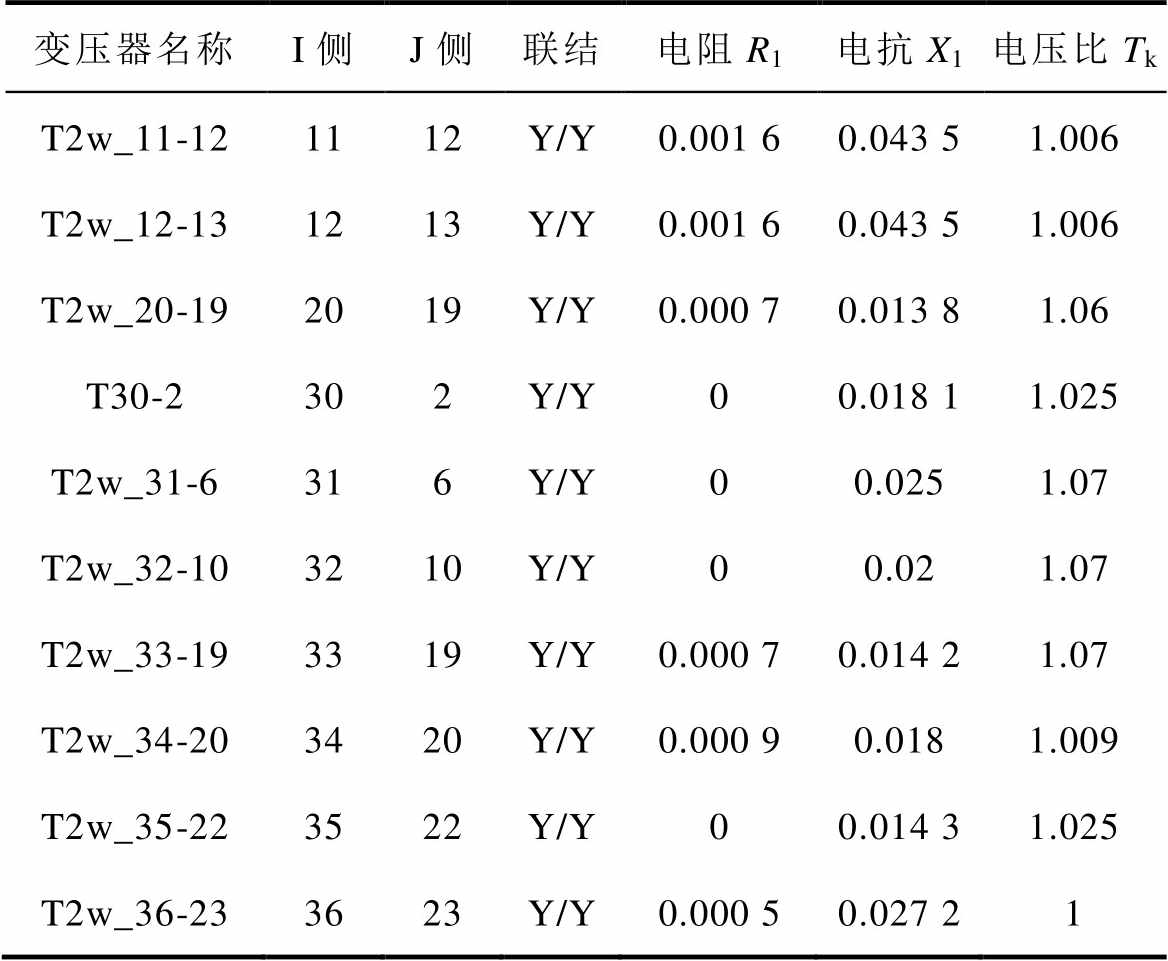
变压器名称I侧J侧联结电阻R1电抗X1电压比Tk T2w_11-121112Y/Y0.001 60.043 51.006 T2w_12-131213Y/Y0.001 60.043 51.006 T2w_20-192019Y/Y0.000 70.013 81.06 T30-2302Y/Y00.018 11.025 T2w_31-6316Y/Y00.0251.07 T2w_32-103210Y/Y00.021.07 T2w_33-193319Y/Y0.000 70.014 21.07 T2w_34-203420Y/Y0.000 90.0181.009 T2w_35-223522Y/Y00.014 31.025 T2w_36-233623Y/Y0.000 50.027 21
附表4 新英格兰10机39节点系统线路参数
App.Tab.4 Line parameters of New England 10-machine 39-bus system (pu)

线路名称I侧节点J侧节点电阻R1电抗X1电纳B1/2 AC_01-02120.003 50.041 10.3493 5 AC_10-1110110.000 40.004 30.036 45 AC_10-1310130.000 40.004 30.036 45 AC_13-1413140.000 90.010 10.086 15 AC_14-1514150.001 80.021 70.183 AC_15-1615160.000 90.009 40.085 5 AC_16-1716170.000 70.008 90.067 1 AC_16-21162100.013 50.127 4 AC_17-1817180.000 70.008 20.065 95 AC_18-031830.001 10.013 30.106 9
(续)

线路名称I侧节点J侧节点电阻R1电抗X1电纳B1/2 AC_19-1619160.001 60.019 50.152 AC_02-252250.0070.008 60.073 AC_02-03230.001 30.015 10.128 6 AC_21-2221220.000 80.0140.128 25 AC_22-2322230.000 60.009 60.092 3 AC_23-2423240.002 20.0350.180 5 AC_24-1624160.000 30.005 90.034 AC_25-2625260.003 20.032 30.256 5 AC_26-2726270.001 40.014 70.119 8 AC_26-2826280.001 40.047 40.390 1 AC_27-1727170.001 30.017 30.160 8 AC_28-29BUS28BUS290.001 40.015 10.124 5 AC_29-26BUS29BUS260.005 70.062 50.514 5 AC_03-04BUS3BUS40.001 30.021 30.110 7 AC_39-01BUS39BUS10.0010.0250.375 AC_04-14BUS4BUS140.000 80.012 90.069 1 AC_04-05BUS4BUS50.000 80.012 80.067 1 AC_05-06BUS5BUS60.000 20.002 60.021 7 AC_05-08BUS5BUS80.000 80.011 20.073 8 AC_06-11BUS6BUS110.000 70.008 20.0694 5 AC_06-07BUS6BUS70.000 60.009 20.056 5 AC_07-08BUS7BUS80.000 40.004 60.039 AC_08-09BUS8BUS90.002 30.036 30.190 2 AC_09-39BUS9BUS390.0010.0250.6
附表5 新英格兰10机39节点系统负荷参数
App.Tab.5 Load parameters of New England 10-machine 39-bus system (pu)

负荷名称负荷节点名节点类型有功功率P无功功率Q电压V电压相位q Load-121210.0750.8810 Load-151513.21.5310 Load-161613.290.32310 Load-181811.580.310 Load-202016.281.0310 Load-212112.741.1510 Load-232312.4750.84610 Load-242413.086-0.92210 Load-252512.240.47210 Load-262611.390.1710
(续)
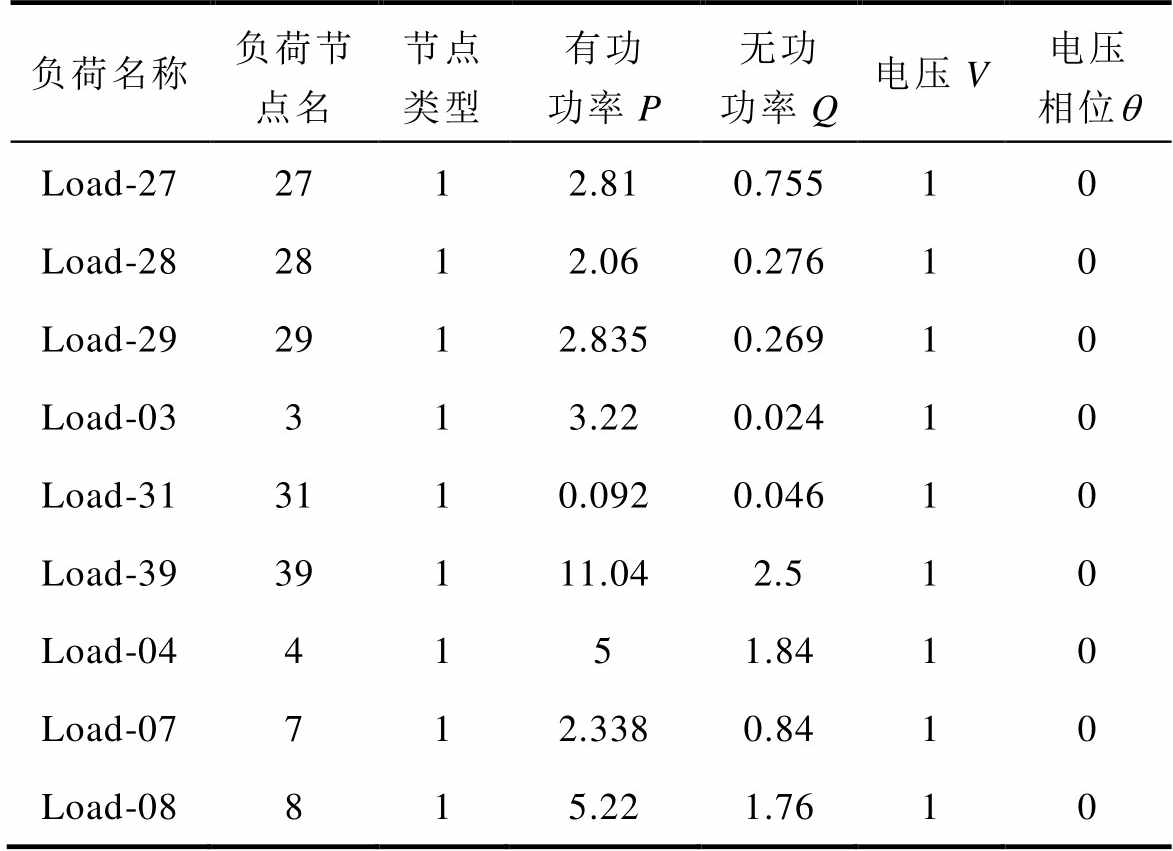
负荷名称负荷节点名节点类型有功功率P无功功率Q电压V电压相位q Load-272712.810.75510 Load-282812.060.27610 Load-292912.8350.26910 Load-03313.220.02410 Load-313110.0920.04610 Load-3939111.042.510 Load-044151.8410 Load-07712.3380.8410 Load-08815.221.7610
参考文献
[1] 汤涌. 电力系统安全稳定综合防御体系框架[J]. 电网技术, 2012, 36(8): 1-5.
Tang Yong. Framework of comprehensive defense architecture for power system security and stability[J]. Power System Technology, 2012, 36(8): 1-5.
[2] 蔡国伟, 穆钢, Chan K W, 等. 基于网络信息的暂态稳定性定量分析: 支路势能法[J]. 中国电机工程学报, 2004, 24(5): 1-6.
Cai Guowei, Mu Gang, Chan K W, et al. Branch potential energy method for power system transient stability assessment based on network dynamic variables[J]. Proceedings of the CSEE, 2004, 24(5): 1-6.
[3] 滕林, 刘万顺, 贠志皓, 等. 电力系统暂态稳定实时紧急控制的研究[J]. 中国电机工程学报, 2003, 23(1): 64-69.
Teng Lin, Liu Wanshun, Yuan Zhihao, et al. Study of real-time power system transient stability emergency control[J]. Proceedings of the CSEE, 2003, 23(1): 64-69.
[4] 葛平娟, 肖凡, 涂春鸣, 等. 考虑故障限流的下垂控制型逆变器暂态控制策略[J]. 电工技术学报, 2022, 37(14): 3676-3687.
Ge Pingjuan, Xiao Fan, Tu Chunming, et al. Transient control strategy of droop-controlled inverter con- sidering fault current limitation[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3676- 3687.
[5] 王科, 秦文萍, 张宇, 等. 双馈风机等效惯量控制比例系数对系统功角首摆稳定的影响机理分析[J]. 电工技术学报, 2023, 38(3): 741-753.
Wang Ke, Qin Wenping, Zhang Yu, et al. Mechanism analysis of effect of equivalent proportional coefficient of inertia control of DFIG on stability of first swing of power angle[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 741-753.
[6] 李生虎, 张亚海, 叶剑桥, 等. 基于双馈风电机组控制参数优化的电网功角振荡控制[J]. 电工技术学报, 2023, 38(5): 1325-1338.
Li Shenghu, Zhang Yahai, Ye Jianqiao, et al. Power angle oscillation control of power grid based on control parameter optimization of doubly-fed wind turbine generator[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1325-1338.
[7] 林伟芳, 汤涌, 孙华东, 等. 巴西“2·4”大停电事故及对电网安全稳定运行的启示[J]. 电力系统自动化, 2011, 35(9): 1-5.
Lin Weifang, Tang Yong, Sun Huadong, et al. Blackout in Brazil power grid on February 4, 2011 and inspirations for stable operation of power grid[J]. Automation of Electric Power Systems, 2011, 35(9): 1-5.
[8] 吴政球, 陈辉华, 唐外文, 等. 以单机等面积稳定判据分析多机系统暂态稳定性[J]. 中国电机工程学报, 2003, 23(4): 48-52.
Wu Zhengqiu, Chen Huihua, Tang Waiwen, et al. Using single machine equal area criterion to analyze multi-machine systems stability[J]. Proceedings of the CSEE, 2003, 23(4): 48-52.
[9] 李锡林, 查晓明, 田震, 等. 考虑频率突变影响的孤岛微电网系统建模和基于Lyapunov第二法的暂态稳定性分析[J]. 电工技术学报, 2023, 38(增刊1): 18-31.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. Modeling of island microgrid considering frequency mutation and transient stability analysis based on Lyapunov second method[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 18-31.
[10] 刘铖, 张昊鑫, 朱晓锋, 等. 基于随机网络能量的电力系统暂态稳定评估[J]. 东北电力大学学报, 2022, 42(6): 90-99.
Liu Cheng, Zhang Haoxin, Zhu Xiaofeng, et al. Transient stability assessment of power system based on random network energy[J]. Journal of Northeast Electric Power University, 2022, 42(6): 90-99.
[11] 刘铖, 王旭, 张宇驰. 基于负荷模式能量的永磁风机电网功率振荡特性分析[J]. 东北电力大学学报, 2022, 42(4): 70-78.
Liu Cheng, Wang Xu, Zhang Yuchi. Analysis of power oscillation characteristics of permanent magnet wind turbine power grid based on load mode energy[J]. Journal of Northeast Electric Power University, 2022, 42(4): 70-78.
[12] 王志文, 孙华东, 易俊, 等. 利用发电机转速实时识别两群暂态功角失稳[J]. 电网技术, 2020, 44(7): 2634-2641.
Wang Zhiwen, Sun Huadong, Yi Jun, et al. Real-time identification of transient angle instability in\r two machine groups using angular velocities[J]. Power System Technology, 2020, 44(7): 2634-2641.
[13] 汤涌. 基于响应的电力系统广域安全稳定控制[J]. 中国电机工程学报, 2014, 34(29): 5041-5050.
Tang Yong. Response-based wide area control for power system security and stability[J]. Proceedings of the CSEE, 2014, 34(29): 5041-5050.
[14] 许树楷, 谢小荣, 辛耀中. 基于同步相量测量技术的广域测量系统应用现状及发展前景[J]. 电网技术, 2005, 29(2): 44-49.
Xu Shukai, Xie Xiaorong, Xin Yaozhong. Present application situation and development tendency of synchronous phasor measurement technology based wide area measurement system[J]. Power System Technology, 2005, 29(2): 44-49.
[15] Zuhaib M, Rihan M, Saeed M T. A novel method for locating the source of sustained oscillation in power system using synchrophasors data[J]. Protection and Control of Modern Power Systems, 2020, 5(4): 1-12.
[16] 谢欢, 张保会, 于广亮, 等. 基于相轨迹凹凸性的电力系统暂态稳定性识别[J]. 中国电机工程学报, 2006, 26(5): 38-42.
Xie Huan, Zhang Baohui, Yu Guangliang, et al. Power system transient stability detection theory based on characteristic concave or convex of trajectory[J]. Proceedings of the CSEE, 2006, 26(5): 38-42.
[17] 郑超, 苗田, 马世英. 基于关键支路受扰轨迹凹凸性的暂态稳定判别及紧急控制[J]. 中国电机工程学报, 2016, 36(10): 2600-2610.
Zheng Chao, Miao Tian, Ma Shiying. Transient stability identification and emergency control based on the convex characteristic of the key branch’s disturbed trajectory[J]. Proceedings of the CSEE, 2016, 36(10): 2600-2610.
[18] 郑超, 孙华东, 李惠玲. 基于响应的支路暂态输电能力指数及紧急控制[J]. 中国电机工程学报, 2021, 41(2): 581-591.
Zheng Chao, Sun Huadong, Li Huiling. Response- based branch transient transmission capability index and transient stability emergency control[J]. Pro- ceedings of the CSEE, 2021, 41(2): 581-591.
[19] 马世英, 朱存浩, 郑超, 等. 扩展相轨迹特征解析及暂态稳定判别方法研究[J]. 中国电机工程学报, 2020, 40(20): 6516-6526.
Ma Shiying, Zhu Cunhao, Zheng Chao, et al. Analysis of extended phase trajectory characteristics and transient stability identification[J]. Proceedings of the CSEE, 2020, 40(20): 6516-6526.
[20] 宋方方, 毕天姝, 杨奇逊. 基于暂态能量变化率的电力系统多摆稳定性判别新方法[J]. 中国电机工程学报, 2007, 27(16): 13-18.
Song Fangfang, Bi Tianshu, Yang Qixun. Multi-swing stability assessment approach based on variation rate of transient energy for power systems[J]. Proceedings of the CSEE, 2007, 27(16): 13-18.
[21] 魏少攀, 杨明, 韩学山, 等. 一种利用机端电压幅值轨迹MLE指标的暂态功角稳定在线辨识方法[J]. 中国电机工程学报, 2017, 37(13): 3775-3786.
Wei Shaopan, Yang Ming, Han Xueshan, et al. An online identification method for transient angle stability using MLE index of generator terminal voltage amplitude trajectory[J]. Proceedings of the CSEE, 2017, 37(13): 3775-3786.
[22] 孙辉, 孙宝硕, 高正男, 等. 基于量测数据时序谱分布特性的电力系统暂态功角稳定在线判别[J]. 电网技术, 2023, 47(3): 1107-1116.
Sun Hui, Sun Baoshuo, Gao Zhengnan, et al. Online identification for power system transient angle stability based on time-series spectral distribution characteristics of measured data[J]. Power System Technology, 2023, 47(3): 1107-1116.
[23] 刘玉田, 林飞. 基于相量测量技术和模糊径向基网络的暂态稳定性预测[J]. 中国电机工程学报, 2000, 20(2): 19-23.
Liu Yutian, Lin Fei. Application of PMU and fuzzy radial basis function network to power system transient stability prediction[J]. Proceedings of the CSEE, 2000, 20(2): 19-23.
[24] 叶圣永, 王晓茹, 刘志刚, 等. 基于支持向量机的暂态稳定评估双阶段特征选择[J]. 中国电机工程学报, 2010, 30(31): 28-34.
Ye Shengyong, Wang Xiaoru, Liu Zhigang, et al. Dual-stage feature selection for transient stability assessment based on support vector machine[J]. Proceedings of the CSEE, 2010, 30(31): 28-34.
[25] 石访, 张林林, 胡熊伟, 等. 基于多属性决策树的电网暂态稳定规则提取方法[J]. 电工技术学报, 2019, 34(11): 2364-2374.
Shi Fang, Zhang Linlin, Hu Xiongwei, et al. Power system transient stability rules extraction based on multi-attribute decision tree[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2364-2374.
[26] 杨浩, 伍柏臻, 刘铖, 等. 基于暂态关键特征逻辑推理的复杂电网响应驱动暂态稳定性判别[J]. 电工技术学报, 2024, 39(13): 3943-3955.
Yang Hao, Wu Baizhen, Liu Cheng, et al. Response- driven transient stability assessment for complex power grids based on logical reasoning with transient key feature[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3943-3955.
[27] 毛安家, 郭志忠, 张学松. 一种基于广域测量系统过程量测数据的快速暂态稳定预估方法[J]. 中国电机工程学报, 2006, 26(17): 38-43.
Mao Anjia, Guo Zhizhong, Zhang Xuesong. A fast transient stability predicting method based on the WAMS process measurement data[J]. Proceedings of the CSEE, 2006, 26(17): 38-43.
[28] 李琰, 周孝信, 周京阳. 基于引入虚拟负荷的发电机暂态稳定预测[J]. 电工技术学报, 2008, 23(3): 103-107, 130.
Li Yan, Zhou Xiaoxin, Zhou Jingyang. The generator transient stability prediction based on additional virtual loads[J]. Transactions of China Electro- technical Society, 2008, 23(3): 103-107, 130.
[29] 彭疆南, 孙元章, 王海风. 基于广域量测数据和导纳参数在线辨识的受扰轨迹预测[J]. 电力系统自动化, 2003, 27(22): 6-11.
Peng Jiangnan, Sun Yuanzhang, Wang Haifeng. Research on the perturbed trajectories prediction based on wide-area measurement and on-line admittance matrix identification[J]. Automation of Electric Power Systems, 2003, 27(22): 6-11.
[30] 王增平, 朱劭璇, 王彤, 等. 基于故障全景信息的电力系统暂态稳定分析方法[J]. 电力系统保护与控制, 2020, 48(15): 34-42.
Wang Zengping, Zhu Shaoxuan, Wang Tong, et al. Transient stability analysis for a power system based on fault panoramic information[J]. Power System Protection and Control, 2020, 48(15): 34-42.
[31] 朱存浩, 马世英, 郑超, 等. 基于实测响应轨迹的电力系统暂态不稳定判别[J]. 中国电机工程学报, 2021, 41(15): 5077-5090.
Zhu Cunhao, Ma Shiying, Zheng Chao, et al. Power system transient instability identification based on real-time response trajectory[J]. Proceedings of the CSEE, 2021, 41(15): 5077-5090.
[32] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[33] 刘道伟, 马世英, 李柏青, 等. 基于响应的电网暂态稳定态势在线量化评估方法[J]. 中国电机工程学报, 2013, 33(4): 85-95.
Liu Daowei, Ma Shiying, Li Baiqing, et al. Quanti- tative method for on-line power system transient stability assessment based on response information[J]. Proceedings of the CSEE, 2013, 33(4): 85-95.
Abstract Compared with the traditional power system, the transient stability dynamic characteristics of the new energy power system have undergone profound changes after large disturbances, which makes the traditional transient stability analysis methods difficult to apply. With the development and improvement of wide-area measurement systems, scholars have proposed discriminant methods based on response information. However, most have the problems with cumbersome calculations, unclear physical meaning, and low accuracy. This paper proposes a transient power-angle stability discrimination method for new energy power systems based on the correlation characteristics of generator current and angular velocity. Based on the transient key characteristics contained in current and angular velocity, the transient power angle stability of the system is quickly and accurately discriminated.
Firstly, the generator current is divided into three sections, and the difference characteristics of the post-fault current are obtained by comparing the current situation of each section in the two cases of power system stability and instability. Secondly, the post-fault current is substituted into the generator rotor motion equation to establish the relationship between the post-fault current and the angular velocity, and the relationship between the two electrical quantities and the transient stability is revealed. Thirdly, by analyzing the characteristics of the relationship curve between current and angular velocity, the key characteristics of transient power angle stability and instability are extracted, and the influence of wind turbine access on the characteristics of the relationship curve is explored. The transient power angle stability criterion is constructed. Finally, the critical generator cluster is identified by comparing the change rate of the phase angle difference of the bus voltage at the terminal after the fault is cleared.
The simulations of the improved New England 10-machine 39-bus system and the actual power grid show that the critical generator cluster can be accurately identified. The transient stability discrimination of system stability and instability scenarios is carried out. When the system is stable, the proposed method can accurately identify from the relationship curve that the current continues to decrease near the inflection point of the angular velocity. When the system is unstable, the current continues to increase near the inflection point of the angular velocity. The method uses 80 ms and 190 ms to distinguish the system instability.
Through simulation analysis, the following conclusions can be drawn. (1) Based on the measured response information, this method can avoid the influence of system operation mode, network structure, model, and parameters. (2) The electrical quantity used in this method is simple and easy to measure. It does not need complicated calculation or coordinate transformation of the response information, which avoids the error caused by calculation or transformation. (3) The proposed criterion is simple and feasible, and the discriminant results can be obtained quickly.
keywords:Power system, transient power angle stability, stability discrimination, response information, key features
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.231893
国家重点研发计划资助项目(2021YFB2400800)。
收稿日期2023-11-13
改稿日期2024-04-30
刘 铖 男,1985年生,博士,教授,博士生导师,研究方向为电力系统稳定分析与控制、新能源并网技术。E-mail: 05dylc@163.com
李守超 男,1998年生,硕士研究生,研究方向为新能源电力系统稳定分析与控制。E-mail: lishouchao131@163.com(通信作者)
(编辑 崔文静)