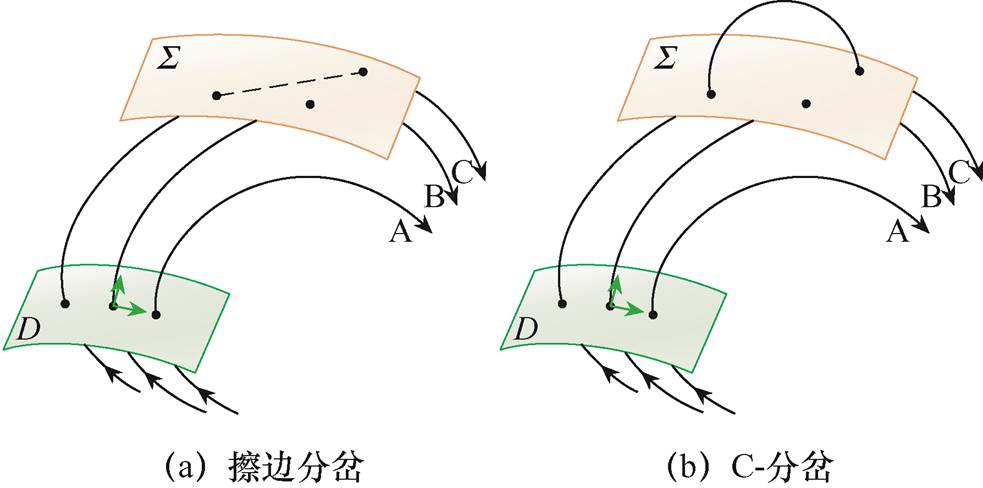
图1 非光滑分岔示意图
Fig.1 Schematic diagram of non-smooth bifurcations
摘要 在大扰动下,基于虚拟同步发电机(VSG)控制的并网逆变器因限幅环节饱和发生的切换型振荡对电力系统的安全稳定运行构成威胁,其振荡机理和影响因素复杂。为此,该文研究大扰动下由VSG限幅环节饱和引发的切换型振荡的机理,并分析限幅环节的类型、限幅值大小和系统参数对切换型振荡特性的影响。首先,介绍切换型振荡和非光滑分岔理论,以及基于VSG控制的并网逆变器及其限幅环节;其次,分析大扰动下VSG并网逆变器切换型振荡现象,并基于相图法揭示其动力学本质是系统发生了非光滑分岔;再次,分析非光滑分岔与限幅环节的类型和限幅值大小的关系,指出非光滑分岔是由多个限幅环节共同作用引发的;最后,分析VSG控制参数和外部参数对系统非光滑分岔特性的影响。结果表明,限幅值越小和故障程度越严重,系统越容易发生切换型振荡。
关键词:虚拟同步发电机 构网型控制 限幅 切换型振荡 非光滑分岔
随着电力低碳转型的推进,电力系统中新能源发电的渗透比例不断提高[1-3],电力系统“双高”(高比例新能源、高比例电力电子设备)特征凸显。然而,与传统同步发电机不同,电力电子并网设备本身缺乏惯量和阻尼,不具备频率调节和电压控制能力,这增加了电网电压和频率的调节难度,给新型电力系统的安全稳定运行带来巨大挑战[4-6]。为此,基于模拟传统同步发电机特性的思想,学者们提出了虚拟同步发电机(Virtual Synchronous Generator, VSG)的控制策略[7-9]。VSG控制借鉴了传统同步发电机的运行原理,使电力电子并网设备模拟同步发电机的惯量和阻尼特性,主动参与电力系统调频调压,极大地提高了电网稳定性。作为一种构网型控制策略,VSG控制具有广阔的应用前景[10-12]。
通过模拟同步发电机的运行特性,VSG控制提高了系统稳定性,但也带来了同步发电机的振荡问题[13]。近年来,国内外学者针对VSG并网逆变器的振荡问题展开了深入研究,在机理分析方面取得了显著成果。文献[14]采用模态分析法研究了VSG控制对系统低频振荡的影响,揭示了VSG控制将改变系统低频振荡的模式。文献[15-16]通过阻尼量化分析方法揭示了VSG并网逆变器低频振荡的机理,分析了VSG控制对系统阻尼特性的影响。文献[17-18]基于功率环小信号模型分析了VSG并网逆变器功率振荡的机理,指出VSG并网逆变器的功率振荡与系统的阻抗和动态响应速度有关。然而,这些研究都忽略了VSG控制中的非线性限幅环节。实际上,由于VSG控制的逆变器表现为电压源特性,所以在大扰动下很容易发生过电流。为保护逆变器免受过电流冲击,在VSG控制中加入限幅环节十分必要。因此,忽略限幅环节的影响不符合VSG在大扰动场景中的实际运行工况[19-20],无法准确地描述VSG并网逆变器的振荡特性。
近年来,大扰动下限幅环节对振荡特性的影响已经引起学者们的广泛关注,主要体现在跟网型逆变器和新能源发电系统振荡现象的研究中[21]。文献[22-23]指出在大扰动下,限幅环节饱和会导致跟网型并网逆变器发生切换型振荡。文献[24-26]指出在水电机组、直驱风机和双馈风机系统中,大扰动下限幅环节饱和均会引发切换型振荡,并基于相图法和非光滑分岔理论分析了振荡机理。文献[27-29]利用描述函数法和广义奈奎斯特判据,分别分析了限幅环节对水电机组、直驱风机和跟网型并网逆变器次同步振荡的影响机理。VSG控制模拟了同步发电机的运行特性,同时含有多个限幅环节[30],在大扰动下很有可能出现上述由限幅环节饱和引发的切换型振荡现象。深入理解VSG并网逆变器切换型振荡的机理可为系统设计提供参考,也有助于制定有效的振荡抑制策略,对维持电力系统安全稳定运行具有重要意义。然而,目前对包括VSG在内的构网型逆变器切换型振荡方面的研究仍鲜有报道。
为此,本文对大扰动下由VSG限幅环节饱和引发的切换型振荡现象展开研究。首先,介绍切换型振荡和非光滑分岔理论,以及基于VSG控制的并网逆变器及其限幅环节;其次,基于相图法分析大扰动下由多个限幅环节共同作用引发的VSG并网逆变器切换型振荡的机理;再次,基于非光滑分岔理论,分析非光滑分岔与限幅环节的类型和限幅值大小的关系;最后,分析VSG控制参数和外部参数对系统非光滑分岔特性的影响,确定影响非光滑分岔特性的关键参数。
在非线性动力学中,含限幅、死区等切换环节的系统对应非光滑动力系统。根据系统向量场、状态空间以及对应Jacobi矩阵的连续性,一般可将非光滑动力系统分为三类:非光滑连续系统、Filippov系统和非光滑脉冲系统[31]。非光滑动力系统可能会发生光滑动力系统所具有的常规分岔,也可能会发生非常规分岔,即非光滑分岔。非光滑分岔会导致系统中复杂动力学行为的产生,表现为轨线与切换面接触后可能会出现不连续、穿越、滑动等非线性动力学行为。
根据系统轨线触碰切换面后与切换面的位置关系,又可将非光滑分岔分为擦边分岔(grazing bifurcation)、C-分岔(C-bifurcation)、滑动分岔(sliding bifurcation)等[32-34]。图1a和图1b分别给出了当系统发生擦边分岔和C-分岔时,轨线在切换面附近的动力学行为示意图[33]。图中,D为Poincaré截面,Σ为切换面。随着分岔参数的连续变化,轨线发生“A→B→C”的变化。其中,轨线B与切换面Σ相切,为临界轨线。如图1a所示,随着分岔参数的进一步变化,若形成了不连续的轨线C,则对应系统发生了擦边分岔;如图1b中轨线C所示,随着分岔参数的进一步变化,当轨线穿过切换面Σ并在切换面Σ的另一侧形成轨线分段时,对应系统发生了C-分岔[33]。

图1 非光滑分岔示意图
Fig.1 Schematic diagram of non-smooth bifurcations
对于VSG并网逆变器而言,当系统运行在稳态时,轨线不会触碰切换面,因此不会发生非光滑分岔;当大扰动发生时,限幅环节很有可能被触发,轨线可能触碰切换面,在切换面处出现不连续、穿越、滑动等复杂动力学行为,发生非光滑分岔,形成非光滑极限环,对应系统出现切换型振荡现象。
VSG并网逆变器的主电路拓扑和控制结构如图2所示。图2中,Udc为逆变器直流侧的恒定电压源;Lf和Cf分别为滤波电感和滤波电容;PCC为公共连接点;Zg1和Zg2分别为当线路中f点发生故障时,故障点f与PCC和电网间的线路阻抗;iL,abc、uabc、iabc和ug,abc分别为静止坐标系下的逆变器输出电流、PCC处电压、PCC处电流和电网电压;IL,dq和Udq分别为dq旋转坐标系下的逆变器输出电流和PCC处电压。
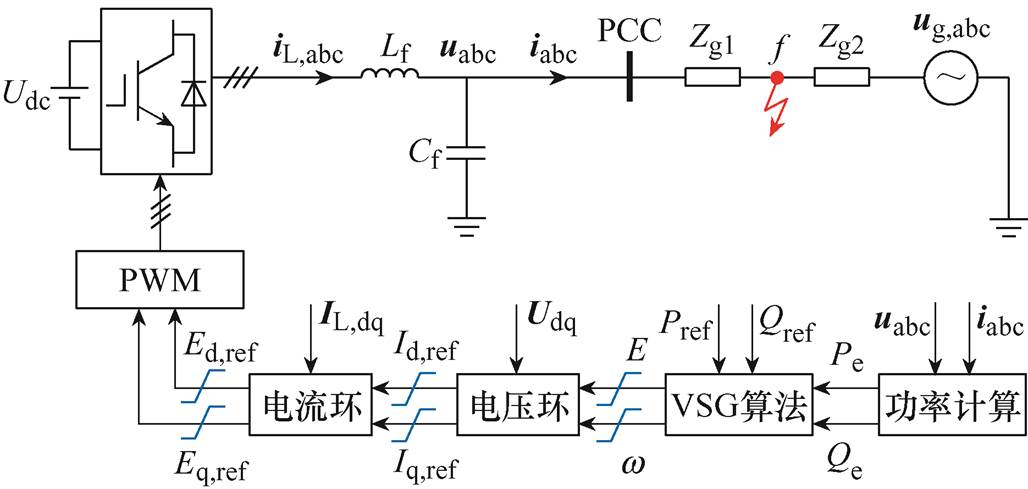
图2 VSG并网逆变器的主电路拓扑及控制结构
Fig.2 Topology and control scheme of a VSG-controlled inverter
VSG控制主要由有功-频率控制环节和无功-电压控制环节组成。有功-频率控制模拟了同步发电机的转子运动方程和一次调频特性,其控制方程为
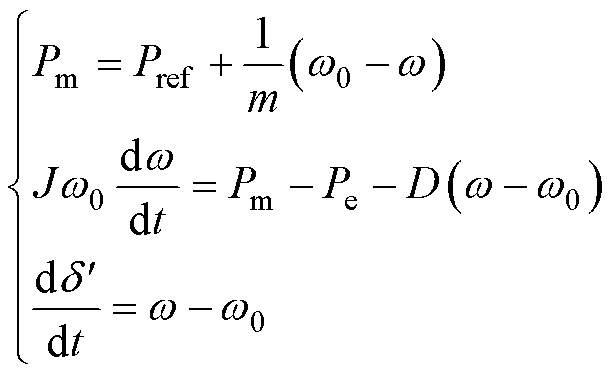 (1)
(1)
式中,Pm为虚拟机械功率;Pref和Pe分别为逆变器输出有功功率的参考值和测量值;m为有功-频率下垂系数;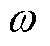 和
和 分别为VSG输出电压角频率和额定电压角频率;J为虚拟转动惯量;D为虚拟阻尼系数;
分别为VSG输出电压角频率和额定电压角频率;J为虚拟转动惯量;D为虚拟阻尼系数;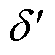 为VSG的虚拟功角,即电网电压与d轴之间的夹角[35]。
为VSG的虚拟功角,即电网电压与d轴之间的夹角[35]。
无功-电压控制模拟了同步发电机的一次调压特性,可表示为
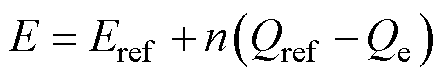 (2)
(2)
式中,E和Eref分别为VSG输出电压幅值的实际值和参考值;n为无功-电压下垂系数;Qref和Qe分别为逆变器输出无功功率的参考值和测量值。
为保证电力系统安全稳定运行,通常在逆变器控制中设置限幅环节。如图2所示,VSG控制中的限幅环节包括四个方面:有功-频率控制环中的角频率限幅、无功-电压控制环中的电压幅值限幅、电压环输出侧的电流限幅和电流环输出侧的调制波限幅。
2.2.1 角频率限幅
通常在有功-频率控制环节中设置角频率限幅以维持电网频率稳定,根据国标GB/T 15945-2008,对于标称频率为50 Hz的容量较小的电力系统,频率偏差限值为±0.5 Hz,即最大频率值fmax= 50.5 Hz,最小频率值fmin=49.5 Hz。对应的角频率限幅方式为
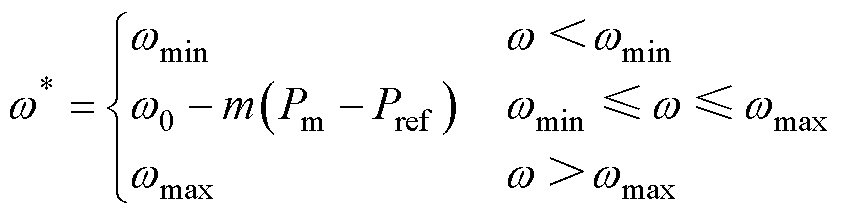 (3)
(3)
式中,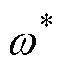 为角频率限幅环节的输出值;
为角频率限幅环节的输出值;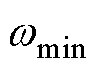 和
和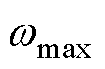 分别为fmin和fmax对应的角频率值。
分别为fmin和fmax对应的角频率值。
2.2.2 电压幅值限幅
无功-电压控制环节中电压幅值限幅的作用在于维持电网电压稳定,根据国标GB/T 12325-2008,本文选定电压偏差限值为±7%,即最大电压幅值Emax=1.07(pu),最小电压幅值Emin=0.93(pu)。可得电压幅值限幅环节的输出为
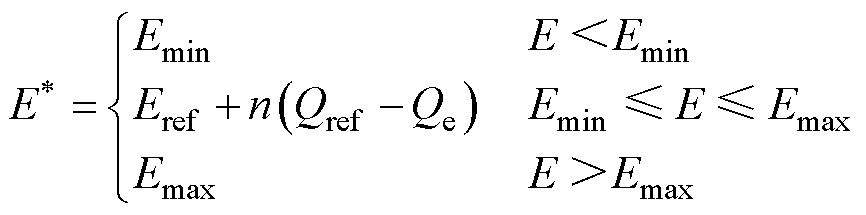 (4)
(4)
2.2.3 电流限幅
为保护逆变器免受过电流冲击,在VSG控制中加入电流限幅环节是十分必要的。本文采用最常用的d轴优先限幅方式来对电压环输出的电流参考值进行限幅,具体限幅方法为
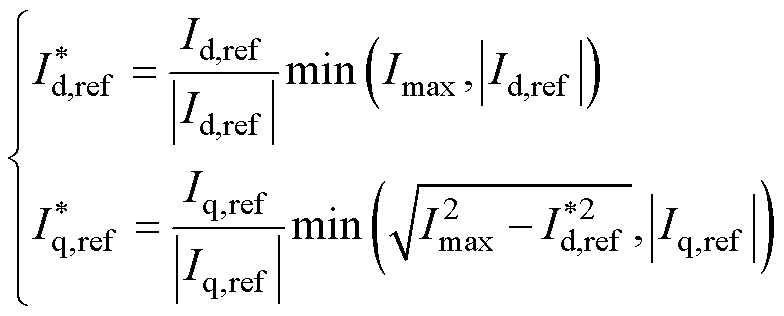 (5)
(5)
式中,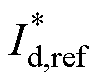 和
和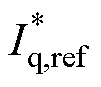 分别为限幅后的d轴和q轴电流参考值;Id,ref和Iq,ref分别为限幅前电压环输出的d轴和q轴电流参考值;Imax为电流限幅值。
分别为限幅后的d轴和q轴电流参考值;Id,ref和Iq,ref分别为限幅前电压环输出的d轴和q轴电流参考值;Imax为电流限幅值。
2.2.4 调制波限幅
当PWM的调制比大于1时,逆变器进入过调制状态,这会引入谐波,降低电力系统的稳定性甚至导致系统失稳。因此,为保持逆变器工作在线性调制状态,通常在电流环输出侧设置调制波限幅,限幅值Er,max=0.5Udc,限幅方式为
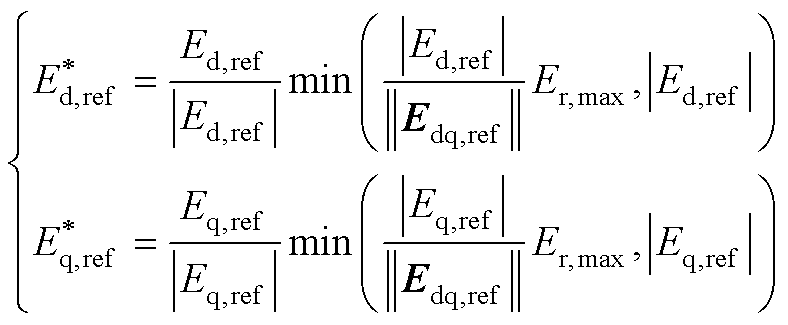 (6)
(6)
式中,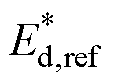 和
和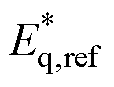 分别为限幅后调制波信号的d轴和q轴分量;Ed,ref和Eq,ref分别为限幅前电流环输出的调制波信号d轴和q轴分量;|| ‧ ||表示dq轴向量幅值。
分别为限幅后调制波信号的d轴和q轴分量;Ed,ref和Eq,ref分别为限幅前电流环输出的调制波信号d轴和q轴分量;|| ‧ ||表示dq轴向量幅值。
基于Matlab/Simulink平台建立图2所示系统的仿真模型,设置t=2 s时在线路中f点处发生三相短路故障,故障持续500 ms后被切除。仿真得到VSG并网点有功功率、电压和电流的时域波形如图3所示。由图3可知,在0~2 s内,系统到达稳态并在稳态运行了一段时间;在2~2.5 s内系统发生三相短路故障,并网点电压瞬间减小,电流瞬间增大,有功功率瞬间增大;当2.5 s故障切除后,经过暂态调节过程,系统出现了周期性功率振荡现象,同时并网点电压和电流也出现了振荡现象。
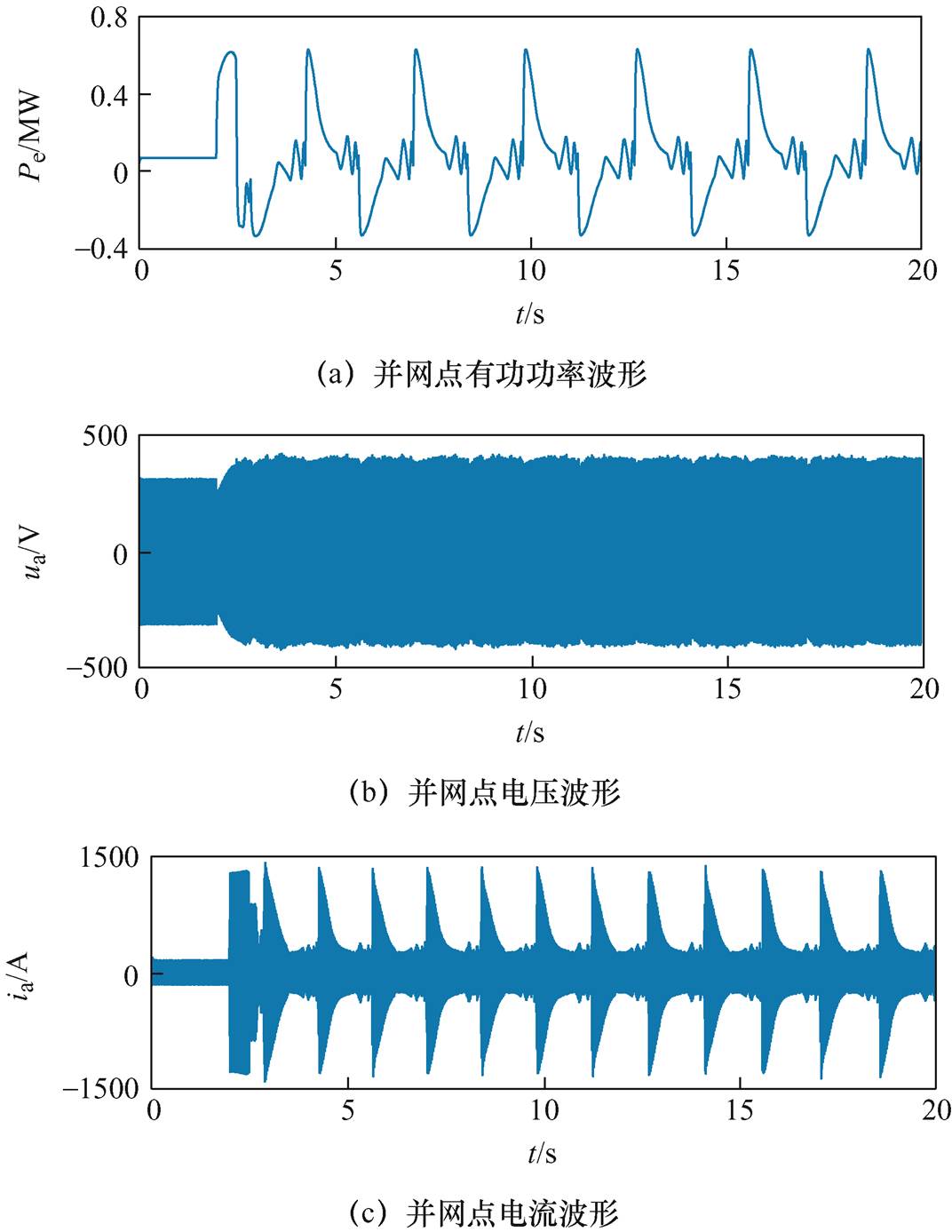
图3 并网点有功功率、电压和电流的时域波形
Fig.3 Time-domain wareforms of active power, voltage, and current at the PCC
对振荡期间的VSG并网点有功功率、电压和电流波形进行频谱分析,结果如图4所示。由图4可知,有功功率的主导振荡频率为0.36 Hz。对应地,并网点电压和电流中包含50.36 Hz(即(50+0.36) Hz)和49.64 Hz(即(50-0.36) Hz)的频率分量。
绘制功率周期振荡过程中角频率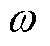 和虚拟功角
和虚拟功角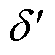 的相图分析如图5所示。观察图5可知,系统轨线连续地穿过切换面Σ1={(w, d')|w=wmin},在切换面的另一侧形成了不同拓扑结构的轨线分段,继而形成了含两个涡卷的非光滑极限环,由此判断轨线在切换面Σ1处发生了C-分岔。对应切换型振荡过程中,角频率限幅环节进入饱和状态一段时间之后,退出饱和状态。
的相图分析如图5所示。观察图5可知,系统轨线连续地穿过切换面Σ1={(w, d')|w=wmin},在切换面的另一侧形成了不同拓扑结构的轨线分段,继而形成了含两个涡卷的非光滑极限环,由此判断轨线在切换面Σ1处发生了C-分岔。对应切换型振荡过程中,角频率限幅环节进入饱和状态一段时间之后,退出饱和状态。
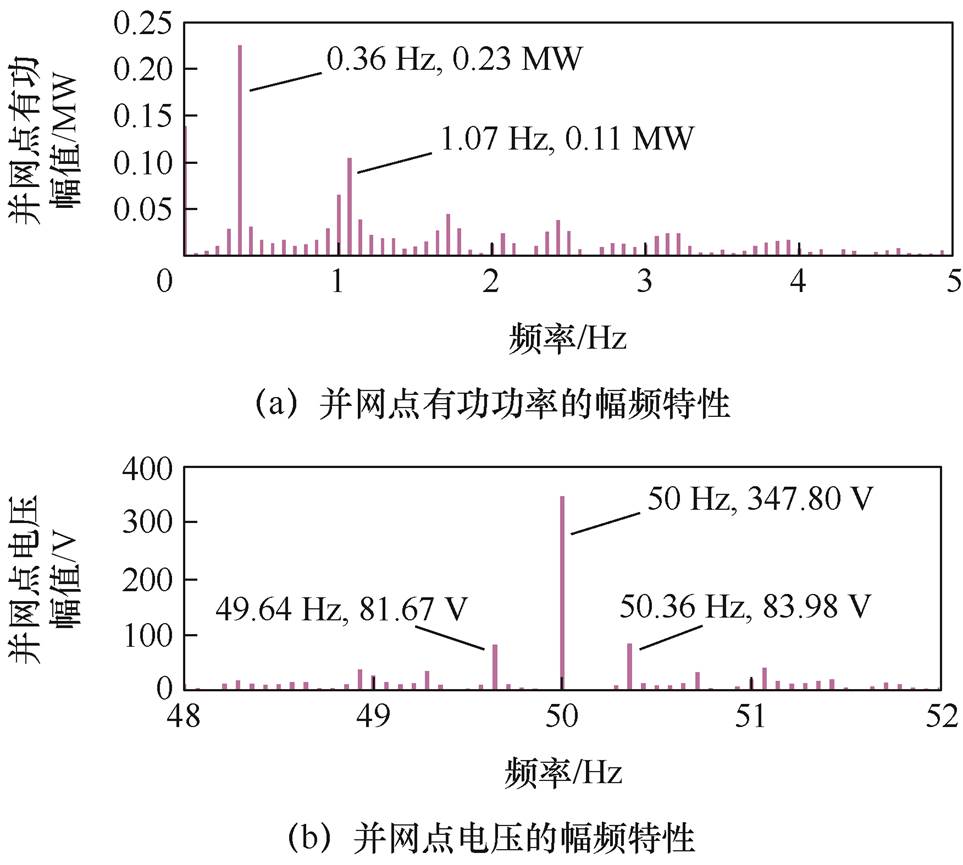
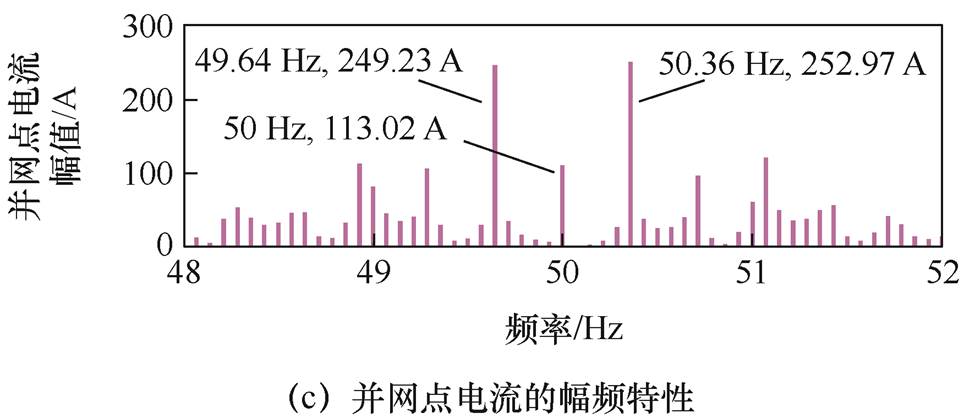
图4 并网点有功功率、电压和电流的频域特性
Fig.4 Amplitude-frequency characteristics of active power, voltage, and current at the PCC
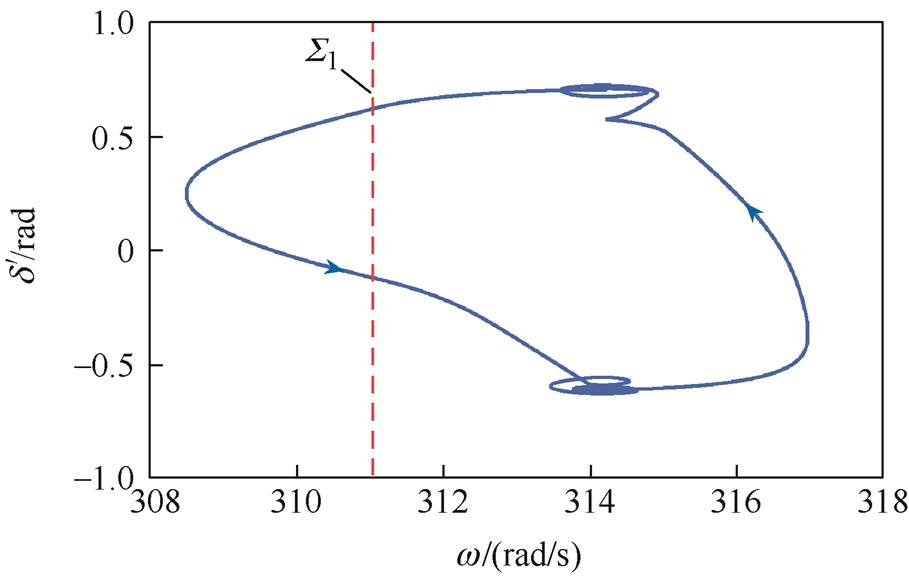
图5 w-d'相图分析
Fig.5 Analysis of phase portrait for w-d'
绘制功率周期振荡过程中d轴电流参考值Id,ref、虚拟磁链q轴分量jq和虚拟功角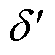 的相图分析如图6所示。由图6可知,系统轨线多次连续地穿过切换面Σ2={(jq, d', Id,ref)| Id,ref =-Imax},形成了非光滑极限环,且在切换面两侧系统轨线的拓扑结构不同,由此判断轨线在切换面Σ2处发生了C-分岔。对应切换型振荡过程中,电流限幅环节多次进入饱和状态。
的相图分析如图6所示。由图6可知,系统轨线多次连续地穿过切换面Σ2={(jq, d', Id,ref)| Id,ref =-Imax},形成了非光滑极限环,且在切换面两侧系统轨线的拓扑结构不同,由此判断轨线在切换面Σ2处发生了C-分岔。对应切换型振荡过程中,电流限幅环节多次进入饱和状态。
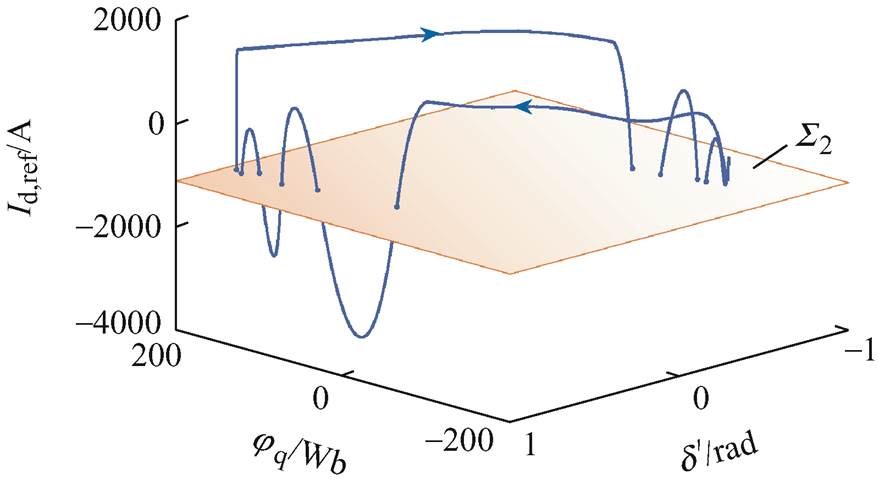
图6 jq-d'-Id,ref相图分析
Fig.6 Analysis of phase portrait for jq-d'-Id,ref
绘制功率周期振荡过程中调制波信号参考值的幅值Er,ref、虚拟功角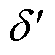 和q轴电流参考值Iq,ref的相图,如图7a所示。进一步地,放大观察轨线在切换面Σ3={(
和q轴电流参考值Iq,ref的相图,如图7a所示。进一步地,放大观察轨线在切换面Σ3={(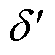 , Iq,ref, Er,ref)|Er,ref=Er,max}处的非光滑分岔行为,如图7b和图7c所示。
, Iq,ref, Er,ref)|Er,ref=Er,max}处的非光滑分岔行为,如图7b和图7c所示。
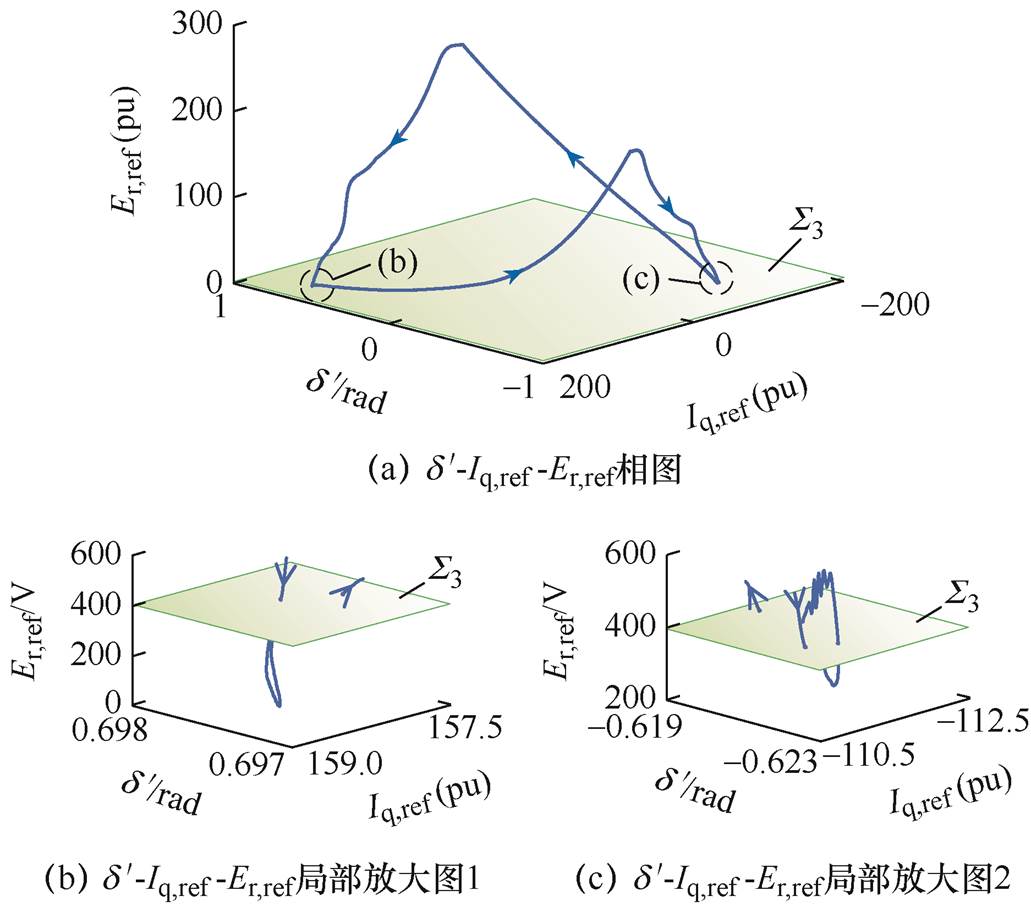
图7 d'-Iq,ref-Er,ref 相图分析
Fig.7 Analysis of phase portrait for d'-Iq,ref-Er,ref
由图7可知,系统轨线多次连续地穿过切换面Σ3,在切换面的另一侧形成了不同拓扑结构的轨线分段,继而形成了非光滑极限环,由此判断轨线在切换面Σ3处发生了C-分岔。对应切换型振荡过程中,调制波限幅环节多次进入饱和状态。值得注意的是,轨线几乎完全位于切换面Σ3上方的区域D= {(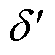 , Iq,ref, Er,ref)|Er,ref >Er,max}内,这表明切换型振荡过程中调制波限幅在较长时间内持续饱和。
, Iq,ref, Er,ref)|Er,ref >Er,max}内,这表明切换型振荡过程中调制波限幅在较长时间内持续饱和。
由上述分析可得,轨线与切换面相交形成了非光滑的交点,当轨线处于非光滑交点之间时,对应VSG控制中限幅环节饱和,此时轨线在切换面处发生了非光滑分岔,导致了系统中的切换型振荡现象。
为了确定非光滑分岔与限幅环节类型的关系,分别假定放开单个限幅环节、放开两个限幅环节和放开三个限幅环节,对比这三种状态,分析不同限幅环节类型对系统非光滑分岔特性的影响。
首先假定放开单个限幅环节,即有:只放开电压限幅、只放开角频率限幅、只放开电流限幅和只放开调制波限幅四种情形。在其他参数和故障条件不变的情况下,得到放开单个限幅时系统的非光滑分岔特性,与保留限幅环节的非光滑分岔特性对比见表1。需要指出的是,由于功率振荡的上下振幅不同而变化趋势一致,所以为了表达的简洁性,本文采用上下振幅的平均值,即平均振幅来表征功率振荡特性。
表1 放开单个限幅对非光滑分岔特性的影响
Tab.1 Non-smooth bifurcation characteristics when a single limiter is released

限幅类型平均振幅/MW振荡频率/Hz 保留限幅环节0.4820.360 放开电压限幅0.4820.360 放开角频率限幅0.4830.196 放开电流限幅系统收敛到稳定平衡点且无振荡 放开调制波限幅系统收敛到稳定平衡点且无振荡
由表1可知,在只放开电压限幅和只放开角频率限幅的两种情形下,系统都发生了第2节中分析的非光滑分岔,导致了系统中的切换型振荡现象,且只放开电压限幅与保留限幅环节的功率振荡特性相同。与保留限幅环节相比,只放开角频率限幅时功率振荡的平均振幅更大,振荡频率更小。在只放开电流限幅和只放开调制波限幅这两种情形下,轨线均未形成非光滑极限环,系统收敛到稳定平衡点且无振荡发生。因此,电流限幅和调制波限幅是决定切换型振荡发生与否的重要因素,角频率限幅对切换型振荡的平均振幅和振荡频率有影响。
假定放开两个限幅环节,也有以下六种情形。
情形1:放开电压限幅和角频率限幅,保留电流限幅和调制波限幅。
情形2:放开电压限幅和电流限幅,保留角频率限幅和调制波限幅。
情形3:放开电压限幅和调制波限幅,保留电流限幅和角频率限幅。
情形4:放开电流限幅和角频率限幅,保留电压限幅和调制波限幅。
情形5:放开电流限幅和调制波限幅,保留电压限幅和角频率限幅。
情形6:放开角频率限幅和调制波限幅,保留电压限幅和电流限幅。
在其他参数和故障条件不变的情况下,得到放开两个限幅时系统的非光滑分岔特性,与保留限幅环节的非光滑分岔特性对比见表2。由表2可知,只有在情形1下,系统发生了第2节中分析的非光滑分岔,引发了系统中的切换型振荡现象,且功率振荡特性与保留限幅环节时相同。在其他五种情形下,轨线均未形成非光滑极限环,系统收敛到稳定平衡点且无振荡发生。因此,当同时保留电流限幅和调制波限幅时,系统就会发生切换型振荡。
表2 放开两个限幅对非光滑分岔特性的影响
Tab.2 Non-smooth bifurcation characteristics when two limiters are released

限幅类型平均振幅/MW振荡频率/Hz 保留限幅环节0.4820.360 情形10.4820.360 情形2系统收敛到稳定平衡点且无振荡 情形3系统收敛到稳定平衡点且无振荡 情形4系统收敛到稳定平衡点且无振荡 情形5系统收敛到稳定平衡点且无振荡 情形6系统收敛到稳定平衡点且无振荡
假定放开三个限幅环节,即只保留单个限幅环节,有以下四种情形:只保留电压限幅、只保留角频率限幅、只保留电流限幅和只保留调制波限幅。在其他参数和故障条件不变的情况下,得到只保留单个限幅时系统的非光滑分岔特性,与保留所有限幅环节的非光滑分岔特性对比见表3。由表3可知,只保留单个限幅时,轨线均未形成非光滑极限环,系统收敛到稳定平衡点且无振荡发生。因此,单个限幅环节不会引发振荡,切换型振荡是多个限幅共同作用的结果。
表3 保留单个限幅对非光滑分岔特性的影响
Tab.3 Non-smooth bifurcation characteristics with a single limiter

限幅类型平均振幅/MW振荡频率/Hz 保留限幅环节0.4820.360 只保留电压限幅系统收敛到稳定平衡点且无振荡 只保留角频率限幅系统收敛到稳定平衡点且无振荡 只保留电流限幅系统收敛到稳定平衡点且无振荡 只保留调制波限幅系统收敛到稳定平衡点且无振荡
根据以上分析结果可得,VSG并网逆变器发生的非光滑分岔是电流限幅和调制波限幅共同作用的结果,当同时保留电流限幅和调制波限幅时,系统可能会发生非光滑分岔,导致切换型振荡发生。此外,角频率限幅对切换型振荡的平均振幅和振荡频率有影响。
进一步地,分析限幅环节的限幅值大小对系统非光滑分岔特性的影响。四个限幅环节中电压限幅和角频率限幅的限幅值为定值,电流限幅环节的限幅值调节范围为1.0~1.5(pu)[36],调制波限幅环节的限幅值由直流母线电压的大小决定。因此分别调节电流限幅值和直流母线电压的大小,分析限幅值大小对系统非光滑分岔特性的影响。
在其他参数保持不变的情况下,获得不同电流限幅值Imax下系统的非光滑分岔特性见表4。表4数据表明,随着Imax的减小,系统呈现出由平衡点到非光滑极限环的非光滑分岔特性。当Imax越小时,系统越容易出现非光滑分岔现象,导致切换型振荡发生,且随着Imax的减小,振荡的平均振幅逐渐减小,振荡频率逐渐减小。
表4 电流限幅值对非光滑分岔特性的影响
Tab.4 Influence of parameter Imax on non-smooth bifurcation characteristics

Imax(pu)平均振幅/MW振荡频率/Hz 1.121.141.161.180.4790.4800.4810.4820.2030.2510.2890.360 1.20系统收敛到稳定平衡点且无振荡
在其他参数保持不变的情况下,获得不同直流母线电压Udc下系统的非光滑分岔特性见表5。表5数据表明,随着Udc的减小,系统呈现出由平衡点到非光滑极限环的非光滑分岔特性。当Udc越小时,系统越容易出现非光滑分岔现象,导致切换型振荡发生,且随着Udc的减小,振荡的平均振幅逐渐减小,振荡频率逐渐减小。
表5 直流母线电压对非光滑分岔特性的影响
Tab.5 Influence of parameter Udc on non-smooth bifurcation characteristics

Udc(pu)平均振幅/MW振荡频率/Hz 3.400.4310.149 3.450.4430.190 3.500.4540.221 3.550.4640.260 4.55系统收敛到稳定平衡点且无振荡
根据上述分析结果可得,当限幅值越小时,系统越容易出现非光滑分岔现象,导致切换型振荡发生,且振荡的平均振幅和振荡频率均随着限幅值的减小而减小。
并网逆变器发生的切换型振荡与VSG控制参数和外部参数密切相关。因此,本节基于切换型振荡的功率振荡特性,初步分析确定影响系统非光滑分岔特性的主导参数,并基于非光滑分岔理论,进一步通过仿真分析系统参数对非光滑分岔特性的具体影响,同时验证功率振荡特性的理论分析结果。
由切换型振荡的相图分析结果可知,在切换型振荡过程中,电流限幅和调制波限幅均发生了多次饱和状态与非饱和状态之间的切换,而且调制波限幅在较长时间内一直处于饱和状态。当调制波限幅饱和时,功率控制环、电压外环、电流内环和电流限幅均失效,因此VSG控制的逆变器可等效为幅值为Er,max的电压源,该等效电压源与d轴的夹角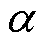 = arctan(Eq,ref/Ed,ref)。此时VSG并网逆变器接入电网的等效电路和电压相量分别如图8a和图8b所示,图中,Zg为线路阻抗值,
= arctan(Eq,ref/Ed,ref)。此时VSG并网逆变器接入电网的等效电路和电压相量分别如图8a和图8b所示,图中,Zg为线路阻抗值,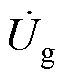 为无穷大电网,
为无穷大电网,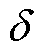 为VSG的功角,即Ėr,max与
为VSG的功角,即Ėr,max与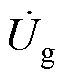 的相位差。VSG输出的有功功率可表示为
的相位差。VSG输出的有功功率可表示为
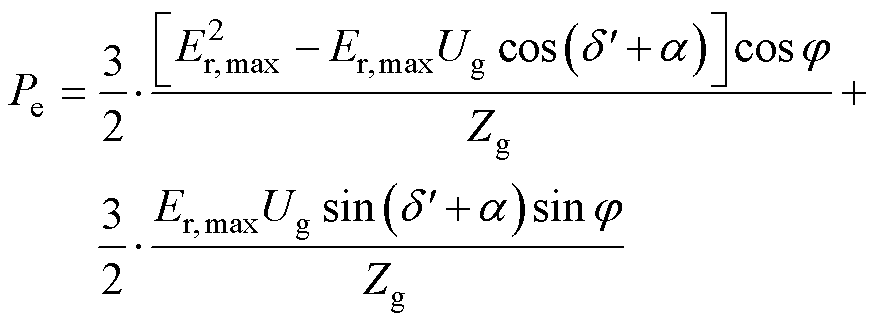 (7)
(7)
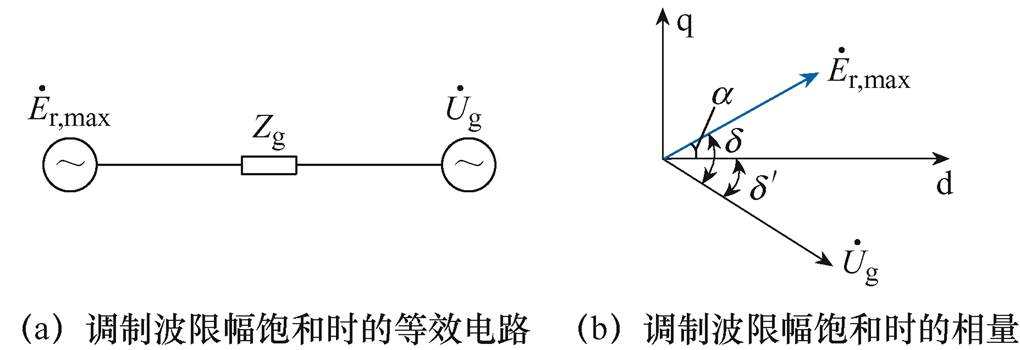
图8 调制波限幅饱和时的系统等效电路及相量
Fig.8 Equivalent circuit diagram and phasor diagram of the system when the modulation signal limiter is saturated
由式(7)可知,功率振荡幅值的直接影响因素有调制波限幅值Er,max、电网电压Ug、线路阻抗值Zg和线路阻抗角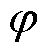 。此外,调制波限幅从非饱和状态到饱和状态的切换点位置不同也会造成功率振荡幅值的差异。切换点位置的影响因素为虚拟功角动态响应速度的控制参数(转动惯量J和阻尼系数D)和影响电压超调程度的因素(电流限幅值Imax和故障程度)。由式(7)可知,功率振荡频率的直接影响因素为VSG频率变化率的有功下垂系数m。此外,控制环路的动态响应速度和切换点位置也会影响功率振荡频率的大小,因此VSG控制参数和外部参数对振荡频率的大小均有一定影响。
。此外,调制波限幅从非饱和状态到饱和状态的切换点位置不同也会造成功率振荡幅值的差异。切换点位置的影响因素为虚拟功角动态响应速度的控制参数(转动惯量J和阻尼系数D)和影响电压超调程度的因素(电流限幅值Imax和故障程度)。由式(7)可知,功率振荡频率的直接影响因素为VSG频率变化率的有功下垂系数m。此外,控制环路的动态响应速度和切换点位置也会影响功率振荡频率的大小,因此VSG控制参数和外部参数对振荡频率的大小均有一定影响。
为了验证第4.1节关于振荡特性影响因素的分析结果,并进一步确定系统参数对非光滑分岔特性的具体影响,本节基于非光滑分岔理论,在第2.3节建立的仿真模型中仿真分析单参数(包括VSG控制参数和外部参数)变化时系统的非光滑分岔特性。具体地,在各系统参数的合理取值范围内均匀取值作为仿真参数值,记录系统参数取不同值时切换型振荡的平均振幅和振荡频率,并记录系统由发生切换型振荡转变为收敛到稳定平衡点时对应的临界参数值。VSG控制参数和外部参数见表6。
表6 VSG并网逆变器参数
Tab.6 Parameters of VSG-controlled inverter

逆变器参数 VSG控制有功下垂系数m 无功下垂系数n 转动惯量J 阻尼系数D 外部控制电网强度短路比RSC 线路参数阻抗角j 故障程度故障持续时间tf
4.2.1 有功下垂系数m对非光滑分岔特性的影响
在其他参数保持不变的情况下,获得不同有功下垂系数m下系统的非光滑分岔特性见表7,绘制振荡过程中的d'-Iq,ref-Er,ref相图如图9所示。表7数据表明,随着m的增大,系统呈现出由平衡点到非光滑极限环的非光滑分岔特性。当m越大时,系统越容易出现非光滑分岔现象,导致切换型振荡发生,且随着m的增大,功率振荡的平均振幅基本不变,振荡频率逐渐减小。结合功率振荡特性的理论分析结果和图9可知,m的增大使频率调节速度减慢,对应极限环逐渐扩大。
表7 有功下垂系数对非光滑分岔特性的影响
Tab.7 Influence of parameter m on non-smooth bifurcation characteristics

m(pu)平均振幅/MW振荡频率/Hz 0.000 1系统收敛到稳定平衡点且无振荡 0.0120.4820.371 0.0140.4820.346 0.0160.4820.315 0.0180.4820.286
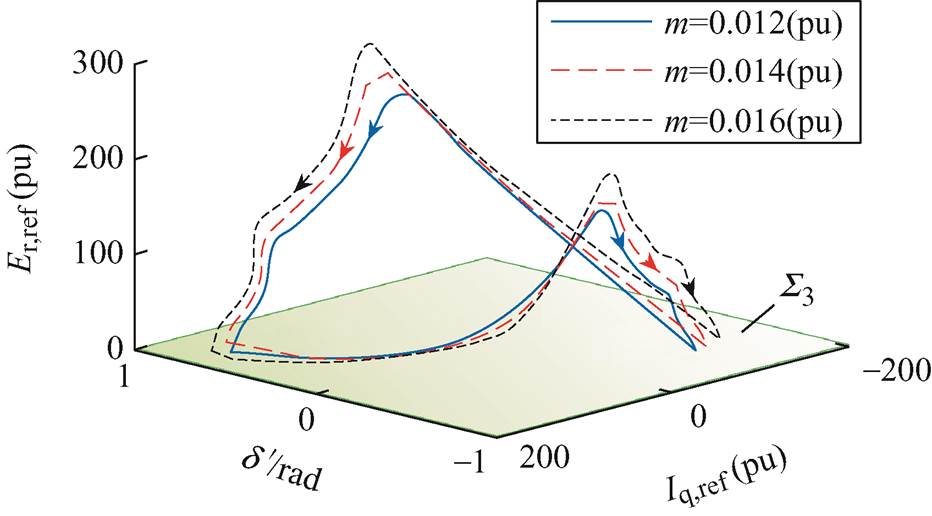
图9 不同m下d'-Iq,ref-Er,ref 相图
Fig.9 Phase portrait for d'-Iq,ref-Er,ref with different m
4.2.2 无功下垂系数n对非光滑分岔特性的影响
在其他参数保持不变的情况下,获得不同无功下垂系数n下系统的非光滑分岔特性见表8,绘制振荡过程中的d'-Iq,ref-Er,ref相图如图10所示。表8数据表明,随着n的减小,系统呈现由平衡点到非光滑极限环的非光滑分岔特性。当n越小时,系统越容易出现非光滑分岔现象,导致切换型振荡发生,且随着n的减小,功率振荡的平均振幅基本不变,振荡频率逐渐减小,这与功率振荡特性的理论分析结果一致。由图10可知,随着n的增大,极限环逐渐缩小,对应电流限幅和调制波限幅的饱和程度逐渐减小。
表8 无功下垂系数对非光滑分岔特性的影响
Tab.8 Influence of parameter n on non-smooth bifurcation characteristics

n(pu)平均振幅/MW振荡频率/Hz 0.0200.0250.0300.0350.4820.4820.4820.4820.2830.3040.3340.367 0.500系统收敛到稳定平衡点且无振荡
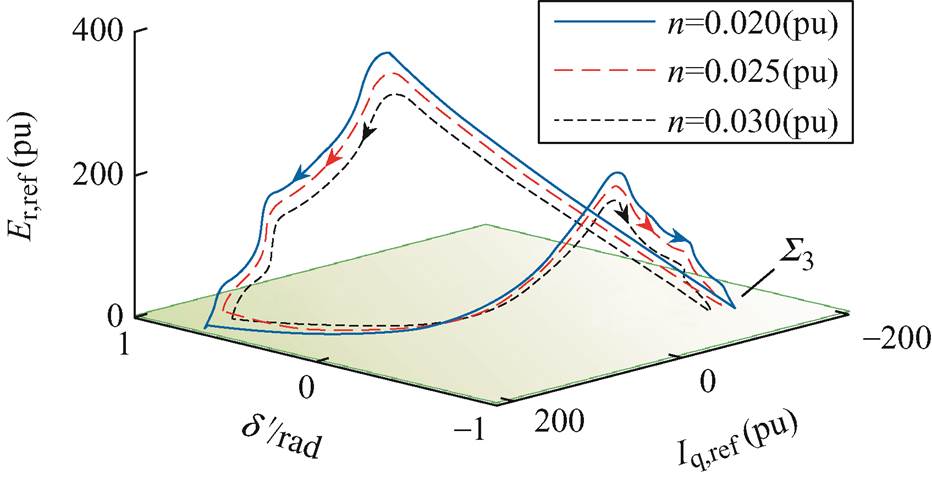
图10 不同n下d'-Iq,ref-Er,ref 相图
Fig.10 Phase portrait for d'-Iq,ref-Er,ref with different n
4.2.3 转动惯量J对非光滑分岔特性的影响
在其他参数保持不变的情况下,获得不同转动惯量J下系统的非光滑分岔特性见表9,绘制振荡过程中的d'-Iq,ref-Er,ref相图如图11所示。表9数据表明,随着J的增大,系统未呈现出平衡点与非光滑极限环转迁的非光滑分岔特性,而是始终形成非光滑极限环,出现切换型振荡现象,且随着J的增大,功率振荡的平均振幅逐渐增大,振荡频率呈先减小后增大,这与功率振荡特性的理论分析结果一致。由图11可知,随着J的增大,极限环先扩大后缩小,对应电流限幅和调制波限幅的饱和程度先增大后减小,同时极限环的形状发生了改变。
表9 转动惯量对非光滑分岔特性的影响
Tab.9 Influence of parameter J on non-smooth bifurcation characteristics

J(pu)平均振幅/MW振荡频率/Hz 24610200.4820.4860.4880.4900.4910.3600.3270.3180.3230.334
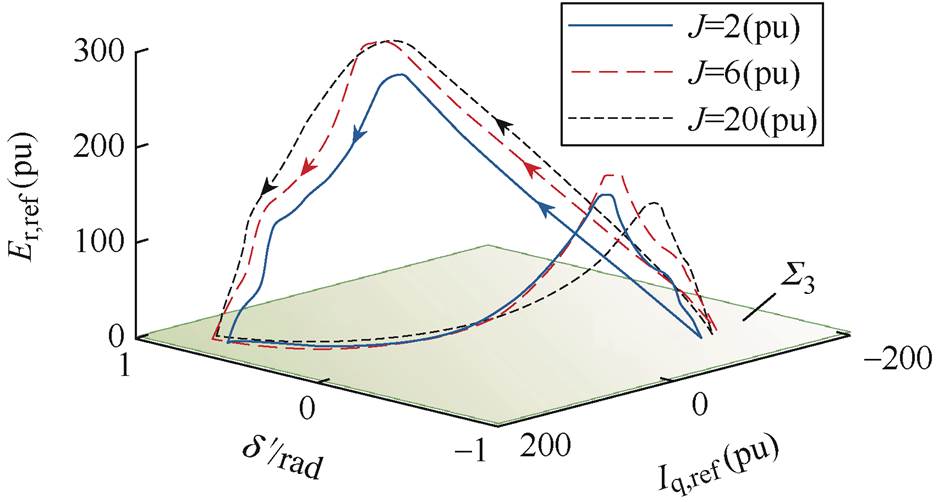
图11 不同J下d'-Iq,ref-Er,ref 相图
Fig.11 Phase portrait for d'-Iq,ref-Er,ref with different J
4.2.4 阻尼系数D对非光滑分岔特性的影响
在其他参数保持不变的情况下,获得不同阻尼系数D下系统的非光滑分岔特性见表10,绘制振荡过程中的d'-Iq,ref-Er,ref相图如图12所示。表10数据表明,随着D的减小,系统呈现由平衡点到非光滑极限环的非光滑分岔特性。当D越小时,即有功动态响应速度越快时,系统越容易出现非光滑分岔现象,导致切换型振荡发生,且随着D的减小,功率振荡的平均振幅逐渐增大,振荡频率逐渐减小,这与功率振荡特性的理论分析结果一致。由图12可知,随着D的增大,极限环逐渐缩小,对应电流限幅和调制波限幅的饱和程度逐渐减小。
表10 阻尼系数对非光滑分岔特性的影响
Tab.10 Influence of parameter D on non-smooth bifurcation characteristics

D(pu)平均振幅/MW振荡频率/Hz 0.020.040.060.080.4820.4820.4810.4790.3510.3840.4040.421 10.00系统收敛到稳定平衡点且无振荡
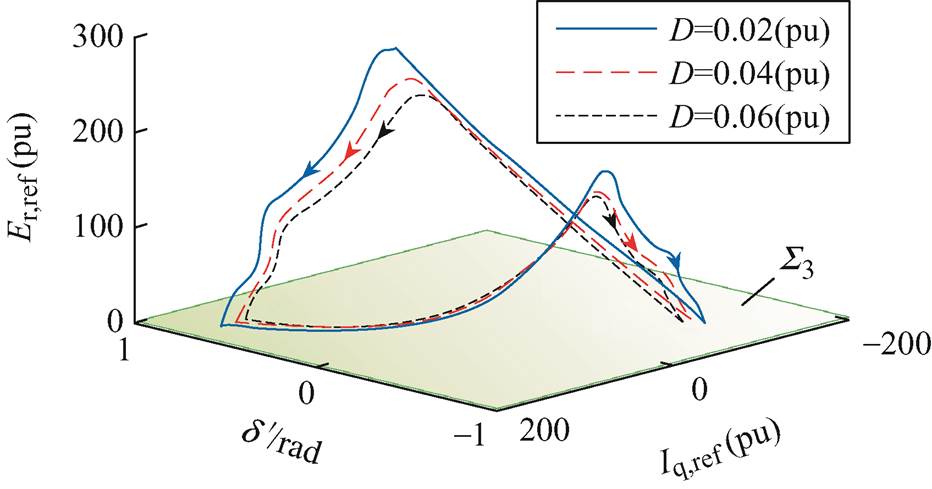
图12 不同D下d'-Iq,ref-Er,ref 相图
Fig.12 Phase portrait for d'-Iq,ref-Er,ref with different D
4.2.5 短路比RSC对非光滑分岔特性的影响
在其他参数保持不变的情况下,获得不同短路比RSC下系统的非光滑分岔特性见表11,绘制振荡过程中的d'-Iq,ref-Er,ref相图如图13所示。表11数据表明,随着RSC的增大,系统呈现出由平衡点到非光滑极限环再到平衡点的分岔特性。对于当前模型参数,使系统发生非光滑分岔,从而出现切换型振荡现象的RSC的取值范围为(0.40, 2.31)。在该取值范围内,随着RSC的增大,即随着线路阻抗值的减小,功率振荡的平均振幅逐渐增大,振荡频率逐渐减小,这与功率振荡特性的理论分析结果一致。此外,由图13可知,随着RSC的增大,极限环逐渐扩大,对应电流限幅和调制波限幅的饱和程度逐渐增大。
表11 短路比对非光滑分岔特性的影响
Tab.11 Influence of parameter RSC on non-smooth bifurcation characteristics

RSC平均振幅/MW振荡频率/Hz 0.40系统收敛到稳定平衡点且无振荡 0.730.880.970.4080.4820.5210.4630.3600.271 2.31系统收敛到稳定平衡点且无振荡
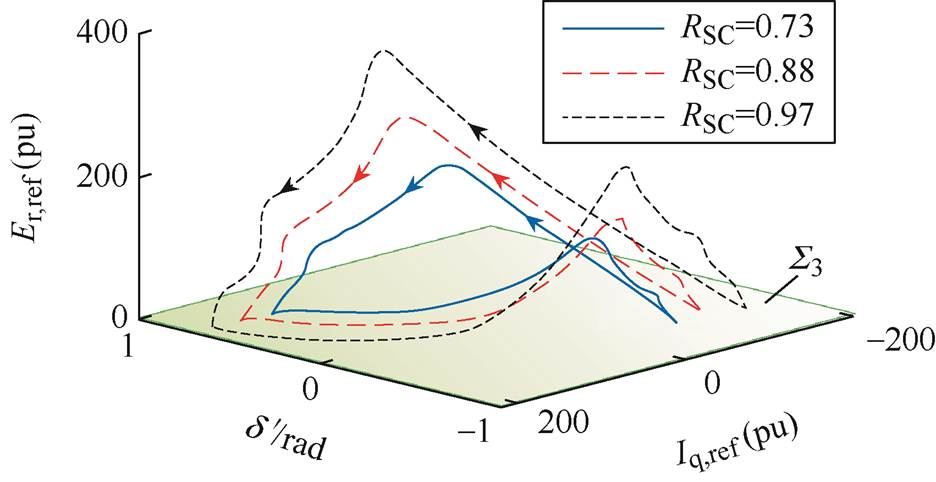
图13 不同RSC下d'-Iq,ref-Er,ref 相图
Fig.13 Phase portrait for d'-Iq,ref-Er,ref with different RSC
4.2.6 线路阻抗角j 对非光滑分岔特性的影响
在其他参数保持不变的情况下,获得不同线路阻抗角j 下系统的非光滑分岔特性见表12,绘制振荡过程中的d'-Iq,ref-Er,ref相图如图14所示。表12数据表明,随着j 的增大,系统呈现出由平衡点到非光滑极限环的非光滑分岔特性。当j 越大时,即线路感性越强时,系统越容易出现非光滑分岔现象,导致切换型振荡发生,且随着j 的增大,功率振荡的平均振幅逐渐增大,振荡频率逐渐减小,这与功率振荡特性的理论分析结果一致。此外,由图14可知,随着j 的增大,极限环逐渐扩大,对应电流限幅和调制波限幅的饱和程度逐渐增大。
表12 阻抗角对非光滑分岔特性的影响
Tab.12 Influence of parameter j on non-smooth bifurcation characteristics

j/(°)平均振幅/MW振荡频率/Hz 66.8系统收敛到稳定平衡点且无振荡 72.374.276.079.50.4820.4850.4880.4910.3600.3180.2900.256
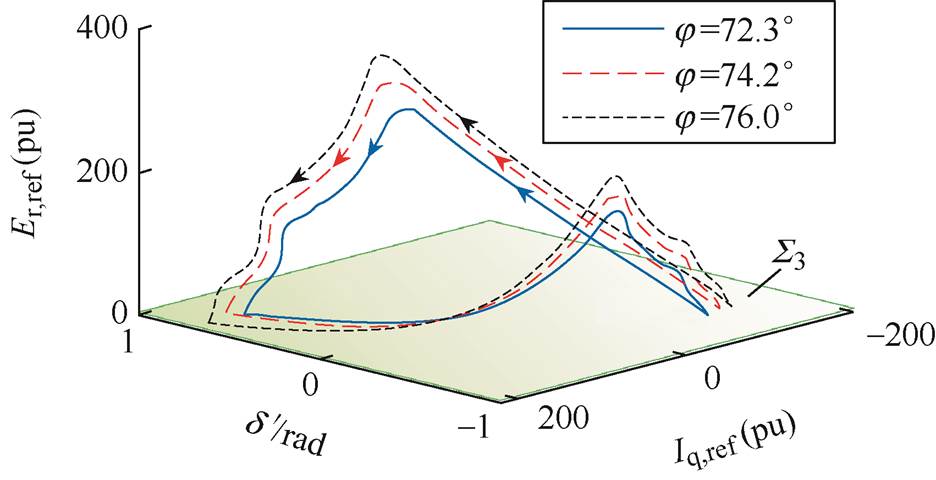
图14 不同j 下d'-Iq,ref-Er,ref 相图
Fig.14 Phase portrait for d'-Iq,ref-Er,ref with different j
4.2.7 故障持续时间tf对非光滑分岔特性的影响
在其他参数保持不变的情况下,获得不同故障持续时间tf下系统的非光滑分岔特性见表13,绘制振荡过程中的d'-Iq,ref-Er,ref相图如图15所示。表13数据表明,随着tf的增大,系统呈现出由平衡点到非光滑极限环的非光滑分岔特性。当tf越大时,此时故障程度越严重,系统越容易出现非光滑分岔现象,导致切换型振荡发生,且随着tf的增大,功率振荡的平均振幅逐渐增大,振荡频率逐渐减小,这与功率振荡特性的理论分析结果一致。此外,由图15可知,随着tf的增大,极限环逐渐扩大,对应电流限幅和调制波限幅的饱和程度逐渐增大。
表13 故障持续时间对非光滑分岔特性的影响
Tab.13 Influence of parameter tf on non-smooth bifurcation characteristics

tf/ms平均振幅/MW振荡频率/Hz 300系统收敛到稳定平衡点且无振荡 4504604704800.4780.4790.4800.4810.5360.5120.4830.449
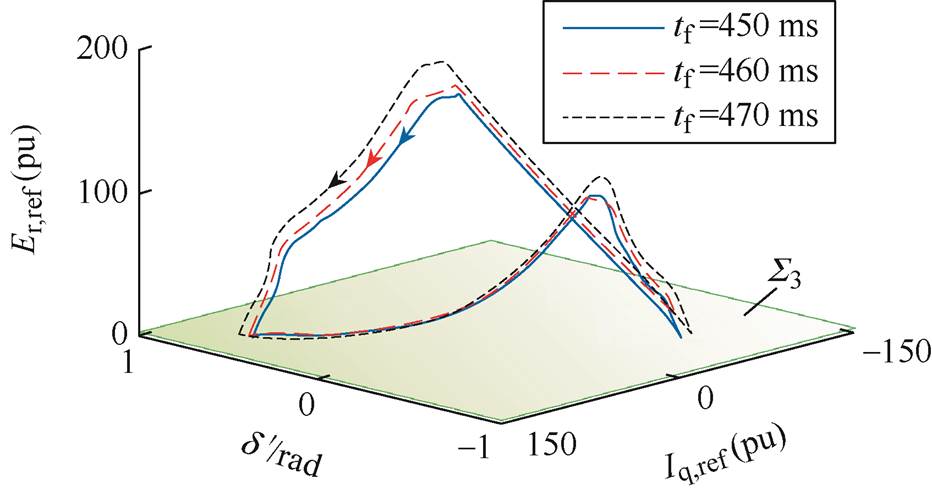
图15 不同tf下d'-Iq,ref-Er,ref 相图
Fig.15 Phase portrait for d'-Iq,ref-Er,ref with different tf
计算并汇总以上参数变化对功率振荡的平均振幅变化率和平均频率变化率的影响见表14。表14数据表明,按照影响程度排序,短路比RSC、直流母线电压Udc、电流限幅值Imax、阻尼系数D和阻抗角j 对平均振幅的影响较大,其他参数的影响较小;而有功下垂系数m、无功下垂系数n、电流限幅值Imax、短路比RSC和阻尼系数D对振荡频率的影响较大,其他参数的影响较小。上述结论均与振荡幅值和频率影响因素的理论分析结果一致。
表14 系统参数对有功功率振荡特性的影响
Tab.14 Influence of system parameters on active power oscillation characteristics

环节参数平均振幅变化率平均频率变化率 VSG限幅环节Imax0.0150.046 Udc0.4500.019 VSG功率控制环m00.288 n00.142 J0.0020 D0.1260.026 电网强度RSC1.5600.033 线路参数j0.1180.015 故障程度tf0.0040.001
本文基于相图法揭示了大扰动下VSG并网逆变器切换型振荡现象的动力学本质,同时基于非光滑分岔理论,分析了非光滑分岔与限幅环节的类型和限幅值大小的关系,以及VSG控制参数和外部参数对系统非光滑分岔特性的影响。得出结论如下:
1)基于VSG控制的并网逆变器在大扰动下会出现由限幅环节饱和引发的切换型振荡现象,其动力学本质为系统发生了非光滑分岔,与传统的光滑系统中发生的振荡现象有着本质区别。对构网型逆变器而言,切换型振荡直观地体现为逆变器控制模式的周期性切换,其失稳机理和影响因素较传统的暂态同步失稳更为复杂,是一种重要的失稳形式。
2)切换型振荡不仅会导致VSG并网逆变器失去同步而无法正常运行,而且会造成并网点电压幅值大幅波动,从而引发新能源机组脱网事故,还会导致有功功率的大幅波动甚至倒吸,进而损坏电力设备,给电力系统的安全稳定运行带来严重影响。
3)VSG并网逆变器发生的非光滑分岔是电流限幅环节和调制波限幅环节共同作用的结果,角频率限幅对切换型振荡的平均振幅和振荡频率有 影响。
4)当限幅值越小和故障程度越严重时,系统越容易发生切换型振荡。此外,对振荡的平均振幅影响较大的参数是短路比、直流母线电压、电流限幅值、阻尼系数和线路阻抗角;而对振荡频率影响较大的参数是有功下垂系数、无功下垂系数、电流限幅值、短路比和阻尼系数。
需要指出的是,本文仅对VSG并网逆变器的切换型振荡现象进行了初步分析,未来的工作将基于研究结果,建立VSG并网逆变器的非光滑动力系统模型,进一步探究VSG并网逆变器的非光滑动力学性质,确定发生切换型振荡的条件。此外,在未来的研究工作中将根据切换型振荡的特征,从控制角度提出有效抑制振荡的措施。
参考文献
[1] 高本锋, 王义, 范辉, 等. 基于阻尼路径的新能源经LCC-HVDC送出系统次同步交互作用分析方法[J]. 电工技术学报, 2023, 38(20): 5572-5589.
Gao Benfeng, Wang Yi, Fan Hui, et al. A sub- synchronous interaction analysis method of renewable energy generations integrated with LCC-HVDC system based on damping path[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5572- 5589.
[2] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system[J]. Transactions of China Electro- technical Society, 2023, 38(21): 5758-5770.
[3] 谢震, 杨曙昕, 代鹏程, 等. 构网型全功率风电机组网侧变流器耦合分析及抑制策略[J]. 电工技术学报, 2023, 38(14): 3745-3758.
Xie Zhen, Yang Shuxin, Dai Pengcheng, et al. Grid-side coupling analysis and suppression strategy of grid-forming full-power wind turbines[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(14): 3745-3758.
[4] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[5] 胡正阳, 高丙团, 张磊, 等. 风电机组双向支撑能力分析与自适应惯量控制策略[J]. 电工技术学报, 2023, 38(19): 5224-5240.
Hu Zhengyang, Gao Bingtuan, Zhang Lei, et al. Bidirectional support capability analysis and adaptive inertial control strategy of wind turbine[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(19): 5224-5240.
[6] 李锡林, 查晓明, 田震, 等. 频率突变影响下基于Lyapunov法的孤岛微电网暂态稳定性分析[J]. 电工技术学报, 2023, 38(增刊1): 18-31, 55.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. Transient stability analysis of islanded microgrid under the influence of frequency mutation based on Lyapunov method[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 18-31, 55.
[7] Zhong Qingchang, Weiss G. Synchronverters: inver- ters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[8] 郑天文, 陈来军, 陈天一, 等. 虚拟同步发电机技术及展望[J]. 电力系统自动化, 2015, 39(21): 165- 175.
Zheng Tianwen, Chen Laijun, Chen Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175.
[9] 吕志鹏, 盛万兴, 刘海涛, 等. 虚拟同步机技术在电力系统中的应用与挑战[J]. 中国电机工程学报, 2017, 37(2): 349-360.
Lü Zhipeng, Sheng Wanxing, Liu Haitao, et al. Application and challenge of virtual synchronous machine technology in power system[J]. Proceedings of the CSEE, 2017, 37(2): 349-360.
[10] 曹炜, 钦焕乘, 陆建忠, 等. 新型电力系统下虚拟同步机的定位和应用前景展望[J]. 电力系统自动化, 2023, 47(4): 190-207.
Cao Wei, Qin Huancheng, Lu Jianzhong, et al. Orientation and application prospect of virtual synchronous generator in new power system[J]. Automation of Electric Power Systems, 2023, 47(4): 190-207.
[11] Rosso R, Wang Xiongfei, Liserre M, et al. Grid-forming converters: control approaches, grid- synchronization, and future trends-a review[J]. IEEE Open Journal of Industry Applications, 2021, 2: 93-109.
[12] Li Yitong, Gu Yunjie, Green T C. Revisiting grid- forming and grid-following inverters: a duality theory[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4541-4554.
[13] 于彦雪, 关万琳, 陈晓光, 等.基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual syn- chronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[14] Zhou Xinyi, Cheng Shu, Wu Xun, et al. Influence of photovoltaic power plants based on VSG technology on low frequency oscillation of multi-machine power systems[J]. IEEE Transactions on Power Delivery, 2022, 37(6): 5376-5384.
[15] 薛翼程, 张哲任, 徐政, 等. 构网型变流器对交流系统低频振荡的影响分析与阻尼控制[J]. 电力系统自动化, 2023, 47(16): 103-113.
Xue Yicheng, Zhang Zheren, Xu Zheng, et al. Impact analysis and damping control of grid-forming con- verter for low-frequency oscillation of AC system[J]. Automation of Electric Power Systems, 2023, 47(16): 103-113.
[16] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1312-1324, 1374.
[17] 马也, 史丽萍, 李衡, 等. 基于VSG控制的微网逆变器工频振荡现象研究[J]. 电力系统保护与控制, 2022, 50(1): 107-115.
Ma Ye, Shi Liping, Li Heng, et al. Power frequency oscillation of a microgrid inverter based on VSG control[J]. Power System Protection and Control, 2022, 50(1): 107-115.
[18] 兰征, 刘祖潭, 何东, 等. 基于暂态电磁功率补偿的VSG并联系统有功振荡抑制策略[J]. 电网技术, 2023, 47(1): 23-33.
Lan Zheng, Liu Zutan, He Dong, et al. Active oscillation suppression strategy of paralleled virtual synchronous generators based on transient electro- magnetic power compensation[J]. Power System Technology, 2023, 47(1): 23-33.
[19] 姜卫同, 胡鹏飞, 尹瑞, 等. 基于虚拟同步机的变流器暂态稳定分析及混合同步控制策略[J]. 电力系统自动化, 2021, 45(22): 124-133.
Jiang Weitong, Hu Pengfei, Yin Rui, et al. Transient stability analysis and hybrid synchronization control strategy of converter based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2021, 45(22): 124-133.
[20] 葛平娟, 肖凡, 涂春鸣, 等. 考虑故障限流的下垂控制型逆变器暂态控制策略[J]. 电工技术学报, 2022, 37(14): 3676-3687.
Ge Pingjuan, Xiao Fan, Tu Chunming, et al. Transient control strategy of droop-controlled inverter con- sidering fault current limitation[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3676- 3687.
[21] 薛安成, 王嘉伟, 刘晓博, 等. 电力系统超低频频率振荡机理分析与抑制研究现状与展望[J]. 中国电机工程学报, 2021, 41(2): 553-568.
Xue Ancheng, Wang Jiawei, Liu Xiaobo, et al. Survey and prospect of ultra-low frequency oscillation mechanism analysis and suppression in power system[J]. Proceedings of the CSEE, 2021, 41(2): 553-568.
[22] 薛安成, 汪云涛, 乔登科, 等. 并网VSC系统正阻尼时的一类切换型振荡分析[J]. 电力自动化设备, 2022, 42(6): 84-89.
Xue Ancheng, Wang Yuntao, Qiao Dengke, et al. Analysis on category of switched oscillation for grid-connected VSC system with positive damping[J]. Electric Power Automation Equipment, 2022, 42(6): 84-89.
[23] 薛安成, 付潇宇, 王嘉伟, 等. 单边限幅参与的并网VSC系统次同步振荡近似分析[J]. 电网技术, 2022, 46(2): 750-758.
Xue Ancheng, Fu Xiaoyu, Wang Jiawei, et al. Approximate analysis of sub-synchronous oscillation for grid-connected VSC system induced by unilateral limit[J]. Power System Technology, 2022, 46(2): 750-758.
[24] 薛安成, 王嘉伟. 基于非光滑分岔的单机水电系统超低频频率振荡机理分析[J]. 电工技术学报, 2020, 35(7): 1489-1497.
Xue Ancheng, Wang Jiawei. Mechanism analysis of ultra-low frequency oscillation of single hydropower system based on non-smooth bifurcation[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(7): 1489-1497.
[25] 薛安成, 王子哲, 付潇宇, 等. 基于非光滑分叉的直驱风机次同步振荡机理分析[J]. 电力系统自动化, 2020, 44(7): 87-92.
Xue Ancheng, Wang Zizhe, Fu Xiaoyu, et al. Mechanism analysis of subsynchronous oscillation in direct-driven wind turbine based on non-smooth bifurcation[J]. Automation of Electric Power Systems, 2020, 44(7): 87-92.
[26] 薛安成, 王永杰, 付潇宇, 等. 含SVG的双馈系统切换型次同步振荡及其非光滑分岔特性分析[J]. 电网技术, 2021, 45(3): 918-926.
Xue Ancheng, Wang Yongjie, Fu Xiaoyu, et al. Analysis of switched subsynchronous oscillation and its non-smooth bifurcation characteristics in doubly- fed system with SVG[J]. Power System Technology, 2021, 45(3): 918-926.
[27] 王嘉伟, 熊鸿韬, 刘晓博, 等. 大扰动后正阻尼单机水电系统频率振荡的近似及适应性分析[J]. 电力自动化设备, 2022, 42(12): 145-150.
Wang Jiawei, Xiong Hongtao, Liu Xiaobo, et al. Approximation and adaptability analysis of frequency oscillation in single hydromachine power system with positive damping after large disturbance[J]. Electric Power Automation Equipment, 2022, 42(12): 145- 150.
[28] Xu Yanhui, Cheng Yundan, Liu Hui, et al. Study on HOPF bifurcation types and dominant parameters of grid-connected voltage source converter considering non-linear saturation elements[J]. IET Renewable Power Generation, 2023, 17(8): 2124-2136.
[29] Xu Yanhui, Gu Zheng, Sun Kai. Characterization of subsynchronous oscillation with wind farms using describing function and generalized nyquist criterion[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2783-2793.
[30] Shuai Zhikang, Shen Chao, Yin Xin, et al. Fault analysis of inverter-interfaced distributed generators with different control schemes[J]. IEEE Transactions on Power Delivery, 2018, 33(3): 1223-1235.
[31] Leine R I, van Campen D H. Bifurcation phenomena in non-smooth dynamical systems[J]. European Journal of Mechanics-A/Solids, 2006, 25(4): 595- 616.
[32] Nusse H E, Yorke J A. Border-collision bifurcations for piecewise smooth one-dimensional maps[J]. International Journal of Bifurcation and Chaos, 1995, 5(1): 189-207.
[33] Di B M, Feigin M I, Hogan S J, et al. Local analysis of C-bifurcations in n-dimensional piecewise-smooth dynamical systems[J]. Chaos Solitons & Fractals, 1999, 10(11): 1881-1908.
[34] di Bernardo M, Kowalczyk P, Nordmark A. Bifurcations of dynamical systems with sliding: derivation of normal-form mappings[J]. Physica D: Nonlinear Phenomena, 2002, 170(3/4): 175-205.
[35] 黄林彬, 章雷其, 辛焕海, 等. 下垂控制逆变器的虚拟功角稳定机理分析[J]. 电力系统自动化, 2016, 40(12): 117-123, 150.
Huang Linbin, Zhang Leiqi, Xin Huanhai, et al. Mechanism analysis of virtual power angle stability in droop-controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-123, 150.
[36] Saffar K G, Driss S, Ajaei F B. Impacts of current limiting on the transient stability of the virtual synchronous generator[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 1509-1521.
Abstract As a grid-forming inverter, the inverter based on virtual synchronous generator (VSG) control can contribute to the regulation of grid voltage and frequency. Power systems with a high penetration of new energy sources and power electronics are prone to stability when applied with VSG-controlled inverters. However, the switched oscillation induced by the saturation of limiters in the grid-connected inverter based on VSG control under large disturbances can threaten the stability of the power system. This paper studies the mechanism of such switched oscillations. The effects of limiter type, limiter value, and system parameters on the switched oscillation are also analyzed.
Firstly, the switched oscillation and non-smooth bifurcation theory are introduced, as well as the VSG-controlled inverter and its limiters. Secondly, the switched oscillation in the VSG-controlled inverter under large disturbances is analyzed in terms of time-domain waveforms and amplitude-frequency characteristics, According to phase diagrams, the switched oscillation is essentially induced by the non-smooth bifurcation. Thirdly, the relationship between non-smooth bifurcation and limiter type and limiter value is analyzed. Non-smooth bifurcation is induced by the saturation of multiple limiters. Finally, the effects of VSG control parameters and external parameters on the non-smooth bifurcation characteristics are analyzed. The results show that the switched oscillation is more likely to occur with smaller limiter values and larger disturbances.
Simulation results show that the power oscillation occurs in the VSG-controlled inverter with limiters under a symmetrical short-circuit fault with a dominant oscillation frequency of 0.36 Hz. The phase diagram during the power oscillation shows that a non-smooth limit cycle occurs, and the C-bifurcation essentially induces the switched oscillation according to the trajectory evolution. Non-smooth bifurcations may occur when both current and modulation signal limiters are included. In addition, as the parameter values are varied, the transition between the equilibrium point and the non-smooth limit cycle occurs, and the oscillation amplitude and frequency are also varied.
The following conclusions can be drawn. (1) Under large disturbances, the switched oscillation may occur in the VSG-controlled inverter with limiters saturated, which is essentially induced by the non-smooth bifurcation. Switched oscillation is an important instability form for the grid-forming inverter, and its mechanism and influencing factors are more complex than the traditional transient synchronous instability. (2) The non-smooth bifurcation in the VSG-controlled inverter results from the saturation of current and modulation signal limiters, and the angular frequency limiter affects the power oscillation characteristics. (3) The switched oscillation is more likely to occur with smaller limiter values and larger disturbances. Furthermore, the SCR and droop coefficients are critical parameters affecting the oscillation amplitude and frequency, respectively.
keywords:Virtual synchronous generator (VSG), grid-forming control, limiter, switched oscillation, non-smooth bifurcation
中图分类号:TM464;TM712
DOI: 10.19595/j.cnki.1000-6753.tces.232024
收稿日期2023-12-04
改稿日期2023-12-31
纪君奇 女,1999年生,博士研究生,研究方向为电力电子装备同步稳定分析与控制。E-mail: jijunqi@stu.xjtu.edu.cn
杨黎晖 女,1980年生,副教授,博士生导师,研究方向为新能源发电系统的分析、运行与控制。E-mail: lihui.yang@mail.xjtu.edu.cn(通信作者)
(编辑 陈 诚)