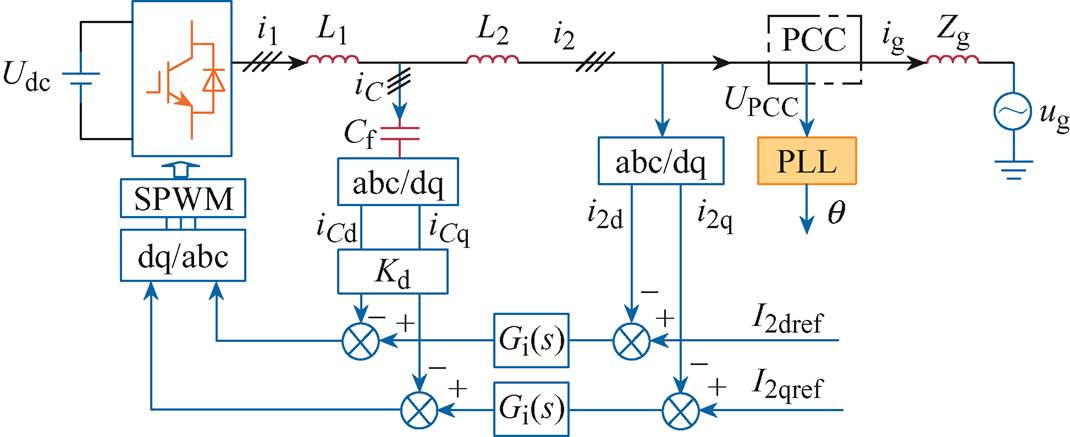
图1 控制在dq域下的GCI结构
Fig.1 Structure diagram of GCI controlled in dq domain
摘要 针对弱电网下并网逆变器(GCI)与电网阻抗交互易失稳的问题,以dq域下控制的GCI为例,构建考虑等效电流源稳定性的GCI的单输入单输出(SISO)阻抗模型,该模型将等效电流源中控制器参数变换到GCI的等效输出阻抗模型中,并将锁相环(PLL)引发的阻抗回路折算到电网侧,实现等效电流源与控制器参数解耦,为控制环参数自适应调整控制策略下GCI的稳定性分析奠定了模型基础。在此基础上,提出一种基于比例权重的控制环参数自适应调整控制方法,并基于所构建阻抗模型实现比例权重系数的分析与设计,该自适应控制方法能够保证GCI在弱电网范围内具有30°以上的充足稳定裕度,促使GCI具有良好的稳态与动态性能。最后,通过仿真和实验验证了该文理论分析的正确性以及所提控制策略的有效性。
关键词:弱电网 并网逆变器 控制器参数解耦 自适应控制 稳定裕度
随着新能源装机容量的不断增加,电网势必会越来越弱[1],低短路比(Short Circuit Ratio, SCR)造成并网逆变器(Grid-Connected Inverter, GCI)与电网之间交互影响所带来的稳定性问题更加突出[2-3],而且GCI自身控制系统的复杂性以及不同控制环节之间的交互耦合性,也导致GCI系统发生失稳的机理难以解析,严重制约新能源电力系统的安全稳定运行[4-6]。
为此,构建准确的GCI数学模型是分析新能源并网系统稳定性以及研究失稳机理的重要前提与基础,而且构建模型的方式不同,所采用的稳定性分析方法也各异[7]。根据分析系统振荡频率范围的不同,可以分为适合于分析低频振荡的阻尼转矩法[8];适合于分析次同步振荡的复转矩系数法[9];适合于分析电力电子设备多时间尺度振荡的建模方法,包括聚焦PLL的主导回路法[10]、聚焦惯性与同步动态的广义转矩系数法[11]、聚焦变流器端口电压/电流相位稳定性的序域阻抗建模法[12-13]、dq域阻抗建模法[14-15]以及极坐标阻抗建模法[16]等。由于阻抗建模法将新能源GCI和电网看作两个相互独立的子系统,当GCI的控制结构发生改变时,只需对该GCI的阻抗模型进行相应修正,无需对整个并网系统进行重新建模,具有使用方便、操作灵活的特点,非常适用于GCI大规模接入下并网系统的模型构建。
基于阻抗分析法带来的优势,现有研究从阻抗的角度出发对新型电力系统下GCI的安全可靠运行方法做出了大量贡献。弱电网下,通过构建阻抗模型,揭示了减小锁相环(Phase Locked Loop, PLL)带宽增加GCI输出阻抗正阻尼频率范围,提升系统稳定性的机理[3,17]。同时,由于PLL只有q轴电压被控制以实现相位与频率跟踪,导致在dq坐标系下阻抗模型中d轴与q轴的不对称交叉耦合,并在PLL与GCI的交互过程中产生频率耦合现象[18-19],威胁并网系统的稳定运行。为此,一种利用d轴通道构造复矢量信息的对称PLL结构被提出[20],消除了由PLL结构激发的频率耦合效应,并通过阻抗分析法验证了所提构造方法的有效性。
除了从PLL角度出发提出抑制GCI系统振荡的方法外,像输出功率调整[21-22]、阻抗重塑[23-24]以及控制参数优化[25-28]等控制方法也被广泛采用,用来增加系统阻尼抑制振荡,提升GCI系统的稳定性。然而,调整输出功率的GCI稳定性提升方法,通常以牺牲部分有功功率为代价来提升系统稳定性,不利于新能源高效消纳;采用阻抗重塑的控制方法,通常需要增加额外的辅助控制环路,极有可能导致控制环及其参数设计变得更加复杂。
值得说明的是,控制参数优化调整方法由于具有操作简单、无需辅助控制环等优良特性而被广泛应用于单机、多机馈入系统。其中,文献[25]针对GCI随电网阻抗增加而稳定性变差的问题,提出一种电网阻抗实时检测的控制环参数自适应调整控制方法,以确保GCI系统的稳定性。为了更好地适应弱电网环境,一种满足弱电网系统稳定运行的控制器参数优化方法被设计[26]。除此之外,文献[27]通过结点电压方程构建GCI系统的网络阻抗矩阵模型,并基于参与因子定位多GCI系统的失稳源,识别关键影响因素,提出优化控制器参数以及电网线路参数的系统振荡稳定性提升方法。同时,文献[28]采用组件连接法构建了GCI系统的网络阻抗矩阵模型,侧重于利用阻抗分析法分析系统稳定性以及识别失稳变流器,其中控制器参数优化设计是提升整个系统在弱电网下稳定性的有效方法。然而,以上采用控制环参数优化调整的稳定性提升方法在利用阻抗模型分析交互系统稳定性的过程中都默认等效电流源是稳定的。但实际情况是,当控制环参数为了适应较大电网阻抗而做调整时[25-27,29],极有可能诱发等效电流源失稳,从而导致阻抗分析法失效,严重制约阻抗分析法在分析交互系统稳定性方面的广泛应用与技术推广。
基于以上分析,为解决控制环参数调整下GCI的稳定性分析及其提升难题,本文以dq域下控制的GCI为例,首先,将dq域下控制GCI的多输入多输出(Multiple-Input Multiple-Output, MIMO)阻抗模型通过等效变换转换成单输入单输出(Single- Input Single-Output, SISO)的阻抗形式;然后,通过阻抗转移与重塑,将等效电流源中的控制器参数变换到GCI的等效输出阻抗模型中,并将PLL引发的阻抗回路折算到电网侧,用来表征PLL经电网阻抗带来的负面影响,实现等效电流源与控制器参数解耦。在此基础上,提出一种基于比例权重的控制环参数自适应调整稳定性提升方法,并基于所构建阻抗模型分析与设计了比例权重系数,保证了GCI在弱电网范围内具有30°以上的充足稳定裕度,促使GCI具有良好的稳态与动态性能。最后,通过仿真和实验进行了验证。
为了能够在GCI控制环参数调整过程中保证等效电流源的稳定性,以便于利用阻抗分析法判定系统的稳定性,本文以dq域下控制的GCI为例来理论推导具有控制器参数解耦的阻抗模型。由于控制在dq域下的GCI的数学模型表现出MIMO的特性,不利于等效电流源控制器参数的解耦以及阻抗等效折算。为此,本文首先将dq域下GCI的MIMO阻抗模型等效变换成SISO阻抗模型的形式。其中,控制在dq域下的GCI的结构如图1所示。

图1 控制在dq域下的GCI结构
Fig.1 Structure diagram of GCI controlled in dq domain
图1中,L1、Cf、L2构成LCL滤波器结构;采用电容电流比例反馈抑制LCL滤波器的谐振尖峰,Kd为比例反馈系数;Zg为电网侧阻抗;Udc为直流母线电压,UPCC为并网点电压,ug为电网电压;i1为逆变桥输出电流;iC为滤波电容电流;i2为GCI输出电流;ig为注入电网电流;iCd、iCq分别为电容电流在d轴、q轴上的分量;i2d、i2q分别为并网电流在d轴、q轴上的分量;I2dref、I2qref分别为并网电流在d轴、q轴上的给定值;Gi(s)为电流控制环的PI控制器,Gi(s)=kp+ki/s,kp为比例系数,ki为积分系数;q 为PLL输出相位。
根据dq域下GCI的小信号建模思想[23, 26, 28],可以得到考虑PLL影响的GCI小信号控制框图,如图2所示。
图2中,Gi(s)为电流环PI控制器传递函数矩阵,Gde(s)为脉宽调制与计算等效延时矩体,KMG为脉宽调制增益矩阵,KMG=diag(KPWM, KPWM),KPWM为调制增益,YL1(s)、YL2(s)、ZCf (s)分别为LCL滤波器滤波电感与滤波电容的传递函数矩阵,它们的具体表达式已经在文献[30]中详细推导,这里不再给出推导过程及表达式具体结构。其中,由PLL小信号扰动在电流参考值、调制信号以及电容电流反馈处所诱发的反馈环路Gasy1(s)、Gasy2(s)、Gasy3(s)分别表示为
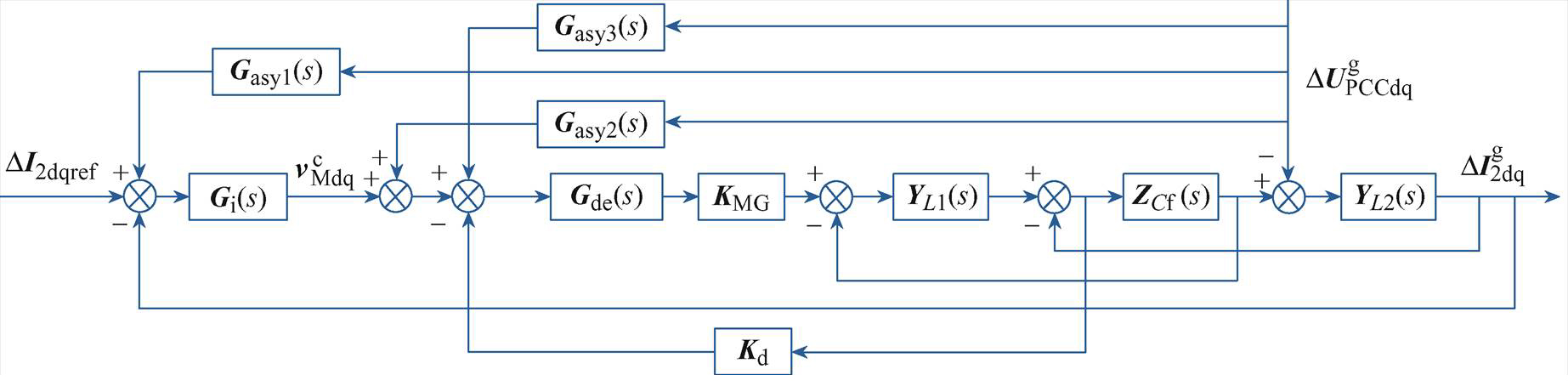
图2 控制在dq域下的GCI的小信号控制框图
Fig.2 Small-signal control structure diagram of GCI controlled in dq domain
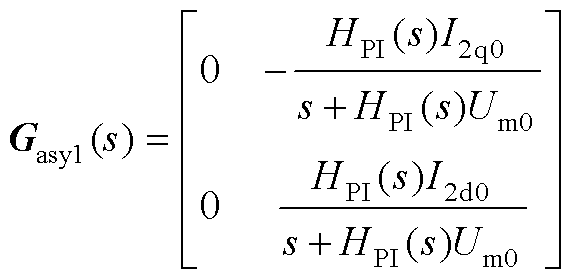 (1)
(1)
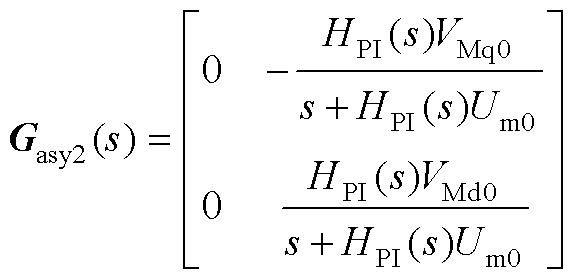 (2)
(2)
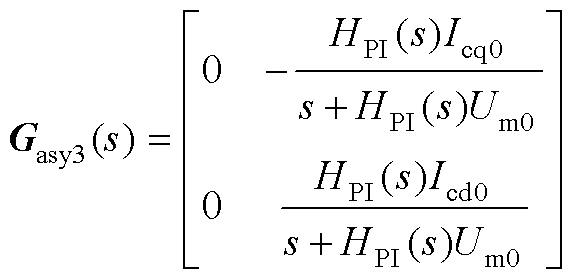 (3)
(3)
式(1)~式(3)中各变量的物理含义与文献[30]中所定义的一样,这里不再重复表述。通过稳态分析与计算,此时基于电容电流比例反馈的GCI调制信号稳态值VMd0、VMq0的表达式分别为
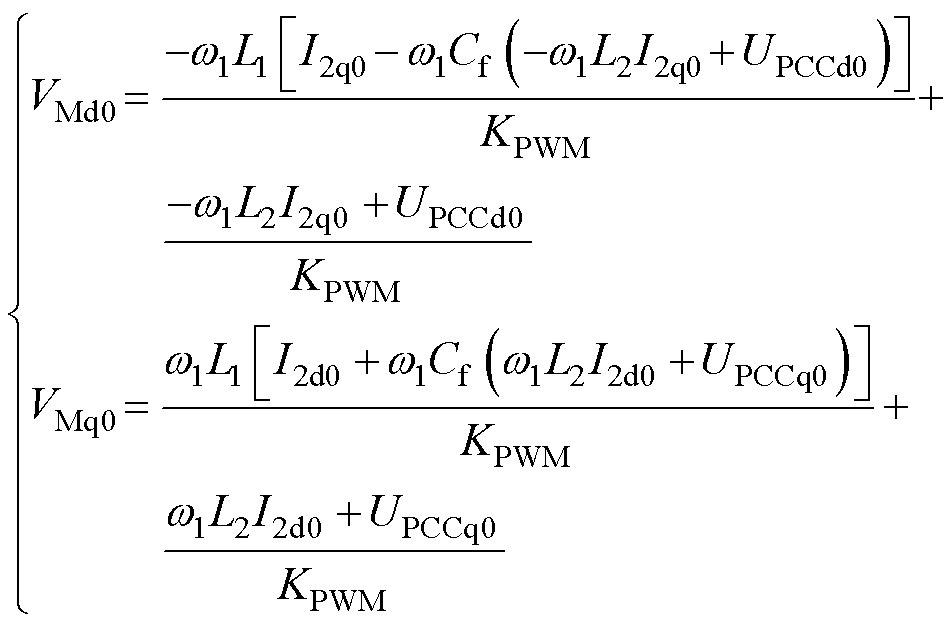 (4)
(4)
式中,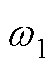 为电网额定角频率。
为电网额定角频率。
电容电流在d轴、q轴上的稳态值ICd0、ICq0的具体数值分别为
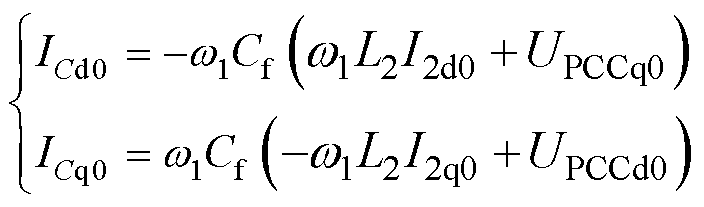 (5)
(5)
借助前期研究所提dq域下GCI的SISO阻抗建模方法[30],将考虑PLL影响的GCI系统的MIMO阻抗模型等效转换至ab 域下的SISO阻抗模型。此时,GCI由dq域转换到ab 域下的SISO小信号模型控制框图如图3所示。
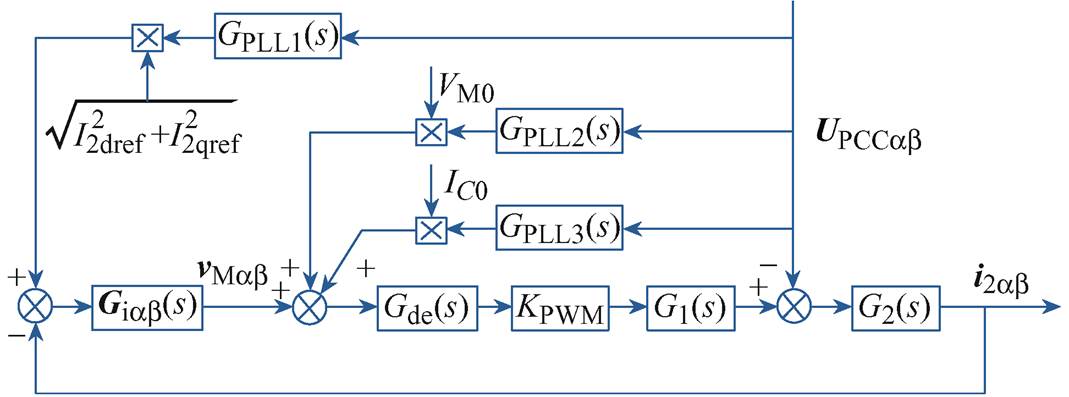
图3 dq域下GCI的等效SISO模型控制框图
Fig.3 Equivalent SISO model control block diagram of GCI controlled in dq domain
考虑到dq域下传递函数等效转换到ab 域下的移频特性,图3中电流环的PI控制器传递函数要转换成Giαβ(s)的形式,有
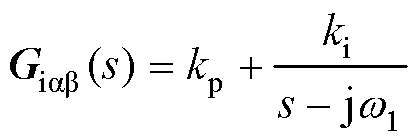 (6)
(6)
通过对图2控制方框图的移频等效变换,可以得到图3中G1(s)、G2(s)的表达式分别为
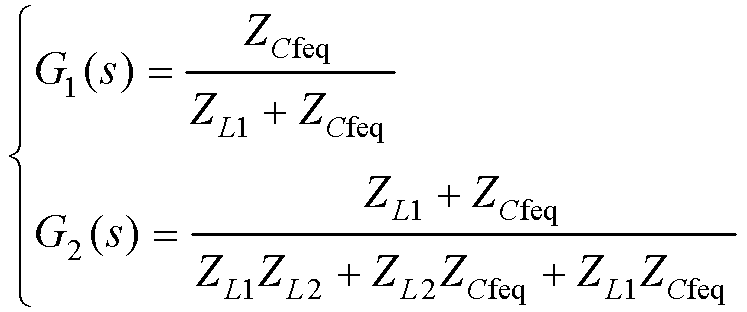 (7)
(7)
式中,ZCfeq为电容电流比例反馈折算到图3控制方框图中的等效传递函数,其表达示为
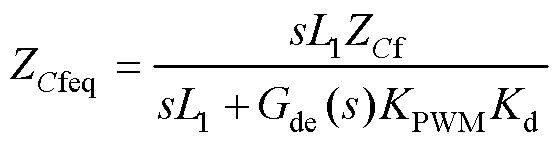 (8)
(8)
图2中,dq域下由PLL小信号扰动诱发的反馈环路Gasy1(s)、Gasy2(s)、Gasy3(s)分别等效转换到图3中ab 域下的GPLL1(s)、GPLL2(s)、GPLL3(s)反馈环路。其中,GPLL1(s)、GPLL2(s)的推导过程与前期研究[30]一致,这里不再详细说明,具体表达式为
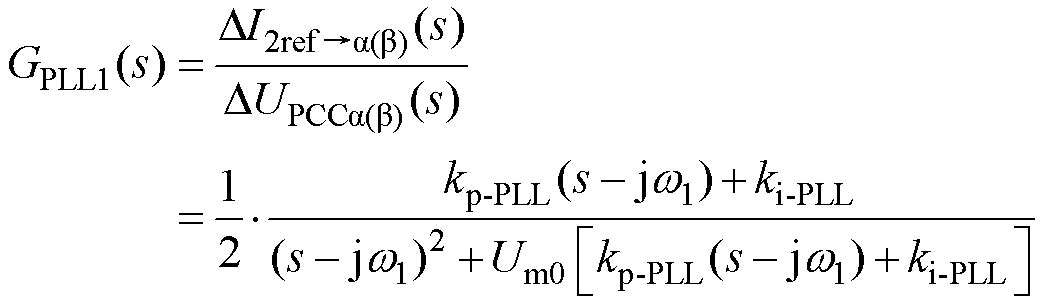 (9)
(9)
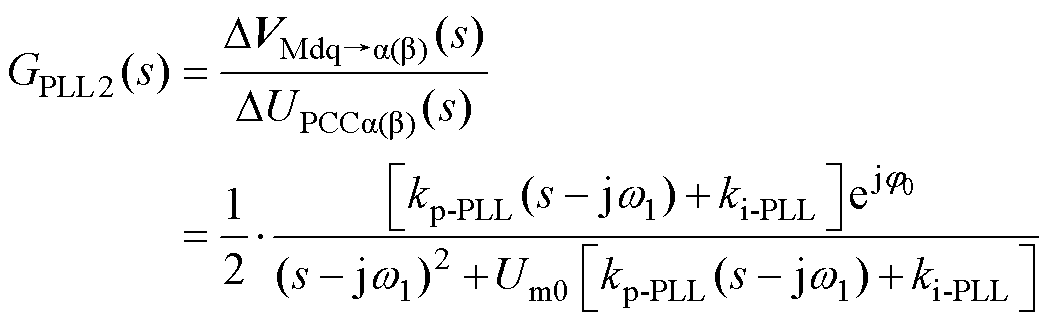 (10)
(10)
式中,KP-PLL、Ki-PLL分别为PLL控制器的比例系数和积分系数。
对于PLL小信号扰动在电容电流比例反馈环节引入的反馈环路GPLL3(s),其具体求解过程与GPLL2(s)类似,这里不妨假设ICdq转换到ICab 的表达式为
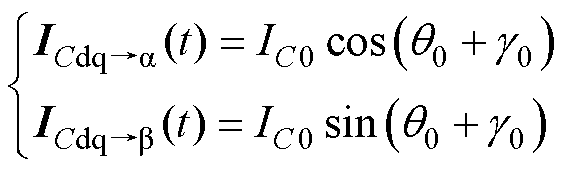 (11)
(11)
式中,IC0为ICab 矢量的幅值;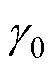 为ICdq矢量的稳态值与d轴之间的夹角。IC0与
为ICdq矢量的稳态值与d轴之间的夹角。IC0与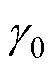 的具体数值分别为
的具体数值分别为
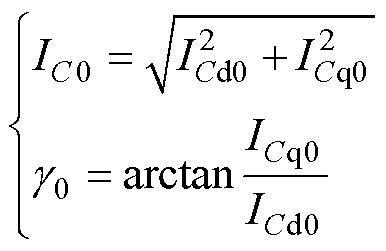 (12)
(12)
式中,ICd0、ICq0的具体数值在式(5)中给出。图2中dq域下的Gasy3(s)环节转换到ab 域下的等效数学模型GPLL3(s)的表达式为
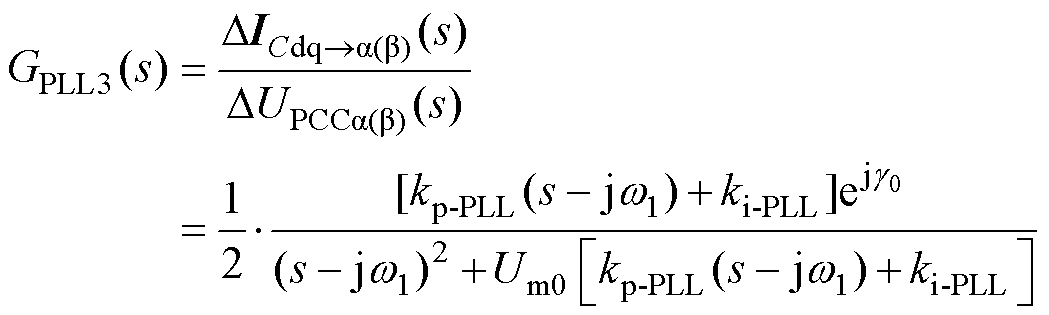 (13)
(13)
根据以上分析,可以求得SISO模型下GCI输出电流表达式为
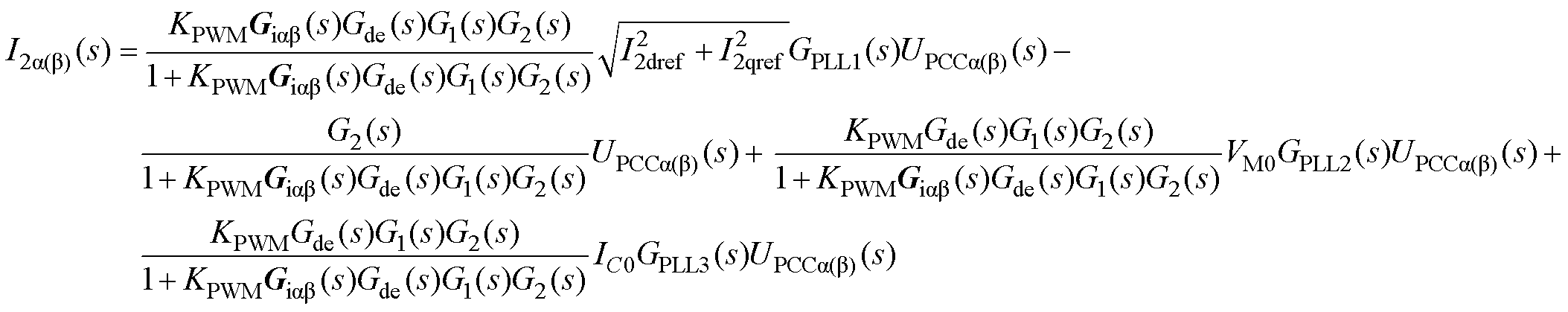
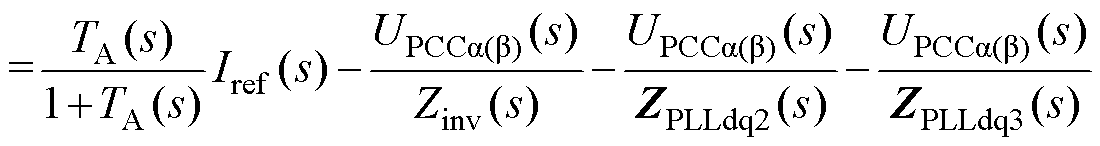 (14)
(14)
式中,TA(s)为GCI系统的等效环路增益,其等效输出阻抗Zinv(s)、ZPLLdq2(s)、ZPLLdq3(s)的具体表达式为
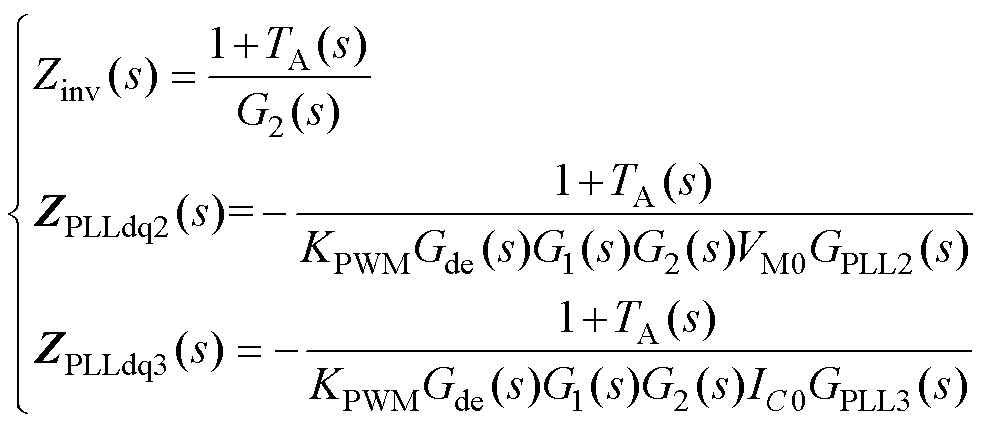 (15)
(15)
根据式(14)、式(15)可以得到考虑PLL影响的GCI在弱电网下的诺顿等效小信号模型,如图4所示。
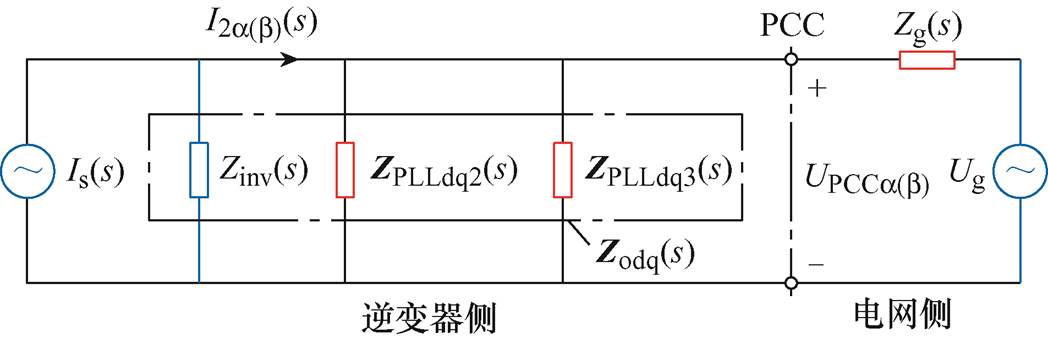
图4 GCI的SISO阻抗模型的诺顿等效小信号模型
Fig.4 Norton equivalent small-signal model of SISO impedance model of GCI
观察图4,此时考虑PLL影响的GCI的SISO等效输出阻抗Zodq(s)的表达式为
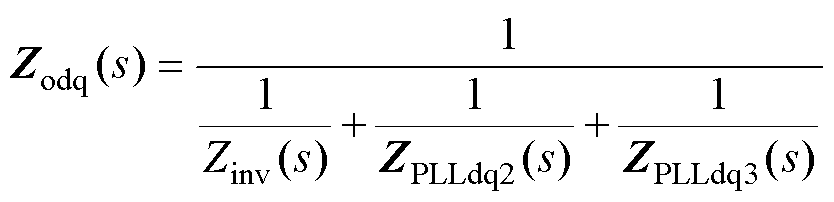 (16)
(16)
GCI系统的稳定性可以通过Zg(s)与Zodq(s)的比值是否满足Nyquist判据来进行识别;然而使用Zg(s)/Zodq(s)的前提条件是首先要保证等效电流源Is(s)是稳定的。但是,当控制器参数为了适应运行工况而变化调整时,极有可能导致TA(s)不稳定,即等效电流源不稳定,此时将无法使用阻抗分析法分析GCI的稳定性,也给控制器参数的分析与设计带来了困难与挑战。
为了能够在控制器参数调整下实现对GCI的稳定性分析以及参数设计,首先,将GCI等效输出阻抗中包含PLL影响的阻抗环路ZPLLdq2(s)、ZPLLdq3(s)折算到电网侧,使其与初始电网阻抗Zg(s)共同构成等效的电网阻抗Zgeq(s)。这种等效折算符合ZPLLdq2(s)、ZPLLdq3(s)的形成规律,因为用ZPLLdq2(s)、ZPLLdq3(s)表征的PLL对GCI稳定性负面效应的形成正是由电网阻抗存在而诱发产生的。
对于包含电流环控制器参数的等效电流源以及输出阻抗Zinv(s)则通过文献[31]中串并联阻抗等效变换法,将电流环控制器参数从等效电流源中分离,实现电流环控制器参数与等效电流源二者之间的 解耦。
通过上述两步处理,可以得到具有控制器参数解耦的GCI诺顿等效电路,如图5所示。
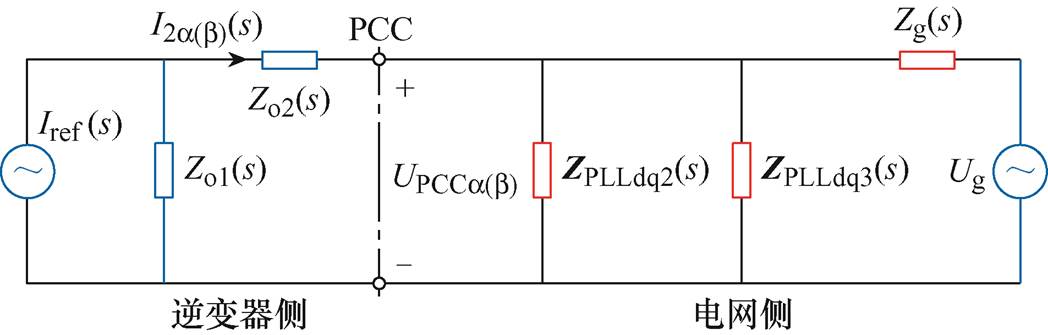
图5 具有控制器参数解耦的GCI诺顿等效电路
Fig.5 Norton equivalent circuit of GCI based on controller parameter decoupling
为了证明图5中本文所提阻抗模型能够实现等效电流源与控制器参数之间的解耦,图6给出了等效电流源Iref(s)的稳定性分析结果。其中,等效电流源的稳定性由式(17)闭环传递函数在复平面右半平面是否有闭环极点来进行判定。
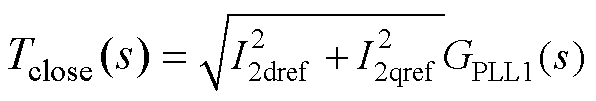 (17)
(17)
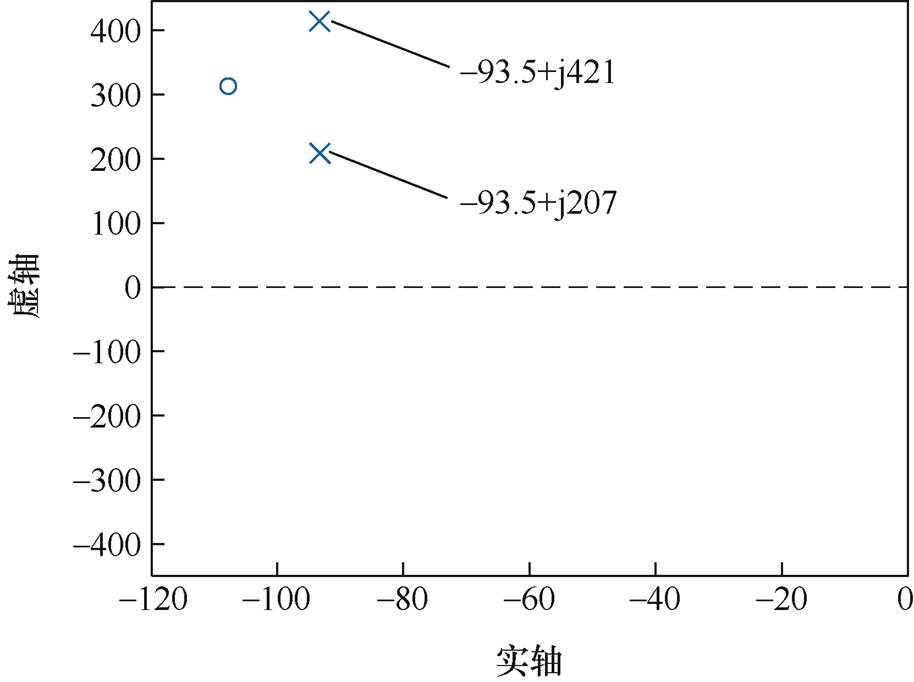
图6 解耦后等效电流源Iref(s)的零极点分布
Fig.6 Pole-zero distribution of the Iref(s) after decoupling
观察图6可以看出,表征等效电流源稳定性的闭环传递函数的极点都位于复平面的左半平面,这意味着等效电流源是闭环稳定的,且与电流控制环参数无关。当电流控制环参数调整时将无法影响等效电流源Iref(s)的稳定性,实现了其与控制环参数之间的解耦。
图5中,Zo1(s)与Zo2(s)的具体表达式分别为
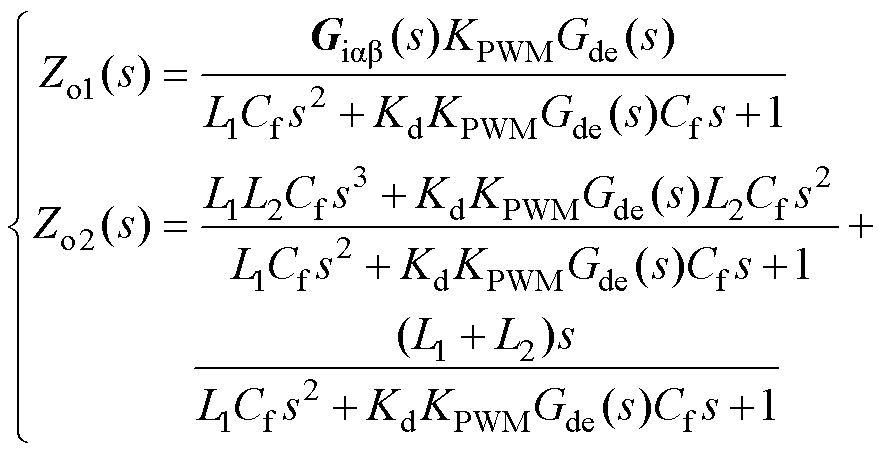 (18)
(18)
ZPLLdq2(s)、ZPLLdq3(s)折算到电网侧的等效电网阻抗Zgeq(s)的表达式为
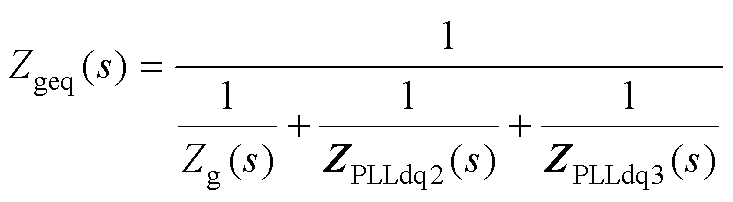 (19)
(19)
此时GCI系统的稳定性可以通过式(20)是否满足Nyquist判据来进行判定,具有无需检查等效电流源稳定性的优良特性。同时,基于所构建具有控制器参数解耦的阻抗模型,可以实现GCI控制器参数自适应调整下的分析与设计。
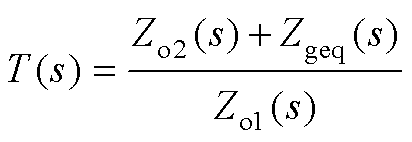 (20)
(20)
为了验证本文所提具有控制器参数解耦的阻抗模型在控制环参数不调整的情况下也能准确识别GCI的稳定性,图7给出了GCI在不同电网阻抗下的稳定性分析结果。其中GCI的主电路与控制参数见表1。
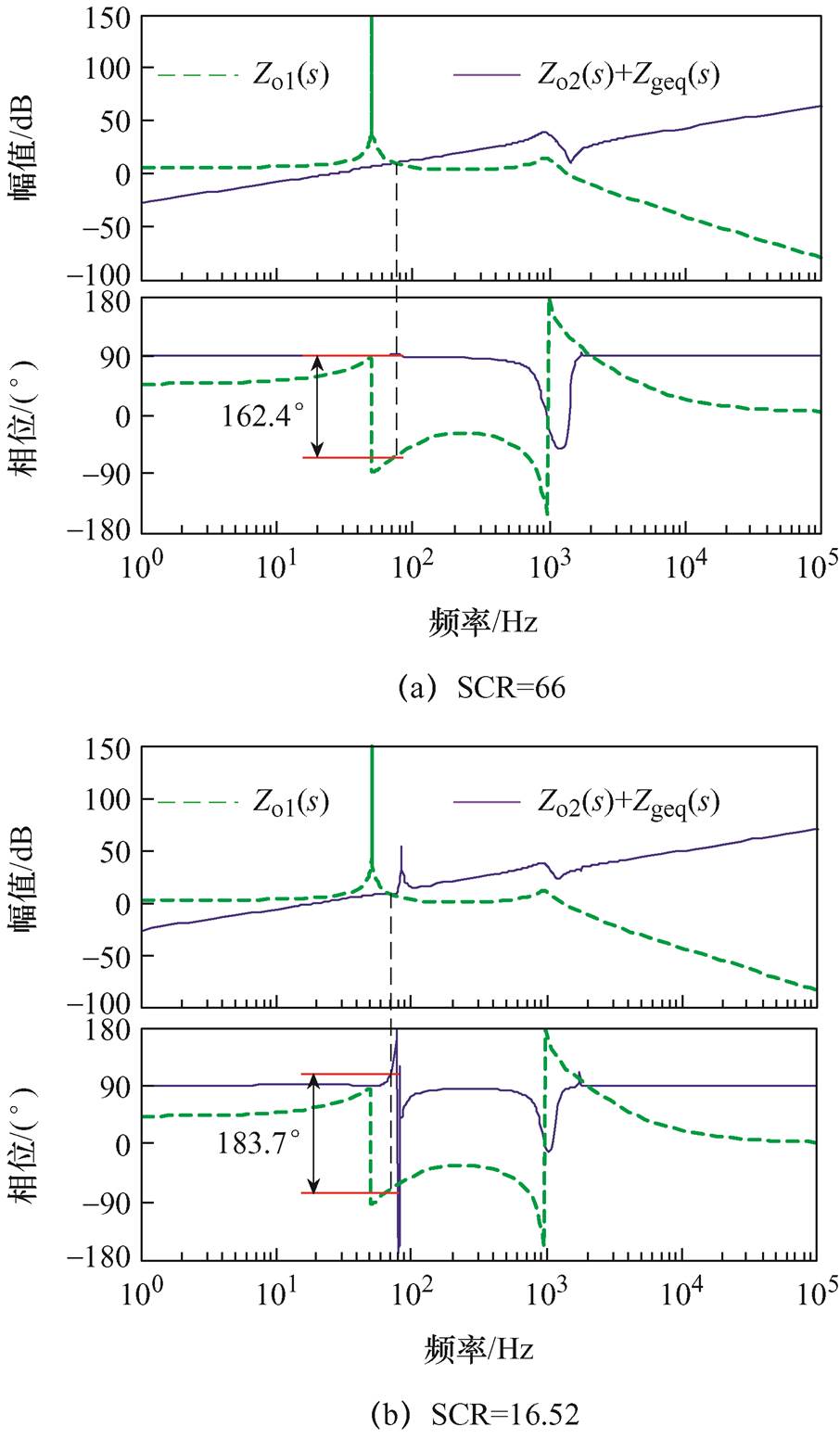
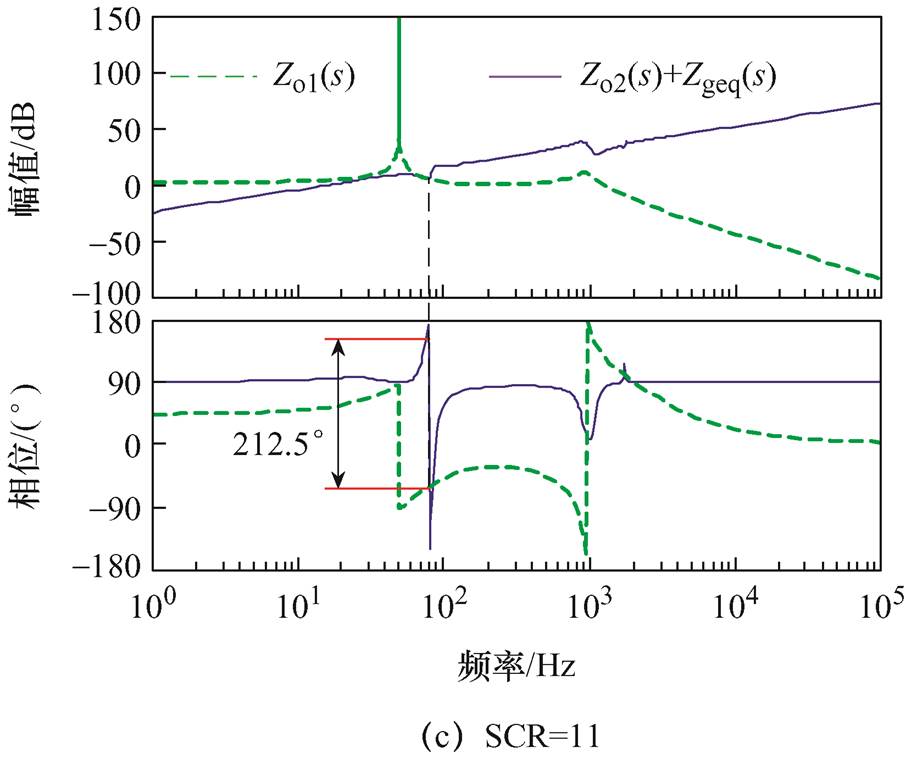
图7 控制环参数不调整下GCI的稳定性分析结果
Fig.7 Stability analysis results of GCI without adjusting the control loop parameters
表1 主要仿真参数
Tab. 1 Main simulation parameters
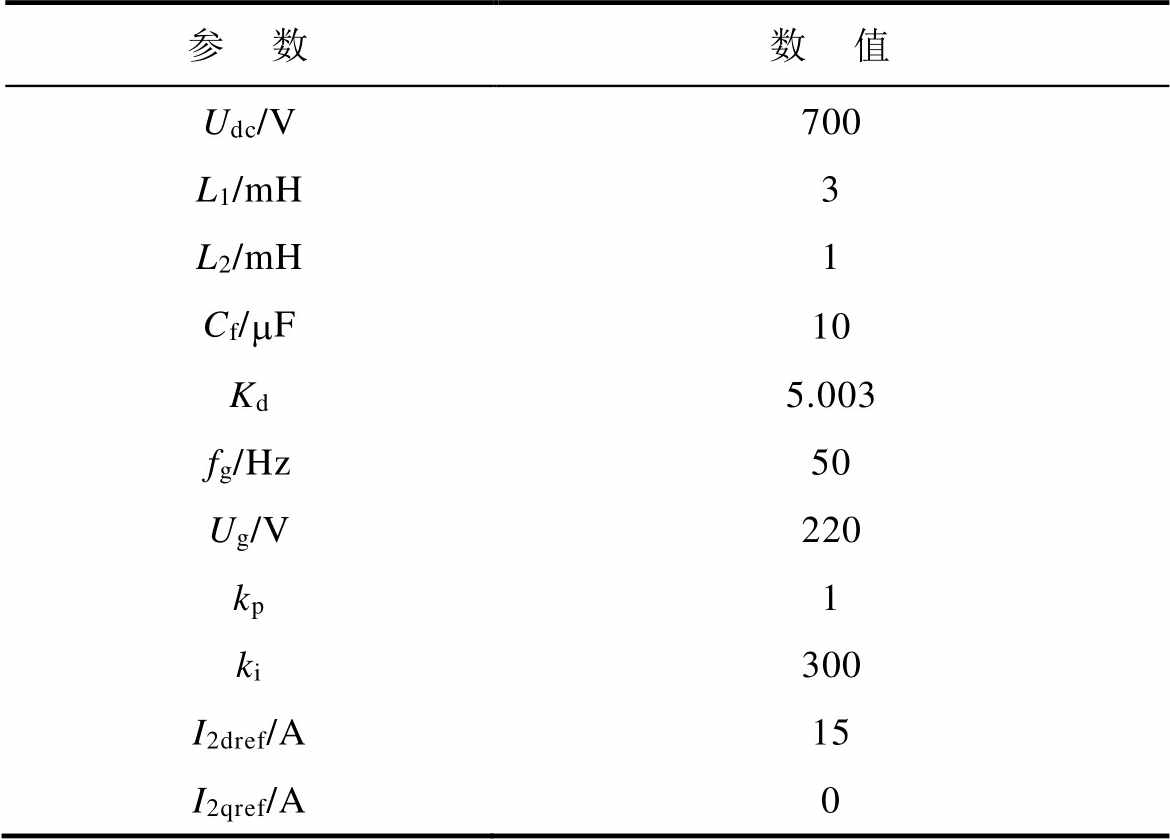
参 数数 值 Udc/V700 L1/mH3 L2/mH1 Cf/mF10 Kd5.003 fg/Hz50 Ug/V220 kp1 ki300 I2dref/A15 I2qref/A0
观察图7可以看出,当电网阻抗从1 mH(SCR= 66.0)逐渐增大到6 mH(SCR=11.0)时,阻抗Zo2(s)+Zgeq(s)与Zo1(s)之间的相位差逐渐增大,这意味着GCI的稳定裕度会随着电网阻抗的增加而逐渐降低。同时,GCI输出电流也会因稳定裕度降低而有逐渐振荡的趋势,严重时甚至会导致系统失稳。如当电网阻抗增加到4 mH(SCR=16.52)时,对应的相位差为183.7°,此时系统的相位裕度为-3.7°<0,这意味着GCI处于失稳运行状态。
为了验证图7理论分析的正确性,图8给出了相应电网阻抗数值下并网电流的仿真结果。从图8b可以看出,当电网阻抗为4 mH时,由于系统相位裕度小于0,并网电流表现出明显的谐波失稳现象。当电网阻抗增加到6 mH时,系统的相位裕度为-32.5°,远远小于0,导致并网电流波形严重畸变,这与图7的理论分析结果一致。
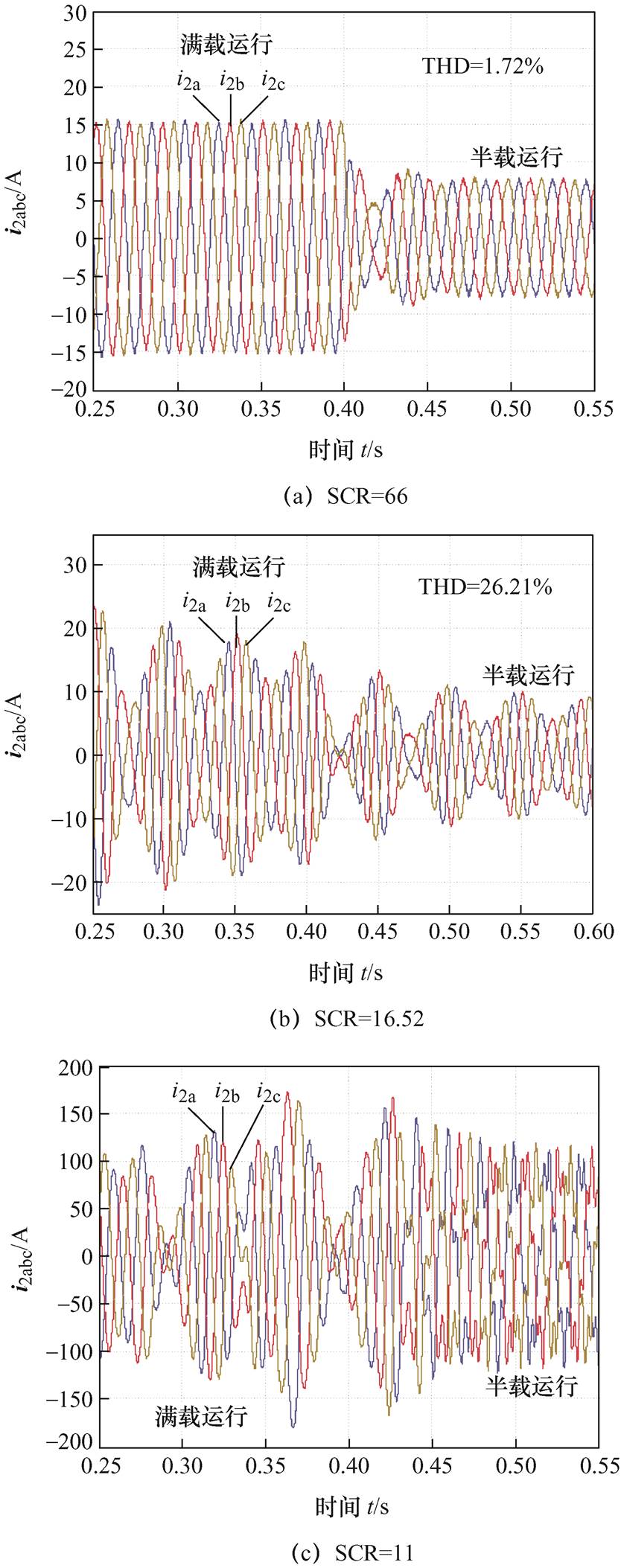
图8 控制环参数不调整下GCI的输出电流波形
Fig.8 Output current waveforms of GCI without adjusting the control loop parameters
通过以上分析不难发现,在控制器参数不调整的情况下,采用本文所提具有控制器参数解耦的阻抗模型同样能够准确识别GCI的稳定性,进一步证明了所构建等效阻抗模型的正确性。
为了提升GCI在弱电网下的稳定性,本文提出一种基于比例权重的控制环参数自适应控制方法。通过考虑电网阻抗影响,调整电流环PI控制器参数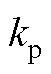 、
、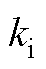 以及电容电流比例反馈系数
以及电容电流比例反馈系数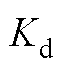 ,以保证GCI在不同电网阻抗下的稳定性。其中,GCI控制环参数随电网阻抗变化的调整原则为
,以保证GCI在不同电网阻抗下的稳定性。其中,GCI控制环参数随电网阻抗变化的调整原则为
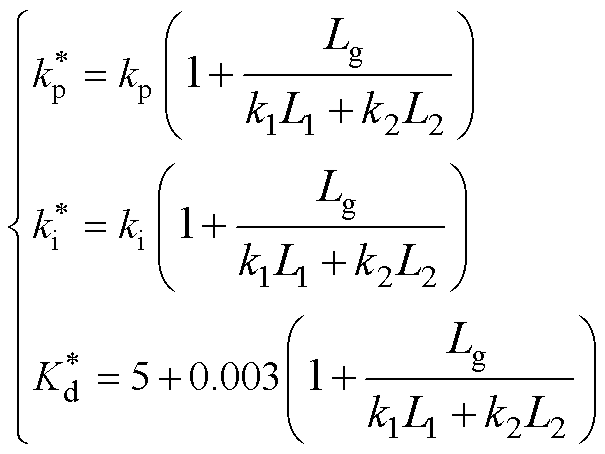 (21)
(21)
式中, 、
、 为比例权重系数,满足
为比例权重系数,满足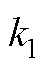 +
+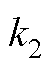 =1的等式关系,调整比例权重系数可以调整考虑电网阻抗Lg影响的GCI系统的稳定裕度;
=1的等式关系,调整比例权重系数可以调整考虑电网阻抗Lg影响的GCI系统的稳定裕度;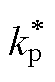 、
、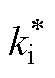 、
、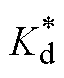 分别为自适应参数调整后的电流环PI控制器参数以及电容电流比例反馈系数。在本文中设计GCI在弱电网范围内,即2≤SCR≤3,都能够保持30°以上的充足相位裕度。由于电网越弱,即电网阻抗越大,GCI的稳定性越差,相位裕度越低,为此本文考虑最恶劣的情况,选择SCR=2,即Lg=33 mH进行
分别为自适应参数调整后的电流环PI控制器参数以及电容电流比例反馈系数。在本文中设计GCI在弱电网范围内,即2≤SCR≤3,都能够保持30°以上的充足相位裕度。由于电网越弱,即电网阻抗越大,GCI的稳定性越差,相位裕度越低,为此本文考虑最恶劣的情况,选择SCR=2,即Lg=33 mH进行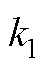 、
、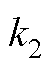 的参数设计。图9a给出了GCI等效阻抗模型随参数
的参数设计。图9a给出了GCI等效阻抗模型随参数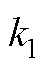 从0变化到1过程中的幅频特性曲线,其中曲面的交点即为阻抗幅值的交截频率。
从0变化到1过程中的幅频特性曲线,其中曲面的交点即为阻抗幅值的交截频率。
在图9a的交截频率处,GCI所对应的相位裕度 ,如图9b所示。此时,可以得到自适应控制参数k1从0变化到1时GCI系统所对应的相位裕度,如图9c所示。
,如图9b所示。此时,可以得到自适应控制参数k1从0变化到1时GCI系统所对应的相位裕度,如图9c所示。
根据图9可以看出,随着自适应控制参数k1减小,GCI系统的相位裕度会不断增加,为了保证GCI具有良好的稳态与动态性能,本文选择k1=0.2,k2=1-k1=0.8成立。由图9c可知,此时所对应的GCI系统相位裕度为35°,满足设计要求。
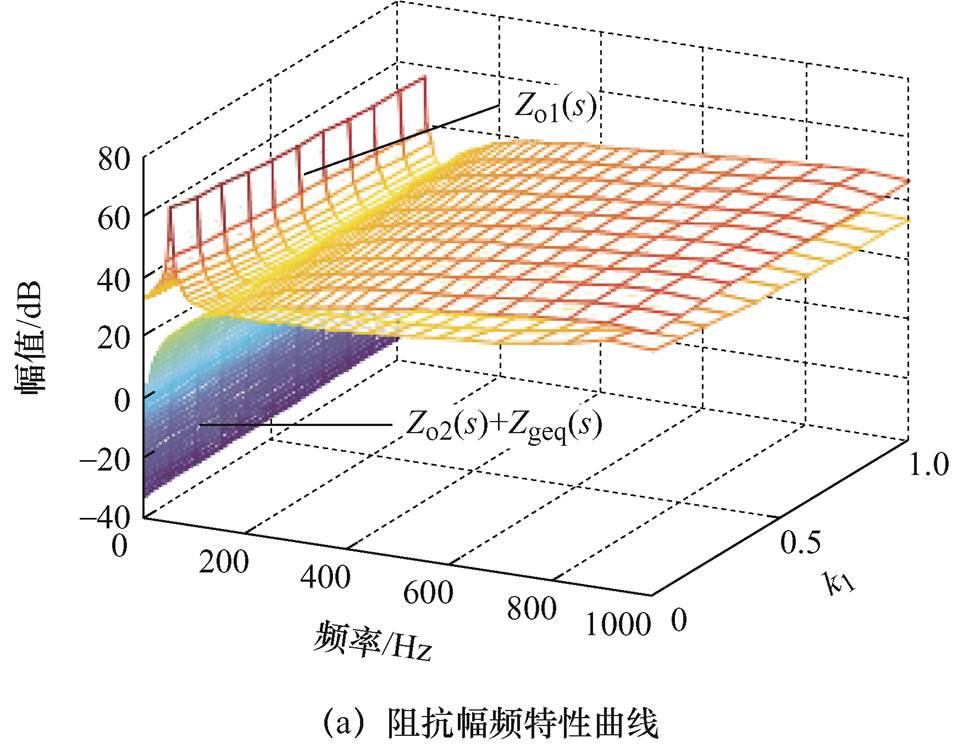
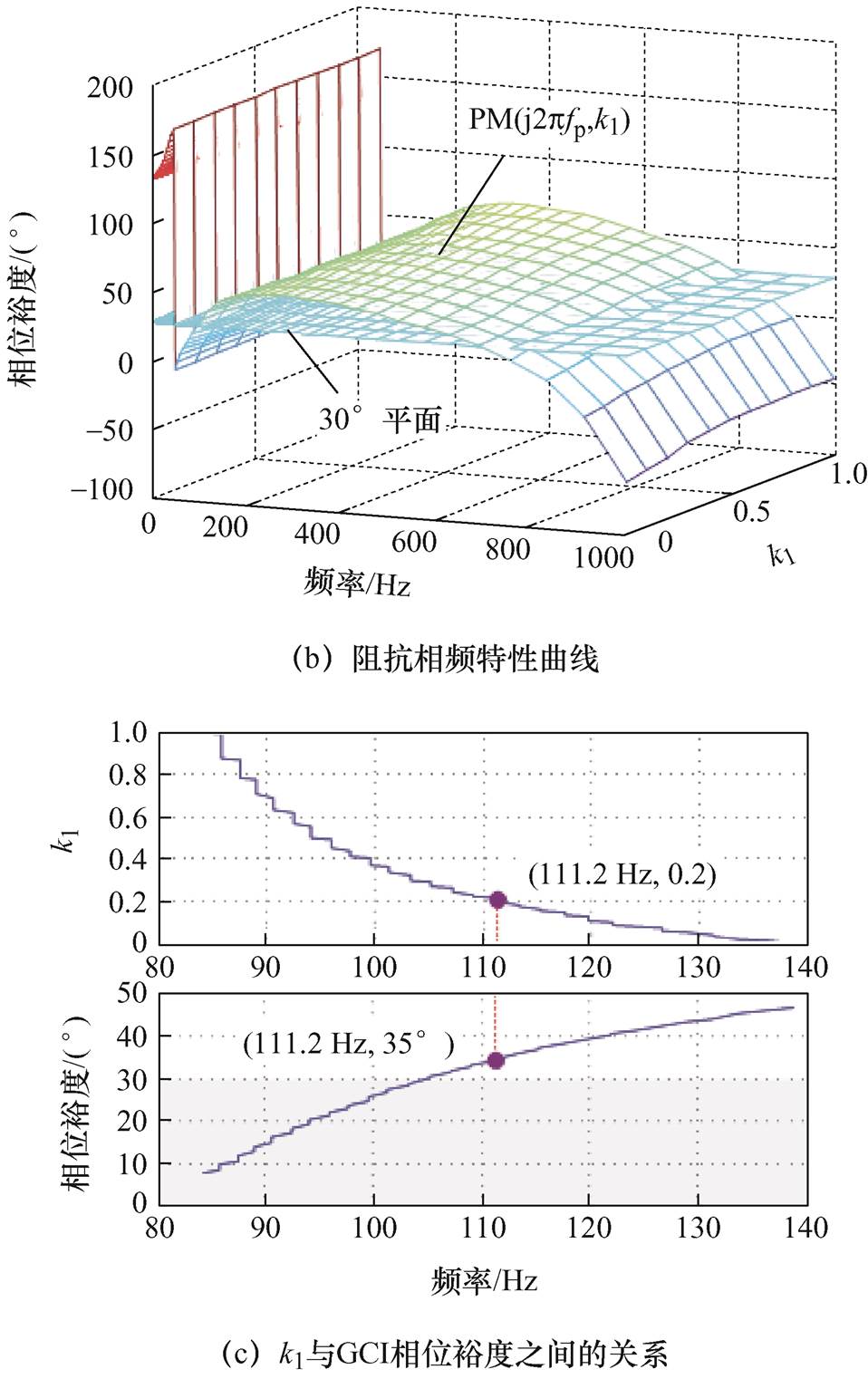
图9 k1变化下GCI的稳定裕度分析
Fig.9 Stability margin analysis of GCI under the change of k1
为了验证本文所提比例权重控制环参数自适应控制方法的有效性,以及所构建控制器参数解耦阻抗模型应用于具有控制环参数自适应的GCI稳定性分析的正确性,图10给出了采用式(21)自适应调整控制策略下GCI在不同电网阻抗下的稳定性分析结果。
观察图10可以看出,当电网阻抗为6 mH,即SCR=11时,采用比例权重控制环参数自适应控制方法后,此时控制环参数修正为kp=5.285 7,ki= 1 585.7,Kd=5.015 9,GCI在阻抗幅值交点频率处所对应的相位差为146.7°,即系统的PM=33.3°,此时GCI能够保持稳定运行。然而,在不采用自适应控制方法前,GCI在电网阻抗为6 mH时就已经严重失稳了,如图7c与图8c所示。当电网阻抗进一步增大,如Lg=22 mH(SCR=3.0)以及Lg=33 mH(SCR=2.0)时,控制环参数分别修正为kp=16.714 3,ki=5 014.3,Kd=5.051以及kp=24.571 4,ki=7 371.4,Kd=5.073 7。GCI系统在阻抗交点频率处的相位裕度基本上都维持在35°左右,系统能够保持良好的运行状态。
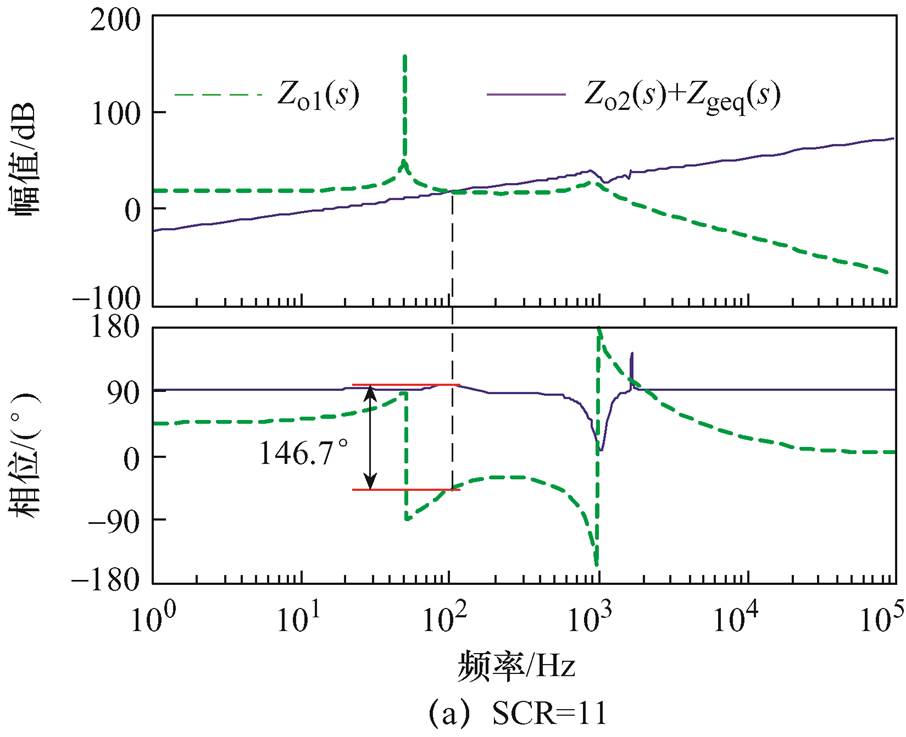
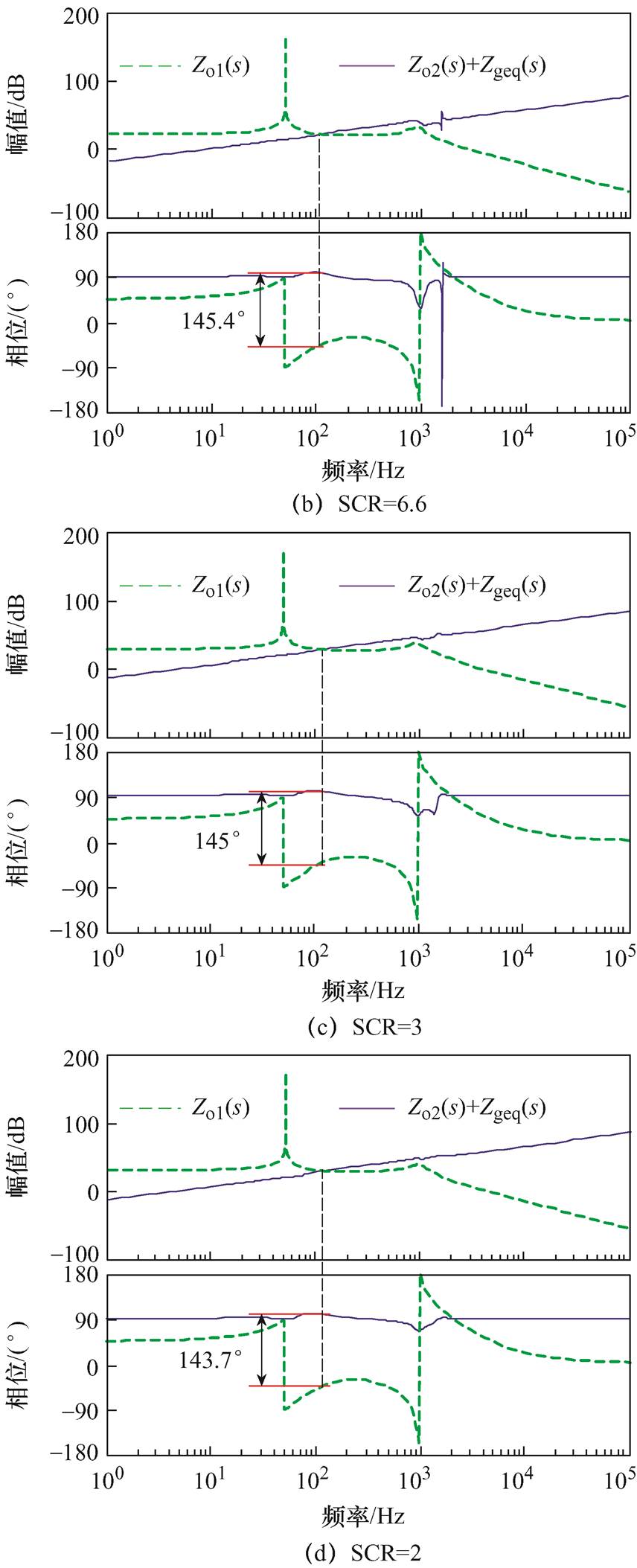
图10 控制环参数自适应调整下GCI的稳定性分析结果
Fig.10 Stability analysis results of GCI under the adaptive adjustment of the control loop parameters
同时,为了验证本文所提具有控制器参数解耦的阻抗模型在识别GCI稳定性上的有效性,图11给出了GCI在相应电网阻抗下的仿真结果。
根据图11可以看出,当Lg从SCR=11逐渐增加到SCR=2时,GCI的输出电流都能够保持稳定运行,且具有良好的电能质量。以上仿真结果验证了图10理论分析的正确性,即在控制环参数实时调整的自适应控制GCI中,本文所提具有控制器参数解耦的阻抗模型依旧能够准确识别GCI的稳定性。
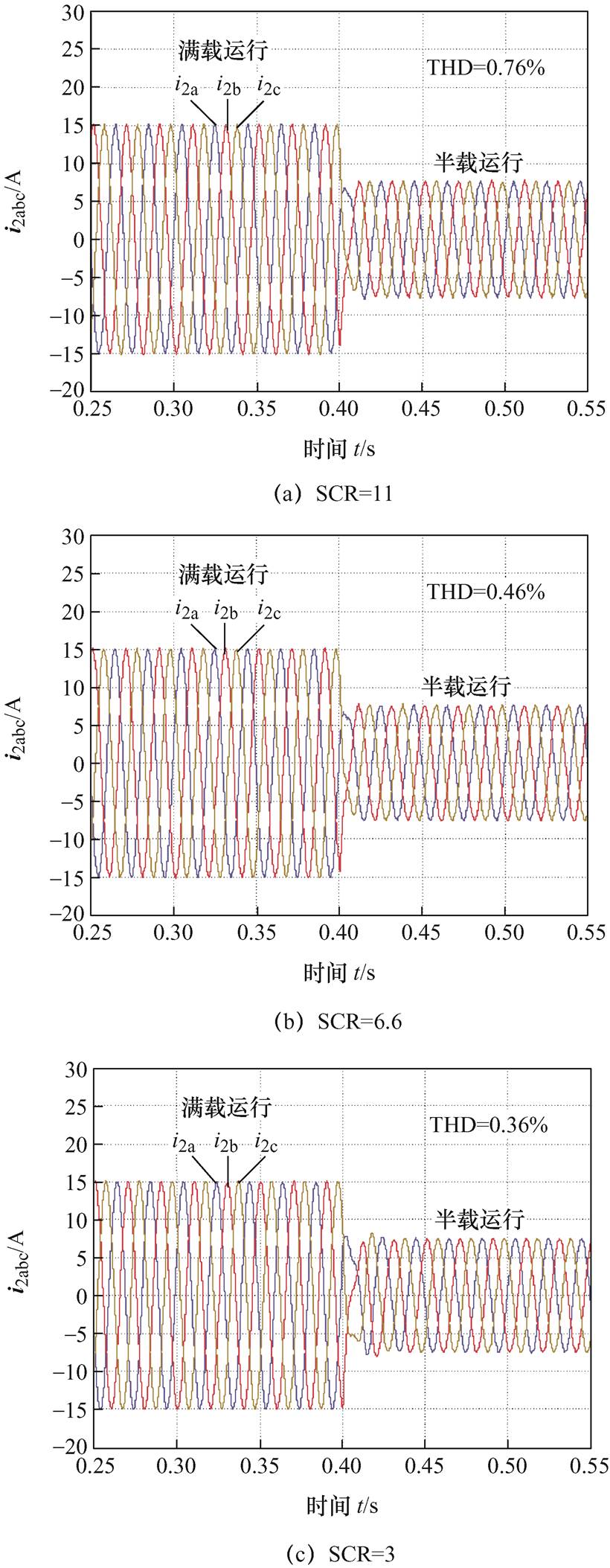
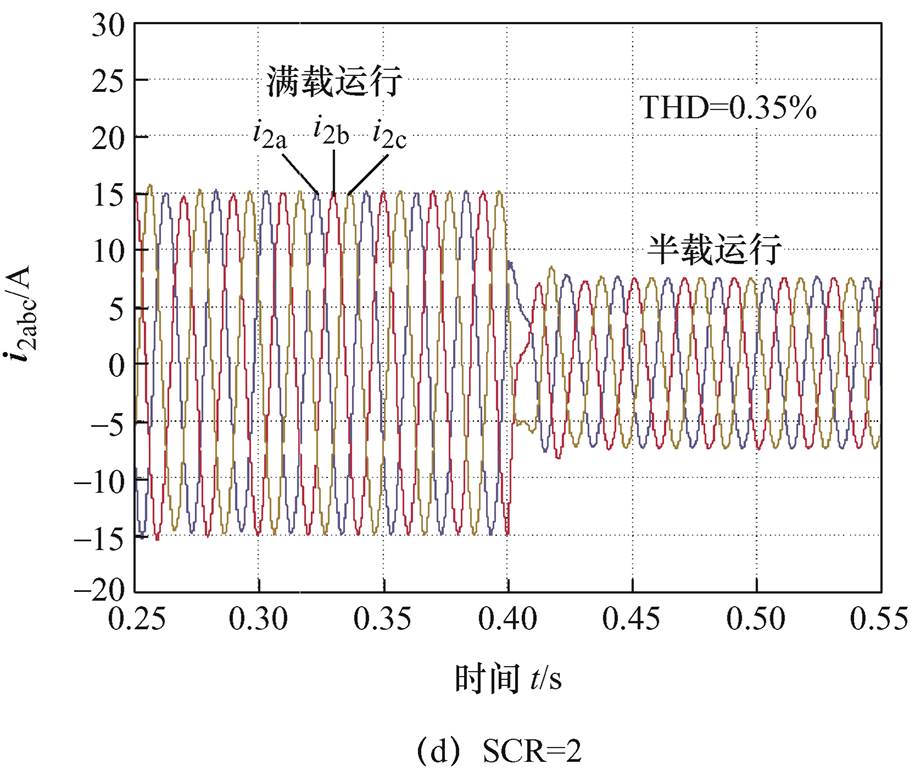
图11 控制环参数调整下GCI的输出电流波形
Fig.11 Output current waveforms of GCI under the adaptive adjustment of the control loop parameters
同时,为了证明本文所提自适应控制策略能够在电网阻抗存在检测误差的情况下实现GCI的稳定运行,图12给出了在SCR=2时,电网阻抗存在20%测量误差下的稳定性分析与仿真结果。由于电网阻抗越大越不利于GCI的稳定运行,为此本文只给出+20%测量误差下的分析结果。此时测量得到的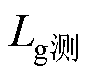 = 33 mH×1.2=39.6 mH,将其代入本文所提自适应控制算法中,得到电流环PI控制参数以及电容电流比例反馈系数分别调整为kp=29.285 7,ki=8 785.7,Kd= 5.087 9。
= 33 mH×1.2=39.6 mH,将其代入本文所提自适应控制算法中,得到电流环PI控制参数以及电容电流比例反馈系数分别调整为kp=29.285 7,ki=8 785.7,Kd= 5.087 9。
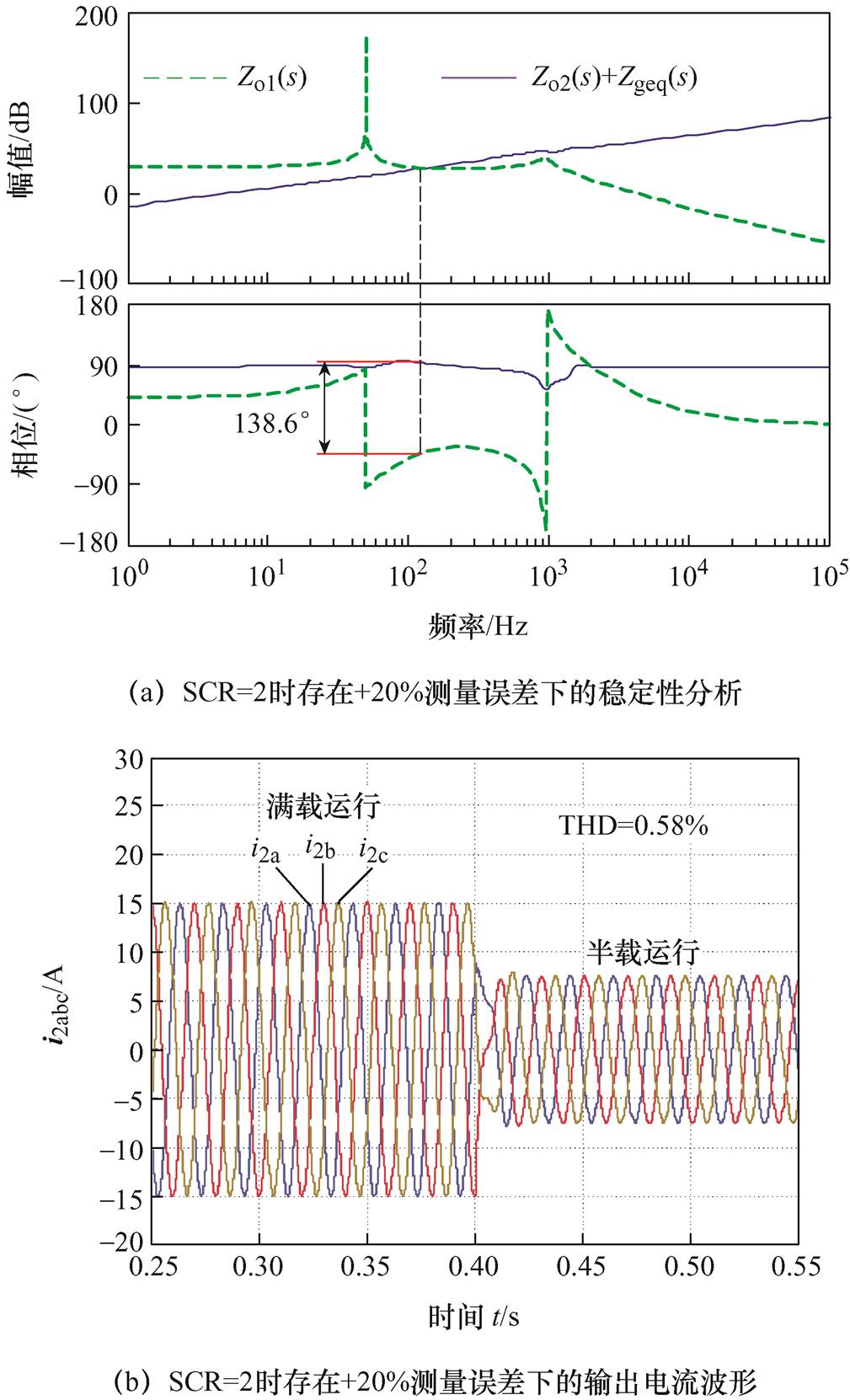
图12 SCR=2时存在+20%测量误差的分析结果
Fig.12 Analysis results of +20% measurement error when SCR=2
观察图12a可以看出,在SCR=2并存在+20%测量误差时,基于所提阻抗模型得到GCI的相位裕度为41.4°>0,系统具有良好的稳定裕度。相应的并网电流波形如图12b所示,可以看出此时并网电流波形在满载运行下的THD仅有0.58%,具有良好的电能质量。基于以上分析发现,当Lg存在较大测量误差时,采用本文所提自适应控制策略依旧能够保持GCI稳定运行,且具有良好的稳定裕度。
为了证明在本文整定参数下GCI在SCR=1时也能够保持稳定运行,图13给出了相应的稳定性分析与仿真结果。
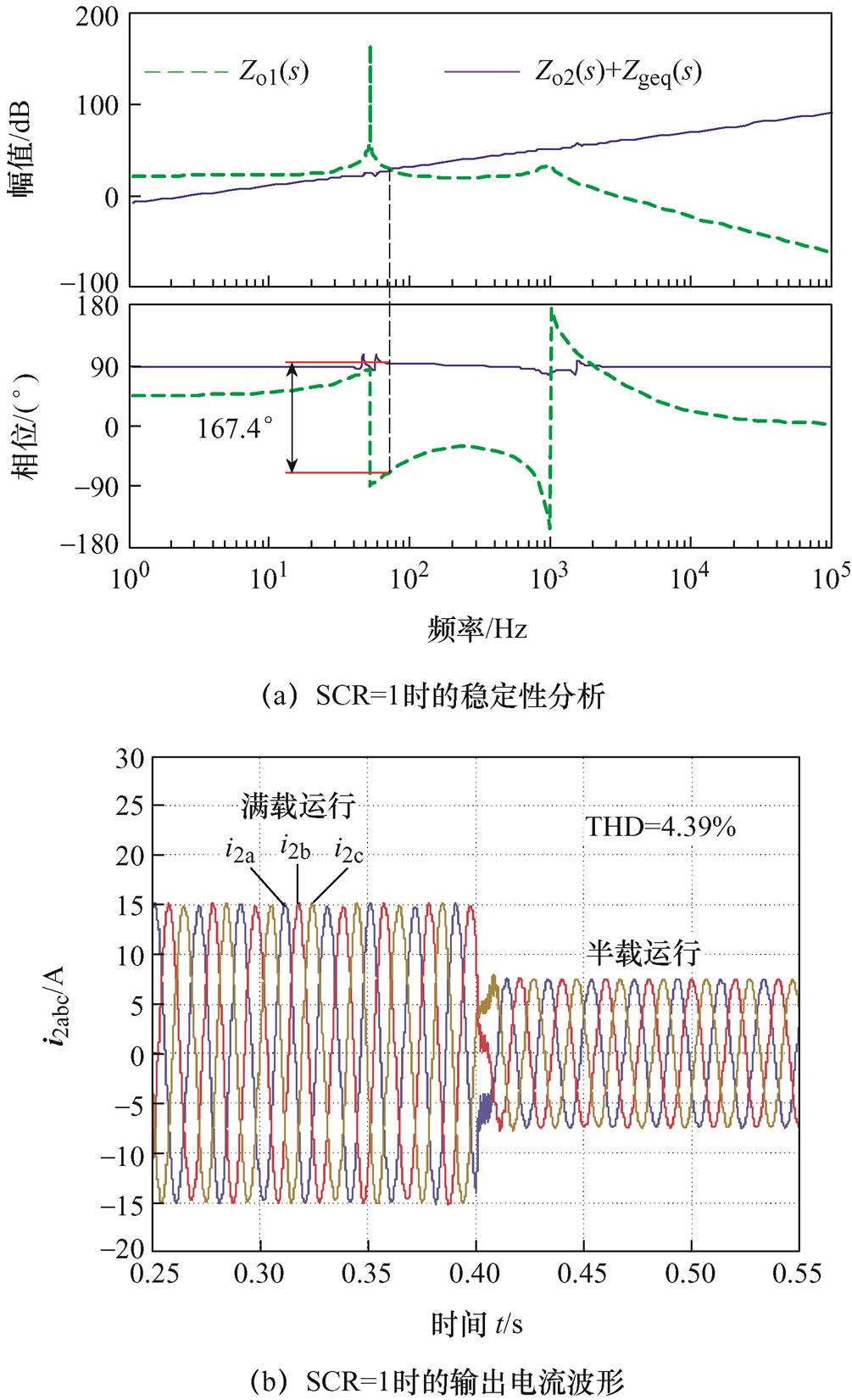
图13 SCR=1时的稳定性分析与仿真结果
Fig.13 Stability analysis and simulation results when SCR=1
观察图13可以看出,当电网阻抗增加到SCR=1时,GCI输出电流在满载运行时的THD达到了4.39%,这是由于此时GCI系统所对应的相位裕度仅有12.6°,稳定裕度不足导致GCI输出电流谐波含量增加[29],但系统依旧保持稳定运行。以上分析进一步证明了本文所提控制策略的有效性。
为验证本文理论分析的正确性,在实验室利用RT-Lab硬件在环平台搭建了一套与表1参数一致GCI模型并进行了实验验证,实验平台照片如图14所示,控制器采用TI公司的TMS320F28335。

图14 实验平台照片
Fig.14 Experimental platform
为了验证本文所构建具有控制器参数解耦的阻抗模型能够在控制环参数不调整的情况下判定GCI的稳定性,图15给出了GCI在电网阻抗分别为3 mH(SCR=22.02)与4 mH(SCR=16.52)时的实验结果。
观察图15的实验结果可以看出,当SCR=22.02时,GCI输出电流波形稳定;当电网阻抗增加到4 mH,即SCR=16.52时,并网电流表现出了明显的谐波振荡现象,此时并网系统处于失稳运行状态。以上实验结果验证了图7理论分析的正确性。
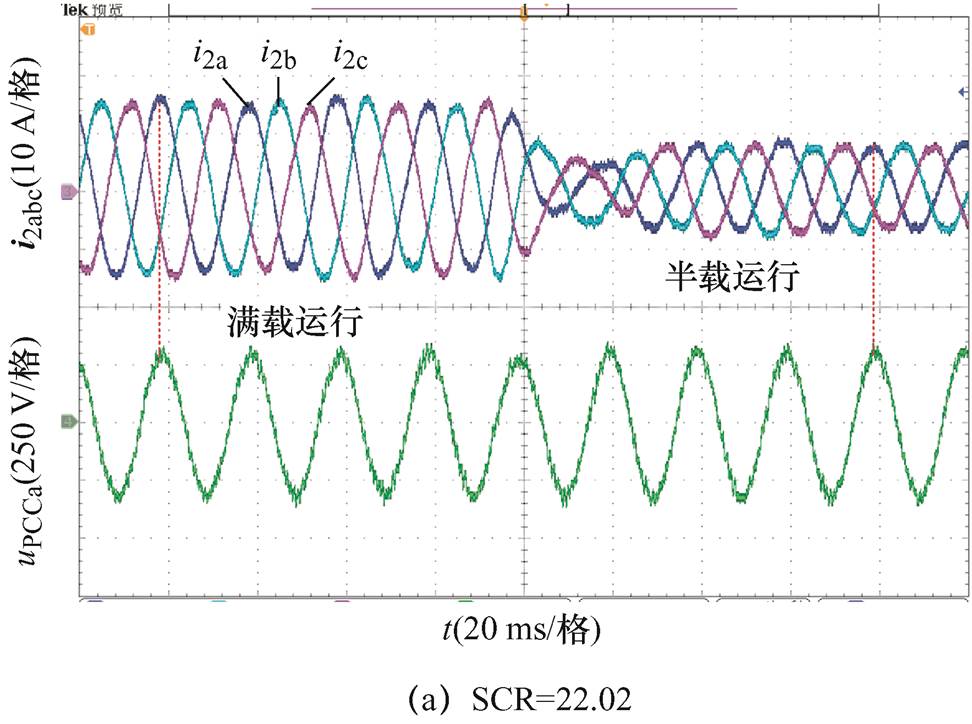
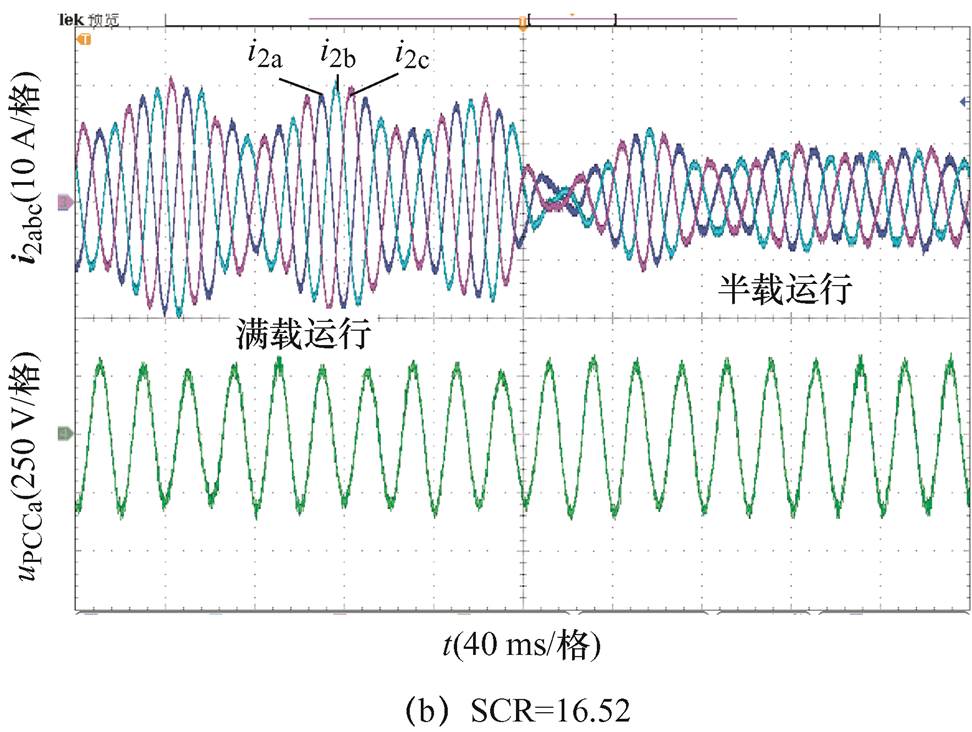
图15 控制环参数不调整下的实验结果
Fig.15 Experimental results under the control loop parameters are not adjusted
为验证本文所提控制环参数自适应调整控制策略对提升弱电网下GCI稳定性的有效性,图16给出了GCI在电网阻抗分别为22 mH(SCR=3)与33 mH(SCR=2)时的实验结果。
观察图16的实验结果可以看出,当采用本文所提比例权重控制环参数自适应调整控制策略后,GCI系统在电网阻抗增加到33 mH(SCR=2)时也能够保持稳定运行,远大于无自适应调整控制策略下GCI所能适应的电网阻抗值,验证了图10理论分析的正确性。
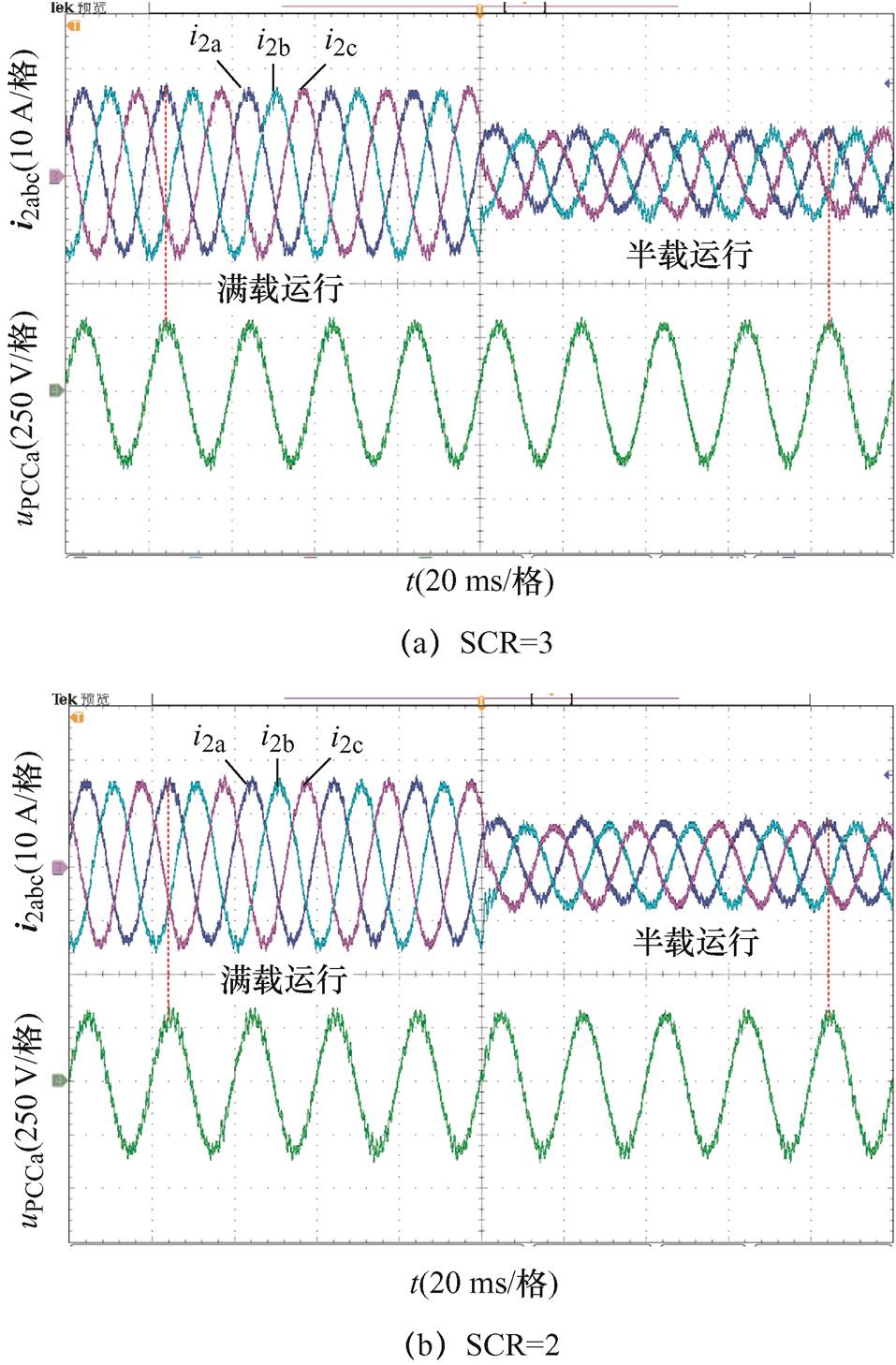
图16 控制环参数调整下的实验结果
Fig.16 Experimental results under the control loop parameters are adjusted
为了进一步证明本文所提自适应控制策略在电网阻抗动态变化过程中依旧能够保持良好的稳态与动态性能,图17给出了SCR从3变化到2,再变化到1时的动态并网电流实验结果。
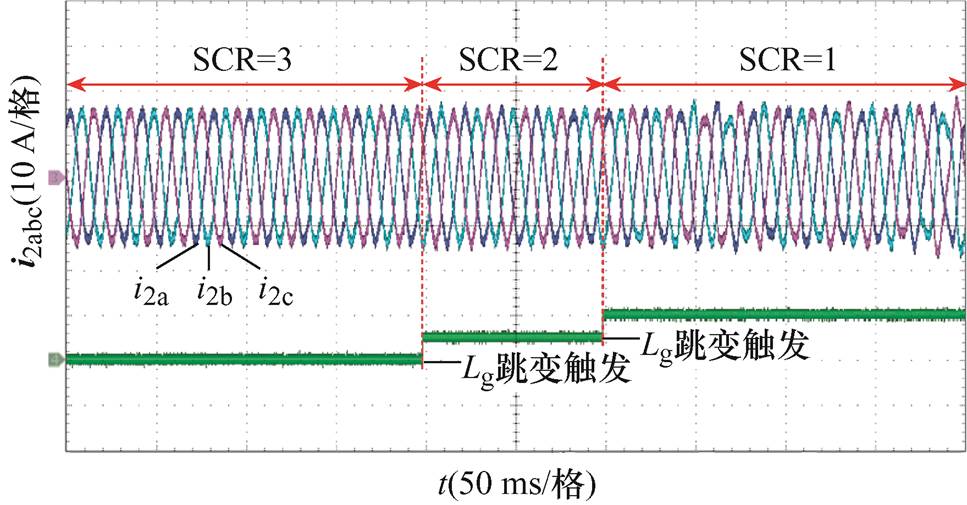
图17 SCR动态变化时的并网电流实验波形
Fig.17 Experimental waveforms of grid-connected current when SCR dynamic change
观察图17可以看出,当电网阻抗由SCR=3跳变到SCR=2时,并网电流保持良好的电能质量;当电网阻抗由SCR=2跳变到SCR=1时,并网电流表现出明显的谐波,电能质量降低,导致这种现象的根本原因在于此时GCI所对应的相位裕度不足,验证了图13理论分析的正确性。
以上实验结果不仅证明了本文所构建具有控制器参数解耦的阻抗模型的正确性,而且也进一步证明了所提比例权重控制环参数自适应控制方法在提升弱电网下GCI稳定性方面的有效性。
为了实现对控制环参数调整下GCI的稳定性分析以及GCI稳定性提升方法的分析与设计,本文首先构建一种具有控制环参数解耦的GCI阻抗模型,实现阻抗模型中等效电流源与控制环参数解耦,以保证控制环参数调整下等效电流源的稳定性;在此基础上提出一种基于比例权重的控制环参数自适应调整稳定性提升方法,并得出以下重要结论:
1)所提具有控制环参数解耦的阻抗模型能够在无需检查等效电流源稳定性的前提条件下实现GCI稳定性的分析与判定。
2)提出一种基于比例权重的控制环参数自适应调整GCI稳定性提升方法,并对比例权重系数给出了详细的分析与设计,在整定参数下所提自适应控制方法显著提升了GCI对弱电网的适应能力;同时,在电网阻抗存在检测误差的情况下依旧能够保持GCI的稳定运行。
3)本文所提具有控制环参数解耦的阻抗模型不仅能够在控制环参数不调整的情况下准确识别GCI的稳定性,而且在控制环参数实时调整的自适应控制GCI中,依旧能够准确地识别GCI的稳定性。
参考文献
[1] 曾祥辰, 刘青, 王嘉晨, 等. 弱电网下并网逆变器恒定带宽及稳定裕度的自适应控制策略[J]. 电工技术学报, 2024, 39(9): 2682-2695.
Zeng Xiangchen, Liu Qing, Wang Jiachen, et al. Adaptive control strategy of grid-connected inverters with constant bandwidth and stability margin in weak grids[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2682-2695.
[2] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability Analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[3] Zhang Chenghui, Li Xiaoyan, Xing Xiangyang, et al. Modeling and mitigation of resonance current for modified LCL-type parallel inverters with inverter-side current control[J]. IEEE Transactions on Industrial Informatics, 2022, 18(2): 932-942.
[4] 杨树德, 李旺, 徐佳, 等. 基于并网电流谐波微分的有源阻尼策略[J]. 电工技术学报, 2023, 38(23): 6305-6317.
Yang Shude, Li Wang, Xu Jia, et al. Research on Active damping strategy based on the differentiation of injected grid current harmonics[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6305- 6317.
[5] 李雨果, 易皓, 姜鑫, 等. 极弱电网下新能源跟网逆变器低频振荡的机理探究与暂态无功过补稳定性提升策略[J]. 中国电机工程学报, 2023, 43(2): 482-496.
Li Yuguo, Yi Hao, Jiang Xin, et al. Mechanism researching on low-frequency resonance of renwable- energy grid-following inverters under very weak grid and the stability-improving strategy based on dynamic reactive power over compensation[J]. Proceedings of the CSEE, 2023, 43(2): 482-496.
[6] 刘芳, 刘威, 徐韫钰, 等. 弱电网条件下并网逆变器控制环路稳定判据及交互作用规律分析[J]. 中国电机工程学报, 2023, 43(2): 466-482.
Liu Fang, Liu Wei, Xu Yunyu, et al. Analysis on stability criterion and interaction law of grid- connected inverter control loop under weak grid condition[J]. Proceedings of the CSEE, 2023, 43(2): 466-482.
[7] Wang Xiongfei, Taul M G, Wu Heng, et al. Grid- synchronization stability of converter-based resources- an overview[J]. IEEE Open Journal of Industry Applications, 2020, 1: 115-134.
[8] 彭技礼, 贾祺, 严干贵, 等. 面向低频振荡分析的直驱风电机组阻尼转矩建模[J]. 电力自动化设备, 2022, 42(8): 39-46.
Peng Jili, Jia Qi, Yan Gangui, et al. Damping torque modeling of direct-drive wind turbine for low- frequency oscillation analysis[J]. Electric Power Automation Equipment, 2022, 42(8): 39-46.
[9] 王一珺, 杜文娟, 王海风. 基于改进复转矩系数法的多风电场接入引发多机电力系统次同步振荡机理分析[J]. 中国电机工程学报, 2021, 41(7): 2383- 2395.
Wang Yijun, Du Wenjuan, Wang Haifeng. Analysis of subsynchronous oscillation in multi-machine power system caused by the integration of multiple wind farms based on improved complex torque coefficient method[J]. Proceedings of the CSEE, 2021, 41(7): 2383-2395.
[10] Huang Linbin, Xin Huanhai, Li Zhiyi, et al. Grid- synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 501-516.
[11] Li Yitong, Gu Yunjie, Green T C. Mapping of dynamics between mechanical and electrical ports in SG-IBR composite grids[J]. IEEE Transactions on Power Systems, 2022, 37(5): 3423-3433.
[12] 伍文华, 陈燕东, 周乐明, 等. 虚拟同步发电机接入弱电网的序阻抗建模与稳定性分析[J]. 中国电机工程学报, 2019, 39(6): 1560-1571, 1853.
Wu Wenhua, Chen Yandong, Zhou Leming, et al. Sequence impedance modeling and stability analysis for virtual synchronous generator connected to the weak grid[J]. Proceedings of the CSEE, 2019, 39(6): 1560-1571, 1853.
[13] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[14] Wu Heng, Wang Xiongfei. Small-signal modeling and controller parameters tuning of grid-forming VSCs with adaptive virtual impedance-based current limitation[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 7185-7199.
[15] 高本锋, 邓鹏程, 梁纪峰, 等. 光伏电站与弱交流电网间次同步交互作用路径及阻尼特性分析[J]. 电工技术学报, 2023, 38(24): 6679-6694.
Gao Benfeng, Deng Pengcheng, Liang Jifeng, et al. Analysis of path and damping characteristics of subsynchronous interaction between photovoltaic plant and weak AC grid[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6679-6694.
[16] 杨超然, 辛焕海, 宫泽旭, 等. 变流器并网系统复电路分析与广义阻抗判据适用性探讨[J]. 中国电机工程学报, 2020, 40(15): 4744-4758.
Yang Chaoran, Xin Huanhai, Gong Zexu, et al. Complex circuit analysis and investigation on applicability of generalized-impedance-based stability criterion for grid-connected converter[J]. Proceedings of the CSEE, 2020, 40(15): 4744-4758.
[17] Davari M, Mohamed Y A R I. Robust vector control of a very weak-grid-connected voltage-source converter considering the phase-locked loop dynamics[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 977-994.
[18] Liu Yifeng, Zhou Xiaoping, Yu Haoqi, et al. Sequence impedance modeling and stability assessment for load converters in weak grids[J]. IEEE Transactions on Industrial Electronics, 2021, 68(5): 4056-4067.
[19] Mohammed N, Ravanji M H, Zhou Weihua, et al. Online grid impedance estimation-based adaptive control of virtual synchronous generators considering strong and weak grid conditions[J]. IEEE Transactions on Sustainable Energy, 2023, 14(1): 673-687.
[20] Yang Dongsheng, Wang Xiongfei, Liu Fangcheng, et al. Symmetrical PLL for SISO impedance modeling and enhanced stability in weak grids[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1473-1483.
[21] Liang Beihua, He Jinwei, Li Yunwei, et al. Aggregated-impedance-based stability analysis for a parallel-converter system considering the coupling effect of voltage feedforward control and reactive power injection[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5954-5970.
[22] 王自力, 陈燕东, 伍文华, 等. 不同容量VSG并联的自适应谐波阻抗重塑均流控制方法及其稳定性分析[J]. 中国电机工程学报, 2021, 41(24): 8571-8585.
Wang Zili, Chen Yandong, Wu Wenhua, et al. Adaptive harmonic impedance reshaping current-sharing control method of parallel VSGs with different capacities and its stability analysis[J]. Proceedings of the CSEE, 2021, 41(24): 8571-8585.
[23] 徐健, 曹鑫, 郝振洋, 等. 基于电网谐波电压前馈的虚拟同步整流器电流谐波抑制方法[J]. 电工技术学报, 2022, 37(8): 2018-2029.
Xu Jian, Cao Xin, Hao Zhenyang, et al. A harmonic- current suppression method for virtual synchronous rectifier based on feedforward of grid harmonic voltage[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2018-2029.
[24] 杨明, 杨倬, 李玉龙, 等. 弱电网下基于电网电压前馈的并网逆变器阻抗重塑控制策略[J]. 电工技术学报, 2024, 39(8): 2553-2566.
Yang Ming, Yang Zhuo, Li Yulong, et al. Impedance remodeling control strategy of grid-connected inverter based on feedforward voltage under weak grid[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2553-2566.
[25] Cespedes M, Sun Jian. Adaptive control of grid- connected inverters based on online grid impedance measurements[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 516-523.
[26] Zhou Shiying, Zou Xudong, Zhu Donghai, et al. An improved design of current controller for LCL-type grid-connected converter to reduce negative effect of PLL in weak grid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(2): 648-663.
[27] Li Yang, Shuai Zhikang, Liu Xuan, et al. Stability analysis and location optimization method for multiconverter power systems based on nodal admittance matrix[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 529-538.
[28] Cao Wenchao, Ma Yiwei, Wang F. Sequence- impedance-based harmonic stability analysis and controller parameter design of three-phase inverter- based multibus AC power systems[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7674-7693.
[29] Chen Xin, Zhang Yang, Wang Shanshan, et al. Impedance-phased dynamic control method for grid- connected inverters in a weak grid[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 274-283.
[30] 高家元, 涂春鸣, 肖凡, 等. 弱电网下基于SISO阻抗模型的LCL滤波并网逆变器在不同域下的稳定性差异分析[J]. 中国电机工程学报, 2022, 42(18): 6777-6789.
Gao Jiayuan, Tu Chunming, Xiao Fan, et al. Analysis of stability differences of LCL-filter grid-connected inverters in different domains based on SISO impedance model in weak grids[J]. Proceedings of the CSEE, 2022, 42(18): 6777-6789.
[31] 高家元, 赵晋斌, 陈晓博, 等. 弱电网条件下基于阻抗的稳定性判据重塑[J]. 电网技术, 2017, 41(9): 2762-2768.
Gao Jiayuan, Zhao Jinbin, Chen Xiaobo, et al. Reconstruction of impedance-based stability criteria in weak grid[J]. Power System Technology, 2017, 41(9): 2762-2768.
Abstract The interaction between grid-connected inverter (GCI) and grid impedance under a weak grid easily induces system instability, threatening the safe and reliable operation of new energy power generation. At present, the method for optimizing and adjusting the parameters of the control loop is widely used to improve the stability of the GCI under a weak grid because of its simple operation and non-auxiliary control loop. The equivalent current source is defaulted to stable when using the impedance model. However, the actual situation is likely to induce instability in the equivalent current source, which leads to the failure of the impedance analysis method and restricts wide applications.
Therefore, the multiple-input multiple-output impedance model of GCI controlled in the dq domain is converted into the impedance form of single-input single-output by equivalent transformation. Then, through impedance transfer and remodeling, the controller parameters in the equivalent current source are transformed into the equivalent output impedance model of GCI, and the impedance loop caused by the phase-locked loop (PLL) is converted to the grid side to characterize the negative impact of the PLL. The impedance modeling method realizes the decoupling between the equivalent current source and the control loop parameters. Under the control loop parameter adjustment, the stability of the equivalent current source can be ensured, and the problem for the stability analysis of GCI is solved.
A stability improvement method of control-loop parameter adaptive adjustment based on proportional weight is proposed. The proportional weight coefficient is analyzed and designed, which ensures that the GCI has a sufficient stability margin of more than 30°in the weak grid range. Meanwhile, the stability analysis and simulation verification are carried out with a short circuit ratio of 2 and 20% detection error. The results show that the adaptive control method can promote the GCI to maintain good steady-state and dynamic performance despite grid impedance detection error. It is worth mentioning that the stable operation of the GCI can be maintained when SCR is equal to 1, although the stability margin of the GCI system is insufficient.
The following important conclusions can be drawn. (1) The proposed impedance model with decoupling control loop parameters can analyze and judge the stability of GCI without checking the stability of equivalent current sources, regardless of whether the control loop parameters are adjusted. (2) A control loop parameter adaptive adjustment GCI stability improvement method is proposed based on proportional weight, and the proportional weight coefficient is analyzed and designed in detail. The proposed adaptive control method under the setting parameters significantly improves GCI’s adaptability to weak grids. Meanwhile, the stable operation of GCI can still be maintained with detection errors of grid impedance.
keywords:Weak grid, grid-connected inverter, controller parameter decoupling, adaptive control, stability margin
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.232043
国家自然科学基金重点基金项目(52130704)和国家自然科学基金面上项目(52077072)资助。
收稿日期 2023-12-07
改稿日期2024-01-17
高家元 男,1991年生,讲师,研究方向为电力电子技术、分布式发电和逆变器控制技术。E-mail: Jiayuan_gao@163.com(通信作者)
黄 帅 男,2001年生,硕士研究生,研究方向为新能源发电及逆变器控制与稳定性分析技术。E-mail: huangshuai02223@163.com
(编辑 陈 诚)