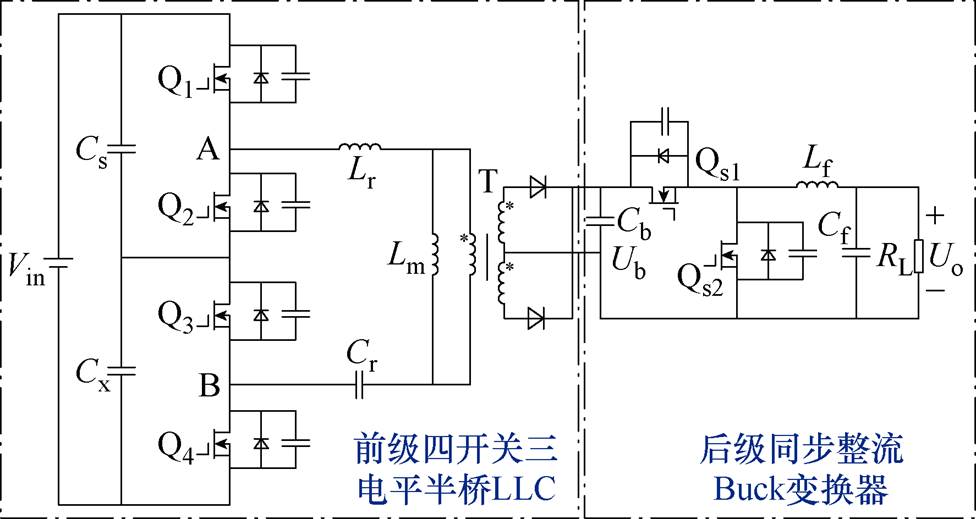
图1 两级式半桥三电平LLC变换器拓扑结构
Fig.1 Diagram of the cascaded half-bridge three-level LLC Converter
摘要 四开关三电平半桥LLC变换器在宽电压范围输入场合应用时具有突出优势。该文首先分析该变换器在定频双模式控制下的工作模态,基于变换器输出增益提出一种模式软切换控制策略,有效地抑制了模式切换过程中的暂态电流过冲现象;进而提出一种均压策略,抑制了输入侧电容电压不均衡现象。为了提升四开关三电平半桥LLC变换器的变换效率,建立变换器损耗模型,并采用布谷鸟搜索算法对变换器的谐振参数进行智能寻优,得到了最优参数。最后,研制了一台500 W的原理样机,验证了所提出控制策略和参数优化方法的正确性和有效性。
关键词:四开关三电平半桥LLC 模式软切换 效率优化 谐振参数 布谷鸟搜索算法
随着多电/全电飞机技术的快速发展,机载用电设备显著增加。冲压空气涡轮(Ram Air Turbine, RAT)是飞机在发动机停车、辅助动力系统失效时的应急动力来源,是保障飞机安全着陆的最后一道防线。受冲压空气涡轮的宽转速变化影响,永磁发电机的输出电压幅值和频率均在宽范围内变化,如线电压有效值变化范围为30~160 V,输出电压频率为500~2 900 Hz。由于大部分机载应急电子设备均为直流电压供电,因此需要将交流电整流为直流电,并经过直流/直流变换后才能使用。可见,对于直流变换器而言,其输入电压范围极宽,常规的隔离型直流变换拓扑难以在如此宽的输入电压范围内稳定且高效的运行。
除了飞机应急电源等宽转速发电应用场景,在航天器太阳能阵列、光伏发电等诸多领域中也存在宽电压范围的类似情况。譬如,光伏阵列受光照强度和温度的影响,其输出特性较软,输出电压也在较宽的范围内变化。因此,研究一款能够适用于超宽输入电压范围的高效率直流变换器及其软开关控制策略,具有非常重要的实际工程意义。
目前,国内外学者已提出了诸多适用于宽电压范围输入的直流变换器拓扑及控制策略。其中,LLC谐振变换器无需额外的辅助电路便可在全范围内实现软开关[1-4],具有运行效率高、结构简单等优点,得到了广泛应用。但是,在输入电压宽范围变化时,变换器的开关频率或占空比会随着输入电压的变化而宽范围变化,造成变换器损耗增加、功率传输效率下降、输入电流纹波变大,以及磁性元器件和控制参数难以优化设计等一系列问题[5-9]。因此,为了提升LLC谐振变换器的工作效率和运行性能,国内外学者重点从拓扑结构及控制、参数优化设计两方面对其进行了深入研究。
首先,在拓扑与控制策略优化方面,文献[10]在传统全桥LLC变换器的基础上,将开关管与变压器一次侧电感进行复用。变换器存在Boost储能、Flyback和LC谐振三种模态,可同时提高工作效率与功率密度。文献[11]提出一种4倍电压增益的变压器串联型LLC谐振变换器,可通过额外控制辅助开关管的开通与关断来改变输出增益,同时减小谐振电流。文献[12]针对宽范围输入的高压场合,将斩波移相(Chopping Plus phase-Shift, CPS)控制应用于桥式LLC变换器当中,变换器可运行在三电平模式或两电平模式。采用CPS控制后,变换器中斩波功率管与超前功率管均可在较宽的负载范围内实现零电压开通,同时也能抑制输入输出电流中高频信号,减小滤波器体积。综合来看,现有方法在实现宽电压增益时相对比较复杂,对于工程实现不够友好。
为了提高LLC变换器的效率,参数优化也极为重要[13-16]。文献[13]采用基波分析法建立了变换器谐振腔模型,在此基础上推导了电压增益表达式,得到了峰值电压增益曲线,并对变换器的品质因数、励磁电感与谐振电感比值等关键参数进行了优化设计,实现了特定电压增益范围内开关器件的导通损耗最小化;文献[14]在分析LLC谐振直流变压器工作原理的基础上,推导了电路损耗与开关管驱动信号死区时间的定量关系,提出了一种死区时间和励磁电感的参数优化设计方法,提高了样机的工作效率。文献[15]采用时域分析法推导了三电平LLC谐振变换器关断损耗与变换器参数的定量关系,在此基础上,采用了粒子群优化(Particle Swarm Optimization, PSO)算法并以变换器关断损耗为目标函数优化了变换器参数值。实际中,LLC谐振变换器的一些关键参数存在相互耦合,如谐振电感与谐振电容。因此,变换器的效率受到诸多因素的制约,需要兼顾多个参数进行综合优化。
目前,参数优化求解算法众多,其中布谷鸟搜索(Cuckoo Search, CS)算法是2009年由英国剑桥大学的Yang Xinshe等[17]提出的一种新颖的仿生进化群算法,主要依据布谷鸟的巢寄生育雏行为和levy飞行搜索原理,可以对存在不可导点的目标函数进行优化求解。CS算法具有参数少、模型简单、收敛速度快、全局搜索能力强、最优求解精度更高等优点,且求解过程中不会出现局部最优的局 面[17]。经过大量函数测试结果表明该算法在许多方面性能要优于遗传算法和粒子群算法。因此,CS算法得到了非常广泛的关注和应用[19-20]。
本文结合宽输入电压范围的应用需求,采用两级结构,如图1所示。前级为四开关三电平半桥LLC谐振变换器,工作在开环状态,以固定其谐振腔输入电压频率,便于变换器参数优化、降低损耗。后级采用同步整流Buck电路。针对前级LLC变换器,提出了一种模式软切换控制策略,可有效抑制模式切换过程中的电流过冲现象。同时,提出了一种均压策略,抑制了输入侧电容电压的不均衡现象。建立了LLC变换器损耗模型,采用CS算法对三电平半桥LLC谐振变换器的谐振参数进行智能寻优,得到了最优参数。最后,设计研制了一台功率为500 W的实验样机,验证了所提控制策略和优化设计方法的有效性。

图1 两级式半桥三电平LLC变换器拓扑结构
Fig.1 Diagram of the cascaded half-bridge three-level LLC Converter
针对输入直流电压为80~400 V,输出电压为28 V的实际需求,若采用单级LLC变换器,其开关频率必然会在很宽的范围内变化,不利于磁性元器件的优化设计,同时也会增加损耗,难以实现高效率和高功率密度。为此,本文考虑采用两级式结构,即前级四开关三电平半桥LLC和后级同步整流Buck。前级LLC变换器采用开环定频控制,运行在DCX模式。为最大程度地减小开关损耗,令谐振腔输入电压频率近似为谐振频率,谐振网络电压增益近似为1。并采用了两种软开关控制模式,通过模式切换使图1中的中间母线(即LLC输出)的变化范围缩小一半,以减小后级Buck输入电压的变化范围。
如图1所示,四开关三电平半桥LLC谐振变换器包含四个开关管,其中Q1、Q2和Q3、Q4分别组成两对半桥桥臂。为了方便分析三电平半桥LLC的工作原理,可按如下规则定义开关管的状态
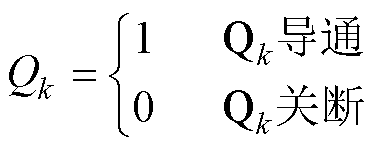 k=1, 2, 3, 4 (1)
k=1, 2, 3, 4 (1)
为了保证电路正常工作,必然需要两个开关管处于同时导通状态。考虑到同一半桥桥臂的开关管不能同时导通,可以得到谐振腔输入电压UAB与开关管状态的对应关系,见表1。
由表1可知,不同的开关管开关状态对应不同的谐振腔输入电压。通过合理分配四个开关管的开关状态的顺序,可以得到不同的谐振腔输入电压的波形(VAB)。根据开关管的开关状态组合不同,可以有两种不同的控制模式,分别是同相控制模式和交错控制模式。
表1 三电平LLC开关状态对应的谐振腔电压
Tab.1 Voltage of resonant tank with different switch states
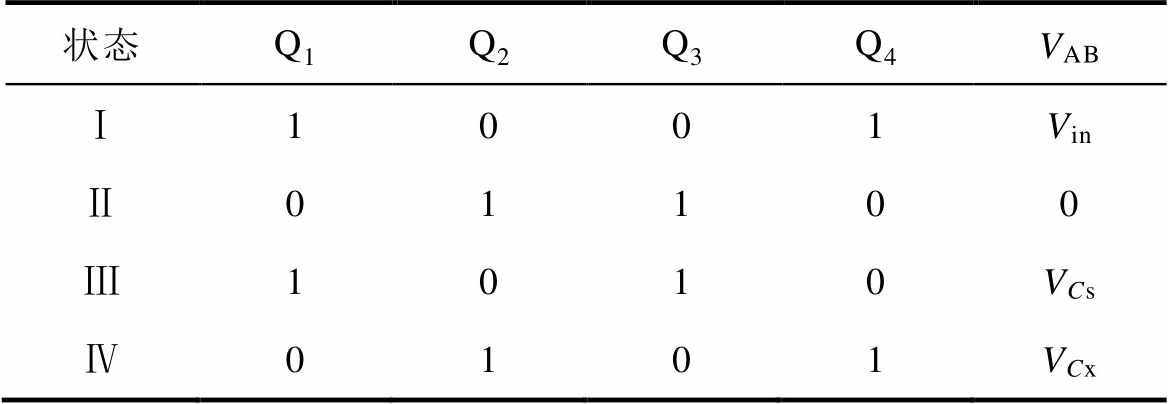
状态Q1Q2Q3Q4VAB Ⅰ1001Vin Ⅱ01100 Ⅲ1010VCs Ⅳ0101VCx
1)同相控制模式
在此模式下,给Q1/Q4和Q2/Q3提供占空比为0.5的相同驱动,Q1与Q2、Q3与Q4互补导通。如图2a所示。此时变换器的开关状态顺序为Ⅰ—Ⅱ—Ⅰ交替进行,谐振腔输入电压VAB存在0和Vin两种电位,输入电压的利用率最高,且谐振腔输入电压VAB的频率与开关频率相同。此模式下变换器的输入输出电压关系为
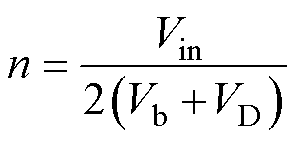 (2)
(2)
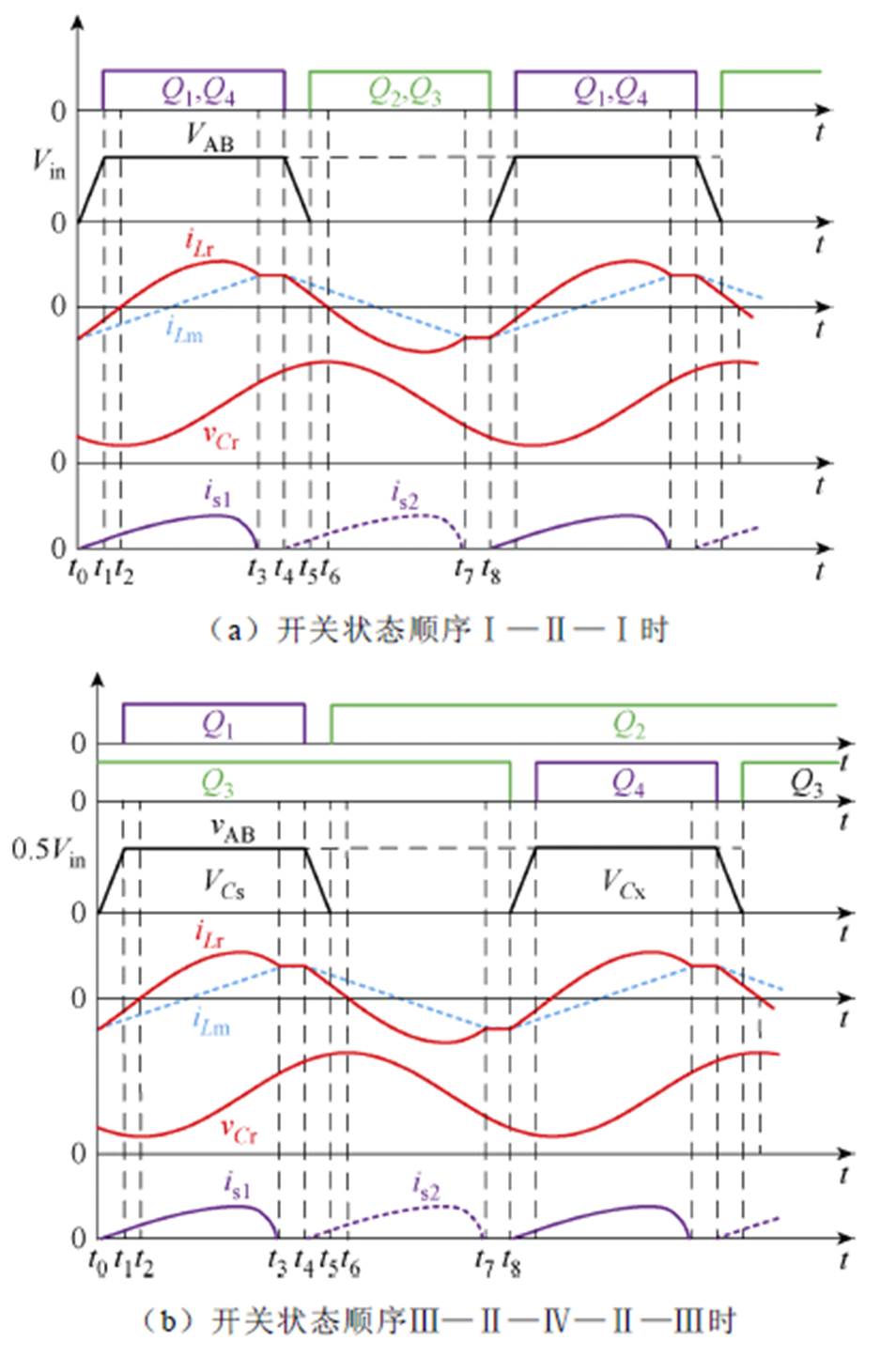
图2 不同控制模态下的开关状态顺序
Fig.2 Switching state sequences of different control mode
式中,Vb为中间母线电压,即LLC的输出电压;VD为LLC二次侧整流二极管的导通压降。
2)交错控制模式
在此模式下,Q1、Q4开关管的占空比为0.25,且保持Q1与Q4、Q2与Q3的占空比相同,但移相180°,Q1与Q2、Q3与Q4互补导通,如图2b所示。此时变换器按Ⅲ—Ⅱ—Ⅳ—Ⅱ—Ⅲ的开关状态顺序重复运行。假设VCs=VCx=Vin/2,则谐振腔的输入电压VAB存在0和Vin/2两种电位。此时的谐振腔输入电压VAB的频率是开关频率的两倍。在交错控制模式下,若维持谐振腔输入电压的频率不变,则开关管的开关频率可降低一半,可有效减小开关损耗。
在交错控制模式下,变换器的输入输出电压关系为
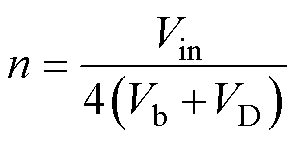 (3)
(3)
对比两种控制模式不难发现,同相控制模式的输出电压增益大,适用于输入电压较低的场合,而交错控制模式的电压增益小,更适用于高压输入的场合。根据输入电压的高低,通过上述两种控制模式的切换,可以将三电平LLC变换器的输出电压变化范围缩小一半。
考虑到实际电路中LLC输入电压会有所波动,且电压采样可能受到干扰,为防止控制模式频繁来回切换,采用迟滞比较方式来进行控制模式的选取。如图3所示,若变换器初始运行于同相控制模式,当输入电压高于200 V时切换为交错控制模式;反之,若变换器初始运行于交错控制模式,当输入电压低于190 V时切换为同相控制模式。
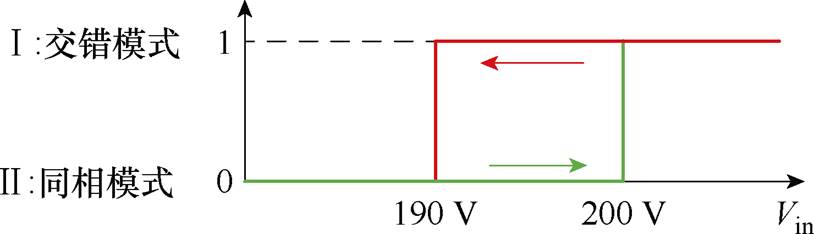
图3 控制模式迟滞比较选择
Fig.3 Hysteresis control method of mode selection
基于上述控制策略,四开关三电平半桥LLC谐振变换器磁性元件的设计和损耗分析,可以按照输入电压较低时的开关频率设计,减小了因开关频率变化范围过宽而导致的较大损耗。同时,得益于采用模式切换控制后LLC变换器输出电压范围的收窄,后级Buck电路也更易得到优化设计。
由前述分析可知,为了降低输入电压范围较宽时LLC谐振变换器的输出电压,可以采用开环定频双模式控制,根据输入电压大小在两种控制模式之间来回切换。由式(2)和式(3)可知,当控制模式发生切换时,变换器的输入输出电压关系将发生明显变化。例如,当LLC变换器从交错控制模式切换到同相控制模式时,变换器的开关频率增加一倍,电压增益也增大了一倍,即前级LLC的输出电压Vb增加一倍。但是,在实际电路中,由于输出滤波电容和谐振腔的存在,变换器是一个高阶系统,在模式切换瞬间,输出电压必然会出现振荡和暂态冲击,如图4所示。
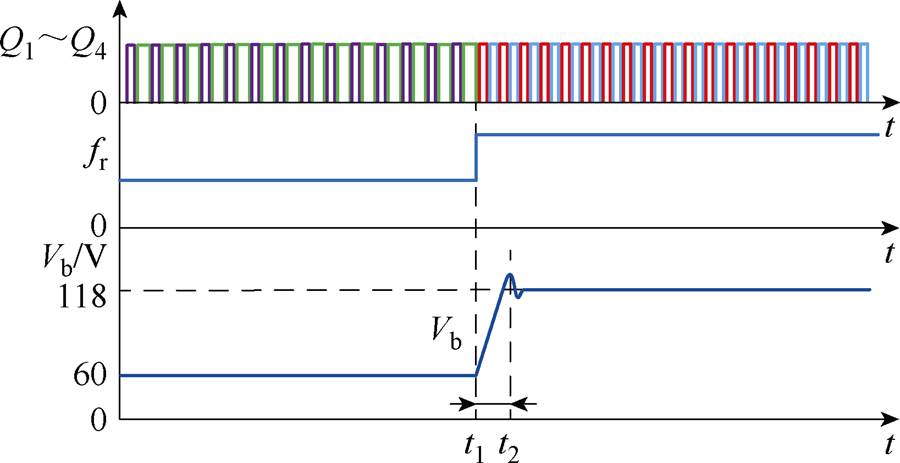
图4 控制模式硬切换波形
Fig.4 Waveforms of control mode hard switching
图5给出了采用双模式切换控制方法后,变换器输出电压随输入电压的变化曲线。可以看出,在输入电压的切换点附近和最大与最小值之间切换时,输出电压的变化范围最大,意味着切换过程的暂态冲击和振荡现象越严重;反之,如果输入电压在图5的A、B两点之间切换,因为输出电压刚好相同,此时的暂态问题最小。
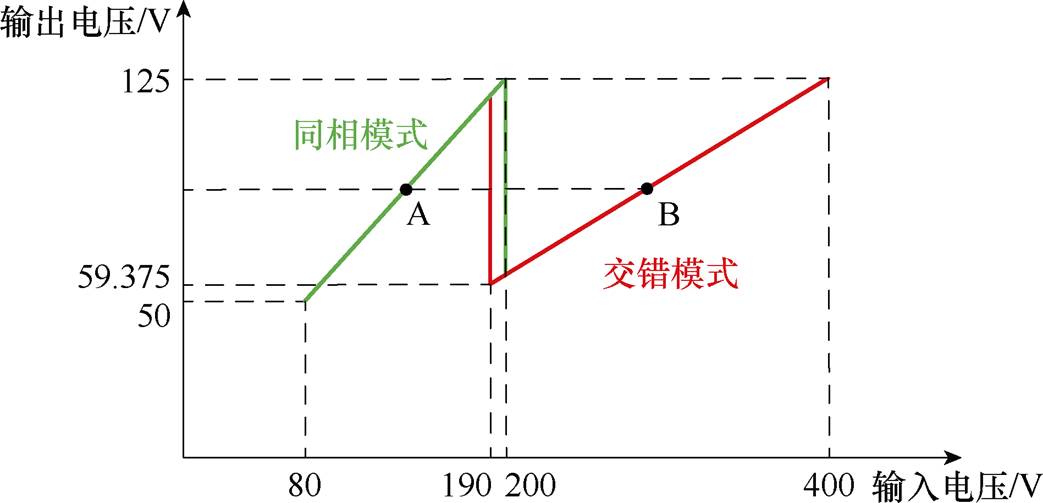
图5 输出电压与输入电压关系曲线
Fig.5 Relationship curves between Vo and Vin
进一步地,可写出电容电压与电流的关系,有
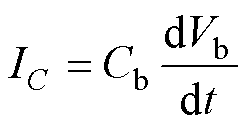 (4)
(4)
由式(4)可知,当输出滤波电容电压变化率越大,其所需要的短时充电电流也越大,即变压器二次侧的输出电流越大,意味着折合到一次侧的谐振电流也会变得很大。
因此,考虑图5中最严重的暂态切换过程,选取输入电压从190 V切换到180 V时进行了初步的仿真验证。图6给出了仿真电压电流波形,仿真参数与第四部分表3所给的实验参数一致。可以看出,当变换器从交错模式切换到同相模式时,变换器谐振腔的谐振电流会产生很大的瞬时过电流,电流峰值高达110 A,约为正常运行时的5倍。如此大的冲击电流,势必会造成变压器磁心饱和或者功率器件损坏,严重威胁变换器的可靠性。可见,双模式直接切换方法无法直接使用。
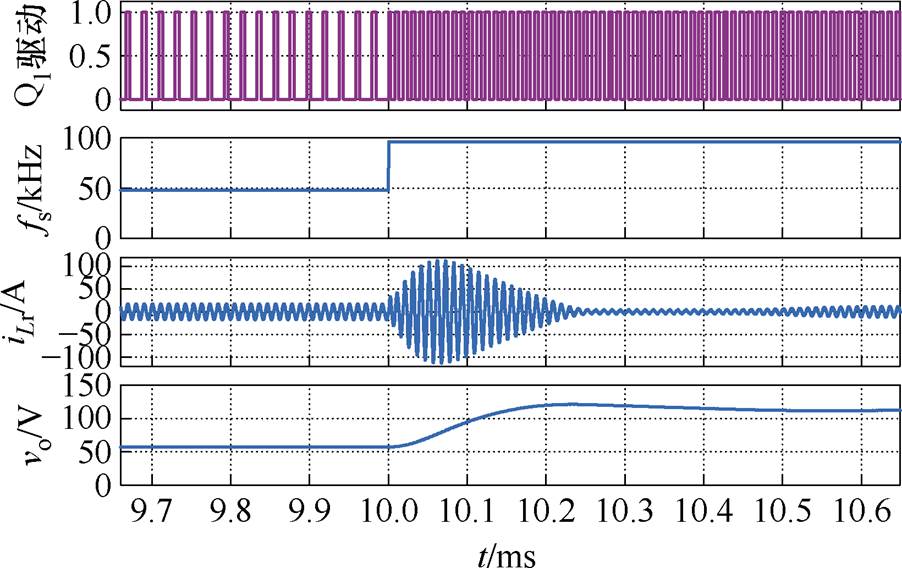
图6 控制模式硬切换仿真波形
Fig.6 Simulation waveforms with hard switching control strategy
采用基波分析法对变换器进行建模,可得其在两种控制模式下的输出电压增益为
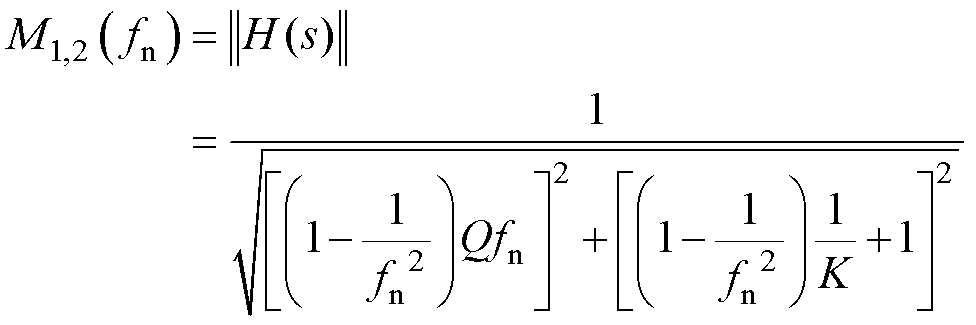 (5)
(5)
其中
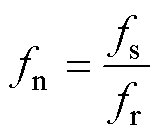 (6)
(6)
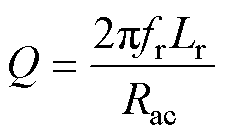 (7)
(7)
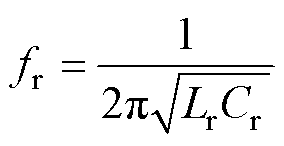 (8)
(8)
式中,Rac为LLC整流网络输出侧折合到变压器一次侧后的等效电阻。
对增益特性进行分析可知,当变换器其余参数都确定后,变换器输出电压增益的变化与归一化频率fn的变化成反比状态。其归一化频率越大,谐振网络输出电压增益越低。因而在控制模式切换时,可考虑对开关频率作短时的变化。例如,在切换瞬间,先降低变换器谐振网络输出增益,使得输出电压基本保持不变,然后再缓慢增加输出电压增益使其恢复到正常值接近于1。对应的工作频率呈现先增大后降低的趋势,如图7所示。如此,可有效解决切换过程的暂态冲击,实现模式软切换。
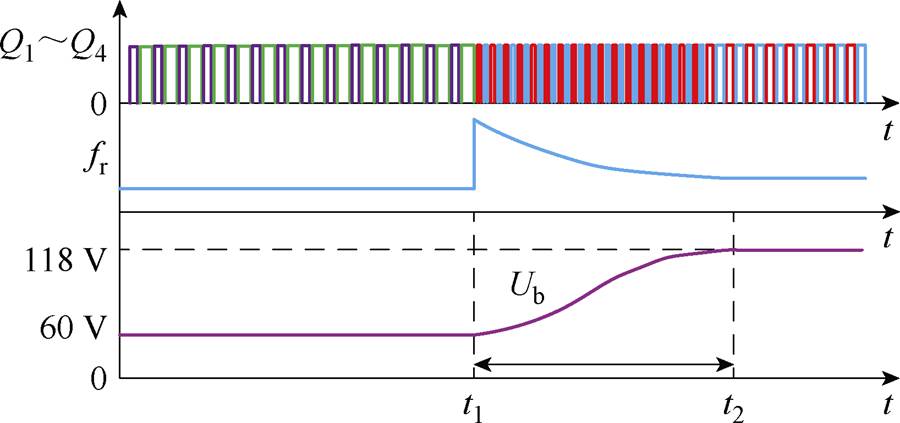
图7 控制模式软切换波形
Fig.7 Waveforms of control mode soft switching
仍然选取输入电压从190 V切换到180 V,即最严重的暂态切换过程进行仿真分析,结果如图8所示。不难看出,采用所提的软切换控制策略后,不再出现电压和电流的暂态冲击问题。在切换瞬间,开关频率也随之变化,即变换器的增益发生变化,使输出电压在切换瞬间维持原有输出不变。然后开关频率再缓慢减小,使输出电压在1.5 ms左右缓慢上升至稳态。对应的谐振电流也只有微小的增大,避免了过电流现象的产生,实现了软切换控制策略的设计目标。实际设计时,切换时长可以根据允许的最大谐振电流进行适当调节。切换过程越快,谐振电流越大。而且,只要确保最恶劣的两个暂态切换工况电流不过大,就可以保证全工况的安全运行。
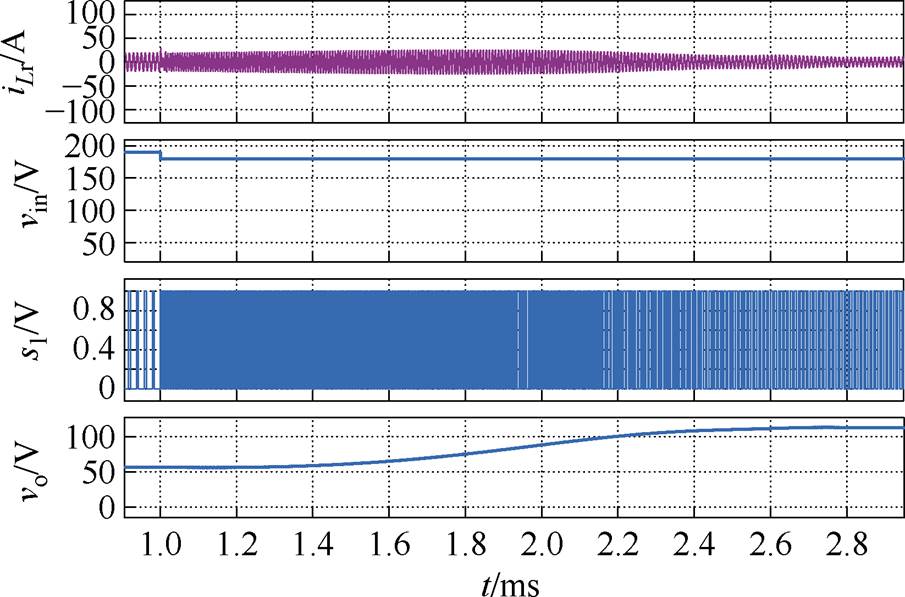
图8 采用软切换控制策略后的仿真波形
Fig.8 Simulation waveforms with soft switching control strategy
对于图1所示三电平半桥LLC变换器,由于存在母线电容和驱动脉宽不对称等非理想因素,实际运行时往往会造成输入母线分压电容电压不均衡,进而导致功率开关管的电压应力变大,失去原本三电平拓扑的优势,严重时甚至存在开关管过电压损坏等潜在风险。
以开关管驱动信号差异为例,分析其对输入母线电容电压不均衡影响结果。为简化分析,近似忽略死区时间。
在同相控制模式下,驱动信号相序实际中可能会出现滞后或超前的现象。以下桥臂滞后上桥臂为例,其波形如图9a所示,其中j 为滞后的相位。在t0~t1时间,谐振腔输入电压等于母线电容Cs的电压,谐振电流负向流通,电容Cs处于充电状态,两端电压逐步上升,电容Cx两端电压逐步下降;在t2~t3时间,谐振腔输入电压等于母线电容Cx的电压,谐振电流正向流通,电容Cx处于放电状态,两端电压逐步下降,电容Cs两端电压逐步上升。由此经过多个周期后,上、下母线分压电容电压逐渐呈现不平衡状态。
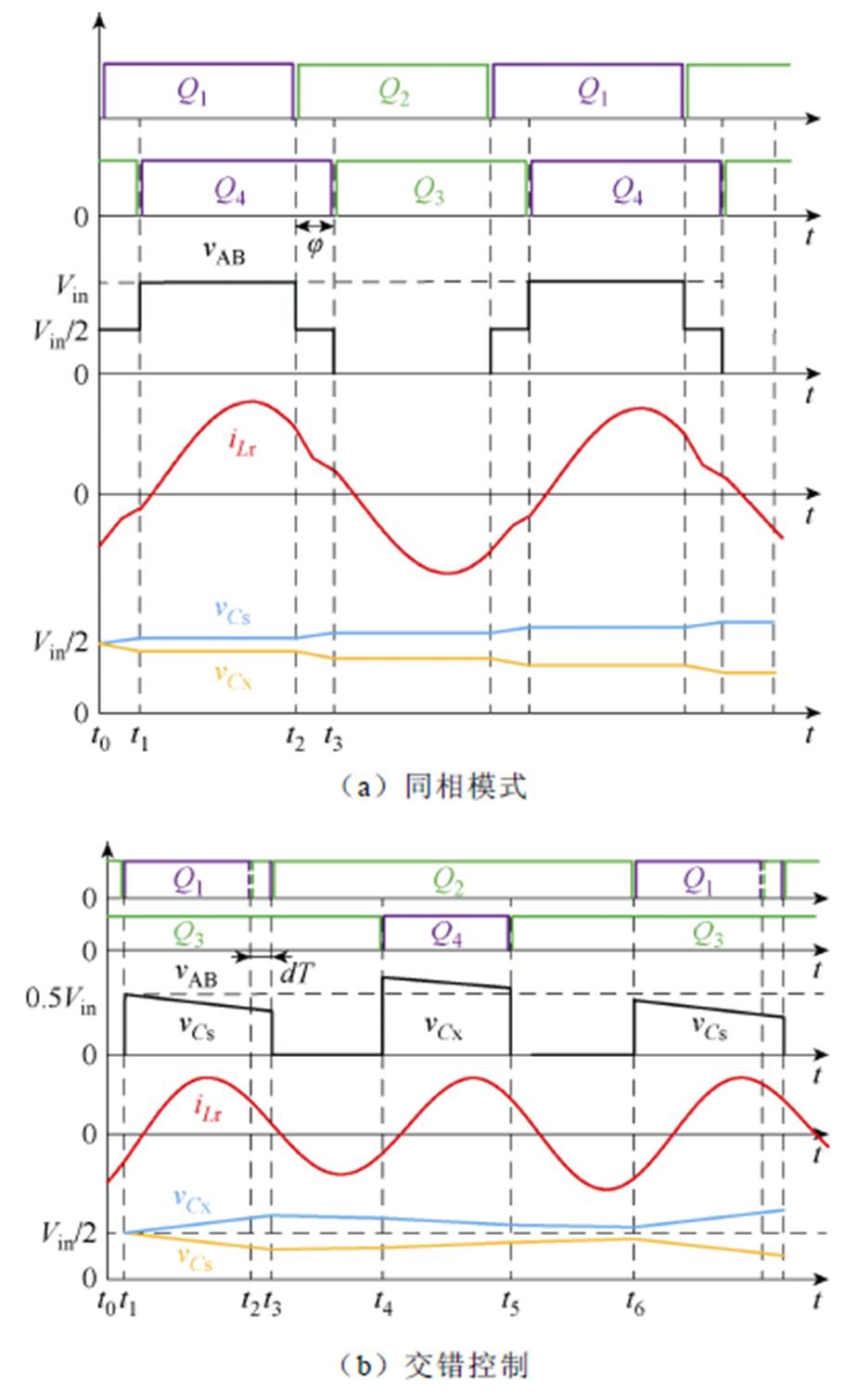
图9 驱动信号对输入电容电压的影响示意图
Fig.9 The impact of drive signal to the voltage of input split capacitor
图9b给出了交错模式下的工作示意图,其中d为驱动信号占空比超出部分,即Q1驱动信号占空比变大,Q2驱动信号占空比变小。类似地,受此影响,上、下母线电容在每个开关周期内电压变化量不等于0,其两端电压逐渐偏离输入电压的一半。
图10给出了两种控制模式下在驱动发生移相或者不对称时的仿真波形。可以看出,两种控制模式下母线电容电压都会产生比较严重的不均衡现象。
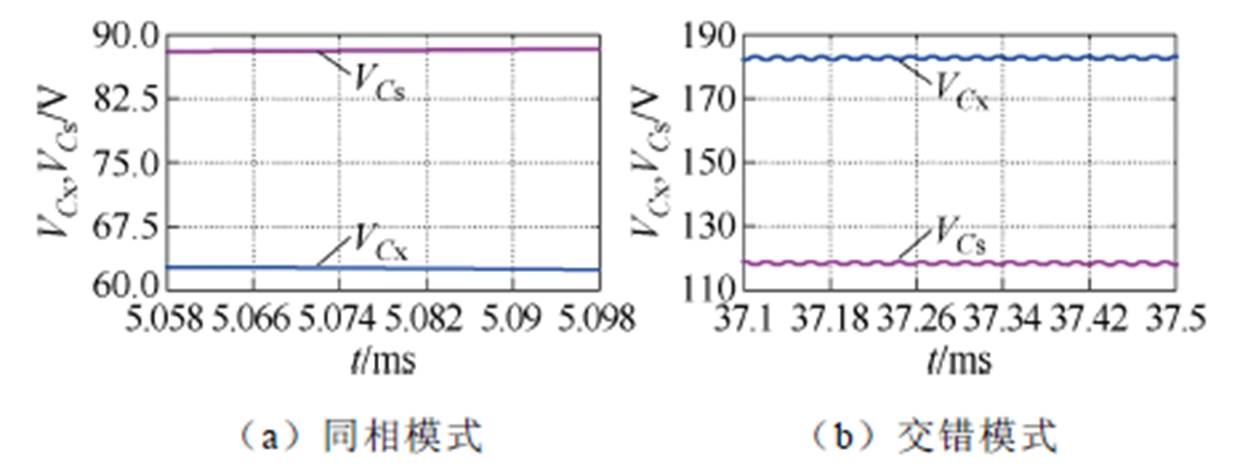
图10 电容电压不均压波形
Fig.10 Voltage waveforms of the split capacitor
由上述分析可知,在两种控制模式下,开关管驱动信号的相位与占空比大小差异均会影响到输入母线分压电容电压的平衡。因而可利用上述规律对电容电压不均衡进行调节,同相控制模式下,调节驱动信号的相位;交错控制模式下,调节驱动信号的占空比。基于该思路,提出了变换器输入母线分压电容电压均压控制方法,如图11所示。
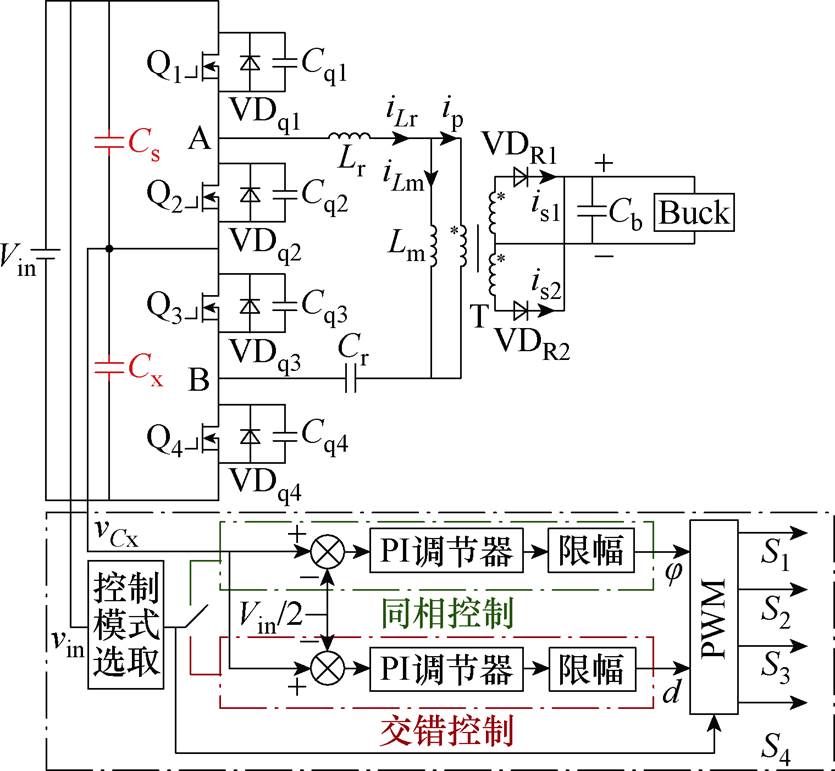
图11 输入母线分压电容电压均压控制框图
Fig.11 Block diagram for voltage sharing control of input bus voltage split-capacitor
为了尽可能地提高LLC变换效率,需要对其关键参数进行优化设计。为此,首先要建立其损耗模型,分析变换器损耗与关键参数之间的量化关系。通常,变换器的总损耗包含一次侧开关管与二次侧整流二极管的损耗、变压器损耗、谐振腔损耗。
2.1.1 一次侧开关管与二次侧整流二极管损耗
一次侧开关管与二次侧整流二极管的损耗主要由开关损耗和导通损耗组成。由于半桥三电平LLC谐振电路实现了全输入电压范围下的一次侧开关管的零电压开通以及二次侧整流二极管的零电流关断。因此一次侧开关管的开通损耗可以忽略不计,只考虑其导通损耗与关断损耗即可。导通损耗和关断损耗分别为
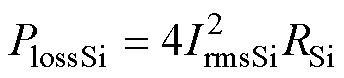 (9)
(9)
 (10)
(10)
式中,IrmsSi为一次侧开关管电流的有效值;RSi为开关管的导通电阻;IoffSi为一次侧开关管关断电流值;fs为开关频率;tr和tf为分别为开关管电压与电流的上升和下降时间。
而二次侧整流二极管只考虑其导通损耗即可,即
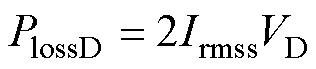 (11)
(11)
式中,Irmss为二次绕组电流的有效值。
2.1.2 变压器损耗
通常,变压器损耗由磁心的铁损和绕组的铜损组成。其中,铜损主要是由一次绕组和二次绕组上的等效直流电阻与等效交流电阻产生,而铁损则主要是由涡流损耗、磁滞损耗和剩余损耗三部分组成。对于磁心而讲,其铁损PlossFe可表示为
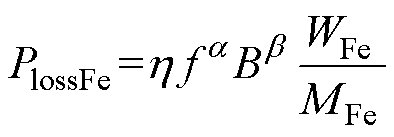 (12)
(12)
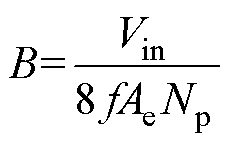 (13)
(13)
式中,h 为磁通波形系数;WFe为变压器磁心质量;MFe为变压器磁心密度;f为磁心的工作频率;a和b为指数常数,对铁氧体材料的磁心而言有h= 0.000 0384,a和b分别为1.63和2.62;Vin为输入电压;Np为变压器一次绕组匝数;Ae为变压器磁心有效截面积。
在高频工作场合,变压器绕组的铜损由交流电阻和直流电阻产生,可表示为
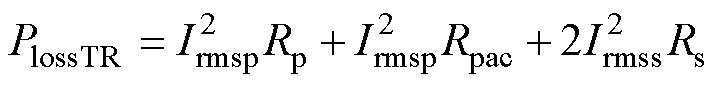 (14)
(14)
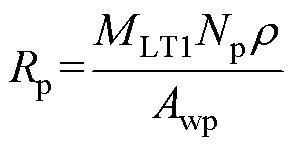 (15)
(15)
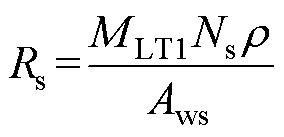 (16)
(16)
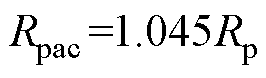 (17)
(17)
式中,Irmsp为一次侧谐振电流有效值;MLT1为变压器磁心截面周长;r 为铜的电阻率;Ns为变压器二次绕组匝数;Awp和Aws为一次、二次侧励磁线的截面积。
2.1.3 谐振腔损耗
LLC变换器的谐振腔由谐振电感与谐振电容组成,故谐振腔损耗同谐振电感与谐振电容直接相关。对谐振电感而言,其损耗与变压器相同,主要由铁损和铜损组成。铁损为
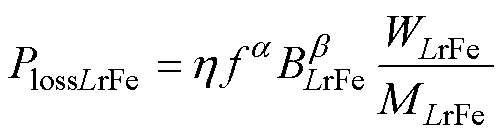 (18)
(18)
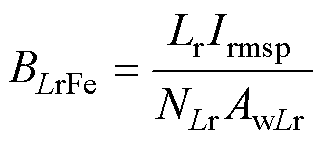 (19)
(19)
式中,WFeLr为谐振电感磁心质量;MFeLr为谐振电感磁心密度;Lr为谐振电感;NLr为谐振电感绕组匝数;AwLr为谐振电感励磁线的截面积。
铜损则表示为
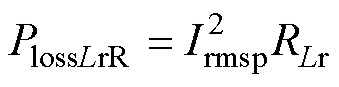 (20)
(20)
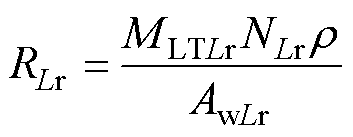 (21)
(21)
式中,MLTLr为谐振电感磁心的截面周长。
对谐振电容而言,其损耗主要集中在谐振电容的等效串联电阻ESRCr。
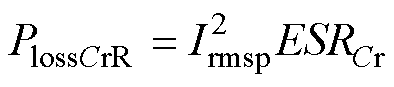 (22)
(22)
综上可知,变换器的总损耗可表示为
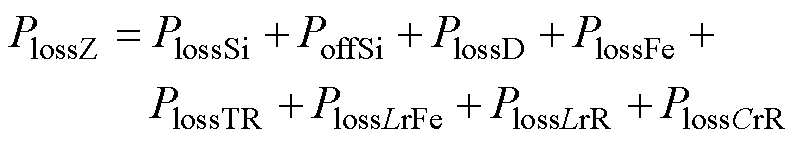 (23)
(23)
定义相对损耗率l 表示为变换器能量转换效率的高低。
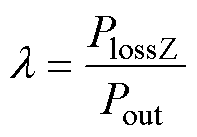 (24)
(24)
从式(24)可知,当变换器负载功率Pout一定时,总损耗PlossZ越小,相对损耗率越低,变换器效率越高。因此,在下文对变换器进行参数优化设计时,将以相对损耗率为优化目标,最大化地减小其相对损耗率。
根据上述理论损耗分析可知,三电平半桥LLC变换器的各部分损耗与Irmsp、Irmss、IrmsSi和IoffSi的大小均存在一定关系。
当变换器工作在欠谐振状态时即谐振腔输入电压频率略小于谐振频率时,其关键工作波形,即准谐振时一次电流与励磁电流波形如图12所示。
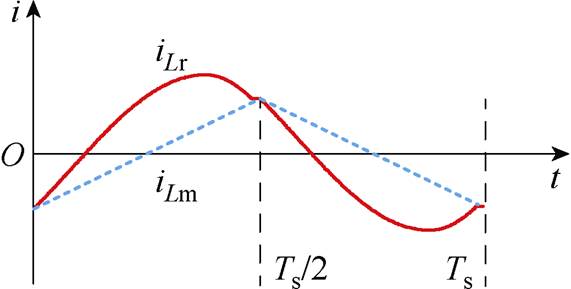
图12 准谐振时一次电流与励磁电流波形
Fig.12 Waveforms of primary current and excitation current in case of quasi resonance mode
从图12中可以看出谐振腔电流可近似为正弦波,其表达式为
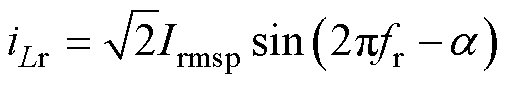 (25)
(25)
式中,a 为一次侧谐振电流的相位。
励磁电感电流近似为三角波,其表达式为
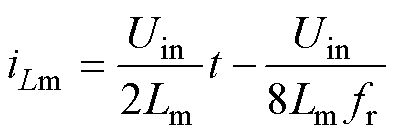 (26)
(26)
在半个开关周期内,谐振电流与励磁电流之差的平均值即为折算到一次侧的二次侧输出电流平均值为
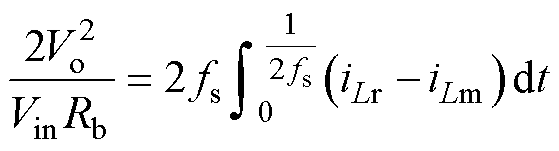 (27)
(27)
式中,Rb为LLC输出等效负载电阻,即Buck变换器输出侧折算到输入侧的等效电阻。
结合式(25)~式(27)可得谐振腔电流有效值为
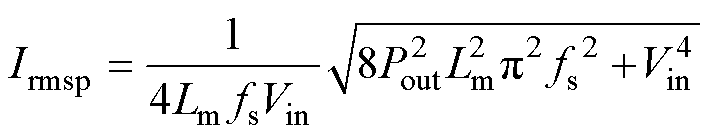 (28)
(28)
同理,可求出开关管导通电流有效值与变压器二次侧单个绕组的电流有效值为
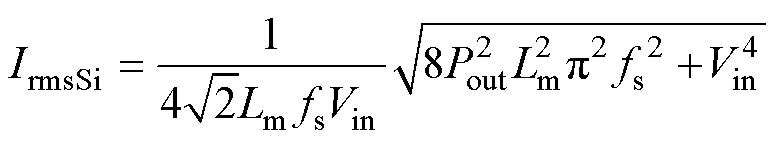 (29)
(29)
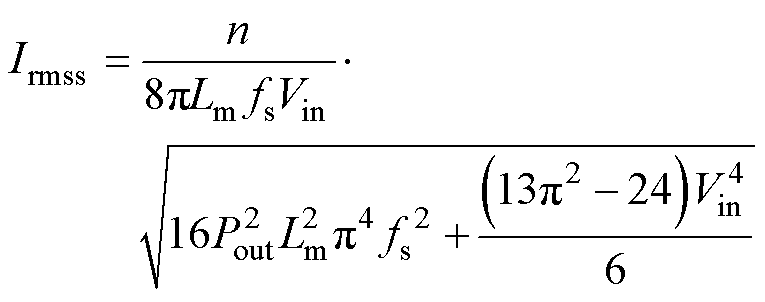 (30)
(30)
从图12中也可看出,开关管的关断电流与励磁电感电流峰值相等,大小为
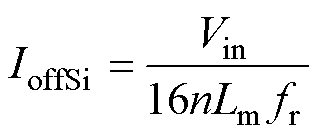 (31)
(31)
图13给出了谐振腔电流、开关管导通电流和关断电流以及变压器二次绕组电流的有效值与励磁电感Lm之间的关系。从图中可知,励磁电感增大后电路中各关键点电流随之减小,尤其是ioffSi的降低较为明显,有利于降低损耗,提升效率。不过,由图13也可以看到,在60 mH之后电感值的增大对电流的影响明显减弱,工程中选在60 mH左右较为合适。
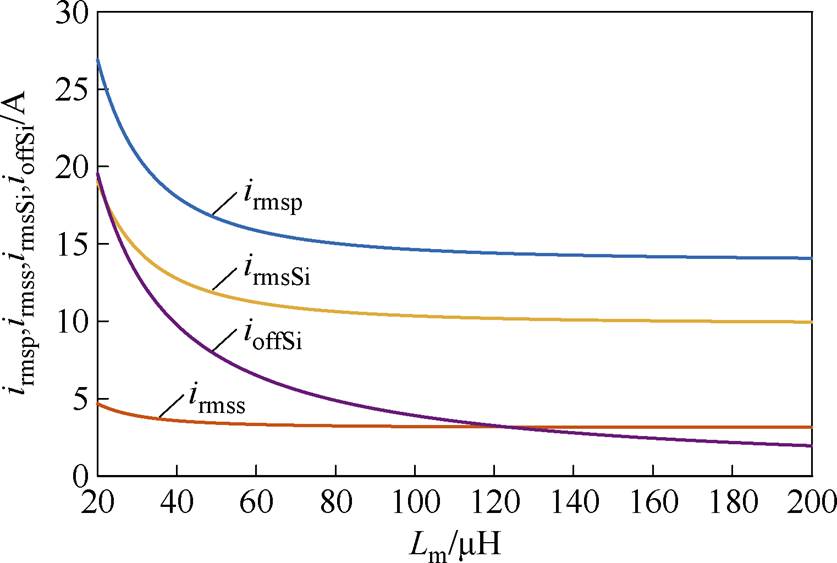
图13 关键点电流与励磁电感Lm的关系曲线
Fig.13 Relationship between key point current and excitation inductance Lm
从上述对变换器损耗以及各关键点电流的分析可知,仅靠优化单一的变换器某个参数并不能最大化地提高变换器的工作效率,因此效率优化的核心问题可表示为:在直流输入电压、谐振频率与额定负载已知时,寻找最优的谐振参数Lr、Lm以及Cr使变换器的相对损耗率最小。考虑到本文LLC变换器采用了开环定频双模式控制策略,因此当谐振频率与开关频率确定时,谐振电感或谐振电容两者取其一进行优化即可,因此可简化为对谐振参数Lr、Lm的优化设计。
而CS算法通过采用Levy飞行搜索方法以及模仿布谷鸟的寄生育雏行为来实现最优问题的求解。相对于其他寻优算法,CS算法具有诸多优点,因此下面将采用该算法对Lr、Lm进行优化求解。
为提高工作效率,定义变换器在不同工况下的相对损耗率为布谷鸟搜索算法的目标函数,即
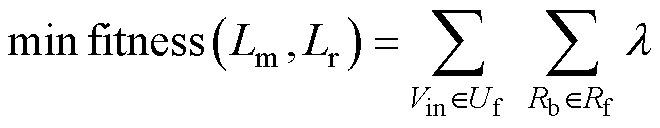 (32)
(32)
式中,Uf为直流输入电压Vin变化范围;Rf为负载电阻Rb变化范围。
3.2.1 变换器输出增益与工作频率约束条件
为便于磁性元器件的设计,提升变换器对宽范围输入电压的适应度,LLC变换器采用了开环定频双模式控制策略,则此时变换器需满足式(33)和式(34)的条件,即LLC输出增益与工作频率约束条件。
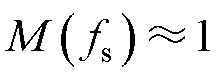 (33)
(33)
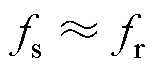 (34)
(34)
3.2.2 功率开关管实现ZVS约束条件
LLC谐振变换器在正常工作时谐振腔阻抗需呈感性状态以及iLr需在死区时间内将结电容的电压释放到0,并且iLr不能反向流通。即
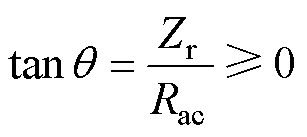 (35)
(35)
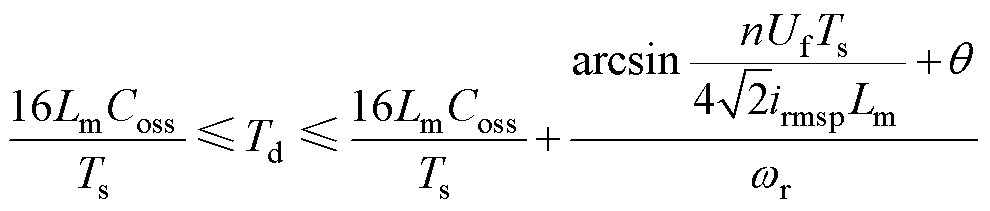 (36)
(36)
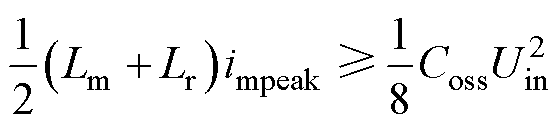 (37)
(37)
式中,Zr为谐振腔阻抗;Coss为功率器件的等效输出电容。
针对上述提出的算法目标函数以及约束条件,采用CS算法对变换器参数进行最优求解,其算法求解流程如图14所示。
根据图14,采用CS算法对变换器的谐振参数进行多次更新迭代后,可得到Lr、Lm以及Cr的优化结果,见表2。图15为CS算法优化流程中适应度函数随迭代次数k的变化曲线,从图中看出,随着迭代次数的变大适应度函数值逐渐减小,当k达到580次左右时,适应度函数值降低速率减缓,k达到600次时适应度函数值逐渐稳定。k越大,则变换器的参数优化求解会更加精准,但需要的时间越长。
为了进一步验证前文理论分析的正确性和可行性,研制了一台500 W的两级式DC-DC实验样机,前级为四开关三电平半桥LLC谐振变换器,其输入电压80~400 V,后级为Buck变换器,其输出电压28 V。表3给出了四开关三电平半桥LLC谐振变换器的主要电气参数。
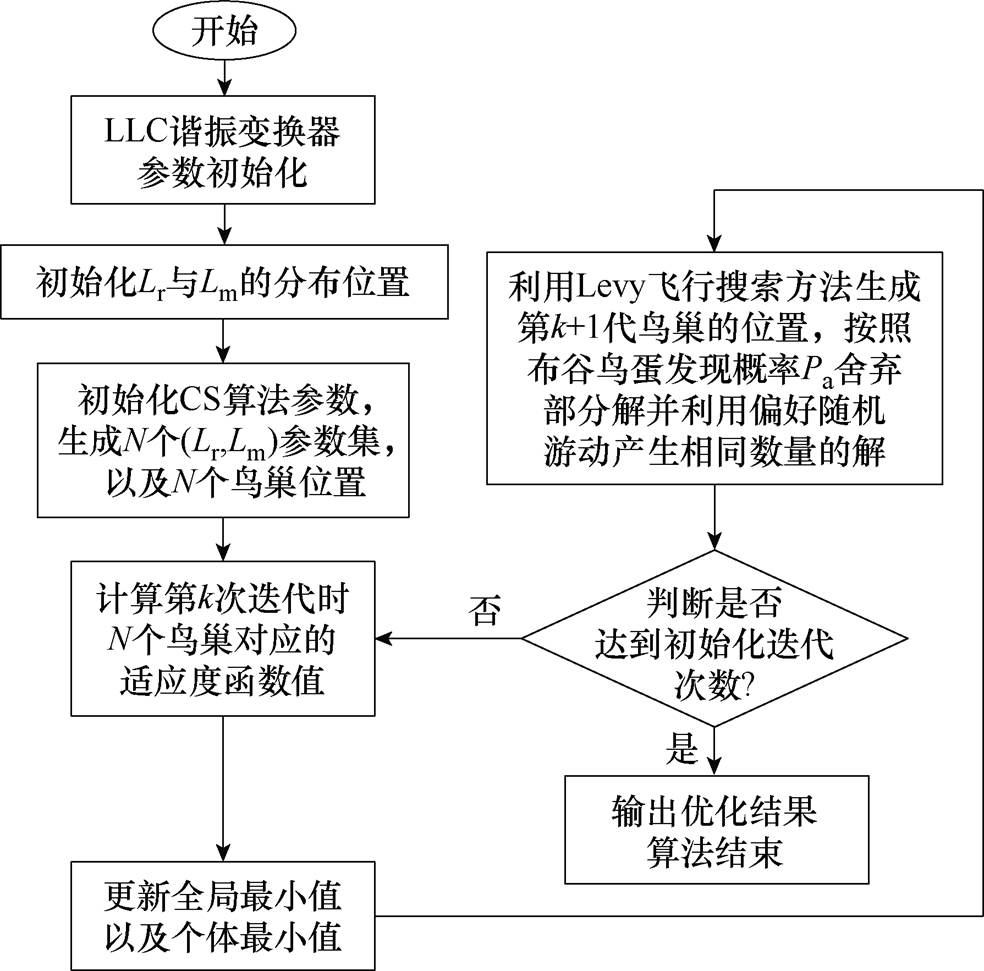
图14 布谷鸟搜索算法优化流程
Fig.14 Optimization flow chart of CS
表2 算法优化结果
Tab.2 Algorithm optimization results
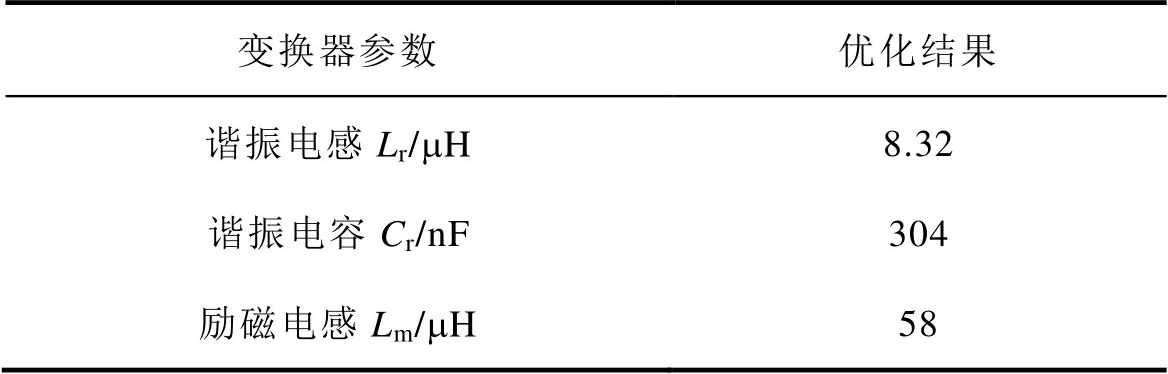
变换器参数优化结果 谐振电感Lr/mH8.32 谐振电容Cr/nF304 励磁电感Lm/mH58
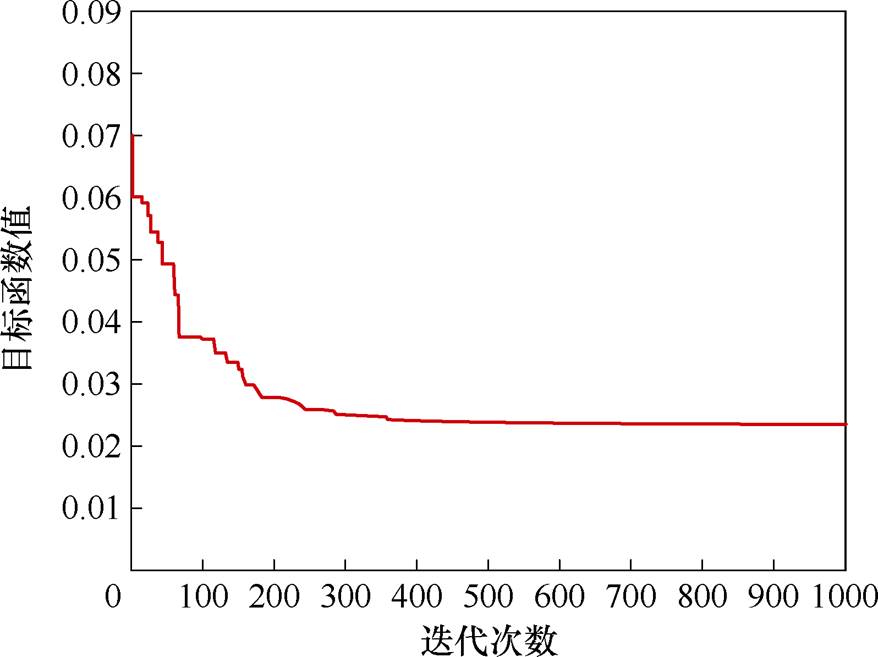
图15 适应度函数值随迭代次数变化曲线
Fig.15 Relationship curve between objective function and iteration number
图16和图17给出了输入电压分别为90 V和360 V时,LLC变换器满载运行时谐振腔输入电压vAB、谐振电流iLr、变压器二次电流it、开关管Q1、Q2驱动电压VQ1、VQ2及漏源驱动电压S1和S2的实验波形。由图可见,在两种输入电压下谐振电流波形都近似呈正弦状,谐振平台明显,LLC谐振变换器工作在欠谐振区域。开关管Q1、Q2的驱动来临前,其漏源电压就已经下降到零,实现了零电压开通;同时从输出电流波形可看出二次侧整流二极管也实现了零电流关断。由图16和图17可知,在90 V和360 V输入时,变换器分别工作于同相控制模式和交错控制模式下。在图16中,谐振腔输入电压vAB的频率等于开关频率;而在图17中,谐振腔输入电压vAB的频率等于开关频率的2倍,符合定频双模式的控制逻辑。
表3 LLC谐振变换器相关参数
Tab.3 Parameters of LLC resonant converter
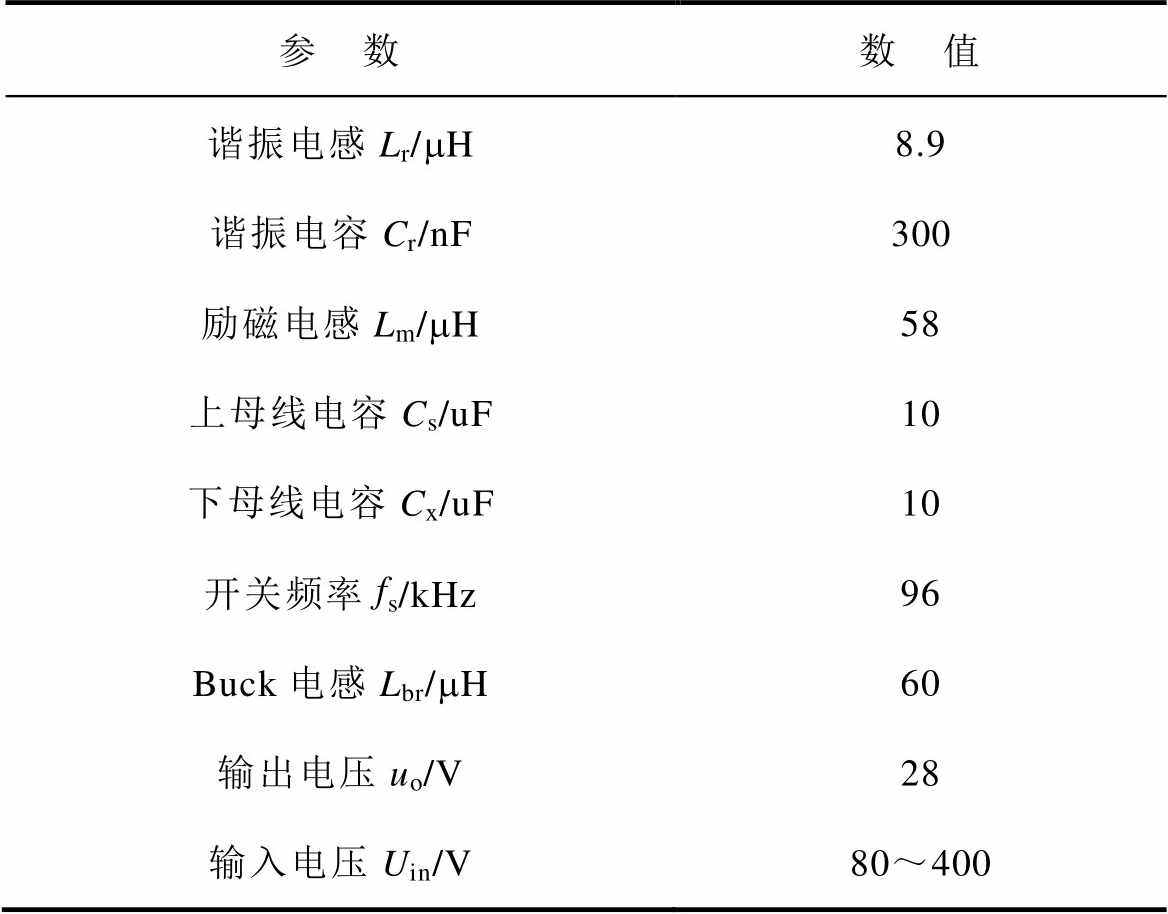
参 数数 值 谐振电感Lr/mH8.9 谐振电容Cr/nF300 励磁电感Lm/mH58 上母线电容Cs/uF10 下母线电容Cx/uF10 开关频率fs/kHz96 Buck电感L /mH60 输出电压uo/V28 输入电压Uin/V80~400
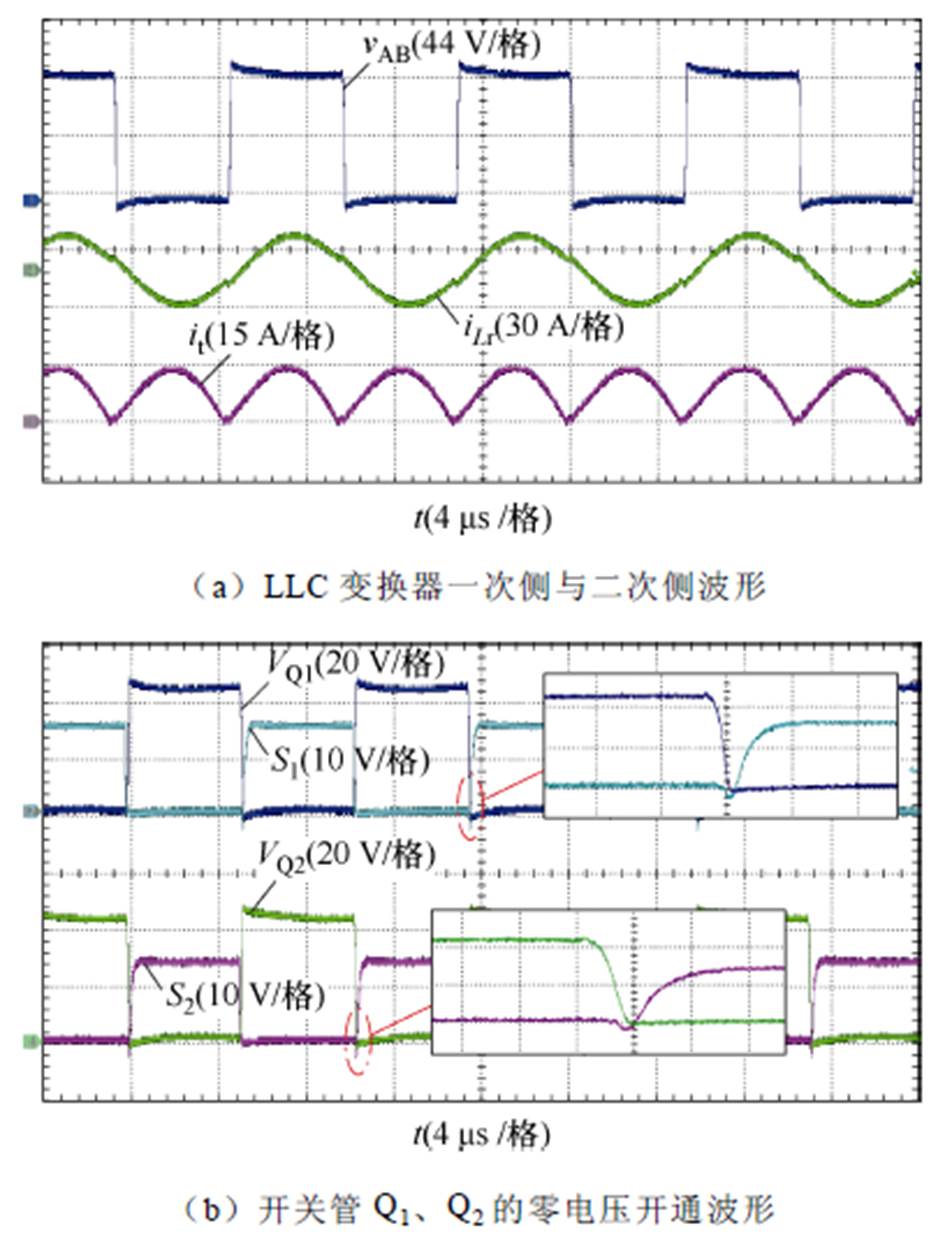
图16 变换器在90 V输入电压下稳态波形
Fig.16 Steady state waveforms of the LLC converter at 90 V input voltage
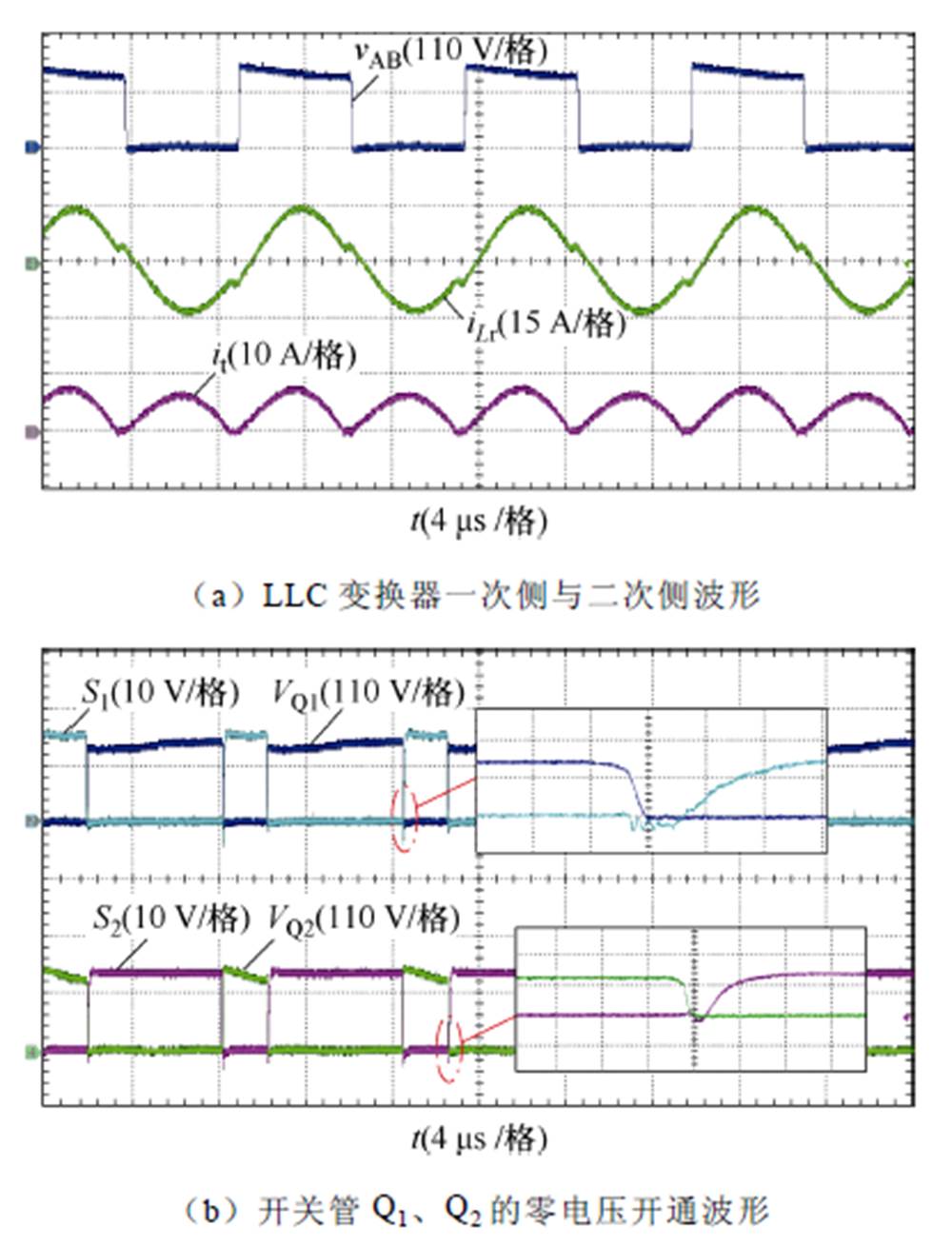
图17 变换器在360 V输入电压下稳态波形
Fig.17 Steady state waveforms of the LLC converter at 360 V input voltage
图18为加入软切换控制策略前后的实测波形。其中,图18a为未加入软切换策略且输入电压从190 V切换到180 V时LLC变换器的动态波形,可以看出,在切换瞬间出现了非常大的谐振电流尖峰,触发了过电流保护。图18b为加入软切换策略后的实测波形。从图中可知,当变换器控制模式改变时,开关频率先瞬间变大后缓慢减小,使得谐振电流基本保持不变,达到消除谐振电流产生过电流现象的目的。
针对提出的电容电压均压控制方法也开展了实验验证。图19为两种控制模式下均压控制的实测波形。从图19中可以看出,两种控制模式在加入均压控制策略后,均可以使输入母线电容电压从不平衡恢复到平衡状态,证明了所提均压控制方法的有效性。相比之下,同相控制模式的用时略长。
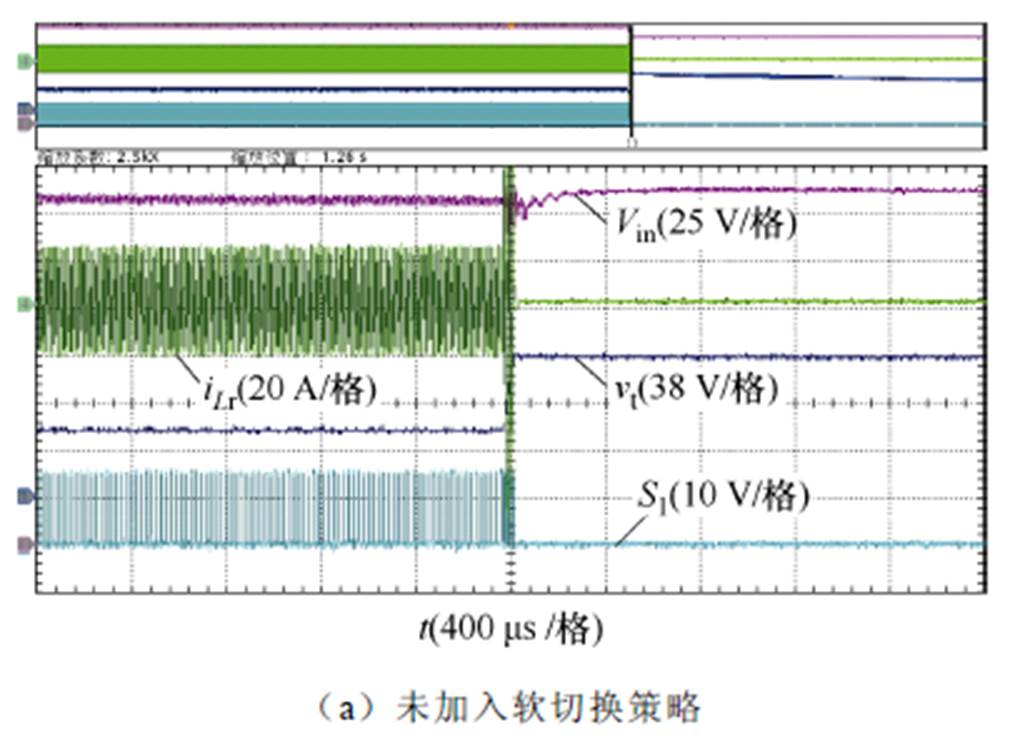
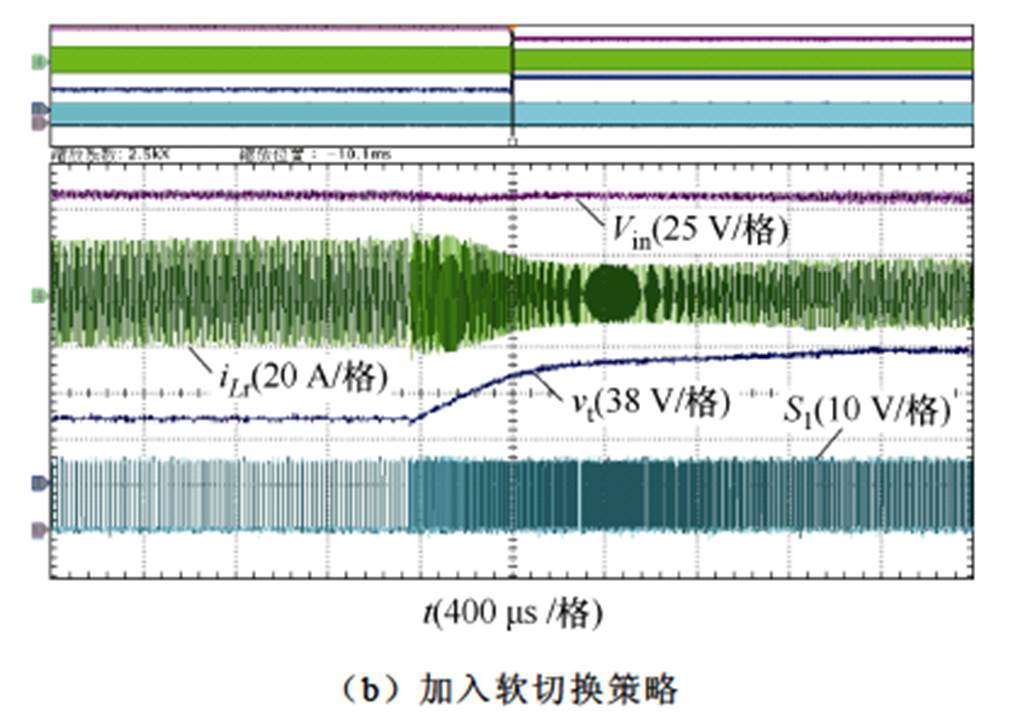
图18 加入软切换控制前后的实测波形
Fig.18 Tested waveforms w/wo soft switching strategy
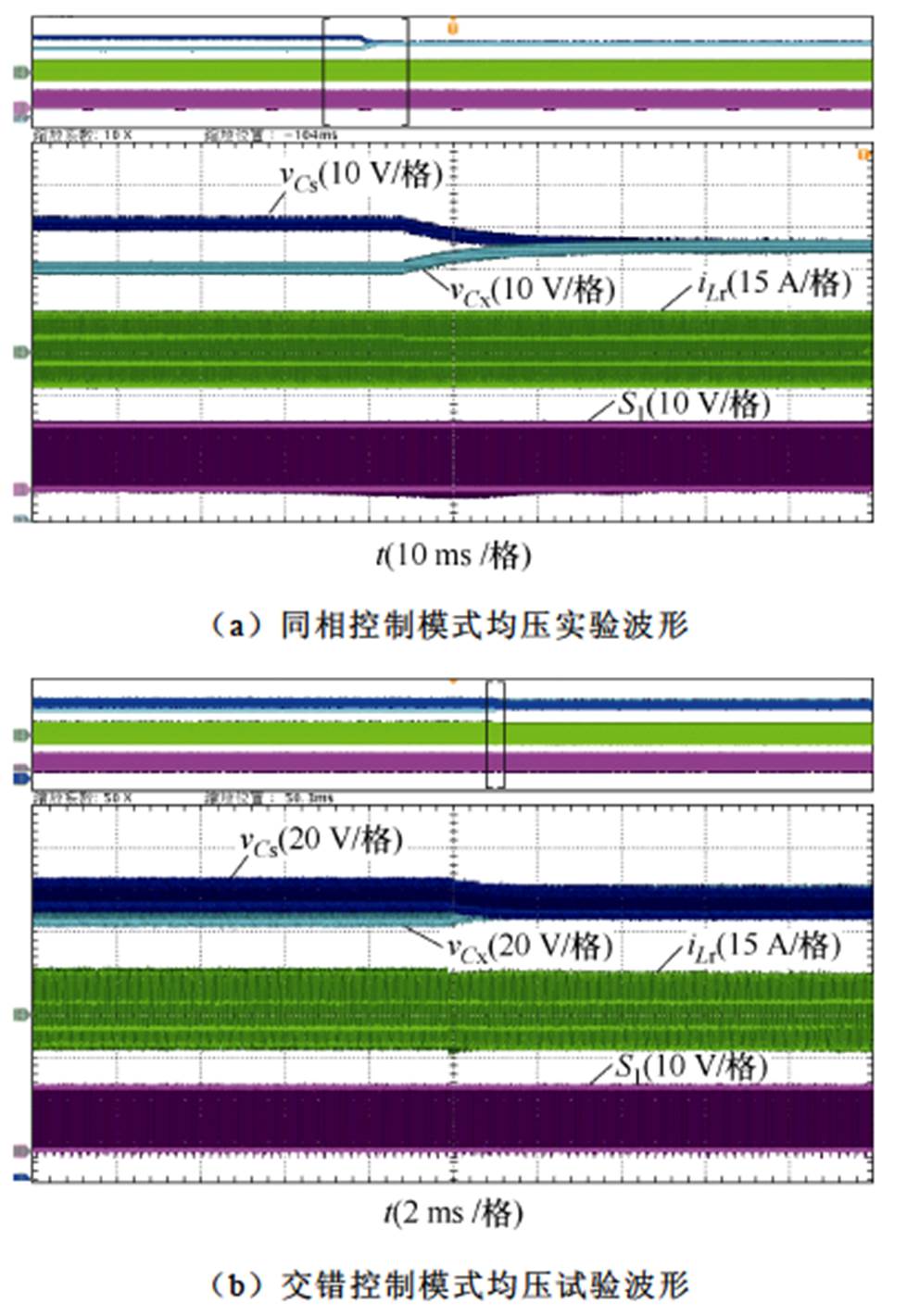
图19 输入母线电容电压波形
Fig.19 Capacitor voltage waveforms of the input DC bus
为了验证基于布谷鸟搜索算法的参数优化设计的有效性,LLC变换器选取了三组不同的谐振参数在三组不同输入电压下进行实验,后级Buck电路参数固定不变。三组实验主要参数见表4,其中第二组数据为理论计算的最佳数值。
图20给出了不同参数和输入电压下的效率实测曲线。由图可见,第2组实验参数在全输入电压范围内的效率比其他两组都高,表明了本文所提优化策略的正确性。
表4 三组实验参数表
Tab.4 Three sets of experimental parameter
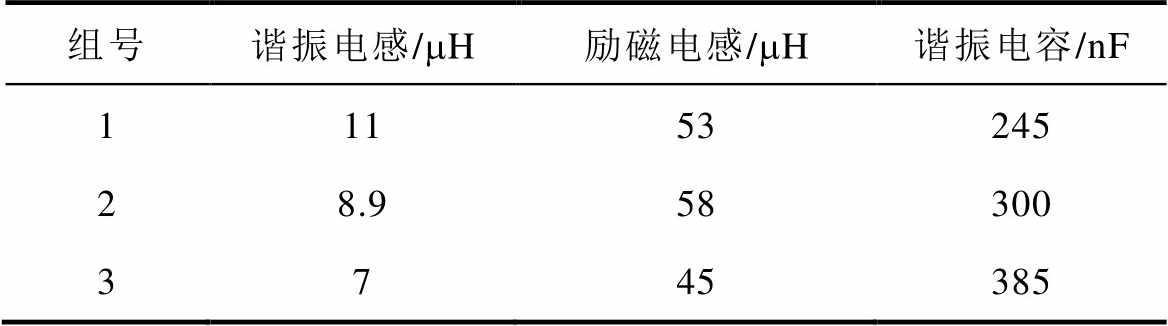
组号谐振电感/mH励磁电感/mH谐振电容/nF 11153245 28.958300 3745385
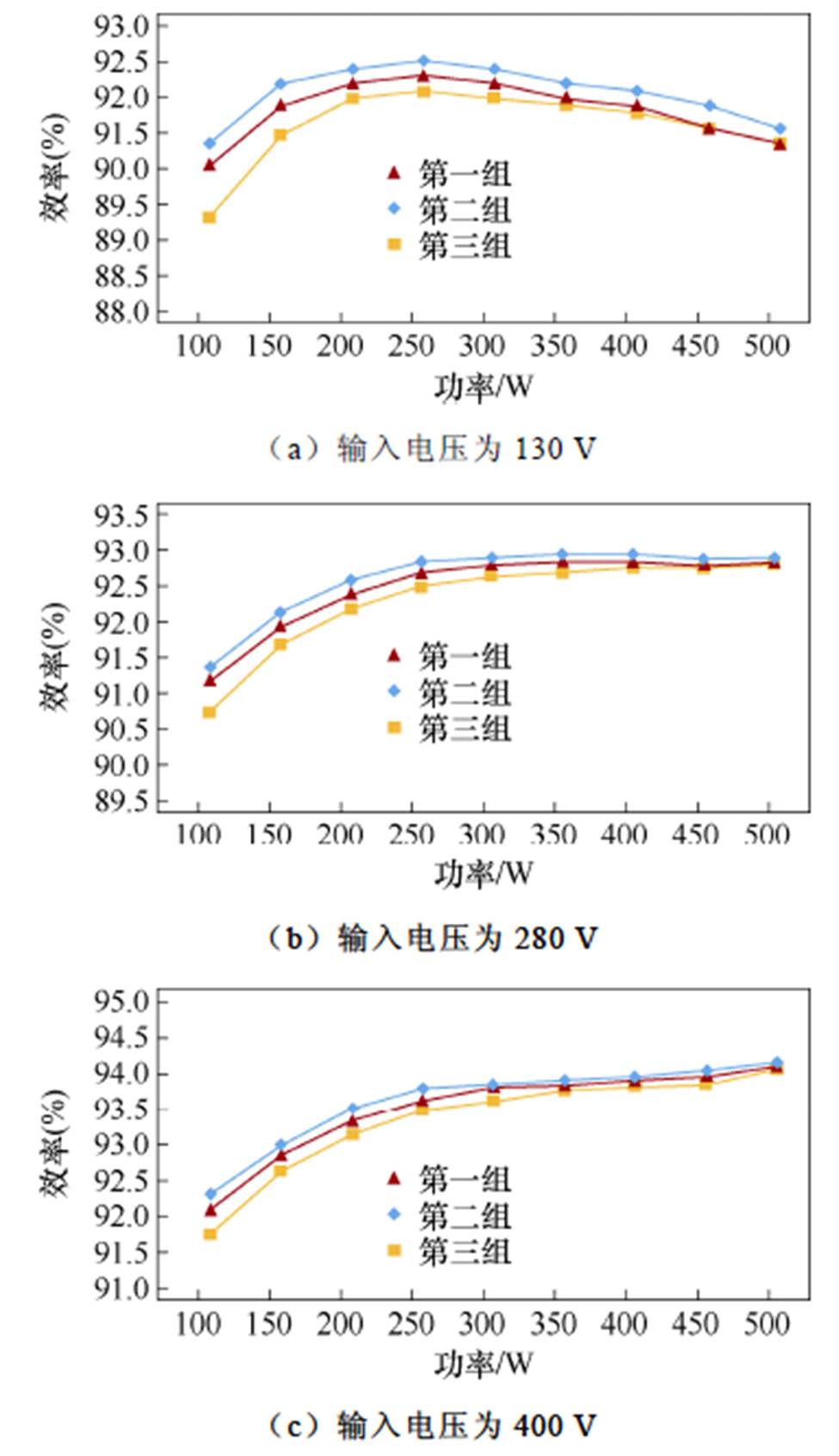
图20 不同参数和输入电压下的效率曲线
Fig.20 Tested efficiency curves under different parameter and input voltage
最后,为了验证LLC变换器损耗模型的正确性,对LLC变换器的单级效率也进行了实际测量,并将其与理论效率进行了对比验证,如图21所示。可以看出,理论效率与实测效率曲线虽然存在微小的偏差,但是整体上具有非常好的吻合度,从而说明理论损耗与实测损耗也是基本吻合的,证明了损耗模型的正确性。
本文对四开关三电平半桥LLC谐振变换器的制策略进行了理论分析,采用了保持谐振腔输入电压频率固定的控制策略。同时分别针对控制模式切换时产生的过电流现象和输入侧电容电压不均压现象提出相应的控制策略进行抑制。并对四开关三电平半桥LLC谐振变换器进行了损耗计算,讨论系统损耗与谐振电感的关系,并利用布谷鸟搜索算法对变换器谐振参数进行优化设计。最后,根据提出的控制策略以及优化设计方法研制了一台500 W的四开关三电平半桥LLC谐振变换器,实验结果验证了所提控制策略及优化设计方法的正确性和有效性。
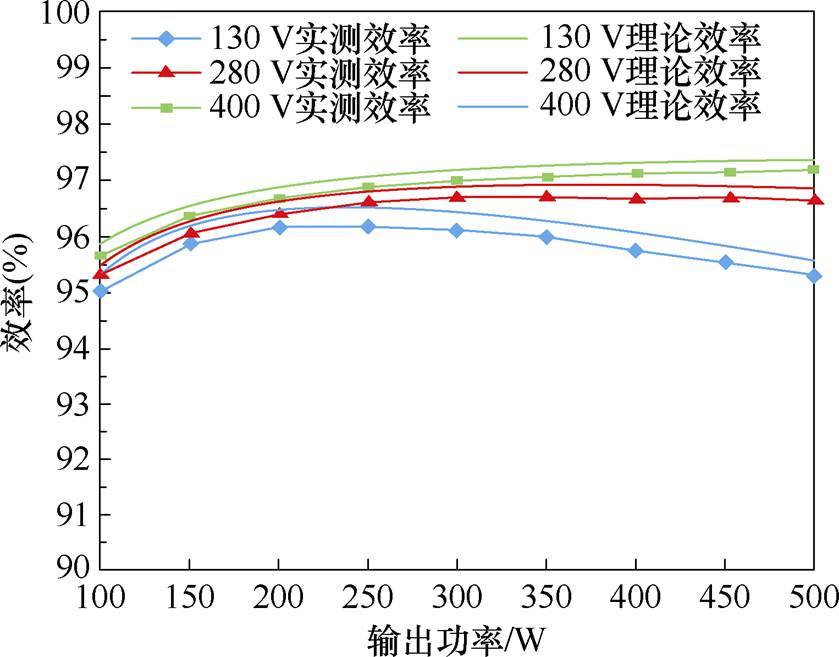
图21 LLC变换器的实测和理论效率曲线
Fig.21 Tested and theoretical efficiency curves of the LLC
参考文献
[1] 缪哲语, 仝昊, 姚文熙, 等. 一种柔性多模态宽范围全桥LLC变换器控制方法[J]. 中国电机工程学报, 2022, 42(2): 747-760.
Miao Zheyu, Tong Hao, Yao Wenxi, et al. A flexible variable-mode control method for wide-range full- bridge LLC converter[J]. Proceedings of the CSEE, 2022, 42(2): 747-760.
[2] Ta L A D, Dao N D, Lee D C. High-efficiency hybrid LLC resonant converter for on-board chargers of plug-in electric vehicles[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8324-8334.
[3] 刘硕. 高效率LLC变换器若干关键问题的研究[D]. 南京: 南京航空航天大学, 2019.
Liu Shuo. Research on some key problems of high efficiency LLC converter[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2019.
[4] Tang Xinxi, Xing Yan, Wu Hongfei, et al. An improved LLC resonant converter with reconfigurable hybrid voltage multiplier and PWM-plus-PFM hybrid control for wide output range applications[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 185-197.
[5] Khan S, Sha Deshang, Jia Xiangshuai, et al. Resonant LLC DC-DC converter employing fixed switching frequency based on dual-transformer with wide input- voltage range[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 607-616.
[6] Sun Wenjin, Xing Yan, Wu Hongfei, et al. Modified high-efficiency LLC converters with two split resonant branches for wide input-voltage range applications[J]. IEEE Transactions on Power Elec- tronics, 2018, 33(9): 7867-7879.
[7] 周国华,邱森林,张小兵. 宽增益高效率级联式四开关Buck-Boost LLC变换器[J]. 电工技术学报, 2024, 39(4): 1103-1115.
Zhou Guohua, Qiu Senlin, Zhang Xiaobing. Cascaded four-switch Buck-Boost LLC converter with wide gain range and high efficiency[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1103-1115.
[8] Zhao Qinglin, Zhang Jianmeng, Gao Yuxia, et al. Hybrid variable frequency LLC resonant converter with wide output voltage range[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 11038-11049.
[9] Awasthi A, Bagawade S, Jain P K. Analysis of a hybrid variable-frequency-duty-cycle-modulated low- Q LLC resonant converter for improving the light- load efficiency for a wide input voltage range[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8476-8493.
[10] 袁义生, 赖立. 一种适用于宽范围输出的复合谐振型全桥变换器[J]. 中国电机工程学报, 2020, 40(20): 6694-6703.
Yuan Yisheng, Lai Li. A compound resonant full- bridge converter suitable for wide range output[J]. Proceedings of the CSEE, 2020, 40(20): 6694-6703.
[11] Hu Haibing, Fang Xiang, Chen F, et al. A modified high-efficiency LLC converter with two transformers for wide input-voltage range applications[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1946-1960.
[12] 张之梁. 零电压开关 PWM全桥三电平变换器[D]. 南京: 南京航空航天大学, 2005.
Zhang Zhiliang. Zero-voltage switching PWM full- bridge three-level converter[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005.
[13] 胡海兵, 王万宝, 孙文进, 等. LLC谐振变换器效率优化设计[J]. 中国电机工程学报, 2013, 33(18): 48-56.
Hu Haibing, Wang Wanbao, Sun Wenjin, et al. Optimal efficiency design of LLC resonant converters[J]. Proceedings of the CSEE, 2013, 33(18): 48-56.
[14] 任仁, 张方华, 刘硕. 基于LLC直流变压器 (LLC- DCT) 效率优化的死区时间与励磁电感设计[J]. 电工技术学报, 2014, 29(10): 141-146.
Ren Ren, Zhang Fanghua, Liu Shuo. Optimal design for efficiency based on the dead time and magnetizing inductance of LLC DC transformer[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 141-146.
[15] 袁义生, 张钟艺, 梅相龙, 等. 三电平LLC谐振变换器关断损耗的优化设计[J]. 电力自动化设备, 2020, 40(2): 28-34.
Yuan Yisheng, Zhang Zhongyi, Mei Xianglong, et al. Optimal design of switching-off loss in three-level LLC resonant converters[J]. Electric Power Auto- mation Equipment, 2020, 40(2): 28-34.
[16] 周子航, 高祎韩, 刘懿静, 等. 基于平面磁元件的LLC变换器相关参数的整体优化设计方法[J]. 电工技术学报, 2024, 39(15): 4820-4829, 4895.
Zhou Zihang, Gao Weihan, Liu Yijing, et al. Para- meters global optimization design method for LLC converter with planar magnetic[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4820- 4829, 4895.
[17] Yang Xinshe, Deb S. Engineering optimisation by cuckoo search[J]. International Journal of MathematicalModelling and Numerical Optimisation, 2010, 1(4): 330.
[18] 张晓凤, 王秀英. 布谷鸟搜索算法综述[J]. 计算机工程与应用, 2018, 54(18): 8-16.
Zhang Xiaofeng, Wang Xiuying. Survey of cuckoo search algorithm[J]. Computer Engineering and Applications, 2018, 54(18): 8-16.
[19] 黄敏丽, 于艾清. 基于改进布谷鸟算法的电动汽车换电站有序充电策略研究[J]. 中国电机工程学报, 2018, 38(4): 1075-1083.
Huang Minli, Yu Aiqing. Study on coordinated charging strategy for battery swapping station based on improved Cuckoo search algorithm[J]. Proceedings of the CSEE, 2018, 38(4): 1075-1083.
[20] Wang Likun, Guo Hai, Marignetti F, et al. Cuckoo search algorithm for multi-objective optimization of transient starting characteristics of a self-starting HVPMSM[J]. IEEE Transactions on Energy Con- version, 2021, 36(3): 1861-1872.
Abstract The ram air turbine (RAT) is an emergency power supply for aircraft when the engine and the auxiliary power system fail. It is the final guarantee to ensure the safe landing of the aircraft. The output voltage amplitude and frequency of permanent magnet synchronous generators vary widely due to the wide speed range of the RAT. Since most onboard emergency electronic devices or loads are powered by DC voltage, it is necessary to rectify the AC voltage to an uncontrolled DC voltage and then convert it to a desired DC voltage by a cascaded DC-DC converter. Therefore, the input voltage range becomes very wide for the DC-DC converter. Similarly, such a wide input voltage range also exists in spacecraft solar arrays and photovoltaic power generation. Thus, converters operating with an extensive wide range of input voltage are necessary. Currently, various topologies and control strategies are suitable for wide input voltage ranges. Among them, the three-level half-bridge (TLHB) LLC resonant converter has a relatively simple topology and low voltage stress. Consequently, this paper analyzes the operational principle, control strategy, and parameter optimization of the TLHB LLC resonant converter.
Firstly, the paper compares different structures of LLC resonant converters suitable for wide input voltage ranges and the commonly used control strategies, analyzes the merits and drawbacks of various topologies and control strategies, and gives the selection consideration of the topology. Considering the broad input voltage range, the two-stage topology is adopted. The four-switch TLHB resonant LLC topology is employed as the front-end converter. It operates in an open-loop state with a fixed resonant cavity input voltage frequency, with the advantage of easy parameter optimization and loss reduction. The second stage uses the synchronous rectification Buck circuit.
Secondly, the operating mode of the LLC converter is analyzed using the constant switching frequency dual mode control strategy. The mathematical model of the TLHB LLC resonant converter is obtained based on the first harmonic approximation (FHA) method, and the relationship between the main parameters and output gain of the resonant converter is analyzed. The impact of switching frequency on the over current phenomenon is revealed, and a soft switching control strategy is proposed for a smooth transition between the two control modes. Additionally, the voltage imbalance mechanism of input bus capacitors is analyzed, the influence of the duty cycle on the capacitor voltage balancing is investigated, and an input bus capacitor voltage balancing control strategy is proposed.
The loss distribution of the TLHB LLC resonant converter is analyzed, and the expressions of power losses and several key currents are quantitatively derived. The optimized parameters of the converter are solved using the cuckoo search algorithm regarding the relative loss rate of the converter as its objective function. The optimized parameters significantly improve the converter’s efficiency. Finally, a 500 W four-switch TLHB LLC resonant converter is developed. Experimental results validate the correctness and effectiveness of the proposed control strategies and the parameter optimization design.
keywords:Four switch three-level half bridge LLC, mode soft switching, efficiency optimization, resonance parameters, Cuckoo search algorithm
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.231847
国家自然科学基金资助项目(52377190, 52237009)。
收稿日期 2023-11-03
改稿日期2024-01-31
陈 杰 男,1982年生,博士,教授,研究方向为电力电子变换装置的建模与控制技术、微电网与分布式发电技术、航空二次电源技术等。E-mail: chen_jie@nuaa.edu.cn
阮新波 男,1970年生,博士,教授,博士生导师,研究方向为高频软开关直直变换器、高频软开关逆变器、变换器建模、电力电子系统集成和新能源供电系统。E-mail: ruanxb@nuaa.edu.cn(通信作者)
(编辑 郭丽军)