一种非对称级联H桥三相逆变器的功率均衡混合随机脉宽调制方法
刘剑锋 龚仁喜 张圆圆
(广西大学电气工程学院 南宁 530004)
摘要 为了降低电压比为1 1
1 1
1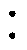 3的非对称级联H桥三相逆变器输出线电压的脉宽调制(PWM)噪声峰值,该文提出一种融合阶梯波调制、同相载波层叠调制、随机调制及功率均衡的功率均衡混合随机脉宽调制(PB-HRPWM)方法。该方法可概述为:①通过高压H桥单元的调制波与参考电位相比较,产生高压H桥单元的驱动脉冲和低压H桥单元的调制波;②通过同相层叠随机载波与低压H桥单元的调制波相比较,产生随机脉冲;③通过脉冲逻辑运算方法对随机脉冲按照0.5Tah进行循环分配,得到低压H桥单元的驱动脉冲;④使用高低压H桥单元的驱动脉冲控制三相逆变器的运行。仿真和实验结果表明:该方法可以降低线电压PWM噪声峰值,同时实现低压H桥单元之间的功率均衡。相比传统的随机和非随机PWM方法,所提PB-HRPWM方法具有更低的线电压PWM噪声峰值和更小的线电压总谐波畸变率(THD)。最后,通过仿真对比和实验验证了所提PB-HRPWM方法的有效性和可行性。
3的非对称级联H桥三相逆变器输出线电压的脉宽调制(PWM)噪声峰值,该文提出一种融合阶梯波调制、同相载波层叠调制、随机调制及功率均衡的功率均衡混合随机脉宽调制(PB-HRPWM)方法。该方法可概述为:①通过高压H桥单元的调制波与参考电位相比较,产生高压H桥单元的驱动脉冲和低压H桥单元的调制波;②通过同相层叠随机载波与低压H桥单元的调制波相比较,产生随机脉冲;③通过脉冲逻辑运算方法对随机脉冲按照0.5Tah进行循环分配,得到低压H桥单元的驱动脉冲;④使用高低压H桥单元的驱动脉冲控制三相逆变器的运行。仿真和实验结果表明:该方法可以降低线电压PWM噪声峰值,同时实现低压H桥单元之间的功率均衡。相比传统的随机和非随机PWM方法,所提PB-HRPWM方法具有更低的线电压PWM噪声峰值和更小的线电压总谐波畸变率(THD)。最后,通过仿真对比和实验验证了所提PB-HRPWM方法的有效性和可行性。
关键词:多电平逆变器 级联H桥 脉宽调制 噪声 功率均衡
0 引言
随着电力电子技术的不断发展,采用脉宽调制(Pulse Width Modulation, PWM)方法控制的三相电压源逆变器已在交流传动系统、电动汽车及船舶舰艇中得到了广泛的应用[1-2]。对于采用固定载波频率PWM方法控制的三相逆变器,其线电压功率谱密度中含有集中在载波频率及其倍频处的高峰值PWM噪声。这类PWM噪声不仅会使电机产生声学噪声,而且还会使逆变器产生电磁噪声。为此,A. M. Trzynadlowski等指出,将集中在载波频率及其倍频处的高峰值PWM噪声分散至较宽的频带能有效降低PWM噪声峰值,进而有效地抑制交流传动系统中电机的声学噪声和逆变器的电磁噪声[3]。据此,学者们提出了大量不同的随机脉宽调制(Random PWM, RPWM)方法,用以抑制逆变器输出电压的PWM噪声峰值[4]。
目前,在降低三相两电平电压源逆变器的线电压PWM噪声峰值上已取得较多研究成果[5]。例如,文献[6]中,揭示了电压功率谱与随机数序列的关系,并据此基于梅森旋转算法设计了改进的随机数生成器,从而为随机空间矢量脉宽调制(Space Vector PMW, SVPWM)方法提供了新的随机数生成方法。但相比三相两电平电压源逆变器,级联H桥(Cascaded H-Bridge, CHB)型三相逆变器不仅输出电压的总谐波畸变率(Total Harmonic Distortion, THD)更小,而且还可以使用低电压开关器件来构造高压大功率逆变器[7]。因而,级联H桥型三相逆变器也在中高压交流传动系统中得到了越来越多的应用。
然而,迄今为止,用于H桥逆变器的RPWM方法的研究却非常缺乏。目前,只见少量文献报道。例如,文献[8]通过将频谱零点法[9]引入基于载波移相的RPWM方法,实现了单H桥逆变器输出电压中PWM噪声的选择性消除;文献[10]通过优化随机三角载波序列的生成方式,解决了载波切换时相位异步问题,进而有效提高了RPWM方法的降噪性能。可见,上述研究主要从随机算法和载波序列等方面优化RPWM方法,并取得了较好的降噪性能。但是,上述研究也还存在如下不足:①这些调制方法主要适用于单H桥逆变器;②这些调制方法均是基于载波移相调制而设计。但相比单H桥逆变器,级联H桥逆变器不仅具有更小的输出电压THD,而且还更适用于高压大功率逆变器。相比载波移相调制,同相载波层叠调制具有更小的线电压THD。另外,对多个随机三角载波进行移相,在工程实践中也存在较大的数字实现困难问题[11]。因而,研究基于同相载波层叠调制的RPWM方法对进一步改善级联H桥逆变器的PWM噪声性能具有重要意义。
相比对称级联H桥逆变器,非对称级联H桥逆变器能以更少的直流电源和开关器件数量获得更大的输出功率和更小的输出电压THD。因而,本文以电压比为1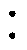 1
1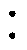 1
1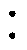 3的非对称级联H桥三相逆变器[7]为研究对象,提出了一种功率均衡混合随机脉宽调制(Power Balanced-Hybrid Random PWM, PB- HRPWM)方法。该调制方法兼顾了阶梯波调制、同相载波层叠调制、随机调制和功率均衡的优势,具有线电压总谐波畸变率较小、线电压PWM噪声峰值较低及低压H桥单元之间功率均衡的优点。
3的非对称级联H桥三相逆变器[7]为研究对象,提出了一种功率均衡混合随机脉宽调制(Power Balanced-Hybrid Random PWM, PB- HRPWM)方法。该调制方法兼顾了阶梯波调制、同相载波层叠调制、随机调制和功率均衡的优势,具有线电压总谐波畸变率较小、线电压PWM噪声峰值较低及低压H桥单元之间功率均衡的优点。
1 PB-HRPWM方法的基本原理
本文所研究的非对称级联H桥三相逆变器拓扑如图1所示。由图1可知,该逆变器由电压比为1 1
1 1
1 3的A、B及C相非对称级联H桥逆变器拓扑构成,A、B及C相逆变器又均由高压H桥单元AH和低压H桥单元AL串联构成,其中低压H桥单元AL是由H桥单元AL1、AL2和AL3级联构成。图1中以A相逆变器为例,H桥单元ALi(i=1, 2, 3)的直流电压为E,高压H桥单元AH的直流电压为3E,QA11、QA12、QA13和QA14为高压H桥单元AH的开关器件,SAx1、SAx2、SAx3和SAx4为低压H桥单元AL的开关器件,x=1, 2, 3。根据级联规律可知,该逆变器的相电压uan有0、±E、±2E、±3E、±4E、±5E和±6E共13种电平,线电压uab有0、±E、±2E、±3E、±4E、±5E、±6E、±7E、±8E、±9E、±10E、±11E和±12E共25种电平。
3的A、B及C相非对称级联H桥逆变器拓扑构成,A、B及C相逆变器又均由高压H桥单元AH和低压H桥单元AL串联构成,其中低压H桥单元AL是由H桥单元AL1、AL2和AL3级联构成。图1中以A相逆变器为例,H桥单元ALi(i=1, 2, 3)的直流电压为E,高压H桥单元AH的直流电压为3E,QA11、QA12、QA13和QA14为高压H桥单元AH的开关器件,SAx1、SAx2、SAx3和SAx4为低压H桥单元AL的开关器件,x=1, 2, 3。根据级联规律可知,该逆变器的相电压uan有0、±E、±2E、±3E、±4E、±5E和±6E共13种电平,线电压uab有0、±E、±2E、±3E、±4E、±5E、±6E、±7E、±8E、±9E、±10E、±11E和±12E共25种电平。
考虑到三相对称关系,仅以A相非对称级联H桥逆变器为例介绍所提PB-HRPWM方法。对于B相和C相逆变器,只需要将A相逆变器的调制波替换为B相或C相的调制波,即可得到用于B相或C相逆变器的PB-HRPWM方法。
1.1 降低PWM噪声峰值
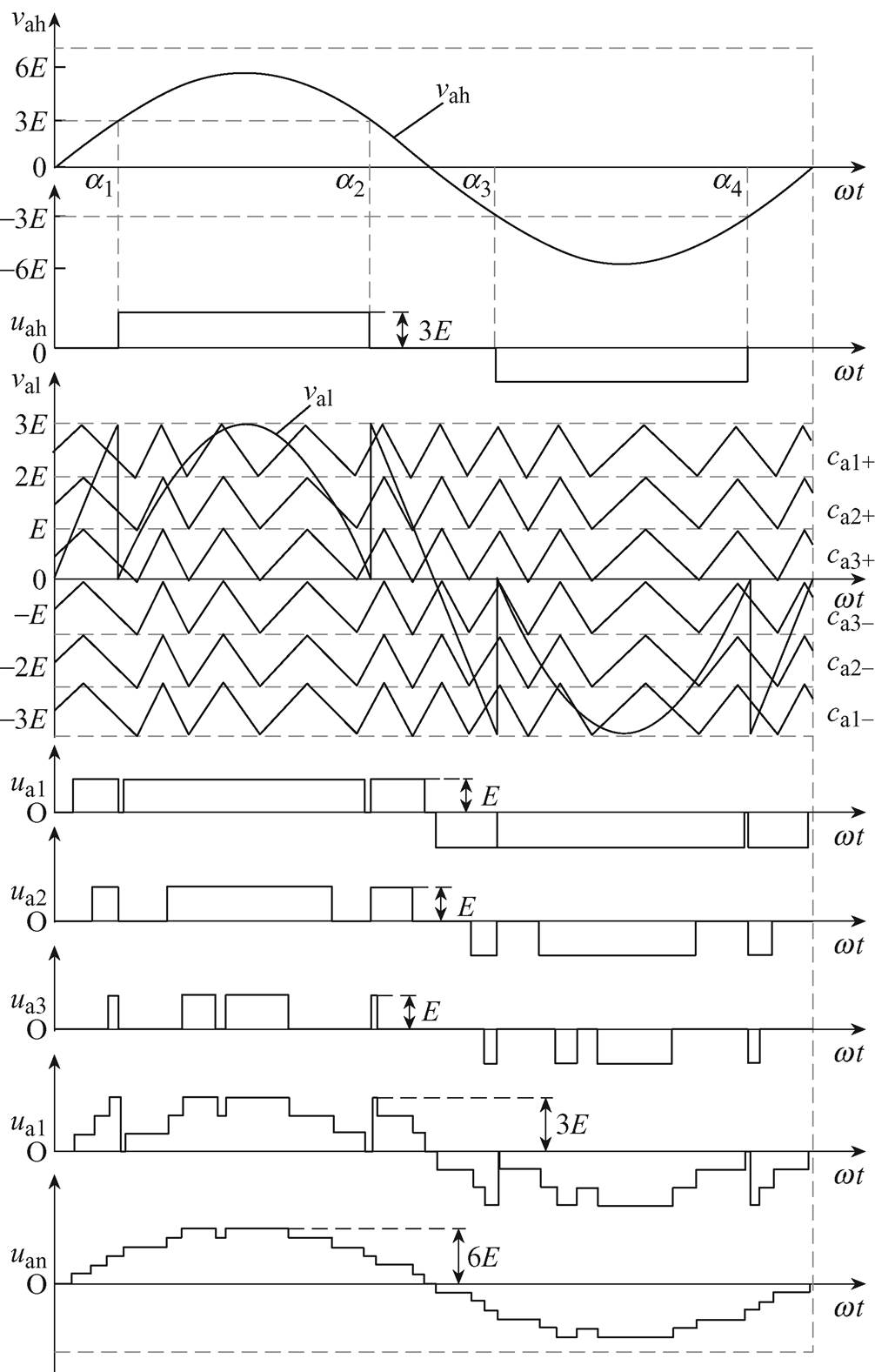
一般而言,在基于三角载波的正弦脉宽调制方法(如载波移相、反相载波层叠及相邻载波反相层叠等)中,同相载波层叠方法具有最小的线电压THD。同时,相比随机脉冲位置调制和双随机调制,随机频率调制不仅能有效地降低PWM噪声峰值,而且线电压的波形畸变也较小[12-13]。基于此,本文将具有随机频率的三角载波引入到同相载波层叠调制中,并结合阶梯波调制,提出了如图2所示的同相载波层叠混合随机脉宽调制(In-Phase Disposition HRPWM, IPD-HRPWM)方法,以期获得良好的线电压THD及PWM噪声性能。
图2中,H桥单元AL1、AL2和AL3的载波分别为具有随机频率的三角载波ca1±、ca2±和ca3±,高压H桥单元AH的参考电位±3E。vah为高压H桥单元AH的调制波,val为低压H桥单元AL的调制波。通过val分别与ca1±、ca2±和ca3±的比较,可获得随机脉冲Xa11和Xa13、Xa21和Xa23、Xa31和Xa33;通过vah与±3E的比较,可得高压H桥单元AH的驱动脉冲Qa11和Qa13。H桥单元AL1、AL2和AL3的输出电压分别为ua1、ua2和ua3,ual为低压H桥单元AL的输出电压,uah为高压H桥单元AH的输出电压,uan为A相逆变器的输出相电压。根据KVL可得
图2中,cai±(i=1, 2, 3)的随机频率fc可表示为
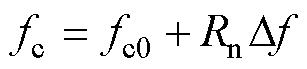 (2)
(2)
式中,fc0为随机频率的中心频率;Df为随机频率的随机带宽,两者均为常数;Rn为随机数,可由Logistic算法、Markov链算法及WELL算法等产生,其取值范围为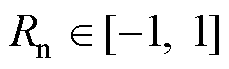 。当调制度
。当调制度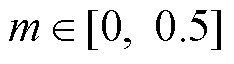 时,vah和val可分别表示为
时,vah和val可分别表示为
当调制度m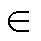 (0.5, 1
(0.5, 1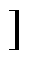 时,vah、val可分别表示为
时,vah、val可分别表示为
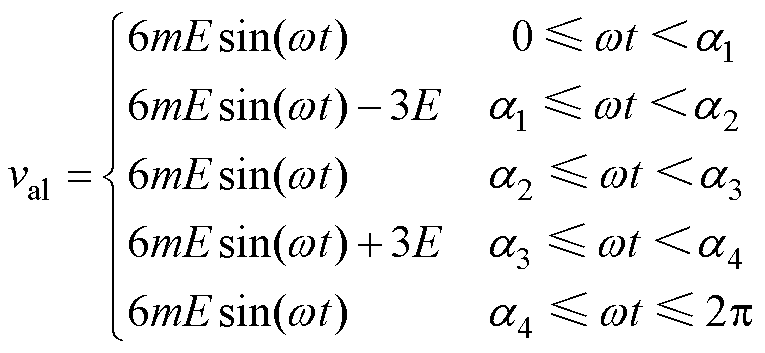 (5)
(5)
其中
由式(3)~式(6)可知,高压H桥单元AH只在调制度m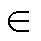 (0.5, 1
(0.5, 1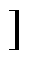 范围内有输出电压,而在调制度m
范围内有输出电压,而在调制度m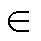 [0, 0.5]范围内没有输出电压;低压H桥单元AL则在全调制度m
[0, 0.5]范围内没有输出电压;低压H桥单元AL则在全调制度m [0, 1]范围内都有输出电压。
[0, 1]范围内都有输出电压。
1.2 功率均衡优化
一般而言,在传统IPD-PWM方法下,级联H桥逆变器中同等电压H桥单元的平均输出功率存在较大差异,即同等电压H桥单元之间存在功率不均衡问题[14-15]。同时,在所提IPD-HRPWM方法中,高压H桥单元AH采用阶梯波PWM方法,低压H桥单元AL采用IPD-PWM方法。因而,在H桥单元AL1、AL2和AL3之间会存在功率不均衡问题,进而使H桥单元AL1、AL2和AL3中各H桥单元及直流电源的寿命存在较大差异。这些差异不仅降低逆变器的可靠性,而且还会增加其维护成本[16-18]。因此,在IPD-HRPWM方法下,有必要对H桥单元AL1、AL2和AL3之间的功率分配进行优化,以在H桥单元AL1、AL2和AL3之间实现功率均衡。
在PWM方法下,当载波频率远大于输出电压频率时,在载波周期内ual的平均值ual等于参考电压val的瞬时值[19-20],即
当m (0.5,1
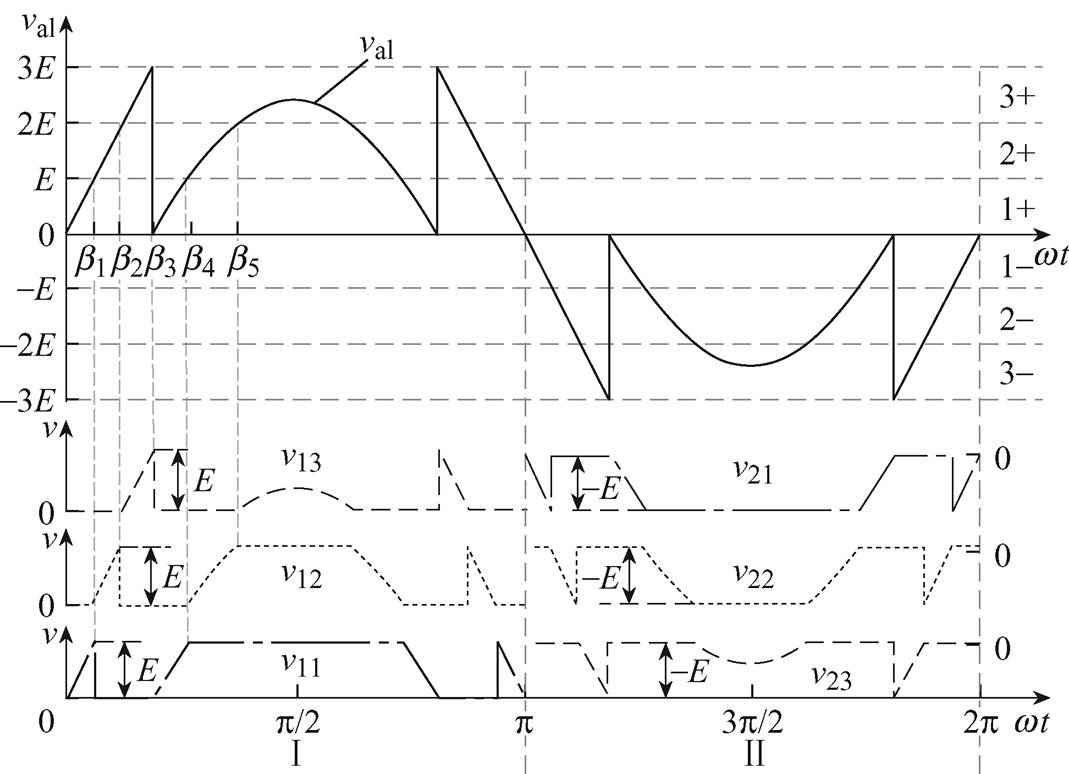
(0.5,1 时,将1个周期内val的分布分为如图3所示的区间Ⅰ和Ⅱ。区间Ⅰ内val可细分为基本电压v11、v12和v13;区间Ⅱ内val可细分为基本电压v2l、v22和v23。此时,结合式(5)和式(6),v1l、v21可分别表示为
时,将1个周期内val的分布分为如图3所示的区间Ⅰ和Ⅱ。区间Ⅰ内val可细分为基本电压v11、v12和v13;区间Ⅱ内val可细分为基本电压v2l、v22和v23。此时,结合式(5)和式(6),v1l、v21可分别表示为
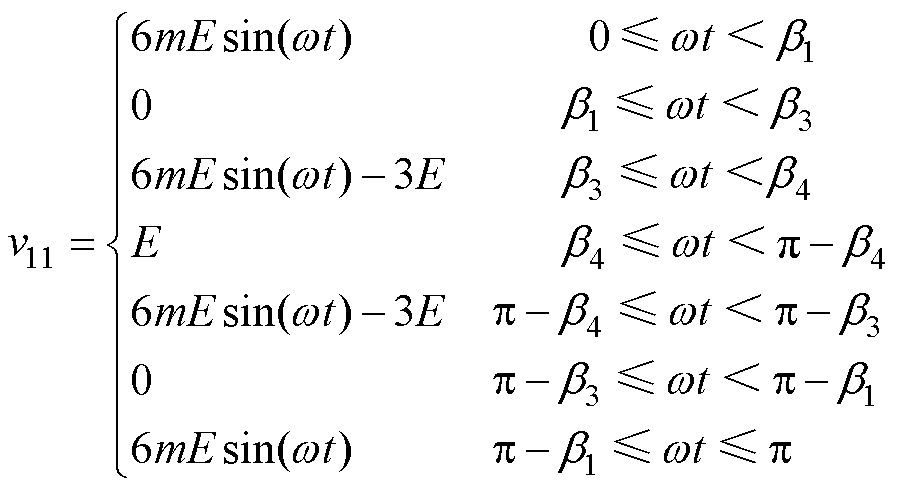 (8)
(8)
其中
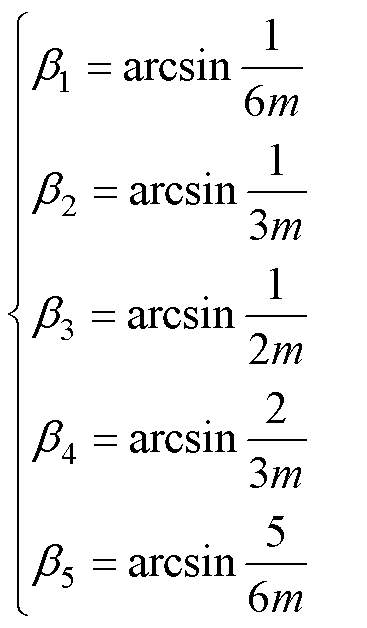 (10)
(10)
设A相逆变器的相电流ia为
结合式(7)可得,在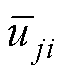 (
(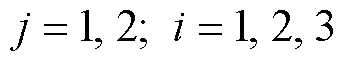 )作用下,H桥单元ALi(i=1, 2, 3)的平均输出功率为
)作用下,H桥单元ALi(i=1, 2, 3)的平均输出功率为
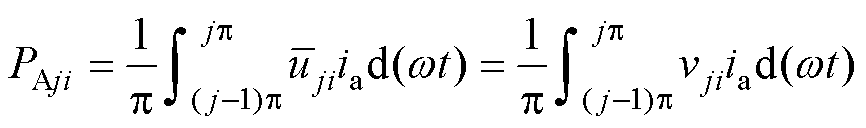 (12)
(12)
结合式(8)、式(9)、式(11)和式(12)可得,H桥单元AL1在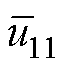 作用下的PA11为
作用下的PA11为
H桥单元AL1在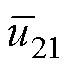 作用下的PA21为
作用下的PA21为
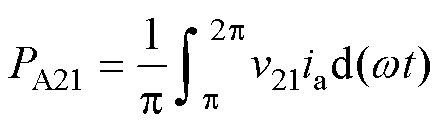 (14)
(14)
计算式(13)和式(14)可得,当m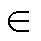 (0.5, 1
(0.5, 1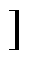 时有
时有
进一步地,还可得
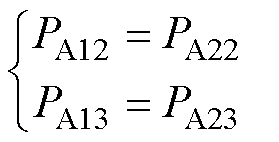 (16)
(16)
同理,当m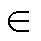 [0, 0.5]时,亦可得
[0, 0.5]时,亦可得
综上所述,只需要使H桥单元ALi(i=1, 2, 3)在一定时间内的输出包含三种基本电压(v11或v21、v12或v22、v13或vA23),即可实现H桥单元AL1、AL2和AL3之间的功率均衡。根据上述原理,学者们提出了一系列基于调制波或载波重构的传统功率均衡方法[14-20],在解决功率均衡问题上都已取得良好的效果。但这些功率均衡方法却将功率均衡目标与调制波或载波重构耦合在一起,即实现功率均衡必须对调制波或载波进行重构。这不仅不利于功率均衡原理的推广和应用,也极大地增加了功率均衡方法的数字实现难度。因为,在数字实现中对调制波或载波进行重构,尤其对随机载波进行重构,是比较困难的且需要消耗处理器大量的存储和计算资源。
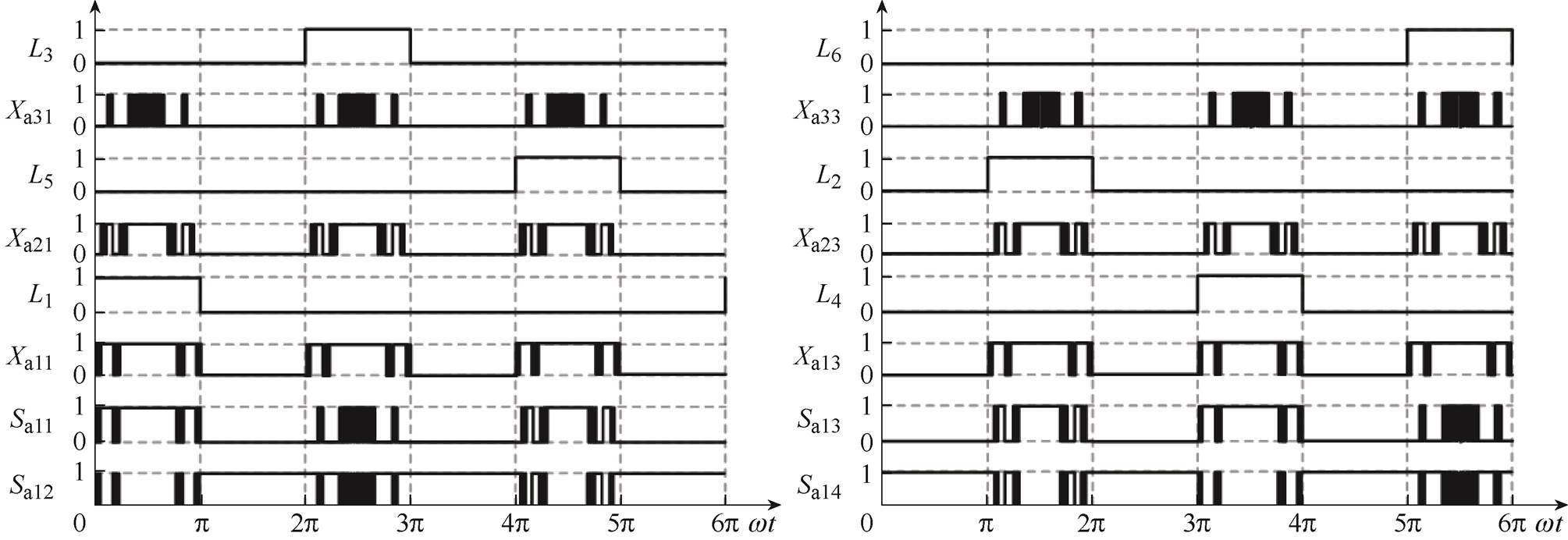
为克服上述问题,从而简化功率均衡方法,以便于解决1.1节所提IPD-HRPWM方法存在的功率不均衡问题,本文提出了一种基于脉冲逻辑运算的功率均衡方法。该方法通过脉冲信号L1、L2、L3、L4、L5、L6与随机脉冲Xa11、Xa13、Xa21、Xa23、Xa31、Xa33的脉冲逻辑运算,将随机脉冲循环分配给H桥单元AL1、AL2和AL3,以获得H桥单元AL1、AL2和AL3的驱动脉冲。调制度m=1时,获得驱动脉冲Sa11、Sa12、Sa13和Sa14的脉冲逻辑运算方法如图4所示。由图4可知,通过脉冲信号与随机脉冲之间的脉冲逻辑运算,即可实现H桥单元AL1在1.5Tah(Tah为vah的周期)内的输出电压包含三种(v11、v22和v13)基本电压。同时可知,该方法通过引入脉冲逻辑运算实现了功率均衡目标与调制波或载波重构的解耦,即避免在数字处理器中构建复杂的调制波或载波重构算法,从而有效降低功率均衡方法的数字实现难度。
图4中,可知Sa11、Sa12、Sa13和Sa14的脉冲逻辑运算式为
同理,可推出Sa21、Sa22、Sa23和Sa24脉冲逻辑运算式为
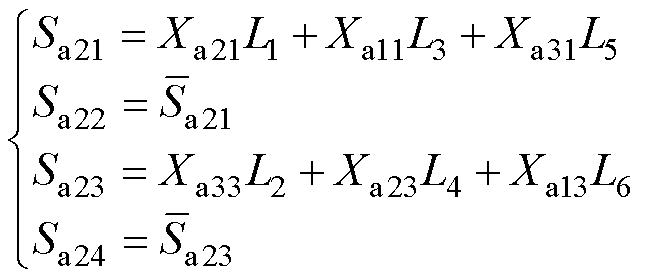 (19)
(19)
Sa31、Sa32、Sa33和Sa34的脉冲逻辑运算式为
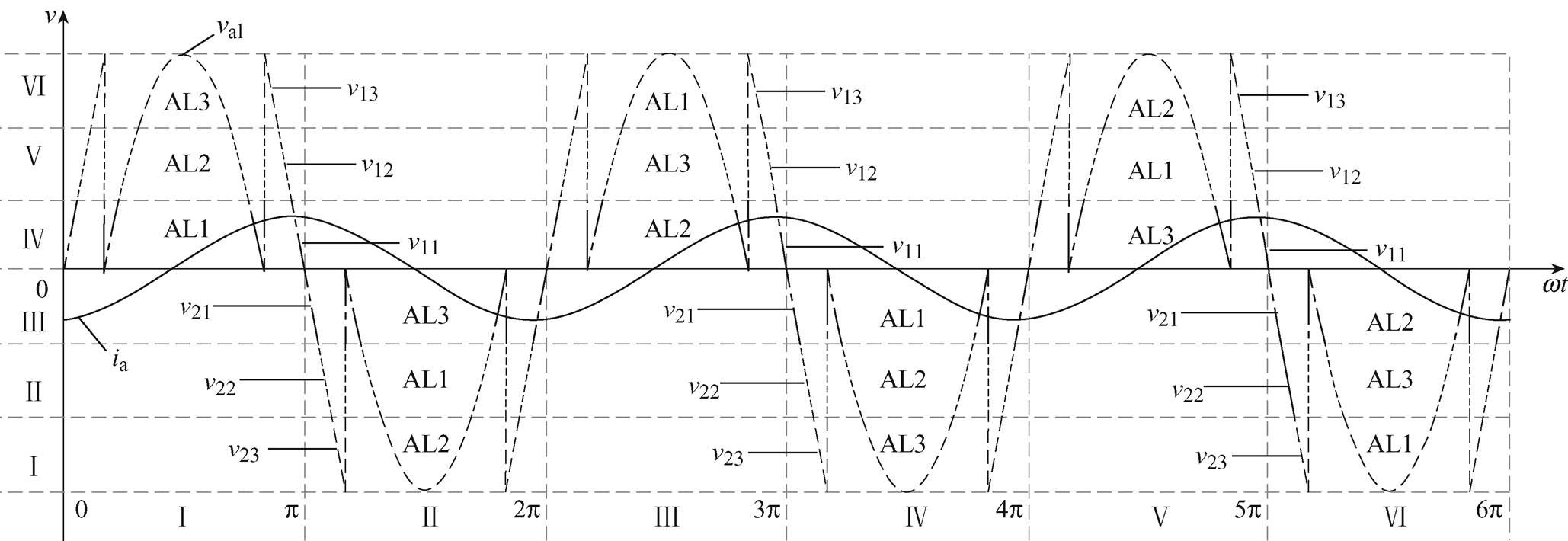
调制度m=1时,在驱动脉冲Saxy(x=1, 2; y=1, 2 , 3, 4)的作用下,H桥单元AL1、AL2和AL3包含的基本电压分布如图5所示。由图5可知,在[0,3π]内,H桥单元AL1平均输出功率PAL1为
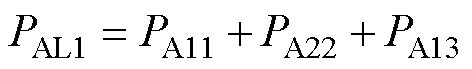 (21)
(21)
H桥单元AL2平均输出功率PAL2为
H桥单元AL3平均输出功率PAL3为
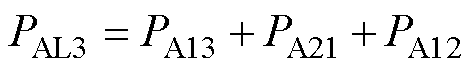 (23)
(23)
结合式(15)和式(16)、式(21)~式(23)可得
即所提功率均衡方法可在1.5Tah内实现H桥单元AL1、AL2和AL3之间的功率均衡。同理,在调制度m≠1时,亦可得到此结论。
1.3 PB-HRPWM方法的总体架构
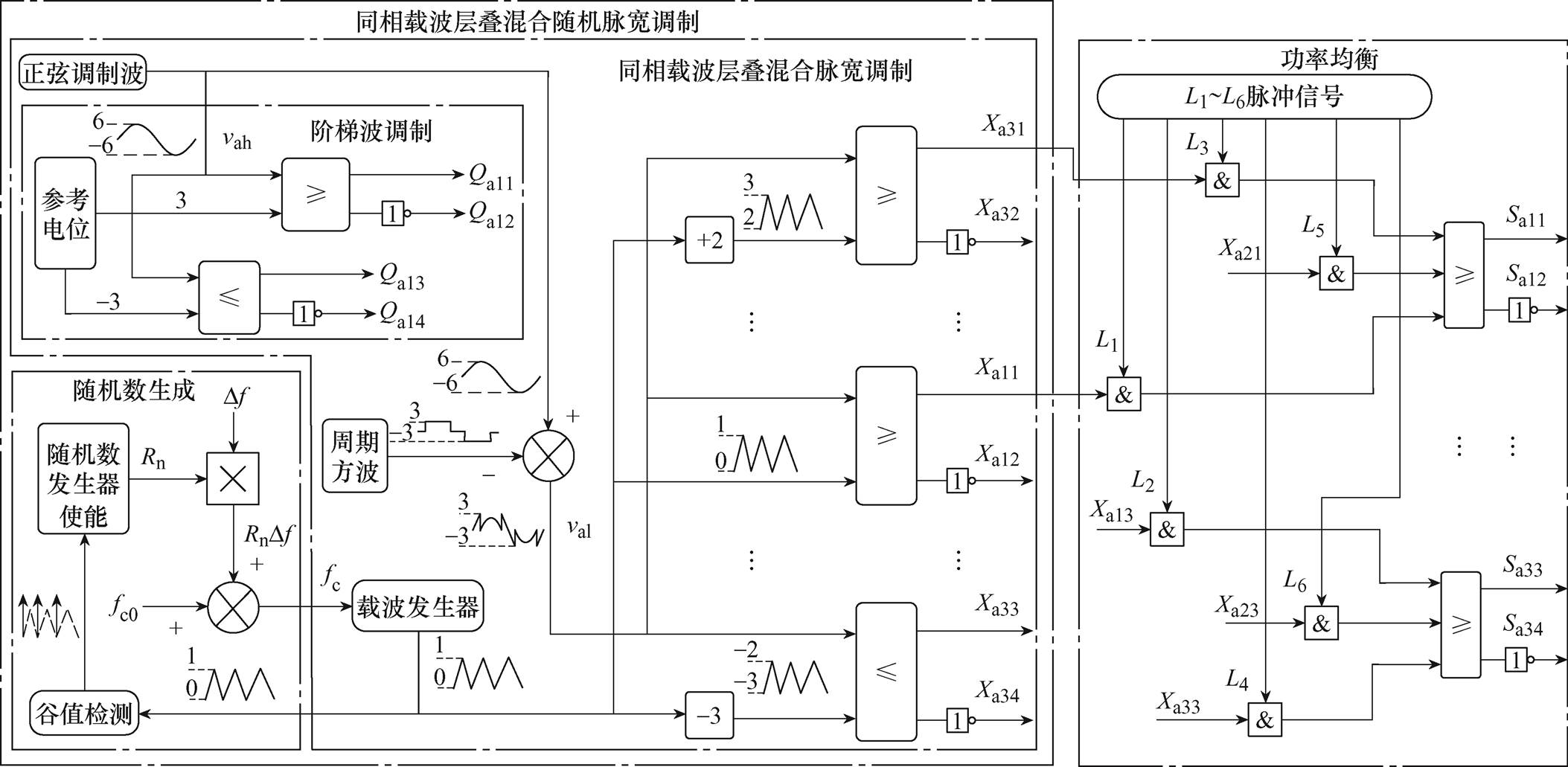
将所提同相载波层叠混合随机脉宽调制(IPD- HRPWM)方法和基于脉冲逻辑运算的功率均衡方法结合即可得功率均衡混合随机脉宽调制(PB- HRPWM)方法,其总体架构如图6所示。由图6可进一步总结PB-HRPWM方法的提出思路:①将阶梯波调制与同相载波层叠调制结合获得同相载波层叠混合脉宽调制(IPD-HPWM)方法,以使高压H桥单元工作在基波频率,低压H桥单元工作在平均等效开关频率,进而降低开关损耗并减小输出线电压的总谐波畸变率;②将随机频率调制引入IPD- HPWM方法获得IPD-HRPWM方法,进而有效降低输出线电压的PWM噪声峰值,并保证较小的THD;③将脉冲逻辑运算引入IPD-HRPWM方法获得PB- HRPWM方法,进而解决低压H桥单元之间的功率不均衡问题,并简化基于调制波或载波重构的传统功率均衡方法。依据上述思路,可将基于同相载波层叠的随机脉宽调制推广应用于其他类型的多电平逆变器,如开关电容型、二极管钳位型、飞跨电容型等多电平逆变器,以有效降低这些多电平逆变器输出电压的PWM噪声峰值。从图6可知,相比IPD- HPWM方法,所提PB-HRPWM方法只增加了随机数生成模块和功率均衡模块,并没有增加更多的复杂运算模块。因而,所提PB-HRPWM方法仍可在高性能数字控制器上实现,如DSP、FPGA和CPLD等。
2 仿真和比较
为对所提PB-HRPWM方法的特性作进一步的分析和比较,本文在Matlab 2019b/Simlink平台上搭建了三相H桥逆变器的仿真模型,其仿真参数见表1。表1中,“1H”表示A(B、C)相逆变器由单H桥单元构成;“4H”表示A(B、C)相逆变器由4个H桥单元级联构成,其拓扑结构如图1所示;“PS”表示基于载波移相的调制方法;“PD”表示基于载波层叠的调制方法。为在输出线电压基波幅值、负载、平均等效开关频率(记为fav)一致的情况下,将PB-HRPWM方法与文献[7, 10, 13-14]中所提调制方法进行对比,在表1中设置了多种不同的仿真参数,具体参数设置如下:①PC-RPWM[10]和PS-RPWM[13]均用于“1H”型三相逆变器,因而,单个H桥单元的直流电压为72 V(记为72 V/HU);②PS-HPWM[7]、POD-HPWM[14]和PB-HRPWM均用于“4H”型三相逆变器,因而,单个低压H桥单元的直流电压为12 V(记为12 V/LH),单个高压H桥单元的直流电压为36 V(记为36 V/HH);③为保证fav均为6 kHz,以最大程度减小不同调制方法损耗特性的差异,所以,POD-HPWM的固定载波频率取6 kHz,PS-HPWM的固定载波频率取1 kHz,PC-RPWM和PS-RPWM的随机载波频率范围取1.5~4.5 kHz,PB-HRPWM的随机载波频率范围取3~9 kHz。
表1 仿真和实验参数
Tab.1 Simulation and experimental parameters

参 数数 值 直流电压 1H(HU)/V72 4H低压(LH)/V高压(HH)/V1236 载波频率PSPS-HPWM:PC-RPWM、PS-RPWM:1 kHz ( fc=1 kHz,fav=6 fc=6 kHz)1.5~4.5 kHz ( fc0=3 kHz,∆f =1.5 kHz,fav=2 fc0=6 kHz) PDPOD-HPWM:PB-HRPWM:6 kHz ( fc=6 kHz,fav=fc=6 kHz)3~9 kHz ( fc0=6 kHz,Df =3 kHz,fav=fc0=6 kHz) 输出频率/Hz50 三相星形负载电阻R/Ω10 电感L/mH3
2.1 线电压波形和功率分配分析
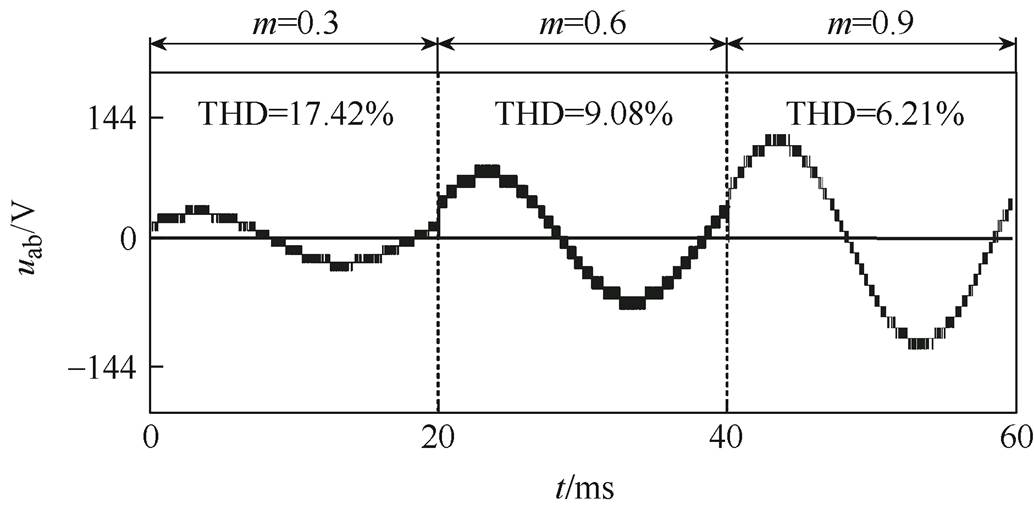
在所提PB-HRPWM方法下,随机载波频率范围为3~9 kHz时,线电压uab的仿真波形及其THD如图7所示。由图7可知,调制度m=0.3、0.6和0.9时,uab分别为9、15和21电平的PWM波形,其THD分别为17.42%、9.08%和6.21%。可知,uab的电平数和THD均随调制度的变化而变化。
H桥单元AL1、AL2和AL3的输出功率仿真波形如图8所示。由图8可知,m=0.3时,PAL1=23.09 W,PAL2=23.09 W,PAL3=23.10 W;m=0.6时,PAL1=37.83 W,PAL2=37.84 W,PAL3=37.83 W;m=0.9时,PAL1=85.49 W,PAL2=85.48 W,PAL3=85.49 W。可见,在3/2 Tah内所提PB-HRPWM方法能使H桥单元AL1、AL2和AL3的平均输出功率基本相等,即实现了H桥单元AL1、AL2和AL3之间的功率均衡。这意味着,对非对称级联H桥逆变器而言,该方法能有效均衡其低压H桥单元中各直流电源和H桥单元的利用率,进而提高其可靠性,同时降低其维护成本。
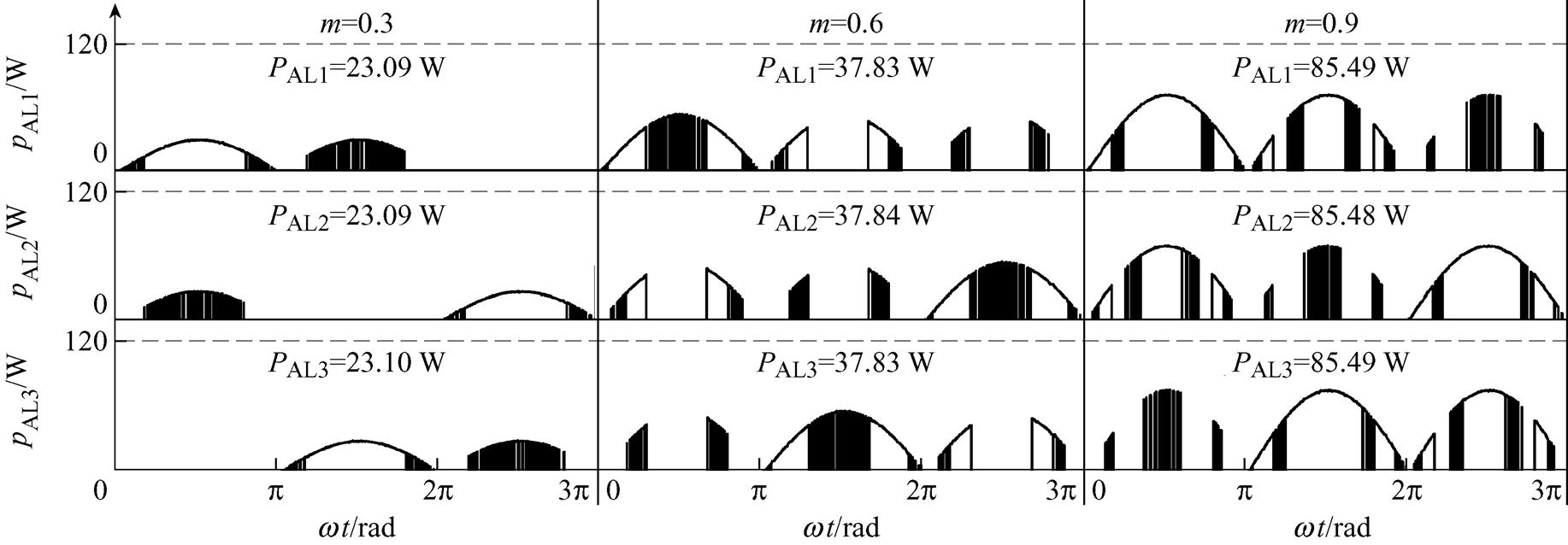
图8 H桥单元AL1、AL2和AL3的输出功率仿真波形
Fig.8 Output power simulation waveforms of H-bridge unit AL1, AL2 and AL3
2.2 线电压PWM噪声峰值分析
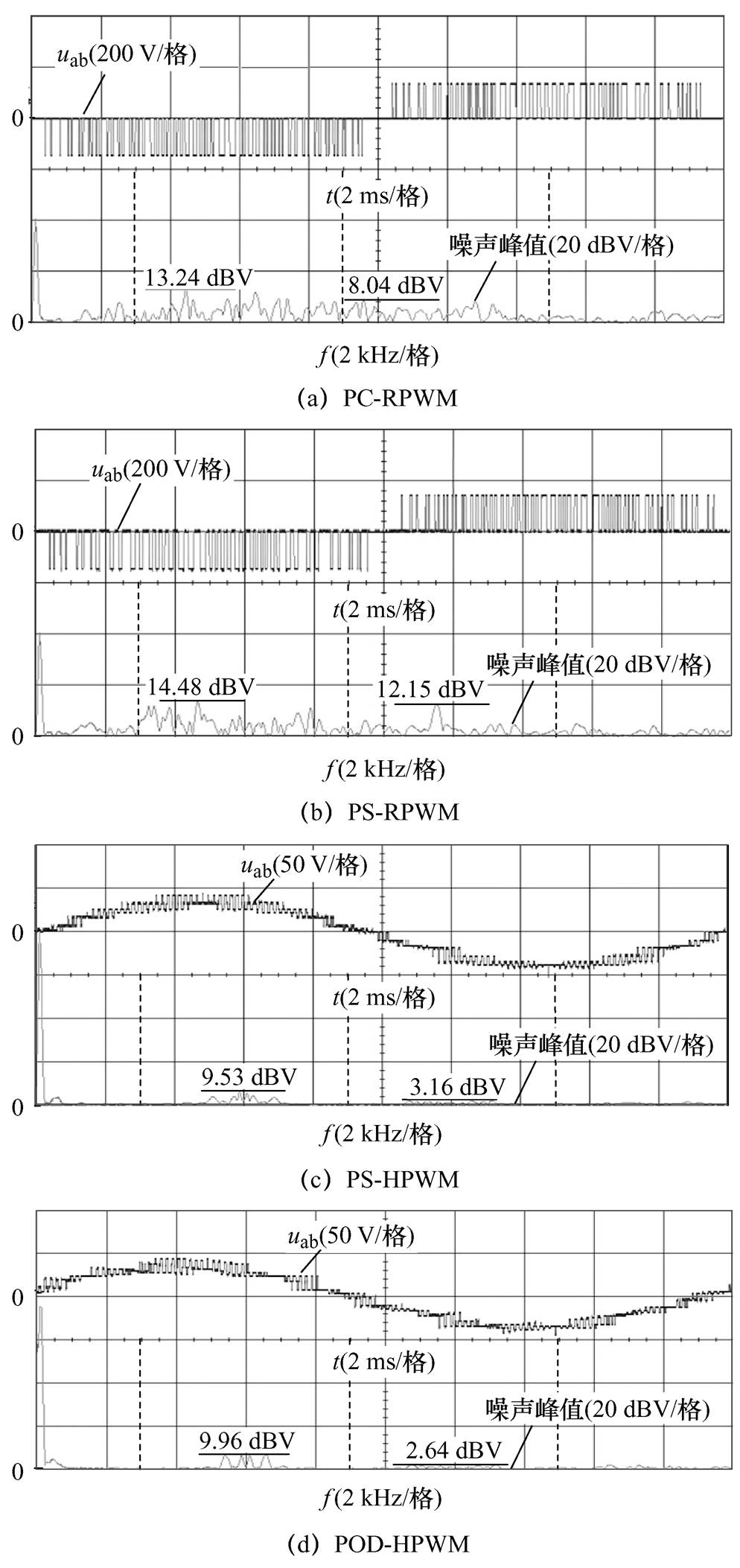
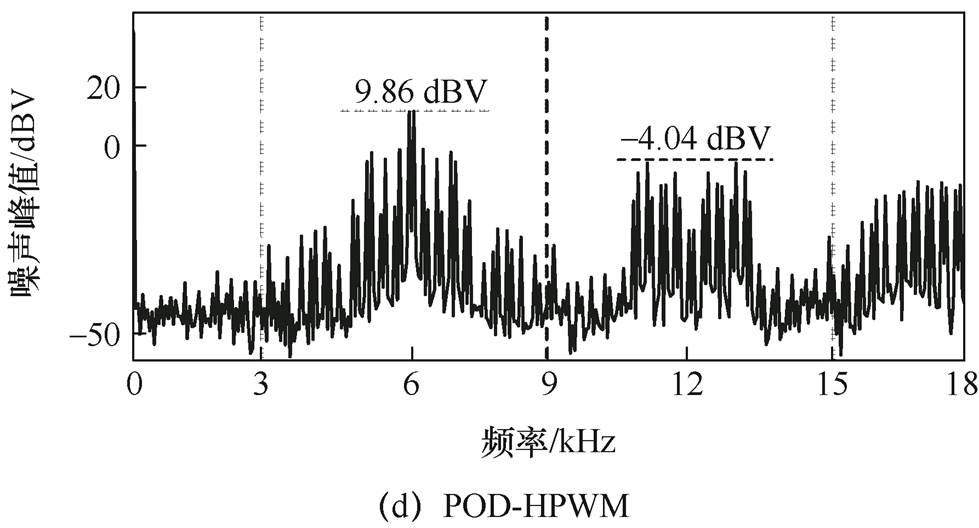
当调制度m=0.6时,在PC-RPWM、PS-RPWM、PS-HPWM、POD-HPWM方法下,uab的仿真频谱如图9所示。由图9可知:①尽管PS-HPWM和POD-HPWM的固定载波频率不同,但两者在6n(n=1, 2, 3, ) kHz附近都集中着大量高峰值PWM噪声,即PWM噪声集中在整数倍平均等效开关频率附近且峰值较高;②尽管PC-RPWM和PS-RPWM的随机载波频率范围不同,但两者在6n(n=1, 2, 3,
) kHz附近都集中着大量高峰值PWM噪声,即PWM噪声集中在整数倍平均等效开关频率附近且峰值较高;②尽管PC-RPWM和PS-RPWM的随机载波频率范围不同,但两者在6n(n=1, 2, 3, ) kHz附近均没有集中大量高峰值PWM噪声,即集中在整数倍平均等效开关频率附近的高峰值PWM噪声被有效分散在整个频带内。将上述差异对比分析可知:相对于非随机频率调制,随机频率调制就是通过将集中在整数倍平均等效开关频率附近的高峰值PWM噪声分散至整个频带来实现PWM噪声峰值的减小。
) kHz附近均没有集中大量高峰值PWM噪声,即集中在整数倍平均等效开关频率附近的高峰值PWM噪声被有效分散在整个频带内。将上述差异对比分析可知:相对于非随机频率调制,随机频率调制就是通过将集中在整数倍平均等效开关频率附近的高峰值PWM噪声分散至整个频带来实现PWM噪声峰值的减小。
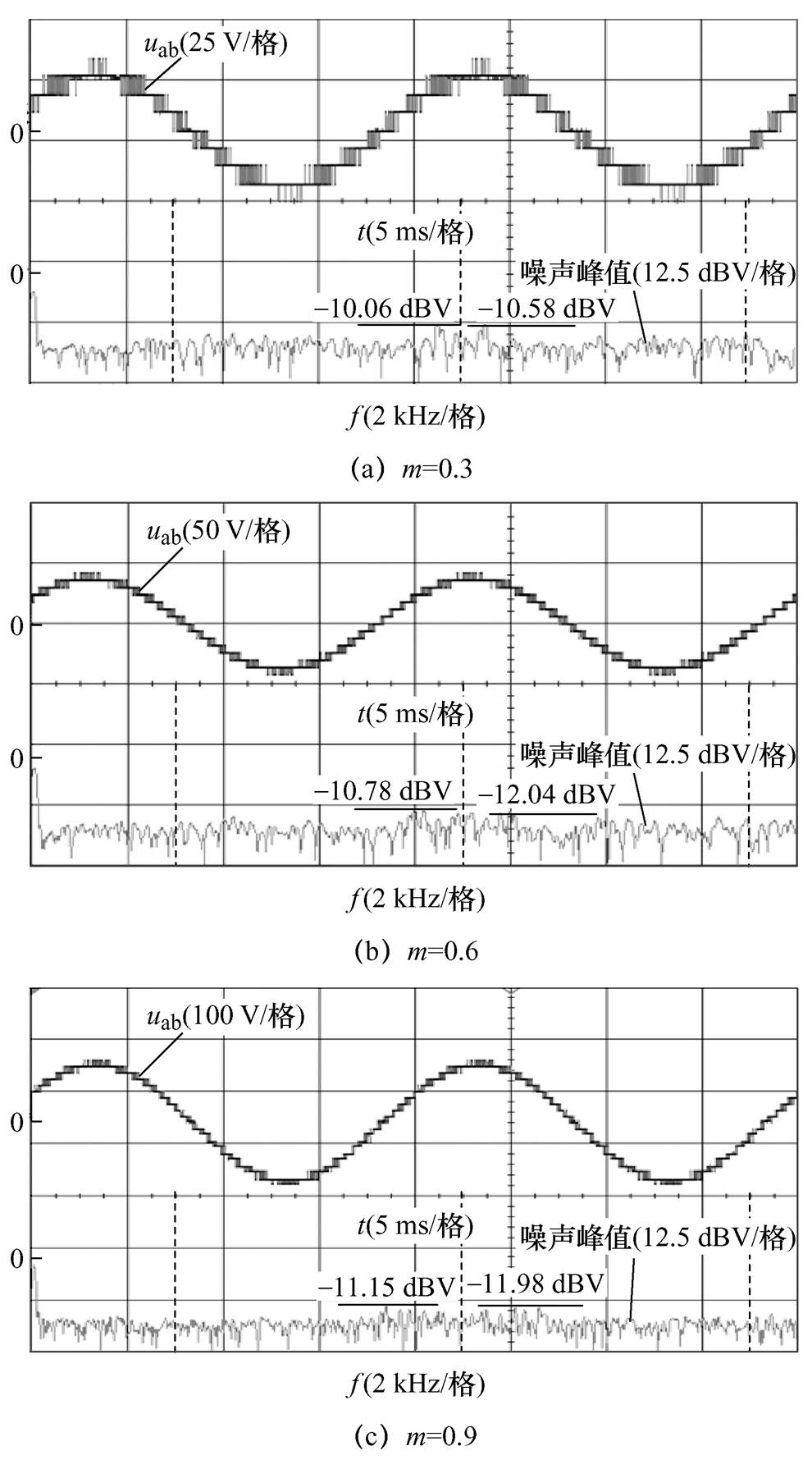
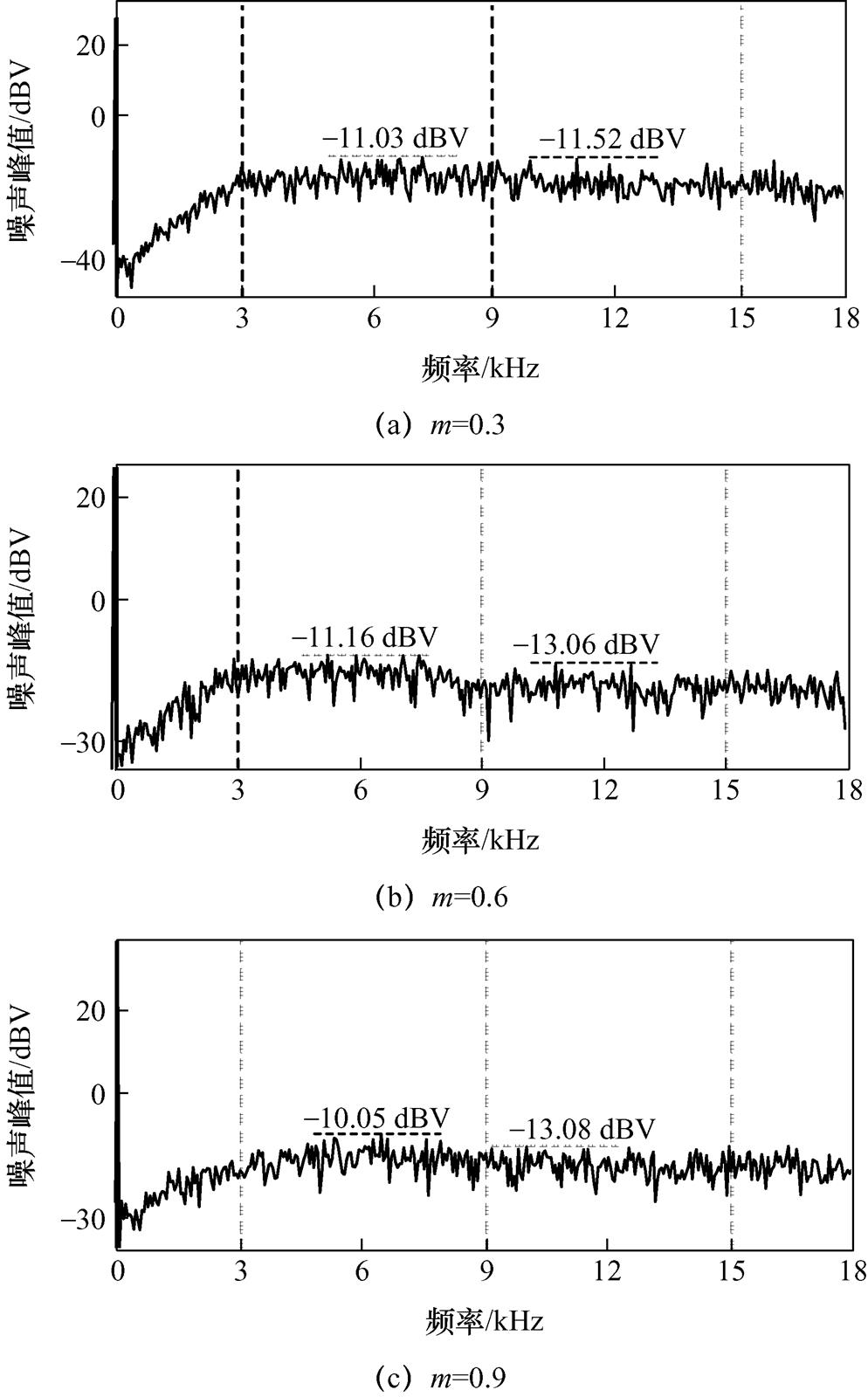
随机和非随机调制的PWM噪声分布都与平均等效开关频率密切相关。因而,为方便更好地比较不同调制方法的PWM噪声性能,本文定义:①第1个PWM噪声峰值为频带3~9 kHz内PWM噪声峰值的最大值;②第2个PWM噪声峰值为频带9~15 kHz内PWM噪声峰值的最大值。在所提PB-HRPWM方法下,且m=0.3、0.6和0.9时,uab的仿真频谱如图10所示。图10中,m=0.3、0.6和0.9时,uab的第1个PWM噪声峰值分别为-11.03、-11.16和-10.05 dBV,uab的第2个PWM噪声峰值分别为-11.52、-13.06和-13.08 dBV。可见,uab的PWM噪声峰值也会随调制度的变化而变化。在所提PB-HRPWM方法下,uab的PWM噪声也被分散至整个频带,因而该方法能有效降低PWM噪声峰值。
2.3 比较分析
当m=[0.1 0.1
0.1 1]时,仿真测得不同调制方法下线电压uab的THD见表2。可以看出,相比PC-RPWM和PS-RPWM方法,所提PB-HRPWM方法均具有更小的线电压THD。这表明:在线电压总谐波畸变率上,相比单H桥逆变器的随机或固定频率载波移相调制,非对称级联H桥逆变器的随机或固定频率载波层叠调制都具有明显的优势。相比PS-HPWM方法,所提PB-HRPWM方法也具有更小的线电压THD。这表明:相比固定频率载波移相调制,在线电压总谐波畸变率方面同相载波层叠随机频率调制也具有更好的性能。相比POD-HPWM方法,所提PB-HRPWM方法同样具有更小的线电压THD。这表明:相比固定频率的反相载波层叠调制,随机频率的同相载波层叠调制具有更好的线电压THD性能。因而,在对线电压波形质量要求较高的场合,可优先考虑非对称级联H桥拓扑和同相载波层叠调制相结合的逆变器设计方案。
1]时,仿真测得不同调制方法下线电压uab的THD见表2。可以看出,相比PC-RPWM和PS-RPWM方法,所提PB-HRPWM方法均具有更小的线电压THD。这表明:在线电压总谐波畸变率上,相比单H桥逆变器的随机或固定频率载波移相调制,非对称级联H桥逆变器的随机或固定频率载波层叠调制都具有明显的优势。相比PS-HPWM方法,所提PB-HRPWM方法也具有更小的线电压THD。这表明:相比固定频率载波移相调制,在线电压总谐波畸变率方面同相载波层叠随机频率调制也具有更好的性能。相比POD-HPWM方法,所提PB-HRPWM方法同样具有更小的线电压THD。这表明:相比固定频率的反相载波层叠调制,随机频率的同相载波层叠调制具有更好的线电压THD性能。因而,在对线电压波形质量要求较高的场合,可优先考虑非对称级联H桥拓扑和同相载波层叠调制相结合的逆变器设计方案。
当m=[0.1 0.1
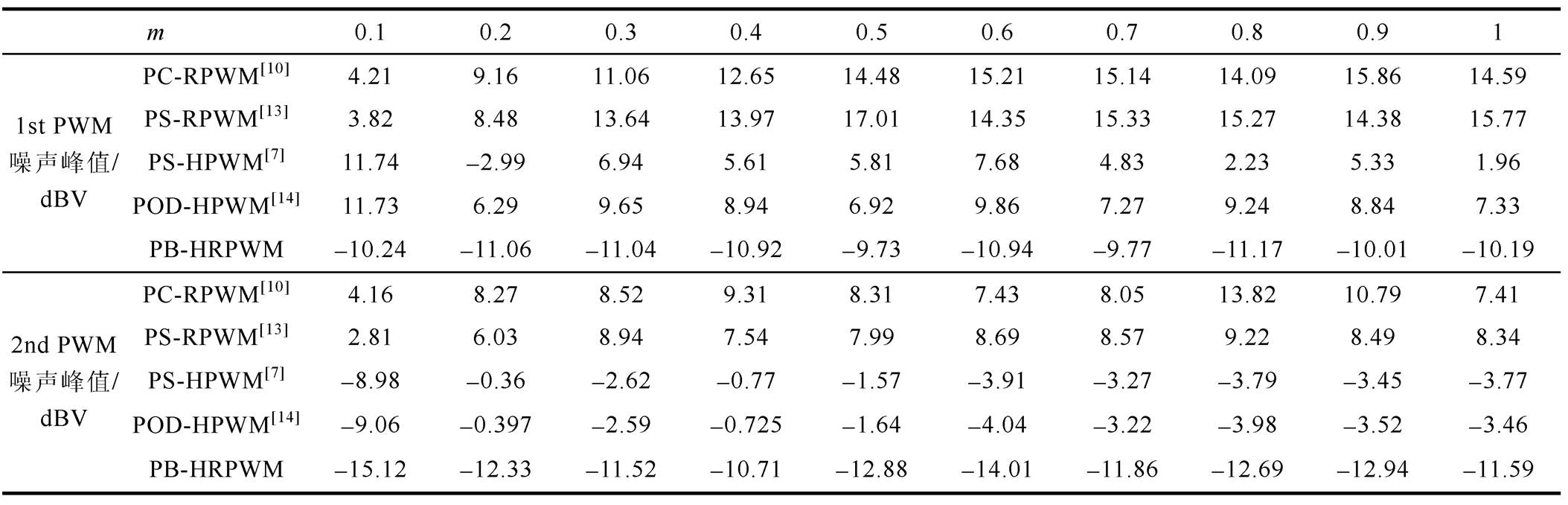
0.1 1]时,仿真测得不同调制方法下线电压uab的1st和2nd PWM噪声峰值见表3。相比PC-RWM、PS-RPWM和PS-HPWM方法,所提PB-HRPWM方法的线电压PWM噪声峰值均是最小的。这表明:相比基于载波移相的随机或固定频率的脉宽调制,基于同相载波层叠的随机频率脉宽调制能更有效地降低线电压PWM噪声峰值。相比POD-HPWM方法,所提PB-HRPWM方法也具有更低的线电压PWM噪声峰值。这表明:相比固定频率的反相载波层叠调制,随机频率的同相载波层叠具有更好的线电压PWM噪声性能。因而,在对线电压PWM噪声峰值敏感的场合,可优先考虑同相载波层叠调制和随机频率调制相结合的逆变器设计方案。
1]时,仿真测得不同调制方法下线电压uab的1st和2nd PWM噪声峰值见表3。相比PC-RWM、PS-RPWM和PS-HPWM方法,所提PB-HRPWM方法的线电压PWM噪声峰值均是最小的。这表明:相比基于载波移相的随机或固定频率的脉宽调制,基于同相载波层叠的随机频率脉宽调制能更有效地降低线电压PWM噪声峰值。相比POD-HPWM方法,所提PB-HRPWM方法也具有更低的线电压PWM噪声峰值。这表明:相比固定频率的反相载波层叠调制,随机频率的同相载波层叠具有更好的线电压PWM噪声性能。因而,在对线电压PWM噪声峰值敏感的场合,可优先考虑同相载波层叠调制和随机频率调制相结合的逆变器设计方案。
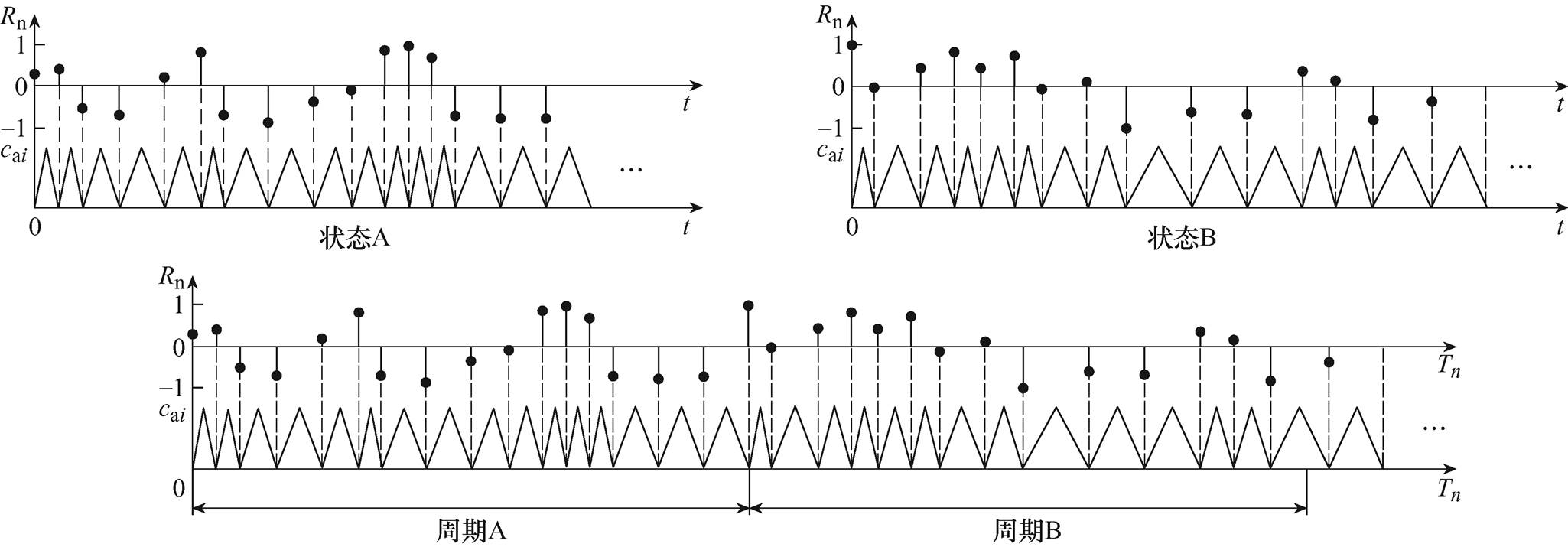
对比图9、图10和表3中的数据,可以发现:①对于随机频率脉宽调制(PC-RPWM、PS-RPWM和PB-HRPWM)方法,调制度m相同时,PWM噪声峰值却不是相同的;②而对于非随机频率脉宽调制(PS-HPWM和POD-HPWM)方法,调制度m相同时,PWM噪声峰值也是相同的。产生该现象的主要原因是:①线电压频谱由载波序列决定,即不同载波序列的线电压PWM噪声分布不同;②随机算法对初始状态敏感,不同初始状态下产生的随机数序列是不相同的,即产生的随机载波序列是不相同的,如图11所示,因而不同初始状态下会观测到不同的PWM噪声峰值;③不同线电压周期使用的随机数组是不相同的,即不同线电压周期使用的随机载波序列是不相同的,如图11所示,因而不同线电压周期也会观测到不同的PWM噪声峰值。对于随机频率脉宽调制,随机载波序列由一系列不同频率的三角载波构成。由图11可见,状态A和状态B、周期A和周期B的随机载波序列中三角载波的频率分布不同,即它们是不同的随机载波序列,进而它们的线电压PWM噪声分布也是不同的。图9、图10和表3中随机频率调制的PWM噪声峰值就是在不同时间、状态和线电压周期下记录的仿真值,所以,这些PWM噪声峰值是不相同的,仅作为参考。对于非随机频率调制,载波频率是固定的,即载波序列中每个三角载波的频率都相同。因而,任何线电压周期的载波序列都是相同的,即任何线电压周期的频谱也相同,所以图9、图10和表3中非随机频率调制的PWM噪声峰值是相同的。在不同随机算法、初始状态、频率范围下也进行了大量的仿真对比分析,结果表明:尽管每次独立观测都会获得不同线电压频谱和PWM噪声峰值,但所提PB-HRPWM方法均具有最小PWM噪声峰值。
表2 不同调制方法下uab的总谐波畸变率
Tab.2 Total harmonic distortions of uabunder different modulation methods
表3 不同调制方法下uab的PWM噪声峰值
Tab.3 PWM noise peak of uab under different modulation methods
综上所述,所提PB-HRPWM方法不仅能减小线电压总谐波畸变率和降低线电压PWM噪声峰值,而且还能实现低压H桥单元之间的功率均衡。另外,还可得如下结论:通过合适的拓扑结构将载波层叠调制、阶梯波调制、随机脉宽调制和功率均衡相融合,可有效减小逆变器输出线电压总谐波畸变率、降低逆变器输出线电压PWM噪声峰值,同时实现相同电压等级H桥之间的功率均衡。
3 实验验证
为进一步验证仿真和比较的结果,本文搭建了“1H”和“4H”型三相逆变器实验样机,其主要参数见表1。当m=0.6时,不同调制方法下线电压uab的实验波形及其频谱如图12所示。由图12可见,PC- RPWM和PS-RPWM的PWM噪声被分散在整个频带内,没有在6n(n=1, 2, 3, ) kHz附近集中大量高峰值PWM噪声;PS-HPWM和POD-HPWM的PWM噪声则集中在6n(n=1, 2, 3,
) kHz附近集中大量高峰值PWM噪声;PS-HPWM和POD-HPWM的PWM噪声则集中在6n(n=1, 2, 3, ) kHz附近且峰值较高。这验证了不同调制方法的PWM噪声分布规律。
) kHz附近且峰值较高。这验证了不同调制方法的PWM噪声分布规律。
当m=0.3、0.6和0.9时,PB-HRPWM方法下线电压uab的实验波形及其频谱如图13所示。由图13可知,m=0.3、0.6和0.9时,uab分别为9、15和21电平的PWM电压波形。进一步地,m=0.3、0.6和0.9时,将实验获得的不同调制方法的uab波形数据导入Matlab 2019b/Simlink以计算线电压THD,其结果见表4。由表4可知,相比PC-RPWM、PS- RPWM、PS-HPWM和POD-HPWM方法,所提PB-HRPWM方法具有最小的线电压THD。
表4 实验测得的总谐波畸变率
Tab.4 Total harmonic distortions through experiments
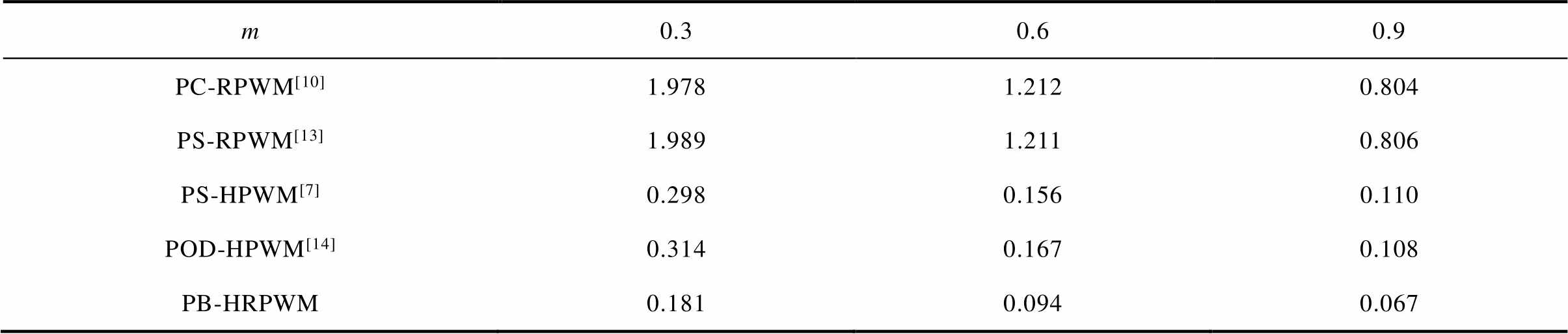
m0.30.60.9 PC-RPWM[10]1.9781.2120.804 PS-RPWM[13]1.9891.2110.806 PS-HPWM[7]0.2980.1560.110 POD-HPWM[14]0.3140.1670.108 PB-HRPWM0.1810.0940.067
当m=0.3、0.6和0.9时,uab的1st PWM噪声峰值分别为-10.06、-10.78和-11.15 dBV;uab的2nd PWM噪声峰值分别为-10.58、-12.04和-11.98 dBV。进一步地,m=0.3、0.6和0.9时,实验测得的不同调制方法下uab的1st和2nd PWM噪声峰值见表5。由表5可知,相比PC-RPWM、PS-RPWM、PS-HPWM和POD-HPWM方法,所提PB-HRPWM方法同样具有最低的线电压PWM噪声峰值。
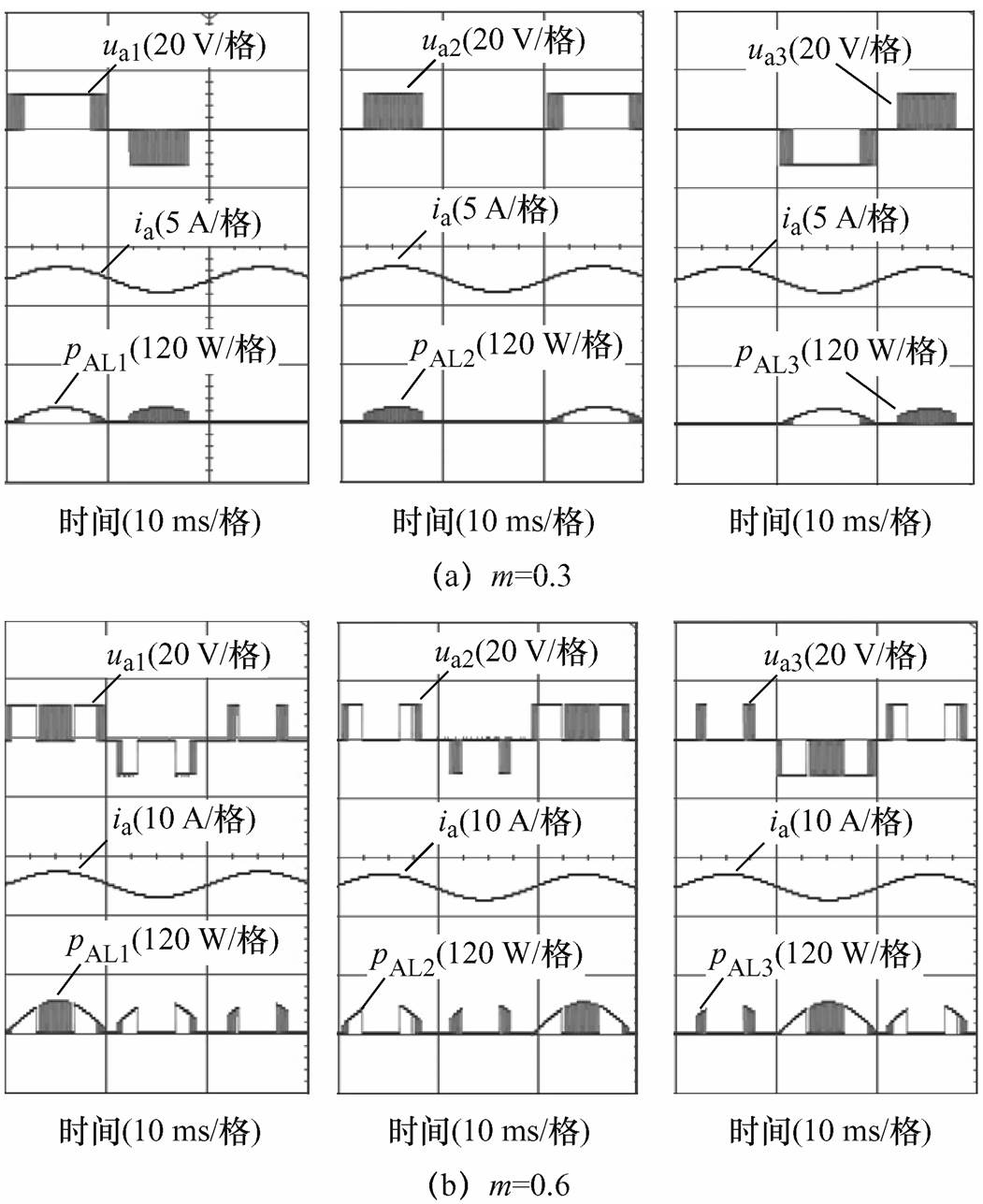
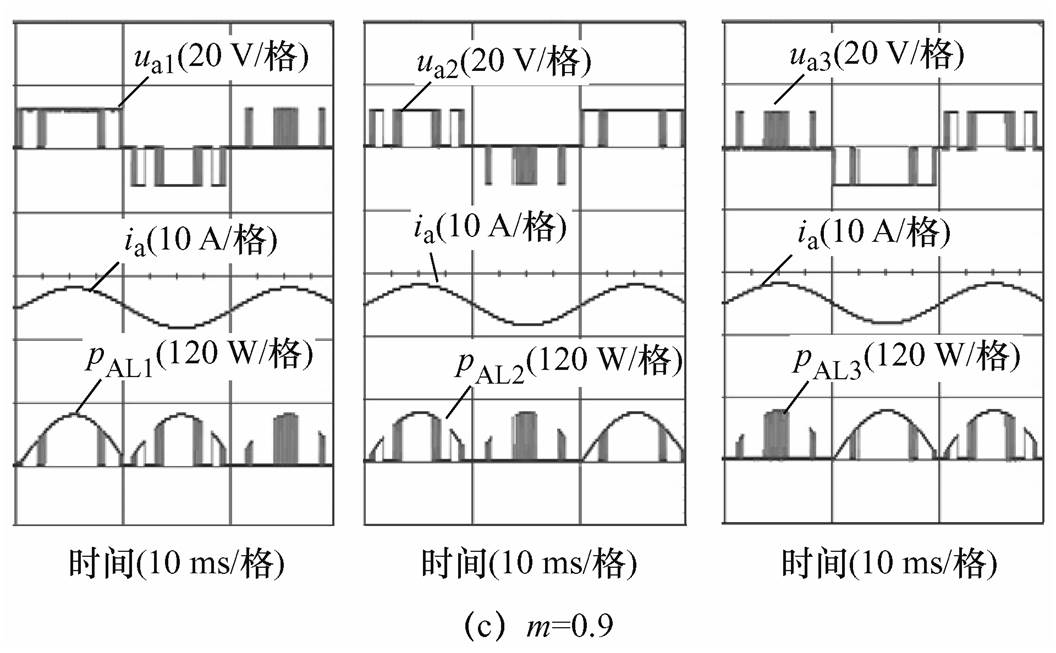
图14给出了m=0.3、0.6和0.9时,H桥单元AL1、AL2和AL3输出电压、电流及功率的实验波形。图14中,uai为H桥单元ALi(i=1,2,3)的输出电压,ia为A相逆变器的相电流(星-星形联结,即相电流等于线电流),pALi为H桥单元ALi(i= 1,2,3)的输出功率。由图14可知,m=0.3时,H桥单元AL1、AL2和AL3的平均输出功率PAL1、PAL2和PAL3分别为21.24、21.24和21.25 W。m=0.6时,H桥单元平均输出功率AL1、AL2和AL3的PAL1、PAL2和PAL3分别为35.56、35.56和35.56 W。m=0.9时,H桥单元AL1、AL2和AL3的平均输出功率PAL1、PAL2和PAL3分别为82.07、82.06和82.07 W。由此可见,H桥单元AL1、AL2和AL3的平均输出功率基本相等,即所提PB-HRPWM方法能有效实现低压H桥单元AL1、AL2和AL2之间的功率均衡,这验证了所提PB-HRPWM方法的功率均衡特性。
表5 实验测得的第1个和第2个PWM噪声峰值
Tab.5 1st and 2nd PWM noise peak through experiments
综上所述,实验结果验证了所提PB-HRPWM方法减小线电压THD降低线电压PWM噪声峰值和实现低压H桥单元之间功率均衡的有效性和可行性。
4 结论
本文提出了一种可有效改善非对称级联H桥三相逆变器中线电压总谐波畸变率、线电压PWM噪声性能和低压H桥单元之间功率分配的PB- HRPWM方法。该方法通过提出的同相层叠随机载波和脉冲逻辑运算将载波层叠调制、阶梯波调制、随机调制和功率均衡有机融合,能有效减小线电压THD和降低线电压PWM噪声峰值,实现非对称级联H桥逆变器中低压H桥单元之间的功率均衡。仿真和实验结果均验证了所提PB-HRPWM方法的有效性和可行性。
参考文献
[1] Liu Senyi, Liu Chunhua. Virtual-vector-based robust predictive current control for dual three-phase PMSM[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2048-2058.
[2] 王晓姬, 王道涵, 王柄东, 等. 电动汽车驱动/充电一体化系统及其控制策略综述[J]. 电工技术学报, 2023, 38(22): 5940-5958.
Wang Xiaoji, Wang Daohan, Wang Bingdong, et al. A review of drive-charging integrated systems and control strategies for electric vehicles[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5940- 5958.
[3] Trzynadlowski A M, Blaabjerg F, Pedersen J K, et al. Random pulse width modulation techniques for converter-fed drive systems-a review[J]. IEEE Transactions on Industry Applications, 1994, 30(5): 1166-1175.
[4] 蒋栋, 沈泽微, 刘自程, 等. 电力推进系统电力电子噪声的主动抑制技术进展[J]. 中国电机工程学报, 2020, 40(16): 5291-5302.
Jiang Dong, Shen Zewei, Liu Zicheng, et al. Progress in active mitigation technologies of power electronics noise for electrical propulsion system[J]. Proceedings of the CSEE, 2020, 40(16): 5291-5302.
[5] Deng Wenzhe, Zuo Shuguang. Electromagnetic vibration and noise of the permanent-magnet synchronous motors for electric vehicles: an overview[J]. IEEE Transactions on Transportation Electrification, 2019, 5(1): 59-70.
[6] 刘剑, 王玉, 鲁炳林, 等. 离散均匀分布随机SVPWM中伪随机数序列的表征与选择[J]. 中国电机工程学报, 2023, 43(9): 3586-3599.
Liu Jian, Wang Yu, Lu Binglin, et al. Characterization and selection of random SVPWM pseudo random number sequence based on discrete uniform distribution[J]. Proceedings of the CSEE, 2023, 43(9): 3586-3599.
[7] 胡文华, 刘剑锋. 一类新型的混合H桥级联逆变器构成方案[J]. 中国电机工程学报, 2019, 39(20): 6044-6055, 6185.
Hu Wenhua, Liu Jianfeng. A new scheme of hybrid H-bridge cascaded inverter[J]. Proceedings of the CSEE, 2019, 39(20): 6044-6055, 6185.
[8] 李国华, 刘春武, 汪玉凤. 单相逆变器随机PWM选择性消谐滞环随机扩频方法[J]. 电工技术学报, 2021, 36(6): 1279-1289.
Li Guohua, Liu Chunwu, Wang Yufeng. A novel hysteresis random spread-spectrum method in random PWM selective harmonic elimination for single-phase inverter[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1279-1289.
[9] Peyghambari A, Dastfan A, Ahmadyfard A. Selective voltage noise cancellation in three-phase inverter using random SVPWM[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4604-4610.
[10] 王亭岭, 熊军华, 张瑾. 基于预设载波的随机开关频率调制方法[J]. 北京航空航天大学学报, 2013, 39(3): 355-360.
Wang Tingling, Xiong Junhua, Zhang Jin. Random PWM method based on pre-determined carrier frequencies[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(3): 355-360.
[11] Chen H C, Chang Y C, Huang C K. Development of optimised carrier sequence in MCU-based random- frequency PWM[J]. IET Electric Power Applications, 2007, 1(1): 43.
[12] 陈少先, 丁树业, 申淑锋, 等. 船舶用表贴式永磁同步电机的电磁振动分析与抑制[J]. 电工技术学报, 2023, 38(5): 1275-1286, 1298.
Chen Shaoxian, Ding Shuye, Shen Shufeng, et al. Analysis and suppression of electromagnetic vibration of surface mounted permanent magnet synchronous motor for ships[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1275-1286, 1298.
[13] Gamoudi R, Elhak Chariag D, Sbita L. A review of spread-spectrum-based PWM techniques-a novel fast digital implementation[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10292-10307.
[14] 胡文华, 刘剑锋, 曹仁赢. 混合级联H桥十三电平逆变器的混合调制[J]. 电力电子技术, 2020, 54(3): 90-92.
Hu Wenhua, Liu Jianfeng, Cao Renying. Hybrid modulation of hybrid cascaded H-bridge thirteen- level inverter[J]. Power Electronics, 2020, 54(3): 90-92.
[15] 顾军, 宋飞, 李平, 等. 混合级联H桥逆变器的调制策略优化方法[J]. 高电压技术, 2022, 48(2): 753-761.
Gu Jun, Song Fei, Li Ping, et al. Modulation strategy optimization method of hybrid cascaded H-bridge inverter[J]. High Voltage Engineering, 2022, 48(2): 753-761.
[16] Ye Manyuan, Peng Ruifan, Tong Ziwei, et al. A generalized scheme with linear power balance and uniform switching loss for asymmetric cascaded H-bridge multilevel inverters[J]. IEEE Transactions on Power Electronics, 2022, 37(3): 2719-2730.
[17] 李金玉, 陈杰, 龚春英, 等. 一种提高级联H桥逆变器功率不平衡运行能力的控制策略[J]. 电工技术学报, 2023, 38(10): 2731-2743.
Li Jinyu, Chen Jie, Gong Chunying, et al. A control strategy to improve working ability of cascaded H-bridge inverter under power imbalance[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(10): 2731-2743.
[18] Guo Xiaoqiang, Wang Xiaoming, Wang Chaozhe, et al. Improved modulation strategy for singe-phase cascaded H-bridge multilevel inverter[J]. IEEE Transactions on Power Electronics, 2022, 37(3): 2470-2474.
[19] 陈仲, 许亚明, 那显龙, 等. 级联型多电平逆变器输出电压循环分配的功率均衡控制及优化[J]. 中国电机工程学报, 2018, 38(4): 1132-1142, 1291.
Chen Zhong, Xu Yaming, Na Xianlong, et al. Power balance control and optimization methods with output voltage rotation for cascaded multilevel inverter[J]. Proceedings of the CSEE, 2018, 38(4): 1132-1142, 1291.
[20] 陈仲, 孙健博, 许亚明, 等. 采用输出周期脉冲循环的级联H桥型逆变器功率均衡方法[J]. 电工技术学报, 2020, 35(4): 827-838.
Chen Zhong, Sun Jianbo, Xu Yaming, et al. Power balance method of cascaded H-bridge inverter based on pulse circulation in output period[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 827- 838.
A Power-Balanced Hybrid Random Pulse Width Modulation Method for Asymmetric Cascaded H-Bridge Three-Phase Inverter
Liu Jianfeng Gong Renxi Zhang Yuanyuan
(School of Electrical Engineering Guangxi University Nanning 530004 China)
Abstract With the continuous development of power electronics technology, three-phase voltage source inverters controlled by pulse width modulation (PWM) have been widely used in AC drive systems, electric vehicles, and ships. Such methods have fixed carrier frequency, and the PWM noise peak of line voltage is very high, causing acoustic noises in the motor and electromagnetic noises in the inverter. Scholars have proposed various random PWM methods to suppress PWM noise peaks, such as RPWM method optimization from random algorithms and carrier sequences.The in-phase disposition pulse width modulation (IPD-PWM) has a smaller THD of line voltage than the phase-shifted pulse width modulation (PS-PWM).
However, these modulation methods are mainly applied to single H-bridge inverters. Compared with single H-bridge inverters, cascaded H-bridge inverters have a smaller total harmonic distortion (THD) of output voltage. In addition, asymmetric cascaded H-bridge inverters have a larger output power and a smaller output voltage THD than symmetric cascaded H-bridge inverters.Therefore, this paper proposes a power-balanced hybrid RPWM (PB-HRPWM) method for asymmetric cascaded H-bridge three-phase inverters with a voltage ratio of 1 1
1 1
1 3. The proposed PB-HRPWM method can be summarized as follows. (1) The driving pulses of the high-voltage H-bridge unit and the modulation wave of the low-voltage H-bridge unit are generated by comparing the modulation wave of the high-voltage H-bridge unit with the reference level. (2) The random pulses are generated by comparing in-phase random level-shifted carriers with the modulation wave of the low-voltage H-bridge unit. (3) The random pulses are circularly distributed according to 1/2 Tah by pulse logic operation method to obtain the driving pulses of the low-voltage H-bridge unit. (4) The driving pulses of high and low-voltage H-bridges control the operation of the three-phase inverter. The proposed PB-HRPWM method effectively reduces the PWM noise peak of line voltage, and the power balance between the low-voltage H-bridge units can be realized. Compared with conventional random and non-random PWM methods, the proposed PB-HRPWM method has a lower PWM noise peak of line voltage and a smaller total harmonic distortion of line voltage. Simulations and experiments verify the effectiveness and feasibility of the proposed PB-HRPWM method.
3. The proposed PB-HRPWM method can be summarized as follows. (1) The driving pulses of the high-voltage H-bridge unit and the modulation wave of the low-voltage H-bridge unit are generated by comparing the modulation wave of the high-voltage H-bridge unit with the reference level. (2) The random pulses are generated by comparing in-phase random level-shifted carriers with the modulation wave of the low-voltage H-bridge unit. (3) The random pulses are circularly distributed according to 1/2 Tah by pulse logic operation method to obtain the driving pulses of the low-voltage H-bridge unit. (4) The driving pulses of high and low-voltage H-bridges control the operation of the three-phase inverter. The proposed PB-HRPWM method effectively reduces the PWM noise peak of line voltage, and the power balance between the low-voltage H-bridge units can be realized. Compared with conventional random and non-random PWM methods, the proposed PB-HRPWM method has a lower PWM noise peak of line voltage and a smaller total harmonic distortion of line voltage. Simulations and experiments verify the effectiveness and feasibility of the proposed PB-HRPWM method.
In summary, the proposed PB-HRPWM method integrates IPD-PWM, step wave modulation, random modulation, and power balance through the proposed in-phase disposition random carriers and pulse logic operations. Therefore, utilizing the low waveform distortion of IPD-PWM and the high-frequency spectrum dispersion of random frequency modulation can decrease the THD and PWM noise peak of line voltage. The power balance target is decoupled from the modulation wave or carrier reconstruction through pulse logic operations between random pulses and pulse signals, avoiding complex modulation wave or carrier design in digital processors.
keywords:Multilevel inverter, cascaded H-bridge, pulse width modulation, noise, power balance
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.231823
国家自然科学基金(61561007)和广西自然科学基金(2017GXNSFAA198168)资助项目。
收稿日期2023-10-31
改稿日期2024-01-23
作者简介
刘剑锋 男,1994年生,博士研究生,研究方向为多电平逆变技术、电机控制技术等。E-mail: dianqi_jfliu@163.com
龚仁喜 男,1962年生,教授,博士生导师,研究方向为新能源发电与智能微电网、电机先进控制技术等。E-mail: rxgong@gxu.edu.cn(通信作者)
(编辑 陈 诚)
 1
1 1
1 3的非对称级联H桥三相逆变器输出线电压的脉宽调制(PWM)噪声峰值,该文提出一种融合阶梯波调制、同相载波层叠调制、随机调制及功率均衡的功率均衡混合随机脉宽调制(PB-HRPWM)方法。该方法可概述为:①通过高压H桥单元的调制波与参考电位相比较,产生高压H桥单元的驱动脉冲和低压H桥单元的调制波;②通过同相层叠随机载波与低压H桥单元的调制波相比较,产生随机脉冲;③通过脉冲逻辑运算方法对随机脉冲按照0.5Tah进行循环分配,得到低压H桥单元的驱动脉冲;④使用高低压H桥单元的驱动脉冲控制三相逆变器的运行。仿真和实验结果表明:该方法可以降低线电压PWM噪声峰值,同时实现低压H桥单元之间的功率均衡。相比传统的随机和非随机PWM方法,所提PB-HRPWM方法具有更低的线电压PWM噪声峰值和更小的线电压总谐波畸变率(THD)。最后,通过仿真对比和实验验证了所提PB-HRPWM方法的有效性和可行性。
3的非对称级联H桥三相逆变器输出线电压的脉宽调制(PWM)噪声峰值,该文提出一种融合阶梯波调制、同相载波层叠调制、随机调制及功率均衡的功率均衡混合随机脉宽调制(PB-HRPWM)方法。该方法可概述为:①通过高压H桥单元的调制波与参考电位相比较,产生高压H桥单元的驱动脉冲和低压H桥单元的调制波;②通过同相层叠随机载波与低压H桥单元的调制波相比较,产生随机脉冲;③通过脉冲逻辑运算方法对随机脉冲按照0.5Tah进行循环分配,得到低压H桥单元的驱动脉冲;④使用高低压H桥单元的驱动脉冲控制三相逆变器的运行。仿真和实验结果表明:该方法可以降低线电压PWM噪声峰值,同时实现低压H桥单元之间的功率均衡。相比传统的随机和非随机PWM方法,所提PB-HRPWM方法具有更低的线电压PWM噪声峰值和更小的线电压总谐波畸变率(THD)。最后,通过仿真对比和实验验证了所提PB-HRPWM方法的有效性和可行性。
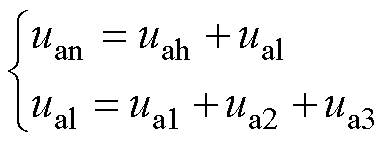 (1)
(1)
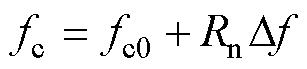 (2)
(2)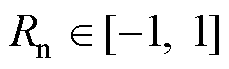 。当调制度
。当调制度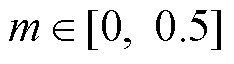 时,v
时,v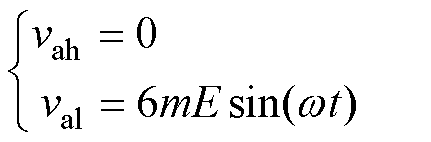 (3)
(3)
 (0.5, 1
(0.5, 1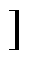 时,v
时,v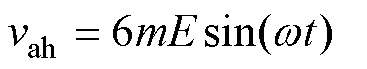 (4)
(4)
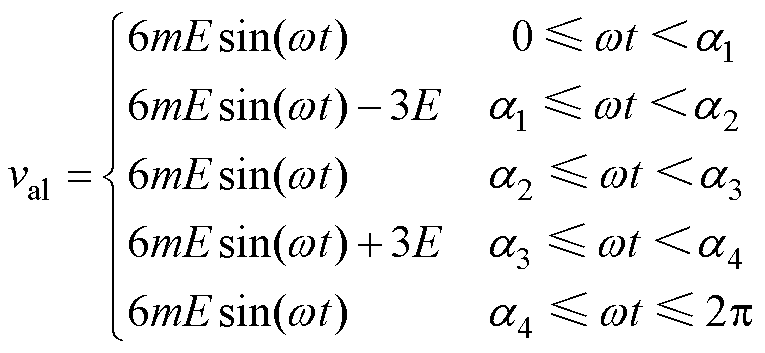 (5)
(5)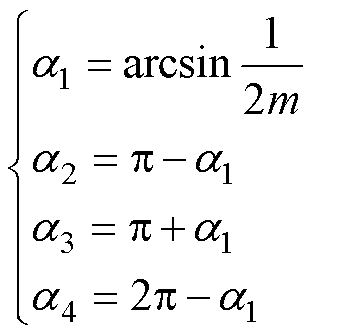 (6)
(6)
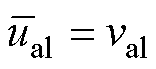 (7)
(7)
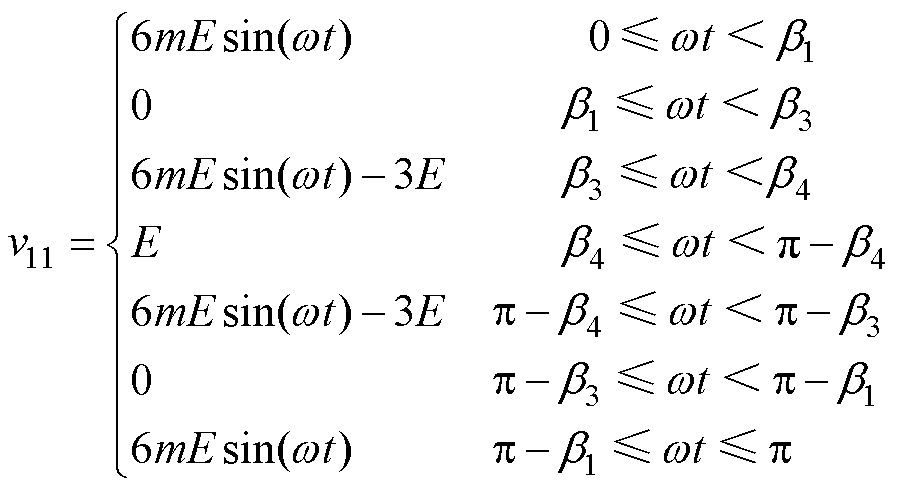 (8)
(8)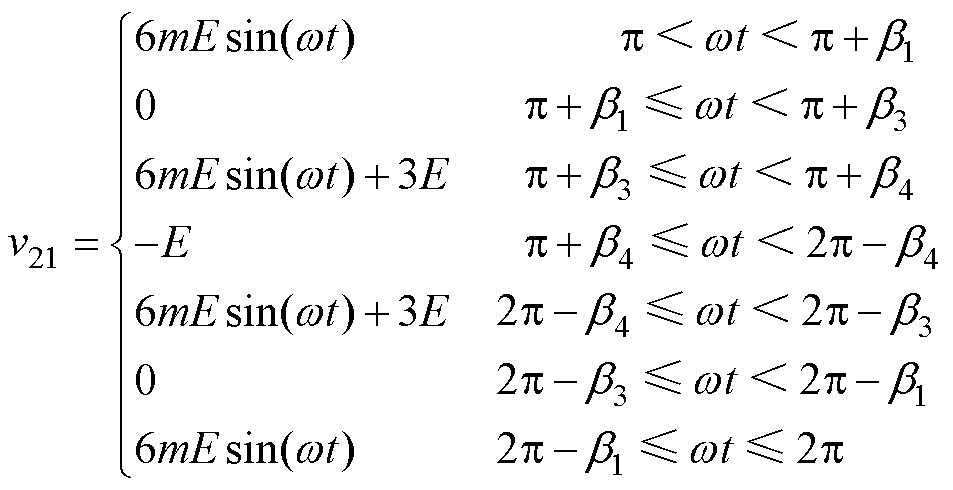 (9)
(9)
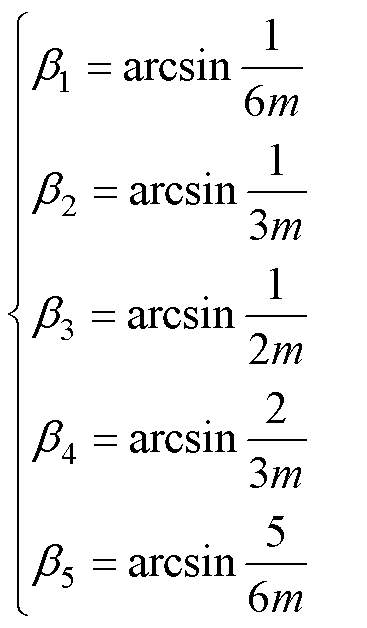 (10)
(10)
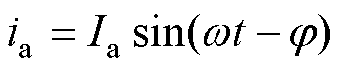 (11)
(11)
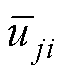 (
(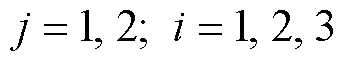 )作用下,H桥单元ALi(i=1, 2, 3)的平均输出功率为
)作用下,H桥单元ALi(i=1, 2, 3)的平均输出功率为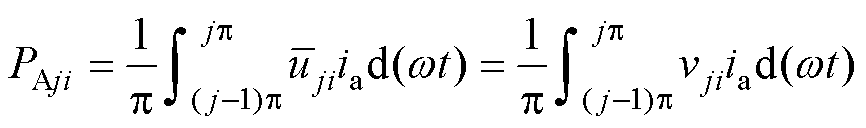 (12)
(12)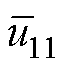 作用下的P
作用下的P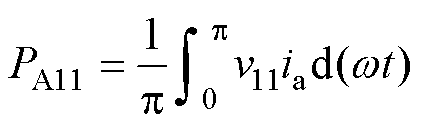 (13)
(13)
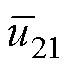 作用下的P
作用下的P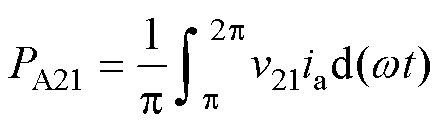 (14)
(14)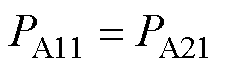 (15)
(15)
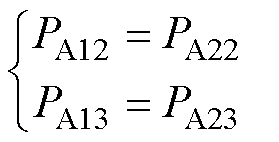 (16)
(16)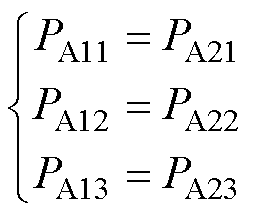 (17)
(17)
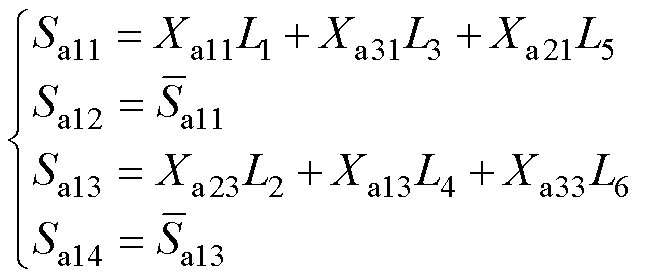 (18)
(18)
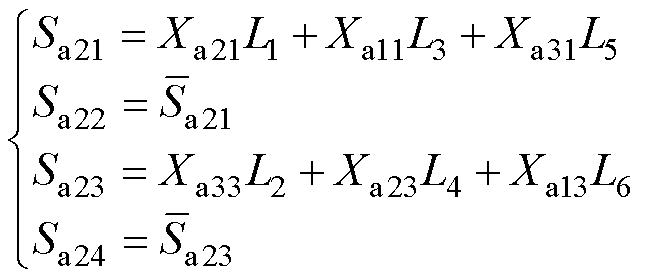 (19)
(19)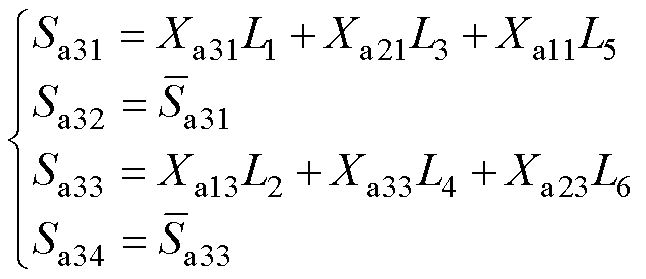 (20)
(20)
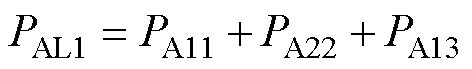 (21)
(21)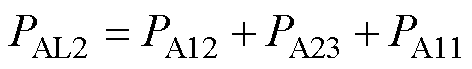 (22)
(22)
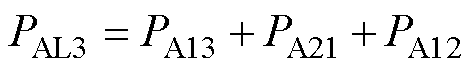 (23)
(23)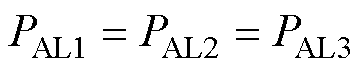 (24)
(24)


 ) kHz附近都集中着大量高峰值PWM噪声,即PWM噪声集中在整数倍平均等效开关频率附近且峰值较高;②尽管PC-RPWM和PS-RPWM的随机载波频率范围不同,但两者在6n(n=1, 2, 3,
) kHz附近都集中着大量高峰值PWM噪声,即PWM噪声集中在整数倍平均等效开关频率附近且峰值较高;②尽管PC-RPWM和PS-RPWM的随机载波频率范围不同,但两者在6n(n=1, 2, 3,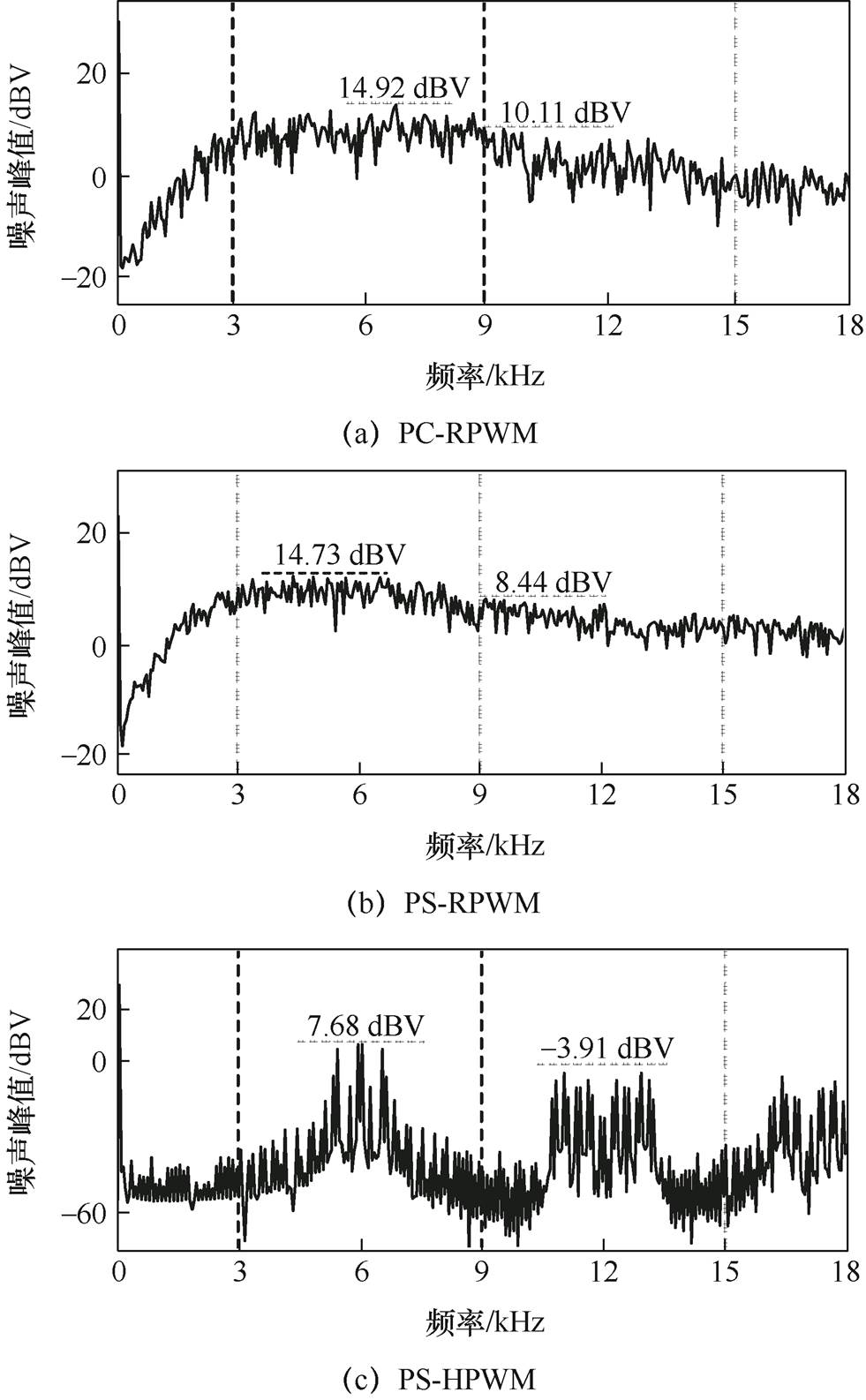
 0.1
0.1