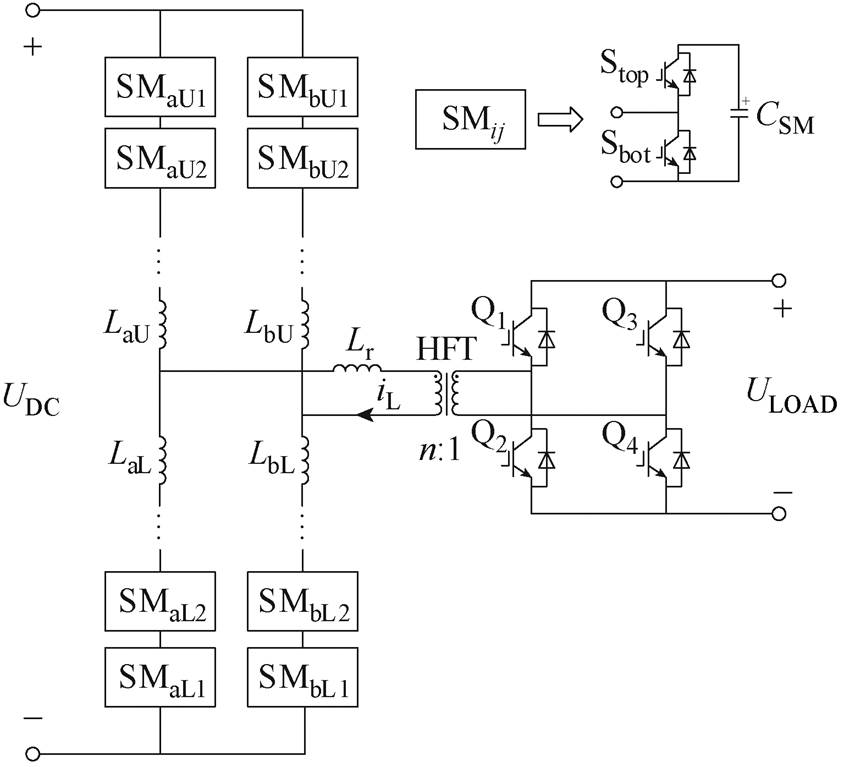
图1 MMC-H SST拓扑
Fig.1 MMC-H SST topology
摘要 相比于双有源桥级联式固态变压器,模块化多电平换流器H桥(MMC-H)固态变压器仅用单个高频隔离变压器且控制灵活,故障容错率高。但现有MMC-H固态变压器主要采用方波-方波调制,存在系统dv/dt应力和电流谐波大的问题。MMC灵活的非方波调制技术具有优化电压和电流性能良好的前景,但其传输模型和特性未知,极大地限制了MMC-H固态变压器的应用。该文提出正弦-方波、三角-方波两类非对称方波调制下的MMC-H固态变压器的精准功率传输建模和控制方法,揭示其功率传输和电流变化特性,确定最大传输功率点。此外,详细对比两类非方波调制和传统方法下的传输特性差异并阐明原因。结果表明,所提两类非对称调制波和控制方法下的传输功率模型平均误差分别为2.8%和3.4%,准确度高;所提正弦-方波调制和控制方法下在最大传输功率、传输电流峰值、谐波量和器件损耗等方面具有综合最优性能,并具有良好的动态稳定性和快速响应能力。
关键词:模块化多电平变流器 固态变压器 功率特性 非方波调制 谐波抑制
固态变压器(Solid State Transformer, SST),是由功率半导体器件和中高频变压器组成的电力变换与控制设备[1-3]。由于其具有多端口集成和优异的控制性能,近年来受到研究人员的广泛关注。典型SST交流部分采用双有源桥(Dual-Active Bridge, DAB)级联拓扑[4],通过每个DAB变压器传递功率,这使得单台固态变压器需要大量的高频隔离变压器。同时,受到DAB结构限制,该拓扑只能采用方波调制,增加了系统dv/dt应力和谐波环流。
固态变压器在高压侧采用模块化多电平换流器(Modular Multilevel Converter, MMC),低压侧H桥结构,是一种新型的中高压大容量SST,其拓扑如图1所示。该拓扑可实现中高压与低压功率的电力变换控制,适用于光伏发电并网、储能直挂、电动汽车充电、船舶配用电等领域[5-6]。与传统DAB级联式固态变压器相比,MMC-H固态变压器仅需单个高频隔离变压器,显著降低了系统的成本和体积,提高了功率密度,简化了系统设计。此外,MMC具有高自由度的调制方法和模块化结构[7],提高了SST装备的控制灵活性和故障容错率。

图1 MMC-H SST拓扑
Fig.1 MMC-H SST topology
现有SST研究主要集中在DAB级联型SST的拓扑演化、传输功率模型构建、传输电流抑制等方面,基于MMC的SST研究还比较少[6]。ABB的S. Kenzelmann等首先提出变压器两侧均采用MMC结构(双MMC型)的直流固态变压器[8],交流部分仅采用单个高频隔离变压器,显著降低了变压器的个数和质量。清华大学的Zhao Biao等[9-10]详细对比了双MMC型和DAB型SST的差异,提出了方波-方波、正弦波-正弦波、三角波-三角波三种对称型功率传输调制方法,后两者降低了变压器dv/dt应力。此外,Sun Changjiang[11-12]等,Zhang Lei[13-15]等提出了针对双MMC型SST电容电压平衡和纹波抑制算法,提高了变压器可靠性。然而,以上研究主要面向高压-高压的双MMC对称式SST建模、特性分析和控制优化。
针对高低压变换应用的MMC-H SST,浙江大学王朝辉等[16]和Shao Shuai等[17-18]提出了基于方波-方波或近方波调制下的SST控制策略和电容电压平衡算法,实现了该新型SST的高效输出电压和内部电容稳定控制;佛罗利达州立大学Mo Ran等[19]针对方波调制较大的谐波环流问题提出了移相方波调制,减小了谐波环流,但存在开关频率较高的问题;俄亥俄州立大学Xing Diang等提出了基于桥臂电感耦合型的MMC-H拓扑[20],并首次应用3.3 kV SiC器件在该SST上。然而,前期研究主要采用DAB结构近似的方波-方波调制,存在系统谐波含量大、环流抑制难等问题。针对高低电压转换和非对称式调制下的更复杂工况的MMC-H固态变压器,其功率传输模型和控制方法未知,特性难以评估,限制了MMC-H SST构建和发展。
因此,本文对正弦-方波,三角-方波两类非对称式调制下MMC-H SST的功率传输机制和特性进行分析,建立了两种非对称式调制下SST精准功率和电流传输模型,揭示了其内部功率传输和电流分布特性。此外,基于传输模型确定了最大传输功率点的位置和功率值,对比分析了正弦-方波、三角-方波和传统方波-方波调制和控制下的传输特性差异并阐述其原因。结果表明,所提传输模型能精准表征传输电流和功率的变化规律,基于正弦-方波调制的MMC-H SST能有效降低传输电流应力和谐波分量,为新型MMC-H SST控制优化、效益评估和应用推广提供了良好理论支撑。
图1显示了MMC-H SST拓扑,主要由高压侧MMC变换器、低压侧H桥变换器、移相电感和单个高频变压器(High Frequency Transformer, HFT)组成。其中,MMC直流侧与高压直流母线相连,UDC为直流母线电压;交流输出侧通过移相电感Lr与高频隔离变压器一次侧连接,n为变压器电压比。H桥变换器与变压器二次侧相连并实现整流功能,ULOAD为输出负载电压。高压端MMC侧包含a、b两相,每相分为上、下两个桥臂,每个桥臂由N个子模块和桥臂电感串联组成,子模块(Sub-Module, SM)电容为CSM。Stop、Sbot分别为上、下两个开关器件。LxU、LxL分别为x相上、下桥臂电感,x=a, b。,iL为系统传输电流(变压器输入电流),Q1~Q4为低压H桥4个开关器件。MMC不同调制方法使各个子模块按照一定的顺序投入或切除,在交流端口输出所需频率下的特定波形[21-22]。低压侧变换器由于采用H桥结构只能输出方波。
基于方波-方波的移相控制是包含MMC-H在内的固态变压器最常用的功率控制方法[23-24],采用移相控制的SST系统电压和电流波形如图2所示。高压侧和低压侧均采用方波,通过调节变压器两侧电压波形移相角,可实现传输功率和方向的调节。图中,U1为MMC输出电压,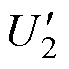 为变压器二次侧等效到一次侧的电压,外移相比D为变压器两侧开关器件移相角j 占半个基频周期的比值,f为MMC一次侧输出电压电流频率。同一桥臂上、下开关信号互补,控制外移相比D即可控制传输功率的大小和方向。传统方波调制下SST移相控制原理和功率传输特性如式(1)~式(5)所示。在该方法中,将电压参考值ULOAD.ref与负载电压ULOAD比较,获得电压差Uerror,通过PI控制调节移相角j,进而调节该功率值下外移相比D,从而控制输出功率的大小和方向。
为变压器二次侧等效到一次侧的电压,外移相比D为变压器两侧开关器件移相角j 占半个基频周期的比值,f为MMC一次侧输出电压电流频率。同一桥臂上、下开关信号互补,控制外移相比D即可控制传输功率的大小和方向。传统方波调制下SST移相控制原理和功率传输特性如式(1)~式(5)所示。在该方法中,将电压参考值ULOAD.ref与负载电压ULOAD比较,获得电压差Uerror,通过PI控制调节移相角j,进而调节该功率值下外移相比D,从而控制输出功率的大小和方向。
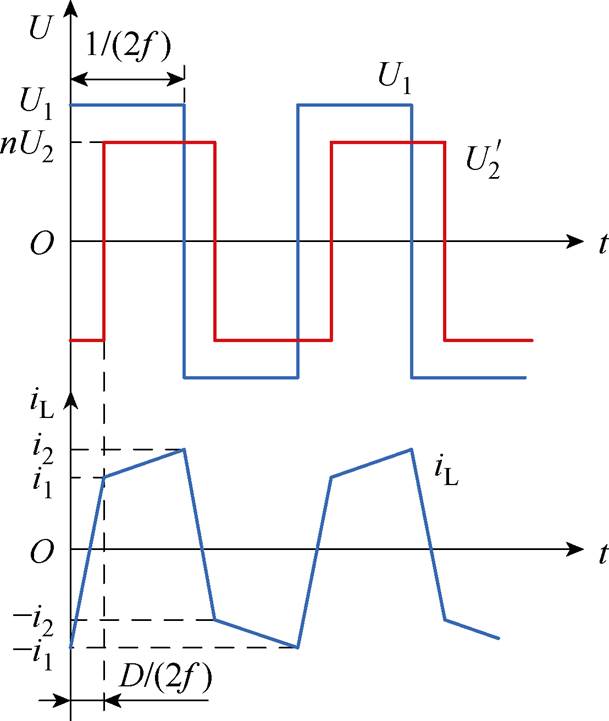
图2 采用移相控制的SST系统电压和电流波形
Fig.2 Voltage and current waveforms of SST using phase shift control
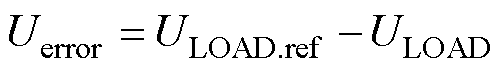 (1)
(1)
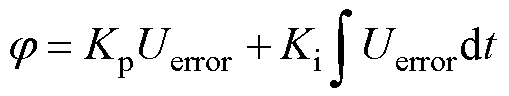 (2)
(2)
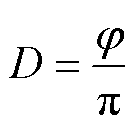 (3)
(3)
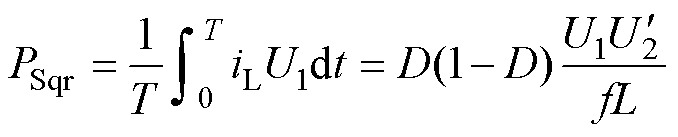 (4)
(4)
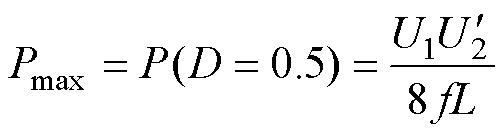 (5)
(5)
式中,PSqr为传统方波调制下SST传输有功功率与D的关系式;T为一次侧输出电压电流周期;L为移相电感;Pmax为最大传输有功功率;Kp和Ki为PI调节参数。
MMC在运行过程中,不同子模块电容因充放电程度不同可能会引发电容电压不平衡问题。因为传统MMC电容排序算法复杂且需要较多的电容电压传感器,而高频下电容电压波动较小,本文参考文献[9]选择单步交替平衡算法来实现电容电压平衡控制,降低系统安装成本的同时保证MMC-H SST内电容电压的平衡稳定。
传统的SST主要采用方波-方波两侧对称型调制方法,已构建精准的功率传输模型并揭示其传输特性。然而对于采用非方波优化调制方法的MMC-H SST并不适应。本节主要对基于正弦-方波和三角-方波非对称型调制方法进行建模和分析,阐明其电流和功率特性并提出综合控制方法。
MMC输出电压等效为电压源U1,变压器输出电压等效到一次电压为nU2。高频变压器等效电路如图3所示。其中,Lr为移相电感,Lσ、R1分别为变压器一次侧漏感和电阻,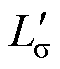 、
、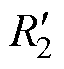 分别为二次侧等效到一次侧的漏感和电阻,Lm和Rm分别为励磁电感和电阻,E为感应电动势,
分别为二次侧等效到一次侧的漏感和电阻,Lm和Rm分别为励磁电感和电阻,E为感应电动势,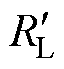 为等效到一次侧的负载电阻。
为等效到一次侧的负载电阻。
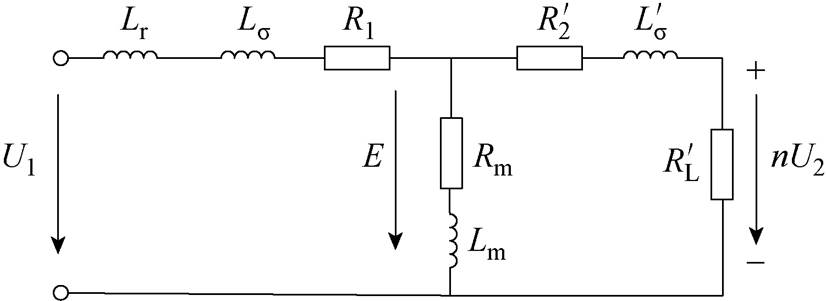
图3 SST高频变压器等效电路
Fig.3 Equivalent circuit diagram of the high frequency transformer in SST
为简化计算,将变压器的励磁电感设为无穷大,忽略变压器漏感及电阻等参数,有
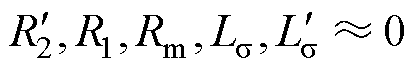 (6)
(6)
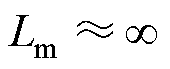 (7)
(7)
因此,二次侧等效为开路,有
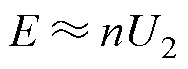 (8)
(8)
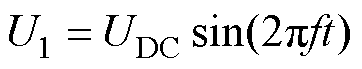 (9)
(9)
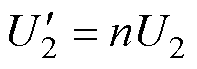 (10)
(10)
进而可以获得系统简化电路模型,如图4所示。
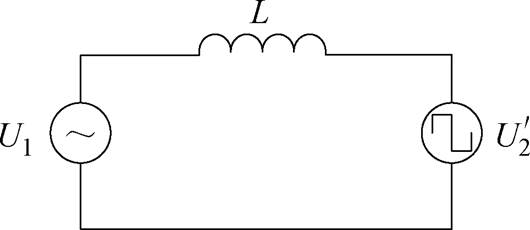
图4 正弦-方波调制下SST简化电路
Fig.4 Circuit model of SST at sine-square modulation
等效电感L为高频变压器的漏感Ls 和移相电感Lr之和,即
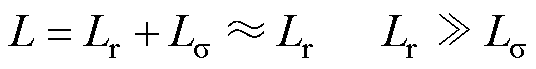 (11)
(11)
图5为MMC-H正弦-方波调制下的系统电压电流特性曲线,利用电感电流公式和基尔霍夫定律,有
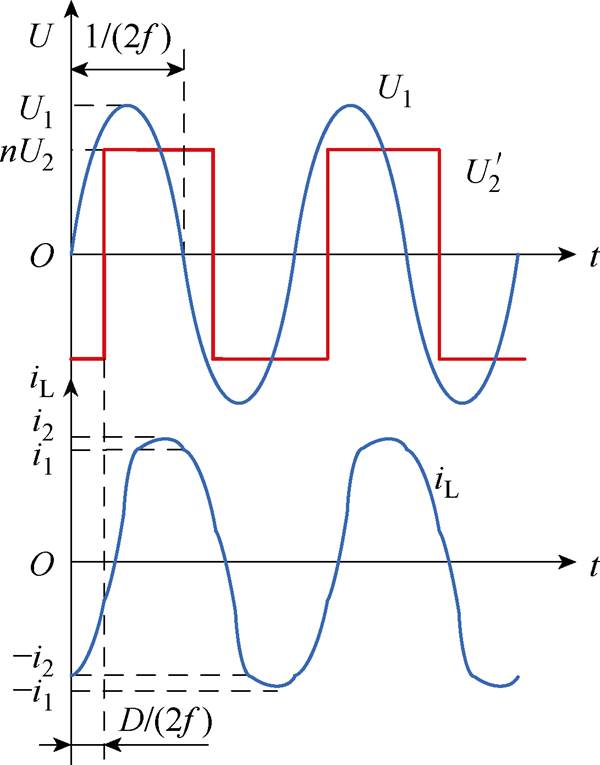
图5 正弦-方波调制下SST电压电流特性
Fig.5 Voltage and current characteristics of the SST at sine-square modulation
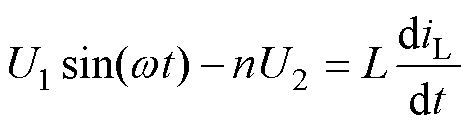 (12)
(12)
考虑半个周期内的电流值,有
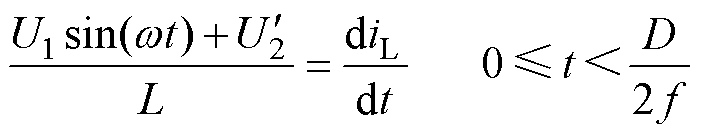 (13)
(13)
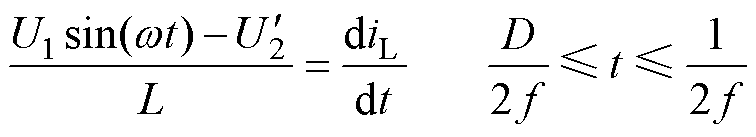 (14)
(14)
式中,w 为系统工作角频率。
电流满足初始值
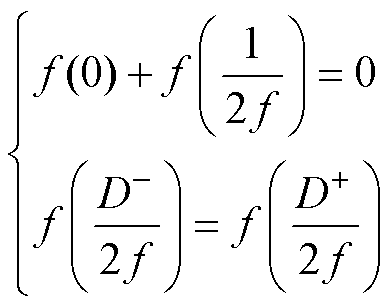 (15)
(15)
结合式(13)~式(15),可求解得到系统在半个周期内传输电流iL(t)的表达式为
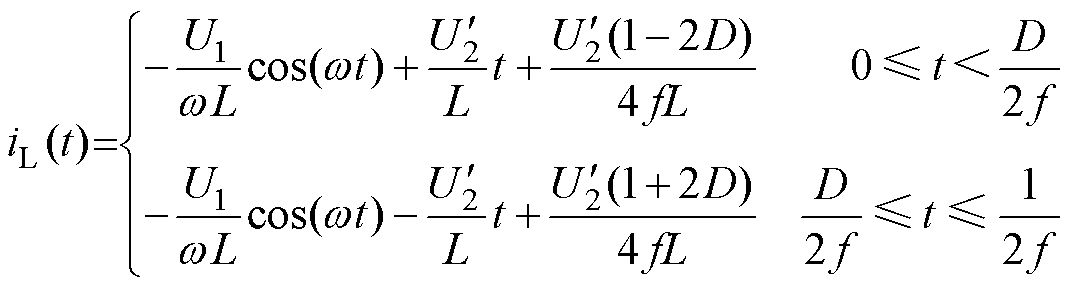 (16)
(16)
由于iL每半个周期改变一次方向,不改变幅值,根据式(16)获得传输电流iL特性如式(17)所示。式(17)显示了传输电流在每个周期内的分布特性。
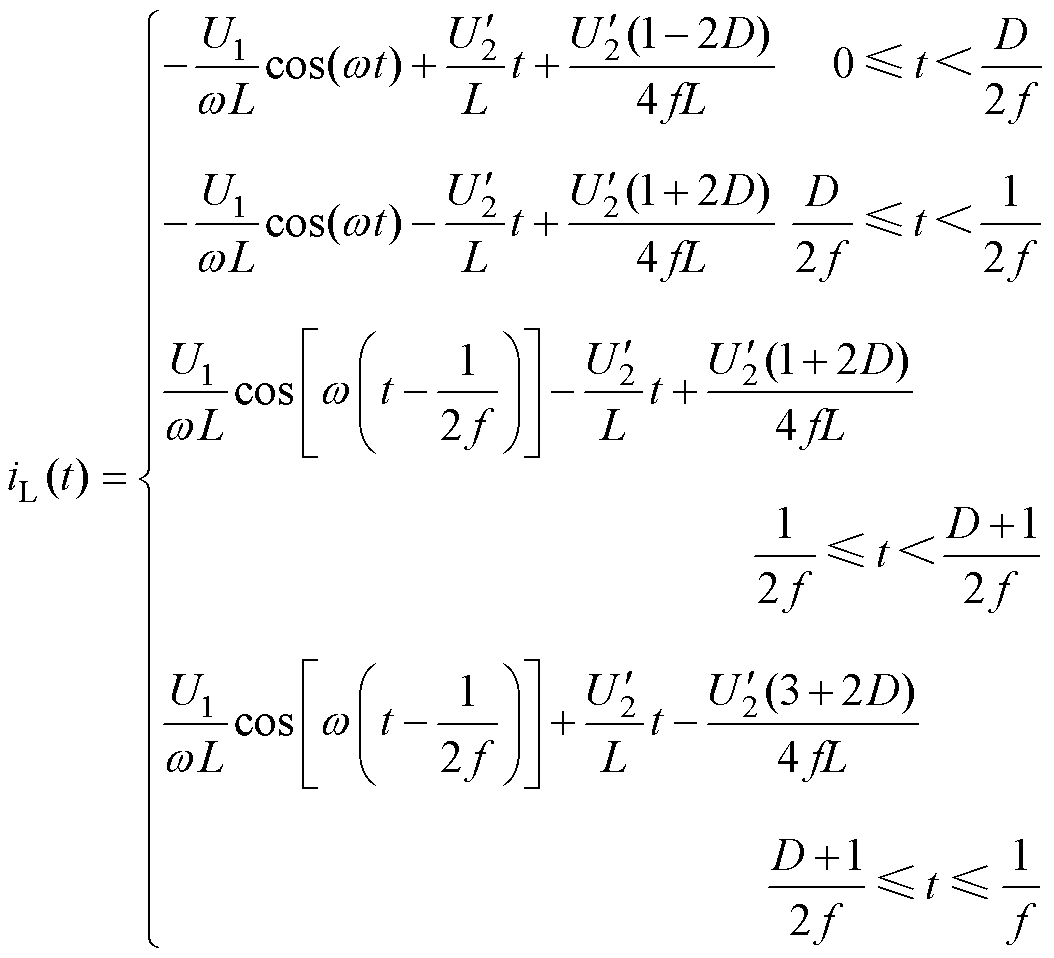 (17)
(17)
利用式(17)即可计算变换器传输有功功率为
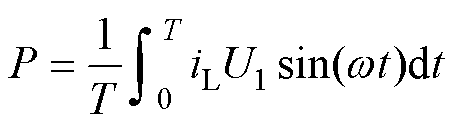 (18)
(18)
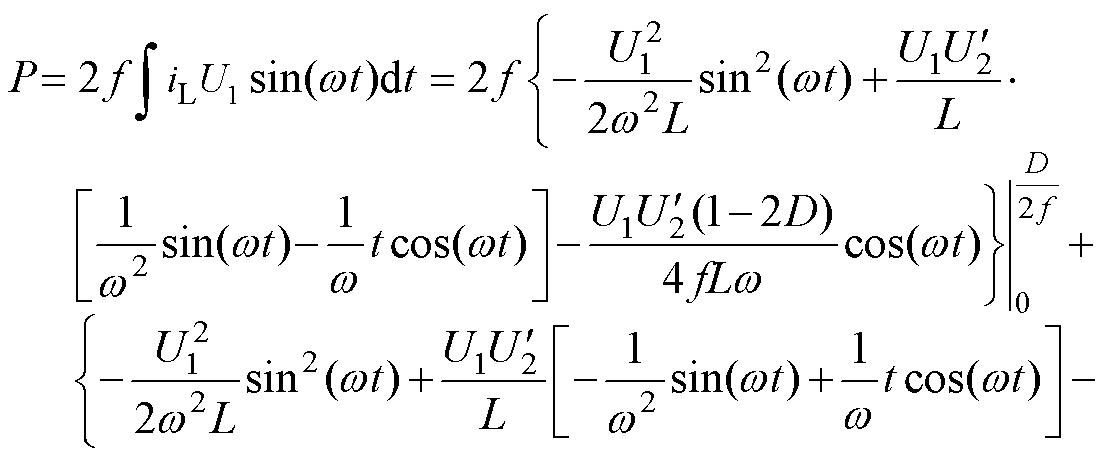
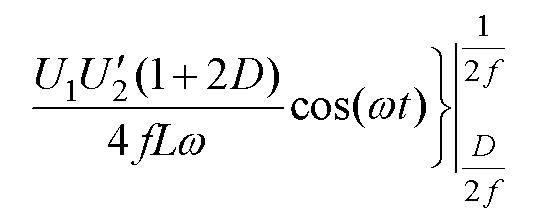 (19)
(19)
化简式(19),得到正弦-方波调制下系统传输有功功率与D的关系式为
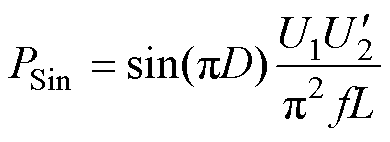 (20)
(20)
系统功率传输模型如式(20)所示,本文用Sqr代表方波-方波调制,Sin代表正弦-方波调制,Tri代表三角-方波调制。在理想正弦(N=∞)调制下,系统传输功率与相移角、输入输出侧电压等级成正比,与变压器漏感和交流链路频率成反比。系统最大功率点在外移相比D=0.5出现,最大功率点表示为
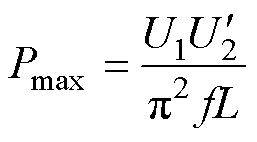 (21)
(21)
三角-方波调制下系统简化模型如图6所示。结合式(9)、式(10),与正弦-方波调制类似,三角-方波调制下系统传输电流iL在第一个周期内的表达式为
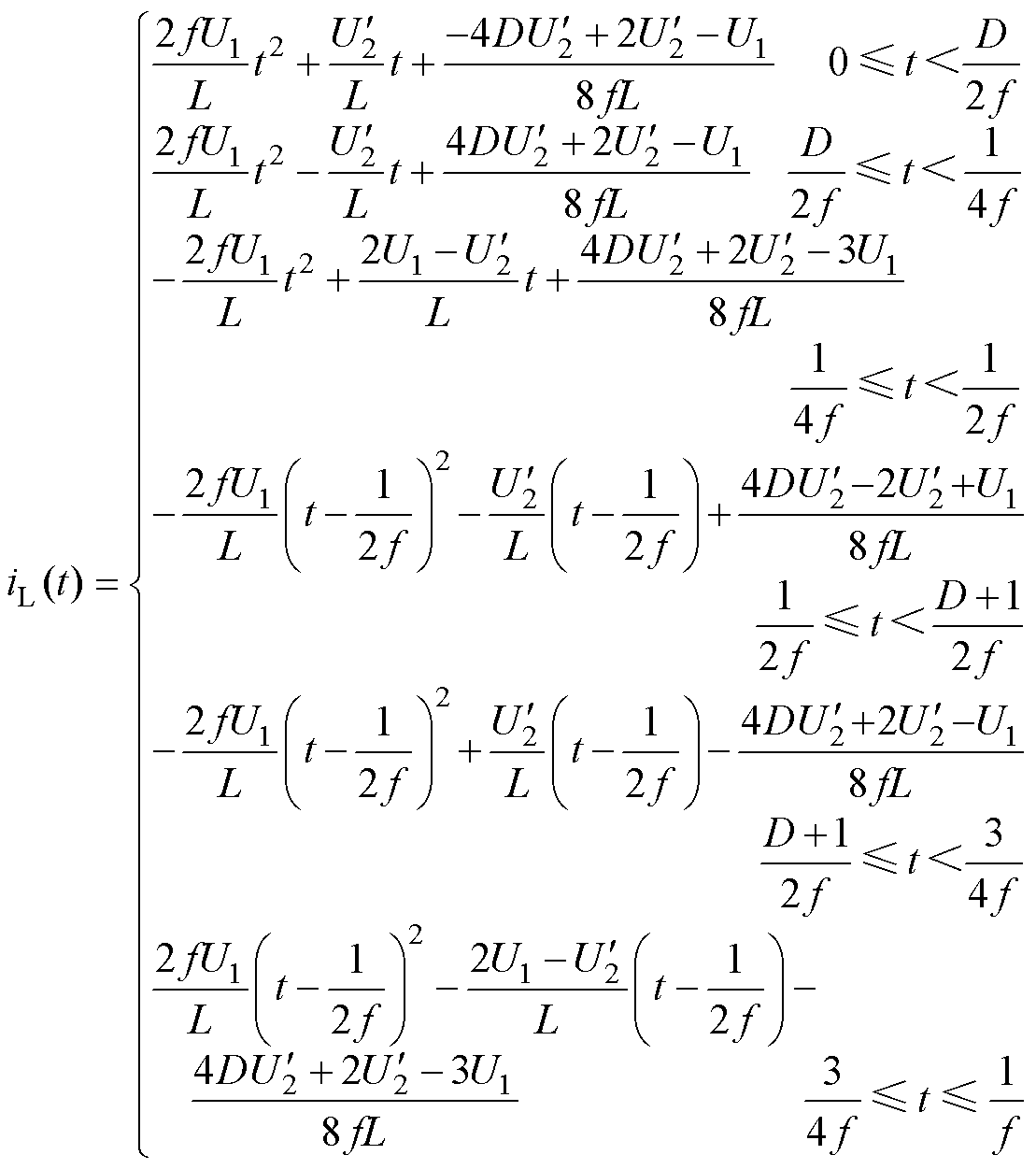 (22)
(22)
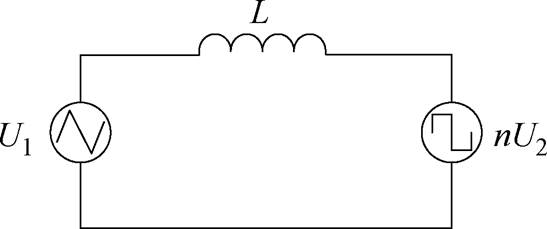
图6 三角-方波下SST简化电路
Fig.6 Circuit model of SST at triangle-square modulation
将电感电流表达式(22)代入式(18),得到三角-方波调制下系统传输有功功率与D的关系式为
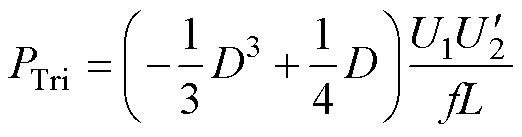 (23)
(23)
系统最大功率点(D=0.5)为
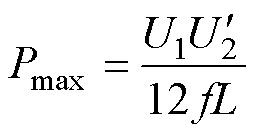 (24)
(24)
本文进一步对移相电感和高频变压器上的传输电流应力进行分析,阐明传输功率与最大传输电流应力的关联关系,揭示正弦-方波和三角-方波调制下的电流应力差异原因。
传统对称方波调制下MMC-H传输电流iL在第一个周期内的表达式如式(25)所示,系统传输功率与移相角关联关系如式(5)所示。
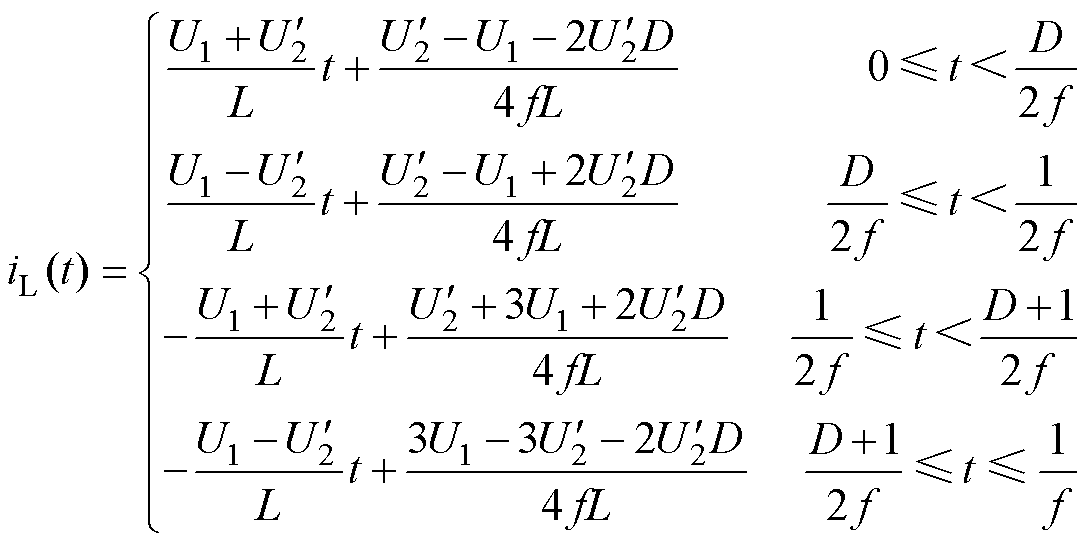 (25)
(25)
记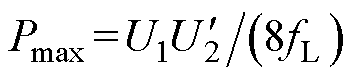 ,同时规定功率标幺值P以正弦-方波调制下的最大功率值
,同时规定功率标幺值P以正弦-方波调制下的最大功率值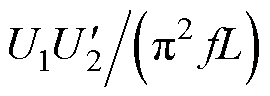 为参考值。结合式(4)、式(20)、式(23),可得方波、正弦波、三角波调制下最大功率P标幺值分别为1.23(pu)、1(pu)、0.82(pu)。说明方波-方波调制方法下最大传输功率会高于正弦-方波调制,三角-方波调制传输功率最小。
为参考值。结合式(4)、式(20)、式(23),可得方波、正弦波、三角波调制下最大功率P标幺值分别为1.23(pu)、1(pu)、0.82(pu)。说明方波-方波调制方法下最大传输功率会高于正弦-方波调制,三角-方波调制传输功率最小。
为对比三种调制方法下最大电流应力差异,本文通过计算同一功率点P下各调制所对应的外移相比,并代入电流特性曲线,可得三种调制方法下传输电流最大值与功率标幺值的关系为
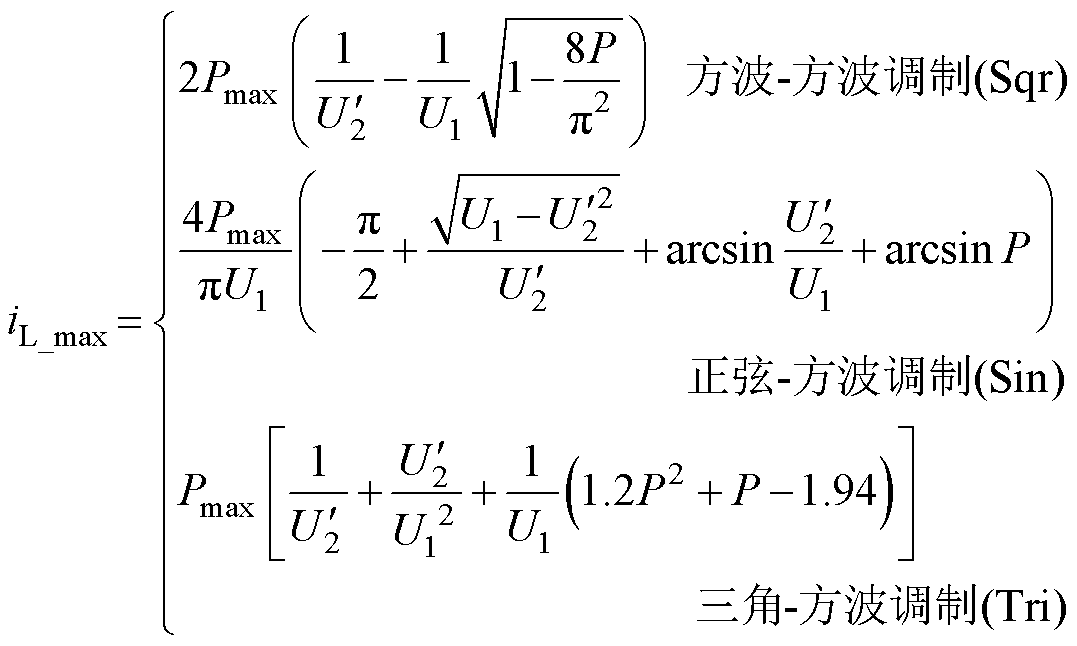 (26)
(26)
同时,将式(26)对P求导,得到传输电流最大值随功率变化的斜率为
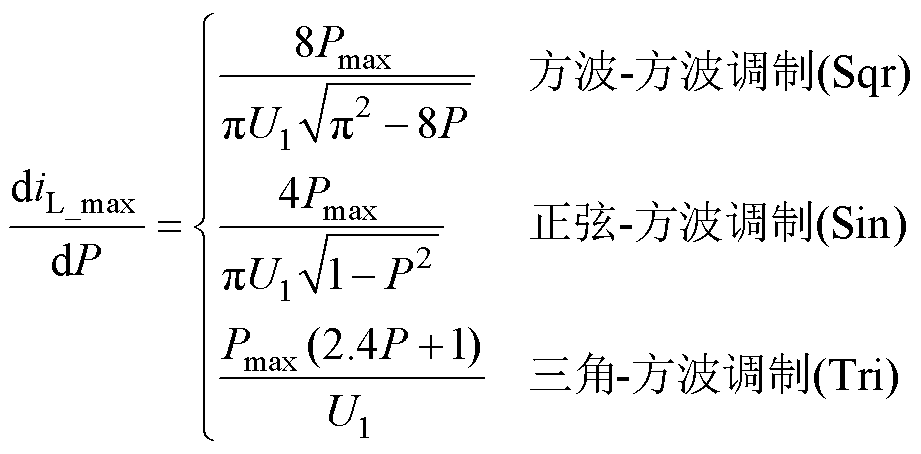 (27)
(27)
因此,式(26)和式(27)从理论上阐明任意传输电压和功率工况下的MMC-H SST传输最大电流应力值及其差异,以及功率从重载到轻载下传输电流最大值的斜率变化特性。本文在仿真部分会结合具体工况对这两个公式进行进一步说明,进而表明三种调制波作用下传输电流应力差异特性。
高频下MMC通过最近电平调制来输出高频交流正弦电压或三角波电压以降低开关频率。MMC单相输出电压与各桥臂电压间的关系为
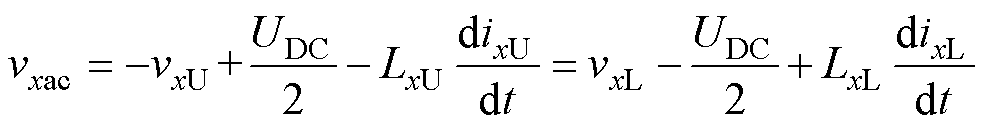 (28)
(28)
式中,vxU和vxL分别为上、下桥臂电压;ixU和ixL分别为上、下桥臂电流,x代表a或b相。忽略桥臂电感,桥臂电压参考值可以用直流母线电压和输出电压参考波表示为
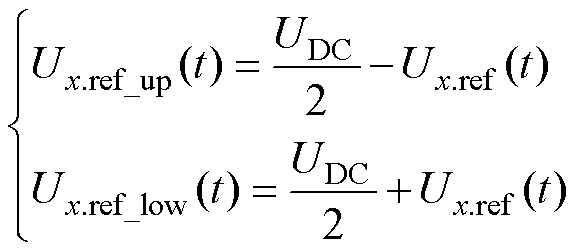 (29)
(29)
式中,Ux.ref(t)为a或b相MMC输出电压参考波;Ux.ref_up(t)、Ux.ref_low(t)分别为各相上、下桥臂电压参考波。
任意时刻上、下桥臂处于导通状态的子模块数量nxU(t)、nxL(t)通过将式(29)分解为N个离散级别来求解,并四舍五入为最接近的整数,N为各桥臂串联子模块数量,ROUND()代表取整函数。
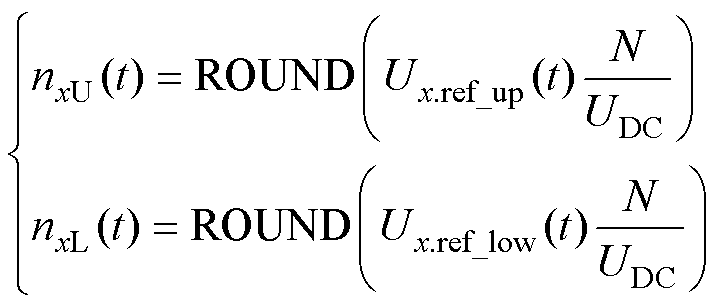 (30)
(30)
因此,通过控制MMC参考电压波形可以实现MMC侧正弦调制或三角调制。同时,调节参考电压频率和幅值能实现SST高频变压器传输频率和输入输出电压幅值的控制。
SST输出电压通过闭环控制来实现。通过负载侧电压闭环控制移相电感两侧外移相比D来控制传输功率大小和方向,如式(1)~式(3)所示。通过调节外移相比D来控制低压侧脉冲移相角,式(31)显示以正弦调制为例的关系,方波和三角调制类似。
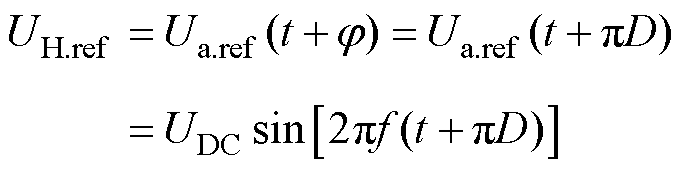 (31)
(31)
将H桥参考电压UH.ref与0电平比较,输出低压侧开关脉冲信号Q1、Q3,并反向输出开关脉冲信号Q2、Q4。开关函数为
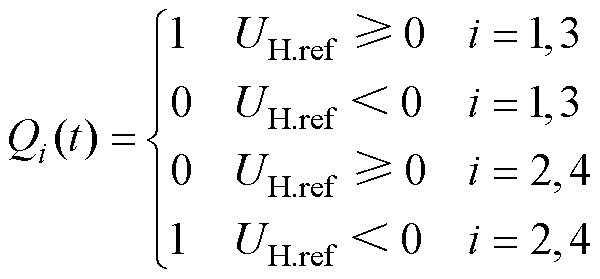 (32)
(32)
图7显示了基于式(28)~式(32)构建的非对称方波MMC-H SST综合控制方法,包含输出电压控制、调制波形和传输频率控制、高压侧MMC模块数计算和电容电压平衡控制、低压H桥侧开关信号控制。其中,MMC两相参考电压为相位互差180°的正弦波或三角波,结合其与高压侧直流母线电压UDC和桥臂电压的关系求得各桥臂参考电压,并采用最近电平控制(Nearest Level Control, NLC)调制方法和电容电压平衡控制输出MMC侧各子模块脉冲信号。低压侧采用输出电压闭环控制外移相比D,并通过两电平调制产生低压侧H桥各开关器件脉冲信号。通过该控制方法,能实现正弦-方波和三角-方波两类非对称方波下的MMC-H SST输出电压、传输频率、传输功率的精准控制。
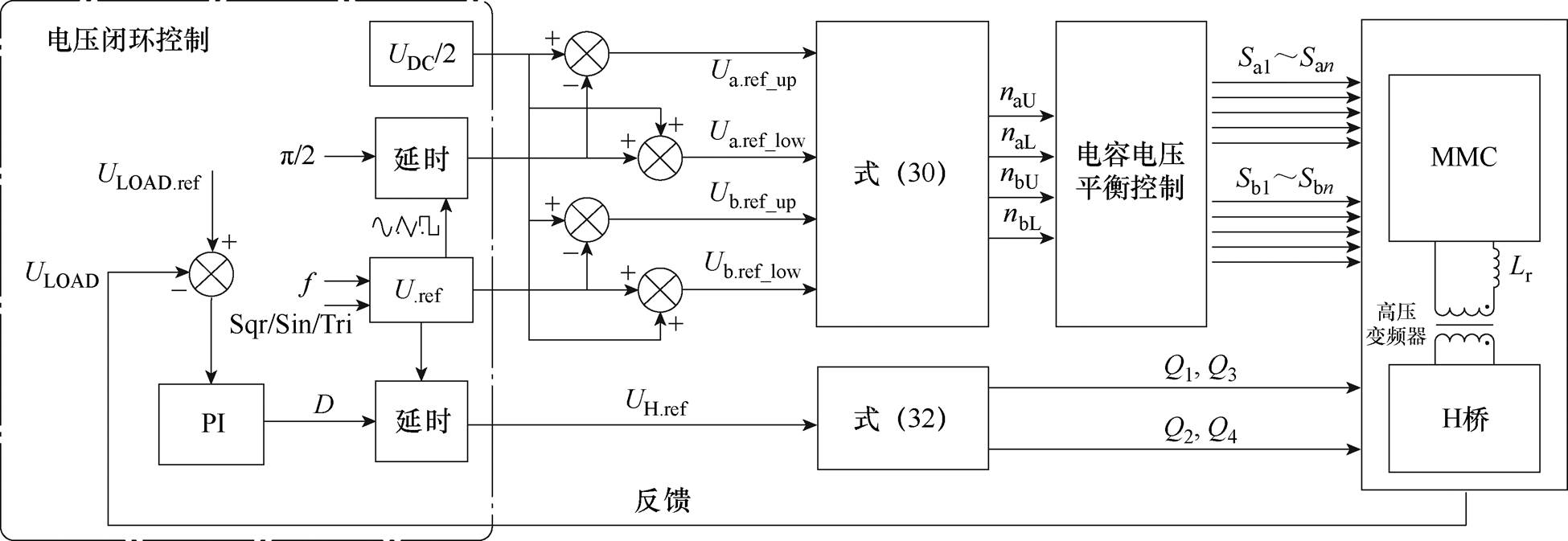
图7 非对称方波调制下MMC-H SST控制方法
Fig.7 Control method of MMC-H SST at asymmetric modulation
本文在PLECS内搭建了10 kV/1 MW的MMC- H SST系统模型并进行上述理论的验证。其中,SST高压侧输入直流电压10 kV,低压侧输出直流电压400 V,系统工作频率10 kHz;高压侧MMC每个桥臂由8个相同参数的子模块串联组成,子模块电容容值0.5 mF。具体参数见表1。
为验证所提正弦-方波和三角波-方波传输模型和理论的有效性,本文在相同传输功率下对基于传统方波-方波和所提两种非方波调制进行了详细仿真和对比分析,结果如图8~图14所示。其中,图8和图9对比了高载和低载下三种调制方法对应的SST高压侧和低压侧传输电压以及传输电流波形。图11和图12分别为高载和低载下SST传输电流的总谐波畸变率(Total Harmonic Distortion, THD)。图13为正弦-方波调制下系统在450 kW工况时仿真的传输电流波形与理论波形对比。图14为传输功率理论模型与仿真结果对比关系。
表1 10 kV/1 MW MMC-H SST仿真参数
Tab.1 10 kV/1 MW MMC-H simulation parameters
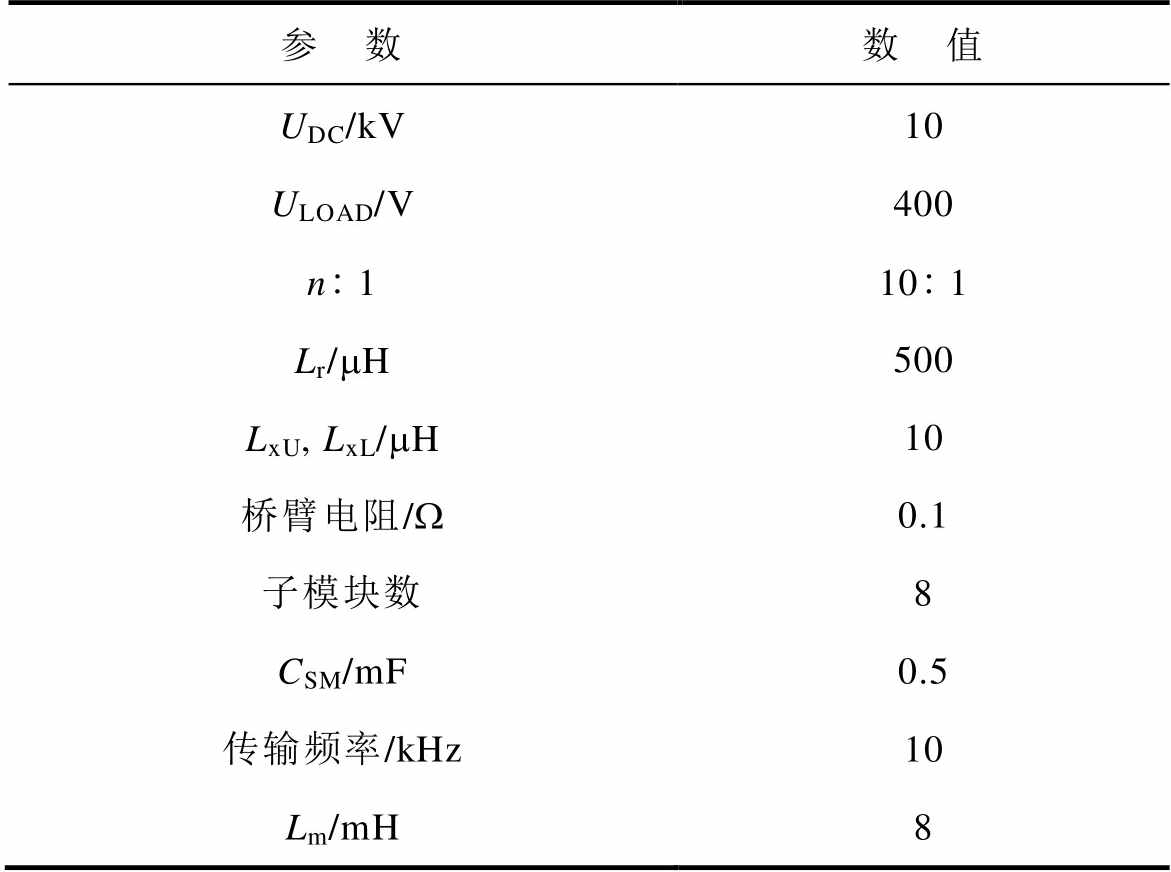
参 数数 值 UDC/kV10 ULOAD/V400 n1101 Lr/mH500 LxU, LxL/mH10 桥臂电阻/W0.1 子模块数8 CSM/mF0.5 传输频率/kHz10 Lm/mH8
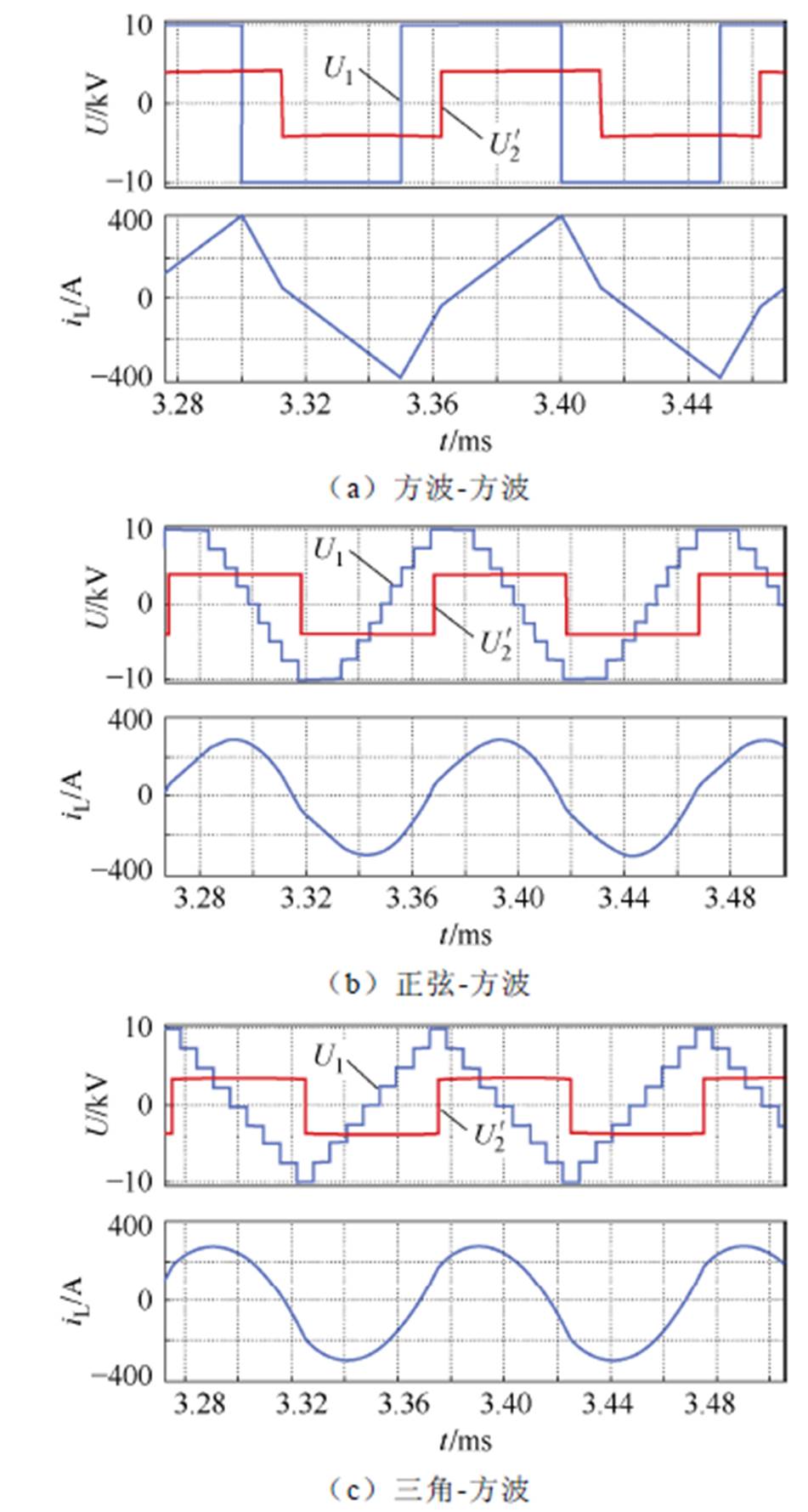
图8 高载下MMC-H SST电压和电流波形(750 kW)
Fig.8 Voltage and current waveforms of MMC-H SST at 750 kW
图8和图9结果显示,正弦-方波调制和三角-方波调制对比方波-方波调制均能使传输电流波形由锯齿波变为类正弦波。传输电流iL幅值在高载下从400 A减小到290 A和288 A,分别减小27.5%和28.0%,低载下从322 A减小到188 A和144 A,分别减小41.6%和55.2%。因此,所提两种调制均显著降低了传输电流与变压器电流应力与损耗,在低负载下三角-方波调制电流应力减小作用更加明显。图10为由式(26)计算所得三种调制波下传输电流峰值应力与不同传输功率的理论关系曲线。带星标记的点为同一传输功率下仿真所得传输电流峰值。由图10可知:①方波-方波调制下系统最大传输功率高于正弦-方波调制,而三角-方波调制下最高传输功率约为正弦-方波的80%;②仿真所得电流峰值与理论曲线上对应值高度吻合,验证了理论曲线的准确性;③同一传输功率下正弦-方波和三角-方波两种调制波下传输电流峰值明显低于方波-方波调制方法,特别是在轻载工况下,正弦-方波和三角-方波调制方法分别下降了43.5%和57.3%。
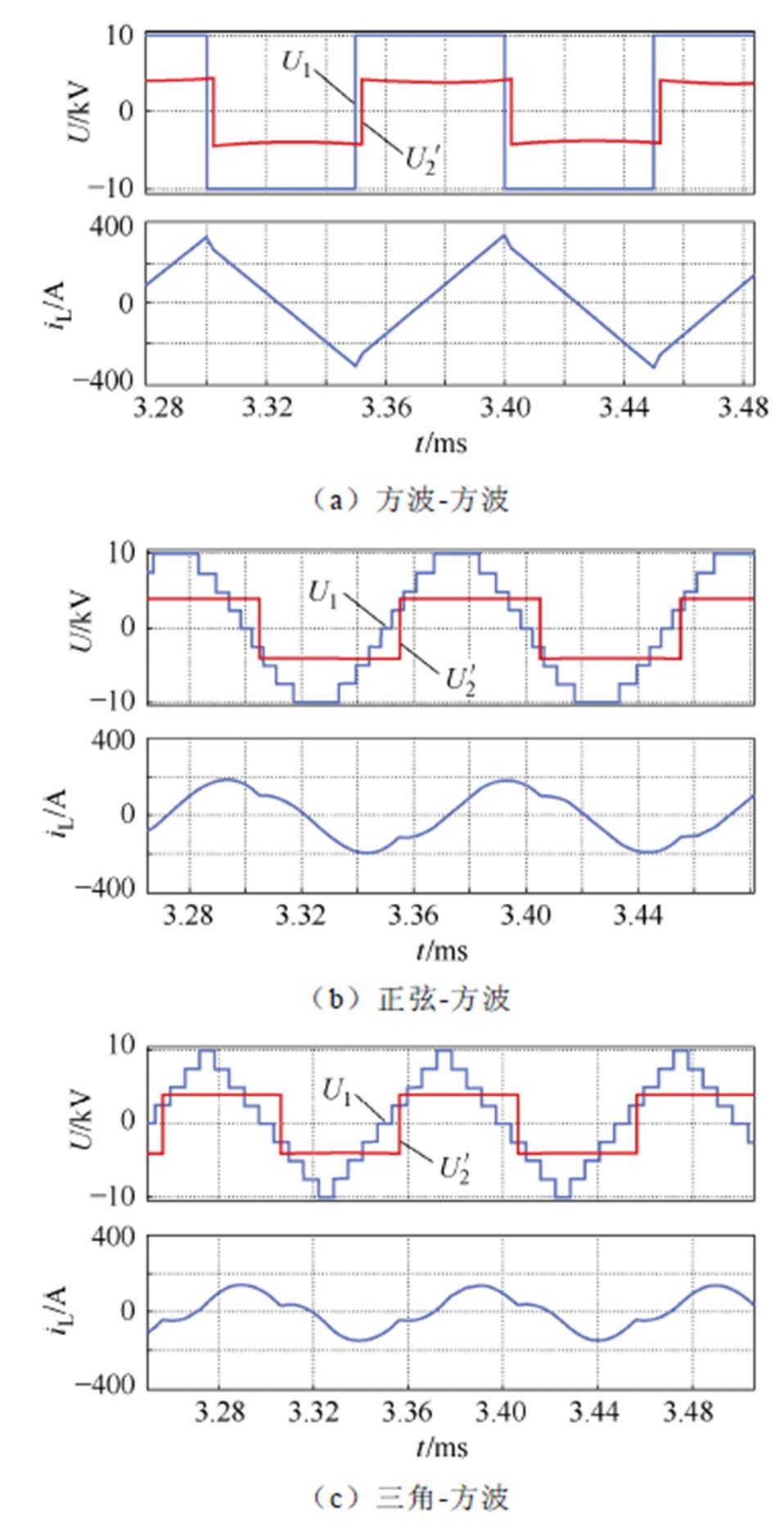
图9 低载下MMC-H SST电压和电流波形(250 kW)
Fig.9 Voltage and current waveforms of MMC-H SST at 250 kW
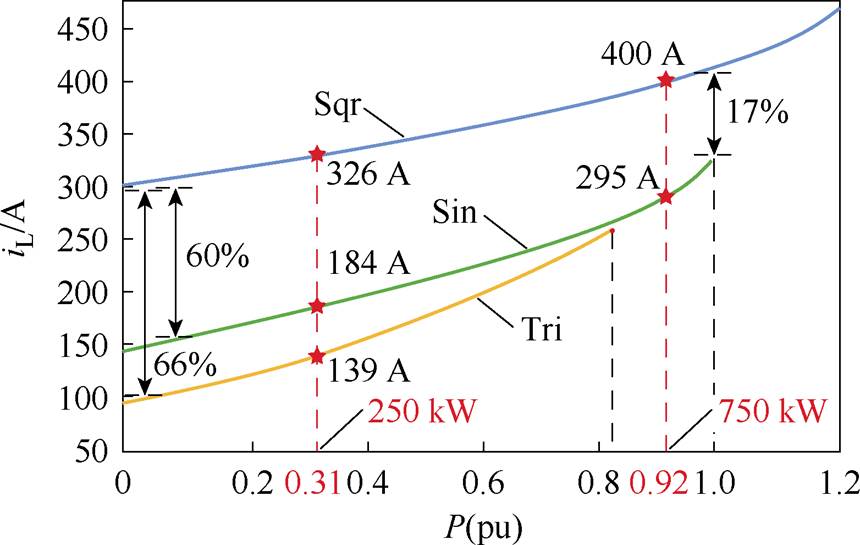
图10 不同调制下传输电流应力峰值随功率变化曲线
Fig.10 Curves between power and transmission current at different modulations
造成正弦-方波和三角-方波传输电流应力峰值显著降低的原因:在宽输出电压调节的MMC-H固态变压器应用中,传统方波-方波调制方法下移相电感两侧较大的电压差会在传输周期内造成无功电流激增,带来额外的内部无功循环功率。而所提正弦或三角调制方法调节高压侧电压缩小了电感上电压差从而减缓电流上升速率,减小无功并降低系统传输电流。在轻载工况下,传统方波调制方法无功电流分量更为显著,正弦和三角波调制下无功电流抑制效果更好,因此轻载下传输电流下降比例更大。
图11和图12结果表明,高载下方波-方波调制传输电流THD=20.3%,正弦-方波调制下THD= 8.1%,三角-方波调制下THD=6.1%;低载下方波-方波调制传输电流THD=15.0%,正弦-方波调制下THD=9.3%,三角-方波调制下THD=17.4%。三角-方波调制虽然高载下略优于正弦-方波调制,但其低载时电流谐波THD反而有所增加。综合比较,正弦-方波调制下传输电流谐波在高载和低载下均具有较好的优化效果,高载下比传统方波调制总谐波含量减小约12.2%。
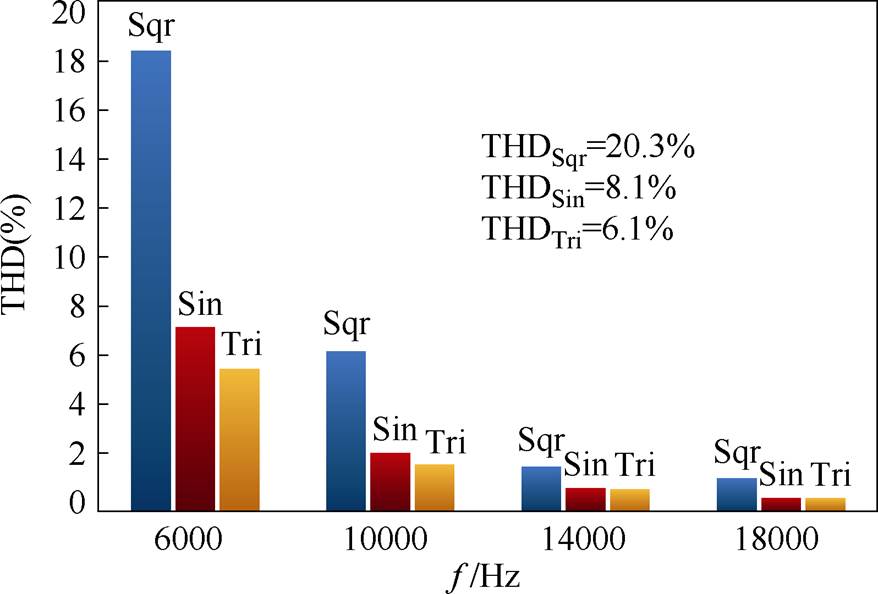
图11 高载下传输电流不同频率谐波含量对比(750 kW)
Fig.11 Comparison of harmonic content at different frequencies of transmission current at 750 kW
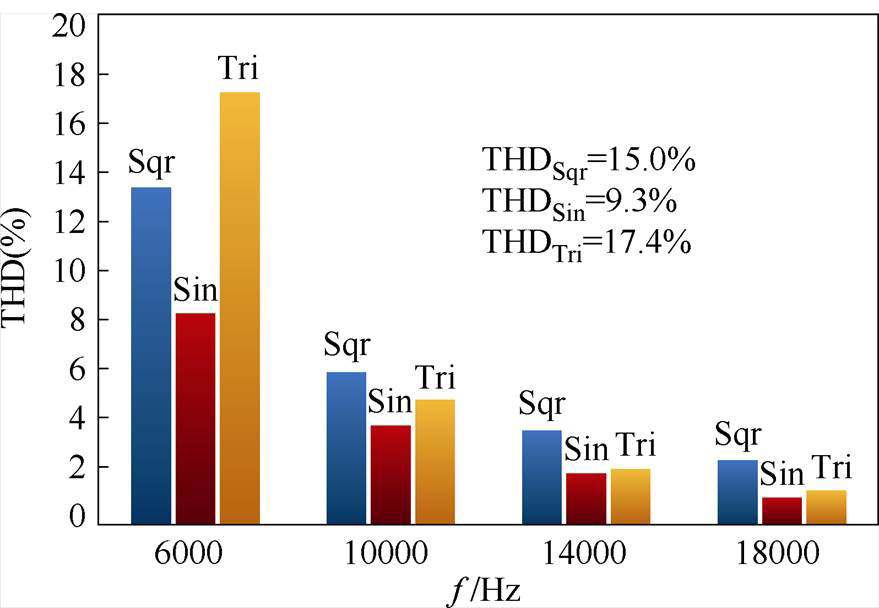
图12 低载下传输电流不同频率谐波含量对比(250 kW)
Fig.12 Comparison of harmonic content at different frequencies of transmission current at 250 kW
图13显示了以传输功率约450 kW工况下的正弦-方波和三角-方波传输电流理论曲线和仿真电流曲线对比。对比容易发现,理论曲线和仿真曲线较为吻合,有效地验证了所提出的非方波调制下传输电流表征关系(见式(17)、式(22))的准确性。
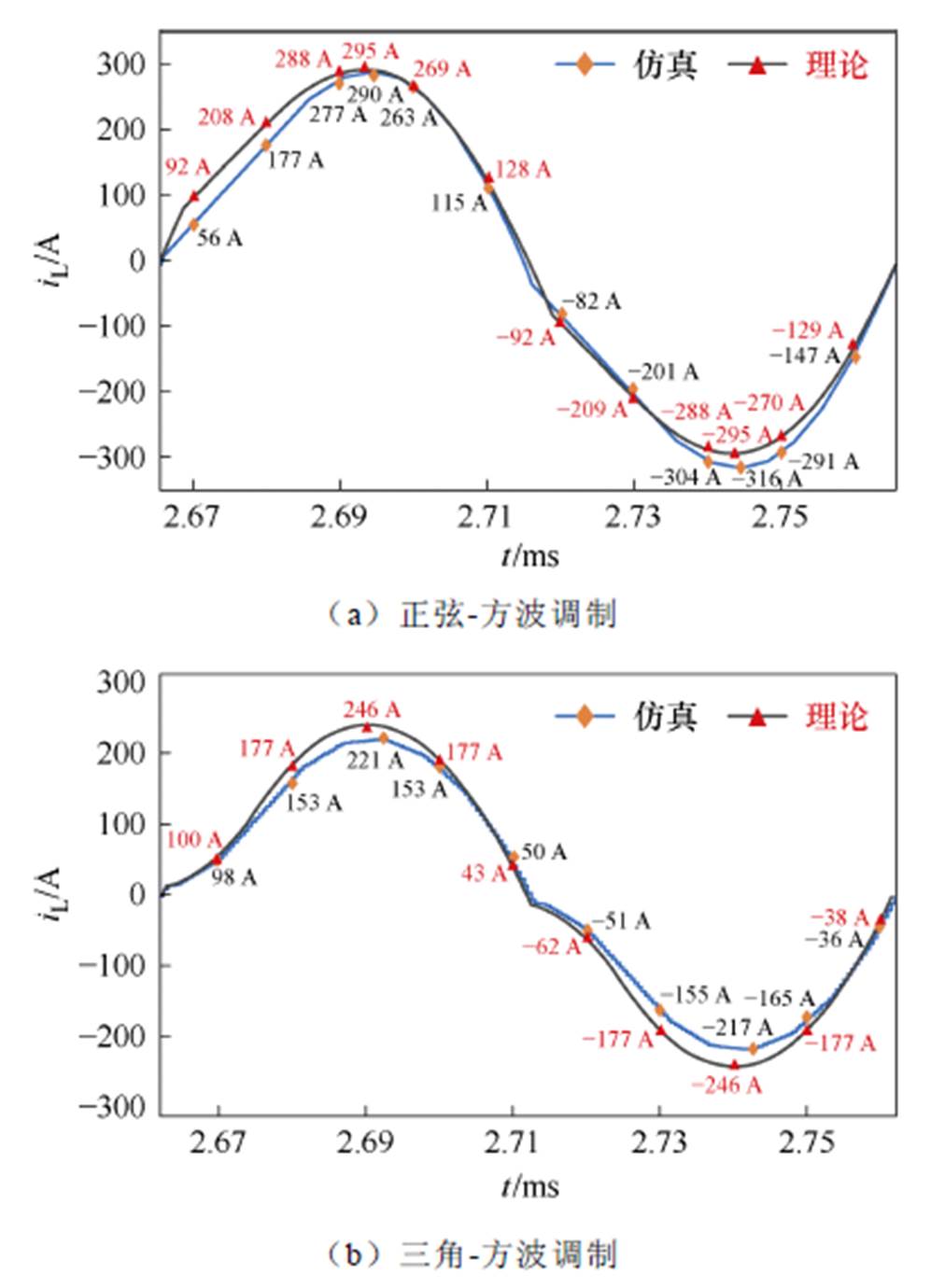
图13 仿真传输电流波形与理论曲线对比
Fig.13 Comparison of currents between simulated and theoretical waveforms
图14显示了所构建的功率传输模型在不同工况下的准确性验证结果。图中分别列出了正弦-方波和三角-方波在传输功率0~100%变化过程中与仿真值的对比结果,同时考虑了不同桥臂子模块数的影响(N=8和20)。其中实线为仿真结果,虚线为理论模型结果。图14显示,所提出的两种调制方法SST功率特性曲线与理论曲线较为吻合。随着桥臂子模块数量的增加(从N=8增加到20),仿真曲线与理论曲线的误差进一步减小;子模块数量为20时,其平均误差e20SM分别降低到2.8%和3.4%。这是因为所提功率传输模型基于纯正弦波和三角波调制分析,实际MMC交流输出电压为阶梯波形,其电压有效值略大于理论电压波形,进而会使仿真所得的传输功率略大于理论传输功率。桥臂子模块数越多,输出电压阶梯波越接近于理想波形,误差越小。因此,图14充分验证了所提正弦-方波和三角-方波传输模型的准确性。
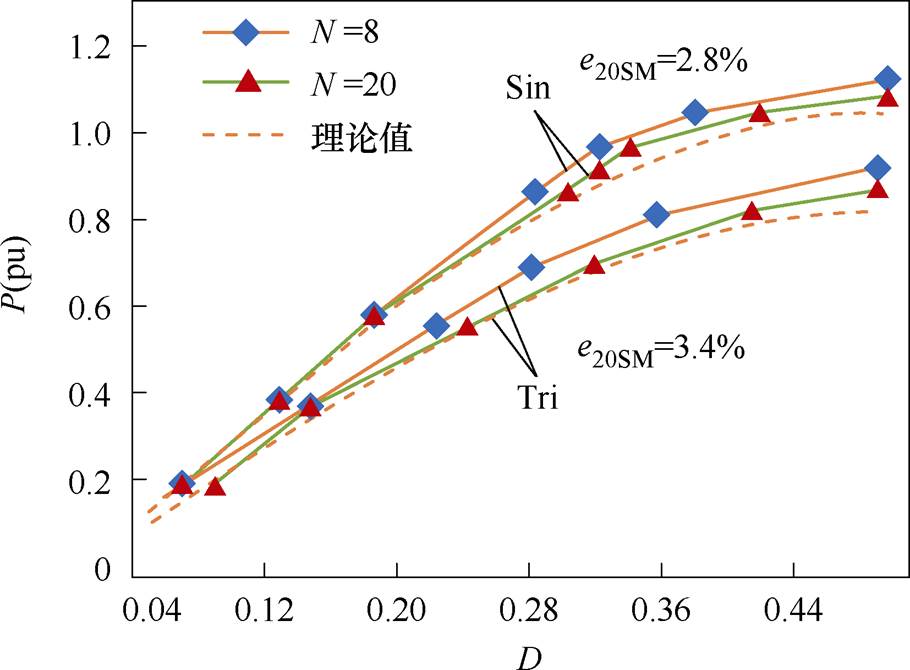
图14 传输功率理论模型与仿真结果对比关系
Fig.14 Comparison between theoretical model and simulation results of transmission power
本文进一步对三种调制方法下的10 kV/1 MW MMC-H SST系统损耗进行分析。其中,SST高压侧器件采用1.7 kV/350 A SiC MOSFET(型号WAS310M17BM3),低压侧器件采用1.2 kV/450 A SiC MOSFET(型号CAB450M12XM3)。器件损耗计算方法参考文献[7],具体为导通损耗通过流经器件的电流值并结合导通电阻RDS_on计算,开关损耗基于器件的开通、关断以及反并联二极管反向恢复能量数据Eon、Eoff、Erec并结合开关频率等效计算。将所有器件导通损耗和开关损耗求和得到SST系统总的器件损耗。变压器损耗包括铜损和铁损,规定RCu为绕组电阻,Irms为绕组电流有效值,PV为磁心损耗密度,Ve为体积。则变压器铜耗和铁耗可分别计算为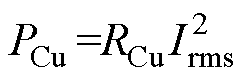 ,
,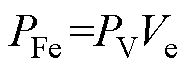 。综合国内外主要研究机构大容量高频变压器技术指标对比[25],中高频变压器功率密度可以按5 MW/m3估计。磁心材料选择纳米晶,其PV约为9.65 MW/cm3[26],可计算变压器10 kV/1 MW MMC-H不同调制下系统损耗对比如图15所示。
。综合国内外主要研究机构大容量高频变压器技术指标对比[25],中高频变压器功率密度可以按5 MW/m3估计。磁心材料选择纳米晶,其PV约为9.65 MW/cm3[26],可计算变压器10 kV/1 MW MMC-H不同调制下系统损耗对比如图15所示。
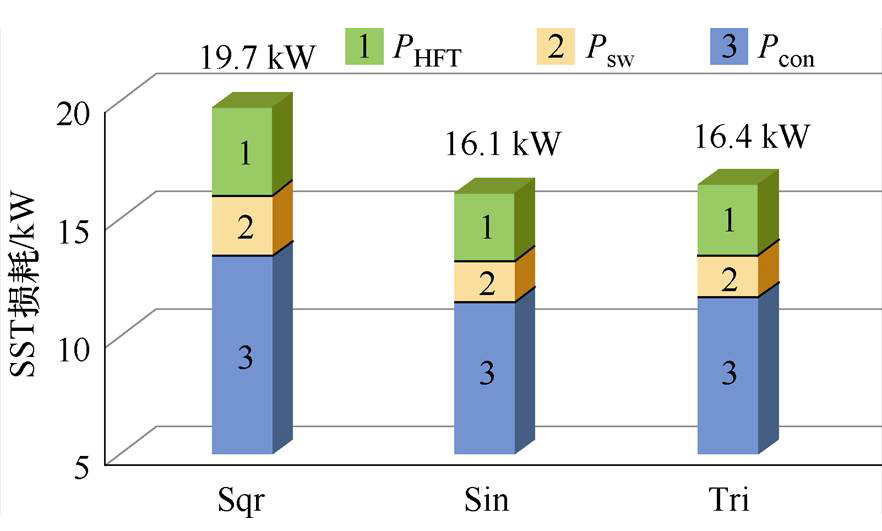
图15 10 kV/1 MW MMC-H不同调制下系统损耗对比
Fig.15 Comparison of losses of 10 kV/1 MW MMC-H system using 3 types modulation
图15显示三种调制波下MMC-H SST器件和变压器损耗对比结果,Psw代表开关损耗,Pcon代表导通损耗,PHFT代表变压器损耗。分析图15可知,1 MW工况下正弦-方波和三角-方波调制比方波-方波调制损耗略低,分别为16.1 kW和16.4 kW。由于电流减小的缘故,所提两种调制下系统的开关损耗和导通损耗均小于传统方波调制。整体比较,正弦-方波调制下系统损耗最低,效率最高。
结合上述对不同调制方法的电流应力、谐波含量、功率传输能力以及损耗分析可知,正弦-方波调制具有整体最佳的结果,更适用于MMC-H SST的应用。
本文基于研制的高性能DSP+FPGA控制板搭建了10 kV/1 MW七电平MMC-H SST硬件在环实验平台,如图16所示。实验平台具体参数见表2。MMC-H作为被控对象,由瑞士PLEXIM公司的RT_box模拟。DSP控制板(TI TMS320F28379D)用于实现输出电压、移相角、传输频率的控制,FPGA控制板(ALTERA Cyclone IV EP4CE40F29C8N)主要实现电容电压平衡算法和开关脉冲信号调制。通过以上分析发现正弦-方波对比三角-方波具有更好的优化效果,因此实验部分主要对正弦-方波调制和所提控制方法下的MMC-H SST进行研究。图17和图18显示了输出电压恒定在400 V不同负载下MMC-H SST采用正弦-方波控制方法下的实验波形。

图16 基于FPGA+DSP的硬件在环实验平台
Fig.16 HIL experimental platform based on FPGA+DSP
表2 10 kV/1 MW MMC-H实验平台参数
Tab.2 10 kV/1 MW MMC-H experimental parameters
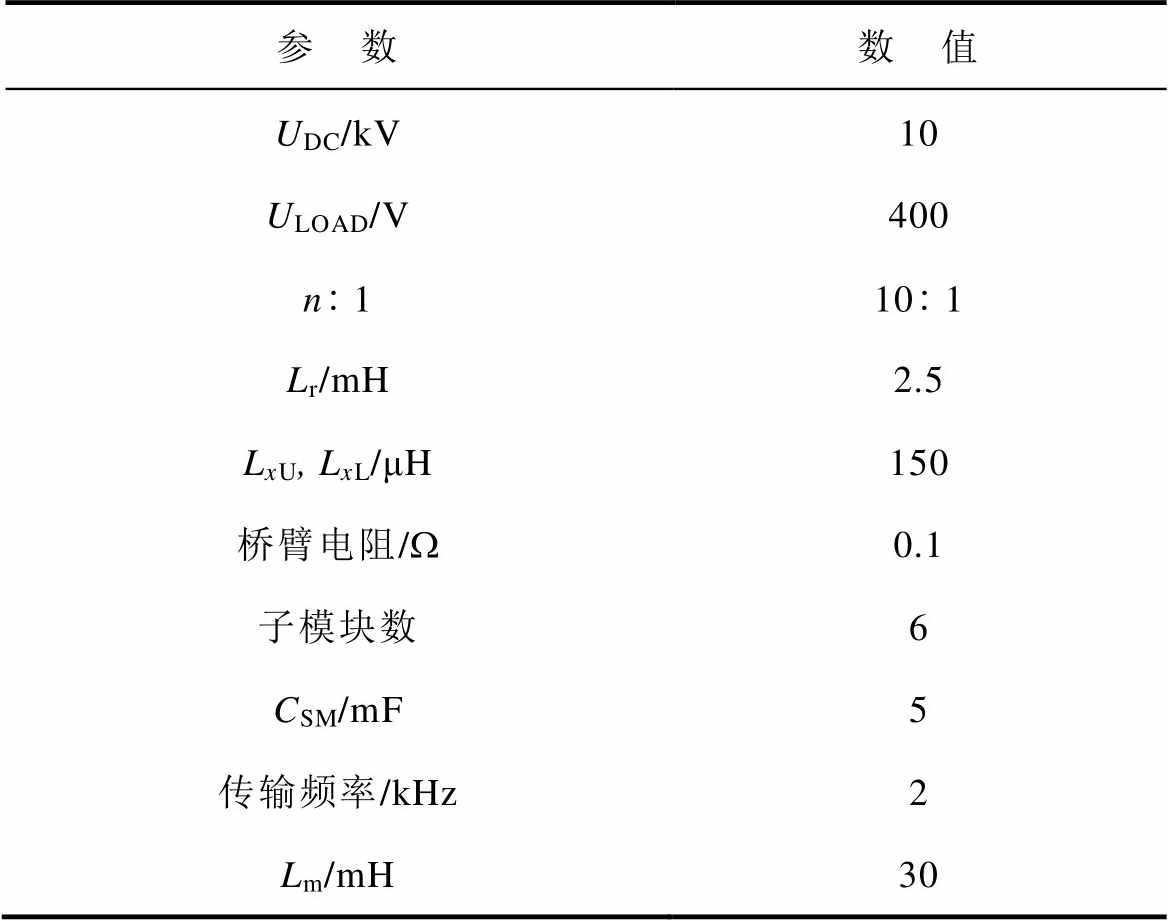
参 数数 值 UDC/kV10 ULOAD/V400 n1101 Lr/mH2.5 LxU, LxL/μH150 桥臂电阻/W0.1 子模块数6 CSM/mF5 传输频率/kHz2 Lm/mH30
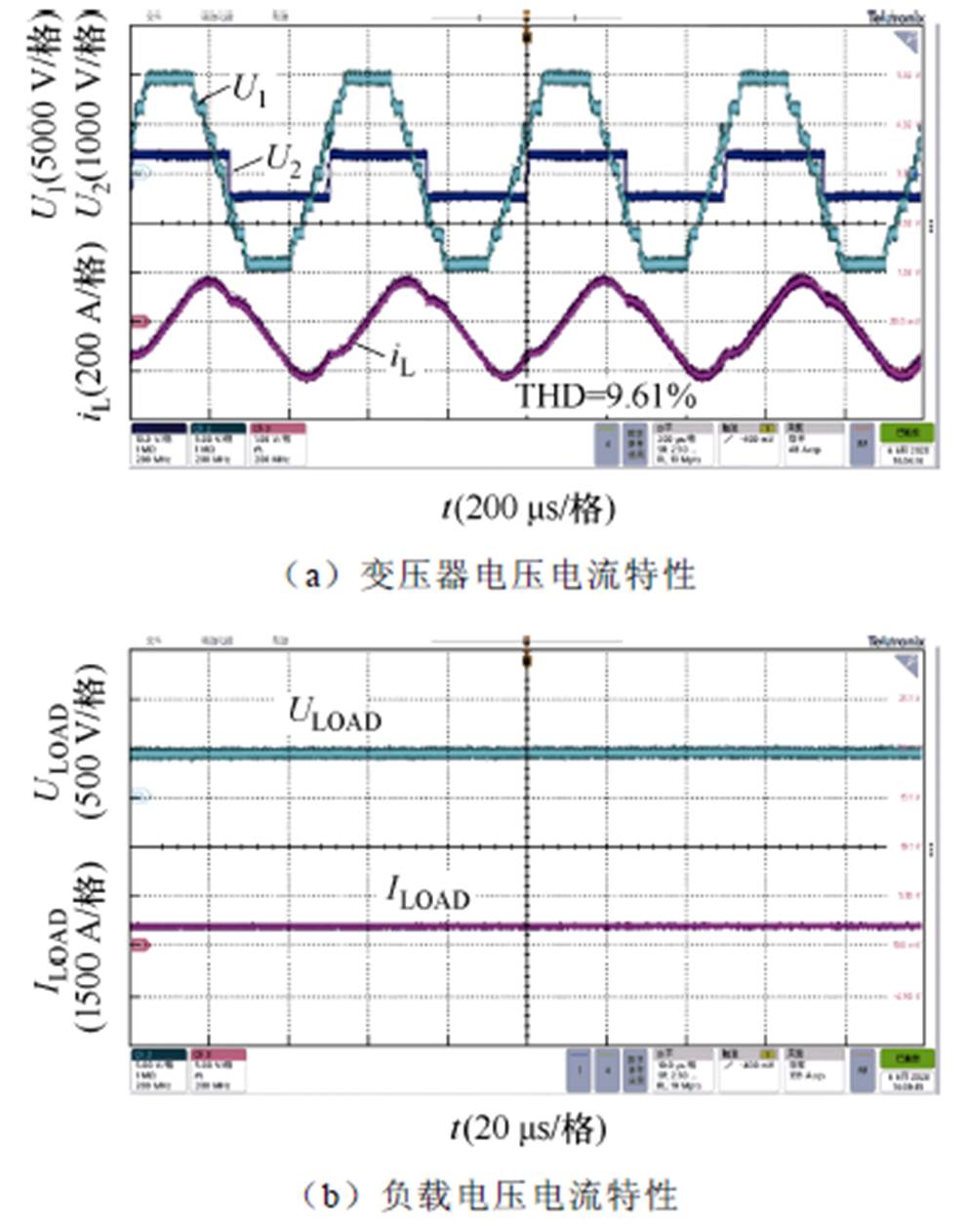
图17 MMC-H系统实验波形(250 kW)
Fig.17 Experimental waveforms of MMC-H SST at 250 kW
图17和图18实验结果显示,MMC侧输出多电平电压阶梯波,H桥侧为方波电压,SST系统实现了MMC多电平波形下的正弦-方波控制;变压器传输电压电流波形与仿真波形吻合,谐波含量与仿真结果较为一致(THD分别为9.61%和7.91%);两侧电压波形移相角随着传输功率增大而增大,但输出电压控制在400 V。图17和图18实验结果验证了正弦-方波调制下MMC-H SST正弦波逼近多电平电压输出波形和低谐波传输电流的特性。
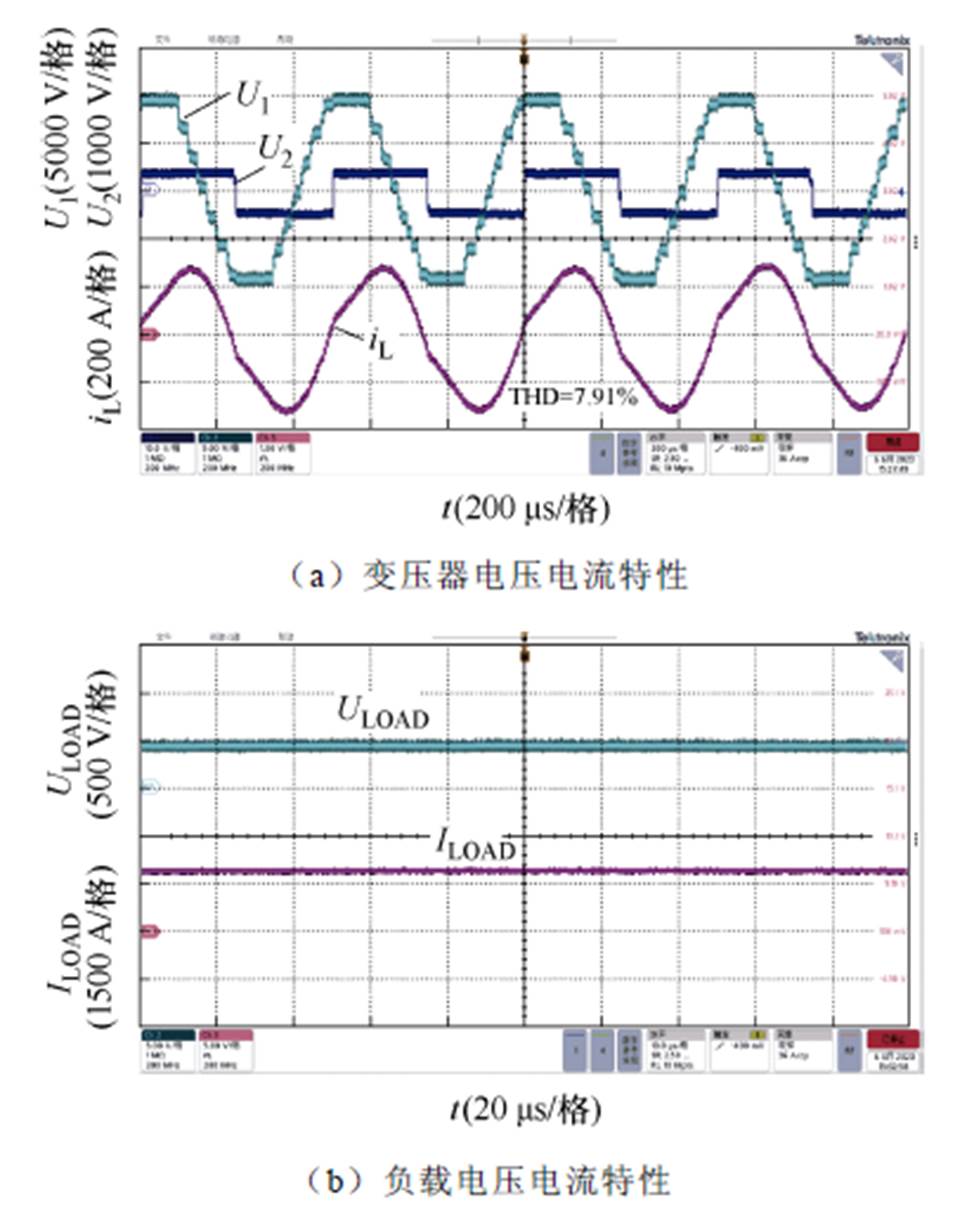
图18 MMC-H系统实验波形(750 kW)
Fig.18 Experimental waveforms of MMC-H SST at 750 kW
图19显示了传输功率约450 kW工况下系统传输电流与理论曲线比较。实验所测传输电流幅值以及各个拐点电流值大小均与理论值非常吻合,验证了所提的传输电流模型的准确性。
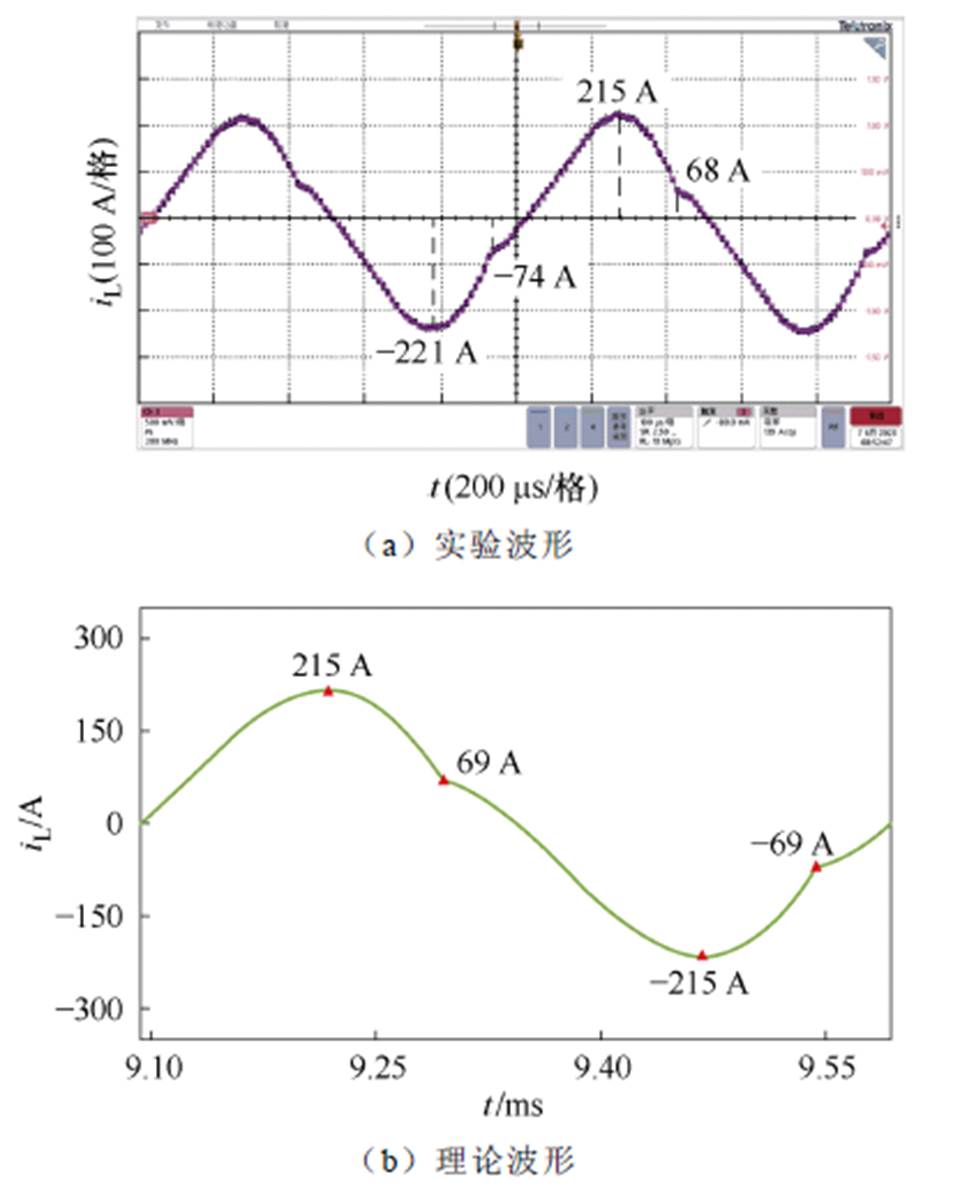
图19 系统传输电流实验波形和理论波形对比
Fig.19 Comparison between experimental and theoretical transfer currents
本文进一步探究了不同移相角(不同负载)下所提功率模型的准确性。通过记录不同移相角下对应的负载电压电流特性计算传输功率大小进而得到两者之间关系。图20所示为实验所得MMC-H SST在各个外移相比D下的功率曲线(虚线为理论值)。由图20可知,系统在不同移相角下的实际功率与传输功率模型得到的理论曲线较为接近,两者平均误差为5.71%。因此,实验结果同样有效地验证了正弦-方波调制下所提出功率传输模型的准确性。实验误差比仿真误差偏大是由于实验中MMC桥臂模块较少(N=6)所致;通过增加MMC子模块数(如N=20),调制阶梯波能够更接近于理论正弦波形进而降低误差。
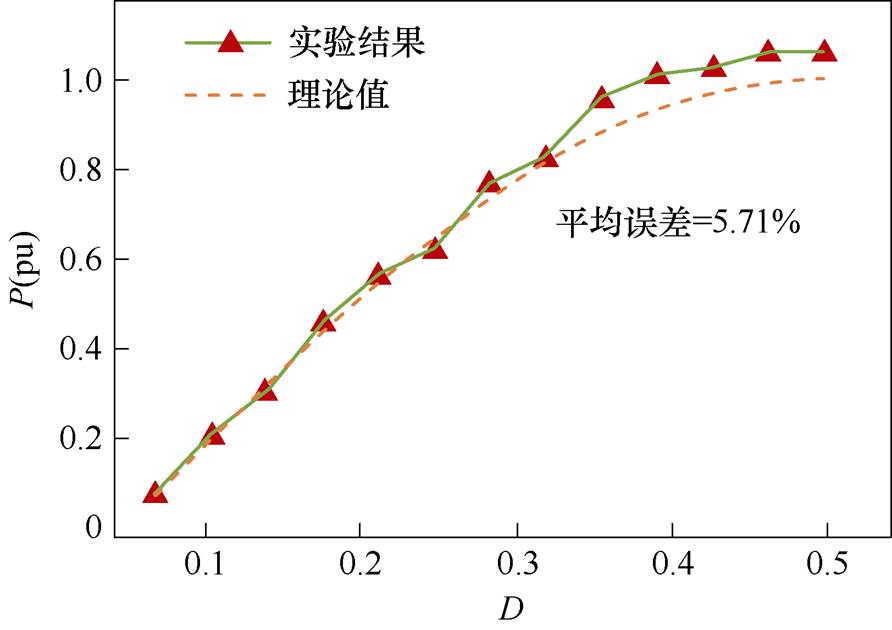
图20 传输功率理论模型与实验结果对比关系
Fig.20 Comparison between theoretical model and experimental results of transmission power
最后,本文进一步对所提方法的动态稳定性进行了实验测试和分析。图21为所提调制波和控制方法下恒负载变电压动态测试时系统动态响应波形,从上到下分别显示了高压侧输出电压、传输电流和低压侧输出电压。输出电压分别由400 V跳跃到800 V和800 V跳跃到400 V,输出负载阻抗不变。区域一和区域二为细节放大图。系统分别在18.5 ms和49.2 ms内进入稳定状态,并准确输出对应的400 V和800 V电压。
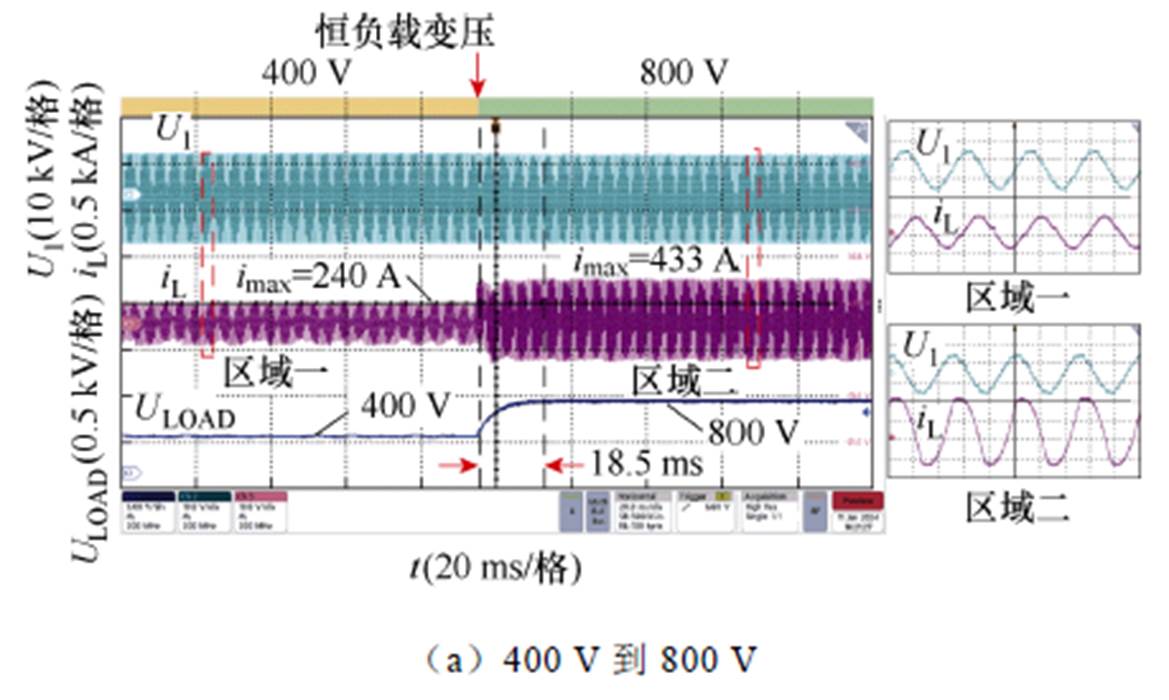
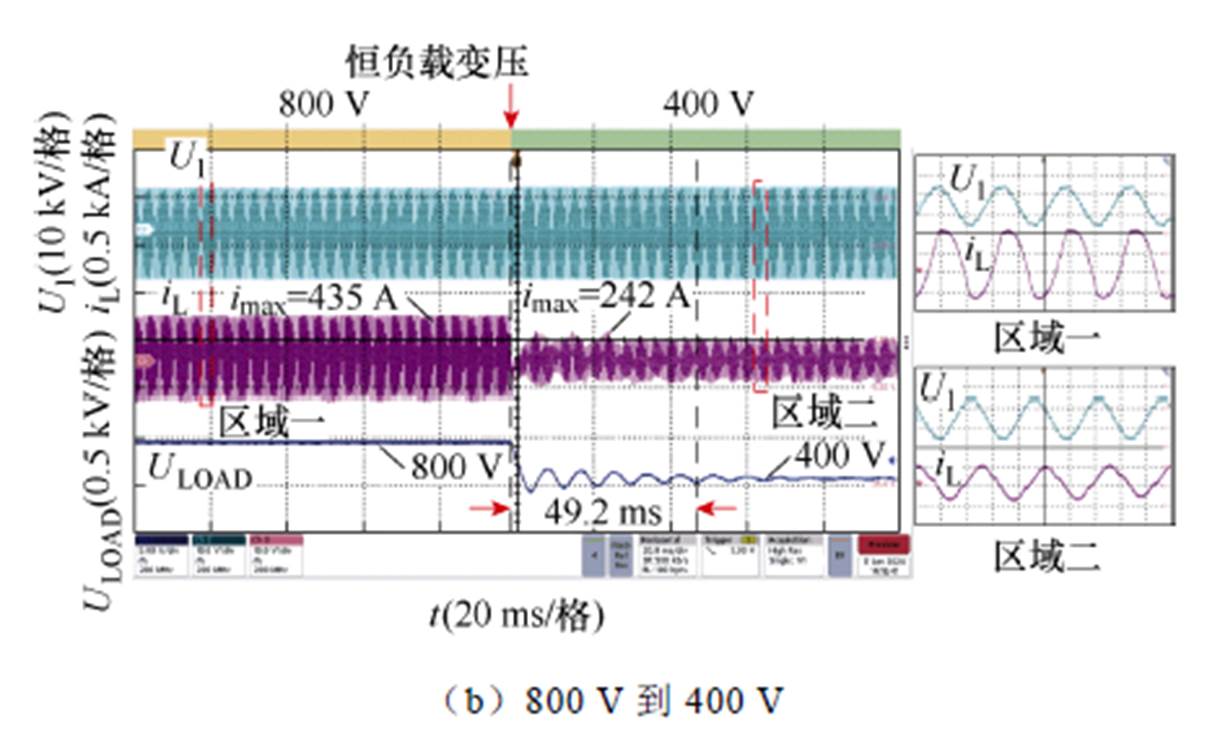
图21 MMC-H恒负载变压时系统动态响应波形
Fig.21 Dynamic response waveforms of MMC-H at voltage disturbance
图22为所提正弦-方波调制和控制方法下恒定输出电压变输出负载工况时系统动态响应波形。输出负载由0.5 MW跳变到0.75 MW,再由0.75 MW跳回到0.5 MW。跳变过程中输出电压会产生一定的扰动,但是在17.0 ms和34.7 ms后快速恢复状态。因此,图21和图22结果显示,所提调制波形和控制方法下整个MMC-H SST具有很强的动态稳定性和快速响应能力。
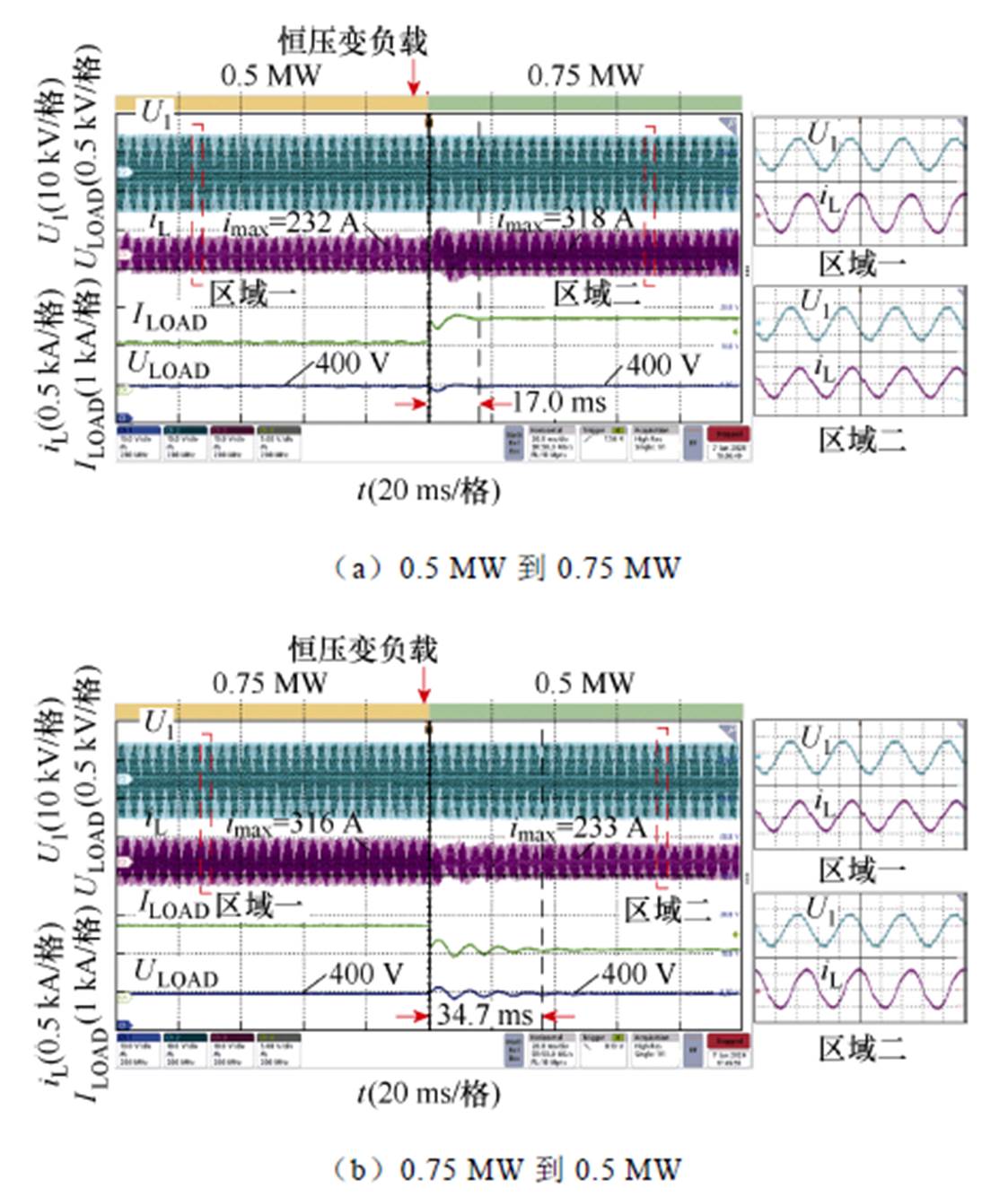
图22 MMC-H恒压变负载时系统动态响应波形
Fig.22 Dynamic response waveforms of MMC-H at load disturbance
本文针对高低压变换应用需求场景提出了基于正弦-方波和三角-方波非对称式调制的MMC-H SST建模和分析方法,进而优化内部电压电流特性。本文建立了MMC-H SST的两种非正弦调制下的精确功率传输模型并提出了控制方法,揭示了其功率和电流传输特性。在此基础上,确定了SST的最大功率传输点,理论分析了两种非对称波形调制下与传统方波-方波调制的电流应力变化规律,并阐明原因。通过仿真和实验结果表明:所提出的正弦-方波和三角-方波功率传输模型在多电平调制下与理论值小于4%,有效验证了所提传输功率和电流模型准确性。对比于方波-方波和三角-方波调制,正弦-方波调制具有最大传输功率、传输电流峰值、谐波、器件损耗综合性能最佳的特点。此外,所提正弦-方波调制和控制方法具有良好的动态稳定性和快速响应能力。本文工作为非对称式调制下的新型MMC-H SST构建、性能评估和优化控制提供了理论支撑。
参考文献
[1] 高范强, 李子欣, 李耀华, 等. 面向交直流混合配电应用的10kV-3MV·A四端口电力电子变压器[J]. 电工技术学报, 2021, 36(16): 3331-3341.
Gao Fanqiang, Li Zixin, Li Yaohua, et al. 10kV- 3MV·A four-port power electronic transformer for AC-DC hybrid power distribution applications[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3331-3341.
[2] 胡钰杰, 李子欣, 罗龙, 等. 串联谐振间接矩阵型电力电子变压器高频电流特性分析及开关频率设计[J]. 电工技术学报, 2022, 37(6): 1442-1454.
Hu Yujie, Li Zixin, Luo Long, et al. Characteristic analysis of high-frequency-link current of series resonant indirect matrix type power electronics transformer and switching frequency design[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1442-1454.
[3] 陈润田, 李楚杉, 姚文熙, 等. 基于等效励磁电感的SiC串联器件型中压双有源桥变换器的软开关技术[J]. 电工技术学报, 2024, 39(12): 3732-3745.
Chen Runtian, Li Chushan, Yao Wenxi, et al. Soft-switching technique for medium voltage dual active bridge converter with series-connected sic devices based on equivalent magnetizing indu- ctance[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3732-3745.
[4] 李福, 邓红雷, 张国驹, 等. 一种中间电容谐振型级联双向DC-DC变换器[J]. 电工技术学报, 2022, 37(20): 5253-5266.
Li Fu, Deng Honglei, Zhang Guoju, et al. A cascaded bidirectional DC-DC converter with intermediate capacitor resonance[J]. Transactions of China Elec- trotechnical Society, 2022, 37(20): 5253-5266.
[5] Shi Yuxiang, Li Hui. Isolated modular multilevel DC-DC converter with DC fault current control capability based on current-fed dual active bridge for MVDC application[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2145-2161.
[6] 郑通, 王奎, 郑泽东, 等. 基于MMC拓扑的电力电子变压器研究综述[J]. 中国电机工程学报, 2022, 42(15): 5630-5648, 21.
Zheng Tong, Wang Kui, Zheng Zedong, et al. Review of power electronic transformers based on modular multilevel converters[J]. Proceedings of the CSEE, 2022, 42(15): 5630-5648, 21.
[7] Pan Jianyu, Ke Ziwei, Al Sabbagh M, et al. 7-kV 1-MVA SiC-based modular multilevel converter prototype for medium-voltage electric machine drives[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10137-10149.
[8] Kenzelmann S, Rufer A, Vasiladiotis M, et al. A versatile DC-DC converter for energy collection and distribution using the modular multilevel con- verter[C]//Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 2011: 1-10.
[9] Zhao Biao, Song Qiang, Li Jianguo, et al. High- frequency-link modulation methodology of DC-DC transformer based on modular multilevel converter for HVDC application: comprehensive analysis and experimental verification[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3413-3424.
[10] Zhao Biao, Song Qiang, Li Jianguo, et al. Modular multilevel high-frequency-link DC transformer based on dual active phase-shift principle for medium- voltage DC power distribution application[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1779-1791.
[11] Sun Changjiang, Zhang Jianwen, Cai Xu, et al. Voltage balancing control of isolated modular multilevelDC-DC converter for use in DC grids with zero voltageswitching[J]. IET Power Electronics, 2016, 9(2): 270-280.
[12] Sun Changjiang, Zhang Jianwen, Cai Xu, et al. Analysis and arm voltage control of isolated modular multilevel DC-DC converter with asymmetric branch impedance[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(8): 5978-5990.
[13] Zhang Lei, Zhao Zhe, Qin Jiangchao. Efficiency optimization design of DC-DC solid state transformer based on modular multilevel converters[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 3508-3513.
[14] Zhang Lei, Qin Jiangchao, Duan Qing, et al. Component sizing and voltage balancing of MMC- based solid-state transformers under various AC-link excitation voltage waveforms[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 371-375.
[15] Zhang Lei, Qin Jiangchao, Zou Yuntao, et al. Analysis of capacitor charging characteristics and low-frequency ripple mitigation by two new voltage- balancing strategies for MMC-based solid-state transformers[J]. IEEE Transactions on Power Elec- tronics, 2021, 36(1): 1004-1017.
[16] 王朝辉, 王天威, 张军明. 模块化多电平直流变压器研究[J]. 中国电机工程学报, 2016, 36(1): 31-39.
Wang Chaohui, Wang Tianwei, Zhang Junming. Research on modular multilevel DC transformer[J]. Proceedings of the CSEE, 2016, 36(1): 31-39.
[17] Zhang Junming, Wang Zhaohui, Shao Shuai. A three-phase modular multilevel DC-DC converter for power electronic transformer applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 140-150.
[18] Shao Shuai, Jiang Mingming, Zhang Junming, et al. A capacitor voltage balancing method for a modular multilevel DC transformer for DC distribution system[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 3002-3011.
[19] Mo Ran, Li Hui, Shi Yanjun. A phase-shifted square wave modulation (PS-SWM) for modular multilevel converter (MMC) and DC transformer for medium voltage applications[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6004-6008.
[20] Xing Diang, Li Xiao, Zhang Yue, et al. MMC-based high gain solid-state transformers for energy storage applications[C]//2021 IEEE Applied Power Elec- tronics Conference and Exposition (APEC), Phoenix, AZ, USA, 2021: 1996-2002.
[21] 王新颖, 汤广福, 陈宇, 等. 一种模块化多电平DC/DC变换器的基频调制策略[J]. 中国电机工程学报, 2016, 36(7): 1987-1998.
Wang Xinying, Tang Guangfu, Chen Yu, et al. A fundamental frequency modulation for module multilevel DC/DC converters[J]. Proceedings of the CSEE, 2016, 36(7): 1987-1998.
[22] Chen Yu, Cui Yuqing, Tao Yupu, et al. High- fundamental-frequency modulation for the DC-DC modular multilevel converter (MMC) with low switching frequency and predicted-based voltage balance strategy[C]//2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 2014: 1-6.
[23] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[24] 管州, 梅军, 丁然, 等. 基于拓展移相控制的直流配电网模块化多电平直流变压器[J]. 电工技术学报, 2019, 34(13): 2770-2781.
Guan Zhou, Mei Jun, Ding Ran, et al. Modular multilevel DC transformer for DC distribution application based on extended phase-shift control[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2770-2781.
[25] 孙凯, 卢世蕾, 易哲嫄, 等. 面向电力电子变压器应用的大容量高频变压器技术综述[J]. 中国电机工程学报, 2021, 41(24): 8531-8545, 24.
Sun Kai, Lu Shilei, Yi Zheyuan, et al. A review of high-power high-frequency transformer technology for power electronic transformer applications[J]. Pro- ceedings of the CSEE, 2021, 41(24): 8531-8545, 24.
[26] Zhang Juanjuan, Du Yumei, Li Zixin, et al. Design of a medium frequency, high voltage transformer for power electronic transformer[C]//2014 IEEE Con- ference and Expo Transportation Electrification Asia- Pacific (ITEC Asia-Pacific), Beijing, China, 2014: 1-5.
Abstract The MMC-H solid-state transformer (SST) uses one high-frequency transformer, greatly reducing the system volume and cost, which is suitable for high to low-voltage conversion scenarios such as distributed energy access and electric vehicle charging stations. However, SST, including MMC-H, typically uses symmetrical square wave modulation to improve transmission power capabilities, leading to the high content of current harmonics. Besides, considering the high voltage level on the MMC side, square wave modulation can make MMC-H experience extremely high dv/dt stress, posing a severe challenge to transformer insulation. Therefore, this paper proposes two asymmetric modulation methods based on MMC topology and studies the current and power variation characteristics of MMC-H SST.
Firstly, this paper proposes the sine-square and triangle-square modulation for MMC-H SST. Based on the proposed SST circuit equivalent model, the power and current expressions for MMC-H under the proposed modulation are presented. The variation of transmission current with power is analyzed, and the reasons for the current difference between different modulations are elucidated. Finally, this paper proposes the overall closed-loop control scheme of MMC-H under asymmetric modulation. The control method includes output voltage closed-loop control, MMC high-frequency nearest level modulation method, and MMC submodules voltage balance control.
The power characteristic curve and current waveform are verified on Matlab/Simulink. Simulation results show that the average errors of the transmission power model with the proposed two modulations are 2.8% and 3.4%, respectively. A hardware-in-the-loop (HIL) experimental platform based on the FPGA and DSP control board has been constructed. The experiment verifies the voltage, current waveform, current peak, and harmonic content of the system at different transmission power. The average error of the proposed modeling method is 5.71%. In addition, dynamic experiments are conducted on the SST system, and the MMC-H SST still has good dynamic stability and fast response ability at asymmetric modulation.
Finally, a comparison is made between the proposed modulation and traditional square wave modulation. Meanwhile, the losses and efficiency of the 1 MW MMC-H SST system are calculated. The following conclusions are drawn from simulation and experimental results. (1) Compared with the traditional square wave modulation, the proposed two modulations reduce the MMC-H system dv/dt stress and current harmonics. (2) The proposed sine-square modulation achieves optimal overall system performance in terms of power variation, current waveform, peak value, and harmonic content. (3) Under steady state and dynamic conditions, the system is stable and consistent with the theoretical waveforms. Therefore, the proposed asymmetric method does not affect the system’s dynamic performance. This paper provides good theoretical support for the optimization and application promotion of the novel MMC-H SST.
keywords:Modular multilevel converter (MMC), solid state transformer (SST), power characteristics, non-square modulation, harmonic suppression
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.231957
重庆市自然科学基金面上项目(cstc2021jcyj-msxmX0871)和重庆英才计划项目(cstc2021ycjh-bgzxm0344)资助。
收稿日期 2023-11-23
改稿日期2024-01-13
潘建宇 男,1989年生,博士,教授,研究方向为中高压电力变换与控制,SiC电驱动和高电压放电防护技术。E-mail: panjianyu@cqu.edu.cn(通信作者)
杜翊豪 男,1999年生,硕士,研究方向为大功率电力变换与控制技术。E-mail: ld10061119@cqu.edu.cn
(编辑 陈 诚)