
图1 SSI-DO-T-TLI的拓扑结构示意图
Fig.1 Proposed SSI-DO-T-TLI topology
摘要 该文提出了一种基于分裂源的双输出T型三电平逆变拓扑结构。所提出的拓扑结构具有直流环节和逆变环节,其中直流环节提供升压能力,逆变环节提供三相双输出三电平逆变功能,并介绍了提出的拓扑结构及其工作原理。然后分析了在正弦脉宽调制方案中,同频同相、同频异相和异频工作模式下,调制参数的可选择值域,保证了电容电压平衡、正确的升压能力和双输出功能的实现,并在分析电感电流的基础上,通过对调制方案的讨论,对电感和电容的性能进行了优化,包括3次谐波注入法以及两种空间矢量调制的载波化调制方法,以使对电感值和电容值的需求最小化。建立了低功耗实验样机,并给出了实验结果,验证了所提拓扑结构的可行性,以及同等硬件参数、不同调制方案下对电感纹波电流、电容纹波电压的改善。
关键词:双输出 三电平 分裂源 逆变器 谐波注入法
世界各地都很重视新能源发电,然而以风电、太阳能发电为主的新能源出力具有波动性和随机性,因而电池储能系统的应用也十分广泛[1-4]。电池储能系统可以用来改善配电网电能质量[5]及满足用户的用电需求[6-7],而这些都需要逆变器的参与。多电平逆变器拓扑由于其良好的输入输出电能质量、较低的共模电压、较弱的电磁干扰,以及优越的系统效率,在众多电力场景中广泛存在[8],如电机驱动[9-10]、新能源并网[11-12]、电能转换与质量优化[13-14]等。
三电平逆变拓扑是多电平逆变拓扑中最基础、发展最早、应用最广泛的一种拓扑结构。常见的三电平逆变拓扑有中点钳位型(Neutral-Point-Clamped, NPC)逆变拓扑、飞跨电容型(Flying Capacitor, FC)逆变拓扑、级联H桥型(Cascaded H-Bridge, CHB)拓扑。NPC拓扑结构使用广泛,发展较久[15]。由于NPC开关管数量大,文献[16]使用飞跨电容代替二极管对电压进行钳位,从而提出了FC逆变拓扑,但FC逆变拓扑由于电容的存在,其体积变大,成本也变高,另外,由于飞跨电容也是有电流出入的,因此其电压也需要额外控制。CHB逆变拓扑就不需要额外进行电压控制,它使用直流电源直接通过开关器件供电,而不是经过母线电容均压后进行供电,因此不需要考虑中点电压不平衡的问题,并且此拓扑结构便于模块化设计,通过相互结合,可以获得更多电平数的多电平电压[17],理论上来说,输出电平数越多,输出电压谐波越少,但输出电平越多,增加的独立直流电源也越多,使得设备体积增大,成本也变高。T形逆变拓扑是NPC逆变拓扑的一种,相比于最开始的NPC逆变拓扑,节省了6个二极管,导通路径更短,效率更高[18]。
出于成本考虑,使用双输出逆变器以减少开关管的使用数量,是电力电子拓扑发展的一种趋势。双输出逆变拓扑最开始是由背靠背拓扑结构转变而来的[19],近些年,双输出逆变结构已经应用在很多电力场景中[20-21]。文献[22]提出了一种经典的九开关逆变(Nine-Switch Inverter, NSI)拓扑,然而NSI拓扑只能提供两电平的输出电压,其性能不如三电平逆变拓扑,因此在双输出逆变拓扑方面,也需要其他更多电平的拓扑结构,以实现更高性能的逆变输出。最直接的方法就是类似背靠背拓扑结构,两个NPC或T形三电平逆变拓扑共用一个直流侧,就可以实现三电平双输出[23-24],此种拓扑性能优越,也有广泛的应用前景,但该拓扑使用器件多、成本高,因此需要寻找其他方法。有一类拓扑增加一相桥臂来控制负载中点电压,从而实现三电平双输出[25],但同样增加了一相桥臂,控制方法更加复杂,同时也增加了成本。还有一种方法是将逆变拓扑中性点连接到输出端口。文献[26]在每个输出端口与逆变拓扑中性点之间使用双向开关连接,从而将中点电压输送到输出端口,实现三电平双输出。文献[27]通过三绕组变压器将单输出转化为双输出,成本较高。文献[28]基于NPC拓扑结构,通过开关管复用的方法,实现了三电平双输出,但由于其拓扑结构特点,无论同频(Common Frequency, CF)还是异频(Different Frequency, DF),其调制度最大不能超过0.5,因而对直流侧电压幅值要求非常高。文献[29]提出了一种基于开关管复用的双T形三电平双输出逆变拓扑结构(Dual-Output T-type Three-Level Converter, DO-T-TLC),并提出了一种可以在同频同相、同频异相、异频情况下正常运行并保持中点电位平衡的控制方法,但其中点电压控制方法计算复杂,且由于其结构特性,同相上下输出电压之间有约束条件,其调制度常常不会很大,因此,对直流侧有高幅值电压要求。为满足直流侧电压高幅值要求,应用中常常会使用一个额外的升压变换器来增加直流侧电压幅值[30],但这种方案会增加系统的复杂度和成本,并且降低能量传递效率。
为降低对直流侧电压高幅值的要求,许多学者和研究人员提出了一系列改进方法。文献[31]使用阻抗网络进行升压,提出Z源逆变(Z-Source Inverter, ZSI)拓扑;文献[32]基于Boost电路拓扑,提出分裂源(Split-Source Inverter, SSI)逆变拓扑,有学者认为,其与Z源逆变拓扑相比,具有更好的特性,并被广泛应用[33]。
本文将使用SSI拓扑结构对DO-T-TLC进行改善,提出了一种基于分裂源的双输出T形三电平逆变(Based on SSI, Dual-Output T-type Three-Level Inverter, SSI-DO-T-TLI)拓扑,主要贡献如下:
(1)使用SSI拓扑,降低了对直流侧电压的高幅值要求,增加了DO-T-TLC的应用场景,降低了硬件成本,提高了功率效率。
(2)利用单独的SSI控制电容电压,简化了对中点电压平衡的控制。
(3)针对调制方案提出了一种基于运行参数中的输入输出参数确定调制参数取值范围的方法。讨论了同频同相、同频异相和异频工作模式下的调制参数取值范围,特别是不同直流电源电压下的调制参数范围,可以保证逆变器在不同直流电源电压下仍能正常工作。
(4)根据电感纹波电流产生的原理,讨论了正弦脉宽调制(Sinusoidal Pulse Width Modulation, SPWM)方案下的电感电流谐波分量,并重新讨论了3次谐波注入PWM(Third-Harmonic Injection PWM, THIPWM)和空间矢量调制载波化调制中的Max-Min PWM中谐波的幅值以及空间矢量调制载波化调制中的不连续PWM(Discontinue PWM, DPWM)中谐波的直流偏置,以最大限度地减少相应调制方案对电感和电容的需求,同时降低调制方案的复杂性。
SSI-DO-T-TLI的拓扑结构如图1所示,与DO- T-TLC拓扑相比,增加两个SSI结构,DO-T-TLC贡献逆变能力,组成逆变环节,SSI结构贡献直流升压能力,组成直流环节。逆变环节由两个直流侧电容与三个桥臂组成,直流环节为两个SSI结构。每个桥臂都由6个开关组成,每个SSI结构都由1个直流电源、1个电感、3个二极管、12个开关以及1个电容组成,其中,有12个开关和1个电容是逆变结构和1个SSI结构共用的,有6个开关是2个SSI结构共用的,以此实现减少器件数量的目的。

图1 SSI-DO-T-TLI的拓扑结构示意图
Fig.1 Proposed SSI-DO-T-TLI topology
开关SA1、SB1、SC1、SA6、SB6、SC6被定义为外部开关。以上SSI结构为例进行分析,VDC1正极接在节点1处,VDC1负极通过电感L1与4个二极管VDA、VDB、VDC、VD1的阴极相连,前3个二极管阳极分别连接在每相桥臂的上输出节点,二极管VD1阳极与中性点0相连。因此,VDC1通过上面三个外部开关SA1、SB1、SC1为电感L1充电,VDC1和电感L1通过开关SA2~SA4、VDA、SB2~SB4、VDB、SC2~SC4、VDC或者VD1对电容C1放电,即上SSI结构控制上电容C1的电压。同理,下SSI结构控制下电容C2的电压。
电压vAO、vBO、vCO分别是节点A、B、C相对于中性点0的电压,定义为上输出的相电压;电压vXO、vYO、vZO分别是节点X、Y、Z相对于中性点0的电压,定义为下输出的相电压;电容C1与电容C2两端的电压均为Ud/2,即UC1=Ud/2,UC2=Ud/2,其中,Ud为直流侧母线电压。
正因为两个电容电压是分别被上、下SSI结构控制的,所以,不需要额外的控制方式来控制中点电压平衡。
根据上述描述,SSI-DO-T-TLI解决了DO-T-TLC需要前级升压的问题,同时还大大简化了中点电压平衡的控制方法。
令中性点为参考点,即v0=0。针对逆变环节,由于开关管复用的限制,每相桥臂上输出相电压与下输出相电压之间存在约束关系,以AX相桥臂为例,vAO≥vXO。因此,以AX相桥臂为例,可用的开关状态及其在逆变环节中的电流路径和输出电压如图2所示。
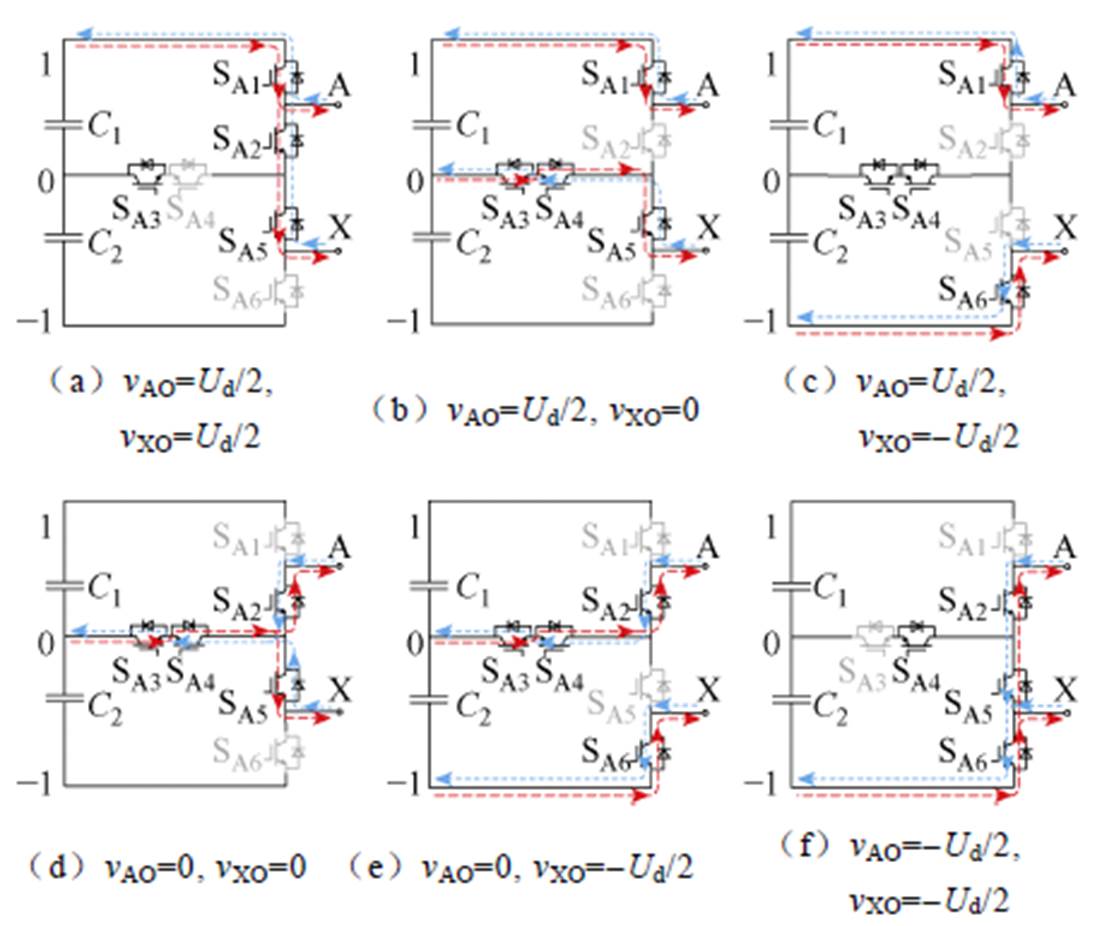
图2 无直流环节,仅逆变环节的AX桥臂的开关状态
Fig.2 Switching states for the AX leg of inverter link without DC link
图2中,黑色开关管代表该开关管被施加了驱动信号,灰色开关管代表该开关管没有被施加驱动信号,带箭头的线条则代表电流路径。
AX支路上开关状态与相电压的关系见表1。
表1 AX桥臂开关状态与输出电压的关系
Tab.1 Relationship between the switching state and the phase voltage of AX leg
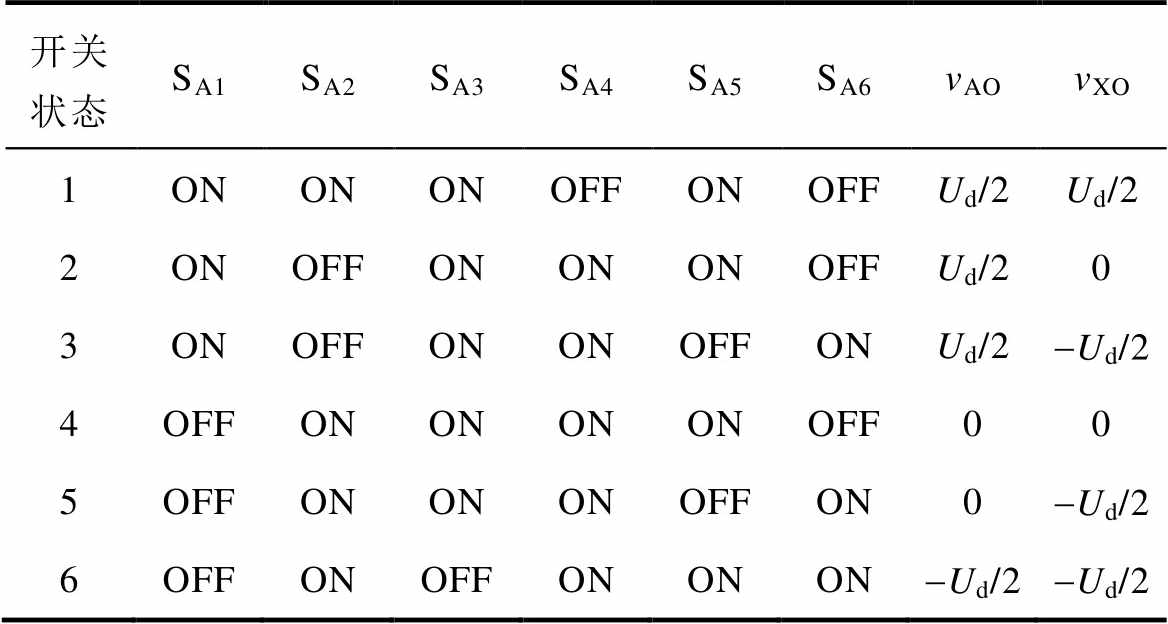
开关状态SA1SA2SA3SA4SA5SA6vAOvXO 1ONONONOFFONOFFUd/2Ud/2 2ONOFFONONONOFFUd/20 3ONOFFONONOFFONUd/2-Ud/2 4OFFONONONONOFF00 5OFFONONONOFFON0-Ud/2 6OFFONOFFONONON-Ud/2-Ud/2
三相桥臂开关状态的组合,除了可以改变逆变结构的输出状态,针对直流环节,还会对SSI结构的工作情况产生影响。经过对SSI各状态的导通路径以及各节点电压的分析可以得到:当开关SA1、SB1、SC1中存在开关为开通状态,那么,直流电源VDC1就一直给电感L1充电,只有当开关SA1、SB1、SC1都关断时,电感L1对电容C1放电。L2的充放电过程与L1类似。
令相电压Ud/2对应输出状态P,相电压0对应输出状态O,相电压-Ud/2对应输出状态N。三条支路输出状态的组合与电感是否对外放电的关系见表2,值得注意的是,上输出的相电压决定L1是否对外放电,下输出的相电压决定L2是否对外放电。
表2 三相输出状态与电感放电的关系
Tab.2 Relationship between output states and discharge of inductance

电感电感放电 是否 L1OOO, OON, ONO, ONN, NOO, NON, NNO, NNN(上输出状态)PPP, PPO, PPN, POP, POO, PON, PNP, PNO, PNN, OPP, OPO, OPN, OOP, ONP, NPP, NPO, NPN, NOP, NNP(上输出状态) L2PPP, PPO, POP, POO, OPP, OPO, OOP, OOO(下输出状态)NPP, NPO, NPN, NOP, NOO, NON, NNP, NNO, NNN, PNP, PNO, PNN, ONP, ONO, ONN, PPN, PON, OPN, OON(下输出状态)
值得注意的是,二极管VD1和VD2分别是为了能够使得SSI结构能单独为对应的电容充电加入的,本文使用的调制方案没有PPP状态和NNN状态,所以,这两个二极管其实是没有作用的。
在1.2节中,为了避免产生无效的开关状态,同一个桥臂,需要满足上输出相电压不能小于下输出相电压的条件,基于本文使用同相层叠载波进行调制,因此,可以通过在两组调制波中增加直流偏移量来满足该条件。此外,选择相位配置载波,可以避免相电压的两级跳变。
首先,取理想正弦波形为
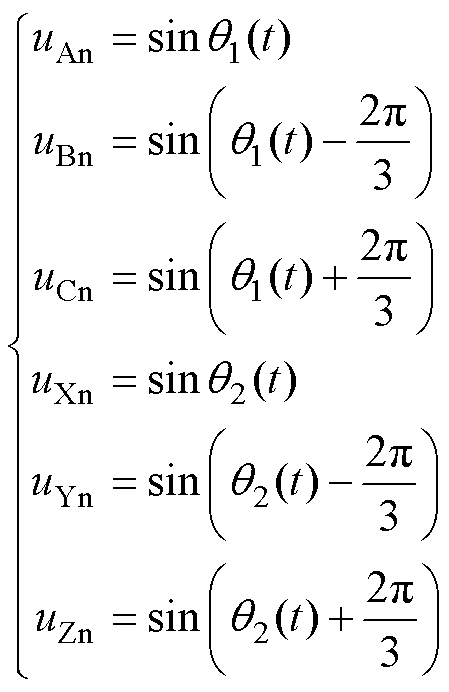 (1)
(1)
在SPWM方案中,两组调制波为
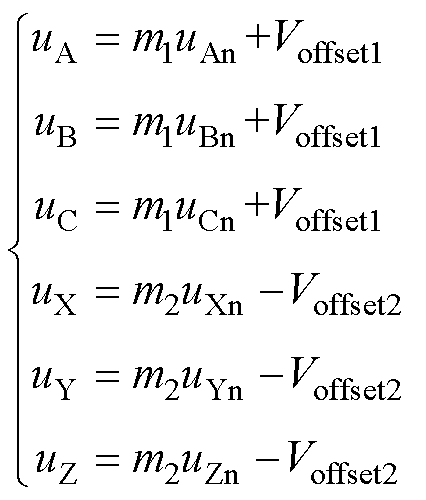 (2)
(2)
式中,q1(t)=w1t+f1、q2(t)=w2t+f2,w1、w2为角频率,且上组调制波的频率为f1=w1/(2p),下组调制波的频率为f2=w2/(2p),f1、f2为初始相位;m1、m2为调制指数,取值范围均为0~1;Voffset1、Voffset2为直流偏移量,取值范围分别为0~1-m1和0~1-m2。
使用了2条三角载波u1和u2,并采用同相层叠方式。2条三角载波u1、u2的相位和频率均相同,u1的变化范围为0~1,u2的变化范围为-1~0。
因为同桥臂上输出相电压不得小于下输出相电压,所以,对于同一个桥臂的调制波,需要上调制波时刻不小于下调制波,即
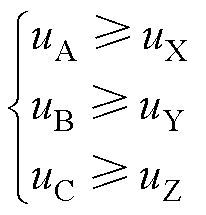 (3)
(3)
对于AX桥臂,当uA>u1时,vAO=Ud/2;当uA<u2时,vAO=-Ud/2;当u1≤uA≤u2时,vAO=0;当uX>u1时,vXO=Ud/2;当uX<u2时,vXO=-Ud/2;当u1≤uX≤u2时,vXO=0。其他桥臂也按照相同的规律,使用该桥臂的调制波与公共载波进行比较来决定上、下输出相电压。
SPWM方案如图3所示(实际载波频率fs是调制波频率的200倍)。
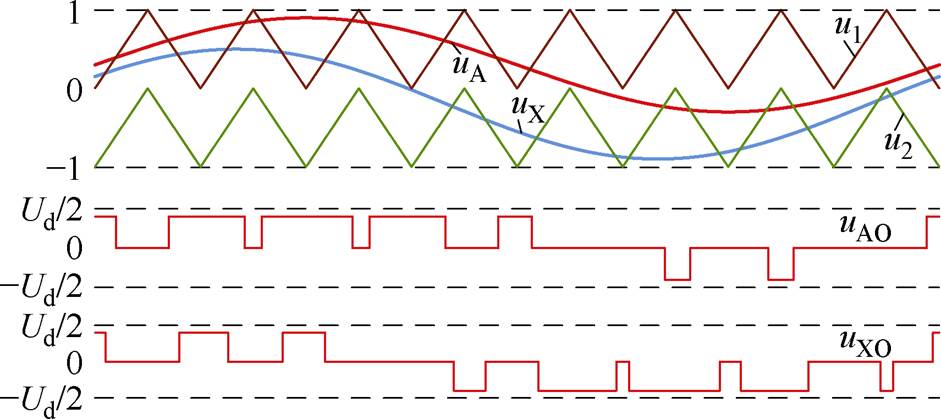
图3 SPWM方案示意图
Fig.3 The reference and carrier signals of the SPWM scheme
对于逆变环节,因为采用了SPWM方式,所以输出线电压的基波峰值分别为
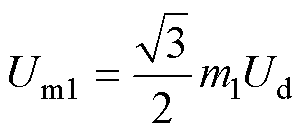 (4)
(4)
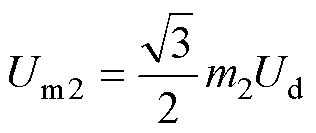 (5)
(5)
式中,Um1为上输出线电压基波幅值;Um2为下输出线电压基波幅值。
对于升压环节,本文针对电感电流连续状态进行讨论。
当上输出状态存在P时,L1充电,当上输出状态没有P时,L1向外放电;同样,当下输出状态存在N时,L2充电,当下输出状态没有N时,L2向外放电。对于上电感L1和上电容C1,只需要考虑上输出状态。因为上输出三相调制波之间存在大小关系,所以当上输出的最大调制波相的输出状态为非P状态时,其余两相就没有P状态,此时电感L1放电,电容C1充电。因此根据式(2)可以得到上电容充电占空比d1(t)为
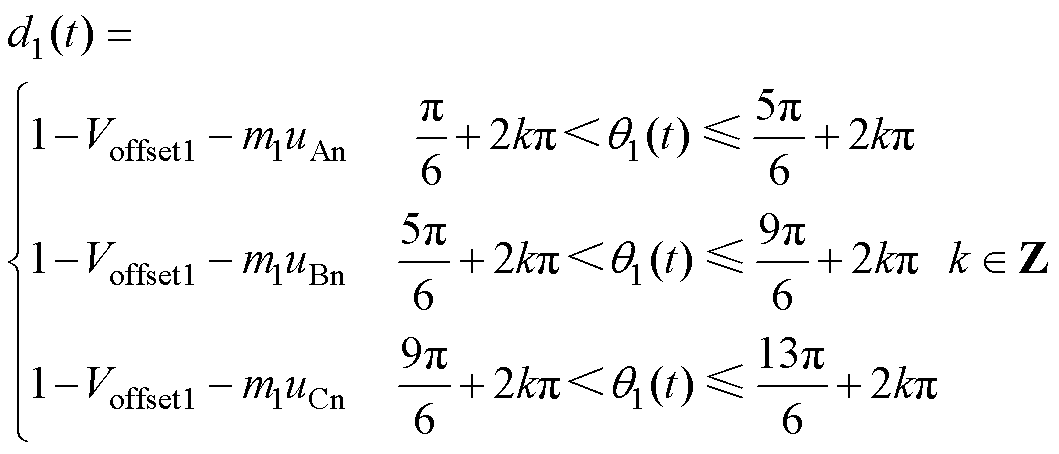 (6)
(6)
同理,根据式(2)可以得到下电容充电占空比d2(t)为
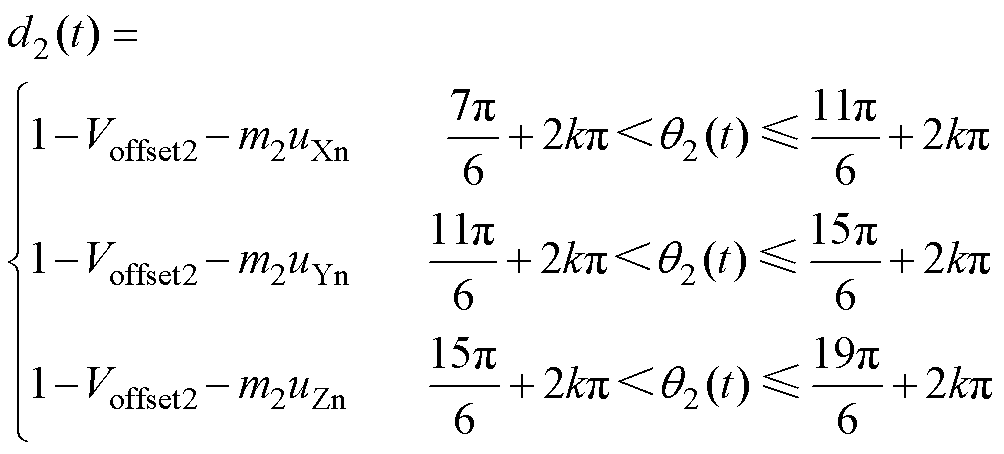
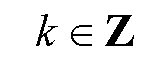 (7)
(7)
显然,d1(t)和d2(t)分别为图4中黄色区域和蓝色区域的高度值,其变化频率为调制波频率的三倍频。使用式(6)、式(7)能够求得上电容充电平均占空比D1和下电容充电平均占空比D2,得到
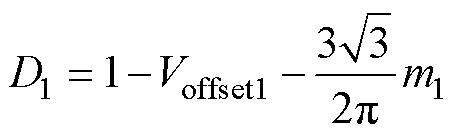 (8)
(8)
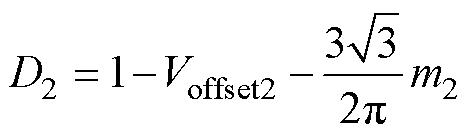 (9)
(9)
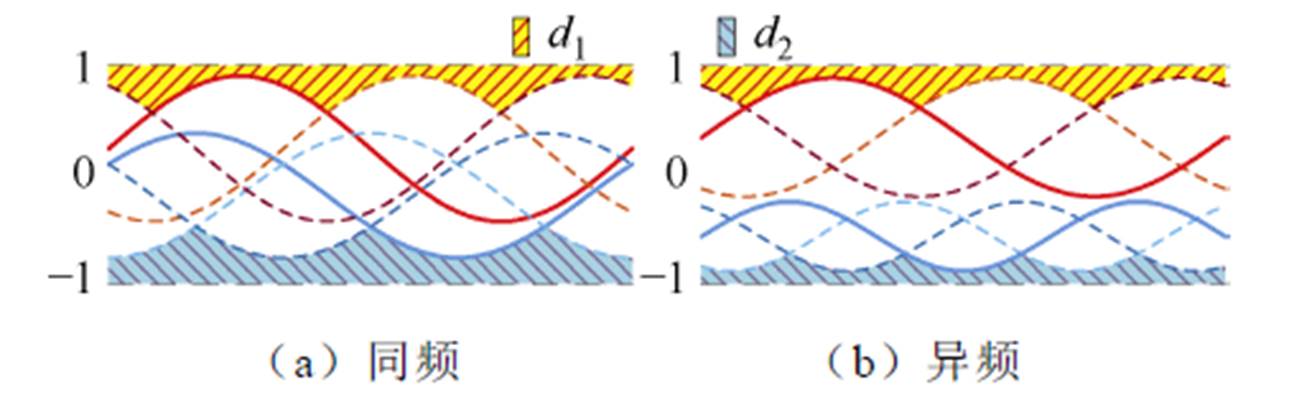
图4 上、下电容充电占空比的变化趋势
Fig.4 Trend of charging duty cycle of upper and lower capacitors
因此
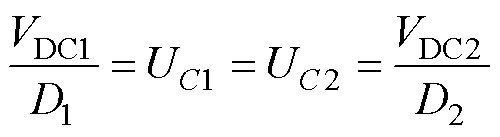 (10)
(10)
对于调制波,如图3所示,需要满足
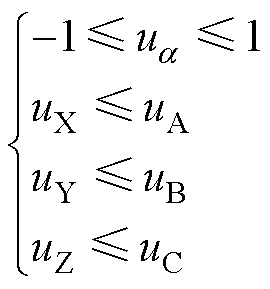 (11)
(11)
式中,a∈{A, B, C, X, Y, Z}。
为进一步确定各调制参数间的关系,以及更广的适用范围,现定义两个直流输入电源电压幅值之间的关系如式(12),两个输出端线电压基波幅值之间的关系如式(13)。
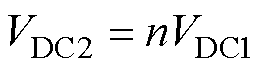 (12)
(12)
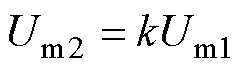 (13)
(13)
式中,n为两个输入电源电压间的比例系数;k为两个输出端线电压基波幅值间的比例系数。
为进一步描述各参数间的约束关系,将式(4)、式(5)、式(8)~式(10)、式(12)、式(13)代入约束关系中,可以得到
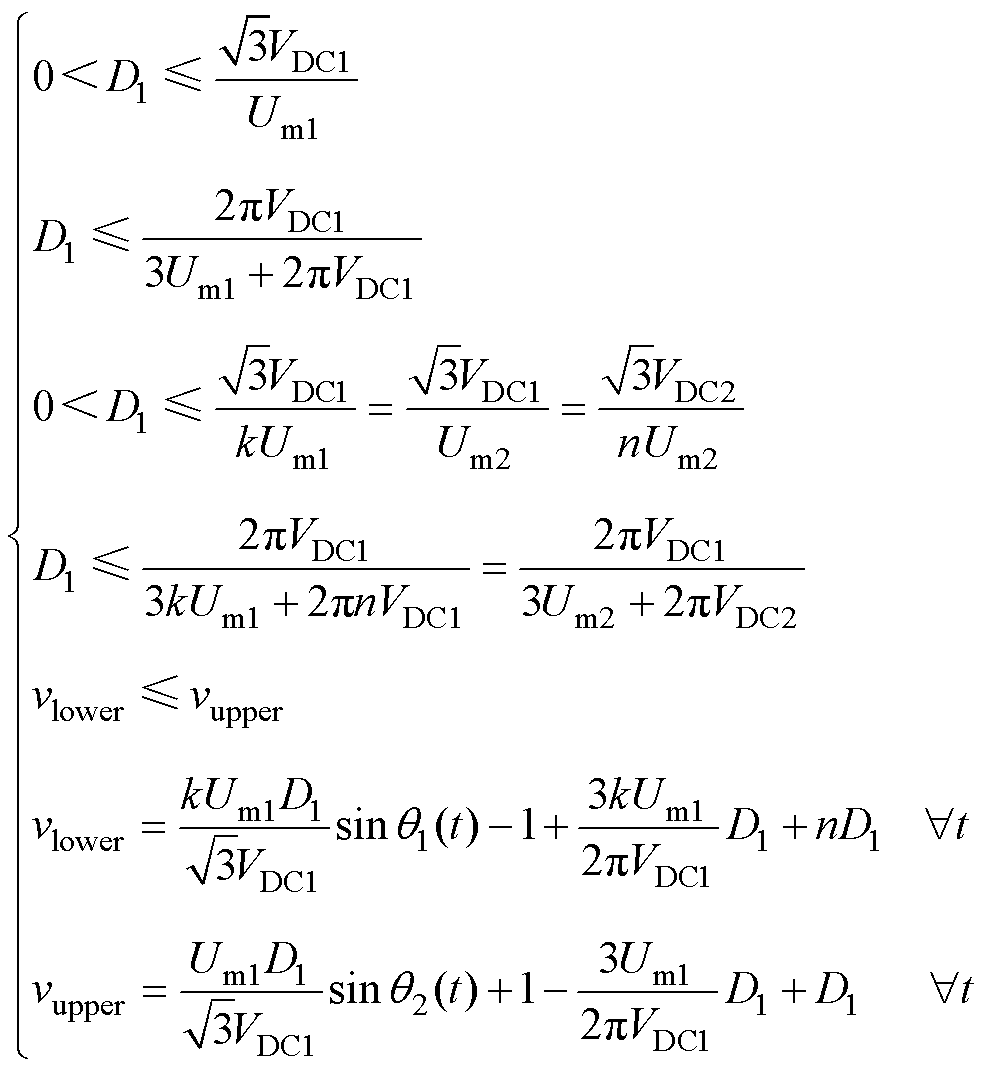 (14)
(14)
很显然,在式(14)中,只有D1是调制参数变量,其余变量均由运行参数提供,因此,可以将式(14)看作是关于D1的不等式方程组,在该不等式方程组的D1的值域中选取合适的D1,再利用前文提到的各变量之间的关系,即可得到一整套满足系统条件的调制参数。
本拓扑中的两个电容电压是分别通过两个SSI结构进行控制的。在调制参数求解过程中可以看出,调制参数的约束建立在可以维持上、下电容电压平衡的基础上,因此基于本调制方法的任何调制参数都可以实现上、下电容电压平衡,大大简化了电容电压平衡控制。
该情况下,令q1(t)=q2(t),则AX相桥臂的调制波uA、uX和公共载波u1、u2的波形如图5所示。
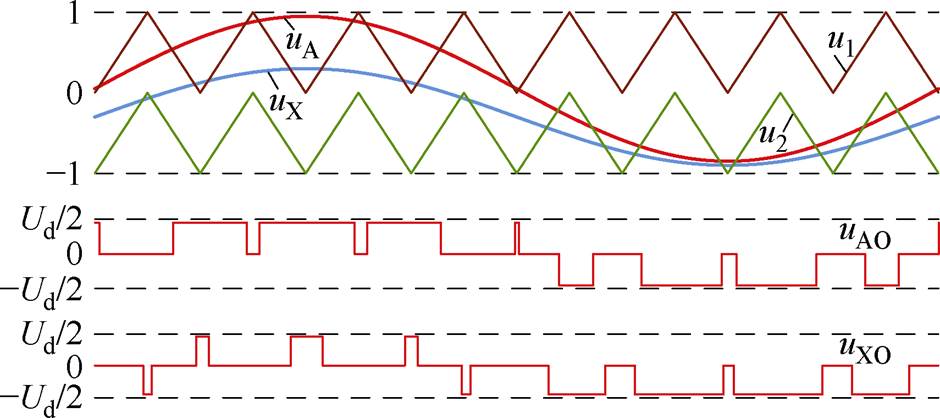
图5 同频同相工作模式下的SPWM方案示意图
Fig.5 SPWM scheme in the in-phase CF operation mode
调制波的范围可以用调制波最大、最小值与±1之间的关系来表示,同频同相上、下调制波的大小关系可转换为两个最大值、两个最小值之间的关系。
因此约束关系可简化为
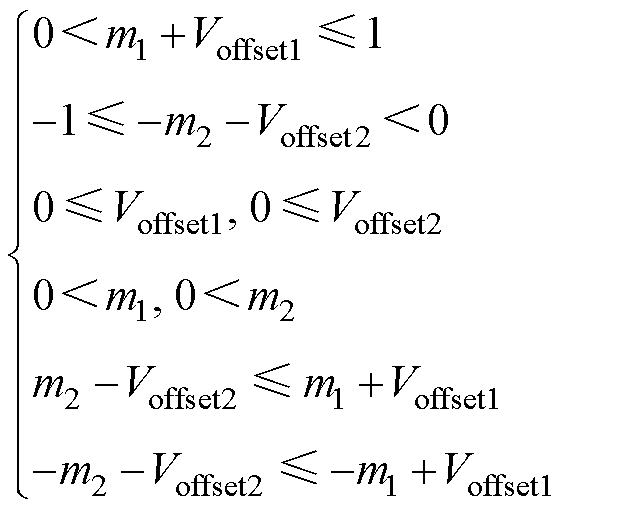 (15)
(15)
此时将式(4)、式(5)、式(8)~式(10)、式(12)、式(13)代入式(15),可以直接推导得出
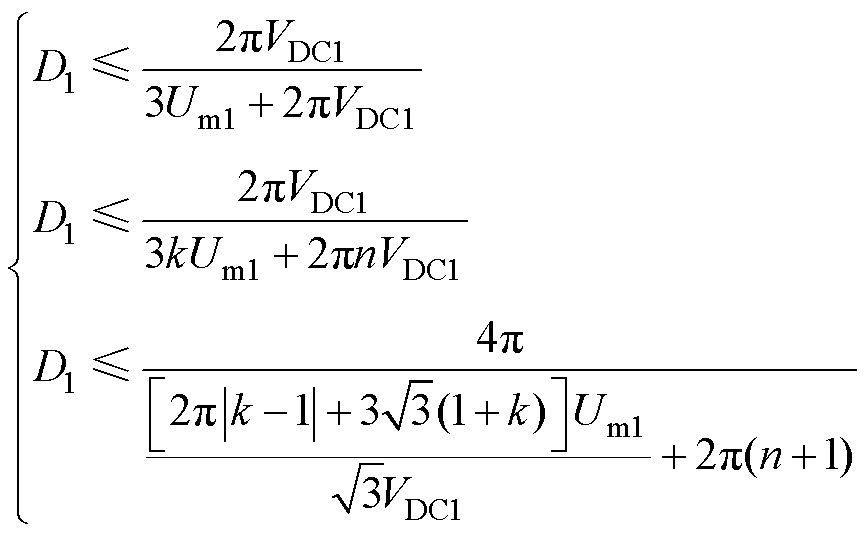 (16)
(16)
由此可以确定,在同频同相情况下,D1的取值范围如式(16)所示,选择合适的D1,再使用式(4)、式(5)、式(10)、式(12)、式(13)确定参数m1、m2、Voffset1和Voffset2,即得到上、下两组调制波。
该情况下,令q1(t)=q2(t)+f,其中f 为上、下同相调制波间的相位差,则AX相桥臂的调制波uA、uX和公共载波u1、u2的波形如图6所示。
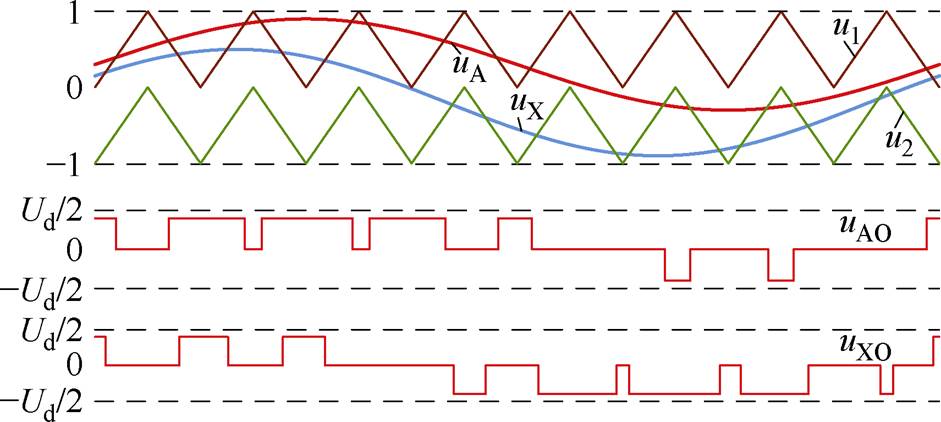
图6 同频异相工作模式下的SPWM方案示意图
Fig.6 SPWM scheme in the non-in-phase CF operation mode
此时两个调制波最大、最小值与±1的关系与同频同相情况相同,只是在同组上下调制波大小关系的表现形式上存在不同,即式(15)中后两个不等式替换为
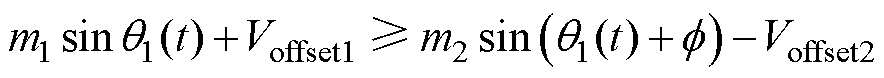 (17)
(17)
其余不等式不变,因此约束关系可简化为
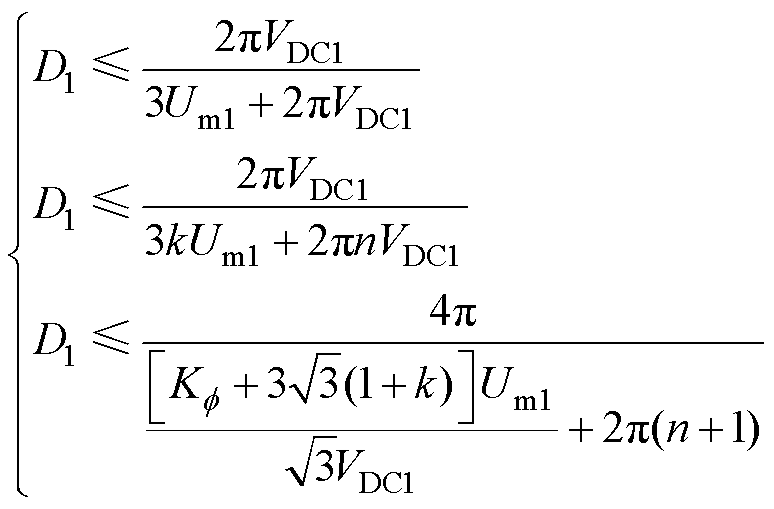 (18)
(18)
式中,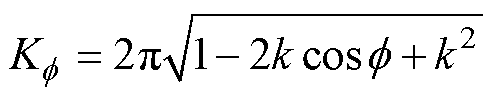 。显然,式(18)是同频情况下,不等关系式的通解域,而式(16)是
。显然,式(18)是同频情况下,不等关系式的通解域,而式(16)是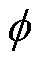 =0的特解域。
=0的特解域。
该情况下,令f1≠f2,则AX相桥臂的调制波uA、uX和公共载波u1、u2的波形如图7所示。
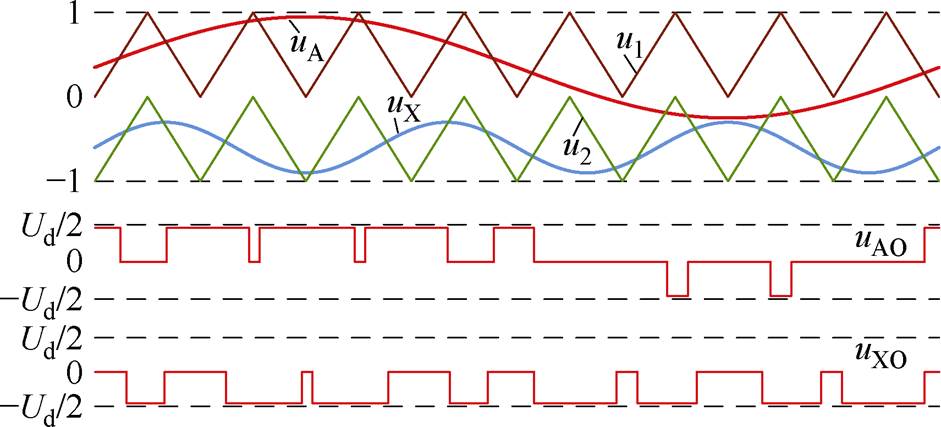
图7 异频工作模式下的SPWM方案示意图
Fig.7 SPWM scheme in the DF operation mode
同样是两个调制波最大、最小值与±1的关系与同频同相情况相同,只是在同组上下调制波大小关系的表现形式上存在不同。
因为上下调制波频率不同,所以,想要满足上调制波每时每刻不小于下调制波的条件,需要上调制波的最小值不小于下调制波的最大值。即式(15)中后两个不等式替换为
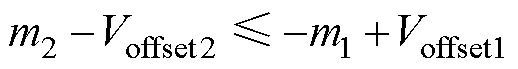 (19)
(19)
其余不等式不变。由此对约束关系化简,可确定在异频情况下的D1的取值范围为
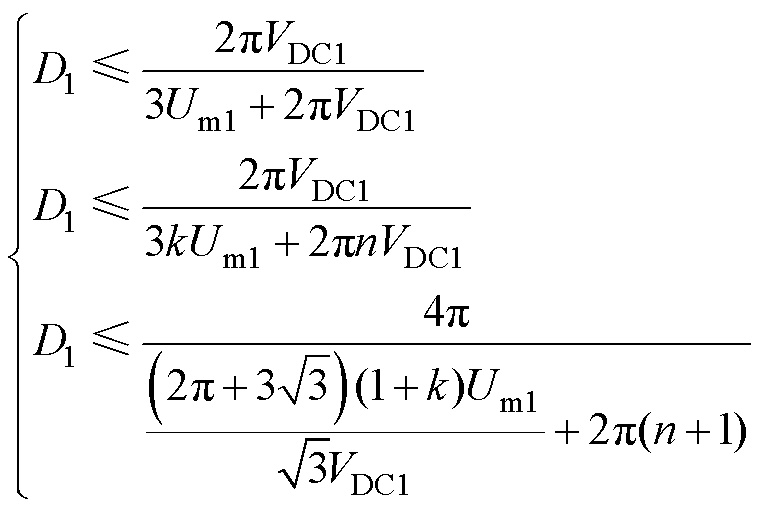 (20)
(20)
但是知道升压电路的输出电压低于理论值,并且由于调制波的波动,电容电压和电感电流也在波动,使得理论输出电压更高。因此,Voffset1和Voffset2应略大于原始计算值。
由文献[32]可以得到,在SPWM方案下,电感参数与电容参数公式为
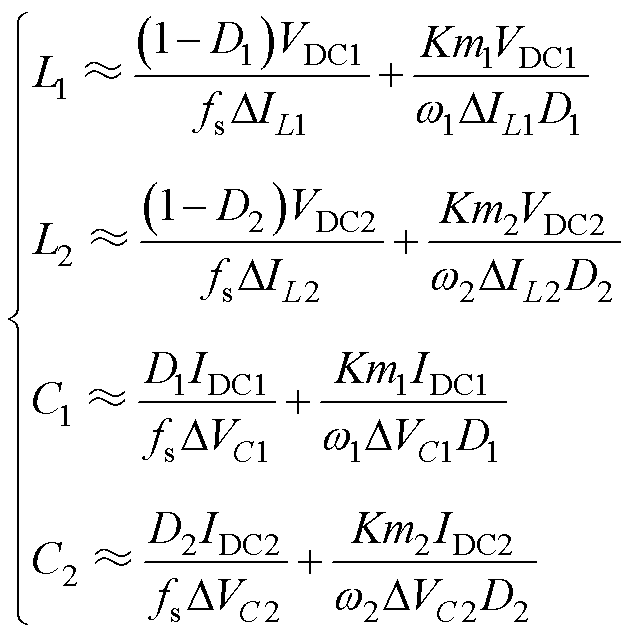 (21)
(21)
式中,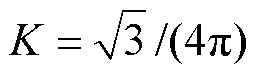 ;DIL1为电感L1的纹波电流;DIL2为电感L2的纹波电流;DVC1为电容C1的纹波电压;DVC2为电容C2的纹波电压。
;DIL1为电感L1的纹波电流;DIL2为电感L2的纹波电流;DVC1为电容C1的纹波电压;DVC2为电容C2的纹波电压。
通过式(21)可以看出,电感和电容都和K有关,因此本节将通过研究电感纹波电流,减小K值,从而减小电感和电容的纹波。这也就意味着,在同等性能要求下,可以降低对电感值、电容值的要求。
电感基本性质如式(22)所示,这体现了电感的能量属性。电感充放电状态的切换会导致电感能量的波动,这体现在电感电流上的波动。
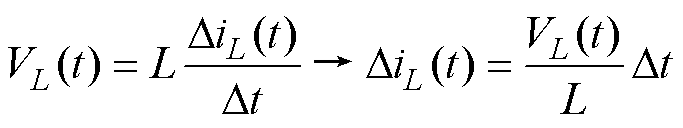 (22)
(22)
接下来,通过微积分思想对该过程进行分析。当电感能量处于稳态时,电感电压在一个稳态周期内的积分是0。但通过式(6)和式(7)可以看出,电感充放电的时间一直在变化,所以并不能总是保持一个开关周期首尾电感能量相等。因此电感纹波电流由两部分组成:一部分是由于开关的频繁通断导致的高频纹波分量,因为开关频率很高,所以这部分占总纹波很小;另一部分是由于电感充放电占空比规律变化导致的低频纹波,占纹波电流的大部分。因此本文只对其低频纹波进行分析。
首先假定电容足够大,使得电容电压不变。以电感L1为例,在t时刻,dt时间内,流过电感L1的电流的变化量diL1(t)为
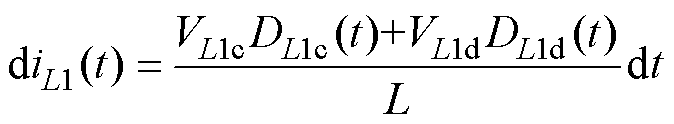 (23)
(23)
式中,VL1c为电感L1充电时两端的电压;VL1d为电感L1放电时两端的电压;DL1c(t)为电感L1在t时刻的充电占空比;DL1d(t)为电感L1在t时刻的放电占空比。
如图4所示,电感充放电的占空比是以基波频率的三倍频进行周期性变化的。将式(7)、式(8)代入到式(23)中,可得
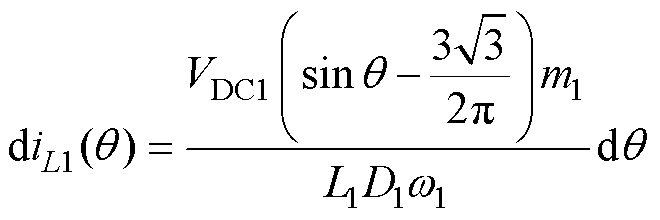 (24)
(24)
式中,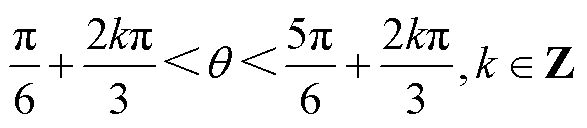 ,其相位在p/6~5p/6范围内电感电流波形如图8所示,其中,q = wt+f,w =w1、f =f1或者w =w2、f =f2,IL1为上电感L1电流的基波分量幅值。
,其相位在p/6~5p/6范围内电感电流波形如图8所示,其中,q = wt+f,w =w1、f =f1或者w =w2、f =f2,IL1为上电感L1电流的基波分量幅值。
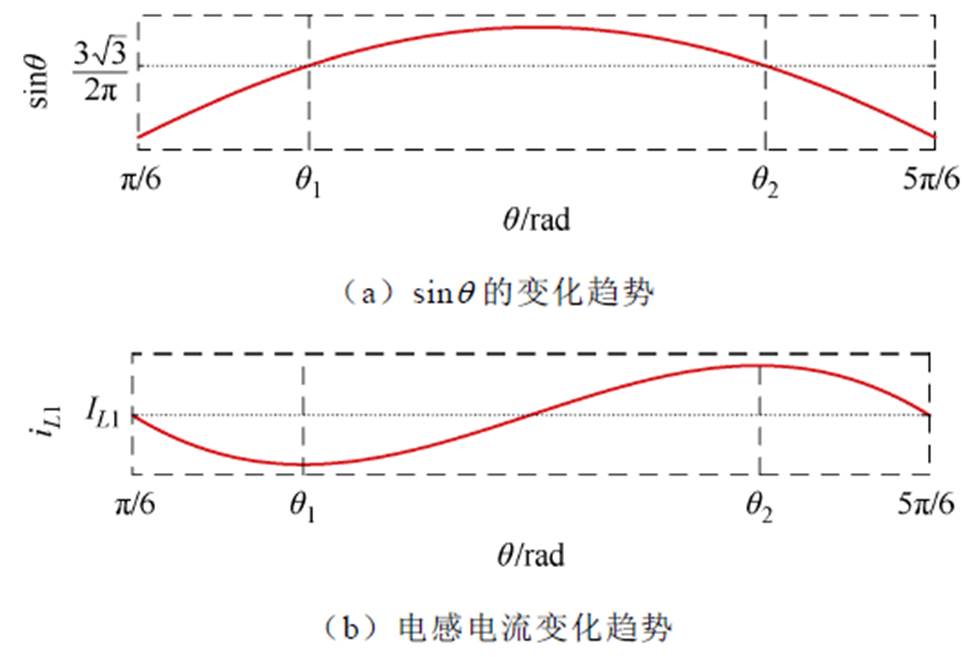
图8 电感电流波形示意图
Fig.8 The waveform of inductive current
显然,如图8a所示,在一个纹波周期内,diL1(q)在 (q1, q2) 中始终为正值,同纹波周期的其余连续区间内恒为非正值,因此电感L1的电流最小值在q1处取得,最大值在q2处取得,电感L1的纹波电流可以通过对式(24)两侧进行积分得到。
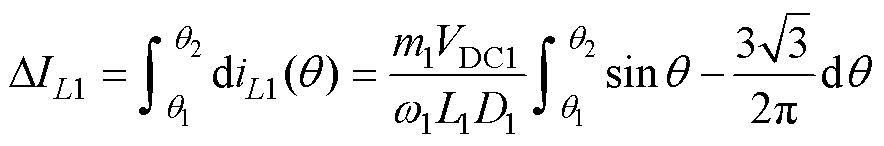 (25)
(25)
因此电感电流波形如图8b所示。同理,可以求得电感L2的纹波电流为
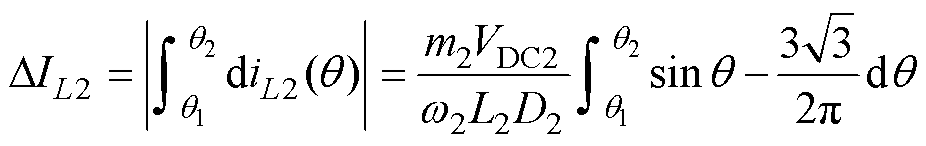 (26)
(26)
由式(4)、式(5)、式(11)可得
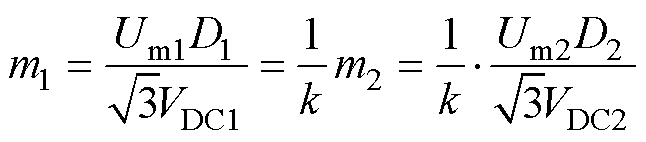 (27)
(27)
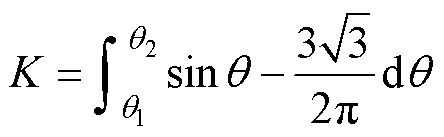 (28)
(28)
可以看出,当系统的输入、输出固定时,只能通过改变调制方案来减小式(26)中的积分,以减小电流纹波。由式(21)、式(25)、式(26)可知,在SPWM方案中,式(28)是成立,该积分值是由于电容充电占空比波动变化引起的,因此可以通过调整电容充电占空比的波动情况,来降低电感纹波电流。
如图4所示,使用SPWM方案时,电容充电占空比波动很大。可以如式(29)、式(30),通过在调制波中加入谐波分量uadb,以达到减小由于占空比变化而产生的纹波电流和纹波电压的目的,而载波不需要变化,其中,b∈{A, B, C, X, Y, Z}。
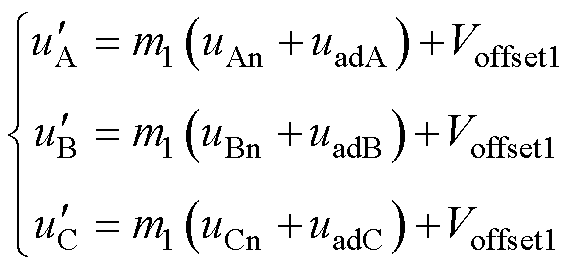 (29)
(29)
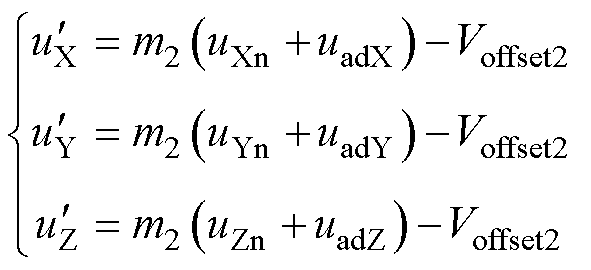 (30)
(30)
下文将通过对THIPWM以及两种SVPWM的载波化调制方案即Max-Min PWM以及DPWM方案的分析,确定合适的谐波成分。
在THIPWM方案中,取谐波为
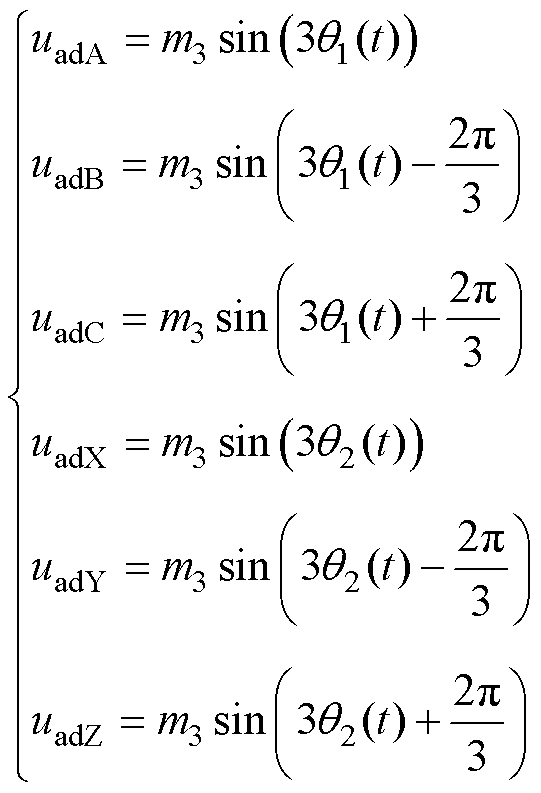 (31)
(31)
在传统THIPWM方案中,为了能够最大限度利用直流电压,常设置m3=1/6。然而,在本文中,使用THIPWM方案的目的是减小纹波,因此,下文将利用与3.1节相同的方法讨论m3的取值。
注入谐波后,THIPWM方案如图9所示。注入的谐波与占空比同样都是以基波频率的三倍频来变化的,因此,注入谐波对电容充电平均占空比无影响。上组调制波相位在(p/6, 5p/6]内时,其上电容充电占空比为
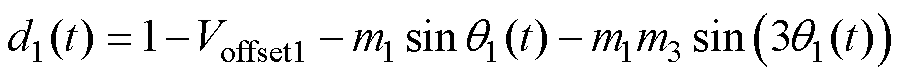 (32)
(32)
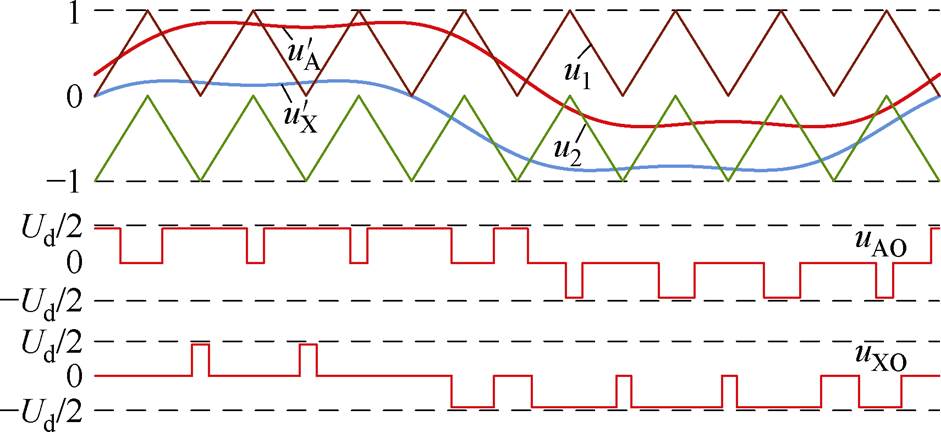
图9 THIPWM方案示意图
Fig.9 The reference and carrier signals of the THIPWM scheme
将式(32)代入式(23)中,可以得到在THIPWM方案下电感L1电流在(p/6, 5p/6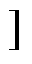 内的变化情况diL1(q)为
内的变化情况diL1(q)为
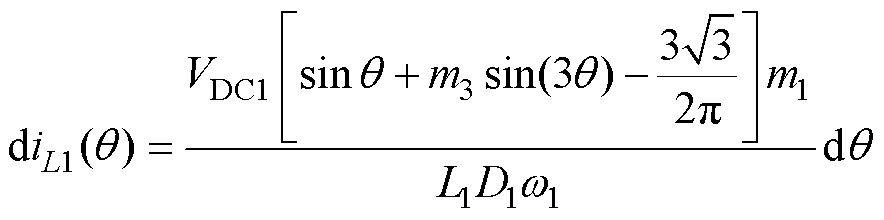 (33)
(33)
对式(33)进行积分之后,即是电流一个纹波周期内的变化情况,电流变化量的最大值与最小值之间的差即为纹波电流。
图10展示了不同m3的情况下,纹波电流标幺值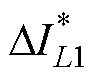 的值(以VDC1m1/(L1D1w1)为基准值),可以得到当m3=0.21时,纹波电流最小,此时的一个电感纹波电流周期内,电感电流波动情况如图11所示。
的值(以VDC1m1/(L1D1w1)为基准值),可以得到当m3=0.21时,纹波电流最小,此时的一个电感纹波电流周期内,电感电流波动情况如图11所示。
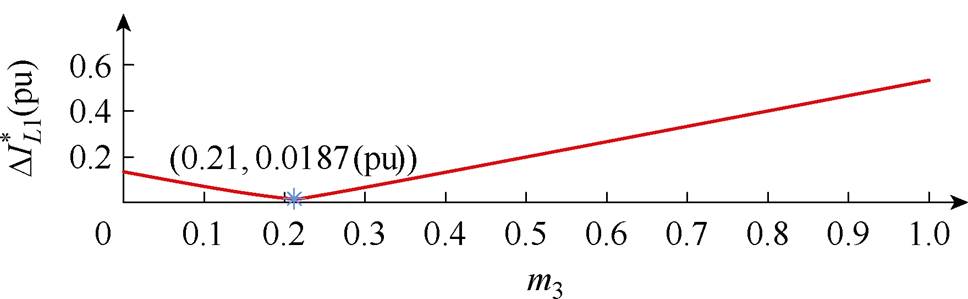
图10 THIPWM方案下电感纹波电流标幺值与m3的关系
Fig.10 Variation of 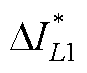 of inductor ripple current (THIPWM)
of inductor ripple current (THIPWM)
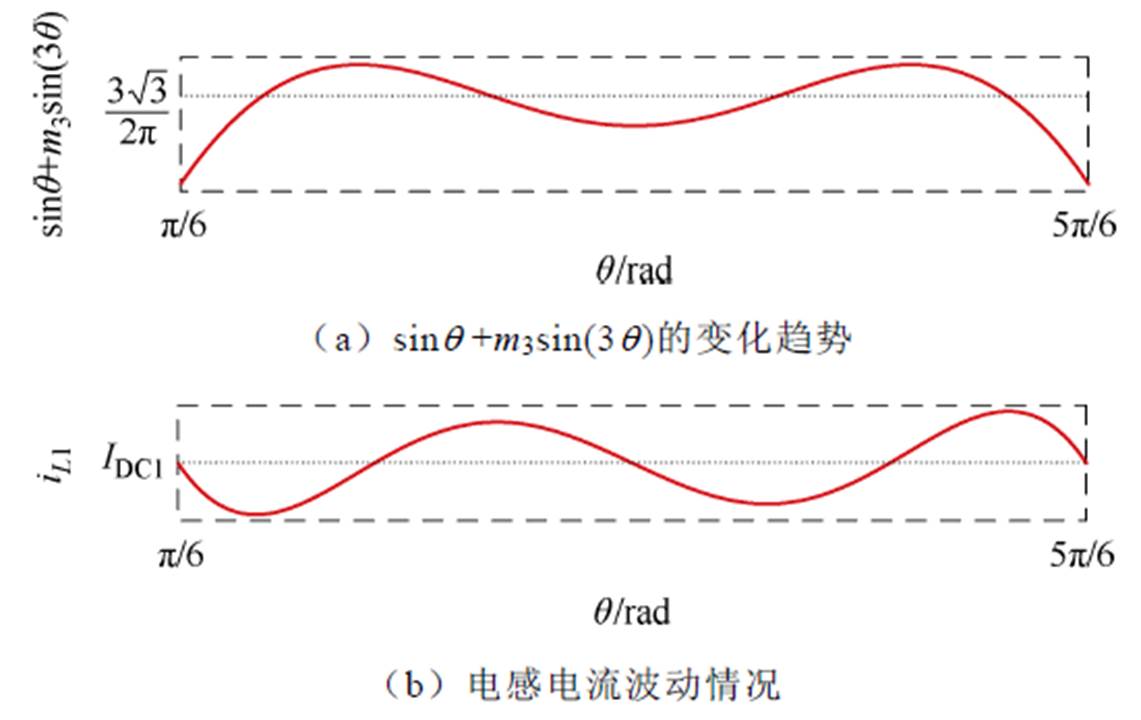
图11 THIPWM方案下电感电流波动示意图
Fig.11 The fluctuation of the inductor current (THIPWM)
因此可以确定,该方法中调制波注入的3次谐波的幅值为基波幅值的0.21,此时K=0.018 7。
在Max-Min PWM方案中,取谐波为
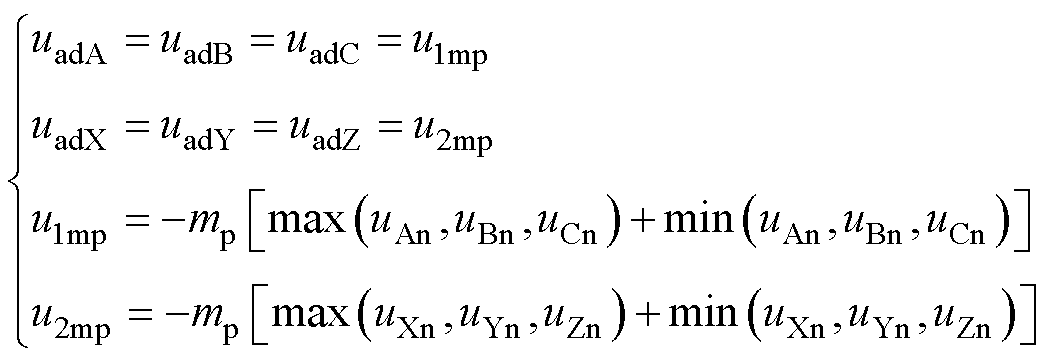 (34)
(34)
式中,mp为一个常数,代表该3次谐波的占比,其大小在下文进行讨论。
注入谐波后,Max-Min PWM方案如图12所示。
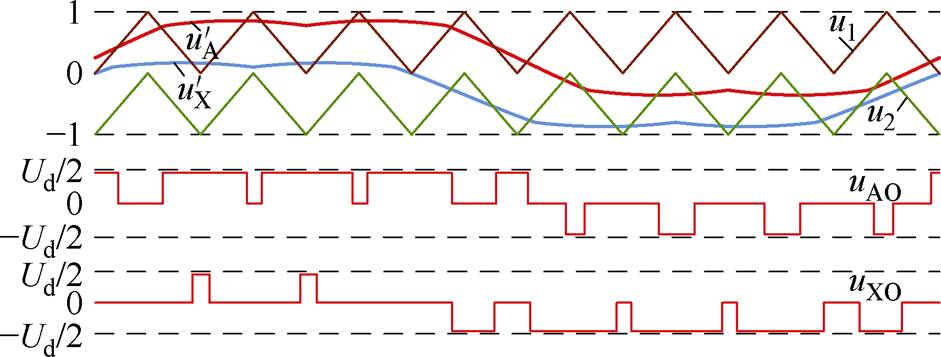
图12 Max-Min PWM方案示意图
Fig.12 The reference and carrier signals of the Max-Min PWM scheme
注入的谐波与占空比变化频率都是基波频率的三倍频,因此,注入谐波对电容充电平均占空比无影响。
因此,上组调制波相位在(p/6, 5p/6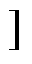 内时,其上电容充电占空比为
内时,其上电容充电占空比为
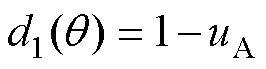 (35)
(35)
将式(35)代入式(23)中,可以得到在Max- Min PWM方案下电感L1电流在(p/6, 5p/6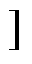 内的变化情况diL1(q)为
内的变化情况diL1(q)为
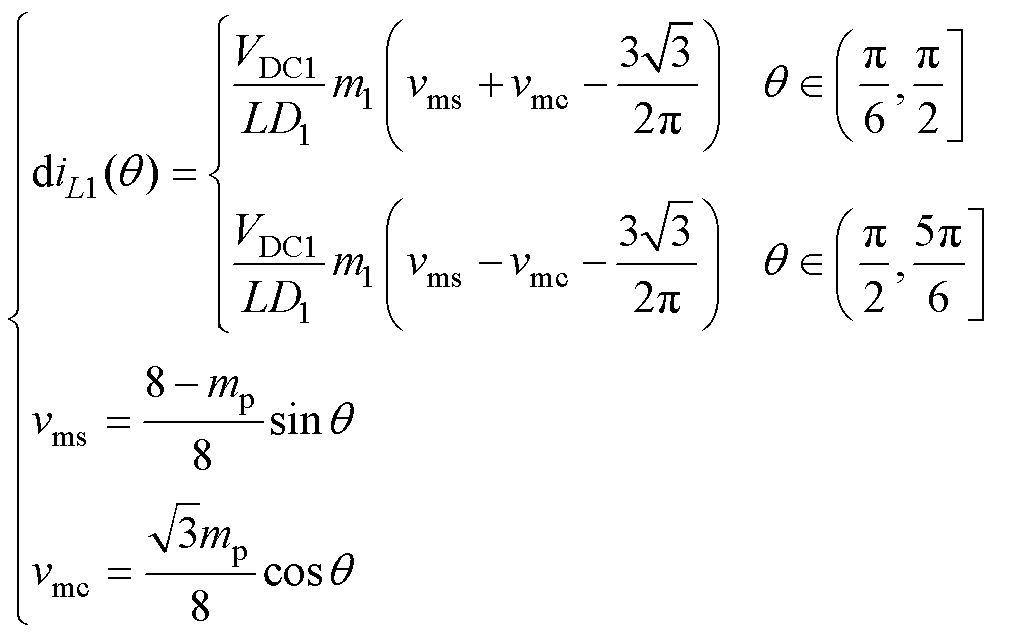 (36)
(36)
对式(36)进行积分之后,即是电流一个纹波周期内的变化情况,电流变化量的最大值与最小值之间的差即为纹波电流。
图13展示了随mp变化而变化的纹波电流标幺值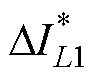 ,可以得到当mp=0.5时,纹波电流最小,此时的一个电感纹波电流周期内,电感电流波形如图14所示。
,可以得到当mp=0.5时,纹波电流最小,此时的一个电感纹波电流周期内,电感电流波形如图14所示。
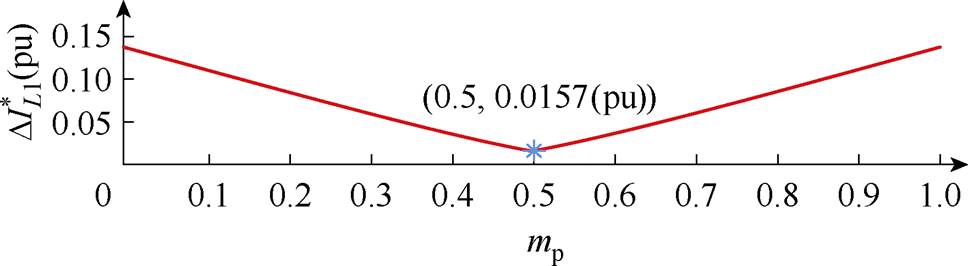
图13 Max-Min PWM调制方案下电感纹波电流标幺值与mp的关系
Fig.13 Variation of 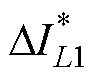 of inductor ripple current (Max-Min PWM)
of inductor ripple current (Max-Min PWM)
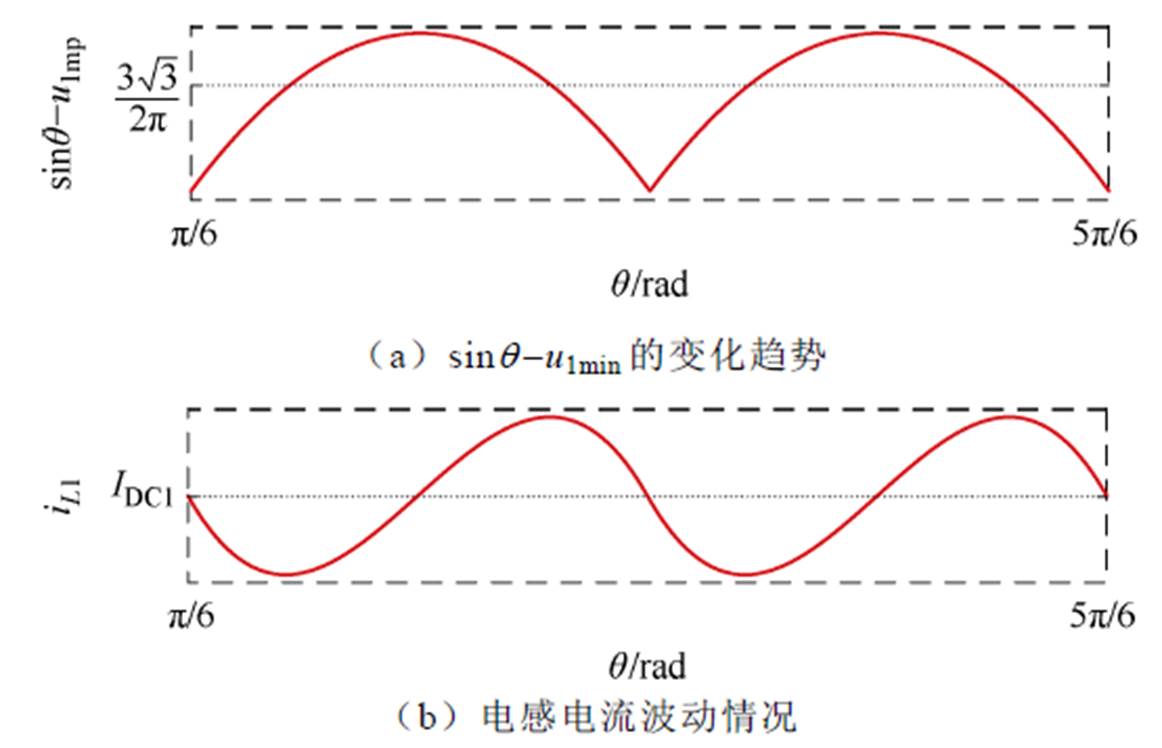
图14 Max-Min PWM方案下电感电流波动示意图
Fig.14 The fluctuation of the inductor current (Max-Min PWM)
因此可以确定,该方法中调制波注入的3次谐波的幅值为基波幅值的0.5,此时K=0.015 7。
基于使得电感纹波电流最小的目的,使用DPWMMAX方案控制上输出,使用DPWMMIN方案控制下输出。
在DPWM方案中,分别取谐波
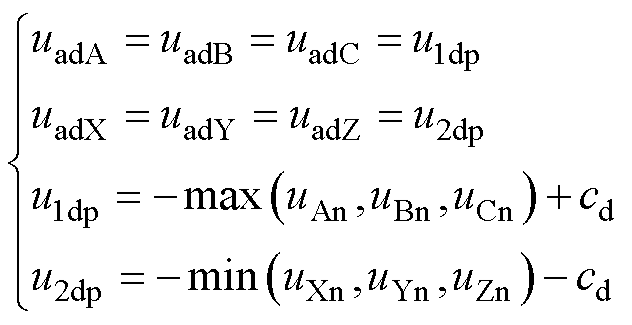 (37)
(37)
式中,cd为一个常数,代表该注入3次谐波中直流偏移量的大小,其取值在下文进行讨论。
注入谐波后,DPWM方案如图15所示。
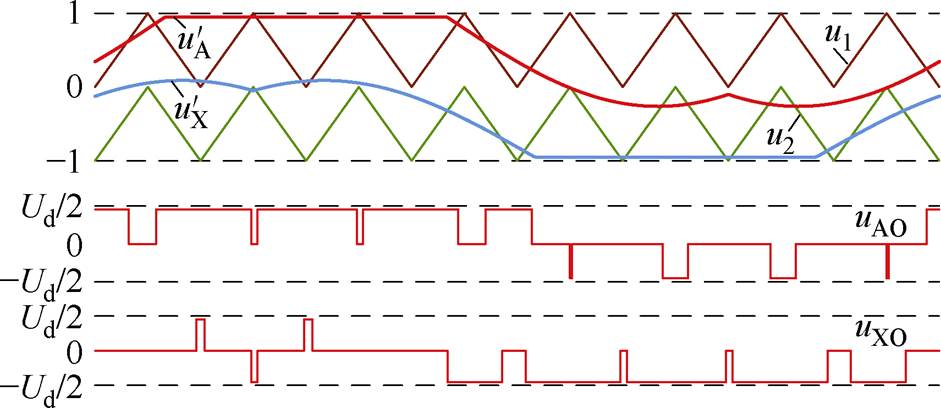
图15 DPWM方案示意图
Fig.15 The reference and carrier signals of the DPWM scheme
因为直流偏移量对相间输出无影响,只对直流侧电容电压的升压倍数有影响,为了更好地确定约束条件,假定cd的加入不对式(8)~式(10)有影响,可以确定3次谐波中注入的直流偏移量cd= 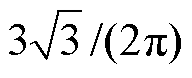 。由于此时电容充电占空比无低频变化,所以,此时电感低频纹波电流为0,K=0,即此时电感纹波电流仅由高频纹波组成。
。由于此时电容充电占空比无低频变化,所以,此时电感低频纹波电流为0,K=0,即此时电感纹波电流仅由高频纹波组成。
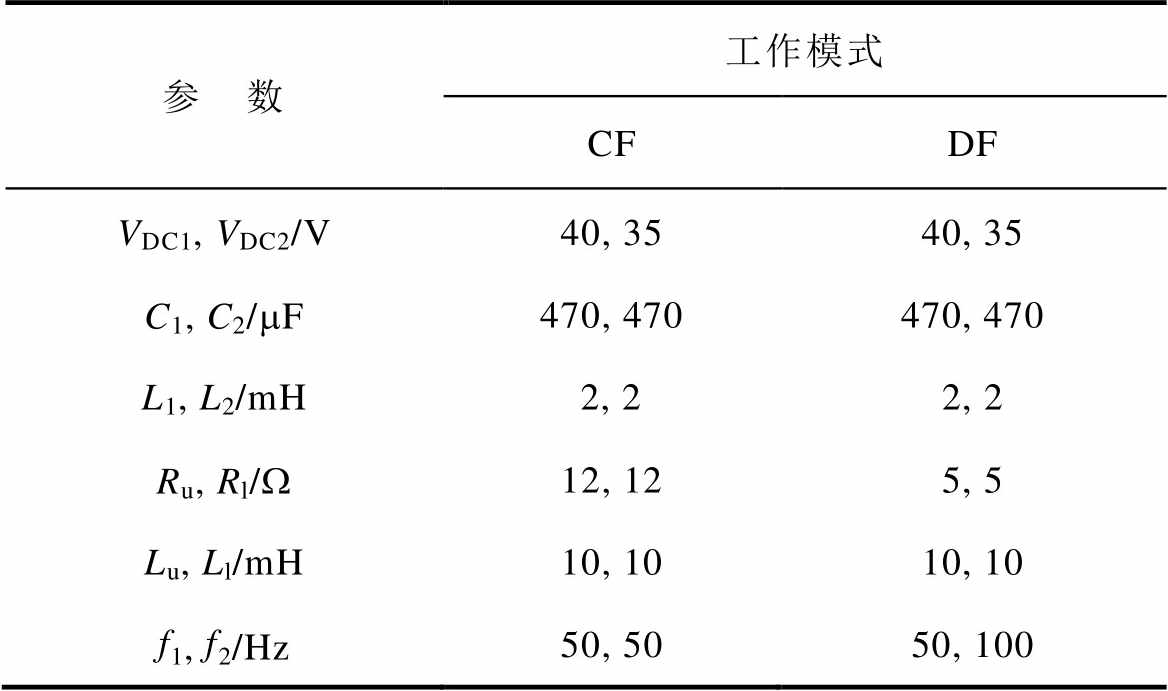
为了验证所提出的拓扑结构和调制方案的可行性,在实验室中构建了一个低功耗SSI-DO-T-TLI样机。该样机由控制板、驱动电路和主电路组成,如图16所示。控制板包括FPGA EP4CE115F23I7N。硬件的其他实验参数见表3,表中Ru、Lu和Rl、Ll分别为上输出和下输出的星形负载单相电阻和电感参数。值得注意的是,由于本文还讨论了两个直流电源具有不同电压的情况,因此在实验中主要验证了拓扑在两个直流电源具有不同电压情况下的可行性。接下来,分别研究了SSI-DO-T-TLI的同频和异频工作模式下的工作情况。

图16 SSI-DO-T-TLI样机
Fig.16 SSI-DO-T-TLI prototype
表3 实验参数
Tab.3 Experimental parameters
参 数工作模式 CFDF VDC1, VDC2/V40, 3540, 35 C1, C2/mF470, 470470, 470 L1, L2/mH2, 22, 2 Ru, Rl/W12, 125, 5 Lu, Ll/mH10, 1010, 10 f1, f2/Hz50, 5050, 100
根据本文提出的方法求解了调制参数。在同频工作模式下,设置上、下目标输出的线路电压基波幅值分别为100 V和105 V。可以计算出D1的取值范围为 (0, 0.455)。理想情况下,为了增加直流侧电压,D1可以做得无限小。但在实际电路中,由于电路损耗问题,它不能取得太小。同时,为了进行对照试验,保证四组调制参数相同,可以取D1=0.44。本文将D1和D2分别降低5%,取Voffset1和Voffset2,得到调制参数见表4。
表4 调制参数
Tab.4 Modulation parameters

工作模式m1Voffset1m2Voffset2 CF0.635 085 30.056 788 70.666 839 60.082 778 1 DF0.317 542 70.341 394 40.317 542 70.396 394 4
图17a和图17b显示了SPWM方案的输出线电压vAB和vXY的波形,以及它们的区域放大波形和快速傅里叶变换(Fast Fourier Transform, FFT)分析,基波幅值分别约为88 V和93 V。图18a、图18b为上、下输出线电流波形,且为正弦波电流,所有输出电压和电流的频率为50 Hz,与预期相符。
但实验输出与理论理想输出之间存在一定的差异,认为这是由于电感电流和电容电压波动引起的。此外,最后三种调制方案可以明显改善输出波形的谐波含量。虽然电容电压和电感电流波动影响输出谐波含量,但由于使用的电容值足够大,其他三种方案的输出波形相似,所以,它们的输出波形不再赘述,更多地关注电感电流和电容电压的波形。
图19显示了四种调制方案在同频工作模式下的iL1、iL2、uC1和uC2的波形。通过对电感电流和电容电压纹波的分析,可以得出在正弦调制波中注入不同的谐波分量可以降低纹波含量的结论,实验得到的改善结果与预期一致。然而,在理论分析中认为DPWM方案应该没有低频纹波,这与实验不同。分析这是不同调制方案使用了相同的电容和电感,使得其值与它们传输的功率不匹配,这在接下来异频工作模式的实验中得到了验证。

图17 SPWM方案下同频同相和异频工作模式的输出线电压波形
Fig.17 Waveforms of the output line voltage in the in-phase CF and DF operation modes (SPWM)

图18 SPWM方案下同频同相和异频工作模式的输出电流波形
Fig.18 Waveforms of the output line current in the in-phase CF and DF operation modes (SPWM)
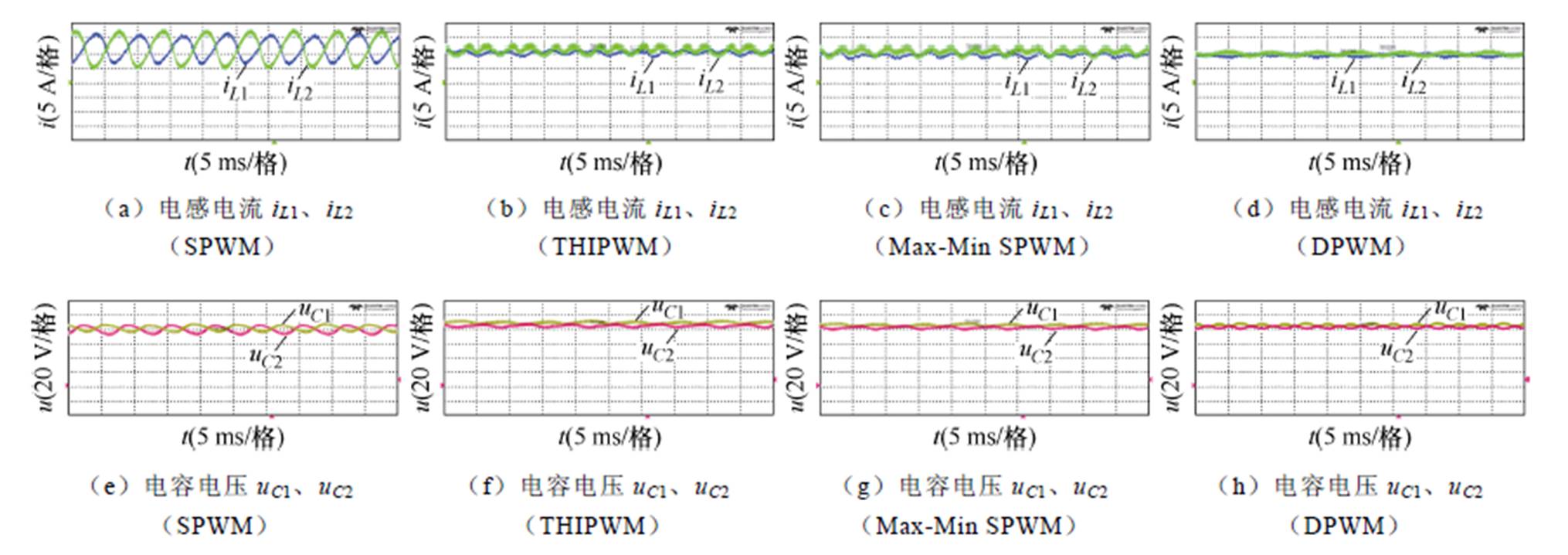
图19 同频同相时,在不同调制方案下,上下电感电流和上下电容电压波形示意图
Fig.19 The current of inductors and the voltage of capacitors in in-phase CF operation mode with different modulation scheme
在异频工作模式下,由于频率不同以及上、下输出相电压的限制,为了保证输出质量,上、下目标输出线电压的基频幅值设置为50 V。可以计算出D1的取值范围为 (0, 0.443)。取D1=0.44,采用与同频工作模式相同的方法可得到表4所示的调制参数。
图17c和图17d显示了SPWM方案的输出线电压vAB和vXY的波形,以及它们的区域放大波形和FFT分析,基本幅值约为50 V。图18c、图18d为上、下输出线电流波形,且为正弦波电流。上、下输出电压、电流频率分别为50 Hz、100 Hz,与预期相符。与同频工作模式相比,异频工作模式的实验输出更接近理论输出。这验证了同频工作方式的实验与理论差异是由电感电流和电容电压波动引起的。与同频工作模式类似,异频工作模式下其他调制的输出波形不再描述。
图20显示了四种调制方式在异频工作模式下的iL1、iL2、uC1和uC2的波形。通过对电感电流和电容电压纹波的分析,也可以得出在正弦调制波中注入不同的谐波分量可以降低纹波含量的结论,实验得到的改善结果与预期一致。
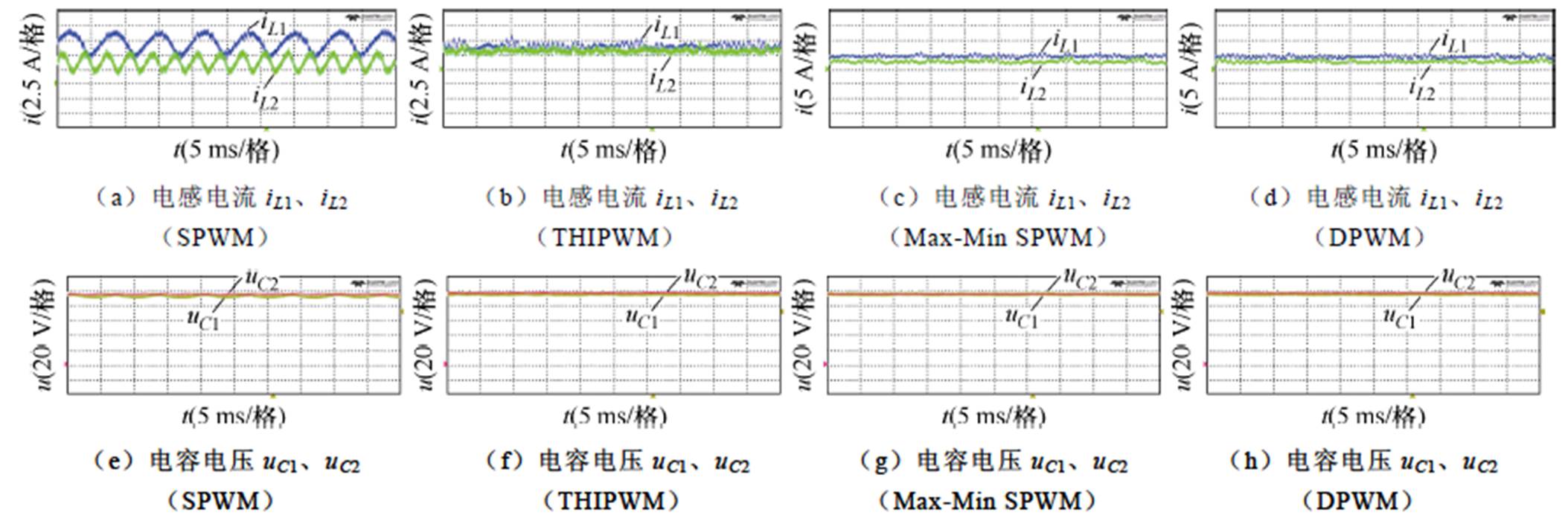
图20 异频时,在不同调制方案下,上下电感电流和上下电容电压波形示意图
Fig.20 The current of inductors and the voltage of capacitors in DF operation mode with different modulation scheme
在图20b~图20d中,可以发现一些意料外的电感电流波动,其波动频率处于开关频率与基频三倍频之间。分析原因为使用的直流电源为非理想电源,在输出电流较低的情况下会出现输出波动,这可以从同频工作模式下的大输出电流中没有出现这些谐波分量得到证实。
在同频或异频工作模式下,电感电流和电容电压的纹波含量都根据第3节中的K值而变化。将四种调制方案从纹波含量最高到最低排序,可以得到SPWM、THIPWM、Max-Min PWM和DPWM的顺序,与预期一致。此外,在实验中证实,由于每个电容的电压都是由一个SSI结构控制的,因此任何调制方案都可以保持上下电容器的电压。如果电容器能正常充放电,电容器的电压就不会失去稳定。
实验总体情况与预期结果一致。
本文提出了一种新颖的SSI-DO-T-TLI拓扑,该拓扑采用同相层叠载波的SPWM方案,解决了原有拓扑对直流输入电压高幅值的要求。此外,由于采用SSI结构,该方案也大大降低了对中性点电压平衡控制的要求。SSI-DO-T-TLI可输出两组三相交流电压,幅值、相位、频率均可调。在分析电感纹波电流产生机理的基础上,提出了减小电感纹波电流和电容纹波电压的思路。在此基础上,讨论了THIPWM、Max-Min PWM和DPWM方案的调制参数,对低频纹波分量较大的情况有一定的参考价值。与原SPWM方案相比,三种调制方案的低频纹波含量均显著降低。最后,对SSI-DO-T-TLI的四种调制方案在同频和异频工作模式下进行了实验,实验结果验证了该拓扑的可行性以及不同调制方案对低频纹波含量的不同影响。
参考文献
[1] 郭立东, 雷鸣宇, 杨子龙, 等. 光储微网系统多目标协调控制策略[J]. 电工技术学报, 2021, 36(19): 4121-4131.
Guo Lidong, Lei Mingyu, Yang Zilong, et al. Multi- objective coordinated control strategy for photo- voltaic and energy-storage microgrid system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4121-4131.
[2] 陆秋瑜, 马千里, 魏韡, 等. 基于置信容量的风场配套储能容量优化配置[J]. 电工技术学报, 2022, 37(23): 5901-5910.
Lu Qiuyu, Ma Qianli, Wei Wei, et al. Optimal configuration of energy storage parameters based on confidence capacity of wind farms[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5901- 5910.
[3] 李建林, 梅生伟, 李军徽. 新型储能系统应用关键技术专题特约主编寄语[J]. 电工技术学报, 2022, 37(23): 5899-5900.
Li Jianlin, Mei Shengwei, Li Junhui. Message from special editor-in-chief on key technologies of new energy storage system application[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5899- 5900.
[4] Peng Weiwen, Chen Qianling, Manandhar U, et al. Event-triggered model predictive control for the inverter of a grid-connected microgrid with a battery- supercapacitor HESS[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(6): 5540-5552.
[5] 韩雪, 贺荣栋, 凌志斌. 部分接入电池储能系统的模块化多电平换流器控制方法[J]. 电力系统自动化, 2024, 48(1): 100-108.
Han Xue, He Rongdong, Ling Zhibin. Control method of modular multilevel converter with partly integrated battery energy storage system[J]. Automation of Electric Power Systems, 2024, 48(1): 100-108.
[6] 时瑞廷, 杨贺钧, 马英浩, 等. 计及峰谷平滑效益的需求响应和电池储能系统调度联合优化策略[J]. 电力自动化设备, 2023, 43(8): 49-55.
Shi Ruiting, Yang Hejun, Ma Yinghao, et al. Joint optimization strategy of demand response and battery energy storage system dispatch considering peak- valley smoothing benefit[J]. Electric Power Auto- mation Equipment, 2023, 43(8): 49-55.
[7] 孙毅, 李飞, 胡亚杰, 等. 计及条件风险价值和综合需求响应的产消者能量共享激励策略[J]. 电工技术学报, 2023, 38(9): 2448-2463.
Sun Yi, Li Fei, Hu Yajie, et al. Energy sharing incentive strategy of prosumers considering con- ditional value at risk and integrated demand response[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2448-2463.
[8] 胡文华, 文森林, 彭修纲, 等. 一种新型多电平逆变器拓扑及调制策略研究[J]. 太阳能学报, 2024, 45(7): 486-493.
Hu Wenhua, Wen Senlin, Peng Xiugang, et al. Research on a novel multilevel inverter topology and modulation strategy[J]. Acta Energiae Solaris Sinica, 2024, 45(7): 486-493.
[9] 于晶荣, 张刚, 邱均成, 等. 一种级联H桥多电平逆变器故障诊断方法[J]. 电机与控制学报, 2023, 27(9): 119-125.
Yu Jingrong, Zhang Gang, Qiu Juncheng, et al. Fault diagnosis method for cascaded H-bridge multilevel inverter[J]. Electric Machines and Control, 2023, 27(9): 119-125.
[10] Bastos R R, Santos de Souza T, de Carvalho M M, et al. Assessment of a nine-phase induction motor drive for metal industry applications[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 7217-7226.
[11] Srivastava A, Seshadrinath J. A new nine-level highly efficient boost inverter for transformerless grid- connected PV application[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(3): 2730-2741.
[12] Zhao Tao, Chen Daolian. A power adaptive control strategy for further extending the operation range of single-phase cascaded H-bridge multilevel PV inverter[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(2): 1509-1520.
[13] 叶满园, 刘文芳, 喻生铭, 等. 新型八开关五电平逆变器及功率均衡调制策略[J]. 电机与控制学报, 2023, 27(5): 138-148.
Ye Manyuan, Liu Wenfang, Yu Shengming, et al. Novel eight-switch five-level inverter and power balance modulation strategy[J]. Electric Machines and Control, 2023, 27(5): 138-148.
[14] Biswas S P, Shamim Anower M, Haq S, et al. A new level shifted carrier based PWM technique for a 5-level multilevel inverter used in induction motor drives[C]//2021 IEEE Industry Applications Society Annual Meeting (IAS), Vancouver, BC, Canada, 2021: 1-6.
[15] 王晓标, 肖华平, 牛晨晖, 等. 高可靠三电平逆变器构造方法研究[J]. 中国电机工程学报, 2023, 43(10): 3928-3937.
Wang Xiaobiao, Xiao Huaping, Niu Chenhui, et al. Research on highly reliable three-level inverters construction principles[J]. Proceedings of the CSEE, 2023, 43(10): 3928-3937.
[16] Meynard T A, Foch H. Multi-level conversion: high voltage choppers and voltage-source inverters[C]// PESC '92 Record. 23rd Annual IEEE Power Elec- tronics Specialists Conference, Toledo, Spain, 1992: 397-403.
[17] 叶满园, 喻生铭, 刘文芳, 等. 不对称级联九电平逆变器线性功率均衡控制策略[J]. 电工技术学报, 2024, 39(14): 4495-4507.
Ye Manyuan, Yu Shengming, Liu Wenfang, et al. Linear power balance strategy for asymmetric cascaded H-bridge nine-level inverter[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(14): 4495-4507.
[18] 申永鹏, 王帅兵, 梁伟华, 等. T型三电平逆变器合成脉冲宽度调制相电流重构策略[J]. 电工技术学报, 2022, 37(20): 5302-5312.
Shen Yongpeng, Wang Shuaibing, Liang Weihua, et al. T-type three-level inverter composite pulse width modulation phase current reconstruction strategy[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5302-5312.
[19] Jayan V, Ghias A M Y M. Operational limits of a cascaded dual-output multilevel converter using model predictive control[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 7026-7037.
[20] 王贵峰, 王建飞. 基于单桥臂独立模型预测电流控制的新型十五开关三电平双输出逆变器研究[J/OL]. 电源学报, 1-12 [2023-11-16]. http://kns.cnki.net/ kcms/detail/12.1420.TM.20231130.0856.002.html.
Wang Guifeng, Wang Jianfei. Novel fifteen-switch three-level dual-output inverter based on single-leg independent model predictive current control[J/OL]. Journal of Power Supply, 1-12 [2023-11-16]. http:// kns.cnki.net/kcms/detail/12.1420.TM.20231130.0856.002.html.
[21] Do D T, Cha H. High-reliability and reduced switch count single-phase dual-output current source inverter using switching-cell structure[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6513-6524.
[22] Kominami T, Fujimoto Y. A novel nine-switch inverter for independent control of two three-phase loads[C]//2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 2007: 2346-2350.
[23] 赵牧天, 葛琼璇, 朱进权, 等. 高速磁浮背靠背三电平ANPC变流器中点电压偏移机理与协同控制策略[J]. 中国电机工程学报, 2024, 44(5): 1932-1947, I0023.
Zhao Mutian, Ge Qiongxuan, Zhu Jinquan, et al. Neutral point voltage offset mechanism and coopera- tive control strategy of high-speed maglev back- to-back three-level ANPC converter[J]. Proceedings of the CSEE, 2024, 44(5): 1932-1947, I0023.
[24] Dong Zhiqiang, Wang Chenchen, Cui Kai, et al. Neutral-point voltage-balancing strategies of NPC- inverter fed dual three-phase AC motors[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3181-3191.
[25] Azizi M, Aznavi S, Fajri P, et al. Space vector modulation scheme for dual-output four-leg inverter[C]// 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 2020: 2937-2943.
[26] Dwivedi D, Roy I, Chinmaya K A. Investigation of three-level dual output T-type NPC for EV appli- cation[C]//2022 International Conference on Smart Energy Systems and Technologies (SEST), Eindhoven, Netherlands, 2022: 1-6.
[27] 王海超, 范学鑫, 杨国润, 等. 超级电容充电三电平双输出直流变换器设计[J]. 高电压技术, 2020, 46(9): 3268-3274.
Wang Haichao, Fan Xuexin, Yang Guorun, et al. Design of three-level dual-output DC-DC converter for ultracapacitor applications[J]. High Voltage Engineering, 2020, 46(9): 3268-3274.
[28] Wang Rutian, Ai Lan, Liu Chuang. A novel three- phase dual-output neutral-point-clamped three-level inverter[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7576-7586.
[29] Wang Rutian, Yuan Shuai, Liu Chuang, et al. A three- phase dual-output T-type three-level converter[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 1844-1859.
[30] 胡雪峰, 汪慧茹, 徐晗, 等. 一种单相非隔离集成升压光伏逆变器[J]. 中国电机工程学报, 2023, 43(16): 6429-6440.
Hu Xuefeng, Wang Huiru, Xu Han, et al. A single- phase non-isolated integrated step-up photovoltaic inverter[J]. Proceedings of the CSEE, 2023, 43(16): 6429-6440.
[31] Peng Fangzheng. Z-source inverter[J]. IEEE Transa- ctions on Industry Applications, 2003, 39(2): 504-510.
[32] Abdelhakim A, Mattavelli P, Spiazzi G. Three-phase split-source inverter (SSI): analysis and modulation[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7451-7461.
[33] Dabour S M, Aboushady A A, Gowaid I A, et al. Analysis and control of simplified dual-output single- phase split-source Boost inverters[C]//2022 23rd International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 2022: 1-5.
Abstract Multi-level inverters perform better than two-level inverters. Using dual output inverters to reduce the number of switching tubes is a trend in developing power electronic topologies for cost reasons. The conventional voltage-source inverter is a buck topology. In many application scenarios, a DC boost topology is often added before the inverter topology to meet the high-magnitude requirements of the output-side voltage. This paper proposed a dual output T-type three-level inverter topology based on a split-source inverter (SSI) using SSI topology to improve the dual output T-type three-level converter.
The SSI topology can reduce the high-magnitude requirements for the DC supply voltage and hardware cost, improving power efficiency. The hardware cost was saved by multiplexing the switching tubes in the inverter and DC boost links. The DC supply voltage passed through the SSI topology and charged the capacitor on the DC side of the inverter link. Thus, the DC side voltage of the inverter link was high, i.e., the high-magnitude requirement of the DC supply voltage was reduced. The energy transfer path was shortened, and the power efficiency was improved.
A separate SSI topology controls the capacitor voltage. The charging of each DC-side capacitor in inverter was completed by a separate SSI topology, and the capacitor charge or discharge duty cycle was controlled by the modulation process of the inverter. If the capacitor is charged and discharged normally, even in the case of open-loop control, the capacitor voltage will not lose stability, thus simplifying the control of the neutral-point potential balance.
A method for determining the range of modulation parameters based on the input and output parameters of the operating parameters was proposed. The boost multiple of the DC link is related to the modulation parameters, and the input parameters are related to the capacitor voltages and modulation parameters of the inverter link. Therefore, combined with the constraint relationship, this paper proposed a method to determine the range of modulation parameters. The range of modulation parameters was discussed under in-phase common frequency (CF), non-in-phase CF, and different frequency (DF) operation modes.
This paper discussed the fluctuation of the inductor current under the sinusoidal pulse width modulation (SPWM) scheme and the harmonic injection SPWM scheme with different harmonics in the sinusoidal modulation wave. Firstly, the harmonic component of the inductor current under the SPWM scheme was discussed. Then, the harmonicamplitude in the third harmonic injection PWM, the Max-Min PWM scheme in the space-vector pulse width carrier modulation, and the DC offset of the discontinuous PWM scheme in the SVPWM were discussed.
Finally, the experimental prototype was built. The experiments were carried out in CF and DF operation modes, which verifies the proposed topology, the modulation parameter selection method, and different modulation schemes on the low-frequency ripple content under the same hardware conditions.
keywords:Dual-output, three level, split source, inverter, harmonic injection
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.232069
国家自然科学基金资助项目(52277170)。
收稿日期 2023-12-11
改稿日期2024-01-23
王汝田 男,1979年生,博士,教授,博士生导师,研究方向为电力电子技术在电力质量控制和输配电系统中的应用,以及新能源发电系统的运行和控制。E-mail: wrtmail@163.com(通信作者)
王 浩 男,1998年生,硕士研究生,研究方向为电力电子技术在功率变换中的应用。E-mail: wang_hao_21@163.com
(编辑 郭丽军)