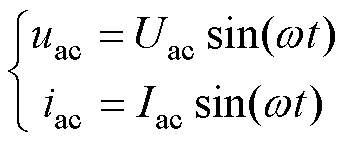 (1)
(1)
摘要 该文提出一种对称半桥功率解耦拓扑。该解耦拓扑串联在变换器直流侧可以起到补偿二倍频脉动电压、减小电感值、降低成本和减小体积的作用。通过对两个解耦电感进行耦合磁集成,进一步减小电路元件和解耦电感的值,使得减小电感值的效果更加显著。该功率解耦拓扑的直流侧输出电流间接闭环控制方法直接对直流侧电流进行采样,无需外加传感器,不需要复杂调节器和计算,在实际应用中更为灵活。最后搭建了基于对称半桥功率解耦拓扑的单相电流型PWM整流器仿真与实验平台,验证了所提拓扑的可行性。
关键词:单相电流型PWM整流器 二倍频纹波脉动 功率解耦技术 磁集成 输出电流间接闭环控制
随着电能在人们日常生活中不断丰富的使用形式,AC-DC变换器已经广泛存在于智能电网的“源-网-荷-储”全过程中[1-7]。而在中小功率系统中,单相脉冲宽度调制(Pulse Width Modulation, PWM)变换器的应用场景更加广阔[8-11],在可再生能源并网发电、机车牵引系统、新能源汽车充电系统、不间断电源和储能等领域[12-17]得到广泛研究。
单相PWM变换器根据不同输出特性,可以分为单相电压型PWM变换器和单相电流型PWM变换器。当前限制单相电流型PWM变换器应用的最大难题是直流侧需要串联大电感来吸收固有的二倍频脉动功率,这使其在体积、成本方面远不如电压型变换器[18-19]。如果能够设法降低单相电流型PWM变换器直流侧电感的取值,使电流型变换器实现轻量化,则单相电流型PWM变换器将会获得更加广泛应用。
目前对单相电流型PWM变换器二倍频脉动抑制的研究分为两种:一种是从调制策略上改进;另一种是从电路拓扑结构上改进,即功率解耦技术。第一种方法通常是在正弦脉宽调制(Sine Pulse Width Modulation, SPWM)策略的基础上进行改进。如文献[20]提出了一种基于调制波修正的非线性调制方法,通过对传统SPWM方法中的调制波进行修正,有效解决了电流型逆变器输出电流中3次谐波较高的问题,减小了直流侧电感值。文献[21]提出一种基于变幅值载波的非线性调制策略,载波幅值根据直流侧电流脉动进行修正,抑制了网侧3次谐波。但非线性调制需要采集多个传感器信号进行复杂的在线计算,对计算精度和速率的要求比较高。同时直流侧电感电流为脉动电流,谐波损耗会比较大,而功率解耦技术将直流侧的二倍频脉动功率转移到外加电路中,从电路拓扑上实现有功功率与无功功率的解耦,抑制直流侧电流纹波脉动,更符合理想电流源的特性。
功率解耦技术可以分为无源功率解耦技术和有源功率解耦技术。无源功率解耦技术[22]指的是在直流侧增加LC滤波器,但由于二倍频纹波的频率很低,体积和质量大的缺点不可避免。有源解耦方法通过一个额外的有源开关电路将纹波功率转移到另一个体积较小的储能元件上,可以消除上述无源解耦方法的缺点。有源功率解耦技术其实不只用于解决单相电流型PWM变换器的二倍频脉动功率抑制问题,在单相功率因数校正电路[23]、单相电压型PWM变换器的电容电压纹波抑制领域中[24]也应用广泛。通过解耦电路来取代电解电容,吸收电路中的二倍频脉动功率,实现电路的无电解电容化,可以有效提高电路的寿命与功率密度。两者都是通过解耦电路来吸收和释放电路中的二倍频脉动功率的,所以有诸多相通之处。因电压型PWM变换器与电流型PWM变换器互为对偶结构,了解电压型PWM变换器功率解耦方案,对解决电流型PWM变换器二倍频脉动抑制问题则很有帮助。
国内外学者将这些研究分类整理,归纳出五种基本功率解耦拓扑,分别为全桥、Buck、Boost、Buck-Boost及对称半桥分裂电容电路[25-26]。由于Buck、Boost、Buck-Boost基本解耦拓扑结构上的限制,进行对偶变换后不能应用在单相电流型变换器中,而将全桥电路进行对偶变换后作为单相电流型变换器功率解耦电路的研究比较热门。文献[27-29]将全桥解耦拓扑串联在单相电流型变换器直流侧,通过控制解耦电容Cpd的充放电来吸收电路中的二倍频脉动功率。解耦电路相对于主电路独立控制,可直流侧电感相对减小。
目前从解耦拓扑单元的角度分析,应用于单相电流型PWM变换器的解耦拓扑单元只有全桥解耦电路一种。本文以现有五类解耦拓扑单元为基础,提出了一种应用于单相电流型PWM变换器的对称半桥解耦拓扑,实现了电感、体积和质量的减小。所提拓扑结构简洁,解耦电感磁集成后电感元件数与简化的全桥独立解耦拓扑中的元件数相同。调制和控制方式简单,采用基于直流侧输出电流间接闭环的控制策略,引入直流侧输出电流信号,无需外加传感器和复杂计算。经对基于对称半桥功率解耦拓扑的单相电流型PWM整流器仿真和实验验证了该方案的可行性。
对于单相电流型PWM变换器,当功率因数为1时,输入侧交流电压uac和电流iac的表达式分别为
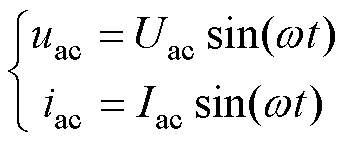 (1)
(1)
式中,Uac和Iac分别为交流电压和交流电流的幅值;w 为交流电压角频率。
此时交流侧功率pac为
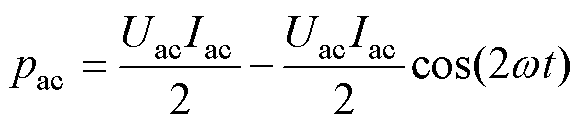 (2)
(2)
直流侧功率Pdc为
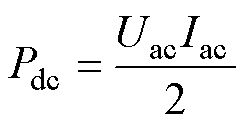 (3)
(3)
从式(2)中可以看出,不管是逆变器还是整流器,其电路中都会存在二倍频的脉动功率,表达式为
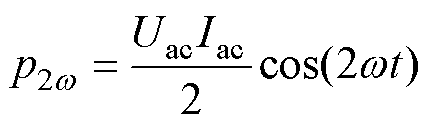 (4)
(4)
该脉动功率由单相电流型PWM变换器的特性决定,不会因为控制策略的不同而消失。
本文所提功率解耦拓扑如图1所示。图1中,uac为交流电源,Lac和Cac为交流侧滤波元件,Cpd为解耦电路电容,L1和L2为解耦电路电感,Rload为负载。该解耦拓扑适用于单相电流型变换器,串联在电路的直流侧代替原来大电感来吸收电路中的二倍频脉动功率。通过增大解耦电路电感电流脉动的方式,使得在吸收相同的二倍频脉动能量的同时可以降低电感取值。
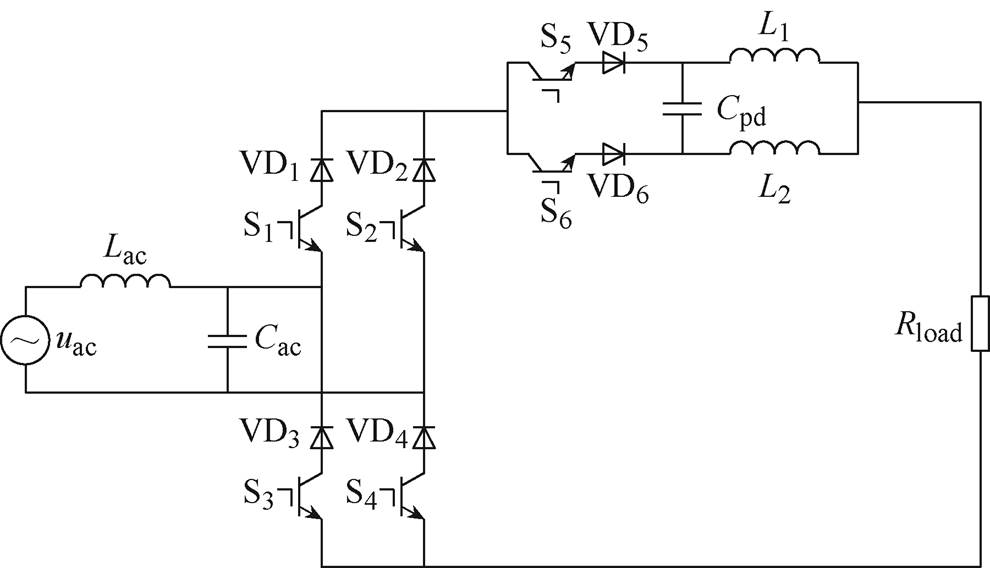
图1 基于对称半桥功率解耦拓扑单相电流型PWM整流器
Fig.1 A single-phase current-source PWM rectifier based on symmetrical half-bridge power decoupling topology
与现有的全桥独立功率解耦拓扑相比,该电路减少了2个开关和2个二极管;与简化的全桥独立解耦拓扑相比,如果同样采用逆阻型IGBT,省略与开关器件串联的二极管,那么该电路减少了2个二极管,只增加了一个电感。经磁集成后,电感元件数与简化的全桥独立解耦拓扑的元件数相同,但调制和控制方式更简单。
对称半桥功率解耦拓扑与单相电流型PWM变换器主电路工作模态独立,主电路工作模态在这里不再赘述。本文所提功率解耦拓扑共有四种工作模态对应的电路状态,如图2所示。图2中,idc为直流侧总电流,iL1和iL2分别为流经电感L1和L2的电流,uCpd为电容Cpd两端电压。该拓扑实质上为“双Buck”电路,具体的模态分析如下:
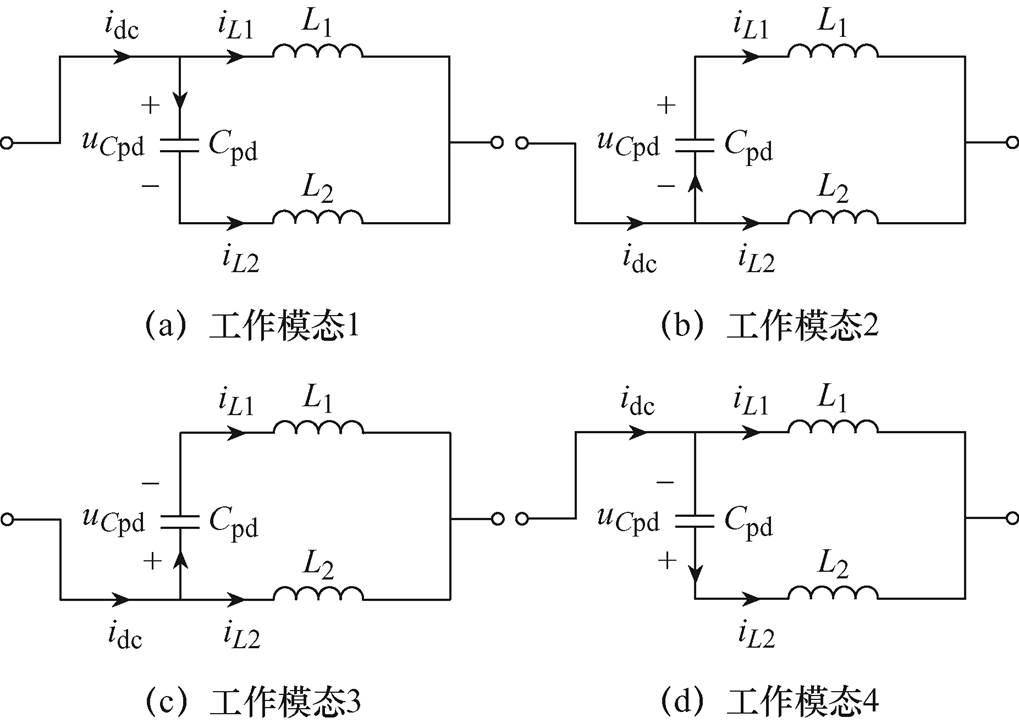
图2 对称半桥功率解耦拓扑工作模态
Fig.2 The operating mode of symmetrical half-bridge power decoupling topology
(1)工作模式1:该模态对应的电路状态如图2a所示。此时S5、VD5导通,而S6、VD6关断,主电路对解耦拓扑电容Cpd充电。
(2)工作模式2:该模态对应的电路状态如图2b所示。此时S6、VD6导通,而S5、VD5关断,解耦拓扑电容Cpd储存的能量为电感L1充电。
(3)工作模式3:该模态对应的电路状态如图2c所示。此时S6、VD6导通,而S5、VD5关断,主电路对解耦拓扑电容Cpd反向充电。
(4)工作模式4:该模态对应的电路状态如图2d所示。此时S5、VD5导通,而S6、VD6关断,解耦拓扑电容Cpd储存的能量为电感L2充电。
工作模式1和2组成一个“Buck电路”,工作模式3和4组成一个反向的“Buck电路”。设d为开关S5占空比,对工作模式1和2中的解耦拓扑电容列出安秒平衡表达式为
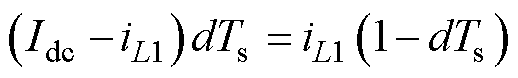 (5)
(5)
可以推导出解耦拓扑电感瞬时电流iL1、iL2与直流侧电流的关系式分别为
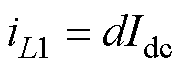 (6)
(6)
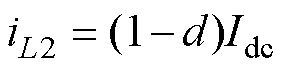 (7)
(7)
为使解耦电感能够吸收二倍频脉动功率,其上电流需带有工频的脉动分量,而两电感又分别承担一半的输出电流。那么解耦电路中两解耦电感的电流iL1与iL2的表达式分别为
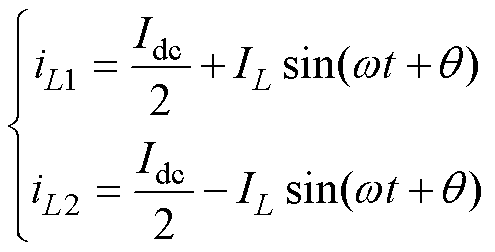 (8)
(8)
式中,Idc为直流侧输出电流平均值;IL为解耦拓扑电感电流脉动幅值。求导可得两解耦电感的电压波形uL1与uL2分别为
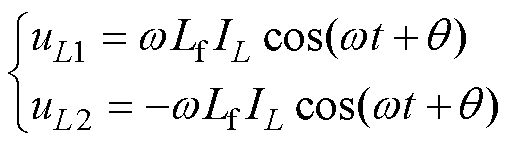 (9)
(9)
式中,Lf为解耦电路中两个解耦电感的数值。结合图3所示解耦等效电路,当开关管S5导通时,解耦拓扑两端电压为电感L1两端电压;当开关管S6导通时,解耦拓扑两端电压为电感L2两端电压。
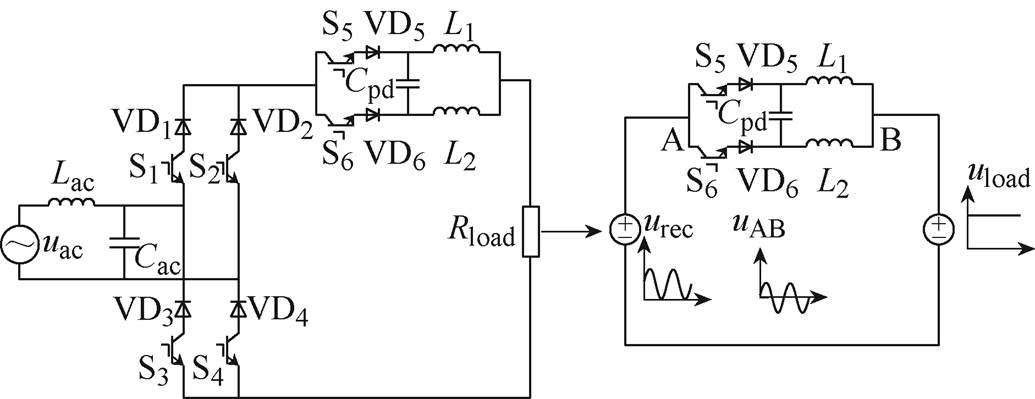
图3 解耦等效电路
Fig.3 Equivalent circuit diagram for decoupling circuit
将式(6)和式(7)代入式(8)可得两开关的占空比表达式为
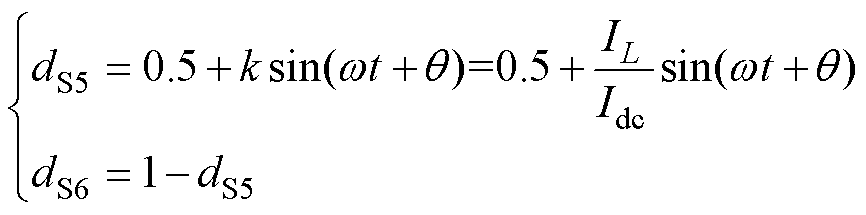 (10)
(10)
式中,dS5为开关管S5占空比;dS6为开关管S6占空比。可以得到解耦拓扑两端电压uAB表达式为
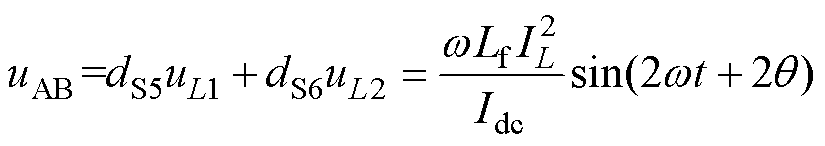 (11)
(11)
忽略交流侧电感电容功率以及开关损耗,Idc为恒定直流,那么整流侧电压urec类似为一个馒头波,即
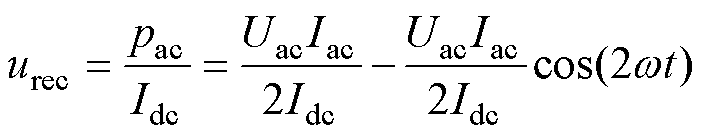 (12)
(12)
使解耦拓扑两端电压uAB与整流侧电压urec的交流分量相等,表达式为
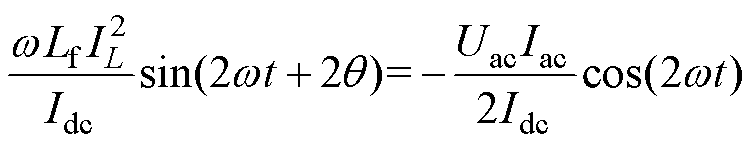 (13)
(13)
可以得到解耦拓扑电感电流相位与幅值分别为
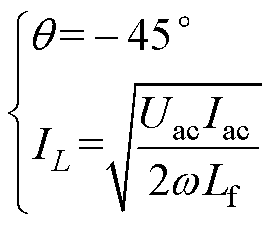 (14)
(14)
可以看出,两电感电流波形的相位与电网相差45°,将式(14)代入式(8)就可以得到解耦电感电流的给定表达式。可以推导出解耦拓扑完全吸收二倍频脉动功率所需电感值为
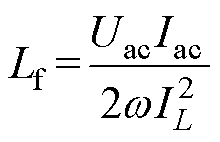 (15)
(15)
由式(15)可知,解耦拓扑所需电感值与输入功率以及电感脉动电流幅值有关系。解耦电感电流脉动幅值越大,所需解耦电感值越小。
解耦拓扑两电感流过的电流波形如图4所示,从吸收和释放脉动功率能量的角度可以将一个工频周期分成四部分。
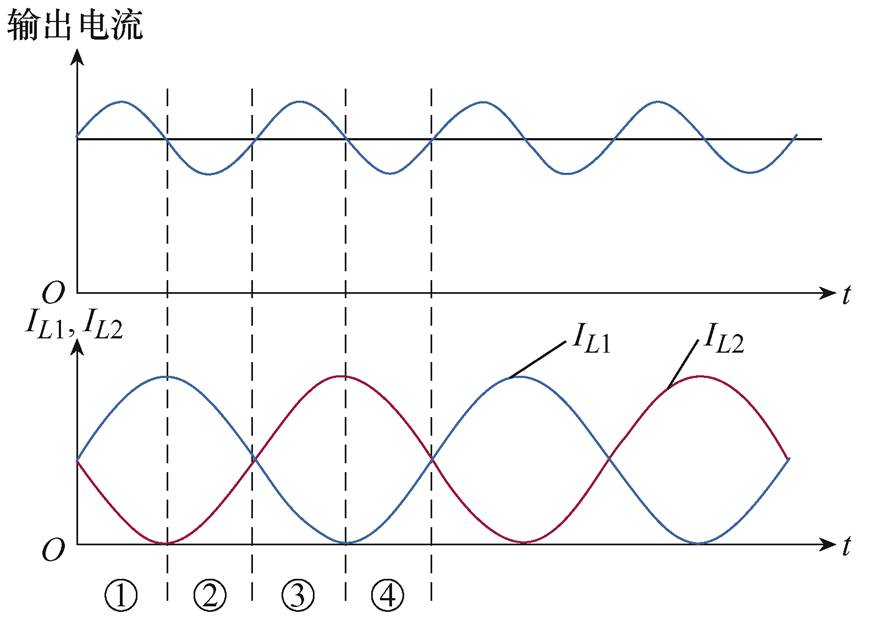
图4 吸收和释放脉动能量示意图
Fig.4 Diagram of absorbing and releasing pulsating energy
电路工作在①区域时,电感L1充电、电感L2放电,由于L1吸收能量大于L2释放的能量,解耦拓扑从直流侧吸收脉动功率。电路工作在②区域时,电感L1放电、电感L2充电,由于L1释放能量大于L2吸收的能量,解耦拓扑从直流侧释放脉动功率,从而达到减小电流纹波和降低电感值的作用。③、④区域同理。
设δ为直流侧输出电流纹波系数,则直流侧输出电流io表达式为
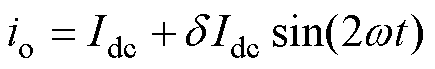 (16)
(16)
大电感所产生的两端电压为
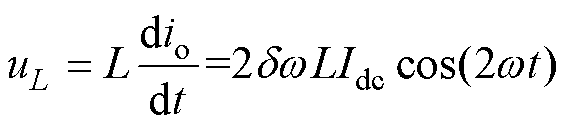 (17)
(17)
令式(11)与式(17)两电压相等,则可得到解耦电路拓扑等效电感值为
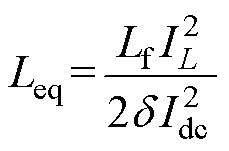 (18)
(18)
则可得解耦电路拓扑等效电感与实际解耦电感的比值同解耦电路脉动占空比k和输出电流纹波系数δ的三维图形如图5所示。可知解耦电路拓扑等效电感与实际解耦电感的比值随解耦电路脉动占空比k的增大而增大,随输出电流纹波d 的减小而减小。当k=0.5,d =1%时,解耦电路拓扑等效电感与实际解耦电感的比值为12.5。
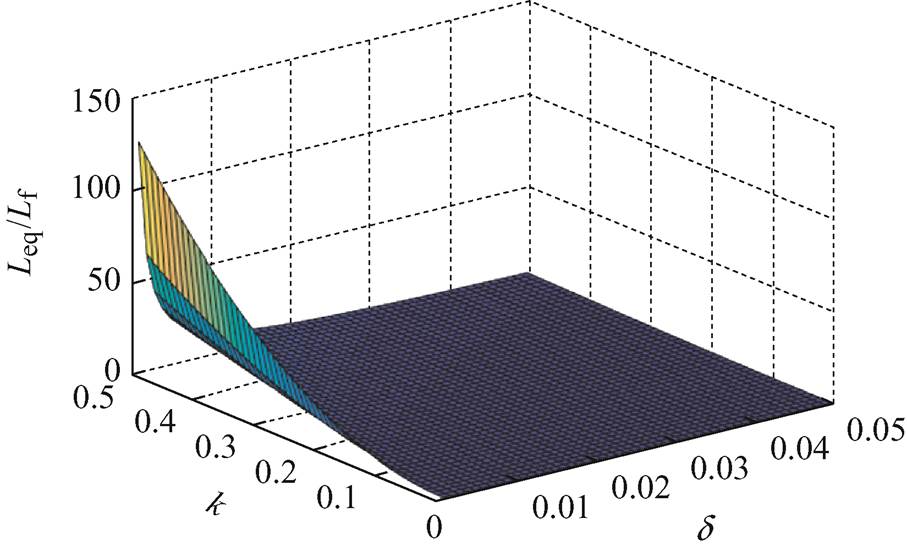
图5 解耦电路拓扑等效电感与实际解耦电感的比值
Fig.5 The ratio of the equivalent inductance of decoupling circuit topology to the actual decoupling inductance
主电路参数设计与传统单相电流型变换器相同,这里不再列写,只介绍本文所提对称半桥解耦电路的参数设计。
对于解耦电路电感值的选择,可以由式(18)选取能够完全吸收二倍频纹波功率的电感,也可以根据系统输出电路纹波要求依据式(15)选取电感值及脉动幅值。而对于解耦电路的滤波电容Cpd的参数设计,根据GB/T 14549-93《电能质量 公用电网谐波》对前20次谐波都有具体的数值要求,综合考虑效果与成本等因素后,为减少Cpd与解耦电感谐振次纹波对电路造成的影响,要使Cpd与解耦电感的谐振频率大于电网频率的21倍[30]。设fw 为电网频率,则电容Cpd的最大值Cpdmax为
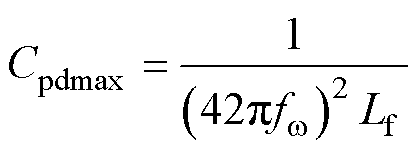 (19)
(19)
为了进一步减少解耦电路的元件数量、体积和质量,利用两电感的电感电流脉动值相反的特点,对对称半桥功率解耦电路的两个解耦电感进行磁集成。电感耦合方式为直流磁通相互抵消,交流磁通相互增强的反向耦合方式。利用耦合集成电感的互感,使得每个解耦等效电感为各自自感与互感之和,不仅减少了电路元件个数,同时也减小了每个解耦电感值,使得直流侧电感值降低,电路体积、质量减小的效果更加显著。耦合电感结构如图6所示,电感L1、L2的电流为相同的直流量叠加可以正负抵消的二倍频脉动量。使L1的电流从同名端流入,L2的电流从同名端流出。
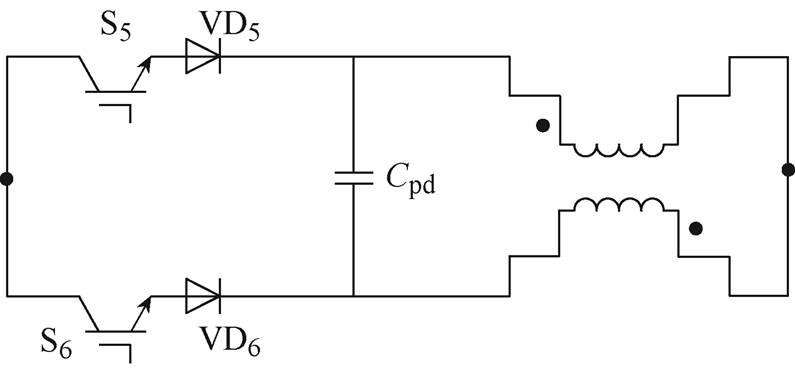
图6 耦合电感结构
Fig.6 Coupled inductor structure diagram
可得流入耦合电感电流i1与i2的关系式为
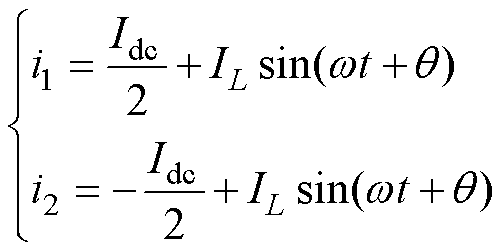 (20)
(20)
那么耦合电感的电压为
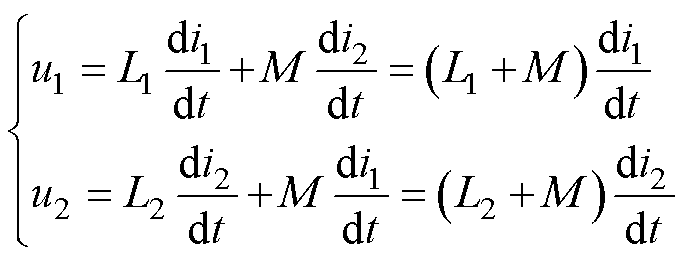 (21)
(21)
经过耦合磁集成后,不仅磁心少了一个,而且耦合电感的互感值也可以起到原电感值的作用,每个解耦等效电感为各自自感与互感之和,使得电感值可以进一步减小。
对称半桥解耦拓扑与单相电流型PWM整流器主电路独立控制,主电路采用传统的直流侧输出电流外环和交流侧输入电流内环的双闭环控制。
传统解耦电路的直接闭环控制都需要外加传感器来测量解耦拓扑元件的电压或电流值且通常需要大量计算,存在成本过高、控制复杂等缺点。本文提出一种基于直流侧输出电流间接闭环的控制策略。此方法引入直流侧输出电流信号,直接利用主电路的输出电流采样值即可,无需外加传感器,不需要复杂计算。直流侧输出电流间接闭环控制方式如图7所示。
当负载功率变小时,解耦拓扑需要吸收的二倍频脉动功率也变小,如果要达到良好的功率解耦效果,脉动幅值也应该减小,从而使得电感电流的波动幅值减小,解耦拓扑需要吸收的二倍频脉动功率也就减小。当负载功率变小时,输出电流会突增,引起PI调节器输出减小,使得脉动幅值也减小,解耦拓扑能够跟随负载变化改变所吸收的脉动功率值。
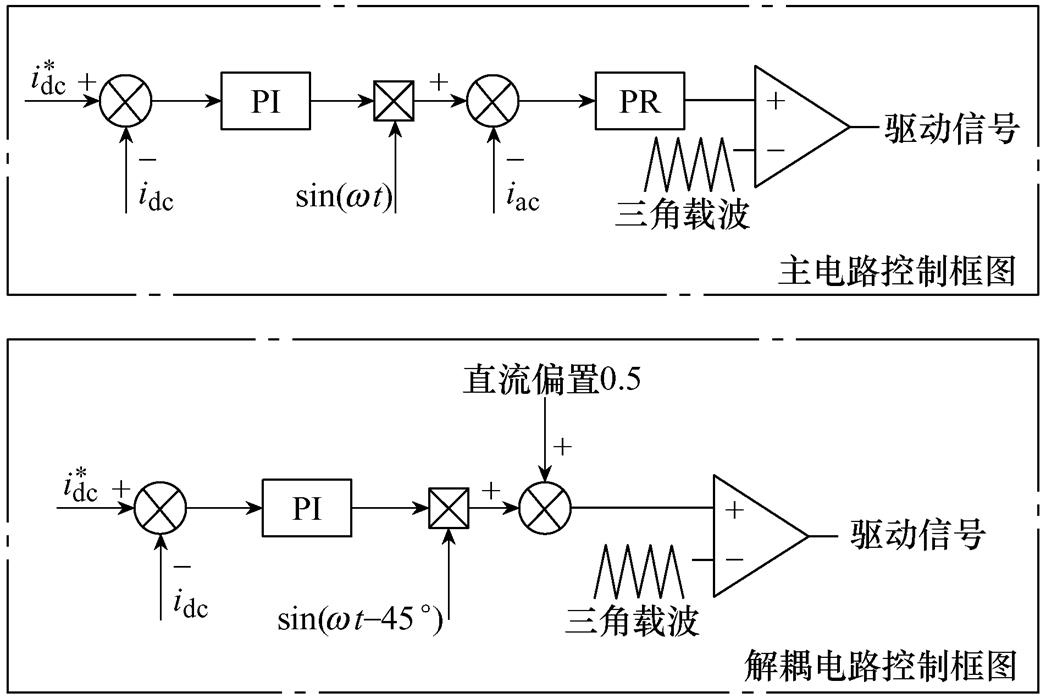
图7 本文所提环闭环控制策略
Fig.7 The proposed closed-loop control strategy
传统单相电流型整流器直流侧电感表示为
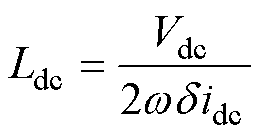 (22)
(22)
由式(22)可知,当直流侧电压一定时,所需电感值与系统功率成反比。直流侧电流越小、功率越小、所需电感值越大。所以从实验的角度,小功率实验更能显示出传统单相电流型整流器与基于对称半桥解耦拓扑单相电流型整流器的对比效果。而由式(20)可知,本文所提功率解耦拓扑在大功率(大直流侧电感电流)工作情况下,电感降低效果更显著,所以完成小功率条件下的仿真分析和对比实验就可以验证对称半桥功率解耦拓扑对直流侧电流二倍频脉动的抑制能力。为验证对称半桥解耦拓扑的解耦能力,进行传统单相电流型PWM整流器和基于对称半桥功率解耦拓扑的单相电流型PWM整流器的对比仿真。
传统单相电流型整流器采用75 mH电感仿真参数见表1,仿真波形如图8所示,输出电流值能够稳定在15 A并带有幅值为0.24 A的二倍频脉动谐波。输入电流波形正弦度良好,功率因数(Power Factor, PF)为0.999,总谐波畸变率(Total Harmonic Distortion, THD)为1.35%,满足相关谐波要求。
表1 传统单相电流型整流器仿真参数
Tab.1 Parameters of simulation of conventional single-phase current-source rectifier

参 数数 值 输入电压(RMS)/VAC 110 输出电流/ADC15 负载电阻/W1 网侧滤波电感Lac/mH2 网侧滤波电容Cac/mF20 解耦电感/mH10 传统电路所用大电感/mH75 开关频率/kHz20
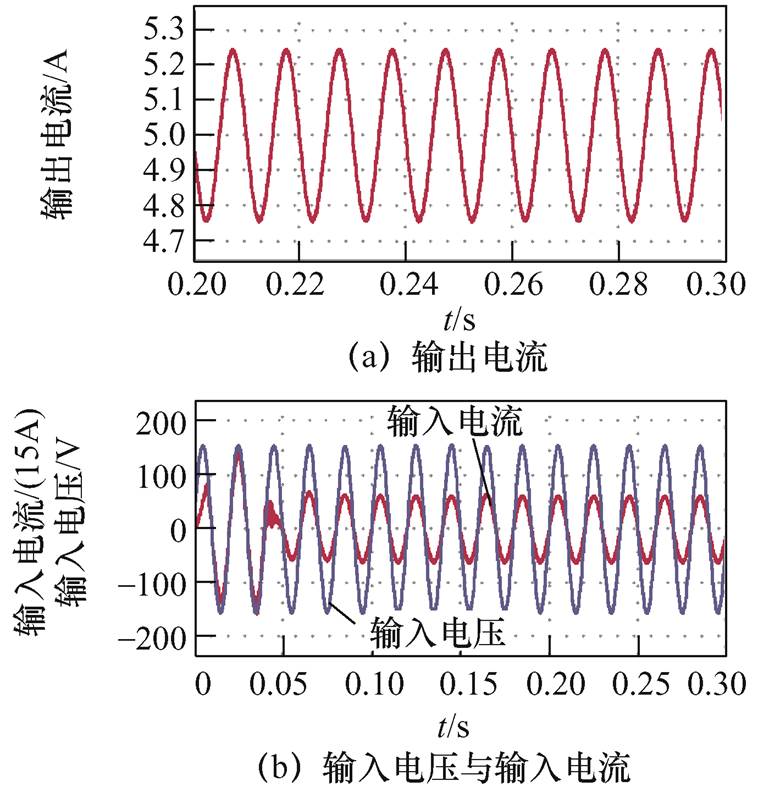
图8 传统单相电流型PWM整流器仿真波形
Fig.8 Simulation waveforms of conventional single-phase current source PWM rectifier
对称半桥解耦拓扑电路参数见表2,主电路参数除直流侧大电感外与传统单相电流型整流器一致。得到的基于对称半桥解耦拓扑单相电流型整流器仿真结果波形如图9所示。
如图9a所示,输出电流稳定在15 A,带有0.16 A的二倍频脉动,证明本文所提对称半桥功率解耦拓扑带有功率解耦作用,能够吸收单相电流型变换器直流侧的二倍频脉动功率,从而降低直流侧电感值。两个10 mH的解耦电感可以起到甚至优于75 mH直流侧电感的滤除二倍频脉动功率的作用。单相电流型整流电路串联解耦拓扑后输入电压与输入电流波形如图9b所示,输入电流波形正弦度良好,PF=0.999,THD=1.22%,满足相关谐波要求。整流侧电压、解耦拓扑两端电压和输出电压波形如图9c所示,脉动电压由解耦拓扑两端电压承担,直流电压为负载电压。解耦拓扑中两解耦电感电流波形如图9d所示,为50%的直流侧输出电流叠加一个二倍频脉动分量的波形,两个电感交替储能来吸收和释放单相电流型整流电路中的二倍频脉动功率,理论分析一致。
表2 对称半桥解耦拓扑仿真参数
Tab.2 Parameters of simulation of single-phase current-source rectifier based on symmetrical half-bridge decoupling topology

参 数数 值 解耦拓扑电感L1,L2/mH10 解耦拓扑电容Cpd/mF47
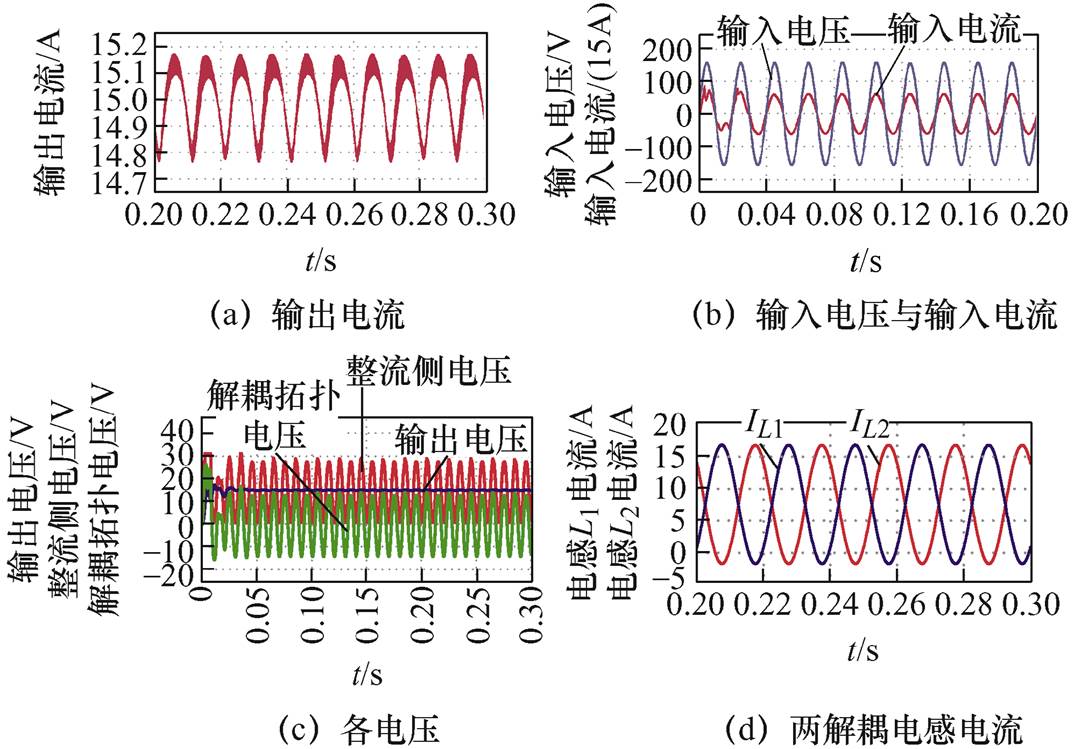
图9 基于对称半桥解耦拓扑单相电流型整流器仿真波形
Fig.9 Simulation waveforms of single-phase current source rectifier based on symmetrical half-bridge decoupling topology
为验证基于对称半桥功率解耦拓扑的单相电流型PWM整流器的抵抗扰动能力,在主电路控制方式双闭环控制中,对称半桥功率解耦拓扑采用输出电流间接闭环控制的前提下进行切载仿真验证。
满载切半载仿真波形如图10所示。电路较快恢复稳定,在输出电流间接闭环控制方式下,不会出现由于解耦拓扑吸收的二倍频功率大于半载时电路的二倍频功率,引起电流纹波增大的问题。满载切半载过程中解耦电路经过输出电流间接闭环控制,使得电感电流脉动值下降,解耦电路从主电路中吸收的二倍频功率下降,从而使得解耦电路吸收的脉动功率能够跟随主电路中的脉动功率发生变化。
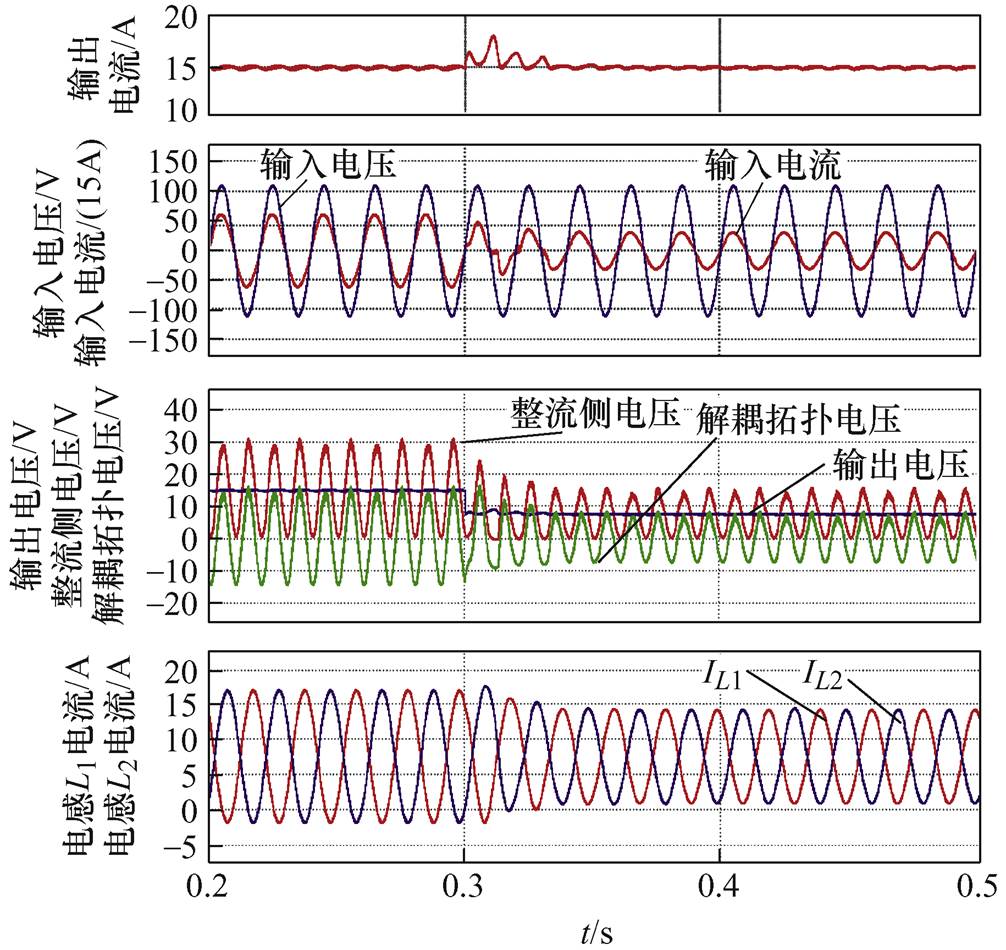
图10 满载切半载仿真波形
Fig.10 Simulation waveforms with changes from full load to half load
半载切满载仿真波形如图11所示。切载后电路较快恢复稳定。由于负载功率增大,此时电路中的二倍频脉动功率也增大,经过输出电流间接闭环控制,使得电感电流脉动值增加,解耦电路从主电路中吸收的二倍频功率增大。
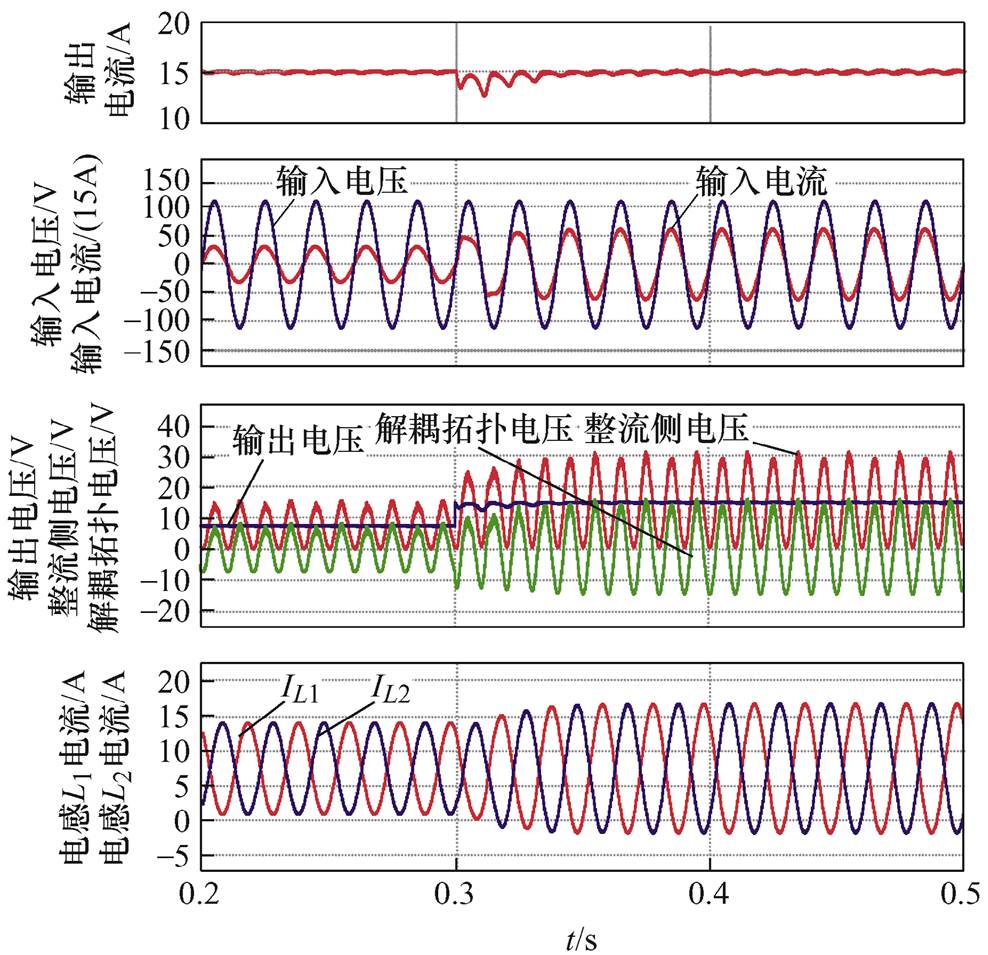
图11 半载切满载仿真波形
Fig.11 Simulation waveforms with changes from half load to full load
采用自感为5.5 mH、互感4.7 mH,耦合系数为0.85的耦合集成电感进行仿真,结果如图12所示。输出电流纹波0.8 A,交流侧电压与电流正弦度良好,交流侧输入电流PF=0.998,符合整流器谐波标准。虽然输出电流纹波略有增大,但每个解耦电感的值进一步降低,仿真分析与理论研究一致。
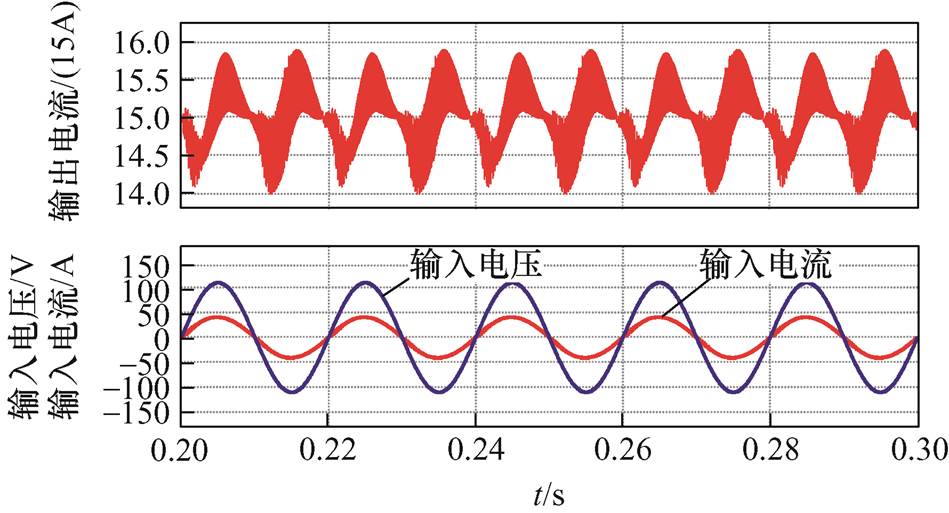
图12 解耦拓扑磁集成仿真波形
Fig.12 Simulation waveforms of magnetic integration
由于实验室电感及调压器耐流限制,实验设定输出电流为10 A,负载电阻为2 W。其余参数与仿真一致。
为验证对称半桥解耦拓扑的解耦能力,进行传统单相电流型PWM整流器和基于对称半桥功率解耦拓扑的单相电流型PWM整流器的对比实验。
图13为200 W工况,直流侧电感为75 mH时,传统单相电流型PWM整流器实验波形。可以看到,交流侧电流质量良好,功率因数为0.97,THD=3.93%,满足THD<5%的相关要求。
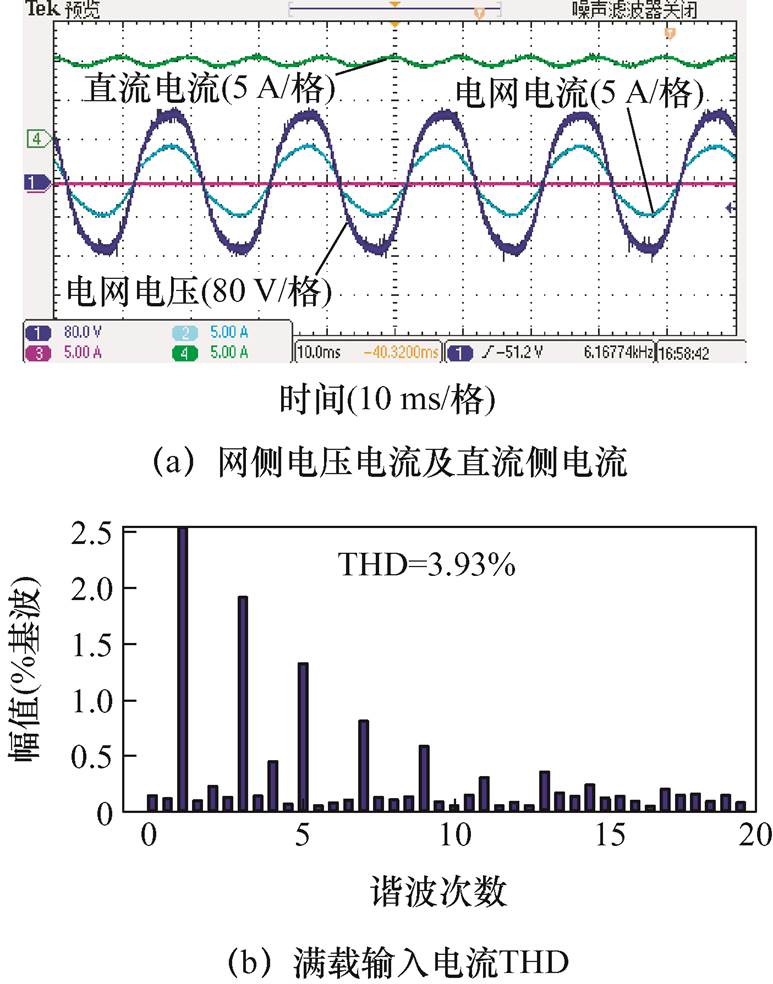
图13 传统单相电流型PWM整流器实验结果
Fig.13 Experimental results of traditional single-phase current source PWM rectifier
从图13a中可见,电网电压本身含有一定的背景谐波,而本文的研究重点是降低直流侧电感,没有对电网背景谐波进行单独的抑制,对此可以引入更加优化的控制方案来抑制背景谐波。
采用两个10 mH电感的基于对称半桥功率解耦拓扑的单相电流型PWM整流器,实验波形如图14所示。图14a为直流侧输出电流、交流侧电压与电流波形,功率因数为0.98,结合图14d可知,THD= 3.79%,交流侧电流谐波质量良好。输出电流稳定为10 A,电流纹波脉动值为0.4 A。
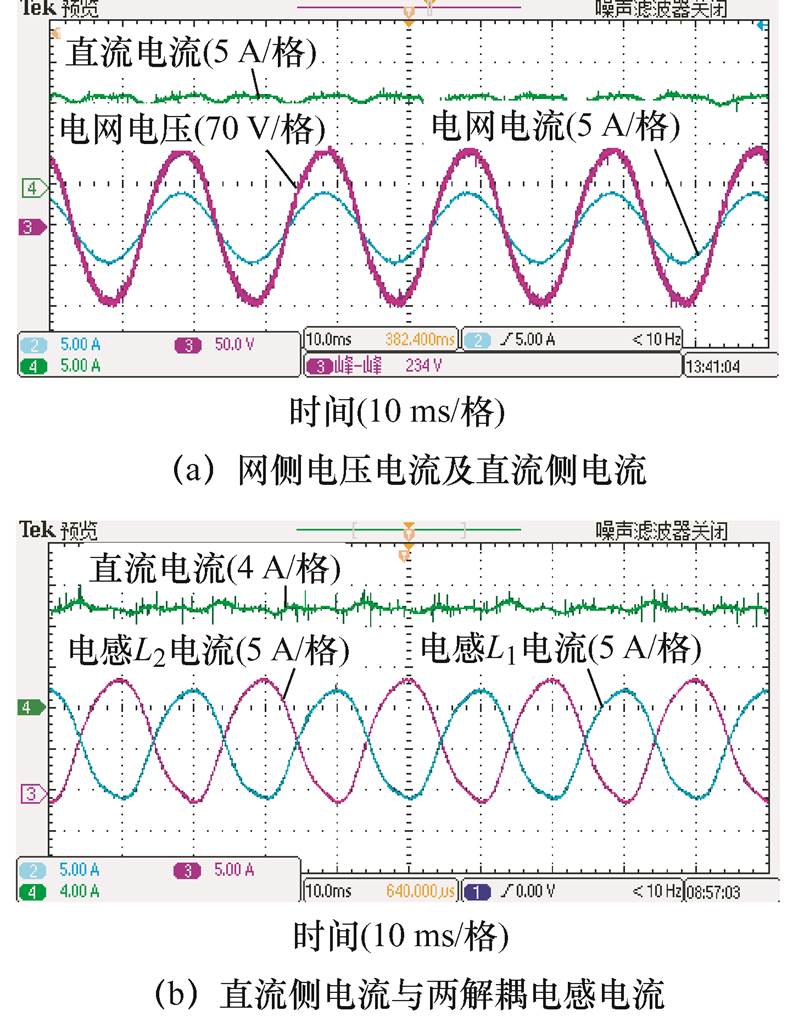
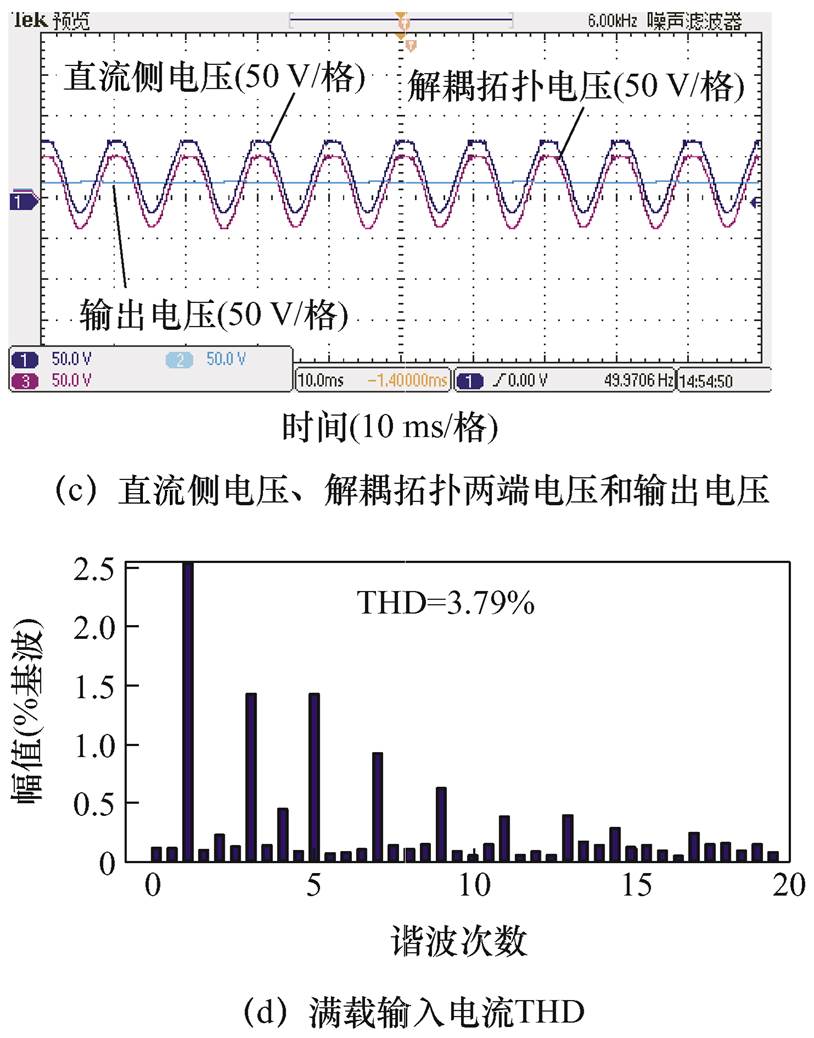
图14 基于对称半桥功率解耦拓扑的单相电流型PWM整流器实验结果
Fig.14 Single-phase current-source PWM rectifier based on symmetrical half-bridge power decoupling topology
直流侧输出电流与解耦电路两电感电流波形如图14b所示,为50%的直流侧输出电流叠加一个工频脉动分量的波形。图14c为直流侧电压、输出电压与解耦拓扑两端电压波形,脉动电压由解耦拓扑两端电压承担,直流电压为负载电压,与理论和仿真一致。
解耦电路输出电流间接闭环控制下,半载切满载实验结果如图15所示,系统的调节时间为120 ms,直流电流降落为20%。
半载切满载由于负载功率增大,此时电路中的二倍频脉动功率也增大,经过输出电流间接闭环控制,使得电感电流脉动值增加,解耦电路从主电路中吸收的二倍频功率增大。满载切半载同理,实验结果如图16所示,调节时间为100 ms,直流电流超调量为20%

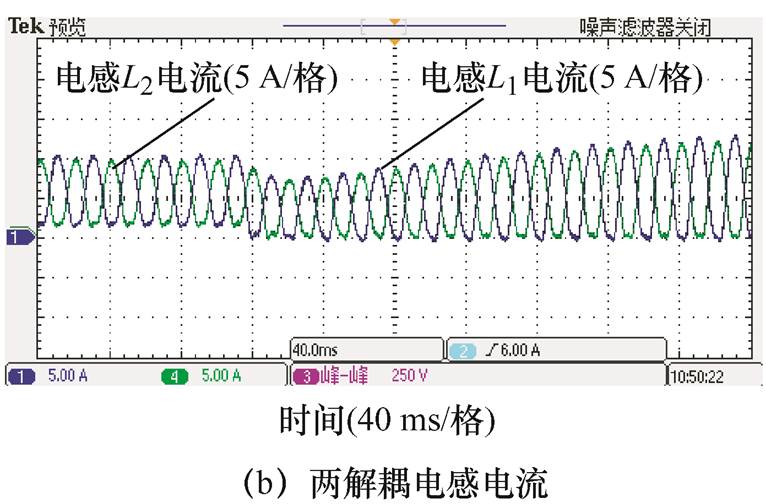
图15 半载切满载实验结果
Fig.15 Experimental results of changes from half load to full load
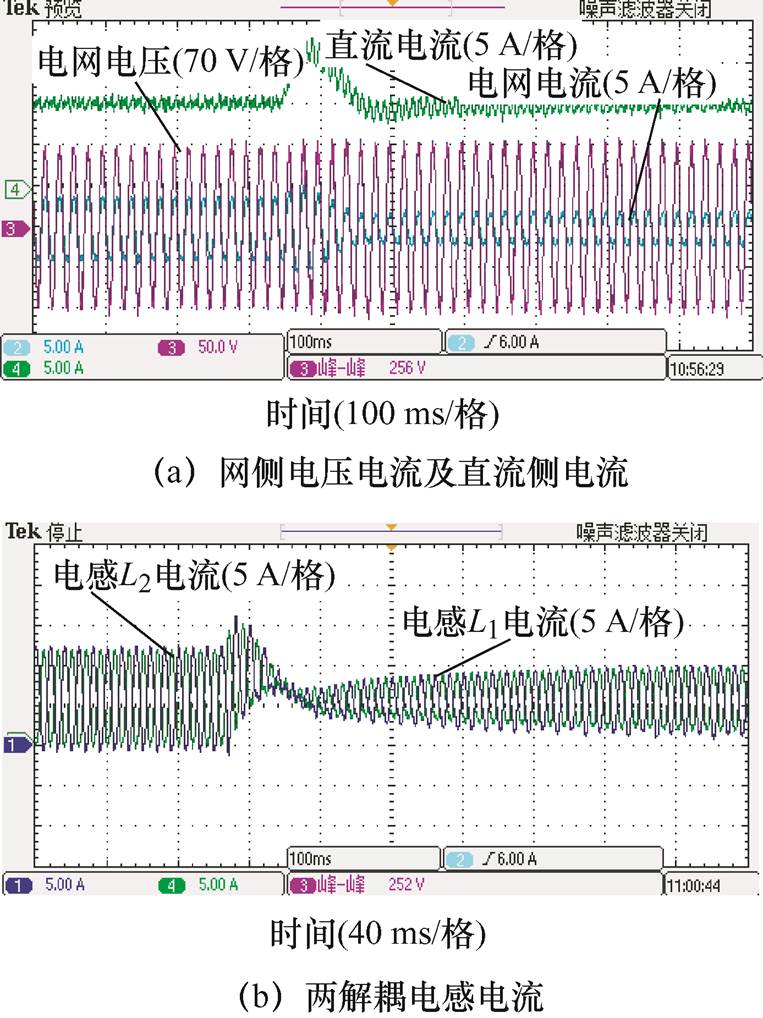
图16 满载切半载实验结果
Fig.16 Experimental results of changes from full load to half load
本文的重点研究目标是降低电流型PWM变换器的直流侧电感取值,并且也达到了明显的降低电感取值的效果。在动态性能设计方面,为简化起见,采用的是基本的PI控制,因此对负载的动态响应较慢。对此,可以引入扰动观测、PID控制等更加优化的方案,提高动态性能。
实验参数与仿真参数一致,得到实验结果如图17所示。直流侧输出电流纹波幅值为0.85 A,交流侧电压与电流正弦度良好,交流侧输入电流PF=0.998,THD=3.83%,符合整流器谐波标准。
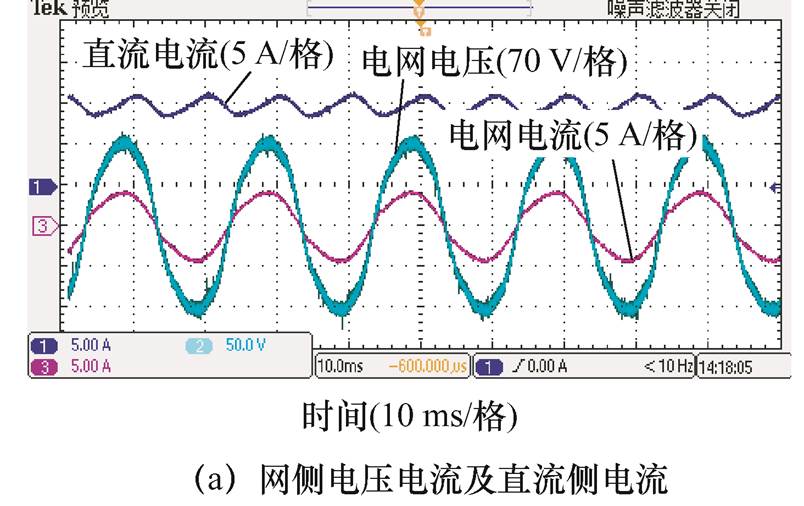

图17 磁集成实验结果
Fig.17 Experimental results of magnetic integration
传统单相PWM整流器所用大电感,解耦电路所用双电感与解耦电路所用集成电感体积数据见表3。由计算可知,当采用解耦电路双电感时,体积可以减少56.9%,当采用集成电感后,体积减少79.7%。基于对称半桥功率解耦拓扑的单相电流型PWM整流器在减小电感值、减少系统体积方面效果显著。
表3 体积比较
Tab.3 Bulk comparation

类 型体积/cm3减小比例(%) 传统大电感12 371.5 (25 mH+25 mH+25 mH) 解耦电路双电感5 326.5 (10 mH+10 mH+解耦电路)56.9 解耦电路集成电感2 511.3 (集成电感+解耦电路)79.7
使用75 mH电感的传统单相电流型PWM整流器和使用两个10 mH电感的基于对称半桥功率解耦拓扑的单相电流型PWM整流器的效率对比如图18所示。
对于电压型的电路,引入解耦拓扑是为了去除电解电容,而电容本身功率损耗不大,若增加解耦电路,引入有源开关,则会增加功率损耗,这是必然发生的问题。因此在电压型电路中,引入解耦拓扑会使得电路效率有所降低。但是电流型电路的储能元件为电感,在电流平均值相等且纹波系数相同的情况下,若采用大电感滤波,电感损耗会很大,是影响电路效率的主要损耗。在电流型电路中引入解耦拓扑后,电路所需的电感更小,可以明显降低电感的损耗。而在本文的研究中,引入解耦拓扑后,降低电感值的能力是很明显的,实验也验证了这一点。如图13和图14所示,在设定了相同的实验输出电流与负载时,传统单相电流型PWM整流器所需直流侧电感为75 mH,而引入了解耦拓扑后,本文所提基于对称半桥功率解耦拓扑的单相电流型PWM整流器仅需要两个10 mH电感,并且对两个电感进行了磁集成的设计和实验,如图17所示。因此,电感值和尺寸大大减小的同时,电感的损耗也大大降低了,由于电感的损耗在电流型PWM变换器的电路损耗中占比很大,在电感损耗降低的同时,即便引入了有源开关的开关损耗,电路整体的损耗也是降低的,因此电路整体的效率必然是上升的。
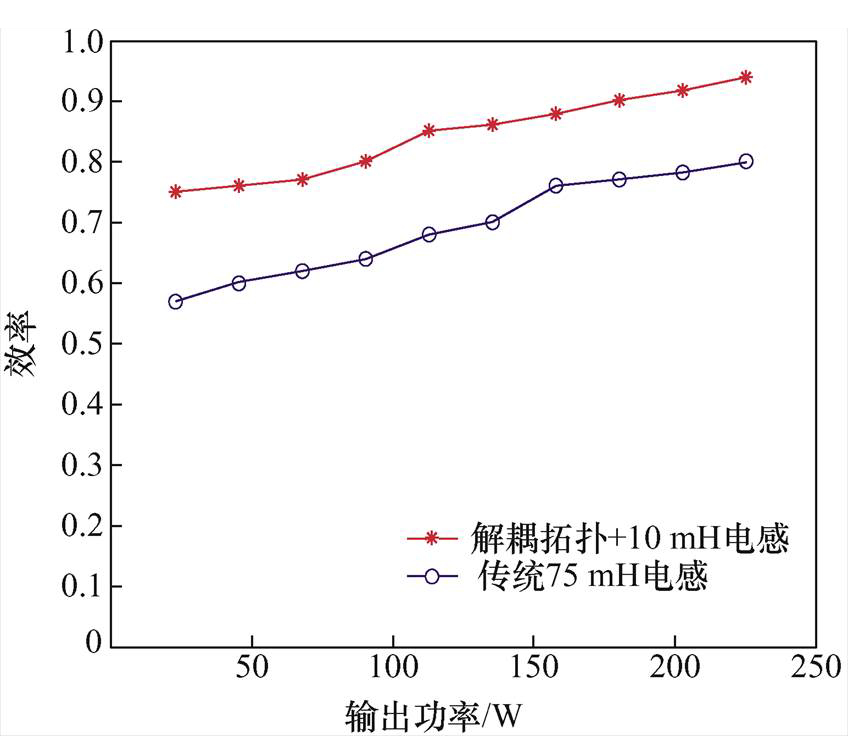
图18 效率对比
Fig.18 Efficiency comparison
本文以抑制单相电流型PWM变换器二倍频脉动功率,降低直流侧电感值,减小变换器体积和成本为出发点,以现有功率解耦技术研究为基础,提出了一种适用于单相电流型PWM变换器的对称半桥功率解耦拓扑,并设计研究了一种基于对称半桥功率解耦拓扑的单相电流型PWM整流器,在其开环、闭环仿真及实验的基础上得出以下结论:
1)本文提出的对称半桥功率解耦拓扑,可有效抑制单相电流型变换器直流侧电流的二倍频纹波脉动,减小直流侧的电感值,降低系统的成本、质量与体积。
2)本文提出的对称半桥功率解耦拓扑,与简化的全桥独立解耦拓扑相比,在都运用逆阻型IGBT的情况下,该电路减少了2个二极管,增加了1个电感。经磁集成后,电感元件数与简化的全桥独立解耦拓扑相同,但调制和控制方式简单。
3)本文提出的输出电流间接闭环功率解耦拓扑控制方式结构简单、实现容易,不需要外加传感器、成本低;不需要复杂计算,对数字处理器的性能要求较小,有利于提升电路的稳定性。
参考文献
[1] 贾焦心, 彭维锋, 颜湘武, 等. 基于余弦定理的旋转潮流控制器功率解耦控制方法[J]. 电工技术学报, 2023, 38(13): 3425-3435.
Jia Jiaoxin, Peng Weifeng, Yan Xiangwu, et al. Research on power decoupling control method rotary power flow controller based on cosine law[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3425-3435.
[2] 姜卫东, 张庆岩, 刘圣宇, 等. 适用于双负载模式的Vienna整流器调制方法[J]. 电力系统自动化, 2023, 47(17): 160-168.
Jiang Weidong, Zhang Qingyan, Liu Shengyu, et al. Modulation method for Vienna rectifier in dual load mode[J]. Automation of Electric Power Systems, 2023, 47(17): 160-168.
[3] 朱艺锋, 赵海龙, 张国澎, 等. 单相五电平整流器滑模模型预测控制[J]. 电工技术学报, 2022, 37(8): 2030-2039.
Zhu Yifeng, Zhao Hailong, Zhang Guopeng, et al. Sliding mode model predictive control of single-phase five-level rectifier[J]. Transactions of China Electro- technical Society, 2022, 37(8): 2030-2039.
[4] 郭强, 周琛力, 李山. 面向电流源型PWM整流器直流侧电压的多环路控制策略[J]. 电工技术学报, 2022, 37(8): 2051-2063.
Guo Qiang, Zhou Chenli, Li Shan. A multiple loops control strategy based on DC link voltage of current source PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2051-2063.
[5] 李山, 马雯, 郭强, 等. 非理想电网条件下PWM整流器优化预测功率控制[J]. 电工技术学报, 2022, 37(18): 4745-4756.
Li Shan, Ma Wen, Guo Qiang, et al. Optimal predictive power control of PWM rectifier under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4745-4756.
[6] 李小强, 马永超, 黄金伟, 等. 基于双脉宽调制的交错Boost集成型CLLLC谐振变换器宽增益控制策略[J]. 电工技术学报, 2022, 37(20): 5313-5323.
Li Xiaoqiang, Ma Yongchao, Huang Jinwei, et al. Wide-gain-range control scheme for interleaved Boost integrated CLLLC resonant converter based on dual pulse width modulation[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5313-5323.
[7] 孟建辉, 吴小龙, 张自力, 等. 三相隔离型AC- DC-DC电源自适应线性自抗扰控制方法及纹波抑制补偿策略[J]. 电工技术学报, 2023, 38(14): 3898- 3908.
Meng Jianhui, Wu Xiaolong, Zhang Zili, et al. Adaptive linear active disturbance rejection control method and ripple suppression compensation strategy for three-phase isolated AC-DC-DC power supply[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3898-3908.
[8] 杨达亮, 彭祖文, 刘金宝, 等. 一种无延时单相并网变换器dq电流解耦控制方法[J]. 电网技术, 2022, 46(4): 1585-1593, 49.
Yang Daliang, Peng Zuwen, Liu Jinbao, et al. d-q current decoupling for single-phase grid-connected converter based on non-delay[J]. Power System Technology, 2022, 46(4): 1585-1593, 49.
[9] 王立乔, 陈建医, 程超然, 等. 单级单相无电解电容Buck-Boost逆变器[J]. 电工技术学报, 2023, 38(24): 6768-6781.
Wang Liqiao, Chen Jianyi, Cheng Chaoran, et al. A single-stage single-phase Buck-Boost inverter without electrolytic capacitor[J]. Transactions of China Elec- trotechnical Society, 2023, 38(24): 6768-6781.
[10] 桑汐坤, 王懿杰, 徐殿国. 基于输入并联输出串联的高效高升压比DC-DC变换器[J]. 电工技术学报, 2023, 38(20): 5488-5502.
Sang Xikun, Wang Yijie, Xu Dianguo. High- efficiency high voltage gain DC-DC converter based on input parallel and output series connection[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5488-5502.
[11] 李慧慧, 皇金锋. 单电感双输出Buck-Boost变换器的非最小相位特性分析及控制策略[J]. 电工技术学报, 2023, 38(14): 3875-3887.
Li Huihui, Huang Jinfeng. Analysis of non-minimum phase characteristics and control strategies for single-inductor dual-output Buck-Boost converters[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3875-3887.
[12] Liu Bin, Wang Hui, Yang Yongheng, et al. Improved model predictive control for single-phase grid-tied inverter with virtual vectors in the compacted solution-space[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 9673-9678.
[13] 王章毅, 陆道荣, 李想, 等.基于移相和调频的单级双向AC-DC变换器临界电流调制策略[J]. 电工技术学报, 2023, 38(14): 3888-3897.
Wang Zhangyi, Lu Daorong, Li Xiang, et al. Boundary current modulation strategy of single-stage bidirectional AC-DC converter based on phase-shift and variable-frequency control[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3888- 3897.
[14] 周国华, 王淇, 邓伦博. 宽增益高效率CLLLC变换器的变频双移相调制策略[J]. 电工技术学报, 2024, 39(8): 2511-2522.
Zhou Guohua, Wang Qi, Deng Lunbo. Variable- frequency dual-phase-shift modulation strategy for CLLLC converter with wide voltage gain and high efficiency[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2511-2522.
[15] 孙瑄瑨, 荣德生, 王宁. 具有谐振软开关的高增益耦合电感组合Boost-Zeta变换器[J]. 电工技术学报, 2024, 39(6): 1830-1842.
Sun Xuanjin, Rong Desheng, Wang Ning. High step- up integrated Boost-Zeta converter with coupled inductor and resonant soft-switching[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1830-1842.
[16] 高娟, 秦岭, 茅靖峰, 等. 分体式储能VSG功率转换系统输出电压鲁棒控制器设计[J]. 电网技术, 2022, 46(1): 213-219, 11-12.
Gao Juan, Qin Ling, Mao Jingfeng, et al. Output voltage robust controller design for the power converter system in the assembled VSG[J]. Power System Technology, 2022, 46(1): 213-219, 11-12.
[17] Wong C S, Liu Junwei, Cao Lingling, et al. A SWISS-rectifier-based single-stage three-phase bidi- rectional AC-DC inductive-power-transfer converter for vehicle-to-grid applications[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 4152-4166.
[18] Zhang Jianhua, Ding Hao, Wang Baocheng, et al. Active power decoupling for current source converters: an overview scenario[J]. Electronics, 2019, 8(2): 197.
[19] Vairavasundaram I, Varadarajan V, Pavankumar P J, et al. A review on small power rating PV inverter topologies and smart PV inverters[J]. Electronics, 2021, 10(11): 1296.
[20] 王立乔, 张检亮, 管成功, 等. 基于非线性载波调制的单相电流型逆变器的研究[J]. 太阳能学报, 2021, 42(12): 435-442.
Wang Liqiao, Zhang Jianliang, Guan Chenggong, et al. Research on single-phase current source inverter based on nonlinear carrier modulation[J]. Acta Energiae Solaris Sinica, 2021, 42(12): 435-442.
[21] 张宇尧. 小储能电感单相电流型并网逆变器研究[D]. 秦皇岛:燕山大学, 2020.
Zhang Yuyao. Research on single-phase current source grid-connected inverter with small energy storage inductor[D]. Qinhuangdao: Yanshan University, 2020.
[22] Wang Haoran, Wang Huai, Zhu Guorong, et al. An overview of capacitive DC-links-topology derivation and scalability analysis[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1805-1829.
[23] Wang Lei, Li Huan, Li Sinan. Burst mode control of active-power-decoupling integrated active clamp flyback PFC rectifiers[J]. IEEE Transactions on Power Electronics, 2023, 38(5): 6337-6350.
[24] Deshmukh N, Prabhakar S, Anand S. Power loss reduction in Buck converter based active power decoupling circuit[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4316-4325.
[25] Sun Yao, Liu Yonglu, Su Mei, et al. Review of active power decoupling topologies in single-phase systems[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4778-4794.
[26] Harb S, Mirjafari M, Balog R S. Ripple-port module-integrated inverter for grid-connected PV applications[J]. IEEE Transactions on Industry Appli- cations, 2013, 49(6): 2692-2698.
[27] Vitorino M A, Hartmann L V, Fernandes D A, et al. Single-phase current source converter with new modulation approach and power decoupling[C]//2014 IEEE Applied Power Electronics Conference and Exposition-APEC, Fort Worth, TX, USA, 2014: 2200- 2207.
[28] Liu Yonglu, Sun Yao, Su Mei. Active power compensation method for single-phase current source rectifier without extra active switches[J]. IET Power Electronics, 2016, 9(8): 1719-1726.
[29] Sun Yao, Liu Yonglu, Su Mei, et al. Active power decoupling method for single-phase current-source rectifier with no additional active switches[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5644-5654.
[30] 林智乐, 何良宗, 周鸿彦. 基于有源负电容的电压源型逆变器直流母线二次功率脉动的抑制方法[J]. 中国电机工程学报, 2021, 41(22): 7772-7781, 21.
Lin Zhile, He Liangzong, Zhou Hongyan. Suppressing secondary power pulsation method for DC bus of voltage source inverter based on active negative capacitor[J]. Proceedings of the CSEE, 2021, 41(22): 7772-7781, 21.
Abstract The voltage reduction characteristics of single-phase current-source PWM converters as rectifiers and the voltage boost characteristics as inverters can meet the current application requirements of single-phase AC-DC converters. Traditional single-phase current-source PWM converters require a large inductor connected in series on the DC side to filter out the naturally occurring second harmonic ripple power, leading to high cost and large volume. The causes and suppression strategies of the second harmonic ripple power on the DC side of single-phase current-source PWM converters are analyzed in this paper. Then, a symmetrical half-bridge power decoupling topology is proposed, and a single-phase current-source PWM rectifier is introduced. The proposed decoupling topology can compensate for the second harmonic ripple power while reducing inductance values, costs, and volume.
The proposed decoupling topology consists of two inverse-blocking IGBTs with series-connected diodes, one capacitor (Cpd), and two inductors (L1 and L2). The decoupling topology compensates for the second harmonic ripple power by charging and discharging inductors L1 and L2 with capacitor Cpd. When one inductor is being charged, the other inductor must be discharged. From the power absorption and release perspective, when the decoupling topology operates in region ①, inductor L1 is charging while inductor L2 is discharging. Because L1 absorbs more energy than L2 releases, the decoupling topology absorbs ripple power from the DC side. In region ②, L1 is discharging while L2 is charging. Because L1 releases more energy than L2 absorbs, the decoupling topology releases ripple power from the DC side. This working mode reduces current ripple and inductance values. Regions ③ and ④ follow a similar logic. The parameter designs for the capacitor and inductors are provided. The capacitor Cpd is 47 mF, and inductors L1 and L2 are 10 mH. After that, the two inductors are coupled magnetically, reducing the number of circuit components. The effect of inductance value reduction is enhanced. Finally, a control method with indirect closed-loop control of output current on the DC side is presented, which directly samples the DC side current and improves the reliability of the system.
Suppose all other parameters are equal, simulations and experiments of a traditional single-phase current-source PWM rectifier with a 75 mH inductor and a single-phase current-source rectifier based on a symmetrical half-bridge decoupling topology with two 10mH inductors are conducted. The proposed symmetrical half-bridge power decoupling topology effectively suppresses the second harmonic ripple of the DC-side current in single-phase current-source converters. The proposed topology significantly reduces the DC-side inductance value, increases efficiency, and reduces the system’s costs, weight, and volume. After magnetic integration, only one inductor component remains, and the value of each inductor is further reduced. The control method based on the indirect closed-loop power decoupling topology has a simple structure and is easy to implement. Compared to traditional decoupling circuit control methods, this method eliminates the need for additional sensors, complex regulators, and calculations, providing greater flexibility in practical applications.
Keywords: Single-phase current-source PWM rectifier, second harmonic ripple power suppression, power decoupling technology, inductive magnetic integration, output current indirect closed-loop control
中图分类号:TM461
DOI: 10.19595/j.cnki.1000-6753.tces.231924
国家自然科学基金(51677162)和河北省自然科学基金(E2017203235)资助项目。
收稿日期2023-11-17
改稿日期2023-12-24
王立乔 男,1974年生,博士,教授,研究方向为高频功率变换、脉冲调制理论、大功率变流技术、可再生能源发电及分布式发电系统。E-mail: brent@ysu.edu.cn(通信作者)
臧 朔 男,1998年生,硕士,研究方向为中小功率电流型变换器轻量化。E-mail: 1031338408@qq.com
(编辑 陈 诚)