
图1 NLS-LDFM结构示意图
Fig.1 Structure diagram of NLS-LDFM
摘要 同心笼次级直线双馈电机是由同心笼转子无刷双馈电机演变而来的一种新型直线电机,具有功率因数可调、可靠性高、中高速区平均推力下降较小、轨道建设成本较低等优点。然而,因物理结构特殊、工作原理复杂等,对同心笼次级直线双馈电机的静态端部效应控制方法的研究仍不够深入,严重限制了该类电机的进一步发展和应用。为此,该文提出了一种带静态端部效应补偿的功率绕组电压定向矢量控制策略。首先,分析了静态端部效应作用规律和补偿方法,建立了考虑静态端部效应的三相静止坐标系数学模型和简化的两相旋转坐标系数学模型;然后,推导了功率绕组电压定向条件下的初、次级电流数学关系,实现了电磁推力方程中两套初级绕组的解耦控制;最后,大量的仿真和实验分析表明,新方法可通过静态端部效应补偿有效提升电机驱动性能,实现平稳运行。
关键词:直线双馈电机 静态端部效应 矢量控制 城轨交通
城轨交通直线牵引系统自1986年开始正式运营,迄今已在全世界有30余条线路,得到了学术界和工业界的广泛关注,未来发展空间巨大。相比当前常规的城轨交通旋转电机系统,直线电机系统具有爬坡能力强、加减速度快、转弯半径小、运行噪声低、整车质量轻、维护量小等优势,特别契合城市轨道交通运输需求,特别是中大城市城区繁华地带[1]。我国“十四五”规划提出要推动先进轨道交通装备创新发展,直线城轨交通建设线路逐年增多,发展趋势良好。
目前,城轨交通直线电机主要分为两大类:一类是主要应用于中低速轮轨和磁悬浮的直线感应电机[2];另一类是主要应用于中高速磁悬浮的直线同步电机[3]。除此之外,直线双馈电机因其功率因数和效率可以调节、运行方式灵活等优势也引起了国内外学者的广泛关注[4-7],其中单边励磁型的同心笼次级直线双馈电机(Nest-Loop Secondary Linear Doubly-Fed Machine, NLS-LDFM)可弥补直线感应电机的部分缺陷,如高速大转差下推力和功率因数显著下降等,同时又能兼顾直线感应电机结构简单、运行维护方便等优势,未来发展潜力较大。
NLS-LDFM的运行原理与笼型转子无刷双馈电机(Brushless Doubly-Fed Machine, BDFM)基本相同。现有的BDFM多应用于风力发电、船舶轴带发电等发电机场合,而作为电动机运行的控制方法相对较少且尚未在工程中得到广泛应用。文献[8-9]研究了BDFM直接转矩控制策略,该方法控制简单,对参数依赖小,但转矩波动较大,可供选择的电压矢量无法同时满足转矩和磁链的控制要求,可能会对电机的稳定运行产生不利影响。文献[10]提出了一种功率绕组磁链定向的矢量控制方法,其中包含三环PI控制,由内到外分别为控制绕组电流环、功率绕组电流环、转速和无功功率环,而BDFM本身存在较强耦合,因此上述三环控制结构较为复杂,不利于实际应用推广。为此,文献[11]简化了控制结构,通过功率绕组电压锁相环实现了基于功率绕组电压定向的矢量控制,避免了对功率绕组磁链的估算,但其功率绕组仍与三相交流电网直接连接,不适用于城轨交通的直流电网供电方式[12]。
此外,因初级铁心开断,NLS-LDFM气隙磁场中包含反向行波磁场和沿运动方向均匀分布的脉振磁场等非工作磁场,三相绕组不对称,纵向静态端部效应较为严重,给电机的分析和控制带来了较大影响。因此,传统BDFM控制方法难以直接应用于NLS-LDFM,亟需研究城轨交通直流电网供电下考虑静态端部效应的控制方法。
在直线电机端部效应研究中,直线感应电机和直线同步电机的研究较为充分,而对于NLS-LDFM端部效应的研究则相对不足。文献[13]提出了一种针对短初级直线电机的绕组分析方法,为研究直线电机端部效应奠定了基础。文献[14]分析了NLS- LDFM的静态纵向端部效应作用机理,表明除三相绕组不对称外,静态端部效应还会导致初级两套绕组产生直接耦合,使电机初级部分功率以变压器的形式传递,而不产生有效的电磁推力,且会引入谐波电动势和谐波电流,对运行性能造成负面影响。文献[15]提出了一种NLS-LDFM静态端部效应补偿方法,有效抑制了初级绕组中的负序电流和直接耦合电流,但谐波电流抑制环路较为复杂,且采用简单的恒电流-频率比控制,电机仅工作在级联异步运行模式,尚未实现双馈闭环调速控制,难以进行实际应用。
本文综合考虑NLS-LDFM静态端部效应和城轨交通牵引系统供电特点,提出了一种带静态端部效应补偿的功率绕组电压定向矢量控制策略。首先,介绍了NLS-LDFM的基本结构与运行原理,分析了静态端部效应作用规律,建立了考虑静态端部效应的三相静止坐标系数学模型和简化的两相旋转坐标系数学模型。然后,推导了在功率绕组电压定向条件下初、次级电流的数学关系,实现了电磁推力方程中初级两套绕组的解耦控制。为适用于直流电网供电,初级两套绕组均通过变频器供电,使功率绕组运行在恒电压-频率比模式下,对控制绕组采用电流-速度双闭环控制,同时对两套绕组施加静态端部效应前馈补偿。最后,通过大量仿真和实验验证了所提控制方法的有效性。分析结果表明:带静态端部效应补偿的矢量控制可抑制初级绕组中由静态端部效应引起的直接耦合电流和负序电流,减小电机推力波动和噪声,提高电机运行性能。
NLS-LDFM采用短初级单边平板型直线电机结构,初级嵌有两套极对数分别为pp和pc的三相交流绕组,一般称作功率绕组和控制绕组,次级采用同心笼结构,每隔初级纵向长度均匀布置pr=pp+pc组,每组含若干个同心式短路笼环,如图1所示。

图1 NLS-LDFM结构示意图
Fig.1 Structure diagram of NLS-LDFM
当次级同心笼产生的两组气隙行波磁通密度与对应的初级行波磁通密度保持相对静止时,电机能够产生稳定的电磁推力,即初级两套绕组产生的气隙行波磁通密度在同心笼中感应的电动势频率相等。两组磁场在次级中的感应电动势频率分别为
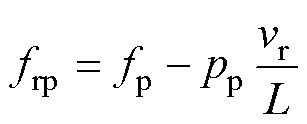 (1)
(1)
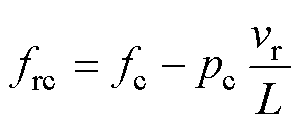 (2)
(2)
式中,fp和fc分别为功率绕组和控制绕组供电频率;vr为次级机械速度;L为初级纵向长度。两组感应电动势频率应满足
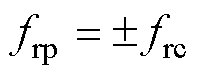 (3)
(3)
式中,正、负号分别对应“差调制”和“和调制”方案。为使电机产生较大的起动推力,本文采用“和调制”方案[16],可得次级速度与初级两套绕组频率满足
 (4)
(4)
当其中一套绕组电流频率为0,即直流激励时,电机工作在同步运行模式,运行速度称为自然同步速,低于自然同步速的速度称为次同步速,高于自然同步速的速度称为超同步速[17]。
传统直线感应电机静态端部效应表现为由脉振磁场引起的三相不平衡,而三相不平衡度与电机极对数呈负相关,因此当极对数较多时可忽略静态端部效应的影响[18]。NLS-LDFM静态端部效应的产生机理与直线感应电机类似,但由于电机主要工作在次同步速,相同供电频率、安装体积和速度限制下绕组极对数一般较小,因此其静态端部效应影响较直线感应电机更为严重,且表现形式更加复杂。
NLS-LDFM静态端部效应产生机理:初级铁心两端开断导致绕组产生沿气隙均匀分布的脉振磁场,进而导致绕组相间互感不等并产生直接耦合。具体表现为,初级两套绕组在两组对称的三相电流激励下均产生正序磁场和脉振磁场,其中,两组正序磁场用于传递稳定的电磁功率,两组脉振磁场将在每一套绕组中同时产生频率为fp和fc的脉振反电动势,其表达式为
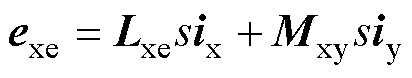 (5)
(5)
式中,s表示微分算子d/dt;下标x、y表示功率绕组或控制绕组;exe为脉振电动势;Lxe为脉振自感矩阵;Mxy为脉振互感(直接耦合互感)矩阵。其中,脉振自感和互感矩阵的表达式分别为
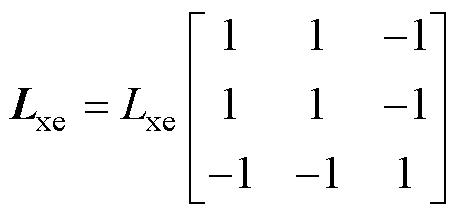 (6)
(6)
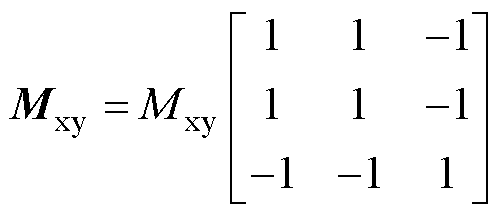 (7)
(7)
式中,Lxe、Mxy为电感幅值。
为简化NLS-LDFM数学模型,可将同心笼次级等效为两套反相级联的次级绕组,其中一套与功率绕组耦合,另一套与控制绕组耦合。对次级而言,两套绕组在次级中产生频率相同、方向相反的行波磁场。电机的电压和磁链方程可以分别表示为
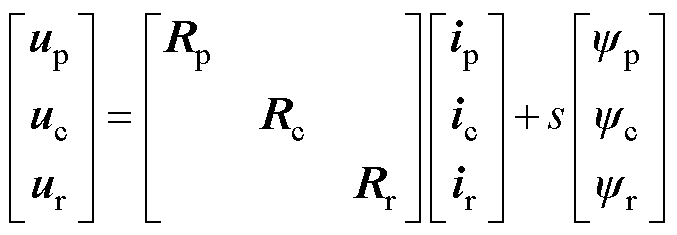 (8)
(8)
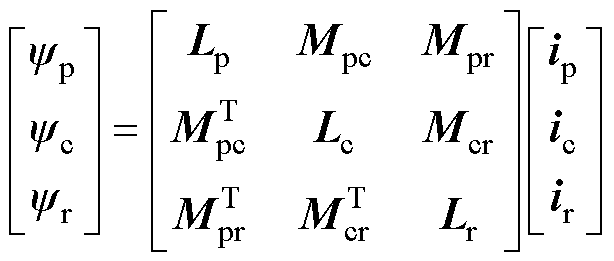 (9)
(9)
式中,u、i、y 分别为三相电压、电流和磁链矢量;下角标p、c、r分别表示功率绕组、控制绕组和次级;Rp、Rc和Rr分别为功率绕组、控制绕组和次级的相电阻矩阵;Lp、Lc和Lr分别为功率绕组、控制绕组和次级的自感矩阵;Mpr、Mcr分别为功率绕组、控制绕组与次级之间的互感矩阵;Mpc为功率绕组和控制绕组之间的直接耦合互感矩阵。其中
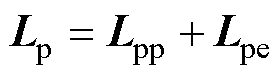 (10)
(10)
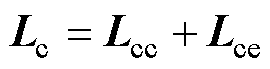 (11)
(11)
式中,Lpp和Lcc分别为BDFM功率绕组和控制绕组的三相自感矩阵;Lpe和Lce分别为功率绕组脉振自感矩阵和控制绕组脉振自感矩阵。
受静态端部效应影响,NLS-LDFM数学模型与BDFM并不相同[19]。如式(8)~式(11)所示,电感矩阵中将出现脉振电感矩阵和直接耦合互感矩阵,电机三相绕组电感不再对称。为便于进行坐标变换和实施控制策略,首先建立忽略三相不对称和直接耦合的数学模型,然后在静止坐标系下对表征静态端部效应的脉振反电动势建模,在实施矢量控制策略时实施前馈电压补偿。NLS-LDFM在功率绕组同步坐标系下的数学模型为
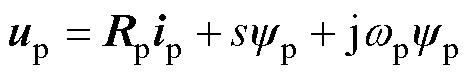 (12)
(12)
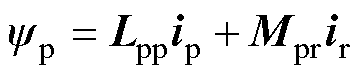 (13)
(13)
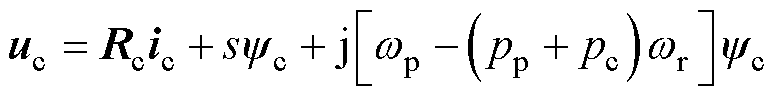 (14)
(14)
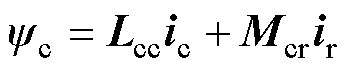 (15)
(15)
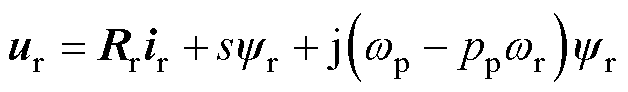 (16)
(16)
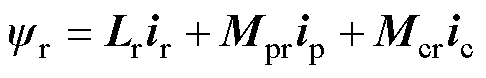 (17)
(17)
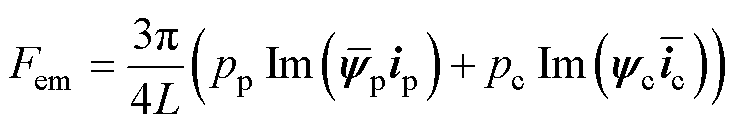 (18)
(18)
其中
u=ud+juq i=id+jiq y =yd+jyq
式中,w 为角频率;Fem为电磁推力。
传统BDFM功率绕组一般直接与三相交流电网相连,需要电压传感器测量电网电压并通过锁相环等锁定电压相位。城轨交通牵引供电系统多采用直流电网供电,本文为模拟城轨交通用电机运行特性,通过变频器为功率绕组和控制绕组供电,如图2所示。为简化控制结构,去掉功率绕组侧的电压传感器和锁相环等,对功率绕组采用电压开环控制,即功率绕组的电压幅值和频率等信息均由控制器给定,并通过空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)输出三相电压为电机功率绕组供电。
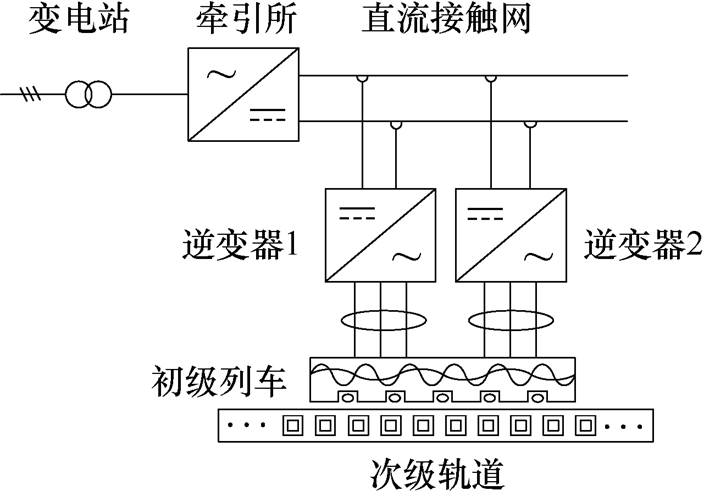
图2 城轨交通直流供电系统
Fig.2 The dc power supply system for urban transit
为简化控制系统结构,功率绕组侧变频器(Power Winding Side Converter, PWSC)采用恒定电压-频率比控制,即恒V/F控制,可根据控制目标灵活调节电压和频率,控制框图如图3所示。
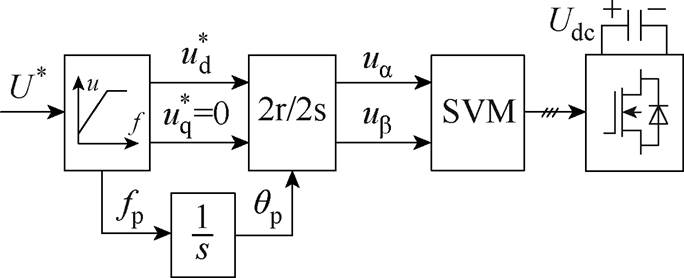
图3 功率绕组侧变频器控制框图
Fig.3 Control diagram of power winding side converter
采用功率绕组电压定向控制时,将功率绕组电压Up定向在同步旋转坐标系d轴上,即upd=Up,upq= 0。与功率绕组反电动势相比,功率绕组电阻上的压降较小,可以将其忽略,则稳态下功率绕组的dq轴磁链可以表示为
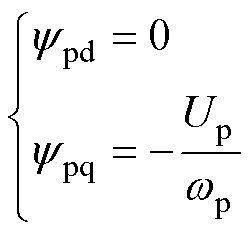 (19)
(19)
由式(19)可知,忽略功率绕组电阻压降后,功率绕组d轴电压定向等价于功率绕组q轴磁链定向,当功率绕组电压和频率比值不变时,功率绕组磁链也不发生变化,由此避免观测功率绕组磁链以及对磁链幅值的闭环控制,简化了控制系统结构。根据给定的磁链幅值yp,可直接得到功率绕组给定电压幅值为wpyp,在基频以下,功率绕组电压和频率比值为2pyp。
控制绕组侧变频器(Control Winding Side Converter, CWSC)除承担调节控制绕组电流的作用,还需对电机的运行速度或电磁推力进行控制。在功率绕组电压定向条件下,仅对控制绕组电流进行闭环控制,而电机的输出功率由功率绕组和控制绕组共同承担。为实现对推力的精确控制,需要将式(18)的推力表达式简化为只含功率绕组磁链和控制绕组电流的形式。
由于次级电流难以直接控制,由式(13)可以得到用功率绕组侧变量表示的次级dq轴电流为
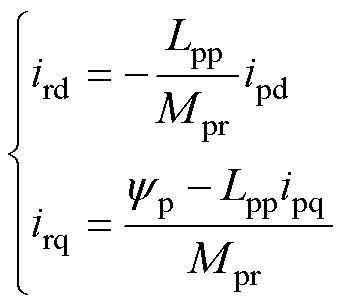 (20)
(20)
将式(20)代入控制绕组磁链方程式(15)并联立控制绕组电压方程式(14),可得
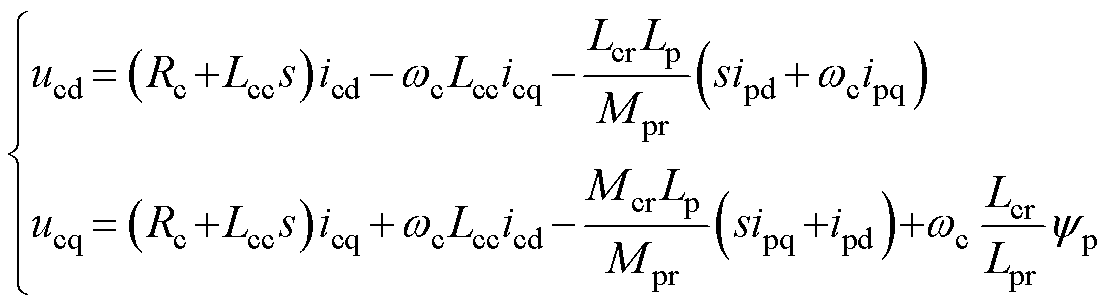 (21)
(21)
由于次级为同心笼短路环结构,次级电压ur=0。联立次级电压方程式(16)和次级磁链方程式(17),消去式(21)中功率绕组电流的导数项,得到控制绕组电压与电流的关系式为
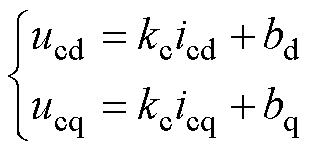 (22)
(22)
其中
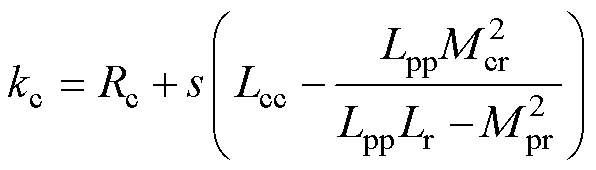 (23)
(23)
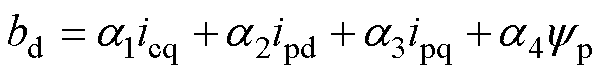 (24)
(24)
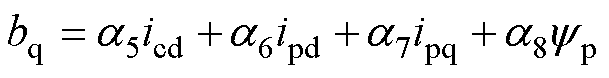 (25)
(25)
式中,ai(i=1, 2,…, 8)为与电机参数及角频率相关的系数,可视为常数。
由控制绕组电压与电流关系式可知,控制绕组电流除了与控制绕组电压直接相关外,还与控制绕组本身及功率绕组存在交叉耦合。由于城轨交通牵引列车惯量较大,对控制绕组电流采用闭环控制时,对于快响应要求不高,在动态时可将交叉耦合项bd和bq视为扰动量,仅会降低系统的动态响应速度,而其在稳态下为直流量,不会对系统的稳态性能产生影响。
在功率绕组电压定向条件下,为实现两套绕组的解耦控制,可将功率绕组和次级同心笼电流用控制绕组电流表示,并将其代入电磁推力方程即式(18)中,忽略次级电阻,得到电磁推力与控制绕组电流的关系为
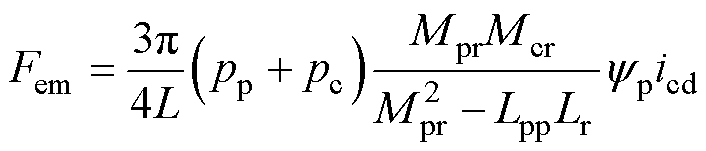 (26)
(26)
由式(26)可知,当功率绕组磁链不变时,可通过调节icd控制电机的电磁推力和速度。基于以上分析,控制绕组侧变频器的控制结构包含内外两环,内环调节控制绕组电流,外环直接控制电机的运行速度。CWSC控制框图如图4所示。
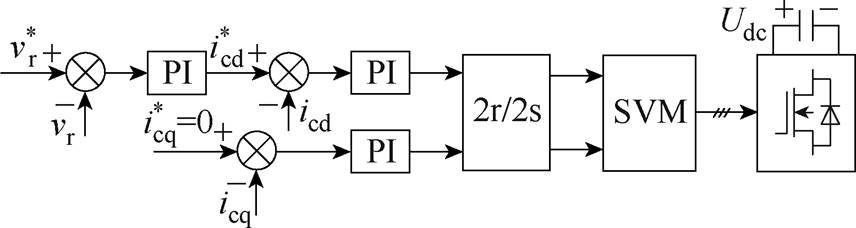
图4 控制绕组侧变频器控制框图
Fig.4 Control diagram of control winding side converter
NLS-LDFM具有多种运行模式,其中级联异步运行模式的起动性能较好,一般多采用异步模式起动后再切换到双馈模式运行。在电机起动前,通过控制CWSC,将三相桥式电路下半桥的开关管全部闭合,上半桥的开关管全部断开,令控制绕组通过下桥臂短路,使电机工作在级联异步运行模式,如图5所示。在电机起动时,逐渐增大功率绕组侧变频器输出电压和频率,直到达到额定值,待电机速度上升到自然同步速附近,再施加闭环控制给控制绕组供电,使电机切换到双馈运行模式。
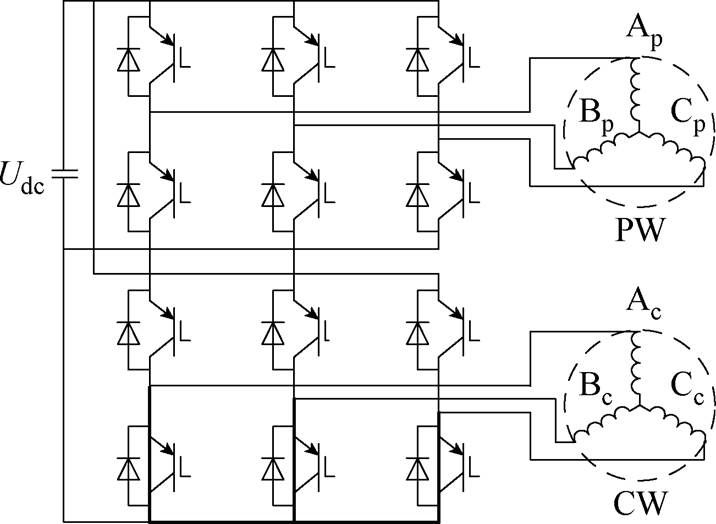
图5 级联异步运行模式IGBT状态
Fig.5 The status of IGBT at cascade asynchronous mode
考虑静态端部效应时,NLS-LDFM的电感矩阵中将出现直接耦合互感和脉振电感。三相静止坐标系下功率绕组电压方程和磁链方程为
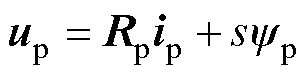 (27)
(27)
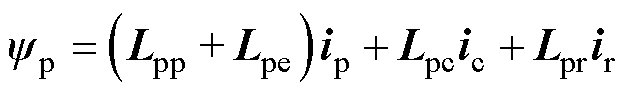 (28)
(28)
将式(28)代入式(27)可得
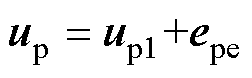 (29)
(29)
其中
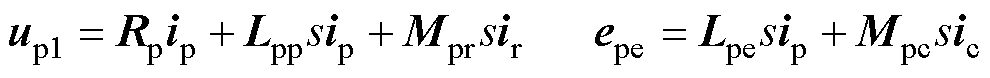
式中,up1为不考虑静态端部效应时的功率绕组电压;epe为静态端部效应产生的脉振反电动势。功率绕组脉振反电动势的两项分别反映了功率绕组脉振磁场引起的三相不对称和直接耦合现象。
为消除脉振反电动势的不利影响,可在功率绕组(控制绕组)供电端加入前馈补偿电压umx,以抵消脉振电动势exe,从而抑制负序电流和直接耦合电流。前馈补偿电压值与脉振电动势的值相等,有
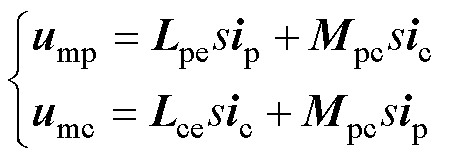 (30)
(30)
式中,ump和umc分别为功率绕组和控制绕组前馈补偿电压矢量。
将脉振电感矩阵和直接耦合互感矩阵代入式(30)中,并由基尔霍夫电流定律消去A、B相电流,可得功率绕组三相电压补偿量为
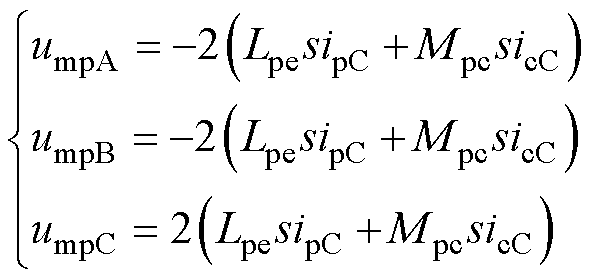 (31)
(31)
式中,umpA、umpB和umpC分别为功率绕组A相、B相和C相前馈补偿电压;ipC和icC分别为功率绕组和控制绕组C相电流。
由式(31)可知,脉振电压补偿值中,三相电压幅值相同。A相电压与B相电压相位相同,且与C相电压相位相反。三相合成电压为一空间位置恒定、幅值随功率绕组和控制绕组电流对时间的导数变化而变化的脉振电压,可表示为
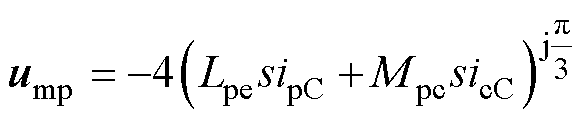 (32)
(32)
将功率绕组脉振电压矢量分解到两相静止坐标系,可得功率绕组补偿电压的ab 分量分别为
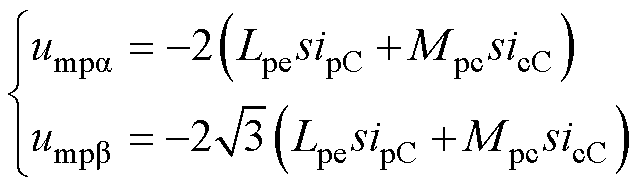 (33)
(33)
同样地,控制绕组补偿电压的ab 分量分别为
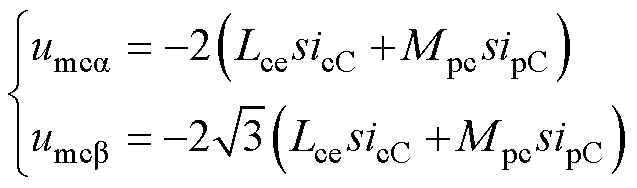 (34)
(34)
结合两套绕组变频器的控制方法及静态端部效应补偿算法,可以构建带静态端部效应补偿的NLS- LDFM功率绕组电压定向控制策略,如图6所示。控制框图主要分为三部分,第一部分为功率绕组侧变频器控制,首先给定参考磁链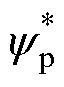 和频率wp,计算得到参考电压
和频率wp,计算得到参考电压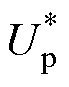 ,令
,令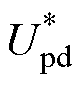 =
=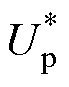 ,
,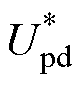 =0,并由频率积分得到坐标变换角qp,以实现功率绕组d轴电压定向。第二部分为控制绕组侧变频器控制,包含速度和电流两个控制环路,速度环的输出为控制绕组d轴电流的参考值
=0,并由频率积分得到坐标变换角qp,以实现功率绕组d轴电压定向。第二部分为控制绕组侧变频器控制,包含速度和电流两个控制环路,速度环的输出为控制绕组d轴电流的参考值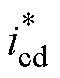 ,由式(26)可知,控制绕组q轴电流不产生推力,因此可令
,由式(26)可知,控制绕组q轴电流不产生推力,因此可令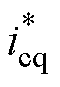 =0。控制绕组三相电流的坐标变换角qc为
=0。控制绕组三相电流的坐标变换角qc为
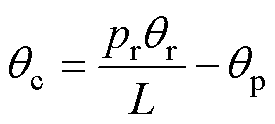 (35)
(35)
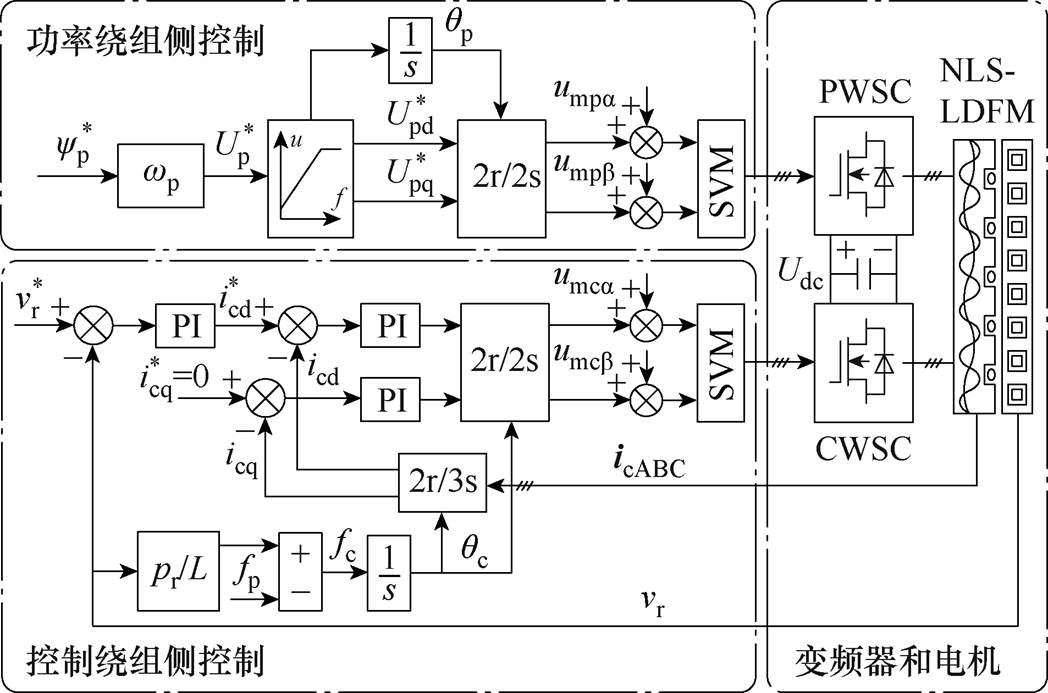
图6 带静态端部效应补偿的电压定向控制
Fig.6 Block diagram of voltage orientation control with static end effect compensation
第三部分为静态端部效应前馈电压补偿,分别由式(33)和式(34)计算得到功率绕组和控制绕组两相静止坐标系下的电压补偿值umpab 和umcab,然后在电压参考值中注入脉振电压以补偿静态端部效应产生的不平衡电流和谐波电流。其中,功率绕组侧变频器未对功率绕组电流进行控制,仍需要电流传感器采集功率绕组相电流(至少是C相电流),用于计算端部效应补偿电压。
由于加工和装配误差等因素影响,实际样机参数和设计参数并不一致,为准确获取样机的脉振电感和直接耦合参数,可以采用文献[20]中实验测定的方法,具体如下:将功率绕组开路,在异步运行模式下测量功率绕组的感应电压,使电机运行于自然同步速,此时调制磁场与开路绕组相对静止,不产生电动势。为控制绕组通入频率和电压恒定的交流电,调整负载大小,使电机稳定运行于自然同步速附近,同时记录功率绕组线电压和控制绕组C相电流,此时功率绕组的感应电动势均是由脉振磁场产生的脉振电动势ump。由于功率绕组三相开路,其三相电流ip=0,脉振自感产生的反电动势为0,反电动势均由直接耦合互感产生,则功率绕组和控制绕组的直接耦合互感矩阵可以表示为
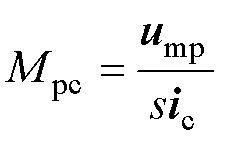 (36)
(36)
式中,sic为控制绕组电流对时间的导数。在实验中直接对电流求导可能会将噪声放大,导致系统失稳。因此,采用跟踪微分器来计算电流的导数[21]。通过实验测定得到直接耦合互感后,可进一步由式(37)和式(38)计算得到功率绕组和控制绕组的脉振自感。
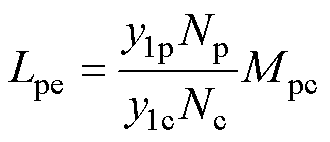 (37)
(37)
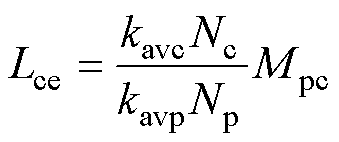 (38)
(38)
式中,y1p和y1c分别为功率绕组和控制绕组的节距;Np和Nc分别为功率绕组和控制绕组的每相串联匝数;kavp和kavc分别为功率绕组和控制绕组的绕组脉振系数。
在电流一定时,脉振电动势的幅值与脉振电感等参数的大小成正比,脉振电动势中的正序和负序分量相等,当参数准确时,补偿电压可基本抵消电压方程中的脉振电动势分量。当参数不准确时,补偿误差基本成比例线性增大。在仿真中分别改变功率绕组脉振电感、直接耦合互感参数至原来的50%~150%,功率绕组三相电流不对称度和直接耦合电流含量的变化曲线如图7和图8所示(三相电流不对称度=负序电流幅值/正序电流幅值)。
当脉振电感的变化率由0变化至±50%时,三相电流不对称度也随之线性变化,由2%均匀变化至7%,当变化率为0时三相电流不对称度最小,补偿效果最好。由于直接耦合和磁场调制(间接耦合)作用同时存在,由直接耦合产生的谐波电流频率丰富。当功率绕组基波频率为50 Hz,控制绕组基波频率为20 Hz时,功率绕组中的直接耦合电流频率除20 Hz外,还有80 Hz和110 Hz等频率成分,图8中绘制出了含量较高的频率为20 Hz和80 Hz的电流随直接耦合互感参数变化的曲线,其中在互感参数变化率为负时频率为20 Hz的电流含量最小,其他频率如80 Hz的电流含量则在互感参数变化率为正时最小,综合起来在互感变化率为0附近时直接耦合电流含量最小,但受到动态端部效应等其他因素影响有所偏移。
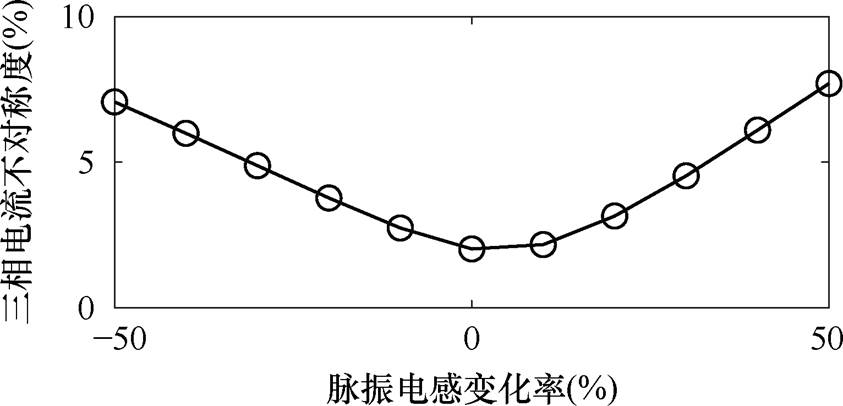
图7 三相电流不对称度随脉振电感变化曲线
Fig.7 The variation curve of three-phase current asymmetry with pulsating inductance
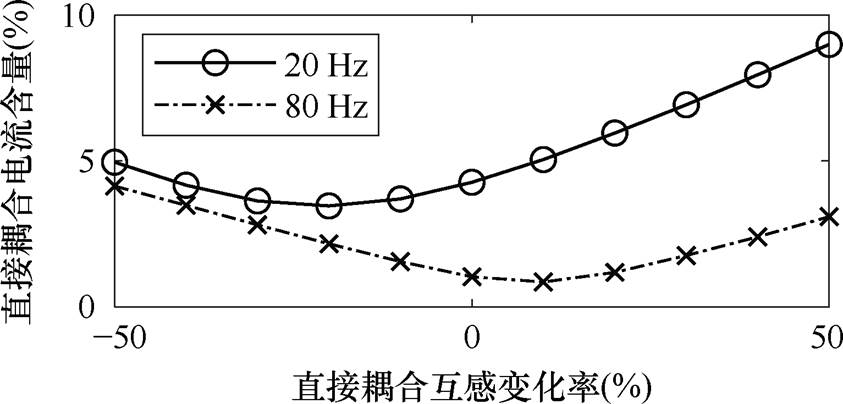
图8 直接耦合电流含量随直接耦合互感变化曲线
Fig.8 The variation curves of direct-coupling current with direct-coupling inductance
为验证所提的NLS-LDFM磁场定向控制及静态端部效应补偿策略的有效性,本文通过Matlab/ Simulink对一台2/4对极的3 kW NLS-LDFM进行仿真分析。仿真中,功率绕组采用恒V/F控制,电压幅值按比例匀速上升,给定线电压有效值为180 V,频率为50 Hz。仿真结果如图9~图14所示。
首先将控制绕组三相短路实现级联异步起动,待电机速度升至自然同步速附近后,在t =1 s时进行速度闭环控制,给定速度为4.5 m/s,此时未施加静态端部效应补偿。在t =3 s时,同时对功率绕组和控制绕组施加补偿电压,补偿初级两套绕组的静态端部效应。电机运行速度曲线如图9所示,功率绕组电压定向控制能够较好地跟踪目标速度。
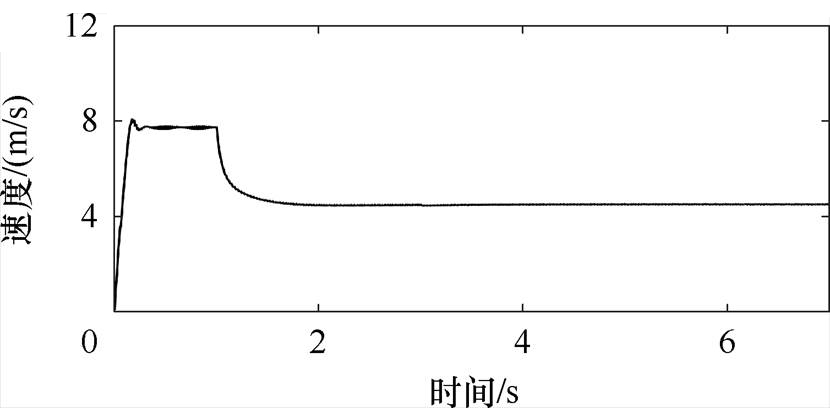
图9 电机运行速度曲线
Fig.9 The curve of mechanical velocity
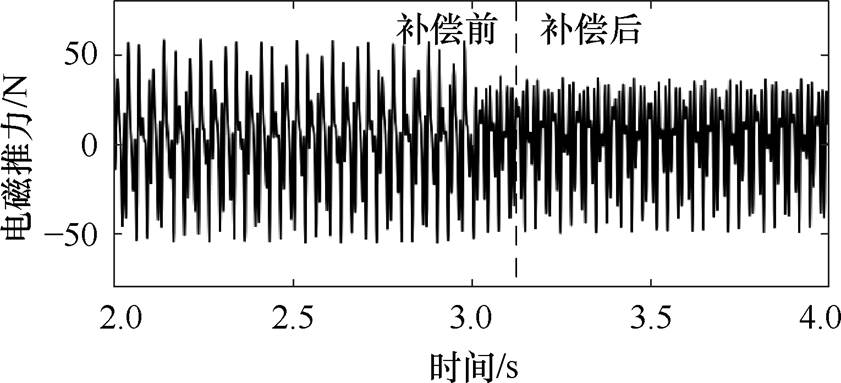
图10 电磁推力波形
Fig.10 Electromagnetic thrust waveform
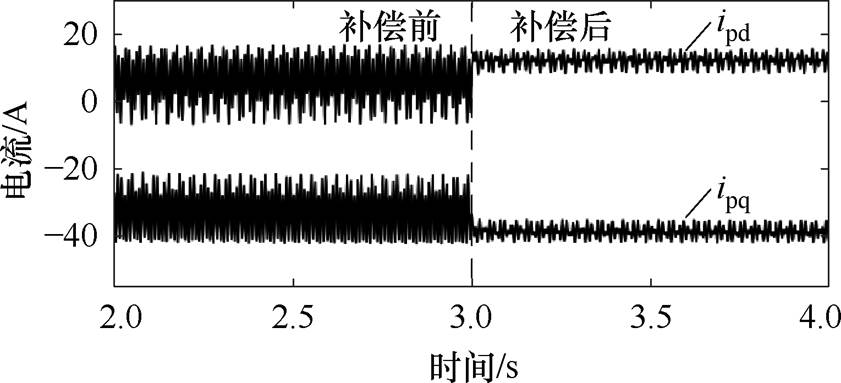
图11 功率绕组dq轴电流
Fig.11 The dq-axis current of power winding
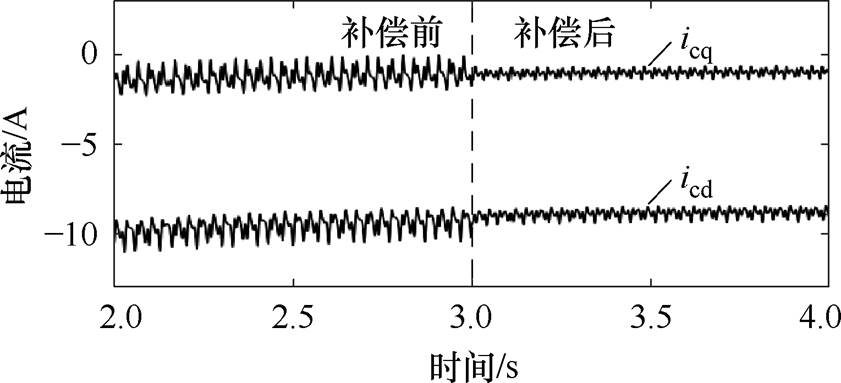
图12 控制绕组dq轴电流
Fig.12 The dq-axis current of control winding
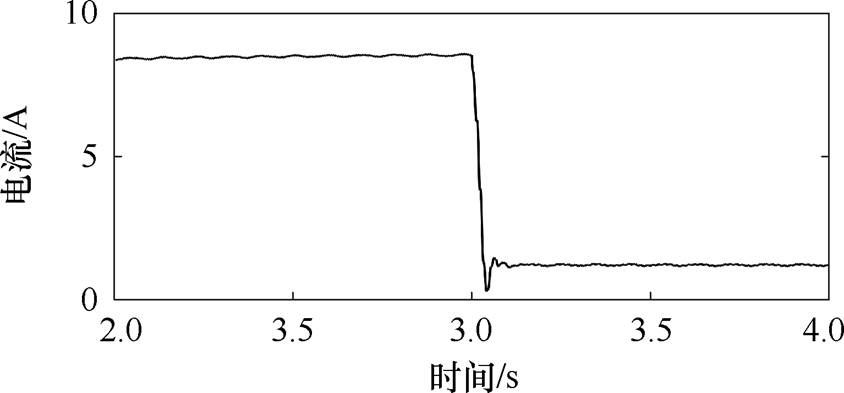
图13 功率绕组负序电流幅值
Fig.13 Negative sequence current amplitude of power winding
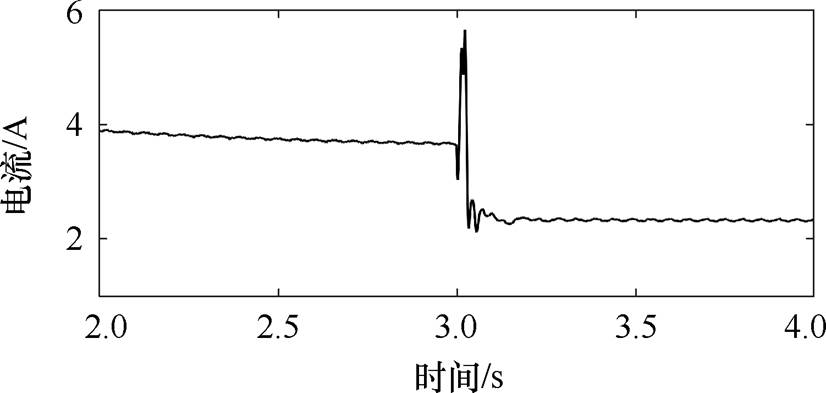
图14 功率绕组直接耦合电流幅值
Fig.14 Direct-coupling current amplitude of power winding
图10为空载时的电磁推力波形,其波动幅值较大,平均值为0。在t=2~3 s时为未补偿静态端部效应时的电磁推力,t=3~4 s为施加补偿后的电磁推力。电磁推力的波动幅值由55 N减小到了38 N,推力波动降低了31%。对比发现,通过静态端部效应补偿可有效减小电磁推力的波动。
图11和图12分别为功率绕组和控制绕组dq轴电流波形,在同步旋转坐标系下,dq轴电流应为直流量,但由于功率绕组和控制绕组中均含有直接耦合电流、负序电流等分量,谐波电流在同步旋转坐标系下为交流量,其幅值越大,dq轴电流的波动越大。静态端部效应补偿后,功率绕组和控制绕组电流波动幅值均有所减小,谐波电流得到抑制。
图13和图14分别给出了功率绕组负序电流幅值和直接耦合电流幅值的波形。补偿前负序电流的幅值为8.6 A,补偿后负序电流幅值减小到了1.7 A。功率绕组直接耦合电流的频率与控制绕组基波频率相同,已知电机的运行速度为4.5 m/s,功率绕组电流频率为50 Hz,可由式(4)计算得到控制绕组电流基波频率为20 Hz,即功率绕组直接耦合电流频率为20 Hz。静态端部效应补偿前直接耦合电流幅值为3.8 A,补偿后直接耦合电流的幅值减小到了2.3 A。
为验证本文所提控制方法的有效性,搭建了如图15所示的3 kW弧形同心笼次级直线双馈电机测试平台,采用弧线段模拟直线运动,可使电机连续运行,以便于实验验证,实验中用到的样机主要参数见表1。
该实验平台的NLS-LDFM电机由两个1/4弧形初级和一个圆形次级组成,可任选一套初级通电;负载由一台永磁同步发电机、调压器和电阻箱提供,通过调节调压器输出电压来调节负载功率;变频器由两台共用直流母线的逆变器及一台三相不控整流器组成,整流器将输入的三相交流电转变为直流电为逆变器供电,逆变器分别与初级两套绕组连接。实验时先控制CWSC下桥臂IGBT全部开通,上桥臂IGBT全部关断,保持恒定压频比逐渐增大功率绕组侧电压,直至相电压幅值达到180 V,频率达到50Hz,以实现控制绕组短路的级联异步起动。待电机起动完成后控制CWSC工作在逆变状态,将电机切入双馈闭环运行模式,设定目标速度为6 m/s,调节调压器给电机施加负载约89 N。实验中控制绕组PI控制器的参数为:电流环kp=30,ki=5;速度环kp=1.5,ki=1。

图15 弧形NLS-LDFM实验平台
Fig.15 The experimental platform of NLS-LDFM
表1 NLS-LDFM样机主要参数
Tab.1 The main parameters of NLS-LDFM prototype
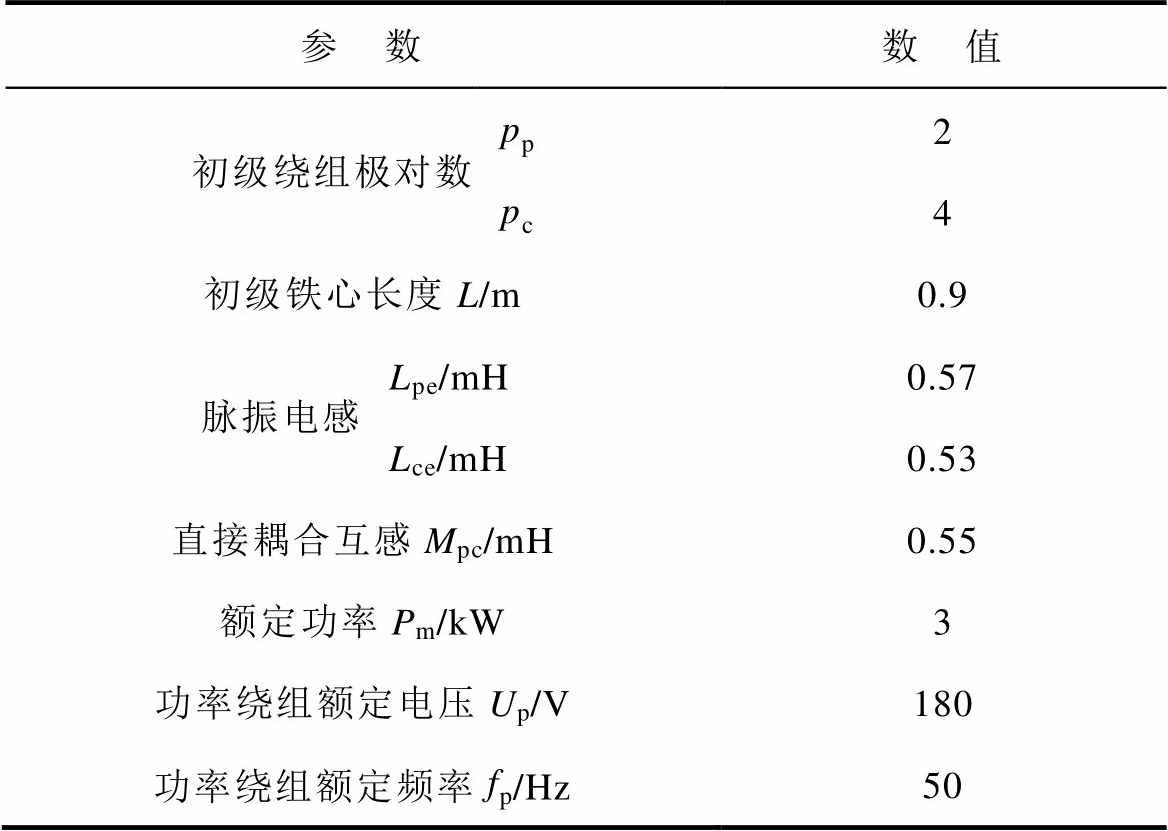
参 数数 值 初级绕组极对数pp2 pc4 初级铁心长度L/m0.9 脉振电感Lpe/mH0.57 Lce/mH0.53 直接耦合互感Mpc/mH0.55 额定功率Pm/kW3 功率绕组额定电压Up/V180 功率绕组额定频率fp/Hz50
图16为功率绕组电流波形,其中图16a为静态端部效益补偿前的三相电流,图16b为补偿后的三相电流。在施加补偿前,功率绕组三相电流不对称度较大,表明在静态端部效应作用下,功率绕组负序电流含量较高。补偿后,电流不对称度明显降低,三相电流幅值基本相等,表明绕组中的负序电流得到了有效抑制。施加补偿后三相电流幅值增大,是由于功率绕组额外施加了补偿电压却并未采用电流闭环。图16c为补偿前后功率绕组相电流快速傅里叶变换(Fast Fourier Transform, FFT)结果对比,由式(4)可以计算得到控制绕组基波电流频率为10 Hz,因此功率绕组中通过直接耦合产生的10 Hz电流含量较高,在经过补偿后其含量由9.9%降低到了2.3%。
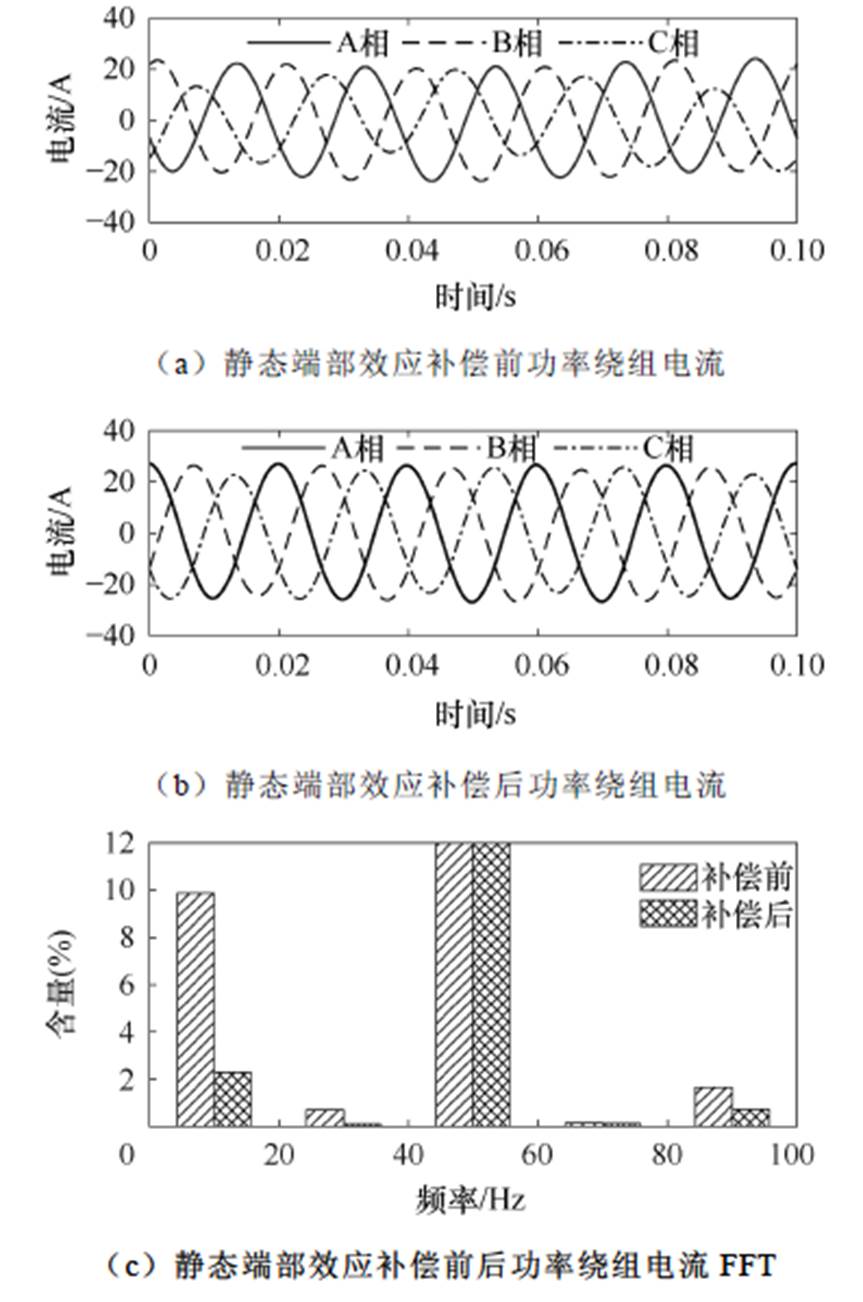
图16 功率绕组电流
Fig.16 The current of power winding
图17为控制绕组三相电流波形,其中图17a为静态端部效应补偿前三相电流波形,图17b为补偿后三相电流波形。与功率绕组类似,静态端部效应补偿前控制绕组三相电流存在一定程度的不对称,补偿后三相电流不对称度减小。除此之外,控制绕组三相电流正弦度更好,表明其中的谐波电流含量有所减小。图17c为补偿前后控制绕组相电流FFT结果对比,由图可知,控制绕组的基波频率为10 Hz,直接耦合电流的频率为50 Hz,经过补偿后其含量由3.7%降低至2.9%。相比功率绕组,控制绕组的三相对称度更好,直接耦合电流含量更低,这是由于控制绕组的极对数较多,静态端部效应产生的影响更小。
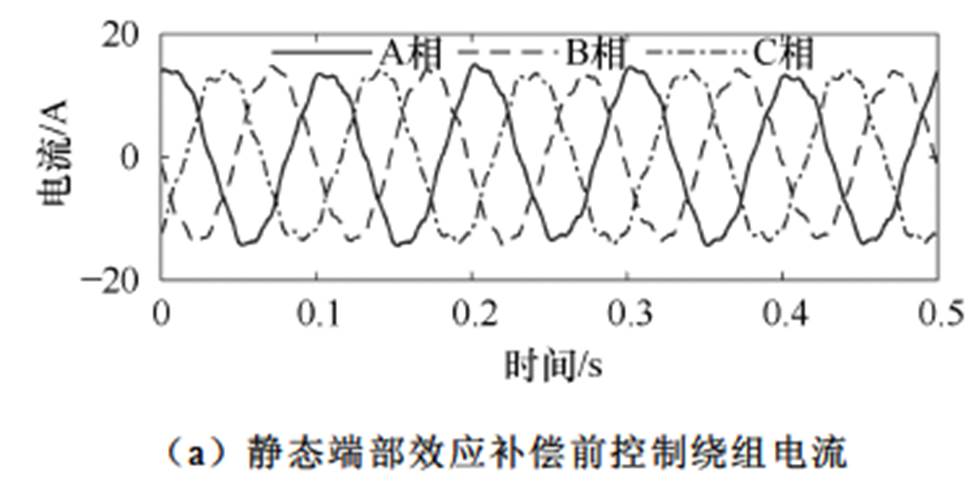
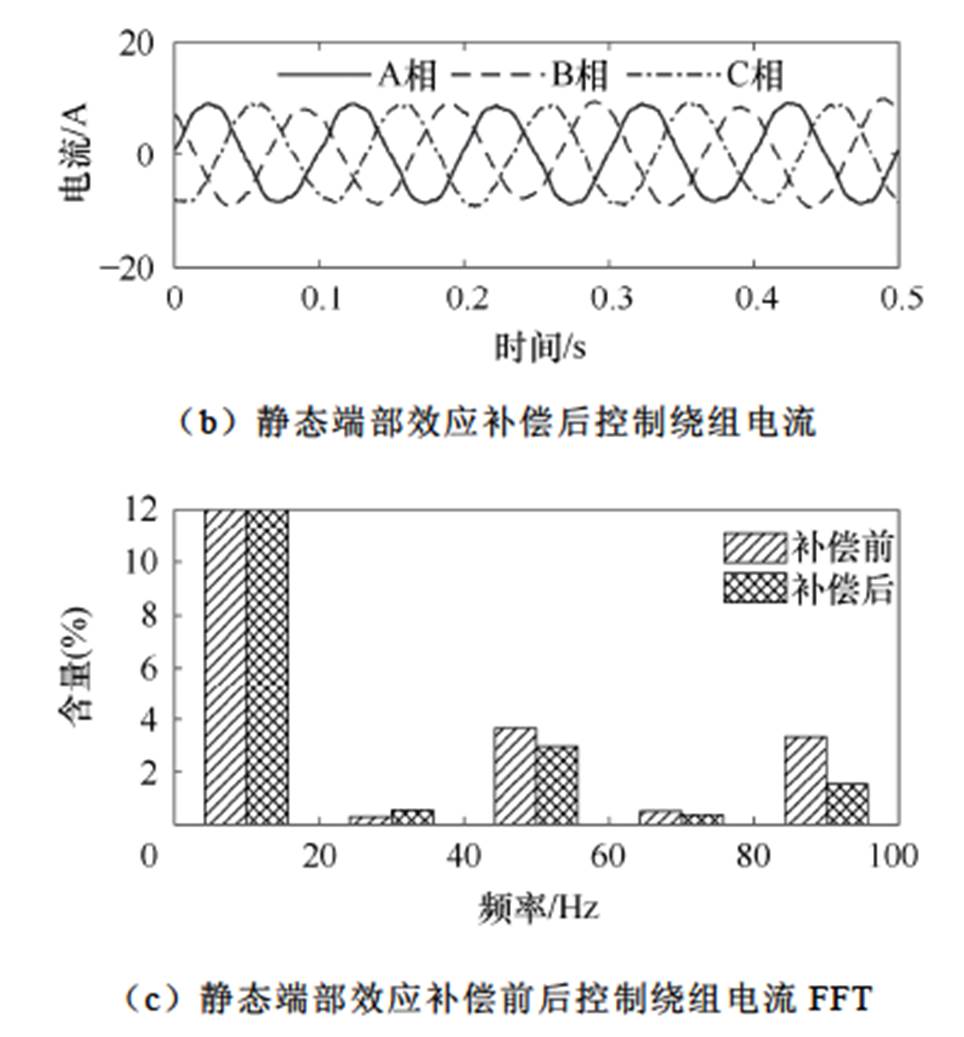
图17 控制绕组电流
Fig.17 The current of control winding
图18为静态端部效应补偿前后的控制绕组dq轴电流波形,施加静态端部效应补偿后控制绕组dq轴电流波动明显减小,表明相电流中的负序电流和直接耦合电流得到了有效抑制。此外,施加补偿后,功率绕组电压增大,导致功率绕组磁链增大,由电磁推力表达式(26)可知,为维持输出推力的恒定,控制绕组d轴电流icd幅值减小,q轴电流icq幅值不变。
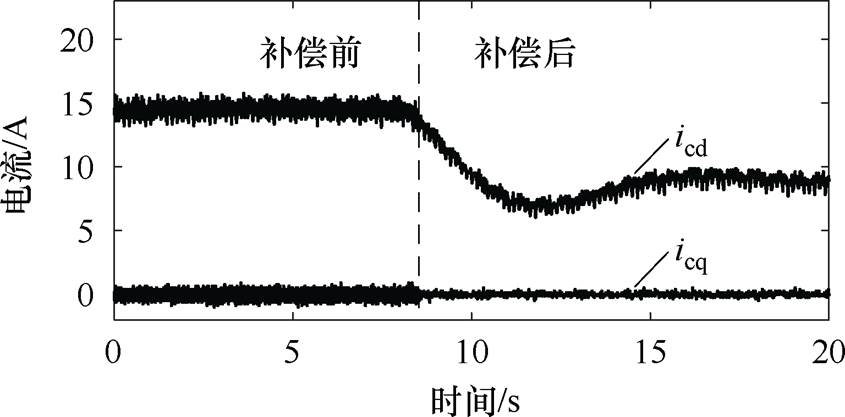
图18 静态端部效应补偿前后控制绕组dq轴电流
Fig.18 The comparison of dq-axis current of control winding before and after static end effect compensation
图19为给定速度由次同步速6 m/s均匀上升至超同步速9 m/s时的电机速度波形,电机能够平稳地越过自然同步速(7.5 m/s)。图20为电机调速过程中的控制绕组dq轴电流,转速上升时d轴电流增大提供的电磁推力,q轴电流保持不变且平均值为0,表明其不提供电磁推力。
除改善电流波形,通过静态端部效应补偿还可有效提升电机推力、效率等性能。由于电磁推力难以直接测量,本文采取测量振动和噪声的方法间接测量推力波动,在电机稳定运行时,通过希玛AR63C笔式测振仪测得电机台架的振动由0.15 mm/s降低至0.12 mm/s,通过德力西分贝测量仪测得电机附近同一位置噪声由64 dB降低至56 dB,表明电机的推力波动得到有效抑制。
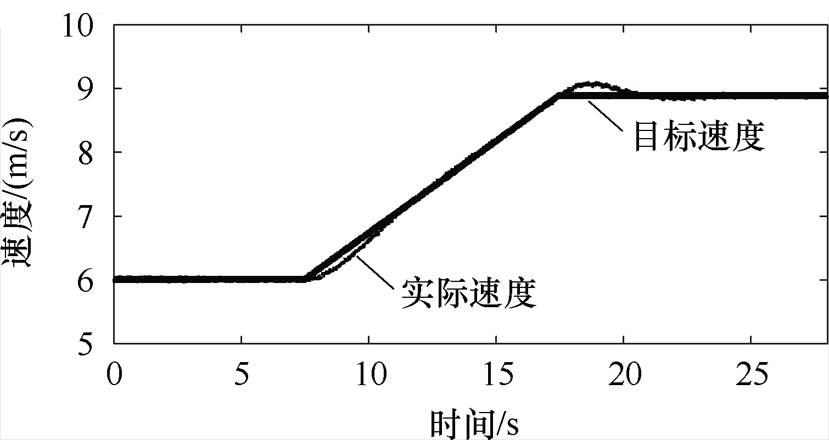
图19 速度上升曲线
Fig.19 The slop curves of speed
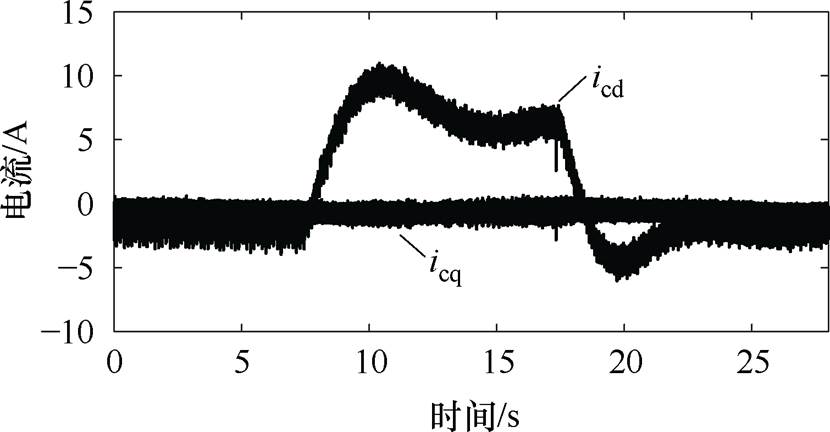
图20 控制绕组dq轴电流
Fig.20 The dq-axis current of control winding
利用电机实测电流和控制器输出电压计算得到电机输入功率,利用转矩测量仪测量转速和平均转矩计算得到输出功率,进而得到电机效率。在保持功率绕组电压和输出功率不变的前提下,通过静态端部效应补偿后效率提升2%~5.5%。
针对城轨交通用同心笼次级直线双馈电机端部效应显著、控制复杂等特点,本文提出了一种简单易行的考虑静态端部效应补偿的功率绕组电压定向控制方法,着重对比分析了静态端部效应补偿前后的电机电流、推力等性能指标。大量仿真和实验结果表明,通过静态端部效应补偿后,新方法可有效抑制初级两套绕组中直接耦合电流和负序电流的含量,明显降低dq轴电流波动幅值,成功实现直流电网下的电机稳态和动态双馈闭环运行,有效抑制电机推力波动,提高运行效率等。
参考文献
[1] 吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665-5675.
Lü Gang. Review of the application and key technology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5675.
[2] 徐伟, 肖新宇, 董定昊, 等. 直线感应电机效率优化控制技术综述[J]. 电工技术学报, 2021, 36(5): 902-915, 934.
Xu Wei, Xiao Xinyu, Dong Dinghao, et al. Review on efficiency optimization control strategies of linear induction machines[J]. Transactions of China Elec- trotechnical Society, 2021, 36(5): 902-915, 934.
[3] 沈燚明, 卢琴芬. 初级励磁型永磁直线电机研究现状与展望[J]. 电工技术学报, 2021, 36(11): 2325- 2343.
Shen Yiming, Lu Qinfen. Overview of permanent magnet linear machines with primary excitation[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2325-2343.
[4] Saifkhani F, Wallace A K. A linear brushless doubly- fed machine drive for traction applications[C]//1993 Fifth European Conference on Power Electronics and Applications, Brighton, UK, 1993: 344-348.
[5] Zhong Zaimin, Shao Zhongshu, Yang Minglei, et al. Quasi-synchronous operation principle of a variable air-gap doubly fed linear motor for high-speed maglev application[J]. IEEE Transactions on Transportation Electrification, 2023, 9(2): 2929-2940.
[6] Seifkhani F. Investigation, analysis and design of the linear brushless doubly-fed machine[D]. USA: Oregon State University, 1991.
[7] Wang Ying, He Hongyun, Lu Weiguo, et al. Calcu- lation and analysis of electromagnetic characteristics of double-fed linear motor[J]. IEEE Access, 2019, 7: 12291-12296.
[8] Sarasola I, Poza J, Rodriguez M A, et al. Direct torque control design and experimental evaluation for the brushless doubly fed machine[J]. Energy Conversion and Management, 2011, 52(2): 1226- 1234.
[9] 张凤阁, 朱连成, 金石, 等. 开绕组无刷双馈风力发电机最大功率点跟踪直接转矩模糊控制研究[J]. 电工技术学报, 2016, 31(15): 43-53.
Zhang Fengge, Zhu Liancheng, Jin Shi, et al. Research on the maximum power point tracking of brushless doubly-fed wind power generator with open winding direct torque fuzzy control strategy[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 43-53.
[10] Poza J, Oyarbide E, Roye D. New vector control algorithm for brushless doubly-fed machines[C]// IEEE 2002 28th Annual Conference of the Industrial Electronics Society, Seville, Spain, 2002: 1138- 1143.
[11] 孔铭. 无刷双馈电动机变频调速系统控制方法研究[D]. 武汉: 华中科技大学, 2018.
Kong Ming. Research on control methods of variable frequency speed regulation system based on a brushless doubly-fed motor[D]. Wuhan: Huazhong University of Science and Technology, 2018.
[12] 王淼, 杨晓峰, 李世翔, 等. 城市轨道交通直流自耦变压器牵引供电系统故障保护研究[J]. 电工技术学报, 2022, 37(4): 976-989.
Wang Miao, Yang Xiaofeng, Li Shixiang, et al. Fault protection of DC auto-transformer traction power supply system for urban rail transit[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 976- 989.
[13] Ge Jian, Xu Wei, Liu Yi, et al. Investigation on winding theory for short primary linear machines[J]. IEEE Transactions on Vehicular Technology, 2021, 70(8): 7400-7412.
[14] 葛健. 同心笼次级直线双馈电机端部效应及运行特性分析[D]. 武汉: 华中科技大学, 2019.
Ge Jian. End effect and Characteristic analysis for linear doubly fed machine with nested-loop secondary[D]. Wuhan: Huazhong University of Science and Technology, 2019.
[15] 包振, 葛健, 徐伟, 等. 同心笼次级直线双馈电机静态端部效应补偿策略[J]. 电工技术学报, 2023, 38(17): 4621-4632.
Bao Zhen, Ge Jian, Xu Wei, et al. Compensation strategy for static end effect in nest-loop secondary linear doubly-fed machine[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4621-4632.
[16] Cheng Yuan, Yu Bo, Kan Chaohao, et al. Design and performance study of a brushless doubly fed generator based on differential modulation[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(12): 10024- 10034.
[17] 于克训, 陈曦, 谢贤飞, 等. 无刷双馈电机研究综述与展望[J]. 电工技术学报, 2024, 39(2): 397-422.
Yu Kexun, Chen Xi, Xie Xianfei, et al. Overview and prospect of the brushless doubly-fed machine research[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 397-422.
[18] 孙兆龙, 马伟明, 鲁军勇, 等. 长初级双边直线感应电动机静态纵向边端效应及阻抗矩阵研究[J]. 中国电机工程学报, 2010, 30(18): 72-77.
Sun Zhaolong, Ma Weiming, Lu Junyong, et al. Research of static longitudinal end effect and impedance matrix for long primary double-sided linear induction motors[J]. Proceedings of the CSEE, 2010, 30(18): 72-77.
[19] Poza J, Oyarbide E, Roye D, et al. Unified reference frame dq model of the brushless doubly fed machine[J]. IET Electric Power Applications, 2006, 153(5): 726-733.
[20] 葛健, 徐伟, 刘毅, 等. 考虑端部效应的同心笼次级直线双馈电机等效电路[J]. 电工技术学报, 2022, 37(19): 4957-4968.
Ge Jian, Xu Wei, Liu Yi, et al. Equivalent circuit for nested-loop secondary linear doubly-fed machine considering end effect[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4957-4968.
[21] Huang Renzhi, Quan Xiangjun, Wu Zaijun, et al. A novel reduced-order generalized differentiator with zero-phase lag and improved noise attenuation[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 1406-1411.
Abstract Compared with the rotating machine, the linear machine has the advantages of strong climbing ability, small turning radius, low noise, light vehicle weight, and low overall energy consumption, which is especially suitable for urban rail transit drive systems. The nest-loop secondary linear doubly-fed machine (NLS-LDFM) is a new linear machine evolved from the nest-loop rotor brushless doubly-fed machine (BDFM), with a simple structure and easy operation and maintenance. It can overcome the significant thrust and power factor decrease under high speed and large slip.
However, traditional control methods for BDFM are unsuitable because of the static end effect and the DC grid supply. Due to the cut-open primary iron core, the static end effect in NLS-LDFM generates the pulsating magnetic field evenly distributed along the motion direction, leading to two sets of asymmetrical three-phase windings and direct coupling. The large harmonic current, including negative sequence current and direct-coupling current, is produced. Furthermore, since the power supply of NLS-LDFM is different from that of BDFM, it is necessary to realize the close loop doubly-fed mode operation in urban transit power supply. Thus, a power winding voltage-oriented vector control strategy with static end effect compensation is proposed.
Firstly, the basic structure and operation principle of NLS-LDFM, similar to the BDFM, is introduced. The static end effect and its compensation principle are analyzed. Then, the mathematical model of the three-phase static coordinate system and simplified two-phase rotating coordinate system are established. Secondly, the mathematical relationship of the primary current under the voltage orientation of the power winding is derived, and the decoupling control of two sets of winding in the electromagnetic thrust equation is realized. The power winding and control winding side converter control methods are presented. The constant voltage and frequency ratio control is employed in power winding, and the double close loop control of speed and current is applied in control winding.
Simulations and experiments have demonstrated that the new method can effectively improve the steady-state drive performance of the NLS-LDFM through vector control with static end effect compensation. With the power winding voltage-oriented vector control, the electromagnetic thrust and speed can be controlled conveniently by adjusting the d-axis current of the control winding. With the static end effect compensation, the three-phase current of two winding sets is symmetrical, effectively suppressing the negative sequence current. The fast Fourier transform results show that the direct-coupling current is also suppressed. Furthermore, the noise and vibration can be decreased, and the efficiency can be improved.
The following conclusions can be drawn. (1) The power winding voltage-oriented vector control easily realizes the start process and close loop doubly-fed operation in the DC power supply. The cross-coupling between power winding and control winding can be ignored. The electromagnetic thrust can be controlled directly by adjusting the d-axis current of the control winding. (2) The proposed static end effect compensation method is realized by pulsating voltage feedforward. Compared with the NLS-LDFM without compensation, the harmonic current and thrust ripple are suppressed effectively.
keywords:Linear doubly-fed machine (LDFM), static end effect, vector control, urban transit
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.231655
国家自然科学基金(52277050)和中国博士后科学基金(2023M731178)资助项目。
收稿日期2023-10-10
改稿日期2023-12-07
葛 健 男,1994年生,博士,研究方向为新型直线电机电磁设计与特性分析。E-mail: gejian1994@hust.edu.cn
包 振 男,1998年生,博士研究生,研究方向为无刷双馈电机与直线电机驱动控制。E-mail: zhenbao@hust.edu.cn(通信作者)
(编辑 崔文静)