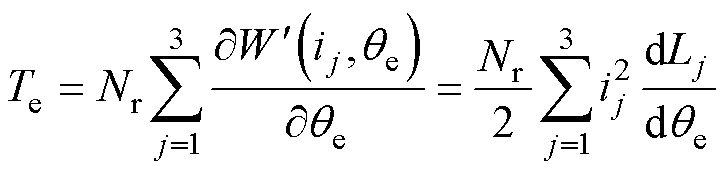 (1)
(1)
摘要 针对开关磁阻电机转矩脉动大,现有开关磁阻电机的转矩脉动抑制方案通常依赖于大量电机电磁特性数据的问题,该文提出一种基于电流平方量约束的新型开关磁阻电机转矩调制方法,既可以有效降低开关磁阻电机转矩脉动,也大大降低了控制过程中对于电机电磁特性数据的依赖。首先,基于开关磁阻电机瞬时转矩公式得出一阶电流平方量对于转矩产生的作用;其次,分析了二阶电流平方量的影响,通过一、二阶电流平方量的协同作用得出最小化开关磁阻电机转矩脉动的约束条件;再次,采用极值点确定法得出电流平方量的最优给定值,对于误差转矩脉动采用瞬时转矩补偿法进行分相直接抑制;最后,基于一台150 W、三相12/8极开关磁阻电机进行了实验,验证了所提方法的可行性与有效性。
关键词:开关磁阻电机 电流平方量 转矩脉动抑制 电磁特性数据 极值点确定法
随着对稀土资源竞争的日益激烈,少稀土或无稀土电机引起了研究人员的极大关注[1-5]。作为无稀土电机的典型代表,开关磁阻电机(Switched Reluctance Motor, SRM)因其结构简单、成本低、鲁棒性强和可靠性高,在家用电器、电动车辆、飞机、轨道牵引等领域显示出巨大的应用潜力[6-9]。
传统的SRM驱动系统中广泛使用了角度位置控制、电流斩波控制和电压脉宽调制控制。然而,由于开关磁阻电机固有的双凸极结构,并且通常采用方波励磁类转矩控制方案,相电流中存在大量不理想高次谐波,导致了严重的转矩脉动、振动和噪声,并严重影响了SRM的推广应用[10-13]。在过去几十年中,许多优化的方波励磁类转矩控制策略被研究以减小SRM的转矩脉动。通过引入矢量控制原理,文献[14-16]研究了应用于开关磁阻电机驱动的直接转矩控制(Direct Torque Control, DTC)。然而,由于需要实时观测磁链与转矩实际值和参考值之间的差值,DTC需要大量的磁链和转矩的电磁特性数据支撑控制运算,并且由于缺少对于开通与关断角的限制,电机运行时会产生较大负转矩影响电机运行效率。在转矩分配函数控制(Torque Sharing Function Control, TSFC)中,首先利用预存的转矩-位置-电流数据查找表将相转矩参考值转化为相应的相位电流参考值,然后通过比较参考值和实际值生成驱动信号[17-18]。在直接瞬时转矩控制(Direct Instantaneous Torque Control, DITC)中,通常根据总转矩参考值和实时转矩之间的误差通过各种先进的转矩滞环算法得到驱动信号以抑制换相过程产生的转矩脉动[19-21],并显示出良好的可实施性和简易性。然而,为了实现SRM的优异转矩性能,这些基于准方波励磁的转矩控制方案通常都依赖于高标准的实时设备,以具备忽略时间延迟的高速计算能力和足够的存储空间来预存电机电磁特性数据。
传统交流电机通常电感为平滑正弦波,并且对称的正弦励磁电流使得电机易于实现对于转矩的精确控制以及更简便的运动控制算法。因此,一些学者对比学习了交流电机的控制概念,文献[22]应用三相全桥功率变换器,将双极性正弦波励磁方法应用于开关磁阻电机,通过正弦波电流来抑制转矩脉动和噪声问题。此外,文献[23-25]还研究了二倍频直流偏置正弦波励磁方案,并且文献[26]通过磁场调制理论对该方案进行进一步解释,该理论引入了磁场定向控制,通过q轴和零轴电流的协同控制来调节SRM的平均转矩,从而简化控制逻辑并提高电机系统效率。文献[27]在直流偏置正弦波励磁的基础上加入d轴电流控制以对正弦电流的相位进行偏移优化。然而,直流偏置正弦波励磁电流在不改变电流波形的情况下总会带来固有偏大的转矩脉动无法消除,并不满足开关磁阻电机的低转矩脉动控制要求。同时,上述研究通常没有考虑高阶电感谐波,这意味着许多影响转矩脉动的因素被忽略,转矩产生过程的分析是不完整的。
本文提出了一种基于电流平方量约束的新型开关磁阻电机转矩调制方法。通过考虑高阶电感谐波的影响,提出了一阶、二阶电流平方量叠加控制策略,抑制了由电感谐波与电流平方量相互作用引起的转矩脉动,并且提出偏置电流平方量优化策略,在提高转矩控制效果的同时确保各相电流运行在最低水平。对于无法调控的误差转矩采用瞬时转矩补偿法通过各相单独补偿转矩。实验结果验证了所提方案的可行性与有效性。
根据机电能量转换原理,开关磁阻电机的瞬时转矩公式可表示为
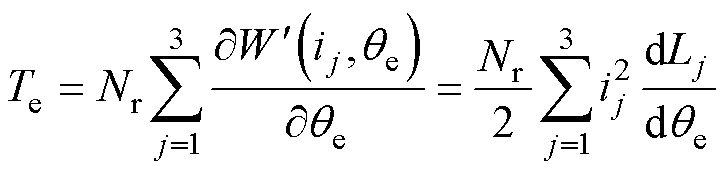 (1)
(1)
式中,Te为瞬时转矩;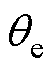 为转子位置电角度;Nr为转子极数;
为转子位置电角度;Nr为转子极数;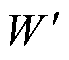 为磁共能;ij与Lj分别为相电流与相电感,其中j为相序,1、2、3分别代表A、B、C相。从式(1)可看出,开关磁阻电机的瞬时转矩由相电流与相电感的相互作用得到。因此,为了阐明电流波形对于转矩产生的影响,应尽可能精确地对相电感进行建模。
为磁共能;ij与Lj分别为相电流与相电感,其中j为相序,1、2、3分别代表A、B、C相。从式(1)可看出,开关磁阻电机的瞬时转矩由相电流与相电感的相互作用得到。因此,为了阐明电流波形对于转矩产生的影响,应尽可能精确地对相电感进行建模。
对于12/8极开关磁阻电机,有限元分析软件中生成的电机电感波形以及对其进行快速傅里叶变换的谐波分析结果如图1所示。由图1a可看出,一个电周期内SRM电感波形类似梯形,其谐波分析结果如图1b所示,以基波为基准值,基波的幅值为100%,电感直流分量的幅值为114.78%,2次谐波的幅值为15.72%,3次谐波幅值为0.26%,4次谐波幅值为4.49%,5次谐波幅值为0.97%,6次谐波为0.24%,7次谐波为1.01%。
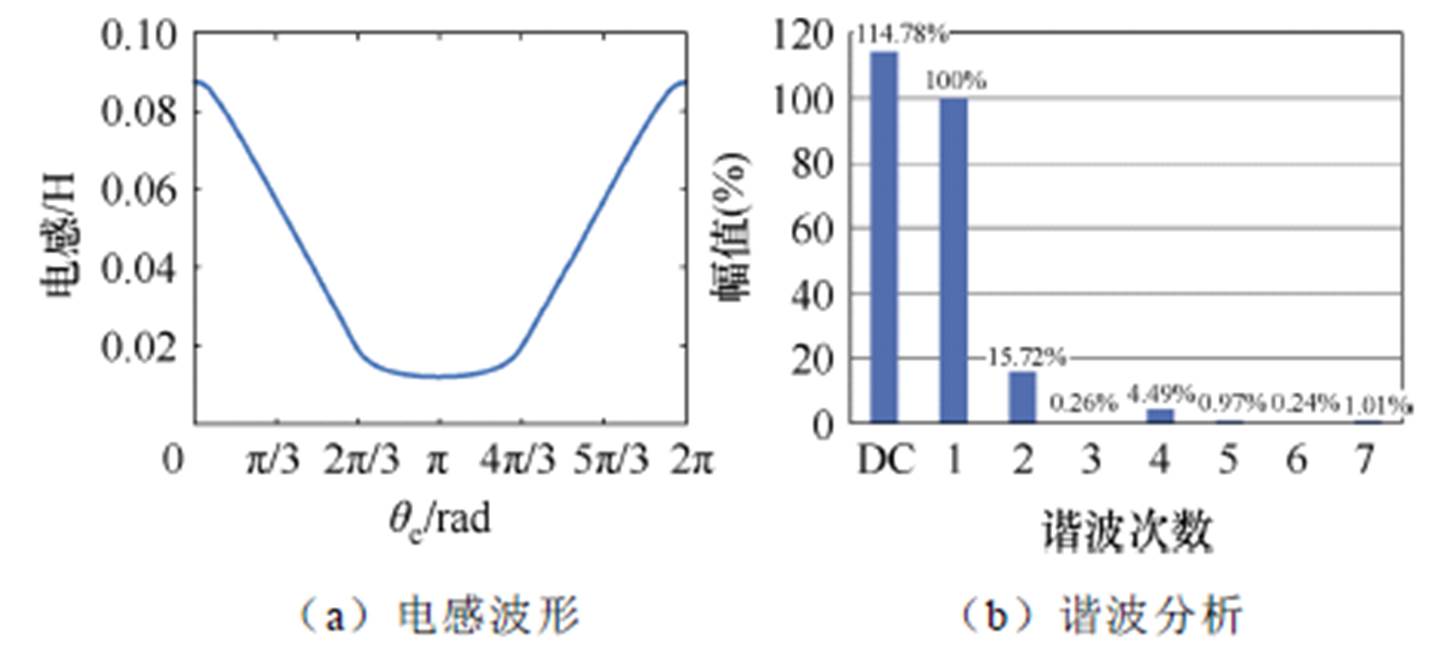
图1 电感波形与谐波分析
Fig.1 Inductance waveform and harmonic analysis
取A相对齐位置电角度为0 rad,相电感的数学模型[28]可表示为
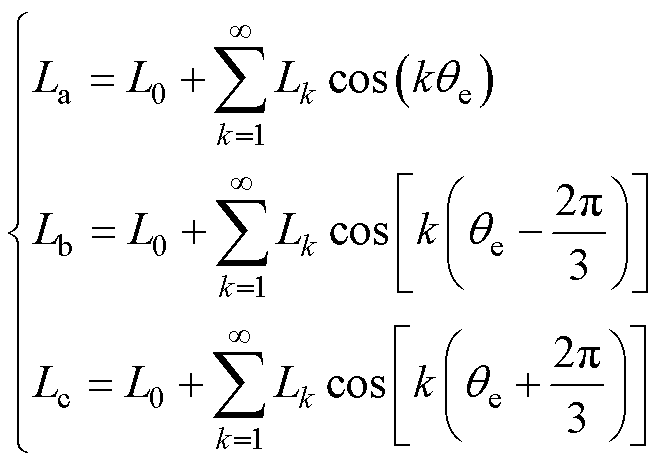 (2)
(2)
式中,La、Lb和Lc分别为A相、B相、C相电感;L0与Lk分别为电感的直流分量与第k次谐波分量的幅值。从图1b中可看出,电感分量中直流分量、基波分量以及第2、4次谐波分量幅值较大,故忽略幅值较小项,相电感可重新表示为
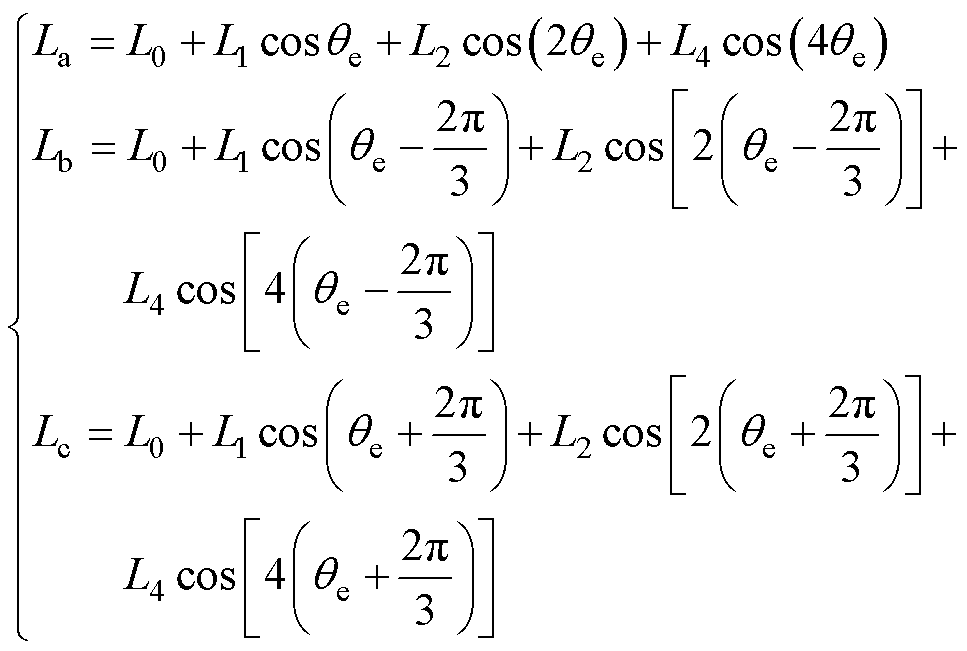 (3)
(3)
式中,L1、L2与L4分别为基波电感、2次谐波电感与4次谐波电感的幅值。
定义相电流的平方为电流平方量,其数值上必须大于零。故基于式(1)和式(3),当电流平方量波形为伴有直流分量的与电感基波同频的正弦波时,电流平方量所产生的电磁转矩为
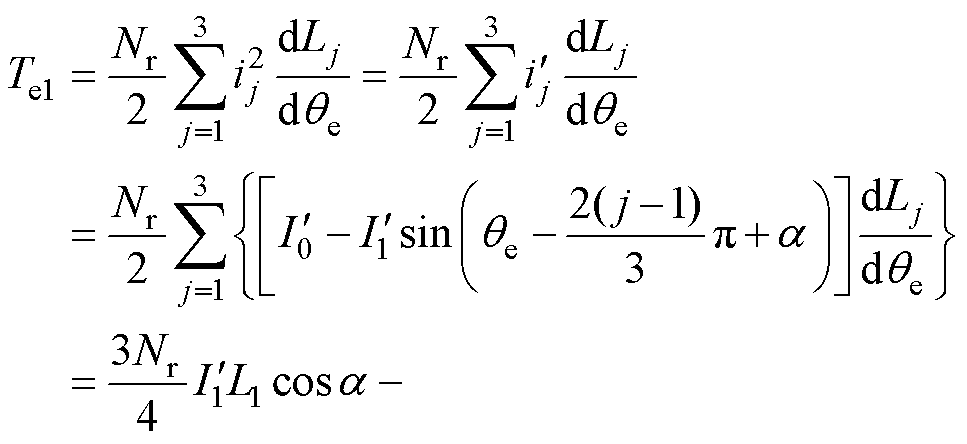
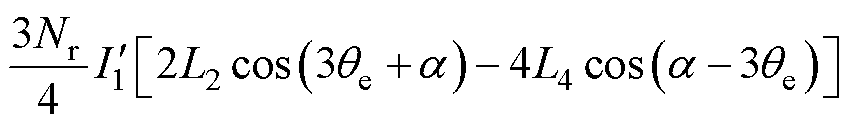 (4)
(4)
式中,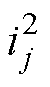 为本文所定义的电流平方量,为了便于分析,将
为本文所定义的电流平方量,为了便于分析,将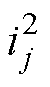 用
用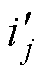 表示;
表示;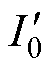 和
和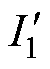 分别为其中所对应的直流分量与交流分量幅值;
分别为其中所对应的直流分量与交流分量幅值;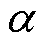 为电流平方量的相位偏移角。将与基波电感为同一交变频率的电流平方量定义为一阶电流平方量,由式(4)可以得出,一阶电流平方量与基波电感作用可以产生恒定的转矩,与2次与4次电感作用将产生三倍频交变转矩,可见,谐波电感的引入导致了转矩交变量即转矩脉动的产生,脉动为三倍频转矩分量。
为电流平方量的相位偏移角。将与基波电感为同一交变频率的电流平方量定义为一阶电流平方量,由式(4)可以得出,一阶电流平方量与基波电感作用可以产生恒定的转矩,与2次与4次电感作用将产生三倍频交变转矩,可见,谐波电感的引入导致了转矩交变量即转矩脉动的产生,脉动为三倍频转矩分量。
为了解决高次电感谐波带来的非理想转矩脉动问题,引入二阶电流平方量,探讨二阶电流平方量对于转矩产生的影响。
将交变频率为一阶电流平方量二倍的电流平方量定义为二阶平方量,三相二阶电流平方量可表 示为
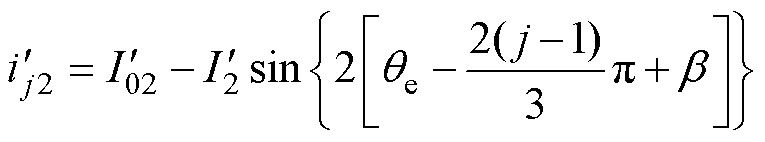 (5)
(5)
式中,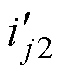 为二阶电流平方量;
为二阶电流平方量;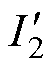 为二阶电流平方量交流分量的幅值;
为二阶电流平方量交流分量的幅值; 为二阶电流平方量的相位偏移角;
为二阶电流平方量的相位偏移角;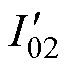 为二阶电流平方量直流偏置量的大小。
为二阶电流平方量直流偏置量的大小。
将式(3)和式(5)代入式(1)可得,当二阶电流平方量作用时,电机产生的电磁转矩为
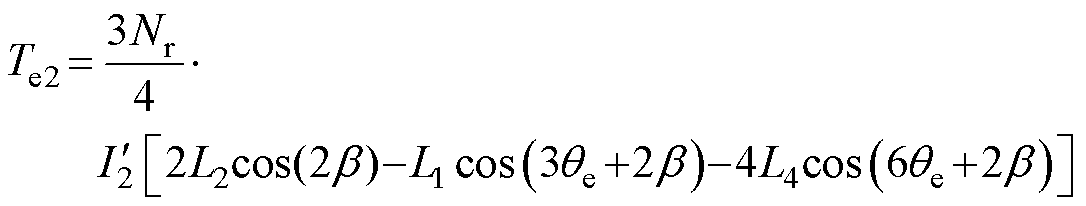 (6)
(6)
由式(6)可得,二阶电流平方量与一次电感相互作用产生三倍频交变转矩,与2次电感相互作用产生恒定转矩,与4次电感相互作用产生六倍频交变转矩。
二阶电流平方量产生的转矩Te2与一阶电流平方量作用时产生的转矩Te1相加可得产生的总转矩为
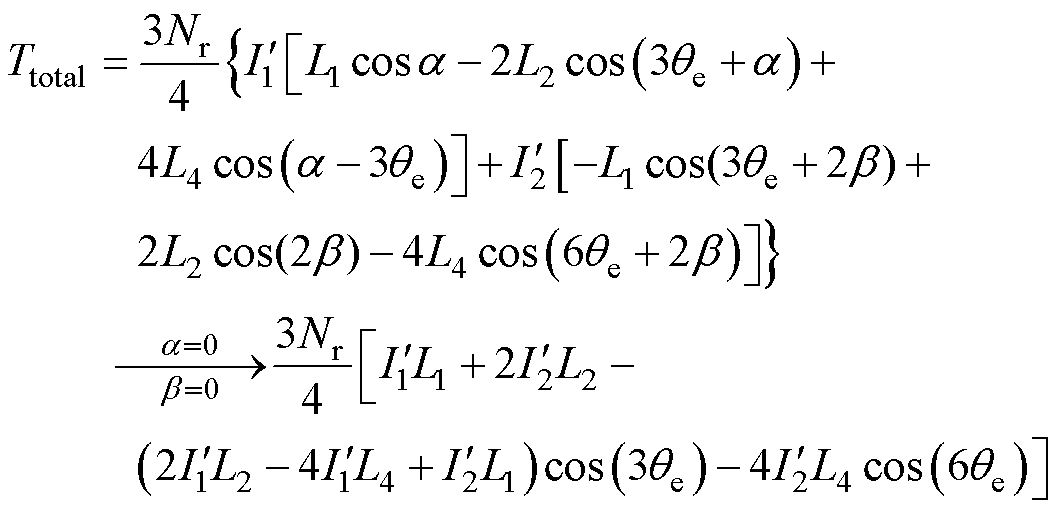 (7)
(7)
当一阶电流平方量相位偏移角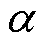 为0 rad时所产生的恒定转矩将达到最大,故取相位偏移角为0 rad。考虑到由一阶电流平方量产生的转矩脉动分量为三倍频分量,而二阶电流平方量产生的转矩主要为三倍频,产生的其余分量幅值相对较小,当相位偏移角
为0 rad时所产生的恒定转矩将达到最大,故取相位偏移角为0 rad。考虑到由一阶电流平方量产生的转矩脉动分量为三倍频分量,而二阶电流平方量产生的转矩主要为三倍频,产生的其余分量幅值相对较小,当相位偏移角 取0 rad时,所产生的三倍频交变转矩与基波电流平方量所产生的三倍频转矩分量相位相同,那么通过一阶、二阶电流平方量的协同作用可优化电机所产生的电磁转矩分量,实现三倍频转矩相抵消,达到转矩调制的目的,实现转矩脉动的最小化控制。
取0 rad时,所产生的三倍频交变转矩与基波电流平方量所产生的三倍频转矩分量相位相同,那么通过一阶、二阶电流平方量的协同作用可优化电机所产生的电磁转矩分量,实现三倍频转矩相抵消,达到转矩调制的目的,实现转矩脉动的最小化控制。
消除三倍频转矩分量的约束条件为
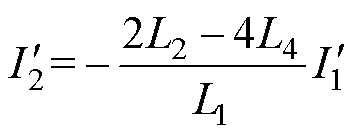 (8)
(8)
当满足上述约束条件时,一、二阶电流平方量所产生的总转矩为
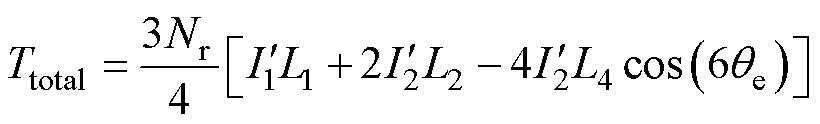 (9)
(9)
此时,各相电流平方量可表示为
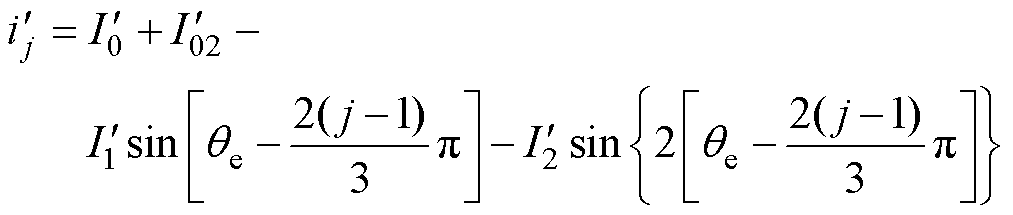 (10)
(10)
电流平方量各分量示意图如图2所示,各相电流平方量可分为交变分量与直流偏置分量。由式(9)可知,电流平方量所产生的转矩为电流平方量中一阶、二阶交变量与各次电感交变量相互作用的结果,与电流平方量中的直流偏置分量无关。由于电流平方量应满足数值上的非负,而过大的直流偏置分量则会导致电机的运行电流增加,损害电机带负载能力,故有必要确定电流平方量偏置量的最优大小。为了确定该大小,本文首先仅考虑电流平方量中的两交变分量,对其进行求导确定极值点,将极值点代入电流平方量公式,求得极值的绝对值即为偏置电流平方量的大小。即当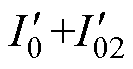 为两交变量叠加后极值的绝对值时最优。
为两交变量叠加后极值的绝对值时最优。
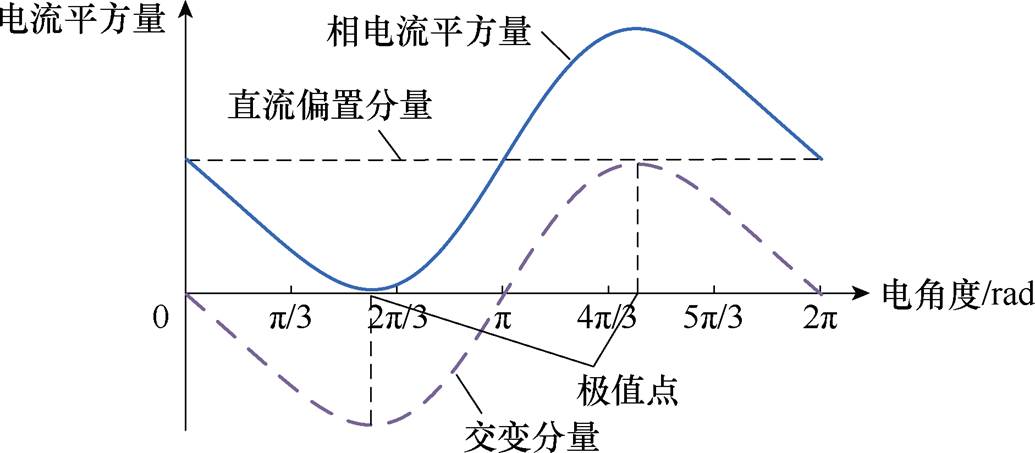
图2 电流平方量各分量示意图
Fig.2 Diagram of current squared components
当设定一阶电流平方量的幅值为同一定值时,一阶电流平方量,一、二阶电流平方量协同作用时的理想电流波形、电流平方量波形以及转矩对比示意图如图3所示,图中,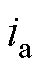 为A相电流,
为A相电流,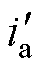 为A相电流平方量。仅一阶电流平方量作用时,电流平方量波形为纯正弦,而当一、二阶电流平方量协同作用时,电流平方量波形为类正弦,且经过偏置电流平方量优化,保证了电流平方量非负的同时整体大小的最小化。对比仅有一阶电流平方量作用,加入二阶电流平方量协同作用后,SRM的转矩脉动明显降低。
为A相电流平方量。仅一阶电流平方量作用时,电流平方量波形为纯正弦,而当一、二阶电流平方量协同作用时,电流平方量波形为类正弦,且经过偏置电流平方量优化,保证了电流平方量非负的同时整体大小的最小化。对比仅有一阶电流平方量作用,加入二阶电流平方量协同作用后,SRM的转矩脉动明显降低。
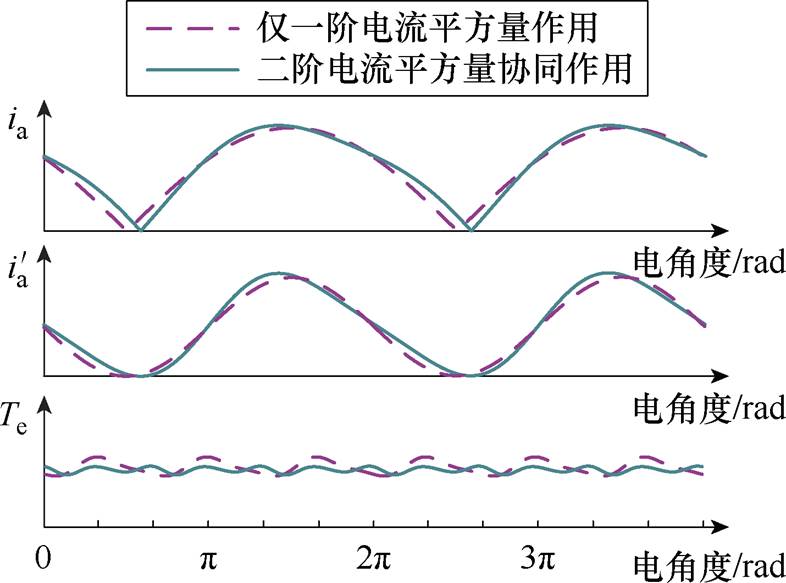
图3 波形对比示意图
Fig.3 Waveformscomparison diagrams
为了计算电流平方量所产生转矩的大小以及所需二阶电流平方量的幅值,开关磁阻电机电感的数学模型通常通过式(3)建立,且该模型在现有研究中广泛应用。然而,实际上由于更高次的电感谐波通常被忽略并且各次电感间的相位一般有少许变化,故存在建模误差。误差的具体表现在于,当定子与转子开始接触与结束相互接触时,电感变化率变化较为激烈,出现了较大偏差,并且由于各相在定转子开始相互接触时电机的相电流较大,因此存在于这一位置的偏差对于转矩的影响更大,导致较大的相转矩波动,最终引起不符合理论分析的转矩脉动。对于三相电机各相而言,所对应的三个存在较大偏差的小区间定义为特征位置区间。
为了抑制特征位置区间的转矩脉动,本文提出瞬时转矩补偿方案,特征位置区间瞬时转矩补偿控制框图如图4所示。忽略式(9)中的交变项,理想的平均转矩可以表示为
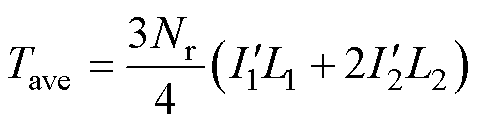 (11)
(11)
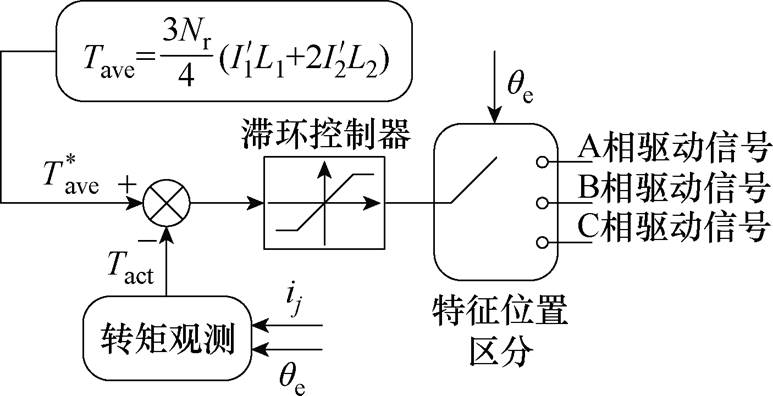
图4 特征位置区间瞬时转矩补偿控制框图
Fig.4 Block diagram of instantaneous torque compensation in the featured regions
实际转矩Tact可通过查找特征位置区间的电流-位置-转矩表得到。将式(11)计算得出的理想平均转矩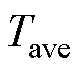 作为参考值
作为参考值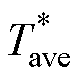 ,取观测到的实际总转矩Tact作为被控量,通过采用转矩滞环控制器,实际总转矩由每相单独补偿。考虑到各相在不同位置区间的转矩控制能力,选取A相补偿临近
,取观测到的实际总转矩Tact作为被控量,通过采用转矩滞环控制器,实际总转矩由每相单独补偿。考虑到各相在不同位置区间的转矩控制能力,选取A相补偿临近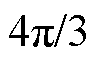 区间的总转矩,临近
区间的总转矩,临近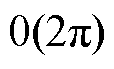 与
与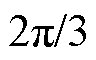 区间的总转矩分别由B相和C相直接补偿。由于观测实际转矩所需要的查找表仅包含特征位置区间的电磁特性数据即可,相对于传统全区间转矩观测方案如DTC、DITC或TSFC,本方案可节省大量电磁特性数据。
区间的总转矩分别由B相和C相直接补偿。由于观测实际转矩所需要的查找表仅包含特征位置区间的电磁特性数据即可,相对于传统全区间转矩观测方案如DTC、DITC或TSFC,本方案可节省大量电磁特性数据。
本文所提整体控制框图如图5所示。首先采用比例积分控制器将给定转速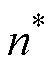 与实际转速n作差转化为参考一阶电流平方量的幅值
与实际转速n作差转化为参考一阶电流平方量的幅值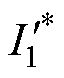 。实际转速n由电机位置检测出的电角度
。实际转速n由电机位置检测出的电角度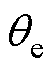 经控制器计算获得。根据快速傅里叶变换解析得到的电机参数L1、L2与L4的大小通过式(8)计算出二阶电流平方量的幅值
经控制器计算获得。根据快速傅里叶变换解析得到的电机参数L1、L2与L4的大小通过式(8)计算出二阶电流平方量的幅值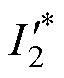 ,通过极值点确定法计算电流平方量中偏置直流分量的大小
,通过极值点确定法计算电流平方量中偏置直流分量的大小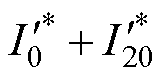 ,进而由式(10)获取参考电流平方量参考值
,进而由式(10)获取参考电流平方量参考值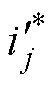 ;以及计算式(11)得到的理想平均转矩
;以及计算式(11)得到的理想平均转矩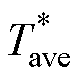 。采用电流平方量滞环控制器比较实际电流平方量大小
。采用电流平方量滞环控制器比较实际电流平方量大小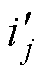 与参考电流平方量大小
与参考电流平方量大小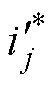 产生驱动信号1。采用转矩滞环控制器比较观测实际转矩大小Tact与参考平均转矩大小
产生驱动信号1。采用转矩滞环控制器比较观测实际转矩大小Tact与参考平均转矩大小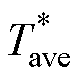 产生驱动信号2,以抑制特殊位置区间的非理想误差转矩脉动,变换器拓扑采用不对称半桥结构。
产生驱动信号2,以抑制特殊位置区间的非理想误差转矩脉动,变换器拓扑采用不对称半桥结构。
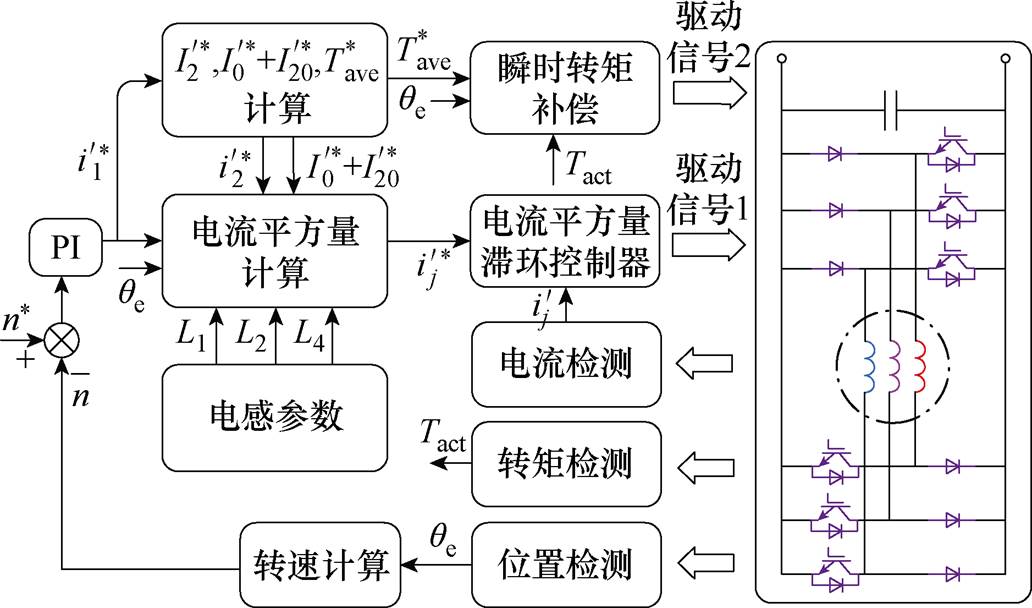
图5 所提策略的整体控制框图
Fig.5 Overall control diagram of the proposed scheme
为了验证本文提出的基于电流平方量约束的开关磁阻电机转矩调制方法的有效性,采用NI公司的FPGA PXIe-7846R芯片实现控制系统搭建,实验平台示意图如图6所示。一台150 W三相12/8极SRM由不对称半桥拓扑驱动,由一个可编程直流电源供电,伺服电机作为负载。所采用的样机参数见表1。

图6 实验平台示意图
Fig.6 Diagram of experimental platform
随着转速的增加,换相时间进一步缩短,并且反电动势进一步增大,大反电动势产生的拖尾电流会形成拖尾转矩,从而引起转矩脉动的变化。故研究不同SRM控制方案在不同转速下的转矩性能对于研究SRM控制方案的有效性至关重要。当电机运行在400 r/min,负载0.95 N∙m时电流斩波控制、直流偏置正弦波励磁控制、一阶电流平方量控制以及所提整体方案的电流波形、总转矩及电角度如图7所示。图7a为电流斩波控制时的实验波形,其电流为非连续准方波,由于对转矩没有控制要求,转矩脉动大小为41.54%。从图7b中可看出,直流偏置正弦波励磁的相电流波形具有正弦性,且该波形具有与交变幅值相同的直流偏置分量,虽然对比电流斩波控制电流波形更加连续顺滑,转矩脉动却并未因此减小,而是更大的75.42%。图7c中为仅一阶电流平方量作用时的实验波形,电流波形既非方波也非正弦,转矩脉动主要为三倍频分量,大小为47.17%。点画线所框阴影部分为一个电周期内样机的三个特征位置区间,由于建模误差的存在,特征位置区间内的转矩波形与图3中理论分析的波形存在较大偏差。当一阶电流平方量与二阶电流平方量协同作用且加入瞬时转矩补偿的所提整体方案运行时,如图7d所示,特征位置区间的电流对转矩进行了瞬时补偿,非特征位置区间转矩也因二阶电流平方量的加入更加平顺,整体转矩脉动被降低至32.9%。
表1 所采用的样机参数
Tab.1 Prototype parameters

参 数数 值 额定功率/W150 额定电压/V132 额定转速/(r/min)1 500 额定负载/(N∙m)0.95 定子极数12 转子极数8
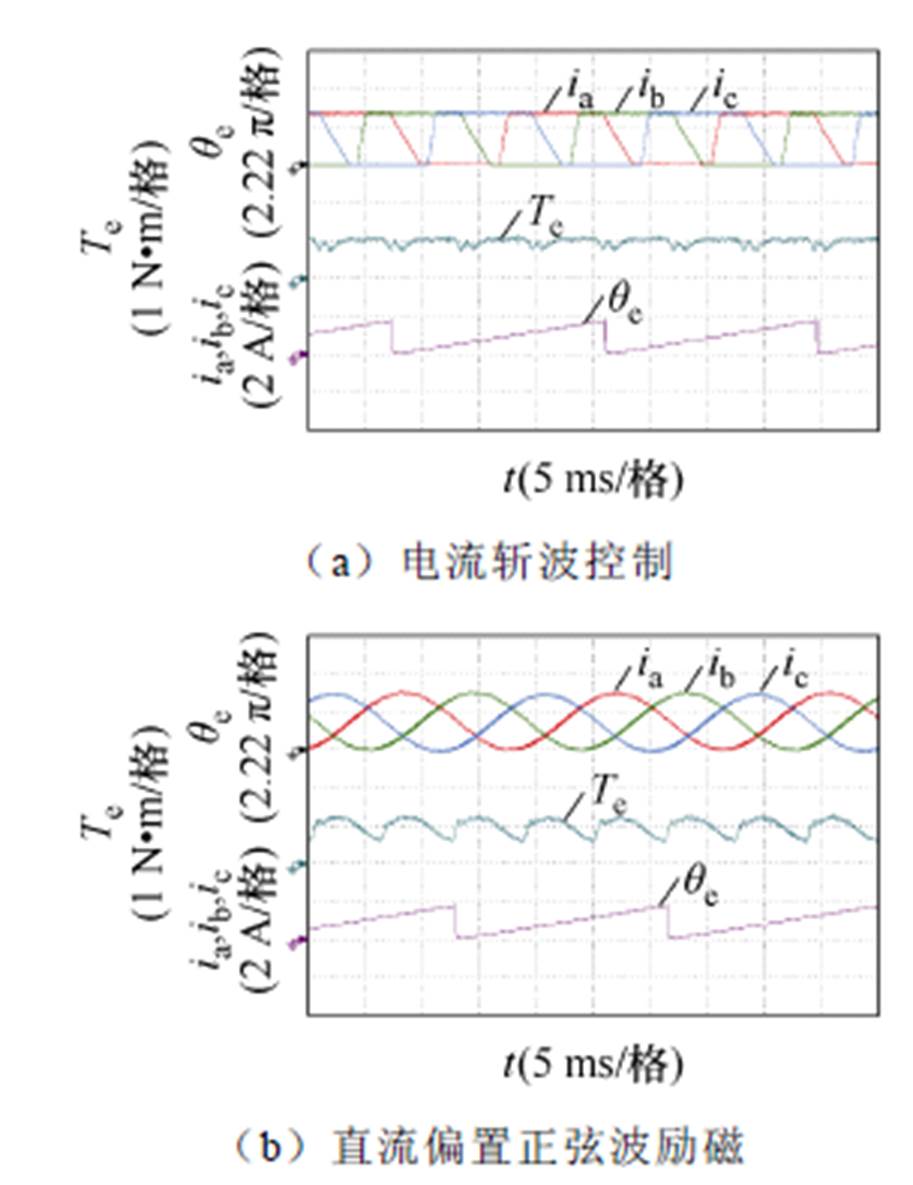
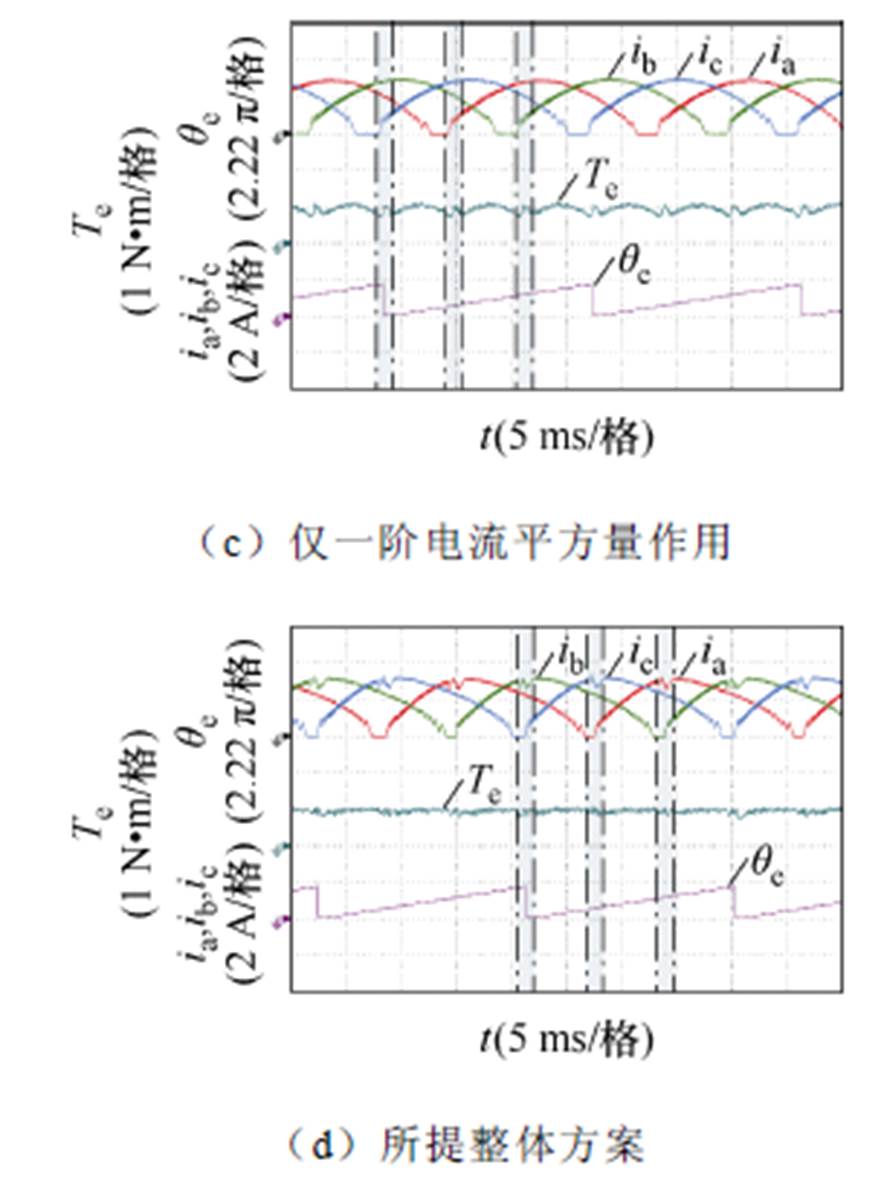
图7 转速400 r/min,负载0.95 N∙m时的实验结果
Fig.7 Experimental results at 400 r/min with 0.95 N∙m load
当转速升至800 r/min时,四种方案的实验结果如图8所示。在图8a中,电流斩波控制方案由于对于电流没有额外调节,随着转速的增加拖尾电流也不断增大,使转矩脉动增加至51.4%。在图8b中直流偏置正弦波励磁由于励磁电流波形没有变化,转矩波形与转矩脉动几乎不变,为75.29%。仅一阶电流平方量控制时转矩波形变化不大,如图8c所示,转矩脉动数值上略增至53.83%。图8d中,所提整体方案的转矩脉动大小为42.95%,相对于前三种方案降低了8.45%、32.34%及10.88%。
当电机运行在1 200 r/min,负载0.95 N∙m的工况时,四种方案的实验结果分别如图9a~图9d所示。随着转速的进一步提升,电流斩波控制的转矩脉动跃升至68.8%;直流偏置正弦波励磁的转矩脉动为76.25%;一阶电流平方量控制下转矩脉动增加至60.87%。而经过二阶电流平方量协同控制以及瞬时转矩补偿,所提整体方案转矩脉动为46.16%,比前三种方案分别降低了22.64%、30.09%与16.71%。
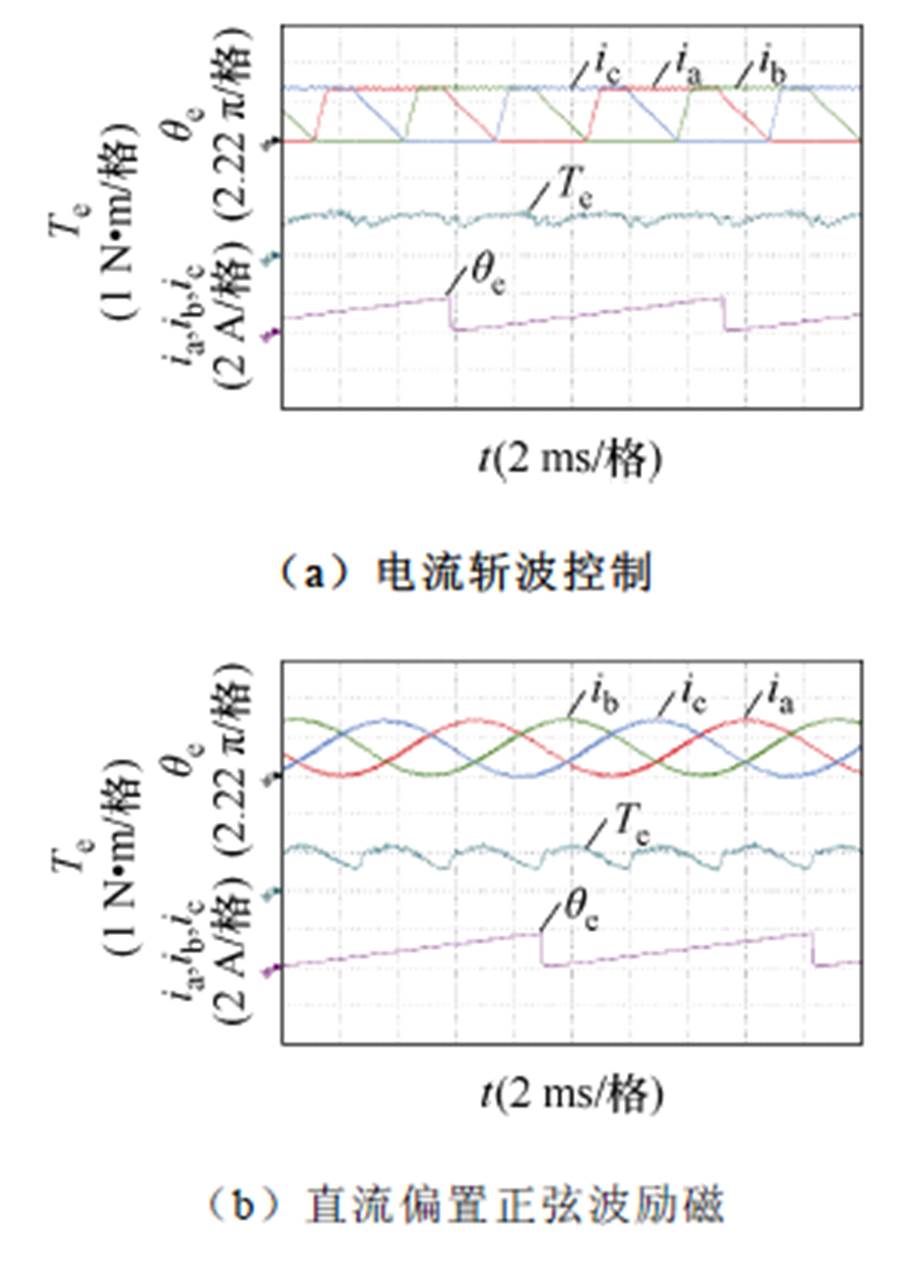
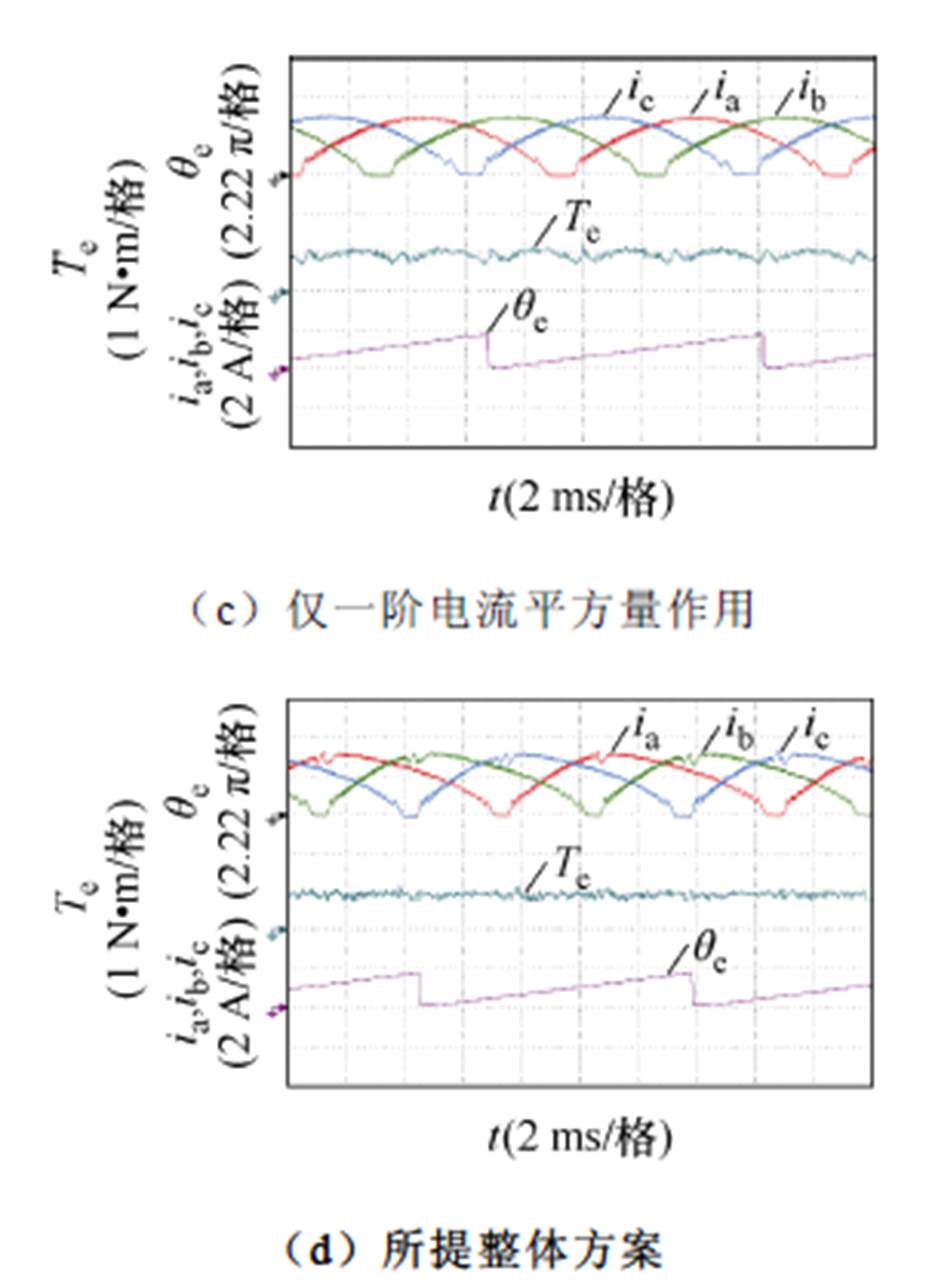
图8 转速800 r/min,负载0.95 N∙m时的实验结果
Fig.8 Experimental results at 800 r/min with 0.95 N∙m load
动态响应实验结果与转矩脉动比较如图10所示。图10a为本文所提方案的动态响应实验结果。电机运行在1 000 r/min转速下,所带负载转矩由0.5 N∙m突增至0.95 N∙m,电机转速因转矩的突增刚开始有所降低,但随着相电流与电磁转矩的增加再次跟随给定值。随后在负载0.95 N∙m的情况下电机参考速度先降低至500 r/min再升高至1 000 r/min,相电流立即先减小再增大以改变电磁转矩,实现转速的快速跟踪。因此,实验结果表明,所提方案具有良好的动态响应能力与稳定性。
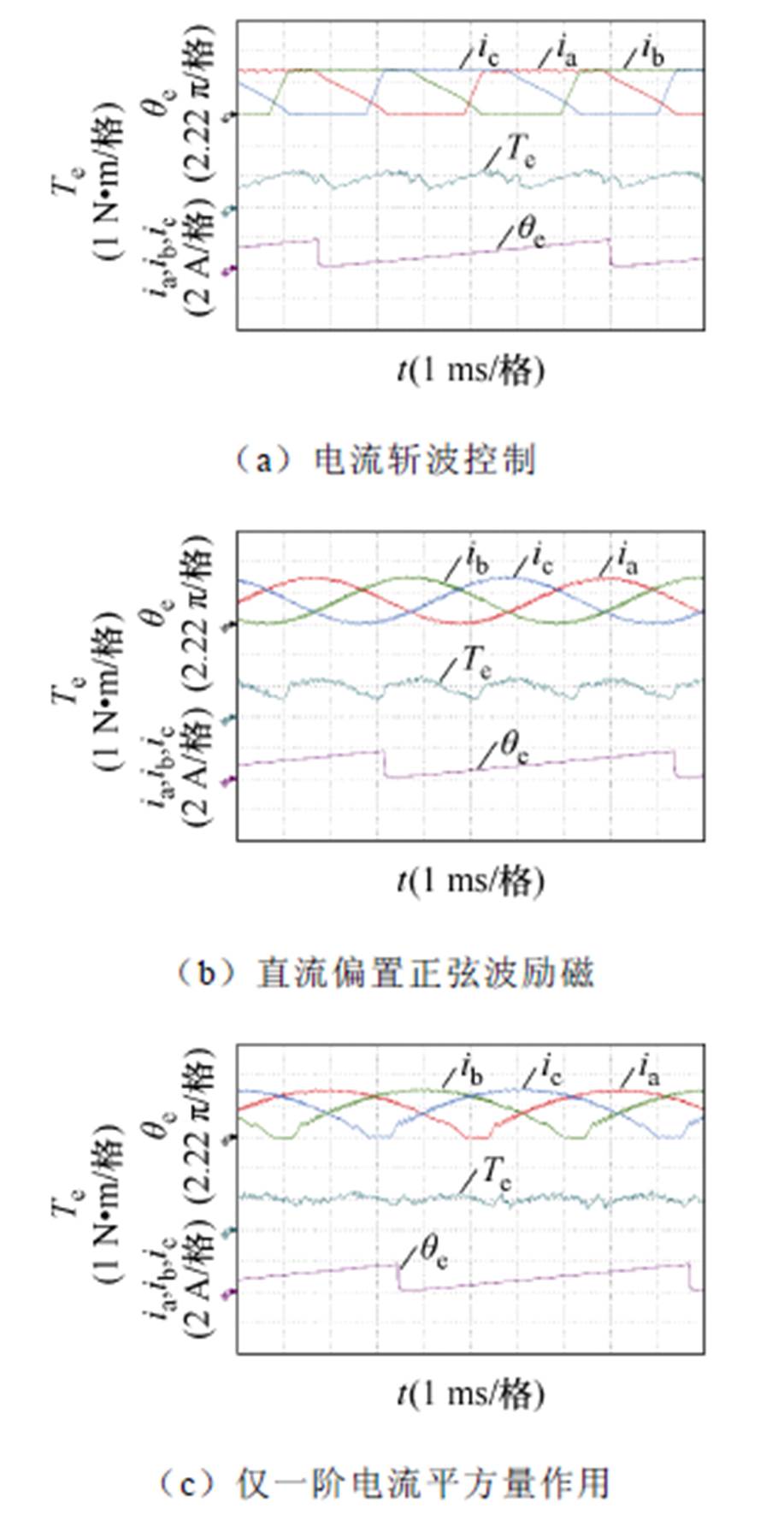
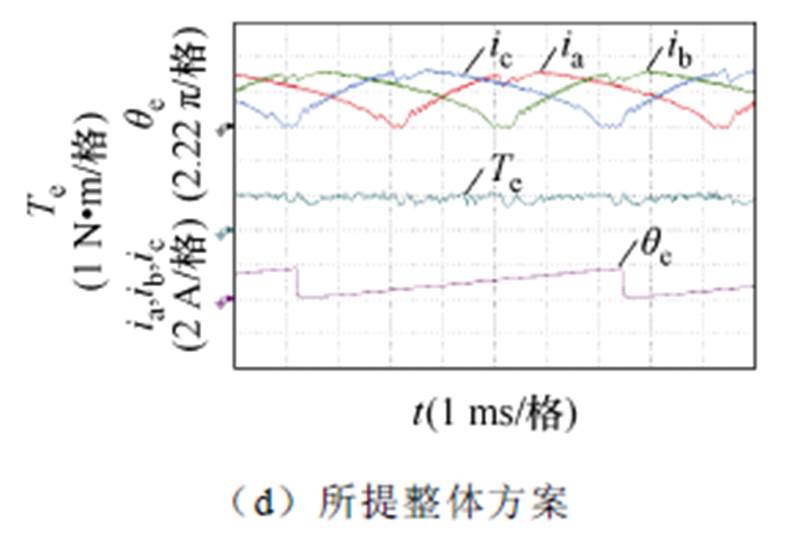
图9 转速1 200 r/min,负载0.95 N∙m时的实验结果
Fig.9 Experimental results at 1 200 r/min with 0.95 N∙m load
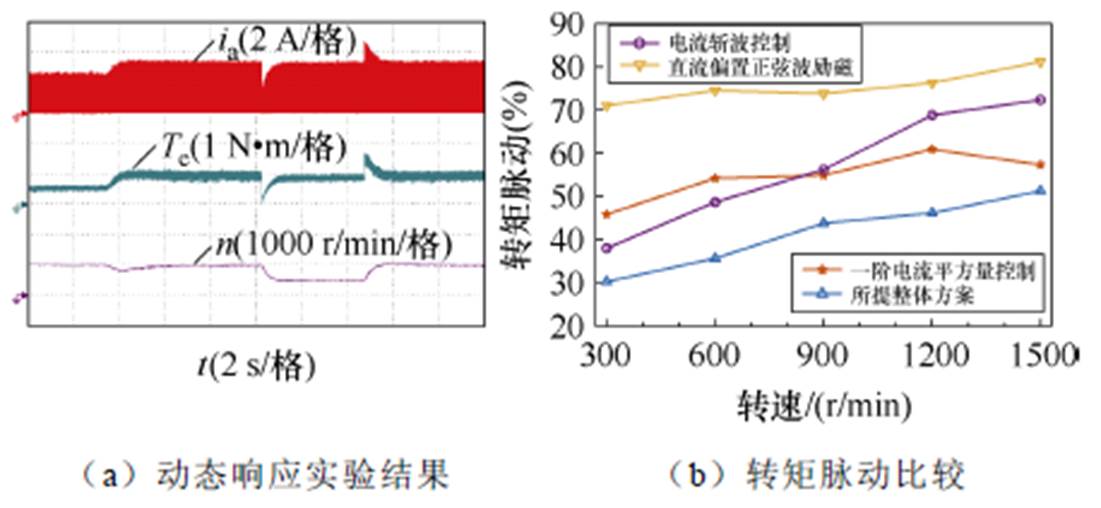
图10 动态响应实验结果与转矩脉动比较
Fig.10 Experimental results of dynamic responses and torque ripple comparison
为表明所提方案的有效性,图10b为不同方案间转矩脉动大小的比较。电流斩波控制因为其励磁电流非连续,在转速增加的同时转矩脉动严重增大。直流偏置正弦波励磁控制由于其并不完全适用于开关磁阻电机转矩控制,转矩脉动一直维持在四种方案中最大的位置。仅一阶电流平方量控制时,由于2、4次电感谐波的存在,电流平方量与电感作用产生的转矩脉动较大,而经过二阶电流平方量协同作用以及瞬时转矩补偿,所提整体方案将转矩脉动抑制在了一个较小的范围内。
本文提出了基于电流平方量约束的新型开关磁阻电机转矩调制方法,首先通过分析所定义的一阶、二阶电流平方量对于SRM产生转矩的影响提出了基于一阶、二阶电流平方量协同作用的电流平方量励磁方案,降低了非特征位置区间的转矩脉动;然后通过分析电机建模误差提出瞬时转矩补偿方案抑制了特征位置区间的转矩脉动。针对开关磁阻电机在运行时转矩脉动较大的问题,所提方法在降低SRM转矩脉动的同时也降低了对于大量电机电磁特性数据的依赖。
参考文献
[1] 于丰源, 陈昊, 闫文举, 等. 宽窄定子极轴向磁通开关磁阻电机的设计与分析[J]. 电工技术学报, 2023, 38(5): 1261-1274.
Yu Fengyuan, Chen Hao, Yan Wenju, et al. Design and characteristic analysis of a wide-narrow stator poles axial flux switched reluctance machine[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1261-1274.
[2] 石国航, 张永昌, 杨海涛. 一种改进的同步磁阻电机无模型预测电流控制[J]. 电气工程学报, 2023, 18(2): 1-8.
Shi Guohang, Zhang Yongchang, Yang Haitao. An improved model-free predictive current control for synchronous reluctance motor drives[J]. Journal of Electrical Engineering, 2023, 18(2): 1-8.
[3] 孙德博, 胡艳芳, 牛峰, 等. 开关磁阻电机调速系统故障诊断和容错控制方法研究现状及展望[J]. 电工技术学报, 2022, 37(9): 2211-2229.
Sun Debo, Hu Yanfang, Niu Feng, et al. Status and prospect of fault diagnosis and tolerant control methods for switched reluctance motor drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2211-2229.
[4] 李存贺, 赵博, 刘剑, 等. 开关磁阻电动机小样本磁链特性精确建模方法[J]. 电气工程学报, 2021, 16(1): 16-25.
Li Cunhe, Zhao Bo, Liu Jian, et al. Accurate modeling method for switched reluctance motors with small sample flux-linkage characteristics[J]. Journal of Electrical Engineering, 2021, 16(1): 16-25.
[5] 孙宇亮, 彭兵. 基于阶梯齿的开关磁阻电机尖峰电流削弱方法[J]. 电气技术, 2022, 23(7): 50-55, 63.
Sun Yuliang, Peng Bing. A method for reducing peak current by stepped tooth in switched reluctance motor[J]. Electrical Engineering, 2022, 23(7): 50-55, 63.
[6] Chen Hao, Yang Jian, Xu Shuai. Electrothermal-based junction temperature estimation model for converter of switched reluctance motor drive system[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 874-883.
[7] Bartolo J, Degano M, Espina J, et al. Design and initial testing of a high-speed 45-kW switched reluctance drive for aerospace application[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 988-997.
[8] 蔡骏, 邓智泉, 胡荣光. 开关磁阻电机在位置检测技术中的应用[J]. 电工技术学报, 2014, 29(3): 150- 159.
Cai Jun, Deng Zhiquan, Hu Rongguang. Applications of switched reluctance motors in position sensing[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 150-159.
[9] Wang Daohan, Du Xingfei, Zhang Dengxu, et al. Design, optimization, and prototyping of segmental- type linear switched-reluctance motor with a toroidally wound mover for vertical propulsion application[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1865-1874.
[10] Nashed M N, Ohyama K, Aso K, et al. Automatic turn-off angle control for high speed SRM drive[C]// 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 2006: 2152-2157.
[11] 田德翔, 曲兵妮, 宋建成, 等. 基于电流斩波控制的开关磁阻电机脉冲宽度调制占空比解析计算法[J]. 电工技术学报, 2019, 34(21): 4449-4457.
Tian Dexiang, Qu Bingni, Song Jiancheng, et al. An analytical method of PWM duty cycle for switched reluctance motors based on current chopping control[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4449-4457.
[12] Sun Qingguo, Wu Jianhua, Gan Chun, et al. Modular full-bridge converter for three-phase switched reluctance motors with integrated fault-tolerance capability[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(3): 2622-2634.
[13] Zhu Z Q, Lee B, Huang Liren, et al. Contribution of current harmonics to average torque and torque ripple in switched reluctance machines[J]. IEEE Transa- ctions on Magnetics, 2017, 53(3): 8100909.
[14] 曹鑫, 户红艳, 颜宁, 等. 扇区实时优化的开关磁阻电机直接转矩控制方法[J]. 电工技术学报, 2018, 33(19): 4526-4534.
Cao Xin, Hu Hongyan, Yan Ning, et al. Direct torque control of switched reluctance motor with real-time optimization of sectors[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4526-4534.
[15] 王雪松, 许爱德, 赵中林, 等. 粒子群优化递归神经网络的SRM磁链观测器[J]. 电气工程学报, 2017, 12(10): 1-8.
Wang Xuesong, Xu Aide, Zhao Zhonglin, et al. Stator flux observer of SRM based on particle swarm optimized recurrent neural network[J]. Journal of Electrical Engineering, 2017, 12(10): 1-8.
[16] Sun Xiaodong, Wu Jiangling, Lei Gang, et al. Torque ripple reduction of SRM drive using improved direct torque control with sliding mode controller and observer[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(10): 9334-9345.
[17] 胡艳芳, 康智勇, 孙德博, 等. 基于区间分段转矩分配函数的开关磁阻电机转矩脉动抑制[J]. 电机与控制学报, 2023, 27(10): 54-62.
Hu Yanfang, Kang Zhiyong, Sun Debo, et al. Torque ripple suppression of switched reluctance motor based on interval segmentation torque sharing function[J]. Electric Machines and Control, 2023, 27(10): 54-62.
[18] 杨帆, 陈昊, 李晓东, 等. 一种优化开关磁阻电机换相区控制策略的高效率转矩分配函数[J]. 电工技术学报, 2024, 39(6): 1671-1683.
Yang Fan, Chen Hao, Li Xiaodong, et al. An efficient torque sharing function for optimizing the com- mutation zone control strategy of switched reluctance motors[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1671-1683.
[19] 蔡燕, 居春雷, 王浩楠, 等. 开关磁阻电机的新型直接瞬时转矩控制方法及其高效率运行[J]. 电工技术学报, 2022, 37(18): 4625-4637.
Cai Yan, Ju Chunlei, Wang Haonan, et al. A new direct instantaneous torque control method of switched reluctance motor and its high efficiency operation[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4625-4637.
[20] 韩国强, 陆哲, 吴孟霖, 等. 基于改进滑模控制策略的开关磁阻电机直接瞬时转矩控制方法[J]. 电工技术学报, 2022, 37(22): 5740-5755.
Han Guoqiang, Lu Zhe, Wu Menglin, et al. Direct instantaneous torque control method for switched reluctance motor based on an improved sliding mode control strategy[J]. Transactions of China Electro- technical Society, 2022, 37(22): 5740-5755.
[21] 任浩天, 甘醇, 曲荣海, 等. 基于电流转矩协同控制的开关磁阻电机新型直接瞬时转矩控制策略[J/OL]. 中国电机工程学报, 2023, DOI: 10.13334/ j.0258-8013.pcsee.230962.
Ren Haotian, Gan Chun, Qu Ronghai, et al. Current- torque coordinated control based direct instantaneous torque control strategy for switched reluctance motor[J/OL]. Proceedings of the CSEE, 2023, DOI: 10.13334/j.0258-8013.pcsee.230962.
[22] Liu Xu, Zhu Z Q, Hasegawa M, et al. Investigation of PWMs on vibration and noise in SRM with sinusoidal bipolar excitation[C]//2012 IEEE International Sympo- sium on Industrial Electronics, Hangzhou, China, 2012: 674-679.
[23] Tungpimolrut K, Kachapornkul S, Jitkreeyarn P, et al. Torque improvement of three-phases full bridge converter based switched reluctance motor with DC assisted winding[C]//2012 15th International Con- ference on Electrical Machines and Systems (ICEMS), Sapporo, Japan, 2012: 1-5.
[24] Nakao N, Akatsu K. Vector control specialized for switched reluctance motor drives[C]//2014 Inter- national Conference on Electrical Machines (ICEM), Berlin, Germany, 2014: 943-949.
[25] 李宏慧, 夏新祥, 蒯松岩. 基于电流矢量分解的开关磁阻电机转矩脉动抑制[J]. 微电机, 2020, 53(9): 40-46, 53.
Li Honghui, Xia Xinxiang, Kuai Songyan. Low torque ripple control of switched reluctance motor based on current vector decomposition[J]. Micromotors, 2020, 53(9): 40-46, 53.
[26] Yu Zhiyue, Gan Chun, Chen Yu, et al. DC-biased sinusoidal current excited switched reluctance motor drives based on flux modulation principle[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10614-10628.
[27] Yu Zhiyue, Gan Chun, Ni Kai, et al. Instantaneous torque modeling and torque ripple reduction strategy for flux modulated doubly-salient reluctance motor drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 9838-9848.
[28] Yu Zhiyue, Gan Chun, Ni Kai, et al. Analytical torque ripple reduction strategy for flux modulated doubly- salient reluctance motor drives based on ZSC harmonic regulation[J]. IEEE Transactions on Indu- strial Electronics, 2024, 71(2): 1365-1376.
Abstract Due to the doubly-salient structure of switched reluctance motors (SRMs), the torque ripple problem always exists and limits the promotion of SRMs. The existing schemes usually rely on a large amount of motor electromagnetic characteristic data to suppress torque ripples during the operation process, which takes up a lot of controller storage space and complicates the control program. In contrast, the schemes independent of the data have an inefficient effect on torque ripple suppression in common. This paper proposes a novel torque modulation method for switched reluctance motors based on current squared constraints to reduce torque ripples and alleviate the dependence on electromagnetic characteristic data during the control process.
Firstly, the effect of the first-order current squared on torque generation is derived based on the instantaneous torque equation of the switched reluctance motor. It is found that the main torque ripple component is the triple frequency torque. Then, the influence of the second-order current squared is analyzed, and the constraint conditions for offsetting the triple frequency torque component are obtained through the synergistic effect of the first-order and the second-order current squared. The extreme point determination method is used to determine the optimal operating state of the current squared, ensuring the numerical value of the current squared is the lowest and positive. Finally, the instantaneous torque compensation method is proposed to suppress the error torque ripple in the specific position regions for each phase.
Experimental verifications are conducted on a 150 W, three-phase, 12/8-pole switched reluctance motor. The torque performance of four schemes is compared: current chopping control, dc-biased sinusoidal-wave excitation, scheme with only the first order current squared acting, and the proposed whole scheme. In the speed range from 300 r/min to 1 500 r/min, the dc-biased sinusoidal-wave excitation has the largest torque ripple because the sinusoidal current waveform excitation scheme for the common alternating current motors is not an effective solution. With speed increasing, the current chopping control scheme has the largest torque ripple increment with no specific control target for the instantaneous torque or current. When only the first-order current squared acts, the torque ripple is large because the second-order and fourth-order inductance harmonics generate the triple-frequency torque component. The proposed scheme has the lowest torque ripple since the largest torque ripple component is offset, and the error torque ripple is compensated.
The contributions of the proposed novel torque modulation method for switched reluctance motor are as follows: (1) The effects of the current squared and inductance harmonics on the torque generation are analyzed. (2) The torque ripple out of the featured position regions can be suppressed combined with the first-order and the second-order current squared. (3) The proposed instantaneous torque compensation method compensates for the torque ripple in the featured position regions. (4) The reliance on electromagnetic characteristic data during the control process is reduced.
keywords:Switched reluctance motor, current squared, torque ripple suppression, electromagnetic characteristics data, extreme point determination method
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.240086
国家自然科学基金(52207045)、河北省省级科技计划(225676163GH)和省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学)优秀青年创新基金(EERI_OY2023002)资助项目。
收稿日期2024-01-12
改稿日期2024-02-20
孙庆国 男,1991年生,副教授,博士生导师,研究方向为高效电机控制、参数辨识与自抗扰控制等。E-mail: qingguosun@hebut.edu.cn(通信作者)
吕广宇 男,1998年生,硕士研究生,研究方向为开关磁阻电机控制。E-mail: 202121401103@stu.hebut.edu.cn
(编辑 崔文静)