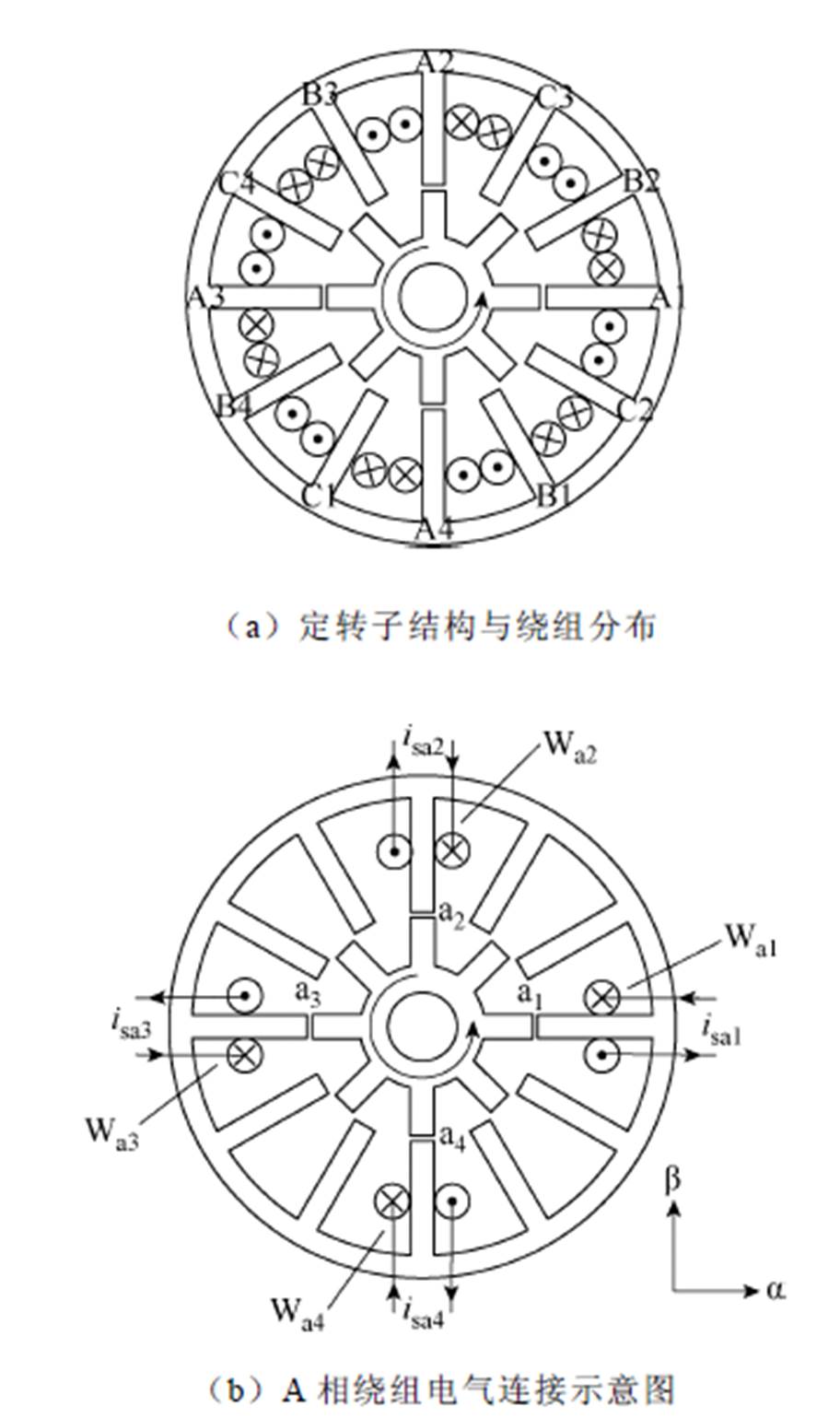
图1 三相12/8极SWBSRM结构示意图
Fig.1 Structure diagram of three-phase 12/8-pole SWBSRM
摘要 该文提出一种计及定转子磁极磁阻的单绕组无轴承开关磁阻电机(SWBSRM)新型数学模型,以解决此电机现有虚位移法建模中存在的径向悬浮力误差较大、定转子齿极中线对齐位置处电磁转矩波形不连续和径向悬浮力波形凹陷以及不便于建立磁饱和模型问题。首先,建立SWBSRM定转子极交叠区线性数学模型:提出一种高精度的计算椭圆形边缘气隙磁路长度的解析方法,解决定转子齿极中线对齐位置处存在的转矩波形不连续和悬浮力波形凹陷问题;此外,提出在建立定转子极交叠区无磁饱和数学模型时计及定转子磁极磁阻,并将气隙磁压表示为关于绕组磁动势的线性函数以更精确地计算气隙磁压,可显著减小悬浮力误差。其次,建立计及磁饱和的SWBSRM定转子极交叠区数学模型:采用分段线性函数拟合气隙磁压和绕组磁动势之间的非线性关系,提出具有高拟合精度的分段点选取规律,可较精确地计算悬浮力和转矩。然后,建立适用于多工况的SWBSRM定转子极非交叠区数学模型,从而与定转子极交叠区数学模型构成一个相周期内的完整数学模型。最后,通过与SWBSRM现有虚位移法模型和有限元模型的计算结果对比,验证了所建模型的优良性能。
关键词:单绕组无轴承开关磁阻电机 边缘气隙磁路 磁极磁阻 磁饱和 数学模型
无轴承开关磁阻电机(Bearingless Switched Reluctance Motor, BSRM)是磁悬浮技术与开关磁阻电机(Switched Reluctance Motor, SRM)的结合。近年来,BSRM因其允许转速高、摩擦功耗小、结构简单、成本低和寿命长等优点逐渐成为高速电机领域的重要研究对象[1-6]。传统BSRM为双绕组无轴承开关磁阻电机(Dual-Winding Bearingless Switched Reluctance Motor, DWBSRM)是利用磁轴承与电机结构的相似特质,将产生径向悬浮力的悬浮绕组和电机主绕组一起安装在电机定子齿极上,并基于电力电子和微机控制使电机转子同时具备旋转和悬浮功能[7-12]。但由于DWBSRM定子齿极上同时绕有主绕组和悬浮绕组,涉及两套绕组的分配设计、装配和磁场叠加控制等问题,故电机设计复杂度和成本均较高[13-14]。而单绕组无轴承开关磁阻电机(Single-Winding Bearing-less Switched Reluctance Motor, SWBSRM)和SRM的本体结构相同,其定子上仅有一套绕组,可降低电机加工难度和成本。因此,BSRM的单绕组悬浮技术成为新的研究热点[15-16]。
图1给出了三相12/8极SWBSRM的结构示意图。图1a为其定转子结构与绕组分布,图1b为其A相绕组电气连接示意图。如图1b所示,每个定子齿极上仅绕有一套绕组,以A相为例:四个定子齿上分别绕有Wa1、Wa2、Wa3、Wa4四组绕组。因需实时控制作用在转子上的径向力,每相四个定子齿极上的绕组电流isa1、isa2、isa3、isa4需独立控制,通过对这四个绕组的不对称励磁,形成在转子径向相对位置的不对称分布的气隙磁通密度,可产生不平衡径向力,以动态控制转子悬浮。基于转子所受磁拉力与电机绕组电流的关系,合理控制绕组电流大小,以产生所需转矩和悬浮力,实现电机稳定旋转和悬浮[17]。因此,SWBSRM数学模型的精度对实现电机稳定旋转和悬浮至关重要,但其亦影响控制复杂度,故在确保数学模型必要精度的同时不应使其过于复杂。

图1 三相12/8极SWBSRM结构示意图
Fig.1 Structure diagram of three-phase 12/8-pole SWBSRM
文献[18-23]采用虚位移法建立了DWBSRM数学模型,文献[24]采用虚位移法建立了SWBSRM数学模型。其中,文献[18]采用气隙磁路近似剖分方法,将边缘气隙磁路近似为椭圆路径,但该模型存在径向悬浮力误差较大、定转子齿极中线对齐位置处电磁转矩波形不连续问题,且未建立磁饱和模型。文献[19]基于文献[18]考虑了转子在a、b两个方向上径向悬浮力的耦合及转子偏心影响,但明显增加了模型复杂度,且仍存在径向悬浮力误差较大、定转子齿极中线对齐位置处电磁转矩不连续和未建立磁饱和模型问题。文献[20]考虑了相互垂直两个方向上径向悬浮力的耦合并提高了模型精度。文献[21]建立了考虑a、b轴方向径向偏移及其耦合时的径向力和转矩的数学模型。文献[22]在建立DWBSRM数学模型时,将椭圆磁路的长度用直线加1/4圆周替代,降低了模型的精度,且该文献未能提供一套计及磁饱和的气隙磁动势差分段点计算规律,不便于直接建立磁饱和模型。文献[23]基于文献[22]建立DWBSRM定转子极交叠区线性数学模型,仍将椭圆磁路的长度用直线加1/4圆周替代,且将气隙磁压等同于绕组磁动势,致使径向悬浮力误差较大。文献[24]将边缘磁通路径近似为椭圆路径,建立了SWBSRM定转子极交叠区数学模型,但该模型仍存在径向悬浮力误差较大、定转子齿极中线对齐时电磁转矩波形不连续和径向悬浮力波形凹陷及未建立磁饱和模型等问题。
此外,值得一提的是,现有文献均在建立BSRM线性数学模型时忽略了定转子磁极磁阻,从而将气隙磁压等同于绕组磁动势,致使径向悬浮力误差较大。这是由于气隙磁压量级较大,是产生悬浮力和电磁转矩的主要来源,其看似较小的差距即可引起较大的悬浮力误差。这一点在定转子齿极中线对齐位置处体现得尤为明显。这是目前基于虚位移法和麦克斯韦应力法的BSRM建模方法中普遍存在的现象,会对BSRM电机本体设计与优化精度产生重要影响。
针对上述问题,本文提出一种计及定转子磁极磁阻的SWBSRM新型建模方法,其创新性如下。首先,建立SWBSRM定转子极交叠区线性数学模型:针对存在于定转子齿极中线对齐位置处的电磁转矩波形不连续和径向悬浮力波形凹陷问题,提出一种计算SWBSRM椭圆形边缘气隙磁路长度的新型解析方法,提高模型精度;此外,揭示了当SWBSRM定转子极交叠区无磁饱和时气隙磁压不等于绕组磁动势且不能忽略定转子磁极磁阻的机理,提出建模时应计及定转子磁极磁阻,并为简化模型将气隙磁压表示为关于绕组磁动势的线性函数,可提高气隙磁压的计算精度,从而有效降低径向悬浮力误差,解决现有BSRM数学模型中普遍存在的定转子齿极中线对齐位置处径向悬浮力误差较大的问题,并提高电机本体设计精度。其次,建立计及磁饱和的SWBSRM定转子极交叠区数学模型:将气隙磁压和绕组磁动势之间的非线性关系进行分段线性化,并提出较精确的分段点选取方法,可获得较高的建模精度。最后,建立SWBSRM定转子极非交叠区数学模型,该模型可应用于无磁饱和及有磁饱和的不同工况,从而与定转子极交叠区数学模型组成一个完整相周期内的数学模型。
本文建立SWBSRM线性数学模型的基本思路为:首先根据磁场有限元分析得出气隙磁路的几何分布形状,对该磁路进行近似等效剖分,利用分割磁场法求解各齿极下的气隙磁导;然后根据等效磁路法计算各支路气隙处的磁压;最后基于气隙磁导和气隙磁压计算气隙处的磁能,并将磁能分别对转子径向位移和位置角求偏导,便可得其径向悬浮力和电磁转矩。
为简化SWBSRM数学建模,做如下假设:
(1)定转子齿极中线对齐位置定义为转子零度位置角。
(2)转子转角规定为逆时针为正。
(3)各相绕组轮流导通。
(4)转子位移远小于气隙长度。
(5)忽略漏磁通和定子交链转子轭部的磁通。
本节建立转子位置角绝对值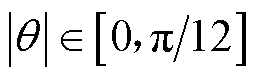 范围内的SWBSRM定转子极交叠区数学模型。定义图1中A相四个定子齿极对应的气隙a1~a4处的磁导分别为Pa1~Pa4。基于定转子极交叠区气隙磁场分布特征,将气隙磁场分割成三个形状规则的区域,先分别求解各区域的气隙磁导,进而计算整个气隙区域的总磁导。
范围内的SWBSRM定转子极交叠区数学模型。定义图1中A相四个定子齿极对应的气隙a1~a4处的磁导分别为Pa1~Pa4。基于定转子极交叠区气隙磁场分布特征,将气隙磁场分割成三个形状规则的区域,先分别求解各区域的气隙磁导,进而计算整个气隙区域的总磁导。
SWBSRM的定转子极交叠区电磁场有限元分析如图2所示。可知,SWBSRM定转子极交叠区中的主气隙磁路近似为直线轨迹,边缘气隙磁路近似为椭圆形轨迹[23],故以气隙a1为例,将其磁路分割,如图3所示。图3中,P1为主气隙磁路磁导,P2和P3为边缘气隙磁路磁导,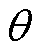 为转子位置角,r为转子极半径,n为椭圆形边缘气隙磁路的短半轴长度,lg为气隙长度,设平均气隙长度为la,转子a方向位移为a,则有lg=la-a。
为转子位置角,r为转子极半径,n为椭圆形边缘气隙磁路的短半轴长度,lg为气隙长度,设平均气隙长度为la,转子a方向位移为a,则有lg=la-a。
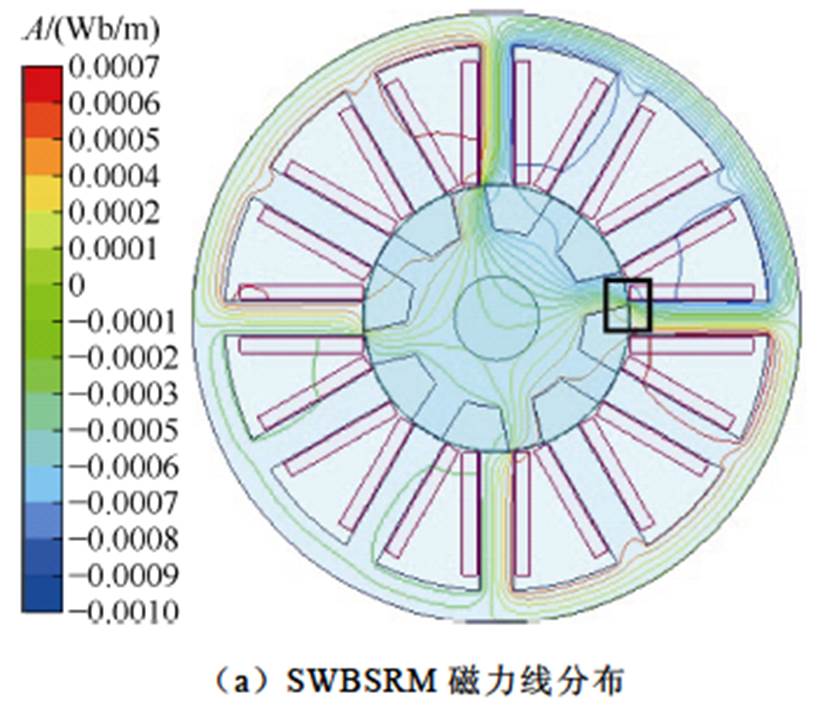
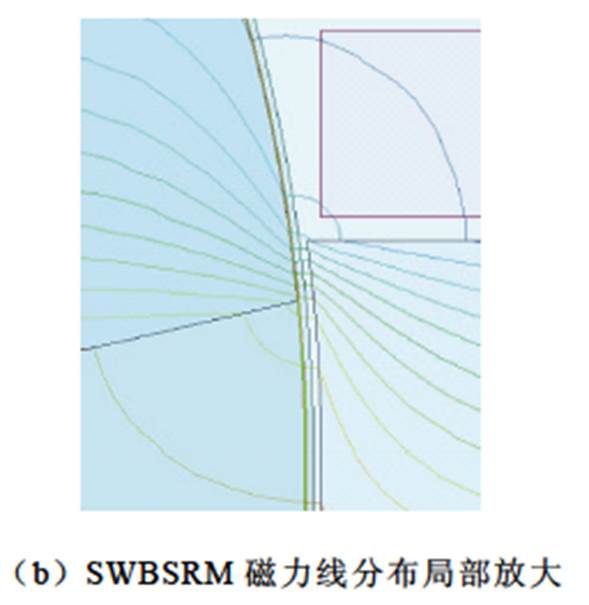
图2 SWBSRM定转子极交叠区电磁场有限元分析(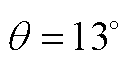 )
)
Fig.2 Finite element analysis of electromagnetic field in the overlapping region of stator and rotor teeth of SWBSRM (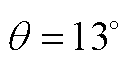 )
)
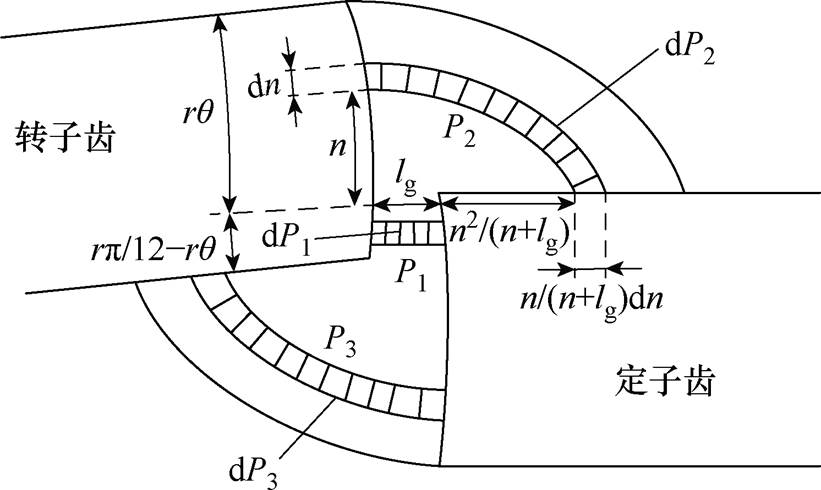
图3 气隙a1处定转子极交叠区磁路分割示意图
Fig.3 Schematic diagram of magnetic circuit segmentation in the overlapping region of stator and rotor teeth at air gap a1
气隙a1处定转子极交叠区的磁导Pa1可分为三部分:主气隙磁路磁导P1、边缘气隙磁路磁导P2和P3[24],即
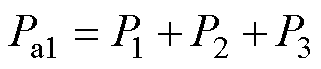 (1)
(1)
式中,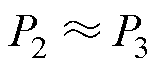 。
。
根据磁导定义可知,主气隙磁路磁导P1为
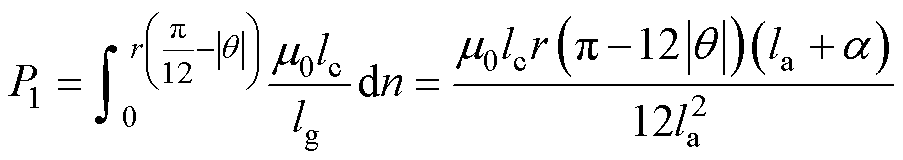 (2)
(2)
式中,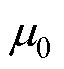 为真空磁导率;lc为铁心叠长。
为真空磁导率;lc为铁心叠长。
易知,在SWBSRM中满足电磁转矩Ta1在定转子齿极中线对齐时连续必有
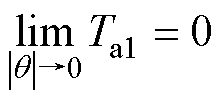 (3)
(3)
由式(1)知,要满足式(3)必有
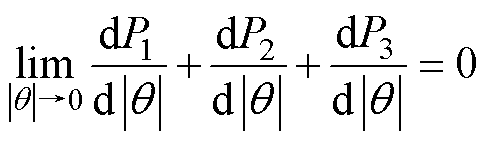 (4)
(4)
由图3中边缘气隙磁路示意图知,可取dP2和dP3的横截面积dS为
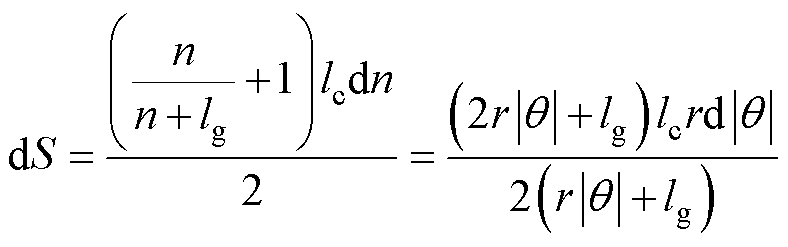 (5)
(5)
据有限元分析可知,边缘气隙磁路长度le为1/4椭圆周长[23],已知椭圆短半轴长度为n,长半轴长度为lg+n2/(n+lg),如图3所示,则1/4椭圆周长为
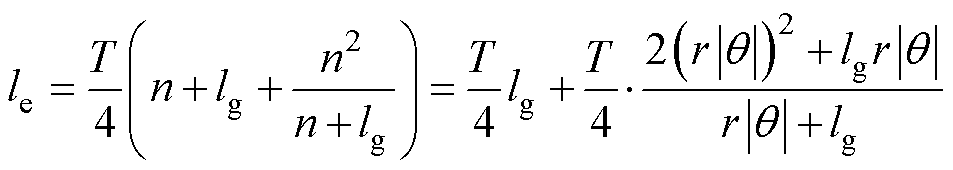 (6)
(6)
式中,T为椭圆系数,可根据椭圆短半轴与长半轴比值查表得到。由查表法计算的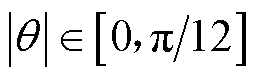 范围内1/4椭圆周长如图4所示,其与
范围内1/4椭圆周长如图4所示,其与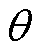 的关系近似为一条直线。
的关系近似为一条直线。
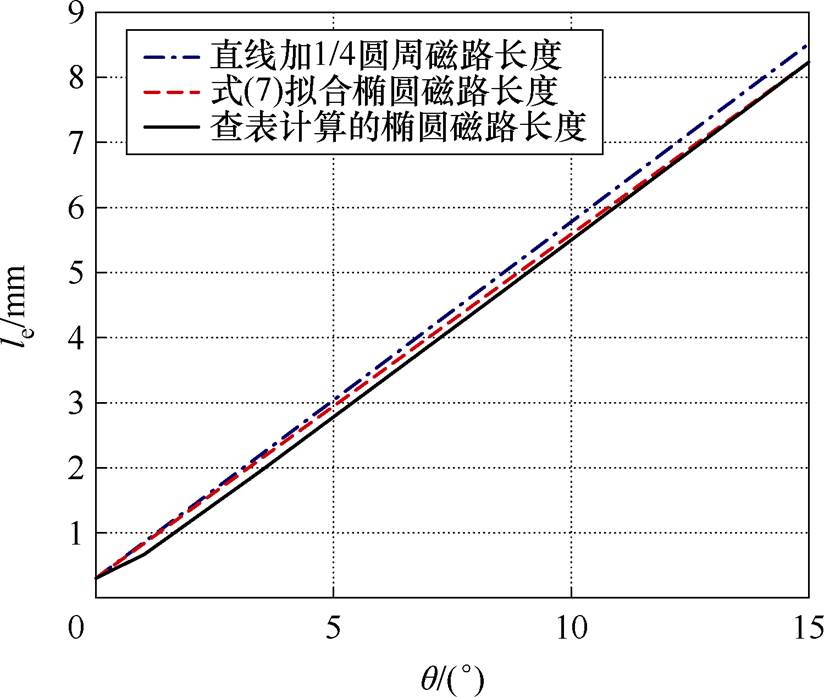
图4 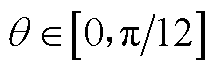 时的椭圆磁路长度le
时的椭圆磁路长度le
Fig.4 The length le of the elliptical magnetic circuit when 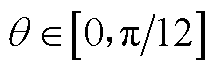
故可用关于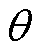 的简单函数拟合该椭圆磁路的长度le,计算得出该函数为
的简单函数拟合该椭圆磁路的长度le,计算得出该函数为
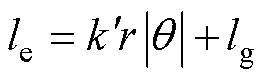 (7)
(7)
式中,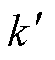 为椭圆磁路长度的斜率因素,其受电机尺寸影响,可近似为
为椭圆磁路长度的斜率因素,其受电机尺寸影响,可近似为
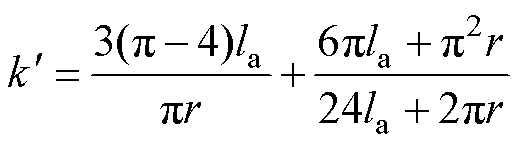 (8)
(8)
如图4所示,与传统算法中将椭圆磁路长度用直线加1/4圆周替代相比,式(7)能更精确地拟合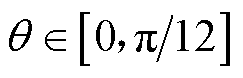 时的椭圆磁路长度。
时的椭圆磁路长度。
将式(5)、式(7)和式(8)结合磁导定义得
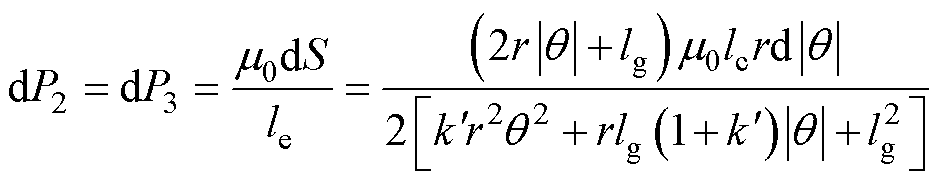 (9)
(9)
可见,式(9)结合式(2)满足式(4),故式(5)、式(7)和式(8)可解决定转子齿极中线对齐位置处存在的电磁转矩波形不连续和径向悬浮力波形凹陷问题。
因此,由式(1)、式(2)和式(9)可得气隙a1处定转子极交叠区磁导Pa1为
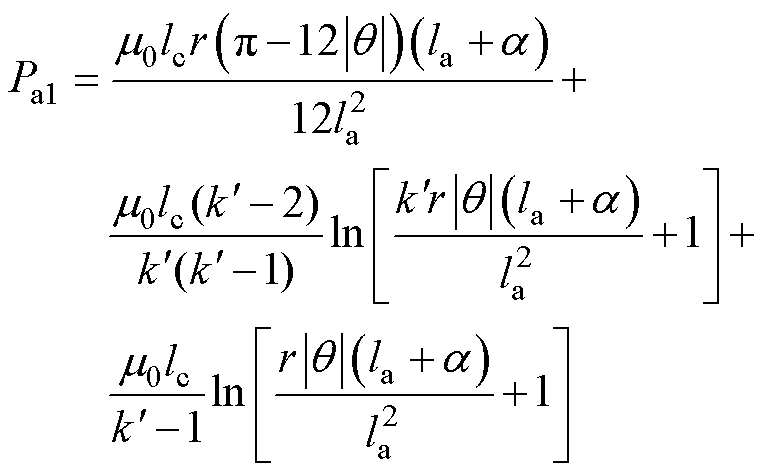 (10)
(10)
将式(10)中a 分别替换为b(转子b 方向位移)、-a、-b 即得气隙a2、a3、a4处定转子极交叠区磁导Pa2、Pa3、Pa4。
需要指出,图3所示的气隙a1处定转子极交叠区磁路对应于定转子齿极中线不对齐即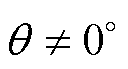 情况。而当定转子齿极中线对齐即
情况。而当定转子齿极中线对齐即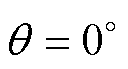 时,图3中仅有主气隙磁路磁导P1,而边缘气隙磁路磁导P2和P3均为0。式(10)对于
时,图3中仅有主气隙磁路磁导P1,而边缘气隙磁路磁导P2和P3均为0。式(10)对于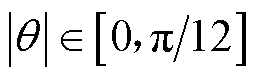 范围内的
范围内的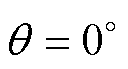 和
和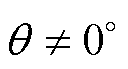 情况均成立。
情况均成立。
1)定转子极交叠区径向悬浮力的比例系数
气隙a1处的磁能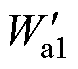 可表示为
可表示为
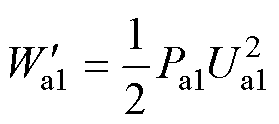 (11)
(11)
式中,Ua1为气隙a1处的磁压。
故气隙a1~a4处的径向悬浮力Fa1~Fa4可分别表示为
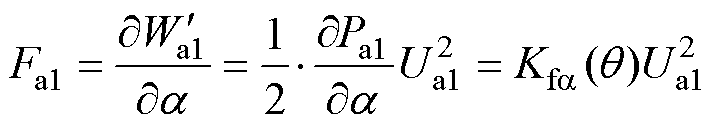 (12)
(12)
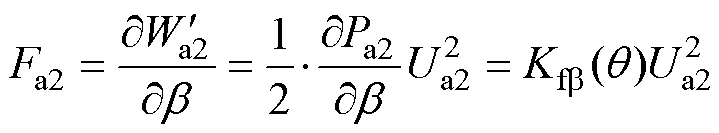 (13)
(13)
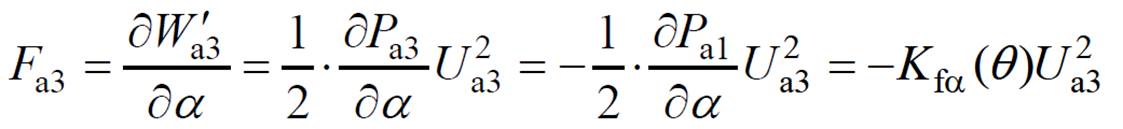 (14)
(14)
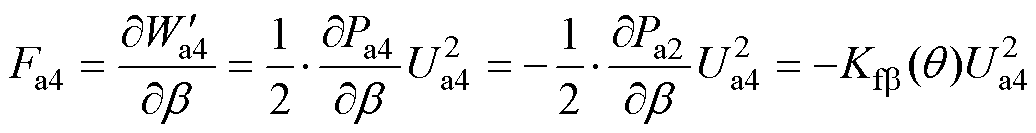 (15)
(15)
式中,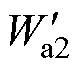 ~
~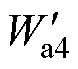 分别为气隙a2~a4处的磁能;Ua2~Ua4分别为气隙a2~a4处的磁压;
分别为气隙a2~a4处的磁能;Ua2~Ua4分别为气隙a2~a4处的磁压;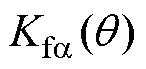 、
、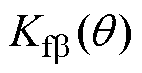 分别为a、b方向径向悬浮力的比例系数。
分别为a、b方向径向悬浮力的比例系数。
从而得到a 方向径向悬浮力合力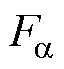 为
为
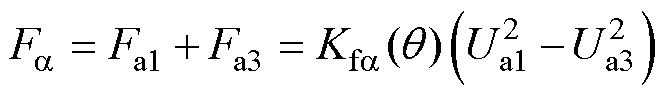 (16)
(16)
b 方向径向悬浮力合力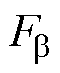 为
为
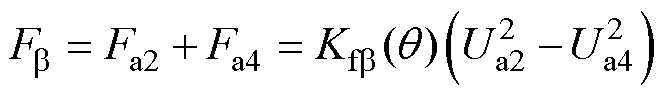 (17)
(17)
由式(10)、式(12)和式(13)可得定转子极交叠区a、b 方向径向悬浮力的比例系数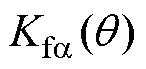 、
、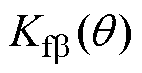 为
为
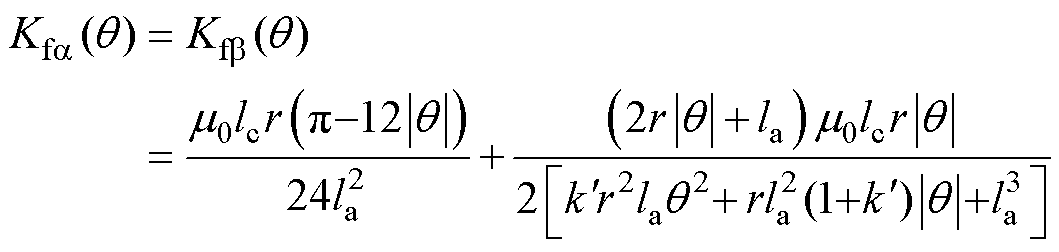 (18)
(18)
2)定转子极交叠区电磁转矩的比例系数
气隙a1~a4处的电磁转矩Ta1~Ta4可分别表示为
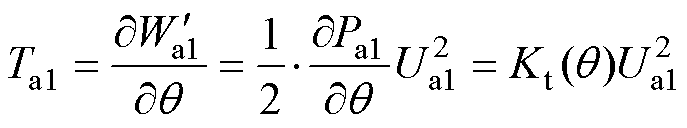 (19)
(19)
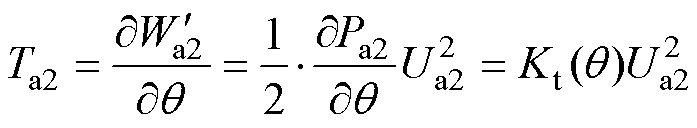 (20)
(20)
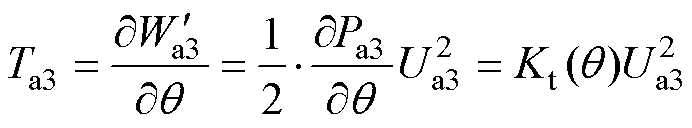 (21)
(21)
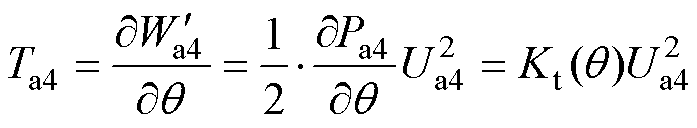 (22)
(22)
式中,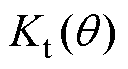 为电磁转矩的比例系数。
为电磁转矩的比例系数。
从而得到总电磁转矩Ta为
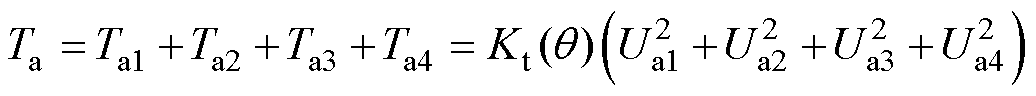 (23)
(23)
由式(10)和式(19)可得定转子极交叠区电磁转矩的比例系数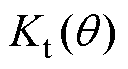 为
为
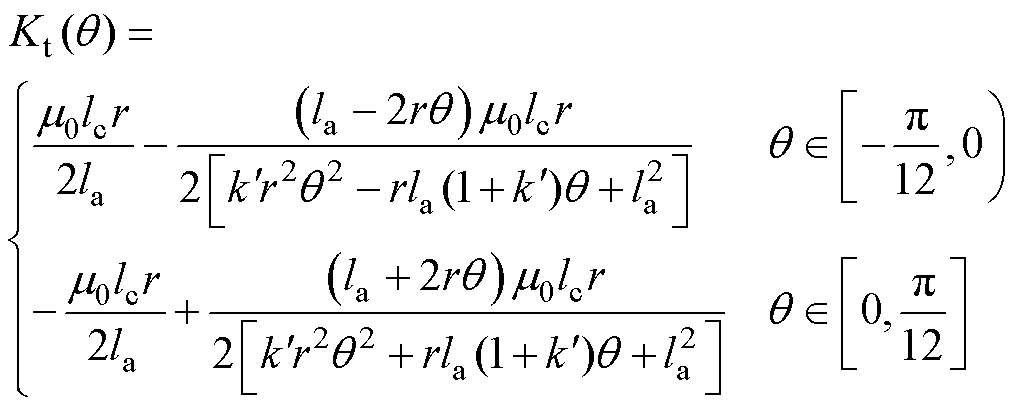 (24)
(24)
以往文献在建立BSRM线性数学模型时,一般忽略定转子磁极磁阻而将气隙磁压近似等于绕组磁动势[18-24],因此都存在径向悬浮力误差较大的问题,尤其在定转子齿极中线对齐位置处。要提高BSRM建模精度和电机本体设计准确度,则需更精确地计算气隙磁压。
为此,计及定转子磁极磁阻,并为确保数学模型的简洁性和实用性,避免一相等效磁路各支路之间磁通耦合,而忽略定转子轭部磁阻,则SWBSRM中的A相a1支路等效磁路如图5所示,同理可得a2~a4支路等效磁路。图5中,Fsa1为a1支路绕组磁动势,Ns为绕组匝数,Uta1为a1支路定转子磁极处的磁压,Pta1为a1支路定转子磁极处的磁导,Pxa1为a1支路绕组端部的轴向磁导,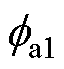 为a1支路磁通。
为a1支路磁通。
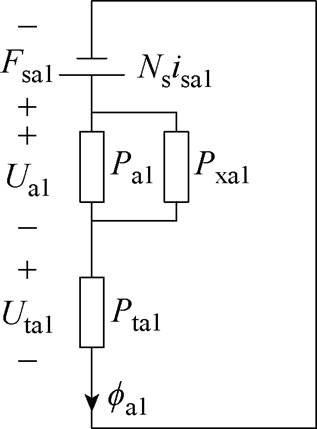
图5 A相a1支路等效磁路
Fig.5 Equivalent magnetic circuit of a1 branch of A phase
气隙磁压Ua1与绕组磁动势Fsa1之间满足
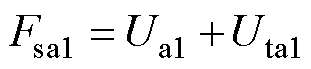 (25)
(25)
由于定转子磁极的铁磁材料具有非线性,关于Uta1计算过于复杂,故仅通过绕组磁动势计算气隙磁压的表达式相对方便。忽略漏磁通时,a1支路中绕组磁通、气隙磁通和定转子磁极处的磁通相等,均为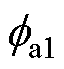 。由磁链和磁通定义并考虑绕组端部的轴向磁导Pxa1,可得定转子极交叠区气隙a1处的磁压Ua1的表达式为
。由磁链和磁通定义并考虑绕组端部的轴向磁导Pxa1,可得定转子极交叠区气隙a1处的磁压Ua1的表达式为
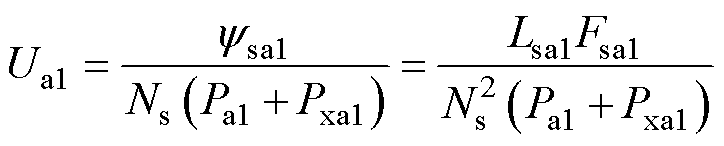 (26)
(26)
其中
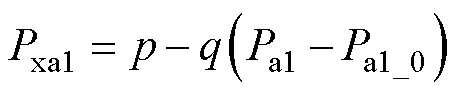 (27)
(27)
式中,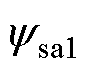 为a1支路中绕组磁链;Lsa1为a1支路中绕组电感;p、q均为常数;Pa1_0为
为a1支路中绕组磁链;Lsa1为a1支路中绕组电感;p、q均为常数;Pa1_0为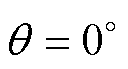 时Pa1的值。
时Pa1的值。
设置电流isa1和isa2均从0 A变化至4 A(样机额定电流IN=5 A,绕组匝数Ns=60),isa3=isa4=1 A,取转子位置角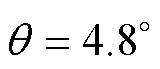 ,式(26)计算的定转子极交叠区气隙磁压Ua1如图6所示,可见在无磁饱和的情况下,定转子极交叠区气隙磁压Ua1并不等于绕组磁动势Fsa1,且其与绕组磁动势Fsa1的关系几乎为一条直线。
,式(26)计算的定转子极交叠区气隙磁压Ua1如图6所示,可见在无磁饱和的情况下,定转子极交叠区气隙磁压Ua1并不等于绕组磁动势Fsa1,且其与绕组磁动势Fsa1的关系几乎为一条直线。
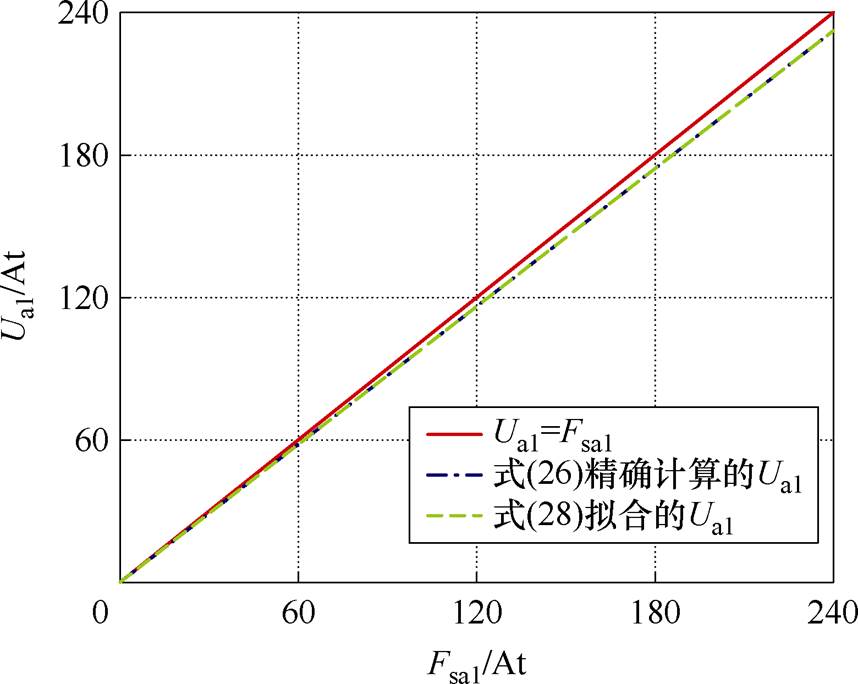
图6 无磁饱和时定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系曲线
Fig.6 Curves of the relationship between the air gap magnetic pressure Ua1 and the winding magnetic potential Fsa1 in the overlapping region of stator and rotor teeth without magnetic saturation
由于式(26)中Lsa1和Pa1均是关于转子位置角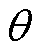 和转子径向位移a、b 的非线性函数,故为简化数学模型可将式(26)描述的气隙磁压Ua1与绕组磁动势Fsa1的关系用简单的线性函数拟合,将其设为
和转子径向位移a、b 的非线性函数,故为简化数学模型可将式(26)描述的气隙磁压Ua1与绕组磁动势Fsa1的关系用简单的线性函数拟合,将其设为
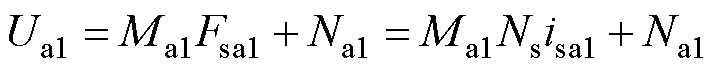 (28)
(28)
式中,Ma1、Na1均为常数,Ma1为无磁饱和时Ua1线性函数的斜率,Na1为其截距。同理可得无磁饱和时定转子极交叠区气隙a2~a4处磁压Ua2~Ua4的表示方法。图6表明,式(28)所用线性函数能精确拟合无磁饱和时定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系。
值得注意的是,由于气隙磁压量级较大,是产生悬浮力和电磁转矩的主要来源,其看似较小的差距即可引起较大的悬浮力误差。将相同气隙磁导计算方式下(如式(10)所示)气隙磁压改进前(Ua1=Fsa1)和改进后(式(28)计算Ua1)以及有限元模型计算的a、b方向径向悬浮力合力Fa和电磁转矩Ta的曲线结果分别对比如图7和图8所示,其中设置各绕组电流isa1=isa2=2 A,isa3=isa4=1 A,转子位置角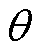 以
以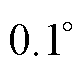 为间隔从
为间隔从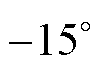 变化至
变化至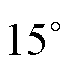 。由图7可见,在建立BSRM线性数学模型时,忽略定转子磁极磁阻而近似认为气隙磁压等于绕组磁动势,会导致径向悬浮力误差较大,尤其在定转子齿极中线对齐位置处,而采用改进的气隙磁压算法更精确地计算气隙磁压后,可显著减小径向悬浮力的误差,气隙磁压改进后模型与有限元模型计算的径向悬浮力合力Fa的曲线结果几乎完全重合。此外,由图8可见,此处气隙磁压算法的精确与否对电磁转矩影响较小。
。由图7可见,在建立BSRM线性数学模型时,忽略定转子磁极磁阻而近似认为气隙磁压等于绕组磁动势,会导致径向悬浮力误差较大,尤其在定转子齿极中线对齐位置处,而采用改进的气隙磁压算法更精确地计算气隙磁压后,可显著减小径向悬浮力的误差,气隙磁压改进后模型与有限元模型计算的径向悬浮力合力Fa的曲线结果几乎完全重合。此外,由图8可见,此处气隙磁压算法的精确与否对电磁转矩影响较小。
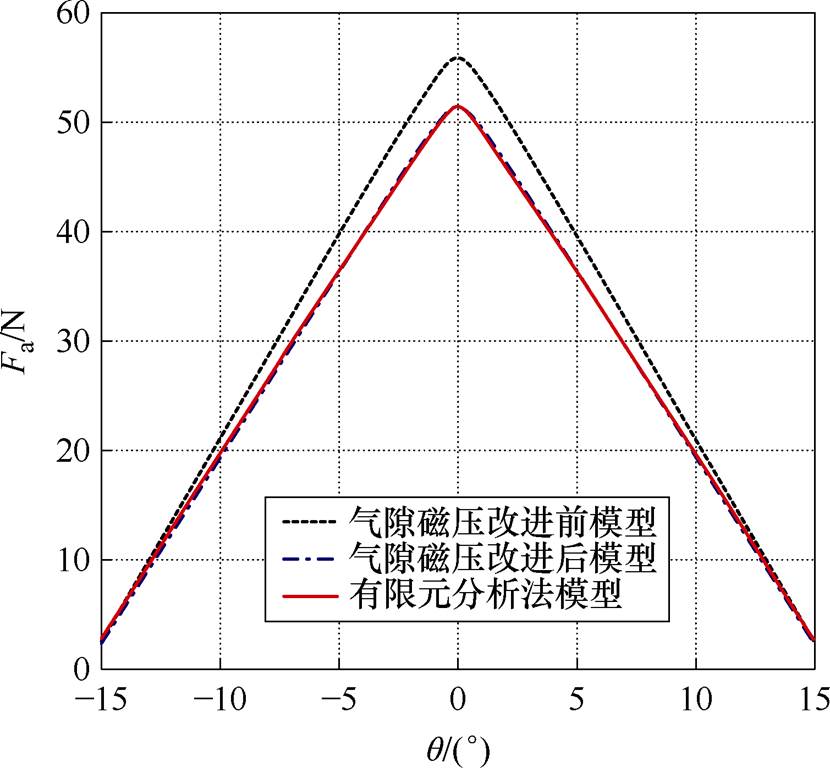
图7 不同气隙磁压计算方式下无磁饱和时定转子极交叠区径向悬浮力合力Fa结果对比
Fig.7 Results comparison of radial suspension force combined force Fa in the overlapping region of stator and rotor teeth without magnetic saturation under different calculation methods of air gap magnetic pressure
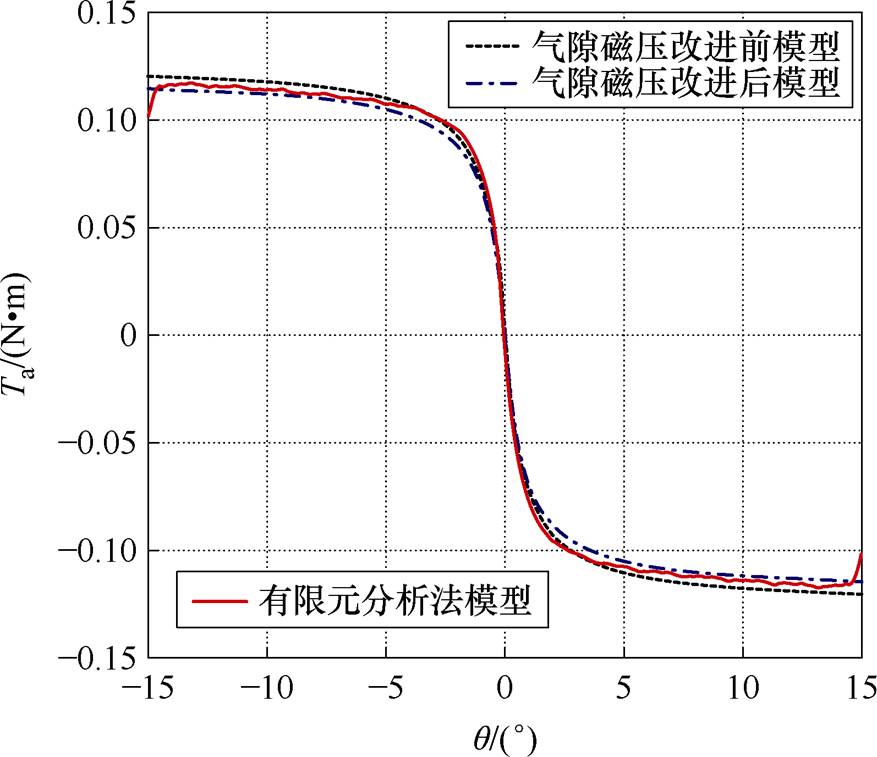
图8 不同气隙磁压计算方式下无磁饱和时定转子极交叠区电磁转矩Ta结果对比
Fig.8 Results comparison of electromagnetic torque Ta in the overlapping region of stator and rotor teeth without magnetic saturation under different calculation methods of air gap magnetic pressure
将式(18)、式(28)代入式(16)和式(17)可得定转子极交叠区a、b方向径向悬浮力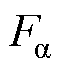 、
、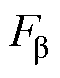 分别为
分别为
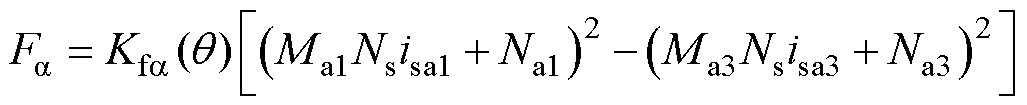 (29)
(29)
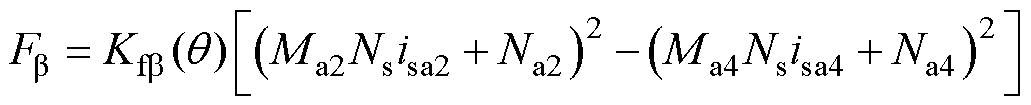 (30)
(30)
式中,Ma2~Ma4、Na2~Na4均为常数,Ma2~Ma4分别为无磁饱和时Ua2~Ua4线性函数的斜率,Na2~Na4为其对应的截距。
定转子极交叠区a、b方向径向悬浮力合力Fa为
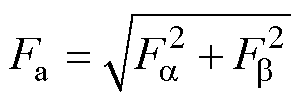 (31)
(31)
将式(24)、式(28)代入式(23)可得定转子极交叠区总电磁转矩Ta为
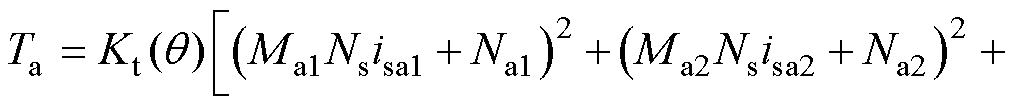
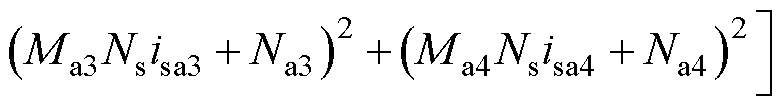 (32)
(32)
由于气隙磁导的空气介质属性,故其不受磁饱和影响。而磁饱和却影响气隙磁压,故建立计及磁饱和的SWBSRM定转子极交叠区数学模型,需对其气隙磁压做进一步分析。
以气隙a1为例,式(26)的本质是磁路欧姆定律,其描述的定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系在无磁饱和及有磁饱和的情况下均成立,区别在于:无磁饱和时,式(26)描述的定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系是一个线性函数;有磁饱和时,式(26)描述的定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系是一个非线性函数。设置电流isa1和isa2均从0 A变化至10 A(样机额定电流IN=5 A,绕组匝数Ns=60),isa3=isa4=1 A,取转子位置角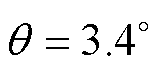 ,对应的定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系曲线如图9所示。
,对应的定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系曲线如图9所示。
由图9可见,随着电流和磁动势的持续增大,磁饱和愈加严重,气隙磁压Ua1的斜率越来越小,呈现出较强的非线性。故为简化数学模型,将式(26)描述的气隙磁压Ua1与绕组磁动势Fsa1的曲线关系用分段线性函数拟合,并总结出一套具有高拟合精度的分段点选取规律,如式(33)所示。同理可得定转子极交叠区气隙a2~a4处磁压Ua2~Ua4的表示方法。
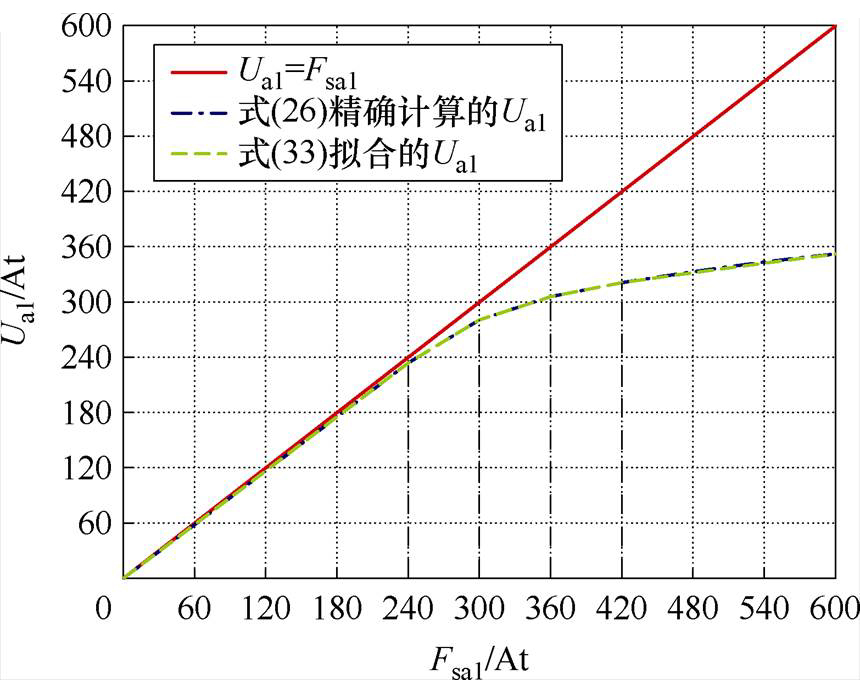
图9 磁饱和时定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系曲线
Fig.9 Curves of the relationship between the air gap magnetic pressure Ua1 and the winding magnetic electromotive force Fsa1 in the overlapping region of stator and rotor teeth with magnetic saturation
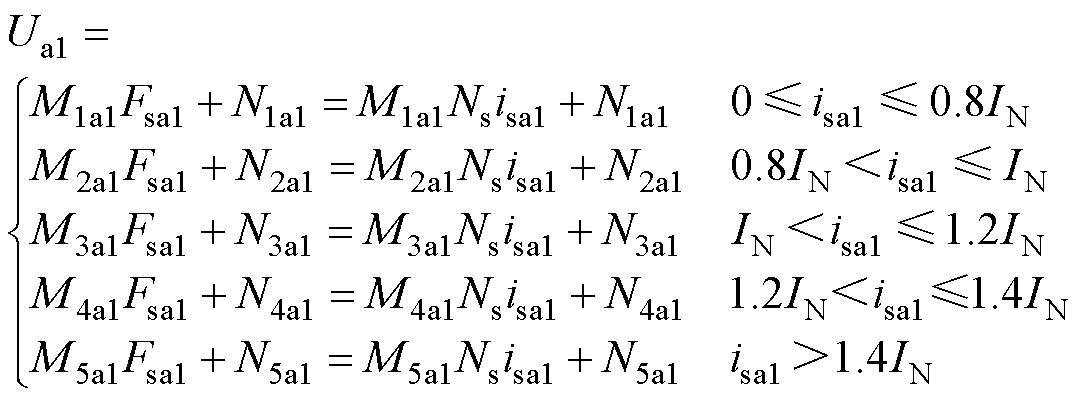 (33)
(33)
式中,M1a1~M5a1、N1a1~N5a1均为常数,M1a1~M5a1为磁饱和时Ua1分段线性函数各段的斜率,N1a1~N5a1为其对应截距;IN为绕组额定电流,也可释义为饱和前允许的最大绕组电流。
如图9所示,式(33)所采用的分段点选取规律下的分段线性函数能够精确地拟合磁饱和情况下定转子极交叠区气隙磁压Ua1与绕组磁动势Fsa1的关系。基于此,可较精确地计算考虑磁饱和情况下的定转子极交叠区径向悬浮力和电磁转矩,且模型相对简洁,实用性强。
值得注意的是,在用式(33)所示的分段线性函数拟合气隙磁压Ua1与绕组磁动势Fsa1的曲线关系过程中,至关重要的是分段点的选取,这充分影响了拟合精度。针对两台不同尺寸和不同绕组额定电流的样机,在不同硅钢材料及不同转子位置角的多种工况下,采用几种可能的分段点取法,并对比其拟合结果的标准误差(Standard Error, SE),见表1和表2。
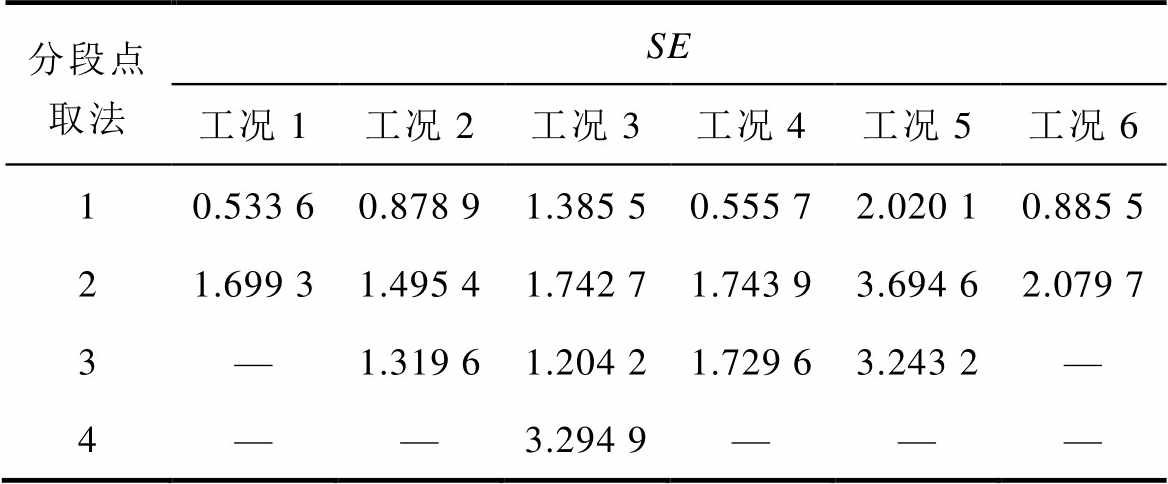
表1 样机1各工况下不同分段点取法的拟合结果标准误差SE对比
Tab.1 Comparison of standard deviations SE of fitting results for different selection methods of piecewise points under different working conditions of prototype 1
分段点取法SE 工况1工况2工况3工况4工况5工况6 10.533 60.878 91.385 50.555 72.020 10.885 5 21.699 31.495 41.742 71.743 93.694 62.079 7 3—1.319 61.204 21.729 63.243 2— 4——3.294 9———
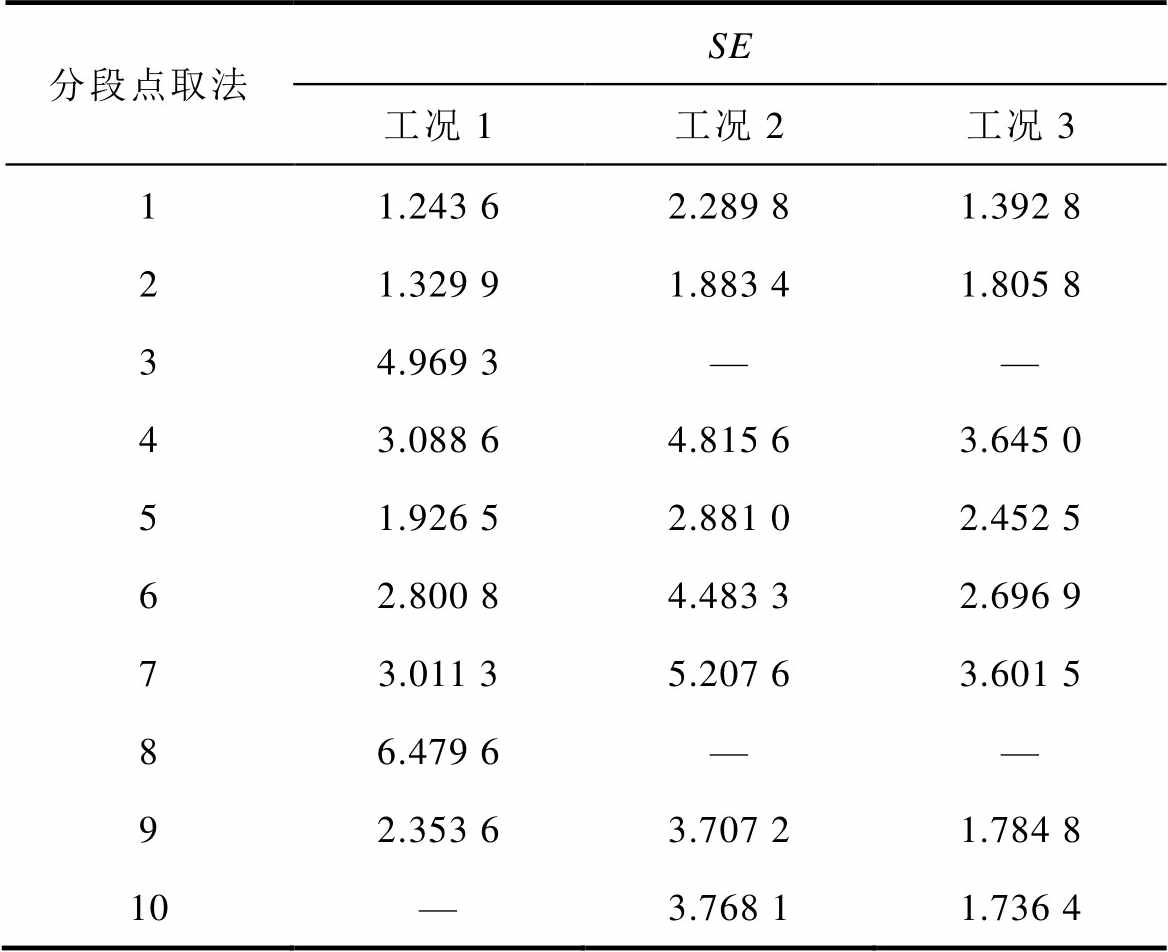
表2 样机2各工况下不同分段点取法的拟合结果标准误差SE对比
Tab.2 Comparison of standard deviations SE of fitting results for different selection methods of piecewise points under different working conditions of prototype 2
分段点取法SE 工况1工况2工况3 11.243 62.289 81.392 8 21.329 91.883 41.805 8 34.969 3—— 43.088 64.815 63.645 0 51.926 52.881 02.452 5 62.800 84.483 32.696 9 73.011 35.207 63.601 5 86.479 6—— 92.353 63.707 21.784 8 10—3.768 11.736 4
其中,对于样机1:额定电流IN=5 A,绕组匝数Ns=60。工况1为绕组电流isa1~isa4均从0 A变化至20 A,取转子位置角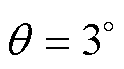 ,硅钢材料为DW310-35;工况2为基于工况1将转子位置角改为
,硅钢材料为DW310-35;工况2为基于工况1将转子位置角改为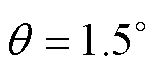 ;工况3为基于工况1将转子位置角改为
;工况3为基于工况1将转子位置角改为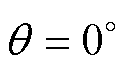 ;工况4为基于工况1将绕组电流改为isa1和isa2均从0 A变化至10 A,isa3=isa4=1 A;工况5为基于工况3将硅钢材料改为D21-50;工况6为基于工况3将硅钢材料改为DW540-50。分段点取法1为4 A,5 A,6 A,7 A(即0.8IN,IN,1.2IN,1.4IN);分段点取法2为4 A,5 A,6 A;分段点取法3为3 A,4 A,5 A,6 A;分段点取法4为3 A,4 A,5 A。
;工况4为基于工况1将绕组电流改为isa1和isa2均从0 A变化至10 A,isa3=isa4=1 A;工况5为基于工况3将硅钢材料改为D21-50;工况6为基于工况3将硅钢材料改为DW540-50。分段点取法1为4 A,5 A,6 A,7 A(即0.8IN,IN,1.2IN,1.4IN);分段点取法2为4 A,5 A,6 A;分段点取法3为3 A,4 A,5 A,6 A;分段点取法4为3 A,4 A,5 A。
对于样机2:额定电流IN=10 A,绕组匝数Ns= 32。工况1为绕组电流isa1和isa2均从0 A变化至30 A,isa3=isa4=1 A,取转子位置角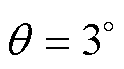 ,硅钢材料为DW310-35;工况2为基于工况1将硅钢材料改为D21-50;工况3为基于工况1将硅钢材料改为DW540-50。分段点取法1为8 A,10 A,12 A,14 A(即0.8IN,IN,1.2IN,1.4IN);分段点取法2为7 A,9 A,11 A,13 A;分段点取法3为7 A,8 A,9 A,10 A;分段点取法4为6 A,8 A,10 A,11 A;分段点取法5为7 A,9 A,11 A,12 A;分段点取法6为9 A,10 A,11 A,12 A;分段点取法7为8 A,9 A,10 A,11 A;分段点取法8为10 A,11 A,12 A,13 A;分段点取法9为9 A,11 A,13 A,15 A;分段点取法10为9 A,11 A,14 A,16 A。
,硅钢材料为DW310-35;工况2为基于工况1将硅钢材料改为D21-50;工况3为基于工况1将硅钢材料改为DW540-50。分段点取法1为8 A,10 A,12 A,14 A(即0.8IN,IN,1.2IN,1.4IN);分段点取法2为7 A,9 A,11 A,13 A;分段点取法3为7 A,8 A,9 A,10 A;分段点取法4为6 A,8 A,10 A,11 A;分段点取法5为7 A,9 A,11 A,12 A;分段点取法6为9 A,10 A,11 A,12 A;分段点取法7为8 A,9 A,10 A,11 A;分段点取法8为10 A,11 A,12 A,13 A;分段点取法9为9 A,11 A,13 A,15 A;分段点取法10为9 A,11 A,14 A,16 A。
由表1可以看出,对于样机1,除工况3以外,其他各工况下均是分段点取法1拟合误差最小,且工况3中分段点取法1的拟合误差与拟合误差最小的分段点取法3最为接近。由表2可以看出,对于样机2,除工况2以外,其他各工况下均是分段点取法1拟合误差最小,且工况2中分段点取法1的拟合误差与拟合误差最小的分段点取法2最为接近。由此可以得出结论,如式(33)中所揭示的拟合气隙磁压Ua1与绕组磁动势Fsa1曲线关系的分段线性函数的分段点选取规律(0.8IN,IN,1.2IN,1.4IN)具有较高的拟合精度。
将式(18)和式(33)代入式(16)和式(17)可得定转子极交叠区a、b方向径向悬浮力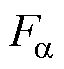 、
、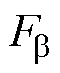 分别为
分别为
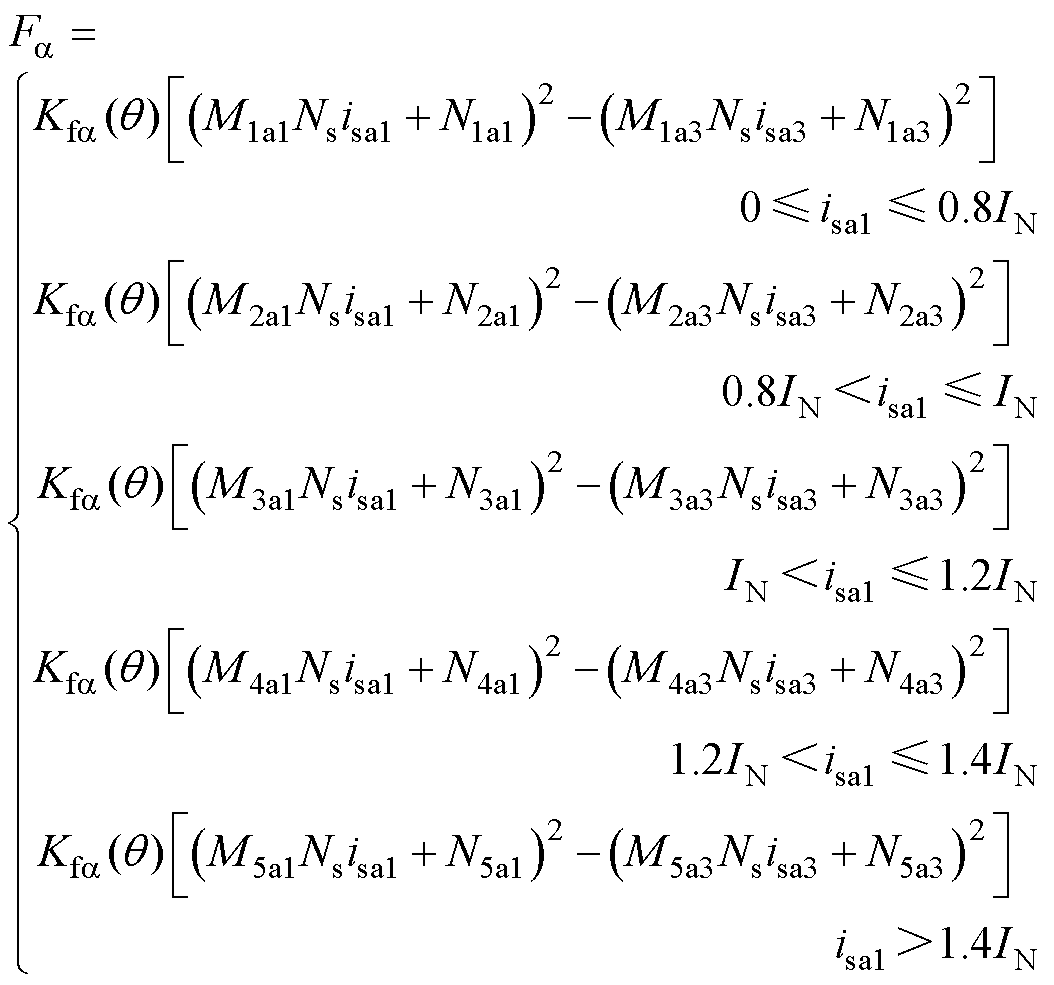 (34)
(34)
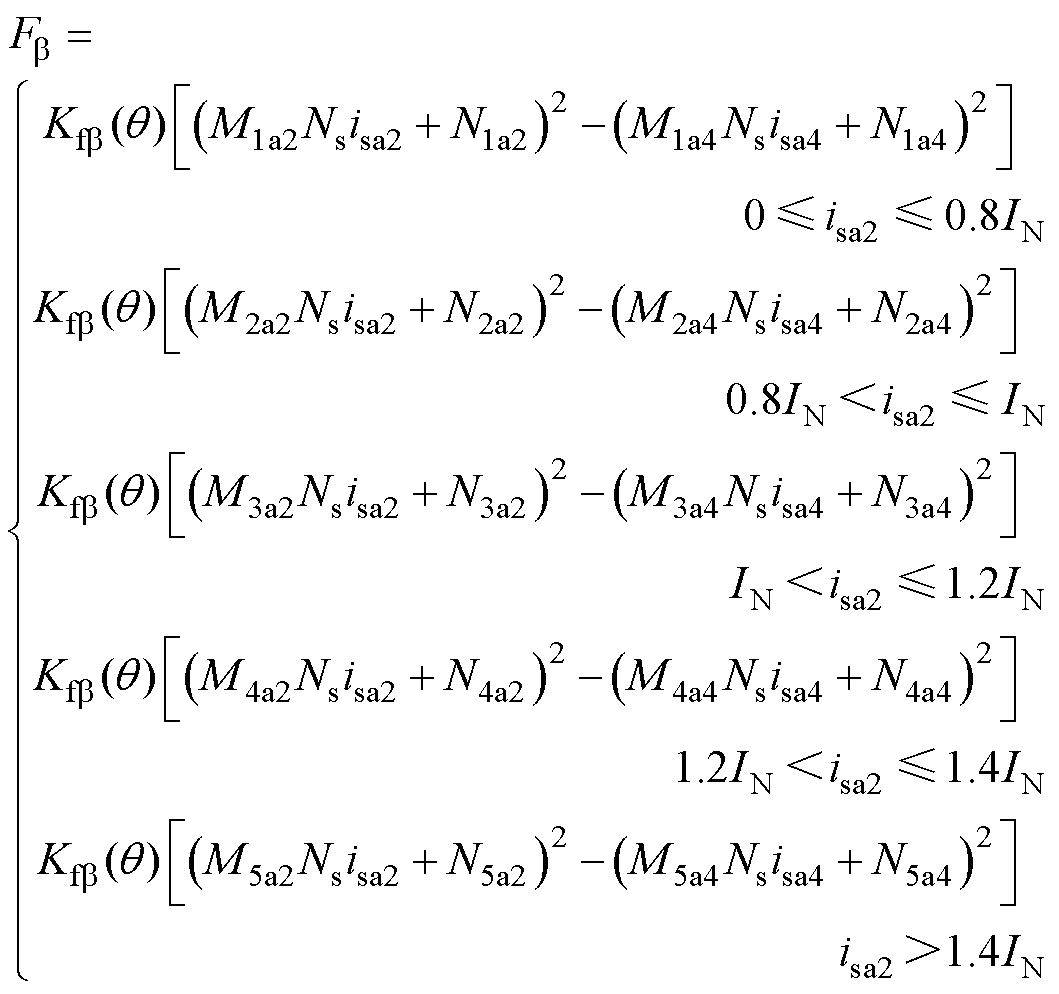 (35)
(35)
式中,M1a2~M5a2、M1a3~M5a3、M1a4~M5a4、N1a2~N5a2、N1a3~N5a3、N1a4~N5a4均为常数,M1a2~M5a2、M1a3~M5a3、M1a4~M5a4分别为磁饱和时Ua2~Ua4分段线性函数各段的斜率,N1a2~N5a2、N1a3~N5a3、N1a4~N5a4为其对应截距。
定转子极交叠区a、b方向径向悬浮力合力Fa算法同式(31)。
将式(24)和式(33)代入式(23)可得定转子极交叠区总电磁转矩Ta为
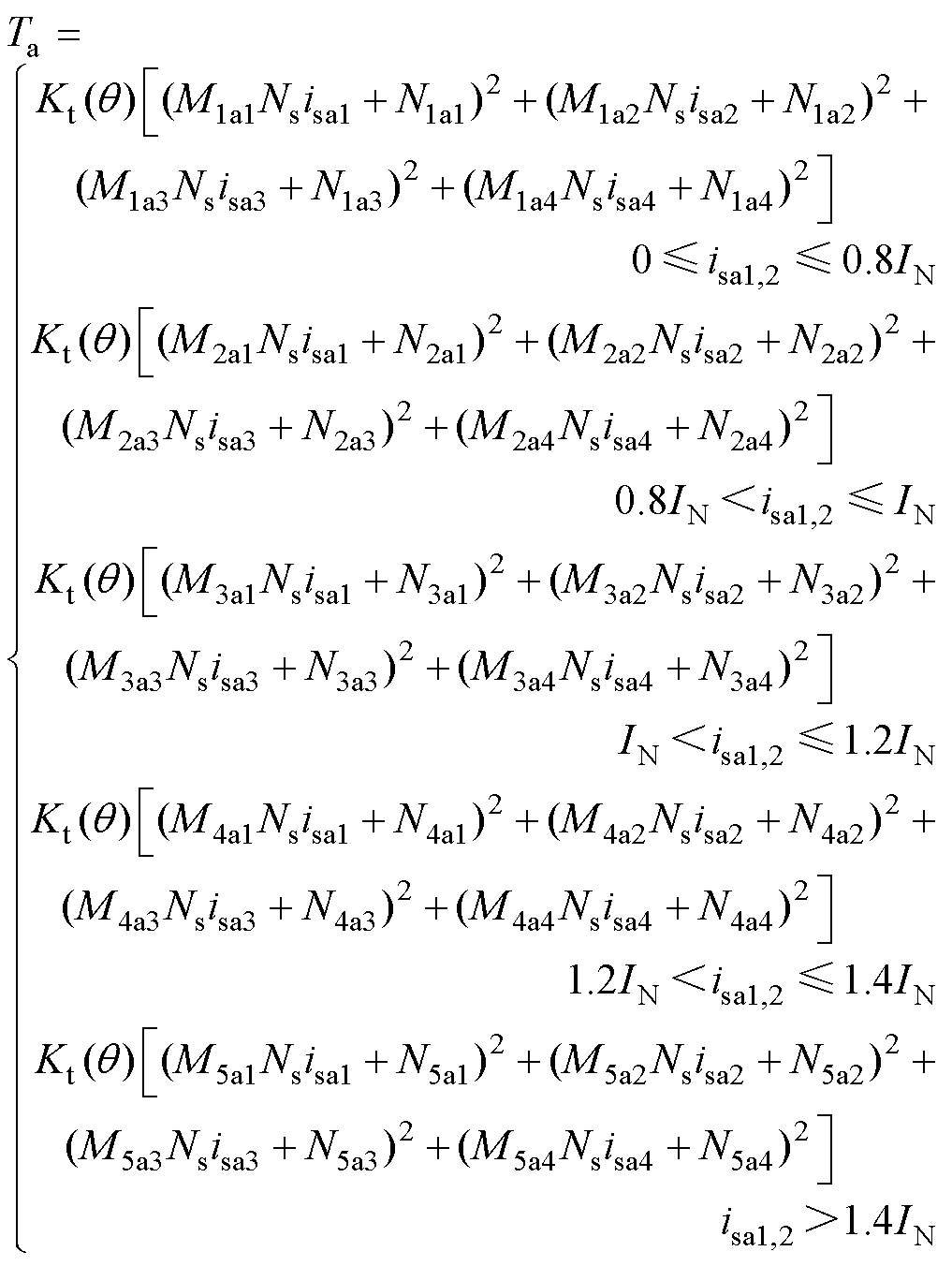 (36)
(36)
本节建立转子位置角绝对值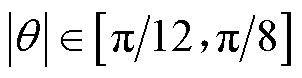 范围内的SWBSRM定转子极非交叠区数学模型。基于定转子极非交叠区气隙磁场分布特征,将气隙磁场分割成四个形状规则的区域,先分别求解各区域的气隙磁导,进而计算整个气隙区域的总磁导。
范围内的SWBSRM定转子极非交叠区数学模型。基于定转子极非交叠区气隙磁场分布特征,将气隙磁场分割成四个形状规则的区域,先分别求解各区域的气隙磁导,进而计算整个气隙区域的总磁导。
SWBSRM定转子极非交叠区电磁场有限元分析如图10示。根据有限元分析可知,SWBSRM定转子极非交叠区中的气隙磁路可分为四个部分的椭圆形轨迹,故以气隙a1为例,将其磁路分割如图11所示。气隙a1处定转子极非交叠区的磁导Pa1可分成四个部分: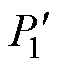 、
、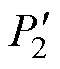 、
、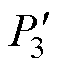 、
、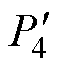 。分别求出这四部分的磁导后,可得气隙a1处磁导Pa1为
。分别求出这四部分的磁导后,可得气隙a1处磁导Pa1为
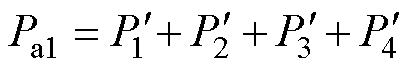 (37)
(37)
式中,由于对称性,有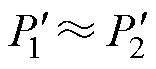 ,
,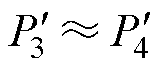 ,且
,且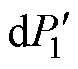 和
和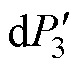 的横截面积dS表达式同式(5)。
的横截面积dS表达式同式(5)。
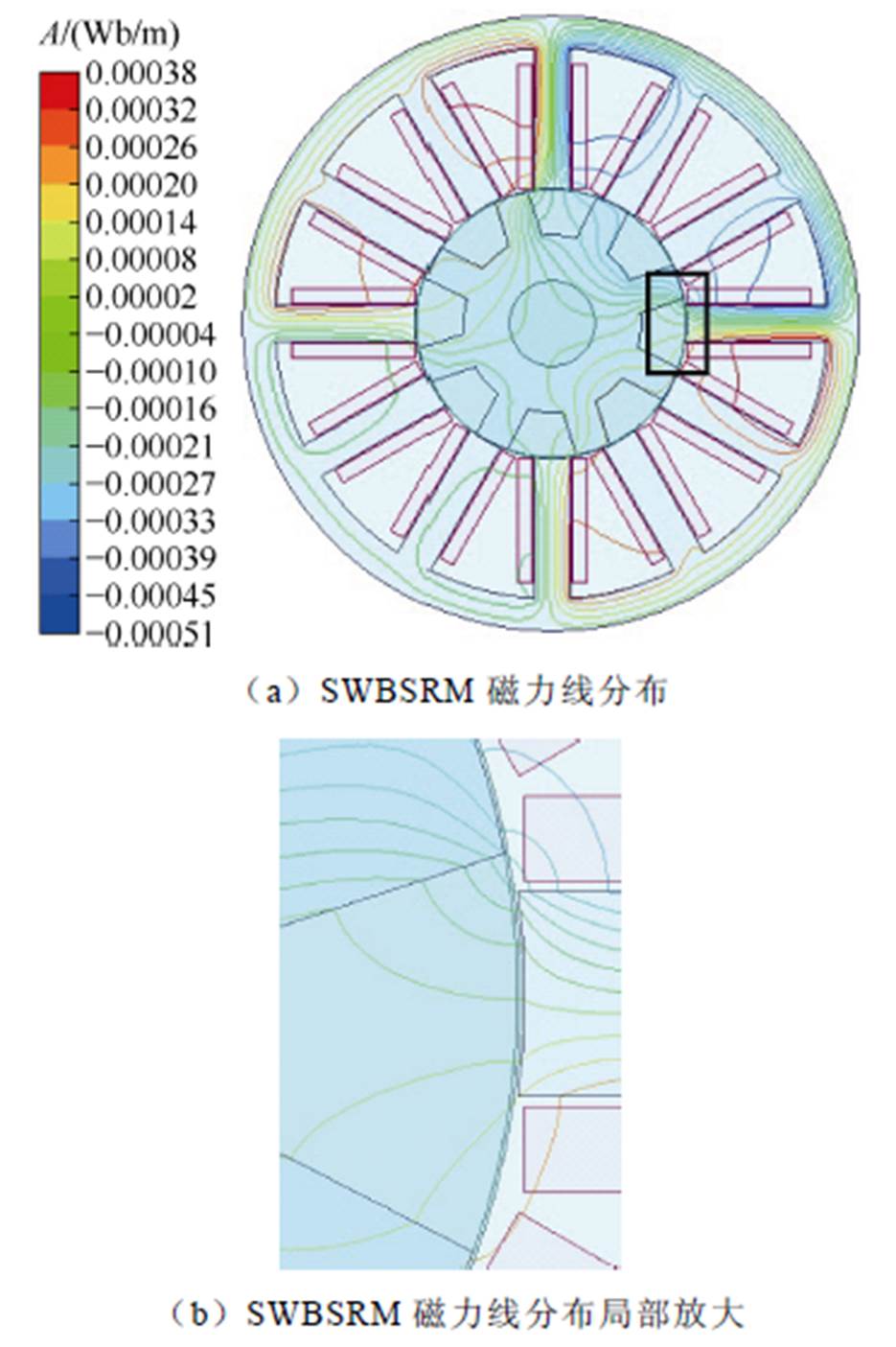
图10 SWBSRM定转子极非交叠区电磁场有限元分析(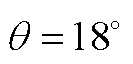 )
)
Fig.10 Finite element analysis of electromagnetic field in the non-overlapping region of stator and rotor teeth of SWBSRM (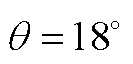 )
)
定转子极非交叠区气隙磁路长度le为1/4椭圆周长,已知椭圆短半轴长度为n,长半轴长度为lg+n2/(n+lg),由查表法计算并画出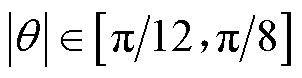 范围内1/4椭圆周长与
范围内1/4椭圆周长与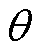 的关系近似为一条直线,如图12所示,故可用关于
的关系近似为一条直线,如图12所示,故可用关于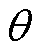 的简单函数拟合该椭圆磁路的长度le,该函数表达式见式(7)和式(8)。由图12所示,与传统算法中将椭圆磁路长度用直线加1/4圆周替代相比,式(7)亦能较好地拟合
的简单函数拟合该椭圆磁路的长度le,该函数表达式见式(7)和式(8)。由图12所示,与传统算法中将椭圆磁路长度用直线加1/4圆周替代相比,式(7)亦能较好地拟合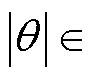
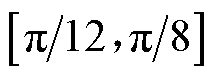 时的椭圆磁路长度。
时的椭圆磁路长度。

图11 气隙a1处定转子极非交叠区磁路分割示意图
Fig.11 Schematic diagram of magnetic circuit segmentation in the non-overlapping region of stator and rotor teeth at air gap a1
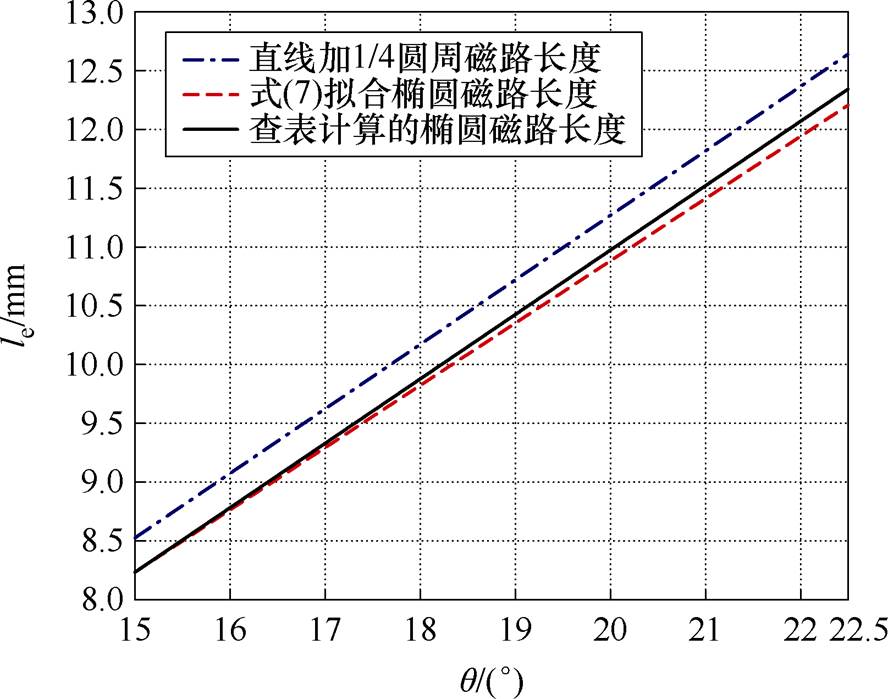
图12 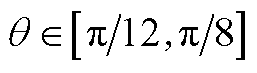 时的椭圆磁路长度le
时的椭圆磁路长度le
Fig.12 The length le of the elliptical magnetic circuit when 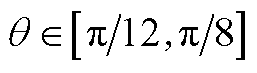
由磁导定义可得,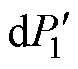 和
和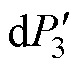 的表达式同式(9)。
的表达式同式(9)。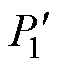 和
和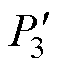 分别为
分别为
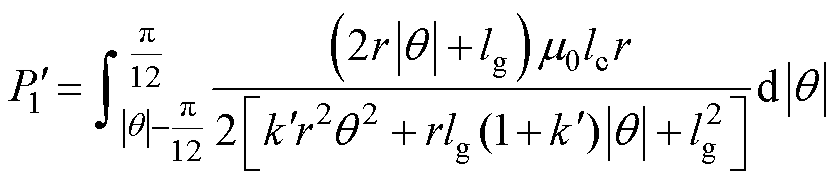 (38)
(38)
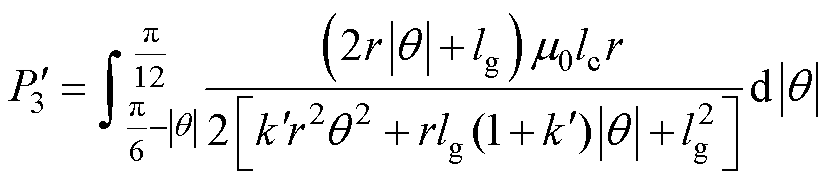 (39)
(39)
因此,由式(37)~式(39)可得气隙a1处定转子极非交叠区磁导Pa1为
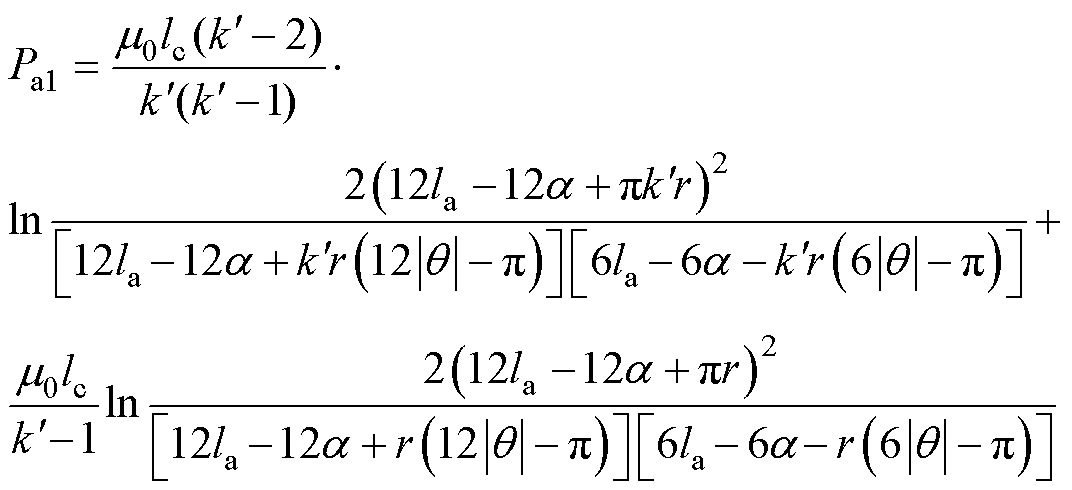 (40)
(40)
同理可得气隙a2~a4处定转子极非交叠区磁导Pa2~Pa4。
1)定转子极非交叠区径向悬浮力的比例系数
由式(40)可得定转子极非交叠区a方向径向悬浮力的比例系数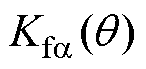 为
为
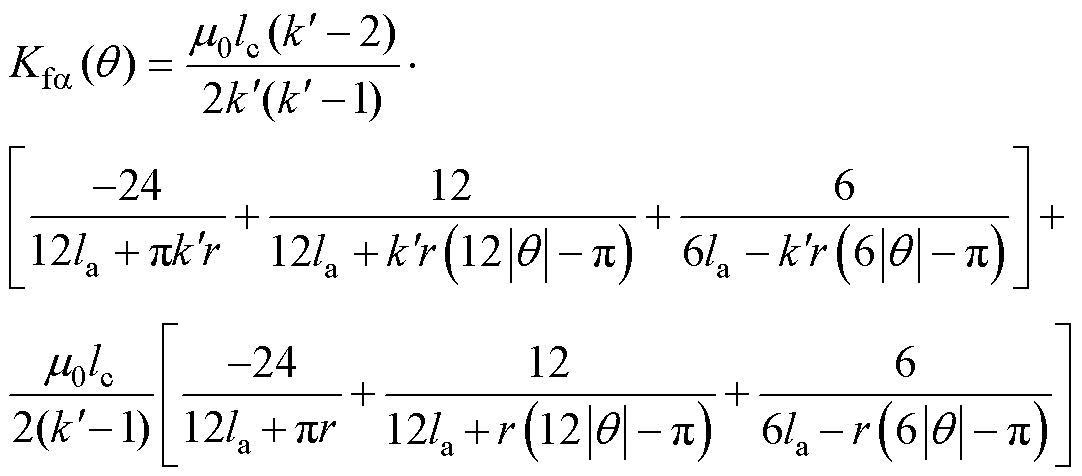 (41)
(41)
b 方向径向悬浮力的比例系数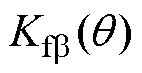 =
=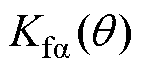 。
。
2)定转子极非交叠区电磁转矩的比例系数
由式(40)可得定转子极非交叠区电磁转矩的比例系数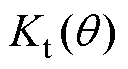 为
为
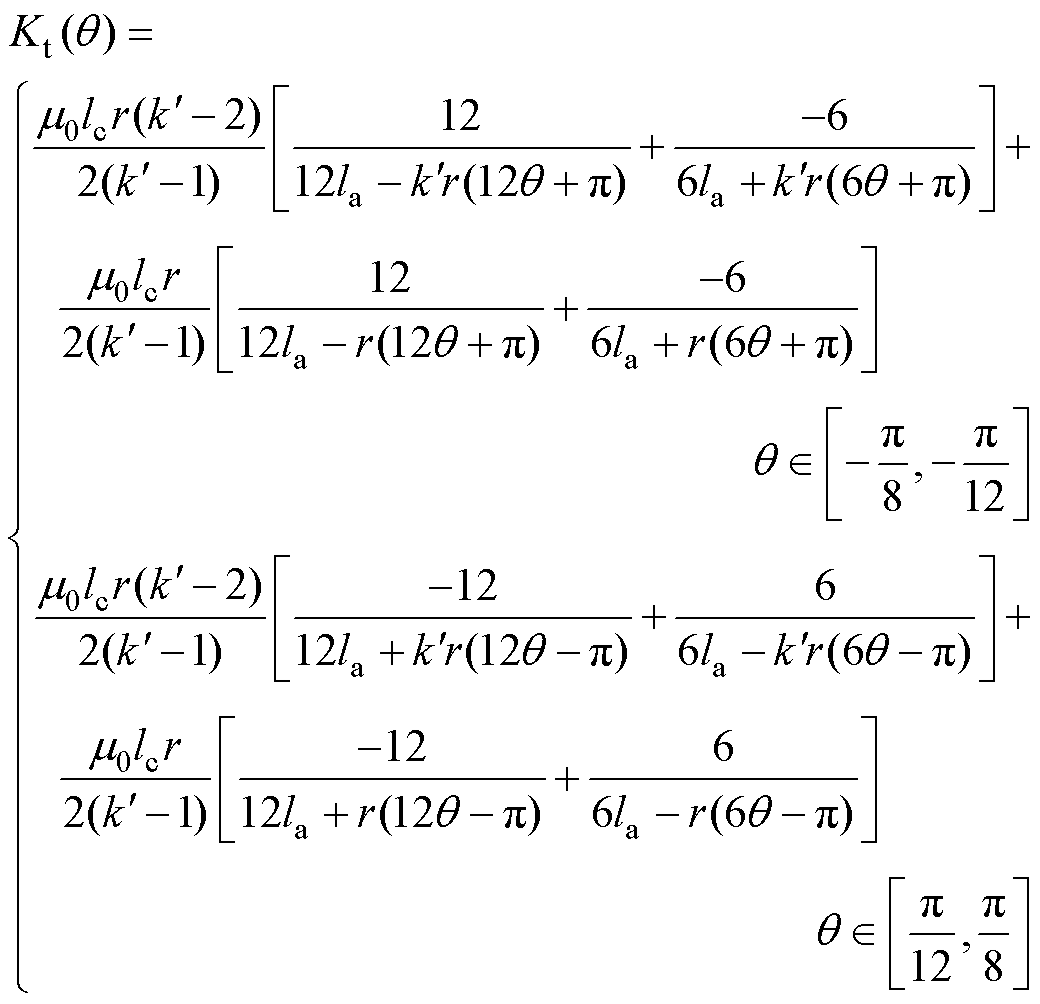 (42)
(42)
在定转子极非交叠区,可近似认为气隙磁压等于绕组磁动势,这种关系即使在大电流情况下也是适用的。这是由于相较于定转子极交叠区,定转子极非交叠区气隙磁路长度增大,导致气隙磁阻增大,因此气隙磁压增大而近似等于绕组磁动势。
结合式(16)、式(17)和式(41)可得定转子极非交叠区a、b方向径向悬浮力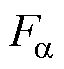 、
、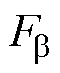 分别为
分别为
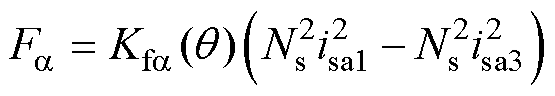 (43)
(43)
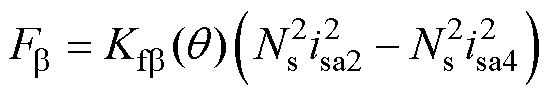 (44)
(44)
定转子极非交叠区a、b 方向径向悬浮力合力Fa算法同式(31)。
结合式(23)和式(42)可得定转子极非交叠区总电磁转矩Ta为
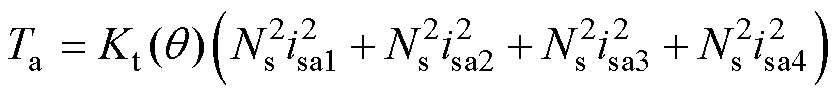 (45)
(45)
为验证本文提出的计及定转子磁极磁阻的SWBSRM新型数学模型的可行性和有效性,将本文模型计算结果分别与SWBSRM现有虚位移法模型和有限元法模型计算结果进行比较和分析。其中,采用样机1参数见表3,绕组额定电流为5 A。
表3 12/8极SWBSRM样机1参数
Tab.3 Parameters of prototype 1 of 12/8-pole SWBSRM
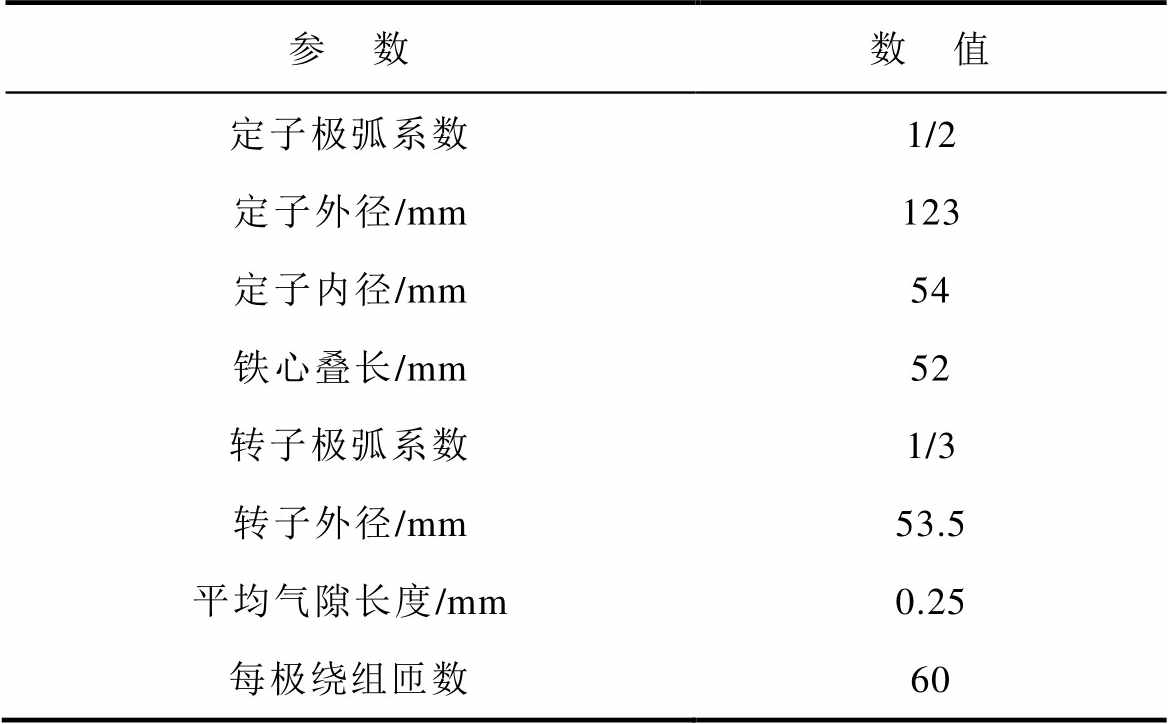
参 数数 值 定子极弧系数1/2 定子外径/mm123 定子内径/mm54 铁心叠长/mm52 转子极弧系数1/3 转子外径/mm53.5 平均气隙长度/mm0.25 每极绕组匝数60
基于样机1,设置各绕组电流isa1=isa2=2 A,isa3= isa4=1 A,转子位置角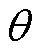 以
以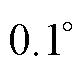 为间隔从
为间隔从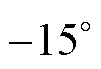 变化至
变化至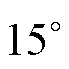 。建模时,式(27)中
。建模时,式(27)中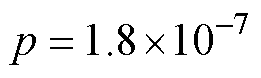 ,
,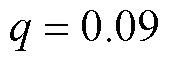 。式(28)中Ma1=0.966 6,Na1=0.386 1,Ma2=0.966 6,Na2=0.386 2,Ma3=1,Na3=0,Ma4=1,Na4=0。基于现有模型、本文模型和有限元法模型计算无磁饱和时SWBSRM定转子极交叠区A相两垂直方向径向悬浮力
。式(28)中Ma1=0.966 6,Na1=0.386 1,Ma2=0.966 6,Na2=0.386 2,Ma3=1,Na3=0,Ma4=1,Na4=0。基于现有模型、本文模型和有限元法模型计算无磁饱和时SWBSRM定转子极交叠区A相两垂直方向径向悬浮力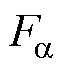 、
、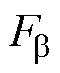 、径向悬浮力合力Fa和电磁转矩Ta的曲线结果如图13所示。
、径向悬浮力合力Fa和电磁转矩Ta的曲线结果如图13所示。
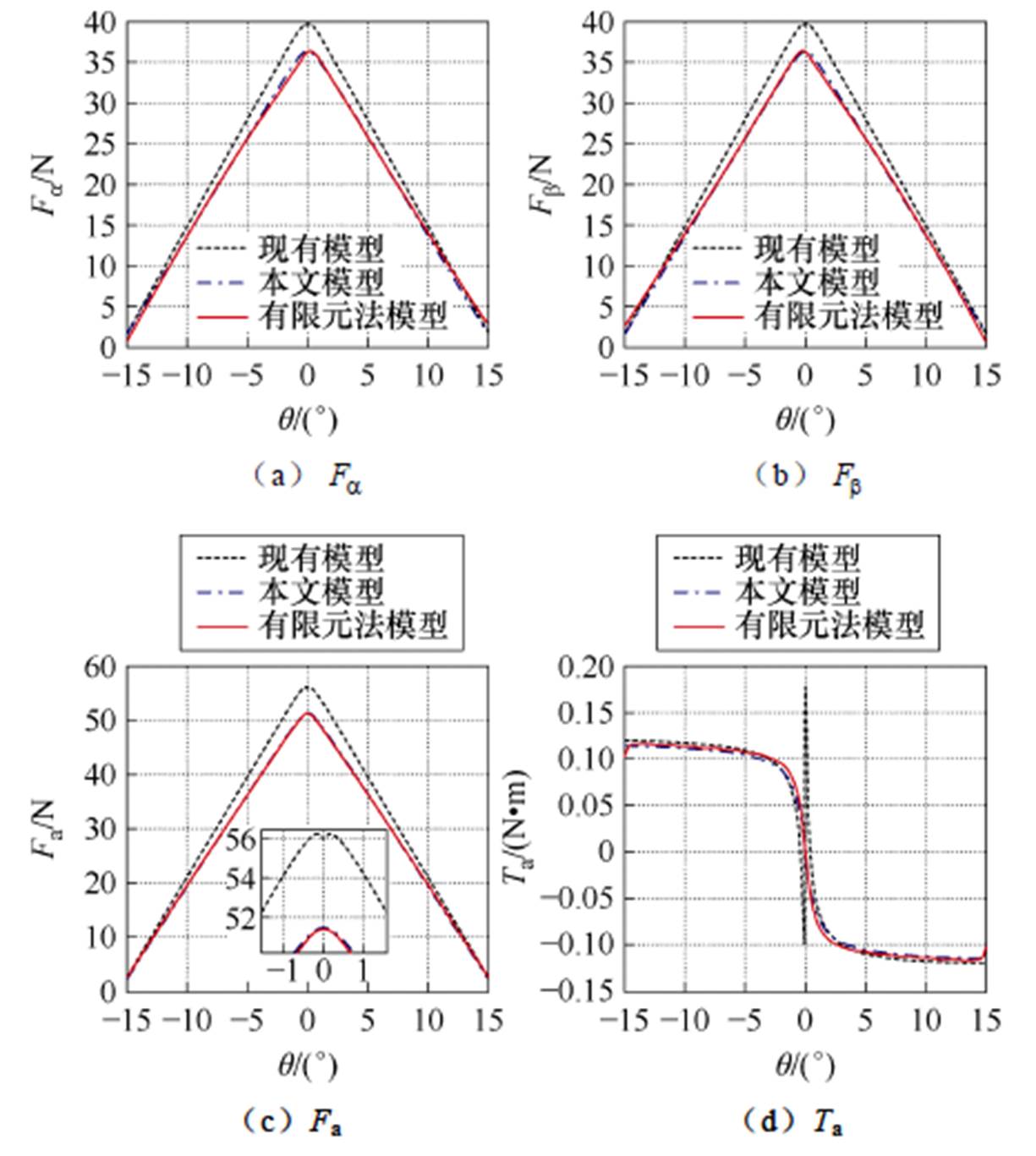
图13 无磁饱和时定转子极交叠区径向悬浮力和电磁转矩结果对比
Fig.13 Results comparison of radial suspension force and electromagnetic torque in the overlapping region of stator and rotor teeth without magnetic saturation
如图13a~图13c所示,与现有模型对比,本文模型能够显著减小a、b方向径向悬浮力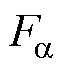 、
、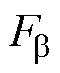 及其径向悬浮力合力Fa的误差,使其非常接近于有限元计算结果,尤其是图13c中的径向悬浮力合力Fa几乎与有限元计算结果完全重合。这正是由于本文建模方法提出当计算SWBSRM定转子极交叠区线性数学模型时计及定转子磁极磁阻,将气隙磁压表示为关于绕组磁动势的线性函数以更精确地计算气隙磁压的原因。从而有效解决了现有BSRM数学模型中普遍存在的定转子齿极中线对齐位置处悬浮力误差较大的问题。
及其径向悬浮力合力Fa的误差,使其非常接近于有限元计算结果,尤其是图13c中的径向悬浮力合力Fa几乎与有限元计算结果完全重合。这正是由于本文建模方法提出当计算SWBSRM定转子极交叠区线性数学模型时计及定转子磁极磁阻,将气隙磁压表示为关于绕组磁动势的线性函数以更精确地计算气隙磁压的原因。从而有效解决了现有BSRM数学模型中普遍存在的定转子齿极中线对齐位置处悬浮力误差较大的问题。
此外,图13a、图13b中径向悬浮力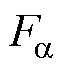 、
、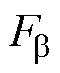 的有限元曲线在横向上有相反方向的微小偏移,而在图13c中径向悬浮力合力Fa曲线没有任何偏移而关于中心点
的有限元曲线在横向上有相反方向的微小偏移,而在图13c中径向悬浮力合力Fa曲线没有任何偏移而关于中心点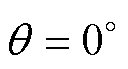 对称,这是由于径向悬浮力
对称,这是由于径向悬浮力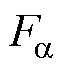 、
、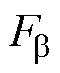 存在耦合作用致使其有限元曲线并非关于中心点对称,各自发生方向相反的微小偏移,而形成径向悬浮力合力Fa后这种方向相反的偏移就会相互抵消,故此,结合简化模型的目的,本文模型并未计及径向悬浮力
存在耦合作用致使其有限元曲线并非关于中心点对称,各自发生方向相反的微小偏移,而形成径向悬浮力合力Fa后这种方向相反的偏移就会相互抵消,故此,结合简化模型的目的,本文模型并未计及径向悬浮力 、
、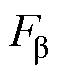 的耦合。
的耦合。
图13a~图13c中,现有模型关于a、b 方向径向悬浮力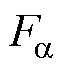 、
、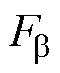 及其径向悬浮力合力Fa的曲线计算结果在定转子齿极中线对齐(
及其径向悬浮力合力Fa的曲线计算结果在定转子齿极中线对齐(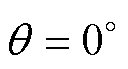 )时均存在凹陷问题,其局部放大如图13c所示。且图13d中,现有模型计算的电磁转矩Ta曲线在
)时均存在凹陷问题,其局部放大如图13c所示。且图13d中,现有模型计算的电磁转矩Ta曲线在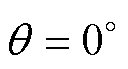 时存在严重的不连续问题。而本文模型却不存在这两个问题,其计算结果更贴近于有限元计算结果。这是因为本文提出一种新的计算SWBSRM椭圆形边缘气隙磁路长度的解析方法,提高了模型精度。
时存在严重的不连续问题。而本文模型却不存在这两个问题,其计算结果更贴近于有限元计算结果。这是因为本文提出一种新的计算SWBSRM椭圆形边缘气隙磁路长度的解析方法,提高了模型精度。
现有模型和本文模型相对于有限元模型计算结果的标准误差(SE)对比见表4,其中本文模型关于径向悬浮力合力Fa计算结果的标准误差比现有模型降低了90%,且其关于电磁转矩Ta计算结果的标准误差比现有模型降低了78%,可见本文模型对比于现有模型显著提高了计算精度。
表4 各模型的径向悬浮力和电磁转矩标准误差SE结果对比
Tab.4 Results comparison of standard deviations SE of radial suspension force and electromagnetic torque of two models

SE 现有模型2.091 22.091 22.898 40.017 8 本文模型0.446 40.446 40.284 60.004 0
设置各绕组电流isa1和isa2均从0 A变化至10 A,isa3=isa4=1 A,取转子位置角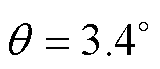 。建模时,式(33)中M1a1=0.972 9,N1a1=0.430 1,M1a2=0.972 9,N1a2= 0.430 2,M1a3=1,N1a3=0,M1a4=1,N1a4=0;M2a1= 0.780 5,N2a1=46.611 3,M2a2=0.780 3,N2a2=46.657 0,M2a3=1,N2a3=0,M2a4=1,N2a4=0;M3a1=0.418 3,N3a1= 155.278 6,M3a2=0.418 1,N3a2=155.310 4,M3a3=1,N3a3=0,M3a4=1,N3a4=0;M4a1=0.262 7,N4a1= 211.302 1,M4a2=0.262 8,N4a2=211.230 5,M4a3=1,N4a3=0,M4a4=1,N3a4=0;M5a1=0.171 3,N5a1= 249.667 0,M5a2=0.171 3,N5a2=249.644 0,M5a3=1,N5a3=0,M5a4=1,N5a4=0。传统不计及磁饱和模型、本文提出的计及磁饱和模型和有限元分析法模型计算的SWBSRM定转子极交叠区A相两垂直方向径向悬浮力
。建模时,式(33)中M1a1=0.972 9,N1a1=0.430 1,M1a2=0.972 9,N1a2= 0.430 2,M1a3=1,N1a3=0,M1a4=1,N1a4=0;M2a1= 0.780 5,N2a1=46.611 3,M2a2=0.780 3,N2a2=46.657 0,M2a3=1,N2a3=0,M2a4=1,N2a4=0;M3a1=0.418 3,N3a1= 155.278 6,M3a2=0.418 1,N3a2=155.310 4,M3a3=1,N3a3=0,M3a4=1,N3a4=0;M4a1=0.262 7,N4a1= 211.302 1,M4a2=0.262 8,N4a2=211.230 5,M4a3=1,N4a3=0,M4a4=1,N3a4=0;M5a1=0.171 3,N5a1= 249.667 0,M5a2=0.171 3,N5a2=249.644 0,M5a3=1,N5a3=0,M5a4=1,N5a4=0。传统不计及磁饱和模型、本文提出的计及磁饱和模型和有限元分析法模型计算的SWBSRM定转子极交叠区A相两垂直方向径向悬浮力 、
、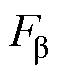 、径向悬浮力合力Fa和电磁转矩Ta的曲线结果对比如图14所示。
、径向悬浮力合力Fa和电磁转矩Ta的曲线结果对比如图14所示。
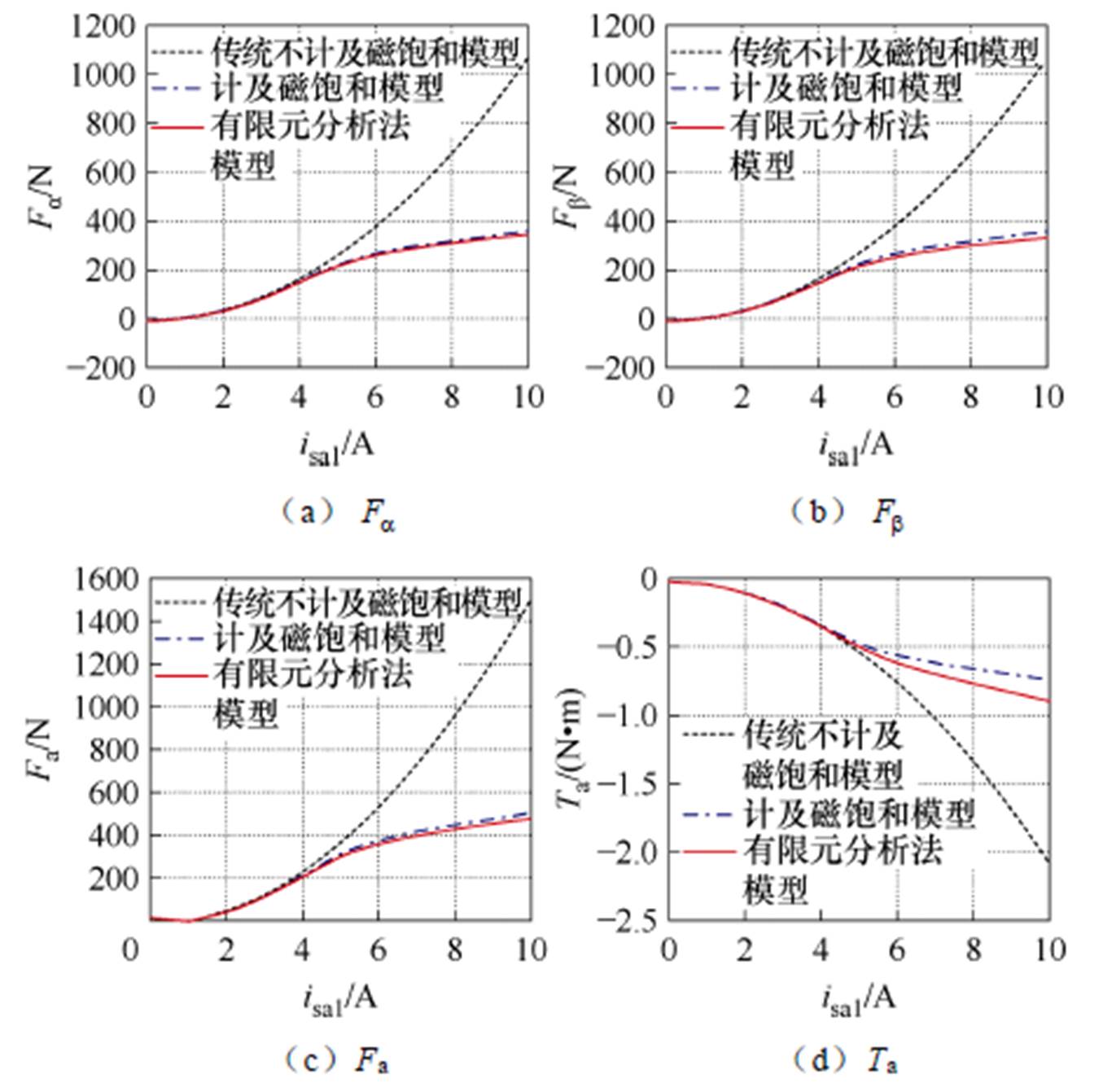
图14 磁饱和时定转子极交叠区径向悬浮力和电磁转矩结果
Fig.14 Results of radial suspension force and electromagnetic torque in the overlapping region of stator and rotor teeth with magnetic saturation
如图14所示,随着绕组电流的不断增大,磁饱和现象愈加明显,传统不计及磁饱和模型对于径向悬浮力和电磁转矩的计算结果均逐渐偏离有限元模型的计算结果且误差逐渐增大,而本文提出的计及磁饱和模型能够始终接近有限元模型的计算结果。这验证了基于所提出的分段点选取规律下的分段线性函数拟合气隙磁压-绕组磁动势关系以建立计及磁饱和的SWBSRM定转子极交叠区数学模型方法的有效性。
设置各绕组电流isa1=isa2=2 A,isa3=isa4=1 A,转子位置角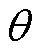 以
以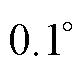 为间隔从
为间隔从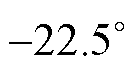 变化至
变化至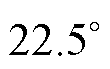 ,基于本文模型和有限元法模型计算无磁饱和时SWBSRM全角度(含定转子极非交叠区)A相两垂直方向径向悬浮力
,基于本文模型和有限元法模型计算无磁饱和时SWBSRM全角度(含定转子极非交叠区)A相两垂直方向径向悬浮力 、
、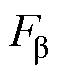 、径向悬浮力合力Fa和电磁转矩Ta的曲线结果对比如图15所示。可知,本文模型能够精确地建立包括定转子极非交叠区在内的SWBSRM全角度数学模型,使其非常接近于有限元计算结果。
、径向悬浮力合力Fa和电磁转矩Ta的曲线结果对比如图15所示。可知,本文模型能够精确地建立包括定转子极非交叠区在内的SWBSRM全角度数学模型,使其非常接近于有限元计算结果。
设置各绕组电流isa1和isa2均从0 A变化至10 A,isa3=isa4=1 A,取转子位置角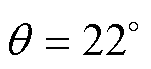 ,本文提出的SWBSRM定转子极非交叠区数学模型和有限元分析法模型计算的各电流下A相两垂直方向径向悬浮力
,本文提出的SWBSRM定转子极非交叠区数学模型和有限元分析法模型计算的各电流下A相两垂直方向径向悬浮力 、
、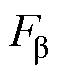 、径向悬浮力合力Fa和电磁转矩Ta的曲线结果对比如图16所示。可知,随着绕组电流的不断增大,该非交叠区数学模型能够始终较精确地接近于有限元模型的计算结果,验证了本文提出的SWBSRM定转子极非交叠区数学模型的正确性和有效性。
、径向悬浮力合力Fa和电磁转矩Ta的曲线结果对比如图16所示。可知,随着绕组电流的不断增大,该非交叠区数学模型能够始终较精确地接近于有限元模型的计算结果,验证了本文提出的SWBSRM定转子极非交叠区数学模型的正确性和有效性。
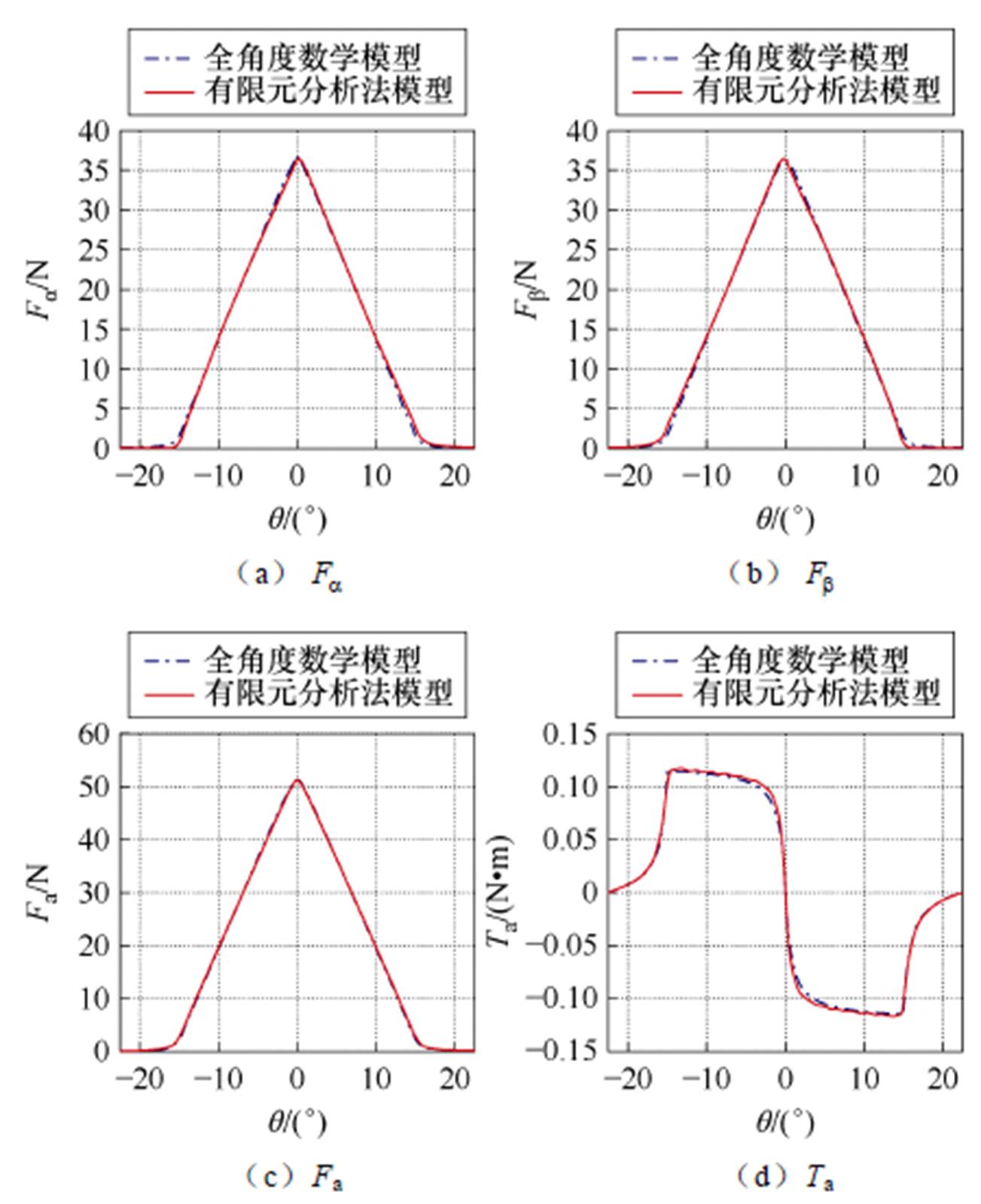
图15 无磁饱和时全角度径向悬浮力和电磁转矩结果对比
Fig.15 Results comparison of radial suspension force and electromagnetic torque for full rotor angular positions without magnetic saturation
针对SWBSRM现有虚位移法模型存在的径向悬浮力误差大、定转子齿极中线对齐时径向悬浮力波形凹陷和电磁转矩波形不连续以及不便于建立磁饱和模型等问题,本文提出了一种计及定转子磁极磁阻的SWBSRM新型数学模型,主要贡献和结论如下:
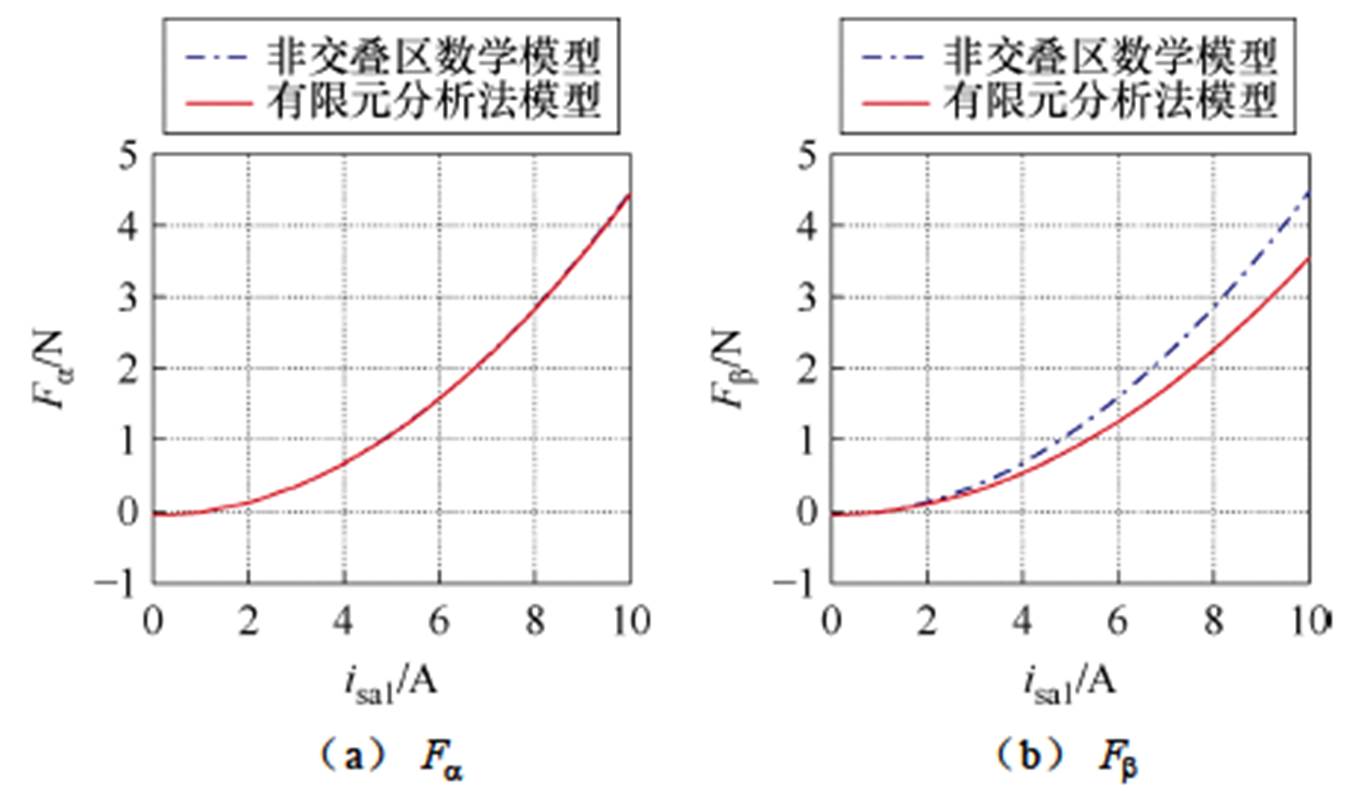
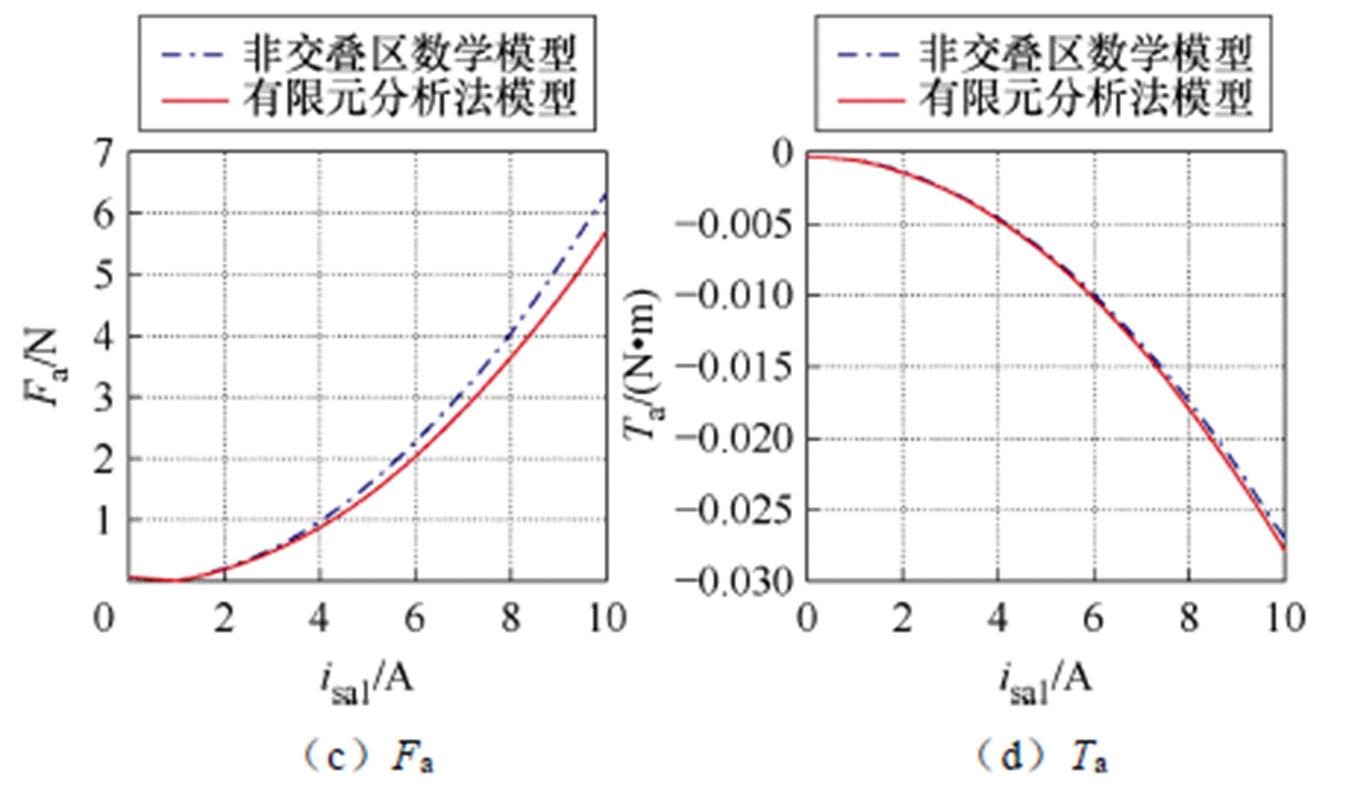
图16 各电流下定转子极非交叠区径向悬浮力和电磁转矩结果对比
Fig.16 Results comparison of radial suspension force and electromagnetic torque in the non-overlapping region of stator and rotor teeth under different currents
1)建立了SWBSRM定转子极交叠区线性数学模型:提出一种关于SWBSRM椭圆形边缘气隙磁路长度的新型计算方法,避免了定转子齿极中线对齐时存在的径向悬浮力波形凹陷和电磁转矩波形不连续问题,提高了建模精度;此外,提出建模时应计及定转子磁极磁阻,令气隙磁压为关于绕组磁动势的线性表达式而非直接使二者相等,在不增加建模复杂度的同时提高了气隙磁压的计算精度,大幅降低了径向悬浮力的误差,有效解决了现有BSRM数学模型中普遍存在的定转子齿极中线对齐时径向悬浮力误差较大的问题,并可进一步提高电机本体设计精度。
2)建立了计及磁饱和的SWBSRM定转子极交叠区数学模型:将气隙磁压表示为关于绕组磁动势的分段线性函数用以拟合磁饱和时二者之间的非线性关系,提出一种高精度的分段点选取方法,基于该分段点选取方法可获取较精确的数学模型,且模型相对简洁,实用性强。
3)建立了SWBSRM定转子极非交叠区数学模型,该模型可适用于无磁饱和及有磁饱和两种工况,与定转子极交叠区数学模型构成了一个完整相周期内的数学模型。
将所建模型与现有虚位移法模型和有限元模型的计算结果进行对比,结果表明,所建的SWBSRM定转子极交叠区线性数学模型关于径向悬浮力和电磁转矩的计算误差分别比现有模型降低了90%和78%,验证了所建模型的准确度。
参考文献
[1] Schweitzer G, Maslen E H, Buehler P, et al. Magnetic bearings: theory, design, and application to rotating machinery[M]. Berlin: Springer-Verlag Berlin Heidelberg, 2009.
[2] Xu Zhenyao, Yu Qingguo, Zhang Fengge. Design and analysis of asymmetric rotor pole type bearingless switched reluctance motor[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 3-10.
[3] 孙德博, 胡艳芳, 牛峰, 等. 开关磁阻电机调速系统故障诊断和容错控制方法研究现状及展望[J]. 电工技术学报, 2022, 37(9): 2211-2229.
Sun Debo, Hu Yanfang, Niu Feng, et al. Status and prospect of fault diagnosis and tolerant control methods for switched reluctance motor drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2211-2229.
[4] 丁文, 李可, 付海刚. 一种12/10极模块化定子混合励磁开关磁阻电机分析[J]. 电工技术学报, 2022, 37(8): 1948-1958.
Ding Wen, Li Ke, Fu Haigang, et al. Analysis of a 12/10-pole modular-stator hybrid-excited switched reluctance machine[J]. Transactions of China Elec- trotechnical Society, 2022, 37(8): 1948-1958.
[5] 贲彤, 王进, 陈龙, 等. 考虑磁致伸缩逆效应的非晶合金开关磁阻电机减振方法[J]. 电工技术学报, 2023, 38(10): 2648-2660.
Ben Tong, Wang Jin, Chen Long, et al. Vibration reduction method of switched reluctance motor with amorphous alloy cores based on inverse- magnetostriction effect[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2648-2660.
[6] 于丰源, 陈昊, 闫文举, 等. 宽窄定子极轴向磁通开关磁阻电机的设计与分析[J]. 电工技术学报, 2023, 38(5): 1261-1274.
Yu Fengyuan, Chen Hao, Yan Wenju, et al. Design and characteristic analysis of a wide-narrow stator poles axial flux switched reluctance machine[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1261-1274.
[7] Shimada K, Takemoto M, Chiba A, et al. Radial forces in switched reluctance type bearingless motor[C]//The 9th Symposium on Electromagnetics and Dynamics, 1997: 547-552.
[8] Takemoto M, Chiba A, Fukao T. A new control method of bearingless switched reluctance motors using square-wave currents[C]//IEEE Power Engin- eering Society Winter Meeting, Singapore, 2000: 375- 380.
[9] Wang Zelin, Cao Xin, Deng Zhiquan, et al. Electromagnetic modeling and investigation for bearingless switched reluctance motor considering magnetic saturation[J]. IEEE Transactions on Energy Conversion, 2023, 38 (1): 122-133.
[10] 孙玉坤, 刘羡飞, 王德明, 等. 基于有限元分析的磁悬浮开关磁阻电机数学模型的全角度拓展[J]. 电工技术学报, 2007, 22(9): 34-39.
Sun Yukun, Liu Xianfei, Wang Deming, et al. Extension of mathematical model to full angle for bearingless switched reluctance motors based on finite-element analysis[J]. Transactions of China Electro-technical Society, 2007, 22(9): 34-39.
[11] 王喜莲, 崔睿珍, 郝毅, 等. 考虑磁饱和的共悬浮绕组式无轴承开关磁阻电机径向力模型[J]. 电机与控制学报, 2021, 25(6): 46-53.
Wang Xilian, Cui Ruizhen, Hao Yi, et al. Radial Force model of a bearingless switched reluctance motor with sharing suspension windings considering magnetic saturation[J]. Electric Machines and Control, 2021, 25(6): 46-53.
[12] 杨帆, 袁野, 祝贵, 等. 12/14磁悬浮开关磁阻电机悬浮力全周期模型构建[J]. 电工技术学报, 2023, 38(2): 330-339.
Yang Fan, Yuan Ye, Zhu Gui, et al. Suspension force modeling for 12/14 bearingless switched reluctance motor considering flux multi teeth hinge[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(2): 330-339.
[13] 李群. 单绕组无轴承开关磁阻电动机控制策略的研究[D]. 南京: 南京航空航天大学, 2013.
[14] 朱志莹, 张巍, 朱海浪, 等. 轴向永磁磁悬浮飞轮电机损耗计算与温度场分析[J]. 电气工程学报, 2022, 17(4): 174-180.
Zhu Zhiying, Zhang Wei, Zhu Hailang, et al. Analysis of loss and temperature field of axial permanent magnet magnetic bearingless flywheel machine[J]. Journal of Electrical Engineering, 2022, 17(4): 174- 180.
[15] 赵丽丹, 邓智泉, 曹鑫, 等. 12/8极单绕组无轴承开关磁阻电机绕组开路故障有限元分析[J]. 电工技术学报, 2013, 28(7): 131-137.
Zhao Lidan, Deng Zhiquan, Cao Xin, et al. Finite element analysis of open circuit fault in a 12/8 single winding bearingless switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 131-137.
[16] 曹鑫, 刘从宇, 邓智泉, 等. 单绕组12/4极无轴承开关磁阻电机转矩和悬浮力的解耦机理与实现[J].电工技术学报, 2018, 33(15): 3527-3534.
Cao Xin, Liu Congyu, Deng Zhiquan, et al. Decoupling mechanism and implementation of torque and levitation force in single-winding 12/4 bearing- less switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3527- 3534.
[17] 曹鑫. 12/8极无轴承开关磁阻电机的研究[D]. 南京: 南京航空航天大学, 2010.
Cao Xin. Research on 12/8 bearingless switched reluctance machine[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.
[18] Takemoto M, Shimada K, Chiba A, et al. A design and characteristics of switched reluctance type bearingless motors[C]//Proceedings of the 4th International Symposium on Magnetic Suspension Technology, NASA, Gifu, Japan, 1998: 49-63.
[19] Takemoto M, Suzuki H, Chiba A, et al. Improved analysis of a bearingless switched reluctance motor[J]. IEEE Transactions on Industry Applications, 2001, 37(1): 26-34.
[20] 邓智泉, 杨钢, 张媛, 等. 一种新型的无轴承开关磁阻电机数学模型[J]. 中国电机工程学报, 2005, 25(9): 139-146.
Deng Zhiquan, Yang Gang, Zhang Yuan, et al. An innovative mathematical model for a bearingless switched reluctance motor[J]. Proceedings of the CSEE, 2005, 25(9): 139-146.
[21] 孙玉坤, 吴建兵, 项倩雯. 基于有限元法的磁悬浮开关磁阻电机数学模型[J]. 中国电机工程学报, 2007, 27(12): 33-40.
Sun Yukun, Wu Jianbing, Xiang Qianwen. The mathematic model of bearingless switched reluctance motor based on the finite-element analysis[J]. Proceedings of the CSEE, 2007, 27(12): 33-40.
[22] Takemoto M, Chiba A, Akagi H, et al. Radial force and torque of a bearingless switched reluctance motor operation in a region of magnetic saturation[J]. IEEE Transactions on Industry Applications, 2004, 40(1): 103-112.
[23] Takemoto M, Chiba A, Akagi H, et al. Torque and suspension force in a bearingless switched reluctance motor[J]. Electrical Engineering in Japan, 2006, 157(2): 72-82.
[24] 项倩雯. 飞轮电池用五自由度单绕组磁悬浮开关磁阻电机参数设计及运行控制[D]. 镇江: 江苏大学, 2013.
Xiang Qianwen. Parameter design and operation control of 5-DOF single-winding bearingless switched reluctance motor for flywheel batteries[D]. Zhenjiang: Jiangsu University, 2013.
Abstract At the center alignment position of the stator and rotor teeth, a large radial suspension force error, discontinuous electromagnetic torque waveform, and concave radial suspension force waveform exist. Moreover, establishing a magnetic saturated model for a single-winding bearingless switched reluctance motor (SWBSRM) is challenging using existing virtual displacement modeling methods. This paper proposes a new mathematical model of SWBSRM considering the reluctance of stator and rotor poles.
Firstly, a mathematical model of the overlapping region of stator and rotor teeth of SWBSRM without magnetic saturation is established. A new analytical method for calculating the length of the elliptical edge air gap magnetic circuit in SWBSRM is proposed to solve the problems of discontinuous electromagnetic torque waveform and concave radial suspension force waveform when the centerlines of stator and rotor teeth are aligned, and improve the accuracy of the model. In addition, the air gap’s magnetic pressure is not equal to the magnetic electromotive force of the winding and the reluctance of stator and rotor poles cannot be ignored when magnetic saturation does not occur in the overlapping region of stator and rotor teeth. Therefore, the reluctance of stator and rotor poles should be considered, and the magnetic pressure of the air gap should be represented as a linear function of the magnetic electromotive force. Thus, the error of radial suspension force can be reduced, and the design accuracy of the motor body is improved.
Secondly, a mathematical model of the overlapping region of stator and rotor teeth of SWBSRM with magnetic saturation is established. A selection rule of piecewise points is proposed using a piecewise linear function to fit the nonlinear relationship between the magnetic pressure of the air gap and the magnetic electromotive force of the winding. As a result, the radial suspension force and electromagnetic torque can be calculated accurately.
Then, a mathematical model of the non-overlapping region of the stator and rotor teeth of SWBSRM is established and applied to multiple working conditions. Thus, A complete mathematical model of SWBSRM within one phase period is formed.
Finally, the calculation results of the proposed new mathematical model of SWBSRM are compared with those of the existing virtual displacement method model and the finite element model. The results indicate that the standard error of the calculation results of the radial suspension force combined force of the proposed mathematical model of the overlapping region of stator and rotor teeth of SWBSRM without magnetic saturation is reduced by 90%, and the standard error of the calculation results of its electromagnetic torque is reduced by 78% compared to those of the existing model, verifying the feasibility and effectiveness of the proposed method.
keywords:Single-winding bearingless switched reluctance motor, edge gap magnetic circuit, magnetic pole reluctance, magnetic saturation, mathematical model
中图分类号:TM352
DOI: 10.19595/j.cnki.1000-6753.tces.232201
国家自然科学基金资助项目(51477042)。
收稿日期2024-01-02
改稿日期2024-04-30
石 凡 女,1994年生,博士研究生,研究方向为无轴承开关磁阻电机优化设计及振动抑制技术。E-mail: 18751809142@163.com
王宏华 男,1963年生,教授,博士生导师,研究方向为电力电子与运动控制系统、先进控制理论及应用。E-mail: wanghonghua@263.net(通信作者)
(编辑 崔文静)