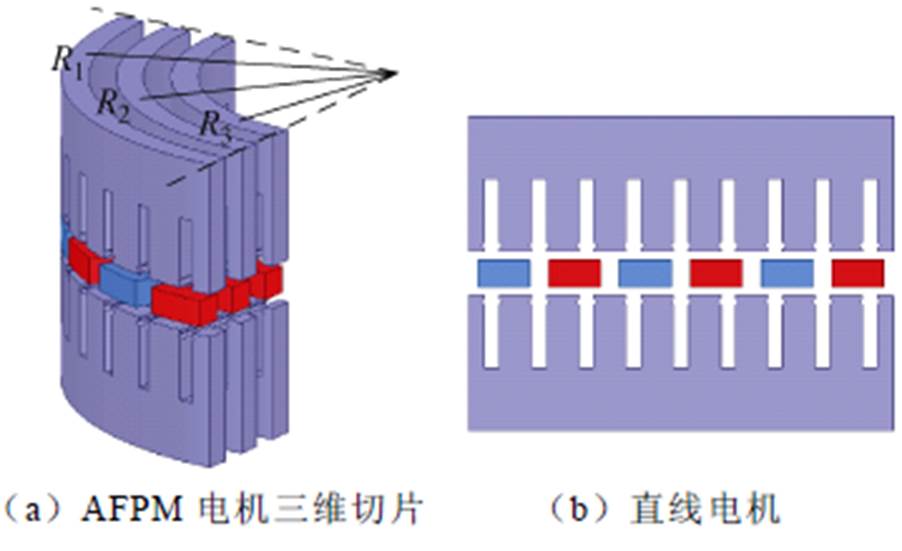
图1 直线电机等效示意图
Fig.1 Equivalent schematic diagram of linear motor
摘要 齿槽效应会对气隙磁场产生较大影响,针对现有保角映射法无法考虑实际槽形以及精确子域法通用性受限的问题,该文基于改进复相对磁导函数提出一种计及定子槽宽、槽深和静态偏心影响的开槽轴向磁通永磁电机气隙磁场通用解析模型。建模时首先将求解域划分为气隙子域和永磁体子域,依据各子域的边界条件求解拉普拉斯方程,借助标量磁位求得无槽空载气隙磁场解析表达式,并引入改进复相对磁导函数考虑齿槽效应。然后分析静态偏心的作用规律,建立计及静态偏心影响的气隙磁场解析模型,在此基础上计算了不同偏心率下的气隙磁通密度、空载反电动势及齿槽转矩,有限元和实验证明了该解析模型的有效性。相较有限元分析,该解析模型具有建模耗时少、计算速度快和求解精度相近的特点,为相关电机的优化设计提供了有益参考。
关键词:齿槽效应 改进复相对磁导函数 静态偏心 轴向磁通永磁电机
轴向磁通永磁(Axial Flux Permanent Magnet, AFPM)电机凭借其特殊的拓扑结构,具有体积小、功率密度高、效率高等优点,特别适用于永磁直驱场合,在航空航天、轨道交通、船舶推进等高转矩密度及高效率应用领域具有极大的应用潜力[1-4]。AFPM电机通常会在定子开槽以嵌放绕组,齿槽效应会对气隙磁场产生较大影响,而气隙磁场的精确求解是计算齿槽转矩、空载反电动势和电磁转矩等电磁性能的前提。当前,主流的电磁场求解方法包含有限元法、等效磁路法和子域法。
有限元法是现今应用最广泛、计算最精确的电磁场求解方法。相关学者采用有限元软件进行电机设计,文献[5]提出一种新型轴向磁通磁齿轮复合电机,相比传统YASA电机大幅提高了转矩密度。文献[6-7]则对电机拓扑结构及材料展开研究,实现了电机转矩输出能力和效率的提升。为了提高三维有限元仿真速度,文献[8]提出虚拟气隙并将其引入电机的三维有限元模型中,通过调整气隙材料相对磁导率适当增大气隙长度,在保证计算精度的前提下,大幅降低了网格剖分数量,在一定程度上缩短了三维有限元的计算时长。有限元法可以考虑定子槽形、铁心材料的非线性以及饱和影响,但磁场的精确求解依赖于大量的网格剖分,因此,在电机的初始设计阶段不宜采用有限元法。
为了提高电磁场计算速度,国内外学者对等效磁路法和子域法展开了大量研究。文献[9]建立了永磁直驱发电机的等效磁路模型,该模型可以考虑定转子的几何尺寸以及磁路的非线性。电机的磁场具有三维分布特性,文献[10-11]对三维等效磁路模型展开研究,由于定转子相对位置在不断变化,因此连接定转子的磁阻单元也会随时间改变,这在一定程度上增加了建模难度。文献[12]借助二维有限元获得气隙磁阻单元随动子运动的变化规律。为了提高电磁场计算精度,通常需要设置大量节点,这使得等效磁路模型过于复杂,而且气隙磁场计算精度相对较低。子域法建模相对容易,通过不同求解域的边界条件解得各子域场量解析表达式,因而子域法具有较高的解析计算精度。文献[13]基于精确子域法建立了AFPM电机电磁场解析模型,该解析模型可以准确计算空载和负载电磁性能,为电机优化设计提供了便利。AFPM电机受制于加工工艺和单边轴向磁拉力的影响,转子容易出现偏心,文献[14-16]总结了电机在不均匀气隙工况下的电磁特性,建立了考虑转子偏心的解析模型。
精确子域法可以考虑定子槽尺寸,从而计及定子的齿槽效应,但由于划分的子域数量众多,会造成方程组难以求解,而且针对不同的极槽配合需要重新建模,其通用性较差。文献[17]针对径向电机采用相对磁导函数考虑定子的齿槽效应,降低了气隙磁场求解难度,但该方法仅能计算气隙磁通密度径向分量,而且计算精度较低。文献[18]提出一种结合等效磁路法的改进相对磁导函数,气隙磁通密度轴向分量计算精度大幅提高,但该方法依旧不能计算气隙磁通密度切向分量。文献[19]引入切向气隙相对磁导函数,从而实现了气隙磁通密度切向分量的计算,但该方法只能近似求解。为提高气隙磁场解析计算精度,文献[20-22]基于保角映射法得到复相对磁导函数,其考虑了齿槽效应对气隙磁通密度切向分量的影响,且适用于任意极槽配合。基于保角映射法的复相对磁导函数求解较为复杂,且定子槽被假定为无限深,定子槽口处的气隙磁导较实际值偏小。文献[23]引入定子槽口与气隙交界面的边界条件,求解单槽区域的气隙磁通密度解析解,由于解析表达式中含有未知系数,需结合卡特系数得到复相对磁导函数,且其未能考虑定子槽深影响。
针对开槽轴向磁通永磁电机,本文在文献[23]的基础上进行改进,提出一种新型复相对磁导函数计算方法,进而建立出一种可同时计及不同定子槽宽、槽深以及偏心影响的气隙磁场通用解析模型。该解析模型可以考虑实际槽形,相较保角映射法大幅提高了气隙磁导的解析计算精度,而且基于单槽模型考虑齿槽效应相比精确子域法具有更好的通用性。此外,结合静态偏心时气隙磁阻的变化规律,建立了考虑静态偏心影响的气隙磁场解析模型,依托该解析模型对不同偏心率下的气隙磁通密度、空载反电动势和齿槽转矩进行计算。最后,以一台7 kW、4 000 r/min的轴向磁通永磁电机开展实验测试,有限元分析和实验测试结果均验证了本文所提解析模型的有效性。该解析模型可进一步拓展,对半闭口槽同样具有适用性,为相关电机的电磁特性快速准确计算带来方便。
本文所采用的样机为一台双定子AFPM电机,其单元电机三维切片如图1a所示,各个切片展开为直线电机如图1b所示。

图1 直线电机等效示意图
Fig.1 Equivalent schematic diagram of linear motor
第l层切片的平均半径Rl为
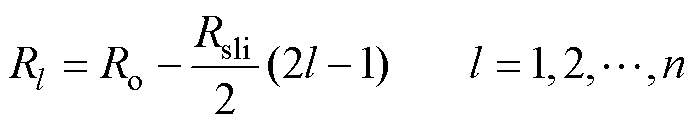 (1)
(1)
其中
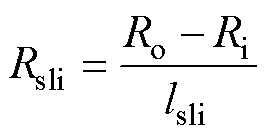 (2)
(2)
式中,Ro为定子铁心外径;Ri为定子铁心内径;lsli为电机切片数量;Rsli为每层电机切片厚度。
为便于解析建模,本文将AFPM电机三维模型等效为直线电机,并在直角坐标系下建立解析模型,解析计算流程如图2所示。

图2 解析计算流程
Fig.2 Analytic calculation flow chart
双定子AFPM电机是对称式结构,可沿转子盘中线分割为两个具有相同电磁特性的单定子AFPM电机,因此,本文对单侧的单定子AFPM电机展开研究,空载气隙磁场二维模型如图3所示,y轴代表电机轴向方向,x轴代表电机切向方向。图3中,hm为单侧永磁体厚度;g为气隙长度,gr=g+hm。
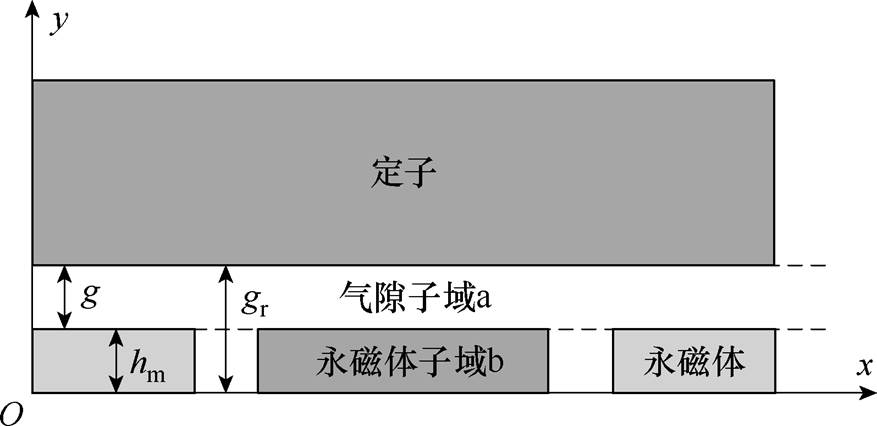
图3 无槽气隙磁场解析模型
Fig.3 Analytical model of slotless air gap magnetic field
鉴于永磁体沿轴向充磁,其磁场强度函数可以表示为傅里叶级数形式,有
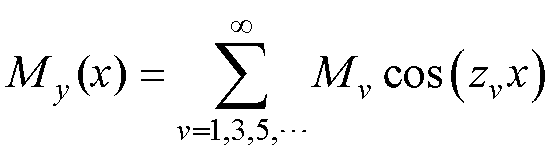 (3)
(3)
其中
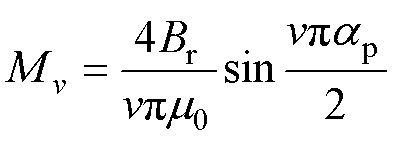 (4)
(4)
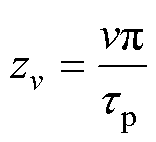 (5)
(5)
式中,Br为永磁体剩磁;v为磁场空间谐波次数;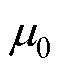 为真空磁导率;
为真空磁导率;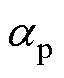 为永磁体极弧系数;
为永磁体极弧系数;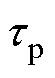 为极距。
为极距。
标量磁动势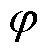 在图3所示的气隙子域a和永磁体子域b满足拉普拉斯方程为
在图3所示的气隙子域a和永磁体子域b满足拉普拉斯方程为
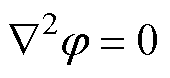 (6)
(6)
由文献[24]可知,定子无槽空载气隙磁通密度轴向和切向分量解析表达式分别为
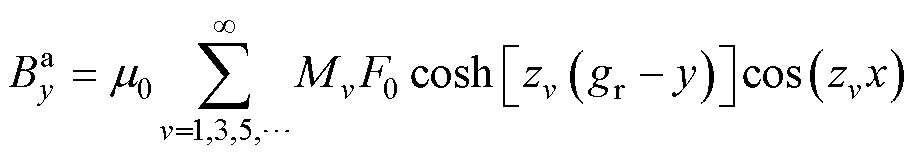 (7)
(7)
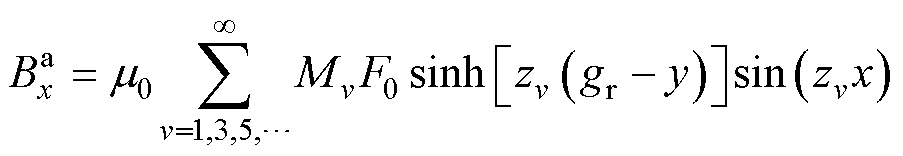 (8)
(8)
其中
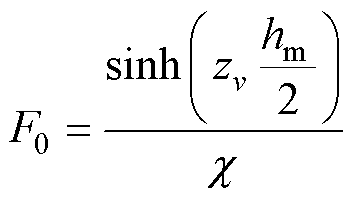 (9)
(9)
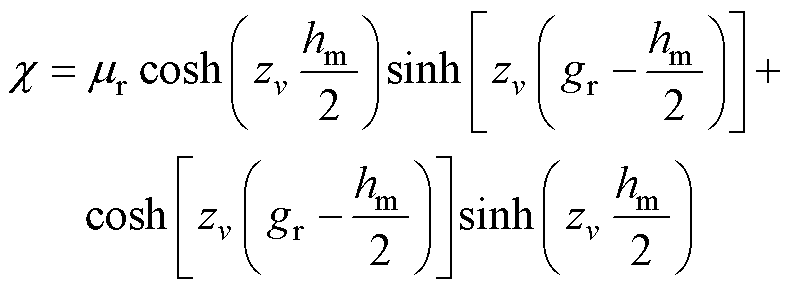 (10)
(10)
式中,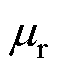 为永磁体相对磁导率。
为永磁体相对磁导率。
式(7)和式(8)没有考虑定子开槽对气隙磁场的影响,因此本文引入基于单槽模型的改进复相对磁导函数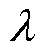 ,定子开槽空载气隙磁通密度轴向和切向分量解析表达式[20]为
,定子开槽空载气隙磁通密度轴向和切向分量解析表达式[20]为
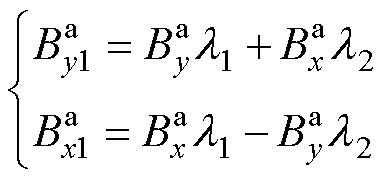 (11)
(11)
其中
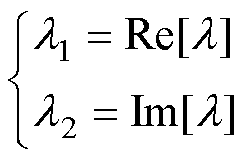 (12)
(12)
为了简化计算,作如下假设[25]:①永磁体相对磁导率接近于1,且为常值;②忽略端部效应;③定转子铁心磁导率趋于无穷大。
将永磁体等效为空气隙,则该单槽区域可划分为气隙子域1和定子槽子域2,单定子槽等效模型如图4所示。由于定转子铁心磁导率趋于无穷大,结合定子的齿槽效应,可认为转子表面与气隙交界面的标量磁位为1,定子表面与气隙交界面的标量磁位为0。图4中,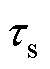 为定子槽距;b0为定子槽口宽度;
为定子槽距;b0为定子槽口宽度;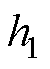 为等效后的气隙长度,
为等效后的气隙长度,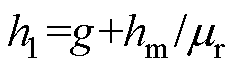 ;h2为转子表面到定子槽底的高度。
;h2为转子表面到定子槽底的高度。
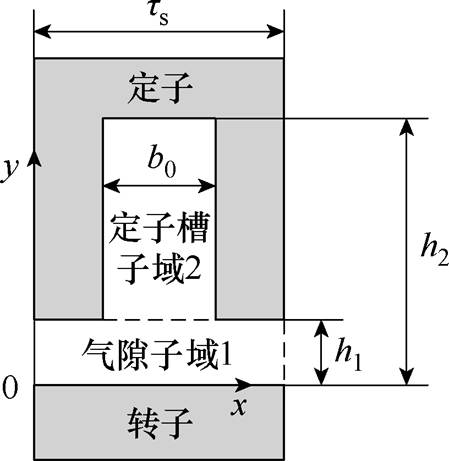
图4 单定子槽等效模型
Fig.4 Single stator slot equivalent model
1.3.1 各子域标量磁位通解
(1)气隙子域1
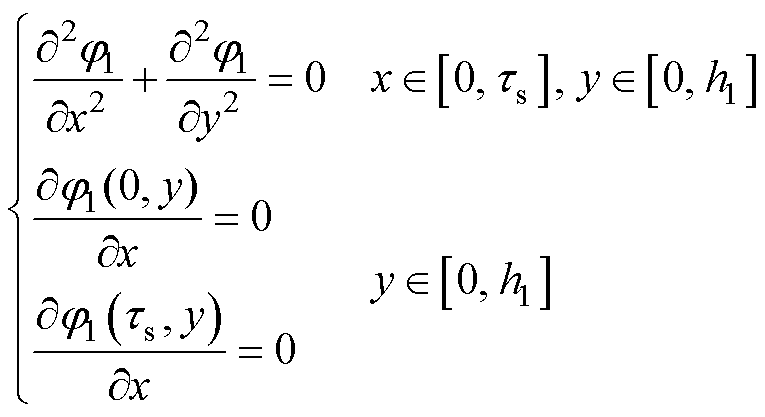 (13)
(13)
气隙子域1标量磁位通解为
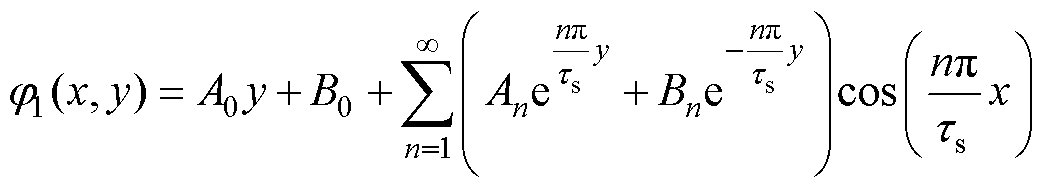 (14)
(14)
式中,A0、B0、An和Bn为气隙子域待求解系数;n为气隙子域磁场谐波次数。
(2)定子槽子域2
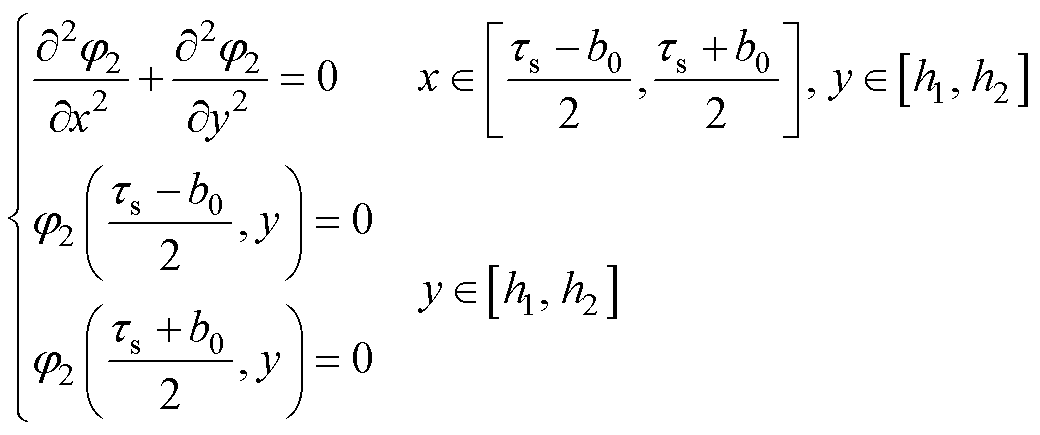 (15)
(15)
定子槽子域2标量磁位通解为
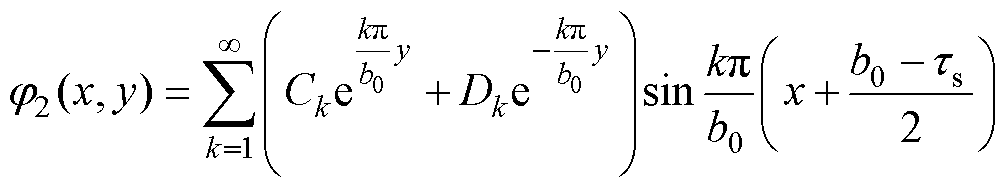 (16)
(16)
式中,Ck和Dk为定子槽子域待求解系数;k为定子槽子域磁场谐波次数。
标量磁位与磁场强度满足
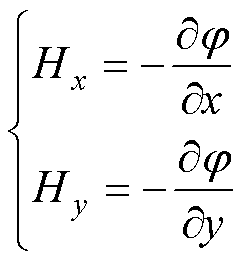 (17)
(17)
气隙子域1磁场强度为
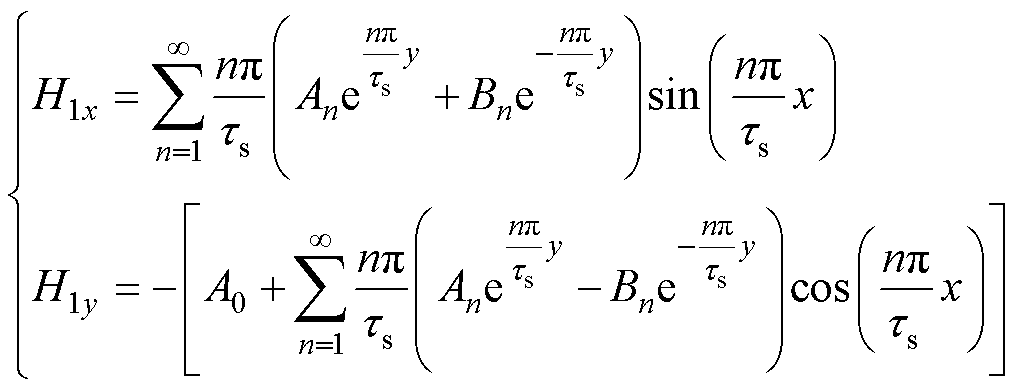 (18)
(18)
定子槽子域2磁场强度为
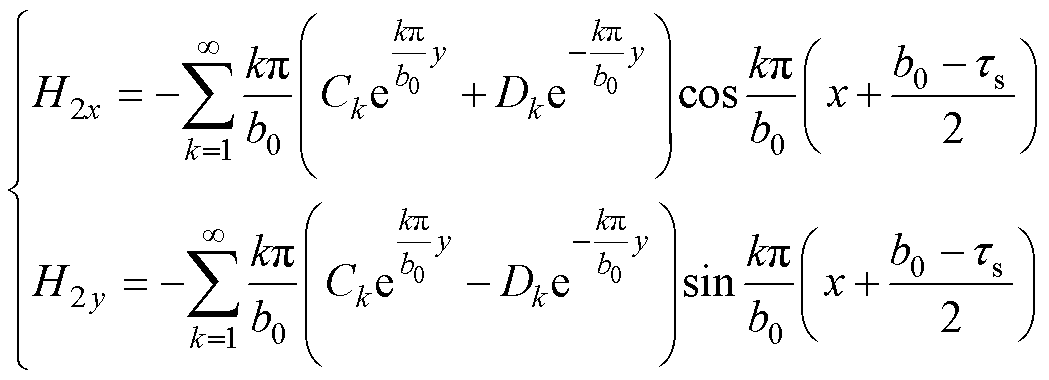 (19)
(19)
1.3.2 边界条件
(1)转子与气隙交界面
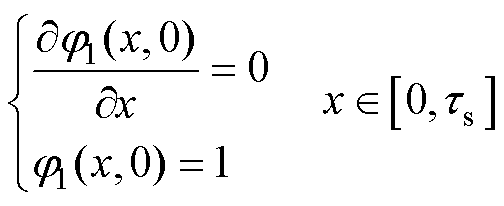 (20)
(20)
由式(14)、式(18)以及式(20)可得
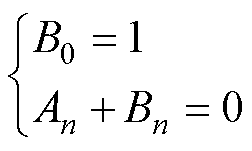 (21)
(21)
(2)定子槽底与气隙交界面
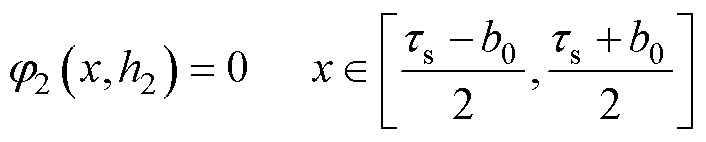 (22)
(22)
由式(16)和式(22)可得
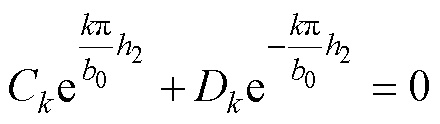 (23)
(23)
(3)气隙子域1与定子槽子域2交界面
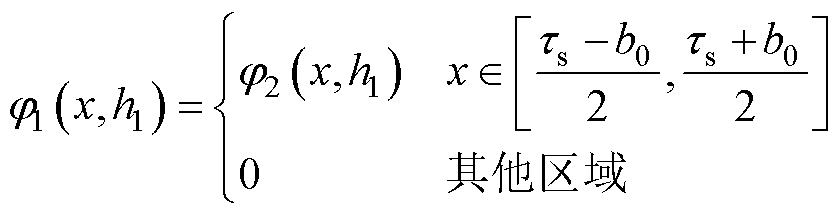 (24)
(24)
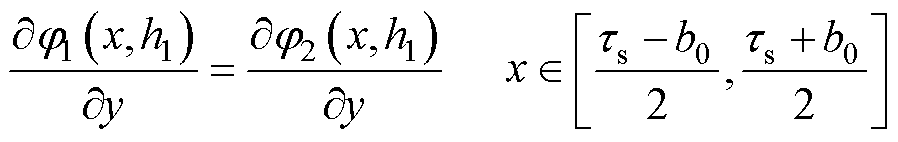 (25)
(25)
由式(24)可得
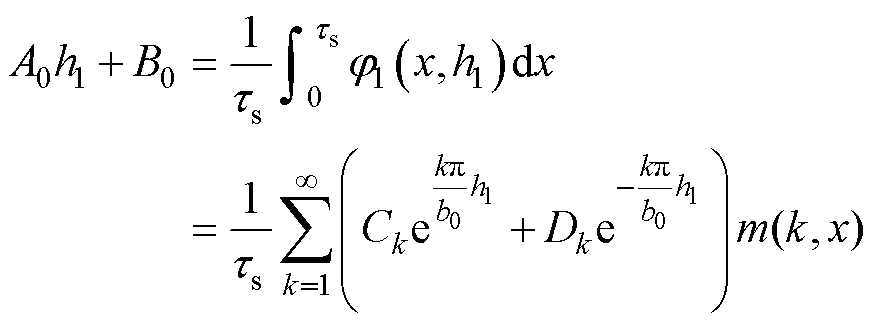 (26)
(26)
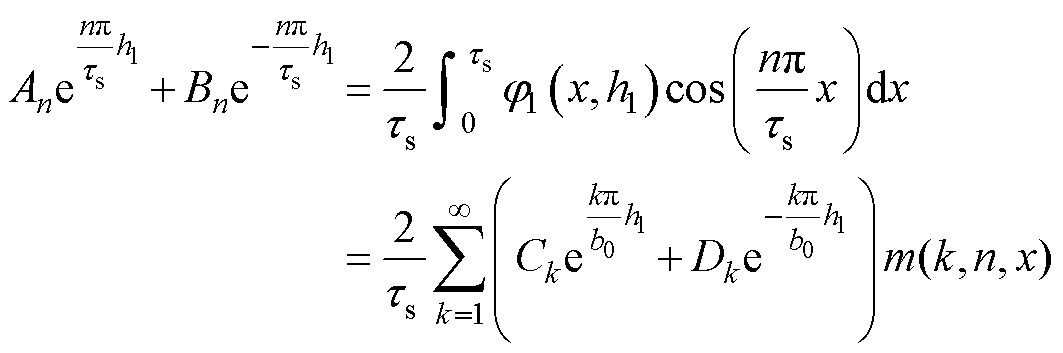 (27)
(27)
由式(25)可得
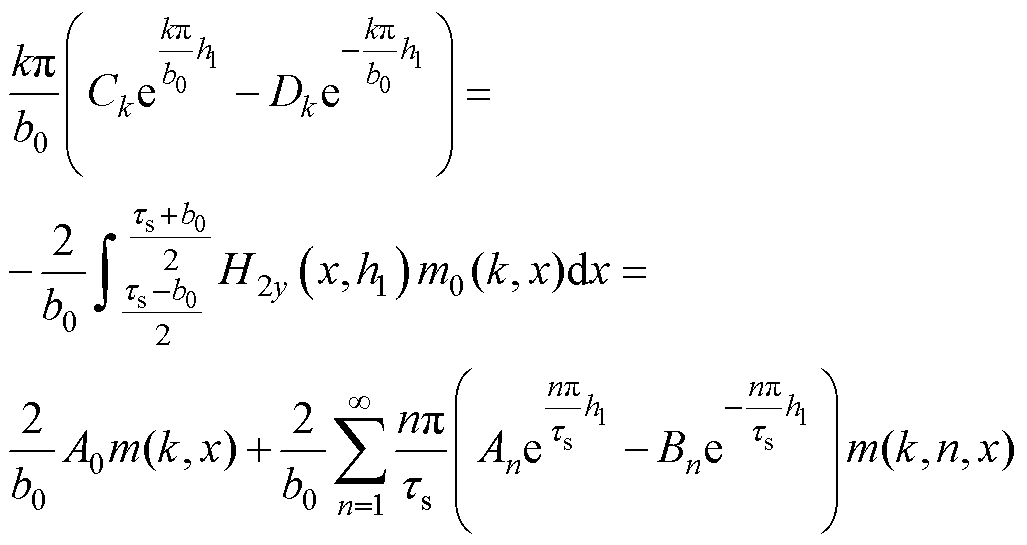 (28)
(28)
其中
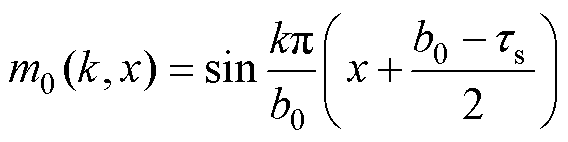 (29)
(29)
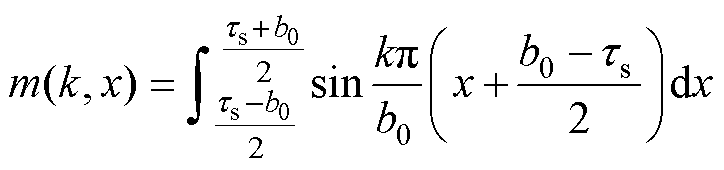 (30)
(30)
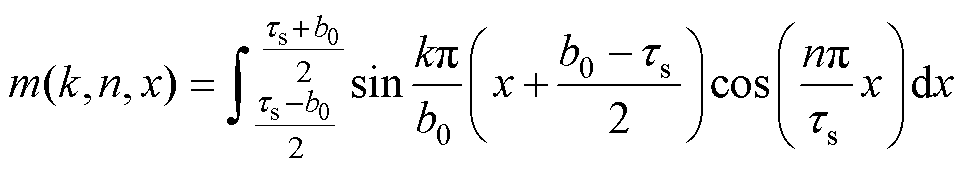 (31)
(31)
1.3.3 子域系数求解
各子域未知系数的求解需要转化成矩阵形式,通常矩阵的阶数会很大,而且解析表达式中含有指数项,这很容易导致求解奇异,因此,对相关未知系数做如下替换
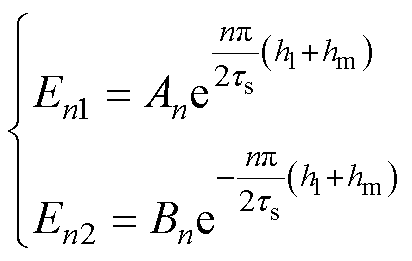 (32)
(32)
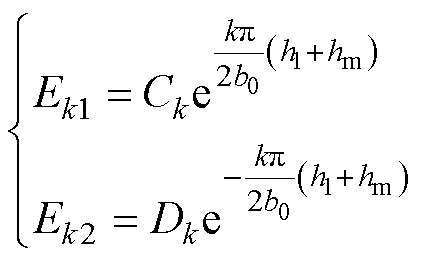 (33)
(33)
式中,En1、En2、Ek1和Ek2为等效后的子域系数。
将式(21)、式(23)、式(26)~式(28)整理成矩阵形式,有
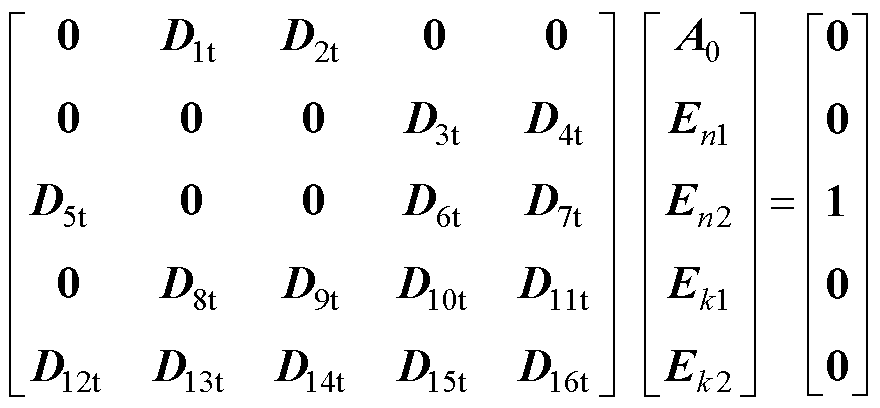 (34)
(34)
式中,A0、En1、En2、Ek1和Ek2为待求解系数矩阵;Dit为已知系数矩阵,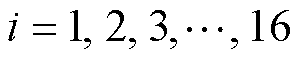 。
。
利用数值软件即可求解式(34),将各系数回代便得到气隙子域磁场强度解析表达式。复相对磁导函数的实部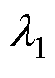 与气隙子域磁场强度的轴向分量H1y有关,而虚部
与气隙子域磁场强度的轴向分量H1y有关,而虚部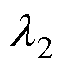 则与气隙子域磁场强度的切向分量H1x有关。考虑到电机机械结构和气隙磁场分布情况,在x=0和x=
则与气隙子域磁场强度的切向分量H1x有关。考虑到电机机械结构和气隙磁场分布情况,在x=0和x=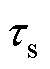 处满足
处满足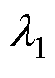 =1。因此,改进复相对磁导函数为
=1。因此,改进复相对磁导函数为
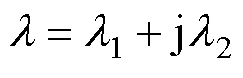 (35)
(35)
其中
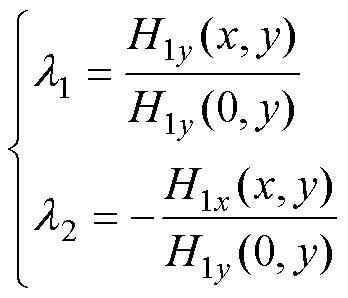 (36)
(36)
本文对一个槽距下气隙中线处的复相对磁导函数的实部和虚部进行计算,并与有限元法及传统复相对磁导函数法作对比,如图5所示。所提解析模型与有限元计算结果吻合良好,且其计及定子槽宽和槽深影响较传统复相对磁导函数法具有更高的解析计算精度,验证了本文所提解析模型的有效性。
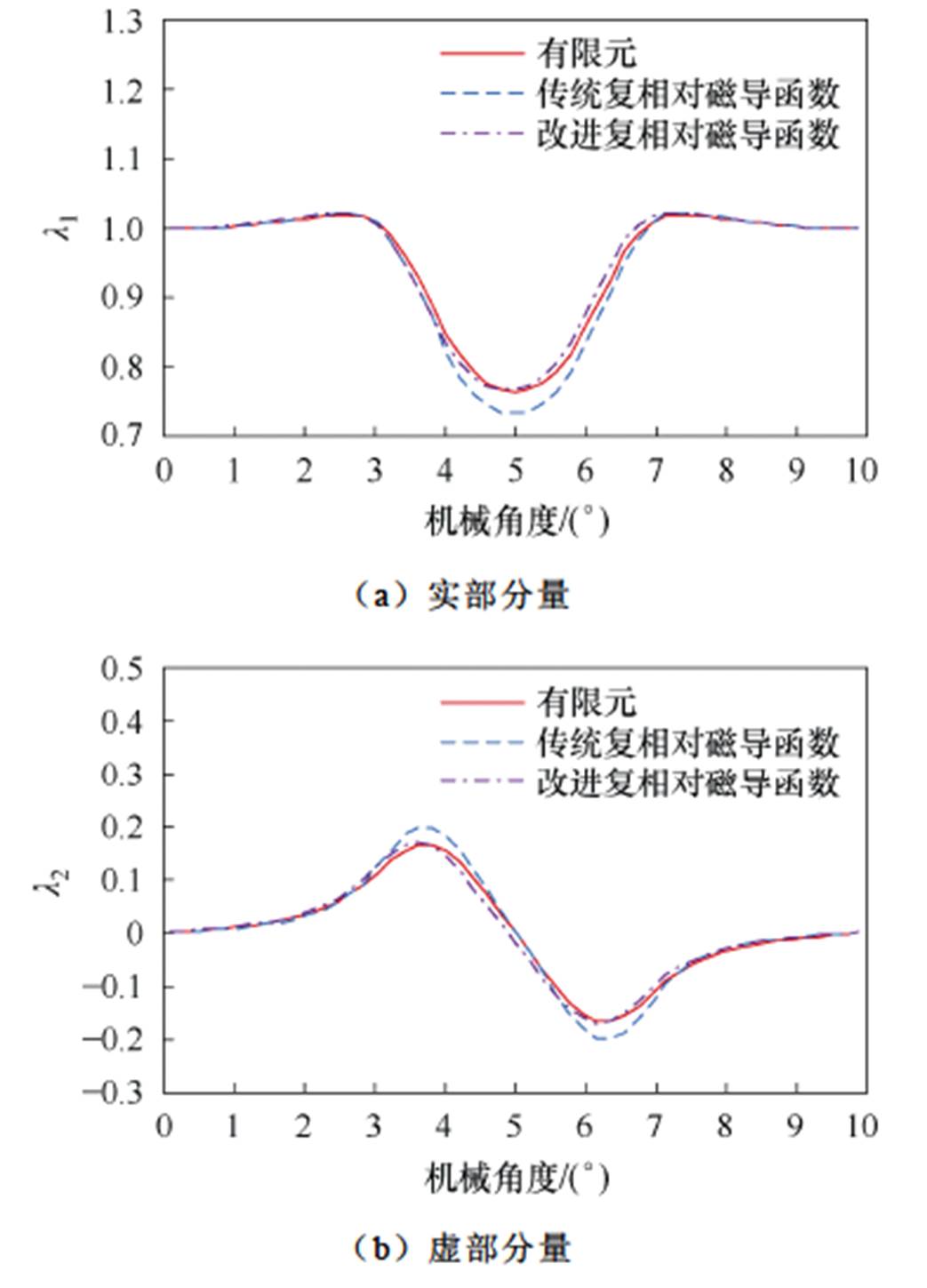
图5 复相对磁导函数对比
Fig.5 Comparison of complex relative permeance function
AFPM电机的拓扑结构较为特殊,存在较大的单边磁拉力。双定子单转子电机具有双气隙结构,受限于加工工艺和运行磨损,通常会存在转子向一侧偏移的情况,导致两侧气隙不均匀,图6为正常和偏心工况示意图。
转子静态偏心率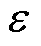 的定义为
的定义为
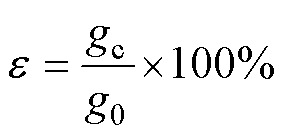 (37)
(37)
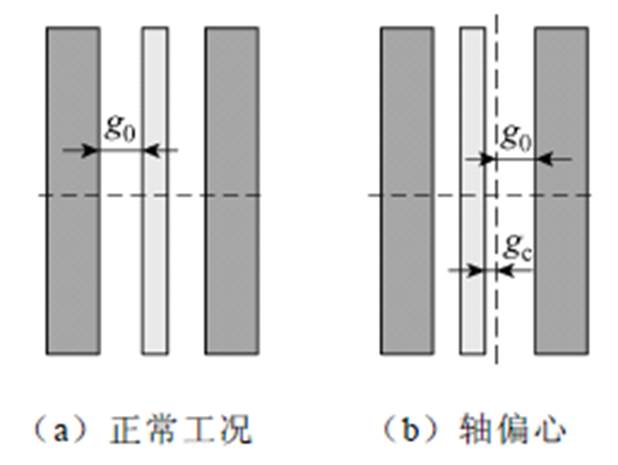
图6 正常和偏心工况
Fig.6 Normal and eccentric conditions
式中,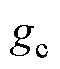 为气隙偏心量;
为气隙偏心量;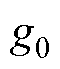 为不偏心单侧气隙长度。
为不偏心单侧气隙长度。
本文采用半模型计算气隙磁通密度,当电机发生轴偏心时,如图7a所示,左侧气隙减小至gmin,右侧气隙增大至gmax。计算左侧气隙磁通密度时对应的等效模型如图7b所示,等效后的右侧气隙相较图7a明显减小,使得总气隙磁阻降低,因此解析计算所得气隙磁通密度幅值偏大;而计算右侧磁通密度时等效模型如图7c所示,等效后的左侧气隙相较图7a明显增大,使得总气隙磁阻增大,因此解析计算所得气隙磁通密度幅值偏小。为此本文提出气隙磁通密度修正系数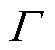 ,有
,有
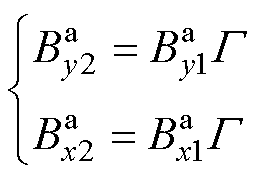 (38)
(38)
其中
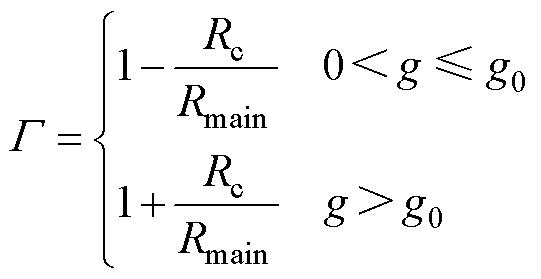 (39)
(39)
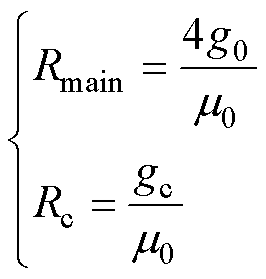 (40)
(40)
式中,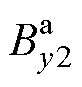 、
、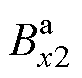 为修正后的气隙磁通密度;
为修正后的气隙磁通密度;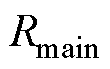 为主磁路总气隙磁阻;
为主磁路总气隙磁阻;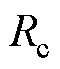 为气隙偏心量磁阻。
为气隙偏心量磁阻。
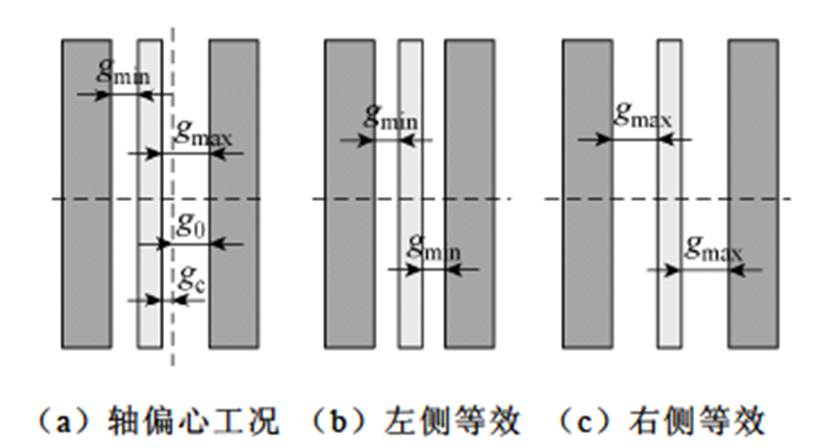
图7 轴偏心下解析模型等效
Fig.7 Analytical model equivalent under axis eccentricity
以转子偏心40%为例,正常气隙长度(单侧)为2.5 mm,偏心后左侧气隙长度gmin=1.5 mm,右侧气隙长度gmax=3.5 mm。图8和图9分别为左侧和右侧气隙磁通密度的对比情况,将偏心后气隙磁阻的变化予以考虑,使得半模型解析计算精度大幅提高,为计算偏心工况下双定子AFPM电机的电磁性能奠定了良好基础。
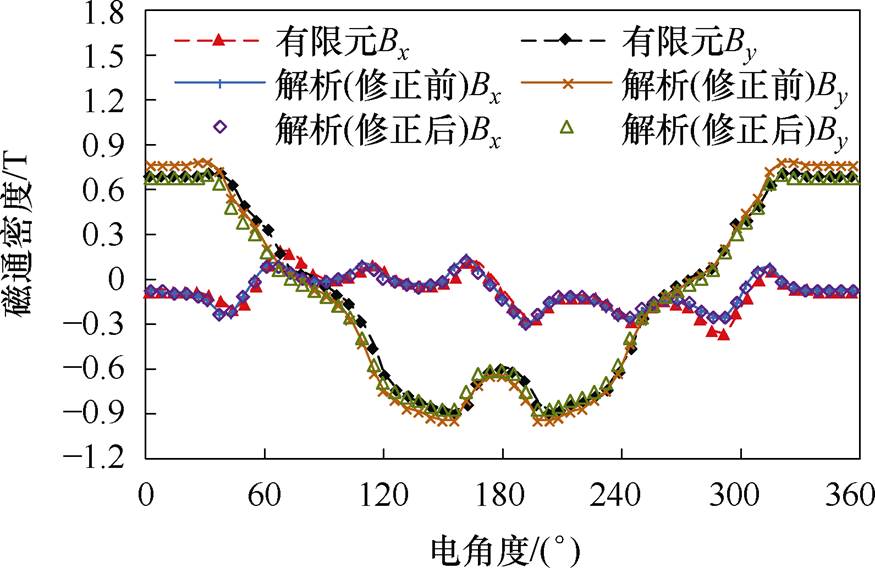
图8 左侧气隙磁通密度对比
Fig.8 Comparison of left air gap flux density
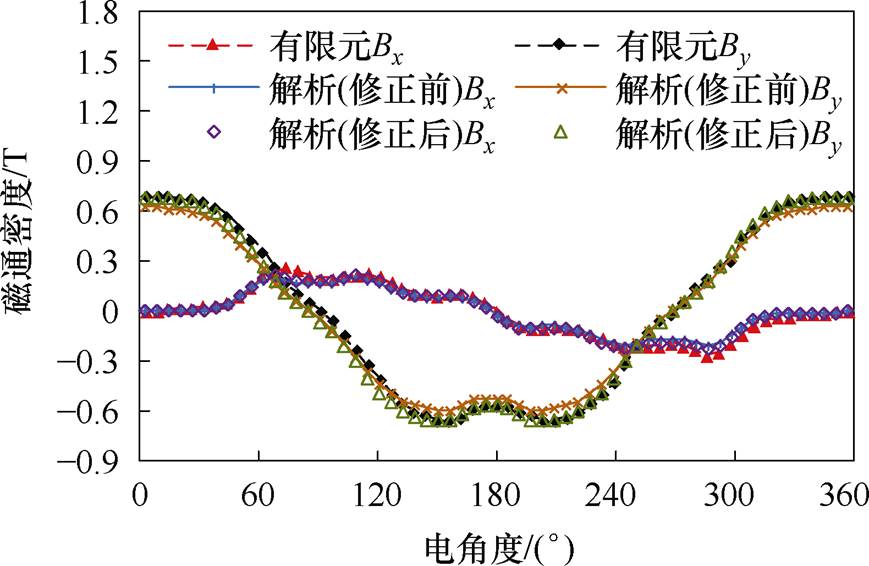
图9 右侧气隙磁通密度对比
Fig.9 Comparison of right air gap flux density
本文所研究的样机为一台双定子AFPM电机,样机参数见表1。
表1 双定子AFPM电机参数
Tab.1 Parameters of double stator AFPM motor
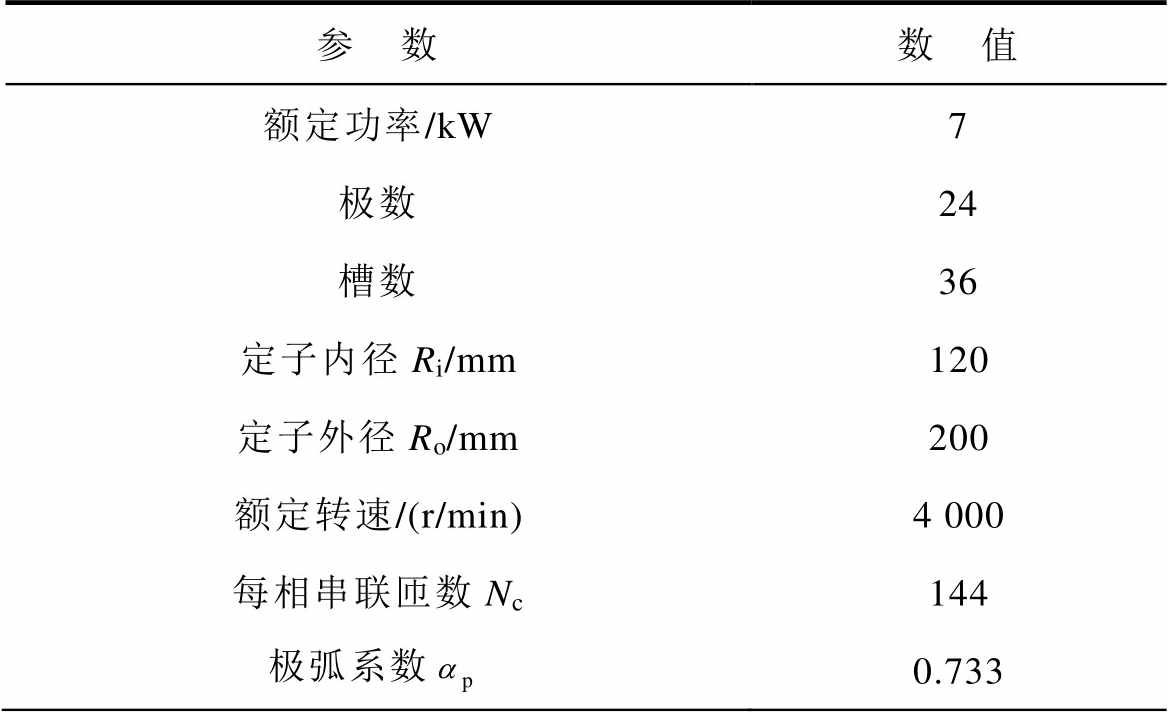
参 数数 值 额定功率/kW7 极数24 槽数36 定子内径Ri/mm120 定子外径Ro/mm200 额定转速/(r/min)4 000 每相串联匝数Nc144 极弧系数0.733
(续)

参 数数 值 气隙长度g/mm2.5 定子槽口宽度b0/mm4.3 定子槽深h0/mm21.5 单侧永磁体厚度hm/mm4 永磁体剩磁Br/T1.25 永磁体相对磁导率1.046
为了验证本文所提出解析模型的高精度,在转子不偏心的情况下,计算了气隙中线处的磁通密度分布情况,如图10所示。传统复相对磁导函数法忽略了定子槽深的影响,在定子槽口处计算精度较低,而本文所提解析模型可以考虑实际定子槽形,与有限元的计算结果一致性较好,证明了基于改进复相对磁导函数的解析模型具有较高的计算精度。
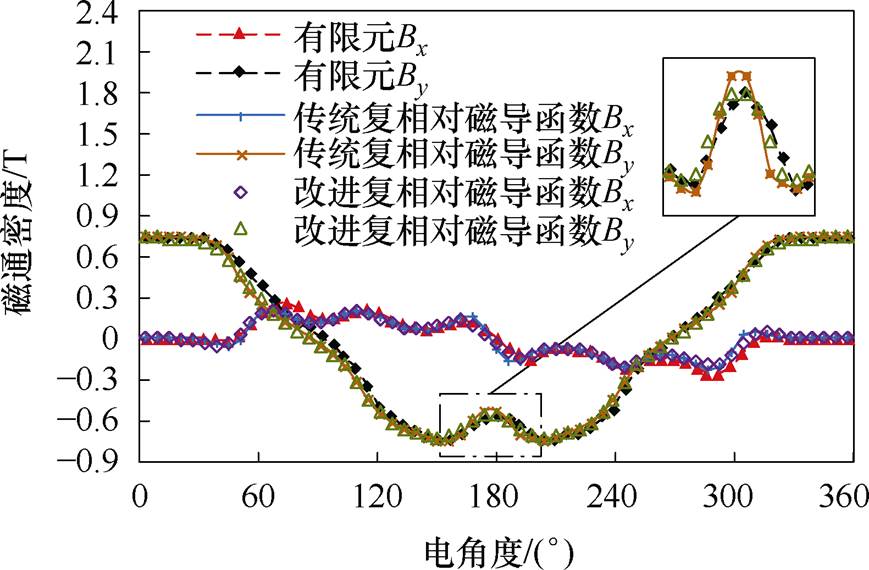
图10 正常工况下气隙磁通密度对比
Fig.10 Comparison of air gap flux density under normal working conditions
样机单侧气隙长度为2.5 mm,转子偏心达到40%已经是电机能够运行的极限条件,因此,本文针对偏心率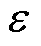 达到20%和40%的工况进行计算,解析计算和有限元分析参考图6b,解析法与有限元计算结果十分吻合,如图11和图12所示。
达到20%和40%的工况进行计算,解析计算和有限元分析参考图6b,解析法与有限元计算结果十分吻合,如图11和图12所示。
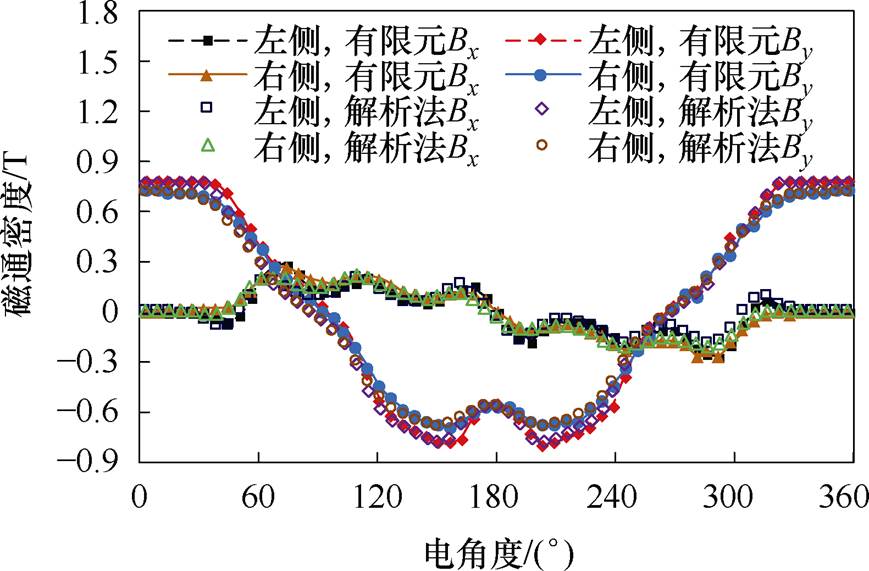
图11 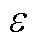 =20%,气隙磁通密度对比
=20%,气隙磁通密度对比
Fig.11 Comparison of air gap flux density, 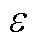 =20%
=20%
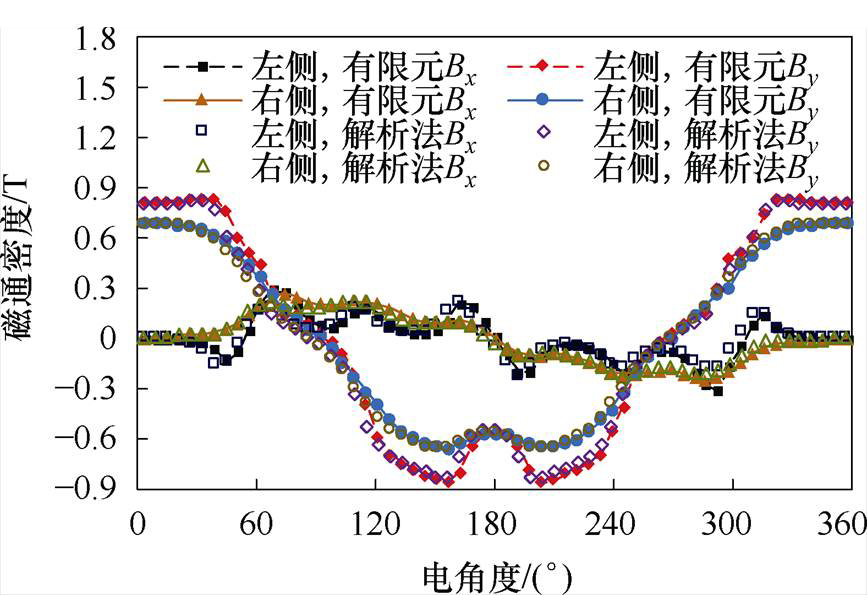
图12 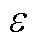 =40%,气隙磁通密度对比
=40%,气隙磁通密度对比
Fig.12 Comparison of air gap flux density, 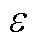 =40%
=40%
线圈中的磁链可认为仅与气隙磁通密度轴向分量有关,因此,单匝线圈中的磁链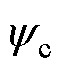 为
为
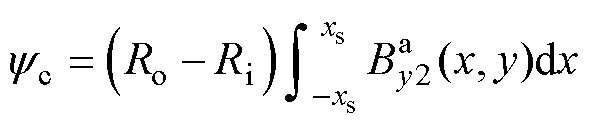 (41)
(41)
其中
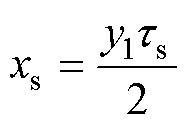 (42)
(42)
式中,y1为线圈的第一节距,表示同一个线圈的两边跨过的槽数。
单匝线圈中产生的空载反电动势为
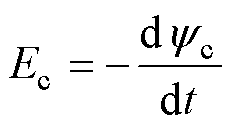 (43)
(43)
由式(43)可以进一步得到单相绕组感应出的空载反电动势为
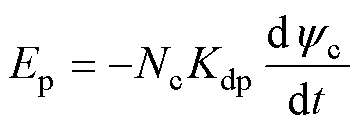 (44)
(44)
式中,Nc为每相串联匝数;Kdp为绕组系数。
空载反电动势对比如图13所示。图13表明两侧定子绕组串联时,空载反电动势不随轴偏心而改变,这是由于主磁路的总气隙长度没有发生变化,与两侧绕组交链的磁链也基本不变,因而空载反电动势不变。
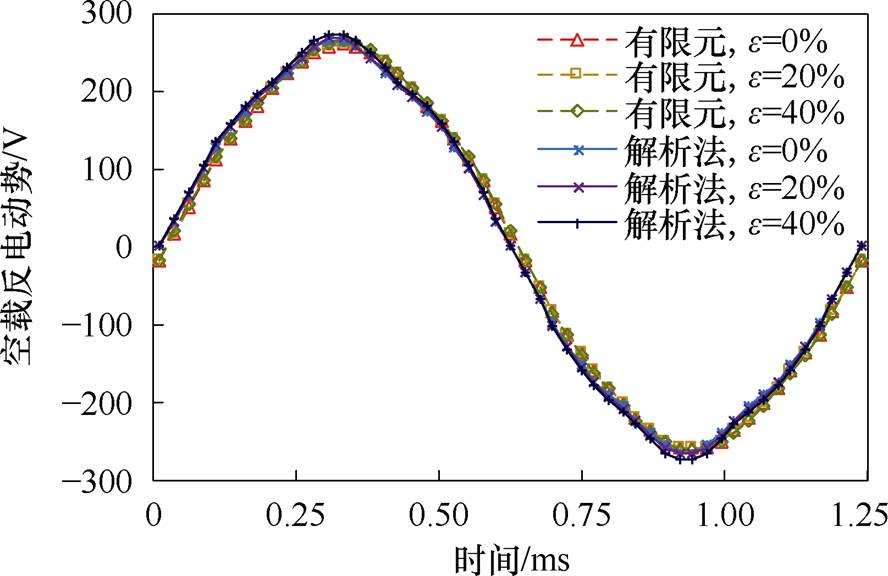
图13 空载反电动势对比
Fig.13 Comparison of no-load back electromotive force
由麦克斯韦张量公式可知,电磁转矩包含四个分量,齿槽转矩可认为是空载气隙磁场轴向分量与切向分量相互作用产生的转矩,有
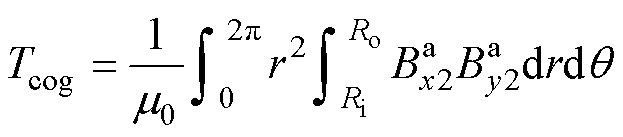 (45)
(45)
本节计算了双定子AFPM电机在不同偏心率下的齿槽转矩,齿槽转矩对比如图14所示,表明解析法在低偏心率的情况下计算精度较高。由文献[26]可知,本文所研究的样机齿槽转矩受静态偏心的影响较小,解析法及有限元计算结果显示,随着轴偏心的增大,齿槽转矩出现小幅下降。
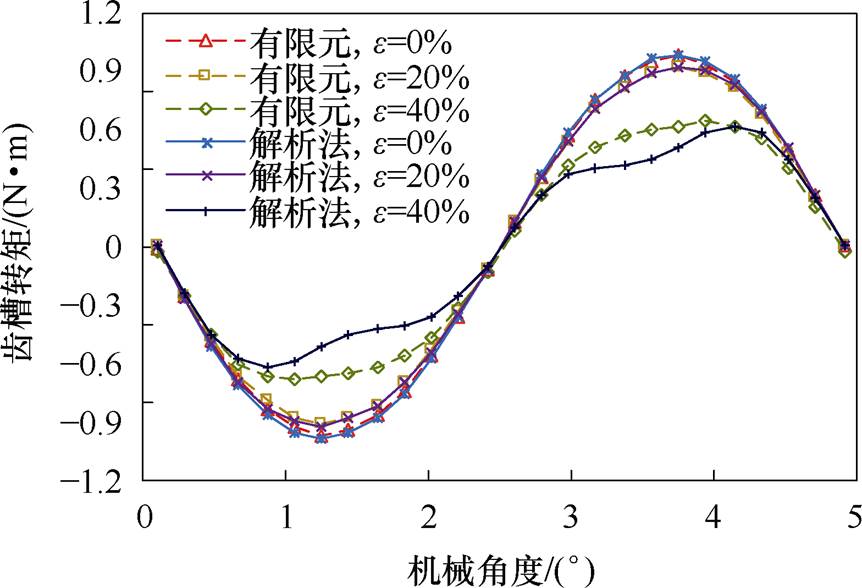
图14 齿槽转矩对比
Fig.14 Comparison of cogging torque
解析法与有限元法的计算耗时对比见表2,在保证求解精度相近的前提下,解析法的计算速度远超有限元法,解析法计算耗时相比有限元法减少了92.2%,这极大地提升了相关电机电磁性能分析的计算效率。
表2 解析法与有限元法计算耗时
Tab.2 The calculation time consumption of analytical method and finite element method

参 数数 值 (型号) 有限元法解析法 计算机CPUi5-12500i5-12500 计算机RAM/GB3232 计算耗时/s83665
AFPM电机实验平台如图15所示。图16为1 000 r/min时空载线反电动势对比情况,有限元、解析法和实验测量得到的空载线反电动势基波幅值依次为110.5、110.4、115.2 V,反电动势波形畸变率依次为1.78%、3.04%和2.11%,三者数据较为吻合,证明了本文所建立的解析模型可以准确计算空载反电动势。

图15 AFPM电机实验平台
Fig.15 Experimental platform of AFPM motor
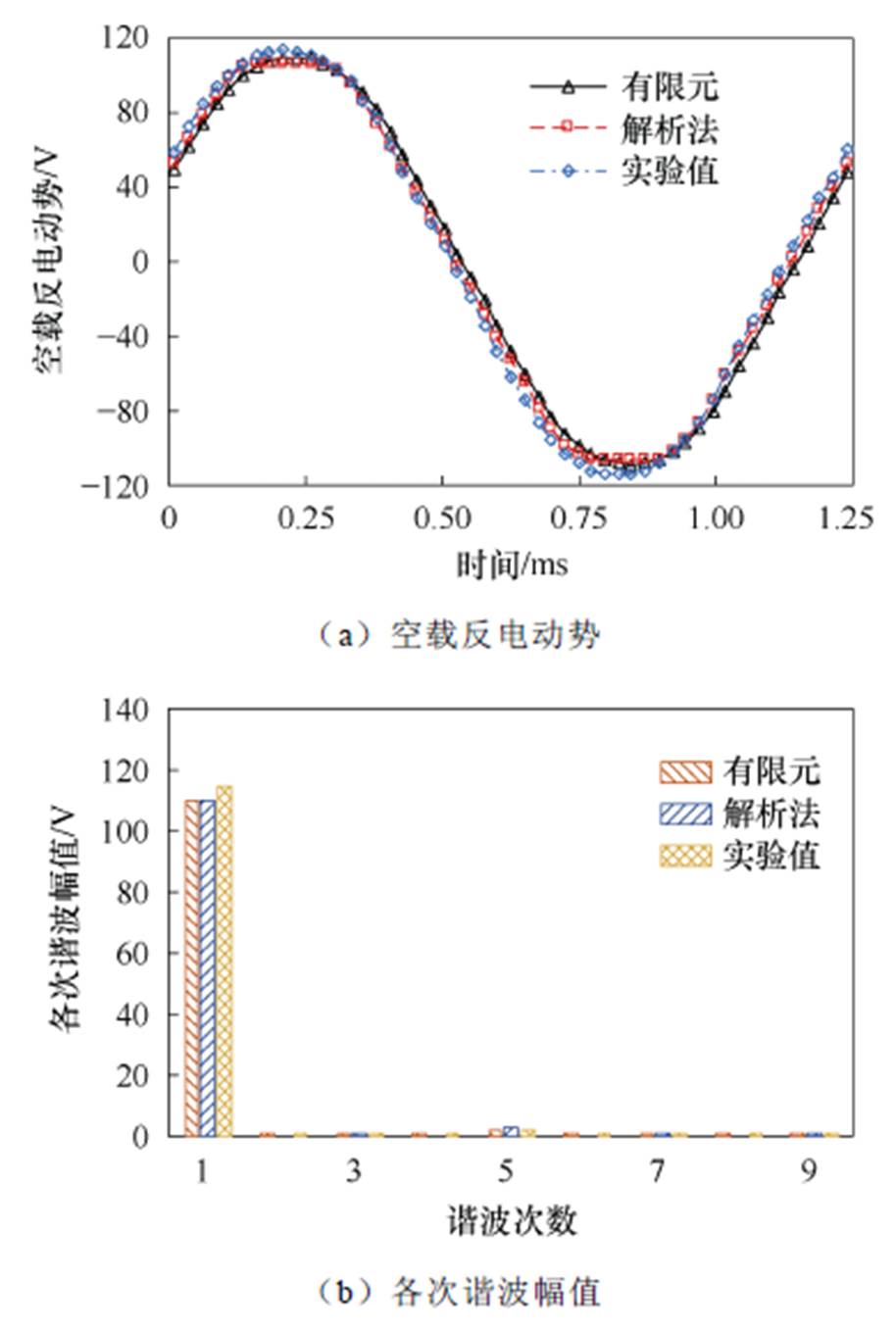
图16 空载反电动势对比
Fig.16 Comparison of no-load back electromotive force
受限于实验条件,无法准确测出齿槽转矩周期,因此,本文采用拉力计法测得未偏心情况下AFPM电机的齿槽转矩幅值。如图17所示,将铜线一端连接电子拉力计,另一端绕制在联轴器上,联轴器直径为65 mm,测量时保持电子拉力计与测试平台垂直,记录电机转轴被拉动瞬间时的拉力值,齿槽转矩幅值为
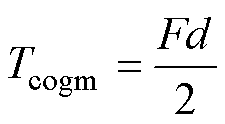 (46)
(46)

图17 拉力计法测齿槽转矩
Fig.17 Measuring cogging torque by tension meter method
式中,F为拉力计测的拉力值;d为联轴器直径。
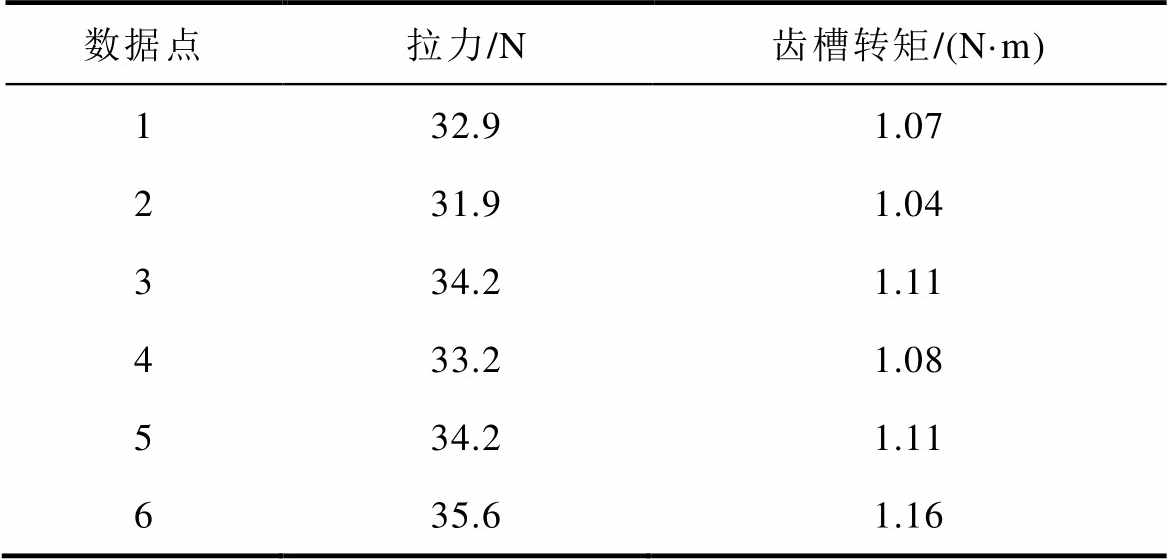
样机齿槽转矩测量数据见表3,双定子AFPM电机齿槽转矩幅值的平均值约为1.10 N·m。
表3 样机齿槽转矩测量值
Tab.3 The measured value of cogging torque of prototype
数据点拉力/N齿槽转矩/(N·m) 132.91.07 231.91.04 334.21.11 433.21.08 534.21.11 635.61.16
齿槽转矩对比如图18所示。从图18可以看出,有限元、解析法和实验测量的齿槽转矩幅值依次为0.97、0.98、1.10 N·m,有限元和解析法较实验测量值分别小了12%和11%,这是因为测量时电机处于冷态,轴承润滑效果一般,实验测量值中包含了摩擦转矩和磁滞转矩,使得测量值偏大。
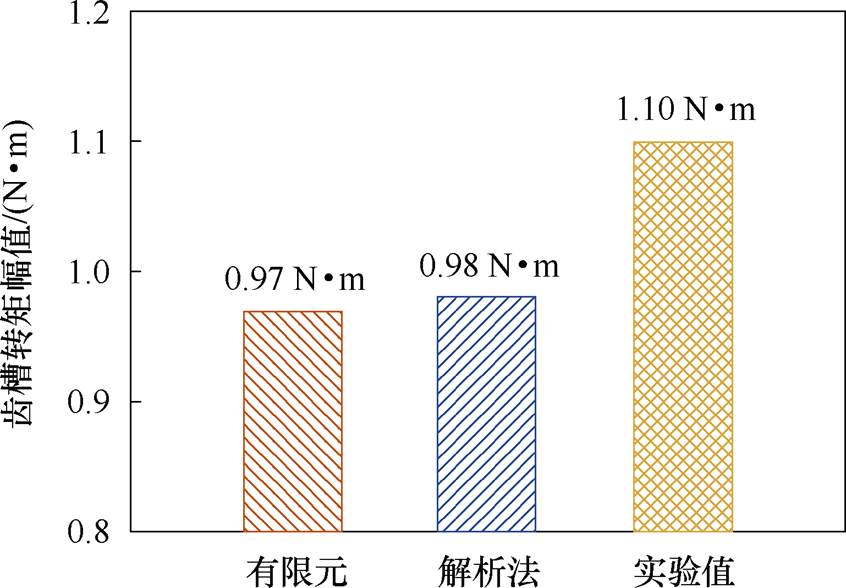
图18 齿槽转矩对比
Fig.18 Comparison of cogging torque
本文基于改进复相对磁导函数提出一种计及定子槽宽、槽深和偏心影响的开槽轴向磁通永磁电机气隙磁场通用解析模型,该解析模型有效地考虑了齿槽效应,大幅提高了静态偏心下半模型的解析计算精度,依托该解析模型可以精确求解任意极槽配合的AFPM电机空载电磁性能。
基于解析模型求解的电磁性能与有限元和实验测量结果吻合良好。其中,解析计算的空载反电动势和齿槽转矩相较有限元误差均在2%以内;解析计算与实验测量结果相比,空载反电动势及齿槽转矩的计算误差分别为4.2%和11%,计算误差满足实际工程要求。相较有限元分析,本文所提解析模型具有计算速度快和求解精度相近的特点,而且该解析模型可进一步拓展至半闭口槽结构,为相关电机的电磁特性快速准确计算带来方便。
参考文献
[1] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[2] Shao Lingyun, Navaratne R, Popescu M, et al. Design and construction of axial-flux permanent magnet motors for electric propulsion applications-a review[J]. IEEE Access, 2021, 9: 158998-159017.
[3] 赵纪龙, 逯卓林, 韩青峰, 等. 轴向磁通永磁电机系统及关键技术前沿发展综述[J]. 中国电机工程学报, 2022, 42(7): 2744-2765.
Zhao Jilong, Lu Zhuolin, Han Qingfeng, et al. An overview on development of axial flux permanent magnet motor system and the key technology[J]. Proceedings of the CSEE, 2022, 42(7): 2744-2765.
[4] 武岳, 张志锋, 平佳齐. 高功率密度轴向磁通永磁电机交流铜耗分析[J]. 电机与控制学报, 2022, 26(5): 65-75.
Wu Yue, Zhang Zhifeng, Ping Jiaqi. Analysis of AC copper loss in high power density axial flux permanent magnet motors[J]. Electric Machines and Control, 2022, 26(5): 65-75.
[5] Khatab M F H, Zhu Z Q, Li H Y, et al. Comparative study of novel axial flux magnetically geared and conventional axial flux permanent magnet machines[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(4): 392-398.
[6] Geng Weiwei, Hou Jining, Li Qiang. Electromagnetic analysis and efficiency improvement of axial-flux permanent magnet motor with yokeless stator by using grain-oriented silicon steel[J]. IEEE Transa- ctions on Magnetics, 2022, 58(2): 8200905.
[7] Zhang Zhuoran, Geng Weiwei, Liu Ye, et al. Feasibility of a new ironless-stator axial flux permanent magnet machine for aircraft electric propulsion application[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 30-38.
[8] 毕云龙, 柴凤, 裴宇龙. 虚拟气隙在轴向磁通永磁电机三维有限元计算中的应用研究[J]. 中国电机工程学报, 2021, 41(6): 1929-1937.
Bi Yunlong, Chai Feng, Pei Yulong. Application and research of virtual air gap in three dimensional finite element analysis of axial flux permanent magnet machines[J]. Proceedings of the CSEE, 2021, 41(6): 1929-1937.
[9] 张志弘, 韩勤锴, 徐学平, 等. 基于保角变换与等效磁路法的永磁直驱发电机气隙磁场计算[J]. 电工技术学报, 2023, 38(3): 703-711.
Zhang Zhihong, Han Qinkai, Xu Xueping, et al. Air gap magnetic field calculation of permanent magnet direct drive generator based on conformal mapping and magnetic equivalent circuit method[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(3): 703-711.
[10] 佟文明, 王萍, 吴胜男, 等. 基于三维等效磁网络模型的混合励磁同步电机电磁特性分析[J]. 电工技术学报, 2023, 38(3): 692-702.
Tong Wenming, Wang Ping, Wu Shengnan, et al. Electromagnetic performance analysis of a hybrid excitation synchronous machine based on 3D equivalent magnetic network[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 692-702.
[11] Huang Rundong, Song Zaixin, Dong Zhiping, et al. An improved magnetic equivalent circuit method for segmented-Halbach axial-flux permanent magnet machines[J]. IEEE Transactions on Transportation Electrification, 2023, 9(2): 3218-3227.
[12] 郭凯凯, 郭有光. 磁通反向直线旋转永磁电机三维非线性等效磁路模型分析[J]. 电工技术学报, 2020, 35(20): 4278-4286.
Guo Kaikai, Guo Youguang. 3D nonlinear equivalent magnetic circuit model analysis of a flux reversal linear rotary permanent magnet machine[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(20): 4278-4286.
[13] Peng Bing, Zhuang Xiaoyu. Design and performance analysis of axial flux permanent magnet machines with double-stator dislocation using a combined wye- delta connection[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 53-59.
[14] Guo Baocheng, Du Yunlu, Peng Fei, et al. Magnetic field calculation in axial flux permanent magnet motor with rotor eccentricity[J]. IEEE Transactions on Magnetics, 2022, 58(9): 8206104.
[15] 刘蓉晖, 刘锦坤, 章君达, 等. 基于双曲余切变换的Halbach阵列表贴式永磁电机转子偏心气隙磁场解析模型[J]. 电工技术学报, 2023, 38(6): 1433- 1446.
Liu Ronghui, Liu Jinkun, Zhang Junda, et al. Analytical model for air-gap magnetic field in halbach arrays surface-mounted permanent magnet motor with rotor eccentricity based on hyperbolic cotangent transformation[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1433-1446.
[16] 秦伟, 马育华, 张洁龙, 等. 不均匀气隙工况下轴向磁通永磁电动式磁悬浮电机的磁场与力特性分析[J]. 电工技术学报, 2023, 38(4): 889-902.
Qin Wei, Ma Yuhua, Zhang Jielong, et al. Characteristic and magnetic field analysis of an axial flux permanent magnets maglev motor with non- uniform air gap[J]. Transactions of China Elec- trotechnical Society, 2023, 38(4): 889-902.
[17] Zhu Z Q, Howe D. Analytical prediction of the cogging torque in radial-field permanent magnet brushless motors[J]. IEEE Transactions on Magnetics, 1992, 28(2): 1371-1374.
[18] Tong Wenming, Wang Shuai, Wu Shengnan, et al. A complete quasi-3-D analytical model of no-load magnetic field of double-sided slotted AFPMMs considering end effect[J]. IEEE Access, 2018, 6: 59557-59566.
[19] 王明杰, 贾宛英, 张志艳, 等. 永磁直线同步电机空载反电动势和推力的解析计算[J]. 电工技术学报, 2021, 36(5): 954-963.
Wang Mingjie, Jia Wanying, Zhang Zhiyan, et al. Analytical calculation of no-load eletromotive force and thrust in permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 954-963.
[20] Zarko D, Ban D, Lipo T A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1828-1837.
[21] Xue Likun, Luo Ling. Semi-analytical calculation of the unsaturated magnetic field distribution of a slotted spoke-type interior permanent magnet machine with conformal mapping method[J]. IEEE Transactions on Magnetics, 2022, 58(5): 8104810.
[22] Ko Y Y, Song J Y, Seo M K, et al. Analytical method for overhang effect of surface-mounted permanent- magnet motor using conformal mapping[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[23] Tessarolo A, Olivo M. A new method for the analytical determination of the complex relative permeance function in linear electric machines with slotted air gap[C]//2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 2016: 1330-1335.
[24] Chan T F, Lai L L, Xie Shuming. Field computation for an axial flux permanent-magnet synchronous generator[J]. IEEE Transactions on Energy Con- version, 2009, 24(1): 1-11.
[25] Zhu Z Q, Howe D, Chan C C. Improved analytical model for predicting the magnetic field distribution in brushless permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2002, 38(1): 229-238.
[26] 冀溥, 王秀和, 王道涵, 等. 转子静态偏心的表面式永磁电机齿槽转矩研究[J]. 中国电机工程学报, 2004, 24(9): 188-191.
Ji Pu, Wang Xiuhe, Wang Daohan, et al. Study of cogging torque in surface-mounted permanent magnet motors with static eccentricity[J]. Proceedings of the CSEE, 2004, 24(9): 188-191.
Abstract The slotting effect has a great influence on the air gap magnetic field. The conformal mapping method is based on the single-slot model to consider the influence of stator slotting, which has good generality. However, it simplifies the stator slot to infinite depth, so the analytical calculation accuracy is low. The exact subdomain method can consider the details of the stator slot with high analytical calculation accuracy. Nevertheless, it needs to be remodeled for different pole-slot combinations, and its generality is poor. This paper proposes a general analytical model of the air gap magnetic field of the slotted axial flux permanent magnet (AFPM) motor, considering the influence of stator slot width, slot depth, and static eccentricity.
Firstly, the topology of the double stator single rotor AFPM motor is introduced, and the analytical expression of the slotless no-load air gap magnetic field is obtained based on the subdomain method. Secondly, the improved complex relative permeance function is used to consider the slotting effect, and then the accurate magnetic field analytical model of the AFPM motor is established. Finally, combined with the variation law of air gap reluctance during static eccentricity, an analytical model of air gap magnetic field considering the influence of static eccentricity is established. The proposed complex relative permeance function calculation method can consider the stator slot width and depth, which has higher analytical calculation accuracy than the traditional complex relative permeance function method.
The calculated air gap flux density, no-load back electromotive force (EMF), and cogging torque are compared with the finite element analysis (FEA) and experimental results. The traditional complex relative permeance function method ignores the stator slot depth, and the calculation accuracy is low at the stator slot opening region. The proposed analytical model agrees with the FEA results, verifying the improved complex relative permeance function method. The air gap flux density, no-load back-EMF, and cogging torque under different eccentricities are calculated. Compared with FEA, the calculation error of the analytical method is within the acceptable range, and the calculation time is reduced by 92.2% under the premise of similar solution accuracy. Compared with the experimental results, no-load back-EMF and cogging torque errors are 4.2% and 11%. The calculation errors meet the actual engineering requirements.
The following conclusions can be drawn. (1) The proposed analytical model considers the slotting effect and improves the analytical calculation accuracy of the static eccentric lower half model. (2) Compared with FEA, the analytical model has the characteristics of fast calculation speed and similar solution accuracy, which improves the calculation efficiency. (3) The analytical model can be further extended to the partly closed slot structure, providing convenience for the fast and accurate calculation of the electromagnetic characteristics of the related motors.
keywords:Slotting effect, improved complex relative permeance function, static eccentricity, axial flux permanent magnet motor
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.231807
国家自然科学基金项目(52222702)和沈阳市创新人才工程项目(RC210067)资助。
收稿日期2023-10-30
改稿日期2023-11-27
佟文明 男,1984年生,教授,博士生导师,研究方向为高性能永磁电机及其控制。E-mail: twm822@126.com(通信作者)
杜绍雨 男,1997年生,硕士研究生,研究方向为高转矩密度轴向磁通永磁电机设计与转矩波动。E-mail: shaoyu_du@163.com
(编辑 崔文静)