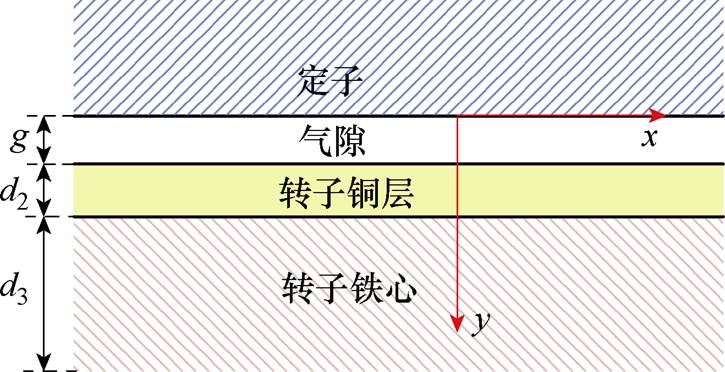
图1 覆铜实心转子感应电机模型
Fig.1 The model of copper-coated solid rotor induction motors
摘要 覆铜实心转子感应电机的转子阻抗参数计算是实心转子感应电机的难点。实心转子铁心材料非线性造成转子磁导率非恒定值,同时非线性导致了电磁场畸变,增加了转子阻抗的计算难度。对此,该文在双层转子模型子域解析的基础上,提出了一种考虑转子材料非线性,利用等效磁化曲线进行阻抗计算的方法,能够对非线性转子铁心在不同转差率下的磁导率进行计算,减小了由转子材料非线性造成的阻抗计算误差。通过二维时谐场有限元仿真验证了该方法的计算精度,并在该方法基础上提出一种考虑温度变化的转子阻抗简化计算方法,能够在转子温度变化情况下快速估算电机性能。
关键词:覆铜实心转子感应电机 转子阻抗 等效磁化曲线 转子材料非线性
实心转子感应电机具有较高的转子强度,相比永磁同步电机和开关磁阻电机更适合在大功率、超高速场合应用[1-2]。覆铜实心转子表面铜层具有高电导率、低磁导率的特点,能够改善实心转子感应电机的电磁性能。文献[3]展示了覆铜实心转子感应电机在高速、大功率磁悬浮空压机领域的应用。
感应电机转子阻抗是T型等效电路的关键参数,但实心转子内电磁场分布复杂,转子材料非线性和趋肤效应增加了计算转子阻抗的困难程度[4]。
国内外学者在二维电磁场子域解析法计算转子阻抗方面进行了大量研究[5-9]。文献[10-11]采用二维子域法对实心转子感应电机建模,并考虑了定子开槽和绕组结构对电磁场的影响,得到较为精确的电磁场参数,但忽略了转子材料非线性的影响。文献[12]以三维静态场和三维时谐场有限元为工具计算覆铜实心转子感应电机空载和堵转状态的性能,间接求解转子阻抗,相比三维瞬态场有限元方法节省了求解时间,但忽略了转子阻抗参数随着转差率变化。
为解决实心转子铁心饱和导致的磁导率变化问题,文献[13-14]应用多层理论计算了覆铜实心转子感应电机的转子阻抗,但没有解决多层累积误差难以消除的问题。对此,J. F. Gieras等提出了等效磁导率的概念,用来计算考虑转子铁心饱和、磁滞效应时的转子磁导率[15-16],并在文献[3]中进行了验证。J. F. Gieras通过转子表面坡印亭矢量将转子铁心磁导率转化为等效复磁导率,从工程上简化了非线性转子阻抗的计算方法,但J. F. Gieras采用的等效磁导率方法只考虑了磁场基波,忽略了转子材料非线性造成的电磁场量高次谐波,因此用似恒电磁场理论进行子域法求解时会带来一定误差[17]。
非线性的磁化曲线(B-H曲线)使磁感应强度B和磁场强度H不能同时为正弦[18],造成了转子内电磁场谐波含量的增加。为解决非线性材料造成磁场高次谐波含量增加的问题,国内外学者提出了大量方法对非线性材料B-H曲线进行等效[19],其中以磁场能量守恒的方法最为常用[20]。
本文在J. F. Gieras提出的方法基础上,将转子铁心原始B-H曲线按照磁场能量守恒的方法进行等效,减小了由电磁场量非正弦带来的误差,进一步提高了转子阻抗的计算精度。
本文首先以子域法求解覆铜实心转子内的矢量磁位,得到转子铜层阻抗、转子铁心阻抗及转子总阻抗[3]。然后采用磁场能量守恒法得到等效后的B-H曲线,进而采用解析迭代的方法得到非线性转子铁心的等效磁导率,最终得到实心转子阻抗,并用二维涡流场有限元法从转子铁心阻抗、铜层阻抗、转子总阻抗、电磁转矩和功率因数方面进行对比。最后在解析法计算转子阻抗基础上,考虑了温度变化对转子材料电阻率和B-H曲线的影响,并提出了一种考虑温度变化情况下的转子阻抗简化计算方法。
覆铜实心转子感应电机模型如图1所示,将电机轴向截面展开,沿y轴方向依次是定子、气隙、转子铜层、转子铁心。图1中,x方向为转子表面切向,y方向为转子径向,电机定、转子电流垂直于平面。

图1 覆铜实心转子感应电机模型
Fig.1 The model of copper-coated solid rotor induction motors
忽略定子开槽影响,假设定子铁心磁导率为∞,气隙磁导率为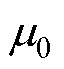 ;铜层电导率为
;铜层电导率为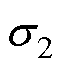 ,铜层磁导率
,铜层磁导率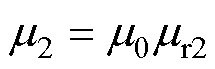 ,其中,
,其中,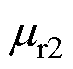 为铜层相对磁导率;转子铁心电导率为
为铜层相对磁导率;转子铁心电导率为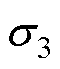 ,转子铁心磁导率
,转子铁心磁导率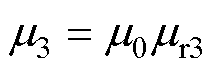 ,其中,
,其中,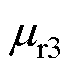 为转子铁心等效相对磁导率;气隙长度为g,铜层厚度为d2,转子铁心半径为d3,定子电压电角速度为
为转子铁心等效相对磁导率;气隙长度为g,铜层厚度为d2,转子铁心半径为d3,定子电压电角速度为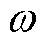 。
。
转子侧阻抗由铜层阻抗和转子铁心阻抗并联组成,如图2对应的T型等效电路所示,定子电阻和定子漏抗分别为r1和X1,励磁电抗为Xm,转子铜层阻抗为ZCu,转子铁心阻抗为ZSteel,转子总阻抗为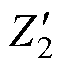 。
。
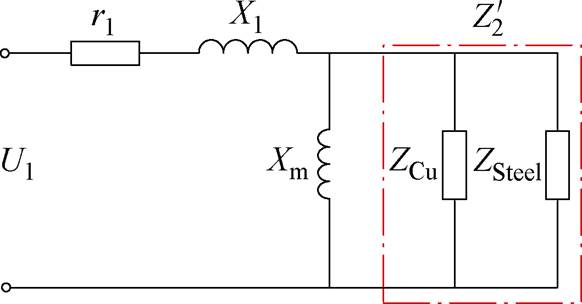
图2 覆铜实心转子感应电机T型等效电路
Fig.2 T type equivalent circuit of copper-coated solid rotor induction motors
引入磁矢量磁位,采用子域法对电机电磁场方程进行求解。对于气隙层的矢量磁位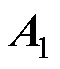 、转子铜层的矢量磁位
、转子铜层的矢量磁位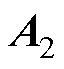 、转子铁心层的矢量磁位
、转子铁心层的矢量磁位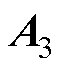 ,有拉普拉斯和泊松方程为
,有拉普拉斯和泊松方程为
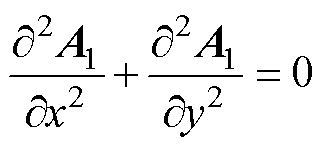 (1)
(1)
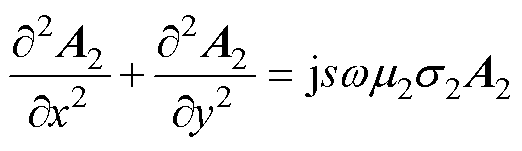 (2)
(2)
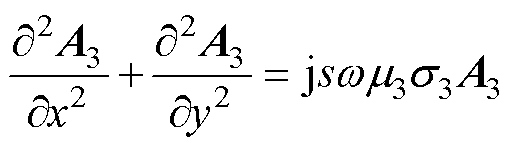 (3)
(3)
气隙与定子分界面的磁场强度切向分量之差等于定子面电流密度。即当y=0时,可得边界条件为
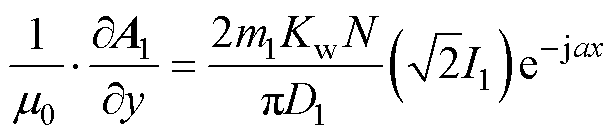 (4)
(4)
其中
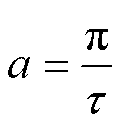
式中,m1为定子相数;Kw为绕组系数;N为每相串联匝数;D1为定子内径;I1为定子相电流有效值;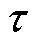 为极距。
为极距。
气隙与转子铜层交界面处,磁矢量磁位连续且磁场强度切向分量相等,即当y=g时,可得边界条件
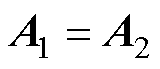 (5)
(5)
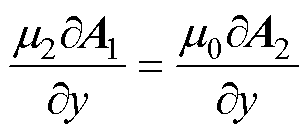 (6)
(6)
转子铜层与转子铁心交界面处,磁矢量磁位连续且磁场强度切向分量相等,即当y=g+d2时,可得边界条件为
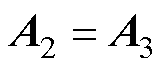 (7)
(7)
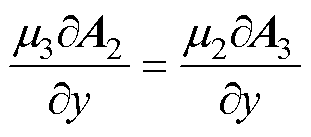 (8)
(8)
当转子铁心半径足够大时,可得边界条件为
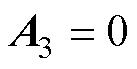 (9)
(9)
单位转子铁心阻抗Z3可用转子铁心表面电场强度轴向分量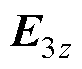 和磁场强度切向分量
和磁场强度切向分量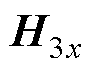 表示为
表示为
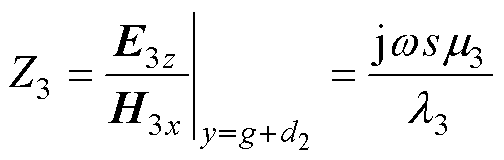 (10)
(10)
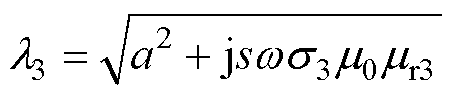 (11)
(11)
归算到定子侧的转子铁心阻抗ZSteel表达式为
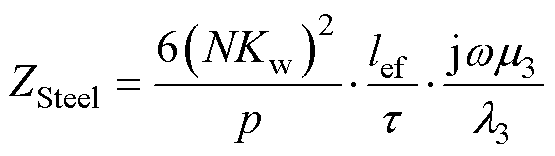 (12)
(12)
式中,lef为电机有效长度;p为极对数。
根据转子外侧铜层表面电场强度轴向分量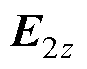 和磁场强度切向分量
和磁场强度切向分量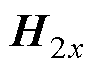 ,单位转子总阻抗Ztot表示为
,单位转子总阻抗Ztot表示为
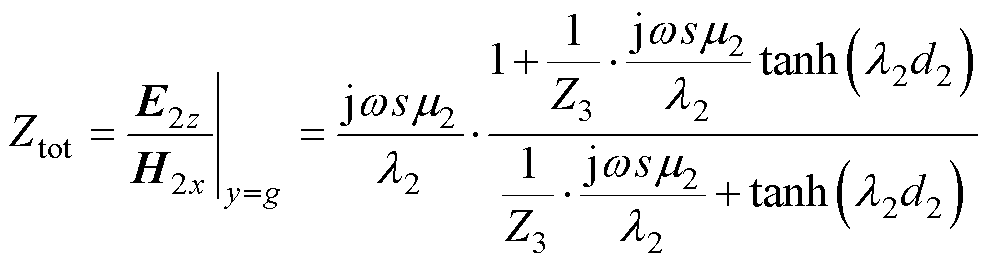 (13)
(13)
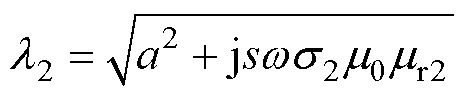 (14)
(14)
因此得到归算后的转子总阻抗值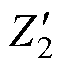 为
为
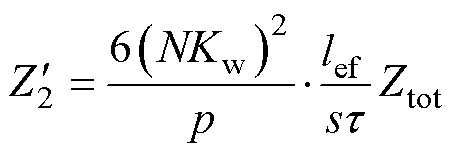 (15)
(15)
ZCu由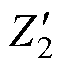 与ZSteel通过并联电路获得,有
与ZSteel通过并联电路获得,有
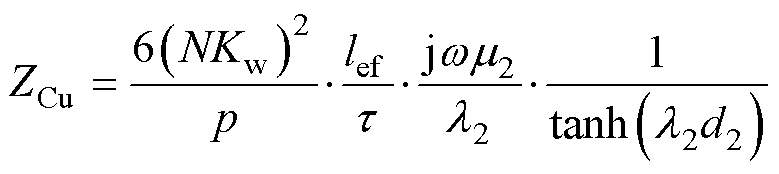 (16)
(16)
转子铁心为非线性材料,磁导率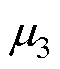 非恒定值,无法直接使用式(12)得到转子铁心阻抗,为此,本文第3节详细介绍了求取非线性转子铁心等效磁导率
非恒定值,无法直接使用式(12)得到转子铁心阻抗,为此,本文第3节详细介绍了求取非线性转子铁心等效磁导率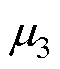 的方法。在求取
的方法。在求取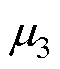 之前,需要对非线性材料原始磁化曲线进行等效,消除由于材料非线性造成的场量非正弦的影响。实心转子阻抗解析计算通常采用端部系数对转子电导率进行修正,但本文主要验证转子材料非线性的解析计算,因此忽略端部效应,端部系数的详细计算方法可参考文献[21]。
之前,需要对非线性材料原始磁化曲线进行等效,消除由于材料非线性造成的场量非正弦的影响。实心转子阻抗解析计算通常采用端部系数对转子电导率进行修正,但本文主要验证转子材料非线性的解析计算,因此忽略端部效应,端部系数的详细计算方法可参考文献[21]。
由于转子铁心材料非线性,当输入电压为正弦量时,B为正弦量,转子铁心材料非线性导致H不是标准的正弦量。
文献[18, 20]从磁场能量守恒的角度对转子铁心材料非线性造成的电磁场量非正弦问题进行了处理,在原始B-H曲线基础上得到了等效B-H曲线。
当B为正弦时,等效磁场强度为
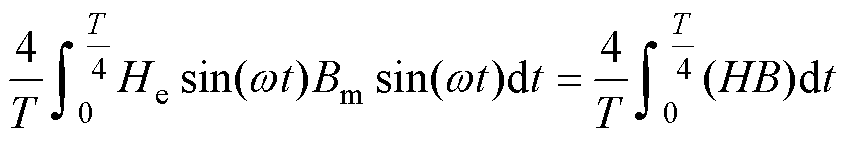 (17)
(17)
式中,T为正弦磁场的电周期;He为等效后磁场强度幅值;Bm为正弦磁感应强度幅值。根据上述能量积分不变的原理,采用数值积分将求出等效后的B-H曲线。
正弦B输入下,分别以原始B-H曲线和等效B-H曲线得到原始磁场强度和等效磁场强度的示意图如图3所示。原始磁场强度波形发生了畸变现象,这与子域法假设电磁场量为正弦的求解条件不符,因此需要对畸变的磁场强度进行等效。以磁场能量守恒法得到的等效磁场强度波形为正弦。尽管等效后的B-H曲线在形状上与原始B-H曲线相似,但采用等效B-H曲线求得的磁场强度为正弦量。
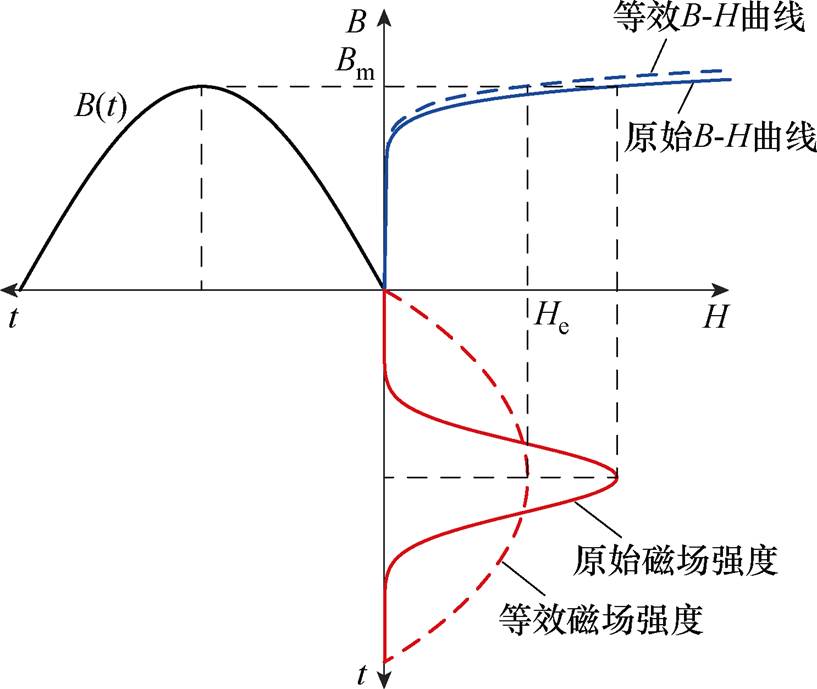
图3 原始B-H曲线和等效B-H曲线对应的原始磁场强度和等效磁场强度
Fig.3 The original magnetic field intensity and the equivalent magnetic field intensity corresponding to the original B-H curves and the effective B-H curve
本文转子铁心材料为10号钢,材料原始B-H曲线采用幂函数拟合,表示为
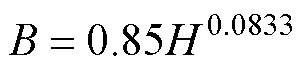 (18)
(18)
使用数值积分法对原始B-H曲线进行等效积分,求解得到等效B-H曲线,表达式为
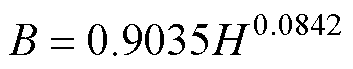 (19)
(19)
图4为原始B-H曲线和采用磁场能量法等效后的B-H曲线。等效后B-H曲线在不饱和区的斜率大于原始B-H曲线。
文献[3]中,J. F. Gieras等提出了一种近似计算的方法,转子铁心相对磁导率表示为
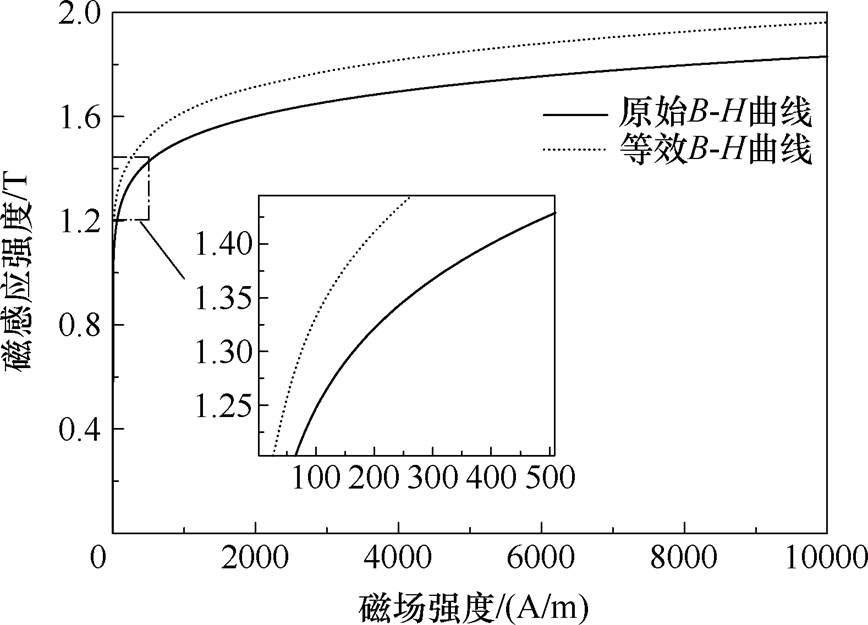
图4 原始B-H曲线与等效B-H曲线
Fig.4 Original B-H curve and effective B-H curve
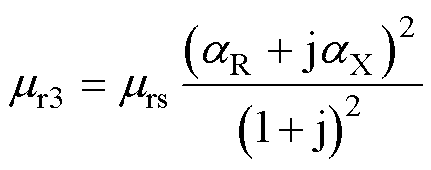 (20)
(20)
式中,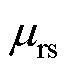 为非线性转子铁心表面相对磁导率;
为非线性转子铁心表面相对磁导率;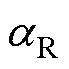 、
、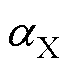 分别为电阻和电抗系数,当
分别为电阻和电抗系数,当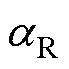 =1.45,
=1.45,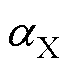 =0.85时,在工程上能够得到较为满意的计算结果,但对于不同材料,上述两个参数的值也在不断变化。文献[15-16]详细阐明了采用坡印廷矢量计算上述两个参数的方法,但转子铁心的磁化曲线采用了原始B-H曲线,并没有采用等效B-H曲线,因此计算精度上存在提升的空间。本节采用等效B-H曲线作为转子铁心的材料参数,将覆铜实心转子分为转子铜层、转子饱和区、转子不饱和区,如图5所示。图中,R1、R2、R3和R4分别为转子不饱和区内径、转子饱和区内径、转子铁心外径和转子铜层外径。铜层为线性材料,相对磁导率近似为1。转子铁心饱和区由于磁场的趋肤效应和饱和效应,相对磁导率变化规律为:从转子铁心表面向内逐渐增大,相对磁导率的值从
=0.85时,在工程上能够得到较为满意的计算结果,但对于不同材料,上述两个参数的值也在不断变化。文献[15-16]详细阐明了采用坡印廷矢量计算上述两个参数的方法,但转子铁心的磁化曲线采用了原始B-H曲线,并没有采用等效B-H曲线,因此计算精度上存在提升的空间。本节采用等效B-H曲线作为转子铁心的材料参数,将覆铜实心转子分为转子铜层、转子饱和区、转子不饱和区,如图5所示。图中,R1、R2、R3和R4分别为转子不饱和区内径、转子饱和区内径、转子铁心外径和转子铜层外径。铜层为线性材料,相对磁导率近似为1。转子铁心饱和区由于磁场的趋肤效应和饱和效应,相对磁导率变化规律为:从转子铁心表面向内逐渐增大,相对磁导率的值从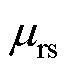 增大到
增大到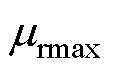 ,根据文献[8],相对磁导率按幂函数的形式变化。转子不饱和区相对磁导率近似为恒定值。
,根据文献[8],相对磁导率按幂函数的形式变化。转子不饱和区相对磁导率近似为恒定值。
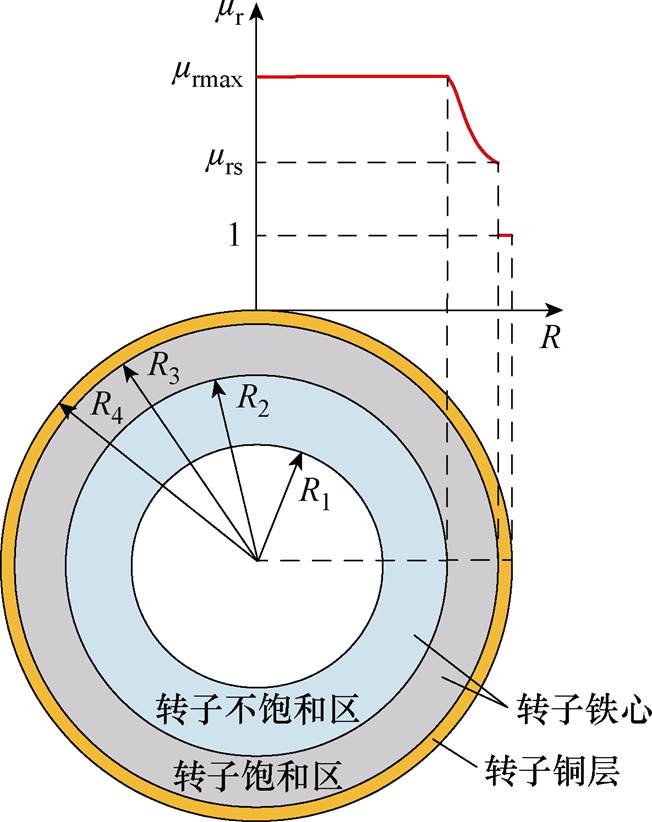
图5 覆铜实心转子相对磁导率分布
Fig.5 Relative permeability distribution of copper-coated solid rotor
分别对转子铁心饱和区、不饱和区磁场扩散方程进行求解。假定磁场强度沿转子表面切向传播,电场强度方向为轴向。转子铁心饱和区磁场强度为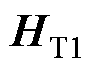 ,电场强度为
,电场强度为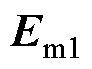 。转子铁心不饱和区磁场强度为
。转子铁心不饱和区磁场强度为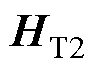 ,电场强度为
,电场强度为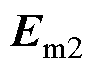 。
。
(1)对于转子饱和区R2<R≤R3,有磁场扩散方程为
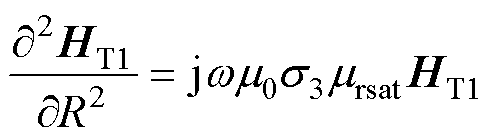 (21)
(21)
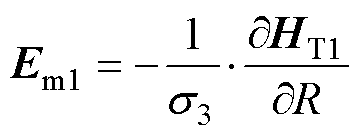 (22)
(22)
式中,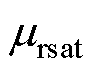 为转子饱和区相对磁导率,可表示为沿半径方向增大的幂函数形式,有
为转子饱和区相对磁导率,可表示为沿半径方向增大的幂函数形式,有
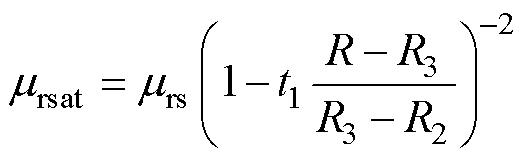 (23)
(23)
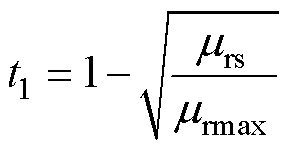 (24)
(24)
(2)对于转子不饱和区R1≤R≤R2,有磁场扩散方程为
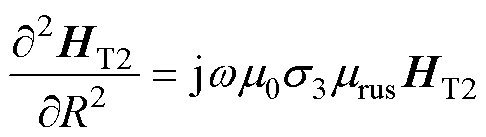 (25)
(25)
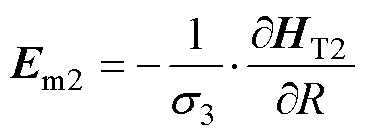 (26)
(26)
式中,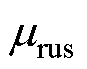 为转子铁心不饱和区的相对磁导率,可由等效B-H曲线近似求取。
为转子铁心不饱和区的相对磁导率,可由等效B-H曲线近似求取。
求解式(21)、式(22)、式(25)、式(26)可得转子铁心饱和区磁场强度和电场强度分别为
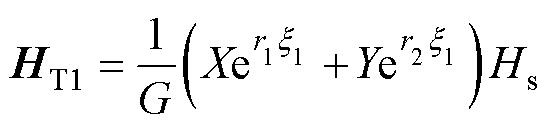 (27)
(27)
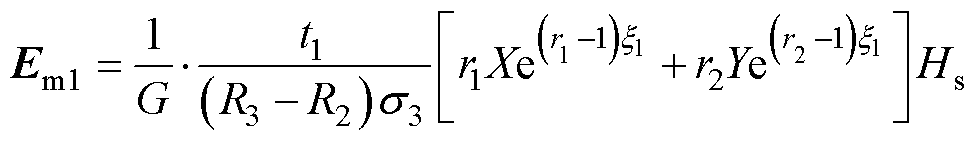 (28)
(28)
其中
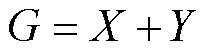 (29)
(29)
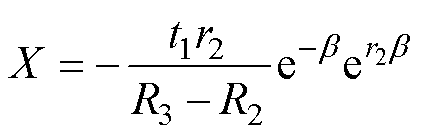 (30)
(30)
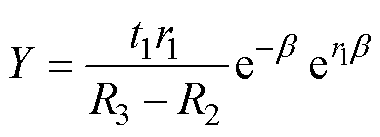 (31)
(31)
式中,Hs为转子铁心表面磁场强度;G、X、Y、r1、r2、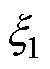 、
、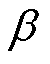 为与等效B-H曲线有关的求解系数。
为与等效B-H曲线有关的求解系数。
根据铁心表面电场强度和磁场强度可以求得转子铁心单位阻抗为
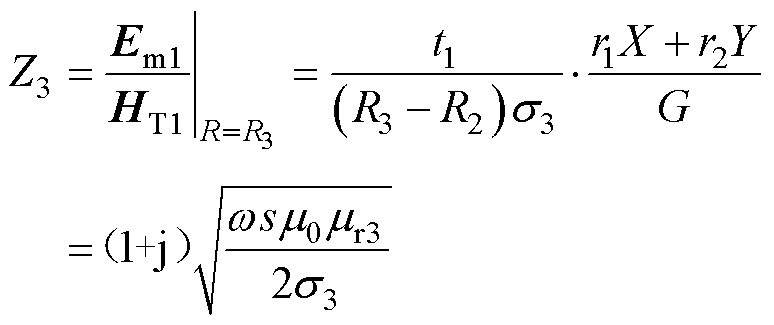 (32)
(32)
式中,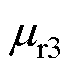 由式(20)计算,
由式(20)计算,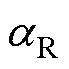 和
和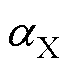 分别为
分别为
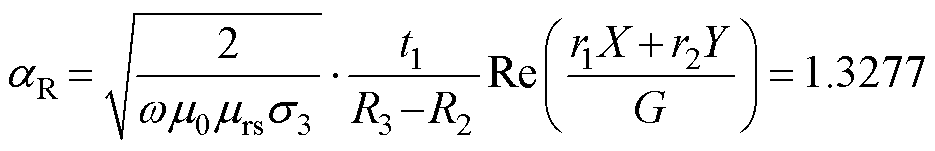 (33)
(33)
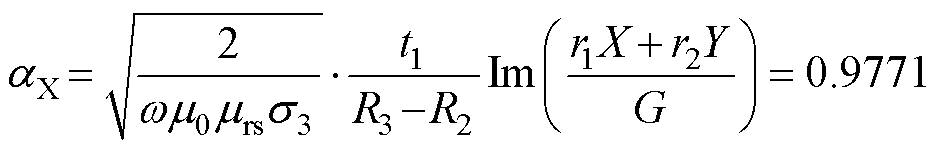 (34)
(34)
从式(20)得出,若已知转子铁心表面的相对磁导率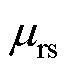 ,就可以将非线性转子铁心等效磁导率
,就可以将非线性转子铁心等效磁导率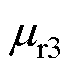 求出。以一台覆铜实心转子感应电机为模型,计算不同转差率下的转子铁心表面相对磁导率
求出。以一台覆铜实心转子感应电机为模型,计算不同转差率下的转子铁心表面相对磁导率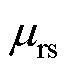 。电机主要尺寸和参数见表1。
。电机主要尺寸和参数见表1。
表1 覆铜实心转子感应电机主要尺寸和参数
Tab.1 Main dimensions and parameters of copper-coated solid rotor induction motor
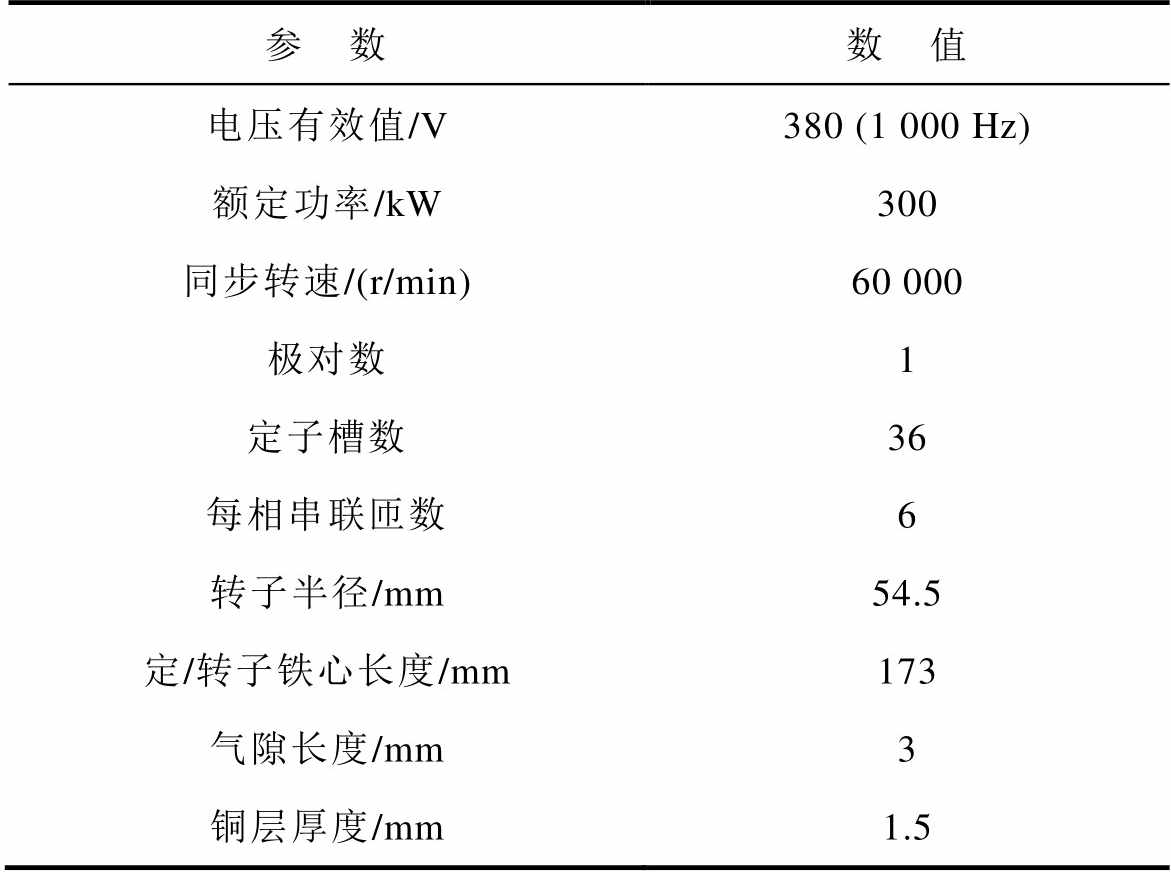
参 数数 值 电压有效值/V380 (1 000 Hz) 额定功率/kW300 同步转速/(r/min)60 000 极对数1 定子槽数36 每相串联匝数6 转子半径/mm54.5 定/转子铁心长度/mm173 气隙长度/mm3 铜层厚度/mm1.5
覆铜实心转子感应电机截面如图6所示。
转差率s为0.005~0.1时,对转子铁心表面相对磁导率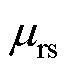 进行迭代计算,迭代计算流程如图7所示,根据式(20)可求得转子铁心表面相对磁导率
进行迭代计算,迭代计算流程如图7所示,根据式(20)可求得转子铁心表面相对磁导率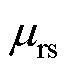 和转子铁心等效相对磁导率
和转子铁心等效相对磁导率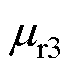 ,见表2。
,见表2。
使用二维涡流场有限元仿真计算转子铁心表面相对磁导率,有限元法与等效B-H曲线解析法结果基本一致,如图8所示。随着转差率逐渐增大,转子铁心表面的相对磁导率呈先减小后增大的趋势,这是因为在转差率较小时,随着转差率增大,转子铁心饱和程度增大,造成转子铁心表面相对磁导率减小;当转差率增大时,趋肤效应造成转子电流集中在转子铜层,转子铁心饱和程度下降,转子铁心表面相对磁导率增大。
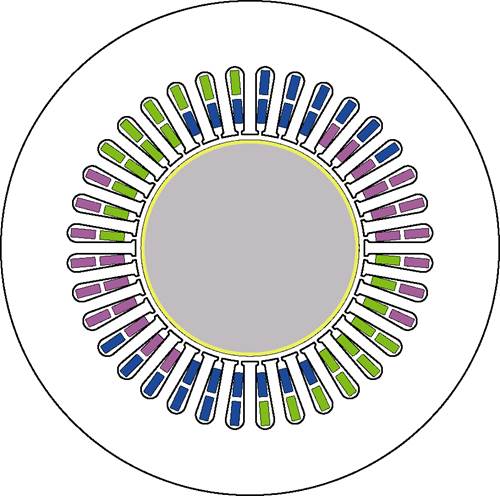
图6 覆铜实心转子感应电机截面
Fig.6 Cross-section of copper-coated solid rotor induction motors
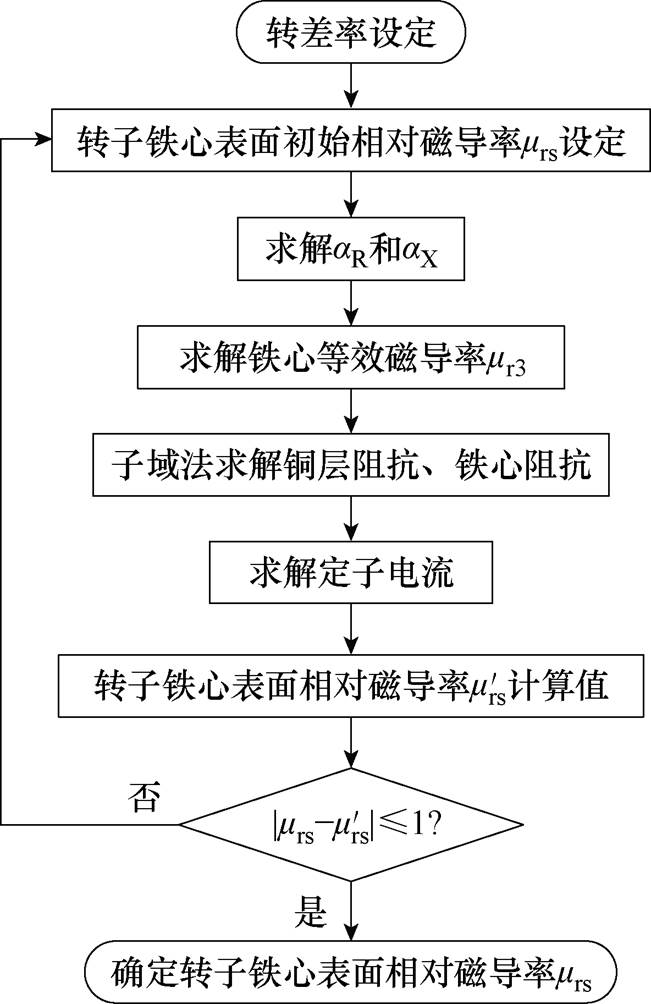
图7 转子铁心表面相对磁导率迭代计算流程
Fig.7 Flow chart of iterative calculation of relative permeability of rotor core surface
表2 不同转差率转子铁心表面相对磁导率与等效磁导率
Tab.2 Relative permeability of rotor core surface and equivalent permeability with different slip

s 0.00549.8664.68-20.15j 0.0134.6945.01-14.02j 0.0228.8037.37-11.64j 0.0328.6237.13-11.56j 0.0429.8638.74-12.07j 0.0531.6641.07-12.79j 0.0633.7143.74-13.62j 0.0735.9146.59-14.51j 0.0838.1849.53-15.43j 0.0940.5052.54-16.36j 0.142.8355.56-17.31j
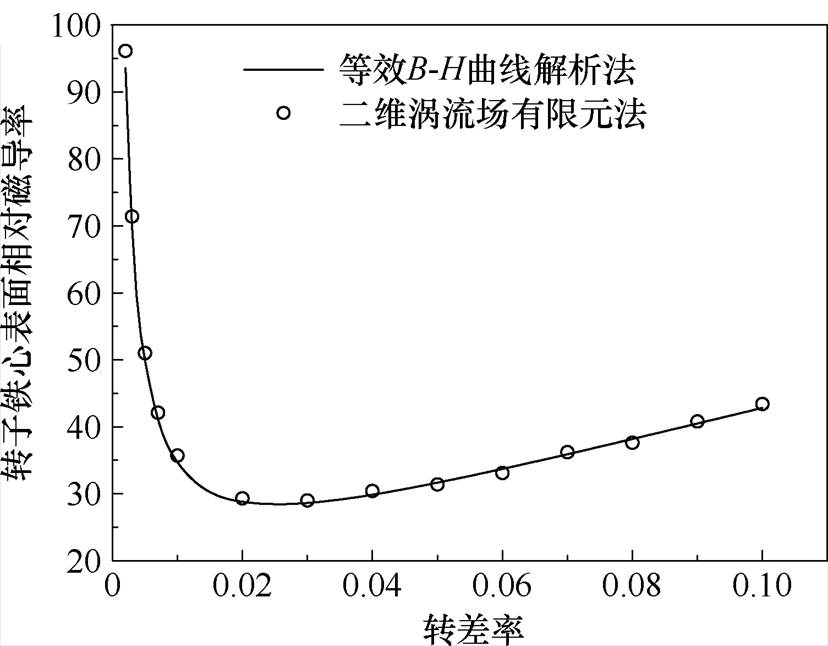
图8 不同转差率下转子铁心表面相对磁导率
Fig.8 Relative permeability of rotor core surface at different slip
转差率为0.005时的转子磁导率如图9所示。图中转子相对磁导率分为两层,即饱和区和不饱和区。
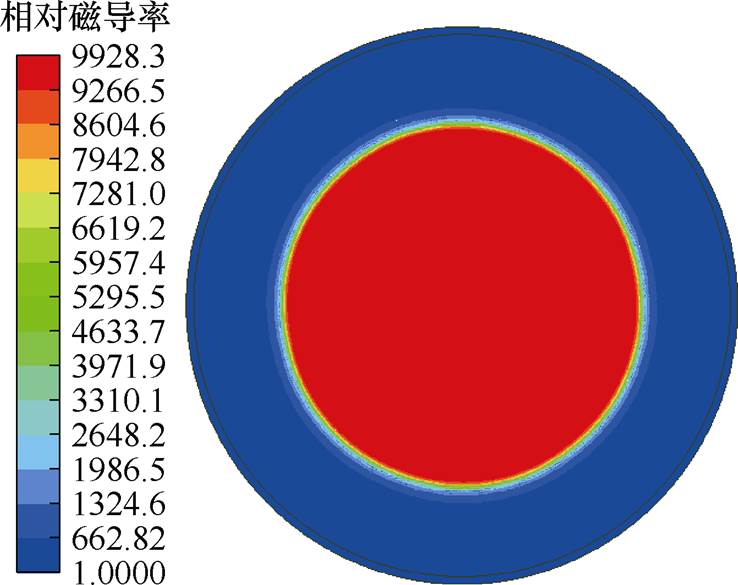
图9 转差率为0.005时转子相对磁导率云图
Fig.9 Cloud image of rotor relative permeability when slip is 0.005
在有限元场计算器中沿着转子半径方向求取转子相对磁导率,如图10所示,转子外侧铜层相对磁导率为1,转子铁心表面相对磁导率为51,与表2中s=0.005时解析计算结果49.86相差约2%。图10中相对磁导率从转子外侧向内逐渐增大,在不饱和区为恒定值,这种变化趋势与图5解析计算模型是一致的。
感应电机采用涡流场有限元计算能够快速达到稳定状态,其计算结果与时步有限元在电机稳定运行工况下一致性较好。在涡流场有限元场编辑器中编辑焦耳热和磁场能量[21],有
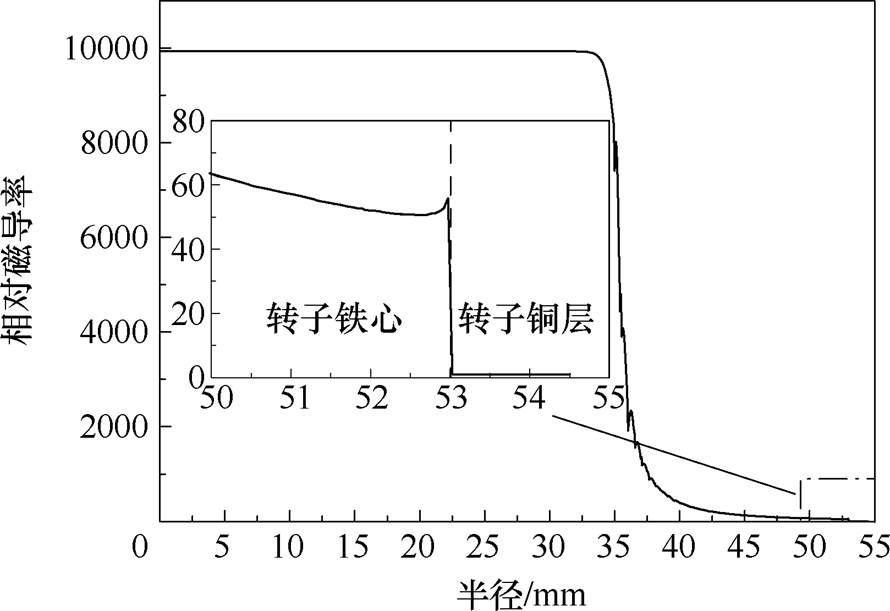
图10 转差率为0.005时转子相对磁导率随半径变化曲线
Fig.10 When the slip is 0.005, the relative permeability of the rotor varies with the radius
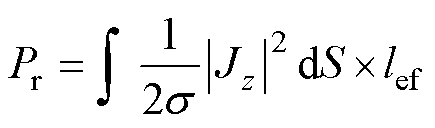 (35)
(35)
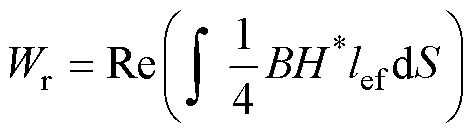 (36)
(36)
式中,Pr为焦耳热能量,当求解转子总电阻时,需要分别计算转子铜层和转子铁心的焦耳热能量进行累加;Jz为轴向电流密度;Wr为磁场能量,当求解转子总电抗时,对转子铜层和铁心的磁场能量进行累加;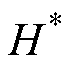 为求解面域内H的共轭复数。
为求解面域内H的共轭复数。
转子总电阻的有限元计算方法如式(37)所示,转子总阻抗可用转子总焦耳热能量Pr2、转子总磁场能量Wr2及转子电流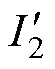 共同表示。
共同表示。
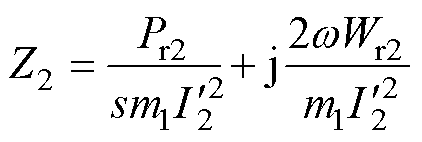 (37)
(37)
转子电流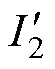 可表示为
可表示为
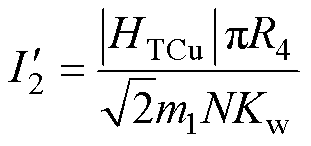 (38)
(38)
式中,HTCu为转子外侧铜层表面处的磁场强度切向分量。
转子铁心阻抗的有限元计算为
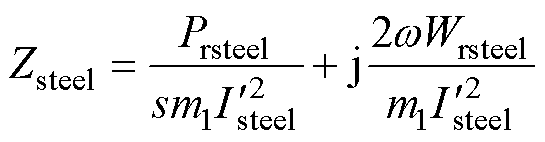 (39)
(39)
式中,Prsteel和Wrsteel分别为转子铁心层的焦耳热和磁场能量;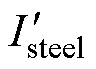 为转子铁心电流,可用铁心层表面磁场强度HTsteel表示,有
为转子铁心电流,可用铁心层表面磁场强度HTsteel表示,有
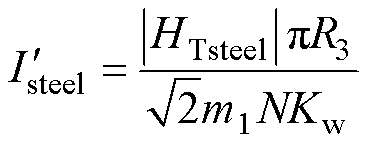 (40)
(40)
分别将等效后B-H曲线和J. F. Gieras采用的原始B-H曲线求得的转子铁心相对磁导率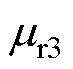 代入式(12)、式(15)和式(16)得到转子阻抗,将结果与二维涡流场有限元结果进行对比。
代入式(12)、式(15)和式(16)得到转子阻抗,将结果与二维涡流场有限元结果进行对比。
图11和图12为转子铁心电阻和电抗采用二维涡流场有限元法和解析法计算的对比。采用等效B-H曲线解析法得到的转子铁心电阻与J. F. Gieras解析法及有限元法得到的结果基本一致。
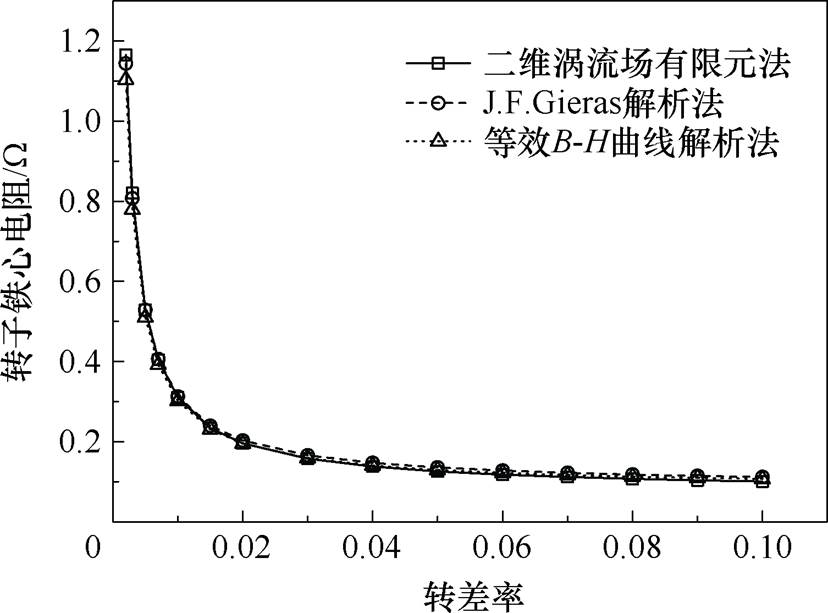
图11 转子铁心电阻解析法与有限元法计算对比
Fig.11 Comparison between the analytical method of rotor core resistance and the finite element method
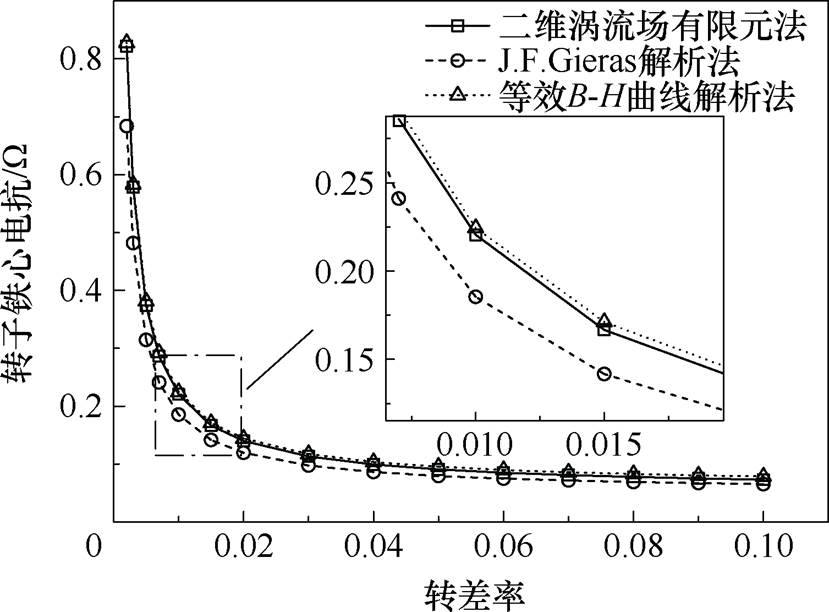
图12 转子铁心电抗解析法与有限元法计算对比
Fig.12 Comparison between the analytical method of rotor core reactance and the finite element method
转子铁心电抗计算采用等效B-H曲线解析法相比J. F. Gieras解析法更接近有限元计算结果。且转差率较小时,等效B-H曲线解析法相比J. F. Gieras解析法明显提升了计算精度。
转子铜层磁导率为恒定值,可以直接采用式(16)求出转子铜层阻抗。图13为转子铜层电阻及电抗随转差率变化的曲线。
图14和图15分别为转子总电阻和总电抗随转差率变化曲线。采用等效B-H曲线的解析法计算转子总电阻相比J. F. Gieras解析法更接近有限元结果,转差率小于0.1时,等效B-H曲线解析法计算误差均小于1%。转子总电抗采用等效B-H曲线解析法相比J. F. Gieras解析法提高了计算精度。
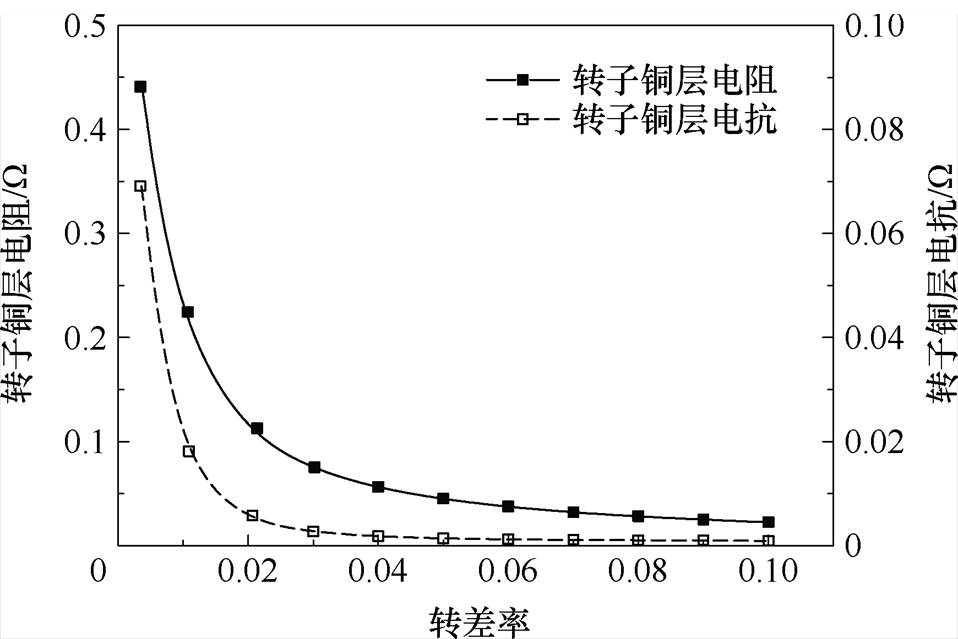
图13 转子铜层电阻及电抗随转差率变化曲线
Fig.13 Curves of rotor copper resistance and reactance with slip
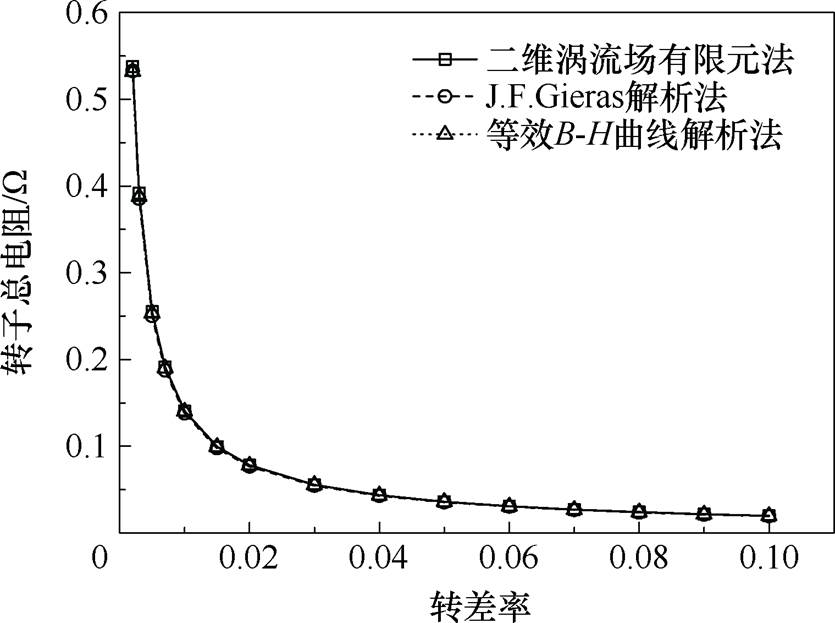
图14 转子总电阻解析法与有限元法计算对比
Fig.14 Comparison between the analytical method of rotor total resistance and the finite element method
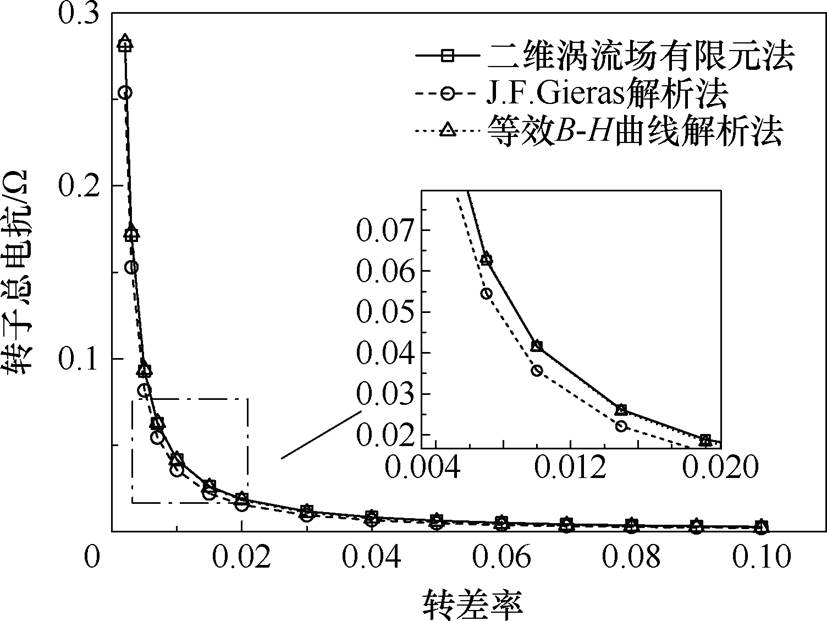
图15 转子总电抗解析法与有限元法计算对比
Fig.15 Comparison between the analytical method of rotor total reactance and the finite element method
为研究转子阻抗对电磁转矩、功率因数的影响,将两种解析法与二维涡流场有限法所得结果进行对比。图16为电磁转矩随转差率变化曲线。从图16可以看出,等效B-H曲线解析法计算的电磁转矩与有限元计算结果基本一致,特别当电机稳定运行时(转差率小于0.02),计算结果更接近有限元仿真结果。
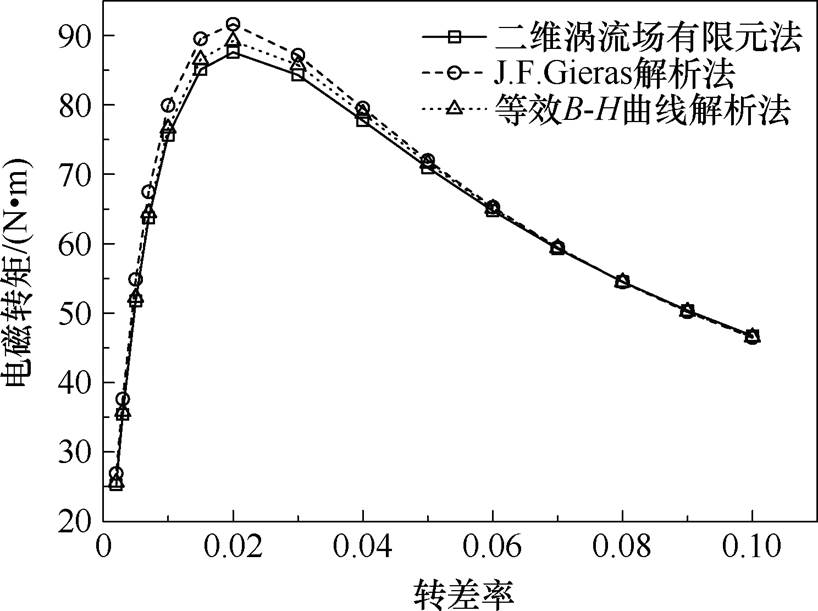
图16 电磁转矩随转差率变化曲线
Fig.16 Electromagnetic torque varies with slip
图17为功率因数随转差率变化曲线,在转差率较低时,等效B-H曲线解析法计算结果更接近有限元结果。
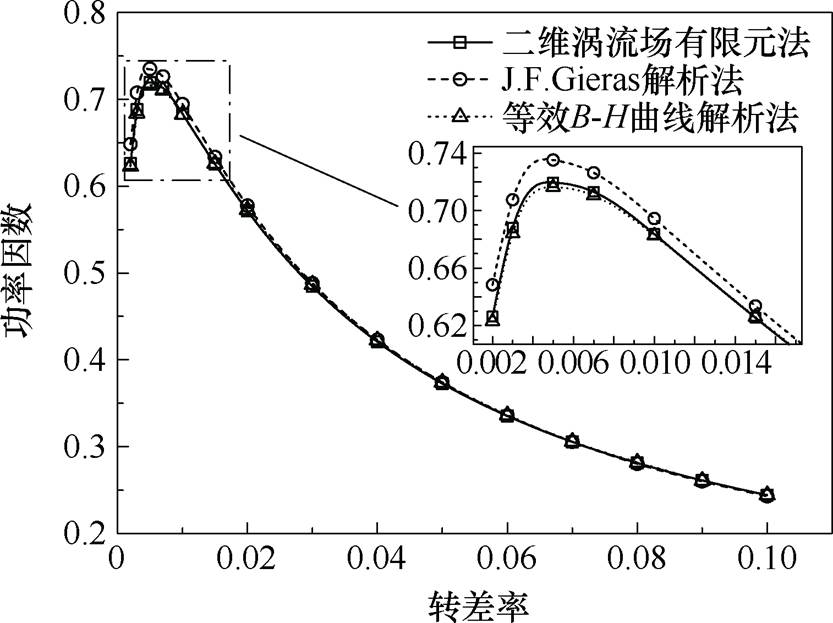
图17 功率因数随转差率变化曲线
Fig.17 The power factor varies with slip
电机运行过程中,转子温度变化引起转子材料电阻率和磁导率变化,造成转子阻抗变化。温度对转子材料电阻率的影响由温度系数得到,有
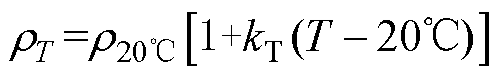 (41)
(41)
式中,T为温度;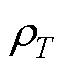 为T摄氏度下的电阻率;
为T摄氏度下的电阻率;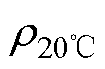 为20℃下的电阻率;kT为电阻率温度系数。转子铜层和转子铁心的电阻率及温度系数见表3。
为20℃下的电阻率;kT为电阻率温度系数。转子铜层和转子铁心的电阻率及温度系数见表3。
表3 转子材料电阻率及温度系数
Tab.3 The resistivity and temperature coefficient of rotor material

参数/(W·m)kT/(℃-1) 转子铜层1.8×10-80.003 93 转子铁心1.1×10-70.006 51
转子铜层磁导率与空气磁导率接近,假定不受温度变化影响。转子铁心磁导率受温度影响较为复杂。文献[22]总结了导磁材料初始磁导率随温度升高而增大,但当达到居里温度时,初始磁导率急剧下降;饱和磁通密度随温度升高而降低。本文以H级绝缘等级的温升作为转子温升的极限值,研究转子在200℃下的阻抗变化。根据文献[23]总结的磁化曲线随温度变化规律,以20℃下的原始B-H曲线为基准,得到200℃下的原始B-H曲线并进行等效,如图18所示。
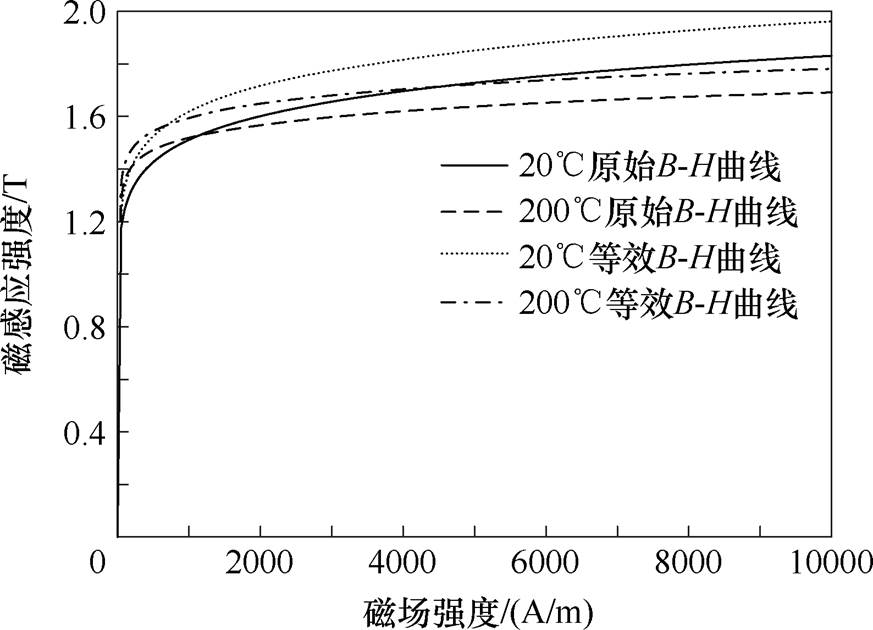
图18 20℃和200℃下转子铁心原始B-H曲线及等效B-H曲线
Fig.18 Original B-H curves and equivalent B-H curves of rotor core at 20℃ and 200℃
当转子温度为200℃时,采用200℃下的材料电阻率和等效B-H曲线可以对转子阻抗进行解析法计算。
然而获得转子铁心在不同温度下的B-H曲线并进行等效处理是困难的,但获得不同温度下的电阻率较为容易,因此提出一种简化的转子阻抗计算方法,即200℃下仍然采用20℃下的转子铁心等效B-H曲线,转子材料电阻率采用200℃下的值,对转子阻抗进行计算。将同时改变电阻率和磁导率的计算结果与只改变电阻率的计算结果进行比较。
200℃下两种方法计算转子铁心电阻、铁心电抗随转差率变化如图19、图20所示。图19、图20表明,在200℃下只改变材料的电阻率,得到的转子铁心电阻和电抗相比同时改变电阻率和磁导率的计算结果最大误差分别为10%和13%。转子总阻抗由转子铁心阻抗与铜层阻抗并联组成,而铜层阻抗的计算结果较为准确。因此并联后的转子总阻抗的计算误差会减小,如图21、图22所示,并联后的总电阻和总电抗误差均小于4%。
将转子处于20℃和200℃下的转矩解析计算结果进行对比。如图23所示,温度变化时转矩变化是明显的,采用仅考虑电阻率变化的简化方法虽然不能完全体现材料属性,但在计算结果上是较为接近实际值的。
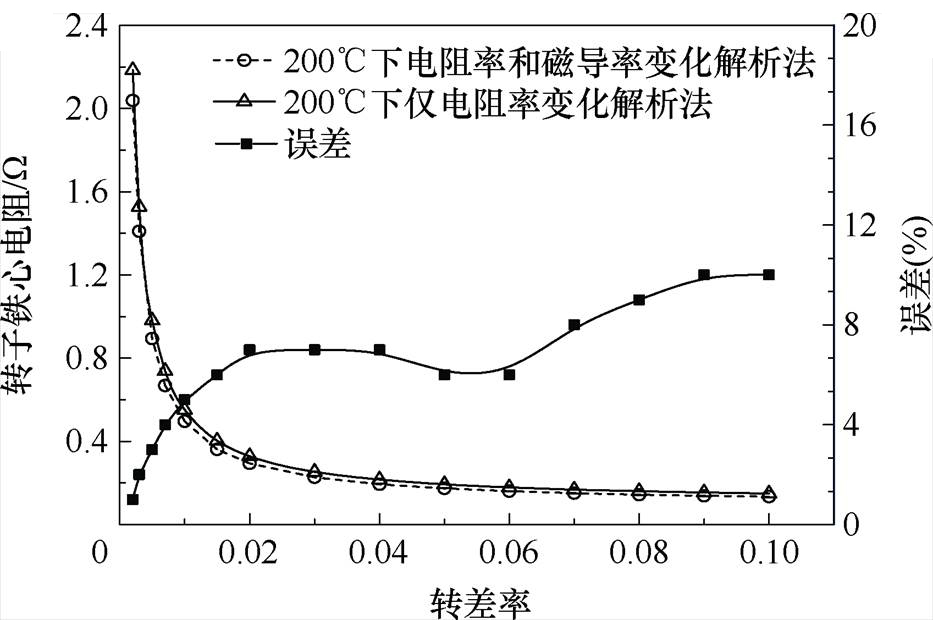
图19 200℃下两种方法计算转子铁心电阻随转差率变化
Fig.19 The change of rotor core resistance with slip calculated by two analytical methods at 200℃
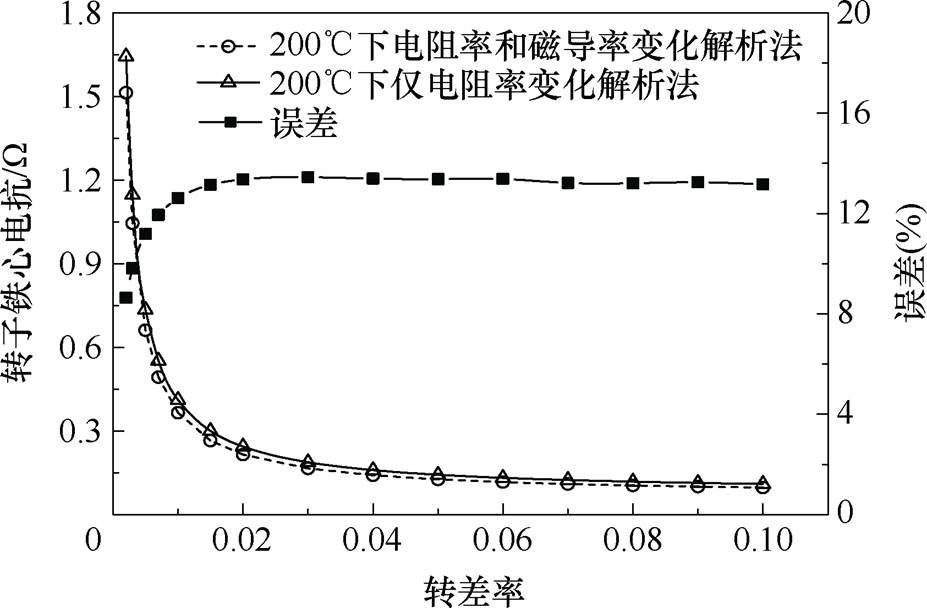
图20 200℃下两种方法计算转子铁心电抗随转差率变化
Fig.20 The change of rotor core reactance with slip calculated by two analytical methods at 200℃
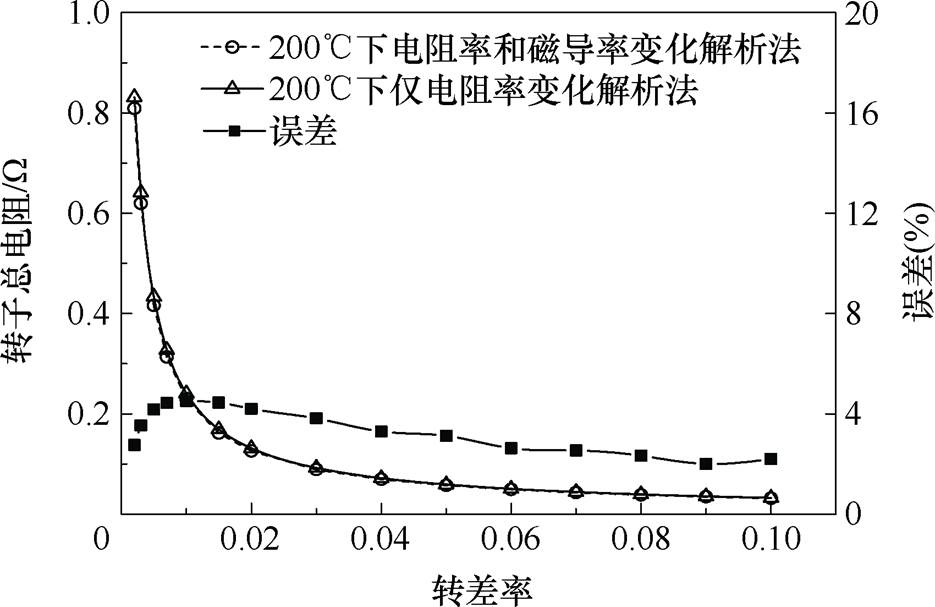
图21 200℃下两种方法计算转子总电阻随转差率变化
Fig.21 The total rotor resistance calculated by two analytical methods varies with the slip at 200℃
尽管并联后的总阻抗误差减小,但转子铁心阻抗的误差仍然存在,需要研究采用这种简化的计算方法对电机性能计算的影响。
图24为200℃下仅考虑电阻率变化的简化计算方法和同时考虑电阻率和磁导率变化的方法对转矩和功率因数的解析计算结果。随着转差率增大,简化方法得到转矩和功率因数均偏大。
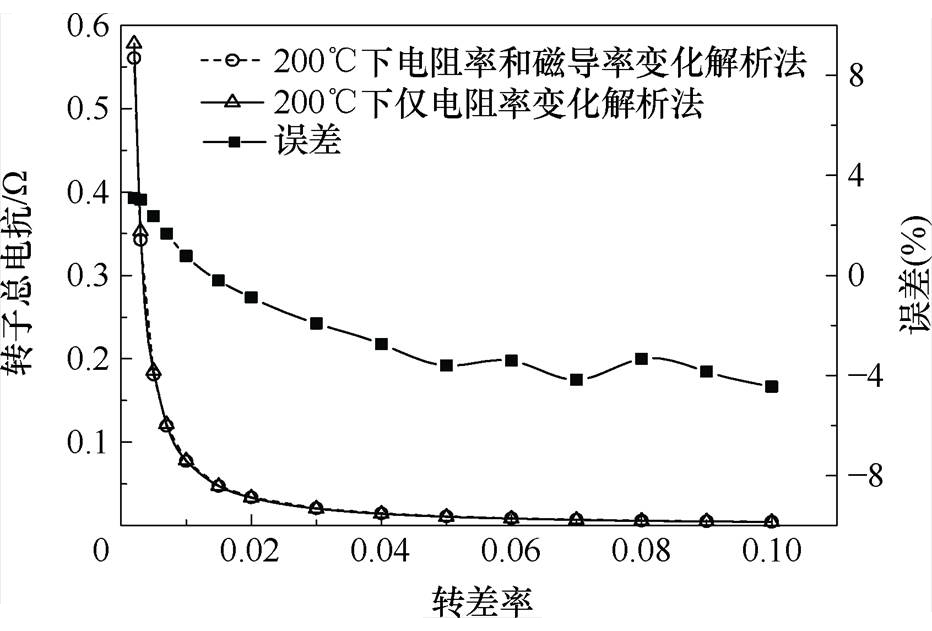
图22 200℃下两种方法计算转子总电抗随转差率变化
Fig.22 The total reactance of the rotor calculated by two analytical methods varies with the slip at 200℃
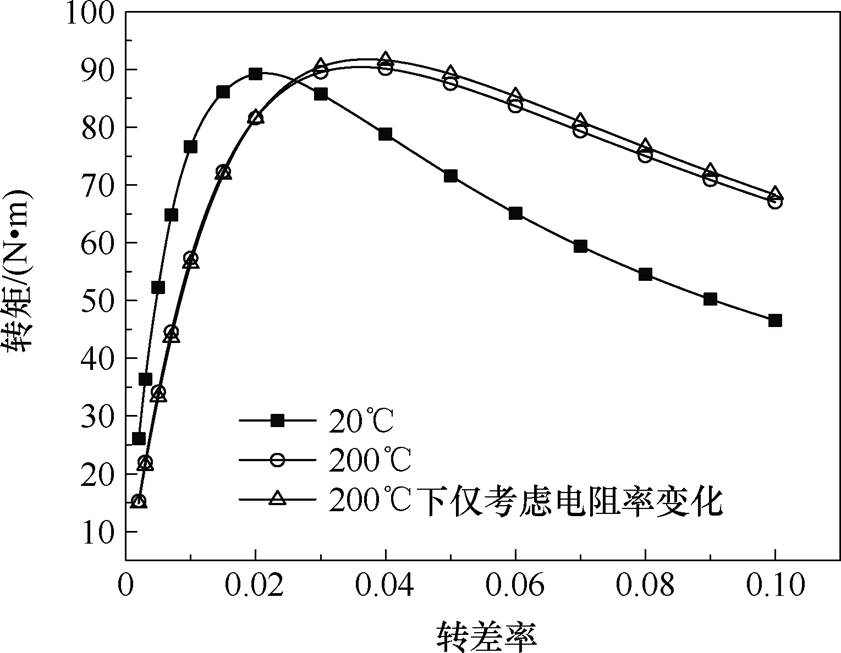
图23 不同温度下计算转矩随转差率变化
Fig.23 The torque varies with the slip at different temperatures
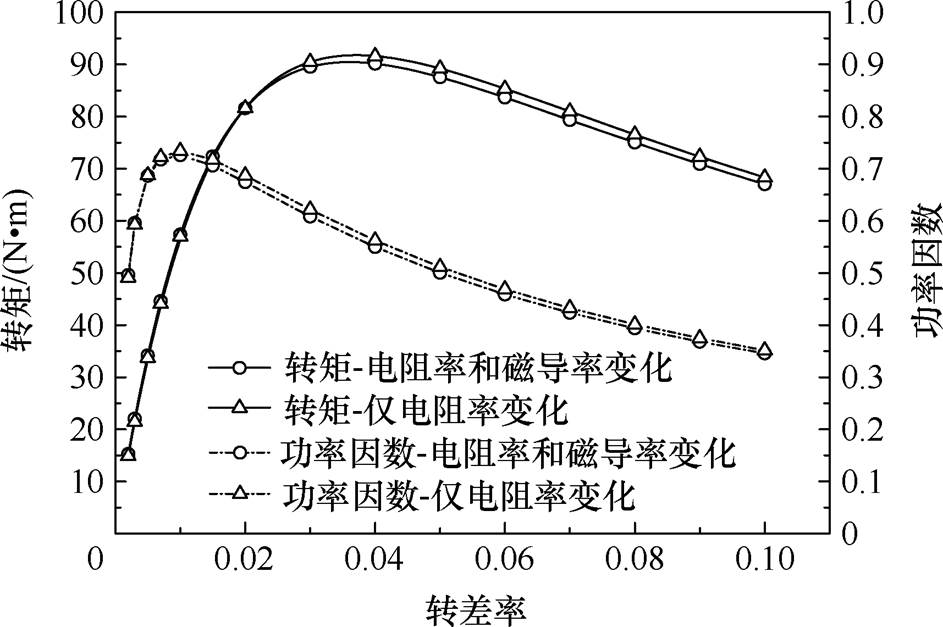
图24 200℃下两种解析方法计算转矩和功率因数随转差率变化
Fig.24 Two analytical methods are used to calculate the variation of torque and power factor with slip at 200℃
仅考虑电阻率变化方法计算转矩偏大的原因是转子铁心阻抗计算误差为正值,转子铁心阻抗与铜层阻抗为并联结构,转子铁心阻抗增大会造成转子电流向铜层集中,相当于加剧了转子趋肤效应,使转矩增大。
图25为200℃下有限元计算转子总涡流损耗与总磁场能量。仅考虑电阻率变化的情况下,转子总涡流损耗计算值偏大,反映无功功率的总磁场能量偏小,因此功率因数计算值偏大。
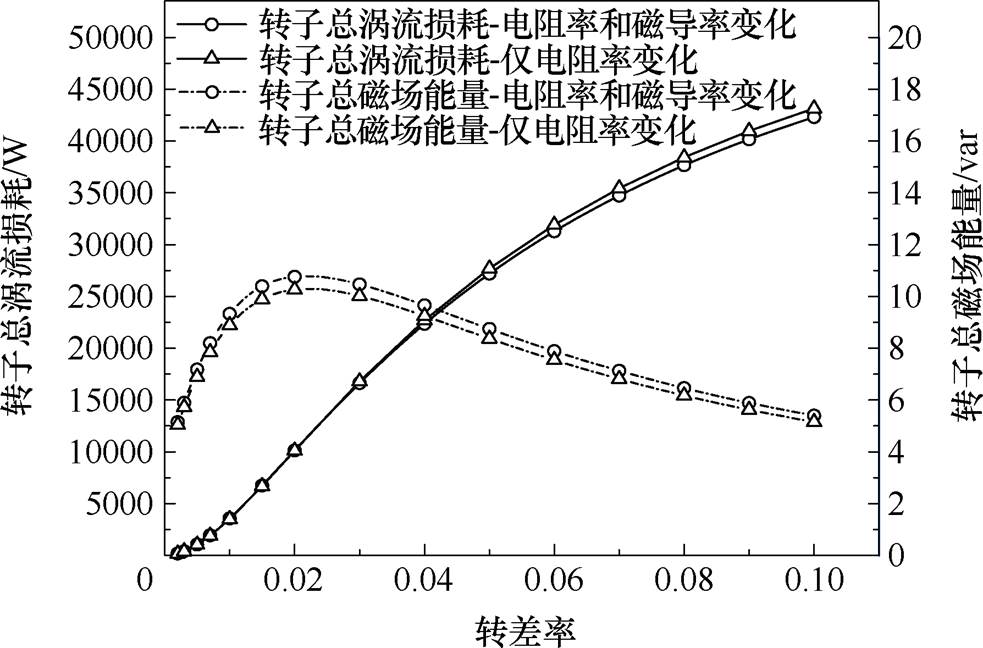
图25 200℃下有限元计算转子总涡流损耗与总磁场能量
Fig.25 The total eddy current loss and magnetic field energy of rotor are calculated by finite element method at 200℃
本节提出的简化计算转子阻抗方法对于转子温度变化情况下,快速计算电机性能存在一定的工程应用价值,但该方法忽略了磁导率变化,造成电机转矩和功率因数偏大。对于覆铜实心转子结构,转子阻抗中铜层阻抗占比较大,铁心阻抗的计算误差对电机性能的影响相对较小,这是能够忽略磁导率变化的原因。但当转子温度变化幅度使转子铁心导磁性能剧变时(如居里温度下失磁),该方法不再适用。对于转子温度变化范围较大的运行工况,可以按照转子温升最大值的温度对误差进行评估。
本文对覆铜实心转子感应电机的转子阻抗解析计算进行了研究,考虑了转子铁心材料非线性造成的电磁场畸变,并在J. F. Gieras解析法基础上,采用等效B-H曲线,将不同转差率下的转子铁心等效磁导率计算出来,提高了转子铁心阻抗的计算精度。考虑了温度变化对转子阻抗的影响,可得如下结论。
1)转子铁心表面相对磁导率随转差率增大呈先减小后增大趋势,这是由于转差率较小时,转子铁心饱和程度随着转差率增大而加剧;转差率较大时,趋肤效应造成转子电流集中在转子铜层,使转子铁心饱和程度下降。在转差率一定时,转子铁心磁导率从转子铁心表面向转子中心呈幂函数趋势增大,在转子铁心不饱和区达到稳定值。
2)等效B-H曲线解析法计算转子总阻抗、电磁转矩及功率因数相比采用原始B-H曲线的J. F. Gieras解析法具有更高精度。
3)转子温度变化时,提出了一种简化计算转子阻抗方法,但此方法计算转子铁心阻抗存在一定误差,在转子温度变化范围较大时,需要对最大温度下的性能误差进行评估,确定该方法的适用性。
参考文献
[1] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[2] 董剑宁, 黄允凯, 金龙, 等. 高速永磁电机设计与分析技术综述[J]. 中国电机工程学报, 2014, 34(27): 4640-4653.
Dong Jianning, Huang Yunkai, Jin Long, et al. Review on high speed permanent magnet machines including design and analysis technologies[J]. Proceedings of the CSEE, 2014, 34(27): 4640-4653.
[3] Gieras J F, Saari J. Performance calculation for a high-speed solid-rotor induction motor[J]. IEEE Transactions on Industrial Electronics, 2012, 59(6): 2689-2700.
[4] 燕婧文, 狄冲, 鲍晓华, 等. 基于二维有限元法的感应电机T型等效电路参数的分析与计算[J]. 中国电机工程学报, 2021, 41(增刊1): 294-302.
Yan Jingwen, Di Chong, Bao Xiaohua, et al. Analysis and calculation of T-type equivalent circuit para- meters of induction machines based on two dimensional finite element method[J]. Proceedings of the CSEE, 2021, 41(S1): 294-302.
[5] 凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(二): 二维多层电磁场模型及其解析计算[J]. 电工技术学报, 2018, 33(17): 4016-4028.
Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor(2): 2D-multilayer electromagnetic model and its analytical calculation[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4016-4028.
[6] 黄子果, 王善铭, 孙宇光, 等. 开槽实心转子电机转子端部系数的计算与比较[J]. 电工技术学报, 2017, 32(15): 59-65.
Huang Ziguo, Wang Shanming, Sun Yuguang, et al. Calculation and comparison of rotor end factors of solid rotor induction machines with axial slits[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 59-65.
[7] 张明玉. 复合转子异步电机的电磁理论及实用计算方法研究[D]. 武汉: 华中理工大学, 1993.
Zhang Mingyu. Research on electromagnetic theory and practical calculation method of compound rotor asynchronous motor[D]. Wuhan: Huazhong University of Science and Technology, 1993.
[8] 唐孝镐, 宁玉泉, 傅丰礼. 实心转子异步电机及其应用[M]. 北京: 机械工业出版社, 1991.
[9] 冯尔健. 铁磁体实心转子异步电机理论与计算[M]. 北京: 科学出版社, 1980.
[10] Boughrara K, Dubas F, Ibtiouen R. 2-D analytical prediction of eddy currents, circuit model parameters, and steady-state performances in solid rotor induction motors[J]. IEEE Transactions on Magnetics, 2014, 50(12): 7028214.
[11] 张守首, 郭思源. 基于子域分析模型的实心转子感应电机磁场解析[J]. 电工技术学报, 2021, 36(20): 4285-4296.
Zhang Shoushou, Guo Siyuan. Analytical solution of magnetic field in solid rotor induction machine based on subdomain model[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4285-4296.
[12] Mellak C, Deuringer J, Muetze A. Impact of aspect ratios of solid rotor, large air gap induction motors on Run-up time and energy input[J]. IEEE Transactions on Industry Applications, 2022, 58(5): 6045-6056.
[13] Feng Haichao, Cui Xu, Si Jikai, et al. Equivalent circuit model of novel solid rotor induction motor with toroidal winding applying composite multilayer theory[J]. Applied Sciences, 2019, 9(16): 3288.
[14] Pyrhonen J. Calculating the effects of solid-rotor material on high-speed induction motor characteri- stics[J]. European Transactions on Electrical Power, 1991, 1(6): 301-310.
[15] Gieras J F, Eastham A R, Dawson G E. Performance calculation for single-sided linear induction motors with a solid steel reaction plate under constant current excitation[J]. IEE Proceedings B Electric Power Applications, 1985, 132(4): 185.
[16] Toliyat H A, Kliman G B. Handbook of electric motors[M]. New York: Marcel Dekker, 2004.
[17] 李锦彪, 谢德馨. 三维稳态涡流场有限元分析的后验误差估计[J]. 电工技术学报, 2010, 25(4): 10-14.
Li Jinbiao, Xie Dexin. A posteriori error estimation of finite element analysis for three dimensional steady state eddy current fields[J]. Transactions of China Electrotechnical Society, 2010, 25(4): 10-14.
[18] 谢德馨. 三维涡流场的有限元分析[M]. 北京: 机械工业出版社, 2001.
[19] Paoli G, Biro O, Buchgraber G. Complex repre- sentation in nonlinear time harmonic eddy current problems[J]. IEEE Transactions on Magnetics, 1998, 34(5): 2625-2628.
[20] Stermecki A, Bíró O, Preis K, et al. Numerical analysis of steady-state operation of three-phase induction machines by an approximate frequency domain technique1[J]. Elektrotechnik und Infor- mationstechnik, 2011, 128(3): 81-85.
[21] 黄子果, 王善铭, 倪守辉. 光滑实心转子异步电机等效电路参数的二维计算方法[J]. 中国电机工程学报, 2016, 36(9): 2505-2512.
Huang Ziguo, Wang Shanming, Ni Shouhui. 2D calculation methods of equivalent-circuit parameters in smooth solid rotor induction machines[J]. Proceedings of the CSEE, 2016, 36(9): 2505-2512.
[22] Fahrner W, Vogelsberger M A, Wolbank T. Identi- fication of induction machine rotor parameters at any operating point considering temperature dependent permeability[C]//45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 2019: 1101-1106.
[23] Krings A, Ali Mousavi S, Wallmark O, et al. Temperature influence of NiFe steel laminations on the characteristics of small slotless permanent magnet machines[J]. IEEE Transactions on Magnetics, 2013, 49(7): 4064-4067.
Abstract This paper aims to establish the impedance calculation model of nonlinear copper-coated solid rotor induction motors. This model takes into account the magnetic field distortion caused by the non-linearity of the rotor core material. A method of impedance calculation based on an effective magnetization curve is proposed, which can calculate the permeability of the nonlinear rotor core at different slips and reduce the impedance calculation error caused by the non-linearity of the rotor material. Based on the effective magnetization curve, a simplified calculation method of rotor impedance considering temperature change is proposed to estimate the performance of the motor quickly.
First, assuming that the magnetic permeability of the rotor core is a fixed value, the vector magnetic potential in the rotor surface domain is solved using the two-dimensional subdomain method of electromagnetic field on the copper-coated solid rotor model. Then, the analytical expression of the rotor core and the total impedance of the rotor is obtained. A method considering the nonlinearity of the rotor core material is proposed to calculate the magnetic permeability of the rotor core by equivalent magnetic field energy conservation from the original magnetization curve of nonlinear materials. The effective magnetization curve is obtained, and the permeability is calculated under different slips.
The rotor core, rotor total impedance, electromagnetic torque, and power factor are calculated using the two-dimensional time-harmonic finite element method, effective magnetization curve analysis method, and original magnetization curve analysis method. The results show that the effective magnetization curve analysis method is more accurate than the original magnetization curve analysis method, especially at the stable operating point with a small slip.
The resistivity and effective magnetization curve of the rotor copper layer and core at 200℃ are applied to the analytical method. A simplified calculation method is presented, which only changes the resistivity of the rotor copper layer and core. Therefore, the performance of the rotor can be calculated quickly when the temperature changes. However, because the change of the rotor core permeability is ignored, errors still exist in the calculated torque and power factor.
The following conclusions can be drawn. (1) The analytical method calculates the permeability of the rotor core under saturation conditions, and the relative permeability of the rotor core surface decreases first and then increases with the slip increase. (2) The equivalent B-H curve analytical method is more accurate in calculating rotor impedance, electromagnetic torque, and power factor than the original B-H curve analytical method. (3) A simplified calculation method that only changes the material resistivity is presented, which can quickly calculate the steady-state performance of the motor when temperature changes. However, when the rotor temperature varies widely, it is necessary to evaluate the performance error at the maximum temperature to determine the applicability of this method.
keywords:Copper-coated solid rotor induction motors, the rotor impedance, effective magnetization curve, nonlinear rotor material
中图分类号:TM346
DOI: 10.19595/j.cnki.1000-6753.tces.231569
国家自然科学基金资助项目(52177049)。
收稿日期2023-09-22
改稿日期2023-12-20
朱利伟 男,1991年生,博士研究生,研究方向为高速实心转子感应电机设计及优化。E-mail: liweizhu@nuaa.edu.cn
邓智泉 男,1969年生,教授,博士生导师,研究方向为高速电机技术、磁轴承技术、无轴承电机等。E-mail: dzq@nuaa.edu.cn(通信作者)
(编辑 崔文静)