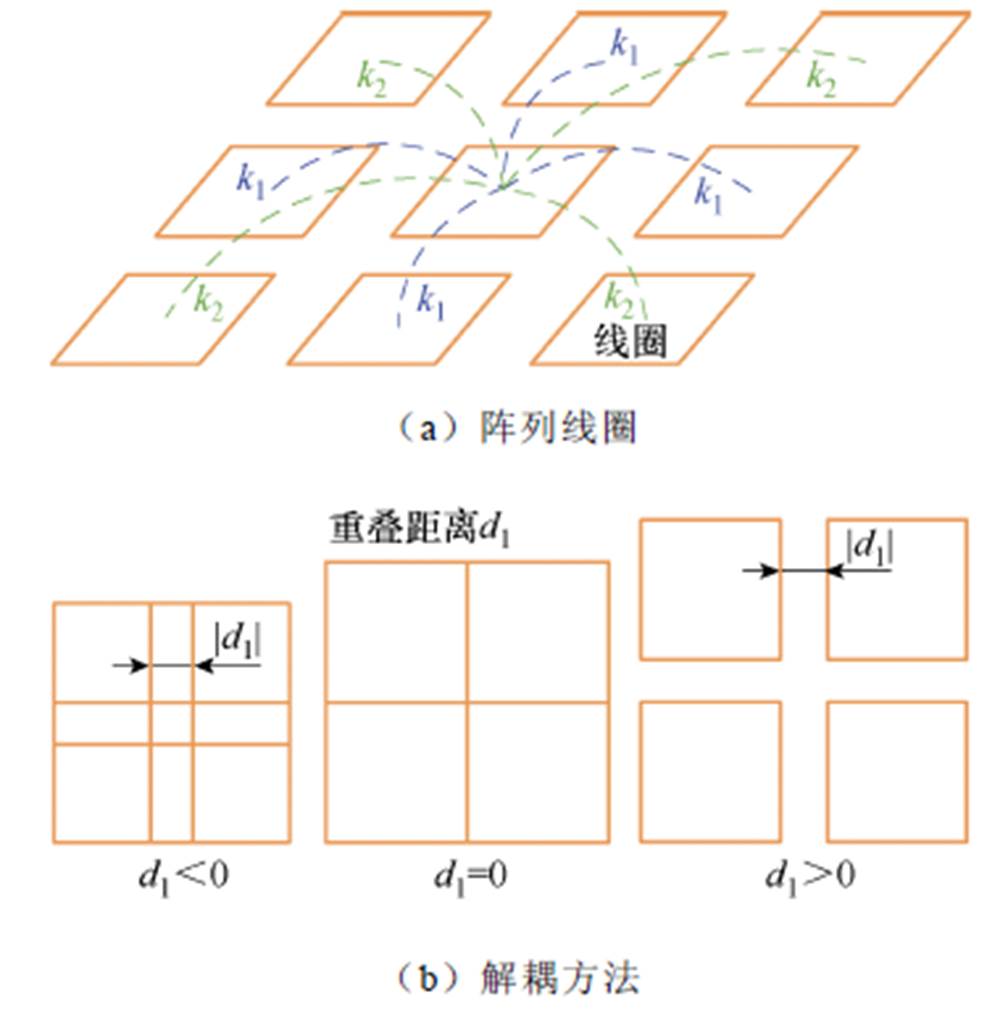
图1 阵列线圈和解耦方法
Fig.1 Array coil and decoupling method
摘要 无线电能传输系统中，发射线圈和接收线圈间不可预知的偏移会显著地降低系统的传输性能。通过阵列式系统的精确定位和功率定向，能够有效地缓解偏移带来的不利影响。该文提出一种基于自适应区域划分的平面阵列式无线电能传输系统接收线圈定位策略。该策略不需要额外的检测线圈或位置传感器，仅通过建立发射线圈电流与接收线圈坐标之间的关系模型，就能推导出坐标计算公式。根据预设定位精度，对随机放置接收线圈的区域进行划分，并动态优化各区域的最佳参考点。通过比较接收线圈在待测定位点与最佳参考点时发射线圈电流的变化量，确定相应坐标的变化量，从而实现对接收线圈的精确定位。通过仿真和实验验证了所提方法的有效性。实验结果表明，在329 mm×329 mm的区域内，平均定位误差为9.98 mm，满足预设的10 mm定位精度。
关键词：无线电能传输 平面阵列式线圈 线圈定位 区域划分 参考点
无线电能传输（Wireless Power Transfer, WPT）技术通过提供一种灵活安全的替代方案，摆脱了传统有线电能传输的限制，彻底改变了电能的使用方式。它在交通、医疗和军事等领域的广泛应用潜力吸引了众多学者的关注[1-2]，未来将会很大程度地改进人类的生产和生活方式。虽然无线电能传输技术消除了电缆的限制，但是要确保发射线圈和接收线圈的精确对准以实现高效稳定的功率传输却面临着不小的挑战。在实际应用中往往难以避免收发线圈间偏移导致的系统传输性能下降问题。学者们通过广泛的研究，包括改进磁心结构[3-5]、优化补偿拓扑[6]和跟踪谐振频率[7]等措施来面对这些挑战。这些方案的应用可能会增加系统的复杂性，而引入发射线圈阵列[8-10]又可以增强无线电能传输系统的可调节性和灵活性。通过发射线圈阵列的功率定向措施可以减轻单个发射线圈下接收线圈偏移导致的传输性能降低问题，为解决偏移提供了一种有效的方法。现有的功率定向研究主要集中在通过阵列线圈的电流相位调制来控制磁场分布，从而增强接收线圈处的磁通量，进而增强传输功率[11]。然而，功率定向的前提是接收线圈的精确定位，因此有必要提出一种接收线圈精确定位的方法。
近年来，学者们对线圈定位进行了广泛的研究，探索了定位传感器、检测线圈和定位算法等各种方法。例如，香港大学利用磁阻传感器阵列[12]来进行接收线圈定位。尽管磁阻传感器具有检测灵敏和输出稳定的优点，但它们的使用增加了系统复杂性、成本和空间需求。韩国科学技术院提出了一种使用铁氧体磁心计数器[13]的车辆位置检测系统，通过计算系统中铁氧体的数量来检测车辆的位置。此外，无线射频（Radio Frequency, RF）模块、红外传感器和激光扫描仪等装置也被用于接收线圈的定位。然而，这些方法通常需要安装大量的传感器模块，给电磁兼容性、分布式电源供电和系统成本带来了不小挑战。
浙江大学提出了将螺线管辅助线圈、双D（Double-D, DD）接收主线圈和方形辅助定位线圈集成为接收线圈，构建两条能量传输路径，并利用接收线圈偏移时测到的螺线管、DD线圈和方形辅助定位线圈的耦合系数来实现定位[14]。东南大学提出了基于检测线圈的精确定位策略[15-16]，通过拟合感应电压随距离变化的曲线来计算坐标。文献[17-19]提出了利用辅助定位线圈或检测器件的定位方法。通过无源辅助器件的定位方法可以降低系统对独立电源的需求，但其精度受到器件数量和安装位置的限制。
文献[20-21]基于Biot-Savart定律和Faraday定律，提出了通过控制发射线圈阵列形成磁场并检测接收线圈的感应电压来实现接收线圈定位的方法。其精度取决于磁场模型的计算精度。然而，在实际应用中，无线电能传输系统往往会受到屏蔽铝板和磁心等因素造成的磁场畸变的影响，导致磁场计算模型出现较大偏差，从而干扰了电磁定位的准确性。目前，还没有准确的物理公式来定量分析金属和磁体对交流电磁场的干扰效应，因此需要研究更精确的磁场校准技术，这将导致系统的复杂性大大增加。此外，上述技术需要多个专用的发射线圈和励磁系统，并且需要收集和处理来自接收侧的传感信号，这限制了其在实际场景中的应用。
目前关于仅利用发射线圈和接收线圈的电压和电流进行定位的研究较为有限。文献[22-24]提出了适用于不同应用场景的耦合机构，并通过测量发射侧电压和电流实现负载定位。文献[25]针对具有中继线圈的三线圈系统提出了一种基于互感扰动的定位方法，通过检测中继线圈在不同位置处发射线圈的电流值实现了三点定位。所提出的定位方法在精度和适应性方面还需改进。
本文提出了一种阵列式无线电能传输系统自适应区域划分定位策略，能够实现高精度低成本的接收线圈定位。该方法利用现有的发射线圈阵列，无需额外的检测线圈或位置传感器，仅通过对发射线圈电流的采集进行定位操作，消除了接收线圈侧信号传递的需求，避免了发射侧和接收侧之间的通信。该定位策略根据系统的预设定位精度，将接收线圈可能放置的区域划分为不同的定位区域，并在每个区域内进行最佳参考点的动态优化选取和定位边界的修正。由此得到满足定位精度的定位区域和相应的最佳参考点。通过拟合发射线圈的电流与接收线圈坐标关系的曲线，结合接收线圈位于最佳参考点和待定位点时的发射线圈电流差值，计算接收线圈的坐标。仿真和实验结果验证了所提方法的有效性。在随机选择的10个点位上，仿真平均定位误差为4.96 mm，每个点的定位误差都低于预设的10 mm精度。实验结果也显示了良好的效果，在相同的10个点位上，平均定位误差为9.98 mm，满足高精度定位的要求。
当发射线圈彼此靠近时，它们之间的交叉耦合是不可忽视的。交叉耦合对正常传输能量的磁场可能产生影响，从而导致无线电能传输系统的传输性能降低。因此，在阵列线圈的研究中，交叉耦合效应是必须考虑的。阵列线圈和解耦方法如图1所示。图1a展示了等间距阵列发射线圈中存在的两种交叉耦合类型。交叉耦合系数k1表示同一行或同一列中相邻发射线圈之间的耦合系数，而k2表示不同行和列中相邻发射线圈之间的耦合系数。由于非相邻线圈之间的交叉耦合相对较小，因此忽略。研究表明，通过优化设计发射线圈间距，可以有效减轻交叉耦合效应[10]。
图1 阵列线圈和解耦方法
Fig.1 Array coil and decoupling method
以2×2阵列线圈为例，如图1b所示，通过理论分析和有限元仿真对发射线圈进行解耦。发射线圈的外部长度为200 mm，匝间距为10 mm，共7匝。图2a和图2b分别给出了耦合系数k1、k2与重叠距离d1的关系。由于使k1和k2最小的重叠距离d1不相同，不可能同时实现所有阵列线圈的最佳解耦，因此必须做出权衡。
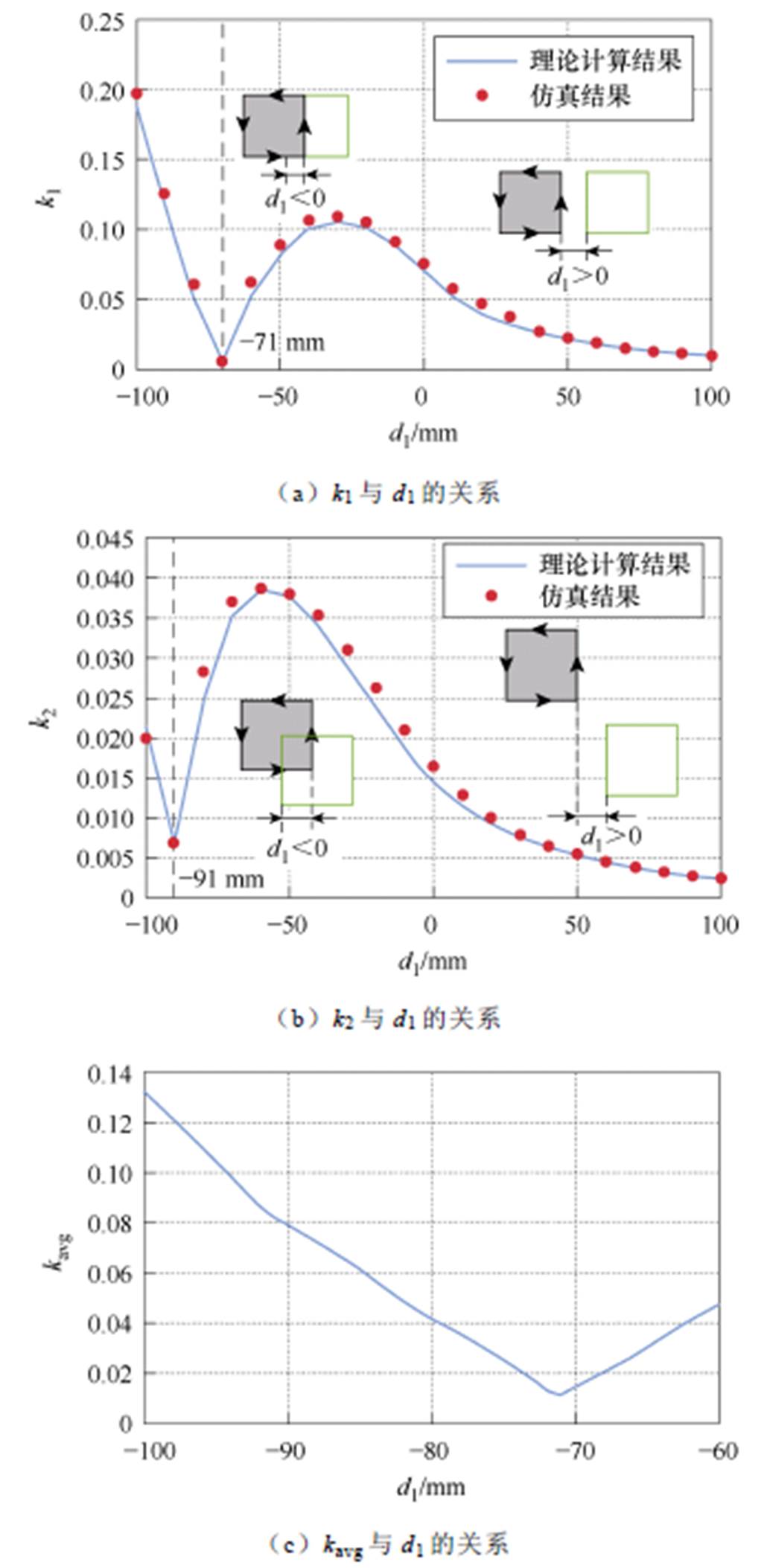
图2 耦合系数与重叠距离的关系
Fig.2 Relationship between coupling coefficient and overlapping distance
对于2×2的线圈阵列，同一行或同一列中相邻线圈之间的耦合共有4个，不同行和列中相邻线圈之间的耦合共有2个。为评价整体交叉耦合效果，将平均交叉耦合系数kavg定义为
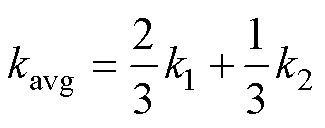（1）
如图2c所示，当重叠距离设置为71 mm时，kavg最小为0.011 3。因此，为实现发射阵列的最佳解耦，本文后续研究均基于这个特定的重叠距离。
图3为阵列线圈简化后的解耦模型。发射线圈1、2、3、4分别表示为A1B1C1D1、A2B2C2D2、A3B3C3D3和A4B4C4D4。发射线圈间的重叠距离为71 mm。接收线圈位于阵列线圈上方两个任意位置，其中心点在Op和Oq位置时4个发射线圈的电流有效值分别表示为Ip1, Ip2, Ip3, Ip4与Iq1, Iq2, Iq3, Iq4。用电流欧几里得距离dp→q来描述接收线圈中心点从Op移动到Oq时发射线圈电流的变化，可以表示为
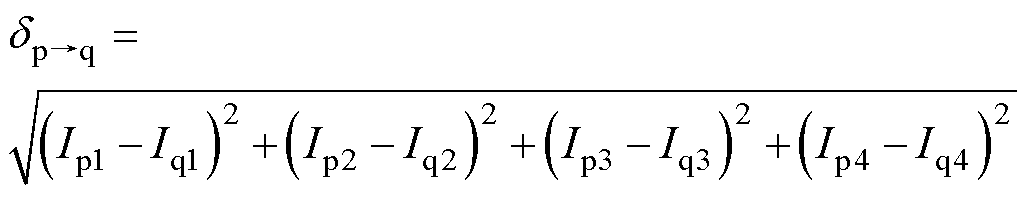（2）
对于式（2），当dp→q=0时，必须满足Ip1=Iq1，Ip2=Iq2，Ip3=Iq3，Ip4=Iq4，此时Op和Oq两点重合。因此，可以在待定位区域内确定一个参考点，通过比较接收线圈在待定位点处与参考点处的电流相似度，计算得到待定位点的坐标。
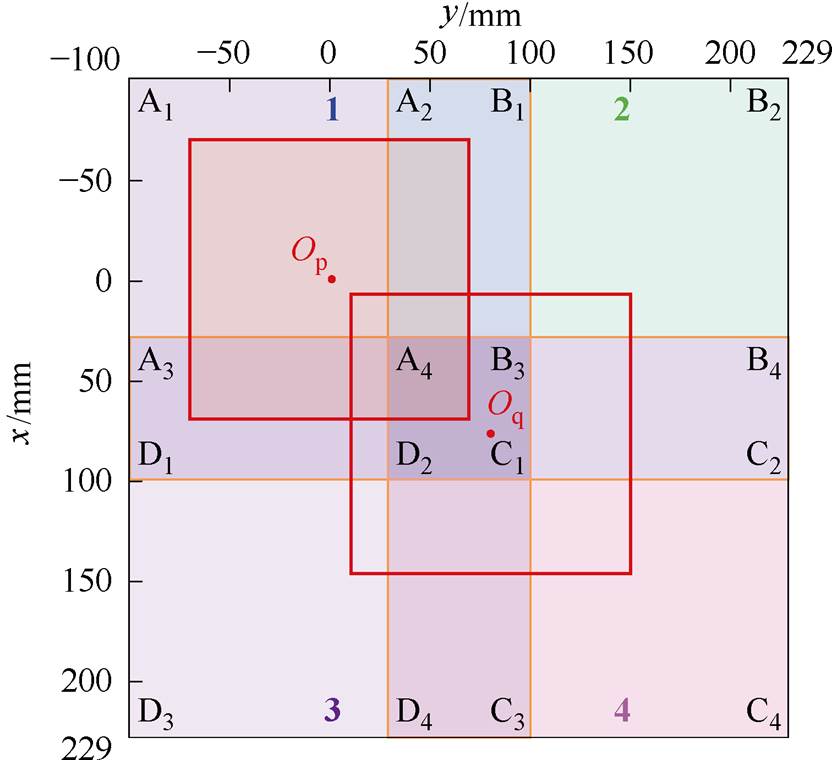
图3 阵列线圈简化解耦模型
Fig.3 Simplified decoupling model of planar coil array
后续研究中，接收线圈长为140 mm，匝数为7，匝间距为7 mm，传输距离为50 mm。发射线圈和接收线圈的电感分别为8.13 mH和5.78 mH。发射线圈阵列和接收线圈通过电容匹配均在200 kHz谐振。在发射线圈平面上建立如图3所示的直角坐标系，接收线圈中心点在不同x、y坐标下发射线圈阵列的电流有效值的变化曲线如图4～图7所示。
这些曲线表明，发射线圈电流和接收线圈坐标之间存在一定程度的相关性。如图4c、图5c、图6a、图7a所示，当接收线圈与发射线圈相距较远时，对应的互感较小，导致发射线圈的电流对接收线圈位置的敏感度较低。例如，在图7a中，对于x坐标为-60 mm和-50 mm，发射线圈4的电流相对于y坐标变化的曲线基本相同，因此图6和图7中省略了部分接近重合的电流曲线。利用Matlab软件进行曲线拟合，将电流I1、I2、I3、I4的波形与y坐标拟合，可以得到
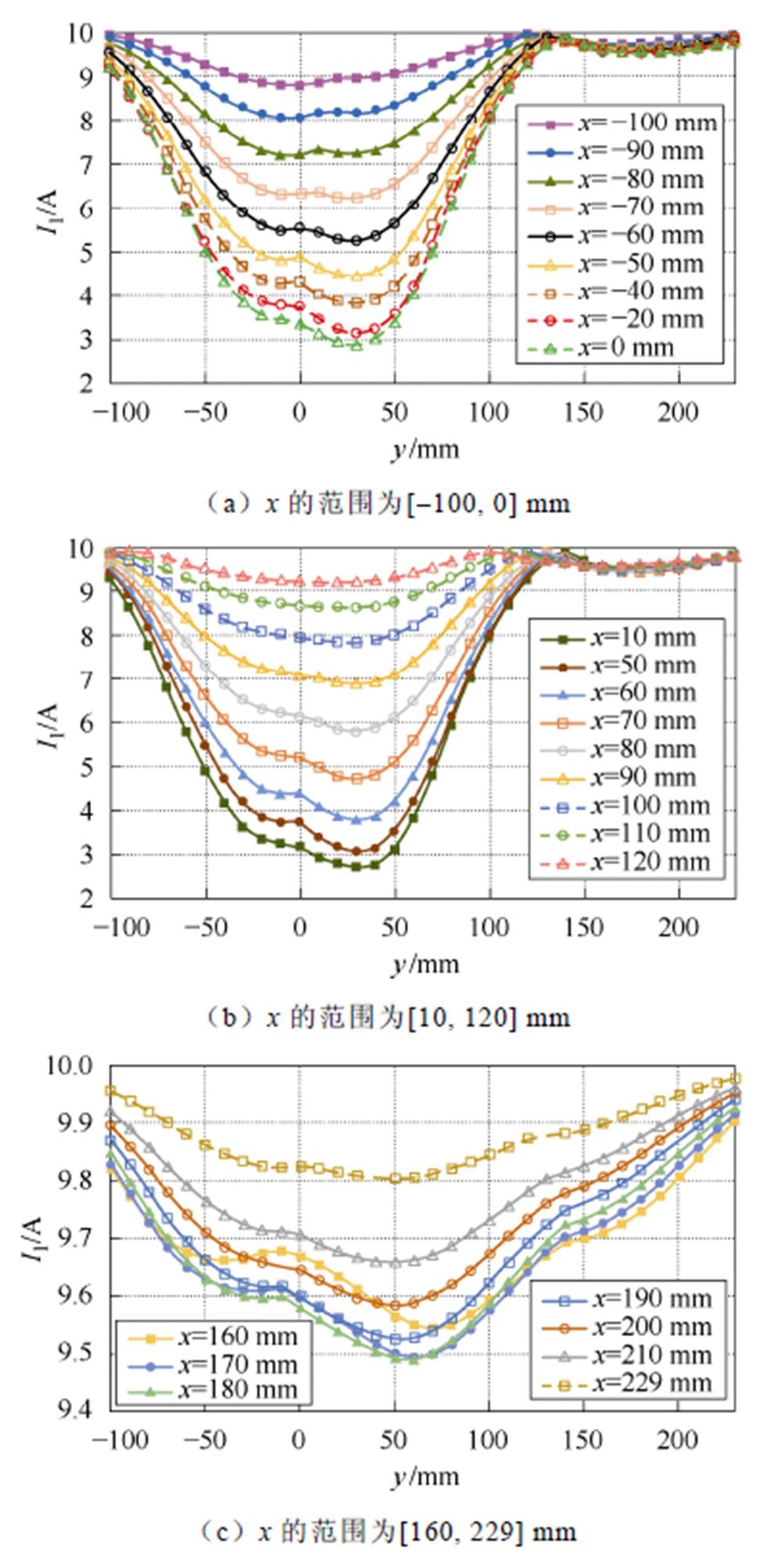
图4 不同坐标下发射线圈电流I1
Fig.4 Transmitter current I1 at different coordinates
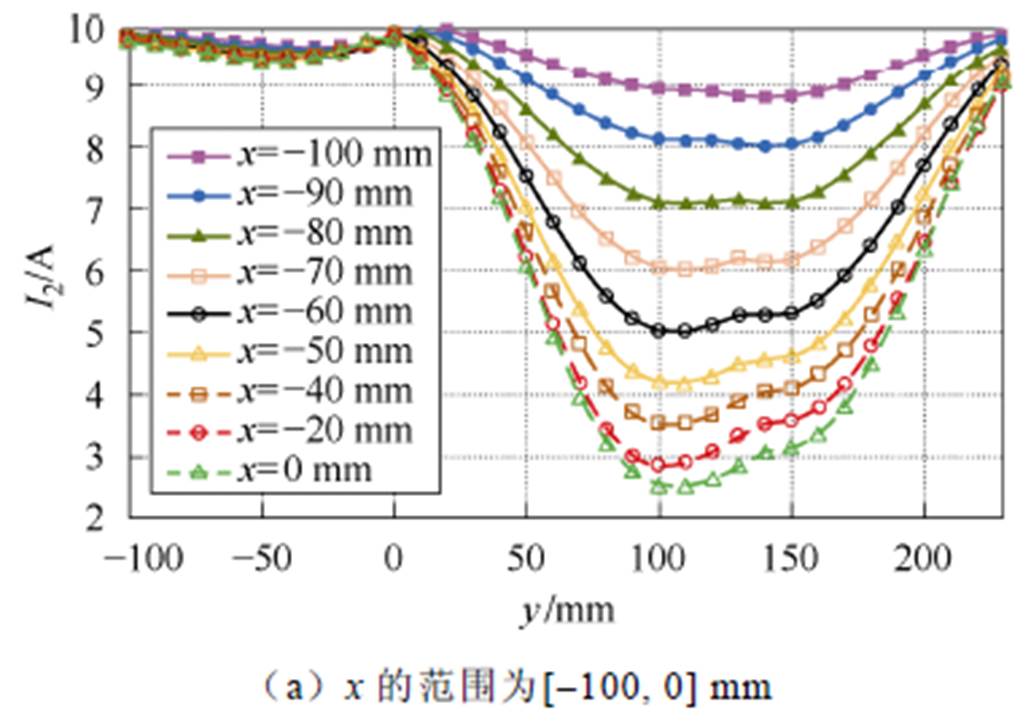
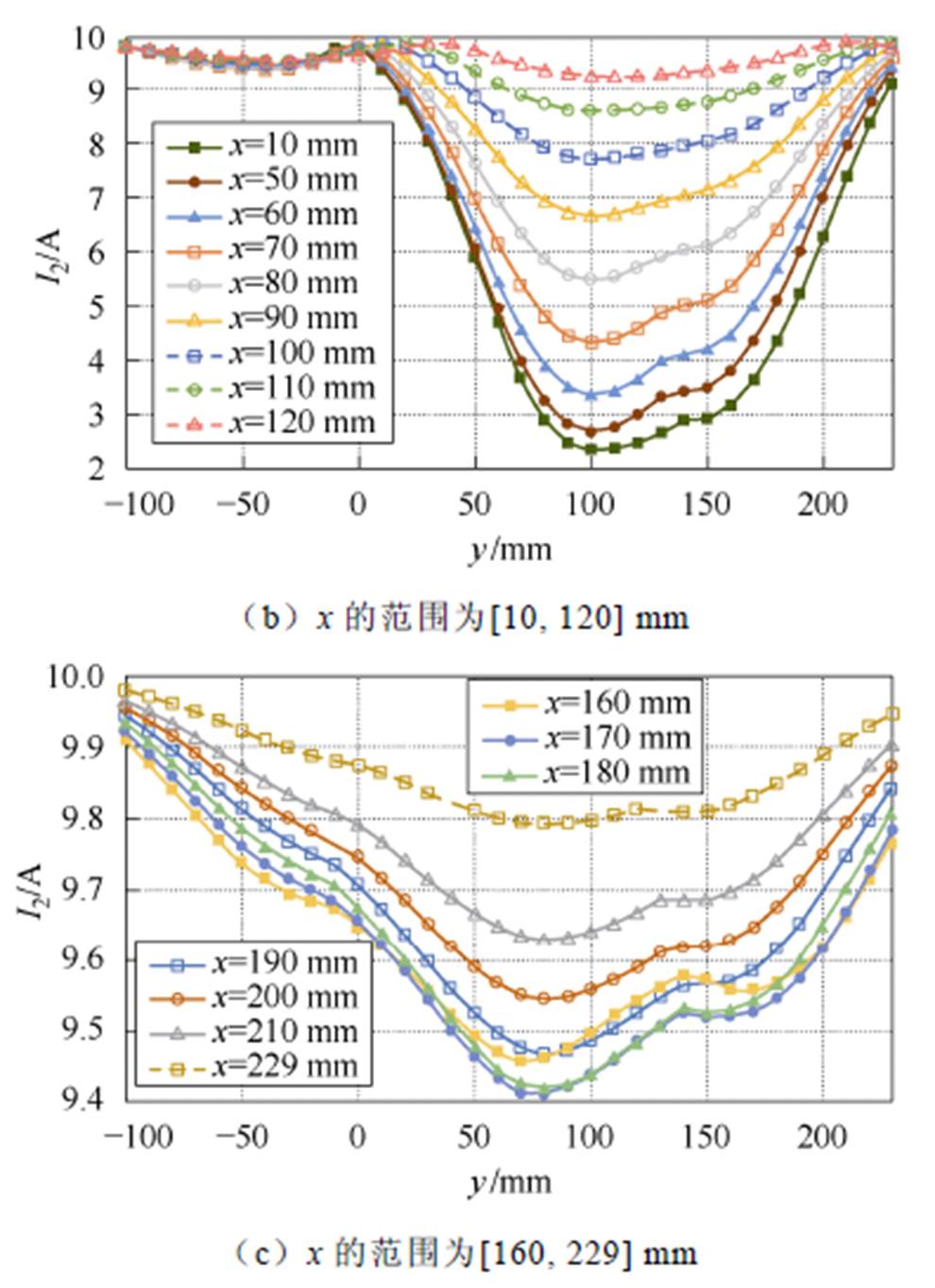
图5 不同坐标下发射线圈电流I2
Fig.5 Transmitter current I2 at different coordinates
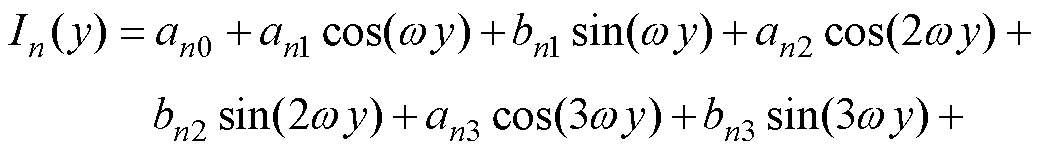
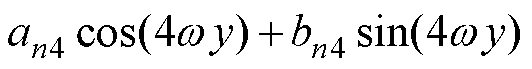（3）
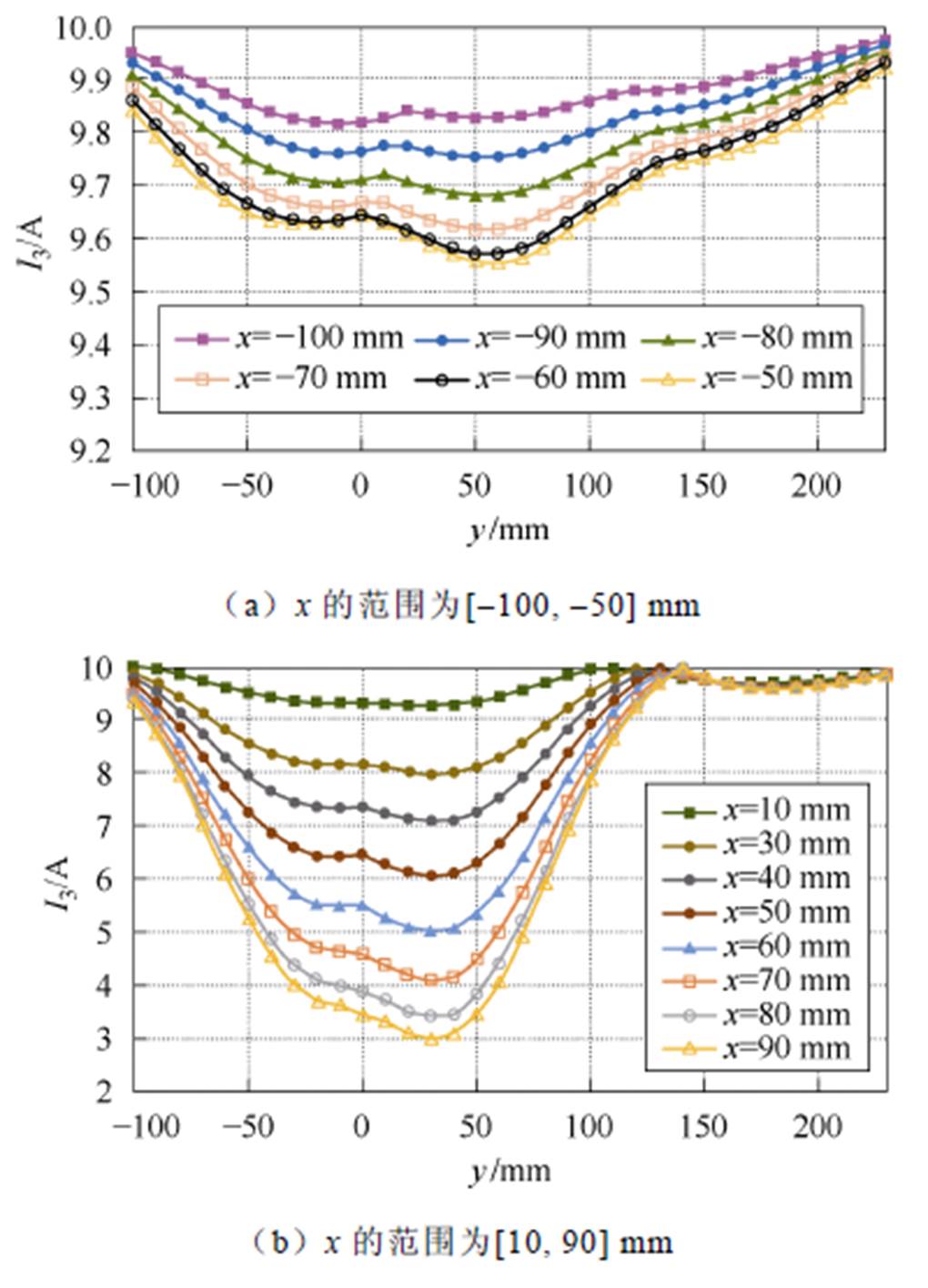
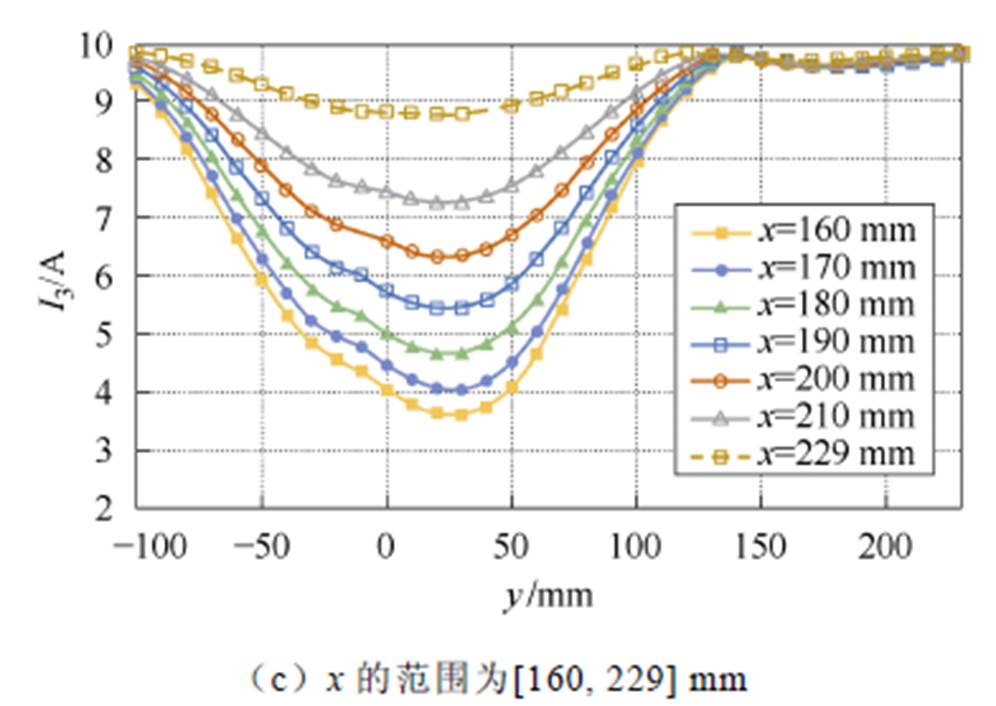
图6 不同坐标下发射线圈电流I3
Fig.6 Transmitter current I3 at different coordinates
图7 不同坐标下发射线圈电流I4
Fig.7 Transmitter current I4 at different coordinates
式中，an0、an1、bn1、an2、bn2、an3、bn3、an4、bn4为第n个发射线圈的系数，n=1, 2, 3, 4。w 为系统工作的角频率，与y无关，y的范围为[-100, 229] mm。因此，可以推导出式（3）的导数如下
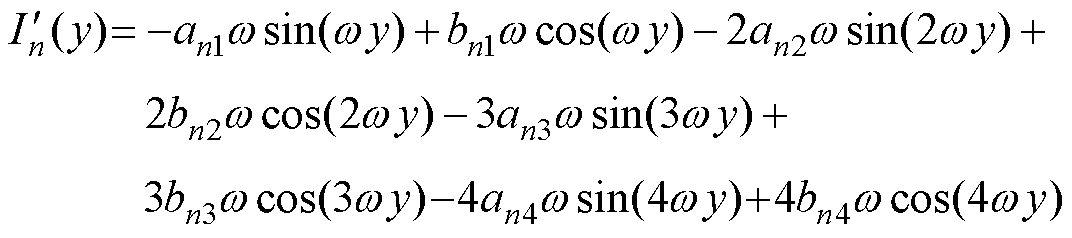（4）
因接收线圈坐标变化Dy而导致的发射线圈电流变化，可近似表示为
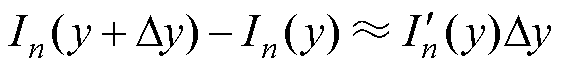（5）
因此，接收线圈在区域Aij中从参考点Oij到待定位点Os，由y坐标变化Ddy导致的电流变化为
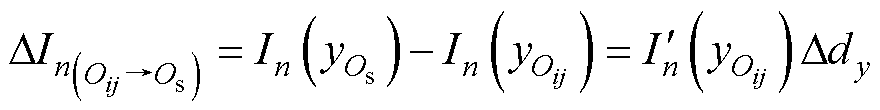（6）
式中，
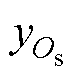和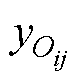
分别为Os和Oij点的y坐标；Ddy为接收线圈中心点从参考点Oij到待定位点Os的y坐标变化量，记为
。
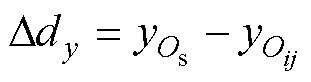将式（4）代入式（6），可以得到
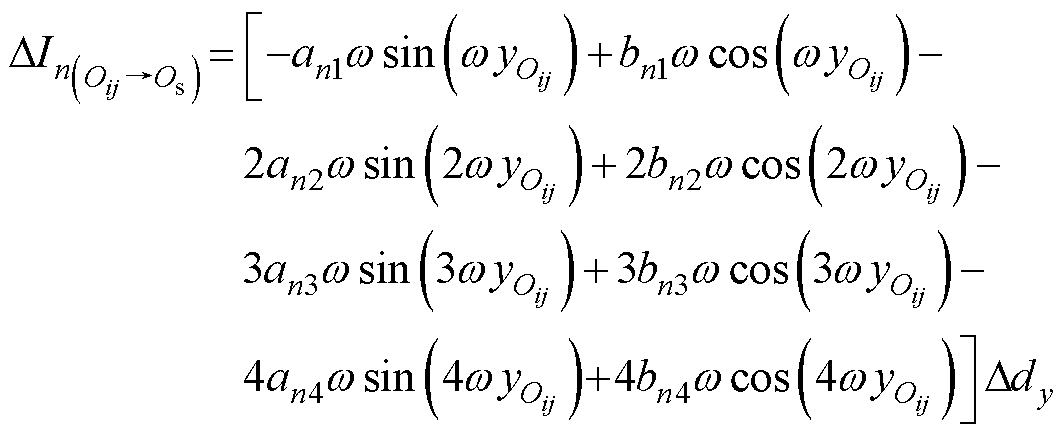（7）
将式（7）简化为
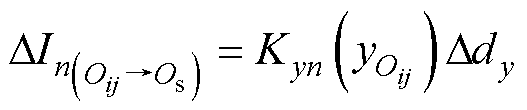（8）
式中，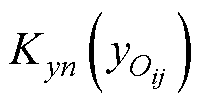
为第n个发射线圈的电流与接收线圈y坐标变化关系的拟合系数。
四个发射线圈的电流变化可计算得到
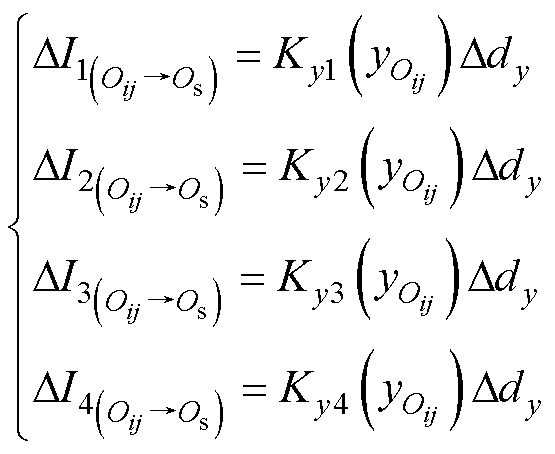（9）
接收线圈中心在点Oij和点Os时，发射阵列电流的欧几里得距离可定义为
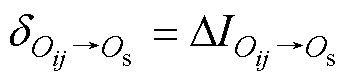（10）
根据式（2），考虑发射阵列四个线圈电流的变化，其欧几里得距离可表示为
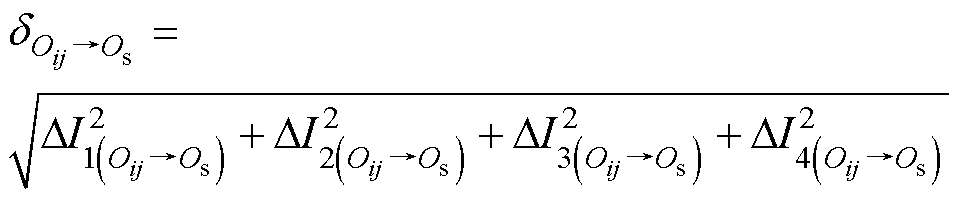（11）
结合式（9）～式（11），从点Oij到点Os的y坐标变化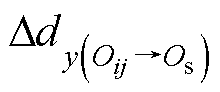
可表示为
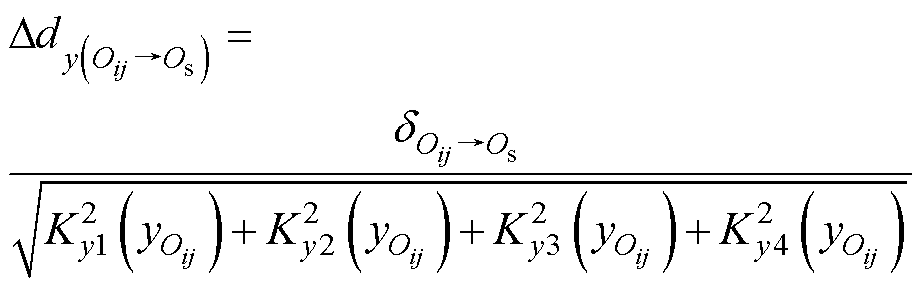（12）
类似地，从点Oij到点Os的x坐标变化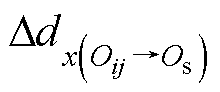
可以表示为
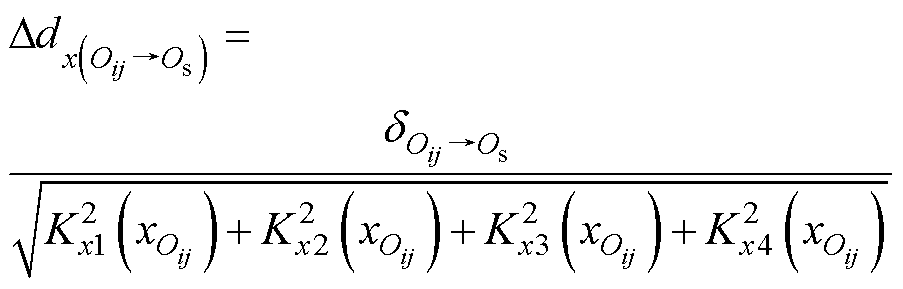（13）
式中，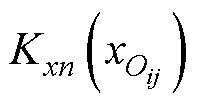
为第n个发射线圈的电流和x坐标变化关系的拟合系数。
为了实现接收线圈在指定区域内的精确定位，需要收集足够数量的定位参考数据。在图3所示的阵列线圈简化解耦模型中，假设接收线圈的位置范围为-100 mm≤x≤229 mm以及-100 mm≤y≤229 mm，并将坐标变化步长设置为s=5 mm，这样可以获得4 489组数据。在进行仿真时，设定发射线圈的输入电压为10 V，频率为200 kHz，补偿网络选用串联-串联（Series-Series, SS）型，并将负载电阻设为15 W。当接收线圈位于x=10 mm，y=110 mm时，最大电流差为7.56 A，对应的最大和最小电流分别为I3=9.95 A和I2=2.39 A。需要特别指出的是，发射线圈的电流在不同区域之间存在显著差异，而电流差较大的区域往往会产生较高的定位误差。因此，为了保证高精度的定位，有必要将定位区域进行划分，并且确定每个区域内的最佳参考点。根据预设的定位精度Ddm来确定区域的划分数量、定位区域的边界以及各区域内的最佳参考点。
在图3所示的定位区域中，点O1, O2, O3, O4, O5, O6沿y轴按步长s分布，如图8所示。
定位参考点的选择对区域内的定位精度起着至关重要的作用。假设选取O3为定位参考点，如果区域内的点O2、O4、O5满足式（14），说明它们在参考点O3下的定位精度满足预设值Ddm；而点O1和O6满足式（15），说明其定位精度低于预设值。
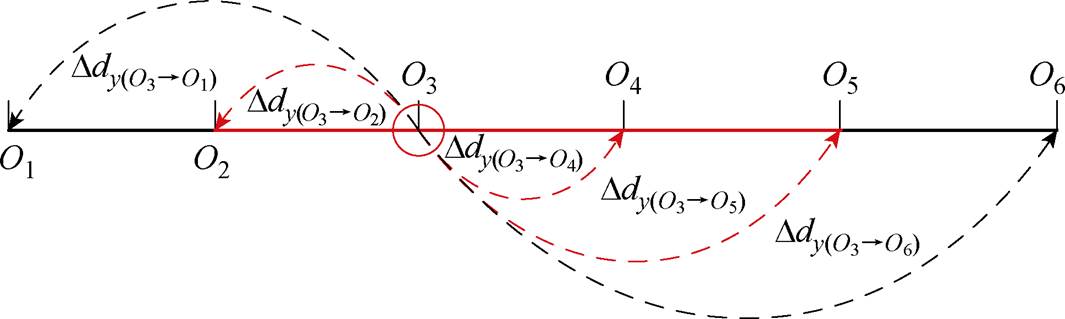
图8 定位参考点的选择
Fig.8 Selection of positioning reference point
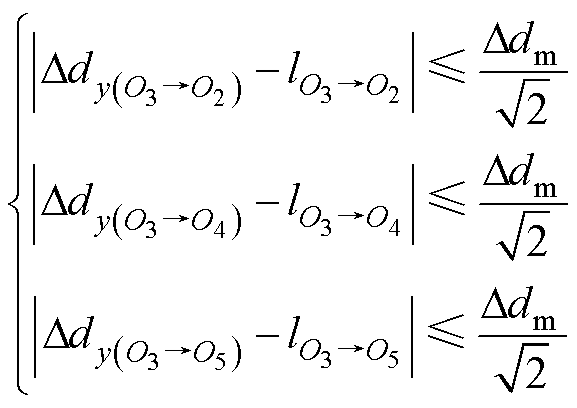（14）
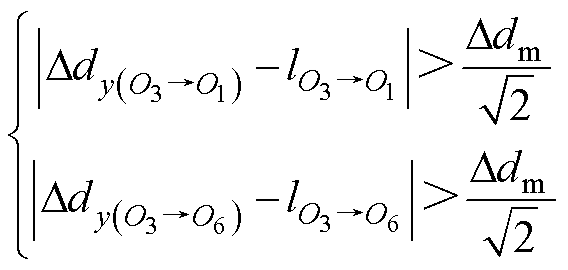（15）
式中，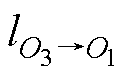
、
、
、
、
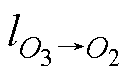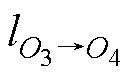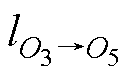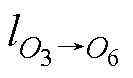为点O1、O2、O4、O5和O6到参考点O3的实际距离，其值分别为2s、s、s、2s和3s。
定位算法流程如图9所示，其核心在于确定区域内的最佳定位参考点和相应的区域边界。该算法包括以下步骤：
（1）搜索y轴最佳参考点：从目标区域的上边界（x=a）开始迭代，寻找满足左侧点定位精度要求的参考点。选择y轴右侧满足定位精度的点数最多的参考点（Oyref），即为x=a处y轴的最佳参考点。
（2）确定y轴区域边界：利用得到的Oyref在y轴上识别满足所有点定位精度要求的区域右边界。
（3）搜索x轴最佳参考点、确定x轴区域边界：采用与步骤（1）类似的方法，从目标区域的左边界（y=b）开始，在x轴上搜索最佳参考点（Oxref）。然后根据参考点确定区域在x轴上的下边界，确保所有点都满足定位精度要求。
（4）确定首个区域边界和区域内最佳参考点：将目标区域的初始边界与步骤（1）～步骤（3）得到的边界合并，形成首个区域A11。在A11中利用上述方法确定区域内的最佳参考点。
（5）初步划分剩余区域：根据首个区域边界，获得A12的初始上、下、左边界和A21的初始上、左、右边界。重复步骤（1）～步骤（3），可以快速将整个区域划分为多个矩形区域。
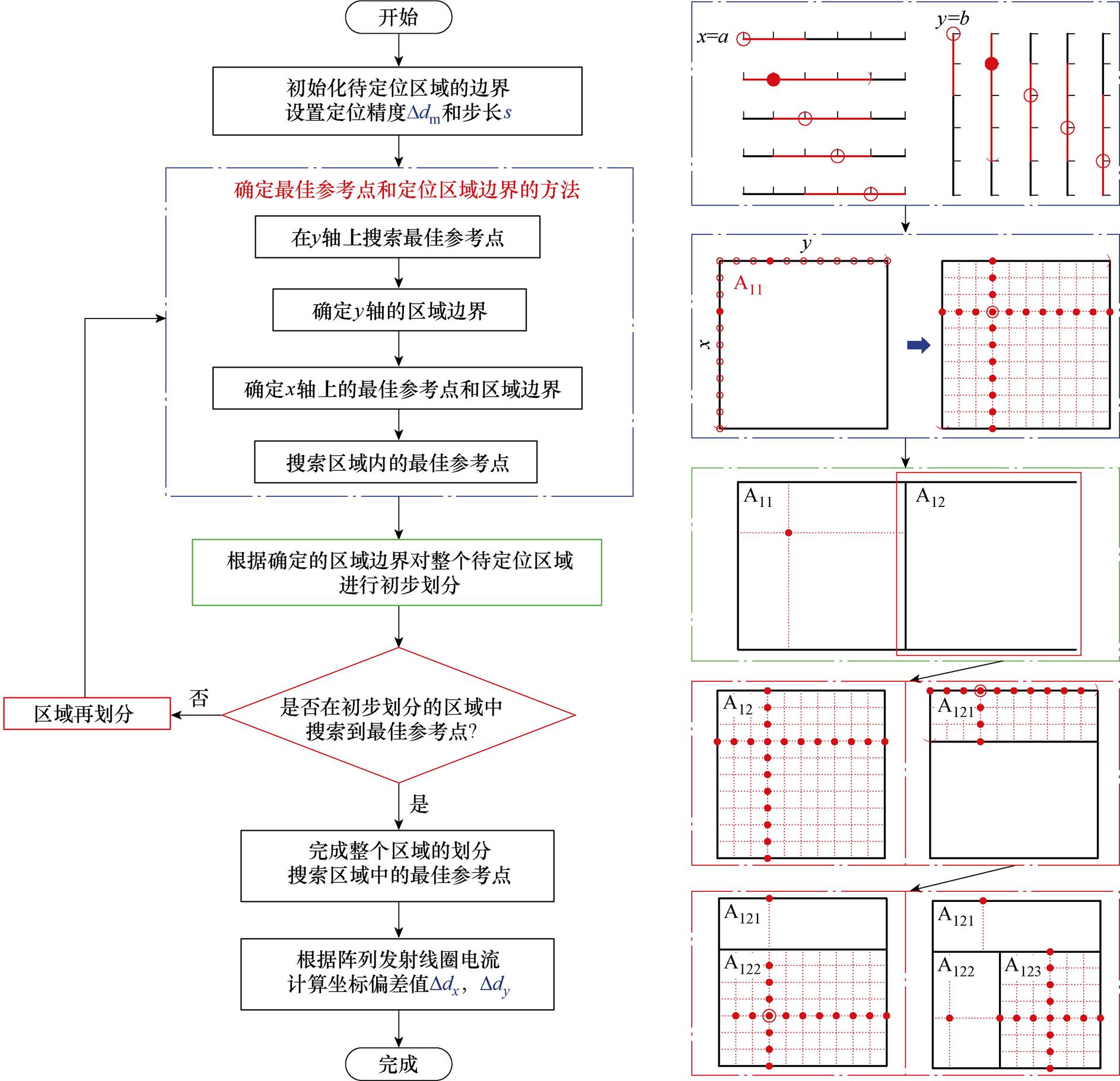
图9 定位算法流程
Fig.9 Flow chart of positioning algorithm
（6）确定区域内最佳参考点、细化区域。由于快速划分的区域只能保证一个或两个边界上的定位精度，因此通过遍历各个区域内的所有点进行精度评估。如果不能找到满足区域内所有点定位精度要求的最佳参考点，则需要细化区域。从该区域的左上角开始，逐渐缩小边界，重复步骤（1）～步骤（4），直到获得所有区域Aij内的最佳参考点Oij。
（7）完成整个区域划分、确定各区域最佳参考点：利用上述算法，进行整个待定位区域的划分和各个区域内最佳参考点的搜索。
（8）计算待定位点坐标。当接收线圈处于未知位置时，测量发射阵列各线圈的电流。利用发射阵列电流与接收线圈坐标的拟合关系，确定接收线圈对应的区域和最佳参考点。计算最佳参考点处的发射阵列电流，利用发射阵列电流的变化量，计算接收线圈与参考点之间的坐标变化量（Ddx和Ddy）。最后，将参考点坐标与计算得到的坐标变化量相结合，精确计算出接收线圈的实际位置。
利用上述定位算法，根据预设的定位精度对图3所示的定位区域进行区域划分和最佳参考点搜索，共得到34个定位区域，结果如图10所示。白色区域和灰色区域的边界坐标以及相应的最佳参考点分别见表1和表2。白色区域的发射线圈电流变化量较小，而灰色区域的变化量较大。为了达到所需的定位精度，将灰色区域进一步细分为多个区域。图10中的“
”的位置表示每个区域的最佳参考点。需要说明的是，灰色区域在整个定位区域的不对称分布归因于有限元仿真模型的误差。在仿真中，四个线圈并不精确地分布在同一平面上，而是具有微小的高度差，导致定位区域的分布呈现出一定的不对称性。
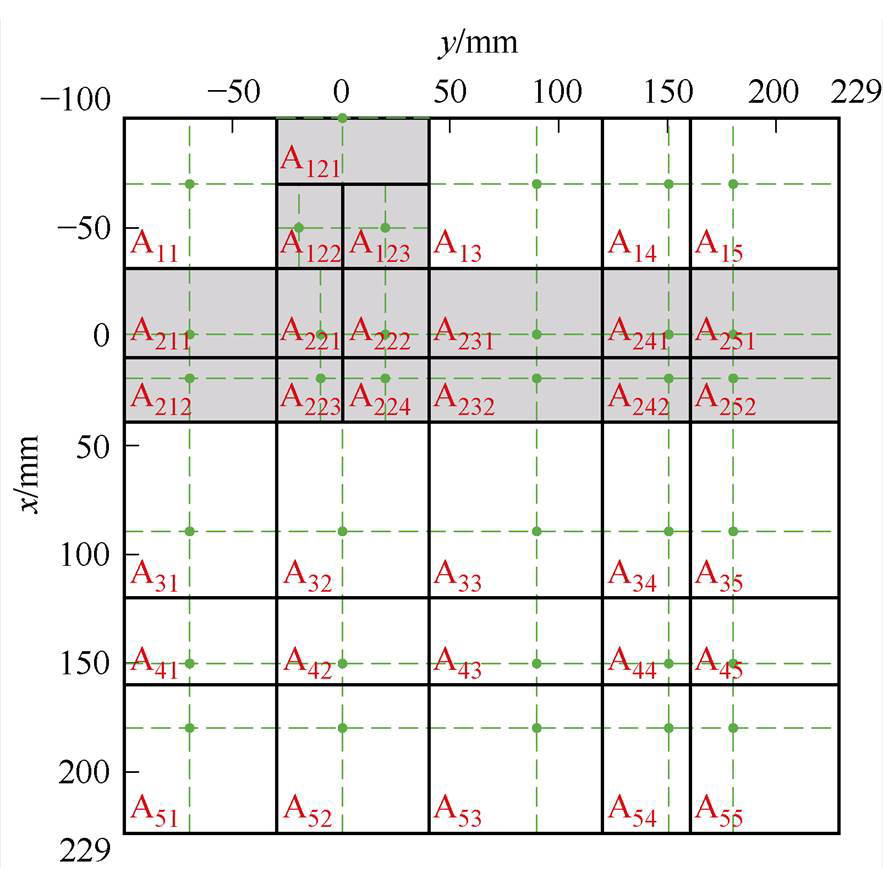
图10 最佳参考点和区域划分结果
Fig.10 The results of the optimal reference points and the subdivided regions of the entire to-be-located area
表1 白色区域边界和最佳参考点的坐标
Tab.1 The boundaries of the white areas and the coordinates of the best reference points
区域x范围/mmy范围/mmOij/mm A11[-100, -30][-100, -30](-70, -70) A13[-100, -30][40, 120](-70, 90) A14[-100, -30][120, 160](-70, 150) A15[-100, -30][160, 229](-70, 180) A31[40, 120][-100, -30](90, -70) A32[40, 120][-30, 40](90, 0) A33[40, 120][40, 120](90, 90) A34[40, 120][120, 160](90, 150) A35[40, 120][160, 229](90, 180) A41[120, 160][-100, -30](150, -70) A42[120, 160][-30, 40](150, 0) A43[120, 160][40, 120](150, 90) A44[120, 160][120, 160](150, 150) A45[120, 160][160, 229](150, 180) A51[160, 229][-100, -30](180, -70) A52[160, 229][-30, 40](180, 0) A53[160, 229][40, 120](180, 90) A54[160, 229][120, 160](180, 150) A55[160, 229][160, 229](180, 180)
表2 灰色区域边界和最佳参考点的坐标
Tab.2 The boundaries of the grey areas and the coordinates of the best reference points
区域x范围/mmy范围/mmOij/mm A12A121[-100, -70][-30, 40](-100, 0) A122[-70, -30][-30, 0](-50, -20) A123[-70, -30][0, 40](-50, 30) A21A211[-30, 10][-100, -30](0, -70) A212[10, 40][-100, -30](20, -70) A22A221[-30, 10][-30, 0](0, -10) A222[-30, 10][0, 40](0, 20) A223[10, 40][-30, 0](20, -10) A224[10, 40][0, 40](20, 20) A23A231[-30, 10][40,120](0, 90) A232[10, 40][40, 120](20, 90) A24A241[-30, 10][120, 160](0, 150) A242[10, 40][120, 160](20, 150) A25A251[-30, 10][160, 229](0, 180) A252[10, 40][160, 229](20, 180)
图11为平面阵列式无线电能传输系统的等效电路模型。
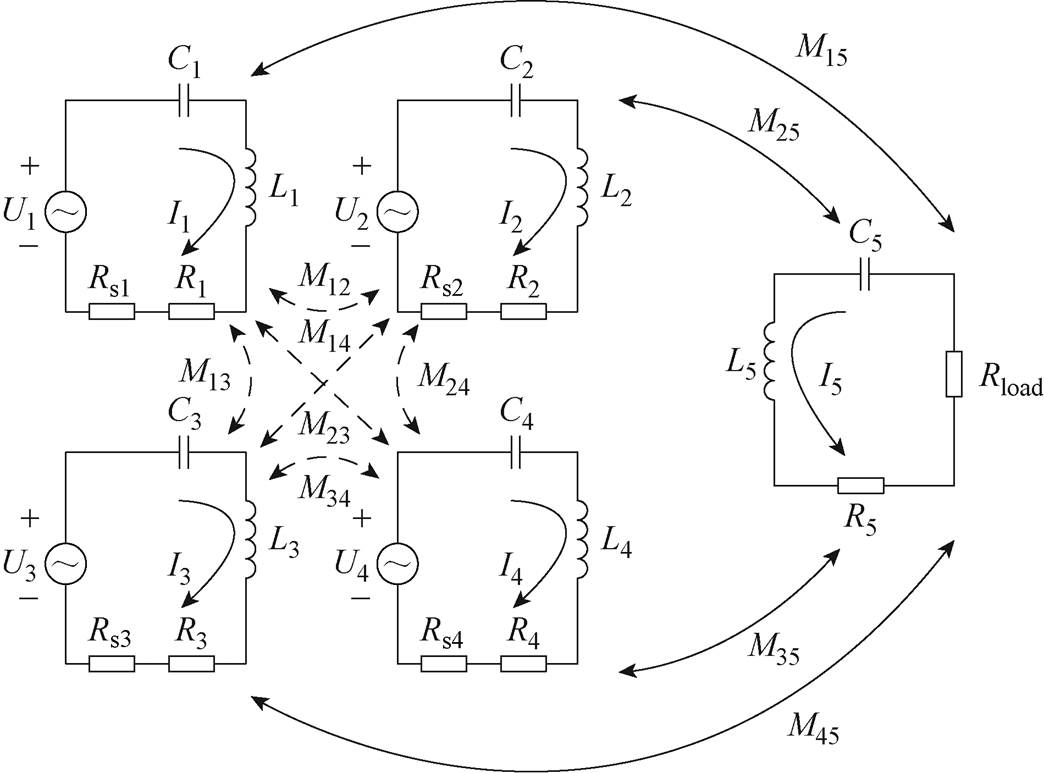
图11 平面阵列式无线电能传输系统等效电路模型
Fig.11 Equivalent circuit model of planar array wireless power transfer system
根据基尔霍夫电压定律（Kirchhoff's Voltage Law, KVL）可得表达式为
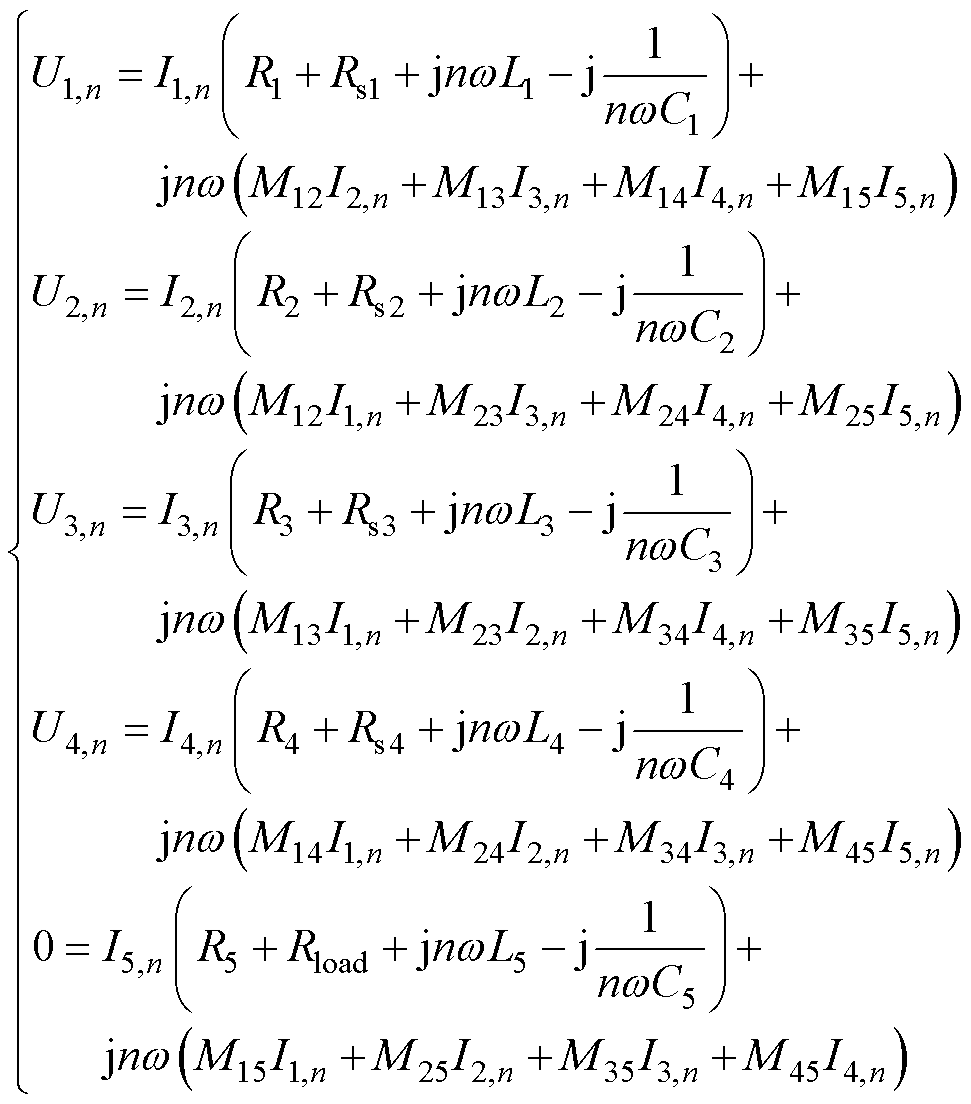（16）
式中，Rload为等效负载电阻；I1,n、I2,n、I3,n、I4,n、I5,n分别为对应线圈电流的各次谐波；U1,n、U2,n、U3,n、U4,n分别为对应线圈输入电压的各次谐波，U1,n=U2,n=U3,n=U4,n=Un；Rs1=Rs2=Rs3=Rs4=Rs为电源寄生内阻，L1、L2、L3、L4、L5分别为发射线圈和接收线圈的自感，相应的补偿电容为C1、C2、C3、C4、C5；M15、M25、M35、M45为发射线圈和接收线圈间的互感；M12、M13、M14、M23、M24、M34为发射线圈间的互感。发射线圈经过最小交叉耦合设计，其互感基本可以忽略。发射线圈的寄生内阻和自感分别满足R1=R2=R3=R4=R0，L1=L2=L3=L4=Lp。因此，发射阵列电流可表示为
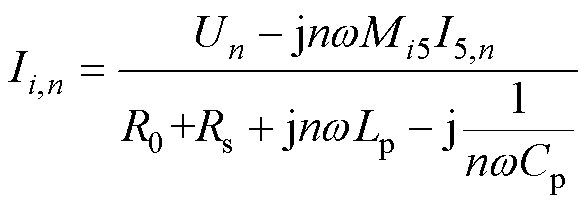（17）
接收线圈电流可表示为
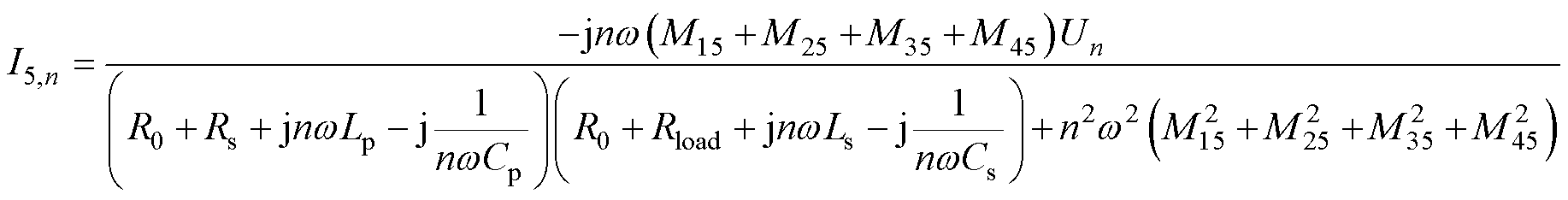（18）
结合式（17）与式（18）可知，发射线圈电流的各次谐波含量极低，基本可以忽略。因此，发射线圈电流可以用对应的基波电流表示为
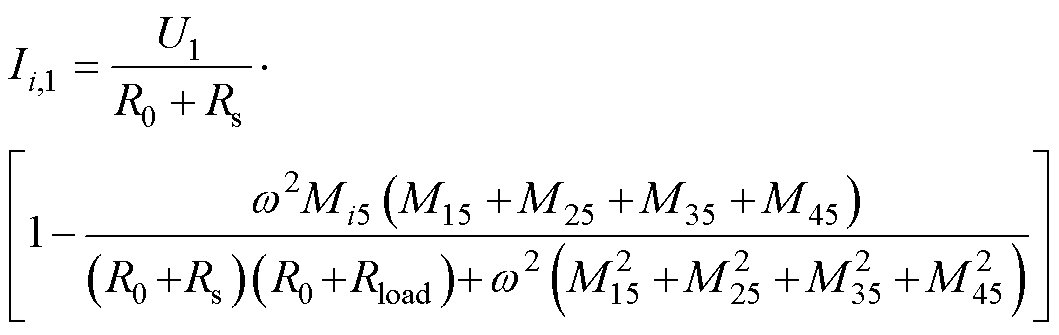（19）
从式（19）可以看出，当接收线圈的位置确定后，发射线圈电流只和等效负载电阻值有关。
输出侧的全桥整流器是无线电能传输系统中的常见环节，而补偿拓扑的形式、接收线圈的自感以及负载电阻等参数对全桥整流电路的导通模式可能存在影响[26-29]。当全桥整流电路维持在连续导通模式时，其等效输入阻抗可以视为电阻，整流桥的输入谐波基本可以忽略；处于断续导通模式时，其输入电流将受到二极管的钳位作用而发生畸变，导致其等效输入阻抗部分出现电抗，且随着断续模式的加深，其电抗将逐渐增大。这对本文所提出的定位方法的精度有一定的影响。目前可以借助多种方法避免全桥整流电路进入断续导通模式，例如：①合理设计系统参数，通过增加接收线圈自感、改变耦合系数、限制负载电阻变化范围等措施；②采用新型的补偿拓扑，采用可以容纳更大范围内负载电阻变化的补偿拓扑；③优化整流桥的结构，利用全控整流桥电路或者在整流桥前并联小电容等方式。其中，方法①、方法②需要对定位数据重新计算、对定位区域重新划分。本文采用全桥整流电路并联小电容[26]的方式验证所提出的定位方法在整流桥存在时的适用性，如图12所示。
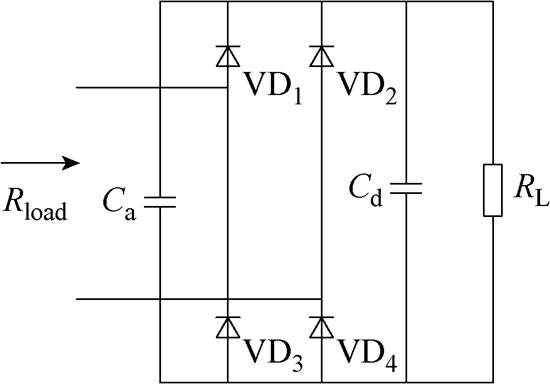
图12 并联小电容的全桥整流电路
Fig.12 Full bridge rectifier with parallel small capacitor
为了评估所提出的定位方法的精度，在Ansys有限元仿真软件中利用上述参数建立仿真模型，如图13所示。在329 mm×329 mm的平面区域内随机选取10个点位。根据电流的仿真结果，应用定位算法确定最佳参考点，得到待定位点的坐标仿真结果。此外，搭建如图14所示的实验平台来验证定位算法的有效性，具体的实验参数见表3。
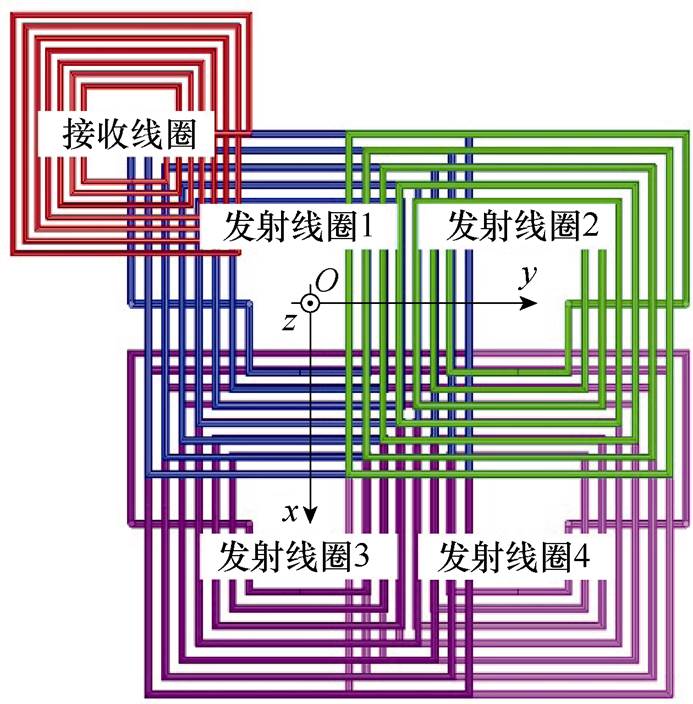
图13 仿真模型
Fig.13 Simulation model
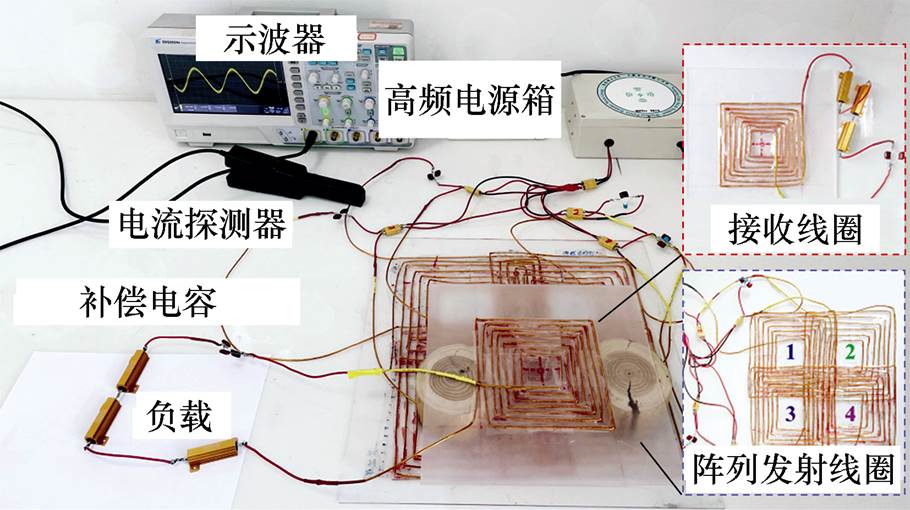
图14 实验平台
Fig.14 Experimental platform
表3 实验参数
Tab.3 Experimental parameters
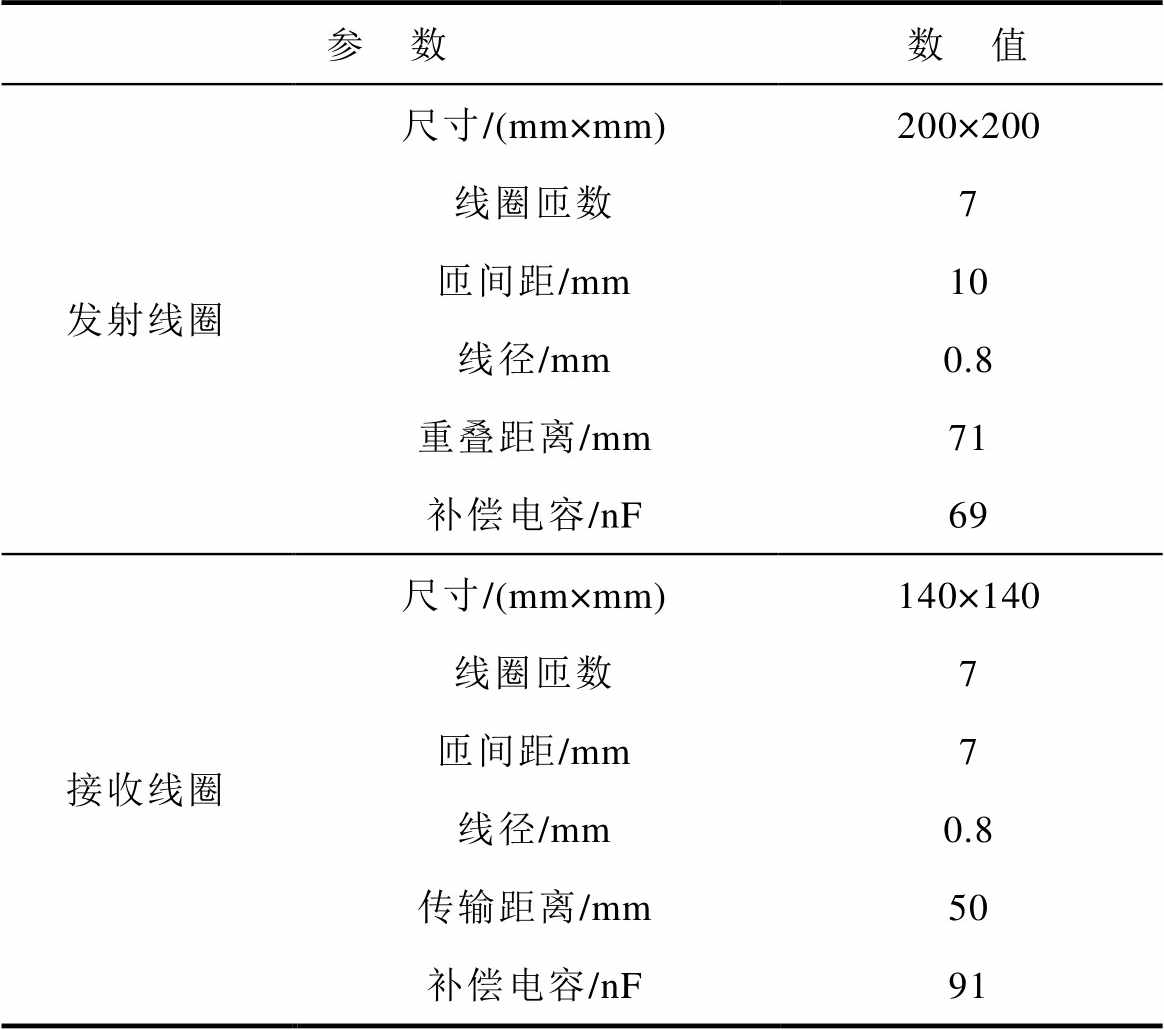
参 数数 值 发射线圈尺寸/(mm×mm)200×200 线圈匝数7 匝间距/mm10 线径/mm0.8 重叠距离/mm71 补偿电容/nF69 接收线圈尺寸/(mm×mm)140×140 线圈匝数7 匝间距/mm7 线径/mm0.8 传输距离/mm50 补偿电容/nF91
电源输出电压为2 V，频率为200 kHz，补偿网络为SS型，负载电阻为15 W。发射阵列与接收线圈之间的传输距离为50 mm。该系统由32位处理器STM32F103C8控制，工作频率为72 MHz，具有128 KB的闪存和20 KB的静态随机存储器。发射线圈均通过串联电容进行补偿后直接并联到高频电源上。利用定位算法计算待定位点的坐标，验证所提方法的精度。
图15展示了待定位点的实际坐标、仿真结果和实验结果。所选择的定位区域、定位结果以及定位误差见表4。定位误差为实际坐标与测量值之间的欧氏距离。结果表明，对于随机选取的10个点，仿真误差均在预设的10 mm定位精度范围内，仿真平均定位误差为4.96 mm。实验结果的平均误差为9.98 mm。实验误差略大，可能由线圈绕组误差、操作误差、测量误差等因素造成。然而，考虑到发射阵列尺寸为329 mm×329 mm、接收线圈尺寸为140 mm×140 mm，10 mm的定位误差在可接受范围内，不会在进一步的功率定向传输中显著影响系统性能。此外，通过降低Ddm的预设值，可以进一步细化定位区域，从而提高定位精度，仿真和实验结果表明，该方法能够实现高精度的负载定位。
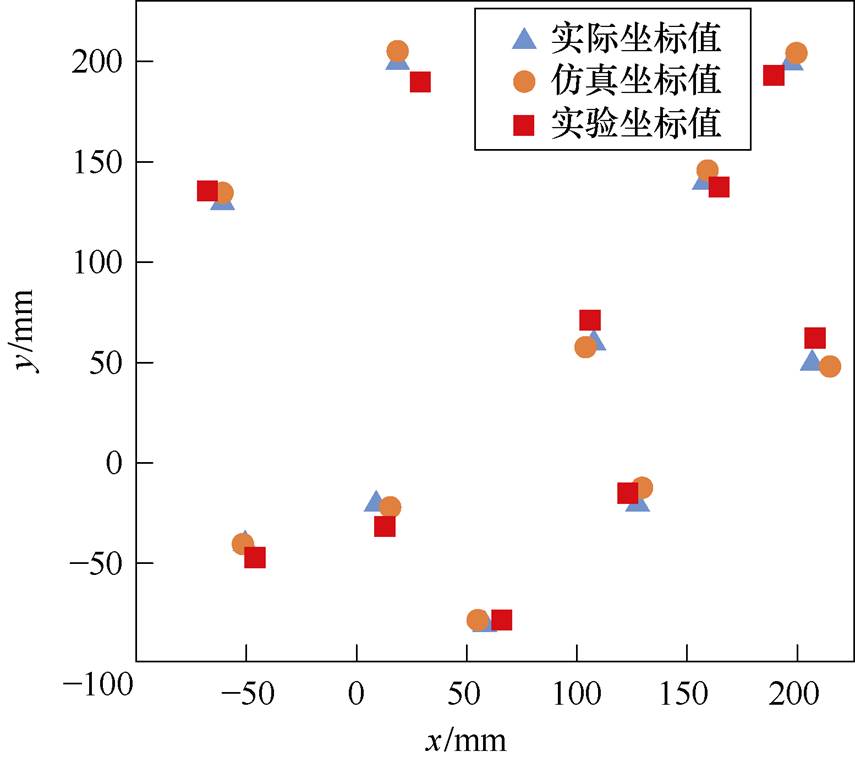
图15 定位结果
Fig.15 Positioning results
表4 仿真和实验结果
Tab.4 The results of simulation and experiment （单位: mm）
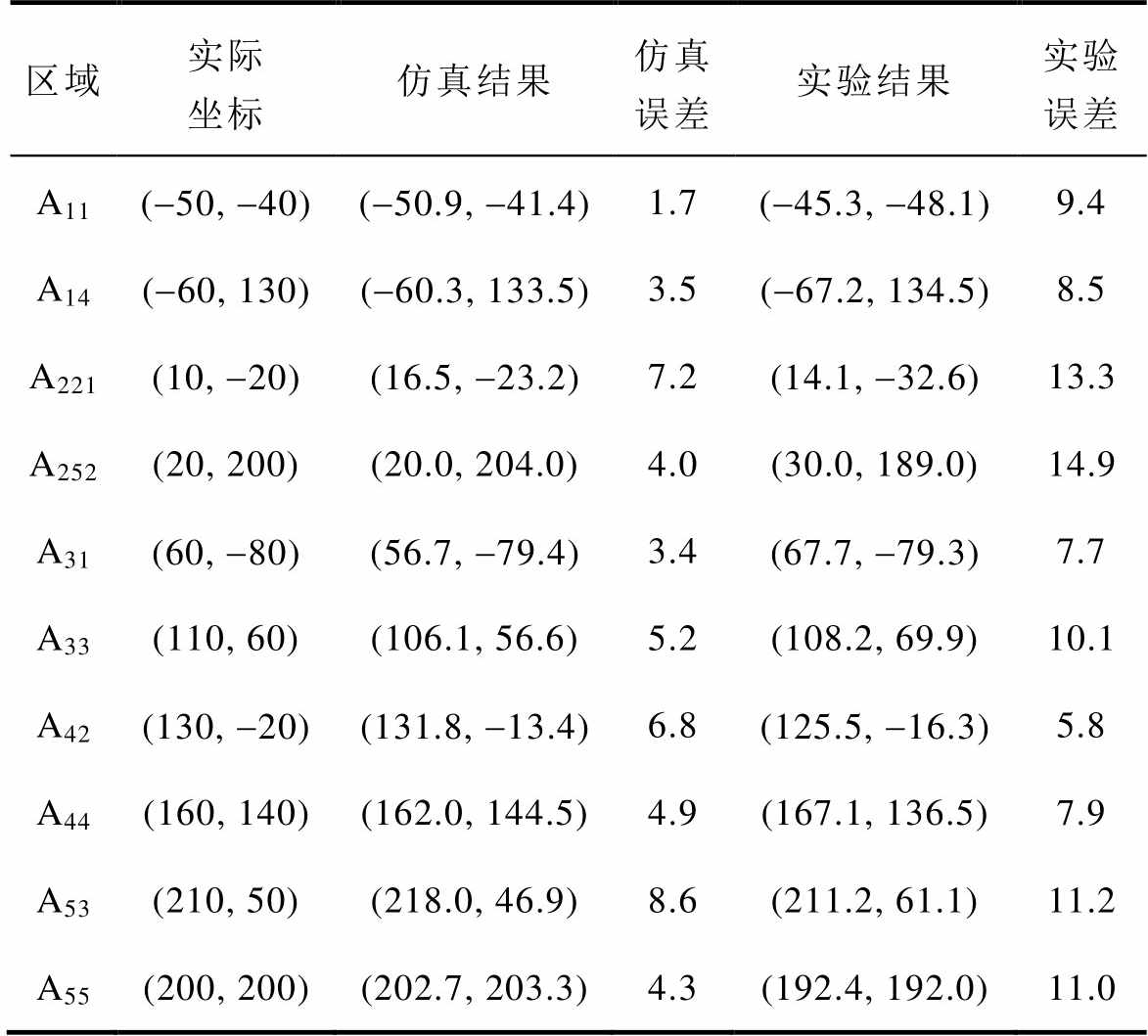
区域实际坐标仿真结果仿真误差实验结果实验误差 A11(-50, -40)(-50.9, -41.4)1.7(-45.3, -48.1)9.4 A14(-60, 130)(-60.3, 133.5)3.5(-67.2, 134.5)8.5 A221(10, -20)(16.5, -23.2)7.2(14.1, -32.6)13.3 A252(20, 200)(20.0, 204.0)4.0(30.0, 189.0)14.9 A31(60, -80)(56.7, -79.4)3.4(67.7, -79.3)7.7 A33(110, 60)(106.1, 56.6)5.2(108.2, 69.9)10.1 A42(130, -20)(131.8, -13.4)6.8(125.5, -16.3)5.8 A44(160, 140)(162.0, 144.5)4.9(167.1, 136.5)7.9 A53(210, 50)(218.0, 46.9)8.6(211.2, 61.1)11.2 A55(200, 200)(202.7, 203.3)4.3(192.4, 192.0)11.0
全桥整流电路对线圈电流的影响如图16所示。图16a、图16c、图16e、图16g分别为无整流桥情况下发射线圈1～4的电流波形，图16b、图16d、图16f、图16h分别为有整流桥情况下发射线圈的电流波形。在无整流桥时，负载电阻为15 W，而有整流桥时，负载电阻为18.5 W，全桥整流电路并联的小电容Ca=3 mF。可以看出，通过合理设置并联小电容的参数，整流桥的存在与否对发射线圈电流波形的影响很小，对所提出的定位方法的精度也几乎没有影响。因此，本文所提出的定位方法可以通过整流桥结构优化等方式来拓展应用的范围。
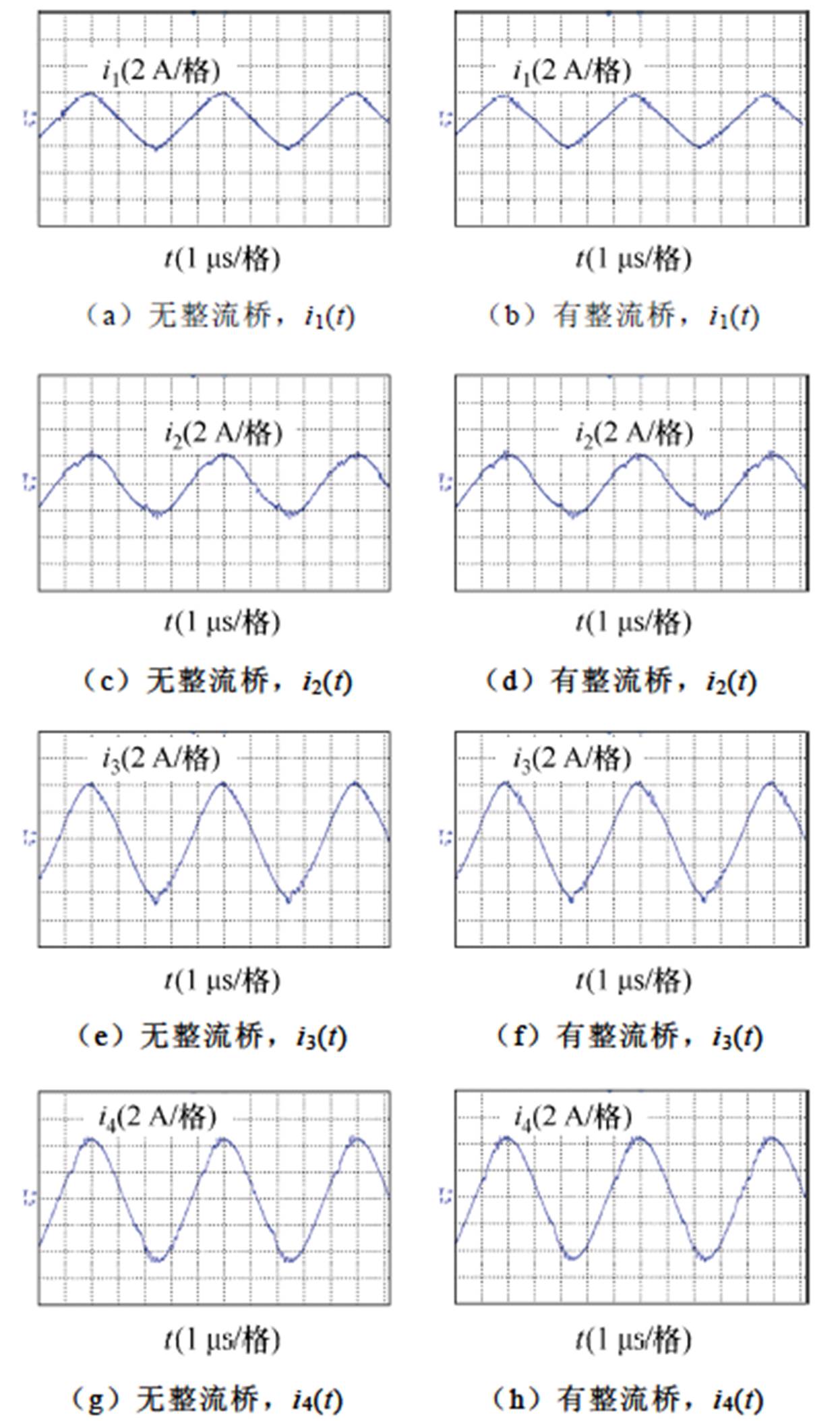
图16 全桥整流电路对线圈电流的影响
Fig.16 Influence of full-bridge rectifier on coil current
表5列出了本文所提出的定位方法与部分现有定位方法的精度对比，均采用最大定位误差表示定位精度。从表5中可以看出，本文提出的定位方法不仅无需额外的辅助定位器件或定位线圈，还能在较大的定位区域内实现较高的定位精度。通过提升预设的定位精度，可以进一步细化区域划分结果，从而提高定位的精度。因此，本文所提出的定位方法具有结构简单的优势，并且适用于不同定位区域和定位精度的应用场合。
表5 定位精度对比
Tab.5 Positioning accuracy comparison
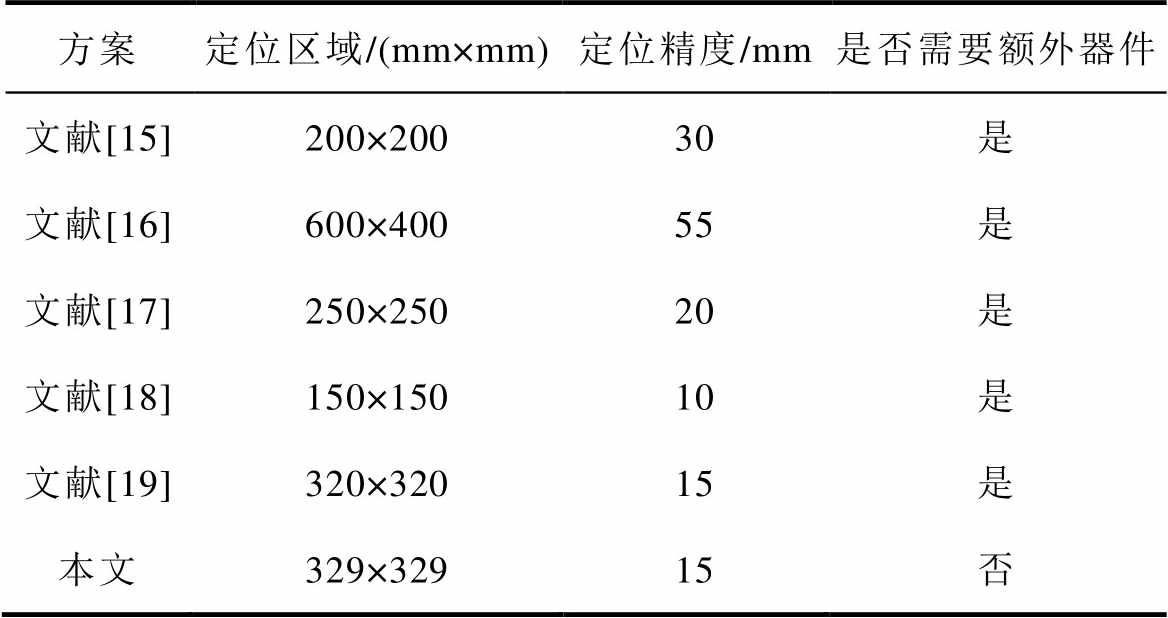
方案定位区域/(mm×mm)定位精度/mm是否需要额外器件 文献[15]200×20030是 文献[16]600×40055是 文献[17]250×25020是 文献[18]150×15010是 文献[19]320×32015是 本文329×32915否
本文提出了一种基于自适应区域划分的阵列式无线电能传输系统接收线圈定位策略。所提出的定位策略只需要采集发射线圈的电流，而不需要额外设备或与接收侧通信。根据预设定位精度对目标区域进行自适应划分，确定各区域的最佳参考点后，利用接收线圈在最佳参考点和待定位点之间发射阵列的电流变化计算出接收线圈坐标。实验结果表明，随机选取的10个点位的平均定位误差为9.98 mm，满足设定的定位精度，可以实现负载的精准定位。所提出的接收线圈定位策略具有高精度、低成本的优势，在各种无线电能传输应用场景中有巨大的潜力，有助于推动技术的进步。
未来研究方向：①系统参数偏移对定位精度的影响研究；②负载三维空间变姿态下的定位策略研究；③阵列扩展时更大定位区域下的定位策略研究；④平面阵列式系统的功率定向策略研究。
参考文献
[1] 杨庆新, 张献, 章鹏程. 电动车智慧无线电能传输云网[J]. 电工技术学报, 2023, 38(1): 1-12.
Yang Qingxin, Zhang Xian, Zhang Pengcheng. Intelligent wireless power transmission cloud network for electric vehicles[J]. Transactions of China Elec- trotechnical Society, 2023, 38(1): 1-12.
[2] 荣灿灿, 严俐慧, 路聪慧, 等. 基于超材料与超表面的无线电能传输技术研究现状与进展综述[J]. 电工技术学报, 2023, 38(20): 5369-5384.
Rong Cancan, Yan Lihui, Lu Conghui, et al. Overview on research status and progress of wireless power transfer technology based on metamaterials and metasurfaces[J]. Transactions of China Electro- technical Society, 2023, 38(20): 5369-5384.
[3] 张献, 韩大稳, 沙琳, 等. 一种共享磁通多耦合模式的无线电能传输系统抗偏移方法[J]. 电工技术学报, 2022, 37(21): 5359-5368.
Zhang Xian, Han Dawen, Sha Lin, et al. An anti-offset method under flux-sharing multi-coupling mode for wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5359-5368.
[4] 谢诗云, 杨奕, 李恋, 等. 基于双极性耦合磁场调控的高抗偏移偏转无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4838-4852.
Xie Shiyun, Yang Yi, Li Lian, et al. Wireless power transfer system with high misalignment tolerance based on bipolar coupling magnetic-field control[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4838-4852.
[5] 谭平安, 许文浩, 上官旭, 等. 无线电能传输系统中组合串绕六边形线圈的互感建模及参数优化[J]. 电工技术学报, 2023, 38(9): 2299-2309.
Tan Ping’an, Xu Wenhao, Shangguan Xu, et al. Mutual inductance modeling and parameter opti- mization of wireless power transfer system with combined series-wound hexagonal coils[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(9): 2299-2309.
[6] 杨云虎, 贾维娜, 梁大壮, 等. LCC-LCC/S自切换恒流-恒压复合型无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4823-4837, 4852.
Yang Yunhu, Jia Weina, Liang Dazhuang, et al. A self-switching wireless power transfer system based on hybrid topology of LCC-LCC/S with constant current and constant voltage[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4823-4837, 4852.
[7] 黄程, 陆益民. 磁谐振无线电能传输系统的频率跟踪失谐控制[J]. 电工技术学报, 2019, 34(15): 3102- 3111.
Huang Cheng, Lu Yimin. Frequency tracking detuning control of magnetic resonant wireless power transfer system[J]. Transactions of China Electro- technical Society, 2019, 34(15): 3102-3111.
[8] 杨奕, 张葛, 曹桂梅, 等. 基于多线圈阵列的单管无线电能传输电路优化[J]. 电工技术学报, 2023, 38(20): 5398-5410.
Yang Yi, Zhang Ge, Cao Guimei, et al. Optimization on single-switch wireless power transfer circuit based on multi-coils array[J]. Transactions of China Elec- trotechnical Society, 2023, 38(20): 5398-5410.
[9] 周玮, 高侨, 陈泽林, 等. 基于同侧解耦型电场耦合机构的多发射多接收无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4811-4822.
Zhou Wei, Gao Qiao, Chen Zelin, et al. Same-sided decoupled electric-field coupler based wireless power transfer system with multi-transmitter and multi- receiver[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4811-4822.
[10] Kang Ning, Shao Yaoxia, Liu Ming, et al. Analysis and implementation of 3D magnetic field shaping via a 2D planar transmitting coil array[J]. IEEE Transa- ctions on Power Electronics, 2022, 37(1): 1172- 1184.
[11] 冯天旭, 史可, 孙跃, 等. 基于互感识别及移相角优化的全方位无线电能传输系统靶向传能方法[J]. 电工技术学报, 2023, 38(24): 6581-6595.
Feng Tianxu, Shi Ke, Sun Yue, et al. Targeted power transfer method for omnidirectional wireless power transfer system based on mutual inductance identi- fication and phase-shift angle optimization[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6581-6595.
[12] Liu Xuyang, Liu Chunhua, Pong P W T. TMR- sensor-array-based misalignment-tolerant wireless charging technique for roadway electric vehicles[J]. IEEE Transactions on Magnetics, 2019, 55(7): 4003107.
[13] Shin Y, Hwang K, Park J, et al. Precise vehicle location detection method using a wireless power transfer (WPT) system[J]. IEEE Transactions on Vehicular Technology, 2019, 68(2): 1167-1177.
[14] Zhang Z, Zheng Shaoting, Yao Zirui, et al. A coil positioning method integrated with an orthogonal decoupled transformer for inductive power transfer systems[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 9983-9998.
[15] Tan Linlin, Li Chengyun, Li Jiacheng, et al. Mesh- based accurate positioning strategy of EV wireless charging coil with detection coils[J]. IEEE Transa- ctions on Industrial Informatics, 2021, 17(5): 3176- 3185.
[16] Tan Linlin, Yu Yongfeng, Wang Jiaqi, et al. Research on grid positioning strategy of coupling mechanism in wireless charging system with offset angle variable[J]. IEEE Transactions on Power Electronics, 2023, 38(5): 6670-6681.
[17] Cortes I, Kim W J. Automated alignment with respect to a moving inductive wireless charger[J]. IEEE Transactions on Transportation Electrification, 2022, 8(1): 605-614.
[18] Wang Wei, Zhang Cun, Wang Jiemin, et al. Multipurpose flexible positioning device based on electromagnetic balance for EVs wireless charging[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10): 10229-10239.
[19] Zhang Bin, Chen Qianhong, Zhang Li, et al. Triple- coil-structure-based coil positioning system for wireless EV charger[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 13515-13525.
[20] Yang Wanan, Zhang Chaoyang, Dai Houde, et al. A novel wireless 5-D electromagnetic tracking system based on nine-channel sinusoidal signals[J]. IEEE/ ASME Transactions on Mechatronics, 2021, 26(1): 246-254.
[21] Sharma A, Srivastava V K. A switched planar multicoil transmitter antenna designed with nonuni- form H-field forming for small device localization[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(11): 10261-10269.
[22] Liu Zhimeng, Wang Lifang, Tao Chengxuan, et al. Receiver position identification method of wireless power transfer system based on magnetic integration inductance[J]. IEEE Transactions on Industry Appli- cations, 2022, 58(1): 1136-1145.
[23] Feng Junjie, Li Qiang, Lee F C. Load detection and power flow control algorithm for an omnidirectional wireless power transfer system[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1422-1431.
[24] Li Xiaofei, Hu Jiefeng, Wang Heshou, et al. A new coupling structure and position detection method for segmented control dynamic wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 6741-6745.
[25] Wen Feng, Chu Xiaohu, Li Qiang, et al. Receiver localization strategy of wireless charging system based on mutual inductance disturbance[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 0600604.
[26] Mai Jianwei, Zeng Xianrui, Yao Yousu, et al. Impedance analysis and design of IPT system to improve system efficiency and reduce output voltage or current fluctuations[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14029-14038.
[27] Qu Xiaohui, Jing Yanyan, Lian Jing, et al. Design for continuous-current-mode operation of inductive- power-transfer converters with load-independent output[J]. IET Power Electronics, 2019, 12(10): 2458-2465.
[28] Mai Ruikun, Liu Yeran, Li Yong, et al. An active- rectifier-based maximum efficiency tracking method using an additional measurement coil for wireless power transfer[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 716-728.
[29] 李树凡, 王丽芳, 郭彦杰, 等. 基于整流性负载补偿的无线充电系统T型阻抗匹配网络设计方法的优化[J]. 电工技术学报, 2017, 32(24): 9-16.
Li Shufan, Wang Lifang, Guo Yanjie, et al. Optimization of design method of T-type impedance matching network for wireless charging system based on rectified load compensation[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 9-16.
Abstract Unforeseen misalignment between transmitter and receiver coils significantly impacts the performance of wireless power transfer (WPT) systems. The array WPT system can extend the effective charging area and reduce the influence of misalignment by optimizing the power orientation of the receiver coil. Accurate positioning of the receiver coil is crucial for achieving optimal power orientation in array WPT systems. Therefore, this paper introduces a region division-based receiver positioning strategy for planar array WPT systems without additional detecting coil or position sensors. The receiver coil can be precisely positioned by analyzing the current of the transmitter array.
A 2×2 array coil is employed as the research subject, requiring only 4 transmitter coils for positioning purposes. The paper demonstrates the theoretical derivation, simulation validation, and experimental results of the precise positioning of the receiver coil. A minimum cross-coupling design of the transmitter coil is carried out. Subsequently, the paper derives a coordinate calculation formula by fitting the relationship between the current of the transmitter coils and the coordinates of the receiver coil. This paper divides the region with randomly placed receiver coil into regions based on preset positioning accuracy. The optimal reference points for each region are dynamically optimized to ensure that positioning accuracy aligns with preset requirements. Finally, by analyzing changes in the transmitter coil current between the undetermined point and the optimal reference point of the receiver coil, the paper calculates the corresponding coordinate changes.
Changes in the load resistance can induce the full-bridge rectifier on the output side to transition into the discontinuous conduction mode, resulting in a surge in harmonic current content in the receiver coil. This paper theoretically analyzes the impact of harmonics at the receiver coil on the transmitter coil current after the full-bridge rectifier enters the discontinuous conduction mode. In continuous conduction mode, the accuracy of the proposed positioning strategy is predominantly influenced by the equivalent resistance of the full-bridge rectifier. Through the parallel small capacitance method, experiments validate that the transmitter coil current remains consistent irrespective of the full-bridge rectifier. Consequently, maintaining equivalent load consistency ensures the positioning accuracy of the proposed strategy, thereby expanding its application scope.
The experimental results show an average positioning error of 9.98 mm within the 329 mm×329 mm area, satisfying the preset positioning accuracy criterion of 10 mm. Moreover, compared to existing positioning strategies in wireless power transfer systems, the proposed approach offers distinct advantages of positioning accuracy and the necessity for additional devices.
keywords：Wireless power transfer, planar coil array, coil positioning, region division, reference point
中图分类号：TM724
DOI: 10.19595/j.cnki.1000-6753.tces.231866
国家自然科学基金（52307205）、江苏省自然科学基金（BK20221491）和中国博士后科学基金（2022M711626）资助项目。
收稿日期 2023-11-28
改稿日期2024-03-02
闻 枫 男，1990年生，博士，副研究员，研究方向为无线电能传输。E-mail: wen@njust.edu.cn（通信作者）
王 磊 男，1999年生，硕士研究生，研究方向为无线电能传输。E-mail: 121110223261@njust.edu.cn
（编辑 陈 诚）