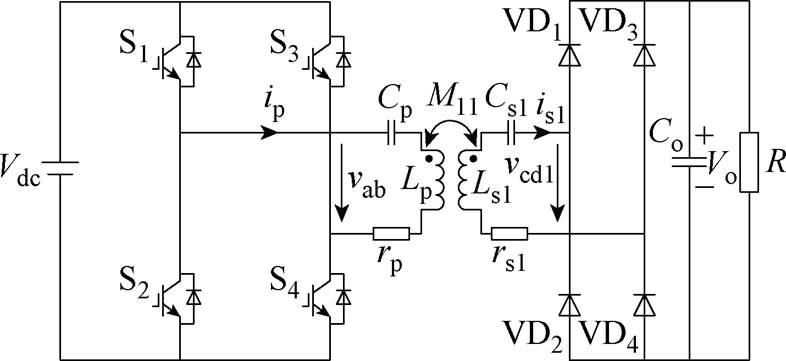
图1 传统ICPT系统拓扑
Fig.1 Topology of the traditional ICPT system
摘要 为抑制感应耦合能量传输（ICPT）系统中高频逆变器的输出电流谐波，提出一种基于辅助拾取模块的电流谐波抑制方法。首先，建立ICPT系统的数学模型，分析了电流谐波的产生机理和影响因素。其次，以抑制3次电流谐波为例，详细分析了辅助拾取模块抑制电流谐波的原理，通过合理设计辅助拾取模块的品质因数，可防止拾取线圈之间的交叉干扰。最后，通过仿真和实验验证了提出方法的有效性。仿真与实验结果表明，提出的方法可有效降低3次电流谐波幅值，减小电流总谐波畸变率（THD），并且轻载工况下系统效率可得到进一步提高。
关键词：感应耦合能量传输 辅助拾取模块 电流谐波抑制 品质因数
感应耦合能量传输（Inductively Coupled Power Transfer, ICPT）系统是通过电磁感应原理将电能由电源端传输到负载端[1-2]。由于ICPT系统具有安全、可靠、美观等优点，已广泛应用于电子设备[3]、生物医疗[4]、电动汽车[5]及轨道交通[6]等领域。
然而，由于ICPT系统中高频逆变器的输出电压为方波，因此，高频逆变器的输出电流中会含有较多的谐波成分，特别是在系统轻载情况下，高频逆变器的输出电流会产生较大的畸变[7]。对应用于轨道交通的ICPT系统来说，发射线圈沿轨道长距离铺设。因此，较大的谐波电流会造成严重的电磁干扰，从而影响开关器件的正常工作以及电路控制，增加开关器件的电流应力，影响列车以及周围环境中电子设备的正常使用，造成系统故障、列车停运甚至威胁人体安全[8-10]。因此，有必要对高频逆变器的输出电流谐波进行有效的抑制。
目前，抑制高频逆变器的输出电流谐波主要有以下四种思路：
（1）提高原边侧发射线圈自感，即提高原边侧的品质因数。但是，对于大功率轨道交通长距离供电系统来说，原边侧常采用单矩形发射线圈结构[11-12]，因此，提高发射线圈自感意味着将延伸发射线圈的铺设距离，导致系统的功率损耗大幅增加[13]，同时发射线圈以及谐振电容的电压应力也会显著增加[14]。所以，该方法并不适用于大功率轨道交通长距离供电系统。
（2）原边侧增加滤波器[15]。由于原边侧电流相对较高，因此，对滤波器的额定电压及额定电流等级要求较高，从而增加系统造价。
（3）采用多套级联高频逆变器[16-18]或引入开关电容变换器[19]输出阶梯波电压。文献[16]分析了逆变器输出电压的总谐波畸变率（Total Harmonic Distortion, THD）与导通角的关系，为降低逆变器输出电压的谐波含量，将逆变器的导通角设定为80°～180°之间。文献[17]采用两套级联逆变器，通过固定一套逆变器的导通角为60°，移相调节另一套逆变器的导通角即可消除3次谐波并实现输出电压基波有效值的连续调节。文献[18]采用三套级联逆变器合成阶梯波，从而消除了3次、5次谐波，并采用脉冲密度调制策略实现了输出功率的连续调节。但是文献[16-18]都限制了逆变器输出电压基波有效值的调节范围。文献[19]通过开关电容逆变器输出阶梯波电压，可抑制逆变器输出电压谐波含量，并且能够有效提高输出基波电压幅值。此外，文献[20-21]在副边侧采用开关电容整流器替代不控整流器，从而减小整流器的输入电压谐波。但是，采用多套高频逆变器或引入开关电容变换器都会提高系统工程造价，并且系统控制相对复杂，不利于工程实施。
（4）采用无源屏蔽线圈[8, 22]。屏蔽线圈产生与谐波分量相反的磁场，从而可以减小谐波分量，抑制电磁干扰，并且几乎不会影响系统效率。该方法简单有效，工程造价相对较低。但是目前研究中没有给出无源屏蔽线圈详细的设计方案。
因此，本文提出一种适用于轨道交通的基于辅助拾取模块的ICPT系统电流谐波抑制方法。针对目前研究中并没有无源屏蔽线圈的设计方法，本文通过理论分析，详细给出了辅助拾取模块的设计方案，从而可有效抑制电磁干扰。
由于高阶电流谐波幅值很小可以忽略不计[15]，因此，本文首先以抑制3次电流谐波为例，详细分析了电流谐波的产生机理以及影响因素。然后分析了提出的基于辅助拾取模块的电流谐波的抑制原理并详细给出了辅助拾取模块的设计方法。通过合理设计辅助拾取模块的品质因数，可防止拾取线圈之间的交叉干扰，从而不会影响主电路功率传输。最后通过仿真和实验验证了提出方法的有效性。
由于基于串联-串联（Series-Series, SS）型补偿电路的ICPT系统具有结构简单、谐振频率与负载和互感无关、系统传输效率较高等优点[22-24]，因此，本文对如图1所示的基于SS型补偿电路的ICPT系统进行分析。图中，Vdc为直流电压源，vab、ip分别为高频逆变器输出电压和电流，vcd1、is1分别为主拾取模块的整流器的输入电压和输入电流，Vo为主拾取模块输出直流电压；Lp、Cp、rp分别为发射线圈电感、补偿电容器电容和发射线圈内阻，Ls1、Cs1、rs1分别为主拾取模块的拾取线圈电感、补偿电容器电容和拾取线圈内阻，M11为发射线圈与主拾取模块的拾取线圈之间的互感，Co为主拾取模块的输出直流电容器电容，R为负载；S1、S2、S3、S4为绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT），VD1、VD2、VD3、VD4为二极管。
图1 传统ICPT系统拓扑
Fig.1 Topology of the traditional ICPT system
为实现ICPT系统的最大功率传输，高频逆变器的工作角频率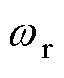
应满足
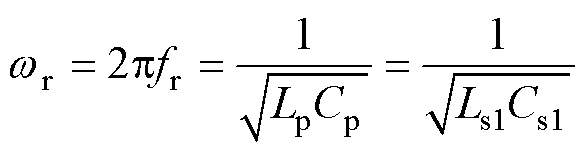（1）
式中，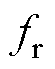
为高频逆变器的工作频率。
传统ICPT系统的等效电路如图2所示。图中，Re1为主拾取模块的交流等效电阻，Re1=8/p2R。
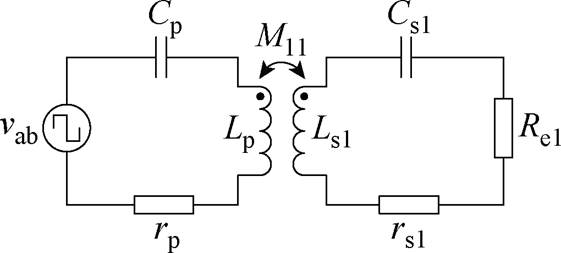
图2 传统ICPT系统的等效电路
Fig.2 Equivalent circuit of the traditional ICPT system
高频逆变器采用移相控制。考虑死区时间[25]，则高频逆变器输出电压vab的k阶电压谐波相量可以表示为
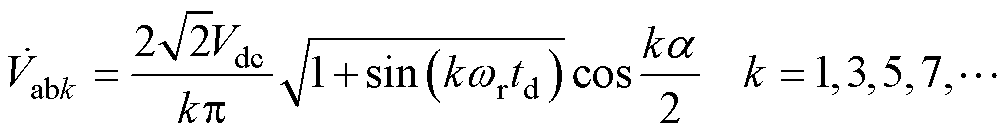（2）
式中，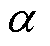
为移相角；td为上桥臂与下桥臂的死区时间。
当移相角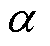=0°时，高频逆变器输出电压vab的基波电压相量表达式为
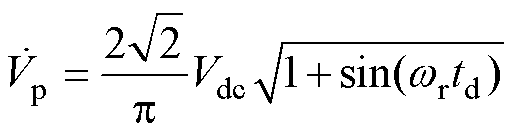（3）
于是，
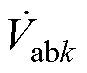与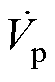
比值的绝对值Gk表示为
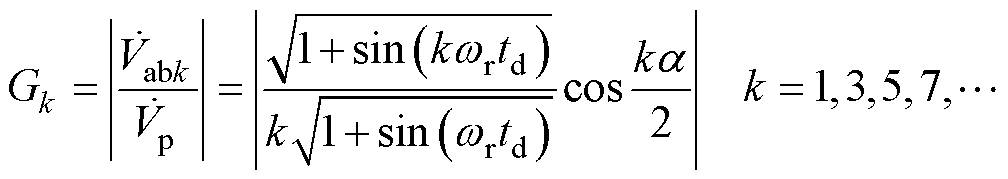（4）
Gk随移相角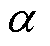变化的曲线如图3所示。图中，1st表示基波分量，3rd、5th、7th、9th分别表示3次、5次、7次、9次谐波分量，其他高阶谐波分量图中不再展示。
于是，可将系统等效为如图4所示的谐波等效电路，vab为各阶电压谐波相量的叠加。图中，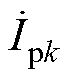
为ip的k阶电流谐波相量，
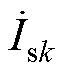为is1的k阶电流谐波相量。
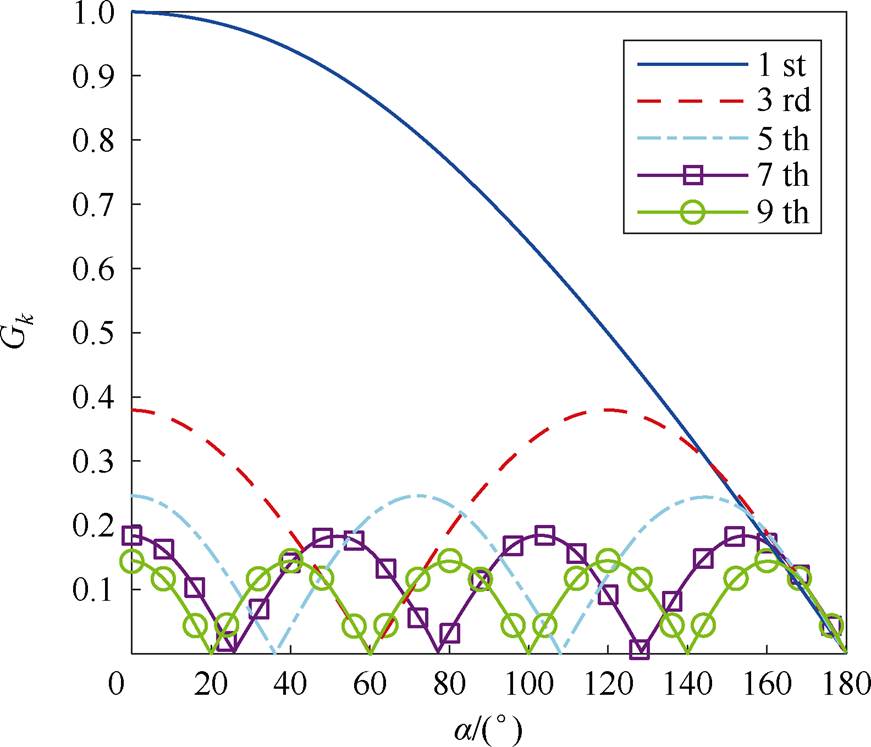
图3 Gk随移相角a 变化的曲线
Fig.3 Curves of Gkversus the phase-shift angle a
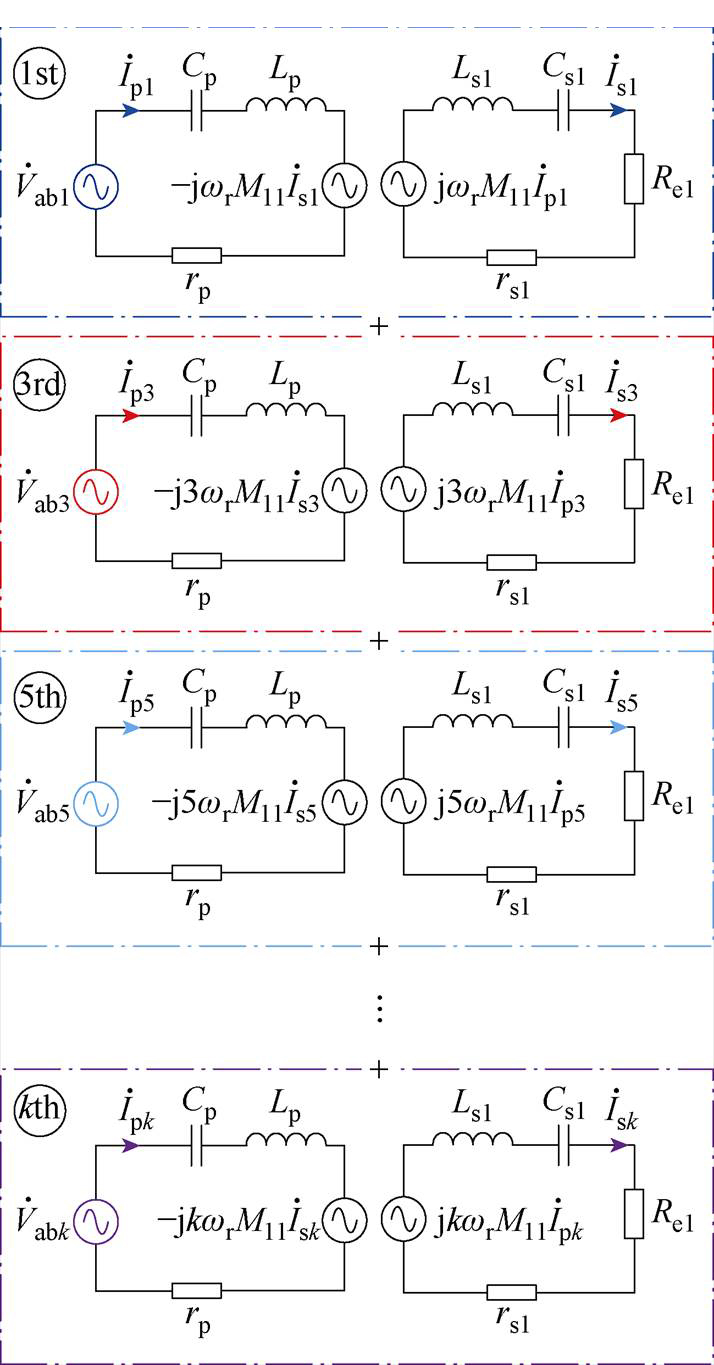
图4 传统ICPT系统的谐波等效电路
Fig.4 Equivalent circuit of the traditional ICPT system for harmonics
以3次电流谐波为例，根据图4可得，传统ICPT系统的基波电流幅值Ip1和3次谐波电流幅值Ip3的表达式分别为
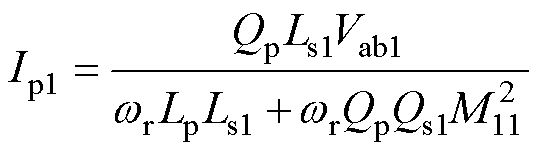（5）
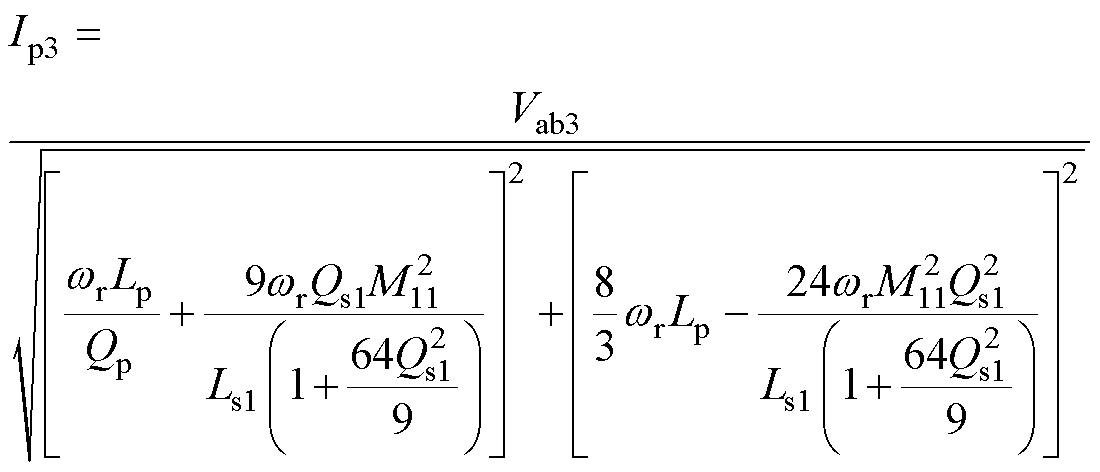（6）
其中
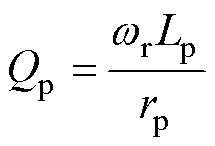
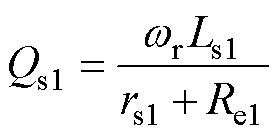
式中，Vabk为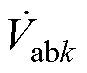的幅值；Qp为原边侧的品质因数；Qs1为主拾取模块的品质因数。
定义3次谐波电流幅值与基波电流幅值的比值为
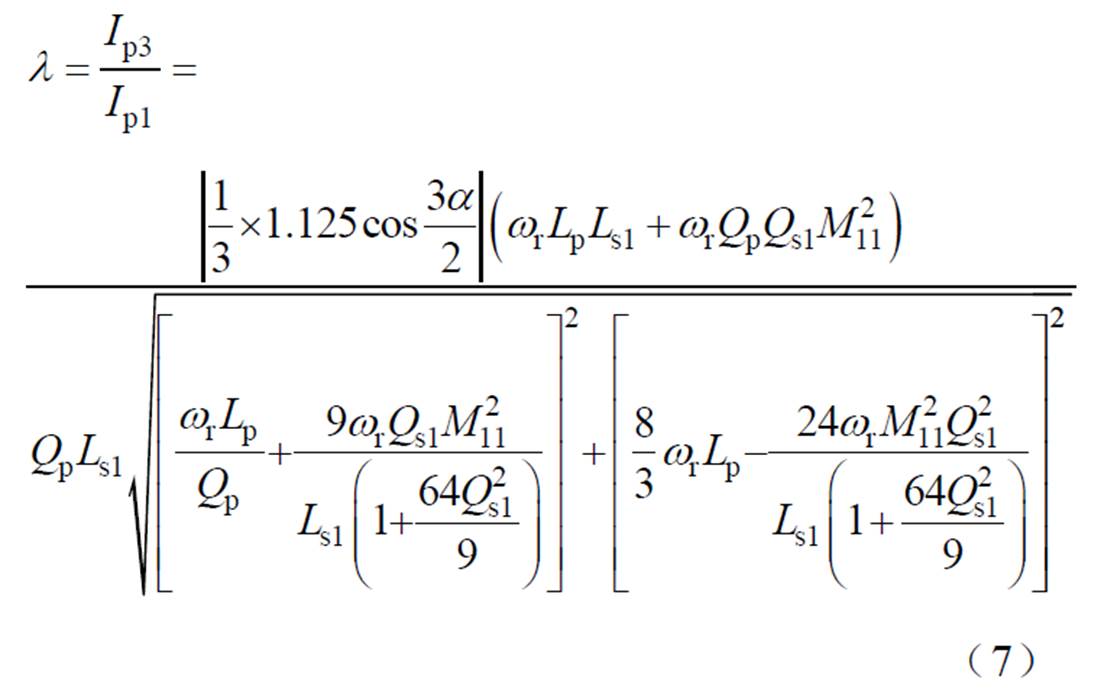
根据表1所示的ICPT系统参数，当Qs1=240时，不同原边侧品质因数下，l 随移相角a 变化的曲线如图5a所示；当Qp=50时，不同主拾取模块品质因数下，l 随移相角a 变化的曲线如图5b所示。
由图5a可知，原边侧品质因数Qp较低时，3次电流谐波分量较高。Qp增加时，3倍频下的系统阻抗增加，因此可有效抑制3次谐波电流。但是，当Qp增加到一定值时，对3次电流谐波的抑制效果将不再明显。由图5b可知，主拾取模块的品质因数Qs1增加，即系统轻载时，基波电流分量减小。同时，3倍频下的系统阻抗降低，导致3次谐波电流分量增加，于是，l 显著增加。因此可知，ICPT系统轻载时，高频逆变器的输出电流会产生较为严重的畸变。
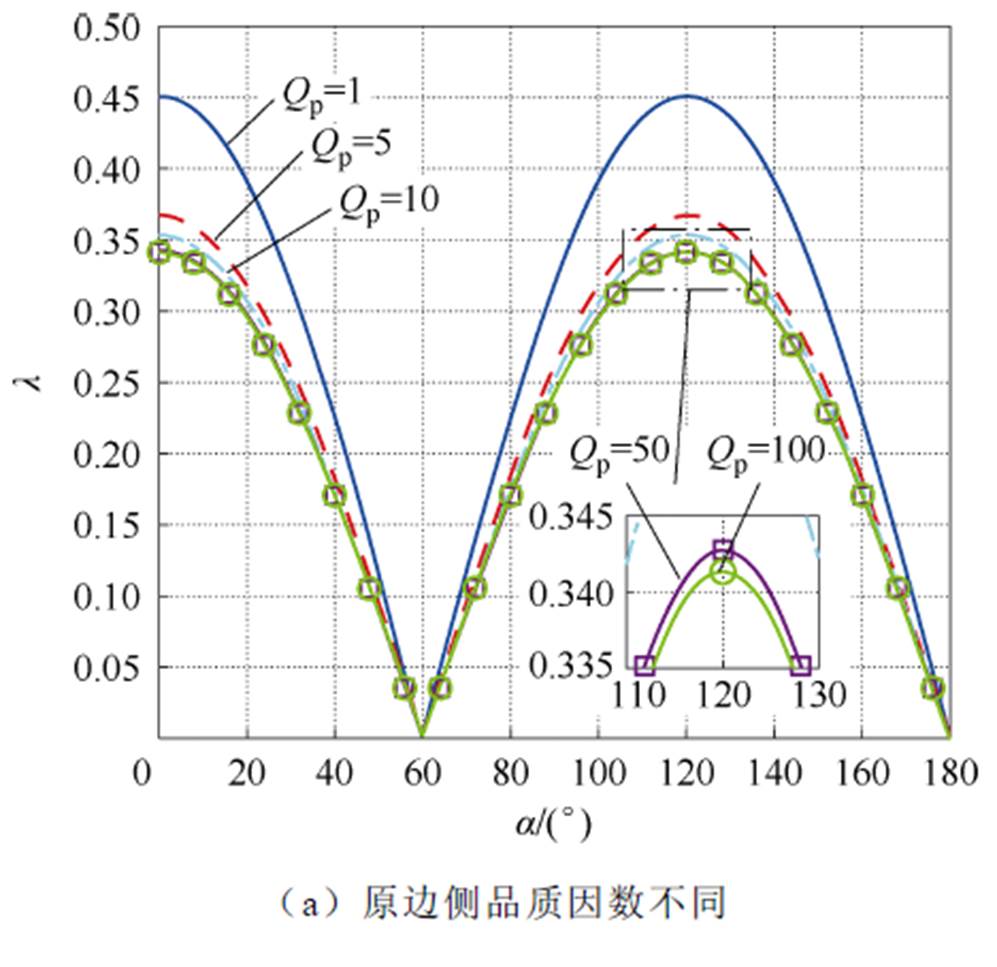
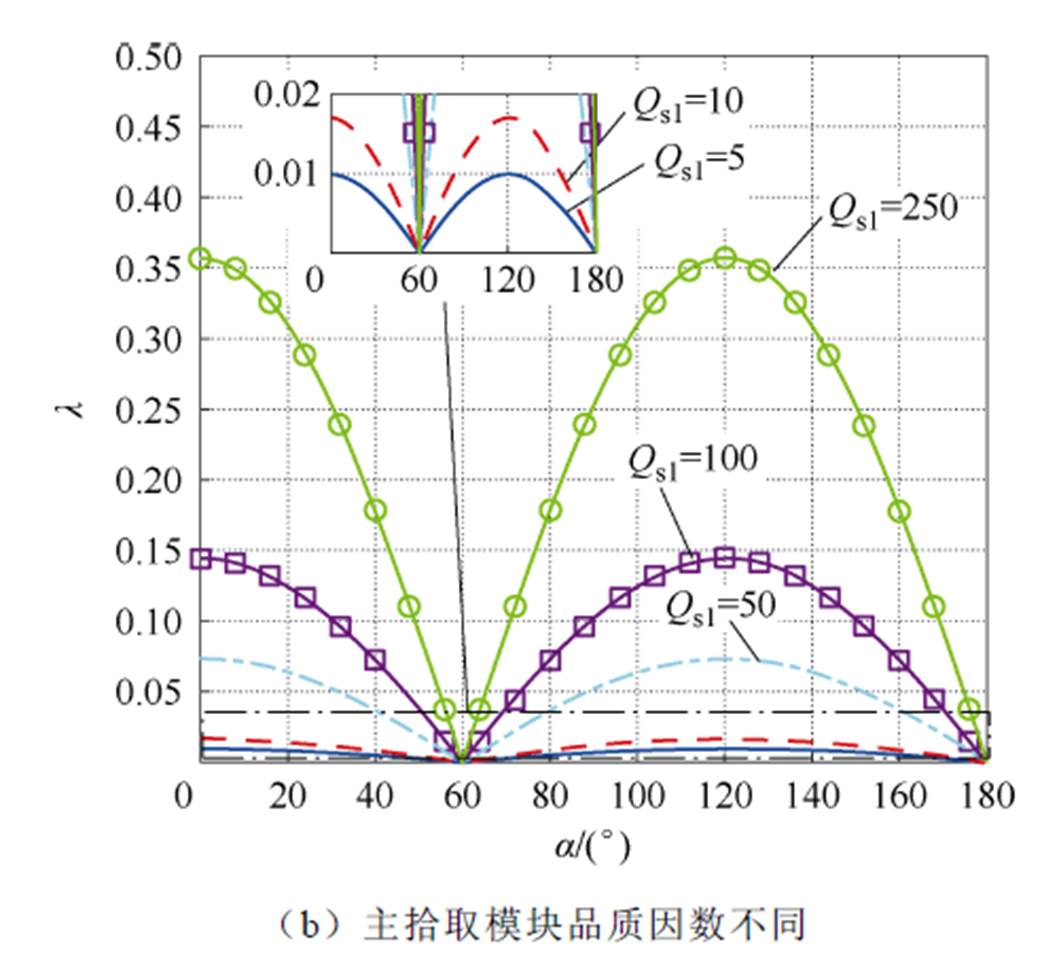
图5 l 随移相角a 变化的曲线
Fig.5 Curves of lversus the phase-shift angle a
以抑制3次电流谐波为例进行分析，基于辅助拾取模块的电流谐波抑制方法分析如下。
为了抑制高频逆变器输出电流ip的3次谐波，基于辅助拾取模块的ICPT系统等效电路如图6所示。主拾取模块与辅助拾取模块沿轨道方向依次排列。由于主拾取模块与辅助拾取模块的距离较远，经实际测量，主拾取模块与辅助拾取模块之间的互感仅为M11的0.63%，因此可忽略主拾取线圈与辅助拾取线圈之间的互感。图6中，Ls3、Cs3、rs3分别为辅助拾取模块的拾取线圈的电感、补偿电容器的电容、拾取线圈内阻；M13为发射线圈与辅助拾取模块的拾取线圈之间的互感；Re3为辅助拾取模块的交流等效电阻，Re3=8/p2R3，其中，R3为辅助拾取模块的负载。
辅助拾取模块的谐振角频率ws3应满足
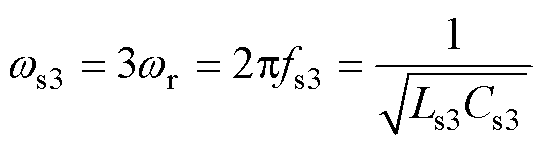（8）
式中，fs3为辅助拾取模块的谐振频率。
辅助拾取模块的品质因数Qs3可以表示为
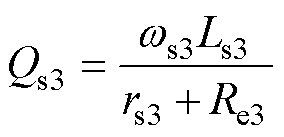（9）
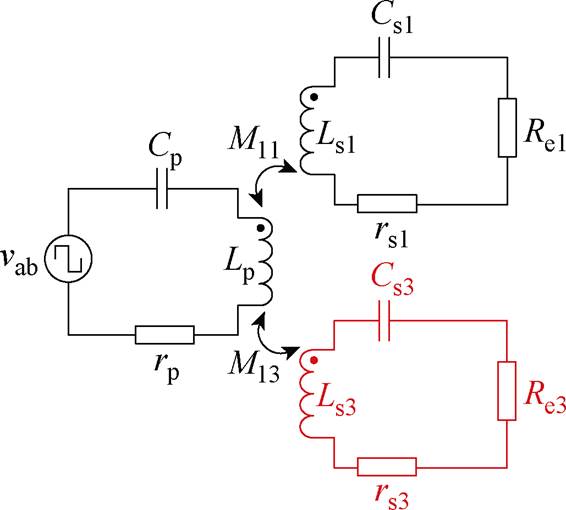
图6 基于辅助拾取模块的ICPT系统补偿电路
Fig.6 Compensation circuit of the ICPT system with auxiliary pickup module
ICPT系统中的拾取模块可以等效为带通滤波器。对于辅助拾取模块来说，辅助拾取模块的电流的幅值表达式为
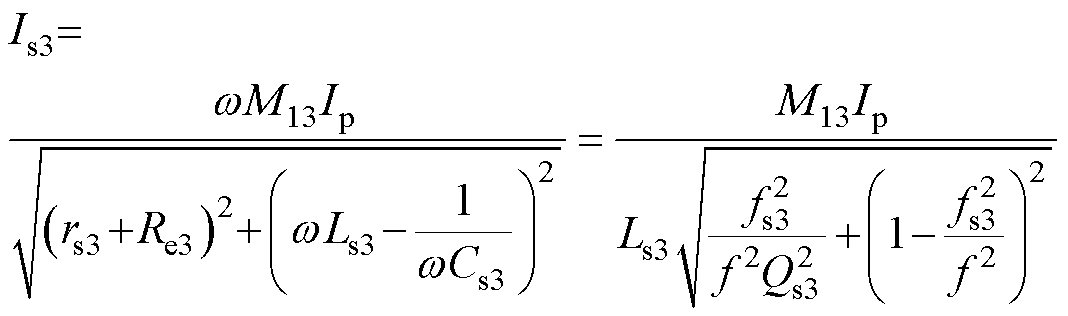（10）
式中，w、f分别为高频逆变器的工作角频率和工作频率，w=2p f；Ip为高频逆变器输出电流ip的幅值。
由式（10）推导可得Is3的最大值Is3max的表达式为
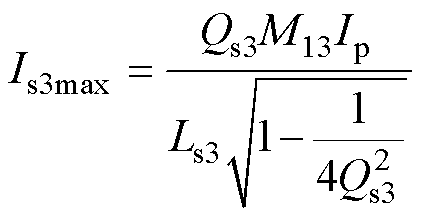（11）
根据式（10）、式（11）可得，不同品质因数Qs3下，辅助拾取模块的单位电流增益随工作频率f变化的曲线如图7所示。图中，fr为基频。
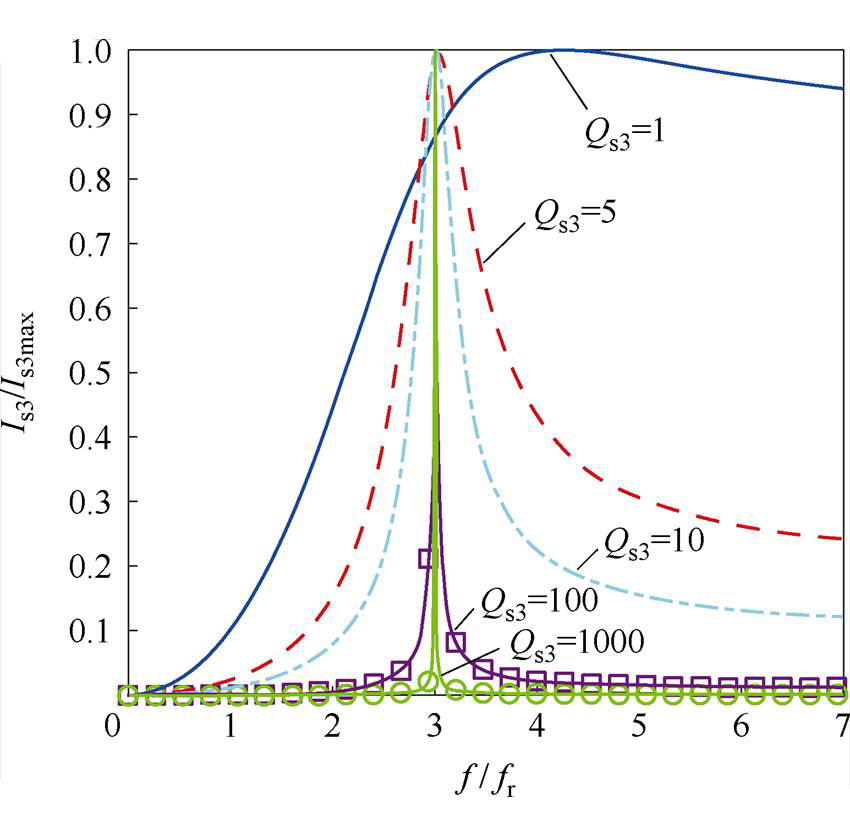
图7 单位电流增益随工作频率变化的曲线
Fig.7 Per-unit current profiles versus the operating frequency under different quality factors
由图7可知，电流-频率特性曲线呈现钟形。在辅助拾取模块的谐振频率点附近，辅助拾取模块的电流幅值达到最大值。同时，当辅助拾取模块的品质因数Qs3较低时，辅助拾取模块会拾取基频fr处的电流，因此造成拾取模块之间的交叉干扰，从而降低系统传输效率。
为了避免拾取模块之间的交叉干扰，需要对辅助拾取模块的品质因数Qs3进行合理的设计，详细的设计过程将在2.2节进行介绍。
根据以上分析，可得基于辅助拾取模块的ICPT系统的等效电路模型如图8所示。图中，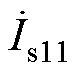
为主拾取模块在fr处的电流相量，
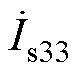为辅助拾取模块在fs3处的电流相量。
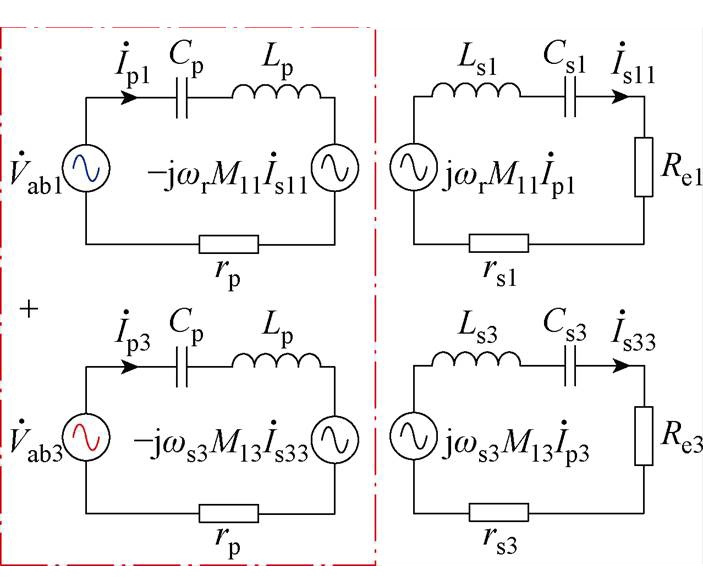
图8 基于辅助拾取模块的ICPT系统等效电路
Fig.8 Equivalent circuit of the ICPT system with auxiliary pickup module
根据图8以及上述分析可得，此时高频逆变器输出电流的3次电流谐波幅值Ip3可以表示为
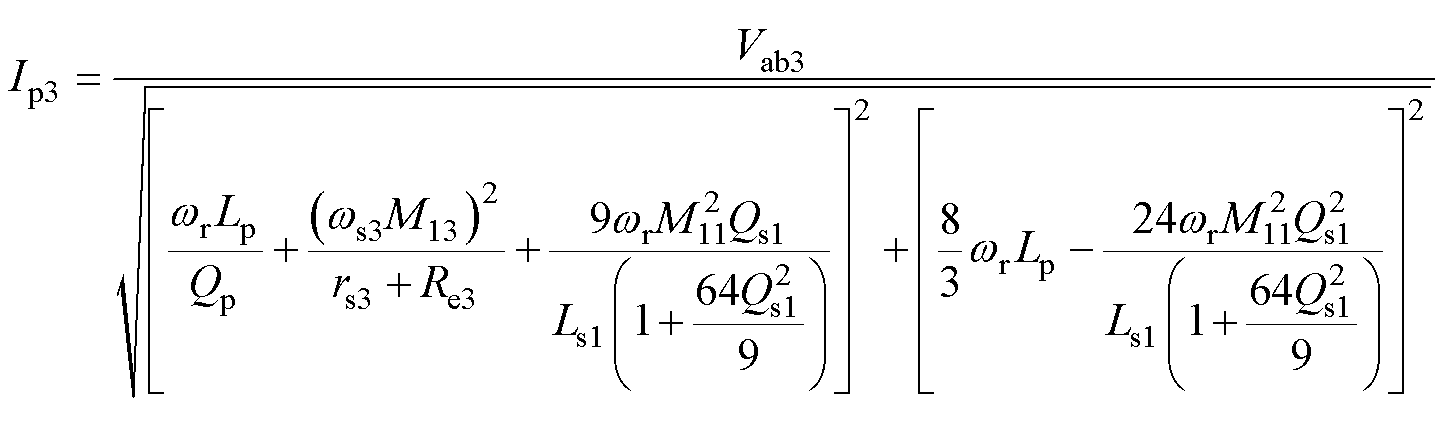（12）
因此，对比式（6）与式（12）可知，辅助拾取模块的增加可以有效减小3次电流谐波幅值。
ICPT系统主电路效率的计算表达式为
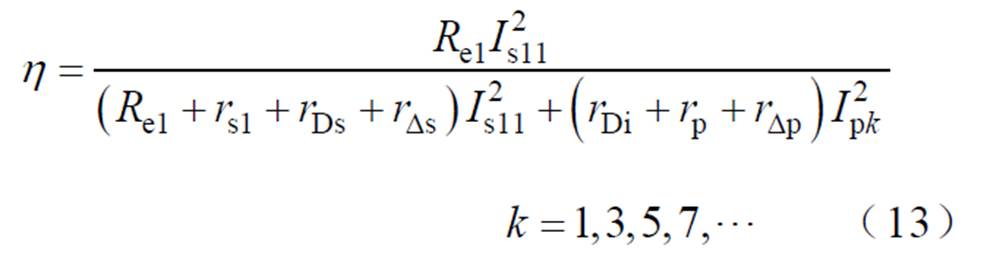
式中，Is11、Ipk分别为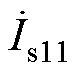、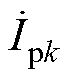的幅值；rDi、rDs分别为高频逆变器、不控整流器的导通电阻；rDp、rDs分别为原、副边侧的其他损耗。
由式（13）可知，电流谐波的存在将会使系统的损耗增加，且谐波畸变率越大，损耗也越大。而本文提出的方法可以较好地抑制轻载工况下高频逆变器输出的谐波电流，因此，系统损耗将进一步减小，系统效率可进一步提高。同时由图5可知，随着系统输出功率增加，谐波畸变率降低，因此，基于辅助拾取模块的ICPT系统效率将与传统ICPT系统效率基本一致。
由式（10）可得，在基频fr处，流经辅助拾取模块的电流幅值Is31的表达式为
（14）
在3倍频fs3处，流经辅助拾取模块的电流幅值Is33的表达式为
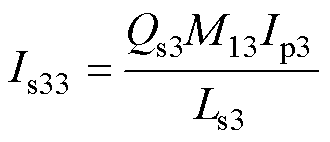（15）
定义k =Is31/Is33，并且当k≤1%时，拾取模块之间的交叉干扰认为可忽略，从而不会影响系统传输效率。因此，辅助拾取模块的品质因数Qs3应满足
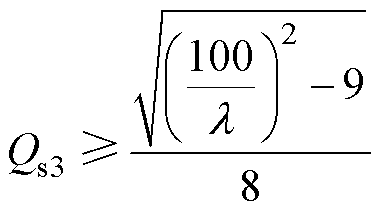（16）
由式（9）可知，提高辅助拾取线圈的品质因数Qs3有两种方法：①增加辅助拾取模块的拾取线圈自感；②减小辅助拾取模块的负载电阻。
但是，增加拾取线圈自感会增加系统的体积和造价。减小负载电阻则不仅可以提高辅助拾取模块的品质因数，同时根据式（12）可知，还可以进一步减小3次电流谐波幅值。Re3=0时，电流谐波抑制效果最好。因此，本文采用减小电阻负载的方法来提高辅助拾取线圈的品质因数。
于是，本文提出的基于辅助拾取模块的ICPT系统拓扑如图9所示，高频逆变器的输出电流谐波因此可得到有效抑制。
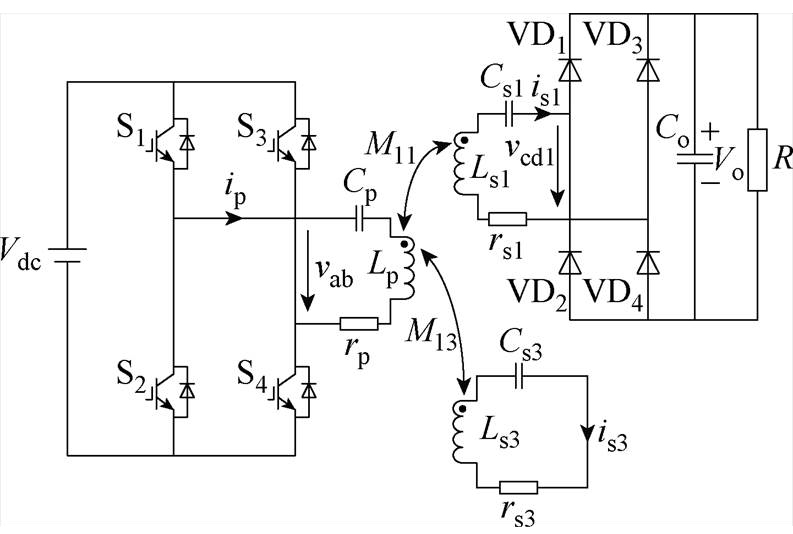
图9 基于辅助拾取模块的ICPT系统拓扑
Fig.9 Topology of the ICPT system with auxiliary pickup module
此外，通过合理设计线圈[26]、改变多层线圈之间的连接方式、采用谐振电容器对线圈进行分段补偿[27]或对多层线圈之间进行补偿[28]，可减小线圈中寄生电容的影响，进一步提高线圈的品质因数。
其他阶次的电流谐波抑制机理、辅助拾取模块设计方法与此类似，此处不再赘述。
搭建的ICPT系统仿真模型和实验平台参数见表1。
表1 ICPT系统参数
Tab.1 Parameters of the ICPT system
参 数数 值 输入直流电压Vdc/V100 发射线圈自感Lp/mH23.2 补偿电容Cp/mF1.3 内阻rp/W0.067 主拾取模块拾取线圈自感Ls1/mH988.32 补偿电容Cs1/nF30.47 内阻rs1/W0.76 辅助拾取模块拾取线圈自感Ls3/mH105.61 补偿电容Cs3/nF30.25 内阻rs3/W0.43 发射线圈与主拾取模块拾取线圈之间的互感M11/mH15.1 发射线圈与辅助拾取模块拾取线圈之间的互感M13/mH6.13 负载电阻R/W0.5 高频逆变器工作频率fr/kHz29.1 死区时间td/ms0.9
辅助拾取线圈的结构如图10所示。辅助拾取线圈采用7圈×2层的结构，线圈的长、宽、高分别为454 mm、164 mm、8.5 mm。为减小线圈的交流损耗，辅助拾取线圈采用利兹线绕制。
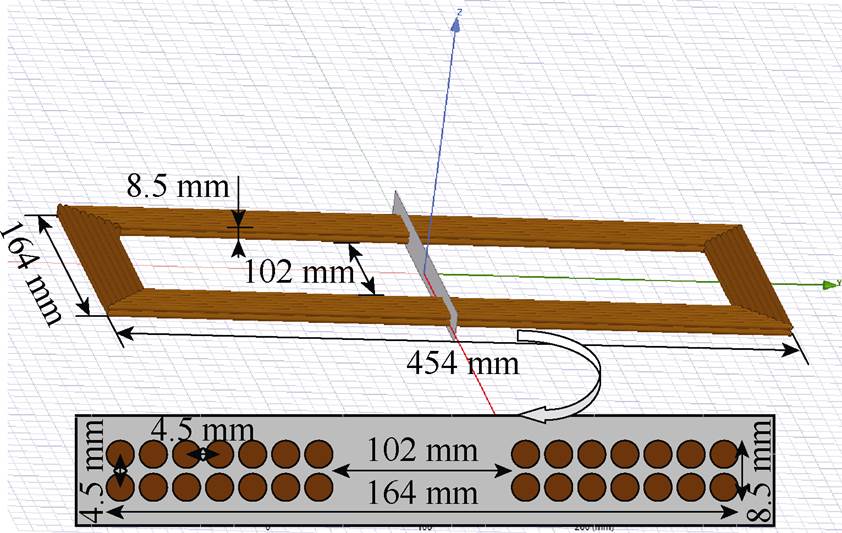
图10 辅助拾取线圈的结构
Fig.10 Structure of the auxiliary pickup coil
辅助拾取线圈的上下两层线圈采用如图11所示[27]的连接方式。上、下两层线圈同方向绕制，其中，一层线圈的内部与另外一层线圈的外部相连，可进一步提高辅助拾取模块的品质因数。
图11 两层线圈的连接方式
Fig.11 Connection method of 2-layer coil
当移相角a=0°时，根据式（7）、式（16）可得，l=0.30且辅助拾取模块的品质因数需满足Qs3≥ 41.66。根据表1可得，Qs3=134.72。因此，设计的辅助拾取模块的品质因数满足式（16）所示的条件。
基于辅助拾取模块的ICPT系统的耦合机构如图12所示。原边侧为单矩形发射线圈结构，为便于安装，发射线圈无铁氧体铺设；副边侧的主拾取线圈的匝数为34匝，为提高发射线圈与主拾取线圈之间的耦合系数，主拾取线圈铺设铁氧体；发射线圈与拾取线圈之间的额定气隙为40 mm。
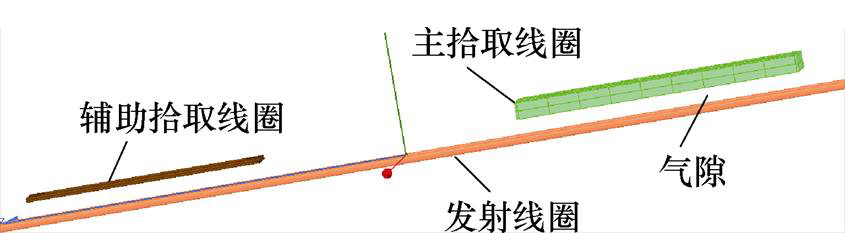
图12 基于辅助拾取模块的ICPT系统的耦合机构
Fig.12 Coupling mechanism of the ICPT system with auxiliary pickup module
当移相角a=0°时，传统与基于辅助拾取模块的ICPT系统的仿真波形分别如图13a和图13b所示。
由图13b可知，辅助拾取模块的电流频率为主拾取模块电流频率的3倍。对比图13a和图13b，基于辅助拾取模块的ICPT系统的高频逆变器的输出电流更加正弦。
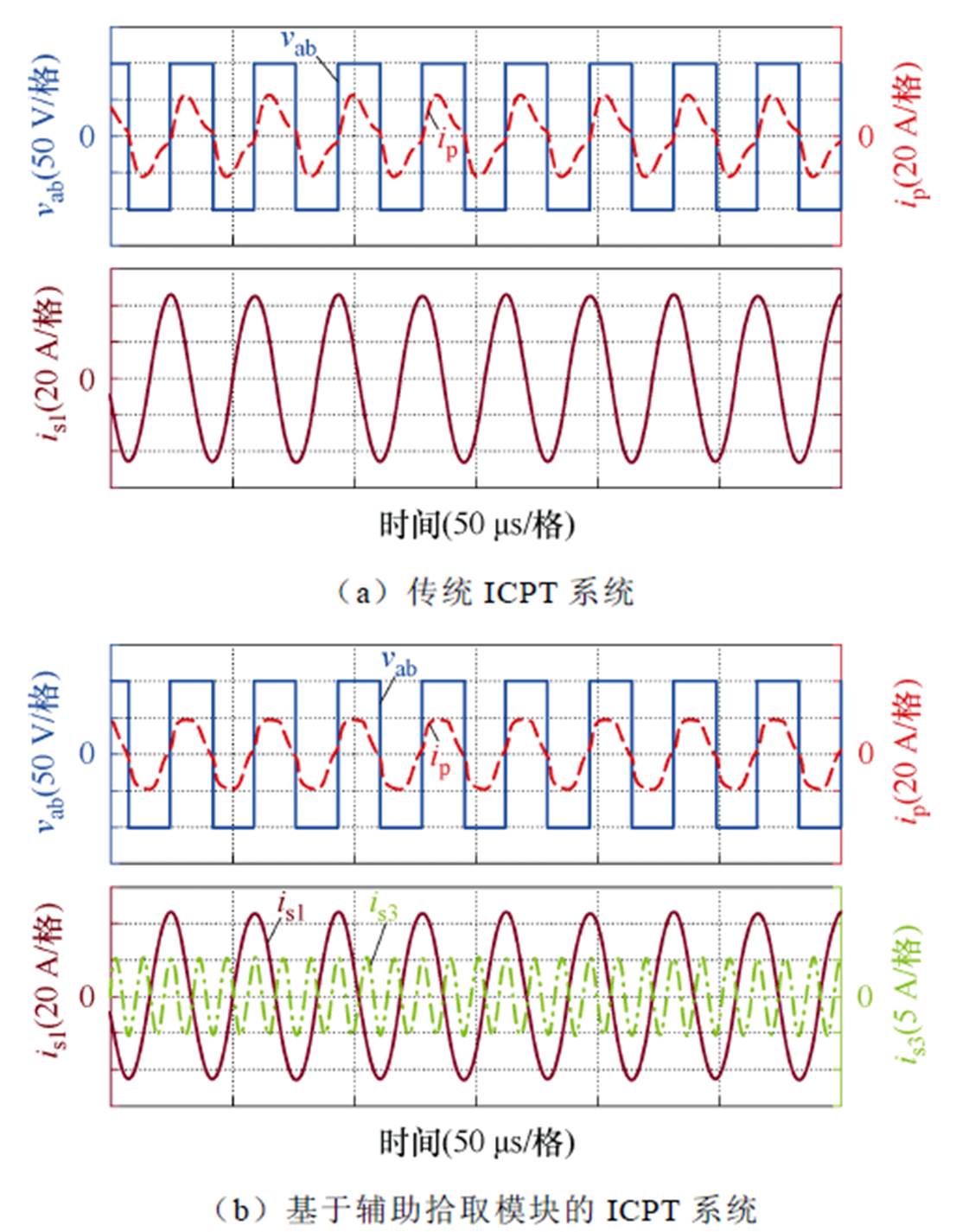
图13 移相角a=0°时，ICPT系统的仿真波形
Fig.13 Simulation waveforms of the ICPT system when phase-shift angleis 0°
当移相角a=60°时，基于辅助拾取模块的ICPT系统的仿真波形如图14所示。由图14可知，当移相角a=60°时，辅助拾取模块的电流为0。
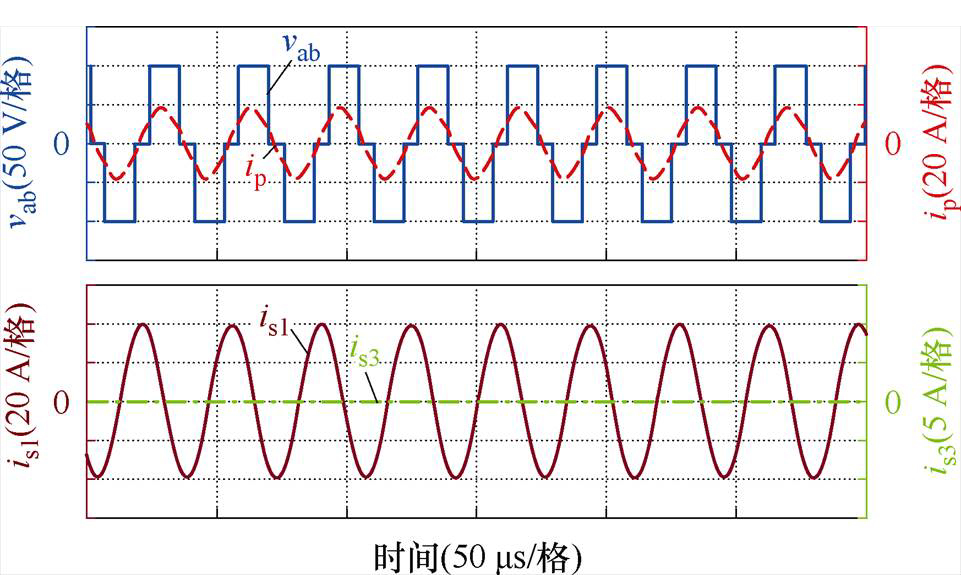
图14 移相角a=60°时，基于辅助拾取模块的ICPT系统的仿真波形
Fig.14 Simulation waveforms of the ICPT system with auxiliary pickup module when phase-shift angleis 60°
仿真情况下，移相角a=0°时，传统ICPT系统、基于辅助拾取模块的ICPT系统与移相角a=60°时，基于辅助拾取模块的ICPT系统的逆变器输出电流的谐波比较如图15所示。
由图15可知，相比于传统ICPT系统，基于辅助拾取模块的ICPT系统的逆变器输出电流的3次谐波幅值明显降低。同时，当移相角a=60°时，3次电流谐波幅值为0，与图3和图5的分析一致。经过计算，传统ICPT系统的逆变器的输出电流的THD= 20.96%，基于辅助拾取模块的ICPT系统的逆变器的输出电流的THD仅为8.39%，降低了12.57%；移相角a=60°时，基于辅助拾取模块的ICPT系统的逆变器输出电流的THD=7.6%。
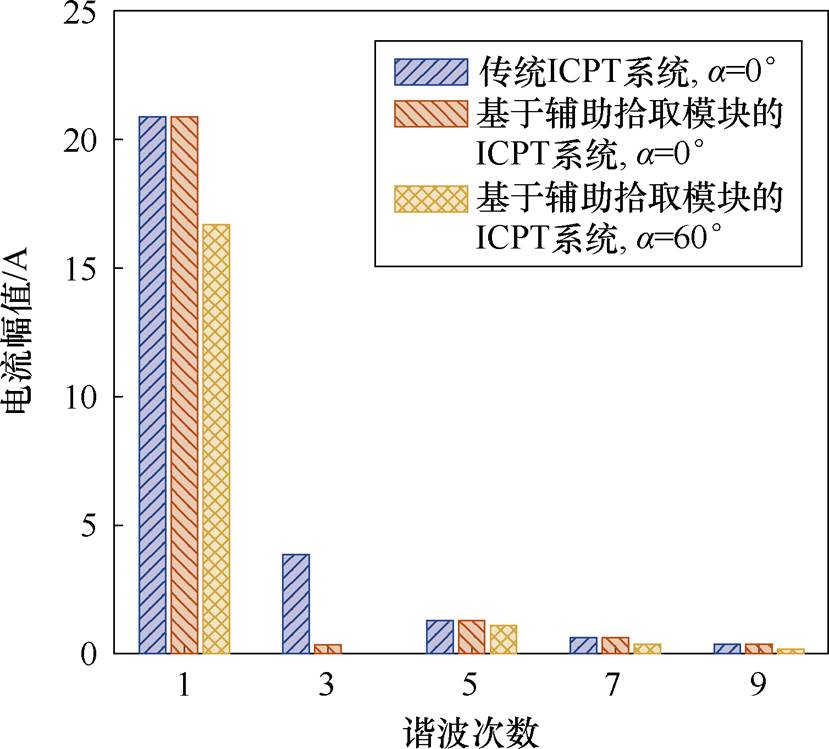
图15 仿真下逆变器输出电流谐波比较
Fig.15 Comparison of the output current harmonics of the inverter under simulation
搭建的ICPT系统实验平台如图16所示。以型号为FF 200R12KT4的IGBT作为功率开关器件，高频逆变器以DSP TMS320F28335和FPGA XC3S400- 4PQ208I作为主控芯片。主拾取模块额定功率Pn= 7.5 kW。
图16 ICPT系统实验平台
Fig.16 Prototype of the ICPT system
当移相角a=0°时，传统ICPT系统与基于辅助拾取模块的ICPT系统的实验波形分别如图17a和图17b所示。
由图17可知，辅助拾取模块的电流频率为主拾取模块电流的3倍，有效地提高了高频逆变器输出电流的正弦度。
当移相角a=60°时，基于辅助拾取模块的ICPT系统的实验波形如图18所示。由图可知，辅助拾取模块的电流显著降低。
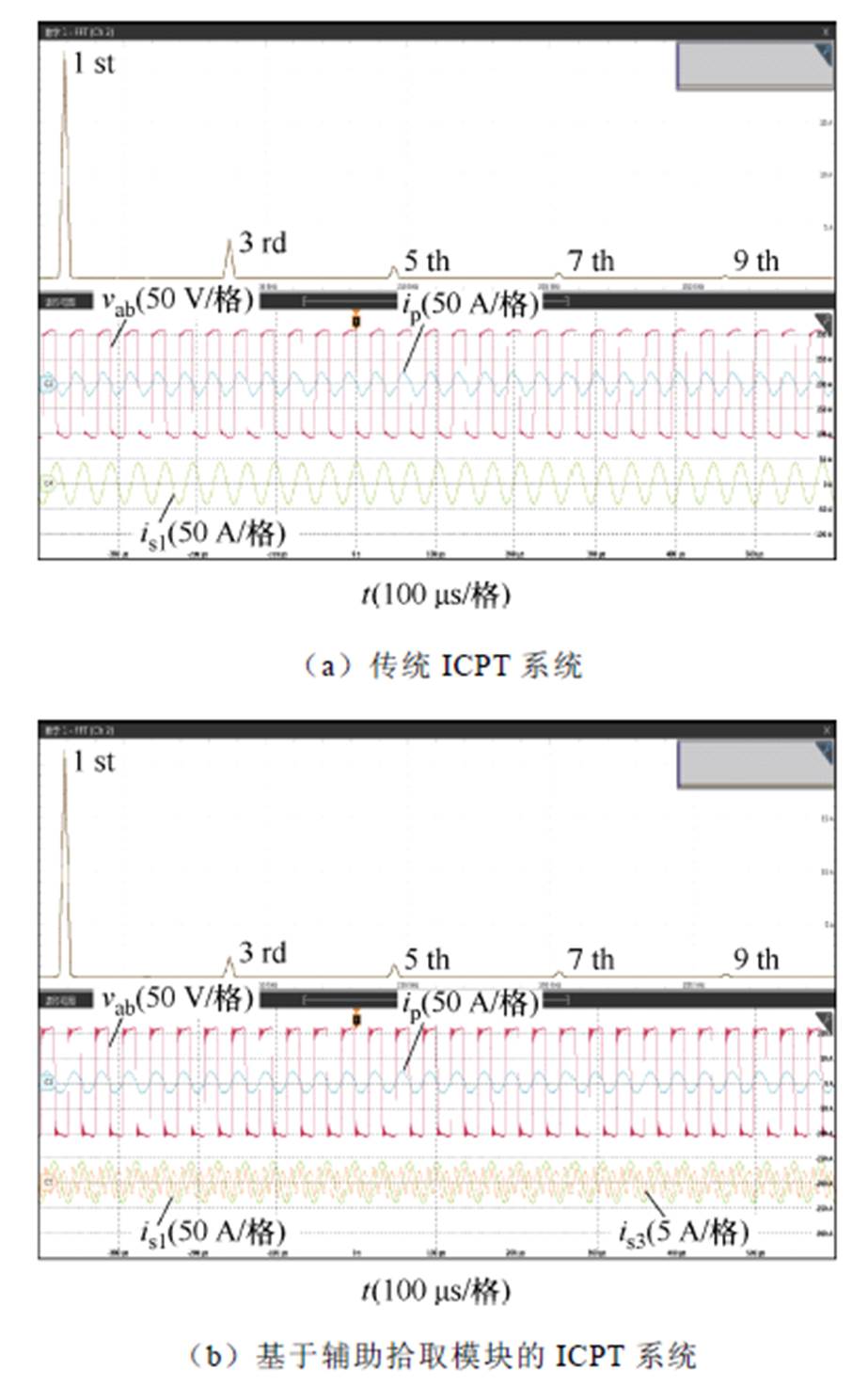
图17 移相角a=0°时，ICPT系统的实验波形
Fig.17 Experimental waveforms of the ICPT system when phase-shift angleis 0°
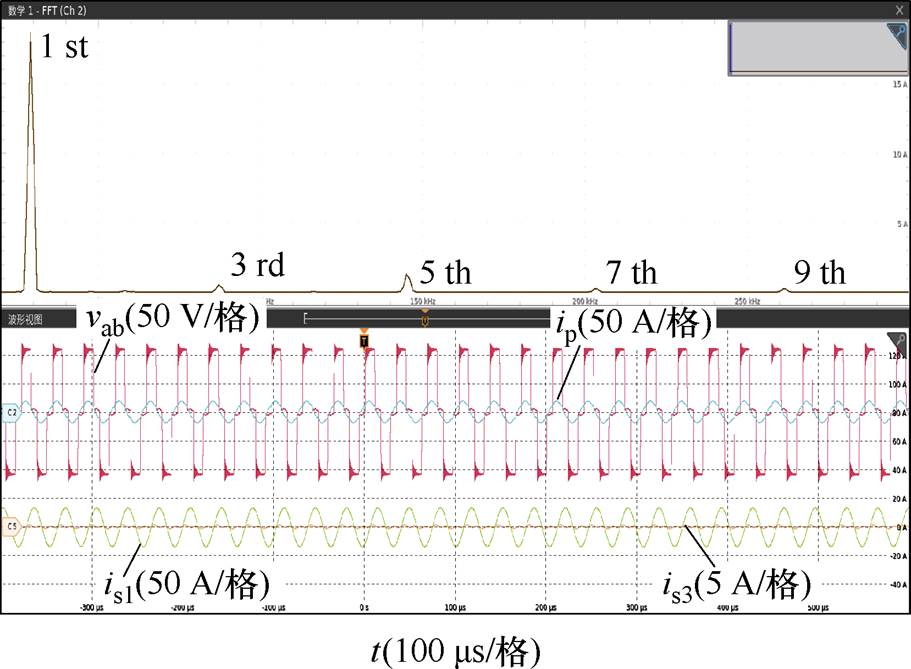
图18 移相角a=60°时，基于辅助拾取模块的ICPT系统的实验波形
Fig.18 Experimental waveforms of the ICPT system with auxiliary pickup module when phase-shift angleis 60°
实验情况下，移相角a=0°时，传统ICPT系统、基于辅助拾取模块的ICPT系统与移相角a=60°时，基于辅助拾取模块的ICPT系统的逆变器输出电流的谐波比较如图19所示。
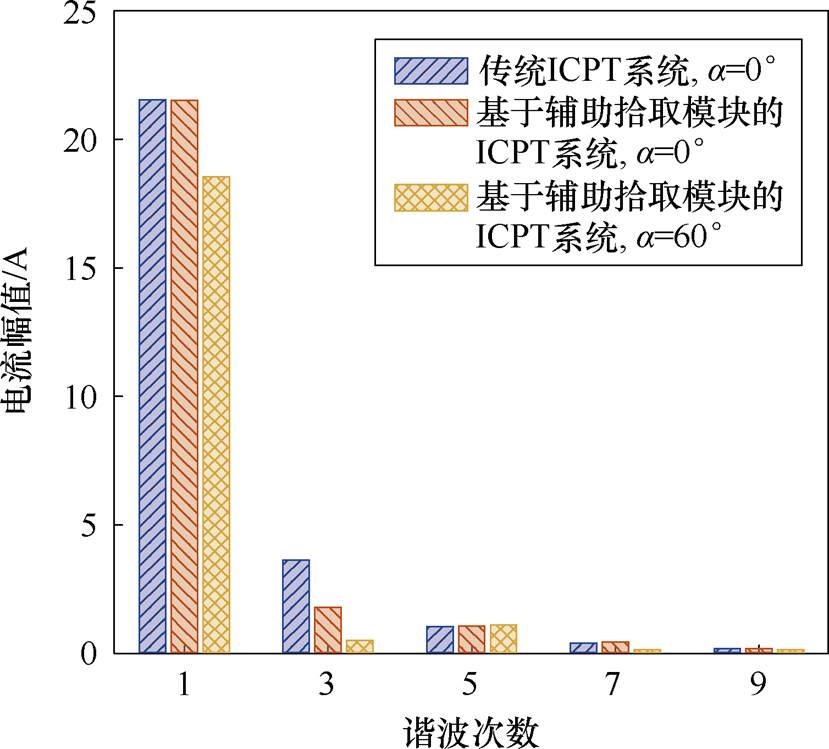
图19 实验下逆变器输出电流谐波比较
Fig.19 Comparison of the output current harmonics of the inverter under experiment
由图19可知，基于辅助拾取模块的ICPT系统逆变器输出电流的3次谐波幅值明显降低。经过计算，传统ICPT系统的逆变器的输出电流的THD= 19.56%，基于辅助拾取模块的ICPT系统的逆变器的输出电流的THD=10.65%，降低了8.91%；移相角a=60°时，基于辅助拾取模块的ICPT系统的逆变器输出电流的THD=7.72%。
相比于传统ICPT系统，基于辅助拾取模块的ICPT系统高频逆变器的输出电流的3次谐波幅值与THD明显降低，验证了理论分析的正确性和本文提出方法的有效性。
基于实验室的ICPT系统实验平台，得到不同功率下，传统ICPT系统与基于辅助拾取模块的ICPT系统的效率对比如图20所示。由图可知，基于辅助拾取模块的ICPT系统的效率与传统ICPT系统的效率基本一致，轻载工况下，系统效率最高提升了0.52%。
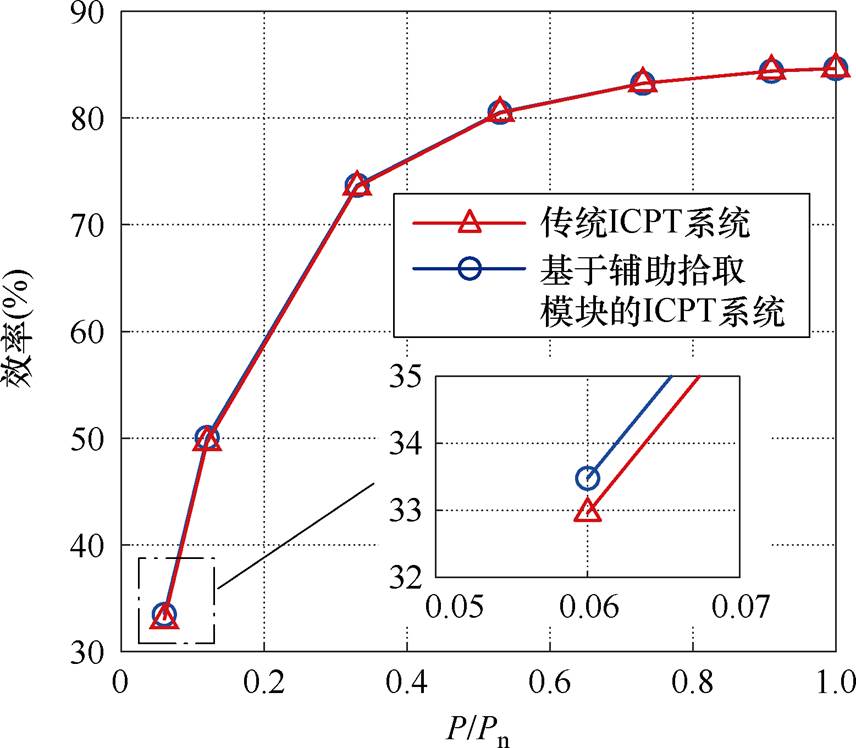
图20 系统效率比较
Fig.20 Comparison of the system efficiency
为抑制高频逆变器的输出电流谐波，本文提出一种基于辅助拾取模块的电流谐波抑制方法。通过将辅助拾取模块的谐振频率设计为基波频率的3、5、7或2k+1倍，并合理设计辅助拾取模块的品质因数，就可以有效降低相应阶次的电流谐波幅值以及高频逆变器输出电流的THD。以抑制3次电流谐波为例进行理论分析、仿真和实验验证，得到以下结论：
1）原边侧品质因数Qp减小或主拾取模块的品质因数Qs1增加时，3次电流谐波含量增加，高频逆变器输出电流畸变率增加；反之，3次电流谐波含量降低。
2）相比于传统ICPT系统，基于辅助拾取模块的ICPT系统高频逆变器输出电流的3次谐波幅值和THD显著降低，并且系统效率基本保持不变。仿真和实验情况下，THD分别降低了12.57%和8.91%，轻载工况下，系统效率提高了0.52%。
3）本文提出的方法简单，工程造价较低，并且不会限制系统的功率调节范围。
参考文献
[1] Zhang Yiming, Chen Kainan, He Fanbo, et al. Closed- form oriented modeling and analysis of wireless power transfer system with constant-voltage source and load[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3472-3481.
[2] 荣灿灿, 严俐慧, 路聪慧, 等. 基于超材料与超表面的无线电能传输技术研究现状与进展综述[J]. 电工技术学报, 2023, 38(20): 5369-5384.
Rong Cancan, Yan Lihui, Lu Conghui, et al. Overview on research status and progress of wireless power transfer technology based on metamaterials and metasurfaces[J]. Transactions of China Electro- technical Society, 2023, 38(20): 5369-5384.
[3] Du Sijun, Chan E K, Wen Bing, et al. Wireless power transfer using oscillating magnets[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(8): 6259- 6269.
[4] 陈伟华, 刘宗旺, 李政兴, 等. 谐振式无线供能心脏起搏器多线圈无功屏蔽研究[J]. 电工技术学报, 2022, 37(11): 2673-2685.
Chen Weihua, Liu Zongwang, Li Zhengxing, et al. Research on multi coil reactive shielding of resonant wireless energy supply cardiac pacemaker[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(11): 2673-2685.
[5] 杨云虎, 贾维娜, 梁大壮, 等. LCC-LCC/S自切换恒流-恒压复合型无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4823-4837, 4852.
Yang Yunhu, Jia Weina, Liang Dazhuang, et al. A self-switching wireless power transfer system based on hybrid topology of LCC-LCC/S with constant current and constant voltage[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4823-4837, 4852.
[6] 陈凯楠, 蒋烨, 檀添, 等. 轨道交通350kW大功率无线电能传输系统研究[J]. 电工技术学报, 2022, 37(10): 2411-2421, 2445.
Chen Kainan, Jiang Ye, Tan Tian, et al. Research on 350kW high power wireless power transfer system for rail transit[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2411-2421, 2445.
[7] Mai Jianwei, Zeng Xianrui, Yao Yousu, et al. Impedance analysis and design of IPT system to improve system efficiency and reduce output voltage or current fluctuations[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14029-14038.
[8] Lee S, Jeong S, Hong S, et al. Design and analysis of EMI shielding method using intermediate coil for train WPT system[C]//2018 IEEE Wireless Power Transfer Conference (WPTC), Montreal, QC, Canada, 2018: 1-4.
[9] Shi Lixin, Rodriguezt J C, Alou P. Modeling and analysis of total harmonic distortion in series-series wireless power transfer system for 6.78 MHz[C]// 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2020: 1016- 1020.
[10] Yao Yousu, Wang Yijie, Liu Xiaosheng, et al. A novel parameter tuning method for a double-sided LCL compensated WPT system with better com- prehensive performance[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8525-8536.
[11] Bauer M, Becker P, Zheng Q. Inductive power supply for the transrapid[C]//Maglev: International Conference on Magnetically Levitated System & Linear Drives, Dresden, Germany, 2006.
[12] Kim J H, Lee B S, Lee J H, et al. Development of 1-MW inductive power transfer system for a high- speed train[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6242-6250.
[13] Shi Liming, Yin Zhenggang, Jiang Longbin, et al. Advances in inductively coupled power transfer technology for rail transit[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(4): 383- 396.
[14] Zhang Jianzhong, Zhao Jin, Zhang Yaqian, et al. A wireless power transfer system with dual switch- controlled capacitors for efficiency optimization[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6091-6101.
[15] Xia Chenyang, Chen Rui, Liu Yuling, et al. Inhibition of current harmonics in LCL/LCC wireless power transfer system[C]//2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 2017: 1-6.
[16] Hao Hao, Covic G A, Boys J T. A parallel topology for inductive power transfer power supplies[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1140-1151.
[17] 李勇, 麦瑞坤, 陆立文, 等. 一种采用级联型多电平技术的IPT系统谐波消除与功率调节方法[J]. 中国电机工程学报, 2015, 35(20): 5278-5285.
Li Yong, Mai Ruikun, Lu Liwen, et al. A harmonic elimination and power regulation approach of a cascaded multilevel technology in IPT systems[J]. Proceedings of the CSEE, 2015, 35(20): 5278-5285.
[18] 范满义, 史黎明, 殷正刚, 等. 感应电能传输系统基于阶梯波合成技术的谐波消除和脉冲密度功率调节方法[J]. 中国电机工程学报, 2017, 37(22): 6516-6523, 6763.
Fan Manyi, Shi Liming, Yin Zhenggang, et al. Harmonic elimination and power regulation with pulse density modulation based on staircase waveform for multilevel inverters in inductive power transfer system[J]. Proceedings of the CSEE, 2017, 37(22): 6516-6523, 6763.
[19] Lee S S. Single-stage switched-capacitor module (S3CM) topology for cascaded multilevel inverter[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8204-8207.
[20] Li Jianting, Wang Puyu, Li Jianke, et al. A resonant modular multilevel rectifier for secondary control in inductive power transfer[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 1391-1397.
[21] Cochran S, Zhao Chongwen, Costinett D. Multilevel switched-capacitor AC-DC step-down rectifier for wireless charging with reduced conduction loss and harmonic content[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 8669-8681.
[22] Shin J, Shin S, Kim Y, et al. Design and imple- mentation of shaped magnetic-resonance-based wireless power transfer system for roadway-powered moving electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3): 1179-1192.
[23] Cai Hua, Shi Liming, Li Yaohua. Harmonic-based phase-shifted control of inductively coupled power transfer[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 594-602.
[24] 周玮, 蓝嘉豪, 麦瑞坤, 等. 无线充电电动汽车V2G模式下光储直流微电网能量管理策略[J]. 电工技术学报, 2022, 37(1): 82-91.
Zhou Wei, Lan Jiahao, Mai Ruikun, et al. Research on power management strategy of DC microgrid with photovoltaic, energy storage and EV-wireless power transfer in V2G mode[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 82-91.
[25] Gao Tian, Cheng Ze, Wang Qi, et al. The analysis of dead time’s influence on the operating characteristics of LLC resonant converter[C]//2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 2019: 85-89.
[26] RamRakhyani A K, Mirabbasi S, Mu Chiao. Design and optimization of resonance-based efficient wireless power delivery systems for biomedical implants[J]. IEEE Transactions on Biomedical Circuits and Systems, 2011, 5(1): 48-63.
[27] Mai Jianwei, Wang Yijie, Zeng Xianrui, et al. A multi-segment compensation method for improving power density of long-distance IPT system[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12795-12806.
[28] Mai Jianwei, Zeng Xianrui, Yao Yousu, et al. Improved winding and compensation methods for the multilayer coil in IPT system[J]. IEEE Transactions on Industrial Electronics, 2022, 69(5): 5375-5380.
Abstract Due to convenience, safety, and aesthetics,inductively coupled power transfer (ICPT) systems have been applied in various applications. However, the output current harmonics of the high-frequency inverter in the ICPT system can cause the switch’s operation and circuit control problems, increasing the additional core loss in coils. Therefore, it is important to suppress the current harmonics. As an example, the 3rd current harmonic is analyzed in detail.
Firstly, the mathematical model of the ICPT system is established based on the S-S compensation circuit. The mechanism of current harmonics generation and the factors affecting the amplitude of current harmonics are analyzed. Due to the square wave output voltage and the existence of dead time, the output current contains a large number of harmonics. A significant distortion of the output current of the high-frequency inverter will be caused under light load conditions.
Then, a current harmonic suppression method for ICPT system based on auxiliary pickup module is proposed to suppress the output current harmonics of the high-frequency inverter. The natural resonant frequency of the auxiliary pickup module is set to three times the fundamental frequency, and the feasibility of suppressing the 3rd current harmonic is demonstrated through theoretical analysis. Furthermore, the quality factor of the auxiliary pickup module is designed to avoid cross interference between pickup coils, thereby not affecting the power transmission of the ICPT system.
Finally, simulation and experimental results verify the theoretical analysis and the proposed method. The amplitude of the 3rd current harmonic and the total harmonic distortion (THD) are reduced. Compared with the traditional ICPT system, the system efficiency is improved effectively under light load conditions.
The following conclusions can be drawn. (1) When the quality factor Qp of the primary side decreases or the quality factor Qs1 increases, the amplitude of the 3rd current harmonic increases, leading to an increase in the THD of the output current. Conversely, the amplitude of the 3rd current harmonic decreases. (2) In the ICPT system based on the auxiliary pickup module, the amplitude of the 3rd current harmonic and THD of the output current of the high-frequency inverter are significantly reduced, and the system efficiency remains almost unchanged. THD decreased by 12.57% and 8.46% in simulation and experiment. Under light load conditions, the system efficiency increased by 0.52%. (3) The proposed method is simple and cost-effective without power adjustment range limitation.
keywords：Inductively coupled power transfer, auxiliary pickup module, current harmonic suppression, quality factor
中图分类号：TM614
DOI: 10.19595/j.cnki.1000-6753.tces.240183
国家重点研发计划项目（2016YFB1200601-B21）和国家自然科学基金项目（52372367）资助。
收稿日期2024-01-26
改稿日期2024-03-19
杨继鑫 男，1995年生，博士研究生，研究方向为轨道交通非接触供电技术及大功率变流器等。E-mail: jixiny@mail.iee.ac.cn
史黎明 男，1964年生，研究员，博士生导师，研究方向为特种电机和驱动控制、新型轨道交通牵引供电、无线电能传输技术等。E-mail: limings@mail.iee.ac.cn（通信作者）
（编辑 崔文静）