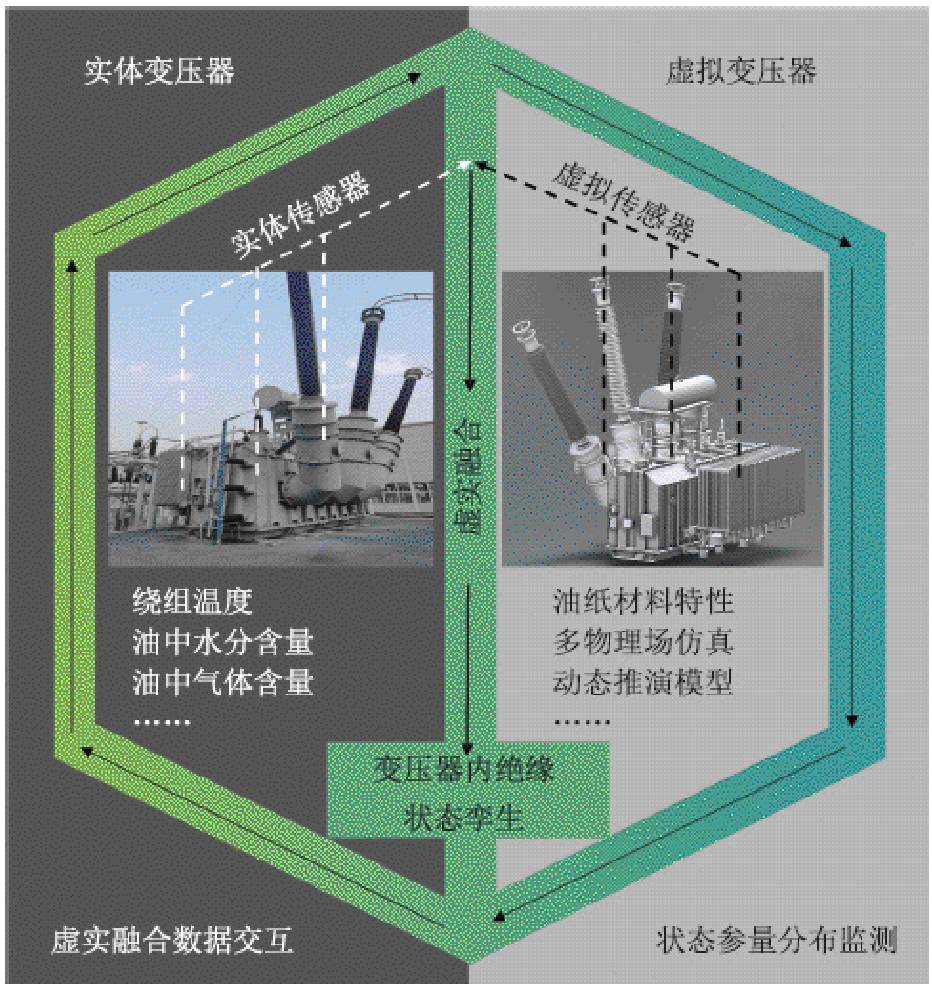
图1 虚实融合的变压器内绝缘状态孪生概念
Fig.1 Concept of transformer internal insulation state twinning by virtual-real fusion
摘要 发展数字孪生变压器对支撑高端电力装备智能化、数字化、可视化运维具有重要意义。然而，由于目前变压器缺乏相应的数字孪生能力，实现变压器的数字孪生还面临巨大挑战。为此，该文开展了虚实融合的变压器内绝缘状态孪生方法研究。首先计算了温度场和水分分布；然后建立了改进水分平移因子的聚合度分布动态推演模型；最后通过Delaunay三角网实现了任意时刻聚合度分布的可视化。结果表明，水分分布主要集中在纸板和底部固体绝缘处，第48年含水量最高值约为3.2%；聚合度分布规律与CIGRE报告基本相符，最低值位于低压绕组热点温度区域，第48年为252.15，验证了该方法的有效性和合理性。该文可实现变压器内绝缘老化状态参量分布评估，为后续全面构建变压器数字孪生体奠定了基础。
关键词：虚实融合 变压器 数字孪生 状态参量 分布监测
“十四五”发展规划要求电力企业进行数智化转型以支撑新型电力系统建设，而数字孪生变压器是实现电网数字化在设备层面的重要保证[1-2]。数字孪生技术是数字化转型的关键技术之一，是指现实空间全要素在数字虚拟空间中全面、准确的映射，在航空航天、建筑建设、城市管理、健康医疗等领域已有成熟应用[3-4]。一般地，构建数字孪生体需要海量高精度、高可靠的分布式传感器，但对于变压器等电力装备而言，由于其内部结构复杂、存在强电磁场、传感器安装困难、特征参量形成的机理不明等因素，导致其数字孪生化进程很慢，还面临许多挑战[5-6]。
目前现场运行变压器的传感措施明显不足，几乎所有实体传感器都安装在箱体外部，内部分布式传感器极少。例如，温度大多采用光纤传感器、溶解气体采用油色谱技术，其监测的都是物理量的平均值或总量，难以准确获取其分布规律[7-8]。变压器其他运行状态参量，如内部固体绝缘的水分、聚合度等参量的分布规律更是无法监测。这是由于绝缘纸的获取需要吊心取纸，过程繁琐，且实际运行中受温度、水分影响不均匀，测量部位没有代表性，也无法安装实体传感器进行监测[9-10]。因此，电力装备领域的现有传感器不足是导致变压器数字孪生进程缓慢的核心原因。
随着国内外电力行业数字化转型，Siemens公司初步建立数字孪生系统并仿真了变压器的温度、应力变化等，用于优化控制变压器的性能和寿命消耗[11]。ABB公司开发了第一台数字化变压器，实现了多个在线监测参量的交互分析和冷却系统的智能控制，延长了绝缘使用寿命[12]。Efacec与MIT联合开展了新一代数字孪生变压器研究，初步实现了变压器的状态评估、多场仿真和可视化建模[13]。此外，Ansys发布了Ansys Twin Builder，用于构建、验证和部署基于仿真模拟的数字孪生体[14]。由此看来，现有变压器数字孪生工作已基本完成了数字孪生的形似部分（多物理场仿真和展示），但如何实现数字孪生的神似部分（性能可视化评估+辅助运维），获得更多状态参量的传感数据以构建具有生命力的数字孪生体还有待深入研究。
为此，本文参考航空航天领域结合虚实传感以丰富传感数据的思想[15]，根据虚拟仿真可有效弥补现场实体传感器不足的痛点问题，增加传感器的种类和数量，提出了虚实融合的变压器内绝缘状态孪生概念，以内绝缘老化寿命最为关心的参量为例开展计算研究，如图1所示。首先，根据变压器内部油纸绝缘材料的多场耦合特性和有限元仿真获得内部稳态的温度场分布；其次，考虑温度分布影响，结合实体油中水分传感数据建立固体绝缘中水分分布推演模型；然后，改进水分平移因子建立时间-温度-水分分布联合老化作用的聚合度分布动态推演模型以计算任意时刻变压器内部的聚合度分布；最后，考虑到推演计算获得的水分、聚合度分布数据是离散的，采用Delaunay三角网来实现变压器内部聚合度分布的可视化。该工作融合虚实传感数据实现了变压器内部水分、聚合度等老化状态参量的分布式监测，大幅提升了运维效率，为支撑数字孪生变压器的智能辅助运维提供了新的解决方案。
图1 虚实融合的变压器内绝缘状态孪生概念
Fig.1 Concept of transformer internal insulation state twinning by virtual-real fusion
在变压器设计、分析及数字化领域，已经实现了变压器的多物理场优化设计、内部三维结构的高精度建模以及内部多物理场的高保真耦合仿真。但与变压器运行相关的老化状态参量如水分、聚合度分布却是无法直接通过仿真获得的，这需要正确认识和深入理解设备中各类材料在不同物理场下的响应特征和性能演化规律，并针对不同的参数类型和预测需求，选择合适的数学物理模型对材料、部件及装备的各种特性进行描述和预测。针对该痛点问题，本文提出了虚实融合的变压器内绝缘状态孪生方法，其整体逻辑和实现框架如图2所示。
由图2可知，本文提出的虚实融合的变压器内绝缘状态孪生方法实现框架具体分为建模仿真层、虚实传感层、数据交互层、可靠验证层、状态评估层。
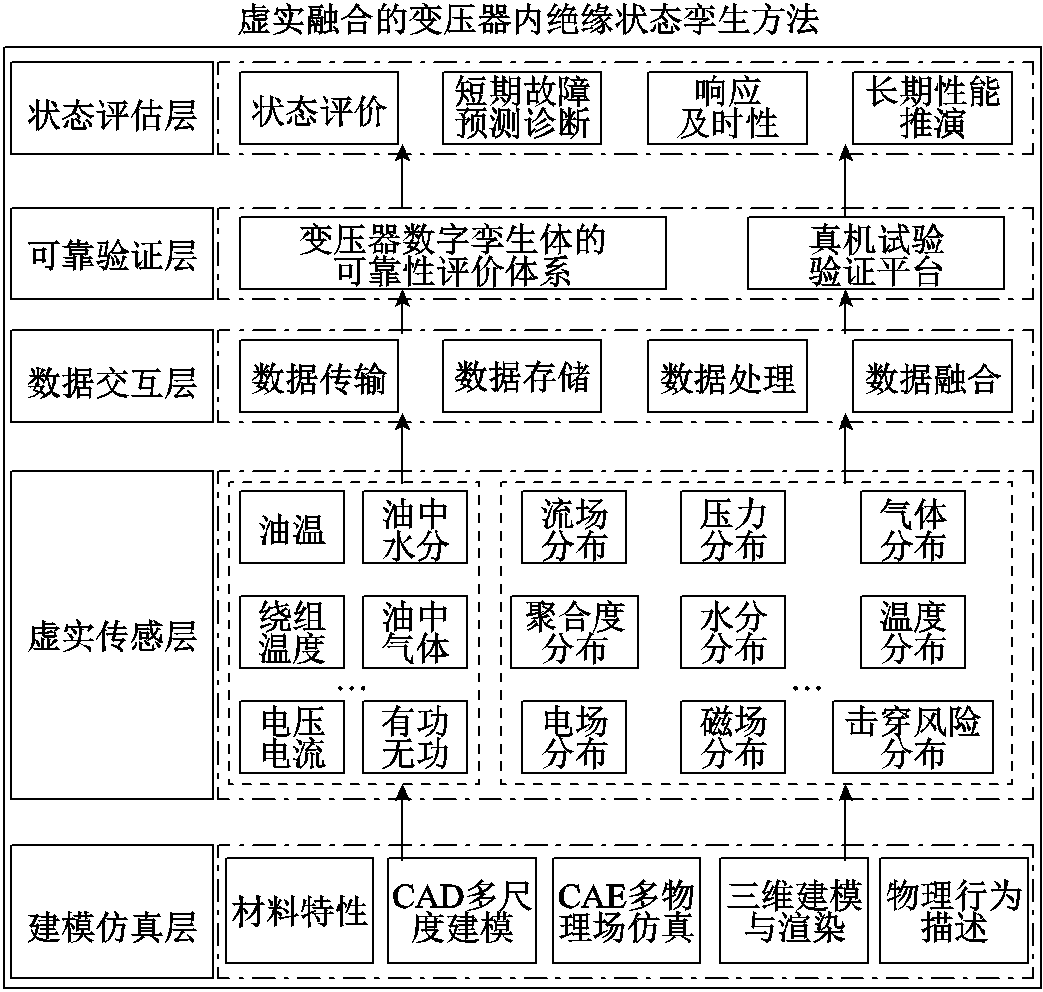
图2 虚实融合的变压器内绝缘状态孪生方法实现框架
Fig.2 A framework for realizing the state twinning method for transformer internal insulation by virtual-real fusion
1）建模仿真层：该层以CAD和CAE软件为基础，基于变压器内部不同材料的非线性特性进行建模和仿真以获得多物理场的计算结果。
2）虚实传感层：该层是在实体感知层的基础上结合有限元仿真和运行状态参量的动态推演模型，实现了变压器内部无法实体传感监测但却对实际运维过程极其重要的状态参量（如水分、聚合度、气体分布等）。
3）数据交互层：该层主要完成数据融合的协同分析，实现不同数据间的融合、处理、传输和存储。
4）可靠验证层：该层为针对虚实融合计算结果的准确性而设定，主要是搭建真型样机试验平台进行运行状态参量分布的验证，同时也为建立一套变压器数字孪生体的可靠性评价体系作支撑。
5）状态评估层：与传统的离线或在线式评估不同，虚实融合的变压器内绝缘状态孪生方法的关键是对设备短期运行性能与长期性能突变过程的准确建模与反演，是具有“生命力”的数字孪生体评估。
根据总的逻辑和实现框架，具体地，虚实融合的变压器内绝缘老化状态参量孪生实现步骤如图3所示。
1）计算温度场分布。基于CAD建模变压器内部结构，将在线监测的传感数据作为输入，借助CAE软件实现多物理场耦合下的稳态温度场分布。
2）计算水分分布。考虑温度分布不均匀的影响获得水分产生、扩散到平衡的数值模型，然后将油中含水量作为输入建立随时间-温度变化的水分分布动态推演模型。
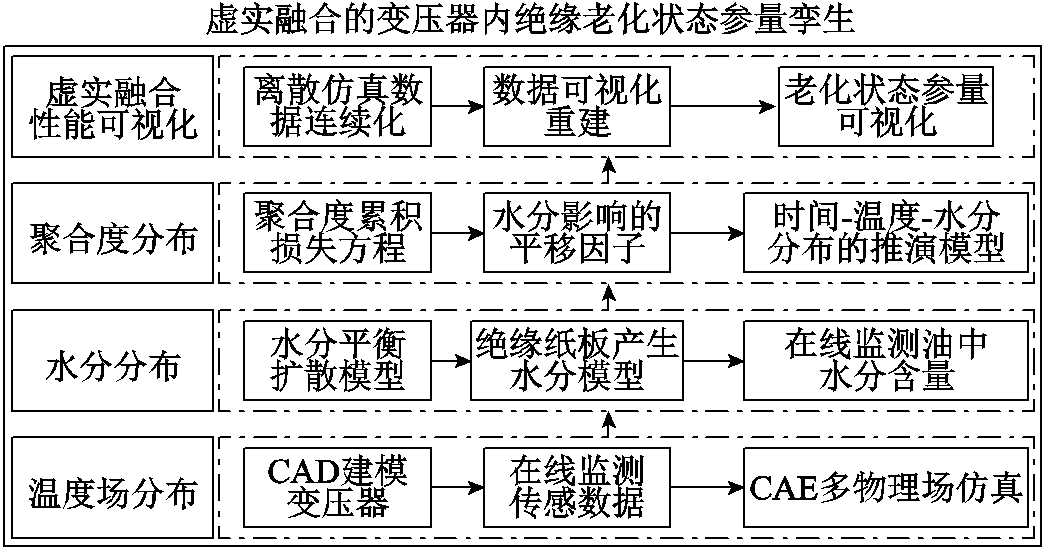
图3 虚实融合的变压器内绝缘状态孪生方法具体步骤
Fig.3 Specific steps of the state twinning method for transformer internal insulation by virtual-real fusion
3）计算聚合度分布。针对水分分布不均匀改进水分平移因子，借助聚合度累积损失动力学方程建立时间-温度-水分分布的聚合度分布动态推演模型。
4）虚实融合实现老化状态参量的可视化。由于CAE软件仿真计算和动态推演获得的水分分布和聚合度分布数据是离散性数据，无法精准孪生可视化，本文采用Delaunay三角网对老化状态参量数据进行可视化重建，实现数字孪生变压器老化状态参量的可视化展示。
变压器内部温度场分布是计算老化状态参量分布的数据基础，准确的温度场分布计算需要考虑变压器复杂的运行环境，即内部电磁场、温度场、流场等多物理场的耦合作用。本文将计算的损耗作为温度场仿真的热源对温度场和流场进行耦合计算。根据现场监测的负载率求解实时负载变化对应的温度场分布，该部分研究内容已有较多报道[16-17]，不再详细说明，本文重点阐述水分分布的计算。目前现场运维对变压器固体绝缘含水量尚无分布式检测手段和感知方法，仅依靠现有的物理传感信息，尚无法实现对变压器内不同部位水分分布的实时监测。因此，研究虚实融合的变压器内绝缘状态孪生方法，能够突破目前物理传感器无法监测部分关键特征参量的技术瓶颈。
首先，根据现场多台变压器纸中总的含水量与运行时间的关系建立经验公式；其次，结合温度场的分布和油中水分监测数据分析变压器内部各个局部位置的纸中水分分布规律；最后，假设变压器油中水分是均匀的，采用油纸平衡方程和水分扩散定律确定其含量及分布。
通过大量统计数据，建立现场变压器运行年限与固体绝缘含水量的经验表达式，用于实现不同负载下不同时刻的变压器内部固体绝缘的含水量及分布[18]。建立的经验公式为
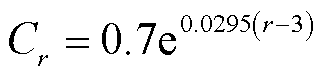（1）
式中，r为变压器运行年限；Cr为第r年的变压器内部固体绝缘总含水量。
值得注意的是，油纸水分平衡方程仅适用于稳态情况，而本文计算变压器内部温度场分布虽然不均匀，但各个局部位置的温度变化并不大，可以认为各个局部位置是处于稳态的。因此，通过水分平衡方程即可获得绝缘纸边界的饱和水分，并通过扩散定律确定其稳态下的分布情况。根据油纸水分平衡曲线[19]，计算相关参数为
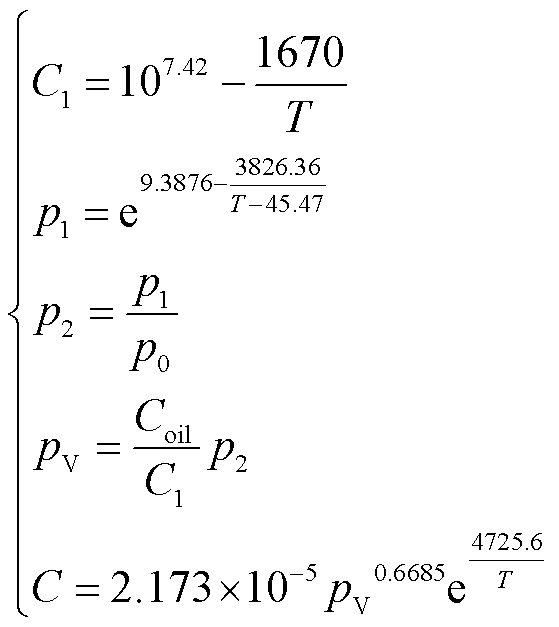（2）
式中，C1为饱和条件下的含水量（10-4%）；p1为饱和条件下的水蒸气分压，MPa；p2为该条件下的标准气压；p0为1个标准大气压，MPa；pV为当前条件下的水蒸气分压；Coil为当前条件下的油中含水量（10-4%）；C为各个局部位置对应温度T（K）的纸中饱和含水量（%）。当获得边界的饱和含水量后，根据Fick扩散定律[20]，局部位置水分沿着纸板扩散，其扩散相关参数计算为
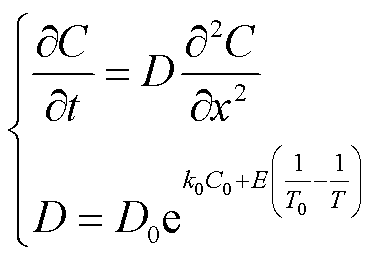（3）
式中，t为时间，s；x为沿厚度l方向上的距离，m；D为水分扩散系数，m2/s；D0为水分扩散系数初值，通常取值为1.34´10-13 m2/s；k0为系数，取值0.5；C0为初始含水量（%）；E为常数，取值为8 074；T0为常温，取值为298 K。当局部位置的水分沿着纸板一侧扩散时，存在水分边界条件为
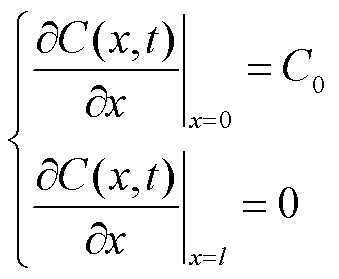（4）
联立式（3）和式（4）可得任意位置、任意时刻的绝缘纸含水量为
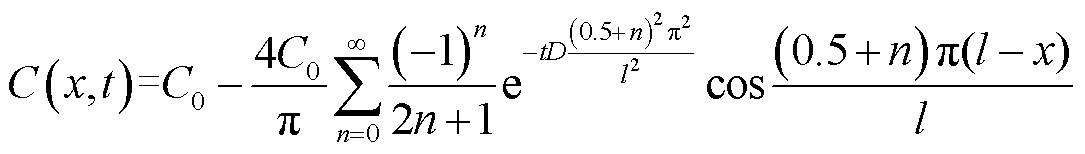（5）
考虑不同影响因素的老化特征参量-聚合度计算已有大量研究，但考虑温度-水分分布影响的固体绝缘聚合度分布推演还鲜有报道。准确地计算聚合度分布对了解变压器内部老化薄弱点和运行寿命有重要参考价值。关于变压器内部纤维素聚合度累积损失的动力学方程[21]为
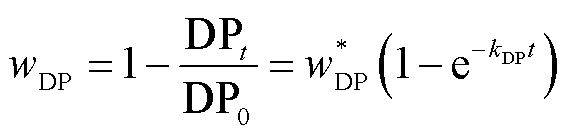（6）
式中，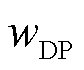
为聚合度的累积损失率；DPt为t时刻的聚合度；DP0为初始聚合度，取值为1 200；
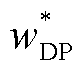为聚合度降解储蓄的能力；kDP为纤维素聚合度的降解速率。结合时温叠加的原理，获得的温度平移因子αT为
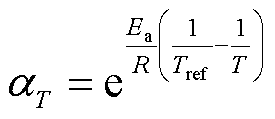（7）
式中，Ea为活化能，在参考温度Tref=363.15 K时取值为91.4 kJ/mol；R为气体常数，R=8.314 J/(mol·K)。考虑含水量及其分布时，文献[21]中的计算会导致考虑温度和水分分布影响的聚合度推演结果反而高于仅考虑温度的情况，这显然与水分会加速纤维素老化的定论不符。因此，本文考虑固体绝缘水分分布的实际情况对水分平移因子进行重新推导和拟合。文献[22]指出水分对活化能影响显著，随着含水量的增加，活化能也逐渐增加，存在较好的线性关系。本文设绝缘纸受水分作用时增加的活化能为γC，则因水分作用而变化的活化能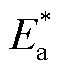
更新为
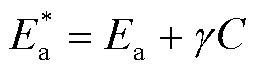（8）
式中，γ为体积量纲的常数。根据反应速度理论，化学反应速率k遵循的Arrhenius方程变为
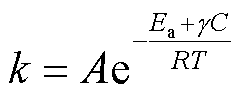（9）
式中，A为指前因子。时间-水分平移因子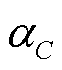
应满足
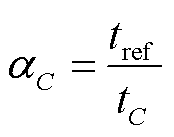（10）
式中，tC为含水量C下拟合曲线上某个数据点对应的时间；tref为拟合曲线经过水平移动后该数据点在主曲线上对应的时间。联立式（8）～式（10）可得
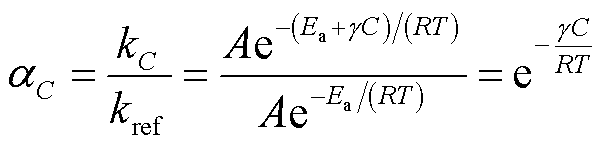（11）
式中，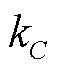
为含水量C下的化学反应速率；
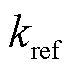为参考水分下的化学反应速率。
从推导结果可看出，时间-水分平移因子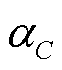与含水量C呈指数关系。结合数据根据式（11）将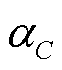与C进行曲线拟合，如图4所示，拟合参数γ= -1 096.112 5，拟合优度为96.44%。
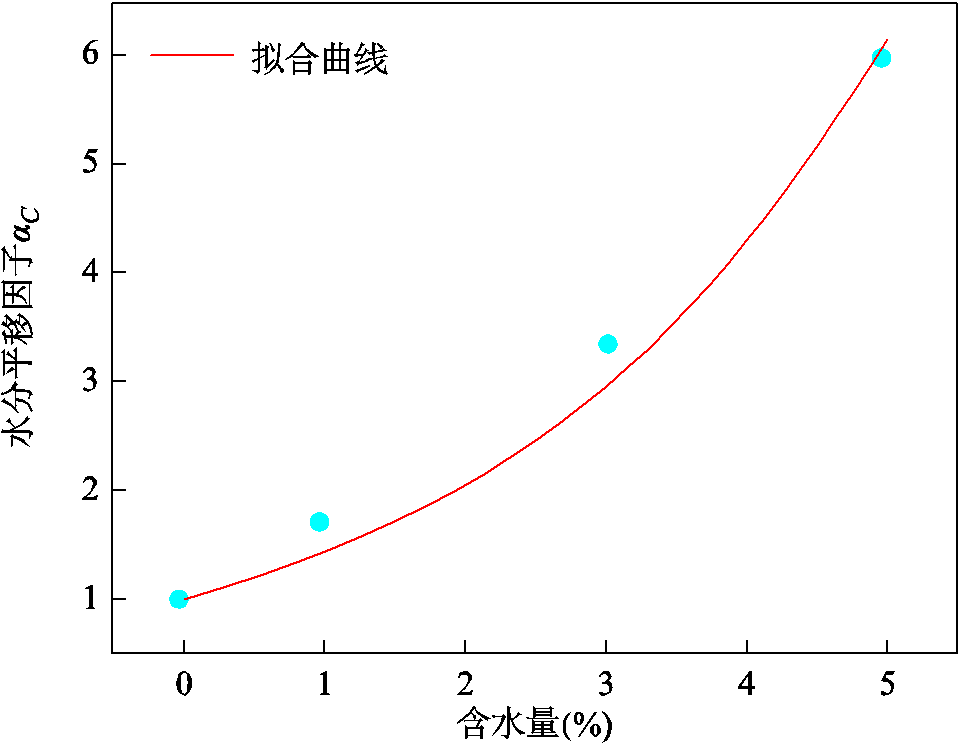
图4 水分平移因子与含水量的拟合关系
Fig.4 Fitting curve of moisture translational factor and moisture content
此外，文献[22]证明了参数wDP和kDP受水分影响较大，会随着水分的增加而增加，其拟合方程为
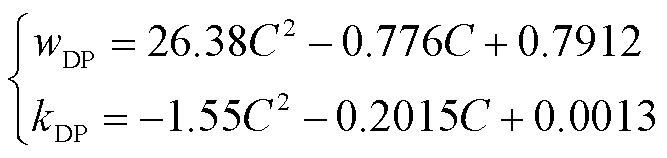（12）
因此，同时考虑时间-温度-水分分布联合老化作用，获得动态推演方程为
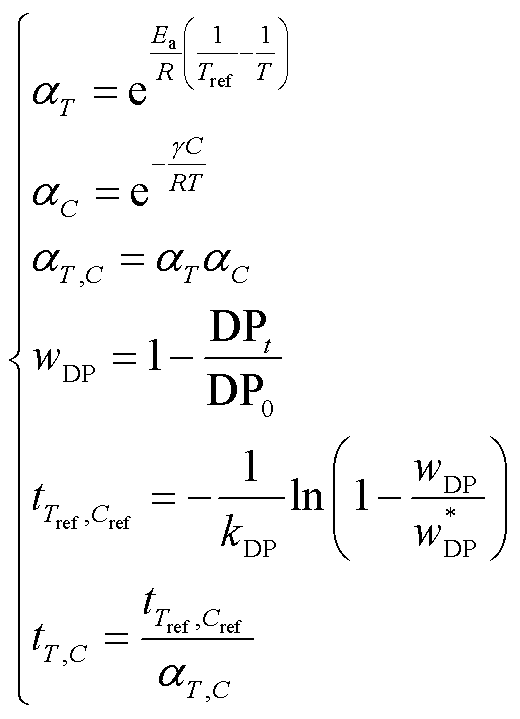（13）
式中，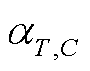
为水分和温度平移因子的乘积；
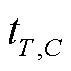为任意温度、水分下聚合度下降至
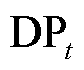的时间；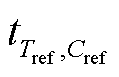
为参考温度和水分下对应的时间。
最后，计算任意时刻下不同温度、水分分布联合老化作用的聚合度分布表达式为
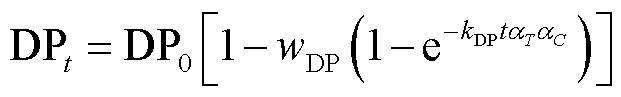（14）
需要指出的是，由于绝缘纸不可能达到完全降解的状态，存在一个极限聚合度DPLodp，本文在负载率为0.74（热点温度为61.29℃、含水量最低为0.18%）的初始条件下计算的DPLodp=DP0(1-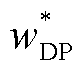)=252.15。
由于变压器仿真计算结果和动态推演结果属于离散点数据，其曲面拟合过程操作复杂、效率低、视化效果模糊，无法精准识别变压器内部具体局部位置。因此还需将推演老化状态参量的离散数据进行可视化重建以满足数字孪生变压器对可视化展示的需求。
本文基于最优的Delaunay三角网，采用逐点插入法将离散点生成连续或光滑的曲面[23]。Delaunay三角网逐点插入算法构网步骤主要分为三步。
1）离散数据点的管理
先对所有推演参量的离散点数据进行统计，获得点集的总数以及点集中最大、最小的坐标值。根据每块的平均点数（一般取值为20～100）进一步计算数据的总行数、总列数、行宽及列宽，表达式分别为
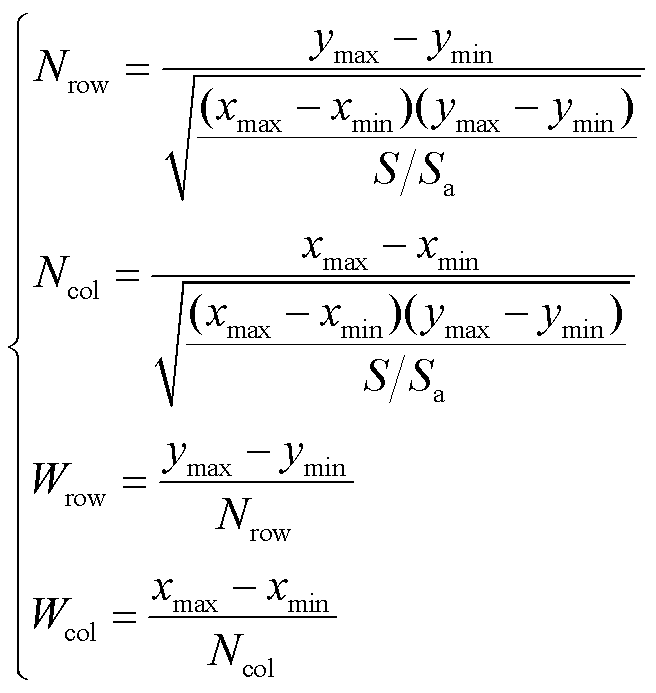（15）
式中，Nrow和Ncol分别为数据域的总行数和总列数；Wrow和Wcol为分别为数据域的行宽和列宽；xmax、xmin、ymax、ymin分别为数据域最大、最小的横纵坐标；S和Sa分别为离散点的总数和平均点数。
2）超三角形的确定
引入三个辅助点（M1、M2、M3）组成一个超三角形将点集M全部包含，构网完成后删除相关三角形即可获得M的Delaunay三角剖分。辅助点坐标的计算式为
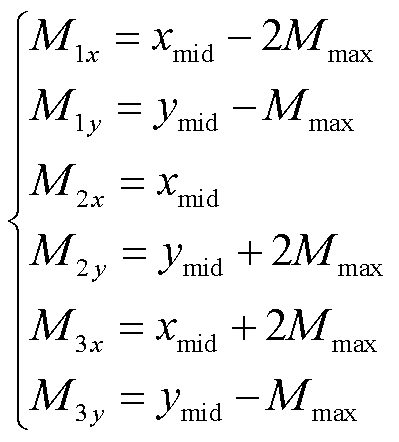（16）
其中
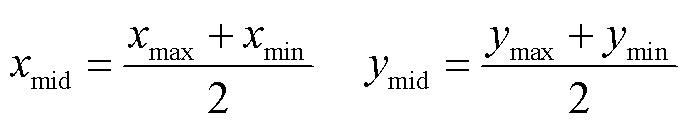
式中，Mmax为横纵坐标差值的最大值；M1x, M1y、M2x, M2y、M3x, M3y分别为M1、M2、M3的横纵坐标值。
3）局部区域的优化
引入Incircle判断法则，即设三角形的三个定点逆时针排列，根据式（17），当计算结果
＜0时，说明插值点M4在三角形外接圆内，此时就可以进行对角线交换，使之满足Delaunay三角网性质。
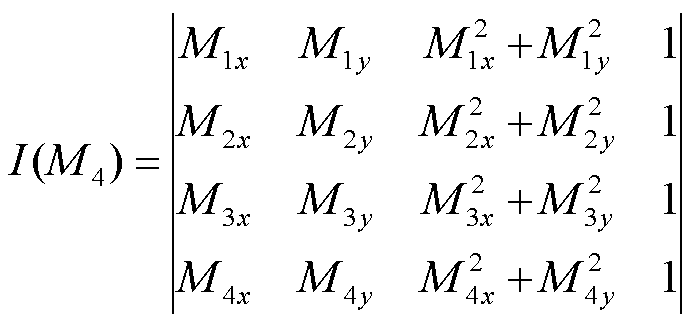（17）
当Delaunay三角网全部构建完成后，其效果如图5所示。可视化重建的数据是连续的，可以清楚地区分变压器内部纸板、角环、绝缘纸的具体位置，这是变压器性能数字孪生对可视化展示的必要要求。
图5 Delaunay三角网的可视化重建效果
Fig.5 Visual reconstruction of Delaunay triangular mesh results
图6展示了现场某变压器一年内运行监测的负载率，可以看出变压器实际运行负载率实时波动，并且大部分时间在额定负载以下运行，这说明通常使用恒定的额定负载直接进行温度场计算和其他参量推演与实际运行情况有较大差距，应按实际负载计算。
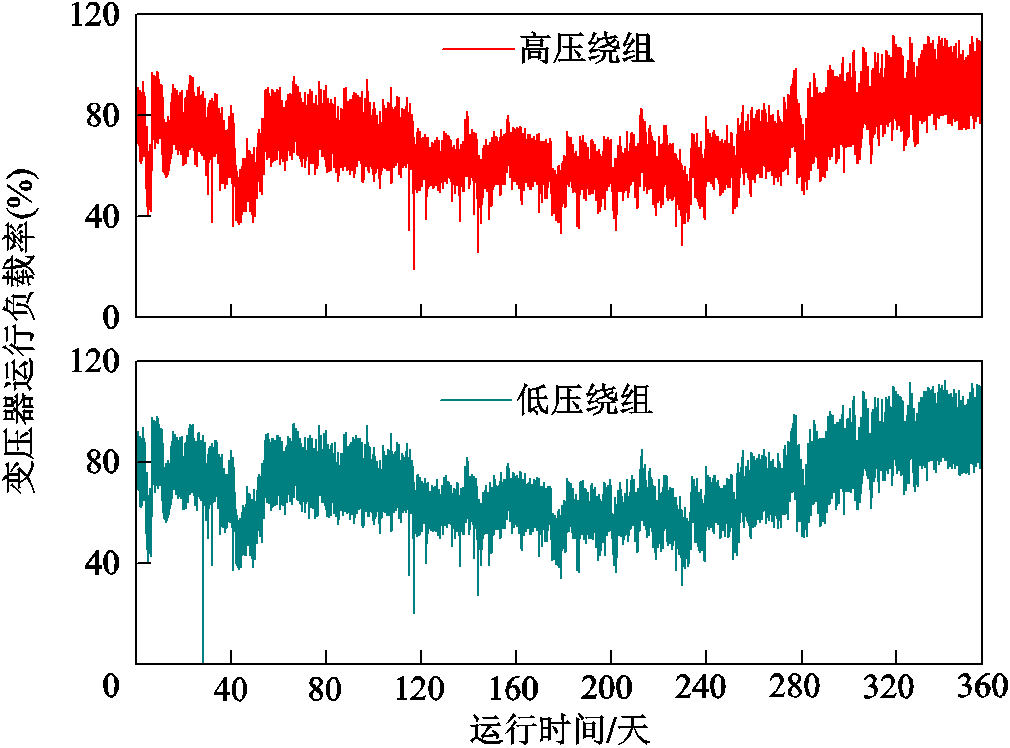
图6 某变压器不同时刻运行的负载率
Fig.6 Operating load rate of a transformer at different moments
为了对变压器老化状态参量进行孪生计算，本文以1月为例，计算并获得了实际运行负载下的温度场分布，如图7所示。可以发现变压器温度场分布不均匀，且低压绕组整体温度高于高压绕组，热点温度位于低压绕组上部90%高度处，平均值约为61.29℃。同时，对比仿真计算的月平均热点温度与现场在线监测热点温度可知，计算结果与传感器监测数据比较相符，误差约为3.5%，因此变压器内部固体绝缘的温度场分布结果也认为是可信的，这为进一步计算固体绝缘的含水量及分布提供了数据基础。
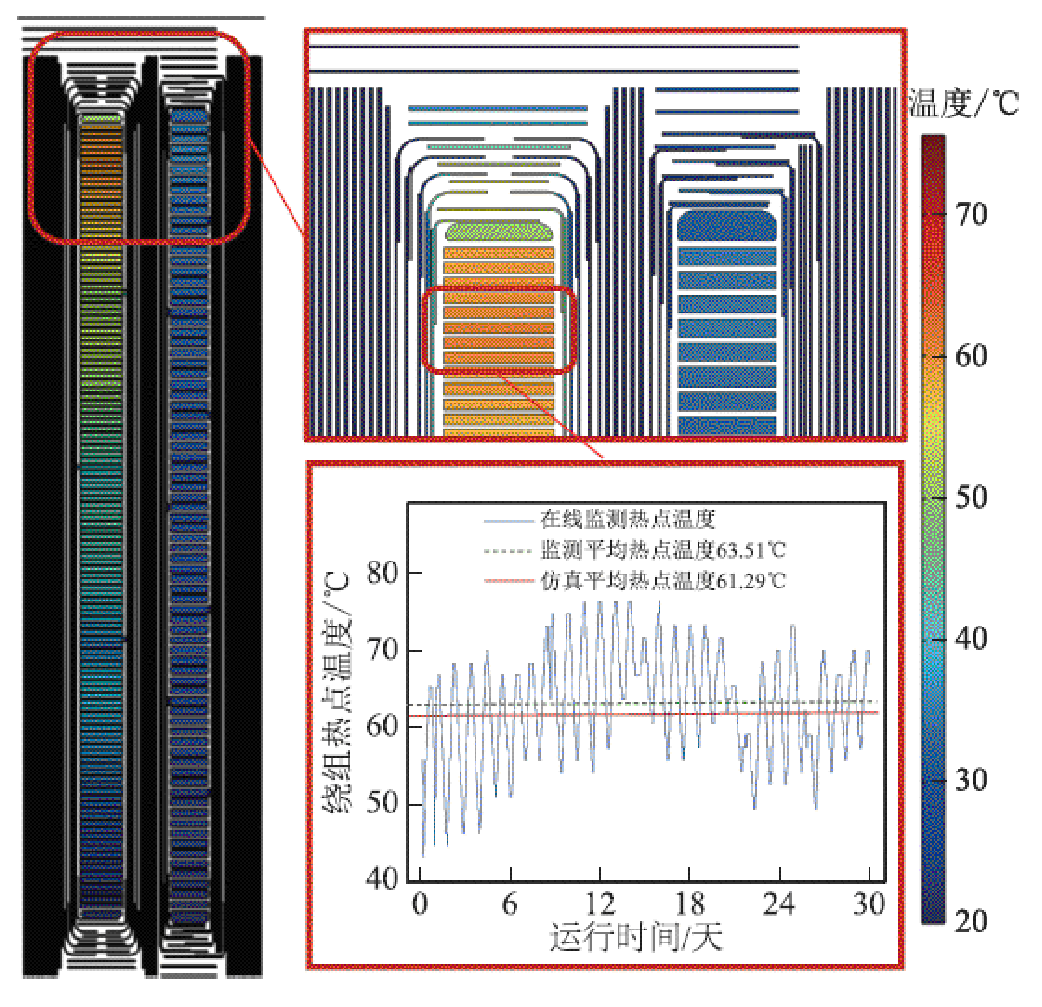
图7 变压器固体绝缘的温度场分布
Fig.7 Temperature field distribution of transformer solid insulation
变压器固体绝缘温度分布不均匀必定导致水分分布不均匀，即总体含水量为3%的变压器局部位置含水量必会大于3%，因此获得固体绝缘的水分分布对现场的实际运维更有利。
通过现场在线监测的油中水分传感数据和仿真计算的温度场分布结果获得了变压器内部水分从初始到稳态的变化规律。假设油中水分是均匀的，投运前期监测的初始油中含水量平均值为10×10-4%。图8展示了固体绝缘底部局部位置的水分扩散变化情况，初始水分扩散快，随后扩散逐渐变缓至趋于平衡，这是由于初始的局部含水量梯度大，扩散系数较大；随着时间的增加，含水量梯度减小，扩散系数明显减小，扩散变慢。
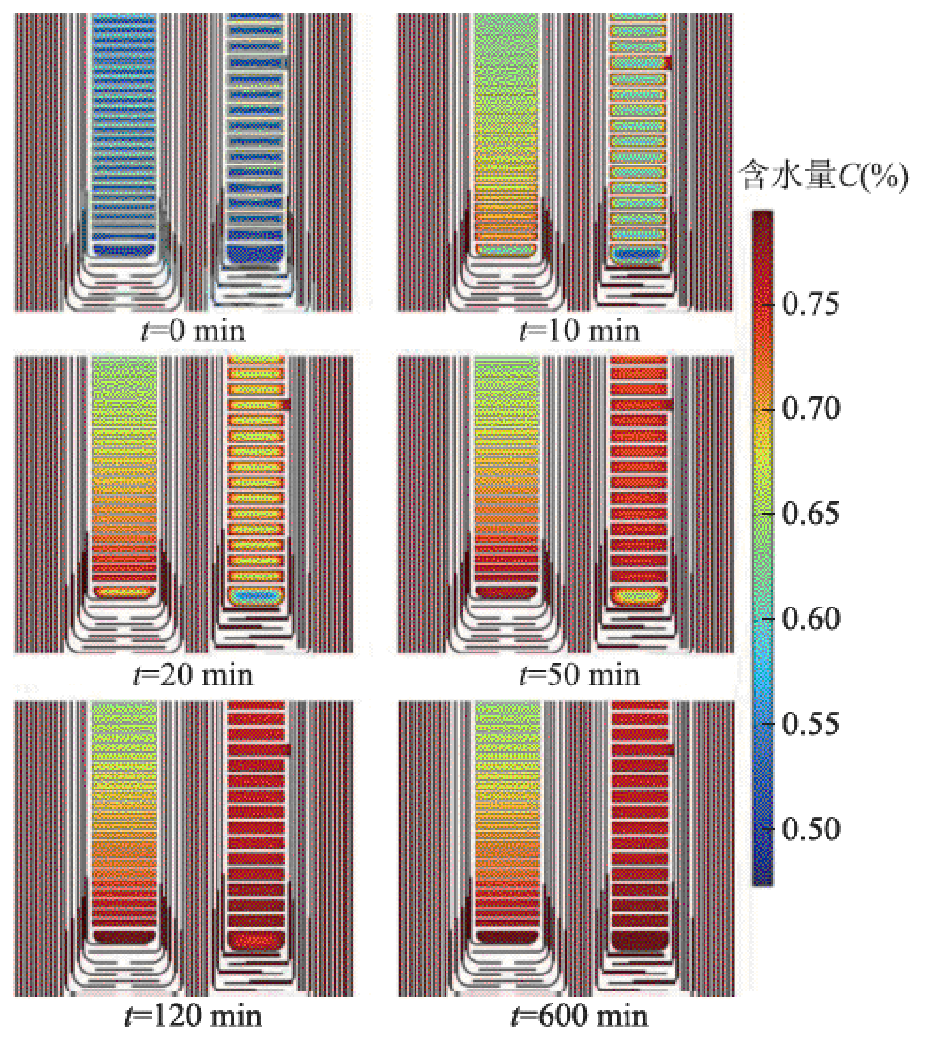
图8 变压器固体绝缘的水分扩散变化
Fig.8 Moisture diffusion variation for transformer solid insulation
当获得水分分布规律后，即可通过现场变压器运行年限与固体绝缘中总含水量的经验表达式来获取不同负载下不同时刻的变压器内部固体绝缘的含水量及分布。本文根据水分分布模型和可视化重建方法获得了该变压器以实际负载运行下不同年限含水量及分布的可视化结果，如图9所示。
从图9可以发现，水分主要集中在低压、高压绕组底部和两侧的层压纸板，这是因为这些位置的温度较低。随着运行年限增加，总的含水量也逐渐积累，当运行到第48年时，最高含水量在变压器底部固体绝缘处达到了3.2%左右，属于重点关注的潮湿部位。变压器内部固体绝缘水分分布计算的实现证明了虚实融合的变压器内绝缘状态孪生方法的可行性，为进一步计算聚合度分布提供了数据基础，同时也为变压器真正实现数字化赋能提供了新思路。
图9 虚实融合的变压器固体绝缘水分分布
Fig.9 Moisture distribution in transformer solid insulation by virtual-real fusion
考虑温度分布影响的聚合度分布推演模型时，通过实际运行负载计算的温度场分布即可获得变压器内部各个局部位置的聚合度，如图10所示。进一步地，考虑水分分布改进的水分平移因子，建立了温度-水分分布联合老化作用下不同年限聚合度分布的动态推演模型，图11展示了不同年限下聚合度分布的可视化结果。
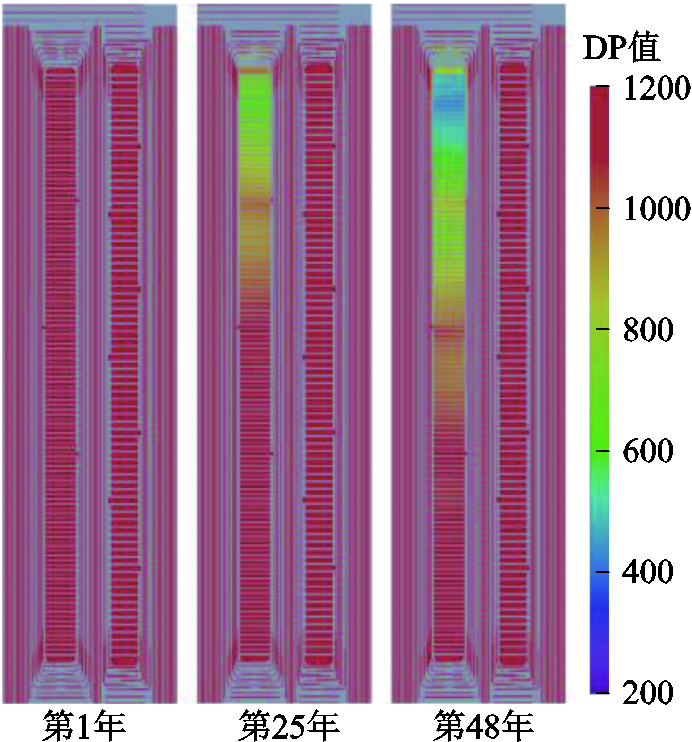
图10 虚实融合的变压器内部聚合度分布（考虑温度分布影响）
Fig.10 Internal degree of polymerization distribution of transformers by virtual-real fusion (considering the effect of temperature distribution)
此外，现场数字孪生变压器的智能运维除了需要实现内部老化状态参量的可视化外，更希望获得当现场突发急剧性过载时会给材料老化带来多大变化，进而如何影响变压器的运行寿命。因此，本文根据运行负载的标准要求，假设平均每年内过载（负载率为130%）运行总共约24 h，其余时间仍按照实际负载率计算聚合度的变化情况。考虑突发过载下聚合度分布的可视化结果如图12所示，此时过载运行的热点温度在短时间内剧增，使得聚合度下降极快。
图11 虚实融合的变压器内部聚合度分布（考虑温度-水分分布影响）
Fig.11 Internal degree of polymerization distribution of transformers by virtual-real fusion (considering the effect of temperature and moisture distribution)
图12 虚实融合的变压器内部聚合度分布（考虑突发过载下温度-水分分布影响）
Fig.12 Internal degree of polymerization distribution of transformers by virtual-real fusion (considering the effect of temperature-moisture distribution under sudden overloads)
根据上述考虑不同因素的虚实融合仿真计算结果，本文以实际运行热点位置为例，比较了考虑温度分布（情况Ⅰ）、温度-水分分布（情况Ⅱ）、突发急剧过载下温度-水分分布（情况Ⅲ）的变压器聚合度可视化评估结果，见表1。
表1 热点位置的变压器内部聚合度计算结果
Tab.1 Results of internal degree of polymerization of the transformer at the hot spot location
运行年限聚合度 情况Ⅰ情况Ⅱ情况Ⅲ 11 167.521 159.461 149.84 25648.27569.91465.24 48429.17368.36252.15
从表1可以看出，按照实际运行负载计算的聚合度随着运行年限的增加逐渐减低，且降低的速率先快后慢，最后由于极限聚合度的存在趋于平稳。当考虑温度-水分分布时，DP值比仅考虑温度时要低，这是由于水分对高温下纤维素老化起加速作用。而在突发急剧过载时，短时间的温度急剧上升会造成固体绝缘DP值大幅下降，DP值到第48年下降至252.15。
最后，本文将第48年的聚合度分布结果与国际大电网会议（CIGRE）中关于服役48年的变压器事后分析报告中聚合度分布测量结果进行对比[24]，如图13所示。本文考虑了温度分布、水分分布和急剧过载的影响，图13a计算的绕组聚合度分布与图13b的CIGRE报告中测量结果的分布规律基本一致，聚合度最低值位于绕组的热点温度位置区域。
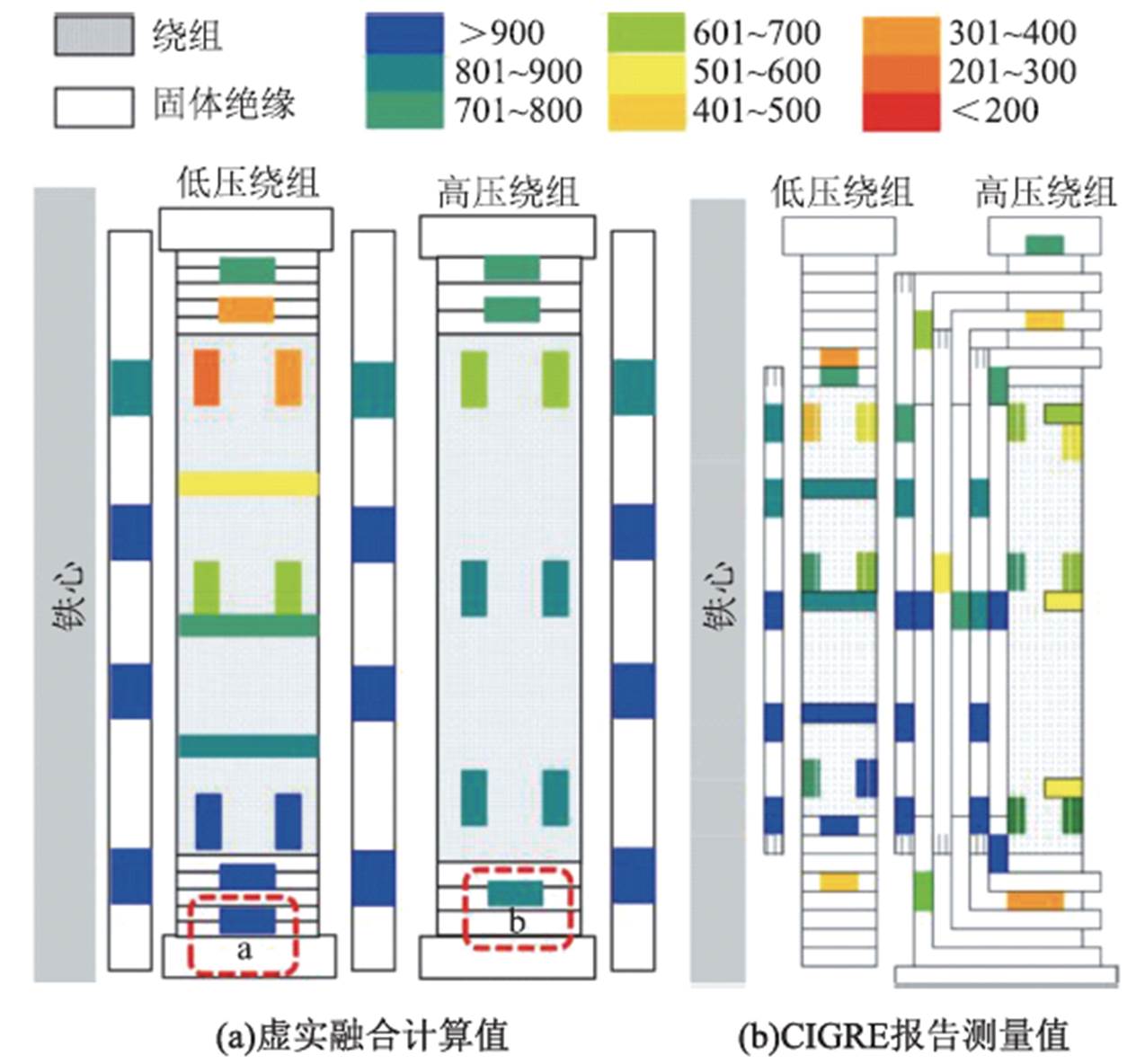
图13 虚实融合推演的聚合度分布与实际退役变压器测量的聚合度分布的对比
Fig.13 Comparison of degree of polymerization distributions inferred from virtual-real fusion with those measured from actual retired transformers
为了定量比较，选取低、高压绕组顶部、中部、底部的聚合度进行对比，见表2。随着绕组高度的增加，DP值逐渐降低，本文计算的数值与CIGRE报告的范围具有较好的一致性，验证了模型的有效性和合理性。但从定量数值上看仍然存在差距，其误差来源是变压器实际的运行负载和环境因素的不同，同时变压器不同的内部结构和有限元仿真也会带来一定的误差。
表2 虚实融合仿真计算结果与CIGRE报告的定量对比
Tab.2 Quantitative comparison of virtual-real fusion simulation calculations with CIGRE reports
位置低压绕组高压绕组 计算值CIGRE计算值CIGRE 顶部252.15201～400645.33501～700 中部676.33601～800811.4601～900 底部927.5＞801879.04＞801
然而，图13a中固体绝缘的a、b两个区域的聚合度与图13b有较大偏差。原因可能是首先本文在计算固体绝缘的水分分布时暂未考虑重力影响，使得目前a、b两处固体绝缘在第48年时计算的含水量最高为3.2%，水分对聚合度的影响还未占据主导作用。这与CIGRE报道的“通常在纸板含水量超过4%时，水对纤维素老化的影响才可能会超过热老化”是一致的。其次，水分加速老化的前提是温度达到了一定数值，底部固体绝缘年平均温度为20～25℃左右，即使在夏季高温天气能达到40～50℃，但该温度也很难引起聚合度大幅度的降低。此外，王俊洪等通过试验研究证明了变压器常年受到的机械应力对绝缘纸板的老化起重要作用[25]，a、b两个区域正好属于与铁轭压紧的固体绝缘位置，常年因受机械应力的作用使得老化加快，然而目前本文暂未考虑机械应力的影响，后续将进一步考虑。
1）本文提出了一种虚实融合的变压器内绝缘状态孪生方法，建立了时间-温度-水分分布联合老化作用的聚合度分布动态推演模型，实现了实际运行负载下变压器内部固体绝缘水分、聚合度的分布式监测和可视化展示。
2）获得了变压器内部老化状态参量——水分和聚合度的分布规律，水分主要集中在绕组底部和两侧纸板，第48年含水量最高约为3.2%；聚合度分布从底部到顶部呈现逐渐降低的趋势，最低位于低压绕组热点区域，为252.15，与CIGRE报告的分布规律一致，验证了本文方法的有效性和合理性。
3）铁轭压紧部位的底部固体绝缘部分计算聚合度仍然存在偏差，关于重力、机械应力等因素将在下一步工作中继续考虑。总的来说，虚实融合初步实现了变压器内部老化状态参量的分布式监测和可视化展示，对构建变压器数字孪生体具有参考意义。
参考文献
[1] 工业和信息化部. “十四五”信息化和工业化深度融合发展规划[Z]. 2021-11-17.
[2] 肖祥武, 王丰, 王晓辉, 等. 面向工业互联网的智慧电厂仿生体系架构及信息物理系统[J]. 电工技术学报, 2020, 35(23): 4898-4911.
Xiao Xiangwu, Wang Feng, Wang Xiaohui, et al. Bionic structure and cyber-physical system for intelligent power plant oriented to the industrial Internet[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4898-4911.
[3] Tuegel E J, Ingraffea A R, Eason T G, et al. Reengineering aircraft structural life prediction using a digital twin[J]. International Journal of Aerospace Engineering, 2011, 2011: 154798.
[4] 江悦, 沈小军, 吕洪, 等. 碱性电解槽运行特性数字孪生模型构建及仿真[J]. 电工技术学报, 2022, 37(11): 2897-2908.
Jiang Yue, Shen Xiaojun, Lü Hong, et al. Construction and simulation of operation digital twin model for alkaline water electrolyzer[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2897-2908.
[5] 杨帆, 吴涛, 廖瑞金, 等. 数字孪生在电力装备领域中的应用与实现方法[J]. 高电压技术, 2021, 47(5): 1505-1521.
Yang Fan, Wu Tao, Liao Ruijin, et al. Application and implementation method of digital twin in electric equipment[J]. High Voltage Engineering, 2021, 47(5): 1505-1521.
[6] 王伟杰, 雍明超, 黄金魁, 等. 高压设备数字孪生体构建及状态分析技术研究[J]. 高压电器, 2023, 59(11): 119-128.
Wang Weijie, Yong Mingchao, Huang Jinkui, et al. Research on construction of condition analysis technology of digital twin for high voltage equipment[J]. High Voltage Apparatus, 2023, 59(11): 119-128.
[7] 杨童亮, 胡东, 唐超, 等. 基于SMA-VMD-GRU模型的变压器油中溶解气体含量预测[J]. 电工技术学报, 2023, 38(1): 117-130.
Yang Tongliang, Hu Dong, Tang Chao, et al. Prediction of dissolved gas content in transformer oil based on SMA-VMD-GRU model[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 117-130.
[8] 江军, 张文乾, 李波, 等. 电力变压器油中溶解气体离群值识别和数据重构[J/OL]. 电工技术学报, 2023: 1-13[2023-12-20]. https://doi. org/10.19595/j. cnki.1000-6753.tces.231033.
Jiang Jun, Zhang Wenqian, Li Bo, et al. Outlier detection and data reconstruction of dissolved gas in oil for power transformers[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-13[2023-12-20]. https://doi.org/10.19595/j.cnki.1000-6753.tces.231033.
[9] 刘云鹏, 黎晏霖, 李欢, 等. 基于布里渊光时域峰值边沿分析的变压器绕组局部热点检测[J]. 电工技术学报, 2024, 39(11): 3486-3498.
Liu Yunpeng, Li Yanlin, Li Huan, et al. Local hot spot detection of transformer windings based on Brillouin optical time domain peak edge analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3486-3498.
[10] 曲岳晗, 赵洪山, 程晶煜, 等. 基于物联感知数据和张量融合的电力变压器绕组绝缘劣化评估方法[J]. 电工技术学报, 2024, 39(4): 1208-1220.
Qu Yuehan, Zhao Hongshan, Cheng Jingyu, et al. Evaluation method for power transformer winding insulation degradation based on IoT sensing data and tensor fusion[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1208-1220.
[11] 西门子低压——西门子面向输电业务的数字化产品落地中国[EB/OL]. (2019-11-26)[2023-11-03]. http:// www.siemensyzs.gongboshi.com/news/itemid-64575. shtml.
[12] ABB电力世界. ABB新品发布！全球首台数字化电力变压器来了[J]. 中国机电工业, 2018(6): 24.
[13] Coutinho C P, Tavares S M O, Gonçalves F, et al. Transformer 4.0: digital revolution of power transformers[EB/OL]. (2020-07-01)[2023-11-03]. https://www.mitportugal.org/research/flagship-projects/ transformer-4p0-digital-revolution-of-power-transformers/.
[14] Ansys Inc. Ansys Twin Builder: simulation-based & hybrid analytics[EB/OL]. (2022-03-30)[2023-11-03]. https://www.ansys.com/content/dam/product/digital-twin/twin-builder/ansys-twin-builder-technical-datasheet. pdf.
[15] 宋振龙, 孙凤伟, 陈锋, 等. 网络化智能传感器及其在航空航天领域中的应用[J]. 电子测试, 2009(9): 10-13, 53.
Song Zhenlong, Sun Fengwei, Chen Feng, et al. Intelligent sensor in network and its application in aeronautics and space domain[J]. Electronic Test, 2009(9): 10-13, 53.
[16] 谭又博, 余小玲, 臧英, 等. 谐波电流对换流变压器绕组损耗及温度分布特性的影响[J]. 电工技术学报, 2023, 38(2): 542-553.
Tan Youbo, Yu Xiaoling, Zang Ying, et al. The influence of harmonic current on the loss and temperature distribution characteristics of a converter transformer winding[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 542-553.
[17] 刘刚, 郝世缘, 朱章宸, 等. 基于动态模态分解-自适应变步长油浸式电力变压器绕组瞬态温升快速计算方法[J]. 电工技术学报, 2024, 39(12): 3895-3906.
Liu Gang, Hao Shiyuan, Zhu Zhangchen, et al. Research on rapid calculation method of transient temperature rise of winding of dynamic mode decomposition-adaptive time stepping oil-immersed power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3895-3906.
[18] Gielniak J, Graczkowski A, Moranda H, et al. Moisture in cellulose insulation of power transformers - statistics[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(3): 982-987.
[19] García B, Villarroel R, García D. A multiphysical model to study moisture dynamics in transformers[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1365-1373.
[20] Zhou Lijun, Wu Guangning, Liu Jun. Modeling of transient moisture equilibrium in oil-paper insulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2008, 15(3): 872-878.
[21] 杨丽君, 邓帮飞, 廖瑞金, 等. 应用时-温-水分叠加方法改进油纸绝缘热老化寿命模型[J]. 中国电机工程学报, 2011, 31(31): 196-203.
Yang Lijun, Deng Bangfei, Liao Ruijin, et al. Improvement of lifetime model on thermal aging of oil-paper insulation by time-temperature-moisture superposition method[J]. Proceedings of the CSEE, 2011, 31(31): 196-203.
[22] 赵洪山, 常杰英, 曲岳晗, 等. 基于二元非线性Wiener随机过程的变压器油纸绝缘剩余寿命预测方法[J]. 电工技术学报, 2023, 38(15): 4040-4049.
Zhao Hongshan, Chang Jieying, Qu Yuehan, et al. Residual life prediction method of transformer oil-paper insulation based on binary nonlinear Wiener random process[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4040-4049.
[23] 赵鑫, 田志峰, 钱卫东, 等. 基于Delaunay三角剖分算法高效构建舰船后处理模型的研究[J]. 现代信息科技, 2018, 2(6): 84-88.
Zhao Xin, Tian Zhifeng, Qian Weidong, et al. The research on post-processing mode establishing of ship based on Delaunay triangled algorithm method[J]. Modern Information Technology, 2018, 2(6): 84-88.
[24] CIGRE WG A2.45. Transformer post-mortem analysis [R]. Paris: CIGRE, 2018.
[25] Wang Junhong, Liao Ruijin, Cheng Li, et al. Effects of winding vibration on the mechanical-thermal aging properties of insulating paper[J]. IEEE Access, 2020, 8: 67912-67920.
Abstract The national development plan calls for the digital and intellectual transformation of power enterprises to support the construction of new power systems. Power transformer as the core equipment of the power grid, its operational reliability is related to the safety of the entire power grid, therefore, the development of digital twin transformer is of great significance to support the intelligent, digital, visualized operation and maintenance of high-end power equipment. However, there are still significant challenges for transformers due to the lack of corresponding digital twin capabilities, such as insufficient sensors, unknown parametric mechanism, and lack of post-processing techniques. For this reason, this paper carries out a research on a state twinning method for transformer internal insulation by virtual-real fusion.
Firstly, the internal temperature field distribution of the transformer is the data basis for calculating the state parameter distribution. Considering the complex multi-physical field coupling effect of the transformer, the calculated losses are used as the heat source of the temperature field simulation for the multi-physical field coupling calculation, and the temperature field distribution corresponding to the real-time load change is derived based on the load rate monitored in the field. Secondly, the temperature field distribution of virtual calculation and the moisture in oil data of physical monitoring are combined to analyze the distribution law of moisture in paper at each local location inside the transformer. Based on the relationship between the total moisture content in the paper of multiple transformers in the field and the operation time, an empirical formula is established, and the oil-paper equilibrium equation and the law of moisture diffusion are utilized to determine the content and distribution. Thirdly, considering the effect of moisture distribution on the moisture translational factor, a dynamic derivation model of degree of polymerization distribution based on the joint action of time-temperature-moisture distribution is established, and the results of the degree of polymerization distribution of the insulating cardboard inside the transformer are obtained. Finally, due to the fact that the multi-physics field simulation calculation results and the dynamic deduction numerical results are discrete point data, this paper adopts the point-by-point insertion method of Delaunay triangular mesh for the continuity of the discrete data, and the state parameter data obtained by virtual-realistic fusion calculation are visualized in this paper.
The results show that the moisture distribution calculated by virtual-real fusion is mainly concentrated in the laminated cardboard on both sides and the bottom of the solid insulation, with the highest moisture content of about 3.2% in the 48th year, which is greatly influenced by the temperature field distribution and environmental factors. The rule of the degree of polymerization distribution in the windings is in general agreement with the measurements reported by CIGRE, and the lowest value is located in the hot spot temperature region of the low-voltage windings, with a value of 252.15 in the 48th year, which verifies the validity and reasonableness of the methodology. This study realizes the assessment of the parametric distribution for the aging state parameter inside the transformer insulation, and lays the foundation for the subsequent comprehensive construction of the digital twin of the transformer.
keywords：Virtual-real fusion, transformer, digital twin, state parameter, distributed monitoring
中图分类号：TM83
DOI: 10.19595/j.cnki.1000-6753.tces.231839
国家重点研发计划资助项目（2021YFB2401700）。
收稿日期 2023-11-03
改稿日期 2023-12-20
罗 豪 男，1997年生，博士研究生，研究方向为电力设备先进数字孪生技术、电气设备寿命评估。E-mail：haoluo@cqu.edu.cn
成 立 男，1989年生，副教授，博士生导师，研究方向为电力设备先进数字孪生技术、电气设备寿命评估、复合材料制备与改性、无损检测新方法等。E-mail：chengl16@cqu.edu.cn（通信作者）
（编辑 李 冰）