图1 间接矩阵变换器-双异步电机调速系统拓扑结构
Fig.1 Topological structure of indirect matrix converter dual asynchronous motor speed control system
摘要 间接矩阵变换器-双异步电机调速系统结构复杂，传统模型预测电压控制中权重因数整定困难。该文提出一种基于层次分析评估的权重因数整定方法，通过对物理量纲、双电机、网侧与电机侧统合将权重因数数量减少至1个，并引入层次分析评估法来实时调整权重因数以满足各种工况的要求，使系统在宽运行范围、多功率流模态下均具有良好的网侧电能质量与电机调速性能。通过仿真和实验证明，采用该文提出的方法，可保证在多种工况下网侧功率因数接近1，网侧电流正弦，电机定子电流畸变小、电机动态调速性能良好。而且，相比于传统的简化模型预测电压控制方法，该文所提出的方法权重因数整定简单易实现，网侧电流质量更好。
关键词：间接矩阵变换器 异步电机 多电机传动 模型预测控制 权重因数整定 层次分析法
近年来，间接矩阵变换器（Indirect Matrix Converter, IMC）被提出，与交-直-交变频器相比，IMC输入输出性能良好，能量可以双向流动，且不存在中间储能器件，其体积小、重量轻、使用寿命长[1-2]。与异步电机构成的间接矩阵变换器-双异步电机（Indirect Matrix Converter-Double Induction Motors, IMC-DIM）调速系统具有控制精度高、能量可双向流动、网侧与电机侧性能良好等优点，在一些对性能和功率密度要求严格的工业传动领域有更深远的应用前景[3-5]。
近年来模型预测控制[6-8]（Model Predictive Control, MPC）由于概念直观、易于理解、多目标优化等优势被引入电力电子领域中。IMC-DIM模型预测控制策略的控制目标多，网侧控制目标有网侧电流、无功功率，电机侧的控制目标有定子电流、磁链、转矩、输出电压。文献[9]提出模型预测转矩控制，控制目标为无功功率、电磁转矩和定子磁链，需要设置三个权重因数并且物理数量级差异较大，给权重因数的设计带来很大困难，难以实现多种工况下的优化控制。文献[10]提出模型预测双电流控制，网侧和电机侧的控制量均为电流，实现了量纲的统一，权重因数的调节范围较小，但对于磁链转矩控制效果较差。文献[11]提出模型预测磁链控制。控制目标为定子电流和磁链矢量，只需设置1个权重因数，但是需要进行大量的迭代计算。权重因数设置得不合理会影响控制效果甚至使系统出现振荡。为了实现对权重因数的优化设计，文献[12]提出双向量模型预测转矩控制，可以利用模糊决策消除权重因数来选择最优切换向量。文献[13]提出模糊控制调节权重因数的直接转矩模型预测方法，对转矩和磁链的控制误差更小。上述控制方法中存在权重因数多和控制效果差的问题，恒定的权重因数无法令IMC-DIM系统在宽范围运行时获得良好的控制性能并且均需要在广泛的操作范围内进行大量实验，计算量较大。
本文针对传统模型预测电压控制方法中恒定权重因数无法在宽运行范围内获得良好系统性能的问题，提出一种IMC-DIM的基于层次分析评估（Analytic Hierarchy Process, AHP）的权重因数整定方法。通过对量纲统合以及多电机统合，将权重因数数量减少至1个，并引入层次分析法来设计基础权重因数，结合工况的变化实时调整权重因数，使系统在宽运行范围、多功率流模态下均具有良好的网侧电能质量与电机调速性能。
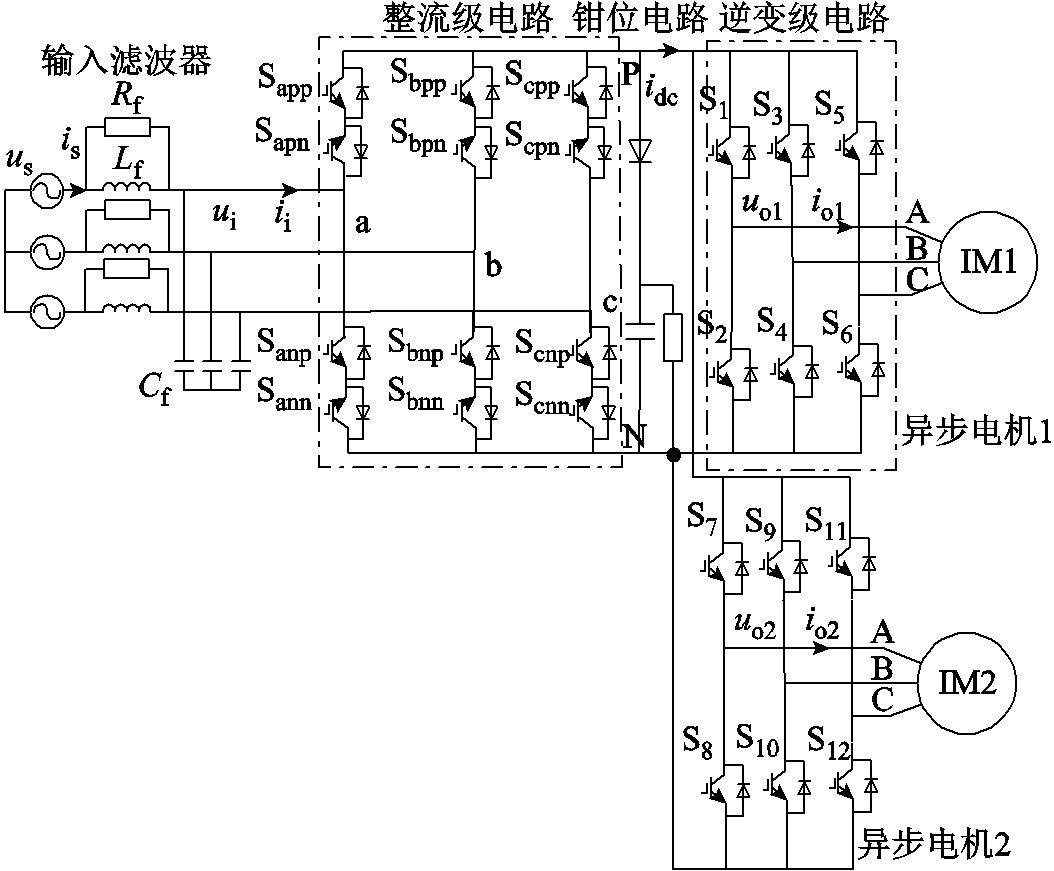
IMC-DIM的拓扑结构如图1所示，该系统由输入滤波器、整流级电路、钳位电路、两个逆变级电路和两台异步电机构成。LC滤波器主要用于消除器件高频开关动作所造成的电流谐波；整流级电路由六组双向开关构成，可以实现系统能量双向流通；钳位电路用于系统的过电压保护；两个逆变级电路的三相输出分别与两台异步电机的定子相连接，用于驱动异步电机运行。
图1 间接矩阵变换器-双异步电机调速系统拓扑结构
Fig.1 Topological structure of indirect matrix converter dual asynchronous motor speed control system
图1中，us、is、ui、ii、uo、io和idc分别为网侧电压电流、输入电压电流、输出电压、电机定子电流和中间环节电流；Rf、Lf和Cf分别为滤波电阻、电感和电容；Sapp～Scnn为整流级电路的开关器件；S1～S12为两个逆变级电路的开关器件。
有限控制集模型预测控制直接利用变换器的离散特性和开关状态有限的特性，根据变换器预测模型采用迭代计算列出所有有限开关组合得到的预测状态变量，筛选出使系统性能指标函数为最小值的开关组合，即通过代价函数优化筛选出最优的开关状态作为下一控制周期的控制信号，结构如图2所示。图2中，X(k)为控制目标，XP(k+1)为对电机模型进行离散化后得到的下一时刻控制目标预测值，X*为控制目标参考值，S(k)为筛选出最优的开关状态。
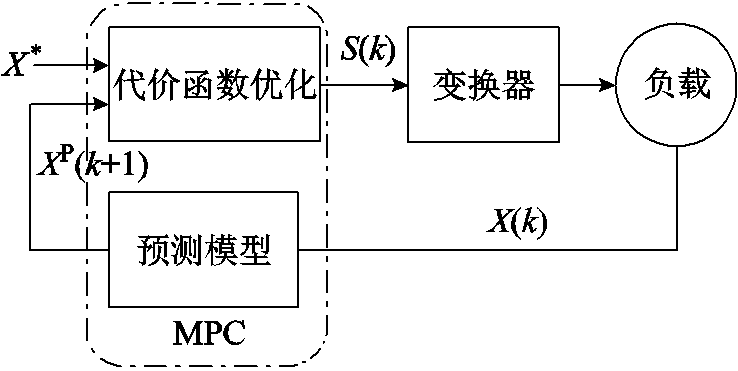
图2 有限控制集模型预测控制方法结构
Fig.2 Structure of finite control set model predictive control method
简化模型预测电压控制（Model Predictive Voltage Control, MPVC）方法的网侧控制目标为可以综合考虑网侧电流谐波和网侧无功功率的网侧电流，电机侧以预测模型部分计算量最小的输出电压为控制目标[14]，传统双机模型预测方法中，整流级可以选出三种开关状态，每个逆变级存在8种开关状态，进行计算时需要进行3×8×8=192次。为了减少计算量，根据输出电压矢量所处扇区选择一种零矢量开关状态和离参考电压矢量最接近的三个非零矢量开关状态，通过对逆变级开关状态进行预筛选，开关状态个数变为3×4×4=48，降低了计算量，实现了较高的控制频率和开关频率，取得了较好的控制效果。
网侧瞬时功率可以表示为
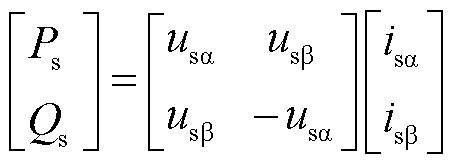（1）
式中，Ps、Qs分别为网侧有功功率和无功功率；usa、usb和isa、isb分别为两相静止坐标系下的两个电压分量和两个电流分量。
网侧无功功率控制目标为无功功率最小化，因此离散化后设定网侧无功功率为零，根据瞬时功率理论可得下一时刻网侧电流参考为
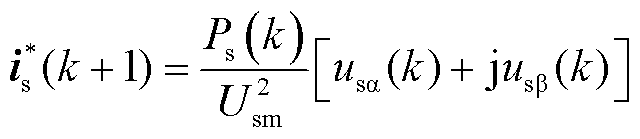（2）
式中，usα(k)和usβ(k)分别为当前时刻两相静止坐标系下的两个电压分量；Ps(k)为当前时刻网侧有功功率；Usm为网侧电压幅值。
异步电机的电磁转矩为
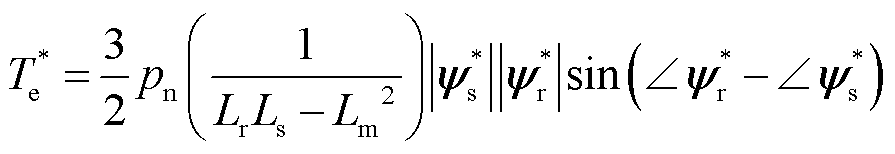（3）
式中，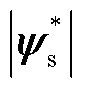
为参考定子磁链幅值；
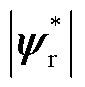为参考转子磁链幅值；pn为极对数；Lr、Ls、Lm分别为电机转子自感、定子自感与互感；
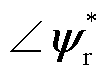和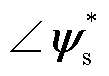
分别为转子磁链和定子磁链的相位。
根据无差拍理论[15]，可以得到参考磁链矢量为
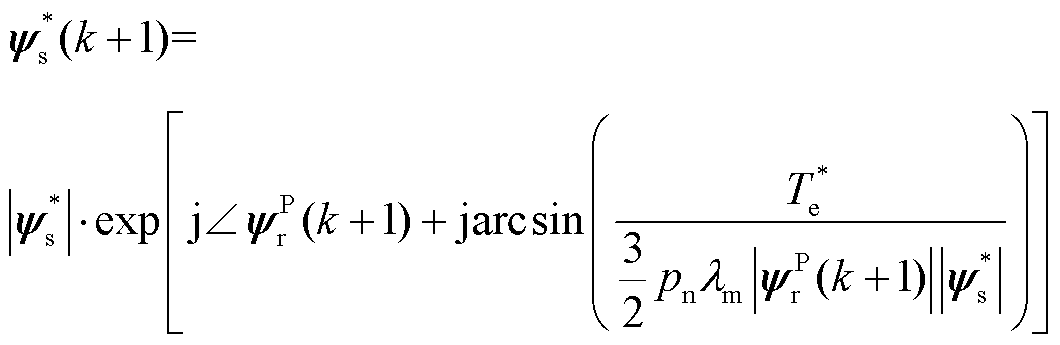（4）
式中，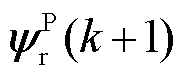
为下一时刻转子磁链矢量预测值，可通过将电机模型离散化得到；
。
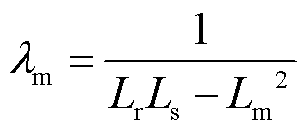异步电机的定子电压方程为
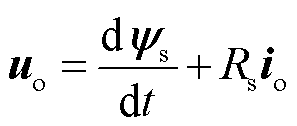（5）
通过对式（5）进行离散化可以得到输出电压参考值为
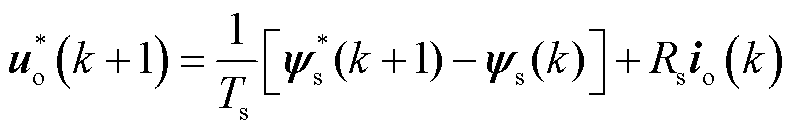（6）
式中，Ts为控制周期；Rs为电机定子绕组电阻值。
输入滤波器的数学模型为
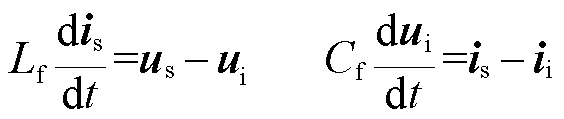（7）
对式（7）进行离散化可以得到网侧电流预测模型为
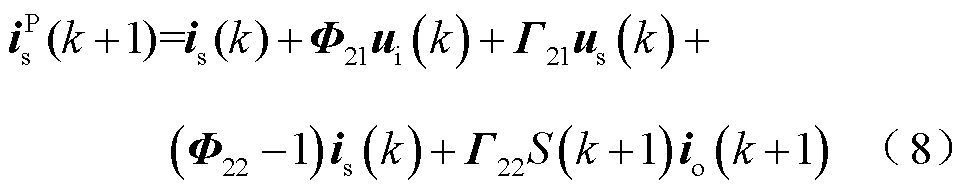
其中
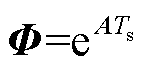
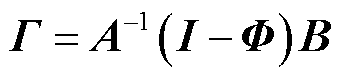
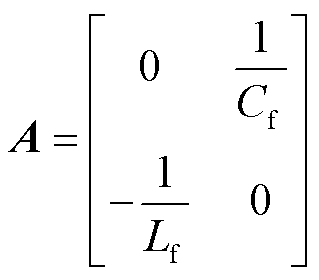
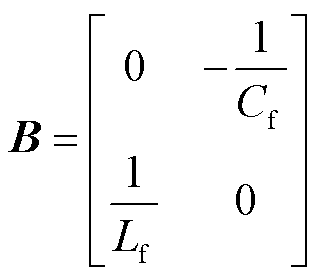
输出电压预测值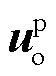
可由下一时刻的输入电压与开关状态得到。同时由于输入电压的频率远小于采样频率，因此相邻两个采样时刻的输入电压近似相等，可以得到
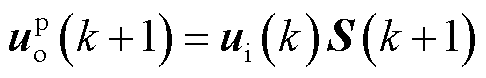（9）
式中，S(k+1)为下一时刻的开关状态。
该方法的代价函数为
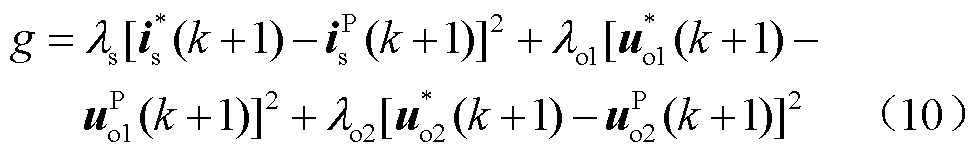
式中，uo1*(k+1)、uo2*(k+1)和is*(k+1)分别为两个电机侧参考输出电压矢量和参考网侧电流矢量；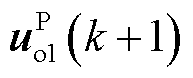
、
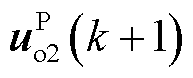和isP(k+1)分别为两个电机侧预测输出电压矢量、预测网侧电流矢量；λs为网侧权重因数；λo1和λo2为两个电机侧权重因数。
虽然相较其他MPC方法，简化MPVC方法的网侧与电机侧性能较好，但简化MPVC方法应用在IMC-DIM时，仍存在下列问题：①简化MPVC方法的权重因数数量多、控制目标间量纲差异大，权重因数整定困难；②即使得到某一工况的最优权重因数，在其他工况也并不一定适用，恒定的权重因数无法保证系统在多模态、宽运行范围内均能实现良好的网侧电能质量与电机调速性能。
针对上述问题，本文提出一种基于层次分析评估的权重因数整定方法，基于层次分析评估权重因数整定的模型预测电压控制方法（Model Predictive Voltage Control Method Based on Analytic Hierarchy Process Weighting Factor Tuning, AHP-MPVC）控制结构如图3所示。其外环为转速闭环、内部控制结构包括磁链观测器、参考网侧电流计算、网侧电流预测模型、参考输出电压计算、输出电压预测模型、量纲统一与双电机统一部分、网侧与电机侧统合部分、参考输出电压估计部分、基于层次分析评估的基础权重因数整定和代价函数优化等部分。
图3中，下角标1、2分别代表两个电机侧；ω(k)、ψsE(k)、ψrE(k)分别为k时刻的电机转速、定子磁链矢量观测值、转子磁链矢量观测值；ω*、Te*、Q*分别为转速参考值、转矩参考值、无功参考值；λ为权重因数。
基于层次分析评估的权重因数整定部分的内部结构如图4所示，其主要包括量纲统一与多电机统一、网侧与电机侧统合、参考输出电压估计、基于层次分析评估的基础权重因数整定和权重因数实时整定五部分。
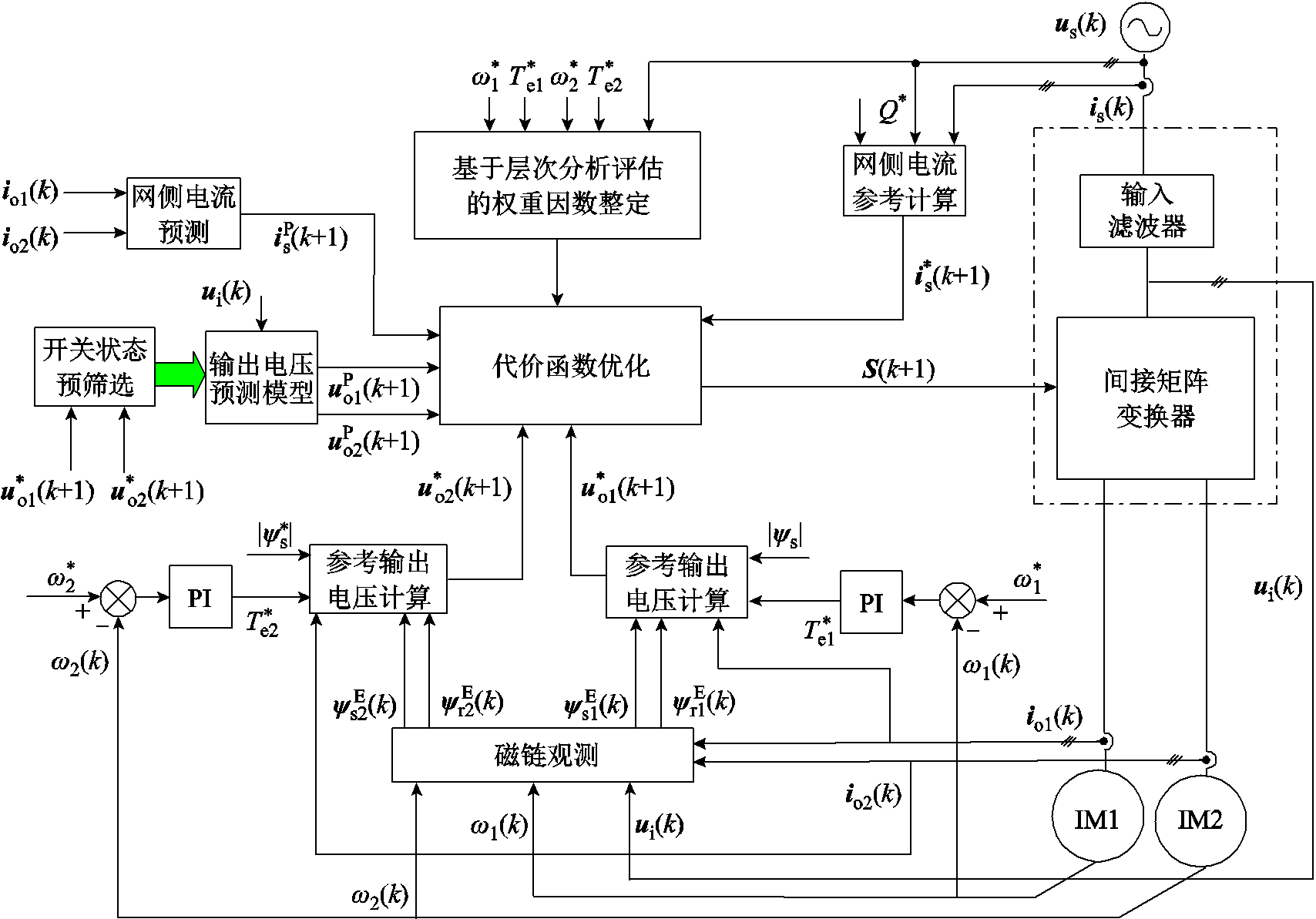
图3 基于层次分析评估方法权重因数整定的模型预测电压控制结构
Fig.3 Model predictive voltage control structure based on analytic hierarchy process evaluation method with weight factor adjustment
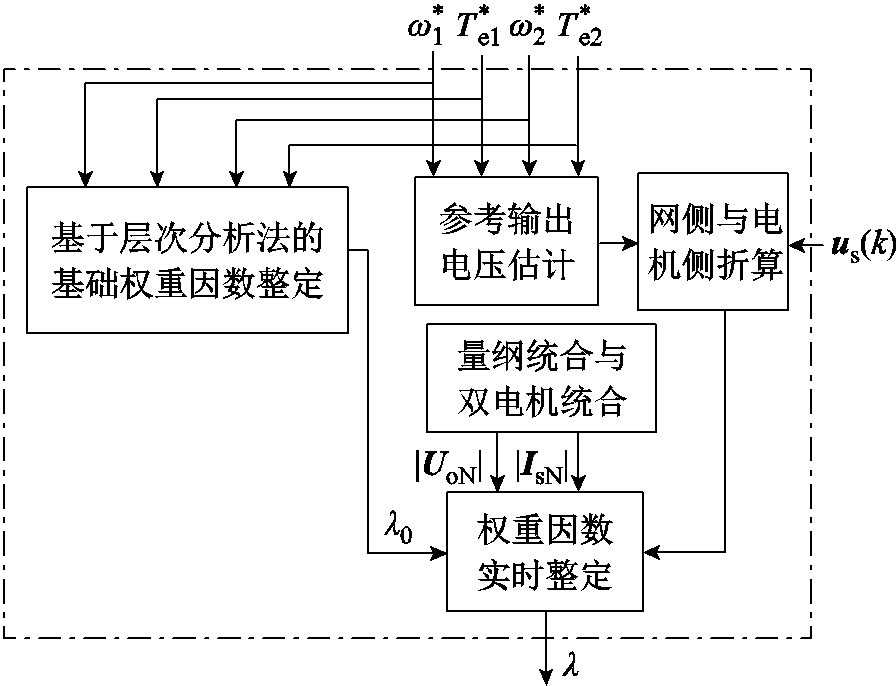
图4 基于层次分析法的权重因数整定结构
Fig.4 Structure based on analytic hierarchy process method with weight factor adjustment
量纲统合与多电机统合通过标幺化，消除了控制目标间的量纲差异，减少了权重因数的数量；网侧与电机侧统合根据有功功率平衡的原则，将网侧与电机侧控制目标统合在一起，实现了权重因数随工况变化实时调整；参考输出电压估计根据两台电机的转速和转矩，通过电机模型得到参考输出电压的基波幅值；基于层次分析评估的基础权重因数整定依据某一工况下的系统性能指标，通过层次分析评估得到基础权重因数λ0；权重因数实时整定部分则是根据上述结果，结合工况条件实时计算权重因数。
由于简化MPVC方法的网侧控制目标为电流，电机侧为电压，这两个物理量之间量纲差异过大，不利于权重因数的整定，因此以额定工况下的网侧电流幅值和电机输入电压幅值为基准值，通过标幺化消除量纲的影响，以降低权重因数整定的难度、标幺化后的代价函数为
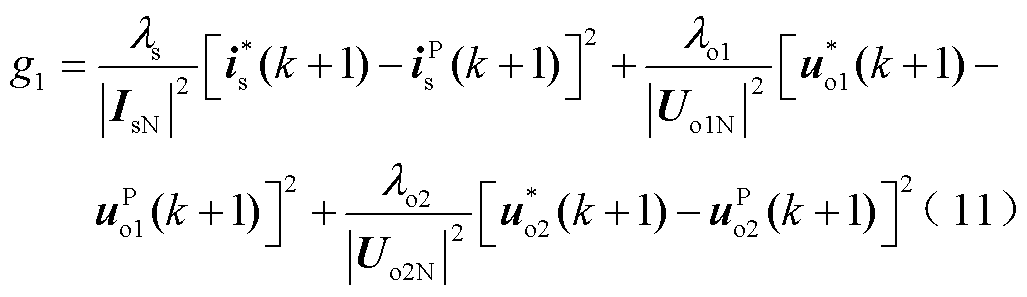
式中，|IsN|为额定工况下网侧电流幅值；|Uo1N|和|Uo2N|分别为两台电机的额定电机输入相电压幅值。
代价函数中存在三个权重因数，权重因数会共同影响控制效果，导致权重因数设置困难。IMC-DIM调速系统在应用中往往两台电机参数一致，具有相同的重要性，因此在标幺化后可以令两个电机侧控制目标共用一个权重因数λo和标幺化参数，最终得到代价函数为
式中，λ1=λs/λo。
此时权重因数从三个减少到一个，且控制目标都处于同一数量级，权重因数整定难度较小。
通过在网侧控制目标上增加统合系数实现网侧与电机侧的统合，用来抵消模态或工况变化时两者之间的非线性变化。统合参数选择为网侧电流预测值与电机定子电流预测值，修改后的代价函数为
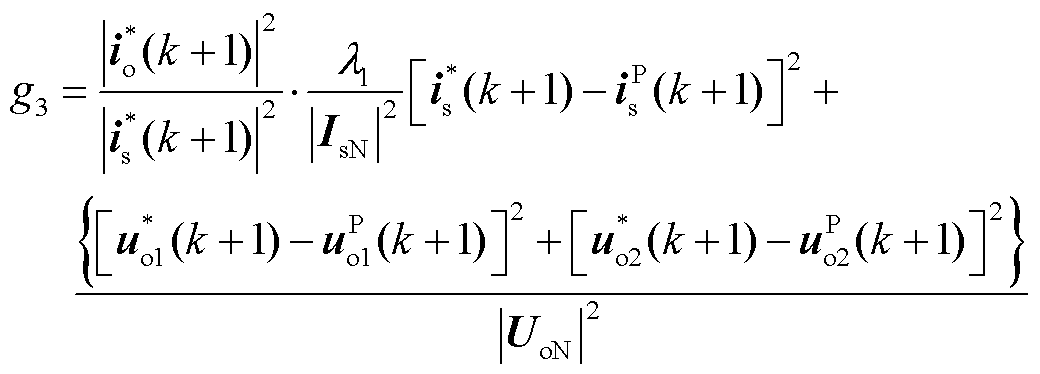（13）
式中，| io*(k+1)|为参考定子电流幅值；| is*(k+1)|为参考网侧电流幅值。
但相比于IMC-IM系统，IMC-DIM存在多种功率流方向模态。功率流模态分类见表1。
表1 功率流模态分类
Tab.1 Power flow modal classification
功率流动方向电机1状态电机2状态 网侧向电机侧电动电动 网侧向电机侧电动发电 电机侧向网侧电动发电 电机侧向网侧发电发电
当系统处于一台电机电动，一台电机发电的情况时，按照式（13）整定出的权重因数过大，导致电机定子电流THD过高，可能会存在权重因数过大使得网侧与电机侧性能都下降的情况。
为避免该情况发生，本节以式（13）所示的代价函数为基础，根据电机侧功率状况对网侧与电机侧进行统合。根据有功功率与电流关系将式（13）中的统合系数表示为网侧相电压幅值|Us|与逆变级的参考输出电压矢量模值|uoh*(k+1)|和功率因数cosφoh的比值，从而得到
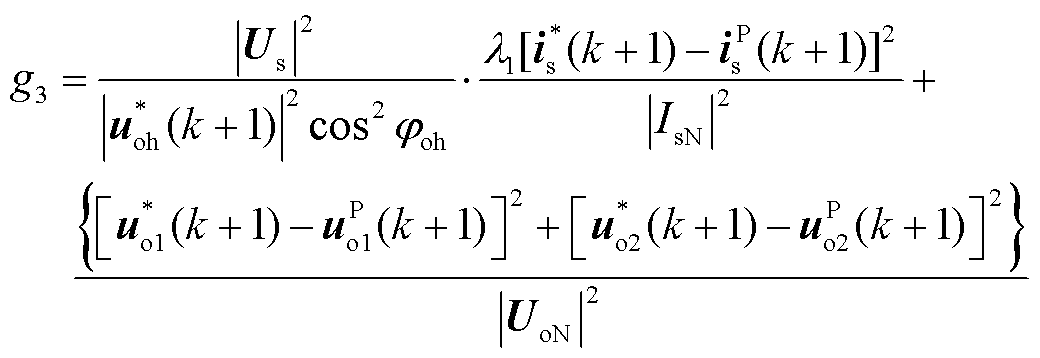（14）
统合后的代价函数可以根据模态和工况变化实时改变权重，解决了简化MPVC方法恒定权重因数无法适应系统需求的问题。同时避免了当两台电机处于不同工作状态时，整定出的权重因数过大的问题。
在理想情况下，稳态时的输出电压矢量参考值与实际输出电压基波应保持一致。但在IMC-DIM实际运行时，参考输出电压中的谐波含量过高，若使用数字滤波器在线提取输出电压基波，其计算量较大且存在时延，因此可通过异步电机电压方程，利用转速和电磁转矩对输出电压和电机侧功率因数进行估计，并代入式（14）得到
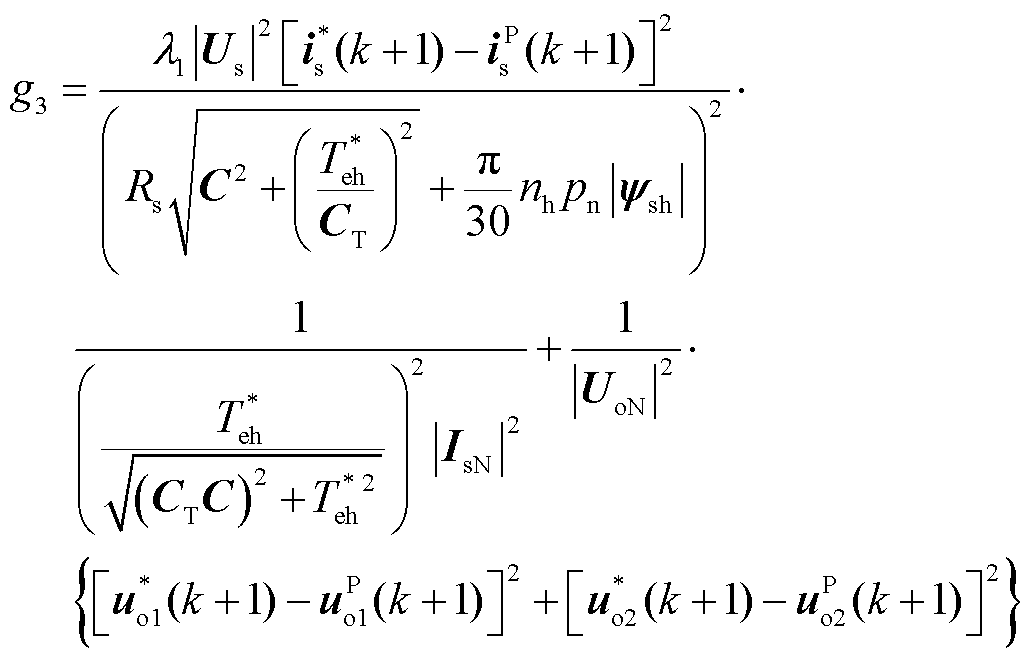（15）
式中，C、CT分别为电机定子电流励磁分量和定子电流转矩分量的相关系数；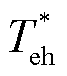
、
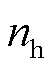和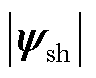
分别为功率较高逆变级的参考电磁转矩、电机转速和电机定子磁链幅值。
本文所使用方法在代价函数优化部分是选择代价函数最小的开关状态，因此可以将式（15）整理为
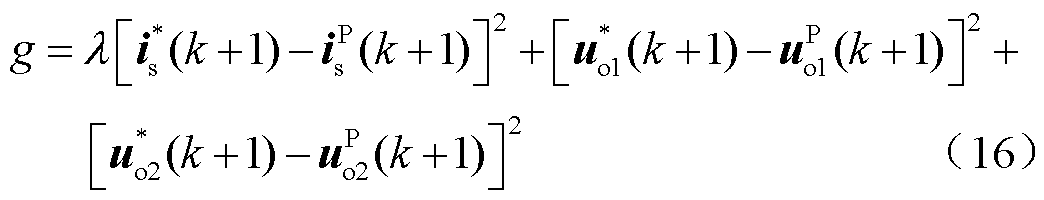
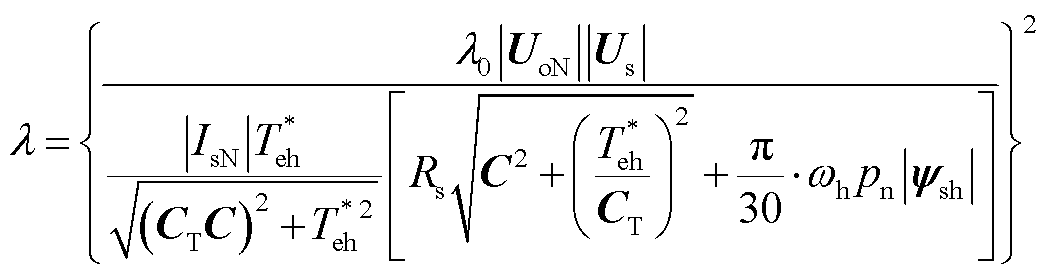
式中，λ0仅体现网侧与机侧间的权重关系，整定难度较低。
权重因数对系统性能作用机理较为复杂，可通过测定某一工况不同权重因数下的网侧与电机侧的不同性能指标，根据层次分析评估方法得到该工况下最优权重因数λop与基础权重因数λ0。本文选择的网侧指标为网侧功率因数与网侧电流总谐波畸变率（Total Harmonic Distortion, THD），电机侧指标为两台电机的定子电流THD。IMC-DIM所使用的层次分析评估方法结构如图5所示。
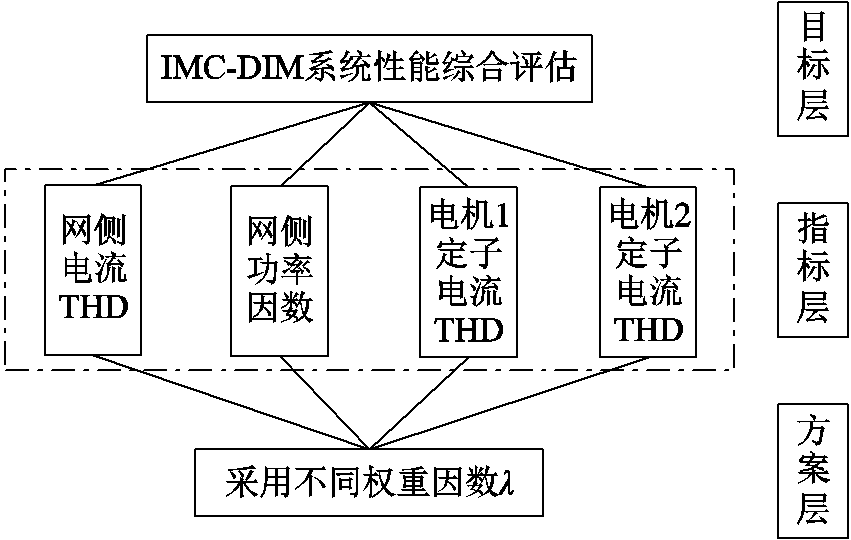
图5 层次分析评估方法结构
Fig.5 Structure of analytic hierarchy process evaluation method
根据九级标度法[16]，对指标层中的指标两两比较重要性，九级标度法取值见表2。
表2 九级标度法取值
Tab.2 Nine level scaling method value
指标n与m重要程度判断anm 同等重要1 稍微重要3 明显重要5 强烈重要7 极端重要9 相邻判断中间值2、4、6、8
构建出IMC-DIM层次分析评估方法的判断矩阵为
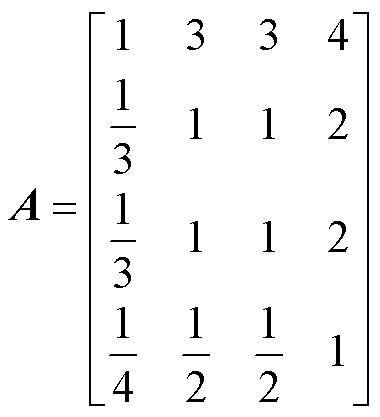（17）
求取判断矩阵的最大特征值所对应的特征向量，其特征向量就是各个指标的权重值。式（17）所示判断矩阵的最大特征值λmax=4.020 6，单位特征向量为α=[0.8732 0.3207 0.3207 0.1784]T。
为了消除主观因素影响，保证权重的合理性，需要采用CR对判断矩阵进行一致性检验，即
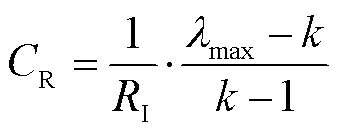（18）
式中，k为指标数量；RI为平均随机一致性指标，当指标数量为4时，RI=0.89[17]。
当CR＜0.1时，一般认为判断矩阵满足要求[18]，式（17）所示判断矩阵的CR=0.007 7，满足要求。
选取某一工况，根据仿真与实验测定结果，构建指标矩阵。由于各指标间量纲、精度等因素存在差异，因此对各指标进行单位化处理，单位化指标矩阵为
（19）
式中，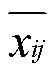
为不同权重因数下的网侧或电机侧单位化性能指标。
通过计算评价矩阵W为
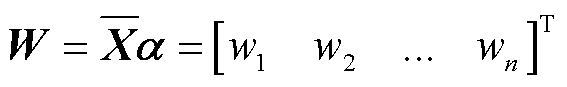（20）
筛选出评价矩阵中的最大值，其对应的权重因数为工况下最优权重因数λop，根据选定工况的参数，计算得到基础权重因数为
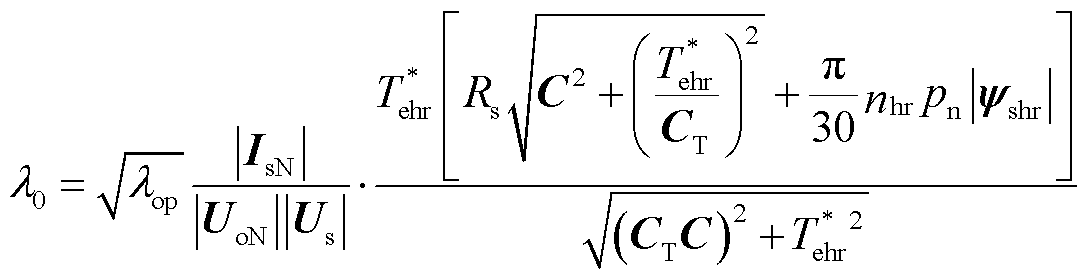（21）
式中，
、
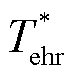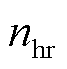和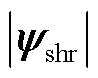
分别为选定工况下功率较高逆变级的参考电磁转矩、电机转速和电机定子磁链幅值。
代价函数优化则是根据上述结果构建代价函数，计算得到48种开关状态的代价函数值，并以代价函数最小为优化原则，筛选出代价函数值最小的开关状态作为系统下一刻的开关状态。
本文利用Matlab/Simulink软件，进行了系统仿真。系统LC滤波器参数与电机参数见表3。网侧电压为160 V/50 Hz，控制频率为50 kHz。
表3 仿真关键参数
Tab.3 Key parameters of simulation
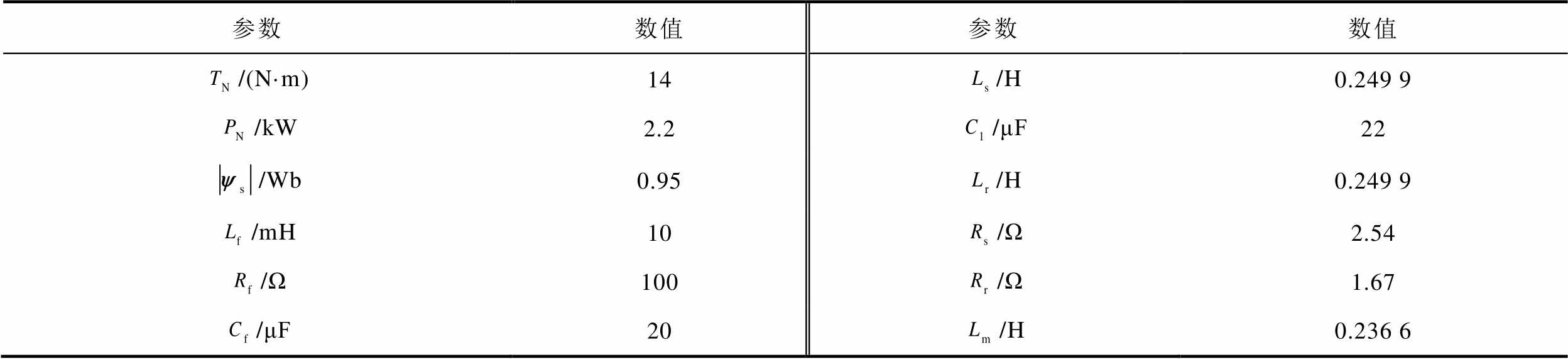
参数数值参数数值 /(N·m)14/H0.249 9 /kW2.2/μF22 /Wb0.95/H0.249 9 /mH10/Ω2.54 /Ω100/Ω1.67 /μF20/H0.236 6
两个转速环PI参数均采用经验法得到，其中KP=5，KI=0.01。
为了确定基础权重因数λ0，对电机1参考转速为600 r/min，负载转矩为10 N·m，电机2参考转速为300 r/min，负载转矩为7 N·m的工况下不同权重因数λ进行性能测试。根据层次分析评估方法得到的不同权重因数方案的评价值如图6所示。
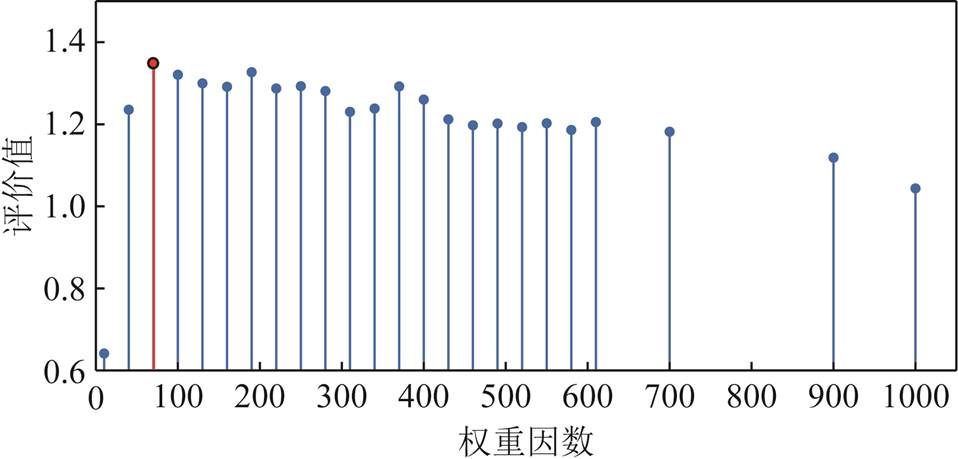
图6 不同权重因数方案的评价值
Fig.6 Evaluation values of different weight factor schemes
可以看出，该工况最优权重因数λop=70，将最优权重因数和工况条件代入式（21）得到基础权重因数λ0=0.55。
图7和图8分别为在电机1参考转速为300 r/min，负载转矩为7 N·m，电机2参考转速为450 r/min，负载转矩为10 N·m的工况下，采用简化MPVC方法和AHP-MPVC方法的网侧电压和电流波形、两台电机定子电流和转速波形。其中，简化MPVC方法的网侧电流THD为6.06%，电机1定子电流THD为2.20%，电机2定子电流THD为1.52%；AHP-MPVC方法的网侧电流THD为4.57%，电机1定子电流THD为2.47%，电机2定子电流THD为2.13%。
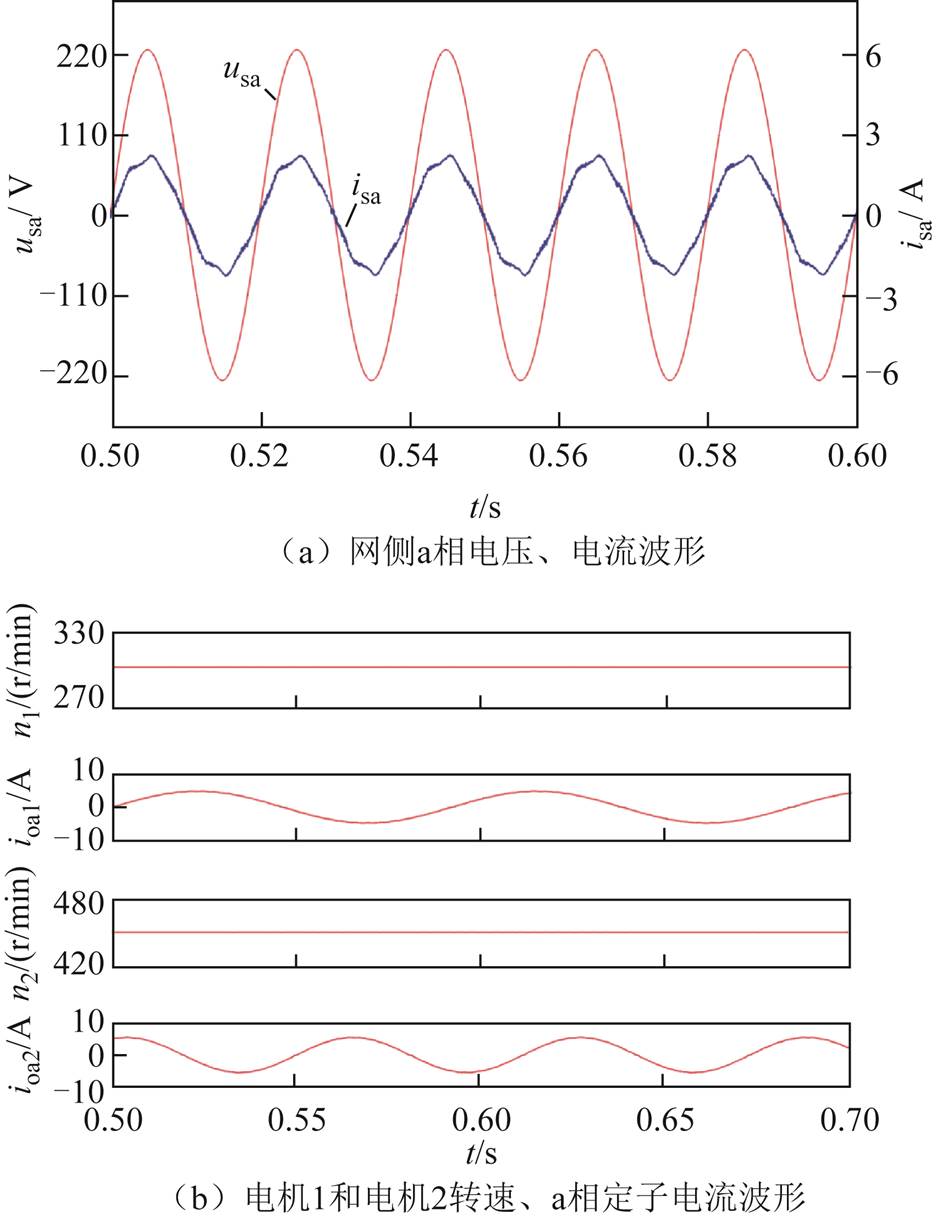
图7 网侧与电机侧稳态波形（简化MPVC）
Fig.7 Steady state waveforms of grid side and motor side（simplify MPVC）
图8 网侧与电机侧稳态波形（AHP-MPVC）
Fig.8 Steady state waveforms of grid side and motor side(AHP-MPVC)
为验证AHP-MPVC方法在不同模态、转速和带载情况下的稳态性能，对多种工况进行了仿真验证。不同功率流状况的网侧电流THD仿真结果如图9所示。
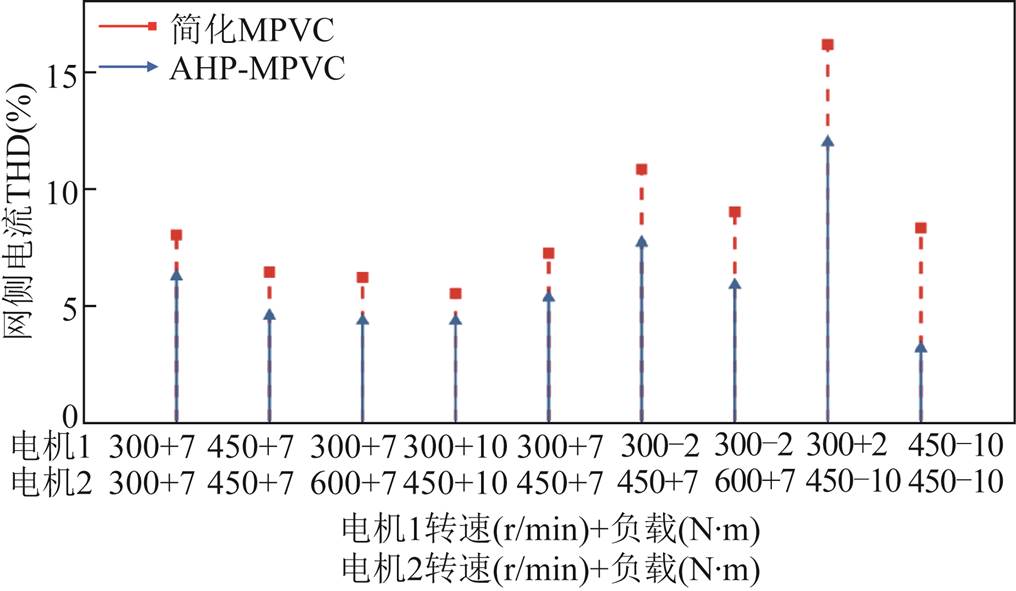
图9 不同工作模态下网侧电流THD
Fig.9 Grid side current THD under different operating modes
仿真结果表明，AHP-MPVC方法在多模态、宽运行范围下网侧电流畸变小。与MPVC方法相比，AHP-MPVC方法在不同模态、转速和带载情况下均具有较好的稳态性能。
本文对AHP-MPVC方法的动态性能进行了仿真验证。在电机1参考转速为600 r/min，负载转矩为10 N·m, 电机2参考转速为300 r/min，负载转矩为7 N·m的工况下，在1.0 s时将电机2转速从300 r/min升至450 r/min。图10和图11分别是简化MPVC方法和AHP-MPVC方法转速突变时的动态性能波形，两种方法的调整时间均为70 ms。
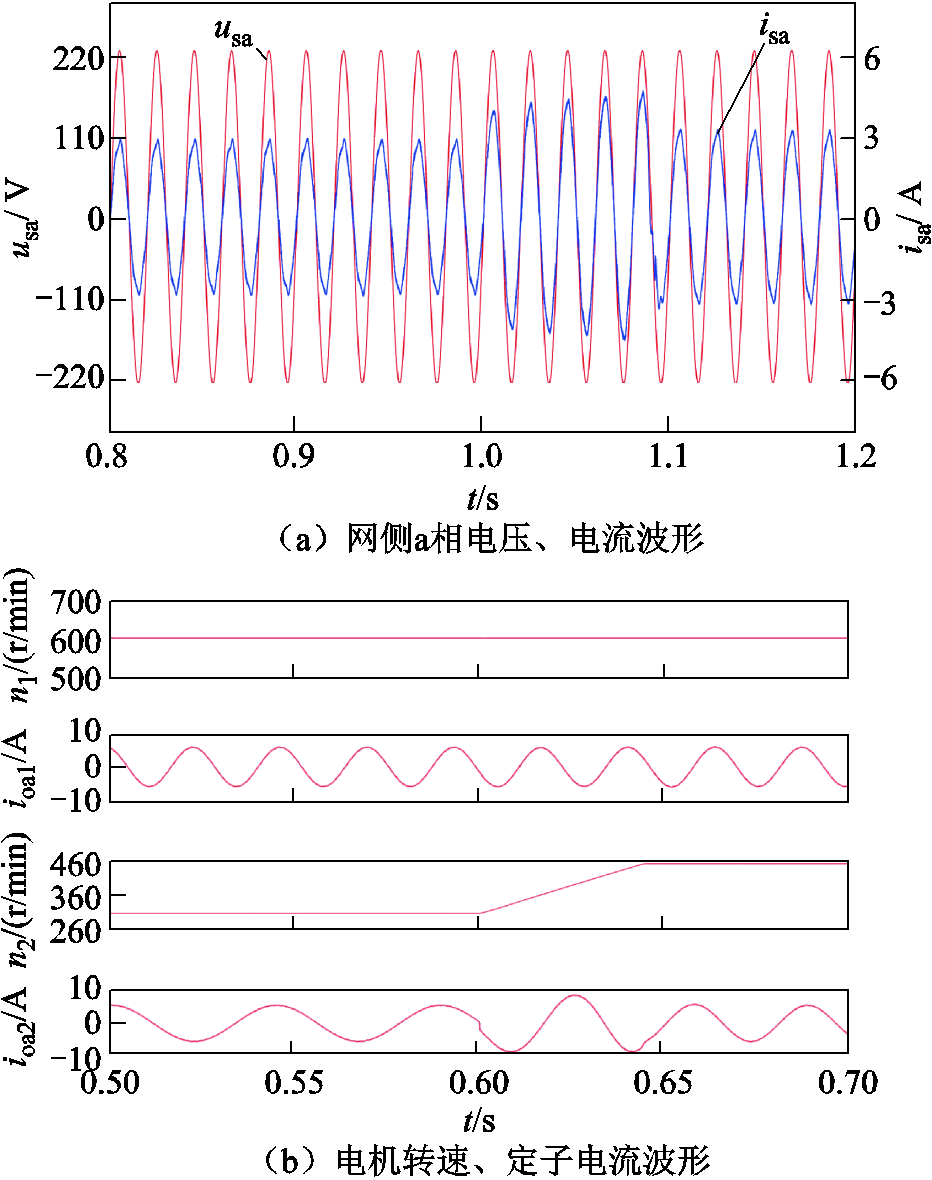
图10 转速突变时动态波形（简化MPVC）
Fig.10 Dynamic waveforms during sudden speed changes（simplify MPVC）
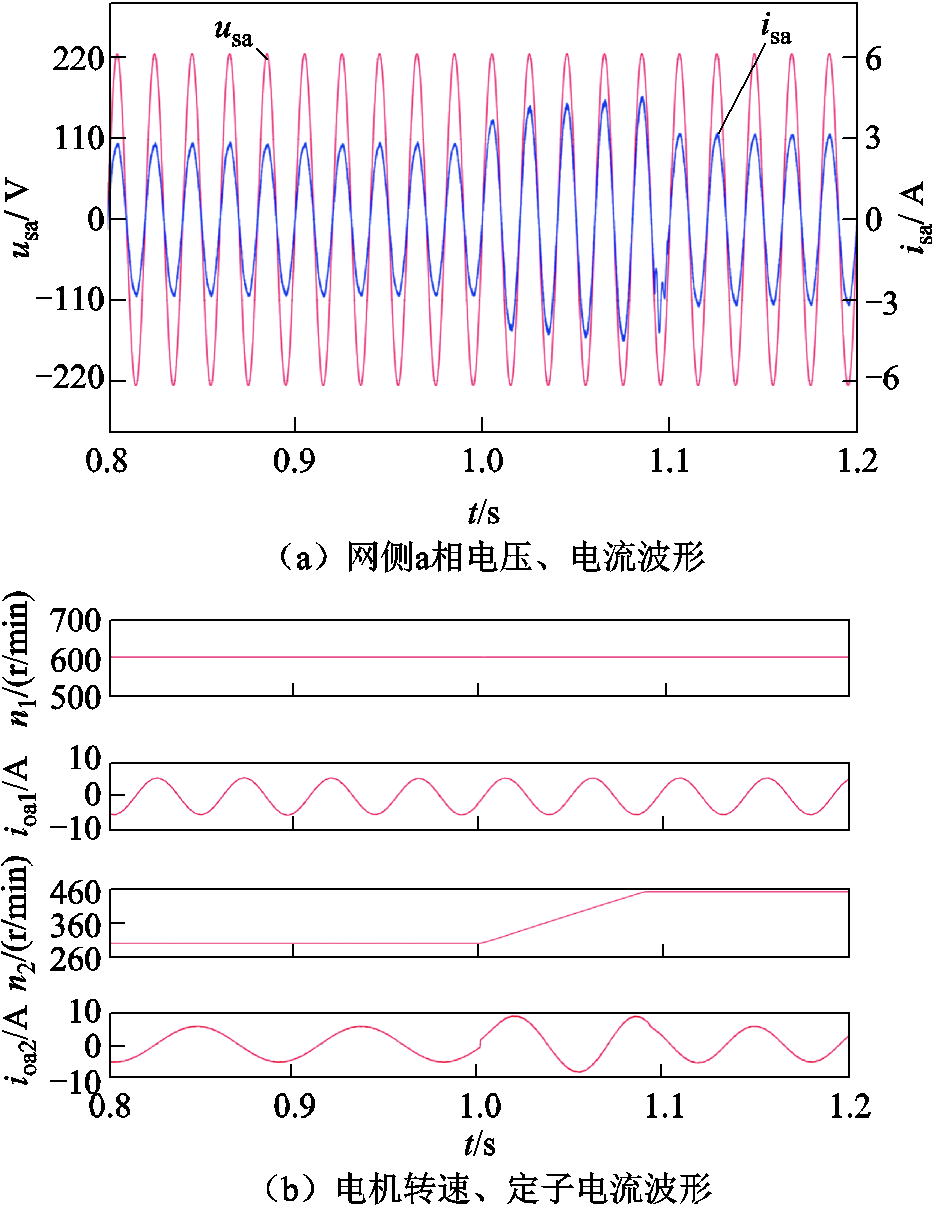
图11 转速突变时动态波形（AHP-MPVC）
Fig.11 Dynamic waveforms during sudden speed changes（AHP-MPVC）
仿真结果表明，简化MPVC和AHP-MPVC这两种方法均可以实现转速的跟踪控制，且电流波形较好，具有良好的动态调速性能。
为验证所提出控制策略的可行性与有效性，利用一台IMC-DIM实验样机进行了实验验证。实验样机如图12所示。实验工况和参数与仿真一致，详见表3。网侧电压为160 V/50 Hz，控制频率为10 kHz。两个转速环PI参数均采用经验法得到，其中KP=0.25，KI=0.15。
图12 实验样机
Fig.12 Experimental prototype
为了确定基础权重因数λ0，对电机1参考转速为600 r/min，负载转矩为10 N·m，电机2参考转速为300 r/min，负载转矩为7 N·m的工况下，不同权重因数λ进行性能测试。根据层次分析评估方法得到的不同权重因数方案的评价值如图13所示。
可以看出，该工况最优权重因数λop=50，将最优权重因数和工况条件代入式（21）得到基础权重因数λ0=0.71。
图14和图15分别为在电机1参考转速为300 r/min，负载转矩为7 N·m，电机2参考转速为450 r/min，负载转矩为10 N·m的工况下，采用简化MPVC方法和AHP-MPVC方法的网侧电压电流、两台电机定子电流和转速波形。其中，简化MPVC方法的网侧电流THD为11.69%，电机1定子电流THD为10.52%，电机2定子电流THD为13.22%；AHP-MPVC方法的网侧电流THD为10.94%，电机1定子电流THD为11.48%，电机2定子电流THD为14.29%。
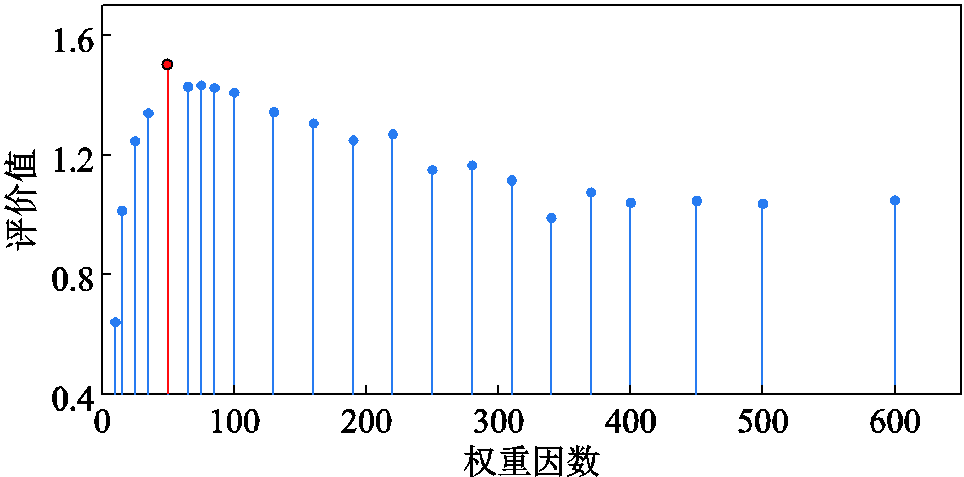
图13 不同权重因数方案的评价值（实验）
Fig.13 Evaluation values of different weight factor schemes (experiment)
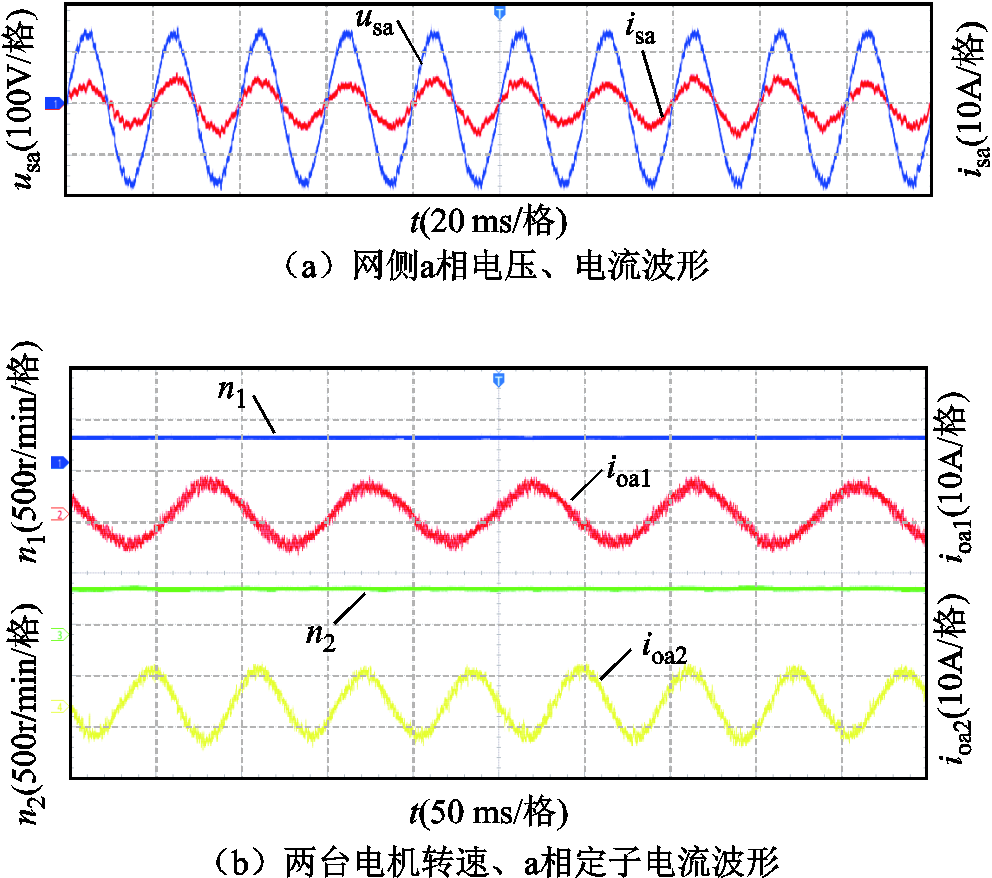
图14 网侧与电机侧稳态波形（简化MPVC）（实验）
Fig.14 Steady state waveform of grid side and motor side（simplify MPVC）(experiment)
图15 网侧与电机侧稳态波形（AHP-MPVC）（实验）
Fig.15 Steady state waveform of grid side and motor side (AHP-MPVC) (experiment)
为验证AHP-MPVC方法在不同模态、转速和带载情况下的稳态性能，对多种工况进行了实验验证。不同功率流状况的网侧电流THD实验结果如图16所示。
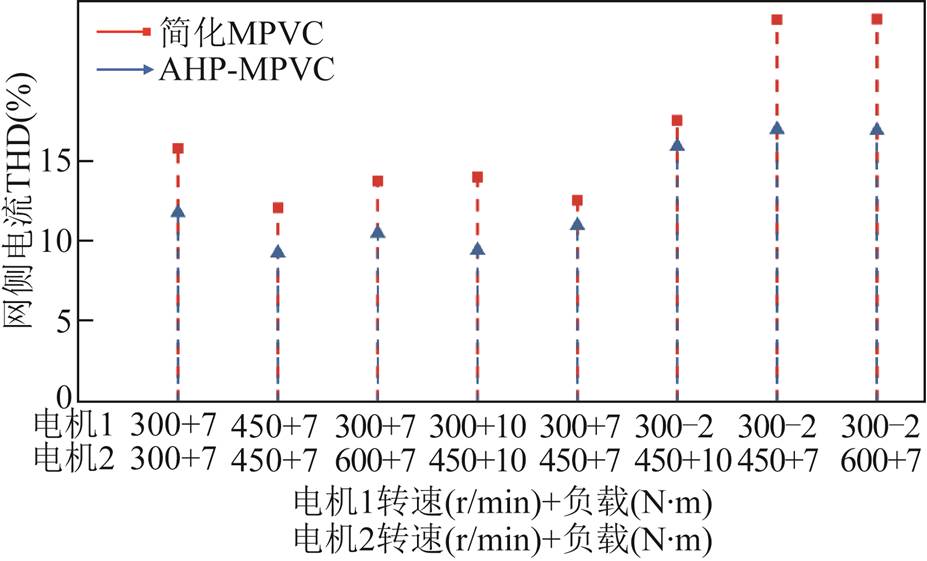
图16 不同工作模态下网侧电流THD（实验）
Fig.16 Grid side current THD under different operating modes (experiment)
实验结果表明，AHP-MPVC方法在多模态、宽运行范围下网侧电流畸变小。与MPVC方法相比，AHP-MPVC方法在不同模态、转速和带载情况下均具有较好的稳态性能。
本文对AHP-MPVC方法的动态性能进行了实验验证。在电机1参考转速为300 r/min，负载转矩为7 N·m, 电机2参考转速为600 r/min，负载转矩为10 N·m的工况下在1.0 s时将电机1转速从300 r/min升至450 r/min。图17和图18分别是简化MPVC方法和AHP-MPVC方法转速突变时的动态性能波形，两种方法的调整时间均为120 ms。
图17 转速突变时动态波形（简化MPVC）（实验）
Fig.17 Dynamic waveform during sudden speed changes (Simplify MPVC) (experiment)
图18 转速突变时动态波形（AHP-MPVC）（实验）
Fig.18 Dynamic waveform during sudden speed changes (AHP-MPVC) (experiment)
实验结果表明，简化MPVC和AHP-MPVC这两种方法均可以实现转速的跟踪控制，且电流波形较好，具有良好的动态调速性能。
本文针对IMC-DIM系统提出一种基于层次分析评估权重因数整定的模型预测电压控制方法。
1）仿真与实验结果表明，该方法可以在多种工况下实现功率因数接近于1，网侧电流正弦且畸变小、电机动态调速性能良好。
2）与简化MPVC相比，该方法权重因数数量少、易于整定。
3）与简化MPVC相比，该方法在多功率流模态以及宽运行范围内均有较好的网侧电能质量与电机调速性能。
参考文献
[1] 鲁紫荆, 李珊瑚, 操孙鹏, 等. 一种大幅度减小间接矩阵变换器高频共模电压的调制策略[J]. 电工技术学报, 2023, 38(16): 4366-4375.
Lu Zijing, Li Shanhu, Cao Sunpeng, et al. A modulation strategy for simultaneously reducing high-frequency common-mode voltage of indirect matrix converter[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4366-4375.
[2] 韩思鹏, 宋卫章, 胥少杰, 等. 不平衡电网电压下精简矩阵变换器扩展直接功率模型预测控制[J]. 电工技术学报, 2023, 38(增刊1): 147-156.
Han Sipeng, Song Weizhang, Xu Shaojie, et al. Extended direct power model predictive control for reduced matrix converter under unbalanced grid voltage operation condition[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 147-156.
[3] Pena R, Cardenas R, Reyes E, et al. Control strategy of an indirect matrix converter with modifying DC voltage[C]//2009 13th European Conference on Power Electronics and Applications, IEEE, Barcelona, Spain, 2009: 1-8.
[4] 程启明, 黄伟, 程尹曼, 等. 双级矩阵变换器驱动永磁同步电机的混合非线性控制系统[J]. 电工技术学报, 2017, 32(4): 101-111.
Cheng Qiming, Huang Wei, Cheng Yinman, et al. Hybrid nonlinear control system of permanent magnet synchronous motor driven by two stage matrix converter [J]. Transactions of China Electrotechnical Society, 2017, 32(4): 101-111.
[5] 叶宇豪, 彭飞, 黄允凯. 多电机同步运动控制技术综述[J]. 电工技术学报, 2021, 36(14): 2922-2935.
Ye Yuhao, Peng Fei, Huang Yunkai. Overview of multi-motor synchronous motion control technology[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2922-2935.
[6] Bordons C, Montero C. Basic principles of MPC for power converters: bridging the gap between theory and practice[J]. IEEE Industrial Electronics Magazine, 2015, 9(3): 31-43.
[7] 王治国, 郑泽东, 李永东, 等. 交流电机模型预测控制综述[J]. 电机与控制学报, 2022, 26(11): 14-30.
Wang Zhiguo, Zheng Zedong, Li Yongdong, et al. A review of model predictive control for AC motor[J]. Electric Machines and Control, 2022, 26(11): 14-30.
[8] 兰志勇, 罗杰, 李延昊, 等. 基于快速选择表的永磁同步电机模型预测转矩控制[J]. 电工技术学报, 2023, 38(21): 5749-5757.
Lan Zhiyong, Luo Jie, Li Yanhao, et al. Model prediction torque control for permanent magnet synchronous motor based on the fast selection table[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5749-5757.
[9] Zhang Yongchang, Yang Haitao, Xia Bo. Model-predictive control of induction motor drives: torque control versus flux control[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 4050-4060.
[10] Mei Yang, Wang Liang, Huang Weichao. An improved model predictive control method for induction motor drives fed by indirect matrix converter[C]//2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-5.
[11] 周奇勋, 刘帆, 吴紫辉, 等. 永磁同步电机转矩与定子磁链模型预测控制预测误差补偿方法[J]. 电工技术学报, 2022, 37(22): 5728-5739.
Zhou Qixun, Liu Fan, Wu Zihui, et al. Model predictive torque and stator flux control method for PMSMs with prediction error compensation[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5728-5739.
[12] Farah N, Lei Gang, Zhu Jianguo, et al. Two-vector dimensionless model predictive control of PMSM drives based on fuzzy decision making[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(4): 393-403.
[13] 史涔溦, 马红如, 陈卓易, 等. 永磁同步电机模糊代价函数预测转矩控制[J]. 电机与控制学报, 2022, 26(1): 1-8.
Shi Cenwei, Ma Hongru, Chen Zhuoyi, et al. Fuzzy tuning of weight coefficient in model predictive torque control of PMSM[J]. Electric Machines and Control, 2022, 26(1): 1-8.
[14] 梅杨, 穆希旺. 间接矩阵变换器-双异步电机调速系统的简化模型预测控制[J]. 电工电能新技术, 2021, 40(3): 1-9.
Mei Yang, Mu Xiwang. Simplified model predictive control for dual induction motor drives fed by indirect matrix converter[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(3): 1-9.
[15] 芮涛, 尹政, 汪凤翔, 等. 基于双矢量的并网逆变器无模型预测电流控制策略[J]. 电工技术学报, 2023, 38(14): 3759-3768.
Rui Tao, Yin Zheng, Wang Fengxiang, et al. Model-free predictive current control strategy of grid-connected inverter based on double-vector[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3759-3768.
[16] Yang Fan, Shen Yu, Cui Xin, et al. Voltage sag severity assessment based on multiobjective decision analytic hierarchy process[C]//2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 2018: 1-6.
[17] Zeng Zheng, Yang Huan, Tang Shengqing, et al. Objective-oriented power quality compensation of multifunctional grid-tied inverters and its application in microgrids[J]. IEEE Transactions on Power Electronics, 2015, 30(3): 1255-1265.
[18] Manusov V Z, Orlov D V. Diagnostics of current technical state of transformer equipment using the analytic hierarchy process[C]//2018 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Moscow, Russia, 2018: 1-6.
Abstract The structure of the indirect matrix converter double induction motor speed control system is complex, and the IMC-DIM system often operates in a wide range of multimodal conditions in practical applications. Traditional MPVC methods are difficult to meet the grid side power quality and motor speed performance requirements of the system under complex operating conditions. To address this issue, this paper proposes a model predictive voltage control (AHP-MPVC) method based on analytic hierarchy process (AHP) evaluation weight factor tuning, solved the problems of multiple weight factors, high tuning difficulty, and inability to ensure good performance of the system under wide range and multimodal conditions in the simplified MPVC method.
This method obtains the grid side reference current, grid side current prediction model, output reference voltage, and output voltage prediction values. The internal structure is divided into five parts: unified dimension and multi motor unified part, integrated grid side and motor side part, reference output voltage estimation part, basic weight factor adjustment based on Analytic Hierarchy Process evaluation, and real-time weight factor adjustment. By combining physical dimensions, dual motors, grid side and motor side, the number of weight factors is reduced to one. By measuring the different performance indicators of grid side and motor side under different weight factors in a certain working condition, the optimal weight factor is obtained based on the Analytic Hierarchy Process evaluation method λop and basic weight factor λ0 At this point, the weight coefficients in the cost function can be adjusted in real-time according to the operating conditions, and the system can achieve better control effects under different operating conditions. In the simulation, the reference speed of motor 1 is 600 r/min, the load torque is 10 N·m, and the reference speed of motor 2 is 300 r/min, and the load torque is 7 N·m under different weight factors λ Conduct performance testing to obtain the optimal weight factor λop=70, basic weight factor λ0=0.55. Then, under another working condition, the simplified MPVC method and AHP-MPVC method are used to obtain the grid side voltage and current, as well as the stator current and speed waveforms of the two motors. The simplified MPVC method has a grid side current THD of 6.06%, motor 1 stator current THD of 2.20%, and motor 2 stator current THD of 1.52%; The grid side current THD of the AHP-MPVC method is 4.57%, the stator current THD of motor 1 is 2.47%, and the stator current THD of motor 2 is 2.13%. In the experiment, the reference speed of motor 1 was 600 r/min, the load torque was 10 N·m, and the reference speed of motor 2 was 300 r/min, and the load torque was 7 N·m, λop=50, λ0=0.71. Under another working condition, the simplified MPVC method and AHP-MPVC method are used to obtain the voltage and current waveforms on the grid side, as well as the stator current and speed waveforms of the two motors. Among them, the THD of the simplified MPVC method for grid side current is 11.69%, the THD of motor 1 stator current is 10.52%, and the THD of motor 2 stator current is 13.22%. The grid side current THD of the AHP-MPVC method is 10.94%, the stator current THD of motor 1 is 11.48%, and the stator current THD of motor 2 is 14.29%.
This article proposes a model predictive voltage control method based on Analytic Hierarchy Process (AHP) evaluation and weight factor tuning for the IMC-DIM system. (1) The simulation and experimental results show that this method can achieve power factor close to 1 under various working conditions, sinusoidal and small distortion of grid side current, and good dynamic speed regulation performance of the motor. (2) Compared with simplified MPVC, this method has fewer weight factors and is easy to tune.(3) Compared with simplified MPVC, this method has better grid side power quality and motor speed regulation performance in multiple power flow modes and wide operating range.
keywords：Indirect matrix converter, induction motors, multi motor drive, model predictive control, weighting factor turning, analytic hierarchy process
中图分类号：TM46; TM343
DOI: 10.19595/j.cnki.1000-6753.tces.231428
北京市自然科学基金资助项目（JL23001, 3222051）。
收稿日期 2023-08-31
改稿日期 2024-01-23
梅 杨 女，1981年生，教授，博士，研究方向为电力电子与电力传动。E-mail：meiy@ncut.edu.cn（通信作者）
吕 宁 男，2000年生，硕士研究生，研究方向为电力电子与电力传动。E-mail：664370619@qq.com
（编辑 赫 蕾）