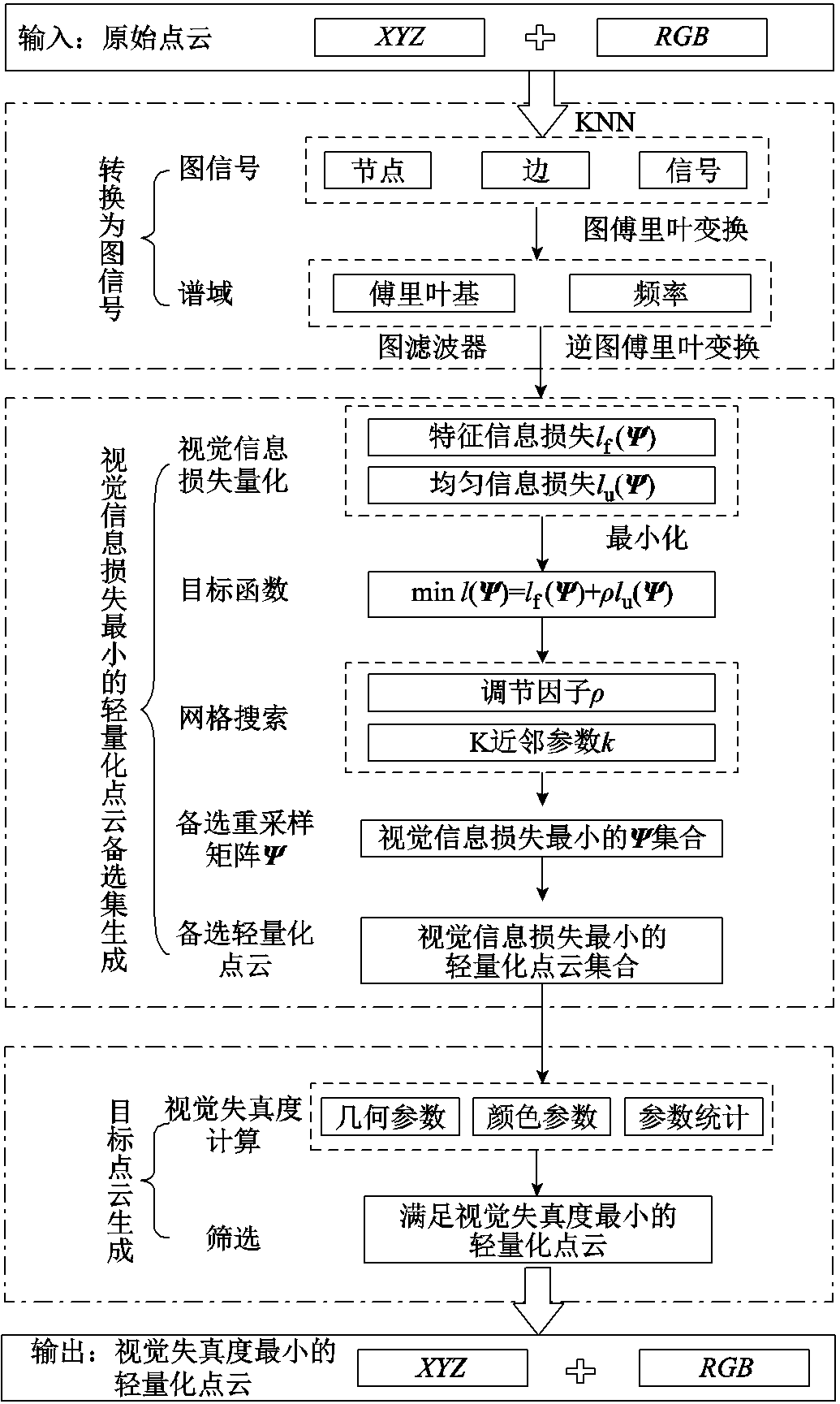
图1 变压器区域大规模点云轻量化方法流程
Fig.1 Flow chart of large-scale point cloud lightweight method for power transformer area
摘要 点云在电网数字化转型中有重要应用价值。现有方法在处理变压器区域大规模点云时难以兼顾点云轻量化后的视觉效果,导致轻量化点云存在较大视觉失真。该文在点云轻量化时引入视觉失真度,以其最小作为约束,实现点云轻量化后视觉效果最优。首先基于谱图理论将原始点云转换为图信号,建立轻量化点云视觉信息损失与重采样矩阵间的函数关系;然后以视觉信息损失最小为目标函数,获得一组满足视觉信息损失最小但特征信息和均匀信息比例不同的轻量化点云;进一步,将原始点云和轻量化点云投影到几何和颜色特征域,用一个低维向量表征点云视觉效果,从而选择出视觉失真度最小的轻量化点云;最后,使用基准数据集和包含8 000余万个点的变压器区域大规模点云进行了验证。结果表明:所提方法与主流的随机降采样法、体素平均法、非均匀网格法、曲率采样法相比,在轻量化点云的视觉效果方面,分别提升了57.4%、69.2%、62.2%、75.6%。
关键词:谱图理论 点云 轻量化 视觉失真 变压器区域
在工业界数字化、智能化转型的背景下,电力行业对实体电网提出数字化、实景化呈现的要求[1-3]。点云由于视觉呈现的逼真性以及建模的快速性,在电力设备三维实景建模领域备受关注[4-6]。对变压器而言,实际生产中的激光扫描对象往往是其整个运行区域[7-9],所得点云包含近亿个点且文件达到GB规模。庞大的数据规模给点云使用带来了困难,因此研究变压器区域大规模点云的轻量化是十分必要的。
目前,点云轻量化方法可分为两类:基于网格的方法和基于点的方法。基于网格的方法将点云转换为网格,然后使用网格简化技术来简化网格,最后从简化后的网格中恢复出轻量化的点云[10]。该方法需要进行网格生成和简化,计算成本高,限制了其在大规模点云轻量化场景中的应用。基于点的方法直接对点云中的点进行操作,主要包括基于局部最优投影的方法[11]、基于空间网格划分的方法[12]、基于准则筛选点的方法[13]。基于局部最优投影的方法生成了一系列点来替换原始点云,缺点在于轻量化后获得的点集不是原始点云的子集。基于空间网格划分的方法将原始点云划分为一系列子空间,然后只保留子空间中最靠近质心的点,以实现点云的轻量化。根据划分子空间的方式,该方法可进一步分为体素平均法和非均匀网格法。体素平均法设置的参数是所划分子空间的几何尺寸[14],该方法可以得到均匀的轻量化点云,但无法保留原始点云中的特征信息。非均匀网格方法设置的参数是子空间中点数量的最大值[15],该方法可以在点密度较高的区域形成更多子空间,缓解了体素平均法在轻量化过程中对原始点云中特征信息丢失严重的问题。基于准则筛选点的方法则是通过设置一些标准来提取原始点云中的某些点以形成轻量化点云。通常,点的几何信息,如法向量[16]、曲率[17]和点密度[18],会被作为筛选点的准则。由于局部熵[19]可用来评估点的重要性,因此它也会被用作点的筛选标准[20-21]。如果筛选标准只有采样率,那么这种方法则退化为随机降采样[22]。上述方法在轻量化时无法对要保留的信息进行灵活控制,鉴于点云和图信号的关联性,有研究人员就提出了借助图滤波器来提升点云轻量化时的可控性[23]。理论上,任何性能的滤波器都可以通过设置滤波参数来实现,但在实际应用中,如何根据轻量化目标设计滤波参数则难度较大。
综上所述,现有点云轻量化方法主要强调对原始点云的几何保真度,即如何保留原始点云中的特征或均匀信息。对电力设备而言,所得轻量化点云会被用于可视化及辅助巡检。这就要求在保留同等数量点的情况下,轻量化点云能够与原始点云视觉效果差异最小,但现有研究尚未充分关注轻量化方法造成的视觉失真,所得轻量化点云无法很好地供电力系统使用。将点云转换为图信号可提升点云轻量化时的可控性,为得到与原始点云视觉效果差异最小的轻量化点云提供了解决思路。
基于此,本研究基于谱图理论提出了一种新的点云轻量化方法,可在保留同等数量点的情况下,得到与原始点云视觉效果差异最小的轻量化点云。首先从图信号处理的角度看待点云轻量化问题;然后对点云轻量化时的视觉信息损失进行理论计算,并以视觉信息损失最小为目标函数得到了一组特征和均匀信息比例不同的轻量化点云;最后,建立轻量化点云的视觉失真度量化准则,进而筛选出与原始点云视觉效果差异最小的轻量化点云。所提方法的有效性在基准数据集和变压器区域的大规模点云上均得到了验证。
点云的视觉信息是指点云中所包含的可被人眼感知到的信息,可以分为特征信息和均匀信息。视觉失真度是指轻量化点云与原始点云相比,呈现到人眼的视觉效果差异。视觉信息损失最小是视觉失真程度最小的前提条件,因为在不同的特征信息和均匀信息比例下都可以满足视觉信息损失最小,需要进一步寻找最佳比例来实现视觉失真度的最小。
变压器区域大规模点云轻量化方法流程如图1所示。所提出的轻量化方法主要包括三个步骤,分别是将原始点云转换为图信号、得到一组满足视觉信息损失最小的轻量化点云、筛选出视觉失真度最小的轻量化点云。
该方法通过K近邻(K-Nearest Neighbor, KNN)算法为原始点云建立边集将,其转换为图信号,并通过图傅里叶变换将图信号转换到频域,进而建立点云轻量化时的特征信息和均匀信息损失表达式。

图1 变压器区域大规模点云轻量化方法流程
Fig.1 Flow chart of large-scale point cloud lightweight method for power transformer area
在量化视觉信息损失后,进一步以视觉信息损失最小为目标函数,对影响特征信息和均匀信息比例的K近邻参数k和调节因子ρ进行网格搜索。在进行网格搜索时,邻域大小参数k=10是一个通用性较好的数值[24]。k的取值越大,对应的图信号就能捕获原始点云中更多的细节特征,因此本方法中取k=[10, 20]且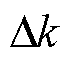 =5。对于不同的点云可保持该区间不变,然后根据计算时间和精度的优先级对
=5。对于不同的点云可保持该区间不变,然后根据计算时间和精度的优先级对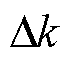 进行设定。参数ρÎ{10-9, 10-7,10-5, 10-3, 10-1, 1, 101, 103, 105, 107, 109},由于原始点云中特征信息和均匀信息的含量是固定的,超过该区间后,轻量化点云中特征信息和均匀信息的比例将不会再发生明显变化。使用时可保持该区间不变,根据时间和精度之间的优先级对
进行设定。参数ρÎ{10-9, 10-7,10-5, 10-3, 10-1, 1, 101, 103, 105, 107, 109},由于原始点云中特征信息和均匀信息的含量是固定的,超过该区间后,轻量化点云中特征信息和均匀信息的比例将不会再发生明显变化。使用时可保持该区间不变,根据时间和精度之间的优先级对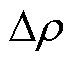 进行设定。经过网格搜索后可得到一组k和ρ的组合参数,进而得到一组满足视觉信息损失最小、但特征信息和均匀信息比例不同的轻量化点云。为从中筛选出视觉失真度最小的轻量化点云,建立了视觉失真度量化准则,将点云投影到与视觉效果相关的几何和颜色特征域下,计算了轻量化点云的视觉失真度,从而选择出与原始点云视觉效果差异最小的轻量化点云。
进行设定。经过网格搜索后可得到一组k和ρ的组合参数,进而得到一组满足视觉信息损失最小、但特征信息和均匀信息比例不同的轻量化点云。为从中筛选出视觉失真度最小的轻量化点云,建立了视觉失真度量化准则,将点云投影到与视觉效果相关的几何和颜色特征域下,计算了轻量化点云的视觉失真度,从而选择出与原始点云视觉效果差异最小的轻量化点云。
1.2.1 点云数学表示
原始点云是通过点云扫描仪获得的,点云扫描仪由激光器、相机以及其他零件组成。激光器用于获得建模对象的几何属性,相机用于获得建模对象的颜色属性。因此,原始点云可表示为
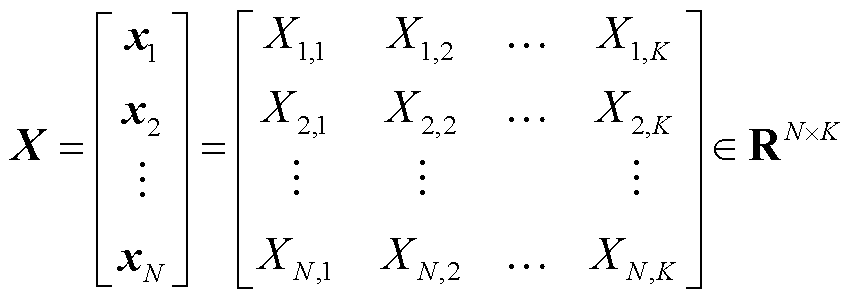 (1)
(1)
式中,原始点云X包含N个点,每个点含K个属性矩阵。X的前三列为点的空间坐标,其余列为点的其他属性,如颜色和纹理等。
变压器区域的原始点云规模庞大,而其通常又呈现在浏览器/服务器(Browser/Server, B/S)架构下的网页端。因此,在使用前对原始点云进行轻量化处理是非常必要的。轻量化过程可以表示为
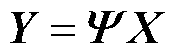 (2)
(2)
式中,Y为轻量化后的点云;Ψ为轻量化过程中使用的重采样矩阵,是一个对角矩阵,在轻量化过程中如果原始点云中的第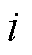 个点要保留,则Ψii=1,反之Ψii=0。所以,点云轻量化的核心在于根据目标函数寻找重采样矩阵Ψ。
个点要保留,则Ψii=1,反之Ψii=0。所以,点云轻量化的核心在于根据目标函数寻找重采样矩阵Ψ。
1.2.2 点云到图信号
基于谱图理论将点云转换为图信号有助于寻找出所需的重采样矩阵。一个典型的图信号如图2所示。
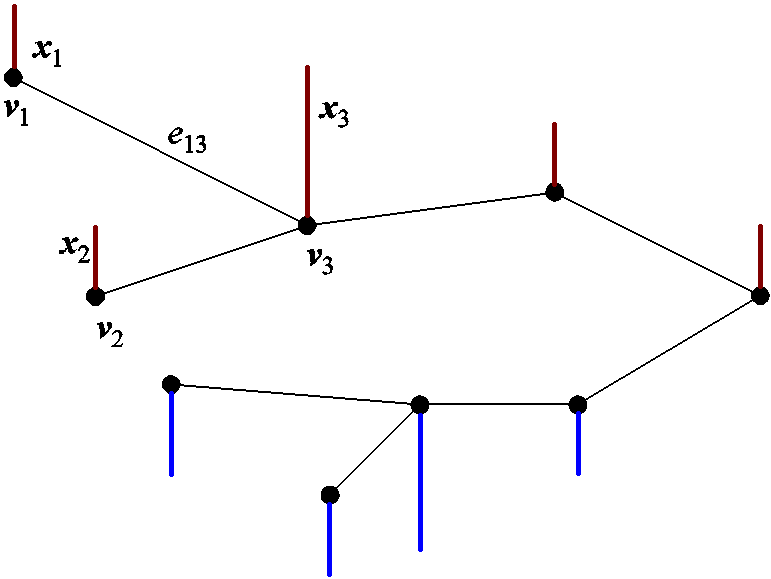
图2 图信号示意图
Fig.2 Schematic diagram of the graph signal
图2可以用G=(V(G),E(G),W)来表示,其中V(G)={v1, v2, ×××,vn}是图顶点的集合,E(G)={×××, eij, ×××}是图中边的集合,W是邻接矩阵,其元素取值为1或0,取决于节点vi和vj之间是否存在连接关系。图信号则是图节点上的信号值,表示成向量的形式为X=[x1 x2 ××× xN]T。
点云中的点可看作图信号的节点集,点的属性可看作图节点上的信号。因此使用KNN方法为原始点云构建拓扑连接后,其就被转换为图信号,可借助图滤波器来完成点云的轻量化。
基于图滤波器的点云轻量化可表示为
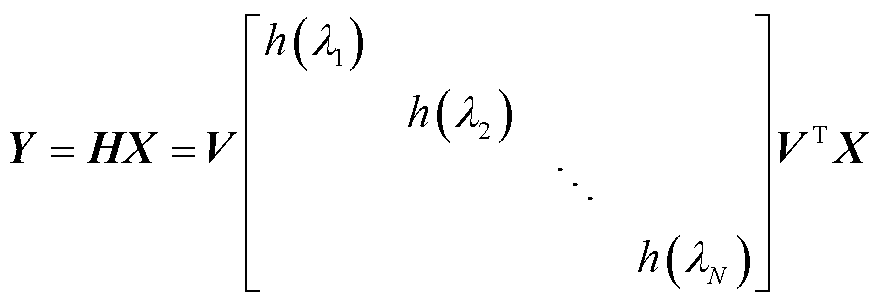 (3)
(3)
式中,H为所使用的图滤波器,HÎRN´N;λi为原始点云所对应图信号的图拉普拉斯矩阵L的特征值;h(∙)为变换函数;V为L的特征矩阵,由L的特征向量组成。
由此看出,通过设置图滤波器的h(λi)项就可以实现原始点云中特定信息的保留或滤除。
点云轻量化过程中产生的视觉信息损失可分为特征信息损失和均匀信息损失。图滤波器可对原始点云中特定信息进行保留或滤除的特性为量化视觉信息损失提供了可行性。基于此,本节进行点云轻量化过程中的视觉信息损失计算。
1.3.1 特征信息损失量化
图信号在谱域中的高频部分对应着空域中的特征信息,所以原始点云中的特征信息可通过高通滤波器进行提取,于是设计了如式(4)所示的高通滤波器。
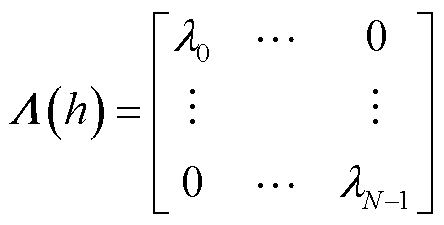 (4)
(4)
式中,Λ(h)为所设计的滤波器;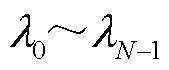 为图信号X的图拉普拉斯矩阵L的特征值。
为图信号X的图拉普拉斯矩阵L的特征值。
进一步基于式(3)和式(4),并结合图拉普拉斯矩阵的定义[25],可得到所设计滤波器的作用为
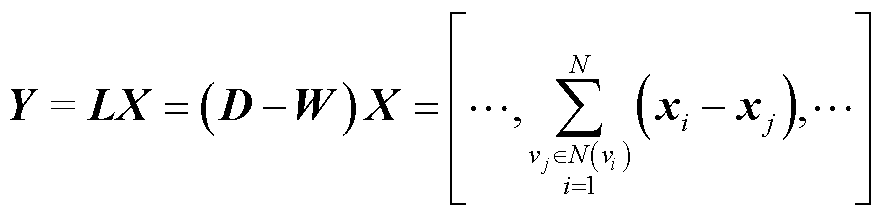 (5)
(5)
式中,D为图信号的度矩阵;N(·)表示领域。
通过式(5)可以看出,上述滤波器提取了原始点云图信号中每个信号与其邻域内信号的差值,而这个差值其实就是原始点云中的特征信息。因此,原始点云的特征信息就可以用LX进行表示。进一步地,当使用重采样矩阵Ψ对原始点云进行轻量化处理时,得到的轻量化点云中包含的特征信息则可以表示成为ΨLX的形式。于是,点云轻量化前后的特征信息损失可以表示为
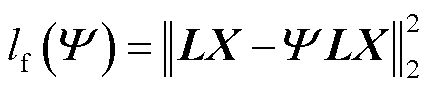 (6)
(6)
式中,lf(Ψ)为点云轻量化前后的特征信息损失。
1.3.2 均匀信息损失量化
当使用矩阵Ψ进行重采样时,假设重采样率为α,如果点云是完全均匀的,那么各个点邻域内的点数量为αk1,这里1ÎRN表示元素都为1的N维列向量。那么αk1可看作是轻量化点云中所能包括均匀信息的最大值。实际上点云不可能是完全均匀的,其邻域内点的数量可以用该节点的度来表示,即D=W∙1,那么经过重采样后,每个点邻域内点的数量可以表示为WΨ1。所以可用WΨ1与αk1的差值来表示轻量化点云中均匀信息实际值与理想值的偏差情况。此外,原始点云中的均匀信息虽然是未知的,但必然是一个恒定值Cori。上述均匀信息损失量化示意图逻辑过程可以用图3表示。
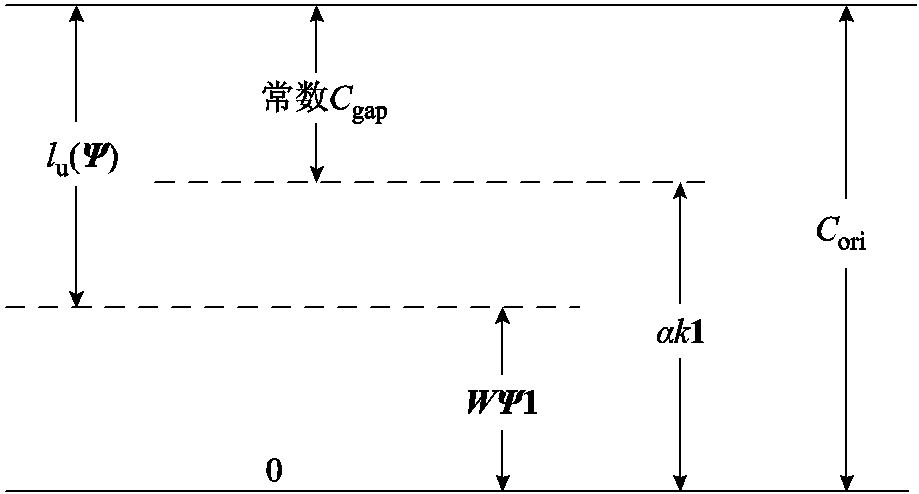
图3 均匀信息损失量化示意图
Fig.3 Schematic diagram of uniform information loss quantification
通过上述分析,点云轻量化前后的均匀信息损失可表示为
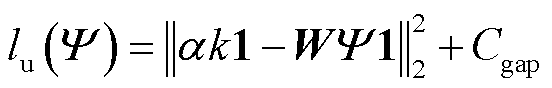 (7)
(7)
式中,lu(Ψ)为点云轻量化前后的均匀信息损失;常数Cgap为轻量化点云均匀信息的最大值αk1与原始点云中均匀信息Cori之间的差值。这里的Cgap和Cori无需确定其具体值,因为在后续最小化视觉信息损失的目标函数中,常数项会被去掉。
1.3.3 目标函数
在得到轻量化前后特征信息损失和均匀信息损失的表达式后,进一步可得到轻量化时总视觉信息损失最小的目标函数为
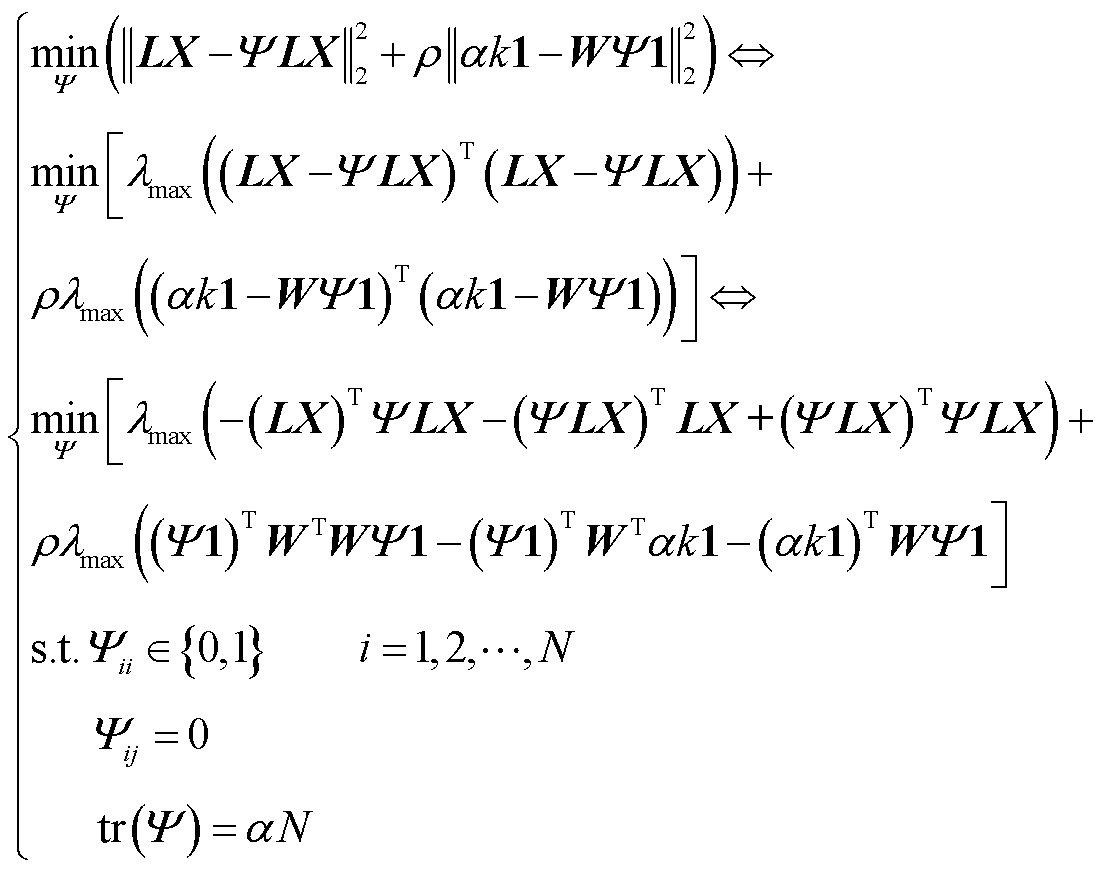 (8)
(8)
式中,λmax(∙)表示矩阵的最大特征值。该目标函数的自变量是重采样矩阵Ψ;约束条件是重采样矩阵Ψ的对角线元素为1或0,非对角线元素为0,且对角线元素的和为αN。考虑到轻量化点云在不同的特征信息和均匀信息比例下均可以达到视觉信息损失最小,但不同的比例对应不同的视觉效果,因此式中引入了比例调节因子ρ。
在式(8)中,该函数上有三个自变量,分别为将点云转换为图信号时的K邻域参数k,比例调节因子ρ和重采样矩阵Ψ。其中参数k和ρ同时影响着轻量化点云中的特征信息和均匀信息比例。因此在该目标函数中,对参数k和ρ进行网格搜索后,借助优化算法就可以得到一组满足信息损失最小的重采样矩阵Ψ,即可以进一步得到一组满足信息损失最小的轻量化点云。所得到轻量化点云的数量等于网格搜索时的网格点个数。这些点云均满足视觉信息损失最小,但具有不同的特征信息和均匀信息比例,因而对应着不同的视觉效果。因此,接下来需要从中选择出与原始点云相比视觉效果差异最小的那个轻量化点云。
为了选择出视觉失真度最小的轻量化点云,本节通过一定的变换将点云的视觉效果转换为低维向量。最后通过比较原始点云和轻量化点云所对应向量之间的差异,量化了轻量化点云的视觉失真度,进而选择出视觉失真度最小的轻量化点云。整体流程如图4所示。
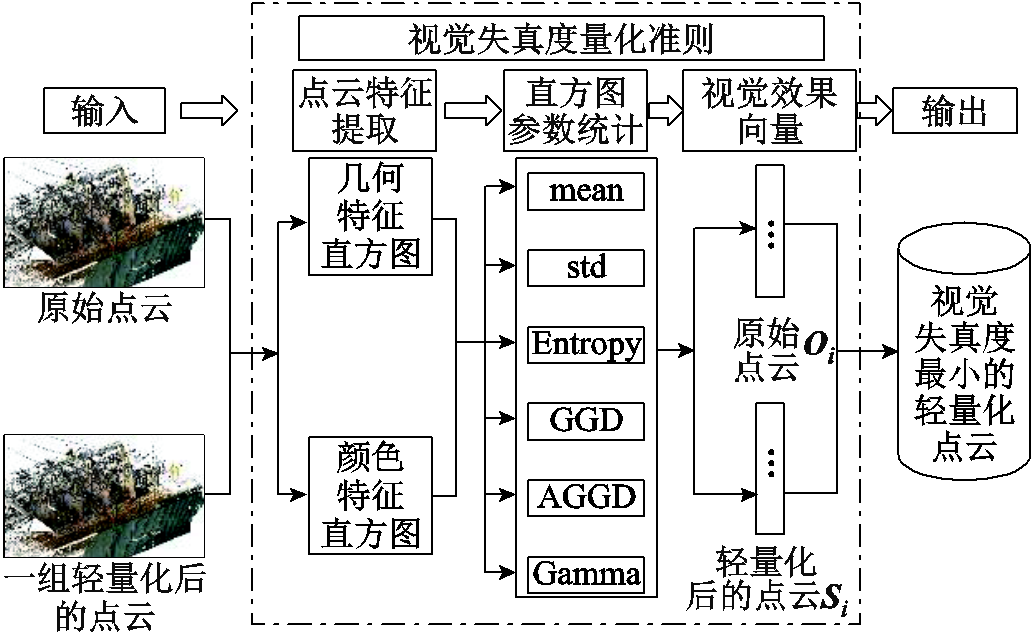
图4 视觉失真度最小的轻量化点云筛选流程
Fig.4 Lightweight point cloud screening process with minimal visual distortion
在图4中,首先将输入的三维点云投影到与视觉效果密切相关的几何和颜色特征构成的特征域,然后每个特征就会对应一个直方图,此时点云被转换为多个直方图。进一步用统计参数对各个特征的直方图进行量化,此时输入的点云就被转换为由点云特征直方图统计结果构成的向量。最后,利用原始点云对应的向量和轻量化点云对应的向量之间的差异就可以计算出轻量化点云的视觉失真度,从而选择出视觉失真度最小的轻量化点云。
1.4.1 视觉效果的几何特征域投影
为了提取点云的几何特征,首先使用KNN方法为点云中的每个点都构建了邻域,即
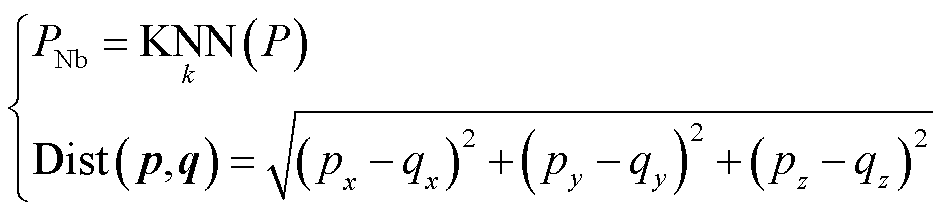 (9)
(9)
式中,PNb为点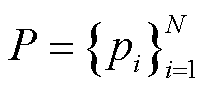 的邻域;KNN(∙)为K近邻函数,即取点
的邻域;KNN(∙)为K近邻函数,即取点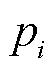 周围距离最近的k个点构成其邻域,且所使用的距离计算函数为Dist(p, q)。
周围距离最近的k个点构成其邻域,且所使用的距离计算函数为Dist(p, q)。
在得到点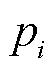 的邻域
的邻域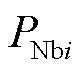 后就可以得到点
后就可以得到点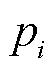 对应的协方差矩阵Ci为
对应的协方差矩阵Ci为
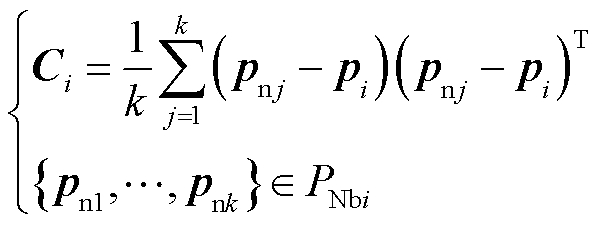 (10)
(10)
式中,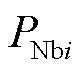 为点
为点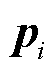 的邻域;
的邻域;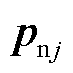 为
为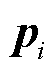 邻域内的点,
邻域内的点,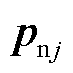 和
和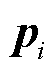 都是3´1的列向量;k为邻域内包含的点的数量;Ci为点
都是3´1的列向量;k为邻域内包含的点的数量;Ci为点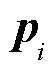 的协方差矩阵。
的协方差矩阵。
文献[26]提出了使用协方差矩阵的特征值来对点云的几何特征进行计算。协方差矩阵Ci的特征值可由式(11)求得。
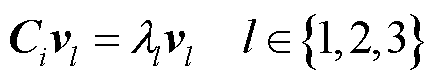 (11)
(11)
式中,λl为Ci的特征值;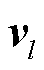 为Ci的特征向量,且假设λ1>λ2>λ3。
为Ci的特征向量,且假设λ1>λ2>λ3。
上述特征值可以计算的几何特征包括:曲率、各向异性、线性度、平面度、球度。这些几何特征的用途如下:
(1)曲率:度量点云内每个点邻域的表面特征。
(2)各向异性:反映在观察点云数据时,在不同方向上的密度、形状等属性差异。
(3)线性度:度量点云的线性一维结构,在高线性度的点云中,点沿着直线排列,反之则分布散乱。
(4)平面度:度量点云的平面二维结构,在高平面度的点云中,点分布在多个平面上,反之则分布不规则。
(5)球度:度量点云的三维体积结构,在高球度的点云中数据点分布较为紧密,接近于一个球体的形状。
文献[27-28]基于上述几何特征开展了点云的识别、语义分割等工作并取得了成功,证明了这些几何特征与视觉效果的相关性。因此,本文选择上述几何特征对点云几何特性进行描述。需要说明的是,上述的几何特征是在点水平上进行计算的,也就是说点云内的每个点都有各自的上述的几何特征。上述特征的计算方式依次为
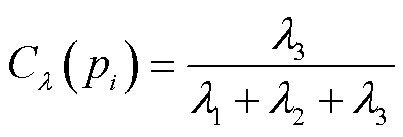 (12)
(12)
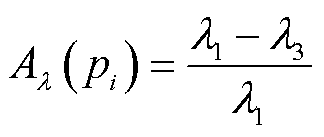 (13)
(13)
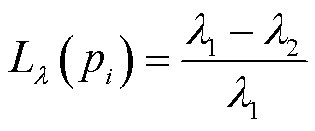 (14)
(14)
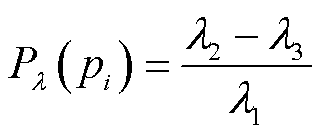 (15)
(15)
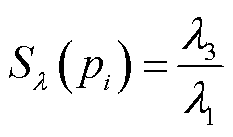 (16)
(16)
通过上述操作,就将空间特征域中的点云投影到了由上述5个参数组成的几何特征域中。
1.4.2 视觉效果的颜色特征域投影
色彩特征是影响视觉质量的另一个关键因素。原始点云的色彩信息是使用RGB数值来存储的,但RGB色空间与人类视觉感知的相关性较差[29],因此本文选择与人眼视觉感知效果更接近的LAB色空间对色彩信息进行描述。
XYZ色空间提供了一种标准的中间色彩空间,可以作为RGB色空间和LAB色空间转换的桥梁。
RGB色空间到XYZ色空间的转换式为
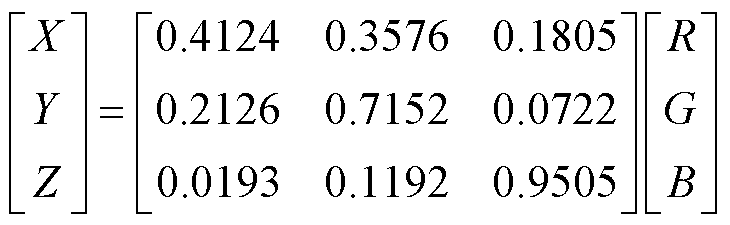 (17)
(17)
XYZ色空间到LAB色空间的转换流程为
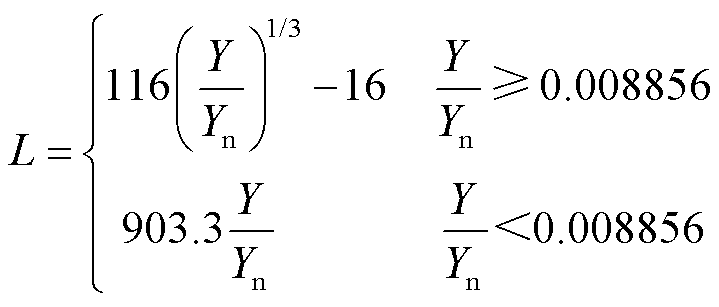 (18)
(18)
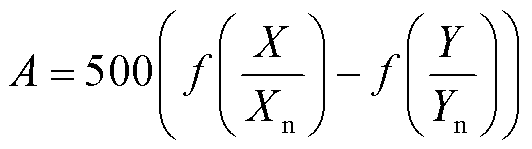 (19)
(19)
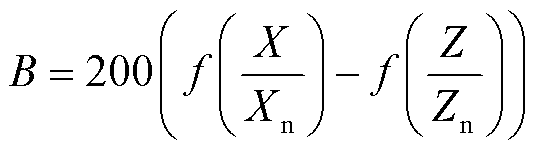 (20)
(20)
式中,Xn、Yn、Zn为白点三刺激值,在D65标准光源下其取值通常为Xn=95.047,Yn=100,Zn=108.883。
1.4.3 视觉效果统计参数
基于1.4.1节和和1.4.2节的变换,点云被投影到了由5个几何特征和3个色彩特征构成的视觉特征域下。由于是在点水平上进行操作的,因此每个特征都会对应一个直方图,直方图的横轴是该特征的值,纵轴是对应值的概率密度。显然,可以通过考查点云轻量化前后各个特征的直方图变化情况来量化点云的视觉失真度。直方图的定量描述就是基于本节的统计参数来完成的。
为了说明统计参数和直方图描述的映射关系,在附图1中,给出了所提方法得到的轻量化点云所对应的视觉特征直方图。可以看出,L、A、B、线性度、平面度的形状可用高斯分布进行拟合,因此选择了广义高斯分布(Generalized Gaussian Distribution, GGD)进行拟合。此外,观察到线性度和平面度的直方图的左右拖尾并不对称,因此也可选择非对称广义高斯分布(Asymmetric Generalized Gaussian Distribution, AGGD)进行拟合。曲率、各向异性、球度的分布则可以用Gamma分布拟合。
因此,共使用了以下四种统计参数对视觉特征的直方图进行考察。
1)3个基本参数
点云的每个特征参数都是一个N´1的数组,因此,首先进行了归一化处理。
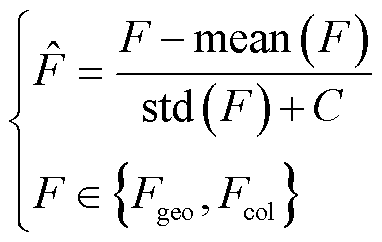 (21)
(21)
式中,F为归一化前的特征参数;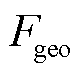 、
、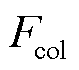 分别为几何特征和视觉特征;
分别为几何特征和视觉特征;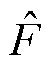 为归一化后的特征参数;mean(∙)为求均值的函数;std(∙)为求标准差的函数;C为一个常数,用于避免分母趋于零时的不稳定性。
为归一化后的特征参数;mean(∙)为求均值的函数;std(∙)为求标准差的函数;C为一个常数,用于避免分母趋于零时的不稳定性。
除均值和标准差外,熵是第三个基本参数,因为熵反映图像中的信息量,与视觉失真程度高度相关。当图像出现失真时,视觉信息会丢失,熵也就会下降。熵E的计算方法为
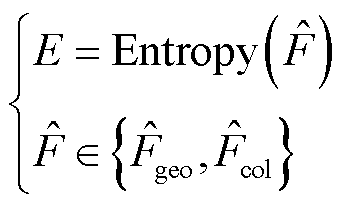 (22)
(22)
式中,Entropy(∙)为计算熵的函数;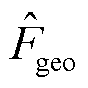 和
和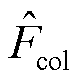 为归一化的几何特征和色彩特征。
为归一化的几何特征和色彩特征。
2)2个GGD参数
GGD是一种概率分布函数,它可以用来描述数据的分布形态。GGD的概率分布函数为
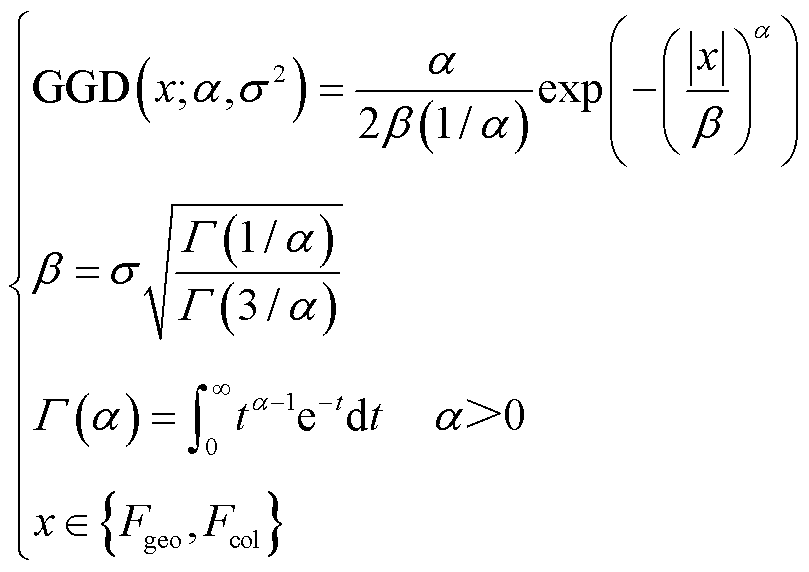 (23)
(23)
式中,α决定高斯分布的形状,σ2决定高斯分布的方差,(α, σ2)共同描述了概率分布的形状。也就是说,将x拟合到GGD概率密度函数上,就可以得到一组用于描述x概率密度分布的(α, σ2)。
此外,考虑归一化后数据的方差固定为1,因此,在式中使用了归一化前的数据来计算GGD参数。
3)4个AGGD参数
非对称广义高斯分布进一步扩展了GGD,用于描述概率密度分布左右不对称的情况,在此同样也将x拟合到了AGGD概率密度函数上。AGGD的概率分布函数为
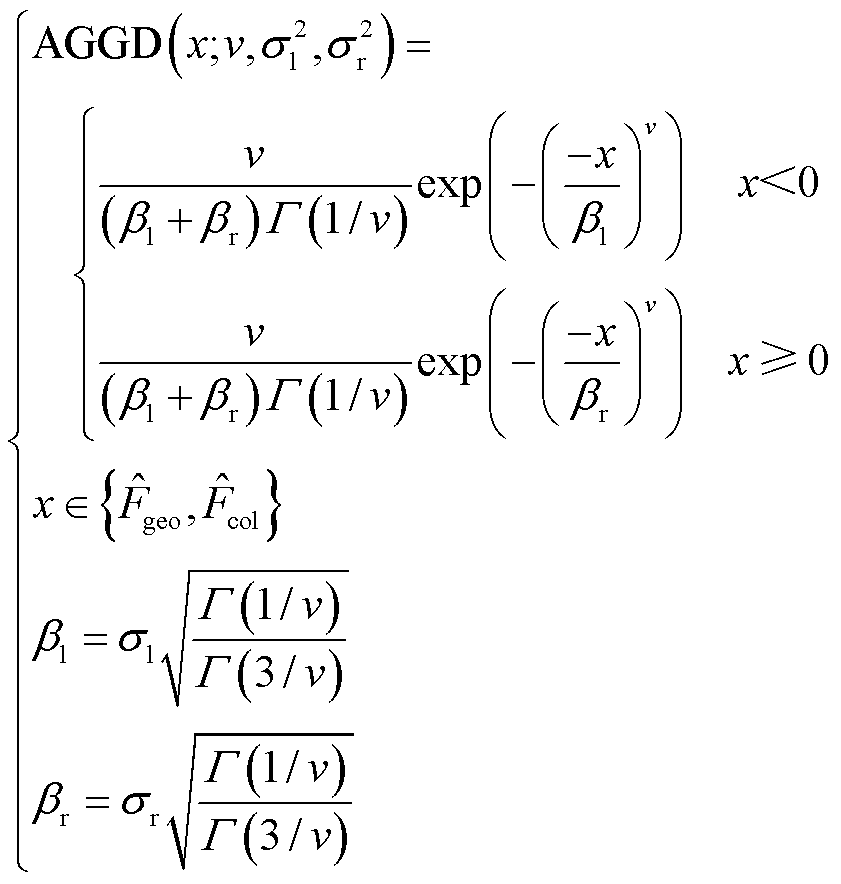 (24)
(24)
AGGD有4个关键参数,分别是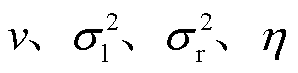 ,η=βl-βr是反映拟合状态的参数,
,η=βl-βr是反映拟合状态的参数,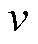 反映了分布的形状,
反映了分布的形状,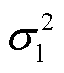 、
、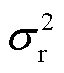 反映了分布的左、右拖尾,当
反映了分布的左、右拖尾,当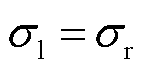 时,AGGD就等价为GGD。
时,AGGD就等价为GGD。
4)2个Gamma参数
Gamma分布也被引入用来拟合直方图的分布,其定义为
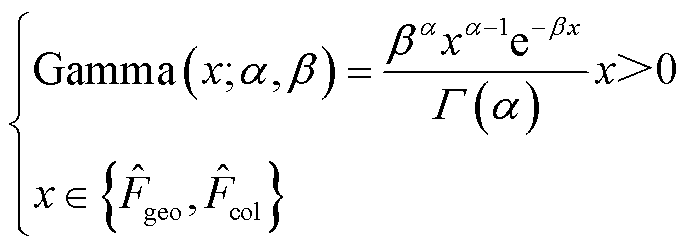 (25)
(25)
式中,α和β分别为形状和尺度参数;α为概率分布曲线的形状;β为概率分布曲线的陡峭程度。
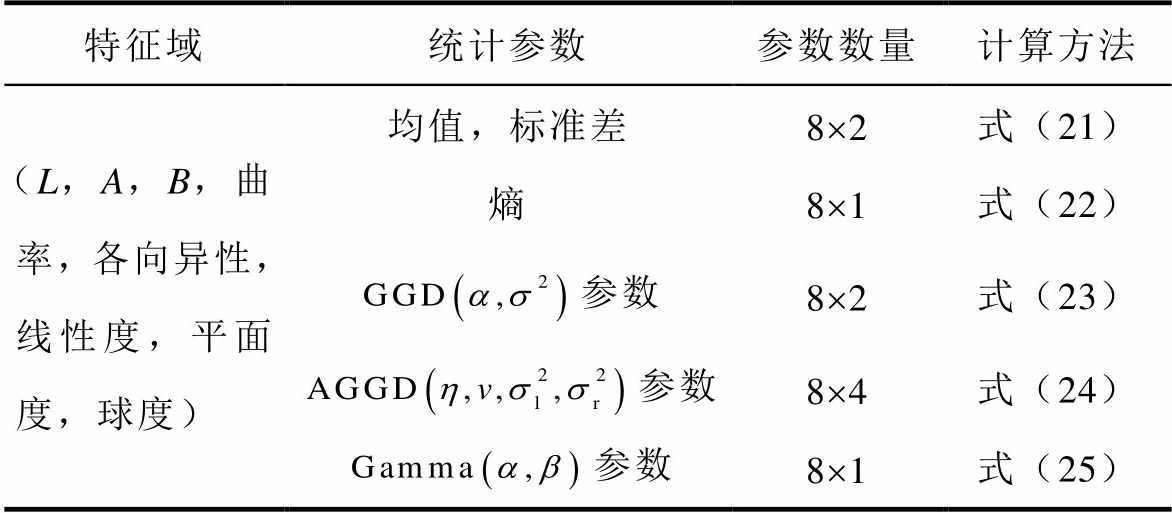
点云中的每个点在特征域内都有8个参数(5个几何参数,3个色彩参数),也就是说一个点云可以用8个直方图来表征。那么在量化点云轻量化时的视觉失真度时只需要比较原始点云的8个直方图和轻量化点云的8个直方图间的差异即可。由于这种差异难以直接比较,因此在本节的1)~ 4)中引入了直方图的统计参数对直方图进行描述。每个直方图均被11个统计参数进行了描述,见表1。
表1 描述直方图的统计参数总结
Tab.1 Summary of statistical parameters to describe the histogram
特征域统计参数参数数量计算方法 (L,A,B,曲率,各向异性,线性度,平面度,球度)均值,标准差8´2式(21) 熵8´1式(22) 参数8´2式(23) 参数8´4式(24) 参数8´1式(25)
从表1可看出,点云的视觉效果可用一个88´1的向量来表达。那么可以通过比较原始点云向量和轻量化点云向量间的差异来计算轻量化点云的视觉失真度,进而选择出失真度最小的轻量化点云。
1.4.4 轻量化点云生成
在将点云转换为一个88维的列向量后,其视觉失真度的计算方法为
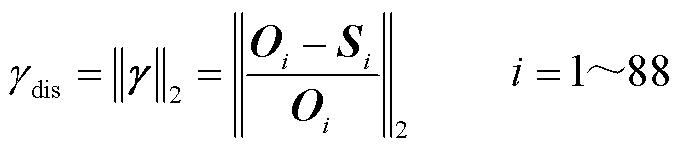 (26)
(26)
式中,Oi为原始点云的向量;Si为轻量化点云的向量;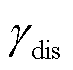 为轻量化点云的视觉失真度。
为轻量化点云的视觉失真度。
由此就可以通过式(26)完成对轻量化点云视觉失真度的量化,进而就可以从1.3节得到的满足视觉信息损失最小的备选轻量化点云集中选择出视觉失真度最小的轻量化点云。
本节使用由滑铁卢大学学者建立的点云基准数据集[30]来定量比较不同轻量化方法导致的视觉失真度。之所以选择该数据集是因为其包括原始点云及原始点云经过三种不同程度轻量化处理后的点云,且其作者为每个轻量化点云都标定了视觉分数。通过比较这些标定的视觉分数与所建立视觉失真度量化准则计算得到的结果,可以首先验证所建立量化准则的有效性。进一步,基于验证后的量化准则可以比较不同轻量化方法的视觉失真度。
2.1.1 基准数据集中点云视觉分数标定方法
数据集中点云的视觉分数是基于观众主观打分来标定的。尽管相关研究已将其作为基准数据集且广泛使用了其中标定的分数,但考虑所标定分数的准确性对于验证本文所提出方法的可靠性至关重要。因此在使用前需要考核该分数的准确性,故本节首先给出了该数据集作者为其中点云进行视觉分数标定的过程。
1)原始数据准备
使用渲染器将每个点云渲染到视频序列。在渲染时将点云置于球心,利用一个虚拟相机,以水平圆和垂直圆为路径为每个点云都生成360帧图像,然后将原始点云和轻量化点云的图像拼接为视频。最终原始点云和某个轻量化程度的点云以视频形式呈现。
2)分数标定开展
得到原始数据后,基于标准ITU-R BT.500-1301/2012开展轻量化点云视觉分数的标定工作[31]。标准中共给出了三种关于观众主观标定视觉分数的方法,该数据集视觉分数的标定采用的是双重刺激损伤评分法(Double-Stimulus Impairment Scale, DSIS)。DSIS方法中,首先向观众提供原始影像数据,然后提供损伤数据,在此之后观众被要求进行打分且根据损伤进行减值打分。DSIS的另一种变体则是提供两遍原始和损伤数据后再进行打分,适用于视觉失真度很小的情况。该数据集中点云视觉分数的标定采用了第一种方法,即只提供一次数据。DSIS方法进行视觉分数标定的流程主要包括:测试环境配置及校准、测试人员选择、测试人员培训、视觉分数标定。
在该数据集视觉分数的标定过程中,首先根据标准对测试环境及显示设备的各项信息进行校准,对于核心的显示设备信息,采用23.6 in(1 in=0.025 4 m)且分辨率为1 920×1 080的LCD显示器。然后根据标准所要求的大于或等于15名观察员,选择了60名观察人员,所有受试者视力均正常或矫正至正常,从两倍于屏幕高度的距离观看。进一步,按照标准要求,播放了18段测试视频,其中人员在测试前就知道了失真类型和程度,由此培训了观察人员如何根据清晰度、几何、颜色、细节进行评分。最后,评分能力达标后才进入视觉分数标定工作。在标定视觉分数时,将1)中形成的点云视频进行播放。每次播放时间持续0.5 h,间隔3~5 min,以消除视觉疲劳的影响。每个视频播放30次且标定分数时采用百分制。
视觉分数在使用前,需要使用Z分数将其标准化后再去除离群值,然后再重新缩放回[0,100]区间内。之所以先标准化后再进行离群值去除,是为了将观察者的得分转换到相同的尺度上,再去除离群值。最后,根据标准取每个点云所有视觉分数的均值作为最终的真值,即标定的视觉分数,结果见附表1。
2.1.2 视觉分数的主观性和随机性分析
为考察2.1.1节所得视觉分数受观察者主观性和随机性影响的情况,其作者考察了60个轻量化点云最终标定的视觉分数向量和每个观察者所得视觉分数向量间的相关性分析结果及其置信区间。相关性分析结果反映受观察者主观性影响的情况,置信区间宽度反映受观察者每次观察随机性影响的情况。
在2.1.1节中,每个观察者均会得到30个视觉分数向量Sco(i)ÎR60´1, i=1~30,而所标定的视觉分数也称为真值向量,可表示为ScorealÎR60´1,那么通过考察Sco(i)和Scoreal的相关性分析结果,就可以考察结果受观察人员主观性和随机性影响的程度。若某观察者的视觉分数向量与真值向量间的相关性越大,说明结果受该观察者主观性的影响越小。此外,由于每个观察者均对应30个视觉分数向量。因此,在比较时将会得到一个置信区间,置信区间的宽度则反映了观察者每次观察时随机性的影响。置信区间宽度越小,表示受观察者每次观察随机性的影响越小。
对于本次的数据[31],个体评分与真值相关性分析统计结果如图5所示。
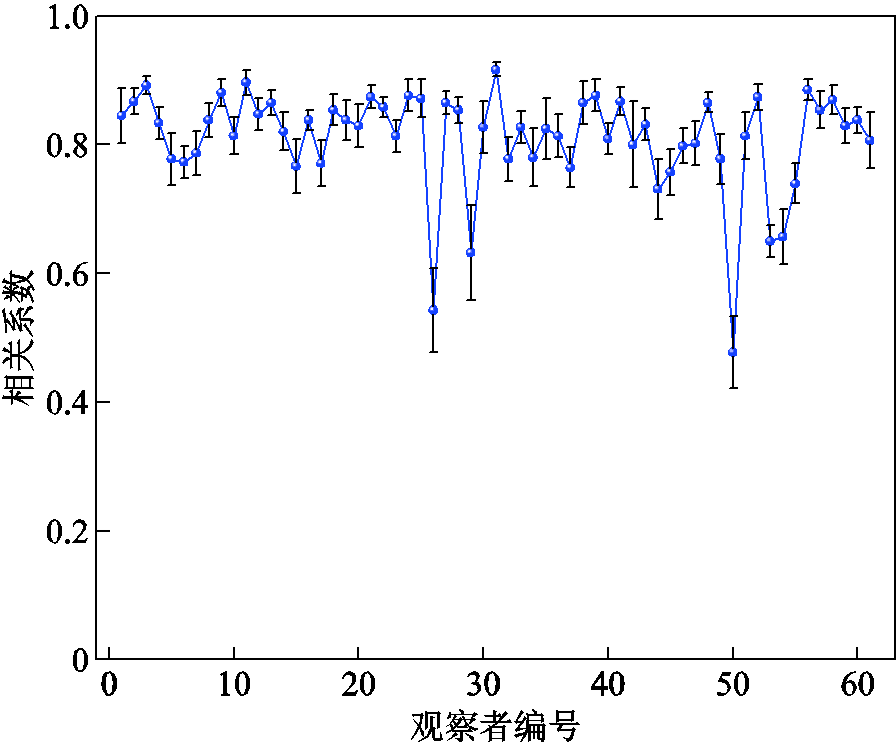
图5 个体评分与真值相关性分析
Fig.5 Correlation analysis between individual scores and truth scores
在图5中,横轴代表观察者编号,纵轴代表该观察者所得视觉分数向量和真值向量间的Spearman相关系数,且存在置信区间。相关系数是绝对值不大于1的数,当绝对值大于0.8时,代表两个变量间满足极强相关;绝对值小于0.2则表示极弱相关或无相关。可以看出,大部分观察者的相关系数都大于0.8,即两者存在极强相关性。进一步统计了所有观察者的平均表现,包括相关系数和置信区间宽度的均值。得到了平均相关系数>0.8,说明2.1.1节所得的视觉分数真值充分规避了观察者主观性的影响,置信区间宽度<0.2,也表明了结果受观察者每次观察随机性的影响很小。
尽管数据集标定的视觉分数被大量文献广泛参考,但为了研究的可靠性和严谨性,本节还是通过上述内容从数据分析的角度论证了数据集标定视觉分数的正确性,证明了其充分规避了人工观察标定视觉分数时的主观性和随机性影响。
2.1.3 不同轻量化方法的视觉失真度对比
这些标定的视觉分数可用于证明所提出的视觉失真度量化准则的有效性。使用1.4节提出的视觉失真度量化准则对数据集中不同轻量化程度的点云进行了评估,并将准则评估结果与标定分数进行了对照,结果见附表1。统计结果显示,同一点云经过不同程度轻量化处理后,标定视觉分数越低的轻量化点云,准则计算得到的失真度就越高。量化准则准确地区分出了不同视觉失真度的轻量化点云,由此证明了视觉失真度量化准则的有效性。
进一步,在数据集中的原始点云上应用了所提出的轻量化方法与主流的四种轻量化方法,并对得到的轻量化点云的视觉失真度进行了比较。在比较时,重采样率都设置为0.1。对于所提出的轻量化方法,其参数按k =10, 15, 20和ρ=10-9, 10-7, 10-5, 10-3, 10-1, 1, 101, 103, 105, 107, 109进行网格搜索。然后根据1.4节的方法选择出了视觉失真度最小的轻量化点云用于比较。最后,使用验证了的视觉失真度量化准则比较了不同方法所得轻量化点云的视觉失真度,如图6所示。
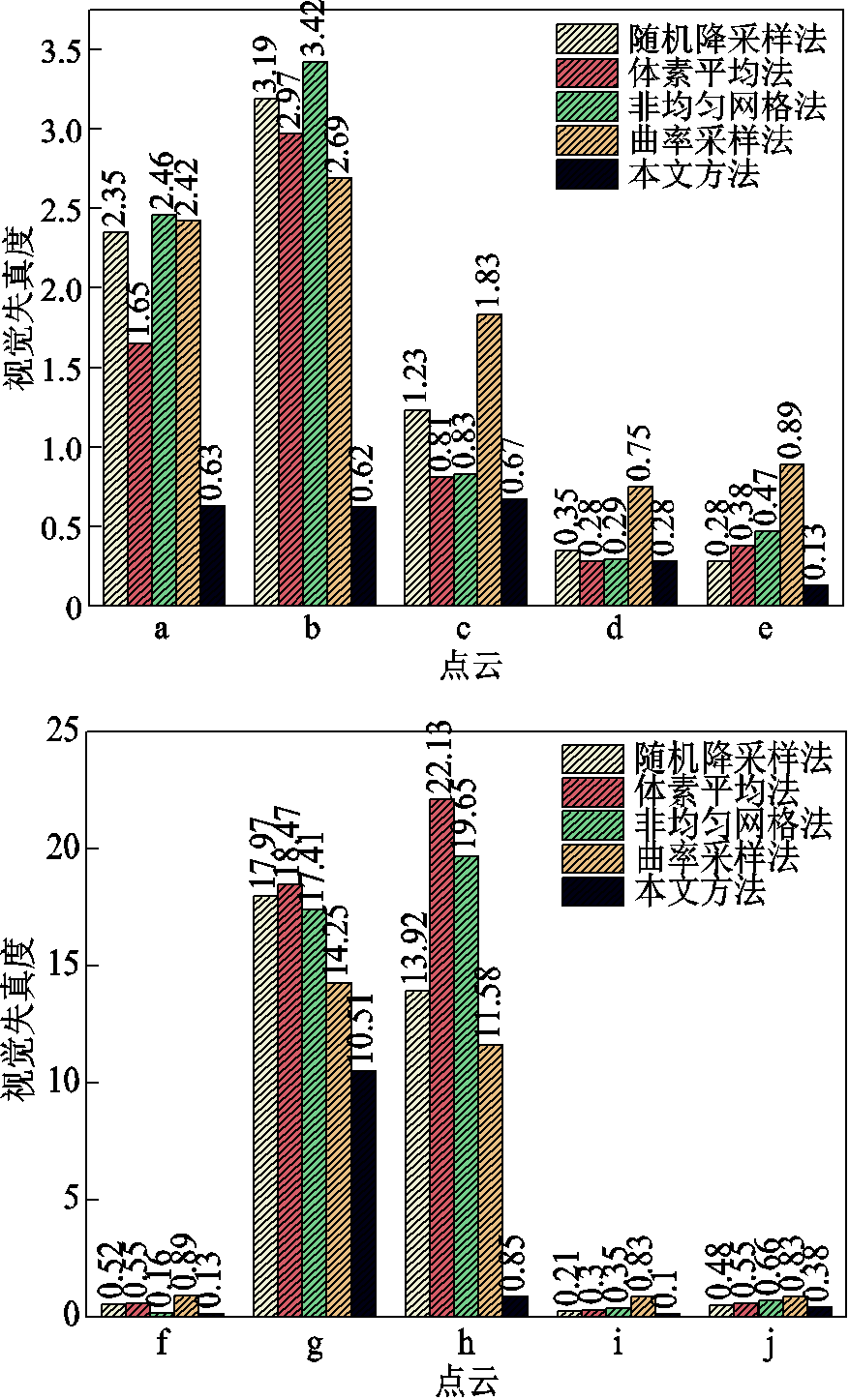
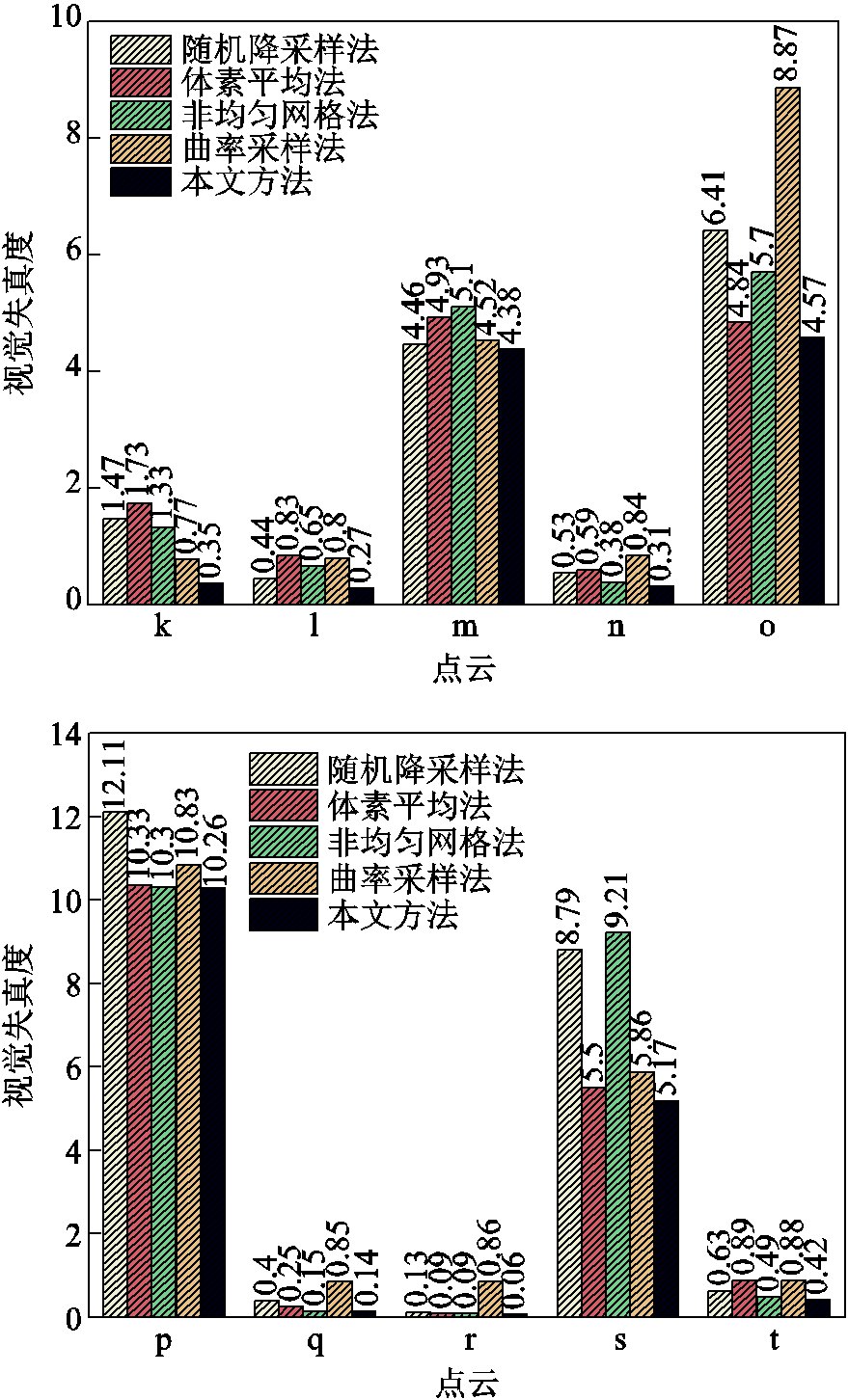
图6 不同轻量化方法在处理数据集中点云时导致的视觉失真度对比
Fig. 6 Comparison of visual distortion caused by different light weight methods in processing point clouds in datasets
从图6可看出,由于基准数据集中的点云具有不同的几何复杂度和颜色纹理复杂度,因此,不同方法导致视觉失真度的大小关系并不恒定。本文方法在轻量化原始点云时引入了视觉失真度最小的约束,因此所得轻量化点云始终拥有最小的视觉失真度。
2.1节在基准数据集上验证了所提方法的有效性。由于本文方法最终目标是服务于电力变压器区域大规模点云的轻量化。因此,本节首先对某变电站的主变区域进行了扫描,获取了包含8 000余万个的原始点云数据。然后使用本文方法和主流轻量化方法对该点云进行了轻量化处理,验证了使用本文方法得到的轻量化点云具有的更好视觉效果。作业所使用的点云扫描系统如图7所示。
整个测量系统由数据采集设备、计算机、连接器和电源组成。采集设备的性能参数见表2。
使用上述扫描系统,获得了某变电站变压器区域的点云。进一步使用不同轻量化方法按0.1的重采样率进行了轻量化处理,结果如图8所示。

图7 点云扫描系统
Fig.7 The point cloud scanning system
表2 点云激光扫描系统性能参数
Tab.2 Parameters of point cloud scanning system

设备数量性能参数 相机4分辨率:1 920´1 080 激光雷达2测量距离:100 m 分辨率:3 cm 垂直视角:-15°~15° 水平视角:360° 点生成速度:600 000/s 旋转速度:5~20 Hz 惯导系统1加速度测量范围:±6 g 角速度测量范围:±120°/s

图8 不同方法得到的变压器区域轻量化点云对比
Fig.8 Comparison of transformer area lightweight point clouds obtained by different methods
在图8中,对于图8b的随机降采样方法,由于在轻量化时是随机采样的,轻量化后点云的视觉效果不固定。基于子空间划分的体素平均法和非均匀网格法得到的图8c和图8d都较好地保留了原始点云的均匀信息而丢失了一定的特征信息。作为对比,基于曲率采样法得到的图8e则较好地保留了特征信息而丢失了均匀信息,这从图8e保留的信息几乎就是图8c和图8d丢失的信息可以直观看出。本文方法由于在最小视觉信息损失的前提下兼顾特征和均匀信息,且得到了二者的最佳比例。因此,本文方法得到的变压器轻量化点云图8f的视觉效果最好。
进一步,使用视觉失真度量化准则,计算了轻量化处理该变压器区域原始点云时各种轻量化方法导致的视觉失真度,如图9所示。
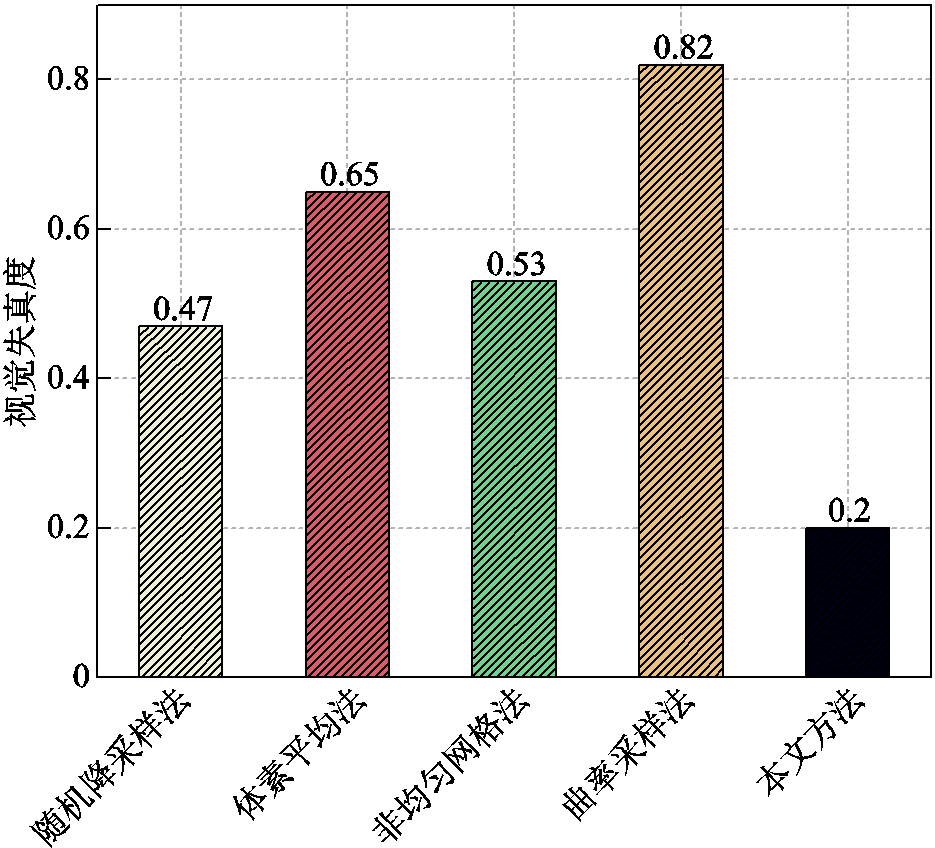
图9 不同轻量化方法的视觉失真度
Fig.9 Visual distortion degree of different lightweight methods
在图9中,所提出方法的参数配置是ρ=109和k=10。可以看出,对于包含8 000余万个点的变压器大规模彩色点云,所提出方法得到的轻量化点云具有最小的视觉失真度。统计后得出,对于该变压器区域的大规模彩色点云,在轻量化后点云的视觉效果方面,与主流的随机降采样法、体素平均法、非均匀网格法、曲率采样法相比,所提出方法分别提升了57.4%、69.2%、62.2%、75.6%。
电力行业在使用点云时,要求在保留同等数量点的情况下,所得轻量化点云与原始点云的视觉效果差异最小。然而,现有点云轻量化方法却尚未充分关注所造成的视觉失真度。为此,本研究提出了基于谱图理论的变压器区域大规模点云轻量化方法,并基于基准数据集和变压器区域大规模点云开展了验证,主要结论如下:
1)进行了点云轻量化时视觉信息损失的计算,得到了视觉信息损失与重采样矩阵间的函数关系。得出轻量化点云的视觉效果除了受视觉信息损失影响外,还受轻量化点云中特征信息和均匀信息比例的影响,需要在最小化视觉信息损失的前提下进一步寻找最佳比例,以获得视觉失真度最小的轻量化点云。
2)建立了轻量化点云的视觉失真度量化准则,得出了把点云投影到与视觉效果相关的几何和颜色特征域下,可以使用向量对点云的视觉效果进行表征,从而实现对轻量化点云视觉失真度的定量描述,由此可选择出视觉效果最好的轻量化点云。
3)在基准数据集和变压器区域大规模点云上将本文方法与主流轻量化方法进行了对比,结果均验证了在保留相同点数的情况下本文方法得到的轻量化点云与主流方法得到的轻量化点云相比具有更好的视觉效果。
附 录
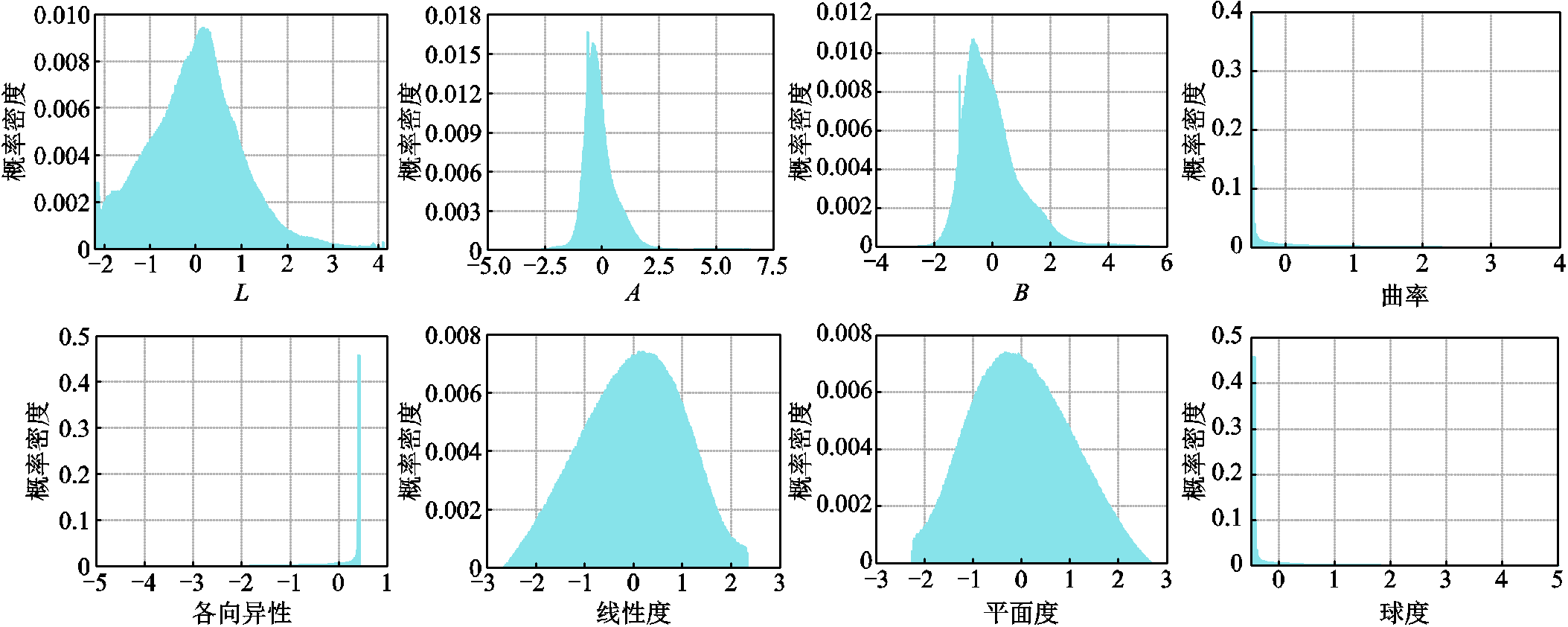
附图1 所提出方法得到的变压器区域轻量化点云的视觉特征直方图
App.Fig.1 The visual feature histogram of the lightweight point cloud in the transformer area obtained by the proposed method
附表1 视觉失真度计算结果与标定的视觉分数对比
App.Tab.1 Comparison of visual distortion calculation results with calibrated visual scores

点云数据集标定的视觉分数量化准则计算得到的视觉失真度一致性 Level 7Level 8Level 9Level 7Level 8Level 9 a9.6018.2482.741.200.750.30R b7.1123.0889.493.711.130.24R c6.9126.0878.911.410.340.23R d7.7717.0964.350.260.090.08R e8.7916.0374.680.620.410.11R f11.4317.7552.630.060.050.05R g10.7019.0469.2510.415.481.71R h5.7420.5687.6226.195.400.80R i2.9515.9463.690.630.330.16R j2.4823.5288.260.750.530.13R k3.8214.8460.860.160.070.05R l2.8021.1269.840.870.220.03R m2.2419.3068.223.932.320.39R n10.6726.1185.720.720.130.04R o3.1516.2677.843.102.250.72R
(续)

点云数据集标定的视觉分数量化准则计算得到的视觉失真度一致性 Level 7Level 8Level 9Level 7Level 8Level 9 p1.8120.6476.037.835.721.54R q5.7915.2751.170.320.110.09R r11.0524.4569.020.100.020.02R s8.5820.6586.873.532.880.84R t7.7925.3672.971.680.390.14R
参考文献
[1] 朱继忠, 骆腾燕, 吴皖莉, 等. 综合能源系统运行可靠性评估评述Ⅰ:模型驱动法[J]. 电工技术学报, 2022, 37(11): 2761-2776.
Zhu Jizhong, Luo Tengyan, Wu Wanli, et al. A review of operational reliability assessment of integrated energysystemsⅠ: model-driven method[J] Transactions of China Electrotechnical Society, 2022, 37(11):2761-2776.
[2] 江悦, 沈小军, 吕洪, 等.碱性电解槽运行特性数字孪生模型构建及仿真[J]. 电工技术学报, 2022, 37(11): 2897-2908.
Jiang Yue, Shen Xiaojun, Lü Hong, et al. Construction and simulation of operation digital twin model for alkaline water electrolyzer[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2897-2908.
[3] 高树国, 汲胜昌, 孟令明, 等. 基于在线监测系统与声振特征预测模型的高压并联电抗器运行状态评估方法[J]. 电工技术学报, 2022, 37(9): 2179-2189.
Gao Shuguo, Ji Shengchang, Meng Lingming, et al. Operation state evaluation method of high-voltage shunt reactorbased on on-line monitoring system and vibro-acoustic characteristic prediction model[J]. Transactions of China Electrotechnical Society, 2022, 37(9):2179-2189.
[4] 田勇, 杨昊, 胡超, 等. 基于毫米波雷达的电动汽车无线充电运动异物检测与跟踪[J]. 电工技术学报, 2023, 38(2): 297-308.
Tian Yong, Yang Hao, Hu Chao, et al. Moving foreign object detection and track for electric vehicle wireless charging based on millimeter wave radar[J]. Transactionsof China Electrotechnical Society, 2023, 38(2): 297-308.
[5] 谢庆, 蔡扬, 谢军, 等. 基于ALBERT的电力变压器运维知识图谱构建方法与应用研究[J].电工技术学报, 2023, 38(1): 95-106.
Xie Qing, Cai Yang, Xie Jun, et al. Research on construction method and application of knowledge graph for power transformer operation and maintenance based on ALBERT[J]. Transactions of China Electro-technical Society, 2023, 38(1): 95-106.
[6] 王小虎, 郭广鑫, 董佳涵, 等. 变电站应用实景复制技术建模和网络安全监控[J]. 中国电力, 2021, 54(11): 221-228.
Wang Xiaohu, Guo Guangxin, Dong Jiahan, et al. Substation modelling and network security monitoring based on scene replication technology[J]. Electric Power, 2021, 54(11): 221-228
[7] 刘云鹏, 刘一瑾, 刘刚, 等. 电力变压器智能运维的数字孪生体构想[J]. 中国电机工程学报, 2023, 43(22): 8636-8652.
Liu Yunpeng, Liu Yijin, Liu Gang, et al. Digital twin conception of intelligent operation and maintenance of power transformer[J]. Proceedings of the CSEE, 2023, 43(22): 8636-8652.
[8] 宋立业, 刘帅, 王凯, 等. 基于改进EfficientDet的电网元件及缺陷识别方法[J]. 电工技术学报, 2022, 37(9): 2241-2251.
Song Liye, Liu Shuai, Wang Kai, et al. Identification method of power grid components and defects based on improved EfficientDet[J]. Transactions of China Electrotechnical Society, 2022, 37(9):2241-2251.
[9] 王伟杰, 雍明超, 黄金魁, 等. 高压设备数字孪生体构建及状态分析技术研究[J]. 高压电器, 2023, 59(11): 119-128.
Wang Weijie, Yong Mingchao, Huang Jinkui, et al. Research on construction of condition analysis technology of digital twin for highvoltage equipment[J]. High Voltage Apparatus, 2023,59(11): 119-128.
[10] 刘衍, 邹阳, 谭舒宁, 等. 基于地面激光雷达的隔离开关合闸状态自动检测方法[J]. 高压电器, 2022, 58(6): 193-198.
Liu Yan, Zou Yang, TanShuning, et al. Automatic detection method of closing state for disconnector based on ground lidar[J]. High Voltage Apparatus, 2022, 58(6): 193-198.
[11] Lipman Y, Cohen-Or D, Levin D, et al. Parameterization-free projection for geometry reconstruction[J]. ACM Transactions on Graphics, 2007, 26(99): 22.
[12] Gezawa A S, Bello Z A, Wang Qicong, et al. A voxelized point clouds representation for object classification and segmentation on 3D data[J]. The Journal of Supercomputing, 2022, 78(1): 1479-1500.
[13] Wang Shuaiqing, Hu Qijun, Xiao Dongsheng, et al. A new point cloud simplification method with feature and integrity preservation by partition strategy[J]. Measurement, 2022, 197: 111173.
[14] Chen Hui, Cui Wen, Bo Caihui, et al. Point cloud simplification for the boundary preservation based on extracted four features[J]. Displays, 2023, 78: 102414.
[15] Lü Chenlei, Lin Weisi, Zhao Baoquan. Voxel structure-based mesh reconstruction from a 3D point cloud[J]. IEEE Transactions on Multimedia, 2022, 24: 1815-1829.
[16] Yang Lina, Li Yuchen, Li Xichun, et al. Efficient plane extraction using normal estimation and RANSAC from 3D point cloud[J]. Computer Standards & Interfaces, 2022, 82: 103608.
[17] Cheng Yuqi, Li Wenlong, Jiang Cheng, et al. A novel point cloud simplification method using local conditional information[J]. Measurement Science and Technology, 2022, 33(12): 125203.
[18] Lü Chenlei, Lin Weisi, Zhao Baoquan. Intrinsic and isotropic resampling for 3D point clouds[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(3): 3274-3291.
[19] Xuan Wei, Hua Xianghong, Chen Xijiang, et al. A new progressive simplification method for point cloud using local entropy of normal angle[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(4): 581-589.
[20] Wei Pengcheng, Yan Li, Xie Hong, et al. Automatic coarse registration of point clouds using plane contour shape descriptor and topological graph voting[J]. Automation in Construction, 2022, 134: 104055.
[21] Song Hao, Feng H Y. A progressive point cloud simplification algorithm with preserved sharp edge data[J]. The International Journal of Advanced Manufacturing Technology, 2009, 45(5): 583-592.
[22] Hu Qingyong, Yang Bo, Xie Linhai, et al. Learning semantic segmentation of large-scale point clouds with random sampling[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(11): 8338-8354.
[23] Qi Junkun, Hu Wei, Guo Zongming. Feature preserving and uniformity-controllable point cloud simplification on graph[C]//2019 IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 2019: 284-289.
[24] Hackel T, Wegner J D, Schindler K. Fast semantic segmentation of 3d point clouds with strongly varying density[J]. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, III3: 177-184.
[25] Ortega A, Frossard P, Kovačević J, et al. Graph signal processing: overview, challenges, and applications[J]. Proceedings of the IEEE, 2018, 106(5): 808-828.
[26] Zhang Zicheng, Sun Wei, Min Xiongkuo, et al. No-reference quality assessment for 3D colored point cloud and mesh models[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2022, 32(11): 7618-7631.
[27] Weinmann M, Schmidt A, Mallet C, et al. Contextual classification of point cloud data by exploiting individual 3d neigbourhoods[J]. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2015, II3: 271-278.
[28] Weinmann M, Jutzi B, Mallet C, et al. Geometric features and their relevance for 3d point cloud classification[J]. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2017, Ⅳ-1/W1: 157-164.
[29] Connolly C, Fleiss T. A study of efficiency and accuracy in the transformation from RGB to CIELAB color space[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 1997, 6(7): 1046-1048.
[30] Su H L. Waterloo-Point-Cloud-Database[EB-OL]. [2019]. https://github.com/qdushl/Waterloo-Point-Cloud- Database.
[31] Liu Qi, Su Honglei, Duanmu Zhengfang, et al. Perceptual quality assessment of colored 3D point clouds[J]. IEEE Transactions on Visualization and Computer Graphics, 2023, 29(8): 3642-3655.
Abstract The three-dimensional visualization based on point clouds has important application value in the digital and intelligent transformation of the power industry. For transformers, the actual production often obtains the point cloud of their entire operating area, and the huge data scale brings difficulties to use. Existing lightweight methods for processing large-scale point clouds always lead to significant visual distortion. Therefore, this paper proposes anew point cloud lightweight method that can take visual effects into account.
Firstly, the K-nearest neighbor (KNN) algorithm establishes an edge set for the original point cloud and converts it into a graph signal. Then, the graph signal is transformed into the frequency domain through the graph Fourier transform. Further, the feature and uniformity loss expressions during point cloud lightweight are derived. After quantifying the visual information loss, an objective function was established to minimize the loss. Then, the grid search was performed on parameters k and ρ, which affect the proportion of features and uniformity in the lightweight point cloud. A set of lightweight point clouds that meet the minimum visual information loss but have different proportions of features and uniformity can be obtained. A visual distortion quantification criterion was established to select the lightweight point cloud with the lowest visual distortion. The criteria project the 3D point cloud onto a feature domain composed of geometric and color features closely related to visual effects, and convert the visual effects of the point cloud into multiple histograms. Furthermore, statistical parameters quantify each feature's histograms, and the point cloud's visual effects are transformed into vectors. The visual distortion was calculated using the difference between vectors, and the lightweight point cloud with the lowest visual distortion was selected. Finally, the effectiveness of the proposed method was validated using a benchmark dataset and a large-scale point cloud of transformer areas containing over 80 million points. Based on the visual scores calibrated on the benchmark dataset, the correctness of the established visual distortion quantification criteria was first verified, further validating the effectiveness of the proposed method. For a large-scale colored point cloud in a specific transformer area, the proposed method has improved the visual effect of the lightweight point cloud by 57.4%, 69.2%, 62.2%, and 75.6% compared to mainstream random down-sampling, voxel averaging, non-uniform grid, and curvature sampling methods, respectively.
The following conclusion can be drawn: the visual effect of lightweight point clouds is not only affected by visual information loss but also by the proportion of feature information and uniformity in the lightweight point cloud. It is necessary to further search for the optimal proportion while minimizing visual information loss to obtain the lightweight point cloud with the lowest visual distortion. Projection of point clouds onto geometric and color feature domains related to visual effects can quantitatively describe the visual distortion of lightweight point clouds and thus select the lightest point cloud with the best visual effect. Compared with mainstream methods, the lightweight point cloud obtained by the proposed method has better visual effects while retaining the same number of points.
keywords:Spectral graph theory, point cloud, lightweight, visual distortion, power transformer area
中图分类号:TM507
DOI: 10.19595/j.cnki.1000-6753.tces.231987
国家电网公司总部科技项目资助(5500-202017468A-0-0-00)。
收稿日期 2023-11-27
改稿日期 2024-03-19
杨 帆 男, 1980年生, 教授,博士生导师,研究方向为输变电设备多物理场计算、电力装备数字孪生。E-mail:yangfan@cqu.edu.cn
吴 涛 男, 1993年生, 博士研究生, 研究方向为输变电设备多物理场计算、电力装备数字孪生。E-mail:Bryant_Mentality@163.com(通信作者)
(编辑 郭丽军)