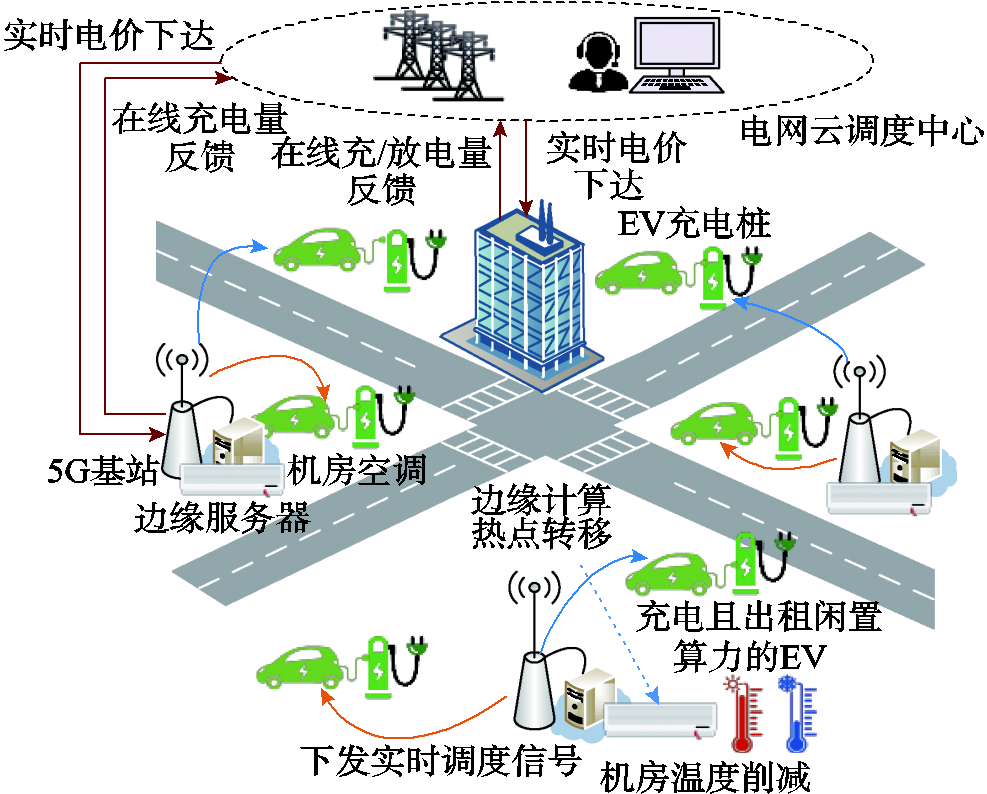
图1 5G车联网能量协同在线管理架构
Fig.1 Energy coordinated management structure of 5G vehicle network
摘要 由于5G基站与电动汽车规模持续增长,亟待开展能量管理,有利于减碳降本,缓解电网压力。但车联网的信息与能量高度耦合,使得基站独立管理能量易恶化车主的通信质量,且基站空调热负荷内部转移能力有限,电动汽车的车载算力调度潜力亟待发掘。为此,该文首先提出联合电动汽车充放电、5G网络与空调负荷和储能调度的能量管理模型,构建车联网时间平均用能成本最小化目标函数;其次,考虑网络状态不确定性,利用改进Lyapunov优化将随机优化问题转换为确定性问题;再次,利用车载计算零热点特性,提出基于主从博弈的计算热点转移策略,此外,考虑电网通信安全需求,提出融合启发式与连续凸近似的求解方法;最后,仿真表明,所提方法与现有实时能量管理方法相比,可有效削减车联网整体用能成本。
关键词:5G边缘计算 电动汽车 能量管理 Lyapunov优化 热点转移 主从博弈
随着车联网的快速发展,电动汽车(Electric Vehicle, EV)与5G宏基站(Macro Base Station, MBS)规模持续上升,并为电网引入可观的用电负荷[1]。截至2021年6月底,EV保有量达603万辆;预计2025年单个5G基站年均耗电量达1.2万kW·h,算力所需电费总额高达490亿元。计算流量与EV规模的增加会产生巨额用电开销,同时导致电网扩容改造成本明显上升[2-3]。此外,在可再生能源(Renewable Energy Sources, RES)消纳困难的背景下,大规模EV与MBS的无序接入将恶化供需功率不平衡和加剧电网损耗等问题[4]。为节能降本并削减电网压力,亟须对EV与MBS开展能量管理。
EV和MBS基于电网协助开展能量管理,有利于削减运营商与车主的用能成本并缓解用电压力[5]。基于电网管理的EV有序充放电方面,文献[6-7]提出考虑地区特征或车主自私性的EV有序充放电策略,以最小化EV车主购电成本。基于电网协同的MBS能量管理方面,文献[8]研究了考虑需求响应的MBS通信负荷调控模型,并基于聚类算法分区调控负荷。文献[9-10]考虑RES出力和网络流量变化不确定性,并提出对应的MBS动态备用储能管理模型以优化用电成本。然而上述工作默认EV调控信号响应过程不受车联网的通信时延影响,MBS能量管理不影响其他业务[7]。但车联网的信息与能量流高度耦合,5G网络开展能量管理将改变通信速率,并延迟EV实际充放电时间造成响应偏差。同时,随着5G机房通信硬件与移动边缘计算(Mobile Edge Computing, MEC)功能融合[11],额外计算能耗迫使MBS在车联网寻求空闲算力转移负荷。
针对上述问题,相关行业与学者讨论了利用EV或MBS的本地资源协助另一方优化购电成本的可行性。基于闲置EV算力协助的5G边缘计算方面,长安汽车等厂商和学者分别提出令停车场或充电站的闲置EV共享算力协助运营商计算换取收益,并间接优化网络负荷分布[12-13]。文献[14]提出联合MBS能量共享与EV计算卸载策略,通过引导EV接入空闲MBS以减少整体基站通信负荷。基于5G边缘计算协同的EV充电方面,文献[15]提出考虑EV储能的基站计算负载迁移策略,利用空闲储能转移计算负荷,间接协助优化EV充放电决策。文献[16]提出EV有序充电与算力交易联合管理协议,允许EV向电网出售空闲算力换取充电优惠,提高EV有序充电收益。文献[17]设计了面向调度时延优化的边缘计算卸载方案,以减少因通信时延造成的EV需求响应容量缩减。然而上述研究仅利用EV或MBS协助另一方转移负荷,未关注协助者的决策对自身能量管理的影响。随着储能设备性能改进,部分学者首次提出协同考虑MBS与EV储能的能量管理方法,其中文献[18]评估了EV与MBS储能的协同调度边界,并提出考虑用户隐私的公平性调度策略以提高整体储能调控潜力。文献[19-20]研究了基站-EV充电站多站融合的储能能量管理模型,分别基于主从博弈与机会约束规划获取最优储能协同充放电功率。文献[21]基于鲁棒优化求解最优5G基站储能与EV协同充放电功率,有效削减网络碳排放。然而,上述研究仍有三个核心问题未解决:
(1)文献[18-21]仅讨论MBS与EV储能协同调度,忽略了车联网信息流对应的负荷转移潜力以及EV与MBS的通信耦合关系。
(2)上述文献均未考虑联合优化基站空调负荷。5G基站的空调功耗约占总功耗的30%[22],且机房制冷功率受计算流量规模影响。车联网海量任务接入致使服务器产热和空调功耗急剧提升,为降低边缘计算热点,基站空调负荷亟待参与能量管理。
(3)文献[12-21]主要为日前离线优化且默认RES与网络流量状态已知。然而实际网络状态具有强随机性,难以获取全局最优解。尽管人工智能算法实现在线优化,但数据库精度不足易陷入次优解。
综上所述,本文针对MBS与EV独立开展能量管理产生的通信质量与购电成本优化性能冲突问题,提出基于计算热点转移的车联网灵活资源协同在线管理策略。以EV与MBS的长期购电成本最小化为目标,提出基于Lyapunov的在线优化算法,并考虑EV与MBS的通信与计算耦合特性,建立EV与MBS的主从博弈模型,激励EV为算力基站提供计算热负荷转移空间。同时设计了考虑EV安全通信的信息与储能调度方法。最后通过仿真验证了所提方法对EV与MBS的购电成本优化性能。
文献[23]指出优化机房空调负荷有利于提升能效节省用电,而空调功耗与机房算力设备的计算负载紧密关联。但现有的基站负载迁移机制仅能转移本地计算产生的热负荷,而无法直接削减机房热量与空调负荷。此外,尽管EV通过有序充放电降低了用能压力,但随着车载算力与EV数量增加,EV可联合空闲算力和储能资源进一步提升车联网用能效益。在5G车联网场景下,停留充电站的EV既接受5G通信服务,也成为MBS能量管理的协助者。在通信方面,EV依赖MBS实时接收聚合商的充放电调度信号。在能量管理方面,MBS可将部分计算任务卸载至停车且算力闲置的EV处理,从而减少MBS的边缘计算热点,有利于优化机房制冷运行功耗,降低基站购电成本。为此,提出5G车联网能量协同在线管理框架,如图1所示。

图1 5G车联网能量协同在线管理架构
Fig.1 Energy coordinated management structure of 5G vehicle network
假设图1架构的运行时段离散化为无穷多个时隙,记时隙集合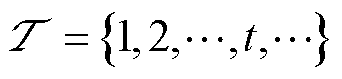 ,每个时隙长度
,每个时隙长度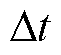 取值5 min。在t时隙开始时,首先,EV确定其在t时隙的充电桩停留时间,MBS采集本地计算流量规模与机房内外温度;其次,基于EV日前调度计划及MBS实时运行功耗,分别得到EV在t时隙的可调度容量及MBS机房热点空间分布;最后,根据电网在t时隙发布的实时电价,对海量灵活资源下达实时能量管理信号,实现EV与MBS经济用电。
取值5 min。在t时隙开始时,首先,EV确定其在t时隙的充电桩停留时间,MBS采集本地计算流量规模与机房内外温度;其次,基于EV日前调度计划及MBS实时运行功耗,分别得到EV在t时隙的可调度容量及MBS机房热点空间分布;最后,根据电网在t时隙发布的实时电价,对海量灵活资源下达实时能量管理信号,实现EV与MBS经济用电。
EV与MBS的能量协同管理将引入EV车主与通信运营商之间的效益冲突。为保障多方经济效益,提出能量协同管理激励补偿原则:①算力交易激励原则。若MBS通过计算卸载转移计算负荷至EV,通信运营商需基于计算任务规模与上网电价差异为EV车主提供使用车载空闲算力的经济补贴。②时效性服务原则。若EV接收MBS的计算负载,为避免车主离开充电桩造成计算结果回传丢包,EV需在当前接收时隙完成计算任务处理。然而,在缺乏能量与网络状态先验知识的前提下,MBS难以确定下一时刻的网络流量变化与EV到达或离开速率,无法开展实时能量管理。为此,第2节将构建车联网灵活资源数学模型,提出用电经济优化目标,并在第3节给出一种无需网络先验知识的能量实时协同管理策略。
融合边缘服务器的5G基站负荷模型如图2所示。融合边缘计算的5G机房由有源天线单元(Active Antenna Unit, AAU)、融合室内基带处理单元(Base Band Unit, BBU)的边缘计算一体机、储能单元、变频空调与机房屋顶光伏组成。5G机房由机房屋顶光伏、本地储能单元及外部电网联合供能。为保证蜂窝网范围的移动用户与EV通信可靠性,5G基站不考虑将屋顶光伏发电余量回馈电网。
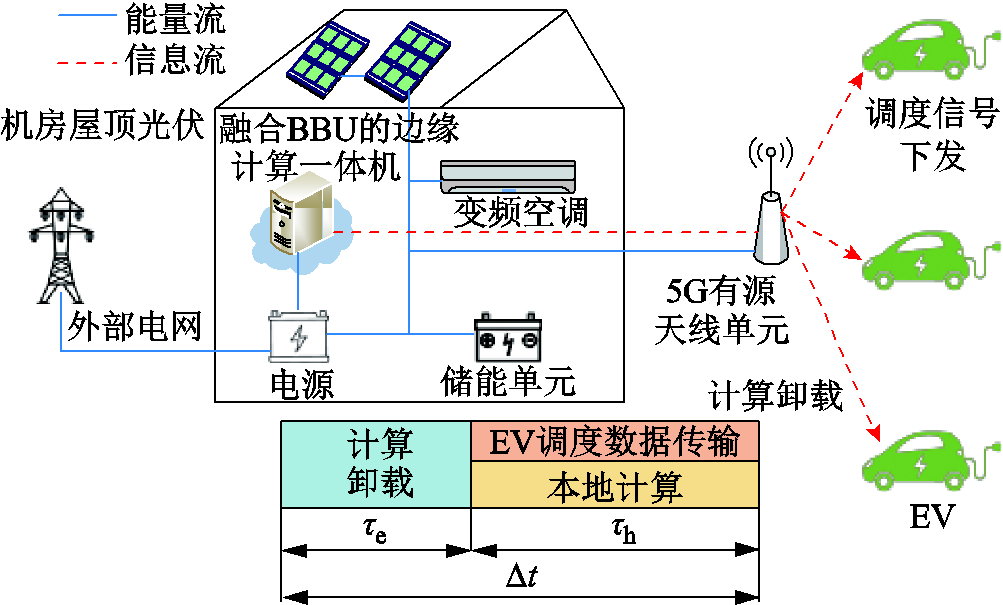
图2 融合边缘服务器的5G基站负荷模型
Fig.2 The model of 5G MBS with edge computing server
设图1场景存在N个MBS,M台EV,记MBS集合为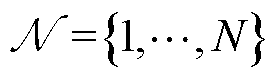 ,
,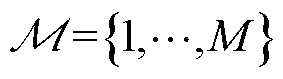 表示EV集合。假设AAU子信道数量足够多,记t时隙开始时,到达第n
表示EV集合。假设AAU子信道数量足够多,记t时隙开始时,到达第n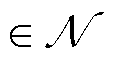 台MBS的本地移动用户计算流量数据规模
台MBS的本地移动用户计算流量数据规模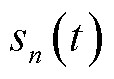 服从独立同分布的随机过程,
服从独立同分布的随机过程,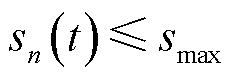 ,
,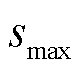 为流量规模上限。记第n台MBS拥有的边缘计算资源由中央处理器(Central Processing Unit, CPU)工作周期
为流量规模上限。记第n台MBS拥有的边缘计算资源由中央处理器(Central Processing Unit, CPU)工作周期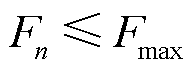 表示。考虑到MBS的计算与储能资源均受限,MBS可将部分任务卸载至EV计算,并留存部分计算流量在任务等待队列中执行本地计算,或留存到下一时隙处理。在时间离散化的车联网能量管理过程中,一个时隙长度划分为
表示。考虑到MBS的计算与储能资源均受限,MBS可将部分任务卸载至EV计算,并留存部分计算流量在任务等待队列中执行本地计算,或留存到下一时隙处理。在时间离散化的车联网能量管理过程中,一个时隙长度划分为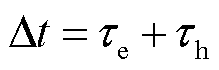 。
。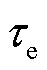 为计算卸载时间,在长度为
为计算卸载时间,在长度为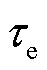 的子时隙中,MBS将部分任务卸载到EV完成计算;
的子时隙中,MBS将部分任务卸载到EV完成计算;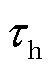 为调度信号传输时间,在长度为
为调度信号传输时间,在长度为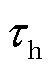 的持续时间里,MBS为EV传输调度信号以开展能量管理。此外,MBS可并行执行本地计算动作,设本地计算时间长度等于
的持续时间里,MBS为EV传输调度信号以开展能量管理。此外,MBS可并行执行本地计算动作,设本地计算时间长度等于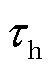 。
。
5G基站网络负荷由本地计算流量接入、EV无线通信、边缘计算任务卸载和本地计算产生的通信与计算功耗组成。为避免重复接入,规定一台EV只接收一个MBS的调度信号,而一个MBS需负责多个EV的调度信号传输,且EV默认选择最优信道接入MBS。令理论最优通信速率用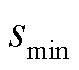 表示,单位Kbit/s。在调度信号传输时间里,第n台MBS为第m个EV提供的无线传输速率为
表示,单位Kbit/s。在调度信号传输时间里,第n台MBS为第m个EV提供的无线传输速率为
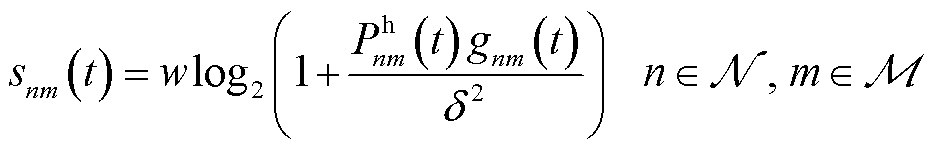 (1)
(1)
式中,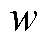 为无线信道带宽;
为无线信道带宽;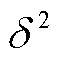 为独立同分布的高斯白噪声,属于随机量;
为独立同分布的高斯白噪声,属于随机量;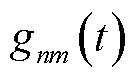 为t时隙第n台MBS与第m个EV之间的信道增益,其计算参考文献[22];
为t时隙第n台MBS与第m个EV之间的信道增益,其计算参考文献[22];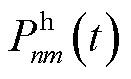 为AAU分配给调度信号传输的子信道瞬时工作功率,
为AAU分配给调度信号传输的子信道瞬时工作功率,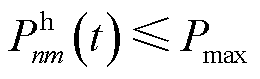 ,
,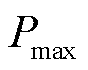 为最大动态工作功率。假设MBS可同时向多个EV卸载计算任务,在长度为
为最大动态工作功率。假设MBS可同时向多个EV卸载计算任务,在长度为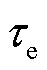 的卸载时间里,第n台MBS卸载至第m个EV的计算任务数量为
的卸载时间里,第n台MBS卸载至第m个EV的计算任务数量为
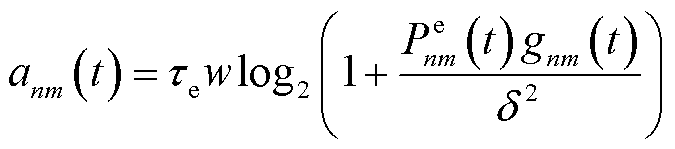 (2)
(2)
式中,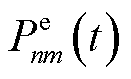 为AAU子信道分配给计算卸载无线通信的工作功率,
为AAU子信道分配给计算卸载无线通信的工作功率,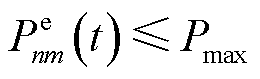 。
。
t时隙第n台MBS总通信能耗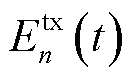 [24]为
[24]为
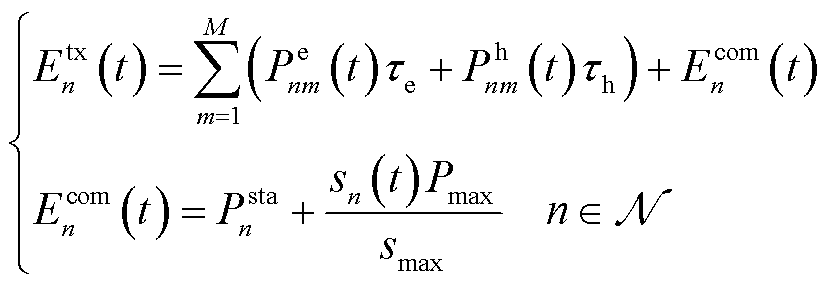 (3)
(3)
式中,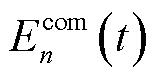 为计算流量接入产生的通信功耗;
为计算流量接入产生的通信功耗;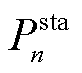 为第n台MBS通信设备静态功耗。
为第n台MBS通信设备静态功耗。
在并行本地计算时间中,第n台MBS计算本地剩余任务量所需计算资源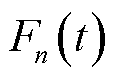 表示为
表示为
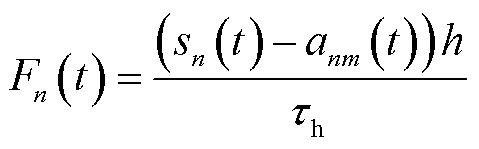 (4)
(4)
式中,h为单位Kbit计算任务所需CPU工作周期。记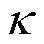 为计算一体机内嵌CPU芯片能耗系数,第n台MBS本地计算能耗为
为计算一体机内嵌CPU芯片能耗系数,第n台MBS本地计算能耗为
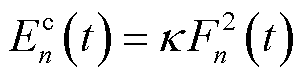 (5)
(5)
MBS的变频空调可将电能转换为热能,为MBS机房内部的边缘服务器运行提供温度调节,其功耗与温度变化满足数学模型式(6)~式(9)。
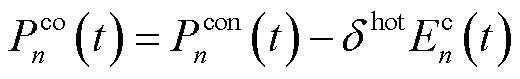 (6)
(6)
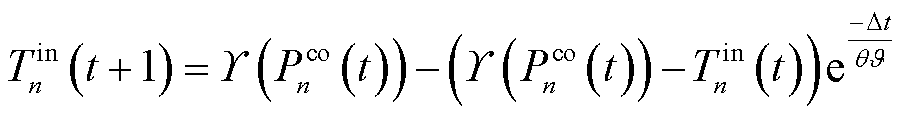 (7)
(7)
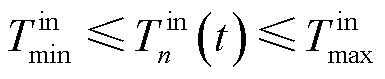 (8)
(8)
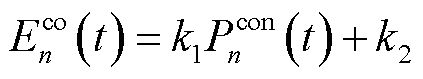 (9)
(9)
式中,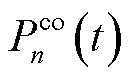 为第n台MBS机房制冷量;
为第n台MBS机房制冷量;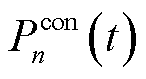 为第n台MBS的变频空调制冷量;
为第n台MBS的变频空调制冷量;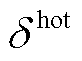 为边缘服务器的散热系数;
为边缘服务器的散热系数;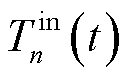 为t时隙的室内温度;
为t时隙的室内温度;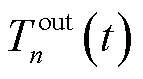 为第n台MBS环境温度,属于环境自变量;
为第n台MBS环境温度,属于环境自变量;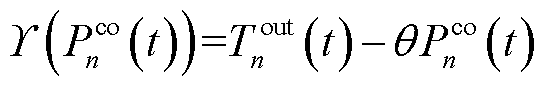 ;
;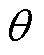 和
和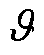 分别为空调负荷的等效热阻与等效热容;
分别为空调负荷的等效热阻与等效热容;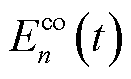 为第n台MBS的变频空调功耗,与变频制冷量有关;
为第n台MBS的变频空调功耗,与变频制冷量有关;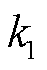 与
与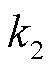 为常系数,仅与空调参数有关;
为常系数,仅与空调参数有关;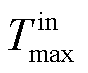 、
、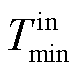 分别为边缘服务器正常工作的机房温度上、下限,取值参考文献[25]。
分别为边缘服务器正常工作的机房温度上、下限,取值参考文献[25]。
MBS闲置储能资源协同参与能量管理可提升能量流与信息流匹配程度及车联网用能经济性。记第n台MBS在t时隙的储能容量为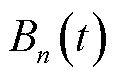 ,5G基站储能单元状态变化满足
,5G基站储能单元状态变化满足
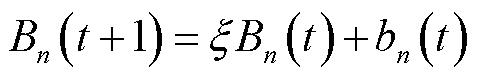 (10)
(10)
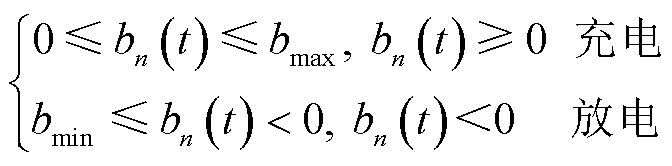 (11)
(11)
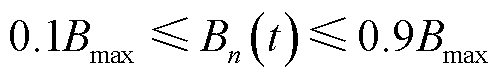 (12)
(12)
式中,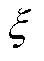 为电能泄漏系数,
为电能泄漏系数,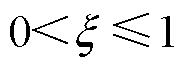 ;
;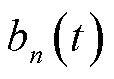 为t时隙第n台MBS的储能充放电功率,
为t时隙第n台MBS的储能充放电功率,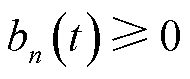 表示储能充电,反之放电;bmax、bmin分别为充电和放电功率上限,
表示储能充电,反之放电;bmax、bmin分别为充电和放电功率上限,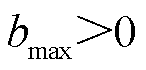 ,
,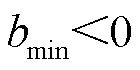 ;
;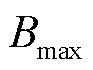 为储能单元容量上限。
为储能单元容量上限。
记第n台MBS的屋顶光伏在t时隙的出力值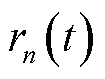 为区间
为区间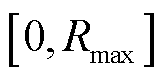 的随机值,
的随机值,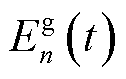 表示第n台MBS从外部电网购入的能量,其供需能量变化满足功率平衡式(13)。
表示第n台MBS从外部电网购入的能量,其供需能量变化满足功率平衡式(13)。
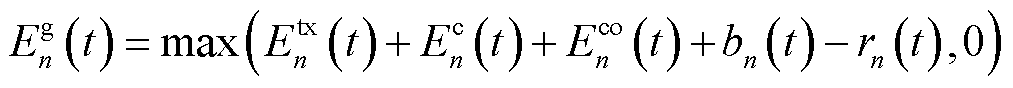 (13)
(13)
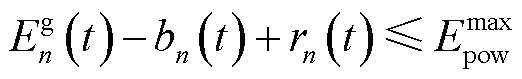 (14)
(14)
式中,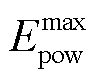 为MBS电源额定功率上限。令
为MBS电源额定功率上限。令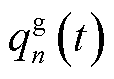 与
与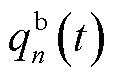 分别为第n台MBS的外部电网实时电价与储能单元损耗成本,通信运营商在t时隙产生的网络用能成本如式(15)所示。
分别为第n台MBS的外部电网实时电价与储能单元损耗成本,通信运营商在t时隙产生的网络用能成本如式(15)所示。
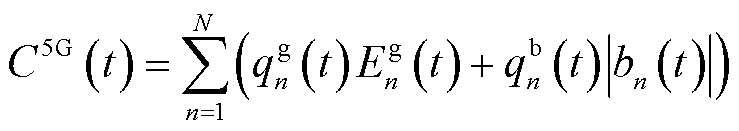 (15)
(15)
2.4.1 EV任务处理与计算负荷模型
假设在各时隙参与协同能量管理的EV均已停留且空闲,车主具有计算资源交易意愿并令车载芯片处于待机状态。为避免EV过载,规定一台EV只接收一个MBS卸载的计算任务。假设EV可在t时隙同时开展边缘计算与响应EV聚合商下发的实时充电调度策略。记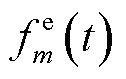 为第m个EV处理MBS卸载数据分配的计算资源,满足
为第m个EV处理MBS卸载数据分配的计算资源,满足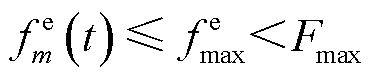 ,其中
,其中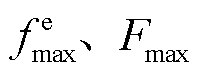 分别表示EV和MBS的计算资源上限。
分别表示EV和MBS的计算资源上限。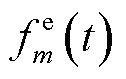 为
为
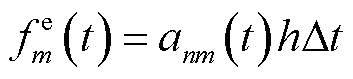 (16)
(16)
EV参与计算卸载产生的本地计算能耗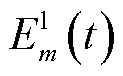 为关于变量的二次方程,表示为
为关于变量的二次方程,表示为
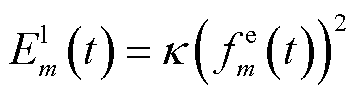 (17)
(17)
2.4.2 计及通信时延影响的EV实时充放电模型
假设EV聚合商通过日前调度模型拟定了各时隙EV充放电总容量的上、下界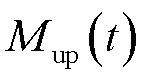 与
与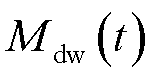 [6]。EV聚合商根据t时隙停留的EV数目制定实时充放电决策,并下发调度指令至各EV。记
[6]。EV聚合商根据t时隙停留的EV数目制定实时充放电决策,并下发调度指令至各EV。记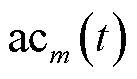 与
与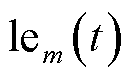 分别为t时隙第m个EV接入与断开充电桩信号时间。记
分别为t时隙第m个EV接入与断开充电桩信号时间。记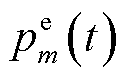 为第m个EV的充/放电功率,当
为第m个EV的充/放电功率,当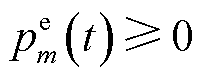 表示EV充电,
表示EV充电,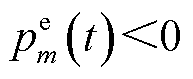 表示EV放电。t时隙的EV有序充/放电过程满足
表示EV放电。t时隙的EV有序充/放电过程满足
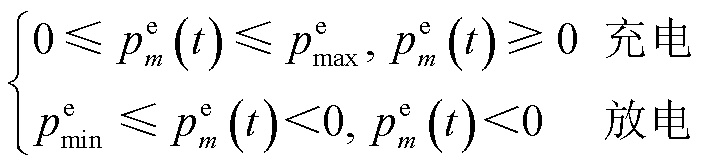 (18)
(18)
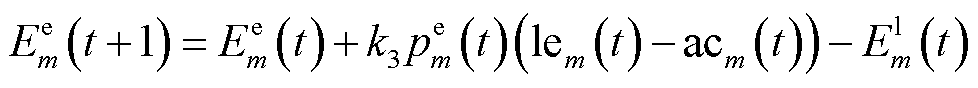 (19)
(19)
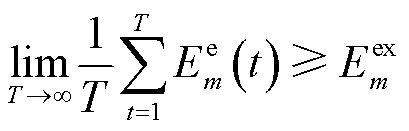 (20)
(20)
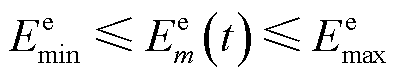 (21)
(21)
式中,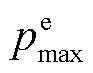 、
、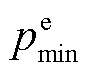 分别为EV的最大充、放电功率,
分别为EV的最大充、放电功率,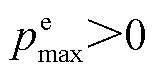 ,
,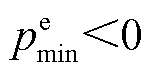 ;
;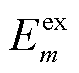 为第m个EV计划出行用电需求;
为第m个EV计划出行用电需求;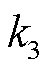 为EV的充/放电效率,当
为EV的充/放电效率,当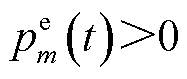 时,
时,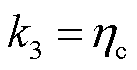 ,反之
,反之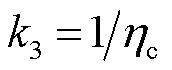 ,
,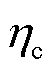 为非负常数,由EV电池性能决定;
为非负常数,由EV电池性能决定;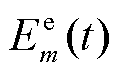 为t时刻第m个EV电池储能容量;
为t时刻第m个EV电池储能容量;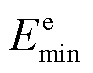 与
与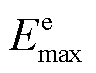 分别为第m个EV电池储能容量的下限和上限。式(20)表示第m个EV电池容量需满足出行计划用电量需求。
分别为第m个EV电池储能容量的下限和上限。式(20)表示第m个EV电池容量需满足出行计划用电量需求。
电网调度中心根据日前决策约束求解当前t时隙的最优实时调度信息并下达至EV。实际情况下,调度数据传输时间将造成EV延迟接收调度信号,并引起实际响应量不足问题。考虑到响应容量与通信时延呈近似线性关系,设在t时隙的第m个EV实际的实时充/放电量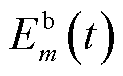 变化满足
变化满足
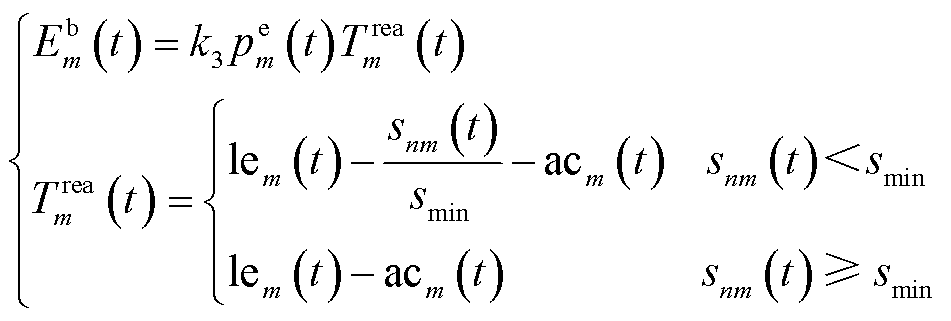 (22)
(22)
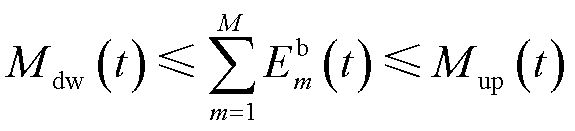 (23)
(23)
式中,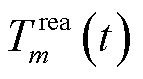 为传输时延影响下的EV实际响应时间。式(23)为日前调度给定的t时隙EV充放电总容量约束。在通信时延影响下,t时隙中第m个EV的实际充电量低于实时计划充电量,MBS需向电力公司支付网络波动补偿。记单位补偿为
为传输时延影响下的EV实际响应时间。式(23)为日前调度给定的t时隙EV充放电总容量约束。在通信时延影响下,t时隙中第m个EV的实际充电量低于实时计划充电量,MBS需向电力公司支付网络波动补偿。记单位补偿为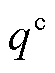 ,第n台MBS因时延支付的网络波动补偿
,第n台MBS因时延支付的网络波动补偿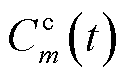 为
为
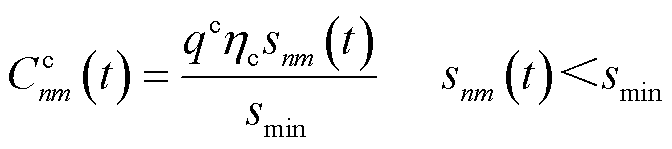 (24)
(24)
记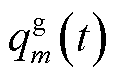 为第m个EV所在充电桩的电网购电电价,t时隙的第m个EV充电成本或放电收益表示为
为第m个EV所在充电桩的电网购电电价,t时隙的第m个EV充电成本或放电收益表示为
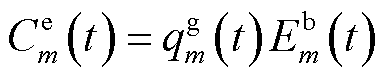 (25)
(25)
实时的灵活资源协同能量管理策略以包括EV充放电成本、MBS的外部购电成本、通信延迟补偿与储能损耗成本在内的整体经济成本最小化为目标,记本文场景下的决策变量集合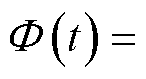
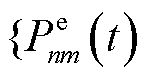 ,
,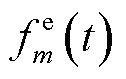 ,
,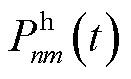 ,
,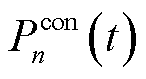 ,
,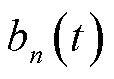 ,
,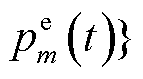 在t时隙的整体服务成本如式(26)所示。
在t时隙的整体服务成本如式(26)所示。
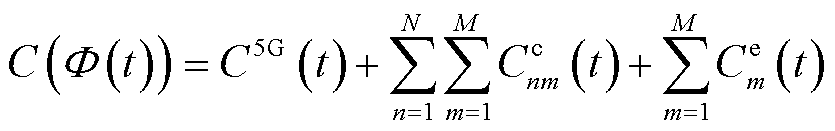 (26)
(26)
在t时隙开始时,能量管理系统获取当前时隙的随机环境变量信息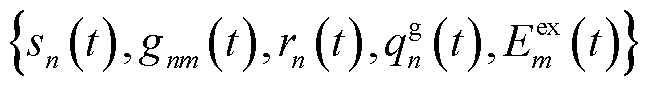 。区别于单时隙问题仅依赖当前状态获取最优解,多时隙优化问题缺乏EV与5G通信网络未来状态的先验知识,其求解无法达到全局最优,令目标函数表达式由时间平均的整体经济成本数学期望值表示,时隙-空间变量耦合的随机优化问题如式(27)所示。
。区别于单时隙问题仅依赖当前状态获取最优解,多时隙优化问题缺乏EV与5G通信网络未来状态的先验知识,其求解无法达到全局最优,令目标函数表达式由时间平均的整体经济成本数学期望值表示,时隙-空间变量耦合的随机优化问题如式(27)所示。
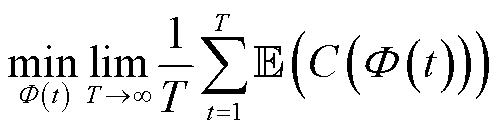 (27)
(27)
约束:式(1)~式(26)
考虑到问题求解面临以下困难:①式(7)、式(10)、式(19)导致前后时隙的系统状态相互耦合,t时隙目标函数的优化结果将影响未来系统状态,无法采用短期优化方法独立实时求解各时隙的目标函数;②实际系统缺乏未来时隙状态的先验知识,离线日前优化方法无法获取全局最优解。为此,第3节基于改进Lyapunov优化将多时隙问题解耦为确定性优化问题,并在线获取问题近似最优解。
为减少机房温度波动并保证市电停电时MBS储能足够维持有限时间运行,首先基于传统Lyapunov优化理论引入辅助变量集合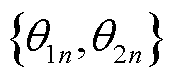 [26],构建MBS的虚拟储能队列
[26],构建MBS的虚拟储能队列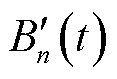 与虚拟温度队列
与虚拟温度队列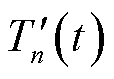 以及EV的虚拟荷电状态(State of Charge, SOC)队列
以及EV的虚拟荷电状态(State of Charge, SOC)队列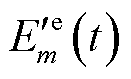 ,即
,即
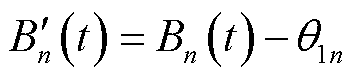 (28)
(28)
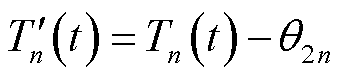 (29)
(29)
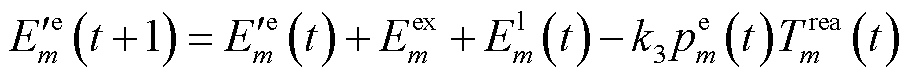 (30)
(30)
区别于实际队列,虚拟队列取值可为负,其含义为实际物理队列状态变化的偏移,视为储能队列的充放电赤字或温度队列的调控偏差值,用于量化实时变化偏离长期运行约束的程度。由于式(7)、式(10)、式(19)受取值约束,虚拟储能与温度队列必然能够达到平均速率稳定,即满足
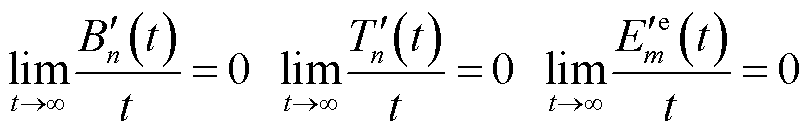 (31)
(31)
其次,记为t时隙的系统状态变量集合为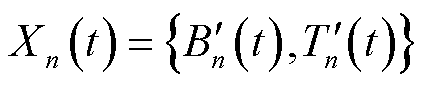 ,
,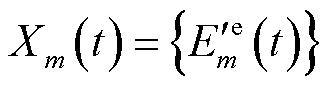 ,分别构建关于式(27)的改进二次Lyapunov方程为
,分别构建关于式(27)的改进二次Lyapunov方程为
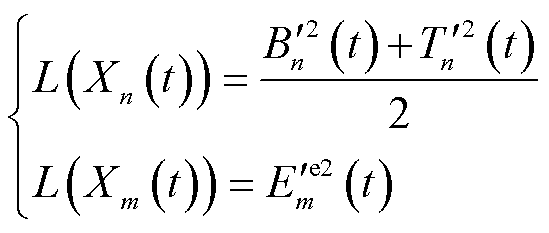 (32)
(32)
各状态变量在t时隙的改进Lyapunov偏移方程由前后时隙的二次Lyapunov方程之差表示,有
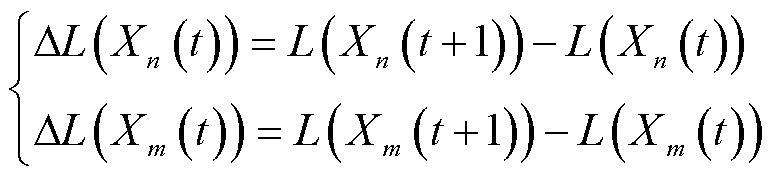 (33)
(33)
引理1。以变量集合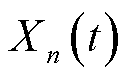 为例,假设所有随机环境变量服从独立随机分布,对于任一MBS
为例,假设所有随机环境变量服从独立随机分布,对于任一MBS 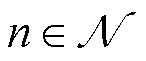 ,满足式(27)约束集合的系统状态变量集合
,满足式(27)约束集合的系统状态变量集合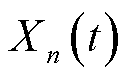 均存在对应的Lyapunov偏移函数上界,即
均存在对应的Lyapunov偏移函数上界,即
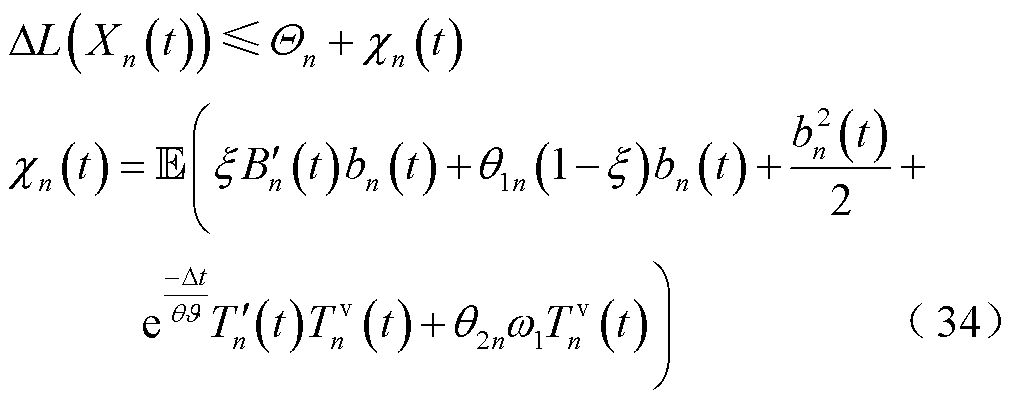
为化简公式,令式(7)中部分环境变量由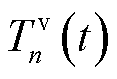 =
=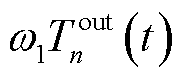 +
+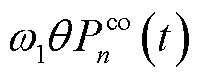 表示,
表示,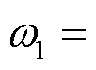
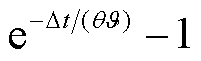 。
。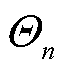 为一个定值。对于任一EV,
为一个定值。对于任一EV, 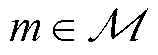 的改进Lyapunov偏移函数
的改进Lyapunov偏移函数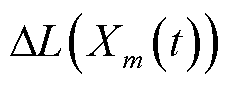 上界推导类似式(34),不再赘述。为松弛系统稳定性与连续性约束式(31),基于引理1和改进后的Lyapunov优化理论,构建式(27)的Lyapunov偏移加罚函数为
上界推导类似式(34),不再赘述。为松弛系统稳定性与连续性约束式(31),基于引理1和改进后的Lyapunov优化理论,构建式(27)的Lyapunov偏移加罚函数为
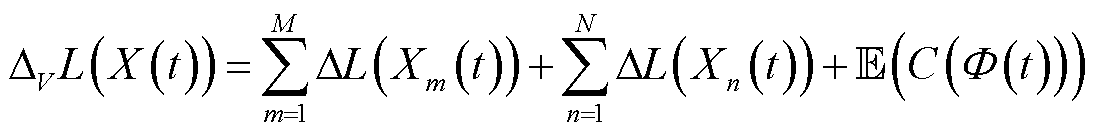 (35)
(35)
尽管无法直接最小化式(35)取值来获取式(27)的全局最优解,但引理1指出能量管理系统可通过优化t时隙的偏移加罚函数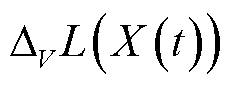 的上界取值以获取原问题的近似最优解。进而在去除无关定值
的上界取值以获取原问题的近似最优解。进而在去除无关定值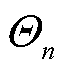 的前提下,基于式(34)、式(35)解耦原问题得到确定性单时隙在线优化问题式(36)。
的前提下,基于式(34)、式(35)解耦原问题得到确定性单时隙在线优化问题式(36)。
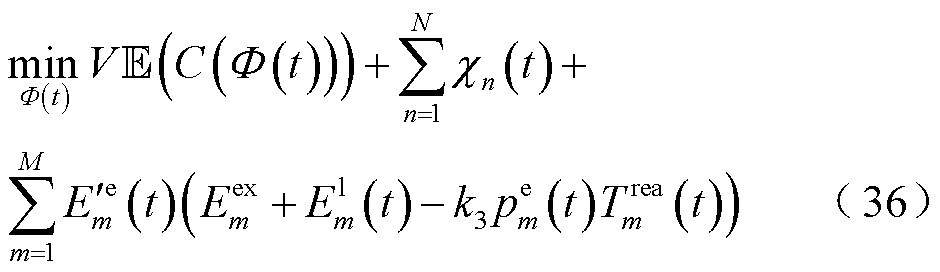
约束:式(1)~式(26)
式中,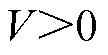 为控制参数。
为控制参数。
解耦后的问题式(36)仅需获取当前与历史时隙的网络环境状态变量即可求解,无需再关注未来网络环境变量的随机变化对多时隙问题耦合关系的影响。为简化表示,问题式(36)去除时隙与数学期望标号重写为
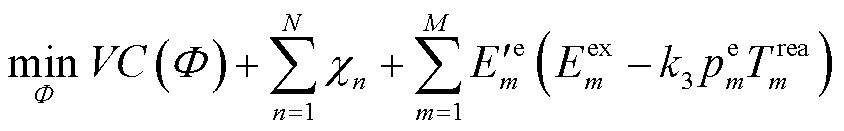 (37)
(37)
在式(37)中,空调热负荷变化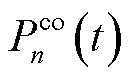 与MBS本地计算能耗有关,而本地计算能耗取决于MBS计算卸载后的剩余任务规模
与MBS本地计算能耗有关,而本地计算能耗取决于MBS计算卸载后的剩余任务规模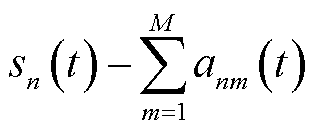 ;MBS的通信功率
;MBS的通信功率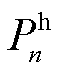 影响EV充放电决策
影响EV充放电决策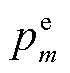 ,而解耦多时隙约束后的EV边缘计算决策仅与EV当前SOC容量有关,与EV充放电决策无关,而EV边缘计算决策决定了MBS空调热负荷优化决策;MBS的储能管理与外部购电决策由MBS的通信与计算能耗组成。基于上述分析,剥离无关项后式(37)可分解成二个上层独立子问题与一个下层子问题,其中上层子问题包括MBS计算卸载、本地计算、空调功率优化与EV车载计算资源分配子问题
,而解耦多时隙约束后的EV边缘计算决策仅与EV当前SOC容量有关,与EV充放电决策无关,而EV边缘计算决策决定了MBS空调热负荷优化决策;MBS的储能管理与外部购电决策由MBS的通信与计算能耗组成。基于上述分析,剥离无关项后式(37)可分解成二个上层独立子问题与一个下层子问题,其中上层子问题包括MBS计算卸载、本地计算、空调功率优化与EV车载计算资源分配子问题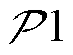 ,MBS调度数据传输与EV充放电子问题
,MBS调度数据传输与EV充放电子问题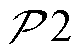 ,下层子问题为MBS储能充放电与外部购电决策子问题
,下层子问题为MBS储能充放电与外部购电决策子问题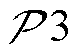 ,分别为
,分别为
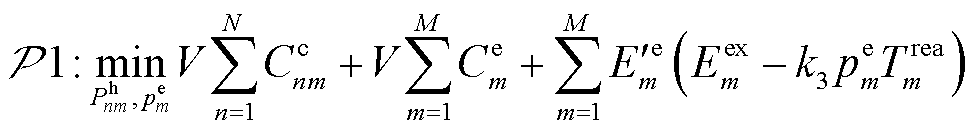 (38)
(38)
约束:式(1),式(18)~式(25)
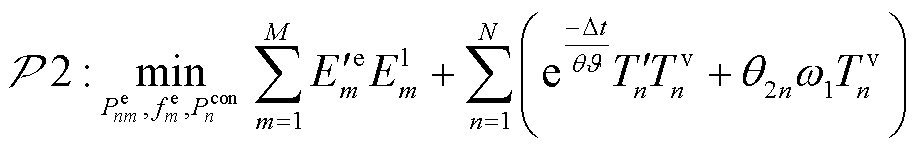 (39)
(39)
约束:式(2), 式(4)~式(9), 式(16),式(17), 式(19)
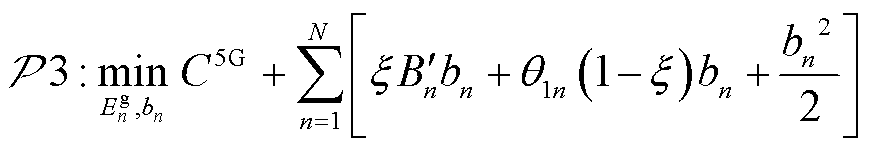 (40)
(40)
约束:式(3), 式(10)~式(15)
由于子问题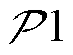 与
与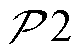 变量互不相关,可独立获取问题可行解。但
变量互不相关,可独立获取问题可行解。但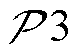 的最优解受功率守恒模型约束,即式(13),其可行解与
的最优解受功率守恒模型约束,即式(13),其可行解与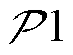 和
和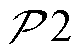 得到的MBS通信及计算能耗取值有关。在给定MBS通信与计算能耗前提下,
得到的MBS通信及计算能耗取值有关。在给定MBS通信与计算能耗前提下,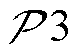 可通过线性优化方法获取最优解。考虑到
可通过线性优化方法获取最优解。考虑到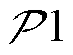 含非凸约束式(22),而
含非凸约束式(22),而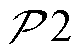 涉及车主与运营商的效益冲突,下文将分别给出子问题
涉及车主与运营商的效益冲突,下文将分别给出子问题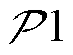 和
和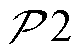 的求解方法。分解后各子问题关系如图3所示。
的求解方法。分解后各子问题关系如图3所示。
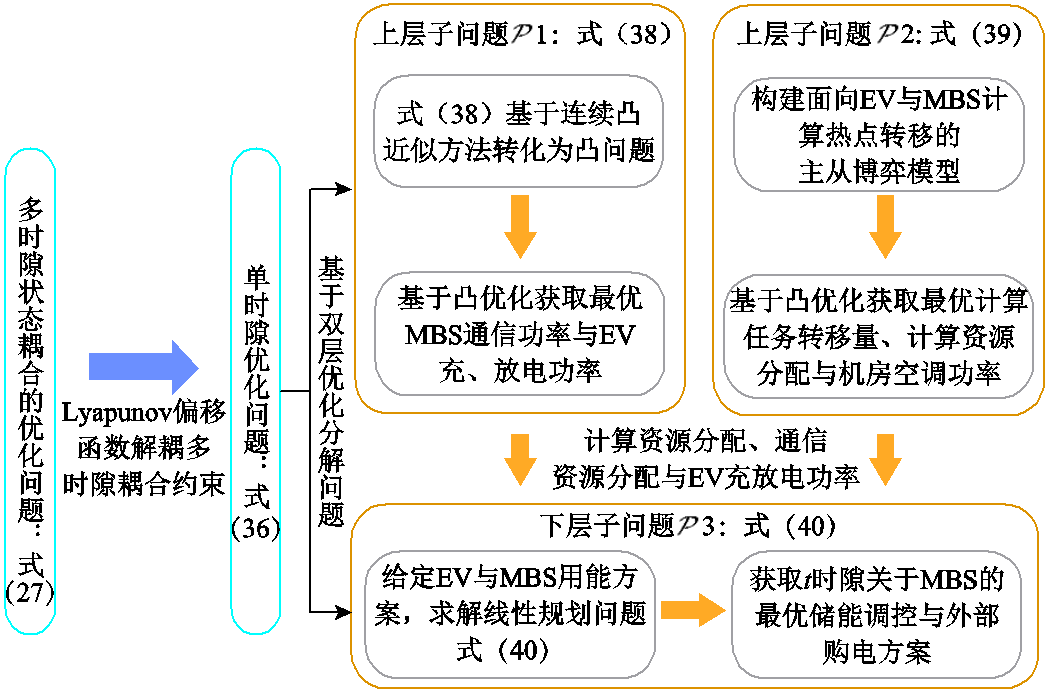
图3 基于双层优化的问题分解与各子问题联系
Fig.3 Problem descomposition based on two-tier optimization and the relationship among subproblems
本节首先提出子问题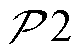 的求解方法。观察式(2)、式(6)和式(39)可知,MBS空调功率
的求解方法。观察式(2)、式(6)和式(39)可知,MBS空调功率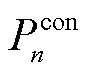 、EV车载计算资源
、EV车载计算资源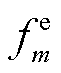 与MBS通信功率
与MBS通信功率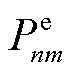 分配均与MBS和EV之间的计算卸载变量
分配均与MBS和EV之间的计算卸载变量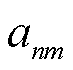 有关,
有关,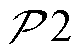 可视为仅关于
可视为仅关于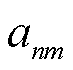 的单变量优化问题。求解式(39)得到
的单变量优化问题。求解式(39)得到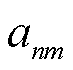 的最优值后,可基于式(2)、式(4)~式(6)和线性规划方法直接获取上述其余变量取值。然而EV车主具有自私性,为避免充电成本上升,不会主动接收运营商的计算任务。为此,视基于计算卸载的MBS热点转移为主从博弈模型,其中EV车主视为领导者,可通过标价车载计算资源并“出售”给MBS转移任务计算产生的热负荷;通信运营商为跟随者,基于EV发布的计算价格购买EV的计算资源以转移任务计算电负荷与空调热负荷。考虑到计算能耗补贴取值与EV计算能耗相关,令
的最优值后,可基于式(2)、式(4)~式(6)和线性规划方法直接获取上述其余变量取值。然而EV车主具有自私性,为避免充电成本上升,不会主动接收运营商的计算任务。为此,视基于计算卸载的MBS热点转移为主从博弈模型,其中EV车主视为领导者,可通过标价车载计算资源并“出售”给MBS转移任务计算产生的热负荷;通信运营商为跟随者,基于EV发布的计算价格购买EV的计算资源以转移任务计算电负荷与空调热负荷。考虑到计算能耗补贴取值与EV计算能耗相关,令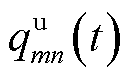 表示第m个EV单位计算资源交易定价,
表示第m个EV单位计算资源交易定价,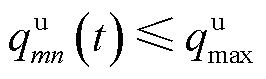 ,
,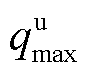 为算力资源定价上限。第n台MBS卸载计算任务至第m个EV提供的计算能耗补贴
为算力资源定价上限。第n台MBS卸载计算任务至第m个EV提供的计算能耗补贴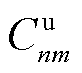 为
为
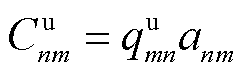 (41)
(41)
记领导者与跟随者的策略空间集合分别为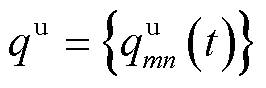 ,
,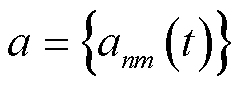 ,则主从博弈过程描述为:首先,各EV通过能量管理系统向MBS发布计算资源交易单价;其次,MBS基于交易单价决定合作EV对象并广播计算资源购买数量给对象EV;最后,EV根据广播结果决定合作或重新定价。假设车主与通信运营商均理性且目标为最大化自身效益,将式(6)代入子问题
,则主从博弈过程描述为:首先,各EV通过能量管理系统向MBS发布计算资源交易单价;其次,MBS基于交易单价决定合作EV对象并广播计算资源购买数量给对象EV;最后,EV根据广播结果决定合作或重新定价。假设车主与通信运营商均理性且目标为最大化自身效益,将式(6)代入子问题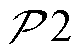 并省略无关时隙标号,引入辅助变量
并省略无关时隙标号,引入辅助变量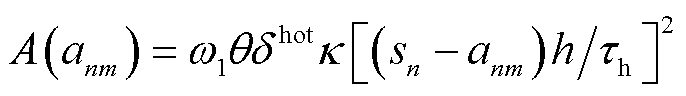 将子问题
将子问题 的空调热负荷优化函数
的空调热负荷优化函数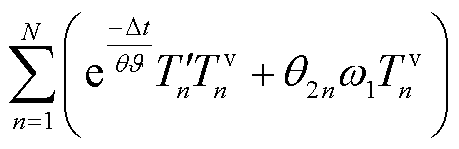 转换为关于跟随者决策
转换为关于跟随者决策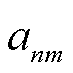 的因变量,并简化公式表述。属于跟随者的第n台MBS效用函数如式(42)所示。
的因变量,并简化公式表述。属于跟随者的第n台MBS效用函数如式(42)所示。
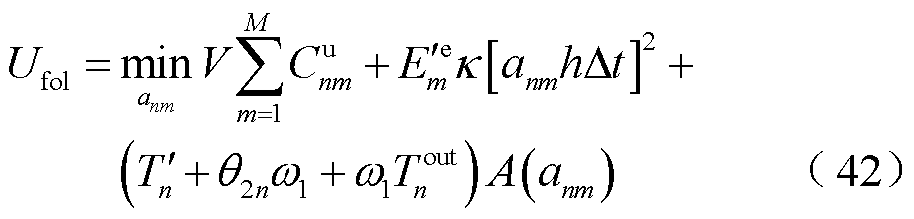
作为领导者的第m个EV效用函数表示为
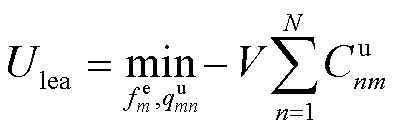 (43)
(43)
基于式(42)、式(43),主从博弈的纳什均衡定义如下:当EV车主与运营商都不能单方面地改变自己的博弈策略来获取更大的效益时,主从博弈达到纳什均衡,即满足
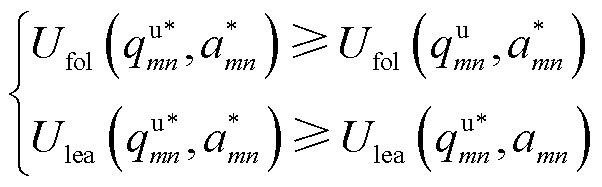 (44)
(44)
式中,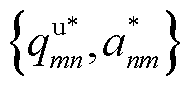 为主从博弈的纳什均衡点。为证明主从博弈的纳什均衡点存在且唯一,基于KKT条件获取跟随者与领导者的最优决策。首先,假设已知领导者的计算单价
为主从博弈的纳什均衡点。为证明主从博弈的纳什均衡点存在且唯一,基于KKT条件获取跟随者与领导者的最优决策。首先,假设已知领导者的计算单价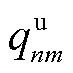 ,构建式(42)关于
,构建式(42)关于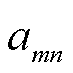 的一阶偏导,关于MBS机房温度变化的最优
的一阶偏导,关于MBS机房温度变化的最优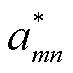 闭合解表示为
闭合解表示为
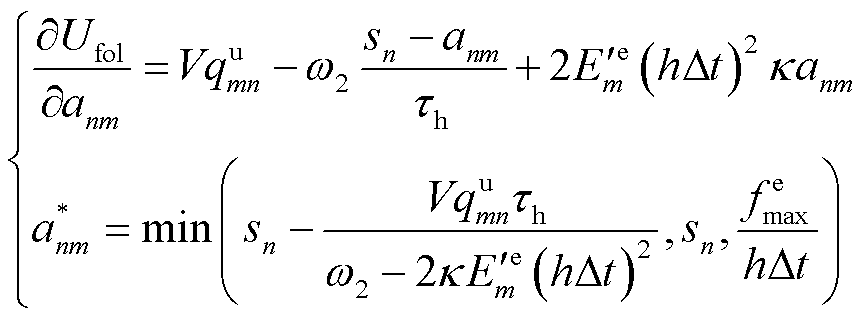 (45)
(45)
式中,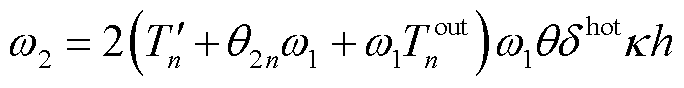 。构建式(45)关于变量
。构建式(45)关于变量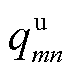 的偏导,得到
的偏导,得到
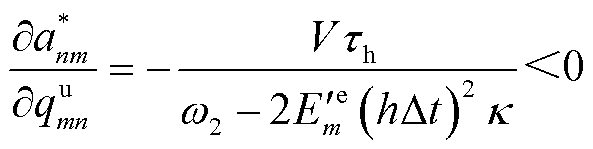 (46)
(46)
明显地,式(46)恒为负值,MBS的计算卸载决策为关于计算单价的单调递减函数,即单价越高卸载数量越低。此外,领导者的效用函数为关于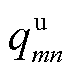 的凸函数,因此EV与MBS的主从博弈必然存在纳什均衡点且唯一,
的凸函数,因此EV与MBS的主从博弈必然存在纳什均衡点且唯一,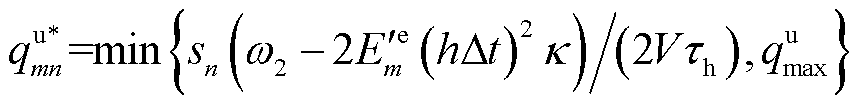 。
。
基于式(45)、式(46)求解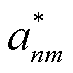 后,MBS在计算卸载阶段的最优通信功率
后,MBS在计算卸载阶段的最优通信功率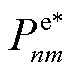 、最优EV的车载计算资源分配决策
、最优EV的车载计算资源分配决策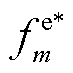 可分别基于式(2)、式(16)、式(17)获取。
可分别基于式(2)、式(16)、式(17)获取。
给定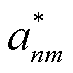 后,式(39)视为仅关于空调功率变量的优化问题,即
后,式(39)视为仅关于空调功率变量的优化问题,即
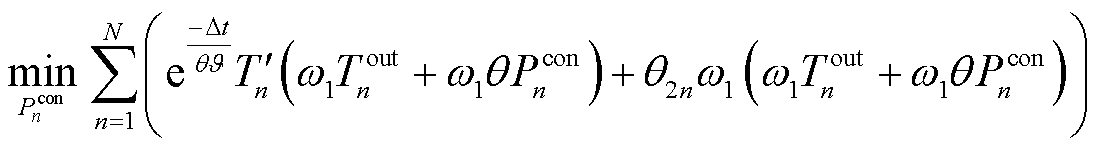 (47)
(47)
观察可知,式(47)属于线性方程,可直接通过凸优化求解器(例如CVX,CPLEX等)获取最优解。下一节将给出子问题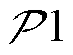 的求解方法。
的求解方法。
由于式(22)存在相乘变量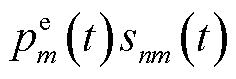 ,导致MBS的传输功率变量
,导致MBS的传输功率变量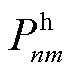 与EV的充放电变量
与EV的充放电变量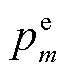 耦合。式(22)属于分段函数,子问题
耦合。式(22)属于分段函数,子问题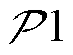 为极度非凸函数,无法直接获取问题最优解。针对上述问题,本节基于连续凸近似方法(Successive Convex Approximation, SCA)将
为极度非凸函数,无法直接获取问题最优解。针对上述问题,本节基于连续凸近似方法(Successive Convex Approximation, SCA)将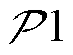 变换为近似凸函数,再利用凸优化方法获取可行解。视
变换为近似凸函数,再利用凸优化方法获取可行解。视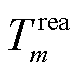 为一个辅助变量,将式(38)的最右项变形为典型的二次方差函数,即
为一个辅助变量,将式(38)的最右项变形为典型的二次方差函数,即
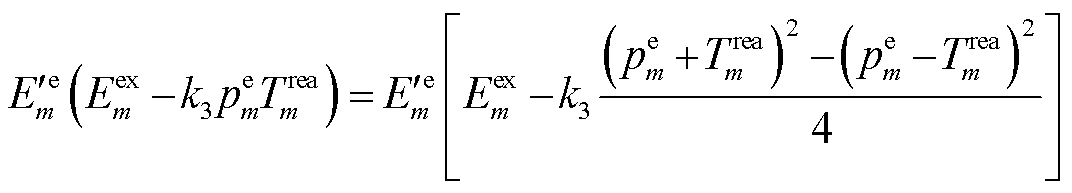 (48)
(48)
式(48)属于典型的凸差分形式,式(23)可转换为
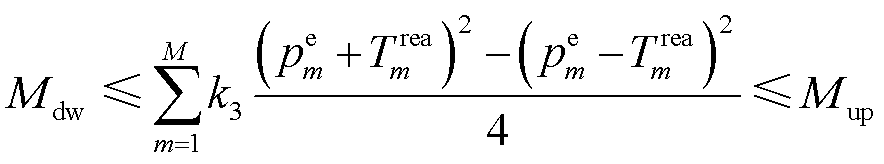 (49)
(49)
为了更方便处理式(49),通过SCA将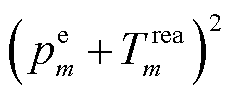 近似展开为一个下凸近似函数
近似展开为一个下凸近似函数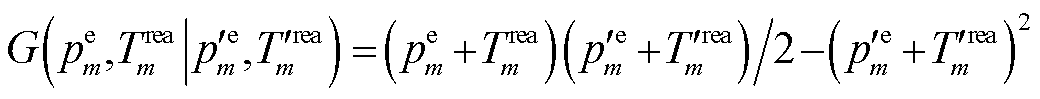 。其中
。其中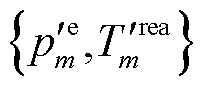 表示满足子问题
表示满足子问题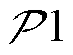 约束的任意可行解集合。进而子问题
约束的任意可行解集合。进而子问题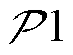 与式(49)分别变形为
与式(49)分别变形为
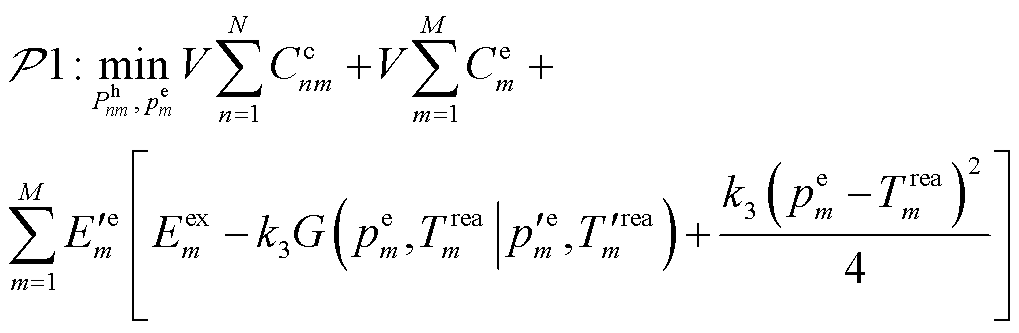 (50)
(50)
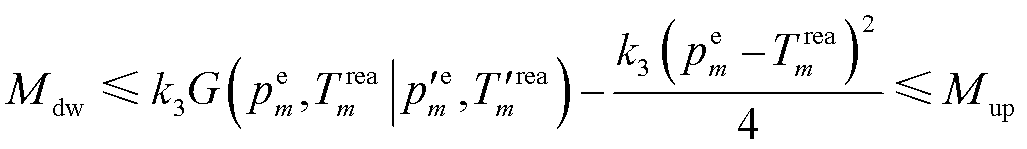 (51)
(51)
将含有相互耦合变量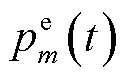 和
和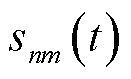 的式(22)变形为式(48),属于
的式(22)变形为式(48),属于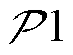 约束的式(23)被限制在优化变量的凸函数集合之中,如式(51)所示。进而,式(38)转换为典型凸函数,即式(50),其可直接应用CVX或CPLEX等求解器获取EV充放电功率与MBS通信功率的最优解。
约束的式(23)被限制在优化变量的凸函数集合之中,如式(51)所示。进而,式(38)转换为典型凸函数,即式(50),其可直接应用CVX或CPLEX等求解器获取EV充放电功率与MBS通信功率的最优解。
基于上述求解过程,进一步讨论实际调控场景下的子问题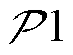 求解。理想情况下,EV必然接入最优信道的MBS以减少通信时延。然而无线链路通常面临旁信道攻击的安全隐患,攻击者会通过攻击接入频率较高的5G接入点造成EV调度数据传输失败。为此,实际场景下的电力公司为保护调度数据的无线传输安全,要求EV通信接入满足安全约束;而通信运营商需联合优化EV的接入决策与MBS通信功率,以均衡安全传输、调度时延与通信能耗。进而,实际场景下的子问题
求解。理想情况下,EV必然接入最优信道的MBS以减少通信时延。然而无线链路通常面临旁信道攻击的安全隐患,攻击者会通过攻击接入频率较高的5G接入点造成EV调度数据传输失败。为此,实际场景下的电力公司为保护调度数据的无线传输安全,要求EV通信接入满足安全约束;而通信运营商需联合优化EV的接入决策与MBS通信功率,以均衡安全传输、调度时延与通信能耗。进而,实际场景下的子问题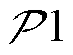 变成考虑EV安全接入约束的MBS功率分配和EV充放电联合优化问题。基于上述介绍,引入二元变量
变成考虑EV安全接入约束的MBS功率分配和EV充放电联合优化问题。基于上述介绍,引入二元变量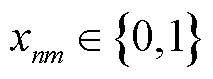 表示EV接入决策,其中
表示EV接入决策,其中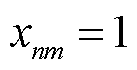 表示第m个EV接入第n台MBS,反之为0。记接入第n台MBS的EV比例
表示第m个EV接入第n台MBS,反之为0。记接入第n台MBS的EV比例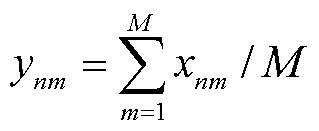 。其次,为量化车联网安全等级,引入信息熵概念描述第n台MBS与第m个EV的通信安全程度,由隐私熵
。其次,为量化车联网安全等级,引入信息熵概念描述第n台MBS与第m个EV的通信安全程度,由隐私熵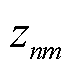 表示为
表示为
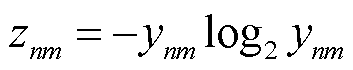 (52)
(52)
若第n台MBS的隐私熵越高,表示在各EV集中接入第n台MBS频率较低,调度数据传输风险越弱。进一步地,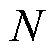 个MBS的平均隐私熵表示为
个MBS的平均隐私熵表示为
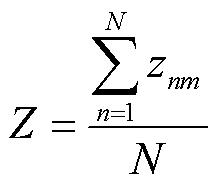 (53)
(53)
令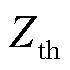 表示接入安全阈值,当平均隐私熵大于该值,表示网络接入混乱程度与安全系数高;反之,无线通信安全程度越低。进而,在考虑EV接入安全约束下,实际场景中的式(38)重写为混合整数非线性规划(Mixed Integer Non-Linear Programming, MINLP)问题,即
表示接入安全阈值,当平均隐私熵大于该值,表示网络接入混乱程度与安全系数高;反之,无线通信安全程度越低。进而,在考虑EV接入安全约束下,实际场景中的式(38)重写为混合整数非线性规划(Mixed Integer Non-Linear Programming, MINLP)问题,即
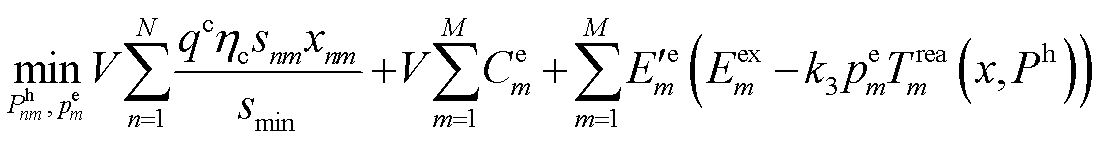 (54)
(54)
约束:
式(1),式(18)~式(21),式(23),式(25)
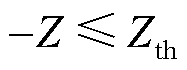 (55)
(55)
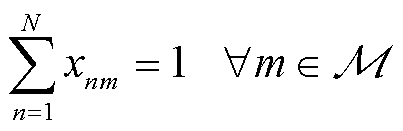 (56)
(56)
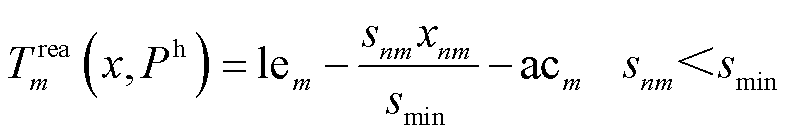 (57)
(57)
由于离散变量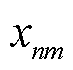 与连续变量
与连续变量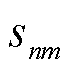 相耦合,为了使属于MINLP的式(54)变成SCA可处理形式,首先松弛
相耦合,为了使属于MINLP的式(54)变成SCA可处理形式,首先松弛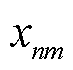 成为取值在
成为取值在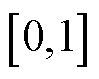 的连续变量
的连续变量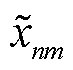 ,其物理意义表示第m个EV接入第n台MBS的概率。接着,将
,其物理意义表示第m个EV接入第n台MBS的概率。接着,将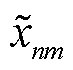 代入式(53)得到其二阶导数
代入式(53)得到其二阶导数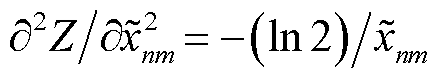 恒小于零,式(55)为凸函数。进而令
恒小于零,式(55)为凸函数。进而令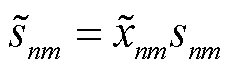 以合并耦合变量,式(54)重写为
以合并耦合变量,式(54)重写为
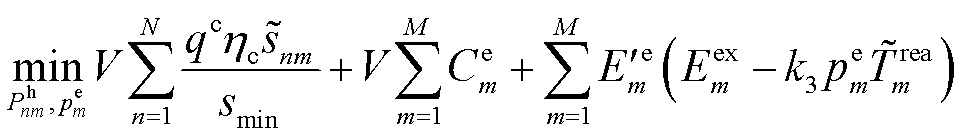 (58)
(58)
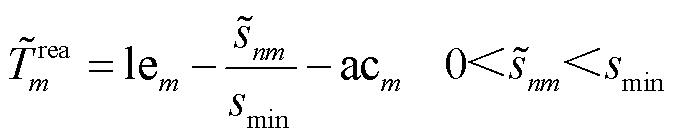 (59)
(59)
基于上述步骤,式(58)从MINLP问题变形为无整数变量的非凸函数,可基于SCA方法变形为凸函数求解,类似流程参考式(48)~式(51)。基于SCA方法得到EV充放电与MBS传输功率分配策略后,需恢复离散变量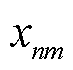 以获取EV接入决策。在离散变量求解方法中,分支定界法的时间复杂度随着EV与MBS数量增多将急剧上升。针对上述问题,提出一种启发式EV安全接入选择策略。首先,将各EV
以获取EV接入决策。在离散变量求解方法中,分支定界法的时间复杂度随着EV与MBS数量增多将急剧上升。针对上述问题,提出一种启发式EV安全接入选择策略。首先,将各EV 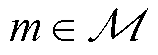 可能接入各MBS的最优传输速率
可能接入各MBS的最优传输速率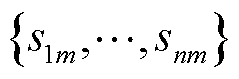 从大到小排序,并令接入速率最高的接入决策
从大到小排序,并令接入速率最高的接入决策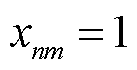 ;然后,判断网络整体隐私熵Z是否满足式(55),若不满足网络约束,从接入EV数量最多的MBS里选择接入速率最优的EV改变其接入到速率次优的MBS;最后,如此重复直到满足约束,视为接入选择策略迭代收敛,获取安全性与通信性能均衡的EV通信接入决策
;然后,判断网络整体隐私熵Z是否满足式(55),若不满足网络约束,从接入EV数量最多的MBS里选择接入速率最优的EV改变其接入到速率次优的MBS;最后,如此重复直到满足约束,视为接入选择策略迭代收敛,获取安全性与通信性能均衡的EV通信接入决策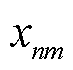 。
。
基于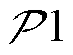 和
和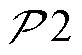 获取MBS的最优通信、计算与空调负荷后,下层子问题
获取MBS的最优通信、计算与空调负荷后,下层子问题 为线性规划问题,可直接应用凸优化求解器求解。基于Lyapunov优化的在线灵活资源协同管理算法流程如图4所示。
为线性规划问题,可直接应用凸优化求解器求解。基于Lyapunov优化的在线灵活资源协同管理算法流程如图4所示。
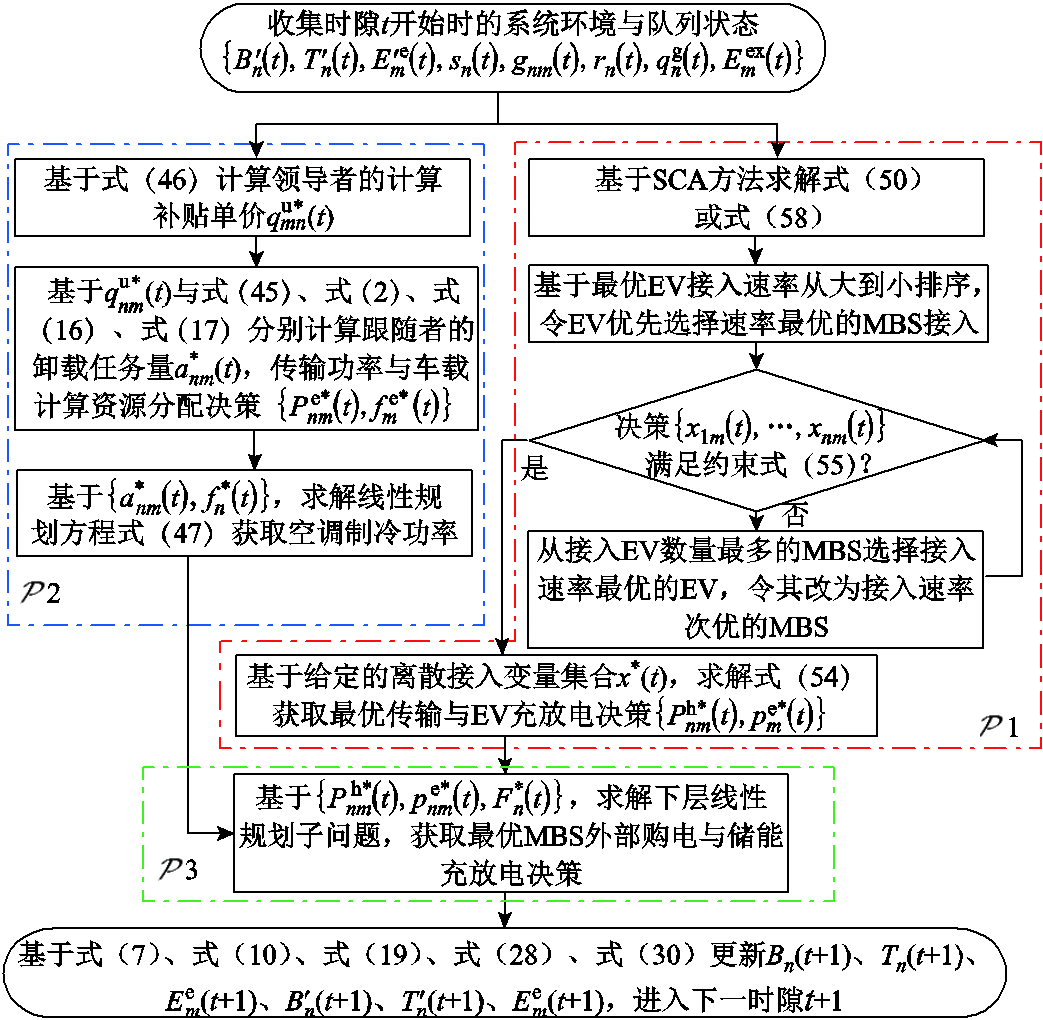
图4 算法流程
Fig.4 Algorithm flow chart
本文基于Matlab R2019a仿真平台进行仿真验证,仿真环境为Intel(R) Core(TM)i7-10700F CPU @2.90GHz,32G内存。考虑一个面积大小为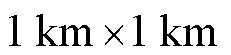 的小区蜂窝通信场景,由3个5G MBS与70台EV组成。各时隙下MBS的生成计算任务规模速率服从参数在
的小区蜂窝通信场景,由3个5G MBS与70台EV组成。各时隙下MBS的生成计算任务规模速率服从参数在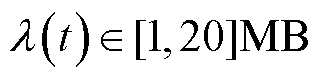 随机浮动的泊松过程,并假设EV在
随机浮动的泊松过程,并假设EV在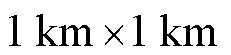 空间的停留位置服从独立同分布的泊松点过程,5G信道增益
空间的停留位置服从独立同分布的泊松点过程,5G信道增益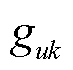 、噪声功率
、噪声功率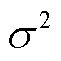 、MBS计算能力上限
、MBS计算能力上限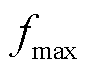 、计算能耗系数
、计算能耗系数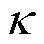 与通信功率
与通信功率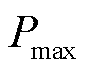 参考文献[27]。5G基站机房配套空调负荷等效热阻
参考文献[27]。5G基站机房配套空调负荷等效热阻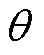 与等效热容、空调固定参数
与等效热容、空调固定参数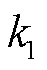 与
与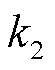 参考文献[8]。各EV的计划出行用电需求
参考文献[8]。各EV的计划出行用电需求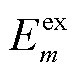 与EV下一天出行概率有关,其概率分布见文献[6]。在不失一般性的前提下,简化各EV的到达与离开时间模型为服从区间
与EV下一天出行概率有关,其概率分布见文献[6]。在不失一般性的前提下,简化各EV的到达与离开时间模型为服从区间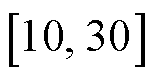 的均匀分布概率模型。5G和EV在各时隙的实时充/放电价设定参考文献[27],其他仿真参数见表1,5G基站外部温度变化趋势参照附图1。在本文仿真中,任何时隙开始时系统不具备未来网络状态先验知识。
的均匀分布概率模型。5G和EV在各时隙的实时充/放电价设定参考文献[27],其他仿真参数见表1,5G基站外部温度变化趋势参照附图1。在本文仿真中,任何时隙开始时系统不具备未来网络状态先验知识。
在下述仿真实例中,本文选取休息日下午时段(15:00)为起点的100个时隙长度,设定五个不同场景进行仿真分析,以分析网络资源、场景规模和变化对购电成本以及EV充放电效率的影响。各场景设定见表2。场景1、2、4、5均采用改进Lyapunov优化解耦问题,场景3采用传统Lyapunov优化解耦问题,其Lyapunov方程采用所有虚拟队列状态总和表示[27],即设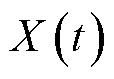 为队列状态集合,则
为队列状态集合,则
表1 仿真参数设定
Tab.1 Simulation parameters

参数数值 单位bit任务数据所需CPU周期/周期数1G 单个时隙长度/min5 计算卸载时间长度/min3 调度通信时间长度/min2 Lyapunov控制参数V10 MBS储能单元容量/(kW·h)3 MBS储能电能泄露系数 0.91 EV车载边缘计算资源/GHz0.5 EV调度信号最优传输速率/(MB/s)0.2 EV电池容量/(kW·h)4 EV充放电效率 0.95 MBS通信延迟补偿/(元/s)0.5
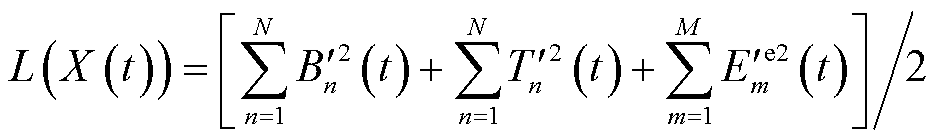
考虑到现有基站能量管理策略均未考虑通信安全约束,而网络能耗优化受通信安全制约,因此,为验证在考虑通信安全前提下的场景2经济成本仍优于对比策略,在下述仿真中若未声明,场景3~5均不考虑电力调度业务通信安全约束式(55)。
表2 场景设定
Tab.2 Scenario setting

场景类型EV策略MBS策略EV通信优化目标 本文场景1接收热点优化传输速率最优 本文场景2接收热点优化传输安全约束下的速率最优 对比场景3无无速率最优 对比场景4[20]无优化传输速率最优 对比场景5[16]接收热点无MBS能耗最优
图5a与图5b分别展示了100个时隙内5G车联网的时间平均用电成本变化。首先,引理1与式(34)保证解耦后的式(36)所得最优解近似收敛于理论最优值,因此场景1和2的MBS时间平均用电成本在时隙30后开始趋于收敛,而EV的时间平均充放电成本也于时隙40开始呈现近似收敛趋势。场景3的EV与MBS未开展协作,导致MBS无法向外部转移热负荷,并为EV调度通信引入额外通信时延,造成EV实际充放电量存在偏差引入额外购电成本。区别于对比场景,场景1和2基于主从博弈为EV提供合作激励,有效地减少计算负荷产生的空调用电量,令MBS具有额外用电空间为EV提供低时延通信服务,以实现充放电决策快速响应。场景2在削减网络负荷的同时需保证EV调度通信安全,EV与MBS的通信链路分布更为均匀但会牺牲部分信道质量较优的EV通信速率,进而在图5b中令EV实际充放电量存在偏差并具有相对较高的时间平均充放电成本。
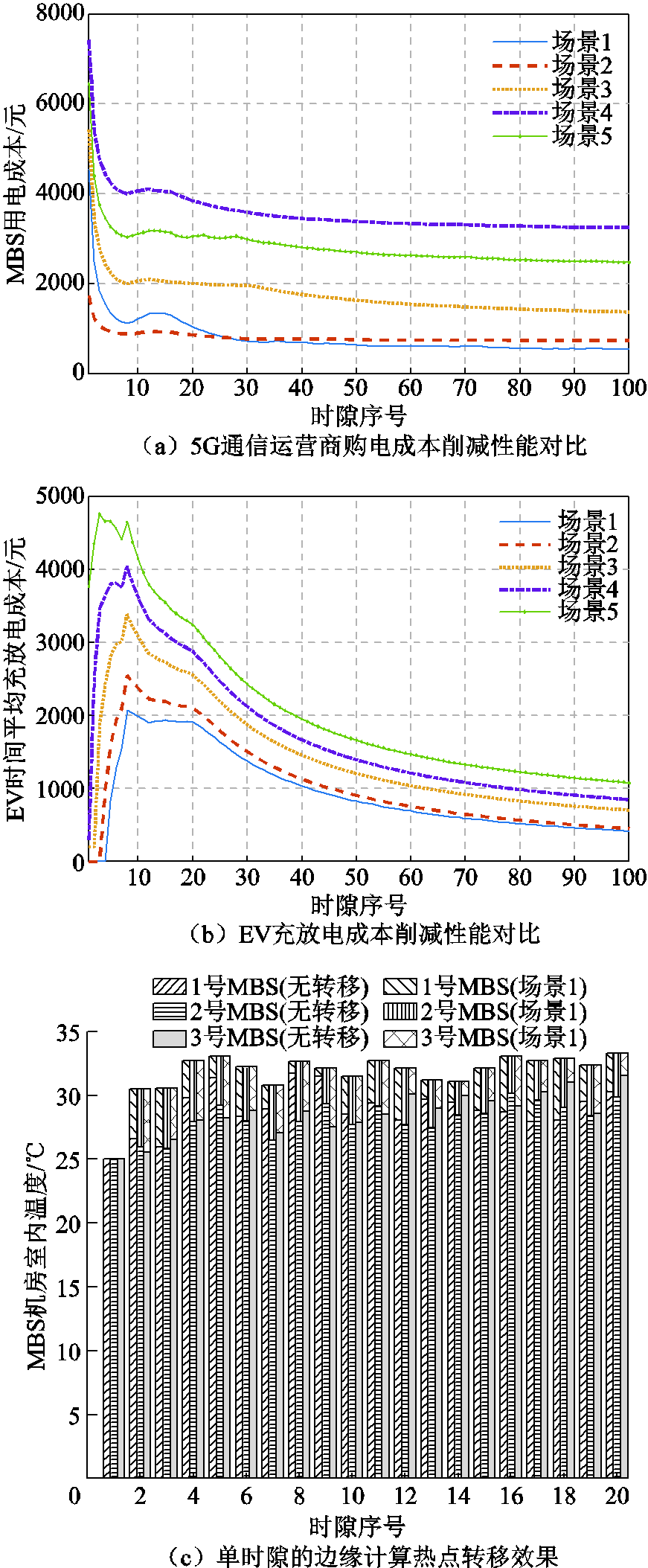
图5 EV与MBS成本优化性能对比
Fig.5 Comparison on cost optimization for EV and MBS
图5c展示了从第1时隙到第20时隙中热点转移机制引导下MBS的热负荷削减性能。在场景3中,由于高计算负载或高实时电价的MBS仅能将计算任务传输至计算负载较低或低电价地区的MBS执行边缘计算,其无法削减边缘计算产生的热负荷,进而造成机房内部温度上升。本文算法基于主从博弈为EV提供计算补偿激励,令MBS具有“零热点”生成特性的额外边缘计算容量,MBS可优先将计算任务转移至EV处理,直接削减了MBS计算负荷。进而,计算负荷削减的同时优化了服务器计算产热与空调制冷用电量,相比于无计算热点转移情况,所提方法平均减少了10.21%的计算热量。
图6与图7分别展示了Lyapunov在线优化框架的控制参数V与引入的虚拟队列对问题近似最优解精度与系统实时控制的影响。图6表明,控制参数V越大,网络整体经济成本越低。随着100时隙的V取值交换,两种曲线也分别呈现相反变化。其中V变小的曲线的经济成本开始上升,V变大的曲线对应的成本开始下降。这是由于Lyapunov优化的控制参数V管理了储能队列稳定性与系统最优解的均衡。Little法则指出,选择恰当的V取值,储能队列保持稳定的同时,EV和MBS用能成本可达到近似长期最优。若V取值过大,实际求解结果与理论最优解近似度越高,储能队列不稳定,存在过度充放电情况。理论证明参考文献[27],本文不做赘述。
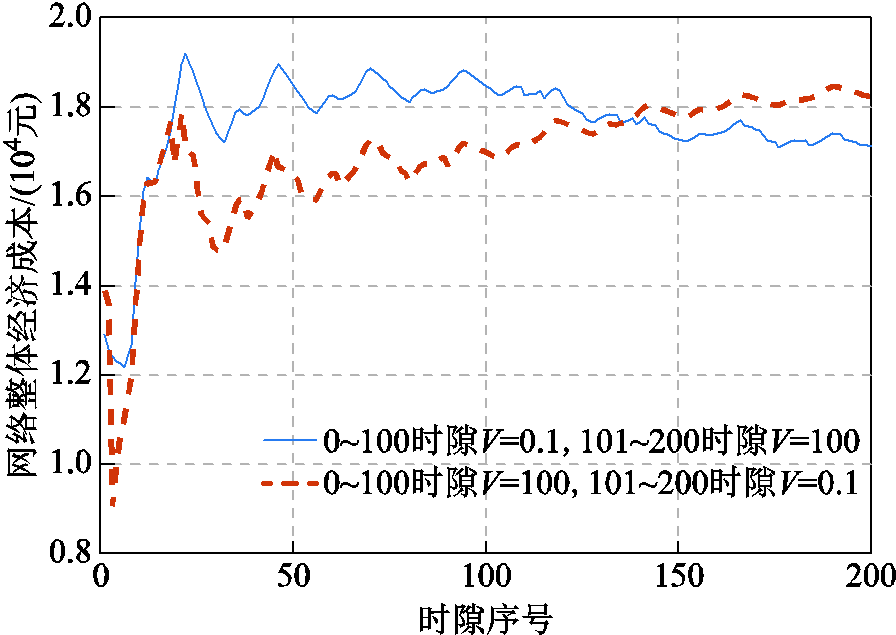
图6 控制参数V对问题求解精度的影响
Fig.6 The impact of control paramter V on solution accuracy
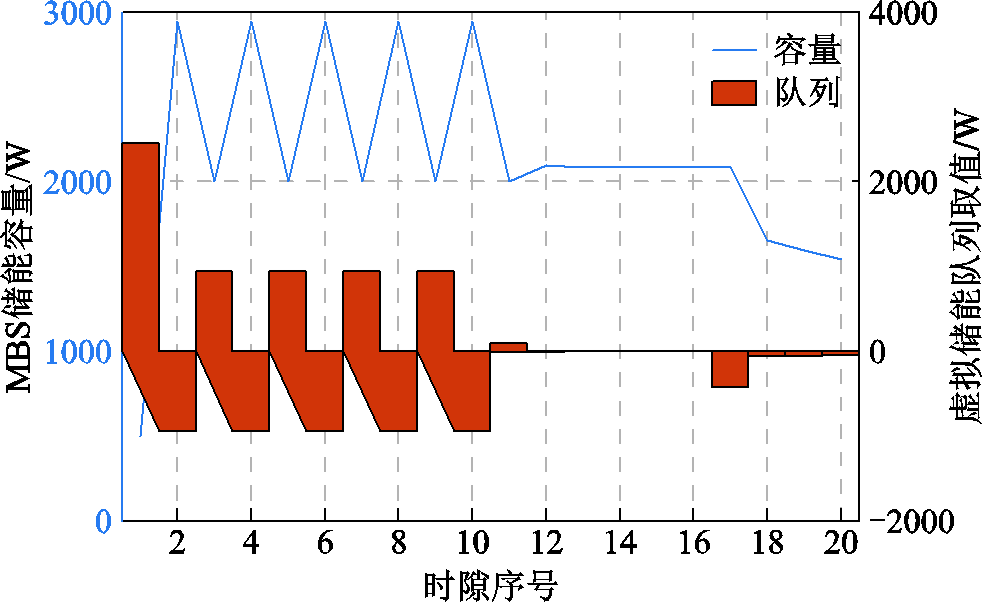
图7 MBS储能容量与虚拟储能队列关系
Fig.7 The relationship between MBS battery storage and virtual battery queue
以20个时隙的MBS储能实时运行为例,图7证明,虚拟储能队列作为实际储能队列的赤字状态,当虚拟储能队列取值为正时,表示储能存储的电量冗余,可以开展放电,即1时隙的虚拟储能队列控制了2时隙的MBS实际储能放电;反之,当虚拟储能队列取值为负,表示储能允许消耗的电量出现赤字,需要充电恢复存储电量,因此下一时隙的实际储能队列进行充电动作。
为证明所提在线算法在车联网异构分布场景下的适用性,图8、图9分别展示了RES配置与不同网络流量分布模式对能量实时管理的影响。图8展示了不同RES配置下的车联网灵活资源能量管理优化性能,其中仅有一台MBS配置有RES,各时隙的实时出力数据基于文献[10]的光伏出力预测数据加上随机预测误差插值得到。2、3号MBS无RES提供混合供能。场景3基于传统Lyapunov优化对车联网整体开展统一控制,无法独立控制各队列状态,其时间平均用电经济成本取值持续波动,但相比于场景4和5具有更优的购电优化性能。这是因为优先为EV或MBS提供资源协助将为另一方增加额外能耗与购电成本,且无法获取协助效益。本文算法除了依赖RES与储能协同管理,还可通过联合调控MBS通信、边缘计算与热负荷的空间分布,实现车联网整体用电成本下降,具有更优的购电成本优化性能。
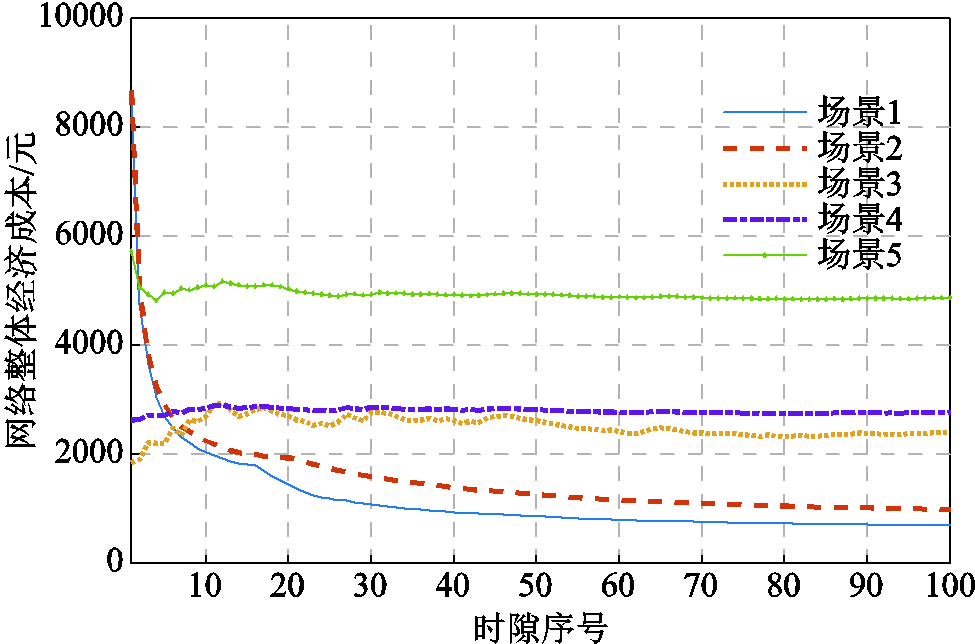
图8 不同可再生能源配置模式对算法性能的影响
Fig.8 The impact of different RES configuration on proposed algorithm
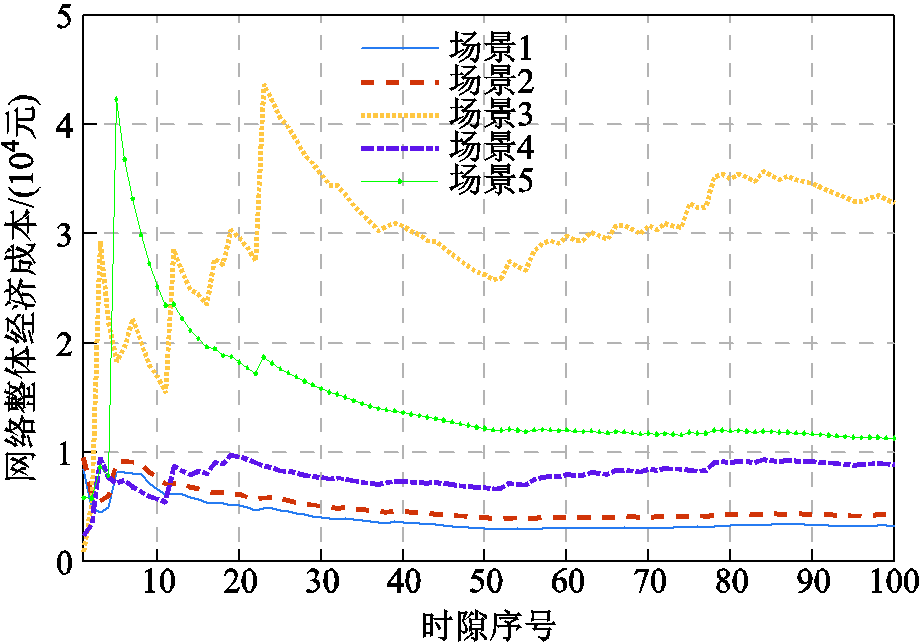
图9 不同计算流量随机分布对算法性能的影响
Fig.9 The impact of different random distribution of task traffic on proposed algorithm
为评估所提改进Lyapunov算法在非平稳的独立随机分布情况下的适用性,图9展示了在突发型计算任务生成速率独立同分布场景下的用电成本优化性能。由于传统Lyapunov优化要求网络流量服从平稳独立随机分布才能满足在线算法优化值必然近似于理论最优值上界,而突发型任务生成速率不满足其充分必要条件,因此场景3呈现优化性能不收敛且急剧上升趋势。不同于场景3,本文算法分别构建了MBS与EV的Lyapunov偏移方程,且EV充放电子问题与MBS计算热点转移子问题相互独立,因此突发计算任务不会引起车联网整体用电负荷急剧上升,具有更优的用电成本优化性能。
图10为工作日下网络整体经济成本对比结果。在仿真示例里,工作日选择与休息日同一时段开始的100个时隙,MBS数量不变,但15:00时段开始的流量分布与EV车辆充电需求高于休息日。明显地,尽管有序充放电业务以及车联网本地计算需求的增加,5个场景的购电成本均远高于图5,但本文方法的整体网络经济成本依旧优于场景3~5。此外,相比于图5休息日情况,场景3~5的时间平均经济成本变化波动大,难以近似收敛至时间平均最优。这是因为随着EV充放电需求增加,EV接入通信要求MBS为充放电调度业务提供高质量通信通道,同时工作日计算流量上升产生更多计算负荷,致使MBS的通信与计算能耗上升;而场景3~5均未同时协同EV与MBS的异构资源开展能量管理,MBS的计算流量转移与负荷削减空间不足,进而受到流量波动影响大,用能削减潜力低于场景1、2。
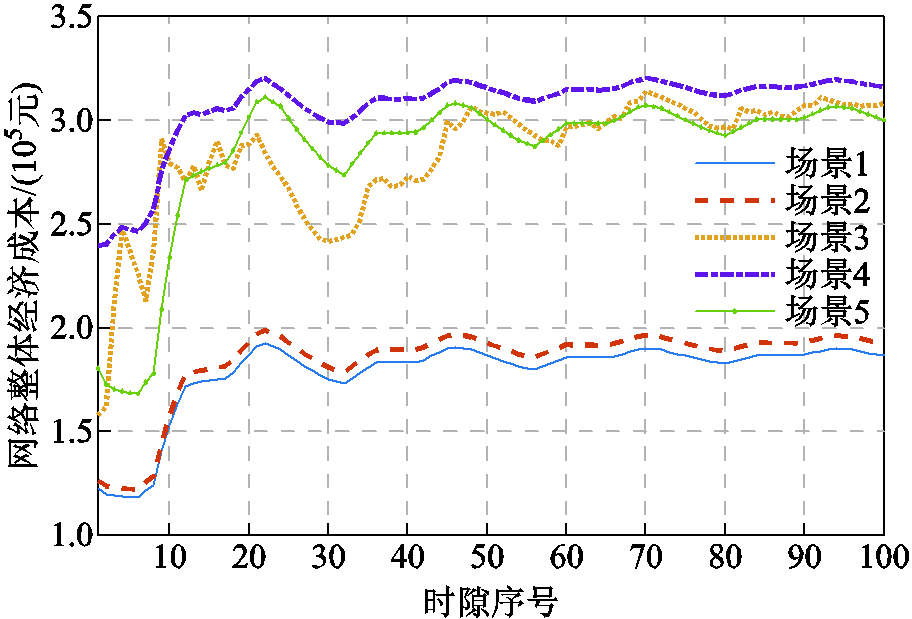
图10 工作日下不同场景的网络整体经济成本对比
Fig.10 The comparison of network total cost in weekday
图11与图12分别展示了单位任务所需计算资源变化对MBS能量管理与EV充放电的影响。如图11所示。随着单位任务所需计算资源上升,五种场景的MBS用电成本均随之上升,而后三种场景的用电成本上升趋势显著高于场景1和2。这是因为场景3无法将计算任务迁移至EV处理。此外,场景5随着任务所需计算资源与边缘计算能耗上升,致使EV计算能耗与用电成本随之上升。场景5优先管控MBS能耗,通信质量下降引入了额外通信服务补偿,致使EV充放电偏差与用能成本上升,如图12所示。本文方法尽管也呈现用电成本上升趋势,但基于主从博弈激励EV车主配合优化MBS空调负荷同时,MBS可通过间接提升通信负荷为EV提供低时延通信服务,进一步为EV提供激励提升空间,有效地降低了车联网整体用电负荷。
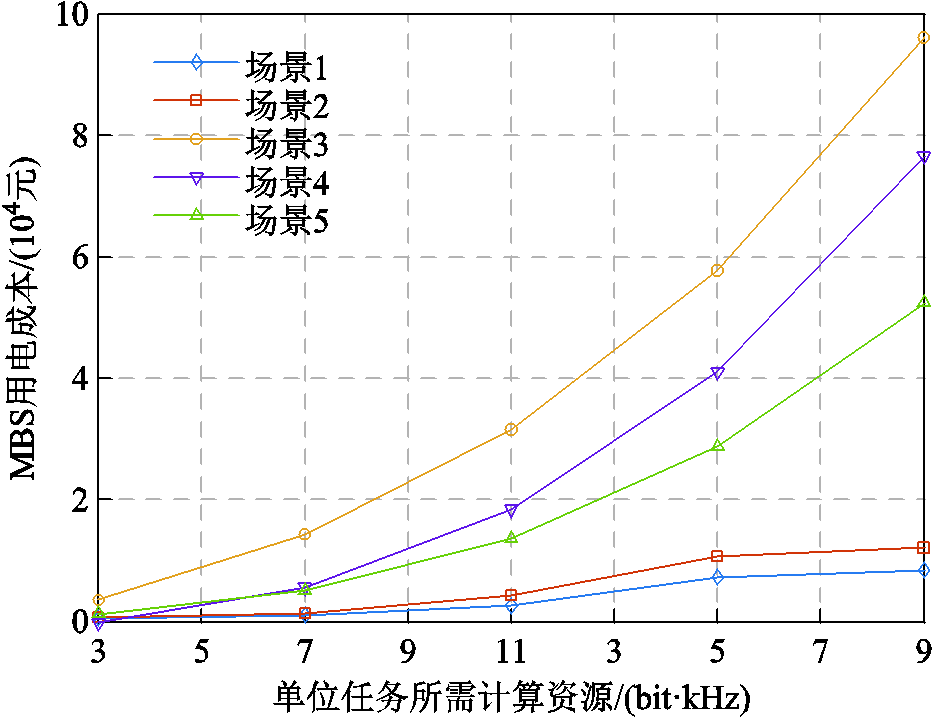
图11 单位任务所需计算资源对MBS能量管理的影响
Fig.11 The impact of variation of computing resource required by unit task on MBS energy management
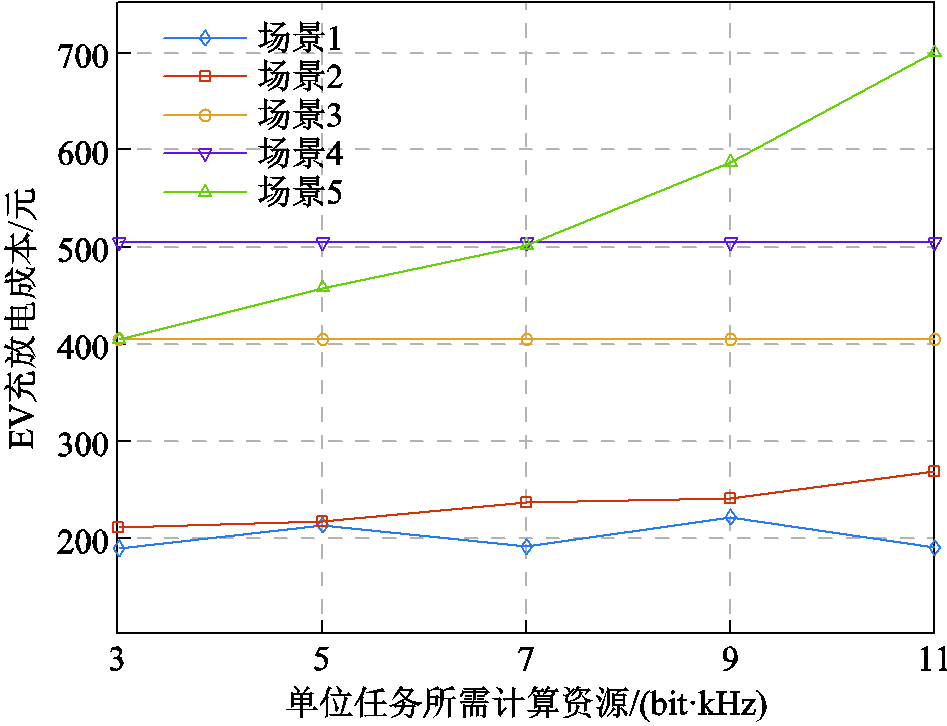
图12 单位任务所需计算资源对EV充放电的影响
Fig.12 The impact of variation of computing resource required by unit task on EV charging
为验证所提算法在异构车联网规模的适用性,图13分别讨论了在130台EV与7组MBS,200台EV与20组MBS的网络规模下,五种场景的5G车联网能量管理性能。图13证明,随着网络规模扩展,在MBS与EV互不提供协助的场景3算法将导致车联网整体用电负荷明显上升,并远高于图5蜂窝小区网络规模下的EV与MBS购电成本。这是因为随着MBS与EV数量上升,MBS不为EV提供通信优化协助致使充电EV的实际响应量偏离总量越来越多,同样地,MBS的计算负载无法向外转移导致电-热负荷持续增长。场景4和场景5尽管利用EV或MBS信息资源为另一方提供了能量调控协助,但由于未考虑另一方经济用能需求致使用电成本仍持续上升。本文的场景1和场景2算法通过博弈机制与充放电通信耦合模型将EV与MBS能量优化需求协同调控,使运营商与EV车主能够在达成效益平衡前提下优化车联网空闲的储能与算力资源利用率;同时,随着EV增加,MBS热电负荷削减空间越高,致使MBS可具备更多的通信资源优化能力,从而具有更低的车联网用能成本。
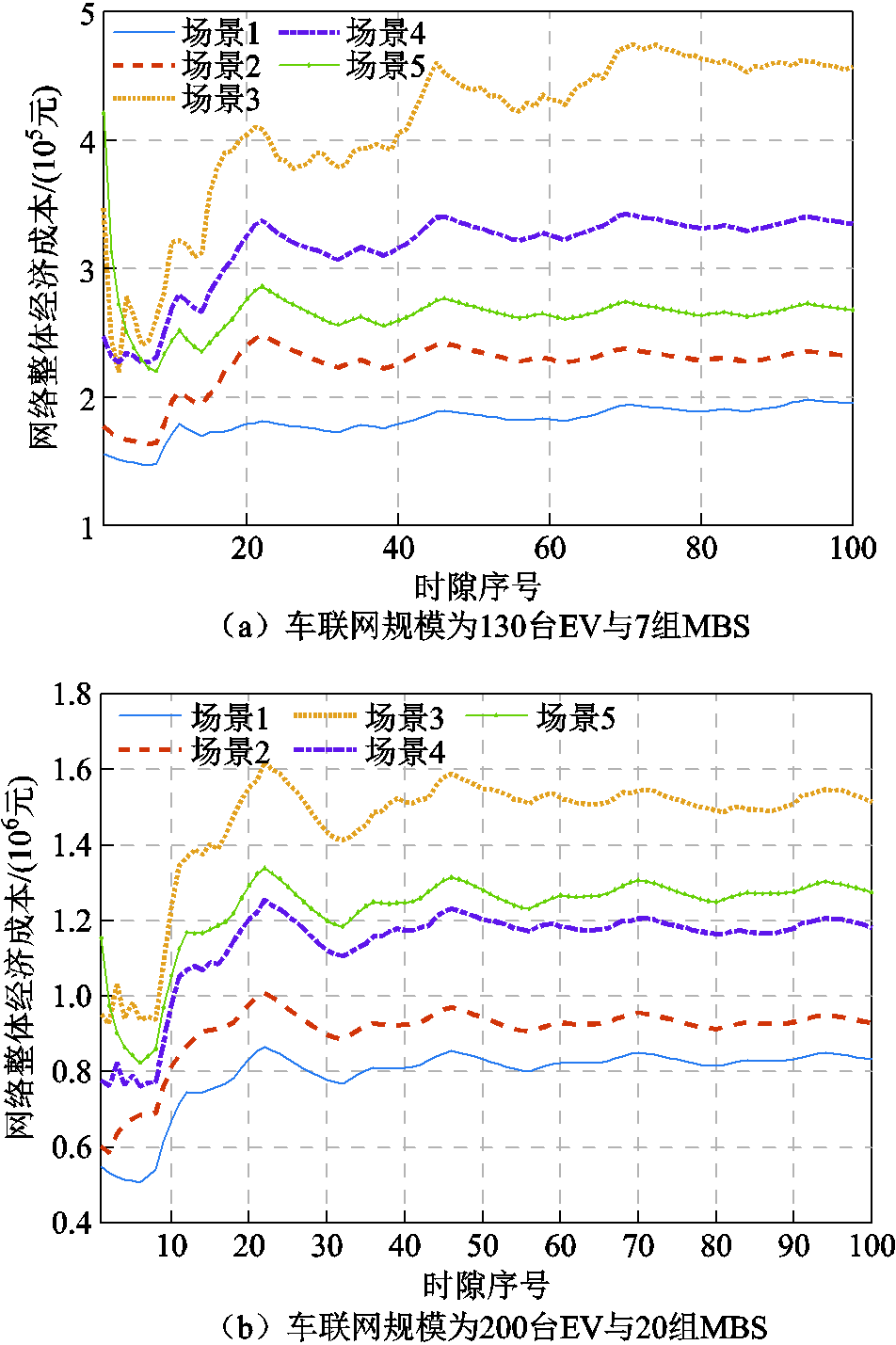
图13 异构车联网规模对算法性能影响分析
Fig.13 Analysis on the impact of heterogeneous vehicle network scale on algorithms
为验证所提算法的寻优精度与收敛速率,图14和图15将本文算法与深度Q算法[28]、结合智能搜索的拍卖算法进行对比,车联网规模参考图13a。深度学习算法用于搜索EV接入MBS的决策,MBS计算热点迁移决策最优解基于平均加权的多目标优化方法获取。为达到整体福利最优,数量远大于MBS的EV将获取更低权重,而MBS获取更高权重,使MBS能耗优化需求远大于EV集群,且深度学习求解取决于数据集精度,这使得该算法在线优化性能弱于本文算法,且收敛速率取决于神经网络参数在线更新优化精度。而智能拍卖优化算法易因启发式搜索算法陷入局部最优解,如图15的第20轮迭代的取值所示,导致在EV数量较大的情况下无法获取最优解。相比于上述算法,本文模型在规定EV只接收一个MBS负载前提下,通过数学推理获取闭合解式(46),令EV与MBS之间的热点转移问题分解为多个一对一独立求解的优化问题。有效降低了求解复杂度同时保证算法可收敛,如图15所示,在第40次迭代时达到渐进最优。
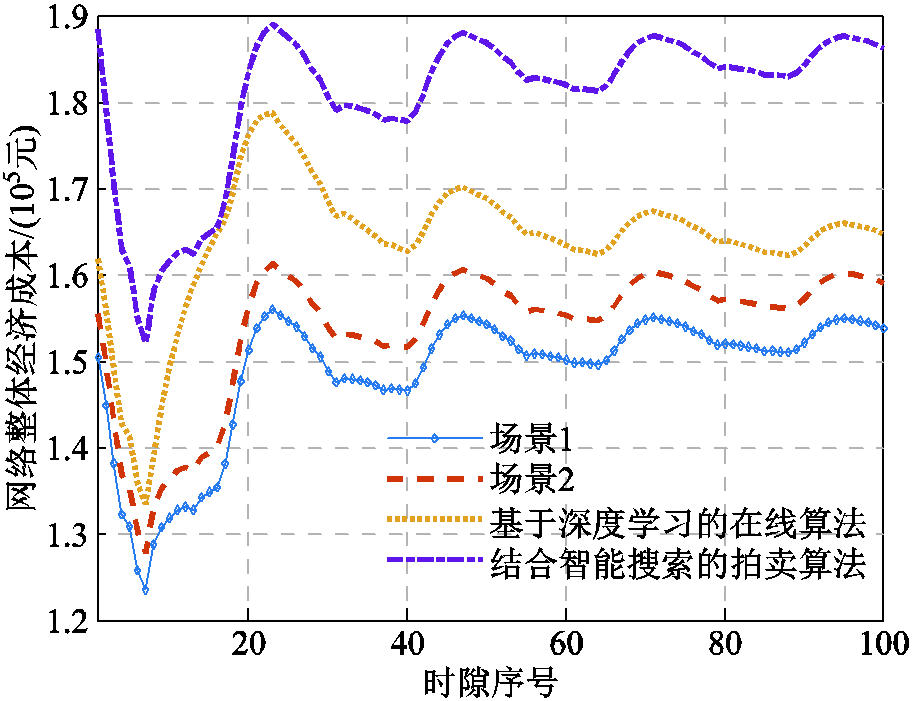
图14 不同算法对模型的寻优精度对比
Fig.14 Comparison of solving accuracy of algorithms
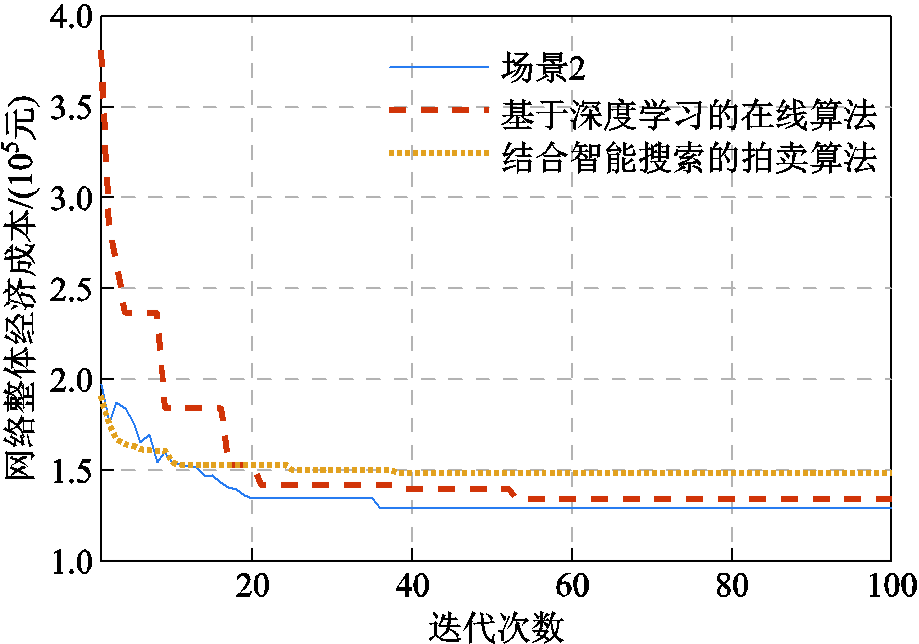
图15 不同算法对模型的寻优速率对比
Fig.15 Comparison of solving rate of algorithms
为对比通信安全约束式(55)存在下各场景的在线能量协同管理效果,图16、图17对比了本文策略与三个对比策略场景在安全通信约束下的时间平均用能成本以及基站隐私熵,其中场景3~5的EV接入策略求解采用粒子群算法获取。如图16所示,在考虑安全接入约束前提下,场景3~5的时间平均用电成本均高于图5。由于MBS首先要满足EV安全接入通信约束,EV将更分散地接入其他MBS以避免信道攻击。若部分EV接入距离较远的MBS,MBS需要提升AAU的工作功率以保证传输速率,进而导致通信运营商用能上升。此外,若以图5的接入模式开展能量协同管理,部分MBS隐私熵将不满足电网业务安全通信需求,如图17所示,会引起EV数据隐私泄露,不满足实际场景运行要求。
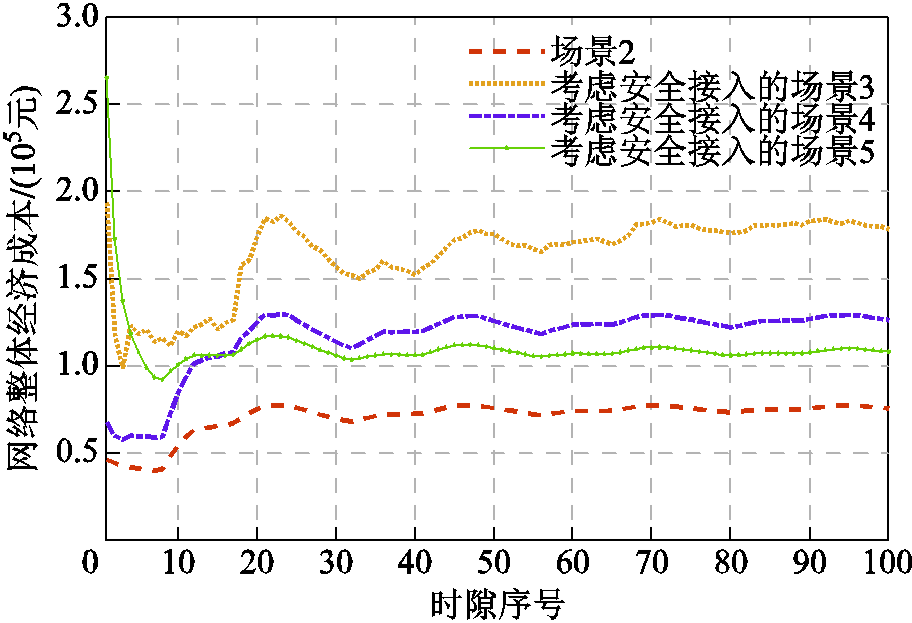
图16 安全接入模式下各场景时间平均用能成本对比
Fig.16 Comparison of time average electrictiy purchasing cost under secure communication mode
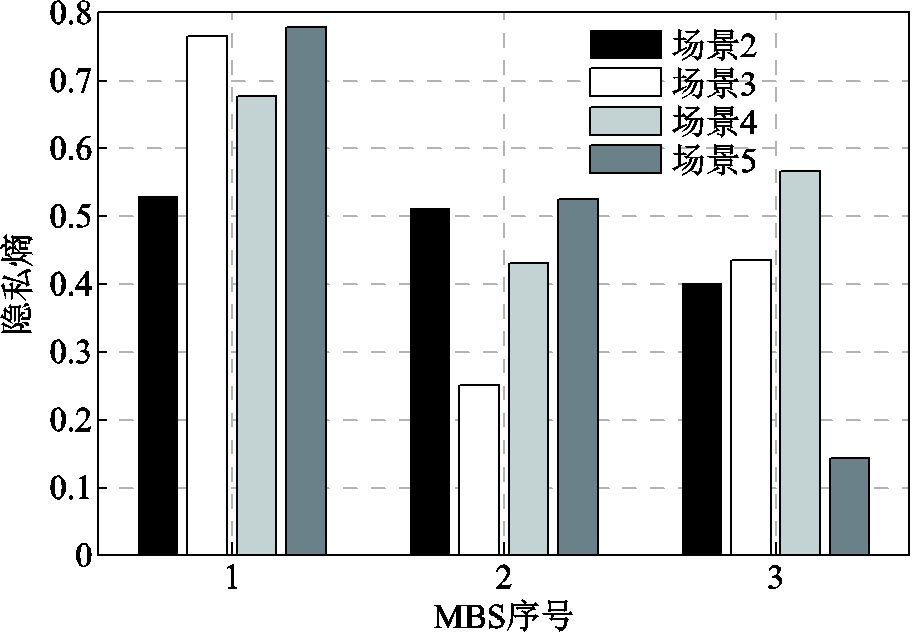
图17 车联网5G基站隐私熵对比
Fig.17 Comparison on privacy entropy
本文研究了面向EV与5G边缘计算网络的能量在线协同管理模型,基于EV车载计算“零”热点特性以及5G通信能耗、时延与EV充放电效率的耦合关系,设计联合计算热点转移与网络资源分配的车联网能量实时管理策略。为鼓励EV参与“零热点”迁移,设计了基于EV-MBS主从博弈的网络热点转移机制,获取关于MBS机房温度变化的最优热点迁移闭合解表达式;提出融合SCA与启发算法的EV充放电与安全调度通信策略;仿真验证了本文策略对车联网系统的节能降本性能,并得出以下结论:
1)在所提能量实时管理框架中,EV与MBS可根据当前时隙的虚拟队列状态,实时调整充放电、RES使用、通信、计算与空调制冷方式,在满足用户基本需求前提下有效削减购电成本。通过协同EV与MBS,能够充分转移与削减机房热负荷,降低高电价地区的基站额外制冷用电需求。
2)所提基于改进Lyapunov和SCA的问题求解方法具有更好的理论最优解近似性能与不同类型场景适应性,能够有效应对突发型计算任务产生或不同比例分布式光伏配置下的5G车联网能量实时管理问题,适用于不同规模的5G车联蜂窝网络能量管理。
附 录
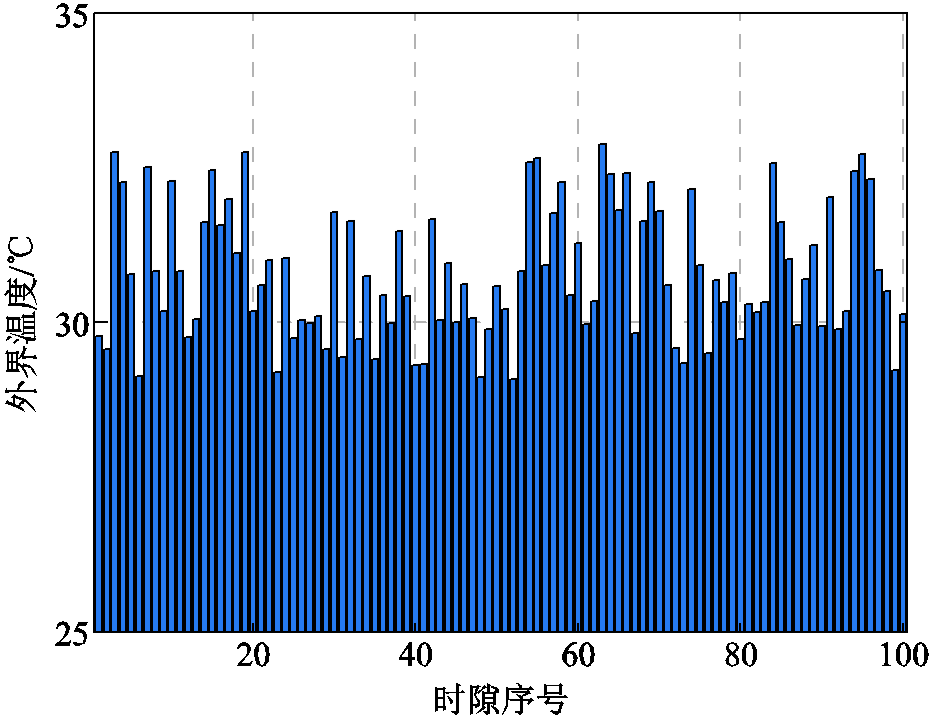
附图1 外界温度变化
App.Fig.1 The variation of outdoor temperature
参考文献
[1] Lü Lin, Yang Xinran, Xiang Yue, et al. Exploring high-penetration electric vehicles impact on urban power grid based on voltage stability analysis[J]. Energy, 2020, 198: 117301.
[2] 王晓卫, 康乾坤, 梁振锋, 等. 考虑5G基站储能参与配网供电恢复研究[J]. 电工技术学报, 2024, 39(11): 3538-3555.
Wang Xiaowei, Kang Qiankun, Liang Zhenfeng, et al. Distribution network restoration supply method considers 5G base station energy storage participation [J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3538-3555
[3] 毛玲, 张钟浩, 赵晋斌, 等. 车-桩-网交融技术研究现状及展望[J]. 电工技术学报, 2022, 37(24): 6357-6371.
Mao Ling, Zhang Zhonghao, Zhao Jinbin, et al. Research status and prospects of fusion technology of vehicle-charging pile-power grid[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6357-6371.
[4] Zhang Qian, Wu Xiaohan, Deng Xiaosong, et al. Bidding strategy for wind power and Large-scale electric vehicles participating in day-ahead energy and frequency regulation market[J]. Applied Energy, 2023, 341: 121063.
[5] 王海鑫, 袁佳慧, 陈哲, 等. 智慧城市车-站-网一体化运行关键技术研究综述及展望[J]. 电工技术学报, 2022, 37(1): 112-132.
Wang Haixin, Yuan Jiahui, Chen Zhe, et al. Review and prospect of key techniques for vehicle-station-network integrated operation in smart city[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 112-132.
[6] 葛晓琳, 曹士鹏, 符杨, 等. 基于区域解耦的时空双尺度电动汽车优化调度[J/OL]. 中国电机工程学报, 2022: 1-13. https://kns.cnki.net/kcms/detail/11. 2107.TM.20220907.1523.006.html.
Ge Xiaolin, Cao Shipeng, Fu Yang, et al. Optimal scheduling of space-time dual-scale electric vehicles based on regional decoupling[J/OL]. Proceedings of the CSEE, 2022: 1-13. https://kns.cnki.net/kcms/ detail/11.2107.TM.20220907.1523.006.html.
[7] 蔡国伟, 姜雨晴, 黄南天, 等. 电力需求响应机制下基于多主体双层博弈的规模化电动汽车充放电优化调度[J]. 中国电机工程学报, 2023, 43(1): 85-98.
Cai Guowei, Jiang Yuqing, Huang Nantian, et al. Large-scale electric vehicles charging and discharging optimization scheduling based on multi-agent two-level game under electricity demand response mechanism[J]. Proceedings of the CSEE, 2023, 43(1): 85-98.
[8] 李昆, 方家琨, 艾小猛, 等. 考虑通信与配套设备协调优化的大规模5G宏基站网络能量管理模型[J]. 中国电机工程学报, 2023, 43(14): 5391-5404.
Li Kun, Fang Jiakun, Ai Xiaomeng, et al. Energy management model of large-scale 5G macro base station network considering the coordinated optimization of communication equipment and standard equipment[J]. Proceedings of the CSEE, 2023, 43(14): 5391-5404.
[9] Munir M S, Abedin S F, Tran N H, et al. Risk-aware energy scheduling for edge computing with microgrid: a multi-agent deep reinforcement learning approach[J]. IEEE Transactions on Network and Service Management, 2021, 18(3): 3476-3497.
[10] 麻秀范, 刘子豪, 王颖, 等. 考虑通信负载迁移及储能动态备电的5G基站光伏消纳能力研究[J]. 电工技术学报, 2023, 38(21): 5832-5845, 5922.
Ma Xiufan, Liu Zihao, Wang Ying, et al. Research on photovoltaic absorption capacity of 5G base station considering communication load migration and energy storage dynamic backup[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5832-5845, 5922.
[11] 浪潮5G MEC边缘计算一体机iAIO V1.0发布[J]. 自动化博览, 2021, 38(2): 7.
Inspur 5G MEC edge computing all-in-one iAIO V1.0 released[J]. Automation Panorama, 2021, 38(2): 7.
[12] 重庆长安汽车股份有限公司. 新时代下智能汽车发展趋势与长安实践[EB/OL]. 2023-09-28.https:// jcpage.jp/jcevent/file/event/upload/file/301/02_automobile_05_changanqiche_he_C_v2.pdf.
[13] Fan Wenhao, Liu Jie, Hua Mingyu, et al. Joint task offloading and resource allocation for multi-access edge computing assisted by parked and moving vehicles[J]. IEEE Transactions on Vehicular Technology, 2022, 71(5): 5314-5330.
[14] Zhang Jieyi, Zhang Biling, Han Zhu. Coalition formation game based information-energy collaboration in vehicle edge computing networks[J]. IEEE Transactions on Vehicular Technology, 2023, 72(6): 7717-7727.
[15] Bahreini T, Brocanelli M, Grosu D. VECMAN: a framework for energy-aware resource management in vehicular edge computing systems[J]. IEEE Transactions on Mobile Computing, 2023, 22(2): 1231-1245.
[16] Wei Zhiwei, Li Bing, Zhang Rongqing, et al. Contract-based charging protocol for electric vehicles with vehicular fog computing: an integrated charging and computing perspective[J]. IEEE Internet of Things Journal, 2023, 10(9): 7667-7680.
[17] 张巍, 王丹. 基于云边协同的电动汽车实时需求响应调度策略[J]. 电网技术, 2022, 46(4): 1447-1458.
Zhang Wei, Wang Dan. Real-time demand response scheduling strategy for electric vehicles based on cloud edge collaboration[J]. Power System Technology, 2022, 46(4): 1447-1458.
[18] 潘建辉, 张宁, 雍培, 等. 面向海量灵活性资源的两阶段分布式协同调度方法[J]. 电力系统自动化, 2023, 47(15): 67-79.
Pan Jianhui, Zhang Ning, Yong Pei, et al. Two-stage distributed collaborative dispatching method for massive flexible resources[J]. Automation of Electric Power Systems, 2023, 47(15): 67-79.
[19] Miao Ankang, Yuan Yue, Wu Han, et al. Planning method and coordinated operation strategy for multi-station integration system[J]. CSEE Journal of Power and Energy Systems, 2023, 9(6): 2394-2408.
[20] 胡龙, 方八零, 樊飞龙, 等.用户-基站-充电站能量共享、互动优化方法及在园区中的应用[J/OL]. 上海交通大学学报, 2023: 1-11. https://doi.org/10.16183/ j.cnki.jsjtu.2023.407.
Hu Long, Fang Baling, Fan Feilong, et al. Energy sharing and interaction optimization method for users, base stations, and charging stations: an application in parks[J/OL]. Journal of Shanghai Jiao Tong University, 2023: 1-11. https://doi.org/10.16183/j. cnki.jsjtu.2023.407.
[21] Bahri R, Zeynali S, Nasiri N, et al. Economic-environmental energy supply of mobile base stations in isolated nanogrids with smart plug-in electric vehicles and hydrogen energy storage system[J]. International Journal of Hydrogen Energy, 2023, 48(10): 3725-3739.
[22] 华为技术有限公司. 绿色5G白皮书[EB/OL]. [2021- 10-1]. https://www.huawei.com/cn/huaweitech/industry- insights/ outlook/green-5g-white-paper.
[23] Chen Xiaojing, Lu Zhouyu, Ni Wei, et al. Cooling-aware optimization of edge server configuration and edge computation offloading for wirelessly powered devices[J]. IEEE Transactions on Vehicular Technology, 2021, 70(5): 5043-5056.
[24] 麻秀范, 孟祥玉, 朱秋萍, 等. 计及通信负载的5G基站储能调控策略[J]. 电工技术学报, 2022, 37(11): 2878-2887.
Ma Xiufan, Meng Xiangyu, Zhu Qiuping, et al. Control strategy of 5G base station energy storage considering communication load[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2878-2887.
[25] ASHRAE. 2021 equipment thermal guidelines for data processing environments [EB/OL]. [2022-06-14]. https://www.ashrae.org/File%20Library/Technical%20Resources/Bookstore/Supplemental%20Files/ReferenceCard_2021ThermalGuidelines.pdf.
[26] Neely M J, Huang Longbo. Dynamic product assembly and inventory control for maximum profit[C]//49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 2010: 2805-2812.
[27] Liu Lilan, Zhang Zhizhong, Wang Ning, et al. Online resource management of heterogeneous cellular networks powered by grid-connected smart micro grids[J]. IEEE Transactions on Wireless Communications, 2022, 21(10): 8416-8430.
[28] Tang Ming, Wong V W S . Deep reinforcement learning for task offloading in mobile edge computing systems[J]. IEEE Transactions on Mobile Computing, 2022, 21(6): 1985-1997.
Abstract With the development of smart vehicle network promoted by China, the number of electric vehicle (EV) and 5G base station (BS) is increasing rapidly, while also bringing huge operation pressure and energy consumption to power grid and network operator, respectively. Therefore, how to coordinate the flexible resource of EV and BS to reduce electric load peak for power grid are important issues. At the same time, as EV equipping with powerful chip, BS can transfer some tasks to idle parked EV for cut down energy consumption of BS. However, due to the communication of EV is coupling with 5G BS, additional communication delay caused by BS energy management will affect the ordered charging scheduling signal between power grid and EV, increasing charging cost of EV. In addition, if 5G BS provided low delay communication for EV, it will bring more energy consumption. Moreover, the optimization of air condition load of BS is still lack of attention, which energy consumption is related with computing hotspot. To this end, this paper establishes a Stackelberg game based online energy management strategy faced to 5G vehicle network, aiming at minimizing the time average battery charging cost of EV and electricity purchasing cost of BS.
First of all, considering vehicle computing characteristics, and the coupling between hot load of air condition and computing tasks, a task migration model between 5G BS and EV is established to transfer the hot load and electric load of BS. Secondly, according to the analysis of communication delay to EV ordered charging, this paper proposes a calculation method of EV real charging capacity considering 5G wireless communication delay, and a communication delay penalty function for 5G network operator. Thirdly, based on above model, considering the stochastic events including task arrival and renewable energy, this paper investigates a long-term average electricity purchasing cost of BS and EV charging cost minimizing problem. Finally, an improved Lyapunov optimization method is proposed to transform the problem to a real time optimization problem. The real time problem can be divided into one upper layer subproblem and two lower layer subproblems, including computing electricity and battery (dis)charging problem, EV charging and communication resource allocation problem, and Stackelberg game-based computing hotspot transferring and BS air condition load control problem, respectively. By introducing an incentive function for EV accepting tasks of BS, the existence of the Nash equilibrium is proved, and this paper gives a close form solution on computing hotspot transferring. Meanwhile, other subproblems can be solved by successive convex approximation method.
In this paper, four scenarios are designed for verifying the performance of our proposed strategy, and analyze the impact of network scale, random task traffic, control parameter, and EV computing capacity on EV charging and BS electricity cost optimization. The simulation results show that proposed method can reduce electricity purchasing cost for both EV and BS without prior knowledge, and the hot load of BS is cut down without adding extra charging cost of parked EV. The following conclusions can be drawn from the simulation analysis: (1) The cooperation between EV and 5G BS can optimize the distribution of energy and information flow, reduce the energy consumption caused by cooling computing hotspot of BS. (2) By introducing improved Lyapunov optimization method, the network resource and energy scheduling of 5G BS and EV can be made online, and the resource scheduling result will not break the backup energy constraint and communication quality.
keywords:5G edge computing, electric vehicle, energy management, Lyapunov optimization, hotspot transfer, Stackelberg game
中图分类号:TM93
DOI: 10.19595/j.cnki.1000-6753.tces.231896
贵州电网有限责任公司科技资助项目(GZKJXM20222149)。
收稿日期 2023-11-04
改稿日期 2024-03-19
陈 恺 男,1997年生,博士研究生,研究方向为能源互联网,电力信息与通信技术等。E-mail:kulewubi@163.com(通信作者)
付 宇 男,1983年生,高级工程师,硕士,研究方向为配网运行分析。E-mail:1641356033@qq.com
(编辑 赫 蕾)