城市电网灾后应急资源的集中匹配-分布调度策略
万海洋 刘文霞 石庆鑫 刘佳怡 张 帅
(新能源电力系统全国重点实验室(华北电力大学) 北京 102206)
摘要 城市电网(UPN)是支撑城市功能正常运行的关键基础设施,及时制定UPN灾后应急资源(ER)的最优调度策略对维护城市各生命线系统功能具有重要意义。与单一输、配电网不同,UPN具有多电压等级交杂和拓扑结构复杂等特点,该文针对灾后UPN负荷应急恢复过程中存在ER总量有限、故障元件(FC)数量繁多、多电压等级电网故障元件的协同抢修存在信息壁垒等问题,提出了UPN灾后ER与FC的集中匹配-分布调度策略。首先,根据ER和FC的实时信息和特征参数,采用二分图法建立二者间的匹配关系;其次,以匹配净收益最大为目标,采用改进后的库恩-曼克尔斯算法,集中制定ER和FC间的最优匹配方式;此外,建立计及UPN中多电压等级电网间耦合关系的双层优化模型,其中,上层高压电网以最大化变电站节点负荷恢复量为目标,下层中压电网以最小化负荷损失成本为目标,制定各电压等级负荷的分布式恢复策略;同时,通过及时更新UPN中新探明的FC和ER的信息,重新确定最优匹配方式和负荷恢复策略,保证所提方法在各时间步长内的最优性;最后,算例部分采用实际UPN对该方法进行仿真分析,结果表明该方法能够在有效地降低UPN负荷损失的同时,大幅缩短求解时间。
关键词:城市电网 极端灾害 故障抢修 负荷恢复 应急资源 赋权二分图 双层优化模型
0 引言
大型城市是一个地区乃至国家的政治、经济、文化中心[1],而城市电网(Urban Power Network, UPN)作为支撑城市各生命线系统功能的重要设施,其正常运行是维护和保障城市功能的基础条件[2-4]。但近年来随着全球气候的变化,以台风、暴雨、暴雪为代表的极端自然灾害发生频率不断升高[5-6],UPN的运行安全受到了极大的威胁。以2021年河南郑州7·20特大暴雨事件为例,全市共计500余条不同电压等级的线路损毁,超过120万居民家中出现长时间停电、停水,居民的焦虑情绪通过网络传播,发生群体性恐慌事件[7]。可以看出,极端灾害所造成的大停电事故不仅会影响居民的衣食住行与生命健康,而且会进一步导致其他城市服务功能瘫痪,造成更加严重的社会动荡和经济损失[8]。
针对极端事件对电网的影响,国内外学者提出了电网韧性的概念,用于表征电网在应对此类低概率-高影响的极端灾害时的抵御冲击和快速恢复供能的能力[9-10],并针对单一配电网的灾后韧性提升过程,开展了调度应急资源(Emergency Resource, ER)抢修故障元件(Fault Component, FC)和恢复负荷供电两方面工作。相较于配电网,以我国北京和上海等城市为例,UPN通常由电压等级为220 kV/500 kV的高/超高压输电网(High-voltage Transmission Network, HTN)、110 kV/35 kV的高压配电网(High-voltage Distribution Network, HDN)、10 kV的中压配电网(Medium-voltage Distribution Network, MDN)和0.4 kV的低压配电网(Low-voltage Distribution Network, LDN)构成[11-15],由于UPN具有多电压等级交杂和拓扑结构复杂等特点[16],导致UPN的灾后恢复过程与单一配电网相比存在三个显著特征:①城市中ER配置的总量有限;②待抢修的FC数量繁多;③需协同调度不同电压等级电网的ER[2]。
对于特征①,现有研究采用的应急资源种类已由固定式ER(分布式电源[17]、储能[18]、微能源网[19]等)逐步扩展至移动式ER(抢修小队[20]、移动式储能车[21-22]、移动式电源车[23]等)。文献[24]从源、网、荷侧总结了各类ER在灾后恢复中的特点,分析得到了当前研究在面向小规模中压配电网时,能够较好地通过灵活调度ER来指导灾后负荷恢复。但在UPN中,由于电力部门通常采用协议储备方式管理ER,即电力部门与物资供应商提前签订协议,物资平常放置在供应商仓库中[25]。因此,灾后UPN中实际能够利用的应急资源总量应当是有限的,需要根据多个电压等级电网故障元件抢修的紧迫程度进行合理分配。但由于现有研究方法通常认为灾后应急资源供应充足,当应用于城市电网时会独立地对各中压配电网进行资源分配,将导致整体资源的分配不均,出现数量稀缺的ER优先分配至受损程度较小的中压配电网中的情况,进而致使受损程度更大的中压配电网难以及时恢复,造成更大范围的停电损失。
对于特征②,现有研究考虑到负荷需求[26]、故障抢修时长[27]、车辆行驶时长[28]的不确定性,采用滚动式优化[28]和多时间断面决策方法[29],即依据最新获得的参数预测值,统一决策并动态更新单一配电网内的故障抢修和负荷恢复的时空协同优化调度计划,能够在一定程度上降低预测误差的影响[29-31]。同时由于单一配电网的故障数量和模型求解维度较小,上述研究中采用的统一决策的方法也能很好地满足计划制定的实时性。但当统一式决策方法适用于多电压等级城市电网时,受灾损范围大、故障数量众多、模型规模庞大等因素的影响,当前基于时空全局最优的恢复决策方法的求解效率会大幅降低,难以在大型城市级电网中应用。
对于特征③,现有研究针对输、配电网协同恢复开展了大量研究,并通常采用分区并行恢复的策略进行供电恢复[32-34]。其中,输电网层面的恢复目标是停电机组的黑启动,使得区内系统尽快获得大量的能量用于恢复配电网[35];配电网层面的恢复目标是尽量保证关键负荷正常运行,减小停电损失。但以上研究均忽略了故障抢修和负荷恢复二者间的时序耦合性[36],并未涉及输、配电网的灾后协同抢修与恢复问题。而在极端事件影响中,UPN中各电压等级电网均会遭遇大规模物理元件毁伤,此时调度抢修小队抢修故障元件和利用应急资源恢复负荷两方面工作应当是同步进行且互相影响的[29],因此针对多电压等级电网的协同抢修与恢复工作仍有待深入研究。
针对上述问题,本文提出了UPN灾后ER与FC间的集中匹配-分布调度策略,建立了多电压等级电网负荷协同恢复的双层优化模型。该策略能够综合考虑UPN中应急资源需求量与可用量的时空变化特性,在短时间内集中式最优匹配ER与FC,并在各电压等级电网中分布式协同调度各类应急资源,实现UPN的全域高效应急恢复,更有利于降低极端灾害对UPN的综合影响。
1 问题描述
1.1 城市电网的结构与功能
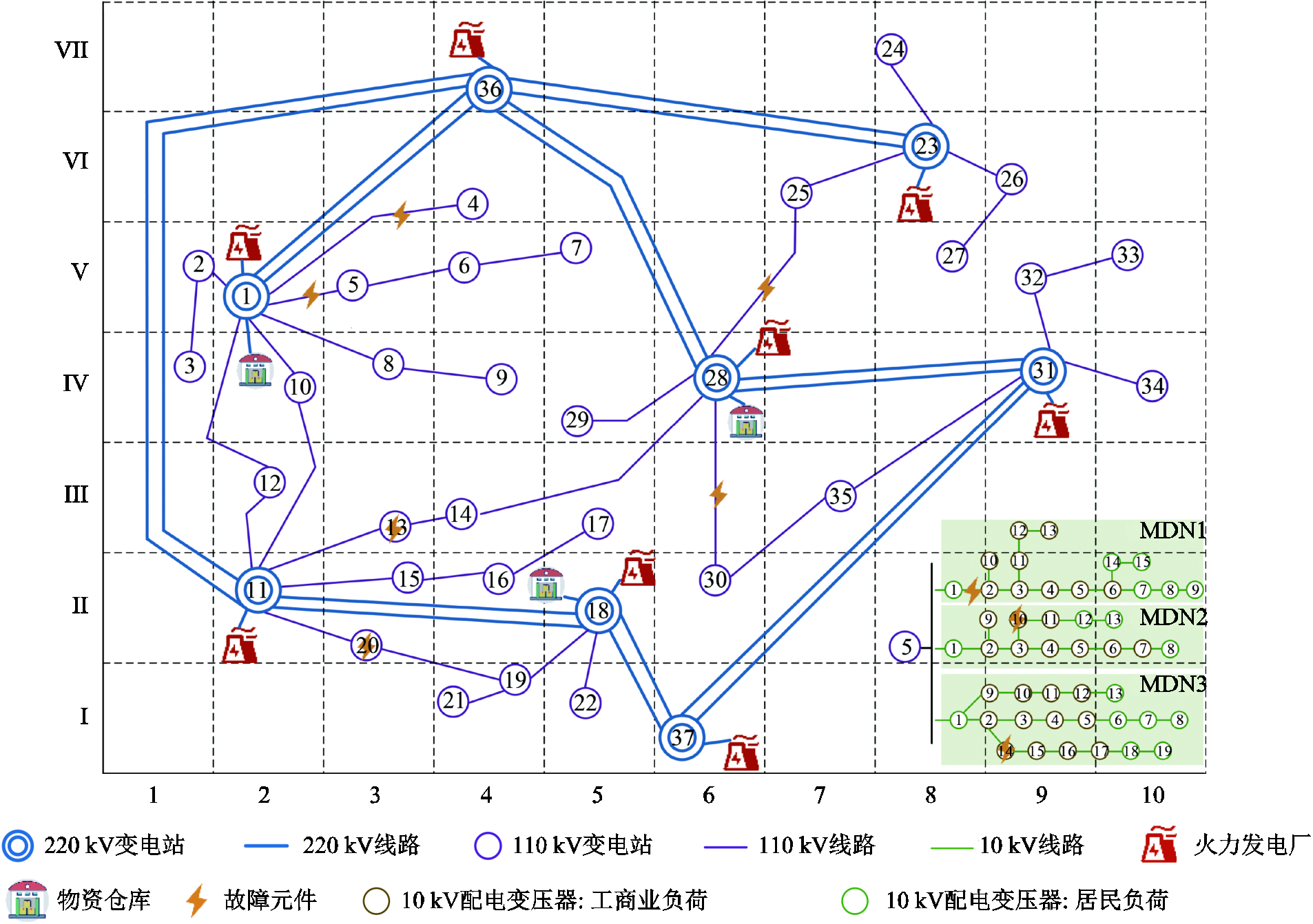
各国家UPN的典型电压等级见表1,灾后UPN应急资源的集中匹配-分布调度框架如图1所示。各电压等级电网的组成和功能包括:①HTN,该电压等级电网负责与发电厂和外部电网交互,接受来自数百千米外区域的电力注入,如图1中蓝线所示;②HDN,该网络结构通常为闭环设计、开环运行,其变电站节点出线侧一般与多条馈线连接,每一条出线即为一个中压配电网,如图1中紫线所示;③MDN,该网络通常为辐射状结构,与建筑物或社区服务变压器直接连接,如图1中绿线所示;④LDN,该网络直接与用户的入户电能装置相连接,本文对该部分不作考虑。
表1 各国城市电网的典型电压等级
Tab.1 Typical voltage levels of UPN in various countries

国家城市HTN/kVHDN/kVMDN/kVLDN/kV 中国[11,15]北京/上海500/220110/35100.4 西安750/330/22011020/100.4 沈阳500/22066100.4 美国[12]纽约34513833/250.4 英国[13]伦敦400/27513222/110.4 日本[14]东京500154/6622/6.60.4 法国[15]巴黎400/27590/63200.4
1.2 灾后城市电网负荷应急恢复问题
灾后UPN负荷应急恢复问题实际上是通过ER和FC的最优匹配与调度,以实现UPN功能尽量维持在正常水平。但受UPN结构的影响,该问题亟须处理两大关键的耦合关系:多资源间协同调度和多电压等级电网间协同恢复。
1.2.1 多资源间协同调度
城市电网中包含的ER和FC的种类和特点总结见表2。故障元件抢修工作顺利开展的前提是相应电压等级和类型的应急资源完备。例如,当高压配电网的杆塔倒塌时,需要等待高压电网抢修人员、起重机和杆塔三类资源均到场后,方可开始抢修。由于灾后UPN中包含的ER和FC的种类和数量繁多,二者间的匹配和调度将是一个多层级、大规模、高维度的问题。而灾后应急策略制定的快速性是降低电力负荷损失的前提条件,因此需要一种具备实时信息更新、高效率求解等条件的方法。目前二分图作为解决大规模变量组间匹配问题的典型方法[37-39],其在处理短期资源分配问题方面具有灵活性强、计算速度快的优势,为大量应急资源在城市电网范围内的高效率优化调度提供了思路。
表2 城市电网中应急资源和故障元件的特点
Tab.2 Characteristics of the ER and FC in UPN

应急资源故障元件 种类人员高压配电网抢修人员、中压配电网抢修人员HTN具有较高的保护措施,假设其在极端灾害下不会发生故障 车辆起重机、抢修车HDN(地下)变电站、线路、杆塔 物资变压器、线路、杆塔MDN变压器、线路(电缆)、杆塔 特点初始部署在物资仓库中、能力不同、总数有限、根据交通网移动数量多、信息获取迟滞性、修复各电压等级故障元件所需资源不同
1.2.2 多电压等级电网间协同恢复
与单一配电网的负荷恢复过程不同,由于城市电网中各电压等级电网间存在耦合关系,以HDN和MDN间为例,HDN作为MDN的能源供应端,MDN中负荷的恢复进程会受限于对应HDN的变电站节点能够承担负荷的上限;MDN作为HDN的能源消耗端,MDN的实际负荷决定了HDN中的潮流和负荷大小,所以在制定恢复计划时应同时考虑各电压等级电网的实际情况与耦合关系。HDN与MDN间的协同恢复过程的直接做法是整合两个电压等级电网调度的通用模型,通过统一优化的方式求解,但该方法意味着调度员应掌握HDN和MDN中的所有数据。然而,在极端灾害场景下,想要同时获取二者的网架结构、负荷大小、故障元件的详细情况等参数是极其困难的[40]。因此,应当采用双层分布式优化,通过模型分解实现区域自治和区域间协同,从而避免集中处理数据和计算困难的问题[34]。
基于上述分析,本文建立了灾后UPN应急资源的集中匹配-分布调度框架,如图1所示。其中,集中匹配指决策平台基于ER和FC的实时信息,采用二分图理论,集中决策二者间的最优匹配关系;分布调度指在各电压等级电网内部,基于ER和FC的匹配结果,互不干涉地最优调度应急资源参与负荷恢复的过程。
2 应急资源与故障元件的集中匹配方法
应急资源和故障元件间的集中匹配过程包含构建表示ER和FC间匹配关系的赋权二分图、提出最优匹配方式的快速求解算法两部分内容。
2.1 应急资源与故障元件的赋权二分图建立
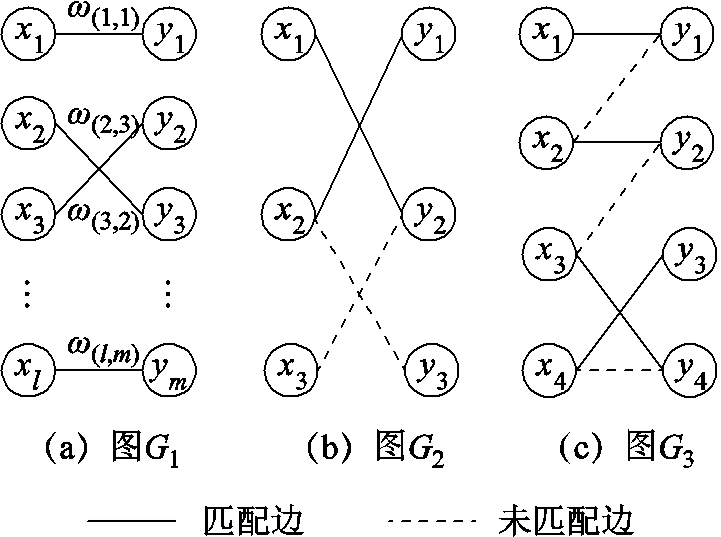
根据赋权二分图的基本概念[40-42](相关内容总结见附录)本节建立的表示应急资源和故障元件间匹配关系的赋权二分图如图2a所示。构成该图的基本元素包括应急资源顶点集合UER={r1, r2,…, rL}、故障元件顶点集合VFC={f1, f2,…, fM}、匹配边(Matching Edge, ME)集合BME={(1,1), (1,2),…, (L,M)}、匹配权重矩阵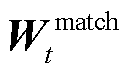 。本节依次计算各部分:首先根据ER和FC的属性,分别建立二者的特征参数集;其次根据ER和FC间的匹配条件,生成二者间的匹配边集合;最后计算各匹配关系的权重大小。
。本节依次计算各部分:首先根据ER和FC的属性,分别建立二者的特征参数集;其次根据ER和FC间的匹配条件,生成二者间的匹配边集合;最后计算各匹配关系的权重大小。
2.1.1 应急资源的顶点集合生成
应急资源具有能力属性、派遣状态、当前地理位置、抢修效率四方面的特征参数,其顶点集合UER用矩阵形式可描述为
式中,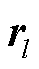 为编号为l的ER的特征参数集合的向量表示;
为编号为l的ER的特征参数集合的向量表示;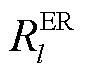 为编号为l的ER的能力属性,取值见表3;
为编号为l的ER的能力属性,取值见表3;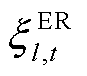 为编号为l的ER在t时刻的派遣状态,当
为编号为l的ER在t时刻的派遣状态,当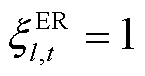 时,表示该ER已被派遣,正在负责处理某一故障元件,否则
时,表示该ER已被派遣,正在负责处理某一故障元件,否则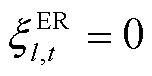 ;
;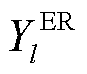 为编号为l的ER的地理位置;
为编号为l的ER的地理位置;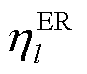 为编号为l的ER的抢修效率。
为编号为l的ER的抢修效率。
表3 故障元件与应急资源的对应关系
Tab.3 Correspondence between the FC and ER
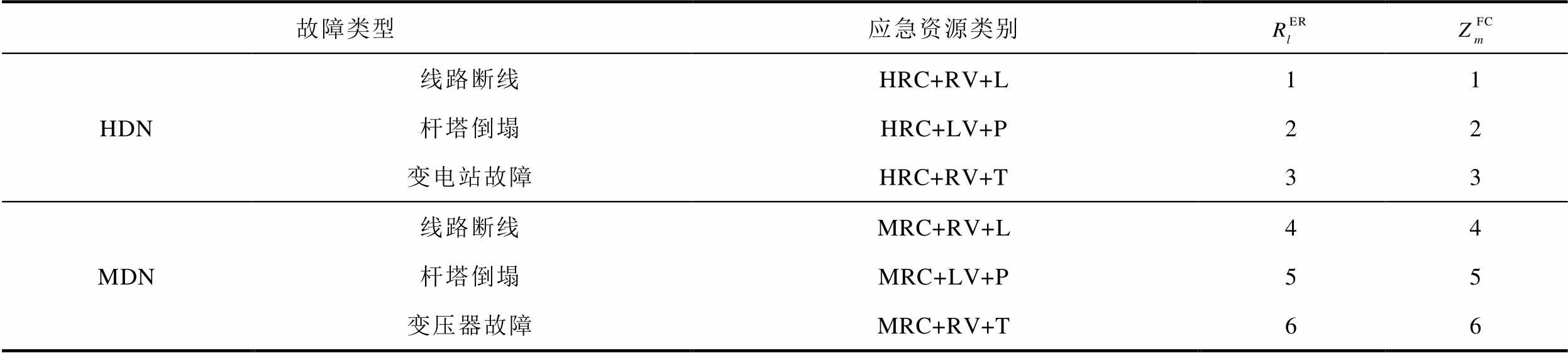
故障类型应急资源类别 HDN线路断线HRC+RV+L11 杆塔倒塌HRC+LV+P22 变电站故障HRC+RV+T33 MDN线路断线MRC+RV+L44 杆塔倒塌MRC+LV+P55 变压器故障MRC+RV+T66
注:HRC—高压配电网抢修人员;MRC—中压配电网抢修人员;LV—起重机;RV—抢修车;T—变压器;L—线路;P—杆塔。
2.1.2 故障元件的顶点集合生成
故障元件具有故障类型、探明故障时长、所需抢修时长、抢修分配情况、地理位置和重要程度六方面的特征参数,其顶点集合VFC用矩阵形式可描述为
式中,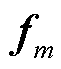 为第m个FC的特征参数集合的向量表示;
为第m个FC的特征参数集合的向量表示;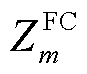 为第m个FC的故障类型,取值见表3;
为第m个FC的故障类型,取值见表3;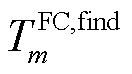 为探明第m个FC位置所需的时间,由于城市电网的故障数量较多且灾损范围较大,巡线员或无人机需要在故障发生的一定时长后,才可探测出故障元件;
为探明第m个FC位置所需的时间,由于城市电网的故障数量较多且灾损范围较大,巡线员或无人机需要在故障发生的一定时长后,才可探测出故障元件;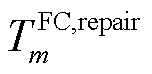 为第m个FC的预估抢修时间,本文设定巡线员或无人机在探明故障的同时,能够预估出故障元件的抢修时间;
为第m个FC的预估抢修时间,本文设定巡线员或无人机在探明故障的同时,能够预估出故障元件的抢修时间;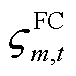 为抢修资源在t时刻对第m个FC的分配情况,当
为抢修资源在t时刻对第m个FC的分配情况,当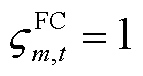 时,表示此时已有应急资源负责抢修该FC,否则
时,表示此时已有应急资源负责抢修该FC,否则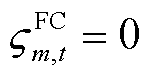 ;
;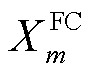 为第m个FC的地理位置,数值上取其距离最近的节点位置;
为第m个FC的地理位置,数值上取其距离最近的节点位置;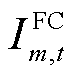 为第m个FC的负荷重要程度,数值上等于相较于电网正常运行时元件单独故障造成的负荷损失,其计算式为
为第m个FC的负荷重要程度,数值上等于相较于电网正常运行时元件单独故障造成的负荷损失,其计算式为
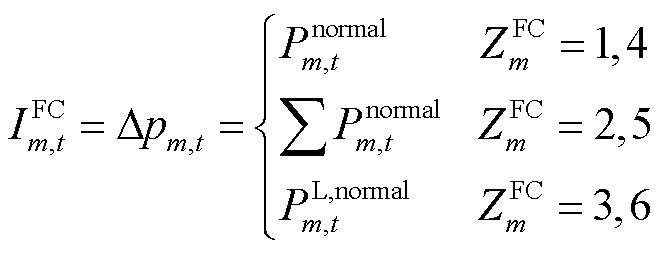 (3)
(3)
式中,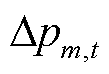 为第m个FC单独故障时会造成的负荷损失。具体地,当第m个FC为线路时,
为第m个FC单独故障时会造成的负荷损失。具体地,当第m个FC为线路时,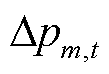 为t时刻系统正常运行时流经线路m的有功潮流
为t时刻系统正常运行时流经线路m的有功潮流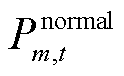 ;当第m个FC为杆塔时,
;当第m个FC为杆塔时,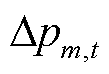 为t时刻系统正常运行时流经杆塔m所有线路的有功潮流和
为t时刻系统正常运行时流经杆塔m所有线路的有功潮流和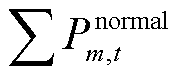 ;当第m个FC为变电站和变压器时,
;当第m个FC为变电站和变压器时,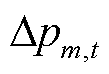 为t时刻系统正常运行时节点m的所连负荷的有功功率
为t时刻系统正常运行时节点m的所连负荷的有功功率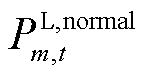 。
。
2.1.3 匹配边集合生成
在生成集合UER与VFC中各顶点间的匹配边时,应先判断应急资源是否具备处理故障元件的能力,以编号为l的ER为例,其需要满足以下条件,方可与第m个FC匹配:①故障类型集合为抢修小队能力属性的子集;②应急资源可用;③故障元件未被分配应急资源;④故障元件已被巡线员或无人机探明情况。上述条件的数学模型为
式中,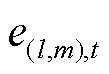 为表征
为表征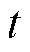 时刻编号为l的ER和第m个FC间匹配关系的0-1变量,当
时刻编号为l的ER和第m个FC间匹配关系的0-1变量,当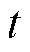 时刻编号为l的ER和第m个FC二者间存在匹配边时,有
时刻编号为l的ER和第m个FC二者间存在匹配边时,有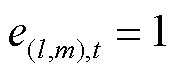 ;否则
;否则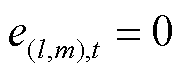 。
。
2.1.4 匹配权重计算
匹配权重矩阵为
式中,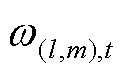 为编号为l的ER和第m个FC在t时刻按照此匹配方式的系统净收益,计算式为
为编号为l的ER和第m个FC在t时刻按照此匹配方式的系统净收益,计算式为
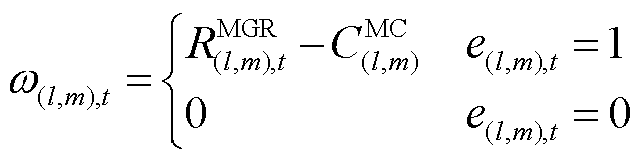 (6)
(6)
式中,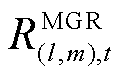 为匹配毛收益(Matching Gross Revenue, MGR);
为匹配毛收益(Matching Gross Revenue, MGR);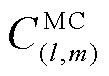 为匹配成本(Matching Costs, MC)。即当
为匹配成本(Matching Costs, MC)。即当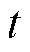 时刻编号为l的ER和第m个FC二者间存在匹配边时,
时刻编号为l的ER和第m个FC二者间存在匹配边时,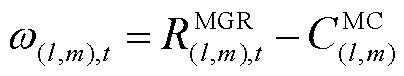 。其中,匹配毛收益
。其中,匹配毛收益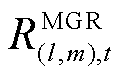 为按照此匹配方式,编号为l的ER修复第m个FC能够减少的负荷损失,其计算式为
为按照此匹配方式,编号为l的ER修复第m个FC能够减少的负荷损失,其计算式为
其中
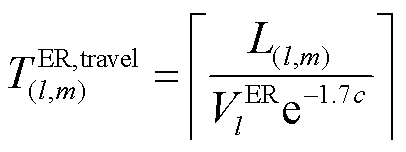 (8)
(8)
式中,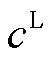 为单位负荷的损失成本;
为单位负荷的损失成本;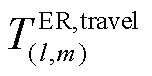 和
和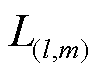 分别为编号为l的ER前往第m个FC最短路径的用时和距离;
分别为编号为l的ER前往第m个FC最短路径的用时和距离; 为向上取整;
为向上取整;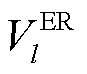 为编号为l的ER的移动速度;c为道路拥塞程度,可以表示灾害对交通网络的影响[43];Dijkstra(×)为最小路径算法;A为交通网络的邻接矩阵,本文以HDN变电站节点为交通网络的节点,HDN线路为交通网络的边,线路长度即为边长。
为编号为l的ER的移动速度;c为道路拥塞程度,可以表示灾害对交通网络的影响[43];Dijkstra(×)为最小路径算法;A为交通网络的邻接矩阵,本文以HDN变电站节点为交通网络的节点,HDN线路为交通网络的边,线路长度即为边长。
匹配成本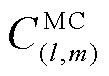 为按照此匹配方式,编号为l的ER修复第m个FC需要消耗的经济成本,其计算式为
为按照此匹配方式,编号为l的ER修复第m个FC需要消耗的经济成本,其计算式为
式中,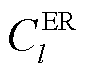 为消耗l号ER的成本;
为消耗l号ER的成本;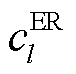 为调度l号ER单位距离的成本。
为调度l号ER单位距离的成本。
2.2 应急资源与故障元件的最优匹配方法
在生成ER和FC间的赋权二分图后,需要在短时间内快速找到二者间的最优匹配。
2.2.1 最优匹配收益模型
ER和FC间的最优匹配即为能够找到一种匹配方式,使得系统的总体净收益(Matching Net Revenue, MNR)最大,即寻找最大权完美匹配。在附图1c中,此时匹配边集合BME={(1,1), (2,2),(3,4),(4,3)},对应总净收益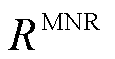 =ω(1,1)+ω(2,2)+ω(3,4)+ω(4,3)。该目标对应的数学模型为
=ω(1,1)+ω(2,2)+ω(3,4)+ω(4,3)。该目标对应的数学模型为
式中,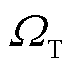 为时间集合;
为时间集合;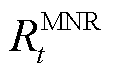 为t时刻ER与FC最优匹配对应的总净收益。
为t时刻ER与FC最优匹配对应的总净收益。
2.2.2 模型求解
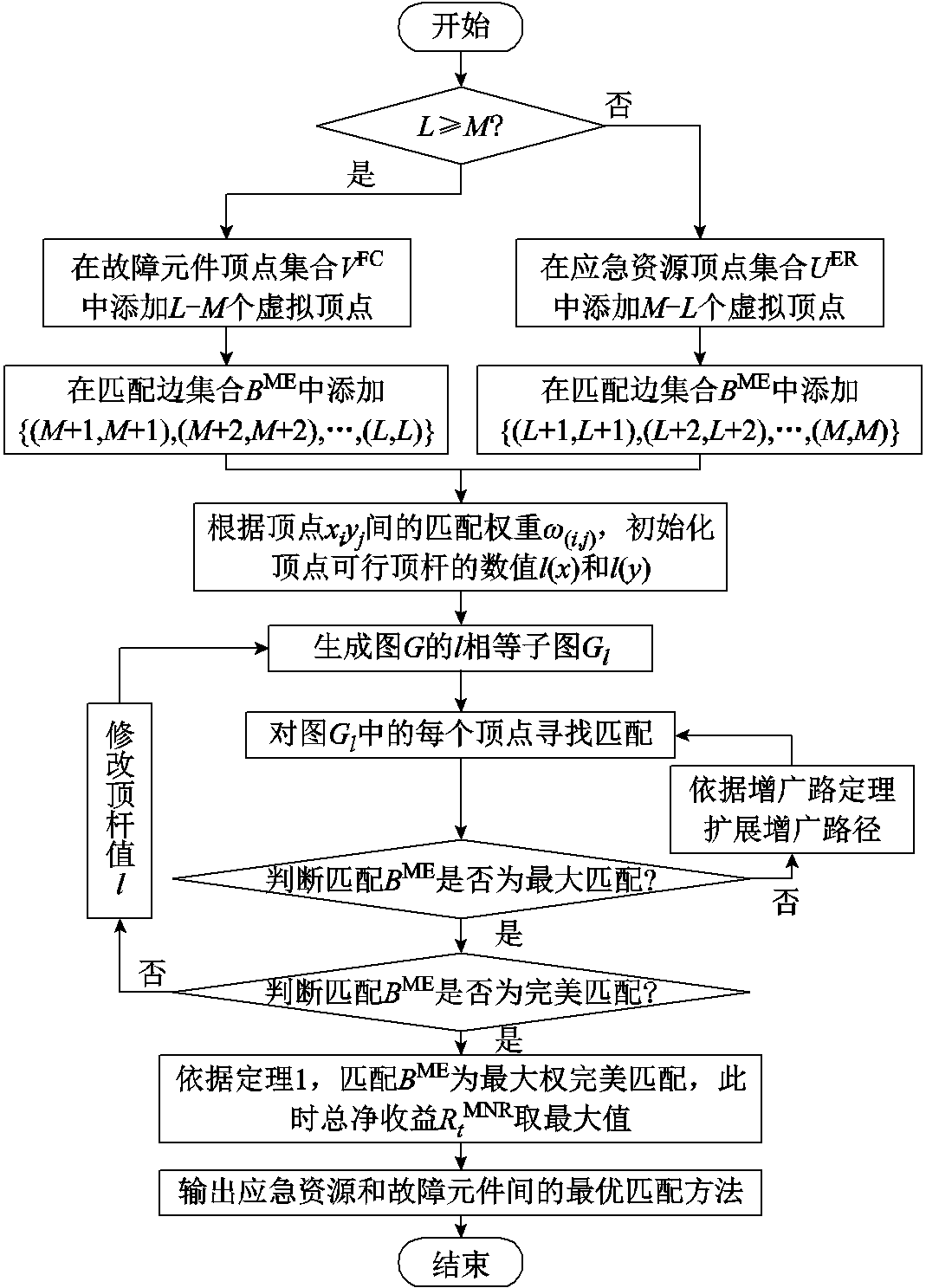
基于补点法的库恩-曼克尔斯(Kuhn-Munkres, KM)算法求解应急资源和故障元件间的最优匹配方法的具体流程如图3所示[39]。该方法首先通过添加|L-M|个虚拟顶点,将ER和FC间的赋权二分图转换为赋权完全二分图,从而解决匹配异常的问题,如图2b所示;其次在设置初始匹配路径的基础上,通过扩展增广路径和修改顶杆值的交替迭代,获取ER和FC的最大权匹配对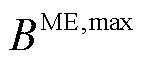 。
。
3 多电压等级电网协同分布式恢复方法
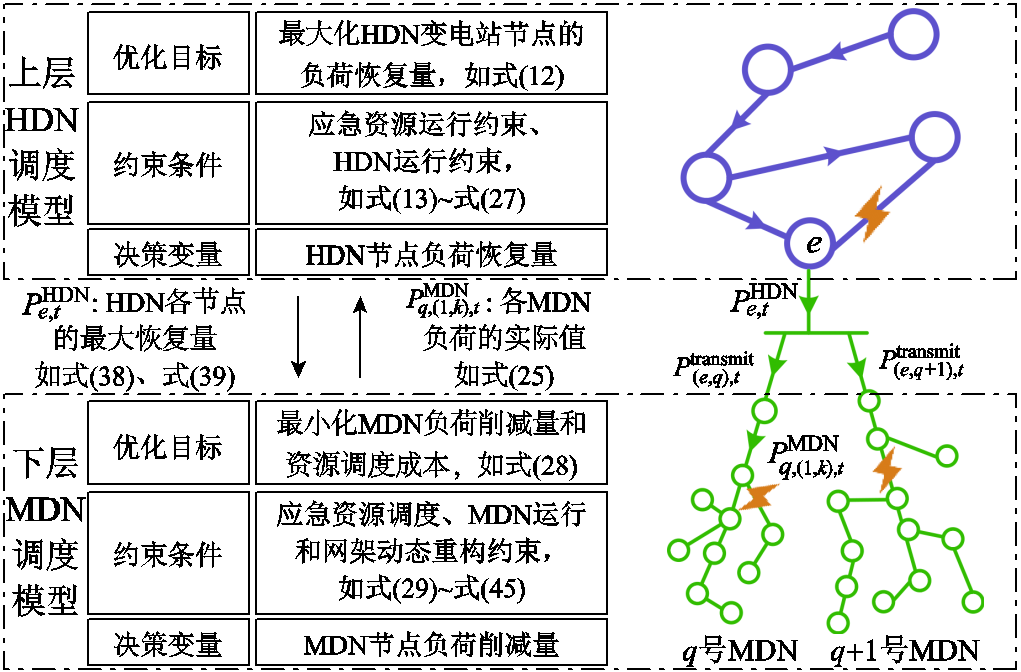
在制定ER和FC的最大权匹配对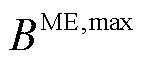 后,UPN在根据匹配对中最优匹配关系执行当前时间步长内故障元件抢修计划的同时,制定各电压等级电网的最优负荷恢复策略。针对1.2.2节中叙述的多电压等级电网间协同恢复中存在的问题,采用双层分布式优化模型对多电压等级电网灾后恢复问题进行建模,模型框架如图4所示。
后,UPN在根据匹配对中最优匹配关系执行当前时间步长内故障元件抢修计划的同时,制定各电压等级电网的最优负荷恢复策略。针对1.2.2节中叙述的多电压等级电网间协同恢复中存在的问题,采用双层分布式优化模型对多电压等级电网灾后恢复问题进行建模,模型框架如图4所示。
上层模型是HDN根据当前网架结构,通过优化线路开关状态和潮流分布,确定各变电站节点负荷的最大恢复量,并传递给MDN作为其恢复过程的上限边界值;下层模型是将每一个HDN变电站节点连接的所有MDN视为一个集团,分别建立以失负荷最小为目标,以应急资源调度、系统运行和网架动态重构为约束条件的优化模型,并在分布式开展灾后故障抢修与负荷恢复工作后,将满足边界条件的负荷实际值传递给高压配电网作为其恢复过程的上限边界值,从而能够达到多电压等级电网协同调度的目的。
3.1 上层:高压配电网调度模型
3.1.1 目标函数
HDN恢复过程的目标是最大化变电站节点的负荷恢复量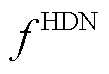 ,表示为
,表示为
式中,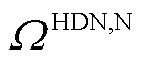 为HDN的变电站节点集合;
为HDN的变电站节点集合;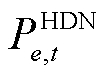 为
为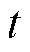 时刻HDN节点
时刻HDN节点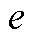 的负荷有功功率的实际值。在每次迭代过程中,该变量的优化结果传递至下层,作为边界条件约束MDN负荷实际大小的上限值,详见后文式(38)和式(39)。
的负荷有功功率的实际值。在每次迭代过程中,该变量的优化结果传递至下层,作为边界条件约束MDN负荷实际大小的上限值,详见后文式(38)和式(39)。
3.1.2 约束条件
1)应急资源运行约束
对于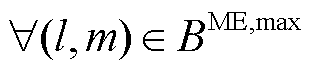 ,
,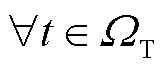 ,
,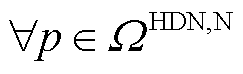 ,
,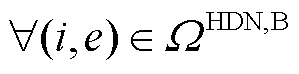 (
(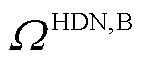 为HDN线路集合),HDN的ER运行约束为
为HDN线路集合),HDN的ER运行约束为
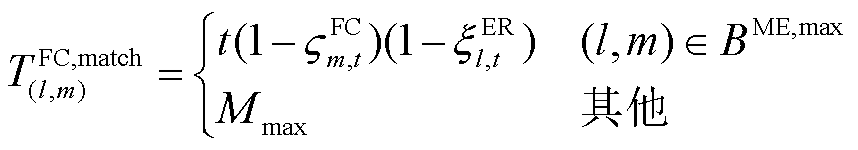 (14)
(14)
 (15)
(15)
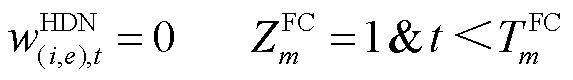 (17)
(17)
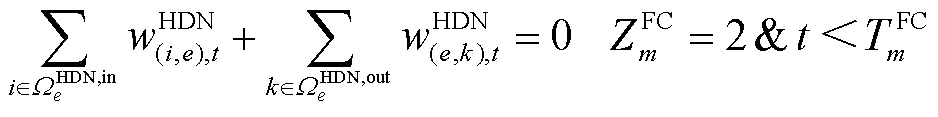 (18)
(18)
式中,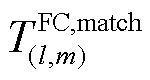 为第m个FC与编号为l的ER最优匹配所需的时长;
为第m个FC与编号为l的ER最优匹配所需的时长;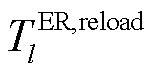 为应急资源l在抢修完某一故障后,返回仓库补充物资所需的时间;
为应急资源l在抢修完某一故障后,返回仓库补充物资所需的时间;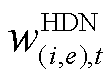 为HDN线路
为HDN线路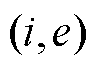 在
在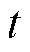 时刻的开关状态,若线路
时刻的开关状态,若线路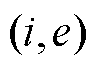 在
在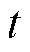 时刻正常运行,则
时刻正常运行,则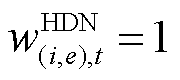 ,否则
,否则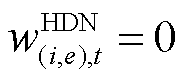 ;
;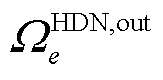 和
和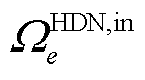 分别为HDN节点
分别为HDN节点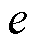 下游、上游节点集合。
下游、上游节点集合。
式(13)为FC的修复总时长,其包含故障探明时长、资源分配时长、资源行驶时长和故障抢修时长四部分,如图5所示;式(14)代表当t时刻FC与ER为最优匹配,即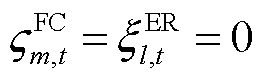 时,等待资源分配时长为t,否则
时,等待资源分配时长为t,否则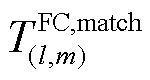 取一极大值
取一极大值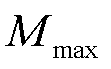 ;式(15)和式(16)表示FC与ER为最优匹配后的相应时段内,二者的分配状态取1;式(17)表示当FC为HDN线路
;式(15)和式(16)表示FC与ER为最优匹配后的相应时段内,二者的分配状态取1;式(17)表示当FC为HDN线路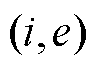 断线时,线路的开关状态受限于其修复状态;式(18)代表当FC为HDN杆塔
断线时,线路的开关状态受限于其修复状态;式(18)代表当FC为HDN杆塔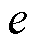 倒塌时,对应节点相连所有线路开关均受限于杆塔
倒塌时,对应节点相连所有线路开关均受限于杆塔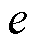 的修复状态;式(19)代表当FC为HDN变电站
的修复状态;式(19)代表当FC为HDN变电站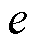 损毁时,对应节点相连的高压线路正常运行,但相连的下游负荷受限于变电站e的修复状态:当元件未修复时,下游负荷功率强制取0。
损毁时,对应节点相连的高压线路正常运行,但相连的下游负荷受限于变电站e的修复状态:当元件未修复时,下游负荷功率强制取0。
2)系统运行约束
对于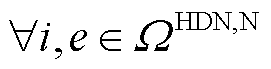 ,
,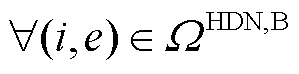 ,
,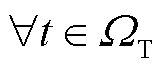 ,系统运行约束如下所示。
,系统运行约束如下所示。
与HTN类似,HDN线路常采用的LGJ-240导线型号满足电抗远大于电阻,可采用直流潮流方程描述系统潮流,表示为
式中,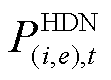 为HDN线路
为HDN线路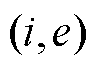 在
在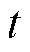 时刻的有功潮流;
时刻的有功潮流;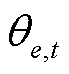 为HDN节点
为HDN节点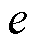 在
在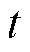 时刻的电压相位;
时刻的电压相位;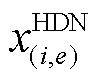 为HDN线路
为HDN线路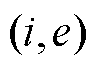 的电抗。
的电抗。
线路容量约束为
式中,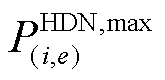 为HDN线路
为HDN线路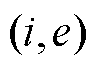 有功潮流的最大值。
有功潮流的最大值。
节点有功功率平衡约束为
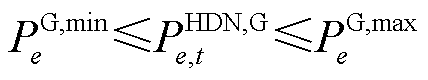 (23)
(23)
式中,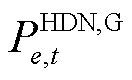 为
为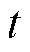 时刻外部电网或火电机组向节点
时刻外部电网或火电机组向节点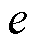 的注入功率;
的注入功率;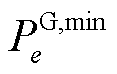 和
和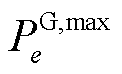 分别为外部电网或火电机组向节点
分别为外部电网或火电机组向节点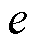 注入功率的最小值和最大值。
注入功率的最小值和最大值。
负荷削减约束为
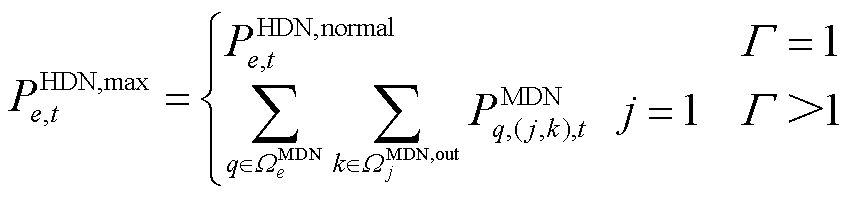 (25)
(25)
式中,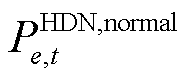 为正常情况下
为正常情况下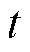 时刻HDN节点
时刻HDN节点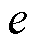 的负荷有功功率的预测值;
的负荷有功功率的预测值;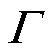 为迭代次数;
为迭代次数;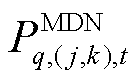 为第q个MDN的线路
为第q个MDN的线路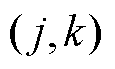 在
在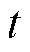 时刻的有功潮流;
时刻的有功潮流;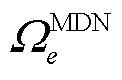 为接入变电站节点
为接入变电站节点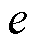 的所有MDN的集合;
的所有MDN的集合;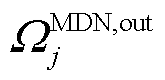 为MDN节点
为MDN节点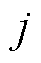 下游节点集合。约束式(25)表示当双层优化过程为第一次迭代时,由于HDN调度过程未知MDN负荷的实际情况,此时令HDN节点负荷有功功率的最大值
下游节点集合。约束式(25)表示当双层优化过程为第一次迭代时,由于HDN调度过程未知MDN负荷的实际情况,此时令HDN节点负荷有功功率的最大值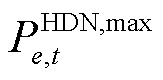 等于正常情况的预测值
等于正常情况的预测值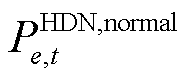 ;当双层优化过程开始第二次迭代之后,此时HDN节点
;当双层优化过程开始第二次迭代之后,此时HDN节点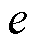 负荷有功功率的最大值应等于节点
负荷有功功率的最大值应等于节点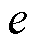 与MDN集团相连联络线的总功率之和。
与MDN集团相连联络线的总功率之和。
节点电压相位约束为
式中,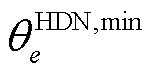 和
和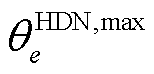 分别为HDN节点
分别为HDN节点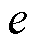 电压相位的最小值和最大值。
电压相位的最小值和最大值。
开环运行约束为
式中,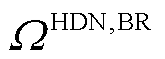 和
和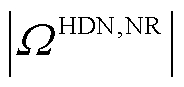 分别为HDN中构成闭环的线路集合和节点数量。约束式(27)表示HDN中闭环设计的线路,运行时应保持开环结构。
分别为HDN中构成闭环的线路集合和节点数量。约束式(27)表示HDN中闭环设计的线路,运行时应保持开环结构。
3.2 下层:中压配电网调度模型
在下层模型中,将每一个HDN变电站节点连接的所有MDN视为一个集团(共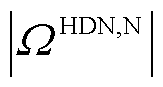 个集团),由于各集团内部的调度模型均相同,本节以接入HDN中
个集团),由于各集团内部的调度模型均相同,本节以接入HDN中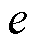 号变电站的MDN为例,建立相应模型。
号变电站的MDN为例,建立相应模型。
3.2.1 目标函数
各MDN集团应急恢复目标为最小化负荷损失,以接入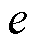 号变电站的MDN集团为例,其相应目标函数
号变电站的MDN集团为例,其相应目标函数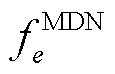 的表达式为
的表达式为
式中,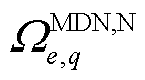 为接入变电站节点
为接入变电站节点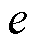 的第
的第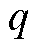 个MDN的节点集合;
个MDN的节点集合;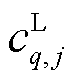 为第
为第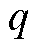 个MDN节点
个MDN节点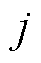 的负荷的单位削减成本,本文将负荷划分为工商业负荷和居民负荷[26];
的负荷的单位削减成本,本文将负荷划分为工商业负荷和居民负荷[26];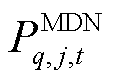 和
和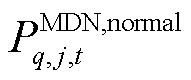 分别为
分别为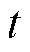 时刻第
时刻第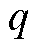 个MDN节点
个MDN节点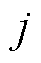 的负荷有功功率的实际值和正常情况下的预测值。
的负荷有功功率的实际值和正常情况下的预测值。
3.2.2 约束条件
1)应急资源调度约束
MDN的ER运行约束与HDN类似,包括式(13)~式(16)和式(29)~式(31),各约束含义此处不再赘述。对于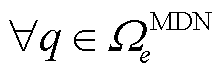 ,
,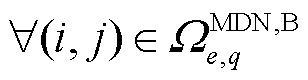 ,
,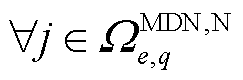 ,
,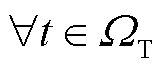 ,有
,有
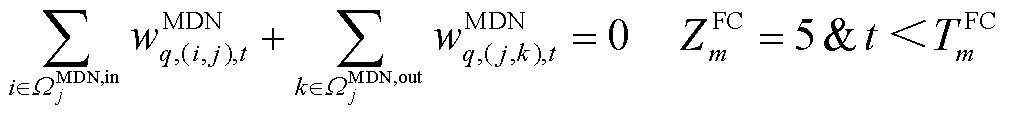 (30)
(30)
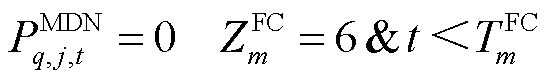 (31)
(31)
式中,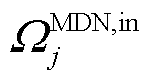 为MDN节点
为MDN节点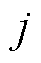 上游节点集合;
上游节点集合;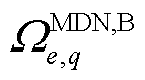 为接入变电站
为接入变电站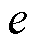 的第q个MDN的线路集合;
的第q个MDN的线路集合;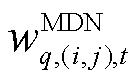 为第
为第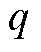 个MDN线路
个MDN线路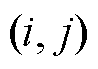 在
在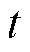 时刻的开关状态。
时刻的开关状态。
2)系统运行约束
对于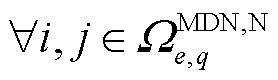 ,
,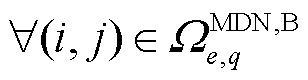 ,
,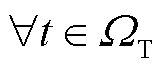 ,
,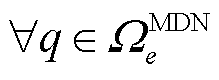 ,MDN系统运行方程包含节点有功、无功功率平衡约束,分别表示为
,MDN系统运行方程包含节点有功、无功功率平衡约束,分别表示为
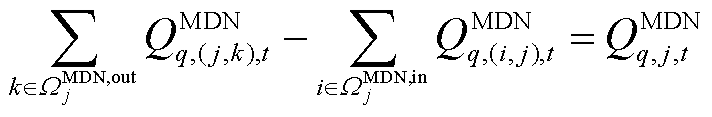 (33)
(33)
式中,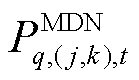 和
和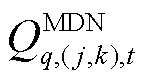 为分别为第
为分别为第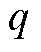 个MDN线路
个MDN线路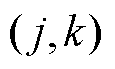 在
在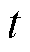 时刻的有功潮流和无功潮流,在每次迭代过程中,变量
时刻的有功潮流和无功潮流,在每次迭代过程中,变量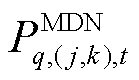 的优化结果传递至上层,作为边界条件约束HDN负荷恢复量的上限值,详见式(25);
的优化结果传递至上层,作为边界条件约束HDN负荷恢复量的上限值,详见式(25);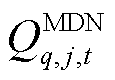 为
为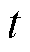 时刻第
时刻第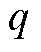 个MDN节点
个MDN节点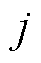 的负荷无功功率的实际值。
的负荷无功功率的实际值。
节点功率削减约束为
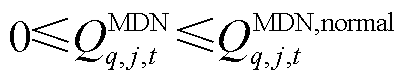 (35)
(35)
式中,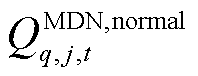 为t时刻第q个MDN节点j的负荷无功功率在正常情况下的预测值。
为t时刻第q个MDN节点j的负荷无功功率在正常情况下的预测值。
采用线性Distflow模型描述线路潮流约束,表示为
式中,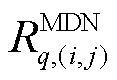 、
、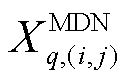 分别为第
分别为第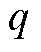 个MDN线路
个MDN线路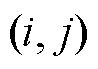 的电阻、电抗值;
的电阻、电抗值;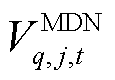 为
为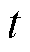 时刻第
时刻第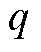 个MDN节点
个MDN节点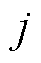 的电压。
的电压。
节点电压约束为
式中,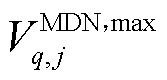 和
和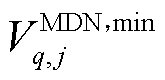 分别为第
分别为第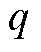 个MDN节点
个MDN节点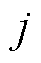 电压的最大值和最小值。
电压的最大值和最小值。
MDN中首节点向下输送的电量受限于上游HDN的注入功率,可表示为
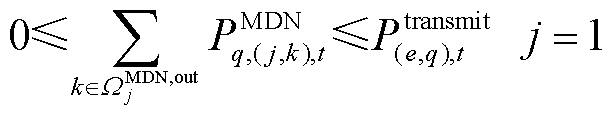 (39)
(39)
式中,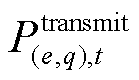 为
为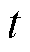 时刻HDN节点
时刻HDN节点 向第
向第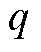 个MDN注入的有功功率。
个MDN注入的有功功率。
线性化后的线路容量约束为
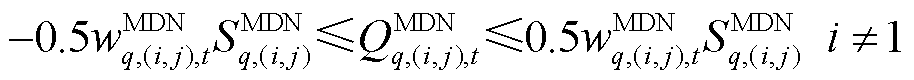 (41)
(41)
式中,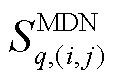 为第
为第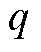 个MDN线路
个MDN线路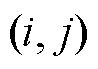 的容量。
的容量。
3)网架动态重构约束
采用单一商品流描述MDN网架动态重构约束,对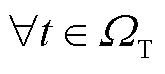 ,
,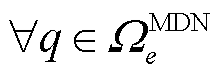 ,有
,有
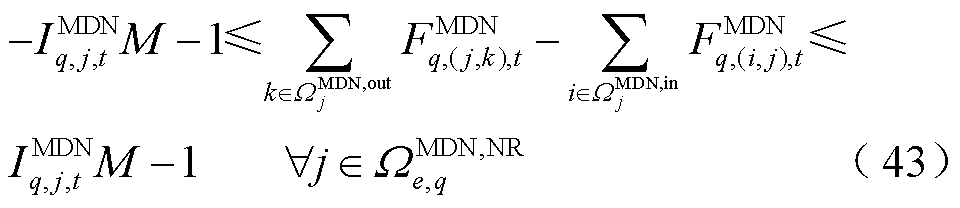
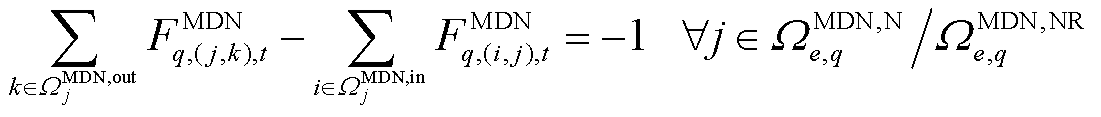 (44)
(44)
式中,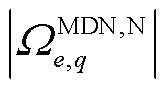 为接入变电站节点e的第q个MDN的节点个数;
为接入变电站节点e的第q个MDN的节点个数;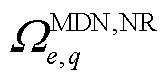 为接入变电站节点e的第q个MDN的潜在根节点集合,包含首节点和故障线路的首末节点;
为接入变电站节点e的第q个MDN的潜在根节点集合,包含首节点和故障线路的首末节点;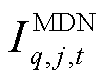 为判断第q个MDN的节点
为判断第q个MDN的节点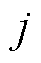 能否作为某一孤岛的根节点的0-1变量,当节点
能否作为某一孤岛的根节点的0-1变量,当节点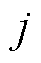 能作为根节点时,
能作为根节点时,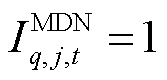 ,否则
,否则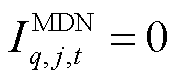 ;
;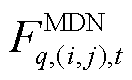 为第q个MDN线路
为第q个MDN线路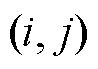 在
在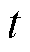 时刻的虚拟潮流。
时刻的虚拟潮流。
3.3 双层优化模型求解算法
本文建立的双层优化模型的求解算法流程如图6所示。首先,在上层优化模型的求解过程中,HDN仅能根据自身内部的网架结构、机组出力、故障元件等信息,决策各HDN变电站节点负荷的最大恢复量,并传递给下层作为MDN恢复过程的上限边界值;其次,在下层优化模型的求解过程中,分别针对每一个HDN变电站所连的MDN集团,在相连联络线总功率之和应不大于上游变电站恢复量的约束条件下,根据自身内部的网架结构、故障元件、重要负荷等信息,制定最优负荷恢复策略,并将满足边界条件的负荷实际值传递至上层;之后,HDN依据该负荷实际值作为恢复过程的边界上限,重复上述流程,直至上层求解的HDN节点负荷恢复量等于下层求解的相连MDN集团的负荷实际值。
4 求解流程
本文整体求解流程如图7所示。具体地,首先基于收集到的ER和FC的实时信息,生成表示二者间潜在匹配关系的赋权二分图;其次,以匹配净收益最大为目标函数,采用改进后的KM算法寻找ER和FC间的最优匹配方式;最后,建立多电压等级电网协同分布式调度的双层优化模型,求解各电网的最优负荷恢复策略。同时,在每个时间步长内,根据城市电网中新探明的FC和ER的信息更新二分图,重新寻找最优匹配方式,并制定负荷恢复策略,直至所有FC均抢修完毕。
5 仿真算例
本文构建的混合整数线性规划问题具体在Matlab R2021a中建模并通过YALMIP-GUROBI进行求解,仿真环境为Intel(R) Core(TM) i7-9700 CPU @ 2.20 GHz,16 GB内存。
5.1 仿真参数
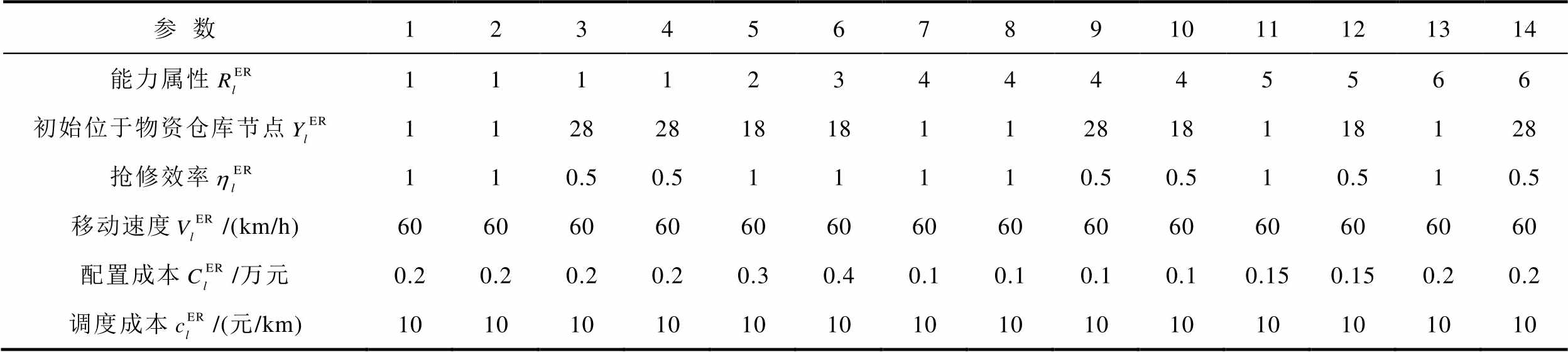
本文采用中国南方一个常住人口为160万的实际城市案例进行算例仿真分析,该城市电力系统网架结构如图8所示。UPN峰值负荷为1 305 MW+ j1 044 Mvar,其中HTN含8个变电站节点,各节点均与火力发电厂相连接,各火电厂的最大出力依次为150、150、150、150、150、150、500、200 MW;HDN含29个变电站节点,各变电站节点均连接三个不同结构的MDN,共计57个MDN。以变电站节点5为例,如图8右下角所示,该变电站共接有三条配电馈线:MDN1的峰值负荷为15 MW+j6 Mvar;MDN2的峰值负荷为12 MW+j4.8 Mvar; MDN3的峰值负荷为18 MW+j7.2 Mvar。工商业负荷和居民负荷的单位削减成本分别为1.5和0.9元/(kW·h)。应急资源参数信息见表4。
假设极端事件发生时刻为t=10 h,导致HDN中的6个元件和MDN中的18个元件故障,故障元件详细信息见表5。
表4 场景1中应急资源的参数信息
Tab.4 Parameters of ERs in Scenario 1
参数1234567891011121314 能力属性11112344445566 初始位于物资仓库节点1128281818112818118128 抢修效率110.50.511110.50.510.510.5 移动速度/(km/h)6060606060606060606060606060 配置成本/万元0.20.20.20.20.30.40.10.10.10.10.150.150.20.2 调度成本/(元/km)1010101010101010101010101010
表5 场景1中故障元件的参数信息
Tab.5 Parameters of FCs in Scenario 1

变电站故障元件编号故障类型故障所在HDN节点位置故障探明时间抢修时间 HDN3,4,29,35,13,201,1,1,1,2,34,5,30,25,13,200,0,0,0,0,04,4,4,4,4,6 MDN12,4,7,8,11,144,4,4,4,5,65,8,12,17,22,290,0,0,0,1,22,2,2,2,2,2 MDN210,2,7,8,4,36,5,4,6,4,45,8,12,17,22,292,0,0,1,0,02,2,2,2,2,2 MDN314,11,5,6,8,105,6,4,5,4,45,8,12,17,22,292,1,0,0,0,12,2,2,2,2,2
5.2 仿真结果及分析
采用本文所提方法对上述场景进行仿真,制定的灾后应急恢复计划共计12 h,系统工商业负荷和居民负荷的总削减量分别为1 020.33 MW和381.20 MW。在双层优化模型的求解迭代过程中,各时间断面内的求解均在两次以内收敛,求解总时间为131.49 s。
5.2.1 二分图最优匹配结果
将14个应急资源和24个故障元件按表4和表5中出现顺序编号,分别采用集合ΩX={x1, x2,…, x14}和ΩY={y1, y2,…, y24}表示后,ER与FC间最优匹配的二分图结果如图9所示,由于篇幅限制,仅展示部分典型时刻。图9中共包含四类顶点:顶点Ⅰ,该时刻最优匹配上的顶点;顶点Ⅱ,在前序时刻已经最优匹配上的顶点;顶点Ⅲ,还未最优匹配的顶点;顶点Ⅳ,保证图为赋权完全二分图而添加的虚拟顶点。例如,图9d中绿色阴影部分,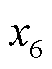 和
和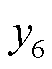 表示ER6与FC6(即HDN的20号故障元件)在t=10 h时已完成最优匹配,并需7 h完成抢修;
表示ER6与FC6(即HDN的20号故障元件)在t=10 h时已完成最优匹配,并需7 h完成抢修;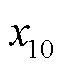 和
和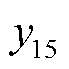 表示ER10与FC15(即MDN2中的7号故障元件)在t=16 h时完成最优匹配,并需3 h完成抢修。
表示ER10与FC15(即MDN2中的7号故障元件)在t=16 h时完成最优匹配,并需3 h完成抢修。
5.2.2 应急资源时空调度结果
位于三个物资仓库的ER的时空移动路径分别如图10a~图10c所示。每一次最优匹配过程包含五类时间,如图10a所示,以ER11与FC19(即MDN3中的14号故障元件)为例简要阐明一次完整的匹配过程:在抢修工作开始的2 h后,FC19被探明(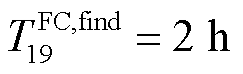 );但由于此时无空闲状态的MDN杆塔抢修小队, FC19需再等待2 h方可与ER11匹配(
);但由于此时无空闲状态的MDN杆塔抢修小队, FC19需再等待2 h方可与ER11匹配(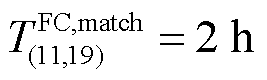 );之后,ER11分别经历1 h前往FC19(
);之后,ER11分别经历1 h前往FC19(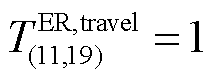 h)和2 h抢修FC19(
h)和2 h抢修FC19(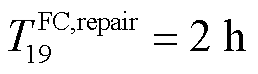 ),于t=17 h完成抢修任务后,花费1 h返回仓库补充物资(
),于t=17 h完成抢修任务后,花费1 h返回仓库补充物资(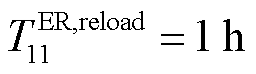 )。
)。
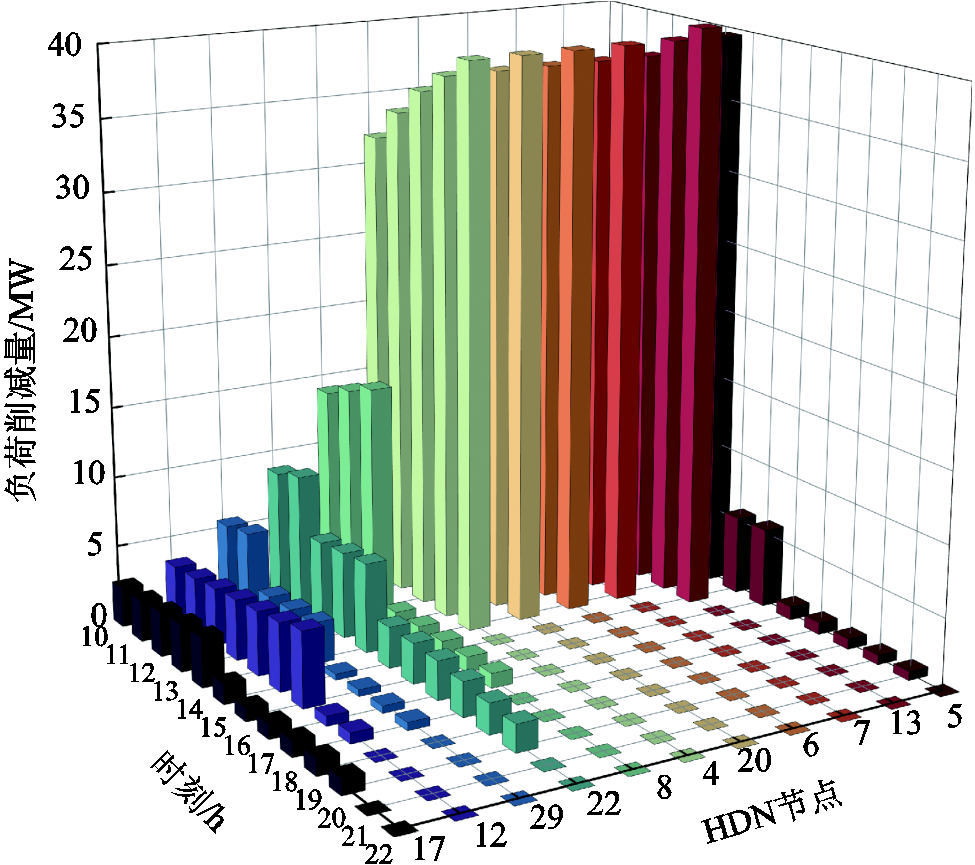
5.2.3 负荷恢复结果
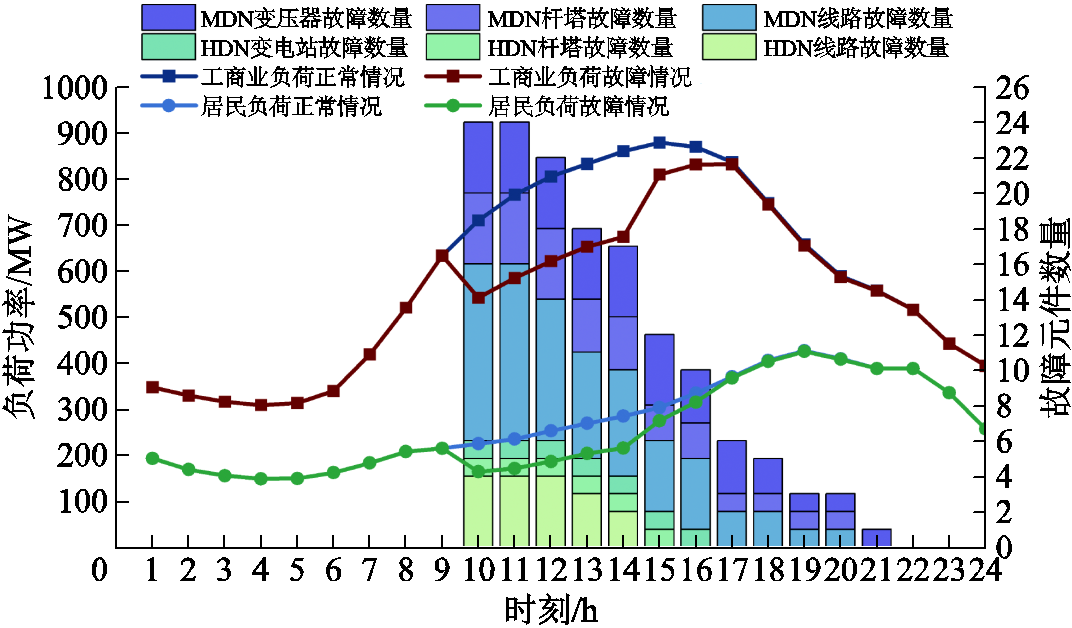
负荷恢复和故障元件抢修的发展过程如图11所示,各HDN变电站节点的负荷削减情况如图12所示,图中仅展示了有负荷削减的变电站节点。观察抢修进程的前几个时间步长(t=10~14 h)可以发现,虽然部分MDN故障元件已被修复,但整个系统的负荷削减量仍然呈现逐渐增加的趋势,这一方面是由于该时段为用电高峰期,负荷总量逐步上升;另一方面,部分优先抢修的MDN故障元件的上游HDN变电站为失电状态,例如,如图10a所示,FC7(MDN1中的2号故障元件)在t=13 h时刻已修复,但受FC2(HDN中的4号故障元件)的影响,其上游HDN5变电站在t=15 h时刻方可恢复供电,导致该时间段内出现了“无效抢修”的情况,即HDN5变电站所连的MDN1并未因首端故障线路7的修复而及时复电。
5.3 对比分析
为验证本文所提方法在协调调度多电压等级电网的灾后恢复时所具有的优势,本节设定了FC数量远大于ER数量的场景2,ER和FC的参数分别见表6和表7,极端事件发生在t=10 h。此外,如表8所示,本节采用现有灾后恢复常用的两种优化方法:集中式优化(策略2[29])、滚动式优化(策略3[28]),并与本文所提方法(策略1)进行对比分析,各类策略的仿真结果见表9。
表6 场景2中应急资源的参数信息
Tab.6 Parameters of ERs in Scenario 2
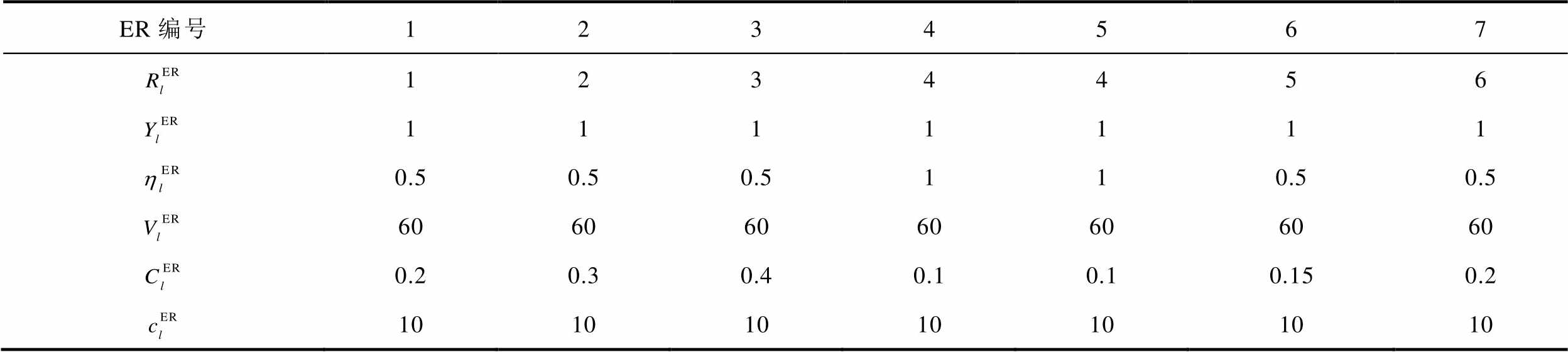
ER编号1234567 1234456 1111111 0.50.50.5110.50.5 60606060606060 0.20.30.40.10.10.150.2 10101010101010
表7 场景2中故障元件的参数信息
Tab.7 Parameters of FCs in Scenario 2

变电站FC编号 HDN3,7,2,51,1,2,34,8,2,50,0,0,04,4,4,6 MDN12,4,5,94,4,5,64,8,2,60,0,1,22,2,2,2 MDN28,9,2,75,6,4,44,8,2,62,0,1,02,2,2,2 MDN39,5,2,66,5,4,44,8,2,62,1,1,02,2,2,2
表8 各类优化策略
Tab.8 Different types of optimization strategies

策略编号求解时间步长故障抢修和负荷恢复 单步长变步长统一求解分立求解 1ÖÖ 2ÖÖ 3ÖÖ
5.3.1 策略1与策略2对比分析
由于策略2在每次决策时考虑了HDN和MDN故障抢修过程的耦合关系,统一制定各电网的故障抢修和负荷恢复计划,能够有效地避免上述出现的“无效抢修”。例如,在场景1中,FC2修复前,策略2会派遣ER8优先抢修位于HDN12变电站节点的FC9,这是由于该故障距离仓库较近且其上游变电站始终为正常状态,故障线路9的修复能够使得MDN1的节点10负荷立即复电;在场景2中,t=10~13 h时段内,由于FC5和FC6的上游HDN4和HDN8节点为失电状态,策略2也会选择优先抢修重要程度较低但上游MDN6节点正常的FC12和FC16。
表9 各类优化策略的仿真结果
Tab.9 Simulation results for each optimization strategy

策略场景1场景2 负荷削减量/MW求解时间/s典型FC(修复时刻/h)负荷总削减量/MW求解时间/s典型FC(修复时刻/h) 11 401.53131.495号(16);7号(13);9号(17)933.4885.771号(17);2号(13);11号(17);15号(17);5号(13);6号(13) 21 379.415 007.875号(16);7号(17);9号(13)904.824 213.201号(13);2号(13);11号(17);15号(17);12号(13);16号(13) 31 398.141 335.195号(16);7号(13);9号(17)931.72868.831号(17);2号(13);11号(17);15号(17);5号(13);6号(13)
但是,由于“无效抢修”出现的概率较小且单个MDN的负荷量较少,导致在两种场景下,策略2较策略1仅分别减小了22.12 MW和28.66 MW的总负荷削减量;此外,策略2由于在每次决策时,均需要将体现各个ER和FC匹配过程的大量二进制变量融入整体模型中求解[29],计算规模大幅扩大,导致求解时间为策略1的近40倍。由于灾后恢复过程相当看重调度计划的制定时间,因此,本文认为用相对较低的精确性换取高效的求解效率是可取的。
5.3.2 策略1与策略3对比分析
策略3借用了模型预测控制方法的思想,能够根据更新后的信息制定当前时步下“全局最优”的调度计划。但实际上,受探明FC迟滞性的影响,策略3以当前的局部信息制定全局计划的意义并不大。与策略1类似地,在场景2中,由于初始时刻FC数量远大于ER数量且大部分较为重要的FC未探明,策略2在最初决策时也会将ER优先派遣至已探明的FC,导致当较为重要的FC探明时,需要等待较长时间才有ER可供调度。此外,策略3的多时步求解也使得所需的计算时间大幅增加,约为策略1的10倍。
5.4 灵敏性分析
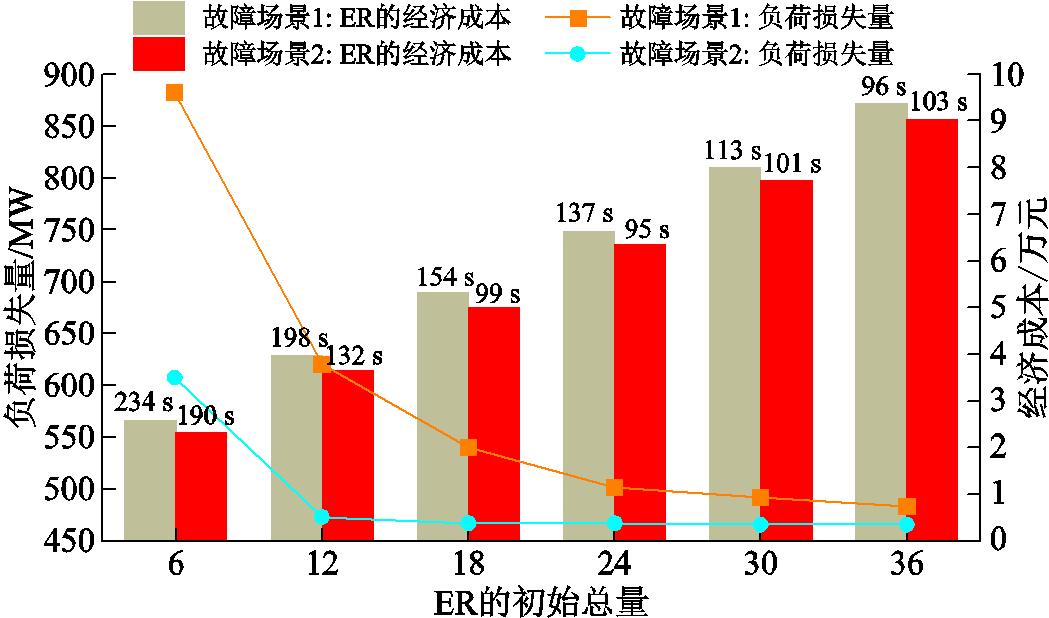
为确定本文方法对应急资源初始配置规模的灵敏性情况,本节按照六种ER的数量比例为1:1:1:1:1:1,设计ER初始总量分别为6、12、18、24、30、36,ER抢修效率均为0.5,初始位置均匀分布在1、18和28三个仓库,极端事件发生在t=1 h,在故障场景1和2下的测试结果如图13所示。其中,各测试场景下的求解时间也表示在图中。
观察图13可以发现,一方面,本文所提方法在各测试场景下均能保持良好的收敛性和计算效率,求解时间均在数分钟之内;另一方面,随着ER初
始配置总量增加,两种故障场景下均呈现出负荷损失量逐步降低且降低幅度逐步减缓,以及配置和调度ER的经济成本逐步增加且增加幅度保持一定的变化趋势。这是由于当ER数量较少时,大量较为重要的FC在抢修初期无法与ER匹配,此时即使额外增加较少数量的ER也能大幅降低负荷损失量;但当ER数量增加至与FC数量持平甚至超过时,各个FC在第一轮匹配中基本均能与ER匹配,继续增加ER能为降低负荷损失起到的效果微乎其微,反而会由于配置ER的固定花费导致经济成本巨大。因此,如何在应急策略经济成本和负荷损失降低程度二者间的杠杆中找到最优的平衡点是很有必要的。
6 结论
本文建立了UPN灾后应急资源与故障元件间的集中匹配-分布调度模型,协同调度了UPN中各电压等级电网的各类型ER,实现了UPN的全域高效应急恢复。具体结论如下:
1)与现有集中式和滚动式调度策略相比,本文所提方法能够得到类似的优化调度结果,且算法具有较好的收敛性,验证了本文方法的有效性。
2)本文所提方法将ER和FC匹配过程独立求解,大幅降低了灾后故障抢修和负荷恢复模型的计算规模,在极端灾害发生后的较短时间内,能够快速高效地制定出较为精确的应急恢复计划。
3)不同类型和数量的ER在城市中预先配置的规模对UPN灾后负荷损失量和经济成本的影响是很大的。在未来研究中,应当进一步在灾前根据灾害的预测信息,研究不同极端灾害对UPN元件的影响机理,分析UPN易损元件的分布情况,制定更加经济、合理的资源预布局策略。
附 录
1. 赋权二分图的名词概念
设G=<V, E, W>是一个无向图,如果顶点集合V可分割为2个互不相交的子集X={x1, x2,…, xl}和Y={y1, y2,…, ym},且边集合E中任意边的两个顶点均分别位于集合X和Y中,此时图G=<X, Y, E, W>被称为赋权二分图[40],W为各条边的匹配权重矩阵。例如,边xi yj的权重值ω(i,j)=W(xi yj),如附图1a所示。当集合X与Y中的节点数目相等时,即有l=m,则为赋权完全二分图,如附图1b所示。
附图1 二分图举例
App.Fig.1 Example of the bipartite graph
在图G中,将两两没有公共顶点的边集合E称为匹配。在附图1b中,边集合E={x1y2}、{x2y3}、{x3y2}、{x1y2, x2y1}等均为图G2的匹配,将匹配边数最大的匹配称为最大匹配,例如边集合{x1y2, x2y1}为图G2的最大匹配。当边集合E包含图中的所有点时,如附图1c所示,匹配E={x1y1, x2y2, x3y4, x4y3}为图G3的完美匹配,并称权值和最大的完美匹配为最大权完美匹配。
2. 赋权二分图的相关定义与定理
定义1:对于赋权完全二分图G,定义各顶点的顶杆l,其满足对G中任意一条边xi yj,一定存在l(x)+l(y)≥ω(i,j)。
定义2:令El={xi yj| xi yjÎE(G), l(x)+l(y)=ω(i,j)},以El为边集的图Gl为图G的生成子图,并称Gl为l相等子图。
定理1:如果相等子图存在完美匹配,那么该完美匹配一定为最大权完美匹配。
参考文献
[1] 孙建平. 上海城市运行安全发展报告(2019-2020) [M]. 上海: 同济大学出版社, 2021.
[2] 何正友, 李波, 廖凯, 等. 新形态城市电网保护与控制关键技术[J]. 中国电机工程学报, 2020, 40(19): 6193-6207.
He Zhengyou, Li Bo, Liao Kai, et al. Key technologies for protection and control of novel urban power grids[J]. Proceedings of the CSEE, 2020, 40(19): 6193-6207.
[3] 何永秀, 朱茳, 罗涛, 等. 城市电网规划自然灾害风险评价研究[J]. 电工技术学报, 2011, 26(12): 205-210.
He Yongxiu, Zhu Jiang, Luo Tao, et al. Risk assessment of natural disaster in urban electric power network planning[J]. Transactions of China Electrotechnical Society, 2011, 26(12): 205-210.
[4] 杨海涛, 祝达康, 李晶, 等. 特大型城市电网大停电的机理和预防对策探讨[J]. 电力系统自动化, 2014, 38(6): 128-135.
Yang Haitao, Zhu Dakang, Li Jing, et al. A discussion on mechanism and countermeasures of blackouts in super megacity power networks[J]. Automation of Electric Power Systems, 2014, 38(6): 128-135.
[5] 周波涛, 钱进. IPCC AR6报告解读:极端天气气候事件变化[J]. 气候变化研究进展, 2021, 17(6): 713-718.
Zhou Botao, Qian Jin. Changes of weather and climate extremes in the IPCC AR6[J]. Climate Change Research, 2021, 17(6): 713-718.
[6] 孙为民, 孙华东, 何剑, 等. 面向严重自然灾害的电力系统韧性评估技术综述[J]. 电网技术, 2024, 48(1): 129-139.
Sun Weimin, Sun Huadong, He Jian, et al. Review of power system resilience assessment techniques for severe natural disasters[J]. Power System Technology, 2024, 48(1): 129-139.
[7] Tao Zhengru, Han Lu. Emergency response, influence and lessons in the 2021 compound disaster in Henan Province of China[J]. International Journal of Environmental Research and Public Health, 2022, 19(1): 488.
[8] 陶然, 赵冬梅, 徐辰宇, 等. 考虑电-气-热-交通相互依存的城市能源系统韧性评估与提升方法[J]. 电工技术学报, 2023, 38(22): 6133-6149.
Tao Ran, Zhao Dongmei, Xu Chenyu, et al. Resilience assessment and enhancement methods for urban energy system considering electricity-gas-heat-transport interdependency[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6133-6149.
[9] Shi Qingxin, Liu Wenxia, Zeng Bo, et al. Enhancing distribution system resilience against extreme weather events: concept review, algorithm summary, and future vision[J]. International Journal of Electrical Power & Energy Systems, 2022, 138: 107860.
[10] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429.
Xu Yin, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhancement[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[11] 王帆. 保定中心城区电网目标网架规划设计[D]. 北京: 华北电力大学, 2014.
Wang Fan. Baoding center city power grid planning and design objectives[D]. Beijing: North China Electric Power University, 2014.
[12] Gilstrap M, Amin S, DeCorla-Souza K. United States electricity industry primer[R/OL]. Washington D. C.: Office of Electricity Delivery and Energy Reliability, U.S. Department of Energy, 2015. https://www.energy. gov/sites/prod/files/2015/12/f28/united-states-electricity- industry-primer.pdf#page=13&zoom =100,93,172.
[13] Electricity Networks Strategy Group. Our electricity transmission network: a vision for 2020[R/OL]. London: Electricity Networks Strategy Group, 2012. https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/48275/4264-ensg-summary.pdf.
[14] 田野, 陈维江, 张薛鸿, 等. 日本配电网中性点接地方式选取原则及接地故障处理方法[J]. 供用电, 2017, 34(5): 14-20.
Tian Ye, Chen Weijiang, Zhang Xuehong, et al. Selection principle of neural grounding mode of distribution power network and its fault processing technology in Japan[J]. Distribution & Utilization, 2017, 34(5): 14-20.
[15] 彭冬, 吴俊玲, 梁才浩, 等. 城市电网电压序列优化配置[J]. 电网技术, 2010, 34(6): 113-118.
Peng Dong, Wu Junling, Liang Caihao, et al. Optimal configuration of voltage grades for urban distribution network[J]. Power System Technology, 2010, 34(6): 113-118.
[16] 周念成, 莫复雪, 肖舒严, 等. 计及多电压等级配电网拓扑约束的协调转供优化[J]. 中国电机工程学报, 2021, 41(9): 3106-3120.
Zhou Niancheng, Mo Fuxue, Xiao Shuyan, et al. Coordinated power transfer optimization of multi-voltage-level distribution network considering topology constraints[J]. Proceedings of the CSEE, 2021, 41(9): 3106-3120.
[17] Shi Qingxin, Li Fangxing, Olama M, et al. Network reconfiguration and distributed energy resource scheduling for improved distribution system resilience[J]. International Journal of Electrical Power & Energy Systems, 2021, 124: 106355.
[18] Liu Wenxia, Wang Yuehan, Shi Qingxin, et al. A multi-stage restoration strategy to enhance distributionsystem resilience with improved conditional generative adversarial nets[J/OL]. CSEE Journal of Power and Energy System, 2022: 1-12[2023-10-08]. doi:10. 17775/CSEEJPES.2021.09080.
[19] 陈厚合, 丛前, 姜涛, 等. 多能协同的配电网供电恢复策略[J]. 电工技术学报, 2022, 37(3): 610-622, 685.
Chen Houhe, Cong Qian, Jiang Tao, et al. Distribution systems restoration with multi-energy synergy[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 610-622, 685.
[20] 卢志刚, 李丹, 吕雪姣, 等. 含分布式电源的冰灾下配电网多故障抢修策略[J]. 电工技术学报, 2018, 33(2): 423-432.
Lu Zhigang, Li Dan, Lü Xuejiao, et al. Multiple faults repair strategy under ice storm for distribution network with distributed generators[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 423-432.
[21] 朱晓荣, 司羽. 考虑物理—信息—交通网耦合的配电网多时段动态供电恢复策略[J]. 电工技术学报, 2023, 38(12): 3306-3320.
Zhu Xiaorong, Si Yu. Multi-period dynamic power supply restoration strategy considering physical-cyber-traffic network coupling[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3306-3320.
[22] 王月汉, 刘文霞, 姚齐, 等. 面向配电网韧性提升的移动储能预布局与动态调度策略[J]. 电力系统自动化, 2022, 46(15): 37-45.
Wang Yuehan, Liu Wenxia, Yao Qi, et al. Pre-layout and dynamic scheduling strategy of mobile energy storage for resilience enhancement of distribution network[J]. Automation of Electric Power Systems, 2022, 46(15): 37-45.
[23] Ye Zhigang, Chen Chen, Chen Bo, et al. Resilient service restoration for unbalanced distribution systems with distributed energy resources by leveraging mobile generators[J]. IEEE Transactions on Industrial Informatics, 2021, 17(2): 1386-1396.
[24] 俞拙非, 刘菲, 刘瑞环, 等. 面向配电网弹性提升的源网荷灵活资源优化研究综述及展望[J]. 中国电力, 2022, 55(4): 132-144.
Yu Zhuofei, Liu Fei, Liu Ruihuan, et al. Resilience-oriented optimization of source-grid-load flexible resources in distribution systems: review and prospect[J]. Electric Power, 2022, 55(4): 132-144.
[25] 李娜. 基于鲁棒规划模型的电力应急物资库网络设计研究[D]. 北京: 华北电力大学, 2019.
Li Na. Research on network design of electric power emergency material warehouse based on robust programming model[D]. Beijing: North China Electric Power Unversity, 2019.
[26] Shi Qingxin, Li Fangxing, Dong Jin, et al. Co-optimization of repairs and dynamic network reconfiguration for improved distribution system resilience[J]. Applied Energy, 2022, 318: 119245.
[27] Sun Xiaotian, Xie Haipeng, Bie Zhaohong, et al. Restoration of high-renewable-penetrated distribution systems considering uncertain repair workloads[J/OL]. CSEE Journal of Power and Energy System, 2022: 1-12[2023-10-08]. doi: 10.17775/CSEEJPES.2021. 06500.
[28] Wan Haiyang, Liu Wenxia, Shi Qingxin, et al. Multi-time-step rolling optimization strategy for post-disaster emergency recovery in distribution system based on model predictive control[J/OL]. CSEE Journal of Power and Energy Systems, 2022: 1-11[2023-10-08]. doi: 10. 17775/CSEEJPES.2021.08050.
[29] 万海洋, 刘文霞, 石庆鑫, 等. 计及交通流量动态变化的配电网灾后修复多时间断面优化策略[J]. 电力系统自动化, 2022, 46(12): 119-129.
Wan Haiyang, Liu Wenxia, Shi Qingxin, et al. Multiple-time-section optimization strategy for post-disaster recovery of distribution network considering dynamic changes of traffic flow[J]. Automation of Electric Power Systems, 2022, 46(12): 119-129.
[30] Yang Lijun, Qin Ying. Research on rolling co-optimization of fault repair and service restoration in distribution network based on combined drive methodology[J]. Electric Power Systems Research, 2023, 220: 109373.
[31] Yao Shuhan, Wang Peng, Liu Xiaochuan, et al. Rolling optimization of mobile energy storage fleets for resilient service restoration[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1030-1043.
[32] 李长城, 和敬涵, 王颖, 等. 考虑分布式电源支撑作用的输配电系统协同恢复方法[J]. 电力自动化设备, 2022, 42(2): 112-119.
Li Changcheng, He Jinghan, Wang Ying, et al. Coordinated restoration of transmission and distribution systems considering DG support[J]. Electric Power Automation Equipment, 2022, 42(2): 112-119.
[33] 王炜歆, 王小君, 许寅, 等. 考虑输配协同的电网并行恢复分区及机组启动次序统一优化决策方法[J]. 中国电机工程学报, 2024, 44(3): 859-872.
Wang Weixin, Wang Xiaojun, Xu Yin, et al. A synthetic optimal decision-making method for parallel restoration sectionalizing and generator start-up sequence of power grids considering transmission and distribution system coordination[J]. Proceedings of the CSEE, 2024, 44(3): 859-872.
[34] Zhao Jin, Wang Hongtao, Liu Yutian, et al. Coordinated restoration of transmission and distribution system using decentralized scheme[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3428-3442.
[35] Wan Haiyang, Liu Wenxia, Zhang Shuai, et al. Pre-disaster and mid-disaster resilience improvement strategy of high proportion renewable energy system considering frequency stability[J]. International Journal of Electrical Power & Energy Systems, 2023, 151: 109135.
[36] Jiang Lizhou, Li Xin, Long Tao, et al. Resilient service restoration for distribution systems with mobile resources using Floyd-based network simplification method[J]. IET Generation, Transmission & Distribution, 2022, 16(3): 414-429.
[37] 胡振涛, 崔南方, 张艳, 等. 基于动态资源权重的多技能项目调度启发式算法[J]. 控制与决策, 2021, 36(10): 2553-2561.
Hu Zhentao, Cui Nanfang, Zhang Yan, et al. Dynamic resource priority-based heuristics for multi-skill resource constrained project scheduling problem[J]. Control and Decision, 2021, 36(10): 2553-2561.
[38] 魏恩伟, 李伟华, 张之涵, 等. 基于改进匈牙利算法的非侵入式负荷匹配方法[J]. 电测与仪表, 2019, 56(22): 58-64.
Wei Enwei, Li Weihua, Zhang Zhihan, et al. Non-intrusive load matching method based on improved Hungarian algorithm[J]. Electrical Measurement & Instrumentation, 2019, 56(22): 58-64.
[39] 韩晓阳, 孟相如, 康巧燕, 等. 基于二分图最优匹配的虚拟网络映射算法[J]. 系统工程与电子技术, 2019, 41(12): 2891-2898.
Han Xiaoyang, Meng Xiangru, Kang Qiaoyan, et al. Virtual network embedding algorithm based on bipartite graph optimal matching[J]. Systems Engineering and Electronics, 2019, 41(12): 2891-2898.
[40] West D B. Introduction to Graph Theory[M]. 2nd ed. Upper Saddle River: Prentice Hall, 2000.
[41] Asratian A S, Denley T M J, Häggkvist R. Bipartite Graphs and Their Applications[M]. Cambridge: Cambridge University Press, 1998.
[42] 杨丽君, 赵宇, 赵优, 等. 考虑交通路网应急电源车调度的有源配电网故障均衡恢复[J]. 电力系统自动化, 2021, 45(21): 170-180.
Yang Lijun, Zhao Yu, Zhao You, et al. Balanced fault recovery of active distribution network considering emergency power supply vehicle scheduling in traffic network[J]. Automation of Electric Power Systems, 2021, 45(21): 170-180.
[43] 赵瑾. 考虑可再生能源参与的时空协调负荷恢复[D]. 济南: 山东大学, 2020.
Zhao Jin. Spatio-temporal coordination of load restoration considering renewable energy participation [D]. Jinan: Shandong University, 2020.
A Post-Disaster Centralized Matching and Decentralized Dispatch Strategy for Emergency Resources in Urban Power Network
Wan Haiyang Liu Wenxia Shi Qingxin Liu Jiayi Zhang Shuai
(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Resources North China Electric Power University Beijing 102206 China)
Abstract The urban power network (UPN) is a critical infrastructure that supports the normal operation of cities. The timely development of optimal post-disaster emergency resource (ER) allocation strategies for the UPN is of great significance for maintaining the functionality of various lifeline systems in cities. Unlike a single transmission and distribution network, the UPN has the characteristics of multiple voltage levels and complex topologies. This paper proposes a centralized matching and decentralized dispatch strategy for post-disaster ERs in the UPN, aiming at the problem of limited emergency resources, numerous fault components (FC), and information barriers for collaborative repair of FCs among multi-voltage power networks in the post-disaster restoration of the UPN.
First, the matching relationship between ER and FC is established using the bipartite graph method based on real-time information and characteristic parameters. Second, with the objective of maximizing the net benefit of matching and using the modified Kuhn-Munkres algorithm, the optimal matching between the ER and the FC is formulated centrally. Additionally, considering the coupling relationship between multi-voltage-level power systems within the UPN, a bi-level optimization model is established. The upper-level high-voltage power system maximizes the load restoration of the substation buses, while the lower-level medium-voltage power system minimizes the load loss cost, and a decentralized recovery strategy for loads of each voltage level is developed. Furthermore, by timely updating the information of newly discovered FC and ER in UPN, the optimal matching method and load restoration strategy are re-determined to ensure that the proposed method is optimal at each time step.
Finally, the case study employs real-world UPN data to perform a simulation analysis of the method proposed in this paper. In comparison to commonly used centralized and rolling optimization approaches in existing research, the method proposed in this paper can swiftly formulate solutions that approach global optimality within a relatively short timeframe. For instance, in Scenario 1, although the load restoration achieved by the proposed method is only 98.42% and 99.76% of the centralized and rolling optimization strategies, respectively, its solving efficiency is 38 times and 10 times faster than the two, respectively. Given the significance of scheduling plan formulation time during post-disaster load restoration, the paper argues that sacrificing some precision for higher solving efficiency is acceptable.
The following conclusions can be drawn from the simulation analysis: (1) The method proposed in this paper independently resolves the ER and FC matching process, significantly reducing the computational complexity of the post-disaster fault repair and load restoration model. It can swiftly and efficiently formulate precise emergency plans in a relatively short time. Also, the algorithm demonstrates good convergence, thereby validating the effectiveness of the method proposed in this paper. (2) The quantities of pre-allocation ERs of different types in UPN has a substantial impact on post-disaster load loss and economic costs. In future research, it is imperative to further explore, based on predictive disaster information, the mechanisms through which different extreme disasters affect UPN components, analyze the location of vulnerable UPN components, and formulate more economical and rational resource pre-allocation strategies.
keywords:Urban power network, extreme disaster, emergency resources, fault repair, load restoration; weighted bipartite graph, two-layer optimization model
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.231836
国家自然科学基金资助项目(52307094)。
收稿日期 2023-11-03
改稿日期 2023-12-06
作者简介
万海洋 男,2000年生,男,博士研究生,研究方向城市电力系统的韧性分析等。E-mail:1398024216@163.com
刘文霞 女,1967年生,女,博士,教授,博士生导师,研究方向为电力系统智能规划、电力系统风险评价、电力系统通信。E-mail:liuwenxia001@163.com(通信作者)
(编辑 李 冰)


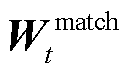 。本节依次计算各部分:首先根据ER和FC的属性,分别建立二者的特征参数集;其次根据ER和FC间的匹配条件,生成二者间的匹配边集合;最后计算各匹配关系的权重大小。
。本节依次计算各部分:首先根据ER和FC的属性,分别建立二者的特征参数集;其次根据ER和FC间的匹配条件,生成二者间的匹配边集合;最后计算各匹配关系的权重大小。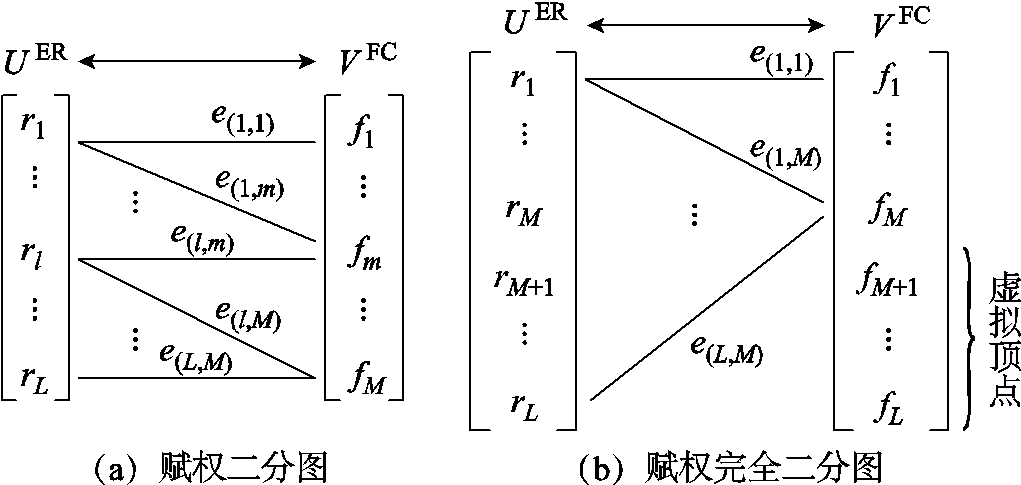
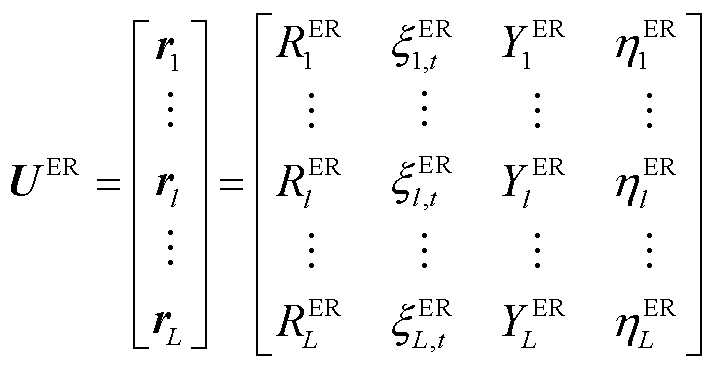 (1)
(1)
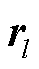 为编号为l的ER的特征参数集合的向量表示;
为编号为l的ER的特征参数集合的向量表示;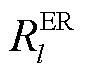 为编号为l的ER的能力属性,取值见表3;
为编号为l的ER的能力属性,取值见表3;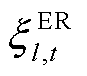 为编号为l的ER在t时刻的派遣状态,当
为编号为l的ER在t时刻的派遣状态,当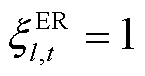 时,表示该ER已被派遣,正在负责处理某一故障元件,否则
时,表示该ER已被派遣,正在负责处理某一故障元件,否则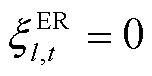 ;
;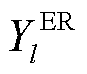 为编号为l的ER的地理位置;
为编号为l的ER的地理位置;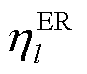 为编号为l的ER的抢修效率。
为编号为l的ER的抢修效率。
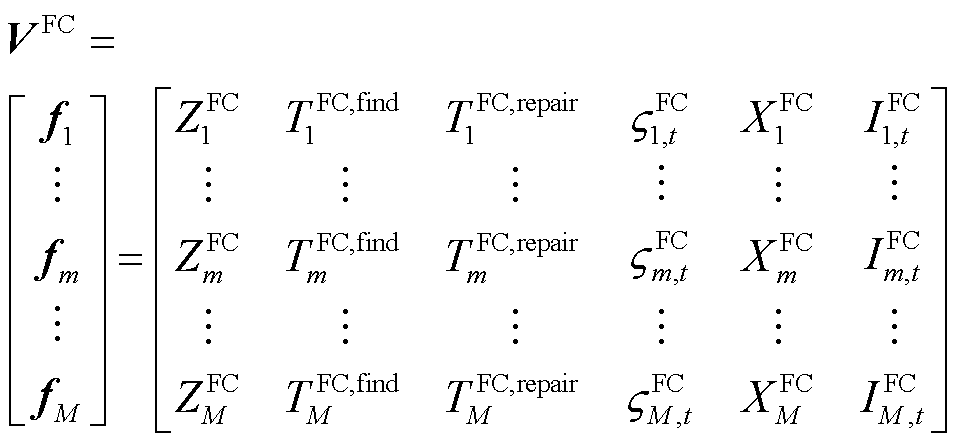 (2)
(2)
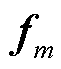 为第m个FC的特征参数集合的向量表示;
为第m个FC的特征参数集合的向量表示;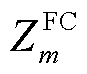 为第m个FC的故障类型,取值见表3;
为第m个FC的故障类型,取值见表3;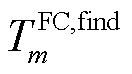 为探明第m个FC位置所需的时间,由于城市电网的故障数量较多且灾损范围较大,巡线员或无人机需要在故障发生的一定时长后,才可探测出故障元件;
为探明第m个FC位置所需的时间,由于城市电网的故障数量较多且灾损范围较大,巡线员或无人机需要在故障发生的一定时长后,才可探测出故障元件;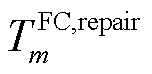 为第m个FC的预估抢修时间,本文设定巡线员或无人机在探明故障的同时,能够预估出故障元件的抢修时间;
为第m个FC的预估抢修时间,本文设定巡线员或无人机在探明故障的同时,能够预估出故障元件的抢修时间;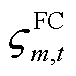 为抢修资源在t时刻对第m个FC的分配情况,当
为抢修资源在t时刻对第m个FC的分配情况,当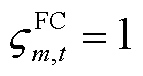 时,表示此时已有应急资源负责抢修该FC,否则
时,表示此时已有应急资源负责抢修该FC,否则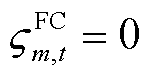 ;
;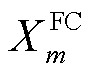 为第m个FC的地理位置,数值上取其距离最近的节点位置;
为第m个FC的地理位置,数值上取其距离最近的节点位置;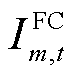 为第m个FC的负荷重要程度,数值上等于相较于电网正常运行时元件单独故障造成的负荷损失,其计算式为
为第m个FC的负荷重要程度,数值上等于相较于电网正常运行时元件单独故障造成的负荷损失,其计算式为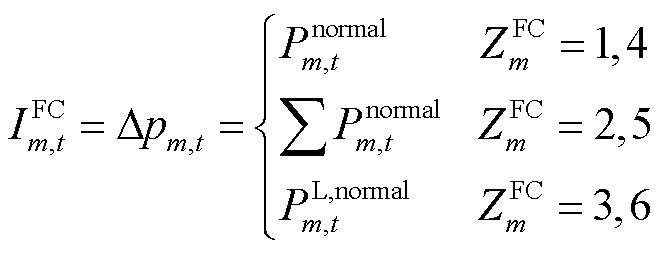 (3)
(3)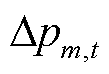 为第m个FC单独故障时会造成的负荷损失。具体地,当第m个FC为线路时,
为第m个FC单独故障时会造成的负荷损失。具体地,当第m个FC为线路时,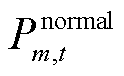 ;当第m个FC为杆塔时,
;当第m个FC为杆塔时,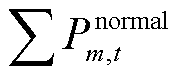 ;当第m个FC为变电站和变压器时,
;当第m个FC为变电站和变压器时,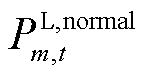 。
。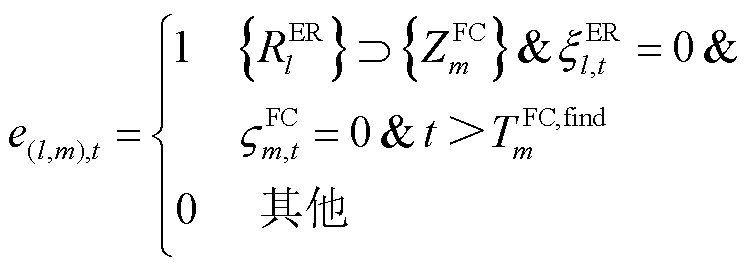 (4)
(4)
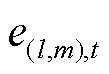 为表征
为表征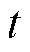 时刻编号为l的ER和第m个FC间匹配关系的0-1变量,当
时刻编号为l的ER和第m个FC间匹配关系的0-1变量,当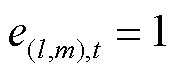 ;否则
;否则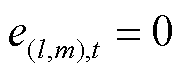 。
。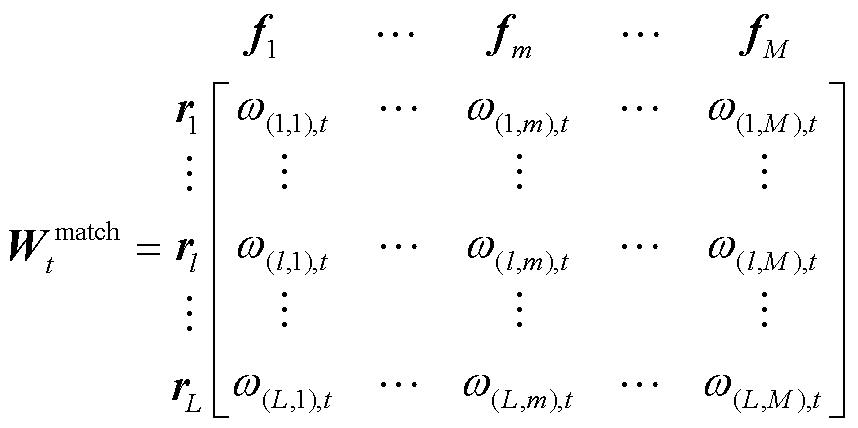 (5)
(5)
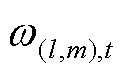 为编号为l的ER和第m个FC在t时刻按照此匹配方式的系统净收益,计算式为
为编号为l的ER和第m个FC在t时刻按照此匹配方式的系统净收益,计算式为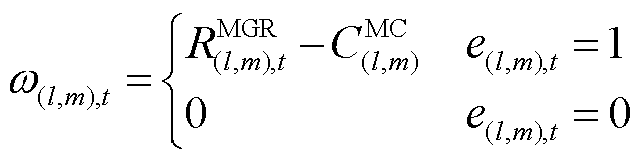 (6)
(6)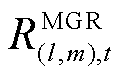 为匹配毛收益(Matching Gross Revenue, MGR);
为匹配毛收益(Matching Gross Revenue, MGR);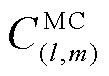 为匹配成本(Matching Costs, MC)。即当
为匹配成本(Matching Costs, MC)。即当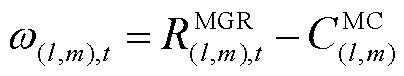 。其中,匹配毛收益
。其中,匹配毛收益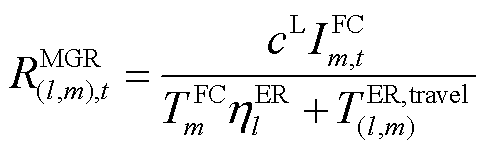 (7)
(7)
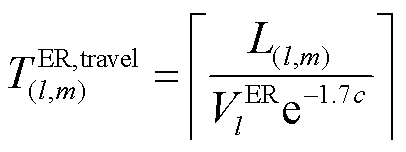 (8)
(8) (9)
(9)
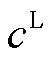 为单位负荷的损失成本;
为单位负荷的损失成本;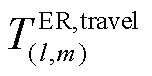 和
和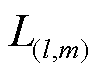 分别为编号为l的ER前往第m个FC最短路径的用时和距离;
分别为编号为l的ER前往第m个FC最短路径的用时和距离; 为向上取整;
为向上取整;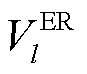 为编号为l的ER的移动速度;c为道路拥塞程度,可以表示灾害对交通网络的影响
为编号为l的ER的移动速度;c为道路拥塞程度,可以表示灾害对交通网络的影响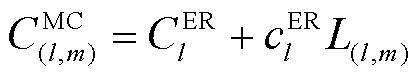 (10)
(10)
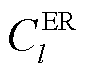 为消耗l号ER的成本;
为消耗l号ER的成本;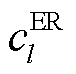 为调度l号ER单位距离的成本。
为调度l号ER单位距离的成本。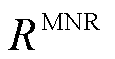 =ω
=ω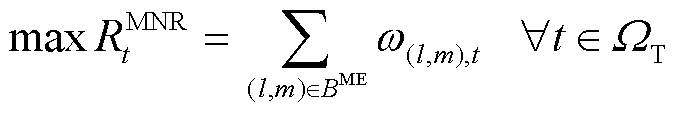 (11)
(11)
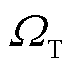 为时间集合;
为时间集合;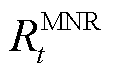 为t时刻ER与FC最优匹配对应的总净收益。
为t时刻ER与FC最优匹配对应的总净收益。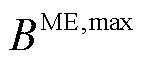 。
。
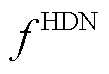 ,表示为
,表示为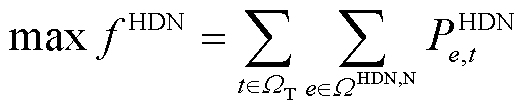 (12)
(12)
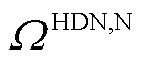 为HDN的变电站节点集合;
为HDN的变电站节点集合;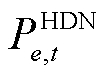 为
为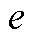 的负荷有功功率的实际值。在每次迭代过程中,该变量的优化结果传递至下层,作为边界条件约束MDN负荷实际大小的上限值,详见后文式(38)和式(39)。
的负荷有功功率的实际值。在每次迭代过程中,该变量的优化结果传递至下层,作为边界条件约束MDN负荷实际大小的上限值,详见后文式(38)和式(39)。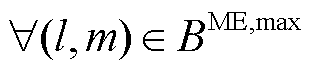 ,
,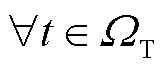 ,
,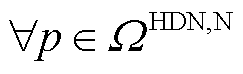 ,
,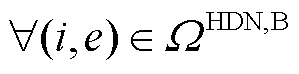 (
(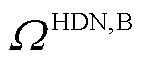 为HDN线路集合),HDN的ER运行约束为
为HDN线路集合),HDN的ER运行约束为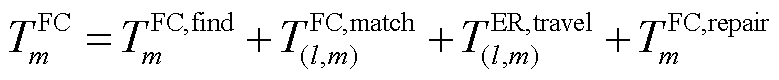 (13)
(13)
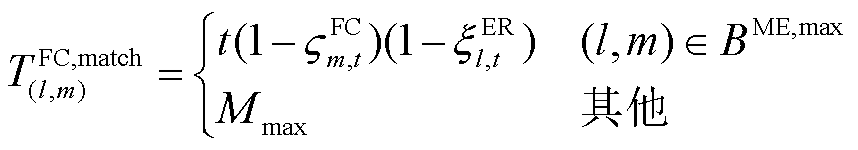 (14)
(14) (15)
(15)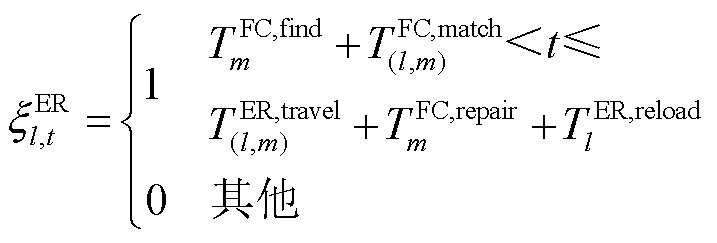 (16)
(16)
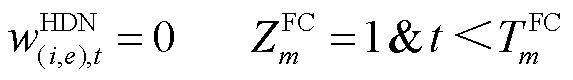 (17)
(17)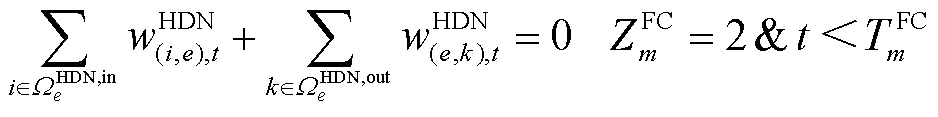 (18)
(18)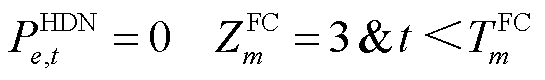 (19)
(19)
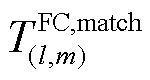 为第m个FC与编号为l的ER最优匹配所需的时长;
为第m个FC与编号为l的ER最优匹配所需的时长;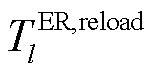 为应急资源l在抢修完某一故障后,返回仓库补充物资所需的时间;
为应急资源l在抢修完某一故障后,返回仓库补充物资所需的时间;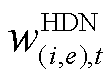 为HDN线路
为HDN线路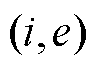 在
在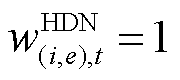 ,否则
,否则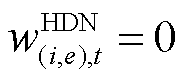 ;
;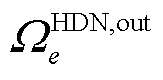 和
和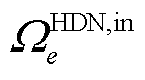 分别为HDN节点
分别为HDN节点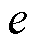 下游、上游节点集合。
下游、上游节点集合。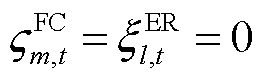 时,等待资源分配时长为t,否则
时,等待资源分配时长为t,否则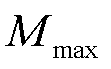 ;式(15)和式(16)表示FC与ER为最优匹配后的相应时段内,二者的分配状态取1;式(17)表示当FC为HDN线路
;式(15)和式(16)表示FC与ER为最优匹配后的相应时段内,二者的分配状态取1;式(17)表示当FC为HDN线路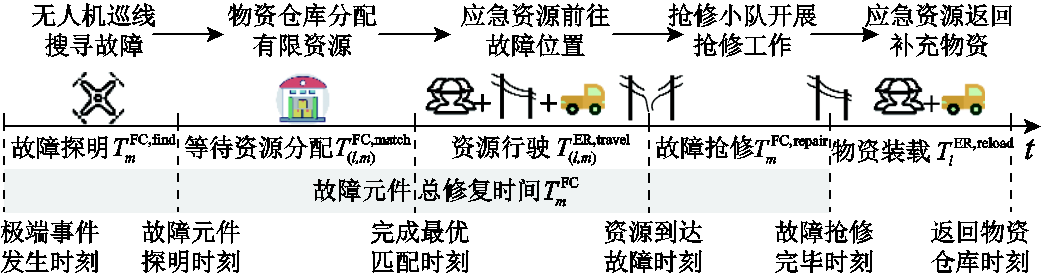
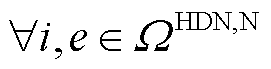 ,
,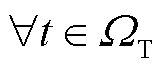 ,系统运行约束如下所示。
,系统运行约束如下所示。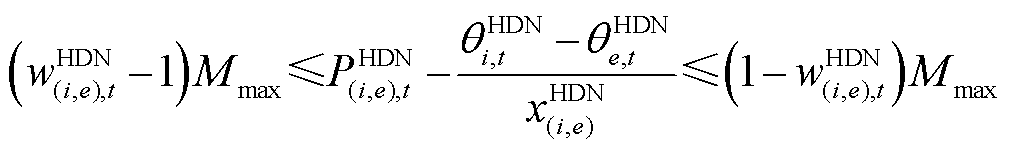 (20)
(20)
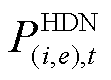 为HDN线路
为HDN线路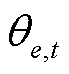 为HDN节点
为HDN节点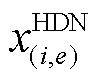 为HDN线路
为HDN线路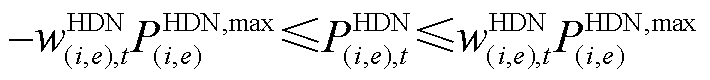 (21)
(21)
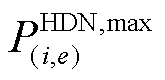 为HDN线路
为HDN线路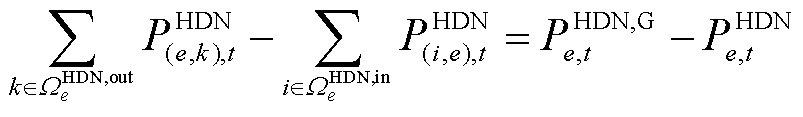 (22)
(22)
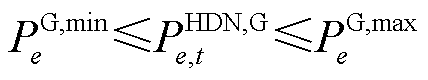 (23)
(23)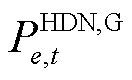 为
为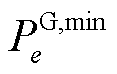 和
和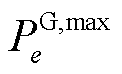 分别为外部电网或火电机组向节点
分别为外部电网或火电机组向节点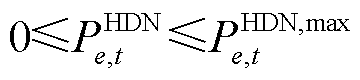 (24)
(24)
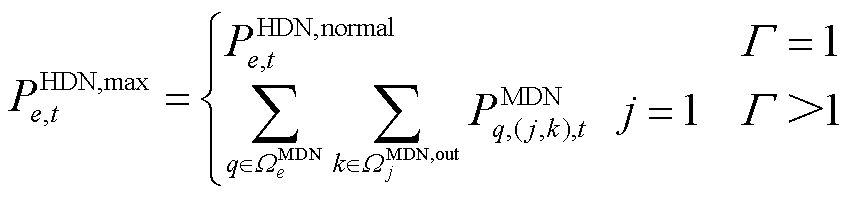 (25)
(25)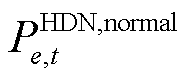 为正常情况下
为正常情况下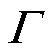 为迭代次数;
为迭代次数;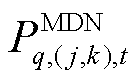 为第q个MDN的线路
为第q个MDN的线路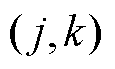 在
在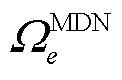 为接入变电站节点
为接入变电站节点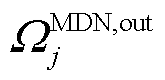 为MDN节点
为MDN节点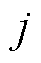 下游节点集合。约束式(25)表示当双层优化过程为第一次迭代时,由于HDN调度过程未知MDN负荷的实际情况,此时令HDN节点负荷有功功率的最大值
下游节点集合。约束式(25)表示当双层优化过程为第一次迭代时,由于HDN调度过程未知MDN负荷的实际情况,此时令HDN节点负荷有功功率的最大值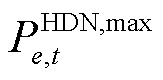 等于正常情况的预测值
等于正常情况的预测值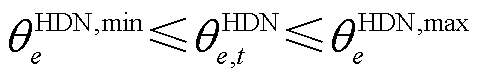 (26)
(26)
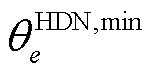 和
和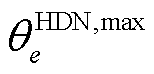 分别为HDN节点
分别为HDN节点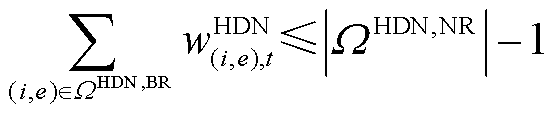 (27)
(27)
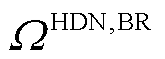 和
和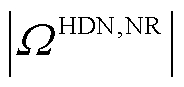 分别为HDN中构成闭环的线路集合和节点数量。约束式(27)表示HDN中闭环设计的线路,运行时应保持开环结构。
分别为HDN中构成闭环的线路集合和节点数量。约束式(27)表示HDN中闭环设计的线路,运行时应保持开环结构。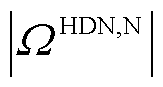 个集团),由于各集团内部的调度模型均相同,本节以接入HDN中
个集团),由于各集团内部的调度模型均相同,本节以接入HDN中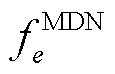 的表达式为
的表达式为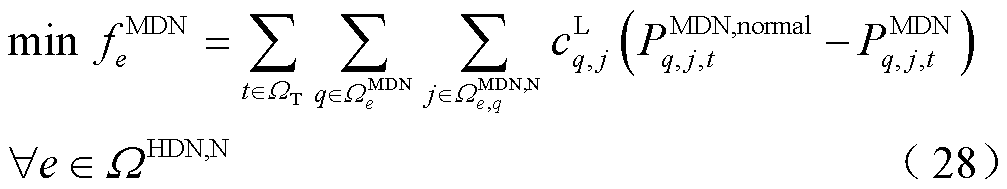
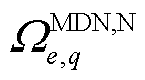 为接入变电站节点
为接入变电站节点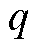 个MDN的节点集合;
个MDN的节点集合;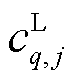 为第
为第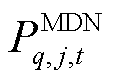 和
和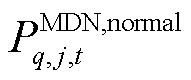 分别为
分别为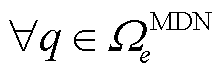 ,
,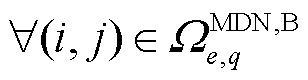 ,
,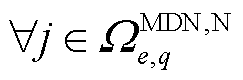 ,
,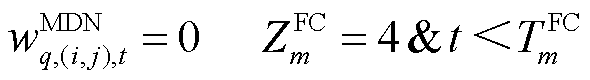 (29)
(29)
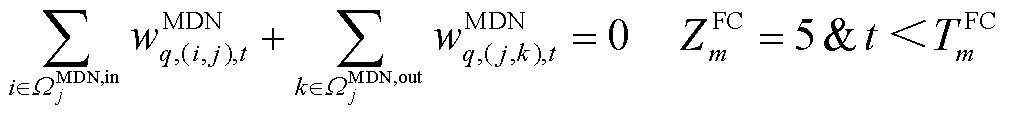 (30)
(30)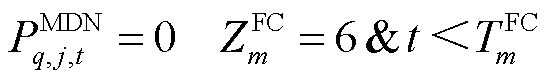 (31)
(31)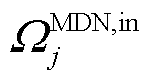 为MDN节点
为MDN节点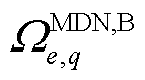 为接入变电站
为接入变电站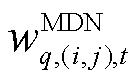 为第
为第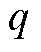 个MDN线路
个MDN线路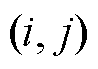 在
在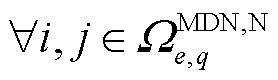 ,
,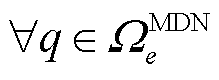 ,MDN系统运行方程包含节点有功、无功功率平衡约束,分别表示为
,MDN系统运行方程包含节点有功、无功功率平衡约束,分别表示为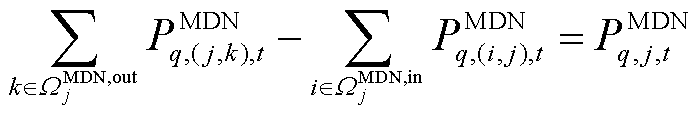 (32)
(32)
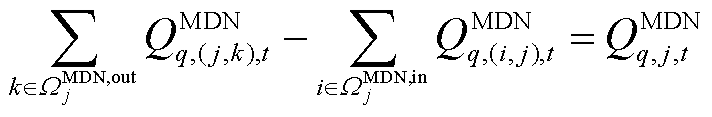 (33)
(33)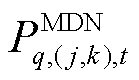 和
和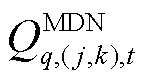 为分别为第
为分别为第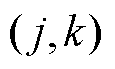 在
在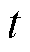 时刻的有功潮流和无功潮流,在每次迭代过程中,变量
时刻的有功潮流和无功潮流,在每次迭代过程中,变量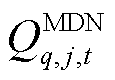 为
为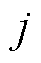 的负荷无功功率的实际值。
的负荷无功功率的实际值。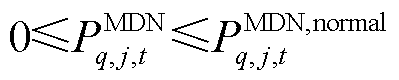 (34)
(34)
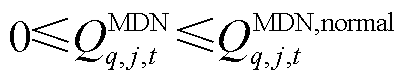 (35)
(35)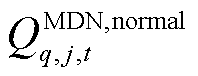 为t时刻第q个MDN节点j的负荷无功功率在正常情况下的预测值。
为t时刻第q个MDN节点j的负荷无功功率在正常情况下的预测值。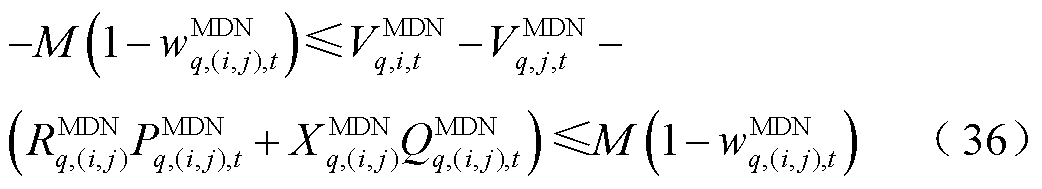
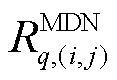 、
、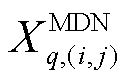 分别为第
分别为第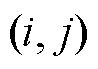 的电阻、电抗值;
的电阻、电抗值;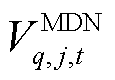 为
为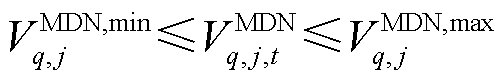 (37)
(37)
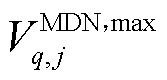 和
和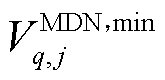 分别为第
分别为第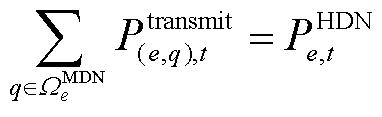 (38)
(38)
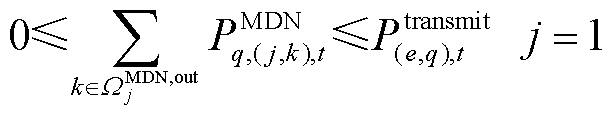 (39)
(39)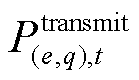 为
为 向第
向第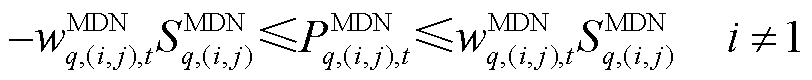 (40)
(40)
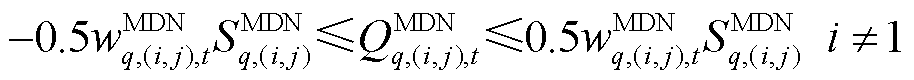 (41)
(41)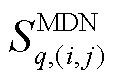 为第
为第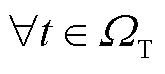 ,
,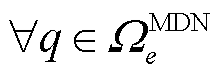 ,有
,有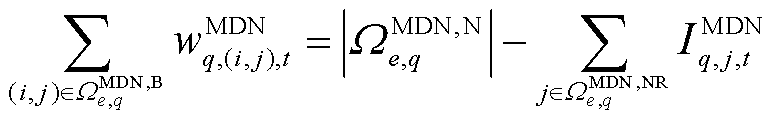 (42)
(42)
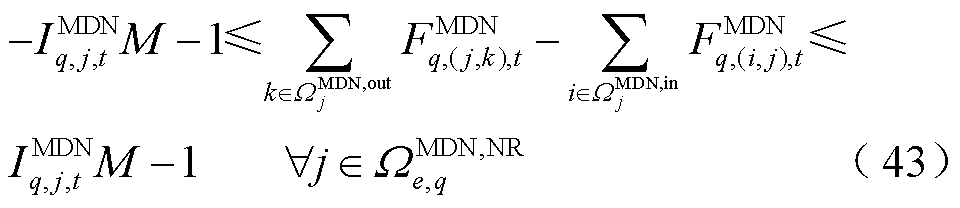
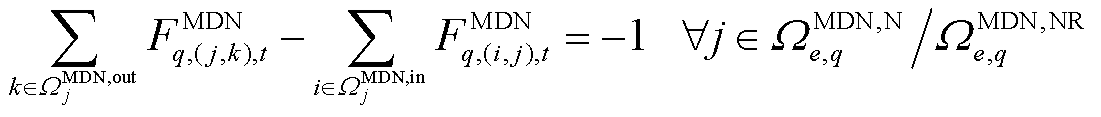 (44)
(44)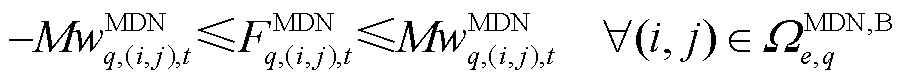 (45)
(45)
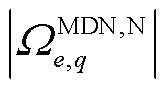 为接入变电站节点e的第q个MDN的节点个数;
为接入变电站节点e的第q个MDN的节点个数;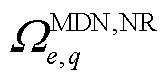 为接入变电站节点e的第q个MDN的潜在根节点集合,包含首节点和故障线路的首末节点;
为接入变电站节点e的第q个MDN的潜在根节点集合,包含首节点和故障线路的首末节点;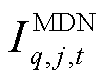 为判断第q个MDN的节点
为判断第q个MDN的节点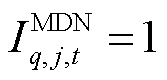 ,否则
,否则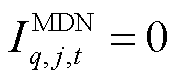 ;
;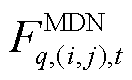 为第q个MDN线路
为第q个MDN线路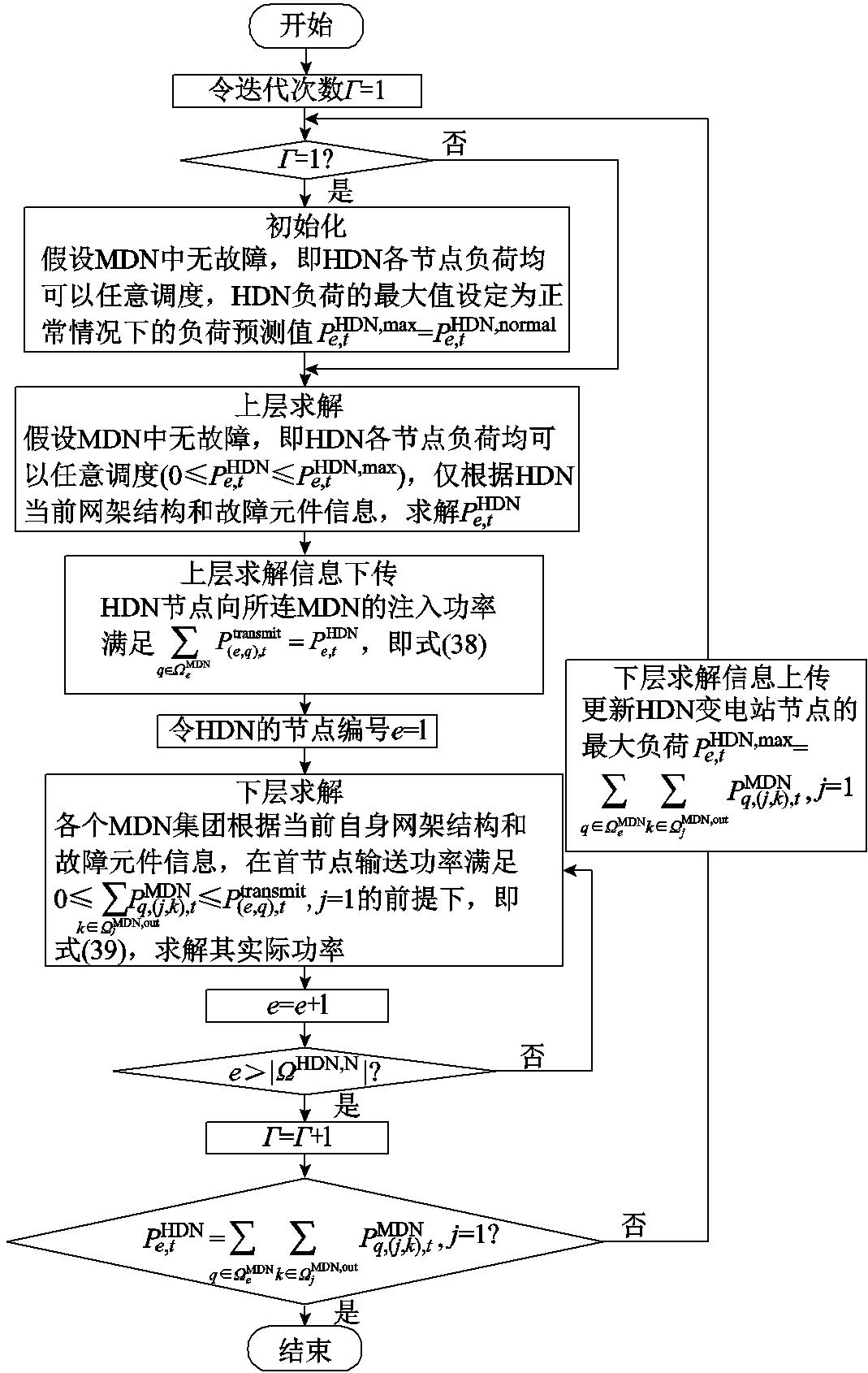



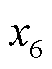 和
和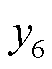 表示ER6与FC6(即HDN的20号故障元件)在t=10 h时已完成最优匹配,并需7 h完成抢修;
表示ER6与FC6(即HDN的20号故障元件)在t=10 h时已完成最优匹配,并需7 h完成抢修;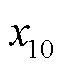 和
和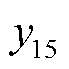 表示ER10与FC15(即MDN2中的7号故障元件)在t=16 h时完成最优匹配,并需3 h完成抢修。
表示ER10与FC15(即MDN2中的7号故障元件)在t=16 h时完成最优匹配,并需3 h完成抢修。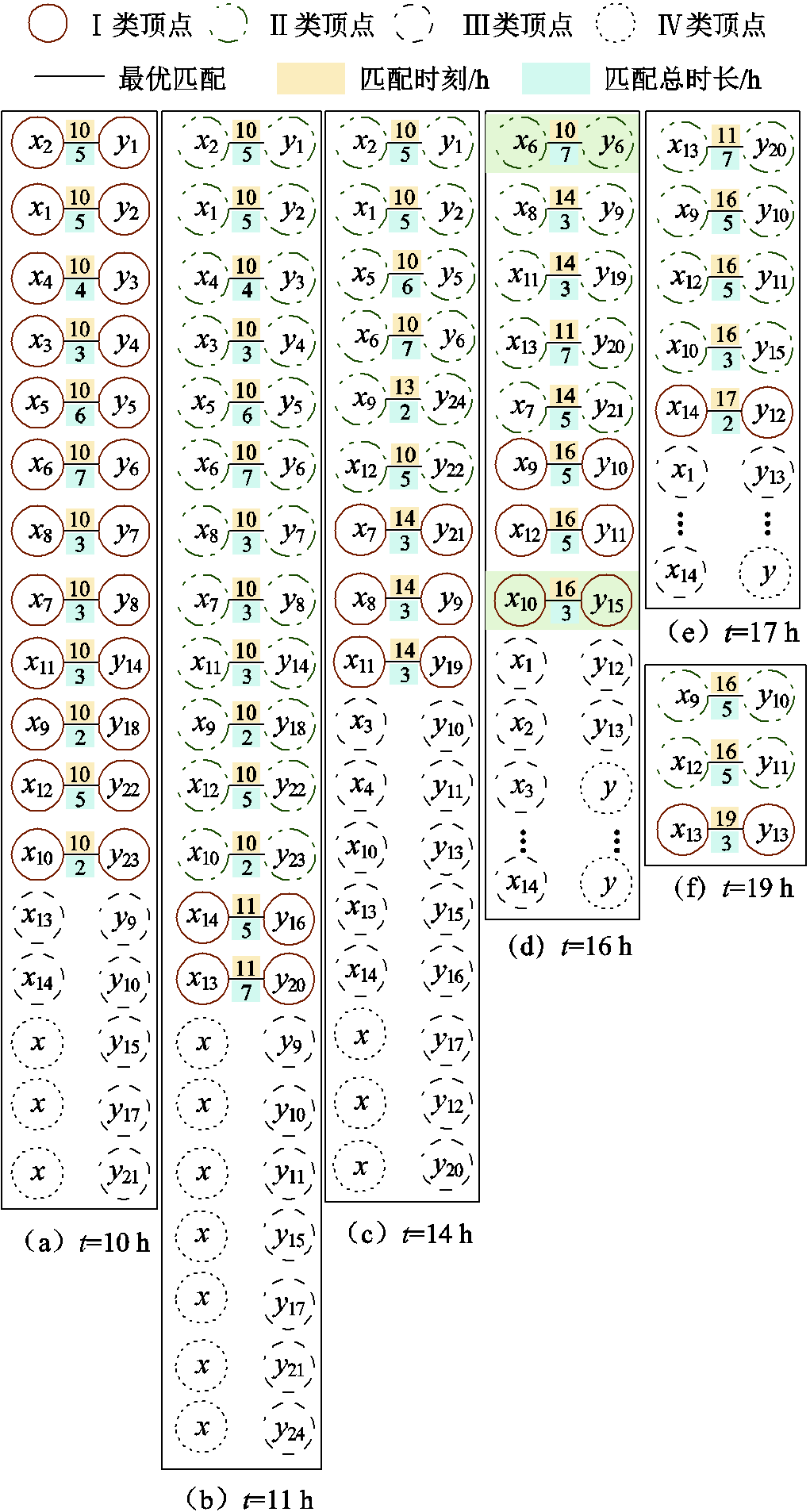
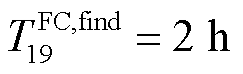 );但由于此时无空闲状态的MDN杆塔抢修小队, FC19需再等待2 h方可与ER11匹配(
);但由于此时无空闲状态的MDN杆塔抢修小队, FC19需再等待2 h方可与ER11匹配(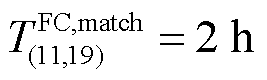 );之后,ER11分别经历1 h前往FC19(
);之后,ER11分别经历1 h前往FC19(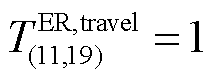 h)和2 h抢修FC19(
h)和2 h抢修FC19(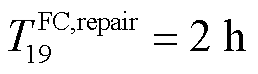 ),于t=17 h完成抢修任务后,花费1 h返回仓库补充物资(
),于t=17 h完成抢修任务后,花费1 h返回仓库补充物资(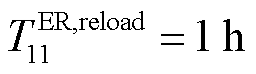 )。
)。