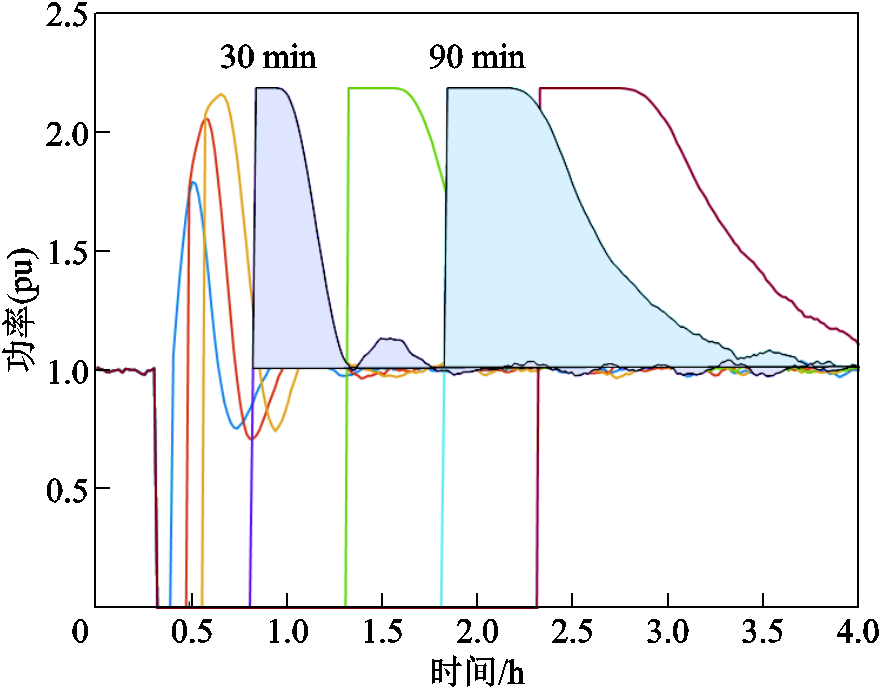
图1 配电网负荷恢复时的冷负荷回流现象[27]
Fig.1 CLPU phenomenon during load recovery in distribution networks[27]
摘要 极端天气、网络攻击等因素造成的配电网故障影响范围广、社会影响恶劣,开展韧性配电网建设以满足经济发展和民生需求。研究表明,配电网恢复过程中负荷特性与负荷恢复决策密切相关,然而当前大部分研究并未对此进行全面考虑,用户负荷行为无法被精准量化,配电网负荷恢复过程中往往面临电压、潮流越限等安全问题。鉴于此,该文首先从客观和主观两个角度分析了配电网恢复过程中的用户负荷决策依赖特性及其演化机理,即冷负荷回流(CLPU)和负荷逐利,并分别利用数据驱动和知识驱动方法精准量化其运行特性,为配电网负荷恢复奠定基础;其次,提出两种考虑用户决策依赖特性的配电网负荷恢复方法,一是基于Karush-Kuhn-Tucher(KKT)条件处理的配电网负荷恢复双层优化模型,二是基于时间标签序列的配电网自适应恢复模型,以实现兼顾用户决策依赖特性的配电网负荷快速恢复;最后,基于系统功能曲线,利用最大负荷损失、负荷中断率、隐私暴露程度等指标对两种方法进行对比分析。算例结果表明,在配电网恢复过程中考虑负荷决策依赖特性能够避免出现配电网负荷恢复过程中电压越限等安全问题,提升配电网运行安全性;相较于双层模型,所提出的自适应模型在提高用户隐私保护程度的同时,求解耗时仅为双层模型的33%。
关键词:配电网 韧性 冷负荷回流 负荷恢复 决策依赖特性
近年来,极端天气与网络攻击常常引发电力系统停电事故,造成巨大的经济损失与恶劣的社会影响。与输电网相比,配电网自动化水平较低、冗余度不足,应对灾害的能力较差,控制保护手段也较为有限[1]。统计数据显示,配电网停电时长占总停电时长的80%[2],是电网故障的主要原因。不仅如此,由于工业、商业和居民用户的终端负荷主要接入配电网,配电网一旦发生故障,便会影响到人们正常的生产生活,社会影响恶劣。因此,国家发改委在《“十四五”全国城市基础设施建设规划》[3]中明确指出需要开展城市韧性电网建设,保证电网在极端情况下能够快速恢复到正常水平,降低电网故障造成的不良影响。
在极端情况下,配电网韧性提升手段主要涵盖故障预防、故障响应和故障恢复三个方面。作为故障恢复的重要组成部分,负荷恢复成功与否直接关系到配电网的韧性强弱,是保障电网安全的重要一环,也是当下研究的热点方向。
随着用户侧可再生能源、电力电子设备和储能的快速发展,配电网负荷恢复策略已经逐步由传统的电源跟踪负荷转变为源-网-储的协同运行,利用分布式电源、配电网拓扑、移动储能[4-5]等提高配电网冗余度。目前对于源测的研究多聚焦于分布式电源在极端情况下的供电能力[6],以弥补故障后配电网供电不足的问题。不仅如此,由于分布式电源的大量接入,在配电网恢复的过程中常常考虑多源协同[7-9]的方式,借助配电网已有的资源,划分出尽可能大的孤岛,利用多源协同向孤岛内的重要负荷供电,以提升负荷恢复的速度与恢复率。在网侧,除了在硬件层面对网络及元件进行加固[10]以外,网络动态重构[11]和网络拓扑优化[12]也已经成为当下的研究热点。网络拓扑动态重构能够更灵活地调度电力网络资源,并借助拓扑优化算法,设计出更加鲁棒和高效的配电网络结构,以实现负荷的快速恢复。储能由于具备在时间上进行能量转移的能力,常与分布式电源结合实现配电网的故障恢复[13],而多种类型储能协调更有助于负荷的快速恢复[14]。文献[15]充分利用储能的时空转移特性实现了配电系统的韧性提升;文献[16]则充分考虑储能的协调作用,构建了极端情况下配电网的源-网-储互动模式。
负荷是配电网恢复对象,其负荷特性能够直接影响配电网恢复进程。目前对于配电网恢复的主流研究是针对负荷恢复过程中源-网-储进行优化协调以实现负荷的快速恢复,而对于用户侧自身的负荷特性则较少涉及。用户侧负荷种类繁多,负荷特性丰富,需要在负荷恢复过程中对其进行精准建模,以实现配电网负荷恢复过程的准确刻画。
目前对配电网负荷恢复中的负荷有以下两种处理方法:
1)负荷曲线在断电前后保持不变[17]。这是目前大部分文献对配电网恢复过程中负荷建模的处理方法。例如,文献[18]采用多能协同方法进行配电网负荷恢复,文中设定恢复时配电网负荷为固定值。文献[19]则提出了一种基于刚性负荷的具有可控开关和分布式发电资源的现代配电系统负荷恢复方法。
2)负荷曲线在断电恢复后发生固定变化[20-23]。部分文献已经关注高比例温控负荷(空调、热水器、热泵等)引起的负荷反弹现象,这是配电网负荷恢复过程中需要重点关注的现象之一。温控负荷(Thermal Control Load, TCL)通常占配电网负荷量的40%左右[24],是配电网负荷的重要组成部分。在电力系统发生停电事故后的恢复过程中,由于配电网中占大比重的温控负荷运行状态多样性的丧失,出现待恢复负荷在恢复初期短时间内的功率远大于基线负荷值的现象[25-26],即冷负荷回流(Cold Load Pick-up, CLPU)现象。
为描述在配电网中占有较大比重的温控负荷在供电恢复时的演化规律,文献[20]采用RC电路模型表示CLPU功耗衰减,然而这种方式假设过于简单,难以准确描述CLPU的实际表现。文献[21]通过温控负荷的一阶或二阶微分式描述CLPU,但其研究的是温控负荷内部温度变化情况,难以准确表征功率变化情况。目前最常见的用于表述CLPU的是延迟指数模型[22-23],借助延迟指数衰减函数来表征断电恢复后温控负荷的实际运行行为。在上述所有的CLPU模型中,都将CLPU描述为与断电时间无关的固定曲线。
然而,以固定曲线表征温控负荷的变化情况只能在一定程度上解释断电过程中温控负荷多样性的缺失,由于存在温控负荷多样性缺失等客观因素,CLPU往往与负荷恢复决策密切相关,固定曲线不能准确地表征在极端情况下的温控负荷演变情况,适用范围较窄。
不仅如此,经研究发现,除了客观的负荷多样性缺失,用户侧用电行为往往还会受到经济等主观因素的影响,最终导致用户侧负荷在重新恢复供电后的表现与恢复前不同,其负荷表现取决于配电网恢复决策,即负荷具有决策依赖性[27]。
综上所述,当下相关研究与负荷实际情况尚有较大出入,显著影响相关理论模型的适用性。若仍按目前大部分文献所认为的以负荷保持不变或是曲线固定进行负荷恢复,会导致负荷特性刻画不全面,容易引起配电网负荷恢复过程中的电压或潮流越限等安全问题。因此,研究负荷决策依赖特性,对其进行精准量化,以快速安全有效地恢复负荷是当下社会迫切的需求。
鉴于此,本文分析了极端情况下负荷产生决策依赖特性的客观与主观原因,建立了配电网负荷恢复双层模型,并针对求解双层模型所使用的Karush-Kuhn-Tucher(KKT)条件隐私保护能力较差的问题,提出了一种基于时间标签序列的配电网自适应恢复模型,以实现对用户侧负荷决策依赖行为多样化的动态选择,在保护用户隐私的同时提高模型的求解效率。本文重点关注极端情况下多样性负荷与决策的依赖特性,从产生原因、解决思路、效果评估等方面进行了框架性的研究,为后续相关研究奠定了基础,创新点可概括如下:
1)从客观与主观两个角度分析配电网恢复过程中负荷决策依赖特性与机理,利用数据驱动与知识驱动相结合的方法对其进行建模,精准量化用户侧负荷的决策依赖特性,为配电网负荷恢复奠定基础。
2)基于用户侧负荷的决策依赖特性,提出配电网负荷恢复双层模型及基于时间标签序列的配电网自适应恢复模型两种负荷恢复方法,在兼顾负荷决策依赖特性的同时快速安全恢复负荷。
3)利用配电网韧性评估指标与基于皮尔逊相似度的用户敏感性评估策略对所提出两种模型进行对比分析。仿真结果表明在不影响配电网韧性的前提下,所提出自适应恢复模型在兼具隐私保护能力的同时,求解时间仅为双层模型的33%。
1.1.1 机理分析
在气候条件较为严苛的冬季与夏季,国内空调负荷在负荷高峰所占峰荷比例高达30%~40%[28-29],在东部沿海地带,部分地区温控负荷占比甚至超过50%[30]。因此,在极端情况下,负荷恢复过程会出现明显的CLPU现象,是必须考虑的因素。
配电网负荷恢复时的冷负荷回流现象如图1所示。由图1可知,配电网的负荷在供电恢复过程中并非一成不变,并且负荷曲线的形状与断电时长密切相关。

图1 配电网负荷恢复时的冷负荷回流现象[27]
Fig.1 CLPU phenomenon during load recovery in distribution networks[27]
冷负荷回流产生的直接原因是温控负荷运行状态多样性的缺失。温控负荷运行状态由开关状态和内部温度决定,图1中温控负荷的接通和断开两种状态分别用方与圆两种几何图形表示,水平位置的不同几何图形表示不同的温度[27]。
正常运行状态:在正常运行时,由于温控负荷只有开(功率为额定功率P)与关(功率为0)两种工作状态,因此温控负荷的内部温度呈现出在一定范围内周期性变化的状态。具体而言,温控负荷存在温度死区宽度δ,若温控负荷设定温度为Tset,当其内部温度超过Tmax(Tmax=Tset+δ)时,温控负荷开始工作,内部温度下降;当其内部温度小于Tmin(Tmin=Tset-δ)时,温控负荷关闭,内部温度升高。最终表现为图2所示的正常运行状态。
温控负荷运行状态的演化随断电时长的变化而变化,大致可分为短时间失电、中长期失电和长期失电三种演化情况,其动态演化机理如图3所示。
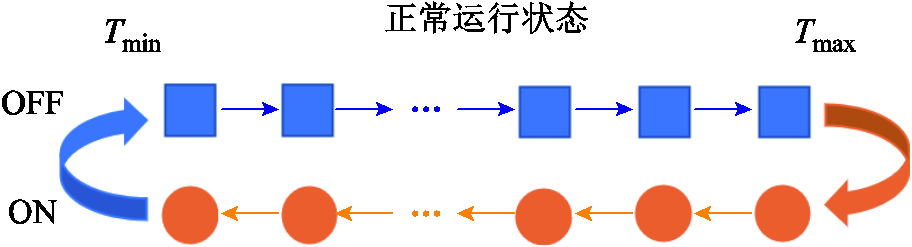
图2 温控负荷的正常运行状态
Fig.2 Normal operating state of TCL
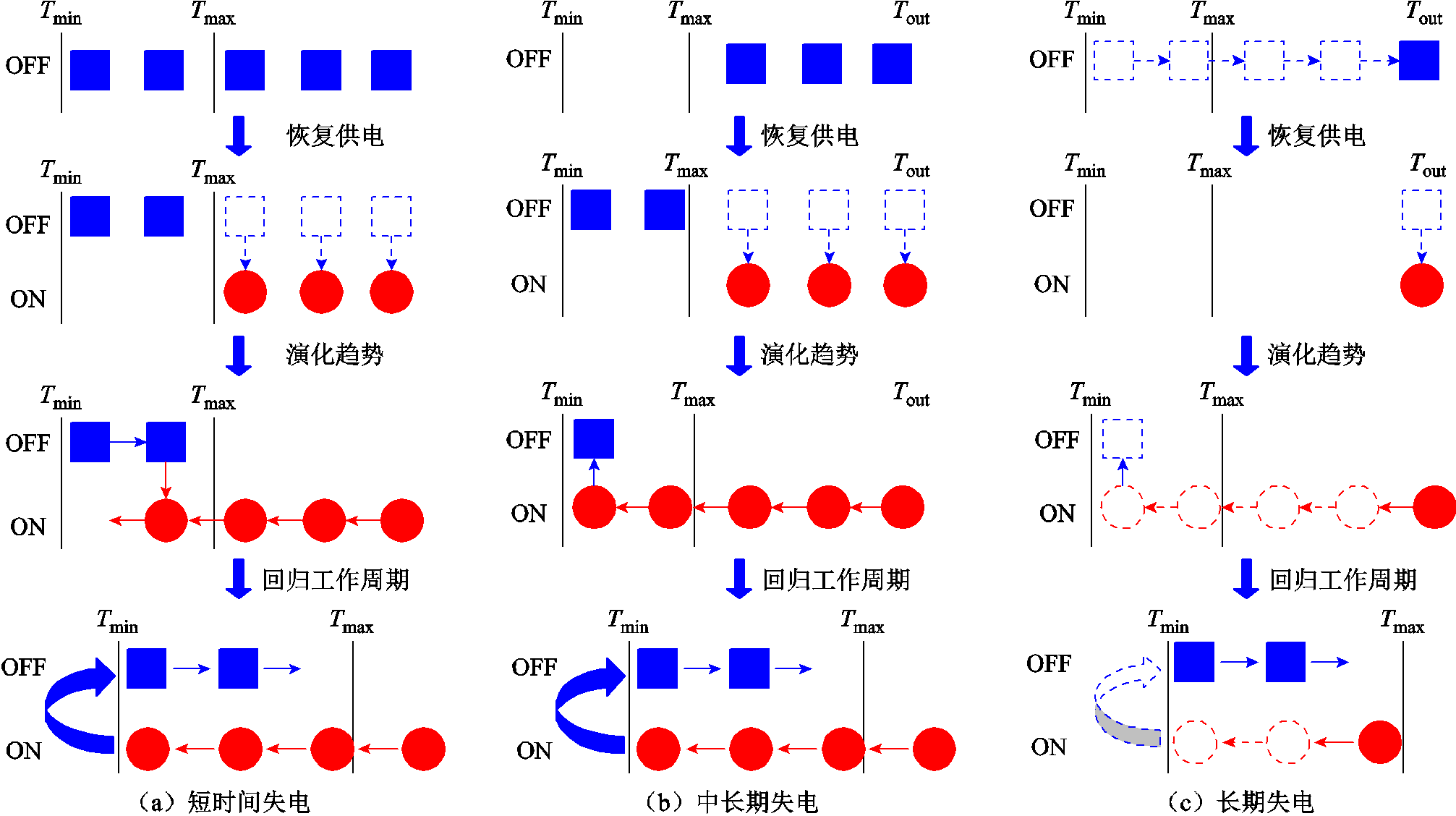
图3 不同失电时间所对应的负荷演化规律[27]
Fig.3 Load evolution law corresponding to different power outage times[27]
短时间失电:当配电网发生停电事件时,由于失去电力供应,所有的温控负荷都处于关闭状态,其内部温度随着时间的推移逐步升高。由于失电时间较短,在恢复供电时,仍有部分的温控负荷温度处于运行周期之内。如图3a所示,当恢复供电时,只有温度处于运行周期之外的温控负荷开通,而处于运行周期之内负荷的开关状态并未改变,仍保持着正常运行状态下的行为。由于在恢复供电时并非所有的温控负荷都处于开通状态,故短时间失电虽使负荷幅值上升,但并不能使其达到最大。
中长期失电:当配电网出现中长期的失电情况时,如图3b所示,由于断电时间较长,在恢复供电时所有温控负荷的内部温度都已跳出正常工作时的运行周期,因此通电瞬间所有的温控负荷都将开通,此时温控负荷总功率达到最大值。而后随着温控负荷的内部温度逐渐降低,回到正常的运行周期,总功率逐渐下降。需要注意的是,在中长期失电的情况下,断电时间越长,温控负荷的内部温度越接近室外温度Tout,需要通过更长的时间才能回到正常运行周期,表现为温控负荷总功率维持在峰值的时间随断电时长的增加而增加。
长期失电:如图3c所示,由于断电时间过长,当供电恢复时,温控负荷的内部温度等于室外温度。与中长期失电类似,在通电瞬间所有的温控负荷都将开通,温控负荷总功率达到最大值。但由于长期失电时温控负荷内部温度与室外一致,断电时间的延长已无法改变温控负荷状态。因此,在长期失电状态下,冷负荷回流的表现是固定的。
综上所述,在不同断电时长下,温控负荷的行为将呈现出不同的演化特点,这也正是冷负荷回流产生决策依赖特性的来源。
1.1.2 建模方法
由于配电网中温控负荷数量巨大,且各个温控负荷的运行参数不尽相同,难以通过知识驱动型的建模方法对温控负荷运行状态进行精准描述。为此,本文采用数据驱动型建模方法对温控负荷的决策依赖特性进行建模,基于文献[31]中的温控负荷运行参数,仿真得到温控负荷运行数据,并以此训练多层感知器(Multiple Layer Perception, MLP)模型,以实现对冷负荷回流现象的准确表征。
MLP本质上是对输入与输出进行非线性拟合,其结构可分为输入层、隐藏层和输出层三个部分。设置MLP输入层神经元数目为2,对应断电时长与恢复供电的时长,隐藏层神经元数目为10,输出层神经元数目设置为1,对应于输出负荷的大小。其数学模型为
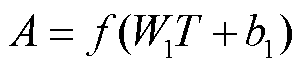 (1)
(1)
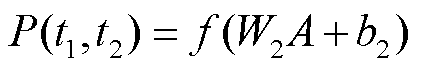 (2)
(2)
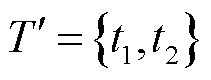 (3)
(3)
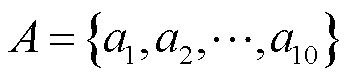 (4)
(4)
式中,W1与b1分别为输入层到隐藏层的权重与偏置;W2与b2分别为隐藏层到输出层的权重与偏置;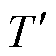 为输入层神经元集合;A为隐藏层神经元集合;P为输出层神经元;f为MLP的激活函数;t1为断电时长;t2为恢复供电时长。所建立MLP的结构示意图如图4所示。
为输入层神经元集合;A为隐藏层神经元集合;P为输出层神经元;f为MLP的激活函数;t1为断电时长;t2为恢复供电时长。所建立MLP的结构示意图如图4所示。
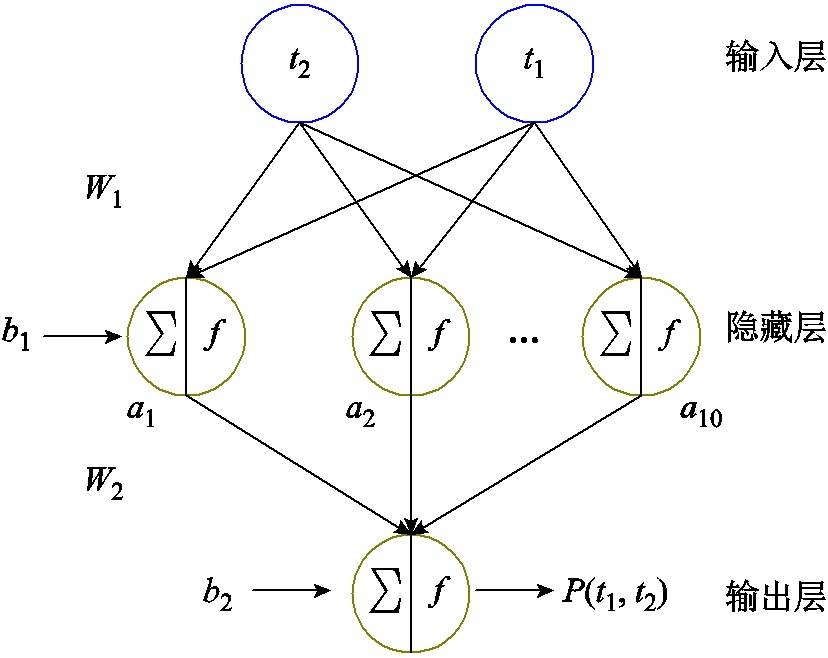
图4 MLP结构示意图
Fig.4 Schematic diagram of MLP structure
在训练的过程中,MLP采用误差反向传播算法对网络进行监督学习,利用梯度下降优化网络的权重与偏置。由于MLP是典型的前馈网络,信息的处理方向是由输入层到隐藏层最终到达输出层,在隐藏层中实现对输入层神经元的非线性映射;并且误差反向传播的方式能够将输出层的误差向前反馈,修正MLP的权重与偏置,进而建立良好的非线性依赖关系的模型。
本文借助MLP实现了由断电时长到负荷量的转换,所训练神经网络以断电时长t1和恢复供电的时长t2为输入,输出层输出数据为与t1、t2相关的负荷大小P,即具备决策依赖特性的CLPU负荷量。本文数据驱动型建模方法在增加模型时间细粒度的同时实现了负荷曲线对停电时间的自适应建模。
1.2.1 机理分析
用户侧负荷含有大量柔性负荷,可以根据电价变化及自身设备运行约束进行调整,以满足用户经济或生产层面的需求。配电网重新恢复供电后,用户基于断电时长对自身生活、生产的影响,及时调整负荷,以最小化经济损失。此时的负荷曲线较断电前已经发生较大改变,传统的固定负荷曲线建模方法不再适用。
以工业园区为例,发生断电事故后若仍按原定计划生产,则无法达成生产目标,给园区造成经济损失。因此在供电恢复后,园区需要扩大产量以保证生产计划顺利完成,出现供电恢复初期负荷量远大于基线负荷的用电行为。极端情况下工业节点负荷曲线如图5所示。
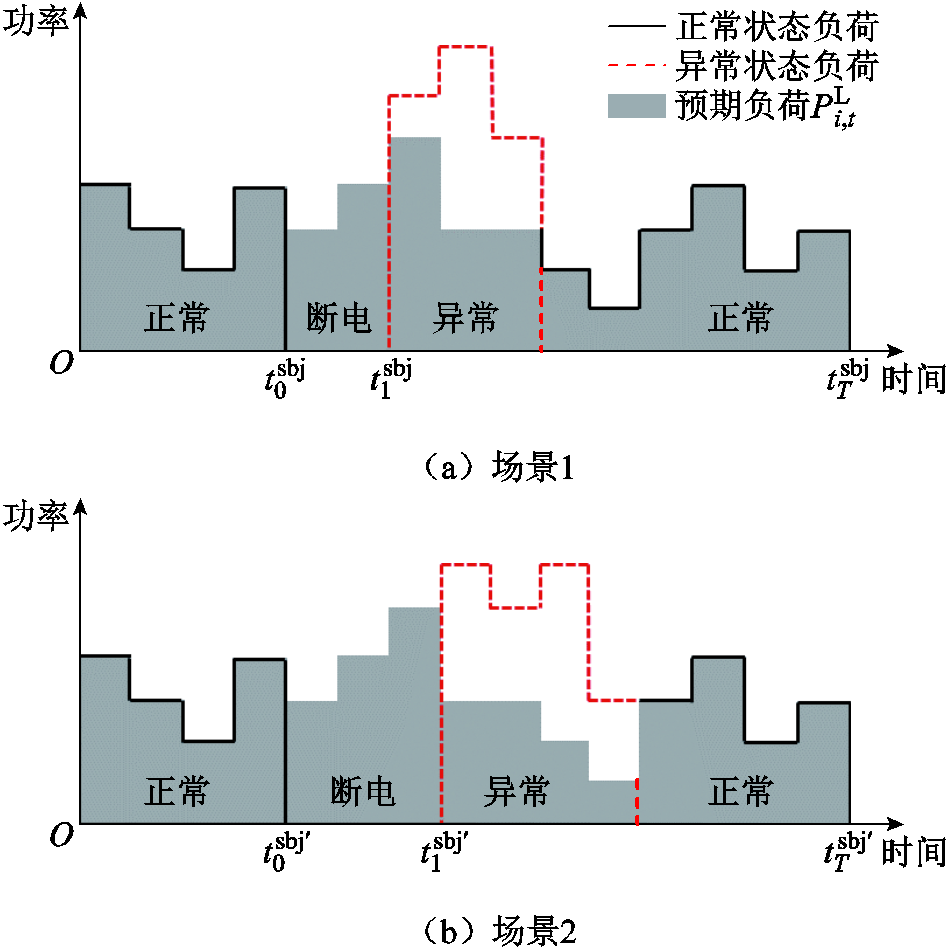
图5 极端情况下工业节点负荷曲线
Fig.5 Industrial node load curve in extreme cases
可以看出,虽然负荷异于常态的表现不尽相同,但都满足总负荷量不超过预期负荷这一关键约束。具有逐利性的负荷在极端情况影响下的负荷表现大致可以分为以下三个阶段。
1)正常运行阶段。正常状态运行时,逐利型负荷的大小为事先规划的基线负荷Pd,在不断电的前提下,按照基线负荷运行能够顺利完成当日生产目标。
2)断电阶段。逐利型负荷因遭遇极端情况产生断电现象,负荷大小瞬间下降为零。断电造成了逐利型负荷的负荷缺失,使其往往无法按照计划达成生产需求。
3)供电恢复阶段。在供电恢复时,由于断电阶段造成的负荷缺失,正常生产难以达到需求,因此,逐利型负荷在供电恢复后往往会扩大生产规模,出现不同于常态的负荷表现。断电时间越长,负荷缺失越大,在恢复供电时异于常态的负荷表现越明显。需要说明的是,由于每日生产目标固定,因此在恢复供电时负荷虽出现高于基线负荷的现象,但总多余负荷不会超过断电时期的总负荷缺失。
节点中所存在的这一类负荷能够在一定范围内调整用电量,可通过用户的主观决策改变负荷大小,本文将这类负荷归结为主观驱动型负荷。主观驱动型负荷断电后的行为可具体概括为受逐利特性影响,以至于在供电恢复时基线负荷大小无法满足用户的需求,最终导致负荷表现改变,其行为改变主要受负荷恢复决策的制约,即主观驱动型负荷的决策依赖特性。
1.2.2 建模方法
在建立主观驱动型负荷模型的过程中需充分考虑负荷逐利特性,主观驱动型负荷不仅要考虑电价Ci,t,如果是工业园区,还需要考虑预期生产目标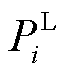 与单位负荷缺失所造成的经济损失
与单位负荷缺失所造成的经济损失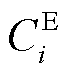 。在恢复供电后一定时间内若未完成生产目标,将造成一定程度上的经济损失。因此主观驱动型负荷约束为
。在恢复供电后一定时间内若未完成生产目标,将造成一定程度上的经济损失。因此主观驱动型负荷约束为
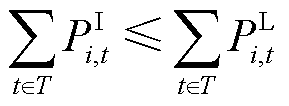 (5)
(5)
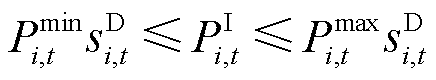 (6)
(6)
式中,PL i,t为在t时刻节点i的预测功率;PI i,t为工业园区i在t时刻的实际功率;T为时间的集合;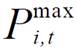 与
与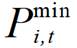 分别为t时刻节点i负荷调节功率范围的上、下限;
分别为t时刻节点i负荷调节功率范围的上、下限;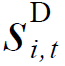 为二进制01变量,表示负荷是否投入使用。
为二进制01变量,表示负荷是否投入使用。
式(5)是主观驱动型负荷最主要的约束条件,其表示在达到预计生产目标之后,工业园区便不再生产,即实际负荷总量不可能超过预期负荷量。也可理解为居民虽调整自身用电负荷,但是用电总量不超过正常情况下的用电量;式(6)表示节点负荷上、下限约束。
需要说明的是,逐利型负荷虽然建模思路与可转移负荷相似,但可转移负荷是被动接受电网公司或聚合商的调控,断电时长大致确定,并且负荷大小通常受电价等经济激励影响,不存在单位负荷缺失所产生的经济损失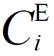 ;而逐利型负荷是用户根据自身运行状况主动决策,且受极端情况影响,断电时长通常无法事前确定。
;而逐利型负荷是用户根据自身运行状况主动决策,且受极端情况影响,断电时长通常无法事前确定。
在电力网络恢复的过程中,配电网的主要目的是尽快恢复负荷,而对于用户而言,负荷特性会受到配电网恢复供电决策影响。配电网决策与用户侧负荷中的部分变量相互被约束为彼此问题的最优解,是典型的双层模型。
2.1.1 上层模型
为了尽可能地减少自然灾害等不确定因素对配电网造成的影响,配电网的优化运行通常以最大化负荷恢复量为目标,即
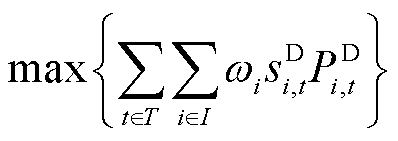 (7)
(7)
式中,PD i,t为节点i负荷在时间t时的有功功率;wi为负荷权重;I为节点集合。
约束条件如下:
1)潮流约束
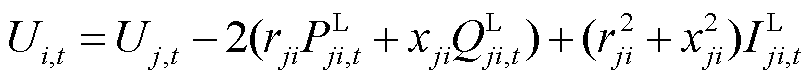 (8)
(8)
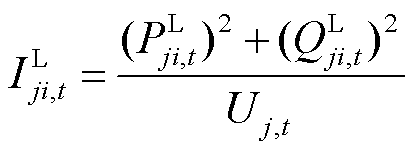 (9)
(9)
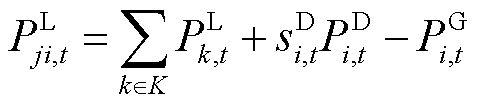 (10)
(10)
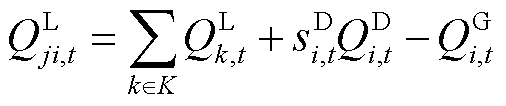 (11)
(11)
式中,Ui,t为节点i电压的二次方;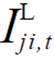 为线路电流的二次方;
为线路电流的二次方;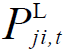 与
与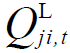 分别为线路上的有功功率和无功功率;rji与xji分别为线路的电阻与电抗;
分别为线路上的有功功率和无功功率;rji与xji分别为线路的电阻与电抗;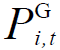 、
、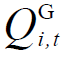 分别为节点i燃气轮机组有功功率、无功功率;K为与节点i相连的节点k的集合。
分别为节点i燃气轮机组有功功率、无功功率;K为与节点i相连的节点k的集合。
由于式(9)是非凸的,因此将其松弛为
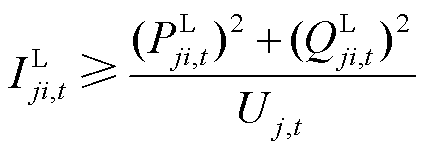 (12)
(12)
2)负荷恢复序列约束
 (13)
(13)
3)电压约束
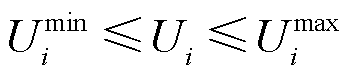 (14)
(14)
式中,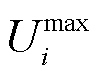 、
、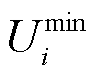 分别为节点i电压二次方最大值与最小值。
分别为节点i电压二次方最大值与最小值。
4)有功无功约束
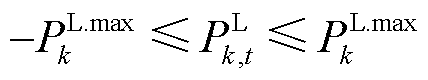 (15)
(15)
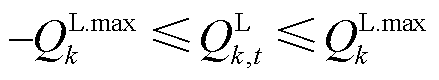 (16)
(16)
式中,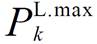 与
与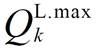 分别为线路所能承受的最大有功功率和无功功率。
分别为线路所能承受的最大有功功率和无功功率。
5)变电站容量限制
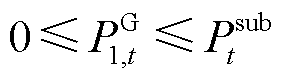 (17)
(17)
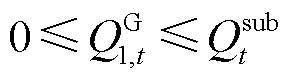 (18)
(18)
6)燃气轮机组的限制
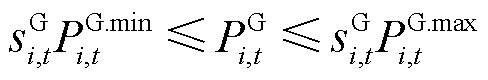 (19)
(19)
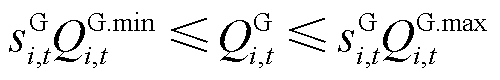 (20)
(20)
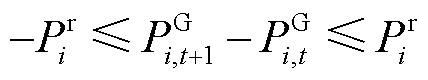 (21)
(21)
式中,Pr i为节点i燃气轮机组的功率的爬坡速率限制;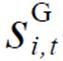 是0-1变量,表示节点i燃气轮机组是否投入使用;
是0-1变量,表示节点i燃气轮机组是否投入使用;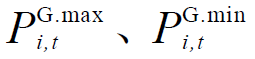 分别为节点i燃气轮机组在t时刻有功功率的最大值与最小值;
分别为节点i燃气轮机组在t时刻有功功率的最大值与最小值;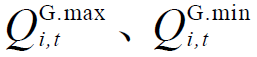 分别为节点i燃气轮机组在t时刻无功功率的最大值与最小值。
分别为节点i燃气轮机组在t时刻无功功率的最大值与最小值。
2.1.2 下层模型
下层模型的决策主体是用户,在极端情况下用户所关心的是经济损失最小,因此下层模型以最小化用电费用为目标,即
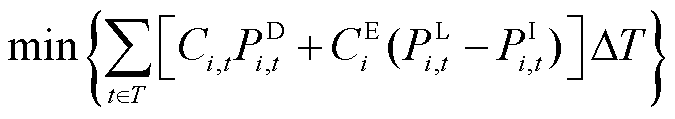 (22)
(22)
式中,Ci,t为节点i在t时刻的电价;ΔT为时间段。
基于以往的历史数据,本文借助MLP构建了负荷大小与断电时长ti,1和恢复时长ti,2的自适应关系,构造出负荷大小与决策序列的关系函数,断电时长与恢复时长可用决策序列sD i,t表述为
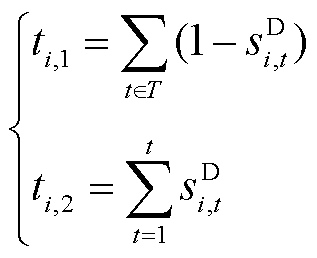 (23)
(23)
因此下层模型约束条件为
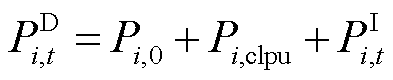 (24)
(24)
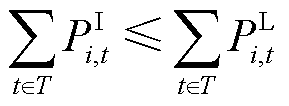 (25)
(25)
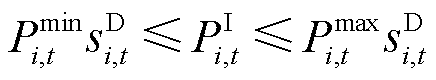 (26)
(26)
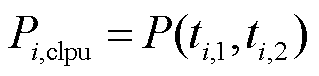 (27)
(27)
式中,Pi,0为节点i负荷中的固定负荷;Pi,clpu为节点i负荷中的温控负荷;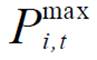 与
与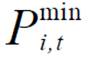 分别为t时刻负荷调节功率范围的上、下限;函数P为本文训练的MLP模型,其输出值仅与断电时长和恢复供电时长有关。
分别为t时刻负荷调节功率范围的上、下限;函数P为本文训练的MLP模型,其输出值仅与断电时长和恢复供电时长有关。
2.1.3 模型求解方法
在负荷恢复序列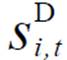 确定以后,下层模型的优化问题属于简单的规划问题,因此,可以通过KKT条件对下层模型进行处理,处理的约束条件除了式(23)~式(27)之外,还具有拉格朗日乘子相关约束条件,即
确定以后,下层模型的优化问题属于简单的规划问题,因此,可以通过KKT条件对下层模型进行处理,处理的约束条件除了式(23)~式(27)之外,还具有拉格朗日乘子相关约束条件,即
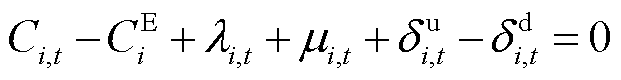 (28)
(28)
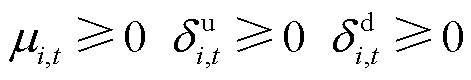 (29)
(29)
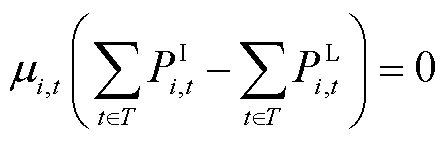 (30)
(30)
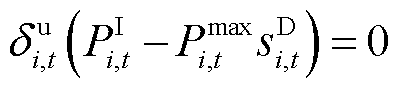 (31)
(31)
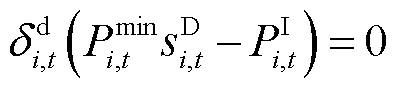 (32)
(32)
式中,λi,t为式(24)的拉格朗日乘子;μi,t为不等式(25)的拉格朗日乘子;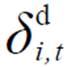 与
与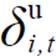 分别为式(26)左右两侧的拉格朗日乘子。
分别为式(26)左右两侧的拉格朗日乘子。
借助KKT条件可将双层模型简化成单层模型,具体表述为
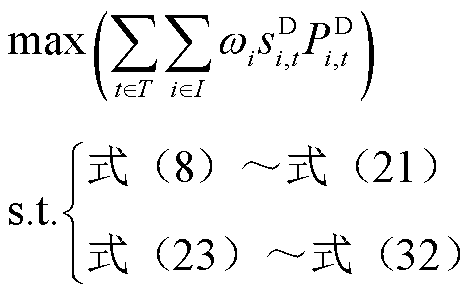 (33)
(33)
经过KKT条件处理之后,原有的双层优化问题被简化为一个能够通过求解器快速求解的混合整数规划问题。然而这种双层模型的方法计算需要下层提供自身所有负荷信息给配电网,对于用户的隐私保护能力较差,在实际的应用中存在一定的局限性。
针对KKT条件存在的隐私保护能力较差等一系列问题,本文提出了一种基于时间标签序列的配电网自适应恢复模型。先由用户侧计算出不同断电时长所对应负荷曲线,再由配电网自主选择负荷曲线参与优化求解,在减少模型计算量、提高模型求解速度的同时,用户传递给配电网运营商的信息也由价格量等隐私信息转变为负荷曲线。自适应模型具体求解步骤如下。
1)求解用户侧在不同断电时长下的负荷曲线簇。
目标函数为用户侧经济损失最小,约束条件为固定负荷、温控负荷和主观驱动型负荷三种类型负荷的特征约束,即
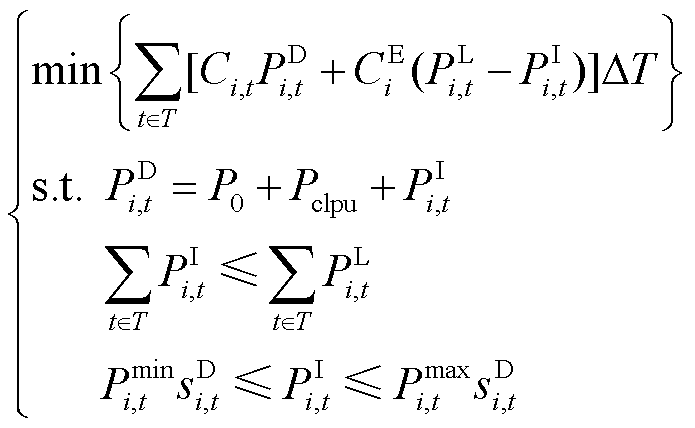 (34)
(34)
将不同的断电时长代入该模型,计算得出带有断电时长标签的负荷曲线,最终得到对应不同断电时间的负荷曲线簇,并将其表征在矩阵Ai中,有
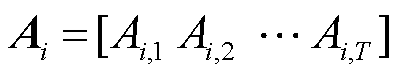 (35)
(35)
2)负荷曲线簇的动态选择。
针对不同的断电时间,节点负荷曲线表示为
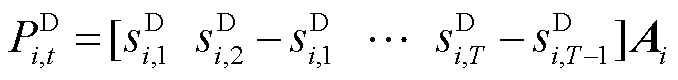 (36)
(36)
使用差分负荷序列能够精准选取所需负荷曲线簇,进而实现对不同断电时长下负荷曲线的动态选择。
3)负荷恢复序列求解。
利用不同断电时间下所求得的负荷曲线矩阵表征优化模型中的负荷量,配电网的自适应恢复模型为
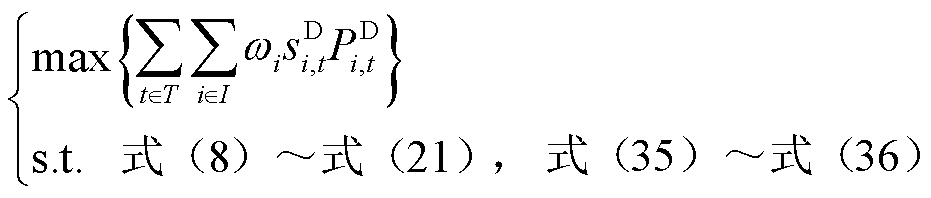 (37)
(37)
采用时间标签序列对负荷曲线进行自主选择的算法伪代码为

算法1:基于时间标签序列的配电网自适应负荷恢复策略 1: Step 1: 初始化2: 初始化全局变量PD i,t和sD i,t3: Step 2: 求解不同断电时长的用户侧负荷曲线4: for t = 1,2,…,tT5: 求解问题,目标函数为式(22),约束条件为式(24)和式(25),得出不同断电时长下的负荷曲线Ai,t6: end for7: Step 3: 求解负荷恢复问题8: 求解问题,目标函数为式(7),约束条件为式(8)~式(21)和式(35)、式(36),得到恢复供电决策sD i,t,以及负荷恢复情况PD i,tOutput: PD i,t、sD i,t
与双层模型相比,该自适应恢复模型仅为单层优化,能够提升模型的计算速度,并且该模型仅需用户侧根据不同的断电时间提供自身的负荷曲线,较好地保护了用户的隐私。
文献[32]中将韧性评估分为静态与动态两种。静态评估手段难以有效地反映受到扰动后的系统性能变化情况,无法准确量化评估系统韧性。而动态韧性评估能准确表述系统的受灾过程,实现对系统韧性的准确评估。系统韧性动态评估主要依赖系统功能曲线,在极端条件下电力系统的功能曲线呈现如图6所示的梯形图状态。
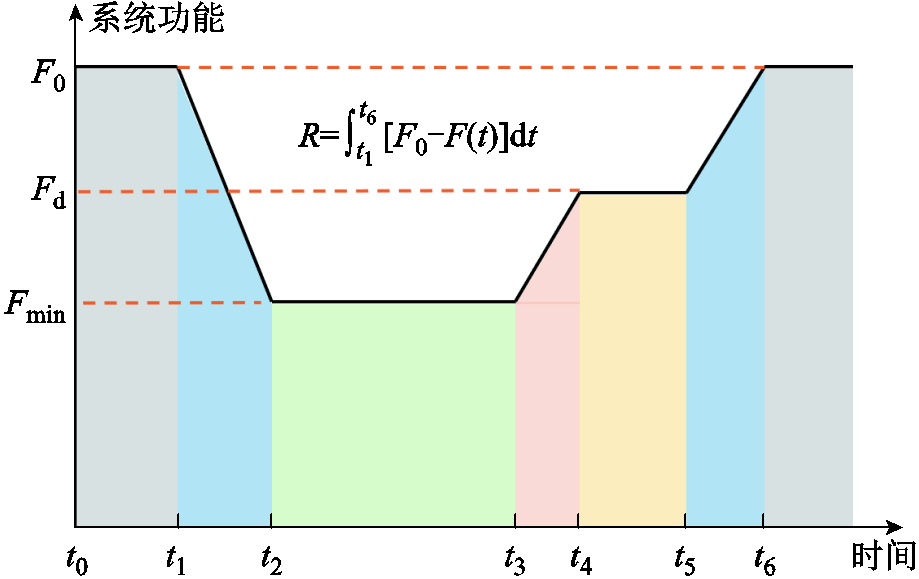
图6 电力系统系统功能曲线[32]
Fig.6 Power system function curve diagram[32]
梯形面积缺失法是韧性评估的传统方式,即计算系统性能曲线在极端事件发生后的面积缺失,即
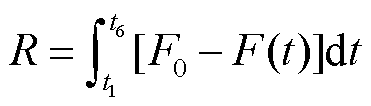 (38)
(38)
梯形缺失面积法可以在一定程度上反映系统的恢复能力和系统的鲁棒性,缺失的面积R越大,表明电力系统的韧性越弱。此外,韧性恢复曲线还包括最大负荷损失R1、负荷中断率R2、自愈恢复时间R3和自愈恢复能力R4等韧性指标。
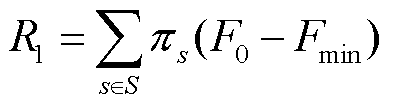 (39)
(39)
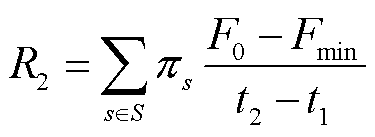 (40)
(40)
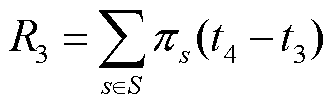 (41)
(41)
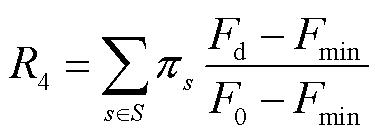 (42)
(42)
式中,F0为故障发生前的系统性能;Fd为采取紧急恢复措施后的系统性能;Fmin为故障适应阶段的系统性能,即在故障时系统的最低性能;S为故障场景集;πs为故障发生概率。各项指标所反映的系统能力见表1。
表1 系统韧性指标及其所反映的系统能力[32]
Tab.1 System resilience indicators and their reflected system capabilities[32]

反映系统能力评估指标 系统韧性R 鲁棒性和吸收能力R1、R2 系统恢复水平R3、R4 决策速度R5
可以看出,除去三种反映系统韧性的指标外,最大负荷损失R1和负荷中断率R2代表了系统的鲁棒性和吸收能力;而自愈恢复时间R3和自愈恢复能力R4用于反映灾害后的系统恢复水平,代表了系统响应的快速性。在此基础之上,本文还使用了模型求解时间R5来衡量负荷恢复模型的求解速度,以此评估系统快速做出决策的能力。
基于皮尔逊相似度的用户敏感性计算方法[33]是一种能够考虑用户对不同信息的隐私偏好等级的隐私泄露量化评估方法,因此本文采用这种方法来评估两种模型的隐私暴露程度。
考虑到用户对于不同的数据有着不同的隐私保护要求,本文对用户断电恢复后的负荷曲线,日前生产目标、单位负荷缺失所造成损失和用户的负荷组成四种信息分别设定不同的隐私偏好等级rik,隐私偏好等级值越大表示用户越不愿意将这些信息告知配电网运营商。可基于四种信息的隐私偏好等级计算出用户信息的平均属性敏感性为
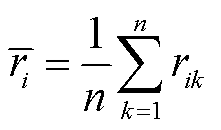 (43)
(43)
式中,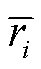 为用户的平均属性敏感性;n为隐私评估指标数量。得到平均属性敏感性后,利用皮尔逊相似度计算用户的隐私敏感性为
为用户的平均属性敏感性;n为隐私评估指标数量。得到平均属性敏感性后,利用皮尔逊相似度计算用户的隐私敏感性为
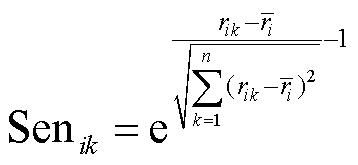 (44)
(44)
在两种方法中,四种隐私评估指标有着不同的曝光程度Expik,用户隐私暴露程度可由曝光程度计算,即
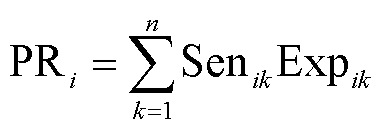 (45)
(45)
式中,PRi为用户的隐私暴露程度;Expik为用户数据的曝光程度,即配电网是否能获取此类隐私信息。设定隐私偏好等级后,便可实现对两种模型隐私泄露程度的准确评估。
本文采用IEEE 33节点和IEEE 123节点进行算例分析。假设配电网在遭遇极端情况断电之后,恢复供电设置5个时间步长,每个时间步长为15 min。为了取得不同断电时长下温控负荷的功率,使用Gurobi求解器在Matlab 2022a中模拟了温控负荷的运行规律,所采用的温控负荷运行参数见文献[31],采用的主观驱动型负荷的运行参数见文献[34]。假设室外温度为34℃,配电网节点为综合节点,由三种不同占比的负荷组成,温控负荷的负荷渗透率为30%,主观驱动型负荷渗透率为20%。假设上级电网也出现故障,但配电网与主网并未完全断开,在供电恢复过程中从主网侧获得功率逐渐增加;且认为恢复过程中处于配电网结构已经确定的负荷恢复阶段,即恢复时不存在线路损坏的现象。为加快负荷恢复,除主变压器外,在IEEE 33节点之中,本文在节点17、节点21和节点24分别接入分布式燃气轮机组。在IEEE 123节点中则在节点6、节点56和节点111设置分布式燃气轮机组。在隐私评估过程中,将负荷曲线、生产目标、负荷组成和单位负荷缺失所造成经济损失四种信息的隐私偏好等级分别设置为0.1、0.9、0.7、0.7。若信息能被配电网运营商获取,则设定其曝光程度为1,反之则设置为0。
为验证所述模型建立方法必要性,本文设置以下四种负荷恢复情景:情景1认为负荷在恢复过程中保持不变;情景2为解释冷负荷回流现象,认为负荷在恢复过程中出现固定变化;情景3在恢复时考虑了负荷的逐利特性;情景4按照本文所提方式恢复,即综合考虑固定负荷、温控负荷和主观驱动型负荷决策。
本文所训练的MLP设置了十个隐藏层神经元,激活函数设置为Sigmoid函数,选取部分输入数值进行差值检验,得到的拟合结果如图7所示。可以看出MLP输出与实际值十分接近,采用MLP能够得到较好的拟合效果。
在负荷恢复的过程中,考虑负荷决策依赖特性与否会使配电网对各节点的负荷理解不同,进而对配电网的开关决策造成影响。
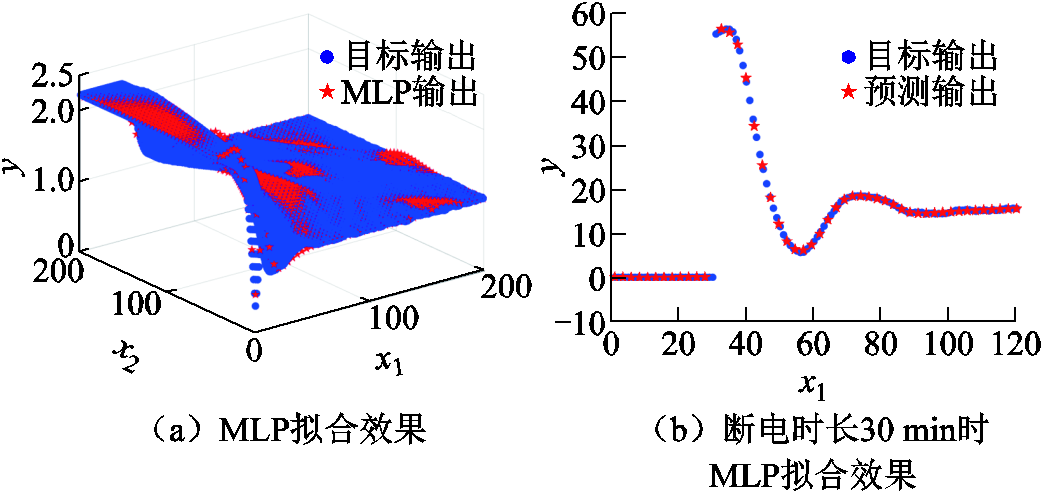
图7 MLP拟合效果
Fig.7 Fitting effect of MLP
配电网的开关决策与供电恢复时的电网潮流密切相关,考虑负荷决策依赖特性与否的负荷表现和开关决策如图8所示。若是将负荷量作为一个恒定不变的量进行供电恢复决策,所得的开关决策与实际情况有着较大的差异。
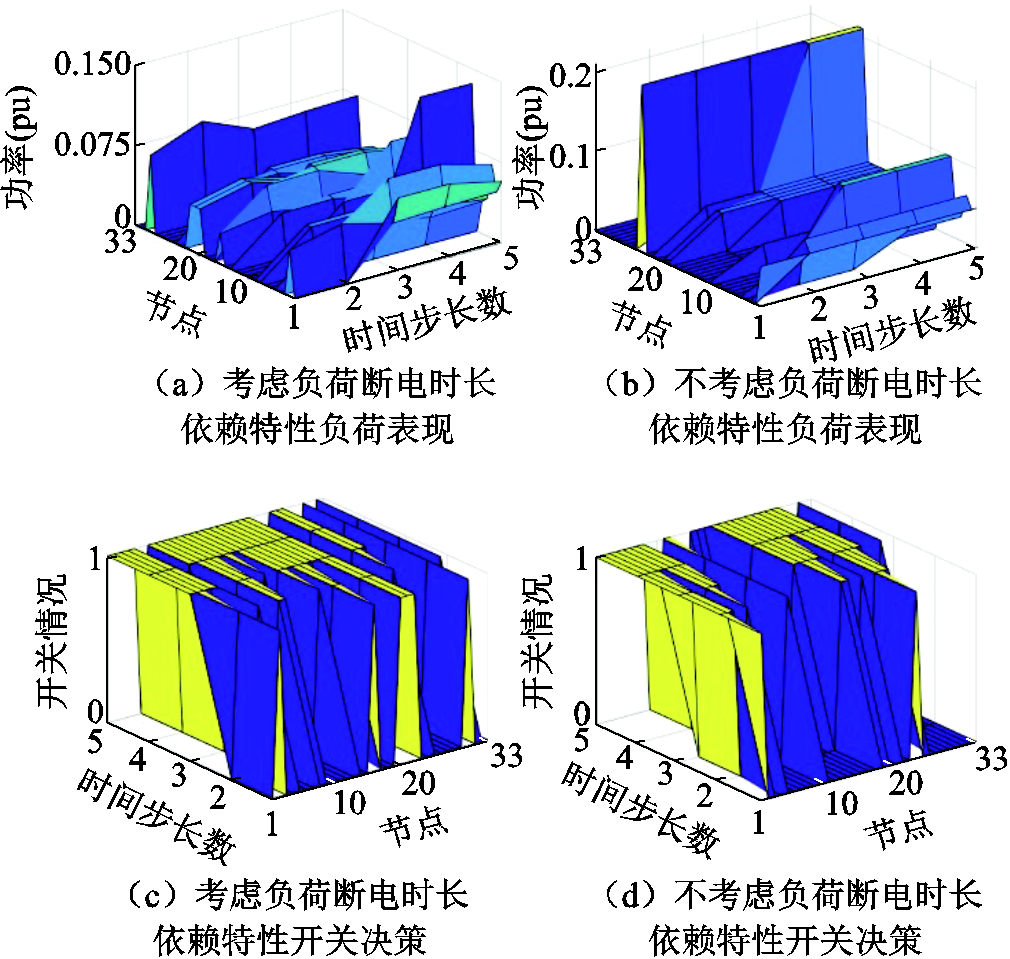
图8 考虑负荷决策依赖特性与否的负荷表现和开关决策
Fig.8 Whether to consider the load performance and switching decision based on decision-dependent behavior
图9和图10分别是IEEE 33节点中负荷恢复30 min时四种情景的节点电压与线路潮流。可以看出,采用情景1~3所作决策的电压与潮流均存在一定程度的越限,其中认为负荷恢复时保持不变(情景1)所做决策越限情况最为严重,出现了大范围的节点越限和四种恢复情景中的最低电压,情景2的越限节点数目较多,情景3的越限程度较为严重。而采用本文所提出的具有决策依赖特性的负荷恢复模型情景4能在恢复过程中确保节点电压与线路潮流不越限,对于配电网安全稳定恢复具有重要意义。
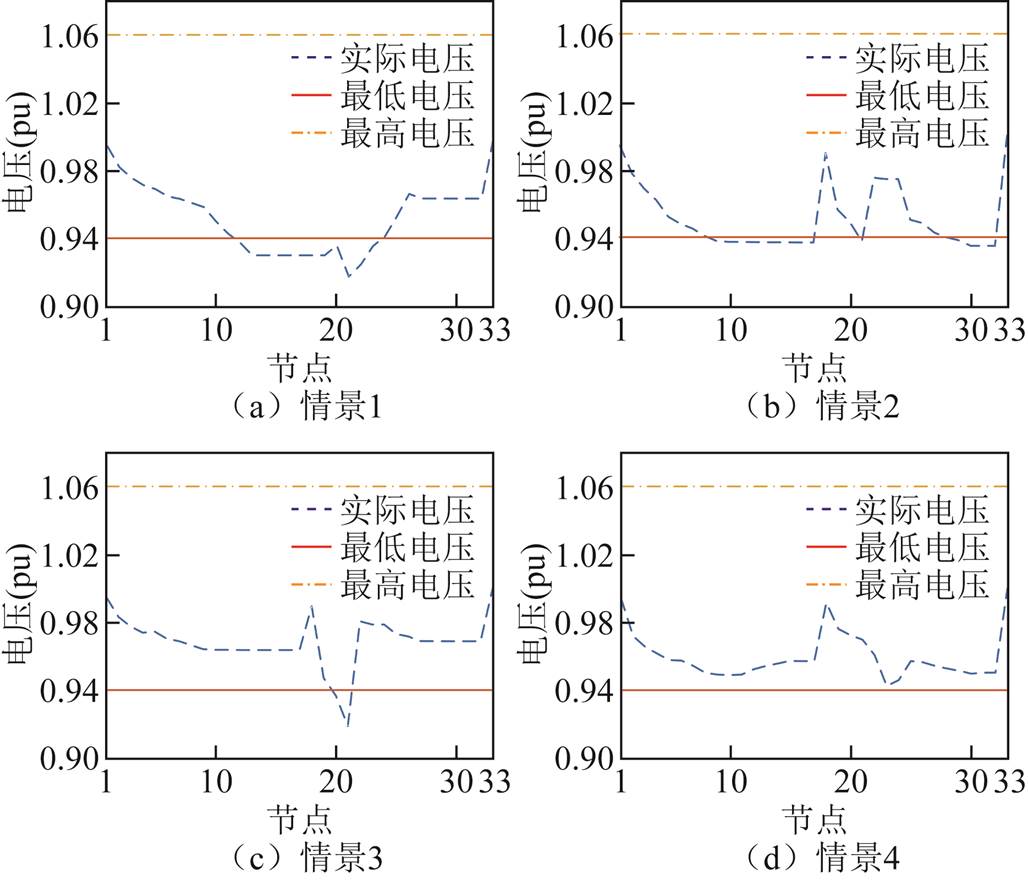
图9 四种情景下的节点电压
Fig.9 Node voltage under four scenarios
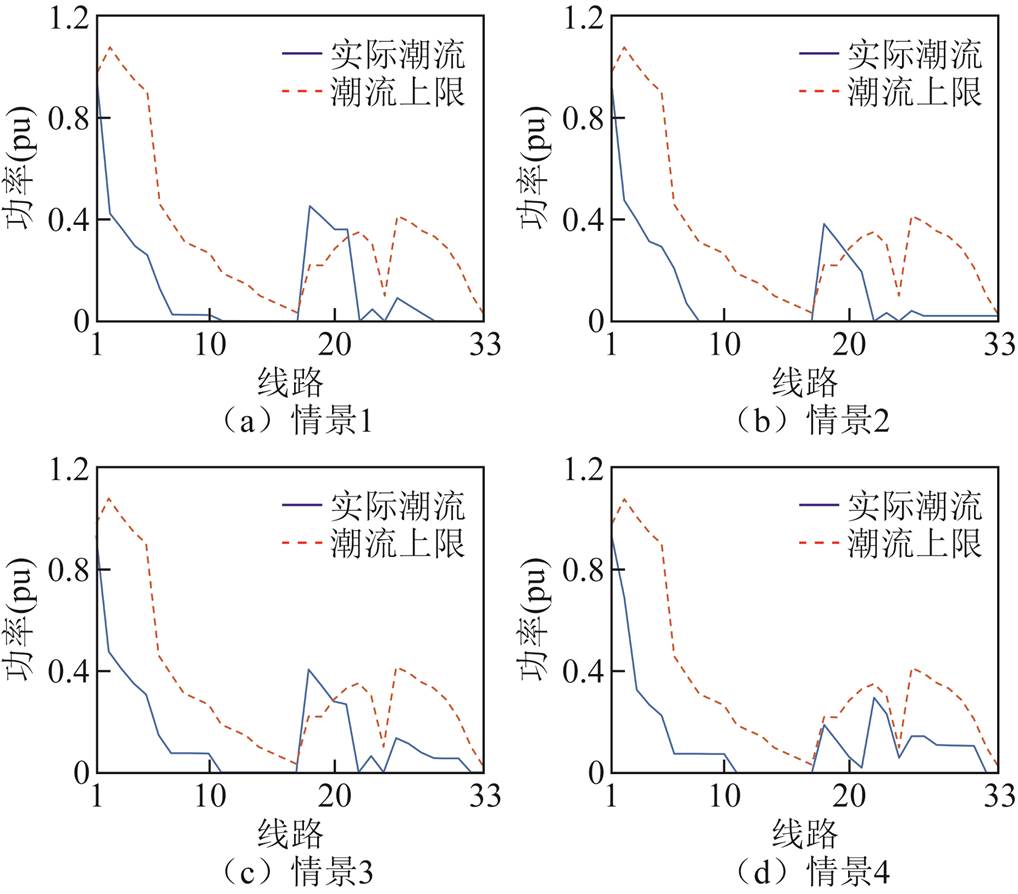
图10 四种情景下的线路潮流
Fig.10 Line trends in four scenarios
四种情景下节点电压与线路潮流具体数据见表2。
表2 四种情景下的节点电压与线路潮流
Tab.2 Line trends and node voltage in four scenarios

情景电压/潮流是否越限电压越限节点数最低电压(pu)潮流越限节点数 情景4否00.941 60 情景1是130.918 74 情景2是130.937 22 情景3是30.919 82
综上所述,在负荷恢复过程中由于存在着多种类型的负荷影响,因此需要对各类负荷的决策依赖特性进行详细分析。若不充分考虑各负荷特性,可能会产生一系列电网电压潮流越限等安全问题。
4.2.1 温控负荷渗透率灵敏度分析
在配电网中,温控负荷的比重能够在很大程度上影响冷负荷回流的负荷表现,温控负荷的渗透率也会直接影响配电网的恢复结果。选取配电网中温控负荷的渗透率分别为10%与50%,求解考虑冷负荷回流与否两种决策的节点电压如图11所示。
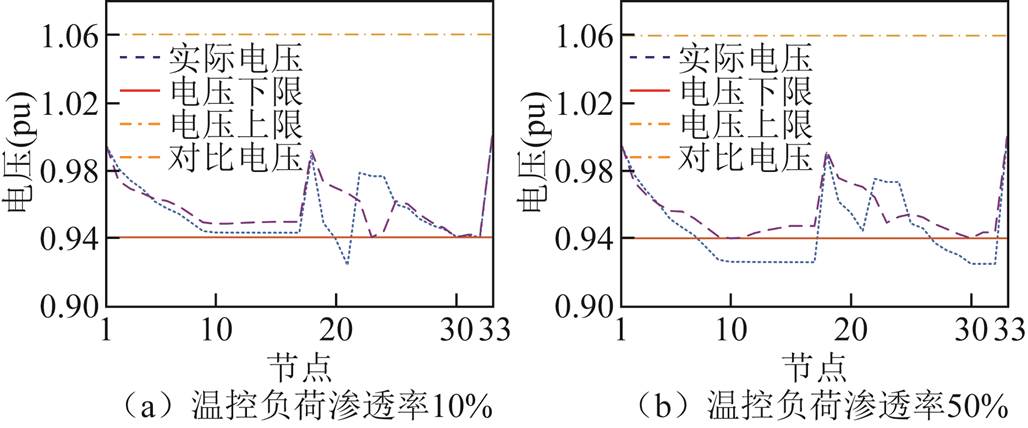
图11 温控负荷渗透率对比分析图
Fig.11 Comparative analysis chart of temperature control load permeability
可以看出,在配电网恢复过程中若不考虑冷负荷回流现象,所做出的配电网恢复决策很可能导致电压的越限,给配电网恢复过程带来极大的不稳定因素。
不同温控负荷渗透率下的节点电压见表3。可以看出,在配电网恢复的过程中不考虑冷负荷回流现象,会造成严重的电压越限,其中电压越限程度和电压越限节点数都会随着温控负荷渗透率的升高而增加。
表3 不同温控负荷渗透率下的节点电压
Tab.3 Node voltage under different temperature control load permeabilities

情况电压是否越限越限节点数最低电压(pu) 考虑冷负荷回流否00.941 6 不考虑冷负荷回流(TCL渗透率10%)是20.929 7 不考虑冷负荷回流(TCL渗透率30%)是100.929 4 不考虑冷负荷回流(TCL渗透率50%)是170.928 2
4.2.2 主观驱动型负荷渗透率灵敏度分析
上述现象不仅局限于温控负荷,同样具有决策依赖特性的主观驱动型负荷也需在负荷恢复过程中充分考虑。
设定配电网中主观负荷渗透率分别为10%与30%,求取考虑主观驱动型负荷与不考虑主观驱动型负荷两种决策情况下的节点电压如图12所示。
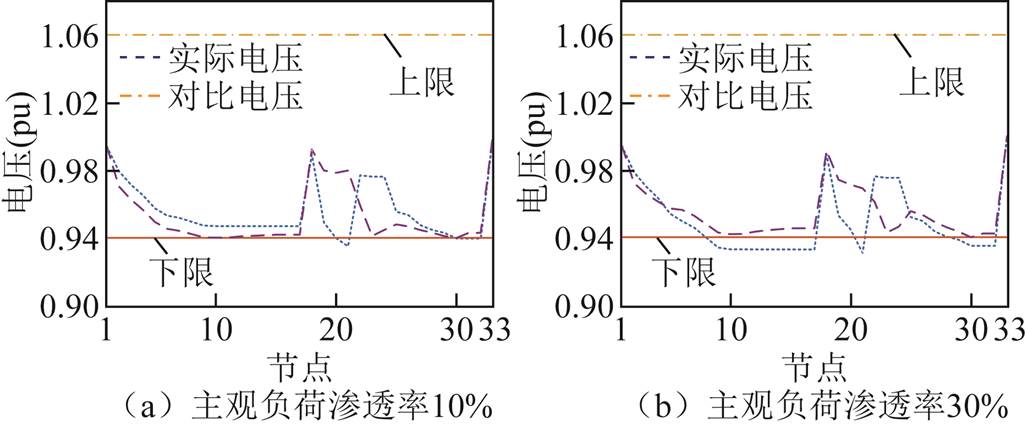
图12 主观负荷渗透率对比分析
Fig.12 Comparative analysis of subjective load permeability
由图12可以看出,若不考虑主观负荷决策,会造成节点电压越限等安全问题,且主观驱动型负荷渗透率越高,电压越限情况越严重。
不同主观驱动型负荷渗透率下的节点电压见表4。可以看出,随着主观驱动型负荷渗透率的增加,越限节点数与电压的越限程度也随之增加。
表4 不同主观驱动型负荷渗透率下的节点电压
Tab.4 Node voltage under different subjective driving load permeability

渗透率(%)越限节点数最低电压(pu) 1020.938 5 20100.929 4 30140.928 5
4.2.3 IEEE 123节点算例分析
上述算例中存在的现象不仅局限于33节点,在IEEE 123节点的负荷恢复过程中也有着类似的负荷表现。在室外温度为34℃时,IEEE 33节点与123节点恢复过程中的负荷组成如图13所示。
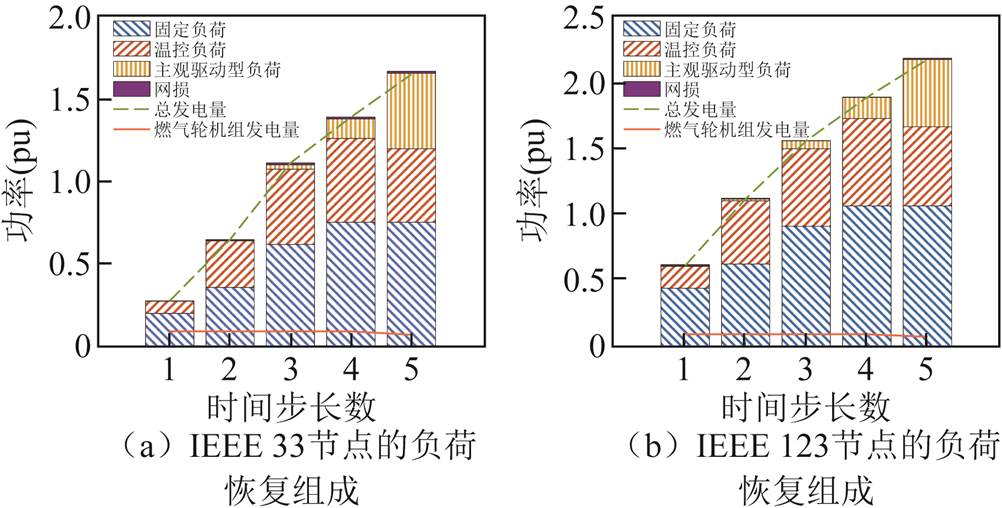
图13 IEEE 123节点恢复过程中的负荷组成
Fig.13 Load composition during recovery process of IEEE 123 nodes
可以看出,在负荷恢复的过程中,IEEE 123节点的负荷表现与IEEE 33节点十分相似,随着恢复时间延长,配电网的功能不断恢复,来自主网的功率不断提升,固定负荷的大小也逐渐增大;而具有冷负荷回流特性的温控负荷,则会先上升到一个负荷最大值,再逐渐回落至定值;对于主观驱动型负荷而言,由于受到电价等因素的调控,在供电恢复初期的负荷量并不大,但为完成计划生产目标,在供电恢复的末期主观驱动型负荷明显上升,呈现出在刚开始恢复供电时主观驱动型负荷量较小,随着时间的推移负荷量明显上升的负荷时变性。
在负荷表现相似的情况下,负荷恢复过程也需对负荷的决策依赖特性进行综合分析。因此选取在负荷恢复30 min时,情景1~3的20号~35号线路,观察其线路潮流越限情况。IEEE 123节点中四种情景下的线路潮流如图14所示。
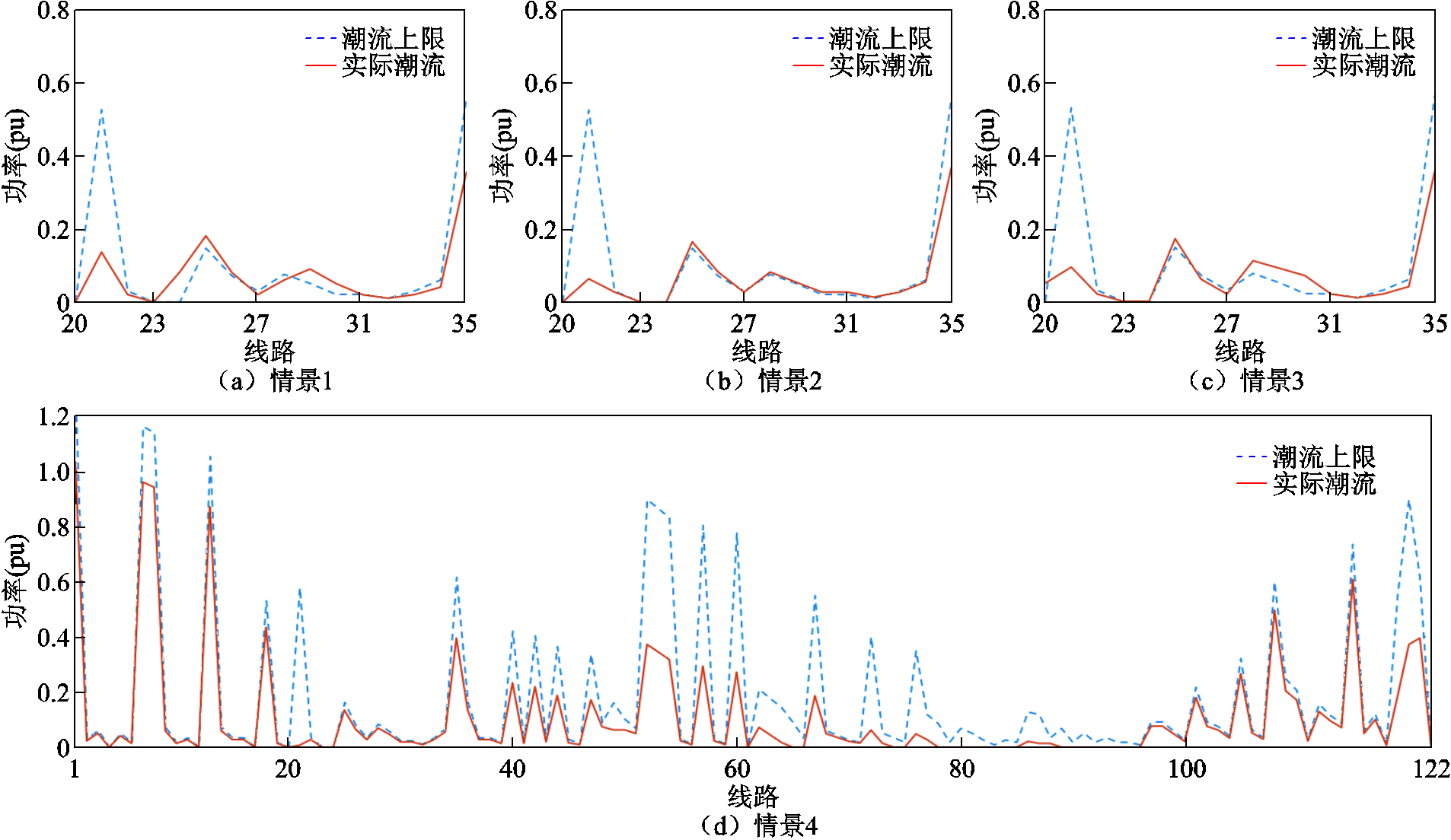
图14 四种情景下的线路潮流(IEEE 123节点)
Fig.14 Line trends in four scenarios(IEEE 123 nodes)
由图14可以看出,在IEEE 123节点中,采用情景1~3所做决策进行负荷恢复,均会造成一定程度的线路潮流越限,其中将负荷视为固定负荷所做决策越限情况最为明显,而采用本文所述方法进行负荷恢复,所有线路均不产生潮流越限。
4.2.4 小结
为验证考虑决策依赖特性的必要性,本文分别在IEEE 33节点与IEEE 123节点中对考虑冷负荷回流现象与否的恢复过程进行仿真模拟,所得差异见表5。
表5 考虑负荷决策依赖特性与否的恢复过程差异
Tab.5 Differences in recovery process considering the decision-dependence behavior

参数数值 考虑决策依赖特性不考虑决策依赖特性 负荷恢复量(33节点,75 min)/MW1.411.97 负荷恢复量(123节点,75 min)/MW1.722.35 潮流是否越限否是 电压是否越限否是
决策依赖特性作为负荷的关键特性,在配电系统恢复中起着重大作用。由表5可以看出,在不考虑负荷决策依赖特性时,恢复的负载将会比实际情况高出30%。若以此做出决策,则实际恢复的负载将远远超过可调度的总发电量,导致系统出现电压、潮流越限等安全问题。
综上所述,负荷决策依赖特性是不可避免的,特别是温控负荷与主观驱动型负荷渗透率高的电力系统。而当模型没有准确描述负荷时变性时,将会导致一系列问题,例如电压、潮流越限和负荷恢复时间的延长。因此,应在模型建立中考虑负荷的决策依赖特性。
在IEEE 33节点算例中,设置温控负荷渗透率为30%,主观驱动型负荷渗透率为20%,室外温度为34℃,每个时间步长为15 min。极端情况发生后,基于时间标签序列的配电网自适应恢复模型计算系统性能曲线及其与KKT条件性能曲线差值如图15所示。由图15可知,两种求解方式所得系统功能曲线十分接近,在同一时间点下的最大差值与系统性能相差四个数量级,可近似认为两种求解方式所得系统性能曲线相等。
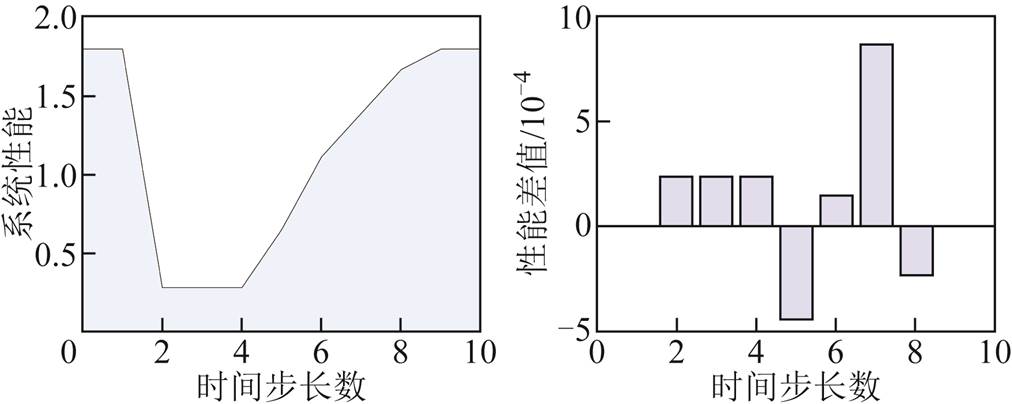
图15 自适应模型性能曲线与性能差值(IEEE 33节点)
Fig.15 Adaptive model performance curve and performance difference graph (IEEE 33节点)
与之相似,在IEEE 123节点算例中,同样设置温控负荷渗透率为30%,主观驱动型负荷渗透率为20%,室外温度为34℃,每个时间步长为15 min。在极端情况发生后,自适应模型系统性能曲线及其与KKT条件性能曲线差值如图16所示,最大差值与系统性能相差三个数量级。
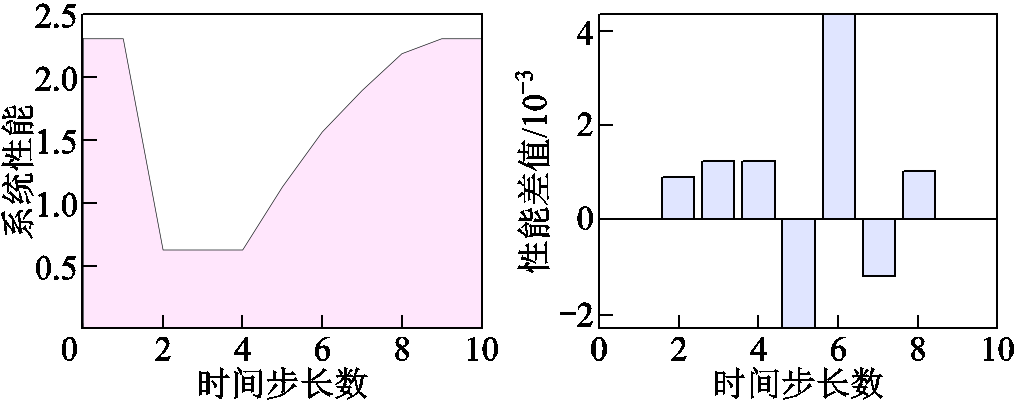
图16 自适应模型性能曲线与性能差值(IEEE 123节点)
Fig.16 Adaptive model performance curve and performance difference graph(IEEE 123 nodes)
将IEEE 33节点与IEEE 123节点的系统性能曲线代入评估模型,KKT条件与自适应模型对比见表6。可以看出,对于相同的电力系统框架,采用双层模型求解与自适应模型求解所得结果并无本质上的不同,求解所得韧性指标近似相等,采用这两种方法并不会影响整个电力系统的鲁棒性与吸收能力,系统灾后恢复水平也并不存在太大的差异,即模型求解方式的不同并不影响系统的韧性。
表6 KKT条件与自适应模型对比
Tab.6 Comparison between KKT conditions and self-adaptive models
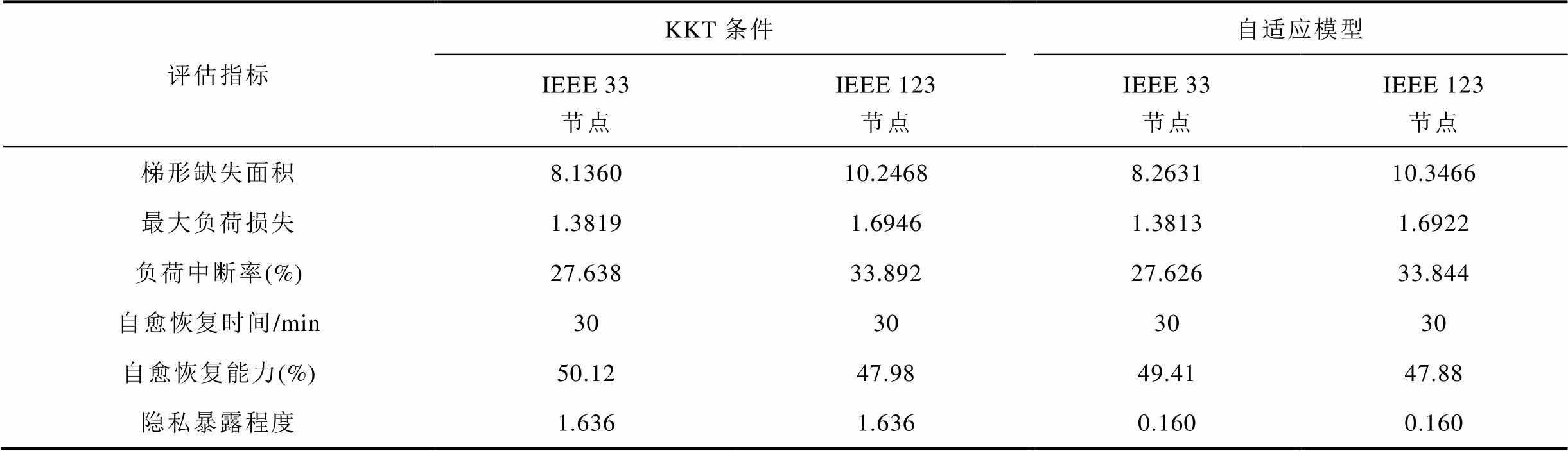
评估指标KKT条件自适应模型 IEEE 33节点IEEE 123节点IEEE 33节点IEEE 123节点 梯形缺失面积8.136010.24688.263110.3466 最大负荷损失1.38191.69461.38131.6922 负荷中断率(%)27.63833.89227.62633.844 自愈恢复时间/min30303030 自愈恢复能力(%)50.1247.9849.4147.88 隐私暴露程度1.6361.6360.1600.160
由于KKT条件增加了模型的约束条件,KKT条件简化双层模型产生的拉格朗日乘子使得决策变量数量上升,增加了模型的复杂程度,因此KKT条件的求解时间比起自适应模型较长。不同拓扑结构下KKT条件与自适应模型求解时间见表7,采用自适应模型的求解速度为双层模型求解速度的三倍,并且大大提高了隐私的保护能力。需要说明的是,由于求解负荷曲线簇可由以往运维数据求解得出,在极端情况发生后的负荷恢复过程,仅需考虑自适应模型的负荷恢复序列求解时间。综上所述,自适应模型能够在保证做出正确决策的前提下缩短求解时间,减小配电网遭受极端情况所带来的经济损失,因此可快速做出决策的自适应模型具有很强的应用价值。
表7 不同拓扑结构下KKT条件与自适应模型求解时间
Tab.7 KKT conditions and solution time of self-adaptive models under different topological structures (单位:s)
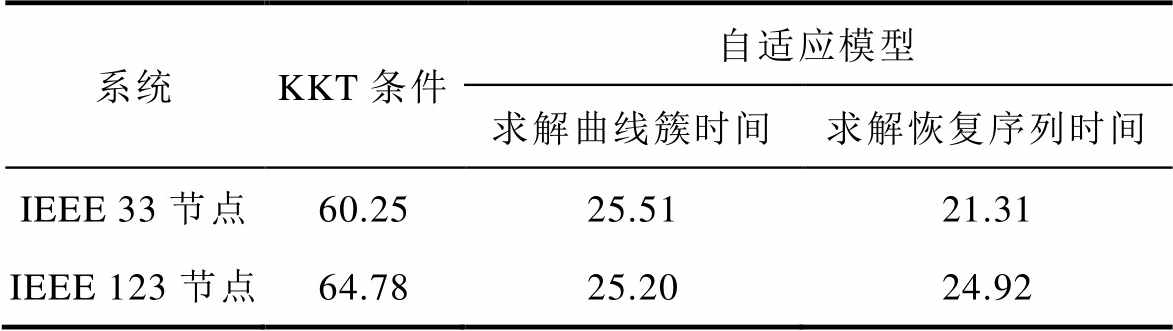
系统KKT条件自适应模型 求解曲线簇时间求解恢复序列时间 IEEE 33节点60.2525.5121.31 IEEE 123节点64.7825.2024.92
针对配电网恢复过程对负荷考量不足的研究现状,本文从主观与客观两个角度深入分析了负荷恢复过程中所出现的决策依赖特性,基于此建立了负荷恢复双层模型。此外,为解决求解双层模型所用KKT条件隐私保护能力不佳的问题,本文提出了一种基于时间标签序列的配电网自适应恢复模型,实现对配电网负荷行为多样化的动态选择。通过算例仿真对比分析,可以得到以下结论:
1)对比结果表明若配电网不考虑负荷的决策依赖特性进行决策,则会产生节点电压、潮流越限等一系列安全隐患。并且不考虑负荷决策依赖特性时,实际恢复的负载将超过可调度的总发电量,进而导致系统安全问题。
2)恢复过程中若不考虑负荷的决策依赖特性进行决策,室外温度越高,温控负荷与主观驱动型负荷渗透率越大,则电压越限的节点数目就越多,超出电压范围的现象也越严重。
3)通过评估指标的对比,本文所提出的基于“时间标签”技术的配电网自适应恢复模型在不影响配电网韧性的情况下,所用时间仅占传统双层模型的33%,而且具有较强的隐私保护能力,能够对配电网在极端情况下快速做出决策提供有力支持。
参考文献
[1] 高海翔, 陈颖, 黄少伟, 等. 配电网韧性及其相关研究进展[J]. 电力系统自动化, 2015, 39(23): 1-8.
Gao Haixiang, Chen Ying, Huang Shaowei, et al. Distribution systems resilience: an overview of research progress[J]. Automation of Electric Power Systems, 2015, 39(23): 1-8.
[2] Chen Kening, Wu Wenchuan, Zhang Boming, et al. Robust restoration decision-making model for distribution networks based on information gap decision theory[J]. IEEE Transactions on Smart Grid, 2015, 6(2): 587-597.
[3] 国家发改委. “十四五”全国城市基础设施建设规划[R/OL]. [2022-07-31]. https://www.gov.cn/zhengce/ zhengceku/2022-07/31/5703690/files/d4ebd608827e 41138701d06fe6133cdb.pdf.
[4] Liu Rongpeng, Hou Yunhe, Li Yujia, et al. Sample robust scheduling of electricity-gas systems under wind power uncertainty[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5889-5900.
[5] Wang Chong, Wang Zhaoyu, Hou Yunhe, et al. Dynamic game-based maintenance scheduling of integrated electric and natural gas grids with a bilevel approach[J]. IEEE Transactions on Power Systems, 2018, 33(5): 4958-4971.
[6] Chen Chen, Wang Jianhui, Qiu Feng, et al. Resilient distribution system by microgrids formation after natural disasters[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 958-966.
[7] 赵冬梅, 王浩翔, 陶然. 计及风电-负荷不确定性的风-火-核-碳捕集多源协调优化调度[J]. 电工技术学报, 2022, 37(3): 707-718.
Zhao Dongmei, Wang Haoxiang, Tao Ran. A multi-source coordinated optimal scheduling model considering wind-load uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 707-718.
[8] 许寅, 王颖, 和敬涵, 等. 多源协同的配电网多时段负荷恢复优化决策方法[J]. 电力系统自动化, 2020, 44(2): 123-131.
Xu Yin, Wang Ying, He Jinghan, et al. Optimal decision-making method for multi-period load restoration in distribution network with coordination of multiple sources[J]. Automation of Electric Power Systems, 2020, 44(2): 123-131.
[9] 罗伟, 李长城, 琚上纯, 等. 考虑孤岛融合的配电系统多源协同恢复策略[J]. 电网技术, 2022, 46(4): 1485-1495.
Luo Wei, Li Changcheng, Ju Shangchun, et al. Multi-source cooperative restoration strategy for distribution system considering islanding integration[J]. Power System Technology, 2022, 46(4): 1485-1495.
[10] Ma Shanshan, Chen Bokan, Wang Zhaoyu. Resilience enhancement strategy for distribution systems under extreme weather events[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1442-1451.
[11] 李超, 苗世洪, 盛万兴, 等. 考虑动态网络重构的主动配电网优化运行策略[J]. 电工技术学报, 2019, 34(18): 3909-3919.
Li Chao, Miao Shihong, Sheng Wanxing, et al. Optimization operation strategy of active distribution network considering dynamic network reconfiguration [J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3909-3919.
[12] 李晓宇. 基于机器学习的配电网络拓扑生成及重构优化研究[D]. 北京: 北京邮电大学, 2019.
Li Xiaoyu. Research on topology generation and reconfiguration of distribution network based on machine learning[D]. BeiJing: Beijing University of Posts and Telecommunications, 2019.
[13] 王维. 考虑间歇性分布式电源出力不确定性的配电网故障恢复策略[D]. 北京: 北京交通大学, 2022.
Wang Wei. Service restoration strategy of distribution network considering output uncertainty of intermittent distributed generation[D]. Beijing: Beijing Jiaotong University, 2022.
[14] 王颖, 祝士焱, 许寅, 等. 考虑多类型储能协同的重要负荷恢复方法[J]. 电力自动化设备, 2022, 42(1): 72-78.
Wang Ying, Zhu Shiyan, Xu Yin, et al. Critical load restoration method considering coordination of multiple types of energy storage[J]. Electric Power Automation Equipment, 2022, 42(1): 72-78.
[15] 刘峰伟, 陈佳佳, 赵艳雷, 等. 端对端交易模式下基于移动储能共享的配电系统韧性提升[J]. 电力系统自动化, 2022, 46(16): 151-159.
Liu Fengwei, Chen Jiajia, Zhao Yanlei, et al. Resilience enhancement for distribution system based on mobile energy storage sharing in peer-to-peer transaction mode[J]. Automation of Electric Power Systems, 2022, 46(16): 151-159.
[16] 陈碧云, 金洋, 徐旗, 等. 计及灾后恢复全过程储能应急响应能力的配电网韧性规划[J/OL]. 电网技术, 2023: 1-8[2023-08-18]. https://doi.org/10.13335/j. 1000-3673.pst.2023.0556.
Chen Biyun, Jin Yang, Xu Qi, et al. Resilience planning of distribution network considering emergency response capability of energy storage throughout the entire process of post-disaster recovery[J/OL]. Power System Technology, 2023, 1-8[2023-08-18]. https://doi.org/10.13335/j.1000-3673. pst.2023. 0556.
[17] Zhang B, Zhang L, Tang W, et al. A coordinated restoration method of electric buses and network reconfiguration in distribution systems under extreme events[J/OL]. CSEE Journal of Power and Energy Systems, 2021. doi: 10.17775/CSEEJPES.2020.04320.
[18] 陈厚合, 丛前, 姜涛, 等. 多能协同的配电网供电恢复策略[J]. 电工技术学报, 2022, 37(3): 610-622, 685.
Chen Houhe, Cong Qian, Jiang Tao, et al. Distribution systems restoration with multi-energy synergy[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 610-622, 685.
[19] Poudel S, Dubey A, Schneider K P. A generalized framework for service restoration in a resilient power distribution system[J]. IEEE Systems Journal, 2022, 16(1): 252-263.
[20] Mirza O H. Usage of CLPU curve to deal with the cold load pickup problem[J]. IEEE Transactions on Power Delivery, 1997, 12(2): 660-667.
[21] Schneider K P, Sortomme E, Venkata S S, et al. Evaluating the magnitude and duration of cold load pick-up on residential distribution using multi-state load models[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3765-3774.
[22] Uçak C, Pahwa A. Optimal step-by-step restoration of distribution systems during excessive loads due to cold load pickup[J]. Electric Power Systems Research, 1995, 32(2): 121-128.
[23] Arif A, Ma Shanshan, Wang Zhaoyu, et al. Optimizing service restoration in distribution systems with uncertain repair time and demand[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6828-6838.
[24] Li Yiyan, Yan Zheng, Chen Sijie, et al. Operation strategy of smart thermostats that self-learn user preferences[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5770-5780.
[25] 宋梦, 周佳妮, 高赐威, 等. CPSS视角下城市建筑与配电网高韧性协调运行:研究述评与展望[J]. 电力系统自动化, 2023, 47(23): 105-121.
Song Meng, Zhou Jiani, Gao Ciwei, et al. High-resilience coordinated operation of urban buildings and distribution networks from cyber-physical-social system perspective: research review and prospect[J]. Automation of Electric Power Systems, 2023, 47(23): 105-121.
[26] 范睿, 孙润稼, 刘玉田. 考虑空调负荷需求响应的负荷恢复量削减方法[J]. 电工技术学报, 2022, 37(11): 2869-2877.
Fan Rui, Sun Runjia, Liu Yutian. A load restoration amount reduction method considering demand response of air conditioning loads[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2869-2877.
[27] Song Meng, Nejad R R, Sun Wei. Robust distribution system load restoration with time-dependent cold load pickup[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3204-3215.
[28] 聂世豪, 李桐, 陈磊, 等. 投切型温控负荷一次调频策略及电网侧聚合建模[J]. 中国电机工程学报, 2022, 42(增刊1): 1-11.
Nie Shihao, Li Tong, Chen Lei, et al. Primary frequency modulation strategy of switching temperature control load and aggregation modeling of power grid side[J]. Proceedings of the CSEE, 2022, 42(S1): 1-11.
[29] 王栋. 参与电网快速调频的变频空调负荷虚拟同步机调控技术研究[D]. 南京: 东南大学, 2020.
Wang Dong. Research on regulation technology of inverter air conditioning load virtual synchronous machine for fast grid frequency modulation[D]. Nanjing: Southeast University, 2020.
[30] 吴润基, 王冬骁, 谢昌鸿, 等. 空调负荷参与配电网电压管理的分布式控制方法[J]. 电力系统自动化, 2021, 45(6): 215-222.
Wu Runji, Wang Dongxiao, Xie Changhong, et al. Distributed control method for air-conditioning load participating in voltage management of distribution network[J]. Automation of Electric Power Systems, 2021, 45(6): 215-222.
[31] Song Meng, Gao Ciwei, Shahidehpour M, et al. State space modeling and control of aggregated TCLs for regulation services in power grids[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4095-4106.
[32] 陈磊, 邓欣怡, 陈红坤, 等. 电力系统韧性评估与提升研究综述[J]. 电力系统保护与控制, 2022, 50(13): 11-22.
Chen Lei, Deng Xinyi, Chen Hongkun, et al. Review of the assessment and improvement of power system resilience[J]. Power System Protection and Control, 2022, 50(13): 11-22.
[33] 谢小杰, 梁英, 王梓森, 等. 社交网络用户隐私泄露量化评估方法[J]. 计算机工程与科学, 2021, 43(8): 1376-1386.
Xie Xiaojie, Liang Ying, Wang Zisen, et al. A quantitative evaluation method of social network users' privacy leakage[J]. Computer Engineering & Science, 2021, 43(8): 1376-1386.
[34] 陆秋瑜, 江里舟, 别朝红, 等. 考虑用户能量优化调度的配电网灾后故障恢复策略[J]. 电力系统自动化, 2023, 47(1): 44-54.
Lu Qiuyu, Jiang Lizhou, Bie Chaohong, et al. Post-disaster fault restoration strategy for distribution network considering optimal scheduling of user-side energy[J]. Automation of Electric Power Systems, 2023, 47(1): 44-54.
Abstract The urban distribution system (DS) serves as a crucial link between end-users and the transmission grid, having a direct impact on the quality of power supply. However, DS is relatively more vulnerable to extreme events in comparison to the transmission network. Hence, it has been an urgent priority to enhance the resilience of DS. In recent years, the approach to enhancing DS resilience moving away from traditional load tracking of power sources to a source-grid-load-storage perspective as the structure evolution of DS caused by the high proportion of renewable generation. However, the study of load behavior on the demand side still has limitations, particularly in terms of precise modeling. Representatively, most literature consider the thermal control loads (TCL) as rigid loads or characterizes their cold load pick-up (CLPU) phenomenon as a fixed curve neglecting the dependence on the outage duration. Similarly, the time-varying, diverse, and complex nature of urban building loads under extreme conditions is seldom addressed in relevant papers. This significant deviation from real-world scenarios greatly impacts the applicability of relevant theoretical models and directly restrict the analysis of the load restoration process.
Therefore, this paper conducts the following works to address the actual scenario of load restorations in DS. Firstly, the study delves into the dynamic coupling evolution law between urban time-varying loads and DS decision sequences under extreme conditions, considering both objective and subjective reasons. It accurately quantifies the complex behavior of urban building loads during the process of DS restoration in a universal and low-dimensional manner. The paper also explains the dependence of loads on DS restoration sequences, analyzing the decision-dependency characteristics of load from both subjective and objective perspectives. Secondly, the interaction between the DS and end-user decision-making constitutes a bi-level model. This paper employs the Karush-Kuhn-Tucker (KKT) conditions to solve and analyze a bi-level model that integrates the load side of the distribution network. This simplifies the model calculation while accurately identifying the optimal solution for the upper distribution network and the lower load side. Additionally, the paper proposes a data-driven modeling method and introduces a differential calculation adaptive model based on “time tag” technology and load restoration decision sequences. This adaptive model enables dynamic selection of diversified load behavior in distribution networks. Finally, the paper summarizes various indicators for evaluating the resilience of distribution networks and utilizes existing research results to compare and analyze the traditional double-layer model with the proposed adaptive model from six perspectives. The evaluation takes the system function curve of DS during the load recovery process as a starting point, allowing for an assessment of the advantages and disadvantages of the two models.
Case studies shows that the lack of consideration for loads’ decision-dependency characteristics leads to the violations of node voltage and line flow, which positively correlated with penetration of TCLs and subjective driven load. Additionally, case studies also shows that the adaptive model can achieve fault restoration without affecting the resilience of the distribution network. While better protecting user privacy, it only takes 33% of the time of traditional bi-level models.
Overall, this research provides valuable insights into load restoration under extreme conditions for urban DS. It provides a comprehensive analysis and optimization method ensures more efficient and effective decision-making processes. Meanwhile, the proposed method facilitates prompt decision-making without affecting the resilience of DS. Its solution time cost only accounts for 33% compared to the traditional bi-level model.
keywords:Distribution system, resilience, cold load pick-up, load restoration, decision-dependent behaviors
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.231828
国家自然科学基金项目(52277085)、江苏省科协青年科技人才托举工程(TJ-2022-042)、东南大学“至善青年学者”支持计划、中国电机工程学会“青年人才托举工程”项目和南京市留学人员科技创新项目资助。
收稿日期 2023-11-03
改稿日期 2024-02-03
邓荣楠 男,2001年生,硕士研究生,研究方向为配电网韧性提升与优化运行。E-mail:220233013@seu.edu.cn
宋 梦 女,1989年生,副教授,博士生导师,研究方向为需求响应与虚拟电厂、配电网韧性提升与优化运行、可交易能源与共享储能等。E-mail:msong_seu@seu.edu.cn(通信作者)
(编辑 赫 蕾)