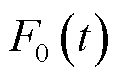 和
和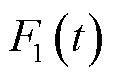 。在极端灾害干扰下,弹性配电网经历以下三个阶段:灾前防御阶段t0~t1、灾害发生阶段t1~t3和灾后恢复阶段t3~t4。本文重点研究台风灾害下配电网对关键负荷的支撑能力和恢复能力,因此,定义弹性指标为台风灾害下受灾配电网的累积失电负荷成本,即附图1中阴影部分的面积
。在极端灾害干扰下,弹性配电网经历以下三个阶段:灾前防御阶段t0~t1、灾害发生阶段t1~t3和灾后恢复阶段t3~t4。本文重点研究台风灾害下配电网对关键负荷的支撑能力和恢复能力,因此,定义弹性指标为台风灾害下受灾配电网的累积失电负荷成本,即附图1中阴影部分的面积 为
为摘要 为准确地刻画台风时空特性造成配电网故障的不确定性,有效地挖掘灵活性资源协同优化的弹性提升潜力,该文提出一种计及台风时空特性和灵活性资源协同优化的配电网弹性提升策略。首先,由台风路径模型和Batts风场模型构建台风时空演变模型;其次,根据结构可靠性原理,分析线路元件强度和荷载效应,计算配电线路的时变故障率,并采用信息熵识别脆弱线路;再次,采用线路加固、分布式电源(DG)、储能(ESS)和智能软开关(SOP)等灵活性资源多维度协调提升配电网弹性,以配电网在台风灾害下的失电负荷成本为弹性量化指标,建立灾前防御和灾后恢复相结合的两阶段三层防御-攻击-防御(DAD)模型,并采用列-约束生成算法进行求解;最后,在我国东部沿海某城市51节点系统上进行仿真测试,分析台风时空特性对配电网的影响,并验证灵活性资源提升配电网弹性的有效性。
关键词:台风灾害 灵活性资源 弹性提升 时空特性 鲁棒优化
近年来,受全球气候变化的影响,台风、地震、洪水、冰雪等极端灾害频发,严重威胁电网的安全可靠运行。尤其是配电网,作为电力用户的直接分配单元,由于基础设施薄弱、网络结构复杂、控制手段匮乏等原因,极易受到极端灾害的影响。极端灾害可在短时间内摧毁大量电力基础设施,引发大规模停电事故,甚至造成严重的人员伤亡和财产损失。为降低极端灾害的影响,亟须提高配电网的弹性水平。弹性配电网具备灾前防御能力和灾后恢复能力,可利用主动防御措施减小故障损失,恢复关键负荷,能够有效地应对极端灾害的干扰[1]。
分布式电源(Distributed Generation, DG)、储能(Energy Storage System, ESS)、智能软开关(Soft Open Point, SOP)、电动汽车等灵活性资源在配电网源网荷侧的大量接入,使得配电网内的资源日趋丰富。这些灵活性资源深度耦合,协调互补,在提升配电网控制灵活性的同时,也为其弹性提升带来新的可能[2]。
目前,提升配电网弹性的措施可分为预防措施和恢复措施[3]。预防措施是从规划角度出发,在灾前通过合理规划各种灵活性资源,提高配电网的坚强性、电力供应充足性和拓扑控制灵活性。为提高坚强性,可通过对配电网基础设施进行加固,降低网络故障概率,提高配电网抗灾能力。为提高电力供应充足性,可通过在配电网中配置应急电源,如分布式电源[4]、电动汽车[5]及移动储能[6]等,或组建孤岛微电网[7],在紧急情况下为关键负荷提供电力支撑。为提高配电网拓扑控制的灵活性,在配电网中配备远程控制开关[8]或智能软开关[9],通过网络重构为关键负荷提供电力恢复路径。恢复措施是从运行角度出发,在灾中/灾后阶段通过应急电源调度、网络重构[10]、多能协同[11]等手段,实现关键负荷的快速复电,减小停电损失。
然而,上述研究大多采用单一的资源或措施提升配电网弹性,忽略了多种灵活性资源协调互补的优势。而多种灵活性资源的协同优化能够给极端灾害防御提供更多的弹性支撑。在考虑多种灵活性资源协同优化提升配电网弹性方面,相关学者也进行了一些研究。文献[12]考虑台风灾害下倒杆和断线的相关性影响,采用燃气轮机、储能和电动汽车等灵活性资源定容选址双层规划方法来增强配电网弹性。在电网与交通网融合的背景下,文献[13]提出一种灾前移动储能预布局与灾后移动储能、电动汽车和柴油发电机动态调度相结合的配电网弹性提升策略。为增强配电网对台风的抵御能力,文献[14]提出一种考虑线路加固、SOP、ESS和发电机协调调度的配电网弹性提升方法。截至目前,该方面的研究还不够完善,多种灵活性资源协同优化提升配电网弹性的潜力还有待进一步挖掘。
极端灾害通常具有时空特性,以台风为例,其时空特性具体表现为:在时间上,表征台风的特征量(比如气压、温度、风速、风向等物理量)随时间而变化;在空间上,台风会波及行进路径上的多个地理区域,造成大范围的破坏。极端灾害的时空特性造成配电网故障时间、位置和规模的不确定性。为处理不确定性,当前研究主要采用随机优化[15-16]和鲁棒优化[17-20]。
随机优化通常假设随机变量服从某种概率分布,比如,风速服从威尔分布[21]、线路故障状态服从伯努利分布[16]、台风发生次数服从泊松分布[22]。然而,由于自然灾害的低概率特性,基于有限历史数据拟合的概率分布与真实分布之间可能存在一定偏差,从而导致次优甚至不合理的优化方案。
考虑到随机优化需要概率分布这一固有限制,有学者提出鲁棒优化方法。鲁棒优化方法一般采用N-K准则建立故障不确定集,然后在故障不确定集中的最恶劣故障场景下进行配电网弹性研究[17,19]。为考虑极端灾害的时空特性,文献[14,20,23]建立多时段多分区的N-K不确定集。但是,文献[20,23]中N-K不确定集建立时仅考虑线路的0/1状态,忽略了配电线路的故障率,可能导致优化方案过于保守。而当前少量考虑配电线路故障率的研究,在对极端灾害时空特性分析时简化处理,分析不透彻。比如,文献[18]假设配电网分布区域远小于台风影响范围,认为在每个时段内所有配电线路承受相同的风速,忽略了台风影响线路故障率的内在机理;文献[16]仅对台风中心周围的台风风场进行建模,未对台风移动路径进行模拟。事实上,时空特性分析时需要综合考虑台风移动路径、风场风速、风向、线路走向、线路元件强度等多方面的因素,以评估台风在时间和空间双重维度下对配电网造成的不确定性影响。
针对上述问题,本文提出计及台风时空特性和灵活性资源协同优化的配电网弹性提升策略。首先,由配电网基本参数和地理位置信息建立直角坐标系,并在获取台风气象信息的基础上构建台风时空演变模型,实时模拟台风移动路径和风场;其次,深入剖析台风致灾机理,建立配电线路故障模型,通过分析线路元件强度和荷载效应,得到配电线路的时变故障率;最后,综合考虑灵活性资源部署成本和弹性量化指标,构建两阶段三层鲁棒优化模型。在灾前防御层,采用线路加固,DG、ESS和SOP优化配置多维度提升配电网弹性;在灾害发生层,基于配电线路时变故障率,采用信息熵识别脆弱线路,并结合故障修复时间确定配电线路的时变故障状态;在灾后恢复层,通过DG和ESS调度,SOP网络重构,实现失电负荷快速复电。
弹性配电网在极端灾害干扰前后的响应过程如附图1所示[23],图中红色虚线和黑色实线分别表示配电网在正常运行状态和极端灾害下的性能曲线,即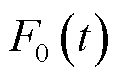 和
和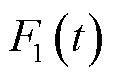 。在极端灾害干扰下,弹性配电网经历以下三个阶段:灾前防御阶段t0~t1、灾害发生阶段t1~t3和灾后恢复阶段t3~t4。本文重点研究台风灾害下配电网对关键负荷的支撑能力和恢复能力,因此,定义弹性指标为台风灾害下受灾配电网的累积失电负荷成本,即附图1中阴影部分的面积
。在极端灾害干扰下,弹性配电网经历以下三个阶段:灾前防御阶段t0~t1、灾害发生阶段t1~t3和灾后恢复阶段t3~t4。本文重点研究台风灾害下配电网对关键负荷的支撑能力和恢复能力,因此,定义弹性指标为台风灾害下受灾配电网的累积失电负荷成本,即附图1中阴影部分的面积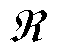 为
为
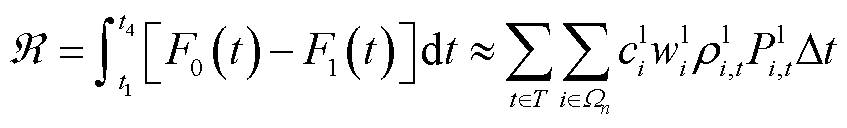 (1)
(1)
式中,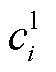 为切负荷单价;i为配电网节点;
为切负荷单价;i为配电网节点;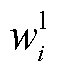 为负荷优先级的权重系数;
为负荷优先级的权重系数;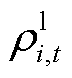 为负荷损失系数;
为负荷损失系数;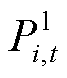 为有功负荷;
为有功负荷;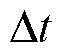 为时长;T为优化时段集合;
为时长;T为优化时段集合;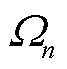 为配电网节点集合。在该指标下,配电网的失电负荷成本
为配电网节点集合。在该指标下,配电网的失电负荷成本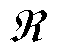 越小,表示配电网弹性水平越高。选取该指标进行弹性计算,可在量化配电网弹性水平的同时兼顾经济性。
越小,表示配电网弹性水平越高。选取该指标进行弹性计算,可在量化配电网弹性水平的同时兼顾经济性。
本文以线路加固、DG、ESS、SOP优化配置作为配电网弹性提升措施,从减小故障规模、降低负荷损失、缩短恢复时间三个维度挖掘灵活性资源的弹性提升潜力。对配电网中的脆弱线路进行加固,可提高电网的坚强性和线路的抗风能力,降低线路在极端灾害下的故障率,从而减小故障规模。考虑到故障后可用供电资源紧缺,灾前部署DG和ESS可在灾后为关键负荷提供电力支撑,提高配电网电力供应的充足性,从而降低负荷损失。基于全控型电力电子器件的智能SOP以柔性互联方式增强拓扑控制灵活性,可在故障后通过网络重构实现关键负荷的快速复电,从而缩短故障恢复时间。
在考虑多种灵活性资源优势互补,多维度提升配电网弹性的基础上,计及台风引发的配电网故障时间、位置和规模的时空不确定性影响,融合灾前防御和灾后恢复策略,构建台风灾害下的配电网弹性提升研究框架如图1所示。
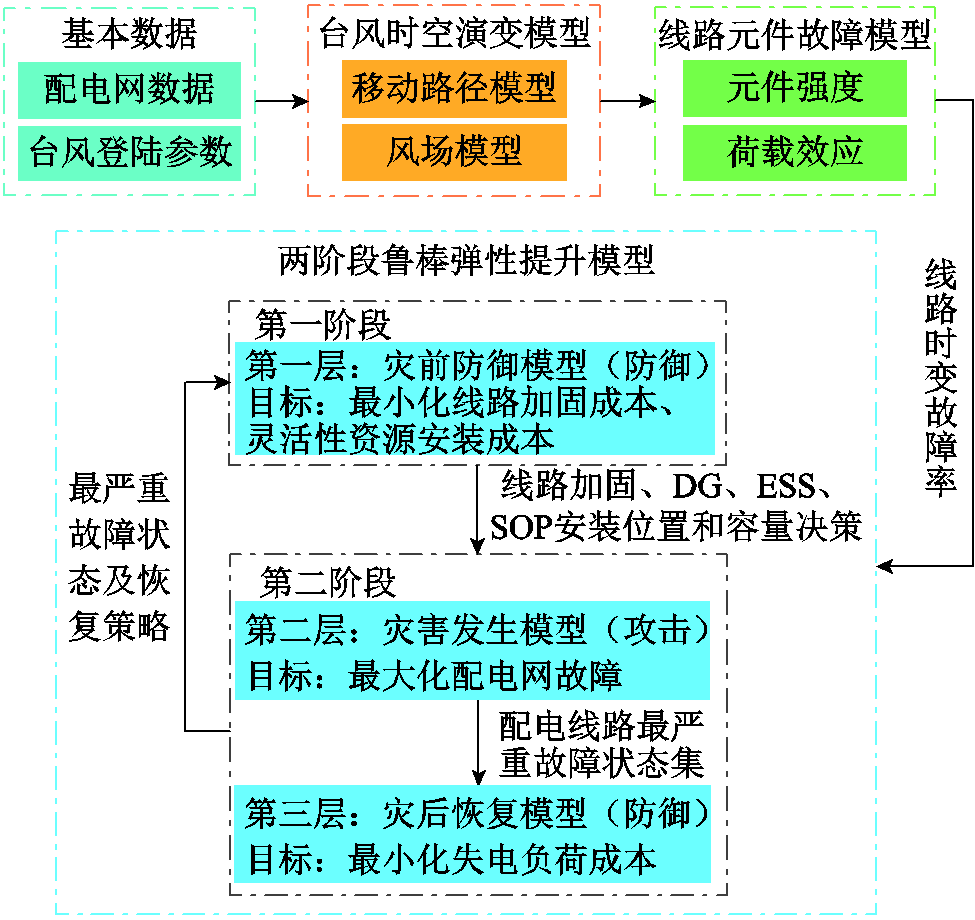
图1 配电网弹性提升研究框架
Fig.1 Research framework for resilience enhancement of distribution networks
首先,根据配电网基本参数和地理位置,建立直角坐标系,确定各线路元件坐标;其次,根据气象中心预报信息获取台风登陆参数,建立台风时空演变模型;再次,通过分析线路元件强度和荷载效应,计算配电线路的时变故障率;最后,基于三层防御-攻击-防御(Defense-Attack-Defense, DAD)结构建立两阶段鲁棒弹性提升模型。第一阶段为DAD模型中的第一层,表示灾前的准备和预防阶段,其数学模型属于配电网规划问题。规划目标为最小化线路加固成本和DG/ESS/SOP部署成本,规划决策为线路加固决策和DG/ESS/SOP安装位置及容量决策,该决策作为初始决策传递到第二阶段。第二阶段包含DAD模型中的第二层和第三层。第二层为灾害发生模型,优化目标是在规划决策已知的条件下,根据配电线路故障概率,采用信息熵识别脆弱线路,并确定在台风灾害下配电线路的最严重故障状态,将其传递到第三层。第三层是在已知配电线路故障状态的条件下,以最小化配电网失电负荷成本为目标,利用第一层的加固措施和部署的灵活性资源对配电网进行故障恢复。同时,第二阶段得到的最严重故障场景和恢复策略形成一个割集,反馈给第一阶段以修正规划决策。最后经过有限次迭代,得到最优的规划决策和恢复决策。
台风是一种沿台风中心旋转的热带气旋,同时又以一定的速度整体移动。台风模型通常由反映其整体移动的路径模型和反映其旋转流场的轴对称圆形风场模型组成。
台风移动路径是由各时刻台风中心位置刻画的。首先根据配电网地理位置建立坐标系;然后由气象中心预报信息得到台风登陆参数,主要包括中心点坐标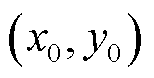 、移动速度
、移动速度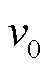 、移动方向角
、移动方向角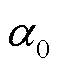 以及台风外围气压与中心气压之差
以及台风外围气压与中心气压之差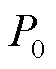 ;最后由台风移动方向和坐标原点的相对位置确定台风路径。
;最后由台风移动方向和坐标原点的相对位置确定台风路径。
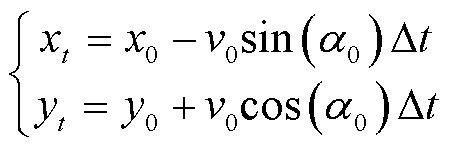 (2)
(2)
式中,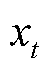 和
和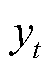 为t时刻台风中心点坐标。
为t时刻台风中心点坐标。
本文采用Batts模型[24]建立台风风场模型,描述台风影响范围内各点的风速和风向。在气象学中,通常将台风风场近似为轴对称的圆形气旋,如附图2所示,图中每个圆被称为一个模拟圆。在北半球,台风气旋的方向为逆时针方向,因此模拟圆上任一点的风速方向为逆时针切线方向。根据Batts模型,模拟圆上任一点的风速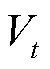 与该点到台风中心的距离有关,如附图3所示,其计算公式为
与该点到台风中心的距离有关,如附图3所示,其计算公式为
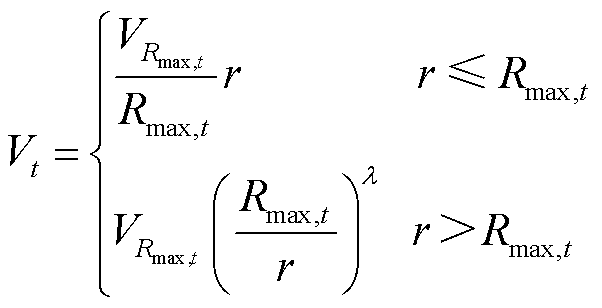 (3)
(3)
式中,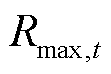 为台风风场的最大风速半径;
为台风风场的最大风速半径;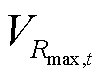 为台风最大风速半径处的风速;
为台风最大风速半径处的风速;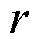 为模拟圆上任一点到台风中心的距离;
为模拟圆上任一点到台风中心的距离;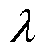 为台风强度衰减系数,在0.5~0.7之间取值。
为台风强度衰减系数,在0.5~0.7之间取值。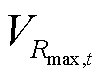 和
和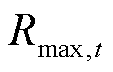 可由台风登陆参数计算得到,计算方法详见文献[24]。
可由台风登陆参数计算得到,计算方法详见文献[24]。
倒杆和断线是台风灾害下配电网故障的主要形式,因此本文以导线和杆塔作为配电线路的主要组成元件,计算配电线路的故障率。
导线和杆塔强度分别指导线的抗拉强度和杆塔的抗弯强度。在实际生产中,由于元件制作工艺、材料力学特性等多方面的差异,元件强度具有不确定性。通常导线/杆塔强度服从正态分布,其概率密度函数可表示为[25]
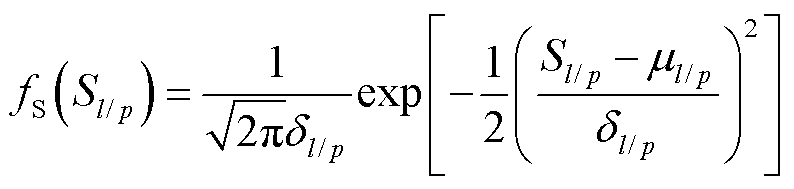 (4)
(4)
式中,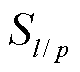 为导线l/杆塔p的强度;
为导线l/杆塔p的强度;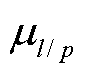 为导线l/杆塔p的强度均值;
为导线l/杆塔p的强度均值;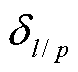 为导线l/杆塔p的强度误差。
为导线l/杆塔p的强度误差。
台风天气下,导线荷载包括水平风荷载和重力荷载;杆塔荷载主要包括悬挂在杆塔上的导线水平风荷载以及杆身风荷载。荷载作用在导线和杆塔上,会引起导线截面应力和杆塔截面弯矩,即荷载效应。
3.2.1 导线截面应力计算
导线通常在最高悬挂点处承受的张力最大,因此本文以该点处的综合张力来计算导线截面应力,即
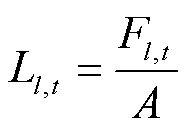 (5)
(5)
式中,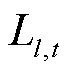 为t时刻导线截面应力;
为t时刻导线截面应力;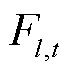 为t时刻导线最高悬挂点处的综合张力;A为导线的计算截面积。
为t时刻导线最高悬挂点处的综合张力;A为导线的计算截面积。
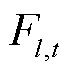 由水平方向的风荷载分量
由水平方向的风荷载分量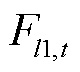 和垂直方向的重力荷载分量
和垂直方向的重力荷载分量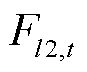 组成,有
组成,有
 (6)
(6)
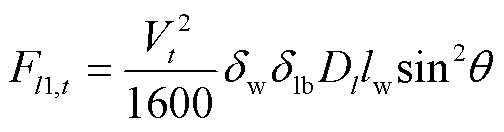 (7)
(7)
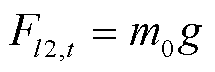 (8)
(8)
式中,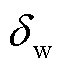 为风压不均匀系数;
为风压不均匀系数;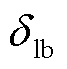 为导线体型系数;
为导线体型系数;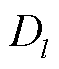 为导线外径;
为导线外径;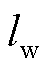 为杆塔档距;
为杆塔档距;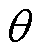 为风向与导线夹角;
为风向与导线夹角;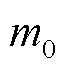 为导线单位长度的质量;g为重力加速度。
为导线单位长度的质量;g为重力加速度。
3.2.2 杆塔截面弯矩计算
杆塔承受的导线水平风荷载为
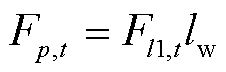 (9)
(9)
杆身风荷载为
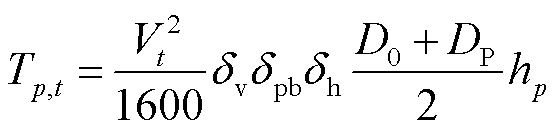 (10)
(10)
式中,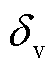 为风振系数;
为风振系数;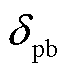 为杆塔体型系数;
为杆塔体型系数;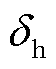 为风压高度变化系数;
为风压高度变化系数;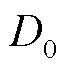 和
和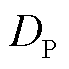 分别为电杆梢径和根径;
分别为电杆梢径和根径;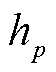 为杆塔高度。
为杆塔高度。
通常杆塔在杆根处弯矩最大,故本文以杆根弯矩来计算杆塔截面弯矩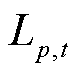 ,计算方法详见文献[24]。
,计算方法详见文献[24]。
根据结构可靠性理论[26],当导线抗拉/杆塔抗弯强度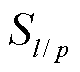 小于导线截面应力/杆塔截面弯矩
小于导线截面应力/杆塔截面弯矩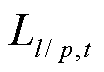 时,元件可能发生故障。因此,导线和杆塔的故障率为
时,元件可能发生故障。因此,导线和杆塔的故障率为
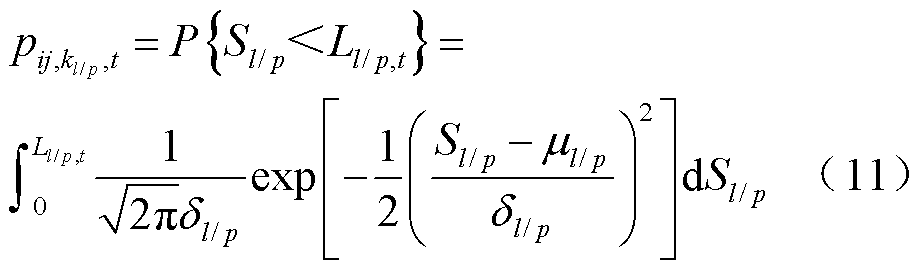
式中,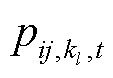 为配电线路ij中导线
为配电线路ij中导线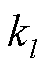 的故障率;
的故障率; 为配电线路ij中杆塔
为配电线路ij中杆塔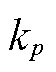 的故障率。
的故障率。
配电线路可看作导线和杆塔串联组成,假设不同元件的故障率相互独立,则配电线路的故障率为
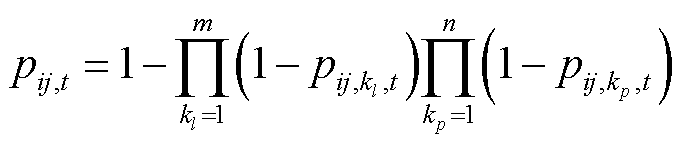 (12)
(12)
式中,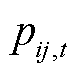 为线路ij的故障率; n为支撑配电线路ij的杆塔数量;m为配电线路ij中相邻杆塔间的导线数量。
为线路ij的故障率; n为支撑配电线路ij的杆塔数量;m为配电线路ij中相邻杆塔间的导线数量。
本文所考虑的目标函数为第一阶段线路加固成本和DG、SOP、ESS部署成本,以及第二阶段的失电负荷成本,目标函数的表达式为
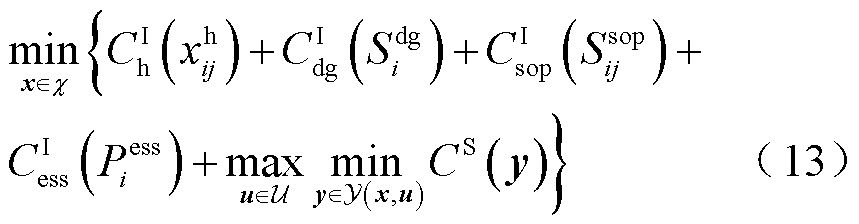
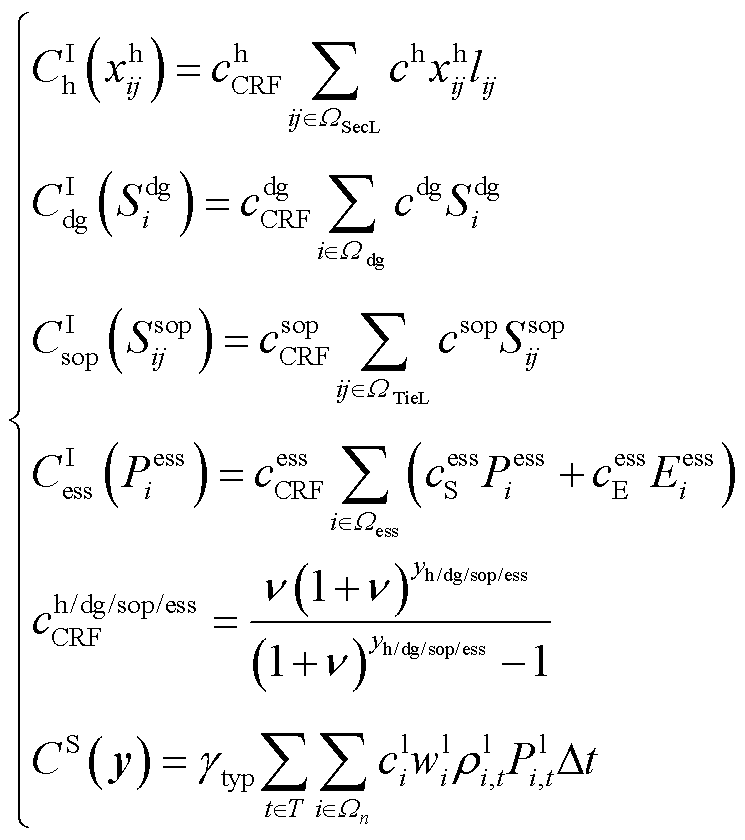 (14)
(14)
式中,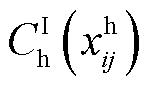 、
、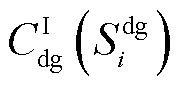 、
、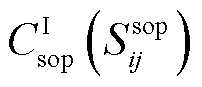 和
和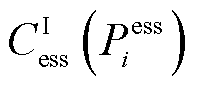 分别为第一阶段的线路加固成本和DG、SOP、ESS部署成本;
分别为第一阶段的线路加固成本和DG、SOP、ESS部署成本;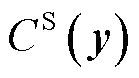 为第二阶段的失电负荷成本,即本文的弹性量化指标;
为第二阶段的失电负荷成本,即本文的弹性量化指标;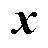 、
、 分别为第一层灾前防御模型的规划决策变量、规划约束集;
分别为第一层灾前防御模型的规划决策变量、规划约束集;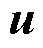 、
、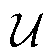 分别为第二层台风灾害下配电线路某一种故障状态、故障状态集;
分别为第二层台风灾害下配电线路某一种故障状态、故障状态集;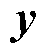 、
、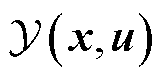 分别为第三层灾后恢复模型的运行状态变量、运行约束集;
分别为第三层灾后恢复模型的运行状态变量、运行约束集; 、
、 分别为分段、联络线路集合,SOP候选部署位置为联络线路集合;
分别为分段、联络线路集合,SOP候选部署位置为联络线路集合;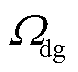 、
、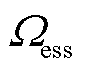 分别为DG、ESS节点集合;
分别为DG、ESS节点集合;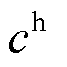 为单位长度线路的加固成本;
为单位长度线路的加固成本;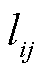 为线路ij的长度;
为线路ij的长度;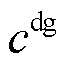 、
、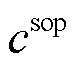 分别为单位容量DG、SOP的配置成本;
分别为单位容量DG、SOP的配置成本; 分别为单位功率和能量ESS的配置成本;
分别为单位功率和能量ESS的配置成本;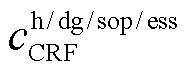 分别为加固线路/DG/SOP/ESS的资本回收系数;
分别为加固线路/DG/SOP/ESS的资本回收系数;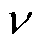 为折旧率;
为折旧率;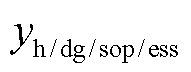 分别为加固线路/DG/SOP/ESS使用年限;
分别为加固线路/DG/SOP/ESS使用年限;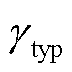 为沿海地区平均一年台风发生次数;
为沿海地区平均一年台风发生次数; 为0-1决策变量,表示线路ij是否加固,若加固,则
为0-1决策变量,表示线路ij是否加固,若加固,则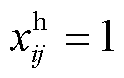 ,否则
,否则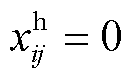 ;
;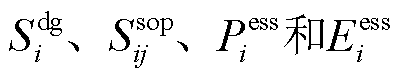 为连续决策变量,分别表示DG安装容量、SOP安装容量、ESS放电功率上限和ESS荷电容量。
为连续决策变量,分别表示DG安装容量、SOP安装容量、ESS放电功率上限和ESS荷电容量。
需要注意的是,优化模型中考虑的两个目标函数之间是相互矛盾和相互影响的,需要进行博弈和均衡。为降低台风灾害造成的失负荷成本,需要各类灵活性资源的协同优化,则相应地会增加部署成本;而降低部署成本则意味着台风灾害后可用资源有限,不能及时有效地恢复失电负荷,从而导致失电负荷成本增加。优化问题同时考虑这两个目标函数具有其合理性。首先台风灾害后需要重点关注的是关键负荷的快速恢复,降低失电负荷成本,因此失电负荷成本是本文首要考虑的目标函数;而考虑部署成本这一目标函数主要有两个方面的原因:①为避免优化问题过度追求配电网弹性提升,而进行大量冗余投资,需要在优化目标中添加部署成本进行限制;②多种规划方案有可能取得相同的弹性提升效果,需要优先选择部署成本较小的规划方案。
计及多种灵活性资源协调互补的优势,本文通过灾前线路加固,DG、SOP、ESS优化配置,分别从减小故障规模、降低负荷损失、缩短恢复时间三个维度提高电网的坚强性、电力供应充足性以及拓扑控制灵活性。灾前防御模型为
 (15)
(15)
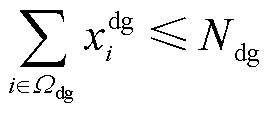 (16)
(16)
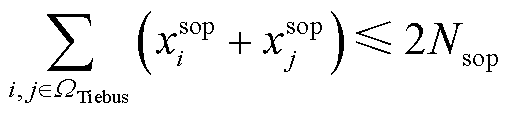 (17)
(17)
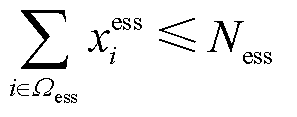 (18)
(18)
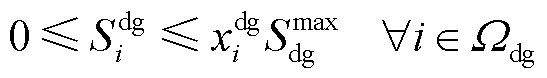 (19)
(19)
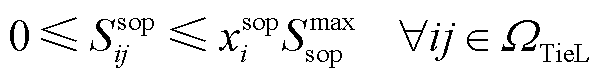 (20)
(20)
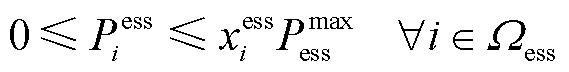 (21)
(21)
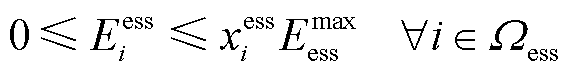 (22)
(22)
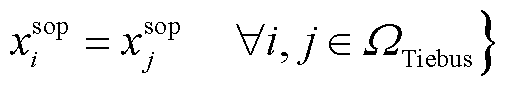 (23)
(23)
式中,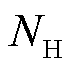 、
、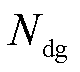 、
、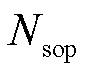 、
、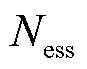 分别为最大线路加固数量,DG、SOP、ESS最大安装数量;
分别为最大线路加固数量,DG、SOP、ESS最大安装数量;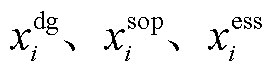 分别为DG、SOP、ESS安装位置0-1决策变量,1表示安装,0表示不安装;
分别为DG、SOP、ESS安装位置0-1决策变量,1表示安装,0表示不安装;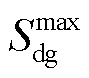 、
、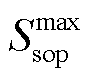 、
、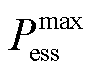 分别为DG最大安装容量、SOP最大安装容量、ESS最大放电功率;
分别为DG最大安装容量、SOP最大安装容量、ESS最大放电功率;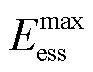 为ESS的最大荷电容量;
为ESS的最大荷电容量; 为联络线端点集合;
为联络线端点集合;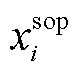 和
和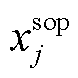 为0-1变量,
为0-1变量,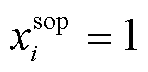 (
(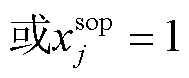 )表示在节点i(或j)处安装SOP。SOP的两个端子分别接在联络线的首末端,式(23)表示两个0-1变量的状态应保持一致。
)表示在节点i(或j)处安装SOP。SOP的两个端子分别接在联络线的首末端,式(23)表示两个0-1变量的状态应保持一致。
三层DAD模型的第二层为灾害发生模型,该模型是在第一阶段规划决策已知的情况下,找到最严重的配电网故障状态。从第3节中配电线路故障模型可知,受台风时空特性的影响,配电线路的故障状态是随机且无序的。本文采用信息熵[18]来量化配电线路故障状态的不确定性,根据已知的配电线路故障率,识别台风天气下配电网脆弱线路,并结合故障修复时间确定配电线路的时变故障状态。灾害发生模型的表达式为
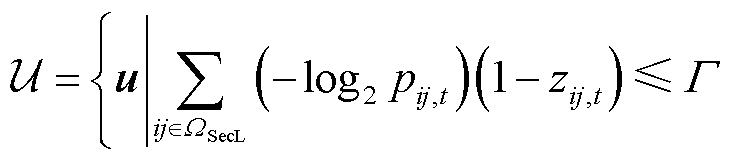 (24)
(24)
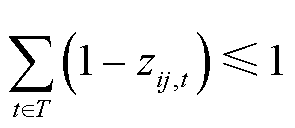 (25)
(25)
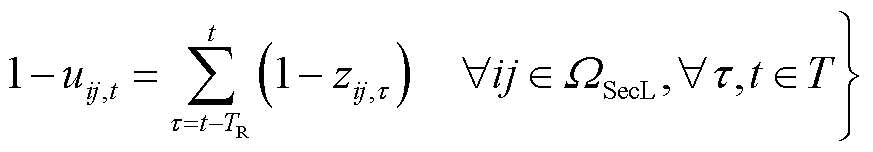 (26)
(26)
式中,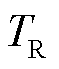 为故障修复时间;
为故障修复时间;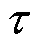 为线路受到攻击的时间;
为线路受到攻击的时间;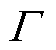 为信息熵预算值;
为信息熵预算值;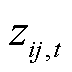 和
和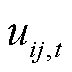 为0-1决策变量。
为0-1决策变量。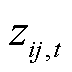 表示配电线路ij在t时段是否因受到台风攻击而故障,若线路ij受到台风攻击后发生故障,则
表示配电线路ij在t时段是否因受到台风攻击而故障,若线路ij受到台风攻击后发生故障,则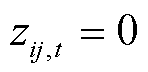 ,否则
,否则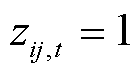 ;
;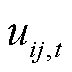 为台风攻击后线路ij在各时段的实际故障状态,若线路处于故障状态,则
为台风攻击后线路ij在各时段的实际故障状态,若线路处于故障状态,则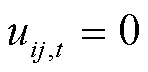 ,否则
,否则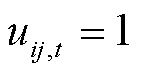 。
。
式(24)为采用信息熵识别脆弱线路的表达式,表示在给定信息熵预算下,高故障率的线路易发生故障。式(25)表示线路ij在整个优化时段T内最多故障一次。式(26)表示线路的故障状态是由其受到攻击的时间和故障修复时间共同决定的,即如果线路在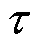 时段被攻击,其会一直处于故障状态直到被修复。
时段被攻击,其会一直处于故障状态直到被修复。
台风灾害发生后,配电网操作者利用第一阶段部署的灵活性资源对配电网进行灾后恢复,以最大限度地降低负荷损失。灾后恢复模型主要包括配电网运行约束和DG/SOP/ESS运行约束。
4.4.1 配电网运行约束
1)功率平衡约束
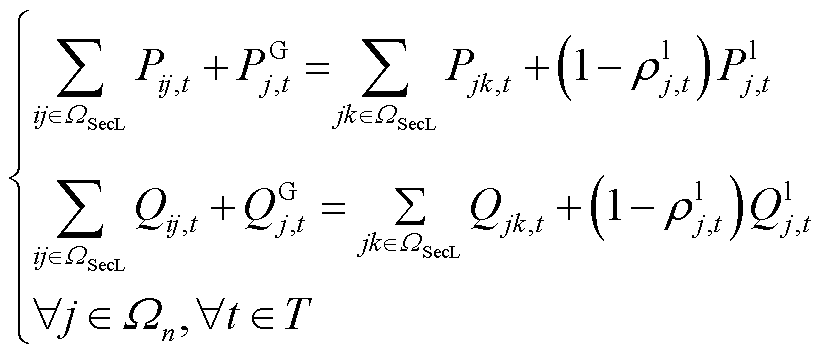 (27)
(27)
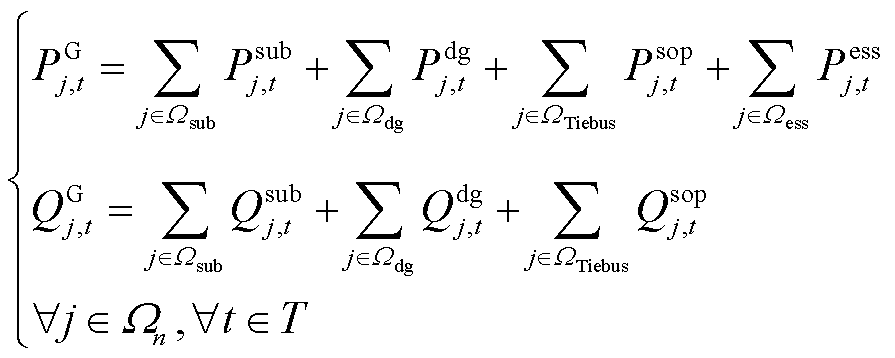 (28)
(28)
式中,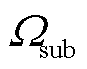 为变电站节点集合;
为变电站节点集合;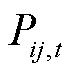 和
和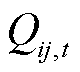 分别为流过线路ij的有功和无功潮流;
分别为流过线路ij的有功和无功潮流;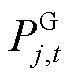 和
和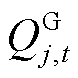 分别为注入节点j的总有功功率和无功功率。
分别为注入节点j的总有功功率和无功功率。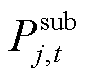 /
/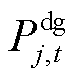 /
/ /
/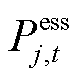 分别为节点j处的变电站/DG/SOP/ESS注入的有功功率;
分别为节点j处的变电站/DG/SOP/ESS注入的有功功率;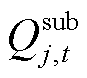 /
/ /
/ 分别为节点j处的变电站/ DG/SOP注入的无功功率。
分别为节点j处的变电站/ DG/SOP注入的无功功率。
2)节点电压约束
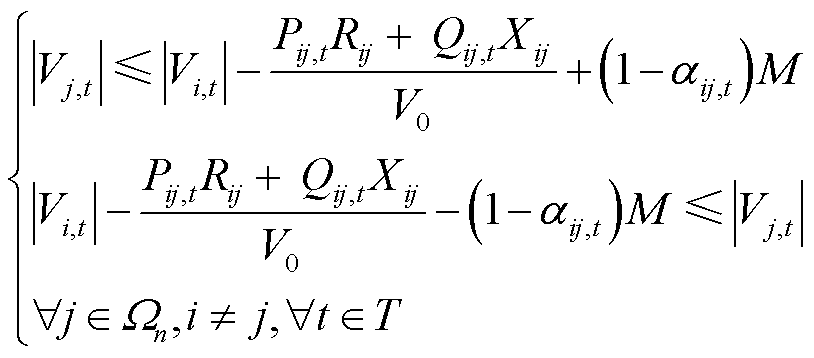 (29)
(29)
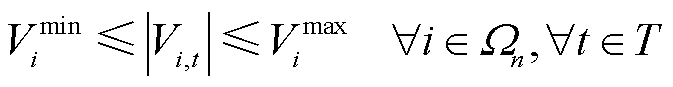 (30)
(30)
式中,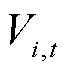 为节点i的电压;
为节点i的电压;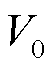 为额定电压;
为额定电压;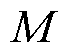 为一个数值较大的参数;
为一个数值较大的参数;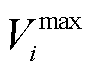 和
和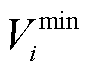 分别为节点i电压的上下限;0-1变量
分别为节点i电压的上下限;0-1变量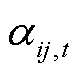 为线路加固措施实施后,在台风袭击下线路的运行状态,若线路正常运行
为线路加固措施实施后,在台风袭击下线路的运行状态,若线路正常运行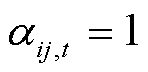 ,否则
,否则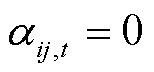 。
。
3)支路潮流方程
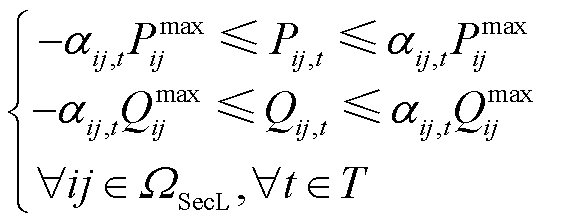 (31)
(31)
式中,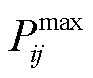 和
和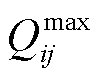 分别为线路ij的有功和无功潮流上限。
分别为线路ij的有功和无功潮流上限。
4)变电站出力约束
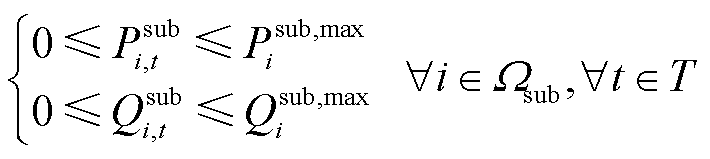 (32)
(32)
式中,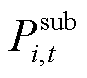 和
和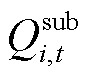 分别为变电站发出的有功功率和无功功率;
分别为变电站发出的有功功率和无功功率;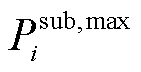 和
和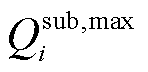 分别为变电站有功功率和无功功率上限。
分别为变电站有功功率和无功功率上限。
5)节点切负荷约束
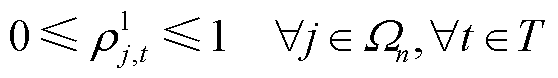 (33)
(33)
6)线路状态约束
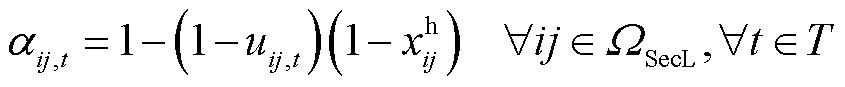 (34)
(34)
本文假设第一阶段被加固的线路能经受住台风的攻击,即若线路被加固(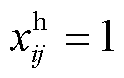 ),当受到攻击后(
),当受到攻击后(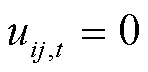 ),其能经受住攻击而正常运行(
),其能经受住攻击而正常运行(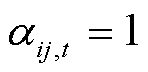 )。
)。
4.4.2 可控DG运行约束
为避免机械故障,受天气影响较大的风电和光伏不参与配网弹性优化,因此本文仅考虑可控DG,即
 (35)
(35)
式中,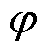 为功率因数角。
为功率因数角。
4.4.3 SOP运行约束
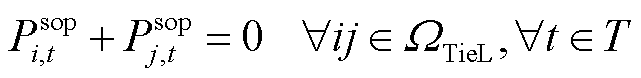 (36)
(36)
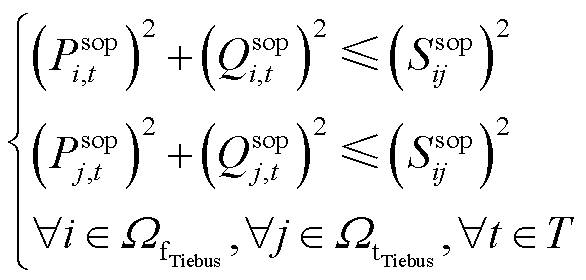 (37)
(37)
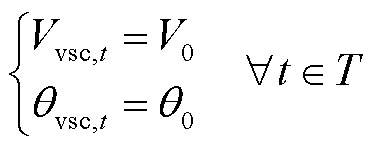 (38)
(38)
式中,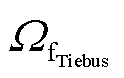 、
、 分别为联络线首、末端节点集合。
分别为联络线首、末端节点集合。
因SOP运行效率较高,其损耗相对网络损耗较小,故在式(36)中忽略SOP损耗。式(37)表示变流器容量约束。式(38)表示故障侧变流器的电压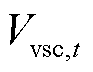 和相位
和相位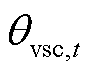 的设定值。另外,式(37)中含二次项,可采用圆的外接正多边形近似法将其线性化[27]。
的设定值。另外,式(37)中含二次项,可采用圆的外接正多边形近似法将其线性化[27]。
4.4.4 ESS运行约束
考虑到灾后供电资源的稀缺性,在故障恢复阶段,本文仅考虑ESS的放电行为。ESS运行约束为
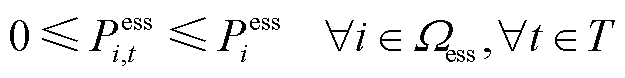 (39)
(39)
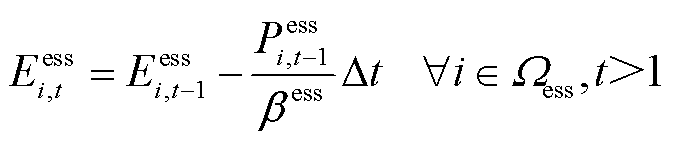 (40)
(40)
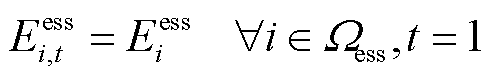 (41)
(41)
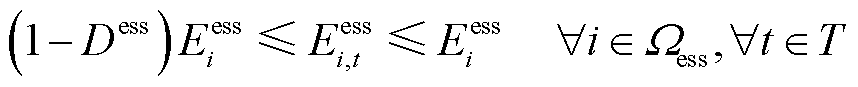 (42)
(42)
式中,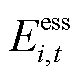 为t时段ESS的荷电量;
为t时段ESS的荷电量;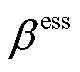 为ESS放电效率;
为ESS放电效率;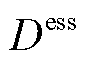 为ESS放电深度系数。
为ESS放电深度系数。
综上所述,灾后恢复模型的运行约束可表示为
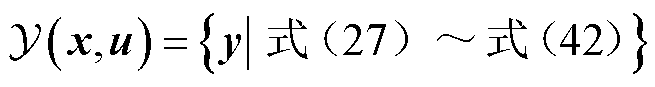 (43)
(43)
本文采用列-约束生成(Column-and-Constraint Generation, C&CG)算法[28]求解两阶段鲁棒弹性提升模型。首先将该模型表示为如下紧凑形式:
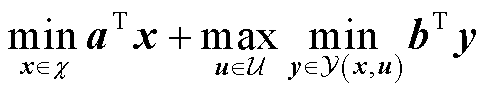 (44)
(44)
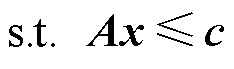 (45)
(45)
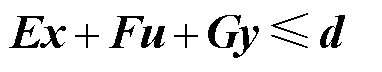 (46)
(46)
式中,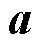 和
和 为目标函数中对应项的系数向量;
为目标函数中对应项的系数向量;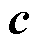 和
和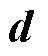 为模型中对应约束的常数向量;
为模型中对应约束的常数向量;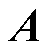 、
、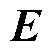 、
、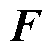 、
、 为对应约束的系数矩阵。式(45)对应灾前防御模型中的约束式(15)~式(23),式(46)对应灾后恢复模型中的约束式(43)。
为对应约束的系数矩阵。式(45)对应灾前防御模型中的约束式(15)~式(23),式(46)对应灾后恢复模型中的约束式(43)。
C&CG算法中主问题的表达式为
 (47)
(47)
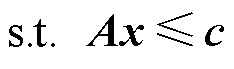 (48)
(48)
 (49)
(49)
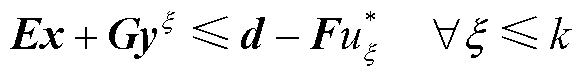 (50)
(50)
式中,k为迭代次数;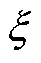 为常数;
为常数;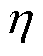 为第k次迭代子问题的优化值;
为第k次迭代子问题的优化值;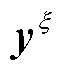 为添加的追索权变量;
为添加的追索权变量;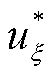 为第k次迭代得到的最严重线路故障状态。式(49)和式(50)为上一次迭代(第k次迭代)过程中求解子问题后添加到主问题的割集。
为第k次迭代得到的最严重线路故障状态。式(49)和式(50)为上一次迭代(第k次迭代)过程中求解子问题后添加到主问题的割集。
C&CG算法中子问题的表达式为
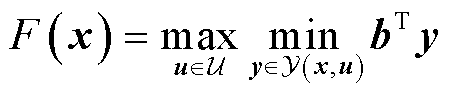 (51)
(51)
 (52)
(52)
子问题仍是一个双层优化问题,采用强对偶理论[29]求出内层最小化问题的对偶问题,将双层问题转换为单层问题进行求解。令式(52)对应的对偶变量为 ,则内层最小化问题的对偶问题为
,则内层最小化问题的对偶问题为
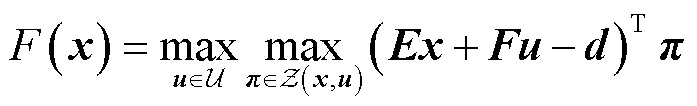 (53)
(53)
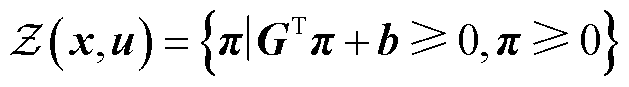 (54)
(54)
式中,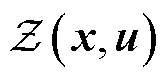 为内层最小化问题之对偶问题的约束集。将式(53)中两个最大化运算合并为单层子问题,有
为内层最小化问题之对偶问题的约束集。将式(53)中两个最大化运算合并为单层子问题,有
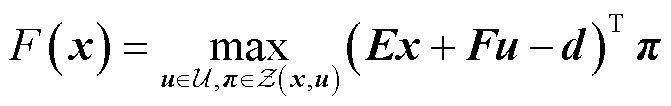 (55)
(55)
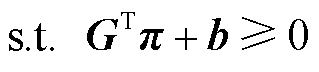 (56)
(56)
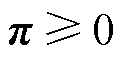 (57)
(57)
式(55)中含双线性项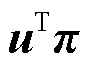 ,可采用文献[30]中的方法对其进行线性化。
,可采用文献[30]中的方法对其进行线性化。
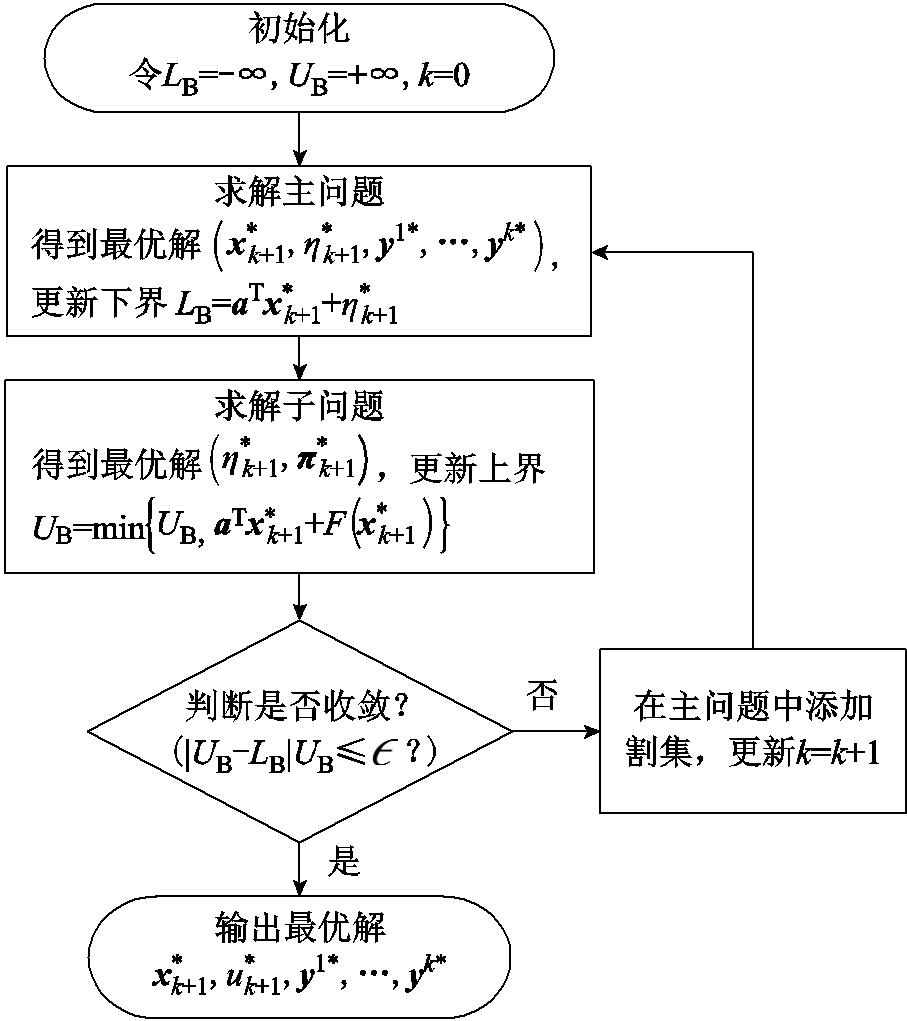
C&CG算法的流程如附图4所示,算法精度设置为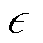 ,具体求解步骤如下。
,具体求解步骤如下。
1)令原问题下界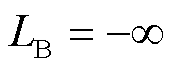 ,上界
,上界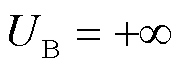 ,迭代次数
,迭代次数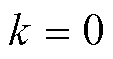 。
。
2)求解主问题,得到最优解(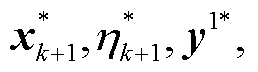
 ),更新下界
),更新下界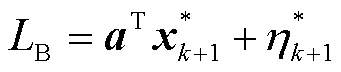 。
。
3)求解子问题,并更新上界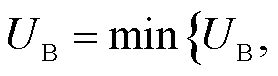
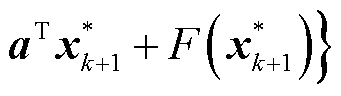 。
。
4)如果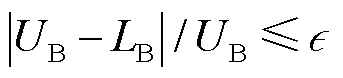 ,返回最优解
,返回最优解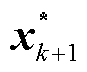 ,并终止算法迭代;否则,在主问题中添加如下割集:
,并终止算法迭代;否则,在主问题中添加如下割集:
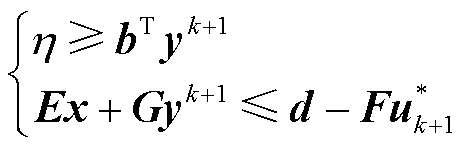 (58)
(58)
更新迭代次数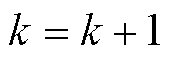 ,并跳转至步骤2)继续执行。
,并跳转至步骤2)继续执行。
为验证本文方法的性能,选取夏季经常受台风影响的我国东部沿海某城市51节点系统[31]作为测试系统,其地理区域覆盖范围为经度(111.2°E~112.4°E)和纬度(21.4°N~22.8°N),其拓扑图如图2所示。
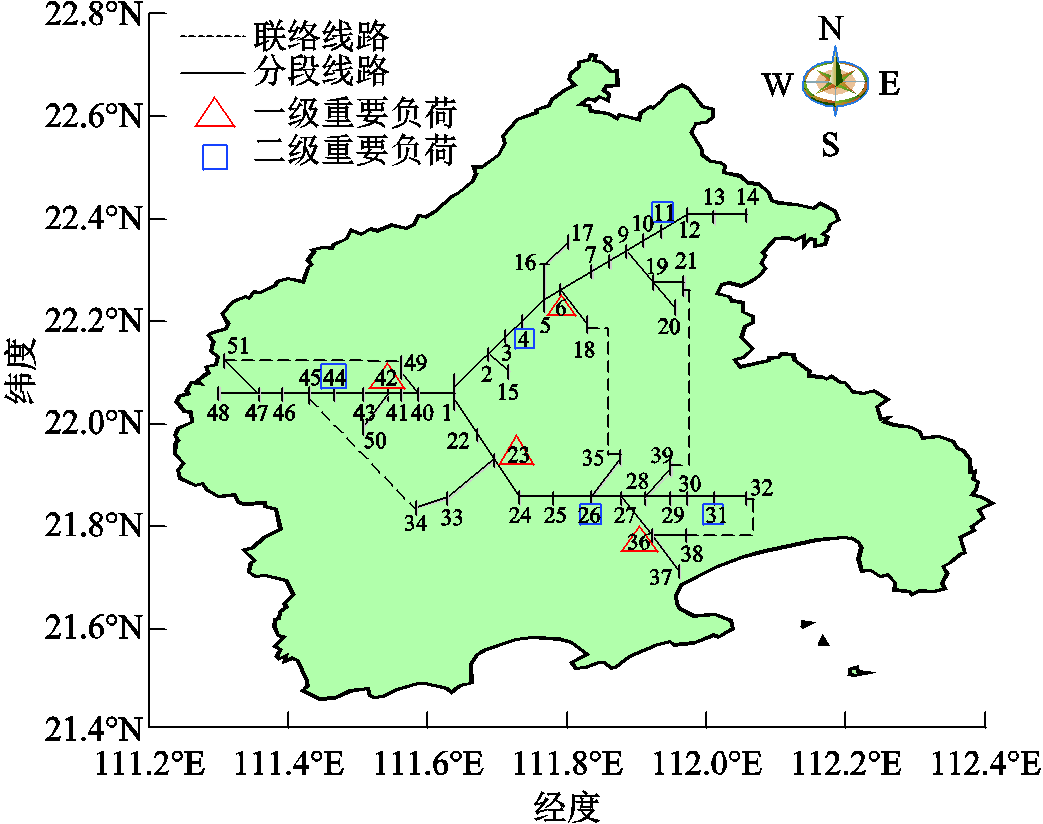
图2 我国东部沿海某城市51节点系统拓扑图
Fig.2 Topology of the 51-bus system in a city along the eastern coast of China
系统有功和无功负荷分别为811 5 kW和 277 7 kvar。变电站节点电压设置为1.0(pu),非变电站节点电压的变化范围设定为0.95(pu)~ 1.05(pu)。根据负荷的重要程度将负荷划分为三个优先级,见附表1,各级负荷权重系数的设置见文献[32]。系统价格参数和DG/SOP/ESS配置参数见表1[14,18,23]。配电线路发生故障后,需要在台风过境后进行人工修复,本文假设故障平均修复时间为6 h[33]。另外,假设我国东部沿海某城市平均每年遭受2次台风袭击[24]。本文建立的两阶段鲁棒弹性提升模型由GAMS 24.4软件求解,C&CG算法的精度设置为1.0×10-4。
表1 系统价格参数和DG/SOP/ESS配置参数
Tab.1 System price parameters and DG/SOP/ESS deployment parameters

系统价格参数数值DG/SOP/ESS配置参数数值 /[元/(kW·h)]98/(MV·A)0.35,0.6 /(元/km)840 000/(MW·h)1.0 /[元/(kV·A)]910/MW0.3 /[元/(kV·A)]1 0500.8, 0.9 /(元/kW)700/年50/20/20/20 /[元/(kW·h)]1 4000.1
本节首先根据台风时空演变模型,对台风登陆后的路径和风速进行模拟。然后,根据配电线路故障模型计算配电线路的故障率,并分析线路故障率的影响因素。
6.2.1 台风模拟
配电线路为LGJ70/10型钢芯铝绞线,按等腰三角形排布,层间距离为0.8 m;杆塔采用高12 m,强度等级为G级的混凝土电杆;导线和杆塔参数见附表2[25]。
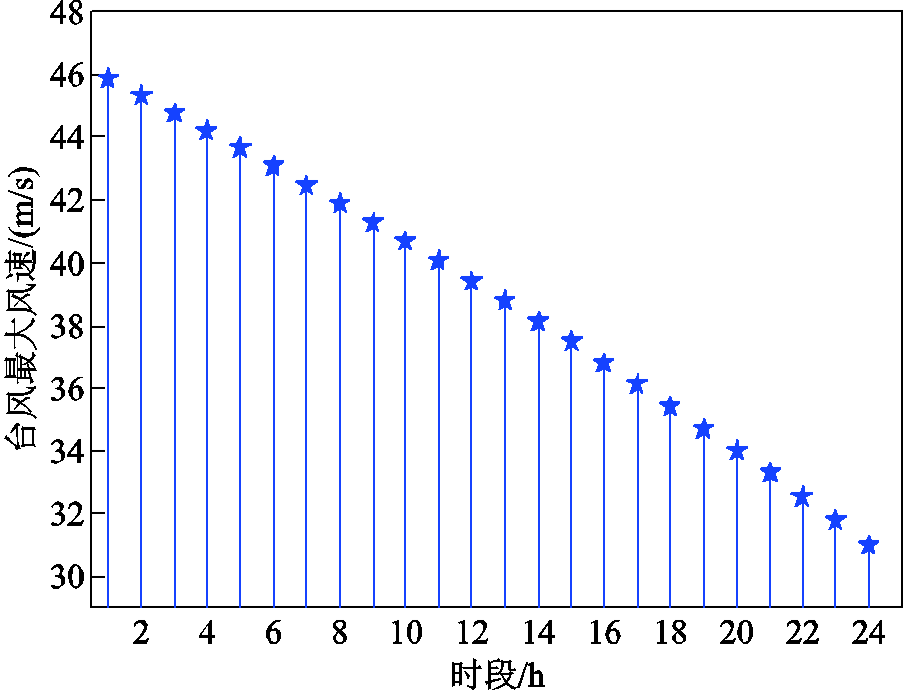
根据测试系统地理分布建立如图2所示的坐标系,台风登陆时中心点坐标为(60, -45) km,对应的经纬度为(112.43°E, 21.36°N),移动速度为 10 km/h,移动方向角为45°,中心点气压为910 hPa,台风外围气压为1 010 hPa[34]。根据台风时空演变模型可得台风登陆后24 h的移动路径,如图3所示。图中浅绿色区域表示我国东部沿海某城市的地理分布图,红色的点表示各时段台风中心的位置,蓝色圆圈表示各时段台风最大风速对应的风圈。台风登陆后,受陆地上建筑物的阻挡,其强度逐渐减弱,中心压差也不断减小。从图3中可以看出,随着中心压差的减小,台风风圈逐渐增大。另外,附图5所示为台风最大风速半径处的风速,可以看出,台风登陆后,风速也逐渐减弱。
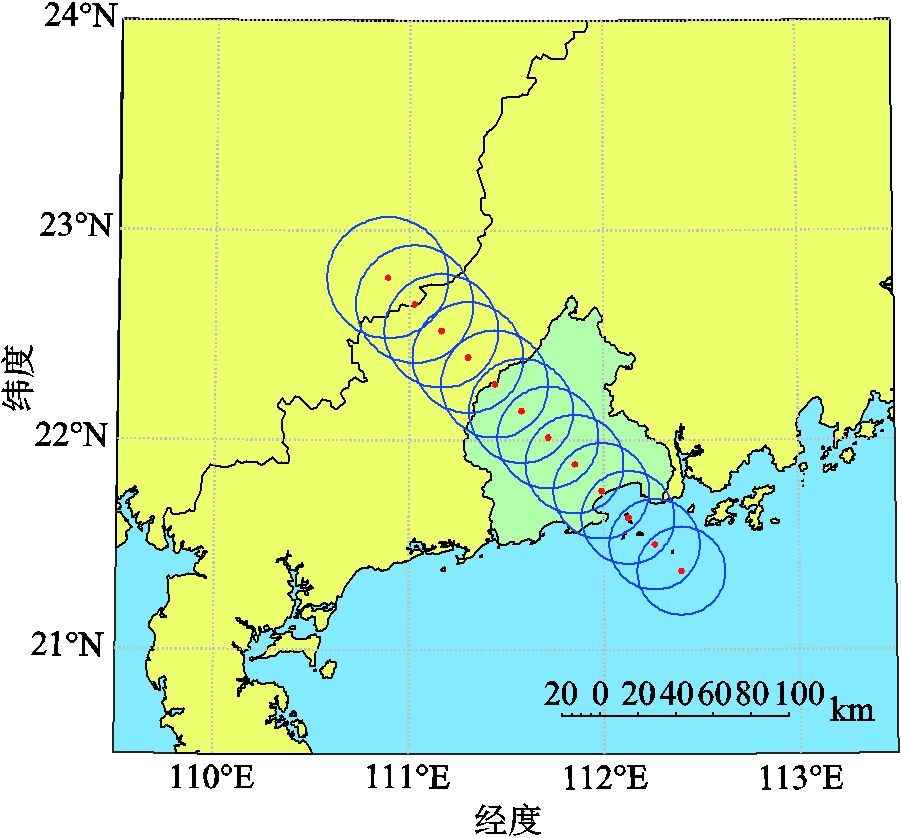
图3 台风登陆24 h的移动路径
Fig.3 Moving path of typhoon in 24 h after landing
6.2.2 线路故障率影响因素
图4给出了配电线路在4时段的故障率。从图4中可以看出,同一时段各线路的故障率不同。显然,若线路坐标不同,则同一时段各线路与台风中心距离不同,导致其承受的风荷载不同,进而使得故障率不同。但线路16(16-17)和17(6-18)地理坐标相近,而故障率相差较大。这是因为两线路与风速夹角不同。类似的情况,如线路19(19-20)和20(19-21),线路36(36-37)和37(36-38)。此外,线路28(28-29)和29(29-30),线路43(43-44)和44(44-45)故障率也不同。这两组线路地理坐标相近,与风速夹角相同,导致线路故障率不同的原因是线路长度。两组线路中线路28和43的长度相对较长,故障率较高。仿真结果表明,线路地理坐标、线路长度以及线路与风速夹角均影响线路故障率。
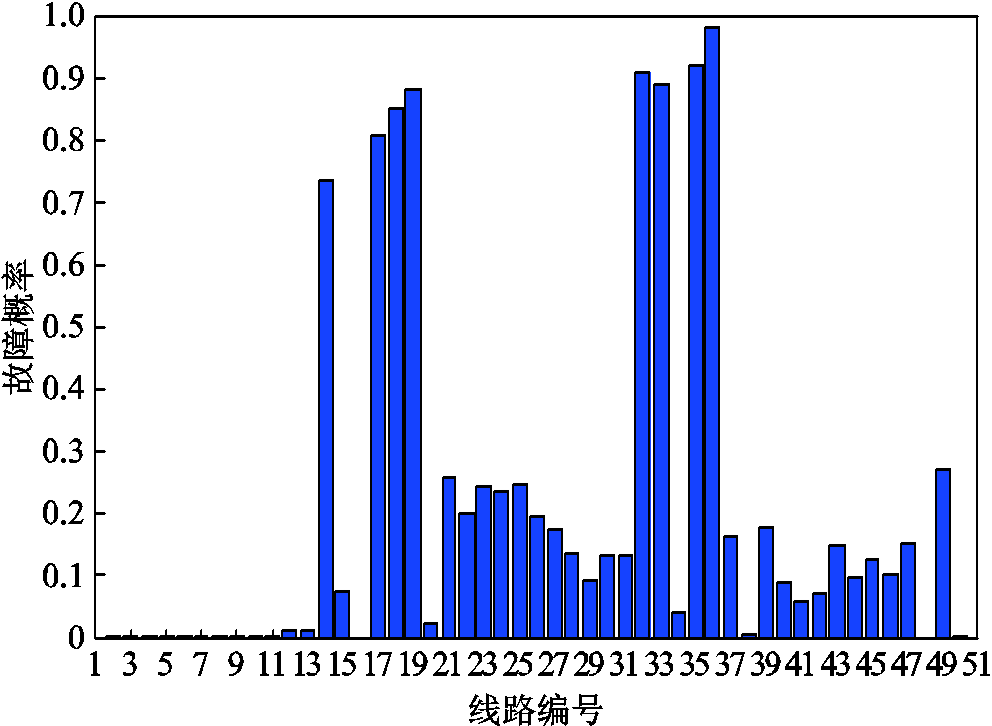
图4 配电线路在4时段的故障概率
Fig.4 Failure probability of distribution lines at 4th time period
进一步地,本节以线路19(19-20)为例,说明线路故障率受线路与台风中心距离的影响。如图5所示,在1~4时段随着台风靠近,线路故障率逐渐增大,该时段线路19处于台风风圈的前沿;接着台风继续向前行进,线路19逐渐接近台风中心,在4~6时段线路故障率逐渐降低;在6~8时段线路19位于台风中心附近,因台风中心附近风速较小,所以线路故障率几乎降为0;在8~10时段台风风圈后沿逐渐靠近线路19,线路故障率上升;在后续时段,随着线路与台风中心距离逐渐增大,线路故障率持续下降直至为0。在台风过境的整个过程中,当线路处于台风风圈附近时易发生故障,因此图5中线路故障率曲线呈现两个尖峰。仿真结果表明,线路与台风中心的距离也是影响线路故障率的重要因素。

图5 线路19的故障率及其与台风中心的距离
Fig.5 Failure probability of line 19 and its distance from the typhoon center
为测试弹性提升措施的性能,本节设置五个案例进行对比分析。案例1:不考虑任何优化措施;案例2:仅考虑DG和ESS部署措施;案例3:考虑DG、ESS部署和线路加固措施;案例4:考虑DG、ESS和SOP部署措施;案例5:综合考虑DG、ESS、SOP部署和线路加固措施。本节测试时设置线路加固数为4,DG、SOP和ESS安装数量分别为4、3、3,信息熵预算值设为1.0,其他参数同上。
6.3.1 弹性提升措施成本分析
五个案例的弹性提升措施成本及失电负荷成本见表2。由表2最后一列可知,相比于没有考虑任何优化措施的案例1,案例2~5的总成本均是降低的,分别降低66%、83%、85%和97%。同时,从表2倒数第二列可看出,失电负荷成本也是逐渐降低的。本文以失电负荷成本作为配电网弹性量化指标,失电负荷成本越低意味着配电网弹性越强。案例5的总成本和失电负荷成本均是最低的,说明多种灵活性资源协同优化不仅能有效提升配电网弹性,还能降低台风造成的经济损失。
6.3.2 线路故障状态分析
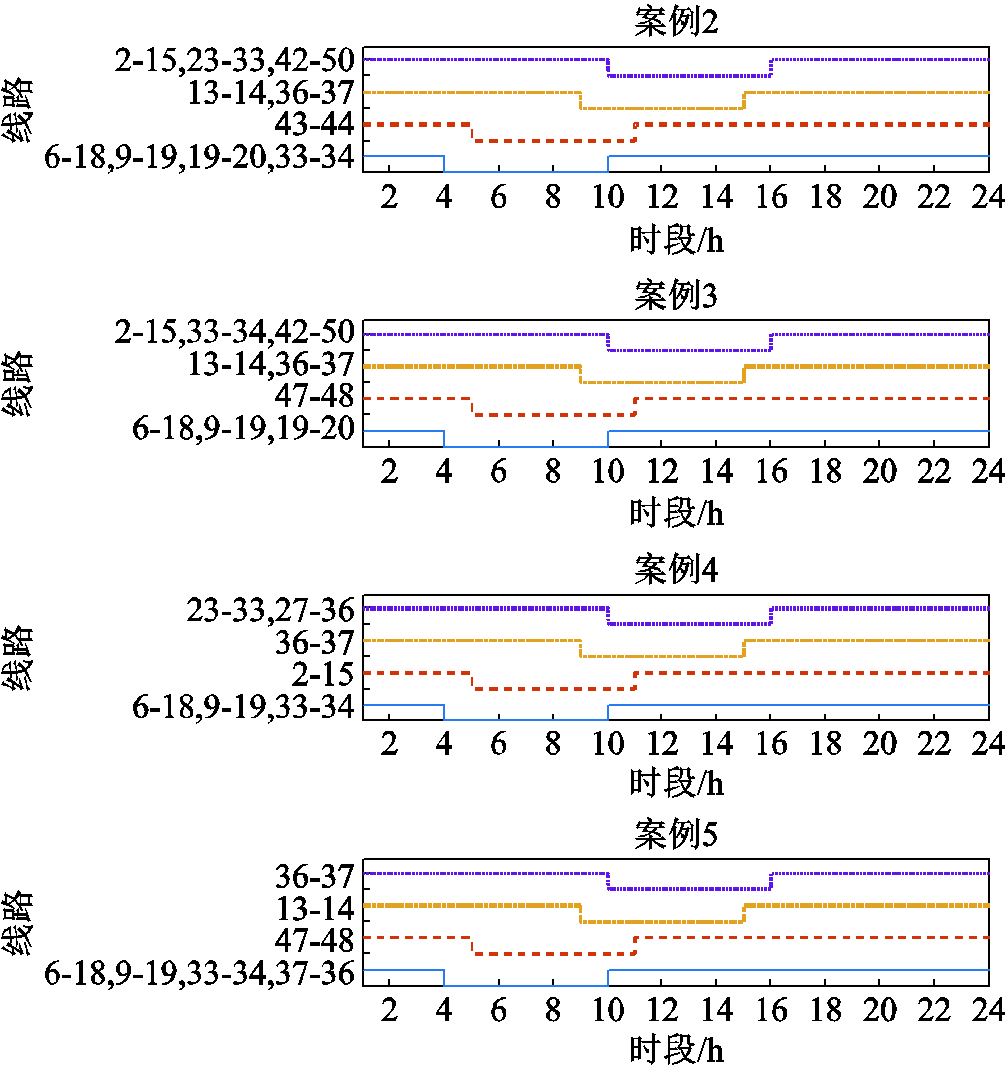
图6所示为案例1的线路故障状态,凹陷部分表示线路处于故障状态,线路故障状态持续时间为6 h,与故障平均修复时间一致。案例1因未考虑优化措施,受台风损害严重,故障数高达10重,并且线路一般在t=3,4,5,9,10时段受到攻击而发生故障。主要是因为在这些时段,配电网多半线路处于台风风圈附近,导致线路故障率升高。另外,附图6给出了案例2~5的线路故障状态。从附图6中可以看出,具有时空特性的台风在不同时段造成不同位置和不同数量的配电线路故障。这说明台风时空演变模型能有效模拟台风时变特性造成配电网故障的不确定性。
表2 不同案例下弹性提升措施成本
Tab.2 Cost of resilience enhancement measures in different cases

案例DG安装成本/万元ESS安装成本/万元SOP安装成本/万元线路加固成本/万元失电负荷成本/万元总成本/万元 1————15 122.7415 122.74 214.9652.40——5 067.785 135.14 314.9652.70—30.652 404.242 502.56 414.9653.3022.20—2 104.462 194.92 514.9649.9622.2032.52270.41390.05
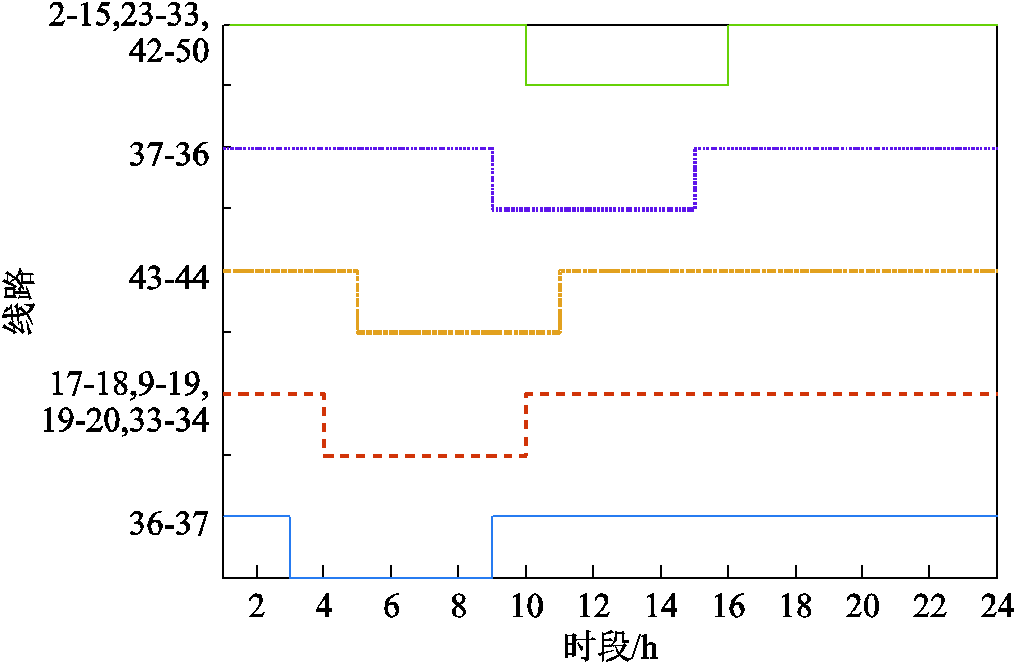
图6 案例1线路故障状态
Fig.6 The fault status of distrubution lines in case 1
6.3.3 优化方案分析
以案例1和案例5为例对优化方案进行具体分析,案例1和案例5的优化结果拓扑图分别如图7和图8所示。案例1中台风袭击后无优化措施实施,该方案造成15 122.74万元的经济损失,失电负荷量高达102 MW。更为严重的是,如图7所示,线路27-36故障导致一级重要负荷36失电,线路43-44故障导致二级重要负荷44失电。重要负荷失电可能造成重大影响,必须采取有效措施保障其供电。
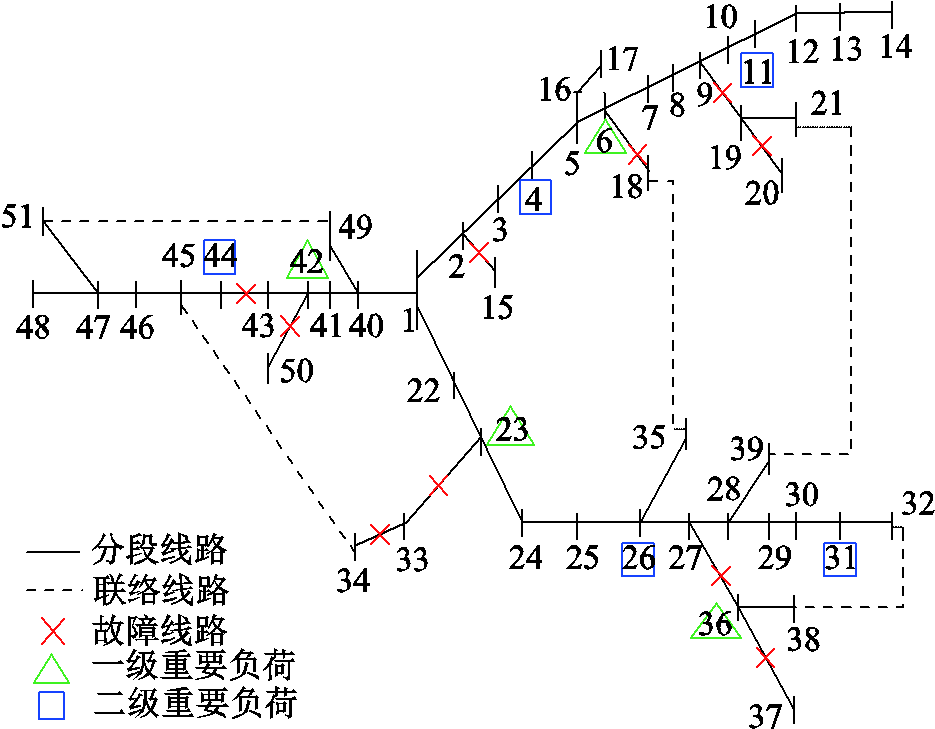
图7 案例1无优化措施的方案
Fig.7 Scheme of case 1 without optimizaiton measures
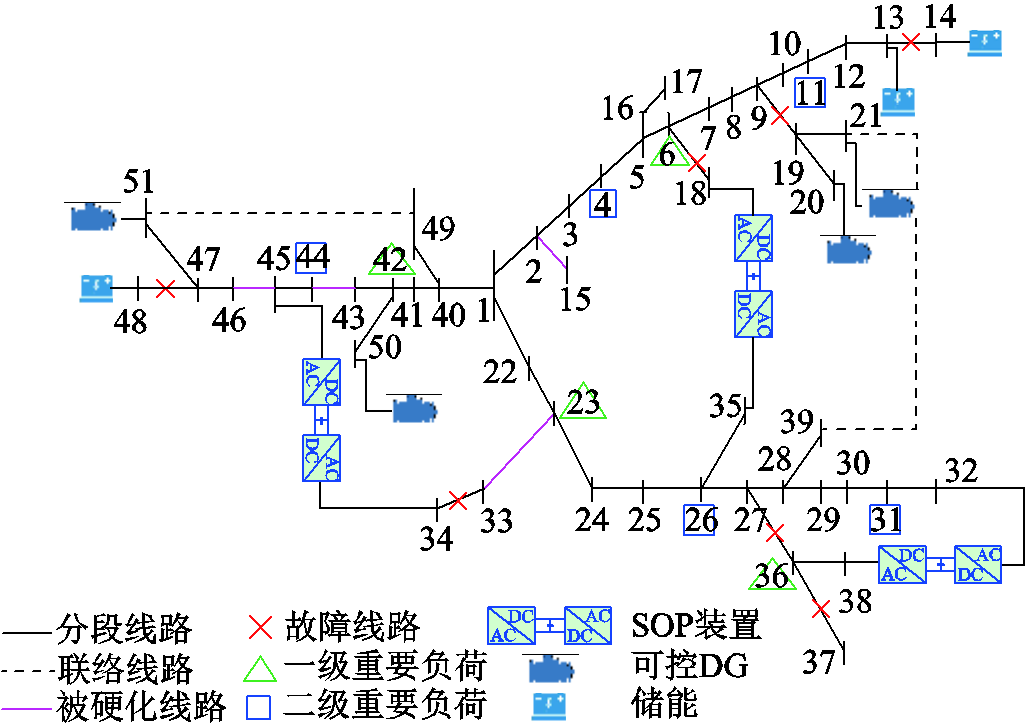
图8 案例5多种措施协调优化方案
Fig.8 The optimiazation scheme of case 5 with the coordination of multiple measures
相比案例1,案例5不仅能保证重要负荷供电,还能有效降低失电负荷量。案例5中失电负荷量仅为3 MW,相比案例1降低了97%,且失电负荷全部为三级负荷。案例5中各优化措施的部署结果如图8所示,联络线32-38处安装SOP,通过灵活的功率控制,优先保证一级重要负荷36的供电;同时线路43-44被加固,使得二级负荷44的供电路径与变电站连通。另外,节点20、21,50和51部署可控DG,节点13、14和48部署ESS,联络线18-35和34-45上安装SOP,这些灵活性资源的部署能够在优先保证一、二级负荷的电力供应后,还可保证失电区域内部分三级负荷的供电。因此,案例5中仅部分三级负荷失电。仿真结果表明,多种灵活性资源协调极大地降低了失电负荷量,提高了配电网弹性。
本节将测试线路加固数量和DG/ESS/SOP安装数量、信息熵预算值、台风登陆位置及方向角对配电网弹性的影响。
6.4.1 线路加固数量和DG/ESS/SOP安装数量的影响
首先将线路加固和DG部署措施划分为一组,将ESS和SOP部署措施划分为另一组,分别进行灵敏度分析。然后设置线路加固数和DG安装数量从1增加到9,SOP安装数量从1增加到5,ESS安装数量从1增加到8,信息熵预算值仍取1.0进行测试。两组测试的优化结果如图9和图10所示。从图9中可以看出,配电网失电负荷成本随着线路加固数量和DG安装数量的增加而降低,但在两种优化措施下失电负荷成本的下降幅度不同,在部署DG优化措施下,失电负荷成本下降幅度较大。线路加固数量和DG安装数量的增加,意味着故障后可用恢复资源增加,则失电负荷成本降低,即配电网弹性提升。在部署DG优化措施下,失电负荷成本降幅明显,说明部署DG对配电网弹性提升效果优于线路加固措施。
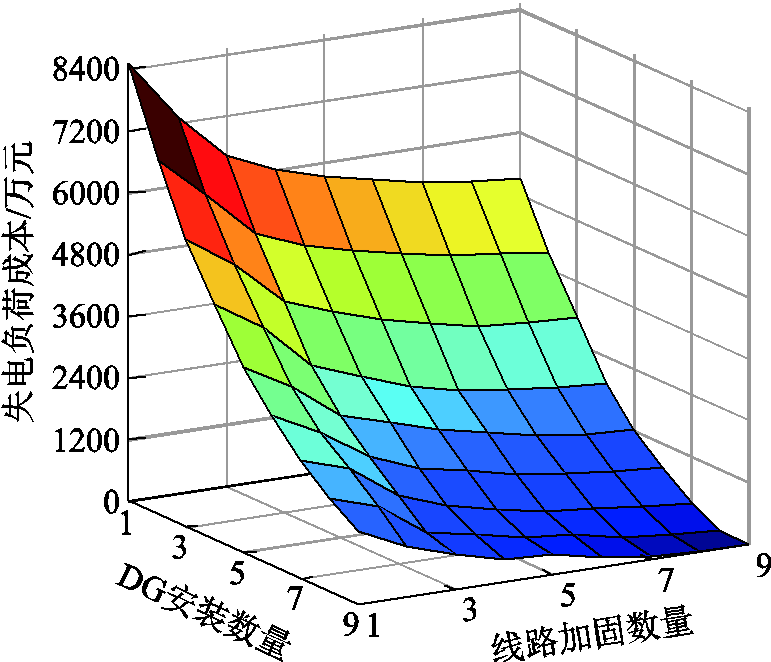
图9 线路加固和DG安装数量对配电网弹性的影响
Fig.9 Influence of line hardening and the number of DG installation on the resilience of distribuiton networks
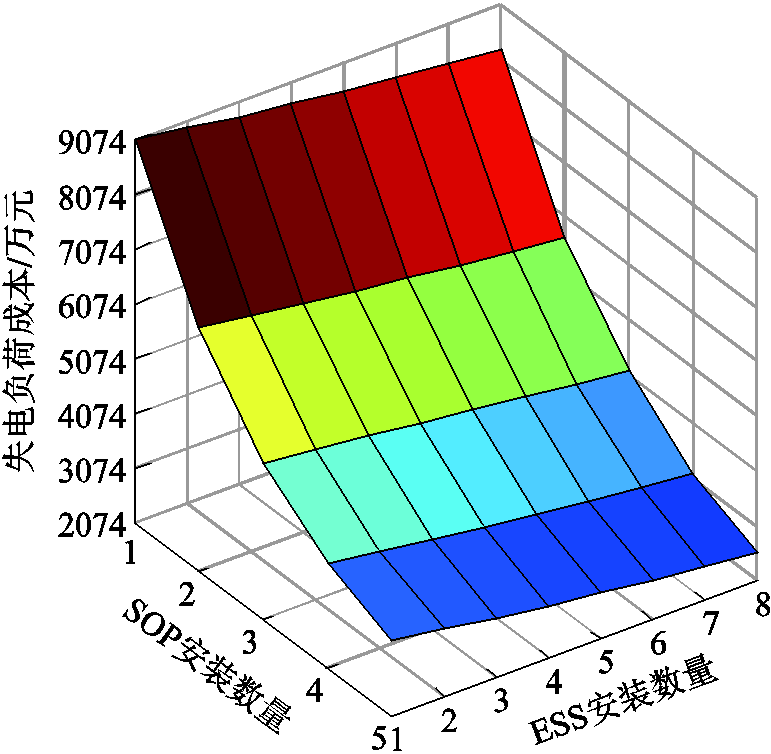
图10 ESS和SOP安装数量对配电网弹性的影响
Fig.10 Influence of the numbers of ESS and SOP installation on the resilience of distribuiton networks
图10所示为配电网在不同ESS和SOP安装数量下的失电负荷成本。类似地,配电网失电负荷成本随着ESS和SOP安装数量的增加而降低。同时,在部署SOP优化措施下,失电负荷成本下降幅度较大。这说明SOP优化措施对弹性的提升效果优于ESS。
仿真结果表明,部署DG和SOP这两种优化措施对配电网弹性的提升效果优于部署ESS和线路加固措施。这是因为单位容量的DG和SOP部署成本比线路加固成本和ESS部署成本低,而本文目标函数在考虑弹性指标的同时也增加了规划成本限制,导致同一规划成本下部署成本低的措施可提供的功率容量相对较大,因此其弹性提升效果相对较优。
6.4.2 信息熵预算值的影响
测试时将线路加固数量、DG/ESS/SOP安装数量分别设置为4、4、3、3,信息熵预算值从0.2起以0.2为步长增加至1.6。不同信息熵预算值下配电网的失电负荷成本如图11所示。从图11中可以看出,信息熵预算值在0.2~0.6之间时,失电负荷成本为0,即所有负荷均被恢复供电;从0.8开始,失电负荷成本随着信息熵预算值的增加而增大。如4.3节所述,信息熵值的大小反映台风危害程度,信息熵值越大表示台风危害越大,反之亦然。图11说明仿真结果符合理论分析。当信息熵值小于0.6时,台风危害相对较小,在给定的优化措施预算下所有负荷均能被恢复供电;而当信息熵值大于0.6时,台风危害程度逐渐增大,在给定的优化措施预算下可用恢复资源逐渐不足,则失电负荷成本逐渐增加,配电网弹性下降。
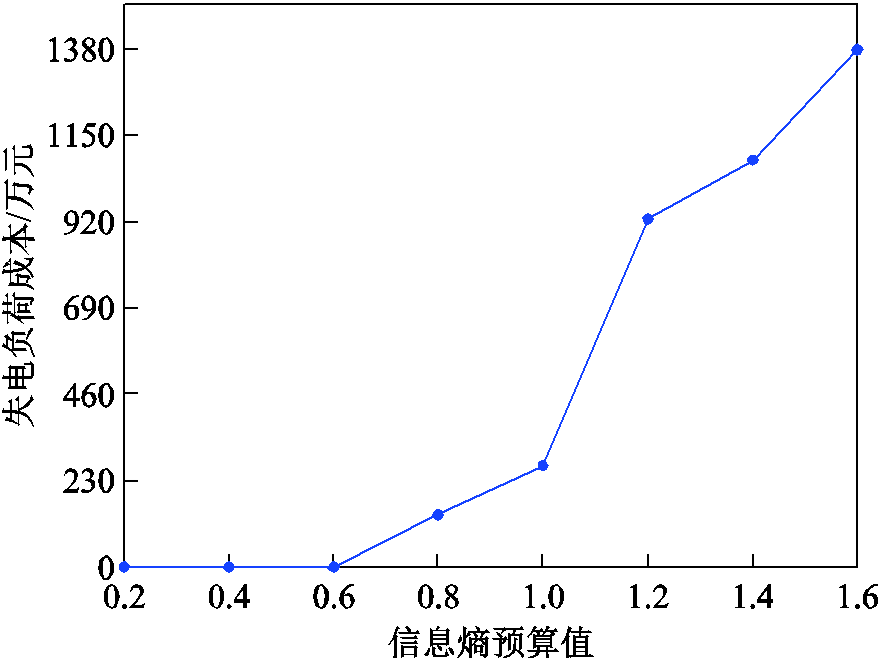
图11 不同信息熵预算值下的失电负荷成本
Fig.11 The load shedding costs under different information entropy budget values
6.4.3 台风登陆位置和方向角的影响
本节以案例5为例,分析不同台风登陆位置和方向角对配电网弹性的影响。如图12所示,选取三个登陆位置:A(80, -20) km、B(60, -45) km、C(40, -50) km,三个方向角:30°、45°、60°,组合为9个场景进行测试。另外,图12中红色五角星表示测试系统地理中心位置。信息熵预算值取0.6,其他参数同上。
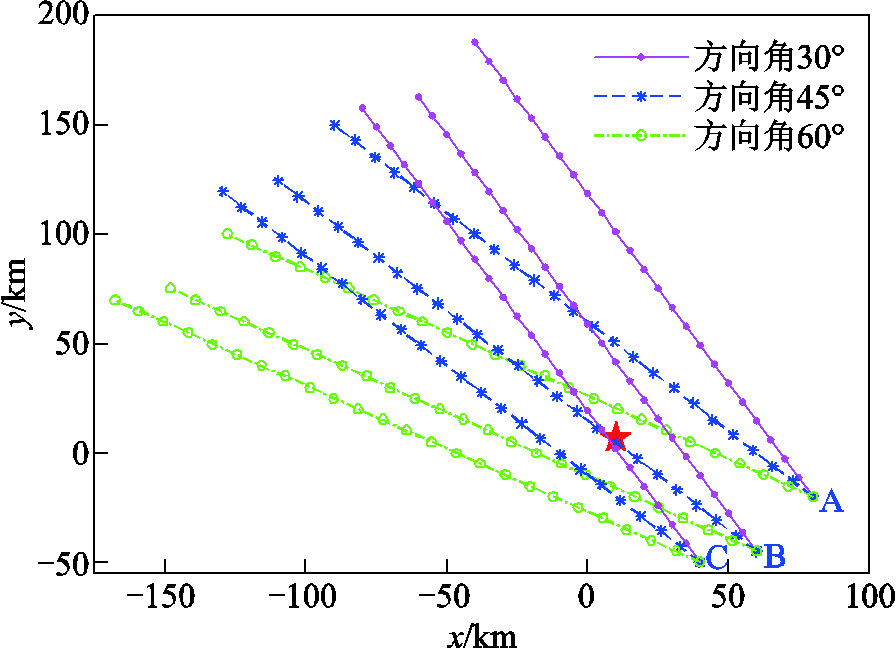
图12 台风不同登陆位置和方向角
Fig.12 Different typhoon landing positions and direction angles
台风在不同登陆位置和方向角时优化措施成本见表3。从表3中可以看出,在登陆位置为A,方向角为60°;登陆位置为B,方向角为30°和60°;登陆位置为C,方向角为45°这四种场景下,失电负荷成本明显大于其他场景。观察图12中这四种场景与配电网的相对位置关系,发现配电网位于这四种场景台风风圈附近,配电网故障线路数增多。因此,在这四种场景下,配电网故障较严重,失电负荷成本较大,配电网弹性较低。从图12中可以看到,在台风登陆位置为B、方向角为45°和台风登陆位置为C、方向角为30°这两种场景下,配电网靠近台风中心点。因台风中心点附近风速较小,所以配电网故障线路较少。相应地,从表3中可以看到,这两种场景下失电负荷成本较小,配电网弹性较高。另外,在登陆位置为A、方向角为30°和45°,以及登陆位置为C、方向角为60°这三种场景下,因配电网距离台风路径较远,受台风影响小,故障线路数较少。从表3中可以看到,这三种场景的失电负荷成本均为0,表明在这三种场景下,本文提出的方法恢复了所有负荷,使得配电网弹性提升至正常运行时的弹性水平。
仿真结果表明,不同登陆位置和方向角的台风对配电网弹性的影响不同。台风登陆位置和方向角通过影响台风和配电网的相对位置关系,影响配电网弹性。根据台风风场模型可知,台风和配电网的相对位置决定了配电网所承受风荷载的大小,进而影响线路故障率,并对配电网弹性产生不同影响。
表3 台风在不同登陆位置和方向角时的优化结果
Tab.3 Optimization results for typhoons at different landing positions and direction angles

登陆位置方向角/(°)DG安装成本/万元ESS安装成本/万元SOP安装成本/万元线路加固成本/万元失电负荷成本/万元总成本/万元 A3011.23018.510029.74 4510.5811.3821.7833.03076.77 6014.9655.7822.1836.352 752.862 882.14 B3014.9653.2822.2037.354 712.434 840.22 4513.687.4221.7528.0949.70120.64 6014.9651.7522.2036.744 259.644 385.28 C3014.9652.0121.2133.59442.93564.71 4514.9651.6121.7533.043 410.013 531.37 6013.36021.5333.59038.49
为有效地降低台风灾害对配电网的影响,本文提出计及台风时空特性和灵活性资源协同优化的配电网弹性提升策略。构建台风时空演变模型,深入分析台风时空特性造成配电网故障时间、位置和规模的不确定性。基于结构可靠性原理,通过分析线路元件强度和荷载效应,计算配电线路时变故障率。挖掘线路加固、DG、ESS和SOP等灵活性资源多维度提升配电网弹性的潜力,建立两阶段三层的DAD模型,并在我国东部沿海某城市51节点系统中进行仿真测试,得到如下结论:
1)本文建立的台风时空演变模型和配电线路故障模型通过对台风实时路径和风场的模拟,以及对线路元件荷载效应的计算,深入剖析台风时空特性影响配电线路故障率的内在机理,明确线路长度、线路与风速夹角、线路位置坐标、线路与台风中心距离是影响线路故障率的主要因素。
2)根据配电线路时变故障率,以信息熵预算值反映台风危害程度,采用信息熵识别脆弱线路,得到配电线路时变故障状态。本文方法能如实反映配电线路时变故障状态与台风危害强度和线路故障率的映射关系。
3)对各灵活性资源的弹性提升效果分析得到,部署DG和SOP这两种优化措施对配电网弹性的提升效果优于部署ESS和线路加固措施,同时多种灵活性资源协调得到最优的弹性提升效果。
附 录
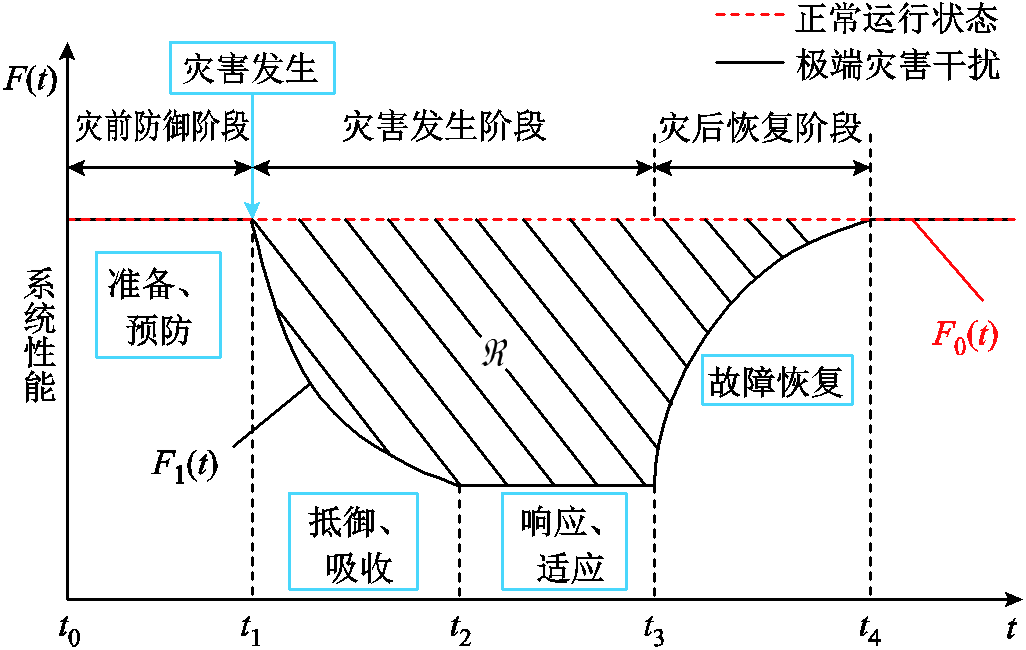
附图1 弹性配电网在极端灾害干扰下的响应过程
App.Fig.1 Response process of resilient distribution network under extreme disaster interference
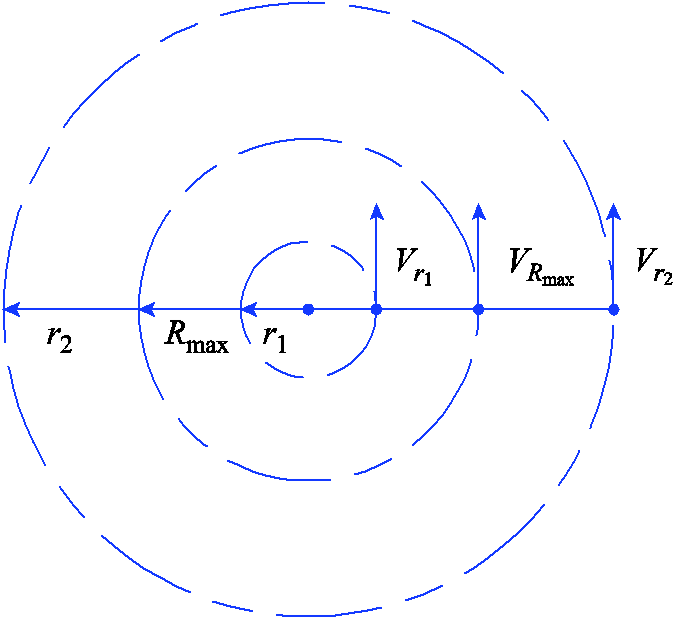
附图2 台风风场
App.Fig.2 Wind field of typhoon
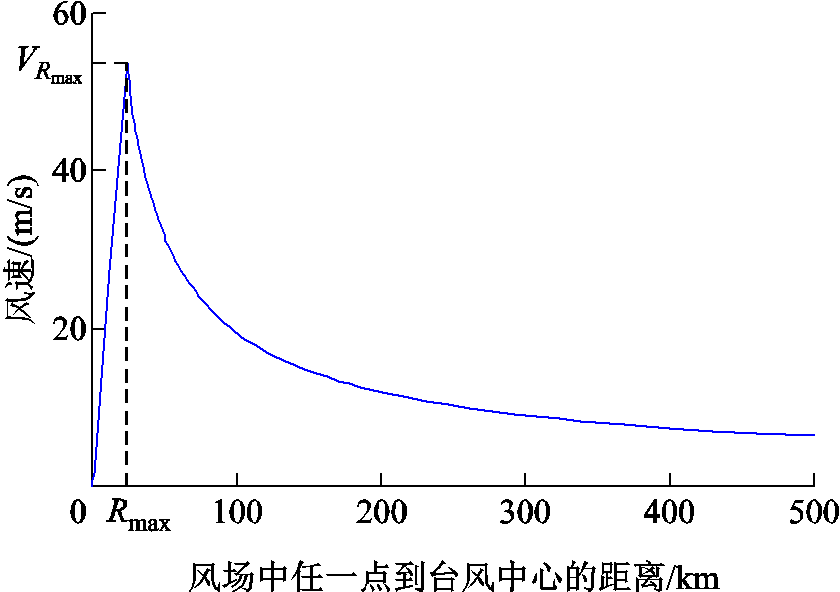
附图3 风场中距离台风中心不同位置处的风速
App.Fig.3 Wind speed at different locations from the typhoon center in the wind field
附图4 C&CG算法流程
App.Fig.4 Flow chart of C&CG algorithm
附表1 负荷优先级
App.Tab.1 Load priority

优先级负荷节点 一级6, 23, 36, 42 二级4, 11, 26, 31, 44 三级1-3, 5, 7-10, 12-22, 24, 25, 27-30, 32-35, 37-41, 43, 45-51
附表2 导线和杆塔参数
App.Tab.2 Parameters of conductor and ploe

导线参数数值杆塔参数数值 0.851.0 1.20.7 /mm11.41.0 A/mm279.39/mm190,350 /(kg/m)0.275/m50 /(N/mm2)15 315 /(N·m)58 512 /(N/mm2)3 333 /(N·m)14 628
附图5 台风最大风速
App.Fig.5 Maximum wind speed of typhoon
附图6 案例2~5线路故障状态
App.Fig.6 The fault status of distribution lines in case 2~5
参考文献
[1] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429.
Xu Yin, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhancement[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[2] 苏译, Teh Jiashen, 柏智, 等. 考虑不确定性扰动的含海量资源配电网弹性研究综述[J]. 电力系统自动化, 2022, 46(16): 17-30.
Su Yi, J.S Teh, Bai Zhi, et al. Review of research on resilience of distribution network with massive resources considering uncertainty disturbance[J]. Automation of Electric Power Systems, 2022, 46(16): 17-30.
[3] 张迪. 提升配电网弹性的微电网技术研究[D]. 上海: 东华大学, 2019.
Zhang Di. Research on microgrid technology for improving the resilience of distribution network[D]. Shanghai: Donghua University, 2019.
[4] 倪萌, 王蓓蓓, 朱红, 等. 能源互联背景下面向高弹性的多元融合配电网双层分布式优化调度方法研究[J]. 电工技术学报, 2022, 37(1): 208-219.
Ni Meng, Wang Beibei, Zhu Hong, et al. Study of two-layer distributed optimal scheduling strategy for highly elastic multi-resource fusion distribution network in energy interconnection environment[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 208-219.
[5] Li Boda, Chen Ying, Wei Wei, et al. Preallocation of electric buses for resilient restoration of distribution network: a data-driven robust stochastic optimization method[J]. IEEE Systems Journal, 2022, 16(2): 2753-2764.
[6] 王育飞, 李可铭, 薛花, 等. 考虑移动式储能调度的配电网灾后多源协同孤岛运行策略[J]. 电力系统自动化, 2024, 48(3): 62-72.
Wang Yufei, Li Keming, Xue Hua, et al. Post-disaster multi-source cooperative islanding operation strategy for distribution network considering mobile energy storage system dispatching[J]. Automation of Electric Power Systems, 2024, 48(3): 62-72.
[7] 蔡胜, 谢云云, 张玉坪, 等. 考虑孤岛微电网建立过程功率冲击的弹性配电网主动预防调度[J]. 电工技术学报, 2023, 38(23): 6419-6432.
Cai Sheng, Xie Yunyun, Zhang Yuping, et al. Proactive scheduling of resilient distribution systems considering power impact during islanded microgrid formation process[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6419-6432.
[8] 卞艺衡, 别朝红. 面向弹性提升的智能配电网远动开关优化配置模型[J]. 电力系统自动化, 2021, 45(3): 33-39.
Bian Yiheng, Bie Zhaohong. Resilience-enhanced optimal placement model of remote-controlled switch for smart distribution network[J]. Automation of Electric Power Systems, 2021, 45(3): 33-39.
[9] 胡玉, 顾洁, 马睿, 等. 面向配电网弹性提升的智能软开关鲁棒优化[J]. 电力自动化设备, 2019, 39(11): 85-91.
Hu Yu, Gu Jie, Ma Rui, et al. SNOP robust optimization for distribution network resilience enhancement[J]. Electric Power Automation Equipment, 2019, 39(11): 85-91.
[10] 王子昊, 王旭, 蒋传文, 等. 基于近端策略优化算法的灾后配电网韧性提升方法[J]. 电力系统自动化, 2022, 46(21): 62-70.
Wang Zihao, Wang Xu, Jiang Chuanwen, et al. Resilience improvement method for post-disaster distribution network based on proximal policy optimization algorithm[J]. Automation of Electric Power Systems, 2022, 46(21): 62-70.
[11] 陈厚合, 丛前, 姜涛, 等. 多能协同的配电网供电恢复策略[J]. 电工技术学报, 2022, 37(3): 610-622, 685.
Chen Houhe, Cong Qian, Jiang Tao, et al. Distribution systems restoration with multi-energy synergy[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 610-622, 685.
[12] 马丽叶, 王海锋, 卢志刚, 等. 计及相关性影响的增强台风灾害下配电网韧性灵活性资源规划[J]. 电力系统自动化, 2022, 46(7): 60-68.
Ma Liye, Wang Haifeng, Lu Zhigang, et al. Flexible resource planning for improving distribution network resilience under typhoon disasters considering relevance impact[J]. Automation of Electric Power Systems, 2022, 46(7): 60-68.
[13] 王月汉, 刘文霞, 姚齐, 等. 面向配电网韧性提升的移动储能预布局与动态调度策略[J]. 电力系统自动化, 2022, 46(15): 37-45.
Wang Yuehan, Liu Wenxia, Yao Qi, et al. Pre-layout and dynamic scheduling strategy of mobile energy storage for resilience enhancement of distribution network[J]. Automation of Electric Power Systems, 2022, 46(15): 37-45.
[14] Huang Zhanghao, Zhang Yachao, Xie Shiwei. A comprehensive strategy for the distribution network resilience enhancement considering the time-varying behaviors of typhoon path[J]. Electric Power Systems Research, 2023, 214: 108819.
[15] Ma Shanshan, Li Shiyang, Wang Zhaoyu, et al. Resilience-oriented design of distribution systems[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2880-2891.
[16] Ma Shanshan, Su Liu, Wang Zhaoyu, et al. Resilience enhancement of distribution grids against extreme weather events[J]. IEEE Transactions on Power Systems, 2018, 33(5): 4842-4853.
[17] Lin Yanling, Bie Zhaohong. Tri-level optimal hardening plan for a resilient distribution system considering reconfiguration and DG islanding[J]. Applied Energy, 2018, 210: 1266-1279.
[18] Ma Shanshan, Chen Bokan, Wang Zhaoyu. Resilience enhancement strategy for distribution systems under extreme weather events[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1442-1451.
[19] Wang Xu, Li Zhiyi, Shahidehpour M, et al. Robust line hardening strategies for improving the resilience of distribution systems with variable renewable resources[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 386-395.
[20] Yuan Wei, Wang Jianhui, Qiu Feng, et al. Robust optimization-based resilient distribution network planning against natural disasters[J]. IEEE Transactions on Smart Grid, 2016, 7(6): 2817-2826.
[21] Najafi Tari A, Sepasian M S, Tourandaz Kenari M. Resilience assessment and improvement of distribution networks against extreme weather events[J]. International Journal of Electrical Power & Energy Systems, 2021, 125: 106414.
[22] Ouyang Min, Dueñas-Osorio L. Multi-dimensional hurricane resilience assessment of electric power systems[J]. Structural Safety, 2014, 48: 15-24.
[23] Zhang Haibo, Ma Shentong, Ding Tao, et al. Multi-stage multi-zone defender-attacker-defender model for optimal resilience strategy with distribution line hardening and energy storage system deployment[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 1194-1205.
[24] Hu Bo, Li Mushui, Niu Tao, et al. Hardening planning of overhead distribution lines in typhoon-prone areas by considering the typhoon motion paths and the line load reliability[J]. International Journal of Electrical Power & Energy Systems, 2021, 129: 106836.
[25] 兰颖. 考虑台风影响的配电网可靠性评估和规划[D]. 重庆: 重庆大学, 2014.
Lan Ying. Distribution system reliability evaluation and design considering influence of typhoon[D]. Chongqing: Chongqing University, 2014.
[26] 贡金鑫, 张勤. 工程结构可靠性设计原理[M]. 2版. 北京: 机械工业出版社, 2022.
[27] Ahmadi H, Martı´ J R. Linear current flow equations with application to distribution systems reconfiguration[J]. IEEE Transactions on Power Systems, 2015, 30(4): 2073-2080.
[28] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477.
Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5462-5477.
[29] Boyd S P, Vandenberghe L. Convex optimization[M]. Cambridge, UK: Cambridge, 2004.
[30] Glover F. Improved linear integer programming formulations of nonlinear integer problems[J]. Management Science, 1975, 22(4): 455-460.
[31] 孙充勃, 李敬如, 罗凤章, 等. 考虑分布式电源接入的配电系统典型算例设计[J]. 电力建设, 2020, 41(10): 47-62.
Sun Chongbo, Li Jingru, Luo Fengzhang, et al. Typical case design of distribution system considering DG integration[J]. Electric Power Construction, 2020, 41(10): 47-62.
[32] Li Yong, Xiao Juanxia, Chen Chun, et al. Service restoration model with mixed-integer second-order cone programming for distribution network with distributed generations[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4138-4150.
[33] 邹波, 孙可, 胡成鹏, 等. 台风天气下配电系统韧性提升策略[J]. 电力系统及其自动化学报, 2021, 33(7): 135-142.
Zou Bo, Sun Ke, Hu Chengpeng, et al. Resilience enhancement strategy for power distribution system under typhoon weather[J]. Proceedings of the CSU-EPSA, 2021, 33(7): 135-142.
[34] 浙江省水利厅. 台风路径[EB/OL]. https://typhoon. slt.zj.gov.cn/.
Abstract Enhancing the resilience of distribution networks is an urgent task to resist the frequent typhoon disasters. Generally, typhoon has the spatiotemporal characteristics, which causes the uncertainty of distribution network failures. However, the current researches ignore this feature and fail to deeply analyze the principle of distribution network failure caused by typhoon. Moreover, most of them overlook the potential of flexible resources in enhancing the resilience of distribution networks. To address these issues, this paper proposes a resilience enhancement strategy that takes into account the spatiotemporal characteristics of typhoon and the coordinated optimization of flexible resources.
Firstly, a spatiotemporal evolution model of typhoon is constructed using the typhoon path model and the Batts wind field model, which is capable of simulating the moving path and wind field of typhoon in real time. Secondly, according to the principle of structural reliability, the time-varying failure probability of distribution lines can be obtained by comparing the strength of line components with load effects. On this basis, the information entropy theory is used to identify fragile lines. Then, a two-stage and three-layer defense-attack-defense (DAD) model combining pre-disaster defense and post-disaster restoration is established, with the load shedding cost as the resilience quantification indicator. In the proposed model, flexible resources such as line hardening, distributed generation (DG), energy storage system (ESS), and soft open point (SOP) are coordinated to enhance the resilience of distribution networks. The proposed model can reflect the uncertain effects of typhoon spatiotemporal characteristics on the time, location and scale of distribution network failures. Meanwhile, flexible resources can be fully utilized to enhance the resilience of distribution networks.
In the numerical test section, two aspects of typhoon simulation and flexible resources performance analysis are tested. In the test of typhoon simulation, the numerical results show that the proposed spatiotemporal evolution model of typhoon is able to simulate the moving path and wind field of typhoon after landfall. Moreover, the failure probability of distribution lines is affected by various factors, such as line length, the angle between the line and the wind speed, the line location coordinates, and the distance between the line and the typhoon center. Besides, the typhoon with spatiotemporal characteristics causes different locations and quantities of distribution line failures at different periods. Several comparison schemes are developed to test the performance of flexible resources in enhancing the resilience of distribution networks. The numerical results show that the number of line hardening and the installation number of DG/ESS/SOP affect the resilience of distribution networks. Compared with the scheme without any optimization measures, the de-energized loads obtained by the optimization scheme considering the coordination of flexible resources is reduced by 97%, and all the de-energized loads are third priority loads.
The following conclusions can be drawn from the study: (1)The proposed spatiotemporal evolution model of typhoon and the fault model of distribution line can effectively simulate the internal mechanism of the influence of typhoonon the failure probability of distribution lines. (2) In terms of resilience enhancement effects, the deployments of DG and SOP are better than line hardening and BSS measure. (3) The coordination of flexible resources greatly reduces the amount of de-energized loads and enhances the resilience of distribution networks compared with the optimization schemes that use only a single measure.
keywords:Typhoon disasters, flexible resources, resilience enhancement, spatiotemporal characteristics, robust optimization
中图分类号:TM73; TM75
DOI: 10.19595/j.cnki.1000-6753.tces.231692
国家重点研发计划政府间国际科技创新合作重点项目(2022YFE0129300)和国家自然科学基金联合基金重点支持项目(U22B200134)资助。
收稿日期 2023-10-12
改稿日期 2024-04-24
肖娟霞 女,1986年生,博士研究生,研究方向为配电网弹性提升,配电网运行优化。E-mail:xiaojuanxia@hnu.edu.cn
李 勇 男,1982年生,教授,博士生导师,研究方向为能源/电力系统优化运行与控制、电能变换系统与装备。E-mail:yongli@hnu.edu.cn(通信作者)
(编辑 赫 蕾)