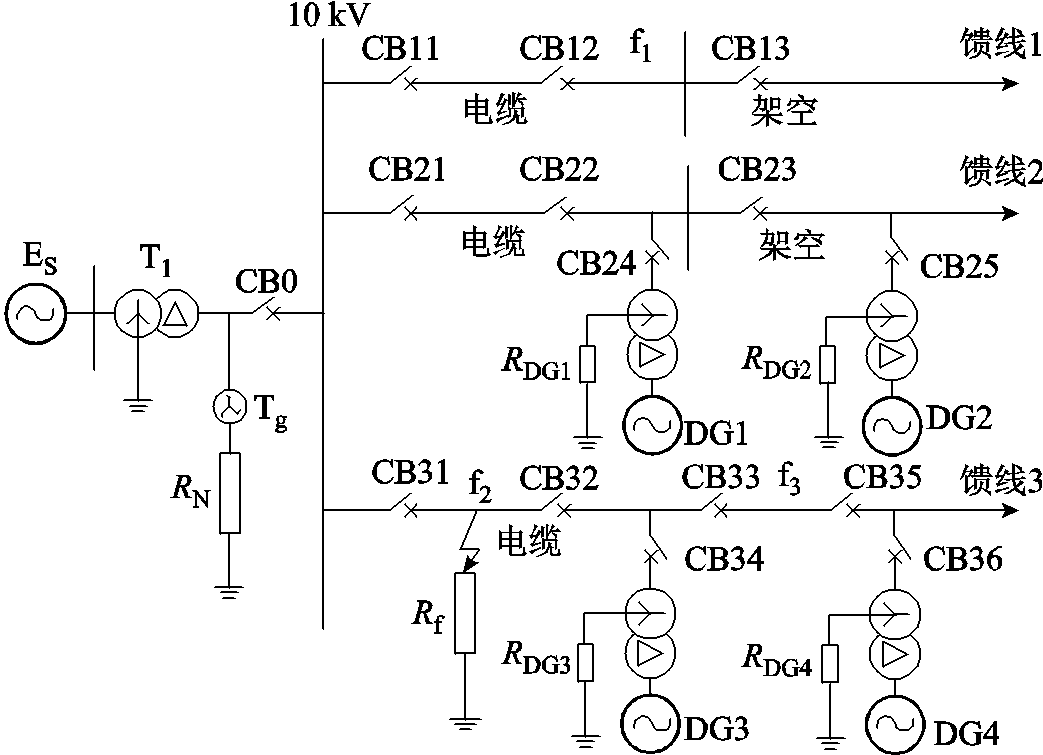
图1 含DG的配电网接地故障电气图
Fig.1 Electrical diagram of grounding fault in distribution network with DG
摘要 大规模分布式电源（DG）接入小电阻接地系统配电网后，故障电流产生明显变化，采用零序电流保护方法切除单相接地故障将出现误动作。为了解决以上问题，首先，提出基于相电压与零序电流相位差的小电阻接地系统有源配电网接地故障保护算法；然后，通过建立包含多个分布式电源的配电网接地故障电气系统结构与模型，对故障时刻相电压与零序电流相位关系进行理论推导与计算，分析得出不同接地故障位置的相位差区间，根据相位差区间进行接地故障判断与保护；最后，进行仿真验证，结果表明该方法在配电网中性点采用小电阻接地系统时，在多种过渡电阻，不同分布电源接入数量与容量，各类型电缆长度等情况下，负载波动，均能可靠判断接地故障，适用于DG中性点经小电阻接地和不接地两种方式。
关键词：有源配电网 相电压与零序电流 相位差 小电阻接地系统 单相接地保护
配电网经小电阻接地系统具有故障过电压水平低、快速切除故障线路等优点，在越来越多的城市得到应用[1-3]。目前小电阻接地系统主要采用定时限零序电流保护方法切除单相接地故障，可准确判断单相接地的过渡电阻值在85～135 Ω[4-5]。当配电网发生数百上千欧的高阻接地故障时，将导致保护拒动，长期存在的故障影响系统运行，可能进一步引发相间短路，造成火灾、设备损坏以及人畜伤亡等事故。
针对小电阻接地系统高阻接地拒动问题，采用反时限零序过电流保护可以提高灵敏度[6]。有学者提出零序电压幅值修正的接地故障差动保护方案[7]，该方案利用零序电压自适应修正两终端电流差，提高接地故障判断灵敏度。这些研究在小电阻接地系统高阻接地故障判断准确度方面取得了较好的效果。
2021年3月，中央财经会议提出将“双碳”目标纳入生态文明建设总体布局，构建以新能源为主体的新型电力系统[8]。高比例分布式电源（Distributed Generation, DG）接入电网，将给电力系统的动态特征分析[9-11]、故障定位与保护准确度带来影响[12-15]。针对小电阻接地方式配电网建立DG并网后的接地故障模型，研究表明DG采用小电阻接地方式时，故障电流产生明显变化，影响系统原有接地保护准确度。文献[16]分析了主网和分布式电源均采用中性点经小电阻接地的配电系统的单相接地故障特性，根据故障线路和非故障线路的零序电流幅值和相位特征，提出基于零序相位差动保护和零序电流幅值比保护的分区域零序保护方案。文献[17]针对含多逆变型分布式电源的小电阻接地有源配电网一般结构，分析了单相接地故障时各出线零序电流、母线零序电压和中性线电流特征，并根据各线路零序电流与中性线电流之间的相位特点提出了基于出线零序电流与中性线电流Pearson相关性的接地保护方案。文献[18]提出小电阻接地有源配电网比幅比相式接地保护方法，需要对各出线及中性线零序电流信息进行集中比较。零序电流相位差动保护方案、Pearson相关性保护法和零序电流集中比较法都需要采集不同监测点零序电流幅值或者相位，将不同监测点的数据上传到主站计算故障位置，或通过设备之间的数据协同判断故障，对通信和主站算法依赖程度较高。
主网中性点采用小电阻接地时，分布式电源侧中性点采用小电阻接地方式具有保护动作性能高、限制过电压和运行安全等优势。针对主网和DG均采用中性点经小电阻接地的有源配电网，建立包含多个DG接入的配电网接地故障电气系统结构与模型。对模型进行理论推导与分析，研究故障时刻相电压与零序电流的相位关系，提出基于相电压与零序电流相位差的小电阻接地系统有源配电网接地故障保护算法。基于Matlab的仿真验证了该方法可以在多种故障情况下可靠判断，同时验证了DG采用不接地方式时也可正确判断接地故障，基于相电压与零序电流相位差的接地故障保护算法，可以在本地完成故障判断，耐受过渡电阻能力达到3 kΩ，不依赖通信和主站进行保护计算，具有较好的工程实用性。
图1所示为含DG的10 kV小电阻接地系统配电网电气图。配电网由系统电源ES、3条馈线、4个DG组成。馈线1不包含DG，馈线2安装DG1和DG2，馈线3安装DG3和DG4，CB0～CB35为断路器，系统电源ES采用中性点经小电阻接地方式，分布式电源DG有中性点经小电阻接地和不接地系统两种方式。T1为主网侧变压器，Tg为主网侧接地变压器，接地电阻为RN，各分布式电源通过升压变压器接入电网。故障时，旋转型DG可等效为恒压源串联阻抗模型[19]，逆变型DG在正序网络中为恒流源输出特征，输出电流与其串联的阻抗无关，在负序网络中开路，不需要考虑正序和负序阻抗，逆变型DG零序电阻受并网变压器中性点接地方式影响[20]，各DG零序电阻等效为RDG1～RDG4，当等效电阻为无穷大时，DG为不接地系统。考虑限制弧光过电压倍数、保护人身安全、零序过电流保护等影响因素，国内10 kV配电网变压器中性点电阻一般为10 Ω[21]。故障点f1位于馈线1，无DG接入；故障点f2位于馈线3，位于母线和DG3之间；故障点f3位于DG3和DG4之间。故障点过渡电阻为Rf。
图1 含DG的配电网接地故障电气图
Fig.1 Electrical diagram of grounding fault in distribution network with DG
根据图1所示含DG的配电网接地故障电气图，建立接地相为C相时的电气特征模型，如图2所示。C01～C03分别为馈线1～馈线3等效零序电容，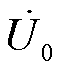
为母线零序电压，
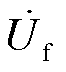为故障点处的等效电源电压（与故障前的相电压幅度相等，方向相反），İ021为非故障馈线2的CB21处零序电流，İ0f为故障点的零序电流。图2a为故障发生在馈线1的f1位置模型图，İ012为馈线1故障点流向母线的CB12处零序电流，İ013为故障点后的CB13处零序电流，İ031为馈线3的CB31处零序电流。图2b为故障发生在馈线3的f2位置模型图，İ012为非故障馈线1的CB12处零序电流，İ031为故障点流向母线的CB31处零序电流，İ032为故障馈线3故障点后CB32处零序电流。图2c为故障发生在馈线3的f3位置模型图，İ033为故障点流向母线的CB33处零序电流，İ035为故障馈线3故障点后CB35处零序电流，İ012与İ021同上述物理意义相同。各零序电流在不同故障位置时，电流方向不相同。
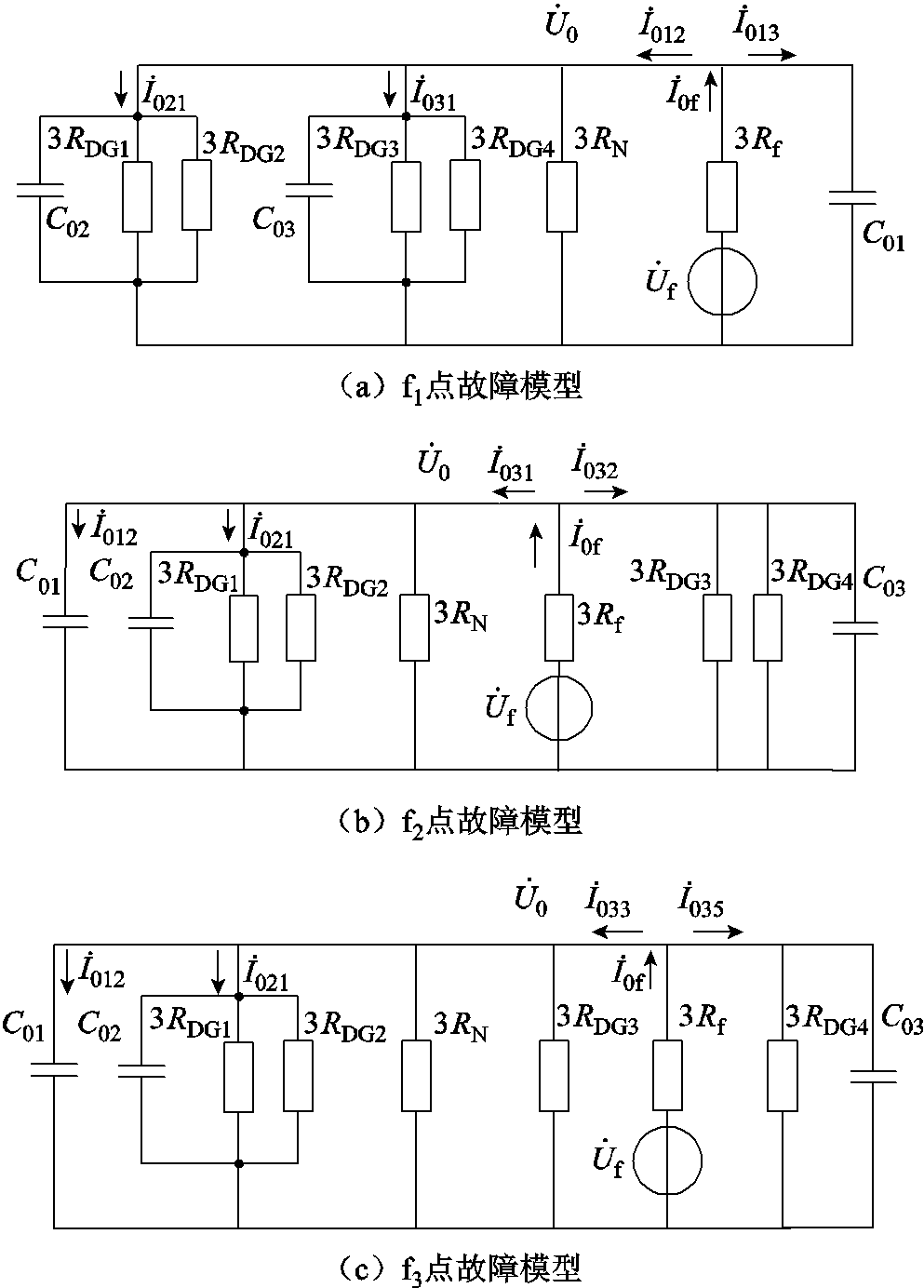
图2 故障特征模型
Fig.2 Fault feature model
1.3.1 f2故障特征分析
图2b为故障发生在馈线3的f2位置模型图，具有典型特征，以图2b模型图为基础进行分析。从故障点向主网侧看等效零序阻抗Z0为
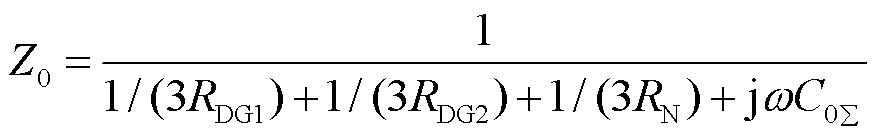（1）
式中，C0S为系统总零序分布电容。零序电压为
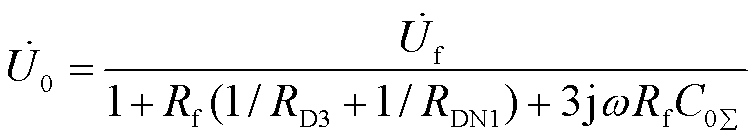（2）
式中，RD3= RDG3// RDG4；RDN1= RDG1// RDG2// RN。
设θU0为零序电压相位，故障点等效电源电压相位与零序电压相位差θUf为
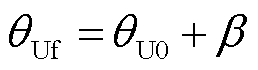（3）
其中
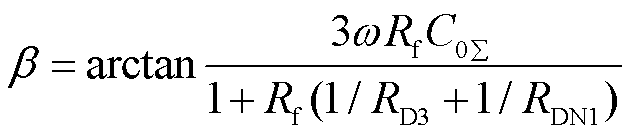（4）
接地相电压和零序电压相位差θUC为
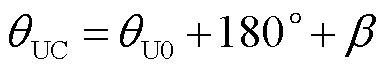（5）
非故障馈线1的零序电流İ012为
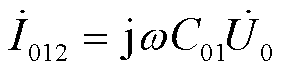（6）
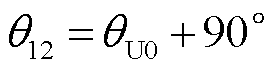（7）
式中，θ12为非故障馈线1的CB12处零序电压和零序电流相位差。非故障馈线1的电容电流呈纯电容特性，İ012比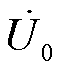零序电压相位超前90°。联立式（5）和式（7），计算出非故障馈线1的故障相电压与零序电流İ012的相位差θUC12为
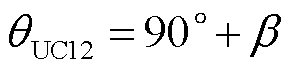（8）
非故障馈线2包含2个DG，CB21处零序电流İ021为
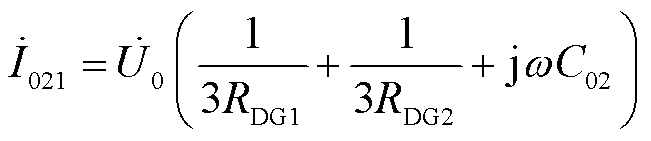（9）
零序电流İ021与零序电压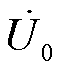的相位差θ21为
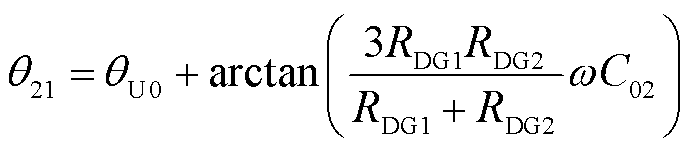（10）
联立式（5）和式（10），计算非故障馈线2的故障相电压与零序电流的相位差θUC21为
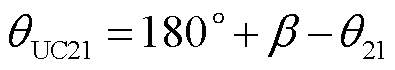（11）
故障馈线3包含2个DG，故障点后CB32处零序电流İ032为
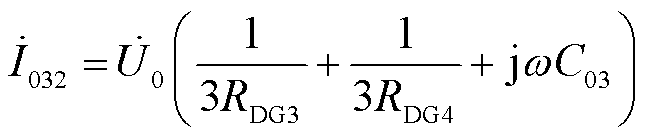（12）
零序电流İ032与零序电压的相位θ32为
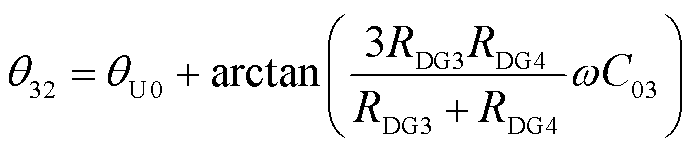（13）
联立式（5）和式（13），计算故障馈线3故障点后故障相电压与零序电流的相位差θUC32为
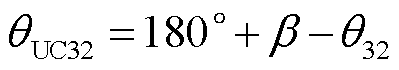（14）
故障馈线3故障点CB31处前零序电流İ031为
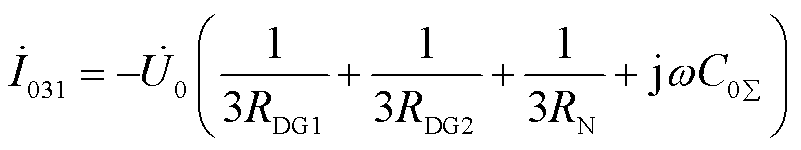（15）
故障馈线3故障点前零序电流İ031与零序电压的相位θ31为
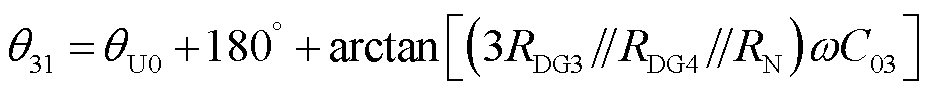（16）
联立式（5）和式（16），计算故障馈线3故障点前故障相电压与零序电流的相位差θUC31为
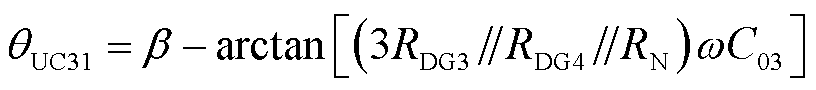（17）
1.3.2 f1故障特征分析
根据f2故障分析过程，对f1故障进行分析，计算故障馈线1故障点前CB12处故障相电压与零序电流的相位差θUC12为
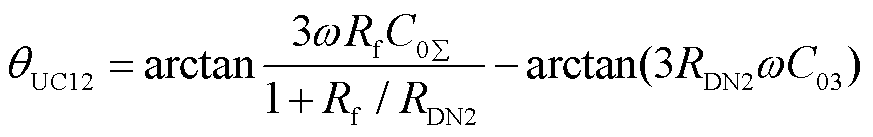（18）
式中，RDN2= RDG1//RDG2//RDG3//RDG4//RN。计算出故障馈线1故障点后CB13处故障相电压与零序电流的相位差θUC13为
（19）
计算非故障馈线2的故障相电压与零序电流的相位差θUC21为
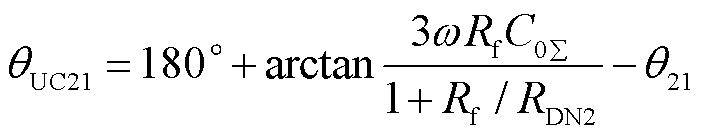（20）
计算非故障馈线3的CB31处故障相电压与零序电流的相位差θUC31为
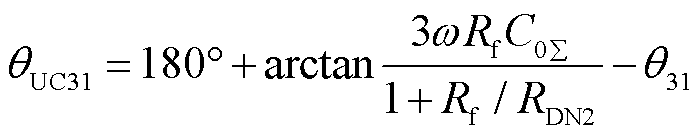（21）
1.3.3 f3故障特征分析
根据f2故障分析过程，对f3故障进行分析，计算出非故障馈线1的CB12处故障相电压与零序电流的相位差θUC12为
（22）
式中，RDN3= RDG1//RDG2//RDG3//RN。计算非故障馈线2的故障相电压与零序电流的相位差θUC21为
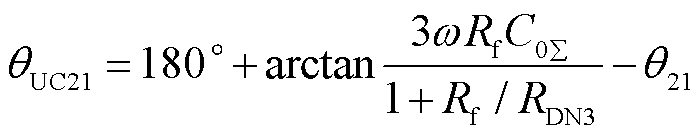（23）
计算故障馈线3故障点前CB33处故障相电压与零序电流的相位差θUC33为
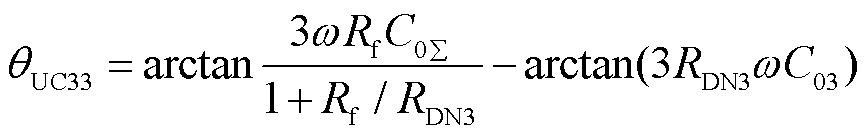（24）
电源侧中性点接地电阻RN取值10 W，DG不接地系统相当于中性点电阻为无穷大，以DG经小电阻接地系统进行计算分析，DG中性点电阻均取值30 W。以故障点在f2的位置进行计算，设接地点过渡电阻为100 W，分别计算故障相电压和不同位置零序电流相位差。根据式（5）计算接地相电压和零序电压相位差θUC=197.1°；根据式（8）计算非故障馈线1的故障相电压与零序电流İ012的相位差θUC12=107.1°；根据式（11）计算非故障馈线2的故障相电压与零序电流İ021的相位差θUC21=193.3°；根据式（14）计算故障馈线3故障点后故障相电压与零序电流İ032相位差θUC32=193.3°；根据式（17）计算故障馈线3故障点前故障相电压与零序电流İ031的相位差θUC31=14.1°。以故障相电压相位θUf的方向为参考方向，各监测点故障相电压和零序电流相位关系如图3所示。
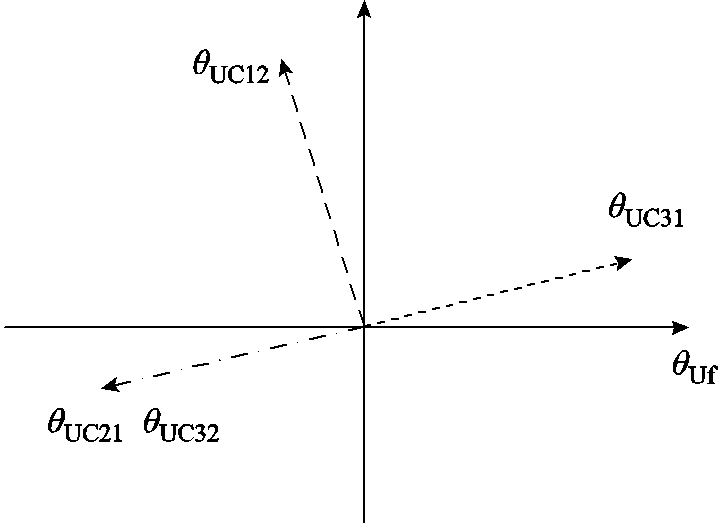
图3 f2故障相位图
Fig.3 f2 fault phase diagram
在过渡电阻为1 W～3 kW情况下，计算故障相电压和不同故障位置零序电流相位差，计算结果见表1。
表1 不同故障位置相位差
Tab.1 Phase difference at different fault positions
监测点不同故障位置相位差/(°) f1f2f3 θUC12(3.4，17.7)(93.5，107)(93.57，110.3) θUC13(93.5，107)(93.5，107)(93.57，110.3) θUC21(179，194)(178，194)(179.7，196.5) θUC31(179，194)(0.5，14.8 )(179.7，196.5) θUC32(179，194)(178，194)(179.7，196.5) θUC33(179，194)(178，194)(3.5，20.3) θUC35(179，194)(178，194)(170.8，187.6)
对表1数据进行整理分析，得出以下结论：
1）故障线路故障点前，无论有无DG，故障相电压和零序电流相位差范围为（0.5°，20.3°）。
2）非故障线路及无DG的故障线路故障点后，故障相电压和零序电流相位差范围为（93.5°，110.3°）。
3）有DG的故障线路故障点后，及有DG的非故障线路，故障相电压和零序电流相位差范围为（170.8°，196.5°）。
根据表1计算出的不同故障位置相位差，提出基于相位差的有源配电网小电阻接地保护算法：
1）实时采集和计算零序电流幅值，当其有效值3In＞Iset，启动保护计算。
2）实时采集和计算相电压幅值，比较三相电压幅值，选取幅值下降的相为故障相。
3）实时计算故障相电压与零序电流的相位差，当相位差θUC∈（-10°，40°），为电源侧界内故障，保护瞬时动作。
4）当相位差θUC∈（80°，130°），为非故障线路或者无DG故障线路故障点后，为界外故障。
5）当相位差θUC∈（150°，230°），为有DG的故障线路故障点后，或有DG的非故障线路，为DG外故障，保护延时动作。
6）算法满足DG经小电阻接地和不接地两种方式的判断。
当10 kV小电阻接地系统发生3 kW接地故障时，根据式（2）和式（12），计算出3In=0.6 A，因此保护启动电流Iset配置为0.5 A。故障相电压与零序电流相位差受过渡电阻、中性点接地电阻、线路分布参数等影响。当电网电容电流达到700 A极端情况时，界内故障范围由（0.5°，14.8°）扩大到（-6.5°，33°）。为了提高判据在极端情况下的适应性，并考虑一定的裕度，在不影响判据的准确性情况下，扩大了相位差的范围，保护判据的动作角度较大于计算结果。故障判据相位差范围如图4所示，相位差处于竖线区域内，判定为电源侧界内故障，相位差处于上对角线区域内，判定为界外故障，相位差处于下对角线区域内，判定为DG外故障。
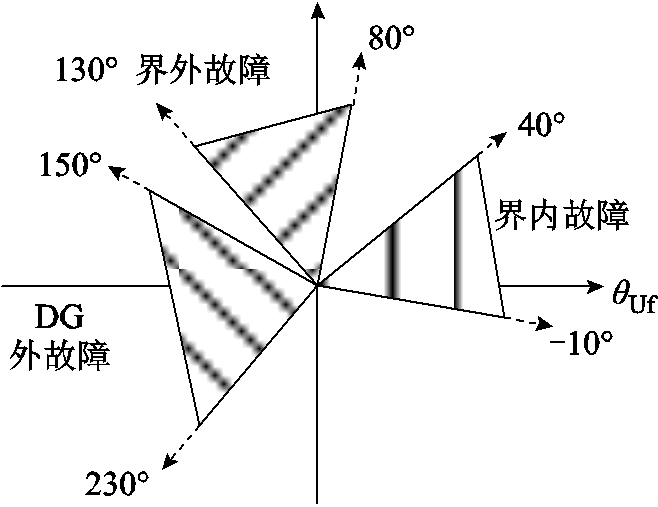
图4 故障判据相位图
Fig.4 Phase diagram of the fault criterion
图1所示含DG的配电网接地故障电气图中，在CB11～CB36各开关节点对应安装保护装置F11～F36，以f3故障位置描述故障判断和隔离过程，算法流程如图5所示。
各保护装置基于相位差的定时限保护配置为：
1）电源侧界内故障，设置零秒延时瞬时速断和200 ms延时分断两种模式，F33设置瞬时速断模式，F31和F32均设置延时分断模式。
2）DG外故障设置为200 ms延时分断模式，F35、F36、F21～F25均为DG外延时分断模式。
各保护装置对开关节点相电压和零序电流进行实时采样和录波，当零序电流大于0.5 A时，启动接地保护算法。比较三相电压幅值，选取幅值较小的相为故障相，计算故障相电压与零序电流的相位差，得出F11～F13相位差满足界外故障判据，上传非故障信号到主站。F31、F32、F33相位差均满足电源侧界内故障判据，F33达到保护条件，零秒延时对开关CB33发出分闸指令，隔离故障并上传故障信息到主站，F31和F32在200 ms内故障消除，退出保护。F21～F25相位差满足DG外故障条件，200 ms延时后故障消除，退出保护并上传非故障信号到主站。主站收集到各保护装置的判断信息后，将故障位置信息推送至运维人员。
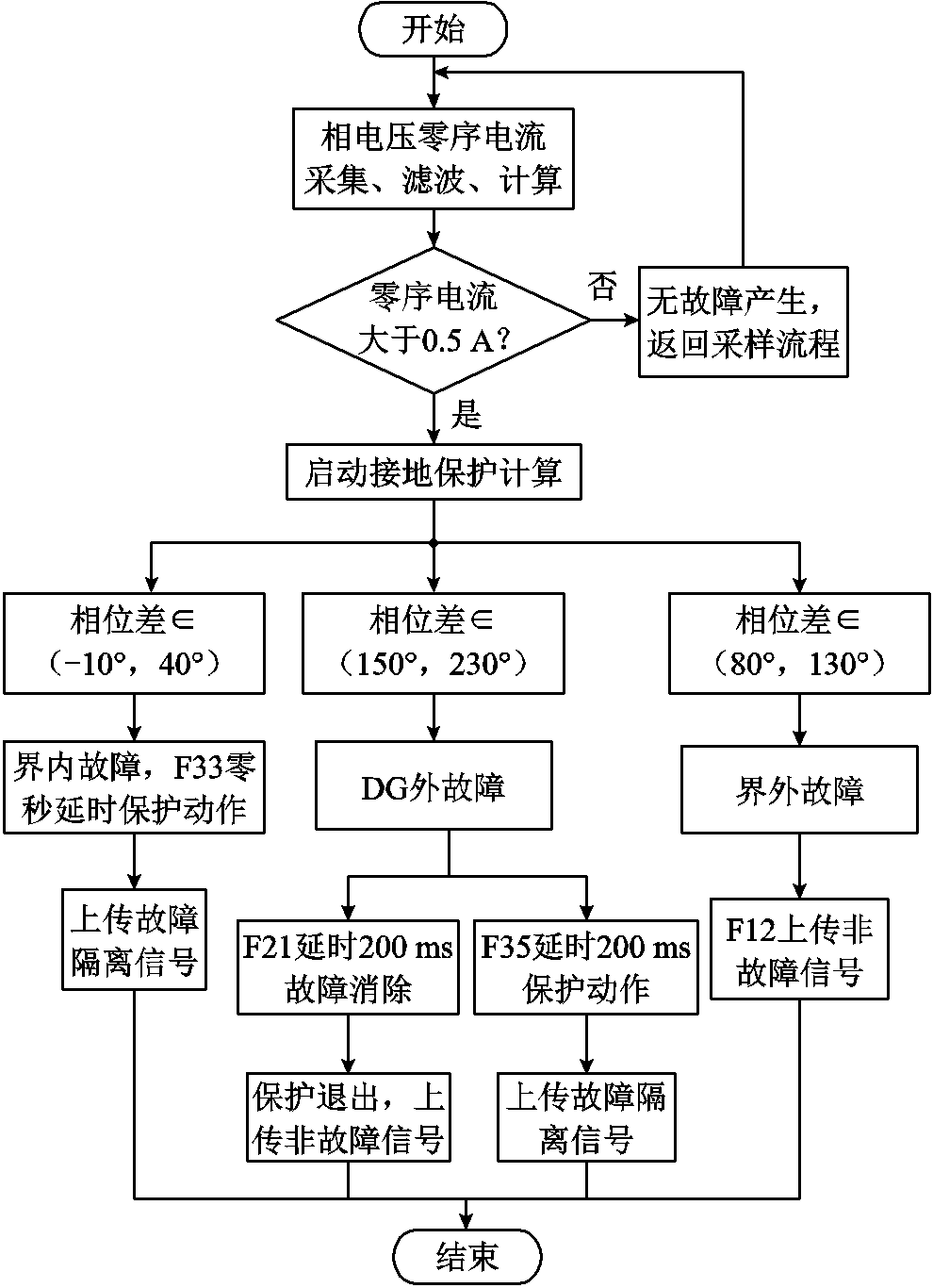
图5 软件算法流程
Fig.5 Flow chart of the software algorithm
F35和F36延时200 ms后，故障仍然存在，对CB35和CB36执行保护跳闸动作，隔离故障，上传故障信号到主站。当允许分布式电源通过孤岛运行方式给非故障区域供电时，F36配置为故障告警模式，可继续向非故障区域供电。不允许孤岛运行时，F36配置为故障分闸模式。
以图1所示含DG的配电网接地故障电气图为基础建立Simulink仿真模型，系统电源ES和分布式电源DG均采用中性点经小电阻接地方式，电源侧中性点接地电阻RN取值10 W，分布式电源中性点电阻均取值30 W。系统电源额定容量为100 MW，各DG额定功率为2 MW。仿真系统主要参数为：电缆线路正序电阻为0.26 Ω/km，正序电抗为 0.255 mH/km，正序电容为0.37 mF/km，零序电阻为2.6 Ω/km，零序电抗为1.109 mH /km，零序电容为0.276 mF/km；架空线路正序电阻为0.17 Ω/km，正序电抗为1.107 mH/km，正序电容为0.115 mF/km，零序电阻为0.32 Ω/km，零序电抗为3.56 mH/km，零序电容为0.006 2 mF /km。
根据3.1节仿真模型进行验证，接地故障点位置处于f3，接地点过渡电阻为10 Ω，接地相为C相。通过仿真计算出三相电压分别为，A相电压6.02 kV，B相电压6.32 kV，C相电压5.07 kV。不含DG非故障馈线1保护装置F12零序电流为4.3 A，含两个DG非故障馈线2保护装置F21零序电流为27.8 A，故障线路故障点前保护装置F33零序电流为154.7 A，故障点后F35零序电流为63.6 A。图6为各装置三相电压和零序电流仿真波形。图7为相电压和零序电流幅值。各保护装置零序电流均达到保护启动值，装置进入保护计算程序，各装置比较三相电压幅值，选择电压较小的C相为故障相，计算故障相电压与零序电流的相位差。
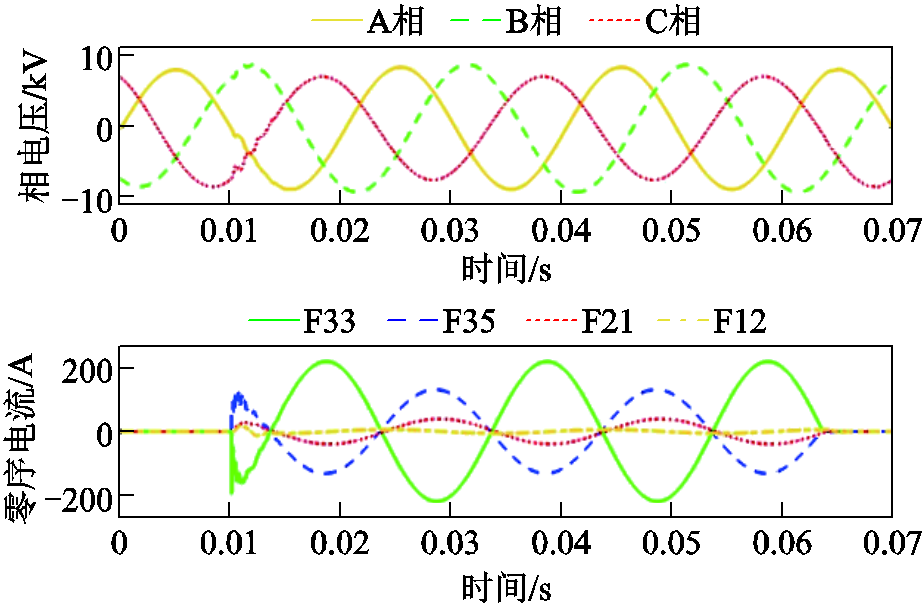
图6 相电压与零序电流波形
Fig.6 Phase voltage and the zero-order current waveforms
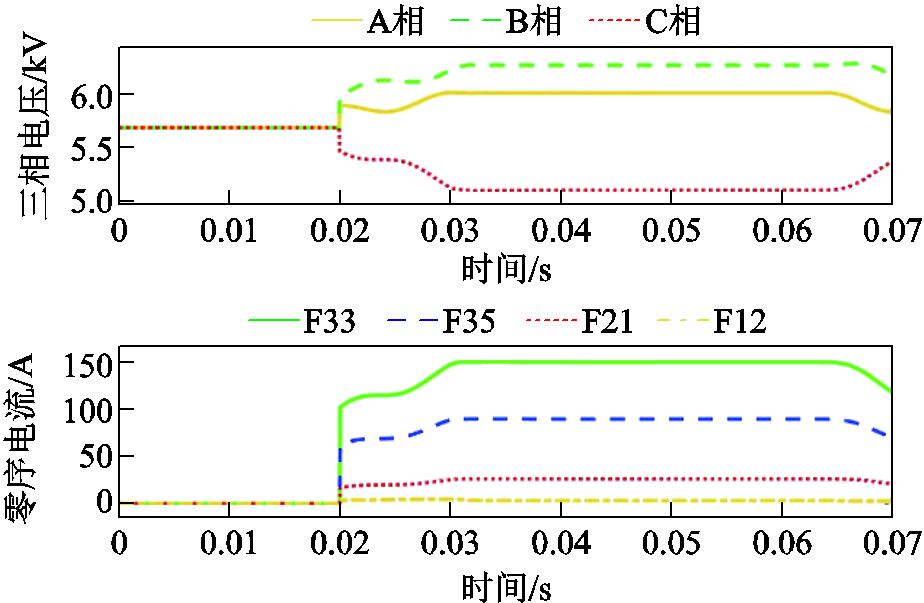
图7 相电压与零序电流幅值
Fig.7 Phase voltage and the zero-order current amplitude
图8为各保护装置故障相与零序电流相位差仿真数据。F12相位差为108°，F21相位差为192.6°，F33相位差为7.1°，F35相位差为176°，上述仿真数据符合表1理论计算。根据2.3节保护判据，F12相位差满足界外故障判据，上传非故障信号到主站。F21相位差满足DG外故障条件，200 ms延时后故障消除，退出保护。F33判定为电源侧界内故障，零秒延时对开关CB33发出分闸指令隔离故障。F35延时200 ms后，故障仍然存在，对CB35执行保护跳闸动作，完成隔离故障。以上动作处理完成后，各保护装置将相应故障信号上传主站。
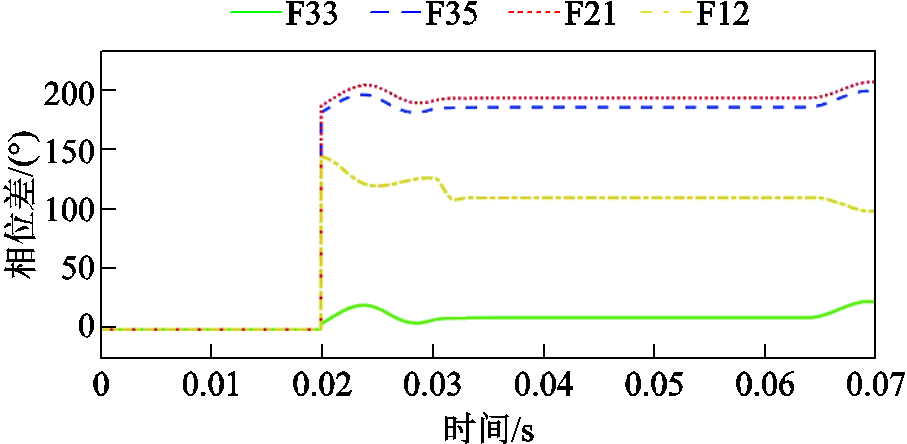
图8 保护装置相位差
Fig.8 Phase difference of the protection device
通过仿真验证过渡电阻为1 Ω～3 kΩ情况下算法准确性，验证结果见表2～表4，所有实验均正确动作。表中符号（×）表示零序电流未达到启动值条件，不启动保护算法；符号（）表示零序电流达到启动值条件，启动保护算法，但未达到相位差条件，保护退出；符号（Ö）表示零序电流达到启动值条件，同时达到相位差条件，保护算法执行跳闸指令。
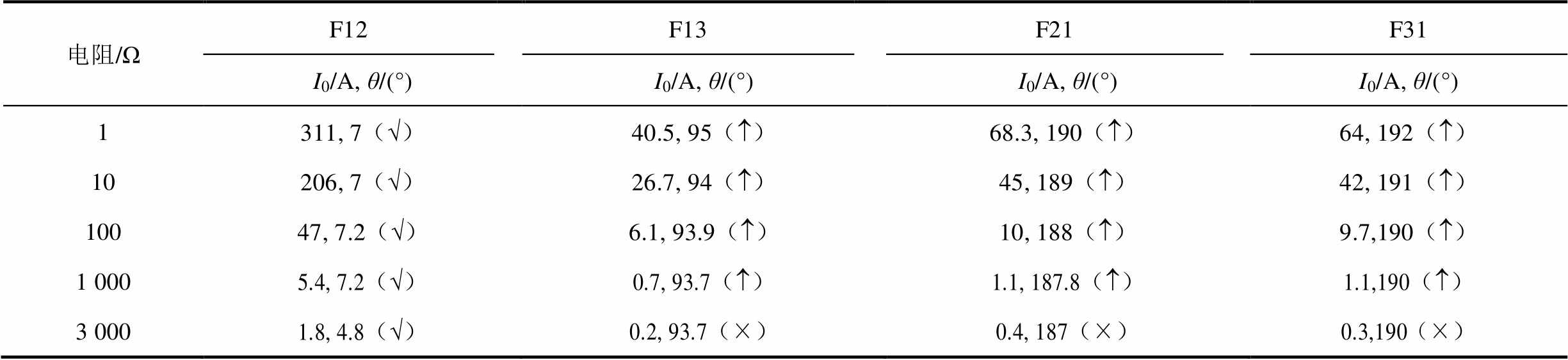
表2 f1故障位置算法结果
Tab.2 Results of the f1 fault location algorithm
电阻/ΩF12F13F21F31 I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°) 1311, 7（Ö）40.5, 95（）68.3, 190（）64, 192（） 10206, 7（Ö）26.7, 94（）45, 189（）42, 191（） 10047, 7.2（Ö）6.1, 93.9（）10, 188（）9.7,190（） 1 0005.4, 7.2（Ö）0.7, 93.7（）1.1, 187.8（）1.1,190（） 3 0001.8, 4.8（Ö）0.2, 93.7（×）0.4, 187（×）0.3,190（×）
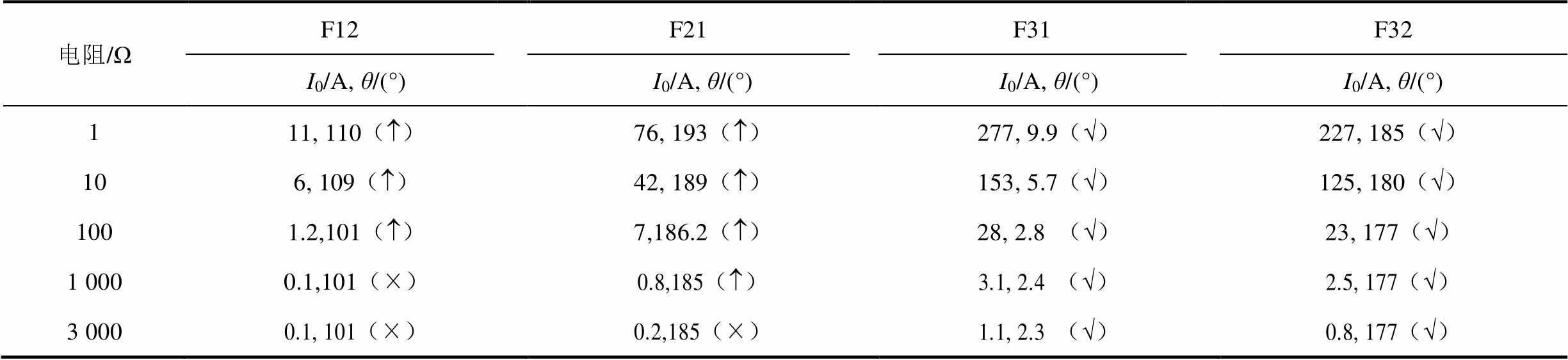
表3 f2故障位置算法结果
Tab.3 Results of the f2 fault location algorithm
电阻/ΩF12F21F31F32 I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°) 111, 110（）76, 193（）277, 9.9（Ö）227, 185（Ö） 106, 109（）42, 189（）153, 5.7（Ö）125, 180（Ö） 1001.2,101（）7,186.2（）28, 2.8 （Ö）23, 177（Ö） 1 0000.1,101（×）0.8,185（）3.1, 2.4 （Ö）2.5, 177（Ö） 3 0000.1, 101（×）0.2,185（×）1.1, 2.3 （Ö）0.8, 177（Ö）
表4 f3故障位置算法结果
Tab.4 Results of the f3 fault location algorithm
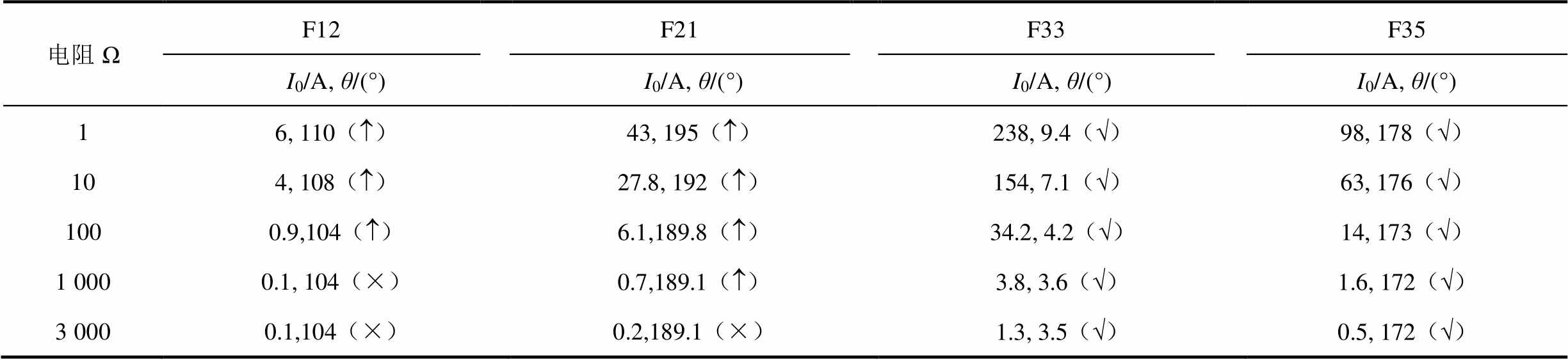
电阻ΩF12F21F33F35 I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°) 16, 110（）43, 195（）238, 9.4（Ö）98, 178（Ö） 104, 108（）27.8, 192（）154, 7.1（Ö）63, 176（Ö） 1000.9,104（）6.1,189.8（）34.2, 4.2（Ö）14, 173（Ö） 1 0000.1, 104（×）0.7,189.1（）3.8, 3.6（Ö）1.6, 172（Ö） 3 0000.1,104（×）0.2,189.1（×）1.3, 3.5（Ö）0.5, 172（Ö）
表2为接地故障处于不含DG馈线1的f1位置算法结果。保护装置F12在不同过渡电阻下全部启动保护计算，正确判断为界内接地故障，并快速执行跳闸指令隔离故障。保护装置F13在过渡电阻为1 Ω～1 kΩ时启动保护计算，但相位计算均为界外故障，退出保护，在过渡电阻为3 kΩ时，零序电流达不到保护计算启动条件。非故障馈线2和3均包含两个DG，保护装置F21和F31在过渡电阻为 1 Ω～1 kΩ时启动保护计算，且相位差达到DG外故障条件，由于配置200 ms延时动作时限，故障已消除，退出保护，在过渡电阻为3 kΩ时，零序电流达不到保护计算启动条件。表2的仿真结果验证了在过渡电阻为1 Ω～3 kΩ情况下，f1故障位置算法计算结果均正确。
表3为接地故障处于含DG馈线3的f2位置算法结果。保护装置F12在过渡电阻1～100 Ω下全部启动保护计算，但相位计算均为界外故障，退出保护；过渡电阻1 Ω～3 kΩ零序电流达不到保护计算启动条件。F21在过渡电阻1 Ω～1 kΩ下全部启动保护计算，且相位差达到DG外故障条件，由于配置200 ms延时动作时限，故障已消除，退出保护；在过渡电阻为3 kΩ时，零序电流达不到保护计算启动条件。保护装置F31在不同过渡电阻下全部启动保护计算，正确判断为界内接地故障，并快速执行跳闸指令隔离故障。F32在过渡电阻1 Ω～3 kΩ下全部启动保护计算，且相位差达到保护动作条件，200 ms延时后，故障仍然存在，执行保护跳闸指令，隔离故障。表3的仿真结果验证了在过渡电阻为 1 Ω～3 kΩ情况下，f2故障位置算法计算结果均正确。
表4为接地故障处于含DG馈线3的f3位置算法结果。F12和F21均未判断出故障，不执行跳闸指令。F33在过渡电阻为1 Ω～3 kΩ下全部正确动作隔离故障。F35在过渡电阻为1 Ω～3 kΩ全部正确判断出故障，在延时200 ms后，故障未消除，发出故障隔离跳闸指令。从以上分析可知，过渡电阻为1 Ω～3 kΩ情况下均可正确判断接地故障，采样量程范围为0.5～800 A。理论上，算法可支持到更高过渡电阻的接地判断，但在产品化时，需要采用双通道进行采样，以满足更大量程范围与较小零序电流采样需求，考虑到成本与现场实际需求情况，算法最高耐受过渡电阻设置为3 kΩ。
配电网DG受电网调度和天气影响，在不同时间段接入电网DG数量情况不相同。2.3节所述保护判据，适应于馈线无DG接入、馈线多个DG接入等情况，通过仿真分析不同DG接入数量算法的准确性。DG并网数量与分布共分五种情况：①数量为4代表4个DG全部并网；②DG数量为3，将馈线2的DG1退出，DG2、DG3、DG4三个DG并网；③DG数量为2，将馈线2的DG1和DG2退出，DG3和DG4两个DG并网；④DG数量为1，将DG1、DG2、DG3退出，DG4并网；⑤DG数量为0，4个DG全部退出。以故障点位置处于馈线1的f1，接地点过渡电阻为10 Ω进行仿真分析，各保护装置仿真结果见表5。
表5 不同DG数量的影响
Tab.5 Effect of different DG amounts
DG数量F12F13F21F31 I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°) 0185, 8.3（Ö）29, 103（）19, 120（）18, 126（） 1189, 8.2（Ö）28, 99.2（）18, 115.3（）25, 190（） 2196, 7.8（Ö）28, 97.2（）16, 111.2（）50, 198（） 3204, 7.4（Ö）27, 95.4（）32, 182（）44, 194（） 4207, 7.3（Ö）26.8, 94.5（）45, 190（）42, 192（）
在五种DG接入情况下，各保护装置零序电流均大于启动值，均启动保护计算。F12相位满足界内故障判据，判断为界内故障，保护动作。F13判断为界外故障，退出保护。F21和F31在其负荷侧有一个或者两个DG投入情况下，均启动保护计算且判断为DG外故障，延时200 ms后，由于故障消除退出保护。F21和F31在其负荷侧没有DG接入情况，判断为界外故障，退出保护。采用相位差的接地故障保护算法，在过渡电阻为1 Ω～3 kΩ情况下，进行了不同DG数量的仿真分析，结果显示，不同数量的DG对零序电流幅值和相位有一定的影响，但都能正确进行故障判断。
按照传统零序过电流保护算法，将零序保护定值设置为40 A，进行接地保护动作分析：在第5种情况DG数量为0时，F12保护动作，而F13、F21、F31未达到保护定值不动作，可正确判断接地故障；在第3种情况下有两个DG接入，F31零序电流达到50 A，仅采用零序过电流算法将会误动作；三个DG接入时，F31零序电流达到44 A，产生误动作；在四个DG接入时，F21和F31均会产生误动作。
不同DG短路容量差异较大，在仿真模型中，对四个DG分别设置1 MW和10 MW短路容量，分析各保护装置在较高过渡电阻情况下接地故障算法的准确性。DG短路容量为1 MW时，接地过渡电阻设置为1 Ω；DG短路容量为10 MW时，接地过渡电阻设置为1 kΩ。仿真数据见表6，各保护装置在1 MW、10 MW短路容量，1 Ω～3 kΩ过渡电阻，不同接地故障位置情况，各保护装置均可正确计算接地故障。
表6 DG短路容量的影响
Tab.6 Effect of DG short-circuit capacity
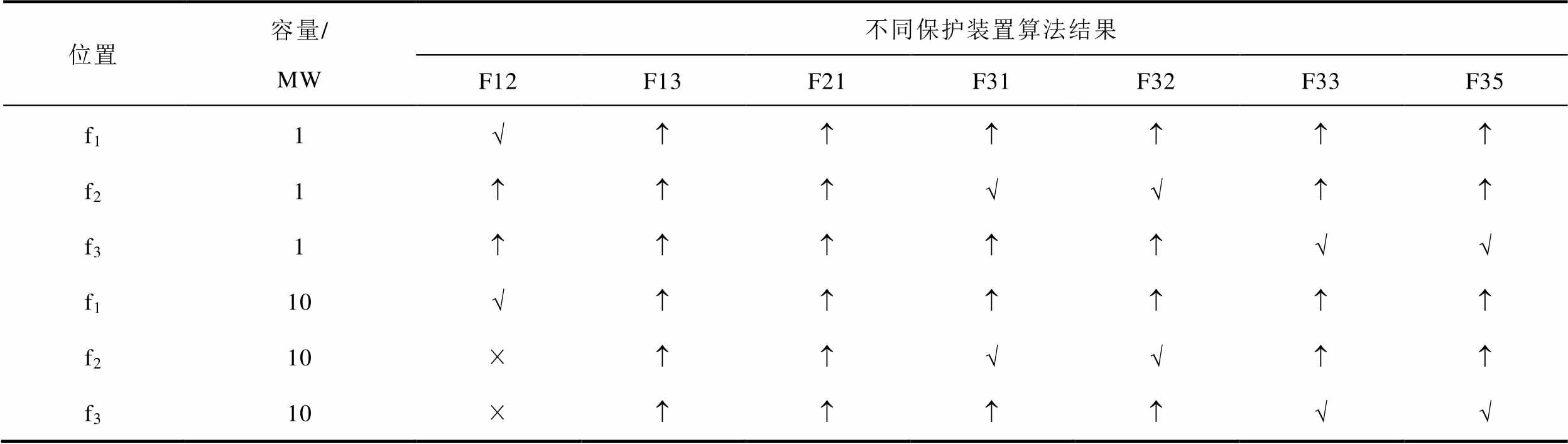
位置容量/MW不同保护装置算法结果 F12F13F21F31F32F33F35 f11Ö f21ÖÖ f31ÖÖ f110Ö f210×ÖÖ f310×ÖÖ
按照零序过电流保护算法，将零序保护定值设置为40 A，进行接地保护动作分析：故障点位于f1，DG短路容量为1 MW，接地过渡电阻为10 Ω，F12正确动作，F13、F21、F31、F32零序电流分别为40.2、100、60.1、60.1 A，达到保护定值，产生误动作，F33和F35零序电流为23.6 A，保护判断准确。
线路长度对相位差有一定影响，选取不同线路长度进行仿真分析。长度类型1代表电缆线路长度60 km，架空线路长度20 km；长度类型2代表电缆线路长度50 km，架空线路长度30 km。过渡电阻为1 kΩ情况下各故障位置仿真结果见表7，针对1 Ω～3 kΩ过渡电阻也进行了仿真分析，各保护装置故障判断准确。
表7 不同长度类型的影响
Tab.7 Effects of the different length types
位置长度类型保护装置仿真结果 F12F13F21F31F32F33F35 f11Ö f21×ÖÖ f31×ÖÖ f12Ö f22×ÖÖ f32×ÖÖ
在不同长度类型影响下，对故障点位于f1进行零序过电流保护算法准确性分析：在接地过渡电阻为10 Ω时，F12正确动作，F13、F21、F31、F32产生误动作，F33和F35保护判断准确。
主网中性点采用小电阻接地时，DG中性点也有采用不接地方式的情况。从图2故障特征模型可知，DG中性点不接地，相当于DG的中性点接地电阻为无穷大。以3.1节仿真模型进行验证，DG中性点不接地，当故障点位于f1时，计算结果见表8。在过渡电阻为1 Ω～3 kΩ情况下，故障线路故障点前F12零序电流均达到启动条件，且故障相电压与零序电流相位差符合电源侧界内故障条件，全部正确判断故障。故障线路故障点后F13，以及非故障线路F21和F31，在1 Ω～1 kΩ情况下，零序电流均达到启动条件，相位差符合界外故障条件，退出保护；在3 kΩ情况下，零序电流未达到启动条件。对故障点位于f2和f3时，进行了仿真计算，仿真结果符合2.3节保护判据，可正确进行接地故障判断。
表8 DG中性点不接地计算结果
Tab.8 Calculation result of DG neutral point is not ground
电阻/ΩF12F13F21F31 I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°) 1266, 8.6（Ö）42, 103（）28, 121（）26, 126（） 10184, 8.3（Ö）29, 103（）19, 120（）18, 126（） 10045, 8.2（Ö）7.1, 102（）4.7, 119（）4.6, 125（） 1 0005.2, 8.2（Ö）0.8, 102（）0.5, 119（）0.5, 125（） 3 0001.7, 8.2（Ö）0.2, 102（×）0.2, 119（×）0.2, 125（×）
按照零序过电流保护算法，将零序保护定值设置为40 A，对故障点位于f1进行零序过电流保护算法准确性分析：当过渡电阻为1 Ω时，F13零序过电流达到了42 A，保护误动作，其他装置故障判断准确。当过渡电阻为1 Ω～3 kΩ情况下，零序电流小于40 A，F12故障判断错误，保护拒动。
线路中有负荷投切时，线路负荷电流产生变化，仿真分析对算法的影响。选择2 kΩ高阻接地进行仿真，故障点位置为f1，在故障点f1下游投入不同负载，变化的负载电流经过故障点f1。投入负载电阻分别为1 kW、10 kW、100 kW、1 MW，仿真结果见表9，对零序电流和相位差影响较小，各保护装置均可以正确判断故障。故障点位于f2和f3时，以及过渡电阻在1 Ω～3 kΩ情况下进行仿真分析，均可正确判断故障。
表9 负荷投切影响
Tab.9 Effect of load casting and cutting
负荷/kWF12F13F21F31 I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°)I0/A, θ/(°) 12.7, 6.9（Ö）0.3, 92（×）0.8, 188（）0.5, 191（） 102.7, 6.9（Ö）0.3, 92（×）0.8, 188（）0.5, 191（） 1002.7, 6.9（Ö）0.3, 92（×）0.8, 188（）0.5, 191（） 1 0002.7, 6.9（Ö）0.3, 93（×）0.8, 189（）0.5, 192（）
在不同负荷影响下，对故障点位于f1进行零序过电流保护算法准确性分析：在接地过渡电阻为 2 kΩ时，由于零序电流均没有达到40 A，F12保护拒动，计算错误。
对基于相电压和零序电流相位差接地故障保护算法进行工程实用性与优势比较，对比分析零序过电流保护算法[4]、零序电流相位差动保护算法[17]、零序电压电流相位接地保护算法[19]等。从多个参数维度进行对比分析，主要参数为是否需要零序电压互感器、不同测量点通信数据量、建设投资成本、工程难度和判断准确度等维度。零序过电流保护算法不需要零序电压互感器，但在分布式电源接入情况下，可能产生误动作。零序电流相位差动保护算法，通过比较故障点两端零序电流相位关系，计算是否产生接地故障，需要高速和高可靠通信网络支持。零序电压电流相位接地保护算法，需要安装零序电压互感器。基于相电压和零序电流相位差的接地故障保护算法，不需要安装零序电压互感器，相电压可以通过电场感应方式获取，也可以通过一、二次深度融合柱上断路器的取电电容获取相电压，零序电流可采用三相电流合成方式，可适应于录波型故障指示器场景，也能应用于一、二次融合柱上断路器场景，成本相对较低，安装简单，接地故障判断准确度高。综上所述，基于相电压和零序电流相位差算法工程实用性最好，四种方法的性能比较见表10。
表10 不同方法的性能比较
Tab.10 Performance comparison of the different methods
参数零序过流零序电流相位差动零序电压电流相位相电压零序电流相位 零序电压不需要不需要需要不需要 通信量小大小小 成本小大大小 工程难度小大大小 准确度较低较高高高
通过建立包含多个分布式电源的小电阻接地系统配电网接地故障模型，对故障时刻相电压与零序电流相位关系进行理论推导与计算，分析得出不同接地故障位置的相位差区间，提出基于相电压与零序电流相位差的接地故障保护算法。经过仿真验证得出以下结论：
１）算法可准确判断界内故障、界外故障和DG外故障，适用DG中性点经小电阻接地和不接地两种方式。
2）算法在不同接地过渡电阻情况能准确判断接地故障，耐过渡电阻能力可达3 kΩ；在不同DG数量，不同DG短路容量，不同电缆长度，负载波动等情况下，能准确判断接地故障。
3）算法在保护装置内部实现接地故障判断，不需要同主站或者装置之间进行通信实现故障判断，不受通信影响。
参考文献
[1] Wang Bin, Geng Jianzhao, Dong Xinzhou. High-impedance fault detection based on nonlinear voltage–current characteristic profile identification[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3783-3791.
[2] 盛亚如, 丛伟, 卜祥海, 等. 基于中性点电流与零序电流投影量差动的小电阻接地系统高阻接地故障判断方法[J]. 电力自动化设备, 2019, 39(3): 17-22, 29.
Sheng Yaru, Cong Wei, Bu Xianghai, et al. Detection method of high impedance grounding fault based on differential current of zero-sequence current projection and neutral point current in low-resistance grounding system[J]. Electric Power Automation Equipment, 2019, 39(3): 17-22, 29.
[3] 李海锋, 陈嘉权, 曾德辉, 等. 小电阻接地系统高灵敏性零序电流保护[J]. 电力自动化设备, 2018, 38(9): 198-204.
Li Haifeng, Chen Jiaquan, Zeng Dehui, et al. High sensitive zero-sequence current protection for low-resistance grounding system[J]. Electric Power Automation Equipment, 2018, 38(9): 198-204.
[4] 杨帆, 刘鑫星, 沈煜, 等. 基于零序电流投影系数的小电阻接地系统高阻接地故障保护[J]. 电网技术, 2020, 44(3): 1128-1133.
Yang Fan, Liu Xinxing, Shen Yu, et al. High resistance ground fault protection of low resistance grounding system based on zero sequence current projection coefficient[J]. Power System Technology, 2020, 44(3): 1128-1133.
[5] 林志超, 汪洋, 罗步升, 等. 小电阻接地系统高灵敏度接地保护配置与整定[J]. 电力系统及其自动化学报, 2020, 32(3): 25-32.
Lin Zhichao, Wang Yang, Luo Busheng, et al. Configuration and tuning of high-sensitivity grounding fault protection for low-resistance grounding system[J]. Proceedings of the CSU-EPSA, 2020, 32(3): 25-32.
[6] 汪洋, 薛永端, 徐丙垠, 等. 小电阻接地系统接地故障反时限零序过电流保护[J]. 电力系统自动化, 2018, 42(20): 150-157.
Wang Yang, Xue Yongduan, Xu Bingyin, et al. Zero-sequence inverse-time overcurrent protection in low resistance grounding system with grounding fault[J]. Automation of Electric Power Systems, 2018, 42(20): 150-157.
[7] 任伟, 薛永端, 徐丙垠, 等. 小电阻接地系统高阻接地故障纵联差动保护[J]. 电网技术, 2021, 45(8): 3276-3282.
Ren Wei, Xue Yongduan, Xu Bingyin, et al. Longitudinal differential protection of high resistance grounding faults in low-resistance grounding system[J]. Power System Technology, 2021, 45(8): 3276-3282.
[8] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[9] 崔庆雪, 李霞林, 葛磊蛟, 等. 计及时滞的含风电配电网节点电压安全分析[J]. 电工技术学报, 2023, 38(5): 1299-1311.
Cui Qingxue, Li Xialin, Ge Leijiao, et al. Analysis on node voltage security of distribution network with wind power considering time delay[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1299-1311.
[10] 秦苏亚, 薛永端, 刘砾钲, 等. 有源配电网小电流接地故障暂态特征及其影响分析[J]. 电工技术学报, 2022, 37(3): 655-666.
Qin Suya, Xue Yongduan, Liu Lizheng, et al. Transient characteristics and influence of small current grounding faults in active distribution network[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 655-666.
[11] 张健磊, 高湛军, 陈明, 等. 考虑复故障的有源配电网故障定位方法[J]. 电工技术学报, 2021, 36(11): 2265-2276.
Zhang Jianlei, Gao Zhanjun, Chen Ming, et al. Fault location method for active distribution networks considering combination faults[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2265-2276.
[12] 乔一达, 吴红斌, 吴通华, 等. 含逆变型分布式电源的配电网分区域电流保护[J]. 电工技术学报, 2022, 37(增刊1): 134-144.
Qiao Yida, Wu Hongbin, Wu Tonghua, et al. Regional current protection of distribution network with inverter distributed power supply[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 134-144.
[13] 詹惠瑜, 刘科研, 盛万兴, 等. 有源配电网故障诊断与定位方法综述及展望[J]. 高电压技术, 2023, 49(2): 660-671.
Zhan Huiyu, Liu Keyan, Sheng Wanxing, et al. Review and prospects of fault diagnosis and location method in active distribution network[J]. High Voltage Engineering, 2023, 49(2): 660-671.
[14] 李君, 何敏, 黄守道, 等. 基于相暂态功率方向的有源配电网接地故障区段定位算法[J]. 高电压技术, 2023, 49(8): 3205-3215.
Li Jun, He Min, Huang Shoudao, et al. Ground fault section positioning algorithm of active distribution network based on phase transient power direction[J]. High Voltage Engineering, 2023, 49(8): 3205-3215.
[15] 朱吉然, 牟龙华, 郭文明. 考虑并网运行微电网故障方向识别的逆变型分布式电源故障控制[J]. 电工技术学报, 2022, 37(3): 634-644.
Zhu Jiran, Mu Longhua, Guo Wenming. Fault control of inverter interfaced distributed generator considering fault direction identification of the grid-connected microgrid[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 634-644.
[16] 乔一达, 吴红斌, 吴通华, 等. 含分布式电源的小电阻接地系统分区域零序保护[J]. 电力系统自动化, 2023, 47(10): 186-194.
Qiao Yida, Wu Hongbin, Wu Tonghua, et al. Regionalized zero-sequence protection for low-resistance grounded system with distributed generator[J]. Automation of Electric Power Systems, 2023, 47(10): 186-194.
[17] 吴娜, 刘子晖, 樊淑娴. 基于Pearson相关性的小电阻接地有源配电网接地保护[J]. 电测与仪表, 2021, 58(4): 136-143.
Wu Na, Liu Zihui, Fan Shuxian. Grounding protection of low resistance grounding active distribution network based on Pearson correlation[J]. Electrical Measurement & Instrumentation, 2021, 58(4): 136-143.
[18] 区伟潮, 廖峰, 陈锦荣, 等. 小电阻接地有源配电网比幅比相式接地保护[J]. 电力系统及其自动化学报, 2023, 35(6): 124-131.
Ou Weichao, Liao Feng, Chen Jinrong, et al. Grounding fault protection based on amplitude and phase comparison for low-resistance grounding active distribution network[J]. Proceedings of the CSU-EPSA, 2023, 35(6): 124-131.
[19] 郭丽伟, 薛永端, 张林利, 等. 含分布式电源的小电阻接地方式配电网单相接地故障分析[J]. 电力系统自动化, 2015, 39(20): 116-123.
Guo Liwei, Xue Yongduan, Zhang Linli, et al. Analysis of single-phase earth fault in low resistance grounded distribution network containing DG[J]. Automation of Electric Power Systems, 2015, 39(20): 116-123.
[20] 徐玉琴, 杨浩, 李鹏. 含逆变型分布式电源的小电阻接地方式配电网单相接地故障分析[J]. 电测与仪表, 2018, 55(16): 57-63, 71.
Xu Yuqin, Yang Hao, Li Peng. Earth fault analysis on low resistance grounded distribution network with inverter interfaced distribution generation[J]. Electrical Measurement & Instrumentation, 2018, 55(16): 57-63, 71.
[21] 李政, 卢继平, 刘加林, 等. 并网光伏电站中性点接地电阻选择与零序保护[J]. 电力自动化设备, 2019, 39(12): 49-55, 147.
Li Zheng, Lu Jiping, Liu Jialin, et al. Neutral grounding resistance selection and zero-sequence protection for grid connected photovoltaic power station[J]. Electric Power Automation Equipment, 2019, 39(12): 49-55, 147.
Abstract After the large scale distributed power supply is connected to the distribution network of the small resistance grounding system, the fault current changes significantly, which affects the original grounding protection accuracy of the system, zero-sequence current protection method is used to remove the single-phase ground fault. In recent years, experts and scholars have put forward the zero-order current phase differential protection scheme, pearson correlation protection method and zero-sequence current centralized comparison method, which is necessary to collect the zero-order current amplitude or phase of different monitoring points to upload it to the main station to calculate the fault location, which depends highly on communication and main station algorithm. In order to solve the above problems, the grounding fault protection algorithm of small resistance grounding system based on phase voltage and zero sequence current is proposed.
By establishing the structure and model of the distribution network grounding fault electrical system containing multiple distributed power sources, we theoretically derive and calculate the phase voltage and zero sequence current at the time of failure, by calculating the phase difference between different grounding fault positions and different grounding transition resistances. Analyzing the phase difference interval characteristic value of ground boundary fault, outboundary fault and DG outboundary fault, according to the interval eigenvalue, the protection algorithm is implemented by: Real-time acquisition and calculation of zero-order current amplitude, when its effective value is 3In＞Iset, start the protection calculation; real-time acquisition and calculating phase voltage amplitude, compare the three-phase voltage amplitude, select the phase with the amplitude drop as the fault phase; calculate the phase difference between the fault phase voltage and the zero-order current in real time, when the phase difference θUC∈ (-10°, 40°), is the power side boundary fault, protect the instantaneous action. When the phase difference θUC∈ (80°, 130°), is the no fault line or no DG fault line, is an extra boundary fault; when the phase difference θUC∈ (150°, 230°), after the fault point with DG, Or a no fault line with a DG, is the DG external failure, protection time-delay action. The phase difference between fault phase voltage and zero sequence voltage is affected by transition resistance, neutral grounding resistance and line distribution parameters. When the capacitor current of the power grid reaches the extreme 700 A, the fault range within the boundary is expanded from (0.5°, 14.8°) to (-6.5°, 33°). In order to improve the adaptability of the criterion in extreme cases and consider a certain margin, the accuracy of the criterion is not affected, and the action angle of the protection criterion is larger than the calculation result.
After simulation verification, the following conclusions are drawn: (1) The algorithm can accurately judge the power side boundary fault, extra boundary fault and DG external failure. Applicable DG neutral point by the small resistance grounding and not grounding two ways. (2) The algorithm can accurately judge the grounding fault in different grounding transition resistance conditions. Transition resistance up to 3 kΩ. At the different numbers of DG, different DG short-circuit capacity, different cable lengths, With load fluctuations and other on, can accurately judge the grounding fault. (3) The algorithm realizes the grounding fault judgment inside the protection device, without communication with the main station or device to achieve fault judgment, not affected by communication. (4) No need to install a zero-sequence voltage transformer, phase voltage can be obtained by electric field induction, the phase voltage can also be obtained by taking the capacitance of the circuit breaker on the primary and secondary deep fusion column, zero-sequence current can be synthesized by three-phase current, can be adapted to the type fault indicator scenario. It can also be applied to the circuit breaker scene on the primary and secondary fusion column.
keywords：Active distribution network, phase voltage and zero sequence current, phase difference, small resistance grounding system, single phase grounding fault protection
中图分类号：TM77
DOI: 10.19595/j.cnki.1000-6753.tces.231742
国家重点研发计划资助项目（2020YFB0906000）。
收稿日期 2023-10-18
改稿日期 2024-03-08
李 君 男，1981年生，博士研究生，研究方向电力系统安全监测与主动防御技术。E-mail：568232496@qq.com（通信作者）
何 敏 女，1977年生，研究员，博士生导师，研究方向为复杂电力系统控制技术。E-mail：hemin607@163.com
（编辑 赫 蕾）