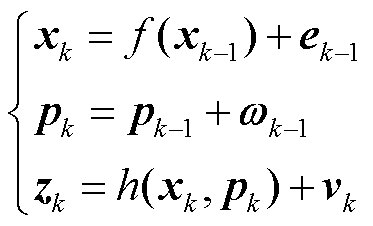 (1)
(1)
摘要 为满足现代电网对于输电线路参数估计和跟踪维护的需求,该文提出一种基于分位数回归双向门控循环单元(QR-BiGRU)神经网络与区间抗差增广状态估计的线路参数区间追踪估计方法。所提方法基于区间估计理论与动态增广状态估计模型,首先采用QR-BiGRU神经网络代替传统Holt指数平滑预测函数进行状态区间预测,并获得了更准确、可信的状态预测区间;其次基于量测值及其所允许的最大误差构建量测区间;再次,基于区间分析理论与误差传播定律求解考虑零注入功率约束的区间抗差增广状态估计模型,获取了由状态预测区间、量测区间所导致的参数估计区间,实现了对输电线路电阻、电抗的区间追踪估计;最后,通过融合了美国纽约独立系统运营商时间序列数据的多个IEEE节点测试系统,验证了所提方法的有效性。
关键词:参数估计 增广状态估计 区间分析 分位数回归 误差传播
输电线路参数的高准确性是电力系统状态估计、潮流计算等应用程序的基础[1]。然而,由于缺乏长期维护,程序中的线路参数存在很多错误,严重影响在线或离线计算的可信度。因此,有必要根据量测数据,对输电线路参数进行估计和跟踪维护。
现有输电线路参数估计方法可分为静态参数估计方法(如增广状态估计法[1-2]、残差灵敏度分析法[3]、拉格朗日乘子法[4-5]、基于多断面相位测量单元(Phase Measurement Unit, PMU)的回归估计法[6-8]等)和基于动态数据的参数追踪估计方法[9-13]。其中,静态参数估计方法对线路参数进行跟踪维护的能力有限,且为提高数据冗余度,因此,静态参数估计方法往往基于多个断面数据联立非线性量测方程组进行求解[5],存在方程规模庞大、求解效率低等问题。相比静态参数估计方法,参数追踪估计方向基于电力系统动态数据,能够更好地对线路参数进行跟踪维护;同时,参数追踪估计无需基于多个断面联立非线性量测方程组以提高数据冗余度,具有模型简单、估计效率高等优点。
文献[9]首次明确提出了参数追踪估计模型,该模型基于动态状态估计模型思想,通过相邻时刻量测值的差值,计算参数修正量以完成对上一时刻参数估计值的修正,从而实现对参数真值的追踪估计。文献[10-12]则提出了基于不同卡尔曼滤波算法的参数追踪估计方法,表明了参数估计问题可以通过动态方法得到更好的解决。然而,文献[10-12]只考虑了待估参数所在支路的量测方程,且依赖于该条支路首、末端PMU及电流测量装置的理想化配置,这在实际电网,尤其配电网中,往往难以实现。文献[13]为解决这一问题提供了思路,提出一种基于动态增广状态估计的参数追踪估计方法,该方法将参数视为状态,通过上一时刻状态、参数下的量测预测值与当前时刻量测值的差值,计算参数修正量以修正参数。相比普通参数追踪估计,动态增广状态估计考虑了全部量测方程,提高了参数估计的数据冗余性,且无需依赖支路量测的理想化配置,只需要系统整体可观测,即可实现对特定参数的估计,因而更具实用性。
然而,动态增广状态估计需对状态进行预测,致使其还受到状态预测误差的影响。现有动态增广状态估计采用Holt指数平滑预测函数[13-14]进行状态预测,这是一种适用于准稳态假设条件下的预测方法,对于波动较大的时间序列数据,其预测精度有限。然而,参数追踪估计无需在准稳态假设条件下进行,状态相差大的多个断面也可进行线路参数估计[5-6, 8]。因此,基于深度学习的预测方法(如长短期记忆(Long Short Term Memory, LSTM)神经网络[15-16]、门控循环单元(Gated Recurrent Unit, GRU)[17-18]神经网络等),因其突出的长时间序列记忆能力以及学习能力,对于波动大的长时间序列预测问题更具优势,因而也更加适合参数追踪估计。
在计及状态预测误差外,参数追踪估计还需考虑测量误差的影响。常见方式是对测量误差的概率分布参数(如均值、方差)进行估计,从而根据估计的误差分布提高模型的准确度与可信度。这种误差考虑方式乃至整个参数追踪估计模型,均属于“点估计”,其缺点在于用抽样指标代替总体指标,从而导致误差参数或线路参数的估计值与真值之间不可避免地存在偏差。针对该问题,统计学家奈曼于1934年提出“区间估计”,即在点估计的基础上,对总体参数的可信范围进行估计;其估计区间通常由样本统计量加减估计误差得到。相比点估计,区间估计被认为是一种更加保险、可信的估计方式。
鉴于此,本文基于区间估计理论与动态增广状态估计模型,提出考虑状态预测误差和量测误差的线路参数区间追踪估计方法。本文首先基于分位数回归双向门控循环单元(Quantile Regression and Bidirectional Gated Recurrent Unit, QR-BiGRU)神经网络获取状态预测区间;然后基于量测值及其所允许的最大误差构建量测区间,从而将动态增广状态估计模型中所有确定性变量替换为区间变量,实现了对状态预测误差、量测误差更可信的考虑;最后基于考虑了零注入功率约束[19-20]的区间抗差增广状态估计(Interval Robust Augmented State Estimation, IRASE)模型,实现了电力系统线路参数更准确、可信的区间估计。估计的线路参数区间能够反映线路参数估计值的可信程度以及估计误差的可能范围,是一种对于线路参数真值的更可信的表征方式;另外,估计的线路参数区间能够为后续错误参数辨识、数据维护等提供边界信息,并为研究参数在一定偏差范围内的状态估计问题提供基础[21-23]。
参数追踪估计的本质是动态参数估计。相比动态状态估计,此时参数作为状态,并通过参数所在支路的量测时间序列数据与量测方程,交替执行“参数修正”与“参数估计”步骤,最终实现参数的动态估计[9]。然而,普通的参数追踪估计依赖于支路首、末端PMU与电流测量装置的理想化配置,这在配电网中往往难以实现。因此基于动态增广状态估计的参数追踪估计方法更具实用性。
根据文献[13],基于动态增广状态估计的参数追踪估计模型为
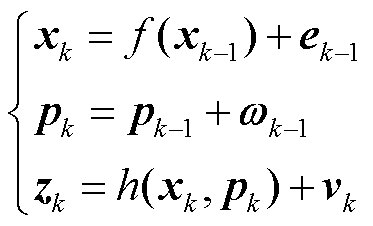 (1)
(1)
式中,k为时刻或断面编号;xk为k时刻状态真值向量;f(·)为状态预测函数;ek-1为k-1时刻状态预测误差向量;pk为k时刻参数真值向量;ωk-1为k-1时刻参数预测误差向量;zk为k时刻量测向量;h(·)为增广状态估计函数;vk为k时刻增广状态估计误差向量。
相比普通参数追踪估计,动态增广状态估计多出了“状态预测”步骤,不仅能追踪特定参数,还能追踪系统状态。另外,动态增广状态估计中的zk为全网量测,并非某条支路首、末端量测;h(·)为全网量测方程,并非某条支路量测方程。因此相比普通参数追踪估计,动态增广状态估计提高了参数估计的数据冗余性,且无需依赖支路量测的理想化配置,只需系统模型可观测,即可实现对特定参数的追踪估计。
区间分析[24],又称区间算术,由R. E. Moore教授等于20世纪50年代提出。该理论的主要思想是在运算过程中用包含某实数的区间来代替该实数,从而分析该实数区间可能造成的结果的上、下界。区间分析最初是从误差理论研究中发展起来的,常被用于区间估计问题的求解。
对于一个给定的有界闭区间实数变量(以下简称区间变量),用符号[x]表示,即
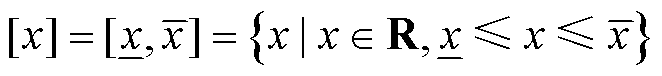 (2)
(2)
式中,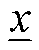 、
、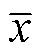 分别为该区间变量的下、上界。
分别为该区间变量的下、上界。
基于区间分析理论,可相应获得参数区间追踪估计模型为
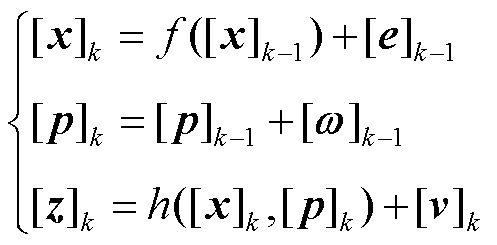 (3)
(3)
式中,[x]k为k时刻状态预测区间向量;[e]k-1为k-1时刻状态预测误差区间向量;[p]k为k时刻参数区间向量;[ω]k-1为k-1时刻参数误差区间向量;[z]k为k时刻量测区间向量;[v]k为k时刻增广状态估计误差区间向量。
[z]k采用国家电网规定的“允许误差率”进行构建[25],即电压幅值量测的允许误差为其测量值的±0.5%,有功功率量测的允许误差为其测量值的±2%,无功功率量测的允许误差为其测量值的±3%。具体构建方法为
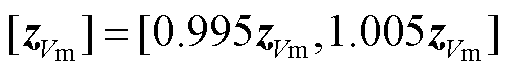 (4)
(4)
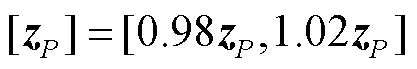 (5)
(5)
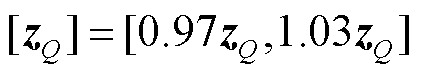 (6)
(6)
式中,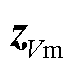 、
、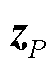 、
、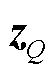 分别为电压幅值量测、有功功率量测、无功功率量测。
分别为电压幅值量测、有功功率量测、无功功率量测。
由式(3)可见,参数区间追踪估计是在动态增广状态估计模型基础上,将确定性变量替换为区间变量,从而实现对于误差的考虑。相比基于概率理论或模糊理论的误差考虑,区间分析无需获取误差的概率密度函数或模糊隶属度函数,只需根据误差统计的边界信息,即可完成对误差的建模与分析。
与确定性动态增广状态估计类似,参数区间追踪估计模型可视为两个内容的融合:①状态区间预测;②基于区间增广状态估计的参数区间估计。
Holt指数平滑预测是一种适用于准稳态假设条件下的预测方法,其预测精度有限,且无法获得预测结果的置信区间。参数区间追踪估计需要获得状态预测区间,从而实现对误差的考虑。因此,本文融合QR与神经网络,提出一种基于QR-BiGRU神经网络的区间预测方法。其中BiGRU神经网络实现更准确的时间序列预测,而QR则实现对于预测结果的置信区间的获取。
本文将基于历史状态估计时间序列数据进行状态预测。其中LSTM神经网络是最经典的时间序列预测方法,但因其较复杂的“门”结构,存在训练参数较多、训练效率低、容易发生过拟合等问题。为解决此问题,K. Cho等于2014年提出一种更简单的门控机制,即GRU。相比LSTM,GRU的参数量减少了三分之一,从而加速了迭代过程,减少了训练时间,也降低了过拟合概率,提升了预测效率[18]。
BiGRU是由两个方向的GRU组成。其中正向GRU是基于时间序列数据由前向后进行预测,而反向GRU则是基于时间序列数据由后向前进行“预测”。正是因为BiGRU中的反向GRU考虑了后文信息,所以BiGRU会比单向GRU预测得更加准确。BiGRU结构示意图如图1所示。
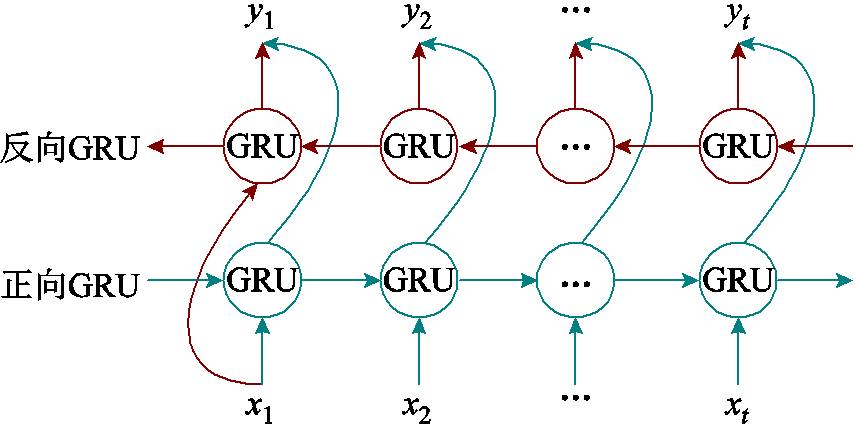
图1 BiGRU结构示意图
Fig.1 Structure of BiGRU
由图1可见,BiGRU摆脱了只能依据前一刻信息预测后一刻状态的限制,能有效地结合输入的前向和后向特征,获得更准确的预测结果。
QR考虑样本的概率分布,并获得该分布下各分位点处的回归结果[26]。具体而言,QR能够回归解释变量X与某分位点处的被解释变量Y之间的函数参数,从而当X取值x*时,能够获得某分位点处y*的数值。假设误差X服从高斯分布,若基于QR获得Y在0.05与0.95分位点的取值,则认为获得了Y的置信度为90%的置信区间。
假设分位数回归模型为
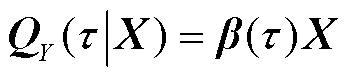 (7)
(7)
式中,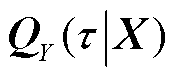 为Y在X=[x1 x2…xk]T给定下的条件分位数;
为Y在X=[x1 x2…xk]T给定下的条件分位数;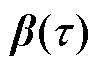 为参数向量,
为参数向量,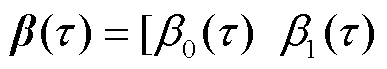
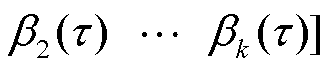 ;τ为分位点。
;τ为分位点。
对式(7)中参数向量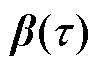 进行估计,可转换为最小二乘优化问题,即
进行估计,可转换为最小二乘优化问题,即
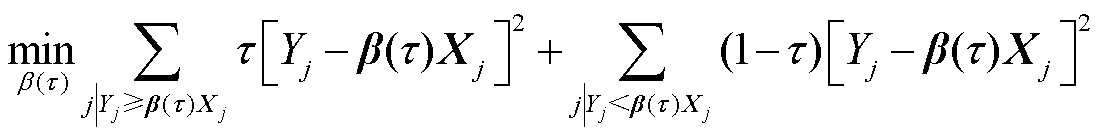 (8)
(8)
式中,j为样本编号。
总之,QR既是对Y的分位点的回归,同时也是对Y的置信区间的估计。本文将式(8)作为损失函数嵌入BiGRU神经网络之中,从而获得QR-BiGRU神经网络,实现各分位点的回归预测与状态预测置信区间的获取。
本文提出的QR-BiGRU神经网络结构示意图如图2所示。
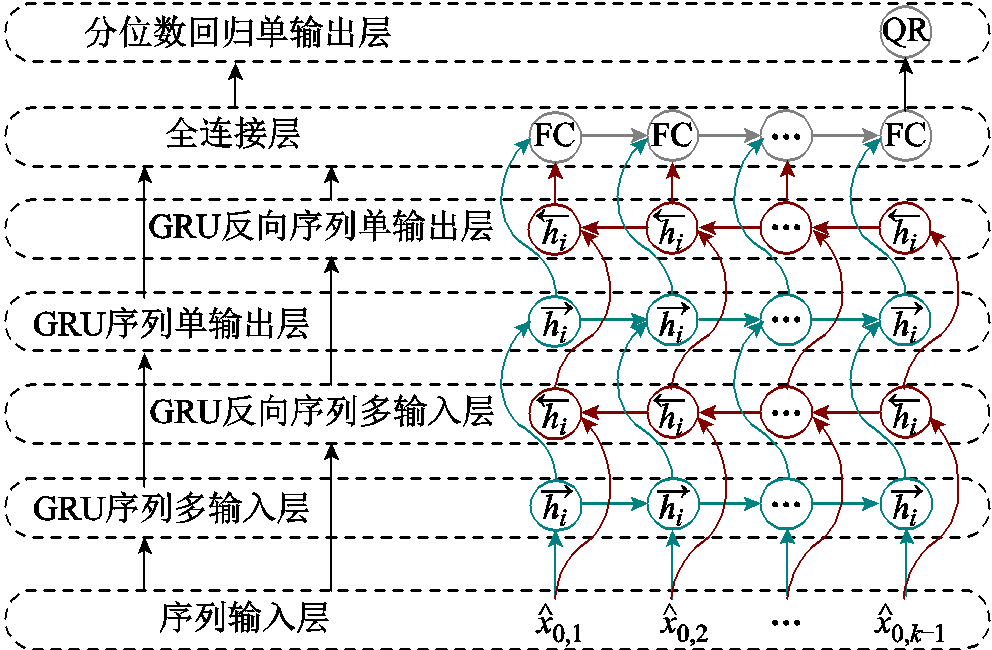
图2 QR-BiGRU结构示意图
Fig.2 Model structure of QR-BiGRU
由图2可见,QR-BiGRU主要由7层神经网络组成,各层功能如下。
1)序列输入层:实现时间序列的输入。本文考虑参数在线追踪的时效性,仅对n个节点的电压幅值、相角共2n条时间序列进行独立预测,不考虑不同节点的电压相关性、电力系统的物理相关性等。因此,所提方法输入为单特征模式,特征维度为1。
2)多对多正向序列GRU层:输入为时间序列数据(即多时刻数据),输出为各时刻GRU单元的训练结果(即多时刻数据)。该层一方面可实现各时刻的“预测结果”保留,从而允许模型功能的扩展;另一方面则可视为对时间序列数据的“预处理”,从而提高预测鲁棒性。
3)多对一正向序列GRU层:输入为各时刻的“预测结果”(即多时刻数据),输出为最后时刻的预测结果(即单一时刻数据)。该层与多对多正向序列GRU层结合,构成典型双层GRU模型。相比单层GRU模型,双层GRU不仅允许更广泛的数据交互与特征挖掘,且相比单层GRU,双层模型中各层GRU只需设置少量神经元隐含层便可达到期望的学习效果,可在一定程度上避免单层GRU由于神经元隐含层数过多而导致的过拟合问题。
4)多对多反向序列GRU层:输入为反向时间序列数据,输出为各时刻GRU单元的训练结果。该层需对时间序列进行翻转处理;该层与多对多正向序列GRU层结合,构成单层BiGRU模型。
5)多对一反向序列GRU层:输入为反向序列各时刻的“预测结果”,输出为第一时刻的预测结果。2)~5)层共同构成双层BiGRU模型。
6)全连接层(Fully Connected layer, FC):该层确保各层之间、各层的神经元隐含层之间相互连接;同时确定输出模式为单步预测模式,特征维度为1。
7)分位数回归层:该层提供神经网络模型的损失函数(目标函数),输出各分位点处的回归结果,决定了模型的最终功能。
上文通过量测允许误差率获取了量测误差并构建量测区间,通过QR-BiGRU神经网络获取了状态预测误差并构建状态预测区间,这是基于IRASE的参数区间估计的必要条件。然而,区间算术具有显著的扩张性问题,因此不能简单地采用区间算术对IRASE模型进行求解,否则将会随着断面数据的不断更新而造成求解区间的无限扩张。
本文基于误差传播定律,提出针对误差区间的计算方法,以避免区间算术求解IRASE模型而产生的区间扩张性问题,实现基于IRASE的有效的参数区间估计。
测量领域中,由于测量值含有误差,导致其函数也含有误差,这种现象称为误差传播。而阐述测量误差与其函数误差之间关系的定律,称为误差传播定律。误差传播定律可推导如下。
函数f(x)在x0处的泰勒展开式为
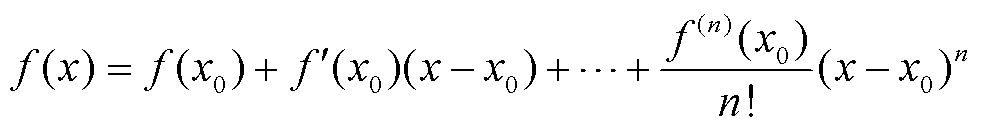 (9)
(9)
假设x0为真值x的一个测量样本,且x0与x之间的测量误差很小,从而可忽略高阶项。若定义测量误差e(x)=x-x0,定义函数误差e(y)=f(x)-f(x0),则根据式(9),可得误差传播定律为
 (10)
(10)
式中,f'(x0)为测量误差到函数误差的传递函数。
假设x的测量置信区间(以下简称:测量区间)为[x],同时[x]也表征了测量误差的置信范围。根据区间分析,[x]仿射形式表示[24]为
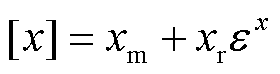 (11)
(11)
式中,xm为区间中心值变量,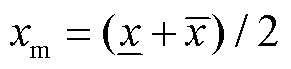 ;xr为区间半径变量,
;xr为区间半径变量,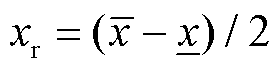 ;εx为自变量x的噪声元,εx=[-1,1]。
;εx为自变量x的噪声元,εx=[-1,1]。
式(11)表明区间变量可采用“区间中心值”和“区间半径”两个确定性变量进行表示;其中“区间半径”内的误差样本可进行传播,从而区间变量的函数结果区间可视为“区间中心值的函数计算结果”与“区间半径内的误差传播结果”的结合。
具体地:若有测量样本xj对应测量误差e(xj),则根据置信区间定义可知:大部分e(xj)<xr,因此可忽略高阶项进行传播。根据式(10),由误差区间传播形成的y的置信区间为
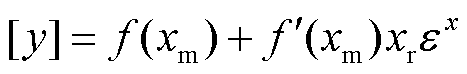 (12)
(12)
上述即为基于误差传播定律的区间分析方法。与直接计算[y]=f([x])不同,上述方法忽略了误差高阶项,将求解过程分为“中心值计算”与“区间计算”两部分。其中,“中心值计算”不存在区间扩张性问题,而“区间计算”则是基于误差传播定律,避免了区间算术中的扩张性问题。总之,基于误差传播定律的区间分析方法克服了区间扩张性问题,适用于由误差区间所导致的结果区间的分析。
IRASE的量测方程为
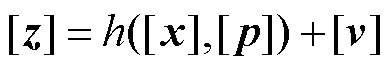 (13)
(13)
式(13)可采用最小二乘法求解,求解方程为
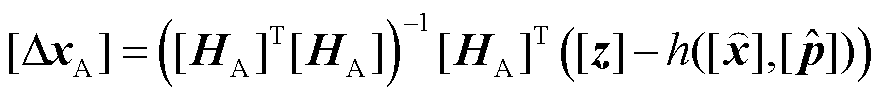 (14)
(14)
式中,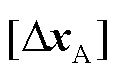 为增广状态修正区间向量;
为增广状态修正区间向量;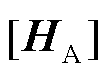 为增广雅可比区间矩阵;
为增广雅可比区间矩阵;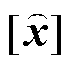 为状态预测区间向量;
为状态预测区间向量;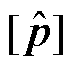 为参数估计区间向量。
为参数估计区间向量。
与静态模型求解不同,IRASE的每一次迭代计算采用不同的断面量测数据,并根据不同断面量测数据与其估计数据的差值,计算参数修正量,最终逼近参数真值。
然而,式(14)若基于区间算术进行求解,将面临严重的区间扩张难题。因此,本文基于误差传播定律的区间分析方法对IRASE进行求解。
IRASE的求解分为“中心值计算”与“参数估计区间计算”两部分。
3.2.1 中心值计算
若考虑零注入功率约束[22],获得IRASE的中心值修正方程为
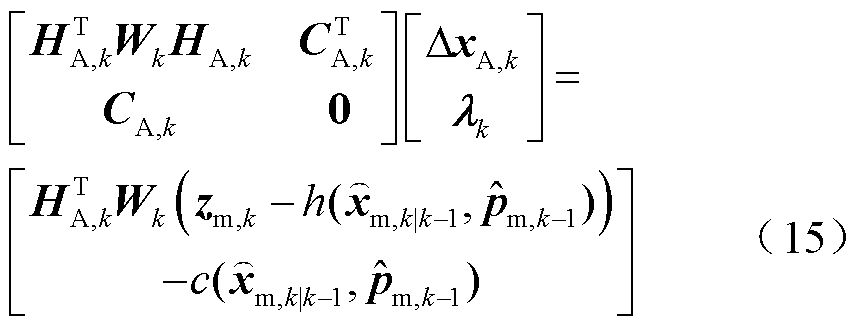
式中,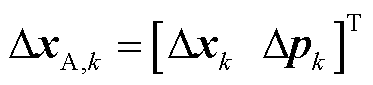 为增广状态修正中心值列向量;
为增广状态修正中心值列向量;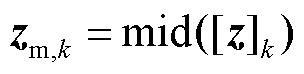 为
为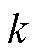 时刻量测中心值列向量;
时刻量测中心值列向量;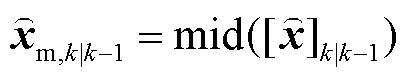 为
为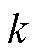 时刻的状态预测中心值列向量;
时刻的状态预测中心值列向量; 为
为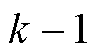 时刻的参数估计中心值列向量;
时刻的参数估计中心值列向量;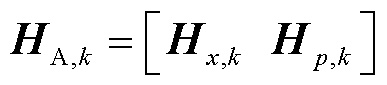 为增广量测函数雅克比矩阵在
为增广量测函数雅克比矩阵在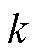 时刻的预测值,
时刻的预测值,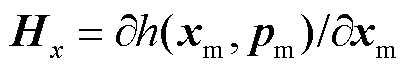 为量测函数对状态变量的雅克比矩阵,
为量测函数对状态变量的雅克比矩阵,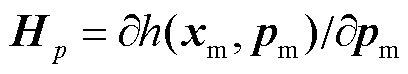 为量测函数对参数误差变量的雅克比矩阵;
为量测函数对参数误差变量的雅克比矩阵;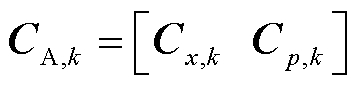 为增广零注入功率函数雅克比矩阵在
为增广零注入功率函数雅克比矩阵在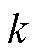 时刻的预测值,
时刻的预测值,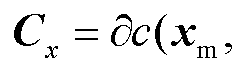
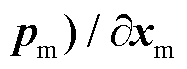 为零注入等式约束对状态变量的雅克比矩阵,
为零注入等式约束对状态变量的雅克比矩阵,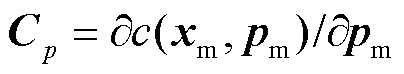 为零注入等式约束对参数误差的维雅克比矩阵。
为零注入等式约束对参数误差的维雅克比矩阵。
从而得到状态估计中心值为
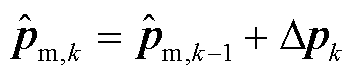 (16)
(16)
式中,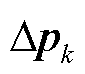 为增广状态修正中心值的参数修正分量。
为增广状态修正中心值的参数修正分量。
3.2.2 参数区间计算
参数估计误差由状态预测误差和量测误差构成,其中,量测误差通过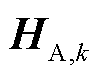 的逆进行传递。然而,
的逆进行传递。然而,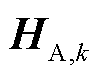 的逆无法直接计算,因此,本文采用
的逆无法直接计算,因此,本文采用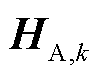 的广义逆
的广义逆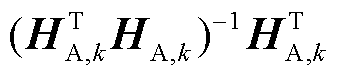 作为误差传递函数,并对参数估计误差区间进行求取。而广义逆也可视为冗余量测误差传递到状态误差的最小二乘解。
作为误差传递函数,并对参数估计误差区间进行求取。而广义逆也可视为冗余量测误差传递到状态误差的最小二乘解。
IRASE的参数区间求取方程为
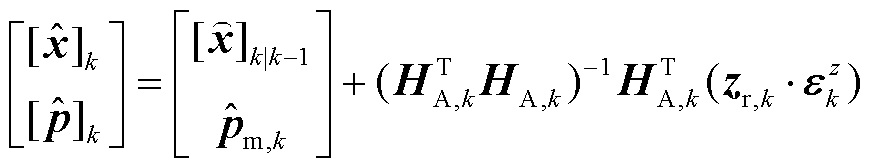 (17)
(17)
式中,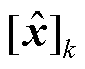 为
为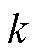 时刻状态估计区间;
时刻状态估计区间;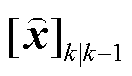 为
为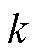 时刻状态预测区间;
时刻状态预测区间;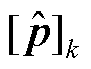 为
为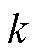 时刻参数估计区间;
时刻参数估计区间;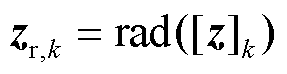 为
为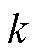 时刻量测半径向量;
时刻量测半径向量;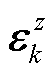 为
为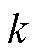 时刻量测z的噪声元向量。
时刻量测z的噪声元向量。
针对短期或固定时长的线路参数追踪维护,可设置收敛条件。IRASE的收敛分为参数中心值收敛与参数区间收敛两部分,具体收敛条件为
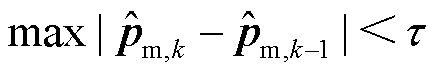 (18)
(18)
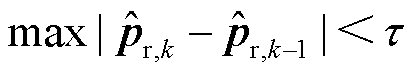 (19)
(19)
式中,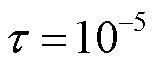 。
。
3.2.3 算法流程
IRASE算法流程如图3所示。由图3可见,参数估计区间实质由“参数估计值”以及“状态预测误差和量测误差传播值”决定。其中,零注入功率约束的考虑提高了模型抗差性,确保了参数估计值的准确性;而基于区间分析理论与误差传播定律的IRASE求解方法则确保了误差区间的可信度。
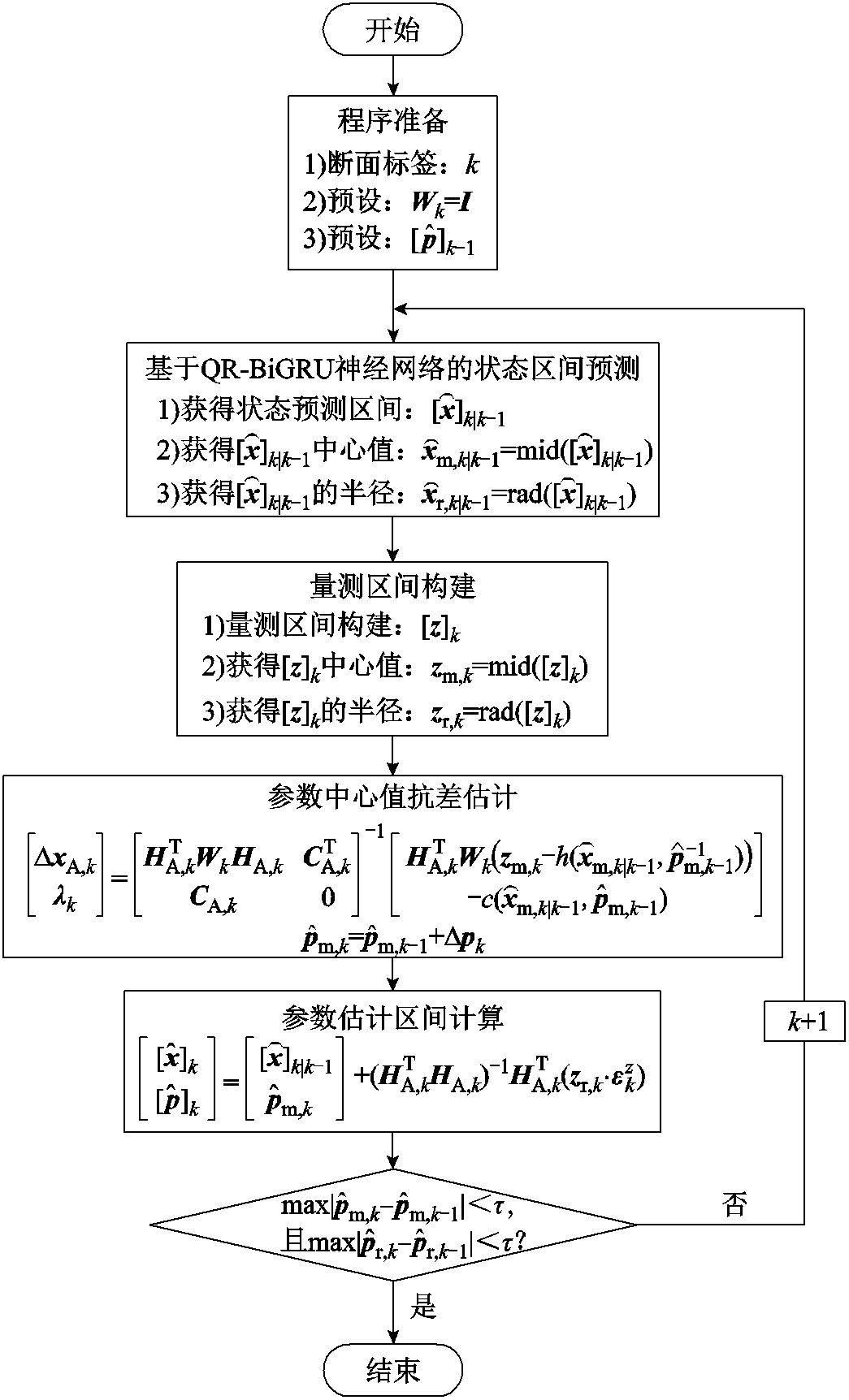
图3 IRASE算法流程
Fig.3 Flow chart of IRASE
参数追踪估计属于一种动态估计模型,可基于时间序列数据不断进行参数估计,无需通过多个断面联立非线性量测方程组来提高数据冗余度,具有模型简单、估计效率高等优点,能够有效实现对电力系统线路参数的长期跟踪与维护。
本文基于Matpower软件包中的IEEE 14、30、118、300节点测试系统,并结合美国纽约独立系统运营商(New York Independent System Operator, NYISO)在2022年10月的数据[28]进行仿真。节点测试系统与NYISO数据的结合方法参考文献[27]。
本文以上述数据的各断面潮流计算结果作为量测的约定真值,并叠加高斯噪声(均值为0、标准差为国家能源局规定的最大允许误差率的1/3)作为量测误差;另随机选择测点,设置3~10倍高斯噪声作为不良量测。量测数据的生成方法详见文献[1]。
完成各断面量测数据生成后,本文根据式(4)~式(6)构建量测区间并进行仿真。
区间估计的常用评价指标为
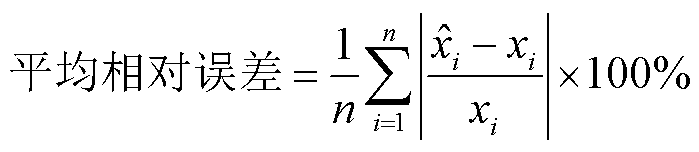 (20)
(20)
式中,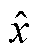 为状态估计/预测值;
为状态估计/预测值;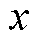 为状态真值;i为节点编号;对于区间预测,n为某个状态的时间序列预测数,对于区间增广状态估计,n表示状态个数。
为状态真值;i为节点编号;对于区间预测,n为某个状态的时间序列预测数,对于区间增广状态估计,n表示状态个数。
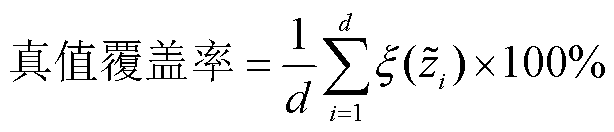 (21)
(21)
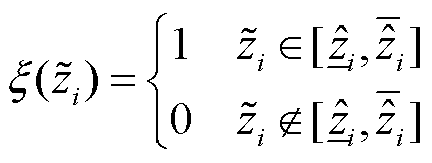 (22)
(22)
式中,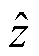 为量测估计/预测值;
为量测估计/预测值;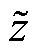 为量测真值;对于区间预测,d为某个量测的时间序列预测数,对于区间增广状态估计,d为量测个数。
为量测真值;对于区间预测,d为某个量测的时间序列预测数,对于区间增广状态估计,d为量测个数。
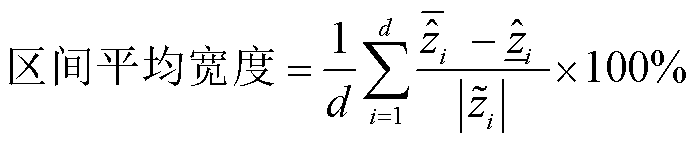 (23)
(23)
区间平均宽度指标表明了区间估计/预测的不确定程度。区间平均宽度越小,表明区间估计/预测的不确定程度越小,区间估计/预测越好。
然而,区间平均宽度与真值覆盖率指标之间具有负相关关系,即真值覆盖率越好,区间平均宽度有可能越坏。因此,本文采用一种简易的方法综合考虑真值覆盖率和区间平均宽度指标,即定义真值覆盖宽度指标为
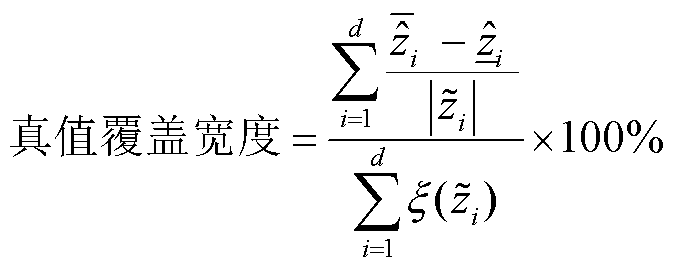 (24)
(24)
真值覆盖宽度是区间估计置信程度与不确定程度的综合考虑。真值覆盖宽度越小,说明区间估计/预测效果越好。
本文的仿真环境和软件为:Intel CPU i5-9400F 2.90 GHz,DDR 8 G,Matlab 2020b,Matpower 6.0,Intlab 12.0。
本节将验证QR-BiGRU神经网络相比其他神经网络的优势。为此本节与如下方法进行比较。
1)QRNN:即文献[26],分位数回归神经网络区间预测方法。
2)QR-LSTM:结合QR的LSTM神经网络区间预测方法。
3)QR-GRU:结合QR的GRU神经网络区间预测方法。
4)QR-BiGRU:即本文所提区间预测方法,具体超参数详见附录。
本文所提区间预测方法是对各节点的电压幅值、相角时间序列数据进行独立的自回归预测,未考虑不同节点的电压相关性以及电力系统的物理相关性等。本文随机抽取某节点电压进行区间预测,并选择约300个时刻的预测结果进行统计分析。其中,预测精度指标详见表1,预测时间详见表2。
表1 电压区间预测精度指标
Tab.1 Prediction indicators for voltage magnitude interval (%)
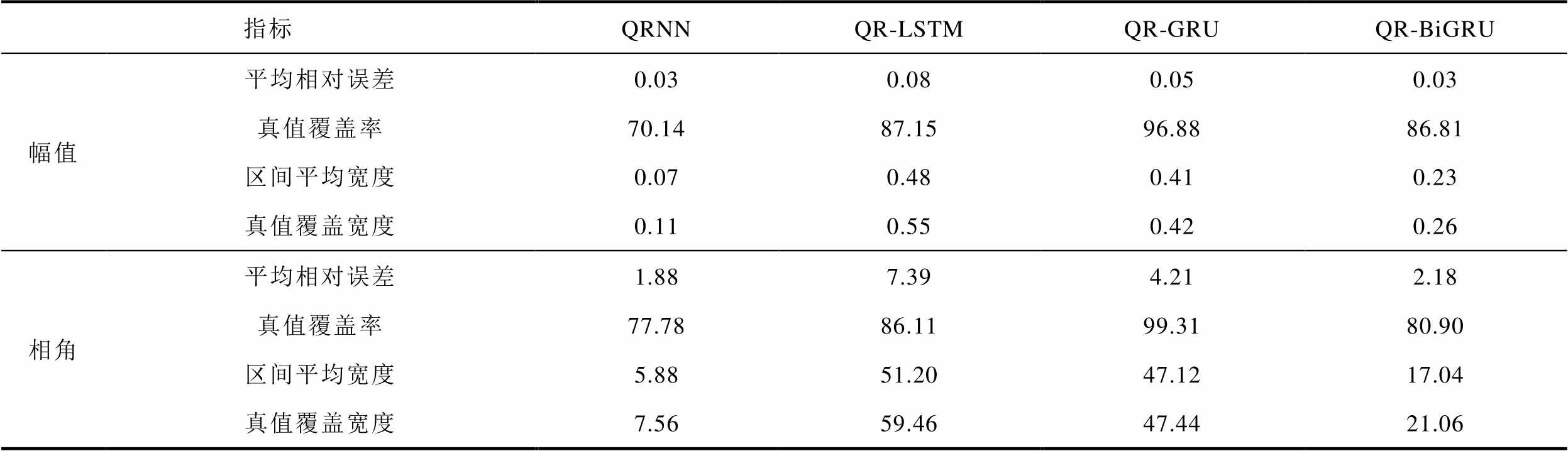
指标QRNNQR-LSTMQR-GRUQR-BiGRU 幅值平均相对误差0.030.080.050.03 真值覆盖率70.1487.1596.8886.81 区间平均宽度0.070.480.410.23 真值覆盖宽度0.110.550.420.26 相角平均相对误差1.887.394.212.18 真值覆盖率77.7886.1199.3180.90 区间平均宽度5.8851.2047.1217.04 真值覆盖宽度7.5659.4647.4421.06
表2 电压区间预测时间
Tab.2 Prediction time for voltage magnitude interval

指标QRNNQR-LSTMQR-GRUQR-BiGRU 训练时间/s0.0013.8313.7733.81 预测时间/s0.185 30.003 60.003 40.005 6
由表1可见,虽然QRNN的平均相对误差最小,但其真值覆盖率也最低,这是因为其区间平均宽度太窄导致;另外,由表2可见,QRNN的平均预测时间太长,不适合大规模电网(比如300节点测试系统)的状态区间预测。因此,在之后讨论中不再考虑QRNN。
对于QR-LSTM、QR-GRU、QR-BiGRU而言,在预测精度方面,QR-BiGRU是最好的。这不仅因为QR-BiGRU具有最小的平均相对误差,即最高的预测精度,更主要的是其真值覆盖宽度也是最好的。而真值覆盖宽度是区间的综合评价指标,表明QR-BiGRU取得了最好的区间预测效果。
而在预测时间方面,无论是训练时间,亦或预测时间,GRU相比LSTM均展现了更高的效率。然而,BiGRU由于采用双向结构,其训练时间、预测时间均高于GRU和LSTM;但即便对于大规模电网的状态区间预测,BiGRU的预测时间仍能满足电网调度自动化系统单次状态估计计算时间限制[25]。
随机抽取QR-LSTM、QR-GRU、QR-BiGRU的电压幅值、相角区间预测结果进行展示,如图4、图5所示。
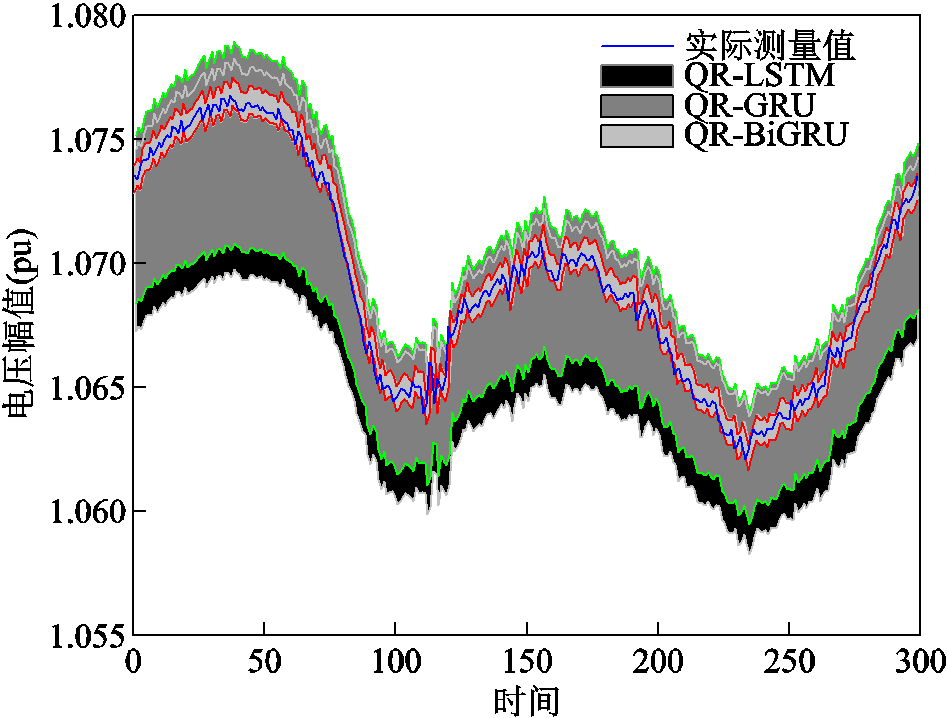
图4 电压幅值区间预测结果比较
Fig.4 Comparison of interval prediction results of voltage magnitude
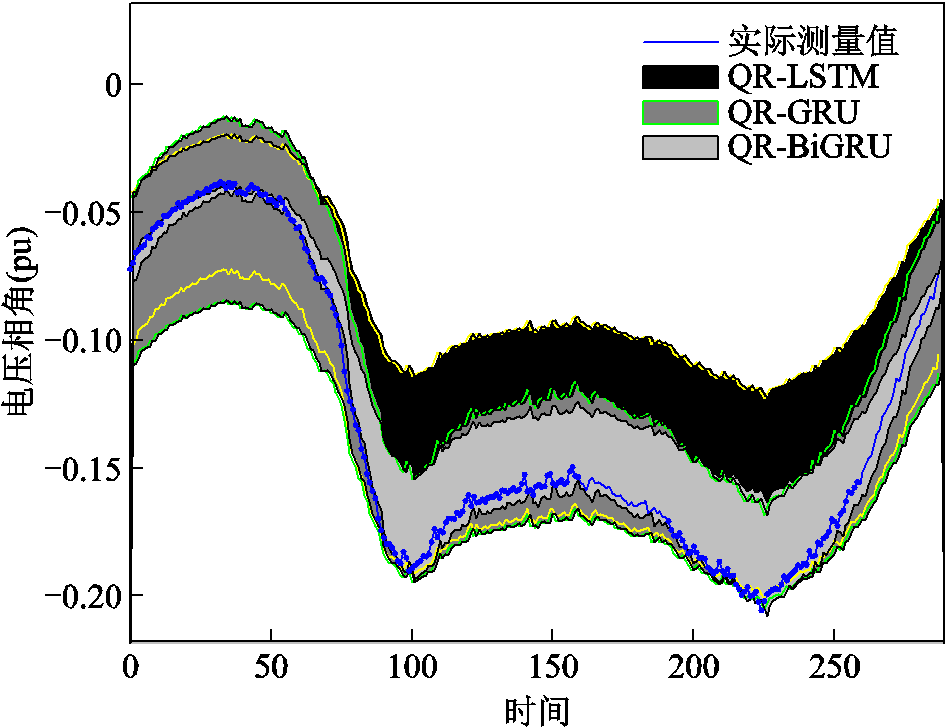
图5 电压相角区间预测结果比较
Fig.5 Comparison of interval prediction results of voltage phase angle
由图4、图5可见,QR-BiGRU的区间平均宽度最小,充分展现了基于双向信息进行预测的优势。
本节将验证:动态增广状态估计方法相比静态参数估计的优势;本文所提区间预测方法相比Holt指数平滑预测方法的优势;本文所提参数区间追踪估计方法相比动态增广状态估计方法的优势。
然而,本文所提方法与动态增广状态估计方法均不太适合线路对地电纳的追踪估计。一方面因为线路的对地电纳相当于特殊的“节点注入无功功率量测”,对其进行估计会受到实际功率量测噪声的影响,导致估计误差很大;另一方面,追踪估计模型的功率量测属于时间序列数据,会导致对地电纳的估计值随着该序列数据的波动而波动,从而难以获得稳定、准确的估计结果。因此,本文只对线路的电阻、电抗进行追踪估计,以论证本文所提方法优势。本文将与以下方案进行比较。
方案一:基于静态增广状态估计的参数估计。
方案二:文献[13]方法,即采用Holt指数平滑预测函数作为状态预测函数,且不考虑抗差的确定性动态增广状态估计方法。
方案三:基于QR-BiGRU状态预测的确定性参数追踪估计方法,但不考虑零注入功率约束抗差。
方案四:本文所提方法,基于QR-BiGRU状态预测与IRASE的参数区间追踪估计方法。
4.3.1 精度分析
上述参数追踪估计方案,即方案二、三、四的追踪结果如图6~图8所示。其中,图6展示了前20个断面的参数追踪估计结果;图7展示了稳定后(第10个断面以后)的参数追踪估计结果;图8则展示了参数追踪估计的误差。
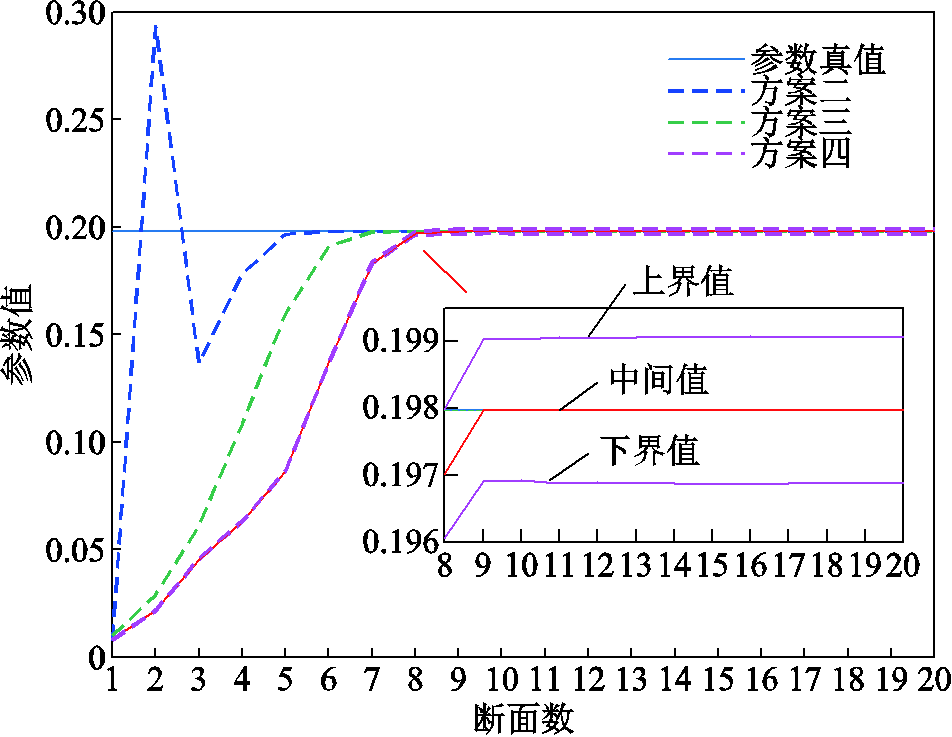
图6 前20断面参数追踪估计结果
Fig.6 Parameter tracking of the first 20 snapshots
由图6可见,各方案的参数估计结果均能“稳定”到参数真值附近。其中方案二、三相比本文所提方法,能够更快速地“稳定”,这是因为方案二、三的模型更简单,因此能够更快速地收敛。另外,方案四输出的是区间结果,大约为[0.197, 0.199],而该参数真值为0.198,位于区间内,表明了基于误差传播的区间求解方法的有效性。
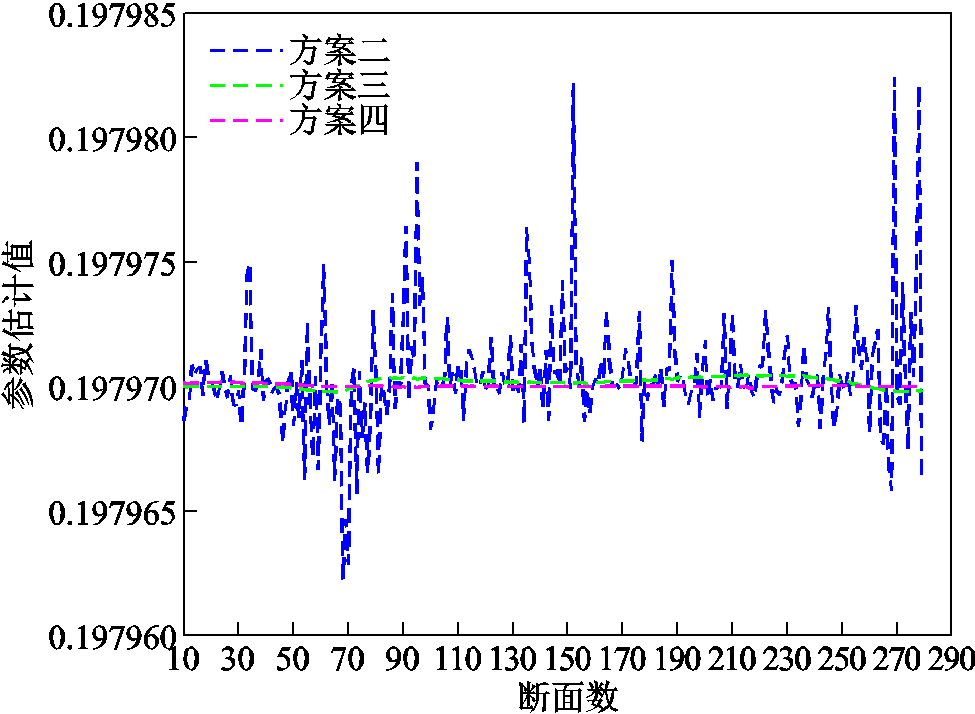
图7 参数追踪估计结果
Fig.7 Results of parameter tracking estimation
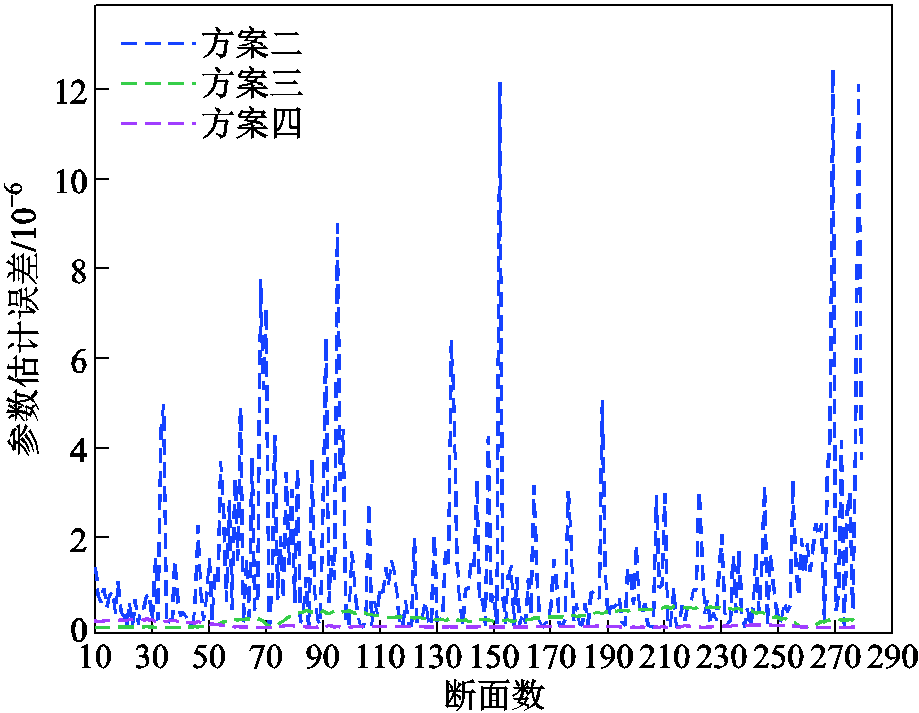
图8 参数追踪估计误差
Fig.8 Error of parameter tracking estimation
由图7、图8可见,方案二、三相比本文所提方法具有更大的估计误差。这是因为方案二采用简易的状态平滑预测,从而将状态预测误差代入参数估计中,降低了参数估计精度;方案三则是缺少抗差机制,从而参数估计过程会受到不良量测的影响,最终导致参数估计偏差。
各方案的平均相对误差见表3。
表3 参数追踪估计误差
Tab.3 Error of parameter tracking estimation

指标测试系统方案二方案三方案四 电阻估计误差14节点系统3.97×10-75.96×10-82.89×10-8 30节点系统6.67×10-66.53×10-63.65×10-6 118节点系统3.51×10-53.42×10-59.02×10-6 300节点系统4.42×10-54.30×10-51.53×10-5
(续)

指标测试系统方案二方案三方案四 电抗估计误差14节点系统1.29×10-62.15×10-75.23×10-8 30节点系统3.12×10-63.47×10-61.18×10-6 118节点系统1.05×10-41.06×10-46.20×10-5 300节点系统1.41×10-51.38×10-59.17×10-6
综上所述,方案二与方案三、四相比,表明了本文所提状态预测方法的有效性;而方案三与方案四相比,表明了本文增加零注入功率约束进行抗差的有效性。
4.3.2 速度分析
追踪估计的思想是将每一次迭代数据替换为不同的断面量测数据,并根据不同断面量测数据与其估计数据的差值,计算参数修正量,最终逼近参数真值。与多断面联立的增广状态估计相比,参数追踪无需通过多断面联立提高数据冗余度,因此降低了方程规模,提高了参数估计效率。
由图5可见,本文所提方法在第9个断面就已稳定在参数真值附近。因此,本文以第10个断面的参数估计结果作为各追踪估计方案(方案二、三、四)的最终结果,并与静态参数估计方法(方案一)进行比较,获得各方案估计时间见表4。
表4 参数追踪估计时间
Tab.4 Time of parameter tracking estimation (单位:s)

测试系统方案一方案二方案三方案四 14节点系统0.081 10.001 90.001 60.023 9 30节点系统0.051 60.0040.003 70.039 9 118节点系统0.723 50.118 10.113 40.361 9 300节点系统2.789 30.618 50.566 42.637 2
由表4可见,各追踪估计方案(方案二、三、四)的估计时间均小于静态参数估计方法(方案一)的估计时间,验证了参数追踪估计的效率优势。
另外,尽管方案四相比方案二、三的估计时间更长,但方案四除了提供参数区间中间值作为最终参数估计值使用外,还提供了考虑量测误差的参数估计区间,为今后错误参数辨识提供边界信息,因此方案四更具工程应用价值。
本文提出一种基于QR-BiGRU神经网络与IRASE的线路参数区间追踪估计方法。所提方法基于区间估计理论,通过融合QR-BiGRU神经网络与IRASE模型,实现了电力系统线路参数更准确、可信的区间估计。其中,QR-BiGRU神经网络考虑了历史状态估计时间序列数据的双向特征,实现了更为准确的状态区间预测;IRASE模型则基于误差传播定律,求取了状态预测误差与冗余量测误差对参数估计误差的传播值,从而获得了由状态预测区间、量测区间所导致的线路电阻、电抗区间,实现了对线路阻抗及其估计误差区间的追踪估计。
仿真结果表明:QR-BiGRU的区间预测结果最好,能够为参数追踪估计提供更为合理、准确的电压区间。在参数追踪估计方面,本文获得的参数估计区间是由“参数估计值”及“状态预测误差、量测误差传播”决定的。其中,零注入功率约束提高了模型抗差性,确保了参数估计值的准确性;而基于区间分析理论与误差传播定律的IRASE则确保了误差区间的可信度。另外,相比静态的多断面增广状态估计,本文所提方法计算效率更高,能够有效实现对参数的长期追踪与维护;获得的参数区间为研究线路参数在一定容差范围内的状态估计问题提供了基础,也为电力系统不确定性建模与分析、数据监测与维护等提供了边界信息。
附 录
附表1 QR-BiGRU神经网络的超参数设置
Tab.1 Hyperparameter setting for QR-BiGRU neural network

网络名称层名称参数数值 主网络序列输入层输入样本维度1 GRU层1隐含层神经元数量16 输出模式sequence 分支网络1连接层输入样本维度1 输入个数2 GRU层3隐含层神经元数量16 输出模式last 分支网络2连接层输入样本维度1 输入个数2 全连接层输出样本维度1 分位数回归层分位数[0.025,0.5,0.975] 分支网络1翻转层1翻转方式默认值 GRU层2 隐含层神经元数量16 输出模式sequence 翻转层2 翻转方式默认值 分支网络2翻转层3 翻转方式默认值 GRU层4隐含层神经元数量16 输出模式last
参考文献
[1] 于尔铿. 电力系统状态估计[M]. 北京: 水利电力出版社, 1985.
[2] 薛安成, 张兆阳, 张建民, 等. 基于最大测点正常率的线路参数增广状态估计方法[J]. 电力系统自动化, 2014, 38(10): 61-65.
Xue Ancheng, Zhang Zhaoyang, Zhang Jianmin, et al. An augmented state estimation method for transmission line parameters based on maximum normal measurement rate[J]. Automation of Electric Power Systems, 2014, 38(10): 61-65.
[3] 何桦, 柴京慧, 卫志农, 等. 基于量测残差的改进参数估计方法[J]. 电力系统自动化, 2007, 31(4): 33-36, 96.
He Hua, Chai Jinghui, Wei Zhinong, et al. Improved method of parameter estimation based on measurement residuals[J]. Automation of Electric Power Systems, 2007, 31(4): 33-36, 96.
[4] Zhu Jun, Abur A. Identification of network parameter errors[J]. IEEE Transactions on Power Systems, 2006, 21(2): 586-592.
[5] Lin Yuzhang, Abur A. Enhancing network parameter error detection and correction via multiple measurement scans[J]. IEEE Transactions on Power Systems, 2017, 32(3): 2417-2425.
[6] 李钦, 项凤雏, 颜伟, 等. 基于SCADA及PMU多时段量测信息的独立线路参数估计方法[J]. 电网技术, 2011, 35(2): 105-109.
Li Qin, Xiang Fengchu, Yan Wei, et al. An approach to estimate parameters of single transmission line based on multi-interval information measured by SCADA and phasor measurement units[J]. Power System Technology, 2011, 35(2): 105-109.
[7] 薛安成, 张兆阳, 毕天姝. 基于自适应抗差最小二乘的线路正序参数在线辨识方法[J]. 电工技术学报, 2015, 30(8): 202-209.
Xue Ancheng, Zhang Zhaoyang, Bi Tianshu. Online identification of transmission line positive-sequence parameters based on adaptive robust least squares[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 202-209.
[8] 刘安迪, 李妍, 谢伟, 等. 基于多源数据多时间断面的配电网线路参数估计方法[J]. 电力系统自动化, 2021, 45(2): 46-54.
Liu Andi, Li Yan, Xie Wei, et al. Estimation method of line parameters in distribution network based on multi-source data and multi-time sections[J]. Automation of Electric Power Systems, 2021, 45(2): 46-54.
[9] Bian Xiaomeng, Li X R, Chen Huimin, et al. Joint estimation of state and parameter with synchrophasors: part II: parameter tracking[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1209-1220.
[10] Ren Pengxiang, Lev-Ari H, Abur A. Tracking three-phase untransposed transmission line parameters using synchronized measurements[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4155-4163.
[11] Pereira R F R, de Albuquerque F P, Liboni L H B, et al. Impedance parameters estimation of transmission lines by an extended Kalman filter-based algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 9003610.
[12] Lin Junjie, Song Jie, Lu Chao. Synchrophasor data analytics: transmission line parameters online estimation for energy management[J]. IEEE Transactions on Engineering Management, 2022, 69(3): 671-681.
[13] Wang Yubin, Xia Mingchao, Yang Qiang, et al. Augmented state estimation of line parameters in active power distribution systems with phasor measurement units[J]. IEEE Transactions on Power Delivery, 2022, 37(5): 3835-3845.
[14] 王玉彬, 夏明超, 李鹏, 等. 基于改进鲁棒自适应UKF的配电网动态状态估计方法[J]. 电力系统自动化, 2020, 44(1): 92-100.
Wang Yubin, Xia Mingchao, Li Peng, et al. Dynamic state estimation method of distribution network based on improved robust adaptive unscented Kalman filter[J]. Automation of Electric Power Systems, 2020, 44(1): 92-100.
[15] 刘雨佳, 樊艳芳, 白雪岩, 等. 基于特征交叉机制和误差补偿的风力发电功率短期预测[J]. 电工技术学报, 2023, 38(12): 3277-3288.
Liu Yujia, Fan Yanfang, Bai Xueyan, et al. Short-term wind power prediction based on feature crossover mechanism and error compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3277-3288.
[16] Wang Ruoheng, Li Chaoshun, Fu Wenlong, et al. Deep learning method based on gated recurrent unit and variational mode decomposition for short-term wind power interval prediction[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(10): 3814-3827.
[17] 高树国, 汲胜昌, 孟令明, 等. 基于在线监测系统与声振特征预测模型的高压并联电抗器运行状态评估方法[J]. 电工技术学报, 2022, 37(9): 2179-2189.
Gao Shuguo, Ji Shengchang, Meng Lingming, et al. Operation state evaluation method of high-voltage shunt reactor based on on-line monitoring system and vibro-acoustic characteristic prediction model[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2179-2189.
[18] 张铄, 吴丽珍. 计及坏数据辨识与修正的配电网状态估计[J]. 电气技术, 2022, 23(11): 1-5, 12.
Zhang Shuo, Wu Lizhen. Distribution network state estimation considering bad data identification and correction[J]. Electrical Engineering, 2022, 23(11): 1-5, 12.
[19] Rakpenthai C, Uatrongjit S, Premrudeepreechacharn S. State estimation of power system considering network parameter uncertainty based on parametric interval linear systems[J]. IEEE Transactions on Power Systems, 2012, 27(1): 305-313.
[20] 卫志农, 颜全椿, 孙国强, 等. 考虑参数不确定性的电力系统区间线性状态估计[J]. 电网技术, 2015, 39(10): 2862-2868.
Wei Zhinong, Yan Quanchun, Sun Guoqiang, et al. Power system interval linear state estimation considering network parameter uncertainty[J]. Power System Technology, 2015, 39(10): 2862-2868.
[21] 邵振国, 林洪洲, 陈飞雄, 等. 采用区间动态状态估计的局部不可观系统谐波源定位[J]. 电工技术学报, 2023, 38(9): 2391-2402.
Shao Zhenguo, Lin Hongzhou, Chen Feixiong, et al. Harmonic source location in the partial unobservable system based on interval dynamic state estimation[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2391-2402.
[22] Lin W M, Teng J H. State estimation for distribution systems with zero-injection constraints[J]. IEEE Transactions on Power Systems, 1996, 11(1): 518-524.
[23] 朱茂林, 刘灏, 毕天姝. 考虑风电场量测相关性的双馈风力发电机鲁棒动态状态估计[J]. 电工技术学报, 2023, 38(3): 726-740.
Zhu Maolin, Liu Hao, Bi Tianshu. Robust dynamic state estimation of doubly-fed induction generator considering measurement correlation in wind farms[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 726-740.
[24] Moore R E, Bierbaum F. Methods and Applications of Interval Analysis[M]. Philadelphia: Siam, 1979.
[25] 国家发展和改革委员会. 电力调度自动化系统运行管理规程: DL/T 516—2006[S]. 北京: 中国电力出版社, 2007.
[26] 李丹, 任洲洋, 颜伟, 等. 基于因子分析和神经网络分位数回归的月度风电功率曲线概率预测[J]. 中国电机工程学报, 2017, 37(18): 5238-5247, 5522.
Li Dan, Ren Zhouyang, Yan Wei, et al. Month-ahead wind power curve probabilistic prediction based on factor analysis and quantile regression neural network[J]. Proceedings of the CSEE, 2017, 37(18): 5238-5247, 5522.
[27] Gu Chaojun, Jirutitijaroen P, Motani M. Detecting false data injection attacks in AC state estimation[J]. IEEE Transactions on Smart Grid, 2015, 6(5): 2476-2483.
[28] Teng W L J. State estimation for distribution systems with zero-injection constraints [J]. IEEE Transactions on Power Systems, 1996, 11(1): 518-524.
Abstract To meet the needs of power systems for parameter estimation and tracking maintenance of transmission lines, this paper proposes an intervals estimation and tracking method for transmission line parameters based on quantile regression bidirectional gated recurrent unit (QR-BiGRU) neural network and interval robust augmented state estimation (IRASE).
The proposed method is based on a dynamic augmented state estimation model in parameter tracking. Compared with static parameter estimation methods, the proposed method does not need to set up nonlinear measurement equations by multiple measurement scans to improve data redundancy, and has the advantages of easy modeling, high estimation efficiency, and better tracking maintenance; Compared with other parameter tracking methods, the proposed method does not require idealized configuration of branch measurements and only requires the system to be observable to realize the estimation, so it is more practical.
The proposed method is based on interval estimation theory. Compared to point estimation, interval estimation can reflect the credibility of estimation values and the possible range of estimation errors and is considered a more secure and reliable estimation method. In addition, the estimated interval of the transmission line parameter can provide boundary information for bad data identification and provide a foundation for interval state estimation considering parameter interval.
The contributions of this paper are as follows:
1) Propose an interval estimation and tracking method for transmission line parameters. The proposed method is based on the interval estimation theory and the improvement of the dynamic augmented state estimation model, including: (1) Interval estimation modeling based on measured values and their maximum allowable errors, predicted values and their prediction errors, etc. (2) Interval prediction based on QR-BiGRU neural network. (3) The improvement of robustness based on zero injection power constraints. The proposed method achieves more accurate and robust interval estimation and tracking maintenance for line parameters.
2) Proposed an interval prediction method based on the QR-BiGRU neural network. The proposed method considers the bidirectional features of historical estimated state time series data, achieving more accurate prediction. In addition, the least squares objective function of quantile regression is used as the loss function of the QR-BiGRU neural network, thereby achieving the interval prediction of the state at the next moment.
3) Propose an IRASE solution method based on interval analysis and error propagation theory. The proposed method is based on the law of error propagation and calculates the propagation values of state prediction error and redundant measurement error on parameter estimation error, thereby obtaining the parameter intervals caused by the state prediction interval and measurement interval.
Finally, the multiple IEEE cases that integrated time series data from independent system operators in New York, USA, validated the following conclusions:
1) Compared with quantile regression long short term memory neural networks and quantile regression gated recurrent unit neural networks, the QR-BiGRU neural network has better interval prediction performance and accepTab.prediction rates.
2) Interval prediction based on the QR-BiGRU neural network can replace Holt exponential smoothing prediction function for parameter tracking, obtaining more accurate state prediction values and reliable state prediction intervals.
3) Zero injection power constraint could improve the robustness of the model and obtain more accurate parameter estimation results.
4) A relatively reasonable parameter estimated interval indicates the feasibility of the proposed IRASE solution method based on interval analysis and error propagation theory.
5) Compared to static augmented state estimation based on multiple measurement scans, the method proposed in this paper has higher computational efficiency and can effectively achieve long-term tracking and maintenance of transmission line parameters.
keywords:Parameter estimation, augmented state estimation, interval analysis, quantile regression, error propagation
中图分类号:TM744
DOI: 10.19595/j.cnki.1000-6753.tces.231882
收稿日期 2023-11-13
改稿日期 2024-01-21
张 栩 男,1988年生,博士研究生,研究方向为电力大数据、状态估计、深度学习。E-mail:626405998@qq.com
颜 伟 男,1968年生,教授,博士生导师,研究方向为电力系统优化运行与控制。E-mail:cquyanwei@cqu.edu.cn(通信作者)
(编辑 赫 蕾)