（1）
摘要 在相量测量单元（PMU）配置数量不足以满足谐波状态估计的可观性条件时，可将电能质量监测装置（PQMD）作为数据补充源。该文针对多源量测数据存在的同步性差异和量测偏差等问题，提出一种融合PMU与PQMD量测数据的区间型抗差谐波状态估计方法。首先，根据PQMD检测起始时刻不同步的特征，提出基于重叠度指标的PMU与PQMD量测数据融合方法；其次，采用量测变换从PQMD功率量测数据得到等效电流相量量测，构建区间型混合量测全集；再次，采用投影统计法和改进Huber权函数计算量测权重，对重叠度低且残差大的量测赋予较小的权重以抑制量测偏差的影响，并根据权重大小优选测点，得到非同步量测偏差最小的量测子集；最后，通过迭代重加权最小二乘法求解状态估计模型，在IEEE 30系统验证了该文所提方法的可行性与有效性。
关键词：同步相量量测 电能质量监测装置 多源量测数据融合 区间算法 谐波状态估计
在以新能源为主体的新型电力系统中，大量电力电子装置以及非线性负荷使得谐波污染问题越发突出[1]。谐波污染严重影响电网的安全、稳定运行，并给用户带来较大的经济损失[2]。
在全网可观的情况下，谐波状态估计方法只需要部分量测数据就可以估计全网谐波电压和谐波电流[3]，进而为谐波治理提供依据[4]。但采用单一数据源往往无法满足系统可观性要求，融合多源量测数据并实现状态估计成为当前的研究热点[5]。文献[6-8]以相量测量单元（Phasor Measurement Unit, PMU）数据为基础，插补生成高级量测体系（Advanced Metering Infrastructure, AMI）、数据采集和监控系统（Supervisory Control and Data Acquisition, SCADA）在PMU采样时刻的伪量测值，并与PMU数据融合实现状态估计。但状态估计精度受制于插值的准确性，在电网状态波动较大的情况下，状态估计误差更大[9-10]。文献[11-12]以SCADA数据为基础，在SCADA的检测时段内存储PMU量测数据，计算缓冲区内PMU量测数据的加权均值，并与SCADA数据融合实现状态估计。但缓冲区越长，状态量变化越大，其量测数据均值的可信度也随之降低[13]。
当前电力系统中主要的谐波量测装置为PMU与电能质量监测装置（Power Quality Monitoring Device, PQMD）[14]，解决这两种量测数据的融合问题可建立更完备的谐波量测数据集。PMU具备同步量测能力，数据精度较高，但由于造价昂贵无法在电网中大量配置，难以满足系统可观性要求[15]。PQMD造价相对低，在电网中配置数量较多，能够为谐波状态估计提供坚实的数据基础，但其谐波量测数据为3 min统计值，如平均值、最大值和最小值等数据，不同测点的统计值之间不满足时间同步关系[16-17]。文献[18]在电网波动较小的情况下，采用PQMD量测数据的平均值进行谐波状态估计。文献[19]采用PQMD谐波数据的最大值和最小值构建区间型谐波量测数据，实现区间动态谐波状态估计，得到相应时段内电网谐波变化范围。
融合PMU与PQMD的量测数据并尽可能减小PQMD量测数据存在的非同步量测偏差，同时在状态估计中抑制该量测偏差的影响，将能为电网谐波分析提供更有效的手段。据此，本文提出了一种考虑量测偏差的多源数据融合方法，并针对该量测偏差提出一种区间型抗差谐波状态估计算法。针对当前PMU无法满足系统完全可观的问题，将PQMD量测数据作为补充源，构建区间型混合量测数据集以实现状态估计；面对PQMD量测数据存在的非同步量测偏差，采用重叠度指标量化偏差大小并引入Huber权函数中，建立考虑量测偏差影响下的区间谐波抗差状态估计模型，并依据权重优选测点获得量测子集，有效提高状态估计的准确性与鲁棒性。
谐波状态估计是在已知网络参数和部分量测数据条件下求解全网谐波状态的过程，其基本方程[20]为
（1）
式中，z为量测量；x为量测误差；x为待求的状态量；h(x)为量测函数。各量测量对应的量测函数如式（2）所示。
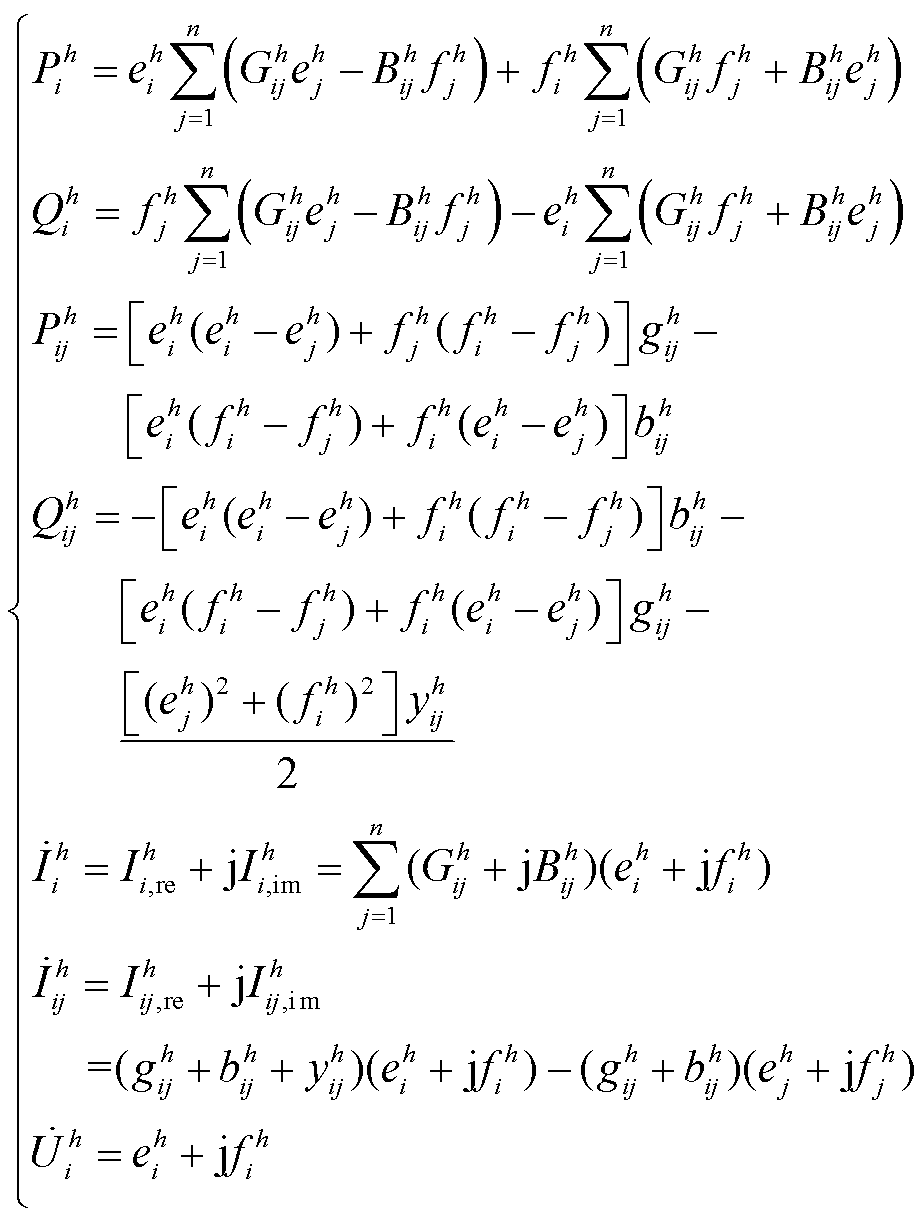（2）
式中，h为谐波次数；i、j为节点编号；n为节点总数；e和f分别为谐波电压的实部和虚部；G和B分别为谐波导纳矩阵的实部和虚部；g和b分别为支路谐波导纳的实部和虚部；y为支路对地导纳；Pij和Qij分别为支路谐波有功和无功功率量测；Pi和Qi分别为节点注入有功和无功量测数据；
和
分别为节点注入谐波电流和支路谐波电流相量；Ire和Iim分别为电流量测的实部和虚部；
为节点谐波电压相量量测。
通常以式（3）所示的量测误差平方和最小为目标，采用如式（4）所示的迭代式求解式（1）。
（3）
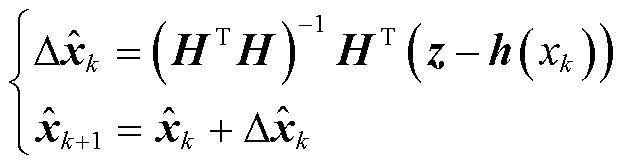（4）
式中，m为量测量维数；l为量测量序号；k为迭代次数；H为雅可比矩阵；
为状态量的修正向量；
为第k次迭代的状态量。
由于式（2）中的功率量测对应的是非线性量测函数，其雅可比矩阵在迭代中随状态量更新，而电流相量量测对应线性量测函数，雅可比矩阵为常数，在迭代中只计算一次，能够有效提高计算效率[21]。
由于PQMD的谐波相角数据均是本地基波电压相角的相对值，各监测点数据间存在相位差，不能直接用于状态估计。因此，本文利用PQMD谐波功率包含的相位差信息，通过量测变换[21]将谐波功率转换为等效谐波电流量测，无需经过基波状态估计求解区间基波同步相角，避免了基波状态估计求解同步相角时造成的区间扩张问题[22]，同时也避免了在量测集中引入求解同步基波相角的误差。
量测变换方程为
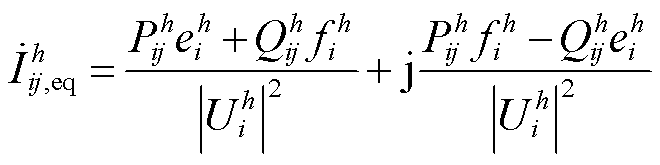（5）
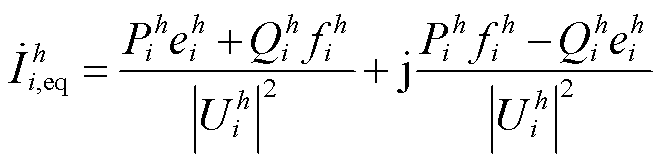（6）
式中，
为PQMD的h次谐波电压幅值量测；
和
分别为等效支路电流和注入电流量测，统称为等效谐波电流量测
。
在量测变换以后，迭代式（4）替换为式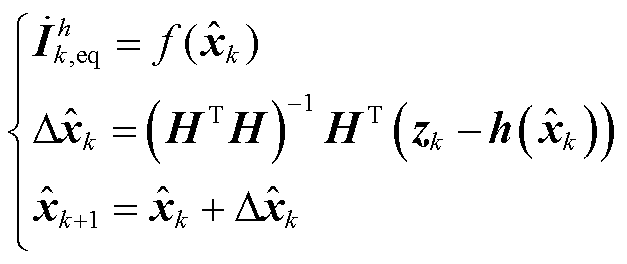（7）。
（7）
式中，
为功率量测变换函数。将z中的功率量测变换为
随迭代更新，形成第k次迭代的量测集zk。
当量测量与状态量为区间变量时，采用功率量测的非线性区间状态估计在迭代中重复计算雅可比矩阵，容易造成区间扩张问题。采用等效电流量测的线性状态估计只计算一次雅可比矩阵，在迭代中保持不变，能够减小区间状态估计的保守性。
由于各PQMD的检测起始时刻不一，量测数据与真实值之间存在不可避免的量测偏差[23]。本文依据电能质量监测装置上传的PQDIF（power quality data interchange format）文件记录的时间序列[24]选取PQMD参与状态估计的检测时段。
定义重叠度l为PQMD测点的检测时段与选定的参考时段重叠部分的占比，来量化非同步造成的检测时段偏差，有
（8）
式中，T为参考时段的时长，取3 min；DT为PQMD检测时段与参考时段的重叠时长；0≤l≤1。
重叠度l越大，代表该检测时段与参考时段之间的时段偏差越小，量测数据与参考时段内的真实值也更为接近。因此，先选择PQMD测点s的某个检测时段作为参考时段，以重叠度最大作为其余PQMD检测时段的选取依据，可以得到在该参考时段下的各PQMD测点检测时段序列Ts。
（9）
式中，Ts,i为PQMD测点i的一个检测时段，且与PQMD测点s的参考时段重叠度最大；q为PQMD测点个数。
依据该时段序列，可以计算出序列中的总重叠度大小
。为了获取最小量测偏差的PQMD谐波量测数据集，遍历所有PQMD测点并计算最大总重叠度
，如式（10）所示。
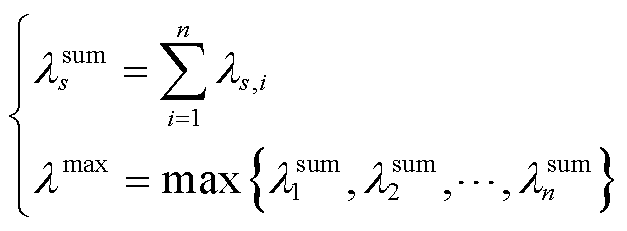（10）
式中，为以PQMD测点s为参考测点时，所选检测时段序列的总重叠度；lmax为最大重叠度。
选择lmax对应的Ts作为PQMD进行状态估计的最佳参考时段，此时各PQMD检测时段之间能够保持最高的重叠率，使得非同步检测造成的量测偏差最小。
基于重叠度指标的PQMD检测时段选取流程如图1所示。
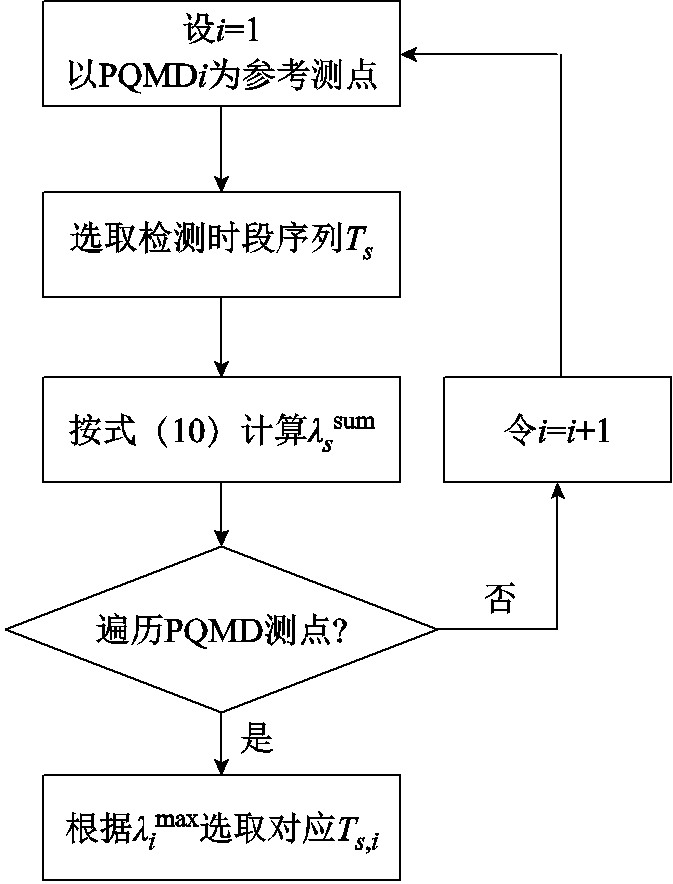
图1 基于重叠度指标选取检测时段流程
Fig.1 Flow chart of detection period is selected based on overlap degree index
本文采用检测时段内谐波数据的最大值和最小值，构建区间型谐波测量样本，进而通过区间谐波状态估计得到电网谐波状态量的变化区间，能够更全面地反映电网谐波的变化。
首先，在选定的各PQMD检测时段中，提取统计数据的最小值
和最大值
，进而经量测变换构建PQMD的区间型谐波数据集{[zPQMD]}。
（11）
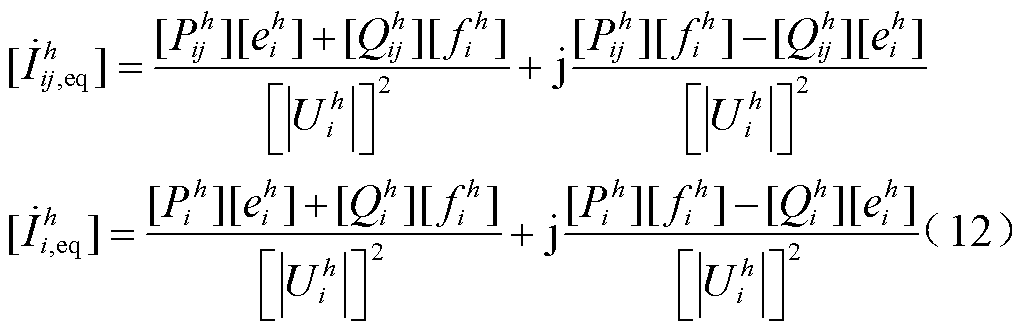
其次，选择PQMD的参考时段作为PMU的缓冲区[11-12]，假设该缓冲区内已经缓存了p个PMU时间断面的量测数据，将同步的幅值与相角转换为直角坐标系后，提取实部与虚部的最大值和最小值，按式（13）建立区间型PMU相量量测集{[zPMU]}。
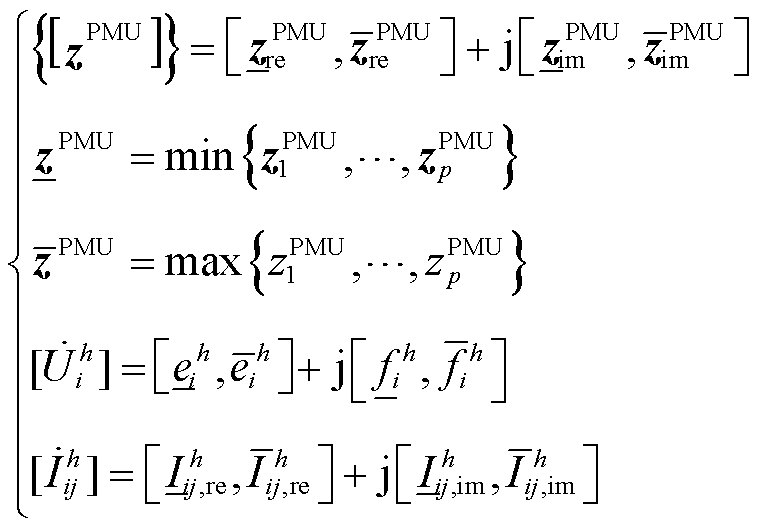（13）
式中，
和
分别为缓冲时段内的PMU量测数据实部或虚部的最小值和最大值；
和
分别为支路谐波电流实部和虚部的最小值；
和
分别为支路谐波电流实部和虚部的最大值。结合PQMD量测集构成区间型混合量测数据集为
（14）
在状态估计中对偏差大的量测量赋予较小的权重，可提高状态估计的鲁棒性[24]。据此可以建立抗差状态估计的目标函数[25]为
（15）
式中，wi为第i个量测量的权重系数；r为抗差权函数；si为第i个量测量的标准化残差。
本文在状态估计前利用投影统计法确定量测量的权重系数w初值；在状态估计过程中通过Huber权函数计算量测权重矩阵Q，并根据权重大小优选测点，构建总量测偏差最小的量测子集；再通过迭代重加权最小二乘法求解区间谐波状态估计模型。
为了尽可能降低量测偏差对状态估计的影响，需要在状态估计前对各量测量赋予先验权重，减小量测偏差数据在状态估计中的影响，然而由于权重的设置具有一定的人为主观性，无法对全局权重的设置客观公正化。投影统计法（Projection Statistics，PS）[26]只需要量测量及对应的雅可比矩阵便可以辨识空间中量测偏差较大的数据，并赋予相应量测量对应的投影统计值作为初始权重。据此，本文采用投影统计法获取各量测量的先验权重，作为后文抗差状态估计模型权函数的初始权重w。
在投影统计法中，第i个量测数据的投影统计值ai为
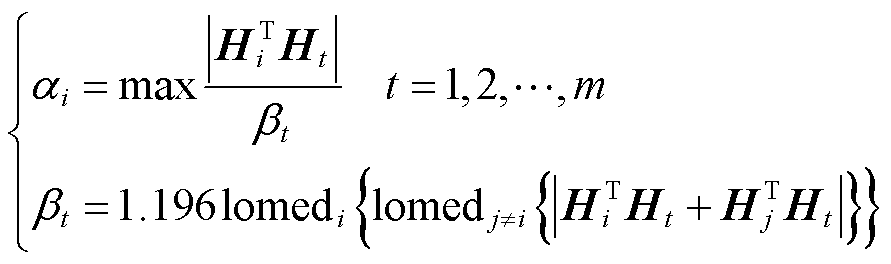（16）
式中，Hi、Ht和Hj分别为雅可比矩阵的第i、t和j行；lomed为低中位数算子。
投影统计量近似服从
分布[27]，假设行向量Hi中有d个非零元，先验权重系数wi计算公式为
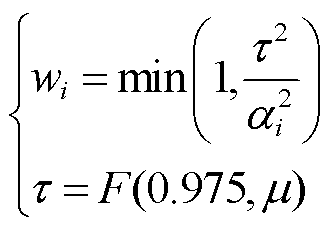（17）
式中，F为分布逆累积分布函数；m为雅可比矩阵的自由度，对应雅克比矩阵第i行的行向量的非零元个数d；t为自由度为m的97.5%分布置信区间。
由于传统加权最小二乘法在迭代中权重保持不变，估计精度受量测偏差影响较大，而Huber权函数[28]在每次迭代中依据量测残差重新调整权重，进而限制量测偏差的影响。综上所述，本文考虑量测偏差影响的改进Huber权函数r定义为
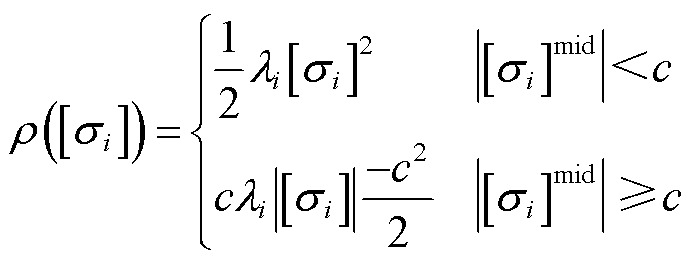（18）
式中，mid表示取区间中心值；c为调节参数；[si]为第i个量测量的区间标准化残差，如式（19）所示。
（19）
对式（15）求导并求最小值，可得
（20）
式中，R为量测误差的方差矩阵；
为区间状态估计量；[Q]为经过Huber权函数调整后的等价权矩阵，由权重系数wi和残差[si]共同确定，计算公式为
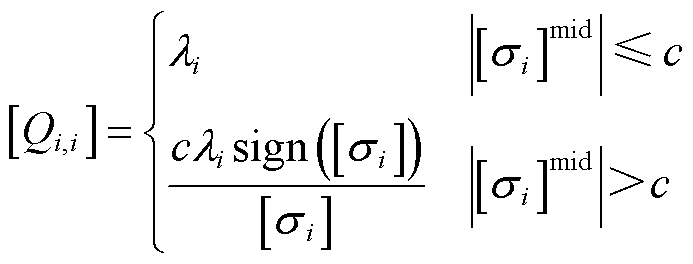（21）
式中，sign(·)为符号函数，若[si]＞0则返回1，[si]＜0返回-1，若[si]包含0点，则用中心值[si]mid确定返回值,且当[si]mid=0时返回0。
采用迭代重加权最小二乘法的迭代方程为
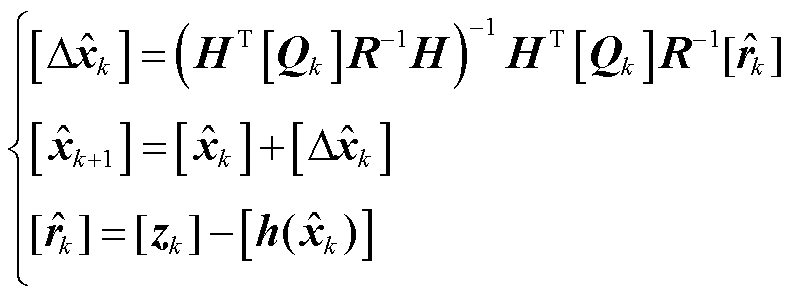（22）
式中，[
]为第k次迭代更新的区间型量测数据集；
为区间状态估计修正量。
采用量测残差的区间中心值表征量测量的偏差程度，将区间权重矩阵[Q]替换为确定值矩阵Q。据此，将式（21）去区间化可得
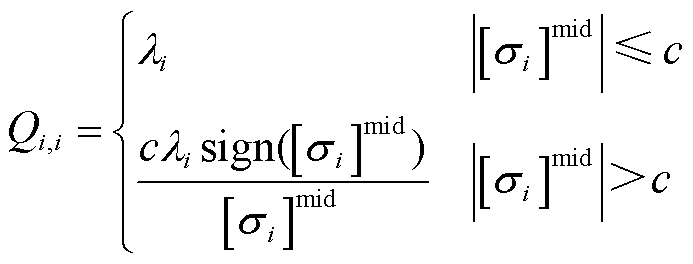（23）
通过去区间化处理可以减少状态估计方程中的区间数，与量测变换后的雅可比矩阵H共同转换为确定值矩阵，减少式（22）中的区间数运算，进一步降低解区间的保守性。
算法的收敛条件如式（24）所示，当前后两次计算的状态量区间宽度的无穷范数均小于设置的收敛精度e时，算法停止迭代，本文取e=10-5。
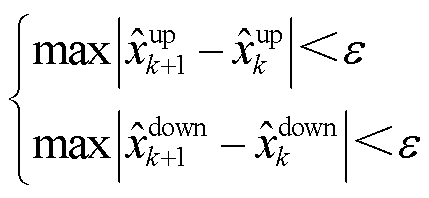（24）
式中，
和
分别为状态量的上、下界。
在抗差状态估计中，权重矩阵Q的系数用于衡量量测数据的可靠性。本文在Huber权函数中引入了重叠度大小表征量测偏差的影响，计算得到的权重系数可以代表量测量的可信度。由于Huber权函数没有淘汰区[29]（即量测权重为0），没有充分利用多源数据融合的量测冗余度优势。因此，本文基于权重矩阵Q优选测点集，新增淘汰区以剔除权重较低的数据，通过优选量测数据进一步减小量测偏差对状态估计精度的影响。
量测数据集的优选方法如下：首先，在不影响系统可观性的前提下，对权重矩阵Q中最小的权重系数置零，淘汰对应测点的数据；然后，重新进行状态估计，直至遍历全部量测数据，若删除的测点数据导致量测残差增大或雅可比矩阵H不满秩，则说明该量测数据影响系统可观性，此时保留该量测数据，重新进行筛选；最后，形成满足系统可观性且非同步量测偏差进一步减小的量测子集，在状态估计环节减小非同步量测偏差对估计精度的影响。
PMU中的相角量测以GPS卫星提供的时间基准为参考，而PQMD中的谐波电压和电流相角是以本地相角为参考，存在相角量测参考坐标系不统一的问题。此外，由于等效电流量测与状态量相关，若状态量的初始值设定不当，可能会导致状态估计结果不收敛或收敛结果错误等问题。因此，状态量初值的设置是影响状态估计结果的重要因素之一。
本文以PMU的相角量测数据为参考系，基于PMU量测数据设置全网状态量初值。选择某一PMU测点为参考节点，将全部PMU测点的相角替换为原相角量测值与参考节点的相位差[30]。全网状态量初始值取与其电气距离最小的PMU测点的电压量测值，实现对全网状态量的初始化。
基于多源量测数据融合的区间型抗差谐波状态估计算法的主要流程为：
1）采用重叠度指标融合多源量测数据，按式（13）和式（14）构建区间型混合量测数据集{[z]},并设置全网状态量初始值。
2）更新等效电流量测，得到混合量测集{[zk]}。
3）构建状态估计的区间量测方程和雅可比矩阵H，按式（16）和式（17）计算先验权重w。
4）根据式（22）计算区间状态量
。
5）通过收敛判据式（24）判断是否收敛，若收敛则转到步骤6）；否则利用状态修正量更新状态量后返回步骤2）。
6）根据Q优选测点后转到步骤3），直至遍历所有PQMD测点，输出谐波状态区间量。
区间型抗差谐波状态估计算法的流程如图2所示。
为了衡量估计结果的精度，定义状态估计解区间的相对误差为
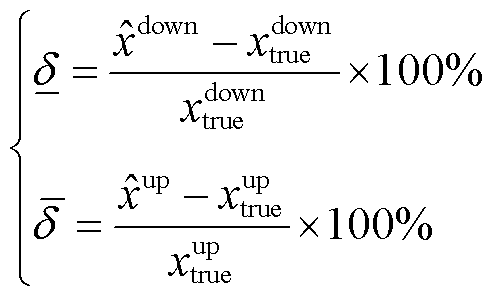（25）
式中，
和
分别为状态量下界和上界的相对误差；
和
分别为潮流计算值的下界和上界。
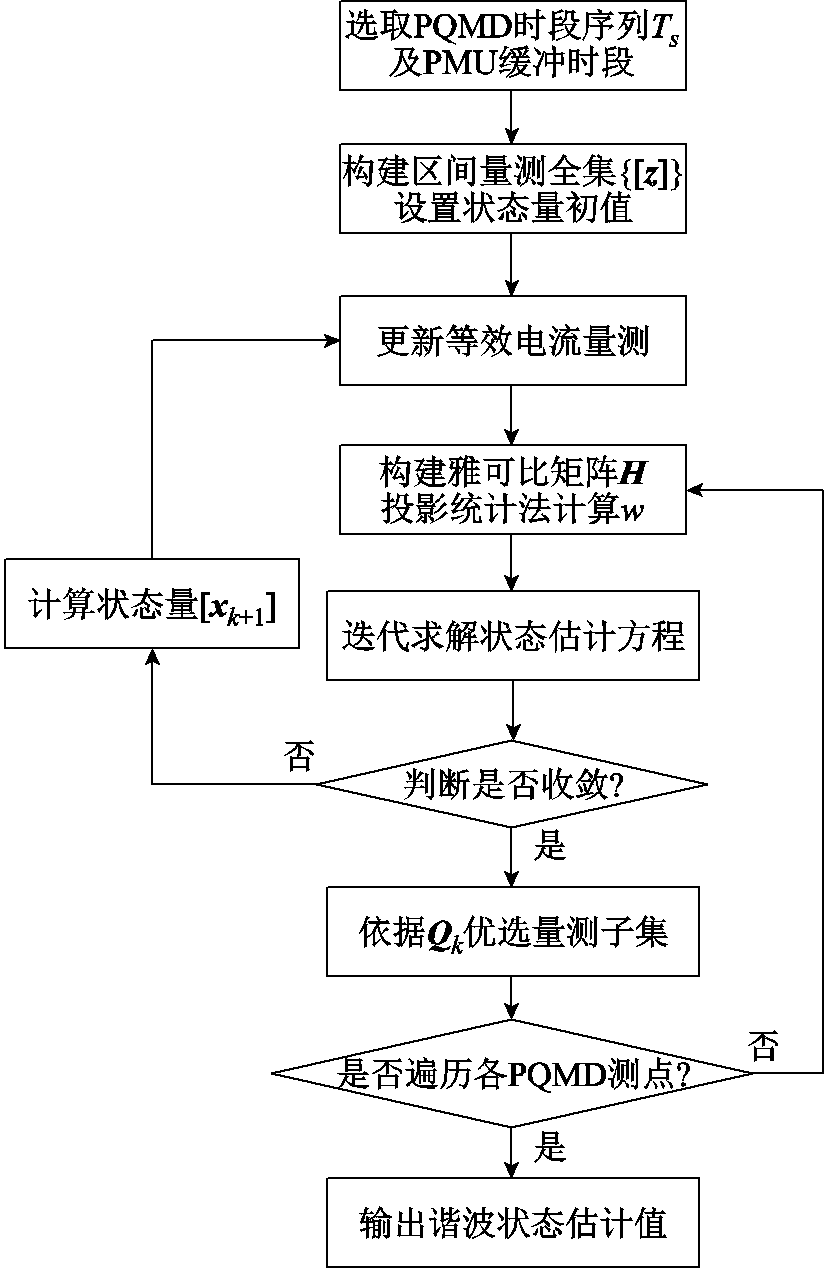
图2 区间型抗差谐波状态估计算法流程
Fig.2 Flow chart of interval resistance harmonic state estimation algorithm
此外，保守性是衡量区间状态估计价值的指标，解区间的保守性越小则越具有参考价值。区间保守性[19]的指标h的计算式为
（26）
本文的仿真算例在IEEE 30节点系统上进行测试，仿真软件为Matlab 2018b，采用Matpower 7.1获取网络拓扑信息，INTLAB V10.2工具箱进行区间运算。将四种算法的状态估计结果与潮流计算值进行对比分析，以验证本文算法的有效性，并测试所提算法在不同量测偏差下的抗差性及不同负荷波动水平下的鲁棒性。
算法1：采用区间型混合谐波数据集，基于加权最小二乘法估计求解谐波状态量。
算法2：采用PQMD电流幅值与相角量测构建区间谐波电流后，与PMU量测数据融合构建区间混合量测集，基于Huber抗差估计求解谐波状态量。
算法3：采用PQMD量测数据的单一量测谐波数据集，基于Huber抗差估计求解谐波状态量。
算法4：采用量测变换后的区间型混合谐波数据集，基于改进Huber抗差估计求解谐波状态量，即本文所提算法。
IEEE 30节点系统拓扑及量测配置如图3所示，在7、14和22号节点接入谐波源，1号节点为参考节点。在量测配置方面，为使系统完全可观且有一定量测冗余度，本文首先基于0-1整数规划算法计算出满足系统可观性所需的PMU数量，配置优化模型[31]为
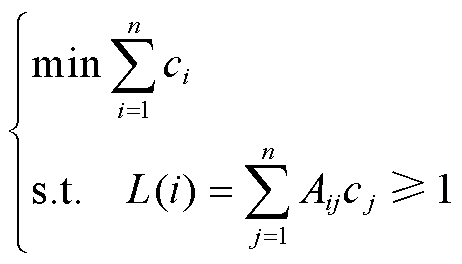（27）
式中，ci=0代表节点i无量测配置，ci=1代表有量测配置；L为约束方程；A为节点关联矩阵。
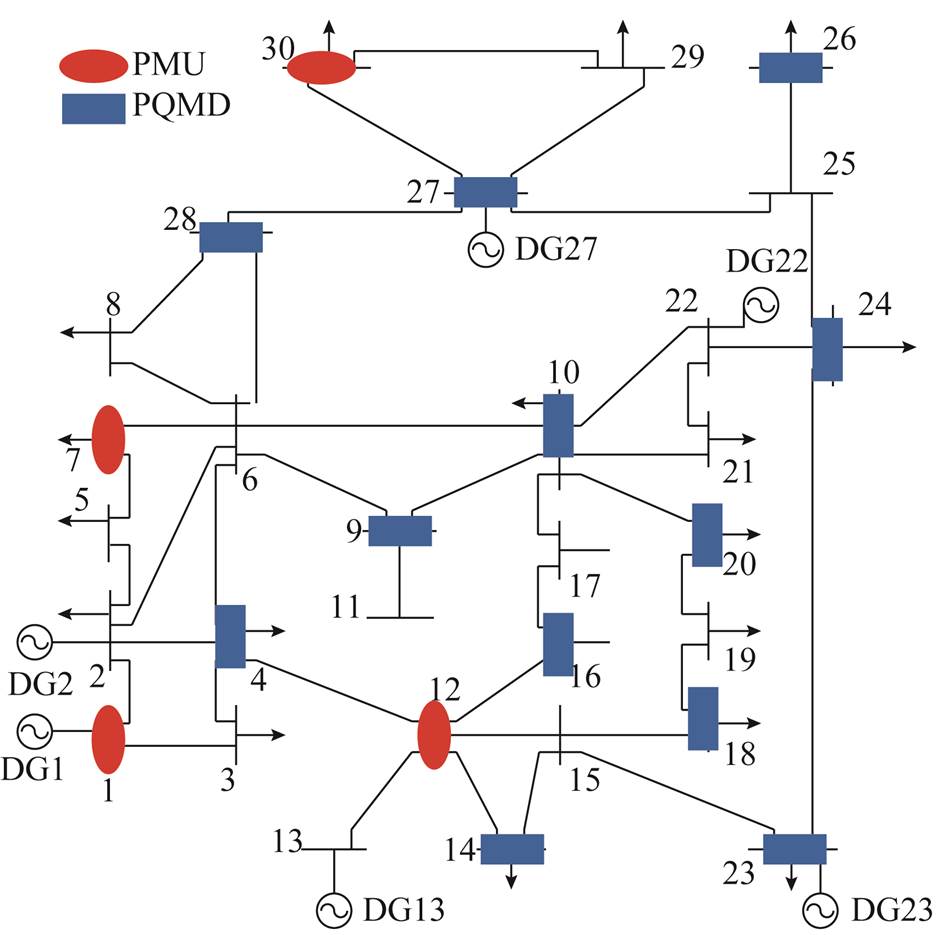
图3 IEEE 30节点系统及多源量测配置
Fig.3 IEEE 30 system and measurement configuration
通过求解式（27）可以得到IEEE 30节点系统至少需要配置10个PMU才能满足系统可观性，考虑到PMU价格昂贵，实际工程中无法满足高密度部署，因此本文只选取四个PMU进行配置。相比于PMU，PQMD在电网中配置数量较多，可以将PQMD作为数据补充源以满足系统可观性，并增加一定的量测冗余度。
本文通过谐波潮流计算获取所需要的谐波量测数据，具体流程如下：采用高斯迭代法求解基波潮流，构建谐波导纳矩阵Yh，由典型谐波源频谱计算注入谐波电流Ih，求解h次谐波电压Uh，根据潮流结果计算相应量测数据。
设置PQ负荷在额定值±10%范围内波动，依次进行谐波潮流计算，以获取各节点的谐波量测数据，将每次谐波潮流计算得到的谐波电压、电流作为PMU按照0.2 s间隔进行采样得到的量测数据。由于PQMD每10个周期进行一次谐波分析计算，每隔3 min计算一次统计值，因此本文取检测时段T=3 min，一个PQMD监测点的一个检测时段内共有900组量测数据，共计算三个检测时段（2 700组）的量测数据，在这个基础上选取检测时段并构建区间混合量测集。
假设全网各PQMD测点的DT服从均值为0.85T、方差为(0.05T)2的正态分布，则各PQMD的重叠度l～N(0.85,0.052)，模拟各PQMD测点的检测起始时刻不同步的现象。将900组含有量测偏差的各次谐波功率、谐波电压幅值作为PQMD在一个检测时段内统计的谐波数据，统计最大值和最小值构建PQMD区间谐波数据，每组潮流计算结果的谐波电压、电流相量作为PMU的量测数据。按2.1节所述的PQMD时段选取方法及和2.2节所述的多源数据融合方法构建区间型混合量测数据全集。
以5次谐波电压幅值和相角状态估计值为例，四种算法的状态估计结果与潮流计算值的对比结果分别如图4、图5所示。
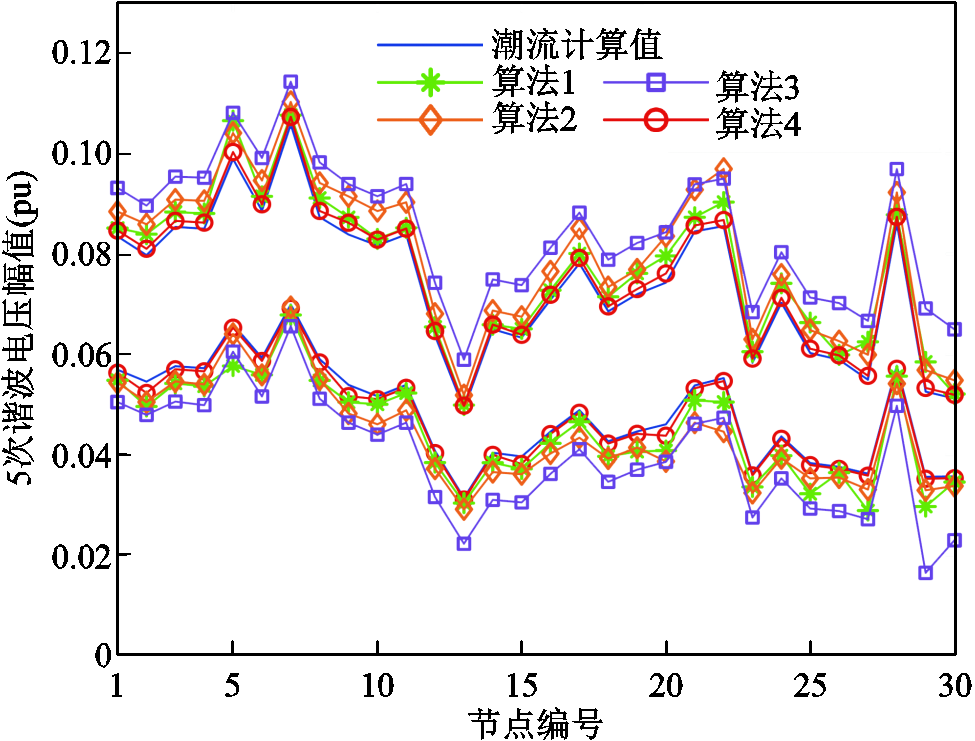
图4 区间谐波电压幅值对比
Fig.4 Interval harmonic voltage amplitude comparison
如图4和图5所示，由于算法1未在状态估计中进行抗差处理，状态量估计值受PQMD非同步量测的影响，导致谐波电压估计值与潮流计算值有较大误差。算法2先通过区间基波状态估计求取区间同步相角，修正得到同步谐波相角后，结合PQMD的谐波电流幅值构建谐波电流相量量测，再进行谐波状态估计。由于区间同步相角在求解过程中存在区间扩张问题，得到的区间谐波电流量测保守性较高，使得估计值与潮流值有较大的误差。算法3只采用PQMD的量测数据集，缺少更加精确的PMU量测数据，且量测集中含有求解同步谐波相角造成的误差，经过抗差处理仍效果不佳。算法4进行等效电流量测变换，构建等效谐波电流相量量测，经过测点优选得到最小量测偏差的数据集，并受量测权重矩阵约束，使得该算法具有较好的鲁棒性，与潮流计算值最为接近。
图5 区间谐波电压相角对比
Fig.5 Interval harmonic voltage phase angle comparison
算法4与算法1相对比，验证了优选量测集及迭代重加权方法的有效性；算法4与算法2相对比，证明了通过量测变换构建的区间电流量测优于PQMD谐波电流幅值、相角的标量数据构造的区间谐波电流数据；算法4与算法3对比，证明了混合量测数据集能够有效减小状态估计区间宽度，降低解区间的保守性。通过以上四种算法的对比分析，证明了算法4在量测数据集及抗差处理方面均能有效提高状态估计的精度，对量测偏差有着较好的抑制作用。
为了量化分析各谐波状态量的精度，分别计算上、下界相对误差，此后取其平均值dmean和最大值dmax进行对比，具体数值见表1。
从表1可以看出，算法4具有最低的估计误差，说明量测变换与优选方法能够提高混合量测数据集的可靠性，且针对量测偏差所提出的改进Huber抗差方法能够有效降低区间状态估计误差，提高区间谐波状态估计的准确性。在算法保守性方面，依据式（25）计算四种算法的保守性指标h1、h2、h3及h4，计算结果见表2。
表1 四种算法的谐波状态估计值相对误差对比
Tab.1 Comparison of the harmonic state estimators relative errors of the four algorithms
类型算法(%)(%)(%)(%) 幅值算法14.4172.72717.9112.08 算法26.6487.06817.7412.76 算法313.4512.3925.9518.36 算法43.2461.9216.1693.589
（续）
类型算法(%)(%)(%)(%) 相角算法17.2394.99843.9824.67 算法220.6612.2563.4028.35 算法328.3818.5283.0247.81 算法44.2252.2687.7455.803
表2 四种算法的谐波状态估计值保守性对比
Tab.2 Conservative comparison of harmonic state estimators of four algorithms
状态量h1h2h3h4 电压幅值0.031 30.035 70.042 30.027 4 电压相角0.472 10.577 40.663 10.411 6
从表2可以看出，在状态量的幅值和相角方面，h4均小于h1、h2和h3，即算法4的保守性更低，即得到的区间宽度更窄，更加接近于潮流计算值。
在本节中，保持重叠度的方差不变，分别取重叠度的数学期望为0.9、0.8、0.7和0.6，形成不同偏差的量测数据集。为避免偶然性，每个重叠度下计算50组区间混合量测数据集，共取200组区间混合量测集对比算法1～算法4的平均相对误差，验证本文所提抗差方法在不同量测偏差下的性能，结果如图6所示。
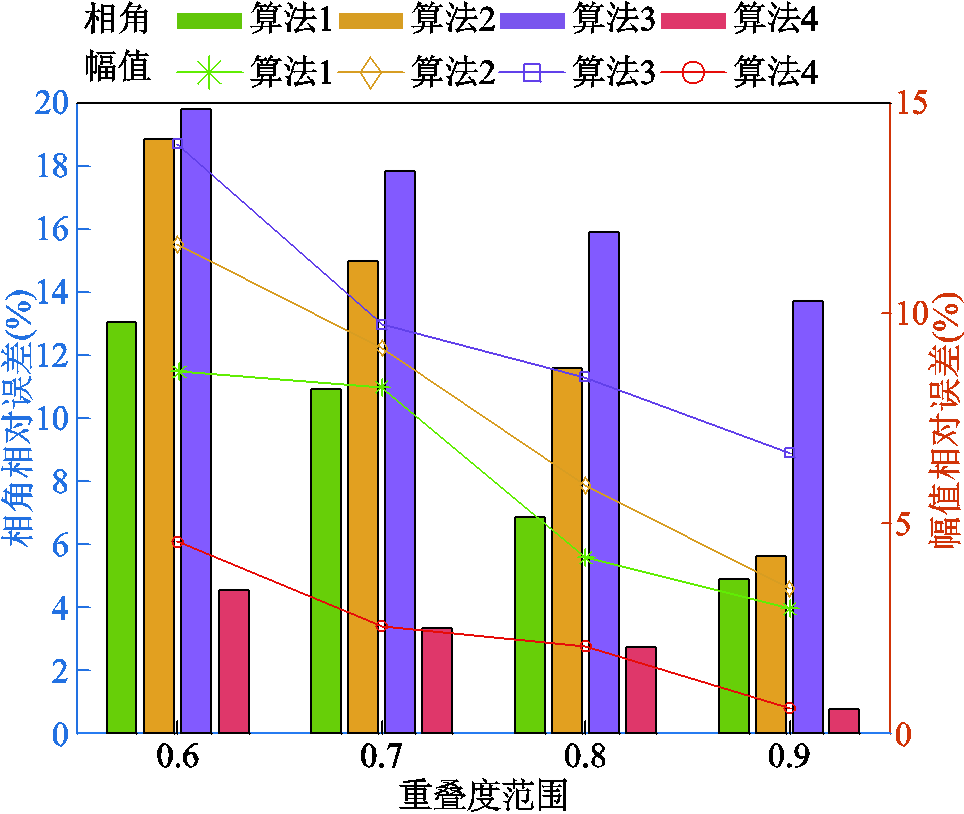
图6 不同量测偏差下算法抗差性对比
Fig.6 Comparison of robustness of algorithms with measurement deviation
由图6可知，当重叠度降低，即PQMD的量测数据偏差增大时，算法4的相对误差虽然增大，但与其他三种算法相比，仍然具有更低的相对误差。当重叠度为0.6时，算法4的平均相对误差约为算法1的1/3，算法2和算法3的1/4。说明即使PQMD量测偏差增大，本文所提抗差算法仍能降低估计误差，验证了算法的有效性和鲁棒性。
为验证所提算法在电网不同波动大小下的有效性，将负荷的波动水平从10%逐次增大至40%，取状态估计量的幅值和相角平均相对误差进行对比，如图7所示。
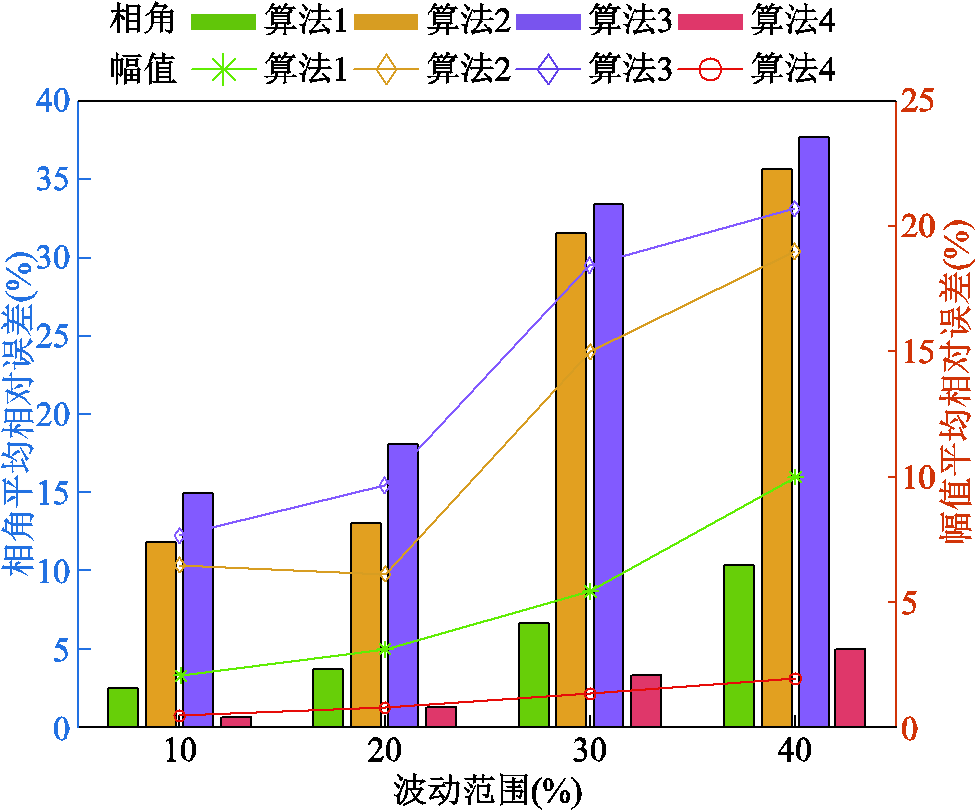
图7 不同负荷波动水平下算法抗差性对比
Fig.7 Comparison of algorithm robustness under different load fluctuation levels
图7展示了不同波动程度下的5次谐波状态估计量的平均相对误差。与算法1～算法3相比，算法4在不同负荷波动水平下的估计值都能有更低的相对误差。在电网波动水平增加时，四种算法对应的估计值相对误差也随之增大。这是由于节点功率波动水平越高，各PQMD检测起始时刻非同步造成的量测偏差也随之增大。在电网的负荷波动水平达到40%时，算法4的状态估计值相对误差仍相对较低，说明了所提算法在面对较大负荷波动水平的情况下仍然具备有效性。
由于目前还无法在电网中大量配置PMU，而PQMD作为数据补充源可以解决系统不可观问题。本文提出PQMD与PMU量测数据的融合方法，解决了多源量测数据融合面临的同步性差异、量测偏差导致的估计精度较低等问题，并提出了相应的区间型抗差谐波状态估计算法。
1）针对数据融合中不可避免的非同步量测偏差问题，提出了区间型抗差谐波状态估计方法。采用重叠度指标量化量测偏差，用于改进抗差状态估计中的权矩阵，并对量测数据进行变换和优选，有效提高区间型混合量测集的可靠性和状态估计的精度。
2）考虑到区间状态估计存在的保守性问题，采用量测变换策略，得到线性量测方程和常数雅可比矩阵，避免区间雅可比矩阵由于迭代运算造成的区间扩张效应。此外，对权重矩阵进行去区间化，进一步减少区间数之间的运算，降低解区间的保守性。
本文验证了融合PMU和PQMD量测数据的区间型抗差谐波状态估计的有效性和鲁棒性，但没有充分利用PMU数据的高采样频率优势，后续将结合PMU量测数据对PQMD数据进行修正，从而进一步提高谐波状态估计的准确性。
参考文献
[1] 杨权, 梁永昌, 魏建荣, 等. 多谐波源下分布式电源并网逆变器的谐波抑制策略[J]. 电工技术学报, 2023, 38(11): 2908-2920.
Yang Quan, Liang Yongchang, Wei Jianrong, et al. Research on harmonic suppression strategy of grid connected inverter under multi-harmonic sources[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2908-2920.
[2] 邵振国, 黄伟达. 考虑出力不确定性的分布式电源谐波传播计算[J]. 电工技术学报, 2019, 34(增刊2): 674-683.
Shao Zhenguo, Huang Weida. Harmonic propagation calculation of distributed generation considering output uncertainty[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 674-683.
[3] 周念成, 谭桂华, 何建森, 等. 基于统计方法的电网谐波状态估计误差分析[J]. 电工技术学报, 2009, 24(6): 109-114.
Zhou Niancheng, Tan Guihua, He Jiansen, et al. Error analysis in harmonic state estimation of power system based on the statistical approach[J]. Transactions of China Electrotechnical Society, 2009, 24(6): 109-114.
[4] 吴笃贵, 徐政. 基于相量量测的电力系统谐波状态估计(Ⅱ): 可观性、质量评估与算例研究[J]. 电工技术学报, 2004, 19(3): 76-81.
Wu Dugui, Xu Zheng. Power system harmonic state estimation based on phasor measurements(II)—observability analysis, quality evaluation algorithm and example studies[J]. Transactions of China Electrotechnical Society, 2004, 19(3): 76-81.
[5] 刘道伟, 谢小荣, 穆钢, 等. 基于同步相量测量的电力系统在线电压稳定指标[J]. 中国电机工程学报, 2005, 25(1): 13-17.
Liu Daowei, Xie Xiaorong, Mu Gang, et al. An on-line voltage stability index of power system based on synchronized phasor mesurement[J]. Proceedings of the CSEE, 2005, 25(1): 13-17.
[6] 王少芳, 刘广一, 黄仁乐, 等. 多采样周期混合量测环境下的主动配电网状态估计方法[J]. 电力系统自动化, 2016, 40(19): 30-36.
Wang Shaofang, Liu Guangyi, Huang Renle, et al. State estimation method for active distribution networks under environment of hybrid measurements with multiple sampling periods[J]. Automation of Electric Power Systems, 2016, 40(19): 30-36.
[7] 薛辉, 贾清泉, 王宁, 等. 基于PMU量测数据和SCADA数据融合的电力系统状态估计方法[J]. 电网技术, 2008, 32(14): 44-49.
Xue Hui, Jia Qingquan, Wang Ning, et al. A novel power system state estimation method based on merging PMU-measured data into SCADA data[J]. Power System Technology, 2008, 32(14): 44-49.
[8] 刘喆林, 王成山, 李鹏, 等. 多源量测数据融合的配电网状态估计及应用[J]. 中国电机工程学报, 2021, 41(8): 2605-2615.
Liu Zhelin, Wang Chengshan, Li Peng, et al. State estimation of distribution networks based on multi-source measurement data and its applications[J]. Proceedings of the CSEE, 2021, 41(8): 2605-2615.
[9] 黄天敏. 基于抗差状态估计的配电网运行状态诊断与分析[J]. 电力电容器与无功补偿, 2022, 43(6): 92-102.
Huang Tianmin. Diagnosisand Analysison operation state of distribution network basedon robust state estimation[J]. Power Capacitor & Reactive Power Compensation, 2022, 43(6): 92-102.
[10] 盛万兴, 方恒福, 沈玉兰, 等. 考虑量测时延时基于3种数据融合的配网状态估计[J]. 电力系统及其自动化学报, 2019, 31(12): 108-115.
Sheng Wanxing, Fang Hengfu, Shen Yulan, et al. Distribution state estimation based on fusion of three data sources considering measurement delay[J]. Proceedings of the CSU-EPSA, 2019, 31(12): 108-115.
[11] Zhang Qing, Chakhchoukh Y, Vittal V, et al. Impact of PMU measurement buffer length on state estimation and its optimization[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1657-1665.
[12] Zhao Junbo, Mili L. A framework for robust hybrid state estimation with unknown measurement noise statistics[J]. IEEE Transactions on Industrial Informatics, 2018, 14(5): 1866-1875.
[13] Murugesan V, Chakhchoukh Y, Vittal V, et al. PMU data buffering for power system state estimators[J]. IEEE Power and Energy Technology Systems Journal, 2015, 2(3): 94-102.
[14] 国家能源局.电能质量数据交换格式规范: DL/T 1608—2016[S]. 北京: 中国电力出版社, 2016.
[15] 吴星, 刘天琪, 李兴源, 等. 基于WAMS/SCADA数据兼容和改进FCM聚类算法的PMU最优配置[J]. 电网技术, 2014, 38(3): 756-761.
Wu Xing, Liu Tianqi, Li Xingyuan, et al. Optimal configuration of PMU based on data compatibility of WAMS/SCADA and improved FCM clustering algorithm[J]. Power System Technology, 2014, 38(3): 756-761.
[16] 张逸, 林焱, 吴丹岳. 电能质量监测系统研究现状及发展趋势[J]. 电力系统保护与控制, 2015, 43(2): 138-147.
Zhang Yi, Lin Yan, Wu Danyue. Current status and development trend of power quality monitoring system[J]. Power System Protection and Control, 2015, 43(2): 138-147.
[17] IEEE. IEEE recommended practice for the transfer of power quality data: IEEE 1159.3—2003[S]. New York: IEEE, 2004.
[18] 肖先勇, 胡誉蓉, 王杨, 等. 基于非同步电能质量监测系统的谐波状态估计[J]. 中国电机工程学报, 2021, 41(12): 4121-4132.
Xiao Xianyong, Hu Yurong, Wang Yang, et al. Harmonic state estimation based on asynchronous power quality monitoring system[J]. Proceedings of the CSEE, 2021, 41(12): 4121-4132.
[19] 邵振国, 林洪洲, 陈飞雄, 等. 采用区间动态状态估计的局部不可观系统谐波源定位[J]. 电工技术学报, 2023, 38(9): 2391-2402.
Shao Zhenguo, Lin Hongzhou, Chen Feixiong, et al. Harmonic source location in the partial unobservable system based on interval dynamic state estimation[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2391-2402.
[20] 林晓婉, 代锋, 刘沈全, 等. 含LCC-HVDC的交直流混联电网统一谐波状态估计方法[J]. 电力系统自动化, 2022, 46(13): 94-103.
Lin Xiaowan, Dai Feng, Liu Shenquan, et al. Unified harmonic state estimation method for AC/DC hybrid power grid with LCC-HVDC[J]. Automation of Electric Power Systems, 2022, 46(13): 94-103.
[21] 徐俊俊, 吴在军, 张腾飞, 等. 融入多源量测数据的配电网分布式区间状态估计[J]. 中国电机工程学报, 2022, 42(24): 8888-8900.
Xu Junjun, Wu Zaijun, Zhang Tengfei, et al. A distributed interval state estimation framework of distribution networks based on multi-source measurements[J]. Proceedings of the CSEE, 2022, 42(24): 8888-8900.
[22] 林洪洲, 邵振国, 陈飞雄, 等. 采用区间型非同步监测数据的鲁棒动态谐波状态估计[J]. 电网技术, 2023, 47(4): 1701-1709.
Lin Hongzhou, Shao Zhenguo, Chen Feixiong, et al. Robust dynamic harmonic state estimation using interval asynchronous monitoring data[J]. Power System Technology, 2023, 47(4): 1701-1709.
[23] Bi Tianshu, Guo Jinrui, Xu Kai, et al. The impact of time synchronization deviation on the performance of synchrophasor measurements and wide area damping control[J]. IEEE Transactions on Smart Grid, 2017, 8(4): 1545-1552.
[24] 张逸, 杨洪耕. 海量电能质量数据交换格式文件快速解析方案[J]. 电力自动化设备, 2013, 33(12): 116-121, 127.
Zhang Yi, Yang Honggeng. Fast parsing of massive PQDIF files[J]. Electric Power Automation Equipment, 2013, 33(12): 116-121, 127.
[25] Zhao Junbo, Wang Shaobu, Mili L, et al. A robust state estimation framework considering measurement correlations and imperfect synchronization[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4604-4613.
[26] Mili L, Cheniae M G, Vichare N S, et al. Robust state estimation based on projection statistics[of power systems[J]. IEEE Transactions on Power Systems, 1996, 11(2): 1118-1127.
[27] 徐艳春, 王格, 孙思涵, 等. 基于改进广义极大似然估计的配电网状态估计方法[J]. 南方电网技术, 2022, 16(6): 23-32.
Xu Yanchun, Wang Ge, Sun Sihan, et al. Distribution network state estimation method based on improved generalized maximum likelihood estimation[J]. Southern Power System Technology, 2022, 16(6): 23-32.
[28] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.
[29] 钱峰, 龚庆武. 基于IGG法的电力系统状态估计[J]. 电力系统自动化, 2005, 29(3): 36-39, 56.
Qian Feng, Gong Qingwu. State estimation of power system based on IGG method[J]. Automation of Electric Power Systems, 2005, 29(3): 36-39, 56.
[30] 秦晓辉, 毕天姝, 杨奇逊. 计及PMU的混合非线性状态估计新方法[J]. 电力系统自动化, 2007, 31(4): 28-32.
Qin Xiaohui, Bi Tianshu, Yang Qixun. A new method for hybrid non-linear state estimation with PMU[J]. Automation of Electric Power Systems, 2007, 31(4): 28-32.
[31] 朱茂林, 刘灏, 毕天姝. 考虑风电场量测相关性的双馈风力发电机鲁棒动态状态估计[J]. 电工技术学报, 2023, 38(3): 726-740.
Zhu Maolin, Liu Hao, Bi Tianshu. Robust dynamic state estimation of doubly-fed induction generator considering measurement correlation in wind farms[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 726-740.
Abstract Harmonic state estimation is a key part of power system operation management, which can be used to monitor the harmonic in the power grid and provide an important reference for the stable operation of the power grid. At present, the number of phasor measurement unit (PMU) configurations are difficult to satisfy the observability requirements of state estimation. It is necessary to adapt power quality monitoring device (PQMD) data to improve the redundancy of measurement and make the harmonic state estimation possible. However, the non-synchronized monitoring data characteristics of PQMD make the fused measurement data still have deviations, which will lead to a large error in harmonic estimation state. Fusing PMU and PQMD measurement data and minimizing the asynchronous measurement bias of PQMD measurement data, as well as suppressing the influence of this measurement bias in state estimation, will provide a more effective means for grid harmonic analysis. Therefore, the paper proposes an interval robust harmonic state estimation method based on PMU and PQMD measurement datafusion.
Firstly, the detection period of PQMD is selected with the overlap index, and the reference period is selected with the maximum overlap as the target. The selected reference period is used as the measurement buffer of PMU, and the PQMD measurement data in this period is fused to form an interval mixed measurement set. The harmonic power measurements of PQMD are converted into equivalent harmonic current phasor measurement by the measurement transformation strategy, which is updated with state quantity in iterative solution. Secondly, the projection statistical method is used to calculate the initial weight of the measurement, and the overlap index is introduced into the Huber weight function to adjust the measurement weight. The measurement with low overlap and large residual is given a small weight to suppress the influence of measurement deviation, and further improve the robustness of the algorithm. Finally, the measurement points are preferring according to the weights, and the measurement subset with the least deviation of non-synchronous measurement is obtained. The harmonic state estimation model is solved by iterative reweighted least square method, and the harmonic state range of the whole network is obtained.The simulation results show that when the load fluctuation is 10% and the average overlap degree is 0.85, the estimated error of the proposed method is 1.92% in the upper bound and 3.24% in the lower bound. The error of phase angle upper bound estimation is 2.27%, and the error of lower bound estimation is 4.22%. When the overlap degree is reduced to 0.6, the average error of amplitude and phase angle of the proposed algorithm is less than 6%. When the level of load fluctuation increases to 40%, the average estimation error of state quantity is less than 5%.
The following conclusions can be obtained through simulation analysis: (1) The overlap index is used to quantify the measurement deviation of PQMD to improve the weight matrix in the state estimation, which can effectively suppress the influence of the measurement deviation on state estimation. In addition, the interval mixed measurement subset is obtained by preferring the measurement points according to the weight coefficient, which can further reduce the non-synchronous measurement deviation of the measurement set, improve the reliability of the interval mixed measurement set and the accuracy of state estimation. (2) Converting the interval weight matrix and Jacobian matrix into a definite value can further reduce the conservatism of the solution interval. (3) The proposed algorithm can effectively reduce the estimation error under different measurement deviations and different load fluctuation sizes which has robustness.
keywords：Phasor measurement units, power quality monitoring device, multi-source measurement data fusion, interval algorithm, harmonic state estimation
中图分类号：TM711
DOI: 10.19595/j.cnki.1000-6753.tces.231815
国家自然科学基金资助项目（52377087）。
收稿日期 2023-10-31
改稿日期 2024-01-02
陈艺煌 男，1998年生，硕士研究生，研究方向为电能质量分析与治理、谐波状态估计等。E-mail：1484984430@qq.com
邵振国 男，1970年生，教授，博士生导师，研究方向为高渗透率新能源电网建模与仿真、电能质量分析与治理等。E-mail：shao.zg@fzu.edu.cn（通信作者）
（编辑 赫 蕾）